初等函数的基本不等式(1)

全部的初等不等式证明

初等不等式证明一、基本不等式及应用基本不等式是指已被人们证明了的较为常用的不等式，它常被当作定理，用于证明其他一些不等式.基本不等式在许多不等式专著中都作过介绍.这里给出几个常用的基本不等式. 1. 平均值不等式设12,,,n a a a ⋅⋅⋅是n 个正实数，记12111n nn H a a a =++⋅⋅⋅+，n G =12n n a a a A n ++⋅⋅⋅+=，n Q =，分别称n n n n H G A Q 、、、为这n 个正数的调和平均、几何平均、算术平均和平方平均，则有n n n n H G A Q ≤≤≤，当且仅当12n a a a ==⋅⋅⋅=时取等号.2. 柯西（Cauchy ）不等式设,(1,2,,)i i a b R i n ∈=⋅⋅⋅，则 222111()()()nn ni i i i i i i a b a b ===≤∑∑∑，当数组12,,,n a a a ⋅⋅⋅；12,,,n b b b ⋅⋅⋅不全为零时，当且仅当(1,2,,,0)i i b a i n λλ==⋅⋅⋅≠时取等号.3. 排序不等式设两组实数12,,,n a a a ⋅⋅⋅；12,,,n b b b ⋅⋅⋅，满足12n a a a ≤≤⋅⋅⋅≤，12n b b b ≤≤⋅⋅⋅≤，则有1211n n n a b a b a b -++⋅⋅⋅+ （反序和） 1212n i i n i a b a b a b ≤++⋅⋅⋅+ （乱序和） 1122n n a b a b a b ≤++⋅⋅⋅+ （同序和）当且仅当12n a a a ==⋅⋅⋅=，或12n b b b ==⋅⋅⋅=时取等号.4. 琴生（Jensen ）不等式设连续函数()f x 的定义域为(,)a b ，如果对于(,)a b 内的任意两个数12,x x ，都有1212()()()22x x f x f x f ++≤，则称()f x 为(,)a b 上的凸函数.若上式不等式反号，则称()f x 为(,)a b 上的凹函数.若()f x 为(,)a b 上的凸函数，则对于任意12,,,(,)n x x x a b ⋅⋅⋅∈有12121()[()()()]n n x x x f f x f x f x n n++⋅⋅⋅+≤++⋅⋅⋅+，当且仅当12n x x x ==⋅⋅⋅=时取等号.若为(,)a b 上的凹函数，则对于任意12,,,(,)n x x x a b ⋅⋅⋅∈有 12121()[()()()]n n x x x f f x f x f x n n++⋅⋅⋅+≥++⋅⋅⋅+，当且仅当12n x x x ==⋅⋅⋅=时取等号.5. 贝努利（Bernoulli ）不等式设1x >-，若0α<，或1α>-，则 (1)1x x αα+≥+. 若01α<<，则(1)1x x αα+≤+.当且仅当0x =时，以上两式均取等号. 6. 赫尔德（H ǒlder ）不等式设,,,(1,2,,)i i i a b l R i n +⋅⋅⋅∈=⋅⋅⋅，又,,,R αβλ+⋅⋅⋅∈，且1αβλ++⋅⋅⋅+=，则有1111()()()nn n nii i i i i i i i i ab l a b l αβλαβλ====⋅⋅⋅≤⋅⋅⋅∑∑∑∑，.当且仅当111(1,2,,)kkknnni i ii i i a b l k n a b l=====⋅⋅⋅==⋅⋅⋅∑∑∑时取等号.特别当1nαβλ==⋅⋅⋅==时，有 11111[()]()()()nn n nnn i iii i i i i i i a b l a b l ====⋅⋅⋅≤⋅⋅⋅∑∑∑∑.7. 切比雪夫(Chebyshev)不等式设两组实数12,,,n a a a ⋅⋅⋅；12,,,n b b b ⋅⋅⋅，若满足12n a a a ≤≤⋅⋅⋅≤，12n b b b ≤≤⋅⋅⋅≤或12n a a a ≥≥⋅⋅⋅≥，12n b b b ≥≥⋅⋅⋅≥，则有111111()()n n ni i i i i i i a b a b n n n ===≥∑∑∑.若满足12n a a a ≤≤⋅⋅⋅≤，12n b b b ≥≥⋅⋅⋅≥，或12n a a a ≥≥⋅⋅⋅≥，12n b b b ≤≤⋅⋅⋅≤，则有111111()()n n ni i i i i i i a b a b n n n ===≤∑∑∑.当且仅当12n a a a ==⋅⋅⋅=，或12n b b b ==⋅⋅⋅=时以上两式均取等号.8. 加权幂平均不等式设,(1,2,,)i i a p R i n +∈=⋅⋅⋅，,r s R ∈，且r s <，则111111nnrsrsi i i i i i nn i i i i p a p a p p ====⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪≤⎪⎪ ⎪ ⎪⎝⎭⎝⎭∑∑∑∑，当且仅当12n a a a ==⋅⋅⋅=时取等号. 9. 其他（1）设,,,,,x y z R αβγ∈，且(21)k αβγπ++=+（k Z ∈），则 i ） 2221cos cos cos ()2yz zx xy x y z αβγ++≤++ 当且仅当sin sin sin yz zx xy αβγ==时取等号.ii ） 22221sin sin sin ()4yz zx xy x y z αβγ++≤++，当且仅当sin 2sin 2sin 2yz zx xy αβγ==时取等号. （2）设,,1,2,,,ij x R i j n ∈=⋅⋅⋅则1n i =≥，当且仅当123::::i i i ni x x x x λ⋅⋅⋅=（常数），1,2,3,,i n =⋅⋅⋅时取等号.（3）设,,,,i i i i x y z l R -⋅⋅⋅∈，22220i i i i x y z l ---⋅⋅⋅-≥，1,2,3,,i n =⋅⋅⋅，则1ni =≤当且仅当::::i i i i x y z l λ⋅⋅⋅=（常数），1,2,3,,i n =⋅⋅⋅时取等号.（4）两个有用定理定理1 设,,u v R λ+∈，记1s u v λ=++，2s uv v u λλ=++，3s uv λ=，x =，y =i ） 23()61(xy xy xy +---(1)(2)3283()61(x xy xy xy ≤≤+-+-ii ）23()61(xy xy xy +---(3)(4)3283()61(y xy xy xy ≤≤+-+-.当且仅当,,u v λ中有两个数相等且不小于第三个数时，（1）、（4）两式取等号；当且仅当,,u v λ中有两个数相等，且不大于第三个数时，（2）、（3）两式取等号.推论1 同定理1条件，有(5)(6)324(1)4(1)164129()219595xy xy xy x xy xy xy xy ---+≤≤++---；(7)(8)324(1)4(1)164129()219595xy xy xy y xy xy xy xy ---+≤≤++---当且仅当u v λ==时，（5）、（6）、（7）、（8）四式取等号.推论2 同定理1条件，有x ≤≤3(11)(12)12728972x y x x-+++≤≤，当且仅当u v λ==时，（9）、（10）、（11）、（12）四式均取等号.定理2 设,,u v R λ∈，记1s u v λ=++，2s uv v u λλ=++，3s uv λ=，w =（10w s ≤≤），则32322323(13)(14)11111111332(2)()(2)()3227272727s s w w s w s w s w s w s s w w s ---++--+=≤≤=，当且仅当,,u v λ中有两个数相等，且不小于113s 时，（13）式取等号；当且仅当,,u v λ中有两个数相等，且不大于113s 时，（14）式取等号. 推论3 同定理2条件，特别当11s =时，有232223(15)(16)132(12)(1)(12)(1)132********w w w w w w w w uv λ---++--+=≤≤=，当且仅当,,u v λ中有两个数相等，且不小于13时，（15）式取等号；当且仅当,,u v λ中有两个数相等，且不大于13时，（16）式取等号. 注：在应用定理2与其推论3时，要特别注意120w -≤的情况，有时要对120w -≤和120w -≥分别加以讨论，尤其在0u λν≥时的情况.（一）算术几何平均值不等式应用例子例1 已知 ,1,2,i a R i +∈=…,n, 且11nii a==∑，求证()()()()3122311*********n n n n a a a a a a a a n -++⋅⋅⋅++≥+++++ （1）当且仅当 121n a a a n==⋅⋅⋅==时，（1）式取等号.例2 （20XX 年全国十八所奥赛协作体学校试题）设 ,,,a b c R +∈且 1bc ca ab ++=，求证1abc≤ （2）提示由1bc =≥∑知，可证更强式（3）⇔3 （※）例3 （2005，第17届亚太地区数学奥林匹克）设 ,,,x y z R +∈且 8xyz =，则243≥（4）当且仅当2x y z ===时，（4）式取等号.注：由本题证明中可知，若将条件改为12yz zx xy ++≥，结论也成立.例4 （自创题，2006.12.17）设,,a b c R +∈，则> （5）例 5 （自创题，1988.10.13）设同一平面上两个凸四边形的边长分别为,,,a b c d 和,,,a b c d ''''，面积分别为∆和'∆，那么aa bb cc dd ''''+++≥ （6）当且仅当这两个凸四边形都内接于圆（不一定要同一个圆），且 ()()()s a s a s b ''--=-⋅()()()()()s b s c s c s d s d ''''''-=--=--时，（6）式取等号. 这里1()2s a b c d =+++，1()2s a b c d '''''=+++.附：凸四边形ABCD 四边长分别为AB a =，BC b =，CD c =，DA d =，当且仅当此四边形ABCD 内接于圆时，其面积最大，最大值为max ()ABCD S =（7）例6 （自创题，2006.12.26）设,,,a b c d R -∈，则32222()4[()()()()]a a c d b d a c a b d b c ≥+++++++∑ （8）当且仅当a c =，b d =时，（8）式取等号.例7 设,,x y z R -∈，求证 25()81x xyz x ≥⋅∑∑ （9）当且仅当x y z ==时，（9）式取等号.（二）柯西不等式应用例子例1 设,i i x y R ∈，1,2,,i n =⋅⋅⋅，且10nii x=≥∑，10ni i y =≥∑，10i j i j nx x ≤<≤≥∑，10i j i j ny y ≤<≤≥∑，1ni i x x ==∑，则1()niii x x y=-≥∑ （1）yxdc baDCBA当且仅当1212n nx x x y y y ==⋅⋅⋅= 时，（1）式取等号. 在（1）式中，当3n =时，被人们称之为“母不等式”.即以下命题1：设123123,,,,,x x x y y y R ∈，且10x≥∑，10y ≥∑，120x x ≥∑，120y y ≥∑，则231()xx y +≥∑ （2）当且仅当312123x x x y y y ==时，（2）式取等号. 命题1应用如下：1.（匹多不等式）ABC ∆与'''A B C ∆边长分别为,,a b c 和,,a b c '''，面积分别为∆与'∆，则2222()16ab c a ''-++≥∆∆∑ （3）当且仅当ABCA B C '''∆∆时，（3）式取等号. 提示：取222x a b c =-++,2222x a b c ''''=-++等，并应用三角形面积公式.2.（程灵提出）若ABC ∆与A B C '''∆边长分别为,,a b c 和,,a b c '''，面积分别为∆与'∆，则()a b c a '-++≥∑ （4）当且仅当ABC ∆与'''A B C ∆均为正三角形时，（4）式取等号.提示：在（2）中取1x a b c '''=-++，1y a b c =-++等，并应用到22bc a-∑∑≥.3.（安振平提出）若ABC ∆与A B C '''∆边长分别为,,a b c 和,,a b c '''，面积分别为∆与'∆，则2()()16a b c a b c a ''-++-≥∆∆∑ （5）当且仅当222()()()a b c a a b c b a b c c a b c '''==-++-++-时，（5）式取等号.提示：在（2）中取2221x a b c '''=-++，1()()y a b c a b c =-++-等.4.（自创题，1983.05.07）若ABC ∆与A B C '''∆边长分别为,,a b c 和,,a b c '''，面积分别为∆与'∆，则()()()16a a b c a b c a b c '''''''-++-++-≥∆∆∑ （6）当且仅当ABCA B C '''∆∆时，（6）式取等号.提示：在（2）中取1()()x a b c a b c =-++-，1()()y a b c a b c ''''''=-++-等. 以上（3）式与（6）式有相同的取等号条件，试讨论他们左边式子的大小.5. 设ABC ∆三边长为,,BC a CA b AB c ===，面积为∆，P 为ABC ∆内部或边界上一点，从P 分别向三边BC 、CA 、AB 所在直线作垂线，垂足分别为D 、E 、F ，记1PD r =，2PE r =，3PF r =，则223242r r bc a∆≤-∑∑∑. （7）提示：12342()()ar a b c r r ∆==-+++∑∑≥≥.我们还可以由（2）式得到或证明更多不等式.又如第六章，“三角几何不等式”中的例6、例22等.注：类似上述方法，应用赫尔德不等式，有命题设x ,,i i i y z R -∈，1,2,3i =，则123123123111222333()()()()x x x y y y z z z x y z x y z x y z ++++++-++≥.（8）例2 （自创题，1988，0.4.20）设,,,,x y z w R λ∈，且0,0xy zw >>，2λ≤，则≤（9）=时，（9）式取等号.注：（9）式可参阅由吴康主编的《奥赛金牌之路》（高中数学）“第一章 §6 三角不等式”（P81—P90），本节系杨学枝所写.利用同上证法可得以下命题（自创题）：设,,,x y z w R +∈，(21)k αβγθπ+++=+ ()k z ∈，则sin sin sin sin x y z w αβγθ+++≤（10）当且仅当，cos cos cos cos x y z w αβγθ=== 时，（9）式取等号.（10）式为笔者首创，可参见同上吴康主编的《奥赛金牌之路》（高中数学）P82. 本命题在《中等数学》杂志社组织的数学竞赛命题评奖中，获一等奖.本命题也可参见《中等数学》，1989年第二期，杨学枝文：《对一个三角不等式的再探讨》.例3 a ,i i b R ∈，1,2,,i n =⋅⋅⋅，则1112nnni i i i i i i a b a b n ===≥∑∑∑. （11）注：（11）式是一个值得关注的不等式，如取3n =时，可证20XX 年中国国家队培训题：,,,,,a b c x y z R ∈，满足()()3a b c x y z ++++=，222222()()4a b c x y z ++++=，求证0ax by cz ++≥.例4 设a,,b c R +∈，且3a b c ++=，则2232a ab ≥+∑. （12）例5 （20XX 年.IMO.46）已知x,y,z ∈R +,且 1xyz ≥，求证525220x x x y z-≥++∑ （13）例6 （20XX 年IMO 预选题）设(1,2,,)i x R i n ∈=⋅⋅⋅,求证1222222211212111n nx x x x x x x x x ++⋅⋅⋅+<++++++⋅⋅⋅+（14）例7 a,b,c 为正数，证明22224()a b c a b a b c b c a a b c-++≥+++++，（15）当且仅当a c b >>，且a b c a c a b c b==---，即a c b >>且3322b c b c +=时，（15）式取等号.例8 （20XX 年国家集训队测试题）设,,,x y z R -∈且1x y z ++=，求证+≤ （16）例9 （自创题，1987.07.20）设 ,,,x y z w R +∈，则 ()2918x x x xy xz xw yz yw zw +⋅≥+++++∑∑∑ （17）当且仅当 x y z w === 时，（17）式取等号.注：（17）式可推广为：设 ,1,2,,i x R i n +∈=⋅⋅⋅，则111n ni i i i x x ==⋅≥∑∑()()2212112n i i i ji j jn x n n x x =≤<≤⎛⎫- ⎪⎝⎭--∑∑ （18）当且仅当12n x x x ==⋅⋅⋅=时,(18)式取等号.若记11ni i s x ==∑，21i j i j ns x x ≤<≤=∑，12n n s x x x =⋅⋅⋅，111n n s s x -=∑，则（18）式可写成如下形式：22212121(2)(1)n n n s s s n n s s n s s -+-≥-.例10 (陈计，2008.08.29提供)对正数,,,a b c d 及0k ≥，有 41a b c d b kd c ka d kb a kc k+++≥+++++. （19）例11 （自创题，2010.11,09）设,,x y z R +∈，求证322x x xy y ≥++∑ （20）当且仅当1x y z ===时（20）式取等号.注：猜想设,,x y z R +∈，有322x x xy y ≥++∑322x x xy y≥++∑.例12 设,,,..a b c x y z 非负，且a b c x y z ++=++，则()()()3()ax a x by b y cz c z abc xyz +++++≥+. （21）例13 （第50届IMO 金牌得主林博提出的猜想）设,,0a b c ≥，求证2a ≤∑∑. （22）例14（自创题，2001.02.02）设,,x y z R +∈,且4yz zx xy xyz +++≤，则x y z yz zx xy ++≥++. （23）注：1.用类似方法，可证以下命题设,,p q r R -∈，,,x y z R ∈，且14p q r pqr +++≤，则222px qy rz yz zx xy ++≥++. （24） 2. 第48届国际数学奥林匹克中国国家集训队有一道测试题（20XX 年3月）与其相似.题目设正实数,,u v w满足4u v w ++=，求证u v w ++. （25）x =y =z =，则原命题等价于：,,x y z R +∈，且4yz zx xy xyz +++=，则x y z yz zx xy ++≥++ ① 式证明可见《数学奥林匹克不等式研究》第八章章练习题64中i ）.例15（第48届IMO 中国国家集训队测试题）设正数12,,,n a a a ⋅⋅⋅，满足12a a +1n a +⋅⋅⋅+=，求证1212231222223311()()1n n a a a na a a a a a a a a a a a n ++⋅⋅⋅+++⋅⋅⋅+≥++++ （26）例16 已知221,a b kab +-= 221c d kcd +-=，,,,,a b c d k R ∈，且 2k <，求证ac bd -≤（27）当且仅当()()()()22a b c d k k a b c d ---=+++，即bc ad k ac bd +=+时，（27）式取等号.例17. （20XX 年IMO 预选题）设(1,2,,)i x R i n ∈=⋅⋅⋅,求证1222222211212111n nx x x x x x x x x ++⋅⋅⋅+<++++++⋅⋅⋅+（28）3. 其他基本不等式应用例子例1 设,,x y z R -∈，则4+≤(1)()2x y z ≤++，例2 （自创题，2010.07.03）若,,a b c 为满足1a b c ++=的正数，19λ≥，则 31()()()(3)3a b c b c a λλλλ+++≥+，（3）推广式，即有以下命题若12,,,n a a a ⋅⋅⋅为满足11ni i a ==∑的正数，21n λ≥，则 122311()()()()n n a a a n a a a nλλλλ++⋅⋅⋅+≥+，（4）当且仅当121n a a a n==⋅⋅⋅==时，（4）式取等号.例3 （自创题，2010.07.03）若,,a b c 为满足1abc ≥的正数，23λ≥，则)a b c ≤++，（5）当且仅当1a b c ===时，（5）式取等号.推广式以下命题若12,,,n a a a ⋅⋅⋅为满足121n a a a ⋅⋅⋅≥的正数，11nλ≥-，则11nni i i a ==≤，（6）当且仅当121n a a a ==⋅⋅⋅==时，（6）式取等号.例4（《不等式研究网站》，“竞赛不等式”专栏，20XX 年1月6日，陈胜利老师提出）设,,0a b c >，且1abc =，求证2112()3a a ≥+-∑ （7）例5 （王雍熙，2011.08.22提供）设,,a b c R -∈，且2a a ≥∑∑，则31aabc bc +≥+∑∑. （8）本题可推广，见以下例6.例6（自创题，2011.08.22）设i a R -∈，1,2,,i n =⋅⋅⋅，2n ≥，记i a （1,2,,i n =⋅⋅⋅）中每k （1,2,,k n =⋅⋅⋅）,个乘积之和为k s ，m 为不大于n 的正整数，且211n ni ii i a a==≥∑∑，则11352411+s 1nn n n ii n n s n s n as s s s n sn --=-⎧⎧++≥+++⋅⋅⋅+⎨⎨⎩⎩∑（为奇数）（为奇数）（为偶数）（为偶数），（9）二、其他方法证明不等式例子例1 （自创题，2006.08.25）设,,x y z R -∈，且2222x y z xyz +++1≤，则 142xyz yz +≥∑，（1）当且仅当12x y z ===，或,,x y z中一个为零，另外二个均等于2时，（1）式取等号.例2（20XX 年全国高中数学联赛A 卷加试题3）给定整数2n >，设正实数12,,,n a a a ⋅⋅⋅满足1,1,2,,k a k n ≤=⋅⋅⋅，记12,1,2,,kk a a a A k n k++⋅⋅⋅+==⋅⋅⋅.求证： 1112nnk k k k n a A ==--<∑∑. （2）例 3 已知123123a a a b b b ++=++，122331122331a a a a a a a a a a a a ++=++，若123123min{,,}min{,,}a a a b b b ≤，求证： 123123max{,,}max{,,}a a a b b b ≤.注. 本例可推广.例4 （自创题，2007.12.28）设,,a b c R +∈，且1bc =∑，则21142a bc ≥-+∑，（3）当且仅当a b c ===时取等号.例5 （宋庆老师在《中学数学研究》（广东），20XX 年第1期，文“两个优美的无理不等式”中提出的猜想）若,,0a b c >，满足1a b c ===，则≥（4）例6 .(20XX 年，Serbian 数学奥林匹克试题) 已知,,a b c 是正数,且1a b c ++=，证明127131bc a a≤++∑. （5）例7（陈计，2008.05.04提供）设,,a b c R ∈，n N ∈，则 2[()()]4[()][()]n n n b c b c b c bc b c +-≥--∑∑∑. （6）例8 （自创题，2008.05.07）设,,a b c R -∈，求使22222233()()()(2)()b c bc c a ca a b ab abc a b c λλλλ++++++≥+++ 成立的最大正数λ的值.例9 (自创题，2008.08.30)设1122,,,a b a b R ∈，且222221122a b a b m -=-=，则2212211122211221122()()()()()4()()a b a b m a b a b a b a b m a b a b ++-+++≥++-++，（7）当且仅当22211a b m -=，12a a =，12b b =时，（7）式取等号.例10 （江苏高三学生顾振同学2010.08.06提供）设,,x y z R -∈，且2221x y z ++=，则411x yzx xyz≤--∑∑∑ ，（8）当且仅当3x y z ===，或,,x y z中，有一个为零，其余两个都等于2时，（8）式取等号.例11 （自创题，2005.12.04）设,,a b c R +∈，且1a b c ++=，则3)5)1080abc abc bc -+≥∑ （9）当且仅当13a b c ===，或,,a b c中有一个等于33-，另外两个都等于6时，（9）式取等号.例12（自创题，2007.09.18）设,,a b c R +∈，且1a b c ++=，则271481abc a-≤∑ （10）当且仅当13a b c ===，或,,a b c 中一个等于23，其余两个都等于16时，（10）式取等号.例13 （美国，Pham Kim Hung ）设,,a b c 是三角形三边长，则222a b a b a≥+∑∑∑， (11) 当且仅当ABC ∆为正三角形时,(11)式取等号.例14 “奥数之家”2010.03.31，“476934847”提出：设,,a b c R +∈，则22222()3a b c a c b c a a b c -++≥+++. （12）例15 假设P 、Q 、R 分别是ABC 的三边BC 、CA 、AB 上三点，且满足13AQ AR BR BP CP CQ +=+=+=，则12PQ QR RP ++≥（13）注：1. 关于本题，有其深刻的背景，可参阅杨之所著《初等数学研究的问题和课题》P297~298；或参阅《数学通讯》1991年第2期“问题征解”栏目杨学枝解答及编者评语；或参阅《中学数学教学参考》（陕西），1992年第6期，杨学枝文《一个几何不等式的再加强》；或参阅《数学通讯》1996年第10期，杨学枝文《从一道命题谈起》：也可以参阅杨学枝主编《不等式研究》(西藏人民出版社，2000年6月出版)一书中杨路教授写的“序”；还可以参阅杨学枝著《数学奥林匹克不等式研究》(哈尔滨工业大学出版社，20XX 年8月出版)一书中杨路教授写的“序”；还可以参见《UNIV, BEOGRAD. PUBL. ELEKTKOTEHN.FAKser. Mat.4(1993).25~27.陈计与杨学枝文:《ON A ZIRAKZADEH INEQUALITY RELATED TO TWO TRIANGLES INSCRIBED ONE IN THE OTHER 》.2. 由以上所得重要不等式1()()(cos cos cos )3QR RP PQ a b c a b c A B C ++≥++-++++（14）可得较（13）式更强的不等式33339()()8QR RP PQ BC CA AB ++≥++ （15）3. 《福建中学数学》，1996年第4期.杨学枝文：《对一道猜想题的证明》中，用与（13）式的类似证法，给出了2221()4RP PQ PQ QR QR RP BC CA AB ⋅+⋅+⋅≥++ （16）其中,,P Q R 分别为,,BC CA AB 边上的周界中点.。

专题0 基本初等函数(Ⅰ)(知识梳理)

专题02基本初等函数(知识梳理)第一节指数与指数函数1．有理数指数幂 (1)幂的有关概念 ①正分数指数幂： am n＝na m (a >0，m ，n ∈N *，且n >1)．②负分数指数幂： a －m n＝1am n＝1n a m(a >0，m ，n ∈N *，且n >1)．③0的正分数指数幂等于0,0的负分数指数幂没有意义． (2)有理数指数幂的性质 ①a r a s ＝a r ＋s (a >0，r ，s ∈Q)； ②(a r )s ＝a rs (a >0，r ，s ∈Q)； ③(ab )r ＝a r b r (a >0，b >0，r ∈Q)． 2．指数函数的图象与性质R1．在进行指数幂的运算时，一般用分数指数幂的形式表示，并且结果不能同时含有根号和分数指数幂，也不能既有分母又含有负指数．2．指数函数y ＝a x (a >0，a ≠1)的图象和性质跟a 的取值有关，要特别注意区分a >1或0<a <1.[谨记通法]指数幂运算的一般原则(1)有括号的先算括号里的，无括号的先做指数运算． (2)先乘除后加减，负指数幂化成正指数幂的倒数．(3)底数是负数，先确定符号，底数是小数，先化成分数，底数是带分数的，先化成假分数． (4)若是根式，应化为分数指数幂，尽可能用幂的形式表示，运用指数幂的运算性质来解答．考点二指数函数的图象及应用重点保分型考点——师生共研[典例引领]1．(2018·嘉兴能力测试)若函数f (x )＝a x －b 的图象如图所示，则( )A ．a >1，b >1B ．a >1,0<b <1C ．0<a <1，b >1D ．0<a <1,0<b <1解析：选D 由f (x )＝a x －b 的图象可以观察出，函数f (x )＝a x －b 在定义域上单调递减，所以0<a <1，又函数f (x )＝a x －b 的图象是在y ＝a x 的基础上向下平移b 个单位长度得到的，所以0<b <1.2．已知a >0，且a ≠1，若函数y ＝|a x －2|与y ＝3a 的图象有两个交点，则实数a 的取值范围是________．解析：①当0<a <1时，作出函数y ＝|a x －2|的图象，如图a.若直线y ＝3a 与函数y ＝|a x －2|(0<a <1)的图象有两个交点，则由图象可知0<3a <2，所以0<a <23.②当a >1时，作出函数y ＝|a x －2|的图象，如图b ，若直线y ＝3a 与函数y ＝|a x －2|(a >1)的图象有两个交点，则由图象可知0<3a <2，此时无解．所以a 的取值范围是⎝⎛⎭⎫0，23. 答案：⎝⎛⎭⎫0，23[由题悟法]指数函数图象的画法及应用(1)画指数函数y ＝a x (a >0，a ≠1)的图象，应抓住三个关键点：(1，a )，(0,1)，⎝⎛⎭⎫－1，1a . (2)与指数函数有关的函数的图象的研究，往往利用相应指数函数的图象，通过平移、对称变换得到其图象．(3)一些指数方程、不等式问题的求解，往往利用相应的指数型函数图象数形结合求解．[即时应用]1．函数f (x )＝1－e |x |的图象大致是( )解析：选A 将函数解析式与图象对比分析，因为函数f (x )＝1－e |x |是偶函数，且值域是(－∞，0]，只有A 满足上述两个性质．2若函数y ＝|3x －1|在(－∞，k ]上单调递减，求k 的取值范围．解：函数y ＝|3x －1|的图象是由函数y ＝3x 的图象向下平移一个单位后，再把位于x 轴下方的图象沿x 轴翻折到x 轴上方得到的，函数图象如图所示．由图象知，其在(－∞，0]上单调递减，所以k 的取值范围是(－∞，0]．考点三指数函数的性质及应用题点多变型考点——多角探明[锁定考向]高考常以选择题或填空题的形式考查指数函数的性质及应用，难度偏小，属中低档题．常见的命题角度有： (1)比较指数式的大小；(2)简单指数方程或不等式的应用； (3)探究指数型函数的性质．[通法在握]应用指数函数性质的常见3大题型及求解策略题型求解策略比较幂值的大小(1)能化成同底数的先化成同底数幂再利用单调性比较大小；(2)不能化成同底数的，一般引入“1”等中间量比较大小解简单指数不等式先利用幂的运算性质化为同底数幂，再利用单调性转化为一般不等式求解探究指数型函数的性质与研究一般函数的定义域、单调性(区间)、奇偶性、最值(值域)等性质的方法一致[提醒]在研究指数型函数的单调性时，当底数与“1”的大小关系不明确时，要分类讨论．第二节对数与对数函数1．对数概念如果a x＝N(a>0，且a≠1)，那么数x叫做以a为底N的对数，记作x＝log a N，其中a叫做对数的底数，N叫做真数，log a N 叫做对数式性质对数式与指数式的互化：a x＝N⇔x＝log a N log a1＝0，log a a＝1，a log a N＝N运算法则log a(M·N)＝log a M＋log a Na>0，且a≠1，M>0，N>0 log aMN＝log a M－log a Nlog a M n＝n log a M(n∈R)换底公式换底公式：log a b＝log c blog c a(a>0，且a≠1，c>0，且c≠1，b>0)2.对数函数的图象与性质y＝log a x a>10<a<1图象性质定义域为(0，＋∞)值域为R过定点(1,0)，即x＝1时，y＝0当x>1时，y>0；当0<x<1时，y<0当x>1时，y<0；当0<x<1时，y>0在区间(0，＋∞)上是增函数在区间(0，＋∞)上是减函数3．反函数指数函数y＝a x(a>0且a≠1)与对数函数y＝log a x(a>0且a≠1)互为反函数，它们的图象关于直线y＝x对称．1．在运算性质log a Mα＝αlog a M中，要特别注意条件，在无M>0的条件下应为log a Mα＝αlog a|M|(α∈N*，且α为偶数)．2．解决与对数函数有关的问题时需注意两点：(1)务必先研究函数的定义域；(2)注意对数底数的取值范围．[谨记通法]对数运算的一般思路(1)将真数化为底数的指数幂的形式进行化简；(2)将同底对数的和、差、倍合并；(3)利用换底公式将不同底的对数式转化成同底的对数式，要注意换底公式的正用、逆用及变形应用．如“题组练透”第1题易错．考点二对数函数的图象及应用重点保分型考点——师生共研[典例引领](2018·杭州模拟)设f(x)＝|ln(x＋1)|，已知f(a)＝f(b)(a<b)，则()A．a＋b>0B．a＋b>1C．2a＋b>0 D．2a＋b>1解析：选A 作出函数f (x )＝|ln(x ＋1)|的图象如图所示，由f (a )＝f (b )，得－ln(a ＋1)＝ln(b ＋1)，即ab ＋a ＋b ＝0.所以0＝ab ＋a ＋b <a ＋b 24＋a ＋b ，即(a ＋b )(a ＋b ＋4)>0，显然－1<a <0，b >0，∴a ＋b ＋4>0.∴a ＋b >0.故选A.[由题悟法]应用对数型函数的图象可求解的问题(1)对一些可通过平移、对称变换作出其图象的对数型函数，在求解其单调性(单调区间)、值域(最值)、零点时，常利用数形结合思想．(2)一些对数型方程、不等式问题常转化为相应的函数图象问题，利用数形结合法求解．[即时应用]1．函数f (x )＝ln|x －1|的图象大致是( )解析：选B 当x >1时，f (x )＝ln(x －1)，又f (x )的图象关于x ＝1对称，故选B.2．(2018·温州适应性训练)若x 1满足2x ＋2x ＝5，x 2满足2x ＋2log 2(x －1)＝5，则x 1＋x 2＝( ) A.52 B ．3 C.72D ．4解析：选C 2x ＝5－2x,2log 2(x －1)＝5－2x ，即2x －1＝52－x ，log 2(x －1)＝52－x ，作出y ＝2x －1，y ＝52－x ，y ＝log 2(x －1)的图象(如图)．由图知y ＝2x－1与y ＝log 2(x －1)的图象关于y ＝x －1对称，它们与y ＝52－x 的交点A ，B 的中点为y ＝52－x 与y ＝x －1的交点C ，x C ＝x 1＋x 22＝74，∴x 1＋x 2＝72，故选C.[通法在握]1．解决与对数函数有关的函数的单调性问题的步骤2．比较对数值大小的方法(1)若底数为同一常数，则可由对数函数的单调性直接进行判断；若底数为同一字母，则需对底数进行分类讨论．(2)若底数不同，真数相同，则可以先用换底公式化为同底后，再进行比较．(3)若底数与真数都不同，则常借助1,0等中间量进行比较．第三节幂函数1．五种常见幂函数的图象与性质函数特征性质y＝x y＝x2y＝x3y＝x12y＝x－1图象定义域R R R{x|x≥0}{x|x≠0}值域R{y|y≥0}R{y|y≥0}{y|y≠0}奇偶性奇偶奇非奇非偶奇单调性增(－∞，0)减，(0，＋∞)增增增(－∞，0)和(0，＋∞)减公共点(1,1)1．对于函数y＝ax2＋bx＋c，要认为它是二次函数，就必须满足a≠0，当题目条件中未说明a≠0时，就要讨论a＝0和a≠0两种情况．2．幂函数的图象一定会出现在第一象限内，一定不会出现在第四象限，至于是否出现在第二、三象限内，要看函数的奇偶性；幂函数的图象最多只能同时出现在两个象限内；如果幂函数图象与坐标轴相交，则交点一定是原点．[小题纠偏]1．已知函数f (x )＝ax 2＋x ＋5的图象在x 轴上方，则a 的取值范围是________．答案：⎝⎛⎭⎫120，＋∞ 2．给出下列命题： ①函数y ＝2x 是幂函数；②如果幂函数的图象与坐标轴相交，则交点一定是原点； ③当n <0时，幂函数y ＝x n 是定义域上的减函数； ④二次函数y ＝ax 2＋bx ＋c ，x ∈[m ，n ]的最值一定是4ac －b 24a. 其中正确的是________(填序号)．答案：②考点一幂函数的图象与性质基础送分型考点——自主练透[题组练透]1．幂函数y ＝f (x )的图象过点(4,2)，则幂函数y ＝f (x )的图象是( )解析：选C 令f (x )＝x α，则4α＝2， ∴α＝12，∴f (x )＝x 12.2．已知幂函数f (x )＝(m 2－3m ＋3)x m ＋1为偶函数，则m ＝( ) A ．1 B ．2 C ．1或2D ．3解析：选A ∵幂函数f (x )＝(m 2－3m ＋3)x m ＋1为偶函数，∴m 2－3m ＋3＝1，即m 2－3m ＋2＝0，解得m ＝1或m ＝2.当m ＝1时，幂函数f (x )＝x 2为偶函数，满足条件．当m ＝2时，幂函数f (x )＝x 3为奇函数，不满足条件．故选A.3．若(a ＋1)12<(3－2a )12，则实数a 的取值范围是________．解析：易知函数y ＝x 12的定义域为[0，＋∞)，在定义域内为增函数，所以⎩⎪⎨⎪⎧a ＋1≥0，3－2a ≥0，a ＋1<3－2a ，解得－1≤a <23.答案：⎣⎡⎭⎫－1，23 [谨记通法]幂函数的指数与图象特征的关系(1)幂函数的形式是y ＝x α(α∈R)，其中只有一个参数α，因此只需一个条件即可确定其解析式． (2)若幂函数y ＝x α(α∈R)是偶函数，则α必为偶数．当α是分数时，一般将其先化为根式，再判断．(3)若幂函数y ＝x α在(0，＋∞)上单调递增，则α>0，若在(0，＋∞)上单调递减，则α<0. 考点二求二次函数的解析式重点保分型考点——师生共研[典例引领]已知二次函数f (x )满足f (2)＝－1，f (－1)＝－1，且f (x )的最大值是8，试确定此二次函数的解析式．解：法一：(利用二次函数的一般式) 设f (x )＝ax 2＋bx ＋c (a ≠0)．由题意得⎩⎪⎨⎪⎧4a ＋2b ＋c ＝－1，a －b ＋c ＝－1，4ac －b 24a ＝8，解得⎩⎪⎨⎪⎧a ＝－4，b ＝4，c ＝7.故所求二次函数为f (x )＝－4x 2＋4x ＋7. 法二：(利用二次函数的顶点式) 设f (x )＝a (x －m )2＋n .∵f (2)＝f (－1)，∴抛物线对称轴为x ＝2＋－12＝12. ∴m ＝12，又根据题意函数有最大值8，∴n ＝8，∴y ＝f (x )＝a ⎝⎛⎭⎫x －122＋8. ∵f (2)＝－1，∴a ⎝⎛⎭⎫2－122＋8＝－1，解得a ＝－4， ∴f (x )＝－4⎝⎛⎭⎫x －122＋8＝－4x 2＋4x ＋7. 法三：(利用两根式)由已知f (x )＋1＝0的两根为x 1＝2，x 2＝－1，故可设f(x)＋1＝a(x－2)(x＋1)，即f(x)＝ax2－ax－2a－1.又函数有最大值y max＝8，即4a－2a－1－a24a＝8.解得a＝－4或a＝0(舍去)，故所求函数解析式为f(x)＝－4x2＋4x＋7.[由题悟法]求二次函数解析式的方法[通法在握]1．二次函数最值问题的3种类型及解题思路(1)类型：①对称轴、区间都是给定的；②对称轴动、区间固定；③对称轴定、区间变动．(2)思路：抓“三点一轴”，三点是指区间两个端点和中点，一轴指的是对称轴．2．由不等式恒成立求参数取值范围的2大思路及1个关键(1)思路：一是分离参数；二是不分离参数．(2)关键：两种思路都是将问题归结为求函数的最值，至于用哪种方法，关键是看参数是否可分离．这两个思路的依据是：a≥f(x)⇔a≥f(x)max，a≤f(x)⇔a≤f(x)min.。

基本初等函数复习课知识总结[1]

⑤在R上是增函数.
⑤在R上是减函数.
底数互为
倒数的两个指数函数
y = ax, y = (1)x a
的函数图像关于y轴对称。
2、对数函数y=logax(a＞0且a≠1)的图象和性质：
a＞1
y
图
象
o
x
0＜a＜1
y
o
x
①x∈ (0,+∞) ； ② y∈ R;
③过定点(1, 0)
性 ④当x＞ 1时,y＞ 0, 质 0＜ x＜ 1时, y＜ 0
A．y3>y1>y2 B．y2>y1>y3 C．y1>y2>y3 D．y1>y3>y2
(2)log323与 log565；
【解析】∵y1＝40.9＝21.8，y2＝80.44＝21.32， y3＝12－1.5=21.5 ,1.8>1.5>1.32.
∴根据指数函数的性质可得，y1>y3>y2.故选D.
知识结构及知识梳理
指数与指数函数
N次方根及其性质根式及其性质指数分数指数幂有理数指数幂的运算性质
定义
指数函数
图像及性质
基本初等函数
定义对数运算性质
对数与对数函数
换底公式
对数函数定义图像和性质
定义幂函数
图像和性质
根式的性质
(1)当n为奇数时，正数的n次方根是一个正数，负数的n次
方根是一个负数，这时，a的n次方根用符号n a 表示.
(2) 已知 log2 3 = a,log3 7 = b,试用a,b表示 log14 56.
指数函数与对数函数 1、指数函数y=ax(a＞0且a≠1)的图象和性质：

高中数学知识点总结(第二章函数的概念与基本初等函数Ⅰ第一节函数及其表示)

第二章函数的概念与基本初等函数Ⅰ第一节函数及其表示一、基础知识1．函数与映射的概念2．函数的有关概念(1)函数的定义域、值域：在函数y＝f(x)，x∈A中，x叫做自变量，x的取值范围A叫做函数的定义域；与x的值相对应的y值叫做函数值，函数值的集合{f(x)|x∈A}叫做函数的值域．求函数定义域的策略(1)确定函数的定义域常从解析式本身有意义，或从实际出发．(2)如果函数y＝f(x)是用表格给出，则表格中x的集合即为定义域．(3)如果函数y＝f(x)是用图象给出，则图象在x轴上的投影所覆盖的x的集合即为定义域．(2)函数的三要素：定义域、值域和对应关系．(3)相等函数：如果两个函数的定义域和对应关系完全一致，则这两个函数相等，这是判断两函数相等的依据.两函数值域与对应关系相同时，两函数不一定相同．(4)函数的表示法：表示函数的常用方法有：解析法、图象法、列表法．3．分段函数若函数在其定义域内，对于定义域内的不同取值区间，有着不同的对应关系，这样的函数通常叫做分段函数．关于分段函数的3个注意(1)分段函数虽然由几个部分构成，但它表示同一个函数．(2)分段函数的定义域是各段定义域的并集，值域是各段值域的并集．(3)各段函数的定义域不可以相交．考点一函数的定义域[典例] (1)(2019·长春质检)函数y ＝ln1－x x ＋1＋1x的定义域是( ) A ．[－1,0)∪(0,1) B ．[－1,0)∪(0,1] C ．(－1,0)∪(0,1]D ．(－1,0)∪(0,1)(2)已知函数f (x )的定义域为(－1,0)，则函数f (2x ＋1)的定义域为( ) A ．(－1,1) B.⎝⎛⎭⎫－1，－12 C ．(－1,0)D.⎝⎛⎭⎫12，1[解析] (1)由题意得⎩⎪⎨⎪⎧1－x >0，x ＋1>0，x ≠0，解得－1<x <0或0<x <1.所以原函数的定义域为(－1,0)∪(0,1)．(2)令u ＝2x ＋1，由f (x )的定义域为(－1,0)，可知－1<u <0，即－1<2x ＋1<0，得－1<x <－12.[答案] (1)D (2)B [解题技法]1．使函数解析式有意义的一般准则(1)分式中的分母不为0； (2)偶次根式的被开方数非负； (3)y ＝x 0要求x ≠0；(4)对数式中的真数大于0，底数大于0且不等于1； (5)正切函数y ＝tan x ，x ≠k π＋π2(k ∈Z)；(6)实际问题中除考虑函数解析式有意义外，还应考虑实际问题本身的要求． 2．抽象函数的定义域问题(1)若已知函数f (x )的定义域为[a ，b ]，其复合函数f (g (x ))的定义域由不等式a ≤g (x )≤b 求出；(2)若已知函数f (g (x ))的定义域为[a ，b ]，则f (x )的定义域为g (x )在x ∈[a ，b ]上的值域． [题组训练] 1.函数f (x )＝1lnx ＋1＋4－x 2的定义域为( ) A ．[－2,0)∪(0,2] B ．(－1,0)∪(0,2] C ．[－2,2]D ．(－1,2]解析：选B 由⎩⎪⎨⎪⎧x ＋1>0，ln x ＋1≠0，4－x 2≥0，得－1<x ≤2，且x ≠0.2.若函数y ＝f (x )的定义域是[1,2 019]，则函数g (x )＝f x ＋1x －1的定义域是________________．解析：因为y ＝f (x )的定义域是[1,2 019]，所以若g (x )有意义，应满足⎩⎪⎨⎪⎧1≤x ＋1≤2 019，x －1≠0，所以0≤x ≤2 018，且x ≠1.因此g (x )的定义域是{x |0≤x ≤2 018，且x ≠1}．答案：{x |0≤x ≤2 018，且x ≠1}考点二求函数的解析式[典例] (1)已知二次函数f (2x ＋1)＝4x 2－6x ＋5，求f (x )； (2)已知函数f (x )满足f (－x )＋2f (x )＝2x ，求f (x )． [解] (1)法一：待定系数法因为f (x )是二次函数，所以设f (x )＝ax 2＋bx ＋c (a ≠0)，则f (2x ＋1)＝a (2x ＋1)2＋b (2x ＋1)＋c ＝4ax 2＋(4a ＋2b )x ＋a ＋b ＋c .因为f (2x ＋1)＝4x 2－6x ＋5，所以⎩⎪⎨⎪⎧4a ＝4，4a ＋2b ＝－6，a ＋b ＋c ＝5，解得⎩⎪⎨⎪⎧a ＝1，b ＝－5，c ＝9，所以f (x )＝x 2－5x ＋9(x ∈R)．法二：换元法令2x ＋1＝t (t ∈R)，则x ＝t －12，所以f (t )＝4⎝⎛⎭⎫t －122－6·t －12＋5＝t 2－5t ＋9(t ∈R)，所以f (x )＝x 2－5x ＋9(x ∈R)．法三：配凑法因为f (2x ＋1)＝4x 2－6x ＋5＝(2x ＋1)2－10x ＋4＝(2x ＋1)2－5(2x ＋1)＋9，所以f (x )＝x 2－5x ＋9(x ∈R)．(2)解方程组法由f (－x )＋2f (x )＝2x ， ① 得f (x )＋2f (－x )＝2－x ，② ①×2－②，得3f (x )＝2x ＋1－2－x . 即f (x )＝2x ＋1－2－x3.故f (x )的解析式是f (x )＝2x ＋1－2－x3(x ∈R)．[解题技法] 求函数解析式的4种方法及适用条件 (1)待定系数法先设出含有待定系数的解析式，再利用恒等式的性质，或将已知条件代入，建立方程(组)，通过解方程(组)求出相应的待定系数．(2)换元法对于形如y ＝f (g (x ))的函数解析式，令t ＝g (x )，从中求出x ＝φ(t )，然后代入表达式求出f (t )，再将t 换成x ，得到f (x )的解析式，要注意新元的取值范围．(3)配凑法由已知条件f (g (x ))＝F (x )，可将F (x )改写成关于g (x )的表达式，然后以x 替代g (x )，便得f (x )的解析式．(4)解方程组法已知关于f (x )与f ⎝⎛⎭⎫1x 或f (－x )的表达式，可根据已知条件再构造出另外一个等式组成方程组，通过解方程组求出f (x )．[提醒] 由于函数的解析式相同，定义域不同，则为不相同的函数，因此求函数的解析式时，如果定义域不是R ，一定要注明函数的定义域．[题组训练]1.[口诀第2句]已知f (x )是二次函数，且f (0)＝0，f (x ＋1)＝f (x )＋x ＋1，则f (x )＝________________.解析：设f (x )＝ax 2＋bx ＋c (a ≠0)，由f (0)＝0，知c ＝0，f (x )＝ax 2＋bx . 又由f (x ＋1)＝f (x )＋x ＋1，得a (x ＋1)2＋b (x ＋1)＝ax 2＋bx ＋x ＋1，即ax 2＋(2a ＋b )x ＋a ＋b ＝ax 2＋(b ＋1)x ＋1，所以⎩⎪⎨⎪⎧2a ＋b ＝b ＋1，a ＋b ＝1，解得a ＝b ＝12.所以f (x )＝12x 2＋12x (x ∈R)．答案：12x 2＋12x (x ∈R)2.[口诀第3句]已知f ⎝⎛⎭⎫2x ＋1＝lg x ，则f (x )＝________________.解析：令2x ＋1＝t ，得x ＝2t －1，则f (t )＝lg 2t －1，又x >0，所以t >1，故f (x )的解析式是f (x )＝lg2x －1(x >1)．答案：lg2x －1(x >1) 3.[口诀第4句]已知f (x )满足2f (x )＋f ⎝⎛⎭⎫1x ＝3x ，则f (x )＝________. 解析：∵2f (x )＋f ⎝⎛⎭⎫1x ＝3x ，①把①中的x 换成1x ，得2f ⎝⎛⎭⎫1x ＋f (x )＝3x.② 联立①②可得⎩⎨⎧2f x ＋f ⎝⎛⎭⎫1x ＝3x ，2f ⎝⎛⎭⎫1x ＋f x ＝3x，解此方程组可得f (x )＝2x －1x(x ≠0)．答案：2x －1x (x ≠0)考点三分段函数考法(一) 求函数值[典例] (2019·石家庄模拟)已知f (x )＝⎩⎪⎨⎪⎧log 3x ，x >0，a x ＋b ，x ≤0(0<a <1)，且f (－2)＝5，f (－1)＝3，则f (f (－3))＝( )A ．－2B ．2C ．3D ．－3[解析] 由题意得，f (－2)＝a －2＋b ＝5，①f (－1)＝a －1＋b ＝3，②联立①②，结合0<a <1，得a ＝12，b ＝1，所以f (x )＝⎩⎪⎨⎪⎧log 3x ，x >0，⎝⎛⎭⎫12x ＋1，x ≤0，则f (－3)＝⎝⎛⎭⎫12－3＋1＝9，f (f (－3))＝f (9)＝log 39＝2. [答案] B[解题技法] 求分段函数的函数值的策略(1)求分段函数的函数值时，要先确定要求值的自变量属于哪一区间，然后代入该区间对应的解析式求值；(2)当出现f (f (a ))的形式时，应从内到外依次求值；(3)当自变量的值所在区间不确定时，要分类讨论，分类标准应参照分段函数不同段的端点．考法(二) 求参数或自变量的值(或范围)[典例] (2018·全国卷Ⅰ)设函数f (x )＝⎩⎪⎨⎪⎧2－x ，x ≤0，1，x >0，则满足f (x ＋1)<f (2x )的x 的取值范围是( )A ．(－∞，－1]B ．(0，＋∞)C ．(－1,0)D ．(－∞，0)[解析] 法一：分类讨论法①当⎩⎪⎨⎪⎧x ＋1≤0，2x ≤0，即x ≤－1时，f (x ＋1)<f (2x )，即为2－(x ＋1)<2－2x，即－(x ＋1)<－2x ，解得x <1. 因此不等式的解集为(－∞，－1]．②当⎩⎪⎨⎪⎧x ＋1≤0，2x >0时，不等式组无解．③当⎩⎪⎨⎪⎧x ＋1>0，2x ≤0，即－1<x ≤0时，f (x ＋1)<f (2x )，即为1<2－2x，解得x <0.因此不等式的解集为(－1,0)．④当⎩⎪⎨⎪⎧x ＋1>0，2x >0，即x >0时，f (x ＋1)＝1，f (2x )＝1，不合题意．综上，不等式f (x ＋1)<f (2x )的解集为(－∞，0)．法二：数形结合法∵f (x )＝⎩⎪⎨⎪⎧2－x ，x ≤0，1，x >0，∴函数f (x )的图象如图所示．结合图象知，要使f (x ＋1)<f (2x )，则需⎩⎪⎨⎪⎧x ＋1<0，2x <0，2x <x ＋1或⎩⎪⎨⎪⎧x ＋1≥0，2x <0， ∴x <0，故选D. [答案] D[解题技法]已知函数值(或范围)求自变量的值(或范围)的方法(1)根据每一段的解析式分别求解，但要注意检验所求自变量的值(或范围)是否符合相应段的自变量的取值范围，最后将各段的结果合起来(求并集)即可；(2)如果分段函数的图象易得，也可以画出函数图象后结合图象求解．[题组训练]1．设f (x )＝⎩⎨⎧x ，0＜x ＜1，2x －1，x ≥1，若f (a )＝f (a ＋1)，则f ⎝⎛⎭⎫1a ＝( ) A ．2 B ．4 C ．6D ．8解析：选C 当0＜a ＜1时，a ＋1＞1，f (a )＝a ，f (a ＋1)＝2(a ＋1－1)＝2a ， ∵f (a )＝f (a ＋1)，∴a ＝2a ，解得a ＝14或a ＝0(舍去)．∴f ⎝⎛⎭⎫1a ＝f (4)＝2×(4－1)＝6.当a ≥1时，a ＋1≥2，f (a )＝2(a －1)，f (a ＋1)＝2(a ＋1－1)＝2a ， ∵f (a )＝f (a ＋1)，∴2(a －1)＝2a ，无解．综上，f ⎝⎛⎭⎫1a ＝6.2．已知函数f (x )＝⎩⎪⎨⎪⎧2x ，x ≤1，f x －1，x >1，则f (f (3))＝________.解析：由题意，得f (3)＝f (2)＝f (1)＝21＝2， ∴f (f (3))＝f (2)＝2. 答案：23．(2017·全国卷Ⅰ)设函数f (x )＝⎩⎪⎨⎪⎧x ＋1，x ≤0，2x ，x >0，则满足f (x )＋f ⎝⎛⎭⎫x －12>1的x 的取值范围是________．解析：由题意知，可对不等式分x ≤0,0<x ≤12，x >12讨论．①当x ≤0时，原不等式为x ＋1＋x ＋12>1，解得x >－14，故－14<x ≤0.②当0<x ≤12时，原不等式为2x ＋x ＋12>1，显然成立．③当x >12时，原不等式为2x ＋2x －12>1，显然成立．综上可知，所求x 的取值范围是⎝⎛⎭⎫－14，＋∞. 答案：⎝⎛⎭⎫－14，＋∞ 4．设函数f (x )＝⎩⎪⎨⎪⎧⎝⎛⎭⎫12x －7，x <0，x ，x ≥0，若f (a )<1，则实数a 的取值范围是____________．解析：若a <0，则f (a )<1⇔⎝⎛⎭⎫12a－7<1⇔⎝⎛⎭⎫12a <8，解得a >－3，故－3<a <0；若a ≥0，则f (a )<1⇔a <1，解得a <1，故0≤a <1. 综上可得－3<a <1. 答案：(－3,1)[课时跟踪检测]1．下列所给图象是函数图象的个数为( )A ．1B ．2C ．3D ．4解析：选B ①中当x ＞0时，每一个x 的值对应两个不同的y 值，因此不是函数图象；②中当x ＝x 0时，y 的值有两个，因此不是函数图象；③④中每一个x 的值对应唯一的y 值，因此是函数图象．故选B.2．函数f (x )＝2x －1＋1x －2的定义域为( ) A ．[0,2)B ．(2，＋∞)C ．[0,2)∪(2，＋∞)D ．(－∞，2)∪(2，＋∞)解析：选C 由题意得⎩⎪⎨⎪⎧2x －1≥0，x －2≠0，解得x ≥0，且x ≠2.3．已知f ⎝⎛⎭⎫12x －1＝2x －5，且f (a )＝6，则a 等于( ) A.74 B ．－74C.43D ．－43解析：选A 令t ＝12x －1，则x ＝2t ＋2，f (t )＝2(2t ＋2)－5＝4t －1，则4a －1＝6，解得a ＝74.4．(2019·贵阳检测)下列函数中，同一个函数的定义域与值域相同的是( ) A ．y ＝x －1 B ．y ＝ln x C ．y ＝13x －1D ．y ＝x ＋1x －1解析：选D 对于A ，定义域为[1，＋∞)，值域为[0，＋∞)，不满足题意；对于B ，定义域为(0，＋∞)，值域为R ，不满足题意；对于C ，定义域为(－∞，0)∪(0，＋∞)，值域为(－∞，－1)∪(0，＋∞)，不满足题意；对于D ，y ＝x ＋1x －1＝1＋2x －1，定义域为(－∞，1)∪(1，＋∞)，值域也是(－∞，1)∪(1，＋∞)．5．(2018·福建期末)已知函数f (x )＝⎩⎪⎨⎪⎧log 2x ＋a ，x >0，4x －2－1，x ≤0.若f (a )＝3，则f (a －2)＝( )A ．－1516B ．3C ．－6364或3D ．－1516或3解析：选A 当a >0时，若f (a )＝3，则log 2a ＋a ＝3，解得a ＝2(满足a >0)；当a ≤0时，若f (a )＝3，则4a －2－1＝3，解得a ＝3，不满足a ≤0，所以舍去．于是，可得a ＝2.故f (a －2)＝f (0)＝4－2－1＝－1516.6．已知函数y ＝f (2x －1)的定义域是[0,1]，则函数f 2x ＋1log 2x ＋1的定义域是( )A ．[1,2]B ．(－1,1] C.⎣⎡⎦⎤－12，0 D ．(－1,0)解析：选D 由f (2x －1)的定义域是[0,1]，得0≤x ≤1，故－1≤2x －1≤1， ∴f (x )的定义域是[－1,1]， ∴要使函数f 2x ＋1log 2x ＋1有意义，需满足⎩⎪⎨⎪⎧－1≤2x ＋1≤1，x ＋1>0，x ＋1≠1，解得－1<x <0.7．下列函数中，不满足f (2 018x )＝2 018f (x )的是( ) A ．f (x )＝|x | B ．f (x )＝x －|x | C ．f (x )＝x ＋2D ．f (x )＝－2x解析：选C 若f (x )＝|x |，则f (2 018x )＝|2 018x |＝2 018|x |＝2 018f (x )；若f (x )＝x －|x |，则f (2 018x )＝2 018x －|2 018x |＝2 018(x －|x |)＝2 018f (x )；若f (x )＝x ＋2，则f (2 018x )＝2 018x ＋2，而2 018f (x )＝2 018x ＋2 018×2，故f (x )＝x ＋2不满足f (2 018x )＝2 018f (x )；若f (x )＝－2x ，则f (2 018x )＝－2×2 018x ＝2 018×(－2x )＝2 018f (x )．故选C.8．已知具有性质：f ⎝⎛⎭⎫1x ＝－f (x )的函数，我们称为满足“倒负”变换的函数，下列函数： ①f (x )＝x －1x ；②f (x )＝x ＋1x ；③f (x )＝⎩⎪⎨⎪⎧x ，0<x <1，0，x ＝1，－1x ，x >1.其中满足“倒负”变换的函数是( ) A ．①② B ．①③ C ．②③D ．①解析：选B 对于①，f (x )＝x －1x ，f ⎝⎛⎭⎫1x ＝1x－x ＝－f (x )，满足题意；对于②，f ⎝⎛⎭⎫1x ＝1x ＋x＝f (x )，不满足题意；对于③，f ⎝⎛⎭⎫1x ＝⎩⎪⎨⎪⎧ 1x ，0<1x <1，0，1x ＝1，－x ，1x >1，即f ⎝⎛⎭⎫1x ＝⎩⎪⎨⎪⎧ 1x ，x >1，0，x ＝1，－x ，0<x <1，故f ⎝⎛⎭⎫1x ＝－f (x )，满足题意．综上可知，满足“倒负”变换的函数是①③. 9．(2019·青岛模拟)函数y ＝ln ⎝⎛⎭⎫1＋1x ＋1－x 2的定义域为________．解析：由⎩⎪⎨⎪⎧ 1＋1x >0，1－x 2≥0⇒⎩⎪⎨⎪⎧x <－1或x >0，－1≤x ≤1⇒0<x ≤1. 所以该函数的定义域为(0,1]．答案：(0,1]10．(2019·益阳、湘潭调研)若函数f (x )＝⎩⎨⎧ lg 1－x ，x <0，－2x ，x ≥0，则f (f (－9))＝________. 解析：∵函数f (x )＝⎩⎨⎧ lg 1－x ，x <0，－2x ，x ≥0，∴f (－9)＝lg 10＝1，∴f (f (－9))＝f (1)＝－2. 答案：－211．(2018·张掖一诊)已知函数f (x )＝⎩⎪⎨⎪⎧2x ，x ＞0，x ＋1，x ≤0，若f (a )＋f (1)＝0，则实数a 的值等于________．解析：∵f (1)＝2，且f (1)＋f (a )＝0，∴f (a )＝－2＜0，故a ≤0. 依题知a ＋1＝－2，解得a ＝－3.答案：－312．已知f (x )＝⎩⎪⎨⎪⎧ 12x ＋1，x ≤0，－x －12，x ＞0，使f (x )≥－1成立的x 的取值范围是________．解析：由题意知⎩⎪⎨⎪⎧ x ≤0，12x ＋1≥－1或⎩⎪⎨⎪⎧ x ＞0，－x －12≥－1，解得－4≤x ≤0或0＜x ≤2，故所求x 的取值范围是[－4,2]．答案：[－4,2]13．设函数f (x )＝⎩⎪⎨⎪⎧ax ＋b ，x ＜0，2x ，x ≥0，且f (－2)＝3，f (－1)＝f (1)． (1)求函数f (x )的解析式；(2)在如图所示的直角坐标系中画出f (x )的图象．解：(1)由f (－2)＝3，f (－1)＝f (1)，得⎩⎪⎨⎪⎧ －2a ＋b ＝3，－a ＋b ＝2，解得⎩⎪⎨⎪⎧ a ＝－1，b ＝1，所以f (x )＝⎩⎪⎨⎪⎧－x ＋1，x ＜0，2x ，x ≥0. (2)函数f (x )的图象如图所示．。

专题二第1讲函数、基本初等函数的图象与性质

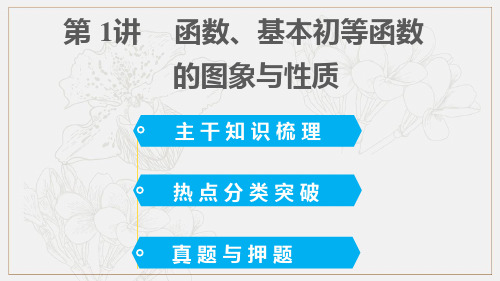
函数，
所以由15<(15)b<(15)a<1 得 0<a<b<1，
所以0<
a b
<1.
所以y＝ax，y＝bx，y＝( a )x在(－∞，＋∞)上都是
b
递减函数，
从而ab<aa，( a)a<1得ba>aa， b
故ab<aa<ba，
答案选B.
答案 B
(2)已知函数 f(x)＝2x－21x，函数 g(x)＝ffx－，xx，≥x0<，0，
变式训练1
(1)(2013·重庆)已知函数f(x)＝ax3＋bsin x＋4(a，b∈R)，
f(lg(log210))＝5，则f(lg(lg 2))等于( C )
A.－5
B.－1 C.3 D.4
解析
lg(log210)＝lg
1 lg 2
＝－lg(lg
2)，
由f(lg(log210))＝5，
得a[lg(lg 2)]3＋bsin(lg(lg 2))＝4－5＝－1，
2
则实数a的取值范围是( )
A.(－1,0)∪(0,1) B.(－∞，－1)∪(1，＋∞) C.(－1,0)∪(1，＋∞) D.(－∞，－1)∪(0,1)
思维启迪可利用函数图象或分
类讨论确定a的范围；
解析方法一由题意作出y＝f(x)的图象如图. 显然当a>1或－1<a<0时，满足f(a)>f(－a).故选C.
方法二对a分类讨论：
当a>0时，log2a>log 1 a，即log2a>0，∴a>1. 2
当a<0时，log 1 (－a)>log2(－a)，即log2(－a)<0，

初等函数基本不等式

初等函数基本不等式以《初等函数基本不等式》为标题，写一篇3000字的中文文章初等函数基本不等式是数学中的基本不等式，涵盖了初等函数及其基本性质，对于许多研究和应用都有着非常重要的意义。

在本文中，我们将重点介绍初等函数基本不等式的形式、历史发展以及在各种应用领域中的表现。

首先，我们介绍初等函数基本不等式的形式。

它是一个比较常见的数学不等式，可以简写为f(x) g(x)或f(x) g(x)，又称为初等不等式。

它可以用来描述数学对象之间的关系，并为其它定理推导提供了依据。

它的实际形式可以是以下几种：1.和不等式：f(x) =aixiaiyi2.分不等式：f(x) =f(x) dxg(x) dx3.量不等式：f(x) = ||f|| ||g||4.函数不等式：f(x) g(x)，其中f(x)是凸函数初等函数基本不等式的发展历史可以追溯到古希腊的数学思想，此时此刻，不等式已经成为数学领域中一种基本概念。

古希腊数学家凯撒若连乌斯（Caesar Eureelius）曾将不等式应用到特殊几何体，他也是初等函数基本不等式的创始人之一。

17世纪，英国数学家约翰汉普顿（John Hampton）将不等式应用到差分方程组中，成为初等函数的第一位开拓者。

随后，法国数学家弗朗西斯得拉克（Francois de Laplace）和英国数学家大卫拉森（David Ranson）也先后推出了自己的初等函数基本不等式理论。

初等函数基本不等式有着丰富的应用范围，主要表现在以下几个方面：1. 优化问题：初等函数基本不等式可以用来解决优化问题，如最小值与最大值求解，极限求解等。

2.数不变性：初等函数基本不等式可以保证函数的不变性，即函数的变化不会影响其他变量的变化。

3.微分方程的解法：初等函数基本不等式可以用于求解偏微分方程，特别是热传导方程的求解。

4.分几何中的应用：初等函数基本不等式在微分几何中也有着重要的作用，它可以用来研究几何图像与函数之间的关系。

第二章函数与基本初等函数1

第1讲函数及其表示【2013年高考会这样考】1．主要考查函数的定义域、值域、解析式的求法．2．考查分段函数的简单应用．3．由于函数的基础性强，渗透面广，所以会与其他知识结合考查．【复习指导】正确理解函数的概念是学好函数的关键，函数的概念比较抽象，应通过适量练习弥补理解的缺陷，纠正理解上的错误．本讲复习还应掌握：(1)求函数的定义域的方法；(2)求函数解析式的基本方法；(3)分段函数及其应用．基础梳理1．函数的基本概念(1)函数的定义：设A、B是非空数集，如果按照某种确定的对应关系f，使对于集合A中的一个数x，在集合B中都有确定的数f(x)和它对应，那么称f：A→B为从集合A到集合B的一个函数，记作：y＝f(x)，x∈A.(2)函数的定义域、值域在函数y＝f(x)，x∈A中，x叫自变量，x的取值范围A叫做，与x的值对应的y值叫函数值，函数值的集合{f(x)|x∈A}叫值域．值域是集合B的子集．(3)函数的三要素：定义域、值域和对应关系．(4)相等函数：如果两个函数的定义域和完全一致，则这两个函数相等；这是判断两函数相等的依据．2．函数的三种表示方法表示函数的常用方法有：解析法、列表法、．3．映射的概念一般地，设A、B是两个非空的集合，如果按某一个确定的对应关系f，使对于集合A 中的任意一个元素x ，在集合B 中都有确定的元素y 与之对应，那么就称对应f ：A →B 为从集合A 到集合B 的一个映射．一个方法求复合函数y ＝f (t )，t ＝q (x )的定义域的方法：①若y ＝f (t )的定义域为(a ，b )，则解不等式得a ＜q (x )＜b 即可求出y ＝f (q (x ))的定义域；②若y ＝f (g (x ))的定义域为(a ，b )，则求出g (x )的值域即为f (t )的定义域．两个防范(1)解决函数问题，必须优先考虑函数的定义域． (2)用换元法解题时，应注意换元前后的等价性．三个要素函数的三要素是：定义域、值域和对应关系．值域是由函数的定义域和对应关系所确定的．两个函数的定义域和对应关系完全一致时，则认为两个函数相等．函数是特殊的映射，映射f ：A →B 的三要素是两个集合A 、B 和对应关系f .双基自测1．函数f (x )＝log 2(3x ＋1)的值域为( )．A ．(0，＋∞)B ．[0，＋∞)C ．(1，＋∞)D ．[1，＋∞) 2．若f (x )＝1log 12(2x ＋1)，则f (x )的定义域为( )．A.⎝ ⎛⎭⎪⎫－12，0B.⎝ ⎛⎦⎥⎤－12，0C.⎝ ⎛⎭⎪⎫－12，＋∞ D ．(0，＋∞) 3．下列各对函数中，表示同一函数的是( )．A ．f (x )＝lg x 2，g (x )＝2lg x B ．f (x )＝lg x ＋1x －1，g (x )＝lg(x ＋1)－lg(x －1)C ．f (u )＝1＋u1－u ，g (v )＝ 1＋v1－vD ．f (x )＝(x )2，g (x )＝x 2 4．某学校要召开学生代表大会，规定各班每10人推选一名代表，当各班人数除以10的余数大于6时再增选一名代表．那么，各班可推选代表人数y 与该班人数x 之间的函数关系用取整函数y ＝[x ]([x ]表示不大于x 的最大整数)可以表示为( )．A ．y ＝⎣⎢⎡⎦⎥⎤x 10 B ．y ＝⎣⎢⎡⎦⎥⎤x ＋310C ．y ＝⎣⎢⎡⎦⎥⎤x ＋410 D ．y ＝⎣⎢⎡⎦⎥⎤x ＋510 5．函数y ＝f (x )的图象如图所示．那么，f (x )的定义域是________；值域是________；其中只与x 的一个值对应的y 值的范围是________．考向一求函数的定义域【例1】►求下列函数的定义域： (1)f (x )＝|x －2|－1log 2(x －1)；(2)f (x )＝ln (x ＋1)－x 2－3x ＋4.【训练1】 (1)已知f (x )的定义域为⎣⎢⎡⎦⎥⎤－12，12，求函数y ＝f ⎝ ⎛⎭⎪⎫x 2－x －12的定义域；(2)已知函数f (3－2x )的定义域为[－1,2]，求f (x )的定义域．考向二求函数的解析式【例2】►(1)已知f ⎝ ⎛⎭⎪⎫2x ＋1＝lg x ，求f (x )；(2)定义在(－1,1)内的函数f (x )满足2f (x )－f (－x )＝lg(x ＋1)，求函数f (x )的解析式．【训练2】 (1)已知f (x )是二次函数，若f (0)＝0，且f (x ＋1)＝f (x )＋x ＋1，试求f (x )的表达式．(2)已知f (x )＋2f (1x )＝2x ＋1，求f (x )．考向三分段函数【例3】设函数f (x )＝⎩⎨⎧21－x，x ≤1，1－log 2x ，x ＞1，则满足f (x )≤2的x 的取值范围是( )．A ．[－1,2]B ．[0,2]C ．[1，＋∞)D ．[0，＋∞)【训练3】已知实数a ≠0，函数f (x )＝⎩⎨⎧2x ＋a ，x ＜1，－x －2a ，x ≥1.若f (1－a )＝f (1＋a )，则a 的值为________．阅卷报告1——忽视函数的定义域【问题诊断】函数的单调区间是函数定义域的子区间，所以求解函数的单调区间，必须先求出函数的定义域．如果是复合函数，应该根据复合函数单调性的判断方法，首先判断两个简单函数的单调性，根据同增异减的法则求解函数的单调区间．由于思维定势的原因，考生容易忽视定义域，导致错误．【防范措施】研究函数的任何问题时，把求函数的定义域放在首位，即遵循“定义域优先”的原则．【示例】►求函数y＝log 13(x2－3x)的单调区间．【试一试】求函数f(x)＝log2(x2－2x－3)的单调区间．第2讲函数的单调性与最值【2013年高考会这样考】1．考查求函数单调性和最值的基本方法．2．利用函数的单调性求单调区间．3．利用函数的单调性求最值和参数的取值范围．【复习指导】本讲复习首先回扣课本，从“数”与“形”两个角度来把握函数的单调性和最值的概念，复习中重点掌握：(1)函数单调性的判断及其应用；(2)求函数最值的各种基本方法；对常见题型的解法要熟练掌握．基础梳理1．函数的单调性(1)单调函数的定义增函数减函数定义一般地，设函数f (x )的定义域为I .如果对于定义域I 内某个区间D 上的任意两个自变量的值x 1，x 2当x 1＜x 2时，都有，那么就说函数f (x )在区间D 上是增函数当x 1＜x 2时，都有，那么就说函数f (x )在区间D 上是减函数图象描述自左向右图象是上升的自左向右图象是下降的(2)单调区间的定义若函数f (x )在区间D 上是增函数或减函数，则称函数f (x )在这一区间上具有(严格的)单调性，区间D 叫做f (x )的单调区间． 2．函数的最值前提设函数y ＝f (x )的定义域为I ，如果存在实数M 满足条件 .①对于任意x ∈I ，都有f (x )≤M ； ①对于任意x ∈I ，都有f (x )≥M ；②存在x 0∈I ，使得f (x 0)＝M②存在x 0∈I ，使得f (x 0)＝M . 结论M 为最大值M 为最小值一个防范函数的单调性是对某个区间而言的，所以要受到区间的限制．例如函数y ＝1x 分别在(－∞，0)，(0，＋∞)内都是单调递减的，但不能说它在整个定义域即(－∞，0)∪(0，＋∞)内单调递减，只能分开写，即函数的单调减区间为(－∞，0)和(0，＋∞)，不能用“∪”连接．两种形式设任意x 1，x 2∈[a ，b ]且x 1＜x 2，那么①f (x 1)－f (x 2)x 1－x 2＞0⇔f (x )在[a ，b ]上是增函数；f (x 1)－f (x 2)x 1－x 2＜0⇔f (x )在[a ，b ]上是减函数．②(x 1－x 2)[f (x 1)－f (x 2)]＞0⇔f (x )在[a ，b ]上是增函数；(x 1－x 2)[f (x 1)－f (x 2)]＜0⇔f (x )在[a ，b ]上是减函数．两条结论(1)闭区间上的连续函数一定存在最大值和最小值．当函数在闭区间上单调时最值一定在端点取到．(2)开区间上的“单峰”函数一定存在最大(小)值．四种方法函数单调性的判断(1)定义法：取值、作差、变形、定号、下结论．(2)复合法：同增异减，即内外函数的单调性相同时，为增函数，不同时为减函数．(3)导数法：利用导数研究函数的单调性． (4)图象法：利用图象研究函数的单调性．双基自测1．设f (x )为奇函数，且在(－∞，0)内是减函数，f (－2)＝0，则xf (x )＜0的解集为 A ．(－2,0)∪(2，＋∞) B ．(－∞，－2)∪(0,2) C ．(－∞，－2)∪(2，＋∞) D ．(－2,0)∪(0,2)2．已知函数f (x )＝e x －1，g (x )＝－x 2＋4x －3.若有f (a )＝g (b )，则b 的取值范围为( )．A ．[2－2，2＋2]B ．(2－2，2＋2)C ．[1,3]D ．(1,3)3．已知f (x )为R 上的减函数，则满足f ⎝ ⎛⎭⎪⎫⎪⎪⎪⎪⎪⎪1x <f (1)的实数x 的取值范围是( )．A ．(－1,1)B ．(0,1)C ．(－1,0)∪(0,1)D ．(－∞，－1)∪(1，＋∞) 4．函数f (x )＝log 5(2x ＋1)的单调增区间是______． 5．若x ＞0，则x ＋2x 的最小值为________．考向一函数的单调性的判断【例1】►试讨论函数f(x)＝xx2＋1的单调性．【训练1】讨论函数f(x)＝axx－1(a≠0)在(－1,1)上的单调性．考向二利用已知函数的单调区间求参数的值(或范围)【例2】►已知函数f(x)＝x2＋ax(a>0)在(2，＋∞)上递增，求实数a的取值范围．【训练2】函数y＝x－5x－a－2在(－1，＋∞)上单调递增，则a的取值范围是A．a＝－3 B．a<3 C．a≤－3 D．a≥－3考向三利用函数的单调性求最值【例3】►已知函数f (x )对于任意x ，y ∈R ，总有f (x )＋f (y )＝f (x ＋y )，且当x ＞0时，f (x )＜0，f (1)＝－23. (1)求证：f (x )在R 上是减函数； (2)求f (x )在[－3,3]上的最大值和最小值．【训练3】已知定义在区间(0，＋∞)上的函数f (x )满足f ⎝ ⎛⎭⎪⎫x 1x 2＝f (x 1)－f (x 2)，且当x ＞1时，f (x )＜0. (1)求f (1)的值； (2)判断f (x )的单调性；(3)若f (3)＝－1，求f (x )在[2,9]上的最小值．规范解答2——如何解不等式恒成立问题【问题研究】在恒成立的条件下，如何确定参数的范围是历年来高考考查的重点内容，近年来在新课标地区的高考命题中，由于三角函数、数列、导数知识的渗透，使原来的分离参数法、根的分布法增添了思维难度，因而含参数不等式的恒成立问题常出现在综合题的位置.【解决方案】解决这类问题的关键是将恒成立问题进行等价转化，使之转化为函数的最值问题，或者区间根的分布问题，进而运用最值原理或者区间根原理使问题获解，常用方法还有函数性质法，分离参数法等.【示例】►(本题满分12分)已知函数f(x)＝x2－2ax＋2，当x∈[－1，＋∞)时，f(x)≥a 恒成立，求a的取值范围．【试一试】当x∈(1,2)时，不等式x2＋mx＋4<0恒成立，则m的取值范围是_____ 第3讲函数的奇偶性与周期性【2013年高考会这样考】1．判断函数的奇偶性．2．利用函数奇偶性、周期性求函数值及求参数值．3．考查函数的单调性与奇偶性的综合应用．【复习指导】本讲复习时应结合具体实例和函数的图象，理解函数的奇偶性、周期性的概念，明确它们在研究函数中的作用和功能．重点解决综合利用函数的性质解决有关问题．基础梳理1．奇、偶函数的概念一般地，如果对于函数f(x)的定义域内任意一个x，都有，那么函数f(x)就叫做偶函数．一般地，如果对于函数f(x)的定义域内任意一个x，都有，那么函数f(x)就叫做奇函数．奇函数的图象关于原点对称；偶函数的图象关于y轴对称．2．奇、偶函数的性质(1)奇函数在关于原点对称的区间上的单调性，偶函数在关于原点对称的区间上的单调性。

三元基本不等式基础

基本不等式在求最值中的应用与完善杨亚军函数的最值是函数这一章节中很重要的部分，它的重要性不仅在题型的多样、方法的灵活上，更主要的是其在实际生活及生产实践中的应用。

高考应用题几乎都与最值问题有关,而基本不等式是解决此类实际问题的有力工具.本文着重就基本不等式在求最值中的应用与完善谈一些个人的体会.只有扎实地掌握好基本不等式求最值的基本技能与注意事项，才能更好地去解决实际应用问题。

一、基本不等式的内容及使用要点1、二元基本不等式：①a，b∈R时，a2+b2≥2ab（当且仅当a=b时“=”号成立）；②a，b≥0时，a+b≥2 （当且仅当a=b时“=”号成立）。

这两个公式的结构完全一致，但适用范围不同。

若在非负实数范围之内，两个公式均成立，此时应根据题目的条件和结论选用合适的公式及公式的变形：ab≤ ，ab≤ 。

对不等式ab≤ ，还有更一般的表达式：|ab|≤ 。

由数列知识可知，称为a，b的等差中项，称为a，b的等比中项，故算术平均数与几何平均数的定理又可叙述为：“两个正数的等比中项不大于它们的等差中项”。

2.三元基本不等式：当a，b，c>0时，a+b+c≥ ，当且仅当a=b=c时，等号成立，……乃至n元基本不等式；当ai >0（i=1，2，…，n）时，a1+a2+…+an≥。

二元基本不等式的其它表达形式也应记住：当a>0，b>0时，≥2，a+ ≥2等。

当字母范围为负实数时，有时可利用转化思想转化为正实数情形，如a<0时，可得到a+ ≤-2。

基本不等式中的字母a，b可代表多项式。

3.利用基本不等式求函数的最大值或最小值是高中求函数最值的主要方法之一。

利用基本不等式求函数最值时，其条件为“一正二定三等”，“一正”指的是在正实数集合内，“二定”指的是解析式各因式的和或积为定值（常数），“三等”指的是等号条件能够成立。

利用基本不等式求函数最值的方法使用范围较广泛，既可适用于已学过的二次函数，又可适用于分式函数，高次函数，无理函数。

基本不等式教学设计

基本不等式教学设计2a b +≤”教学设计一、教学内容解析本节内容选自《普通高中课程标准实验教科书数学必修（5）》（人教A 版）第三章第四节第一课时。

基本不等式是关于不等式的证明、求解最值问题的重要工具，在高中数学知识体系中占有重要的地位。

作为本章最后一节内容，基本不等式承前启后，即为解决最值问题提供了新的依据和方法，也为后续内容如“直接证明与间接证明”、“均值不等式（推广）”等知识的学习作好知识储备。

本节课的学习任务主要是探索几何背景赵爽弦图(勾股圆方图)中所蕴含的不等关系，通过对重要不等式（222a b ab +≥，当且仅当a b =时取“=”2a b +且a b R +∈、，当且仅当a b =时取“=”）的初步认识，在此基础之上引导学生多角度探索基本不等式的证明方法及几何意义，并在解决简单的最值问题过程中体会基本不等式的重要作用。

教学重点：基本不等式的探究过程及多角度探索基本不等式的证明方法。

突出重点的手段：教师在教学过程中要善于捕捉学生情感的兴奋点，激发他们的学习兴趣，鼓励学生大胆猜想，积极探索，以积极的评价，促使他们知难而进。

另外，以数形结合为主导思想选择知识的切入点，从学生已有的认知水平和知识基础入手，在以学生为主体的前提下教师给以适当的引导。

二、教学目标设置《课程标准》对本节内容的要求是：①探索并了解基本不等式的证明过程；②会用基本不等式解决简单的最值问题。

依据《课程标准》并结合本节教学内容及学情，将本节课的教学目标确定为：1.结合赵爽弦图探究概括基本不等式，直观理解基本不等式的几何背景，体会数形结合的思想方法；2.在多角度探究基本不等式的证明方法的过程中，培养学生的探索精神和逻辑推理能力；3.通过解决简单的最大（小）值问题，深化对基本不等式的理解，感受基本不等式在解决实际问题中的作用。

三、学生学情分析学生比较熟悉勾股定理、圆的简单性质、相似三角形的性质等知识，高中阶段已经学习了基本初等函数及其性质、不等关系与不等式的性质，学生对不等式有了初步的了解和应用，对数形结合、转化与化归等数学思想方法有了一定的体会，这为本节课奠定了思想基础。

人教A版高中数学教材目录（全）

人教A 版高中数学目录必修1第一章集合与函数概念1 1．．1 1 集合集合 1 1．．2 2 函数及其表示函数及其表示 1 1．．3 3 函数的基本性质函数的基本性质第二章基本初等函数（Ⅰ）2．1 1 指数函数指数函数 2 2．．2 2 对数函数对数函数 2 2．．3 3 幂函数幂函数第三章函数的应用3．1 1 函数与方程函数与方程 3 3．．2 2 函数模型及其应用函数模型及其应用必修2第一章空间几何体1 1．．1 1 空间几何体的结构空间几何体的结构 1 1．．2 2 空间几何体的三视图和空间几何体的三视图和直观图1 1．．3 3 空间几何体的表面积与空间几何体的表面积与体积第二章点、直线、平面之间的位置关系2 2．．1 1 空间点、直线、平面之空间点、直线、平面之间的位置关系2 2．．2 2 直线、平面平行的判定直线、平面平行的判定及其性质 2 2．．3 3 直线、平面垂直的判定直线、平面垂直的判定及其性质第三章直线与方程3．1 1 直线的倾斜角与斜率直线的倾斜角与斜率 3 3．．2 2 直线的方程直线的方程3 3．．3 3 直线的交点坐标与距离直线的交点坐标与距离公式必修3第一章算法初步1 1．．1 1 算法与程序框图算法与程序框图 1 1．．2 2 基本算法语句基本算法语句 1 1．．3 3 算法案例算法案例阅读与思考割圆术第二章统计2 2．．1 1 随机抽样随机抽样阅读与思考一个著名的案例阅读与思考广告中数据的可靠性阅读与思考如何得到敏感性问题的诚实反应 2 2．．2 2 用样本估计总体用样本估计总体阅读与思考生产过程中的质量控制图2 2．．3 3 变量间的相关关系变量间的相关关系阅读与思考相关关系的强与弱第三章概率3 3．．1 1 随机事件的概率随机事件的概率阅读与思考天气变化的认识过程 3 3．．2 2 古典概型古典概型 3 3．．3 3 几何概型几何概型必修4第一章三角函数1 1．．1 1 任意角和弧度制任意角和弧度制 1 1．．2 2 任意角的三角函数任意角的三角函数1 1．．3 3 三角函数的诱导公式三角函数的诱导公式 1 1．．4 4 三角函数的图象与性质三角函数的图象与性质 1 1．．5 5 函数函数y=Asin y=Asin（（ωx+ψ） 1 1．．6 6 三角函数模型的简单应三角函数模型的简单应用第二章平面向量 2 2．．1 1 平面向量的实际背景及平面向量的实际背景及基本概念 2 2．．2 2 平面向量的线性运算平面向量的线性运算 2 2．．3 3 平面向量的基本定理及平面向量的基本定理及坐标表示 2 2．．4 4 平面向量的数量积平面向量的数量积 2 2．．5 5 平面向量应用举例平面向量应用举例第三章三角恒等变换3 3．．1 1 两角和与差的正弦、余两角和与差的正弦、余弦和正切公式 3 3．．2 2 简单的三角恒等变换简单的三角恒等变换必修5第一章解三角形1.1正弦定理和余弦定理1.2应用举例1.3实习作业第二章数列2.1数列的概念与简单表示法2.2等差数列2.3等差数列的前n 项和2.4等比数列2.5等比数列的前n 项和第三章不等式3.1不等关系与不等式3.2一元二次不等式及其解法3.3二元一次不等式（组）与简单的线性规划问题3.3.1二元一次不等式（组）与平面区域3.3.2简单的线性规划问题3.4基本不等式选修1-1第一章常用逻辑用语1.1命题及其关系1.2充分条件与必要条件1.3简单的逻辑联结词1.4全称量词与存在量词第二章圆锥曲线与方程2.1椭圆2.2双曲线2.3抛物线第三章导数及其应用3.1变化率与导数3.2导数的计算3.3导数在研究函数中的应用的应用3.4生活中的优化问题举例举例选修1-2第一章第一章统计案例统计案例 1．1 回归分析的基本思想及其初步应用思想及其初步应用 1．2 独立性检验的基本思想及其初步应用本思想及其初步应用第二章第二章推理与证明推理与证明 2．1 合情推理与演绎证明证明2．2 直接证明与间接证明证明第三章第三章数系的扩充与复数的引入与复数的引入3．1数系的扩充和复数的概念的概念3．2复数代数形式的四则运算则运算第四章第四章框图框图 4．1流程图流程图 4．2结构图结构图选修2-1第一章第一章常用逻辑用语1.1 命题及其关系命题及其关系 1.2 充分条件与必要条件条件1.3 简单的逻辑联结词1.4 全称量词与存在量词量词第二章第二章圆锥曲线与方程方程2.1 曲线与方程曲线与方程2.2 椭圆椭圆 2.3 双曲线双曲线 2.4 抛物线抛物线第三章第三章空间向量与立体几何立体几何3.1 空间向量及其运算3.2 立体几何中的向量方法量方法选修2-2第一章第一章导数及其应用1.1 变化率与导数变化率与导数1.2 导数的计算导数的计算1.3 导数在研究函数中的应用中的应用1.4 生活中的优化问题举例题举例1.5 定积分的概念定积分的概念 1.6 微积分基本定理微积分基本定理 1.7 定积分的简单应用第二章第二章推理与证明推理与证明 2.1 合情推理与演绎推理推理2.2 直接证明与间接证明证明2.3 数学归纳法数学归纳法第三章数系的扩充与复数的引入与复数的引入3.1 数系的扩充和复数的概念数的概念3.2 复数代数形式的四则运算四则运算选修2-3第一章第一章计数原理计数原理1.1 分类加法计数原理与分步乘法计数原理理与分步乘法计数原理1.2 排列与组合排列与组合 1.3 二项式定理二项式定理第二章第二章随机变量及其分布其分布2.1 离散型随机变量及其分布列及其分布列2.2 二项分布及其应用2.3 离散型随机变量的均值与方差的均值与方差2.4 正态分布正态分布第三章第三章统计案例统计案例3.1 回归分析的基本思想及其初步应用思想及其初步应用 3.2 独立性检验的基本思想及其初步应用本思想及其初步应用选修3-1第一讲第一讲早期的算术与几何与几何第二讲第二讲古希腊数学古希腊数学第三讲第三讲中国古代数学瑰宝学瑰宝第四讲第四讲平面解析几何的产生何的产生第五讲第五讲微积分的诞生第六讲第六讲近代数学两巨星巨星第七讲第七讲千古谜题千古谜题第八讲第八讲对无穷的深入思考入思考第九讲第九讲中国现代数学的开拓与发展学的开拓与发展选修3-2选修3-3第一讲第一讲从欧氏几何看球面看球面第二讲第二讲球面上的距离和角离和角第三讲第三讲球面上的基本图形本图形第四讲第四讲球面三角形球面三角形第五讲第五讲球面三角形的全等的全等第六讲第六讲球面多边形与欧拉公式与欧拉公式第七讲第七讲球面三角形的边角关系边角关系第八讲第八讲欧氏几何与非欧几何非欧几何选修3-4第一讲第一讲平面图形的对称群对称群第二讲第二讲代数学中的对称与抽象群的概念对称与抽象群的概念第三讲第三讲对称与群的故事故事选修4-1第一讲第一讲相似三角形的判定及有关性质的判定及有关性质第二讲直线与圆的位置关系位置关系第三讲圆锥曲线性质的探讨质的探讨选修4-2第一讲线性变换与二阶矩阵二阶矩阵第二讲变换的复合与二阶矩阵的乘法与二阶矩阵的乘法第三讲逆变换与逆矩阵矩阵第四讲变换的不变量与矩阵的特征向量量与矩阵的特征向量选修4-3 选修4-4第一讲第一讲坐标系坐标系第二讲第二讲参数方程参数方程选修4-5第一讲不等式和绝对值不等式对值不等式第二讲证明不等式的基本方法的基本方法第三讲柯西不等式与排序不等式与排序不等式第四讲数学归纳法证明不等式证明不等式选修4-6第一讲第一讲整数的整除整数的整除第二讲第二讲同余与同余方程方程第三讲第三讲一次不定方程第四讲第四讲数伦在密码中的应用中的应用选修4-7第一讲第一讲优选法优选法第二讲第二讲试验设计初步选修4-8选修4-9第一讲第一讲风险与决策的基本概念的基本概念第二讲第二讲决策树方法决策树方法第三讲第三讲风险型决策的敏感性分析的敏感性分析第四讲第四讲马尔可夫型决策简介决策简介高中人教版（高中人教版（B B ）教材目录介绍必修一第一章第一章集合集合1．1 1 集合与集合的表示方法集合与集合的表示方法集合与集合的表示方法 1 1．．2 2 集合之间的关系与运算集合之间的关系与运算集合之间的关系与运算第二章第二章函数函数2 2．．1 1 函数函数函数 2 2．．2 2 一次函数和二次函数一次函数和二次函数一次函数和二次函数 2 2．．3 3 函数的应用（Ⅰ）函数的应用（Ⅰ）函数的应用（Ⅰ） 2 2．．4 4 函数与方程函数与方程函数与方程第三章第三章基本初等函数（Ⅰ）3 3．．1 1 指数与指数函数指数与指数函数指数与指数函数 3 3．．2 2 对数与对数函数对数与对数函数对数与对数函数3 3．．3 3 幂函数幂函数幂函数 3 3．．4 4 函数的应用（Ⅱ）函数的应用（Ⅱ）函数的应用（Ⅱ）必修二第一章第一章立体几何初步立体几何初步1．1 1 空间几何体空间几何体空间几何体 1 1．．2 2 点、线、面之间的位置点、线、面之间的位置关系关系第二章第二章平面解析几何初步平面解析几何初步 2 2．．1 1 平面真角坐标系中的基平面真角坐标系中的基本公式本公式2 2．．2 2 直线方程直线方程直线方程 2 2．．3 3 圆的方程圆的方程圆的方程 2 2．．4 4 空间直角坐标系空间直角坐标系空间直角坐标系必修三第一章第一章算法初步算法初步1．1 1 算法与程序框图算法与程序框图算法与程序框图 1 1．．2 2 基本算法语句基本算法语句基本算法语句 1 1．．3 3 中国古代数学中的算法中国古代数学中的算法案例案例第二章第二章统计统计2．1 1 随机抽样随机抽样随机抽样 2 2．．2 2 用样本估计总体用样本估计总体用样本估计总体 2 2．．3 3 变量的相关性变量的相关性变量的相关性第三章第三章概率概率3．1 1 随机现象随机现象随机现象 3 3．．2 2 古典概型古典概型古典概型 3 3．．3 3 随机数的含义与应用随机数的含义与应用随机数的含义与应用 3 3．．4 4 概率的应用概率的应用概率的应用必修四第一章第一章基本初等函基本初等函((Ⅱ) 1 1．．1 1 任意角的概念与弧度制任意角的概念与弧度制任意角的概念与弧度制 1 1．．2 2 任意角的三角函数任意角的三角函数任意角的三角函数 1 1．．3 3 三角函数的图象与性质三角函数的图象与性质三角函数的图象与性质第二章第二章平面向量平面向量 2 2．．1 1 向量的线性运算向量的线性运算向量的线性运算 2 2．．2 2 向量的分解与向量的坐向量的分解与向量的坐标运算标运算 2 2．．3 3 平面向量的数量积平面向量的数量积平面向量的数量积2 2．．4 4 向量的应用向量的应用向量的应用第三章第三章三角恒等变换三角恒等变换3．1 1 和角公式和角公式和角公式 3 3．．2 2 倍角公式和半角公式倍角公式和半角公式倍角公式和半角公式 3 3．．3 3 三角函数的积化和差与三角函数的积化和差与和差化积和差化积必修五第一章第一章解直角三角形解直角三角形1．1 1 正弦定理和余弦定理正弦定理和余弦定理正弦定理和余弦定理 1 1．．2 2 应用举例应用举例应用举例第二章第二章数列数列2 2．．1 1 数列数列数列 2 2．．2 2 等差数列等差数列等差数列 2 2．．3 3 等比数列等比数列等比数列第三章第三章不等式不等式3 3．．1 1 不等关系与不等式不等关系与不等式不等关系与不等式 3 3．．2 2 均值不等式均值不等式均值不等式3 3．．3 3 一元二次不等式及其解一元二次不等式及其解法 3 3．．4 4 不等式的实际应用不等式的实际应用不等式的实际应用 3 3．．5 5 二元一次不等式（组）二元一次不等式（组）与简单线性规划问题与简单线性规划问题选修1－1第一章第一章常用逻辑用语常用逻辑用语1．1 1 命题与量词命题与量词命题与量词 1 1．．2 2 基本逻辑联结词基本逻辑联结词基本逻辑联结词 1 1．．3 3 充分条件、必要条件与充分条件、必要条件与命题的四种形式命题的四种形式第二章第二章圆锥曲线与方程圆锥曲线与方程2．1 1 椭圆椭圆椭圆 2 2．．2 2 双曲线双曲线双曲线 2 2．．3 3 抛物线抛物线抛物线第三章第三章导数及其应用导数及其应用3 3．．1 1 导数导数导数 3 3．．2 2 导数的运算导数的运算导数的运算 3 3．．3 3 导数的应用导数的应用导数的应用选修1－2第一章第一章统计案例统计案例第二章第二章推理与证明推理与证明第三章第三章数系的扩充与复数的引入的引入第四章第四章框图框图选修4－5第一章第一章不等式的基本性质和证明的基本方法和证明的基本方法1 1．．1 1 不等式的基本性质和一不等式的基本性质和一元二次不等式的解法元二次不等式的解法 1 1．．2 2 基本不等式基本不等式基本不等式1 1．．3 3 绝对值不等式的解法绝对值不等式的解法绝对值不等式的解法 1 1．．4 4 绝对值的三角不等式绝对值的三角不等式绝对值的三角不等式 1 1．．5 5 不等式证明的基本方法不等式证明的基本方法不等式证明的基本方法第二章第二章柯西不等式与排序不等式及其应用不等式及其应用2．1 1 柯西不等式柯西不等式柯西不等式 2 2．．2 2 排序不等式排序不等式排序不等式 2 2．．3 3 平均值不等式平均值不等式平均值不等式((选学选学) ) 2 2．．4 4 最大值与最小值问题，最大值与最小值问题，优化的数学模型优化的数学模型第三章第三章数学归纳法与贝努利不等式利不等式3．1 1 数学归纳法原理数学归纳法原理数学归纳法原理 3 3．．2 2 用数学归纳法证明不等用数学归纳法证明不等式，贝努利不等式式，贝努利不等式。

初等函数的基本不等式

x
不等式转化为 x x1 源自x2 1, 即 f (x)
x ln x 1 ln ( x2 1) 0,x 1.
2
x 1
2
2
而
f
' (x)

ln x (x 1)2

1 x 1
x x2 1

0

ln
x

x x
2 2
1 1
,x
1.
由不等式
2(1)有 ln (1
x)

x 1 x
2
2
后一结果，一般称为指数平均不等式. 3. 指数数型不等式
(1) ex 1 x x2 ... xm (m 1,x 0; 或x 0, m为奇数);
2!
m!
(2) ex 1 x x2 ... xm (x 0, m为偶数).
2!
m!
(3) ex ex (x 1)2,x 0(x 0,1 取等号).
1 2(x 1)
1 x
0, 即 2 x(x 1)(x2 1) (x 1)2 ,
x 1 x 1 x(x 1)(x2 1)
也就是 4x(x2 1) (x 1)3,(3x2 1)(x 1) 0, 显然成立.
x
y
右边的另一证明：由赫尔德不等式知 x x y y x y

2x 2 x
,
x
0,
2
于是 ln
x

1 ln x2 2

1 2(x2 1) 2 2 (x2 1)

x2 x2
1 1
,x
1.
这样
f
' ( x)

2.2.2 第2课时对数函数的性质应用--第二章基本初等函数(I)《新课程同步进阶攻略(人教A版必修一》

第2课时对数函数的性质应用[目标] 1.会利用对数函数的单调性比较两个对数的大小或解对数不等式；2.会求与对数函数有关的函数的最大(小)值或值域；3.能综合应用对数函数的图象和性质解决有关问题．[重点] 对数函数的图象和性质的应用．[难点] 对数函数的图象和性质的综合应用.知识点一对数函数的单调性[填一填]1．对数函数的单调性：当a>1时，y＝log a x为增函数，当0<a<1时，y＝log a x为减函数．2．对于y＝log a x，若a>1，当x>1时，y>0，当0<x<1时，y<0；若0<a<1，当0<x<1时，y>0，当x>1时，y<0.[答一答]1．若a>1，且m>n，则log a m与log a n的大小关系是log a m>log a n.若0<a<1，且m>n，则log a m与log a n的大小关系是log a m<log a n.2．若a>1，且log a m>log a n，则m与n的大小关系是m>n；若0<a<1，且log a m>log a n，则m与n的大小关系是m<n.知识点二复合函数的单调性[填一填]复合函数y＝log a f(x)，x∈D的单调性：设集合M⊆D，若a>1，且u＝f(x)在x∈M上单调递增(减)，则集合M对应的区间是函数y＝log a f(x)的增(减)区间；若0<a<1，且u＝f(x)在x∈M上单调递增(减)，则集合M对应的区间是函数y＝log a f(x)的减(增)区间．[答一答]3．f(x)＝log3(x＋5)的单调区间是否只有一个？是否就是y＝x＋5的单调区间？提示：是只有1个，但不是y＝x＋5的单调增区间(－∞，＋∞)，而是(－5，＋∞)．知识点三反函数[填一填]函数y ＝log a x (a >0，且a ≠1)与y ＝a x (a >0，且a ≠1)互为反函数，其图象关于直线y ＝x 对称．[答一答]4．指数函数与对数函数有哪些主要的相同点？两种函数之间有哪些关系？提示：(1)底数及其范围相同；(2)a >1时同为增函数，0<a <1时同为减函数；(3)互为反函数，图象关于直线y ＝x 对称；(4)指数函数的定义域是对数函数的值域，指数函数的值域是对数函数的定义域．类型一比较大小[例1] 比较下列各组值的大小． (1)log 534与log 543；(2)log 13 2与log 15 2；(3)log 23与log 54.[解] (1)法一：对数函数y ＝log 5x 在(0，＋∞)上是增函数，而34<43，∴log 534<log 543.法二：∵log 534<0，log 543>0，∴log 534<log 543.对数式比较大小的三种类型和求解方法 (1)底数相同时，利用单调性比较大小.(2)底数与真数均不相同时，借助于0或1比较大小.(3)真数相同时，可利用换底公式换成同底，再比较大小，但要注意对数值的正负.[变式训练1] 设a ＝log 36，b ＝log 510，c ＝log 714，则( D ) A ．c >b >a B ．b >c >a C ．a >c >bD ．a >b >c解析：由对数运算法则得a ＝log 36＝1＋log 32，b ＝1＋log 52，c ＝1＋log 72，由对数函数图象得log 32>log 52>log 72，所以a >b >c ，故选D. 类型二解对数不等式[例2] (1)若log a 25<1(a >0，且a ≠1)，求实数a 的取值范围．(2)已知log 0.7(2x )<log 0.7(x －1)，求x 的取值范围．[分析] 对于(1)“1”变为log a a 讨论单调性；对于(2)直接根据单调性列不等式组求解． [解] (1)log a 25<1，即log a 25<log a a .当a >1时，函数y ＝log a x 在定义域内是增函数，所以log a 25<log a a 总成立；当0<a <1时，函数y ＝log a x 在定义域内是减函数，由log a 25<log a a ，得a <25，即0<a <25.所以实数a 的取值范围为⎝⎛⎭⎫0，25∪(1，＋∞)． (2)∵函数y ＝log 0.7x 在(0，＋∞)上为减函数， ∴由log 0.7(2x )<log 0.7(x －1)，得⎩⎪⎨⎪⎧2x >0，x －1>0，2x >x －1，解得x >1.∴x 的取值范围为(1，＋∞)．解对数不等式时，要防止定义域扩大，应在解的过程中加上限制条件，使定义域保持不变，即进行同解变形.若非同解变形，最后一定要检验.[变式训练2] 若－1<log a 34<1(a >0，且a ≠1)，求实数a 的取值范围．解：∵－1<log a 34<1，∴log a 1a <log a 34<log a a .当a >1时，1a <34<a ，则a >43；当0<a <1时，1a >34>a ，则0<a <34.故实数a 的取值范围是⎝⎛⎭⎫0，34∪⎝⎛⎭⎫43，＋∞. 类型三对数复合型函数的值域[例3] 求下列函数的值域： (1)y ＝log 12(－x 2＋2x ＋3)；(2)y ＝log 3⎣⎡⎦⎤⎝⎛⎭⎫13x －2，x ∈[－3，－1]． [分析] 先求出真数的范围，再利用对数函数的单调性求原函数的值域． [解] (1)设u ＝－x 2＋2x ＋3＝－(x －1)2＋4≤4， ∵y ＝log 12 u 在(0，＋∞)上是减函数， ∴log 12 (－x 2＋2x ＋3)≥log 12 4＝－2.∴函数的值域为[－2，＋∞)． (2)设u ＝⎝⎛⎭⎫13x －2，∵x ∈[－3，－1]． ∴3≤⎝⎛⎭⎫13x ≤27，即1≤u ≤25.∵函数y ＝log 3u 在(0，＋∞)上是增函数，∴0≤log 3⎣⎡⎦⎤⎝⎛⎭⎫13x －2≤log 325. ∴原函数的值域为[0，log 325]．1.与对数函数有关的复合函数的值域：求与对数函数有关的复合函数的值域，一方面，要抓住对数函数的值域；另一方面，要抓住中间变量的取值范围，利用对数函数的单调性来求其值域(多采用换元法).2.对于形如y ＝log a f (x )(a >0，且a ≠1)的复合函数的值域的求解的步骤：①分解成y ＝log a u ，u ＝f (x )两个函数；②求f (x )的定义域；③求u 的取值范围；④利用y ＝log a u 的单调性求解.[变式训练3] 设函数f (x )＝log 2(4x )·log 2(2x )，14≤x ≤4.若t ＝log 2x .(1)求t 的取值范围． (2)求f (x )的值域．解：(1)因为t ＝log 2x ，14≤x ≤4，所以log 214≤t ≤log 24，即－2≤t ≤2.(2)函数f (x )＝log 2(4x )·log 2(2x )，即f (x )＝(log 2x )2＋3log 2x ＋2，又t ＝log 2x ，则y ＝t 2＋3t ＋2＝⎝⎛⎭⎫t ＋322－14(－2≤t ≤2)．当t ＝－32时，即log 2x ＝－32，x ＝2－32时，f (x )min ＝－14；当t ＝2时，即log 2x ＝2，x ＝4时，f (x )max ＝12. 综上可得，函数f (x )的值域为⎣⎡⎦⎤－14，12. 类型四对数复合型函数的单调性[例4] 已知f (x )＝log 12 (x 2－ax －a )在⎝⎛⎭⎫－∞，－12上是增函数，求a 的取值范围． [解] 令u (x )＝x 2－ax －a ，∵f (x )＝log 12 u (x )在⎝⎛⎭⎫－∞，－12上是增函数，∴u (x )在⎝⎛⎭⎫－∞，－12上是减函数，且u (x )>0在⎝⎛⎭⎫－∞，－12上恒成立．∴⎩⎨⎧a 2≥－12，u ⎝⎛⎭⎫－12≥0，即⎩⎪⎨⎪⎧a ≥－1，14＋a 2－a ≥0.∴－1≤a ≤12.∴满足条件的a 的取值范围是{a |－1≤a ≤12}．与对数函数有关的复合函数y ＝log a g (x )的单调性的求解步骤：(1)确定定义域，研究函数的单调区间一定要在函数的定义域上进行.(很多同学忽略了定义域，即要满足g (x )>0导致错误)(2)弄清函数是由哪些基本初等函数复合而成的，将复合函数分解成基本初等函数：外层函数y ＝log a u ，内层函数u ＝g (x ).(3)分别确定这两个函数的单调区间.(4)若这两个函数同增或同减，则y ＝log a g (x )为增函数；若一增一减，则y ＝log a g (x )为减函数，即“同增异减”.[变式训练4] 已知f (x )＝log a (8－3ax )在[－1,2]上是减函数，则实数a 的取值范围是( B )A ．(0,1) B.⎝⎛⎭⎫1，43 C.⎣⎡⎭⎫43，4D ．(1，＋∞)解析：由题意，知8－3ax >0，x ∈[－1,2]，∴8＋3a >0,8－6a >0，∴－83<a <43.又易知a >0，且a ≠1，∴0<a <1或1<a <43，此时可知函数g (x )＝8－3ax 是减函数．若f (x )在[－1,2]上是减函数，则必有a >1.所以实数a 的取值范围为⎝⎛⎭⎫1，43.故选B.1．若0<x <y <1，则下列关系式正确的一组是( D ) A ．log 3x >log 3y B ．log 12 x <log 12 yC ．log x 3<log y 3D ．log 4x <log 4y解析：∵y ＝log 3x 是增函数，∴当x <y 时，log 3x <log 3y .∵y ＝log 12 x 是减函数，∴当x <y 时，log 12 x >log 12 y .∵log 3x <log 3y <0，∴1log 3y <1log 3x <0.∴log y 3<log x 3.∵y ＝log 4x 是增函数，且0<x <y <1知log 4x <log 4y . 2．函数y ＝2x 的反函数是( C ) A ．y ＝log 2x B ．y ＝log 12 xC ．y ＝log 2x (x >0)D ．y ＝log 12x (x >0)解析：函数y ＝2x 的值域是(0，＋∞)．又其反函数为y ＝log 2x .故选C.3．函数y ＝log 12 (x 2－6x ＋17)的值域是(－∞，－3]．解析：由x 2－6x ＋17＝(x －3)2＋8>0恒成立，知x ∈R .设u ＝x 2－6x ＋17.∵0<12<1，∴函数y ＝log 12 u 是减函数．又∵x 2－6x ＋17＝(x －3)2＋8≥8，∴log 12 (x 2－6x ＋17)≤log 12 8＝log 12 23＝log 12⎝⎛⎭⎫12－3＝－3.故函数y ＝log 12(x 2－6x ＋17)的值域为(－∞，－3]．4．函数f (x )＝ln(3＋2x －x 2)的单调递增区间是(－1,1)，单调递减区间是(1,3)．解析：∵3＋2x －x 2>0，∴x 2－2x －3<0. ∴－1<x <3.令u ＝3＋2x －x 2＝－(x 2－2x －3)＝－(x －1)2＋4，∴当x ∈(－1,1)时，u 是x 的增函数，y 是ln u 的增函数，故函数f (x )＝ln(3＋2x －x 2)的单调递增区间是(－1,1)．同理，函数f (x )＝ln(3＋2x －x 2)的单调递减区间是(1,3)． 5．已知f (x )＝log a (a x －1)(a >0，且a ≠1)． (1)求f (x )的定义域； (2)讨论函数f (x )的单调性．解：(1)使f (x )＝log a (a x －1)有意义，则a x －1>0，即a x >1.当a >1时，x >0；当0<a <1时，x <0，∴当a >1时，函数的定义域为{x |x >0}；当0<a <1时，函数的定义域为{x |x <0}．(2)①当a >1时，设0<x 1<x 2，则1<ax 1<ax 2，∴0<ax 1－1<ax 2－1，∴log a (ax 1－1)<log a (ax 2－1)，∴f (x 1)<f (x 2)，∴当a >1时，函数f (x )在(0，＋∞)上为增函数；②当0<a <1时，设x 1<x 2<0，则ax1>ax2>1，∴ax1－1>ax2－1>0，∴log a(ax1－1)<log a(ax2－1)，∴f(x1)<f(x2)，∴当0<a<1时，函数f(x)在(－∞，0)上为增函数．综上可知：函数f(x)＝log a(a x－1)在其定义域上为增函数．——本课须掌握的三大问题1．利用对数的单调性可解简单的对数不等式．解对数不等式的关键是把真数视为一个整体，用对数函数的单调性构造不等式，但一定要注意真数大于零这一隐含条件．2．求与对数函数有关的复合函数的单调区间，首要的是弄清楚这个函数是怎样复合而成的，再按“同增异减”的方法来求其单调区间．3．对于对数型复合函数的综合应用的题目，无论是求最值还是求参数的取值范围，必须抓住两点：一是先求出原函数的定义域，二是在定义域内求出函数的单调区间，然后由函数的单调性求出其最值或参数的取值范围．此外在解题过程中一定要注意数形结合方法的灵活应用．学习至此，请完成课时作业21。

全部的初等不等式证明

初等不等式证明一、基本不等式及应用基本不等式是指已被人们证明了的较为常用的不等式，它常被当作定理，用于证明其他一些不等式.基本不等式在许多不等式专著中都作过介绍.这里给出几个常用的基本不等式. 1. 平均值不等式设12,,,n a a a ⋅⋅⋅是n 个正实数，记12111n nn H a a a =++⋅⋅⋅+，n G =12n n a a a A n ++⋅⋅⋅+=，n Q =，分别称n n n n H G A Q 、、、为这n 个正数的调和平均、几何平均、算术平均和平方平均，则有n n n n H G A Q ≤≤≤，当且仅当12n a a a ==⋅⋅⋅=时取等号.2. 柯西（Cauchy ）不等式设,(1,2,,)i i a b R i n ∈=⋅⋅⋅，则 222111()()()nn ni i i i i i i a b a b ===≤∑∑∑，当数组12,,,n a a a ⋅⋅⋅；12,,,n b b b ⋅⋅⋅不全为零时，当且仅当(1,2,,,0)i i b a i n λλ==⋅⋅⋅≠时取等号.3. 排序不等式设两组实数12,,,n a a a ⋅⋅⋅；12,,,n b b b ⋅⋅⋅，满足12n a a a ≤≤⋅⋅⋅≤，12n b b b ≤≤⋅⋅⋅≤，则有1211n n n a b a b a b -++⋅⋅⋅+ （反序和） 1212n i i n i a b a b a b ≤++⋅⋅⋅+ （乱序和） 1122n n a b a b a b ≤++⋅⋅⋅+ （同序和）当且仅当12n a a a ==⋅⋅⋅=，或12n b b b ==⋅⋅⋅=时取等号.4. 琴生（Jensen ）不等式设连续函数()f x 的定义域为(,)a b ，如果对于(,)a b 内的任意两个数12,x x ，都有1212()()()22x x f x f x f ++≤，则称()f x 为(,)a b 上的凸函数.若上式不等式反号，则称()f x 为(,)a b 上的凹函数.若()f x 为(,)a b 上的凸函数，则对于任意12,,,(,)n x x x a b ⋅⋅⋅∈有12121()[()()()]n n x x x f f x f x f x n n++⋅⋅⋅+≤++⋅⋅⋅+，当且仅当12n x x x ==⋅⋅⋅=时取等号.若为(,)a b 上的凹函数，则对于任意12,,,(,)n x x x a b ⋅⋅⋅∈有 12121()[()()()]n n x x x f f x f x f x n n++⋅⋅⋅+≥++⋅⋅⋅+，当且仅当12n x x x ==⋅⋅⋅=时取等号.5. 贝努利（Bernoulli ）不等式设1x >-，若0α<，或1α>-，则 (1)1x x αα+≥+. 若01α<<，则(1)1x x αα+≤+.当且仅当0x =时，以上两式均取等号. 6. 赫尔德（H ǒlder ）不等式设,,,(1,2,,)i i i a b l R i n +⋅⋅⋅∈=⋅⋅⋅，又,,,R αβλ+⋅⋅⋅∈，且1αβλ++⋅⋅⋅+=，则有1111()()()nn n nii i i i i i i i i ab l a b l αβλαβλ====⋅⋅⋅≤⋅⋅⋅∑∑∑∑，.当且仅当111(1,2,,)kkknnni i ii i i a b l k n a b l=====⋅⋅⋅==⋅⋅⋅∑∑∑时取等号.特别当1nαβλ==⋅⋅⋅==时，有 11111[()]()()()nn n nnn i iii i i i i i i a b l a b l ====⋅⋅⋅≤⋅⋅⋅∑∑∑∑.7. 切比雪夫(Chebyshev)不等式设两组实数12,,,n a a a ⋅⋅⋅；12,,,n b b b ⋅⋅⋅，若满足12n a a a ≤≤⋅⋅⋅≤，12n b b b ≤≤⋅⋅⋅≤或12n a a a ≥≥⋅⋅⋅≥，12n b b b ≥≥⋅⋅⋅≥，则有111111()()n n ni i i i i i i a b a b n n n ===≥∑∑∑.若满足12n a a a ≤≤⋅⋅⋅≤，12n b b b ≥≥⋅⋅⋅≥，或12n a a a ≥≥⋅⋅⋅≥，12n b b b ≤≤⋅⋅⋅≤，则有111111()()n n ni i i i i i i a b a b n n n ===≤∑∑∑.当且仅当12n a a a ==⋅⋅⋅=，或12n b b b ==⋅⋅⋅=时以上两式均取等号.8. 加权幂平均不等式设,(1,2,,)i i a p R i n +∈=⋅⋅⋅，,r s R ∈，且r s <，则111111nnrsrsi i i i i i nn i i i i p a p a p p ====⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪≤⎪⎪ ⎪ ⎪⎝⎭⎝⎭∑∑∑∑，当且仅当12n a a a ==⋅⋅⋅=时取等号. 9. 其他（1）设,,,,,x y z R αβγ∈，且(21)k αβγπ++=+（k Z ∈），则 i ） 2221cos cos cos ()2yz zx xy x y z αβγ++≤++ 当且仅当sin sin sin yz zx xy αβγ==时取等号.ii ） 22221sin sin sin ()4yz zx xy x y z αβγ++≤++，当且仅当sin 2sin 2sin 2yz zx xy αβγ==时取等号. （2）设,,1,2,,,ij x R i j n ∈=⋅⋅⋅则1n i =≥，当且仅当123::::i i i ni x x x x λ⋅⋅⋅=（常数），1,2,3,,i n =⋅⋅⋅时取等号.（3）设,,,,i i i i x y z l R -⋅⋅⋅∈，22220i i i i x y z l ---⋅⋅⋅-≥，1,2,3,,i n =⋅⋅⋅，则1ni =≤当且仅当::::i i i i x y z l λ⋅⋅⋅=（常数），1,2,3,,i n =⋅⋅⋅时取等号.（4）两个有用定理定理1 设,,u v R λ+∈，记1s u v λ=++，2s uv v u λλ=++，3s uv λ=，x =，y =i ） 23()61(xy xy xy +---(1)(2)3283()61(x xy xy xy ≤≤+-+-ii ）23()61(xy xy xy +---(3)(4)3283()61(y xy xy xy ≤≤+-+-.当且仅当,,u v λ中有两个数相等且不小于第三个数时，（1）、（4）两式取等号；当且仅当,,u v λ中有两个数相等，且不大于第三个数时，（2）、（3）两式取等号.推论1 同定理1条件，有(5)(6)324(1)4(1)164129()219595xy xy xy x xy xy xy xy ---+≤≤++---；(7)(8)324(1)4(1)164129()219595xy xy xy y xy xy xy xy ---+≤≤++---当且仅当u v λ==时，（5）、（6）、（7）、（8）四式取等号.推论2 同定理1条件，有x ≤≤3(11)(12)12728972x y x x-+++≤≤，当且仅当u v λ==时，（9）、（10）、（11）、（12）四式均取等号.定理2 设,,u v R λ∈，记1s u v λ=++，2s uv v u λλ=++，3s uv λ=，w =（10w s ≤≤），则32322323(13)(14)11111111332(2)()(2)()3227272727s s w w s w s w s w s w s s w w s ---++--+=≤≤=，当且仅当,,u v λ中有两个数相等，且不小于113s 时，（13）式取等号；当且仅当,,u v λ中有两个数相等，且不大于113s 时，（14）式取等号. 推论3 同定理2条件，特别当11s =时，有232223(15)(16)132(12)(1)(12)(1)132********w w w w w w w w uv λ---++--+=≤≤=，当且仅当,,u v λ中有两个数相等，且不小于13时，（15）式取等号；当且仅当,,u v λ中有两个数相等，且不大于13时，（16）式取等号. 注：在应用定理2与其推论3时，要特别注意120w -≤的情况，有时要对120w -≤和120w -≥分别加以讨论，尤其在0u λν≥时的情况.（一）算术几何平均值不等式应用例子例1 已知 ,1,2,i a R i +∈=…,n, 且11nii a==∑，求证()()()()3122311*********n n n n a a a a a a a a n -++⋅⋅⋅++≥+++++ （1）当且仅当 121n a a a n==⋅⋅⋅==时，（1）式取等号.例2 （20XX 年全国十八所奥赛协作体学校试题）设 ,,,a b c R +∈且 1bc ca ab ++=，求证1abc≤ （2）提示由1bc =≥∑知，可证更强式（3）⇔3 （※）例3 （2005，第17届亚太地区数学奥林匹克）设 ,,,x y z R +∈且 8xyz =，则243≥（4）当且仅当2x y z ===时，（4）式取等号.注：由本题证明中可知，若将条件改为12yz zx xy ++≥，结论也成立.例4 （自创题，2006.12.17）设,,a b c R +∈，则> （5）例 5 （自创题，1988.10.13）设同一平面上两个凸四边形的边长分别为,,,a b c d 和,,,a b c d ''''，面积分别为∆和'∆，那么aa bb cc dd ''''+++≥ （6）当且仅当这两个凸四边形都内接于圆（不一定要同一个圆），且 ()()()s a s a s b ''--=-⋅()()()()()s b s c s c s d s d ''''''-=--=--时，（6）式取等号. 这里1()2s a b c d =+++，1()2s a b c d '''''=+++.附：凸四边形ABCD 四边长分别为AB a =，BC b =，CD c =，DA d =，当且仅当此四边形ABCD 内接于圆时，其面积最大，最大值为max ()ABCD S =（7）例6 （自创题，2006.12.26）设,,,a b c d R -∈，则32222()4[()()()()]a a c d b d a c a b d b c ≥+++++++∑ （8）当且仅当a c =，b d =时，（8）式取等号.例7 设,,x y z R -∈，求证 25()81x xyz x ≥⋅∑∑ （9）当且仅当x y z ==时，（9）式取等号.（二）柯西不等式应用例子例1 设,i i x y R ∈，1,2,,i n =⋅⋅⋅，且10nii x=≥∑，10ni i y =≥∑，10i j i j nx x ≤<≤≥∑，10i j i j ny y ≤<≤≥∑，1ni i x x ==∑，则1()niii x x y=-≥∑ （1）yxdc baDCBA当且仅当1212n nx x x y y y ==⋅⋅⋅= 时，（1）式取等号. 在（1）式中，当3n =时，被人们称之为“母不等式”.即以下命题1：设123123,,,,,x x x y y y R ∈，且10x≥∑，10y ≥∑，120x x ≥∑，120y y ≥∑，则231()xx y +≥∑ （2）当且仅当312123x x x y y y ==时，（2）式取等号. 命题1应用如下：1.（匹多不等式）ABC ∆与'''A B C ∆边长分别为,,a b c 和,,a b c '''，面积分别为∆与'∆，则2222()16ab c a ''-++≥∆∆∑ （3）当且仅当ABCA B C '''∆∆时，（3）式取等号. 提示：取222x a b c =-++,2222x a b c ''''=-++等，并应用三角形面积公式.2.（程灵提出）若ABC ∆与A B C '''∆边长分别为,,a b c 和,,a b c '''，面积分别为∆与'∆，则()a b c a '-++≥∑ （4）当且仅当ABC ∆与'''A B C ∆均为正三角形时，（4）式取等号.提示：在（2）中取1x a b c '''=-++，1y a b c =-++等，并应用到22bc a-∑∑≥.3.（安振平提出）若ABC ∆与A B C '''∆边长分别为,,a b c 和,,a b c '''，面积分别为∆与'∆，则2()()16a b c a b c a ''-++-≥∆∆∑ （5）当且仅当222()()()a b c a a b c b a b c c a b c '''==-++-++-时，（5）式取等号.提示：在（2）中取2221x a b c '''=-++，1()()y a b c a b c =-++-等.4.（自创题，1983.05.07）若ABC ∆与A B C '''∆边长分别为,,a b c 和,,a b c '''，面积分别为∆与'∆，则()()()16a a b c a b c a b c '''''''-++-++-≥∆∆∑ （6）当且仅当ABCA B C '''∆∆时，（6）式取等号.提示：在（2）中取1()()x a b c a b c =-++-，1()()y a b c a b c ''''''=-++-等. 以上（3）式与（6）式有相同的取等号条件，试讨论他们左边式子的大小.5. 设ABC ∆三边长为,,BC a CA b AB c ===，面积为∆，P 为ABC ∆内部或边界上一点，从P 分别向三边BC 、CA 、AB 所在直线作垂线，垂足分别为D 、E 、F ，记1PD r =，2PE r =，3PF r =，则223242r r bc a∆≤-∑∑∑. （7）提示：12342()()ar a b c r r ∆==-+++∑∑≥≥.我们还可以由（2）式得到或证明更多不等式.又如第六章，“三角几何不等式”中的例6、例22等.注：类似上述方法，应用赫尔德不等式，有命题设x ,,i i i y z R -∈，1,2,3i =，则123123123111222333()()()()x x x y y y z z z x y z x y z x y z ++++++-++≥.（8）例2 （自创题，1988，0.4.20）设,,,,x y z w R λ∈，且0,0xy zw >>，2λ≤，则≤（9）=时，（9）式取等号.注：（9）式可参阅由吴康主编的《奥赛金牌之路》（高中数学）“第一章 §6 三角不等式”（P81—P90），本节系杨学枝所写.利用同上证法可得以下命题（自创题）：设,,,x y z w R +∈，(21)k αβγθπ+++=+ ()k z ∈，则sin sin sin sin x y z w αβγθ+++≤（10）当且仅当，cos cos cos cos x y z w αβγθ=== 时，（9）式取等号.（10）式为笔者首创，可参见同上吴康主编的《奥赛金牌之路》（高中数学）P82. 本命题在《中等数学》杂志社组织的数学竞赛命题评奖中，获一等奖.本命题也可参见《中等数学》，1989年第二期，杨学枝文：《对一个三角不等式的再探讨》.例3 a ,i i b R ∈，1,2,,i n =⋅⋅⋅，则1112nnni i i i i i i a b a b n ===≥∑∑∑. （11）注：（11）式是一个值得关注的不等式，如取3n =时，可证20XX 年中国国家队培训题：,,,,,a b c x y z R ∈，满足()()3a b c x y z ++++=，222222()()4a b c x y z ++++=，求证0ax by cz ++≥.例4 设a,,b c R +∈，且3a b c ++=，则2232a ab ≥+∑. （12）例5 （20XX 年.IMO.46）已知x,y,z ∈R +,且 1xyz ≥，求证525220x x x y z-≥++∑ （13）例6 （20XX 年IMO 预选题）设(1,2,,)i x R i n ∈=⋅⋅⋅,求证1222222211212111n nx x x x x x x x x ++⋅⋅⋅+<++++++⋅⋅⋅+（14）例7 a,b,c 为正数，证明22224()a b c a b a b c b c a a b c-++≥+++++，（15）当且仅当a c b >>，且a b c a c a b c b==---，即a c b >>且3322b c b c +=时，（15）式取等号.例8 （20XX 年国家集训队测试题）设,,,x y z R -∈且1x y z ++=，求证+≤ （16）例9 （自创题，1987.07.20）设 ,,,x y z w R +∈，则 ()2918x x x xy xz xw yz yw zw +⋅≥+++++∑∑∑ （17）当且仅当 x y z w === 时，（17）式取等号.注：（17）式可推广为：设 ,1,2,,i x R i n +∈=⋅⋅⋅，则111n ni i i i x x ==⋅≥∑∑()()2212112n i i i ji j jn x n n x x =≤<≤⎛⎫- ⎪⎝⎭--∑∑ （18）当且仅当12n x x x ==⋅⋅⋅=时,(18)式取等号.若记11ni i s x ==∑，21i j i j ns x x ≤<≤=∑，12n n s x x x =⋅⋅⋅，111n n s s x -=∑，则（18）式可写成如下形式：22212121(2)(1)n n n s s s n n s s n s s -+-≥-.例10 (陈计，2008.08.29提供)对正数,,,a b c d 及0k ≥，有 41a b c d b kd c ka d kb a kc k+++≥+++++. （19）例11 （自创题，2010.11,09）设,,x y z R +∈，求证322x x xy y ≥++∑ （20）当且仅当1x y z ===时（20）式取等号.注：猜想设,,x y z R +∈，有322x x xy y ≥++∑322x x xy y≥++∑.例12 设,,,..a b c x y z 非负，且a b c x y z ++=++，则()()()3()ax a x by b y cz c z abc xyz +++++≥+. （21）例13 （第50届IMO 金牌得主林博提出的猜想）设,,0a b c ≥，求证2a ≤∑∑. （22）例14（自创题，2001.02.02）设,,x y z R +∈,且4yz zx xy xyz +++≤，则x y z yz zx xy ++≥++. （23）注：1.用类似方法，可证以下命题设,,p q r R -∈，,,x y z R ∈，且14p q r pqr +++≤，则222px qy rz yz zx xy ++≥++. （24） 2. 第48届国际数学奥林匹克中国国家集训队有一道测试题（20XX 年3月）与其相似.题目设正实数,,u v w满足4u v w ++=，求证u v w ++. （25）x =y =z =，则原命题等价于：,,x y z R +∈，且4yz zx xy xyz +++=，则x y z yz zx xy ++≥++ ① 式证明可见《数学奥林匹克不等式研究》第八章章练习题64中i ）.例15（第48届IMO 中国国家集训队测试题）设正数12,,,n a a a ⋅⋅⋅，满足12a a +1n a +⋅⋅⋅+=，求证1212231222223311()()1n n a a a na a a a a a a a a a a a n ++⋅⋅⋅+++⋅⋅⋅+≥++++ （26）例16 已知221,a b kab +-= 221c d kcd +-=，,,,,a b c d k R ∈，且 2k <，求证ac bd -≤（27）当且仅当()()()()22a b c d k k a b c d ---=+++，即bc ad k ac bd +=+时，（27）式取等号.例17. （20XX 年IMO 预选题）设(1,2,,)i x R i n ∈=⋅⋅⋅,求证1222222211212111n nx x x x x x x x x ++⋅⋅⋅+<++++++⋅⋅⋅+（28）3. 其他基本不等式应用例子例1 设,,x y z R -∈，则4+≤(1)()2x y z ≤++，例2 （自创题，2010.07.03）若,,a b c 为满足1a b c ++=的正数，19λ≥，则 31()()()(3)3a b c b c a λλλλ+++≥+，（3）推广式，即有以下命题若12,,,n a a a ⋅⋅⋅为满足11ni i a ==∑的正数，21n λ≥，则 122311()()()()n n a a a n a a a nλλλλ++⋅⋅⋅+≥+，（4）当且仅当121n a a a n==⋅⋅⋅==时，（4）式取等号.例3 （自创题，2010.07.03）若,,a b c 为满足1abc ≥的正数，23λ≥，则)a b c ≤++，（5）当且仅当1a b c ===时，（5）式取等号.推广式以下命题若12,,,n a a a ⋅⋅⋅为满足121n a a a ⋅⋅⋅≥的正数，11nλ≥-，则11nni i i a ==≤，（6）当且仅当121n a a a ==⋅⋅⋅==时，（6）式取等号.例4（《不等式研究网站》，“竞赛不等式”专栏，20XX 年1月6日，陈胜利老师提出）设,,0a b c >，且1abc =，求证2112()3a a ≥+-∑ （7）例5 （王雍熙，2011.08.22提供）设,,a b c R -∈，且2a a ≥∑∑，则31aabc bc +≥+∑∑. （8）本题可推广，见以下例6.例6（自创题，2011.08.22）设i a R -∈，1,2,,i n =⋅⋅⋅，2n ≥，记i a （1,2,,i n =⋅⋅⋅）中每k （1,2,,k n =⋅⋅⋅）,个乘积之和为k s ，m 为不大于n 的正整数，且211n ni ii i a a==≥∑∑，则11352411+s 1nn n n ii n n s n s n as s s s n sn --=-⎧⎧++≥+++⋅⋅⋅+⎨⎨⎩⎩∑（为奇数）（为奇数）（为偶数）（为偶数），（9）二、其他方法证明不等式例子例1 （自创题，2006.08.25）设,,x y z R -∈，且2222x y z xyz +++1≤，则 142xyz yz +≥∑，（1）当且仅当12x y z ===，或,,x y z中一个为零，另外二个均等于2时，（1）式取等号.例2（20XX 年全国高中数学联赛A 卷加试题3）给定整数2n >，设正实数12,,,n a a a ⋅⋅⋅满足1,1,2,,k a k n ≤=⋅⋅⋅，记12,1,2,,kk a a a A k n k++⋅⋅⋅+==⋅⋅⋅.求证： 1112nnk k k k n a A ==--<∑∑. （2）例 3 已知123123a a a b b b ++=++，122331122331a a a a a a a a a a a a ++=++，若123123min{,,}min{,,}a a a b b b ≤，求证： 123123max{,,}max{,,}a a a b b b ≤.注. 本例可推广.例4 （自创题，2007.12.28）设,,a b c R +∈，且1bc =∑，则21142a bc ≥-+∑，（3）当且仅当a b c ===时取等号.例5 （宋庆老师在《中学数学研究》（广东），20XX 年第1期，文“两个优美的无理不等式”中提出的猜想）若,,0a b c >，满足1a b c ===，则≥（4）例6 .(20XX 年，Serbian 数学奥林匹克试题) 已知,,a b c 是正数,且1a b c ++=，证明127131bc a a≤++∑. （5）例7（陈计，2008.05.04提供）设,,a b c R ∈，n N ∈，则 2[()()]4[()][()]n n n b c b c b c bc b c +-≥--∑∑∑. （6）例8 （自创题，2008.05.07）设,,a b c R -∈，求使22222233()()()(2)()b c bc c a ca a b ab abc a b c λλλλ++++++≥+++ 成立的最大正数λ的值.例9 (自创题，2008.08.30)设1122,,,a b a b R ∈，且222221122a b a b m -=-=，则2212211122211221122()()()()()4()()a b a b m a b a b a b a b m a b a b ++-+++≥++-++，（7）当且仅当22211a b m -=，12a a =，12b b =时，（7）式取等号.例10 （江苏高三学生顾振同学2010.08.06提供）设,,x y z R -∈，且2221x y z ++=，则411x yzx xyz≤--∑∑∑ ，（8）当且仅当3x y z ===，或,,x y z中，有一个为零，其余两个都等于2时，（8）式取等号.例11 （自创题，2005.12.04）设,,a b c R +∈，且1a b c ++=，则3)5)1080abc abc bc -+≥∑ （9）当且仅当13a b c ===，或,,a b c中有一个等于33-，另外两个都等于6时，（9）式取等号.例12（自创题，2007.09.18）设,,a b c R +∈，且1a b c ++=，则271481abc a-≤∑ （10）当且仅当13a b c ===，或,,a b c 中一个等于23，其余两个都等于16时，（10）式取等号.例13 （美国，Pham Kim Hung ）设,,a b c 是三角形三边长，则222a b a b a≥+∑∑∑， (11) 当且仅当ABC ∆为正三角形时,(11)式取等号.例14 “奥数之家”2010.03.31，“476934847”提出：设,,a b c R +∈，则22222()3a b c a c b c a a b c -++≥+++. （12）例15 假设P 、Q 、R 分别是ABC 的三边BC 、CA 、AB 上三点，且满足13AQ AR BR BP CP CQ +=+=+=，则12PQ QR RP ++≥（13）注：1. 关于本题，有其深刻的背景，可参阅杨之所著《初等数学研究的问题和课题》P297~298；或参阅《数学通讯》1991年第2期“问题征解”栏目杨学枝解答及编者评语；或参阅《中学数学教学参考》（陕西），1992年第6期，杨学枝文《一个几何不等式的再加强》；或参阅《数学通讯》1996年第10期，杨学枝文《从一道命题谈起》：也可以参阅杨学枝主编《不等式研究》(西藏人民出版社，2000年6月出版)一书中杨路教授写的“序”；还可以参阅杨学枝著《数学奥林匹克不等式研究》(哈尔滨工业大学出版社，20XX 年8月出版)一书中杨路教授写的“序”；还可以参见《UNIV, BEOGRAD. PUBL. ELEKTKOTEHN.FAKser. Mat.4(1993).25~27.陈计与杨学枝文:《ON A ZIRAKZADEH INEQUALITY RELATED TO TWO TRIANGLES INSCRIBED ONE IN THE OTHER 》.2. 由以上所得重要不等式1()()(cos cos cos )3QR RP PQ a b c a b c A B C ++≥++-++++（14）可得较（13）式更强的不等式33339()()8QR RP PQ BC CA AB ++≥++ （15）3. 《福建中学数学》，1996年第4期.杨学枝文：《对一道猜想题的证明》中，用与（13）式的类似证法，给出了2221()4RP PQ PQ QR QR RP BC CA AB ⋅+⋅+⋅≥++ （16）其中,,P Q R 分别为,,BC CA AB 边上的周界中点.。

专题一第2讲基本初等函数、函数与方程

第2讲基本初等函数、函数与方程[考情分析] 1.基本初等函数的图象与性质是高考考查的重点，利用函数性质比较大小、解不等式是常见题型.2.函数零点的个数判断及参数范围是常考题型，常以压轴题的形式出现.3.函数模型及应用是近几年高考的热点，通常考查指数函数、对数函数模型．考点一基本初等函数的图象与性质核心提炼指数函数y＝a x(a>0，且a≠1)与对数函数y＝log a x(a>0，且a≠1)互为反函数，其图象关于y ＝x对称，它们的图象和性质分0<a<1，a>1两种情况，着重关注两种函数图象的异同．例1(1)(2022·杭州模拟)已知lg a＋lg b＝0(a>0且a≠1，b>0且b≠1)，则函数f(x)＝a x与g(x) x的图象可能是()log＝1b(2)若e a＋πb≥e－b＋π－a，则下列结论一定成立的是()A．a＋b≤0 B．a－b>0C．a－b≤0 D．a＋b≥0规律方法(1)指数函数、对数函数的图象与性质受底数a的影响，解决与指数函数、对数函数有关的问题时，首先要看底数a的取值范围．(2)基本初等函数的图象和性质是统一的，在解题中可相互转化．跟踪演练1(1)(2022·山东名校大联考)若a＝log32，b＝log52，c＝e0.2，则a，b，c的大小关系为()A．b<a<c B．c<a<bC．b<c<a D．a<b<c(2)(2022·邯郸模拟)不等式10x－6x－3x≥1的解集为________．考点二函数的零点核心提炼判断函数零点个数的方法(1)利用函数零点存在定理判断．(2)代数法：求方程f (x )＝0的实数根．(3)几何法：对于不易求根的方程，将它与函数y ＝f (x )的图象联系起来，利用函数的性质找出零点或利用两个函数图象的交点求解．在利用函数性质时，可用求导的方法判断函数的单调性．考向1 函数零点个数的判断例2 已知f (x )是定义在R 上周期为2的偶函数，且当x ∈[0,1]时，f (x )＝2x －1，则函数g (x )＝f (x )－log 5|x |的零点个数是( )A ．2B ．4C ．6D ．8考向2 求参数的值或范围例3 (2022·河北联考)函数f (x )＝e x 和g (x )＝kx 2的图象有三个不同交点，则k 的取值范围是________．规律方法利用函数零点的情况求参数值(或取值范围)的三种方法跟踪演练2 (1)(2022·合肥模拟)若f (x )为奇函数，且x 0是y ＝f (x )－2e x 的一个零点，则－x 0一定是下列哪个函数的零点( )A ．y ＝f (－x )e －x －2B ．y ＝f (x )e x ＋2C ．y ＝f (x )e x －2D ．y ＝f (－x )e x ＋2(2)已知函数f (x )＝⎩⎨⎧－x ，x <0，x ，x ≥0，若关于x 的方程f (x )＝a (x ＋1)有三个不相等的实数根，则实数a 的取值范围是________．考点三函数模型及其应用核心提炼解函数应用题的步骤(1)审题：缜密审题，准确理解题意，分清条件和结论，理清数量关系．(2)建模：将自然语言转化为数学语言，将文字语言转化为符号语言，利用数学知识，建立相应的数学模型．(3)求模：求解数学模型，得出数学结论．(4)反馈：将得到的数学结论还原为实际问题的意义．例4 (1)(2022·西安模拟)2022年4月16日，神舟十二号3名航天员告别了工作生活183天的中国空间站，安全返回地球．中国征服太空的关键是火箭技术，在理想情况下，火箭在发动机工作期间获得速度增量的公式Δv ＝v e ln m 0m 1，其中Δv 为火箭的速度增量，v e 为喷流相对于火箭的速度，m 0和m 1分别代表发动机开启和关闭时火箭的质量，在未来，假设人类设计的某火箭v e 达到5公里/秒，m 0m 1从100提高到600，则速度增量Δv 增加的百分比约为( ) (参考数据：ln 2≈0.7，ln 3≈1.1，ln 5≈1.6)A ．15%B ．30%C ．35%D ．39%(2)(2022·福州模拟)深度学习是人工智能的一种具有代表性的实现方法，它是以神经网络为出发点的．在神经网络优化中，指数衰减的学习率模型为L ＝00GG L D ，其中L 表示每一轮优化时使用的学习率，L 0表示初始学习率，D 表示衰减系数，G 表示训练迭代轮数，G 0表示衰减速度．已知某个指数衰减的学习率模型的初始学习率为0.5，衰减速度为22，且当训练迭代轮数为22时，学习率衰减为0.45，则学习率衰减到0.05以下(不含0.05)所需的训练迭代轮数至少为(参考数据：lg 3≈0.477 1)( )A ．11B ．22C ．227D ．481易错提醒构建函数模型解决实际问题的失分点(1)不能选择相应变量得到函数模型．(2)构建的函数模型有误．(3)忽视函数模型中变量的实际意义．跟踪演练3 (1)(2022·荆州联考)“绿水青山就是金山银山”，党的十九大以来，城乡深化河道生态环境治理，科学治污．某乡村一条污染河道的蓄水量为v 立方米，每天的进出水量为k 立方米．已知污染源以每天r 个单位污染河水，某一时段t (单位：天)河水污染质量指数为m (t )(每立方米河水所含的污染物)满足m (t )＝r k ＋⎝⎛⎭⎫m 0－r k e kt -v (m 0为初始质量指数)，经测算，河道蓄水量是每天进出水量的80倍．若从现在开始关闭污染源，要使河水的污染水平下降到初始时的10%，需要的时间大约是(参考数据：ln 10≈2.30)()A．1个月B．3个月C．半年D．1年(2)(2022·广东大联考)水果采摘后，如果不进行保鲜处理，其新鲜度会逐渐流失，某水果产地的技术人员采用一种新的保鲜技术后发现水果在采摘后的时间t(单位：小时)与失去的新鲜度y满足函数关系式：y＝220301,010100012,10100,20tt tt+⎧<⎪⎪⎨⎪⋅⎪⎩≤，≤≤为了保障水果在销售时的新鲜度不低于85%，从水果采摘到上市销售的时间间隔不能超过(参考数据：log23≈1.6)() A．20小时B．25小时C．28小时D．35小时。

高中数学第二章基本初等函数(ⅰ)2.1.2指数函数及其性质(第1课时)指数函数的图象及性质

12/13/2021
第十二页，共三十八页。
(1)判断一个函数是指数函数的方法 ①看形式：只需判断其解析式是否符合 y＝ax(a>0，且 a≠1)这一结构特征； ②明特征：看是否具备指数函数解析式具有的三个特征．只要有一个特征不具备，则该函数不是指数函数．
12/13/2021
第十三页，共三十八页。
解析：选 B.法一：由图象可知③④的底数必大于 1，①②的底
数必小于 1.
作直线 x＝1，在第一象限内直线 x＝1 与各曲线的交点的纵坐
标即各指数函数的底数，则 1＜d＜c，b＜a＜1，从而可知 a，b，
c，d 与 1 的大小关系为 b＜a＜1＜d＜c.
法二：根据图象可以先分两类：
③④的底数大于 1，①②的底数小于 1，再Байду номын сангаас③④比较 c，d 的
12/13/2021
第十八页，共三十八页。
求解指数函数图象问题的策略 (1)抓住特殊点：指数函数的图象过定点(0，1)． (2)巧用图象变换：函数图象的平移变换(左右平移、上下平移)． (3)利用函数的性质：奇偶性与单调性．
12/13/2021
第十九页，共三十八页。
1．指数函数①f(x)＝mx，②g(x)＝nx 满足不等式 0<m<n<1，则它们的图象是( )
第二十一页，共三十八页。
2．已知 0＜a＜1，b＜－1，则函数 y＝ax＋b 的图象必定不经过
() A．第一象限
B．第二象限
C．第三象限
D．第四象限
解析：选 A.函数恒过点(0，1＋b)，因为 b＜－1，所以点(0，1 ＋b)在 y 轴负半轴上．故图象不经过第一象限．
12/13/2021

人教版高中数学基本初等函数(1)复习课(共21张PPT)教育课件

2 2
,
1
小结：1、构造两个函数，研究函数图象，利用数形结合求解；
2、数形结合是解决方程、不等式的重要工具；
3、考查函数思想、数形结合思想、分类讨论思想
四、核心考点突破练
例2：复习参考题B组第3题 (课后练习）
对于函数f
x
a
2 2x 1
a
R ：
1 探索函数f x的单调性；
2是否存在实数a使函数f x为奇函数？
•
: 其实兴趣真的那么重要吗？很多事情我们提不起兴趣可能就是运维我们没有做好。想想看，如果一件事情你能做好，至少做到比大多数人好，你可能没有办法岁那件事情没有兴趣。再想想看，一个刚来到人世的小孩，白纸一张，开始什么都不会，当然对事情开始的时候也没有兴趣这一说了，随着年龄的增长，慢慢的开始做一些事情，也逐渐开始对一些事情有兴趣。通过观察小孩的兴趣，我们可以发现一个规律，往往不是有了兴趣才能做好，而是做好了才有了兴趣。人们总是搞错顺序，并对错误豪布知晓。尽管并不绝对是这样，但大多数事情都需要熟能生巧。做得多了，自然就擅长了；擅长了，就自然比别人做得好；做得比别人好，兴趣就大起来，而后就更喜欢做，更擅长，更。。更良性循环。教育小孩也是如此，并不是说买来一架钢琴，或者买本书给孩子就可以。事实上，要花更多的时间根据孩子的情况，选出孩子最可能比别人做得好的事情，然后挤破脑袋想出来怎样能让孩子学会并做到很好，比一般人更好，做到比谁都好，然后兴趣就自然出现了。

基本初等函数知识点归纳

函数及其基本初等函数〖1.1〗函数及其表示【1.1.1】函数的概念（1）函数的概念①设A 、B 是两个非空的数集，如果按照某种对应法则f ，对于集合A 中任何一个数x ，在集合B 中都有唯一确定的数()f x 和它对应，那么这样的对应（包括集合A ，B 以及A 到B 的对应法则f ）叫做集合A 到B 的一个函数，记作:f A B →．②函数的三要素:定义域、值域和对应法则．（所以进行已知对应关系()f x 的函数，一定先求出函数的定义域）③只有定义域相同，且对应法则也相同的两个函数才是同一函数．（2）区间的概念及表示法①设,a b 是两个实数，且a b <，满足a x b ≤≤的实数x 的集合叫做闭区间，记做[,]a b ；满足a x b <<的实数x 的集合叫做开区间，记做(,)a b ；满足a x b ≤<，或a x b <≤的实数x 的集合叫做半开半闭区间，分别记做[,)a b ，(,]a b ；满足,,,x a x a x b x b ≥>≤<的实数x 的集合分别记做[,),(,),(,],(,)a a b b +∞+∞-∞-∞．注意：对于集合{|}x a x b <<与区间(,)a b ，前者a 可以大于或等于b ，而后者必须a b <，（前者可以不成立，为空集；而后者必须成立）．而且无论闭区间或者开区间，,a b 均称为端点。

（3）求函数的定义域时，一般遵循以下原则：①()f x 是整式时，定义域是全体实数．②()f x 是分式函数时，定义域是使分母不为零的一切实数．③()f x 是偶次根式时，定义域是使被开方式为非负值时的实数的集合．④对数函数的真数大于零，当对数或指数函数的底数中含变量时，底数须大于零且不等于1．⑤tan y x =中，()2x k k Z ππ≠+∈．⑥零（负）指数幂的底数不能为零．⑦若()f x 是由有限个基本初等函数的四则运算而合成的函数时，则其定义域一般是各基本初等函数的定义域的交集．⑧对于求复合函数定义域问题，一般步骤是：若已知()f x 的定义域为[,]a b ，其复合函数[()]f g x 的定义域应由不等式()a g x b ≤≤解出．⑨对于含字母参数的函数，求其定义域，根据问题具体情况需对字母参数进行分类讨论． ⑩由实际问题确定的函数，其定义域除使函数有意义外，还要符合问题的实际意义．（4）求函数的值域或最值求函数最值的常用方法和求函数值域的方法基本上是相同的．事实上，如果在函数的值域中存在一个最小（大）数，这个数就是函数的最小（大）值．因此求函数的最值与值域，其实质是相同的，只是提问的角度不同．求函数值域与最值的常用方法： ①观察法：对于比较简单的函数，我们可以通过观察直接得到值域或最值．②配方法：将函数解析式化成含有自变量的平方式与常数的和，然后根据变量的取值范围确定函数的值域或最值．③判别式法：若函数()y f x =可以化成一个系数含有y 的关于x 的二次方程2()()()0a y x b y x c y ++=，则在()0a y ≠时，由于,x y 为实数，故必须有2()4()()0b y a y c y ∆=-⋅≥，从而确定函数的值域或最值．④不等式法：利用基本不等式确定函数的值域或最值．⑤换元法：通过变量代换达到化繁为简、化难为易的目的，三角代换可将代数函数的最值问题转化为三角函数的最值问题． ⑥反函数法：利用函数和它的反函数的定义域与值域的互逆关系确定函数的值域或最值． ⑦数形结合法：利用函数图象或几何方法确定函数的值域或最值． ⑧函数的单调性法．例1 已知函数32()f x x ax bx c =+++，下列结论中错误的是（）A 00,()0x R f x ∃∈=B 函数()y f x =的图像是中心对称图形C 若0x 是()f x 的极小值点，则()f x 在区间（-∞，0x ）上单调递减D 若0x 是()f x 的极值点，则'()0f x =例2 已知偶函数()f x 在[0,)+∞上单调递减，(2)f =0，若(1)0f x ->，则x 的取值范围是（）例 3 设函数()xf x mπ=，若存在()f x 的极值点0x 满足22200[(()]x f x m +<，则m 的取值范围是（）A （-∞，-6）∪（6，+∞）B （-∞，-4）∪（4，+∞）C （-∞，-2）∪（2，+∞）D （-∞，-1）∪（1，+∞）例4 下列函数与y=x 有相同图像的一个函数是（）A y =B 2x y x=C log (01)xy aa a =>≠且 D log xa a y =【1.2.2】函数的表示法（5）函数的表示方法表示函数的方法，常用的有解析法、列表法、图象法三种．解析法：就是用数学表达式表示两个变量之间的对应关系．列表法：就是列出表格来表示两个变量之间的对应关系．图象法：就是用图象表示两个变量之间的对应关系．（6）映射的概念①设A 、B 是两个集合，如果按照某种对应法则f ，对于集合A 中任何一个元素，在集合B 中都有唯一的元素和它对应，那么这样的对应（包括集合A ，B 以及A 到B 的对应法则f ）叫做集合A 到B 的映射，记作:f A B →．②给定一个集合A 到集合B 的映射，且,a A b B ∈∈．如果元素a 和元素b 对应，那么我们把元素b 叫做元素a 的象，元素a 叫做元素b 的原象．〖1.3〗函数的基本性质【1.3.1】单调性与最大（小）值（1）函数的单调性①定义及判定方法②在公共定义域内，两个增函数的和是增函数，两个减函数的和是减函数，增函数减去一个减函数为增函数，减函数减去一个增函数为减函数．③对于复合函数[()]y f g x =，令()u g x =，若()y f u =为增，()u g x =为增，则[()]y f g x =为增；若()y f u =为减，()u g x =为减，则[()]y f g x =为增；若()y f u =为增，()u g x =为减，则[()]y f g x =为减；若()y f u =为减，()u g x =为增，则[()]y f g x =为减．（2）打“√”函数()(0)af x x a x=+>的图象与性质 ()f x 分别在(,]a -∞-、[,)a +∞上为增函数，分别在[,0)a -、(0,]a 上为减函数（判定方法2）．（3）最大（小）值定义①一般地，设函数()y f x =的定义域为I ，如果存在实数M满足：（1）对于任意的x I ∈，都有()f x M ≤；（2）存在0x I ∈，使得0()f x M =．那么，我们称M 是函数()f x 的最大值，记作max ()f x M =．②一般地，设函数()y f x =的定义域为I ，如果存在实数m 满足：（1）对于任意的x I ∈，都有()f x m ≥；（2）存在0x I ∈，使得0()f x m =．那么，我们称m 是函数()f x 的最小值，记作max ()f x m =．【1.3.2】奇偶性（4）函数的奇偶性①定义及判定方法函数的性质定义图象判定方法函数的奇偶性如果对于函数f(x)定义域内任意一个x ，都有f(．．－．x)=．．．－．f(x)．．．．,那么函数f(x)叫做奇函数．．．．（1）利用定义（要先判断定义域是否关于原点对称）（2）利用图象（图象关于原点对称）yxo如果对于函数f(x)定义域内任意一个x ，都有f(．．－．x)=．．．f(x)．．．．,那么函数f(x)叫做偶函数．．．．（1）利用定义（要先判断定义域是否关于原点对称）（2）利用图象（图象关于y 轴对称）②若函数()f x 为奇函数，且在0x =处有定义，则(0)0f =．③奇函数在y 轴两侧相对称的区间增减性相同，偶函数在y 轴两侧相对称的区间增减性相反．④在公共定义域内，两个偶函数（或奇函数）的和（或差）仍是偶函数（或奇函数），两个偶函数（或奇函数）的积（或商）是偶函数，一个偶函数与一个奇函数的积（或商）是奇函数．〖补充知识〗函数的图象（1）作图利用描点法作图：①确定函数的定义域； ②化解函数解析式； ③讨论函数的性质（奇偶性、单调性）； ④画出函数的图象．利用基本函数图象的变换作图：要准确记忆一次函数、二次函数、反比例函数、指数函数、对数函数、幂函数、三角函数等各种基本初等函数的图象．①平移变换0,0,|()()h h h h y f x y f x h ><=−−−−−−−→=+左移个单位右移|个单位0,0,|()()k k k k y f x y f x k ><=−−−−−−−→=+上移个单位下移|个单位②伸缩变换01,1,()()y f x y f x ωωω<<>=−−−−→=伸缩 01,1,()()A A y f x y Af x <<>=−−−−→=缩伸③对称变换()()x y f x y f x =−−−→=-轴()()y y f x y f x =−−−→=-轴 ()()y f x y f x =−−−→=--原点1()()y x y f x y f x -==−−−−→=直线 ()(||)y y y y f x y f x =−−−−−−−−−−−−−−−→=去掉轴左边图象保留轴右边图象，并作其关于轴对称图象()|()|x x y f x y f x =−−−−−−−−−→=保留轴上方图象将轴下方图象翻折上去（2）识图对于给定函数的图象，要能从图象的左右、上下分别范围、变化趋势、对称性等方面研究函数的定义域、值域、单调性、奇偶性，注意图象与函数解析式中参数的关系．（3）用图函数图象形象地显示了函数的性质，为研究数量关系问题提供了“形”的直观性，它是探求解题途径，获得问题结果的重要工具．要重视数形结合解题的思想方法．第二章基本初等函数(Ⅰ)〖2.1〗指数函数【2.1.1】指数与指数幂的运算（1）根式的概念①如果,,,1nx a a R x R n =∈∈>，且n N +∈，那么x 叫做a 的n 次方根．当n 是奇数时，a 的n 次方根用符号n a 表示；当n 是偶数时，正数a 的正的n 次方根用符号n a 表示，负的n 次方根用符号n a -表示；0的n 次方根是0；负数a 没有n 次方根．②式子n a 叫做根式，这里n 叫做根指数，a 叫做被开方数．当n 为奇数时，a 为任意实数；当n 为偶数时，0a ≥．③根式的性质：()n n a a =；当n 为奇数时，nn a a =；当n 为偶数时，(0)|| (0) nn a a a a a a ≥⎧==⎨-<⎩．（2）分数指数幂的概念①正数的正分数指数幂的意义是：(0,,,mn m na a a m n N +=>∈且1)n >．0的正分数指数幂等于0．②正数的负分数指数幂的意义是： 11()()(0,,,m m m nn n aa m n N a a-+==>∈且1)n >．0的负分数指数幂没有意义．注意口诀：底数取倒数，指数取相反数．（3）分数指数幂的运算性质①(0,,)rsr sa a aa r s R +⋅=>∈ ②()(0,,)r s rs a a a r s R =>∈③()(0,0,)r r rab a b a b r R =>>∈ 【2.1.2】指数函数及其性质（4）指数函数函数名称指数函数定义函数(0xy a a =>且1)a ≠叫做指数函数图象1a > 01a <<xa y =xy(0,1)O1y =xa y =xy(0,1)O1y =〖2.2〗对数函数【2.2.1】对数与对数运算（1）对数的定义①若(0,1)xa N a a =>≠且，则x 叫做以a 为底N 的对数，记作log a x N =，其中a 叫做底数，N 叫做真数．②负数和零没有对数．③对数式与指数式的互化：log (0,1,0)xa x N a N a a N =⇔=>≠>．（2）几个重要的对数恒等式log 10a =，log 1a a =，log b a a b =．（3）常用对数与自然对数常用对数：lg N ，即10log N ；自然对数：ln N ，即log e N （其中 2.71828e =…）．（4）对数的运算性质如果0,1,0,0a a M N >≠>>，那么①加法：log log log ()a a a M N MN += ②减法：log log log a a aM M N N-= ③数乘：log log ()na a n M M n R =∈ ④log a N a N =⑤log log (0,)b n a a nM M b n R b=≠∈ ⑥换底公式：log log (0,1)log b a b NN b b a=>≠且【2.2.2】对数函数及其性质（5）对数函数函数名称对数函数定义函数log (0a y x a =>且1)a ≠叫做对数函数图象1a > 01a <<定义域 (0,)+∞值域 R过定点图象过定点(1,0)，即当1x =时，0y =．奇偶性非奇非偶单调性在(0,)+∞上是增函数在(0,)+∞上是减函数函数值的变化情况log 0(1)log 0(1)log 0(01)a a a x x x x x x >>==<<<log 0(1)log 0(1)log 0(01)a a a x x x x x x <>==><<a 变化对图象的影响在第一象限内，a 越大图象越靠低；在第四象限内，a 越大图象越靠高．(6)反函数的概念设函数()y f x =的定义域为A ，值域为C ，从式子()y f x =中解出x ，得式子()x y ϕ=．如果对于y 在C 中的任何一个值，通过式子()x y ϕ=，x 在A 中都有唯一确定的值和它对应，那么式子()x y ϕ=表示x是y 的函数，函数()x y ϕ=叫做函数()y f x =的反函数，记作1()x f y -=，习惯上改写成1()y f x -=．x yO(1,0)1x =log a y x=xyO (1,0)1x =log a y x=（7）反函数的求法①确定反函数的定义域，即原函数的值域；②从原函数式()y f x =中反解出1()x f y -=；③将1()x f y -=改写成1()y f x -=，并注明反函数的定义域（即原函数的值域）．（8）反函数的性质①原函数()y f x =与反函数1()y f x -=的图象关于直线y x =对称．②函数()y f x =的定义域、值域分别是其反函数1()y f x -=的值域、定义域．③若(,)P a b 在原函数()y f x =的图象上，则'(,)P b a 在反函数1()y f x -=的图象上．④一般地，函数()y f x =要有反函数则它必须为单调函数．〖2.3〗幂函数（1）幂函数的定义一般地，函数y x α=叫做幂函数，其中x 为自变量，α是常数．（2）幂函数的图象（3）幂函数的性质①图象分布：幂函数图象分布在第一、二、三象限，第四象限无图象．幂函数是偶函数时，图象分布在第一、二象限(图象关于y 轴对称)；是奇函数时，图象分布在第一、三象限(图象关于原点对称)；是非奇非偶函数时，图象只分布在第一象限． ②过定点：所有的幂函数在(0,)+∞都有定义，并且图象都通过点(1,1)．③单调性：如果0α>，则幂函数的图象过原点，并且在[0,)+∞上为增函数．如果0α<，则幂函数的图象在(0,)+∞上为减函数，在第一象限内，图象无限接近x 轴与y 轴． ④奇偶性：当α为奇数时，幂函数为奇函数，当α为偶数时，幂函数为偶函数．当q pα=（其中,p q 互质，p 和q Z ∈），若p 为奇数q 为奇数时，则qpy x =是奇函数，若p 为奇数q 为偶数时，则q py x =是偶函数，若p 为偶数q 为奇数时，则q py x =是非奇非偶函数．⑤图象特征：幂函数,(0,)y x x α=∈+∞，当1α>时，若01x <<，其图象在直线y x =下方，若1x >，其图象在直线y x =上方，当1α<时，若01x <<，其图象在直线y x =上方，若1x >，其图象在直线y x =下方．〖补充知识〗二次函数（1）二次函数解析式的三种形式①一般式：2()(0)f x ax bx c a =++≠②顶点式：2()()(0)f x a x h k a =-+≠③两根式：12()()()(0)f x a x x x x a =--≠（2）求二次函数解析式的方法①已知三个点坐标时，宜用一般式．②已知抛物线的顶点坐标或与对称轴有关或与最大（小）值有关时，常使用顶点式． ③若已知抛物线与x 轴有两个交点，且横线坐标已知时，选用两根式求()f x 更方便．（3）二次函数图象的性质①二次函数2()(0)f x ax bx c a =++≠的图象是一条抛物线，对称轴方程为,2bx a=-顶点坐标是24(,)24b ac b a a--． ②当0a >时，抛物线开口向上，函数在(,]2b a -∞-上递减，在[,)2ba-+∞上递增，当2b x a =-时，2min 4()4ac b f x a -=；当0a <时，抛物线开口向下，函数在(,]2ba -∞-上递增，在[,)2b a -+∞上递减，当2bx a=-时，2max 4()4ac b f x a -=．③二次函数2()(0)f x ax bx c a =++≠当240b ac ∆=->时，图象与x 轴有两个交点11221212(,0),(,0),||||M x M x M M x x =-．（4）一元二次方程20(0)ax bx c a ++=≠根的分布一元二次方程根的分布是二次函数中的重要内容，这部分知识在初中代数中虽有所涉及，但尚不够系统和完整，且解决的方法偏重于二次方程根的判别式和根与系数关系定理（韦达定理）的运用，下面结合二次函数图象的性质，系统地来分析一元二次方程实根的分布．设一元二次方程20(0)ax bx c a ++=≠的两实根为12,x x ，且12x x ≤．令2()f x ax bx c =++，从以下四个方面来分析此类问题：①开口方向：a ②对称轴位置：2bx a=-③判别式：∆ ④端点函数值符号． ①k ＜x 1≤x 2 ⇔②x 1≤x 2＜k ⇔③x 1＜k ＜x 2 ⇔ af (k )＜0④k 1＜x 1≤x 2＜k 2 ⇔x y1x 2x 0>a O ••1k 2k 0)(1>k f 0)(2>k f ab x 2-=xy1x 2x O•<a 1k •2k 0)(1<k f 0)(2<k f a b x 2-=⑤有且仅有一个根x 1（或x 2）满足k 1＜x 1（或x 2）＜k 2 ⇔ f (k 1)f (k 2)<0，并同时考虑f (k 1)=0或f (k 2)=0这两种情况是否也符合x y1x 2x 0>a O ••1k 2k 0)(1>k f 0)(2<k fxy1x 2x O•<a 1k •2k 0)(1>k f 0)(2<k f⑥k 1＜x 1＜k 2≤p 1＜x 2＜p 2 ⇔ 此结论可直接由⑤推出．（5）二次函数2()(0)f x ax bx c a =++≠在闭区间[,]p q 上的最值设()f x 在区间[,]p q 上的最大值为M ，最小值为m ，令01()2x p q =+．（Ⅰ）当0a >时（开口向上） ①若2b p a -<，则()m f p = ②若2b p q a ≤-≤，则()2b m f a =- ③若2b q a->，则()m f q =①若02b x a -≤，则()M f q = ②02b x a->，则()M f p =f(p) f (q) ()2b f a-f (p)f(q)()2bf a-f (p)f (q)()2b f a-f(p) f (q)()2b f a-0x f(p) f(q)()2b f a-0x(Ⅱ)当0a <时(开口向下) ①若2b p a -<，则()M f p = ②若2b p q a ≤-≤，则()2b M f a =- ③若2b q a->，则()M f q =①若02b x a -≤，则()m f q = ②02b x a->，则()m f p =．第三章函数的应用〖3.1〗方程的根与函数的零点一、方程的根与函数的零点1、函数零点的概念：对于函数))((D x x f y ∈=，把使0)(=x f 成立的实数x 叫做函数))((D x x f y ∈=的零点。

(完整版)基本初等函数知识点及函数的基本性质

指数函数及其性质一、指数与指数幂的运算（一）根式的观点1、假如 x na, a R, x R, n 1，且 nN ，那么 x 叫做 a 的 n 次方根．当 n 是奇数时， a的 n 次方根用符号 n a 表示；当 n 是偶数时，正数 a 的正的 n 次方根用符号 na 表示，负的 n 次方根用符号 na 表示； 0 的 n 次方根是 0；负数 a 没有 n 次方根．2、式子 n a 叫做根式，这里 n 叫做根指数， a 叫做被开方数．当n 为奇数时， a 为随意实数；当 n 为偶数时， a0 ．3 、根式的性质： ( n a )na ；当 n 为奇数时， n a na ；当 n 为偶数时，na n|a |a (a 0) ． a (a 0)（二）分数指数幂的观点mna m (a 0,m, n1、正数的正分数指数幂的意义是：a n N , 且 n1) ．0 的正分数指数幂等于 0．mm1)m (a2、正数的负分数指数幂的意义是：a n( 1) nn ( 0, m, n N , 且 n 1)． 0 的负aa分数指数幂没存心义．注意口诀：底数取倒数，指数取相反数． 3、a 0=1 ( a 0) a p1/a p ( a 0； p N )4、指数幂的运算性质a r a sa r s (a 0, r , s R)( a r )s a rs (a 0, r , s R)( ab) r a r b r (a 0, b0, r R)5 、 0 的正分数指数幂等于 0,0 的负分数指数幂无心义。

二、指数函数的观点一般地，函数 xy a ( a 0, 且a 1) 叫做指数函数，此中 x是自变量，函数的定义域为R．注意：○1 指数函数的定义是一个形式定义；○2 注意指数函数的底数的取值范围不可以是负数、零和 1．三、指数函数的图象和性质函数名称指数函数定义函数 ya x ( a 0 且 a 1) 叫做指数函数a 10 a 1y图象y 1Oya xya xy(0,1) y 1(0,1)xOx定义域 R值域（ 0,+ ∞）过定点图象过定点（ 0,1 ），即当 x=0 时， y=1．奇偶性非奇非偶单一性在 R 上是增函数在 R 上是减函数函数值的 y ＞ 1(x ＞ 0), y ＞ 1(x ＜ 0),y=1(x=0),y=1(x=0),变化状况0＜ y ＜ 1(x ＜ 0)0 ＜ y ＜ 1(x ＞ 0)a 变化对在第一象限内， a 越大图象越高，越凑近在第一象限内， a 越小图象越高，越凑近y 轴； a 越大图象越低，越凑近 y 轴；a 越小图象越低，越凑近图象影响在第二象限内，在第二象限内， x 轴． x 轴．注意：利用函数的单一性，联合图象还能够看出：（ 1）在 [a ， b] 上， f (x )a x (a 0且 a 1) 值域是 [ f (a), f ( b)] 或 [ f (b), f (a)] （ 2）若 x 0，则 f (x ) 1； f ( x) 取遍全部正数当且仅当 x R （ 3）对于指数函数 f (x ) a x (a 0 a 1)，总有 f (1) a 且（ 4）当 a 1 时，若 x 1 x 2 ，则 f (x 1 ) f ( x 2 )四、底数的平移对于任何一个存心义的指数函数：在指数上加上一个数，图像会向左平移；减去一个数，图像会向右平移。

基本初等函数讲义(全)

基本初等函数讲义(全)一、一次函数一次函数可以表示为y=kx+b（k不等于0），其中k表示斜率，b表示截距。

当k大于0时，函数图像随着x的增大而增大，当k小于0时，函数图像随着x的增大而减小。

当b大于0时，函数图像在y轴上方，当b小于0时，函数图像在y轴下方。

当b等于0时，函数图像经过原点。

二、二次函数1）二次函数有三种解析式形式：一般式、顶点式和两根式。

一般式为f(x)=ax^2+bx+c（a不等于0），顶点式为f(x)=a(x-h)^2+k（a不等于0），两根式为f(x)=a(x-x1)(x-x2)（a不等于0）。

2）求二次函数解析式的方法有三种情况：已知三个点坐标时，宜用一般式；已知抛物线的顶点坐标或与对称轴有关或与最大（小）值有关时，常使用顶点式；若已知抛物线与x轴有两个交点，且横线坐标已知时，选用两根式求f(x)更方便。

3）二次函数的图像是一条抛物线，对称轴方程为x=-b/2a，顶点坐标为(-b/2a。

-Δ/4a)。

当a大于0时，抛物线开口向上，函数在(-∞。

-b/2a)上递增，在[-b/2a。

+∞)上递减，最小值为f(-b/2a)；当a小于0时，抛物线开口向下，函数在(-∞。

-b/2a]上递增，在[-b/2a。

+∞)上递减，最大值为f(-b/2a)。

三、幂函数1）幂函数可以表示为y=x^α，其中x为自变量，α是常数。

2）所有的幂函数在(0.+∞)都有定义，并且图像都通过点(1,1)。

四、指数函数1）根式的概念是指，如果xn=a，a属于实数，x属于实数，n大于1，且n属于正整数，那么x叫做a的n次方根。

2）正数的正分数指数幂的意义是，a的n次方根的正分数指数幂等于a的n次方。

正数的负分数指数幂没有意义。

非奇非偶函数指的是在定义域为(0.+∞)上的减函数。

对于loga x，当x>1时，函数值递增；当x<1时，函数值递减；当x=1时，函数值为0.在第一象限内，a越大，函数图像越靠低；在第四象限内，a越大，函数图像越靠高。

初等函数的基本不等式(1)

全部的初等不等式证明

专题0 基本初等函数(Ⅰ)(知识梳理)

基本初等函数复习课知识总结[1]

高中数学知识点总结(第二章 函数的概念与基本初等函数Ⅰ第一节 函数及其表示)

专题二 第1讲 函数、基本初等函数的图象与性质

初等函数基本不等式

第二章 函数与基本初等函数1

三元基本不等式基础

基本不等式教学设计

人教A版高中数学教材目录（全）

初等函数的基本不等式

2.2.2 第2课时 对数函数的性质应用--第二章基本初等函数(I)《新课程同步进阶攻略(人教A版必修一》

全部的初等不等式证明

专题一 第2讲 基本初等函数、函数与方程

高中数学第二章基本初等函数(ⅰ)2.1.2指数函数及其性质(第1课时)指数函数的图象及性质

人教版高中数学基本初等函数(1)复习课(共21张PPT)教育课件

基本初等函数知识点归纳

(完整版)基本初等函数知识点及函数的基本性质

基本初等函数讲义(全)

高中数学知识点总结(第二章函数的概念与基本初等函数Ⅰ第一节函数及其表示)

专题二第1讲函数、基本初等函数的图象与性质

第二章函数与基本初等函数1

2.2.2 第2课时对数函数的性质应用--第二章基本初等函数(I)《新课程同步进阶攻略(人教A版必修一》

专题一第2讲基本初等函数、函数与方程