弹性力学2013-_第二章_应力状态
合集下载
弹性力学 第二章应力状态理论
同理，由 Fy 0, Fz 0 :
fvx , fvy , fvz为fv在 x, y, z轴上的投影
fvy ms y n zy l xy fvz ns z l xy m yz
➢应力张量为对称张量。
➢ 一点的应力状态完全 由应力张量确定。
应力状态理论
§2－4 与坐标倾斜的微分面上的应力
z
C
o x
v
xy sx
sy
yx
xzfv
yz P zy zx
B
A
sz
PABC 的体积为 V
体力为 Fx，Fy，Fz
ABC 上的应力为 fv
v ― 平面ABC的外法线 v的方向弦为：
cos(v, x) l cos(v, y) m cos(v, z) n
应力状态理论
x面的应力： s x , xy , xz
y面的应力： s y , yx , yz
z面的应力： s z , zx , zy
应力状态理论
➢ 一点的应力状态： 过一点有无数的截面，这一点的各个截面上应力情况的集合，
称为这点的应力状态（State of Stress at a Given Point）。
偶排列 有序数组1，2，3逐次对换两个相邻的数字而得到的 排列 奇排列
e123 e231 e312 1
e132 e321 e213 1
应力状态理论
二阶对称张量 反对称张量
Tij T ji Tij T ji
任意一个二阶张量，总是可以分解为一个对称张 量和一个分对称张量之和。
张量的对称和反对称性质，可以推广到二阶以上 高阶张量。
应力状态理论
第二章 应力状态理论
§2－1 张量分析基础
张量——在数学上，如果某些量依赖于坐标轴的选择， 并在坐标变换时，按某种指定的形式变化，则称这些 量的总体为张量。简化缩写记号表达物理量的集合。 显著优点——基本方程以及其数学推导简洁 张量的特征——整体与描述坐标系无关
弹性力学_第二章__应力状态分析
弹性⼒学_第⼆章__应⼒状态分析第⼆章应⼒状态分析⼀、内容介绍弹性⼒学的研究对象为三维弹性体，因此分析从微分单元体⼊⼿，本章的任务就是从静⼒学观点出发，讨论⼀点的应⼒状态，建⽴平衡微分⽅程和⾯⼒边界条件。
应⼒状态是本章讨论的⾸要问题。
由于应⼒⽮量与内⼒和作⽤截⾯⽅位均有关。
因此，⼀点各个截⾯的应⼒是不同的。
确定⼀点不同截⾯的应⼒变化规律称为应⼒状态分析。
⾸先是确定应⼒状态的描述⽅法，这包括应⼒⽮量定义，及其分解为主应⼒、切应⼒和应⼒分量；其次是任意截⾯的应⼒分量的确定—转轴公式；最后是⼀点的特殊应⼒确定，主应⼒和主平⾯、最⼤切应⼒和应⼒圆等。
应⼒状态分析表明应⼒分量为⼆阶对称张量。
本课程分析中使⽤张量符号描述物理量和基本⽅程，如果你没有学习过张量概念，请进⼊附录⼀，或者查阅参考资料。
本章的另⼀个任务是讨论弹性体内⼀点－微分单元体的平衡。
弹性体内部单元体的平衡条件为平衡微分⽅程和切应⼒互等定理；边界单元体的平衡条件为⾯⼒边界条件。
⼆、重点1、应⼒状态的定义：应⼒⽮量；正应⼒与切应⼒；应⼒分量；2、平衡微分⽅程与切应⼒互等定理；3、⾯⼒边界条件；4、应⼒分量的转轴公式；5、应⼒状态特征⽅程和应⼒不变量；知识点：体⼒；⾯⼒；应⼒⽮量；正应⼒与切应⼒；应⼒分量；应⼒⽮量与应⼒分量；平衡微分⽅程；⾯⼒边界条件；主平⾯与主应⼒；主应⼒性质；截⾯正应⼒与切应⼒；三向应⼒圆；⼋⾯体单元；偏应⼒张量不变量；切应⼒互等定理；应⼒分量转轴公式；平⾯问题的转轴公式；应⼒状态特征⽅程；应⼒不变量；最⼤切应⼒；球应⼒张量和偏应⼒张量§2.1 体⼒和⾯⼒学习思路:本节介绍弹性⼒学的基本概念——体⼒和⾯⼒，体⼒F b和⾯⼒F s的概念均不难理解。
应该注意的问题是，在弹性⼒学中，虽然体⼒和⾯⼒都是⽮量，但是它们均为作⽤于⼀点的⼒，⽽且体⼒是指单位体积的⼒；⾯⼒为单位⾯积的作⽤⼒。
体⼒⽮量⽤F b表⽰，其沿三个坐标轴的分量⽤F b i（i=1，2，3）或者F b x、F b y和F b z表⽰，称为体⼒分量。
高等材料力学课件第二章应力状态
§2.3 平衡微分方程
平衡
物体整体平衡，内部任 何部分也是平衡的。 对于弹性体，必须讨论 一点的平衡。
微分平行六面体单元
§2.5 平衡方程2
• x截面,应力分量 • σ x Շxy Շxz • x+dx截面,应力分量
x x xd,xx y x xy d,xx z x xd z ,x
数必须等于3个。
§2.6 主应力与应力主方向
转轴公式描述了应力随坐标转动的变化规律
结构强度分析需要简化和有效的参数
——最大正应力、最大切应力以及方位 主应力和主平面——应力状态分析重要参数 应力不变量——进一步探讨应力状态
§2.6 主应力2
主应力和主平面
切应力为零的微分面称为 主微分平面，简称主平面。 主平面的法线称为应力主 轴或者称为应力主方向。 主平面上的正应力称为主 应力。
zx zy z
代数主子式之和
应力张量元素 构成的行列式
•§2.6应主应力力6 状态特征方程
• ——确定弹性体内部任意一点主应力和应力 主轴方向。
• 主应力和应力主轴方向取决于载荷、形状和 边界条件等，与坐标轴的选取无关。
• 因此，特征方程的根是确定的，即I1、I2、I3 的值是不随坐标轴的改变而变化的。
§2.5 边界条件
弹性体的表面，应力分量必须与表面力满足面 力边界条件，维持弹性体表面的平衡。
边界面力已知——面力边界S
面力边界条件——
确定的是弹性体表面 外力与弹性体内部趋 近于边界的应力分量 的关系。
§2.5 边界条件2
面力边界条件
Fsj ijni
§2.5 边界条件3
面力边界条件描述弹性体表面的平衡， 平衡微分方程描述弹性体内部的平衡。 这种平衡只是静力学可能的平衡。 真正处于平衡状态的弹性体，还必须满足变 形连续条件。
弹性力学 第二章 应力分析
ν
∫∫ ∫∫∫ eijkr j T k dS + eijk rj Fkdv = 0
S
V
ν
因为Tk = σ rkν r ，所以由 Gauss 公式有
∫∫ ∫∫∫( ) eijkr jσ rkν r dS =
eijk rjσ rk ,r dv
S
V
又因为
rj ,r
= δ jr
=
∂x j ∂xr
故使上式成为
方程(2.5.3)式有根，应有三个根，即σ1 ,σ 2 ,σ 3 ，称为主应力，(2.5.3) 和 (2.5.4)式可重写成
(σ − σ1 )(σ − σ 2 )(σ − σ 3 ) = 0
J1 = σ1 + σ 2 +σ 3
J 2 = σ 1σ 2 + σ 2σ 3 + σ 3σ 1
J 3 = σ1σ 2σ 3
消去公因子得 (2.3.1a) 式的第二式，同理由另两个方向的平衡得到其余的两式，
∂σ xx ∂x
+
∂σ yx ∂y
+
∂σ zx ∂z
+
X
=
0
∂σ xy ∂x
+
∂σ yy ∂y
+
∂σ zy ∂z
+Y
=0
∂σ xz ∂x
+
∂σ yz ∂y
+
∂σ zz ∂z
+
Z
=0
或
(2.3.1a)
2
对应σ 2 , 可求出 ν j = a j − ib j ，因此 (4) 式中的因子
( )( ) 1 2
② 积分方程法 上述的平衡方程也可用积分方程的方法得到。作用在被分割出物体上的合力为零的矢量 方程为
弹性力学简明教程第二章 (1)
其中：l=cos(n,x), m=cos(n,y)。
(a)
第二章
平面应力问题和平面应变问题
斜面应力
(2)求（ σ n , τ n ）
将 p ( px , p y ) 向法向，切向投影，得
2 2 n lp y mpx lm(σ y σ x ) (l m ) xy . σ n lpx mp y l σ x m σ y 2lm xy ,
定义
§ 2－ 2
平衡微分方程
平衡微分方程--表示物体内任一点
的微分体的平衡条件。
第二章
平面应力问题和平面应变问题
定义
在任一点（x，y）取出一微小的平行六 面体 d xd y1 ,作用于微分体上的力：
体力： f x , f y 。 应力：作用于各边上， 并表示出正面上
由坐标增量引起
的应力增量。
第二章
第二章
平面应力问题和平面应变问题
说明
⑷ 几何方程是变形后物体连续性条件 的反映和必然结果。 ⑸ 形变和位移之间的关系： 位移确定 形变完全确定： 从物理概念看，各点的位臵确定，则 微分线段上的形变确定 。 从数学推导看，位移函数确定，则其 导数（形变）确定 。
第二章
平面应力问题和平面应变问题
形变与位移的关系
第二章
平面应力问题和平面应变问题
平面应变
坐标系选择如图：
对称面
oz
x
ox
z
zy
y y
第二章
平面应力问题和平面应变问题
平面应变
简化为平面应变问题：
（1）截面、外力、约束沿z 向不变，外力、约束 平行xy面，柱体非常长； 故任何z 面（截面）均为对称面。
(a)
第二章
平面应力问题和平面应变问题
斜面应力
(2)求（ σ n , τ n ）
将 p ( px , p y ) 向法向，切向投影，得
2 2 n lp y mpx lm(σ y σ x ) (l m ) xy . σ n lpx mp y l σ x m σ y 2lm xy ,
定义
§ 2－ 2
平衡微分方程
平衡微分方程--表示物体内任一点
的微分体的平衡条件。
第二章
平面应力问题和平面应变问题
定义
在任一点（x，y）取出一微小的平行六 面体 d xd y1 ,作用于微分体上的力：
体力： f x , f y 。 应力：作用于各边上， 并表示出正面上
由坐标增量引起
的应力增量。
第二章
第二章
平面应力问题和平面应变问题
说明
⑷ 几何方程是变形后物体连续性条件 的反映和必然结果。 ⑸ 形变和位移之间的关系： 位移确定 形变完全确定： 从物理概念看，各点的位臵确定，则 微分线段上的形变确定 。 从数学推导看，位移函数确定，则其 导数（形变）确定 。
第二章
平面应力问题和平面应变问题
形变与位移的关系
第二章
平面应力问题和平面应变问题
平面应变
坐标系选择如图：
对称面
oz
x
ox
z
zy
y y
第二章
平面应力问题和平面应变问题
平面应变
简化为平面应变问题：
（1）截面、外力、约束沿z 向不变，外力、约束 平行xy面，柱体非常长； 故任何z 面（截面）均为对称面。
弹性力学一点应力状态01
水坝
—— 近似认为无限长
(2) 外力特征
外力（体力、面力）平行于横截面作 用，且沿长度 z 方向不变化。
约束 —— 沿长度 z 方向不变化。
(3) 变形特征
滚柱
厚壁圆筒
如图建立坐标系：以任一横截面为 xy 面，任一纵线为 z 轴。
设 z方向为无限长，则 x, x, u, 沿 z 方向都不变化，
仅为 x，y 的函数。 任一横截面均可视为对称面
由 1 2 x y 得
2 y (1 x )
tan 2
xy 1
x
显然有 tan1 tan2 1
表明： σ1 与 σ2 互相垂直。
结论
任一点P，一定存在两 互相
垂直的主应力σ1 、 σ2 。
（3）σN 的主应力表示
O
x
2
1
P
dy
dx ds
A
y
N
N
B
sN
由 N l 2 x m2 y 2lm xy
P dx x dy ds
A XN
N lYN mX N
将式（2-3）（2-4）代入，并整理得： y
N l 2 x m2 y 2lm xy （2-5）
xy N
B YN
N sN
N lm( y x ) (l 2 m2 ) xy （2-6）—— 任意斜截面上应力计算公式
说明： （1）运用了剪应力互等定理： xy yx
剪应力互等定理
应力符号的意义：
z
zx
zy
z
y
yx xz
yz x zy
xy
zx
yz yx y
O
y z
x
xy
第1个下标 x 表示τ所在面的垂线线方向； 第2个下标 y 表示τ的方向.
弹性力学第二章
（2）平面应变问题的物理方程 由于平面应力问题中：εz = γ zx = γ zy = 0
µ 1− µ2 σx − εx = σy 1− µ E 1− µ2 µ σy − εy = σy E 1− µ
——平面应变问题 ——平面应变问题 物理方程
第三节
平面问题中一点的应力状态
一点的应力
2. 一点的主应力与应力主向 （1）主应力 若某一斜面上τn = 0 ，则该斜面上的正应力σn 称为该点一个主应力σ； 当τn = 0 时，有 σn =σ = p
px =lσ py = m σ
lσx +m xy =lσ τ m y +lτxy = m σ σ
γ xy =
2(1+ µ) τ xy E
在z方向，εz = 0, σz = µ(σx +σy )
变换关系 ： 平面应力物理方程 →平面应变物理方程：
E µ E→ ， → µ 2 1− µ 1− µ
平面应变物理方程 →平面应力物理方程：
E→
E(1+ 2µ)
(1+ µ)2
， → µ 1+ µ
µ
思考题 1. 试证：由主应力可以求出主应变，且两者方 向一致。 2. 试证：三个主应力均为压应力，有时可以产 生拉裂现象。 3. 试证：在自重作用下，圆环（平面应力问题） 比圆筒（平面应变问题）的变形大。
E
µ
2.平面应变问题 2.平面应变问题 条件是：⑴很长的常截面柱体 ； ⑵体力、面力、约束平行于柱面横截面， 沿长度方向不变。 应力：
σz = µ(σx +σy )
τ zx =τ zy = 0
应变：
εz = 0 γ zx = 0 γ zy = 0
弹性力学第二章 应力理论
主应力 & 应力不变量
应力1、第二主应力2和第三主应力3 ，且
1 2 3
Chapter 3.3
主应力 & 应力不变量
主应力的性质
3I12I2I30
➢ 不变性 由于特征方程的三个系数是不变量，所以作为特征 根的主应力及相应主方向都是不变量。
1, 2, 3
1, 2 , 3
➢ 实数性 即特征方程的根永远是实数。
Chapter 3.3
主应力 & 应力不变量
➢ 极值性
主应力1和3是一点正应力的最大值和最小值。
在主坐标系中，任意斜截面上正应力的表达式：
n==ijij =11 222 233 2
= 1 (1 2 )2 2 (2 3 )3 2 1 = (1 3 )1 2 (2 3 )2 2 3 3
Chapter 3.3
e3
11
e1
32
31
23
13
22
12 21
x2 e2
x1
Chapter 3.1
外力、内力与应力
把作用在正面dSi上的应力矢量沿坐标轴正向分解得：
(1) 11e1 12e2 13e3 1jej
(2) 21e1 22e2 23e3 2jej
(3) 31e1 32e2 33e3 Nhomakorabea 3jej x3 33
主应力 & 应力不变量
x l xym xzn 0
xyl y m yzn 0
xzl yzm z n 0
由于l2m2n21，所以要有非零解，则上述三
个方程必须是线性相关的，亦即系数行列式为零：
x xy xz
xy y
yz
xz yz 0 z
弹性力学 应力状态
Fby 0
ij , i Fbj 0
§2.3 平衡方程5
考察主矩为零条件：
M
x
O ;
yz 1 1 yz y dy dxdz 2 dy yz dxdz 2 dy zy 1 1 zy dz dxdy dz zy dxdy dz 0 z 2 2
§2.4 应力状态1
•应力状态对于结构强度是十分重要的。
•为了探讨各个截面应力的变化趋势，确定可以 描述应力状态的应力参数。 如果应力张量能够描述一点的应力状态，则 1. 应力张量可以描述其它应力参数
——斜面应力公式； 2. 坐标变换与应力张量关系 ——转轴公式。
§2.4 应力状态2
应力矢量与应力分量的关系
这就是著名的哥西公式，又称为斜面应力公式。它说明； 过一点三个互相垂直微分面上的九个应力分量完全确定了该点 的应力状态。这样，我们就可以把要了解各点应力状态的问
题，转化为去求各点的九个应力分量的问题。
§2.4 应力状态6
应力矢量不仅随位置改 变而变化，而且随截面 方位改变而变化。 同一点由于截面的法线 方向不同，截面上的应 力矢量也不同。
第二章 应力状态
弹性力学的研究对象为三维弹性体， 分析从微分单元体入手， 本章的任务就是从静力学观点出发，讨 论一点的应力状态，建立平衡微分方程 和面力边界条件。
目录
§2.1 §2.2 §2.3 §2.4 §2.5 §2.6 §2.7 体力和面力 应力与应力张量 平衡微分方程 应力状态的描述 应力边界条件 主应力与应力主方向 应力球张量和球应力偏张量
§2.3 平衡方程2
主矢为零：
微分平行六面体单元
F 静力平衡条件:
塑性力学-第二章 应力状态和应变状态
（2—36）
T～等效剪应力或剪应力强度。 其意义是，原来的应力状态，在某种意义上可以用等效的，大小为 T 的纯剪切应力状态来代 替。 也就是说，纯剪切状态 1 T , 2 0, 3 T ，的剪应力强度等于 T，而实际应力状态的 剪应力强度也等于 T。 8， 、σi、T 和 J2 一样，在塑性本构关系中起重要作用。 ，它们之间的换算关系如下：
（2—25） 在后面的第三章可以看到，应力偏量的第二不变量在研究塑性本构关系时具有特殊的重要意 义。由于 sij 是对称张量， （2—24）式也可以写为：
1 J 2 sij sij 2
（2—26）
（二）几种特定截面上的应力 求得一点处的主平面的方向和主应力大小以后，可以求得通过该点任意倾斜方向截面上的正 应力和剪应力。选三个主应力方向 1、2、3 为坐标轴，设任意斜截面的法线为 n，它对于 1、2、3 轴的方向余弦为 l1，l2，l3。图 2.3 所示的微元四面体即由三个与主平面一致的坐标面及一个斜截 面组成。设斜截面上的总应力 p 分解为沿三个主轴的分量 p1，p2，p3，由微元体的平衡得到
pj=σijli
σn= pjlj
（2—2）代入（2—3）得：
（2—3） （2—4）
n = ij lilj= xl12 y l22 z l32 2 xyl1l2 2 yzl2l3 2 zx l3l1
斜截面上的剪应力 τn 为：
2 2 2 2 2 2 n p2 n px py pz n
第二章
应力状态和应变状态
§2.1
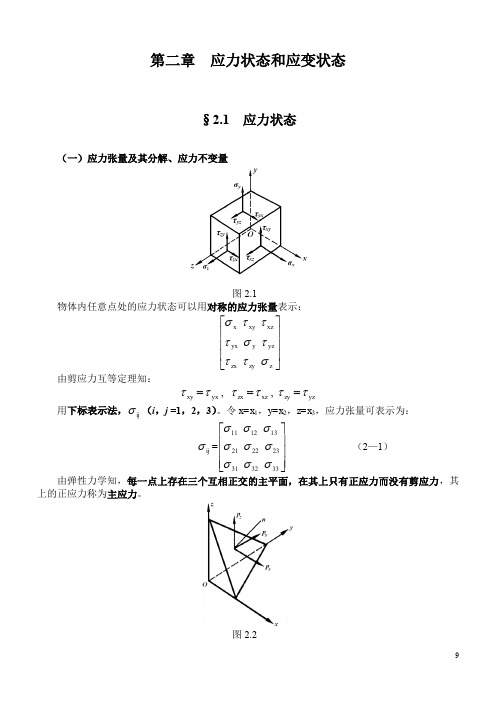
（一）应力张量及其分解、应力不变量
应力状态
图 2.1 物体内任意点处的应力状态可以用对称的应力张量表示：
x xy xz yx y yz zx zy z
弹性力学-第二章
(a)
(b)
y
o
z
a
b
x
(c) 刚性槽
2.平面问题的应力边界条件 设在S 部分边界上给定了面力分量 f x ( s) 和 f y ( s) ， 则可由边界上任一点微分体的平衡条件，导出应力 与面力之间的关系式。
0 o y P y
tyx txy
x
B
y
fx
A
x
P
x
fy
fx
n
fy
f
斜面上的应力
由式 (2-3)
x=-b为负x 面
l cos n, x cos180 1
m cos n, y cos 90 0
(σ x ) xb f x , (t xy ) x b f y
n
b a x
fx fy
σx
σx
fx fy
t xy
y
t xy
应力边界条件的两种表达式： （1）公式写法 公式写法通常只用于 边界为非坐标面时
x=a为正x 面
l cos n, x cos 0 1
m cos n, y cos 90 0
(σ x ) xa f x , (t xy ) xa f y
b a x
n
fx fy
σx
σx
fx fy
t xy
y
t xy
当边界面为坐标面时
(l x mt xy ) s f x ( s) (m y lt xy ) s f y ( s)
( 2) 斜边 y x tan
l cos n, x cos 90 sin
m cos n, y cos
第二章_应力讲解
第二章 应力分析研究弹性力学问题要从三方面规律（条件）：平衡、几何、物理来建立，本章就是研究第一个规律：平衡规律。
第1节 内力和外力1.1 外力：物体承受外因而导致变形，外因可以是热力作用、化学力作用、电磁力作用和机械力作用；另一方面从量纲分类，外力主要为体积力和表面积力。
我们讨论的外力是属于机械力中的体力和面力的范围。
1． 外部体力：作用在物体单位体积（质量）上的力如重力（惯性力）。
量纲：力/（长度）3。
求V 中任意点P 上承受体力采用极限方法：X X 2X X 2第2节 应力和应力张量2.1 应力当变形体受外力作用时，要发生变形，同时引起物体内部各点之间相互作用力（抵抗力）——内力，为了描述物体内任意点P 的内力可采取如下方法：过P 点设一个截面S 将V 分为两部分：（作用力与反作用力）FF -l n n x ==1、m n n y ==2、n n n z ==3。
即n t m t l t n t n t n t n t t z y x i i n )()()(3)3(2)2(1)1()()( ++=++==,,1S n P B C S A B C ∆∆∆∆==0)()(=++-V f S t S t i i n ∆∆∆而 S n S t t i i i i ∆∆=-=-,)()(代入上式，并忽略高阶微量 0)()(=-S n t S t i i n ∆∆或 )()(i i n t n t =展开为 3)3(2)2(1)1()(n t n t n t t n++= 或n t m t l t t z y x n )()()()( ++=2.1 应力张量每个坐标面上的应力矢量又可以沿三个坐标面分解三个分量，比如坐标面法线为x 1jxj j j z xz y xy x xx x e e e e e e e e t t σσσσσσσσ==++=++==1313212111)()1(x 2x 1 x 1(x)x 3,,32S n PAB S n PAC ∆=∆∆=∆同理，得j yj j j z yz y yy x yx y e e e e e e e e t t σσσσσσσσ==++=++==2323222121)()2(jzj j j z zz y zy x zx z e e e e e e e e t t σσσσσσσσ==++=++==3333232131)()3(将法线方向n 取为单位长度，则将式（3.25）代入式（3.26），得3.3.2.讨论：） （ ３３３３３３２２２２２２253.l p l p l p l p ⎪⎪⎪⎭⎪⎬====σσσσ） （2631232221.l l l =++７）＝１ （）（）＋（） （２３３２２２２2311.p p p σσσ+（1）：如果以p 1，p 2，p 3为坐标轴建立直角坐标系，则在此坐标系中，上式为一椭球面方程，主半轴分别为σ1，σ2，σ3，称为应力椭球面。
《弹性力学》第二章_平面问题的基本理论
o
xy
x
y
P
yx
y
A
XN
x
设AB面在xy平面内的长度为dS， 厚度为一个单位长度，N为该面的外 法线方向，其方向余弦为：
B
N
N
N
cos(N , x) l , cos(N , y) m
9
YN S
图2 － 4
斜面AB上全应力沿x轴及y轴的投影分别为XN和YN。由PAB 的平衡条件 Fx 0 可得： X N dS xldS yxmdS
2.主应力的方向
1 与 2 互相垂直。
11
§2-4
几何方程、刚体位移
在平面问题中，弹性体中各点都可能产生任意方向的位移。 通过弹性体内的任一点P，取一单元体PAB，如图2-5所示。弹性 体受力以后P、A、B三点分别移动到P′、A′、B′。 一、P点的正应变
u (u dx) u u x x dx x
二、P点的剪应变
线段PA的转角：
同理可得线段PB的转角：
u y
所以
xy
v u x y
13
因此得到平面问题的几何方程：
u x x v y y v u xy x y
由几何方程可见，当物体的位移分量完全确定时，形变 分量即可完全确定。反之，当形变分量完全确定时，位移分 量却不能完全确定。
z
E
( x y )
16
二、平面应变问题的物理方程 1 2 x ( x y ) E 1 1 2 y ( y x ) E 1 2(1 ) xy xy E 三、平面应力的应力应变关系式与平面应变的关系式之间的 变换关系 1 ( ) y 将平面应力中的关系式： x E x
第二章应力状态理论(弹性力学)
应力状态理论
第二章
应力状态理论
§2－1 张量分析基础
张量——在数学上，如果某些量依赖于坐标轴的选择， 并在坐标变换时，按某种指定的形式变化，则称这些 量的总体为张量。简化缩写记号表达物理量的集合。 显著优点——基本方程以及其数学推导简洁 张量的特征——整体与描述坐标系无关 ——分量需要通过适当的坐标系定义 一般张量——曲线坐标系定义
2 2 2 2 ∴ v = fvx + fvy + fvz −σv τ2
如已知 σ x ,σ y ,σz ,τ yz ,τ zx,τ xy, 就可求得任一斜截面 正应力和切应力。 正应力和切应力
应力状态理论
如果ABC是物体边界面：
lσx + m yx + n zx = fx τ τ
z
C v
fz
fxP
应力状态理论
§2－2 体力和面力
外力：构件外物体作用在构件上的力。 外力：构件外物体作用在构件上的力。
面力：作用在物体表面上的力，如接触力、 面力：作用在物体表面上的力，如接触力、液体压 力等。 表示。单位： 力等。用 fx , f y , fz 表示。单位：N/m2。 体力：分布在物体整个体积内部的力，如重力、 体力：分布在物体整个体积内部的力，如重力、惯
F 5
m
F 4
F 1 F 2
Ι
m
ΙΙ
F 3
F 5
F 4
F 1F 2ຫໍສະໝຸດ ΙΙΙF 3
应力状态理论
§2－3 应力和一点的应力状态 应力和一点的应力状态
应力：内力的分布集度。 应力：内力的分布集度。 r 平均应力： ①平均应力： r ∆ F f = ∆S 全应力： ②全应力： r r r ∆ F dF f v = lim = dS ∆S → 0 ∆ S
第二章
应力状态理论
§2－1 张量分析基础
张量——在数学上，如果某些量依赖于坐标轴的选择， 并在坐标变换时，按某种指定的形式变化，则称这些 量的总体为张量。简化缩写记号表达物理量的集合。 显著优点——基本方程以及其数学推导简洁 张量的特征——整体与描述坐标系无关 ——分量需要通过适当的坐标系定义 一般张量——曲线坐标系定义
2 2 2 2 ∴ v = fvx + fvy + fvz −σv τ2
如已知 σ x ,σ y ,σz ,τ yz ,τ zx,τ xy, 就可求得任一斜截面 正应力和切应力。 正应力和切应力
应力状态理论
如果ABC是物体边界面：
lσx + m yx + n zx = fx τ τ
z
C v
fz
fxP
应力状态理论
§2－2 体力和面力
外力：构件外物体作用在构件上的力。 外力：构件外物体作用在构件上的力。
面力：作用在物体表面上的力，如接触力、 面力：作用在物体表面上的力，如接触力、液体压 力等。 表示。单位： 力等。用 fx , f y , fz 表示。单位：N/m2。 体力：分布在物体整个体积内部的力，如重力、 体力：分布在物体整个体积内部的力，如重力、惯
F 5
m
F 4
F 1 F 2
Ι
m
ΙΙ
F 3
F 5
F 4
F 1F 2ຫໍສະໝຸດ ΙΙΙF 3
应力状态理论
§2－3 应力和一点的应力状态 应力和一点的应力状态
应力：内力的分布集度。 应力：内力的分布集度。 r 平均应力： ①平均应力： r ∆ F f = ∆S 全应力： ②全应力： r r r ∆ F dF f v = lim = dS ∆S → 0 ∆ S
第二章弹性力学的基本方程
在二维笛卡尔空间中, 下标用小写希腊字母表示,并取
, , 1, 2
由此,向量 a可表示为
3
a a1e1 a2e2 a3e3 ai ei i 1
三阶线性代数方程组
a11x a12 y a13 z P1
a21
x
a22
y
a23
z
P2
a31
x
a32
y
a33
z
P3
可表示为
ai1x1 ai2 x2 ai3x3 Pi
(c) 非循环序列:i, j, k中有两个以上得指标取
相同值
e112 e222 e323 0
利用置换符号可以简化公式
(1)行列式
a11 a12 a13 a a21 a22 a23
( xix j
) ,ij
例如:
xi
,i
ui x j
ui, j
2ui x j xk
ui, jk
ui xi
ui,i
u1,1
u2,2
u3,3
f xi
dxi
f ,i dxi
f ,1dx1
f ,2 dx2
f ,3dx3
4、 克罗内克(Kroneker)符号
定义: ij ei e j cos(ei ˆ e j )
Fx
1 dh 3
0
同理可得:
Tx xl yx m zx n Ty xyl y m zy n Tz xzl yz m z n
上式称为斜面应力公式,又称Cauchy公式。
2、斜面上得正应力与剪应力
Tν Txl Tym Tz n
xl 2 y m 2 z n 2 2 xylm 2 yz mn 2 zx nl
ei
, , 1, 2
由此,向量 a可表示为
3
a a1e1 a2e2 a3e3 ai ei i 1
三阶线性代数方程组
a11x a12 y a13 z P1
a21
x
a22
y
a23
z
P2
a31
x
a32
y
a33
z
P3
可表示为
ai1x1 ai2 x2 ai3x3 Pi
(c) 非循环序列:i, j, k中有两个以上得指标取
相同值
e112 e222 e323 0
利用置换符号可以简化公式
(1)行列式
a11 a12 a13 a a21 a22 a23
( xix j
) ,ij
例如:
xi
,i
ui x j
ui, j
2ui x j xk
ui, jk
ui xi
ui,i
u1,1
u2,2
u3,3
f xi
dxi
f ,i dxi
f ,1dx1
f ,2 dx2
f ,3dx3
4、 克罗内克(Kroneker)符号
定义: ij ei e j cos(ei ˆ e j )
Fx
1 dh 3
0
同理可得:
Tx xl yx m zx n Ty xyl y m zy n Tz xzl yz m z n
上式称为斜面应力公式,又称Cauchy公式。
2、斜面上得正应力与剪应力
Tν Txl Tym Tz n
xl 2 y m 2 z n 2 2 xylm 2 yz mn 2 zx nl
ei
弹性力学_第二章__应力状态分析
第二章应力状态分析一、内容介绍弹性力学的研究对象为三维弹性体，因此分析从微分单元体入手，本章的任务就是从静力学观点出发，讨论一点的应力状态，建立平衡微分方程和面力边界条件。
应力状态是本章讨论的首要问题。
由于应力矢量与内力和作用截面方位均有关。
因此，一点各个截面的应力是不同的。
确定一点不同截面的应力变化规律称为应力状态分析。
首先是确定应力状态的描述方法，这包括应力矢量定义，及其分解为主应力、切应力和应力分量；其次是任意截面的应力分量的确定—转轴公式；最后是一点的特殊应力确定，主应力和主平面、最大切应力和应力圆等。
应力状态分析表明应力分量为二阶对称张量。
本课程分析中使用张量符号描述物理量和基本方程，如果你没有学习过张量概念，请进入附录一，或者查阅参考资料。
本章的另一个任务是讨论弹性体内一点－微分单元体的平衡。
弹性体内部单元体的平衡条件为平衡微分方程和切应力互等定理；边界单元体的平衡条件为面力边界条件。
二、重点1、应力状态的定义：应力矢量；正应力与切应力；应力分量；2、平衡微分方程与切应力互等定理；3、面力边界条件；4、应力分量的转轴公式；5、应力状态特征方程和应力不变量；知识点：体力；面力；应力矢量；正应力与切应力；应力分量；应力矢量与应力分量；平衡微分方程；面力边界条件；主平面与主应力；主应力性质；截面正应力与切应力；三向应力圆；八面体单元；偏应力张量不变量；切应力互等定理；应力分量转轴公式；平面问题的转轴公式；应力状态特征方程；应力不变量；最大切应力；球应力张量和偏应力张量§2.1 体力和面力学习思路:本节介绍弹性力学的基本概念——体力和面力，体力F b和面力F s的概念均不难理解。
应该注意的问题是，在弹性力学中，虽然体力和面力都是矢量，但是它们均为作用于一点的力，而且体力是指单位体积的力；面力为单位面积的作用力。
体力矢量用F b表示，其沿三个坐标轴的分量用F b i（i=1，2，3）或者F b x、F b y和F b z表示，称为体力分量。
弹性力学3-应力状态、几何方程
s x ,s y ,t xy t yx
应力张量： tsyxx
t xy sy
t t
xz yz
t zx t zy s z
s x t xy
t yx
s
y
第二章 平面问题的基本理论 2.3 平面问题中一点的应力状态
一点的应力状态可以用以下三种方法表示：
用包围该点的微元体（微正六面体）表征 过该点的任意斜截面上的应力 用一点的主应力与主方向表征
2.1 平面应力与平面应变 2.2 平衡微分方程 2.3 一点的应力状态 2.4 几何方程 2.5 物理方程 2.6 边界条件 2.7 圣维南原理 2.8 按位移求解平面问题 2.9 按应力求解平面问题 2.10 常体力情况下的简化
第二章 平面问题的基本理论 2.4几何方程
几何方程：应变分量与位移分量之间的关系。
fx
dxdy 2
1 0
上式分别将dx、dy用ds 表达：
pxds
s xlds
t yxmds
fx
ldsmds 2
0
ds趋于零时
O
x
t yx s y
P
A
t t xy
Px
n
px ls x mt xy
(2-3a)
sx
微元体竖直静力平衡条件： Fy 0 可得：
Py s n n
B
y pyds 1 s ydx 1 t xydy 1
过P点的微小三角形，两个边分别 O
平行于坐标轴，当面积SAPB无限减小， 趋近于P点时，平面AB上的应力即成
x
t yx s y
P
A
为过P点斜面上的应力。
P点应力分量（直角坐标面上的应
力）已知：s x ,s y ,t xy t yx
弹性力学第2章—应力
⎡σ x τ xy τ xz ⎤ ⎢ ⎥ [σ ij ] = ⎢τ yx σ y τ yz ⎥ ⎢ ⎥ τ τ σ zx zy z ⎣ ⎦
i, j = x, y , z
τzx
σy
σz
τzy
σx
τyx τ xyτ τ xz yx τ xz τ xy τyz
σxτ
τ yz Δz σ
y
O
σz Δy
zy
τzx
截面上的切应力：
2 n
τyz
px
x
A
τzy
τzx
σz
τxz p y
σx
B
y
τ = pi pi − σ = σ ij n jσ ik nk − (σ ij n j ni )
2
2.2 一点的应力状态
应力分量的转换方程
应力张量在坐标变换时的转换公式 和 Ox ′y ′z ′ ，其中 x ′ 轴取为斜截面的 法向 n ，并通过O点。 沿 x ′ 轴方向的正应力为 令变换前后的坐标系分别为Oxyz
Δx
y
x
2.1 应力的概念
应力张量的特点:
当坐标系变换时， 另一坐标系
σ ij 能够按照一定的变换式变换成 Ox ′y ′z ′ 中的九个分量 σ i′j′
i ′, j ′ = x ′, y ′, z ′
⎡ σ x′ τ x′y′ τ x′z′ ⎤ ⎥ [σ i′j′ ] = ⎢ τ σ τ y′ y ′z ′ ⎥ ⎢ y′x′ ⎢ ⎣τ z′x′ τ z′y′ σ z′ ⎥ ⎦
同理可得 σ 1′ 2′ = l1′i l2′ jσ ij ，
σ 1′ 3′ = l1′il3′ jσ ij
2.2 一点的应力状态
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
§2.4 应力状态13
• ——应力分量满足张量变化规则
• 应力张量为二阶对称张量
• 转轴公式表明：新坐标系下的六个应力分 量可通过原坐标系的应力分量确定。
• 应力张量可以确定一点的应力状态。
• 坐标轴转轴后，应力分量发生改变。但是 作为整体所描述的应力状态没有变化。
§2.4 应力状态14
平面应力状态转轴公式
过物体内部点M的三个彼此垂直的微分面（使之与坐标平面平 行）则在这三个微分面上的应力矢量可分别表示为
px, py, pz
§2.2 应力4
p x x i xy j xz k p y yxi y j yz k p z zx i zy j z k
体力
• 方向约定
2.1.2 面力
§2.2
• 内力
应力与应力张量
– 物体在外界因素作用下，例如外力，温度变化等，物体内部各个部分 之间将产生相互作用，这种物体一部分与相邻部分之间的作用力称为
内力。当物体内部形成的内力厂足以和外力相平衡时，变形不再继 续，物体达到稳定平衡状态。 • 应力
– 内力的分布一般是不均匀的。为了描述任意一点M的内力，利用假想 平面将物体截为两部分，将希望计算内力F的截面暴露出来，计算微 面积ΔS 上内力的平均值称平均应力
§2.5 边界条件
弹性体的表面，应力分量必须与表面力满足面 力边界条件，维持弹性体表面的平衡。
应力状态分析——首先是确定应力状态的描述方法， 这包括应力矢量定义，及其分解为主应力、切应力 和应力分量；其次是任意截面的应力分量的确定— 转轴公式；最后是一点的特殊应力确定，主应力、 最大切应力等。 应力状态分析表明应力分量为二阶对称张量。本课 程分析中使用张量符号描述物理量和基本方程，如 果你没有学习过张量概念，请查阅参考资料。 本章的另一个任务是讨论弹性体内一点——微分单 元体的平衡。弹性体内部单元体的平衡条件为平衡 微分方程和切应力互等定理；边界单元体的平衡条 件为面力边界条件。
应力张量可以描述一点应力状态
§2.3 平衡微分方程
平衡 物体整体平衡，内部任 何部分也是平衡的。 对于弹性体，必须讨论 一点的平衡。
考察微分平行六面体单元
dx,dy,dz， 在体力、面力作用下处 于平衡。 负面、正面（约定）
§2.3 平衡方程1
X轴方向负面上；
x x, y, z , xy x, y, z , xz x, y, z
X轴方向正面上，因为应力是坐标的连续函数，所以有
x x dx, y , z , xy x dx, y , z , xz x dx, y , z
xy x xz x x, y , z dx, xy dx , xz dx x x x
x yx zx Fbx 0 x y z
§2.3 平衡方程4
平衡微分方程
x yx zx Fbx 0 x y z xy y zy
x xz z Fbz 0 x y z y yz z
xy l1m3 l3m1 yz m1n3 m3n1 zx l1n3 l3n1
§2.4 应力状态11
通过 x , y , z 三者的轮换， 可得到其余六个应力分量；
y , yx , yz z , zx , zy
§2.1 体力和面力
• 物体外力 • ——分为两类 • 体力 _体积力；电磁力；惯性力；也称质量力。 • [ F / LLL ]
• 面力_面积力；指分布在物体表面上的外力，如液体压力、接 触力等 。
•
[ F / LБайду номын сангаас ]
• 体力和面力分别为物体单位体积或者单位面积的载荷。
2.1.1
• 体力 _[ F/LLL ]
xy l2 px m2 p y n2 pz l2 x l1 yx m1 zx n1
x l1l2 y m1 m2 z n1 n2
m2 xy l1 y m1 zy n1 n2 xz l1 yz m1 z n1
,
并可证明
y x
x y
,
x z
z x
y z
z y
•转轴公式
i ` j ` ij nii ` n jj `
§2.4 应力状态12
• 转轴公式——又称为应力分量转换公式。它表
明：当坐标作转轴变换时，应力分量遵循二阶 张量的变换规律。
• 因此从数学上证明了一点的应力状态是一个二 阶张量，在坐标转换时具有不变性。即物体内 一点的客观受力状态不会因人为地选择参考坐 标而改变。 • 通俗地讲，坐标改变后各应力分量都改变了， 但九个分量作为一个“整体”，所描述的一点 的应力状态是不会改变的。 • 由于 i ` j ` j `i ` • 因此应力张量是对称张量。
§2.4 应力状态4
§2.4 应力状态5
张量表达式：
pi ij n j
•公式表明：已知应力张量，可以确定任意方位
微分面的应力矢量。
•当然可以确定正应力 n与切应力 n。
这就是著名的哥西公式，又称为斜面应力公式。它说明； 过一点三个互相垂直微分面上的九个应力分量完全确定了该点 的应力状态。这样，我们就可以把要了解各点应力状态的问题，
§2.4 应力状态8
§2.4 应力状态9
§2.4 应力状态10
x l1 p x m1 p y n1 pz l1 x l1 yx m1 zx n1
m1 xy l1 y m1 zy n1 n1 xz l1 yz m1 z n1 x l12 y m12 z n12 2 xy l1m1 2 yz m1n1 2 zx n1l1
简化为去求各点的九个应力分量的问题。
§2.4 应力状态6
应力矢量不仅随位置改 变而变化，而且随截面 方位改变而变化。 同一点由于截面的法线 方向不同，截面上的应 力矢量也不同。
讨论应力分量在坐标
变换时的变化规律。
§2.4 应力状态7
• 坐标变换的应力分量和应力张量 • 坐标平动时，n方向无变化，应力分量不变化。 • 转轴公式：
Fby 0
ij , i Fbj 0
§2.3 平衡方程5
考察主矩为零条件：
M
x
O ;
yz 1 1 yz y dy dxdz 2 dy yz dxdz 2 dy zy 1 1 zy dz dxdy dz zy dxdy dz 0 z 2 2
应力张量
x xy xz 11 12 13 ij yx y yz 21 22 23 z 31 32 33 zx zy
•应力分量是标量、箭头仅是说明方向
—弹性力学以坐标系定义应力分量；
材料力学以变形效应定义应力分量。
正应力二者定义没有差异
而切应力定义方向不同（顺时针为正）
§2.4 应力状态15
平面问题转轴公式：
x ` x cos 2 y sin 2 2 xy cos sin ) y ` x sin 2 y cos 2 2 xy (cos sin ) x `y ` ( x y ) cos sin 1 xy (cos 2 sin 2 )
pn随截面的法线方向n的方向改变而变化
§2.2 应力2
应力状态及应力矢量pn的分解
§2.2 应力3
应力矢量沿坐标分解
p n px i p y j pz k
正应力和切应力——应力矢量沿其作用面的法向和切向分解，称
为正应力，称为剪应力。
p n n n nt
同一点各方位上的应力集合称为一点的应力状态。
• 应力矢量
F pn S
– 应力pn是矢量，随点的位置和截面的法线方向n的方向改变而变化。 这种性质称为应力状态。因此凡是应力均必须说明是物体内哪一点， 并且通过该点哪一个微分面的应力。
23
§2.2 应力1
内力——外界因素作用下，物体内部各个部 分之间的相互作用力。
附加内力
应力 应力矢量
F pn lim S 0 S
§2.3 平衡方程2
主矢为零：
微分平行六面体单元
F 静力平衡条件:
x
O , Fy O , Fz O
主矩为零：
M
x
O,M y O,Mz O
§2.3 平衡方程3
F
x
O ;
yx x dx dydz x dydz yx dy dxdz yx dxdz x x y zx dz dxdy zx dxdy Fbx dxdydz 0 zx z
xy l1m2 l2m1 yz m1n2 m2n1 zx l1n2 l2n1
xz l3 px m3 p y n3 pz l3 x l1 yx m1 zx n1
m3 xy l1 y m1 zy n1 n3 xz l1 yz m1 z n1 x l1l3 y m1 m3 z n1 n3
§2.4 应力状态1
•应力状态对于结构强度是十分重要的。
•为了探讨各个截面应力的变化趋势，确定可以 描述应力状态的应力参数。 如果应力张量能够描述一点的应力状态，则 1. 应力张量可以描述其它应力参数