河海大学大二上大学物理答案 磁学作业
河海大学电磁学作业答案-电磁场
M=0
m B dS
d a
d
μ 0 Ib μ0I d a dx ln 2π x 2π d
μ 0b d a M ln I 2π d
m
b
d
3、
m1
N0 r nIS
m 2 0
a
x dx x
m1 m 2 Nn0 r IS q R R
l
方向从a到b
ε i ε ao ε ob ε ba ε ab ε
1 i 2 l 2 dB R 4 dt
2
电磁场
一、选择题 1.B 2. D 二、填空题
μ 0 rI 1、 B1 2π a 2
(三) 自感、互感和能量
μ 0μ r I , B2 2π r
, B3 0
w m1
磁通量不变
b
Q
B
ε i总=ε i PS ε i SQ ε i PQ 0
ε
iSQ
1 Bω a 2 方 向 Q S 2
2、
A
E B r o R0 C
r dB E 2 dt εi π r 2 dB I R R dt
B
RAB
A
RAc
C
ε BA
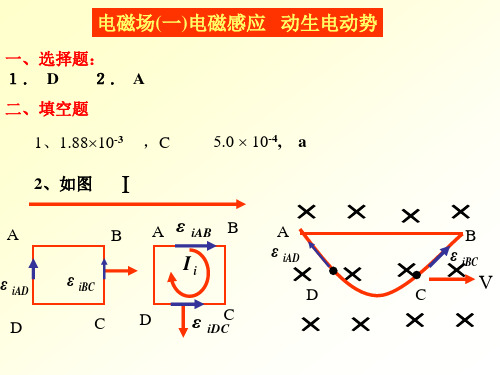
2、如图
A
I
B
A
ε iAB B
ε பைடு நூலகம்AD
D
ε iBC
C D
Ii
C ε iDC
ε iAD
A
D
C
ε iBC V
B
三、计算题
解1:从法拉弟电磁感应定律求解: 设t时刻AD边距直导线为x, 此时线圈中 的磁通量为: xa I 0 m B dS l dr x 2r S
河海大学电磁学作业答案

r
0
2 π x 2 Ahdx
2 π Ahr 3 3
由高斯定理可得
2 Ahr 3 2Erh 0 3 0 Ar 2 E r R 3ε 0
q
(b) 当r>R时,其电量为
q
ρ dV
R
0
由高斯定理可得
2 π AhR 3 2 π x 2 Ahdx 3 q 2 π AhR 3 2Erh 0 3ε 0
AR 3 E 3 ε 0r rR
2、求电势
(1)
r R
φ
l
r
Edr
R
r
A r 2 dr 3ε 0
l
R
A R 3 dr 3 ε 0r
A AR 3 l 3 3 (R r ) ln 9ε 0 3ε 0 R
(2)、
r R
φ
l
r
Edr
q
45 伏,
15伏。 .
A
B
C
A A B
1 1 45V 4 0 0.1 0.2 q q
1 1 C C B 15V 4 0 0.3 0.2
三、计算题
1. 解: (1) 以O为对称点作垂直于平板平面的圆柱面为高斯面, 设底面积为S,长度为2xP,如图所示。 高斯面内所包含的电量为:
由高斯定理:
2 rlE
πρ l r 2 R 2 4 ε 0 l 2 2 r R / 4 E 2 0 r
E
( 3)
r R
作以r为半径,高为l的同轴封闭圆柱面为高斯面,高斯面 上的电通量为
河海大学大二上大学物理答案--第8章-电磁感应

合上闸刀开关后,此灯缓慢变亮 自感 线圈
电阻
BATTERY
电池
拉开闸刀后此灯先亮后暗
BATTERY
电池
自感 线圈
拉开闸刀后此灯先亮后暗
BATTERY
电池
自感 线圈
拉开闸刀后此灯先亮后暗
BATTERY
电池
自感 线圈
拉开闸刀后此灯先亮后暗
BATTERY
电池
自感 线圈
B I ,又Ψ B
LI
L称为自感系数简称自感。 单位:“亨利”(H)
1H 1Wb A1
1H 103 mH 106 μH
自感系数 L 取决于回路线圈自身的性质(回路大 小、形状、周围介质等)
L
d dt
d(LI ) dt
(L
dI dt
I
dL ) dt
如果回路自身性质不随时间变化,则:
L
L
dI dt
结论 : 回路中的自感系数,在量值上等于电流随
i
d
dt
i 0
0
d 0
dt
i 0
Φ0
d 0
dt
i 0
Φ0
d 0
dt
i 0
由N 匝导线构成的线圈时:
i
d dt
(1
2
N )
d dt
(
N i 1
i
)
d
dt
N
全磁通: i i 1
磁通链数: N
i
N
d
dt
伏特 1V 1Wb s1
设闭合线圈回路的电阻为R
感应电流:
Ii
i
R
1 R
i
l2
2
r
《大学物理》磁学习题及答案
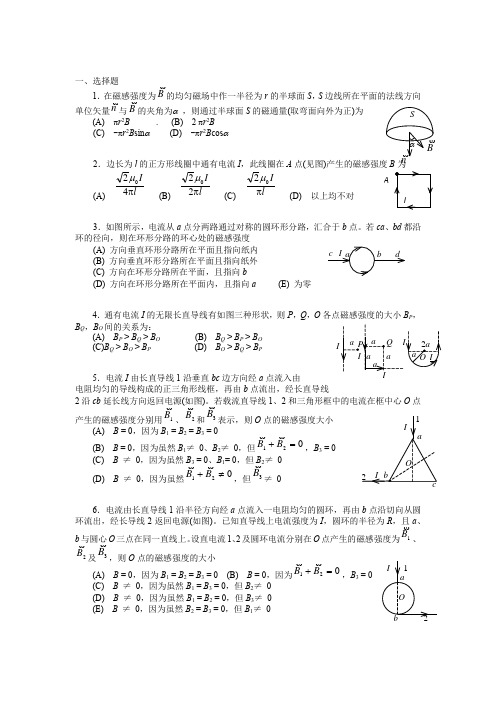
AI I一、选择题1.在磁感强度为的均匀磁场中作一半径为r 的半球面S ,S 边线所在平面的法线方向单位矢量与的夹角为α ,则通过半球面S 的磁通量(取弯面向外为正)为 (A) πr 2B . (B) 2 πr 2B (C) -πr 2B sin α (D) -πr 2B cos α 2.边长为l 的正方形线圈中通有电流I ,此线圈在A 点(见图)产生的磁感强度(A)(B) (C) (D) 以上均不对3.如图所示,电流从a 点分两路通过对称的圆环形分路,汇合于b 点。
若ca 、bd 都沿环的径向,则在环形分路的环心处的磁感强度(A) 方向垂直环形分路所在平面且指向纸内 (B) 方向垂直环形分路所在平面且指向纸外 (C) 方向在环形分路所在平面,且指向b(D) 方向在环形分路所在平面内,且指向a (E) 为零4.通有电流I 的无限长直导线有如图三种形状,则P ,Q ,O 各点磁感强度的大小B P ,B Q ,B O 间的关系为:(A) B P > B Q > B O (B) B Q > B P > B O(C)B Q > B O > B P (D) B O > B Q > B P5.电流I 由长直导线1沿垂直bc 边方向经a 点流入由电阻均匀的导线构成的正三角形线框,再由b 点流出,经长直导线2沿cb 延长线方向返回电源(如图)。
若载流直导线1、2和三角形框中的电流在框中心O 点产生的磁感强度分别用、和表示,则O 点的磁感强度大小(A) B = 0,因为B 1 = B 2 = B 3 = 0(B) B = 0,因为虽然B 1≠ 0、B 2≠ 0,但,B 3 = 0(C) B ≠ 0,因为虽然B 3 = 0、B 1= 0,但B 2≠ 0(D) B ≠ 0,因为虽然,但≠ 06.电流由长直导线1沿半径方向经a 点流入一电阻均匀的圆环,再由b 点沿切向从圆环流出,经长导线2返回电源(如图)。
大学物理习题答案磁场

大学物理练习题八一、选择题1.有两个点电荷电量都是+q ,相距为2 a 。
今以左边的点电荷所在处为球心,以a 为半径作一球形高斯面。
在球面上取两块相等的小面积S 1和S 2,其位置如图所示。
设通过S 1和S 2的电场强度通量分别为1Φ和2Φ,通过整个球面的电场强度通量为s Φ,则 [ D ](A)s ΦΦ>Φ,21=0/εq (B)021/2,εq s =ΦΦ<Φ(C)021/,εq s =ΦΦ=Φ (D)021/,εq s =ΦΦ<Φ解∶对整个球面,由高斯定理有0εqs =Φ对左、右两小面元处:0][412201=-=aqa q E πε, 0111==ΦS E ])2([412202a q a q E +=πε向左,S 2法向向左,0222>=ΦS E 由此可知,答案为D 。
2.图示为一具有球对称性分布的静电场的E-r 关系曲线。
请指出该静电场是由下列哪种带电体产生的? [ D ] (A) 半径为R 的均匀带电球面。
(B) 半径为R 的均匀带电球体。
(C) 半径为R 、电荷体密度Ar =ρ(A 为常数)的非均匀带电球体。
(D) 半径为R 、电荷体密度r A /=ρ (A 为常数)的非均匀带电球体。
解:(1)在球面内(r<R ):在半径为r 处取厚度为dr 的球壳,体积元dr r dV 24π=。
球壳内的电荷dr r rA dr r dq 2244ππρ=⋅= 球面内的电荷2202244r A dr r r A dr r q rr i πππρ===⎰∑⎰ 由高斯定理有200212114r A q r E i πεεπ==⋅∑,012εAE =(2)在球面外(r ≥R ):由高斯定理有0224επQr E =⋅,故0224επr QE =3. 在磁感应强度为B ϖ的均匀磁场中作一半径为r 的半球面S ,S 边线所在平面的法线方向单位矢量n ϖ与B ϖ的夹角为α,则通过半球面S 的磁通量为 [ D ](A)B r 2π (B) 2B r 2π (C) απsin 2B r - (D) Bcos απr 2-解:穿过半球面的磁通量与穿过底面的相等,且0<Φm 。
大学物理磁场部分习题

大学物理磁场部分习题磁学部分一、选择题1. 一载有电流I的细导线分别均匀密绕在半径为R和r的长直圆筒上形成两个螺线管(R=2r),两螺线管单位长度上的匝数相等。
两螺线管中的磁感应强度大小BR和Br应满足:(A)BR=2Br (B)BR=Br [ ] (C)2BR=Br (D)BR=4Br??2.磁场的高斯定理??B?dS?0说明了下面的哪些叙述是正确的?( A )a 穿入闭合曲面的磁感应线条数必然等于穿出的磁感应线条数;b 穿入闭合曲面的磁感应线条数不等于穿出的磁感应线条数;c 一根磁感应线可以终止在闭合曲面内;d 一根磁感应线可以完全处于闭合曲面内。
(A)ad;(B)ac;(C)cd;(D)ab。
3.下列说法正确的是( A )? (A)电荷在空间各点要激发电场,电流元Idl在空间各点也要激发磁场(B) 静止电荷在磁场中不受磁场力,运动电荷在磁场中必受磁场力 (C) 所有电场都是保守力场,所有磁场都是涡旋场(D) 在稳恒磁场中,若闭合曲线不围绕有任何电流,则该闭合曲线上各点的磁感应强度必为零4.洛仑兹力可以 ( B )(A)改变带电粒子的速率;(B)改变带电粒子的动量;(C)对带电粒子作功;(D)增加带电粒子的动能。
5. 取一闭合积分回路L,使三根载流导线穿过它所围成的面。
现改变三根导线之间的相互间隔,但不越出积分回路,则 [ ]?(A)回路L内的ΣI不变,L上各点的B不变。
?(B)回路L内的ΣI不变,L上各点的B改变。
?(C)回路L内的ΣI改变,L上各点的B不变。
?(D)回路L内的ΣI改变,L上各点的B改变。
6. 如图所示,在无限长载流直导线附近作一球形闭合曲面S,当曲面S向长直导线靠近时,穿过曲面S的磁通量?和面上各点的磁感应强度B将如何变化?( D )(A)?增大,B也增大; S I (B)?不变,B也不变;(C)?增大,B不变;(D)?不变,B增大。
7. 如图所示,螺线管内沿轴向放入一小磁针,当电键K闭合时,小磁针的N极的指向: [ ](A)向外转90°(B)向里转90° (C)图示位置不动(D)旋转180° (E)不能确定8.将形状完全相同的铜环和木环静止放置,并使通过两环面的磁通量随时间的变化率相等,则( D )(A)铜环中有感应电动势,木环中无感应电动势(B) 铜环中感应电动势大,木环中感应电动势小 (C) 铜环中感应电动势小,木环中感应电动势大 (D) 两环中感应电动势相等 10. 有一无限长通电流的扁平铜片,宽度为a,厚度不计,电流 I在铜片上均匀分布,在铜片外与铜片共面,离铜片右边缘?为b处的P点(如图)的磁感应强度B的大小为:[ ] (A)2??a?b??0I (B)?0Ia?bln 2?ab (C)?0I?0Ia?bln (D) 12?ba2?(a?b)211. 磁场由沿空心长圆筒形导体的电流产生,圆筒半径为R, x坐标轴垂直圆筒轴线,原点在中心轴线上,图(A)~(E) 哪一条曲线表示B-X的关系 ???d12.在感应电场中电磁感应定律可写成?EK?dl??dt?,式中EK为感应电场的电场强度。
大学物理电磁学考试试题及答案

大学物理电磁学考试试题及答案(总7页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除大学电磁学习题1一.选择题(每题3分)1.如图所示,半径为R 的均匀带电球面,总电荷为Q ,设无穷远处的电势为零,则球内距离球心为r 的P 点处的电场强度的大小和电势为: (A) E =0,RQ U 04επ=. (B) E =0,rQU 04επ=.(C) 204r QE επ=,r Q U 04επ= .(D) 204r Q E επ=,RQU 04επ=. [ ]2.一个静止的氢离子(H +)在电场中被加速而获得的速率为一静止的氧离子(O +2)在同一电场中且通过相同的路径被加速所获速率的: (A) 2倍. (B) 22倍.(C) 4倍. (D) 42倍. [ ]3.在磁感强度为B的均匀磁场中作一半径为r 的半球面S ,S 边线所在平面的法线方向单位矢量n 与B 的夹角为 ,则通过半球面S 的磁通量(取弯面向外为正)为 (A) r 2B . . (B) 2r 2B .(C) -r 2B sin . (D) -r 2B cos . [ ]4.一个通有电流I 的导体,厚度为D ,横截面积为S ,放置在磁感强度为B 的匀强磁场中,磁场方向垂直于导体的侧表面,如图所示.现测得导体上下两面电势差为V ,则此导体的霍尔系数等于(A) IB VDS . (B) DS IBV .(C) IBD VS . (D) BD IVS . (E) IBVD . [ ]O R rP Qn Bα SDI S V B5.两根无限长载流直导线相互正交放置,如图所示.I 1沿y 轴的正方向,I 2沿z 轴负方向.若载流I 1的导线不能动,载流I 2的导线可以自由运动,则载流I 2的导线开始运动的趋势是 (A) 绕x 轴转动. (B) 沿x 方向平动. (C) 绕y 轴转动. (D) 无法判断. [ ]6.无限长直导线在P 处弯成半径为R 的圆,当通以电流I 时,则在圆心O 点的磁感强度大小等于(A) R I π20μ. (B) RI 40μ.(C) 0. (D) )11(20π-R I μ.(E) )11(40π+R I μ. [ ]7.如图所示的一细螺绕环,它由表面绝缘的导线在铁环上密绕而成,每厘米绕10匝.当导线中的电流I 为 A 时,测得铁环内的磁感应强度的大小B 为 T ,则可求得铁环的相对磁导率r 为(真空磁导率0 =4×10-7 T ·m ·A -1) (A) ×102 (B) ×102 (C) ×102 (D) [ ]8.一根长度为L 的铜棒,在均匀磁场 B中以匀角速度绕通过其一端的定轴旋转着,B 的方向垂直铜棒转动的平面,如图所示.设t =0时,铜棒与Ob 成角(b 为铜棒转动的平面上的一个固定点),则在任一时刻t 这根铜棒两端之间的感应电动势的大小为:(A) )cos(2θωω+t B L . (B) t B L ωωcos 212.(C) )cos(22θωω+t B L . (D) B L 2ω.(E)B L 221ω. [ ]9.面积为S 和2 S 的两圆线圈1、2如图放置,通有相同的电流I .线圈1的电流所产生的通过线圈2的磁通用21表示,线圈2的电流所产生的通过线圈1的磁通用12表示,则21和12的大小关系为: (A) 21 =212. (B) 21 >12.(C) 21 =12. (D) 21 =2112. [ ]y z xI 1 I 2O RI B ω LO θ b12S 2 SII10.如图,平板电容器(忽略边缘效应)充电时,沿环路L 1的磁场强度H 的环流与沿环路L 2的磁场强度H的环流两者,必有:(A) >'⎰⋅1d L l H ⎰⋅'2d L l H.(B) ='⎰⋅1d L l H ⎰⋅'2d L l H.(C) <'⎰⋅1d L l H⎰⋅'2d L l H.(D) 0d 1='⎰⋅L l H. [ ]二.填空题(每题3分)1.由一根绝缘细线围成的边长为l 的正方形线框,使它均匀带电,其电荷线密度为,则在正方形中心处的电场强度的大小E =_____________.2.描述静电场性质的两个基本物理量是___________ ___;它们的定义式是____________ ____和__________________________________________.3.一个半径为R 的薄金属球壳,带有电荷q ,壳内充满相对介电常量为r 的各向同性均匀电介质,壳外为真空.设无穷远处为电势零点,则球壳的电势U = ________________________________.4.一空气平行板电容器,电容为C ,两极板间距离为d .充电后,两极板间相互作用力为F .则两极板间的电势差为______________,极板上的电荷为______________.5.真空中均匀带电的球面和球体,如果两者的半径和总电荷都相等,则带电球面的电场能量W 1与带电球体的电场能量W 2相比,W 1________ W 2 (填<、=、>).6.若把氢原子的基态电子轨道看作是圆轨道,已知电子轨道半径r =×10-10 m ,绕核运动速度大小v =×108 m/s, 则氢原子基态电子在原子核处产生的磁感强度B 的大小为HL 1L 2____________.(e = ×10-19 C ,0 =4×10-7 T ·m/A)7.如图所示.电荷q (>0)均匀地分布在一个半径为R 的薄球壳外表面上,若球壳以恒角速度0绕z 轴转动,则沿着z 轴从-∞到+∞磁感强度的线积分等于____________________.8.带电粒子穿过过饱和蒸汽时,在它走过的路径上,过饱和蒸汽便凝结成小液滴,从而显示出粒子的运动轨迹.这就是云室的原理.今在云室中有磁感强度大小为B = 1 T 的均匀磁场,观测到一个质子的径迹是半径r = 20 cm 的圆弧.已知质子的电荷为q = ×10-19 C ,静止质量m = ×10-27 kg ,则该质子的动能为_____________.9.真空中两只长直螺线管1和2,长度相等,单层密绕匝数相同,直径之比d 1 / d 2 =1/4.当它们通以相同电流时,两螺线管贮存的磁能之比为W 1 / W 2=___________.10.平行板电容器的电容C 为 F ,两板上的电压变化率为d U /d t =×105 V ·s -1,则该平行板电容器中的位移电流为____________. 三.计算题(共计40分)1. (本题10分)一“无限长”圆柱面,其电荷面密度为:= 0cos ,式中为半径R 与x 轴所夹的角,试求圆柱轴线上一点的场强.2. (本题5分)厚度为d 的“无限大”均匀带电导体板两表面单位面积上电荷之和为 .试求图示离左板面距离为a 的一点与离右板面距离为b 的一点之间的电势差.zRO ωO R zy xφ 1σd a3. (本题10分)一电容器由两个很长的同轴薄圆筒组成,内、外圆筒半径分别为R 1 = 2 cm ,R 2 = 5 cm ,其间充满相对介电常量为r 的各向同性、均匀电介质.电容器接在电压U = 32 V 的电源上,(如图所示),试求距离轴线R = cm 处的A 点的电场强度和A 点与外筒间的电势差.4. (本题5分)一无限长载有电流I 的直导线在一处折成直角,P 点位于导线所在平面内,距一条折线的延长线和另一条导线的距离都为a ,如图.求P 点的磁感强度B.5. (本题10分)无限长直导线,通以常定电流I .有一与之共面的直角三角形线圈ABC .已知AC 边长为b ,且与长直导线平行,BC 边长为a .若线圈以垂直于导线方向的速度v向右平移,当B 点与长直导线的距离为d 时,求线圈ABC 内的感应电动势的大小和感应电动势的方向.基础物理学I 模拟试题参考答案一、选择题(每题3分,共30分)1.[A]2.[B]3.[D]4.[E]5.[A]6.[D]7.[B]8.[E]9.[C] 10.[C]二、填空题(每题3分,共30分)1.0 3分 2. 电场强度和电势 1分 3. q / (40R ) 3分0/q F E=, 1分lE q W U aa ⎰⋅==00d /(U 0=0) 1分AR 1R 2R εrUaaP IIv ABCab c d4. C Fd /2 2分5. < 3分6. T 3分 FdC 2 1分7. π200qωμ 3分参考解:由安培环路定理 ⎰⋅⎰⋅+∞∞-=l B l Bd d I 0μ=而 π=20ωq I , 故 ⎰⋅+∞∞-l B d =π200q ωμ8. ×10-13 J 3分参考解∶ r m B q 2v v = ==m qBrv ×107 m/s质子动能 ==221v m E K ×10-13 J9. 1∶16 3分参考解:02/21μB w =nI B 0μ=)4(222102220021d l I n V B W π==μμμ)4/(21222202d l I n W π=μ16:1::222121==d d W W10. 3 A 3分三、计算题(共40分)1. (本题10分)解:将柱面分成许多与轴线平行的细长条,每条可视为“无限长”均匀带电直线,其电荷线密度为= 0cos R d , 它在O 点产生的场强为:φφεσελd s co 22d 000π=π=R E 3分 它沿x 、y 轴上的二个分量为:d E x =-d E cos =φφεσd s co 2200π- 1分OxRyφd φd E x d E yd Ed E y =-d E sin =φφφεσd s co sin 20π 1分 积分: ⎰ππ-=2020d s co 2φφεσx E =002εσ 2分 0)d(sin sin 2200=π-=⎰πφφεσy E 2分 ∴ i i E E x02εσ-== 1分2. (本题5分)解:选坐标如图.由高斯定理,平板内、外的场强分布为: E = 0 (板内) )2/(0εσ±=x E (板外) 2分1、2两点间电势差 ⎰=-2121d x E U U xx x d b d d d a d 2d 22/2/02/)2/(0⎰⎰+-+-+-=εσεσ)(20a b -=εσ 3分3. (本题10分)解:设内外圆筒沿轴向单位长度上分别带有电荷+和, 根据高斯定理可求得两圆筒间任一点的电场强度为 rE r εελ02π= 2分则两圆筒的电势差为 1200ln 22d d 2121R R r r r E U r R R r R R εελεελπ=π==⎰⎰⋅解得 120ln 2R R Ur εελπ=3分 于是可求得A点的电场强度为 A E )/ln(12R R R U== 998 V/m 方向沿径向向外 2分A 点与外筒间的电势差: ⎰⎰=='22d )/ln(d 12R R R Rr rR R U r E U RR R R U212ln )/ln(== V 3分4. (本题5分)解:两折线在P 点产生的磁感强度分别为: 1σd abxO)221(401+π=a IB μ 方向为 1分)221(402-π=a I B μ 方向为⊙ 2分 )4/(2021a I B B B π=-=μ 方向为 各1分5. (本题10分)解:建立坐标系,长直导线为y 轴,BC 边为x 轴,原点在长直导线上,则斜边的方程为 a br a bx y /)/(-= 式中r 是t 时刻B 点与长直导线的距离.三角形中磁通量⎰⎰++-π=π=Φr a r r a r x axbra b I x x y I d )(2d 200μμ)ln (20r r a a br b I +-π=μ 6分 trr a a r r a a Ib t d d )(ln 2d d 0+-+π=Φ-=μE 3分 当r =d 时,v )(ln 20da a d d a a Ib +-+π=μE 方向:ACBA (即顺时针) 1分。
大学物理电磁学练习题及答案

大学物理电磁学练习题及答案题目一:1. 电场和电势a) 一个均匀带电圆环上各点的电势如何?答:电场和电势是描述电荷之间相互作用的物理量。
对于一个均匀带电圆环上的各点,其电势是相同的,因为圆环上的每个点与圆心的距离相等且圆环上的电荷密度是均匀分布的。
所以,圆环上任意一点的电势与其它点是等势的。
b) 电势能和电势的关系是什么?答:电势能是电荷在电场中由于位置而具有的能量,而电势则是描述电荷因所处位置而具有的势能单位的物理量。
电势能和电势之间的关系可以用公式:电势能 = 电荷 ×电势来表示。
题目二:2. 高斯定律a) 高斯定律适用于哪些情况?答:高斯定律适用于具有球对称性、圆柱对称性和平面对称性的问题,其中球对称性是最常见和最简单的情况。
b) 高斯定律的数学表达式是什么?答:高斯定律的数学表达式是∮E·dA = ε₀q/ε,其中∮E·dA表示电场E通过闭合曲面积分得到的通量,ε₀是真空介电常数,q表示闭合曲面内的电荷总量,ε表示物质的介电常数。
题目三:3. 电动力学a) 什么是电感?答:电感是指电流在变化时产生的电磁感应现象所引起的抗拒电流的能力。
电感的单位是亨利(H)。
b) 电感的大小与什么因素有关?答:电感的大小与线圈的匝数、线圈的形状以及线圈中的铁芯材料的性质有关。
线圈匝数越多,电感越大;线圈形状越复杂,电感越大;线圈中的铁芯材料磁导率越大,电感越大。
题目四:4. 交流电路a) 直流电和交流电有什么区别?答:直流电是指电流方向始终保持不变的电流,而交流电是指电流方向以一定频率周期性地变化的电流。
直流电是恒定电流,交流电是变化电流。
b) 交流电流的形式有哪些?答:交流电流的形式可以是正弦波、方波、锯齿波等。
其中,正弦波是最常见和最基本的交流电流形式,用于描述交流电路中电压和电流的变化规律。
以上是关于大学物理电磁学练习题及答案的一些内容。
希望这些问题和答案能够帮助你更好地理解和学习物理电磁学的知识。
河海大学大二上大学物理答案--第5章-静电场

dl a
P. L
dE = 2πdε 0a = 2σπεdl0a
dl y
由电荷分布的对称性:
Ey =0
d o
x
E = dEx= dE sin
= 2σπεdl0a sin
a
dE
= 2σπεad0a sin
dl = ad
=
σ
2πε0
π
sind 0
σ
= 2πε0
cos
π
0
=πσε0
§5-3 高斯定理及应用
电荷元dq在P点的场强:
dE
dq
4or 2
e
带电体在P点的场强:
dE
dq P
E
dE
dq
4 o r
2
der
V
4
dV
or
2
er
矢量积分,计算时首先将电荷元的电场强度矢量沿各坐 标轴进行分解,然后对电荷元沿各坐标轴方向的电场强 度分量分别求标量积分,最后求出合电场强度E.
三种带电形式:
线的夹角分别为1和2 。求P点的场强。(设电荷线密度
为)
已知: q 、a 、θ 1 、θ 2 。
x
dEy y dE
解题步骤:
1. 选电荷元 d q =λ dx
P dEx
2. 确定d E 的方向
3. 确定d E 的大小
dx
ra
1
2 x
dx x o
dE
4.
4or 2
建立坐标,将
dE
投影到坐标轴上
dEx dE cos dEy dE sin
解:
E
q
4o r l
22
E
q
大学物理电磁学综合练习题(含答案)

ev
1 R2
−
1 R1
,方向向下。
2.一长直导线通有电流 I1 = 20 A ,旁边放一直导线 AB ,通有电流 I 2 = 10 A 。两导线在
同一平面内,且相互垂直(如图),则导线 AB 受到的作用力为 9.21 10 −5 N 。
解: B
=
0 I1 2r
,d
f
=
I2
d
B
变化,在磁场中有
A
、
B
dt
×××
两点,其间可放直导线 AB 和弯曲的导线 AB ,则
(A) 电动势只在 AB 导线中产生; (B) AB 导线中的电动势小于 AB 导线中的电动势;
×× ×××
o•
×× A
×
× B×
× ××
5-3
(C)电动势在 AB 、 AB 中都产生,且两者大小相等;
(D)电动势只在 AB 导线中产生。
H
=
I 2r
,磁感应强度 B
=
I 2r
,磁场能量密度 wm
=
I 2 8 2r 2
。
解:由安培环路定理, 2rH = I , H = I 2r
B
=
H
=
I 2r
,
w
m
=
1 BH
2
=
I 2 8 2r 2
9.如图所示,半径为 R ,电荷线密度为 ( 0) 的均匀带电圆线圈,绕过圆心与动势 i
=
5 2
BR 2 ;
O 点电势高。
解:添 ob 后,整个线圈的感应电动势为零,所以
oacb
=
ob
=
ob(v
B) dl
大学物理(第四版)课后习题及答案 磁场
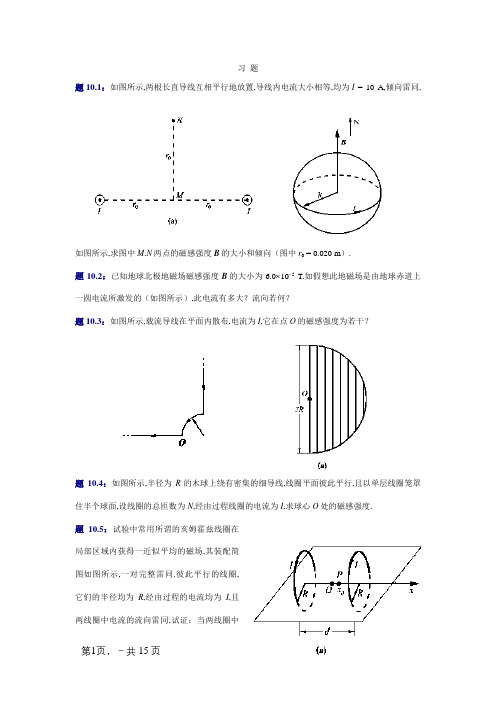
习题题10.1:如图所示,两根长直导线互相平行地放置,导线内电流大小相等,均为I= 10 A,倾向雷同,如图所示,求图中M.N两点的磁感强度B的大小和倾向(图中r0 = 0.020 m).题10.2:已知地球北极地磁场磁感强度B的大小为6.0⨯10-5T.如假想此地磁场是由地球赤道上一圆电流所激发的(如图所示),此电流有多大?流向若何?题10.3:如图所示,载流导线在平面内散布,电流为I,它在点O的磁感强度为若干?题10.4:如图所示,半径为R的木球上绕有密集的细导线,线圈平面彼此平行,且以单层线圈笼罩住半个球面,设线圈的总匝数为N,经由过程线圈的电流为I,求球心O处的磁感强度.题10.5:试验中常用所谓的亥姆霍兹线圈在局部区域内获得一近似平均的磁场,其装配简图如图所示,一对完整雷同.彼此平行的线圈,它们的半径均为R,经由过程的电流均为I,且两线圈中电流的流向雷同,试证:当两线圈中间之间的距离d 等于线圈的半径R 时,在两线圈中间连线的中点邻近区域,磁场可算作是平均磁场.(提醒:如以两线圈中间为坐标原点O ,两线圈中间连线为x 轴,则中点邻近的磁场可算作是平均磁场的前提为x B d d = 0;0d d 22=xB)题10.6:如图所示,载流长直导线的电流为I ,试求经由过程矩形面积的磁通量.题10.7:如图所示,在磁感强度为B 的平均磁场中,有一半径为R 的半球面,B 与半球面轴线的夹角为α,求经由过程该半球面的磁通量.题10.8:已知10 mm 2裸铜线许可经由过程50 A 电流而不会使导线过热.电流在导线横截面上平均散布.求:(1)导线内.外磁感强度的散布;(2)导线表面的磁感强度.题10.9:有一同轴电缆,其尺寸如图所示,两导体中的电流均为I ,但电流的流向相反,导体的磁性可不斟酌.试盘算以下遍地的磁感强度:(1)r <R 1;(2)R 1<r <R 2;(3)R 2<r <R 3;(4)r >R 3.画出B -r 图线.题10.10:如图所示.N 匝线圈平均密绕在截面为长方形的中空骨架上.求通入电流I 后,环表里磁场的散布.题10.11:设有两无穷大平行载流平面,它们的电流密度均为j ,电流流向相反,如图所示,求:(1)两载流平面之间的磁感强度;(2)两面之外空间的磁感强度.题10.12:测定离子质量的质谱仪如图所示,离子源S 产生质量为m ,电荷为q 的离子,离子的初速很小,可看作是静止的,经电势差U 加快后离子进入磁感强度为B 的平均磁场,并沿一半圆形轨道到达离进口处距离为x 的感光底片上,试证实该离子的质量为228x Uq B m =题10.13:已知地面上空某处地磁场的磁感强度B = 0.4×10-4 T,倾向向北.若宇宙射线中有一速度17s m 105.0-⋅⨯=v 的质子,垂直地经由过程该处.如图所示,求:(1)洛伦兹力的倾向;(2) 洛伦兹力的大小,并与该质子受到的万有引力比拟较.题10.14:在一个显像管的电子束中,电子有eV 101.24⨯的能量,这个显像管安放的地位使电子程度地由南向北活动.地球磁场的垂直分量5105.5-⊥⨯=B T,并且倾向向下,求:(1)电子束偏转倾向;(2)电子束在显像管内经由过程20 cm 到达屏面时光点的偏转间距.题10.15:如图所示,设有一质量为m e 的电子射入磁感强度为B 的平均磁场中,当它位于点M 时,具有与磁场倾向成α角的速度v ,它沿螺旋线活动一周密达点N ,试证M .N 两点间的距离为eBαv m MN cos π2e =题10.16:应用霍耳元件可以测量磁场的磁感强度,设一霍耳元件用金属材料制成,其厚度为0.15mm,载流子数密度为1.0×1024 m —3.将霍耳元件放入待测磁场中,测得霍耳电压为42V μ,电流为10 mA.求此时待测磁场的磁感强度.题10.17:试证实霍耳电场强度与稳恒电场强度之比ρne B E E //C H =这里ρ为材料电阻率,n 为载流子的数密度.题10.18:载流子浓度是半导体材料的主要参数,工艺上经由过程掌握三价或五价掺杂原子的浓度,来掌握p 型或n 型半导体的载流子浓度,应用霍耳效应可以测量载流子的浓度和类型,如图所示一块半导体材料样品,平均磁场垂直于样品表面,样品中经由过程的电流为I ,现测得霍耳电压为U H ,证实样品载流子浓度为n =HedU IB题10.19:一通有电流为I 的导线,弯成如图所示的外形,放在磁感强度为B 的平均磁场中,B 的倾向垂直纸面向里,求此导线受到的安培力为若干?题10.20:一向流变电站将电压为500 kV 的直流电,经由过程两条截面不计的平行输电线输向远方,已知两输电导线间单位长度的电容为111103.0--⋅⨯m F ,若导线间的静电力与安培力正好抵消,求:(1)经由过程输电线的电流;(2)输送的功率.题10.21:将一电流平均散布的无穷大载流平面放入磁感强度为B 0的平均磁场中,电流倾向与磁场垂直,放入后,平面两侧磁场的磁感强度分离为B 1和B 2(图),求该载流平面上单位面积所受的磁场力的大小和倾向.题10.22:在直径为1.0 cm 的铜棒上,切割下一个圆盘,假想这个圆盘的厚度只有一个原子线度那么大,如许在圆盘上约有 6.2⨯1014个铜原子,每个铜原子有27个电子,每个电子的自旋磁矩为224e m A 109.3⋅⨯=-μ,我们假设所有电子的自旋磁矩倾向都雷同,且平行于铜棒的轴线,求:(1)圆盘的磁矩;(2)如这磁矩是由圆盘上的电流产生的,那么圆盘边缘上须要有多大的电流.题10.23:通有电流I 1 = 50 A 的无穷长直导线,放在如图所示的弧形线圈的轴线上,线圈中的电流I 2 = 20 A,线圈高h = 7R /3.求感化在线圈上的力.题10.24:如图所示,在一通有电流I 的长直导线邻近,有一半径为R ,质量为m 的渺小线圈,渺小线圈可绕经由过程个中间与直导线平行的轴迁移转变,直导线与渺小线圈中间相距为d ,设d >>R ,经由过程小线圈的电流为I '.若开端时线圈是静止的,它的处死线矢量n e 的倾向与纸面法线ne '的倾向成0θ角.问线圈平面转至与屏幕面重叠时,其角速度的值为多大?题10.25:如图所示,电阻率为ρ的金属圆环,其表里半径分离为R 1和R 2,厚度为d .圆环放入磁感强度为α的平均磁场中,B 的倾向与圆环平面垂直,将圆环表里边缘分离接在如图所示的电动势为ε的电源南北极,圆环可绕经由过程环心垂直环面的轴迁移转变,求圆环所受的磁力矩.题10.26:如图所示,半径为R 的圆片平均带电,电荷面密度为σ,令该圆片以角速度ω绕经由过程个中间且垂直于圆平面的轴扭转.求轴线上距圆片中间为x 处的点P 的磁感强度和扭转圆片的磁矩.题10.27:如图所示是一种正在研讨中的电磁轨道炮的道理图.该装配可用于发射速度高达10km.s -1的炮弹,炮弹置于两条平行轨道之间与轨道相接触,轨道是半径为r 的圆柱形导体,轨道间距为d .炮弹沿轨道可以自由滑动.恒流电源ε.炮弹和轨道组成一闭合回路,回路中电流为I .(1)证实感化在炮弹上的磁场力为rrd I μF +=ln)π(2120 (2)假设I = 4 500 kA,d = 120 mm,r = 6.7 cm,炮弹从静止起经由一段旅程L = 4.0 m 加快后的速度为多大?(设炮弹质量m = 10.0 kg )习 题 解 答题10.1解:距离无穷长直载流导线为r 处的磁感强度RIμB B π2021== 磁感强度1B 和2B 的倾向可以依据右手定章剖断.依据磁场叠加道理B = B 1+B 2,斟酌到磁场的对称性,点M 的磁感强度00021M π2π2r Iμr I μB B B -=-= = 0 点N 的磁感强度T100122π24πcos )(40021N -⨯=⋅=+=. r I μB B B由右手定章可知N B 的倾向沿程度向左.题10.2解:设赤道电流为I ,则圆电流轴线上北顶点的磁感强度RI μR R IR μB /24)(20232220=+=是以赤道上的等效圆电流为A 107312490⨯==.μRBI 因为在地球内部,地磁场由南极指向北极,依据右手螺旋轨则可以断定赤道圆电流应当是由西向东流,与地球自转倾向一致.题10.3解:将载流导线看作圆电流和长直电流,由叠加道理可得RIμR I μB π22000-=0B 的倾向垂直屏幕向里.题10.4解:现将半球面朋分为很多薄圆盘片,则任一薄圆盘片均可等效为一个圆电流,任一薄圆盘片中的电流为I θR RNN I I ⋅⋅==d π2d d 该圆电流在球心O 处激发的磁场为I y x y μB /d )(2d 232220+=球心O 处总的磁感强度B 为θR RN y x I y μ/d π2)(2B 2/0232220⋅+⋅=⎰π 由图可知θR y R x sin cos ==;θ,将它们代入上式,得RNIμR NI μB π/4d sin π02200==⎰θθ 磁感强度B 的倾向由电流的流向依据右手定章肯定.题10.5证:取两线圈中间连线的中点为坐标原点O ,两线圈中间轴线为x 轴,在x 轴上任一点的磁感强度232220232220])2([2])2([2//x d/R IR μx d/R IR μB +++-+=则当 0}])2([)2(3)2()2(3{2d )(d 22220=+++--+-=x d/R x d/x d/R x d/IR μx x B0=++-++-+--=}])2([)2(4])2([)2(4{23d )(d 272222722222022//x d/R R x d/x d/R R x d/IR μx x B时,磁感强度在该点邻近小区域内是平均的,该小区域的磁场为平均磁场. 由0d )(d =xx B ,解得0=x 由0d )(d 022==x x x B ,解得R d =这表明在d = R 时,中点(x = 0)邻近区域的磁场可视为平均磁场.题10.6解:在矩形平面上取一矩形面元d S = I d x ,载流长直导线的磁场穿过该面元的磁通量为x l xIμΦd π2d d 0=⋅=S B 矩形平面的总磁通量⎰==ΦΦd ⎰=211200ln π2d π2d d d dl I μx l x I μ 题10.7解:由磁场的高斯定理⎰=⋅,0d S B 穿过半球面的磁感线全体穿过圆面S,是以有αcos π2B R Φ=⋅=S B题10.8解:(1)环绕轴线取齐心圆为环路L,取其绕向与电流成右手螺旋关系,依据安培环路定理,有⎰∑=⋅=⋅I r B 0π2d μl B在导线内∑==<2222ππR Ir r R I I R r ,,因而20π2R r I μB =在导线外∑=>,I I R r ,因而rIμB π20=(2)在导线表面磁感强度持续,由3101.78/π A,50-⨯===S R I m,得T 1065π2300-⨯==.RIμB 题10.9解:由安培环路定理⎰∑=⋅I 0d μl B ,得1R r < 2211πππ2r R Iμr B =⋅ 2101π2R IrμB =R 1<r <R 2 I r B 02π2μ=⋅B 2 =rμπ2I0 R 2<r <R 3 r B π23⋅=]π22232220I )R π(R )R (r I ---[μ B 3 =22232230 π2R R rR r I --⋅μ r >R 3 r B π24⋅=μo (I -I ) = 0B 4 = 0磁感强度B(r )的散布曲线如图.题10.10解:由安培环路定理,有r B π2⋅=μ0∑I R <R 1 r B π21⋅= 0 B 1 = 0R 2>r >R 1 r B π22⋅=μ0NI B 2 =rNIμπ20 r >R 2 r B π23⋅= 0 B 3 = 0在螺线管内磁感强度B 沿圆周,与电流成右手螺旋,若R 2-R 1<<R 1和R 2,则环内的磁场可以近似视作平均散布,设螺线环的平均半径R =21(R 1+R 2),则环内的磁感强度近似为 B RNIμπ20≈题10.11解:由安培环路定理,可求得单块无穷大载流平面在两侧的磁感强度大小为2/0j μ,倾向如图所示,依据磁场的叠加道理可得(1)取垂直于屏幕向里为x 轴正向,合磁场为B =i i i j μjμj μ00022=+ (2)两导体载流平面之外,合磁场的磁感强度B =02200=-i i jjμμ题10.12证:由离子源产生的离子在电势差为U 的电场中加快,依据动能定理,有qU mv =221(1) 离子以速度v 进入磁场后,在洛伦兹力的感化下作圆周活动,其动力学方程为qvB = m 2/2x v由上述两式可得228x Uq B m =题10.13解:(1)按照F L = q v ⨯B 可知洛伦兹力F L 倾向为B v ⨯的倾向,(2)因v ⊥B ,质子所受的洛伦兹力F L = qvB = 3.2⨯10-16 N在地球表面质子所受的万有引力G = m p g = 1.64⨯10-26 N因而,有F L /G = 1.95⨯1010,即质子所受的洛伦兹力弘远于重力题10.14解:(1)如图所示,由洛伦兹力F = q v ⨯B可以断定电子束将倾向东侧(2)在如图所示的坐标中,电子在洛伦兹力感化下,沿圆周活动,其轨道半径R 为R =m 6.712k ==eBmE eBmv由题知y = 20cm,并由图中的几何干系可得电子束倾向东侧的距离m 102.98322-⨯=--=∆y R R x即显示屏上的图像将整体向东平移近3 mm,这种平移并不会影响整幅图像的质量题10.15证:将入射电子的速度沿磁场倾向和垂直磁场倾向分化⊥v 和v //,在磁场倾向进步一螺距MN所需的时光T =αcos //v MNv MN =(1) 在垂直磁场倾向的平面内,电子作匀速圆周活动的周期T =eBv R em π2π2=⊥ (2) 由式(1)和式(2),可得eBv m MN αcos π2e =题10.16解:由霍耳效应中霍耳电压与电流.磁感强度的关系,有B =T 010H H H .nq IdU I R d U == 题10.17证:由欧姆定律的微分情势知,在导体内稳恒电场强度为v j ne E c ρρ==由霍耳效应,霍耳电场强度E H =B v ⨯-因载流子定向活动倾向与磁感强度正交,故E H = vB ,因而ρρρne Bnev vB j vB E E ===C H 题10.18证:通电半导体的载流子在洛伦兹力的感化下,逐渐积累在相距为b 的导体两侧,形成霍耳电压U H = vBb而流经导体横截面S (S = bd )的电流I = jbd = nevbd由此可解得载流子浓度n =HedU IB题10.19解:由对称性可知,半圆弧所受安培力F 1的水等分量互相抵消为零,故有F 1 =⎰⎰==πBIR BIR F 0y 12d sin d θθ两段直线部分所受安培力大小相等,但倾向相反,当导体外形不变时,该两力均衡,因而,全部导线所受安培力F = 2BIR j题10.20解:(1)单位长度导线所受的安培力和静电力分离为f B = BI =dI μπ22f E = E λ=dU C 022π2ε由f B +f E = 0可得dU C d I 02220π2π2εμ= 解得 I =A 105.4300⨯=μεCU(2)输出功率N = IU = 2.25⨯109 W题10.21解:无穷大载流平面两侧为平均磁场,磁感强度大小为j 021μ,则 B 1 = B 0j 2μ- (1)B 2 = B 0+j 2μ (2) 由式(1).(2)解得B 0 =)(2121B B +)(1120B B j -=μ外磁场B 0感化在单位面积载流平面上的安培力)(21d d d d d d 2122000B B μjB y x yB x j S F -=== 按照右手定章可知磁场力的倾向为程度指向左侧.题10.22解:(1)因为所有电子的磁矩倾向雷同,则圆盘的磁矩27e m A 10651--⋅⨯==.N μm(2)由磁矩的界说,可得圆盘边缘等效电流I = m /S = 2.0⨯10-3 A题10.23解:树立如图坐标,将闭合线圈分化为圆弧⋂bc 和⋂da ,直线ab 和cd 四段,由安培力B ⨯=l F d d I 可知圆弧线所受磁力为零,直线ab 和cd 上I 1激发的磁感强度大小均为B =RI μπ210,则直线ab 和cd 所受磁力大小均为F 0 =i IlB -,其合力F = 2F 0 = -2I 2lB i = -9.33⨯10-4i N.题10.24解:小线圈在随意率性地位受到的磁力矩 B m M ⨯=0则 M = θμsin π2π02dIR I '依据迁移转变惯量的界说,由图可求得小线圈绕OO ′轴迁移转变的迁移转变惯量J = ⎰⎰==πββ20222221d π2sin d mR m R m r 式中m 为圆环的质量,因为磁力矩倾向和角位移倾向相反,由动能定理有⎰-=⋅0θ20021d J ωθM ⎰='-0θ2202041d sin 2ωmR θθd I μR I 积分后即可解得1/200)cos (12⎥⎦⎤⎢⎣⎡-'=θmd I I μω题10.25解:若在金属环上取如图所示的微元,该微元沿径向的电阻d R =rdrπ2d ρ积分可得金属圆环的径向电阻R =⎰=2112ln π2π2d R R R R d ρrd r ρ径向电流I =)/R (R ρdR ε12ln π2ε=将圆环径向电流朋分为线电流θII d 2πd =,线电流元受到的磁力为,d d d rB I F =倾向沿圆周切向,该力对轴的磁力矩大小为r I rB F r M d d d d ==圆环面上电流元对轴的磁力矩倾向雷同,为垂直屏幕沿转轴向外,因而金属圆环所受的磁力矩⎰⎰=I r rB M d d=⎰⎰-=21)()/ln(πd d )/ln(212212π2012R R R R R R d B r r R R Bd ρεθρω磁力矩倾向垂直屏幕沿轴线向外题10.26解:扭转的带电圆盘可以等效为一组齐心圆电流,如图所示,在圆盘面上取宽度为d r 的细圆环,其等效圆电流Trr σI d π2d ⋅=此圆电流在轴线上点P 处激发的磁感强度的大小为3/22220)(d 2d x r I r μB +=积分,得 ⎥⎥⎦⎤⎢⎢⎣⎡-++=+=⎰x R x x R μx r r μB R222)(dr 22222 03/22230σωσω 圆片的磁矩m 的大小为⎰==R R σr r m 043π41d πωσωB 和m 的倾向均沿Ox 轴正向题10.27解:取对称轴线为x 轴,由题意,炮弹处的磁感强度可近似当作两根半无穷长的载流圆柱在该点激发的磁感强度之和y)d/r Iμy)d/r I μB -++++=2(π42(π400 炮弹所受磁场力的大小为⎰-=d/2d/2d y BI F = y y)d/(r y)d/(r I μd/d/d ]2121[π42220⎰--++++ = rrd I μ+lnπ220 炮弹出口时的速度132120s m 10821ln π2-⋅⨯=⎭⎬⎫⎩⎨⎧+==.r r d m I L μaL v。
大学物理——电磁学习题答案

静电场1直角三角形ABC 的A 点上,有电荷C 108.191-⨯=q ,B 点上有电荷C 108.492-⨯-=q ,试求C 点的电场强度(设m 03.0m,04.0==AC BC ). 解:1q 在C 点产生的场强 20114AC q E πε= 2q 在C 点产生的场强 22204q E BC πε=C 点的合场强43.2410V E m ==⨯ 方向如图2. 带电细线弯成半径为R 的半圆形,电荷线密度为φλλsin 0=,式中0λ为一常数,φ为半径R 与x 轴所成的夹角,如图所示.试求环心O 处的电场强度. 解:R d R dl dE 00204sin 4πεϕϕλπελ==ϕcos dE dE x = 考虑到对称性 0=x E ϕsin dE dE y =RR d dE E y 0000284sin sin λϕϕλϕπ===⎰⎰ 方向沿y 轴负向3.一半径为R 的半球面,均匀地带有电荷,电荷面密度为σ,求球心O 处的电场强度. 解:把球面分割成许多球带,球带所带电荷 dl r dq σπ2=2322023220)(42)(4r x dlrx r x xdqdE +=+=πεσππεθcos R x = θs i n R r = θRd dl =20001sin2224E d i πσσθθεε==⎰ 4如图所示,真空中一长为L 的均匀带电细直杆,总电荷为q ,试求在直杆延长线上距杆的一端距离为d 的P 点的电场强度.解:设杆的左端为坐标原点O ,x 轴沿直杆方向.带电直杆的电荷线密度为λ=q / L ,在x 处取一电荷元d q = λd x = q d x / L ,它在P 点的场强:()204d d x d L q E -+π=ε()204d x d L L xq -+π=ε 2分L Pd EO总场强为 ⎰+π=L x d L x L q E 020)(d 4-ε()d L d q+π=043分 方向沿x 轴,即杆的延长线方向.5一个细玻璃棒被弯成半径为R 的半圆形,沿其上半部分均匀分布有电荷+Q ,沿其下半部分均匀分布有电荷-Q ,如图所示.试求圆心O 处的电场强度.解:把所有电荷都当作正电荷处理. 在θ处取微小电荷d q = λd l = 2Q d θ / π它在O 处产生场强 θεεd 24d d 20220R QR q E π=π= 按θ角变化,将d E 分解成二个分量:θθεθd sin 2sin d d 202RQ E E x π==,θθεθd cos 2cos d d 202R Q E E y π-=-=对各分量分别积分,积分时考虑到一半是负电荷⎥⎦⎤⎢⎣⎡-π=⎰⎰πππθθθθε2/2/0202d sin d sin 2R QE x =0, 2022/2/0202d cos d cos 2R QR Q E y εθθθθεππππ-=⎥⎦⎤⎢⎣⎡-π-=⎰⎰ 所以j RQ j E i E E y x202επ-=+=6边长为b 的立方盒子的六个面,分别平行于xOy 、yOz 和xOz 平面.盒子的一角在坐标原点处.在此区域有一静电场,场强为j i E300200+= .试求穿过各面的电通量.解:由题意知E x =200 N/C , E y =300 N/C ,E z =0平行于xOy 平面的两个面的电场强度通量 01=±==⋅S E S E z eΦ 平行于yOz 平面的两个面的电场强度通量2002±=±==⋅S E S E x eΦ b 2N ·m 2/C“+”,“-”分别对应于右侧和左侧平面的电场强度通量平行于xOz 平面的两个面的电场强度通量 3003±=±==⋅S E S E y eΦ b 2 N ·m 2/C“+”,“-”分别对应于上和下平面的电场强度通量.xz7图中所示, A 、B 为真空中两个平行的“无限大”均匀带电平面,A 面上电荷面密度σA =-17.7×10-8 C ·m -2,B 面的电荷面密度σB =35.4 ×10-8 C ·m -2.试计算两平面之间和两平面外的电场强度.(真空介电常量ε0=8.85×10-12 C 2·N -1·m -2 )解:两带电平面各自产生的场强分别为:()02/εσA A E = 方向如图示()02/εσB B E = 方向如图示由叠加原理两面间电场强度为()()02/εσσB A B A E E E +=+= =3×104 N/C 方向沿x 轴负方向两面外左侧()()02/εσσA B A B E E E -=-=' =1×104 N/C 方向沿x 轴负方向两面外右侧 E ''= 1×104 N/C 方向沿x 轴正方向8 一球体内均匀分布着电荷体密度为ρ的正电荷,若保持电荷分布不变,在该球体中挖去半径为r 的一个小球体,球心为O ',两球心间距离d O O =',如图所示. 求:(1) 在球形空腔内,球心O '处的电场强度0E .(2) 在球体内P 点处的电场强度E .设O '、O 、P 三点在同一直径上,且d OP =.解:(1)利用补偿法,以O 为圆心,过O '点作一个半径为d 的高斯面。
大学物理课后习题答案 电磁感应 电磁场

第十三章 电磁感应 电磁场 1、[D]分析:应用楞次定律为分析的根据,若要产生乙线圈中的,则乙线圈中电流产生的电感应强度是由右向左,说明甲线圈中电流产生的由右向左的电感应强度在减小,即产生该磁场的电流在减小,由此可见,将抽出甲中铁心,nI B r 0μμ=,在I 不变时,B 减小。
2、[D]依据法拉第电磁感应规律,td d φε-=在上述条件下,ε应相同。
依据欧姆定律,RI ε=因为是不同的导体电阻率不同,所以R 不同,I 也不同。
3、[B]应用楞次定律分析,在I 增长时,垂直通过线圈平面内向外的磁通量是增大,因此感应电流产生的磁感强度垂直平面向里,为顺时针方向。
4、[C]分析:当a >>r 时,有以r 为半径的圆周内各点的B可视为常矢量。
断电前通过导体环的磁通量:2012r aIBS S B ππμφ==⋅=。
断电后通过导体环的磁通量:02=φ。
对纯电阻电路有:aRIr RRq 2)(120112μφφφ==--=5、[D]θαεcos d sin d )(d l vB l B v =⋅⨯=)(B v ⨯和l d 之间夹角2πθ=,∴0d =ε 0d ==⎰εε6、[D]在t ωθθ+=,θαεcos d sin d l vB =其中θ是)(B v⨯和l d 之间夹角r r l vB d cos d sin d ωθαε-== 2OP 21d BL r r B ωωε-=-=⎰O 处为高电势 221BL ωε=7、[D]两自感线圈顺接和反接的自感系数:M L L L 221++=顺21L L KM =10≤≤KM L L L 221-+=反图(1)为反接:1111ab 2L L K L L L -+=,由于1<K ,∴0ab >L 图(2)为反接:1111ab 2L L KL L L -+=,由于1=K ,∴0ab =L8、[C]V 0.8161225.0d d 11=-⨯-=∆∆-=-=tI LtI Lε9、[C]a Ia IaIB πμπμπμ000P 22=+=10、tS B td d d d )( ⋅-=-=φεt mIa nI a nI BS BS S B mωπμπμθcos cos 2020====⋅t mIa nI mωωπμεcos 20-=11、解:Wb 1057.1)1.0(1416.310562521--⨯=⨯⨯⨯===⋅=rB BS S B πφWb 1057.1612-⨯-=-=φφC 1014.3)(1612-⨯=--=φφRq12、(1)向右移动时,垂直纸面向内的φ减小。
大学物理课后习题答案14电磁场习题_图文_图文

习题总目录
结束 目录
)EyBy
+
(1
v2 c2
)EzBz
=ExBx+EyBy+EzBz = E .B
结束 目录
(2) E´2 c2B´2=
= E´x 2+E´y2+E´z 2 c2B´x2 c2B´y2 c2B´z2
= Ex2 c Bx2
+ g 2 Ey2+v2Bz2 2EyBz + Ez2+v2By2+2EzBy
c2( cv42Ey2 + Bz2
cosω
t
结束 目录
14-8 已知无限长载流导线在空间任一点 的磁感应强度为:m0I/2pr 。试证明满足方 程式
.B
=
Bx x
+
By y
+
Bz z
=0
结束 目录
证明: Bx = =
.B
=
Bx x
+
By y
+
Bz z
=0
m0I
2pr
sinq
m0Iy
2pr2
=
m0Iy
2p(x2+y2)
g
2pf
=
5.7×107
8.85×10-12×2p×3×1011
= 2.0×1016
结束 目录
14-5 有一平板电容器,极板是半径为R 的圆形板,现将两极板由中心处用长直引线 连接到一远处的交变电源上,使两极板上的 电荷量按规律q=q0sinω t变化。略去极板边 缘效应,试求两极板间任一点的磁场强度。
By
=
m0Ix
2p(x2+y2)
Bz =0
电磁学(第二版)___习题解答

电磁学(第二版)___习题解答本文档旨在概述《大学物理通用教程_电磁学(第二版)___题解答》的内容和目的。
章节结构本教程共包含以下章节:第一章:电磁学基础概念第二章:库仑定律和电场第三章:电场的高斯定理第四章:静电场的电势第五章:电场中的运动带电粒子第六章:稳恒电流第七章:磁场的基本特性第八章:安培定律和磁场的高斯定理第九章:磁场的矢量势与法拉第电磁感应定律第十章:电磁感应中的动生电动势第十一章:电磁感应中的感生电流第十二章:电磁场的能量与动量第十三章:交变电路理论第十四章:交变电磁场中的能流与坡印廷矢量第十五章:电磁波概论第十六章:辐射和天线每一章节都提供了对应题的解答,帮助读者更好地理解和应用所学的电磁学知识。
该题解答本是《大学物理通用教程_电磁学(第二版)___》的附属部分,旨在补充教材内容,提供题的详细解答,便于读者巩固所学知识。
本文档总结了《大学物理通用教程_电磁学(第二版)___题解答》中的题解答内容特点和方法。
本解答提供了《大学物理通用教程_电磁学(第二版)___题解答》中的题解答方式和思路的例子。
问题:如何计算两个点电荷间的电势差?答案:根据库仑定律可以计算出两个点电荷间的力,将该力乘以电荷间的距离即可得到电势差。
问题:如何确定一个圆环上的电场强度大小与方向?答案:根据环上各点的电荷之间的静电力作用,可以确定该点的电场强度大小和方向。
可以施用库仑定律以及数学公式来计算。
问题:如何计算一个球体内的电势分布?答案:根据球内各点的电荷密度以及球内各处的距离关系,利用电场的定义公式,可以计算出球体内各点的电势。
以上是一些《大学物理通用教程_电磁学(第二版)___题解答》的题目解答示例,希望对你的研究有所帮助。
本文档是《大学物理通用教程_电磁学(第二版)___题解答》的一部分,旨在为读者提供对电磁研究题的解答。
以下是总结本文档的重要性和帮助的几点观点:方便研究:本文档提供了电磁研究题的解答,可以帮助读者更好地理解和掌握这门学科。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2π a 2π 2a µ 0 I 3 µ 0 I1 导线Ⅱ处 B2 = − 2πa 2πa µ 0 I 2 µ 0 I1 + Ⅰ 导线Ⅱ 处 B 3 = 2π a 2π 2a F1 = I1B1l F2 = I2 B2l
F : F2 = I1B1l : I2 B2l = 7 : 8 1
2 7:8 µ0I2 µ0I3 + 导线Ⅰ处 B1 =
迭加 平行 r2 2π ×10 −7 T 2 ×10 −4 T 增大
B
IR 2 B = 4π ( R + x 2 ) 3 / 2 dB = 0 2 dR x = ± 2
0 2
µ
2x
R
I = I1 + I 2
I 1l1 = I 2 l2 ;
l1 : l 2 = 3 : 1
C
A I
E F
∴ I 2 : I1 = 3 : 1
µ
0
d I = j 0 d r dB = R2µ j µ 0 j0 R2 0 0 ∴B = ∫ d B = ∫ dr = ln = 2.9 ×10−5 T R1 2r 2 R1
方向:垂直纸面向里 方向 垂直纸面向里
dI µ 0 j0 d r = 2r 2r
dr
O.R1 r R2
1A (8A) 2A 磁(六)磁介质 二、1 2 .0T 64 3 . 1 × 10 − 2 2 .5 × 10 4 1 . 6 × 10 µ 0 nI nI µ nI 2 nI I r r 三、 r < R 1. B ⋅ d l = B 2π r = µ I ′
1. 解:
r 设沿 x轴电流在 P点产生 B P1 :
µ 0I π µ 0I 2 1 − = cos 0 − cos = 2 4π a 4 4π a
y
B P1
方向垂直纸面向外, 轴正方向。 方向垂直纸面向外,沿 z轴正方向。 r 设沿 y轴电流在 P点产生 B P2 :
f = evB = ev
µ 0I 2π a
方向:垂直导线轴线,沿矢径方向向外(背离导线向外) 方向:垂直导线轴线,沿矢径方向向外(背离导线向外)
=1.6×10 ×1.0×10 × 2π ×5.0×10−2 = 3.2×10 N
7
−19
∴ f = e v B = 3.2 × 10−16 N 方向:于行于导线中电流方向 方向: r r r (3) 垂直于导线与电子构成的平面,此时 与该处B 平行或反平行 V 垂直于导线与电子构成的平面, V
L1
利用安培环路定律求B的分布。(因为B有对称分布) 。(因为 2.解: 利用安培环路定律求B的分布。(因为B有对称分布) 分析得知: 分析得知: y
r B
⊗⊗ ⊗⊗ ⊗⊗
x
2 hB = µ
0
2xh j
∴ B =µ
r B
矢量表示
r B =−µ
0
0
r j0 x j
j0 x
x> , x<− :
d 2 d 2
C
A I
E F
方向: 方向 垂直纸面向外
r r r r B= B +B2 +B3 1
µ 0I ∴B = 4π R
I2 B
内电流(电流密度) 内电流(电流密度) 向里
D
I
2.解:矢经方向上电流均匀分布, 矢经方向上电流均匀分布, 矢经方向上单位长度 j 0 = n I = 10 3 × 0 . 01 = 10 A m
r µ 0I r µ 0I r 矢量表达式: i + j 矢量表达式: B 2 = 4π R 4π R
相交点到 P 点距离为 r。
r B
r µ 0I r µ 0I 2µ 0 I r j B= i + + 4π R 4π R 8R
磁场( 磁场(四 )安培环路定理 一、选择题 1.C .C 2.D 二、填空题 1.积分回路 回路所包围的面积的电流 回路上的磁 感应强度 回路内包围的 回路外 回路内
1 2 R M = pmB = 2 π I B π(0.1)2×10×0.5 R =2 =7.85×10-2 N.m
Φm1 = BS cos
I
B
图示位置线圈内磁通量: (2) 图示位置线圈内磁通量:
π
2 =0
转过60度后线圈内磁通量: 转过 度后线圈内磁通量: 度后线圈内磁通量
Φm2 = BS cos(
0, µ 0 I 0 ,
0
r > R 2 : 2π rB = µ 0(I 2 − I1)
B=−
B=−
µ 0 பைடு நூலகம் I 2 − I1 ) 2π r
B
r
r 的方向沿Y x>0 B 的方向沿Y轴负向 r 的方向沿Y x<0 B 的方向沿Y轴正向 r r d d − 2 < x< 2: ∫ B ⋅ dl = B ⋅ 2 h
2.
三、计算题: 计算题: 1.解: 利用安培环路定律求B的分布。(因为B的对称性) 利用安培环路定律求B的分布。(因为B的对称性) 。(因为 r r r < R1 : B=0 ∫ L 1 B ⋅ drl = 2π rB = ∑ I = 0 r µ 0 I1 R1 < r < R2 : ∫ B ⋅ d l = 2π rB = ∑ I = − I 1 L2 2π r
π
2
−
π
3
) = BS cos
π
6
在转动过程中磁力矩作功: 在转动过程中磁力矩作功
A = I (Φm2 − Φm1 ) = IBS cos
π
6
= 6.8 ×10−2 J
磁场( 磁场(三)毕萨定理 一、选择题 1. A 2. B
µ 0I
二、填空题
2 µ 0 I 解题思路: 园电流圆心处: B0 = 解题思路: 园电流圆心处: 1. 2R 2R ⊗ ⊗ ⊗ 解题思路: 各边在 点产生的磁感应强 解题思路: 各边在O点产生的磁感应强 2. 2 2 µ 0 I ⊗ 度相同,大小为: ⊗ 度相同,大小为: πa ⊗ ⊗ ⊗ 2 2µ 0 I µ 0I π 3π B = 4 B1 = B1 = cos − cos 4π a 2 4 4 πa
1B
2D 3C
− 14
磁(七)综合练习二
r r r 提示 ( F = qV × B = L)
二、1 8.0 × 10
r k
r r r r r 6 6 − 19 F = − 1 . 6 × 10 ⋅ (1 . 0 × 10 i + 0 . 5 × 10 j ) × ( 0 . 2 i − 0 . 4 j ) N
一、
1
6
∫
l
0
µ0 Ir B 得: = 2πR2
I ′ = j ∫ ds =
S
π r π R
2 2
R2
R1
I
R1 < r < R 2
µ0µr I B= 2πr
µ0 I B= 2πr
Ir H= 2πR2 B 2π r = µ 0 µ r I
dS
R2 < r
B 2π r = µ 0 I
I H= 2πr
µr
1 并联电路 I1 = I 可求得: 可求得: 4
3 BEA = 0 ; I2 = I 4 3 µ 0 I1 3µ 0 I 垂直 1 µ 0 I 2 3µ 0 I 垂直 = BACB = 4 2R 32R 纸面 BADB = 4 2 R = 32R 纸面 向外
向里
I2 B
D
I
BBF
µ0 I µ 0I π (cos − cosπ ) = = 4π R 2 4π R
3. B =
µ 0I
µ 0I , 方向是:垂直纸面向里 。 方向是: + 4 R 2π R
解题思路: 解题思路: 在O点产生的磁感应强度可以看作是两条半无限长直电 点产生的磁感应强度可以看作是两条半无限长直电 流与一个半圆形弧电流产生的磁感应强度的叠加,大小为: 流与一个半圆形弧电流产生的磁感应强度的叠加,大小为:
∴f =0
r (2) V
平行于导线电流, 平行于导线电流,则该处仍有
v r B⊥V
一、1 A
2 B
磁场( 磁场(二)安培力 磁力的功
二、1
提示 : ( M = Pm × B × sin 60 o = 4 .3 × 10 − 3 牛米 )
IBR
整圆受力为0 整圆受力为0,半圆受力如图 F=IB2R,F-2T=0,T=IBR , , 2 3.0×10−3 − 7.5×10−4 (W )
一、选择题 1.B .B 二、填空题 1.vBd
磁场 (一)洛仑兹力 一 洛仑兹力
2.B 上极板 2. n
2 .86 × 10 14
3. 1 : 1 : 2 1: 2 : 2 三、计算题 r :(1 V 平行于导线电流, 解:(1) 平行于导线电流,则该处
r r B ⊥V
4π ×10−7 ×50 −16
B P2 µ 0I π µ 0I = cos − cos π = 4π a 4 4π a 2 + 1 2
• P (a , a ) I I
O
x
方向垂直纸面向里, 方向垂直纸面向里,沿
z 轴负方向。 轴负方向。
r r r µ 0I µ 0I 2 2 1 − = B P = B P1 + B P2 , B P = + 1 − 4π a 4π a 2 2 方向垂直纸面向里, 轴负方向。 方向垂直纸面向里,沿 z轴负方向。
3
M磁力矩 = P ⋅ B ⋅ sin( m
π
