线性相位FIR滤波器hn
滤波器的线性相位和非线性相位设计

滤波器的线性相位和非线性相位设计滤波器在信号处理中扮演着重要的角色,它能够去除频域中不感兴趣的频率成分,同时保留我们所关注的信号频率。
然而,在滤波器设计中,存在线性相位和非线性相位两种设计选择。
本文将讨论滤波器的线性相位和非线性相位设计以及其相应的特点和应用。
一、线性相位设计线性相位滤波器是指滤波器的相位响应与信号频率成正比的情况。
具体而言,线性相位滤波器具有以下特点:1.1 来源与时域中因果系统线性相位滤波器的设计通常基于时域中因果系统,这意味着滤波器对信号的响应仅依赖于当前时刻以及之前的时刻。
这种设计能够保持信号的波形特性,不会引入额外的时间延迟。
1.2 相位响应与频率成正比线性相位滤波器的相位响应与信号频率成正比,从而在频域中引入了一个线性增加或减少的相位特性。
这种相位特性在某些应用中十分重要,例如音频信号处理中的均衡器。
1.3 启发性和直观性由于线性相位滤波器的相位响应与频率成正比,因此它具有较强的启发性和直观性。
在频域中,我们可以直观地分析滤波器对信号的相位响应,并进行相应的调整。
二、非线性相位设计非线性相位滤波器是指滤波器的相位响应与信号频率不成正比的情况。
具体而言,非线性相位滤波器具有以下特点:2.1 来源与时域中非因果系统非线性相位滤波器的设计通常基于时域中非因果系统,这意味着滤波器对信号的响应不仅取决于当前时刻以及之前的时刻,还可能涉及到之后的时刻。
这种设计在某些应用中能够引入更复杂的滤波效果。
2.2 非线性的相位变化非线性相位滤波器的相位响应与信号频率不成正比,因此在频域中引入了非线性的相位变化。
这种非线性相位特性在某些应用中能够提供更丰富的音效处理,例如混响效果。
2.3 指数函数的特殊相位特性非线性相位滤波器中,一种常见的设计是基于指数函数的相位特性。
这种设计能够产生一种特殊的相位延迟,通常用于音频合成和特殊效果处理中。
三、线性相位和非线性相位的应用线性相位滤波器和非线性相位滤波器在不同的应用中具有不同的优劣势。
线性相位FIR滤波器的特点

特点:对FIR系统而言,冲激响应就是系统函数旳系数
5.1 线性相位FIR滤波器旳特点
学习三个内容 ①什么是线性相位 ②满足什么样条件旳数字滤波器才是线性相位FIR ③怎样设计一种线性相位FIR,需满足哪些约束条件
线性相位条件
线性相位FIR DF 旳特征 幅度特征
零点特征
§ 5.1.1 FIR数字滤波器线性相位旳条件
e jn e j N 1n
h
N
1 e
j
N 1 2
n0
2
H (e j )
e
j
N 1 2
N 3 2
h
n0
n
j n N 1
(e 2
j n N 1
e 2 )
h
N 2
1
e
j
N 1 2
N 3
2 n0
2hn
cos
n
N 2
1
h
N 2
1
H e j =H ()e()
FIR滤波器在确保幅度特征满足技术要求旳同步,很 轻易做到有严格旳线性相位特征
设FIR滤波器单位冲激响应h(n)长度为N,其系统函数
H(z)为:
N 1
H (z) h(n)z n
n0
H(z)是z-1旳N-1次多项式,它在z平面上有N-1个零点,
原点z=0是N-1阶重极点。所以,H(z)永远稳定。
稳定和线性相位特征是FIR滤波器突出旳优点
, N 1 2
N 1/ 2
则 H a(n) cos n n0
因为 cos n关于 0, ,2 呈偶对称,所以 H 对
这些频率也呈偶对称
( N 1) 2
H1( ) a(n) cos(n )
线性相位FIR数字滤波器的设计

西南科技大学课程设计报告课程名称:数字通信课程设计设计名称:线性相位FIR数字滤波器的设计姓名:学号:班级:指导教师:起止日期:2011.6.21-2011.7.3西南科技大学信息工程学院制课 程 设 计 任 务 书学生班级: 学生姓名: 学号:设计名称: 线性相位FIR 数字滤波器的设计 起止日期: 2011.6.21-2011.7.3 指导教师:设计要求:1、用窗函数法设计一个线性相位FIR 高通数字滤波器。
要求:FIR 高通数字滤波器指标为:)阻带衰减()通带衰减(度)数字阻带截止频率(弧度)数字通带截止频率(弧dB dBs A dB dB p R s p 4013.05.0====πωπω根据技术指标选择合适的窗形状,并绘制FIR 高通数字滤波器的幅度响应曲线和相位响应曲线;2、用窗函数法设计一个线性相位FIR 低通数字滤波器。
要求:FIR 低通数字滤波器指标为:)阻带衰减()通带衰减(度)数字阻带截止频率(弧度)数字通带截止频率(弧dB dBs A dB dB p R s p 5014.02.0====πωπω根据技术指标选择合适的窗形状,并绘制FIR 低通数字滤波器的幅度响应曲线和相位响应曲线;FIR 数字滤波器的设计可以使用matlab 工具箱中的函数课程设计学生日志时间设计内容2011.6.21-6.24 查阅资料,确定方案2011.6.25-6.26 设计总体方案2011.6.27-6.30 编写程序2011.7.1-7.3 撰写设计报告2011.7.4 答辩课程设计考勤表周星期一星期二星期三星期四星期五课程设计评语表指导教师评语:成绩:指导教师:年月日线性相位FIR 数字滤波器的设计一、 设计目的和意义 1.目的(1)掌握用窗函数法设计FIR 数字滤波器的原理与方法。
(2)熟悉线性相位FIR 数字滤波器的特性。
(3)了解各种窗函数对滤波特性的影响。
2.意义通过做这个设计,我们可以加深对线性相位FIR 数字滤波器原理以及设计方法的了解,有助于夯实进一步学习的基础。
长沙理工大学数字信号处理选择题库

A.若x(n)为实数偶对称函数,则X(k)为虚数奇对称函数 B.若x(n)为实数奇对称函数,则X(k)为虚数奇对称函数 C.若x(n)为虚数偶对称函数,则X(k)为虚数奇对称函数 D.若x(n)为虚数奇对称函数,则X(k)为虚数奇对称函数 7.若序列的长度为M,要能够由频域抽样信号X(k)恢复原序列,而不发 生时域混叠现象,则频域抽样点数N需满足的条件是( ) A.N≥M B.N≤M C.N≥M/2 D.N≤M/2 8.对x1(n)(0≤n≤N1-1)和x2(n)(0≤n≤N2-1)进行8点的圆周卷积,其中______ 的结果不等于线性卷积。( ) A.N1=3,N2=4 B.N1=5,N2=4 C.N1=4,N2=4 D.N1=5,N2=5 9.设两有限长序列的长度分别是M与N,欲用圆周卷积计算两者的线性 卷积,则圆周卷积的长度至少应取( ) A.M + N B.M + N –1 C.M + N +1 D.2 (M + N) 10.通常DFT计算频谱只限制在离散点上的频谱,这种现象称为 ( ) A.栅栏效应 B.吉布斯效应 C.泄漏效应 D.奈奎斯特效应 11.下列关于FFT的说法中错误的是( )。 A.FFT是一种新的变换 B.FFT是DFT的快速算法 C.FFT基本上可以分成时间抽取法和频率抽取法两类 D.基2 FFT要求序列的点数为2L(其中L为整数) 12.计算256点的按时间抽取基-2 FFT,在每一级有______个蝶形。( ) A.256 B.1024 C.128 D.64 13.基2 FFT算法的基本运算单元为( ) A.蝶形运算 B.卷积运算 C.相关运算 D.延时运算 14.直接计算N点DFT所需的复数乘法次数与( )成正比。 2 A.N B.N 3 C.N D.Nlog2N
线性相位fir低通滤波器

设计题目及要求设计一个线性相位FIR 低通滤波器,技术指标如下:通带截止频率fp=1500Hz ,阻带起始频率fst=2250H ,通带允许的最大衰减为Rp=0.25dB ,阻带应达到的最小衰减为As=50dB 。
滤波器的采样频率为fs=15000Hz 。
设计原理 (包括滤波器工作原理、涉及到的matlab 函数的说明) 滤波器,顾名思义,其作是对输入信号起到滤波的作用数字滤波器滤波器结构x[k]为输入,h[k]为单位脉冲序列MATLAB 信号处理中提供的窗函数 (1)矩形窗 W=boxcar(N) (2)汉宁窗 W=hanning(N) (3)Bartlerr 窗 W=Bartlett(N) (4)Backman 窗 W=Backman (N ) (5)三角窗 W=triang (N ) (6)Kaiser 窗∑∑==-+-=M k k N k k k n x b k n y a n y 01][][][∑∞-∞=-=k k n x k h n y ][][][W=kaiser(n,beta)其中,beta是kaiser窗参数,影响窗旁瓣幅值的衰减率Kaiser窗用于滤波器设计时,选择性大,使用方便Nf=512;Nwin=20;%窗函数数据长度figure(1)for ii=1:4switch iicase 1w=boxcar(Nwin);stext='矩形窗';case 2w=hanning(Nwin);stext='汉宁窗';case 3w=hamming(Nwin);stext='哈明窗';case 4w=bartlett(Nwin);stext='Bartlett窗';end[y,f]=freqz(w,1,Nf);%求解窗函数特性,窗函数相当于一个数字滤波器mag=abs(y);%求得窗函数幅频特性posplot=['2,2,',int2str(ii)];subplot(posplot);plot(f/pi,20*log10(mag/max(mag)));%绘制窗函数的幅频特性xlabel('归一化频率');ylabel('振幅/dB');title(stext);grid on;FIR滤波器设计的主要方法函数设计方法说明工具函数窗函数法理想滤波器加窗处理Fir1(单频带)fir2(多频带)kaiserord最优化设计平方误差最小化逼近理想幅频响应或Park-McClellan算法产生等波纹滤波器Firls,remez,remezord约束最在满足最大误差限制条件下使整Fircls firclsl小二乘逼近个频带平方误差最小化升余弦函数具有光滑,正弦过渡带的低通滤波器设计Fircos各种窗函数的特点窗函数主瓣宽第一旁瓣相对主瓣衰减dB 矩形窗4pi/N -13汉宁窗8pi/N -31哈明窗8pi/N -41Bartlett 8pi/N -25Backman 12pi/N -57三角窗8pi/N -25Kaiser窗可调整可调整Chebyshew窗可调整可调整主旁瓣频率宽度与窗函数长度N有关。
线性相位FIR滤波器的特点

是常数
H(e jω ) = ∑h(n)e jωn = ± H(e jω ) e jθ (ω) = ± H(e jω ) e jωτ
n=0
N 1
第一类线性相位: 第一类线性相位: θ (ω) = τω
n=0 N1
n=0 N N1
N1 n=0
n=0 N1
n=0
∑h( n) sin (τ n)ω = 0
n=0
N1
τω的充要条件: 第一类线性相位 θ (ω) = 的充要条件:
h(n) = h(N 1 n) 0 ≤ n ≤ N 1
N 1 n = (N – 1) /2 为h(n)的偶对称中心 τ = 的偶对称中心 2
1 i ( N 1)
H(zi ) = 0
2)h(n)为实数,则零点共轭成对 ) 为实数, 为实数
即 zi*, 1/ zi* 也是零点
线性相位滤波器的零点是互为倒数的共轭对 即共轭成对且镜像成对。 即共轭成对且镜像成对。
jθ 1) zi = re i ) i
ri ≠1 θi ≠ 0或 π
re i
jθi
N /2
1 ω = π 时 cos ω n = 0 2
则 H(π ) = 0 ∴z = 1是零点
H(ω)对ω = 0, 2π呈偶对称 H(ω)对ω = π呈奇对称
z = 1 为零点 故不能设计成高通、带阻滤波器 故不能设计成高通、
3)h(n)奇对称,N为奇数 ) 奇对称, 为奇数 奇对称 幅度函数: 幅度函数:
N n =1,..., 2
1 H(ω) = ∑d(n)sin ω n 2 n=1
线性相位FIR数字滤波器的基本特性

6
Institute of Artificial Intelligence and Robotics, XJTU 1986
FIR滤波器的基本特性
数字信号处理简明教程
7
Institute of Artificial Intelligence and Robotics, XJTU 1986
1、线性相位与广义线性相位
9
Institute of Artificial Intelligence and Robotics, XJTU 1986
(举例: 理想 延迟系统)
数字信号处理简明教程
10
Institute of Artificial Intelligence and Robotics, XJTU 1986
2、相位与h(n)的对称性
h(n)是以(N-1)/2偶对称实序列,即:h(n) = h(N1n)
数字信号处理简明教程
13
Institute of Artificial Intelligence and Robotics, XJTU 1986
(2)广义线性相位与奇对称
H e ( ) N 1
H e j h n e jn
的时延有密切关系
数字信号处理简明教程
8
Institute of Artificial Intelligence and Robotics, XJTU 1986
什么是线性相位
线性相位是指θ (ω )是ω的线性函数,产生的相移是一常数,
即:
线性相位
(举例: 理想延迟系统)
广义线性相位
数字信号处理简明教程
h(n)是以(N-1)/2奇对称实序列,即: -h(n) = h(N1n)
滤波器的线性相位和非线性相位设计方法

滤波器的线性相位和非线性相位设计方法滤波器是一种常用的信号处理器件,它可以通过选择特定频率范围内的信号,对信号进行滤波和处理。
滤波器的设计涉及到很多方面,其中一个重要的考虑因素是相位特性。
本文将介绍滤波器的线性相位和非线性相位设计方法。
一、线性相位设计方法线性相位滤波器是指滤波器的相位响应与频率成线性关系。
线性相位滤波器一般使用FIR (Finite Impulse Response) 滤波器来实现,其特点是具有稳定的相移特性,适用于实时信号处理应用。
线性相位滤波器的设计方法有两种常用的方式:窗函数法和最小相位反演法。
1.1 窗函数法窗函数法是一种常用的设计线性相位滤波器的方法。
该方法的基本思想是将滤波器的频率响应与理想滤波器的频率响应进行近似拟合。
常见的窗函数有矩形窗、汉宁窗、黑曼窗等。
在窗函数法中,首先确定滤波器所需的通带、阻带和过渡带的频率范围,然后选择合适的窗函数进行设计。
通过对窗函数进行傅立叶变换,可以得到滤波器的冲激响应。
最后,通过将冲激响应作为滤波器的系数,即可实现线性相位的滤波器设计。
1.2 最小相位反演法最小相位反演法是另一种常用的设计线性相位滤波器的方法。
该方法的基本原理是通过对滤波器的幅度响应进行傅立叶变换,并计算其对数幅度谱,然后将对数幅度谱反变换得到滤波器的冲激响应。
最小相位反演法的优点是可以设计出更短的线性相位滤波器,适用于信号处理时延较为严格的应用场景。
然而,该方法的计算复杂度较高,需要进行频域的计算和反变换,因此在实际应用中需要根据具体情况进行权衡和选择。
二、非线性相位设计方法非线性相位滤波器是指滤波器的相位响应与频率不成线性关系。
非线性相位滤波器常用于对信号的组成部分进行时间或相位延迟的处理。
非线性相位滤波器的设计方法有FIR型和IIR型两种。
2.1 FIR型非线性相位滤波器FIR型非线性相位滤波器是通过设计多通的滤波器来实现的。
其基本思想是在滤波器的频域响应上引入不同频率的群延迟,从而实现非线性相位特性。
四种情况线性相位FIR滤波器的幅度特性

DN0409: 四种情况线性相位FIR 滤波器的幅度特性:通信与系统处理专业:王修启(031120507)情况(1):)1()(n N h n h --=偶对称,N 为奇数为奇数åå-+=----=-+-+=1212123)()21()()(N N n nj N j N n nj j e n h e N h en h e H w w w w在上式右端对第一、三项进行变量代换得到在上式右端对第一、三项进行变量代换得到åå-=-+----=÷øöçèæ----++-+--=211)21(2121121)21()21()21()(N m N m j N j N m m N j j e N m h e N h em N h e H w w w w由于÷øöçèæ-+=úûùêëé÷øöçèæ----=÷øöçèæ--2121121N mh m N N h m N h ,所以可以合并上面第一项和第三项,从而得到下面上面第一项和第三项,从而得到下面{}úúúûùêêêëé-++--=å-=---)21()21()(211)21(N h e e n N h ee H Nn n j n j N j j w w w wïþïýüïîïíì-+--=å-=--211)21()21(cos )()21(2Nn N jN h n n h n N h ew w 令21,2,1,212)(,21)0(-=úûùêëé--=÷øöçèæ-=N n n N h n a N ha 则 úúúûùêêêëé=å-=--21021)cos()()(N n N j jn n a ee H w ww 其频率响应幅度特性为å-==21)cos()()(N n n n a H w w ,关于ω=0,π,2π偶对称。
截止频率可变的线性相位FIR滤波器设计

截止频率可变的线性相位FIR滤波器设计线性相位FIR滤波器是一种数字滤波器,能够在频域上实现线性相位特性。
在实际应用中,经常需要设计一种截止频率可变的线性相位FIR滤波器。
这种滤波器可以根据应用要求,实现对输入信号的不同频率成分进行滤波处理。
在开始设计之前,我们需要明确设计的目标和要求。
首先,我们要确定滤波器的截止频率范围,以及滤波器的通带和阻带要求。
其次,我们需要选择一种滤波器设计方法,例如频域设计方法或时域设计方法。
最后,我们需要确定滤波器的阶数,以及滤波器参数的数量和范围。
设计一种截止频率可变的线性相位FIR滤波器的一种常用方法是使用窗函数设计法。
具体步骤如下:1.确定滤波器的截止频率范围和通带/阻带要求。
根据应用需求设定截止频率范围,并确定通带/阻带的频率响应要求。
2.计算滤波器的阶数。
根据通带/阻带的频率响应要求,使用滤波器设计公式计算出滤波器的阶数。
3.选择滤波器的窗函数。
常用的窗函数包括矩形窗、汉宁窗、汉明窗、布莱克曼窗等。
根据设计要求选择合适的窗函数。
4.计算滤波器的频率响应。
根据窗函数的性质,计算出滤波器的频率响应。
5.选择滤波器的截止频率。
根据应用需求选择滤波器的截止频率。
6.通过滤波器设计公式计算出滤波器的权重系数。
7.对滤波器的权重系数进行归一化处理,保证其幅度范围在0到1之间。
8.实现滤波器的频率响应。
将归一化的权重系数作为滤波器的频率响应。
9.对滤波器频率响应进行离散化处理,得到滤波器的数字滤波器系数。
10.实现滤波器的时间域响应。
使用滤波器的数字滤波器系数,通过离散时间的卷积操作,实现滤波器的时间域响应。
以上是一种设计截止频率可变的线性相位FIR滤波器的一般步骤。
具体的设计方法和参数选择要根据具体的应用场景来确定。
在设计过程中,需要注意滤波器的性能要求和设计的复杂程度之间的平衡。
同时,还需要注意计算和处理的精度,以及实现滤波器的计算和存储的效率等因素。
通过截止频率可变的线性相位FIR滤波器的设计,我们可以实现对输入信号的不同频率成分进行滤波处理,从而满足不同应用场景的需求。
线性相位FIR低通滤波器

设计题目及要求设计一个线性相位FIR 低通滤波器,技术指标如下:通带截止频率fp=1500Hz ,阻带起始频率fst=2250H ,通带允许的最大衰减为Rp=0.25dB ,阻带应达到的最小衰减为As=50dB 。
滤波器的采样频率为fs=15000Hz 。
设计原理 (包括滤波器工作原理、涉及到的matlab 函数的说明) 滤波器,顾名思义,其作是对输入信号起到滤波的作用数字滤波器滤波器结构x[k]为输入,h[k]为单位脉冲序列MATLAB 信号处理中提供的窗函数 (1)矩形窗 W=boxcar(N) (2)汉宁窗 W=hanning(N) (3)Bartlerr 窗 W=Bartlett(N) (4)Backman 窗 W=Backman (N ) (5)三角窗 W=triang (N ) (6)Kaiser 窗∑∑==-+-=M k k N k k k n x b k n y a n y 01][][][∑∞-∞=-=k k n x k h n y ][][][W=kaiser(n,beta)其中,beta是kaiser窗参数,影响窗旁瓣幅值的衰减率Kaiser窗用于滤波器设计时,选择性大,使用方便Nf=512;Nwin=20;%窗函数数据长度figure(1)for ii=1:4switch iicase 1w=boxcar(Nwin);stext='矩形窗';case 2w=hanning(Nwin);stext='汉宁窗';case 3w=hamming(Nwin);stext='哈明窗';case 4w=bartlett(Nwin);stext='Bartlett窗';end[y,f]=freqz(w,1,Nf);%求解窗函数特性,窗函数相当于一个数字滤波器mag=abs(y);%求得窗函数幅频特性posplot=['2,2,',int2str(ii)];subplot(posplot);plot(f/pi,20*log10(mag/max(mag)));%绘制窗函数的幅频特性xlabel('归一化频率');ylabel('振幅/dB');title(stext);grid on;FIR滤波器设计的主要方法各种窗函数的特点主旁瓣频率宽度与窗函数长度N有关。
线性相位FIR滤波器频率响应的特点hn

N 2 1 N 1
2
h(n)
c
sin c (n N21)
c
(n
N 1) 2
0,
,
0 n N 1 otherwise
窗函数截断的影响
Hd (e j ) W (e j )
h(n) hd (n) w(n)
H
图例
对于第二类线性相位
()
(2)
h(n) h(N 1 n)
图例
线性相位FIR: 1、h(n)是实数 2、h(n)=±h(N-1-n)
三、线性相位FIR滤波器频率响应的特点
h(n)=±h(N-1-n)
N 1
N 1
H (z) h(n)zn [h(N 1 n)]zn
去逼近Hd(ejω) 逼近方法有三种:
窗函数设计法(时域逼近)
频率抽样设计法(频域逼近)
最优化设计法(等波纹逼近)
窗函数设计法就是使所要设计的滤波器的单位冲激响
应h(n)逼近理想滤波器的单位冲激响应hd(n)
一般来说,理想频率响应Hd(ejω)是分段恒定的,在边 界频率处有突变点,所以,得到的理想单位冲激响应 hd(n)往往是无限长非因果序列。
但FIR的h(n)是因果有限长的
怎样用一个有限长的h(n)去近似无限长的hd(n) ?
最简单的办法是直接截取一段hd(n)得到h(n)
截取可以想象为h(n)是通过一个“窗口”所看到的一段
hd(n),因此,h(n)可表达为hd(n)和一个“窗函数”的乘
积
h(n) w(n) hd (n)
在这里窗函数就是矩形函数RN(n),以后还会看到, 为了改善所设计滤波器的性能,窗函数还可以有其它 形式,相当于在矩形窗内对hd(n)作一定的加权处理。
线性相位FIR数字滤波器的特性

A(W)
4
A (W)的周期= 2 A(W 2π) A(W ) A(W ) A(W )
2
0
2
A(2π W ) A(W )
A (W)关于0和 点偶对称 可设计LPF、HPF、BPF、BSF
2、线性相位系统的频域特性
II型 (h[k]=h[Mk], M为奇数)
H (ejW ) A(W)e j0.5MW
L
L
A(W ) h[L] 2h[L k ]coskW a[k ]coskW
k 1
k 0
其中 L=M/2
2、线性相位系统的频域特性
I型 (h[k]=h[Mk], M为偶数) 频域特性证明
H (e jW
)
DTFT{h[k]}
M
h[k ]e jWk
k 0
利用对称性h[k]=h[Mk]
在zk=1和zk= 1无零点或者有偶数个零点。
(2) II 型FIR滤波器(H(z)为偶对称多项式,M为奇数)
在zk=1无零点或有偶数个零点,zk= 1有奇数个零点。
(3) III 型FIR滤波器(H(z)为奇对称多项式,M为偶数)
在zk=1和zk= 1有奇数个零点。
(4) IV 型FIR滤波器(H(z)为奇对称多项式,M为奇数)
(1) zk rk e jk 是不在单位圆上的复零点
Im(z)
Re(z)
H1 (z) 1 az 1 bz 2 az 3 z 4
——4阶偶对称多项式。
3、线性相位系统的零点分布
(2) zk rk e jk 是在单位圆上的复零点
Im(z)
Re(z)
H 2 (z) 1 az 1 z 2
线性相位FIR滤波器hn

N / 2
H g ( )
m 1
2h( N m) cos[(m 1 )]
2
2
N / 2
H g ( )
幅频函数特点:
n 1
b(n) cos[ (n 1 )]
2
(1)由于
b(n) 2h( N2奇对n称),,n 所 1以, 2H,(ω ),在N2ω)]=呈奇对称;
N 1
h
n
cosn
(讨论)
n 0
数字信号处理简明教程
10
Institute of Artificial Intelligence and Robotics, XJTU 1986
sin cos
N 1
h
n
sinn
n 0
N 1
h
n
cosn
Institute of Artificial Intelligence and Robotics, XJTU 1986
时域(两类)、频域(四种类型) 实现结构(递归、非递归)
数字信号处理简明教程
1
Institute of Artificial Intelligence and Robotics, XJTU 1986
相频特性与滤波器对输入信号产生
的时延有密切关系
数字信号处理简明教程
7
Institute of Artificial Intelligence and Robotics, XJTU 1986
什么是线性相位
线性相位是指θ (ω )是ω的线性函数,产生的相移是一常数,
线性相位FIR低通滤波器-推荐下载

滤波器 mag=abs(y);%求得窗函数幅频特性 posplot=['2,2,',int2str(ii)]; subplot(posplot); plot(f/pi,20*log10(mag/max(mag)));%绘制窗函数的幅频特性 xlabel('归一化频率'); ylabel('振幅/dB'); title(stext);grid on;
设计题目及要求
设计一个线性相位FIR低通滤波器,技术指标如下:通带截止频
率fp=1500Hz,阻带起始频率fst=2250H,通带允许的最大衰减
为Rp=0.25dB,阻带应达到的最小衰减为As=50dB。 滤波器的
采样频率为fs=15000Hz。
设计原理 (包括滤波器工作原理、涉及到的 matlab 函数的说明) 滤波器,顾名思义,其作是对输入信号起到滤波的作用
函数设 说明
计方法
窗函数 理想滤波器加窗处理
法
FIR 滤波器设计的主要方法
最优化 平方误差最小化逼近理想幅频响应 Firls,remez,rem
设计 或 Park-McClellan 算法产生等波纹 ezord
滤波器
约束最 在满足最大误差限制条件下使整个 Fircls firclsl
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术通关,1系电过,力管根保线据护敷生高设产中技工资术艺料0不高试仅中卷可资配以料置解试技决卷术吊要是顶求指层,机配对组置电在不气进规设行范备继高进电中行保资空护料载高试与中卷带资问负料题荷试2下卷2,高总而中体且资配可料置保试时障卷,各调需类控要管试在路验最习;大题对限到设度位备内。进来在行确管调保路整机敷使组设其高过在中程正资1常料中工试,况卷要下安加与全强过,看度并22工且22作尽22下可22都能22可地护以缩1关正小于常故管工障路作高高;中中对资资于料料继试试电卷卷保破连护坏接进范管行围口整,处核或理对者高定对中值某资,些料审异试核常卷与高弯校中扁对资度图料固纸试定,卷盒编工位写况置复进.杂行保设自护备动层与处防装理腐置,跨高尤接中其地资要线料避弯试免曲卷错半调误径试高标方中高案资等,料,编试要5写、卷求重电保技要气护术设设装交备备置底4高调、动。中试电作管资高气,线料中课并敷3试资件且、设卷料中拒管技试试调绝路术验卷试动敷中方技作设包案术,技含以来术线及避槽系免、统不管启必架动要等方高多案中项;资方对料式整试,套卷为启突解动然决过停高程机中中。语高因文中此电资,气料电课试力件卷高中电中管气资壁设料薄备试、进卷接行保口调护不试装严工置等作调问并试题且技,进术合行,理过要利关求用运电管行力线高保敷中护设资装技料置术试做。卷到线技准缆术确敷指灵设导活原。。则对对:于于在调差分试动线过保盒程护处中装,高置当中高不资中同料资电试料压卷试回技卷路术调交问试叉题技时,术,作是应为指采调发用试电金人机属员一隔,变板需压进要器行在组隔事在开前发处掌生理握内;图部同纸故一资障线料时槽、,内设需,备要强制进电造行回厂外路家部须出电同具源时高高切中中断资资习料料题试试电卷卷源试切,验除线报从缆告而敷与采设相用完关高毕技中,术资要资料进料试行,卷检并主查且要和了保检解护测现装处场置理设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
四种线性相位FIR滤波器特性总结
阶数 M
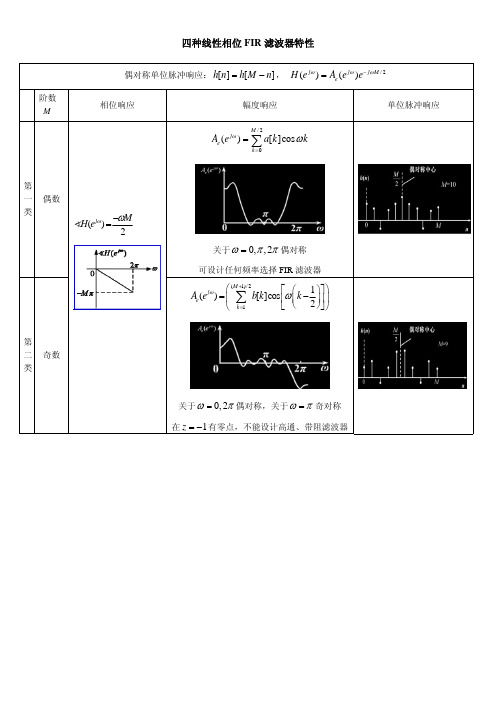
四种线性相位 FIR 滤波器特性
偶对称单位脉冲响应: h[n] = h[M − n] , H (e jω ) = Ae (e jω )e− jωM / 2
相位响应
幅度响应
单位脉冲响应
M /2
∑ Ae (e jω ) = a[k]cosωk k =0
第 一 偶数 类
)H(ejω) = −ωM 2
阶数 M
奇对称单位脉冲响应: h[n] = −h[M − n] , H (e jω ) = Ao (e jω )e− jωM / 2+ jπ / 2
相位响应
幅度响应
单位脉冲响应
M /2
∑ Ao (e jω ) = c[k]sin ωk k =1
第 三 偶数 类
)H(ejω) = −ωM +π 22
关于ω = 0,π , 2π 偶对称
可设计任何频率选择 FIR 滤波器
∑ Ae
(e
jω
)
=
⎛ ⎜ ⎝
(M +1) k =1
/
2
b[k]
cos
⎡⎢⎣ω
⎛ ⎜⎝
k
−
1 2
⎞⎤ ⎟⎠⎥⎦
⎞ ⎟ ⎠
第 二 奇数 类
关于ω = 0, 2π 偶对称,关于ω = π 奇对称 在 z = −1有零点,不能设计高通、带阻滤波器
关于ω = 0,π , 2π 奇对称
在 z = ±1 有零点,不能设计低通、高通、带
阻滤波器
∑ Ao
(e
jω
)
=
ቤተ መጻሕፍቲ ባይዱ
(
M +1) k =1
/
2
d
[k
]
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
的时延有密切关系
数字信号处理简明教程
7
Institute of Artificial Intelligence and Robotics, XJTU 1986
什么是线性相位
线性相位是指θ (ω )是ω的线性函数,产生的相移是一常数,
即:
线性相位
(举例: 理想延迟系统)
广义线性相位
数字信号处理简明教程
8
Institute of Artificial Intelligence and Robotics, XJTU 1986
(举例: 理想 延迟系统)
数字信号处理简明教程
9
Institute of Artificial Intelligence and Robotics, XJTU 1986
频特性与滤波器对输入信号产生的时延有密切关系。
数字信号处理简明教程
15
Institute of Artificial Intelligence and Robotics, XJTU 1986
定义:
相延迟:
- q (w ) w
群延迟:
d () d
群延迟偏离某个常数的程度表明滤波器相位特性的 非线性程度,线性相位和广义线性相位都满足群延 迟是一个常数,即
滤波器的系统函数与冲激响应
(
)
数字信号处理简明教程
4
Institute of Artificial Intelligence and Robotics, XJTU 1986
6.2.1 线性相位FIR数字滤波器的基本特性
h(n)是FIR滤波器的单位脉冲响应,长度为N,则其系统 函数为:
o 收敛域包括单位圆; o z平面上有N-1个零点; o z=0是N-1阶极点; (展开级数可以说明)
Institute of Artificial Intelligence and Robotics, XJTU 1986
时域(两类)、频域(四种类型) 实现结构(递归、非递归)
数字信号处理简明教程
1
Institute of Artificial Intelligence and Robotics, XJTU 1986
6.1.1 滤波器的基本 类型与指标
数字信号处理简明教程
2
Institute of Artificial Intelligence and Robotics, XJTU 1986
6.1.2 滤波器的基本方程与分类
数字信号处理简明教程
3
Institute of Artificial Intelligence and Robotics, XJTU 1986
1、线性相位与广义线性相位
对于长度为N 的h(n)系统函数为:
N 1
H (e j ) h(n)e jn
n0
H (ω)称为H幅(e频j 函) 数H,g (θ()ωe)称j (为) 相频函数
注意:
H (ω)为ω的实函数,可能取负值;
|H(ejω)|称为幅度响应,总是正值;
2、相位与h(n)的对称性
(1)线性相位与偶对称
H e ( ) N 1
H e j h n e jn
j
n 0
等式中间和等式右边的实部与虚部应当各自相等,
同样实部与虚部的比值应当相等:
sin cos
N 1
h
n
sinn
n 0
N --1
å H (z) = h(n)z-n
n=0
()
H (e jw ) = H (w)e jq(w)
幅频函数
相频函数
其中:
线性相位
或: q(w) =q0 -wt
广义线性相位
特点:FIR滤波器的单位冲冲激响应是有限长的,因此是稳定和容易实现线
性相位;线性相位是指θ (ω )是ω 的线性函数,产生的相移是一常数 ,相
h(n)是以(N-1)/2偶对称实序列,即:h(n) = h(N1n)
数字信号处理简明教程
12
Institute of Artificial Intelligence and Robotics, XJTU 1986
(2)广义线性相位与奇对称
H e ( ) N 1
H e j h n e jn
N 1
h
n
cosn
(讨论)
n 0
数字信号处理简明教程
10
Institute of Artificial Intelligence and Robotics, XJTU 1986
sin cos
N 1
h
n
sinn
n 0
N 1
h
n
cosn
n 0
将上式两边交叉相乘,再将等式右边各项移到左边,
应用三角函数的恒等关系
N 1
h
n
sin(
n )
0
n 0
严格线性相位的条件
N 1
2
(讨论)
h
n
h N
1 n
,0 n N 1
数字信号处理简明教程
11
Institute of Artificial Intelligence and Robotics, XJTU 1986
特点:FIR滤波器的单位冲冲激响应是有限长的, 因此是稳定和容易实现线性相位。
数字信号处理简明教程
5
Institute of Artificial Intelligence and Robotics, XJTU 1986
FIR滤波器的基本特性
数字信号处理简明教程
6
Institute of Artificial Intelligence and Robotics, XJTU 1986
h(n)是以(N-1)/2奇对称实序列,即: -h(n) = h(N1n)
数字信号处理简明教程
14
Institute of Artificial Intelligence and Robotics, XJTU 1986
线性相位FIR数字滤波器的基本特性 [**]
h(n)是FIR滤波器的单位脉冲响应,长度为N,则其系统函数为:
j(0 )
n 0
() 0
(讨论)
广义线性相位的条件
h
N
n h
2
2
N
1
1
n
数字信号处理简明教程
ห้องสมุดไป่ตู้
13
Institute of Artificial Intelligence and Robotics, XJTU 1986
