定积分及应用题库A

合集下载

定积分的应用题

六、定积分应用题
23x x 7x 1、求抛物线与直线所围成的平面图形的面积.（要求作图）（6分）
24y =−2y x =+2、求抛物线与直线所围成的平面图形的面积. （要求作图）（6分）
24y =−2y x =−+3、求抛物线与直线所围成的平面图形的面积. （要求作图）（6分）
24y x =+2y x =−+4、求抛物线与直线所围成的平面图形的面积. （要求作图）（6分）
24y x =+27y x =+5、求抛物线22y =与直线4y x =−+所围成的平面图形的面积. （要求作图）（6分）
6、求抛物线与直线22y =x 4y x =−所围成的平面图形的面积. （要求作图）（6分）
7、求抛物线212y x =
与直线4y x =+所围成的平面图形的面积. （要求作图）（6分） 8、求抛物线212
y x =
与直线4y x =−+所围成的平面图形的面积. （要求作图）（6分）
9、求抛物线24y x =与直线3y x =−+所围成的平面图形的面积. （要求作图）（6分）
10、求抛物线24y x =与直线所围成的平面图形的面积. （要求作图）（6分）
3y x =−。

不定积分+定积分及其应用习题附带答案

1．设是在上的一个原函数,且为奇函数,则是 ( )()F x ()f x (),-∞+∞()F x ()f x A ．偶函数 B ．奇函数C ．非奇非偶函数 D ．不能确定2．已知的一个原函数为,的一个原函数为,则的一个原函数()f x cos x ()g x 2x ()f g x ⎡⎤⎣⎦为 ( )A ．B ． 2x 2cos x C ． D ．2cos x cos x3．设为连续导函数,则下列命题正确的是 ( )()f x A ． ()()1222f x dx f x c '=+⎰B ．()()22f x dx f x c'=+⎰C ． ()()()222f x dx f x ''=⎰D ．()()2f x dx f x c'=+⎰4．设且()22cos sin f x x '= ,则=( )()00f =()f x A ． B ． 212x x -212x -C ． D ．1x -313x x-5．设是的一个原函数,则2xe-()f x ( )()02()limx f x x f x x∆→-∆-=∆A ． B ．22xe -28xe-C ． D ．22xe--24xe-6．设,则=( )()xf x e -=()ln f x dx x'⎰A ．B ． 1x-c +ln x c -+C ．D ． 1c x+ln x c +7．若是的一个原函数,则ln x x ()f x =()f x '8．设的一个原函数为()()tan 2f x k x =,则 2ln cos 23x k =9．若,则()2f x dx x c =+⎰=()231x f x dx -⎰10．()()2cos 2sin 2d θθθ=⎰11．若,则()()f x dx F x c =+⎰()xx ef e dx --=⎰12．若,则()ln cos f x x '=⎡⎤⎣⎦()f x =13．计算()23x xe dx +⎰14．计算()()sin ln cos ln x x dx x⎡⎤⎡⎤⎣⎦⎣⎦⎰15．计算ln(tan )sin cos x dxx x ⎰16．计算21arctan1x dx x +⎰17．计算11sin dx x+⎰18．计算19．计算20．计算21．计算22．计算23. 计算()221tan xex dx+⎰24．已知的一个原函数为,求()f x sin x x()3x f x dx '⎰1、解:可导奇函数的导函数必为偶函数.必为偶函数.选A()()f x F x '∴=2、解:(1),()()cos sin f x x x '==- ()()()22sin 2g x x x f g x x'==∴=-⎡⎤⎣⎦(2)()2cos 2cos (sin )xx x '=- 选B sin 2x =-∴3、解:()()12222f x dx f x d x''=⎰⎰()122f x c =+选A4、解：(1)()22cos 1cos f x x '=- ()1f x x'∴=- (2)()22x f x x c=-+且得()00f =0c =,选A ()22x f x x =-5、解：(1)原式=()()()022limx f x x f x x∆→-∆--⎡⎤⎣⎦-2∆()2f x '=-(2)()2xF x e-= ()()222x xf x e e --'∴==-(3) 原式= 选D222(2)4xx ee ----=6、解：(1)()()ln ln ln f x dx f x d xx''=⎰⎰()ln f x c=+(2)(),xf x e -= ()1lnln 1ln x xf x e ex-∴===(3)原式=选C 1c x+7、解：(1)()ln F x x x= ()()1ln f x F x x'∴==+(2) ()()11ln f x x x''=+=8、解：()2ln cos 23F x x =()()2sin 223cos 2xf x x -∴=-故 ()()4tan 21ln 3x F x x '=-=+43k =-9、解：原式=()()331113f x d x ---⎰()3113x c =--+10、解：原式=2222cos sin 4sin cos d θθθθθ-⎰221144sin cos d d θθθθ=-⎰⎰11cot tan 44t cθθ=--+或1csc 2c θ⎛⎫=-+ ⎪⎝⎭11、解：原式=()()xxx f edeF e c----=-+⎰12、解：()ln cos f x dx xdx'=⎡⎤⎣⎦⎰⎰()1ln sin f x x c =+()1sin sin c x xf x e c e -==⋅13、解:原式=()22323x xx x e e dx ⎡⎤++⋅⎢⎥⎣⎦⎰()2923xxxe dx dx e dx=++⎰⎰⎰219232ln 91ln 3x x xx e e c ⋅⋅=++++14、解:原式=()()sin ln cos ln ln x x d x⋅⎰()()sin ln sin ln x d x =⎰=()21sin ln 2x c +⎡⎤⎣⎦15、解:原式=()2ln tan tan cosx dxx x⎰()ln tan tan tan x d xx=⎰()()ln tan ln tan x d x =⎰ ()21ln tan 2x c =+⎡⎤⎣⎦16、解:原式=221arctan11x dx x x ⎛⎫+ ⎪⎝⎭⎰21arctan111x d x x ⎛⎫=- ⎪⎝⎭⎛⎫+ ⎪⎝⎭⎰11arctan arctand x x=-⎰211arctan 2cx ⎛⎫=-+ ⎪⎝⎭17、解:原式=21sin 1sin xdx x --⎰21sin cos cos x dx dx x x=-⎰⎰2cos tan cos d xx x =+⎰1tan cos x cx=-+18、解:2,1,2t x t dx tdt==-=原式=()2221211tdt dt tt t=++⎰⎰=2arctan t c+c+回代19、解:令2tan ,sec x t dx tdt==原式=32tan sec sec ttdtt⎰=2tan sec td t⎰()2sec 1sec t d t=-⎰31sec sec 3t t c =-+()()3122221113x x c +-++回代20、解:令2sin ,2cos x t dx tdt ==原式=2cos 2sin cos t dtt t ⎰1csc 2tdt =⎰()1ln csc cot 2t t c -+公式12c 回代21、解:(倒代换)令211,x dx dt t t-==原式==-11arcsin 333t c =-=-+13arcsin 3c x-+回代13arccos 3c x=+(注:(三角代换)令3sec ,x t =,3sec tan dx t tdt =原式=3sec tan 19sec tan 3t t dt t c t t =+⎰)13arccos 3c x+回代22、解:2,1,xt e t ==+ ()222ln 1,1tx tdx dtt=+=+原式=222211211t t t dt dtt t ⋅+-=++⎰⎰=()2arctan t t c-+2c-+回代23、解：原式=()221tan2tan xex x dx++⎰2tan 2tan x d x e xdx=+⎰⎰2x e 222tan tan 22tan x x x e x x e dx e xdx =-⋅⋅+⎰⎰22tan 2tan x x e x x e dx =-⋅⎰22tan x xe dx +⎰2tan x e x c=+24、解： ()sin x F x x= ()()2cos sin x x xf x F x x -'∴==原式()3x df x =⎰()()323x f x f x x dx=-⋅⎰2222cos sin cos sin 3x x x x x x x x dx x x --=⋅-⎰2cos sin 3sin 3sin x x x x xd x xdx=--+⎰⎰2cos sin 3sin 3sin 3sin x x x x x x xdx xdx =--++⎰⎰2cos 4sin 6cos x x x x x c=--+1．设初等函数在区间有定义，则在上一定（）()f x [],a b ()f x [],a b A ．可导 B ．可微C ．可积D ．不连续2．若连续，下列各式正确的是（）f A ．()()ba d f x dx f x dx =⎰B ．()()df x dx f x dx dx =⎰C ． ()()bx d f t dt f x dx =⎰D ．()()xad f t dt f x dx =⎰3. 下列关系式中正确的是（）A ．B ．21100x x e dx e dx =⎰⎰211x x e dx e dx≥⎰⎰C ．D ．以上都不对211x x e dx e dx ≤⎰⎰4．下列各式中，正确的是（）A ．B ．2101x e dx ≤≤⎰211x e dx e≤≤⎰C ． D ．以上都不对2120x e e dx e ≤≤⎰5．下列函数在区间上可用牛顿——莱布尼兹公式的是（）[]1,1-AB ．C1x 6．设在上，[],a b ()()()0,'0,''0f x f x f x ><>记，，，则有（）()110S f x dx =⎰()()2S f b b a =⋅-()()32b aS f b f a -=+⎡⎤⎣⎦A ． B ．123S S S <<213S S S <<C ． D ．312S S S<<231S S S <<7．xx →=8．设连续，且，则 ()f x ()()xe xF x f t dt -=⎰()'F x =9．设连续，则 ()'f x 1'2x f dx ⎛⎫= ⎪⎝⎭⎰10．设则()()120121f x f x dx x=-+⎰ ()1f x dx =⎰11．设连续，且则 ()f x ()21301,(1)x f t dt x x -=+>⎰()8f =12．设，则y 的极小值为()01xy t dt =-⎰13．方程，确定，求cos 0yx t e dt tdt +=⎰⎰()y y x =0x dydx=14．设在连续，且满足，求 ()f x []0,1()()13243f x x x f x dx =-⎰()f x 15．讨论方程在区间内实根的个数4013101xx dt t --=+⎰()0,116．设在连续，且在单调减少，讨论在区间()f x [],a b (),a b ()()1xa F x f t dt x a=-⎰的单调性(),a b 17．求()22220limx t xx t e dt te dt→⎰⎰18．设其中为连续函数，求()()2xa x F x f t dt x a=-⎰f ()lim x a F x →19．设，且可导，，求()()01122xf t dt f x =-⎰()f x ()0f x ≠()f x20．若为连续的奇函数，判别的奇偶性()f x ()0xf t dt ⎰21．1321sin x x x dx-⎡⎤⎣⎦⎰22．已知，求221x t e dt -⎰()1xf x dx⎰23．1⎰24．设连续，证明()f x 并由此计算()()20sin 2sin f x dx f x dx ππ=⎰⎰0π⎰1、解：初等函数在定义区间内必连续，连续必可积。

高考数学定积分应用选择题

高考数学定积分应用选择题1. 定积分在几何应用中，计算一个矩形的面积，面积为10平方单位，则该矩形的长和宽分别为（）A. 2, 5B. 10, 2C. 5, 2D. 2, 22. 定积分在物理应用中，一个物体从静止开始沿直线加速运动，已知初速度为2m/s，加速度为5m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程3. 定积分在物理应用中，已知物体沿直线运动的位移s与时间t 的关系为s=3t^2-2t+1，求物体在t=1秒时的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程4. 定积分在物理应用中，一个物体沿直线加速运动，已知初速度为5m/s，加速度为2m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程5. 定积分在物理应用中，一个物体沿直线加速运动，已知初速度为3m/s，加速度为4m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程6. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为5m/s，加速度为-2m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程7. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为3m/s，加速度为-4m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程8. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为2m/s，加速度为-5m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程9. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为1m/s，加速度为-3m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程10. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为2m/s，加速度为-4m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程11. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为3m/s，加速度为-5m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分D. 积分方程12. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为4m/s，加速度为-2m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程13. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为5m/s，加速度为-3m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程14. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为6m/s，加速度为-4m/s^2，求物体运动1秒后的速度，应使用（）B. 不定积分C. 微积分D. 积分方程15. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为7m/s，加速度为-5m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程16. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为8m/s，加速度为-2m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程17. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为9m/s，加速度为-3m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程18. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为10m/s，加速度为-4m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程19. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为11m/s，加速度为-5m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程20. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为12m/s，加速度为-2m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程21. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为13m/s，加速度为-3m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程22. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为14m/s，加速度为-4m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程23. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为15m/s，加速度为-5m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程24. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为16m/s，加速度为-2m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程25. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为17m/s，加速度为-3m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程26. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为18m/s，加速度为-4m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程27. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为19m/s，加速度为-5m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程28. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为20m/s，加速度为-2m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程29. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为21m/s，加速度为-3m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程30. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为22m/s，加速度为-4m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程31. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为23m/s，加速度为-5m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程32. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为24m/s，加速度为-2m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程33. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为25m/s，加速度为-3m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程34. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为26m/s，加速度为-4m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程35. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为27m/s，加速度为-5m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程36. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为28m/s，加速度为-2m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程37. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为29m/s，加速度为-3m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程38. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为30m/s，加速度为-4m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程39. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为31m/s，加速度为-5m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程40. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为32m/s，加速度为-2m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程41. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为33m/s，加速度为-3m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程42. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为34m/s，加速度为-4m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程43. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为35m/s，加速度为-5m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程44. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为36m/s，加速度为-2m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程45. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为37m/s，加速度为-3m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程46. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为38m/s，加速度为-4m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程47. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为39m/s，加速度为-5m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程48. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为40m/s，加速度为-2m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程49. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为41m/s，加速度为-3m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程50. 定积分在物理应用中，一个物体沿直线减速运动，已知初速度为42m/s，加速度为-4m/s^2，求物体运动1秒后的速度，应使用（）A. 定积分B. 不定积分C. 微积分D. 积分方程。

定积分应用练习题

定积分的应用练习题1. 抛物线22y x = 把圆228x y +=分为两部分，分别求出这两部分的面积。

2. 直线将椭圆2236x y y +=分成两部分，分别求出这两部分的面积。

3. 在抛物线21y x =-上找一点00(,)P x y ，其中00x ≠，过00(,)P x y 作抛物线的切线，使该切线与抛物线及两坐标轴所围成的图形的面积最小。

4. 从抛物线21y x =-上的点00(,)P x y 引另一条抛物线2y x =的切线，求该切线与2y x=所围成的图形的面积。

5. 求有抛物线24(0)y ax a =>与过焦点的弦所围成图形面积的最小值。

6. 求星形线33cos (02)sin x a t t y a tπ⎧=≤≤⎨=⎩所围成的图形的面积A ，全长L ，绕Ox 轴旋转一周所形成的旋转体的体积，和该旋转体的侧表面积。

7. 求伯努利双纽线22cos 2a ρθ=的面积A ，及绕Ox 轴旋转的旋转体的体积和侧表面积。

8. 求圆域222()()x y b ab a +-≤>绕Ox 轴旋转而成的圆环体的体积。

9. （1）求曲线32y x x =-与2y x =所围成的图形的面积；（2）若该图形绕Oy 绕一周，求所得旋转体的体积。

10. 求螺线(0)m ae θρθπ=≤≤与Ox 轴所围成的面积A ，弧长L ，绕Ox 轴旋转一周所形成的旋转体的体积，和该旋转体的侧表面积。

11. 在曲线2(04)3y x =≤≤上人一点的密度等于该点至原点一段曲线的弧线长度，求其质量。

12. 半径为R ，长为l 的圆柱体平放在深度为2R 的水池中（柱体的侧面与水面相切），设柱体的密度为(1)ρρ>，问将柱体移出水中需要做多少功？13. 设半径为R ，高为h 的圆柱体水池盛满了水，若将水池中的水吸干，要做多少功？14. 将半径为的半圆形板竖直放入水中，是其直径与水面相齐。

（1）求该板一侧所受的压力；（2）欲使压力增加一倍，该板应下移多少米？15. 一根半径为R 的圆环金属丝，其线密度为ρ，以等角速度ω绕其某一条直径旋转，求金属丝的动能。

(完整版)定积分应用题附答案

《定积分的应用》复习题一．填空：1．曲线ln ,ln ,ln (0)y x y a y b a b y ===<<及轴所围成的平面图形的面积为A =ln ln by ae dy ⎰=b-a______2.2y x y ==曲线和 ____13____二．计算题：1．求由抛物线 y 2 = 2x 与直线 2x + y – 2 = 0 所围成的图形的面积。

解：（1）确定积分变量为y ，解方程组2222y x y x ⎧=⎨=-+⎩ 得12121/22,12x x y y ==⎧⎧⎨⎨==-⎩⎩ 即抛物线与直线的交点为（21，1）和( 2 , - 2 ).故所求图形在直线y = 1和y = - 2 之间，即积分区间为［－2，1 ］。

（2）在区间［－2，1］上，任取一小区间为［ y , y + dy ］,对应的窄条面积近似于高为［(１－21y ）-21y 2 ］,底为dy 的矩形面积，从而得到面积元素 dA = [(１－21y)- 21y 2 ]dy (3)所求图形面积 A =⎰-12[（1- 21y ）-21y 2 ]dy = [y - 41y 2 – 61y 3]12-= 942．求抛物线 y = - x 2 + 4x - 3 及其在点（0，- 3）和（3，0）处的切线所围成的图形的面积。

解：由y = - x 2 + 4x – 3 得 '24,'(0)4,'(3)2y x y y =-+==-。

抛物线在点（0，- 3）处的切线方程为 y = 4x – 3 ;在点（3，0）处的切线方程为 y = - 2x + 6 ; 两切线的交点坐标为（ 32，3 ）。

故面积A =332223029[(43)(43)][(26)(43)]4x x x dx x x x dx --+-+-+-+-=⎰⎰3．求由摆线 x = a (t – sint) , y = a( 1- cost) 的一拱（02t π≤≤）与横轴所围成的图形的面积。

第6章定积分的应用习题集及答案

第六章习题定积分的应用一．选择题1．曲线x y ln =、a y ln =、b y ln =（b a <<0）和y 轴所围图形的面积为（ C ）（A ）⎰ba xdx ln ln ln ；（B ）⎰be a e xdx e ；（C ）⎰ba ydy e ln ln ；（D ）⎰ae b e xdx ln ．2．曲线x e y =下方与该曲线过原点的切线左方和y 轴右方所围图形的面积为（a ）（A ）⎰-10)(dx ex e x ；（B ）⎰-edy y y y 1)ln (ln ；（C ）⎰-e x x dx x e e 1)(；（D ）⎰-10)ln (ln dy y y y ．3．摆线)sin (t t a x -=、)cos 1(t a y -=（0>a ）的一拱（π20≤≤t ）与x 轴所围图形绕x 轴旋转一周所成旋转体的体积为（ D ）（A ）⎰-ππ2022)cos 1(dt t a ；（B ）⎰--at t a d t a ππ2022)]sin ([)cos 1(；（C ）⎰-a dt t a ππ2022)cos 1(；（D ）⎰--ππ2022)]sin ([)cos 1(t t a d t a ． 4．曲线θρcos 2a =(0>a )所围图形的面积为（ D ）（A ）⎰22)cos 2(21πθθd a ；（B ）⎰-ππθθd a 2)cos 2(21；（C ）⎰πθθ202)cos 2(21d a ；（D ）⎰202)cos 2(212πθθd a ．5．连续曲线)(x f y =与直线a x =、b x =（b a <≤0）及x 轴围成的图形绕y 轴旋转一周生成的旋转体体积为（ B ）（A ）⎰ba dx x xf )(2π；（B ）⎰ba dx x f x )(2π；（C ）⎰ba dx x xf )(22π；（D ）⎰ba dx x f x )(22π． 6．半径为R 的半球形水池已装满水．要将水全部吸出水池，需做功的为（ C ）（A ）⎰-Rdy y R 022)(π；（B ）⎰Rdy y 02π；（C ）⎰-Rdy y R y 022)(π；（D ）⎰Rdy y 03π．二．计算题1．求曲线221x y =与822=+y x 所围图形（上半平面部分）的面积．解：易知：曲线221x y =与822=+y x 的交点为(2,2)±。

数学选修2-2定积分的简单应用练习题含答案

数学选修2-2定积分的简单应用练习题含答案学校：__________ 班级：__________ 姓名：__________ 考号：__________1. 曲线y=sin x与x轴在区间[0, 2π]上所围成阴影部分的面积为（）A.−4B.−2C.2D.42. 由直线x=0，x=2，y=0和抛物线x=√1−y所围成的平面图形绕x轴旋转所得几何体的体积为（）A.46 15πB.43π C.1615π D.83π3. 由直线x=1，x=2，y=0与抛物线y=x2所围成的曲边梯形的面积为（）A.1 3B.53C.73D.1134. 由曲线y=x2+2与y=3x，x=0，x=1所围成的平面图形的面积为（）A.5 6B.1C.53D.25. 曲线y=x2和y2=x所围成的平面图形绕x轴旋转一周后，所形成的旋转体的体积为（）A.3π10B.π2C.π5D.7π106. 函数y=sin x，y=cos x在区间(π4，5π4)内围成图形的面积为（）A.√2B.2√2C.3√2D.4√27. 一物体在力F(x)=3+e2x(x的单位：m，F的单位：N)的作用下，沿着与力F相同的方向，从x=0处运动到x=1处，力F(x)所做的功为（）A.(3+e2)JB.(3+12e2)J C.(52+12e2)J D.(2+e2)J8. 由曲线y=√x，y=x−2及x轴所围成的封闭图形的面积是()A.4B.103C.163D.1549. 下列表示图中f(x)在区间[a, b]上的图象与x 轴围成的面积总和的式子中，正确的是（）A.∫f ba (x)dx B.|∫f ba (x)dx|C.∫f c 1a (x)dx +∫f c 2c 1(x)dx +∫f cc 2(x)dxD.∫f c 1a (x)dx −∫f c 2c 1(x)dx +∫f cc2(x)dx10. 直线y =x 与曲线y =√x 3围成的平面图形的面积是．（） A.14 B.2 C.1D.1211. 设函数f(x)=ax 2+c(a ≠0)，若∫f 10(x)dx =f(x 0)，0≤x 0≤1，则x 0的值为________．12. y =cos x 与直线x =0，x =π及x 轴围成平面区域面积为________．13. 由曲线y =|x|，y =−|x|，x =2，x =−2合成的封闭图形绕y 轴旋转一周所得的旋转体的体积为V ，则V =________．14. 两曲线x −y =0，y =x 2−2x 所围成的图形的面积是________．15. 由曲线y =x 2和直线x =0，x =1，以及y =0所围成的图形面积是________． 16.若在平面直角坐标系xOy 中将直线y =x 2与直线x =1及x 轴所围成的图形绕x 轴旋转一周得到一个圆锥，则该圆锥的体积V 圆锥=∫π10(x 2)2dx =π12x 3|10=π12据此类比：将曲线y =x 2与直线y =9所围成的图形绕y 轴旋转一周得到一个旋转体，则该旋转体的体积V =________．17. 在直角坐标平面内，由直线x=1，x=2，y=0和曲线y=1所围成的平面区域的x面积是________．18. 在xOy平面上，将抛物线弧y=1−x2(0≤x≤1)、x轴、y轴围成的封闭图形记为D，如图中曲边三角形OAB及内部．记D绕y轴旋转一周而成的几何体为Ω，过点(0, y)(0≤y≤1)作Ω的水平截面，所得截面面积为(1−y)π，试构造一个平放的直三棱柱，利用祖暅原理得出Ω的体积值为________．19. 函数f(x)=x3−x2+x+1在点(1, 2)处的切线与函数g(x)=x2−x围成的图形的面积等于________．2ax2−a2x)dx，则f(a)的最大值为________．20. 已知f(a)=∫(1x2在第一象限内的交点为P.21. 已知曲线C1：y2=2x与C2：y=12(1)求曲线C2在点P处的切线方程；(2)求两条曲线所围成图形的面积S.22. 求由曲线y=x2+2与y=3x，x=0，x=2所围成的平面图形的面积．23. 已知曲线C:y=x2(x≥0)，直线l为曲线C在点A(1, 1)处的切线．（1）求直线l的方程；（2）求直线l与曲线C以及x轴所围成的图形的面积．24. 如图一是火力发电厂烟囱示意图．它是双曲线绕其一条对称轴旋转一周形成的几何体，烟囱最细处的直径为10m，最下端的直径为12m，最细处离地面6m，烟囱高14m，试求该烟囱占有空间的大小．（精确到0.1m3）25.(1)已知复数z的共轭复数是z¯，且z⋅z¯−3iz=10，求z；1−3ix所围成的平面图形的面积．(2)求曲线y=√x与直线x+y=2，y=−1326.（1）已知(√x +2√x4)n 展开式的前三项系数成等差数列．求n ．（2）如图所示，在一个边长为1的正方形AOBC 内，曲线y =x 2和曲线y =√x 围成一个叶形图（阴影部分），向正方形AOBC 内随机投一点（该点落在正方形AOBC 内任何一点是等可能的），求所投的点落在叶形图内部的概率．27. 求由下列给出的边界所围成的区域的面积：（1）y ＝sin x(π4≤x ≤π)，x =π4，y ＝0；（2）y ＝x 2，y ＝2x 2，x ＝1；（3）y ＝x 2，y =√x ．28. 求由y =4−x 2与直线y =2x −4所围成图形的面积．29. 已知曲线y =sin x 和直线x =0，x =π，及y =0所围成图形的面积为S 0．（1）求S 0．（2）求所围成图形绕ox 轴旋转所成旋转体的体积．30. 已知函数y =f(x)的图形如图所示，给出y =f(x)与x =10和x 轴所围成图形的面积估计值；要想得到误差不超过1的面积估计值，可以怎么做？31. 已知曲线C:y =√x 和直线：x −2y =0由C 与围成封闭图形记为M ．（1）求M 的面积；（2）若M 绕x 轴旋转一周，求由M 围成的体积．32. 已知f(x)为一次函数，且f(x)=x ∫f 20(t)dt +1，（1）求函数f(x)的解析式；（2）若g(x)=x ⋅f(x)，求曲线y =g(x)与x 轴所围成的区域绕x 轴旋转一周所得到的旋转体的体积．33. 已知圆锥的高为ℎ，底半径为r ，用我们计算抛物线下曲边梯形面积的思路，推导圆锥体积的计算公式． [提示：（1）用若干张平行于圆锥底面的平面把它切成n 块厚度相等的薄片；（2）用一系列圆柱的体积近似地代替对应的薄片，圆柱的高为ℎn ，底半径顺次为：rn ，2r n，3r n…，(n−1)r n，r ；（3）问题归结为计算和式V(n)=ℎn ×(12+22+...+n 2)×πr 2n 2，当n 越来越大时所趋向的值．]．34. 求曲线y =√x(0≤x ≤4)上的一条切线，使此切线与直线x =0，x =4以及曲线y =√x 所围成的平面图形的面积最小．35. 过点(0, 1)作曲线L:y =ln x 的切线，切点为A ．又L 与x 轴交于B 点，区城D 由L 、x 轴与直线AB 围成，求区域D 的面积及D 绕x 轴旋转一周所得旋转体的体积．36. 求曲线y =2x −x 2，y =2x 2−4x 所围成图形的面积．37. 已知∫(103ax +1)(x +b)dx =0，a ，b ∈R ，试求ab 的取值范围．38. 求下列曲线所围成图形的面积：曲线y=cos x，x=π2，x=3π2，y=0．39. 求曲线y=sin x与直线x=−π2，x=5π4，y=0所围成的平面图形的面积．40. 如图，直线y＝kx分抛物线y＝x−x2与x轴所围图形为面积相等的两部分，求k的值．参考答案与试题解析数学选修2-2定积分的简单应用练习题含答案一、选择题（本题共计 10 小题，每题 3 分，共计30分） 1.【答案】 D【考点】定积分在求面积中的应用【解析】由积分的几何意义可得，S =2∫sin π0xdx ，即可得出结论．【解答】解：由积分的几何意义可得，S =2∫sin π0xdx =(−cos x)|0π=4．故选：D ． 2.【答案】 A【考点】用定积分求简单几何体的体积【解析】由题意此几何体的体积可以看作是∫π20(1−x 2)2dx ，求出积分即得所求体积．【解答】解：由题意几何体的体积； ∫π20(1−x 2)2dx=π(x −23x 3+15x 5)|02=π(2−23×23+15×25) =4615π 故选A ． 3. 【答案】 C【考点】定积分在求面积中的应用【解析】先根据题意画出区域，然后依据图形利用定积分表示出曲边梯形的面积，最后用定积分的定义求出所求即可．【解答】解：直线x =1，x =2，y =0与抛物线y =x 2所围成的曲边梯形的面积为S =∫x 221dx =13x 3|12=83−13=73，故选：C ．4.【答案】 A【考点】定积分的简单应用【解析】因为所求区域均为曲边梯形，所以使用定积分方可求解，然后求出曲线y =x 2+2与y =3x 的交点坐标，然后利用定积分表示所围成的平面图形的面积，根据定积分的定义解之即可．【解答】解：联立{y =x 2+2y =3x，解得x 1=1，x 2=2∴ S =∫(10x 2+2−3x)d x =[13X 3+2X −32X 2]01=56 故选：A 5.【答案】 A【考点】用定积分求简单几何体的体积【解析】欲求曲线y =x 2和y 2=x 所围成的平面图形绕x 轴旋转一周后所形成的旋转体的体积，可利用定积分计算，即求出被积函数y =π(x −x 4)在0→1上的积分即可．【解答】解：设旋转体的体积为V ，则v =∫π10(x −x 4)dx =π(12x 2−15x 5)|01=3π10．故旋转体的体积为：3π10．故选A ． 6. 【答案】 B【考点】定积分在求面积中的应用【解析】根据定积分的几何意义，所求面积为S =∫(5π4π4sin x −cos x)dx ，然后利用公式求出sin x −cos x 的原函数F(x)，算出F(5π4)−F(π4)的值，即为所求图形的面积．【解答】解：根据题意，所求面积为S =∫(5π4π4sin x −cos x)dx =(−cos x −sin x +C)|π45π4 （其中C 为常数） ∴ S =(−cos 5π4−sin5π4+C)−(−cos π4−sin π4+C)=(√22+√22+C)−(−√22−√22+C)=2√2 故选B 7.【答案】 C【考点】定积分的简单应用【解析】先根据题意建立关系式∫(103+e 2x )dx ，然后根据定积分的计算法则求出定积分的值即可．【解答】解：根据题意可知F(x)所做的功为∫(103+e 2x )dx =(3x +12e 2x )|01=3+12e 2−12=52+12e 2故选C ．8.【答案】 B【考点】定积分在求面积中的应用【解析】根据定积分的几何意义，先求出积分的上下限，即可求出所围成的图形的面积【解答】解：联立直线y =x −2，曲线y =√x 构成方程组，解得{x =4,y =2,联立直线y =x −2，y =0构成方程组，解得{x =2,y =0,如图所示：∴曲线y=√x，y=x−2及x轴所围成的封闭图形的面积S=∫√x40dx−∫(42x−2)dx=2x32|04 −(1x2−2x)|24=163−2=103．故选B．9.【答案】D【考点】定积分在求面积中的应用定积分定积分的简单应用【解析】先根据定积分的几何意义可知将区间[a, b]分成三段，然后利用上方曲线方程减下方的曲线方程，求积分即为面积，从而求出所求．【解答】解：根据定积分的几何意义可知将区间[a, b]分成三段利用上方曲线方程减下方的曲线方程，求积分即为面积S=∫fc1a (x)dx−∫fc2c1(x)dx+∫fcc2(x)dx故选：D10.【答案】D【考点】定积分在求面积中的应用【解析】先画出画出直线y=x与曲线y=√x3围成的平面图形，然后求出交点横坐标得到积分上下限，然后利用定积分表示出图形的面积，根据定积分的运算法则进行求解即可．【解答】解：画出直线y=x与曲线y=√x3围成的平面图形图形关于原点对称，交点的横坐标为−1，1∴直线y=x与曲线y=√x3围成的平面图形的面积是∫(1−1√x3−x)dx=2∫(1√x3−x)dx=2(34x43−12x2)|01=2(34−12−0)=12故选D ．二、填空题（本题共计 10 小题，每题 3 分，共计30分） 11.【答案】 √33【考点】定积分的简单应用【解析】求出定积分∫f 10(x)dx ，根据方程ax 02+c =∫f 10(x)dx 即可求解．【解答】解：∵ f(x)=ax 2+c(a ≠0)，∴ f(x 0)=∫f 10(x)dx =[ax 33+cx]01=a3+c ．又∵f(x 0)=ax 02+c ．∴ x 02=13，∵ x 0∈[0, 1]∴ x 0=√33． 12.【答案】2【考点】定积分在求面积中的应用【解析】本题利用直接法求解，根据三角函数的对称性知，曲线y =cos x 与直线x =0，x =π所围成的平面区域的面积S 为：曲线y =cos x 与直线x =0，x =π2所围成的平面区域的面积的两倍，最后结合定积分计算面积即可．【解答】解：根据对称性，得：曲线y =cos x 与直线x =0，x =π所围成的平面区域的面积S 为：曲线y =cos x 与直线x =0，x =π2所围成的平面区域的面积的两倍， ∴ S =2∫cos π20xdx =2 故答案为2．13.【答案】323π【考点】旋转体（圆柱、圆锥、圆台）用定积分求简单几何体的体积【解析】作出曲线围成的封闭图象，根据旋转得到旋转体的结构即可得到结论．【解答】解：曲线y=|x|，y=−|x|，x=2，x=−2合成的封闭图形绕y轴旋转一周所得的旋转体为底面半径为2，高为4的圆柱，去掉2个底面半径为2，高为2的圆锥，则对应的体积为π×42−2×13π×22×2=16π−16π3=323π，故答案为：323π14.【答案】92【考点】定积分在求面积中的应用【解析】先根据题意画出区域，然后依据图形得到积分上限为3，积分下限为0，从而利用定积分表示出曲边梯形的面积，最后用定积分的定义求出所求即可．【解答】解：先根据题意画出图形，得到积分上限为3，积分下限为0；两曲线x−y=0，y=x2−2x所围成的图形的面积是∫(33x−x2)dx而∫(303x−x2)dx=(32x2−13x3)|03=272−9=92∴曲边梯形的面积是92故答案为92．15. 【答案】13【考点】定积分在求面积中的应用【解析】作出两个曲线的图象，求出它们的交点，由此可得所求面积为函数y =x 2在区间[0, 1]上的定积分的值，再用定积分计算公式加以运算即可得到本题答案．【解答】解：∵ 曲线y =x 2和直线L:x =1的交点为A(1, 1)，∴ 曲线C:y =x 2、直线L:x =1与x 轴所围成的图形面积为 S =∫x 210dx =13x 3|01=13．故答案为：13．16. 【答案】81π2【考点】用定积分求简单几何体的体积【解析】根据类比推理，结合定积分的应用，即可求出旋转体的体积．【解答】解：根据类比推理得体积V =∫π90(√y)2dy =∫π90ydy =12πy 2|09=81π2，故答案为：81π2.17.【答案】 ln 2【考点】定积分在求面积中的应用【解析】先根据所围成图形的面积利用定积分表示出来，然后根据定积分的定义求出面积即可．【解答】解：由题意，S =∫1x 21dx =ln x|12=ln 2．故答案为：ln 2． 18. 【答案】√34π 【考点】用定积分求简单几何体的体积【解析】(1−y)π看作是把一个底面边长为1，高为π的直三棱柱平放得到的，根据祖暅原理，每个平行水平面的截面积相等，故它们的体积相等，即可得出结论．【解答】解：(1−y)π看作是把一个底面边长为1，高为π的直三棱柱平放得到的，根据祖暅原理，每个平行水平面的截面积相等，故它们的体积相等，即Ω的体积为π⋅√34=√34π．故答案为√34π． 19. 【答案】92【考点】定积分在求面积中的应用【解析】求出函数的切线方程，利用积分的几何意义即可求出区域的面积．【解答】解：函数的导数为f′(x)=3x 2−2x +1，则在(1, 2)处的切线斜率k =f′(1)=3−2+1=2，则对应的切线方程为y −2=2(x −1)，即y =2x ，由{y =x 2−x y =2x，解得x =3或x =0，则由积分的几何意义可得阴影部分的面积S =∫(302x −x 2+x)dx =(32x 2−13x 3)| 30 =92，故答案为：92．20. 【答案】29【考点】定积分的简单应用【解析】先根据定积分的运算公式求出f(a)的解析式，然后利用二次函数的图象和性质即可求出f(a)的最大值．【解答】解：f(a)=∫(102ax 2−a 2x)dx =(23ax 3−12a 2x 2)|01=23a −12a 2∴ 当a =23时，f(a)取最大值，最大值为29 故答案为：29三、解答题（本题共计 20 小题，每题 10 分，共计200分） 21.【答案】解：(1)∵ 交点为P(2,2),∴ 曲线C 2的导函数为：y ′=x ∴ 切点坐标为(2,2)，故该点的切线方程为：2x −y −2=0. (2)两曲线交点坐标(0,0),(2,2), S ∈∫(√2x −12x 2)20dx =43.【考点】定积分在求面积中的应用利用导数研究曲线上某点切线方程【解析】此题暂无解析【解答】解：(1)∵ 交点为P(2,2),∴ 曲线C 2的导函数为：y ′=x ∴ 切点坐标为(2,2)，故该点的切线方程为：2x −y −2=0. (2)两曲线交点坐标(0,0),(2,2), S ∈∫(√2x −12x 2)20dx =43. 22. 【答案】解：联立{y =x 2+2y =3x，解得x 1=1，x 2=2∴ S =∫(10x 2+2−3x)d x +∫(213x −x 2−2)d x =[13X 3+2X −32X 2]01+[32X 2−13X 3−2X]12=1【考点】定积分的简单应用【解析】因为所求区域均为曲边梯形，所以使用定积分方可求解．【解答】解：联立{y =x 2+2y =3x，解得x 1=1，x 2=2∴ S =∫(10x 2+2−3x)d x +∫(213x −x 2−2)d x =[13X 3+2X −32X 2]01+[32X 2−13X 3−2X]12=1 23. 【答案】解：（1）由y′=2x ，则切线l 的斜率k =y′|x=1=2×1=2，切线l 的方程为y −1=2(x −1)即2x −y −1=0；（2）如图，所求的图形的面积s =∫x 2120dx +∫[112x 2−(2x −1)]dx =112．【考点】定积分在求面积中的应用利用导数研究曲线上某点切线方程【解析】（1）根据导数的几何意义即可求出切线方程；（2）根据定积分的几何意义即可求出所围成的图形的面积．【解答】解：（1）由y′=2x ，则切线l 的斜率k =y′|x=1=2×1=2，切线l 的方程为y −1=2(x −1)即2x −y −1=0；（2）如图，所求的图形的面积s =∫x 2120dx +∫[112x 2−(2x −1)]dx =112．24.【答案】解：由题意，将烟囱横截面按照如图放置，建立坐标系如图，双曲线的短轴长为2A =10，并且过(−6, 6)，所以双曲线方程为y 225−11x 225×36=1，所以V =π∫(8−611x 236+25)dx =1659.2m 3【考点】用定积分求简单几何体的体积双曲线的特性【解析】由题意建立坐标系，得到如图的双曲线，烟囱最细处的直径为10m 即2a =10，最下端的直径为12m ，最细处离地面6m ，即双曲线经过(−6, 6)，烟囱高14m ，即自变量范围为−6到8，由此利用定积分的值得到体积．【解答】解：由题意，将烟囱横截面按照如图放置，建立坐标系如图，双曲线的短轴长为2A =10，并且过(−6, 6)，所以双曲线方程为y 225−11x 225×36=1，所以V =π∫(8−611x 236+25)dx =1659.2m 325.【答案】解：(1)设z =a +bi (a,b ∈R )，则z ¯=a −bi ，∴ z ⋅z ¯−3iz =a 2+b 2+3b −3ai . 又∵ z ⋅z ¯−3iz =101−3i =1+3i ， ∴ {a 2+b 2+3b =1，−3a =3，解得 {a =−1，b =0，或{a =−1，b =−3，∴ z =−1或z =−1−3i . (2)由{y =√x ，x +y =2，解得{x =1，y =1，即曲线y =√x 与直线x +y =2的交点坐标为(1,1)，同理可得，曲线y =√x 与直线y =−13x 的交点坐标为(0,0)，直线x +y =2与直线y =−13x 的交点坐标为(3,−1)，所以围成的平面图形的面积为： S =∫(√x +13x)10dx +∫(2−x +13x)31dx=(23x 32+16x 2)|01+(2x −13x 2)|13=136．【考点】复数的运算共轭复数复数代数形式的混合运算定积分在求面积中的应用【解析】此题暂无解析【解答】解：(1)设z =a +bi (a,b ∈R )，则z ¯=a −bi ，∴ z ⋅z ¯−3iz =a 2+b 2+3b −3ai . 又∵ z ⋅z ¯−3iz =101−3i =1+3i ， ∴ {a 2+b 2+3b =1，−3a =3，解得 {a =−1，b =0，或{a =−1，b =−3，∴ z =−1或z =−1−3i . (2)由{y =√x ，x +y =2，解得{x =1，y =1，即曲线y =√x 与直线x +y =2的交点坐标为(1,1)，同理可得，曲线y =√x 与直线y =−13x 的交点坐标为(0,0)，直线x +y =2与直线y =−13x 的交点坐标为(3,−1)，所以围成的平面图形的面积为： S =∫(√x +13x)10dx +∫(2−x +13x)31dx=(23x 32+16x 2)|01+(2x −13x 2)|13=136．26. 【答案】解：（1）∵ (√x 2x4)n 展开式的前三项系数成等差数列，∴ C n 0+C n 2(12)2=2C n 1⋅12…∴ 1+n(n−1)2×14=n ，整理得n 2−9n +8=0，n 1=1（舍） n 2=8…（2）所投的点落在叶形图内记为事件A ，由几何概型的概率公式得： P(A)=叶形图面积AOBC 的面积=∫(10√x−x 2)dx1=(23x 32−13x 3)|01=13…【考点】二项式定理的应用定积分在求面积中的应用等差数列的性质几何概型计算（与长度、角度、面积、体积有关的几何概型）【解析】（1）由题意可得，C n 0+C n 2(12)2=2C n 1⋅12，解关于n 的方程即可；（2）由几何概型的概率公式可知，需求叶形图的面积，利用定积分∫(10√x −x 2)dx 可求叶形图的面积，从而使问题解决．【解答】解：（1）∵ (√x 2√x4)n 展开式的前三项系数成等差数列，∴ C n 0+C n 2(12)2=2C n 1⋅12…∴1+n(n−1)2×14=n，整理得n2−9n+8=0，n1=1（舍）n2=8…（2）所投的点落在叶形图内记为事件A，由几何概型的概率公式得：P(A)=叶形图面积AOBC的面积=∫(1√x−x2)dx1=(23x32−13x3)|01=13…27.【答案】利用S=∫ππ4sin xdx=(−cos x)|π4π=1+√22．利用S=∫10(2x2−x2)dx=23x3|01−13x3|01=13．由于{y=x2y=√x，解得{x=0y=0或{x=1y=1，所以S=∫10(√x−x2)dx=23x32|01−13x3|01=23−13=13．【考点】定积分的简单应用【解析】首先求出被积函数的原函数，进一步利用定积分知识求出结果．【解答】利用S=∫ππ4sin xdx=(−cos x)|π4π=1+√22．利用S=∫10(2x2−x2)dx=23x3|01−13x3|01=13．由于{y=x2y=√x，解得{x=0y=0或{x=1y=1，所以S=∫10(√x−x2)dx=23x32|01−13x3|01=23−13=13．28.【答案】解：由y=4−x2与直线y=2x−4联立，可得交点(−4, −12)，(2, 0)，∴y=4−x2与直线y=2x−4所围成图形的面积S=∫(2−44−x2−2x+4)dx=(−13x3−x2+8x)|−42=36．【考点】定积分在求面积中的应用【解析】先联立方程，组成方程组，求得交点坐标，可得被积区间，再用定积分表示出y=4−x2与直线y=2x−4所围成图形的面积，即可求得结论．【解答】解：由y=4−x2与直线y=2x−4联立，可得交点(−4, −12)，(2, 0)，∴y=4−x2与直线y=2x−4所围成图形的面积S=∫(2−44−x2−2x+4)dx=(−13x 3−x 2+8x)|−42=36．29. 【答案】解：（1）S 0=∫sin π0xdx =[−cos x]0π=(−cos π)−(−cos 0)=1+1=2 （2）V =π∫sin 2π0xdx =π[x2−14sin 2x]0π=π(π2−14×0)=π22【考点】用定积分求简单几何体的体积定积分在求面积中的应用【解析】（1）根据题意可知曲线y =sin x 和直线x =0，x =π，及y =0所围成图形的面积为S 0=∫sin π0xdx ，解之即可；（2）所围成图形绕ox 轴旋转所成旋转体的体积为V =π∫sin 2π0xdx ，根据定积分的定义解之即可．【解答】解：（1）S 0=∫sin π0xdx =[−cos x]0π=(−cos π)−(−cos 0)=1+1=2 （2）V =π∫sin 2π0xdx=π[x 2−14sin 2x]0π=π(π2−14×0)=π2230.【答案】解：设f(x)=ax 3+bx 2+cx +d ，则f′(x)=3ax 2+2bx +c ，由图象可知{ f(0)=0f(1)=1f′(4)=0f′(7)=0，即{ d =0a +b +c =0c 3a =28−2b 3a =11，解得{ a =2137b =−33137c =168137d =0， ∴ f(x)=2137x 3−33137x 2+168137x ． ∴ S =∫f 100(x)dx =(2137×x 44−33137×x 33+168137×x 22)|10≈17.5．若要想得到误差不超过1的面积估计值，可使用分段函数求出f(x)的解析式，然后使用定积分求出面积．【考点】定积分在求面积中的应用【解析】设f(x)=ax 3+bx 2+cx +d ，利用待定系数法确定函数关系式，利用定积分求出面积估计值；若要误差小可分段求出f(x)的解析式，然后使用定积分求出面积．【解答】解：设f(x)=ax 3+bx 2+cx +d ，则f′(x)=3ax 2+2bx +c ，由图象可知{ f(0)=0f(1)=1f′(4)=0f′(7)=0，即{ d =0a +b +c =0c 3a =28−2b 3a =11，解得{ a =2137b =−33137c =168137d =0， ∴ f(x)=2137x 3−33137x 2+168137x ． ∴ S =∫f 100(x)dx=(2137×x 44−33137×x 33+168137×x 22)|10≈17.5．若要想得到误差不超过1的面积估计值，可使用分段函数求出f(x)的解析式，然后使用定积分求出面积． 31. 【答案】解：（1）曲线C:y =√x 和直线：x −2y =0联立，可得交点坐标为(4, 2)，则 S =∫(40√x −12x)dx =(23x 32−x 24)|04=43；（2）V =∫[40π(√x)2−π(x2)2]dx =π(x 22−x 312)|04=8π3．【考点】用定积分求简单几何体的体积旋转体（圆柱、圆锥、圆台）【解析】（1）求得交点坐标，可得积分区间，即可求M 的面积；（2）旋转一周所得旋转体的体积应该用定积分来求．【解答】解：（1）曲线C:y =√x 和直线：x −2y =0联立，可得交点坐标为(4, 2)，则 S =∫(40√x −12x)dx =(23x 32−x 24)|04=43；（2）V =∫[40π(√x)2−π(x2)2]dx=π(x 22−x 312)|04=8π3．32.【答案】解：（1）设f(x)=kx +b ， ∵ f(x)=x ∫f 20(t)dt +1， ∴ kx +b =x •(kt 22+bt)|02+1，∴ kx +b =(2k +2b)x +1，∴ k =−2，b =1， ∴ f(x)=−2x +1，；2)g(x)=xf(x)=−2x 2+x ， ∴ V =π∫[120xf(x)]2dx =π240．【考点】用定积分求简单几何体的体积定积分【解析】（1）利用待定系数法，结合定积分的定义求函数f(x)的解析式；（2）求出g(x)，应用定积分来求旋转体的体积．【解答】解：（1）设f(x)=kx+b，∵f(x)=x∫f2(t)dt+1，∴kx+b=x•(kt22+bt)|02+1，∴kx+b=(2k+2b)x+1，∴k=−2，b=1，∴f(x)=−2x+1，；2)g(x)=xf(x)=−2x2+x，∴V=π∫[120xf(x)]2dx=π240．33.【答案】解：（1）若干张平行于圆锥底面的平面把它切成n块厚度相等的薄片；（2）用一系列圆柱的体积近似地代替对应的薄片，圆柱的高为ℎn ，底半径顺次为：rn，2r n ，3rn…，(n−1)rn，r；（3）问题归结为计算和式V(n)=ℎn ×(12+22+...+n2)×πr2n2，当n越来越大时所趋向的值．（对V求极限V=limn→∞ℎn×(12+22+...+n2)×πr2n2=lim n→∞ℎn⋅16n(n+1)(2n+1)⋅πr2n2=ℎπr26limn→∞2n2+3n+1n2=πr2ℎ3=13S底ℎ故圆锥的体积等于13的圆柱体的体积【考点】用定积分求简单几何体的体积【解析】利用极限的定义进行分割、近似代换和求极限的方法，进行推到【解答】解：（1）若干张平行于圆锥底面的平面把它切成n块厚度相等的薄片；（2）用一系列圆柱的体积近似地代替对应的薄片，圆柱的高为ℎn ，底半径顺次为：rn，2r n ，3rn…，(n−1)rn，r；（3）问题归结为计算和式V(n)=ℎn ×(12+22+...+n2)×πr2n2，当n越来越大时所趋向的值．（对V求极限V=limn→∞ℎn×(12+22+...+n2)×πr2n2=lim n→∞ℎ⋅1n(n+1)(2n+1)⋅πr22=ℎπr26limn→∞2n2+3n+1n2=πr2ℎ3=13S底ℎ故圆锥的体积等于13的圆柱体的体积34.【答案】解：设(x0, y0)为曲线y=√x(0≤x≤4)上任一点，得曲线于该点处的切线方程为：y−y0=2√x −x0)即y=y02+2√x．得其与x=0，x=4的交点分别为(0,y02)，(4,y02+2y0)于是由此切线与直线x=0，x=4以及曲线y=√x所围的平面图形面积为：S=∫(4 0y022x√x)dx=2y0+x−163=2√x0x−163应用均值不等式求得x0=2时，S取得最小值．即所求切线即为：y=22+√22．【考点】定积分在求面积中的应用【解析】先根据导数的几何意义求出曲线y=√x(0≤x≤4)上任一点处的切线方程，再求出积分的上下限，然后利用定积分表示出图形面积，最后利用定积分的定义进行求解即可．【解答】解：设(x0, y0)为曲线y=√x(0≤x≤4)上任一点，得曲线于该点处的切线方程为：y−y0=2x −x0)即y=y02+2x．得其与x=0，x=4的交点分别为(0,y02)，(4,y02+2y0)于是由此切线与直线x=0，x=4以及曲线y=√x所围的平面图形面积为：S=∫(4 0y022√x√x)dx=2y0+√x−163=2√x0√x−163应用均值不等式求得x0=2时，S取得最小值．即所求切线即为：y=2√2+√22．35.【答案】解：设切线方程为y =kx +1，切点坐标为(a, b)，则{k =1aka +1=b ln a =b ，解得a =e 2，b =2，∴ 切线方程为y =1e 2x +1．将y =0代入y =1e 2x +1得x =−e 2，∴ B(−e 2, 0)． ∴区域D 的面积为∫(e 2−e 21e 2x+1)dx −∫ln e 21xdx=x 22e 2+x|e 2−e 2−x(ln x −1)|e 21=2e 2+e 2=3e 2．区域D 绕x 轴旋转一周所得几何体体积为13⋅π⋅22⋅2e 2−π⋅∫(e 21ln x)2dx =8πe 23−π⋅x[(ln x)2−2ln x +2]|e 21=8πe 23−(2e 2−2)⋅π=2πe 23+2π．【考点】用定积分求简单几何体的体积【解析】求出A 的坐标和切线方程，则所求面积和体积均可用两个定积分的差来表示．【解答】解：设切线方程为y =kx +1，切点坐标为(a, b)，则{k =1aka +1=b ln a =b，解得a =e 2，b =2，∴ 切线方程为y =1e 2x +1．将y =0代入y =1e 2x +1得x =−e 2，∴ B(−e 2, 0)． ∴区域D 的面积为∫(e 2−e 21e 2x+1)dx −∫ln e 21xdx=x 22e 2+x|e 2−e 2−x(ln x −1)|e 21=2e 2+e 2=3e 2．区域D 绕x 轴旋转一周所得几何体体积为13⋅π⋅22⋅2e 2−π⋅∫(e 21ln x)2dx=8πe 23−π⋅x[(ln x)2−2ln x +2]|e 21=8πe 23−(2e 2−2)⋅π=2πe 23+2π．36. 【答案】解：由{y =2x −x 2y =2x 2−4x ，得{x =0y =0或{x =2y =0， ∴ 所求图象的面积为：∫[20(2x −x 2)−(2x 2−4x)]dx =∫(206x −3x 2)dx =(3x 2−x 3)|02=3×22−23=12−8=4．【考点】定积分在求面积中的应用【解析】先求出两曲线的交点坐标，利用定积分的应用即可求出对应图形的面积．【解答】解：由{y =2x −x 2y =2x 2−4x ，得{x =0y =0或{x =2y =0， ∴ 所求图象的面积为：∫[20(2x −x 2)−(2x 2−4x)]dx =∫(206x −3x 2)dx =(3x 2−x 3)|02=3×22−23=12−8=4． 37. 【答案】解：∫(103ax +1)(x +b)dx =∫[103ax 2+(3ab +1)x +b]dx=[ax 3+12(3ab +1)x 2+bx]|01 =a +12(3ab +1)+b =0即3ab +2(a +b)+1=0 设ab =t ∴ a +b =−3t+12则a ，b 为方程x 2+3t+12x +t =0两根△=(3t+1)24−4t ≥0∴ t ≤19或t ≥1∴ a ⋅b ∈(−∞, 19]∪[1, +∞) 【考点】定积分的简单应用【解析】先根据定积分的运算法则建立a 与b 的等量关系，然后设ab =t 则a +b =−3t+12，再利用构造法构造a ，b 为方程x 2+3t+12x +t =0两根，然后利用判别式可求出a ．b 的取值范围．【解答】解：∫(103ax +1)(x +b)dx =∫[103ax 2+(3ab +1)x +b]dx=[ax 3+12(3ab +1)x 2+bx]|01 =a +12(3ab +1)+b =0即3ab +2(a +b)+1=0 设ab =t ∴ a +b =−3t+12则a ，b 为方程x 2+3t+12x +t =0两根△=(3t+1)24−4t ≥0∴ t ≤19或t ≥1∴ a ⋅b ∈(−∞, 19]∪[1, +∞) 38.【答案】解：根据对称性，得：曲线y =cos x 与直线x =π2、x =3π2、y =0所围成的平面区域的面积S 为：曲线y =cos x与直线x =π2，x =π所围成的平面区域的面积的二倍， ∴ S =−2∫cos ππ2xdx =−2sin x =2．故曲线y =cos x 与直线x =π2、x =3π2、y =0所围成的面积为2．【考点】定积分在求面积中的应用【解析】本题利用直接法求解，根据三角函数的对称性知，曲线y =cos x 与直线x =π2、x =3π2、y =0所围成的平面区域的面积S 为：曲线y =cos x 与直线x =π2，x =π所围成的平面区域的面积的二倍，最后结合定积分计算面积即可．【解答】解：根据对称性，得：曲线y =cos x 与直线x =π2、x =3π2、y =0所围成的平面区域的面积S 为：曲线y =cos x与直线x =π2，x =π所围成的平面区域的面积的二倍， ∴ S =−2∫cos ππ2xdx =−2sin x =2．故曲线y =cos x 与直线x =π2、x =3π2、y =0所围成的面积为2．39. 【答案】解：s =∫|5π4−π2sin x|dx =−∫sin 0−π2xdx+∫sin π0xdx−∫sin 5π4πxdx=cos x|−π20−cos x|0π+cos x|π5π4=1+2+(−√22+1)=4−√22．【考点】定积分在求面积中的应用【解析】求曲线y =sin x 与直线x =−π2，x =5π4，y =0所围成的平面图形的面积【解答】解：s =∫|5π4−π2sin x|dx =−∫sin 0−π2xdx+∫sin π0xdx−∫sin 5π4πxdx=cos x|−π20−cos x|0π+cos x|π5π4=1+2+(−√22+1)=4−√22． 40.【答案】由 {y =kx y =x −x2 得 {x =1−k y =k −k 2 (0<k <1)．由题设得∫10−k[(x −x 2)−kx]dx =12∫(10x −x 2)dx 即∫10−k[(x −x 2)−kx]dx =12( 12x 2−13x 3)|01=112 ∴ (1−k)3=12 ∴ k ＝1−√432∴ 直线方程为y ＝(1−√432)x ．故k 的值为：k =1−√432．【考点】定积分的简单应用【解析】先由 {y =kx y =x −x 2 得 {x =1−k y =k −k 2 ，根据直线y ＝kx 分抛物线y ＝x −x 2与x 轴所围成图形为面积相等的两个部分得∫10−k[(x −x 2)−kx]dx =12∫(10x −x 2)dx 下面利用定积分的计算公式即可求得k 值．【解答】由 {y =kx y =x −x 2得 {x =1−k y =k −k 2 (0<k <1)．由题设得∫10−k[(x −x 2)−kx]dx =12∫(10x −x 2)dx 即∫10−k[(x −x 2)−kx]dx =12( 12x 2−13x 3)|01=112试卷第31页，总31页 ∴ (1−k)3=12 ∴k ＝1−√432∴ 直线方程为y ＝(1−√432)x ．故k 的值为：k =1−√432．。

11-12学年高中数学 1.7 定积分的简单应用同步练习新人教A版选修2-2

定积分的简单应用一、选择题1．如图所示，阴影部分的面积为( )A.⎠⎛a b f (x )d xB.⎠⎛a b g (x )d xC.⎠⎛ab [f (x )－g (x )]d xD.⎠⎛ab [g (x )－f (x )]d x[答案] C[解析] 由题图易知，当x ∈[a ，b ]时，f (x )>g (x )，所以阴影部分的面积为⎠⎛ab [f (x )－g (x )]d x .2．如图所示，阴影部分的面积是( )A ．2 3B ．2－ 3 C.323D.353[答案] C[解析] S ＝⎠⎛1－3(3－x 2－2x )d x即F (x )＝3x －13x 3－x 2，则F (1)＝3－1－13＝53，F (－3)＝－9－9＋9＝－9.∴S ＝F (1)－F (－3)＝53＋9＝323.故应选C.3．由曲线y ＝x 2－1、直线x ＝0、x ＝2和x 轴围成的封闭图形的面积(如图)是( ) A.⎠⎛02(x 2－1)d xB ．|⎠⎛02(x 2－1)d x |C.⎠⎛02|x 2－1|d xD.⎠⎛01(x 2－1)d x ＋⎠⎛12(x 2－1)d x[答案] C[解析] y ＝|x 2－1|将x 轴下方阴影反折到x 轴上方，其定积分为正，故应选C.4．设f (x )在[a ，b ]上连续，则曲线f (x )与直线x ＝a ，x ＝b ，y ＝0围成图形的面积为( ) A.⎠⎛a b f (x )d xB ．|⎠⎛ab f (x )d x |C.⎠⎛ab |f (x )|d xD ．以上都不对[答案] C[解析] 当f (x )在[a ，b ]上满足f (x )<0时，⎠⎛ab f (x )d x <0，排除A ；当阴影有在x 轴上方也有在x 轴下方时，⎠⎛ab f (x )d x 是两面积之差，排除B ；无论什么情况C 对，故应选C.5．曲线y ＝1－1681x 2与x 轴所围图形的面积是( )A ．4B ．3C ．2D.52[答案] B[解析] 曲线与x 轴的交点为⎝ ⎛⎭⎪⎫－94，0，⎝ ⎛⎭⎪⎫94，0故应选B.6．一物体以速度v ＝(3t 2＋2t )m/s 做直线运动，则它在t ＝0s 到t ＝3s 时间段内的位移是( )A ．31mB ．36mC ．38mD ．40m[答案] B[解析] S ＝⎠⎛03(3t 2＋2t )d t ＝(t 3＋t 2)| 30＝33＋32＝36(m)，故应选B.7．(2010·山东理，7)由曲线y ＝x 2，y ＝x 3围成的封闭图形面积为( )A.112B.14 C.13D.712[答案] A[解析] 由⎩⎪⎨⎪⎧y ＝x2y ＝x 3得交点为(0,0)，(1,1)．∴S ＝⎠⎛01(x 2－x 3)d x ＝⎪⎪⎪⎝⎛⎭⎪⎫13x 3－14x 410＝112.8．一物体在力F (x )＝4x －1(单位：N)的作用下，沿着与力F 相同的方向，从x ＝1运动到x ＝3处(单位：m)，则力F (x )所做的功为( )A ．8JB ．10JC ．12JD ．14J[答案] D[解析] 由变力做功公式有：W ＝⎠⎛13(4x －1)d x ＝(2x 2－x )| 31＝14(J)，故应选D.9．若某产品一天内的产量(单位：百件)是时间t 的函数，若已知产量的变化率为a ＝36t，那么从3小时到6小时期间内的产量为( )A.12B ．3－32 2C ．6＋3 2D ．6－3 2[答案] D [解析] ⎠⎛3636tdt ＝66t | 63＝6－32，故应选D.10．过原点的直线l 与抛物线y ＝x 2－2ax (a >0)所围成的图形面积为92a 3，则直线l 的方程为( )A ．y ＝±axB ．y ＝axC ．y ＝－axD ．y ＝－5ax[答案] B[解析] 设直线l 的方程为y ＝kx ，由⎩⎪⎨⎪⎧y ＝kx y ＝x 2－2ax 得交点坐标为(0,0)，(2a ＋k,2ak ＋k 2) 图形面积S ＝∫2a ＋k[kx －(x 2－2ax )]d x＝⎝ ⎛⎭⎪⎫k ＋2a 2x 2－x 33| 2a ＋k 0＝(k ＋2a )32－(2a ＋k )33＝(2a ＋k )36＝92a 3∴k ＝a ，∴l 的方程为y ＝ax ，故应选B. 二、填空题11．由曲线y 2＝2x ，y ＝x －4所围图形的面积是________． [答案] 18[解析] 如图，为了确定图形的范围，先求出这两条曲线交点的坐标，解方程组⎩⎪⎨⎪⎧y 2＝2x y ＝x －4得交点坐标为(2，－2)，(8,4)．因此所求图形的面积S ＝⎠⎛4－2(y ＋4－y 22)d y取F (y )＝12y 2＋4y －y 36，则F ′(y )＝y ＋4－y22，从而S ＝F (4)－F (－2)＝18.12．一物体沿直线以v ＝1＋t m/s 的速度运动，该物体运动开始后10s 内所经过的路程是________．13．由两条曲线y ＝x 2，y ＝14x 2与直线y ＝1围成平面区域的面积是________．[答案] 43[解析] 如图，y ＝1与y ＝x 2交点A (1,1)，y ＝1与y ＝x 24交点B (2,1)，由对称性可知面积S ＝2(⎠⎛01x 2d x＋⎠⎛12d x －⎠⎛0214x 2d x )＝43.14．一变速运动物体的运动速度v (t )＝⎩⎪⎨⎪⎧2t (0≤t ≤1)a t(1≤t ≤2)b t (2≤t ≤e )则该物体在0≤t ≤e 时间段内运动的路程为(速度单位：m/s ，时间单位：s)______________________． [答案] 9－8ln2＋2ln2[解析] ∵0≤t ≤1时，v (t )＝2t ，∴v (1)＝2；又1≤t ≤2时，v (t )＝a t， ∴v (1)＝a ＝2，v (2)＝a 2＝22＝4；又2≤t ≤e 时，v (t )＝bt， ∴v (2)＝b2＝4，∴b ＝8.∴路程为S ＝⎠⎛012t d t ＋⎠⎛122td t ＋⎠⎛2e 8td t ＝9－8ln2＋2ln2 .三、解答题15．计算曲线y ＝x 2－2x ＋3与直线y ＝x ＋3所围图形的面积．[解析] 由⎩⎪⎨⎪⎧y ＝x ＋3y ＝x 2－2x ＋3解得x ＝0及x ＝3.从而所求图形的面积S ＝⎠⎛03(x ＋3)d x －⎠⎛03(x 2－2x ＋3)d x＝⎠⎛03[(x ＋3)－(x 2－2x ＋3)]d x＝⎠⎛03(－x 2＋3x )d x＝⎝ ⎛⎭⎪⎫－13x 3＋32x 2| 30＝92.16．设y ＝f (x )是二次函数，方程f (x )＝0有两个相等的实根，且f ′(x )＝2x ＋2. (1)求y ＝f (x )的表达式；(2)若直线x ＝－t (0＜t ＜1)把y ＝f (x )的图象与两坐标轴所围成图形的面积二等分，求t 的值．[解析] (1)设f (x )＝ax 2＋bx ＋c (a ≠0)，则f ′(x )＝2ax ＋b ，又已知f ′(x )＝2x ＋2，∴a ＝1，b ＝2， ∴f (x )＝x 2＋2x ＋c .又方程f (x )＝0有两个相等实根． ∴判别式Δ＝4－4c ＝0，即c ＝1. 故f (x )＝x 2＋2x ＋1.(2)依题意有⎠⎛－1－t (x 2＋2x ＋1)d x ＝⎠⎛0－t (x 2＋2x ＋1)d x ，∴⎝ ⎛⎭⎪⎫13x 3＋x 2＋x | －t －1＝⎝ ⎛⎭⎪⎫13x 3＋x 2＋x | 0－t 即－13t 3＋t 2－t ＋13＝13t 3－t 2＋t .∴2t 3－6t 2＋6t －1＝0， ∴2(t －1)3＝－1，∴t ＝1－132.17．A 、B 两站相距7.2km ，一辆电车从A 站开往B 站，电车开出t s 后到达途中C 点，这一段速度为1.2t (m/s)，到C 点的速度达24m/s ，从C 点到B 站前的D 点以等速行驶，从D 点开始刹车，经t s 后，速度为(24－1.2t )m/s ，在B 点恰好停车，试求：(1)A 、C 间的距离； (2)B 、D 间的距离；(3)电车从A 站到B 站所需的时间． [解析] (1)设A 到C 经过t 1s ，由1.2t ＝24得t 1＝20(s)，所以AC ＝∫2001.2t d t ＝0.6t 2| 200＝240(m)．(2)设从D →B 经过t 2s ，由24－1.2t 2＝0得t 2＝20(s)，所以DB ＝∫200(24－1.2t )d t ＝240(m)． (3)CD ＝7200－2×240＝6720(m)．从C 到D 的时间为t 3＝672024＝280(s)．于是所求时间为20＋280＋20＝320(s)．18．在曲线y ＝x 2(x ≥0)上某一点A 处作一切线使之与曲线以及x 轴所围成的面积为112，试求：(1)切点A 的坐标； (2)过切点A 的切线方程．[解析] 如图所示，设切点A (x 0，y 0)，由y ′＝2x ，过A 点的切线方程为y －y 0＝2x 0(x －x 0)，即y ＝2x 0x －x 20.令y ＝0得x ＝x 02，即C ⎝ ⎛⎭⎪⎫x 02，0.设由曲线和过A 点的切线及x 轴所围成图形的面积为S ，S ＝S 曲边△AOB －S △ABC . S 曲边△AOB ＝∫x 00x 2d x ＝13x 30， S △ABC ＝12|BC |·|AB | ＝12⎝ ⎛⎭⎪⎫x 0－x 02·x 20＝14x 30，即S ＝13x 30－14x 30＝112x 30＝112.所以x 0＝1，从而切点A (1,1)，切线方程为y ＝2x －1.。

五、定积分及其应用

2
sin
xd sin
x
.
0
0
2
3.【解】
令
1
f
xdx
A ，则由
f
x
1 x2
1 2x4
f xdx ，得
1
A
1
1 x2
dx
A 2
1
1 x4
dx
1
A ，解得 A 6 ，所以
6
7
f x
1 x2
3 7x4
.
4.【解】
1 0
f
xdx
x
1
2 0
f
xd
x 2
x
f
x
1
0
1
2 0
x f xdx
0
20
0
2
x t
x cos x dx
t cost dt
t cost dt
cost dt 2 3 ，
0
0
0
3
x 2 t
x cos xdx
t 2 cost dt
t cost dt 2
cost dt 5 ，
2
0
0
0
则 n x cos x dx 3 2n 1 n2 . 0
arcsin2x
1
1 1
，
1 2 x 1 2
22
2 2
3
2
1
dx
3
2
x2 x 1
d x 1
2 ln x 1
x 1 2 1 2
2
3
x2 x 2 ln 2 1
3，
2 2
原式 ln 2 3 . 2
8.【证明】

高等数学(定积分的应用)习题及解答

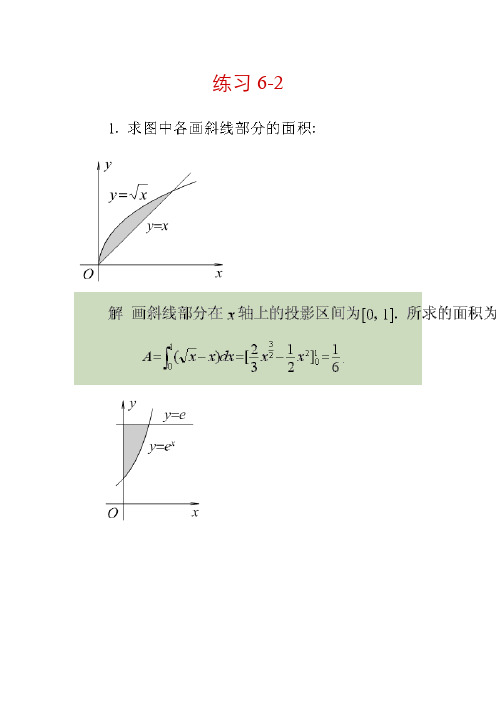
练习6-2练习6-2练习6-3总习题六高等数学（文专）练习题A一、单项选择题在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。

错选、多选或未选均无分。

下列函数是奇函数的是（）．（A）1y x=+；（B）e e2x xy-+=；（C）e e2x xy--=；（D）2y x x=+．2．ln(2)y x=-的定义域为（）．（A）(,2)-∞；（B）(2,)+∞；（C ）(,2)(2,)-∞+∞；（D ）(,)-∞+∞．3．设2()sin f x x x =+，则2f π⎛⎫= ⎪⎝⎭（）．（A ）24π；（B ）214π+；（C ）214π-；（D ）424πππ⎛⎫+⎪⎝⎭． 4．3d (e )d xx x+=（）．（A ）3e 1x +；（B ）33e 1x +；（C ）31e 13x +；（D ）3211e 32x x +．5．ln d xx x=⎰（）．（A ）ln |ln |x ；（B ）ln ln ||x c + （C ）21(ln )2x（D ）21(ln )2x c +．6．10(1)d x x +=⎰（）．（A ）2；（B ）1；（C ）32；（D ）12． 7．设)(x f 在点x a =处可导，那么=--+→h h a f h a f h )2()(lim（）.A ． )(3a f 'B ． )(2a f 'C ． )(a f 'D ．)(31a f '8. 函数2x e y -=的图形的水平渐近线方程为（） A ．1=yB ．1=xC ．0=yD ．0=x9.cos()x dx +=⎰5( )A. 155cos()x c ++ B.55sin()x c ++ C.55cos()x c ++ D. sin()x c ++5 二、填空题 10．xxx 23sin lim0→ ___________.11．x x e y x sin ln 2-+=则='y ． 12．dx x ⎰--3329 =．13．曲线y =在1x =处的切线方程为 _______________.14．已知某商品的成本函数为221020)(q q q C +-= (万元),则20=q 时的边际成本为___________．15．若函数⎪⎩⎪⎨⎧=≠--=2,2,242x a x x x y 在2=x 处连续，则=a ______.16．x x f sin )(=在[]π,0上满足罗尔中值定理的条件, 当ξ= 时,0)(='ξf ．三、计算题 17．求)32(13lim23--+-→x x x x x .18．求由方程423=+y x 所确定的隐函数y=y(x)的dxdy . 19．求极限1lim(13)xx x →-．20．求极限201cos lim2x xx →-．21．设)0()1(>+++=a ax x a y aax，求.dy 22．计算⎰+edx xx1ln 2 23．求dx xex ⎰-22四、综合题24．求函数212x xy +=的极值与拐点.25．证明：当1x >时，22(1)ln (1)x x x ->-。

高考数学定积分应用选择题

高考数学定积分应用选择题1. 定积分可以用来求解什么问题？A. 曲线下的面积B. 物体的质量C. 物体的体积D. 以上都是2. 定积分表示的物理意义是什么？A. 曲线下的面积B. 物体的质量C. 物体的体积D. 以上都是3. 求解曲线下的面积，应该使用哪种积分？A. 定积分B. 不定积分C. 双重积分D. 三重积分4. 定积分的基本性质是什么？A. 定积分与被积函数单调性无关B. 定积分与积分区间长度无关C. 定积分与积分上下限无关D. 以上都是5. 定积分在物理学中的一个应用是求解什么？A. 物体的质量B. 物体的速度C. 物体的加速度D. 物体的位移6. 求解物体的质量，应该使用哪种积分？A. 定积分B. 不定积分C. 双重积分D. 三重积分7. 定积分可以用来求解物体的体积，这是因为在三维空间中，物体的体积可以表示为什么？A. 曲线下的面积B. 物体的质量C. 物体的体积D. 以上都是8. 定积分在物理学中的一个应用是求解物体的位移，这是因为在物理学中，物体的位移可以表示为什么？A. 曲线下的面积B. 物体的质量C. 物体的体积D. 物体的速度与时间的积分9. 求解物体的速度，应该使用哪种积分？A. 定积分B. 不定积分C. 双重积分D. 三重积分10. 求解物体的加速度，应该使用哪种积分？A. 定积分B. 不定积分C. 双重积分D. 三重积分11. 定积分可以用来求解物体的速度，这是因为在物理学中，物体的速度可以表示为什么？A. 曲线下的面积B. 物体的质量C. 物体的体积D. 物体的位移与时间的积分12. 定积分在物理学中的一个应用是求解物体的加速度，这是因为在物理学中，物体的加速度可以表示为什么？A. 曲线下的面积B. 物体的质量C. 物体的体积D. 物体的速度与时间的积分13. 求解物体的位移，应该使用哪种积分？A. 定积分B. 不定积分C. 双重积分D. 三重积分14. 定积分可以用来求解物体的加速度，这是因为在物理学中，物体的加速度可以表示为什么？A. 曲线下的面积B. 物体的质量C. 物体的体积D. 物体的速度与时间的积分15. 求解物体的速度，应该使用哪种积分？A. 定积分B. 不定积分C. 双重积分16. 定积分可以用来求解物体的质量，这是因为在物理学中，物体的质量可以表示为什么？A. 曲线下的面积B. 物体的质量C. 物体的体积D. 物体的位移与时间的积分17. 定积分在物理学中的一个应用是求解物体的位移，这是因为在物理学中，物体的位移可以表示为什么？A. 曲线下的面积B. 物体的质量C. 物体的体积D. 物体的速度与时间的积分18. 求解物体的加速度，应该使用哪种积分？A. 定积分B. 不定积分D. 三重积分19. 定积分可以用来求解物体的速度，这是因为在物理学中，物体的速度可以表示为什么？A. 曲线下的面积B. 物体的质量C. 物体的体积D. 物体的位移与时间的积分20. 定积分在物理学中的一个应用是求解物体的加速度，这是因为在物理学中，物体的加速度可以表示为什么？A. 曲线下的面积B. 物体的质量C. 物体的体积D. 物体的速度与时间的积分21. 求解物体的位移，应该使用哪种积分？A. 定积分C. 双重积分D. 三重积分22. 定积分可以用来求解物体的加速度，这是因为在物理学中，物体的加速度可以表示为什么？A. 曲线下的面积B. 物体的质量C. 物体的体积D. 物体的速度与时间的积分23. 求解物体的速度，应该使用哪种积分？A. 定积分B. 不定积分C. 双重积分D. 三重积分24. 定积分可以用来求解物体的质量，这是因为在物理学中，物体的质量可以表示为什么？A. 曲线下的面积B. 物体的质量C. 物体的体积D. 物体的位移与时间的积分25. 定积分在物理学中的一个应用是求解物体的位移，这是因为在物理学中，物体的位移可以表示为什么？A. 曲线下的面积B. 物体的质量C. 物体的体积D. 物体的速度与时间的积分26. 求解物体的加速度，应该使用哪种积分？A. 定积分B. 不定积分C. 双重积分D. 三重积分27. 定积分可以用来求解物体的速度，这是因为在物理学中，物体的速度可以表示为什么？A. 曲线下的面积B. 物体的质量C. 物体的体积D. 物体的位移与时间的积分28. 定积分在物理学中的一个应用是求解物体的加速度，这是因为在物理学中，物体的加速度可以表示为什么？A. 曲线下的面积B. 物体的质量C. 物体的体积D. 物体的速度与时间的积分29. 求解物体的位移，应该使用哪种积分？A. 定积分B. 不定积分C. 双重积分D. 三重积分30. 定积分可以用来求解物体的加速度，这是因为在物理学中，物体的加速度可以表示为什么？A. 曲线下的面积B. 物体的质量C. 物体的体积D. 物体的速度与时间的积分31. 求解物体的速度，应该使用哪种积分？A. 定积分B. 不定积分C. 双重积分D. 三重积分32. 定积分可以用来求解物体的质量，这是因为在物理学中，物体的质量可以表示为什么？A. 曲线下的面积B. 物体的质量C. 物体的体积D. 物体的位移与时间的积分33. 定积分在物理学中的一个应用是求解物体的位移，这是因为在物理学中，物体的位移可以表示为什么？A. 曲线下的面积B. 物体的质量C. 物体的体积D. 物体的速度与时间的积分34. 求解物体的加速度，应该使用哪种积分？A. 定积分B. 不定积分C. 双重积分D. 三重积分35. 定积分可以用来求解物体的速度，这是因为在物理学中，物体的速度可以表示为什么？A. 曲线下的面积B. 物体的质量C. 物体的体积D. 物体的位移与时间的积分36. 定积分在物理学中的一个应用是求解物体的加速度，这是因为在物理学中，物体的加速度可以表示为什么？A. 曲线下的面积B. 物体的质量C. 物体的体积D. 物体的速度与时间的积分37. 求解物体的位移，应该使用哪种积分？A. 定积分B. 不定积分C. 双重积分D. 三重积分38. 定积分可以用来求解物体的加速度，这是因为在物理学中，物体的加速度可以表示为什么？A. 曲线下的面积B. 物体的质量C. 物体的体积D. 物体的速度与时间的积分39. 求解物体的速度，应该使用哪种积分？A. 定积分B. 不定积分C. 双重积分D. 三重积分40. 定积分可以用来求解物体的质量，这是因为在物理学中，物体的质量可以表示为什么？A. 曲线下的面积B. 物体的质量C. 物体的体积D. 物体的位移与时间的积分41. 定积分在物理学中的一个应用是求解物体的位移，这是因为在物理学中，物体的位移可以表示为什么？A. 曲线下的面积B. 物体的质量D. 物体的速度与时间的积分42. 求解物体的加速度，应该使用哪种积分？A. 定积分B. 不定积分C. 双重积分D. 三重积分43. 定积分可以用来求解物体的速度，这是因为在物理学中，物体的速度可以表示为什么？A. 曲线下的面积B. 物体的质量C. 物体的体积D. 物体的位移与时间的积分44. 定积分在物理学中的一个应用是求解物体的加速度，这是因为在物理学中，物体的加速度可以表示为什么？A. 曲线下的面积C. 物体的体积D. 物体的速度与时间的积分45. 求解物体的位移，应该使用哪种积分？A. 定积分B. 不定积分C. 双重积分D. 三重积分46. 定积分可以用来求解物体的加速度，这是因为在物理学中，物体的加速度可以表示为什么？A. 曲线下的面积B. 物体的质量C. 物体的体积D. 物体的速度与时间的积分47. 求解物体的速度，应该使用哪种积分？A. 定积分C. 双重积分D. 三重积分48. 定积分可以用来求解物体的质量，这是因为在物理学中，物体的质量可以表示为什么？A. 曲线下的面积B. 物体的质量C. 物体的体积D. 物体的位移与时间的积分49. 定积分在物理学中的一个应用是求解物体的位移，这是因为在物理学中，物体的位移可以表示为什么？A. 曲线下的面积B. 物体的质量C. 物体的体积D. 物体的速度与时间的积分50. 求解物体的加速度，应该使用哪种积分？B. 不定积分C. 双重积分D. 三重积分。

(完整版)§定积分的应用习题与答案

第六章定积分的应用（A ）1、求由下列各曲线所围成的图形的面积 1）221x y =与822=+y x （两部分都要计算）2）xy 1=与直线x y =及2=x3）xe y =，xe y -=与直线1=x4）θρcos 2a =5）t a x 3cos =，t a y 3sin =１、求由摆线()t t a x sin -=，()t a y cos 1-=的一拱()π20≤≤t 与横轴所围成的图形的面积２、求对数螺线θρae=()πθπ≤≤-及射线πθ=所围成的图形的面积３、求由曲线x y sin =和它在2π=x 处的切线以及直线π=x 所围成的图形的面积和它绕x 轴旋转而成的旋转体的体积４、由3x y =，2=x ，0=y 所围成的图形，分别绕x 轴及y 轴旋转，计算所得两旋转体的体积５、计算底面是半径为R 的圆，而垂直于底面上一条固定直径的所有截面都是等边三角形的立体体积６、计算曲线()x y -=333上对应于31≤≤x 的一段弧的长度７、计算星形线t a x 3cos =，t a y 3sin =的全长８、由实验知道，弹簧在拉伸过程中，需要的力→F （单位：N ）与伸长量S （单位：cm ）成正比，即：kS =→F （k 是比例常数），如果把弹簧内原长拉伸6cm ，计算所作的功９、一物体按规律3ct x =作直线运动，介质的阻力与速度的平方成正比，计算物体由0=x 移到a x =时，克服介质阻力所作的功１０、设一锥形储水池，深15m ，口径20m ，盛满水，将水吸尽，问要作多少功？１１、有一等腰梯形闸门，它的两条底边各长10cm 和6cm ，高为20cm ，较长的底边与水面相齐，计算闸门的一侧所受的水压力１２、设有一长度为λ，线密度为u 的均匀的直棒，在与棒的一端垂直距离为a 单位处有一质量为m 的质点M ，试求这细棒对质点M 的引力(B)1、设由抛物线()022>=p px y 与直线p y x 23=+ 所围成的平面图形为D 1）求D 的面积S ;2）将D 绕y 轴旋转一周所得旋转体的体积2、求由抛物线2x y =及x y =2所围成图形的面积，并求该图形绕x 轴旋转所成旋转体的体积3、求由x y sin =，x y cos =，0=x ，2π=x 所围成的图形的面积，并求该图形绕x 轴旋转所成旋转体的体积4、求抛物线px y 22=及其在点⎪⎭⎫⎝⎛p p ,2处的法线所围成的图形的面积5、求曲线422+-=x x y 在点()4,0M 处的切线MT 与曲线()122-=x y 所围成图形的面积6、求由抛物线ax y 42=与过焦点的弦所围成的图形面积的最小值7、求由下列曲线所围成图形的公共部分的面积 1）θρcos 3=，θρcos 1+=2）θρsin a =，()θθρsin cos +=a ，0>a8、由曲线()16522=-+y x 所围成图形绕x 轴旋转所成旋转体的体积9、求圆心在()b ,0半径为a ，()0>>a b 的圆，绕x 轴旋转而成的环状体的体积10、计算半立方抛物线()32132-=x y 被抛物线32x y =截得的一段弧的长度(C)1、用积分方法证明半径为R 的球的高为H 的球缺的的体积为⎪⎭⎫ ⎝⎛-=32H R H V π2、分别讨论函数x y sin =⎪⎭⎫⎝⎛≤≤20πx 在取何值时，阴影部分的面积1S ，2S 的和21S S S +=取最大值和最小值3、求曲线x y =()40≤≤x 上的一条切线，使此切线与直线0=x ， 4=x 以及曲线x y =所围成的平面图形的面积最小4、半径为r 的球沉入水中，球的上部与水面相切，球的密度与水相同，现将球从水中取出，需作多少功？第六章定积分应用习题答案（A ）1、1）342+π，346-π 2）2ln 23- 3）21-+ee 4）2a π 5）283a π2、23a π 3、()ππ2224--e e a 4、12-π，42π 5、7128π，564π 6、3334R 7、3432- 8、a 6 9、kJ 18.0 10、3732727a kc （其中k 为比例常数）11、()kJ 5.57697 12、()kN 14373 13、取y 轴经过细直棒⎪⎪⎭⎫⎝⎛+-=2211t a aGmu F y 22t a a Gmu F x +-=λ(B)1、1）⎰-=⎪⎪⎭⎫ ⎝⎛--=pp p dy p y y p S 322316223 或()⎰⎰=⎪⎭⎫⎝⎛+-++=20229231622322pp p p dx px x p dx px px S2）⎰⎰--=⎪⎪⎭⎫⎝⎛-⎪⎭⎫⎝⎛-=pp p p p dy p y dy y p V 33322215272223πππ 2、()⎰=-=10231dx x x A ()()ππ⎰=⎪⎭⎫⎝⎛-=10222103dx x x V3、()()⎰⎰-=-+-=244222cos sin sin cos πππdx x x dx x x A()()()()()()⎰⎰=-+-=24224022cos sin sin cos πππππdx x x dx x x V4、抛物线在点⎪⎭⎫⎝⎛p p ,2处的法线方程为： p y x 23=+，以下解法同第一题2316p A = 5、MT ：x y 24-=，切线MT 与曲线()122-=x y 的交点坐标为⎪⎭⎫⎝⎛1,23，()2,3- ⎰-=⎪⎪⎭⎫ ⎝⎛---=122491224dy y y A 6、提示：设过焦点()0,a 的弦的倾角为α则弦所在直线的方程为()a x y -=αtan由()a x y -=αtan ，ax y 42=得两交点纵坐标为()()21csc 2csc 2y ctg a ctg a y =+<-=αααα所以()()dy a y yctg a A y y ⎰⎥⎦⎤⎢⎣⎡-+=2142αα ()()32222csc 34csc 4csc 4ααααa ctg a a -+=()()3232csc 34csc 4ααa a -=()32csc 38αa =因为πα<<0 当2πα=时 ()3csc α取得最小值为1所以当2πα=时过焦点的弦与抛物线ax y 42=所围成的图形面积()32csc 382απa A =⎪⎭⎫ ⎝⎛最小7、1）()()πθθθθπππ45cos 321cos 1212232302=⎥⎦⎤⎢⎣⎡++=⎰⎰d d A2）()()[]⎰⎰-=++=ππππθθθθθ22220241cos sin 21sin 21a d a d a A 8、()()⎰⎰------+=44442222165165dx xdx xV ππ()()⎰-=⎭⎬⎫⎩⎨⎧----+=4422222160165165ππdx xx9、解法同题810、提示：()32132-=x y ，32x y = 联立得交点⎪⎪⎭⎫ ⎝⎛36,2，⎪⎪⎭⎫ ⎝⎛-36,2 所求弧长()⎰+=212'12dx y s由()32132-=x y 得()yx y 2'1-=于是()()()()()1231321134222'-=--=⎪⎪⎭⎫ ⎝⎛-=x x x y x y于是得()⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛=⎥⎦⎤⎢⎣⎡-+=⎰12598123122321221dx x S(C)1、证明：此处球缺可看作由如图阴影（图222R y x =+的一部分）绕y 轴旋转而成所以()⎰⎰---==RHR RHR dy y R dy x V 222ππR HR R HR y yR ---=332ππ()[]()[]3323H R R H R R R -----=ππ⎪⎭⎫ ⎝⎛-=32H R H π2、解：()⎰-=tdx x t S 11sin sin ()⎰-=22sin sin πtdx t x S()()⎰-=tdx x t t S 1sin sin +()⎰-2sin sin πtdx t x=⎪⎭⎫ ⎝⎛≤≤-⎪⎭⎫⎝⎛-+201sin 22cos 2ππt t t t ()0cos 22'=⎪⎭⎫⎝⎛-=t t t S π，得驻点2421ππ==t t易知()()002''1''<>t S t S122max -=⎪⎭⎫ ⎝⎛=∴ππS S ，124min -=⎪⎭⎫⎝⎛=πS S3、解：设()00,y x 为曲线x y =()40≤≤x 上任一点，易得曲线于该点处的切线方程为：()00021x x x y y -=- 即0022x x y y +=得其与0=x ， 4=x 的交点分别为⎪⎭⎫ ⎝⎛2,00y ，⎪⎪⎭⎫⎝⎛+0022,4y y 于是由此切线与直线0=x ， 4=x 以及曲线x y =所围的平面图形面积为：3164222004000-+=⎪⎪⎭⎫ ⎝⎛-+=⎰x y dx x x x y S3164200-+=x x 问题即求31642-+=xx S ()40≤≤x 的最小值令022321=+=--xxS 得唯一驻点2=x 且为唯一极小值所以当2=x 时，S 最小即所求切线即为：2222+=x y 4、如图：以水中的球心为原点，上提方向作为坐标轴建立坐标系易知任意[]dx x x +,段薄片在提升过程中在水中行程为r －x ，而在水上的行程为2r －（r －x ）＝r ＋x因为求的密度与水相同，所以在水中提升过程中浮力与重力的合力为零，不做功，而在水面上提升时，做功微元为()()dx x r x r g dW +-=22π()()g r dx x r x r g dW W r r r r 42234ππ⎰⎰--=+-==。

第5章定积分及其应用单元自测题

1
f ( x )dx
0
1
xdx
0
1 0
x
2
1 0
f
(
x
)dx
dx
1 x2 1
1 x 2 dx
1
f ( x )dx
20
0
0
1 1 x3 1 23 0
1 f ( x )dx 1 1
0
23
1
0 f ( x )dx 。
得 2 1 f ( x )dx 1 1 f ( x )dx 3 。故，f ( x ) x 3 x 2 。
六、定积分的应用 1、微元法
2、平面图形的面积 (1)直角坐标情形 (2)极坐标情形
3、体积 (1)平行截面面积为已知的立体体积 (2)旋转体体积
第五章定积分及其应用自测题
一、填空题：
1．
x4 sin xdx
0。
分析设 f ( x ) x4 sin x ，则
f ( x ) ( x )4 sin( x ) x4 sin x f ( x ) ，
a
a
当f ( x)是偶函数时， f ( x)dx 2 f ( x)dx.
a
0
二、积分上限的函数及其导数
x
1、定义：( x) f (t )dt (a b) a
2、导数：
d
x
x
f (t)dt ( f (t)dt) f ( x)
dx a
a
第五章定积分及其应用自测题
d
u( x)
上的表达式为（ A ）。
2x, 0 x 1
2 x ,
（A）( x ) x2 1,
1 x 2 ；（B）( x )
x
2

定积分及应用

例9 求
∫
2 0
x 2 − 4 x + 4dx
2
解
∫
2
0
x − 4x + 4dx = ∫
2
x
0
1 (x − 2) dx = ∫ x − 2 dx = ∫ (2 − x)dx = (2x − x2 ) = 2 0 0 2 0
2 2 2
2
例 10
∫ t (t + sin t )dt 求 lim ∫ t dt
）
此题属于
0 型未定式的极限，由洛必达法则有 0
原式= lim
sin x 2 1 = x →0 3x 2 3
例6
∫
a
−a
x sin 8 xdx = (
)
解例7
因 x sin 8 x 为奇函数且积分区间[-a,a]关于原点对称，故
∫
a
−a
x sin 8 xdx =0
d x 1 + t 4 dt = （ dx ∫ 0
0
a2
1 2 t
π
0
dt = ∫ tf (t )dt = ∫ xf ( x)dx
π
例2
设
∫
x 0
f ( t )dt = x sin x ，则 f（x）=（
(B)sinx-xcosx，
x 0
） (D) －（sinx+xcosx）
(A)sinx+xcosx，解例3 由
(C)xcosx-sinx，
∫
x 0
f (t )dt = x sin x ，则 ( ∫ f (t )dt )′ = ( x sin x)′ ，即 f（x）=sinx+xcosx，应选 B。

第六章定积分及应用习题

第六章定积分及应用一、填空题 1．250cos sin x xdx π=⎰_______2．当0b ≠时，1ln 0bx dx =⎰，则b =_______3．325425sin 21x xdx x x -=++⎰_______ 4．设()f x 为连续函数则[]2()()a ax f x f x dx ---=⎰.5.() 122 1sin 5x x x dx -+=⎰6. 已知=+=⎰)(,)(2)(1x f dx x f x x f 则_______7．若===⎰⎰⎰2121)(,2)(,3)(dx x f dx x f dx x f 则8．利用定积分性质比较下列积分的大小： dx e I x ⎰=11 dx x I ⎰+=12)1(，则 _______33234ln ,(ln )eeI xdx I x dx ==⎰⎰，则_______9. 估计定积分3013sin dx xπ+⎰的取值范围_______10. 设()f x 可导，且lim ()1x f x →+∞=，则23lim sin()x xx t f t dt t+→+∞=⎰11. 设23()1x dxg x x =+⎰，则(1)g ''= _______ 12． 20cos limxx t dt x→=⎰113． arctan ba d x dx dx=⎰ . 14．求曲线2sin xty dt t π=⎰在2x π=处的切线方程，_______ 15．设2221()x t t xF x e dt e dt -+⎰⎰＝，则()F x '=_______16. 2()x t xf x e dt -⎰＝，则()f x '=_______17．⎰=-xdt x t dx d 0)cos(_______ 18．已知当0→x时，⎰''-=xdt t f t x x F 022)()()(的导数)(x F '与2x 为等价无穷小，则)0(f ''= _______19.211dx x +∞-∞=+⎰_______二、选择题1.)(x f 在],[b a 上连续是⎰badx x f )(存在的（）.（A ）必要条件（B ）充分条件（C ）充要条件（D ）既不充分也不必要 2. ⎰⎰==2122211)(ln ,ln dx x I dx x I 设，则（）（A ） 21I I < （B ） 21I I > （C ） 21I I = （D ）无法比较3.设 dx x x x P dx x x N xdx x x M )cos sin (,)cos (sin ,cos 1sin 4223242254222⎰⎰⎰----=+=+=ππππππ （）（A ） M P N << （B ） N P M << （C ） P M N << （D ）N M P << 4. 22222lim 12n n n n n n n n →∞⎛⎫+++=⎪+++⎝⎭ ( ) （A ）0；（B ）12；（C ）4π；（D ）2π5.⎰+-=+ππdx x x e x )sin (2cos （）3π.A 33π2.B 3 32π2e .C 3-1+ 32πe-e .D 3-1+ 6.203sin lim xx t dt x →⎰=( )（A ）0；（B ）1；（C ）13；（D ）∞ . 7. 下列结果正确的是（）（A ）22s i n )s i n (a dx x da d b a =⎰ （B ） 22s i n )s i n (b dx x db d ba =⎰ （C ）22s i n )s i n (x dx x dx d b a=⎰ （D ）22sin 2)sin (x x dx x dx d b a =⎰ 8. 设)(x f 为已知函数,⎰>>=t st s dx tx f tI 0,0,0)(，其中则I 的值依赖于（）（A ）依赖于s 和t ；（B ）依赖于s ，x t ,；（C ）依赖于x 和t ，不依赖于s ；（D ）依赖于s ，不依赖于t 。

定积分及应用题库A

定积分的应用题

不定积分+定积分及其应用习题附带答案

高考数学定积分应用选择题

定积分应用练习题

最新定积分的几何应用例题与习题(学生用)

(完整版)定积分应用题附答案

第6章定积分的应用习题集及答案

数学选修2-2定积分的简单应用练习题含答案

11-12学年高中数学 1.7 定积分的简单应用同步练习 新人教A版选修2-2

五、定积分及其应用

高等数学(定积分的应用)习题及解答

高考数学定积分应用选择题

(完整版)§定积分的应用习题与答案

第5章定积分及其应用单元自测题

定积分及应用

第六章 定积分及应用习题

11-12学年高中数学 1.7 定积分的简单应用同步练习新人教A版选修2-2

第六章定积分及应用习题