坐标转换之计算公式
84坐标转平面坐标公式

84坐标转平面坐标公式在平面直角坐标系中,一点的坐标表示为(x,y),其中x表示在x轴上的距离,y表示在y轴上的距离。
而在三维空间中,我们需要一个额外的坐标来表示点的位置,即z轴坐标。
为了将三维坐标转换为平面坐标,我们可以使用投影的概念。
在投影中,我们可以将一个三维点投影到一个平面上,从而得到平面坐标。
当我们想要将一个三维点投影到 xy 平面上时,我们可以忽略 z 坐标,即将 z 坐标设为 0。
这样,我们就得到了 x 和 y 坐标。
所以,可以使用以下公式将三维坐标转换为平面坐标:(x,y,z)->(x,y)例如,假设有一个三维点 P(3, 4, 5)。
如果我们想要将其投影到 xy 平面上,我们可以忽略 z 坐标,得到平面坐标为 (3, 4)。
同样地,如果我们想要将一个平面点转换为三维坐标,我们可以将其z坐标设为0。
所以,可以使用以下公式将平面点转换为三维坐标:(x,y)->(x,y,0)例如,假设有一个平面点Q(2,6)。
如果我们想要将其转换为三维坐标,我们可以将其z坐标设为0,得到三维坐标为(2,6,0)。
这种方式是一种简单且常用的将三维坐标转换为平面坐标的方法。
在实际应用中,还有其他的方式可以进行坐标转换,例如使用矩阵变换等方法。
总结起来,三维坐标与平面坐标之间的转换可以通过将z坐标设为0或忽略z坐标来实现。
这样可以得到一个简单的投影关系,将三维点投影到平面上,或者将平面点转换为三维坐标。
需要注意的是,在进行坐标转换时,要确保选择的平面为适合要求的平面,以避免产生误差或计算错误。
希望以上内容能够帮助你理解三维坐标与平面坐标之间的转换公式。
如有需要,请随时追问。
经纬度换算公式

经纬度换算公式
经纬度换算公式又称经纬度转换公式,是从一个地名到另一个地
名的经纬度之间的转换计算方法。
它是由两个相关的算术公式构成的。
这些公式可以用来将地球上任何一个地名的经纬度坐标,转换为另一
个地名的经纬度坐标。
经纬度换算公式通常只有两部分,分别是换算经度公式和换算纬
度公式。
换算经度公式类似于“x = a * x”的形式,其中“x”表示
要转换的经度坐标,“a”代表转换系数,以千米单位表示。
换算纬度
公式则类似“y = b * y”的形式,其中“y”表示要转换的纬度坐标,“b”代表转换系数,以千米单位表示。
经纬度换算公式是一种根据地点间距离来确定经纬度坐标之间的
转换关系,而不是根据地名来确定。
经纬度换算公式也可以用来计算
相对位置,例如在全球定位系统(GPS)中。
经纬度换算公式的最大优
势在于它消除了地名的影响,可以更为精确地使用经纬度坐标作为查
找位置的标准。
因此,经纬度换算公式是从一个地名到另一个地名的经纬度之间
的转换算法,其优势在于它消除了地名的影响,可以更准确地进行定位。
另外,经纬度换算公式还可以用来计算全球定位系统中相对位置。
对数坐标与普通坐标的转换计算

对数坐标与普通坐标的转换计算对数坐标与普通坐标是数学中常见的两种坐标系统。
它们在不同的场景中都有着各自的优势和适用性。
本文将介绍对数坐标与普通坐标的转换计算方法。
普通坐标系统是我们通常使用的坐标系统,也称为直角坐标系统。
在这个坐标系统中,任意点可以表示为一个有序数对(x, y),其中x表示横坐标,y表示纵坐标。
这种表示方法通过两个数值的大小和正负关系来确定点的位置。
而对数坐标系统则是以对数函数为基础的坐标系统。
在对数坐标系统中,数值的大小代表了对数函数的值,而点的位置则通过数值的指数来表示。
对数坐标系统常用于表示非线性关系,可以将数据的广度差异较大的部分更好地展示出来。
在对数坐标系统中,横坐标通常是以对数形式表示的。
常见的对数坐标包括常用对数坐标(以10为底)、自然对数坐标(以e为底)等。
对于对数坐标与普通坐标之间的转换,下面将分别介绍两种情况的计算方法:1.对数坐标转换为普通坐标:对数坐标转换为普通坐标时,我们需要知道坐标轴上的起始点和单位长度。
以常用对数坐标为例,起始点为(0, 0),单位长度为1,指数表示坐标轴上的位置。
假设需要将对数坐标(x, y)转换为普通坐标(X, Y),计算公式如下:X = 10^xY = 10^y例如,对于对数坐标(2, 3):X = 10^2 = 100Y = 10^3 = 1000则对应的普通坐标为(100, 1000)。
2.普通坐标转换为对数坐标:普通坐标转换为对数坐标时,我们需要知道坐标轴上的起始点和单位长度。
以常用对数坐标为例,起始点为(0, 0),单位长度为1,指数表示坐标轴上的位置。
假设需要将普通坐标(X, Y)转换为对数坐标(x, y),计算公式如下:x = log10(X)y = log10(Y)例如,对于普通坐标(100, 1000):x = log10(100) = 2y = log10(1000) = 3则对应的对数坐标为(2, 3)。
以上就是对数坐标与普通坐标之间的转换计算方法。
2000坐标值转经纬度 公式

2000坐标值转经纬度公式从2000坐标值转换为经纬度的公式是什么?在地理信息系统中,经纬度是用来表示地球上的位置的坐标系统。
经度用来表示位置在东西方向上的偏移,纬度用来表示位置在南北方向上的偏移。
在转换2000坐标值为经纬度时,我们可以使用以下公式:纬度 = arctan( exp(y / R) ) - π/4经度 = x / R其中,x和y代表2000坐标值,R是地球的半径,π是圆周率。
这个公式的原理是将2000坐标值转换为直角坐标系下的点,然后通过反三角函数计算出对应的经纬度。
具体解释如下:1. 首先,我们需要确定地球的半径R。
地球的平均半径约为6371公里,我们可以使用这个数值作为R。
2. 将2000坐标值的x除以R,得到以地球半径为单位的经度。
3. 将2000坐标值的y除以R,然后使用指数函数和反三角函数计算出纬度。
这是因为纬度的取值范围是[-π/2, π/2],而y的取值范围是[-R * π/2, R * π/2]。
使用指数函数可以将y的取值范围映射到[-1, 1],然后使用反三角函数将值映射到[-π/2, π/2]。
4. 最后,我们得到的经纬度是以弧度为单位的,如果需要将其转换为度数,可以将其乘以180/π。
使用这个公式,我们可以将2000坐标值转换为对应的经纬度。
这在地理信息系统和导航系统中非常有用,可以帮助我们准确定位和导航。
不过需要注意的是,这个公式是在假设地球是一个完美的球体的情况下成立的。
实际上,地球的形状是稍微扁平的,所以在进行精确的坐标转换时,可能需要考虑地球的椭球形状和地理坐标系统的变换。
总结起来,通过使用上述公式,我们可以将2000坐标值转换为对应的经纬度。
这个公式是在假设地球是一个完美的球体的情况下成立的,对于一般的位置定位和导航应用已经足够准确。
但是在进行精确的坐标转换时,可能需要考虑地球的椭球形状和地理坐标系统的变换。
希望这篇文章能帮助你理解2000坐标值转换为经纬度的公式。
坐标系转换步骤以及公式

一、各坐标系下椭球参数WGS84大地参数北京54大地参数西安80大地参数参考椭球体:WGS 84 长半轴:6378137短半轴:6356752.3142 扁率:1/298.257224 参考椭球体:Krasovsky_1940长半轴:6378245短半轴:6356863.0188扁率:1/298.3参考椭球体:IAG 75长半轴:6378140短半轴:6356755.2882扁率:1/298.257000二、WGS84转北京54一般步骤(转80一样,只是椭球参数不同)前期工作:收集测区高等级控制点资料。
在应用手持GPS接收机观测的区域内找出三个以上分布均匀的等级点(精度越高越好)或GPS“B”级网网点,点位最好是周围无电磁波干扰,视野开阔,卫星信号强。
并到测绘管理部门抄取这些点的54北京坐标系的高斯平面直角坐标(x、y),大地经纬度(B、L),高程h ,高程异常值ξ和WGS-84坐标系的大地经纬度(B、L),大地高H。
如果没有收集到WGS-84下的大地坐标,则直接用手持GPS测定已知点B、L、H值。
转换步骤:1、把从GPS中接收到84坐标系下的大地坐标(经纬度高程B、L, H,其中B为纬度,L为经度,H为高程),使用84坐标系的椭球参数转换为84坐标系下的地心直角坐标(空间坐标):式中,N为法线长度,为椭球长半径,b为椭球短半径,为第一偏心率。
2、使用七参数转换为54坐标系下的地心直角坐标(x,y,z):x = △x + k*X- β*Z+ γ*Y+ Xy = △y + k*Y + α*Z - γ*X + Yz = △z + k*Z - α*Y + β*X + Z其中,△x,△y,△z为三个坐标方向的平移参数;α,β,γ为三个方向的旋转角参数;k为尺度参数。
(采用收集到的控制点计算转换参数,并需要验证参数)在小范围内可使用七参数的特殊形式即三参数,即k、α、β、γ都等于0,变成:x = △x+ Xy = △y+ Yz = △z + Z3、根据54下的椭球参数,将第二步得到的地心坐标转换为大地坐标(B54,L54,H54)计算B时要采用迭代,推荐迭代算法为:4、根据工程需要以及各种投影(如高斯克吕格)规则进行投影得到对应的投影坐标,即平面直角坐标。
测量坐标转换建筑坐标公式

测量坐标转换建筑坐标公式引言在建筑测量过程中,坐标转换是一项重要的工作。
它涉及将不同坐标系下的位置信息进行转换,以满足具体测量需求。
本文将介绍测量坐标转换中常用的建筑坐标公式,包括平面坐标转换、高程坐标转换以及三维坐标转换。
1. 平面坐标转换平面坐标转换主要涉及将不同测量坐标系下的平面坐标互相转换。
常见的平面坐标系有国家大地坐标系、UTM坐标系等。
建筑测量中常用的公式如下:1.1 国家大地坐标系转化为局部坐标系国家大地坐标系是基于地球的椭球体模型建立的坐标系。
当需要将国家大地坐标系转换为局部坐标系时,可以使用以下公式进行计算:X_Local = X_Geo - X_OriginY_Local = Y_Geo - Y_Origin其中,X_Local和Y_Local表示转换后的局部坐标,X_Geo和Y_Geo表示国家大地坐标系下的坐标,X_Origin和Y_Origin表示局部坐标系的原点坐标。
1.2 UTM坐标系转化为局部坐标系UTM坐标系是一种经纬度的投影坐标系,以地区为单位进行划分。
当需要将UTM坐标系转换为局部坐标系时,可以使用以下公式进行计算:X_Local = X_UTM - X_OriginY_Local = Y_UTM - Y_Origin其中,X_Local和Y_Local表示转换后的局部坐标,X_UTM和Y_UTM表示UTM坐标系下的坐标,X_Origin和Y_Origin表示局部坐标系的原点坐标。
2. 高程坐标转换高程坐标转换主要涉及将不同坐标系下的高程信息互相转换。
常见的高程坐标系有大地水准面、局部高程坐标系等。
建筑测量中常用的公式如下:2.1 大地水准面转化为局部高程坐标系大地水准面是以地球引力为基准的坐标系,用于表示地球表面高程。
当需要将大地水准面转换为局部高程坐标系时,可以使用以下公式进行计算:H_Local = H_Geo - H_Origin其中,H_Local表示转换后的局部高程坐标,H_Geo表示大地水准面下的高程,H_Origin表示局部高程坐标系的起始高程。
EXCEL公式进行经纬度与XY坐标的相互转换

EXCEL公式进行经纬度与XY坐标的相互转换在Excel中,我们可以使用一些公式来进行经纬度与XY坐标的相互
转换。
这对于地理信息系统(GIS)或地理定位系统(GPS)相关的数据处
理非常有用。
下面我们将介绍两种方法,分别是将经纬度转换为XY坐标
和将XY坐标转换为经纬度。
1.经纬度转换为XY坐标:
在Excel中,我们可以使用以下公式将经纬度转换为XY坐标:
XY坐标=(经度-经度原点)*2*PI(*R*COS(纬度原点)/360
其中,经度原点和纬度原点是你选择的参考点的经纬度,R是地球的
半径(通常为6371千米)。
2.XY坐标转换为经纬度:
在Excel中,我们可以使用以下公式将XY坐标转换为经纬度:
经度=经度原点+(XY坐标/(2*PI(*R*COS(纬度原点)/360))
纬度=纬度原点+(XY坐标/(2*PI(*R/360))
在上述公式中,需要注意的是,使用的经纬度应采用十进制度数格式。
这些公式可以帮助我们在Excel中进行经纬度与XY坐标的相互转换。
根据具体的数据和参考点的经纬度,我们可以应用相应的公式进行计算。
这对于处理地理信息数据非常有用,特别是在需要将数据在GIS或GPS中
进行处理和显示时。
平面坐标系之间转换计算
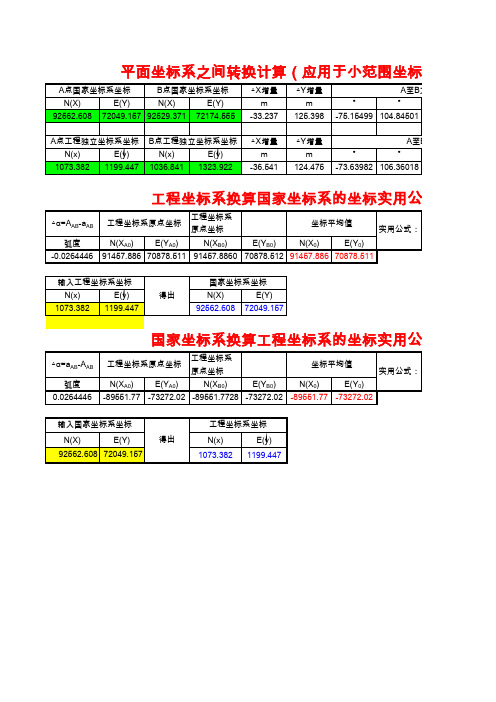
A点国家坐标系坐标 N(X) 92562.608 E(Y) B点国家坐标系坐标 N(X) E(Y) 72174.555 △X增量 m -33.237 △X增量 m -36.541 △Y增量 m 125.398 △Y增量 m 124.475 ° ° ° A至B方位角( ° -75.15499 104.84501 A至B -73.63982 106.36018 72049.157 92529.371
输入工程坐标系坐标 N(x) 1073.382 E(y) 1199.447 得出
国家坐标系坐标 N(X) 92562.608 E(Y) 72049.157
国家坐标系换算工程坐标系的坐标实用公式
△α=aAB-AAB 弧度 0.0264446 工程坐标系原点坐标 N(XA0) E(YA0) 工程坐标系原点坐标 N(XB0) E(YB0) 坐标平均值 N(X0) E(Y0) 实用公式: -89551.77 -73272.02 -89551.7728 -73272.02 -89551.77 -73272.02 工程坐标系坐标 得出 N(x) 1073.382 E(y) 1199.447
标实用公式
xP=Xp*COS(△α)-Y*SIN(△α)+X0 yP=Xp*SIN(△α)+Y*COS(△α)+Y0
A点工程独立坐标系坐标 N(x) 1073.382 E(y) 1199.441 E(y) 1323.922
工程坐标系换算国家坐标系的坐标实用公式
△α=AAB-aAB 弧度 -0.0264446 工程坐标系原点坐标 N(XA0) E(YA0) 工程坐标系原点坐标 N(XB0) E(YB0) 坐标平均值 N(X0) E(Y0) 实用公式: 91457.886 70878.511 91457.8860 70878.512 91457.886 70878.511
极坐标方程与直角坐标方程之间的转换公式

极坐标方程与直角坐标方程之间的转换公式引言在数学中,极坐标系和直角坐标系是常用的两种坐标系。
它们分别通过极坐标方程和直角坐标方程来描述平面上的点的位置。
而在实际问题中,有时我们需要在两个坐标系之间进行转换。
本文将介绍极坐标方程和直角坐标方程之间的转换公式。
极坐标系的定义与公式极坐标系是通过一个有向线段和一个非负实数来描述平面上的点的位置。
对于极坐标系中的一个点 P,其坐标用(r, θ) 表示,其中 r 表示点 P 到原点 O 的距离,θ 表示从 x 轴正半轴到 OP 的角度,逆时针方向为正。
在极坐标系中,点 P 的直角坐标可以通过以下公式计算得到: - x = r * cos(θ) -y = r * sin(θ)直角坐标系的定义与公式直角坐标系是在平面上通过两个垂直坐标轴来描述点的位置。
对于直角坐标系中的一个点 Q,其坐标用 (x, y) 表示,其中 x 表示点 Q 在 x 轴上的投影,y 表示点Q 在 y 轴上的投影。
在直角坐标系中,点 Q 的极坐标可以通过以下公式计算得到: - r = √(x^2 +y^2) - θ = arctan(y / x)极坐标方程到直角坐标方程的转换已知某个点 P 在极坐标系中的坐标为(r, θ),我们可以通过前述的公式将其转换为直角坐标系中的坐标 (x, y): - x = r * cos(θ) - y = r * sin(θ)直角坐标方程到极坐标方程的转换对于直角坐标系中的一个点 Q,其坐标为 (x, y),我们可以通过前述的公式将其转换为极坐标系中的坐标(r, θ): - r = √(x^2 + y^2) - θ = arctan(y / x)需要注意的是,在进行直角坐标方程到极坐标方程的转换时,要特别注意点 Q的坐标 (x, y) 是否在特殊情况下,例如 x = 0 或 y = 0,此时需要额外讨论。
总结极坐标方程和直角坐标方程是描述平面上点位置的两种常用形式。
经纬度转换公式范文

经纬度转换公式范文经纬度是用来描述地球上其中一点位置的坐标系统。
一般来说,经度用来表示东西方向的位置,纬度用来表示南北方向的位置。
经度的取值范围是-180到180度,纬度的取值范围是-90到90度。
经纬度转换公式可以用来在不同坐标系统之间进行坐标转换,比如将经纬度坐标转换为其他坐标系的坐标,或者将其他坐标系的坐标转换为经纬度坐标。
下面介绍几种常见的经纬度转换公式:1.经纬度转换为直角坐标系坐标:经度转换为直角坐标系坐标的公式为:x = R*cos(纬度)*cos(经度)y = R*cos(纬度)*sin(经度)z = R*sin(纬度)其中,R是地球的平均半径。
2.直角坐标系坐标转换为经纬度:直角坐标系坐标转换为经纬度的公式为:经度 = atan2(y, x)纬度 = atan2(z, sqrt(x^2 + y^2))3.经纬度转换为UTM坐标:UTM(Universal Transverse Mercator)坐标是一种具有划分区域的平面坐标系统。
首先,根据经度的正负确定所处的UTM带;然后,计算起始经度和中央经度差值,根据差值和中央经度确定UTM 带原点;最后,根据地球椭球体参数和转换公式,将经纬度转换为UTM坐标。
4.UTM坐标转换为经纬度:UTM坐标转换为经纬度的公式也较为复杂,需要进行以下计算:首先,根据UTM带的中央经度确定UTM带原点;然后,根据UTM坐标和UTM带原点,计算经度差值;最后,根据地球椭球体参数和转换公式,将UTM坐标转换为经纬度。
5.经纬度转换为高斯克吕格坐标:高斯克吕格(Gauss-Krüger)坐标是一种常用的平面坐标系统,常用于全球的测量和地理信息系统。
首先,根据经度的正负确定所处的高斯带;然后,根据经度差值和高斯带的中央经度,计算高斯带原点;最后,根据地球椭球体参数和高斯投影公式,将经纬度转换为高斯克吕格坐标。
这些是常见的经纬度转换公式,根据具体需求和坐标系统,可以选择不同的公式进行转换。
坐标转换四参数解算

坐标转换四参数解算
分享⼀个前段时间项⽬中遇到的⼀个姿势点,就是求解平⾯坐标四参数转换的转换参数;当时学渣⼩编还是花了些时间研究,其实原理很Easy,过程也很Easy,理解起来更Easy。
废话不多说,下⾯开整
已知:
转换前坐标点(x1,y1),转换后坐标点(x2,y2);
⼆维四参数转换模型:
求解:平移参数、旋转参数、尺度参数。
开始求解:
Step1:为了简化计算公式,我们先设定:
以上转换模型公式表达为:
Step2:经过矩阵运算变化,将我们要求解的参数变换到同⼀个矩阵中:
Step3:利⽤间接平差法得到以下计算公式:
Step4:计算旋转参数和尺度参数:
⾄此,我们要求解的参数已经全部计算出来了,很Easy吧。
当然实际⽣产中,我们的坐标是坐标点对,可以结合上述计算公式利⽤最⼩⼆乘法来进⾏计算,同时也可以计算误差。
施工坐标换算公式大全

施工坐标换算公式大全1. 引言在施工过程中,经常需要进行不同坐标系之间的换算。
同时,施工坐标换算也是一项重要的技术,它能够保证施工工程的精确度和高效性。
本文将介绍施工中常用的坐标系,并提供了一些常用的施工坐标换算公式。
2. 坐标系介绍2.1. 大地坐标系(WGS84)大地坐标系是地理学中使用最广泛的坐标系,它基于地球椭球体建立,用经度、纬度和高程三个量来表示一个点的位置。
大地坐标系以世界大地测量系统第1984年修订版(World Geodetic System 1984, WGS84)为基础,是全球定位系统(GPS)使用的基准坐标系。
2.2. 投影坐标系(UTM)投影坐标系是将地球表面的经纬度坐标用X、Y坐标来表示的坐标系。
其中通用横轴墨卡托投影(Universal Transverse Mercator, UTM)是最常用的投影坐标系之一,主要用于地图绘制和工程测量。
3. 施工坐标换算公式3.1. 大地坐标系与投影坐标系之间的换算大地坐标系与投影坐标系之间的换算,常用的方法是通过坐标转换公式进行计算。
以下是大地坐标系(WGS84)与投影坐标系(UTM)之间的换算公式:•大地坐标系转投影坐标系公式:–X = f(L, B, H) - X0–Y = f(L, B, H) - Y0•投影坐标系转大地坐标系公式:–L = f(X + X0, Y + Y0, H)– B = f(X + X0, Y + Y0, H)–H = f(X + X0, Y + Y0, Z0)其中,X、Y表示投影坐标系下的坐标,L、B表示大地坐标系下的经度和纬度,H表示高程,X0、Y0表示投影坐标系的原点。
3.2. 坐标系之间的高程换算在施工过程中,经常需要进行不同坐标系之间的高程换算。
以下是常用的坐标系之间的高程换算公式:•大地水准面高程与正高差的换算公式:–H = N + h其中,H表示大地水准面高程,N表示大地法线高,h表示正高差。
计算器极坐标与直角坐标的互化

计算器极坐标与直角坐标的互化极坐标与直角坐标是两种常见的坐标系统,用于描述平面上的点的位置,它们可以互相转换。
本文将介绍极坐标和直角坐标的互化方法以及相关的计算公式和参考内容。
一、极坐标转换为直角坐标极坐标是以点到某个固定点的距离(称为极径)和与某条固定线段的夹角(称为极角)来描述点的位置。
我们可以通过以下公式将极坐标转换为直角坐标:x = r * cos(θ)y = r * sin(θ)其中,(x, y)为直角坐标系下的坐标,r为点到原点的距离,θ为与x轴正半轴的夹角(弧度制)。
参考内容:1. 参考教材《高等数学》(同济大学数学系编著)第三章“极坐标与空间直角坐标系”。
该教材详细介绍了极坐标与直角坐标之间的转换关系,包括公式推导和实例计算。
2. 网上教学视频:许多在线教育平台和视频分享网站,如YouTube、Bilibili等,都有关于极坐标与直角坐标转换的教学视频。
这些视频通常具有形象生动的动画和示例,能够更直观地展示转换过程。
3. 网上教学文档:一些知名学术网站和教育网站,如维基百科、百度百科、中国大学MOOC等,提供了关于极坐标和直角坐标转换的详细介绍和计算公式。
二、直角坐标转换为极坐标直角坐标是以点在x轴和y轴上的投影长度表示点的位置。
我们可以通过以下公式将直角坐标转换为极坐标:r = sqrt(x^2 + y^2)θ = arctan(y / x)其中,r为与原点的距离,θ为与x轴正半轴的夹角,arctan()是反正切函数。
参考内容:1. 同上,《高等数学》第三章中也包含了直角坐标转换为极坐标的公式和实例计算。
2. 网上教学视频:同样,可以在各大在线教育平台和视频分享网站上搜索直角坐标转换为极坐标的教学视频,以获得直观的展示和示例。
3. 数学类论坛和问答平台:可以参考一些数学类论坛和问答平台,如知乎、百度知道、数学之都等,查找关于直角坐标转换为极坐标的相关问题和解答。
总之,对于极坐标和直角坐标的互化,可以参考教材、教学视频、网络教学文档以及数学类论坛和问答平台。
直角坐标系和极坐标系的转化公式

直角坐标系和极坐标系的转化公式直角坐标系和极坐标系是数学中常用的两种坐标系。
它们分别用于描述平面上的点的位置,并且可以通过一定的转化公式进行相互转化。
本文将介绍直角坐标系和极坐标系的定义以及它们之间的转化公式。
直角坐标系直角坐标系,也称为笛卡尔坐标系,是通过垂直的x轴和y轴构成的平面坐标系。
直角坐标系中,每个点的位置都可以用一个有序对(x, y)来表示,其中x是点到y轴的距离,y是点到x轴的距离。
x轴和y轴的交点称为原点,原点的坐标为(0, 0)。
在直角坐标系中,任意一个点P的坐标可以通过计算P到x轴和y轴的距离得到。
假设P的坐标为(x, y),那么点P到x轴的距离为y,点P到y轴的距离为x。
极坐标系极坐标系是通过一个原点O和一个极轴构成的平面坐标系。
极坐标系中,每个点的位置都可以用一个有序对(r, θ)来表示,其中r是点到原点O的距离,θ是点到极轴正向的角度,通常以弧度表示。
在极坐标系中,角度θ的取值范围通常是[0, 2π)或[-π, π]。
若θ为正,则表示从极轴正向逆时针旋转的角度;若θ为负,则表示从极轴正向顺时针旋转的角度。
当θ=0时,点位于极轴上;当θ=π/2时,点位于极轴正向与x轴正向之间的直线上。
直角坐标系到极坐标系的转化从直角坐标系到极坐标系的转化,需要根据直角坐标(x, y)计算出极坐标(r, θ)。
根据勾股定理,我们可以得到公式如下:r = √(x^2 + y^2)在计算r时,需要注意r的正负号。
若(x, y)位于第一、二象限,则r为正;若(x, y)位于第三、四象限,则r为负。
计算角度θ的公式如下:θ = arctan(y / x)其中,arctan函数为反正切函数,用于计算两个直角边之比的反正切值。
在计算θ时,需要考虑x的值。
若x>0,则θ取值在(-π/2, π/2)范围内;若x<0,则θ取值在(-π, -π/2)和(π/2, π)范围内;若x=0,则θ的值需要额外考虑y的值来确定。
坐标转换之计算公式

坐标转换之计算公式、参心大地坐标与参心空间直角坐标转换1名词解释:A :参心空间直角坐标系:Y 轴在赤道面上与 X 轴垂直,构成右手直角坐标系 0-XYZ ;2参心大地坐标转换为参心空间直角坐标:X =(N +H )*cosB*cosL Y = ( N + H ) * cosB * sin L Z =[N*(1—e 2) +H]*sin B J公式中,N 为椭球面卯酉圈的曲率半径, e 为椭球的第一偏心率,a 、b 椭球的长短半径,f 椭球扁率,W 为第一辅助系数J a 2 -b 2亠 72* f -1 e = -------- 或 e = ----------a f3参心空间直角坐标转换参心大地坐标a) 以参心0为坐标原点;b) Z 轴与参考椭球的短轴(旋转轴)相重合; C ) X 轴与起始子午面和赤道的交线重合;d) e) 地面点P 的点位用(X ,Y ,Z )表示; B :参心大地坐标系:a) 以参考椭球的中心为坐标原点,椭球的短轴与参考椭球旋转轴重合;b) 大地纬度B :以过地面点的椭球法线与椭球赤道面的夹角为大地纬度C) 大地经度L:以过地面点的椭球子午面与起始子午面之间的夹角为大地经度d) 大地高H :地面点沿椭球法线至椭球面的距离为大地高 H ;e) 地面点的点位用(B ,L ,H )表示。
2 2-e * sin 2 BYL =arcta n㈠XB=arctan( _______J(X2+Y2)* N *(1-e2) + HcosB高斯投影及高斯直角坐标系1、高斯投影概述中^^子午«、Q高斯-克吕格投影的条件:1.是正形投影;2.中央子午线不变形高斯投影的性质: 1.投影后角度不变;2.长度比与点位有关,与方向无关3.离中央子午线越远变形越大为控制投影后的长度变形,采用分带投影的方法。
常用3度带或6度带分带,城市或工程控制网坐标可采用不按 3度带中央子午线的任意带。
2、高斯投影正算公式:N 2 N 3 2 ** 2 **4 4x=X+—sin B cos Bl + ——sin BcosB(5-t +9* +4") l2 24+ —sin Bcos5 B(61 —58t2 +t4)|6720y =N cosBl +W COS3B(1 —t2T2)|36唱cosTim58^53、高斯投影反算公式:2X 12 2〔 y1 (1+2t 2+口2)丄6(N f 丿1+-(5+2&2+2硏+6"2+时訂表1 BJ54与 WGS84基准参数榊球体氏却轴a 〔米)叙T 轴b (米】Kr<ssscivsky 〔北京 5^ 采ni)637S2456356863. 01881 ZiC- 75 (西城 8U f Hj 36J7S1 IG 6336755.肥 IG5 816378137O3.jG753 u1 12十丄(61+90t 2 +45t 4 丨- 360 "丿cosB f 参考椭球体 长半轴 短半轴 扁率BJ54基准参数 Krasovsky_1940 6378245 6356863.0188 298.3WGS84基准参数WGS 84 6378137 6356752.3142 298.257224附2高斯正反算参数pi =0.0174532925 探※0.0174532925199133 //n长半轴A二6378245.0;扁申f=l-0 298. 3; //54年北京坐标系参数长半轴泸6378140.0; M率匸1/29& 257: //80邙西安坐标系参数长半轴a=6378137m;f=l:298. 257223563. /9GS・8芒加杯系x=E|+ sin B CQS B-严+ —^sin B cos' 5(5 -『+ 9h + 4?/)严」2//2 2 计J '"+ —~- sin B cos' 5(61-58?+Z720Q"y = £gsB・r + -^^cos' B(1 一尸 + 〃2)严,p" 6Q"3 / + 12, "55(5 — 18尸 + 严+147/2 -587/2尸)严t = tanB,Tf = cos^ B2、高斯投影坐标反算公式:x.y^B. /满足以下三个条件:①左坐标轴投影后为中央子午线是投影的对称轴;②X坐标轴投彩后长度不变;③投影具有正形性质,即正形投影条件。
旋转坐标转换公式

旋转坐标转换公式在数学和计算机图形学领域,旋转是一种常见的变换操作。
通过旋转,我们可以改变对象在平面或空间中的位置和方向。
在进行旋转操作时,需要使用旋转矩阵来进行坐标转换。
本文将介绍旋转坐标转换的公式及其应用。
二维空间的旋转坐标转换在二维空间中,我们通常使用逆时针旋转为正方向的方式进行坐标转换。
假设一个点P在二维直角坐标系中的坐标为(x,y),我们希望将这个点绕原点O逆时针旋转θ角度,得到新的坐标P’(x’,y’)。
点P经过旋转之后,新的坐标可以通过以下公式计算得出:x’ = x * cos(θ) - y * sin(θ) y’ = x * sin(θ) + y * cos(θ)其中,θ为旋转角度,cos(θ)和sin(θ)分别代表旋转角度的余弦和正弦值。
三维空间的旋转坐标转换在三维空间中,我们同样使用逆时针旋转为正方向的方式进行坐标转换。
假设一个点P在三维直角坐标系中的坐标为(x,y,z),我们希望将这个点绕坐标轴进行旋转,得到新的坐标P’(x’,y’,z’)。
点P经过旋转之后,新的坐标可以通过旋转矩阵的运算得到:x' = x * cos(θ) - y * sin(θ)y' = x * sin(θ) + y * cos(θ)z' = z其中,θ为旋转角度,cos(θ)和sin(θ)分别代表旋转角度的余弦和正弦值。
旋转坐标转换的应用旋转坐标转换在计算机图形学、游戏开发等领域有着广泛的应用。
通过旋转坐标转换,我们可以实现物体的旋转、变换和动画效果。
在3D建模软件中,旋转坐标转换可以用来控制物体的姿态和方向,使得模型呈现出真实的效果。
此外,旋转坐标转换也可以用于机器人运动学中。
通过旋转坐标转换,我们可以计算机器人的末端执行器在运动时相对于基准坐标系的位置和姿态,从而实现精确的运动控制和轨迹规划。
总的来说,旋转坐标转换是一种重要的数学变换,它不仅可以帮助我们理解物体在空间中的位置和方向变化,还可以应用于各种领域,拓展了数学和计算机科学的应用范围。
测量坐标转换公式推导过程

测量坐标转换公式推导过程一、二维坐标转换(平面坐标转换)(一)平移变换。
1. 原理。
- 设原坐标系O - XY中的一点P(x,y),将坐标系O - XY平移到新坐标系O' - X'Y',新坐标系原点O'在原坐标系中的坐标为(x_0,y_0)。
2. 公式推导。
- 对于点P在新坐标系中的坐标(x',y'),根据平移的几何关系,我们可以得到x = x'+x_0,y = y'+y_0,则x'=x - x_0,y'=y - y_0。
(二)旋转变换。
1. 原理。
- 设原坐标系O - XY绕原点O逆时针旋转θ角得到新坐标系O - X'Y'。
对于原坐标系中的点P(x,y),我们要找到它在新坐标系中的坐标(x',y')。
- 根据三角函数的定义,设OP = r,α是OP与X轴正方向的夹角,则x = rcosα,y = rsinα。
- 在新坐标系中,x'=rcos(α-θ),y'=rsin(α - θ)。
2. 公式推导。
- 根据两角差的三角函数公式cos(A - B)=cos Acos B+sin Asin B和sin(A -B)=sin Acos B-cos Asin B。
- 对于x'=rcos(α-θ)=r(cosαcosθ+sinαsinθ),因为x = rcosα,y = rsinα,所以x'=xcosθ + ysinθ。
- 对于y'=rsin(α-θ)=r(sinαcosθ-cosαsinθ),所以y'=-xsinθ + ycosθ。
(三)一般二维坐标转换(平移+旋转)1. 原理。
- 当既有平移又有旋转时,先进行旋转变换,再进行平移变换。
2. 公式推导。
- 设原坐标系O - XY中的点P(x,y),先将坐标系绕原点O逆时针旋转θ角得到中间坐标系O - X_1Y_1,根据旋转变换公式,P在O - X_1Y_1中的坐标(x_1,y_1)为x_1=xcosθ + ysinθ,y_1=-xsinθ + ycosθ。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
创作编号:
GB8878185555334563BT9125XW
创作者: 凤呜大王*
坐标转换之计算公式
一、参心大地坐标与参心空间直角坐标转换
1名词解释:
A :参心空间直角坐标系: a) 以参心0为坐标原点;
b) Z 轴与参考椭球的短轴(旋转轴)相重合; c) X 轴与起始子午面和赤道的交线重合;
d) Y 轴在赤道面上与X 轴垂直,构成右手直角坐标系0-XYZ ; e) 地面点P 的点位用(X ,Y ,Z )表示; B :参心大地坐标系:
a) 以参考椭球的中心为坐标原点,椭球的短轴与参考椭球旋转轴重合; b) 大地纬度B :以过地面点的椭球法线与椭球赤道面的夹角为大地纬度B ; c) 大地经度L :以过地面点的椭球子午面与起始子午面之间的夹角为大地经度
L ;
d) 大地高H :地面点沿椭球法线至椭球面的距离为大地高H ; e) 地面点的点位用(B ,L ,H )表示。
2 参心大地坐标转换为参心空间直角坐标:
⎪⎭
⎪
⎬⎫
+-=+=+=B H e N Z L B H N Y L B H N X sin *])1(*[sin *cos *)(cos *cos *)(2 公式中,N 为椭球面卯酉圈的曲率半径,e 为椭球的第一偏心率,a 、b 椭球的长短半径,f 椭球扁率,W 为第一辅助系数
a
b a e 2
2-=
或 f
f e 1
*2-= W a N B W e =
-=22
sin *1(
3 参心空间直角坐标转换参心大地坐标
[
]
N
B
Y X H H
e N Y X H N Z B X Y
L -+=
+-++==cos ))1(**)()
(*arctan()
arctan(2
22
2
2
二 高斯投影及高斯直角坐标系
1、高斯投影概述
高斯-克吕格投影的条件:1. 是正形投影;2. 中央子午线不变形
高斯投影的性质:1. 投影后角度不变;2. 长度比与点位有关,与方向无关; 3. 离中央子午线越远变形越大
为控制投影后的长度变形,采用分带投影的方法。
常用3度带或6度带分带,城市或工程控制网坐标可采用不按3度带中央子午线的任意带。
2、高斯投影正算公式:
52224253
2236
425442232)5814185(cos 120
)1(cos 6
cos )5861(cos sin 720
495(cos sin 24cos sin 2l t t t B N l t B N
Bl N y l t t B B N l t B B N
Bl B N X x ηηηηη-++-++-+=+-+++-++
=)
3、高斯投影反算公式:
()()()⎥⎥⎦
⎤⎪⎪⎭⎫ ⎝⎛+++⎪⎪⎭
⎫
⎝⎛⎢⎣⎡-++-⎪⎪⎭⎫ ⎝⎛-=⎥⎥⎥⎥⎦
⎤⎪⎪⎭⎫ ⎝⎛+++++⎢⎢⎣⎡⎪⎪⎭
⎫
⎝⎛++-⎪⎪⎭⎫ ⎝⎛=
4422
22224222422
22
4590613601 935121128624285120
1 )21(6
11cos 1f f f f
f f f f f
f
f f f
f f f f f f
f f f
f N y t t N y t t N y y M t B B N y t t t N y t N y B l ηηηηη
创作编号:
GB8878185555334563BT9125XW
创作者: 凤呜大王*。
