不同坐标系之间的变换
常用坐标系及其间的转换

将式(1.4)中之φ0、 α0 分别用 B0、 A0 代替。即可得到。
3. 发射坐标系与箭体坐标系间的欧拉角及方向余弦阵 这两个坐标系的关系用以反映箭体相对于发射坐标系的姿态角。为使一般一状态下
这两坐标系转至相应轴平行,现采用下列转动顺序:先绕 oz 轴正向转动ϕ 角,然后绕
新的 y′ 轴正向转动ψ 角,最后绕新的 x1 轴正向转γ 角。两坐标系的欧拉角关系如图 1.4
用该坐标系与其它坐标系的关系反映出火箭的飞行速度矢量状态。
1.1.2 坐标系间转换
1. 地心惯性坐标系与地心坐标之间的方向余弦阵
由定义可知这两坐标系的 oE ZI , oE ZE 是重合的,而 oE X I 指向平春分点 oE X E 指
向所讨论的时刻格林威治天文台所在子午线一赤道的交点, oE X I 与 oE X E 的夹角要通
cosα0 cosλ0 + sinα0 sinφ0 sin λ0
cosα0 cosφ0 ⎤
sinφ0
⎥ ⎥
−sinα0 cosφ0 ⎦⎥
(1.4)
若将地球考虑为总地球椭球体,则发射点在椭球体上的位置可用经度 λ0 ,地理纬
度 B0 确定, ox 轴的方向则以射击方位角 A0 表示。这样两坐标系间的方向余弦阵只需
过天文年历年表查算得到,记该角为 ΩG ,显然,这两个坐标系之间仅存在一个欧拉角
ΩG ,因此不难写出两个坐标系的转换矩阵关系。
⎡XE⎤
⎡XI ⎤
⎢ ⎢
YE
⎥ ⎥
= EI
⎢ ⎢
YI
⎥ ⎥
(1.1)
⎢⎣ ZE ⎥⎦
⎢⎣ ZI ⎥⎦
其中
பைடு நூலகம்
⎡ cos ΩG sin ΩG 0⎤
常用坐标系之间的关系与转换

7.5 常用坐标系之间的关系与转换一、大地坐标系和空间大地直角坐标系及其关系大地坐标系用大地纬度企丈地经度L 和丈地髙H 来表示点的位置°这种坐标系是经 典大地测量甬:両用座标紊7屜据地图投影的理论,大地坐标系可以通过一定的投影转 化为投影平面上的直角坐标系,为地形测图和工程测量提供控制基础。
同时,这种坐标系 还是研究地球形状和大小的 种有用坐标系°所以大地坐标系在大地测量中始终有着重要 的作用.空间大地直角坐标系是-种以地球质心为原点购亘墮®坐标系,一般用X 、化Z 表 示点BSSTSTT 逐碇SS 範菇飞両H 绕禎扭转冻其轨道平面随时通过 地球质心。
对它们的跟踪观测也以地球质心为坐标原点,所以空间大地直角坐标系是卫星 大地测量中一种常用的基本坐标系。
现今,利用卫星大地测量的手段*可以迅速地测定点的空间大地直角坐拯,广泛应用于导航定位等空间技术。
同时经过数学变换,还可求岀点 的大地坐标I 用以加强和扩展地面大地网,进行岛屿和洲际联测,使传统的大地测量方法 发生了深刻的变化,所以空间大地宜角坐标系对现今大地测量的发展’具有重要的意义。
、大地坐标系和空间大地直角坐标系的转换如图7- 23所示’尸点的位置用空间 大地直角坐标〔X, Y, Z)表示,其相应 的大地坐标为(E, L)a 将该图与图?一5上式表明了 2种基本坐标系之间的关系。
加以比较可见,图7-5中的子午椭圆平面 相当于图7-23中的OJVP 平面.其中 PPz=Z.相当于图7-5中的j7;OP 3相当 丫于图7-5中的仏两平面的经度乙可视为相同,等于"叽 于是可以直接写岀X=jrcQsi f Y=jrsinL, Z=y将式(7-21).式(7-20)分别代入上式, 井考虑式(7-26)得X=Ncos^cosZr ”Y =NcQsBsinL > (7—78)Z=N (1—护〉sin^ ;BB 7-231.由大地坐标求空间大地直角坐标当已知椭球面上任一点P 的大地坐标(B, L)时,可以按式(7-78)直接求该点的 空间大地直角坐标(X, Y, Z)。
工程测量中不同坐标系变换与精度

工程测量中不同坐标系变换与精度
工程测量中,不同坐标系之间的变换和精度非常重要。
其中,常用的坐标系包括平面
直角坐标系、大地坐标系、投影坐标系等,不同坐标系之间的变换需要考虑到坐标系的基
准面、坐标轴方向、单位等因素。
一、坐标系的基准面
1. 平面直角坐标系的基准面为水平面,通常采用大地水准面作为参考面。
3. 投影坐标系的基准面通常为椭球面或平面,不同的投影方式会导致不同的基准面。
二、坐标轴方向的变换
不同坐标系的坐标轴方向也可能不同,因此需要进行某些坐标轴的转换。
1. 平面直角坐标系通常采用右手坐标系,其中x轴与东向、y轴与北向成正交关系。
2. 大地坐标系中,通常采用地心坐标系或以某个恒星为基准的坐标系,其中z轴与
地轴或某个恒星的指向相同。
3. 投影坐标系的坐标轴方向也有所不同,例如通常采用高斯投影系统的平面坐标系中,x轴指向中央经线的正方向,y轴指向赤道正方向。
三、单位的变换
2. 大地坐标系中,通常采用度或弧度作为单位。
四、变换精度的影响
不同坐标系之间的变换会影响精度,因此需要进行适当的考虑和处理。
1. 坐标系的变换会引入误差,误差的大小与变换参数的精度有关。
2. 不同坐标系之间的误差也有所不同,例如平面直角坐标系与大地坐标系之间的误
差通常比两个大地坐标系之间的误差更小。
综上所述,工程测量中的不同坐标系之间的变换和精度是非常重要的,需要进行适当
的考虑和处理。
为了保证测量的精度和稳定性,应选择合适的坐标系和变换方法,并进行
精确的计算和校正。
不同空间直角坐标系的转换

不同空间直角坐标系的转换
欧勒角
不同空间直角坐标系的转换,包括三个坐标轴的平移和坐标轴的旋转,以及两个坐标系的尺度比参数,坐标轴之间的三个旋转角叫欧勒角。
三参数法
三参数坐标转换公式是在假设两坐标系间各坐标轴相互平行,轴系间不存在欧勒角的条件下得出的。
实际应用中,因为欧勒角不大,可以用三参数公式近似地进行空间直角坐标系统的转换。
公共点只有一个时,采用三参数公式进行转换。
七参数法
用七参数进行空间直角坐标转换有布尔莎公式,莫洛琴斯基公式和范氏公式等。
下面给出布尔莎七参数公式:
坐标转换多项式回归模型
坐标转换七参数公式属于相似变换模型。
大地控制网中的系统误差一般呈区域性,当区域较小时,区域性的系统误差被相似变换参数拟合,故局部区域的坐标转换采用七参数公式模型是比较适宜的。
但对全国或一个省区范围内的坐标转换,可以采用多项式回归模型,将各区域的系统偏差拟合到回归参数中,从而提高坐标转换精度。
两种不同空间直角坐标系转换时,坐标转换的精度取决于坐标转换的数学模型和求解转换系数的公共点坐标精度,此外,还与公共点的分布有关。
鉴于地面控制网系统误差在⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡000111222Z Y X Z Y X Z Y X ⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡000111111222000)1(Z Y X Z Y X Z Y X m Z Y X X Y X Z Y Z εεεεεε
不同区域并非是一个常数,所以采用分区进行坐标转换能更好地反映实际情况,提高坐标转换的精度。
测量学中的坐标系和他们之间相互转换
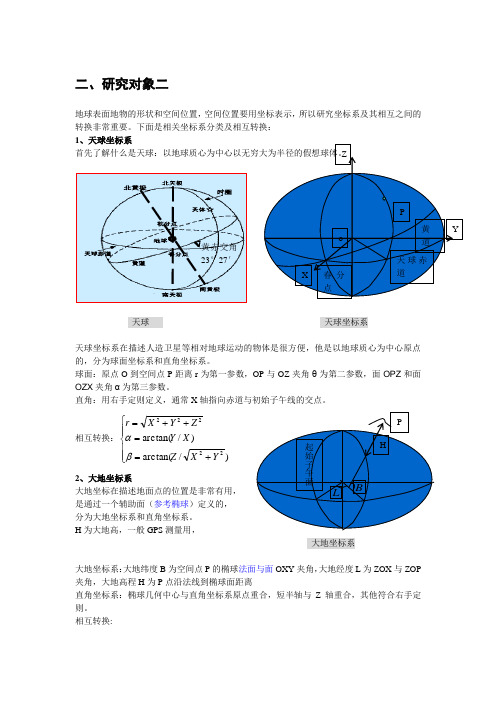
二、研究对象二地球表面地物的形状和空间位置,空间位置要用坐标表示,所以研究坐标系及其相互之间的转换非常重要。
下面是相关坐标系分类及相互转换: 1、天球坐标系首先了解什么是天球:以地球质心为中心以无穷大为半径的假想球体。
天球 天球坐标系天球坐标系在描述人造卫星等相对地球运动的物体是很方便,他是以地球质心为中心原点的,分为球面坐标系和直角坐标系。
球面:原点O 到空间点P 距离r 为第一参数,OP 与OZ 夹角θ为第二参数,面OPZ 和面OZX 夹角α为第三参数。
直角:用右手定则定义,通常X 轴指向赤道与初始子午线的交点。
相互转换:⎪⎪⎩⎪⎪⎨⎧+==++=)/arctan()/arctan(22222Y X Z X Y Z Y X r βα 2、大地坐标系大地坐标在描述地面点的位置是非常有用, 是通过一个辅助面(参考椭球)定义的, 分为大地坐标系和直角坐标系。
H 为大地高,一般GPS 测量用,大地坐标系大地坐标系:大地纬度B 为空间点P 的椭球法面与面OXY 夹角,大地经度L 为ZOX 与ZOP 夹角,大地高程H 为P 点沿法线到椭球面距离直角坐标系:椭球几何中心与直角坐标系原点重合,短半轴与Z 轴重合,其他符合右手定则。
相互转换:黄赤交角23°27′X YZ oP春分点黄道 天球赤道 起始子午面L B PH[]⎪⎩⎪⎨⎧+=+=-=+-=L B H N X L B H N Y B e a N B H e N Z cos cos )(sin cos )(e ,2sin 21/ sin )21(为第一扁率卯酉全曲率半径,其中3、惯性坐标系(CIS )与协议天球坐标系① 惯性坐标系(CIS ):在空间不动或做匀速直线运动的坐标系.② 协议天球坐标系:以某一约定时刻t0作为参考历元,把该时刻对应的瞬时自转轴经岁差和章动改正后作为Z 轴,以对应的春分点为X 轴的指向点,以XOZ 的垂直方向为Y 轴方向建立的天球坐标系。
坐标系的转换

对于坐标系之间的转换,目前我们国家有以下几种:1、大地坐标(BLH)对平面直角坐标(XYZ);2、北京54全国80及WGS84坐标系的相互转换;3、任意两空间坐标系的转换。
坐标转换就是转换参数。
常用的方法有三参数法、四参数法和七参数法。
以下对上述三种情况作转换基本原理描述如下:1、大地坐标(BLH)对平面直角坐标(XYZ)常规的转换应先确定转换参数,即椭球参数、分带标准(3度,6度)和中央子午线的经度。
椭球参数就是指平面直角坐标系采用什么样的椭球基准,对应有不同的长短轴及扁率。
一般的工程中3度带应用较为广泛。
对于中央子午线的确定的一般方法是:平面直角坐标系中Y坐标的前两位*3,即可得到对应的中央子午线的经度。
如x=3888888m,y=388888666m,则中央子午线的经度=38*3=114度。
另外一些工程采用自身特殊的分带标准,则对应的参数确定不在上述之列。
确定参数之后,可以用软件进行转换,以下提供坐标转换的程序下载。
2、北京54全国80及WGS84坐标系的相互转换这三个坐标系统是当前国内较为常用的,它们均采用不同的椭球基准。
其中北京54坐标系,属三心坐标系,大地原点在苏联的普而科沃,长轴6378245m,短轴6356863,扁率1/298.3;西安80坐标系,属三心坐标系,大地原点在陕西省径阳县永乐镇,长轴6378140m,短轴6356755,扁率1/298.25722101;WGS84坐标系,长轴6378137.000m,短轴6356752.314,扁率1/298.257223563。
由于采用的椭球基准不一样,并且由于投影的局限性,使的全国各地并不存在一至的转换参数。
对于这种转换由于量较大,有条件的话,一般都采用GPS联测已知点,应用GPS软件自动完成坐标的转换。
当然若条件不许可,且有足够的重合点,也可以进行人工解算。
详细方法见第三类。
3、任意两空间坐标系的转换由于测量坐标系和施工坐标系采用不同的标准,要进行精确转换,必须知道至少3个重合点(即为在两坐标系中坐标均为已知的点。
测量中常见的坐标转换方法和注意事项

测量中常见的坐标转换方法和注意事项在测量工作中,坐标转换是一个非常关键的步骤。
它可以将不同坐标系下的测量数据进行转换,以便更好地进行分析和比较。
本文将讨论测量中常见的坐标转换方法和注意事项,以帮助读者更好地理解和应用这些知识。
一、常见的坐标转换方法1. 直角坐标系与极坐标系的转换直角坐标系和极坐标系是我们常见的两种坐标系,它们在不同的情况下都有各自的优势。
当我们在进行测量时,有时需要将直角坐标系转换为极坐标系,或者反过来。
这时我们可以使用以下公式进行转换:直角坐标系 (x, y) 转换为极坐标系(r, θ):r = √(x^2 + y^2)θ = arctan(y/x)极坐标系(r, θ) 转换为直角坐标系 (x, y):x = r * cosθy = r * sinθ2. 地理坐标系与平面坐标系的转换在地理测量中,我们常常需要将地理坐标系与平面坐标系进行转换。
地理坐标系是以地球表面为基准的坐标系,而平面坐标系则是在局部范围内采用平面近似地球的坐标系。
转换的目的是为了将地球上的经纬度转换为平面上的坐标点,或者反过来。
这时我们可以使用专门的地图投影算法进行转换,例如常见的墨卡托投影、UTM投影等。
3. 坐标系之间的线性转换有时,我们需要将一个坐标系中的点的坐标转换到另一个坐标系中。
这时我们可以通过线性变换来实现。
线性变换定义了一个坐标系之间的转换矩阵,通过乘以这个转换矩阵,我们可以将一个坐标系中的点的坐标转换到另一个坐标系中。
常见的线性变换包括平移、旋转、缩放等操作,它们可以通过矩阵运算进行描述。
二、坐标转换的注意事项1. 坐标系统选择的准确性在进行坐标转换时,必须保证所选择的坐标系统是准确可靠的。
不同的坐标系统有不同的基准面和基准点,选择错误可能导致转换结果出现较大误差。
因此,在进行测量时,我们应该仔细选择坐标系统,了解其基本原理和适用范围。
2. 数据质量的控制坐标转换所依赖的输入数据必须具有一定的质量保证。
坐标变换原理

坐标变换原理
坐标变换是一种数学操作,用来在不同的坐标系间进行转换。
它是将一个点或对象的位置从一个坐标系转换到另一个坐标系的方法。
在二维平面坐标系中,通常使用笛卡尔坐标系和极坐标系。
笛卡尔坐标系使用x和y轴来表示一个点的位置,而极坐标系使用半径和角度来表示。
坐标变换可以通过简单的公式来实现:
1. 笛卡尔坐标系转换为极坐标系:给定一个点的笛卡尔坐标(x, y),可以通过以下公式计算其极坐标(r, θ):
r = √(x² + y²)
θ = arctan(y/x)
2. 极坐标系转换为笛卡尔坐标系:给定一个点的极坐标(r, θ),可以通过以下公式计算其笛卡尔坐标(x, y):
x = r * cos(θ)
y = r * sin(θ)
这些公式将一个点在不同坐标系中的位置进行相互转换。
通过这些转换,可以在不同坐标系之间准确地描述和定位对象的位置。
除了坐标系之间的转换,还可以进行其他类型的坐标变换,如平移、缩放和旋转。
在平移中,点的位置通过添加一个固定的偏移量来改变。
在缩放中,点的位置通过乘以一个缩放因子来改变。
在旋转中,点的位置通过应用旋转矩阵来改变。
通过这些坐标变换,可以单独或组合地对对象进行不同类型的变换,使其在平面内按照所需的方式移动、缩放和旋转。
这在计算机图形学和计算机视觉中经常使用,用于实现图像转换、模型变换等应用。
坐标变换为我们提供了一种非常有用的工具,可以方便地在不同坐标系中进行准确的位置描述与处理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
不同坐标系之间的变换 SANY GROUP system office room 【SANYUA16H-
§10.6不同坐标系之间的变换
10.6.1欧勒角与旋转矩阵
对于二维直角坐标,如图所示,有:
⎥⎦
⎤
⎢⎣⎡⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡1122cos sin sin cos y x y x θθθθ(10-8)
在三维空间直角坐标系中,具有相同原点的两坐标系间的变换一般需要在三个坐标平面上,通过三次旋转才能完成。
如图所示,设旋转次序为:
①绕1OZ 旋转Z ε角,11,OY OX 旋
转至0
0,OY OX ;
②绕0
OY 旋转Y ε角
10
,OZ OX 旋转至0
2
,OZ OX ; ③绕2OX 旋转X ε角,
0,OZ OY 旋转至22,OZ OY 。
Z Y X εεε,,为三维空间直角坐标变换的三个旋转角,也称欧勒角,与
它相对应的旋转矩阵分别为:
⎥⎥⎥⎦
⎤
⎢⎢⎢⎣⎡-=X X
X X X R εεεεεcos sin 0sin cos 00
01
)(1 (10-10)
⎥⎥⎥⎦⎤
⎢⎢⎢⎣⎡-=Y Y Y Y
Y R εεεεεcos 0sin 010sin 0cos )(2 (10-11)
⎥⎥⎥⎦
⎤
⎢⎢⎢⎣⎡-=10
0cos sin 0sin cos )(3Z
Z Z Z
Z R εεεεε (10-12)
令 )()()(3210Z Y X R R R R εεε=
(10-
13) 则有:
⎥⎥⎥⎦
⎤
⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡1110111321222)()()(Z Y X R Z Y X R R R Z Y X Z Y X εεε (10-14) 代入:
⎥⎥⎥⎦
⎤⎢⎢
⎢⎣⎡
+-+++--=Y X Z Y X Z X Z Y X Z X Y X Z Y X Z X Z Y X Z X Y Z Y Z Y R εεεεεεεεεεεεεεεεεεεεεεεεεεεεεcos cos sin sin cos cos sin cos sin cos sin sin cos sin sin sin sin cos cos cos sin sin sin cos sin sin cos cos cos 0一般Z Y X εεε,,为微小转角,可取:
sin sin sin sin sin sin sin ,sin ,sin 1cos cos cos =========Z Y Z X Y X Z
Z Y Y X X Z Y X εεεεεεεεεεεεεεε
于是可化简
⎥⎥
⎥⎦
⎤
⎢⎢⎢⎣⎡---=1110X
Y
X Z
Y Z
R εεεεεε (10-16) 上式称微分旋转矩阵。
10.6.2不同空间直角坐标之间的变换
当两个空间直角坐标系的坐标换算既有旋转又有平移时,则存在三个平移参数和三个旋转参数,再顾及两个坐标系尺度不尽一致,从而还有
一个尺度变化参数,共计有七个参数。
相应的坐标变换公式为:
⎥⎥⎥⎦
⎤
⎢⎢⎢⎣⎡∆∆∆+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡000111111222000
)1(Z Y X Z Y X Z Y X m Z Y X X
Y
X Z Y Z
εεεεεε(10-17) 上式为两个不同空间直角坐标之间的转换模型,其中含有7个转换参数,为了求得7个转换参数,至少需要3个公共点,当多于3个公共点时,可按最小二乘法求得个参数的最或是值。
10.6.3不同大地坐标系的变换
对于不同大地坐标系的换算,除包含三个平移参数、三个旋转参数和一个尺度变化参数外,还包括两个地球椭球元素变化参数,以下推导不同大地坐标系的换算公式。
由(7-30)式
⎥⎥⎥
⎦
⎤⎢⎢⎢⎣⎡+-++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡B H e N L B H N L B H N Z Y X sin ])1([sin cos )(cos cos )(2
取全微分得
⎥⎦⎤
⎢⎣⎡+⎥⎥⎥⎦
⎤
⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡αd da A dH dB dL J dZ dY dX (10-19) 式中
⎥⎥⎥
⎦
⎤⎢⎢
⎢
⎣⎡++-++-+-=⎥⎥⎥⎥⎥⎥⎦
⎤
⎢⎢⎢⎢
⎢⎢⎣⎡∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂=B B H M L B L B H M L B H N L B L B H M L B H N H Z B
Z L
Z H Y B Y L Y H X B X
L X
J sin cos )(0cos cos sin sin )(cos sin )(cos cos cos sin )(sin cos )((10-20)
⎥⎥⎥⎥⎥⎥⎦
⎤
⎢⎢⎢⎢⎢⎢⎣⎡-+-----=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢
⎢⎢⎣⎡∂∂∂∂∂∂∂∂∂∂∂∂=)sin cos 1(sin 1sin )1(sin sin cos 1sin cos sin cos cos 1cos cos 222222
B e B B M B e a
N B
L B M L B a
N B L B M L B a N Z a
Z Y a Y X
a X
A ααα
α
αα (10-21)
上式两端乘以1-J 并加以整理得:
⎥⎦⎤
⎢⎣⎡-⎥⎥⎥⎦
⎤
⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--αd da A J dZ dY dX J dH dB dL 11 (10-22)
式中
⎥⎥⎥
⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡111222Z Y X Z Y X dZ dY dX ⎥⎥⎥
⎦
⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡111222H B L H B L dH dB dL 顾及(10-21)式及
⎥⎥
⎥⎥
⎥⎥⎦⎤⎢⎢⎢⎢⎢
⎢⎣
⎡++-
+-++-=-B L
B L B H M B H M L B H M L B B H N L B H N L J sin sin cos cos cos cos sin sin cos sin 0
cos )(cos cos )(sin 1
(10-23) (10-22)式可写为:
=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡dH dB dL ⎥⎥⎥⎦
⎤
⎢⎢⎢⎣⎡∆∆∆⎥⎥⎥⎥⎥⎥
⎦
⎤⎢⎢
⎢⎢⎢⎢⎣
⎡''+'
'+-''+-'
'+''+-000sin sin cos cos cos cos sin sin cos sin 0
cos )(cos cos )(sin Z Y
X B L
B L B H
M B H M L B H
M L B B H N L
B H N L ρρρρρ ⎥⎥⎥⎦⎤
⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎦
⎤⎢⎢⎢⎢⎢
⎣
⎡
'
'''---+Z Y X L
B B Ne L B B Ne L
L
L tgB L tgB εεερρ0cos cos sin sin cos sin 0cos sin 1sin cos 2
2
m
H B e N B B e H M N ⎥⎥⎥⎦⎤⎢⎢⎢⎣
⎡+-''+-+)sin 1(cos sin 0
2
22ρ
⎥
⎦⎤⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦
⎤
⎢
⎢⎢⎢⎢⎢⎣⎡----''-+-''++ααραρd da B B e M B e a N B B H M B e M B B e a H M N 2
222
2222sin )sin 1(1)sin 1(cos sin )1)(()
sin 2(cos sin )(0
(10-24)
上式通常称为广义大地坐标微分公式或广义变换椭球微分公式。
如略去旋转参数和尺度变化参数的影响,即简化为一般的大地坐标微分公式。
根据3个以上公共点的两套大地坐标值,可列出9个以上(10-24)式的方程,可按最小二乘法求得8个转换参数。
