第2讲(空间组合)-要点
第二讲线性子空间一、线性子空间的定义及其性质定义:设是数域上的

第二讲 线性子空间一、线性子空间的定义及其性质1. 定义:设1V 是数域K 上的线性空间V 的一个非空子集合,且对V 已有的线性运算满足以下条件 (1) 如果1,V y x ∈,则1V y x ∈+; (2) 如果1V x ∈,K k ∈,则1V kx ∈, 则称1V 是V 的一个线性子空间或子空间。
2. 性质:(1)线性子空间1V 与线性空间V 享有共同的零元素; (2)1V 中元素的负元素仍在1V 中。
[证明](1)O x =0V V x ⊂∈1∴ V 中的零元素也在1V 中,1V 与V 享有共同的零元素。
(2)1V x ∈∀1)()1(V x x ∈-=- 封闭性∴ 1V 中元素的负元素仍在1V 中3. 分类:子空间可分为平凡子空间和非平凡子空间平凡子空间:{0}和V 本身 非平凡子空间:除以上两类子空间4. 生成子空间:设m x x x ,,21 为V 中的元素,它们的所有线性组合的集合⎭⎬⎫⎩⎨⎧=∈∑=m i i i i m i K k x k 1,2,1,也是V 的线性子空间,称为由m x x x ,,21 生(张)成的子空间,记为),,(21m x x x L 或者),,(21m x x x Span 。
若m x x x ,,21 线性无关,则{}m x x x L m =),,(dim 215. 基扩定理:设1V 是数域K 上的线性空间n V 的一个m 维子空间,m x x x ,,21 是1V 的一个基,则这m 个基向量必可扩充为n V 的一个基;换言之,在n V 中必可找到m n -个元素n m m x x x ,,21 ++,使得n x x x ,,21 成为n V 的一个基。
这m n -个元素必不在1V 中。
二、子空间的交与和1.定义:设1V 、2V 是线性空间V 的两个子空间,则 {}2121,V x V x x V V ∈∈={}2121,V y V x y x V V ∈∈+=+分别称为1V 和2V 的交与和。
高中数学空间几何组合教案

高中数学空间几何组合教案
一、教学目标:
1. 熟练掌握空间几何基本概念和相关定理;
2. 能够运用组合的方法解决空间几何问题;
3. 培养学生逻辑思维和空间想象能力。
二、教学内容:
1. 空间几何基本概念和相关定理复习;
2. 组合的概念和性质;
3. 运用组合解决实际空间几何问题。
三、教学过程:
1. 导入:通过展示一些空间几何问题的图片或视频,引起学生的兴趣,并激发他们的空间想象能力。
2. 学习与讨论:教师讲解空间几何的相关概念和定理,学生跟随着思考和讨论。
特别是介绍组合的概念和性质,让学生了解如何利用组合的方法解决空间几何问题。
3. 练习:布置一些练习题,让学生独立或小组完成,加深他们对空间几何和组合的理解。
4. 分析与解答:教师对学生的练习成果进行分析和解答,指导他们在解题过程中注意的问题和方法。
5. 总结与拓展:总结本节课的重点内容,拓展空间几何和组合的应用领域,激发学生的学习兴趣。
四、作业布置:
1. 完成课堂练习题目;
2. 完成一些实际空间几何问题的分析与解答;
3. 阅读相关空间几何和组合的知识,并做好笔记。
五、教学反馈:
1. 教师对学生作业进行批阅和评价,及时反馈学生的学习情况;
2. 针对学生存在的问题进行指导和辅导,帮助学生提高空间几何和组合的能力。
第二篇建筑设计空间构成及组合

2 平面组合的形式
建筑由于使用功能不同,房间之间的相互关系也不同。 平面组合是根据使用功能特点及交通路线的组织,将不 同房间组合起来。平面组合大致可以归纳为如下几种形 式:
• (1)走道式组合
走道式组合的特点是使用房间与交通联系部分明确分 开,各房间沿走道(走廊)一侧或两侧并列布置,房间 门直接开向走道,通过走道相互联系;各房间基本上不 被交通穿越,能较好地保持相对独立性;走道式组合的 优点是:各房间有直接的天然采光和通风,结构简单, 施工方便等。这种形式建筑特别适用于房间面积不大、 数量较多的重复空间组合,如学校、宿舍、医院、旅馆 等。
第二层人数不超过 30人
第二篇建筑设计空间构成及组合
4 电梯、扶梯、坡道设计
A 电梯
电梯按其使用性质可分为乘客电梯、载货电梯、 消防电梯、客货两用电梯、杂物梯等几类。
电梯的布置形式一般有单面式和对面式
B 扶梯
自动扶梯是一种在一定方向上能大量、连续输
送流动客流的装置。除了提供乘客一种既方便又
舒适的上下楼层间的运输工具外,自动扶梯还可
厨房设计应有良好的采光和通风条件;尽量利 用厨房的有效空间布置足够的贮藏设施,如壁龛、 吊柜等;厨房的墙面、地面应考虑防水、便于清 洁;室内布置应符合操作流程,并保证必要的操 作空间,为使用方便、提高效率、节约时间创造 条件。
PPT文档演模板
第二篇建筑设计空间构成及组合
厨房的布置形式有单排、双排、L形、U形等几种
A 家具或设备所占面积;
B 人在室内的使用活动面积(包括使用 家具及设备时,近旁所需面积);
C 房间内部的交通面积。
PPT文档演模板
第二篇建筑设计空间构成及组合
部分民用建筑房间面积定额参考指标
《空间构成》空间组合与形式

第五节 线性
1. 线性组合是沿某条线若干单位空间组合构成一个 空间系列。这些单位空间可以作接触排列.并相 互串通。也可以由另一个单独的线型空间来联系。 这些单位空间的视觉特征可以是重复的.渐变 的.类似的。交替的.特异的.线性组合排列方 式还可以细分为:直线型.折线型、曲线.环型、 鱼刺型.轴线型、树枝型。每一种线型又可分别 采取直串式.内廊式、外廊式、双廊式。所以线 型的排列组合能创造出无穷无尽的组合形式。
2. 空间序列的整体由动线贯穿,由分区来整理: (1)空间动线不能太直.”畅则浅”原理同样适应用创造序列。 (2)深远而狭长的空间是令人讨厌的.是否引入一段曲线或折线以增加视 觉艺术感?如何在横向通过渗透来丰富空间表现? (3)忌走回头略.可采用环形线设计。 (4)动线分主次.用非对称性形式以便识别序列。 (5)动线上的空间形态不能平铺.应设支点。
2 线性内空间组合的特点是。 (1)具有鲜明的运动.延伸.增长及节奏感。还具 有扩展的灵活性和利于空间的发展。 (2)既可以水平方向组合也可以垂直方向竖立或综 合展开排列.又可以将某个水平组织作为单 位.再沿垂直方向重叠组合.或将某个有水平高 差的空间组织沿垂直方向重叠组合. (3)无论线型简单或复杂.总有明确的方向和主 线.即使连接形状.大小不同的内空间.也能形 成有序的组织。
互锁
互锁是体接触又一形式.特指两个内空间有一部分 穿插.透叠.复叠、减缺和差叠后形成空间的模糊性.不 定性.多异性、灰色性.多用于空间联系.过渡、引 伸.成为共有空间地带.并保持各自的界限和完整。 1 共享。共享是由于二空间互锁(形态间的透叠)后仍能维 持各自空间形状的特性。共享处既可以属于A空间.又可 以属于B空间.它们的共享部分给人以曖昧多意的空间感 觉。共享空间的条件是该部分天覆、地载皆备.而围闭则 可有可无(若有也只能取半隔式通透的形式)。 2 主次。二空间互锁(形成形态与形态的复叠与减缺)时, 相叠部分与一个空间合并.成为主空间。相当于平面构成 两形相遇时的复叠.从而使相叠部分与空间联合并保持主 空间的完整性.而另一空间形态则因此成为减缺形态而变 得从属。主次空间中主空间天覆.地載与围闭皆备。
原理 第 节 空间组合方式

演变类型
双内廊 双外廊
实例: CHANNEL4电视台总部——Richard Rogers
巴黎大学生住宅
一栋具有两个朝向,双重 机理,双重意义的建筑
挑战: 表达人们想要看到的 掩蔽人们不想要的感觉
靠环形道路一边, 一座曲线形墙, 30m*100m的盾形物是 一个巨大的屏幕。
靠绿化一边,一条 静悄悄的绿色带,三 栋11层的顶端尖形高 楼仅靠着防护墙。
通过十字架的 聚中,通过透 过着色玻璃窗 的光线,通过 体量的表达等 几个方面,人 们的聚集特征 都由十字形表
现出来。
5、单元式
以竖向交通空间(楼梯)来连接各使用房间的 空间组合方式
特点:集中、紧凑、易于保持安静、不受干扰
实例
所
大阪NAKED SQUARE集合住宅区——HEXA事务
在实际设计中,空间组合的方式千变万化,往往是基 本组合方式的综合应用。因而,在一幢建筑中,单一 的空间组合方式是很少见的。
灵活分隔——各个空间之间相互穿插贯通,没有 明确界限
这种空间形式打破了 传统的“组合”概念,它 不是把若干个独立的空 间通过某种方式或媒介 连接在一起而形成整体, 而是把一个大空间分成 若干个部分。这些部分 有所区分又相互穿插贯 通,没有明确、肯定的 界限,从而失去了各自 的独立性。 这种空间形式打破了 古典建筑空间组合的机 械性,为创造高度灵活、复杂的空间开辟了可能性。
实例
巴塞罗那展览馆德国馆——Mies van der Rohe
实例
德国国家美术馆——Mies van der Rohe
4、大空间式
以体量巨大的主体空间为中心,其它附属空间环绕四 周布置的空间组合形式(注意与广厅式的区别)
大空间不仅是主要使用空间,而且体量巨大 常用建筑类型:体育馆、影剧院、大型市场……
第2讲 空间几何体的表面积和体积

思维点拨:由三视图知此几何体为圆锥. 思维点拨:由三视图知此几何体为圆锥. 解析:由三视图可知,该几何体是底面半径为 解析:由三视图可知,该几何体是底面半径为3 cm, , 母线长为5 的圆锥, 母线长为 cm的圆锥,其侧面积为 =π×3×5=15π cm2. 的圆锥 其侧面积为πrl= × × = 答案: 答案:B
1.一个长方体上一个顶点所在的三个面的面积分别是 . 这个长方体的对角线是( 这个长方体的对角线是 A.2 . B.3 . ) C.6 . D.
解析:设长方体的长、宽、高为a、b、c 解析:设长方体的长、 高为 、 、 则ab= = ,bc= = ,ac= = ,解得:a= 解得: = ,b=1,c= = , =
则
解得: = , 解得:R=1,∴2R=2. =
答案: 答案:B
如图,一个空间几何体的正视图、侧视图、 3. .如图,一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角 形,如果直角三角形的直角边长为1,那么这个几何体的表面积为 如果直角三角形的直角边长为 ,那么这个几何体的表面积为( )
2.体积公式 . (1)柱体的底面积为 ,高为 ,则柱体的体积为 Sh 柱体的底面积为S,高为h, 柱体的底面积为 (2)锥体的底面积为 ,高为 ,则锥体的体积为 锥体的底面积为S,高为h, 锥体的底面积为 .
Sh . (S′+ ′ +S)h.
(3)棱台的上、下底面面积为S′、S,高为 ,则体积为 棱台的上、下底面面积为 ′ 棱台的上 ,高为h, (4)球的半径为 ,则体积为 球的半径为R, 球的半径为 πR3 .
高考中对该部分的考查常以几何体的三视图为条件,来求表面积和体积, 高考中对该部分的考查常以几何体的三视图为条件,来求表面积和体积, 解题时要将图形还原为空间几何体,根据面积和体积公式求解. 解题时要将图形还原为空间几何体,根据面积和体积公式求解. (2009· 浙江绍兴第一次质检 若某几何体的三视图 单位 : cm)如 若某几何体的三视图(单位 · 浙江绍兴第一次质检)若某几何体的三视图 单位: 如 【例2】 】 右图所示,则此几何体的侧面积等于 右图所示,则此几何体的侧面积等于( A.12π cm2 . C.24π cm2 . B.15π cm2 . D.30π cm2 . )
建筑空间组合论精华

重复地排列而形成,各时而减小,有穿插而形成。
各要素互-从这一点出发,进一步认像圆、?经过长期的研究、探索、比较,终于发现其,亦称“黄金比”若干毗邻的长方形,如果它们的对角线互相),一般可以现代著名的建筑师勒.柯布西耶把比例和人体尺度结合在一2·26m,肚脐至地面高度为1 13m,698mm,两者之商为1130rcan除以698得1.618,自古以来还有许多建筑家曾以各种不同的方法来分析研究建筑中的比例问题。
其中最流行的一种看法是:虽然有一但其中也包含着一些合理6度感。
部都必须认真地对待并给予恰当的处理第七章处理间——环境——又何偿不是一个领域呢?当然,当然,群体组合并不限于环境处理这一方面的问题。
顾及到自身的完整统一而“独善其身”,的范围内建立起一种秩序。
任何建筑,只有当它和环境融合在一起,现力。
群体组合分以下五个方面.一、建筑与环境任何建筑都必然要处在一定的环境之中,联系,环境的好坏对于建筑的影响甚大。
为此,首先面临的问题就是选择合适的建筑地段。
对于环境——自然——应当取何种态度呢?也很不相同。
脱离自然而孤立地存在,他在同一本书又说:“建筑就是建筑,合”从这里可以看_出:尽管他们所强调的侧重有所不同,的效果。
建筑与环境的统一主要是指两者联系的有机性,安排上。
用莱特自己的话来讲:房子做成它所在地段的—部分。
此外,对于自然环境的结合和利用.地形、地貌,而且还可以大到相当远的范围。
限度地利用自然条件来美化环境。
二、关于结合地形的问题[图124]14种秩序感和互相吸引的关系,从而结成有机统一的整体。
现代建筑,比较强调功能对于形式的影响和作用,序感,或秩序感,这其中自然也就包含有统一的因素了。
筑与地形之间发生某种内在的联系.成群体的各单体建筑具有统一的形式和风格处理。
—而结合成为同一个“族类”,从而达到群体组合的统一。
一。
这是因为居住建筑于达到风格上的统一。
即使有很多困难,至少也应当争取大体上的统一。
【精品复习】立体几何篇-第2讲 空间几何体的表面积与体积
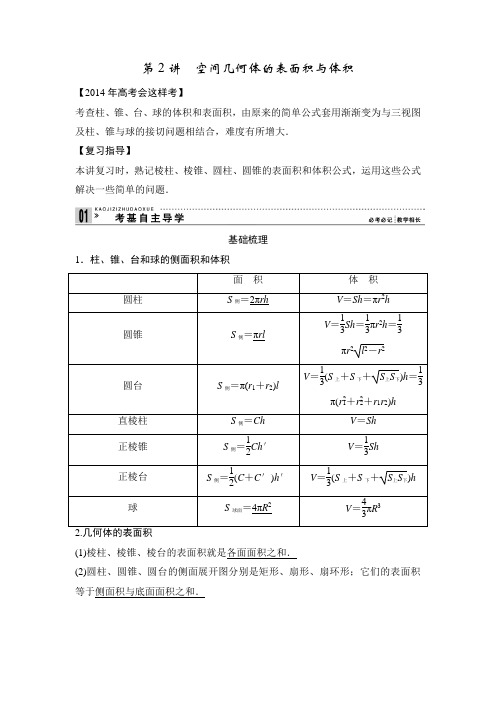
第2讲空间几何体的表面积与体积【2014年高考会这样考】考查柱、锥、台、球的体积和表面积,由原来的简单公式套用渐渐变为与三视图及柱、锥与球的接切问题相结合,难度有所增大.【复习指导】本讲复习时,熟记棱柱、棱锥、圆柱、圆锥的表面积和体积公式,运用这些公式解决一些简单的问题.基础梳理1.柱、锥、台和球的侧面积和体积面积体积圆柱S侧=2πrh V=Sh=πr2h圆锥S侧=πrlV=13Sh=13πr2h=13πr2l2-r2圆台S侧=π(r1+r2)lV=13(S上+S下+S上S下)h=13π(r21+r22+r1r2)h直棱柱S侧=Ch V=Sh正棱锥S侧=12Ch′V=13Sh正棱台S侧=12(C+C′)h′V=13(S上+S下+S上S下)h球S球面=4πR2V=43πR32.几何体的表面积(1)棱柱、棱锥、棱台的表面积就是各面面积之和.(2)圆柱、圆锥、圆台的侧面展开图分别是矩形、扇形、扇环形;它们的表面积等于侧面积与底面面积之和.两种方法(1)解与球有关的组合体问题的方法,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.球与旋转体的组合,通常作它们的轴截面进行解题,球与多面体的组合,通过多面体的一条侧棱和球心或“切点”、“接点”作出截面图.(2)等积法:等积法包括等面积法和等体积法.等积法的前提是几何图形(或几何体)的面积(或体积)通过已知条件可以得到,利用等积法可以用来求解几何图形的高或几何体的高,特别是在求三角形的高和三棱锥的高.这一方法回避了具体通过作图得到三角形(或三棱锥)的高,而通过直接计算得到高的数值.双基自测1.(人教A版教材习题改编)圆柱的一个底面积为S,侧面展开图是一个正方形,那么这个圆柱的侧面积是().A.4πS B.2πSC.πS D.23 3πS解析设圆柱底面圆的半径为r,高为h,则r=S π,又h=2πr=2πS,∴S圆柱侧=(2πS)2=4πS.答案 A2.(2012·东北三校联考)设长方体的长、宽、高分别为2a、a、a,其顶点都在一个球面上,则该球的表面积为().A.3πa2B.6πa2C.12πa2D.24πa2解析由于长方体的长、宽、高分别为2a、a、a,则长方体的体对角线长为(2a)2+a2+a2=6a.又长方体外接球的直径2R等于长方体的体对角线,∴2R=6a.∴S球=4πR2=6πa2.答案 B3.(2011·北京)某四面体的三视图如图所示,该四面体四个面的面积中最大的是( ).A .8B .6 2C .10D .8 2解析 由三视图可知,该几何体的四个面都是直角三角形,面积分别为6,62,8,10,所以面积最大的是10,故选择C. 答案 C 4.(2011·湖南)设右图是某几何体的三视图,则该几何体的体积为( ). A.92π+12 B.92π+18 C .9π+42 D .36π+18解析 该几何体是由一个球与一个长方体组成的组合体,球的直径为3,长方体的底面是边长为3的正方形,高为2,故所求体积为2×32+43π⎝ ⎛⎭⎪⎫323=92π+18.答案 B5.若一个球的体积为43π,则它的表面积为________. 解析 V =4π3R 3=43π,∴R =3,S =4πR 2=4π·3=12π. 答案 12π考向一几何体的表面积【例1】►(2011·安徽)一个空间几何体的三视图如图所示,则该几何体的表面积为().A.48 B.32+817C.48+817 D.80[审题视点] 由三视图还原几何体,把图中的数据转化为几何体的尺寸计算表面积.解析换个视角看问题,该几何体可以看成是底面为等腰梯形,高为4的直棱柱,且等腰梯形的两底分别为2,4,高为4,故腰长为17,所以该几何体的表面积为48+817.答案 C以三视图为载体考查几何体的表面积,关键是能够对给出的三视图进行恰当的分析,从三视图中发现几何体中各元素间的位置关系及数量关系.【训练1】若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积等于().A. 3 B.2C.2 3 D.6解析由正视图可知此三棱柱是一个底面边长为2的正三角形、侧棱为1的直三棱柱,则此三棱柱的侧面积为2×1×3=6.答案 D考向二 几何体的体积【例2】►(2011·广东)如图,某几何体的正视图(主视图)是平行四边形,侧视图(左视图)和俯视图都是矩形,则该几何体的体积为( ).A .18 3B .12 3C .9 3D .6 3[审题视点] 根据三视图还原几何体的形状,根据图中的数据和几何体的体积公式求解.解析 该几何体为一个斜棱柱,其直观图如图所示,由题知该几何体的底面是边长为3的正方形,高为3,故V =3×3×3=9 3. 答案 C以三视图为载体考查几何体的体积,解题的关键是根据三视图想象原几何体的形状构成,并从三视图中发现几何体中各元素间的位置关系及数量关系,然后在直观图中求解.【训练2】 (2012·东莞模拟)某几何体的三视图如图所示,则该几何体的体积等于( ).A.283πB.163π C.43π+8 D .12 π解析 由三视图可知,该几何体是底面半径为2,高为2的圆柱和半径为1的球的组合体,则该几何体的体积为π×22×2+43π=283π.答案 A考向三 几何体的展开与折叠【例3】►(2012·广州模拟)如图1,在直角梯形ABCD 中,∠ADC =90°,CD ∥AB ,AB =4,AD =CD =2,将△ADC 沿AC 折起,使平面ADC ⊥平面ABC ,得到几何体DABC ,如图2所示.(1)求证:BC ⊥平面ACD ; (2)求几何体DABC 的体积.[审题视点] (1)利用线面垂直的判定定理,证明BC 垂直于平面ACD 内的两条相交线即可;(2)利用体积公式及等体积法证明. (1)证明 在图中,可得AC =BC =22,从而AC 2+BC 2=AB 2,故AC ⊥BC , 取AC 的中点O ,连接DO ,则DO ⊥AC ,又平面ADC ⊥平面ABC ,平面ADC ∩平面ABC =AC ,DO ⊂平面ADC ,从而DO ⊥平面ABC ,∴DO ⊥BC , 又AC ⊥BC ,AC ∩DO =O ,∴BC ⊥平面ACD .(2)解 由(1)可知,BC 为三棱锥BACD 的高,BC =22,S △ACD =2,∴V BACD = 13S △ACD ·BC =13×2×22=423,由等体积性可知,几何体DABC 的体积为423.(1)有关折叠问题,一定要分清折叠前后两图形(折前的平面图形和折叠后的空间图形)各元素间的位置和数量关系,哪些变,哪些不变.(2)研究几何体表面上两点的最短距离问题,常选择恰当的母线或棱展开,转化为平面上两点间的最短距离问题.【训练3】已知在直三棱柱ABCA1B1C1中,底面为直角三角形,∠ACB=90°,AC=6,BC=CC1=2,P是BC1上一动点,如图所示,则CP+P A1的最小值为________.解析P A1在平面A1BC1内,PC在平面BCC1内,将其铺平后转化为平面上的问题解决.计算A1B=AB1=40,BC1=2,又A1C1=6,故△A1BC1是∠A1C1B=90°的直角三角形.铺平平面A1BC1、平面BCC1,如图所示.CP+P A1≥A1C.在△AC1C中,由余弦定理得A1C=62+(2)2-2·6·2·cos 135°=50=52,故(CP+P A1)min=5 2.答案5 2难点突破17——空间几何体的表面积和体积的求解空间几何体的表面积和体积计算是高考的一个常见考点,解决这类问题,首先要熟练掌握各类空间几何体的表面积和体积计算公式,其次要掌握一定的技巧,如把不规则几何体分割成几个规则几何体的技巧、把一个空间几何体纳入一个更大的几何体中的补形技巧、对旋转体作其轴截面的技巧、通过方程或方程组求解的技巧等,这是化解空间几何体面积和体积计算难点的关键.【示例1】►(2010·安徽)一个几何体的三视图如图,该几何体的表面积为().A .280B .292C .360D .372【示例2】► (2011·全国新课标)已知两个圆锥有公共底面,且两圆锥的顶点和底面的圆周都在同一个球面上.若圆锥底面面积是这个球面面积的316,则这两个圆锥中,体积较小者的高与体积较大者的高的比值为________.。
建筑平面的功能分析和平面组合设计第2讲精品PPT课件

2. 宽度 :应符合人流、货流通畅和消防安全的要求 通常单股人流的通行宽度为550~700mm。因此考虑两人并列行走或迎面
交叉,较少人流使用的过道净宽度,包括消防楼梯的最小净宽度都不得小于 1100mm 。
对于有大量人流通过的走道,其宽度根据使用情况,相关规范都作出了下 限的要求。例如民用建筑中中小学的设计规范中规定,当走道为内廊,也就是 两侧均有使用房间的情况下,其净宽度不得小于2100mm;而当走道为外廊, 也就是单侧连接使用房间,并为开敞式明廊时,其净宽度不得小于1800mm。
●建筑物交通联系部分包括: 1.走道——建筑物中最大量使用的交通联系部分 2.门厅和过厅 ——门厅是在建筑物的主要出入口处起内外过渡、集散人流 作用的交通枢纽。过厅一般位于体型较复杂的建筑物各分段的连接处或建 筑物内部某些人流或物流的集中交汇处,起到缓冲的作用 3.楼梯和电梯 ——建筑物中起垂直交通枢纽作用的重要部分
指满足主要使用功能和辅助使用功 能的那部分空间。例如住宅中的起 居室、卧室等起主要功能作用的空 间和卫生间、厨房等起次要功能作 用的空间,工业厂房中的生产车间 等起主要功能作用的空间和仓库、 更衣室、办公室等起次要功能作用 的空间
指专门用来连通建筑物的各使用部 分的那部分空间。例如许多建筑物 的门厅、过厅、走道(水平交通)、 楼梯、电梯(垂直交通)等等
名称
位于两个外部出口或楼梯间之间的房间
位于袋形走道两侧或尽端的房间
耐火等级
耐火等级
一、二级
三级
四级
一、二级
三级Leabharlann 四级托儿所、幼儿25
20
—
20
15
—
园
医院、疗养院
35
30
—
2021版高考数学一轮复习第八章立体几何第2讲空间几何体的表面积与体积教案文新人教A版

第2讲 空间几何体的表面积与体积一、知识梳理1.多面体的表(侧)面积多面体的各个面都是平面,则多面体的侧面积就是所有侧面的面积之和,表面积是侧面积与底面面积之和.2.圆柱、圆锥、圆台的侧面展开图及侧面积公式圆柱 圆锥 圆台侧面展开图侧面积公式S 圆柱侧=2πrl S 圆锥侧=πrlS 圆台侧=π(r +r ′)l表面积 体积柱体 (棱柱和圆柱)S 表面积=S 侧+2S 底 V =S 底h锥体 (棱锥和圆锥)S 表面积=S 侧+S 底 V =13S 底h 台体 (棱台和圆台)S 表面积=S 侧+S 上+S 下V =13(S 上+S 下+S 上S 下)h 球S =4πR 2 V =43πR 31.正方体与球的切、接常用结论 正方体的棱长为a ,球的半径为R ,(1)若球为正方体的外接球,则2R =3a ; (2)若球为正方体的内切球,则2R =a ;(3)若球与正方体的各棱相切,则2R=2a .2.长方体共顶点的三条棱长分别为a ,b,c ,外接球的半径为R ,则2R =a 2+b 2+c 2. 二、习题改编1.(必修2P27练习1改编)已知圆锥的表面积等于12π cm 2,其侧面展开图是一个半圆,则底面圆的半径为 cm.解析:由题意,得S 表=πr 2+πrl =πr 2+πr ·2r =3πr 2=12π,解得r 2=4,所以r =2(cm).答案:22.(必修2P27例4改编)圆柱的底面直径与高都等于球的直径,则球的体积与圆柱的体积比V 球∶V 柱为 .解析:设球的半径为R ,则V 球V 柱=43πR 3πR 2×2R =23.答案:23一、思考辨析判断正误(正确的打“√”,错误的打“×”) (1)多面体的表面积等于各个面的面积之和.( ) (2)锥体的体积等于底面积与高之积.( ) (3)球的体积之比等于半径比的平方.( )(4)简单组合体的体积等于组成它的简单几何体体积的和或差.( ) (5)长方体既有外接球又有内切球.( ) 答案:(1)√ (2)× (3)× (4)√ (5)× 二、易错纠偏常见误区(1)锥体的高与底面不清楚致误; (2)不会分类讨论致误.1.如图,长方体ABCD A 1B 1C 1D 1的体积是120,E 为CC 1的中点,则三棱锥E BCD 的体积是 .解析:设长方体中BC =a ,CD =b ,CC 1=c ,则abc =120,所以V E BCD=13×12ab ×12c =112abc =10. 答案:102.将一个相邻边长分别为4π,8π的矩形卷成一个圆柱,则这个圆柱的表面积是 .解析:当底面周长为4π时,底面圆的半径为2,两个底面的面积之和是8π;当底面周长为8π时,底面圆的半径为4,两个底面的面积之和为32π.无论哪种方式,侧面积都是矩形的面积32π2,故所求的表面积是32π2+8π或32π2+32π.答案:32π2+8π或32π2+32π空间几何体的表面积(师生共研)(1)(2018·高考全国卷Ⅰ)已知圆柱的上、下底面的中心分别为O 1,O 2,过直线O 1O 2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( )A .122πB .12πC .82πD .10π(2)(2020·湖南省五市十校联考)某四棱锥的三视图如图所示,其侧视图是等腰直角三角形,俯视图的轮廓是直角梯形,则该四棱锥的各侧面面积的最大值为( )A .8B .4 5C .8 2D .12 2【解析】 (1)因为过直线O 1O 2的平面截该圆柱所得的截面是面积为8的正方形,所以圆柱的高为22,底面圆的直径为22,所以该圆柱的表面积为2×π×(2)2+22π×22=12π.(2)由三视图可知该几何体是一个底面为直角梯形,高为4的四棱锥,如图,其中侧棱PA ⊥平面ABCD ,PA =4,AB =4,BC =4,CD =6,所以AD =25,PD =6,PB =42,连接AC ,则AC =42,所以PC =43,显然在各侧面面积中△PCD 的面积最大,又PD =CD =6,所以PC 边上的高为62-⎝ ⎛⎭⎪⎫4322=26,所以S △PCD =12×43×26=122,故该四棱锥的各侧面面积的最大值为122,故选D.【答案】 (1)B (2)D空间几何体表面积的求法(1)以三视图为载体的几何体的表面积问题,关键是分析三视图确定几何体中各元素之间的位置关系及数量关系.(2)多面体的表面积是各个面的面积之和;组合体的表面积问题应注意衔接部分的处理. (3)旋转体的表面积问题应注意其侧面展开图的应用.1.(2020·江西七校第一次联考)一个半径为1的球对称削去了三部分,其俯视图如图所示,那么该立体图形的表面积为( )A .3πB .4πC .5πD .6π解析:选C.由题中俯视图可知该球被平均分成6部分,削去了3部分,剩余的3部分为该几何体,所以该立体图形的表面积为2×π×12+3×π×12=5π,故选C.2.(2020·辽宁丹东质量测试(一))一个圆锥的轴截面是面积为1的等腰直角三角形,则这个圆锥的侧面积为 .解析:设圆锥的底面圆半径为r ,因为圆锥的轴截面是面积为1的等腰直角三角形,所以等腰直角三角形的斜边长为2r ,斜边上的高为r ,所以12×2r ×r =1,解得r =1,圆锥的母线长l =12+12=2,圆锥的侧面积为πrl =2π. 答案:2π空间几何体的体积(多维探究) 角度一 求简单几何体的体积(1)(2020·石家庄质量检测)某几何体的三视图如图所示(图中小正方形网格的边长为1),则该几何体的体积是( )A .8B .6C .4D .2(2)将一张边长为12 cm 的正方形纸片按如图(1)所示将阴影部分的四个全等的等腰三角形裁去,余下部分沿虚线折叠并拼成一个有底的正四棱锥,如图(2)放置,如果正四棱锥的主视图是正三角形,如图(3)所示,则正四棱锥的体积是( )A.3236 cm 3B.6436 cm 3C.3232 cm 3D .6432 cm 3【解析】 (1)由三视图可得该几何体为底面是直角梯形的直四棱柱(如图所示),其中底面直角梯形的上、下底分别为1,2,高为2,直四棱柱的高为2,所以该几何体的体积为(1+2)×22×2=6,故选B.(2)设折成的四棱锥的底面边长为a cm ,高为h cm ,则h =32a cm ,由题设可得四棱锥侧面的高等于四棱锥的底面边长,所以12a +a =12×22⇒a =42,所以四棱锥的体积V =13×(42)2×32×42=6463cm 3,故选B. 【答案】 (1)B (2)B简单几何体体积的求法对于规则几何体,直接利用公式计算即可.若已知三视图求体积,应注意三视图中的垂直关系在几何体中的位置,确定几何体中的线面垂直等关系,进而利用公式求解.角度二 求组合体的体积(2020·唐山市摸底考试)已知某几何体的三视图如图所示(俯视图中曲线为四分之一圆弧),则该几何体的表面积为( )A .1-π4B .3+π2C .2+π4D .4【解析】 由题设知,该几何体是棱长为1的正方体被截去底面半径为1的14圆柱后得到的,如图所示,所以表面积S =2×(1×1-14×π×12)+2×(1×1)+14×2π×1×1=4.故选D.【答案】 D(1)处理体积问题的思路(2)求体积的常用方法 直接法 对于规则的几何体,利用相关公式直接计算割补法把不规则的几何体分割成规则的几何体,然后进行体积计算;或者把不规则的几何体补成规则的几何体,不熟悉的几何体补成熟悉的几何体,便于计算 等体积法选择合适的底面来求几何体体积,常用于求三棱锥的体积,即利用三棱锥的任一个面作为三棱锥的底面进行等体积变换1.(2019·高考北京卷)某几何体是由一个正方体去掉一个四棱柱所得,其三视图如图所示.如果网格纸上小正方形的边长为1,那么该几何体的体积为 .解析:如图,由三视图可知,该几何体为正方体ABCD A 1B 1C 1D 1去掉四棱柱B 1C 1GF A 1D 1HE 所得,其中正方体ABCD A 1B 1C 1D 1的体积为64,VB 1C 1GF A 1D 1HE =(4+2)×2×12×4=24,所以该几何体的体积为64-24=40.答案:402.(2019·高考全国卷Ⅲ)学生到工厂劳动实践,利用3D 打印技术制作模型.如图,该模型为长方体ABCD A 1B 1C 1D 1挖去四棱锥O EFGH 后所得的几何体,其中O 为长方体的中心,E ,F ,G ,H 分别为所在棱的中点,AB =BC =6 cm ,AA 1=4 cm.3D 打印所用原料密度为0.9 g/cm 3.不考虑打印损耗,制作该模型所需原料的质量为 g.解析:长方体ABCD A 1B 1C 1D 1的体积V 1=6×6×4=144(cm 3),而四棱锥O EFGH 的底面积为矩形BB 1C 1C 的面积的一半,高为AB 长的一半,所以四棱锥O EFGH 的体积V 2=13×12×4×6×3=12(cm 3),所以长方体ABCD A 1B 1C 1D 1挖去四棱锥O EFGH 后所得几何体的体积V =V 1-V 2=132(cm 3),所以制作该模型所需原料的质量为132×0.9=118.8(g).答案:118.8球与空间几何体的接、切问题(师生共研)(1)若直三棱柱ABC A 1B 1C 1的6个顶点都在球O 的球面上,且AB =3,AC =4,AB⊥AC ,AA 1=12,则球O 的表面积为 .(2)(一题多解)(2019·高考天津卷)已知四棱锥的底面是边长为2的正方形,侧棱长均为 5.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为 .【解析】 (1)将直三棱柱补形为长方体ABEC A 1B 1E 1C 1,则球O 是长方体ABEC A 1B 1E 1C 1的外接球.所以体对角线BC 1的长为球O 的直径. 因此2R =32+42+122=13. 故S 球=4πR 2=169π.(2)法一:由题意得圆柱的高为四棱锥高的一半,底面圆的直径为以四棱锥侧棱的四个中点为顶点的正方形的对角线,易求得圆柱的底面圆的直径为1,高为1,所以该圆柱的体积V =π×⎝ ⎛⎭⎪⎫122×1=π4.法二:由题可得,四棱锥底面对角线的长为2,则圆柱底面的半径为12,易知四棱锥的高为5-1=2,故圆柱的高为1,所以该圆柱的体积为π×⎝ ⎛⎭⎪⎫122×1=π4. 【答案】 (1)169π (2)π4处理球的“切”“接”问题的求解策略解决与球有关的切、接问题,其通法是作截面,将空间几何问题转化为平面几何问题求解,其解题的思维流程是:1.正四棱锥P ABCD 的侧棱和底面边长都等于22,则它的外接球的表面积是( ) A .16π B .12π C.8πD .4π解析:选A.设正四棱锥的外接球半径为R ,顶点P 在底面上的射影为O ,因为OA =12AC=12 AB 2+BC 2=12(22)2+(22)2=2,所以PO =PA 2-OA 2=(22)2-22=2.又OA =OB =OC =OD =2,由此可知R =2,于是S 球=4πR 2=16π.2.设球O 内切于正三棱柱ABC A 1B 1C 1,则球O 的体积与正三棱柱ABC A 1B 1C 1的体积的比值为 .解析:设球O 半径为R ,正三棱柱ABC A 1B 1C 1的底面边长为a ,则R =33×a 2=36a ,即a =23R ,又正三棱柱ABC A 1B 1C 1的高为2R ,所以球O 的体积与正三棱柱ABC A 1B 1C 1的体积的比值为43πR 334a 2×2R =43πR 334×12R 2×2R =23π27.答案:23π27核心素养系列14 直观想象——数学文化与空间几何体(2020·甘肃、青海、宁夏3月联考)汉朝时,张衡得出圆周率的平方除以16等于58.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,俯视图中的曲线为圆,利用张衡的结论可得该几何体的体积为( )A .32B .40 C.32103D .40103【解析】 将三视图还原成如图所示的几何体:半个圆柱和半个圆锥的组合体,底面半径为2,高为4,则体积V =12π×22×4+13×12π×22×4=323π,因为圆周率的平方除以16等于58,即π216=58,所以π=10,所以V =32103.故选C.【答案】 C本题是数学文化与三视图结合,主要是根据几何体的三视图及三视图中的数据,求几何体的体积或侧(表)面积.此类问题难点:一是根据三视图的形状特征确定几何体的结构特征;二是将三视图中的数据转化为几何体的几何度量.考查了直观想象这一核心素养.(2020·安徽六安一中模拟(四))我国南北朝时期的数学家祖暅提出了一条原理:“幂势既同,则积不容异”.意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.椭球体是椭圆绕其轴旋转所成的旋转体.如图,将底面直径都为2b ,高皆为a 的半椭球体和已被挖去了圆锥体的圆柱放置于同一平面β上,用平行于平面β且与平面β任意距离d 处的平面截这两个几何体,可横截得到S 圆及S 环两截面.可以证明S 圆=S 环总成立.据此,短半轴长为1,长半轴长为3的椭球体的体积是 .解析:因为S 圆=S 环总成立,所以半椭球体的体积为πb 2a -13πb 2a =23πb 2a ,所以椭球体的体积V =43πb 2a .因为椭球体的短半轴长为1,长半轴长为3. 所以椭球体的体积V =43πb 2a =43π×12×3=4π.答案:4π[基础题组练]1.(2020·安徽合肥质检)已知圆锥的高为3,底面半径为4,若一球的表面积与此圆锥侧面积相等,则该球的半径为( )A .5 B. 5 C .9D .3解析:选B.因为圆锥的底面半径r =4,高h =3,所以圆锥的母线l =5,所以圆锥的侧面积S =πrl =20π,设球的半径为R ,则4πR 2=20π,所以R =5,故选B.2.(2020·蓉城名校第一次联考)已知一个几何体的正视图和侧视图如图1所示,其俯视图用斜二测画法所画出的水平放置的直观图是一个直角边长为1的等腰直角三角形(如图2所示),则此几何体的体积为( )A .1 B. 2 C .2D .2 2解析:选B.根据直观图可得该几何体的俯视图是一个直角边长分别是2和2的直角三角形(如图所示),根据三视图可知该几何体是一个三棱锥,且三棱锥的高为3,所以体积V =13×⎝ ⎛⎭⎪⎫12×2×2×3= 2.故选B.3.(2020·武汉市武昌调研考试)中国古代数学名著《九章算术》中记载了公元前344年商鞅监制的一种标准量器——商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其体积为12.6(单位:立方寸),则图中的x 为( )A .1.2B .1.6C .1.8D .2.4解析:选B.该几何体是一个组合体,左边是一个底面半径为12的圆柱,右边是一个长、宽、高分别为5.4-x ,3,1的长方体,所以组合体的体积V =V 圆柱+V 长方体=π·⎝ ⎛⎭⎪⎫122×x +(5.4-x )×3×1=12.6(其中π=3),解得x =1.6.故选B.4.(2020·辽宁大连第一次(3月)双基测试)我国古代数学名著《九章算术》中有如下问题:“今有羡除,下广六尺,上广一丈,深三尺,末广八尺,无深,袤七尺.问积几何 ”.羡除是一个五面体,其中三个面是梯形,另两个面是三角形,已知一个羡除的三视图如图中粗线所示,其中小正方形网格的边长为1,则该羡除的表面中,三个梯形的面积之和为( )A .40B .43C .46D .47解析:选C.由三视图可知,该几何体的直观图如图所示,其中平面ABCD ⊥平面ABEF ,CD =2,AB =6,EF =4,等腰梯形ABEF 的高为3,等腰梯形ABCD 的高为4,等腰梯形FECD的高为9+16=5,三个梯形的面积之和为2+62×4+4+62×3+2+42×5=46,故选C.5.(2020·辽宁沈阳东北育才学校五模)将半径为3,圆心角为2π3的扇形围成一个圆锥,则该圆锥的内切球的表面积为( )A .πB .2πC .3πD .4π解析:选B.将半径为3,圆心角为2π3的扇形围成一个圆锥,设圆锥的底面圆半径为R ,则有2πR =3×2π3,所以R =1.设圆锥的内切球半径为r ,圆锥的高为h ,内切球球心必在圆锥的高线上,因为圆锥的母线长为3,所以h =9-1=22,所以有rh -r =R 3,解得r =22,因此内切球的表面积S =4πr 2=2π.故选B. 6.现有橡皮泥制作的底面半径为5、高为4的圆锥和底面半径为2、高为8的圆柱各一个.若将它们重新制作成总体积与高均保持不变,但底面半径相同的新的圆锥和圆柱各一个,则新的底面半径为 .解析:设新的底面半径为r ,由题意得13πr 2·4+πr 2·8=13π×52×4+π×22×8,解得r =7.答案:77.(2020·沈阳质量监测)某四棱锥的三视图如图所示,则该四棱锥的侧面积是 .解析:由三视图可知该几何体是一个四棱锥,记为四棱锥P ABCD ,如图所示,其中PA ⊥底面ABCD ,四边形ABCD 是正方形,且PA =2,AB =2,PB =22,所以该四棱锥的侧面积S 是四个直角三角形的面积和,即S =2×⎝ ⎛⎭⎪⎫12×2×2+12×2×22=4+4 2.答案:4+4 28.(2020·长春市质量监测(一))已知一所有棱长都是2的三棱锥,则该三棱锥的体积为 .解析:记所有棱长都是2的三棱锥为P ABC ,如图所示,取BC 的中点D ,连接AD ,PD ,作PO ⊥AD 于点O ,则PO ⊥平面ABC ,且OP =63×2=233,故三棱锥P ABC 的体积V =13S △ABC·OP =13×34×(2)2×233=13.答案:139.如图,在四边形ABCD 中,∠DAB =90°,∠ADC =135°,AB =5,CD =22,AD =2,求四边形ABCD 绕AD 旋转一周所成几何体的表面积及体积.解:由已知得CE =2,DE =2,CB =5,S 表面积=S圆台侧+S圆台下底+S圆锥侧=π(2+5)×5+π×25+π×2×22=(60+42)π,V =V 圆台-V圆锥=13(π·22+π·52+22·52π2)×4-13π×22×2=1483π. 10.(应用型)现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥P A 1B 1C 1D 1,下部的形状是正四棱柱ABCD A 1B 1C 1D 1(如图所示),并要求正四棱柱的高O 1O 是正四棱锥的高PO 1的4倍,若AB =6 m ,PO 1=2 m ,则仓库的容积是多少?解:由PO 1=2 m ,知O 1O =4PO 1=8 m.因为A 1B 1=AB =6 m ,所以正四棱锥P A 1B 1C 1D 1的体积V 锥=13·A 1B 21·PO 1=13×62×2=24(m 3);正四棱柱ABCD A 1B 1C 1D 1的体积V 柱=AB 2·O 1O =62×8=288(m 3),所以仓库的容积V =V 锥+V 柱=24+288=312(m 3). 故仓库的容积是312 m 3.[综合题组练]1.(2019·高考全国卷Ⅰ)已知三棱锥PABC的四个顶点在球O的球面上,PA=PB=PC,△ABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为( )A.86πB.46πC.26πD.6π解析:选D.因为点E,F分别为PA,AB的中点,所以EF∥PB,因为∠CEF=90°,所以EF⊥CE,所以PB⊥CE.取AC的中点D,连接BD,PD,易证AC⊥平面BDP,所以PB⊥AC,又AC∩CE=C,AC,CE⊂平面PAC,所以PB⊥平面PAC,所以PB⊥PA,PB⊥PC,因为PA=PB=PC,△ABC为正三角形,所以PA⊥PC,即PA,PB,PC两两垂直,将三棱锥PABC放在正方体中如图所示.因为AB=2,所以该正方体的棱长为2,所以该正方体的体对角线长为6,所以三棱锥PABC的外接球的半径R=62,所以球O的体积V=43πR3=43π⎝⎛⎭⎪⎫623=6π,故选D.2.如图,正方体ABCDA1B1C1D1的棱长为3,线段B1D1上有两个动点E,F且EF=1,则当E,F移动时,下列结论不正确的是( )A.AE∥平面C1BDB.四面体ACEF的体积不为定值C.三棱锥ABEF的体积为定值D.四面体ACDF的体积为定值解析:选B.对于A,如图1,AB1∥DC1,易证AB1∥平面C1BD,同理AD1∥平面C1BD,且AB 1∩AD 1=A ,所以平面AB 1D 1∥平面C 1BD ,又AE ⊂平面AB 1D 1,所以AE ∥平面C 1BD ,A 正确;对于B ,如图2,S △AEF =12EF ·h 1=12×1×(32)2-⎝ ⎛⎭⎪⎫3222=364,点C 到平面AEF的距离为点C 到平面AB 1D 1的距离d 为定值,所以V A CEF=V C AEF=13×364×d =64d 为定值,所以B 错误;对于C ,如图3,S △BEF =12×1×3=32,点A 到平面BEF 的距离为A 到平面BB 1D 1D 的距离d 为定值,所以V A BEF=13×32×d =12d 为定值,C 正确;对于D ,如图4,四面体ACDF 的体积为V A CDF=V F ACD=13×12×3×3×3=92为定值,D 正确.3.(2020·东北师大附中、重庆一中等校联合模拟)若侧面积为4π的圆柱有一外接球O ,当球O 的体积取得最小值时,圆柱的表面积为 .解析:设圆柱的底面圆半径为r ,高为h , 则球的半径R =r 2+⎝ ⎛⎭⎪⎫h 22.因为球的体积V =4π3R 3,故V 最小当且仅当R 最小.圆柱的侧面积为2πrh =4π,所以rh =2.所以h 2=1r,所以R =r 2+1r 2≥2,当且仅当r 2=1r2.即r =1时取等号,此时k 取最小值,所以r =1,h =2,圆柱的表面积为2π+4π=6π.答案:6π4.(2020·新疆第一次毕业诊断及模拟测试)如图,A 1B 1C 1D 1是以ABCD 为底面的长方体的一个斜截面,其中AB =4,BC =3,AA 1=5,BB 1=8,CC 1=12,求该几何体的体积.解:过A 1作A 1E ⊥BB 1于点E , 作A 1G ⊥DD 1于点G , 过E 作EF ⊥CC 1于点F ,过D 1作D 1H ⊥CC 1于点H ,连接EH ,GF , 因为平面ABB 1A 1∥平面DCC 1D 1, 所以A 1B 1∥D 1C 1.因为AA 1=BE =5,所以EB 1=8-5=3,C 1H =EB 1=3,GD 1=HF =12-5-3=4,则几何体被分割成一个长方体ABCD A 1EFG ,一个斜三棱柱A 1B 1E D 1C 1H 和一个直三棱柱A 1D 1G EHF .故该几何体的体积为V =3×4×5+12×3×4×4+12×3×4×3=102.。
赣美版初中美术九年级上册1丰富多彩的建筑风格教案

《1丰富多彩的建筑风格》课程教案一、教学目的:1、培养学生建立基本的建筑设计思维和正确的建筑观:帮助学生了解初步的建筑概念、理论和基础知识——建筑空间、环境、功能,组成一般建筑的元素,中外建筑发展的背景知识等;2、帮助学生掌握科学的工作方法,对设计过程形成初步的感性认识和一般了解:帮助学生初步掌握形态构成在建筑艺术创作中的作用;3、能运用所有的基本建筑概念、理论和基础知识,对中外建筑名作及自己的设计进行初步的理性评价;4、加强基于建筑设计的专业基本技能训练;帮助学生掌握规范的建筑设计表达;工作模型的制作,口头及文字表达与交流。
二、教学重点与难点:1、学生了解初步的建筑概念、理论和基础知识——建筑空间、环境、功能,组成一般建筑的元素。
2、加强基于建筑设计的专业基本技能训练;帮助学生掌握规范的建筑设计表达:徒手及工具的铅笔与墨线效果表现,工作模型的制作,口头及文字表达与交流。
三、教学方法:教师在授课中采用启发式教学,注重课堂教学中是互动,既重视基本原理、基本方法的教授,也重视学生在课程作业中对知识的掌握和灵活运用,让学生参与教学的过程,以唤起学生的学习兴趣。
四、教学过程设计:教学过程以理论教学和实践教学结合为主。
首先讲解建筑设计的基础知识,然后通过学生作业的过程继续补充建筑知识。
五、教学内容:(第1讲)讲课要点:1、建筑设计的基本知识;2、建筑设计的发展概况;3、设计的一般要求和依据;4、建筑设计的内容、程序和方法;5、建筑使用构成和功能组织;6、建筑材料的选择与设计1、建筑设计的基本知识1)、建筑的分类一、建筑是按照功能来分类,建筑还可以按照时间、规模、民族文化特征、材料技术特征等分类:(1)按照建筑功能分类,可分为公共建筑、居住建筑、农业建筑、工业建筑。
(2)按照建筑时间分类,可分为方代建筑、近代建筑、现代建筑、当代建筑、未来建筑。
(3):按照规模分类,可分为小型建筑、中型建筑、大型建筑、巨大型建筑等。
建筑空间的构成及组合

厨房的布置形式有单排、双排、L形、U形等几种
四 交通联系部分的设计
1 建筑物交通联系部分的设计要求 A 满足使用高峰时段人流、货流通 过所需的安全尺度。 B 符合紧急情况下规范所规定的疏 散要求。 C 方便各使用空间之间的联系。 D 满足采光、通风等方面的要求。
2走道设计
走道又称为过道、走廊。凡走道一侧或 两侧空旷者称为走廊。 按走道的使用性质不同,可分为三种情 况: A 完全为交通需要而设置的走道,不允 许安排作其它功能的用途。 B 主要为交通联系同时也兼有其它功能 的走道,这时过道的宽度和面积应相应增 加。
(2)套间式组合
套间式组合的特点是用穿套的方式按一定的序 列组织空间。房间与房间之间相互穿套,不再通 过走道联系。这种形式通常适用于房间的使用顺 序和连续性较强,使用房间不需要单独分隔的情 况下形成的组合方式,如展览馆、火车站、浴室 等建筑类型。套间式组合按其空间序列的不同又 可分为串联式和放射式两种。串联式是按一定的 顺序关系将房间连接起来;放射式将各房间围绕 交通枢纽呈放射状布置。 可分为串联式和放射式两种组合方式。
门窗位置应有利于采光通风。门的位 置应方便交通,利于疏散
D 门窗的开启方向
门窗的开启方向一般有外开 和内开,大多数房间的门均采用 内开方式,可防止门开启时影响 室外的人行交通。
三 辅助使用房间的设计
1 厕所设计 A 厕所设备及数量 厕所卫生设备主要有大便器、小便 器、洗手盆、污水池等 一般民用建筑每一个卫生器具可供 使用的人数参考表如下:
C 坡道
坡道的特点是上下比较省力(楼梯的坡度在 25~45度左右,室内坡道的坡度通常<10度), 通行人流的能力几乎和平地相当,但是坡道的最 大缺点是所占面积比楼梯面积大得多。
空间组合论

空间组合论一.总论建筑发展中的本质联系(两个要求一个手段):一是人们对建筑提出的功能和使用方面的要求;二是人们对建筑提出的精神和审美要求;三是必要的物质技术手段来达到前述的两个方面(一)从使用功能看建筑形式是指它的内部空间和外部体形。
功能对建筑形式既有规定性又有灵活性。
建筑作为巨大的物质财富主要是为统治阶级服务的,它必须首先满足统治阶级对它提出的功能要求(二)从精神与审美要求看形式美的基本原则:按照使用经济美观的原则,恰如其分地处理好空间和体形,整体和局部的关系而使之符合统一与变化,对比与微差,均衡与稳定等形式美的基本原则。
形式美与艺术性是不同的,凡具有艺术性的作品都必须符合形式美的规律,反正凡是符合形式美规律的建筑不一定具有艺术性。
形式美和艺术性的区别在于,前者对现实的审美关系只限于外部形式本身是否符合统一与变化,对比与微差,均衡与稳定等与形式美有关的法则,而后者要求通过自身的艺术形象表现一定得思想内容建筑艺术只能运用一些抽象的集合体形,运用线。
面,体各部分的比例,均衡,对称,色彩,质感,韵律等的统一和变化而获得一定得艺术气氛诸如庄严,雄伟,明朗,优雅,忧郁,沉闷,神秘,恐怖,亲切,宁静等的统一和变化而获得一定的艺术气氛一切艺术都是立意在先的,建筑表现与性格特征,建筑的共性表现风格特征,风格可分为时代的,民族的,地区的和个人的,建筑艺术是上层建筑的组成部分(三)从物质技术手段看功能结构式形成建筑的手段,功能与空间形式的矛盾,某种意义上讲表现为功能与工程技术,特别是与结构的矛盾。
功能对建筑结构促进工程结构的发展具有相对独立性新结构有优越性,新结构更符合力学规律性自身必然有内在的和谐统一性,反应在外部形式上必须符合均衡,稳定的原则。
古典建筑的形式是美的,它的美体现了上述各方面的和谐哦拿故意,但是这种统一是建立在当时的材料和结构方法的基础之上的。
不同地区民族其建筑形式仍然保留着民族特点的差别,这些差别表现在对材料结构的处理方法不同(四)从建筑发展趋势看恩格斯在《自然辩证法》中写到辩证法是关于普遍联系的科学。
空间的形态构成2

1.大空间之 间的衔接与 过渡
过渡空间的设置
2.内、外空间的衔接与过渡
内部空间组织
对比与变化 衔接与过渡 重复与再现 渗透与层次 引导与暗示 空间序列组织
• 当人们从外界进入到建筑物的内部空间时,为 了不致产生过分突然的感觉,也有必要在内、 外空间之间插进一个过渡性的空间,从而通过 它把人很自然地由室外引入室内。
常见空间类型
运用流动的光影、水体、楼电梯等 动态要素 来丰富空间,形成富有动感的空间。
常见空间类型
舒适沉稳的色彩、良好的空间比例,形成安静 的学习工作环境。
常见空间类型
3.凹入空间与外凸空间
凹入空间
•在室内某一墙面或 角落局部凹入的空 间,通常只有一面 或两面开放,所以 受干扰较少, •其领域感与私密性 随凹入的深度而加 强。 •可作为休憩、交谈 、进餐、睡眠等用 途的空间。
空间的形态构成(二)
Composition of Space Morphology
本讲框架
基本形态要素
本讲框架
要素介绍
空间限定 空 间 的 形 态 构 成 单一空间的形成
建筑空间形态构成 常见的空间类型 建筑空间序列的组织 空间形态的属性
教学目标
教学目标
通过本次课的学习,使同学们了解有关建筑空间 的基本属性及建筑二元空间的形成规律,在设计 时能灵活运用各种空间类型和设计手法,为空间 的组合打下基础。
开敞空间经常作为室内外的过渡空间有一定的流 动性和很高的趣味性。
常见空间类型
某博物馆室内开敞空间
常见空间类型
封闭空间
封闭空间是用限定性较强的围护实体包围起来的, 具有较强的内向性,领域感和私密性较强,强调空 间的独立性和完整性,与周围环境的流动性较差。
建筑空间组合分析(2)

建筑空间组合专业:城市规划分指导老师:蔡家伟组员:焦晓强张振李帅孙慧敏郜慧云析意大利建筑理论家赛维指出:“建筑空间是我们生活的场地、生活的环境、生活的舞台。
而且空间是人们人为的为了满足人们生产或生活的需要,运用各种建筑要素与形式所构成的内部空间与外部空间的统称。
内部空间包括墙、地面、屋顶、门窗等围城建筑,而外部空间是建筑物与周围环境中的树木、山峦、水面、街道、广场等形成建筑的。
由此可以看出建筑空间对我们生活的重要性,正应为如此,我们应该进一步对空间进行了解,尤其是建筑空间的组合,但空间组合形式是指若干独立空间以何种方式衔接在一起的,使之形成一种连续、有序的有机整体。
在建筑设计实践中,空间组合的形式是千变万化的,初看起来似乎很难分类总结,然而形式的变化最终总要反映建筑功能的联系特点,因此我们可以从错综复杂的现象中概括出若干种具有典型意义的空间组合形式,以便在实践中加以把握和应用。
空间组合方式有很多种,选择的依据一是考虑建筑本身的设计要求,如功能分区、交通组织、采光通风以及景观需要等等;二是要考虑建筑基地的外部条件,周围环境的不同直接会影响到空间组合方式上的选择。
空间的组合方式根据各自的特征,概括起来有并联式、串联式、集中式、辐射式、组团式、网格式、轴线对位式等,北京故宫空间组合分析北京故宫的空间组合为串联式空间组合和轴线对应组合。
一串联式空间组合说它是串联式组合,是由于功能和形式等方面的要求,先后次序明确,相互串联形成一个空间序列,呈线性排列,规规矩矩,都有严格要求,因此这种组合方式也称为“序列组合”或“线性组合”。
如北京故宫,整个建筑先后次序明确,前是前后是后,都有一定的规定,它们互相串联而形成一个空间序列,并且都沿一条线分布,是一个典型的串联式组合,如下图:图一整个故宫的空间组合图及序列组合图一图二整个故宫的空间组合图及序列组合图一由图一和图二可以看出故宫的组合故宫宫殿是沿着一条南北向中轴线排列,三大殿、后三宫、御花园都位于这条中轴线上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
集中式小中型体量
布拉格国家Tecnical图书馆-Projektil Architek主从式组合 1. 组成特征 2. 形体特征 3. 实例分析 二、廊道式组合 1.适用类型 2.变化类型 三、厅堂式组合 四、统间式组合
Zollverein School of Management and Design
一、主从式组合 1. 组成特征 2. 形体特征 3. 实例分析 二、廊道式组合 1.适用类型 2.变化类型 三、厅堂式组合 四、统间式组合
不适宜集中体量,宜处理成网络式
11
第二讲 空间组合分析
一、主从式组合 1. 组成特征 2. 形体特征 3. 实例分析 二、廊道式组合 1.适用类型 2.变化类型 三、厅堂式组合 四、统间式组合
2
运动俱乐部 (若干主体空间组合) 第二讲 空间组合分析
一、主从式组合 1. 组成特征 2. 形体特征 3. 实例分析 二、廊道式组合 1.适用类型 2.变化类型 三、厅堂式组合 四、统间式组合
3
第二讲 空间组合分析
一、主从式组合 1. 组成特征 2. 形体特征 3. 实例分析 二、廊道式组合 1.适用类型 2.变化类型 三、厅堂式组合 四、统间式组合
西班牙毕尔巴鄂体育中心-ACXT
形体多为集中式体量。
4
第二讲 空间组合分析
一、主从式组合 1. 组成特征 2. 形体特征 3. 实例分析 二、廊道式组合 1.适用类型 2.变化类型 三、厅堂式组合 四、统间式组合
2011深圳大运会宝安体育场“竹林” - GMP
城堡式集中体量,围绕交通疏散空间
5
第二讲 空间组合分析
18
第二讲 空间组合分析
一、主从式组合 1. 组成特征 2. 形体特征 3. 实例分析 二、廊道式组合 1.适用类型 2.变化类型 三、厅堂式组合 四、统间式组合
19
第二讲 空间组合分析
四、统间式空间组合
一、主从式组合 1. 组成特征 2. 形体特征 3. 实例分析 二、廊道式组合 1.适用类型 2.变化类型 三、厅堂式组合 四、统间式组合
第二讲 空间组合分析
一、主从式空间组合
从属空间 主要使用空间
一、主从式组合 1. 组成特征 2. 形体特征 大体量的主体空间,与辅 3. 实例分析 助房间具有联系紧密、体 二、廊道式组合 量悬殊、功能主从关系显 1.适用类型 著; 2.变化类型 具有以大型空间为主,穿 三、厅堂式组合 插组合辅助空间的特点。 四、统间式组合
体育馆、影剧院、商场、 车站、航空港、会堂等类 型的建筑;
中学风雨操场
共同特性:人流量大
1
第二讲 空间组合分析
交通空间 主体空间
一、主从式组合 1. 组成特征 2. 形体特征 3. 实例分析 二、廊道式组合 1.适用类型 2.变化类型 三、厅堂式组合 四、统间式组合
辅助空间 辅助空间
影剧院 (单一主体空间)
24
第二讲 空间组合分析
一、主从式组合 1. 组成特征 2. 形体特征 3. 实例分析 二、廊道式组合 1.适用类型 2.变化类型 三、厅堂式组合 四、统间式组合
澳大利亚Cooroy社区图书馆
25
二年级茶室设计学生作业——摘自ABBS
第二讲 空间组合分析
一、主从式组合 1. 组成特征 2. 形体特征 3. 实例分析 二、廊道式组合 1.适用类型 2.变化类型 三、厅堂式组合 四、统间式组合
综合大厅实例
Hanamidori Cultural Center _ Atelier Bow-Wow
20
第二讲 空间组合分析
一、主从式组合 1. 组成特征 2. 形体特征 3. 实例分析 二、廊道式组合 1.适用类型 2.变化类型 三、厅堂式组合 四、统间式组合
Hanamidori Cultural Center _ Atelier Bow-Wow
单内廊
第二讲 既以较小的辅助面积服务于较多的主要使用房间,又以较大的总进深增加建筑保暖性,适用 空间组合分析 于北方冬季保暖。在结构上比较优越。但是位于两侧的房间得不到同样理想的朝向。且当走廊较
长时,天然采光的不足,使廊内偏于阴暗。
使用中,通常将主要房间布置在朝向较好的一侧,将辅助房间及楼梯间安排在朝向较差的一
设计要点2: 空间排列方式,按大小归类,大空 间放置在“尽端”或独立设置;
14
主要房间的体量增加到一定程度,
第二讲 由于人流量的累计,廊道的宽度不断加 空间组合分析 大而产生“质”的飞跃——以厅堂为枢
纽的放射式组合。
一、主从式组合 1. 组成特征 2. 形体特征 3. 实例分析 二、廊道式组合 1.适用类型 2.变化类型 三、厅堂式组合 四、统间式组合
集中式小体量
17
第二讲 空间组合分析
一、主从式组合 1. 组成特征 2. 形体特征 3. 实例分析 二、廊道式组合 1.适用类型 2.变化类型 三、厅堂式组合 四、统间式组合
Rauner Special Collections, Dartmouth College, Hanover, NH, 1998
一、主从式组合 1. 组成特征 2. 形体特征 3. 实例分析 二、廊道式组合 1.适用类型 2.变化类型 三、厅堂式组合 四、统间式组合
斯特林·美国表演艺术中心
室内同样呈现出交通特质
6
第二讲 空间组合分析
一、主从式组合 1. 组成特征 2. 形体特征 3. 实例分析 二、廊道式组合 1.适用类型 2.变化类型 三、厅堂式组合 单外廊 四、统间式组合
三、厅堂式空 间组合
15
第二讲 空间组合分析
一、主从式组合 1. 组成特征 2. 形体特征 3. 实例分析 二、廊道式组合 1.适用类型 2.变化类型 三、厅堂式组合 四、统间式组合
放射形体量
16
第二讲 空间组合分析
一、主从式组合 1. 组成特征 2. 形体特征 3. 实例分析 二、廊道式组合 1.适用类型 2.变化类型 三、厅堂式组合 四、统间式组合
一、主从式组合 侧。而最为合理的方式是将内外廊结合运用,将不同功用的房间按照功能分区分别布置在走廊的 1. 组成特征 两侧。 2. 形体特征 3. 实例分析 二、廊道式组合 1.适用类型 2.变化类型 三、厅堂式组合 四、统间式组合
8
第二讲 空间组合分析
一、主从式组合 1. 组成特征 2. 形体特征 3. 实例分析 二、廊道式组合 1.适用类型 2.变化类型 三、厅堂式组合 四、统间式组合
结合外廊,缩短走廊长度,改善通风采光
双内廊
9
第二讲 空间组合分析
一、主从式组合 1. 组成特征 2. 形体特征 3. 实例分析 二、廊道式组合 1.适用类型 2.变化类型 三、厅堂式组合 四、统间式组合
主空 次间 分组 明 合 有原 机则 结 合 联 系 方 便 关 系 紧 凑
10
第二讲 空间组合分析
27
Akershus University Hosptial C.F.Mø ller Architects
12
第二讲 空间组合分析
一、主从式组合 1. 组成特征 2. 形体特征 3. 实例分析 二、廊道式组合 1.适用类型 2.变化类型 三、厅堂式组合 四、统间式组合
13
第二讲 空间组合分析
一、主从式组合 1. 组成特征 2. 形体特征 3. 实例分析 二、廊道式组合 1.适用类型 2.变化类型 三、厅堂式组合 四、统间式组合
内外不清,主次不明,空间组织混乱
26
第二讲 空间组合分析
一、主从式组合 1. 组成特征 2. 形体特征 3. 实例分析 二、廊道式组合 1.适用类型 2.变化类型 三、厅堂式组合 四、统间式组合
Cafe Pavilion - Architekten martenson und nagel theissen
二、廊道式空间组合
具有大量的、体量相同或相 近,使用上各自具有独立性,无 一定的序列性要求、可共用辅助 房间(如公共卫生间、贮藏室) 的主要房间。如办公室、教室、 诊疗室、病房等。之间的联系紧 密却无须直接。所以用走廊提供 间接联系。
7
解决日照、采光、通风、 观景、防噪声干扰等问 题,具有得天独厚的有 利条件,非常适用于南 方湿热地区。
21
第二讲 空间组合分析
一、主从式组合 1. 组成特征 2. 形体特征 3. 实例分析 二、廊道式组合 1.适用类型 2.变化类型 三、厅堂式组合 四、统间式组合
布拉格国家Tecnical图书馆-Projektil Architekti
22
第二讲 空间组合分析
一、主从式组合 1. 组成特征 2. 形体特征 3. 实例分析 二、廊道式组合 1.适用类型 2.变化类型 三、厅堂式组合 四、统间式组合
