青岛大学817固体物理2014--2015年考研专业课初试真题
青岛大学固体物理2016年考研真题考研试题硕士研究生入学考试试题

1 青岛大学2016年硕士研究生入学考试试题 科目代码:817 科目名称:固体物理 (共2页) 请考生写明题号,将答案全部答在答题纸上,答在试卷上无效
一、简答(本题20分)
1.晶体中声子数目是否守恒?同一温度下,一个光学波的声子数目多还是一个声学波的声子数目多(说明理由)?
2.简述固体的能带理论的三步近似。
3.简述布洛赫定理(文字描述及公式表示)。
4.晶体有哪几种宏观对称操作?写出其独立的基本对称元素。
二、(本题30分)
对于金刚石结构:
(1)说明其布拉菲点阵类型、基元的原子坐标、所属晶系、特征对称操作元素。
(2)分别画出(110)和(011)面上原子的分布。
(3)求出金刚石结构的几何结构因子,讨论衍射极大的条件,写出前3个衍射峰对应的衍射面指数。
(4)分别写出其晶格振动色散曲线的支数,光学支格波和声学支格波的支数。
三、(本题20分) 已知某晶体中相邻原子间的相互作用势能可表示为n m r r u βα
+-=,
n m ,,,βα均为正常数。
(1) 说明右式两项代表的物理意义,并求平衡态时近邻原子间距。
(2) 证明此系统可以处于稳定平衡态的条件是m n >。
(3) 写出由N 个相同原子组成的该晶体的总相互作用能的表达式。
(4) 证明其体积弹性模量009V mn U K =,(0U ,0V 分别是晶体处于热平
衡时的能量和体积)。
青岛大学657数学分析2014--2015年考研专业课初试真题

e
D
( x2 是以 A(a, 0, 0 ) , B(0, a, 0 ) , C(0, 0, a ) 为顶点的三角形,沿
ABCA 方向,计算积分
( z y)dx ( x z)dy ( y x)dz
L
2 2
.
2
四、 (满分 12 分)求函数 f ( x1 , x2 , , xn ) x1 x2 xn
九、 (满分 12 分)确定幂级数 数。
n 1
xn 的收敛半径,并求其和函 n (n 1)
十、 (满分 12 分)设 f ( x) x ,在区间 ( , ) 内将其展开成傅里叶 级数。
2
青岛大学 2015 年硕士研究生入学考试试题
科目代码: 657 科目名称: 数学分析 (共 2 页) 请考生写明题号,将答案全部答在答题纸上,答在试卷上无效
0
x s 1e x dx 在 ( 0, ) 内连续。
1 八、 (满分 12 分)确定幂级数 1 n n 1
n2 x n 的收敛半径和收敛域。
九、 (满分 12 分)计算曲线积分
xdy ydx ,其中 L 是一按段光 L x2 y2
滑的封闭曲线,取正向, (0,0) 是 L 所围区域 D 的内点。
3 yzdydz 2 zxdzdx xydxdy
S
.
1
三、 (满分 12 分)设函数 f ( x) 在 [a, b] 上可导, a b 0 ,证明存在
(a, b) 使得
3 2 ( f (b) f (a)) (b 3 a 3 ) f ( ) .
n a0 (a k cos kx bk sin kx) , f ( x) 在 2 k 1
青岛大学2014年硕士研究生入学考试试题

青岛大学2014年硕士研究生入学考试试题科目代码:897科目名称:教育管理学(共1页)请考生写明题号,将答案全部答在答题纸上,答在试卷上无效一、名词解释:(40分,每题8分)1. 学校效能2. 教育行政的服务职能3. 帕累托改进4. 教育信息公开5. 学校形象二、简答题:(60分,每题20分)1. 试述课程实施评价的主要类型2. 试述教育部门在实施信息公开时面临的困境3. 试述教师考核的主要内容三、论述题:(50分,每题25分)1.试论学校危机管理预警系统的构建2.党的十八届三中全会做出的《中共中央关于若干改革问题的决定》指出:“深入推进管办评分离,扩大省级政府教育统筹和学校办学自主权,完善学校内部治理结构。
强化国家教育督导,委托社会组织开展教育评估监测。
”青岛大学2013 年硕士研究生入学考试试题科目代码: 897 科目名称:教育管理学(共1 页)请考生写明题号,将答案全部答在答题纸上,答在试卷上无效一、名词解释:(40 分,每题8 分)1. 教育管理科学化2. 课程实施3. 派任制4. 教育信息5. 学校发展战略二、简答题:(60 分,每题20 分)1. 试述我国教师培训存在的问题及改进对策?2. 我国中小学教师职业专业性没有得到社会承认的原因是什么?3. 我国目前高等教育学生资助体系包括哪些方式?各有什么侧重点?三、论述题:(50 分)请就下列新闻进行分析论述。
要求:至少用一个教育管理学原理进行分析。
问题的分析可从某一个方面切入,不必面面俱到,能阐述清楚即可。
视点犀利,欢迎发表自己的独到见解,但是必须有理论依据。
抓住要点,条理清晰,文字简练。
近一个月内,长春大学师生茶余饭后议论着该校原副校长门树廷受贿一案:2003 年至2011 年间,门树廷利用自己负责学校后勤和基建的职务之便,索取和收受他人贿赂939 万余元。
长春市中级人民法院以受贿罪判处门树廷无期徒刑,剥夺政治权利终身,并没收财产100 万元。
青岛大学2020年817 固体物理

物理学专业硕士入学考试大纲
考试科目代码及名称:817 固体物理
一、考试要求
了解并掌握固体物理学的基本概念、基本原理和基本方法,能够利用基础知识解决固体物理领域相关问题。
二、考试内容
(1)晶体结构和X射线衍射
(2)晶体中原子的结合
(3)晶格振动
(4)金属自由电子理论
(5)能带理论
(6)晶体中电子的输运性质
(7)晶体中的缺陷和扩散
三、试卷结构(题型分值)
1.本科目满分为150分,考试时间为180分钟。
2. 题型结构
(1)简答题:占总分的33.3%
(2)计算证明题: 占总分的66.7%
四、参考书目
《固体物理学》,方俊鑫,陆栋,上海科学技术出版社。
《固体物理基础》,王淑华,济南出版社。
青岛大学827固体物理2016-2017年考研专业课真题试卷

青岛大学2017年硕士研究生入学考试试题科目代码:817科目名称:固体物理(共2页)请考生写明题号,将答案全部答在答题纸上,答在试卷上无效一、简答(本题20分)1.按顺序写出下列晶体的布拉菲点阵,并写出基元中原子在晶胞中的坐标:NaCl,CsCl,Si,Na.2.共价键有什么特点?说明原子晶体的基本特征。
3.为什么晶体原胞中电子数目为奇数,相应的晶体具有金属导电性?4.什么是金属的脱出功?用你以前学过的一个实例说明脱出功的应用。
二、(本题20分)晶格常数为a 的体心立方:(1)证明密勒指数为)(hkl 的晶面族的面间距为:222hkl l k h a d ++=(2)说明密勒指数简单的晶面容易解理。
(3)若体心立方看成是等体积的硬球组成,证明其致密度π=ρ83。
三、(本题20分)惰性气体元素晶体,原子间的相互作用势⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛σ-⎪⎭⎫ ⎝⎛σε=1612r r 4)r (u ,其中σ和ε为待定常数,r 为两原子间距。
(1)说明上式中两项的物理意义;(2)证明由N 个惰性气体原子组成的晶体,总互作用势能可表示为()⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=6612122R A R A N R U σσε(3)若惰性气体元素晶体为面心立方结构,计算6A 、12A 的值(计及最近邻和次近邻原子)。
(4)证明平衡时最近邻原子间距0R 与σ之比是与晶体结构有关的常数。
四、(本题30分)用德拜模型讨论由N 个原子组成的晶体的比热问题。
(1)证明模式密度239)(ωω=ωρDN ;(2)写出晶体振动能和晶体比热的表达式;(3)讨论高低温极限下晶体比热与温度的关系。
五、(本题20分)一个有N 个自由电子的电子气系统中,能量在E E E d ~+间的电子数为()EE f E C N d d =(1)证明()23023F E N C =(2)证明绝对零度时能量在T k E B F 230-到0F E 之间的电子数()049F B E T k N N ≈'六、(本题20分)简单正交晶格在最近邻近似下,应用紧束缚法推导由原子S 态电子形成的能量表达式,并求出电子沿x k 方向的速度()x k v 表达式、画出()x k v 曲线。
青岛大学物理基础综合2013-2015,2017年考研初试真题

分)
10、以白光垂直照射在一块平面衍射光栅上,要求能在 30 度的衍射方向
观察到 600nm 的第二级主最大,并能在该处分辨波长差为 0.005nm 的两条
光谱线,但是 400nm的谱线在此缺级。试求:(1)光栅常数;(2)光栅的
总宽度;(3)光栅的缝宽;(4)用这块光栅总共能看到 590nm 的哪几条谱
1
6、如图所示一平行板电容器,两极板间距为 d , 板的面积为 S ,中间插入一块厚度为 t 、相对介电 常数为 r 的电介质平板(介质板贴近电容器的下 极板)。求:(1)未加入电介质之前电容器的电容; (2)加入电介质后的电容;(3)向上平移电介质, 是否改变电容器的电容?为什么?(15 分)
Fmax (M m)g mg
1 2kh (M m)g
(15 分)
4、如图所示,一长为 l ,质量为 M 的杆可绕支点 O 自由
转动。一质量为
m
、速度为
v
的子弹射入下端而不复出,
此后杆摆至水平位置又开始回落;设从子弹射入到停在杆
内为时极短。求:(1)子弹进入杆前的速度;(2)子弹刚
青岛大学目名称: 物理基础综合 (共 2 页)
请考生写明题号,将答案全部答在答题纸上,答在试卷上无效
1、已知质点的运动学方程为 r 2ti (2 t 2 )j ,式中 r 的单位为 m ,t 的单位为 s 。求:(1)质点的运动轨迹;(2) t 0 及 t 2s 时,质点的 位置矢量;(3)由 t 0 到 t 2s 内质点的位移 r ;(4) t 2s 时质点 的速度;(5) t 2s 时质点的加速度。 (15 分)
2、轻型飞机连同驾驶员总质量为 m ,飞机以 v0 的速率在水平跑道上着陆 后,驾驶员开始制动,若阻力与时间 t 成正比,即 f kt ,空气对飞机升 力不计,求:飞机任意时刻的加速度、速度,和其运动学方程。(以驾驶 员开始制动处为坐标原点)(15 分)
青岛大学834化工原理2014--2015年考研专业课初试真题

二、计算题(20 分)
1
如图所示,液体循环系统,即液体由容器A进入离心泵,又由泵打回 容器A.液体循环量为1.8m3/h,液体密度为1000kg/m3,输送管路 为内径25mm 的光滑管。从液面至泵入口C的压头损失为0.55m,泵 出口至容器A的全部压头损失为1.6m, 泵入口处的静压头比容器A液面 上方静压头高出2m,容器内液面恒定. 试求: (1)泵的压头 H (2)容器A液面至泵入口的垂直距离 h0 三、计算题(20 分) 流量为 2000kg/h 的某气体在列管式换热器的管程流过, 温度由 150℃降至 80℃;壳程冷却用水,进口温度为 15℃,出口温度为 65℃,与气体作逆 流流动,两者均处于湍流。已知气体侧的对流传热膜系数远小于冷却水侧 的对流传热膜系数,管壁热阻 、 污垢热阻和热损失均可忽略不计即
一、 简答题(共 60 分,每题 12 分) 1. 理想伯努利方程能量式和成立条件。 2. 旋风分离器的临界粒径概念及影响因素。 3. 牛顿冷却定律和影响因素。 4. 气膜控制现象和强化传质的措施。 5. 干燥过程的结合水分和非结合水分概念 二、 计算题(30 分) 如图所示,用离心泵将水从敞口的水池输送到敞口的高位储槽内,吸 入管为852.5mm 的钢管,管长 L1=6m,摩擦系数可取1=0.02,压出管 为652.5mm 的钢管,管长 L2=13m,摩擦系数2 可取为 0.03,吸入和压 出各有 900 的弯头, 其阻力系数为 0.75, 压出管路上的阀门阻力系数为 6.4, 水池及储槽内的液面高度保持不变。H10m,泵进口高于水池面 2m,管 内流量为 0.012m3/s,试求:每 kg 水需从离心泵获得多少机械能?Βιβλιοθήκη 七、计算题(5 分)3
今有一干燥器,处理湿物料量为 800kg/h。要求物料干燥后含水量由 30% 减至 4%(均为湿基) 。试求水分的蒸发量。
青岛大学固体物理考研真题2010年、2011年

青岛大学2010年项士研究生入学考试试题科目代码: 817 科目名称: 固体物理学 (共2页)请考生写明题号,将答案全部答在答题纸上,答在此试卷上无效一、简答题 (本题共80分,每小题10分)1.说明晶体的对称操作类型并说明晶体有哪几种独立的宏观的对称元素。
2.说明晶体有哪几种基本的结合类型,并说明其特点。
3.对于含有N 个固体物理学原胞(初基晶胞)的金刚石晶体,按顺序写出格波支数、光学波支数、声学波支数、每支格波含的格波数、总格波数(即独立的振动模数)。
4.说明晶体周期场中运动的电子具有哪些一般属性。
5.当磁场方向沿<111>方向时,银的德哈斯范阿尔芬效应中磁化率振荡出现两个周期,当磁场方向沿其它方向时,磁化率振荡有时出现一个周期,有时甚至没有振荡存在。
请说明这一现象反映出的费米面的特征。
6.说明你对晶体中电子有效质量的了解。
7.请写出布里渊区边界方程,并说明面心立方第一布里渊区的形状及体积。
设面心立方晶格常数为a 。
8.说明你对晶体比热德拜模型的了解。
二、(本题10分)证明晶带轴[]uvw 与该晶带中的平面)(321h h h 满足下列关系:0321=++wh vh uh三、(本题10分)已知某晶体中相邻原子间的相互作用势可表示为:nm r r u βα+-=,其中βα,,,n m 都是大于零的常数。
1.说明右式两项的物理意义并求出处于平衡态时的原子间距0r ;2.证明此系统可以处于稳定平衡态的条件是m n >。
四、(本题10分)体心立方晶格,原子总数为N。
设电子的等能面为球面,试求当费密面恰好与第一布里渊区的界面相切时,第一布里渊区实际填充的电子数。
五、(本题20分)由N 个质量为m 、原子间距为a 的相同原子组成的一维单原子晶格,恢复力系数为β,若只考虑近邻原子间的相互作用,并用简谐近似。
1.证明其色散关系为:2sin 2aq m βω=; 2.在简约布里渊区内画出色散关系曲线;3.求模式密度()ωρ。
青岛大学821机械控制工程基础2014—2015年考研专业课初试真题
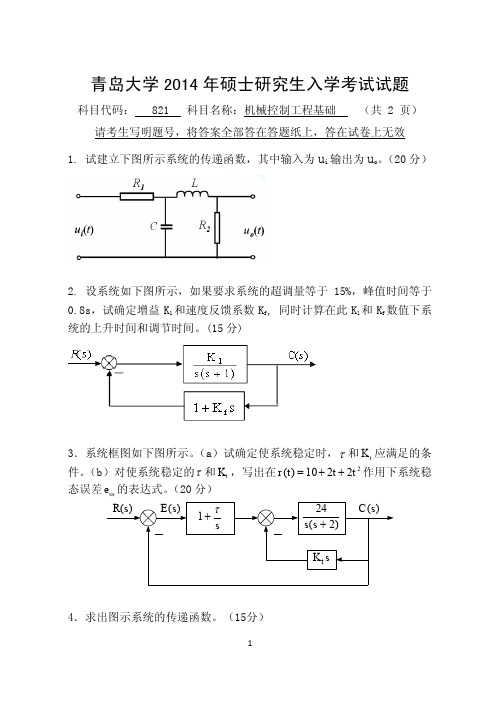
3.系统框图如下图所示。 (a)试确定使系统稳定时, 和 K t 应满足的条 件。 (b)对使系统稳定的 和 K t ,写出在 r (t ) 10 2t 2t 2 作用下系统稳 态误差 e ss 的表达式。 (20 分)
R(s)
E (s)
1
s
24 s ( s 2) Kt s
C (s)
4.求出图示系统的传递函数。(15分)
1
5. 设系统的开环传递函数为 Gk(s)=k(2s+1)/s2(0.5s+1)(s+1), 试粗略绘 制其 Nyquist 图,并分析闭环系统的稳定性。 (30 分)
6. 已知单位反馈的最小相位系统, 其开环对数幅频特性如下图所示, 试 求 (1)开环传递函数;(2)计算系统的相位裕度,并判断系统的稳定性。 (20分)
(15 分) 五.对图示控制系统,求输入 xi(t)=1(t),扰动 n(t)=1(t)时,系统的总 稳态误差。 (1Байду номын сангаас 分)
六. (15 分)
(15 分) 七.已知系统开环传递函数 G ( s ) H ( s )
20 ,应用 Nyquist 判 ( s 1)(2 s 1)(5s 1)
据判别闭环系统的稳定性。若不稳定,闭环系统有几个正实部的根? (15 分) 八.设控制系统如下图所示 k=10,试 1)画出系统开环 BODE 图(10 分) ; 2)求出系统的相位裕度和幅值裕度(10 分) 。
2
九. 已知某单位反馈系统, 其 G(s)和 Gc(s)的对数幅频特性渐近线如下图 所示。
青岛大学 2014 年硕士研究生入学考试试题
科目代码: 821 科目名称:机械控制工程基础 (共 2 页) 请考生写明题号,将答案全部答在答题纸上,答在试卷上无效 1. 试建立下图所示系统的传递函数,其中输入为 ui 输出为 uo。 (20 分)
青岛大学物理基础综合考研真题2015年、2017年

青岛大学2015年硕士研究生入学考试试题 科目代码: 913 科目名称: 物理基础综合 (共2页) 请考生写明题号,将答案全部答在答题纸上,答在试卷上无效1、质点由坐标原点出发时开始计时,沿x 轴运动,其速度12-=t v x 。
求:(1)瞬时加速度随时间的变化规律;(2)质点的运动学方程;(3)01=t到12=t 时间内质点的位移,以及运动的路程。
(15分)2、天平左端挂一定滑轮,一轻绳跨过滑轮,绳的两端分别系上质量为1m 、2m 的物体(21m m ≠)。
天平右端的托盘内放有砝码。
问天平托盘和砝码共重若干,才能保持天平平衡?不计滑轮和绳的质量及轴承摩擦,绳不伸长。
(15分)3、质量M 的物块与弹簧(劲度系数为k )原来处于静止,另一质量为m 的质点从离M 为h 的高度自由落下,m 和M 做完全非弹性碰撞。
证明:弹簧对地面的最大压力为gm M kh mg g m M F )(21)(max ++++= (15分)4、如图所示,一长为l ,质量为M 的杆可绕支点O 自由转动。
一质量为m 、速度为v 的子弹射入下端而不复出,此后杆摆至水平位置又开始回落;设从子弹射入到停在杆内为时极短。
求:(1)子弹进入杆前的速度;(2)子弹刚停在杆内时轴O 受杆的力。
(15分)5、空间有两块面积为S 的平行放置的金属平板A 和B ,两板长宽均比板间距离大得多,如图所示。
令每板带上A q 及B q 的电量,求每板表面的电荷密度。
(15分)6、半径为R 的金属球带电荷Q ,球外套一个同心球壳的均匀电介质,其内外半径分别为a 和b ,相对介电常数为r ε(如图所示)。
求:(1)介质球壳内外的电场强度E 和电位移D ;(2)导体球的电位。
(15分)7、把能量为E 的电子射入磁感应强度为B 的匀强磁场中,其速度矢量与B 成θ角,路径成螺旋线,其轴在B 的方向。
试求这螺旋线运动的周期T ,螺距h 和半径r 。
(15分)8、一长直导线中通有I 的电流,在与其相距d 处放有一矩形线圈,线圈以速度v 沿垂直长直导线的方向向右离开导线时,线圈中的感应电动势是多少?指出感应电流方向。
617固体物理

青岛大学2021年硕士研究生入学考试题科目代码: 617 科目名称: 固体物理(共2页) 请考生写明题号,将答案全部答在答题纸上,答在试卷上无效一、简答题 (80分,每题10分)1.请说明当电子的波矢落在布里渊区边界上时,电子有效质量与真实质量有显著差别的原因。
2.请说明导体、半导体、绝缘体能带结构的特点,并从能带结构的角度分析说明能否实现导体和绝缘体间的转变,如果能,如何实现。
3.请说明你对晶体衍射理论中反射球概念的理解。
4.请说明什么是金属的脱出功,并说出两种与脱出功有关的物理现象。
5.当磁场方向沿[111]方向时,银的德哈斯-范·阿尔芬效应中磁化率振荡出现两个周期,请说明原因(先说明什么是德哈斯-范·阿尔芬效应,再说明原因)。
6.请说明晶体中原子结合的基本类型,并说明各种结合类型的特点。
7.两个声子相互作用产生第三个声子,有正常过程和反常过程。
请列式说明你对正常过程和反常过程的理解。
8.请说明你对金属电阻率的了解。
二、证明与计算(70分,第1、2题各15分, 第3、4题各10分,第5题20分)1.对于金刚石结构,若晶格常数为a,试完成以下各问:(1)写出其固体物理学原胞基矢;(2)计算其倒格基矢,说明倒格点阵类型、第一布里渊区形状及体积;(3)说明在X射线衍射图中,找不到(321)、(221)及(442)等面的一级衍射斑点的原因。
2.用德拜比热模型求一维单原子链的热容)(T C V的表达式,并证明在低温极限下,它与温度T 成正比。
3.对于由N 个正、负离子组成的离子晶体。
(1)证明其结合能为)4(202n RB R q N U --=πεμ (R 为离子间最近邻距离) (2)求平衡时体积弹性模量,并说明如何确定n 。
4.设有一个由相同原子组成的二维正方点阵,原子质量为M ,晶格常数为a ,取近邻原子间的恢复力系数为β,设原子只作垂直表面的横向振动,在简谐近似下,试求(1)横向晶格振动的色散关系;(2)长波极限下格波的传播速度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Fhkl f j e in K hkl R j f j e
j j
i 2n( hu j kv j lw1 )
(1)计算体心立方结构的几何结构因子,并说明衍射极大条件。 (2) 具有体心立方结构的元素晶体, 它的多晶样品 X 射线衍射谱中,
1
散射角最小的三个衍射峰相应的面指数是什么? 三、 (本题 10 分) 具有简单立方结构的晶体,原子间距为 2 A ,由于晶体中非简 谐 项 作 用 的 存 在 , 一 个 沿 [ 100 ] 方 向 传 播 的 波 矢 为
ak y ak ak E s ( k ) E sat J SS 8J cos x cos cos z ; 2 2 2
2.写出能带顶部和能带底部电子的波矢,并求能带宽度; 3.求能带顶部及底部电子的倒有效质量张量。 4. 求出电子运动速度表达式。
2
2
2
青岛大学 2015 年硕士研究生入学考试试题
科目代码: 817 科目名称: 固体物理 (共 2 页) 请考生写明题号,将答案全部答在答题纸上,答在试卷上无效 一、简述题 (80 分,每题 10 分) 1.晶体有哪几种基本对称操作,并写出晶体独立的宏观的对称元素。 2.写出晶体衍射的劳厄方程的三种形式,并说明其物理意义。 3.对于含有 N 个固体物理学原胞(初基晶胞)的金刚石晶体,按顺序写出 格波支数、光学波支数、声学波支数、每支格波含的格波数、总格波数 (即独立的振动模数) 。 4.当磁场方向沿<111>方向时,银的德哈斯范阿尔芬效应中磁化率振荡出 现两个周期,当磁场方向沿其它方向时,磁化率振荡有时出现一个周期。 请说明这一现象反映出的费米面的特征。 5.说明你对晶体中电子有效质量的了解。当电子的波矢落在布里渊区 边界上时,为什么其有效质量与真实质量有显著差别? 6.请写出布里渊区边界方程,并说明面心立方第一布里渊区的形状及体积。 设面心立方晶格常数为 a 。 7. 写出索末菲自由电子论的电子分布函数 f ( E ) 的表达式, 画出两条有 代表性的 f ( E ) ~ E E F 的曲线,并对其加以解释。 8.由 N 个原子组成的半导体材料硅晶体,试分析说明该晶体中一个能 带最多可填充多少个电子? 二、 (本题 10 分) 由几何结构因子的定义式:
青岛大学 2014 年硕士研究生入学考试试题
科目代码:817 科目名称:固体物理 (共 2 页) 请考生写明题号,将答案全部答在答题纸上,答在试卷上无效 一、 简答题(50 分)
1. 试解释“基元+点阵=晶格结构”的公式(要求说明:(1)什么是布喇菲 点阵?(2)什么是基元?(3)点阵和结构间的区别和联系。 ) (10分) 2. 根据结合力的不同,晶体可分为哪几种不同类型,并简述它们的基本特点。 (10 分) 3. 费米分布函数 f E 及 f / E 有哪些特性?其物理意义是什么?(10 分) 4. 定性画出导体、 半导体和绝缘体的能带示意图,并解释为什么晶体会有导体、 半导体和绝缘体之分。 (10 分) 5. 什么叫 F 心?并简述它是如何形成的。 (10 分) 二、 (20 分) 用波长为 1.5405 A 的X射线投射到钽的粉末上,得到前面几条衍射谱线的布 喇格角 如下: 谱线
q100 1.3 1010 m 1 的声子同另一个波矢大小相等、但沿[110]方
0
向传播的声子相互作用,合并成第三个声子。试求新形成的第三个 声子的波矢。 四、 (本题 15 分) 设晶体由 N 个原子组成,按德拜模型求其晶格振动热容量的表 达式,并讨论高低温极限下热容量与温度的关系 ( 已知模式密度
1 19.61
2 2ቤተ መጻሕፍቲ ባይዱ.14
3 35.16
4 41.16
5 47.77
已知钽为体心立方结构,试求: (1)各谱线对应的衍射晶面族的面指数; (2)上述各晶面族的面间距; (3)利用上两项结果计算晶格常数a。 (其中sin19.61=0.3356,sin28.14=0.4716,sin41.16=0.6582,sin47.77=0.7405.) 三、 (20 分) 面心立方晶格常数为 a ,原子总数为 N。 (1)证明其倒格子是边长为 4 的体心立
3 )。 ( ) 9 N 2 D
五、 (本题 15 分) 体心立方晶格,原子总数为N。设电子的等能面为球面, 试求当费密面恰好与第一布里渊区的界面相切时,第一布里渊 区实际填充的电子数。 六、 (本题20分) 用紧束缚近似方法处理体心立方晶格的s态电子, 若只计及最近 邻原子间的相互作用。 1.证明其能量表达式为:
试用德拜模型求出由 N 个原子组成的单原子晶体晶格振动的比热, 并求其在高温 和低温极限情况下的表达式。 五、 (15 分) 已知一维金属晶体共含有N个电子,晶体的长度为L。设T=0K,试求 (1)电子的能态密度; (2)晶体的费密能级; (3)晶体电子的平均能量。
六、 (30 分) 用紧束缚近似方法处理体心立方晶格的s态电子,若只计最近邻原子的相互作 用, (1)试导出其能带表达式; (2)写出能带顶部和能带底部电子的波矢,并求能带宽度; (3)求能带顶部及底部附近电子的有效质量。
a
方。 (2)说明第一布里渊区的形状及体积。 (3)设电子等能面是球面,试求当费 密面是第一布里渊区中最大、 最完整的球面时,第一布里渊区中实际填充的电子 数。
1
1
四、 (15 分) 已知一个频率为
i 的简谐振动在温度T下的平均能量
i
1 i i k BTi 2 e 1
