八(上)数学竞赛练习题(5)

合集下载

八年级(上)数学竞赛试题及答案(新人教版)

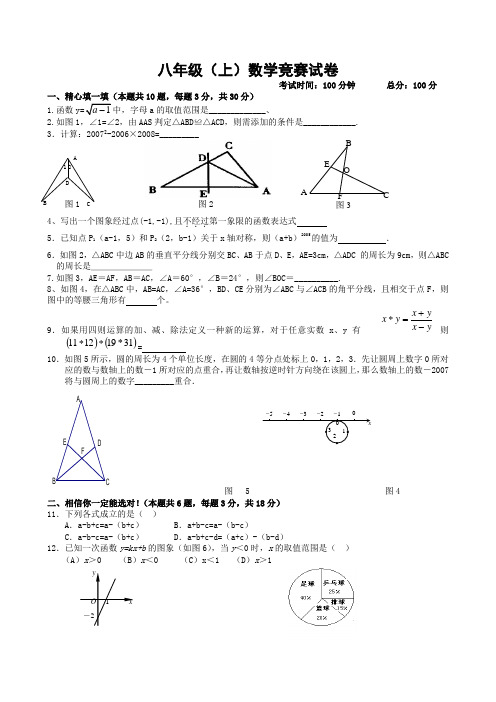
八年级（上）数学竞赛试卷考试时间：100分钟总分：100分一、精心填一填（本题共10题，每题3分，共30分）1.函数a 的取值范围是_____________、2.如图1，∠1=∠2，由AAS 判定△ABD ≌△ACD ，则需添加的条件是____________. 3．计算：20072-2006×2008=_________图1 图24、写出一个图象经过点(-1,-1),且不经过．．．第一象限的函数表达式 5．已知点P 1（a-1，5）和P 2（2，b-1）关于x 轴对称，则（a+b ）2005的值为．6．如图2，△ABC 中边AB 的垂直平分线分别交BC 、AB于点D 、E ，AE=3cm ，△ADC•的周长为9cm ，则△ABC 的周长是＿＿＿＿＿＿＿7.如图3，AE ＝AF ，AB ＝AC ，∠A ＝60°，∠B ＝24°，则∠BOC ＝__________.8、如图4，在△ABC 中，AB=AC ，∠A=36°，BD 、CE 分别为∠ABC 与∠ACB 的角平分线，且相交于点F ，则图中的等腰三角形有个。

9．如果用四则运算的加、减、除法定义一种新的运算，对于任意实数x 、y 有y x y x y x -+=* 则()()31*191211**=10．如图5所示，圆的周长为4个单位长度，在圆的4等分点处标上0，1，2，3．先让圆周上数字0所对应的数与数轴上的数－1所对应的点重合，再让数轴按逆时针方向绕在该圆上，那么数轴上的数－2007将与圆周上的数字_________重合．FEDACB图 5图4 二、相信你一定能选对！（本题共6题，每题3分，共18分） 11．下列各式成立的是（）A ．a-b+c=a-（b+c ）B ．a+b-c=a-（b-c ）C ．a-b-c=a-（b+c ）D ．a-b+c-d=（a+c ）-（b-d ） 12．已知一次函数y=kx+b 的图象（如图6），当y ＜0时，x 的取值范围是（）（A ）x ＞0 （B ）x ＜0 （C ）x ＜1 （D ）x ＞1A B C D12 AEBO F C图3图6 图713.在△ABC 中，∠B ＝∠C ，与△ABC 全等的三角形有一个角是100°，那么在△ABC 中与这100°角对应相等的角是（）A.∠AB.∠BC.∠CD.∠B 或∠C 14．某校八（2）班的全体同学喜欢的球类运动用图7所示的扇形统计图来表示，下面说法正确的是（） A 、从图中可以直接看出喜欢各种球类的具体人数； B 、从图中可以直接看出全班的总人数；C 、从图中可以直接看出全班同学初中三年来喜欢各种球类的变化情况；D 、从图中可以直接看出全班同学现在喜欢各种球类的人数的大小关系 15．已知一次函数y=mx+│m+1│的图像与y 轴交于点（0，3），且y 随x 的增大而减小，则m 的值为（）． A ．2 B ．-4 C ．-2或-4 D ．2或-416．设y=ax 15+bx 13+cx 11-5(a 、b 、c 为常数)，已知当x=7时，y=7，则x= -7时，y 的值等于( )A 、-7B 、-17C 、17D 、不确定三、认真解答，一定要细心哟！（各6分，共18分） 17. 先化简再求值：[]y y x y x y x 4)4()2)(2(2÷+--+，其中x =5，ｙ=2。

第一学期八年级数学竞赛练习题6份

第一学期八年级数学竞赛练习题1 (1)第一学期八年级数学竞赛练习题2 (7)第一学期八年级数学竞赛练习题3 (13)第一学期八年级数学竞赛练习题4 (17)第一学期八年级数学竞赛练习题5 (22)第一学期八年级数学竞赛练习题6 (25)第一学期八年级数学竞赛练习题1(满分120分,时间120分钟)一、选择题(每小题5分,共40分)1．已知一列数a 1，a 2，a 3…a n 中，a 1=0，a 2=2a 1+1，a 3=2a 2+1，…a n+1=2a n +1 ，则a 2004-a 2003的个位数字是（）A. 2B. 4C. 6D. 82. 在△ABC 中，AB=13，AC=15，高AD=12，则BC 的长是（） A.14 B.4 C.14或4 D.以上都不正确3. 如图，四边形ABCD 是正方形，直线l 1，l 2，l 3分别通过A ，B ，C 三点，且a//b//c ，若a 与b 的距离为5，b 与c 的距离为7，则正方形ABCD 的面积等于（）A. 70B.74C.144D.1484.已知对于任意有理数a 、b,关于x,y 的二元一次方程：(a ＋b)x －(a －b)y ＝a －b 都有一组公共解，则这个公共解为（） A.00x y =⎧⎨=⎩ Ｂ.11x y =-⎧⎨=⎩ Ｃ. 12x y =⎧⎨=⎩ D.01x y =⎧⎨=-⎩5. 把自然数n 的各位数字之和记S(n),如：n ＝38,S(n)＝3＋8＝11；n ＝247,S(n)＝2＋4＋7＝13, 若对于某个自然数n 满足:n －S(n)＝2007,则n 的最大值是（） A.2019 B.2021 C.2023 D.20256. 如图是一个由几块相同的小正方体搭成的立体图形的三视图，则这堆立体图形中的小正方体共有（）块。

A. 7B. 8C. 9D. 107. 已知p 、q 均是质数，且满足5p 2+3q=59，则以p+3、1-p+q 、2p+q-4为边长的三角形的形状（）A ．锐角三角形B ．直角三角形C ．钝角三角形D ．等腰三角形8. 某校准备开办一些学生课外活动的兴趣班，有计算机班、奥数班、英语口语班和音乐艺术班，结果反映热烈。

八年级上数学竞赛练习题含答案

八年级上数学竞赛练习题含答案文档编制序号：[KKIDT-LLE0828-LLETD298-POI08]八年级（上）数学竞赛题一、选择题1、设x 、y 、z 均为正实数,且满足z x+y <x y+z <yz+x ,则x 、y 、z 三个数的大小关系是（） A 、z<x<yB 、y<z<xC 、x<y<zD 、z<y<x2、已知a 、b 都是正整数,那么以a 、b 和8为边组成的三角形有（） A 、3个B 、4个C 、5个D 、无数个3、将一长方形切去一角后得一边长分别为13、19、20、25和31的五边形（顺序不一定按此）,则此五边形的面积为（） A 、680B 、720C 、745D 、7604、如果不等式组⎩⎨⎧<-≥-0809b x a x 的整数解仅为1，2，3，那么适合这个不等式组的整数a 、b 的有序数对（a 、b ）共有（）个个个个5、设标有A 、B 、C 、D 、E 、F 、G 记号的7盏灯顺次排成一行，每盏灯安装一个开关，现在A 、C 、E 、G 4盏灯开着，其余3盏灯是关的，小岗从灯A 开始，顺次拉动开关，即从A到G，再顺次拉动开关，即又从A到G，…，他这样拉动了1999次开关后，则开着的灯是（）A、、 C、 D、、已知13xx-=，那么多项式3275x x x--+的值是（）A．11 B．9 C．7 D．57、线段12y x a=-+（1≤x≤3，），当a的值由-1增加到2时，该线段运动所经过的平面区域的面积为（）A．6 B．8 C．9 D．108、已知四边形ABCD为任意凸四边形，E、F、G、H分别是边AB、BC、CD、DA的中点，用S、P分别表示四边形ABCD的面积和周长；S1、P1分别表示四边形EFGH的面积和周长．设K = SS1，K1 =PP1，则下面关于K、K1的说法正确的是（）．、K1均为常值为常值，K1不为常值不为常值,K1为常值、K1均不为常值二、填空题1、如图，△ABC是一个等边三角形，它绕着点P旋转，可以与等边△ABD重合，则这样的点P有_______个。

八年级上学期数学竞赛试题(含答案)

八年级上学期数学竞赛试题（含答案）题号一二三四五得分得分一、选择题（每题3分，共42分）将唯一正确答案的代号字母填在下面的表格内：题号 1 2 345 6 7 8 9 10 11 12 13 14 答案1.在以下绿色食品、回收、节能、节水四个标志中，是轴对称的图形有2．已知三角形两边长分别为3和5，则第三边a 的取值范围是 A ．53<<a B ．83<<a C ．52<<a D ．82<<a 3．下列运算错误的是 A ．333532a a a -=B ．633a a a ÷=C ．325()()()a b b a a b --=-D ．236m n m n +⨯=4. 一个正多边形的外角与它相邻的内角之比为1：4，那么这个多边形的边数为 A ．8 B ．9 C ．10 D ．125. 计算45(210)(410)-⨯⨯⨯的正确结果是A. 20210-⨯B. 9210⨯C. 9810⨯D. 9810-⨯ 6．下列各式由左边到右边的变形中，是分解因式的为A B C DA ．ay ax y x a +=+)(B ．4)4(442+-=+-x x x xC ．)12(55102-=-x x x xD ．x x x x x 3)4)(4(3162++-=+-7. 若321()44m n x y x y x ÷=，则,m n 的值分别是A.6,1m n ==B.5,1m n ==C.5,0m n ==D.6,0m n ==8.下列分式运算中正确的是 A. a acb bc= B.x y y x x y x y --=+- C.321x y x xy x +=+ D. 0.33100.20.525a b a ba b a b++=++9．如图，∠1＝∠2，要证明△ABC≌△ADE，还需补充的条件是A. AB ＝AD ，AC ＝AEB. AB ＝AD ，BC ＝DEC. AC ＝AE ，BC ＝DED. 以上都不对10．在平面直角坐标系中，已知点(,3)A m 与点(4,)B n 关于y 轴对称，那么2015()m n + 的值为A ．1-B ．1C ．20157-D ．2015711.如果214x x c ++是一个完全平方式，那么常数c 的值可以是 A ．49 B ．169 C ．49±D ．169±12.对于任何整数a ，多项式2(35)4a +-都能第9题图A.被9整除B.被a 整除C.被1a +整除D.被1a -整除13.如图，在直角ABC △中，90C =∠，30B =∠，AB 的垂直平分线交AB 于点D ，交BC 于点E ，若3AC =，1CE =，则△DBE 的周长为 A ．13+ B ．23+C ．231+D ．33+14. 如图为杨辉三角系数表，它的作用是指导读者按规律写出形如()n a b +（其中 n 为正整数）展开式的系数，例如：（a ＋b ）＝a ＋b ，（a ＋b ）2＝a 2＋2ab ＋b 2，（a ＋b ）3＝a 3＋3a 2b ＋3ab 2＋b 3，那么6()a b +展开式中前四项系数分别为A ．1,5,6,8B ．1,5,6,10C ．1,6,15,18D ．1,6,15,20二、填空题：（每题3分，共15分）答案直接填在题中横线上. 15. 计算：()2323x x ⋅-= .16. 分解因式：(1)(3)4x x -++=___________． 17．若分式2244x x x --+的值为0，则x 的值为．18. 如图，在△ABC 中，AB ＝6，BC ＝8，∠B ＝60°，将第18题图第13题图E DCBA△ABC沿射线BC 的方向平移2个单位后，得到△'''A B C ，连接'A C ，则△''A B C 的周长为________.19. 新定义一种运算：22@()()a b a b a b =+--，下面给出关于这种运算的几个结论：①1@(2)8-=-；②@@a b b a =；③若@0a b =，则a 一定为0；④若0a b +=，那么2(@)(@)8a a b b a +=.其中正确结论的序号是．三、开动脑筋，你一定能做对！（本大题共3小题，共19分）20. （本题共6分）如图，在△ABC 和△BDE 中，点C 在边BD 上，边AC 交边BE 于点F ，若AC ＝BD ， AB ＝ED ，BC ＝BE ，求证：∠ACB =12∠AFB ．21.（本题共7分）先化简再求值：已知y x A +=2，y x B -=2，求代数式22()(2)A B x y --的值，其中1x =-，2y =.F E DCBA第20题图22．（本题共6分）如图所示，ABC △中，110BAC ∠=︒，点D,E,F 分别在线段AB 、BC 、AC 上，且BD ＝BE ，CE ＝CF ，求DEF ∠的度数.四、认真思考，你一定能成功！（本大题共2小题，共21分）23．(12分)如图，在平面直角坐标系中，直线l 是第一、三象限的角平分线．实验与探究：（1）由图观察易知A （0，4）关于直线l 的对称点A '的坐标为（4，0），请在图中分别标明B(5,2) 、C(-2,3) 关于直线l 的对称第22题图FEDCBA点B'、C'的位置，并写出他们的坐标:B'、C'；归纳与发现：（2）结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点(,)P a b关于第一、三象限的角平分线l的对称点P'的坐标为（不必证明）；运用与拓广：（3）已知两点D(1，-2)、E(-1，-3)，试在直线l上确定一点Q，使点Q到D、E两点的距离之和最小．（要有必要的画图说明，并保留作图痕迹）24.（本题共9分）设kxy=，是否存在实数k，使得代数式5x？若能，请求出所有满足条件的k的值；----能化简为2()(2)3(2)x y x y x x y若不能，请说明理由．五、相信自己，加油呀！（本大题共2小题，共23分）25. （11分）已知：△ABC中，∠A＝90°，AB＝AC，D为BC的中点.（1）如图1，E，F分别是AB，AC上的点，且BE＝AF，求证：△DEF为等腰直角三角形．（2）如图2，若E，F分别为AB，CA延长线上的点，仍有BE＝AF，其他条件不变，那么，△DEF是否仍为等腰直角三角形？如果是，请写出证明过程；如果不是，请说明理由．26.（本题12分）阅读材料：分解因式：223x x +-解：原式＝22113x x ++-- ＝2(21)4x x ++-＝2(1)4x +- ＝(12)(12)x x +++-＝(3)(1)x x +-此种方法抓住了二次项和一次项的特点，然后加一项，使这三项成为完全平方式，我们把这种分解因式的方法叫配方法.请仔细体会配方法的特点，然后尝试用配方法解决下列问题：（1）分解因式： 2243m mn n -+；（2）无论m 取何值，代数式232015m m -+总有一个最小值，请你尝试用配FE DCBA方法求出它的最小值.八年级数学试题参考答案及评分建议15. 518x 16. 2(1)x + 17． 2x =- 18. 18 19.①②④三、解答题（共63分）20. （本题共6分）证明：∵AC ＝BD ， AB ＝ED ，BC ＝BE ， ∴△ABC ≌△DEB ，……………………………………………2分 ∴∠ACB=∠EBD,…………………………………………………3分 ∵∠AFB 是△BFC 的外角，∴∠AFB=∠ACB+∠EBD ， ∴∠AFB=2∠ACB ，即∠ACB =12∠AFB.…………………………………………………6分 21.（本题共7分）解：原式＝8(2)xy x y -＝22816x y xy -…………………………… 5 分当1,2x y =-=时，原式＝16＋64＝80. ……………………………… 7 分 22．（本题共6分）解：不妨设∠B＝x ，∠C ＝y ，则在△BDE 中，∵BD ＝BE ，∴∠B ED ＝12（180°－x ），同理在在△CEF中，∵CE ＝CF ，∴∠CEF ＝12（180°－y ），………………2分因为∠B ED ＋∠DEF ＋∠CEF ＝180°，FEDCBA∴∠DEF ＝180°－（∠B ED ＋∠CEF ）＝180°－11(180)(180)22x y ⎡⎤-+-⎢⎥⎣⎦＝1()2x y +……………………………4分又∵110BAC ∠=︒，∴18011070x y +=︒-︒=︒，故∠DEF ＝170352⨯︒=︒.………6分 23.（本题共9分）解：能．……………………………………………………………1分假设存在实数k ，因为()(2)3(2)x y x y x x y ----=224x y -+，………………3分将kx y =代入，原式＝224()x kx -+=22(4)k x -，………………………………5分∵22(4)k x -＝25x ，∴245k -=，………………………………………………7分29k =，得3k =±．……………………………………………………………………9分24．(12分) 解:(1)由图可知，'(2,5)B ，'(3,2)C -；…………………………4分（2）由（1）可知，关于直线l 对称的点'(,)P b a ；……………………………………7分（3）作出点E 关于直线l 对称点F ，连接FD ，则QF ＝QE ，故EQ ＋QD ＝FQ ＋QD ＝FD.……………………………………………………12分25. （11分）证明：（1）连结AD ， ∵AB AC =，∠BAC ＝90°，D 为BC 的中点，∴AD ⊥ BC ，BD ＝AD ，∴∠B ＝∠DAC ＝45°又BE ＝AF ，∴△BDE ≌△ADF （SAS ）∴ED ＝FD ，∠BDE ＝∠ADF∴∠EDF ＝∠EDA ＋∠ADF ＝∠EDA ＋∠BDE ＝∠BDA ＝90°∴△DEF 为等腰直角三角形 …………………………… 5分（2）若E ，F 分别是AB ，CA 延长线上的点，如图所示．连结AD ∵AB ＝AC ，∠BAC ＝90°， D 为BC 的中点，∴AD ＝BD ，AD ⊥BC ∴∠DAC ＝∠ABD ＝45°，∴∠DAF ＝∠DBE ＝135°，又AF ＝BE ，∴△DAF ≌△DBE （SAS ），∴FD ＝ED ，∠FDA ＝∠EDB ， ∴∠EDF ＝∠EDB ＋∠FDB ＝∠FDA ＋∠FDB ＝∠ADB ＝90°，∴△DEF 仍为等腰直角三角形.…………………………………………………11分26.（本题12分）解：（1）222224344m mn n m mn n n -+=-+- …………1分22(2)m n n =-- ………………………………3分 (3)()m n m n =--；………………………………6分（2）232015m m -+222333()()201522m m =-+-+…………………………7分 2233()()201522m =--+233()201224m =-+，………………………………8分 ∵23()02m -≥，∴2333()20122012244m -+≥，…………………………11分即代数式232015m m -+的最小值为320124.…………………………………12分（备注：在解答题中，考生若用其它解法，应参照本评分标准给分）。

八年级上学期数学竞赛试题(含答案)

26.（本题12分）阅读材料：
分解因式：
解：原式＝
＝
＝
＝
＝
此种方法抓住了二次项和一次项的特点,然后加一项,使这三项成为完全平方式,我们把这种分解因式的方法叫配方法.请仔细体会配方法的特点,然后尝试用配方法解决下列问题：
（1）分解因式：；
（2）无论取何值,代数式总有一个最小值,请你尝试用配方法求出它的最小值.
∵ ＝ ,∴ ,………………………………………………7分
,得．……………………………………………………………………9分
24．(12分)解:(1)由图可知, , ；…………………………4分
（2）由（1）可知,关于直线对称的点；……………………………………7分
（3）作出点E关于直线对称点F,连接FD,则QF＝QE,故EQ＋QD＝FQ＋QD＝FD.
∴∠EDF＝∠EDB＋∠FDB＝∠FDA＋∠FDB＝∠ADB＝90°,
∴△DEF仍为等腰直角三角形.…………………………………………………11分
26.（本题12分）解：（1） …………1分
………………………………3分
；………………………………6分
（2） …………………………7分
,………………………………8分
∴△DEF为等腰直角三角形 …………………………… 5分
（2）若E,F分别是AB,CA延长线上的点,如图所示．连结AD
∵AB＝AC,∠BAC＝90°, D为BC的中点,∴AD＝BD,AD⊥BC
∴∠DAC＝∠ABD＝45°,∴∠DAF＝∠DBE＝135°,
又AF＝BE,∴△DAF≌△DBE（SAS）,∴FD＝ED,∠FDA＝∠EDB,
3．下列运算错误的是
A． B．

八年级上数学竞赛练习题含答案

八年级上数学竞赛练习题含答案Newly compiled on November 23, 2020八年级（上）数学竞赛题一、选择题1、设x 、y 、z 均为正实数,且满足z x+y <x y+z <yz+x ,则x 、y 、z 三个数的大小关系是（） A 、z<x<yB 、y<z<xC 、x<y<zD 、z<y<x2、已知a 、b 都是正整数,那么以a 、b 和8为边组成的三角形有（） A 、3个B 、4个C 、5个D 、无数个3、将一长方形切去一角后得一边长分别为13、19、20、25和31的五边形（顺序不一定按此）,则此五边形的面积为（） A 、680B 、720C 、745D 、7604、如果不等式组⎩⎨⎧<-≥-0809b x a x 的整数解仅为1，2，3，那么适合这个不等式组的整数a 、b 的有序数对（a 、b ）共有（）个个个个5、设标有A 、B 、C 、D 、E 、F 、G 记号的7盏灯顺次排成一行，每盏灯安装一个开关，现在A 、C 、E 、G 4盏灯开着，其余3盏灯是关的，小岗从灯A 开始，顺次拉动开关，即从A到G，再顺次拉动开关，即又从A到G，…，他这样拉动了1999次开关后，则开着的灯是（）A、、 C、 D、、已知13xx-=，那么多项式3275x x x--+的值是（）A．11 B．9 C．7 D．57、线段12y x a=-+（1≤x≤3，），当a的值由-1增加到2时，该线段运动所经过的平面区域的面积为（）A．6 B．8 C．9 D．108、已知四边形ABCD为任意凸四边形，E、F、G、H分别是边AB、BC、CD、DA的中点，用S、P分别表示四边形ABCD的面积和周长；S1、P1分别表示四边形EFGH的面积和周长．设K = SS1，K1 =PP1，则下面关于K、K1的说法正确的是（）．、K1均为常值为常值，K1不为常值不为常值,K1为常值、K1均不为常值二、填空题1、如图，△ABC是一个等边三角形，它绕着点P旋转，可以与等边△ABD重合，则这样的点P有_______个。

初中数学八年级上数学竞赛试题含答案

初中数学八年级上数学竞赛试题含答案Newly compiled on November 23, 20200 1 2－1A 八年级（上）数学竞赛试题一、填空题:（40分）1、在ABC Rt ∆中，b a 、为直角边，c 为斜边，若14=+b a ，10=c ，则ABC ∆的面积是；2、计算：=⋅27 311 ；3 313÷⨯＝；2 3 2 +-＝； 3、某位老师在讲实数时，画了一个图（如图1），即以数轴的单位长线段为边作一个正方形，然后以0点为圆心，正方形的对角线长为半径画图，交x 轴于一点A ，作这样的图是用来说明；42，又出现了一个方格体正向下运动，为了使所有图案消失，你必须按后才能拼一个完整图案，从而使图案自动消失（游戏机有此功能）。

5、如图3，=∠+∠+∠+∠+∠+∠F E D C B A ；6、图4是一住宅小区的长方形花坛图样，阴影部分是草地，空地是四块同样的菱形，则草地与空地的面积之比为；(6)7、如图5，一块白色的正方形木板，边长是cm 18，上面横竖各有两根木条（阴影部分），宽都是cm 2，则白色部分面积是 2cm ；8、如图6，一块正方形地板由全等的正方形瓷砖铺成，这地板上的两条对角线上的瓷砖全是黑色，其余的瓷砖是白色的，如果有101块黑色瓷砖，那么瓷砖的总数是；二、选择题:（30分）9、CD 是ABC Rt ∆斜边AB 上的高，若2=AB ，1:3:=BC AC ，则CD 为（）A 、51B 、52 C 、53D 、5410、如图，长方形ABCD 中，3=AB ，4=BC ，若将该矩形折叠，使C 点与A 点重合，则折痕EF 的长为（）A 、B 、3.75C 、D 、 11、如果a a -=-1 1 ，则a 的取值范围是（）A 、1=aB 、10<<aC 、0≥aD 、10≤≤a 12、若2 2 -+-x x 有意义，则x 的取值为（）A 、2>xB 、2<xC 、2≤xD 、2=x13、如上中图所示，一块边长为cm 10的正方形木板ABCD ，在水平桌面上绕点D 按顺时针方向转到D C B A ''''的位置时，顶点B 从开始到结束所经过的路径为（） A 、cm 20 B 、cm 220 C 、cm 10π D 、cm 25π14、如上右图所示，设ABCD 边上任意一点，设CMB ∆的面积为2S ，CDM ∆的面积为S ，AMD ∆的面积为1S ，则有（）A 、21S S S +=B 、21S S S +> C 、21S S S +< D 、不能确定三、画图题:（12分）15、如图，历史上最有名的军师诸葛亮，率精骑兵与司马懿对阵，诸葛亮一挥羽扇，军阵瞬时由左图变为右图，其实只移动了其中的3骑而己，请问如何移动（在图形上画出来即可）16、有一等腰梯形纸片，其上底和腰长都是a ，下底的长是a 2，你能将它剪成形状、大小完全一样的四块吗若能，请画出图形。

八年级上册数学竞赛题试卷

一、选择题（每题5分，共25分）1. 下列各数中，正数是（）A. -2.5B. -3.6C. -0.5D. 02. 已知a=2，b=-3，那么a²+b²的值是（）A. 7B. 13C. 17D. 233. 下列各数中，有理数是（）A. √9B. √16C. √25D. √-94. 已知x=3，y=-2，那么x+y的值是（）A. 5B. 1C. -5D. -15. 下列各式中，分式是（）A. 2xB. 3x+4C. 5/xD. x-1二、填空题（每题5分，共25分）6. 3/4的倒数是______。

7. 已知x²=16，那么x的值是______。

8. （-2）³的值是______。

9. 下列各数中，负数是______。

10. 2/3的平方根是______。

三、解答题（每题15分，共45分）11. （1）已知a=2，b=-3，求a²+b²的值。

（2）已知x²=9，求x的值。

12. 已知一元二次方程2x²-3x+1=0，求该方程的解。

13. 已知一元一次方程3x-5=2x+4，求x的值。

四、应用题（每题20分，共40分）14. 某班有男生x人，女生y人，已知男生人数是女生人数的2倍，求男生和女生人数之和。

15. 小明有若干个苹果，第一天吃了1/3，第二天又吃了2个，这时还剩12个苹果，求小明原来有多少个苹果。

答案：一、选择题1. C2. B3. C4. A5. C二、填空题6. 4/37. ±38. -89. -2 10. ±√6三、解答题11. （1）a²+b²=2²+(-3)²=4+9=13（2）x²=9，则x=±312. 2x²-3x+1=0x²-3/2x+1/2=0(x-1/2)²=0x-1/2=0x=1/213. 3x-5=2x+4x=9四、应用题14. 男生人数是女生人数的2倍，设女生人数为y，则男生人数为2y。

八年级(上)竞赛数学试题(含答案)

八年级竞赛数学试题及答案一、选择题：（每小题3分，本题满分共36分，）下列每小题中有四个备选答案，其中只有一个．．．．是符合题意的，把正确答案前字母序号填在下面表格相应的题号下。

题号 1 2 3 4 5 6 7 8 9 10 11 12答案1．分式有意义，则x的取值范围是（）A．x＞1 B．x≠1 C．x＜1 D．一切实数2．下列运算正确的是（）A．3a+2a=5a2B．x2﹣4=（x+2）（x﹣2）C．（x+1）2=x2+1 D．（2a）3=6a33．把x3﹣2x2y+xy2分解因式，结果正确的是( )A．x（x+y）（x﹣y）B．x（x2﹣2xy+y2）C．x（x+y）2D．x（x﹣y）2 4．如图，将等腰直角三角形沿虚线裁去顶角后，∠ 1+∠ 2=（）A．225°B．235°C．270°D．300°5．如图，△ABC和△DEF中，AC=DE，∠B=∠DEF，添加下列哪一个条件无法证明△ABC≌△DEF( )A．AC∥DF B．∠A=∠D C．AB=DE D．∠ACB=∠F 6．如图，在△ABC中，∠A=50°，∠ABC=70°，BD平分∠ABC，则∠BDC的度数是( )A．85°B．80°C．75°D．70°7．如图，小敏做了一个角平分仪ABCD，其中AB=AD，BC=D C．将仪器上的点A与∠PRQ 的顶点R重合，调整AB和AD，使它们分别落在角的两边上，过点A，C画一条射线AE，AE就是∠PRQ的平分线．此角平分仪的画图原理是：根据仪器结构，可得△ABC≌△ADC，这样就有∠QAE=∠P AE．则说明这两个三角形全等的依据是( ) A．SAS B．ASA C．AAS D．SSS8．若3x=4，9y=7，则3x﹣2y的值为( )A．B．C．﹣3 D．9．如图，在方格纸中，以AB为一边作△ABP，使之与△ABC全等，从P1，P2，P3，P4四个点中找出符合条件的点P，则点P有( )A．1个B．2个C．3个D．4个10．如图，在△ABC中，AD是角平分线，DE⊥AB于点E，△ABC的面积为7，AB=4，DE=2，则AC的长是（）A．4 B．3 C．6 D．511.如图，平面直角坐标系中，已知定点A(1，0)和B(0，1)，若动点C在x轴上运动，则使△ABC为等腰三角形的点C有( )个A. 5B. 4C. 3D. 212、.当x=1时，ax+b+1的值为﹣2，则（a+b﹣1）（1﹣a﹣b）的值为（）A．﹣16 B．﹣8 C．8D．16二、填空（每题4分，共32分）13. 如图，直线a ∥b ，一块含60°角的直角三角板ABC （∠A =60°）按如图所示放置．若∠1=55°，则∠2的度数为 .14．如图，△ABC 中，∠C =90°，∠BAC =60°，AD 是角平分线，若BD =8，则CD 等于 .15．分解因式：﹣x 2+4xy ﹣4y 2= ．16．若9x 2﹣kxy +4y 2是一个完全平方式，则k 的值是． 17．一个多边形的内角和是它的外角和的4倍，这个多边形是边形． 18．已知x 为正整数，当时x = 时，分式的值为负整数．19. 已知1024x y xy +==，，则()2x y -的值是 .20.比较255，344，433，522的大小，用“<”号连接为：三、解答下列各题（满分52分）21.（每小题4分，本题满分8分）分解因式：（1）3x 2﹣12x +12 （2）ax 2﹣4a ．22. （每小题5分，本题满分15分）计算与化简（1）(3-x )(3+x ）+(1+x )2,（2）（﹣）÷．（3）÷23. （本题满分8分）如图，△ACB和△ECD都是等边三角形，点A、D、E在同一直线上，连接BE．（1）求证：△ACD≌△BCE；（2）若CE=16，BE=21，求AE的长．24．（本题满分10分）如图，AD为△ABC的角平分线，DE⊥AB于点E，DF⊥AC于点F，连接EF交AD 于点G．（1）求证：AD垂直平分EF；（2）若∠BAC=60°，猜测DG与AG间有何数量关系？请说明理由．25. （本题满分5分）阅读材料：若m2﹣2mn+2n2﹣8n+16=0，求m、n的值．解：∵m2﹣2mn+2n2﹣8n+16=0，∴（m2﹣2mn+n2）+（n2﹣8n+16）=0∴（m﹣n）2+（n﹣4）2=0，∴（m﹣n）2=0，（n﹣4）2=0，∴n=4，m=4．根据你的观察，探究下面的问题：已知x2﹣2xy+2y2+6y+9=0，求xy的值；26. （本题满分6分）．我们在学习完全平方公式（a+b）2=a2+2ab+b2时，了解了一下它的几何背景，即通过图来说明上式成立．在习题中我们又遇到了题目“计算：（a+b+c）2”，你能将知识进行迁移，从几何背景说明（大致画出图形即可）并计算（a+b+c）2吗？八年级数学试题参考答案及评分标准（这里只提供了一种解法或证法，其他证法，只要合理，照常得分）一、1-12，BBDCC A DACB BA二、13．115°14.4 15. ﹣（x﹣2y）2．16、±12．17、十．18、3，4，5，8；19、4；20、522<255<433<344三、解答题．21、（1）解：原式=3（x2﹣4x+4）--------------------2分=3（x﹣2）2，-------------4分（2）解：ax2﹣4a=a（x2﹣4）--------------------------2分=a（x﹣2）（x+2）．-----------------------4分22、（1）解：原式=9-x2+1+2x+x2 -------------------3分=2x+10 ---------------------------5分（2）解：原式=•--------------------3分=•---------------------------4分=，------------------------------5分（3）解：÷=--------------------3分=----------------------------5分23、（1）证明：∵△ACB和△ECD都是等边三角形，∴AC=BC，CD=CE，∠ACB=∠DCE=60°，----------------1分∵∠ACD=∠ACB﹣∠DCB，∠BCE=∠DCE﹣∠DCB，∴∠ACD=∠BCE，--------------------2分在△ACD和△BCE中，，∴△ACD≌△BCE（SAS）；----------------------5分（2）∵△ACD≌△BCE，∴AD=BE=21，----------------6分∵△ECD是等边三角形，∴DE=CE=16，----------------------------7分∴AE=AD+DE=21+16=37．--------------------------8分24、（1）证明：∵ A D为△ABC的角平分线，DE⊥AB，DF⊥AC，∴DE=DF，∠AED=∠AFD=90°，---------1分∴∠DEF=∠DFE，∴∠AEF=∠AFE，∴AE=AF------------------------------------3分∴点A、D都在EF的垂直平分线上，∴AD垂直平分EF．--------------------------------5分（2）答：AG=3DG．-----------------------6分理由：∵∠BAC=60°，AD平分∠BAC，∴∠EAD=30°，∴AD=2DE，∠EDA=60°，-------------7分∵AD⊥EF，∴∠EGD=90°，∴∠DEG=30°--------------8分∴DE=2DG，∴AD=4DG，∴AG=3DG．---------------------------------10分25解：∵x2﹣2xy+2y2+6y+9=0，∴（x2﹣2xy+y2）+（y2+6y+9）=0，---------------------2分∴（x﹣y）2+（y+3）2=0，∴x﹣y=0，y+3=0，∴x=﹣3，y=﹣3，---------------------------------4分∴xy=（﹣3）×（﹣3）=9，即xy的值是9．--------------------------------5分26．解：（a+b+c）2的几何背景如图，-----------------------3分整体的面积为：（a+b+c）2，用各部分的面积之和表示为：（a+b+c）2=a2+b2+c2+2ab+2ac+2bc，所以（a+b+c）2=a2+b2+c2+2ab+2ac+2bc．-----------------------6分。

初二数学竞赛训练题5

练习卷51. 1．若实数a 、b 、c 、d 满足a ＋1＝b －2＝c ＋3＝d －4，则a 、b 、c 、d 这四个实数中最大的是（）A ．aB ．bC ．cD ．d2．一个凸多边形的每一个内角都等于150°，则这个多边形所有对角线的条数共有（）A 、42条B 、54条C 、66条D 、78条3．如图是一个正方体的表面展开图，已知正方体相对两个面上的数值相同，且不相对两个面上的数值不相同，则“★”面上的数为（）A ．1B ．1或2C ．2D ．2或34．关于x 满足32537213x x x +-≥--，且23+--x x 的最大值为p ，最小值为q ，则pq 的值是（）A ．6B ．5C ．－5D ．45．如图，直角梯形ABCD 中，AD ∥BC ，AB ⊥BC ，AD ＝3，BC ＝5，将腰DC 绕点D 的逆时针方向旋转90°至DE ，连结AE ，则△ADE 的面积是（）A ．1B ．2C ．3D ．46.如图，矩形ABCD 的对角线相交于点O ，AE 平分∠BAD 交BC 于E ，若∠CAE=15°则∠BOE=（）A 、30°B 、45°C 、60°D 、75°7. 若不等式a x x ≤-+-3312有解，则实数a 最小值是（）A 、1B 、2C 、4D 、68. 若实数a 、b 、c 、d 满足4321-=+=-=+d c b a ，则a 、b 、c 、d 这四个实数中最大的是（）A 、aB 、bC 、cD 、d9.已知=++++++++2009200913312211112222 （） A 、1 B 、20092008 C 、20102009 D 、20092010 10. 已知51=-a a ，则aa 1-=______________. 11. 一次函数)(111为正整数k k x k k y +++-=的图像与x 轴、y 轴的交点是A 、B ，O 为原点，设Rt△AB O 的面积是k S ，则=++++2009321S S S S ____________.12. 规定任意两个实数对()()d c b a ,,和：当且仅当a=c 且b=d 时，()()d c b a ,,=.定义运算“⊗”: ()()()bc ad bd ac d c b a +-=⊗,,,.若()()()0,5,2,1=⊗q p ,则=+q p _____.13. 已知△ABC 中，AB=39；BC=6；CA=3.点M 是BC 中点，过点B 作AM 延长线的垂线，垂足为D ，则线段BD 的长度是 .14. 一次棋赛，有n 个女选手和9n 个男选手，每位参赛者与其110-n 个选手各对局一次，计分方式为：胜者的2分，负者得0分，平局各自得1分。

初中数学八年级(上)数学竞赛试题(含答案)

1 2－1A 八年级〔上〕数学竞赛试题一、填空题:〔40分〕1、在ABC Rt ∆中,b a 、为直角边,c 为斜边,若14=+b a ,10=c ,则ABC ∆的面积是；2、计算：=⋅27 311 ；3 313÷⨯＝；2 3 2 +-＝；3、某位老师在讲实数时,画了一个图〔如图1〕,即以数轴的单位长线段为边作一个正方形,然后以0点为圆心,正方形的对角线长为半径画图,交x 轴于一点A ,作这样的图是用来说明；〔1〕4、在电子游戏中有一种方格拼图游戏,若在游戏过程中,已拼好的图案如图2,又出现了一个方格体正向下运动,为了使所有图案消失,你必须按后才能拼一个完整图案,从而使图案自动消失〔游戏机有此功能〕。

5、如图3,=∠+∠+∠+∠+∠+∠F E D C B A ；6、图4是一住宅小区的长方形花坛图样,阴影部分是草地,空地是四块同样的菱形,则草地与空地的面积之比为；<4> <5> <6>7、如图5,一块白色的正方形木板,边长是cm 18,上面横竖各有两根木条〔阴影部分〕,宽都是cm 2,则白色部分面积是2cm ；8、如图6,一块正方形地板由全等的正方形瓷砖铺成,这地板上的两条对角线上的瓷砖全是黑色,其余的瓷砖是白色的,如果有101块黑色瓷砖,则瓷砖的总数是；二、选择题:〔30分〕9、CD 是ABC Rt ∆斜边AB 上的高,若2=AB ,1:3:=BC AC ,则CD 为〔〕A 、51B 、52 C 、53 D 、5410、如图,长方形ABCD 中,3=AB ,4=BC ,若将该矩形折叠,使C 点与A 点重合,则折痕EF 的长为〔〕A 、3.74B 、3.75 C 、3.76 D 、3.77DFD)(A '11、如果a a -=-1 1 ,则a 的取值范围是〔〕A 、1=aB 、10<<aC 、0≥aD 、10≤≤a 12、若2 2 -+-x x 有意义,则x 的取值为〔〕A 、2>xB 、2<xC 、2≤xD 、2=x13、如上中图所示,一块边长为cm 10的正方形木板ABCD ,在水平桌面上绕点D 按顺时针方向转到D C B A ''''的位置时,顶点B 从开始到结束所经过的路径为〔〕A 、cm 20B 、cm 220C 、cm 10πD 、cm 25π14、如上右图所示,设M 是边上任意一点,设CMB ∆的面积为2S ,CDM ∆的面积为S ,AMD ∆的面积为1S ,则有〔〕A 、21S S S +=B 、21S S S +>C 、21S S S +<D 、不能确定三、画图题:〔12分〕15、如图,历史上最有名的军师诸葛亮,率精骑兵与司马懿对阵,诸葛亮一挥羽扇,军阵瞬时由左图变为右图,其实只移动了其中的3骑而己,请问如何移动？〔在图形上画出来即可〕16、有一等腰梯形纸片,其上底和腰长都是a ,下底的长是a 2,你能将它剪成形状、大小完全一样的四块吗？若能,请画出图形。

八上数学竞赛(含答案)

八年级上数学竞赛试题 (时间90分钟,满分100分)一、填空题(每小题5分，共40分) 1、若01223344555)12(a x a x a x a x a x a x +++++=-，则024a a a ++的值是_2、已知b a 82=（b a ,是正整数）且,52=+b a 那么b a 82+的值是3、如图，在Rt △ABC 中，∠C=90°，∠A=35°，以直角顶点C 为旋转中心，将△ABC 旋转到△A ’B ’C 的位置，其中A ’、B ’分别是A 、B 的对应点，且点B 在斜边A ’B ’上，直角边CA ’交AB 于点D ，则∠DCA 的度数_____。

4、小王与同学约好下午4：30在学校门口见，不见不散，为此，他们在早上8：00钟两人均把自己的表对准，小王于4：30正点走到学校门口，可是同学没来，原来同学的手表比正确时间每小时慢4分钟，如果同学按他自己的手表4：30到达，则小王还要等分钟（正确时间）5、甲、乙两位探险者到沙漠进行探险。

某日早晨7∶00甲先出发，他以6千米/时的速度向东行走，1小时后乙出发，他以5千米/时的速度向北行进。

上午10∶00，甲、乙二人的距离的平方是_____。

6、一个等腰三角形的周长为16，底边上的高是4，则这个三角形的三边长分别是______，_____，_______。

7、已知:如图2，E 、F 分别是正方形ABCD 的边BC 、CD 上的点，AE 、AF 分别与对角线BD 相交于M 、N ，若∠EAF=500，则∠CME +∠CNF =________。

8、如图3，将面积为2a 的正方形与面积为2b 的正方形(b>a)放在一起，则△ABC 的面积是__________。

二、选择题(每小题5分，共40分)1、如图5，正方形ABCD 的边长为1cm ，以对角线AC 为边长再作一个正方形，则正方形ACEF 的面积是( )A 、3cm 2B 、4cm 2AE D BFC图3 A BCDFE 图5ABC D FENM图2BA ∙甲组AE CD F 图612C 、5cm 2D 、2cm 22、以线段16,13,10,6ab c d ====为边，且使a ∥c 作四边形，这样的四边形( )A 、能作一个 B 、能作两个 C 、能作三个 D 、能作无数个 E 、不能作3、如图6，正方形的面积为256，点F 在AD 上，点E 在AB 的延长线上，Rt △CEF 的面积为200，则BE 的值为( )A 、10 B 、11 C 、12 D 、154、实数a 、b 满足ab=1,若11,1111a b M N a b a b=+=+++++，则M 、N 的关系为( )A 、M>N B 、M=N C 、M<N D 、不确定 5、一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如左图),那么B 点从开始至结束走过的路径长度为( )A 、23πB 、34π C 、 4 D 、2+23π6、在甲组图形的4个图中，每个图示由4种简单图形A 、B 、C 、D （不同的线段或圆）中的某两个图形组成的，例如由A 、B 组成的图形记为B A ∙，在乙组图形的（a ）、(b)、 (c)、（d ）4个图中，表示“D A ∙”和“C A ∙”的是（）A 、 (a),(b)B 、 (b),(c)C 、 (c),(d)D 、 (b),(d) 7、如图所示的4个的半径均为1，那么图中的阴影部分的面积为（） A 、1+πB 、π2 C 、 4 D 、68、设标有A 、B 、C 、D 、E 、F 、G 记号的7盏灯顺次排成一行，每盏灯安装一个开关，现在A 、C 、E 、G 4盏灯开着，其余3盏灯是关的，小岗从灯A 开始，顺次拉动开关，即从A 到G ，再顺次拉动开关，即又从A 到G ，…，他这样拉动了1999次开关后，则开着的灯是（）A 、A.C.E.G B 、 A.C.F C 、 B.D.F D 、C.E.G乙组B A ∙C B ∙D C ∙ D B ∙ 甲组三、解答题(20分)1、已知四边形ABCD中，AB=AD，∠BAD=60°，∠BCD=120°，请说明：BC+DC=AC2、如图，四边形ABCD中，AB∥CD，且AB+BC=CD+AD。

初二上数学竞赛试卷及答案

一、选择题（每题5分，共50分）1. 下列数中，是质数的是（）A. 15B. 16C. 17D. 182. 一个等腰三角形的底边长为10cm，腰长为12cm，则这个三角形的面积是（）A. 60cm²B. 70cm²C. 80cm²D. 90cm²3. 已知方程2x+3=7，则x的值是（）A. 2B. 3C. 4D. 54. 下列图形中，是轴对称图形的是（）A. 正方形B. 等腰三角形C. 矩形D. 等边三角形5. 一个长方体的长、宽、高分别为5cm、3cm、2cm，则这个长方体的体积是（）A. 30cm³B. 40cm³C. 50cm³D. 60cm³6. 已知x²-5x+6=0，则x的值是（）A. 2或3B. 1或4C. 1或6D. 2或57. 下列数中，是偶数的是（）A. 3B. 4C. 5D. 68. 一个梯形的上底长为8cm，下底长为12cm，高为6cm，则这个梯形的面积是（）A. 48cm²B. 60cm²C. 72cm²D. 84cm²9. 已知方程3x-4=9，则x的值是（）A. 1B. 2C. 3D. 410. 下列图形中，是旋转对称图形的是（）A. 正方形B. 等腰三角形C. 矩形D. 等边三角形二、填空题（每题5分，共50分）1. 5的倒数是_________。

2. 2的平方根是_________。

3. 下列数中，最小的负数是_________。

4. 下列数中，最大的正数是_________。

5. 一个圆的半径是3cm，则这个圆的直径是_________。

6. 下列图形中，是中心对称图形的是_________。

7. 下列图形中，是轴对称图形的是_________。

8. 下列图形中，是旋转对称图形的是_________。

9. 一个长方体的长、宽、高分别为5cm、3cm、2cm，则这个长方体的体积是_________。

第一学期八年级数学竞赛练习题6份

初二上数学竞赛试题及答案

初二上数学竞赛试题及答案一、选择题（每题3分，共30分）1. 下列哪个数是最小的正整数？A. 0B. 1C. -1D. 22. 如果一个数的平方等于9，那么这个数是多少？A. 3B. -3C. ±3D. 93. 一个直角三角形的两条直角边分别为3和4，斜边的长度是多少？A. 5B. 6C. 7D. 84. 一个数的绝对值是5，这个数可以是？A. 5B. -5C. ±5D. 05. 以下哪个是合数？A. 2B. 3C. 4D. 56. 一个数的立方等于-8，这个数是多少？A. -2B. 2C. -8D. 87. 一个数除以2余1，除以3余2，这个数最小是多少？A. 5B. 7C. 8D. 98. 一个圆的半径是5，那么它的面积是多少？A. 25πB. 50πC. 75πD. 100π9. 一个数的平方根是4，这个数是多少？A. 16B. -16C. ±4D. ±1610. 以下哪个是偶数？A. 1B. 2C. 3D. 5答案：1-5 B C A C B；6-10 A B B D B二、填空题（每题2分，共20分）1. 一个数的平方是16，这个数是______。

2. 如果一个数的绝对值是4，那么这个数可以是______或______。

3. 一个数的立方是27，这个数是______。

4. 一个数的倒数是1/2，这个数是______。

5. 一个数的平方根是2，这个数是______。

6. 如果一个数除以4余3，那么这个数可以是______（答案不唯一）。

7. 一个数的平方是25，这个数是______或______。

8. 一个数的立方根是3，这个数是______。

9. 一个数的平方根是-3，这个数是______。

10. 如果一个数的绝对值是3，那么这个数可以是______或______。

答案：1. ±4 2. 4, -4 3. 3 4. 2 5. 4 6. 7（答案不唯一） 7.±5 8. 27 9. 无实数解 10. 3, -3三、计算题（每题10分，共40分）1. 计算下列表达式的值：(2+3)² - 4×5 + 6。

八年级数学竞赛试题上

八年级数学竞赛试题上一、选择题（每题3分，共30分）1. 若a，b，c是三角形的三边长，且满足a^2 + b^2 = c^2，那么这个三角形是：A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不能确定2. 已知x^2 - 5x + 6 = 0，求x的值：A. 2B. 3C. 1, 6D. 2, 33. 下列哪个不是有理数？A. πB. √2C. 1/3D. -24. 如果一个数的平方根等于它本身，那么这个数是：A. 0B. 1C. -1D. 0或15. 一个数的立方根等于它本身，这个数可能是：A. 1B. -1C. 0D. A, B, C都是6. 一个圆的直径是10cm，那么它的半径是：A. 5cmB. 10cmC. 15cmD. 20cm7. 一个数的绝对值是它本身，那么这个数：A. 一定是正数B. 一定是负数C. 一定是非负数D. 一定是非正数8. 一个数的相反数是它本身，这个数是：A. 正数B. 负数C. 0D. 无法确定9. 一个数的倒数是它本身，这个数是：A. 1B. -1C. 0D. 1或-110. 如果一个分数的分子和分母同时乘以或除以同一个不为0的数，分数的值：A. 变大B. 变小C. 不变D. 无法确定二、填空题（每题3分，共15分）11. 一个数的平方是36，这个数是________。

12. 一个数的立方是-8，这个数是________。

13. 如果一个圆的周长是2πr，那么它的面积是________。

14. 一个三角形的内角和是________度。

15. 如果一个分数的分子是5，分母是10，那么它的倒数是________。

三、解答题（每题5分，共25分）16. 已知a和b是方程x^2 - 4x + 4 = 0的两个根，求a^2 + b^2的值。

17. 一个长方形的长是宽的两倍，如果长增加2cm，宽增加1cm，面积增加了10平方厘米，求原长方形的长和宽。

18. 一个数列的前三项是1，2，4，求第10项的值。