计算题专练(一)
高考政治复习 经济生活计算题专项练习1 商品价值量、

2013高考政治复习:经济生活计算题专项练习一一:关于商品价值量、价值总量、价格问题的计算1、基本概念:(1)单位商品价值量:指商品价值的大小,即单价。
(2)商品价值总量:指在一定时间内生产一定数量的商品的价值总和。
(3)商品使用价值量:指商品的数量。
(4)劳动时间:指生产某种商品所耗费的时间。
分为社会必要劳动时间和个别劳动时间。
社会必要劳动时间:是指在现有的社会正常的生产条件下,在社会平均的劳动熟练程度和劳动强度下,制造某种商品所需要的劳动时间。
个别劳动时间:是指某一商品生产者生产某种商品所耗费的劳动时间。
(5)劳动生产率:指劳动者的生产效率。
分为个别劳动生产率和社会劳动生产率。
两种表示方法:①数量表示法:用单位时间内生产的产品数量来表示。
②时间表示法:用生产同一产品所需的时间来表示。
2.基本关系:(1) 商品价值量是由社会必要劳动时间决定的,与社会必要劳动时间成正比,与社会劳动生产率成反比,不受个别劳动时间和个别劳动生产率的影响。
(2) 商品价值总量与个别劳动生产率成正比,与个别劳动时间成反比,不受社会必要劳动时间和社会劳动生产率的影响。
(3) 无论个别还是社会的劳动时间都与劳动生产率成反比。
(4)商品使用价值总量(商品数量)与(个别或社会)劳动生产率成正比。
(5)商品价值总量与生产规模(劳动数量)成正比。
(6)商品价格与商品本身价值成正比,与货币价值(升值)成反比例1:假定去年生产一件A商品的社会必要劳动时间是生产B商品的2倍、C商品的5倍。
如果今年生产A商品的社会劳动生产率提高了3倍,生产C商品的社会劳动生产率却降低了20%,那么A、B、C三者形成新的等量关系是()ArrayA.3A=2 B=0.8CB. 5A=2B=0.8CC.2A=1B=2CD. 4A=2.5B=1C训练:1、如果现在1只羊=2袋大米符合等价交换原则,现在生产羊的社会劳动生产率提高了二倍,生产大米的社会劳动生产率不变,那么,一只羊可以换A.1袋大米B.4袋大米C.3袋大米D.2/3袋大米2、(2001年·广东政治卷、河南卷·18)在商品生产中,商品的价值量与社会劳动生产率成反比。
2020-2021中考化学综合题专练∶计算题含详细答案(1)

一、中考初中化学计算题1.为测定一瓶久置的烧碱中氢氧化钠的含量,某同学取25.0g样品,溶于水得到100g溶液,再加入100g足量稀硫酸,充分反应至不再产生气体,测得溶液质量为197.8g。
请计算:(1)反应产生CO2的质量。
(2)样品中NaOH的质量分数(结果保留至0.1%)。
(3)最后所得溶液中的钠元素的质量(结果保留至0.1)。
【答案】(1)2.2g;(2)78.8%;(3)13.6g【解析】(1)根据质量守恒定律,反应过程中所生成的气体的质量等于反应前后溶液质量的减少;(2)样品中NaOH的质量分数等于样品中NaOH的质量除以样品的总质量,所以我们可以根据上一步所求得二氧化碳的质量,根据质量守恒定律,求得样品中NaOH的质量,而后再求样品中NaOH的质量分数;(3)根据NaOH的质量、碳酸钠的质量分别乘以它们的质量分数可求得钠元素的质量;解:(1)根据质量守恒定律,反应前后溶液质量的减少就等于反应过程中所生成的气体的质量,所以反应产生的CO2的质量为100 g+100 g-197.8 g=2.2g。
(2)解:设所取样品中含有Na2CO3的质量为x。
Na2CO3+H2SO4═Na2SO4+H2O+CO2↑106 44x 2.2g10644x 2.2g解之得:x═5.3g烧碱样品中NaOH的质量为:25g-5.3 g=19.7 g样品中NaOH的质量分数为:19.7g25g×100%=78.8%(3)所得溶液中钠元素的质量=19.7g×2340 +5.3g×46106=13.6g2.为测定某纯碱(Na2CO3)样品中(含有少量的氯化钠杂质)碳酸钠的质量分数,现称取6g 试样放在烧杯中并滴入稀盐酸,当稀盐酸滴加至36.5g时,烧杯内溶液的总质量为40.3g (产生的气体全部逸出)。
产生气体的质量与滴入稀盐酸的质量关系如图所示,试计算:⑴A 点产生气体的质量为 ;⑵试样中碳酸钠的质量分数(结果精确到0.1%); ⑶B 点时,烧杯内溶液中溶质的化学式 。
人教版一年级上册数学专项练习-计算题50道带答案(黄金题型)

人教版一年级上册数学专项练习-计算题50道一.计算题(共50题,共425分)1.看图列式计算。
1. 2.2.看谁算得又快又准。
3.看谁算得又对又快。
2+5= 1+4= 2+3= 0+6=7+2= 7-7= 5+3= 4+4=3+1= 9-8= 6+4= 5+5= 3-3= 6-2= 5-2= 10-2= 4.先说一说图意,再列式计算。
□○□=□(条)5.数字“开屏”。
(1)(2)6.我能列得对。
7.算一算。
6+2= 5-4= 0+10= 15-10= 4-3= 2+4=5+2= 6-3= 13-10= 9-4= 10-2= 11+8=0+13= 13-1= 6+10= 8-6= 17-7= 13+3=6+3= 10-3= 1+11= 11-1= 14-10= 2+5=8.列式计算。
9.看图列式计算。
女孩踢了□下,男孩踢了□下,两人一共踢了几下?□○□=□(下)10.计算:8+7= 8-6= 6+10= 9+4= 7+5= 8+5= 2+8= 9+6= 7-3= 9+9= 4+8= 10+5= 10-6= 9-7= 5+8= 9-4= 11-10= 4+5=7-7= 6+9= 9+3= 14-4= 9+8= 2+8= 11.在□里填上合适的数。
12.填一填。
13.看谁都算对.14.看图列式计算。
15.看图列式计算。
□○□=□(个)16.看谁算得又对又快。
2+3= 2-2= 4-0= 1+1= 5+0= 0+1= 5-4= 1+4= 4-4= 2-0= 4-3= 0+3=4-1= 1+3= 2+0= 3-1=17.算一算。
2+1= 1+5= 10-4= 5-5= 3+5=7+2= 6-5= 7-5= 5+5= 1+6=8-5= 4+3= 9-5= 3+7= 2+8=0+9= 1+1= 9+0= 10-5= 0+8=18.算一算。
1+2=________ 1+1=________ 9+0=________ 3+1=________ 6+1=________ 1+3=________ 2+2=________ 9+1=________ 3+2=________ 6+2=________19.看图写算式,并计算。
【强烈推荐】人教版六年级数学上册计算题专项训练

【强烈推荐】⼈教版六年级数学上册计算题专项训练六年级数学上册计算题专项练习⼀1、直接写出得数67 ÷3= 35 ×15= 2-37 = 1+2%= 78 ÷710 = 5÷23 = 43 ×75% = 78 ×4×87 = 16 +56 ×15 = 12 ×99+99×12 = 2、解⽅程X -27 X=114 X ÷18 =15×23 40%X-14 =7123、下⾯各题怎样简便就怎样算72 ×58 -32 ÷85 1-58 ÷2528 -310 (23 +415 ×56 )÷2021 45 ÷[(35 +12 )×2]4、列综合算式或⽅程计算1、⼀个数的20%是100;这个数的35 是多少? 2、⼀个数的58 ⽐20少4;这个数是多少?计算题专项练习⼆1、直接写出得数。
6×45= 94109?= 755÷= 100×25%==÷331 =-5131 51:201=(⽐值) 4)2141(?+= 3285÷= 21)211(÷+= 2、解⽅程。
92×x =181 16%20=-x x 6543=÷x21441=+x 10212=+x x 3、计算下⾯各题;能简算的就简算。
61946594?+? 1185185367-÷- 52835383?+? 514365512+??? ??+? 722110233-?- 4、列式计算。
① 4减去41的差乘53;积是多少?②⽐18的20%多0.35的数是多少?③⼀个数与71的和相当于94的45%;这个数是多少?④ 28⽐某数的3倍少2;求这个数。
(列⽅程解)⑤甲数的52和⼄数相等;甲数和⼄数的⽐是多少?计算题专项练习三(1)直接写出得数。
小学数学六年级应用题、计算题专项练习[1]
![小学数学六年级应用题、计算题专项练习[1]](https://img.taocdn.com/s3/m/fc6e5ed9192e45361166f540.png)
1.某个体户,去年12月份营业收入5000元,按规定要缴纳3%的营业税。
纳税后还剩多少钱?2.一块合金内,铜和锌的比是2:3,现在再加入6克锌,共得新合金36克。
求新合金中锌的重量。
3.如图,在一只圆形钟面上,时针长3厘米,分针长5厘米。
经过12小时,时针扫过的面积是多少平方厘米?分针走了多少厘米?4.信息:去年由于受非典影响,5月份全南京市餐饮业营业额为3.5亿元,比前年同期下降30%。
前年5月份全市餐饮业营业额235496785.小明要买不同档次的文具盒。
高档的5个,中档的占总数的75%,低档的占总数的61。
你知道小明一共要买多少个文具盒吗? 6.为了学生的卫生安全,学校给每个住宿生配一个水杯,每只水杯3元,大洋商城打九折,百汇商厦“买八送一”。
学校想买180只水杯,请你当“参谋”,算一算:到哪家购买较合算?请写出你的理由。
7.某村去年产粮食40吨,今年比去年增产二成五,今年计产粮食多少吨?8.果园里有果树1200棵,其中梨树占40%,桃树占20%,两种果树共有多少棵?9.修路队修一条路,已经修了4.5千米,还剩下55%没有修,这条路长多少千米?10.李大伯饲养鸡的只数的60%与鹅的只数的45相等。
已知李大伯饲养了120只鸡,那么李大伯饲养了多少只鹅?11.一批树苗540棵,分给五、六年级同学去种,五年级有120人,六年级有150人,如果按照人数进行分配,每个年级各应分得多少棵树苗?12.李师傅加工一批零件,第一天完成的个数与零件总数的比是1:3。
如果再加工15个,就可以完成这批零件的一半。
这批零件共有多少个?13.一项工程,甲队独做要10天完成,乙队独做要15天完成,甲队先做2天后,剩下的再由两队合做,还要多少天可以完成任务?14. 甲仓库存粮食100吨,乙仓库存粮食80吨,甲仓库运了一批粮食到乙仓库,这时乙仓库的粮食正好是甲仓库的45。
甲仓库运了多少吨粮食到乙仓库?15. 五年级体育“达标”人数比四年级多92,实际多12人。
八年级物理上册第一章机械运动计算题专项练习
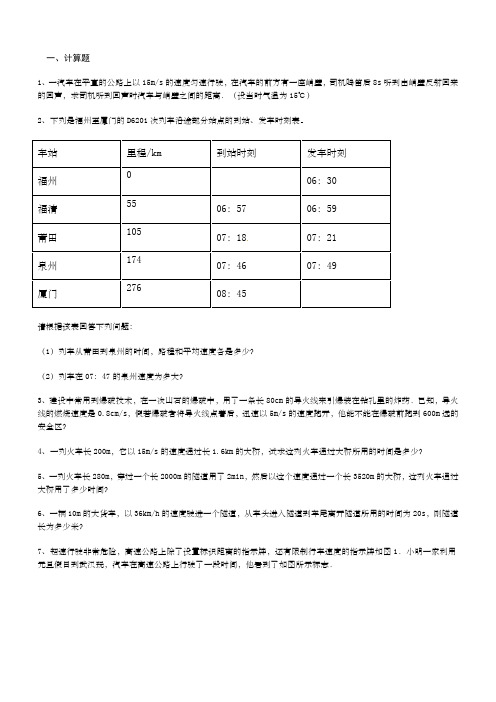
一、计算题1、一汽车在平直的公路上以15m/s的速度匀速行驶,在汽车的前方有一座峭壁,司机鸣笛后8s听到由峭壁反射回来的回声,求司机听到回声时汽车与峭壁之间的距离.(设当时气温为15℃)2、下列是福州至厦门的D6201次列车沿途部分站点的到站、发车时刻表。
车站里程/km 到站时刻发车时刻福州0 06:30福清55 06:57 06:59莆田105 07:1807:21泉州174 07:46 07:49厦门276 08:45请根据该表回答下列问题:(1)列车从莆田到泉州的时间,路程和平均速度各是多少?(2)列车在07:47的泉州速度为多大?3、建设中常用到爆破技术,在一次山石的爆破中,用了一条长80cm的导火线来引爆装在钻孔里的炸药.已知,导火线的燃烧速度是0.8cm/s,假若爆破者将导火线点着后,迅速以5m/s的速度跑开,他能不能在爆破前跑到600m远的安全区?4、一列火车长200m,它以15m/s的速度通过长1.6km的大桥,试求这列火车通过大桥所用的时间是多少?5、一列火车长280m,穿过一个长2000m的隧道用了2min,然后以这个速度通过一个长3520m的大桥,这列火车通过大桥用了多少时间?6、一辆10m的大货车,以36km/h的速度驶进一个隧道,从车头进入隧道到车尾离开隧道所用的时间为20s,则隧道长为多少米?7、超速行驶非常危险,高速公路上除了设置标识距离的指示牌,还有限制行车速度的指示牌如图1.小明一家利用元旦假日到武汉玩,汽车在高速公路上行驶了一段时间,他看到了如图所示标志.(1)从图1可知,汽车在高速公路上最快时速不能超过km/h.(2)在不违规的前提下,若汽车以最快的速度行驶,从图1的标志牌到武汉至少需要的时间是多少h?(3)若以图2所示的速度行驶1.5h,通过的路程是多少km?8、为了减少超速事故,我市计划将“区间测速”作为判断是否超速的依据之一.所谓的“区间测速”,就是测算出汽车在某一区间行驶的平均速度,如果超过了该路段的最高限速即被判为超速.若监测点A、B相距18km,全程限速40km/h,由“电子眼”抓拍到某辆货车通过监测点A、B的速度分别为30km/h和45.6km/h,通过A、B两个监测点的时间为20min.请你通过计算解答:(1)该货车通过监测段AB时是否超速?(2)为了不超速,至少需要的时间.9、一辆长200m的火车匀速行驶通过一条电线杆,用时10s.(1)求火车运行速度.(2)若这辆火车以同样的速度匀速通过一条长1km的隧道,需要多少时间?10、小明家与学校的直线距离AB为1500m。
高中数学计算题专项练习1-(3096)

2019年高中数学计算题专项练习1一.解答题(共30 小题)1.计算:( 1);( 2).2.计算:( 1) lg1000+log 342﹣ log 314﹣ log 48;(2) .3.( 1)解方程: lg ( x+1) +lg ( x ﹣ 2)=lg4 ; ( 2)解不等式: 21﹣ 2x> .4.( 1)计算: 2× ×( 2)计算: 2log 510+log 50.25.5.计算:( 1) ;( 2).6.求 log 89×log 332﹣log 1255 的值.7.( 1)计算 .( 2)若 ,求 的值.8.计算下列各式的值0.75( 1) 0.064﹣(﹣ ) +16 +0.25( 2) lg5+ ( log 32)?( log 89) +lg2 .9.计算:( 1) lg 22+lg5?lg20 ﹣ 1;(2).10.若 lga 、 lgb 是方程 2x 2﹣ 4x+1=0 的两个实根,求的值.11.计算(Ⅰ)(Ⅱ) .12.解方程:.13.计算:(Ⅰ)(Ⅱ).14.求值:( log 62) 2+log 63×log 612.15.( 1)计算( 2)已知 ,求 的值.16.计算(Ⅰ);(Ⅱ) 0.0081 ﹣() + ? ? .17.(Ⅰ)已知全集 U={1 , 2, 3, 4, 5,6} , A={1 , 4, 5} , B={2 , 3, 5} ,记 M= ( ?U A ) ∩B ,求集合 M ,并写出 M 的所有子集;(Ⅱ)求值:.18.解方程: log 2( 4x ﹣ 4) =x+log 2( 2x+1﹣ 5)219.(Ⅰ)计算( lg2) +lg2 ?lg50+lg25 ;(Ⅱ)已知a=,求÷.20.求值:( 1) lg14 ﹣+lg7 ﹣ lg18(2).21.计算下列各题:(1)( lg5)2+lg2 ×lg50 ;﹣1,求的值.( 2)已知 a﹣ a =122.( 1)计算;( 2)关于 x 的方程 3x 2﹣ 10x+k=0 有两个同号且不相等的实根,求实数k 的取值范围.23.计算题(1)(2)24.计算下列各式:(式中字母都是正数)(1)(2).25.计算:( 1);(2) lg25+lg2 ×lg50+ ( lg2)2.26.已知 x+y=12 , xy=27 且 x< y,求的值.27.( 1)计算:;b,用 a, b 表示.( 2)已知 a=log3 2, 3 =528.化简或求值:( 1);( 2).29.计算下列各式的值:( 1);( 2).30.计算log( 1) lg20 ﹣ lg2 ﹣ log 23?log32+2(2)(﹣1)0+()+().参考答案与试题解析一.解答题(共30 小题)1.计算:( 1);( 2).考点:有理数指数幂的化简求值;对数的运算性质.专题:函数的性质及应用.分析:(1)利用指数幂的运算法则即可得出;( 2)利用对数的运算法则即可得出.解答:解:( 1)原式 ===.( 2)原式 ===.点评:熟练掌握指数幂的运算法则、对数的运算法则是解题的关键.2.计算:(1) lg1000+log 342﹣ log 314﹣ log48;(2).考点:有理数指数幂的化简求值;对数的运算性质.专题:函数的性质及应用.分析:(1)利用对数的运算性质即可得出;( 2)利用指数幂的运算性质即可得出.解答:解:( 1)原式 =;( 2)原式 =.点评:熟练掌握对数的运算性质、指数幂的运算性质是解题的关键.3.( 1)解方程: lg( x+1) +lg ( x﹣ 2)=lg4 ;( 2)解不等式:21﹣2x>.考点 : 对数的运算性质;指数函数单调性的应用.专题 : 计算题.分析:( 1)原方程可化为 lg (x+1 )( x ﹣ 2) =lg4 且可求( 2)由题意可得1﹣ 2x ﹣2,结合指数函数单调性可求x 的范围2> =2解答:解:( 1)原方程可化为 lg ( x+1 )(x ﹣ 2)=lg4 且∴( x+1 )(x ﹣ 2) =4 且 x > 2∴ x 2﹣ x ﹣ 6=0 且 x >2 解得 x= ﹣2(舍)或 x=3( 2)∵ 21﹣ 2x> =2 ﹣2∴ 1﹣ 2x >﹣ 2 ∴点评: 本题主要考查了对数的运算性质的应用,解题中要注意对数真数大于0 的条件不要漏掉,还考查了指数函数单调性的应用.4.( 1)计算: 2× ×( 2)计算: 2log 510+log 50.25.考点 : 对数的运算性质.专题 : 计算题;函数的性质及应用.分析: ( 1)把各根式都化为 6 次根下的形式,然后利用有理指数幂的运算性质化简;( 2)直接利用对数式的运算性质化简运算.解答:× ×解( 1)计算: 2= ===6;( 2) 2log 510+log 50.25==log 5100×0.25 =log 525 =2log 55=2 .点评: 本题考查了指数式的运算性质和对数式的运算性质,解答的关键是熟记有关运算性质,是基础的运算题.5.计算:(1) ;(2).考点:对数的运算性质.专题:计算题.分析:(1)利用有理指数幂的运算法则,直接求解即可.( 2)利用对数的运算形状直接求解即可.解答:解:( 1)﹣ 13﹣ 1+8=12⋯(6 分)=0.2﹣ 1+2 =5( 2)===⋯(12 分)点评:本题考查指数与对数的运算性质的应用,考查计算能力.6.求 log 9×log32﹣log 5 的值.83125考点:对数的运算性质.专题:计算题.分析:利用对数的运算性质进及对数的换底公式行求解即可解答:解:原式 ====3点评:本题主要考查了对数的运算性质的基本应用,属于基础试题7.( 1)计算.( 2)若,求的值.考点:对数的运算性质.专题:计算题.分析:( 1)把对数式中底数和真数的数4、8、 27 化为乘方的形式,把底数的分数化为负指数幂,把真数的根式化为分数指数幂,然后直接利用对数的运算性质化简求值;( 2)把已知条件两次平方得到﹣ 12﹣ 2得答案.x+x与 x +x,代入解答:解:( 1)===2 ﹣ 4﹣ 1=﹣ 3;( 2)∵,∴,∴ x+x﹣ 1.=5 则( x+x ﹣122 ﹣ 2) =25 ,∴ x +x=23 ∴=.点评: 本题考查了有理指数幂的化简与求值,考查了对数的运算性质,是基础的计算题.8.计算下列各式的值0 0.75( 1) 0.064﹣(﹣ ) +16 +0.25( 2) lg5+ ( log 32)?( log 89) +lg2 .考点 : 对数的运算性质;有理数指数幂的化简求值.专题 : 计算题. 分析:( 1)化小数指数为分数指数, 0 次幂的值代1,然后利用有理指数幂进行化简求值;( 2)首先利用换底公式化为常用对数,然后利用对数的运算性质进行化简计算.解答:0.75解:( 1) 0.064﹣(﹣ ) +16 +0.25==( 0.4) ﹣1﹣1+8+0.5=2.5﹣ 1+8+0.5=10 ;( 2) lg5+ ( log 32)?( log 89) +lg2= =1+=1+ = .点评: 本题考查了对数的运算性质,考查了有理指数幂的化简与求值,是基础的运算题.9.计算:( 1) lg 22+lg5?lg20 ﹣ 1;(2).考点 : 对数的运算性质;有理数指数幂的化简求值.专题 : 计算题.分析: ( 1)把 lg5 化为 1﹣ lg2, lg20 化为 1+lg2 ,展开平方差公式后整理即可;( 2)化根式为分数指数幂, 化小数指数为分数指数, 化负指数为正指数, 然后进行有理指数幂的化简求值.2解答: 解:( 1) lg 2+lg5 ?lg20 ﹣12=lg 2+( 1﹣ lg2 )( 1+lg2)﹣ 122;=lg 2+1﹣ lg 2﹣ 1=0( 2)==2 3=2 ?3 ﹣ 7﹣2﹣ 1=98.点评: 本题考查了有理指数幂的化简与求值,考查了对数的运算性质,解答的关键是熟记有关性质,是基础题.10.若 lga 、 lgb 是方程 2x 2﹣ 4x+1=0 的两个实根,求的值.考点 : 对数的运算性质;一元二次方程的根的分布与系数的关系.专题 : 计算题;转化思想.分析:lga 、 lgb 是方程 2x 2﹣4x+1=0 的两个实根,先由根与系数的关系求出,再利用对数的运算性质对化简求值.解答:解: ,2=( lga+lgb )( lga ﹣ lgb )2=2[ (lga+lgb ) ﹣ 4lgalgb ]=2(4﹣ 4× )=4点评: 本题考查对数的运算性质,求解的关键是熟练掌握对数的运算性质,以及一元二次方程的根与系数的关系.11.计算(Ⅰ)(Ⅱ) .考点 : 对数的运算性质;有理数指数幂的化简求值.专题 : 计算题.分析: ( 1)根据对数运算法则化简即可( 2)根据指数运算法则化简即可解答:解:( 1)原式 =(2)原式 ==点评:本题考查对数运算和指数运算,注意小数和分数的互化,要求能灵活应用对数运算法则和指数运算法则.属简单题12.解方程:.考点:对数的运算性质.专题:计算题;函数的性质及应用.分析:利用对数的运算性质可脱去对数符号,转化为关于x 的方程即可求得答案.解答:解:∵,∴log5( x+1) +log 5(x﹣ 3) =log 55,∴( x+1 )?( x﹣ 3)=5,其中, x+1> 0 且 x﹣ 3> 0解得 x=4 .故方程的解是4点评:本题考查对数的运算性质,考查方程思想,属于基础题.13.计算:(Ⅰ)(Ⅱ).考点:对数的运算性质;运用诱导公式化简求值.专题:计算题;函数的性质及应用.分析:( I)利用诱导公式,结合特殊角的三角函数值即可求解( II )利用对数的运算性质及指数的运算性质即可求解解答:解:(I)(每求出一个函数值给( 1 分),6 分( II )(每求出一个式子的值可给( 1 分), 12 分)点评:本题主要考查了诱导公式在三角化简求值中的应用及对数的运算性质的简单应用,属于基础试题14.求值:( log62)2+log 63×log 612.考点:对数的运算性质.分析:先对后一项:log 63×log 612 利用对数的运算法则进行化简得到:log63+log 63×log 62,再和前面一项提取公因式 log62 后利用对数的运算性质: log a( MN ) =log a M+log a N 进行计算,最后再将前面计算的结果利用log 62+log 63=1 进行运算.从而问题解决.解答:解:原式=(log62+log63)log62+log63=log 62+log 63=1.∴( log62)2+log 63×log 612=1.点评:本小题主要考查对数的运算性质、对数的运算性质的应用等基础知识,考查运算求解能力.属于基础题.对数的运算性质:log a( MN ) =log a M+log a N; log an=log a M ﹣ log a N ;log a M =nlog a M 等.15.( 1)计算( 2)已知,求的值.考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:(1)化根式为分数指数幂,把对数式的真数用同底数幂相除底数不变,指数相减运算,然后利用对数式的运算性质化简;( 2)把给出的等式进行平方运算,求出﹣ 1的结果.x+x ,代入要求的式子即可求得解答:解( 1)===;(2)由,得:,所以, x+2+x ﹣1=9,故x+x ﹣1=7,所以,.点评:本题考查了有理指数幂的化简与求值,考查了对数式的运算性质,解答的关键是熟记有关性质,是基础题.16.计算(Ⅰ);(Ⅱ) 0.0081﹣()+??.考对数的运算性质;根式与分数指数幂的互化及其化简运算.点:专函数的性质及应用.题:分 (Ⅰ)利用对数的运算法则,由已知条件能求出结果.析 (Ⅱ)利用指数的运算法则,由已知条件,能求出结果.:解 解:(Ⅰ)答 ===:= = =﹣ .(Ⅱ)0.0081 ﹣()+??4 3=0.3﹣ +3=.=[( 0.3) ] ﹣([ )]+ 点 本题考查指数和对数的运算法则,是基础题,解题时要认真解答,避免出现计算上的低级错误. 评 :17.(Ⅰ)已知全集 U={1 , 2, 3, 4, 5,6} , A={1 , 4, 5} , B={2 , 3, 5} ,记 M= ( ?U A ) ∩B ,求集合 M ,并写出 M 的所有子集;(Ⅱ)求值:.考点 : 对数的运算性质;交、并、补集的混合运算.专题 : 函数的性质及应用.分析: ( I )利用集合的运算法则即可得出.( II )利用对数的运算法则即可得出. 解答: 解:(Ⅰ)∵ U={1 , 2, 3, 4, 5, 6} , A={1 , 4,5} ,∴ C U A={2 , 3, 6} ,∴ M= ( ?U A ) ∩B={2 , 3, 6} ∩{2 , 3,5}={2 , 3} .∴ M 的所有子集为: ? , {2} , {3} , {2 , 3} .(Ⅱ)= = = .点评: 本题考查了集合的运算法则、对数的运算法则,属于基础题.18.解方程: log 2( 4x ﹣ 4) =x+log 2( 2x+1﹣ 5)考点 : 对数的运算性质.专题 : 计算题.分析:利用对数的运算法则将方程变形为 ,将对数式化为指数式得到 ,通过换元转化为二次方程,求出x 的值,代入对数的真数检验.xx+1解答: 解: log 2( 4 ﹣ 4) =x+log 2( 2 ﹣ 5)即为log 2(4x ﹣ 4)﹣ log 2( 2x+1﹣ 5)=x即为所以令 t=2x即解得 t=4 或 t=1所以 x=2 或 x=0 (舍)所以方程的解为x=2.点评:本题考查对数的真数大于0、对数的运算法则、二次方程的解法,解题过程中要注意对数的定义域,属于基础题.19.(Ⅰ)计算( lg2)2;+lg2 ?lg50+lg25(Ⅱ)已知 a= ,求÷.考点:对数的运算性质;根式与分数指数幂的互化及其化简运算.专题:计算题.分析:(Ⅰ)利用对数的运算法则进行运算,利用结论lg2+lg5=0 去求.(Ⅱ)先将根式转化为同底的分数指数幂,利用指数幂的运算性质,化为最简形式,然后在将 a 值代入求值.解答:解:(Ⅰ)原式=lg2(lg2+lg50)+lg25=2lg2+lg25=lg100=2.(Ⅱ)原式 =.∵ a= ,∴原式 =.点评:本题考查对数的四则运算法则,根式与分数指数幂的互化,以及同底数幂的基本运算性质,要求熟练掌握相应的运算公式.20.求值:( 1) lg14 ﹣+lg7 ﹣ lg18(2).考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:(1)应用和、差、积、商的对数的运算性质计算即可;( 2)利用指数幂的运算性质(m n mn计算即可.a) =a解答:解:( 1)∵ lg14﹣+lg7﹣ lg18=( lg7+lg2 )﹣ 2(lg7﹣ lg3 )+lg7 ﹣( lg6+lg3 )=2lg7 ﹣ 2lg7+lg2+2lg3 ﹣ lg6 ﹣ lg3( 2)∵=﹣1﹣+=﹣+=.(8分)点评:本题考查对数与指数的运算性质,关键在于熟练掌握对数与指数幂的运算性质进行计算,属于中档题.21.计算下列各题:(1)( lg5)2+lg2 ×lg50 ;﹣ 1的值.( 2)已知 a﹣ a =1,求考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:(1)直接利用对数的运算性质,求出表达式的值;﹣ 12﹣ 2的值,然后化简,求出它的值( 2)通过 a﹣ a =1,求出 a +a解答:2×lg50=2×(lg5+1) =lg5( lg2+lg5) +lg2=1 ;解:( 1)( lg5) +lg2( lg5 ) +lg2﹣ 12﹣ 2( 2)因为 a﹣ a =1,所以 a +a﹣ 2=1,2﹣2∴a +a =3,==0 .点评:本题主要考查对数的运算性质和有理数指数幂的化简求值的知识点,解答本题的关键是熟练对数的运算性质,此题难度一般.22.( 1)计算;( 2)关于 x 的方程 3x 2﹣ 10x+k=0 有两个同号且不相等的实根,求实数k 的取值范围.考点:根式与分数指数幂的互化及其化简运算;一元二次方程的根的分布与系数的关系.专题:计算题.分析:( 1)转化为分数指数幂,利用指数幂的运算法则进行计算;( 2)由维达定理的出k 的关系式,解不等式即可.解答:( 1)解:原式 ===a 0(∵ a≠0)( 2)解:设 3x 2﹣ 10x+k=0 的根为 x 1,x 2由 x 1+, x 1 ?由条件点评: 本题考查根式和分数指数幂的转化、指数的运算法则、及二次方程根与系数的关系,属基本运算的考查.23.计算题( 1)( 2)考点 : 根式与分数指数幂的互化及其化简运算;对数的运算性质.专题 : 计算题.分析: ( 1)根据分数指数与根式的互化以及幂的乘方运算法则,还有零指数、负指数的运算法则,化简可得值;( 2)运用对数运算性质及对数与指数的互逆运算化简可得.解答:解:( 1)原式 = ﹣(﹣ 2) 24﹣ = ﹣64+ +1﹣ =﹣;×(﹣ 2) +( 2)原式 =83224×8﹣ log 3 32+log 3 ﹣log 3 ﹣ 3 =log 3 ﹣ 9=﹣ 9.点评: 考查学生灵活运用根式与分数指数幂互化及其化简运算的能力,以及分母有理化的应用能力.24.计算下列各式: (式中字母都是正数)( 1)(2).考点 : 根式与分数指数幂的互化及其化简运算;有理数指数幂的化简求值.专题 : 函数的性质及应用. 分析:( 1)利用及其根式的运算法则即可;( 2)利用立方和公式即可得出. 解答:解:( 1)原式 == ?= ==.( 2)原式 ===.点评:熟练掌握根式的运算法则、立方和公式是解题的关键.25.计算:( 1);( 2) lg25+lg2 ×lg50+ ( lg2)2.考点:有理数指数幂的运算性质;对数的运算性质.专题:计算题.分析:( 1)由指数幂的含义和运算法则,,=|3﹣π|,求解即可.( 2)利用对数的运算法则,各项都化为用lg2 表达的式子即可求解.解答:解:( 1)==1+2+ π﹣3=π(2) lg25+lg2 ×lg50+ ( lg2)2=2﹣ 2lg2+lg2 (2﹣ lg2 ) +( lg2)2=2.点评:本题考查指数和对数式的化简和求值、考查指数和对数的运算法则、属基本运算的考查.26.已知 x+y=12 , xy=27 且 x< y,求的值.考点:有理数指数幂的运算性质.专题:计算题.分析:利用已知条件求出x﹣ y 的值,利用分母有理化直接求解所求表达式的值.解答:解:∵ x+y=12 , xy=27∴( x﹣ y)2=( x+y )2﹣ 4xy=122﹣ 4×27=36(3分)∵ x< y∴x﹣ y= ﹣ 6(5 分)∴===(9分)==(12分)点评:本题考查有理指数幂的运算,考查计算能力.27.( 1)计算:;(b,用 a, b 表示.2)已知 a=log3 2, 3 =5考点:有理数指数幂的运算性质;对数的运算性质.专题:计算题.分析:( 1)根据指数幂的运算性质和恒等式0a,进行化简求值;a =1、0 =1( 2)根据指对互化的式子把3b化成对数式,再把化为分数指数幂的形式,由对数的运算性质将30 =5拆成 3×2×5 后,再进行求解.解答:解:( 1)原式 =(7 分)(2)∵ 3b=5∴ b=log 35∴(14 分)点评:本题考查了指数和对数运算性质的应用,常用的方法是将根式化为分数指数幂的形式,指数式和对数式互化,以及将真数拆成几个数的积或商的形式.28.化简或求值:( 1);( 2).考点:有理数指数幂的化简求值;对数的运算性质.专题:计算题.分析:(1)由原式有意义,得到a≥1,然后把各根式进行开平方和开立方运算,开方后合并即可.(2)直接运用对数式的运算性质进行求解计算.解答:解:( 1)因为 a﹣ 1≥0,所以 a≥1,所以=a﹣1+|1﹣ a|+1﹣ a=|1﹣ a|=a﹣ 1;( 2)=2lg5+2lg2+lg5 ( 1+lg2 ) +( lg2)2=2 ( lg2+lg5 ) +lg5+lg2 ( lg5+lg2 ) =2+lg5+lg2=3 .点评:本题考查了有理指数幂的化简求值,考查了对数的运算性质,解答此题的关键是由根式有意义得到 a 的取值范围,此题是基础题.29.计算下列各式的值:(1);(2).考点:有理数指数幂的化简求值;对数的运算性质.专题:计算题.分析:(1)根据分数指数与根式的互化以及幂的乘方运算法则,还有零指数、负指数的运算法则,化简可得值;( 2)运用对数运算性质化简可得.解答:解:( 1)原式 =;.点评:考查学生灵活运用根式与分数指数幂互化及其化简运算的能力,以及分母有理化的应用能力.30.计算log( 1) lg20 ﹣ lg2 ﹣ log 23?log32+2(2)(﹣1)0+()+().考点:有理数指数幂的化简求值;对数的运算性质.专题:函数的性质及应用.分析:(1)利用对数的运算法则、对数的换底公式及其对数恒等式即可得出;( 2)利用指数幂的运算法则即可得出.解答:解:( 1)原式 ==1﹣1+ = ;(2)原式 =1===2 .点评:数列掌握对数的运算法则、对数的换底公式及其对数恒等式、指数幂的运算法则是解题的关键.。
四年级数学下册计算题专练1-30

四(下)计算专练四则运算(-)1、口算:11×70= 0×536= 34×5= 84×2= 35×30=180×4= 19×6= 24÷12= 99÷11= 36÷18=96÷6= 60÷12= 91÷13= 85÷17= 51÷17=2、用递等式计算:17+83-25 41×3-76÷28×(54-49)-33 284-27 ×473-6×12+34 81÷(21-12)×13四则运算(二)1、口算:15×80= 80×60= 101×40= 48×50= 17×20=130×7= 75×2= 25×4= 52÷13= 74÷37= 54÷27= 100÷4= 86÷43= 60÷2÷5= 45×2÷9=12÷3×4= 111×40≈ 208×20≈ 197×50≈ 93×21≈2、用递等式计算:145÷5×6 27+(18 -12)×752-18×2+31 125-15÷5(75+25)×(43-36) 120÷4-360÷4四则运算(三)1、口算:25×40= 104×4= 200×8= 12×50= 300×20=21×7= 15×6= 13×4= 48÷12= 90÷30=54÷27= 320÷4= 420÷21= 48÷2÷3= 30×2÷1=12×3÷6= 482×20≈ 751÷3≈ 99×33≈ 604÷60≈2、用递等式计算:6×(4×25) 43×4-65×2960÷5+56×20 69÷3×(85-65)(76+54)÷5 168÷4+17×6四则运算(四)1、口算:15×80= 80×60= 101×40= 48×50= 17×20=130×7= 75×2= 25×4= 52÷13= 74÷37= 54÷27= 100÷4= 86÷43= 60÷2÷5= 45×2÷9=12÷3×4= 111×40≈ 208×20≈ 197×50≈ 93×21≈2、用递等式计算:13×24÷12 (119-8)÷3(32-14)÷(36÷6) 43×4-65×20×54+84÷3 20+30×0-6四则运算(五)1、递等式计算:29×(3+9) 36×13-552÷8125-54÷9 56÷(102-94)+126 0×(35÷7)+86 (18-18)÷(18+18)179-4×9÷6 63+24÷8-2×3=75 2、把合适的数填在□里。
人教版一年级上册数学专项练习-计算题50道及答案1套

人教版一年级上册数学专项练习-计算题50道一.计算题(共50题,共426分)1.算一算。
10-4=1+2= 5-3= 0+8= 10-7=2+4= 6-5= 4+4= 5-1= 1+9=8-4= 6+0= 3-3= 1+5= 10-5=1+1= 8+1= 4-1= 9-3= 3+6=2.看图写算式。
(1)(2)3.看图列出加法算式。
(1)□+□=□(2)□+□=□(3)□+□=□4.先说一说图意,再列式计算。
□○□=□(条)5.我能列得对。
6.看谁先到家:7.看图列式计算。
8.看图列算式。
_____ _____ _____ = _____(个)9.算一算。
12+7= 14+5= 5+9= 17-6= 2+6= 3+9= 1+19= 11+7= 5+6= 5+15= 10.看谁算得又对又快。
2+3= 2-2= 4-0= 1+1=5+0= 0+1= 5-4= 1+4=4-4= 2-0= 4-3= 0+3=4-1= 1+3= 2+0= 3-1=11.看图列式计算。
(1)(2)12.算一算。
8-2= 0+8= 3+1= 6+1= 7+3=10-2=7-2= 6-4= 9-2= 10-9=5+5= 5+2= 9-4= 8+1= 2-1=4+6= 2+7= 9-5= 3+3= 4-2=13.列式计算。
14.看图列式计算。
15.算一算。
10+2= 7-6= 6-6= 9-1= 10-10= 13+5=1+17= 15-10= 12+7= 8-2= 5-5= 2+6=11+3= 14-4= 3+10= 8-3= 15-5= 12+7=4+3= 7-5= 13+2= 20-10= 10-5= 11+4=16.看图写算式。
□○□=□(朵)17.看图列式计算。
(1)(2)18.开心算一算。
8+6=_______ 16-3=_______ 17-6=_______ 13+6=_______9+5=_______ 14-10=_______ 17-4=_______ 18-1=_______19.算一算。
一元一次方程计算题专练(含答案)

一元一次方程计算题专练(含答案)1.解方程:212132x x -+=+2.解方程:(1)()104x 32x 1+-=-; (2)14y 2y 1y 25-+=-.3.解方程(1)2x 13x 2x 1124+--=-. (2)x 0.160.1x 80.50.03--=4.解方程.(1)()83520x x -+= (2)1:225%:0.753x =(3) 2940%316x ÷=5.解方程(1)5322x -=; (2)3254x x -=-(2)5(31)2(42)8-=+-x x ; (4)2114135-+=-x x6.解下列方程或方程组(1)2x ﹣1=x+9 (2)x+5=2(x ﹣1)(3)43135x x --=- (4)3717245x x -+-=-7.解方程:(1)()12142x x x ⎛⎫--=- ⎪⎝⎭ (2)132123x x +-+=8.解方程:(1) 2534x x -=+ (2)341125x x -+-=9.解方程(1)2x+5=5x-7; (2)3(x-2)=2-5(x+2);(4)12x + +43x -=2; (4)12311463x x x -++-=+.10.解方程:(1)4(x﹣2)=2﹣x;(2)3121243y y+-=-.11.解方程:21122 323 x xx-++=-12.解方程:(1)2x+3=x+5;(2)2(3y–1)–3(2–4y)=9y+10;(3)3157146y y-+-=;(4)3(1)1126x x++=+.13.解方程25321 68x x+--=14.解方程:(1)51312423-+--=x x x;(2)30.4110.50.3---=x x15.解方程x ﹣13x -=36x -﹣116.解方程:(1)3x 158+=; (2)()7x 22x 310--=; (3)x 22x 1146+--=17.解方程 (1)5y ﹣2(y +4)=6 (2)2121136x x -+-=-18.111(9)(9)339x x x x ⎡⎤---=-⎢⎥⎣⎦19.解方程并在每一步后面写出你的依据.212163+--x x =120.解方程:32384x -=.21.解下列方程:(1)11(32)152x x --=; (2)131122x x +-=--;(3)243148x x --=-; (4)113(1)(21)234x x x ⎡⎤--=+⎢⎥⎣⎦ 参考答案1.14x =【解析】【分析】按照解一元一次方程的步骤,去分母,去括号,移项,合并同类项,系数化为1,即可求出解.【详解】解:去分母得:2(21)3(2)6x x -=++,去括号得:42366x x -=++,移项得:43662x x -=++,合并同类项得:14x =.【点睛】本题考查了解一元一次方程,熟练掌握解一元一次方程的一般步骤是解题关键.2.(1)1x 2=;(2)y 2=-. 【解析】【分析】 ()1方程去括号,移项合并,把x 系数化为1,即可求出解;()2方程去分母,去括号,移项合并,把y 系数化为1,即可求出解..【详解】解:()1去括号得:104x 122x 1+-=-,移项得:4x 2x 11012-=--+,合并得:2x 1=, 解得:1x 2=; ()2去分母得:()5y 1024y 210y +=--,去括号得:5y 108y 410y +=--,移项得:5y 8y 10y 410-+=--,合并得:7y 14=-,解得:y 2=-.此题考查了解一元一次方程,解题关键在于掌握其步骤为:去分母,去括号,移项合并,把x 系数化为1,求出解.3.(1)x=1(2)x=52【解析】【分析】(1)先分母,再去括号,合并移项即可求解;(2)先把分母化成整数,再求解方程的解.【详解】(1)2x 13x 2x 1124+--=-()12x 21123(32)x x -+=--12x-2x-1=12-9x+619x=19,x=1(2)x 0.160.1x80.50.03--=1610x283x --=6x-16+10x=2416x=40 x=52此题主要考查一元一次方程的求解,解题的关键是熟知一元一次方程的解法.4.(1)20x;(2)12x =;(3)1516x = 【解析】【分析】(1)原式去括号,移项然后系数化为1即可得出答案;(2)把原式中的百分数转化为分数的形式,然后比例转化为乘法计算,运用乘法法则计算即可得出答案;(3)把原式中的百分数转化为分数的形式,然后等式两边乘以23,再利用除法法则计算即可得出结果.【详解】(1)解:83520x x --= 20x(2)解:1120.7543x ⨯=⨯ 12x = (3)解:2925163x =⨯ 1516x = 【点睛】本题主要考查解一元一次方程,根据等式的性质进行解答即可.5.(1)5x =;(2)1x =;(3)17x =;(4)72x =.【分析】(1)(2)依次移项,合并同类项,系数化为1即可得解;(3)依次去括号、移项,合并同类项,系数化为1即可得解;(4)依次去分母、去括号、移项,合并同类项,系数化为1即可得解【详解】解:(1)移项得5223x =+,合并同类项得525x =系数化为1得5x =;(2)移项得3524x x -=-合并同类项得22x -=-系数化为1得1x =;(3)去括号得155848x x -=+-移项得158485x x -=+-+合并同类项得71x =系数化为1得17x =;(4)去分母得5(21)3(14)15x x -=+-去括号得10531215x x -=+-移项得10123515x x -=+-合并同类项得27x -=-系数化为1得72x =.本题考查解一元一次方程,需注意,移项要变号,去分母时,没有分母的项也要乘以分母的最小公倍数,去括号时,括号外面的数与括号里面的每一项都要相乘.6.(1)10x = (2)7x = (3) 5.5x = (4)13x =【解析】【分析】解:(1)对移项合并2x ﹣1=x+9即可得到答案;(2)先去括号得x+5=2x ﹣2,移项合并,再系数化为1即可得到答案;(3)去分母得20﹣5x =3x ﹣9﹣15,移项合并,再系数化为1即可得到答案;(4)去分母得40﹣15x+35=﹣4x ﹣68,移项合并,再系数化为1即可得到答案.【详解】解:(1)对2x ﹣1=x+9移项合并得:x =10;(2)去括号得:x+5=2x ﹣2,移项合并得:﹣x =﹣7,系数化为1得:x =7;(3)去分母得:20﹣5x =3x ﹣9﹣15,移项合并得:﹣8x =﹣44,系数化为1得:x =5.5;(4)去分母得:40﹣15x+35=﹣4x ﹣68,移项合并得:﹣11x =﹣143,系数化为1得:x =13.本题考查解一元一次方程,解题的关键是掌握解一元一次方程的基本解题步骤.7.(1)1x =;(2)3x =【解析】【分析】利用等式的性质解一元一次方程即可解答.【详解】(1)()12142x x x ⎛⎫--=- ⎪⎝⎭解:去括号得:2142x x x -+=-移项合并同类项得:33x -=-系数化为1得:1x =(2)132123x x +-+= 解:去分母得:3(1)2(32)6x x ++-=去括号得:33646x x ++-=移项合并同类项得:3x -=-系数化为1得:3x =【点睛】本题考查了解一元一次方程,难度较低,熟练掌握等式的性质以及解一元一次方程是解题关键. 8.(1)x=14-(2)x=-9【分析】(1)根据一元一次方程移项合并即可求解;(2)去分母后,再根据一元一次方程的解法即可求解.【详解】(1) 2534x x -=+-8x=2 x=14- (2)341125x x -+-= 5(x-3)-2(4x+1)=105x-15-8x-2=10-3x=27x=-9【点睛】此题主要考查一元一次方程的求解,解题的关键是熟知一元一次方程的解法.9.(1)x=4;(2)14x =-;(3)751x =;(4)5x =-. 【解析】【分析】(1)通过移项、合并同类项、系数化为1即可得解;(2)通过去括号、移项、合并同类项、系数化为1即可得解;(3)(4)都是通过去分母去括号、移项、合并同类项、系数化为1即可得解.【详解】(1)2x+5=5x−7移项得:2x−5x=−7−5合并同类项得:−3x=−12系数化为1得:x=4.(2)3(x−2)=2−5(x+2)去括号得:3x−6=2−5x -10移项得:3x+5x=2-10+6合并同类项得:8x=-2系数化为1得:x=14- .(3)12x + +43x -=2;去分母得: 3(1)2(4)12x x ++-=去括号得: 332812x x ++-=移项得: 321283x x +=+-合并同类项得: 517x =.系数化为1得751x =.(4)12311463x x x-++-=+去分母得: 3(1)122(23)4(1)x x x --=+++去括号得: 33124644x x x --=+++移项得: 34464312x x x --=+++合并同类项得: 525x -=系数化为1得: 5x =-.【点睛】本题考查解一元一次方程,解一元一次方程的一般步骤是:(1)去分母(即在方程两边都乘以各分母的最小公倍数,去各项中的分母);(2)去括号(即按先去小括号,再去中括号,最后去大括号的顺序,逐层把括号去掉);(3)移项(即把含有未知数的项都移到方程的一边,其它项都移到方程的另一边。
初中化学计算专练50题1

(1)计算Vc中碳、氢元素的质量比_______。
(2)通过计算确定Vc的化学式____________。
(3)新鲜的水果和蔬菜富含Vc,若100g西红柿含Vc30mg,则每天食用多少质量的西红柿也可达到服用上述Vc片的效果(请写出解题过程)。
28.戊二醛(C5H8O2)是防控新冠肺炎疫情的消毒剂请计算:
6.褪黑激素(C13H16O2N2)具有促进睡眠、调节时差、抗衰老、调节免疫,抗肿瘤等多项生理功能。根据上述信息回答下列问题:
(1)褪黑激素中碳元素和氧元素的质量之比是______________;
(2)每个分子中共有___________个原子。
7.已知用作相对原子质量基准的碳原子的质量为1.993×10-26kg,1个铝原子的质量为4.482×10-26kg,请列式求铝原子的相对原子质量。(保留整数)
(1)由题意可知,反应生成氢气的质量共_______g
(2)若欲计算反应后所得溶液的质量,你认为至少还应该补充的一个条件是_______
(3)弹壳中铜的质量______(计算结果精确至0.1,请书写出计算过程)
27.如图是已破损的维生素C(简写为Vc)片剂说明书的部分信息。已知维生素C由碳、氢、氧三种元素组成。
18.黄铜(铜锌合金),为了测定黄铜中锌的含量。取20g黄铜样品加入足量稀硫酸充分反应,生成氢气的质量为0.2g。
(1)该反应属于_______(填基本反应类型)。
(2)求黄铜样品中锌的质量分数。
19.鸡蛋壳的主要成分是CaCO3,现在取15g干燥的鸡蛋壳放入20g的烧杯中,向其中加入40g稀盐酸恰好完全反应(杂质不溶于水,且不与稀盐酸反应),反应后烧杯和物质的总质量为70.6g,计算鸡量中的CaCO3的质量分数是多少?(结果保留到0.1%)
新人教版六年级下册数学计算题专项练习试题1

计算专项训练(一)一、 计算题:(共38分)1、 直接写出得数(每小题1分,共6分)=-2143 =⨯%7524=++32.03268.0 =⨯÷3319=⎪⎭⎫ ⎝⎛-÷4.0541 =⨯÷⨯41724172 2、 合理、灵活地计算(每小题4分,共16分)32125.15.2÷⨯ %502013100113.203.20115⨯+÷-⨯⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--⨯411454392 ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+⨯-÷312.05.475.435.23、 求未知数x (每小题3分,共6分)323264=⨯-x 3.0:53%24:=x4、 列综合算式或方程解答(4分) 96的61比一个数的21多2.5,求这个数。
计算专项训练(二)一、计算。
(共35分)1、直接写出得数。
(每题0.5分,共4分)1787-998=58+0.25=1021×35=21÷37=5 9×15÷59×15=18÷18÷18=111×12.1-1=35+25÷15=2、用递等式计算。
(每题3分,共18分,多做不给分。
)①987+104×65-1747 ②86.4÷3.2-6.4×3.2 ③3763÷7 +17×266317-16.8÷(1.8+7.2×112) (79+421-37)×6.3 15÷〔(57-12)÷328〕-0.53、求未知数X。
(每題2分,共6分)0.4 X-0.4×10.8 =20 13X+34X =134856: X =34:25一、计算。
(共26分) 1.直接写出得数。
(每小题1分,共8分) 6.3÷0.1=65÷76= 97-(75-92)= 8×(2.5+0.25)= 3.37+6.73=65-91= (0.18+0.9)÷9= 7×61÷7×61= 2.计算下面各题。
四年级数学下册计算题专练1-30

四则运算(-)班级姓名1、口算:11×70= 0×536= 34×5= 84×2= 35×30=180×4= 19×6= 24÷12= 99÷11= 36÷18=96÷6= 60÷12= 91÷13= 85÷17= 51÷17=2、用递等式计算:17+83-25 41×3-76÷28×(54-49)-33 284-27 ×4 73-6×12+34 81÷(21-12)×13四则运算(二)班级姓名1、口算:15×80= 80×60= 101×40= 48×50= 17×20=130×7= 75×2= 25×4= 52÷13= 74÷37= 54÷27= 100÷4= 86÷43= 60÷2÷5= 45×2÷9=12÷3×4= 111×40≈ 208×20≈ 197×50≈ 93×21≈2、用递等式计算:145÷5×6 27+(18 -12)×752-18×2+31 125-15÷5(75+25)×(43-36) 120÷4-360÷4四则运算(三)班级姓名1、口算:25×40= 104×4= 200×8= 12×50= 300×20=21×7= 15×6= 13×4= 48÷12= 90÷30= 54÷27= 320÷4= 420÷21= 48÷2÷3= 30×2÷1=12×3÷6= 482×20≈ 751÷3≈ 99×33≈ 604÷60≈2、用递等式计算:6×(4×25) 43×4-65×2960÷5+56×20 69÷3×(85-65)(76+54)÷5 168÷4+17×6四则运算(四)班级姓名1、口算:15×80= 80×60= 101×40= 48×50= 17×20=130×7= 75×2= 25×4= 52÷13= 74÷37= 54÷27= 100÷4= 86÷43= 60÷2÷5= 45×2÷9=12÷3×4= 111×40≈ 208×20≈ 197×50≈ 93×21≈2、用递等式计算:13×24÷12 (119-8)÷3(32-14)÷(36÷6) 43×4-65×20×54+84÷3 20+30×0-6四则运算(五)班级姓名1、递等式计算:29×(3+9) 36×13-552÷8125-54÷9 56÷(102-94)+126 0×(35÷7)+86 (18-18)÷(18+18)179-4×9÷6 63+24÷8-2×3=752、把合适的数填在□里。
高中数学计算题专项练习1

2019年高中数学计算题专项练习1一.解答题(共30 小题)1.计算:( 1);( 2).2.计算:( 1) lg1000+log 342﹣ log 314﹣ log 48;(2) .3.( 1)解方程: lg ( x+1) +lg ( x ﹣ 2)=lg4 ; ( 2)解不等式: 21﹣ 2x> .4.( 1)计算: 2× ×( 2)计算: 2log 510+log 50.25.5.计算:( 1) ;( 2).6.求 log 89×log 332﹣log 1255 的值.7.( 1)计算 .( 2)若 ,求 的值.8.计算下列各式的值0.75( 1) 0.064﹣(﹣ ) +16 +0.25( 2) lg5+ ( log 32)?( log 89) +lg2 .9.计算:( 1) lg 22+lg5?lg20 ﹣ 1;(2).10.若 lga 、 lgb 是方程 2x 2﹣ 4x+1=0 的两个实根,求的值.11.计算(Ⅰ)(Ⅱ) .12.解方程:.13.计算:(Ⅰ)(Ⅱ).14.求值:( log 62) 2+log 63×log 612.15.( 1)计算( 2)已知 ,求 的值.16.计算(Ⅰ);(Ⅱ) 0.0081 ﹣() + ? ? .17.(Ⅰ)已知全集 U={1 , 2, 3, 4, 5,6} , A={1 , 4, 5} , B={2 , 3, 5} ,记 M= ( ?U A ) ∩B ,求集合 M ,并写出 M 的所有子集;(Ⅱ)求值:.18.解方程: log 2( 4x ﹣ 4) =x+log 2( 2x+1﹣ 5)219.(Ⅰ)计算( lg2) +lg2 ?lg50+lg25 ;(Ⅱ)已知a=,求÷.20.求值:( 1) lg14 ﹣+lg7 ﹣ lg18(2).21.计算下列各题:(1)( lg5)2+lg2 ×lg50 ;﹣1,求的值.( 2)已知 a﹣ a =122.( 1)计算;( 2)关于 x 的方程 3x 2﹣ 10x+k=0 有两个同号且不相等的实根,求实数k 的取值范围.23.计算题(1)(2)24.计算下列各式:(式中字母都是正数)(1)(2).25.计算:( 1);(2) lg25+lg2 ×lg50+ ( lg2)2.26.已知 x+y=12 , xy=27 且 x< y,求的值.27.( 1)计算:;b,用 a, b 表示.( 2)已知 a=log3 2, 3 =528.化简或求值:( 1);( 2).29.计算下列各式的值:( 1);( 2).30.计算log( 1) lg20 ﹣ lg2 ﹣ log 23?log32+2(2)(﹣1)0+()+().参考答案与试题解析一.解答题(共30 小题)1.计算:( 1);( 2).考点:有理数指数幂的化简求值;对数的运算性质.专题:函数的性质及应用.分析:(1)利用指数幂的运算法则即可得出;( 2)利用对数的运算法则即可得出.解答:解:( 1)原式 ===.( 2)原式 ===.点评:熟练掌握指数幂的运算法则、对数的运算法则是解题的关键.2.计算:(1) lg1000+log 342﹣ log 314﹣ log48;(2).考点:有理数指数幂的化简求值;对数的运算性质.专题:函数的性质及应用.分析:(1)利用对数的运算性质即可得出;( 2)利用指数幂的运算性质即可得出.解答:解:( 1)原式 =;( 2)原式 =.点评:熟练掌握对数的运算性质、指数幂的运算性质是解题的关键.3.( 1)解方程: lg( x+1) +lg ( x﹣ 2)=lg4 ;( 2)解不等式:21﹣2x>.考点 : 对数的运算性质;指数函数单调性的应用.专题 : 计算题.分析:( 1)原方程可化为 lg (x+1 )( x ﹣ 2) =lg4 且可求( 2)由题意可得1﹣ 2x ﹣2,结合指数函数单调性可求x 的范围2> =2解答:解:( 1)原方程可化为 lg ( x+1 )(x ﹣ 2)=lg4 且∴( x+1 )(x ﹣ 2) =4 且 x > 2∴ x 2﹣ x ﹣ 6=0 且 x >2 解得 x= ﹣2(舍)或 x=3( 2)∵ 21﹣ 2x> =2 ﹣2∴ 1﹣ 2x >﹣ 2 ∴点评: 本题主要考查了对数的运算性质的应用,解题中要注意对数真数大于0 的条件不要漏掉,还考查了指数函数单调性的应用.4.( 1)计算: 2× ×( 2)计算: 2log 510+log 50.25.考点 : 对数的运算性质.专题 : 计算题;函数的性质及应用.分析: ( 1)把各根式都化为 6 次根下的形式,然后利用有理指数幂的运算性质化简;( 2)直接利用对数式的运算性质化简运算.解答:× ×解( 1)计算: 2= ===6;( 2) 2log 510+log 50.25==log 5100×0.25 =log 525 =2log 55=2 .点评: 本题考查了指数式的运算性质和对数式的运算性质,解答的关键是熟记有关运算性质,是基础的运算题.5.计算:(1) ;(2).考点:对数的运算性质.专题:计算题.分析:(1)利用有理指数幂的运算法则,直接求解即可.( 2)利用对数的运算形状直接求解即可.解答:解:( 1)﹣ 13﹣ 1+8=12⋯(6 分)=0.2﹣ 1+2 =5( 2)===⋯(12 分)点评:本题考查指数与对数的运算性质的应用,考查计算能力.6.求 log 9×log32﹣log 5 的值.83125考点:对数的运算性质.专题:计算题.分析:利用对数的运算性质进及对数的换底公式行求解即可解答:解:原式 ====3点评:本题主要考查了对数的运算性质的基本应用,属于基础试题7.( 1)计算.( 2)若,求的值.考点:对数的运算性质.专题:计算题.分析:( 1)把对数式中底数和真数的数4、8、 27 化为乘方的形式,把底数的分数化为负指数幂,把真数的根式化为分数指数幂,然后直接利用对数的运算性质化简求值;( 2)把已知条件两次平方得到﹣ 12﹣ 2得答案.x+x与 x +x,代入解答:解:( 1)===2 ﹣ 4﹣ 1=﹣ 3;( 2)∵,∴,∴ x+x﹣ 1.=5 则( x+x ﹣122 ﹣ 2) =25 ,∴ x +x=23 ∴=.点评: 本题考查了有理指数幂的化简与求值,考查了对数的运算性质,是基础的计算题.8.计算下列各式的值0 0.75( 1) 0.064﹣(﹣ ) +16 +0.25( 2) lg5+ ( log 32)?( log 89) +lg2 .考点 : 对数的运算性质;有理数指数幂的化简求值.专题 : 计算题. 分析:( 1)化小数指数为分数指数, 0 次幂的值代1,然后利用有理指数幂进行化简求值;( 2)首先利用换底公式化为常用对数,然后利用对数的运算性质进行化简计算.解答:0.75解:( 1) 0.064﹣(﹣ ) +16 +0.25==( 0.4) ﹣1﹣1+8+0.5=2.5﹣ 1+8+0.5=10 ;( 2) lg5+ ( log 32)?( log 89) +lg2= =1+=1+ = .点评: 本题考查了对数的运算性质,考查了有理指数幂的化简与求值,是基础的运算题.9.计算:( 1) lg 22+lg5?lg20 ﹣ 1;(2).考点 : 对数的运算性质;有理数指数幂的化简求值.专题 : 计算题.分析: ( 1)把 lg5 化为 1﹣ lg2, lg20 化为 1+lg2 ,展开平方差公式后整理即可;( 2)化根式为分数指数幂, 化小数指数为分数指数, 化负指数为正指数, 然后进行有理指数幂的化简求值.2解答: 解:( 1) lg 2+lg5 ?lg20 ﹣12=lg 2+( 1﹣ lg2 )( 1+lg2)﹣ 122;=lg 2+1﹣ lg 2﹣ 1=0( 2)==2 3=2 ?3 ﹣ 7﹣2﹣ 1=98.点评: 本题考查了有理指数幂的化简与求值,考查了对数的运算性质,解答的关键是熟记有关性质,是基础题.10.若 lga 、 lgb 是方程 2x 2﹣ 4x+1=0 的两个实根,求的值.考点 : 对数的运算性质;一元二次方程的根的分布与系数的关系.专题 : 计算题;转化思想.分析:lga 、 lgb 是方程 2x 2﹣4x+1=0 的两个实根,先由根与系数的关系求出,再利用对数的运算性质对化简求值.解答:解: ,2=( lga+lgb )( lga ﹣ lgb )2=2[ (lga+lgb ) ﹣ 4lgalgb ]=2(4﹣ 4× )=4点评: 本题考查对数的运算性质,求解的关键是熟练掌握对数的运算性质,以及一元二次方程的根与系数的关系.11.计算(Ⅰ)(Ⅱ) .考点 : 对数的运算性质;有理数指数幂的化简求值.专题 : 计算题.分析: ( 1)根据对数运算法则化简即可( 2)根据指数运算法则化简即可解答:解:( 1)原式 =(2)原式 ==点评:本题考查对数运算和指数运算,注意小数和分数的互化,要求能灵活应用对数运算法则和指数运算法则.属简单题12.解方程:.考点:对数的运算性质.专题:计算题;函数的性质及应用.分析:利用对数的运算性质可脱去对数符号,转化为关于x 的方程即可求得答案.解答:解:∵,∴log5( x+1) +log 5(x﹣ 3) =log 55,∴( x+1 )?( x﹣ 3)=5,其中, x+1> 0 且 x﹣ 3> 0解得 x=4 .故方程的解是4点评:本题考查对数的运算性质,考查方程思想,属于基础题.13.计算:(Ⅰ)(Ⅱ).考点:对数的运算性质;运用诱导公式化简求值.专题:计算题;函数的性质及应用.分析:( I)利用诱导公式,结合特殊角的三角函数值即可求解( II )利用对数的运算性质及指数的运算性质即可求解解答:解:(I)(每求出一个函数值给( 1 分),6 分( II )(每求出一个式子的值可给( 1 分), 12 分)点评:本题主要考查了诱导公式在三角化简求值中的应用及对数的运算性质的简单应用,属于基础试题14.求值:( log62)2+log 63×log 612.考点:对数的运算性质.分析:先对后一项:log 63×log 612 利用对数的运算法则进行化简得到:log63+log 63×log 62,再和前面一项提取公因式 log62 后利用对数的运算性质: log a( MN ) =log a M+log a N 进行计算,最后再将前面计算的结果利用log 62+log 63=1 进行运算.从而问题解决.解答:解:原式=(log62+log63)log62+log63=log 62+log 63=1.∴( log62)2+log 63×log 612=1.点评:本小题主要考查对数的运算性质、对数的运算性质的应用等基础知识,考查运算求解能力.属于基础题.对数的运算性质:log a( MN ) =log a M+log a N; log an=log a M ﹣ log a N ;log a M =nlog a M 等.15.( 1)计算( 2)已知,求的值.考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:(1)化根式为分数指数幂,把对数式的真数用同底数幂相除底数不变,指数相减运算,然后利用对数式的运算性质化简;( 2)把给出的等式进行平方运算,求出﹣ 1的结果.x+x ,代入要求的式子即可求得解答:解( 1)===;(2)由,得:,所以, x+2+x ﹣1=9,故x+x ﹣1=7,所以,.点评:本题考查了有理指数幂的化简与求值,考查了对数式的运算性质,解答的关键是熟记有关性质,是基础题.16.计算(Ⅰ);(Ⅱ) 0.0081﹣()+??.考对数的运算性质;根式与分数指数幂的互化及其化简运算.点:专函数的性质及应用.题:分 (Ⅰ)利用对数的运算法则,由已知条件能求出结果.析 (Ⅱ)利用指数的运算法则,由已知条件,能求出结果.:解 解:(Ⅰ)答 ===:= = =﹣ .(Ⅱ)0.0081 ﹣()+??4 3=0.3﹣ +3=.=[( 0.3) ] ﹣([ )]+ 点 本题考查指数和对数的运算法则,是基础题,解题时要认真解答,避免出现计算上的低级错误. 评 :17.(Ⅰ)已知全集 U={1 , 2, 3, 4, 5,6} , A={1 , 4, 5} , B={2 , 3, 5} ,记 M= ( ?U A ) ∩B ,求集合 M ,并写出 M 的所有子集;(Ⅱ)求值:.考点 : 对数的运算性质;交、并、补集的混合运算.专题 : 函数的性质及应用.分析: ( I )利用集合的运算法则即可得出.( II )利用对数的运算法则即可得出. 解答: 解:(Ⅰ)∵ U={1 , 2, 3, 4, 5, 6} , A={1 , 4,5} ,∴ C U A={2 , 3, 6} ,∴ M= ( ?U A ) ∩B={2 , 3, 6} ∩{2 , 3,5}={2 , 3} .∴ M 的所有子集为: ? , {2} , {3} , {2 , 3} .(Ⅱ)= = = .点评: 本题考查了集合的运算法则、对数的运算法则,属于基础题.18.解方程: log 2( 4x ﹣ 4) =x+log 2( 2x+1﹣ 5)考点 : 对数的运算性质.专题 : 计算题.分析:利用对数的运算法则将方程变形为 ,将对数式化为指数式得到 ,通过换元转化为二次方程,求出x 的值,代入对数的真数检验.xx+1解答: 解: log 2( 4 ﹣ 4) =x+log 2( 2 ﹣ 5)即为log 2(4x ﹣ 4)﹣ log 2( 2x+1﹣ 5)=x即为所以令 t=2x即解得 t=4 或 t=1所以 x=2 或 x=0 (舍)所以方程的解为x=2.点评:本题考查对数的真数大于0、对数的运算法则、二次方程的解法,解题过程中要注意对数的定义域,属于基础题.19.(Ⅰ)计算( lg2)2;+lg2 ?lg50+lg25(Ⅱ)已知 a= ,求÷.考点:对数的运算性质;根式与分数指数幂的互化及其化简运算.专题:计算题.分析:(Ⅰ)利用对数的运算法则进行运算,利用结论lg2+lg5=0 去求.(Ⅱ)先将根式转化为同底的分数指数幂,利用指数幂的运算性质,化为最简形式,然后在将 a 值代入求值.解答:解:(Ⅰ)原式=lg2(lg2+lg50)+lg25=2lg2+lg25=lg100=2.(Ⅱ)原式 =.∵ a= ,∴原式 =.点评:本题考查对数的四则运算法则,根式与分数指数幂的互化,以及同底数幂的基本运算性质,要求熟练掌握相应的运算公式.20.求值:( 1) lg14 ﹣+lg7 ﹣ lg18(2).考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:(1)应用和、差、积、商的对数的运算性质计算即可;( 2)利用指数幂的运算性质(m n mn计算即可.a) =a解答:解:( 1)∵ lg14﹣+lg7﹣ lg18=( lg7+lg2 )﹣ 2(lg7﹣ lg3 )+lg7 ﹣( lg6+lg3 )=2lg7 ﹣ 2lg7+lg2+2lg3 ﹣ lg6 ﹣ lg3( 2)∵=﹣1﹣+=﹣+=.(8分)点评:本题考查对数与指数的运算性质,关键在于熟练掌握对数与指数幂的运算性质进行计算,属于中档题.21.计算下列各题:(1)( lg5)2+lg2 ×lg50 ;﹣ 1的值.( 2)已知 a﹣ a =1,求考点:对数的运算性质;有理数指数幂的化简求值.专题:计算题.分析:(1)直接利用对数的运算性质,求出表达式的值;﹣ 12﹣ 2的值,然后化简,求出它的值( 2)通过 a﹣ a =1,求出 a +a解答:2×lg50=2×(lg5+1) =lg5( lg2+lg5) +lg2=1 ;解:( 1)( lg5) +lg2( lg5 ) +lg2﹣ 12﹣ 2( 2)因为 a﹣ a =1,所以 a +a﹣ 2=1,2﹣2∴a +a =3,==0 .点评:本题主要考查对数的运算性质和有理数指数幂的化简求值的知识点,解答本题的关键是熟练对数的运算性质,此题难度一般.22.( 1)计算;( 2)关于 x 的方程 3x 2﹣ 10x+k=0 有两个同号且不相等的实根,求实数k 的取值范围.考点:根式与分数指数幂的互化及其化简运算;一元二次方程的根的分布与系数的关系.专题:计算题.分析:( 1)转化为分数指数幂,利用指数幂的运算法则进行计算;( 2)由维达定理的出k 的关系式,解不等式即可.解答:( 1)解:原式 ===a 0(∵ a≠0)( 2)解:设 3x 2﹣ 10x+k=0 的根为 x 1,x 2由 x 1+, x 1 ?由条件点评: 本题考查根式和分数指数幂的转化、指数的运算法则、及二次方程根与系数的关系,属基本运算的考查.23.计算题( 1)( 2)考点 : 根式与分数指数幂的互化及其化简运算;对数的运算性质.专题 : 计算题.分析: ( 1)根据分数指数与根式的互化以及幂的乘方运算法则,还有零指数、负指数的运算法则,化简可得值;( 2)运用对数运算性质及对数与指数的互逆运算化简可得.解答:解:( 1)原式 = ﹣(﹣ 2) 24﹣ = ﹣64+ +1﹣ =﹣;×(﹣ 2) +( 2)原式 =83224×8﹣ log 3 32+log 3 ﹣log 3 ﹣ 3 =log 3 ﹣ 9=﹣ 9.点评: 考查学生灵活运用根式与分数指数幂互化及其化简运算的能力,以及分母有理化的应用能力.24.计算下列各式: (式中字母都是正数)( 1)(2).考点 : 根式与分数指数幂的互化及其化简运算;有理数指数幂的化简求值.专题 : 函数的性质及应用. 分析:( 1)利用及其根式的运算法则即可;( 2)利用立方和公式即可得出. 解答:解:( 1)原式 == ?= ==.( 2)原式 ===.点评:熟练掌握根式的运算法则、立方和公式是解题的关键.25.计算:( 1);( 2) lg25+lg2 ×lg50+ ( lg2)2.考点:有理数指数幂的运算性质;对数的运算性质.专题:计算题.分析:( 1)由指数幂的含义和运算法则,,=|3﹣π|,求解即可.( 2)利用对数的运算法则,各项都化为用lg2 表达的式子即可求解.解答:解:( 1)==1+2+ π﹣3=π(2) lg25+lg2 ×lg50+ ( lg2)2=2﹣ 2lg2+lg2 (2﹣ lg2 ) +( lg2)2=2.点评:本题考查指数和对数式的化简和求值、考查指数和对数的运算法则、属基本运算的考查.26.已知 x+y=12 , xy=27 且 x< y,求的值.考点:有理数指数幂的运算性质.专题:计算题.分析:利用已知条件求出x﹣ y 的值,利用分母有理化直接求解所求表达式的值.解答:解:∵ x+y=12 , xy=27∴( x﹣ y)2=( x+y )2﹣ 4xy=122﹣ 4×27=36(3分)∵ x< y∴x﹣ y= ﹣ 6(5 分)∴===(9分)==(12分)点评:本题考查有理指数幂的运算,考查计算能力.27.( 1)计算:;(b,用 a, b 表示.2)已知 a=log3 2, 3 =5考点:有理数指数幂的运算性质;对数的运算性质.专题:计算题.分析:( 1)根据指数幂的运算性质和恒等式0a,进行化简求值;a =1、0 =1( 2)根据指对互化的式子把3b化成对数式,再把化为分数指数幂的形式,由对数的运算性质将30 =5拆成 3×2×5 后,再进行求解.解答:解:( 1)原式 =(7 分)(2)∵ 3b=5∴ b=log 35∴(14 分)点评:本题考查了指数和对数运算性质的应用,常用的方法是将根式化为分数指数幂的形式,指数式和对数式互化,以及将真数拆成几个数的积或商的形式.28.化简或求值:( 1);( 2).考点:有理数指数幂的化简求值;对数的运算性质.专题:计算题.分析:(1)由原式有意义,得到a≥1,然后把各根式进行开平方和开立方运算,开方后合并即可.(2)直接运用对数式的运算性质进行求解计算.解答:解:( 1)因为 a﹣ 1≥0,所以 a≥1,所以=a﹣1+|1﹣ a|+1﹣ a=|1﹣ a|=a﹣ 1;( 2)=2lg5+2lg2+lg5 ( 1+lg2 ) +( lg2)2=2 ( lg2+lg5 ) +lg5+lg2 ( lg5+lg2 ) =2+lg5+lg2=3 .点评:本题考查了有理指数幂的化简求值,考查了对数的运算性质,解答此题的关键是由根式有意义得到 a 的取值范围,此题是基础题.29.计算下列各式的值:(1);(2).考点:有理数指数幂的化简求值;对数的运算性质.专题:计算题.分析:(1)根据分数指数与根式的互化以及幂的乘方运算法则,还有零指数、负指数的运算法则,化简可得值;( 2)运用对数运算性质化简可得.解答:解:( 1)原式 =;.点评:考查学生灵活运用根式与分数指数幂互化及其化简运算的能力,以及分母有理化的应用能力.30.计算log( 1) lg20 ﹣ lg2 ﹣ log 23?log32+2(2)(﹣1)0+()+().考点:有理数指数幂的化简求值;对数的运算性质.专题:函数的性质及应用.分析:(1)利用对数的运算法则、对数的换底公式及其对数恒等式即可得出;( 2)利用指数幂的运算法则即可得出.解答:解:( 1)原式 ==1﹣1+ = ;(2)原式 =1===2 .点评:数列掌握对数的运算法则、对数的换底公式及其对数恒等式、指数幂的运算法则是解题的关键.。
北师大版数学五年级下册专项练习题 计算题练习10套

北师大版五年级数学下册专项练习五年级计算题练习一班级 姓名 得分一、直接写出得数。
(4分)101-201= 2+21= 41+43-51= 97 -92= 1-21-51= 51+21-51= 31+35-2= 52+101= 二、解方程或比例。
(9分)① 0.3χ= 45 ②52χ+53χ=28 ③χ-54 =125三、计算,要写出主要计算过程,能用简便方法的要用简便方法计算。
(18分)51+21+31 21+31-4151+21+54 2-125-12779+61+65+75 1513-(1513-52)五年级计算题练习二班级 姓名 得分一.直接写出得数。
(4分)21+21= 31+32= 1-65= 65-65=51+51= 54-51= 83+83= 1-21= 二.解方程或比例。
(9分)Ⅹ-21=54 61+Ⅹ=21 2Ⅹ-65=61三.计算下列各题,要写出主要计算过程,能用简便方法的要用简便方法计算。
(18分)(1)54 +(83-41) (2)2-73-74 (3)85-31+125(4)68- 7.5 + 32-2.5 (5)125 -(121 -21)班级 姓名 得分一.直接写出得数。
(4分)92+21= 76-32= 103+41= 73+91= 31-51= 61+41= 75-51= 2017-203-209= 92+83-85= 7-75=141+145+143= 41+41+43= 1-32-31=二.解方程或比例。
(9分)X +13 =67 712 —x = 14 X -(716 -524 )=724三.计算下列各题,要写出主要计算过程,能用简便方法的要用简便方法计算。
(18分)51+31+54 1-115-11672+61+65+75 1513-(1513-52)89 -(29 +13 ) 1115 +1017 +415 +517班级姓名得分一.直接写出得数。
(4分)0.15×0.6= 7÷40= 2-13=25+45=1 2+23= 1.2÷2.4=13-14= 0.64÷8=0.75÷0.25= 10-0.06=512+712= 12.5×80=5 8+78= 0.53=13+16= 5—16=二.解方程或比例。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算题专练(一)
(限时:25分钟)
24.(12分)如图1所示,有一个可视为质点的质量为m =1 kg 的小物块,从光滑平台上的A 点以v 0=2 m/s 的初速度水平抛出,到达C 点时,恰好沿C 点的切线方向进入固定在水平地面上的光滑圆弧轨道,最后小物块滑上紧靠轨道末端D 点的质量为M =3 kg 的长木板,已知木板上表面与圆弧轨道末端切线相平,木板下表面与水平地面之间光滑,小物块与长木板间的动摩擦因数μ=0.3,圆弧轨道的半径为R =0.4 m ,C 点和圆弧的圆心连线与竖直方向的夹角θ=60°,不计空气阻力,g 取10 m/s 2.求:
图1
(1)小物块刚要到达圆弧轨道末端D 点时对轨道的压力;
(2)若长木板长度L =2.4 m ,小物块能否滑出长木板?
答案 见解析
解析 (1)物块到达C 点的速度与水平方向的夹角为60°,则
v C =v 0cos 60°
=2v 0=4 m/s 小物块由C 到D 的过程中,由动能定理得:
mgR (1-cos 60°)=12m v D 2-12
m v C 2 代入数据解得:v D =2 5 m/s
小物块在D 点时,由牛顿第二定律得:F N -mg =m v D 2R
解得:F N =60 N
由牛顿第三定律得:小物块刚要到达圆弧轨道末端D 点时对轨道的压力F N ′=F N =60 N ,方向竖直向下.
(2)设小物块始终在长木板上,共同速度大小为v ,小物块在木板上滑行的过程中,小物块与长木板组成的系统动量守恒,取向左为正方向
由动量守恒定律得:m v D =(M +m )v
解得:v =52
m/s 设物块与木板的相对位移为l ,由功能关系得:
μmgl =12m v D 2-12
(m +M )v 2 解得:l =2.5 m>L =2.4 m ,所以小物块能滑出长木板.
25.(20分)如图2所示,在平面直角坐标系中,第三象限里有一加速电场,一个电荷量为q 、质量为m 的带正电粒子(不计重力),从静止开始经加速电场加速后,垂直x 轴从A (-4L,0)点进入第二象限,在第二象限的区域内,存在着指向O 点的均匀辐射状电场,距O 点4L 处的
电场强度大小均为E =qLB 02
16m
,粒子恰好能垂直y 轴从C (0,4L )点进入第一象限,如图所示,在第一象限中有两个全等的直角三角形区域Ⅰ和Ⅱ,均充满了方向垂直纸面向外的匀强磁场,区域Ⅰ的磁感应强度大小为B 0,区域Ⅱ的磁感应强度大小可调,D 点坐标为(3L,4L ),M 点为CP 的中点.粒子运动轨迹与磁场区域相切时认为粒子能再次进入磁场.从磁场区域Ⅰ进入第二象限的粒子可以被吸收掉.求:
图2
(1)加速电场的电压U ;
(2)若粒子恰好不能从OC 边射出,求区域Ⅱ磁感应强度大小;
(3)若粒子能到达M 点,求区域Ⅱ磁场的磁感应强度大小的所有可能值.
答案 见解析
解析 (1)粒子在加速电场中加速,根据动能定理有:
qU =12
m v 2 粒子在第二象限辐射状电场中做半径为R 的匀速圆周运动,则:qE =m v 2
4L
联立解得:v =qB 0L 2m ,U =qL 2B 02
8m
(2)粒子在区域Ⅰ中运动的速度大小
v =qB 0L 2m
, 根据洛伦兹力提供粒子在磁场中做匀速圆周运动的向心力,
有qB 0v =m v 2r ,得半径r =m v qB 0=L 2
, 若粒子在区域Ⅱ中的运动半径R 较小,则粒子会从OC 边射出磁场. 恰好不从OC 边射出时,作出对应的运动轨迹,如图.
满足∠O 2O 1Q =2θ,
sin 2θ=2sin θcos θ=2425
, 又sin 2θ=r R -r
解得:R =4924r =4948
L 又R =m v qB
, 代入v =qB 0L 2m
可得:B =24B 049
(3)①若粒子由区域Ⅰ达到M 点
每次前进CP 2=2(R -r )cos θ=85
(R -r ) 由周期性得:CM =n CP 2(n =1,2,3……),
即52L =85
n (R -r ) R =r +2516n L ≥4948
L ,解得n ≤3
n =1时R =3316L ,B =833
B 0 n =2时R =4132L ,B =1641
B 0 n =3时R =4948L ,B =2449
B 0 ②若粒子由区域Ⅱ达到M 点 由周期性:CM =CP 1+n CP 2(n =0,1,2,3……) 即52L =85R +85
n (R -r ) 解得:R =52+45n 85
(1+n )L ≥4948L 解得:n ≤2625
n =0时R =2516L ,B =825
B 0 n =1时R =3332L ,B =1633B 0.。
