第三单元分数除法整理复习ppt
合集下载
六年级上册数学课件-第三单元分数除法(60张PPT)

180 ÷ 9 = 2000(个) 100
答:可以插入2000个零件。
17. 按下面的步骤计算,再把最后的得数与开始的
P36 数比较,你能发现什么?你知道为什么吗?
2
7 ÷3 15
7
÷
3 4
14
÷
1 2
7
10
15
15
23
1
我发现得数等于本来的数。因为 , 的倒数与 的
积正好是1。也就是除以 2
,
3
10
水的体积和这块冰的体积相等,这桶水有多重?
9÷(1 - 1 )= 10(kg) 10
答:这桶水10 kg。
9.
P40
平均每车运走这批大米几分之几?剩下的大米还要几
车才能运完?
2
2 11
÷4=
×=
7
7 4 14
( 1- 2 ) ÷ 1 = 10 (车)
7
14
1
答:平均每车运走大米的 。
14
剩下的大米还需要10车才能运 完。
25 1分钟可以检测多少瓶?
1分 = 60秒
60 ÷ 1 = 1500(个) 25
答:一分钟可以检测1500瓶。
8. 我 们 平 时 看 到 的 电 影 画 面 实 际 上 是 有 许
P35
1
多 连 续 拍 摄 照 片 以 每 张 24 秒 的 速 度 连 续
播放。请你算一算:半秒可以播放多少张
照片?1分钟呢?
33
21
(4 - 16) × ( 9 + 3 )
=5 16
P35
10. 照 这 个 速 度 , 老 爷 爷 每 天 慢 跑 要 用
多少时间?
第三单元分数除法整理和复习
32
3
再如6.3:0.7的比值是9,那么6.3:0.7的最简比是 9:1,即把比值化成最简分数—9— ,看成9比1。)
1
★回忆思考:比和除法、分数有
什么联系和区别?
联 系(相 当 于) 区别
比
比的前项 :比号 比的后项 比值
一种 关系
除法 被除数 ÷除号 除数
商
一种 运算
分数 分 子 —分数线 分母 分数值 一种数
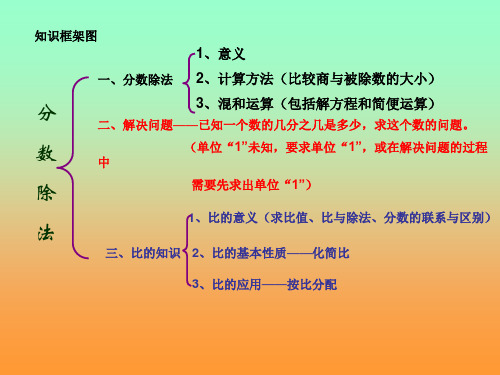
知识框架图
1、意义
一、分数除法 2、计算方法(比较商与被除数的大小)
分
3、混和运算(包括解方程和简便运算)
二、解决问题——已知一个数的几分之几是多少,求这个数的问题。
数
中
(单位“1”未知,要求单位“1”,或在解决问题的过程
除
需要先求出单位“1”)
1、比的意义(求比值、比与除法、分数的联系与区别)
法
三、比的知识 2、比的基本性质——化简比
0 .25 : 2
2) 求比值和化简比有什么联系,又有什么区别?
区别:比值是一个数,它可以是整数、小数和 分数;而最简比是一个比,前项和后项是互质的。
※联系:都可以用比的前项除以比的后项去计 算。
讨论:根据比值怎样很快说出它的最简比呢?根据 最简比你能直接说出比值吗?
如1:1 的最简比2:3, 那么它的比值是2 ,
3、比的应用——按比分配
一、分数除法的意义
• 已知两个因数的积与其中一个因数, 求另个因数的运算。
二、复习分数除法的计算法则。
除以一个数(0除外),等于( 乘这个数的倒数)。
1、计算
2 6 5
15 26
讨论: 1) 2 6的商为什么比被除数( 2) 小?
人教版数学六年级上册第3单元分数除法-整理和复习课件(共19张PPT)

鹅 7 0 0 5 0 0 = 2 0 0 只
拓展提升
拓展提升
5、小明和爷爷一起去操场漫步。小明走一圈需要8分钟, 爷爷走一圈需要10分钟。
(1)如果两人同时同地出发,相背而行,多少分钟后相遇?
(2)如果两人同时同地出发,同方向而行,多少分钟后小明超过爷爷一整圈?
( 1)
1
1 1 8 10
人教版六年级上第3单元 第9课时:整理和复习
视察思考
回顾:本单元知识点
A.倒数的认识 B.分数除法的计算方法 C.用分数除法解决问题
视察思考
倒数的认识
分数除以整数
分 数
分数除法计算
分数除以分数
除
分数除法混合运算
法
已知一个数的几分之几是多少,求这个数
已知比一个数多或少几分之几是多少,求这个数 解决问题
拓展提升
2、张大爷养了200只鹅,鹅的只数比鸭少 3 ,
养了多少只鸭?
5
200
1
3 5
= 200 2 5
200 5 2
5 0 0 只
拓展提升
3、张大爷养的鸭和鹅共有700只,其中鹅的只数是鸭的 2
,
5
鸭和鹅各多少只?
鸭
700
1
Байду номын сангаас
2 5
=700 7 5
=700 5 7
= 5 0 0 只
和倍问题
工程问题
探究新知
什么叫倒数?
乘积是1的两个数互为倒数,那我们称其 中一个数是另一个数的倒数。
1的倒数是1;0没有倒数。
探究新知
倒数的复习
乘积是1的两个数互为倒数。
3 8
和
第三单元《分数除法》(单元复习课件)六年级数学上册 人教版

找出下面各数的倒数。
3
5
5
3
0.6
5
3
1
3
2
2
7
找分数的倒数: 把分子和分母颠倒位置。
找小数的倒数: 先把小数化成分数,再求这个分数的倒数。
找带分数的倒数:先把带分数化成假分数,再求这个假分数的倒数。
重难易错点剖析
重难易错点剖析
Text here
Text here
分数的除法
3.分数除法的计算方法
计算下列各题。
35 7
64 8
35 8
64 7
5
8
1.有括号的先算小括号里
面的,再算中括号里面的,
最后算括号外面的。
2.没有括号的,先算乘除
法,再算加减法。
3.同级运算,从左往右依
次计算。
重难易错点剖析
Text here
解决问题
5.已知比一个数多(少)几分之几的数是多少,求这个数
公园的园丁栽了2500盆杜鹃花,比种植的月季花少1 ,
15
)。
16
5
7
1
(3)甲数比乙数多 ,是把( 乙数
)看作单位“1”,甲数是乙数的( );乙数
4
4
1
3
甲
数
比甲数少 ,是把(
)看作单位“1”,乙数是甲数的( )。
4
4
3
3
(4) kg花生仁可以榨出花生油 kg,照这样计算,1kg花生仁可以榨油( )
10
42
5
kg;榨1kg花生油需要( )kg花生仁。
2
5
第3单元 分
数除法
• 人教版·六年级上册
人教版第三单元 分数除法整理和复习(一)课件(15张ppt)

最小的自然数: 最小的合数: 最小的质数: 最小的偶数: 最小的奇数: 一个数的最小倍数:
整
除
一个数的最大因数:
二、探索新知
(1)倒数的认识 1、先计算,再观察,看看有什么规律。
2 7 7 2
4 3 3 4
6
1 6
1 11 11
规律:两个数的乘积都是1;相乘的两个数分子、分母正好颠倒 了位置。
9 12 22
36
9 11
2 1 7 3
7 14 9 27
3 10 5 13 13
24
8 23 17 51
(2)解下列方程
12 6x 17
5 x 15 13
5 1 x 2 8 8
2 3 x x 50 3 8
2 8 6 x - 1 7 9 7
(3)脱式计算
4、
小明平均每小时走: 1 3 2 1 2 2 3 2 3 3 2 2 1 小红平均每小时走? 1 2
5 5 51 5 12 12 2 6 12 65 65
1 求小明的速度如何画线段图? 1
除以一个不等于0的数, 等于乘这个数的倒数。
三、巩固练习
(1)计算下面各题
②六年级上午比下午多植树多少棵?
(6)思考题
21 21 21 23
甲、乙、丙、丁四人参加军训,在一次组队
负重比赛中他们四人进行了如下操作:丙把
自己负重的 1 给了丁,丁把自己负重的 1
给了乙,乙又把自己负重的 1 给了甲,这时
2
3
4
四人的负重都是36kg,求原来甲乙丙丁四人 各负重多少kg?
• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •
第三单元:分数除法(单元复习课件)-人教版六年级数学上册

( 180
)元。若按原价的 出售,售价应是(
162 )元。
把背包的原价看成单位“1”,根据已知一个数的几分之几是多少,
求这个数,用除法,算出这件上衣的原价;
160÷ = 160×
=180(元);
根据求一个数几分之几是多少,用乘法,求出这件上衣售价。
180×
=162(元)。
【例14】哥哥今年16岁,弟弟今年的年龄是哥哥年龄的
150÷(1- )
=150÷
=180(万元)
答:下半年的营业额是180万元。
,
每一份努力,都将
在学习中得到最好
的回报。加油!
(3)列出方程并解答;
(4)检验并写出答案。
4、工程问题
(1)工作时间=工作总量÷工作效率
(2)利用抽象的“1”解决实际问题:
工程问题是分数问题的特例,工作总量与工作效率都不是具体的
数,而是用抽象的分数来表示。一般地,工作总量用单位“1”
来表示,工作效率则用完成总量所需时间的倒数来表示。
【例13】一个背包按原价的 出售是160元,这件上衣原价是
)。
x、y互为倒数且都不等于0,那么x×y=1。
×
=
÷
×
×
=
= ×
=63;
=
×
×
=
。
【例8】如图可以表示用分数除法计算的算
式是( B )。
A、 ÷
人教版六年级上册数学第3单元分数除法复习课件(共20张ppt)

复习课件
6.分数除法的计算法则: 除以一个不为0的数,等于乘这个数的倒数。 7.分数除法比较大小时的规律: (1)当除数大于1,商小于被除数; (2)当除数小于1(不等于0),商大于被除数; (3)当除数等于1,商等于被除数。
练习
1.写出下面各数的倒数。
4 11
16 9
35
7 8
4 15
11
9
1
1÷5 ( × 5 )=16
3
34
8 17
4
(2)一个数的 3 是75,这个数的 2 是多少?
4
5
75÷ 3× =240
45
复习课件
7.能简算的要简算。
3 7 48 78 77 (3 4) 8 77 7 1 8
7 8
7
11 1 5 1 18 9 18 9
(11 5 ) 9 18 18
8
15
4
16
35
7
4
复习课件
复习课件
2.计算下面各题。
9 10
÷3=((190 ))×((
1 3
))=((
3 10
) )
3 8
÷2=( (
3 8
))×× ((
1 2
))=((
3 16
) )
复习课件
3.不用计算,你知道下面哪几道题的商大于被除数,哪几道题的商 小于被除数吗?
6 7
÷3
1 2
÷
2 3
1÷( 1 + 1 )=2(次) 63
复习课件
3
甲乙两列火车同时从相距240km的两地相对开出,经过 4 小时两 车相遇,甲车每小时行152km,乙车每小时行多少千米? 2答4:0÷乙34车-每15小2时=1行6186(8kkmm)。
六年级上册数学课件-第三单元分数除法整理与复习(共17张PPT)青岛版(2019秋)

4
解:设这袋面粉重X 千克.
X×
3 4
X
X
X
= 15
= 15 ÷
3 4
= 15 × 4
= 20
3
15 ÷
3 4
- 15
= 20 - 15
= 5(千克)
20 - 15 = 5(千克) 答:这袋面粉还剩5千克
小麦 棉花
小麦 棉花
?公顷
1 4
公顷
有棉花田
1 4
公顷,占小麦的
田有多少公顷?
2 5
,小麦
5 8
8 9
÷2=
4 9
5 9
÷3=
5 27
5 8
÷
7 6
=
15 28
4÷
4 9
=
9
5÷
2 7
=
35 2
4 3
÷
3 4
=
16 9
讨论:为什么第一行算式的商比被除数小? 而第二行算式的商比被除数大?
(在除法里,当除数大于1时,商比被除数(0除 外)小,当除数小于1时,商大于被除数,除数 等于1,商等于被除数。)
5
面积占12,草地面积约是多少万平方千米?草地面积
5
是森林面积的 2 ,森林面积大约是多少万平方千米?
草地:
森林面积:
960 5 40(0 万平方千米)400 5 16(0 万平方千米)
12
2
答:草地面积大约是400万平方千米;森林面积 大约是160万平方千米。
3、小刚家买来一袋面粉,吃了15千克正好是 这袋面粉的 3 ,这袋面粉还剩多少千克?
( 原计划造价)×
9 10
=( 实际造价 )
解:设原计划造价为 元。
解:设这袋面粉重X 千克.
X×
3 4
X
X
X
= 15
= 15 ÷
3 4
= 15 × 4
= 20
3
15 ÷
3 4
- 15
= 20 - 15
= 5(千克)
20 - 15 = 5(千克) 答:这袋面粉还剩5千克
小麦 棉花
小麦 棉花
?公顷
1 4
公顷
有棉花田
1 4
公顷,占小麦的
田有多少公顷?
2 5
,小麦
5 8
8 9
÷2=
4 9
5 9
÷3=
5 27
5 8
÷
7 6
=
15 28
4÷
4 9
=
9
5÷
2 7
=
35 2
4 3
÷
3 4
=
16 9
讨论:为什么第一行算式的商比被除数小? 而第二行算式的商比被除数大?
(在除法里,当除数大于1时,商比被除数(0除 外)小,当除数小于1时,商大于被除数,除数 等于1,商等于被除数。)
5
面积占12,草地面积约是多少万平方千米?草地面积
5
是森林面积的 2 ,森林面积大约是多少万平方千米?
草地:
森林面积:
960 5 40(0 万平方千米)400 5 16(0 万平方千米)
12
2
答:草地面积大约是400万平方千米;森林面积 大约是160万平方千米。
3、小刚家买来一袋面粉,吃了15千克正好是 这袋面粉的 3 ,这袋面粉还剩多少千克?
( 原计划造价)×
9 10
=( 实际造价 )
解:设原计划造价为 元。
西师大版六年级数学上册第三单元《整理与复习》课件

黑兔的只数:18× = 12(只)
解:设灰兔有x只。
x =12
=12÷
x
x =20
答:灰兔有20只。
返回
西师大版
整理与复习数学
六年级
上册
3 分数除法
整理与复习
整体回顾
综合运用
知识梳理
课后作业
返回
整理与复习
整体回顾
倒数的意义
倒数
分
数
除
法
分数
除法
怎样找一个数的倒数
分数除以整数
整数除以分数、分数除以分数
分数连除、乘除混合运算
问题
解决
探索规律
问题解决
稍复杂的分数问题
返回
整理与复习
知识梳理
意义
1.倒数
乘积是1的两个数互为倒数。
把除法转化为乘法,再计算,能约分
的要约分。
注意
事项
在分数连除或者分数乘除混合运算
中,遇到除以一个数时,只要乘以
这个数的倒数就可以了。
返回
整理与复习
5.问题解决
问题解决
已知一个数的几分之几是多少,求这个数
方 ①找出单位“1”,设未知量为x。
程 ②找出题中的数量关系式。
法 ③列出方程。
①找出单位“1”。
返回
整理与复习
(3)饲养小组养了白、黑、灰3种兔,其中白兔18只,黑
兔的只数是白兔的 ,又是灰兔的 。灰兔有多少只?
画线段图:
18只
白兔:
白兔只数的 =黑兔的只数
黑兔:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
钢笔的单价 10 元 , 正好比钢笔的单价少 价是多少元? 黑兔 (2) 李明家有白兔450只, 白兔的只数比黑兔 多
2 3
3 8
1) 小张买了一本书和一支钢笔,书的单价是 , 钢笔的单
,黑兔有多少只?
食堂运来大米80千克,运 1 来的大米比面粉多 ,运 7 来面粉多少千克?
妈妈买了一盒巧克力,已
强调:互为倒数,即倒数是 两个数的关系,它们互相依 存,倒数不能单独存在。 (要说清楚谁是谁的倒数, 谁和谁互为倒数。)
注意:倒数必须是成对的两个数,单 独的一个数不能称做倒数。
3 写出2 的倒数。 8
__ 3 28
先化成假分数
8 __ 19
再交换分子、分母的位置
__ 8 19
__ 3 的倒数是__ 8 28 19
1 2 1 ( [ ) 15] 5 3 5
3 4 1 ÷ 3 + × 5 5 3 3 1 4 1 = × + × 5 3 5 3 3 4 1 =( + )× 5 5 3 1 =1× 3 1 = 3
3 10 2 3- 2 ×21 - 7 2 5 =3- - 7 7 2 5 =3-( + 7 ) 7 =3-1 =2
3 5
①一个数(0除外)除以大于1的数,商小于被除数; ②一个数(0除外)除以小于1的数,商大于被除数; ③一个数(0除外)除以等于1的数,商等于被除数。
(1)在一个没有括号的算式里,只有 乘除法或加减法,应该从左往右依次计 算;如果既有加减法又有乘除法,应该 先算乘除法,后算加减法。 (2)在一个有小括号的算式里,应该 先算小括号里面的,后算小括号外面的。 (3)在一个既有小括号又有中括号的 算式里,应该先算小括号里面的,后算 中括号里面的,最后算中括号外面的。
15、 求一个小数的倒数,要先把这个小数化成分数,再求它 的倒数。 (√ )
计算
3 4 7 ÷ ÷ 5 8 8 3 4 7 ÷ ÷ 8 5 9 3 4 7 ÷6
6
9
6
4
6
÷ 14
计算时应注意什么什么?
(2)在括号里填>、<或=
3 1 4 2
(
3 >) 4
)
5 20 ( < )20 4
3 9( < 5
一个水池有两个进水管,一个出 水管。开甲管12小时可把空池注 满,开乙管15小时可把满池的水 放完,开丙管20小时可把空池注 满,三管同时开,多少小时可把 空池注满水?
果园里桃树有80棵,正好是苹果树 的
4
5
,梨树又是苹果树的
3
4
,
梨树有多少棵?
修路队修一个条路,第一天修了总长的 8分之3,第二天修了总长的4分之1, 还剩80米没有修完,这条路一共有多长?
)。
)。
分数除法的计算方法
分数除以整数
一个分数除以一个整 数(0除外),就用 这个分数去乘这个整 数的倒数。
一个数除以分数
除以一 个数 (0除 外), 等于乘 一个数除以一个分 数,就用这个数去 这个数 乘这个分数的倒数。 的倒数。
11、
5 6
5 3 除以 4 ,等于 6 乘
4 。 3
(√ )
12、 一个数除以一个真分数,其结果要比这个数大。(√ ) 13、 求一个带分数的倒数,要先把这个带分数化成假分数, 然后再求它的倒数。 (√ ) 14、 一个数除以一个假分数,其结果要比这个数小。(× )
单位“1”的量=对应量 ÷ (1+分率)
我们学校有教师28人, 是全校学生总数的
1 20
全校学生共有多少人?
1、停车场停着 18辆大客车,大客车的 1 辆数比小汽车少 。小汽车有多少辆? 7 2、某工厂十月份用水 4800 吨,比原计划 1 节约了 ,十月份原计划用水多 少吨? 9
2、根据条件列方程解答。
梨树有多少棵?
打一份稿件,小红单独需8小 时完成,小明打完需12小时, 两人合作打需几小时?
从甲站到乙站,快车要行6小 时,慢车要行9小时。两车同 时从两站对开,几小时相遇?
一堆货物,甲车单独运,4小时 可以运完;乙单独运6小时可以运 完。现在由甲、乙两车合运这堆 货物的3/4,需要多少小时?
1 1 3 X X 2 3 4
5 5 2 x 4 6 3
1 7 X 1 2 8
9 3 (1)一个数的 10 是 4 ,这个数是多少? 3 4 3 (2) 减去 与 的积,所得的差除 5 4 4
以3,商是几?
我们还学会了在单位“1”未知时用乘 法列方程和用分数除法解决分数除法 的实际问题,解这样的题你认为最关 键的步骤是什么?
1、看清分率。 2、找准单位“1”的量,列出数量关系式。 。 3、确定单位“1”是已知还是未知? 4、如果单位“1”的量是未知的,则可以用分数 除法或用乘法列方程解答。
(已知一个数的几分之几是多少,求这个数?) (单位“1”是未知的。)
解答方法: 方程解: (1)确定单位“1”,把单位“1”设为未知数X。 (2)根据含有分率的句子找出等量关系。 (3)根据一个数乘分数的意义用乘法列方程解答。
2 经吃了 3
,还剩8块没吃,
这盒巧克力共有多少块?
图书馆运来一批新书,第一
3 周卖出1200本,还剩下 4 ,
这批新书一共有多少本?
修一条公路,第一天修了全长
1 1 的 ,第二天修了全长的 3 ,还 6
剩下360米没有修,这条路全长多 少米?
一个修路队修一条路,第一天修了全
1 长的 4 2 ,第二天修了全长的 5 ,
1 =3 7
10 =1 11
1 x+ x 42 6 1 1+ ) x 42 解: ( 6
7 x 42 6 7 7 7 x 42 6 6 6
6 x 42 7
x 36
4 8 (1) x 5 15 2 8 ( 2) x 9 15
2 1 (3) x 12 3 4 22 8 ( 4) x 41 15
带分数的倒数小于1。
写出0.75 的倒数。
先化成分数
0.75
__ 3 4
再交换分子、分母的位置
__ 4 3
__ 4 0.75的倒数是3
火眼金睛
1、得数是1的两个数互为倒数。( × 2、0的倒数是0 。 (× 3、乘积是1的几个数互为倒数。( × 4、1的倒数是1 。 (√ 5、假分数的倒数是真分数。 (× ) ) ) ) )
什么叫倒数?
这两个数可以是分数, 也可以是小数或整数。
乘积是1的两个数互为倒数, 那我们称其中一个数是另一 个数的倒数。
1的倒数是1;
0没有倒数。
真分的倒数一定大于 1 。 假分数的倒数小于 或等于1 。
带分数的倒数小于1。
分子是 1 的分数,它的倒数一定是整数 。
不为 0 的整数,它的 倒数的分子一定是 1 。
6、 真分数的倒数是假分数。
(√ )
7、
8、
任何自然数的倒数都是真分数。( × )
1
1 3
的倒数是
9、
0.2的倒数是2.0 .
7
3 4
。
(√ )
( ×)
(√ )
10、 0.7的倒数是 10。
分数除法的意义 • 已知两个因数的积与其中一个因数, 求另个因数的运算。
说出下面各除法算式的意义。
3 2 表示( 5 3 9 表示( 4 10
第一天比第二天少修300米,这条路 全长多少米?
万佳超市昨天运来蜜梨和柿子两
种水果432千克,蜜梨是柿子重 量的
4
多少千克?
5
,运来柿子和蜜柚各
返
1 小明做题的数量是小华的 4 ,已知小明比小华少 做6道,小明和小华分别做多少道?
果园里桃树有80棵,正好是苹果树 的
4
5
,梨树又是苹果树的
3
4
,
5 (0.75- 8 ) ×40 10 9 5.4× 9 +3.6÷ 10
你会简算吗?
(18+ =(18+ =18× =3+
6 7 6 7
+
)÷6 )×
(
5 8
11 11 + 16 )÷ 16 16 )× 11 + 16 11 × 11 16
1 6 1 7
6 7
×
1 6 1 6
11 5 =( 8 + 16 16 5 × = 11 8 = 10 11 +1
如果分率前是“的”:单位“1”的量×对应分率=对应量
如果分率前是“多(少)”的意思: 单位“1”的量×(1+分率)=对应量
单位“1”的量+单位“1”的量×分率=对应量
算术解: 根据“分数除法的意义”用除法计算。
如果分率前是“的”: 单位“1”的量=对应量 ÷ 对应分率
如果分率前是“多(少)”的意思:
2 3
3 8
1) 小张买了一本书和一支钢笔,书的单价是 , 钢笔的单
,黑兔有多少只?
食堂运来大米80千克,运 1 来的大米比面粉多 ,运 7 来面粉多少千克?
妈妈买了一盒巧克力,已
强调:互为倒数,即倒数是 两个数的关系,它们互相依 存,倒数不能单独存在。 (要说清楚谁是谁的倒数, 谁和谁互为倒数。)
注意:倒数必须是成对的两个数,单 独的一个数不能称做倒数。
3 写出2 的倒数。 8
__ 3 28
先化成假分数
8 __ 19
再交换分子、分母的位置
__ 8 19
__ 3 的倒数是__ 8 28 19
1 2 1 ( [ ) 15] 5 3 5
3 4 1 ÷ 3 + × 5 5 3 3 1 4 1 = × + × 5 3 5 3 3 4 1 =( + )× 5 5 3 1 =1× 3 1 = 3
3 10 2 3- 2 ×21 - 7 2 5 =3- - 7 7 2 5 =3-( + 7 ) 7 =3-1 =2
3 5
①一个数(0除外)除以大于1的数,商小于被除数; ②一个数(0除外)除以小于1的数,商大于被除数; ③一个数(0除外)除以等于1的数,商等于被除数。
(1)在一个没有括号的算式里,只有 乘除法或加减法,应该从左往右依次计 算;如果既有加减法又有乘除法,应该 先算乘除法,后算加减法。 (2)在一个有小括号的算式里,应该 先算小括号里面的,后算小括号外面的。 (3)在一个既有小括号又有中括号的 算式里,应该先算小括号里面的,后算 中括号里面的,最后算中括号外面的。
15、 求一个小数的倒数,要先把这个小数化成分数,再求它 的倒数。 (√ )
计算
3 4 7 ÷ ÷ 5 8 8 3 4 7 ÷ ÷ 8 5 9 3 4 7 ÷6
6
9
6
4
6
÷ 14
计算时应注意什么什么?
(2)在括号里填>、<或=
3 1 4 2
(
3 >) 4
)
5 20 ( < )20 4
3 9( < 5
一个水池有两个进水管,一个出 水管。开甲管12小时可把空池注 满,开乙管15小时可把满池的水 放完,开丙管20小时可把空池注 满,三管同时开,多少小时可把 空池注满水?
果园里桃树有80棵,正好是苹果树 的
4
5
,梨树又是苹果树的
3
4
,
梨树有多少棵?
修路队修一个条路,第一天修了总长的 8分之3,第二天修了总长的4分之1, 还剩80米没有修完,这条路一共有多长?
)。
)。
分数除法的计算方法
分数除以整数
一个分数除以一个整 数(0除外),就用 这个分数去乘这个整 数的倒数。
一个数除以分数
除以一 个数 (0除 外), 等于乘 一个数除以一个分 数,就用这个数去 这个数 乘这个分数的倒数。 的倒数。
11、
5 6
5 3 除以 4 ,等于 6 乘
4 。 3
(√ )
12、 一个数除以一个真分数,其结果要比这个数大。(√ ) 13、 求一个带分数的倒数,要先把这个带分数化成假分数, 然后再求它的倒数。 (√ ) 14、 一个数除以一个假分数,其结果要比这个数小。(× )
单位“1”的量=对应量 ÷ (1+分率)
我们学校有教师28人, 是全校学生总数的
1 20
全校学生共有多少人?
1、停车场停着 18辆大客车,大客车的 1 辆数比小汽车少 。小汽车有多少辆? 7 2、某工厂十月份用水 4800 吨,比原计划 1 节约了 ,十月份原计划用水多 少吨? 9
2、根据条件列方程解答。
梨树有多少棵?
打一份稿件,小红单独需8小 时完成,小明打完需12小时, 两人合作打需几小时?
从甲站到乙站,快车要行6小 时,慢车要行9小时。两车同 时从两站对开,几小时相遇?
一堆货物,甲车单独运,4小时 可以运完;乙单独运6小时可以运 完。现在由甲、乙两车合运这堆 货物的3/4,需要多少小时?
1 1 3 X X 2 3 4
5 5 2 x 4 6 3
1 7 X 1 2 8
9 3 (1)一个数的 10 是 4 ,这个数是多少? 3 4 3 (2) 减去 与 的积,所得的差除 5 4 4
以3,商是几?
我们还学会了在单位“1”未知时用乘 法列方程和用分数除法解决分数除法 的实际问题,解这样的题你认为最关 键的步骤是什么?
1、看清分率。 2、找准单位“1”的量,列出数量关系式。 。 3、确定单位“1”是已知还是未知? 4、如果单位“1”的量是未知的,则可以用分数 除法或用乘法列方程解答。
(已知一个数的几分之几是多少,求这个数?) (单位“1”是未知的。)
解答方法: 方程解: (1)确定单位“1”,把单位“1”设为未知数X。 (2)根据含有分率的句子找出等量关系。 (3)根据一个数乘分数的意义用乘法列方程解答。
2 经吃了 3
,还剩8块没吃,
这盒巧克力共有多少块?
图书馆运来一批新书,第一
3 周卖出1200本,还剩下 4 ,
这批新书一共有多少本?
修一条公路,第一天修了全长
1 1 的 ,第二天修了全长的 3 ,还 6
剩下360米没有修,这条路全长多 少米?
一个修路队修一条路,第一天修了全
1 长的 4 2 ,第二天修了全长的 5 ,
1 =3 7
10 =1 11
1 x+ x 42 6 1 1+ ) x 42 解: ( 6
7 x 42 6 7 7 7 x 42 6 6 6
6 x 42 7
x 36
4 8 (1) x 5 15 2 8 ( 2) x 9 15
2 1 (3) x 12 3 4 22 8 ( 4) x 41 15
带分数的倒数小于1。
写出0.75 的倒数。
先化成分数
0.75
__ 3 4
再交换分子、分母的位置
__ 4 3
__ 4 0.75的倒数是3
火眼金睛
1、得数是1的两个数互为倒数。( × 2、0的倒数是0 。 (× 3、乘积是1的几个数互为倒数。( × 4、1的倒数是1 。 (√ 5、假分数的倒数是真分数。 (× ) ) ) ) )
什么叫倒数?
这两个数可以是分数, 也可以是小数或整数。
乘积是1的两个数互为倒数, 那我们称其中一个数是另一 个数的倒数。
1的倒数是1;
0没有倒数。
真分的倒数一定大于 1 。 假分数的倒数小于 或等于1 。
带分数的倒数小于1。
分子是 1 的分数,它的倒数一定是整数 。
不为 0 的整数,它的 倒数的分子一定是 1 。
6、 真分数的倒数是假分数。
(√ )
7、
8、
任何自然数的倒数都是真分数。( × )
1
1 3
的倒数是
9、
0.2的倒数是2.0 .
7
3 4
。
(√ )
( ×)
(√ )
10、 0.7的倒数是 10。
分数除法的意义 • 已知两个因数的积与其中一个因数, 求另个因数的运算。
说出下面各除法算式的意义。
3 2 表示( 5 3 9 表示( 4 10
第一天比第二天少修300米,这条路 全长多少米?
万佳超市昨天运来蜜梨和柿子两
种水果432千克,蜜梨是柿子重 量的
4
多少千克?
5
,运来柿子和蜜柚各
返
1 小明做题的数量是小华的 4 ,已知小明比小华少 做6道,小明和小华分别做多少道?
果园里桃树有80棵,正好是苹果树 的
4
5
,梨树又是苹果树的
3
4
,
5 (0.75- 8 ) ×40 10 9 5.4× 9 +3.6÷ 10
你会简算吗?
(18+ =(18+ =18× =3+
6 7 6 7
+
)÷6 )×
(
5 8
11 11 + 16 )÷ 16 16 )× 11 + 16 11 × 11 16
1 6 1 7
6 7
×
1 6 1 6
11 5 =( 8 + 16 16 5 × = 11 8 = 10 11 +1
如果分率前是“的”:单位“1”的量×对应分率=对应量
如果分率前是“多(少)”的意思: 单位“1”的量×(1+分率)=对应量
单位“1”的量+单位“1”的量×分率=对应量
算术解: 根据“分数除法的意义”用除法计算。
如果分率前是“的”: 单位“1”的量=对应量 ÷ 对应分率
如果分率前是“多(少)”的意思:
