专题突破练25 直线与圆及圆锥曲线
高考大题专项突破 直线与圆及圆锥曲线

高考大题专项突破五5.1直线与圆及圆锥曲线1.(优质试题河南南阳、信阳等六市一模,理20)如图,抛物线C:y2=2px的焦点为F,抛物线上一定点Q(1,2).(1)求抛物线C的方程及准线l的方程;(2)过焦点F的直线(不经过点Q)与抛物线交于A,B两点,与准线l交于点M,记QA,QB,QM的斜率分别为k1,k2,k3,问是否存在常数λ,使得k1+k2=λk3成立?若存在λ,求出λ的值;若不存在,说明理由.〚优质试题21500816〛2.已知抛物线C:y2=2x的焦点为F,平行于x轴的两条直线l1,l2分别交C于A,B两点,交C的准线于P,Q两点.(1)若F在线段AB上,R是PQ的中点,证明AR∥FQ;(2)若△PQF的面积是△ABF的面积的两倍,求AB中点的轨迹方程.3.已知抛物线C:x2=2py(p>0)的焦点为F,过F的直线l交抛物线C于点A,B,当直线l的倾斜角是时,AB的垂直平分线交y轴于点Q(0,5).(1)求p的值;(2)以AB为直径的圆交x轴于点M,N,记劣弧的长度为S,当直线l绕点F 旋转时,求的最大值.4.在平面直角坐标系xOy中,以坐标原点O为圆心的圆与直线x-y=4相切.(1)求圆O的方程;(2)若圆O上有两点M,N关于直线x+2y=0对称,且|MN|=2,求直线MN的方程;(3)圆O与x轴相交于A,B两点,圆内的动点P使|PA|,|PO|,|PB|成等比数列,求的取值范围.5.(优质试题山西吕梁二模,理20)如图,已知圆N:x2+(y+)2=36,P是圆N上的点,点Q在线段NP上,且有点D(0,)和DP上的点M满足=2=0.(1)当点P在圆上运动时,求点Q的轨迹方程;(2)若斜率为的直线l与(1)中所求点Q的轨迹交于不同的两点A,B,又点C,求△ABC面积最大值时对应的直线l的方程.〚优质试题21500817〛6.(优质试题安徽黄山二模,理20)已知椭圆E:=1(a>)的离心率e=,右焦点F(c,0),过点A的直线交椭圆E于P,Q两点.(1)求椭圆E的方程;(2)若点P关于x轴的对称点为M,求证:M,F,Q三点共线;(3)当△FPQ面积最大时,求直线PQ的方程.参考答案高考大题专项突破五5.1直线与圆及圆锥曲线1.解 (1)把Q(1,2)代入y2=2px,得2p=4,所以抛物线方程为y2=4x,准线l的方程为x=-1.(2)由条件可设直线AB的方程为y=k(x-1),k≠0.由抛物线准线l:x=-1,可知M(-1,-2k).又Q(1,2),所以k3==k+1.把直线AB的方程y=k(x-1),代入抛物线方程y2=4x,并整理,可得k2x2-2(k2+2)x+k2=0.设A(x1,y1),B(x2,y2),则x1+x2=,x1x2=1.又Q(1,2),故k1=--,k2=--.因为A,F,B三点共线, 所以k AF=k BF=k,即--=k.所以k1+k2=----=--=2(k+1),即存在常数λ=2,使得k1+k2=2k3成立.2.解由题知F.设l1:y=a,l2:y=b,则ab≠0且A,B,P-,Q-,R-.记过A,B两点的直线为l,则l的方程为2x-(a+b)y+ab=0.(1)证明:由于点F在线段AB上,因此1+ab=0.记AR的斜率为k1,FQ的斜率为k2,则k1=---=-=-b=k2.所以AR∥FQ.(2)设直线l与x轴的交点为D(x1,0),则S△ABF=|b-a||FD|=|b-a|-,S△PQF=-.由题设可得|b-a|-=-,所以x1=0(舍去),x1=1.设满足条件的AB的中点为E(x,y).当AB与x轴不垂直时,(x≠1 .由k AB=k DE可得-又=y,所以y2=x-1(x≠1 .当AB与x轴垂直时,点E与点D重合.故所求轨迹方程为y2=x-1.3.解 (1)抛物线C:x2=2py(p>0)的焦点为F,当l的倾斜角为时,l的方程为y=x+.设A(x1,y1),B(x2,y2),由得x2-2px-p2=0,则x1+x2=2p,y1+y2=x1+x2+p=3p,得AB中点为D,AB的垂直平分线为y-p=-(x-p),把x=0代入得y=p=5.∴p=2.(2)设直线l的方程为y=kx+1,代入x2=4y得x2-4kx-4=0,∴|AB|=y1+y2+2=k(x1+x2)+4=4k2+4,AB中点为D(2k,2k2+1).令∠MDN=2α,S=2α·|AB|=α·|AB|,∴=α,点D到x轴的距离|DE|=2k2+1,cos α==1-.当k2=0时cos α取最小值,α的最大值为.故的最大值为.4.解 (1)依题意,圆O的半径r等于原点O到直线x-y=4的距离,即r==2.所以圆O的方程为x2+y2=4.(2)由题意,可设直线MN的方程为2x-y+m=0.则圆心O到直线MN的距离d=,故+()2=22,即m=±.所以直线MN的方程为2x-y+=0或2x-y-=0.(3)设P(x,y),由题意得A(-2,0),B(2,0).由|PA|,|PO|,|PB|成等比数列,得-=x2+y2,即x2-y2=2.因为=(-2-x,-y)·(2-x,-y)=2(y2-1).因为点P在圆O内,所以-由此得y2<1.所以的取值范围为[-2,0).5.解 (1)由题意,MQ是线段DP的垂直平分线,∴|NP|=|NQ|+|QP|=|QN|+|QD|=6>|DN|=2.∴点Q的轨迹是以D,N为焦点的椭圆,且c=,a=3,b=2.∴点Q的轨迹方程是=1.(2)设直线l:y=x+m,A(x1,y1),B(x2,y2),与椭圆联立,可得9x2+6mx+2m2-18=0,∴x1+x2=-m,x1·x2=(2m2-18),∴|AB|=--=-.点C到直线l的距离d=,∴S=|AB|d=-,∴当m=±3时,S最大,此时直线l的方程为y=x±3.6.(1)解由-得a=,c=ea==2,则b2=a2-c2=2,∴椭圆E的方程是=1.(2)证明由(1)可得A(3,0),设直线PQ的方程为y=k(x-3),由方程组-得(3k2+1)x2-18k2x+27k2-6=0,依题意Δ=12(2-3k2)>0,得-<k<.设P(x1,y1),Q(x2,y2),则x1+x2=,x1x2=-.∵F(2,0),M(x1,-y1),=(2-x1,y1),=(x2-2,y2),由(2-x1)y2-(x2-2)y1=(2-x1)·k(x2-3)-(x2-2)·k(x1-3)=k[5(x1+x2)-2x1x2-12]=k---=0,得,∴M,F,Q三点共线.(3)解设直线PQ的方程为x=my+3.。
高考数学专项突破圆锥曲线专题

高考数学专项突破:圆锥曲线专题目录一、知识考点讲解 (2)第一部分了解基本题型 (3)第二部分掌握基本知识 (6)第三部分掌握基本方法 (8)二、知识考点深入透析 (15)三、圆锥曲线之高考链接 (18)四、基础知识专项训练 (22)五、解答题专项训练 (30)附录:圆锥曲线之高考链接参考答案 (35)附录:基础知识专项训练参考答案 (39)附录:解答题专项训练参考答案 (41)一、知识考点讲解一、圆锥曲线的考查重点:高考试卷对圆锥曲线的考查主要是:给出曲线方程,讨论曲线的基本元素和简单的几何性质;或给出曲线满足的条件,判断(或求)其轨迹;或给出直线及曲线、曲线及曲线的位置关系,讨论及其有联系的有关问题(如直线的方程、直线的条数、弦长、曲线中参数的取值范围等);或讨论直线及曲线、曲线及曲线的关系;或考查圆锥曲线及其它知识的综合(如及函数、数列、不等式、向量、导数等)等。
二、圆锥曲线试题的特点:1、突出重点知识的考查。
直线及圆的方程、圆锥曲线的定义、标准方程、几何性质等是圆锥曲线命题的根本,在对圆锥曲线的考查中,直线及圆锥曲线的位置关系仍然是重点。
2、注重数学思想及方法的考查。
3、融合代数、三角、不等式、排列组合、向量和几何等知识,在知识网络的交汇点处设计问题是高考的一大特点,由于向量具有代数和几何的双重身份,使得圆锥曲线及平面向量的整合交汇成为高考命题的热点,导数知识的引入为我们解决圆锥曲线的最值问题和切线问题提供了新的视角和方法。
三、命题重点趋势:直线及圆锥曲线或圆及圆锥曲线1、高考圆锥曲线内容重点仍然是直线及圆锥曲线或圆及圆锥曲线,直线及圆锥曲线联系在一起的综合题在高考中多以高档题、压轴题出现。
2、热点主要体现在:直线及圆锥曲线的基础题;涉及位置关系的判定;轨迹问题;范围及位置问题;最值问题;存在性问题;弦长问题;对称问题;及平面向量或导数相结合的问题。
3、直线及圆锥曲线的题型涉及函数的及方程,数形结合,分类讨论,化归及转化等重要的数学思想方法,是高考必考内容之一,这类题型运算量比较大,思维层次较高,要求考生分析问题和解决问题的能力、计算能力较高,起到了拉开考生“档次”,有利于选拔的功能,对学生的能力要求也相对较高,是每年高考中平面几何部分出题的重点内容第一部分了解基本题型一、高考中常见的圆锥曲线题型1、直线及圆锥曲线结合的题型(1)求圆锥曲线的轨迹方程:这类题主要考查学生对圆锥曲线的标准方程及其相关性质,要求较低,一是出现在选择题,填空题或者解答题的第一问,较容易。
直线和圆、圆锥曲线综合测试卷(新高考专用)(解析版)—2025年高考数学一轮复习

直线和圆、圆锥曲线综合测试卷专练(考试时间:120分钟;满分:150分)注意事项:1.本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第I卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。
写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第I卷(选择题)一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合要求的。
则由椭圆的中心对称性可知可知AF1BF2为平行四边形,则可得△ABF2的周长为|AF当AB位于短轴的端点时,当围成的等腰三角形底边在x轴上时,当围成的等腰三角形底边在直线l因为tanα=2tanα21―tan2α2=2,且tanα2>所以k=tanθ=tanα2=5―12,或故选:B.5.(5分)(2024·西藏拉萨的最小值为()A.1453【解题思路】先设点的坐标,结合轨迹方程求参,再根据距离和最小值为两点间距离求解即可6.(5分)(2024·湖南邵阳点B在C上且位于第一象限,B.8 A.453【解题思路】由点A―1,8由点A―1,8在抛物线y23所以抛物线C的方程为y2设B(x0,y0),则x0>0,y0>由题意知F p2,0,又OP 显然直线AB的斜率不为由y2=2pxx=ty+p2,得y2―2pty显然直线BD的斜率不为由y2=2pxλp,得y2故选:C.二、多项选择题:本题共3小题,每小题6分,共18分,在每小题给出的四个选项中,有多项符合题目的要求,全部选对的得6分,部分选对的得部分分,有选错的得0分。
如图,因为K OA=∠PDA=∠ODB,所以×|PA|⋅S△PAB=12故选:ABD.11.(6分)(2024·福建龙岩|AB|=8.过焦点F的直线C的准线与坐标轴的交点,则(A.若MF=3FN,则直线C.∠MON为钝角设M(x1,y1),N(x2,y 得y2―8my―16=所以y1y2=―16,x1∴x1x2+y1y2=4⟨⟩三、填空题:本题共3小题,每小题5分,共15分。
直线、圆、圆锥曲线提升训练答案

1.直线210x y -+=关于直线1x =对称的直线方程是( )A .210x y +-=B .210x y +-=C .230x y +-=D .230x y +-= 【答案】D 【解析】试题分析:直线210x y -+=和直线1x =的交点为()1,1,直线210x y -+=关于直线1x =对称的直线方程的斜率为12k =-,故所求直线方程为()1112y x -=--,化简可得230x y +-=,故选D .考点:与直线关于点、直线对称的直线方程 2.已知点A (2,3),B (-3,-2),若直线l 过点P (1,1)且与线段AB 相交,则直线l 的斜率k 的取值范围是( ) A .324k k ≥≤或 B .324k ≤≤ C .34k ≥D .2k ≤ 【答案】A 【解析】试题分析:用数形结合,建立坐标系直线PA 的斜率31221-=-k=,直线PB 的斜率213314--'=--k =,结合图象可得直线l 的斜率取值范围是324k k ≥≤或;考点:1.数形结合思想;2.直线的斜率公式;3.过点()2,3P 且在两坐标轴上截距相等的直线方程为( ) A .230x y -= B .50x y +-=C .320x y -=或50x y +-=D .230x y -=或50x y +-=【答案】C 【解析】试题分析:当截距都为0时,过点()0,0时直线为320x y -=,当截距不为零时,设直线为1x ya a+=,代入点()2,3P 得550a x y =∴+-= 考点:直线方程4.直线l 经过点(2,),(3,A y B ,且倾斜角范围是2[,]33ππ,则y 的范围是( )A 、[-B 、(,0])-∞⋃+∞C 、(,[0,)-∞-⋃+∞D 、 【答案】C 【解析】 试题分析:)2[,]tan 33k πθπθ∈∴=∈+∞(,-∞([),0,k y =∈-∞-+∞ 考点:直线倾斜角与斜率的关系5.对于直线x sin α+y+1=0,其斜率的取值范围是( )A .-,-1][1,+)∞⋃∞( B .[1,1]- C .[-,]44ππD .[-,]22ππ【答案】B【解析】试题分析:直线的斜率为αsin -=k ,因此斜率的取值范围是[-1,1],答案选B . 考点:直线的一般方程与斜率6.若直线ax+2y+6=0与直线x+a(a+1)y+a 2-1=0垂直,则实数a 的值为( ) A .-32 B .0 C .1 D .0或-32【答案】D . 【解析】试题分析:根据一般式直线方程中,两直线垂直的等价条件,则有2(1)0a a a ++=,即2230a a +=,解得a=0或a=-32,故选D .考点:直线的一般式方程中,两直线垂直的等价参数关系.7.平行线0943=-+y x 和620x my ++=的距离是( ) A .58 B .2 C .511 D .57 【答案】B 【解析】试题分析:根据两直线平行,可以断定8m =,所以直线方程可化为3410x y ++=,由公式可得两直线之间的距离1925d +==,故选B . 考点:平行线间的距离公式.8.直线30x y -+=被圆()()22222x y ++-=截得的弦长等于( )A .2. 【答案】D 【解析】试题分析:圆心为()2,2-,半径r =圆心到直线的距离为d ==,所以弦长l 满足2222l d r l ⎛⎫+=∴= ⎪⎝⎭考点:直线与圆相交问题9.圆221:(2)(3)1C x y -+-=,圆222:(3)(4)9C x y -+-=,M 、N 分别是圆1C ,2C 上的动点,P 为x 轴上的动点,则||||PM PN +的最小值A .4B 1C .6-【答案】A 【解析】试题分析:作2C 关于x 轴的对称点)4,3(-A ,连接1AC 得1AC 所在直线方程0177=-+y x ,与x 轴的交点为)0,717(P ,此时21PC PC +最小,连接1PC 、2PC 分别交圆于N M 、,则PNPM +最小,PN PM +==--+3121PC PC 425-考点:1.圆与最值问题;10.圆012222=+--+y x y x 上的点到直线2=-y x 的距离最大值是( )A .2B .21+C .221+D .221+【答案】B 【解析】试题分析:先将圆012222=+--+y x y x 配方得1)1()1(22=-+-y x ,知此圆的圆心坐标为),1,1( 半径r=1,再求出圆心到已知直线的距离:12)1(121122>=-+--=d ,画出草图可知:所求最大值应为1+2,故选B .考点:直线与圆的位置关系.11.设抛物线28y x =的焦点为F ,准线为l ,P 为抛物线上一点,且,PA l A ⊥为垂足,如果直线AF 的斜率为1-,则PF 等于( )A .2B .4C . 8D .12 【答案】B 【解析】试题分析:∵抛物线方程为28y x =,∴焦点20F (,),准线方l 程为2x =-,∵直线AF 的斜率为1-,直线AF 的方程为2y x =--(),当2x =-时,4y =,由可得A 点坐标为()2,4A -,PA l A ⊥ 为垂足,∴P 点纵坐标为4,代入抛物线方程,得点P 坐标为()2,4P , 224PF PA ∴==--=(). 考点:抛物线的定义12.已知双曲线22221(0,0)x y a b a b-=>>与抛物线28y x =有一个公共的焦点F ,且两曲线的一个交点为P ,若5PF =,则双曲线的离心率为( )A 、5B 、2C 、332 D 、3 【答案】B 【解析】试题分析:()02,F ,4=p ,所以422=+b a ,根据抛物线的焦半径公式,522=+=+=x px PF ,解得3=x ,代入抛物线有242=y ,因为点P 是交点,所以代入双曲线,有124922=-b a ,解得:3,122==b a ,所以离心率2==a c e .考点:1.抛物线的几何性质;2.双曲线的方程;3.抛物线的方程.13.已知点()0,2A ,抛物线C:2(0)y ax a =>(0a >)的焦点为F ,射线FA 与抛物线C 相交于点M,与其准线相交:KM MN =于点N ,若则a 的值等于( ) A .41 B .21C .1D .4【答案】D 【解析】 试题分析:(,0),:1:54a F M F M K M M N =∴ ,42421:2:=∴=∴=a a KM KN . 考点:抛物线的性质.14.已知双曲线)0,0(12222>>=-b a bx a y 的离心率为3,则双曲线的渐近线方程为( )A .xy 22±= B .x y 2±= C .x y 2±= D .x y 21±= 【答案】A【解析】试题分析:根据题意,焦点在y 轴上的双曲线的标准方程,则a b ====则所求双曲线的渐近线方程为xy 22±=,所以答案为A .考点:1.双曲线的标准方程;2,双曲线的渐近线方程.15.抛物线2x y =上一点到直线042=--y x 的距离最短的点的坐标是 ( ) A .(1,1) B .(41,21) C .)49,23( D .(2,4)【答案】A 【解析】试题分析:设抛物线上的点为()200,x x点到直线的距离为d =,当01x =时取得最小值,所以点的坐标为(1,1)考点:1.点到直线的距离;2.函数求最值16.已知抛物线的方程为x y 42=,过其焦点F 的直线l 与抛物线交于B A ,两点,若BOF AOF S S ∆∆=(O 为坐标原点),则=AB ( ) A .316 B .38 C .34D .4 【答案】D 【解析】试题分析:设B A ,的纵坐标为21,y y ,则由BOF AOF S S ∆∆=,得212121y OF y OF =,即021=+y y ;即x AB ⊥轴,即()1,1y A ,则21=y ,所以4=AB . 考点:直线与抛物线的位置关系.17.已知椭圆C :22221(0)x y a b a b +=>>的左右焦点为F 1、F 2F 2的直线l 交C 与A 、B 两点,若△AF 1B的周长为C 的方程为( )A .22132x y += B .2213x y += C .221128x y += D .221124x y += 【答案】A【解析】试题分析:由椭圆的定义可知三角形的周长为344)(221111==+++=++a BF AF BF AF AB BF AF ,解得3=a ,又离心率33=a c ,所以1=c ,由222c b a +=得2=b ,所以椭圆的方程为12322=+y x ,答案选A .考点:椭圆的方程与几何性质18.已知F 是抛物线24y x =的焦点,A B , 是抛物线上的两点,12AF BF +=,则线段AB 的中点到y 轴的距离为( ) A. 4 B. 5 C. 6 D. 11 【答案】B 【解析】试题分析:∵212A B AF BF x x +=++=,∴10A B x x +=,∴52A Bx x +=,∴线段AB 的中点到y 轴的距离为5,故选B. 考点:直线与抛物线的位置关系.19.已知1F ,2F 是椭圆和双曲线的公共焦点,P 是它们的一个公共点,且321π=∠PF F ,椭圆的离心率为1e ,双曲线的离心率2e ,则=+222131e e . 【答案】4【解析】试题分析:设11ce a =,22ce a =,则221222212313a a e e c ++=,又2221212122cos3PF PF PF PF F F π+-=,所以22121212()3PF PF PF PF F F +-=,22121212()PF PF PF PF F F -+=,即22112434a PF PF c -=,2221244a PF PF c +=,因此222222121241216,34,a a c a a c +=+=2212134.e e +=考点:椭圆及双曲线定义20.将一个半径为2的半圆面围成一个圆锥,所得圆锥的轴截面面积等于 .【解析】试题分析:半径为2的半圆面的半周长是π2,那么围成圆锥的半径为r ,ππ22=r ,1=r ,所以轴截面是以2为边长的等边三角形,面积是3432==a S . 考点:圆锥的基本计算21.椭圆221259x y +=上的点M 到左焦点1F 的距离为2,N 是1MF 中点,则||ON = .【答案】4 【解析】试题分析:根据椭圆的定义:1021=+MF MF ,所以82=MF ,N 是1MF 中点,O 是21F F 的中点,所以4212==MF ON . 考点:1.椭圆的定义;2.椭圆的几何意义.22.已知抛物线24x y =的焦点F 和点(1,8)A -,P 为抛物线上一点,则PA PF +的最小值是______________ 【答案】9 【解析】试题分析:根据题意,过P 作抛物线的准线的垂线垂足为P ' ,根据抛物线的定义PF PP '=,所以PA PF PA PP '+=+的最小值即为抛物线上一个动点P 到一个定点()1,8A -的距离与到定直线1y =-的距离之和的最小值,显然,最小值即为点A 到直线1y =-的距离为()819--=.考点:1.抛物线的定义;2.距离的最小值.23.已知椭圆22221(0)x y a b a b+=>>的右顶点为A ,上顶点为B ,点M 为线段AB 的靠近点B 的三等分点,∠MOA=45°,则椭圆的离心率为 .【解析】试题分析:A (a,0),B (0,b ),M 的靠近点B 的三等分点,所以M (2,33a b ),又因为∠MOA=45°,所以2233a b a b =∴=,222222223344a c a b e e a a a -====∴=考点:本题考查椭圆的离心率点评:通过M 是三等分点,相似三角形求得M 点坐标,再利用∠MOA=45°,可得M 的横纵坐标相等,找到a,b 的关系24.设抛物线22y x =的焦点为F ,过F 的直线交该抛物线于A ,B 两点,则4AF BF +的最小值为_____________. 【答案】4.5 【解析】试题分析:根据题意抛物线的焦点坐标为:()1,0F ,过焦点的直线与抛物线22y x =交于两点,直线斜率一定存在,设过焦点()1,0F 与抛物线交于()()1122,,,A x y B x y 的直线方程为:()1y k x =-带入22y x =中,化简为:()22221204k x k x k -++=,根据韦达定理得:1214x x =,根据抛物线的定义知:4AF BF +121211555944222222x x x x ⎛⎫=+++=++≥== ⎪⎝⎭(当且仅当“1241x x ==”时取“=”),所以4AF BF +的最小值为4.5. 考点:1.抛物线的定义;2.基本不等式求最值.25.已知P 是双曲线1366422=-y x 上一点,F 1,F 2是双曲线的两个焦点,若|PF 1|=17,则|PF 2|的值为________. 【答案】33 【解析】试题分析:根据双曲线定义知;1216PF PF -==,所以2116161733PF PF =+=+=或21PF =(舍去),故答案为33. 考点:1.双曲线定义;2.计算.26.在平面直角坐标系中,已知两点(3,0)A -及(3,0)B ,动点Q 到点A 的距离为10,线段BQ 的垂直平分线交AQ 于点P . (Ⅰ)求||||PA PB +的值;(Ⅱ)求点P 的轨迹方程【答案】(Ⅰ)10;(Ⅱ)2212516x y += 【解析】试题分析:(Ⅰ)由线段的垂直平分线的性质及抛物线的定义易得||||PA PB +=||PA +||PQ =||AQ =10(Ⅱ)由(Ⅰ)及椭圆的定义可知点P 的轨迹是中心在原点,以,A B 为焦点,长轴在x 轴上的椭圆,则椭圆方程可求试题解析:(Ⅰ)因为线段BQ 的垂直平分线交AQ 于点P ,∴||PB =||PQ , ∴||||PA PB +=||PA +||PQ =||AQ =10;(Ⅱ)由(Ⅰ)知||||PA PB +=10(常数),又||||PA PB +=10>6=||AB ,∴点P 的轨迹是中心在原点,以,A B 为焦点,长轴在x 轴上的椭圆,其中210,26a c ==,所以椭圆的轨迹方程为2212516x y +=. 考点:椭圆、抛物线的定义。
2020高考数学大二轮专题突破文科通用直线与圆圆锥曲线精选试题及答案解析(10页)

2020高考数学大二轮专题突破文科通用直线与圆圆锥曲线精选试题1.(节选)已知圆M:x2+y2=r2(r>0)与直线l1:x-y+4=0相切,设点A为圆上一动点,AB⊥x轴于B,且动点N满足=2,设动点N的轨迹为曲线C.(1)求曲线C的方程;(2)略.2.(2019甘肃武威第十八中学高三上学期期末考试)已知圆C1:x2+y2-2x-6y-1=0和C2:x2+y2-10x-12y+45=0.(1)求证:圆C1和圆C2相交;(2)求圆C1和圆C2的公共弦所在直线的方程和公共弦长.3.已知圆O:x2+y2=4,点A(,0),以线段AB为直径的圆内切于圆O,记点B的轨迹为Γ.(1)求曲线Γ的方程;(2)直线AB交圆O于C,D两点,当B为CD的中点时,求直线AB的方程.4.(2019全国卷1,理19)已知抛物线C:y2=3x的焦点为F,斜率为的直线l与C的交点为A,B,与x轴的交点为P.(1)若|AF|+|BF|=4,求l的方程;(2)若=3,求|AB|.5.(2019天津河北区高三二模)已知椭圆C:=1(a>b>0)过点P(2,1),且短轴长为2.(1)求椭圆C的方程;(2)过点P作x轴的垂线l,设点A为第四象限内一点且在椭圆C上(点A不在直线l上),点A关于l的对称点为A',直线A'P与椭圆C交于另一点B.设O为坐标原点,判断直线AB与直线OP的位置关系,并说明理由.6.(2019天津第一中学高三下学期第五次月考)已知椭圆C1:=1(a>b>0)的左、右焦点为F1,F2,F2的坐标满足圆Q方程(x-)2+(y-1)2=1,且圆心Q满足|QF1|+|QF2|=2a.(1)求椭圆C1的方程;(2)过点P(0,1)的直线l1:y=kx+1交椭圆C1于A,B两点,过P与l1垂直的直线l2交圆Q于C,D两点,M为线段CD中点,若△MAB的面积为,求k的值.参考答案专题突破练24直线与圆及圆锥曲线1.解(1)设动点N(x,y),A(x0,y0),因为AB⊥x轴于B,所以B(x0,0).已知圆M的方程为x2+y2=r2,由题意得r==2,所以圆M的方程为x2+y2=4.由题意,=2,所以(0,-y0)=2(x0-x,-y),即将A(x,2y)代入圆M:x2+y2=4,得动点N的轨迹方程为+y2=1.(2)略.2.(1)证明圆C1的圆心C1(1,3),半径r1=,圆C2的圆心C2(5,6),半径r2=4, 两圆圆心距d=|C1C2|=5,r1+r2=+4,|r1-r2|=4-,所以|r1-r2|<d<r1+r2.所以圆C1和C2相交.(2)解将圆C1和圆C2的方程相减,得4x+3y-23=0,所以两圆的公共弦所在直线的方程为4x+3y-23=0.因为圆心C2(5,6)到直线4x+3y-23=0的距离为d==3,故两圆的公共弦长为2-=2.3.解(1)设AB的中点为M,切点为N,连接OM,MN,则|OM|+|MN|=|ON|=2,|AB|=|ON|-(|OM|-|MN|)=2-|OM|+|AB|,即|AB|+2|OM|=4.取A关于y轴的对称点A',连接A'B,则|A'B|=2|OM|,故|AB|+2|OM|=|AB|+|A'B|=4.所以点B的轨迹是以A',A为焦点,长轴长为4的椭圆.其中a=2,c=,b=1,则曲线Γ的方程为+y2=1.(2)因为B为CD的中点,所以OB⊥CD,则.设B(x0,y0),则x0(x0-)+=0.又=1,解得x0=,y0=±.则k OB=±,k AB=∓,则直线AB的方程为y=±(x-),即x-y-=0或x+y-=0.4.解设直线l:y=x+t,A(x1,y1),B(x2,y2).(1)由题设得F,故|AF|+|BF|=x1+x2+,由题设可得x1+x2=.由可得9x2+12(t-1)x+4t2=0,则x1+x2=--.从而--,得t=-.所以l的方程为y=x-.(2)由=3可得y1=-3y2.由可得y2-2y+2t=0.所以y1+y2=2.从而-3y2+y2=2,故y2=-1,y1=3.代入C的方程得x1=3,x2=.故|AB|=.5.解(1)由题意得解得∴椭圆C的方程为=1.(2)直线AB与直线OP平行,证明如下:由题意知,直线PA的斜率存在且不为零.PA,PA'关于l:x=2对称,则直线PA与PA'斜率互为相反数.设直线PA:y-1=k(x-2),PB:y-1=-k(x-2).设A(x1,y1),B(x2,y2).由消去y得(4k2+1)x2-(16k2-8k)x+16k2-16k-4=0, -∴2x1=--.∴x1=--.同理,x2=-.∴x1-x2=-.∵y1=k(x1-2)+1,y2=-k(x2-2)+1,∴y1-y2=k(x1+x2)-4k=-.∵A在第四象限,∴k≠0 且A不在直线OP上,∴k AB=-.-又k OP=,∴k AB=k OP.故直线AB与直线OP平行.6.解(1)因为F2的坐标满足圆Q方程(x-)2+(y-1)2=1,故当y=0时,x=,即F2(,0),故c=.因为圆心Q满足|QF1|+|QF2|=2a,所以点Q(在椭圆上,故有=1.联立方程组解得所以椭圆方程为=1.(2)因为直线l2交圆Q于C,D两点,M为线段CD的中点,所以QM与直线l2垂直.又因为直线l1与直线l2垂直,所以QM与直线l1平行.所以点M到直线AB的距离即为点Q到直线AB的距离.即点M到直线AB的距离为d=.设点A(x1,y1),B(x2,y2).联立方程组解得(1+2k2)x2+4kx-2=0,Δ=b2-4ac=16k2+8(2k2+1)=32k2+8>0,由韦达定理可得--则|x1-x2|=----.所以AB=|x1-x2|=.所以△MAB的面积为.所以.即·|k|=,两边同时平方,化简得,28k4-47k2-18=0,解得k2=2或k2=-(舍).故k=±.此时l2:y=±x+1.圆心Q到l2的距离h=-<1成立.综上所述,k=±.。
2019年高考数学二轮复习专题7解析几何2直线圆圆锥曲线小综合题专项练课件理

关闭
设点CA..圆[[P2心2,到6,3]到直直2线]线ABA的B 的距D.距离[2B离为.[24,dd,38='.]易|22+]知02+2|=2 2.
d-r≤d'≤d+r,即 2 ≤d'≤3 2.
又 AB=2 2,
∴S△ABP=12 ·|AB|·d'= 2d', ∴2≤S△ABP≤6.
关闭
A
解析 答案
=
������-������ ������������
, 代入
������1 + ������2 = 2������,
������1 + ������2 = 2������������,
得B a2=bc,即 a4=(c2-a2)c2,有 e4-e2-1=0,得 e=
1+ 2
5.
关闭
解析 答案
一、选择题 二、填空题
近 的由则线 离题F2的 心意到对 率,F渐1称 为(近0点(,-线c恰)的,F好2距)(0落离,c在)为,一以条���F���渐������1 为近=圆线b.心方,程|O为F1|y为=半������������x,径的圆上,则双曲线 关闭
A.3
B. 3 ������2+������2 C.2
D. 2
5.过圆及圆锥曲线上一点的切线方程
(1)过圆x2+y2=r2上一点M(x0,y0)的切线方程为x0x+y0y=r2; (2)过圆(x-a)2+(y-b)2=r2上一点M(x0,y0)的切线方程为(x0-a)(xa)+(y0-b)(y-b)=r2; 为(A3)x过0x+曲B线y0Cy+:ADx���2���0+2+B������y+2+E���D���0x2++������E+yF+=F0=. 0上的一点P(x0,y0)的切线方程
2025年高考数学一轮复习-第九章-直线与圆、圆锥曲线【课件】

间的距离.
卷·T15
7.回顾确定圆的几何要素,在平面直角坐标系中,探索并掌握圆的标准方程 2021年:新高考Ⅰ
与一般方程.
卷·T11
8.能根据给定直线、圆的方程,判断直线与圆、圆与圆的位置关系.
2021年:新高考Ⅱ
9.能用直线和圆的方程解决一些简单的数学问题与实际问题.
卷·T11
角度 考查内容
课程标准
3.重视数学思想方法的应用 (1)解析法:用代数方法研究几何问题是本章的基本方法,一是依据条件求曲线 的方程;二是由曲线的方程,研究曲线的几何性质. (2)数形结合思想:在解决与直线的倾斜角、斜率有关的最值问题、对称问题, 与参数有关的问题,与弦的中点有关问题时,往往用到数形结合思想. (3)函数与方程思想:在求解直线、圆、椭圆、抛物线等的方程,解决参数问题、 最值问题时,经常利用函数与方程思想. (4)分类与整合思想:在解决与参数有关的问题时,往往依据解析式特点、函数 取最值的条件,或题设条件对参数进行分类讨论.
高考真题
1.了解圆锥曲线的实际背景,感受圆锥曲线在刻
平面 解析 几何
画现实世界和解决实际问题中的作用. 2.经历从具体情境中抽象出椭圆的过程,掌握椭 圆的定义、标准方程及简单几何性质. 圆锥曲线 3.了解抛物线与双曲线的定义、几何图形和标 与方程 准方程,以及它们的简单几何性质. 4.通过对圆锥曲线与方程的学习,进一步体会数 形结合的思想.
角度 考查内容
课程标准
1.题型设置:各种题型均有涉及. 命题
2.内容考查:主要考查直线和圆的位置关系及圆锥曲线的方程与性质. 趋势
3.能力考查:注重运算求解能力与逻辑推理能力的考查.
高考真题
备考策略 根据近三年新高考卷命题特点和规律,复习本章时,要注意以下几个方面: 1.全面系统复习,深刻理解知识本质 (1)概念:直线的倾斜角、斜率,直线、圆、椭圆、双曲线、抛物线的定义,两直
2019-2020年高考数学一轮复习专题突破提升练4直线圆与圆锥曲线的交汇问题

由
x2 4+
y
2=
1
,
y= kx+ m,
得 (1 + 4k2 ) x2+ 8kmx+ 4m2- 4= 0.
则
Δ
=
(8
km)
2-
4(1
+
4k2)(4
m2-
4)
=
16(1
+
4k 2-
m2)
>0,
x1+
x2 =-
8km 1+ 4k2 , x1x2 =
4m2 -4
m2- 4k2
1+ 4k2,则 y1y2=( kx1+ m)( kx2=- x2 联立得
3x2- 4x-t
= 0,由
Δ= 16+ 12t
=0
得
t
=-
4 ,两条平行线间的距
3
离即为所求最小距离,由两平行线的距离公式得
4 d= 3.
【答案】 A x2 y2
2.双曲线 a2- b2= 1( a> 0, b>0) 的左、右焦点分别为
F1 , F2,渐近线分别为
l 1, l 2,
率为 1 的直线 l 与抛物线 C交于 A,B 两点,则弦 AB的中点到抛物线准线的距离为 ________. 【解析】 设抛物线方程为 y2= 2px( p> 0) ,因为焦点 F 与双曲线的右焦点重合,故
p F(3,0) ,所以 2= 3, p= 6,抛物线方程为
y2=12x,设 A( x1, y1) , B( x2, y2) ,过点 P(2,0)
1 PF1 ⊥PF2,即 | OP| = 2| F1F2| =c,即
x20+y20 =c2. 又因为
b y0 = ax0 ,代入得
x 20+
b ax0
高考数学(文科)2轮专题突破训练:专题6 直线、圆、圆锥曲线 专题能力训练15 Word版含答案

本资源的初衷 ,是希望通过网络分享 ,能够为广阔读者提供更好的效劳 ,为您水平的提高提供坚强的动力和保证 .内容由一线名师原创 ,立意新 ,图片精 ,是非常强的一手资料 .专题能力训练15直线与圆一、能力突破训练1.圆(x +1)2 +y2 =2的圆心到直线y =x +3的距离为()A.1B.2C.D.22.三点A(1,0),B(0,),C(2,),那么△ABC外接圆的圆心到原点的距离为()A. B. C. D.3.直线y =kx +3与圆(x -1)2 +(y +2)2 =4相交于M,N两点,假设|MN|≥2,那么实数k的取值范围是()A. B.C. D.4.过三点A(1,3),B(4,2),C(1, -7)的圆交y轴于M,N两点,那么|MN| =()A.2B.8C.4D.105.(2021全国Ⅰ,文15)直线y =x +1与圆x2 +y2 +2y -3 =0交于A,B两点,那么|AB| =.6.a∈R,方程a2x2 +(a +2)y2 +4x +8y +5a =0表示圆,那么圆心坐标是,半径是.7.假设直线 =1(a>0,b>0)过点(1,2),那么2a +b的最|小值为.8.P是抛物线y2 =4x上的动点,过P作抛物线准线的垂线,垂足为M,N是圆(x -2)2 +(y -5)2 =1上的动点,那么|PM| +|PN|的最|小值是.9.在平面直角坐标系xOy中,以坐标原点O为圆心的圆与直线x -y =4相切.(1)求☉O的方程;(2)假设☉O上有两点M,N关于直线x +2y =0对称,且|MN| =2,求直线MN的方程;(3)设☉O与x轴相交于A,B两点,假设圆内的动点P使|PA|,|PO|,|PB|成等比数列,求的取值范围.10.☉O:x2 +y2 =4,点A(,0),以线段AB为直径的圆内切于☉O,记点B的轨迹为Γ.(1)求曲线Γ的方程;(2)直线AB交☉O于C,D两点,当B为CD的中点时,求直线AB的方程.11.过点A(0,1)且斜率为k的直线l与☉C:(x -2)2 +(y -3)2 =1交于M,N两点.(1)求k的取值范围;(2)假设 =12,其中O为坐标原点,求|MN|.二、思维提升训练12.圆M:x2 +y2 -2ay =0(a>0)截直线x +y =0所得线段的长度是2.那么圆M与圆N:(x -1)2 +(y -1)2 =1的位置关系是()A.内切B.相交C.外切D.相离13.(2021全国Ⅲ,文8)直线x +y +2 =0分别与x轴、y轴交于A,B两点,点P在圆(x -2)2 +y2 =2上,那么△ABP面积的取值范围是()A.[2,6]B.[4,8]C.[,3]D.[2,3]14.在平面直角坐标系xOy中,A( -12,0),B(0,6),点P在圆O:x2 +y2 =50上.假设≤20,那么点P的横坐标的取值范围是.15.在平面直角坐标系中,当P(x,y)不是原点时,定义P的 "伴随点〞为P';当P是原点时,定义P的 "伴随点〞为它自身.现有以下命题:①假设点A的 "伴随点〞是点A',那么点A'的 "伴随点〞是点A;②单位圆上的点的 "伴随点〞仍在单位圆上;③假设两点关于x轴对称,那么它们的 "伴随点〞关于y轴对称;④假设三点在同一条直线上,那么它们的 "伴随点〞一定共线.其中的真命题是.(写出所有真命题的序号)16.在平面直角坐标系xOy中,☉C1:(x +3)2 +(y -1)2 =4和☉C2:(x -4)2 +(y -5)2 =4.(1)假设直线l过点A(4,0),且被☉C1截得的弦长为2,求直线l的方程;(2)设P为平面上的点,满足:存在过点P的无穷多对互相垂直的直线l1和l2,它们分别与☉C1和☉C2相交,且直线l1被☉C1截得的弦长与直线l2被☉C2截得的弦长相等,试求所有满足条件的点P的坐标.如图,在平面直角坐标系xOy中,以M为圆心的圆M:x2 +y2 -12x -14y +60 =0及其上一点A(2,4).(1)设圆N与x轴相切,与圆M外切,且圆心N在直线x =6上,求圆N的标准方程;(2)设平行于OA的直线l与圆M相交于B,C两点,且BC =OA,求直线l的方程;(3)设点T(t,0)满足:存在圆M上的两点P和Q,使得,求实数t的取值范围.专题能力训练15直线与圆一、能力突破训练1.C解析由题意可知圆心坐标为( -1,0),故圆心到直线y =x +3的距离d =,应选C.2.B解析由题意知,△ABC外接圆的圆心是直线x =1与线段AB垂直平分线的交点,设为P,而线段AB垂直平分线的方程为y -,它与x =1联立得圆心P坐标为,那么|OP|=.3.B解析当|MN| =2时,在弦心距、半径和半弦长构成的直角三角形中,可知圆心(1, -2)到直线y =kx +3的距离为 =1,即 =1,解得k = -.假设使|MN|≥2,那么k≤ -.4.C解析设圆的方程为x2 +y2 +Dx +Ey +F =0,将点A,B,C代入,得解得那么圆的方程为x2 +y2 -2x +4y -20 =0.令x =0得y2 +4y -20 =0,设M(0,y1),N(0,y2),那么y1,y2是方程y2 +4y -20 =0的两根,由根与系数的关系,得y1 +y2 = -4,y1y2 = -20,故|MN| =|y1 -y2| = =4.5.2解析圆的方程可化为x2 +(y +1)2 =4,故圆心C(0, -1),半径r =2,圆心到直线y =x +1的距离d =,所以弦长|AB| =2 =2 =2.6.( -2, -4)5解析由题意,可得a2 =a +2,解得a = -1或2.当a = -1时,方程为x2 +y2 +4x +8y -5 =0,即(x +2)2 +(y +4)2 =25,故圆心为( -2, -4),半径为5;当a =2时,方程为4x2 +4y2 +4x +8y +10=0, +(y +1)2 = -不表示圆.7.8解析∵直线 =1过点(1,2),∴ =1.∵a>0,b>0,∴2a +b =(2a +b) =4 +≥4 +2 =8.当且仅当b =2a时 " =〞成立.8. -1解析抛物线y2 =4x的焦点为F(1,0),圆(x -2)2 +(y -5)2 =1的圆心为C(2,5),根据抛物线的定义可知点P到准线的距离等于点P到焦点的距离,进而推断出当P,C,F三点共线时,点P到点C的距离与点P到抛物线的焦点距离之和的最|小值为|FC| =,故|PM| +|PN|的最|小值是|FC| -1 = -1.9.解(1)依题意,☉O的半径r等于原点O到直线x -y =4的距离,即r = =2.所以☉O的方程为x2 +y2 =4.(2)由题意,可设直线MN的方程为2x -y +m =0.那么圆心O到直线MN的距离d =.由垂径定理,得 +()2 =22,即m =±.所以直线MN的方程为2x -y + =0或2x -y - =0.(3)设P(x,y),由题意得A( -2,0),B(2,0).由|PA|,|PO|,|PB|成等比数列,得 =x2 +y2,即x2 -y2 =2.因为 =( -2 -x, -y)·(2 -x, -y) =2(y2 -1),且点P在☉O内,所以由此得y2<1.所以的取值范围为[ -2,0).10.解(1)设AB的中点为M,切点为N,连接OM,MN,那么|OM| +|MN| =|ON| =2,|AB| =|ON| -(|OM| -|MN|) =2 -|OM| +|AB|,即|AB| +2|OM| =4.取A关于y轴的对称点A',连接A'B,那么|A'B| =2|OM|,所以|AB| +2|OM| =|AB| +|A'B| =4>|A'A|.所以点B的轨迹是以A',A为焦点,长轴长为4的椭圆.其中,a =2,c =,b =1,故曲线Γ的方程为 +y2 =1.(2)因为B为CD的中点,所以OB⊥CD,那么.设B(x0,y0),那么x0(x0 -) + =0.又 =1,解得x0 =,y0 =±.那么k OB =±,k AB =∓,那么直线AB的方程为y =±(x -),即x -y - =0或x +y -=0.11.解(1)由题设,可知直线l的方程为y =kx +1.因为l与C交于两点,所以<1.解得<k<.所以k的取值范围为.(2)设M(x1,y1),N(x2,y2).将y =kx +1代入方程(x -2)2 +(y -3)2 =1,整理得(1 +k2)x2 -4(1 +k)x +7 =0.所以x1 +x2 =,x1x2 =.=x1x2 +y1y2=(1 +k2)x1x2 +k(x1 +x2) +1 = +8.由题设可得 +8 =12,解得k =1,所以l的方程为y =x +1.故圆心C在l上,所以|MN| =2.二、思维提升训练12.B解析圆M的方程可化为x2 +(y -a)2 =a2,故其圆心为M(0,a),半径R =a.所以圆心到直线x +y =0的距离d = a.所以直线x +y =0被圆M所截弦长为2 =2a,由题意可得 a =2,故a =2.圆N的圆心N(1,1),半径r =1.而|MN| =,显然R -r<|MN|<R +r,所以两圆相交.13. A解析设圆心到直线AB的距离d = =2.点P到直线AB的距离为d'.易知d -r≤d'≤d +r,即≤d'≤3.又AB =2,∴S△ABP =·|AB|·d' =d',∴2≤S△ABP≤6.14.[ -5,1]解析设P(x,y),由≤20,易得x2 +y2 +12x -6y≤20.把x2 +y2 =50代入x2 +y2 +12x -6y≤20得2x -y +5≤0.由可得由2x -y +5≤0表示的平面区域及P点在圆上,可得点P在圆弧EPF上,所以点P横坐标的取值范围为[ -5,1].15.②③解析对于①,假设令P(1,1),那么其伴随点为P',而P'的伴随点为( -1, -1),而不是P,故①错误;对于②,令单位圆上点的坐标为P(cos x,sin x),其伴随点为P'(sin x, -cos x)仍在单位圆上,所以②正确;③设A(x,y)与B(x, -y)为关于x轴对称的两点,那么A的 "伴随点〞为A',B点的伴随点为B',A'与B'关于y轴对称,故③正确;对于④,取直线l:y =1.设其 "伴随曲线〞为C,其上任一点M(x,y),与其对应的直线l上的点为N(t,1).那么由定义可知①2 +②2得x2 +y2 = =x,整理得x2 +y2 -x =0,显然不是一条直线.故④错误.所以正确的序号为②③.16.解(1)设直线l的方程为y =k(x -4),即kx -y -4k =0,由垂径定理,得圆心C1到直线l的距离d = =1.由点到直线距离公式,得 =1,化简,得24k2 +7k =0,解得k =0或k = -.当k =0时,直线l的方程为y =0;当k = -时,直线l的方程为y = -(x -4),即7x +24y -28 =0.故所求直线l的方程为y =0或7x +24y -28 =0.(2)设点P坐标为(m,n),直线l1,l2的方程分别为y -n =k(x -m)和y -n = -(x -m),即kx -y +n -km =0, -x -y +n +m =0.∵直线l1被☉C1截得的弦长与直线l2被☉C2截得的弦长相等,两圆半径相等,∴由垂径定理得圆心C1到直线l1与圆心C2到直线l2的距离相等.∴,化简,得(2 -m -n)k =m -n -3或(m -n +8)k =m +n -5.∵关于k的方程有无穷多解,∴解得故点P坐标为.17.解圆M的标准方程为(x -6)2 +(y -7)2 =25,所以圆心M(6,7),半径为5.(1)由圆心N在直线x =6上,可设N(6,y0).因为圆N与x轴相切,与圆M外切,所以0<y0<7,于是圆N的半径为y0,从而7 -y0 =5 +y0,解得y0 =1.因此,圆N的标准方程为(x -6)2 +(y -1)2 =1.(2)因为直线l∥OA,所以直线l的斜率为 =2.设直线l的方程为y =2x +m,即2x -y +m =0,那么圆心M到直线l的距离d =.因为BC =OA = =2,而MC2 =d2 +,所以25 = +5,解得m =5或m = -15.故直线l的方程为2x -y +5 =0或2x -y -15 =0.(3)设P(x1,y1),Q(x2,y2).因为A(2,4),T(t,0),,所以①因为点Q在圆M上,所以(x2 -6)2 +(y2 -7)2 =25.②将①代入②,得(x1 -t -4)2 +(y1 -3)2 =25.于是点P(x1,y1)既在圆M上,又在圆[x -(t +4)]2 +(y -3)2 =25上,从而圆(x -6)2 +(y -7)2 =25与圆[x -(t +4)]2 +(y -3)2 =25有公共点, 所以5 -5≤≤5 +5,解得2 -2≤t≤2 +2.因此,实数t的取值范围是[2 -2,2 +2].。
高考数学命题热点名师解密:专题(25)圆的解题方法(文)(含答案)

专题26 圆的解题方法一.【学习目标】1.掌握圆的标准方程和一般方程,会用圆的方程及其几何性质解题.2.能根据所给条件选取适当的方程形式,利用待定系数法求出圆的方程,解决与圆有关的问题.3.能利用直线与圆、圆与圆的位置关系的几何特征判断直线与圆、圆与圆的位置关系,能熟练解决与圆的切线和弦长等有关的综合问题;体会用代数法处理几何问题的思想.二.方法规律总结1.在求圆的方程时,应根据题意,合理选择圆的方程形式.圆的标准方程突出了圆心坐标和半径,便于作图使用;圆的一般方程是二元一次方程的形式,便于代数运算;而圆的参数方程在求范围和最值时应用广泛.同时,在选择方程形式时,应熟悉它们的互化.如果问题中给出了圆心与圆上的点两坐标之间的关系或圆心的特殊位置时,一般用标准方程;如果给出圆上的三个点的坐标,一般用一般方程.2.在二元二次方程中x2和y2的系数相等并且没有xy项,只是表示圆的必要条件而不是充分条件.3.在解决与圆有关的问题时,要充分利用圆的几何性质,这样会使问题简化.涉及与圆有关的最值问题或范围问题时应灵活、恰当运用参数方程.4.处理直线与圆、圆与圆的位置关系常用几何法,即利用圆心到直线的距离,两圆心连线的长与半径和、差的关系判断求解.5.求过圆外一点(x0,y0)的圆的切线方程:(1)几何方法:设切线方程为y-y0=k(x-x0),即kx-y-kx0+y0=0.由圆心到直线的距离等于半径,可求得k,切线方程即可求出.(2)代数方法:设切线方程为y-y0=k(x-x0),即y=kx-kx0+y0,代入圆方程,得一个关于x的一元二次方程,由Δ=0,求得k,切线方程即可求出.(以上两种方法只能求斜率存在的切线,斜率不存在的切线,可结合图形求得).6.求直线被圆截得的弦长(1)几何方法:运用弦心距、半径及弦的一半构成的直角三角形,计算弦长|AB|=2·r2-d2.(2)代数方法:运用韦达定理.弦长|AB|=[(x A+x B)2-4x A·x B](1+k2).7.注意利用圆的几何性质解题.如:圆心在弦的垂直平分线上,切线垂直于过切点的半径,切割线定理等,在考查圆的相关问题时,常结合这些性质一同考查,因此要注意灵活运用圆的性质解题. 三.【典例分析及训练】例1.圆:与轴正半轴交点为,圆上的点,分别位于第一、二象限,并且,若点的坐标为,则点的坐标为()A. B. C. D.【答案】B【解析】由题意知,,设的坐标为,则, ,,因为,所以,即,又,联立解得或,因为在第二象限,故只有满足,即.故答案为B.练习1.已知圆上的动点和定点,则的最小值为()A. B. C. D.【答案】D【解析】如图,取点,连接,,,,,,,因为,当且仅当三点共线时等号成立,的最小值为的长,,,故选D.【点睛】本题主要考查圆的方程与几何性质以及转化与划归思想的应用,属于难题. 转化与划归思想解决高中数学问题的一种重要思想方法,尤其在解决知识点较多以及知识跨度较大的问题发挥着奇特功效,运用这种方法的关键是将题设条件研究透,这样才能快速找准突破点.以便将问题转化为我们所熟悉的知识领域,进而顺利解答,解答本题的关键是将转化为.练习2.已知点为函数的图象上任意一点,点为圆上任意一点,则线段的长度的最小值为()A. B. C. D.【答案】A【解析】依题意,圆心为,设点的坐标为,由两点间距离公式得,设,,令解得,由于,可知当时,递增,时,,递减,故当时取得极大值也是最大值为,故,故时,且,所以,函数单调递减.当时,,,当时,,即单调递增,且,即,单调递增,而,故当时,函数单调递增,故函数在处取得极小值也是最小值为,故的最小值为,此时.故选A.练习3.直线l是圆C1:(x+1)2+y2=1与圆C2:(x+4)2+y2=4的公切线,并且l分别与x轴正半轴,y轴正半轴相交于A,B两点,则△AOB的面积为A. B. C. D.【答案】A【解析】如图,设OA=a,OB=b,由三角形相似可得:,得a=2.再由三角形相似可得:,解得b=.∴△AOB的面积为.故选A.(二)圆的一般方程例2.若由方程x2-y2=0和x2+(y-b)2=2所组成的方程组至多有两组不同的实数解,则实数b的取值范围是( )A.b≥2或b≤-2 B.b≥2或b≤-2 C.-2≤b≤2 D.-2≤b≤2【答案】B练习1.若圆的圆心在第一象限,则直线一定不经过()A.第一象限 B.第二象限 C.第三象限 D.第四象限【答案】A【解析】因为圆的圆心坐标为,由圆心在第一象限可得,所以直线的斜率,轴上的截距为,所以直线不过第一象限.练习2.若方程a2x2+(a+2)y2+2ax+a=0表示圆,则a的值为A.a=1或a=–2 B.a=2或a=–1 C.a=–1 D.a=2【答案】C【解析】若方程a2x2+(a+2)y2+2ax+a=0表示圆,则,解得a=–1.故答案为:C(三)点与圆的位置关系例3.例3.过点作直线的垂线,垂足为M,已知点,则当变化时,的取值范围是A. B. C. D.【答案】B练习 1.已知点,,是圆内一点,直线,,,围成的四边形的面积为,则下列说法正确的是()A. B. C. D.【答案】A【解析】由已知,四条直线围成的四边形面积,故选A.练习2.设点M(3,4)在圆外,若圆O上存在点N,使得,则实数r的取值范围是()A. B. C. D.【答案】C【解析】如图,要使圆O:x2+y2=r2(r>0)上存在点N,使得∠OMN=,则∠OMN的最大值大于或等于时一定存在点N,使得∠OMN=,而当MN与圆相切时∠OMN取得最大值,此时OM=5,ON=,又点M(3,4)在圆x2+y2=r2(r>0)外,∴实数r的取值范围是.故选:C.(四)圆的几何性质例4.如图,在平面直角坐标系内,已知点,,圆C的方程为,点P为圆上的动点.求过点A的圆C的切线方程.求的最大值及此时对应的点P的坐标.【答案】(1)或;(2)最大值为,.【解析】当k存在时,设过点A切线的方程为,圆心坐标为,半径,,解得,所求的切线方程为,当k不存在时方程也满足;综上所述,所求的直线方程为:或;设点,则由两点之间的距离公式知,要取得最大值只要使最大即可,又P为圆上的点,,,此时直线OC:,由,解得舍去或,点P的坐标为练习1.已知圆心在x轴正半轴上的圆C与直线相切,与y轴交于M,N两点,且.Ⅰ求圆C的标准方程;Ⅱ过点的直线l与圆C交于不同的两点D,E,若时,求直线l的方程;Ⅲ已知Q是圆C上任意一点,问:在x轴上是否存在两定点A,B,使得?若存在,求出A,B两点的坐标;若不存在,请说明理由.【答案】(I);(II)或;(III)存在,或,满足题意.【解析】Ⅰ由题意知圆心,且,由知中,,,则,于是可设圆C的方程为又点C到直线的距离为,所以或舍,故圆C的方程为,Ⅱ设直线l的方程为即,则由题意可知,圆心C到直线l的距离,故,解得,又当时满足题意,因此所求的直线方程为或,Ⅲ方法一:假设在x轴上存在两定点,,设是圆C上任意一点,则即,则,令,解得或,因此存在,,或,满足题意,方法二:设是圆C上任意一点,由得,化简可得,对照圆C的标准方程即,可得,解得解得或,因此存在,或,满足题意.练习2.设点P是函数图象上任意一点,点Q坐标为,当取得最小值时圆与圆相外切,则的最大值为A. B. C. D.【答案】C【解析】根据题意,函数y,即(x﹣1)2+y2=4,(y≤0),对应的曲线为圆心在C(1,0),半径为2的圆的下半部分,又由点Q(2a,a﹣3),则Q在直线x﹣2y﹣6=0上,当|PQ|取得最小值时,PQ与直线x﹣2y﹣6=0垂直,此时有2,解可得a=1,圆C1:(x﹣m)2+(y+2)2=4与圆C2:(x+n)2+(y+2)2=9相外切,则有3+2=5,变形可得:(m+n)2=25,则mn,故选:C.练习3.已知,是单位向量,•0.若向量满足||=1,则||的最大值为()A. B. C. D.【答案】C【解析】∵||=||=1,且,∴可设,,.∴.∵,∴,即(x﹣1)2+(y﹣1)2=1.∴的最大值.故选:C.练习4.设P,Q分别是圆和椭圆上的点,则P,Q两点间的最大距离是( )A. B.C. D.【答案】C【解析】圆的圆心为M(0,6),半径为,设,则,即,∴当时,,故的最大值为.故选C.(五)轨迹问题例 5.已知线段AB的端点B的坐标为(3,0),端点A在圆上运动;(1)求线段AB中点M的轨迹方程;(2)过点C(1,1)的直线m与M的轨迹交于G、H两点,当△GOH(O 为坐标原点)的面积最大时,求直线m的方程并求出△GOH面积的最大值.(3)若点C(1,1),且P在M轨迹上运动,求的取值范围.【答案】(1);(2);(3)【解析】(1)解:设点由中点坐标公式有又点在圆上,将点坐标代入圆方程得:点的轨迹方程为:(2)令,则当,即时面积最大为2又直线过点,,∴到直线的距离为,当直线斜率不存在时,到的距离为1不满足,令故直线的方程为:(3)设点,由于点则,令有,由于点在圆上运动,故满足圆的方程.当直线与圆相切时,取得最大或最小故有所以练习1.已知线段AB的端点B的坐标为(3,0),端点A在圆上运动;(1)求线段AB中点M的轨迹方程;(2)过点C(1,1)的直线m与M的轨迹交于G、H两点,求以弦GH 为直径的圆的面积最小值及此时直线m的方程.学-科网(3)若点C(1,1),且P在M轨迹上运动,求的取值范围.(O 为坐标原点)【答案】(1);(2)圆的面积最小值(3)【解析】(1)解:设点由中点坐标公式有又点在圆上,将点坐标代入圆方程得:点的轨迹方程为:(2)由题意知,原心到直线的距离∴当即当时,弦长最短,此时圆的面积最小,圆的半径,面积又,所以直线斜率,又过点故直线的方程为:(3)设点,由于点法一:所以,令有,由于点在圆上运动,故满足圆的方程. 当直线与圆相切时,取得最大或最小故有所以法二:∴从而练习2.四棱锥P-ABCD中,AD⊥面PAB,BC⊥面PAB,底面ABCD为梯形,AD=4,BC=8,AB=6,∠APD=∠CPB,满足上述条件的四棱锥的顶点P的轨迹是()A.圆的一部分 B.椭圆的一部分 C.球的一部分 D.抛物线的一部分【答案】A练习3.已知椭圆的左右焦点分别为,过的直线与过的直线交于点,设点的坐标,若,则下列结论中不正确的是()A.B.C.D.【答案】A【解析】由椭圆的左右焦点分别为F1(﹣1,0),F2(1,0),过F1的直线l1与过F2的直线l2交于点P,且l1⊥l2,∴P在线段F1F2为直径的圆上,故x02+y02=1,∴1,故A错误,B正确;3x02+2y02>2x02+2y02=2(x02+y02)=2>1,故C正确;由圆x2+y2=1在P(x0,y0)的切线方程为:x0x+y0y=1,如图,∵坐标原点O(0,0)与点()在直线x0x+y0y=1的同侧,且x0×0+y0×0=0<1,∴,故D正确.∴不正确的选项是A.故选:A.练习4.已知圆C: (为锐角) ,直线l:y=kx,则A.对任意实数k与,直线l和圆C相切 B.对任意实数k与,直线l和圆C有公共点C.对任意实数k与,直线l和圆C相交 D.对任意实数k与,直线l和圆C相离【答案】B【解析】由题意,圆心坐标为:,所以圆心的轨迹方程为:,所以圆心与原点的距离为1,所以圆必过原点.由于直线过原点,所以直线与圆必有交点.故选B.(六)直线与圆的位置关系例6.已知抛物线的顶点在坐标原点,其焦点在轴正半轴上,为直线上一点,圆与轴相切(为圆心),且,关于点对称.(1)求圆和抛物线的标准方程;(2)过的直线交圆于,两点,交抛物线于,两点,求证:.【答案】(1)的标准方程为.的标准方程为(2)见证明【解析】(1)设抛物线的标准方程为,则焦点的坐标为.已知在直线上,故可设因为,关于对称,所以,解得所以的标准方程为.因为与轴相切,故半径,所以的标准方程为.(2)由(1)知,直线的斜率存在,设为,且方程为则到直线的距离为,所以,由消去并整理得:.设,,则,,.所以因为,,,所以所以,即.练习1.已知以点为圆心的圆经过点和,线段的垂直平分线交圆于点和,且.(1)求直线的方程;(2)求圆的方程.【答案】(1);(2)或.【解析】(1)直线的斜率,的中点坐标为直线的方程为(2)设圆心,则由点在上,得.①又直径,,.②由①②解得或,圆心或圆的方程为或练习2.已知直线,曲线,若直线与曲线相交于、两点,则的取值范围是____;的最小值是___.【答案】【解析】直线l:kx﹣y k=0过定点(1,),曲线C为半圆:(x﹣2)2+y2=4(y≥0)如图:由图可知:k OP,k PE,∴;要使弦长AB最小,只需CP⊥AB,此时|AB|=22,故答案为:[,];.练习3.阿波罗尼斯是古希腊著名数学家,与欧几里得、阿基米德被称为亚历山大时期数学三巨匠,他对圆锥曲线有深刻而系统的研究,主要研究成果集中在他的代表作《圆锥曲线》一书,阿波罗尼斯圆是他的研究成果之一,指的是:已知动点M与两定点A、B的距离之比为λ(λ>0,λ≠1),那么点M的轨迹就是阿波罗尼斯圆.下面,我们来研究与此相关的一个问题.已知圆:x2+y2=1和点,点B(1,1),M为圆O上动点,则2|MA|+|MB|的最小值为_____.【答案】【解析】如图所示,取点K(﹣2,0),连接OM、MK.∵OM=1,OA=,OK=2,∴,∵∠MOK=∠AOM,∴△MOK∽△AOM,∴,∴MK=2MA,∴|MB|+2|MA|=|MB|+|MK|,在△MBK中,|MB|+|MK|≥|BK|,∴|MB|+2|MA|=|MB|+|MK|的最小值为|BK|的长,∵B(1,1),K(﹣2,0),∴|BK|=.故答案为:.练习4.已知直线l:mx﹣y=1,若直线l与直线x+m(m﹣1)y=2垂直,则m的值为_____,动直线l:mx﹣y=1被圆C:x2﹣2x+y2﹣8=0截得的最短弦长为_____.【答案】0或2 .(七)圆与圆的位置关系例1.在平面直角坐标系中,已知点和直线:,设圆的半径为1,圆心在直线上.(Ⅰ)若圆心也在直线上,过点作圆的切线.(1)求圆的方程;(2)求切线的方程;(Ⅱ)若圆上存在点,使,求圆心的横坐标的取值范围.【答案】(Ⅰ)(1)或(2)或(Ⅱ)【解析】(Ⅰ)(1)由得圆心为,∵圆的半径为1,∴圆的方程为:.(2)由圆方程可知过的切线斜率一定存在,设所求圆的切线方程为,即,∴,解之得:或,∴所求圆的切线方程为:或.即或.(Ⅱ)∵圆的圆心在直线:上,设圆心为,则圆的方程为:,又∵,∴设为,则整理得:,设为圆,∴点应该既在圆上又在圆上∴圆和圆有公共点,∴,即:,解之得:即的取值范围为:.练习1.在平面直角坐标系中,已知的顶点坐标分别是,,,记外接圆为圆.(1)求圆的方程;(2)在圆上是否存在点,使得?若存在,求点的个数;若不存在,说明理由.【答案】(1)(2)存在,且个数为2【解析】(1)设外接圆的方程为,将代入上述方程得:解得则圆的方程为(2)设点的坐标为,因为,所以化简得:.即考查直线与圆的位置关系点到直线的距离为所以直线与圆相交,故满足条件的点有两个。
2019版高考数学二轮复习专题七圆锥曲线专题突破练21直线与圆及圆锥曲线文.docx

专题突破练21直线与圆及圆锥曲线1.(节选)己知圆必py j2(,o)与直线厶:/?户4刃相切,设点A为圆上一动点fAB_Lx轴于B,且动点/V满足AB=2“B,设动点艸的轨迹为曲线Q(1)求曲线Q的方程;⑵略.2.(2018河北唐山一模,文20)已知椭圆厂:/ b2=l SZ以))的左焦点为F,上顶点为力,长轴长为2、® 〃为直线7: *-3上的动点,M5, 0)(/7/<0), AMLBM.当初丄1时,"与F重合. (1)求椭圆厂的方程;⑵若C为椭圆厂上一点,满足AC//mf,,求刃的值.3.已知圆0: QyX,点J (A 0),以线段初为直径的圆内切于圆0,记点〃的轨迹为r.(1)求曲线厂的方程;(2)直线M交圆。
于两点,当〃为Q的中点吋,求直线处的方程.4 14.己知圆M的圆心〃在x轴上,半径为1,直线l:y=3x-2被圆〃所截的弦长为且圆心〃在直线Z的下方.(1)求圆於的方程;⑵设力(0, Z),E(0, f)(~5WfW-2),若圆〃是的内切圆,求的面积S的最大值和最小值.5.(2018山西吕梁一模,文20)已知椭圆C:/ 於=1 @%x))过/ 1,2),且离心率为巨.(1)求椭圆C的方程;(2)过右焦点厂的直线1与椭圆交于/, 〃两点,〃点坐标为(4, 3),求直线DA,仞的斜率之和.x y--- 1—6.(2018河南六市联考一,文20)已知椭圆Q2於二1(爲肋刈的左右焦点分别为R,甩上顶点为M若直线沏S的斜率为1,且与椭圆的另一个交点为汕 MMN的周长为dV2.(1)求椭圆的标准方程;(2)过点月的直线"直线1的斜率不为1)与椭圆交于只0两点,点戶在点0的上方,若, _2S △ F、NQ = £S △ F M p1 3 1 ,求直线/的斜率.参考答案专题突破练21直线与圆及圆锥曲线1.解⑴设动点A f(y, y), A(xo f旳),因为AB Lx轴于B y所以B(XQ, 0).设圆必的方程为必/孑-A由题意得+ 3吃,所以圆M的方程为M\ x -i-y=\.x0 = X&y° = 2y.所以(0, -必)=2(Xo-X, -y),即将力匕,2y)代入圆^x2+y=4,得动点TV的轨迹方程为°勺耳. (2)略.2.解⑴依题意得水0"),尸(p,0),当個丄/时,〃(-3,b b—•I由AFA.BF得屁■ k£・ 3 + C=_],又E +c =6,解得c=2,所以,椭圆厂的方程为62司.(2)由⑴得水0,厲,所以k AM=-m f又仙丄他AC//mf,所以AC丄BM, △4忆为直角三角形,m所以k沪k\c=-kg忆,2 -1 联立得(2^3zff2) x十12/脳=0,-12m所以捡二2 +珈[⑷#』2 + 加/二Q 2 + 3m]〃炖),在Rt△加T中,由ZAI/T-600得/化/斯加",整理得(2/〃八忆)m,解得m=- 3 .3.解⑴设肋的中点为必切点为N,连接0乩MN,则-12m所以直线sc的方程为IOW+[MN]=IONi丸,lABl=ION/-{ / W-/MO -2 -/购“2 /肋/,取M关于y轴的对称点/I;连接A,B,则〃'BT/OMh 故〔AB]也 IOMl=/ABl-hlA 'BE.所以点〃的轨迹是以A\A为焦点,长轴t为4的椭圆.其中岚,c/,方二1,则曲线厂的方程为°勺r. ⑵因为〃为C〃的中点,所以OBLCD,则处丄朋设Bg如,则肮(《-、角Jop.72则ko尸土 2 ,局斗、任,则直线/〃的方程为y二土溟,即才一y -7^0 或卫x+y-芬=0.4.解(1)设圆心Ma, 0),由已知得圆心"到直线Z:8x-6y-3=0的距离为|8a- 3| _ 1用+ (-6尸,又:•圆心必在直线/的下方,Z8a-3A), Z8a~3^5, a-1.故圆〃的方程为匕-1)2龙二1.(2)由题意设化的斜率为仏,力的斜率为免则直线化的方程为y二hx+t,直线力的方程为y 二k?x+t代.(L,y — y + t, ______由方程组® = k2x+t + 6,得c点的横坐标为』-由于圆〃与sc 相切,所以1二1 + "1,・:脸2t ; i. a + 6)2同理,/、. = 2( t + 6)3(t 2 + 6t + 1)/.k }-k 2=产+ 6t , 6( t 2 + 6t) 1.:s 二* + 6t + 1书(i£ + 6t + 1):・-5WFW —2,・:—2WT3W1,1 15(H 4).T1 2715 27的面积S 的最大值为2 ,最小值为4 .1 亠 9 cl 十 _ = _ 5.解 ⑴由己知得a 二i, a 2,孑二川痔,解得曰羽,治筋,^=1,2 2x y —+ —所以椭圆方程为4 3 =1.⑵设水山」),〃(疋,比),由⑴得F (i,o ),设直线1的方程为 尸心1)与椭圆联立得2 2x y . ----- 1---- -- 1,4 3 y = kx ■匕消去/得(3创护)#-8处¥创用-12弐),8/c 2 4/ - 12所以山总二缺+ 3 xm 二Ak + 3,71-3 y 2-3所以 kg+k 』l ■ 4 *2 - 4kx x - k - 3 kx 2 - k - 3 Ml + t\ 1 -12•门AB=t 代-t=d 18X6*l - k2f----------------- 1 ------------------ 4 兀2・43/c- 3 3/c- 3----------- F ---------汝严「4 X2-4(3/c - 3)(兀i + x2 - 8)丸k+(心-4)(%2-4)3(/c ・ 1)(8/ ・ 32/c2 - 24)毛kA^ -12-4x8/c2 + 16(4/ + 3)3(k - 1)( - 24/c2 - 24)龙后36/c2 + 363 3当直线/斜率不存在时,*1,・2)“(1,2),也祕加2. 所以必,防的斜率之和为2.6.解⑴•・• \邸的周长为4A/2・:4$N\/2,即b由直线」%[的斜率为1,得°=1,-f-c,.:方=1, c-1,・:椭圆的标准方程为2^y=l.' y = % + 1. x22—-4- y2 = 1. ⑵rti题意可得直线胎方程为尸卅1,联立124 1解得A(-3,-3),眄I _ 1•师为• ♦ ,* ,1 21即2/“歼//如/sinZ 的心32/扔 / ・ I PF J S WP F ], ・・・ lQF\lmJPF\l,当直线1的斜率为0吋,不符合题意,故设直线1的方程为x=my~\t Pg, 口),QU 刃),由 点、P 在点、0的上方,则刃=-2儿■ x = my -1,x' 2可+ y =i,联立12所以(/772 *2)声-2仍yT2m - 12 2所以门少二m + 2, +2,8m 2 _ 1所以(亦+ 2)2 m 2 + 22 714解得分二7,则沪土 7 , 714 又由画图可知刃二7不符合题意, V14所以於-7 ,£卫故直线1的斜率为九二一 2 . 消去乃得 2y[= 1m z + 2。
高考数学直线圆、圆锥曲线练习
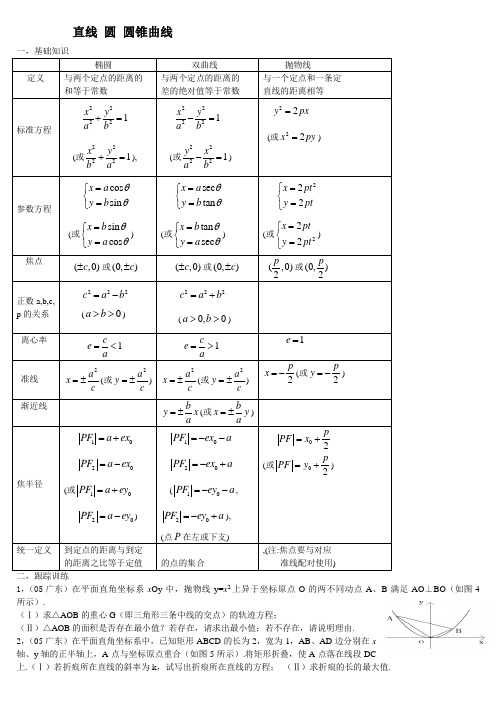
直线 圆 圆锥曲线椭圆双曲线抛物线 定义 与两个定点的距离的 和等于常数与两个定点的距离的 差的绝对值等于常数与一个定点和一条定 直线的距离相等标准方程22221x y a b += (或22221x y b a+=),22221x y a b -= (或22221y x a b-=)22y px =(或22x py =)参数方程cos sin x a y b θθ=⎧⎨=⎩(或sin cos x b y a θθ=⎧⎨=⎩)sec tan x a y b θθ=⎧⎨=⎩(或tan sec x b y a θθ=⎧⎨=⎩)222x pt y pt⎧=⎨=⎩ (或222x pt y pt=⎧⎨=⎩)焦点 (,0)c ±或(0,)c ± (,0)c ±或(0,)c ± (,0)2p 或(0,)2p正数a,b,c, p 的关系 222c a b =-(0a b >>)222c a b =+(0,0a b >>)离心率 1ce a=< 1c e a=> 1e =准线 2a x c =±(或2a y c =±) 2a x c =±(或2a y c=±)2p x =-(或2p y =-) 渐近线b y x a =±(或b x y a=±)焦半径10PF a ex =+ 20PF a ex =-(或10PF a ey =+20PF a ey =-)10PF ex a =-- 20PF ex a =-+(10PF ey a =--,20PF ey a =-+),(点P 在左或下支) 02pPF x =+(或02pPF y =+)统一定义到定点的距离与到定 的距离之比等于定值的点的集合,(注:焦点要与对应准线配对使用)二,跟踪训练 1,(05广东)在平面直角坐标系x Oy 中,抛物线y=x 2上异于坐标原点O 的两不同动点A 、B 满足AO ⊥BO (如图4所示).(Ⅰ)求△AOB 的重心G (即三角形三条中线的交点)的轨迹方程;(Ⅱ)△AOB 的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由. 2,(05广东)在平面直角坐标系中,已知矩形ABCD 的长为2,宽为1,AB 、AD 边分别在x 轴、y 轴的正半轴上,A 点与坐标原点重合(如图5所示).将矩形折叠,使A 点落在线段DC 上.(Ⅰ)若折痕所在直线的斜率为k ,试写出折痕所在直线的方程; (Ⅱ)求折痕的长的最大值.3,(04全国I)双曲线C :2221x y a-=(0a >)与直线l :1x y +=相交于两个不同的点A ,B .(I )求双曲线C 的离心率e 的取值范围;(II )设直线l 与y 轴的交点为P ,且512PA PB =u u u v u u u v,求a 的值。
新高考数学二轮专题总复习突破练习直线与圆及圆锥曲线

专题突破练25直线与圆及圆锥曲线1.(2020全国Ⅱ,理19)已知椭圆C1:x 2a2+y2b2=1(a>b>0)的右焦点F与抛物线C2的焦点重合,C1的中心与C2的顶点重合.过F且与x轴垂直的直线交C1于A,B两点,交C2于C,D两点,且|CD|=43|AB|.(1)求C1的离心率;(2)设M是C1与C2的公共点.若|MF|=5,求C1与C2的标准方程.2.已知圆O:x2+y2=4,点A(√3,0),以线段AB为直径的圆内切于圆O,记点B的轨迹为Γ.(1)求曲线Γ的方程;(2)直线AB交圆O于C,D两点,当B为CD的中点时,求直线AB的方程.3.(2019全国Ⅰ,理19)已知抛物线C :y 2=3x 的焦点为F ,斜率为32的直线l 与C 的交点为A ,B ,与x 轴的交点为P.(1)若|AF|+|BF|=4,求l 的方程; (2)若AP ⃗⃗⃗⃗⃗ =3PB ⃗⃗⃗⃗⃗ ,求|AB|.4.(2020山东威海一模,20)已知椭圆x 2a 2+y 2b2=1(a>b>0)的左、右焦点分别为F 1,F 2,点P (-1,32)是椭圆上一点,|F 1F 2|是|PF 1|和|PF 2|的等差中项. (1)求椭圆的标准方程;(2)若A 为椭圆的右顶点,直线AP 与y 轴交于点H ,过点H 的另一条直线与椭圆交于M ,N 两点,且S △HMA =6S △PHN ,求直线MN 的方程.5.(2020重庆名校联盟高三二诊,19)已知椭圆C :x 2a2+y 2b2=1(a>b>0),F 1,F 2为椭圆的左、右焦点,P (1,√22)为椭圆上一点,且|PF 1|=3√2. (1)求椭圆的标准方程;(2)设直线l :x=-2,过点F 2的直线交椭圆于A ,B 两点,线段AB 的垂直平分线分别交直线l 、直线AB 于M ,N 两点,当∠MAN 最小时,求直线AB 的方程.6.(2020天津河北一模,19)已知椭圆C :x 2a 2+y 2b2=1(a>b>0)的离心率为12,直线x+y-√6=0与圆x 2+y 2=b2相切.(1)求椭圆C 的方程;(2)过点P (4,0)的直线l 与椭圆C 交于不同两点A ,B ,线段AB 的中垂线为l 1,若l 1在y 轴上的截距为413,求直线l 的方程.专题突破练25 直线与圆及圆锥曲线1.解(1)由已知可设C 2的方程为y 2=4cx ,其中c=√a 2-b2.不妨设A ,C 在第一象限,由题设得A ,B 的纵坐标分别为b 2a ,-b2a ;C ,D 的纵坐标分别为2c ,-2c ,故|AB|=2b2a,|CD|=4c.由|CD|=43|AB|得4c=8b 23a ,即3×c a =2-2(c a )2,解得c a =-2(舍去),c a=12.所以C 1的离心率为12. (2)由(1)知a=2c ,b=√3c ,故C 1:x 24c 2+y 23c 2=1.设M (x 0,y 0),则x 024c 2+y 023c 2=1,y 02=4cx 0,故x 024c 2+4x03c =1.①由于C 2的准线为x=-c ,所以|MF|=x 0+c ,而|MF|=5,故x 0=5-c ,代入①得(5-c )24c 2+4(5-c )3c=1,即c 2-2c-3=0,解得c=-1(舍去),c=3.所以C 1的标准方程为x 236+y 227=1,C 2的标准方程为y 2=12x.2.解(1)设AB 的中点为M ,切点为N ,连接OM ,MN ,则|OM|+|MN|=|ON|=2,|AB|=|ON|-(|OM|-|MN|)=2-|OM|+12|AB|,即|AB|+2|OM|=4.取A 关于y 轴的对称点A',连接A'B ,则|A'B|=2|OM|, 故|AB|+2|OM|=|AB|+|A'B|=4.所以点B 的轨迹是以A',A 为焦点,长轴长为4的椭圆. 其中a=2,c=√3,b=1,则曲线Γ的方程为x 24+y 2=1.(2)因为B 为CD 的中点,所以OB ⊥CD ,则OB ⃗⃗⃗⃗⃗ ⊥AB ⃗⃗⃗⃗⃗ .设B (x 0,y 0),则x 0(x 0-√3)+y 02=0.又x 024+y 02=1,解得x 0=√3,y 0=±√2√3.则k OB =±√22,k AB =∓√2,则直线AB 的方程为y=±√2(x-√3),即√2x-y-√6=0或√2x+y-√6=0. 3.解设直线l :y=3x+t ,A (x 1,y 1),B (x 2,y 2).(1)由题设得F (34,0), 故|AF|+|BF|=x 1+x 2+3, 由题设可得x 1+x 2=52. 由{y =32x +t ,y 2=3x ,可得9x 2+12(t-1)x+4t 2=0,则x 1+x 2=-12(t -1)9. 从而-12(t -1)9=52,得t=-78.所以l 的方程为y=32x-78. (2)由AP ⃗⃗⃗⃗⃗ =3PB ⃗⃗⃗⃗⃗ 可得y 1=-3y 2. 由{y =32x +t ,y 2=3x可得y 2-2y+2t=0.所以y 1+y 2=2.从而-3y 2+y 2=2,故y 2=-1,y 1=3. 代入C 的方程得x 1=3,x 2=13. 故|AB|=4√133.4.解(1)因为|F 1F 2|是|PF 1|和|PF 2|的等差中项,所以a=2c ,得a 2=4c 2,则b 2=a 2-c 2=3c 2.又P (-1,32)在椭圆上,所以14c 2+94b2=1,即14c 2+34c 2=1,所以c=1.则a 2=4,b 2=3,椭圆的标准方程为x 24+y 23=1.(2)因为P (-1,32),由(1)计算可知A (2,0),H (0,1),当直线MN 与x 轴垂直时,易验证,不合题意.当直线MN 与x 轴不垂直时,设直线MN 的方程为y=kx+1,联立直线与椭圆的方程{y =kx +1,x 24+y 23=1,消去y ,可得(4k 2+3)x 2+8kx-8=0,设M (x 1,y 1),N (x 2,y 2),由韦达定理可得{x 1+x 2=-8k4k 2+3,x 1x 2=-84k 2+3.①由S △HMA =6S △PHN ,可得|AH||MH|=6|NH||PH|,又|AH|=2|PH|, 所以|MH|=3|NH|,得x 1=-3x 2, 代入①,可得{-2x 2=-8k4k 2+3,-3x 22=-84k 2+3,所以3×16k2(4k 2+3)2=84k 2+3,解得k=±√62,所以直线MN 的方程为y=±√62x+1.5.解(1)设椭圆的左焦点F 1(-c ,0)(c>0),则|PF 1|=√(1+c )2+12=3√22,解得c=1,所以|PF 2|=√22,则由椭圆定义|PF 1|+|PF 2|=2a=2√2,∴a=√2,b=1.故椭圆的标准方程为x 22+y 2=1.(2)由题意直线AB 的斜率必定不为零,于是可设直线AB :x=ty+1,联立方程{x =ty +1,x 22+y 2=1,得(t 2+2)y 2+2ty-1=0,∵直线AB 交椭圆于A (x 1,y 1),B (x 2,y 2), ∴Δ=4t 2+4(t 2+2)=8(t 2+1)>0, 由韦达定理得y 1+y 2=-2tt 2+2,y 1y 2=-1t 2+2, 则y N =-t t 2+2,∴x N =ty N +1=-t 2t 2+2+1=2t 2+2.∵MN ⊥AB ,∴k MN =-t ,∴|MN|=√1+t 2·-2-2t 2+2=√1+t 2·2t 2+6t 2+2. 又|AN|=12|AB|=12√1+t 2·|y 1-y 2|=√1+t 2·√2√1+t 2t 2+2,∴tan ∠MAN=|MN |=√2(2√t +1=√2(√t 2+1+√t +1)≥√2·2√2=4.当且仅当√t 2+1=√t +1,即t=±1时取等号.此时直线AB 的方程为x+y-1=0或x-y-1=0.6.解(1)由题意得,{e =c a =12,b =√6|1+1=√3,又a 2=b 2+c 2,∴a=2.∴椭圆C 的方程为x 24+y 23=1.(2)由题意,直线l 的斜率k 存在且不为零. 设直线l 的方程为y=k (x-4),k ≠0.设A (x 1,y 1),B (x 2,y 2),AB 的中点Q (x 0,y 0). 由{y =k (x -4),x 24+y 23=1,消去y ,整理得(3+4k 2)x 2-32k 2x+64k 2-12=0. 由Δ=(-32k 2)2-4(3+4k 2)(64k 2-12)>0, 解得-12<k<12,且k ≠0,∴x 1+x 2=32k23+4k2.∴x 0=16k 23+4k2,y 0=k (x 0-4)=-12k 3+4k2.∴Q (16k23+4k2,-12k 3+4k2).由题意可知,l 1:y-y 0=-1(x-x 0),即y+12k3+4k 2=-1(x -16k23+4k2). 化简得,y=-1k x+4k 3+4k 2.令x=0,4k 3+4k 2=413.解得k=14或k=3.∵-12<k<12,且k ≠0,∴k=14.故直线l 的方程为y=14(x-4),即x-4y-4=0.。
圆锥曲线中的定点、定值、定线与探索性问题-专题突破

证明:点 P 在定直线上.
解 (1)设双曲线 C 的方程为ax22-by22=1(a>0,b>0),由焦点坐标可知 c=2 5,
则由 e=ac= 5可得 a=2,b= c2-a2=4, 故 C 的方程为x42-1y62 =1.
所以 y1y2=-8,又yy2122==22xx12,, 所以 y21y22=4x1x2=64,
即 x1x2=16,则 k1k2=yx11·yx22=-168=-12.
目录 精做大题 1 2 3 4 5 6 7 8
解
②设直线 PQ 的方程为 x=ty+n(n≠0),P(x3,y3),Q(x4,y4),
因为 A(-2,0),则直线 AP:y=x1y+1 2(x+2),
令 x=0,解得 y=x12+y12,即 M0,x12+y12,
目录 精做大题 1 2 3 4 5 6 7 8
解
同理可得 N0,x22+y22,
则x12+y12+2 x22+y22=k(x1x+1+2)2 +3+k(x2x+2+2)2 +3
解 (1)易知直线 2x+4y-1=0 与 x 轴交于点12,0, 即焦点坐标为12,0,所以p2=12,p=1,则抛物线 C 的标准方程为 y2=2x.
(2)证明:①设直线 MN 的方程为 x=my+4,M(x1,y1),N(x2,y2),
联立方程组yx2==m2yx+,4,得 y2-2my-8=0,Δ=4m2+32>0,
目录 精做大题 1 2 3 4 5 6 7 8
解
二、模拟大题 3.(2024·四川巴蜀中学高三适应性月考(二))如图 所示,点 F1,A 分别为椭圆 E:ax22+by22=1(a>b>0)的 左焦点和右顶点,点 F 为抛物线 C:y2=16x 的焦点, 且|OF|=2|OA|=4|OF1|(O 为坐标原点). (1)求椭圆 E 的方程; (2)过点 F1 作直线 l 交椭圆 E 于 B,D 两点,连接 AB,AD 并延长交抛物线的准线于点 M,N,求证:∠MF1N 为定值.
2024年高考数学第一轮复习专题训练第八章 §8.9 圆锥曲线压轴小题突破练[培优课]
![2024年高考数学第一轮复习专题训练第八章 §8.9 圆锥曲线压轴小题突破练[培优课]](https://img.taocdn.com/s3/m/8b7124317ed5360cba1aa8114431b90d6d858940.png)
§8.9 圆锥曲线压轴小题突破练题型一 离心率范围问题例1 (1)已知F 是椭圆x 2a 2+y 2b 2=1(a >b >0)的右焦点,若直线x =a 2c与x 轴的交点为A ,在椭圆上存在点P 满足线段AP 的垂直平分线过点F ,则椭圆的离心率的取值范围是( )A.⎝⎛⎦⎤0,22B.⎝⎛⎭⎫0,12 C .[2-1,1]D.⎣⎡⎭⎫12,1 (2)(2022·哈尔滨模拟)已知双曲线的方程是x 2a 2-y 2b2=1(a >0,b >0),点F 1,F 2为双曲线的两个焦点,以F 1F 2为直径的圆与双曲线相交于点P (点P 在第一象限),若∠PF 1F 2≤π6,则双曲线离心率的取值范围是( )A.⎣⎢⎡⎭⎪⎫1+32,+∞ B .[3+1,+∞) C.⎝⎛⎦⎥⎤1,3+12 D .(1,3+1] 听课记录:______________________________________________________________ ________________________________________________________________________ 思维升华 求解圆锥曲线离心率范围问题的策略(1)利用圆锥曲线的定义,以及余弦定理或勾股定理,构造关于a ,b ,c 的不等式或不等式组求解,要注意椭圆、双曲线离心率自身的范围.(2)利用圆锥曲线的性质,如:椭圆的最大角、通径、三角形中的边角关系、曲线上的点到焦点距离的范围等,建立不等式(不等式组).(3)利用几何图形中几何量的大小,例如线段的长度、角的大小等,构造几何度量之间的关系. 跟踪训练1 (1)(2022·南京市宁海中学模拟)设e 1,e 2分别为具有公共焦点F 1与F 2的椭圆和双曲线的离心率,P 为两曲线的一个公共点,且满足∠F 1PF 2=π3,则e 1e 2的最小值为( ) A.32 B.32 C.34 D.34(2)已知椭圆C :x 2a 2+y 2b2=1(a >b >0),点P 是C 上任意一点,若圆O :x 2+y 2=b 2上存在点M ,N ,使得∠MPN =120°,则C 的离心率的取值范围是( )A.⎝⎛⎦⎤0,32B.⎣⎡⎭⎫32,1 C.⎝⎛⎦⎤0,12 D.⎣⎡⎭⎫12,1题型二 圆锥曲线中二级结论的应用命题点1 椭圆、双曲线中二级结论的应用例2 (1)(2022·咸宁模拟)已知椭圆C :x 2a 2+y 2b 2=1(a >b >0),其左、右焦点分别为F 1,F 2,其离心率e =12,点P 为该椭圆上一点,且满足∠F 1PF 2=π3,已知△F 1PF 2的内切圆半径为r =3,则该椭圆的长轴长为( )A .2B .4C .6D .12(2)(2022·石家庄模拟)已知双曲线C :x 2a 2-y 2b2=1(a >0,b >0),过原点O 的直线交C 于A ,B 两点(点B 在右支上),双曲线右支上一点P (异于点B )满足BA →·BP →=0,直线P A 交x 轴于点D ,若∠ADO =∠AOD ,则双曲线C 的离心率为( )A. 2 B .2 C. 3 D .3听课记录:______________________________________________________________ ________________________________________________________________________ 思维升华 焦点三角形的面积公式:P 为椭圆(或双曲线)上异于长轴端点的一点,且∠F 1PF 2=θ,则椭圆中12PF F S △=b 2·tan θ2, 双曲线中12PF F S △=b 2tan θ2.周角定理:已知A ,B 为椭圆(或双曲线)上关于原点对称的两点,点P 为椭圆(或双曲线)上异于A ,B 的任一点,则椭圆中k P A ·k PB =-b 2a2, 双曲线中k P A ·k PB =b 2a2. 跟踪训练2 (1)如图,F 1,F 2是椭圆C 1:x 24+y 2=1与双曲线C 2的公共焦点,A ,B 分别是C 1,C 2在第二、四象限的公共点.若四边形AF 1BF 2为矩形,则C 2的离心率是( )A. 2B. 3C.32D.62(2)设椭圆x 2a 2+y 2b 2=1(a >b >0)的左、右焦点分别为F 1,F 2,上、下顶点分别为A ,B ,直线AF 2与该椭圆交于A ,M 两点,若∠F 1AF 2=90°,则直线BM 的斜率为( )A.13B.12 C .-1 D .-12命题点2 抛物线中二级结论的应用例3 (1)(2022·“四省八校”联考)已知抛物线y 2=4x 过焦点F 的直线与抛物线交于A ,B 两点,则2|AF |+|BF |的最小值为( )A .2B .26+3C .4D .3+22(2)(2023·长沙模拟)已知抛物线C :y 2=16x ,倾斜角为π6的直线l 过焦点F 交抛物线于A ,B 两点,O 为坐标原点,则△ABO 的面积为________.听课记录:______________________________________________________________ ________________________________________________________________________ 思维升华 与抛物线的焦点弦有关的二级结论:若倾斜角为α⎝⎛⎭⎫α≠0,π2的直线l 经过抛物线y 2=2px (p >0)的焦点,且与抛物线相交于A (x 1,y 1),B (x 2,y 2)(y 1>y 2)两点,则①焦半径|AF |=x 1+p 2=p 1-cos α, |BF |=x 2+p 2=p 1+cos α, ②焦点弦长|AB |=x 1+x 2+p =2p sin 2α, ③S △OAB =p 22sin α(O 为坐标原点), ④x 1x 2=p 24,y 1y 2=-p 2, ⑤1|AF |+1|BF |=2p, ⑥以AB 为直径的圆与准线相切,以F A 为直径的圆与y 轴相切.跟踪训练3 已知A ,B 是过抛物线y 2=2px (p >0)焦点F 的直线与抛物线的交点,O 是坐标原点,且满足AB →=3FB →,S △OAB =23|AB |,则|AB |的值为( ) A.92 B.29C .4D .2 题型三 圆锥曲线与其他知识的综合例4 (多选)油纸伞是中国传统工艺品,至今已有1 000多年的历史,为宣传和推广这一传统工艺,某市文化宫于春分时节开展油纸伞文化艺术节.活动中,某油纸伞撑开后摆放在户外展览场地上,如图所示,该伞的伞沿是一个半径为1的圆,圆心到伞柄底端的距离为1,阳光照射油纸伞在地面上形成了一个椭圆形的影子(春分时,该市的阳光照射方向与地面的夹角为60°),若伞柄底端正好位于该椭圆的左焦点位置,则( )A .该椭圆的离心率为3-12B .该椭圆的离心率为2-3C .该椭圆的焦距为32-63D .该椭圆的焦距为23-1听课记录:______________________________________________________________ ________________________________________________________________________思维升华 高考对圆锥曲线的考查,经常出现一些与其他知识交汇的题目,如与平面向量交汇、与三角函数交汇、与不等式交汇、与导数交汇等等,这些问题的实质是圆锥曲线问题,体现出数学的应用性.跟踪训练4 (多选)(2022·福州质检)如图为陕西博物馆收藏的国宝——唐·金筐宝钿团花纹金杯,杯身曲线内收,巧夺天工,是唐代金银细作的典范.该杯的主体部分可以近似看作是双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的右支与直线x =0,y =4,y =-2围成的曲边四边形ABMN 绕y 轴旋转一周得到的几何体,若该金杯主体部分的上口外直径为1033,下底外直径为2393,双曲线C 与坐标轴交于D ,E 两点,则( )A .双曲线C 的方程为x 23-y 29=1 B .双曲线y 23-x 2=1与双曲线C 共渐近线 C .存在一点,使过该点的任意直线与双曲线C 有两个交点D .存在无数个点,使它与D ,E 两点的连线的斜率之积为3。
圆锥曲线(学生版)--2024年高考数学大题突破

圆锥曲线目录【题型一】轨迹【题型二】新结构卷中19题“定义”型轨迹【题型三】直线所过定点不在坐标轴上【题型四】面积比值范围型【题型五】非常规型四边形面积最值型【题型六】“三定”型:圆过定点【题型七】“三定”型:斜率和定【题型八】“三定”型:斜率积定【题型九】圆锥曲线切线型【题型十】“韦达定理”不能直接用【题型十一】“非韦达”型:点带入型【题型一】轨迹求轨迹方程的常见方法有:(1)直译法:直接将条件翻译成等式,整理化简后即得动点的轨迹方程;(2)定义法:如果能确定动点的轨迹满足某种已知曲线的定义,则可利用曲线的定义写出方程;(3)相关点法:用动点Q的坐标x、y表示相关点P的坐标x0、y0,然后代入点P的坐标x0,y0所满足的曲线方程,整理化简可得出动点Q的轨迹方程;(4)参数法:当动点坐标x、y之间的直接关系难以找到时,往往先寻找x、y与某一参数t得到方程,即为动点的轨迹方程;(5)交轨法:将两动曲线方程中的参数消去,得到不含参数的方程,即为两动曲线交点的轨迹方程.1(2024·重庆·模拟预测)已知点F-1,0和直线m:x=2,点P到m的距离d=4-2PF.(1)求点P的轨迹方程;(2)不经过圆点O的直线l与点P的轨迹交于A,B两点. 设直线OA,OB的斜率分别为k1,k2,记k1k2 =t,是否存在t值使得△OAB的面积为定值,若存在,求出t的值;若不存在,说明理由.2(2024·辽宁·一模)已知平面上一动点P到定点F12,0的距离比到定直线x=-2023的距离小40452,记动点P的轨迹为曲线C.(1)求C的方程;(2)点A2,1,M,N为C上的两个动点,若M,N,B恰好为平行四边形MANB的其中三个顶点,且该平行四边形对角线的交点在第一、三象限的角平分线上,记平行四边形MANB的面积为S,求证:S≤86 9.3(2024·山东淄博·一模)在平面直角坐标系xOy 中,点.F 5,0 ,点P x ,y 是平面内的动点.若以PF 为直径的圆与圆D :x 2+y 2=1相切,记点P 的轨迹为曲线C .(1)求C 的方程;(2)设点A (1,0),M (0,t ),N (0,4-t )(t ≠2),直线AM ,AN 分别与曲线C 交于点S ,T (S ,T 异于A ),过点A 作AH ⊥ST ,垂足为H ,求|OH |的最大值.【题型二】新结构卷中19题“定义”型轨迹1(2024·新疆乌鲁木齐·二模)在平面直角坐标系xOy 中,重新定义两点A x 1,y 1 ,B x 2,y 2 之间的“距离”为AB =x 2-x 1 +y 2-y 1 ,我们把到两定点F 1-c ,0 ,F 2c ,0 c >0 的“距离”之和为常数2a a >c 的点的轨迹叫“椭圆”.(1)求“椭圆”的方程;(2)根据“椭圆”的方程,研究“椭圆”的范围、对称性,并说明理由;(3)设c =1,a =2,作出“椭圆”的图形,设此“椭圆”的外接椭圆为C ,C 的左顶点为A ,过F 2作直线交C 于M ,N 两点,△AMN 的外心为Q ,求证:直线OQ 与MN 的斜率之积为定值.2(2024·湖南·二模)直线族是指具有某种共同性质的直线的全体,例如x=ty+1表示过点(1,0)的直线,直线的包络曲线定义为:直线族中的每一条直线都是该曲线上某点处的切线,且该曲线上的每一点处的切线都是该直线族中的某条直线.(1)若圆C1:x2+y2=1是直线族mx+ny=1(m,n∈R)的包络曲线,求m,n满足的关系式;(2)若点P x0,y0不在直线族:Ω:(2a-4)x+4y+(a-2)2=0(a∈R)的任意一条直线上,求y0的取值范围和直线族Ω的包络曲线E;(3)在(2)的条件下,过曲线E上A,B两点作曲线E的切线l1,l2,其交点为P.已知点C0,1,若A,B,C三点不共线,探究∠PCA=∠PCB是否成立?请说明理由.3(2024·全国·模拟预测)已知复平面上的点Z对应的复数z满足z2-z2-9=7,设点Z的运动轨迹为W.点 O 对应的数是0.(1)证明W是一个双曲线并求其离心率e;(2)设W的右焦点为 F1 ,其长半轴长为L,点Z到直线x=Le的距离为d(点Z在W的右支上),证明:ZF1=ed;(3)设W的两条渐近线分别为 l1,l2 ,过Z分别作 l1,l2 的平行线l3,l4分别交l2,l1于点 P,Q ,则平行四边形OPZQ的面积是否是定值?若是,求该定值;若不是,说明理由.【题型三】直线所过定点不在坐标轴上存在性问题求解的思路及策略(1)思路:先假设存在,推证满足条件的结论,若结论正确则存在;若结论不正确则不存在.(2)策略:①当条件和结论不唯一时要分类讨论;②当给出结论而要推导出存在的条件时,先假设成立,再推出条件;③当条件和结论都不知,按常规法解题很难时,可先由特殊情况探究,再推广到一般情况.1已知点M 是抛物线C :x 2=2py p >0 的对称轴与准线的交点,过M 作抛物线的一条切线,切点为P ,且满足PM =22.(1)求抛物线C 的方程;(2)过A -1,1 作斜率为2的直线与抛物线C 相交于点B ,点T 0,t t >0 ,直线AT 与BT 分别交抛物线C 于点E ,F ,设直线EF 的斜率为k ,是否存在常数λ,使得t =λk ?若存在,求出λ值;若不存在,请说明理由.2已知双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的离心率为233,点P 2,3 到其左右焦点F 1,F 2的距离的差为2.(1)求双曲线C 的方程;(2)在直线x +2y +t =0上存在一点Q ,过Q 作两条相互垂直的直线均与双曲线C 相切,求t 的取值范围.3已知双曲线C :x 2a 2-y 2b2=1(a >0,b >0)上任意一点Q (异于顶点)与双曲线两顶点连线的斜率之积为19,E 在双曲线C 上,F 为双曲线C 的右焦点,|EF |的最小值为10-3.(1)求双曲线C 的标准方程;(2)过椭圆x 2m 2+y 2n2=1(m >n >0)上任意一点P (P 不在C 的渐近线上)分别作平行于双曲线两条渐近线的直线,交两渐近线于M ,N 两点,且|PM |2+|PN |2=5,是否存在m ,n 使得椭圆的离心率为223?若存在,求出椭圆的方程,若不存在,说明理由.【题型四】面积比值范围型圆锥曲线中取值范围问题的五种求解策略:(1)利用圆锥曲线的几何性质或判别式构造不等关系,从而确定参数的取值范围;(2)利用已知参数的范围,求新的参数的范围,解这类问题的核心是建立两个参数之间的等量关系;(3)利用隐含的不等关系建立不等式,从而求出参数的取值范围;(4)利用已知的不等关系建立不等式,从而求出参数的取值范围;(5)利用求函数值域的方法将待求量表示为其他变量的函数,求其值域,从而确定参数的取值范围.1(2022·全国·高三专题练习)F c,0是椭圆C:x2a2+y2b2=1a>b>0的右焦点,其中c∈N*.点A、B分别为椭圆E的左、右顶点,圆F过点B与坐标原点O,P是椭圆上异于A、B的动点,且△PBF的周长小于8.(1)求C的标准方程;(2)连接BP与圆F交于点Q,若OQ与AP交于点M,求S△OPQS△MBQ的取值范围.2(2023下·福建福州·高三校考)如图,已知圆C:x2a2+y2b2=1(a>b>0)的左顶点A(-2,0),过右焦点F的直线l与椭圆C相交于M,N两点,当直线l⊥x轴时,|MN|=3.(1)求椭圆C的方程;(2)记△AMF,△ANF的面积分别为S1,S2,求S1S2的取值范围.3(2022·湖北黄冈·蕲春县第一高级中学校考模拟预测)已知椭圆C :x 2a 2+y 2b2=1(a >b >0)的左、右顶点分别为A 1,A 2,左、右焦点分别为F 1,F 2,圆A 2:(x -2)2+y 2=r 2(r >0),椭圆C 与圆A 2交于点D ,且k DA2⋅k DA 1=-34.(1)求椭圆方程.(2)若过椭圆右焦点F 2的直线l 与椭圆C 交于P ,Q 两点,与圆A 2交于M ,N 两点,且S △A 1PQS △A 2MN=3,求r 的取值范围.【题型五】非常规型四边形面积最值型求非常规型四边形的面积最大值,首先要选择合适的面积公式,对于非常规四边形,如果使用的面积公式为S DMEN=12x N-x My1-y2,为此计算y1-y2,x N-x M代入转化为k的函数求最大值.1(2023·全国·高三专题练习)已知圆O:x2+y2=4,O为坐标原点,点K在圆O上运动,L为过点K的圆的切线,以L为准线的拋物线恒过点F1-3,0,F23,0,抛物线的焦点为S,记焦点S的轨迹为S.(1)求S的方程;(2)过动点P的两条直线l1,l2均与曲线S相切,切点分别为A,B,且l1,l2的斜率之积为-1,求四边形PAOB面积的取值范围.2(2023·全国·高三专题练习)已知F1,F2是椭圆C:x2a2+y2b2=1(a>b>0)的左右焦点,以F1F2为直径的圆和椭圆C在第一象限的交点为G,若三角形GF1F2的面积为1,其内切圆的半径为2-3.(1)求椭圆C的方程;(2)已知A是椭圆C的上顶点,过点P-2,1的直线与椭圆C交于不同的两点D,E,点D在第二象限,直线AD、AE分别与x轴交于M,N,求四边形DMEN面积的最大值.3(2023·全国·高三专题练习)如图.已知圆M :(x -2)2+y 2=81,圆N :(x +2)2+y 2=1.动圆S 与这两个圆均内切.(1)求圆心S 的轨迹C 的方程;(2)若P 2,3 、Q 2,-3 是曲线C 上的两点,A 、B 是曲线C 上位于直线PQ 两侧的动点.若直线AB 的斜率为12,求四边形APBQ 面积的最大值.【题型六】“三定”型:圆过定点圆过定点思维:1.可以根据特殊性,计算出定点,然后证明2.利用以“某线段为直径”,转化为向量垂直计算2.利用对称性,可以猜想出定点,并证明。
高考数学(文科)2轮专题突破训练:专题6 直线、圆、圆锥曲线 专题能力训练17 Word版含答案

本资源的初衷 ,是希望通过网络分享 ,能够为广阔读者提供更好的效劳 ,为您水平的提高提供坚强的动力和保证 .内容由一线名师原创 ,立意新 ,图片精 ,是非常强的一手资料 .专题能力训练17直线与圆锥曲线一、能力突破训练1.过抛物线C:y2 =4x的焦点F,且斜率为的直线交C于点M(M在x轴的上方),l为C的准线,点N 在l上且MN⊥l,那么M到直线NF的距离为()A.B.2C.2D.32.与抛物线y2 =8x相切倾斜角为135°的直线l与x轴和y轴的交点分别是A和B,那么过A,B两点的最|小圆截抛物线y2 =8x的准线所得的弦长为()A.4B.2C.2D.3.设抛物线C:y2 =4x的焦点为F,直线l过F且与C交于A,B两点.假设|AF| =3|BF|,那么l的方程为()A.y =x -1或y = -x +1B.y =(x -1)或y = -(x -1)C.y =(x -1)或y = -(x -1)D.y =(x -1)或y = -(x -1)4.在平面直角坐标系xOy中,双曲线C1: =1(a>0,b>0)的渐近线与抛物线C2:x2 =2py(p>0)交于点O,A,B.假设△OAB的垂心为C2的焦点,那么C1的离心率为.5.(2021全国Ⅱ,文20)设抛物线C:y2 =4x的焦点为F,过点F且斜率为k(k>0)的直线l与C交于A,B 两点,|AB| =8.(1)求l的方程.(2)求过点A,B且与C的准线相切的圆的方程.6.椭圆C的两个顶点分别为A( -2,0),B(2,0),焦点在x轴上,离心率为.(1)求椭圆C的方程;(2)点D为x轴上一点,过D作x轴的垂线交椭圆C于不同的两点M,N,过D作AM的垂线交BN于点E.求证:△BDE与△BDN的面积之比为4∶5.7.在平面直角坐标系xOy中,过椭圆M: =1(a>b>0)右焦点的直线x +y - =0交M于A,B两点,P为AB的中点,且OP的斜率为.(1)求M的方程;(2)C,D为M上两点,假设四边形ACBD的对角线CD⊥AB,求四边形ACBD面积的最|大值.8.椭圆C的中|心在坐标原点,右焦点为F(1,0),A,B是椭圆C的左、右顶点,D是椭圆C上异于A,B的动点,且△ADB面积的最|大值为.(1)求椭圆C的方程.(2)是否存在一定点E(x0,0)(0<x0<),使得当过点E的直线l与曲线C相交于M,N两点时,为定值?假设存在,求出定点和定值;假设不存在,请说明理由.二、思维提升训练9.(2021全国Ⅲ,文20)斜率为k的直线l与椭圆C: =1交于A,B两点,线段AB的中点为M(1,m)(m>0).(1)证明:k< -;(2)设F为C的右焦点,P为C上一点,且 =0.证明:2|| =|| +||.10.椭圆E: =1(a>b>0)的一个焦点与短轴的两个端点是正三角形的三个顶点,点P在椭圆E上.(1)求椭圆E的方程;(2)设不过原点O且斜率为的直线l与椭圆E交于不同的两点A,B,线段AB的中点为M,直线OM与椭圆E交于C,D,证明:|MA|·|MB| =|MC|·|MD|.11.如图,在平面直角坐标系xOy中,椭圆E: =1(a>b>0)的左、右焦点分别为F1,F2,离心率为,两准线之间的距离为8.点P在椭圆E上,且位于第|一象限,过点F1作直线PF1的垂线l1,过点F2作直线PF2的垂线l2.(1)求椭圆E的标准方程;(2)假设直线l1,l2的交点Q在椭圆E上,求点P的坐标.专题能力训练17直线与圆锥曲线一、能力突破训练1.C解析由题意可知抛物线的焦点F(1,0),准线l的方程为x = -1,可得直线MF:y =(x -1),与抛物线y2 =4x联立,消去y得3x2 -10x +3 =0,解得x1 =,x2 =3.因为M在x轴的上方,所以M (3,2).因为MN⊥l,且N在l上,所以N( -1,2).因为F(1,0),所以直线NF:y = -(x -1).所以M到直线NF的距离为 =2. 2.C解析设直线l的方程为y = -x +b,联立直线与抛物线方程,消元得y2 +8y -8b =0.因为直线与抛物线相切,所以Δ =82 -4×( -8b) =0,解得b = -2,故直线l的方程为x +y +2 =0,从而A( -2,0),B(0, -2).因此过A,B两点的最|小圆即为以AB为直径的圆,其方程为(x +1)2 +(y +1)2 =2,而抛物线y2 =8x的准线方程为x = -2,此时圆心( -1, -1)到准线的距离为1,故所截弦长为2 =2.3.C解析由题意可得抛物线焦点F(1,0),准线方程为x = -1.当直线l的斜率大于0时,如图,过A,B两点分别向准线x = -1作垂线,垂足分别为M,N,那么由抛物线定义可得,|AM| =|AF|,|BN| =|BF|.设|AM| =|AF| =3t(t>0),|BN| =|BF| =t,|BK| =x,而|GF| =2,在△AMK中,由,得,解得x =2t,那么cos∠NBK =,∴∠NBK =60°,那么∠GFK =60°,即直线AB的倾斜角为60°.∴斜率k =tan 60° =,故直线方程为y =(x -1).当直线l的斜率小于0时,如图,同理可得直线方程为y = -(x -1),应选C.4.解析双曲线的渐近线为y =±x.由得A.由得B.∵F为△OAB的垂心,∴k AF·k OB = -1,即 = -1,解得,∴,即可得e =.5.解(1)由题意得F(1,0),l的方程为y =k(x -1)(k>0).设A(x1,y1),B(x2,y2).由得k2x2 -(2k2 +4)x +k2 =0.Δ =16k2 +16>0,故x1 +x2 =.所以|AB| =|AF| +|BF| =(x1 +1) +(x2 +1) =;由题设知 =8,解得k = -1(舍去),k =1.因此l的方程为y =x -1.(2)由(1)得AB的中点坐标为(3,2),所以AB的垂直平分线方程为y -2 = -(x -3),即y = -x +5.设所求圆的圆心坐标为(x0,y0),那么解得因此所求圆的方程为(x -3)2 +(y -2)2 =16或(x -11)2 +(y +6)2 =144.6.(1)解设椭圆C的方程为 =1(a>b>0).由题意得解得c =.所以b2 =a2 -c2 =1.所以椭圆C的方程为 +y2 =1.(2)证明设M(m,n),那么D(m,0),N(m, -n).由题设知m≠±2,且n≠0.直线AM的斜率k AM =,故直线DE的斜率k DE = -.所以直线DE的方程为y = -(x -m),直线BN的方程为y =(x -2).联立解得点E的纵坐标y E = -.由点M在椭圆C上,得4 -m2 =4n2.所以y E = -n.又S△BDE =|BD|·|y E| =|BD|·|n|,S△BDN =|BD|·|n|,所以△BDE与△BDN的面积之比为4∶5.7.解(1)设A(x1,y1),B(x2,y2),P(x0,y0),那么 =1, =1, = -1,由此可得 = - =1.因为x1 +x2 =2x0,y1 +y2 =2y0,,所以a2 =2b2.又由题意知,M的右焦点为(,0),所以a2 -b2 =3.所以a2 =6,b2 =3.所以M的方程为 =1.(2)由解得因此|AB| =.由题意可设直线CD的方程为y =x +n,设C(x3,y3),D(x4,y4).由得3x2 +4nx +2n2 -6 =0.于是x3,4 =.因为直线CD的斜率为1,所以|CD| =|x4 -x3| =.由,四边形ACBD的面积S =|CD|·|AB| =.当n =0时,S取得最|大值,最|大值为.所以四边形ACBD面积的最|大值为.8.解(1)设椭圆的方程为 =1(a>b>0),由可得△ADB的面积的最|大值为·2a·b =ab =.①∵F(1,0)为椭圆右焦点,∴a2 =b2 +1.②由①②可得a =,b =1,故椭圆C的方程为 +y2 =1.(2)过点E取两条分别垂直于x轴和y轴的弦M1N1,M2N2,那么,即,解得x0 =,∴E假设存在必为,定值为3.证明如下:设过点E的直线方程为x =ty +,代入C中得(t2 +2)y2 +ty - =0.设M(x1,y1),N(x2,y2),那么y1 +y2 = - = -,y1y2 = -,=== =3.综上得定点为E,定值为3.二、思维提升训练9.证明(1)设A(x1,y1),B(x2,y2),那么 =1, =1.两式相减,并由 =k得·k =0.由题设知 =1, =m,于是k = -.由题设得0<m<,故k< -.(2)由题意得F(1,0).设P(x3,y3),那么(x3 -1,y3) +(x1 -1,y1) +(x2 -1,y2) =(0,0).由(1)及题设得x3 =3 -(x1 +x2) =1,y3 = -(y1 +y2) = -2m<0.又点P在C上,所以m =,从而P,|| =.于是|| == =2 -.同理|| =2 -.所以|| +|| =4 -(x1 +x2) =3.故2|| =|| +||.10.(1)解由,a =2b.又椭圆 =1(a>b>0)过点P,故 =1,解得b2 =1.所以椭圆E的方程是 +y2 =1.(2)证明设直线l的方程为y =x +m(m≠0),A(x1,y1),B(x2,y2),由方程组得x2 +2mx +2m2 -2 =0,①方程①的判别式为Δ =4(2 -m2).由Δ>0,即2 -m2>0,解得 -<m<.由①得x1 +x2 = -2m,x1x2 =2m2 -2.所以M点坐标为,直线OM方程为y = -x.由方程组得C,D.所以|MC|·|MD| =( -m +)· +m) =(2 -m2).又|MA|·|MB| =|AB|2 =[(x1 -x2)2 +(y1 -y2)2] =[(x1 +x2)2 -4x1x2] =[4m2 -4(2m2 -2)] =(2 -m2).所以|MA|·|MB| =|MC|·|MD|.11.解(1)设椭圆的半焦距为c.因为椭圆E的离心率为,两准线之间的距离为8,所以 =8,解得a =2,c =1,于是b =,因此椭圆E的标准方程是 =1.(2)由(1)知,F1( -1,0),F2(1,0).设P(x0,y0),因为P为第|一象限的点,故x0>0,y0>0.当x0 =1时,l2与l1相交于F1,与题设不符.当x0≠1时,直线PF1的斜率为,直线PF2的斜率为.因为l1⊥PF1,l2⊥PF2,所以直线l1的斜率为 -,直线l2的斜率为 -,从而直线l1的方程:y = -(x +1),①直线l2的方程:y = -(x -1).②由①②,解得x = -x0,y =,所以Q.因为点Q在椭圆上,由对称性,得 =±y0,即 =1或 =1.又P在椭圆E上,故 =1.由解得x0 =,y0 =无解.因此点P的坐标为.。
2023年高考数学总复习第12讲:直线与圆、圆锥曲线(附答案解析)

2023年高考数学总复习第12讲:直线与圆、圆锥曲线
一.选择题(共10小题,满分50分,每小题5分)
1.(5分)(2022春•温州期末)已知直线kx﹣y+k﹣1=0与圆(x﹣2)2+y2=1有两个不同的交点,则实数k的取值范围是()
A .
B .
C .
D .
2.(5分)(2022春•萧县校级月考)直线l的方程为:x=﹣3,则直线l的倾斜角是()A .B .C.πD.0
3.(5分)(2022春•海淀区校级月考)不论m为何实数,直线x﹣2my﹣1+3m=0恒过一个定点,则这个定点的坐标为()
A.(1,0)B.(2,3)C.(3,2)D .
4.(5分)(2022春•海淀区校级月考)已知直线l:y=k(x﹣2)+2,当k变化时,点P(﹣1,2)到直线l的距离的取值范围是()
A.[0,+∞)B.[0,2]C.[0,3]D.[0,3)
5.(5分)(2022春•南京月考)已知椭圆C :=1(a>b>0)的左、右焦点分别为F1、F2,P为C上的一点,且∠F1PF2=60°,|PF1|=3|PF2|,则椭圆C的离心率为()A .B .C .D .
6.(5分)(2022•甲卷)椭圆C
:+=1(a>b>0)的左顶点为A,点P,Q均在C
上,且关于y轴对称.若直线AP,AQ 的斜率之积为,则C的离心率为()
A .
B .
C .
D .
7.(5分)(2022•甲卷)已知椭圆C :+=1(a>b>0)的离心率为,A1,A2分别
为C的左、右顶点,B为C
的上顶点.若•=﹣1,则C的方程为()
A .+=1
B .+=1
第1页(共47页)。
高考数学二轮复习 专题七 圆锥曲线 专题突破练21 直线与圆及圆锥曲线 文

亲爱的同学:这份试卷将再次记录你的自信、沉着、智慧和收获,我们一直投给你信任的目光……学习资料专题专题突破练21 直线与圆及圆锥曲线1.(节选)已知圆M:x2+y2=r2(r>0)与直线l1:x-y+4=0相切,设点A为圆上一动点,AB⊥x轴于B,且动点N满足=2,设动点N的轨迹为曲线C.(1)求曲线C的方程;(2)略.2.(2018河北唐山一模,文20)已知椭圆Γ:=1(a>b>0)的左焦点为F,上顶点为A,长轴长为2,B为直线l:x=-3上的动点,M(m,0)(m<0),AM⊥BM.当AB⊥l时,M与F重合.(1)求椭圆Γ的方程;(2)若C为椭圆Γ上一点,满足AC∥BM,∠AMC=60°,求m的值.3.已知圆O:x2+y2=4,点A(,0),以线段AB为直径的圆内切于圆O,记点B的轨迹为Γ.(1)求曲线Γ的方程;(2)直线AB交圆O于C,D两点,当B为CD的中点时,求直线AB的方程.4.已知圆M的圆心M在x轴上,半径为1,直线l:y=x-被圆M所截的弦长为,且圆心M在直线l的下方.(1)求圆M的方程;(2)设A(0,t),B(0,t+6)(-5≤t≤-2),若圆M是△ABC的内切圆,求△ABC的面积S的最大值和最小值.5.(2018山西吕梁一模,文20)已知椭圆C:=1(a>b>0)过E1,,且离心率为e=.(1)求椭圆C的方程;(2)过右焦点F的直线l与椭圆交于A,B两点,D点坐标为(4,3),求直线DA,DB的斜率之和.6.(2018河南六市联考一,文20)已知椭圆=1(a>b>0)的左右焦点分别为F1,F2,上顶点为M,若直线MF1的斜率为1,且与椭圆的另一个交点为N,△F2MN的周长为4.(1)求椭圆的标准方程;(2)过点F1的直线l(直线l的斜率不为1)与椭圆交于P,Q两点,点P在点Q的上方,若,求直线l的斜率.参考答案专题突破练21直线与圆及圆锥曲线1.解 (1)设动点N(x,y),A(x0,y0),因为AB⊥x轴于B,所以B(x0,0).设圆M的方程为M:x2+y2=r2,由题意得r==2,所以圆M的方程为M:x2+y2=4.由题意,=2,所以(0,-y0)=2(x0-x,-y),即将A(x,2y)代入圆M:x2+y2=4,得动点N的轨迹方程为+y2=1.(2)略.2.解 (1)依题意得A(0,b),F(-c,0),当AB⊥l时,B(-3,b),由AF⊥BF得k AF·k BF==-1,又b2+c2=6,解得c=2,b=.所以,椭圆Γ的方程为=1.(2)由(1)得A(0,),所以=-,又AM⊥BM,AC∥BM,所以AC⊥BM,△AMC为直角三角形,所以k BM=k AC=-k AM=,所以直线AC的方程为y=x+,y=x+=1联立得(2+3m2)x2+12mx=0,所以x C=,|AM|=,|AC|=(m<0), 在Rt△AMC中,由∠AMC=60°得|AC|=|AM|,整理得(m+)2=0,解得m=-.3.解(1)设AB的中点为M,切点为N,连接OM,MN,则|OM|+|MN|=|ON|=2,|AB|=|ON|-(|OM|-|MN|)=2-|OM|+|AB|,即|AB|+2|OM|=4.取A关于y轴的对称点A',连接A'B,则|A'B|=2|OM|,故|AB|+2|OM|=|AB|+|A'B|=4.所以点B的轨迹是以A',A为焦点,长轴长为4的椭圆.其中a=2,c=,b=1,则曲线Γ的方程为+y2=1.(2)因为B为CD的中点,所以OB⊥CD,则.设B(x0,y0),则x0(x0-)+=0.又=1,解得x0=,y0=±.则k OB=±,k AB=∓,则直线AB的方程为y=±(x-),即x-y-=0或x+y-=0.4.解 (1)设圆心M(a,0),由已知得圆心M到直线l:8x-6y-3=0的距离为,∴,又∵圆心M在直线l的下方,∴8a-3>0,∴8a-3=5,a=1.故圆M的方程为(x-1)2+y2=1.(2)由题意设AC的斜率为k1,BC的斜率为k2,则直线AC的方程为y=k1x+t,直线BC的方程为y=k2x+t+6.由方程组得C点的横坐标为x0=.∵|AB|=t+6-t=6,∴S=×6=,由于圆M与AC相切,所以1=,∴k1=;同理,k2=,∴k1-k2=,∴S==61-,∵-5≤t≤-2,∴-2≤t+3≤1,∴-8≤t2+6t+1≤-4,∴S max=6×1+=,S min=6×1+=,∴△ABC的面积S的最大值为,最小值为.5.解 (1)由已知得=1,,a2=b2+c2,解得a=2,b=,c=1,所以椭圆方程为=1.(2)设A(x1,y1),B(x2,y2),由(1)得F(1,0),设直线l的方程为y=k(x-1)与椭圆联立得消去x得(3+4k2)x2-8k2x+4k2-12=0,所以x1+x2=,x1x2=,所以k DA+k DB===2k+=2k+=2k+=2k+=2.当直线l斜率不存在时,A1,-,B1,,k DA+k DB=2.所以DA,DB的斜率之和为2.6.解 (1)∵△F2MN的周长为4,∴4a=4,即a=,由直线MF1的斜率为1,得=1,∵a2=b2+c2,∴b=1,c=1,∴椭圆的标准方程为+y2=1.(2)由题意可得直线MF1方程为y=x+1,联立解得N-,-,∴,∵,即|NF1||QF1|sin∠QF1N=|MF1|·|PF1|sin∠PF1M,∴|QF1|=2|PF1|,当直线l的斜率为0时,不符合题意,故设直线l的方程为x=my-1,P(x1,y1),Q(x2,y2),由点P在点Q的上方,则y2=-2y1,联立所以(m2+2)y2-2my-1=0,所以y1+y2=,y1y2=,消去y2得所以.解得m2=,则m=±,又由画图可知m=不符合题意,所以m=-,故直线l的斜率为=-.。
通用版高考数学大二轮复习专题突破练24直线与圆及圆锥曲线(理科)

专题突破练24 直线与圆及圆锥曲线1.(节选)已知圆M:x2+y2=r2(r>0)与直线l1:x-y+4=0相切,设点A为圆上一动点,AB⊥x轴于B,且动点N满足=2,设动点N的轨迹为曲线C.(1)求曲线C的方程;(2)略.2.(2019甘肃武威第十八中学高三上学期期末考试)已知圆C1:x2+y2-2x-6y-1=0和C2:x2+y2-10x-12y+45=0.(1)求证:圆C1和圆C2相交;(2)求圆C1和圆C2的公共弦所在直线的方程和公共弦长.3.已知圆O:x2+y2=4,点A(,0),以线段AB为直径的圆内切于圆O,记点B的轨迹为Γ.(1)求曲线Γ的方程;(2)直线AB交圆O于C,D两点,当B为CD的中点时,求直线AB的方程.4.(2019全国卷1,理19)已知抛物线C:y2=3x的焦点为F,斜率为的直线l与C的交点为A,B,与x 轴的交点为P.(1)若|AF|+|BF|=4,求l的方程;(2)若=3,求|AB|.5.(2019湖南长沙第一中学高三下学期高考一模)已知椭圆=1(a>b>0)的离心率e=,过焦点且垂直于x轴的直线被椭圆截得的线段长为3.(1)求椭圆的方程;(2)已知P为直角坐标平面内一定点,动直线l:y=x+t与椭圆交于A,B两点,当直线PA与直线PB的斜率均存在时,若直线PA与PB的斜率之和为与t无关的常数,求出所有满足条件的定点P的坐标.6.(2019天津第一中学高三下学期第五次月考)已知椭圆C1:=1(a>b>0)的左、右焦点为F1,F2,F2的坐标满足圆Q方程(x-)2+(y-1)2=1,且圆心Q满足|QF1|+|QF2|=2a.(1)求椭圆C1的方程;(2)过点P(0,1)的直线l1:y=kx+1交椭圆C1于A,B两点,过P与l1垂直的直线l2交圆Q于C,D两点,M为线段CD中点,若△MAB的面积为,求k的值.参考答案专题突破练24直线与圆及圆锥曲线1.解(1)设动点N(x,y),A(x0,y0),因为AB⊥x轴于B,所以B(x0,0).已知圆M的方程为x2+y2=r2,由题意得r==2,所以圆M的方程为x2+y2=4.由题意,=2,所以(0,-y0)=2(x0-x,-y),即将A(x,2y)代入圆M:x2+y2=4,得动点N的轨迹方程为+y2=1.(2)略.2.(1)证明圆C1的圆心C1(1,3),半径r1=,圆C2的圆心C2(5,6),半径r2=4, 两圆圆心距d=|C1C2|=5,r1+r2=+4,|r1-r2|=4-,所以|r1-r2|<d<r1+r2.所以圆C1和C2相交.(2)解将圆C1和圆C2的方程相减,得4x+3y-23=0,所以两圆的公共弦所在直线的方程为4x+3y-23=0.因为圆心C2(5,6)到直线4x+3y-23=0的距离为d==3,故两圆的公共弦长为2-=23.解(1)设AB的中点为M,切点为N,连接OM,MN,则|OM|+|MN|=|ON|=2,|AB|=|ON|-(|OM|-|MN|)=2-|OM|+|AB|,即|AB|+2|OM|=4.取A关于y轴的对称点A',连接A'B,则|A'B|=2|OM|,故|AB|+2|OM|=|AB|+|A'B|=4.所以点B的轨迹是以A',A为焦点,长轴长为4的椭圆.其中a=2,c=,b=1,则曲线Γ的方程为+y2=1.(2)因为B为CD的中点,所以OB⊥CD,则设B(x0,y0),则x0(x0-)+=0.又=1,解得x0=,y0=±则k OB=±,k AB=,则直线AB的方程为y=±(x-),即x-y-=0或x+y-=0.4.解设直线l:y=x+t,A(x1,y1),B(x2,y2).(1)由题设得F,故|AF|+|BF|=x1+x2+,由题设可得x1+x2=由可得9x2+12(t-1)x+4t2=0,则x1+x2=--从而--,得t=-所以l的方程为y=x-(2)由=3可得y1=-3y2.由可得y2-2y+2t=0.所以y1+y2=2.从而-3y2+y2=2,故y2=-1,y1=3.代入C的方程得x1=3,x2=故|AB|=5.解(1)设椭圆的半焦距为c,则c2=a2-b2,且e=由题意得解得y=±依题意,=3,结合a2=b2+c2,解得c=1,a=2,b=于是椭圆的方程为=1.(2)设A x1,x1+t,B x2,x2+t,P(m,n).将l:y=x+t代入椭圆方程得x2+tx+t2-3=0.则Δ=t2-4(t2-3)>0,t2<4,则有x1+x2=-t,x1x2=t2-3.直线PA,PB的斜率之和k PA+k PB=------=--------=---,当n=m,2mn=3时斜率的和恒为0,解得或--综上所述,所有满足条件的定点P的坐标为1,或-1,-.6.解(1)因为F2的坐标满足圆Q方程(x-)2+(y-1)2=1,故当y=0时,x=,即F2(,0),故c=因为圆心Q满足|QF1|+|QF2|=2a,所以点Q(,1)在椭圆上,故有=1.联立方程组解得所以椭圆方程为=1.(2)因为直线l2交圆Q于C,D两点,M为线段CD的中点,所以QM与直线l2垂直.又因为直线l1与直线l2垂直,所以QM与直线l1平行.所以点M到直线AB的距离即为点Q到直线AB的距离.即点M到直线AB的距离为d=设点A(x1,y1),B(x2,y2).联立方程组解得(1+2k2)x2+4kx-2=0,Δ=b2-4ac=16k2+8(2k2+1)=32k2+8>0,由韦达定理可得--则|x1-x2|=----所以AB=|x1-x2|=所以△MAB的面积为所以即|k|=,两边同时平方,化简得,28k4-47k2-18=0,解得k2=2或k2=-(舍).故k=±此时l2:y=±x+1.圆心Q到l2的距离h=-<1成立.综上所述,k=±。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题突破练25 直线与圆及圆锥曲线1.(2020全国Ⅱ,理19)已知椭圆C 1:x 2a2+y 2b2=1(a>b>0)的右焦点F 与抛物线C 2的焦点重合,C 1的中心与C 2的顶点重合.过F 且与x 轴垂直的直线交C 1于A ,B 两点,交C 2于C ,D 两点,且|CD|=43|AB|. (1)求C 1的离心率;(2)设M 是C 1与C 2的公共点.若|MF|=5,求C 1与C 2的标准方程. 2.已知圆O :x 2+y 2=4,点A (√3,0),以线段AB 为直径的圆内切于圆O ,记点B 的轨迹为Γ. (1)求曲线Γ的方程;(2)直线AB 交圆O 于C ,D 两点,当B 为CD 的中点时,求直线AB 的方程.3.(2019全国Ⅰ,理19)已知抛物线C :y 2=3x 的焦点为F ,斜率为32的直线l 与C 的交点为A ,B ,与x 轴的交点为P.(1)若|AF|+|BF|=4,求l 的方程; (2)若AP⃗⃗⃗⃗⃗ =3PB ⃗⃗⃗⃗⃗ ,求|AB|. 4.(2020山东威海一模,20)已知椭圆x 2a 2+y 2b2=1(a>b>0)的左、右焦点分别为F 1,F 2,点P (-1,32)是椭圆上一点,|F 1F 2|是|PF 1|和|PF 2|的等差中项. (1)求椭圆的标准方程;(2)若A 为椭圆的右顶点,直线AP 与y 轴交于点H ,过点H 的另一条直线与椭圆交于M ,N 两点,且S △HMA =6S △PHN ,求直线MN 的方程.5.(2020重庆名校联盟高三二诊,19)已知椭圆C :x 2a 2+y 2b2=1(a>b>0),F 1,F 2为椭圆的左、右焦点,P (1,√22)为椭圆上一点,且|PF 1|=3√22. (1)求椭圆的标准方程;(2)设直线l :x=-2,过点F 2的直线交椭圆于A ,B 两点,线段AB 的垂直平分线分别交直线l 、直线AB 于M ,N 两点,当∠MAN 最小时,求直线AB 的方程.6.(2020天津河北一模,19)已知椭圆C :x 2a2+y 2b2=1(a>b>0)的离心率为12,直线x+y-√6=0与圆x 2+y 2=b2相切.(1)求椭圆C 的方程;(2)过点P (4,0)的直线l 与椭圆C 交于不同两点A ,B ,线段AB 的中垂线为l 1,若l 1在y 轴上的截距为413,求直线l 的方程.专题突破练25 直线与圆及圆锥曲线1.解 (1)由已知可设C 2的方程为y 2=4cx ,其中c=√a 2-b2.不妨设A ,C 在第一象限,由题设得A ,B 的纵坐标分别为b 2a ,-b2a ;C ,D 的纵坐标分别为2c ,-2c ,故|AB|=2b2a,|CD|=4c.由|CD|=43|AB|得4c=8b 23a ,即3×c a =2-2(c a )2,解得c a =-2(舍去),c a=12.所以C 1的离心率为12. (2)由(1)知a=2c ,b=√3c ,故C 1:x 24c 2+y 23c 2=1.设M (x 0,y 0),则x 024c 2+y 023c 2=1,y 02=4cx 0,故x 024c 2+4x03c =1.①由于C 2的准线为x=-c ,所以|MF|=x 0+c ,而|MF|=5,故x 0=5-c ,代入①得(5-c )24c 2+4(5-c )3c=1,即c 2-2c-3=0,解得c=-1(舍去),c=3.所以C 1的标准方程为x 236+y 227=1,C 2的标准方程为y 2=12x.2.解(1)设AB 的中点为M ,切点为N ,连接OM ,MN ,则|OM|+|MN|=|ON|=2,|AB|=|ON|-(|OM|-|MN|)=2-|OM|+1|AB|,即|AB|+2|OM|=4.取A 关于y 轴的对称点A',连接A'B ,则|A'B|=2|OM|, 故|AB|+2|OM|=|AB|+|A'B|=4.所以点B 的轨迹是以A',A 为焦点,长轴长为4的椭圆. 其中a=2,c=√3,b=1,则曲线Γ的方程为x 24+y 2=1.(2)因为B 为CD 的中点,所以OB ⊥CD ,则OB ⃗⃗⃗⃗⃗ ⊥AB ⃗⃗⃗⃗⃗ .设B (x 0,y 0),则x 0(x 0-√3)+y 02=0.又x 024+y 02=1,解得x 0=√3,y 0=±√2√3.则k OB =±√22,k AB =∓√2,则直线AB 的方程为y=±√2(x-√3), 即√2x-y-√6=0或√2x+y-√6=0. 3.解 设直线l :y=32x+t ,A (x 1,y 1),B (x 2,y 2).(1)由题设得F (34,0), 故|AF|+|BF|=x 1+x 2+32, 由题设可得x 1+x 2=52.由{y =32x +t ,y 2=3x ,可得9x 2+12(t-1)x+4t 2=0,则x 1+x 2=-12(t -1)9. 从而-12(t -1)=5,得t=-7.所以l 的方程为y=32x-78. (2)由AP ⃗⃗⃗⃗⃗ =3PB ⃗⃗⃗⃗⃗ 可得y 1=-3y 2. 由{y =32x +t ,y 2=3x可得y 2-2y+2t=0.所以y 1+y 2=2.从而-3y 2+y 2=2,故y 2=-1,y 1=3. 代入C 的方程得x 1=3,x 2=13. 故|AB|=4√133.4.解 (1)因为|F 1F 2|是|PF 1|和|PF 2|的等差中项,所以a=2c ,得a 2=4c 2,则b 2=a 2-c 2=3c 2.又P (-1,32)在椭圆上,所以14c 2+94b2=1,即14c 2+34c 2=1,所以c=1.则a 2=4,b 2=3,椭圆的标准方程为x 24+y 23=1.(2)因为P (-1,32),由(1)计算可知A (2,0),H (0,1),当直线MN 与x 轴垂直时,易验证,不合题意.当直线MN 与x 轴不垂直时,设直线MN 的方程为y=kx+1,联立直线与椭圆的方程{y =kx +1,x 24+y 23=1,消去y ,可得(4k 2+3)x 2+8kx-8=0, 设M (x 1,y 1),N (x 2,y 2),由韦达定理可得{x 1+x 2=-8k4k 2+3,x 1x 2=-84k 2+3.①由S △HMA =6S △PHN ,可得|AH||MH|=6|NH||PH|,又|AH|=2|PH|, 所以|MH|=3|NH|,得x 1=-3x 2, 代入①,可得{-2x 2=-8k4k 2+3,-3x 22=-84k 2+3,所以3×16k2(4k 2+3)2=84k 2+3,解得k=±√62,所以直线MN 的方程为y=±√62x+1.5.解 (1)设椭圆的左焦点F 1(-c ,0)(c>0),则|PF 1|=√(1+c )2+12=3√22,解得c=1,所以|PF 2|=√22,则由椭圆定义|PF 1|+|PF 2|=2a=2√2,∴a=√2,b=1.故椭圆的标准方程为x 22+y 2=1.(2)由题意直线AB 的斜率必定不为零,于是可设直线AB :x=ty+1,联立方程{x =ty +1,x 22+y 2=1,得(t 2+2)y 2+2ty-1=0,∵直线AB 交椭圆于A (x 1,y 1),B (x 2,y 2), ∴Δ=4t 2+4(t 2+2)=8(t 2+1)>0, 由韦达定理得y 1+y 2=-2tt 2+2,y 1y 2=-1t 2+2, 则y N =-t t 2+2,∴x N =ty N +1=-t 2t 2+2+1=2t 2+2.∵MN ⊥AB ,∴k MN =-t ,∴|MN|=√1+t 2·-2-2t 2+2=√1+t 2·2t 2+6t 2+2. 又|AN|=12|AB|=12√1+t 2·|y 1-y 2|=√1+t 2·√2√1+t 2t 2+2,∴tan ∠MAN=|MN |=√2(2√t +1=√2(√t 2+1+√t +1)≥√2·2√2=4.当且仅当2+1=√t +1,即t=±1时取等号.此时直线AB 的方程为x+y-1=0或x-y-1=0. 6.解 (1)由题意得,{e =ca =12,b =√6|1+1=√3,又a 2=b 2+c 2, ∴a=2.∴椭圆C 的方程为x 24+y 23=1.(2)由题意,直线l 的斜率k 存在且不为零. 设直线l 的方程为y=k (x-4),k ≠0.设A (x 1,y 1),B (x 2,y 2),AB 的中点Q (x 0,y 0).由{y =k (x -4),x 24+y 23=1,消去y ,整理得(3+4k 2)x 2-32k 2x+64k 2-12=0. 由Δ=(-32k 2)2-4(3+4k 2)(64k 2-12)>0, 解得-1<k<1,且k ≠0,∴x 1+x 2=32k23+4k2.∴x 0=16k 23+4k2,y 0=k (x 0-4)=-12k 3+4k2.∴Q (16k23+4k2,-12k 3+4k2).由题意可知,l 1:y-y 0=-1k(x-x 0),即y+12k3+4k 2=-1k (x -16k23+4k2). 化简得,y=-1k x+4k 3+4k 2.令x=0,4k 3+4k 2=413.解得k=14或k=3.∵-12<k<12,且k ≠0,∴k=14.故直线l 的方程为y=14(x-4),即x-4y-4=0.。
