北京各区初中一模数学分类汇编27题及答案#优选、

合集下载

2022北京中考数学一模分类《几何综合压轴题》含答案解析

2022北京中考一模数学分类——几何综合压轴题一、倍长八字共5小题1.（2022朝阳一模27题）在ABC △中，D 是BC 的中点，且90BAD ∠≠︒，将线段AB 沿AD 所在直线翻折，得到线段AB '，作//CE AB 交直线AB '于点E ．（1）如图，若AB AC >， ①依题意补全图形；②用等式表示线段,,AB AE CE 之间的数量关系，并证明；（2）若AB AC <，上述结论是否仍然成立？若成立，简述理由；若不成立，直接用等式表示线段,,AB AE CE 之间新的数量关系（不需证明）．2.（2022顺义一模27题）如图，在Rt ABC △中，90ACB ∠=︒，CD 是斜边AB 上的中线，EF 垂直平分CD ，分别交AC ，BC 于点E ，F ，连接DE ，DF ．（1）求∠EDF 的度数；（2）用等式表示线段AE ，BF ，EF 之间的数量关系，并证明．3.（2022平谷一模27题）如图，在△ABC 中，∠ACB =90°，AC =BC ,点D 为AB 边上一点（不与点A ，B 重合），作射线C D ，过点A 作AE ⊥CD 于E ，在线段AE 上截取EF=EC ，连接BF 交CD 于G.(1)依题意补全图形； (2)求证：∠CAE=∠BCD(3)判断线段BG 与GF 之间的数量关系，并证明.4.（2022丰台一模27题）如图，在△ABC 中，∠BAC=α,点D 在边BC 上（不与B,C 重合），连接AD,以点A 为中心，将线段AD 逆时针旋转180°-α得到线段AE,连接BE. （1）∠BAC+∠DAE= °（2）取CD 的中点F ，连接AF ，用等式表示线段AF 与BE 的数量关系，并证明。

5.（2022石景山一模27题）如图，△ACB 中，AC =BC ，∠ACB =90°，D 为边BC 上一点（不与点C 重合），CD ＜BD ，点E 在AD 的延长线上，且ED =AD ，连接BE ，过点B 作BE 的垂线，交边AC 于点F ．（1）依题意补全图形；（2）求证：BE =BF ；（3）用等式表示线段AF 与CD 的数量关系，并证明．ABCDABCD二、一线三垂直共1小题6.（2022通州一模27题）如图，在Rt ACB △中， 90ACB ∠=︒ ，AC BC =．点D 是BC 延长线上一点，连接AD ．将线段AD 绕点A 逆时针旋转90°，得到线段AE ．过点E 作//EF BD ，交AB 于点F ．（1）①直接写出AFE ∠的度数是____________；②求证：DAC E ∠=∠；（2）用等式表示线段AF 与DC 的数量关系，并证明．三、三线合一共1小题7.（2022大兴一模27题）已知：如图，OB =BA ，∠OBA =150°，线段BA 绕点A 逆时针旋转90°得到线段AC .连接BC ，OA ，OC ，过点O 作OD ⊥AC 于点D .（1）依题意补全图形；（2）求∠DOC 的度数.四、手拉手共5小题8.（2022燕山一模27题）如图，在三角形ABC 中，AB =AC ，∠BAC <60°，AD 是BC 边的高线，将线段AC 绕点A 逆时针旋转60°得到线段AE ，连接BE 交AD 于点F ．（1）依题意补全图形，写出∠CAE= ° （2）求∠BAF+∠ABF 和∠FBC 的度数；（3）用等式表示线段AF ，BF ，EF 之间的数量关系，并证明．9.（2022门头沟一模27题）如图，在等边△ABC 中，将线段AC 绕点A 顺时针旋转(060)αα<<，得到线段AD ，连接CD ，作∠BAD 的平分线AE ，交BC 于E ．（1）① 根据题意，补全图形；② 请用等式写出∠BAD 与∠BCD 的数量关系，并证明．（2）分别延长CD 和AE 交于点F ，用等式表示线段AF ，CF ，DF 的数量关系，并证明．AB C A B C AB C10.（2022房山一模27题）已知：等边ABC，过点B作AC的平行线l．点P为射线AB上一个动点（不与点,A B重合），将射线PC绕点P顺时针旋转60°交直线l于点D．（1）如图1，点P在线段AB上时，依题意补全图形；∠=∠；①求证：BDP PCBBC BD BP之间的数量关系，并证明；②用等式表示线段,,BC BD BP之间的数量关系．（2）点P在线段AB的延长线上，直接写出线段,,11.（2022海淀一模27题）27．在Rt ABC △中，90ABC ∠=︒，30BAC ∠=︒，D 为边BC 上一动点，点E 在边AC 上， C E CD =．点D 关于点B 的对称点为点F ，连接AD ，P 为AD 的中点，连接,,PE PF EF ．（1）如图1，当点D 与点B 重合时，写出线段PE 与PF 之间的位置关系与数量关系；（2）如图2，当点D 与点,B C 不重合时，判断（1）中所得的结论是否仍然成立？若成立，请给出证明，若不成立，请举出反例。

2024年北京海淀区初三一模考试数学及答案

2024北京海淀初三一模数学2024.04学校________姓名__________准考证号________第一部分选择题一、迭择题（共16分，每题2分）第1-8题均有四个选项，符合题意的选项只有一个. 1.下列几何体放置在水平面上，其中俯视图是圆的几何体为2.据报道，2024年春节假期北京接待游客约1750万人次，旅游收入同比增长近四成.将17 500 000用科学记数法表示应为 (A)175×105(B)1.75×106(C)1.75×107(D)0.175×1083.如图，AB ⊥BC ，AD ∥BE ，若∠BAD=28°，则∠CBE 的大小为 (A)66° (B)64° (C)62°(D)60°4.实数a 在数轴上的对应点的位置如图所示，下列结论中正确的是(A)a ≥-2(B)a<-3(C)-a>2(D)-a ≥35.每一个外角都是40°的正多边形是（A ）正四边形（B ）正六边形（C ）正七边形（D）正九边形6.若关于x 的一元二次方程x 2+2x +m =0有两个相等的实数根，则实数m 的值为 (A)1(B)-1(C)4(D)-47.现有三张背面完全一样的扑克牌，它们的正而花色分别为◆，，，若将这三张扑克牌背面朝上，洗匀后从中碗机抽取两张，则抽取的两张牌花色相同的概率为(A)16(B)13(C)12(D)238.如图.AB 经过圆心O ，CD 是⊙O 的一条弦，CD ⊥AB ，BC 是⊙O 的切线.再从条件①，条件②，条件③中选择一个作为已知，便得AD=BC. 条件①：CD 平分AB条你②OA 条件③：AD 2=AO ·AB 则所有可以添加的条件序号是 (A) ①(B) ①③(C) ②③(D) ①②③第二部分非选择题二、填空题(共16分，每题2分)9.x 的取值范围是_______. 10.分解因式：a 3-4a=_______. 11.方程1231x x =− 的解为_______.12.在平面直角坐标系xOy 中,若函数(0)ky k x=≠的图象经过点A (a ，2)和B (b ，-2).则a +b 的值为_______.13.如图，在△ABC 中，∠ACB=90°,AB=5,AC=3.点D 在射线BC上运动(不与点B 重合).当BD 的长为______时, AB=AD. 14.某实验基地为全面掌握“无絮杨”树苗的生长规律，定期对2000棵该品种树苗进行抽测.近期从中随机抽测了100棵树苗，获得了它们的高度x (单位：cm).数据经过整理后绘制的频数分布直方图如右图所示.若高度不低于300cm 的树苗为长势良好，则估计此时该基地培育的2000棵“无絮杨”树苗中长势良好的有_________棵.15.如图，在正方形ABCD 中.点E ，F ，G 分别在边CD ，AD ，BC 上，FD<CG.若FG=AE ，∠1=a ，则∠2的度数为_____（用含a 的式子表示）.16.2019年11月，联合国教科文组织将每年的3月14日定为“国际数学日”，也被许多人称为“π节”.某校今年“π节”策划了五个活动，规则见下图：小云参与了所有活动.（1）若小云只挑战成功一个，则挑战成功的活动名称为__________;（2）若小云共挑战成功两个，且她参与的第四个活动成功，则小云最终剩下的“π币”数量的所有可能取值为______.三、解答题（共68分，第17-19题,每题5分，第20-21题，每题6分，第22-23题,每题5分，第24题6分，第25题5分，第26题6分，第27-28题，每题7分）解答应写出文字说明、演算步骤或证明过程. 17.计算：112sin 601()2−︒+−+18.解不等式组：435,212.3x x x −<⎧⎪+⎨>−⎪⎩19.已知240b a −=,求代数式241(1)2a b b+−+的值.20.如图，在ABCD 中，O 为AC 的中点，点E ，F 分別在BC ，AD 上，EF 经过点O ，AE=AF.(1)求证：四边形AECF 为菱形；(2)若E 为BC 的中点，AE=3，AC=4.求AB 的长.21.下图是某房屋的平面示意图.房主准备将客厅和卧室地面铺设木地板，厨房和卫生间地面铺设瓷砖.将房间地面全部铺设完预计需要花费10 000元，其中包含安装费1270元.若每平方米木地板的瓷砖的价格之比是5:3，求每平方米木地板和瓷砖的价格.22.在平面直角坐标系xOy 中，函数y =kx +b (k ≠0)的图象经过点A(1，2)和B(0，1). (1)求该函数的解析式；(2)当x <l 时.对于x 的每一个值，函数y =mx -1(m ≠0)的值小于函数y =kx +b (k ≠0)的值，直接写出m 的取值范围.23.商品成本影响售价，为避免因成本波动导致售价剧烈波动，需要控制售价的涨跌幅.下面给出了商品售价和成本（单位：元）的相关公式和部分信息： a.计算商品售价和成本涨跌幅的公式分别为：100%100%−−=⨯⨯当周售价前周售价当周成本前周成本售价涨跌幅，成本涨跌幅=；前周售价前周成本b.规定当周售价涨跌幅为当周成本涨跌幅的一半；c.甲、乙两种商品成本与售价信息如下：根据以上信息，回答下列问题：（1）甲商品这五周成本的平均数为___________,中位数为___________;（2）表中m 的值为____________,从第三周到第五周，甲商品第_______周的售价最高；（3）记乙商品这40周售价的方差为 21S ，若将规定“当周售价涨跌福为当周成本涨跌福的一半”更改为“当周售价涨跌幅为当周成本涨跌辐的四分之一”，重新计算每周售价，记这40周新售价的方差为22S ,则21S ____22S ；（填“>”“=”或“<”）.24.如图.AB 、CD 均为⊙O 的直径.点E 在BD ̂上，连接AE ，交CD 于点F,连DE ，∠EDB+∠EAD=45°,点G 在BD 的延长线上，AB=AG. (I)求证：AG 与⊙O 相切；(2)若BG=1tan 3EDB ∠=，求EF 的长.25.某校为培养学生的阅读习惯，发起“阅读悦听”活动，现有两种打卡奖励方式：方式一：每天打卡可领取60min 听书时长；方式二：第一天打卡可领取5min 听书时长，之后每天打卡领取的听书时长是前一天的2倍. （1）根据上述两种打卡奖励方式补全表二：表一每天领取听书时长达了变化趋势.其中表示方式二变化趋势的虚线是________（填a 或b ）,从第_______天完成打卡时开始，选择方式二累计领取的听书时长超过方式一；（3）现有一本时长不超过60min 的有声读物，小云希望通过打卡领取该有声读物.若选择方式二比选择方式一所需的打卡天数多两天，则这本有声读物的时长t （单位：min ）的取值范围是______.26.在平面坐标系xOy 中，点(m ，n )在抛物线2(0)y ax bx a =+>上，其中m ≠0. (1)当m =4，n =0时.求抛物线的对称轴； (2)已知当0<m <4时，总有n <0. ①求证：4a +b ≤0;②点12(,),(3,)P k y Q k y 在该抛物线上，是否存在a ，b ，使得当1<k <2时，都有12y y <?若存在，求出a 与b 之间的数量关系；若不存任，说明理由.27.在△ABC 中.∠ACB=90°,∠ABC=30°，将线段AC 绕点A 顺时针旋转α((0°<α≤60°)得到线段AD.点D 关于直线BC 的对称点为E.连接AE ，DE.(1)如图1，当α=60°时，用等式表示线段AE 与BD 的数量关系，并证明； (2)连接BD ，依题意补全图2.若AE=BD ，求α的大小.28.在平面直角坐标系xOy中，对于图形M与图形N给出如下定义：P为图形N上任意一点，将图形M绕点P顺时针旋转90°得到M’，将所有M’组成的图形记作M’,称M’是图形M关于图形N的“关联图形”.(1)已知A(-2，0)，B(2，0)，C(2，t)，其中t≠0.①若t=1,请在图中画出点A关于线段BC的“关联图形”；②若点A关于线段BC的“关联图形”与坐标轴有公共点.立接写出t的取值范围；(2)对于平面上一条长度为a的线段和一个半径为r的圆，点S在线段关于圆的“关联图形”上，记点S的纵坐标的最大值和最小值的差为d，当这条线段和圆的位置变化时，直接写出d的取值范围(用含a和r的式子表示).海淀区九年级第二学期期中练习数学试卷参考答案第一部分选择题一、选择题（共16分，每题2分）第二部分非选择题二、填空题（共16分，每题2分）9．1x ≥ 10．(2)(2)a a a −+11．1x = 12．0 13．8 14．94015．180α︒−16．（1）鲁班锁；（2）1，2，3三、解答题（共68分，第17-19题，每题5分，第20-21题，每题6分，第22-23题，每题5分，第24题6分，第25题5分，第26题6分，第27-28题，每题7分）解答应写出文字说明、演算步骤或证明过程．17. 解：原式212=++− 12=+−3=18. 解：原不等式组为435212.3x x x −<⎧⎪⎨+>−⎪⎩，①②解不等式①，得2x <.解不等式②，得1x >. ∴原不等式组的解集为12x <<. 19. 解：原式241212a b b b +=−++2411a b +=+.∵240b a−=，∴24b a=.∴原式41 41aa+ =+1 =.20．（1）证明：∵四边形ABCD为平行四边形，∴AD // BC.∴AFO CEO∠=∠，FAO ECO∠=∠.∵O为AC的中点，∴AO CO=.∴△AOF≌△COE.∴AF EC=.∵AF//EC，∴四边形AECF为平行四边形.∵AE AF=，∴四边形AECF为菱形.（2）解：∵O为AC的中点，4AC=，∴122OA AC==.∵四边形AECF为菱形，∴AC EF⊥.∴90AOE∠=︒.∴在Rt△AOE中，由勾股定理得OE=.∵E为BC的中点，∴2AB OE==.21. 解：设每平方米木地板的价格为5x元，则每平方米瓷砖的价格为3x元.由题意可得，123(3615)5100001270x x⨯++⨯=−.解得30x=.∴5150x=，390x=.答：每平方米木地板的价格为150元，每平方米瓷砖的价格为90元.22．解：（1）∵函数(0)y kx b k =+≠的图象经过点(1,2)A 和(0,1)B ，∴21.k b b +=⎧⎨=⎩，解得11.k b =⎧⎨=⎩，∴该函数的解析式为1y x =+. （2）13m ≤≤.23．解：（1）32，25；（2） 60，四；（3）＞.24.（1）证明：∵BE BE =，∴BAE BDE ∠=∠. ∵45EDB EAD ∠+∠=︒，∴45BAE EAD ∠+∠=︒，即45BAD ∠=︒. ∵AB 为O 的直径， ∴90ADB ∠=︒. ∴AD BG ⊥. ∵AB AG =，∴45BAD GAD ∠=∠=︒. ∴90BAG ∠=︒. ∴AB AG ⊥.∵AB 为O 的直径， ∴AG 与O 相切.（2）解：连接BE ，如图.∵AB AG =，AD BG ⊥，BG =∴12BD BG == 在Rt △ADB 中，90ADB ∠=︒，45BAD ∠=︒，可得AB =∴12OA AB ==. ∵BAE BDE ∠=∠， ∴1tan tan 3BAE BDE ∠=∠=.∵AB 为O 的直径，∴90AEB ∠=︒.在Rt △AEB 中，1tan 3BAE ∠=，可得13BE AE =.由勾股定理得 222BE AE AB +=.∴2221()3AE AE +=.∴6AE =. ∵290BOD BAD ∠=∠=︒. ∴90AOF ∠=︒.在Rt △AOF 中，1tan 3BAE ∠=，OA =OF =.由勾股定理得 103AF =. ∴108633EF AE AF =−=−=. 25.解：（1）60n ，525n ⨯−；（2） a ，7；（3）1535t <≤.26.解：（1）由题意可知，点(40)，在抛物线2(0)y ax bx a =+>上，∴1640a b +=. ∴4b a =−. ∴4222b aa a−==−−. ∴抛物线的对称轴为直线2x =.（2）① 法一：令0y =，则20(0)ax bx a +=>. 解得0x =或b x a=−. ∴抛物线2(0)y ax bx a =+>与x 轴交于点(00)，，(0)b a−，. ∵0a >，∴抛物线开口向上. (ⅰ)当0b <时，0ba−>.∴当0bx a <<−时，0y <；当0x <或b x a>−时，0y >. ∵当04m <<时，总有0n <. ∴4ba−≥.∵0a >， ∴40a b +≤. (ⅱ)当0b >时，0ba−<. ∴当0bx a −<<时，0y <；当b x a<−或0x >时，0y >. ∴当04m <<时，0n >，不符合题意. 综上，40a b +≤. 法二：∴由题意可知，2am bm n +=.若0n <，则2()0am bm m am b +=+<. ∵0m >， ∴0am b +<. ∵0a >， ∴b m a<−. ∴当0bm a<<−时，0n <. ∵当04m <<时，总有0n <. ∴4ba−≥.∵0a >， ∴40a b +≤. ② 存在.设抛物线的对称轴为x t =，则2b t a=−. ∵，∴当x t ≥时，y 随x 的增大而增大；当x t ≤时，y 随x 的增大而减小. ∵12k <<，∴336k <<，3k k <. (ⅰ)当1t ≤时，∵3t k k ≤<. ∴12y y <，符合题意. (ⅱ)当12t <≤时，当2t k ≤<时， ∵3t k k <<. ∴12y y <. 当1k t <<时，设点1()P k y ，关于抛物线对称轴x t =的对称点为点01'(,)P x y ，则0x t >，0t k x t −=−. ∴02x t k =−. ∵1k t <<，12t <≤， ∴23t k −<. ∴03t x <<. ∵336k <<. ∴03t x k <<. ∴12y y <.∴当12t <≤时，符合题意. (ⅲ)当23t <≤时，令12k t =，332k t =，则12y y =，不符合题意.(ⅳ)当36t <<时，令3k t =，则3k k t <≤. ∴12y y >，不符合题意. (ⅴ)当6t ≥时，∵3k k t <<，∴12y y >，不符合题意. ∴ 当2t ≤，即22ba−≤时，符合题意. ∵0a >， ∴40a b +≥. 由①可得40a b +≤. ∴40a b +=.27.（1）线段AE 与BD的数量关系：AE .证明：连接BE ，如图1.∵点D ，E 关于直线BC 对称， ∴直线BC 是线段DE 的垂直平分线. ∴BD BE =.∴30DBC EBC ∠=∠=. ∴60DBE ∠=.∴△DBE 是等边三角形.∴BD BE DE ==，60BDE BED ∠=∠=. ∵△ABC 中，90ACB ∠=，30ABC ∠=， ∴2AB AC =.依题意，得AD AC =，点D 在AB 上. ∴2AB AD =. ∴.BD AD = ∴.DE AD =∴30.DAE DEA ∠=∠= ∴90.BEA ∠= ∴在Rt △ABE 中，tan tan 60 3.AEABE BE=∠== ∴AE. ∴.AE =（2）依题意补全图2，如图.B图1方法一：解：延长AC 至F ，使CF AC =，连接BF ，BE ，EF ，CD ，CE ，如图2. ∵90ACB ∠=， ∴.AB BF = ∵60BAC ∠=，∴△ABF 是等边三角形. ∴AB AF BF ==,60BFC ∠=. ∵点D ，E 关于直线BC 对称， ∴直线BC 是线段DE 的垂直平分线. ∴BD BE =，CD CE =. ∴DCB ECB ∠=∠. ∵90ACB DCF ∠=∠=， ∴DCA ECF ∠=∠. ∵AC FC =， ∴△DAC ≌△EFC . ∴CAD CFE ∠=∠. ∵AE BD =, ∴BE AE =.∵EF EF =,BF AF =， ∴△BEF ≌△AEF .∴30BFE AFE ∠=∠=. ∴30CAD AFE ∠=∠=. ∴30.α= 方法二：解：如图3，取AB 中点F ，连接DF ，BE ，CD ，CE ，设DBC β∠=.F∵点D ，E 关于直线BC 对称， ∴直线BC 是线段DE 的垂直平分线. ∴BD BE =，CD CE =. ∴DBC EBC β∠=∠=.∴30EBA β∠=︒+，30DBA β∠=︒−. ∵AE BD =, ∴AE BE =.∴30EAB EBA β∠=∠=︒+. ∵90ACB ∠=︒，30ABC ∠=︒， ∴60BAC ∠=︒. ∴30EAC β∠=︒−. ∴EAC DBA ∠=∠. 由（1）可得2.AB AC = ∵F 为AB 中点， ∴22.AB AF BF == ∴.AC AF BF ==∵AC BF =，EAC DBA ∠=∠,AE BD =, ∴△ACE ≌△BFD . ∴CE FD =. ∴CD FD =.∵AD AD =，AF AC =, ∴△ADF ≌△ADC . ∴30FAD CAD ∠=∠=︒. ∴30α=︒.28.（1）①如图，线段B'C'即为所求.②4t ≤−或2t ≥.图3FD≤≤+. （2）d a。

北京市中考数学一模分类27题二次函数及答案

2017年北京中考数学一模 27题“二次函数综合题”西城. 在平面直角坐标系xOy 中，二次函数5)12(2-++-=m x m mx y 的图象与x 轴有两个公共点. （1）求m 的取值范围；（2）若m 取满足条件的最小的整数，①写出这个二次函数的解析式；②当n ≤x ≤1时，函数值y 的取值范围是-6≤y ≤4-n ，求n 的值；③将此二次函数图象平移，使平移后的图象经过原点O . 设平移后的图象对应的函数表达式为k h x a y +-=2)(，当x ＜2时，y 随x 的增大而减小，求k 的取值范围东城．二次函数2(2)2(2)5y m x m x m =+-+-+，其中20m +>．（1）求该二次函数的对称轴方程；（2）过动点C (0, n )作直线l ⊥y 轴.① 当直线l 与抛物线只有一个公共点时, 求n 与m 的函数关系；② 若抛物线与x 轴有两个交点，将抛物线在x 轴下方的部分沿x 轴翻折，图象的其余部分保持不变，得到一个新的图象. 当n =7时，直线l 与新的图象恰好有三个公共点，求此时m 的值；（3）若对于每一个给定的x 的值，它所对应的函数值都不小于1，求m 的取值范围．xy直线lCBA–1–21234–1–2–31234O朝阳．在平面直角坐标系中xOy 中，抛物线2211222y x mx m m =-++-的顶点在x 轴上．（1）求抛物线的表达式；（2）点Q 是x 轴上一点，①若在抛物线上存在点P ，使得∠POQ =45°，求点P 的坐标； ②抛物线与直线y =2交于点E ，F （点E 在点F 的左侧），将此抛物线在点E ，F （包含点E 和点F ）之间的部分沿x 轴平移n 个单位后得到的图象记为G ，若在图象G 上存在点P ，使得∠POQ =45°，求n 的取值范围．房山. 在平面直角坐标系xOy 中，直线32-=x y 与y 轴交于点A ，点A 与点B 关于x 轴对称，过点B 作y 轴的垂线l ，直线l 与直线32-=x y 交于点C. （1）求点C 的坐标；（2）如果抛物线n nx nx y 542+-= (n ＞0)与线段BC 有唯一公共点，求n 的取值范围．顺义．如图，已知抛物线28(0)y ax bx a =++≠与x 轴交于A （-2，0），B 两点，与y 轴交于C点，tan ∠ABC =2．（1）求抛物线的表达式及其顶点D 的坐标；（2）过点A 、B 作x 轴的垂线，交直线CD 于点E 、F ，将抛物线沿其对称轴向上平移m 个单位，使抛物线与线段EF （含线段端点）只有1个公共点．求m 的取值范围．平谷．直线33y x =-+与x 轴，y 轴分别交于A ，B 两点，点A 关于直线1x =-的对称点为点C ．（1）求点C 的坐标；（2）若抛物线()230y mx nx m m =+-≠经过A ，B ，C 三点，求该抛物线的表达式；（3）若抛物线()230y ax bx a =++≠ 经过A ，B 两点，且顶点在第二象限，抛物线与线段AC 有两个公共点，求a 的取值范围．yx–2–112345–5–4–3–2–112O门头沟. 在平面直角坐标系xOy 中，抛物线()()13y a x x =+-与x 轴交于A ,B 两点，点A 在点B 的左侧，抛物线的顶点为P ,规定：抛物线与x 轴围成的封闭区域称为“G 区域”（不包含边界）.（1）如果该抛物线经过（1, 3），求a 的值，并指出此时“G 区域”有______个整数点；（整数点就是横纵坐标均为整数的点）（2）求抛物线()()13y a x x =+-的顶点P 的坐标（用含a 的代数式表示）；（3）在（2）的条件下，如果G 区域中仅有4个整数点时，直接写出a 的取值范围.海淀．平面直角坐标系xOy 中，抛物线2222y mx m x =-+交y 轴于A 点，交直线x =4于B 点．（1）抛物线的对称轴为x = （用含m 的代数式表示）；（2）若AB ∥x 轴，求抛物线的表达式；（3）记抛物线在A ，B 之间的部分为图象G （包含A ，B 两点），若对于图象G 上任意一点P （P x ，P y ），2P y ≤，求m 的取值范围．丰台．在平面直角坐标系xOy 中，抛物线()01242≠-+-=m m mx mx y 与平行于x 轴的一条直线交于A ，B 两点．（1）求抛物线的对称轴；（2）如果点A 的坐标是（-1，-2），求点B 的坐标；（3）抛物线的对称轴交直线AB 于点C ，如果直线AB 与y 轴交点的纵坐标为-1，且抛物线顶点D 到点C 的距离大于2，求m 的取值范围．石景山．在平面直角坐标系xOy 中，抛物线2443(0)y ax ax a a =-+-≠的顶点为A ．（1）求顶点A 的坐标；（2）过点(0,5)且平行于x 轴的直线l ，与抛物线 2443(0)y ax ax a a =-+-≠交于B ，C 两点．①当2a =时，求线段BC 的长；②当线段BC 的长不小于6时，直接写出a 的取值范围．通州．在平面直角坐标系xOy 中，抛物线2222+-+-=m m mx x y 的顶点为D.线段AB 的两个端点分别为A （-3，m ），B （1，m ）.（1）求点D 的坐标（用含m 的代数式表示）；（2）若该抛物线经过点B （1，m ），求m 的值；（3）若线段AB 与该抛物线只有一个公共点，结合函数的图象，求m 的取值范围.怀柔．已知二次函数122-++=a ax axy （a>0）.（1）求证：抛物线与x 轴有两个交点；（2）求该抛物线的顶点坐标；（3）结合函数图象回答：当x ≥1时，其对应的函数值y 的最小值范围是2≤y ≤6，求a 的取值范围.西城.解：（1）∵ 二次函数5)12(2-++-=m x m mx y 的图象与x 轴有两个交点，∴ m ≠0[]054122>)()+(---m m m解得 241->m 且m ≠0. ∴m 的取值范围是241->m 且m ≠0. ·········································· 2分（2）①m 取满足条件的最小的整数，由（1）可知m =1.∴ 二次函数的表达式为234y x x =--. ·································· 3分② 图象的对称轴为直线23=x .当n ≤x ≤1＜32时，函数值y∵ 函数值y 的取值范围是-6≤y ≤4-n ， ∴ 当x =1时，函数值为- 6. 当x =n 时，函数值为4-n.∴ n 2 – 3n - 4 = 4-n.，解得n = - 2或n = 4（不合题意，舍去）. ∴ n 的值为- 2. ③由①可知，a =1. 又函数图像经过原点， ∴k =-h 2，∵当x ＜2时，y 随x 的增大而减小， ∴h ≥ 2 ∴k ≤-4.············································································································ 7分东城.解：（1）对称轴方程：2(2)12(2)m x m -+=-=+. …………1分（2）①∵直线l 与抛物线只有一个公共点,∴23n m =-+. …………3分② 依题可知：当237m -+=-时，直线l 与新的图象恰好有三个公共点. ∴5m =. …………5分（3）抛物线2(2)2(2)5y m x m x m =+-+-+的顶点坐标是(1,23)m -+.依题可得 20,23 1.m m +>⎧⎨-+≥⎩解得2,1.m m >-⎧⎨≤⎩∴ m 的取值范围是21m -<≤. …………7分朝阳．解：（1）222111-2()2222y x mx m m x m m =++-=-+-. 由题意，可得m -2=0． ∴2m =． ∴21(2)2y x =-．（2）①由题意得，点P 是直线y x =与抛物线的交点.∴21-222x x x =+. 解得 135x =+，235x =-. ∴P 点坐标为(35,35)++或 (35,35)--.②当E 点移动到点（2,2）时，n =2.当F 点移动到点（-2,2）时，n =-6. 由图象可知，符合题意的n 的取值范围是26-≤≤n .房山解：（1）∵直线y=2x-3与y 轴交于点A （0，-3） ------1分 ∴点A 关于x 轴的对称点为B （0，3），l 为直线y=3 ∵直线y=2x-3与直线l 交于点C ，∴点C 的坐标为（3，3） ------2分（2）∵抛物线n nx nx y 542+-= (n ＞0) ∴y = nx2-4nx+4n+n = n(x-2)2+n∴抛物线的对称轴为直线x=2，顶点坐标为（2，n ） ------3分 ∵点B （0，3），点C （3，3）①当n ＞3时，抛物线最小值为n ＞3，与线段BC 无公共点； ②当n=3时，抛物线顶点为（2，3），在线段BC 上，此时抛物线与线段BC 有一个公共点； ------4分 ③当0＜n ＜3时，抛物线最小值为n ，与直线BC 有两个交点如果抛物线y=n(x-2)2+ n 经过点B （0，3），则3=5n ，解得53=n由抛物线的对称轴为直线x=2，可知抛物线经过点（4，3）点（4，3）不在线段BC 上，此时抛物线与线段BC 有一个公共点B ------5分如果抛物线y=n(x-2)2+ n 经过点C （3，3），则3=2n ，解得23=n 由抛物线的对称轴为直线x=2，可知抛物线经过点（1，3）点（1，3）在线段BC 上，此时抛物线与线段BC 有两个公共点 ------6分综上所述，当53≤n ＜23或n=3时，抛物线与线段BC 有一个公共点. ------7分顺义27．解：（1）由抛物线的表达式知，点C （0，8），即 OC =8；Rt △OBC 中，OB =OC •tan ∠ABC =8×12=4，则点B （4，0）． ………………………… 1分将A 、B 的坐标代入抛物线的表达式中，得：428016480a b a b -+=⎧⎨++=⎩，解得12a b =-⎧⎨=⎩， ∴抛物线的表达式为228y x x =-++．…… 3分∵2228(1)9y x x x =-++=--+ ，∴抛物线的顶点坐标为D （1，9）． ………… 4分（2）设直线CD 的表达式为y =kx +8,∵点D （1，9），∴直线CD 表达式为y =x +8．∵过点A 、B 作x 轴的垂线，交直线CD 于点E 、F ，可得：E （-2，6），F （4，12）． ………… 6分设抛物线向上平移m 个单位长度（m ＞0），则抛物线的表达式为：2(1)9y x m =--++；当抛物线过E （-2，6）时，m =6，当抛物线过F （4，12）时，m =12， ∵抛物线与线段EF （含线段端点）只有1个公共点，∴m 的取值范围是6<m ≤12． ………………………………………… 7分平谷27．解：（1）令y =0，得x =1．∴点A 的坐标为（1,0）． ···································································· 1 ∵点A 关于直线x =﹣1对称点为点C ， ∴点C 的坐标为（﹣3,0）． ··················· 2 （2）令x =0，得y =3．∴点B 的坐标为（0,3）． ∵抛物线经过点B ， y 2345B∴﹣3m =3，解得m =﹣1． ····················· 3 ∵抛物线经过点A ，∴m+n ﹣3m =0，解得n =﹣2．∴抛物线表达式为223y x x =--+． (4)（3）由题意可知，a <0．根据抛物线的对称性，当抛物线经过（﹣1,0）时，开口最小，a =﹣3， ·········· 5 此时抛物线顶点在y 轴上，不符合题意.当抛物线经过（﹣3,0）时，开口最大，a =﹣1. (6)结合函数图像可知，a 的取值范围为31a -<≤-. (7)门头沟27. （1）()()3a 1113=+- ……………1分解得：34a =-………………………2分 6个 ………………………3分（2）由()()y a 13x x =+-配方或变形()()()2y a 13=14x x a x a =+--- .所以顶点P 的坐标为（1，-4a ）. ……………………………………5分（3） a ＜0时，；分a ＞0时， 7分分 22x +与y 轴交于A 点，分 ∵ AB ∥x 轴，B 点在直线x =4上，∴ B （4，2），抛物线的对称轴为直线x =2. --------------------------------------------- 4分 ∴ m =2．2132a --≤＜12≤∴ 抛物线的表达式为2282y x x =-+． --------------------------------------------------- 5分（3）当0m >时，如图1．∵()02A ，，∴要使04P x ≤≤时，始终满足2P y ≤，只需使抛物线2222y mx m x =-+的对称轴与直线x=2重合或在直线x=2的右侧． ∴2m ≥． -------------------------------------------- 6分当0m <时，如图2，0m <时，2P y ≤恒成立． ------------------- 7分综上所述，0m <或2m ≥．丰台27. 解：（1）∵抛物线()12212422---=-+-=m x m m mx mx y ，∴对称轴为x = 2．…………………………………2分（2）①∵抛物线是轴对称图形，∴点A 点B 关于x = 2轴对称，∵A (﹣1，-2) ，∴B （5，-2）．……………………………………………3分 ②∵抛物线()12212422---=-+-=m x m m mx mx y ，∴顶点D （2，﹣2m -1）． …………………………………………………4分∵直线AB 与y 轴交点的纵坐标为-1，∴C （2，-1）． ……………………………………………………………5分∵顶点D 到点C 的距离大于2，∴﹣2m ﹣1 +1 > 2或﹣1+ 2m +1 > 2，∴m <﹣1或m > 1．………………………………………………………… 7分石景山27．解：（1）解法一： ∵2443y ax ax a =-+-2(2)3a x =--， ………………………………… 1分∴顶点A 的坐标为(2,3)-． ………………………………… 2分图2解法二： ∵244(43)(4)2,324a a a a aa-⨯----==-，∴顶点A 的坐标为(2,3)-． ………………………………… 2分（2）①当2a =时，抛物线为2285y x x =-+，如图．令5y =，得22855x x -+=， ……………… 3分解得，1204x x ==，．……………… 4分∴线段BC 的长为4． ……………… 5分② 80<9a ≤． ……………… 7分通州27. 解：（1）D (m ，-m +2) （2）m =3或m =1 ……………………..(5分)（3）1≤m ≤3 ……………………..(7分) 怀柔27．解：（1）令y=0. ∴0122=-++a ax ax .∵△=)1(442--a a a=4a,……………………………1分 ∵a>0,∴4a>0.∴△>0.∴抛物线与x 轴有两个交点. …………………2分（2）212ax a=-=-.……………………………3分把x=-1代入122-++=a ax ax y .∴y=-1.∴顶点坐标（-1，-1）.…………………4分（3）①把（1,2）代入122-++=a ax ax y . ∴43=a .……………………………5分 ②把（1,6）代入122-++=a ax axy . ∴74a =.……………………………6分 ∴由图象可知：43≤a ≤74.……………………………7分 y xB x =2–1–2–3–4–512345–1–2–3–41234567CA (2,-3)O。

2024年北京大兴区初三一模考试数学及答案

大兴区2023～2024学年度第二学期初三期中检测数学参考答案及评分标准一、选择题（共16分，每题2分）题号1 2 3 4 5 6 7 8 答案D B C B C D A D二、填空题（共16分，每题2分）题号910 11 12 13 14 15 16 答案3x ≥ ()()22a x x +− 1x = -5 45 1 240 60，30三、解答题（共68分，第17-20题，每题5分，第21题6分，第22-23题，每题5分，第24-26题，每题6分，第27，28题，每题7分）解答应写出文字说明、演算步骤或证明过程.17．解：原式=2312222++−⨯························································· 4分 =42+． ··········································································· 5分18. 解：4125213x x x x ⎧⎪⎨⎪⎩-≥+,①-＜.②解不等式①，得x ≥3. ································································· 2分解不等式②，得x ＞-1. ······························································· 4分所以不等式组的解集为x ≥3. ························································ 5分19.解：··························································· 2分. ·········································································· 3分∵，∴. ············································································· 4分∴.∴原式=2-1=1. ················································································ 5分2(1)(4)2a a a +++−222142a a a a =++++−2261a a =+−2310a a +−=231a a +=2262a a +=2261a a =+−原式20.解：设每本A 书籍厚度为x cm ，桌子高度为y cm. ····································· 1分由题意可得37965825,.x y x y ⎧+=⎪⎨⨯+=⎪⎩····································································· 3分解得176x y ⎧=⎨=⎩,.············································································· 4分答：每本A 书籍厚度为1cm. ···································································· 5分21. (1)证明：∵四边形ABCD 是正方形，∴AD ∥BC ，AD =BC . …………………………1分∵BE =FD ，∴AD -FD =BC -BE.即AF =CE . …………………………2分又∵AF ∥CE ，∴ 四边形AECF 是平行四边形. ……………………………………3分(2)解：∵四边形ABCD 是正方形，∴AB ∥CD ，∠BCD=∠D =90°，AD =CD. ……………………………4分∴∠BAE=∠G ，∠ECG =90°，∴tan ∠BAE = tan G =. 在Rt △ADG 中，∵ tan G =AD DG =，DG =9， ∴ AD =6.∴ CD =6.…………………………………………………………5分∴ CG =3.在Rt △ECG 中，∵ tan G = =CE CG ， ∴ CE=2 . ··········································································· 6分22.解：(1)4； …………………………………………………………………………1分(2)7.55； ……………………………………………………………………………2分(3)①；………………………………………………………………………………4分(4)乙. ………………………………………………………………………………5分23232323. 解：(1)将A (1，3)，B (-1，-1)代入0()y kx b k =+≠中，得3 1.，k b k b +=⎧⎨−+=−⎩ ············································································· 1分解得21.，k b =⎧⎨=⎩∴函数的表达式为21=+y x . ························································ 2分 ∵过点(-2，0)且平行于y 轴的直线交于点C ，∴点C 的横坐标为-2.把x =-2代入，得y =-3.∴点C 的坐标为(-2，-3)． ····························································· 3分 (2) 312≤≤n .··············································································· 5分24. (1) ②，①； ···················································································· 2分(2)①不能. ························································································ 3分理由如下：由题意可得OE =2.6+3=5.6.把x =5.6代入上边缘抛物线表达式，得2156220388()==−−+y ..<0.5 所以绿化带不全在喷头口的喷水区域内.所以洒水车不能浇灌到整个绿化带. ················································· 4分 ②2≤OD ≤231−. ······································································ 6分25. (1)证明：∵AB 为⊙O 的切线，∴∠OBA =90°.∴∠A +∠AEB =90°.∵BC 为⊙O 的直径，∴∠CDB =90°.∴∠CDE +∠BDE =90°.∵BD =BA ，∴∠BDA =∠A .∴∠CDE =∠AEB. ···················································································· 1分又∵∠CDE=∠CBF，∴∠AEB=∠CBF.∴EF=BF. ···························································································2分(2) 解：连接CF.∵AB为⊙O的切线，∴∠OBA=90°.∴∠AEB+∠A=90°，∠EBF+∠FBA=90°.∵∠AEB=∠CBF，∴∠FBA=∠A.∴AF=BF.∴AF=BF=EF. ························································································3分设BF =EF=AF=x，则AE=2x.在Rt△ABE中，∵sin A=13，AE=2x，∴BE=23x. ·····························································································4分∵BC为直径，∴∠CFB=90°.∵∠BCF=∠BDA，∠BDA=∠A，∴∠BCF=∠A. ························································································5分∴sin A=sin∠BCF=1 3 .在Rt△BFC中，∵BF=x，∴BC=3x.∵BC=2OB=2(OE+BE)，∴3x=2(52+23x).解得x=3.∴OB=9 2 .∴⊙O半径的长为92. ················································································6分26.解：(1)∵x 2=2，y 2=c ，∴4a +2b +c =c. ………………………………………………………………………………1分 ∴b =-2a .∴12b t .a=−= ························································································ 2分 (2) ∵ 2(0)y ax bx c a =++<，∴抛物线开口向下.∵ 抛物线的对称轴为x =t ，t +1＜x 1＜t +2，∴点M 在对称轴的右侧. …………………………………………………………………3分 ①当点N 在对称轴上或对称轴右侧时，∵抛物线开口向下，∴在对称轴右侧，y 随x 的增大而减小.由y 1>y 2,∴x 1＜x 2.∴424≤≤t ,t .⎧⎨+⎩解得42≤≤t ,t .⎧⎨⎩∴2≤t . ……………………………………………………………………………4分 ②当点N 在对称轴上或对称轴左侧时，设抛物线上的点N （x 2, y 2）关于x =t 的对称点为()2N d ,y ',∴ t - x 2=d -t ，解得d =2t - x 2,∴()222N t x ,y '−.∵4＜x 2＜5∴2t -5＜2t -x 2＜2t -4.在对称轴右侧，y 随x 的增大而减小.由y 1>y 2,∴x 1＜2t -x 2.∴5225≥≤t,t t .⎧⎨+−⎩解得57≥≥t ,t .⎧⎨⎩∴7≥t .综上所述，t 的取值范围是27≤或≥t t .…………………………………………………6分27. (1)补全图形如下：…………………………………………….1分(2) 解：∵AC= BC ，∠ACB ＝90°，∴∠A =∠ABC =45°.∴∠CDB =∠A +∠ACD =45°+α. ………………………………………………………….2分 ∵∠CDE =90°，∴∠EDB =∠CDE -∠CDB =45°-α.……………………………………………………….3分(3) 用等式表示线段BE ，BC ，AD 之间的数量关系是BC=AD+BE. ………………………4分证明：过点D 作DM ⊥AB ，交AC 于点F ，交BC 的延长线于点M .∵∠MDB =∠CDE =90°，∴∠CDM =∠EDB .∵∠MBD =45°，∴∠M =∠MBD =45°.∴DM=DB.又∵DC=DE ，∴△DCM ≌△DEB .∴CM=BE .···························································································· 5分 ∵∠M =45°，∠ACB ＝90°，∴∠CFM =∠M =45°.∴CF=CM .∴CF=BE. ···························································································· 6分 E CA BD2在Rt △F AD 中，∵∠A =45°，∴cos A =. ∴AF=AD .∵AC=AF+FC ，∴AC=AD+FC.∵CF=BE ，BC=AC ，∴BC=AD+BE.············································································ 7分28.解：(1)① …………………………………………………………………….2分 ②如图1：设射线与⊙T 相切于点，连接. ∴TM ⊥PM .当∠P =45°时，在Rt △PMT 中，.∴当点在⊙T 外且∠P ≥ 45°时，1＜PT . ∴点在以T 为圆心，以为半径的圆上或圆内且在以1为半径的圆外. ············ 3分如图2：直线上有且只有一个⊙T 的“伴随点”， ∴直线与以为圆心，为半径的圆相切. ∴b ≠0.设直线与轴，轴分别交于点，，与以为圆心，为半径的圆相切于点，连接， ∴.令，则；令，则，.，.在Rt △ATB 中，，90° . ， 22AD AF =22223P P ，PM M TM 2222112PT MP MT =+=+=P 12∴＜PT ≤P 21:2l y x b =+12y x b =+T 212y x b =+x y A B T 2C TC TC AB ⊥0x =y b =0y =2x b =−2,0),(0,)A b B b ∴−（2AT b ∴=−BT b =1tan 122b BT AT b ∠===−1290∠+∠=TC AB ⊥图2图190°... 在Rt △TCB 中， 1322tan =BC BC .CT ∠== . . . . ···························································································· 5分 (2)或. ································································ 7分 2390∴∠+∠=13∴∠=∠1tan 1tan 32∴∠=∠=22BC ∴=2222210(2)()22BT CT BC ∴=+=+=102b ∴=102b ∴=±213312,2222t t −−−＜≤≤＜213312,2222t t −−−＜≤≤＜。

2024北京朝阳区初三一模数学试卷和答案

2024北京朝阳初三一模数学考生须知1．本试卷共6页，共三道大题， 28道小题，满分100分．考试时间120分钟．2．在试卷和答题卡上认真填写学校名称、班级、姓名和考号．3．试题答案一律填涂或书写在答题卡上，在试卷上作答无效．4．在答题卡上，选择题、作图题用2B 铅笔作答，其他试题用黑色字迹签字笔作答．5．考试结束，请将本试卷、答题卡和草稿纸一并交回．一、选择题（共16分，每题2分）第1-8题均有四个选项，其中符合题意的选项只有一个．1. 2024年1月21日北京市第十六届人民代表大会第二次会议开幕，在政府工作报告中提到，2023年北京向天津、河北输出技术合同成交额74870000000元，将74870000000用科学记数法表示应为（）A. 974.8710⨯ B. 107.48710⨯ C. 97.48710⨯ D. 110.748710⨯2. 下列图形中，既是轴对称图形又是中心对称图形的是（）A. B. C. D.3. 如图，直线AB ，CD 相交于点O ，若50AOC ∠=︒，15DOE ∠=︒，则∠BOE 的度数为（）A. 15︒B. 30︒C. 35︒D. 65︒4. 如果一个几何体的三视图都是矩形，那么这个几何体可能是（）A. 三棱柱B. 长方体C. 圆柱D. 圆锥5. 若a b <，则下列结论正确的是（）A. a b-<- B. 2a a b<+ C. 11a b-<- D. 2121a b +>+6. 正十边形的内角和为（）A. 144︒B. 360︒C. 1440︒D. 1800︒7. 掷一枚质地均匀的骰子，骰子的六个面上分别刻有1到6的点数，向上一面的点数为5的概率是（）A.23B. 12C.13D.168. 如图，四边形ABCD 是正方形，点E F ，分别在AB BC ，的延长线上，且BE CF =，设AD a AE b AF c ===，，．给出下面三个结论：①a b c +>；②22ab c <；2a >．上述结论中，所有正确结论的序号是（）A. ①②B. ②③C. ①③D. ①②③二、填空题（共16分，每题2分）9. x 的取值范围是______．10. 分解因式：3x 2+6xy+3y 2＝_____．11. 方程21345x x =-的解为______．12. 关于x 的一元二次方程250x x m ++=有两个不相等的实数根，则实数m 的取值范围是_____．13. 某种植户种植了1000棵新品种果树，为了解这1000棵果树的水果产量，随机抽取了50棵进行统计，获取了它们的水果产量（单位：千克），数据整理如下：水果产量50x <5075x ≤<75100x ≤<100125x ≤<125x ≥果树棵数11520122根据以上数据，估计这1000棵果树中水果产量不低于75千克的果树棵数为_____．14. 在数学活动课上，小南利用镜子、尺子等工具测量学校教学楼高度（如图所示），当他刚好在点C 处的镜子中看到教学楼的顶部D 时，测得小南的眼睛与地面的距离 1.6m AB =，同时测得 2.4m BC =，9.6m CE =，则教学楼高度DE =_____m ．15. 如图，O 是Rt ABC △的外接圆，OE AB ⊥于点D ，交O 于点E ，若8AB =，2DE =，则BC 的长为_____．16. 甲、乙两位同学合作为班级联欢会制作A B C D 、、、四个游戏道具，每个道具的制作都需要拼装和上色两道工序，先由甲同学进行拼装，拼装完成后再由乙同学上色．两位同学完成每个道具各自的工序需要的时间（单位：分钟）如下表所示： A B C D 甲9568乙7793（1）如果按照A B C D →→→的顺序制作，两位同学合作完成这四个道具的总时长最少为_______分钟；（2）两位同学想用最短的时间完成这四个道具的制作，他们制作的顺序应该是_______．三、解答题（共68分，第17-19题，每题5分，第20-21题，每题6分，第22-23题，每题5分，第24题6分，第25题5分，第26题6分，第27-28题，每题7分）解答应写出文字说明、演算步骤或证明过程．17. ()012π2sin45--︒18. 解不等式组：()2431432x x x x ⎧-<-⎪⎨--<⎪⎩，．19. 已知220x y ++=，求代数式 2422yxx x x y ⎛⎫-⋅⎪-⎝⎭的值．20. 如图，在ABCD Y 中，AB AC =，过点D 作AC 的平行线与BA 的延长线相交于点 E ．（1）求证：四边形ACDE 是菱形；（2）连接CE ，若5tan 2AB B ==，，求CE 的长．21. 燕几（即宴几）是世界上最早的一套组合桌，设计者是北宋进士黄伯思．全套燕几一共有七张桌子，每张桌子高度相同．其桌面共有三种尺寸，包括2张长桌、2张中桌和3张小桌，它们的宽都相同．七张桌面可以拼成一个大的长方形，或者分开组合成不同的图形，其方式丰富多样，燕几也被认为是现代七巧板的前身．右图给出了《燕几图》中列出的名称为“函三”和“回文”的两种桌面拼合方式．若全套七张桌子桌面的总面积为61.25平方尺，则长桌的长为多少尺？22. 在平面直角坐标系xOy 中，正比例函数()0y mx m =≠的图象和反比例函数 ()0ky k x=≠的图象都经过点()24A ，．（1）求该正比例函数和反比例函数的解析式；（2）当3x >时，对于x 的每一个值，函数()0y mx n m =+≠的值都大于反比例函数 ()0k y k x=≠的值，直接写出n 的取值范围．23. 某广场用月季花树做景观造型，先后种植了两批各12棵，测量并获取了所有花树的高度（单位：cm ），数据整理如下：a ．两批月季花树高度的频数： 131135136140144148149第一批13422第二批12351b ．两批月季花树高度的平均数、中位数、众数（结果保留整数）：平均数中位数众数第一批140140n 第二批141m144（1）写出表中m ，n 的值；（2）在这两批花树中，高度的整齐度更好的是（填“第一批”或“第二批”）；（3）根据造型的需要，这两批花树各选用10棵，且使它们高度的平均数尽可能接近．若第二批去掉了高度为135cm 和149cm 的两棵花树，则第一批去掉的两棵花树的高度分别是 cm 和 cm ．24. 如图，AB 是O 的直径，点C 在O 上，D 是 BC的中点，AD 的延长线与过点B 的切线交于点E ，AD 与BC 的交点为F ．（1）求证：BE BF =；（2）若O 的半径是2，3BE =，求AF 的长．25. 某款电热水壶有两种工作模式：煮沸模式和保温模式，在煮沸模式下将水加热至100C ︒后自动进入保温模式，此时电热水壶开始检测壶中水温，若水温高于50C ︒水壶不加热；若水温降至50C ︒，水壶开始加热，水温达到100C ︒时停止加热……此后一直在保温模式下循环工作．某数学小组对壶中水量a （单位：L ），水温T （单位： C ︒）与时间t （单位：分）进行了观测和记录，以下为该小组记录的部分数据．表1从20C ︒开始加热至100C ︒水量与时间对照表a0.51 1.522.53t4.5811.51518.522表2 1L 水从20C ︒开始加热，水温与时间对照表煮沸模式保温模式t036m 101214161820222426…T 205080100898072666055505560对以上实验数据进行分析后，该小组发现，水壶中水量为1L 时，无论在煮沸模式还是在保温模式下，只要水壶开始加热，壶中水温T 就是加热时间t 的一次函数．（1）写出表中m 的值；（2）根据表2中的数据，补充完成以下内容：①在下图中补全水温与时间的函数图象；②当60t =时，T = ；（3）假设降温过程中，壶中水温与时间的函数关系和水量多少无关．某天小明距离出门仅有30分钟，他往水壶中注入2.5L 温度为 20C ︒的水，当水加热至100C ︒后立即关闭电源．出门前，他（填“能”或“不能”）喝到低于50C ︒的水．26. 在平面直角坐标系xOy 中，抛物线 ()20y ax bx a =+>上有两点()()1122,,x y x y ，，它的对称轴为直线x t =．（1）若该抛物线经过点()40，，求t 的值；（2）当()101x <<时，①若1t >，则1y 0；（填“>”“=”或“<” ）②若对于122x x +=，都有120y y >，求t 的取值范围．27. 如图，在菱形ABCD 中，120BAD ∠=︒，E 是CD 边上一点（不与点C ，D 重合）．将线段AE 绕点A 逆时针旋转60︒得到线段AF ，连接DF ，连接BF 交AC 于点G ．（1）依据题意，补全图形；（2）求证：GB GF =；（3）用等式表示线段BC ，CE ，BG 之间的数量关系．28. 在平面直角坐标系xOy 中，O 的半径为1，对于直线l 和线段PQ ，给出如下定义：若线段PQ 关于直线l 的对称图形是O 的弦P Q ''（P '，Q '分别为P ，Q 的对应点），则称线段PQ 是O 关于直线l 的“对称弦”（1）如图，点1A ，2A ，3A ，1B ，2B ，3B 的横、纵坐标都是整数．线段11A B ，22A B ，33A B 中，是O 关于直线1y x =+的“对称弦”的是；（2）CD 是O 关于直线()0y kx k =≠的“对称弦”，若点C 的坐标为()1,0-，且1CD =，求点D 的坐标；（3）已知直线y x b =-+和点(3,M ，若线段MN 是O 关于直线y b =-+的“对称弦”，且1MN =，直接写出b 的值．参考答案一、选择题（共16分，每题2分）第1-8题均有四个选项，其中符合题意的选项只有一个．1. 【答案】B【分析】本题考查了科学记数法的表示方法．科学记数法的表示形式为10n a ⨯的形式，其中110a ≤<，n 为整数，解题的关键要正确确定a 的值以及n 的值．【详解】解：10748700000007.48710=⨯；故选：B ．2. 【答案】D【分析】本题考查了中心对称图形以及轴对称图形，根据中心对称图形是指图形绕着某个点旋转180°能与原来的图形重合；轴对称图形是指图形沿一条直线折叠，直线两旁的部分能够完全重合；逐项分析即可得出答案．【详解】解：A 、正三角形是轴对称图形不是中心对称图形，A 不符合题意；B 、等腰直角三角形是轴对称图形不是中心对称图形，B 不符合题意；C 、正五边形是轴对称图形不是中心对称图形，C 不符合题意；D 、正六边形既是轴对称图形又是中心对称图形，D 符合题意；故选：D ．3. 【答案】C【分析】本题考查了对顶角相等，角的运算；根据对顶角的性质得50BOD AOC ∠=∠=︒，根据BOE BOD DOE ∠=∠-∠即可求解．【详解】解：∵直线AB ，CD 相交于点O ，50AOC ∠=︒，∴50BOD AOC ∠=∠=︒，∵15DOE ∠=︒，∴501535BOE BOD DOE ∠=∠-∠=︒-︒=︒．故选：C ．4. 【答案】B【分析】本题考查了简单几何图的三视图，根据几何体的三视图逐项判断即可求解．【详解】解：三棱柱的两个底面是三角形，所以不可能三视图都是矩形，故选项A 不符合题意；长方体的三视图都是矩形，故选项B 符合题意；圆柱的两个底面是三角形，所以不可能三视图都是矩形，故选项C 不符合题意；正立的圆锥的主视图和左视图都是等腰三角形，俯视图是带圆心的圆，故选项D 不符合题意．故选：B ．5. 【答案】B【分析】本题主要考查不等式的基本性质，解题的关键是根据不等式的两边同时加上（或减去）同一个数或同一个含有字母的式子，不等号的方向不变逐项判定．【详解】解：A 、若a b <，则a b ->-，故不合题意；B 、若a b <，则2a a b <+，故符合题意；C 、若a b <，则11a b ->-，故不合题意；D 、若a b <，则2121a b +<+，故不合题意，故选：B ．6. 【答案】C【分析】本题主要考查多边形的内角和，解题的关键是利用多边形的内角和公式进行计算即可．【详解】解：正十边形的内角和为180(102)︒⨯-1808=︒⨯1440=︒．故选C ．7. 【答案】D【分析】本题主要考查概率公式，解题的关键是根据概率公式求解，随机事件A 的概率()P A =事件A 可能出现的结果数÷所有可能出现的结果数．【详解】解：∵骰子的六个面上分别刻有1到6的点数，∴向上一面的点数为5的概率是16，故选：D ．8. 【答案】A【分析】本题考查正方形的性质，全等三角形的判定和性质，勾股定理，证明DAE BAF △≌△，结合三角形的三边关系判断①；完全平方公式结合勾股定理判定②；勾股定理判断③．【详解】解：∵正方形ABCD ，∴,90AD AB BC DAB ABC ==∠=∠=︒，∵BE CF =，∴AE BF =，∴DAE BAF △≌△，∴AF DE c ==，∵AD AE DE +>，∴a b c +>；故①正确；∵222AD AE DE +=，即：222+=a b c ，∴()2222220b a a ab b c ab -=-+=->，∴22ab c <；故②正确；c =，且,E F 为动点，∴无法确定c 和2a 的关系，故③错误；故选A ．二、填空题（共16分，每题2分）9. 【答案】14x ≥【分析】本题考查了二次根式有意义的条件，解一元一次不等式，根据被开方数不小于零列出不等式，解不等式即可．∴140x -≥，解得：14x ≥．故答案为：14x ≥．10. 【答案】3（x+y ）2．【分析】先利用提取公因式法提取数字3，再利用完全平方公式继续进行分解．【详解】3x 2+6xy +3y 2=3（x 2+2xy +y 2）=3（x +y ）2．故答案为3（x +y ）2．【点睛】本题考查了用提公因式法和公式法进行因式分解，一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解，同时因式分解要彻底，直到不能分解为止．11. 【答案】2x =【分析】本题考查了解分式方程，根据去分母，去括号，移项，合并同类项，系数化为1的步骤解方程，然后检验即可得出答案．【详解】解：21345x x =-去分母得：()2453x x -=，去括号得：8103x x -=，移项得：8310x x -=，合并同类项得：510x =，系数化为1得：2x =．检验：当2x =时，()3450x x -≠，∴原分式方程的解为2x =．故答案为：2x =．12. 【答案】254m <【分析】根据有两个不相等的实数根，直接得到判别式＞0，即可求解本题．【详解】解：∵方程250x x m ++=有两个不相等的实数根，∴25410＞∆=-⨯⨯m ，解得：254m <；故答案为：254m <．【点睛】本题考查的是一元二次方程根的判别式，注意记忆判别式大于0时有两个不相等的实数根，判别式等于0时有两个相等的实数根，判别式小于0时方程无实数根．13. 【答案】680【分析】本题考查了频数（率）分布表和用样本估计总体，解题的关键是利用样本估计总体思想的运用．用1000乘以水果产量不低于75千克的果树的百分比即可求解．【详解】解：估计这1000棵果树中水果产量不低于75千克的果树棵数为20122100068050++⨯=（棵）．故答案为：680．14. 【答案】6.4【分析】本题考查了相似三角形的应用，根据相似三角形的判定和性质列出比例式，即可求解．【详解】解：由题意可知，AB DE ∥，∴ABC DEC ∽△△，∴AB BCDE CE=，即1.62.49.6DE =，解得 6.4DE =，则教学楼高度 6.4m DE =，故答案为：6.4．15. 【答案】6【分析】本题考查了垂径定理，勾股定理和中位线定理，由垂径定理得142AD BD AB ===，90ADO BDO ∠=∠=︒，则可得OD 是ABC 的中位线，设半径为r ，由勾股定理得222OA OD AD =+，求出=5r 即可求解，熟练掌握知识点的应用是解题的关键．【详解】解：∵OE AB ⊥，∴142AD BD AB ===，90ADO BDO ∠=∠=︒，∵OA OC =，∴OD 是ABC 的中位线，∴12OD BC =，即2BC OD =，设半径为r ，则2OD OE DE r =-=-，在Rt AOD 中，由勾股定理得：222OA OD AD =+，∴()22224r r =-+，解得=5r ，∴23OD r =-=，∴26BC OD ==．16. 【答案】 ①. 35 ②. B C A D→→→【分析】本题主要考查最优化时间的使用的有理数加减运算，()1根据甲乙各自的拼装和上色所需时间进行分解，求出对应的用时再求得总时长即可；()2由于甲乙开始都需要时间，为甲选择B ，再结合各自所需时间排序即可．【详解】解：（1）甲先拼装A 需9分钟，乙开始上色A ，与此同时甲可以拼装B 和2分钟的C ，乙给B 上色时，甲可以继续拼装C 和3分钟D ，乙为C 上色5分钟时甲可以完成D 的拼装，此时乙还需要4分钟为C 上色，接着为D 上色3分钟，时间分解如图，（其中字母表示制作的游戏道具，数字表示相应的时间）故总时长最少为97754335+++++=分钟，故答案为35；（2）甲先拼装B 需5分钟，乙开始上色B ，与此同时甲可以拼装C 和1分钟的A ，乙给C 上色时，甲可以继续拼装A 和1分钟D ，乙为A 上色7分钟时甲可以完成D 的拼装，此时乙还需要3分钟为D 上色，时间分解如图，选择B C A D →→→这种方案即可用时最少．（其中字母表示制作的游戏道具，数字表示相应的时间）故答案为B C A D→→→．三、解答题（共68分，第17-19题，每题5分，第20-21题，每题6分，第22-23题，每题5分，第24题6分，第25题5分，第26题6分，第27-28题，每题7分）解答应写出文字说明、演算步骤或证明过程．17.【答案】【分析】此题主要考查了实数运算，解题的关键是直接利用二次根式的性质、绝对值的性质、特殊角的三角函数值、零整数指数幂的性质分别化简得出答案．()012π2sin45+---︒112=-+-11=+-+=18. 【答案】12x-<<【分析】本题考查了解一元一次不等式组，分别解出每个不等式的解集，然后确定不等式组的解集即可，熟练掌握不等式组的解法是解题的关键．【详解】解：()2431432x xxx⎧-<-⎪⎨--<⎪⎩①②，解不等式①得，1x>-，解不等式②得，2x<，∴不等式组的解集为12x-<<．19. 【答案】24x y+，4-【分析】本题考查了分式的化简求值，先根据分式的混合运算化简所求式子，再根据220x y++=，可以得到22+=-x y，代入化简后的式子计算即可．【详解】解：2422y xxx x y⎛⎫-⋅⎪-⎝⎭22422x y x x x y -=⋅-()()2222x y x y xxx y-+=⋅-()22x y =+24x y =+，∵220x y ++=，∴22+=-x y ，∴原式()()22422x y ==⨯-=-+．20. 【答案】（1）见解析（2）【分析】（1）由平行四边形的性质得AB CD =，AB CD ∥，再证明四边形ACDE 是平行四边形，进而证明CD AC =，然后由菱形的判定即可得出结论；（2）设AD 与CE 交于点F ，证明FAC ACB B ∠=∠=∠，再由菱形的性质得AF DF =，CF EF =，AD CE ⊥，进而由锐角三角函数定义得CF 2AF =，设CF x =，则2CF x =，然后在Rt AFC △中，由勾股定理得出方程，解方程即可．【小问1详解】证明：四边形ABCD 是平行四边形，AB CD ∴=，AB CD ∥，DE AC ∥ ，∴四边形ACDE 是平行四边形，AB AC = ，CD AC ∴=，∴平行四边形ACDE 是菱形；【小问2详解】如图，设AD 与CE 交于点F ，5AB AC == ，B ACB ∴∠=∠，四边形ABCD 是平行四边形，AD BC ∴∥，FAC ACB B ∴∠=∠=∠，由（1）可知，四边形ACDE 是菱形，AB CD AE ∴==，AD BC ∥，AD CE ⊥，90BCE AOE ∴∠=∠=︒，在Rt BCE △中，tan 2CEB BC==，设BC x =，则2CE x =，∵AB =5∴BE =2AB =10∵222BC CE BE += ，222(2)10x x ∴+=，解得12)x x ==-舍即CE 的长为【点睛】本题考查了菱形的判定与性质、平行四边形的判定与性质、锐角三角函数定义以及勾股定理等知识．21. 【答案】7【分析】本题考查了一元二次方程的应用，结合图形表示出小桌、中桌、长桌的长是解题的关键．设每张桌面的宽为x 尺，结合图形分别表示出小桌、中桌、长桌的长，根据题意列出方程，解方程即可求解．【详解】解：设每张桌面的宽为x 尺，根据图形可得：小桌的长为2x 尺，中桌的长为3x 尺，长桌的长为4x 尺，故可得22224233261.25x x x ⨯+⨯+⨯=，解得：174x =，274x =-（舍去），∴47x =，答：长桌的长为7尺．22. 【答案】（1）2y x =，8y x=（2）103n ≥-【分析】本题考查了反比例函数与一次函数的交点问题，解题的关键是：（1）将A 点坐标代入两个函数解析式求出,m k 值即可；（2）当3x =时，26y mx n x n n =+=+=+，883y x ==，根据题意863n +>，解出不等式解集即可．【小问1详解】解：正比例函数(0)y mx m =≠的图象和反比例函数(0)kyk x=≠的图象都经过点(2,4)A ，422m ∴==，428k =⨯=，∴正比例函数解析式为：2y x =；反比例函数解析式为：8y x=；【小问2详解】当3x =时，26y mx n x n n =+=+=+，883y x ==，当3x >时，对于x 的每一个值，函数(0)ymx n m =+≠的值都大于反比例函数(0)ky k x=≠的值，863n ∴+≥，解得103n ≥-．23. 【答案】（1）140n =，142m = （2）第二批（3）131，135【分析】本题考查了众数，中位数，平均数等．（1）根据众数和中位数的定义直接进行解答即可；（2）从平均数，众数和中位数三个方面进行分析，即可得出答案；（3）根据表中给出的数据，分别进行分析，即可得出答案．【小问1详解】解：∵在第一批中，140出现了4次，出现的次数最多，∴众数是140cm ，即140n =；把第二批花的高度从小到大排列，中位数是第6、第7个数的平均数，则中位数是1401441422+=（cm ），即142m =；【小问2详解】（2）第一批的方差是：112×[（131-140）2+3×（135-140）2+4×（140-140）2+2×（144-140）2+2×（148-140）2]=793，第二批的方差是：112×[（135-141）2+2×（136-141）2+3×（140-141）2+5×（144-141）2+（149-141）2]=16.5，则在这两批花树中，高度的整齐度更好的是第二批；故答案为：第二批；【小问3详解】解：第二批去掉了高度为135cm 和149cm 的两棵花树后的平均数为：14112135149140.810⨯--=（cm ），第一批花树的平均数为140cm ，去掉的两棵且使高度尽可能接近平均高度，则需要去掉高度最小的两颗，即去掉的两棵花树的高度分别是131cm ，135cm ；故答案为：131，135．24. 【答案】（1）证明见解析（2）75【分析】（1）根据在同圆中等弧所对的圆周角相等得出BAD CAD ∠=∠，根据直径所对的圆周角是直角可得90C ∠=︒，根据直角三角形中两个锐角互余可得90CAD AFC ∠+∠=︒，根据对顶角相等可得90CAD EFB ∠+∠=︒，根据圆的切线垂直于经过切点的半径可得90ABE ∠=︒，根据直角三角形中两个锐角互余可得90E BAD ∠+∠=︒，根据等角的余角相等可得EEFB ∠=∠，根据等角对等边即可证明；（2）连接BD ，根据直径所对的圆周角是直角可得90ADB ∠=︒，根据直角三角形中两个锐角互余可得90EAB ABD ∠+∠=︒，根据等角的余角相等可得EAB EBD ∠=∠，根据题意可得4AB =，根据直角三角形中两直角边的平方和等于斜边的平方求得5AE =，根据锐角三角形函数的定义可求得95ED =，根据等腰三角形底边上的高与底边上的中点重合可得185EF =，即可求解．【小问1详解】证明：∵D 是 BC的中点，∴ BDCD =，∴BAD CAD ∠=∠，∵AB 是O 的直径，∴90C ∠=︒，∴90CAD AFC ∠+∠=︒，∵AFC EFB ∠=∠，∴90CAD EFB ∠+∠=︒，∵BE 与O 相切于点B ，∴90ABE ∠=︒，∴90E BAD ∠+∠=︒，∴EEFB ∠=∠，∴BE BF =．【小问2详解】解：连接BD ，如图：∵AB 是O 的直径，∴90ADB ∠=︒，∴90EAB ABD ∠+∠=︒，∵90ABE EBD ABD ∠=∠+∠=︒，∴EAB EBD ∠=∠，∵O 的半径是2， ∴4AB =，∵3BE =，在Rt ABE △中，5AE ===，∴3sin sin 5DE BE EBD EAB BE AE ====∠∠，∴39sin 355ED BE EBD =⋅=⨯=∠，∵BE BF =，BD EF ⊥，∴9182255EF DE ==⨯=，∴187555AF AE EF =-=-=．【点睛】本题考查了圆周角定理，直角三角形的性质，切线的性质，等腰三角形的性质，勾股定理，锐角三角形函数的定义，等角的余角相等等，熟练掌握圆周角定理、等腰三角形的性质和勾股定理是解题的关键．25. 【答案】（1）8（2）①图见解析；②60℃ （3）不能【分析】本题考查了一次函数的应用，理解题意并分析表格中数据变化的规律是解题的关键．（1）在煮沸模式下，加热时间每增加3分钟，水温就上升30℃，从而计算出每增加1分钟水上升的温度，据此列方程并求解即可；（2）①描点并连线即可；②当时间从26分开始，设时间为t 时，水温加热到100℃．在这个过程中每2分钟，水温升高5℃，从而求出每增加1分钟水上升的温度，据此列方程求出t ，再计算出剩下的时间，根据表2，得到在剩下的时间内水温可以变化到多少；（3）由表1可知，2.5L 的水从20℃加热到100℃需要18.5分，此时离出门还剩3018.511.5-=（分）；根据表2，计算水温从100℃降到50℃需要的时间，将这个时间与21.5分比较，在关闭电源的基础上即可得到结论．【小问1详解】解：在煮沸模式下，加热时间每增加3分钟，水温就上升30℃，30310÷=（℃），∴在煮沸模式下，加热时间每增加1分钟，水温就上升10℃，∴()10610080m -=-，∴8m =．【小问2详解】解：①补全水温与时间的函数图象如图所示：②当时间从26分开始，设时间为t 时，水温加热到100℃．在这个过程中每2分钟，水温升高5℃，则每1分钟水温升高52 2.5÷=（℃），由此得()2.52610060t -=-，解得42t =，604218-=（分），根据表2的数据可知，100T =℃经过18分后水温降到了60℃，∴当60t =时，60T =℃．故答案为：60℃；【小问3详解】解：由表1可知，2.5L 的水从20℃加热到100℃需要18.5分，3018.511.5-=（分），由表2可知，水温从100℃降到50℃需要22814-=（分），∵11.513<，且电源已关闭，∴出门前，他不能喝到低于50℃的水．故答案为：不能．26. 【答案】（1）2t = （2）①<，②1t ≤或0t ≤【分析】本题主要考查二次函数的性质，()1将点代入抛物线求得4b a =-，结合对称轴定义即可求得；()2①根据题意得抛物线开口向上，且过原点，即可得10y<；②由已知求得212x <<，结合120y y >恒成立，则有点()()1122,,x y x y ，在x 的同侧即可．【小问1详解】解：将点()40，代入()20y ax bx a =+>得1640a b +=，解得4b a =-，∴4222b a x a a-=-=-=，则2t =；【小问2详解】①根据题意得抛物线开口向上，且过原点，∵1t >，101x <<，∴10y <；②∵122x x +=， 101x <<，∴212x <<，∵有120y y >恒成立，∴点()()1122,,x y x y ，在x 的同侧，则1t ≤或0t ≤．27. 【答案】（1）图见解析（2）证明见解析（3）22234BC CE BG +=【分析】（1）根据题意连线即可；（2）连接BD ，与AC 相交于点O ，根据旋转的性质可得60EAF ∠=︒，AE AF =，根据菱形的性质可得AB BC =，1602BAC CAD BAD ∠=∠=∠=︒，BO OD =，根据等边三角形的判定和性质可得AC AD =，60ACD ∠=︒，根据全等三角形的的判定和性质可得60ADF ACD ==︒∠∠，根据平行线的判定得出DF AC ∥，根据平行线分线段成比例定理即可证明；（3）根据勾股定理可得2224BD DF BG +=，根据等边三角形的性质可得30OBC ∠=︒，根据锐角三角函数可求得BC =，推得223BC BD =，即可求解．【小问1详解】解：如图：【小问2详解】证明：连接BD ，与AC 相交于点O ，如图：∵线段AE 绕点A 逆时针旋转60︒得到线段AF ，∴60EAF ∠=︒，AE AF =，∵在菱形ABCD 中，120BAD ∠=︒，∴AB BC =，1602BAC CAD BAD ∠=∠=∠=︒，BO OD =，∴ABC 、ACD 是等边三角形，∴AC AD =，60ACD ∠=︒，∴CAE DAF ∠=∠,∴ACE ADF ≌，∴60ADF ACD ==︒∠∠，∴DF AC ∥，∴BGBOGF OD =，∵BO OD =，∴GB GF =；【小问3详解】解：22234BC CE BG +=，理由如下：∵DF AC ∥，BD AC ⊥，∴DF BD ⊥，在Rt BFD 中，()2222224BD DF BF BG BG +===，∵ABC 是等边三角形，BO AC ⊥，∴1302OBC ABC ==︒∠，cos30cos OB OBC BC ︒===∠，∴BC =，则2243BC BO =，则()2222342BC BO BO BD ===，∴2222234BC CE BD DF BG +=+=，即22234BC CE BG +=．【点睛】本题考查了旋转的性质，菱形的性质，等边三角形的判定和性质，平行线的判定和性质，全等三角形的判定和性质，平行线分线段成比例定理，勾股定理，解直角三角形等，解题的关键是根据全等三角形的性质和平行线的判定推得DF AC ∥．28. 【答案】（1）11A B（2）1,2⎛- ⎝或12⎛- ⎝（3【分析】（1）根据题中定义即可画图得出；（2）根据题意可得直线()0y kx k =≠垂直平分CC '，DD '，结合点C 的坐标，推得点D 在O 上，即可得出点D 是C 与O 交点，根据等边三角形的性质和勾股定理即可求得点1D 、2D 的坐标；（3）结合（2）可得点1N 是点1M 与O 交点，先求出直线y x b =-+与x ，y 轴的交点坐标，结合三角形的面积求得OH 的值，根据锐角三角函数可求得点O '的坐标3,2b ⎫⎪⎪⎭，根据两点间的距离公式即可列出方程，解方程即可．【小问1详解】解：如图所示：∴O 关于直线1y x =+的“对称弦”的是线段11A B ；【小问2详解】解：设点C ，D 关于直线()0y kx k =≠的对称点为C ',D ¢，∴直线()0y kx k =≠垂直平分CC '，DD '，∵CD 是O 关于直线()0y kx k =≠的“对称弦”，∴C ',D ¢在O 上，∵点C 的坐标为()1,0-，即点C 在O 上，∵直线()0y kx k =≠经过圆心O ，∴点D 也在O 上，∵1CD =，故点D 在以点C 为圆心，CD 为半径的圆上，如图：C 与O 交于点1D 与点2D ；∵11OC CD OD ==，即1OCD △是等边三角形，故点1D 的横坐标为12-，点1D同理，点2D 的横坐标为12-，点2D 的纵坐标为-，综上，点D 的坐标为1,2⎛- ⎝或12⎛- ⎝；【小问3详解】解：设点M 关于直线y x b =-+的对称点为1M ,∴直线y x b =-+垂直平分1MM ，∵线段MN 是O 关于直线y x b =-+的“对称弦”， ∴1M 在O 上，由（2）可得点1N 在以点1M 为圆心，MN 为半径的圆上，又∵1MN =，即11OM =；令直线y x b =-+与x ，y 轴交于点P ，Q ，过点O 作OO '⊥直线y x b =-+交于点H ，点O '作O E x '⊥轴交于点E ，如图：令0x =，则y b =，即点()0,Q b ，OQ b =,令0y =，则x =，即点),0P ，OP =，则2PQ b ===，则OQ OP OH PQ ⋅===，∴2OO OH =='，∵90OQP QOH ∠+∠=︒，90OQP QPO ∠+∠=︒，∴QOH QPO ∠=∠，∵OQ O E ' ，∴OO E QOH QPO ∠=∠=∠'，∵1sin 2OQ QPO PQ ∠==，cos OP QPO PQ ∠==，∴1sin 2OE OO E OO ∠==''，cos O E OO E OO ''=='∠∴sin OE OO OO E ''=⋅∠=，3cos 2O E OO OO E b ='∠'⋅='，即点O '的坐标为3,2b ⎫⎪⎪⎭，∵(3,M ，11O M OM '==；∴1O M '==，整理得：23200b -+=，解得：b =或b =，故b 的值为【点睛】本题考查了轴对称的性质，一次函数与坐标轴的交点问题，解直角三角形，勾股定理，等边三角形的判定和性质等，正确理解新定义的含义，灵活应用数形结合思想是解题的关键．。

2024北京大兴区初三一模数学试卷和答案

2024北京大兴初三一模数学考生须知：1．本试卷共6页，共28道题．满分100分．考试时间120分钟．2．在试卷和答题卡上准确填写姓名、准考证号、考场号和座位号．3．试题答案一律填涂或书写在答题卡上，在试卷上作答无效．4．在答题卡上，选择题、作图题用2B 铅笔作答，其他试题用黑色字迹签字笔作答．5．考试结束，将本试卷、答题卡和草稿纸一并交回．一、选择题（共16分，每题2分）第1-8题均有四个选项，符合题意的选项只有一个．1. 下面几何体中，是圆锥的为（）A. B. C. D.2. 2024年是京津冀协同发展十周年，高标准建设雄安新区成效显著．从新区设立至2023年底，累计开发面积184平方公里，4017栋楼宇拔地而起，总建筑面积4370万平方米．将43700000用科学记数法表示应为（）A. 643.710⨯B. 74.3710⨯C. 84.3710⨯D. 90.43710⨯3. 五边形的内角和为（）A. 180︒B. 360︒C. 540︒D. 720︒4. 如图，直线AB ，CD 相交于点O ，OE AB ⊥，若30AOC ∠=︒，则EOD ∠的大小为（）A. 30︒B. 60︒C. 120︒D. 150︒5. 实数a ，b ，c 在数轴上的对应点的位置如图所示，下列结论中正确的是（）A. 0b c ->B. 0ac >C. 0b c +<D. 1ab <6. 不透明的盒子中装有3个小球，每个小球上面写着一个汉字分别是“向”、“前”、“冲”，这3个小球除汉字外无其他差别，从中随机摸出一个小球，记录其汉字，放回并摇匀，再从中随机摸出一个小球，记录其汉字，则两次都摸到“冲”字的概率是（）A. 23 B. 13 C. 16 D. 197. 若关于x 的一元二次方程220x x m +-=有两个不相等的实数根，则实数m 的取值范围是（）A. 1m >-B. 1m ≥-C. 1m >D. m 1≥8. 如图，在ABC 中，90BAC ∠=︒，AD BC ⊥于点D ，设BD a =，DC b =，AD c =，给出下面三个结论：①2c ab =；②2a b c +≥；③若a b >，则a c >．上述结论中，所有正确结论的序号是（）A.①②B. ①③C. ②③D. ①②③二、填空题（共16分，每题2分）9. 在实数范围内有意义，则实数x 的取值范围是______．10.分解因式：24ab a -=_______.11. 方程1341x x =-的解为______．12. 在平面直角坐标系xOy 中，若点(5,2)A 和(,2)B m -在反比例函数(0)k y k x=≠的图象上，则m 的值为______．13. 如图，AB 是O 的直径，点C ，D 在O 上，若AC BC =，则D ∠的度数为______︒．14. 如图，在矩形ABCD 中，AC 与BD 相交于点O ，OE BC ⊥于点E ．若4AC =，30DBC ∠=︒，则OE 的长为______．15. 某年级为了解学生对“足球”“篮球”“排球”“乒乓球”“羽毛球”五类体育项目的喜爱情况，现从中随机抽取了100名学生进行问卷调查，根据数据绘制了如图所示的统计图．若该年级有800名学生，估计该年级喜爱“篮球”项目的学生有______人．16. 某公园门票价格如下表：某学校组织摄影、美术两个社团的学生游览该公园，两社团的人数分别为a 和()b a b >．若两社团分别以各自社团为单位购票，共需1560元；若两社团作为一个团体合在一起购票，共需1170元，那么这两个社团的人数为=a ______，b =______．购票人数1~4041~8080以上门票价格20元/人16元/人13元/人三、解答题（共68分，第17-20题，每题5分，第21题6分，第22-23题，每题5分，第24-26题，每题6分，第27-28题，每题7分）解答应写出文字说明、演算步骤或证明过程．17. 计算：0|3|(2024)2cos 45π-+++-︒18. 解不等式组：4125213x x x x -≥+⎧⎪-⎨<⎪⎩19. 已知2310a a +-=，求代数式2(1)(4)2a a a +++-的值．20. 某学校开展“浸书香校园，品诗词之美”读书活动．现有A ，B 两种诗词书籍整齐地叠放在桌子上，每本A 书籍和每本B 书籍厚度的比为5:6，根据图中所给出的数据信息，求每本A 书籍的厚度．21. 如图，在正方形ABCD 中，点E ，F 分别在BC ，AD 上，BEDF =，连接CF ，射线AE 和线段DC 的延长线交于点G ．（1）求证：四边形AECF 是平行四边形；（2）若2tan 3BAE ∠=，9DG =，求线段CE 的长．22. 种子被称作农业的“芯片”，粮安天下，种子为基．农科院计划为某地区选择合适的甜玉米种子，随机抽取20块自然条件相同的试验田进行试验，得到各试验田每公顷产量（单位：t ），并对数据（每公顷产量）进行了整理、描述和分析，下面给出了部分信息：a ．20块试验田每公顷产量的频数分布表如下：每公顷产量(t)频数7.407.45x ≤<37.457.50x ≤<27.507.55x ≤<m 7.557.60x ≤<67.607.65x ≤≤5b ．试验田每公顷产量在7.557.60x ≤<这一组的是：7.55 7.55 7.57 7.58 7.59 7.59c ． 20 块试验田每公顷产量的统计图如下：（1）写出表中m 的值；（2）随机抽取的这20块试验田每公顷产量的中位数为______．（3）下列推断合理的是______（填序号）；①20块试验田的每公顷产量数据中，每公顷产量低于7.50t 的试验田数量占试验田总数的25%；②3号试验田每公顷产量在20块试验田的每公顷产量数据中从高到低排第5名．（4）1~10号试验田使用的是甲种种子，11~20号试验田使用的是乙种种子，已知甲、乙两种种子的每公顷产量的平均数分别为7.537t 及7.545t ，若某种种子在各试验田每公顷产量的10个数据的方差越小，则认为这种种子的产量越稳定．据此推断：甲、乙两种种子中，这个地区比较适合种植的种子是______（填“甲”或“乙”）．23. 在平面直角坐标系xOy 中，函数(0)y kx b k =+≠的图象经过点(1,3)A 和(1,1)B --，与过点(2,0)-且平行于y 轴的直线交于点C ．（1）求该函数的表达式及点C 的坐标；（2）当2x <-时，对于x 的每一个值，函数(0)y nx n =≠的值大于函数(0)y kx b k =+≠的值且小于2-，直接写出n 的取值范围．24. 某洒水车为绿化带浇水，图1是洒水车喷水区域的截面图，其上、下边缘都可以看作是抛物线的一部分，下边缘抛物线是由上边缘抛物线向左平移得到的．喷水口H 距地面的竖直高度OH 为1.5m ，喷水区域的上、下边缘与地面交于A ，B 两点，上边缘抛物线的最高点C 恰好在点B 的正上方，已知6m OA =，2m OB =，2m CB =．建立如图2所示的平面直角坐标系．（1）在①21(2)28y x =-++，②21(2)28y x =--+两个表达式中，洒水车喷出水的上边缘抛物线的表达式为______，下边缘抛物线的表达式为______（把表达式的序号填在对应横线上）；（2）如图3，洒水车沿着平行于绿化带的公路行驶，绿化带的横截面可以看作矩形DEFG ，水平宽度3m DE =，竖直高度0.5m DG =．如图4，OD 为喷水口距绿化带底部的最近水平距离（单位：m ）．若矩形DEFG 在喷水区域内，则称洒水车能浇灌到整个绿化带．①当 2.6m OD =时，判断洒水车能否浇灌到整个绿化带，并说明理由；②若洒水车能浇灌到整个绿化带，则OD 的取值范围是______．25. 如图，过O 外一点A 作O 的切线，切点为点B ，BC 为O 的直径，点D 为O 上一点，且BD BA =，连接CD ，AD ，线段AD 交直径BC 于点E ，交O 于点F ，连接BF ．（1）求证：EF BF =；（2）若1sin 3A =，25OE =，求O 半径的长．26. 在平面直角坐标系xOy 中，()11,M x y ，()22,N x y 是抛物线2(0)y ax bx c a =++<上任意两点．设抛物线的对称轴为直线x t =．（1）若22x =，2y c =，求t 的值；（2）若对于112t x t +<<+，245x <<，都有12y y >，求t 的取值范围．27. 在ABC 中，AC BC =，90ACB ∠=︒，点D 是线段AB 上一个动点（不与点A ，B 重合），()045ACD αα∠=<<︒，以D 为中心，将线段DC 顺时针旋转90︒得到线段DE ，连接EB ．（1）依题意补全图形；（2）求EDB ∠的大小（用含α的代数式表示）；（3）用等式表示线段BE ，BC ，AD 之间的数量关系，并证明．28. 在平面直角坐标系xOy 中，已知点(,0)T t ，T e 的半径为1，过T e 外一点P 作两条射线，一条是T e 的切线，另一条经过点T ，若这两条射线的夹角大于或等于45︒，则称点P 为T e 的“伴随点”．（1）当0=t 时，①在1(1,0)P ，2P ，3(1,1)P -，4(1,2)P -中，T e 的“伴随点”是______．②若直线12y x b =+上有且只有一个T e 的“伴随点”，求b 的值；（2）已知正方形EFGH 的对角线的交点(0,)M t ，点11,22E t ⎛⎫-+ ⎪⎝⎭，若正方形上存在T e 的“伴随点”，直接写出t 的取值范围．参考答案一、选择题（共16分，每题2分）第1-8题均有四个选项，符合题意的选项只有一个．1. 【答案】D【分析】本题考查了常见几何体的识别，观察所给几何体，可以直接得出答案．【详解】解：A 选项为正方体，不合题意；B 选项为球，不符合题意；C 选项为五棱锥，不合题意；D 选项为圆锥，符合题意．故选：D ．2. 【答案】B【分析】本题考查科学记数法，科学记数法的表示形式为 10n a ⨯ 的形式，其中 110a ≤<，n 为整数（确定 n 的值时，要看把原数变成 a 时，小数点移动了多少位）．【详解】解：43700000=74.3710⨯，故选：B ．3. 【答案】C【分析】本题考查了n 边形内角和公式，熟练记忆公式是解题的关键．代入公式即可求解．【详解】解：五边形的内角和为()52180540-⨯︒=︒，故选：C ．4. 【答案】B【分析】本题主要考查的是对顶角的性质和垂线，依据垂线的定义可求得90EOB ∠=︒，然后依据对顶角的性质可求得BOD ∠的度数，最后依据EOD EOB DOB ∠=∠-∠求解即可．【详解】解：∵OE AB ⊥，∴90EOB ∠=︒．∵30DOB AOC ∠=∠=︒，∴903060EOD EOB DOB ∠=∠-∠=︒-︒=︒．故选：B ．5. 【答案】C【分析】本题考查了根据点在数轴的位置判断式子的正负．熟练掌握根据点在数轴的位置判断式子的正负是解题的关键．由数轴可知，32101a b c -<<-<<-<<<，则0b c -<，0ac <，0b c +<，1ab >，然后判断作答即可．【详解】解：由数轴可知，32101a b c -<<-<<-<<<，∴0b c -<，0ac <，0b c +<，1ab >，∴A 、B 、D 错误，故不符合要求；C 正确，故符合要求；故选：C ．6. 【答案】D【分析】本题考查的是列表法或画树状图求解概率，根据题意列出表格即可求解．【详解】解：根据题意列表如下：向前冲向向，向前，向冲，向前向，前前，前前，冲冲向，冲前，冲冲，冲共有9种等可能得情况，其中两次都摸到“冲”字的情况有1种，则两次都摸到“冲”字的概率是：19，故选：D ．7. 【答案】A【分析】本题考查了根的判别式：一元二次方程()200ax bx c a ++=≠的根与24b ac ∆=-有如下关系：当0∆>时，方程有两个不相等的实数根；当Δ0=时，方程有两个相等的实数根；当Δ0<时，方程无实数根．根据判别式的意义得到()22410m ∆=-⨯⨯->，然后求出不等式的解集即可．【详解】解：根据题意得()22410m ∆=-⨯⨯->，解得1m >-．故选：A ．8. 【答案】D【分析】由90BAC ∠=︒，AD BC ⊥，得到ABD CAD ∽△△，BD AD AD DC =，将BD a =，DC b =，AD c =代入，即可判断①正确，由()2222a b a b ab -=+-，()2222a b a b ab +=++，将2c ab =代入，整理后即可判断②正确，将2c b a=，代入a b >，即可判断③正确，本题考查了，相似三角形的性质与判定，完全平方公式的应用，解不等式，解题的关键是：熟练掌握完全平方公式的变形及应用．【详解】解：∵90BAC ∠=︒，AD BC ⊥，∴90BAD CAD ∠+∠=︒，90BAD ABD ∠+∠=︒，90BAD ADC ∠=∠=︒，∴CAD ABD ∠=∠，∴ABD CAD ∽△△，∴BD AD AD DC=即：a c c b =，整理得：2c ab =，故①正确，∵()2222a b a b ab -=+-，即：()2222a b a b ab +=-+， ∴()()()222222244a b a b ab a b ab a b c +=++=-+=-+，∵()20a b -≥，∴()224a b c +≥，∵0a >、0b >、0c >，∴2a b c +≥，故②正确，∵a b >，2c b a=，∴2c a a>，∵0a >，∴22a c >，∴a c >，故③正确，综上所述，①②③正确，故选：D ．二、填空题（共16分，每题2分）9. 【答案】3x ≥【分析】此题主要考查了分式有意义及二次根式有意义的条件，正确掌握相关定义是解题关键．由分式有意义及二次根式有意义的条件，进而得出x 的取值范围．【详解】由二次根式的概念，可知30x -≥，解得3x ≥.故答案为：3x ≥10. 【答案】()()22a b b +-．【分析】要将一个多项式分解因式的一般步骤是首先看各项有没有公因式，若有公因式，则把它提取出来，之后再观察是否是完全平方公式或平方差公式，若是就考虑用公式法继续分解因式．因此，先提取公因式a 后继续应用平方差公式分解即可【详解】解：()()()224422a a a a b b b b -=-=+-，故答案为：()()22a b b +-．11. 【答案】1x =【分析】本题考查了解分式方程，先将分式方程化为一元一次方程，再解一元一次方程，最后检验即可求解，注意分式的方程需要检验是解题的关键．【详解】解：1341x x =-∴413x x -=，解得：1x =，经检验，1x =是原分式方程的解，∴1x =，故答案为：1x =．12. 【答案】5-【分析】本题考查了反比例函数图象上点的坐标特征，先把(5,2)A 代入(0)k y k x=≠求出10,k =再把(,2)B m -代入10y x=，求出5m =-．【详解】解：把(5,2)A 代入(0)k y k x =≠得：25k =，解得，10,k =∴反比例函数解析式为10y x =，把(,2)B m -代入10y x =，得：102m-=，解得，5m =-，故答案为：5-13. 【答案】45【分析】本题主要考查了圆周角定理，先由直径所对的圆周角为90︒，可得90ACB ∠=︒，然后由AC BC =得：45CAB CBA ∠=∠=︒，然后根据同弧所对的圆周角相等，即可求出D ∠的度数．【详解】解：∵AB 是O 的直径，∴90ACB ∠=︒，∵AC BC =，∴45CAB CBA ∠=∠=︒，∴45D CAB ∠=∠=︒．故答案为：4514. 【答案】1【分析】本题考查矩形的性质，等腰三角形的判定和性质，解直角三角形，根据矩形的性质，得到OB OC =，根据三线合一结合30度角的直角三角形的性质，求解即可．【详解】解：∵矩形ABCD ，∴OB OC =，90BCD ∠=︒，4BD AC ==，∵30DBC ∠=︒，∴122CD BD ==，∴BC =，∵OB OC =，OE BC ⊥，∴12BE BC ==，∴tan 301OE BE =⋅︒==；故答案为：1．15. 【答案】240【分析】本题主要考查了样本估计总体．用800乘以喜爱“篮球”项目所占的百分比，即可．【详解】解：30800240100⨯=人，即该年级喜爱“篮球”项目的学生有240人．故答案为：24016. 【答案】 ①. 60 ②. 30【分析】本题考查了二元一次方程组的应用，由两次门票费用，列出方程组，可求解．【详解】解：∵1170不能整除16，∴两个部门的人数81a b +≥，又1560不能整除16，∴每个部门的人数不可能同时在41~80之间，由于a b >，所以，当140,4180b a ≤≤≤≤，则有：()20161560131170b a a b +=⎧⎨+=⎩解得，6030a b =⎧⎨=⎩故答案为：60，30．三、解答题（共68分，第17-20题，每题5分，第21题6分，第22-23题，每题5分，第24-26题，每题6分，第27-28题，每题7分）解答应写出文字说明、演算步骤或证明过程．17. 【答案】4+【分析】本题考查了实数的混合运算，掌握相关运算法则是解题关键．先计算绝对值、零指数幂、二次根式、特殊角的三角函数值，再计算加减法即可．【详解】解：0|3|(2024)2cos 45π-+++-︒312=++-⨯31=++-4=．18. 【答案】3x ≥【分析】本题主要考查了解一元一次不等式组，先求出每个不等式的解集，再根据 “同大取大，同小取小，大小小大中间找，大大小小找不到（无解）”求出不等式组的解集即可．【详解】解：4125213x x x x -≥+⎧⎪⎨-<⎪⎩①②解不等式①，得3x ≥．解不等式②，得1x >-．∴不等式组的解集为3x ≥．19. 【答案】1【分析】本题考查整式的混合运算、代数式求值，熟练掌握运算法则是解答的关键．先根据整式的混合运算法则结合完全平方公式化简原式，再将已知化为2262a a +=代入求解即可．【详解】解：2(1)(4)2a a a +++-222142a a a a =++++-2261a a =+-．2310a a +-= ，231a a ∴+=．2262a a ∴+=．∴原式2261a a =+-21=-1=．20. 【答案】每本A 书籍厚度为1cm【分析】本题主要考查了二元一次方程的应用，设每本A 书籍厚度为cm x ，桌子高度为cm y ，根据等量关系，列出方程组，解方程组即可．【详解】解：设每本A 书籍厚度为cm x ，桌子高度为cm y ，由题意可得：37965825x y x y +=⎧⎪⎨⨯+=⎪⎩，解得176x y =⎧⎨=⎩，答：每本A 书籍厚度为1cm ．21. 【答案】（1）见解析（2）2CE =【分析】本题考查了平行四边形的判定，正方形的性质，正切的定义；（1）根据正方形的性质得出AD BC ∥，AD BC =．根据题意得出AF CE =，即可得证；（2）根据正方形的性质得出2tan tan 3BAE G ∠==，在Rt ADG 中，得出6CD =则3CG =，根据2tan 3CEG CG ==，即可求解．【小问1详解】证明：四边形ABCD 是正方形，∴AD BC ∥，AD BC =．BE FD =，∴AD FD BC BE -=-．即AF CE =．又 AF CE ∥，∴四边形AECF 是平行四边形．【小问2详解】解：四边形ABCD 是正方形，∴AD BC ∥，90BCD D ∠=∠=︒，AD CD =．∴BAE G ∠=∠，90ECG ∠=︒，∴2tan tan 3BAE G ∠==．在Rt ADG 中， 2tan 3ADG DG ==，9DG =，∴6AD =．∴6CD =．∴3CG =．在Rt ECG 中， 2tan 3CEG CG ==，∴2CE =．22. 【答案】（1）4 （2）7.55（3）① （4）乙【分析】本题考查了频数分布表，求中位数，根据方差判断稳定性：（1）运用频数总数减去已知频数即可得出m ；（2）根据中位数的定义可求解；（3）从统计图中可得每公顷产量低于7.50t 的试验田数量有5块，可判断①；3号试验田每公顷产量在20块试验田的每公顷产量数据中从高到低排第4名可判断②．（4）根据图象判断稳定性即可得出结果．【小问1详解】解：2032654m =----=【小问2详解】解：随机抽取的这20块试验田每公顷产量的中位数是7.557.60x ≤<这一组的第1个和第2个数据，即：7.55和7.55，故中位数为：7.557.557.552+=，故答案为：7.55；【小问3详解】解：20块试验田的每公顷产量数据中，每公顷产量低于7.50t 的试验田数量有5块，所以，占试验田总数的百分数为510025%20⨯=，故①正确；3号试验田每公顷产量在20块试验田的每公顷产量数据中从高到低排第4名，故②错误，故答案为：①【小问4详解】解：从20 块试验田每公顷产量的统计图中可看出甲种种子每公顷产量波动大，乙种种子每公顷产量波动小，据此推断：甲、乙两种种子中，这个地区比较适合种植的种子是乙；故答案为：乙23. 【答案】（1）21y x =+；(2,3)--（2）312n ≤≤【分析】本题考查待定系数法求一次函数解析式，一次函数图象及性质，用数形结合思想考虑本题是解答本题的关键．（1）将两点代入函数解析式中即可求得函数解析式，再将2x =-代入解析式即可求出点C 坐标；（2）根据题意将(2,2)--代入(0)y nx n =≠求出n 的最小值，再根据题意将C 代入求出n 的最大值，即为本题答案．【小问1详解】解：∵函数(0)y kx b k =+≠的图象经过点(1,3)A 和(1,1)B --，∴将点(1,3)A 和(1,1)B --代入(0)y kx b k =+≠中，31k b k b +=⎧⎨-+=-⎩，解得：21k b =⎧⎨=⎩，∴该函数的表达式为：21y x =+，∵与过点(2,0)-且平行于y 轴的直线交于点C ，∴将2x =-代入21y x =+中，得=3y -，∴(2,3)C --；【小问2详解】解：∵当2x <-时，对于x 的每一个值，函数(0)y nx n =≠的值大于函数(0)y kx b k =+≠的值且小于2-，，通过图象可知，当(0)y nx n =≠的函数值小于2-时，即将(2,2)--H 代入(0)y nx n =≠中，1n =，当(0)y nx n =≠的函数值大于函数(0)y kx b k =+≠的值将(2,3)C --代入(0)y nx n =≠中，32n =，∴n 的取值范围为：312n ≤≤．24. 【答案】（1）②，① （2）①不能；理由见解析；②21OD ≤≤-【分析】本题考查了二次函数的实际应用，（1）由题意可知：顶点坐标()2,2C ，()0,1.5H ，利用待定系数法即可求出函数解析式为：()21228y x =--+，利用()0,1.5H 关于对称轴2x =的对称点为：()4,1.5，可知下边缘抛物线是由上边缘抛物线向左平移4个单位得到，求出下边缘抛物线为：()21228=-++y x ；（2）①根据 2.6m OD =，将 5.6x =代入上边缘抛物线的函数解析式得出0.380.5y =<，即可求解；②当点B 和点D 重合时，d 有最小值，此时2d =；当上边缘抛物线过点F 时，d 有最大值，231=+-=-d ；所以21d ≤≤-．【小问1详解】解：由题意可知：()2,2C ，故设上边缘抛物线的函数解析式为：()222y a x =-+，∵()0,1.5H ，将其代入()222y a x =-+可得：()21.5022=-+a ，解得：18a =-，∴上边缘抛物线的函数解析式为：()21228y x =--+，解：∵()0,1.5H 关于对称轴2x =的对称点为：()4,1.5，∴下边缘抛物线是由上边缘抛物线向左平移4个单位得到，∴下边缘抛物线为：()21228=-++y x ，故答案为：②，①．【小问2详解】①不能，理由如下，依题意， 2.63 5.6OE =+=将 5.6x =代入上边缘抛物线的函数解析式()21228y x =--+得()215.6220.380.58y =--+=<∴绿化带不全在喷头口的喷水区域内，∴洒水车不能浇灌到整个绿化带；②解：设灌溉车到绿化带的距离OD 为d ，要使灌溉车行驶时喷出的水能浇灌到整个绿化带，则当点B 和点D 重合时，d 有最小值，此时2d =；当上边缘抛物线过点F 时，d 有最大值，3m DE =，0.5m EF =．∴令()21220.58=--+=y x ，解得：2x =+2x =-，结合图像可知：()2+Fd ∴的最大值为：231=+-=-d ；∴21d ≤≤-．故答案为：21OD ≤≤-．25. 【答案】（1）证明见解析（2）92【分析】（1）由切线的定义可得出90A AEB ∠+∠=︒，由直径所对的圆周角等于90︒得出90CDE BDE ∠+∠=︒，由等边对等角得出BDA A ∠=∠，等量代换得出CDE AEB ∠=∠，由同弧所对的圆周角相等得出C D E C B F ∠=∠，进而可得出AEB CBF ∠=∠ ，由等角对等边得出EF BF =．（2）连接CF ，先证明==AF BF EF ，设BF EF AF x ===，则2AE x =，解直角三角形Rt ABE 得出23BE x =，再证明BCF A ∠=∠，得出1sin sin 3A BCF =∠=，进一步得出22()BC OB OE BE ==+，即523223x x ⎛⎫=+ ⎪⎝⎭，解出x 即可求解．【小问1详解】证明： AB 为O 的切线，∴90OBA ∠=︒．∴90A AEB ∠+∠=︒．BC 为O 的直径，∴90CDB ∠=︒．∴90CDE BDE ∠+∠=︒．BD BA =，∴BDA A ∠=∠．∴CDE AEB ∠=∠．又CDE CBF ∠=∠ ，AEB CBF ∴∠=∠．EF BF ∴=．【小问2详解】连接CF ．AB 为O 的切线，∴90OBA ∠=︒．∴90AEB A ∠+∠=︒，90EBF FBA ∠+∠=︒．AEB CBF ∠=∠，∴FBA A ∠=∠．∴AF BF =．∴==AF BF EF ．设BF EF AF x ===，则2AE x =．在Rt ABE 中， 1sin 3A =，2AE x =，∴23BE x =．BC 为直径，∴90CFB ∠=︒．BCF BDA ∠=∠，BDA A ∠=∠，∴BCF A ∠=∠．∴1sin sin 3A BCF =∠=．在Rt BFC △中，BF x =，∴3BC x =．22()BC OB OE BE ==+，∴523223x x ⎛⎫=+⎪⎝⎭．解得3x =．∴92OB =．∴O 半径的长为92．【点睛】本题主要考查了切线的定义，直径所对的圆周角等于90︒，同弧所对的圆周角相等，解直角三角形的相关计算，等角对等边等知识，掌握这些性质是解题的关键．26. 【答案】（1）1t =（2）2t ≤或7t ≥【分析】本题主要考查了二次函数的图象和性质等知识，（1）将22x =，2y c =代入解析式，得出2b a =-即可得解；（2）分①当点N 在对称轴上或对称轴右侧时，②当点N 在对称轴上或对称轴左侧时两种情况讨论组成不等式组即可得解；解题的关键是理解题意，灵活运用所学知识解决问题．【小问1详解】22x =，2y c =，42a b c c ∴++=，2b a ∴=-，12bt a ∴=-=，【小问2详解】2(0)y ax bx c a =++<，∴抛物线开口向下，抛物线的对称轴为x t =，112t x t +<<+，∴点M 在对称轴的右侧，①当点N 在对称轴上或对称轴右侧时，抛物线开口向下，∴在对称轴右侧，y 随x 的增大而减小．由12y y >，∴12x x <，∴4,24t t ≤⎧⎨+≤⎩，解得42t t ≤⎧⎨≤⎩，∴2t ≤，②当点N 在对称轴上或对称轴左侧时，设抛物线上的点()22,N x y 关于x t =的对称点为()2,N d y '，2t x d t ∴-=-，解得22d t x =-，∴()222,N t x y '-，245x <<，∴225224t t x t -<-<-，在对称轴右侧，y 随x 的增大而减小，由12y y >，∴122x t x <-，∴5225t t t ≥⎧⎨+≤-⎩，解得57t t ≥⎧⎨≥⎩，∴7t ≥，综上所述，t 的取值范围是2t ≤或7t ≥．27. 【答案】（1）补全图形见解析（2）45α︒-（3）BC BE =+；证明见解析【分析】本题主要考查旋转的性质，全等三角形的性质与判定，三角形外角的性质，勾股定理等：（1）根据题目叙述作图即可；（2）由三角形外角性质得45CDB A ACD α∠=∠+∠=︒+，根据90CDE ∠=︒可得结论；（3）过点D 作DM AB ⊥，交AC 于点F ，交BC 的延长线于点M ．证明DCM DEB △≌△，得出CM BE =，再证明CF CM =，CF BE =，在Rt FAD △中，由勾股定理得出AF =，得出AC FC =+，由CF BE =，BC AC =可得出结论【小问1详解】补全图形如下：【小问2详解】解： AC BC =，90ACB ∠=︒，∴45A ABC ∠=∠=︒．∴45CDB A ACD α∠=∠+∠=︒+．90CDE ∠=︒，∴45EDB CDE CDB α∠=∠-∠=︒-．【小问3详解】解：用等式表示线段BE ，BC ，AD 之间的数量关系是BC BE =+．证明：过点D 作DM AB ⊥，交AC 于点F ，交BC 的延长线于点M ．90MDB CDE ∠=∠=︒，∴CDM EDB ∠=∠．45MBD ∠=︒，∴45M MBD ∠=∠=︒．∴DM DB =．又 DC DE =，∴DCM DEB △≌△．∴CM BE =．45M ∠=︒，90ACB ∠=︒，∴45CFM M ∠=∠=︒．∴CF CM =．∴CF BE =．在Rt FAD △中，45A ∠=︒，∴45AFD A ∠=∠=︒,∴,AD FD =AF ∴==．AC AF FC =+ ，AC FC ∴=+．CF BE = ，BC AC =，BC BE ∴=+．28. 【答案】（1）①2P ，3P ；②b =（232t <≤或32t -≤<【分析】（1）①设射线PM 与T e 相切于点M ，连接TM ，根据题目中的定义得出1PT <≤，分别求出四个点与()0,0T 间的距离，然后进行判断即可；②根据直线12y x b =+上有且只有一个T e 的“伴随点”，得出直线12y x b =+与以()0,0T为半径的圆相切，设直线12y x b =+与x 轴，y 轴分别交于点A 、B ，与以()0,0T 为半径的圆相切于点C ，连接TC ，求出BT ===，得出b =，即可求出结果；（2）分两种情况进行讨论：当0t >时，当0t <时，分别画出图形，列出不等式组，解不等式组即可．【小问1详解】解：①如图1，设射线PM 与T e 相切于点M ，连接TM ，∴TM PM ⊥，当45P ∠=︒时，PTM △为等腰直角三角形，∴1PM TM ==，PT ===，∴当点P 在T e 外，45P ≥︒∠时，1PT <≤，当0=t 时，点()0,0T ，∵11PT =，2PT =，3PT ==4PT ==>∴在1(1,0)P ，2P ，3(1,1)P -，4(1,2)P -中，T e 的“伴随点”是2P ，3P ；故答案为：2P ，3P②∵当点P 在T e 外，45P ≥︒∠时，1PT <≤∴点P 在以T 为半径的圆上或圆内且在以1为半径的圆外，如图2：∵直线12y x b =+上有且只有一个T e 的“伴随点”，∴直线12y x b =+与以()0,0T 为圆心，为半径的圆相切，∴0b ≠，设直线12y x b =+与x 轴，y 轴分别交于点A 、B ，与以()0,0T 为半径的圆相切于点C ，连接TC ，∴TC AB ⊥，令0x =，y b =，令0y =，2x b =-，∴()2,0A b -，()0,B b ，∴2AT b =-，BT b =，在Rt ATB △中，1tan 122bBTAT b ∠===-，1290∠+∠=︒，∵TC AB ⊥，∴2390∠+∠=︒，∴13∠=∠，∴1312tan tan ==∠∠，在Rt TCB 中132tan BC CT ===∠，∴BC =∴BT ===，∴b =∴b =；【小问2详解】解：∵正方形EFGH 的对角线的交点(0,)M t ，点11,22E t ⎛⎫-+ ⎪⎝⎭，∴点11,22G t ⎛⎫- ⎪⎝⎭，11,22F t ⎛⎫+ ⎪⎝⎭，11,22H t ⎛⎫-- ⎪⎝⎭，当0t >时，如图所示：此时正方形EFGH 上的点到圆心T 的最大距离为ET ，最小距离为GT ，∵正方形上存在T e 的“伴随点”，且点P 在以T为圆心，以为半径的圆上或圆内且在以1为半径的圆外，∴1ET >，GT ≤，∵12ET t ⎫==+⎪⎭，12GT ==-，∴11212t ⎫+>⎪⎭-≤，32t <≤；当0t <时，如图所示：此时正方形EFGH 上的点到圆心T 的最大距离为GT ，最小距离为ET ，∵正方形上存在T e 的“伴随点”，且点P 在以T为圆心，以为半径的圆上或圆内且在以1为半径的圆外，∴ET ≤，1GT >，∵12ET ==+，12GT t ⎫==-⎪⎭，∴12112t +≤⎫->⎪⎭，解得：32t -≤<；综上分析可知：t 32t <≤或32t -≤<．【点睛】本题主要考查了切线的性质，解直角三角形，勾股定理，两点间距离公式，等腰直角三角形的性质，解不等式组，解题的关键是数形结合，注意进行分类讨论．。

2024年北京西城区九年级初三一模数学试卷及答案

北京市西城区九年级统一测试试卷数学 2024.4考生须知1. 本试卷共7页，共两部分， 28道题。

满分 100分。

考试时间120分钟。

2. 在试卷和草稿纸上准确填写姓名、准考证号、考场号和座位号。

3. 试题答案一律填涂或书写在答题卡上，在试卷上作答无效。

4. 在答题卡上，选择题、作图题用2B 铅笔作答，其他试题用黑色字迹签字笔作答。

5. 考试结束，将本试卷、答题卡和草稿纸一并交回。

第一部分选择题一、选择题 (共16分,每题2分)第1-8题均有四个选项，符合题意的选项只有一个.1.右图是某几何体的展开图，该几何体是 (A) 圆锥 (B)三棱柱 (C)三棱锥 (D)四棱锥2. 2024年5.5G 技术正式开始商用，它的数据下载的最高速率从5G 初期的1Gbps 提升到10Gbps,给我们的智慧生活“提速”.其中10Gbps 表示每秒传输10000000000 位(bit)的数据. 将 10000000000用科学记数法表示应为(A )0.1×10¹¹ (B )1×10¹⁰ (C )1×10¹¹ (D) 10×10⁹3.下列图形中，既是中心对称图形也是轴对称图形的是4. 直尺和三角板如图摆放，若∠1=55°，则∠2的大小为 (A)35° (B)55° (C) 135° (D) 145°北京市西城区九年级统一测试试卷数学2024.4 第1页 (共7页)15.如图，两个边长相等的正六边形的公共边为BD，点A，B，C在同一直线上，点O₁， O₂分别为两个正六边形的中心. 则tan∠O₂AC的值为.16. 将1, 2, 3, 4, 5, …, 37这37个连续整数不重不漏地填入37个空格中. 要求: 从左至右，第1个数是第2个数的倍数，第1个数与第2个数之和是第3个数的倍数，第1，2，3个数之和是第4个数的倍数，…，前36个数的和是第37个数的倍数.若第 1 个空格填入 37，则第 2 个空格所填入的数为，第 37 个空格所填入的数为 .37三、解答题(共68分,第17-22题,每题5分,第23-26题,每题6分,第27-28题,每题7分)解答应写出文字说明、演算步骤或证明过程.17. 计算:|−3|−+2sin60∘−12.18.解不等式组: 2(+1)<x+5, x+23≥x−12.19. 已知x²−x−4=0,求代数式 (x−2)²+(x−1)(x+3)的值.20. 如图,点E在▱ABCD的对角线DB的延长线上,AE=AD.AF⊥BD于点F,EG∥BC交AF的延长线于点G, 连接DG.(1) 求证: 四边形AEGD是菱形;(2)若AF=BF,tan∠AEF=12,AB=4,求菱形AEGD的面积.21.某学校组织学生社团活动，打算恰好用1000元经费购买围棋和象棋，其中围棋每套40元，象棋每套30元.所购买围棋的套数能否是所购买象棋套数的2倍?若能，请求出所购买的围棋和象棋的套数，若不能，请说明理由.22. 在平面直角坐标系xOy中,函数y=kx+b(k≠0)的图象经过点A(3,5), B(-2,0), 且与y轴交于点 C.(1)求该函数的解析式及点C的坐标；(2)当x<2时, 对于x的每一个值, 函数y=-3x+n的值大于函数y=kx+b(k≠0)的值，直接写出n的取值范围.北京市西城区九年级统一测试试卷数学2024.4 第3页 (共7页)24. 如图, AB 为⊙O 的直径, 弦CD⊥AB 于点H, OO 的切线CE 与BA 的延长线交于点E, AF∥CE, AF 与⊙O 的交点为F.(1) 求证: AF=CD;(2) 若⊙O 的半径为6, AH=2OH,求AE 的长.25. 如图，点O 为边长为1的等边三角形ABC 的外心. 线段PQ 经过点O，交边AB 于点P, 交边AC 于点Q. 若 AP =x,AQ =y 1,S APQ :S ABC =y 2,下表给出了x, y ₁, y ₂的一些数据 (近似值精确到0.0001).x 0.50.550.60.650.70.750.80.850.90.951y ₁10.84620.750.68420.63640.60.57140.54840.52940.51350.5y ₂0.46540.450.44470.44550.450.45710.46610.47650.48780.5(1)补全表格;(2)在同一平面直角坐标系xOy 中描出了部分点( x ,y ₁,x ,y ₂..请补全表格中数据的对应点，并分别画出y ₁与y ₂关于x 的函数图象；(3)结合函数图象，解决下列问题：①当△APQ 是等腰三角形时， y ₁关于x 的函数图象上的对应点记为(a ，b)，请在x轴上标出横坐标为a 的点；C ②当y ₂取最大值时，x 的值为 .北京市西城区九年级统一测试试卷数学2024.4 第5页 (共7页)5.不透明袋子中装有红、蓝小球各一个，除颜色外无其他差别，随机摸出一个小球后，放回并摇匀，再从中随机摸出一个小球，则两次都摸到蓝球的概率为(A) 14(B) 13(C) 12(D)236. 已知-2<a<-1, 则下列结论正确的是(A) a<1<-a<2 (B) 1<a<-a<2 (C) 1<-a<2<a (D) -a<1<a<27.若关于x 的一元二次方程 lnx²+x−2=0有两个实数根，则实数k 的取值范围是(A )k ≤−18 (B )k >−18且k≠0 (C )k ≥−18且k≠0 (D )k ≥−14且k≠08. 如图, 在Rt△ABC 中, ∠ACB=90°, BC=a, AC=b(其中a<b). CD⊥AB 于点D,点E 在边AB 上, BE=BC. 设CD=h, AD=m, BD=n, 给出下面三个结论:①n²+h²<(m+n)²;②2h²>m²+n²;③AE 的长是关于 x 的方程 x²+2ax−b²=0的一个实数根.上述结论中，所有正确结论的序号是(A)① (B) ①③ (C) ②③ (D) ①②③第二部分非选择题二、填空题 (共16分,每题2分)9. 若 x−3在实数范围内有意义，则实数x 的取值范围是 .10. 分解因式:x²y-12xy+36y= .11. 方程43x−1=3x−2的解为 .12.在平面直角坐标系xOy 中，若函数 y =kx(k ≠0)的图象经过点(-1,8)和(2,n), 则n 的值为.13. 如图, 在▱ABCD 中, 点E 在边AD 上, BA, CE 的延长线交于点F. 若AF=1, AB=2, 则 AEED =¯.14. 如图, 在⊙O 的内接四边形ABCD 中, 点A 是 ⌢BD 的中点，连接AC, 若∠DAB=130°, 则∠ACB= °.北京市西城区九年级统一测试试卷数学2024.4 第2页 (共7页)23.某学校组织学生采摘山楂制作冰糖葫芦(每串冰糖葫芦由5颗山楂制成).同学们经过采摘、筛选、洗净等环节，共得到7.6kg的山楂.甲、乙两位同学各随机分到了15颗山楂，他们测量了每颗山楂的重量(单位：g)，并对数据进行整理、描述和分析.下面给出了部分信息.a.甲同学的山楂重量的折线图：b.乙同学的山楂重量：8, 8.8, 8.9, 9.4, 9.4, 9.4, 9.6, 9.6, 9.6, 9.8, 10, 10, 10, 10,10c.甲、乙两位同学的山楂重量的平均数、中位数、众数：平均数中位数众数甲9.5m9.2乙9.59.6n根据以上信息，回答下列问题：(1)写出表中m, n的值;(2)对于制作冰糖葫芦，如果一串冰糖葫芦中5颗山楂重量的方差越小，则认为这串山楂的品相越好.①甲、乙两位同学分别选择了以下5颗山楂制作冰糖葫芦.据此推断：品相更好的是(填写“甲”或“乙”);甲9.29.29.29.29.1乙9.49.49.48.98.8②甲同学从剩余的 10颗山楂中选出5颗山楂制作一串冰糖葫芦参加比赛，首先要求组成的冰糖葫芦品相尽可能好，其次要求冰糖葫芦的山楂重量尽可能大.他已经选定的三颗山楂的重量分别为9.4，9.5，9.6，则选出的另外两颗山楂的重量分别为和；(3)估计这些山楂共能制作多少串冰糖葫芦.北京市西城区九年级统一测试试卷数学2024.4 第4页 (共7页)26. 在平面直角坐标系xOy中，点A−2y₁,B2y₂,C m y₃在抛物线y=ax²+bx+3(a⟩0)上.设抛物线的对称轴为直线x=t.(1)若y₁=3,,求t的值;(2) 若当t+1<m<t+2时，都有y₁>y₃>y₂,求t的取值范围.27. 在△ABC中,∠ABC=∠ACB=45°,AM⊥BC于点M.D是射线AB上的动点 (不与点 A, B重合), 点 E 在射线 AC 上且满足.AE=AD,，过点D 作直线 BE 的垂线交直线BC于点F, 垂足为点 G, 直线BE交射线AM于点P.(1) 如图1, 若点D在线段AB上, 当AP=AE时,求∠BDF的大小；(2)如图2，若点D在线段AB的延长线上，依题意补全图形，用等式表示线段CF，MP, AB的数量关系, 并证明.北京市西城区九年级统一测试试卷数学2024.4第6页 (共7页)28.在平面直角坐标系xOy 中，已知⊙O 的半径为1.对于⊙O 上的点 P 和平面内的直线l:y =ax 给出如下定义：点P 关于直线l 的对称点记为 P¹,，若射线OP 上的点Q 满足 OQ =PP ′,则称点Q 为点P 关于直线l 的“衍生点”.(1)当a=0时,已知⊙O 上两点 PP 2−22,在点Q ₁(1,2), QQ 3(−1,−1),Q 4(−2,−2)中，点P ₁关于直线l 的“衍生点”是，点P ₂关于直线l 的“衍生点”是；(2) P 为⊙O 上任意一点, 直线y=x+m (m≠0)与x 轴, y 轴的交点分别为点 A,B.若线段AB 上存在点S ，T ，使得点S 是点P 关于直线l 的“衍生点”，点T 不是点P 关于直线l 的“衍生点”，直接写出m 的取值范围；(3) 当-1≤a≤1时，若过原点的直线s 上存在线段 MN，对于线段 MN 上任意一点R，都存在⊙O 上的点P 和直线l ，使得点R 是点P 关于直线l 的“衍生点”. 将线段MN 长度的最大值记为D(s)，对于所有的直线s ，直接写出D(s)的最小值.北京市西城区九年级统一测试试卷数学2024.4 第7页 (共7页)北京市西城区九年级统一测试试卷数学答案及评分参考 2024.4一、选择题(共16分，每题2分)题号12345678答案C B D D A A C B二、填空题(共16分，每题2分)9. x≥3 10.y(x−6)² 11. x=-1 12. -413.1214. 25 15.3516. 1, 19三、解答题(共68分, 第17-22题, 每题5分, 第23-26题, 每题6分, 第27-28题,每题7分)17. 解: |−3|−+2sin60∘−12=3−5+2×32−23 4分 =-5 . 5分18.解：原不等式组为2(x+1)<x+5, x+23≥x−12.解不等式①, 得x<3. ·2分解不等式②, 得x≤7. 4分 ∴ 原不等式组的解集为x<3. 5分19. 解: (x−2)²+(x−1)(x+3)=(x²−4x+4)+(x²+2x−3)=2x²−2x+1.…… 3分∵x²−x−4=0,∴x²−x=4.∴原式=2(x²−x)+1=9. ·5分20. (1) 证明: 如图1.∵ AE=AD, AF⊥BD于点F,∴ ∠EAG=∠DAG, EF=DF.∵ 四边形 ABCD 是平行四边形,北京市西城区九年级统一测试试卷数学答案及评分参考 2024.4 第1页(共6页)①②∴ AD∥BC.∵ EG∥BC,∴ AD∥EG.∴ ∠AGE=∠DAG.∴ ∠EAG=∠AGE.∴ AE=EG.∴ AD=EG.∴ 四边形AEGD 是平行四边形.又∵ AE=AD,∴四边形AEGD是菱形.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3分(2) 解: 在Rt△ABF中, ∠AFB=90°, AF=BF, AB=4,∴ ∠ABF=45° , AF=AB·sin45°=22.在Rt△AEF中,∠AFE=90∘,tan∠AEF=12,AF=22,∴EF=AFtan∠AEF=4 2.∵ 四边形 AEGD 是菱形,∴AG=2AF=42,DE=2EF=8 2.∴S差πAEGD =12AG×DE=12×42×82=32. …5分21.解:设购买x套围棋,y套象棋 (1)假设所购买围棋的套数能是所购买象棋套数的2倍，①则40x+30y=1000,x=2y.② 3分解得y=10011. 4分此时 y不为正整数，不合题意.答：所购买围棋的套数不能是所购买象棋套数的2倍.⋯⋯⋯⋯⋯⋯⋯⋯5分22. 解: (1) ∵ 函数y=kx+b (k≠0) 的图象经过点 A(3,5), B(-2,0),∴3k+b=5,−2k+b=0.解得k=1,b=2.∴该函数的解析式为y=x+2,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分点C的坐标为C(0,2).⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3分(2)n≥10.……………………………………………………………………………5分北京市西城区九年级统一测试试卷数学答案及评分参考 2024.4 第2页 (共6页)23.解:(1)9.4,10;⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分(2)①甲;⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3分②9.3,9.6;⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5分(3)76009.5×5=160(串).答：估计这些山楂共能制作160串糖葫芦.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6分24. (1) 证明: 如图2, 连接OC, OC与AF交于点 G.∵ CE 与⊙O 相切, 切点为C,∴CE⊥OC.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分∴ ∠OCE=90° .∵ AF∥CE,∴ ∠OGA=∠OCE=90° .∴ OC⊥AF于点 G.∴ AF=2AG.∵ CD⊥AB 于点 H,∴ ∠OHC=90° , CD=2CH .∴ ∠OGA=∠OHC.又∵ ∠AOG=∠COH, OA=OC,∴ △OAG≌△OCH.∴ AG=CH.∴AF=CD.…………………………………………………… 3分(2) 解: ∵ ⊙O的半径为6, AH=2OH,∴ OH=2, AH=4.在Rt△OCH中,∠OHC=90∘,cos∠COH=OHOC =13.在Rt△OCE中,∠OCE=90∘,cos∠COE=13,OC=6,∴OE=OCcos∠COE=18.∴AE=OE-OA=18-6=12.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6分北京市西城区九年级统一测试试卷数学答案及评分参考 2024.4 第3页(共6页)25. 解: (1)0.5; ……………………… 1分(2)3分(3)①见图3; ·4分 ②0.5, 1. …6分26. 解: (1) 抛物线 y =ax²+bx +3与y 轴的交点的坐标为(0，3).∵ 抛物线. y =ax²+bx +3过A(-2,y ₁), y ₁=3,∴ A(-2,3)与(0,3)关于直线x=t 对称.∴t =−2+02=−1. 2分(2) ∵ a>0,∴ 当x≤t 时, y 随x 的增大而减小; 当x≥t 时, y 随x 的增大而增大.A(-2,y ₁), B(2,y ₂), C(m,y ₃).①当t≤-2时,∵ t≤-2<2,|.y₁<y₂,不合题意.②当-2<t<2时, A(-2,y ₁)关于对称轴x=t 的对称点为 A ′(2t +2,y ₁).∵ 当t+1<m<t+2时, 都有 y₁>y₃>y₂,∴t +1≥2,t +2≤2t +2.解得 t≥1.∴ 1≤t<2.③当t≥2时,A(-2,y ₁),B(2,y ₂)关于对称轴x=t 的对称点分别为 A ′(2t +2,y ₁), B ′(2t−2,y ₂).北京市西城区九年级统一测试试卷数学答案及评分参考 2024.4 第4页(共6页)∵当t+1<m<t+2时, 都有. y₁>y₃>y₂,∴t +1≥2t−2,t +2≤2t +2.解得 0≤t≤3.∴ 2≤t≤3.综上所述,t 的取值范围是1≤t≤3.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6分27. 解: (1) 如图4.∵在△ABC 中, ∠ABC=∠ACB=45° ,∴ AB=AC, ∠BAC=90° , ∠1+∠2=90°.∵ AM⊥BC 于点 M,∴∠3=∠BAC 2=45∘,BM =CM.∵ AP=AE, ∴∠2=180∘−∠32=180∘−45∘2=67.5∘.∵ DF⊥BE 于点 G,∴ ∠1+∠BDF=90°.∴∠BDF=∠2=67.5°.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分(2)补全图形见图5.CF =2MP +2AB.证明: 如图4, 作 CQ∥AP 交BE 于点 Q.∵ CQ∥AP, BM=CM, AM⊥BC, ∴MP CQ =BM BC =12,∠BCQ =∠AMC =90∘ ∴CQ =2MP,∠5=180°−∠ACB−∠BCQ =45°.∵∠4=∠ABC =45°,∴ ∠4=∠5.北京市西城区九年级统一测试试卷数学答案及评分参考 2024.4 第5页 (共6页)∵∠DBG=∠ABE,DG⊥BE于点 G,∠BAC=90°,∴ ∠D=∠E.∵AD=AE,AB=AC,∴AD−AB=AE−AC, 即BD=CE.∴△BDF≅△CEQ.:.BF=CQ.∵CF=BF+BC,BC=2AB,∴CF=CQ+2AB=2MP+2AB. ……………… 7分28. 解: (1)Q₂,Q₃; · ·2分(2)−22≤m≤−2或 2≤m≤22; ·5分(3)2−2. 7分北京市西城区九年级统一测试试卷数学答案及评分参考 2024.4 第6页(共6页)。

北京市各区2022届中考数学一模试题分类汇编几何综合

（2）若边AD上存在一点F，使得AF+CE=EF，请你在图2中探究∠ABF与
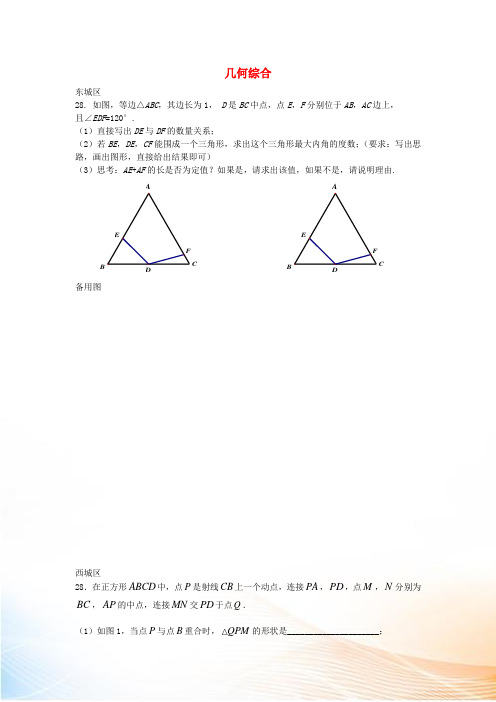
∠CBE的数量关系并证明；
（3）在（2）的条件下，若点E为边CD的三等分点，且CE<DE，请写出求
cos∠FED的思路．（可以不写出计算结果）．
图1图2备用图
顺义区
28．已知：在△ABC中，∠BAC=60°．
如图1，若AB=AC，点P在△ABC内，且∠APC=150°，PA=3，PC=4，把△APC绕着点A顺时针旋转，使点C旋转到点B处，得到△ADB，连接DP
图1图2
图1图2图3
朝阳区
28．在等腰三角形ABC中，AC=BC，点P为BC边上一点（不与B、C重合），连接PA，以P为旋转中心，将线段PA顺时针旋转，旋转角与∠C相等，得到线段PD，连接DB．
（1）当∠C=90º时，请你在图1中补全图形，并直接写出∠DBA的度数；
（2）如图2，若∠C=α，求∠DBA的度数（用含α的代数式表示）；
（2）判断AE与BD的数量关系与位置关系并加以证明；
（3）若0°＜α≤64°，AB=4，AE与BD相交于点G，求点G到直线AB的距离的最大值．请写出求解的思路（可以不写出计算结果）．
房山区
28.如图1，在四边形ABCD中，BA=BC，∠ABC=60°，∠ADC=30°，连接对角线BD.
（1）将线段CD绕点C顺时针旋转60°得到线段CE，连接AE.
（3）连接AD，若∠C =30º，AC=2，∠APC=135º，请写出求AD长的思路．（可以不写出计算结果）
海淀区
28．在△ABC中，AB=AC，∠BAC= ，点D在射线BC上（与B、C两点不重合），以
AD为边作正方形ADEF，使点E与点B在直线AD的异侧，射线BA与射线CF相交于点G．

2024年北京市西城区九年级中考复习一模数学试卷(含答案)

北京市西城区九年级统一测试试卷数学答案及评分参考 2024.4 第1页（共6页）北京市西城区九年级统一测试试卷数学答案及评分参考 2024.4一、选择题（共16分，每题2分）题号 1 2 3 4 5 6 7 8 答案CBDDAACB二、填空题（共16分，每题2分）9．x ≥3 10．2(6)y x 11．1x 12．4 13．1214．2515．3516．1，19三、解答题（共68分，第17-22题，每题5分，第23-26题，每题6分，第27-28题，每题7分）17．解： 11()2sin 60552 4分 5 ． ……………………………………………………………………………… 5分18．解：原不等式组为2+1+5,21.32x x x x≥（）解不等式①，得3x ．……………………………………………………………2分解不等式②，得x ≤7．……………………………………………………………4分 ∴ 原不等式组的解集为3x ．………………………………………………… 5分19．解： 2(2)(1)(3)x x x22(44)(23)x x x x2221x x ．……………………………………………………………………… 3分∵240x x ， ∴ 24x x ．∴ 2219x x 原式（）．…………………………………………………………5分20．（1）证明：如图1．∵ AE=AD ，AF ⊥BD 于点F ， ∴ ∠EAG=∠DAG ，EF=DF ． ∵ 四边形ABCD 是平行四边形，① ②北京市西城区九年级统一测试试卷数学答案及评分参考 2024.4 第2页（共6页）①② ∴ AD//BC ． ∵ EG//BC ， ∴ AD // EG ． ∴ ∠AGE=∠DAG ． ∴ ∠EAG=∠AGE ． ∴ AE=EG ． ∴ AD=EG ．∴ 四边形AEGD 是平行四边形．又∵ AE=AD ，∴ 四边形AEGD 是菱形． ……………………………………………… 3分（2）解：在Rt △ABF 中，∠AFB=90°，AF=BF ，AB=4，∴ ∠ABF=45°，sin 45AF AB ．在Rt △AEF 中，∠AFE=90°，1tan 2AEF，AF ， ∴tan AFEF AEF∵ 四边形AEGD 是菱形，∴2AG AF，2DE EF ∴ AEGD S菱形113222AG DE．…………………………5分 21．解：设购买x 套围棋，y 套象棋．………………………………………………………1分假设所购买围棋的套数能是所购买象棋套数的2倍，则40301000,2.x y x y…………………………………………………… 3分解得10011y．…………………………………………………………………… 4分此时 y 不为正整数，不合题意．答：所购买围棋的套数不能是所购买象棋套数的2倍．…………………………… 5分 22．解：（1）∵ 函数y kx b （k ≠0）的图象经过点(3,5)A ，(2,0)B ，∴ 35,20.k b k b解得 1,2.k b∴ 该函数的解析式为2y x ， ………………………………………… 2分点C 的坐标为(0,2)C ．………………………………………………… 3分（2）n ≥10．…………………………………………………………………………5分图1北京市西城区九年级统一测试试卷数学答案及评分参考 2024.4 第3页（共6页）23．解：（1）9.4，10；……………………………………………………………………… 2分（2）①甲；………………………………………………………………………… 3分②9.3，9.6；……………………………………………………………………5分（3）76001609.55（串）．答：估计这些山楂共能制作160串糖葫芦．…………………………………6分24．（1）证明：如图2，连接OC ，OC 与AF 交于点G ．∵ CE 与⊙O 相切，切点为C ，∴ CE ⊥OC ．……………………………………………………………… 1分 ∴ ∠OCE=90°． ∵ AF //CE ，∴ ∠OGA=∠OCE=90°． ∴ OC ⊥AF 于点G ． ∴ 2AF AG ． ∵ CD ⊥AB 于点H ，∴ ∠OHC=90°，2CD CH ． ∴ ∠OGA=∠OHC ．又∵ ∠AOG=∠COH ，OA=OC ， ∴ △OAG ≌△OCH ． ∴ AG=CH ．∴ AF=CD ．……………………………………………………………… 3分（2）解：∵ ⊙O 的半径为6，AH=2OH ，∴ OH=2，AH=4．在Rt △OCH 中，∠OHC=90°，1cos 3OH COH OC．在Rt △OCE 中，∠OCE=90°，1cos 3COE ，OC=6，∴ 18cos OCOE COE．∴ 18612AE OE OA ．…………………………………………… 6分图2北京市西城区九年级统一测试试卷数学答案及评分参考 2024.4 第4页（共6页）25．解：（1）0.5； ……………………………………………………………………………1分（2）图3…………………………………………………………………………… 3分（3）①见图3；………………………………………………………………………4分②0.5，1．………………………………………………………………………6分26．解：（1）抛物线23y ax bx 与y 轴的交点的坐标为(0,3)．∵ 抛物线23y ax bx 过1(2,)A y ，13y ， ∴ (2,3)A 与(0,3)关于直线x t 对称． ∴ 2012t．………………………………………………………… 2分（2）∵ a ＞0，∴ 当x ≤t 时，y 随x 的增大而减小；当x ≥t 时，y 随x 的增大而增大． 1(2,)A y ，2(2,)B y ，3(,)C m y ．①当t ≤2 时， ∵ t ≤2 ＜2， ∴ 12y y ，不合题意．②当2 ＜t ＜2时，1(2,)A y 关于对称轴x=t 的对称点为1(22,)A t y ． ∵ 当12t m t 时，都有132y y y ，∴ 12,22 2.t t t≥≤ 解得 t ≥1． ∴ 1≤t ＜2．③当t ≥2时，1(2,)A y ，2(2,)B y 关于对称轴x=t 的对称点分别为1(22,)A t y ，2(22,)B t y ．北京市西城区九年级统一测试试卷数学答案及评分参考 2024.4 第5页（共6页）∵ 当12t m t 时，都有132y y y ，∴ 122,22 2.t t t t≥≤ 解得 0≤t ≤3． ∴ 2≤t ≤3．综上所述，t 的取值范围是1≤t ≤3．……………………………………… 6分27．解：（1）如图4．∵ 在△ABC 中，∠ABC=∠ACB =45°， ∴ AB=AC ，∠BAC=90°，1290 ． ∵ AM ⊥BC 于点M ， ∴ 3452BAC，BM=CM ． ∵ AP=AE ， ∴ 180318045267.522． ∵ DF ⊥BE 于点G ， ∴ 190BDF ．∴ 267.5BDF ．…………………………………………………… 2分（2）补全图形见图5．2CF MP ．证明：如图4，作CQ ∥AP 交BE 于点Q ．∵ CQ ∥AP ，BM=CM ，AM ⊥BC ， ∴12MP BM CQ BC ，∠BCQ =∠AMC=90°． ∴ CQ=2MP ，518045ACB BCQ ． ∵ ∠4=∠ABC =45°， ∴ ∠4=∠5．图4图5∵∠DBG=∠ABE，DG⊥BE于点G，∠BAC=90°，∴∠D=∠E．∵AD= AE，AB=AC，∴AD AB AE AC，即BD=CE．∴△BDF≌△CEQ．∴BF=CQ．∵CF BF BC，BC ，∴2CF CQ MP．…………………………… 7分28．解：（1）2Q，3Q；………………………………………………………………………2分（2） m≤2 或2≤m≤5分（3）2 7分北京市西城区九年级统一测试试卷数学答案及评分参考2024.4 第6页（共6页）北京市西城区九年级统一测试试卷数学2024.4 第1页（共7页）北京市西城区九年级统一测试试卷数学 2024.4考生须知1．本试卷共7页，共两部分，28道题。

2023年北京市初三一模数学试题汇编：几何综合(第27题)

2023北京初三一模数学汇编几何综合（第27题）一、解答题∠平分线的一点，点M，N分1.（2023·北京西城·统考一模）如图，直线AB，CD交于点O，点E是BOC别是射线OA，OC上的点，且ME=NE.∠=∠；（1）求证：MEN AOC（2）点F在线段NO上，点G在线段NO延长线上，连接EF，EG，若EF=EG，依题意补全图形，用等式表示线段NF，OG，OM之间的数量关系，并证明.2.（2023·北京朝阳·统考一模）如图，∠MON=α，点A在ON上，过点A作OM的平行线，与∠MON的平分线交于点B，点C在OB上（不与点O，B重合），连接AC，将线段AC绕点A顺时针旋转180°-α，得到线段AD，连接BD.（1）直接写出线段AO与AB之间的数量关系，并证明∠MOB=∠DBA；（2）连接DC并延长，分别交AB，OM于点E，F. 若α=60°，用等式表示线段EF与AC之间的数量关系，并证明.3.（2023·北京海淀·统考一模）如图，正方形ABCD中，点E，F分别在BC，CD上，BE=CF，AE，BF交于点G.（1）求∠AGF的度数；（2）在线段AG上截取MG=BG，连接DM，∠AGF的角平分线交DM于点N.①依题意补全图形；②用等式表示线段MN与ND的数量关系，并证明.备用图4.（2023·北京房山·统考一模）如图，正方形ABCD 中，点E 是边BC 上的一点，连接AE ，将射线AE 绕点A 逆时针旋转90°交CD 的延长线于点F ，连接EF ，取EF 中点G ，连接DG . （1）依题意补全图形；用等式表示∠ADG 与∠CDG 的数量关系，并证明；（2）若DG，用等式表示线段BC 与BE 的数量关系，并证明.5.（2023·北京丰台·统考一模）在正方形ABCD 中，点O 为对角线AC 的中点，点E 在对角线AC 上，连接EB ，点F 在直线AD 上（点F 与点D 不重合），且EF = EB. （1）如图1，当点E 在线段AO 上（不与端点重合）时，①求证：∠AFE = ∠ABE ；②用等式表示线段AB ，AE ，AF 的数量关系并证明；（2）如图2，当点E 在线段OC 上（不与端点重合）时，补全图形，并直接写出线段AB ，AE ，AF 的数量关系.图1 图26．（2023·北京门头沟·统考一模）已知正方形ABCD 和一动点E ，连接CE ，将线段CE 绕点C 顺时针旋转90°得到线段CF ，连接BE ，DF ．（1）如图1，当点E 在正方形ABCD 内部时， ①依题意补全图1；G FED CBA G FEDCBA ABCD E②求证：BE DF =；（2）如图2，当点E 在正方形ABCD 外部时，连接AF ，取AF 中点M ，连接AE ，DM ，用等式表示线段AE 与DM 的数量关系，并证明．7．（2023·北京顺义·统考一模）已知：如图，△ABC 中，AC=BC ，∠ACB =90°，点D 在AB 边上，点A 关于直线CD 的对称点为E ，射线BE 交直线CD 于点F ，连接AF ．（1）设∠ACD =α，用含α的代数式表示∠CBF 的大小，并求∠CFB 的度数；（2）用等式表示线段AF ，CF ，BF 之间的数量关系，并证明．8．（2023·北京通州·统考一模）直线MO 是线段AB 的垂直平分线，垂足为点O ，点C 是直线OM 上一点，连接AC ．以AC 为斜边作等腰直角ACD △，连接OD ．（1）如图1，若CO AB =，求AOD ∠的度数；（2）如图2所示，点E 是直线MO 上一点，且CE AB =，连接DE ，延长DO 至点F ，使得OF OD =，连接AF ．根据题意补全图2，写出线段,DE AF 之间的关系，并证明．9.（2023·北京延庆·统考一模）如图，在△ABC 中，∠BAC =90°，AB=AC ，AD 是BC 边上的高，点E 是边 AB 上的一动点（不与点A ，B重合），连接CE 交AD 于点F ．将线段CF 绕点C 顺时针旋转90°得到线段CG ，连接AG ．（1）如图1，当CE 是∠ACB 的角平分线时，①求证：AE=AF ；②直接写出∠CAG= °．（2）依题意补全图2，用等式表示线段AF ，AC ，AG 之间的数量关系，并证明．图1 图2 10．（2023·北京燕山·统考一模）如图，△ABC 中，∠ACB ＝90°，AC ＝BC ，D 为边BC 上一点(不与点B ， C 重合)，连接AD ，过点C 作CE ⊥AD 于点E ，过点B 作BF ⊥CE ，交直线CE 于点F ．(1) 依题意补全图形；用等式表示线段CE 与BF 的数量关系，并证明； (2) 点G 为AB 中点，连接FG ，用等式表示线段AE ，BF ，FG 之间的数量关系，并证明．GFEDCBADB图1图2 参考答案1．（1）证明：作EH ⊥CD ，EK ⊥AB ，垂足分别是H ，K ，如图1． ∵ OE 是∠BOC 的平分线， ∴ EH ＝EK ． ∵ ME ＝NE ，∴ Rt △EHN ≌Rt △EKM ． ∴ ∠ENH ＝∠EMK ．记ME 与OC 的交点为P ，∴ ∠EPN ＝∠OPM ．∴ ∠MEN ＝∠AOC ． ····························································· 3分（2）OM ＝ NF ＋OG ．证明：在线段OM 上截取OG 1＝OG ，连接EG 1，如图2．∵ OE 是∠BOC 的平分线，∴ ∠EON ＝∠EOB ． ∵ ∠MOF ＝∠DOB ， ∴ ∠EOM ＝∠EOD ． ∵ OE =OE ，∴ △EOG 1≌△EOG ．∴ EG 1=EG ，∠EG 1O =∠EGF ．∵ EF ＝EG ，∴ EF =EG 1EFG =∠EGF ． ∴ ∠EFG =∠EG 1O ． ∴ ∠EFN =∠EG 1M ． ∵ ∠ENF =∠EM G 1．∴ △ENF ≌△EM G 1． ∴ NF ＝M G 1． ∵ OM ＝M G 1＋O G 1，∴ OM ＝NF ＋OG ． ······························································· 7分2．解：（1）AO =AB.证明：∵OB 平分∠MON ， ∴∠MOB =∠NOB. ∵OM //AB ， ∴∠MOB =∠ABO. ∴∠NOB =∠ABO. ∴AO =AB.根据题意，得AC=AD ，∠OAB=∠CAD.∴∠CAO=∠DAB.∴△OAC ≌△BAD. ∴∠COA=∠DBA. ∴∠MOB=∠DBA.（2）EF =.证明：如图，在OM 上截取OH=BE ，连接CH.∵△OAC ≌△BAD ， ∴OC=BD. 又OH=BE ，∴△OHC ≌△BED.∴CH=DE ，∠OHC=∠BED ， ∵OM//AB ， ∴∠MFC=∠BED. ∴∠MFC=∠OHC. ∴CF=CH. ∴CF=DE. ∴CD=EF. ∵α=60°，∴∠CAD=180°－α=120°，作AK ⊥CD 于点K. ∵AC=AD ，∴∠ACK=30°，1.2CK CD =∴.CK AC =∴CD .∴EF =.3.（本题满分7分）（1）∵ 四边形ABCD 是正方形， ∴ AB =BC ，∠ABE =∠BCF =90°. 又∵ BE =CF ，∴ △ABE ≌△BCF （SAS ）. ………………………………………………………1分 ∴ ∠BAE =∠FBC .∵ ∠FBC +∠ABG =90°， ∴ ∠BAE +∠ABG =90°.∴ ∠AGF =90°. …………………………………………………………………2分（2）① 依题意补全图形.…………………………………………………………………………………3分 ② 线段MN 与ND 的数量关系为MN =ND . …………………………………4分证明：过点A 作AH ⊥AE 交GN 延长线于点H ，连接DH . ∵ ∠AGF =90°，GN 平分∠AGF ， ∴ ∠AGN =12∠AGF =45°. ∵ AH ⊥AE ， ∴ ∠GAH =90°. ∴ ∠AHG =∠AGH =45°. ∴ AG =AH .∵ 四边形ABCD 是正方形， ∴ ∠BAD =90°，AB =AD .∵ ∠GAH =90°，∴ ∠BAG =∠DAH .∴ △BAG ≌△DAH （SAS ）. ∴ BG =DH ，∠AHD =∠AGB =90°. ∵ BG =GM ，∠AHG =45°， ∴ GM =DH ，∠DHN =∠NGM =45°.∵ ∠HND =∠GNM ，∴ △HND ≌△GNM （AAS ）.∴ MN =ND . ……………………………………………………………7分4.（1）补完图形如下：……………………1分∠ADG =∠CDG . ……………………2分M NG F EDC BAH M NG F EDCBA证明：如图，连接AG 、CG∵∠EAF =90° ，点G 是EF 中点， ∴AG =12EF ∵正方形ABCD ，∠ECF =90° ，∴CG =12EF∴AG =CG ……………………3分 ∵AD =CD ，DG =DG ∴△ADG ≌△CDG∴∠CDG =∠ADG ……………………4分（2）BC =3BE ……………………5分过点G 作GH ⊥CD 于点H ，易证GH 是△CEF 的中位线，∴CE =2GH . ……………………6分易证△GDH 是等腰直角三角形，∴DG .又∵DG =DF ，∴DF =GH . 易证△ADF ≌△ABE ∴DF =BE ， ∴BE =GH . ∵CE =2GH ， ∴CE =2BE∴BC =3BE ……………………7分（其它证法酌情给分）5.（1） ①证明：连接DE . ∵四边形ABCD 是正方形，∴AB =AD ，∠BAD =90°. ∵点E 在对角线AC 上，∴∠BAC =∠DAC =45°. ∵AE =AE ，∴△ABE ≌△ADE . ∴BE =DE ,∠ABE =∠ADE . ∵EF =BE ,∴DE =EF . ∴∠F =∠ADE .∴∠F =∠ABE . ……2分 ②AB=AF +2AE ; ……3分证明：过点E 作EG ⊥AE 交AB 于点G .∴ ∠AEG =90°. ∵∠BAE =45°， ∴ ∠AGE =∠BAE =45°. ∴AG =2AE ,∠EGB =135°. ∵∠F AE =∠F AB +∠BAE =135°, ∴ ∠EGB =∠F AE . ∵∠F =∠ABE ,EF=EB , ∴△AEF ≌△GEB . ∴BG=AF . ∴AB=BG+GA=AF +2AE . ……5分（2）正确补全图形；AB+AF=2AE . ……7分 6．（本小题满分7分）解：（1）① 图1；……………………………………………1分②∵正方形ABCD ，∴BC =DC ，∠BCD =90°. ……………………2分∵线段CE 绕点C 顺时针旋转90°得到线段CF ，∴CE =CF ，∠ECF =90°. ∴∠BCE+∠ECD =∠DCF+∠ECD =90°.∴∠BCE =∠DCF . ……………………………3分图1 ∴△BCE ≌△DCF .∴BE =DF . …………………………………………………………………………4分ADBM（2）猜想：AE =2DM .证明：如图2，延长AD 到N ，使得DN =AD .∵M 是AF 中点，∴NF =2DM .………………………5分 ∵由（1）得△BCE ≌△DCF ， ∴∠EBC =∠FDC ，EB =FD .又∵正方形ABCD ，∴AB =AD ，∠ABC =∠ADC = 90°. ∵DN =AD ，∠ADC +∠CDN =180°，∴AB =DN ，∠CDN = 90°.∴EBC ABC FDC CDN ∠−∠=∠−∠，图2即：∠ABE =∠NDF .∴△ABE ≌△NDF . ……………………………………………………………6分 ∴AE =NF .∴AE =2DM .……………………………………………………………………7分7．（1）解：∵A 、E 关于直线CD 对称，∴∠ACF =∠ECF =α，AC =CE ． ∵∠ACB =90°，∴∠BCE =90°-2α． …………………………………………… 1分 ∵AC =CE ， ∴CB =CE ． ∴∠CBF =∠CEB =12(180°-∠BCE )=45°+α． …………………… 2分 ∠CFB =∠CEB -∠ECF =45°+α-α=45°． …………………… 3分（2）线段AF ，CF ，BF 之间的数量关系AF +BF CF ． ……………… 4分证明：过C 作MC ⊥CF 于C 交F A 的延长线于点M ． ∵A 、E 关于FC 对称 ∴∠AFC =∠CFE =45°． ∵MC ⊥CF∴∠M =∠AFC =45°． ∴MC =FC ．∵∠ACB =∠MCF =90° ∴∠MCA =∠BCF ．又∵AC =BC ∴△MCA ≌△FCB ．NFE∴MA=FB．∴MF=AF+MA=AF+BF．∵MC=FC，∠MCF=90°∴MF．∴AF+BF．……………………………………………………7分8.暂缺9．（本小题满分7分）（1）①证明：∵在△ABC中，∠BAC=90°，AB=AC，∴∠ACB =∠B= 45°．∵AD是BC边上的高，∴∠BAD =∠CAD= 45°．∵CE是∠ACB的角平分线，∴∠ACE =∠BCE．∵∠AFE =∠CAD+∠ACE，∠AEF =∠B+∠BCE．∴∠AFE =∠AEF．∴AE = AF．②∠CAG= 45°．（2）依题意补全图形．AC=AF+AG．证明：过点C作CM⊥AC于点C，交AD的延长线于点M．∵∠CAD= 45°，∴∠M= 45°．∴CA = CM．∴AM．∵∠ACM= 90°，∴∠ACF+∠MCF = 90°．∵∠FCG= 90°，∴∠ACF+∠ACG = 90°．∴∠MCF =∠ACG．∵CF= CG，∴△MCF≌△ACG．∴MF = AG．∴AM =AF +AG．AC=AF+AG．GFED CBAB………… 2分………… 3分………… 7分10．(本题满分7分)解：(1)依题意补全图形，如图．线段CE与BF的数量关系：CE＝BF．证明：∵∠ACB＝90°，∴∠CAE＋∠CDE＝90°．∵CE⊥AD，∴∠CED＝90°，∴∠DCE＋∠CDE＝90°，∴∠CAE＝∠DCE．在△ACE和△CBF中，∠AEC＝∠CFB＝90°，∠CAE＝∠BCF，AC＝BC，∴△ACE≌△CBF，∴CE＝BF．……………………………………………3分(2)线段AE，BF，FG之间的数量关系：AE－BF．证明：连接CG，EG，设CF与AB交于点H．∵∠ACB＝90°，AC＝BC，点G为AB中点，∴CG⊥AB，CG＝BG＝12 AB．∵∠CGH＝∠BFH＝90°，∠CHG＝∠BHF，∴∠GCH＝∠FBH．由(1)得△ACE≌△CBF，∴AE＝CF，CE＝BF．在△GCE和△中，CG＝BG，∠GCE＝∠GBF，CE＝BF，∴△GCE≌△GBF，∴GE＝GF，∠CGE＝∠BGF，∴∠EGF＝∠EGB＋∠BGF＝∠EGB＋∠CGE＝∠CGB＝90°，∴△GEF是等腰直角三角形，∴EF．∵CF－CE＝EF，CF＝AE，CE＝BF，∴AE－BF．……………………………………………7分GFE DCB AH。

北京市各区九年级中考一模数学试卷精选汇编：压轴题专题(含答案）

北京市各区九年级中考一模数学试卷精选汇编压轴题专题东城区28．给出如下定义：对于⊙O的弦MN和⊙O外一点P（M，O，N三点不共线，且P，O 在直线MN的异侧），当∠MPN＋∠MON=180°时，则称点P是线段MN关于点O 的关联点．图1是点P为线段MN关于点O的关联点的示意图.在平面直角坐标系xOy中，⊙O的半径为1.（1）如图2，2222M⎛⎫⎪⎪⎝⎭，2222N⎛-⎝⎭.在A（1，0），B（1，1），)2,0C三点中, 是线段MN关于点O的关联点的是；（2）如图3，M（0，1），N3122⎛⎫-⎪⎪⎝⎭，点D是线段MN关于点O的关联点.①∠MDN的大小为°；②在第一象限内有一点E)3,m m，点E是线段MN关于点O的关联点，判断△MNE的形状，并直接写出点E的坐标；③点F在直线32y x=+上，当∠MFN≥∠MDN时，求点F的横坐标Fx的取值范围．28. 解：（1）C ； --------------2分（2）① 60°；② △MNE 是等边三角形，点E 的坐标为)31，；--------------5分③ 直线32y x =+交 y 轴于点K （0，2），交x 轴于点()23T ，0. ∴2OK =，23OT =∴60OKT ∠=︒.作OG ⊥KT 于点G ,连接MG . ∵()M 0，1， ∴OM =1. ∴M 为OK 中点 . ∴ MG =MK =OM =1.∴∠MGO =∠MOG =30°，OG 3∴33.2G ⎫⎪⎪⎝⎭， ∵120MON ∠=︒, ∴ 90GON ∠=︒. 又3OG =1ON =， ∴30OGN ∠=︒. ∴60MGN ∠=︒.∴G 是线段MN 关于点O 的关联点. 经验证，点)31E，在直线32y =+上. 结合图象可知，当点F 在线段GE 上时，符合题意. ∵G F E x x x ≤≤， ∴33F x ≤分西城区28．对于平面内的⊙C 和⊙C 外一点Q ，给出如下定义：若过点Q 的直线与⊙C 存在公共点，记为点A ，B ，设AQ BQk CQ+=，则称点A （或点B ）是⊙C 的“k 相关依附点”，特别地，当点A 和点B 重合时，规定AQ BQ =，2AQ k CQ =（或2BQCQ）．已知在平面直角坐标系xOy 中，(1,0)Q -，(1,0)C ，⊙C 的半径为r ．（1）如图，当2r =①若1(0,1)A 是⊙C 的“k 相关依附点”，则k 的值为__________．②2(12,0)A +是否为⊙C 的“2相关依附点”．答：__________（填“是”或“否”）．（2）若⊙C 上存在“k 相关依附点”点M ， ①当1r =，直线QM 与⊙C 相切时，求k 的值． ②当3k r 的取值范围．（3）若存在r 的值使得直线3y x b =-+与⊙C 有公共点，且公共点时⊙C 的3附点”，直接写出b 的取值范围．备用图CyO Q图1CyxO A 1A 2Q【解析】（12．②是．（2）①如图，当1r =时，不妨设直线QM 与⊙C 相切的切点M 在x 轴上方（切点M 在x 轴下方时同理），连接CM ，则QM CM ⊥，2QO xyCM∵(1,0)Q -，(1,0)C ，1r =， ∴2CQ =，1CM =， ∴3MQ =，此时23MQk CQ== ②如图，若直线QM 与⊙C 不相切，设直线QM 与⊙C 的另一个交点为N （不妨设QN QM <，点N ，M 在x 轴下方时同理），作CD QM ⊥于点D ，则MD ND =，N 2QO xyCM D∴()222MQ NQ MN NQ NQ ND NQ DQ +=++=+=， ∵2CQ =， ∴2MQ NQ DQk DQ CQ CQ+===，∴当3k 3DQ = 此时221CD CQ DQ -=，假设⊙C 经过点Q ，此时2r =， ∵点Q 早⊙C 外，∴r 的取值范围是12r <≤．（3）333b -<．海淀区28．在平面直角坐标系xOy 中，对于点P 和C ，给出如下定义：若C 上存在一点T 不与O 重合，使点P 关于直线OT 的对称点'P 在C 上，则称P 为C 的反射点．下图为C的反射点P 的示意图．yxPOC T P’（1）已知点A 的坐标为(1,0)，A 的半径为2，①在点(0,0)O ，(1,2)M ，(0,3)N -中，A 的反射点是____________；②点P 在直线y x =-上，若P 为A 的反射点，求点P 的横坐标的取值范围；（2）C 的圆心在x 轴上，半径为2，y 轴上存在点P 是C 的反射点，直接写出圆心C的横坐标x 的取值范围．28．解（1）①A 的反射点是M ，N ． ………………1分②设直线y x =-与以原点为圆心，半径为1和3的两个圆的交点从左至右依次为D ，E ，F ，G ，过点D 作⊥DH x 轴于点H ，如图．可求得点D 的横坐标为32．同理可求得点E ，F ，G 的横坐标分别为2232 点P 是A 的反射点，则A 上存在一点T ，使点P 关于直线OT 的对称点'P 在A 上，则'OP OP =.∵1'3≤≤OP ，∴13≤≤OP ．反之，若13≤≤OP ，A 上存在点Q ，使得OP OQ =，故线段PQ 的垂直平分线经过原点，且与A 相交．因此点P 是A 的反射点．∴点P 的横坐标x 的取值范围是322≤x 232x ．………………4分（2）圆心C 的横坐标x 的取值范围是44≤≤x -． ………………7分丰台区28．对于平面直角坐标系xOy 中的点M 和图形1W ，2W 给出如下定义：点P 为图形1W 上一点，点Q 为图形2W 上一点，当点M 是线段PQ 的中点时，称点M 是图形1W ，2W 的“中立点”．如果点P (x 1，y 1)，Q (x 2，y 2)，那么“中立点”M 的坐标为⎪⎭⎫⎝⎛++2,22121y y x x ．已知，点A (-3，0)，B (0，4)，C (4，0)．（1）连接BC ，在点D (12，0)，E (0，1)，F (0，12)中，可以成为点A 和线段BC 的“中立点”的是____________；（2）已知点G (3，0)，⊙G 的半径为2．如果直线y = - x + 1上存在点K 可以成为点A 和⊙G 的“中立点”，求点K 的坐标；（3）以点C 为圆心，半径为2作圆．点N 为直线y = 2x + 4上的一点，如果存在点N ，使得y 轴上的一点可以成为点N 与⊙C 的“中立点”，直接写出点N 的横坐标的取值范围．54411231213xOy687654327654326528．解：（1）点A 和线段BC 的“中立点”的是点D ，点F ； ………2分（2）点A 和⊙G 的“中立点”在以点O 为圆心、半径为1的圆上运动. 因为点K 在直线y =- x +1上，设点K 的坐标为（x ，- x +1），则x 2+（- x +1）2=12，解得x 1=0，x 2=1.所以点K 的坐标为（0，1）或（1，0）. ………5分（3）（说明：点N 与⊙C 的“中立点”在以线段NC 的中点P 为圆心、半径为1的圆上运动.圆P 与y 轴相切时，符合题意.）所以点N 的横坐标的取值范围为-6≤x N ≤-2. ………8分石景山区28．对于平面上两点A ，B ，给出如下定义：以点A 或B 为圆心，AB 长为半径的圆称为点A ，B 的“确定圆”．如图为点A ，B 的“确定圆”的示意图．．．． xy xyAB（1）已知点A 的坐标为(1,0)-，点B 的坐标为(3,3)，则点A ，B 的“确定圆”的面积为_________；（2）已知点A 的坐标为(0,0)，若直线y x b =+上只存在一个点B ，使得点A ，B 的“确定圆”的面积为9π，求点B 的坐标；（3）已知点A 在以(0)P m ，为圆心，以1为半径的圆上，点B 在直线33y = 若要使所有点A ，B 的“确定圆”的面积都不小于9π，直接写出m 的取值范围．28．解：（1）25π； ………………… 2分（2）∵直线y x b =+上只存在一个点B ，使得点,A B 的“确定圆”的面积为9π，∴⊙A 的半径3AB =且直线y x b =+与⊙A 相切于点B ，如图， ∴AB CD ⊥，45DCA ∠=°．①当0b >时，则点B 在第二象限．过点B 作BE x ⊥轴于点E ，∵在Rt BEA ∆中，45BAE ∠=°，3AB =， ∴322BE AE ==．y xl'lECD BB'3A∴323222B-（，）． ②当0b <时，则点'B 在第四象限．同理可得3232'22B -（．综上所述，点B 的坐标为323222-（，或323222-（． ………………… 6分（3）5m -≤或11m ≥． ………………… 8分朝阳区28. 对于平面直角坐标系xOy 中的点P 和线段AB ，其中A (t ，0)、B (t +2，0)两点，给出如下定义：若在线段AB 上存在一点Q ，使得P ，Q 两点间的距离小于或等于1，则称P 为线段AB 的伴随点．（1）当t =-3时，①在点P 1（1，1），P 2（0，0），P 3（-2，-1）中，线段AB 的伴随点是； ②在直线y =2x +b 上存在线段AB 的伴随点M 、N ，且MN 5=b 的取值范围；（2）线段AB 的中点关于点（2，0）的对称点是C ，将射线CO 以点C 为中心，顺时针旋转30°得到射线l ，若射线l 上存在线段AB 的伴随点，直接写出t 的取值范围．28. 解：（1）①线段AB 的伴随点是: 23,P P . …………………2分②如图1，当直线y =2x +b 经过点（-3，-1）时，b =5，此时b 取得最大值.…………………………………………4分如图2，当直线y =2x +b 经过点（-1，1）时，b =3，此时b 取得最小值.……………………………………………5分∴b的取值范围是3≤b≤5. ……………………………………6分（2）t的取值范围是-12.2t≤≤…………………………………………8分燕山区28．在Rt△ABC中,∠ACB=90°,CD是AB边的中线，DE⊥BC于E, 连结CD，点P在射线CB上（与B，C不重合）．（1）如果∠A=30°①如图1，∠DCB= °②如图2，点P在线段CB上，连结DP，将线段DP绕点D逆时针旋转60°，得到线段DF,连结BF，补全图2猜想CP、BF之间的数量关系，并证明你的结论；( 2 )如图3，若点P在线段CB的延长线上，且∠A=α（0°<α<90°），连结DP, 将线段DP绕点逆时针旋转α2得到线段DF,连结BF, 请直接写出DE、BF、BP三者的数量关系（不需证明）．图1图228.解：(1) ①∠DCB=60°…………………………………1′②补全图形CP=BF …………………………………3′△ DCP ≌△ DBF …………………………………6′（2）BF-BP=2DE ⋅tan α…………………………………8′门头沟区28. 在平面直角坐标系xOy 中，点M 的坐标为11(,)x y ，点N 的坐标为22(,)x y ，且12x x ≠，12y y =,我们规定：如果存在点P ，使MNP ∆是以线段MN 为直角边的等腰直角三角形，那么称点P 为点M 、N 的 “和谐点”. （1）已知点A 的坐标为)3,1(，①若点B 的坐标为)3,3(，在直线AB 的上方，存在点A ，B 的“和谐点”C ，直接写出点C 的坐标；②点C 在直线x =5上，且点C 为点A ，B 的“和谐点”，求直线AC 的表达式.（2）⊙O 的半径为r ，点D (1,4)为点E (1,2)、F ),(n m 的“和谐点”，若使得△DEF 与⊙O 有交点，画出示意图．．．直接．．写出半径r 的取值范围.备用图1 备用图228．（本小题满分8分）解： (1)①)5,3()5,1(21C C 或. ……………………………………………2分②由图可知，B )3,5( ∵A (1,3) ∴AB =4∵ABC ∆为等腰直角三角形 ∴BC =4∴)1,5()7,5(21-C C 或设直线AC 的表达式为(0)y kx b k =+≠ 当)7,5(1C 时，⎩⎨⎧=+=+753b k b k ⎩⎨⎧==∴21b k 2+=∴x y …………………………………3分当)1,5(2-C 时，⎩⎨⎧-=+=+153b k b k ⎩⎨⎧=-=∴41b k4+-=∴x y …………………………………4分 ∴综上所述，直线AC 的表达式是2+=x y 或4+-=x y (2)当点F 在点E 左侧时：xyOxyO大兴区28.在平面直角坐标系xOy 中，过y 轴上一点A 作平行于x 轴的直线交某函数图象于点D ，点P 是x 轴上一动点，连接D P ，过点P 作DP 的垂线交y 轴于点E （E 在线段OA 上，E 不与点O 重合），∠DPE 则称为点D ，P ,E 的“平横纵直角”.图1为点D ，P ,E 的“平横纵直角”的示意图.图1 图2如图2，在平面直角坐标系xOy 中，已知二次函数图象与y 轴交于点(0,)F m ，与x 轴分别交于点B （3-，0），C （12，0）. 若过点F 作平行于x 轴的直线交抛物线于点N .（1）点N 的横坐标为；（2）已知一直角为点,,N M K 的“平横纵直角”，若在线段OC 上存在不同的两点1M 、2M ，使相应的点1K 、2K 都与点F 重合，试求m 的取值范围；（3）设抛物线的顶点为点Q ，连接BQ 与FN 交于点H ,当4560QHN ︒≤≤︒∠时，求m 的取值范围．28.（1）9 ………………………………………………………………… 1分（2）方法一:MK ⊥MN ，∴要使线段OC 上存在不同的两点M 1、M 2，使相应的点K 1、K 2都与点F 重合，也就是使以FN 为直径的圆与OC 有两个交点，即m r >．29=r ， 29<∴m ．又0>m ， 290<<∴m ． ………………………………………………4分方法二：0>m ，∴点K 在x 轴的上方．过N 作NW ⊥OC 于点W ，设OM x =，OK y =，则 CW ＝OC －OW ＝3，WM ＝9x -．由△MOK ∽△NWM ，得，∴9y x x m=-． ∴x mx m y 912+-=．当m y =时，219m x x m m=-+，化为0922=+-m x x ．当△=0，即22940m -=，解得92m =时，线段OC 上有且只有一点M ，使相应的点K 与点F 重合．0>m ，∴ 线段OC 上存在不同的两点M 1、M 2，使相应的点K 1、K 2都与点F 重合时，m 的取值范围为290<<m ． ………………………………………………………………………………4分（3）设抛物线的表达式为：)12)(3(-+=x x a y (a ≠0)，又抛物线过点F （0，m ），a m 36-=∴．m a 361-=∴．m x m x x m y 1625)29(361)12)(3(3612+--=-+-=∴．…………………………………5分过点Q 做QG ⊥x 轴与FN 交于点RFN ∥x 轴 ∴∠QRH =90°tan BG BQG QG∠=，2516QG m =，152BG =∴，又4560QHN ︒≤∠≤︒，∴3045BQG ︒≤∠≤︒∴当30BQG ∠=︒时，可求出3524=m ，………………………………… 6分当45BQG ∠=︒时，可求出524=m ． ……………………………………7分m ∴的取值范围为2424355m ≤≤． …………………………………8分平谷区28. 在平面直角坐标系xOy 中，点M 的坐标为()11,x y ，点N 的坐标为()22,x y ，且12x x ≠，12y y ≠，以MN 为边构造菱形，若该菱形的两条对角线分别平行于x 轴，y 轴，则称该菱形为边的“坐标菱形”.（1）已知点A （2,0），B （0,23），则以AB 为边的“坐标菱形”的最小内角为_______；（2）若点C （1,2），点D 在直线y =5上，以CD 为边的“坐标菱形”为正方形，求直线CD 表达式；（3）⊙O 的半径为2，点P 的坐标为(3,m ) .若在⊙O 上存在一点Q ，使得以QP 为边的“坐标菱形”为正方形，求m 的取值范围．28．解：（1）60； ·························································································· 1 （2）∵以CD 为边的“坐标菱形”为正方形， ∴直线CD 与直线y =5的夹角是45°．过点C 作CE ⊥DE 于E ．∴D （4,5）或()2,5-． ........................................ 3 ∴直线CD 的表达式为1y x =+或3y x =-+． (5)（3）15m ≤≤或51m -≤≤-． (7)怀柔区28. P 是⊙C 外一点，若射线．．PC 交⊙C 于点A ，B 两点，则给出如下定义：若0＜PAPB≤3，则点P 为⊙C 的“特征点”． (1)当⊙O 的半径为1时．①在点P 1（2,0）、P 2（0,2）、P 3（4，0）中，⊙O 的“特征点”是； ②点P 在直线y=x+b 上，若点P 为⊙O 的“特征点”．求b 的取值范围；(2)⊙C 的圆心在x 轴上，半径为1，直线y=x+1与x 轴，y 轴分别交于点M ，N ，若线段MN 上的所有点都不是．．．⊙C 的“特征点”，直接写出点C 的横坐标的取值范围．yx–1–2–3–4–512345–1–2–3–4–512345O28.(1)①P 1（2,0）、P 2（0,2）…………………………………………………………………2分yxE Hy=x+b 2y=x+b–1–2–3–41234–1–2–3–41234OD②如图，在y=x+b 上，若存在⊙O 的“特征点”点P ，点O 到直线y=x+b 的距离m≤2. 直线y=x+b 1交y 轴于点E ，过O 作OH ⊥直线y=x+b 1于点H. 因为OH=2，在Rt △DOE 中，可知OE=22. 可得b 1=22.同理可得b 2=-22.∴b 的取值范围是:22-≤b ≤22. …………………………………………………6分 (2)x>3或 3-<x . …………………………………………………………………………8分延庆区28．平面直角坐标系xOy 中，点1(A x ，1)y 与2(B x ，2)y ，如果满足120x x +=，120y y -=，其中12x x ≠，则称点A 与点B 互为反等点．已知：点C (3，4)（1）下列各点中，与点C 互为反等点； D (-3，-4)，E （3，4），F （-3，4）（2）已知点G （-5，4），连接线段CG ，若在线段CG 上存在两点P ，Q 互为反等点，求点P 的横坐标p x 的取值范围；（3）已知⊙O 的半径为r ，若⊙O 与（2）中线段CG 的两个交点互为反等点，求r 的取值范围．-1-2-3-4-5-6-6-5-4-3-2-1y123456x654321O28．(1)F ……1分 (2) -3≤p x ≤3 且p x ≠0 ……4分(3)4 < r≤5 ……7分顺义区点P 任意引出一条射线分别与1L 、2L 交于1Q 、2Q ，总有12PQ PQ 是定值，我们称曲线1L 与2L “曲似”，定值12PQ PQ 为“曲似比”，点P 为“曲心”．例如：如图2，以点O'为圆心，半径分别为1r 、2r （都是常数）的两个同心圆1C 、2C ，从点O'任意引出一条射线分别与两圆交于点M 、N ，因为总有12''r O M O N r =是定值，所以同心圆1C 与2C 曲似，曲似比为12r r ，“曲心”为O'．（1）在平面直角坐标系xOy 中，直线y kx =与抛物线2y x =、212y x =分别交于点A 、B ，如图3图2C 2C 1NMO'所示，试判断两抛物线是否曲似，并说明理由；（2）在（1）的条件下，以O 为圆心，OA 为半径作圆，过点B 作x 轴的垂线，垂足为C ，是否存在k 值，使⊙O 与直线BC 相切？若存在，求出k 的值；若不存在，说明理由；（3）在（1）、（2）的条件下，若将“212y x =”改为“21y x m=”，其他条件不变，当存在⊙O 与直线BC 相切时，直接写出m 的取值范围及k 与m 之间的关系式．28．（1）是．21 / 21。

2022北京各区初中一模数学分类汇编27题及答案

2022北京各区初中一模数学分类汇编27题及答案27．在△ABC中，AB=AC，CD⊥BC于点C，交∠ABC的平分线于点D，AE平分∠BAC交BD于点E，过点E作EF∥BC交AC于点F，连接DF．（1）补全图1；（2）如图1，当∠BAC=90°时，①求证：BE=DE；②写出判断DF与AB的位置关系的思路（不用写出证明过程）；（3）如图2，当∠BAC=α时，直接写出α，DF，AE的关系．AADEEBBC图2图1DC西城27．正方形ABCD的边长为2，将射线AB绕点A顺时针旋转，所得射线与线段BD交于点M，作CEAM于点E，点N与点M关于直线CE对称，连接CN．（1）如图，当045时，①依题意补全图．②用等式表示NCE与BAM之间的数量关系：__________．（2）当4590时，探究NCE与BAM之间的数量关系并加以证明．（3）当090时，若边AD的中点为F，直接写出线段EF长的最大值．AMBABD图1CD备用图C延庆27．如图1，正方形ABCD中，点E是BC延长线上一点，连接DE，过点B作BF⊥DE于点F，连接FC．（1）求证：∠FBC=∠CDF．（2）作点C关于直线DE的对称点G，连接CG，FG．①依据题意补全图形；②用等式表示线段DF，BF，CG之间的数量关系并加以证明．海淀27．如图，已知AOB60，点P为射线OA上的一个动点，过点P 作PEOB，交OB于点E，点D在AOB内，且满足DPAOPE，DPPE6.（1）当DPPE时，求DE的长；（2）在点P的运动过程中，请判断是否存在一个定点M，使得值不变？并证明你的判断.OEBAADFADFB图1CEB备用图CEDM的MEPD大兴27．如图，在等腰直角△ABC中，∠CAB=90°，F 是AB边上一点，作射线CF，过点B作BG⊥CF于点G，连接AG．（1）求证：∠ABG=∠ACF；（2）用等式表示线段CG，AG，BG之间的等量关系，并证明．怀柔27.如图，在△ABC中，∠A=90°，AB=AC，点D是BC上任意一点，将线段AD绕点A逆时针方向旋转90°，得到线段AE，连结EC.(1)依题意补全图形；(2)求∠ECD的度数；(3)若∠CAE=7.5°，AD=1，将射线DA绕点D顺时针旋转60°交EC 的延长线于点F，请写出求AF长的思路．顺义27.如图，在正方形ABCD中，E是BC边上一点，连接AE，延长CB至点F，使BF=BE，过点F作FH⊥AE于点H，射线FH分别交AB、CD于点M、N，交对角线AC于点P，连接AF．（1）依题意补全图形；（2）求证：∠FAC=∠APF；（3）判断线段FM与PN的数量关系，并加以证明．门头沟27.如图，在△ABC中，AB=AC，A2，点D是BC的中点，DEAB 于点E，DFAC于点F.（1）EDB_________°；（用含的式子表示）（2）作射线DM与边AB交于点M，射线DM绕点D顺时针旋转1802，与AC边交于点N．①根据条件补全图形；A②写出DM与DN的数量关系并证明；③用等式表示线段BM、CN与BC之间的数量关系，（用含的锐角三角函数表示）并写出解题思路.EBDFC丰台27．如图，Rt△ABC中，∠ACB=90°，CA=CB，过点C在△ABC外作射线CE，且∠BCE=，点B关于CE的对称点为点D，连接AD，BD，CD，其中AD，BD分别交射线CE于点M，N.（1）依题意补全图形；（2）当=30°时，直接写出∠CMA的度数；（3）当0°<45°时，用等式表示线段AM，CN之间的数量关系，并证明．CEAB东城27.已知△ABC中，AD是BAC的平分线，且AD=AB，过点C作AD的垂线，交AD的延长线于点H．（1）如图1，若BAC60①直接写出B和ACB的度数；②若AB=2，求AC和AH的长；（2）如图2，用等式表示线段AH与AB+AC之间的数量关系，并证明．房山27.如图，已知Rt△ABC中，∠C=90°，∠BAC=30°，点D为边BC上的点，连接AD，∠BAD=α，点D关于AB的对称点为E，点E关于AC的对称点为G，线段EG交AB于点F，连接AE，DE，DG，AG.（1）依题意补全图形；（2）求∠AGE的度数（用含α的式子表示）；（3）用等式表示线段EG与EF，AF之间的数量关系，并说明理由.线CB上（与B，C不重合）．（1）如果∠A=30°①如图1，∠DCB=°②如图2，点P在线段CB上，连结DP，将线段DP绕点D逆时针旋转60°，得到线段DF,连结BF，补全图2猜想CP、BF之间的数量关系，并证明你的结论；(2)如图3，若点P在线段CB的延长线上，且∠A=（0°<90°），连结DP,将线段DP绕点逆时针旋转2得到线段DF,连结BF,请直接写出DE、BF、BP三者的数量关系（不需证明）．αABDC燕山28．在Rt△ABC中,∠ACB=90°,CD是AB边的中线，DE⊥BC于E,连结CD，点P在射。

2024北京丰台区初三一模数学试卷和答案

2024北京丰台初三一模数学2024.04考生须知1．本试卷共8页，共28道小题．满分100分．考试时间120分钟．2．在试卷和答题卡上认真填写学校名称、姓名和考号．3．试题答案一律填涂或书写在答题卡上，在试卷上作答无效．4．选择题用2B 铅笔作答，其他试题用黑色字迹签字笔作答．5．考试结束，将本试卷和答题卡一并交回．一、选择题（共16分，每题2分）第1—8题均有四个选项，符合题意的选项只有一个．1．2023年5月28日，我国自主研发的C919国产大飞机商业首航取得圆满成功．一架C919飞机最大储油量超过19000千克．将数据19000用科学记数法表示为（）A ．50.1910⨯B ．41.910⨯C ．31.910⨯D ．31910⨯2．窗花是中国传统民间艺术之一，下列四个窗花作品既是轴对称图形又是中心对称图形的是（）A ．B ．C ．D ．3．如图，直线a b ∥，直线l 与直线a ，b 分别交于点A ，B ，点C 在直线b 上，且CA CB =．若132∠=︒，则2∠的大小为（）A ．32︒B ．58︒C ．74︒D ．106︒4．已知实数a ，b 满足1a b >-，则下列结论正确的是（）A ．a b>B ．a b<C ．21a b +>+D ．21a b +<+5．我国古代园林连廊常采用八角形的窗户设计，如图1所示，其轮廓是一个正八边形，从窗户向外观看，景色宛如镶嵌于一个画框之中．图2是八角形窗户的示意图，它的一个外角1∠的大小为（）A ．22.5︒B ．45︒C ．60︒D ．135︒6．若关于x 的方程230ax x c -+=有两个不相等的实数根，则满足条件的实数a ，c 的值可以是（）A ．0a =，1c =B ．1a =，3c =C ．2a =-，4c =-D ．1a =-，3c =7．不透明的袋子中装有四个小球，上面分别写有数字“1”，“2”，“3”，“4”，除数字外这些小球无其他差别．从袋中随机同时摸出两个小球，那么这两个小球上的数字之和是5的概率是（）A ．12B ．13C ．14D ．168．如图，在正方形ABCD 中，点E ，F 分别是AD ，AB 边上的点，AE AF =，且0AE ED <<，过点E 作EH BC ⊥于点H ，过点F 作FG CD ⊥于点G ，EH ，FG 交于点O ，连接OB ，OD ，BD ．设AE a =，ED b =，BD c =，给出下面三个结论：①a b +>；②c >；③a b +>．上述结论中，所有正确结论的序号是（）A ．①②B ．①③C ．②③D ．①②③二、填空题（共16分，每题2分）9．若代数式3xx -有意义，则实数x 的取值范围是______．10．分解因式：224ax ay -=______．11．方程3102x x-=+的解为______．12．在平面直角坐标系xOy 中，若函数()0ky k x=≠的图象经过点(),6A m 和()3,4B -，则m 的值为______．13．如图，DE 是ABC △的中位线，点F 在DB 上，2DF BF =，连接EF 并延长，与CB 的延长线交于点M ．若8BC =，则线段CM 的长为______．14．2011年国际数学协会正式宣布：将每年的3月14日设为“国际数学节”．某学校在3月14日举办了校园数学节活动，学生可通过参加多项数学活动获得积分（百分制），次日兑换奖品．为了更好地准备奖品，学生会干部从全校300名学生中随机抽取60名学生的积分，得到数据的频数分布直方图如下（数据分成6组：4050x ≤<，5060x ≤<，6070x ≤<，7080x ≤<，8090x ≤<，90100x ≤≤）：根据以上数据，估计该校300名学生中积分不低于70分的学生人数约为______．第14题图15．如图，A ，B ，C 是O 上的点，OA BC ⊥，点D 在优弧 BC上，连接BD ，AD ．若30ADB ∠=︒，BC =，则O 的半径为______．第15题图16．车间里有五台车床同时出现故障．已知第一台至第五台修复的时间如下表：车床代号A B C D E 修复时间（分钟）15829710若每台车床停产一分钟造成经济损失10元，修复后即可投入生产．（1）若只有一名修理工，且每次只能修理一台车床，则下列三个修复车床的顺序：①D B E A C →→→→；②D A C E B →→→→；③C A E B D →→→→中，经济损失最少的是______（填序号）；（2）若由两名修理工同时修理车床，且每台车床只由一名修理工修理，则最少经济损失为______元．三、解答题（共68分，第17—20题，每题5分，第21题6分，第22—23题，每题5分，第24—26题，每题6分，第27—28题，每题7分）17．计算：1132cos303-⎛⎫-+︒- ⎪⎝⎭．18．解不等式组：2335,2623x x x x ->-⎧⎪+⎨<-⎪⎩．19．已知320x y --=，求代数式22264693x y x xy y x y-+-+-的值．20．如图，在Rt ABC △中，90C ∠=︒，延长CB 至D ，使得BD CB =，过点A ，D 分别作AE BD ∥，DE BA ∥，AE 与DE 交于点E ，连接BE ．（1）求证：四边形ACBE 是矩形；（2）连接AD，若AD =，2tan 3BAC ∠=，求AC 的长．21．小刚对诗仙李白的诗作《早发白帝城》中“朝辞白帝彩云间，千里江陵一日还”的说法产生疑问：李白真能在一日之内从白帝城到达江陵吗?小刚经过查阅资料得知，白帝城是现今的重庆奉节，而江陵是现今的湖北荆州．假设李白乘坐的轻舟从奉节到宜昌的速度约为14 km/h ，从宜昌到荆州的速度约为10 km/h ．从奉节到荆州的水上距离约为350 km ．经过分析资料，小刚发现从奉节到宜昌的时间比从宜昌到荆州多1 h ．根据小刚的假设，回答下列问题：（1）奉节到宜昌的水上距离是多少km ？（2）李白能在一日（24h ）之内从白帝城到达江陵吗？说明理由．22．在平面直角坐标系xOy 中，函数()0y kx b k =+≠的图象经过点()2,1A 和()0,1B -．（1）求该函数解析式；（2）当2x >-时，对于x 的每一个值，函数12y x n =+的值小于函数()0y kx b k =+≠的值且大于4-，直接写出n 的取值范围．23．为了增强学生体质，某校九年级举办了小型运动会．其中男子立定跳远项目初赛成绩前10名的学生直接进入决赛．现将进入决赛的10名学生的立定跳远成绩（单位：厘米），数据整理如下：a ．10名学生立定跳远成绩：244，243，241，240，240，238，238，238，237，236b ．10名学生立定跳远成绩的平均数、中位数、众数：平均数中位数众数239.5mn（1）写出表中m ，n 的值；（2）现有甲、乙、丙三名未进入决赛的学生，要通过复活赛进人决赛．在复活赛中每人要进行5次测试，每人的5次测试成绩同时满足以下两个条件方可进入决赛：i ．平均成绩高于已进入决赛的10名学生中一半学生的成绩；ii ．成绩最稳定．①若甲学生前4次复活赛测试成绩为236，238，240，237，要满足条件i ，则第5次测试成绩至少为______（结果取整数）；②若甲、乙、丙三名学生的5次复活赛测试成绩如下表：第一次第二次第三次第四次第五次甲236238240237237乙237239240244235丙237242237239240则可以进入决赛的学生为______（填“甲”“乙”或“丙”）．24．如图，四边形ABCD 是O 的内接四边形，AB 是直径，C 是 BD的中点，过点C 作O 的切线CE 交AD 的延长线于点E ．（1）求证：CE AE ⊥；（2）连接BD ，若6BC =，8AC =，求BD 的长．25．一般来说，市面上某种水果出售量较多时，水果的价格就会降低．这时，将水果进行保鲜存储，等到价格上升之后再出售，可获得更高的出售收入．但是保鲜存储是有成本的，而且成本会随着时间的延长而增大，因此出售水果获得的收益要从出售价格中扣除保鲜存储成本．某水果公司的调研小组收集到去年一段时间内某种水果当日每千克的出售价格和保鲜存储成本的部分数据如下：设水果保鲜存储的时间为t 天（120t ≤≤），当日每千克水果出售价格为1y 元，每千克水果保鲜存储成本为2y 元．t12581012141618201y 4.0 6.310.812.512.712.412.211.812.013.02y 2.42.84.05.26.06.87.68.49.210.0（1）根据表格中的数据，第8天每千克水果的收益为______元；（2）通过分析表格中的数据，发现1y ，2y 都可近似看作t 的函数，在平面直角坐标系xOy 中，描出表中各组数值所对应的点()1,t y ，并用平滑曲线连接这些点；（3）结合函数图象，将水果保鲜存储第______天至第______天（结果取整数）时，出售每千克水果所获得的收益超过4元．26．在平面直角坐标系xOy 中，()12,M y ，()25,N y 是抛物线22y x ax =-上的两点．（1）直接写出一个a 的值，使得12y y <成立；（2）()33,P x y 是抛物线22y x ax =-上不同于M ，N 的点，若对于301x <≤，都有132y y y <<，求a的取值范围．27．在ABC △中，AB AC =，BAC α∠=，点D 是BC 中点，点E 是线段BC 上一点，以点A 为中心，将线段AE 逆时针旋转α得到线段AF ，连接EF ．（1）如图1，当点E 与点D 重合时，线段EF ，AC 交于点G ，求证：点G 是EF 的中点；（2）如图2，当点E 在线段BD 上时（不与点B ，D 重合），若点H 是EF 的中点，作射线DH 交AC 于点M ，补全图形，直接写出AMD ∠的大小，并证明．图1图228．在平面直角坐标系xOy 中，O 的半径为1，对于O 的弦AB 和O 外一点C ，给出如下定义：若直线CA ，CB 都是O 的切线，则称点C 是弦AB 的“关联点”．（1）已知点()1,0A -．①如图1，若O 的弦AB =(1C -，()21,1C -，(31,C -中，弦AB 的“关联点”是______；②如图2，若点1,2B ⎛-⎝，点C 是O 的弦AB 的“关联点”，直接写出OC 长；图1图2（2）已知点()3,0D ，线段EF 是以点D 为圆心，以1为半径的D 的直径，对于线段EF 上任意一点S ，存在O 的弦AB ，使得点S 是弦AB 的“关联点”．当点S 在线段EF 上运动时，将其对应的弦AB 长度的最大值与最小值的差记为t ，直接写出t 的取值范围．备用图参考答案一、选择题（共16分，每题2分）题号12345678答案BDCCBDBA二、填空题（共16分，每题2分）9．3x ≠10．()()22a x y x y +-11．1x =12．2-13．1014．20015．216．①，1010三、解答题（共68分，第17—20题，每题5分，第21题6分，第22—23题，每题5分，第24—26题，每题6分，第27—28题，每题7分）17．解：原式32333=+--=+--=．18．解：解不等式①，得2x <，解不等式②，得0x <，∴不等式组的解集为0x <．19．解：原式()()223424633333x y x y x y x y x yx y -=+=+=-----．∵320x y --=．∴32x y -=，∴原式632==．20．证明：（1）∵AE BD ∥，DE BA ∥，∴四边形ABDE 是平行四边形．∴AE BD =．∵BD CB =，∴AE CB =．∵AE BD ∥，∴四边形ACBE 是平行四边形．∵90C ∠=︒，∴四边形ACBE 是矩形．（2）∵在Rt ABC △中，90C ∠=︒，2tan 3BC BAC AC ∠==，∴设2BC x =，3AC x =．∴2BD BC x ==．∴4DC x =．在Rt ADC △中，90C ∠=︒，AD =，∵222AC DC AD +=，∴()()(22234x x +=．解得，x =．∴3AC x ==．21．解：（1）设奉节到宜昌的水上距离是x km ．根据题意得：35011410x x--=，解得210x =．答：奉节到宜昌的水上距离为210km ．（2）∵210350210151429241410-+=+=>，∴李白不能在一日之内从白帝城到达江陵．22．解：（1）∵函数()0y kx b k =+≠的图象经过点()2,1A 和()0,1B -，∴211k b b +=⎧⎨=-⎩．解得：11k b =⎧⎨=-⎩．∴该函数解析式为1y x =-．（2）32n -≤≤-．23．解：（1）239m =，238n =．（2）①240．②丙．24．（1）证明：连接OC ，∵CE 为O 的切线，∴OC CE ⊥．∴90OCE ∠=︒．∵C 是 BD的中点，∴ CB CD =．∴EAC CAO ∠=∠．∵OA OC =，∴CAO ACO =∠．∴EAC ACO ∠=∠．∴OC AE ∥，∴180E OCE ∠+∠=︒，∴90E ∠=︒，∴CE AE ⊥．（2）解：∵AB 为直径，∴90ACB ADB ∠=∠=︒．∵6BC =，8AC =，∴10AB =．∵EAC CAO ∠=∠，E ACB ∠=∠，∴ACE ABC ∽△△．∴CE ACBC AB=．∴ 4.8CE =．∵90E BDE ECO ∠=∠=∠=︒，∴四边形EDFC 是矩形．∴ 4.8DF EC ==，OC BD ⊥．∴29.6BD DF ==．25．解：（1）7.3；（2）（3）3，14．26．解：（1）答案不唯一，例如：3a =．（2）∵二次函数解析式为22y x ax =-，∴函数图像开口向上，对称轴为x a =．①当3a x ≤时，∴点P ，M ，N 均在对称轴右侧．∴由二次函数性质，必有312y y y <<，不符题意舍去．②当32x a ≤<时，∵点P 在对称轴左侧，设P 点关于x a =的对称点为P '，则点P '的坐标为()312,a x y -．∵点P '，M ，N 在对称轴右侧，且132y y y <<，∴322a x <-．∴322a <<．③当25a ≤≤时，∵点P 和M 在对称轴左侧，由函数性质，有13y y <，∵点P '，N 在对称轴右侧，且32y y <，∴325a x -<．∴522a ≤≤．④当5a >时，∴点P ，M ，N 均在对称轴左侧．∴由二次函数性质，必有312y y y >>，不符题意舍去．由①②③④可知，3522a <≤．27．（1）证明：∵AB AC =，点D 是BC 中点，∴1122DAC BAC α∠=∠=．∵DAF α∠=，∴12CAF DAC α∠=∠=．试题11∵AE AF =，∴点G 是EF 的中点．（2）依题意补全图形．解：90AMD ∠=︒．证明：连接FC ，截取KC BE =，连接FK 交AC 于N ．∵BAC EAF α∠=∠=，∴BAE CAF ∠=∠．∵AE AF =，AB AC =，∴BAE CAF ≌△△．∴BE CF =，B ACF ∠=∠．∵B ACB ∠=∠，∴ACB ACF ∠=∠．∵KC BE =，∴KC CF =．∴KF AC ⊥于N ．∵点D 是BC 中点，∴BD CD =．∴DE DK =．∵点H 是EF 的中点，∴DH KF ∥．∴90AMD ANK ∠=∠=︒．28．解：（1）①1C ，3C ；②OC．（2t ≤≤．。

13.2020年北京初三数学一模分类汇编：几何综合 27题 (教师版)

2020中考一模汇编---27题几何综合教师版（2020海淀一模）27.已知∠MON=α,A为射线OM上一定点，OA=5,B为射线ON上一动点，连接AB，满足∠OAB，∠OBA均为锐角.点C在线段OB上(与点O，B不重合)，满足AC=AB，点C关于直线OM的对称点为D，连接AD,OD.(1)依题意补全图1;(2)求∠BAD的度数(用含α的代数式表示);(3)若tanα=3,点P在OA的延长线上，满足AP=OC，连接BP，写出一个AB的值，使得4BP//OD，并证明.（2020西城一模）27.如图，在等腰直角△ABC中，∠ACB=90点P在线段BC上，延长BC 至点Q,使得CQ=CP，连接AP,AQ.过点B作BD⊥AQ于点D,交AP于点E,交AC于点F.K是线段AD上的一个动点(与点A,D不重合),过点K作GN⊥AP于点H,交AB于点G,交AC于点M,交FD的延长线于点N.(1)依题意补全图1;(2)求证：NM=NF；(3)若AM=CP,用等式表示线段AE,GN与BN之间的数量关系，并证明.（2020朝阳一模）27．四边形ABCD 是正方形，将线段CD 绕点C 逆时针旋转2α(045)α︒︒＜＜,得到线段CE ，连接DE ，过点B 作BF ⊥DE 交DE 的延长线于F ,连接BE ．（1）依题意补全图1；（2）直接写出∠FBE 的度数；（3）连接AF ，用等式表示线段AF 与DE 的数量关系，并证明．图1备用图（2020丰台一模）27. 已知∠AOB =120°，点P为射线OA上一动点（不与点O重合），点C为∠AOB内部一点，连接CP，将线段CP绕点C顺时针旋转60°得到线段CQ，且点Q 恰好落在射线OB上，不与点O重合.（1）依据题意补全图1；（2）用等式表示∠CPO与∠CQO的数量关系，并证明；（3）连接OC，写出一个OC的值，使得对于任意点P，总有OP+OQ=4，并证明.O ABO AB图1备用图（2020延庆一模）27．如图1，在等腰直角△ABC 中，△A =90°，AB =AC=3，在边AB 上取一点D （点D 不与点A ，B 重合），在边AC 上取一点E ，使AE =AD ，连接DE . 把△ADE 绕点A 逆时针方向旋转α（0°＜α＜360°），如图2. （1）请你在图2中，连接CE 和BD ，判断线段CE 和BD 的数量关系，并说明理由；（2）请你在图3中，画出当α =45°时的图形，连接CE 和BE ，求出此时△CBE 的面积；（3）若AD =1，点M 是CD 的中点，在△ADE 绕点A 逆时针方向旋转的过程中，线段AM的最小值是________________．【答案】（1）CE ＝BD ，理由见解析；（2）图形见解析，92CBES ；（3）1．【解析】【分析】（1）连接CE 和BD ，求出∠EAC ＝∠DAB ，即可利用SAS 证明△AEC ≌△ADB ，进而得到CE ＝BD ；（2）连接CE 和BE ，延长AD 交BC 于F ，首先求出∠BAF ＝∠CAF ＝∠EAC ＝45°，然后可得AF ＝BF ＝CF ，∠EAB ＝135°，进而证明AE ∥BC ，再根据12CBES BC AF 进行计算；（3）判断出在△ADE 绕点A 逆时针方向旋转的过程中，点M 在以G 为圆心，12长为半径的圆上，即可得到点M 与点E 重合时AM 取最小值．图1 图3图2【详解】解：（1）CE＝BD；理由：连接CE和BD，如图2所示，由题意可知，△ABC和△ADE都是等腰直角三角形，∵∠EAD＝∠CAB＝90°，∴∠EAC＝∠DAB，又∵AE＝AD，AC＝AB，∴△AEC≌△ADB(SAS)，∴CE＝BD；（2）当α =45°时，连接CE和BE，如图所示，延长AD交BC于F，∵α =45°，△ABC和△ADE都是等腰直角三角形，∴∠BAF＝∠CAF＝∠EAC＝45°，∴AF＝BF＝CF，∠EAB＝135°，∴∠EAB＋∠ABC＝135°+45°＝180°，∴AE∥BC，∵BC=，∴AF＝132 22 BC，∴11329322222 CBES BC AF；（3）如图4，当点M不在AC上时，取AC中点G，连接GM，∵M是CD′的中点，∴GM＝111 222 AD AD，当点M在AC上时，由M是CD′的中点可得GM＝12，∴在△ADE绕点A逆时针方向旋转的过程中，点M在以G为圆心，12长为半径的圆上，∴当点M与点E重合时AM取最小值，此时AM＝AE＝1．【点睛】本题考查了等腰直角三角形的性质、全等三角形的判定和性质、旋转的性质、勾股定理、三角形面积计算以及三角形中位线定理等知识，熟练掌握旋转的性质是解答本题的关键．（2020房山一模）27．如图27-1，在等腰Rt△ABC中，∠BAC=90°，AB=AC=2，点M为BC中点.点P为AB边上一动点，点D为BC边上一动点，连接DP，以点P为旋转中心，将线段PD逆时针旋转90°，得到线段PE，连接EC.（1）当点P与点A重合时，如图27-2.①根据题意在图27-2中完成作图；②判断EC与BC的位置关系并证明.（2）连接EM，写出一个BP的值，使得对于任意的点D总有EM EC，并证明.（2020平谷一模）27．△ABC中，AB=BC，△ABC=90°，将线段AB绕点A逆时针旋转α（0°<α <90°）得到线段AD．作射线BD，点C关于射线BD的对称点为点E．连接AE，CE．（1）依题意补全图形；（2）若α=20°，直接写出△AEC的度数；（3）写出一个α的值，使AE=2时，线段CE的长为31，并证明．备用图27.（1）补全图形...........................................................１（2）135°...................................................................................................2 （３）︒=30α......................................................３证明：过A 作AG ⊥ＣＥ于Ｇ．连接ＡＣ．..................４由题意，BC=BE=BA ∴∠BCE=∠2，∠BAE=∠1∵∠BCE+∠2+∠BAE+∠1+∠ABC=360° ∵∠ABC=90° ∴2（∠2+∠1）=270° ∴∠2+∠1=135°·················································································································· ５ ∴∠AEG=45°∵AE =2∴AG=GE=1 当︒=30α时， ∴∠EBC=30° ∵BC=BE ∴∠BCG=75° ∵∠BCA=45° ∴∠ACG=30° ∴CG=3 ∴CE=3-1·················································································································· ６图1EDCB A（2020顺义一模）27.已知，如图，△ABC 是等边三角形.（1）如图1，将线段AC 绕点A 逆时针旋转90°，得到AD ，连接BD ，∠BAC 的平分线交BD 于点E ，连接CE . ①求∠AED 的度数；②用等式表示线段AE 、CE 、BD 之间的数量关系（直接写出结果）.（2）如图2，将线段AC 绕点A 顺时针旋转90°，得到AD ，连接BD ，∠BAC 的平分线交DB 的延长线于点E ，连接CE . ①依题意补全图2；②用等式表示线段AE 、CE 、BD 之间的数量关系，并证明.27．（1）解：①∵△ABC 是等边三角形，∴AB=AC ，∠BAC =60°． ∵AE 平分∠BAC ，∴∠BAE =12∠BAC = 30°．由旋转可知：AD=AC ，∠CAD =90°． ∴AB=AD ，∠BAD =150°．∴∠ABD =∠D =15°．∴∠AED =∠ABD +∠BAE =45°．……………………………………2分②用等式表示线段AE 、CE 、BD之间的数量关系为2BD CE =． ………………………………………………………………………3分图2图1ABCEDCBA654321F CBA图3E D（2）解：①依题意补全图2．……………………………………………………4分②用等式表示线段AE 、CE 、BD………………………………………………………………………5分证明：过点A 作AF ⊥AE ，交ED 的延长线于点F （如图3）．∵△ABC 是等边三角形， ∴AB=AC ，∠BAC =60°． ∵AE 平分∠BAC ， ∴∠1=12∠BAC = 30°．由旋转可知：AD=AC ，∠CAD =90°． ∴AB=AD ，∠2=∠CAD -∠BAC =30°． ∴∠3=∠4=75°． ∴∠5=∠4-∠1=45°． ∵AF ⊥AE ，∴∠F =45°=∠5．∴AF=AE ． ∴AE ．∵∠6=∠EAF -∠1-∠2=30°， ∴∠6=∠1=30°．又∵∠F =∠5=45°，AD=AB ， ∴△ADF ≌△ABE ． ∴DF=BE ．∵AB=AC ，AE 平分∠BAC ， ∴AE 垂直平分BC ． ∴CE=BE ．∵BD =EF -DF -BE ，∴BD AE -2CE ．……………………………………………7分DE 图2ABC（2020密云一模）27. 已知∠MCN=45°，点B在射线CM上，点A是射线CN上的一个动点（不与点C重合）. 点B关于CN的对称点为点D，连接AB、AD和CD，点F在直线BC 上，且满足AF=AB. 小明在探究图形运动的过程中发现：AF⊥AD始终成立.（1）如图1，当0°＜∠BAC＜90°时.①求证：AF⊥AD②用等式表示线段CF、CD与CA之间的数量关系，并证明；（2）当90°＜∠BAC＜135° 时，直接用等式表示线段CF、CD与CA之间的数量关系是.27 . (1) ① ∵点B 关于CN 的对称点为点D ∴ABC ADC ∆≅∆∴∠ABC=∠ADC ，∠ACB=∠ACD=45° ∴∠BCD =90° ∵AF=AB ∴∠ABC=∠AFB ∴∠AFB =∠ADC ∵∠AFB+∠AFC=180°∴∠ADC+∠AFC=180°在四边形AFCD 中，∠FAD=90°∴AF ⊥AD ………………………………3分 ②CD CF +=………………………………4分解：过点A 作AC 边的垂线交CB 延长线于点P ∴△APC 是等腰直角三角形，∠PAC =90°，AP=AC∵∠PAF+∠FAC=∠DAC +∠FAC =90°∴∠PAF=∠DAC ∵∠AFB =∠ADC∴ APF ACD ∆≅∆ ∴ PF=CD 在等腰Rt △APC中，PF CF +=∴CD CF += ………………………………6分（2）CD CF -= ………………………7分DD(2020通州一模)（2020燕山一模）27．△ABC 中，∠ACB ＝90°，AC ＝BC ＝2，M 为BC 边上的一个动点(不与点B ，C 重合)，连接AM ，以点A 为中心，将线段AM 逆时针旋转135°，得到线段AN ，连接BN ．(1)依题意补全图1；(2)求证：∠BAN ＝∠AMB ；(3)点P 在线段BC 的延长线上，点M 关于点P 的对称点为Q ，写出一个PC 的值，使得对于任意的点M ，总有AQ ＝BN ，并证明．图1 M C B A A BC 备用图27．(1)补全图形，如图． ………………………………1分(2)证明：∵∠ACB ＝90°，AC ＝BC ，∴∠ABM ＝45°．∵∠MAB ＋∠ABM ＋∠AMB ＝180°，∴∠AMB ＝135°－∠MAB ．又∵∠MAN ＝135°，∴∠BAN ＝135°－∠MAB ，∴∠BAN ＝∠AMB ．………………………………3分 (3) PC 的值为1．………………………………4分证明：∵∠ACB ＝90°，AC ＝BC ＝2，∴AB ＝2．如图，任取满足条件的点M ，作点M 关于点C 的对称点M'，连接AM'，∴AM'＝AM ＝AN ，MM'＝2CM ，∴∠AM'C ＝∠AMC ，∴∠AM'Q ＝∠AMB ＝∠BAN ．∵点M 关于点P 的对称点为Q ，∴MQ ＝2MP ，∴M'Q ＝MQ －MM'＝2MP －2MC ＝2PC ＝2，∴M'Q ＝AB ，∴△AM'Q ≌△ANB ，∴AQ ＝BN ．………………………………7分 NC BAA C N M'Q。

2024年北京市中考数学一模26题汇编含答案

2024北京数学一模第26题汇编1.（2024平谷一模）在平面直角坐标系xoy 中,抛物线22y x bx =-．（1）当抛物线过点（2,0）时,求抛物线的解析式.（2）若抛物线上存在两点11(x ,y )A 和22(x ,y )B ,若对于11x 2,≤≤2x 2b =+都有120y y <,求b 的取值范围． 2．（2024 石景山一模）在平面直角坐标系xOy 中,抛物线222y x m x m =-++()的对称轴为直线x t =．（1）求t 的值（用含m 的代数式表示）.（2）点1A t y -(，),2B t y (，),31C t y +(，)在该抛物线上．若抛物线与x 轴的一个交点为00x (，),其中002x <<,比较1y ,2y ,3y 的大小,并说明理由．3．（2024燕山一模）在平面直角坐标系xOy 中,M (m ,1y ),N (m ＋2,2y )是抛物线2(0)y ax bx c a =++>上两点．设该抛物线的对称轴为x t =．(1) 若对于m ＝1,有1y ＝2y ,求t 的值.(2) 若对于1＜m ＜2,都有1y ＜2y ,求t 的取值范围．4．（2024北京汇文中学）（6分）在平面直角坐标系xOy 中,已知抛物线y ＝x 2﹣2tx +t 2﹣t ．（1）求抛物线的顶点坐标（用含t 的代数式表示）.（2）点P （x 1,y 1）,Q （x 2,y 2）在抛物线上,其中t ﹣1≤x 1≤t +2,x 2＝1﹣t ． ①若y 1的最小值是﹣2,求y 1的最大值. ②若对于x 1,x 2,都有y 1＜y 2,求出t 的取值范围．5．（2024人大附一模）（6分）在平面直角坐标系xOy 中,抛物线y ＝x 2﹣2mx +m 2+1与y 轴的交点为A ,过点A 作直线l 垂直于y 轴．（1）求抛物线的对称轴（用含m 的式子表示）．（2）将抛物线在y 轴左侧的部分沿直线l 翻折,其余部分保持不变,组成图形G ．点M （x 1,y 1）,N （x 2,y 2）为图形G 上任意两点．①当m ＝0时,若x 1＜x 2,判断y 1与y 2的大小关系,并说明理由. ②若对于x 1＝m ﹣2,x 2＝m +2,都有y 1＞y 2,求m 的取值范围．6．（2024北京陈经纶一模）（6分）如图,AB 是⊙O 的一条弦,E 是AB 的中点,过点E 作EC ⊥OA 于点C ,过点B 作⊙O 的切线交CE 的延长线于点D ．（1）求证：DB ＝DE .（2）若AB ＝12,BD ＝5,求⊙O 的半径．7．（2024北京四中一模）（本题9分）如图,四边形ABCD 为正方形,点E 为BC 延长线上一点,连接AE ,交BD 于点F ,交CD 于点G ,连接CF ．(1)求证：CF 与CEG 的外接圆相切.(2)当CE CF =时,判断CG 和EF 有怎样的数量关系？并说明理由. (3)在（2）的条件下,求DG 与CG 的比值．8. （2024北京西城一模）在平面直角坐标系xOy 中,点 ()()()2,2,,A y B y C m y -₁，₂，₃在抛物线 ²3y ax bx =++ (0)a >上．设抛物线的对称轴为直线x =t ．（1）若 3y =₁,求t 的值.（2）若当 12t m t +<<+时,都有 y y y >>₁₃₂，求t 的取值范围．9.（2024北京朝阳一模）在平面直角坐标系xOy 中,抛物线 ()20y ax bx a =+>上有两点()()1122,,x y x y ，, 它的对称轴为直线x t =．（1）若该抛物线经过点()40，,求t 的值. （2）当()101x <<时.①若1t >, 则1y 0, （填“>”“=”或“<” ） ②若对于122x x +=,都有120y y >,求t 的取值范围．10.（2024北京首师大附中一模）如图,在等边ABC 中,点D 在BC 边上,点E 在AC 的延长线上,且DE DA =．（1）求证：BAD EDC ∠=∠.（2）点E 关于直线BC 的对称点为M ,连接DM ,AM . ①根据题意将图补全.②在点D 运动的过程中,DA 和AM 有什么数量关系并证明．11．（2024北京顺义一模）在平面直角坐标系xOy 中,M 11()x y ，,N 22()x y ，是抛物线2(0)y ax bx c a =++＞上任意两点,设抛物线的对称轴为x t =.（1）当12x =时,1y c =,求抛物线的对称轴.（2）若对于11t x t --＜＜2,2t x t ＜＜+2,都有12y y ＞,求t 的取值范围.12．（2024北京丰台一模）在平面直角坐标系xOy 中,()12,M y ,()25,N y 是抛物线22y x ax =-上的两点．（1）直接写出一个a 的值,使得12y y <成立.（2）()33,P x y 是抛物线22y x ax =-上不同于M ,N 的点,若对于301x <≤,都有132y y y <<,求a 的取值范围．13. （2024北京大兴一模）在平面直角坐标系xOy 中,()11,M x y ,()22,N x y 是抛物线2(0)y ax bx c a =++<上任意两点．设抛物线的对称轴为直线x t =．（1）若22x =,2y c =,求t 的值.（2）若对于112t x t +<<+,245x <<,都有12y y >,求t 的取值范围．14. （2024北京房山一模）在平面直角坐标系xOy 中,11()A x y ，,22()B x y ，是抛物线2222y x a x a =-+-上任意两点. （1）当1a =时,求抛物线与y 轴的交点坐标及顶点坐标. （2）若对于1102x <<,2112x <<,都有12y y >,求a 的取值范围． 15.（2024北京门头沟一模）在平面直角坐标系xoy 中,点()1,A x m ,()2,B x n 在抛物线24y ax bx =++()0a >上,设抛物线的对称轴为直线x h =. （1）如果抛物线经过点()2,4,求h 的值.（2）如果对于14x h =-,23x h =,都有m n >,求h 取值范围.（3）如果对于142h x h -+≤≤,22112x x ≤或≥,存在m n >,直接写出h 的取值范围.16.（2024北京延庆一模）在平面直角坐标系xOy 中,点A （3,m ）,点B （5,n ）在抛物线2(0)y ax bx c a =++> 上.设抛物线的对称轴为直线x t =. （1）若m =n ,求t 的值.（2）点)(0p x C ，在该抛物线上,若对于100＜＜x ,都有p n m ＜＜,求t 的取值范围.17．（2024北京人朝分校一模）在平面直角坐标系xOy 中,点M （x 1,y 1）,N （x 2,y 2）是抛物线y ＝ax 2﹣2ax +c （a ＞0）上任意两点．（1）直接写出抛物线的对称轴.（2）若x 1＝a +1,x 2＝a +2,比较y 1与y 2的大小,并说明理由.（3）若对于m ＜x 1＜m +1,m +1＜x 2＜m +2,总有y 1＜y 2,求m 的取值范围．26题答案解析1.（1）抛物线的对称轴为x=b (1)∵抛物线过点（0,0）和（2,0） ∴b=1························································2 ∴抛物线的解析式为22y x x =-（2）∵抛物线的对称轴为x=b.∴（b+2,0）点一定位于对称轴的右侧························································3 情况1：当原点位于对称轴的左侧时此时,有2222b bb+>⎧⎨<⎩解得12b <<························································4 情况2：当原点位于对称轴的右侧时此时,有220b b <+<解得22b b <⎧⎨<-⎩解得2b <-························································5 综上.1∴<b<2或b<-2························································6 2．解：（1）由题意,得22m t -+=-(). 即22mt +=． ………………………… 2分（2）231y y y <<．理由如下：令0y =,得2220x m x m -++=()． ∴122x x m ==，．∴抛物线与x 轴的两个交点为20(，),0m (，)． ∵抛物线与x 轴的一个交点为00x (，),其中002x <<. ∴02m <<．∵22mt +=. ∴12t <<．∴21t -<-<-,213t <+<．设点1A t y -(，)关于抛物线的对称轴x t =的对称点为1A n y '(，)． ∵点1A t y -(，)在抛物线上. ∴点1A n y '(，)也在抛物线上．由n t t t -=--(),得3n t =． ∴336t <<． ∴13t t t <+<．∵抛物线的解析式为222y x m x m =-++(). ∴此抛物线开口向上．当x t ≥时,y 随x 的增大而增大．∵点2B t y (，),31C t y +(，),13A t y '(，)在抛物线上,且13t t t <+<. ∴231y y y <<． ………………………… 6分 2．解：(1) ∵对于m ＝1,有1y ＝2y . ∴点M (1,1y ),N (3,2y )关于直线x ＝t 对称.∴t －1＝3－t .∴t ＝2． ……………………………………………2分 (2) ∵a ＞0.∴当x ≥t 时,y 随x 增大而增大,当x ＜t 时,y 随x 增大而减小． ①当t ≤1时. ∵1＜m ＜2. ∴3＜m ＋2＜4. ∴t ＜m ＜m ＋2. ∴1y ＜2y ,符合题意． ②当1＜t ≤2时. （i ）当t ≤m ＜2时. ∵3＜m ＋2＜4. ∴t ≤m ＜m ＋2. ∴1y ＜2y ,符合题意．（ii ）当m ＜t ≤2时.设点M (m ,1y )关于x ＝t 的对称点为M ′,则点M ′的坐标为(2t －m ,1y )．∵1＜m ＜t ≤2. ∴m ＜2t －m ＜3． ∵3＜m ＋2＜4. ∴2t －m ＜m ＋2. ∴1y ＜2y ,符合题意．③当2＜t ＜3时,令m ＝t －1,则m ＋2＝t ＋1. ∴1y ＝2y ,不符合题意． ④当t ≥3时,令m ＝32,则m ＋2＝72. ∴1y ＞2y ,不符合题意．综上所述,t 的取值范围是t ≤2． …………………………………………6分 3．解：(1) ∵对于m ＝1,有1y ＝2y . ∴点M (1,1y ),N (3,2y )关于直线x ＝t 对称.∴t －1＝3－t .∴t ＝2． ……………………………………………2分 (2) ∵a ＞0.∴当x ≥t 时,y 随x 增大而增大,当x ＜t 时,y 随x 增大而减小． ①当t ≤1时. ∵1＜m ＜2. ∴3＜m ＋2＜4. ∴t ＜m ＜m ＋2. ∴1y ＜2y ,符合题意． ②当1＜t ≤2时. （i ）当t ≤m ＜2时. ∵3＜m ＋2＜4. ∴t ≤m ＜m ＋2. ∴1y ＜2y ,符合题意．（ii ）当m ＜t ≤2时.设点M (m ,1y )关于x ＝t 的对称点为M ′,则点M ′的坐标为(2t －m ,1y )． ∵1＜m ＜t ≤2. ∴m ＜2t －m ＜3． ∵3＜m ＋2＜4. ∴2t －m ＜m ＋2. ∴1y ＜2y ,符合题意．③当2＜t ＜3时,令m ＝t －1,则m ＋2＝t ＋1. ∴1y ＝2y ,不符合题意．④当t ≥3时,令m ＝32,则m ＋2＝72. ∴1y ＞2y ,不符合题意．综上所述,t 的取值范围是t ≤2． …………………………………………6分4．【解答】解：（1）∵y ＝x 2﹣2tx +t 2﹣t ＝（x ﹣t ）2﹣t . ∴抛物线的顶点坐标为（t ,﹣t ）.（2）①∵y ＝x 2﹣3tx +t 2﹣t ＝（x ﹣t ）2﹣t . ∴抛物线的对称轴为x ＝t . ∵8＞0.∴抛物线开口向上. ∵t ﹣1≤x 4≤t +2.∴当x ＝t 时,y 1的最小值为﹣t . ∵y 4的最小值是﹣2. ∴t ＝2.∵|t ﹣3﹣t |＝1,|t +2﹣t |＝4.∴当x ＝t +2时,y 1最大＝（t +3﹣t ）2﹣t ＝4﹣t ＝2﹣2＝2. 即y 4的最大值为2.②∵点P （x 1,y 2）,Q （x 2,y 2）在抛物线y ＝（x ﹣t ）8﹣t 上. ∴y 1＝（x 1﹣t ）7﹣t ,y 2＝（x 2﹣t ）6﹣t . ∵对于x 1,x 2,都有y 4＜y 2.∴y 2﹣y 2＝（x 2﹣t ）2﹣t ﹣（x 2﹣t ）2+t ＝（x 2﹣t ）2﹣（x 1﹣t ）2＝（x 5﹣x 1）（x 2+x 2﹣2t ）＞0. ∴或.Ⅰ,当时.由①知,x 5＞x 1.∵t ﹣1≤x 2≤t +2,x 2＝5﹣t . ∴1﹣t ＞t +2. ∴t ＜﹣. 由②知,x 2+x 8＞2t . ∵t ﹣1≤x 3≤t +2,x 2＝6﹣t . ∴0≤x 2+x 8≤3.∴2t＜2.∴t＜0.即t＜﹣.Ⅱ,当时.由③知,x2＜x4.∵t﹣1≤x1≤t+4,x2＝1﹣t.∴6﹣t＜t﹣1.∴t＞1.由④知,x2+x1＜2t.∵t﹣3≤x1≤t+2,x8＝1﹣t.∴0≤x3+x1≤3.∴5t＞3.∴t＞.即t＞.即满足条件的t的取值范围为t＜﹣或t＞．5．【分析】（1）根据抛物线的对称轴公式求解即可.（2）①由题意可得出二次函数解析式是y＝x2+1,对称轴为y轴,即可画出图形G,如图1,得出图形G上的点的横纵坐标x和y,满足y随x的增大而增大,即可得出结论,②通过计算可知,P（m﹣2,5）,Q（m+2,5）为抛物线上关于对称轴x ＝m对称的两点,下面讨论当m变化时,y轴于点P,Q的相对位置：分三种情形：如图2,当y轴在点P左侧时（含点P）,如图3,当y轴在点Q右侧时（含点Q）,如图4,当y轴在点P,Q之间时（不含P,Q）,分别求解即可．【解答】解：（1）∵该抛物线解析式为y＝x2﹣2mx+m2+1.∴抛物线的对称轴为直线.（2）①y1＜y2．理由：当m＝0时,二次函数解析式是y＝x2+1,对称轴为y轴.∴图形G大致图象如下.∴图形G上的点的横纵坐标x和y,满足y随x的增大而增大．∵x1＜x2.∴y1＜y2.②对于y＝x2﹣2mx+m2+1,令x＝m﹣2,则y＝（m﹣2）2﹣2m（m﹣2）+m2+1＝5.令x＝m+2,则y＝（m+2）2﹣2m（m+2）+m2+1＝5.∴该抛物线上两点P（m﹣2,5）,Q（m+2,5）为抛物线上关于对称轴x＝m对称的两点．分类讨论：如图2,当y轴在点P左侧时（含点P）,经翻折后,点P,Q位置不动.∴y1＝y2,不符题意.如图3,当y轴在点Q右侧时（含点Q）,点P,Q经翻折之后的对应点为点M,N.∴y1＝y2,不符题意.如图4,当y轴在点P,Q之间时（不含P,Q）,经翻折后,点N在l下方,点M,P重合,在l上方.∴y1＞y2,符合题意.此时有m﹣2＜0＜m+2,即﹣2＜m＜2.综上所述,m的取值范围为﹣2＜m＜2．【点评】本题属于二次函数综合题,考查了二次函数的性质,轴对称翻折变换,函数的增减性等知识,解题的关键是学会用分类讨论的思想思考问题,正确作出图形是解决问题的关键．6．【分析】（1）欲证明DB＝DE,只要证明∠DEB＝∠DBE.（2）作DF⊥AB于F,连接OE．只要证明∠AOE＝∠DEF,可得sin∠DEF＝sin∠AOE＝＝,由此求出AO即可解决问题．【解答】（1）证明：∵AO＝OB.∴∠OAB＝∠OBA.∵BD是切线.∴OB⊥BD.∴∠OBD＝90°.∴∠OBE+∠EBD＝90°.∵EC⊥OA.∴∠CAE+∠CEA＝90°.∵∠CEA＝∠DEB.∴∠EBD＝∠BED.∴DB＝DE．（2）作DF⊥AB于F,连接OE．∵DB＝DE,AE＝EB＝6.∴EF＝BE＝3,OE⊥AB.在Rt△EDF中,DE＝BD＝5,EF＝3.∴DF ＝＝4.∵∠AOE +∠A ＝90°,∠DEF +∠A ＝90°. ∴∠AOE ＝∠DEF . ∴sin ∠DEF ＝sin ∠AOE ＝＝.∵AE ＝6. ∴AO ＝．∴⊙O 的半径为．【点评】本题考查切线的性质,勾股定理,垂径定理,锐角三角函数,等腰三角形的性质等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题,属于中考常考题型．7．(1)见解析 (2)3EF CG =．理由见解析 (3)DG CG =【分析】本题主要考查切线的判定,全等石匠判定与性质,直角三角形的性质等知识：（1）证明ADF CDF △≌△得2DAF ∠=∠,由AD BE 得2E DAF ∠=∠=∠,取EG 的中点H ,连接CH ,证明2+4=90∠∠︒即可得出结论.（2）证明30E ∠=︒,得出2,EG CG =进一步得出结论.（3）设CG x =,可求出)1AG x =,)1,2x DG =从而可得结论．【详解】（1）证明：如图.四边形ABCD 为正方形.,AD CD ADF CDF ∴=∠=∠. 又DF DF =. ,ADF CDF ∴△≌△2DAF ∴∠=∠.,AD BE ∥ ,DAF E ∴∠=∠ 2E ∴∠=∠.取EG 的中点H ,连接CH .则CH EH GH ==为CEG 外接圆的半径.1,45,E ∴∠=∠∠=∠ 12∴∠=∠.1490,∠+∠=︒2490∴∠+∠=︒.CF CH ∴⊥.所以CF 与CEG 的外接圆相切．（2）解：3EF CG =．理由如下：CE CF =.312,E ∴∠=∠=∠=52E ∠=∠.而590,E ∠+∠=︒30E ∴∠=︒. 2,EG CG ∴=3EF CG ∴=．（3）解：设CG x =,则,FG x CE CF AF ====. )1AG x ∴=.由（2）知30DAF E ∠=∠=︒.)11,22x DG AG ∴==DG CG ∴=8. 【答案】（1）1- （2）13t ≤≤【分析】本题考查了二次函数的性质,二次函数图象上点的坐标特征,熟练掌握二次函数的性质是解题的关键．（1）把A 点的坐标代入解析式求得2b a =,然后利用对称轴公式即可求得.（2）由题意可知点1(2,)A y -在对称轴的左侧,3(,)C m y 在对称轴的右侧,点1(2,)A y -关于直线x t =的对称点为(22)t +,2(2,)B y 关于直线x t =的对称点为(22)t -,分两种情况讨论,得到关于t 的不等式组,解不等式组从而求得t的取值范围．解：点(2,3)A -在抛物线23(0)y ax bx a =++>上.3423a b ∴=-+.2b a ∴=.12bt a∴=-=-. 【小问2详解】解：0a >.∴抛物线23(0)y ax bx a =++>开口向上.当x t >时,y 随x 的增大而增大.当12t m t +<<+时,都有132y y y >>.∴点1(2,)A y -在对称轴的左侧,3(,)C m y 在对称轴的右侧.点1(2,)A y -,2(2,)B y ,3(,)C m y 在抛物线23(0)y ax bx a =++>上.∴点1(2,)A y -关于直线x t =的对称点为(22)t +,2(2,)B y 关于直线x t =的对称点为(22)t -.当2t ≥时,则222221t t t t +>+⎧⎨-≤+⎩,解得03t <≤.23t ∴≤≤.当2t <时,则22212t t t +>+⎧⎨+≤⎩,解得12t ≤<.综上所述,t 的取值范围为13t ≤≤． 9. 【答案】（1）2t = （2）①<,②1t ≤或0t ≤【分析】本题主要考查二次函数的性质,()1将点代入抛物线求得4b a =-,结合对称轴定义即可求得.()2①根据题意得抛物线开口向上,且过原点,即可得10y<.②由已知求得212x <<,结合120y y >恒成立,则有点()()1122,,x y x y ，在x 的同侧即可．【小问1详解】解：将点()40，代入()20y ax bx a =+>得1640a b +=,解得4b a =-. ∴4222b a x a a-=-=-=. 则2t =.①根据题意得抛物线开口向上,且过原点. ∵1t >,101x <<. ∴10y <.②∵122x x +=, 101x <<. ∴212x <<. ∵有120y y >恒成立.∴点()()1122,,x y x y ，在x 的同侧. 则1t ≤或0t ≤．26. 【答案】（1）见解析（2）①见解析,②DM AM =,证明见解析【分析】本题考查了等腰三角形的性质,等边三角形的判定与性质,轴对称的性质等知识点,利用轴对称的性质求解是解题关键．（1）根据等边三角形的性质可得60BAC ACB ∠=∠=︒,根据等腰三角形的性质及三角形外角的性质即可得出BAD EDC ∠=∠.（2）①根据题意补全图形即可,②根据轴对称的性质得出MDC EDC ∠=∠,DE DM =,结合（1）中结论可得60ADM B ∠=∠=︒,即可证明ADM △是等边三角形,可得DM AM =．【小问1详解】解：∵ABC 是等边三角形. ∴60BAC ACB ∠=∠=︒.∵BAD DAC BAC ∠+∠=∠,EDC DEC ACB ∠+∠=∠. ∴BAD DAC EDC DEC ∠+∠=∠+∠. ∵DE DA =. ∴DAC DEC ∠=∠. ∴BAD EDC ∠=∠．【小问2详解】 ①补全图形如图所示：x=h②DM AM =,理由如下：如①中图,连接CM .∵点M ,E 关于直线BC 对称. ∴MDC EDC ∠=∠,DE DM =. 由（1）知BAD EDC ∠=∠. ∴MDC BAD ∠=∠.∵ADC BAD B ∠=∠+∠,即ADM MDC BAD B ∠+∠=∠+∠. ∴60ADM B ∠=∠=︒. ∵DA DE DM ==. ∴ADM △是等边三角形. ∴DM AM =．11．解：（1）∵抛物线2(0)y ax bx c a =++＞经过（0,c ）和（2,c ）.∴抛物线对称轴为x =1．…………………………………………………..…………….2分（2）2x t t x t =∵抛物线的对称轴为，＜＜+2，2'x N N ∴点在对称轴右侧，设点关于对称轴对称点的横坐标为2'2,t x t -∴＜＜12y y ∵＞，11t x t --＜＜2∴①当点M 在对称轴左侧时.2t t t --≤2≥2②当点M 对称轴右侧时. 11t t t -+≥2≤-21.t t ≥2或≤综述，-所2上…………………………………………………..…………….6分12．解：（1）答案不唯一,例如：3a =．（2）∵二次函数解析式为22y xax =-,∴函数图像开口向上,对称轴为x a =．t1x=h①当3a x ≤时,∴点P ,M ,N 均在对称轴右侧． ∴由二次函数性质,必有312y y y <<,不符题意舍去． ②当32x a ≤<时.∵点P 在对称轴左侧,设P 点关于x a =的对称点为P '. 则点P '的坐标为()312,a x y -．∵点P ',M ,N 在对称轴右侧,且132y y y <<. ∴322a x <-．∴322a <<． ③当25a ≤≤时.∵点P 和M 在对称轴左侧,由函数性质,有13y y <. ∵点P ',N 在对称轴右侧,且32y y <. ∴325a x -<．∴522a ≤≤． ④当5a >时,∴点P ,M ,N 均在对称轴左侧．∴由二次函数性质,必有312y y y >>,不符题意舍去．由①②③④可知,3522a <≤． 13. 【答案】（1）1t = （2）2t ≤或7t ≥【分析】本题主要考查了二次函数的图象和性质等知识. （1）将22x =,2y c =代入解析式,得出2b a =-即可得解.（2）分①当点N 在对称轴上或对称轴右侧时,②当点N 在对称轴上或对称轴左侧时两种情况讨论组成不等式组即可得解.解题的关键是理解题意,灵活运用所学知识解决问题．【小问1详解】22x =,2y c =.42a b c c ∴++=. 2b a ∴=-. 12bt a∴=-=. 【小问2详解】2(0)y ax bx c a =++<.∴抛物线开口向下.抛物线的对称轴为x t =,112t x t +<<+. ∴点M 在对称轴的右侧.①当点N 在对称轴上或对称轴右侧时. 抛物线开口向下.∴在对称轴右侧,y 随x 的增大而减小．由12y y >. ∴12x x <. ∴4,24t t ≤⎧⎨+≤⎩.解得42t t ≤⎧⎨≤⎩.∴2t ≤.②当点N 在对称轴上或对称轴左侧时.设抛物线上的点()22,N x y 关于x t =的对称点为()2,N d y '.2t x d t ∴-=-,解得22d t x =-.∴()222,N t x y '-.245x <<.∴225224t t x t -<-<-.在对称轴右侧,y 随x 的增大而减小. 由12y y >. ∴122x t x <-. ∴5225t t t ≥⎧⎨+≤-⎩.解得57t t ≥⎧⎨≥⎩. ∴7t ≥.综上所述,t 的取值范围是2t ≤或7t ≥．14.解：（1）令0x =,则22y a =-.当1a =时,1y =-.∴抛物线与y 轴的交点坐标为(01)-，, ∵22222()2y x ax a x a =-+-=--.当1a =时,抛物线的顶点坐标为(12)-，.（2）∵11()A x y ，,22()B x y ，是抛物线2222y x ax a =-+-上任意两点.∴211()2y x a =--,222()2y x a =--.∴2212121212()()()(2)y y x a x a x x x x a -=---=-+-.∵1102x <<,2112x <<. ∴12x x <,121322x x <+<.∵12x x <,12y y >. ∴1220x x a +-<.即122x x a +<.∴322a ≥.∴34a ≥. 15．（本小题满分6分）方案2解：（1）由题意知,442.a b c =++ ∴ 2b a =-.∴12=-=a b h . …………………………2分（2）∵0a >.∴当x h ≥时,y 随x 的增大而增大,当x h ≤时,y 随x 的增大而减小.点()4A h m -，关于对称轴x h =的对称点为()'4A h m +，……………………3分 ①当0h ≤,时3h h ≤,4h h -<.m n >∴43h h -<∴20h -<≤②当0h >,时2h h >,4h h +>.m n >∴43h h +> ∴02h <<综上22h -<<. ……………………5分（3）5h <或8h > ……………………6分16.（1）解：∵点A （3,m ）,点B （5,n ）在抛物线2(0)y ax bx c a =++>上,且m =n ,抛物线的对称轴为x=t . ∴5-t =t -3. ∴t =4.（2）∵点A （3,m ）,点B （5,n ）,点)(0p x C ，在抛物线2(0)y ax bx c a =++>上. ∴c b a m ++=39. c b a n ++=525. c bx ax p ++=020. ∵ p n m <<.∴n m <且p n <.①当n m ＜时,有c b a c b a ++<++52539. ∴b a b a 52539+<+. ∴08>+b a . ∴a b 8->. ∵0>a .∴0<-a . ∴42<-ab. ∵t ab=-2. ∴4<t .②当p n ＜时,有c bx ax c b a ++<++020525. ∴a ax bx b 255200-<-. ∴)5)(5()5(000-+<-x x a x b .∵100＜＜x . ∴)5(0+<x a b . ∴2520+>-x a b . ∴3≥t . 综上：43<≤t .……………………5分 ……………………2分……………………4分……………………3分……………………6分17．【分析】（1）更近抛物线对称轴公式求出即可.（2）根据条件点M,N都在对称轴右侧,根据函数增减性进行解答即可.（3）根据二次函数图象上点的坐标特征,分析MN中点坐标与对称轴的关系得到不等式,解不等式即可得到m的取值范围．【解答】解：（1）抛物线y＝ax2﹣2ax+c（a＞0）的对称轴为：x＝﹣＝1.∴抛物线的对称轴为直线x＝1.（2）∵a＞0,抛物线开口向上,对称轴为直线x＝1.∴M（x1,y1）,N（x2,y2）都在对称轴右侧.∵当x＞1时,y随x的增大而增大,且x1＜x2.∴y1＜y2.（3）∵m＜x1＜m+1,m+1＜x2＜m+2.∴＜.∵y1＜y2,a＞0.∴M（x1,y1）距离对称轴更近,x1＜x2,则MN的中点在对称轴的右侧.∴解得：m．【点评】本题考查了二次函数的性质,熟练掌握二次函数的性质是解答本题的关键．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2018北京各区初中一模数学分类汇编27题及答案平谷27．在△ABC 中，AB=AC ，CD ⊥BC 于点C ，交∠ABC 的平分线于点D ，AE 平分∠BAC 交BD 于点E ，过点E 作EF ∥BC 交AC 于点F ，连接DF ．（1）补全图1；（2）如图1，当∠BAC =90°时，①求证：BE=DE ；②写出判断DF 与AB 的位置关系的思路（不用写出证明过程）；（3）如图2，当∠BAC=α时，直接写出α，DF ，AE 的关系．西城27．正方形ABCD 的边长为2，将射线AB 绕点A 顺时针旋转α，所得射线与线段BD 交于点M ，作CE AM ⊥于点E ，点N 与点M 关于直线CE 对称，连接CN ．（1）如图，当045α︒<<︒时， ①依题意补全图．②用等式表示NCE ∠与BAM ∠之间的数量关系：__________．（2）当4590α︒<<︒时，探究NCE ∠与BAM ∠之间的数量关系并加以证明．（3）当090α︒<<︒时，若边AD 的中点为F ，直接写出线段EF 长的最大值．CDBA图1备用图C DBAM图1BB 图2延庆27．如图1，正方形ABCD 中，点E 是BC 延长线上一点，连接DE ，过点B 作BF ⊥DE于点F ，连接FC ．（1）求证：∠FBC =∠CDF ．（2）作点C 关于直线DE 的对称点G ，连接CG ，FG ．①依据题意补全图形；②用等式表示线段DF ，BF ，CG 之间的数量关系并加以证明．海淀27．如图，已知60AOB ∠=︒，点P 为射线OA 上的一个动点，过点P交OB 于点E ，点D 在AOB ∠内，且满足DPA OPE ∠=∠，6DP PE +=.（1）当DP PE =时，求DE 的长；（2）在点P 的运动过程中，请判断是否存在一个定点M ，使得DMME的值不变？并证明你的判断.图1备用图FDEC BA FDEC BA大兴27．如图，在等腰直角△ABC中，∠CAB=90°，F是AB边上一点，作射线CF，过点B作BG⊥C F于点G，连接AG．（1）求证：∠ABG=∠ACF；（2）用等式表示线段C G，AG，BG之间的等量关系，并证明．怀柔27.如图，在△ABC中，∠A=90°，AB=AC，点D是BC上任意一点，将线段AD绕点A 逆时针方向旋转90°，得到线段AE，连结EC.(1)依题意补全图形；(2)求∠ECD的度数；(3)若∠CAE=7.5°，AD=1，将射线DA绕点D顺时针旋转60°交EC的延长线于点F，请写出求AF长的思路．顺义27. 如图，在正方形ABCD中，E是BC边上一点，连接AE，延长CB至点F，使BF=BE，过点F作FH⊥AE于点H，射线FH分别交AB、CD于点M、N，交对角线AC于点P，连接AF．（1）依题意补全图形；（2）求证：∠FAC=∠APF；（3）判断线段FM与PN的数量关系，并加以证明．门头沟27.如图，在△ABC中，AB=AC，2Aα∠=，点D是BC的中点，DE AB E⊥于点，DF AC F⊥于点.（1）EDB∠=_________°；（用含α的式子表示）（2）作射线DM与边AB交于点M，射线DM绕点D顺时针旋转1802α︒-，与AC边交于点N．①根据条件补全图形；②写出DM与DN的数量关系并证明；③用等式表示线段BM CN、与BC之间的数量关系，（用含α的锐角三角函数表示）并写出解题思路.FE丰台27．如图，Rt △ABC 中，∠ACB = 90°，CA = CB ，过点C 在△ABC 外作射线CE ，且∠BCE = α，点B 关于CE 的对称点为点D ，连接AD ，BD ，CD ，其中AD ，BD 分别交射线CE 于点M ，N .（1）依题意补全图形；（2）当α= 30°时，直接写出∠CMA 的度数；（3）当0°<α< 45°时，用等式表示线段AM ，CN 之间的数量关系，并证明．ABCE东城27. 已知△ABC 中，AD 是BAC ∠的平分线，且AD =AB ，过点C 作AD 的垂线，交 AD的延长线于点H ．（1）如图1，若60BAC ∠=︒①直接写出B ∠和ACB ∠的度数； ②若AB =2，求AC 和AH 的长；（2）如图2，用等式表示线段AH 与AB +AC 之间的数量关系，并证明．房山27. 如图，已知Rt △ABC 中，∠C =90°，∠BAC =30°，点D 为边BC 上的点，连接AD ，∠BAD =α，点D 关于AB 的对称点为E ，点E 关于AC 的对称点为G ，线段EG 交AB 于点F ，连接AE ，DE ，DG ，AG . （1）依题意补全图形；（2）求∠AGE 的度数（用含α的式子表示）；（3）用等式表示线段EG 与EF ，AF 之间的数量关系，并说明理由.燕山28．在Rt △ABC 中, ∠ACB =90°,CD 是AB 边的中线，DE ⊥BC 于E , 连结CD ，点P 在射线CB 上（与B ，C 不重合）．（1）如果∠A =30°①如图1，∠DCB =°②如图2，点P 在线段CB 上，连结DP ，将线段DP 绕点D 逆时针旋转60°，得到线段DF ,连结BF ，补全图2猜想CP 、BF 之间的数量关系，并证明你的结论；( 2 )如图3，若点P 在线段CB 的延长线上，且∠A =α （0°<α<90°），连结DP , 将线段DP 绕点逆时针旋转 α2得到线段DF ,连结BF , 请直接写出DE 、BF 、BP 三者的数量关系（不需证明）．αD CB A平谷27．解：（1）补全图1； (1)B（2）①延长AE ，交BC 于点H ． ················· 2 ∵AB=AC ， AE 平分∠BAC ，∴AH ⊥BC 于H ，BH=HC ．∵CD ⊥BC 于点C ， ∴EH ∥CD ． ∴BE=DE ． (3)②延长FE ，交AB 于点G ．由AB=AC ，得∠ABC =∠ACB ．由EF ∥BC ，得∠AGF =∠AFG ．得AG=AF ．由等腰三角形三线合一得GE=E F ． ······· 4 由∠GEB =∠FED ，可证△BEG ≌△DEF ．可得∠ABE =∠FDE ． (5)从而可证得DF ∥AB ． ························ 6 （3）tan 2DF αAE =． (7)西城27. （1）①补全的图形如图所示：NEMABDC②2NCE BAM ∠=∠．BB（2）1902MCE BAM ∠+∠=︒，连接CM ，NQM ABDC EDAM DCM ∠=∠，DAQ ECQ ∠=∠，∴2NCE MCE DAQ ∠=∠=∠，∴12DCM NCE ∠=∠，∵BAM BCM ∠=∠， 90BCM DCM ∠+∠=︒，∴1902NCE BAM ∠+∠=︒．（3）∵90CEA ∠=︒， ∴点E 在以AC 为直径的圆上，E∴max 1EF FO r =+=+延庆27.（1）证明：∵四边形ABCD 是正方形，∴∠DCB =90°． ∴∠CDF +∠E =90°． ∵BF ⊥DE ， ∴∠FBC +∠E =90°．图1FDEC BA∴∠FBC =∠CDF ．……2分（2）① ……3分②猜想：数量关系为：BF =DF +CG ．证明：在BF 上取点M 使得BM =DF 连接CM ．∵四边形ABCD 是正方形， ∴BC =DC ．∵∠FBC =∠CDF ，BM =DF ， ∴△BMC ≌△DFC ． ∴CM =CF ，∠1=∠2． ∴△MCF 是等腰直角三角形．∴∠MCF =90°，∠4=45°． ……5分 ∵点C 与点G 关于直线DE 对称， ∴CF =GF ，∠5=∠6． ∵BF ⊥DE ，∠4=45°， ∴∠5=45°， ∴∠CFG =90°， ∴∠CFG =∠MCF ， ∴CM ∥GF ． ∵CM =CF ，CF =GF ， ∴CM =GF ，∴四边形CGFM 是平行四边形， ∴CG =MF ．∴BF =DF +CG ． ……7分海淀27．.解：（1）作PF ⊥DE 交DE 于F .∵PE ⊥BO ，60AOB ∠=，∴30OPE ∠=.∴30DPA OPE ∠=∠=.∴120EPD ∠=.…1分 ∵DP PE =,6DP PE +=,∴30PDE ∠=,3PD PE ==.∴cos30DF PD =⋅︒=∴2DE DF ==……3分（2）当M 点在射线OA 上且满足OM =DMME的值不变，始终为1.理由如下：…………4分当点P 与点M 不重合时，延长EP 到K 使得PK PD =.GFDECBA∵,DPA OPE OPE KPA ∠=∠∠=∠,∴KPA DPA ∠=∠. ∴KPM DPM ∠=∠.∵PK PD =,PM 是公共边, ∴KPM △≌DPM △.∴MK MD =. ………………5分作ML ⊥OE 于L ,MN ⊥EK 于N . ∵23,60MO MOL =∠=，∴sin 603ML MO =⋅=. ………………6分∵PE ⊥BO ,ML ⊥OE ,MN ⊥EK ，∴四边形MNEL 为矩形.∴3EN ML ==. ∵6EK PE PK PE PD =+=+=,∴EN NK =.∵MN ⊥EK ,∴MK ME =.∴ME MK MD ==,即1DMME=. 当点P 与点M 重合时，由上过程可知结论成立. ………………7分大兴27.（1）证明 :∵ ∠CAB=90°. ∵ BG ⊥CF 于点G ， ∴ ∠BGF =∠CAB =90°.∵∠GFB =∠CFA . ………………………………………………1分 ∴ ∠ABG =∠ACF . ………………………………………………2分（2）CG =2AG +BG . …………………………………………………3分证明：在CG 上截取CH =BG ，连接AH ， …………………………4分 ∵ △ABC 是等腰直角三角形， ∴ ∠CAB =90°，AB =AC . ∵ ∠ABG =∠ACH .∴ △ABG ≌△ACH . …………………………………………………… 5分 ∴ AG =AH ,∠GAB =∠HAC . ∴ ∠GAH =90°.∴ 222AG AH GH +=.∴ GH =2AG . ………………………………………………………6分 ∴ CG =CH +GH =2AG +BG . ………………………………………7分NMD KOBA PB怀柔27. (1)如图 …………………………………………………………………………………………1分 (2) ∵线段AD 绕点A 逆时针方向旋转90°，得到线段AE. ∴∠DAE=90°，AD=AE. ∴∠DAC+∠CAE =90°.∵∠BAC=90°, ∴∠BAD+∠DAC =90°.∴∠BAD=∠CAE . …………………………………………………………………………2分又∵AB=AC,∴△ABD ≌△ACE. ∴∠B=∠ACE.∵△ABC 中，∠A=90°，AB=AC, ∴∠B=∠ACB=∠ACE=45°.∴∠ECD=∠ACB+∠ACE=90°. ……………………………………………………………4分(3)Ⅰ.连接DE,由于△ADE 为等腰直角三角形，所以可求DE=2；……………………5分 Ⅱ.由∠ADF=60°,∠CAE=7.5°，可求∠EDC 的度数和∠CDF 的度数，从而可知DF 的长； …………………………………………………………………………………………………6分Ⅲ.过点A 作AH ⊥DF 于点H ，在Rt △ADH 中, 由∠ADF=60°，AD=1可求AH 、DH 的长； Ⅳ. 由DF 、DH 的长可求HF 的长；Ⅴ. 在Rt △AHF 中, 由AH 和HF,利用勾股定理可求AF 的长．…………………………7分顺义27．（1）补全图如图所示． ………………………………………………………… 1分（2）证明∵正方形ABCD ， ∴∠BAC =∠BCA =45°，∠ABC =90°， ∴∠PAH =45°-∠BAE ． ∵FH ⊥AE ．∴∠APF =45°+∠BAE ． ∵BF=BE ，∴AF=AE ，∠BAF =∠BAE ． ∴∠FAC =45°+∠BAF ．∴∠FAC =∠APF ．…………………………… 4分（3）判断：FM =PN ． …………………………………… 5分证明：过B 作BQ ∥MN 交CD 于点Q ，∴MN =BQ ，BQ ⊥AE ．∵正方形ABCD，∴AB=BC，∠ABC=∠BCD=90°．∴∠BAE=∠CBQ．∴△ABE≌△BCQ．∴AE=BQ．∴AE=MN．∵∠FAC=∠APF，∴AF=FP．∵AF=AE，∴AE=FP．∴FP=MN．∴FM=PN．……………………………………………………………8分门头沟27．（本小题满分7分）（1）EDBα∠=……………………………………………1分（2）①补全图形正确……………………………………2分②数量关系：DM DN=…………………………………3分∵,AB AC BD DC==∴DA平分BAC∠∵DE AB E⊥于点，DF AC F⊥于点∴DE DF=，MED NFD∠=∠……………………4分∵2Aα∠=∴1802EDFα∠=︒-∵1802MDNα∠=︒-∴MDE NDF∠=∠∴MDE NDF△≌△……………………5分∴DM DN=③数量关系：sinBM CN BCα+=⋅……………………6分证明思路：a.由MDE NDF△≌△可得EM FN=b. 由AB AC=可得B C∠=∠,进而通过BDE CDF△≌△,可得BE CF=进而得到2BE BM CN=+c.过BDERt△可得sinBEBDα=,最终得到sinBM CN BCα+=⋅……………7分丰台27．解：（1）如图；…………………1分（2）45°；…………………2分（3）结论：AMCN．…………………3分证明：作AG⊥EC的延长线于点G．∵点B与点D关于CE对称，∴CE是BD的垂直平分线．∴CB=CD．∴∠1=∠2=α．∵CA=CB，∴CA=CD．∴∠3=∠CAD．B87654321GNMCEB ∵∠4=90°，∴∠3=12（180°-∠ACD ）=12（180°-90°-α-α）=45°-α．∴∠5=∠2+∠3=α+45°-α=45°．…………………5分 ∵∠4=90°，CE 是BD 的垂直平分线， ∴∠1+∠7=90°，∠1+∠6=90°． ∴∠6=∠7． ∵AG ⊥EC ， ∴∠G =90°=∠8．∴在△BCN 和△CAG 中， ∠8=∠G ， ∠7=∠6， BC =CA ，BCN ≌△CAG ．∴CN =AG ． ∵Rt △AMG 中，∠G =90°，∠5=45°， ∴AM 2．∴AM 2． …………………7分东城27. （1）①75B ∠=︒，45ACB ∠=︒；--------------------2分②作DE ⊥AC 交AC 于点E .Rt △ADE 中，由30DAC ∠=︒，AD =2可得DE =1，AE 3=. Rt △CDE 中，由45ACD ∠=︒，DE=1，可得EC =1. ∴AC 31.Rt △ACH 中，由30DAC ∠=︒，可得AH 33+=； --------------4分（2）线段AH 与AB +AC 之间的数量关系：2AH =AB +AC证明：延长AB 和CH 交于点F ，取BF 中点G ，连接GH .易证△ACH ≌△AFH .∴AC AF =,HC HF =. ∴GH BC ∥. ∵AB AD =，∴ ABD ADB ∠=∠. ∴ AGH AHG ∠=∠ . ∴ AG AH =.∴()2222AB AC AB AF AB BF AB BG AG AH +=+=+=+==. --------------7房山27. 解（1）G………………………………………………1分（2）由轴对称性可知，AB 为ED 的垂直平分线，AC 为EG 的垂直平分线.∴AE =AG =AD .∴∠AEG =∠AGE ，∠BAE =∠BAD =α ∴∠EAC =∠BAC +∠BAE =30°+α ∴∠EAG =2∠EAC =60°+2α∴∠AGE =12(180°－∠EAG ) =60°－α………………………………………………3分或：∠AGE =∠AEG =90°－∠EAC =90°－（∠BAC +∠EAB ）=90°－（30°+α）=60°－α……………………………………………………………………3分（3）EG =2EF +AF ……………………………………………………………………………4分法1：设AC 交EG 于点H ∵∠BAC =30°，∠AHF =90°∴FH =12AF …………………………5分∴EH =EF +FH =EF +12AF …………6分又∵点E ，G 关于AC 对称 ∴EG =2EH∴EG =2(EF +12AF )=2EF +AF ………………………………………………………7分法2：在FG 上截取NG =EF ，连接AN. 又∵AE =AG ， ∴∠AEG =∠AGE ∴△AEF ≌△AGNH∴AF=AN∵∠EAF=α，∠AEG=60°－α∴∠AFN=60°…………………………………………………………………………6分∴△AFN为等边三角形∴AF=FN∴EG=EF+FN+NG=2EF+AF…………………………………………………………7分燕山28.解：(1) ①∠DCB=60°…………………………………1′②补全图形CP=BF …………………………………3′△DCP≌△DBF …………………………………6′（2）BF-BP=2DE⋅tanα…………………………………8′最新文件仅供参考已改成word文本。