数学花园探秘真题及详解
“数学花园探秘”5年级数学试卷及解答

经验证符合题目要求. 7. 将 1 至 8 填入方格中,使得数列□□,9,□□,□□,□□从第三个项开始,每一项都等于前面 两项的和,那么这个数列的所有项之和是 【作者】学而思培优 胡浩 【答案】198 【分析】第三个数比第一个数多 9,第四个数比第三个数多 9; 若第一个数除以 9 余 a , 则第三个数和第四个数也余 a , 第五个数则余 2a , 五个数总和除以 9 余 4a ; 而由于 1 2 3 .
2015 年“数学花园探秘”科普活动 五年级组初试试卷 A
(测评时间:2014 年 12 月 20 日 8:30—9:30) 一.填空题Ⅰ(每小题 8 分,共 32 分)
1. 算式 5
(2014 12) 20 的计算结果是 930 830
.
【作者】顺天府学 叶培臣 【答案】2002 【分析】原式= 5
× 1 0 2
.
5
【作者】学而思培优 胡浩 【答案】118
1 是被乘数的 5 倍,其百位数字不可能是 9,则乘积的百位处加法没有进 【分析】如下左图所示, □□
位,易知 □0□ 的百位为 2,如右图所示;
× 1 0 2 2 0 2 5 × 1 5
20□ 作为一个两位数和一位知 a 0 ,即这五个数都是 9 的倍数;
若设第一个数为 18,则这五个数分别为 18,9,27,36,63;6 出现两次不符合要求; 若设第一个数为 27,则这五个数分别为 27,9,36,45,81;符合要求. 所有项之和为 27 9 36 45 81 198 . 8. 甲、乙、丙三户人家打算订阅报纸,共有 5 种不同的报纸可供选择,已知每户人家都订两份不同 的报纸,并且知道这三户人家每两户所订的报纸恰好有一份相同,那么三户人家共有 种不同的订阅方式. 【作者】高思教育 方非 【答案】180 【分析】每两户恰有 1 份报纸相同,只有两种类型: (ab,ac,ad)和(ab,ac,bc) ;
“迎春杯”数学花园探秘初赛试卷(五年级d卷)

2016年“迎春杯”数学花园探秘初赛试卷(五年级D卷)一、填空题(共4小题,每小题8分,满分32分)1.(8分)算式20.15÷(1.2+1.9)×(42﹣32+22﹣12)的计算结果是.2.(8分)有一种细胞,每隔1小时死亡2个细胞,余下的每个细胞分裂成2个.若经过5小时后细胞的个数记为164.最开始的时候有个细胞.3.(8分)如图,一道乘法竖式中已经填出了2、0、1、6,那么乘积是.4.(8分)有四个人甲、乙、丙、丁,乙欠甲1元,丙欠乙2元,丁欠丙3元,甲欠丁4元.要想把他们之间的欠款结清,只因要甲拿出元.二、填空题(共4小题,每小题10分,满分40分)5.(10分)一个自然数A连着写2遍(例如把12写成1212)得到一个新的数B,如果B是2016的倍数,则A最小是.6.(10分)图中,A、B、C、D、E是正五边形各边的中点,那么,图中共有个梯形.7.(10分)对于自然数N,如果在1﹣9这九个自然数中至少有七个数是N的因数,则称N是一个“七星数”,则在大于2000的自然数中,最小的“七星数”是.8.(10分)如图中,A、B、C、D为正六边形四边的中点,六边形的面积是16,阴影部分的面积是.三、填空题(共3小题,每小题12分,满分36分)9.(12分)如图,魔术师在一个转盘上的16个位置写下来了1﹣16共16个数,四名观众甲、乙、丙、丁参与魔术表演.魔术师闭上眼,然后甲从转盘中选一个数,乙、丙、丁按照顺时针方向依次选取下一个数,图示是一种可能的选取方式,魔术师睁开眼,说:“选到偶数的观众请举手.”,这时候,只有甲和丁举手,这时候魔术师就大喝一声:“我知道你们选的数了!”.你认为甲和丁选的数的乘积是.10.(12分)小张驾驶汽车从山脚下A地出发,经过山顶,到山另一边的山脚下B地,然后沿原路返回.汽车上山速度30千米每小时,下山速度40千米每小时.小张回到A地时,发现归程时间比去时少花了10分钟,汽车里程表增加了240千米.小张这一次往返一个用了小时.11.(12分)在空格中填入数字1﹣5,使得每行和每列数字不重复,每个除法从上向下或者从左到右运算都能够整除.那么第二行的前三个数字依次组成的三位数是.2016年“迎春杯”数学花园探秘初赛试卷(五年级D卷)参考答案与试题解析一、填空题(共4小题,每小题8分,满分32分)1.(8分)算式20.15÷(1.2+1.9)×(42﹣32+22﹣12)的计算结果是65 .【解答】解:20.15÷(1.2+1.9)×(42﹣32+22﹣12)=20.15÷3.1×10=6.5×10=65;故答案为:65.2.(8分)有一种细胞,每隔1小时死亡2个细胞,余下的每个细胞分裂成2个.若经过5小时后细胞的个数记为164.最开始的时候有9 个细胞.【解答】解:第5小时开始时有:164÷2+2=84(个)第4小时开始时有:84÷2+2=44(个)第3小时开始时有:44÷2+2=24(个)第2小时开始时有:24÷2+2=14(个)第1小时开始时有:14÷2+2=9(个)答:最开始的时候有 9个细胞.故答案为:9.3.(8分)如图,一道乘法竖式中已经填出了2、0、1、6,那么乘积是612 .【解答】解:首先根据数字0判断,第一个数的十位是5,只有2×5=10是满足条件的.所以0前边的数字是1.再根据数字6判断是1+5=6,6上面的数字是5.出现第一个两位数51.所以在乘法中2前面只有数字1满足条件,0后面就是数字2.即51×12=612.故答案为:6124.(8分)有四个人甲、乙、丙、丁,乙欠甲1元,丙欠乙2元,丁欠丙3元,甲欠丁4元.要想把他们之间的欠款结清,只因要甲拿出 3 元.【解答】解:根据分析,从甲开始,乙欠甲1元,故甲应得1元,甲欠丁4元,故甲应还4元;清算时,甲还应拿出4﹣1=3元,此时甲的账就结清了;再看看丁的账,丁得到甲的4元后,还给丙3元,即可结清;再看看丙的账,丙得到丁的3元后,还给乙2元,丙的账也清了;再看看乙的账,乙得到丙的2元后,还给甲1元,乙的账也结清;综上,甲只须先拿出4元还给丁,后得到乙的1元,故而甲总共只须拿出3元.故答案是:3.二、填空题(共4小题,每小题10分,满分40分)5.(10分)一个自然数A连着写2遍(例如把12写成1212)得到一个新的数B,如果B是2016的倍数,则A最小是288 .【解答】解:2016=25×7×32,因为B是2016的倍数,即B=2016k;则A至少是两位数,则两位数表示为,B==×101,101与2016没有公因数,所以A不是最小;因此换成A是三位数,表示为,则B=×1001=×13×11×7,则×13×11×7=25×7×32k,×13×11=25×32k,因为后面,A×(10001、100001…,都不是2和3的倍数),所以要使A最小,则A==25×32=288;答:A最小是 288.故答案为:288.6.(10分)图中,A、B、C、D、E是正五边形各边的中点,那么,图中共有15 个梯形.【解答】解:根据分析可得,3×5=15(个)答:图中共有 15个梯形.故答案为:15.7.(10分)对于自然数N,如果在1﹣9这九个自然数中至少有七个数是N的因数,则称N是一个“七星数”,则在大于2000的自然数中,最小的“七星数”是2016 .【解答】解:根据分析,在2000~2020之间排除掉奇数,剩下的偶数还可以排除掉不能被3整除的偶数,最后只剩下:2004、2010、2016,再将三个数分别分解质因数得:2004=2×2×3×167;2010=2×3×5×67;2016=2×2×2×2×2×3×3×7,显然2014和2010的质因数在1~9中不到7个,不符合题意,排除,符合题意的只有2016,此时2016的因数分别是:2、3、4、6、7、8、9.故答案是:2016.8.(10分)如图中,A、B、C、D为正六边形四边的中点,六边形的面积是16,阴影部分的面积是8 .【解答】解:如图:连接正方形的一条对角线,延长DA,与最上边正六边形边的延长线交与一点,这样可得两个三角形①、②三角形①和三角形②是全等三角形,它们的面积相等,进而可得出阴影部分两侧的三角形可补到六边形的角上,这样就成了一个长方形,阴影部分的面积等于空白部分的面积,所以阴影部分的面积是正六边形面积的一半16÷2=8答:阴影部分的面积是8.故答案为:8.三、填空题(共3小题,每小题12分,满分36分)9.(12分)如图,魔术师在一个转盘上的16个位置写下来了1﹣16共16个数,四名观众甲、乙、丙、丁参与魔术表演.魔术师闭上眼,然后甲从转盘中选一个数,乙、丙、丁按照顺时针方向依次选取下一个数,图示是一种可能的选取方式,魔术师睁开眼,说:“选到偶数的观众请举手.”,这时候,只有甲和丁举手,这时候魔术师就大喝一声:“我知道你们选的数了!”.你认为甲和丁选的数的乘积是120 .【解答】解:依题意可知:2个偶数中间间隔是2个奇数.发现只有数字10,11,9,12是符合条件的数字.乘积为10×12=120.故答案为:12010.(12分)小张驾驶汽车从山脚下A地出发,经过山顶,到山另一边的山脚下B地,然后沿原路返回.汽车上山速度30千米每小时,下山速度40千米每小时.小张回到A地时,发现归程时间比去时少花了10分钟,汽车里程表增加了240千米.小张这一次往返一个用了7 小时.【解答】解:根据分析,总路程为240,那么来回的上坡、下坡都是120,则所花的时间是:120÷40+120÷30=7即一次往返用的总时间为:7小时.故答案是:7.11.(12分)在空格中填入数字1﹣5,使得每行和每列数字不重复,每个除法从上向下或者从左到右运算都能够整除.那么第二行的前三个数字依次组成的三位数是531 .【解答】解:首先根据已知数字5下面的数字不能是偶数只能是3,那么5上面的数字只能是1.再根据第三行的数字3只能和1一组,那么前边是4÷2后面是3除以1.再根据第一行的数字规律最后只能填写数字3.即42÷3.继续推理得:故答案为:531声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2019/5/5 18:16:59;用户:小学奥数;邮箱:pfpxxx02@;学号:20913800。
“迎春杯”数学花园探秘初赛试卷(四年级b卷)

2016年“迎春杯”数学花园探秘初赛试卷(四年级B卷)一、填空题(共4小题,每小题8分,满分32分)1.(8分)计算:(18×23﹣24×17)÷3+5,所得结果是.2.(8分)8位老人下两副象棋.8人轮流下,他们从早上8点,一直下到当天下午6点,则平均每个人下了小时.3.(8分)三年级一班期末数学考试中,前10名的成绩恰好构成一个等差数列,已知考试满分100分,每个同学的得分都是整数,而且第3、4、5、6名同学一共得了354分,又知道小悦得了96分,那么第10名同学得了多少分?4.(8分)如图乘法算式中只有四个位置上的数已知,它们分别是2,0,1,6请你在空白位置填上数字,使得算式能够成立.那么乘积为.二、填空题(共4小题,每小题10分,满分40分)5.(10分)羊圈里有若干只鸡和羊.如果一半的鸡被赶出羊圈,则羊圈里剩余的鸡和羊的总腿数恰好是羊圈里鸡的总腿数的2倍;如果有4只羊被赶出羊圈,则羊圈里剩余的鸡和羊的总腿数恰好是羊圈里羊的总腿数的4倍.那么一共有只羊.6.(10分)数列1,1,2,3,5,8,…从第二项起每一项都等于它前面两项之和,这个数列成为斐波那契数列.其中每一项都叫做斐波那契数.可以证明“任意正整数n都可以成若干个不同的斐波那契数之和”,那么把100表示成若干个不同的斐波那契数之和有种表示方法.(只是交换加数的顺序算作同一种)7.(10分)男生戴红帽,女生带黄帽,老师带蓝帽,每人看不到自己的帽子,小强(男生)看到的红帽比黄帽多2顶,小花(女生)看到的黄帽是蓝帽的2倍,老师看到的蓝帽比红帽少11顶,那么其中有名女生.8.(10分)表格中每个字母代表一个数字,不同的字母代表不同数字.每个数的首位不得为零.每一行从左到右的三个数为等差数列,每一列从上到下的三个数也为等差数列,那么五位数=.A BA AAAB CA EFCD GA BDC三、填空题(共3小题,每小题12分,满分36分)9.(12分)A、B两地相距30厘米,甲、乙两根细绳在玩具车的牵引下从A,B两地同时出发相向而行.甲绳长151厘米,前行速度每秒2厘米;乙绳长187厘米,前行速度每秒3厘米.如果出发时两绳尾端同时被点燃,甲绳燃烧速度为每秒1厘米,乙绳燃烧速度为每秒2厘米.两绳从相遇到完全错开共需秒.10.(12分)如图,一个面积为420平方厘米的长方形被四条线段分割成了五个三角形,且这五个三角形的面积S1,S2,S3,S4,S5依次构成等差数列,那么S5是平方厘米.11.(12分)大毛、二毛、三毛兄弟三人,大毛对三毛说:“爸爸36岁时,我的年龄是你的4倍,二毛的年龄是你的3倍.”二毛说:“是啊,那时候我们三人的年龄加起来恰好是爸爸现在年龄的一半.”三毛说:“现在我们父子4人的年龄和已经有108岁了.”那么三毛今年岁.2016年“迎春杯”数学花园探秘初赛试卷(四年级B卷)参考答案与试题解析一、填空题(共4小题,每小题8分,满分32分)1.(8分)计算:(18×23﹣24×17)÷3+5,所得结果是7 .【解答】解:(18×23﹣24×17)÷3+5=(6×3×23﹣6×4×17)÷3+5=6×(3×23﹣4×17)÷3+5=6×(69﹣68)÷3+5=6÷3+5=7故答案为:7.2.(8分)8位老人下两副象棋.8人轮流下,他们从早上8点,一直下到当天下午6点,则平均每个人下了 5 小时.【解答】解:12+6﹣8=10(小时),10×4÷8=40÷8=5(小时)答:平均每个人下了 5小时.故答案为:5.3.(8分)三年级一班期末数学考试中,前10名的成绩恰好构成一个等差数列,已知考试满分100分,每个同学的得分都是整数,而且第3、4、5、6名同学一共得了354分,又知道小悦得了96分,那么第10名同学得了多少分?【解答】解:设第10名同学得了a分,前10名的成绩由低到高构成的等差数列公差是d,则第3、4、5、6名同学分别得了a+7d、a+6d、a+5d、a+4d,第3、4、5、6名同学一共得分为:(a+7d)+(a+6d)+(a+5d)+(a+4d)=4a+22d=354,整理,可得2a+11d=177…①,设小悦第m名,则1≤m≤10,则a+(10﹣m)d=96…②,②×2﹣①,可得(9﹣2m)d=15,(1)当9﹣2m=3,d=5时,解得,此时a=61;(2)当9﹣2m=5,d=3时,解得,此时a=72;(3)当9﹣2m=1,d=15时,解得,此时小悦第4名,第三名的得分是96+15=111(分),因为111>100,所以不符合题意;综上,可得第10名同学得了61分或72分.答:第10名同学得了61分或72分.4.(8分)如图乘法算式中只有四个位置上的数已知,它们分别是2,0,1,6请你在空白位置填上数字,使得算式能够成立.那么乘积为2205 .【解答】解:答:乘积是2205.故答案为:2205.二、填空题(共4小题,每小题10分,满分40分)5.(10分)羊圈里有若干只鸡和羊.如果一半的鸡被赶出羊圈,则羊圈里剩余的鸡和羊的总腿数恰好是羊圈里鸡的总腿数的2倍;如果有4只羊被赶出羊圈,则羊圈里剩余的鸡和羊的总腿数恰好是羊圈里羊的总腿数的4倍.那么一共有10 只羊.【解答】解:根据一半的鸡被赶出羊圈,则羊圈里剩余的鸡和羊的总腿数恰好是羊圈里鸡的总腿数的2倍,可知这时鸡的只数是羊只数的2倍设原来有羊x只,则一半的鸡赶出羊圈后,圈里鸡有2x只(x﹣4)×4×(4﹣1)=2x×2(x﹣4)×4×3=4x12x﹣48=4x12x﹣4x=488x=48x=66+4=10(只)答:一共有10只羊.故答案为:10.6.(10分)数列1,1,2,3,5,8,…从第二项起每一项都等于它前面两项之和,这个数列成为斐波那契数列.其中每一项都叫做斐波那契数.可以证明“任意正整数n都可以成若干个不同的斐波那契数之和”,那么把100表示成若干个不同的斐波那契数之和有9 种表示方法.(只是交换加数的顺序算作同一种)【解答】解:首先枚举出小于100的斐波那契数.1,1,2,3,5,8,13,21,34,55,89.①100=89+3+8②=89+1+2+8③=89+1+2+3+5④=55+34+1+2+3+5⑤=55+34+1+2+8⑥=55+34+3+8⑦=55+13+21+1+2+3+5⑧=55+13+21+3+8⑨=55+13+21+1+2+8故答案为:97.(10分)男生戴红帽,女生带黄帽,老师带蓝帽,每人看不到自己的帽子,小强(男生)看到的红帽比黄帽多2顶,小花(女生)看到的黄帽是蓝帽的2倍,老师看到的蓝帽比红帽少11顶,那么其中有13 名女生.【解答】解:设有x名女生,则有x+3(x+2+1=x+3)名男生,所以(x﹣1)÷2=x+3﹣11+10.5x﹣0.5=x﹣70.5x﹣7=﹣0.50.5x=6.5x=13答:其中有13名女生.故答案为:13.8.(10分)表格中每个字母代表一个数字,不同的字母代表不同数字.每个数的首位不得为零.每一行从左到右的三个数为等差数列,每一列从上到下的三个数也为等差数列,那么五位数=40637 .A BA AAAB CA EFCD GA BDC【解答】解:(1)因为A、BA、AA为等差数列,所以A+AA=2BA,所以A+11A=2×(10B+A),所以12A=20B+2A,整理,可得B=0.5A.(2)因为A、AB、CD为等差数列,所以A+CD=2AB,所以A+CD=2×(10A+0.5A),整理,可得:CD=20A,所以D=0,C=2A,因为0<2A<10,所以A=1,2,3或4,结合B=0.5A,则A=4或2,B=2或1.(3)因为AB、CA、EF为等差数列,所以AB+EF=2CA,所以10A+0.5A+EF=2×(20A+A),整理,可得:EF=31.5A,只有A=2时满足.(4)因为BA、CA、GA为等差数列,所以BA+GA=2CA,所以5A+A+10G+A=2×(20A+A),整理,可得:G=3.5A=7,所以A=2,C=2×2=4,D=0,EF=31.5×2=63,G=7,所以五位数=40637.故答案为:40637.三、填空题(共3小题,每小题12分,满分36分)9.(12分)A、B两地相距30厘米,甲、乙两根细绳在玩具车的牵引下从A,B两地同时出发相向而行.甲绳长151厘米,前行速度每秒2厘米;乙绳长187厘米,前行速度每秒3厘米.如果出发时两绳尾端同时被点燃,甲绳燃烧速度为每秒1厘米,乙绳燃烧速度为每秒2厘米.两绳从相遇到完全错开共需40 秒.【解答】解:30÷(2+3)=6(秒),(151+187)﹣(1+2)×6=320(厘米),320÷(2+3+1+2)=320÷8=40(秒),答:两绳从相遇到完全错开共需40秒.10.(12分)如图,一个面积为420平方厘米的长方形被四条线段分割成了五个三角形,且这五个三角形的面积S1,S2,S3,S4,S5依次构成等差数列,那么S5是112 平方厘米.【解答】解:设这五个三角形的面积S1,S2,S3,S4,S5依次构成的等差数列的公差是d,则5S5﹣d=420,整理,可得:S5﹣2d=84 ①根据图示,可得:S4+S5=2S5﹣d=420÷2=210,所以2S5﹣d=210 ②②×2﹣①,可得3S5=336,解得S5=112.所以S5是112平方厘米.故答案为:112.11.(12分)大毛、二毛、三毛兄弟三人,大毛对三毛说:“爸爸36岁时,我的年龄是你的4倍,二毛的年龄是你的3倍.”二毛说:“是啊,那时候我们三人的年龄加起来恰好是爸爸现在年龄的一半.”三毛说:“现在我们父子4人的年龄和已经有108岁了.”那么三毛今年15 岁.【解答】解:设爸爸36岁时,三毛x岁,则二毛3x岁,大毛4x岁,所以爸爸现在的年龄是:2(x+3x+4x)=16x(岁),4x+3x+x+(16x﹣36)×3+16x=10872x﹣108=10872x=216x=3则三毛为:(16×3﹣36)+3=48﹣36+3=12+3=15(岁)答:三毛今年15岁.故答案为:15.声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2019/5/5 18:16:33;用户:小学奥数;邮箱:****************;学号:20913800第11页(共11页)。
数学花园探秘(迎春杯)六年级初赛试题及详解

一、 填空题 I(每题 8 分,共 32 分) 1 1 1 1 1、算式( + )×2016+12+3 的计算结果是________. 36 54 72 108 2、相邻两个自然数,如果他们的数字和都是 8 的倍数,我们就称他为“8 和数组”,那么最 小的一组“8 和数组”中两数之和是________. 1 3、侠客岛的人,原来有 是卧底,后来卧底中有 30%的人被驱离出岛,而不是卧底的人有 13 3 转变成了卧底。如果侠客岛上现在还有 810 人,那么现在侠客岛上有_____人是卧底。 4、如图,一道除法竖式中已经填出了“2017”,那么被除数是_______.
二、填空题 II(每小题 10 分,共 40 分) 5、今年“天宫二号”成功发射,中国科学家在太空进行植物生长实验,如果一种奇怪的 植物,它的生长之和温度有关,如果某一天的温度是 n 摄氏度,那么该株植物在当天增重 n2 克。5 天过去,这株植物共增重 88 克,已知这 5 天太空舱里的温度的数值都是互不相同的飞 0 自然数,且前 3 天的总增重量都不是 3 的倍数,则第 3 天的气温是_______摄氏度。 6、如图,在一直角三角形中,剪掉一个最大的半圆,使得半圆的直径在斜边 AB 上,已知 AC 长 210 厘米,BC 长 280 厘米,那么图中阴影部分的面积是_________平方厘米。(π 取 3.14)
98
比例法解行程,此题比以往考查的行程问题要稍微容易一些,只要找到速度之比就可 以迎刃而解。 8、答案:124 解析:通过俯视图可以知道,从 A 到 B 需要经过 4 根管道,但是题 目要求经过 6 根管道,故而分成两种情况,第一种是指在中间这个平面移动,第二种 是经过上平面或者下平面。第一种情况可以轻易数出只有 4 种。 第二种情况,需要上下爬行一次,那么水平爬行还是 4 根管道,通过俯视图标数可以 知道水平移动要经过 5 个点,而且标出爬到 B 的爬行情况。最后加上需要在五个点内 选两个点上下,一定是靠近 A 的点向下、靠近 B 的点向上或者靠近 A 的点向上、靠近 2 B 的点向下两种情况,所以是 6×C5 ×2=120,两种情况相加 120+4=124 种。
数学花园探秘笔试题

2 3 2
1
图1
图2
若图4中隐藏的4个宝箱如图3所示,请在图4中找出这4个宝箱,将宝物用○表示出来.请把答
案写在答题纸上.
343222
4
0
5
3
0
4
图3
图4
第12关 胶囊数独
在空格内填入数字1、2、3、4、5,使得每行、每列都有数字1、2、3、4、5且不重复,
表示胶囊,每个胶囊中必须是一个单数和一个双数(如图1).请问图2中从左数第2列从. 上. 到. 下. 的 五个数字依次是多少?请把答案写在答题纸上.
1234 56
第10关 淘气的数字宝宝
九个数字宝宝1、2、3、4、5、6、7、8、9要坐在九宫格的饭桌吃饭,不同的图形代表不同 的数字,相同的图形代表相同的数字,连续的两个数字的座位不能挨在一起,不能有公共边,比 如数字 2、 3 就不能左右或上下紧挨在一起坐 ,如图1每个宝宝占一个座位.
图1
九个数字宝宝自己有各种各样的要求:
5
第11关 宝箱探秘
下图中隐藏了一些放有宝物的宝箱,宝物的放法遵守3个规则: (1)宝物都放在宝箱里,每个宝箱都由四个小方块组成,每个小方块里都有一个宝物, 用○ 表示; (2)方格周围的数字表示该行或者该列宝物的数量; (3)两个宝箱之间互不相邻(包括横、列、斜). 例:图1的两个宝箱放入图2
310 4
示例:图1
图2
2
第5关
铁丝的长度
用一根固定长度的铁丝去围一些一样大小的正方形,结果如图1 和图2,围1个正方形一圈, 铁丝还多出20厘米,围着两个挨在一起的正方形一圈,铁丝还多出8厘米.请想一想,这根铁丝的 长度为多少厘米?请把答案写在答题纸上.
20厘米
“迎春杯”数学花园探秘科普活动试卷(六年级初赛b卷)

2015年“迎春杯”数学花园探秘科普活动试卷(六年级初赛B卷)一、填空题(共4小题,每小题8分,满分32分)1.(8分)算式(+++)×2015的计算结果是.2.(8分)如图,一道除法竖式中已经填出了“2015”和“0”,那么被除数是3.(8分)A电池的广告语是“一节更比六节强”.意义是A电池比其他电池更耐用.我们就假定1节A电池的电量是B电池的6倍,有两种耗电速度一样的时钟,现在同时在甲钟里装了2节A电池,乙钟里装了2节B电池,结果乙时钟正常工作了2个月电池就耗尽了,那么甲时钟的正常工作时间比乙时钟多个月.4.(8分)如图六角星的6个顶点恰好是一个正六边形的6个顶点,那么阴影部分面积是空白部分面积的倍.二、填空题(共4小题,每小题10分,满分40分)5.(10分)一个正整数A乘以6后所得结果的因数个数变为原来的3倍,那么符合条件的A最小是.6.(10分)在2014年北京APEC会议期间,京津冀实施道路限行和污染企业停工等措施,来保证空气质量达到良好水平,在经历了一个月三场雾霾,北京11月3日空气达到一级优水平,人们称为“APEC蓝”,2013年北京优良空气天数仅占47.9%,2014上半年实行减排30%的措施,优良空气天数比2013年同期增加20天,要达到全年优良空气天数增加20%的目标,下半年需要使优良天气相比2013年同期至少增加天.7.(10分)甲、乙、丙三户人家打算订阅报纸,共有5种不同的报纸可供选择,已知每户人家都订两份不同的报纸,并且知道这三户人家每两户所订的报纸恰好有一份相同,那么三户人家共有几种不同的订阅方式?8.(10分)6个半径相等的小圆和1个大圆如图摆放.图中大圆的面积是120,那么,一个小圆面积是.三、填空题(共3小题,每小题12分,满分36分)9.(12分)希希和姗姗各有若干张积分卡.希希对姗姗说:“如果你给我3张,我的张数就是你的3倍”姗姗对希希说:“如果你给我4张,我的张数就是你的4倍”希希对姗姗说:“如果你给我5张,我的张数就是你的5倍”已知以上三句话中恰有一句不正确,那么,原来希希有张积分卡.10.(12分)如图,A、B为圆形轨道一条直径的两个端点,甲、乙、丙三个微型机器人在圆形轨道上同时出发,作匀速圆周运动,甲、乙从A出发,丙从B出发;乙顺时针运动,甲、丙逆时针运动,出发后12秒钟甲到达B,再过9秒钟甲第一次追上丙时恰好也和乙第一次相遇;那么当丙第一次到达A后,再过秒钟,乙才第一次到达B.11.(12分)在空格内填入数字1﹣6,使得每行每列数字不重复,黑点两边的数是两倍的关系,白点两边的数差为1.那么第四行所填数字从左往右前5位组成的五位数是.2015年“迎春杯”数学花园探秘科普活动试卷(六年级初赛B卷)参考答案与试题解析一、填空题(共4小题,每小题8分,满分32分)1.(8分)算式(+++)×2015的计算结果是2418 .【解答】解:(+++)×2015=()×2015==2418故答案为:2418.2.(8分)如图,一道除法竖式中已经填出了“2015”和“0”,那么被除数是20685【解答】解:依题意可知:首先根据图中方框代表的是金三角,只能唯一情况是10﹣9.所以结果1中的百位和十位为10,那么除数的百位和十位就是10,商的首位是1.再根据结果2的首位数字是9,那么商的十位数字是9,根据尾数是5,推理出除数为105.商的前两位是19.最后结果3的数字经尝试不能是600多只能是105的7倍735.被除数为105×197=20685.故答案为:206853.(8分)A电池的广告语是“一节更比六节强”.意义是A电池比其他电池更耐用.我们就假定1节A电池的电量是B电池的6倍,有两种耗电速度一样的时钟,现在同时在甲钟里装了2节A电池,乙钟里装了2节B电池,结果乙时钟正常工作了2个月电池就耗尽了,那么甲时钟的正常工作时间比乙时钟多10 个月.【解答】解:根据分析,因都是正常耗电,正常工作,故耗电速度一样,甲时钟耗尽电量所需时间是乙时钟的电池耗尽电量所需时间的6倍,所以甲时钟可以正常工作:6×2=12个月,比乙时钟多工作:12﹣2=10个月.故答案是:10.4.(8分)如图六角星的6个顶点恰好是一个正六边形的6个顶点,那么阴影部分面积是空白部分面积的 3 倍.【解答】解:根据分析,如图所示,将图进行分割成面积相等的三角形,阴影部分由18个小三角形组成,而空白部分有6个小三角形,故阴影部分面积是空白部分面积的18÷6=3倍.故答案是:3.二、填空题(共4小题,每小题10分,满分40分)5.(10分)一个正整数A乘以6后所得结果的因数个数变为原来的3倍,那么符合条件的A最小是 2 .【解答】解:假设原数分解质因数后为2a×3b,乘6后变为2a+1×3b+1,由题意:3(a+1)(b+1)=(a+2)(b+2),由于A要尽可能小,因此令a=1,b=0即可得到答案.所以满足条件的A最小值为2.6.(10分)在2014年北京APEC会议期间,京津冀实施道路限行和污染企业停工等措施,来保证空气质量达到良好水平,在经历了一个月三场雾霾,北京11月3日空气达到一级优水平,人们称为“APEC蓝”,2013年北京优良空气天数仅占47.9%,2014上半年实行减排30%的措施,优良空气天数比2013年同期增加20天,要达到全年优良空气天数增加20%的目标,下半年需要使优良天气相比2013年同期至少增加15 天.【解答】解:365×47.9%×20%﹣20≈174.8×20%﹣20≈35.0﹣20=15(天)答:下半年需要使优良天气相比2013年同期至少增加15天.故答案为:15.7.(10分)甲、乙、丙三户人家打算订阅报纸,共有5种不同的报纸可供选择,已知每户人家都订两份不同的报纸,并且知道这三户人家每两户所订的报纸恰好有一份相同,那么三户人家共有几种不同的订阅方式?【解答】解:由题意可知,有ab,ac,ad和ab,ac,bc两种不同的订阅类型:ab,ac,ad有×=5×(4×3×2)=5×24=120种;ab,ac,bc有×=10×6=60种.所以共有120+60=120种不同的订阅方式.8.(10分)6个半径相等的小圆和1个大圆如图摆放.图中大圆的面积是120,那么,一个小圆面积是40 .【解答】解:根据分析,如图1所示,由对称性可知,△ADE与△OBE面积相等,因此可知,△AOD的面积与△AOB的面积相等,都等于△ABC面积的三分之一,由于△AOD与△ABC都是圆的内接正三角形,因此可以得到小圆的面积为大圆面积的三分之一,依此小圆面积为40故答案是:40.三、填空题(共3小题,每小题12分,满分36分)9.(12分)希希和姗姗各有若干张积分卡.希希对姗姗说:“如果你给我3张,我的张数就是你的3倍”姗姗对希希说:“如果你给我4张,我的张数就是你的4倍”希希对姗姗说:“如果你给我5张,我的张数就是你的5倍”已知以上三句话中恰有一句不正确,那么,原来希希有15 张积分卡.【解答】解:根据分析,假设第一、二句是对的,那么总和应该是20的倍数,根据第一句,希希与珊珊积分卡之比应该为15:5,根据第二句,希希与珊珊卡数之比应该为4:16,每个人差的11倍对应了7张卡,不是整数,舍去.假设第一、三句是对的,总和应该是12的倍数,根据第一句,二人积分卡之比为9:3,根据第二句,二人积分卡之比为10:2,差的1份为多给的2张,成立,因此希希和珊珊积分卡之比为6:24,根据第三句,希望和珊珊积分卡之比为25:5,相差的19份为9张,不是整数,不成立,舍去.综上,第一、三句是对的,希希有15张积分卡.故答案是:15.10.(12分)如图,A、B为圆形轨道一条直径的两个端点,甲、乙、丙三个微型机器人在圆形轨道上同时出发,作匀速圆周运动,甲、乙从A出发,丙从B出发;乙顺时针运动,甲、丙逆时针运动,出发后12秒钟甲到达B,再过9秒钟甲第一次追上丙时恰好也和乙第一次相遇;那么当丙第一次到达A后,再过56 秒钟,乙才第一次到达B.【解答】解:甲经过12秒钟到从A到达B,则再过9秒钟后甲到达C点,且BC的长度等于AB长度的,则AC的长度等于AB长度的,即21秒钟的时间内,甲的路程为AB+BC=AB段,乙的路程为AC=AB,丙的路程为BC=AB,则速度比甲:乙:丙=7:1:3,丙从C到达A所用时间=21×=7(秒),此时乙从C点到达D点,所用时间也为7秒,因为CA=BC,则CD=AC,则CB=8CD,丙到达A后乙到达B的所需时间:8×7=56(秒)故答案为:5611.(12分)在空格内填入数字1﹣6,使得每行每列数字不重复,黑点两边的数是两倍的关系,白点两边的数差为1.那么第四行所填数字从左往右前5位组成的五位数是21436 .【解答】解:依题意可知:如图所示,D,E,F必然是1,2,4或者4,2,1.因此B,C一定是3和6.故可知A是5.而G,H,I为三个连续自然数,I存在2倍关系,则只能是1,2,3.故右上角为6.左上角为4.并可以判定B是6,C是3.因此C的右边临格为6.以此为突破口,可以填表如图所示:故答案为:21436声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2019/5/5 18:12:42;用户:小学奥数;邮箱:pfpxxx02@;学号:20913800第11页(共11页)。
数学花园探秘 迎春杯 六年级初赛试题及详解

6、8 至少取一个,要么取 8、要么取 6; 3、如果取 8,那么 4 必须取,否则
XYZ8 (Z 为奇)一定不是 4 的倍数,进而发现无数可取,否则必然不是 3 的倍数或
者能被本身的数整除; 4、那么必须取 6,进而必须取 3、9,这样我们取的数就
是 3、6、9、5;
5、为了是 8 的倍数则末尾必须为 6,剩下的 3 个数,共可组
5. 答案:3 解析:该题的本质是找到 5 个互不相同的平方数,使得他们的和为 88,
由于平方数除以 3 的余数只能是 0 或 1,要使得最终的和为除以 3 余 1 的数(88),
那么有两种情况,要么除以 3 余 1,1,0,1,1;要么除以 3 余 0,0,1,0,0.显然
后一种情况可以排除,因为最小的 4 个除以 3 余 0 的平方数的和已经超过 88
角形 BGH 的面积都是 27.5 平方厘米,那么,梯形 GFAB 的面积是_______平方厘米。
10、从 1 至 9 这 9 个数字中选出 4 个不同数字,组成一个四位数,使得这个四位数能被 未选出的 5 个数字整除,而不能被选出的 4 个数字整除,那么,这个四位数是_______.
11、在空格里填入数字 1 至 6 中的某个数字,使得每行、每列和每个 2×3 的宫内的数字 不重复,图中两格之间的分数表示两个数中较小数除以较大数得到的商,那么,最后一行从 左到右前五个数组成的五位数是________.
97
2017 年“数学花园探秘”解析
1. 答案:43 解析:原式=118 (12 -13 +14 -16 )×2016+15=118 ×14 ×2016+15=43
提取公因数是重要考点,该题设计到分数的提取公因数,较为创新,如果直接通分会
2021数学花园探秘详解

2021数学花园探秘详解2021“数学花园探秘”科普活动(小低组)视听题(注:具体题意请参看视听题动画演示)第一关看看谁算是的慢1)5+5+5+5+1=2)21+13+9=3)26+28+74=4)48-2-2-2-2-2=5)169-(16+23+61)=【难度】★【题目解析】此题实地考察加减法排序基础,牵涉巧算方法和小括号的认知与采用.1)5+5+5+5+1=212)21+13+9=433)26+28+74=1284)48-2-2-2-2-2=385)169-(16+23+61)=69【实地考察科学知识】速算巧算第二关镜子里的画秋天至了,树叶掉下来了,右图就是大君用树叶在一张纸上搞的一幅画.当小君拿着画站在镜子前,答小君看见的镜子中的图像就是a、b、c中的哪一个?恳请把恰当选项写下在答题纸的对应边线.答案:b【难度】★【题目解析】动画模拟中镜子在图画的前面,所以图形照镜后将左右恰好相反,a和原图的关系就是上下恰好相反,c和原图短一样,没变化,只有b图和得出的画左右恰好相反.【实地考察科学知识】生活中的等距思想答案:5下【难度】★【题目解析】短时记忆的考查,在图形变化和声音两种因素的影响下,孩子与否能够忘记星星手挥的次数.【考察知识】专注力、记忆力第四关转一转回小朋友,接下来屏幕上将出现一个由四个小方块粘在一起组合而成的图形,认真观察下面abcde五个选项,有两个选项不能由原图旋转或者翻转得来,请你把这两个不能由原图旋转或者翻转得来的选项找出来,填写在答题纸对应位置.答案:a、e【难度】★★【题目解析】仔细观察所给的图,不管是旋转还是翻转,那么至少有一个方向是有三层的.再观察所给的选项,a和e中不管哪个方向,最多都只有两层,所以a和e选项不能由上图旋转或者翻转而成.通过尝试,b、c、d都可以由上图旋转或翻转而成.【考察知识】立体空间想象能力大朋友们,我们现在用的数字1、2、3、4、5、6、7、8、9、0就是由欧洲传至,被称作阿拉伯数字.其实,最早阿拉伯数字就是和古印度人发明者的.曾经在一个时期,这些印度数字的读法并不是现在的读法,而是后来慢慢演进过来的.下面是阿拉伯数字的一些古老写法,请你仔细观察并记忆,然后回答问题.代表的三位数就是___________.答案:347【难度】★★【题目解析】通过对古老数字读法的观测,我们能够找出一些相近的形状,比如说古老数字中的2与现在我们所采用的2比较相近,那也可以辨认出古老数字版的4更像是现在的8,通过两种对照找到相似性和差异性,就可以防止最后跳入陷阱中.【实地考察科学知识】记忆力、观测能力接下来屏幕上会出现一张卡片,卡片从图①开始顺时针旋转,旋转成图②,再旋转一次成图③,按照这样的规律,请问图③旋转到图④,应该旋转成a、b、c、d中的哪一个?请把正确选项填写在答题纸的对应位置.【难度】★★★【题目解析】仔细观察图形的变化,根据图形顺时针的旋转进行答案的排除,a和b存在明显的不同,其中漏掉了部分格子,d旋转的方向不同,排除法锁定答案为c.【考察知识】观察力第七关装盒子下课后,乐乐帮老师把所有的正方体小木块收到一个立方体大盒子里,已经放了一部分,请问再放多少块就能把盒子全部装满?请把正确答案填写在答题纸对应位置.【难度】★★★【题目解析】根据观察我们发现整个大立方体盒子一共需要27块小方块,再减去已经放好的17块,答案为10块.【考察知识】立体图形计数接下来,屏幕中存有一个全等直角三角形的纸,大朋友们认真看看,将下面这张纸对折一次,再对折一次,然后沿着虚线包住,答整张纸被剪了几个单独的小纸片?恳请把恰当答案核对在答题纸对应边线.答案:4个【难度】★★★【题目解析】通过看看动画中的动手模拟,展开空间想象,通过两次对折纸片变为四层,抠回去后的如下图,刚好4个单独的小纸片:【考察知识】空间想象能力第九第一关抽牌游戏花花和园园两个小朋友一起玩翻牌游戏.花花拿了20张不一样的扑克牌,园园从中抽出一张发现是黑桃a,之后便把黑桃a还给花花,插在了从下往上数的第11张.接着花花把手里的牌依次从左到右、从上到下的摆好.聪明的小朋友,请你找一找,现在这张幸运黑桃a在第几行第几列.答案:第2行及第5列【难度】★★★【题目解析】排队问题的变形,从小往上第11张就从上往下的第10张,那按照排序顺序,第10张就必须在第2行及的第5列【实地考察科学知识】排队问题第十关拼接小方块下面的图形就是由右侧图形中的两块图形堆叠构成的,恳请你认真看看,它就是由a、b、c、d、e当中的哪两块图形拆成的?答案:a和d【难度】★★★【题目解析】仔细观察给的图,如果最下一层右后方无方块,那么这个图由7个小方块组成;如果最下一层右后方有方块,那么这个图由8个小方块组成.5个选项是由4或5个小方块组成的,那么可以判断,最下一层右后方有方块.再观察选项,得出所选的选项应有一块有三层,推出其中一块选择a或者c,另一块就需要在b和d中选择(因为e有5个小方块组成,超过了总数).如果选择a,那么另一块需要填满a右下角的空,通过尝试,d符合要求.所以a和d可以拼成上图.如果选择c,那么另一块需要使c左列为两行,经过尝试b和d都不符合要求.所以本题选择a和d.有的小朋友空间感特别好,可以通过原图对照法,迅速观察到a和d是可以不通过任何翻转就直接拼组成所给图形的.【考察知识】立体图形与空间想象答案:2021【难度】★★【题目解析】根据第一个算式,找到突破口“花”.三个数字相加,“花”只有两种可能,1或者2,假设花为“2”,发现“数+花+园”的结果最大只能为19,所以排除“花”为2,“花”只能为1;根据“花”为1,“花+花=数”,推理出“数=2”,所以第一个算式变为“2+1+园=1学”,这个算式要凑两位数,园只可能是7、8、9,通过依次尝试,推理出园=7,学=0;所以得出数学花园代表的四位数为2021.【考察知识】数字谜答案:a【难度】★★【题目解析】通过观察发现图1是由5个小方格组成的图形,观察尝试发现a可以用图1拼成,而且,图b是23个小放歌,图c是21个小方格,不能由5凑出来总数,所以不能是由图1拼成的.【实地考察科学知识】图形抠比拼【难度】★★★【题目解析】根据图中未知的2、5、6三个数字可以推理小说出来:①这六个数字存有两种可能性,1、2、3、4、5、6或者2、3、4、5、6、7;②2、5、6这三个数字就是相连的,无法相对.六个数字如果为1~6,则1+6=2+5=3+4合乎对面数字和成正比,但是这样2和5就须要相对,与题目未知条件相符;六个数字如果为2~7,则2+7=3+6=4+5合乎对面数字和成正比,且2、5、6这三个数字相连,合乎题意.所以这六个数字就是2、3、4、5、6、7,恰当答案为2+3+4+5+6+7=27.【实地考察科学知识】正方体打听对面答案:19个【难度】★★★【题目解析】发生改变灯光涵盖两种情况,哪知的小方块灯关上灯,已经暗的小方块灯停用.根据左右两边的数字对照,2变为0须要动3个小方块灯,0变为1须要变7个小方块灯,1变为0一样就是7个小方块灯,7变为1须要动2个小方块灯,所以加在一起共须要变动3+7+7+2=19个小方块灯.【实地考察科学知识】图形计数答案:7点【难度】★★★【题目解析】根据老师的描述,从昨晚9点到中午12点有15个小时,被分成了相等的三份,得出一份是5个小时,所以距中午12点吃饭还有5个小时,得出现在是早上7点.【考察知识】逻辑推理【难度】★★★【题目解析】根据第一个天平推理小说出来a>b,通过第一个与第二个天平对照,得出结论a+d>a+c,所以d>c,通过第三个天平推理小说出来b>d,综合前面的结论,得出结论a>b>d>c,所以a最轻.【实地考察科学知识】等量赋值【难度】★★★★【题目解析】首先2颗糖,第一次放置1颗,第二次刚好就是在两个间隔之间放置2颗,第三次就是4个间隔放置4颗,第四次就是8个间隔放置8颗,第五次16个间隔放置16颗,加之最后的3颗糖,2+1+2+4+8+16+3=36(颗).【实地考察科学知识】间隔问题、打听规律【难度】★★★★【题目解析】从三位数中最高位开始有序的尝试,百位到十位、个位,从大的数字9开始凑,得出最大的三位数为995;最小三位数通过有序的尝试,百位为1的话,用掉两根火柴棒,个位十位没有能凑15根火柴棒的,由此发现百位最小只能是2,则最小三位数为200,最后得出两数的差为995-200=795.【考察知识】动手操作、计算【难度】★★★★【题目解析】根据东东的话,猜测出西西和南南手上的四张牌刚好为1、3、5、7四个奇数,东东自己拿2、8;乙说东东、南南两人自己的两张牌和相等,已经知道东东手中的牌的和为2+8=10,则南南为3+7=10,推理出西西的两张牌为1、5,所以西西的两张牌数字和为1+5=6.【考察知识】逻辑推理【难度】★★★★【题目解析】观察发现后从一宫突破,圆圈在角上,说明圆圈中不能填写2或者3,如果填写2或者3,圆圈周围的3个格子在同一个宫,同一宫中只能有一个△,则圆圈中只能填写1;再根据第二列圆圈中的3推理出第一个宫的3,找到突破口后按照数独规则推理即可.【实地考察科学知识】数独【难度】★★★★【题目解析】想斩获最多金币,最出色的情况从起点至终点的过程中走到所有小岛,尝试后辨认出一定会跑重复路线,全部金币都领到就是不可能将同时实现的;那已经开始尝试退出一些金币比较太少的小岛,从退出通过3个金币的小岛已经开始尝试,辨认出退出3没用,退出通过存有4个金币的小岛可以同时实现.所以路线就是:起点-6-3-8-16-14-9-7-5-10-11-15-12-13-终点,顺序不唯一.【实地考察科学知识】枚举法答案:110101【难度】★★★★【题目解析】认知规则后,从同行、同列、同一条斜线已经发生3个相同数字入学,层层推理小说,思路步骤不唯一.【考察知识】数独。
2-6二年级数学花园探秘

2年级数学花园探秘1、今天是2017年1月1日“数学花园探秘”科普活动,在下面的两个算式中,相同汉字表示相同数字,不同汉字表示不同数字,那么“数学花园”所代表的四位数是多少? 数+花+园=花学 花+花=数2、我来拼一拼:小朋友玩拼图游戏,妈妈只给图1形状的图片,小朋友想一想,下图A 、B 、C 中哪一幅图是用图1拼成的作品图1图A图B图C3、数字的和有一个正方体,六个面分别有一个数字,这六个数字恰好是连续的,且每两个相对面上的数字和想等,这个正方体你能看到其中三个面,上面写着数字2、5、6,问这六个数字之和是多少?4、新年的灯光今年是2017年1月1日元旦节,广场上的灯板由许多个小方块灯组成,亮其中部分小方块灯就会显示一个数,比如最早显示的是年份2017,接下来这块灯板需要关闭一些小方块灯,打开另一些小方块灯,将灯板显示日期为“0101”,请问至少需要多少小方块灯改变状态才能实现?→5算一算时间欢欢到学校后,与老师进行对话。
欢欢:“老师,你能告诉我几点么?”老师:“可以,不过你要根据我的话猜一猜,从现在到中午十二点吃饭的时间,刚好是昨晚你9点睡觉到现在所过时间一半”,那么你帮欢欢猜一猜,这段对话发生时的准确时间是早上几点?6、哪一个最重?把A、B、C、D四个重量不相等的正方体块摆放在天平山,轻重情况如图所示,想一想A、B、C、D中哪一个正方体块最重?7、共有几颗糖:星星想数一数自己有多少颗糖,于是他将糖果摆成一排。
首先把两颗糖摆在两端,第一次在两颗糖的正中央摆第一颗糖,第二次在每组相邻的两颗糖的正中间各摆放一颗糖,第三次又在每组相邻的两颗糖的正中间各摆放一颗糖,直到第五次摆放完成后,星星手上还剩3颗糖,问星星原来共有多少颗糖?8、火柴棒游戏:用火柴棒摆成数字0-9,如下图所示:按照上面的摆法,用17根火柴棒先摆出一个最大的三位数,再用17根火柴棒摆出一个最小的三位数,请计算一下,这个最大的三位数和最小的三位数的差是多少?老师和东东、西西、南南三位小朋友玩猜纸牌游戏,这三个小朋友都很聪明且都不说谎。
2017年“迎春杯”数学花园探秘决赛试卷(小中组A卷)

2017年“迎春杯”数学花园探秘决赛试卷(小中组A卷)一、解答题(共11小题,满分0分)1.算式67×67﹣34×34+67+34的计算结果是.2.在横式×+C×D=2017中,相同的字母代表相同的数字,不同的字母代表不同的数字,若等式成立,那么代表的两位数是.3.如图中共有个平行四边形.4.小兔与蜘蛛共50名学员参加舞蹈训练营,小兔学员走了一半,蜘蛛学员增加了一倍,但老师发现学员的脚既没有增加也没有减少,那么原有小兔只.(注:蜘蛛有8只脚)5.一组有两位数组成的偶数项等差数列,所有奇数项的和为100,若从第1项开始,将每个奇数项与它后面相邻的偶数项不改变次序地合并成一个四位数,形成一个新的数列,那么新数列的和与原数列的和相差.6.最常见的骰子是六面骰,它是一个正方体,6个面上分别有1到6个点,其相对两面点数的和都等于7,现在从空间一点看一个骰子,能看到所有点数之和最小是1,最大是15(15=4+5+6),那么在1~15中,不可能看到的点数和是.7.一排格子不到100个,一开始仅有两端的格子内各放有一枚棋子,几名同学依次轮流向格子中放棋子.每人每次只放一枚且必须放在相邻两个棋子正中间的格子中(如从左到右第3格,第7格中有棋子,第4、5、6格中没棋子,则可以在第5格中放一枚棋子;但第4格,第7格中有棋子,第5、6格没棋子,则第5、6格都不能放).这几名同学每人都放了9次棋子,使得每个格子中都恰好放了一枚棋子,那么共有名同学.8.蕾蕾买了一些山羊和绵羊,如果她多买2只山羊,那么每只羊的平均价格会增加60元,如果她少买2只山羊,那么每只羊的平均价格会减少90元.蕾蕾一共买了只羊.9.现有A、B、C、D、E五名诚实的安保在2016年12月1日~5日各值班三天,每天将有3名安保值班,每位安保值班安排5天一循环.今天(2017年1月1日周日),关于他们在上个月的值班情况,5人进行了如下对话:A:我和B在周末(周六、周日)值班的日子比其他3人都多;B:我与其余4人在这个月都一起值过班;C:12月3日本来我休息,但那天恰逢数学花园探秘初赛,于是我也来帮忙,可惜不算值班;D:E每次都和我安排在一起;E:圣诞节(12月25日)那天我和A都值班了.那么,安保A在12月份中第2次、第6次、第10次值班日期顺次排列组成的五位数是.(如果第2次、第6次、第10次值班分别在12月3日、12月17日,则答案为,31217)10.如图中每个小正三角形的面积是12平方厘米,那么大正三角形的面积为平方厘米.11.如图,圆圈表示房间,实线表示地上通道,虚线表示地下通道,开始时,一个警察和一个小偷在两个不同房间中,每一次警察从所在房间的地上通道转移到相邻的房间;同时,小偷从所在房间沿着地下通道转移到相邻的房间,如果警察和小偷转移了3次都没有在任何房间相遇,那么他们有种不同的走法.2017年“迎春杯”数学花园探秘决赛试卷(小中组A卷)参考答案与试题解析一、解答题(共11小题,满分0分)1.算式67×67﹣34×34+67+34的计算结果是3434 .【分析】根据乘法的分配律简算即可.【解答】解:67×67﹣34×34+67+34=67×(67+1)﹣34×34+34=67×2×34﹣34×34+34=101×34=3434故答案为:3434.【点评】此题重点考查了学生对运算定律的掌握与运用情况,要结合数据的特征,灵活选择简算方法.2.在横式×+C×D=2017中,相同的字母代表相同的数字,不同的字母代表不同的数字,若等式成立,那么代表的两位数是14 .【分析】由于0<C×D<100,所以1900<×<2017,根据130×13=1690,140×14=1960,150×15=2250,即可得出结论.【解答】解:由于0<C×D<100,所以1900<×<2017,因为130×13=1690,140×14=1960,150×15=2250,所以=14,进一步可得C×(14+D)=57,C=3,D=5.故答案为14.【点评】本题考查位值原则,考查学生的计算能力,确定1900<×<2017是关键.3.如图中共有15 个平行四边形.【分析】把图中的平行四边形分三类计数:①单个的(红色);②两个组成的(蓝色);③6部分组成的(黄色).【解答】解:根据分析可得,①单个的(红色)有:4个;②两个组成的(蓝色)有8个;③6部分组成的(黄色)有:3个;共有:4+8+3=15(个);答:图中共有 15个平行四边形.故答案为:15.【点评】本题要注意按顺序分类计数,防止遗漏.4.小兔与蜘蛛共50名学员参加舞蹈训练营,小兔学员走了一半,蜘蛛学员增加了一倍,但老师发现学员的脚既没有增加也没有减少,那么原有小兔40 只.(注:蜘蛛有8只脚)【分析】每走一只小兔,总腿数少了4,每增加一只蜘蛛,总腿数多了8,由此要总腿数不变,减少的兔子数量应该是增加蜘蛛数量的两倍,从而可得原有动物共5份,即可得出结论.【解答】解:每走一只小兔,总腿数少了4,每增加一只蜘蛛,总腿数多了8,由此要总腿数不变,减少的兔子数量应该是增加蜘蛛数量的两倍,把增加的蜘蛛当作1份,那么原蜘蛛数量也是1份,走了的兔子数量是2份,原有兔子数量为4份,则原有动物共5份,是50只,1份有10只,所以原有兔子4×10=40只.故答案为40.【点评】本题考查差倍问题,考查学生转化问题的能力,确定要总腿数不变,减少的兔子数量应该是增加蜘蛛数量的两倍是关键.5.一组有两位数组成的偶数项等差数列,所有奇数项的和为100,若从第1项开始,将每个奇数项与它后面相邻的偶数项不改变次序地合并成一个四位数,形成一个新的数列,那么新数列的和与原数列的和相差9900 .【分析】将每个奇数项与后面相邻的偶数项合并,由于每一项都是两位数,所以合并后的四位数列和与原数列的和相差所有奇数项的和的99倍,即可得出结论.【解答】解:设这个等差数列的奇数项分别为a1,a3,a5,…,公差为d,那么将每个奇数项与后面相邻的偶数项合并,由于每一项都是两位数,所以合并后的四位数列可以表示为a1×100+a1+d,a2×100+a2+d,…,所以新数列的和与原数列的和相差99×(a1+a3+a5+…),由于奇数项的和为100,所以99×(a1+a3+a5+…)=99×100=9900,故答案为9900.【点评】本题考查等差数列,考查学生的计算能力,确定合并后的四位数列和与原数列的和相差所有奇数项的和的99倍是关键.6.最常见的骰子是六面骰,它是一个正方体,6个面上分别有1到6个点,其相对两面点数的和都等于7,现在从空间一点看一个骰子,能看到所有点数之和最小是1,最大是15(15=4+5+6),那么在1~15中,不可能看到的点数和是13 .【分析】骰子上相对的两面点数分别为(1,6),(2,5),(3,4),从空间一点看一个骰子,可能只看到骰子的一个面,也可以看到相邻的两个面,还可以看到相邻的三个面,在1~15中,点数1~6显然可以看到,7~15进行分拆,即可得出结论.【解答】解:骰子上相对的两面点数分别为(1,6),(2,5),(3,4),从空间一点看一个骰子,可能只看到骰子的一个面,也可以看到相邻的两个面,还可以看到相邻的三个面,在1~15中,点数1~6显然可以看到,7=1+2+7,8=6+2,9=6+3,10=6+4,11=6+5,12=6+2+4,14=6+5+3,15=4+5+6,13无法拆出,即在1~15中,不可能看到的点数和是13.故答案为13.【点评】本题考查筛选与枚举,考查学生分析解决问题的能力,解题的关键是从空间一点看一个骰子,可能只看到骰子的一个面,也可以看到相邻的两个面,还可以看到相邻的三个面.7.一排格子不到100个,一开始仅有两端的格子内各放有一枚棋子,几名同学依次轮流向格子中放棋子.每人每次只放一枚且必须放在相邻两个棋子正中间的格子中(如从左到右第3格,第7格中有棋子,第4、5、6格中没棋子,则可以在第5格中放一枚棋子;但第4格,第7格中有棋子,第5、6格没棋子,则第5、6格都不能放).这几名同学每人都放了9次棋子,使得每个格子中都恰好放了一枚棋子,那么共有7 名同学.【分析】由题意可得,若相邻两枚棋子之间有偶数个空格子,则无法再往其中放棋子,那么若想要在每个格子中都放上棋子,每次放完相邻两棋子间空格数应为奇数.进而推出总共放下的棋子个数应该为等比数列1,2,4,8,…的和,而由于每人都放9次,因此这个和为9的倍数,且该和不能超过100,枚举可得1+2+4+8+16+32=63,满足条件,则共有63÷9=7名同学.【解答】解:由题意可得,若相邻两枚棋子之间有偶数个空格子,则无法再往其中放棋子,那么若想要在每个格子中都放上棋子,每次放完相邻两棋子间空格数应为奇数.第一轮只能在最中间放1枚棋子,此时将格子分为前半部分和后半部分,那么第二轮在每一部分的中间,都可以放1枚棋子,总共可以放2枚,此时将格子分成了4,第三轮在每一部分的中间,都可以放1枚棋子,总共可以放4枚,以此类推,总共放下的棋子个数应该为等比数列1,2,4,8,…的和,而由于每人都放9次,因此这个和为9的倍数,且该和不能超过100,枚举可得1+2+4+8+16+32=63,满足条件,则共有63÷9=7名同学,棋子分布依次为:1,651,33,651,17,33,49,651,9,17,25,33,41,49,57,65,…故答案为7.【点评】本题考查找规律,考查枚举与筛选,解题的关键是若想要在每个格子中都放上棋子,每次放完相邻两棋子间空格数应为奇数.8.蕾蕾买了一些山羊和绵羊,如果她多买2只山羊,那么每只羊的平均价格会增加60元,如果她少买2只山羊,那么每只羊的平均价格会减少90元.蕾蕾一共买了10 只羊.【分析】如果她多买2只山羊,那么每只羊的平均价格会增加60元,如果她少买2只山羊,那么每只羊的平均价格会减少90元,两次变化都是两只山羊的价钱,变化的总价格应该相等,即可得出结论.【解答】解:假设蕾蕾买了x只羊,原平均价格为a元,买2只山羊,每只羊的平均价格会增加60元,总价格增加60x+2(a+60)元;少买2只山羊,那么每只羊的平均价格会减少90元,总价格减少90x+2(a﹣90)元,两次变化都是两只山羊的价钱,应该相等,所以60x+2(a+60)=90x+2(a﹣90),解得x=10,故答案为10.【点评】本题考查等量关系与方程,考查学生分析解决问题的能力,正确建立等量关系是关键.9.现有A、B、C、D、E五名诚实的安保在2016年12月1日~5日各值班三天,每天将有3名安保值班,每位安保值班安排5天一循环.今天(2017年1月1日周日),关于他们在上个月的值班情况,5人进行了如下对话:A:我和B在周末(周六、周日)值班的日子比其他3人都多;B:我与其余4人在这个月都一起值过班;C:12月3日本来我休息,但那天恰逢数学花园探秘初赛,于是我也来帮忙,可惜不算值班;D:E每次都和我安排在一起;E:圣诞节(12月25日)那天我和A都值班了.那么,安保A在12月份中第2次、第6次、第10次值班日期顺次排列组成的五位数是41016 .(如果第2次、第6次、第10次值班分别在12月3日、12月17日,则答案为,31217)【分析】画出12月份值班表,分析A在12月份中第2,6,10次值班日期依次为4,10,16,即可得出结论.【解答】解:12月份值班表如下:由E说的话可知,25日A和E都值班,又由D的话可知D和E永远在一起,那么可以判断5日这一竖列值班人为A,D,E.由C的话可知,3日他不值班,由于每天必须有3人值班,所以D,E中必须有一个,又因为D,E在一起,所以3日这一竖列,D,E都值班.通过A的话判断,A,B在周末值班的日子比C,D,E多,统计出每一列中的周末数量,为2,1,2,2,2,每人都要在三列中值班,若要A,B比其他人多,那么1那一列必须是C,D,E值班,每天都要有3人值班,D,E现在已经排满,因此第1,4列为A,B,C值班.还剩第3列没有排完,B要跟每个人都搭配过,因此此处为B.A在12月份中第2,6,10次值班日期依次为4,10,16,故五位数为41016.故答案为41016.【点评】本题考查逻辑推理,考查学生分析解决问题的能力,确定A在12月份中第2,6,10次值班日期依次为4,10,16是关键.10.如图中每个小正三角形的面积是12平方厘米,那么大正三角形的面积为84 平方厘米.【分析】如图所示,补出右边的一些小等边三角形,则△ABC被分为面积相等的三个钝角三角形△AMB,△BNC,△APC,以及一个小正三角形△PMN,其中△AMB面积是所在的平行四边形ADBM的一半,即可得出结论.【解答】解:如图所示,补出右边的一些小等边三角形,则△ABC被分为面积相等的三个钝角三角形△AMB,△BNC,△APC,以及一个小正三角形△PMN,其中△AMB面积是所在的平行四边形ADBM的一半为12×4÷2=24平方厘米,那么△ABC面积为3×24+12=84平方厘米.故答案为84.【点评】本题考查面积的计算,考查补形方法的运用,正确补形是关键.11.如图,圆圈表示房间,实线表示地上通道,虚线表示地下通道,开始时,一个警察和一个小偷在两个不同房间中,每一次警察从所在房间的地上通道转移到相邻的房间;同时,小偷从所在房间沿着地下通道转移到相邻的房间,如果警察和小偷转移了3次都没有在任何房间相遇,那么他们有1476 种不同的走法.【分析】考虑起始时,警察与小偷所在房间有三类关系相邻、相隔、相对,分别求出各种情况的不同的走法,即可得出结论.【解答】解:考虑起始时,警察与小偷所在房间有三类关系相邻、相隔、相对.相邻:如1与2,那么下一步都顺时针走,可变为2与3,都逆时针走,变为6与1,一个顺时针,一个逆时针变为2与1或6与3,都有3种可能相邻,1种可能相对;相隔:如1与3,那么下一步可能变为2与4,6与2,6与4,都有3种可能相邻;相对:如1与4,那么下一步可能变为2与3,6与5,6与3,2与5,即有2种相邻的可能和2种相对的可能.假设警察初始房间为1,小偷与其相邻可能为2或6,那么3次之后不相遇的走法有2×(27+9+6+6+6+2+4+4)=128种相隔⇌3相隔⇌9相隔⇌27相隔.假设警察初始房间为1,小偷与其相邻可能为3或5,那么3次之后不相遇的走法有2×27=54种,假设警察初始房间为1,小偷与其相对为4,那么3次之后不相遇的走法有18+6+4+4+12+4+8+8=64种,综上所述,警察若初始位置为1,满足题目条件的走法有128+54+64+246种,那么警察初始位置还能选择2~6,因此共有246×6=1476种走法.故答案为1476.【点评】本题考查排列组合知识的运用,考查分类讨论的数学思想,正确分类讨论是关键.。
2016年数学花园探秘五年级初赛(解析)_74

2016年“数学花园探秘”科普活动五年级组初试试卷A 详解一.填空题Ⅰ(每小题8分,共32分)1. 算式()1912191912121219⎛⎫⨯-⨯÷- ⎪⎝⎭的计算结果是__________.【考点】计算,分数计算,整体约分 【难度】★ 【答案】228【分析】原式19191212(19191212)1219⨯-⨯=⨯-⨯÷⨯1219(19191212)19191212⨯=⨯-⨯⨯⨯-⨯1219228=⨯=2. 有一种细胞,每隔1小时死亡2个细胞,余下的每个细胞分裂成2个.如果经过8小时后细胞的个数为1284,那么,最开始的时候有__________个细胞. 【考点】计算,数列,递推 【难度】★★ 【答案】9【分析】方法一(逆推):128422644 ,64422324 ,32422164 ,1642284 ,842244 ,442224 ,242214 ,14229 .方法二(不动点/通项):若有4个细胞,则每小时细胞数目均不变,故知通项式为0(4)24n n a a ,故801284(4)24a ,09a .3. 如图,一道乘法竖式中已经填出了2、0、1、6,那么乘积是__________.×612【考点】数字谜,乘法竖式谜 【难度】★★ 【答案】6156【分析】第二个部分积小于第一个部分积,故第二乘数的十位比个位小,只能是1.进而第一部分积必为106□,第二部分积十位(即第一乘数十位)为0或1.若乘数为503,则503126036 ,百位不符合进位要求; 若乘数为508,则508126036 ,百位不符合进位要求; 若乘数为513,则513126156 ,符合要求;若乘数为518,则518126216 ,百位不符合进位要求. 综上,本题有唯一答案6156.4. 有一个数列,第一项为12,第二项为19,从第三项起,如果它的前两项和是奇数,那么该项就等于前两项的和,如果它的前两项和是偶数,该项就等于前两项的差(较大数减较小数).那么,这列数中第__________项第一次超过2016. 【考点】计算,数列,等差数列 【难度】★★★ 【答案】252【分析】即奇偶性不同求和,奇偶性相同求差.12、19、31、12、43、55、12、67、79、12、…可见凡是31n 项都是12,除去这些项,得到的数列即为首项为19,公差为12的等差数列.第167项1912(1671)2011 ,第168项1912(1681)2023 第一次超过2016,这个数列的第168项是原数列的第16823252 项.二.填空题Ⅱ(每小题10分,共40分)5. 四位数双成成双的所有因数中,有3个是质数,其它39个不是质数.那么,四位数成双双成有__________个因数.【考点】数论,因数个数定理及其逆用 【难度】★★★ 【答案】12【分析】由题意,双成成双恰有三种质因数,其中必有11,设11x y z p q 双成成双=⨯⨯,(1)(1)(1)42x y z +++=,得双成成双最小是12611326336⨯⨯=,其他可能值都至少是五位数,故有唯一解6336双成成双=,进而211366331137成双双成==⨯⨯,有(21)(11)(11)12+⨯+⨯+=个因数.6. 右图中,A 、B 、C 、D 、E 是正五边形各边的中点,那么,图中共有__________个梯形.ECBA【考点】计数,几何计数 【难度】★★★ 【答案】35【分析】图中有5组平行线,例如AB 、EC 及过D 的边(所在直线设为l )是一组平行线,AB 、EC 之间枚举知有2个梯形;AB 、l 之间没有梯形;EC 、l 之间枚举知有5个梯形,故这组平行线共有7个梯形.梯形总数为7535⨯=个.7.对于自然数N,如果在1~9这九个自然数中至少有六个数可以整除N,则称N是一个“六合数”,则在大于2000的自然数中,最小的“六合数”是__________.【考点】数论,分解质因数【难度】★★【答案】2016【分析】6个数中必有偶数,故“六合数”是偶数,枚举知:=⨯⨯⨯只能被1、2、7整除,不符要求;20022711132=⨯⨯只能被1、2、3、4、6整除,不符要求;200423167200621759=⨯⨯只能被1、2整除,不符要求;3=⨯只能被1、2、4、8整除,不符要求;20082251=⨯⨯⨯只能被1、2、3、5、6整除,不符要求;2010235672=⨯只能被1、2、4整除,不符要求;20122503201421953=⨯⨯只能被1、2整除,不符要求;52=⨯⨯能被1、2、3、4、6、7、8、9整除,符合要求.20162378.如图,魔术师在一个转盘上的16个位置写下来了1~16共16个数,四名观众甲、乙、丙、丁参与魔术表演.魔术师闭上眼,然后甲从转盘中选一个数,乙、丙、丁按照顺时针方向依次选取下一个数,图示是一种可能的选取方式.魔术师睁开眼,说:“选到偶数的观众请举手.”这时候,只有甲和丁举手,这时候魔术师就大喝一声:“我知道你们的选的数了!”,你认为甲和丁选的数的乘积是__________.【考点】组合,进位制,构造【难度】★★★【答案】120【分析】甲、乙、丙、丁四个人所选数分别为偶数、奇数、奇数、偶数,图中连续的位置只有10、11、9、12符合要求,所以甲、丁所选的数必为10和12,其积为1012120⨯=.其实连续四个数有16种取法,恰好连续四个数的奇偶情况也是16种,此图的任何连续四个数的奇偶情况都不同,这是魔术的数学原理.三.填空题Ⅲ(每小题12分,共48分)9. 正八边形边长是16,那么阴影部分的面积是__________.【考点】几何,正八边形 【难度】★★★★ 【答案】512【分析】如图,连接正八边形的对角线,可知其中12S S =,34S S =,所以图中左、右两个阴影部分的面积之和等于中间正方形的面积,也就是1616256⨯=.同理,上、下两个阴影部分的面积之和也等于256.所以阴影部分的总面积是2562512⨯=.10. 某城市早7:00到8:00是高峰时段,所有车辆的行驶速度变为原来的一半.每天早上6:50,甲、乙两人从这城市的A 、B 两地同时出发,相向而行,在距离A 地24千米的地方相遇.如果乙早出发20分钟,两人将在距离A 地20千米的地方相遇;如果甲晚出发20分钟,两人恰好在AB 中点相遇.那么,AB 两地相距__________千米. 【考点】行程,方程行程 【难度】★★★★ 【答案】42【分析】同时出发的情况中,由于两人要减速也是同时减速(当然也许两人并未减速过),故无论哪个时段,甲乙的速度比是固定的,所以任意时段行走的距离比也是固定的.总之,相遇点左、右距A 、B 的距离比代表了两人的初始速度比.乙先行的情况中,乙所先行的20分钟是以原速运动的,之后的过程类似上一段分析.故设甲、乙原速分别为x 、y 千米每分,全长S 千米,有方程:2420242020x y S S y ==---,得120S y =. 甲晚行的情况中,乙先以原速独行了10分钟,又以原速的一半独行了10分钟,之后的过程类似第一段分析.有方程:240.5241050.5x S y S S y y S ==----,即242430S S S y=--,将120S y =代入,得14513y =-,故207y =,12042S y ==.11.在空格里填入数字1~5,使得每行和每列数字不重复.每个除法从上向下或者从左到右运算都能够整除.问:第二行的前三个数依次是__________.【考点】数独【难度】★★【答案】531【分析】首先确定下图1中的数字;再确定出下图2中的数字;最终填出此图中所有的数字(如图3).所以所求的三个数依次为531.图1 图2 图3。
四年级下册数学试题2019年“迎春杯”数学花园探秘决赛试卷(小中组a卷)(含答案解析)全国通用

2019年“迎春杯”数学花园探秘决赛试卷(小中组A卷)一、填空题(共4小题,每小题8分,满分32分)1.(8分)算式33+43+53+63+73+83+93的计算结果是.2.(8分)蓉蓉从一班转到了二班,蕾蕾从二班转到了一班,于是一班学生的平均身高增加了2厘米,二班学生的平均身高减少了3厘米,如果蕾蕾身高158厘米,蓉蓉身高140厘米,那么两个班共有学生人.3.(8分)如图,图中3个大三角形都是等边三角形,则图中共有个三角形.4.(8分)今天是1月30日,我们先写下130;后面写数的规则是:如果刚写下的数是偶数就把它除以2再加上2写在后面,如果刚写下的数是奇数就把它乘以2再减去2写在后面,于是得到:130、67、132、68…,那么这列数中第2016个数是.二、填空题(共4小题,每小题10分,满分40分)5.(10分)请将1~6分别填入如图的6个圆圈中,使得每条直线上的圆圈中填的所有数的和都相等(图中有3条直线上各有3个圆圈,有2条直线上各有2个圆圈);那么两位数=.6.(10分)在A、B、C三个连续的小水池中各放入若干条金鱼,若有12条金鱼从A池游到C池中,则C池内的金鱼将是A池的2倍,若有5条金鱼从B池游到A池中,则A 池与B池的金鱼数将相等,此外,若有3条金鱼从B池游到C池中,则B池与C池中的金鱼数也会相等,那么A水池中原有条金鱼.7.(10分)如图,长方形ABCD的长AB为20厘米,宽BC为16厘米,长方形内放着两个重叠的正方形DEFG和BHIJ,已知三个阴影长方形的周长相等,那么长方形INFM的面积为平方厘米.8.(10分)在如图所示每个格子里填入数字1~5中的一个,使得每一行和每一列数字都不重复,每个“L”状大格子跨了两行和两列,上圆圈中的数表示相邻两个格子内数字的和(如图给出了一个填1~4的例子,如中图第3行从左到右四格依次为3,4,1,2)那么图中最下面一行的五个数字按从左到右的顺序依次组成的五位数是.三、填空题(每小题12分,满分36分)9.(12分)用数字1至9组成一个没有重复数字的九位数要求、、、、、、、这八个两位数均能写成两个一位数的乘积;那么算式++的计算结果是.10.(12分)图③是由6个图①这样的模块拼成的,如果最底层已经给定两块的位置(如图②),那么剩下部分一共有种不同的拼法.11.(12分)甲乙两人轮流从1~9这9个自然数中取不同的数,对方取过的数不能再取,谁取得的数中先有三个数成等差数列谁就获胜;甲先取了8,乙接着取了5;为了确保甲必胜,甲接下来取的一个数的所有可能值的乘积是.2019年“迎春杯”数学花园探秘决赛试卷(小中组A卷)参考答案与试题解析一、填空题(共4小题,每小题8分,满分32分)1.(8分)算式33+43+53+63+73+83+93的计算结果是2016.【解答】解:33+43+53+63+73+83+93=13+23+33+43+53+63+73+83+93﹣13﹣23=(1+2+3+…+9)2﹣1﹣8=[(1+9)×9÷2]2﹣9=452﹣9=2025﹣9=2016;故答案为:2016.2.(8分)蓉蓉从一班转到了二班,蕾蕾从二班转到了一班,于是一班学生的平均身高增加了2厘米,二班学生的平均身高减少了3厘米,如果蕾蕾身高158厘米,蓉蓉身高140厘米,那么两个班共有学生15人.【解答】解:158﹣140=18(厘米),18÷2+18÷3=9+6=15(人)答:两个班共有学生15人.故答案为:15.3.(8分)如图,图中3个大三角形都是等边三角形,则图中共有30个三角形.【解答】解:根据分析,小三角形的个数为:9个;含有两个小三角形的三角形的个数为:18个;大三角形的个数为:3个,故总的三角形的个数是:9+18+3=30个.4.(8分)今天是1月30日,我们先写下130;后面写数的规则是:如果刚写下的数是偶数就把它除以2再加上2写在后面,如果刚写下的数是奇数就把它乘以2再减去2写在后面,于是得到:130、67、132、68…,那么这列数中第2016个数是6.【解答】解:依题意可知:数字规律是130、67、132、68、36、20、12、8、6、5、8、6、5、8、6、5、去掉钱7项是循环周期数列2016﹣7=2009.每3个数字一个循环2009÷3=667 (2)循环数列的第二个数字就是6.故答案为:6二、填空题(共4小题,每小题10分,满分40分)5.(10分)请将1~6分别填入如图的6个圆圈中,使得每条直线上的圆圈中填的所有数的和都相等(图中有3条直线上各有3个圆圈,有2条直线上各有2个圆圈);那么两位数=63.【解答】解:依题意可知:A+C+D=A+B=B+D+F=E+F=E+B+C.B=C+D.B+D=E.E+C=A.①D=1,C=2,B=3,E=4,A=6,F=5.②D=2,C=1,B=3,E=5,A=6,F=4.那么两位数=63.故答案为:63.6.(10分)在A、B、C三个连续的小水池中各放入若干条金鱼,若有12条金鱼从A池游到C池中,则C池内的金鱼将是A池的2倍,若有5条金鱼从B池游到A池中,则A 池与B池的金鱼数将相等,此外,若有3条金鱼从B池游到C池中,则B池与C池中的金鱼数也会相等,那么A水池中原有40条金鱼.【解答】解:若5条金鱼从B游到A,则A和B相等,那么B池水中的鱼比A中的多10条.若有3条金鱼从B池游到C池中,则B池与C池中的金鱼数也会相等,说明B池水中的鱼比C多6条.所以A池水中的鱼比C池水中的金鱼少4条.若有12条金鱼从A池游到C池中,说明C比A多4+12+12=28条.则C池内的金鱼将是A池的2倍.那么一份就是28条.A中有28条.那么原来A中的金鱼数量为28+12=40条.故答案为:40条.7.(10分)如图,长方形ABCD的长AB为20厘米,宽BC为16厘米,长方形内放着两个重叠的正方形DEFG和BHIJ,已知三个阴影长方形的周长相等,那么长方形INFM的面积为32平方厘米.【解答】解:阴影部分的总周长为:(20+16)×2=72,四边形IMFN的周长是72÷3=24,所以MF+FN=12 ①,因为正方形的边长相等:MF+MG=FN+EN,则MF﹣FN=EN﹣GM,所以EN﹣GM=EN+BJ﹣(GM+BH)=AB﹣BC=4,则MF﹣FN=4 ②,根据①②式可得:(12+4)÷2=8,(12﹣4)÷2=4,长方形IMFN的面积为4×8=32.故答案为:32.8.(10分)在如图所示每个格子里填入数字1~5中的一个,使得每一行和每一列数字都不重复,每个“L”状大格子跨了两行和两列,上圆圈中的数表示相邻两个格子内数字的和(如图给出了一个填1~4的例子,如中图第3行从左到右四格依次为3,4,1,2)那么图中最下面一行的五个数字按从左到右的顺序依次组成的五位数是24531.【解答】解:图1,左上角8=3+5,若5在左边,则第一列的第4行的9无法确定,则必须是左3右5.同理右下角的4=1+3,若1在左边,第四列的第4行和第5行无法确定,所以左3右1.图2,第一列的第2行和第6行的和是3,只能是1和2,而第6行有1了,所以第一列的第2行是1,第6行是2,同理可知第6列的第1行是2,第4行是3.图3,第一行还有1和4两个数,1在第4列,则7无法确定,所以第3列是1,第4列是4,第2行第4列是3,第5列第4行是2,第4列第4行是1,因为第2行4已经存在,所以第6列,第第2行是5,第4行是5,由此可以推出第1列的第4行是5,第5行是4.图4,其他按此方法,填入即可,故答案为24531.三、填空题(每小题12分,满分36分)9.(12分)用数字1至9组成一个没有重复数字的九位数要求、、、、、、、这八个两位数均能写成两个一位数的乘积;那么算式++的计算结果是1440.【解答】解:跟数字9组合的数字只有4.所以放在最后.和数字7组合的只有2,27或者72,只能有一个数字所以.再分析数3,组合只有63和35.数字5后面只能有54.∴=35.再分析数字8,组合可以是28,18,81,所..=728+163+549=1440.故答案为:1440.10.(12分)图③是由6个图①这样的模块拼成的,如果最底层已经给定两块的位置(如图②),那么剩下部分一共有2种不同的拼法.【解答】解:如图:答:剩下部分一共有2种不同的拼法.故答案为:2.11.(12分)甲乙两人轮流从1~9这9个自然数中取不同的数,对方取过的数不能再取,谁取得的数中先有三个数成等差数列谁就获胜;甲先取了8,乙接着取了5;为了确保甲必胜,甲接下来取的一个数的所有可能值的乘积是168.【解答】解:若甲接下来取的一个数是1,则乙取4,那么下一轮无论甲取几,均不能构成等差数列,且下一轮乙再取一个数均能构成等差数列(4、5、6或3、4、5),甲输;若甲接下来取的一个数是2,则乙取4,同理,甲输;若甲接下来取的一个数是3,则乙取6,同理,甲输;若甲接下来取的一个数是4,则乙取6(否则甲下一轮取6直接获胜),则甲只能取7(否则乙下一轮取7直接获胜),这样,乙这轮不可能构成等差数列,下一轮可以取1或9均能构成等差数列(1、4、7或7、8、9),甲胜;若甲接下来取的一个数是6,则无论乙取几,甲再取一个数均能构成等差数列(4、6、8或者6、7、8);若甲接下来取的一个数是7,则无论乙取几,甲再取一个数均能构成等差数列(6、7、8或者7、8、9);若甲接下来取的一个数是9,则乙取7(否则甲下一轮取7直接获胜),则下一轮无论甲取几,乙再取一个数均能构成等差数列(3、5、7或5、6、7).综上,为了确保甲必胜,甲接下来取的一个数可以是4、6、7,所有可能值的乘积是:4×6×7=168.故答案为:168.。
“迎春杯”数学花园探秘网试试卷(三年级)

2015年“迎春杯”数学花园探秘网试试卷(三年级)一、填空题Ⅰ(每题8分,共24分)1.(8分)如图2中共有个与如图1形状完全一样的月牙.2.(8分)僵尸正在走来,火龙草负责防卫:一阶火龙草总是吐红色火焰;二阶火龙草一半时间吐红色火焰,一半时间吐蓝色火焰;三阶火龙草总是吐蓝色火焰.如果二阶火龙草的攻击能力是一阶火龙草的2倍,那么三阶火龙草的攻击能力是一阶火龙草的倍.3.(8分)老师手里有一个计算器,每个同学依次过来输入一个自然数,第一个同学输入1,第二个同学输入2,第三个同学输入3,由于计算器上的按键4和8坏掉了,下一个同学只能输入5,以后的同学依次输入6、7、9、10、11、12、13、15…,按照此输入法,小明是第100个同学,小明输入的自然数是.二、填空题Ⅱ(每题10分,共30分)4.(10分)小明买了4个苹果、6个梨和8个桃,小红买了5个苹果、7个梨和6个桃.在接下去的18天中,他们每人每天吃一个水果,有三天两人都吃苹果;有两天两人都吃梨,还有三天一人吃苹果,另一人吃梨,那么有天两人都吃桃.5.(10分)帅帅在如图的16个房间中玩“秘密逃脱”游戏.任务是从1号房间走到16号房间,密室间的门都是单向门,只有从正确的方向经过门才能打开(如图).帅帅要完成任务并使得经过的房间尽可能的少,那么他所经过房间(含1号和16号)的编号总和是.6.(10分)三个天平的托盘中形状相同的物体重量相等.图中的前两个天平处于平衡状态,要使第3个天平也保持平衡,则需要在它的右盘中放置个球.三、填空题Ⅲ(每题15分,共30分)7.(15分)某“趣味游戏”的游戏规则如下:玩家手中有水、火、风、土四个技能.发动每个技能都需要消耗一定数量的水晶,各技能具体效果如下:水:消耗4个水晶,同时使敌人的血量减少4点(如敌人血量不足4点则直接击杀);火:消耗10个水晶,同时使敌人的血量减少11点(如敌人血量不足11点则直接击杀);风:消耗10个水晶,同时使敌人的血量减少5点(如敌人血量不足5点则直接击杀)并且下一个技能发动消耗水晶数除以2(例如:在风技能后面发动水技能,水技能只消耗两个水晶);土:消耗18个水晶,同时使敌人的血量除以2(如敌人血量是奇数,则先加1再除以2):如果敌人的血量为120点,那么合理选择技能,至少需要个水晶将敌人击杀(敌人血量减少至0则死亡).8.(15分)在如图的9宫格中填入9个不同的自然数,满足:每一行中,左边两个数的和等于最右边的数;每一列中,上面两个数的和等于最下面的数,那么右下角的数最小是.四、亲子互动操作题Ⅳ(每小题18分,共36分)9.(18分)在空格中填入数字1﹣5使得每行、每列和每宫(在数独中被粗线分割开的每块称为宫)数字都不重复,斜线相邻的数字也不能相同.那么,第一行从左至右5个数字依次组成的五位数是.10.(18分)试一试:上面是中国结中草花结的简易编法,编好草花结后将它外面的5个环如图剪开,在将所有的结打开,看看绳子被剪成了段.想一想:如图是中国结编制高手小兰花的作品,她用一根绳子编成如此美丽的蝴蝶结,如果将蝴蝶的两支大翅膀各7个环都一刀剪开,再将所有的结打开,那么这根绳子一共被剪成了段.2015年“迎春杯”数学花园探秘网试试卷(三年级)参考答案与试题解析一、填空题Ⅰ(每题8分,共24分)1.(8分)如图2中共有7 个与如图1形状完全一样的月牙.【解答】解:方法一::①横方向放的有3个;②竖方向放的有4个;共有:3+4=7(个);方法二:14÷2=7(个);答:图2中共有 7个与如图1形状完全一样的月牙.故答案为:7.2.(8分)僵尸正在走来,火龙草负责防卫:一阶火龙草总是吐红色火焰;二阶火龙草一半时间吐红色火焰,一半时间吐蓝色火焰;三阶火龙草总是吐蓝色火焰.如果二阶火龙草的攻击能力是一阶火龙草的2倍,那么三阶火龙草的攻击能力是一阶火龙草的 3 倍.【解答】解:由题意,二阶火龙草一半时间吐蓝色火焰,使得攻击力变为2倍,即增加了1倍;若三阶火龙草一半时间吐蓝色火焰,则使得攻击力比二阶火龙草增加1倍,因为二阶火龙草比一阶火龙草增加1倍,所以三阶火龙草的攻击能力是一阶火龙草的3倍.故答案为3.3.(8分)老师手里有一个计算器,每个同学依次过来输入一个自然数,第一个同学输入1,第二个同学输入2,第三个同学输入3,由于计算器上的按键4和8坏掉了,下一个同学只能输入5,以后的同学依次输入6、7、9、10、11、12、13、15…,按照此输入法,小明是第100个同学,小明输入的自然数是155 .【解答】解:依题意可知:1﹣100中去掉的数字是个位数字是4的4,14,24,34,44,54,64,74,84,94共10个和8的共20个.十位数字是4的40,41,42,43,44,45,46,47,48,49和8的共计20个.但是44,48,88,84分别多计数1次.则有40﹣4=36个数字不能使用,需要从100开始再计算36个数字.101﹣110共8个数字.111﹣120共8个数字.121﹣130共8个数字.131﹣139共7个数字.共8+8+8+7=31个数字.150,151,152,153,155共5个,则最后是155.故答案为:155.二、填空题Ⅱ(每题10分,共30分)4.(10分)小明买了4个苹果、6个梨和8个桃,小红买了5个苹果、7个梨和6个桃.在接下去的18天中,他们每人每天吃一个水果,有三天两人都吃苹果;有两天两人都吃梨,还有三天一人吃苹果,另一人吃梨,那么有 4 天两人都吃桃.【解答】解:(1)有三天两人都吃苹果,有两天两人都吃梨,5天后小明还剩下1个苹果4个梨,小红还剩下2个苹果5个梨;(2)有三天一人吃苹果一人吃梨,所以小明吃剩下的1个苹果时,小红吃梨;小红吃剩下的2个苹果时,小明吃梨;(3)小明吃剩下的2个梨时小红只能吃桃;小红吃剩下的4个梨时,小明只能吃桃;(4)这时两人都只剩下4个桃子,所以共同吃桃子4天.答:有4天两人都吃桃.答案填:4.5.(10分)帅帅在如图的16个房间中玩“秘密逃脱”游戏.任务是从1号房间走到16号房间,密室间的门都是单向门,只有从正确的方向经过门才能打开(如图).帅帅要完成任务并使得经过的房间尽可能的少,那么他所经过房间(含1号和16号)的编号总和是114 .【解答】解:根据题意,画出树状图可知经过的房间尽可能的少的路线是1→2→6→5→9→13→14→10→11→7→8→12→16.所以经过房间(含1号和16号)的编号总和是1+2+6+5+9+13+14+10+11+7+8+12+16=114.故答案为114.6.(10分)三个天平的托盘中形状相同的物体重量相等.图中的前两个天平处于平衡状态,要使第3个天平也保持平衡,则需要在它的右盘中放置 5 个球.【解答】解:设球的质量是x,小正方形的质量是y,小正三角形的质量是z.根据题意得到:解得:第三图中左边是:x+2y+z=x+2x+2x=5x,因而需在它的右盘中放置5个球.答:需在它的右盘中放置5个球.故答案为:5.三、填空题Ⅲ(每题15分,共30分)7.(15分)某“趣味游戏”的游戏规则如下:玩家手中有水、火、风、土四个技能.发动每个技能都需要消耗一定数量的水晶,各技能具体效果如下:水:消耗4个水晶,同时使敌人的血量减少4点(如敌人血量不足4点则直接击杀);火:消耗10个水晶,同时使敌人的血量减少11点(如敌人血量不足11点则直接击杀);风:消耗10个水晶,同时使敌人的血量减少5点(如敌人血量不足5点则直接击杀)并且下一个技能发动消耗水晶数除以2(例如:在风技能后面发动水技能,水技能只消耗两个水晶);土:消耗18个水晶,同时使敌人的血量除以2(如敌人血量是奇数,则先加1再除以2):如果敌人的血量为120点,那么合理选择技能,至少需要63 个水晶将敌人击杀(敌人血量减少至0则死亡).【解答】解:观察发现,先用风再用土可以消耗较少的水晶,使用下列方式最少(如表),只需要63个水晶,故答案为63.8.(15分)在如图的9宫格中填入9个不同的自然数,满足:每一行中,左边两个数的和等于最右边的数;每一列中,上面两个数的和等于最下面的数,那么右下角的数最小是12 .【解答】解:1+2+3+4+5+6+7+8+9=45,所以右下角的数最小不能小于:45÷4=11…1,则数字最小为12,例如:.故答案为:12.四、亲子互动操作题Ⅳ(每小题18分,共36分)9.(18分)在空格中填入数字1﹣5使得每行、每列和每宫(在数独中被粗线分割开的每块称为宫)数字都不重复,斜线相邻的数字也不能相同.那么,第一行从左至右5个数字依次组成的五位数是53124 .【解答】解:根据分析,L、H与4斜线相邻,故不能为4,第二列中只有能是D为4;L、H处只能是1和5,由于H与5在一条斜线上,故不能为5,所以L为5,H为1;而F与5同列,故不能为5,而E、F与1、2同行,只能是3和5,故F 为3,E为5;在第一宫中,D为4,A、B只能是1和5,因B与5相邻,故B不能是5,故B是1,A是5;在第一行中,只剩下C必为4.综上,第一行从左至右5个数字依次组成的五位数是:53124.故答案是:53124.10.(18分)试一试:上面是中国结中草花结的简易编法,编好草花结后将它外面的5个环如图剪开,在将所有的结打开,看看绳子被剪成了6段.想一想:如图是中国结编制高手小兰花的作品,她用一根绳子编成如此美丽的蝴蝶结,如果将蝴蝶的两支大翅膀各7个环都一刀剪开,再将所有的结打开,那么这根绳子一共被剪成了15 段.【解答】解:(1)5+1=6(段)答:绳子被剪成了 6段.(2)(7×2×2+2)÷2第12页(共12页)=30÷2=15(段)答:这根绳子一共被剪成了 15段.故答案为:6;15.声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2019/5/5 18:12:10;用户:小学奥数;邮箱:pfpxxx02@;学号:20913800第12页(共12页)。
“迎春杯”六年级数学花园探秘科普活动总决赛试卷
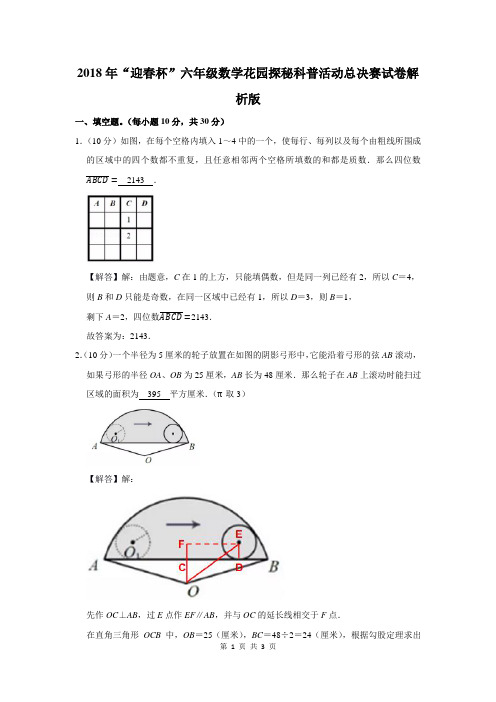
第 1 页 共 3 页
2018年“迎春杯”六年级数学花园探秘科普活动总决赛试卷解
析版
一、填空题。
(每小题10分,共30分)
1.(10分)如图,在每个空格内填入1~4中的一个,使每行、每列以及每个由粗线所围成
的区域中的四个数都不重复,且任意相邻两个空格所填数的和都是质数.那么四位数ABCD = 2143 .
【解答】解:由题意,C 在1的上方,只能填偶数,但是同一列已经有2,所以C =4, 则B 和D 只能是奇数,在同一区域中已经有1,所以D =3,则B =1,
剩下A =2,四位数ABCD =2143.
故答案为:2143.
2.(10分)一个半径为5厘米的轮子放置在如图的阴影弓形中,它能沿着弓形的弦AB 滚动,
如果弓形的半径OA 、OB 为25厘米,AB 长为48厘米.那么轮子在AB 上滚动时能扫过区域的面积为 395 平方厘米.(π取3)
【解答】解:
先作OC ⊥AB ,过E 点作EF ∥AB ,并与OC 的延长线相交于F 点.
在直角三角形OCB 中,OB =25(厘米),BC =48÷2=24(厘米)
,根据勾股定理求出。
数学花园探秘(迎春杯)六年级决赛试卷及详解

数学花园探秘(迎春杯)六年级决赛试卷及详解1002017 年“数学花园探秘”科普活动⼩学⾼年级组决赛试卷 A(测评时间:2017 年 1 ⽉ 1 ⽇ 8:00—9:30)⼀.填空题Ⅰ(每⼩题 8 分,共 40 分)2.⼀个边长为 100 厘⽶的正五边形和五个扇形拼成如图的“海螺”,那么这个图形的周长是厘⽶(π取 3.14).3.在 2016 年⾥约奥运会⼥排决赛中,中国队战胜了塞尔维亚队获得冠军.统计 4 局⽐赛中中国队的得分,发现前 2 局的得分之和⽐后 2 局的得分之和少 12%,前 3 局的得分之和⽐后 3 局的得分之和少8%.已知中国队在第 2 局和第 3 局中各得了 25 分,那么中国队在这 4 局中的得分总和为分.4.右⾯三个算式中,相同汉字代表相同数字,不同汉字代表不同数字;那么四位数“ 李⽩杜甫 ”=.5. n 个数排成⼀列,其中任意连续三个数之和都⼩于30,任意连续四个数之和都⼤于 40,则n 的最⼤值为.⼆.填空题Ⅱ(每⼩题 10 分,共 50 分)6.算式的计算结果是.7.有⼀个四位数,它和 6 的积是⼀个完全⽴⽅数,它和 6 的商是⼀个完全平⽅数;那么这个四位数是.8.在空格⾥填⼊数字 1~6,使得每⾏、每列和每个 2×3的宫(粗线框)内数字不重复.若虚线框A,B,C,D,E,F 中各⾃数字和依次分别为 a ,b ,c ,d ,e ,f ,且 a =b ,c =d ,e >f .那么第四⾏的前五个数字从左到右依次组成的五位数是.10120 C P 179. 抢红包是微信群⾥⼀种有趣的活动,发红包的⼈可以发总计⼀定⾦额的⼏个红包,群⾥相应数量的成员可以抢到这些红包,并且⾦额是随机分配的.⼀天陈⽼师发了总计 50 元的 5 个红包,被孙、成、饶、赵、乔五个⽼师抢到.陈⽼师发现抢到红包的 5 个⼈抢到的⾦额都不⼀样,都是整数元的,⽽且还恰好都是偶数.孙⽼师说:“我抢到的⾦额是10 的倍数.” 成⽼师说:“我和赵⽼师抢到的加起来等于孙⽼师的⼀半.” 饶⽼师说:“乔⽼师抢到的⽐除了孙⽼师以外其他所有⽼师抢到的总和还多.” 赵⽼师说:“其他所有⽼师抢到的⾦额都是我的倍数.” 乔⽼师说:“饶⽼师抢到的是我抢到的 3 倍.” 已知这些⽼师⾥只有⼀个⽼师没说实话,那么这个没说实话的⽼师抢到了元的红包.D10. 如图,P 为四边形 ABCD 内部的点,AB :BC :DA =3:1:2,∠DAB =∠ CBA =60°.图中所有三⾓形的⾯积都是整数.如果三⾓形PAD 和三⾓形 PBC 的⾯积分别为 20 和 17,那么四边形ABCD 的⾯积最⼤是.三.填空题Ⅲ(每⼩题 12 分,共 60 分)A B11. 有⼀列正整数,其中第 1 个数是 1,第 2 个数是 1、2 的最⼩公倍数,第 3 个数是 1、2、3 的最⼩公倍数,……,第 n 个数是1、2、……、n 的最⼩公倍数.那么这列数的前 100个数中共_______个不同的值.12. 如图,有⼀个固定好的正⽅体框架,A 、B 两点各有⼀只电⼦跳蚤同时开 A 始跳动.已知电⼦跳蚤速度相同,且每歩只能沿棱跳到相邻的顶点,两只电⼦跳蚤各跳了 3 歩,途中从未相遇的跳法共有种.13. 甲以每分钟 60 ⽶的速度从 A 地出发去 B 地,与此同时⼄从 B 地出发匀速去 A 地;过了 9 分钟,丙从 A 地出发骑车去 B 地,在途中 C 地追上了甲甲、⼄相遇时,丙恰好到 B 地;丙到 B 地后⽴即调头,且速度下降为原来速度的⼀半;当丙在 C 地追上⼄时,甲恰好到 B 地.那么AB 两地间的路程为⽶.10214. 在⼀个 8×8 的⽅格棋盘中放有 36随后的空格棋⼦,则不能进⾏操作.那么最后在棋盘上最少剩下枚棋⼦. 15. 你认为本试卷中⼀道最佳试题是第题(答题范围为01~14);你认为本试卷整体的难度级别是(最简单为“1”,最难为“9”,答题范围为 1~9);你认为本试卷中⼀道最难试题是第题;(答题范围为 01~14).(所有答题范围内的作答均可得分,所有的评定都将视为本⼈对本试卷的有效评定,不作答或者超出作答范围不得分.)2017数学花园探秘科普活动⼩⾼决赛A解析1.答案:64 解析:原式=(632-163)+(1-163)=63+1=642.答案:2384 解析:500+15×2×π×(100+200+300+400+500)=23843.答案:94 解析:注意到前三局⽐前两局多25分,后三局⽐后两局多25分,所以中国队得分总和为25+(18%-112%)÷12%×(1+1-12%)=94分。
“迎春杯”数学花园探秘初赛试卷(五年级b卷)

2016年“迎春杯”数学花园探秘初赛试卷(五年级B卷)一、填空题(共4小题,每小题8分,满分32分)1.(8分)算式2016×(﹣)×(﹣)的计算结果是.2.(8分)一位牧羊人赶着一群羊去放牧,跑出一只公羊后,他数了数羊的数量,发现剩下的羊中,公羊与母羊的只数比是7:5,过来一会跑出的公羊又回到羊群,却又跑了一只母羊,牧羊人又数了羊的只数,发现公羊与母羊的只数之比是5:3.这群羊原来有只.3.(8分)如图,一道乘法竖式中已经填出了2、0、1、6,那么乘数中较小的是.4.(8分)对于自然数N,如果1﹣9这九个自然数中至少有五个数可以整除N,则称N是一个“五顺数”,则在大于2000的自然数中,最小的“五顺数”是.填空题Ⅱ5.(10分)一个自然数A连着写2遍(例如把12写成1212)得到一个新的数B,如果B是2016的倍数,则A最小是.6.(10分)将如图所示的“b”型多联方块覆盖到8×8网格里:要求方块必须与网格线对齐,覆盖后所有横、竖列网格内的方块总数都分别相等,则一共能再放入个这样的“b”型多联方块.(注意:放入的多联方块允许旋转,但不允许翻转).7.(10分)如图的两个竖式中,相同汉字代表相同数字,不同汉字代表不同数字.两个△和两个□中填入的数字分别相同:那么,“花园探秘”的值是.8.(10分)12个蓝精灵围着圆桌坐着,每个蓝精灵都讨厌与他为邻的2个蓝精灵,但不讨厌其余的9个蓝精灵.蓝爸爸要派出一个由5个蓝精灵所组成的小队来营救格格巫抓走的蓝妹妹,小队中不能有互相讨厌对方的人,则有种方法来组队.二、填空题Ⅲ(共3小题,每小题12分,满分36分)9.(12分)如图,在直角三角形ABC中,AB、BC的长度分别是15、20,四边形BDEF是正方形,如果三角形EMN的高EH的长度是2,那么,正方形BDEF的面积为.10.(12分)甲、乙、丙三人在一条周长为360米环形跑道上的同一出发点:甲先出发,逆时针方向跑步;在甲还未完成一圈时,乙、丙同时出发,顺时针方向跑步;当甲、乙第一次相遇时,丙刚好距他们半圈;一段时间后,当甲、丙第一次相遇时,乙刚好也距他们半圈.如果乙的速度是甲的4倍,那么,当乙、丙出发时,甲已经跑了米.11.(12分)动物王国里的老虎总说真话,狐狸总说假话,猴子有时说真话、有时说假话.现有这三种动物各100只,分成100组,每组3只动物恰好一种2只,另一种1只.分好组后,功夫熊猫问每只动物“你组内有老虎吗”,结果恰有138只回答“有”;功夫熊猫又问每只动物“你组内有狐狸吗”,结果恰有188只回答“有”.问两次都说真话的猴子有只.2016年“迎春杯”数学花园探秘初赛试卷(五年级B卷)参考答案与试题解析一、填空题(共4小题,每小题8分,满分32分)1.(8分)算式2016×(﹣)×(﹣)的计算结果是8 .【解答】解:2016×(﹣)×(﹣)=63×8×4×(﹣)×(﹣)=4×[(﹣)×8]×[(﹣)×63]=4×[×8﹣×8]×[×63﹣×63]=4×[2﹣1]×[9﹣7]=4×1×2=8故答案为:8.2.(8分)一位牧羊人赶着一群羊去放牧,跑出一只公羊后,他数了数羊的数量,发现剩下的羊中,公羊与母羊的只数比是7:5,过来一会跑出的公羊又回到羊群,却又跑了一只母羊,牧羊人又数了羊的只数,发现公羊与母羊的只数之比是5:3.这群羊原来有25 只.【解答】解:根据分析,刚开始,少了一只公羊,比为7:5=14:10,后来,公羊回到羊群,则公羊须加1只,而母羊则须减去1只,此时比为15:10=(14+1):(10﹣1),因此,原来公羊数量为15只,母羊数量为:10只,羊的总数为:15+10=25只.故答案是:25.3.(8分)如图,一道乘法竖式中已经填出了2、0、1、6,那么乘数中较小的是152 .【解答】解:答:乘数较小的数是152.故答案为:152.4.(8分)对于自然数N,如果1﹣9这九个自然数中至少有五个数可以整除N,则称N是一个“五顺数”,则在大于2000的自然数中,最小的“五顺数”是2004 .【解答】解:依题意可知:2001是1,3,倍数不满足题意;2002=2×13×11×7不满足题意;2003不满足题意;2004是1,2,3,4,6的倍数,满足题意.故答案为:2004填空题Ⅱ5.(10分)一个自然数A连着写2遍(例如把12写成1212)得到一个新的数B,如果B是2016的倍数,则A最小是288 .【解答】解:2016=25×7×32,因为B是2016的倍数,即B=2016k;则A至少是两位数,则两位数表示为,B==×101,101与2016没有公因数,所以A不是最小;因此换成A是三位数,表示为,则B=×1001=×13×11×7,则×13×11×7=25×7×32k,×13×11=25×32k,因为后面,A×(10001、100001…,都不是2和3的倍数),所以要使A最小,则A==25×32=288;答:A最小是 288.故答案为:288.6.(10分)将如图所示的“b”型多联方块覆盖到8×8网格里:要求方块必须与网格线对齐,覆盖后所有横、竖列网格内的方块总数都分别相等,则一共能再放入7 个这样的“b”型多联方块.(注意:放入的多联方块允许旋转,但不允许翻转).【解答】解:根据分析,如图要使方块必须与网格线对齐,覆盖后所有横、竖列网格内的方块总数都分别相等,可以再放进去7这样的b型方块.故答案是:7.7.(10分)如图的两个竖式中,相同汉字代表相同数字,不同汉字代表不同数字.两个△和两个□中填入的数字分别相同:那么,“花园探秘”的值是9713 .【解答】解:根据加法和减法竖式的第一步可以知道:□=6再根据0+学=爱,结合”相同汉字代表相同数字,不同汉字代表不同数字”所以1+花的结果必须进位,探还是四位数的最高位,所以探不能为0所以花=9,探=1,爱=5则6+园必须进位根据加法竖式可知:学=4因为花=9所以习﹣花时必须借位,所以学﹣探只能是2故△=2因为6+园必须进位,根据前面汉字所代表的数字及其条件只能推出:秘=3,园=7故:数=6,我=8如图:答:花园探秘”是9713故答案为:9713.8.(10分)12个蓝精灵围着圆桌坐着,每个蓝精灵都讨厌与他为邻的2个蓝精灵,但不讨厌其余的9个蓝精灵.蓝爸爸要派出一个由5个蓝精灵所组成的小队来营救格格巫抓走的蓝妹妹,小队中不能有互相讨厌对方的人,则有36 种方法来组队.【解答】解:按要求分成三大类情况:一类是全选奇数号的,其组数是=6,二类是全选偶数号的,其组数是=6,三类是奇偶数混合的,因情况复杂,再分为4小类:1类:1偶4奇的(或4奇1偶),其所组成的小组有:2﹣5﹣7﹣9﹣11、4﹣7﹣9﹣11﹣1、6﹣9﹣11﹣1﹣3、8﹣11﹣1﹣3﹣5、10﹣1﹣3﹣5﹣7、12﹣3﹣5﹣7﹣9计6种.2类:2偶3奇(或3奇2偶)所组成的小组有:2﹣4﹣7﹣9﹣11、4﹣6﹣9﹣11﹣1、6﹣8﹣11﹣1﹣3、8﹣10﹣1﹣3﹣5、10﹣12﹣3﹣5﹣7、12﹣2﹣5﹣7﹣9计6种.3类:3偶2奇(或2奇3偶)所组成的小组有:2﹣4﹣6﹣9﹣11、4﹣6﹣8﹣11﹣1、6﹣8﹣10﹣1﹣3、8﹣10﹣12﹣3﹣5、10﹣12﹣2﹣5﹣7、12﹣2﹣4﹣7﹣9计6种.4类:4偶1奇(或1奇4偶)所组成的小组有:2﹣4﹣6﹣8﹣11、4﹣6﹣8﹣10﹣1、6﹣8﹣10﹣12﹣3、8﹣10﹣12﹣2﹣5、10﹣12﹣2﹣4﹣7、12﹣2﹣4﹣6﹣9计6种.根据计算法得:6+6+(6+6+6+6)=6+6+24=36(种).故:共有36种方法组队.二、填空题Ⅲ(共3小题,每小题12分,满分36分)9.(12分)如图,在直角三角形ABC中,AB、BC的长度分别是15、20,四边形BDEF是正方形,如果三角形EMN的高EH的长度是2,那么,正方形BDEF的面积为100 .【解答】解:在直角三角形ABC中,因为AB、BC的长度分别是15、20,所以AC=25,在△ABC和△EHM中,∵==,∴==,∴HM=,EM=,设正方形BDEF的边长为x,在△ADM和△EHM中,∵=,∴=,解得x=10,∴正方形BDEF的面积为100,故答案为100.10.(12分)甲、乙、丙三人在一条周长为360米环形跑道上的同一出发点:甲先出发,逆时针方向跑步;在甲还未完成一圈时,乙、丙同时出发,顺时针方向跑步;当甲、乙第一次相遇时,丙刚好距他们半圈;一段时间后,当甲、丙第一次相遇时,乙刚好也距他们半圈.如果乙的速度是甲的4倍,那么,当乙、丙出发时,甲已经跑了90 米.【解答】解:由于甲、乙第一次相遇时,丙刚好距他们半圈;一段时间后,当甲、丙第一次相遇时,乙刚好也距他们半圈.所以,甲、乙第一次相遇之后,甲乙继续跑一圈半,乙丙相差半圈,即:甲乙跑:360+×360=540米,甲丙一共跑:×360=180(米),所以,甲跑了540×=108(米),乙跑了540﹣108=432(米),丙跑了180﹣108=72(米),所以,乙的速度是丙速度的=6倍,即:丙的速度是甲的,180÷(4﹣)=54(米),360﹣5×54=90(米)答:乙、丙出发时,甲已经跑了90米,故答案为:9011.(12分)动物王国里的老虎总说真话,狐狸总说假话,猴子有时说真话、有时说假话.现有这三种动物各100只,分成100组,每组3只动物恰好一种2只,另一种1只.分好组后,功夫熊猫问每只动物“你组内有老虎吗”,结果恰有138只回答“有”;功夫熊猫又问每只动物“你组内有狐狸吗”,结果恰有188只回答“有”.问两次都说真话的猴子有76 只.【解答】解:设与老虎在一起的猴子有x只,与老虎在一起的狐狸有y只,在与老虎一起的猴子中说假话的猴子有m只(m≤x),在与狐狸一起的猴子中说假话的猴子有n只(n≤100﹣x),与猴子在一起的老虎有z只,则(x﹣m)+(100﹣y)+n=38①,m+(100﹣x﹣n)+(100﹣z)=188②,①+②整理可得z=74﹣y③,所以x只猴子与(74﹣y)只老虎在一起,y只狐狸与(y+26)只老虎在一起,(100﹣x)猴子与(100﹣y)只狐狸在一起,因为每组中只有2种共3只动物,所以x≤2(74﹣y),y+26≤2y,(100﹣x)≤2(100﹣y),所以100≤348﹣4y,所以y≤62,所以100﹣y≥38,所以(x﹣m)+(100﹣y)+n≥38(当且仅当x=m,n=0时取等号),结合①②③得到y=62,z=12,因为x≤2(74﹣y),(100﹣x)≤2(100﹣y),所以x=24,所以说真话的猴子有100﹣24=76只.可得分组的方法有24只猴子和12只老虎在一起,共12组,62只狐狸和88只老虎在一起,共50组,76只猴子和38只狐狸在一起,共38组,功夫熊猫问每只动物“你组内有老虎吗”,结果恰有138只回答“有”,表示100只老虎和38只狐狸回答“有”;76只猴子回答没有;功夫熊猫又问每只动物“你组内有狐狸吗”,结果恰有188只回答“有”.表示24只猴子、88只老虎和76只猴子回答“有”,故答案为76.声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2019/5/5 18:14:59;用户:小学奥数;邮箱:pfpxxx02@;学号:20913800。
四年级数学花园探秘初赛真题+解析

名师提醒:奥数学不好,我们来支招!1、心态平和是前提;2、系统学习最重要;3、技巧策略不可少;4、针对练习是必要。
2015年“数学花园探秘”科普活动四年级组初试试卷A一.填空题(每题8分,共32分)1.计算()=÷⨯⨯⨯-57532235。
2.在下面算式的每个方框中填入一个适当的数字,使得乘法竖式成立,两个乘数之和为。
3.五个人站成一排,每人戴一顶不同的帽子,编号为1、2、3、4、5的帽子,每人只能看到前面的人的帽子.小王一顶都看不到;小孔只看到4号帽子;小田没有看到3号帽子,但看到了1号帽子;小严看到了有3顶帽子,但没有看到3号帽子;小韦看到了3号帽子和2号帽子,小田戴________号帽子。
4.右图中共有________个三角形。
二.填空题(每题10分,共40分)5.王伯伯养了一些鸡、兔和鹤。
其中鹤白天双足站立,夜间则单足站立;鸡晚上睡觉时则把头藏起来。
细心的悦悦发现:不论白天还是晚上,足数和头数的差都一样,那么,如果白天悦悦可以数出56条腿,晚上会数出________个头。
6.在下图中可以取出一个由三个小方格组成的“L”形,现在要求取出的都是全白色的,共有________种不同的取法(允许“L”形旋转)。
7.在空格内填入数字1-6,使得每个雪花和三个方向上六个格内数字都不重复,如下左图是一个完整的例子.请填出右图空格中的数字,那么图中四个英文字母所代表的四位数ABCD是________。
8.有11个小朋友围成一圈玩游戏,按照顺时针分别编号为1,2,3,…,11号,游戏规则是从1号开始,每个人说一个两位数,要求这个两位数数字和不能是6和9,而且后说的小朋友不能说之前说过的数,直到有人说不出新的数,游戏就结束,说不出数的人就作为游戏的输家,那么最后________号是游戏的输家。
三.填空题(每题12分,共48分)9.甲、乙、丙三人从A地出发前往B地。
甲8:00出发,乙8:20出发,丙8:30出发。
2020年数学花园探秘三年级详解

2020年“数学花园探秘”详解
解析:
所以30+30=60cm
解析:每次快递小哥说4个字,鹦鹉说2个字,最后一次他们说的字数相同,所以前面每次快递小哥比鹦鹉每次多2个字,12÷2=6次6×2+4=16个字
解析:假设公鸡有10只,母鸡有10+17=27只兔子有10+27—13=24只母兔=19只公兔=5只27—19=8只
解析:
2020÷40=50余数是20和第20次的是同样的就是在10号
解析:重复的汉字是你是我的没有重复的是诗正如梦要求相邻的和为一位数要求和最大那么“你”最大取8,的取0时梦可以取9.
8+1+7+0+6+3+2+9=36
解析:在除法和乘法的哪里找突破口,
解析:年龄差不变,4个人与一个人的年龄差。
