2011高教社杯全国大学生数学建模竞赛题目
高教社杯全国大学生数学建模竞赛题目(四套ABCD)

高教社杯全国大学生数学建模竞赛题目(四套ABCD)当我第一遍读一本好书的时候,我仿佛觉得找到了一个朋友;当我再一次读这本书的时候,仿佛又和老朋友重逢。
我们要把读书当作一种乐趣,并自觉把读书和学习结合起来,做到博览、精思、熟读,更好地指导自己的学习,让自己不断成长。
让我们一起到店铺一起学习吧!2017年高教社杯全国大学生数学建模竞赛题目A题 CT系统参数标定及成像CT(Computed T omography)可以在不破坏样品的情况下,利用样品对射线能量的吸收特性对生物组织和工程材料的样品进行断层成像,由此获取样品内部的结构信息。
一种典型的二维CT系统如图1所示,平行入射的X射线垂直于探测器平面,每个探测器单元看成一个接收点,且等距排列。
X射线的发射器和探测器相对位置固定不变,整个发射-接收系统绕某固定的旋转中心逆时针旋转180次。
对每一个X射线方向,在具有512个等距单元的探测器上测量经位置固定不动的二维待检测介质吸收衰减后的射线能量,并经过增益等处理后得到180组接收信息。
CT系统安装时往往存在误差,从而影响成像质量,因此需要对安装好的CT系统进行参数标定,即借助于已知结构的样品(称为模板)标定CT系统的参数,并据此对未知结构的样品进行成像。
请建立相应的数学模型和算法,解决以下问题:(1) 在正方形托盘上放置两个均匀固体介质组成的标定模板,模板的几何信息如图2所示,相应的数据文件见附件1,其中每一点的数值反映了该点的吸收强度,这里称为“吸收率”。
对应于该模板的接收信息见附件2。
请根据这一模板及其接收信息,确定CT系统旋转中心在正方形托盘中的位置、探测器单元之间的距离以及该CT系统使用的X射线的180个方向。
(2) 附件3是利用上述CT系统得到的某未知介质的接收信息。
利用(1)中得到的标定参数,确定该未知介质在正方形托盘中的位置、几何形状和吸收率等信息。
另外,请具体给出图3所给的10个位置处的吸收率,相应的数据文件见附件4。
2010高教社杯全国大学生数学建模竞赛官方题目(含ABCD)
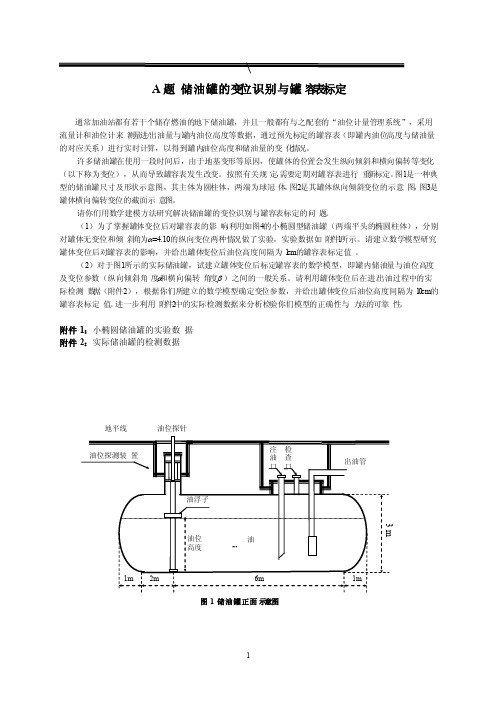
\A 题 储油罐的变位识别与罐容表标定通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表发生改变。
按照有关规定,需要定期对罐容表进行重新标定。
图1是一种典型的储油罐尺寸及形状示意图,其主体为圆柱体,两端为球冠体。
图2是其罐体纵向倾斜变位的示意图,图3是罐体横向偏转变位的截面示意图。
请你们用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题。
(1)为了掌握罐体变位后对罐容表的影响,利用如图4的小椭圆型储油罐(两端平头的椭圆柱体),分别对罐体无变位和倾斜角为α=4.10的纵向变位两种情况做了实验,实验数据如附件1所示。
请建立数学模型研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm 的罐容表标定值。
(2)对于图1所示的实际储油罐,试建立罐体变位后标定罐容表的数学模型,即罐内储油量与油位高度及变位参数(纵向倾斜角度α和横向偏转角度β )之间的一般关系。
请利用罐体变位后在进/出油过程中的实际检测数据(附件2),根据你们所建立的数学模型确定变位参数,并给出罐体变位后油位高度间隔为10cm 的罐容表标定值。
进一步利用附件2中的实际检测数据来分析检验你们模型的正确性与方法的可靠性。
附件1:小椭圆储油罐的实验数据 附件2:实际储油罐的检测数据油油浮子出油管油位探测装置注油口 检查口地平线 2m6m1m1m3 m油位高度图1 储油罐正面示意图油位探针油位探针α地平线 图2 储油罐纵向倾斜变位后示意图油油浮子出油管油位探测装置注油口 检查口水平线(b) 小椭圆油罐截面示意图α油油浮子出油管油位探针注油口水平线2.05mcm 0.4m1.2m1.2m1.78m(a) 小椭圆油罐正面示意图图4 小椭圆型油罐形状及尺寸示意图图3 储油罐截面示意图(b )横向偏转倾斜后正截面图地平线β地平线垂直线油位探针(a )无偏转倾斜的正截面图油位探针油位探测装置地平线油3m油B题2010年上海世博会影响力的定量评估2010年上海世博会是首次在中国举办的世界博览会。
2011高教社杯全国大学生数学建模竞赛B题(题目改变)参考答案

交巡警服务平台的设置与调度优化分析摘要本文综合应用了Floyd算法,匈牙利算法,用matlab计算出封锁全市的时间为1.2012小时。
并在下面给出了封锁计划。
为了得出封锁计划,首先根据附件2的数据将全市的道路图转为邻接矩阵,然后根据邻接矩阵采用Floyd算法计算出该城市任意两点间的最短距离。
然后从上述矩阵中找到各个交巡警平台到城市各个出口的最短距离,这个最短距离矩阵即可作为效益矩阵,然后运用匈牙利算法,得出分派矩阵。
根据分派矩阵即可制定出封锁计划:96-151,99-153,177-177,175-202,178-203,323-264,181-317, 325-325,328-328,386-332,322-362,100-387,379-418,483-483, 484-541,485-572。
除此以外,本人建议在编号为175的路口应该设置一个交巡警平台,这样可以大大减少封锁全市的时间,大约可减少50%。
关键词: Floyd算法匈牙利算法 matlab一、问题重述“有困难找警察”,是家喻户晓的一句流行语。
警察肩负着刑事执法、治安管理、交通管理、服务群众四大职能。
为了更有效地贯彻实施这些职能,需要在市区的一些交通要道和重要部位设置交巡警服务平台。
每个交巡警服务平台的职能和警力配备基本相同。
由于警务资源是有限的,如何根据城市的实际情况与需求合理地设置交巡警服务平台、分配各平台的管辖范围、调度警务资源是警务部门面临的一个实际课题。
试就某市设置交巡警服务平台的相关情况,建立数学模型分析研究下面的问题:警车的时速为60km/h, 现有突发事件,需要全市紧急封锁出入口,试求出全市所有的交巡警平台最快的封锁计划,一个出口仅需一个平台的警力即可封锁。
二、模型假设1、假设警察出警时的速度相同且不变均为60/km h 。
2、假设警察出警的地点都是平台处。
3、假设警察接到通知后同时出警,且不考虑路面交通状况。
三、符号说明及一些符号的详细解释A 存储全市图信息的邻接矩阵 D 任意两路口节点间的最短距离矩阵X 01-规划矩阵ij a ,i j 两路口节点标号之间直达的距离 ij d 从i 路口到j 路口的最短距离 ij b 从i 号平台到j 号出口的最短距离ij x 取0或1,1ij x =表示第i 号平台去封锁j 号出口在本文中经常用到,i j ,通常表示路口的编号,但是在ij d ,ij b ,ij x 不再表示这个意思,i 表示第i 个交巡警平台,交巡警平台的标号与附件中给的略有不同,如第21个交巡警平台为附件中的标号为93的交巡警平台,本文的标号是按照程序的数据读取顺序来标注的,在此声明;j 表示第j 个出口,如:第5个出口对应于附件中的路口编号为203的出口。
201x高教社杯全国大学生数学建模竞赛-天然肠衣搭配问题

2011高教社杯全国大学生数学建模竞赛承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写):我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):参赛队员(打印并签名) :1.2.3.指导教师或指导教师组负责人(打印并签名):日期:年月日赛区评阅编号(由赛区组委会评阅前进行编号):2011高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):题目摘要天然肠衣搭配问题优化模型摘要:本文通过对题目中所给数据和参考资料以及网站上获得的数据进行分析,利用多种模型对数据规律进行归纳提炼.首先我们建立了,方程和不等式,利用线性归回求最优,利用matelab求解,通过常识和分析我们知道,由于受到人为和多种外在和内在因素的影响,是不可能实现的,它只是在理想情况下的一种模式.在这个模型中,由于两个因素的变化,使得在预测时只能简单的预测下数据,虽然精度很大,但是预测的时间太短。
于是,在分析了天然糖衣的搭配问题。
首先我们是将数据进行处理,利用四舍五入以0.5为一个等级划分并作图。
而后我们是对两表的数据信息进行分类,总共分为三类。
解本题的思路是,利用线性归回求最优解,将最优的搭配一一列好,将剩余的材料进行降级处理后再次搭配。
2011年全国大学生数学建模竞赛B题一等奖论文

我们参赛选择的题号是(从 A/B/C/D 中选择一项填写) : 我们的参赛报名号为(如果赛区设置报名号的话) : 所属学校(请填写完整的全名) : 参赛队员 (打印并签名) :1. 赵东辉 2. 张晓凤 3. 汪立 指导教师或指导教师组负责人 (打印并签名) : 林军 日期: 日 西
交巡警服务平台的设置与调度
摘要:在我国经济社会快速发展进程中, 警察的工作任务日益繁重。由于警 务资源是有限的,如何根据城市的实际情况与需求合理地设置交巡警服务平台、 分配各平台的管辖范围、调度警务资源是警务部门面临的一个实际课题。 问题一: (1)题目要求在城区 A 的 20 个巡警服务台位置确定的情况下,按照尽量 3min 到达案发地的原则为各服务平台分配管辖范围。对于此问题本文建立最大 集合覆盖模型,并利用数学软件 MATLAB 进行分配求解,最后得到 A 区现有每个 巡警服务台的管辖范围如表 1。 (2)我们对于 13 条交通要道实现快速全封锁的问题,以所用时间最小为目 标,引入 0-1 变量,建立该问题的 0-1 规划模型,并借助数学软件 LINGO 进行求 解,求解结果见表 4。 (3)由问题(1)的分配结果可知,在现有巡警服务台的设置下:①还有 6 个路口在案发时巡警不能在 3min 之内到达, 即必然导致某些地方出警时间过长; ②我们根据每个巡警服务台的工作量的方差定义了工作量不均衡度,结果显示: 此时服务台的工作量不均衡度为 8.4314。 为了解决上述出警时间过长与工作量不均衡的问题。我们建立集合覆盖的 0-1 规划模型,求解结果表明:在增加 4 个平台的情况下,可以解决出警时间过 长的问题。 在此基础上我们又解决了工作量不均衡的问题,在增加 4 个巡警服务 台的情况下, 使平台的工作量的不均衡度降为 3.0742。 增加的 4 个巡警服务台的 路口标号见表 8。 问题二: (1) 本文定义了两个评价原则, 原则一: 巡警能在 3min 之内到达案发路口; 原则二: 巡警服务台的工作量均衡度尽量小。 根据以上两个原则对该市现有巡警 服务台的设置方案的合理性进行评价, 评价结果显示, 有下述两种不合理的情况: ①有 138 个路口,在案发时巡警不能在 3min 之内到达;②此时的不均衡度已达 40.3。基于上述两点,现有的巡警服务台设置极其不合理。 针对现有巡警服务台设置不合理的情况下, 本文提出三种方案对设置进行优 化调整。方案一:保持现有巡警服务台的个数和位置,再在其他路口增设巡警服 务台;方案二:保持现有巡警服务台的个数,但对其位置进行调整;方案三:不 考虑现有巡警服务台的设置情况,重新确定全城的最佳巡警服务台数目与位置。 (2)本问题实质是单目标规划问题,以巡警围堵时间最短为目标,以成功围 堵为条件。对于巡警的成功围堵,可以转化为二部图的完全匹配,利用匈牙利算 法,求得最佳围堵方案。
高教社杯全国大学生数学建模竞赛题目

高教社杯全国大学生数学建模竞赛题目高教社杯全国大学生数学建模竞赛已经成为了我国大学生数学建模领域一项极具影响力的赛事之一。
作为一项旨在提高大学生数学建模能力和创新能力的比赛,其题目的设计非常关键。
从2009年开始,高教社杯全国大学生数学建模竞赛就引入了“数学、建模和计算机”三个方面相结合来设置竞赛题目,旨在充分体现创新性、实际性和时代性。
每年的竞赛题目独具特色,既注重基础,又注重应用,给参赛选手提供了一个广泛展示科技创新成果的舞台,极大地推动了我国大学生数学建模水平的提升。
以下是近几年高教社杯全国大学生数学建模竞赛的题目:2019年:多元时空数据的融合与应用该题目要求选手用数据分析和模型建模技术进行多元时空数据融合,制作出能应用于数据分析、可视化和预测等领域的模型。
该题目考验选手的计算机应用能力和数据处理能力。
2018年:海洋环境与生态建设该题目需要选手从海洋生态、环境污染、资源利用、气候变化等方面出发,结合数学模型和计算机技术,探究关键问题。
选手要能积极运用大数据技术,分析丰富的海洋数据,并针对不同海洋问题给出行之有效的数学和计算模型。
2017年:共享单车智能管理与优化该题目以共享单车为研究对象,要求选手分析共享单车智能管理的效能,探究如何在现有的单车停放、调度、维修等方面研究出更优的管理模式,实现精准的数量分配和智能的管理系统。
以上三个题目从不同的角度出发,分别涉及了数据分析、海洋环境、共享单车等多个领域。
它们都融合了计算机技术和数学建模思想,是一道技术与创新相结合的精彩之作。
总体而言,高教社杯全国大学生数学建模竞赛的题目设计体现了需求实际、具有挑战性和创新性等特点,能够有效地提高大学生的数学建模和创新能力。
同时,它也为推进我国大学生数学建模水平的提升做出了重大贡献。
相信未来会有更多具有前瞻性和实践性的竞赛题目出现,让更多大学生通过数学建模实现梦想。
高教社杯全国大学生数学建模竞赛题目 穿越沙漠

高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)B 题 穿越沙漠考虑如下的小游戏:玩家凭借一张地图,利用初始资金购买一定数量的水和食物(包括食品和其他日常用品),从起点出发,在沙漠中行走。
途中会遇到不同的天气,也可在矿山、村庄补充资金或资源,目标是在规定时间内到达终点,并保留尽可能多的资金。
游戏的基本规则如下:(1)以天为基本时间单位,游戏的开始时间为第0天,玩家位于起点。
玩家必须在截止日期或之前到达终点,到达终点后该玩家的游戏结束。
(2)穿越沙漠需水和食物两种资源,它们的最小计量单位均为箱。
每天玩家拥有的水和食物质量之和不能超过负重上限。
若未到达终点而水或食物已耗尽,视为游戏失败。
(3)每天的天气为“晴朗”、“高温”、“沙暴”三种状况之一,沙漠中所有区域的天气相同。
(4)每天玩家可从地图中的某个区域到达与之相邻的另一个区域,也可在原地停留。
沙暴日必须在原地停留。
(5)玩家在原地停留一天消耗的资源数量称为基础消耗量,行走一天消耗的资源数量为基础消耗量的2倍。
(6)玩家第0天可在起点处用初始资金以基准价格购买水和食物。
玩家可在起点停留或回到起点,但不能多次在起点购买资源。
玩家到达终点后可退回剩余的水和食物,每箱退回价格为基准价格的一半。
(7)玩家在矿山停留时,可通过挖矿获得资金,挖矿一天获得的资金量称为基础收益。
如果挖矿,消耗的资源数量为基础消耗量的3倍;如果不挖矿,消耗的资源数量为基础消耗量。
到达矿山当天不能挖矿。
沙暴日也可挖矿。
(8)玩家经过或在村庄停留时可用剩余的初始资金或挖矿获得的资金随时购买水和食物,每箱价格为基准价格的2倍。
请根据游戏的不同设定,建立数学模型,解决以下问题。
1. 假设只有一名玩家,在整个游戏时段内每天天气状况事先全部已知,试给出一般情况下玩家的最优策略。
求解附件中的“第一关”和“第二关”,并将相应结果分别填入Result.xlsx 。
2011高教社杯全国大学生数学建模竞赛A题

城市表层土壤重金属污染分析摘要随着城市经济的快速发展和城市人口的不断增加,人类活动对城市环境质量的影响日益突出,研究人类活动影响下城市地质环境的演变模式日益成为人们关注的焦点。
按照功能划分,可将城市划分为生活区、工业区、山区、主干道路区和公园绿地区等,不同区域环境受人类活动影响的程度不同。
对于问题一,利用附件中所给数据,通过MATLAB插值法建立城市地形的三维模型,以及八种重金属元素空间浓度分布图(共8幅),通过模型我们可以清楚地看到不同元素在不同区域的分布情况。
分析不同地区污染程度时我们采用了Muller指数将污染情况分成0—6共7个等级,并列表统计不同功能区不同金属元素的污染等级。
通过比较可以清楚地看到该城区不同区域重金属的污染程度,按严重程度依次为工业区主干道路区生活区公园绿地区山区。
对于问题二,通过问题一我们发现工业区、主干道路区和生活区是重金属污染较为严重的区域。
由于目前我国在重金属冶炼、开采、加工等领域生产方式粗放,造成了大量的重金属元素如Pb、Hg、Cu等进入空气、水体以及土壤,造成了严重的重金属污染。
人类生活中日常使用的一些物品含有大量重金属元素,如电池中含有大量Hg、Zn、Ni等重金属元素,他们通过自然和生物降解,随雨水进入水体和土壤中。
对于问题三,我们通过分析前两问得出的结论,即重金属元素从高海拔向低海拔,从高浓度向低浓度扩散,我们建立数学模型,通过求解函数极值,可确定污染源位置。
对于问题四,我们仔细分析了上述数学模型的优缺点,为了更好地研究城市地质环境的演变模式,还应收集该城市盛行风风向、水流流向、人类活动、土壤中生物活动情况、土壤本身的性质情况以及各污染源污染强度、持续时间、当地的空气污染情况等信息。
综合各因子的作用效果,通过回归分析解决新模型。
关键词:插值法;Muller;扩散模型;回归分析1一、问题重述随着城市经济的快速发展和城市人口的不断增加,人类活动对城市环境质量的影响日显突出。
2012高教社杯全国大学生数学建模竞赛 C题

其中, 2.对标准化阵Z求相关系数矩阵
,得标准化阵Z。
R [rij ] p
ZTZ xp n 1
kj
其中, rij
z
z kj
n 1
, i, j 1,2...p
3.解样本相关矩阵R的特征方程 R I p 0 得p个特征根,确定主成分
按
m j 1 p
j
j 1 j
四.问题分析
问题的重要性:
脑卒中俗称“中风”,是由向大脑输送血液的血管疾病引起的一种急 性疾病。脑卒中或脑血管意外( CVA )会对大脑组织造成突发性损坏,通常 发生在向大脑输送氧气和其它营养物的血管爆裂之时,或发生在血管被血 凝块或其它颗粒物质阻塞之时。如果神经细胞缺乏足够的氧气供给,几分 钟内就会死亡。接着,受这些神经细胞控制的身体机能也会随之失去作用。 由于死亡的大脑细胞无法替换,因此脑卒中造成的后果通常是永久的。患 有大血管急性缺血性发作的患者,每小时损失 1 亿 2 千万神经细胞、 8300 亿神经键、 和 714 千米有髓纤维。 每分钟有 190 万神经细胞、 140 亿神经键、 12 千米有髓纤维受损。与因大脑老化而产生的神经细胞的正常死亡速率相 比,缺血性大脑如果不接受治疗,则每小时老化 3.6 年。 专家指出:全国每年新发脑卒中患者达 200 万人,因此我们应该引起 关注,到底有哪些因素导致脑卒中患者逐年增加?接下来我们就对导致脑 卒中发病率的因素进行分析。
我们参赛选择的题号是(从 A/B/C/D 中选择一项填写) : 我们的参赛报名号为(如果赛区设置报名号的话) : 所属学校(请填写完整的全名) : 参赛队员 (打印并签名) :1. 2. 3. 指导教师或指导教师组负责人 (打印并签名): 日期: 2012 年 9
大学生数学建模竞赛试题(全套)

2011年大学生数学建模竞赛试题(全套)12011高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)A题城市表层土壤重金属污染分析随着城市经济的快速发展和城市人口的不断增加,人类活动对城市环境质量的影响日显突出。
对城市土壤地质环境异常的查证,以及如何应用查证获得的海量数据资料开展城市环境质量评价,研究人类活动影响下城市地质环境的演变模式,日益成为人们关注的焦点。
按照功能划分,城区一般可分为生活区、工业区、山区、主干道路区及公园绿地区等,分别记为1类区、2类区、……、5类区,不同的区域环境受人类活动影响的程度不同。
现对某城市城区土壤地质环境进行调查。
为此,将所考察的城区划分为间距1公里左右的网格子区域,按照每平方公里1个采样点对表层土(0~10 厘米深度)进行取样、编号,并用GPS 记录采样点的位置。
应用专门仪器测试分析,获得了每个样本所含的多种化学元素的浓度数据。
另一方面,按照2公里的间距在那些远离人群及工业活动的自然区取样,将其作为该城区表层土壤中元素的背景值。
附件1列出了采样点的位置、海拔高度及其所属功能区等信息,附件2列出了8种主要重金属元素在采样点处的浓度,附件3列出了8种主要重金属元素的背景值。
现要求你们通过数学建模来完成以下任务:(1) 给出8种主要重金属元素在该城区的空间分布,并分析该城区内不同区域重金属的污染程度。
(2) 通过数据分析,说明重金属污染的主要原因。
(3) 分析重金属污染物的传播特征,由此建立模型,确定污染源的位置。
(4) 分析你所建立模型的优缺点,为更好地研究城市地质环境的演变模式,还应收集什么信息?有了这些信息,如何建立模型解决问题?B题交巡警服务平台的设置与调度“有困难找警察”,是家喻户晓的一句流行语。
警察肩负着刑事执法、治安管理、交通管理、服务群众四大职能。
为了更有效地贯彻实施这些职能,需要在市区的一些交通要道和重要部位设置交巡警服务平台。
2011数学建模B题

2011高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)B题交巡警服务平台的设置与调度“有困难找警察”,是家喻户晓的一句流行语。
警察肩负着刑事执法、治安管理、交通管理、服务群众四大职能。
为了更有效地贯彻实施这些职能,需要在市区的一些交通要道和重要部位设置交巡警服务平台。
每个交巡警服务平台的职能和警力配备基本相同。
由于警务资源是有限的,如何根据城市的实际情况与需求合理地设置交巡警服务平台、分配各平台的管辖范围、调度警务资源是警务部门面临的一个实际课题。
试就某市设置交巡警服务平台的相关情况,建立数学模型分析研究下面的问题:(1)附件1中的附图1给出了该市中心城区A的交通网络和现有的20个交巡警服务平台的设置情况示意图,相关的数据信息见附件2。
请为各交巡警服务平台分配管辖范围,使其在所管辖的范围内出现突发事件时,尽量能在3分钟内有交巡警(警车的时速为60km/h)到达事发地。
对于重大突发事件,需要调度全区20个交巡警服务平台的警力资源,对进出该区的13条交通要道实现快速全封锁。
实际中一个平台的警力最多封锁一个路口,请给出该区交巡警服务平台警力合理的调度方案。
根据现有交巡警服务平台的工作量不均衡和有些地方出警时间过长的实际情况,拟在该区内再增加2至5个平台,请确定需要增加平台的具体个数和位置。
(2)针对全市(主城六区A,B,C,D,E,F)的具体情况,按照设置交巡警服务平台的原则和任务,分析研究该市现有交巡警服务平台设置方案(参见附件)的合理性。
如果有明显不合理,请给出解决方案。
如果该市地点P(第32个节点)处发生了重大刑事案件,在案发3分钟后接到报警,犯罪嫌疑人已驾车逃跑。
为了快速搜捕嫌疑犯,请给出调度全市交巡警服务平台警力资源的最佳围堵方案。
附件1:A区和全市六区交通网络与平台设置的示意图。
附件2:全市六区交通网络与平台设置的相关数据表(共5个工作表)。
附图1:A区的交通网络与平台设置的示意图附图2:全市六区交通网络与平台设置的示意图说明:(1)图中实线表示市区道路;红色线表示连接两个区之间的道路;(2)实圆点“·”表示交叉路口的节点,没有实圆点的交叉线为道路立体相交;(3)星号“*”表示出入城区的路口节点;(4)圆圈“○”表示现有交巡警服务平台的设置点;(5)圆圈加星号“○*”表示在出入城区的路口处设置了交巡警服务平台;(6)附图2中的不同颜色表示不同的区。
2011年高教杯四川赛区最终成绩

丁川 骆川义 樊胜 樊胜 孙云龙 李绍文 粱涛 蒲伟 薛长虹 薛长虹 杨晗 蒲伟 何平 王璐 于凯 赵联文 蒲伟 马丽琼 黄雪梅 张兴元 万美凯 张雁 马骁 马志霞 马志霞 李玲娜 数学建模组 数模指导组 数模指导组 数模指导组 左莉 沈荣泸 陈新娟 郭小林 李开友 教师指导组 教师指导组 刘鸿博 张 瑞 张森 陈东 陈龙 陈琼 陈延礼 戴岱
甲组 62队
四川省一等奖(77 队) 参赛学校 参赛队员 成都学院 王政,白燚焱,邓敏 电子科技大学 廖庆,李憬宇,张亚萍 电子科技大学 彭贵强,蒋太翔,莫念凯 乐山师范学院 陈强,余慷,张小欢 内江师范学院 张密,赵凤,张菊 四川大学 马毓,聂颖,吴博剑 四川大学 孔凡航,孙玉欣,陈豪 四川大学 许译方,迟雄香,刘洋 四川大学 付仕辉,张军,李敏 四川大学 鲁宏,刘潇婧,陈阳晴 四川大学 李晓萌,王峰,蒋珏 四川大学 刘丹青,王玉东,席磊磊 四川大学 徐强,蔡颖,罗志一 四川理工学院 张勇卫,岳智慧,肖 晴 四川师范大学 何鹏,张婷,张倩 四川师范大学 邓泽培,谢杨晓洁,邱忠娟 四川师范大学 付如意,王艳飞,姜仁志 四川师范大学 李承旭,王庆,李振国 四川师范大学 管天彦,李代江,陈巧丹 四川师范大学文理学院 苟祝、赵梦霞、祝芸菲 四川师范大学文理学院 董燕、钟凤梅、张艳伟 西华大学 彭彪,刘德富,宋新新 西华大学 马万里,刘腾飞,黄冉 西南财经大学 谢宏蕾,张会彦,徐薪凯 2
4
西南财经大学 西南财经大学 西南财经大学 西南财经大学 西南财经大学 西南财经大学 西南交通大学 西南交通大学 西南交通大学 西南交通大学 西南交通大学 西南交通大学 西南交通大学 西南交通大学 西南交通大学 西南交通大学 西南交通大学 西南交通大学峨眉校区 西南交通大学峨眉校区 西南交通大学峨眉校区 西南交通大学峨眉校区 西南交通大学峨眉校区 西南交通大学峨眉校区 西南民族大学 西南民族大学 西南石油大学
高教社杯全国大学生数学建模竞赛题目 中小微企业的信贷决策

高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)C题中小微企业的信贷决策在实际中,由于中小微企业规模相对较小,也缺少抵押资产,因此银行通常是依据信贷政策、企业的交易票据信息和上下游企业的影响力,向实力强、供求关系稳定的企业提供贷款,并可以对信誉高、信贷风险小的企业给予利率优惠。
银行首先根据中小微企业的实力、信誉对其信贷风险做出评估,然后依据信贷风险等因素来确定是否放贷及贷款额度、利率和期限等信贷策略。
某银行对确定要放贷企业的贷款额度为10~100万元;年利率为4%~15%;贷款期限为1年。
附件1~3分别给出了123家有信贷记录企业的相关数据、302家无信贷记录企业的相关数据和贷款利率与客户流失率关系的2019年统计数据。
该银行请你们团队根据实际和附件中的数据信息,通过建立数学模型研究对中小微企业的信贷策略,主要解决下列问题:(1) 对附件1中123家企业的信贷风险进行量化分析,给出该银行在年度信贷总额固定时对这些企业的信贷策略。
(2) 在问题1的基础上,对附件2中302家企业的信贷风险进行量化分析,并给出该银行在年度信贷总额为1亿元时对这些企业的信贷策略。
(3) 企业的生产经营和经济效益可能会受到一些突发因素影响,而且突发因素往往对不同行业、不同类别的企业会有不同的影响。
综合考虑附件2中各企业的信贷风险和可能的突发因素(例如:新冠病毒疫情)对各企业的影响,给出该银行在年度信贷总额为1亿元时的信贷调整策略。
附件1 123家有信贷记录企业的相关数据附件2 302家无信贷记录企业的相关数据附件3 银行贷款年利率与客户流失率关系的2019年统计数据附件中数据说明:(1) 进项发票:企业进货(购买产品)时销售方为其开具的发票。
(2) 销项发票:企业销售产品时为购货方开具的发票。
(3) 有效发票:为正常的交易活动开具的发票。
(4) 作废发票:在为交易活动开具发票后,因故取消了该项交易,使发票作废。
2011年数学建模D题天然肠衣搭配优化问题答案

2011高教社杯全国大学生数学建模竞赛题目D题天然肠衣搭配问题摘要该题主要研究生产天然肠衣及其搭配问题,并且要求在一定的原料情况下,生产的成品捆数越多越好,该问题属于线性规划并且为取整线性规划来求最优解问题。
根据每种规格的规定,在解题的过程中,我们建立线性方程组作为第一层优化,然后将建立的模型带入到lingo软件中,得到第一层优化最优方案,之后又根据实际进行了第二层优化,得到规格一成品捆数的上限为15捆;规格二成品的捆数的上限为37捆;规格三成品的捆数的上限为137捆;总捆数为188捆。
在一定的误差允许范围内,该方案较符合题目所属要求和实际生产情况。
并且生产后的剩余废弃原料少,做到了在限定原料内创造最大利润的好处。
问题简述:原料按长度分档,通常以0.5米为一档,如:3-3.4米按3米计算,3.5米-3.9米按3.5米计算,其余的依此类推。
成品规格和原料描述如图所示:表1 成品规格表最短长度最大长度根数总长度3 6.5 20 897 13.5 8 8914 ∞ 5 89表2 原料描述表长度3-3.4 3.5-3.9 4-4.4 4.5-4.9 5-5.4 5.5-5.9 6-6.4 6.5-6.9根数43 59 39 41 27 28 34 21长度7-7.4 7.5-7.9 8-8.4 8.5-8.9 9-9.4 9.5-9.910-10.410.5-10.9根数24 24 20 25 21 23 21 18长度11-11.411.5-11.9 12-12.412.5-12.913-13.413.5-13.914-14.414.5-14.9根数31 23 22 59 18 25 35 29长度15-15.415.5-15.9 16-16.416.5-16.917-17.417.5-17.918-18.418.5-18.9根数30 42 28 42 45 49 50 64长度19-19.419.5-19.9 20-20.420.5-20.921-21.421.5-21.922-22.422.5-22.9根数52 63 49 35 27 16 12 2长度23-23.423.5-23.9 24-24.424.5-24.925-25.425.5-25.9根数0 6 0 0 0 1本题要求建立数学模型设计一个原料搭配方案,按题中所给规格完成原料搭配方案,并符合如下要求:(1) 对于给定的一批原料,装出的成品捆数越多越好;(2) 对于成品捆数相同的方案,最短长度最长的成品越多,方案越好;(3) 为提高原料使用率,总长度允许有± 0.5米的误差,总根数允许比标准少1根;(4) 某种规格对应原料如果出现剩余,可以降级使用。
高教社杯全国大学生数学建模竞赛题目

高教社杯全国大学生数学建模竞赛题目
(请先阅读“全国大学生数学建模竞赛论文格式规范”)
题 机器人避障问题
图是一个×的平面场景图,在原点(, )点处有一个机器人,它只能在该平面场景范围内活动。
图中有个不同形状的区域是机器人不能与之发生碰撞的障碍物,
点与障碍物的距离至少超过个单位)。
规定机器人的行走路径由直线段和圆弧组成,其中圆弧是机器人转弯路径。
机器人不能折线转弯,转弯路径由与直线路径相切的一段圆弧组成,也可以由两个或多个相切的圆弧路径组成,但每个圆弧的半径最小为个单位。
为了不与障碍物发生碰撞,同时要求机器人行走线路与障碍物间的最近距离为个单位,否则将发生碰撞,若碰撞发生,则机器人无法完成行走。
机器人直线行走的最大速度为50=v 个单位秒。
机器人转弯时,最大转弯速度为21.0100e
1)(ρρ-+==v v v ,其中ρ是转弯半径。
如果超过该速度,机器人将发生侧 翻,无法完成行走。
请建立机器人从区域中一点到达另一点的避障最短路径和最短时间路径的数学模型。
对场景图中个点(, ),(, ),(, ),(, ),具体计算:
() 机器人从(, )出发,→、→、→和→→→→的最短路径。
() 机器人从 (, )出发,到达的最短时间路径。
注:要给出路径中每段直线段或圆弧的起点和终点坐标、圆弧的圆心坐标以及机器人行走的总距离和总时间。
图×平面场景图。
数学建模“教你如何进行人员分配”的问题
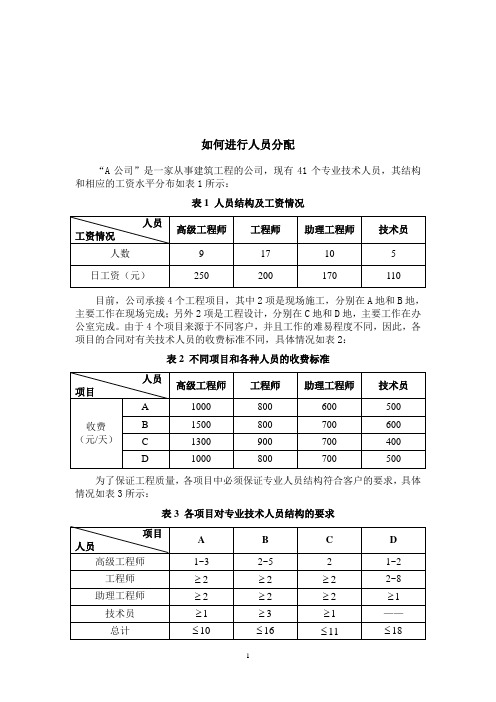
如何进行人员分配“A公司”是一家从事建筑工程的公司,现有41个专业技术人员,其结构和相应的工资水平分布如表1所示:表1 人员结构及工资情况目前,公司承接4个工程项目,其中2项是现场施工,分别在A地和B地,主要工作在现场完成;另外2项是工程设计,分别在C地和D地,主要工作在办公室完成。
由于4个项目来源于不同客户,并且工作的难易程度不同,因此,各项目的合同对有关技术人员的收费标准不同,具体情况如表2:表2 不同项目和各种人员的收费标准为了保证工程质量,各项目中必须保证专业人员结构符合客户的要求,具体情况如表3所示:表3 各项目对专业技术人员结构的要求说明:(1)项目D,由于技术要求较高,人员配备必须是助理工程师以上,技术员不能参加;(2)高级工程师相对稀少,而且是保证质量的关键,因此,各项目客户对高级工程师的配备要求不能少于一定数目的限制。
各项目对其他专业人员也有不同的限制或要求;(3)各项目客户对总人数都有限制;(4)由于C,D两项目是在办公室完成,所以每人每天有50元的管理费开支;由于收费是按人工计算的,而且4个项目总共同时最多需要的人数是10+16+11+18=55,多于公司现有人数41,应如何合理地分配现有的人员力量,使公司每天的直接受益最大?2011年高教社杯全国大学生数学建模竞赛选拔赛题目如何进行人员分配摘要人力资源管理是一个公司进行人力资源分配的重要工作,合理地安排人力资源,能够为企业带来最大的经济效益。
公司不只要对现有的人员进行任务分配,还要使公司的人力资源结构保持一个科学的比例。
本模型旨在为A建筑公司提供一个良好的人员分配方案,达到公司获利最大的目的,以及怎样在以后的人员招聘中使人力资源结构保持一个良好的比例。
在公司现有的情况下,通过分析各种影响因素,排除掉一些不必要的干扰因素,运用整数线性规划和分支定界法的知识建立数学模型,并使用LINGO软件进行编程求解,得出公司人员分配的最佳方案。
高教社杯全国大学生数学建模竞赛上海赛区获奖名单-2011年
2011年高教社杯全国大学生数学建模竞赛上海赛区获奖名单(公示版,按奖级、学校名和题号排列)序奖级题号参赛学校队员1队员2311A复旦大学吴梦月翟晓宇沅21A复旦大学舒天民秦瑛迪炜31A复旦大学王桑原王之光沅41A复旦大学许珂诚吴俣霖沅51A复旦大学黎明嘉薛钧元沅61A265复旦大学何怡琳周卉侃沅71A复旦大学王腾熊丝纬81A复旦大学马淑敏张艳梅沅91B复旦大学周晔何洋101B复旦大学姜宛悦马浩君沅111B复旦大学杨可人张骁沅121A上海交通大学丁星光朱文浩131A上海交通大学蔡元楠牛文昊141A上海交通大学陈宸刘天骥151A上海交通大学于晨刘思妍161A上海交通大学杨元辉余论171A上海交通大学郑博方徐欢乐波181A上海交通大学裘明达吴穹聪191A上海交通大学陈婧姝盛立霏201B上海交通大学阳煜东李一璇211B上海交通大学陈曦仑邱航221B上海交通大学钱臻之张颖异231B上海交通大学王宏剑张一鸣鑫241B上海交通大学吴嘉杰陈之弘251B上海交通大学周光远王翊时瑛261A同济大学冯建设赵云波271A同济大学乔亚丹关响生281A同济大学王威彭子逸291A华东师范大学乌金一唐宇洋301A华东师范大学张一帆薛旻辉311A华东师范大学柴柯辰张晓民衍321A华东师范大学陈诗芸陈婧超尧331A华东理工大学蔡文甫高梁衍341A华东理工大学晋海波李俊挺351B华东理工大学李君楠任翔361B华东理工大学张越宇王硕鸿371B华东理工大学秦奋杨健科381B华东理工大学冯田佳点陈俊睿391B华东理工大学蒋瑞王佳远401A东华大学荀宇豪冉芸云411A东华大学马珂陈晓鹏421A东华大学李璇张柏阳伯洁431A东华大学陈维贾曼妮萍441A东华大学曾佳玉翟相和平451B东华大学张捷奕永峰伟461B东华大学沈天云周吉陆471B东华大学李梦雅胡贤伟涛481B东华大学潘旻欣王淯舒佳491A上海财经大学杜溦陈卫华501A上海财经大学茅颖逸杨弋菁鑫511A上海财经大学王超潘弘521A上海财经大学杨潇周也舒531B上海财经大学张潇傅建龙541A上海理工大学蓝锦龙何睿琦551A042上海理工大学王鹏程吴文威舰561A上海海事大学杨启凡肖玲571B上海海事大学魏晨金泽璐聪581C上海海事大学许婷柳静静591D上海海事大学赵云雨周帅601D上海海事大学赵亚会袁欣欣611A上海电力学院林颜锦王巨波621A380上海电力学院戎建鹏刘宝宣631A上海师范大学沈昊张晓晗641A上海工程技术大学杜瑞倩蔡晓蓓651A上海工程技术大学王禹钦潘春林曦661B上海工程技术大学刘喆江婷671C上海工程技术大学严平张亮681A上海应用技术学院李一帆刘祥691A上海应用技术学院孙鹏宋林蒙701A上海金融学院王凡石炜昕711B上海第二工业大学倪玲燕唐瑛芝721C上海第二工业大学贾春峰刘绍贵731B上海电机学院高育新康屹峰741C上海新侨职业技术学院项磊李锋751C上海出版印刷高等专科学校石振威闫文婷761A上海海关学院吴精华黄启智研771A上海海关学院冯丹婷陈小漪781B上海海关学院郑玲宇林之千12A复旦大学沈超郝关胜睿22A复旦大学楼平易沈忱32A复旦大学任龙飞郑泽嘉42A复旦大学杨洁李莹菲52A复旦大学钱华杰易江南62A复旦大学张启航周泽人沅72A复旦大学李一寒张旭晖沅82B复旦大学王亮张宇鸣沅92B复旦大学马祥袁之日沅102B复旦大学吴世宇张嘉然衡112B复旦大学沈云骢张航沅122A上海交通大学岳建亭李粤龙洋132A上海交通大学杨帆许凌云142A上海交通大学奚申佳王子悦辰152A上海交通大学雷正新江淼滔162A上海交通大学危尊豪姚均霖172A上海交通大学张骁男张道天182A上海交通大学范刘洋李集佳光192A上海交通大学潘多昭张驰202A上海交通大学王小维黄鹏涛212A上海交通大学韩崔泽汪洋222A上海交通大学黄一展王鹏232A上海交通大学罗涛鲁海昊242A上海交通大学荣任远曾笮组252B上海交通大学罗施博王召光262B上海交通大学寇琪李致静272B上海交通大学张翼王灏新282B上海交通大学王中胜茅元琦292B上海交通大学杜若飞凌宇霄金302B上海交通大学冯征凯丁维贤宇312B上海交通大学江屹斌杨珏322B同济大学黎金星陆荻332A华东师范大学田木洪文嘉342B华东师范大学吴奕沈之一煜352A华东理工大学李桂传郜煜竞362A华东理工大学黄磊时强功372A华东理工大学张益东万宇雷382A华东理工大学侯若男张成龙昊392A华东理工大学周萧潇冯泽权骏402B华东理工大学尤越钱天威珊412B华东理工大学李风雷郑常昊422B华东理工大学尹芹吴曾睿432A东华大学陈程吕凤娇442A东华大学刘圆刘一452A东华大学王鹤翔罗世操462A东华大学王超新杨静懿艳472B东华大学张可帆刘荡健482B东华大学朱雄伟张晓波彪492B东华大学蔡梦沁王晓丹502A上海财经大学梁爽黄治森艺512A上海财经大学佘昀刘文颖群522A上海财经大学韩洲枫刘孟雷532A上海财经大学孔潇郑敏542A上海财经大学刘骏秦沈林552B上海财经大学王晔楠施京奇562B上海财经大学舒云鹏周文静正572A上海理工大学叶超兵范本喆良582A上海理工大学杜飞鹏叶一汀柯592A上海海事大学倪玮郎璟来译602A上海海事大学王腾骅沈连才612A上海海洋大学张喆昊刘冰清622B上海师范大学张洁俞顺成康632A上海工程技术大学王文怡裴彧642A上海工程技术大学陈博文顾小君652A上海工程技术大学刘鑫韩玉婷662A上海工程技术大学赵洋黄乐骏672B上海工程技术大学陆琴琴黄慧敏682C上海工程技术大学徐志能范涵692A上海应用技术学院杨亚楠林海702A上海金融学院谢生耀陈杰锋712A上海金融学院薛菲毛冰清轩722A上海立信会计学院王胤奎曾晓迪舒辉732A上海立信会计学院陈志成龚敬诚742A上海第二工业大学余婵娟厉丹璐752A上海第二工业大学吴敏洁陶舒娴762A上海第二工业大学吴微肖艳涛772C上海第二工业大学荣夫弟贾强强782D上海第二工业大学周刚张燕兰娜792D上海第二工业大学方建业沈婷婷钰802B上海电机学院董昱刘邓富812C上海新侨职业技术学院邹雯漪吴柳822C上海电子信息职业技术学院赵祖雄李志强832C上海科学技术职业学院郝凯刘东泉烨842C上海科学技术职业学院王学田田然852C上海出版印刷高等专科学校顾建群顾晓玉探862D上海医疗器械高等专科学校魏凤佳邵娟娟程872D上海医疗器械高等专科学校唐夕麟颜文卿瑞13A复旦大学杨秦枝李含韵沅23A复旦大学章丹颂陈功伟33A复旦大学郁杰周瀛沅43A复旦大学江武钟策敏帆53A复旦大学孙赫雍正婧63A复旦大学侯佳麟斯逸卿德73A复旦大学叶博艺倪辛辰83A复旦大学韩启阳丁骁同沅93A复旦大学钱云浩王越沅103A复旦大学罗嘉良陆丛希113A复旦大学何少杰李宜来123A复旦大学李恒李晓沅133A复旦大学章少骏储骏吉沅143A复旦大学周剑帆朱历轩天沅153A复旦大学梁济寰高翔163A复旦大学王茂实邓宇晨正沅173A复旦大学王雪孙田园183B复旦大学盛益彬潘剑阳晶193B复旦大学李怡鑫王学彬欣沅203B复旦大学张冰洁韦笑沅213B复旦大学郑家仑郑宜立223B复旦大学郁星炜孔陆洋征233A上海交通大学刘炅陶鑫龚243A上海交通大学王佳晨李豪253A上海交通大学杨勇吉雍彬263A上海交通大学张巍戴晓武273A255上海交通大学江梦洋高卓旸283A上海交通大学刘庆祥王小戏293A上海交通大学涂伟康赵弈韬303A上海交通大学毛晓军毛琪涛珞313A上海交通大学杨锡灿王思齐铎323A上海交通大学朱旻杨蒙蒙兰333A上海交通大学朱惠康朱皇儒模指导组343A上海交通大学帅杰许准353A上海交通大学蒋辉宏洪翔363B上海交通大学高鹏李之恒373B上海交通大学李巍龚郝383B上海交通大学屈正阳栾文韬393B上海交通大学郝骥腾陆奕骞祥403B上海交通大学佟帅王煌鑫璐413B上海交通大学王泽宇林敏华423B上海交通大学钟磊高凯晔433B上海交通大学郑可琛李强炜443B上海交通大学董洪信褚夫峰453B上海交通大学陈逸尘徐志诚威463B上海交通大学陈程肖涛组473B上海交通大学周凯唐爱民483A同济大学谢磊徐昊进493A同济大学陈曦欧阳君未503A同济大学张元张帆513A同济大学辛梓幸许骏森523A同济大学张晨谭思录533A同济大学朱静怡姚震洲晨翔543B同济大学陈元清吕慧洁553B同济大学李玮峰杨雨林563B同济大学戴天翔张丹聃573B同济大学陆旸盛凡迪583B同济大学王坦周宸章593A华东师范大学曹远韬宋坚骏603A华东师范大学张月霞许可茜613A华东师范大学胡立明梁晖浩623B华东师范大学邵溪濛张磊633A华东理工大学陆毅成秦鸣雷衍643A华东理工大学赵江坤刘宝653A华东理工大学杨剑王傲雪663A华东理工大学成茂徐颖婷衍673A华东理工大学曹亚强施镇昊衍683A华东理工大学何靖恺陈辰衍693B华东理工大学牟树兆惠龙武703B华东理工大学谢梦金祎713B华东理工大学曹鑫马绍之超723A东华大学袁茂恺林华733A东华大学陈京军陈梓兮743A东华大学解书垚陈霞凯753A东华大学徐慧军尹然763A东华大学胡炳然孙昭苏訸773A东华大学火耀乔文杰蒙芳783B东华大学王佩青周多793B东华大学宇菲刘月乔803A上海财经大学徐驾屹朱钱胜813A上海财经大学罗浩昇杨洋823A上海财经大学王方王任达飞833A上海财经大学曹珏左士蕊843A上海财经大学许骁昱葛璐澜853A上海财经大学石睿智普绍增863A上海财经大学谭梦昕蔡晓羽873A上海财经大学陈熠君申翔渝883A上海财经大学季凯明黄灿帅893B上海财经大学杨光汤成轶靖903A上海理工大学胡望燚张东东乐913A上海理工大学方凯何冬霜高923A上海理工大学马泓苗森高933A上海理工大学杨波王元宏943A上海理工大学阳波夏大雨953B上海理工大学颜雄亮翟雨浩963A上海海事大学刘强袁铭泽973C上海海事大学林怡林凯强983A上海海洋大学随宏运齐晓宝杜993B上海电力学院石晓菲闫玉婷1003B上海电力学院杨铁军汪韧岩1013A上海大学齐济高群1023A上海大学林法卡束俊辉1033A上海大学徐奕哲李启通1043A上海大学马健铭陈恺超1053A上海大学朱骏飞王斌宇1063B上海大学江含琤赵文迪伟1073A上海师范大学唐英智陆晓霞1083A上海师范大学郑轶吕阳1093A上海师范大学季政方征阳梦阳1103A上海师范大学王宇郎敏毅1113A上海工程技术大学赵德安马承坤雁1123A上海工程技术大学曲嘉骏吴超号1133A上海工程技术大学龚弛宇张蕴文1143A上海工程技术大学朱云婷江偲偲亚1153A上海工程技术大学沈翠翠李建云组1163A上海工程技术大学郭凤于玮勇1173A上海工程技术大学柳俊莫洲骐苗1183A上海工程技术大学余国喜张富祥海1193B上海工程技术大学丁亦俊阎婉婷1203B上海工程技术大学范柳斌胡昱1213B上海工程技术大学蒋辰艳徐小静1223B上海工程技术大学茹晓洁柯银清驰1233B上海工程技术大学李杨余超1243B上海工程技术大学盛驰骋申雄琼1253B上海工程技术大学李江波赵静静龙1263C上海工程技术大学刘欢段涛超1273D上海工程技术大学刘泽瑞王森勇1283A上海应用技术学院刘旭晨冯俊衔攀1293A上海应用技术学院丁彬王佳斌1303A上海应用技术学院姜丽丽崔羚1313B上海应用技术学院孙传辉张艺健1323A上海金融学院刘江城蔡纪森1333A上海金融学院林冰倩牟芝颖1343A上海金融学院方晏荷朱振兴1353A上海金融学院杨磊王天宠1363A上海金融学院田鹏飞陈冰1373A上海金融学院施扬军马涛旸1383B上海金融学院杨益丰黄家玉涛1393C上海立信会计学院郑泽丰单方会1403C上海立信会计学院梅磊贾丽蒙祥1413C上海立信会计学院钟素玲付志红1423C上海立信会计学院杨驰铭尹莹珍1433A上海第二工业大学沈佳美柴晓桦1443A上海第二工业大学刘文通孙勇超强1453A上海第二工业大学唐勤郑文焘1463A上海第二工业大学李旭董浩1473B上海第二工业大学王宇刘杉杉1483C上海第二工业大学禹永根安平1493A上海电机学院齐军印徐朋敏玲1503A上海电机学院陈龙崔亚飞欣1513A上海电机学院苏丹郑小华峰富1523B上海电机学院程国明何金鑫峰1533A上海商学院周鑫李鑫1543A上海商学院尹子都何晓楠1553B上海建桥学院施闻华郭建崟斌1563C上海新侨职业技术学院龚佳琪叶明珠浪1573C上海行健职业学院胡扬旭聂文景1583C上海交通职业技术学院王滔徐吉伟1593D上海电子信息职业技术学院赵正恩邱文宇桥练组1603C上海科学技术职业学院吴航宋尚朴伟1613C上海建峰职业技术学院张立郜阿东1623D上海邦德职业技术学院陆一灏郭海金进1633C上海中华职业技术学院黄萍王晓冬超珅1643C上海中华职业技术学院王绪陆黄马帅珅1653C上海城市管理职业技术学院丁灿袁吉海婧、陈从衡1663D上海城市管理职业技术学院刘柯严丽丽崇、陈从衡1673D上海城市管理职业技术学院陆琛玮董陈江、陈从衡1683D上海出版印刷高等专科学校孙徐坦姜徐婷1693C上海医疗器械高等专科学校覃曼琦胡存根妍1703A上海师范大学天华学院施凯钱荣欣梦1713B上海师范大学天华学院戴力汪丹妮1723B上海师范大学天华学院胡方洁徐海燕1733B上海师范大学天华学院陈庆焦大明1743B上海师范大学天华学院付明罗昊阳1753A上海海关学院薛翔文陈家本强1763A上海海关学院刘京梅黛萍1773B上海海关学院戴金华胡佳芸1783B上海海关学院薛梁朱容俊1793A第二军医大学梁萌陈瑞兵1803A第二军医大学宋泽宇孙平新1813A第二军医大学吕奕鹏马跃宇2011年高教社杯全国大学生数学建模竞赛上海赛区组委会,2011.10.7。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)
D题天然肠衣搭配问题
天然肠衣(以下简称肠衣)制作加工是我国的一个传统产业,出口量占世界首位。
肠衣经过清洗整理后被分割成长度不等的小段(原料),进入组装工序。
传统的生产方式依靠人工,边丈量原料长度边心算,将原材料按指定根数和总长度组装出成品(捆)。
原料按长度分档,通常以0.5米为一档,如:3-3.4米按3米计算,3.5米-3.9米按3.5米计算,其余的依此类推。
表1是几种常见成品的规格,长度单位为米,∞表示没有上限,但实际长度小于26米。
表1 成品规格表
为了提高生产效率,公司计划改变组装工艺,先丈量所有原料,建立一个原料表。
表2为某批次原料描述。
根据以上成品和原料描述,设计一个原料搭配方案,工人根据这个方案“照方抓药”进行生产。
公司对搭配方案有以下具体要求:
(1) 对于给定的一批原料,装出的成品捆数越多越好;
(2) 对于成品捆数相同的方案,最短长度最长的成品越多,方案越好;
(3) 为提高原料使用率,总长度允许有± 0.5米的误差,总根数允许比标准少1根;
(4) 某种规格对应原料如果出现剩余,可以降级使用。
如长度为14米的原料可以和长度介于7-13.5米的进行捆扎,成品属于7-13.5米的规格;
(5) 为了食品保鲜,要求在30分钟内产生方案。
请建立上述问题的数学模型,给出求解方法,并对表1、表2给出的实际数据进行求解,给出搭配方案。
