古代数学家杨辉的故事
杨辉与杨辉三角

数学家杨辉杨辉,中国南宋末年杰出的数学家和数学教育家。
在13世纪中叶活动于苏杭一带,其著作甚多。
他著名的数学书共五种二十一卷。
著有《详解九章算法》十二卷(1261年)、《日用算法》二卷(1262年)、《乘除通变本末》三卷(1274年)、《田亩比类乘除算法》二卷(1275年)、《续古摘奇算法》二卷(1275年)。
其中在《详解九章算法》一书中载有二项(a+b)n展开系数的数字三角形,被称为“杨辉三角”,它的发现比国外同类发现至少早3O0年。
杨辉的数学研究与教育工作的重点是在计算技术方面,他对筹算乘除捷算法进行总结和发展,有的还编成了歌决,如九归口决。
他在《续古摘奇算法》中介绍了各种形式的"纵横图"及有关的构造方法,同时"垛积术"是杨辉继沈括"隙积术"后,关于高阶等差级数的研究。
杨辉在"纂类"中,将《九章算术》246个题目按解题方法由浅入深的顺序,重新分为乘除、分率、合率、互换、二衰分、叠积、盈不足、方程、勾股等九类。
他非常重视数学教育的普及和发展,在《算法通变本末》中,杨辉为初学者制订的"习算纲目"是中国数学教育史上的重要文献。
=================================================================杨辉介绍杨辉,字谦光,中国南宋(1127~1279)末年钱塘(今杭州市)人。
其生卒年月及生平事迹均无从详考。
据有关著述中的字句推测,杨辉大约于13世纪中叶至末叶生活在现今浙江杭州一带,曾当过地方官,到过苏州、台州等地。
是当时有名的数学家和数学教育家,他每到一处都会有人慕名前来请教数学问题。
杨辉一生编写的数学书很多,但散佚也很严重。
据史料记载,他至少有以下书,曾在国内或国外刊行:《详解九章算法》12卷(1261)《详解算法》若干卷《日用算法》(1262)《乘除通变算宝》3卷(1274)《续古摘奇算法如卷》(1275)《田亩比类乘除捷法如卷》(1275)其中《详解九章算法》残缺不全,《详解算法》、《日用算法》迄今未见传本。
南宋数学家杨辉生平简介

南宋数学家杨辉生平简介杨辉,字谦光,汉族,南宋杰出的数学家和数学教育家,生平履历不详。
曾担任过南宋地方行政官员,为政清廉,足迹遍及苏杭一带。
下面是为大家整理的南宋数学家杨辉生平简介,希望大家喜欢!南宋杨辉是杭州人,是南宋著名的数学家。
关于杨辉的出生年月和生平阅历没有详细的记载,只知道杨辉曾在南宋朝廷任职,多数时间都在苏州杭州一带。
杨辉为官清廉而有正义感,深得百姓称颂。
说起杨辉的贡献,不得不提的就是他在算数上的成就,后人将杨辉、秦九韶、李冶、朱世杰并称“宋元数学四大家”。
南宋杨辉一生写过很多著作,都是数学相关的理论知识。
其中,他写有《详解九章算法》、《日用算法》、《乘除通变本末》、《田亩比类乘除捷法》等书籍。
杨辉根据日常需要的运算总结出算法理论,帮助百姓们计算需求。
值得一提的是,杨辉是世界上第一个排列纵横图,并且从中总结出构成规律的理论知识,推动了世界算术进程,具有很高的现实意义。
杨辉生活年间,手工业和商业已经有了较大发展,社会经济得到提升的同时,商人和百姓们都需要用到数学计算。
社会对算术的需求引发了杨辉的重视。
事实上,资本经济萌芽时期,就有数学家总结了日常计算方法。
晚唐时期,出现可一些较为实用的计算书籍,到了南宋年间时,诸如《夏侯阳算经》等书籍已经失传了。
随后,南宋杨辉在总结前人算术基础上,又总结出一种更为简单便捷的算法。
所以,后人们在提到杨辉在数学方面的贡献时,也会想起他改进乘除计算技术,让运算更加便捷化和简单化。
不仅提高了运算速度,也提高了准确率。
杨辉的故事杨辉担任台州官吏时,一次,看着窗外春光无限好,杨辉便打算巡游台州。
一边体察民情,一边欣赏美丽的春景,实在是一件很美妙的事情。
杨辉坐在轿子中,看见大自然一片万物复苏的场景,心情非常愉悦。
他撩起轿帘正在欣赏沿途的春光,突然轿子停住了。
杨辉问侍卫为何立即停下,侍卫回答说,前方路上有个小男孩正蹲在不知在干什么。
另一位侍卫急忙上前呵斥这位小男孩,让他赶紧让路。
三年级数学传统文化故事稿

三年级数学传统文化故事稿中国传统数学文化拥有丰富的历史和独特的特点。
三年级的数学教学中,可以通过讲述一些与传统文化相关的故事,帮助学生更好地理解和学习数学知识。
一、九九乘法表的故事在中国传统文化中,九是一个重要的数字,被视为吉利之数。
九九乘法表是小学时期必须掌握的基础算术表。
这个故事可以激发学生的学习兴趣,同时帮助他们记住九九乘法表。
故事内容:很久很久以前,有一个叫杨辉的老人,他非常聪明。
有一天,天空突然响起雷声,杨辉出去看到了一只长有九个翅膀的仙鹤。
仙鹤告诉杨辉,它是来教他九九乘法表的。
仙鹤对杨辉说:“九是一个很特别的数字,你只要掌握了九九乘法表,就能解决很多问题。
”于是,仙鹤开始对杨辉教九九乘法表。
首先,仙鹤对杨辉说:“1乘以1等于多少呢?”杨辉答道:“等于1。
”仙鹤赞赏地点点头,又问:“1乘以2等于多少呢?”杨辉回答:“等于2。
”仙鹤高兴地继续问下去,杨辉全都能答对。
最后,仙鹤兴奋地对杨辉说:“九九乘法表就是这么简单!你要记住这个表格,它对你以后做数学题非常有用。
”从那时起,杨辉开始学习九九乘法表,每天背诵、练习。
在练习的过程中,他发现了一些有趣的规律,比如任何两个相邻的数相乘,结果都是一样的。
最后,杨辉成功地掌握了九九乘法表,并成为了一位杰出的数学家。
他还把九九乘法表传授给了后人,为中国的数学事业做出了巨大贡献。
这个故事可以让学生了解九九乘法表的来历,激发他们的学习兴趣,并通过九九乘法表的记忆和运用,提高他们的计算能力。
二、《三弄》的乐理故事中国传统音乐中,有一种叫《三弄》的乐曲,它独特的音调和复杂的乐理结构,可以用数学的方法来解释。
通过讲述《三弄》的故事,可以帮助学生理解乐理知识,并培养他们对音乐的兴趣。
故事内容:在古代,有一个天赋异禀的音乐家叫许逍遥。
他非常喜欢音乐,但是却对它的乐理一直感到困惑。
有一天,许逍遥遇到了一位神秘的老人,老人告诉他:“你想要了解音乐的乐理吗?我可以教你。
”许逍遥高兴地接受了老人的教导。
中国著名数学家的故事

中国著名数学家的故事
中国著名数学家的故事有很多,以下是其中一些:
1. 杨辉(公元1238年-公元1298年):杨辉是中国元代著名
数学家,他以其发现的杨辉三角而闻名。
杨辉三角是一个由数字组成的三角形,其中每个数字是由上方两个数字相加得出的。
杨辉的杨辉三角在组合数学和概率论中有广泛应用。
2. 程大位(1628年-1696年):程大位是中国明朝末年和清朝
初年的数学家,他被誉为中国代数学的先驱。
程大位的代表作品是《程大位开宗明义几何学》,这本书将欧几里德的几何学与中国传统思维相结合,并提出了一种新的几何学理论,对中国数学影响深远。
3. 华罗庚(1910年-1985年):华罗庚是中国现代数学的奠基
人之一,被尊称为“中国数学之父”。
他在数论和代数几何等领域做出了重要贡献,尤其是他解决了古老数论问题“哥德巴赫
猜想”的一部分。
华罗庚还一直致力于培养年轻数学家的能力,并在中国数学事业的发展中起到了重要的推动作用。
以上只是中国著名数学家的一些故事,他们每个人都有着独特而令人钦佩的贡献,对中国数学的发展产生了巨大的影响。
神奇的三角---杨辉三
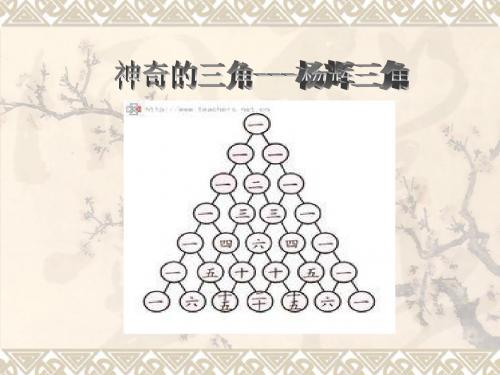
1 1 1 1 1 1 1 1 1 1 9 8 36 7 28 84 6 21 56 126 5 15 35 70 126 4 10 20 35 56 84 3 6 10 15 21 28 36 2 3 4 5 6 7 8 9 1 1 1 1 1 1 1 1 1
用杨辉三角求高次方
将各行数字相排列,可得 11的N次方: 1=11º 11=11¹ 121=11³ 注:15101051≠11的5次 方 ,应为:
杨辉三角形,又称贾宪三角形,帕斯卡三 角形,是二项式系数在三角形中的一种几 何排列。
0行 1 1行 1 1 2行 1 2 1 3行 1 3 3 1 4行 1 4 6 4 1 ……
从上倒下,都是上面两个数加起来的和就是对应下面一
个数,列如:1+1=2,1+2=3,1+3=4
.
性质
1 1 1 1 1 1 1 1 8 9 36 7 28 84 6 21 56 126 5 15 35 70 126 4 10 20 35 56 84 3 6 10 15 21 28 36 2 3 4 5 6 7 8 9 1 1 1 1 1 1 1 1 1
杨辉三角与斐波那契数列
将第2n+1行第1个数,跟第2n+2行第3个数、 9、将第2n+1行第1个数,跟第2n+2行第3
第2n+3行第5个数……连成一线,这些数的 个数、第2n+3行第5个数……连成一线,这 和是第4n+1个斐波那契数;将第2n行第2个 些数的和是第4n+1个斐波那契数;将第2n 数(n>1),跟第2n-1行第4个数、第2n-2行第 行第2个数(n>1),跟第2n-1行第4个数、第 6个数……这些数之和是第4n-2个斐波那契 2n-2行第6个数……这些数之和是第4n-2个 数 斐波那契数
南宋数学家杨辉主要故事概括

南宋数学家杨辉主要故事概括
杨辉(约公元1238年-公元1298年),字西城,号永昌,是中国南宋时期的
一位著名数学家。
他在数学领域的贡献被后人称为“杨辉三角”,这一成就至今仍然被广泛应用于数学和计算机科学领域。
杨辉的主要故事可以追溯到他在南宋时期的求学生涯。
据传记记载,杨辉自幼
聪慧好学,勤奋好学,对数学和天文颇有研究。
他曾拜南宋著名数学家秦九韶为师学习数学,深受秦九韶的影响。
杨辉在学习数学的过程中,善于观察总结,喜欢探索数学规律,因此逐渐形成了自己独特的数学思维和方法。
杨辉最著名的成就就是“杨辉三角”。
据传记载,杨辉在研究二项式定理和多项
式的展开过程中,发现了一种奇妙的数学规律,这就是杨辉三角。
杨辉三角是一种数学图形,其特点是每个数字等于它上方两个数字的和,这种规律被称为杨辉三角的性质。
杨辉三角在数学和计算机科学领域有着广泛的应用,被称为“数学之美”。
除了杨辉三角,杨辉在数学领域还有许多其他重要的贡献。
他在数学计算和代
数方面有深入研究,提出了许多重要的数学定理和算法,对数学学科的发展做出了积极的贡献。
杨辉的数学成就不仅在当时引起了广泛的关注,而且对后人的学习和研究产生了深远的影响。
总的来说,杨辉是中国南宋时期的一位杰出的数学家,他的数学成就和研究在
数学领域有着重要的地位,被后人广泛认可和尊重。
杨辉的故事不仅令人敬佩,而且启发了许多数学学者对数学的热爱和探索,为数学学科的发展做出了杰出的贡献。
杨辉的数学成就在中国数学史上有着重要的地位,对数学的发展和传承具有重要的意义。
杨辉的故事

中国古代数学家在数学 的许多重要领域中处于 遥遥领先的地位。 中国古代数学史曾经 有自己光辉灿烂的篇章, 而杨辉三角的发现就是 十分精彩的一页。
幻方,在我国也称纵横图, 它的神奇特点 吸引了无数人 对它的痴迷。 “河出图,洛出 书,圣人则之”
九宫者,二四为肩,六八为足,左三右 七,戴九履一,五居中央。 把1到9的数字分行 排列,不论竖着加、 横着加,还是斜着 加,结果都等于15。
杨辉三角简史
1、北宋人贾宪约1050年首先使用“贾宪 三角”进行高次开方运算。 2、南宋数学家杨辉在《详解九章算法》 (1961年)记载并保存了“贾宪三角”。 3、元朝数学家朱世杰在《四元玉鉴》扩 充了“贾宪三角”成“古法七乘方图”。 4、杨辉在他1261年所著的《详解九章算 法》一书中,辑录了如图所示的三角形 数表,称之为“开方作法本源”图。在国 外,这也叫做“帕斯卡三角形”。
专注研究 成就辉煌 —数学家杨辉
七三班 曹赛如
杨辉:字谦光,
钱塘人(今杭州), 南宋时期杰出的 数学家、数学教 育家。与秦九韶、 李冶、朱世杰并称 宋元四九章算法》十二卷 《日用算法》两卷 《乘除通变本末》三卷 《田亩比类乘除算法》两卷 《续古摘奇算法》两卷
元代数学家杨辉的故事

元代数学家杨辉的故事杨辉 ,字谦光 ,汉族 ,钱塘〔今杭州〕人 ,中国古代数学家和数学教育家 ,生平履历不详。
由现存文献可推知 ,杨辉担任过南宋地方行政官员 ,为政清廉 ,足迹普及苏杭一带 ,他署名的数学书共五种二十一卷。
他是世界上第一个排出丰富的纵横图和讨论其构成规律的数学家。
与秦九韶、李治、朱世杰并趁称宋元数学四大家。
杨辉一生留下了大量的著述 ,他著名的数学书共五种二十一卷 ,它们是:?详解九章算法?12卷(1261年) ,?日用算法?2卷(1262年) ,?乘除通变本末?3卷(1274年 ,第3卷与他人合编) ,?田亩比类乘除捷法?2卷(1275年) ,?续古摘奇算法?2卷(1275年 ,与他人合编) ,其中后三种为杨辉后期所著 ,一般称之为?杨辉算法?。
他非常重视数学教育的普及和开展 ,在?算法通变本末?中 ,杨辉为初学者制订的"习算纲目"是中国数学教育史上的重要文献。
杨辉在?详解九章算法?一书中还画了一张表示二项式展开后的系数构成的三角图形 ,称做“开方做法根源〞 ,现在简称为“杨辉三角〞。
杨辉的故事说起杨辉的这一成就 ,还得从偶然的一件小事说起。
一天 ,台州府的地方官杨辉出外巡游 ,路上 ,前面铜锣开道 ,后面衙役殿后 ,中间 ,大轿抬起 ,好不威风。
迷人的春天慷慨地散布着芳香的气息 ,带来了生活的欢乐和幸福。
杜鹃隐藏在芒果树的枝头。
用它那圆润、甜蜜、动人心弦的鸣啭来唤醒人们的希望。
成群的画眉鸟像迎亲似的蹲在树的枝丫上 ,发出婉丽的啼声。
楝树、花梨树和栗树都仿佛被自身的芬芳熏醉了。
杨辉撩起轿帘 ,看那杂花生树 ,飞鸟穿林 ,真乃春色怡人淡复浓 ,唤侣黄鹂弄晓风。
更是一年好景 ,旖旎风光。
走着、走着 ,只见开道的镗锣停了下来 ,前面传来孩童的大声喊叫声 ,接着是衙役恶狠狠的训斥声。
杨辉忙问怎么回事 ,差人来报:“孩童不让过 ,说等他把题目算完后才让走 ,要不就绕道。
古今中国的数学家故事

古今中国的数学家故事
中国有许多杰出的数学家,他们为数学的发展做出了重要贡献。
以下是一些古今中国数学家的故事:
1. 刘徽(约公元3世纪)
刘徽是中国古代著名的数学家和工程师,他在数学领域的贡献
极为重要。
他编写了《九章算术》,这是中国古代最早的数学专著
之一,包含了许多数学问题和解法。
他的工作对后世的数学研究产
生了深远影响。
2. 杨辉(公元5世纪)
杨辉是中国古代数学家和诗人,他最著名的贡献是杨辉三角。
杨辉三角是一个由数字排列而成的三角形,其中每个数字是上方两
个数字之和。
这个三角形在组合数学和概率论中有广泛应用。
3. 程大位(公元11世纪)
程大位是北宋时期的数学家,他是中国古代数学发展的重要推
动者之一。
他的主要贡献是整理了古代数学著作《数书九章》。
这
本著作收集了中国古代数学的重要成果,对后世的数学研究起到了重要的指导作用。
4. 华罗庚(1910-1985年)
华罗庚是中国现代著名的数学家,他对代数几何和数论做出了重要贡献。
他的研究在国际数学界享有很高的声誉。
华罗庚还培养了许多杰出的数学学生,对中国数学事业的发展起到了重要的推动作用。
5. 丘成桐(1949年至今)
丘成桐是中国当代著名的数学家,他的研究领域主要是微分几何和数学物理。
丘成桐是第一个获得菲尔兹奖的中国数学家,这是数学界最高荣誉之一。
他的研究成果为中国数学的国际地位提升做出了重要贡献。
中国的数学家们在古代和现代都为数学的发展做出了巨大的贡献。
他们的故事激励着新一代的数学爱好者,推动着数学的不断进步。
数学家杨辉的简短故事

数学家杨辉的简短故事
杨辉(公元约1238年-约1298年),是中国南宋时期的数学家和数学思想家。
他是中国古代著名的数学家之一,被誉为“中国组合数学之父”。
以下是关于杨辉的一个简短故事:
据传说,杨辉小时候非常聪明好学,对数学有着浓厚的兴趣。
有一天,他在田地里捡到了一只受伤的乌鸦,他心生怜悯,决定将它养大并疗伤。
他给乌鸦取名为"乌乌",并经常喂食和照顾它。
乌乌逐渐恢复了健康,变得活泼起来。
杨辉发现它有着惊人的智慧,能够理解一些基本的数学概念。
他开始用乌乌来进行数学实验和探索。
有一次,杨辉给乌乌展示了他最著名的发现之一——杨辉三角形。
他把数字按照一定规律排列成一个三角形的形状,每个位置上的数字是它上方两个数字之和。
杨辉发现,这个三角形可以用来解决组合数学中的许多问题,特别是在数列、排列组合和二项式定理等方面。
乌乌似乎也理解了这个三角形的规律,它开始用它的爪子指着不同的数字,仿佛在与杨辉交流。
这一幕让杨辉惊叹不已,他意识到乌乌已经成为了他最好的数学助手。
从那以后,杨辉和乌乌一起研究数学问题,探索数学的奥秘。
他们合作发表了许多重要的数学著作,对中国数学的发展做出了巨大贡献。
这个故事展示了杨辉对数学的早期兴趣和才华,以及他与乌乌之间的特殊关系。
虽然这只乌鸦可能只是一个寓言中的形象,但它象征着杨辉那种对数学的热爱和创造力,以及他在数学领域的重要贡献。
杨辉三角的发展史

杨辉三角的发展史杨辉三角是一种由数字排列而成的三角形,其中每个数字等于它上方两个数字的和。
它最早出现在中国古代数学经典著作《九章算术》中,被称为“杨辉数”。
杨辉三角的发展史可以追溯到古代,经历了漫长的历史变迁。
古代中国数学家杨辉(约公元5世纪)是杨辉三角的创始人,他首次将这一数学现象进行了系统的研究和描述。
在他的著作《九章算术》中,他详细地介绍了杨辉三角的构造方法和特性。
杨辉通过逐行相加的方式,将数字排列成三角形的形式,这就是我们现在所熟知的杨辉三角。
杨辉三角的发展并非一蹴而就,它在中国古代的数学研究中经历了多次改进和完善。
在唐代,数学家贾宪三进一步发展了杨辉三角,他提出了一种更加简便的构造方法,不再需要逐行相加,而是通过一种特殊的排列方式,使得每个数字都等于其上方两个数字的和。
这种构造方法被称为“杨辉法”,成为了杨辉三角的一种重要形式。
随着时间的推移,杨辉三角逐渐传播到其他国家和地区。
在欧洲,杨辉三角最早出现在16世纪的意大利数学家帕斯卡的著作中。
帕斯卡对杨辉三角进行了深入研究,并发现了一些有趣的性质,如杨辉三角中的对角线上的数字构成了帕斯卡三角形,它具有一些特殊的数学性质。
在现代数学中,杨辉三角不仅仅是一个有趣的数学现象,它还有着广泛的应用。
在组合数学中,杨辉三角被用来解决排列组合问题,计算二项式系数等。
在概率论中,杨辉三角被用来计算二项分布的概率。
在计算机科学中,杨辉三角被用来生成杨辉三角矩阵,用于图像处理和模式识别等领域。
总结来说,杨辉三角的发展史可以追溯到古代中国,经历了多次改进和完善。
它是中国古代数学的重要成果之一,也是世界数学史上的重要里程碑。
杨辉三角不仅仅是一个有趣的数学现象,它还有着广泛的应用领域。
无论是在数学领域还是在其他领域,杨辉三角都展示了其独特的魅力和价值,为人们带来了无尽的思考和探索的乐趣。
中国古代数学家杨辉

“杨辉三角”比 西方的“帕斯卡三 角”早出现300多年。
找规律填数
1 11 1 21 1331 14641 1 () ()() () 1
1 22 3 43 47 7 4 5 () ()() 5
通过这节课的学习, 你有什么收获?
两条斜边都是由数字1组成,其余的数则是 等于上一行左右两个数字之和。
每行数字左右对称,由1开始逐渐变大,然 后变小,最后再回到1。
每一行的数字个数与行数同样多。
杨辉是南宋时期杭州人,在他1261年所著书中, 记录了如图所示的三角形数表,这三角形就被称为杨 辉三角。在欧洲直到1623年以后,法国数学家帕斯卡 才发现了同样的规律,因此欧洲人又称这个三角“帕 斯卡三角”。但是大家从杨辉发现这 个规律的年代与帕斯卡发现这个规律 年代相比就会知道,我国的杨辉发现 此规律比帕斯卡早了300多年。近年 来国外也逐渐承认这项成果属于中国, 开始称这个三角为“中国三角的数学家,与 秦九韶、李治、朱世杰一起 被誉为“宋元数学四大家”。
杨辉一生写了很多 数学著作,流传很广, 朝鲜、日本等国均有译 本出版。
杨辉为初学者制 定的“习算纲目”, 集中体现了他的数学 教育思想和方法。
杨辉在计算方面很有 研究,“杨辉三角”为其 代表作,具有很大的实 用价值。
数学家杨辉三角的故事

数学家杨辉三角的故事
杨辉三角,也被称为贾宪三角或帕斯卡三角形,是二项式系数在三角形中的一种几何排列。
在中国古代,数学家杨辉在南宋时期(1261年)的著作《详解九章算法》中首次描绘了这一三角形,并称之为“开方作法本源”图。
在欧洲,法国数学家帕斯卡在1654年也发现了这一规律,因此这个表在欧洲也被叫做帕斯卡三角形。
杨辉三角的发现是中国古代数学的杰出研究成果之一。
这个三角形把二项式系数图形化,把组合数内在的一些代数性质直观地从图形中体现出来,是一种离散型的数与形的优美结合。
杨辉三角的每个数等于它上方两数之和,这一性质使得其在数学中有着广泛的应用。
例如,在组合数学中,杨辉三角可以用来计算组合数;在代数中,它可以用来展开二项式;在概率论中,它可以用来计算某些事件的概率等。
此外,杨辉三角还与一些数学游戏和问题有关,如“堆垛术”问题、纵横路线图问题等。
这些问题都可以通过杨辉三角来找到解决方案。
总之,杨辉三角是一个在数学中有着广泛应用和深远影响的数学概念,它的发现和应用展示了中国古代数学的卓越成就和独特魅力。
古代数学家杨辉的故事

古代数学家杨辉的故事
宋、元数学四大家之一的杨辉是世界上第一个排出丰富的纵横图和讨论构成规律的数学家.
说起杨辉的这一成就,还得从一件偶然的小事说起.一天台州府的地方官杨辉坐轿出外巡游,半路上被一个在路中间算题的孩童拦住道路不能通过.杨辉一看来了兴趣,连忙下轿,抬步来到前面.
杨辉摸着孩童的头说:“为何不让本官从此经过?”
孩童答道:“不是不让经过,我是怕你们把我的算式踩掉,我又想不起来了.”
“什么算式?”
“就是把1到9九个数字分三行排列,不论直着加、横着加还是斜着加,结果都是等于15.我们先生说下午一定要把这道题做好.我正算到关键之处.”
杨辉连忙蹲下身,仔细地看孩童的算式,觉得这个算式在哪儿见过,仔细一想,原来是西汉学者戴德编纂的《大戴礼》中所写的文章中提及的.杨辉和孩童两人连忙一起运算起来,直到天过午,两人才舒了一口气,结果出来了,他们又验算了一下,结果全是15,这才站了起来.结果如图1所示:
杨辉回到家中反复琢磨,一有空闲就在桌上摆弄这些数字,终于发现了其中的规律,按照类似的规律,杨辉又得到了“花16图”——把从1到16的数字排列在四行四列的方格中,使每一横行、纵行、斜行四数之和均为34.后来,杨辉又将散见于前人著作和流传于民间的有关这类问题加以整理,得到了“五五图”“六六图”“衍数图”“易数图”“九九图”“百子图”等许多类似的图.杨辉把这些图总称为纵横图,于1275年写进自己的数学著作《续古
摘奇算法》一书中,并流传后世.
但长期以来,人们习惯于把它当做纯粹的数学游戏,并没有给予应有的重视.随着近代组合数学的发展,纵横图显示了越来越强大的生命力,在图论、组合分析、对策论、计算机科学领域中都找到了用武之地.。
有趣的中国古代数学故事

中国古代数学故事——杨辉三角的奇妙之旅中国古代的数学学问博大精深,在古代数学的发展历程中,不乏许多有趣的故事。
其中,杨辉三角是一种独特的数学图形,它曾经给人们带来无限的惊喜和启发。
本文将为你讲述杨辉三角的奇妙之旅。
杨辉三角的诞生与发展杨辉三角最早出现在公元5世纪,也就是南北朝时期的中国。
这一数学图形是由中国古代数学家杨辉发现并研究的,因此得名杨辉三角。
杨辉三角是一种规律的数字阵列,它的构造方法很简单:首先在第一行放置一个数字1,然后从第二行开始,每个数字都是它上方两个数字之和。
通过这样的方法,一个奇妙的图形便逐渐形成。
杨辉三角的神奇与应用杨辉三角不仅仅是一个数学图形,它还蕴含着许多神奇的特性和应用。
下面,让我们一起来探索其中的奥秘。
二项式定理的发现杨辉三角中最为人津津乐道的神奇特性之一,就是它与二项式定理的关系。
二项式定理是数学中的重要定理之一,它表达了任意整数幂的多项式展开式中各项的系数。
通过观察杨辉三角的一些特点,我们可以发现每一行的数字之和正好是2的n次方,其中n代表行数。
这个规律与二项式定理中的二项展开系数恰好吻合,从而使杨辉三角与二项式定理紧密联系在一起。
杨辉三角在概率中的应用杨辉三角还可以应用于概率的计算中。
我们知道,概率是描述事物发生可能性的数值,而杨辉三角中的数字又与组合数相关联。
在杨辉三角中,每个数字都可以表示为它所在位置的行数和列数,也就是组合数C(n, k)。
通过计算不同行数和列数的组合数,我们可以得到一系列与概率相关的数值。
这种方法在离散数学和概率统计中有着广泛的应用。
加密中的利用——编码与解码在古代,人们常常使用杨辉三角进行加密和解码。
通过特定的编码规则,将明文转化为杨辉三角中的数字,然后通过解码规则将数字重新还原为明文。
杨辉三角加密法的基本思想是,将明文的每个字母与阵列中的数字相对应,然后将这些数字按照特定的规律排列成杨辉三角。
通过这种加密方式,即使有人获得了密文,也很难通过逆向推理得到明文的内容。
宋代著名的数学教育家杨辉

杨辉,字谦光,中国南宋(1127~1279)末年钱塘(今杭州市)人。
其生卒年月及生平事迹均无从详考。
据有关著述中的字句推测,杨辉大约于13世纪中叶至末叶生活在现今浙江杭州一带,曾当过地方官,到过苏州、台州等地。
是当时有名的数学家和数学教育家,他每到一处都会有人慕名前来请教数学问题。
杨辉一生编写的数学书很多,但散佚也很严重。
据史料记载,他至少有以下书,曾在国内或国外刊行:《详解九章算法》12卷(1261)《详解算法》若干卷《日用算法》(1262)《乘除通变算宝》3卷(1274)《续古摘奇算法如卷(1275)《田亩比类乘除捷法如卷(1275)其中《详解九章算法》残缺不全,《详解算法》、《日用算法》迄今未见传本。
而后3种共7卷合刊在一起,被称为《杨辉算法》。
杨辉继承中国古代数学传统,他广征博引数学典籍,引用了现已失传的宋代的许多算书,使我们才()得知其部分内容。
其中,刘益的“正负开方术”,贾宪的“增乘开方法”与“开方作法本源”图(即误传为“杨辉三角”),就是极其宝贵的数学史料。
杨辉继沈括研究“隙积术”之后,研究了“垛积术”,即关于高阶等差数列的研究。
他首次将所谓“幻方”问题作为数学问题研究,并创“纵横图”之名。
他给出了三阶至十阶幻方的实例,对某些构成原理也有所研究。
杨辉之前在中国尚无这方面的研究成果,杨辉之后,明、清两代中国数学家关于纵横图的研究相继不绝,因此杨耀的著述也是研究关于幻方乃至组合数学历史的珍贵资料。
杨辉还非常关心日常计算技巧,改进算法程序。
杨辉不仅著述甚丰,而且是一位杰出的数学教育家。
他特别注重数学的普及教育,其许多著作都是为此而编写的教科书。
杨辉主张在数学教育中贯彻理论联系实际的原则,在《日用算法》中,他说:“以乘除加减为法,称斗尺田为问;用法必载源流,命题须责实用。
”他还主张贯彻循序渐进的原则,在《算法通变本末》(即《乘除通变算宝》上卷)中,专门为初学者制了一份“司算纲目”,要求学习者抓住要领,反复练习,这是我国历史上第一部数学教学大纲。
数学家杨辉的简短故事

数学家杨辉的简短故事杨辉,一位伟大的数学家,他在数学领域做出了举世瞩目的贡献。
他的生平故事不仅仅是一段简短的叙述,更是关于智慧、勇气和奉献精神的诠释。
在这篇文章中,我们将聚焦于数学家杨辉的简短故事,探索他在数学领域的成就和对后世的影响。
杨辉生于公元约1238年的宋朝,他的名字被无数数学爱好者所熟知,主要因为他发现了一个重要的数学现象,即杨辉三角。
他这一发现不仅是数学史上的重要突破,更为我们的数学学习和研究提供了巨大的帮助。
杨辉三角是一个数字构成的三角形,每个数字等于它上方两个数字之和。
这一特殊的结构被广泛应用于组合数学、代数学和数论等领域。
在杨辉三角中,每行数字与二项式定理的展开系数相关,也有着许多有趣的数学性质,例如它与著名的斐波那契数列存在着一定的联系。
杨辉三角的发现,不仅提供了一种数学工具,更为我们理解数学本质和发现更多数学规律铺平了道路。
杨辉的成就不仅限于杨辉三角,他在数学研究中表现出了卓越的才华和深刻的洞察力。
他的研究领域涵盖了数论、代数和几何等多个方面,其中最杰出的成果之一是他对二次方程的研究。
杨辉通过严谨的数学推演和辩证思考,成功地解决了很多复杂的数学问题,并提出了许多数学理论和定理。
除了在学术领域取得的巨大成就,杨辉还积极投身于社会公益事业。
他致力于推广数学教育,将自己所掌握的知识传授给更多的人。
他相信,数学不仅是理性思维的重要工具,更是一种培养逻辑思维、分析问题和解决困难的能力的方法。
因此,他编写了许多数学教材,推广了数学知识的传播,培养了一批批年轻的数学人才。
杨辉的贡献和影响远不止于数学领域,他的研究思想和方法也对其他学科产生了积极的影响。
他坚持细致入微的观察,注重数学问题本身的推导和分析,这种方法为后来的科学和哲学研究提供了重要的启示。
不可否认,杨辉是一位伟大而值得敬佩的数学家。
他的数学成就不仅体现了个人智慧和才华,更是对人类智慧的卓越展示。
他用自己的学识和研究造福了人类,并激励着无数年轻的数学学子追求卓越。
杨辉数学家作文

杨辉数学家作文
我听说过一个关于他的故事。
有一天,杨辉外出巡游,路上遇到一个小孩在算题,小孩说他正在算把1到9的数字分三行排列,不论直着加、横着加还是斜着加,结果都等于15。
杨辉听了很感兴趣,就和小孩一起
算了起来。
嘿呀,他们算得可认真了,一直到天过午才算出来。
杨辉回到家后,还在琢磨这个问题,终于发现了其中的规律。
他把这个规律总结成了四句话:九子斜排,上下对易,左右相更,四维挺出。
哈哈,是不是很有趣呢?
杨辉还写了一本很有名的书,叫《详解九章算法》。
这本书里有很多数学知识,对后来的数学发展有很大的影响呢!
我真的很佩服杨辉,他的数学成就让我觉得数学真是一门神奇的学科!我也要向他学习,努力探索数学的奥秘!嘿嘿!。
南宋数学家杨辉主要故事概括

南宋数学家杨辉主要故事概括杨辉,字谦光,钱塘(今杭州)人,我国南宋时期杰出的数学家,与秦九韶、李冶、朱世杰并称宋元四大数学家,他在我国古代数学史和数学教育史上占有十分重要的地位。
杨辉对幻方的研究源于一个小故事。
当时杨辉是台州的地方官,一次外出巡游,碰到一孩童挡道,杨辉问明原因方知是一孩童在做一道数学算题,杨辉一听来了兴趣,下轿来到孩童旁问是什么算题。
原来,这个孩童在算一位老先生出的一道趣题:把1到9的数字分行排列,不论竖着加、横着加,还是斜着加,结果都等于15。
杨辉看到这个算题时想起来他在西汉学者戴德编纂的《大戴礼》一书中也见过。
杨辉想到这儿,和孩童一起算了起来,直到午后,两人终于将算式摆出来了。
后来,杨辉随孩童来到老先生家里,与老先生谈论起数学问题来。
老先生说:“北周的甄弯注《数术记遗》一书中写过九宫者,二四为肩,六八为足,左三右七,戴九履一,五居中央。
”杨辉听了,这与自己与孩童摆出来的完全一样。
便问老先生:“你可知这个九宫图是如何造出来的?”老先生说不知道。
杨辉回到家中,反复琢磨。
一天,他终于发现一条规律,并总结成四句话:“九子斜排,上下对易,左右相更,四维挺出”。
就是说:先把l~9九个数依次斜排,再把上l下9两数对调,左7右3两数对调,最后把四面的2、4、6、8向外面挺出,这样三阶幻方就填好了。
杨辉研究出三阶幻方(也叫络书或九宫图)的构造方法后,又系统的研究了四阶幻方至十阶幻方。
在这几种幻方中,杨辉只给出了三阶、四阶幻方构造方法的说明,四阶以上幻方,杨辉只画出图形而未留下作法。
但他所画的五阶、六阶乃至十阶幻方全都准确无误,可见他已经掌握了高阶幻方的构成规律。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
古代数学家杨辉的故事
宋、元数学四大家之一的杨辉是世界上第一个排出丰富的纵横图和讨论构成规律的数学家.
说起杨辉的这一成就,还得从一件偶然的小事说起.一天台州府的地方官杨辉坐轿出外巡游,半路上被一个在路中间算题的孩童拦住道路不能通过.杨辉一看来了兴趣,连忙下轿,抬步来到前面.
杨辉摸着孩童的头说:“为何不让本官从此经过?”
孩童答道:“不是不让经过,我是怕你们把我的算式踩掉,我又想不起来了.”
“什么算式?”
“就是把1到9九个数字分三行排列,不论直着加、横着加还是斜着加,结果都是等于15.我们先生说下午一定要把这道题做好.我正算到关键之处.”
杨辉连忙蹲下身,仔细地看孩童的算式,觉得这个算式在哪儿见过,仔细一想,原来是西汉学者戴德编纂的《大戴礼》中所写的文章中提及的.杨辉和孩童两人连忙一起运算起来,直到天过午,两人才舒了一口气,结果出来了,他们又验算了一下,结果全是15,这才站了起来.结果如图1所示:
杨辉回到家中反复琢磨,一有空闲就在桌上摆弄这些数字,终于发现了其中的规律,按照类似的规律,杨辉又得到了“花16图”——把从1到16的数字排列在四行四列的方格中,使每一横行、纵行、斜行四数之和均为34.后来,杨辉又将散见于前人著作和流传于民间的有关这类问题加以整理,得到了“五五图”“六六图”“衍数图”“易数图”“九九图”“百子图”等许多类似的图.杨辉把这些图总称为纵横图,于1275年写进自己的数学著作《续古
摘奇算法》一书中,并流传后世.
但长期以来,人们习惯于把它当做纯粹的数学游戏,并没有给予应有的重视.随着近代组合数学的发展,纵横图显示了越来越强大的生命力,在图论、组合分析、对策论、计算机科学领域中都找到了用武之地.。
