紧束缚近似
紧束缚近似理论

§5-4 紧束缚近似理论原子结合为原子时,电子的状态发生了根本性的变化,电子从孤立原子的束缚态变为晶体中的共有化状态。
电子状态变化的大小取决于电子在某原子附近所受该原子势场的作用与其它诸原子势场作用的相对大小。
若原子所处原子势场的作用较之其它原子势场的作用要大得多,例如对于原子中内层电子,或晶体间距较大时,上面讨论的近自由电子近似就不适用,这时共有化运动状态与束缚态之间有直接联系,即紧束缚近似理论。
紧束缚理论的实质是把原子间相互作用影响看成微扰的简并微扰方法,微扰后的状态是N 个简并态的线性组合,即用原子轨道()i m ϕ-r R 的线性组合来构成晶体中的电子共有化运动的轨道(,)ψk r ,也称原子轨道线性组合法,简写为LCAO 。
5.4.1 原子轨道线性组合设晶体中第m 个原子的位矢为:112233m m m m =++R a a a ……………………………………………………………………………(5-4-1)若将该原子看作一个孤立原子,则在其附近运动的电子将处于原子的某束缚态()i m ϕ-r R ,该波函数满足方程:22()()()2m i m i i m V m ϕεϕ⎡⎤-∇+--=-⎢⎥⎣⎦r R r R r R ………………………………………………(5-4-2) 其中()m V -r R 为上述第m 个原子的原子势场,i ε是与束缚态i ϕ相对应的原子能级。
如果晶体为N 个相同的原子构成的布喇菲格子,则在各原子附近将有N 个相同能量i ε的束缚态波函数i ϕ。
因此不考虑原子之间相互作用的条件下,晶体中的这些电子构成一个N 个简并的系统:能量为i ε的N 度简并态()i m ϕ-r R ,m=1,2,…,N 。
实际晶体中的原子并不是真正孤立、完全不受其它原子影响的。
由于晶体中其它诸原子势场的微扰,系统的简并状态将消除,而形成由N 个能级构成的能带。
根据以上的分析和量子力学的微扰理论,我们可以取上述N 个简并态的线性组合(,)()()mi m maψϕ=-∑k r k r R ………………………………………………………………………(5-4-3)作为晶体电子共有化运动的波函数,同时把原子间的相互影响当作周期势场的微扰项,于是晶体中电子的薛定谔方程为:22()()()2U E m ψψ⎡⎤-∇+=⎢⎥⎣⎦r r r …………………………………………………………………(5-4-4) 其中晶体势场U (r )是由原子势场构成的,即 ()()()nl nU V U =-=+∑r r Rr R …………………………………………………………………(5-4-5)5.4.2 微扰计算(5-4-4)式可以转化为如下形式:()()22()()()2m m V U V E m ψψ⎡⎤-∇+-+--=⎢⎥⎣⎦r R r r R r r 代入(5-4-2)和(5-4-3)后,可得:[()()()]()0mi m i m maE U V εϕ-+---=∑r r R r R ………………………………………………(5-4-5)在紧束缚近似作用下,可认为原子间距较i ϕ态的轨道大得多,不同原子的i ϕ重叠很小,从而有:()()*in i m nm d ϕϕδ--=⎰r R r R r …………………………………………………………………(5-4-6)现以()*in ϕ-r R 左乘方程(5-4-5),并对整个晶体积分,可以得: *()()[()()]()n i m i m m i m ma E a U V d 0εϕϕ-+---⋅-∑⎰r R r r R r R r =…………………………(5-4-7)首先讨论(5-4-7)式中的积分。
固体物理学:4-5-紧束缚近似
紧束缚模型 —— 只考虑不同原子、相同原子态 之间的相互作用
不考虑不同原子态之间的作用
对于内层电子能级和能带有一一对应的关系 对于外层电子,能级和能带的对应关系较为复杂
一般的处理方法 1) 主要由几个能量相近的原子态相互组合形成能带 2) 略去其它较多原子态的影响
讨论分析同一主量子数中的s态和p态之间相互作用 略去其它主量子数原子态的影响
处理思路和方法 1) 将各原子束缚态的波函数组成布洛赫和 2) 再将能带中的电子的波函数写成布洛赫和的线性组合 3) 最后代入薛定谔方程求解组合系数和能量本征值
同一量子数s态和 p态之间的作用 原子态组成布洛赫和
能带中的电子态 布洛赫和的线性组合
能带中的电子态
代入薛定谔方程 求解组合系数 能量本征值
§4-5 紧束缚近似
一、 模型
电子在一个原子(格 点)附近时,主要受 到该原子势场的作 用,其它原子势场 的作用较弱。
设晶体有N个原子组成,每个原子只有一个价电子,处于S态。
1)孤立原子中的电子
第m个格点附近,第i个电子的束缚态波函数写 为
—— 满足薛定谔方程
—— 格点的原子在 处的势场
—— 电子第i 个束缚态的能级 —— 电子第i 个束缚态的波函数
Wannier 函数
一个能带的Wannier 函数是由同一个能带的布洛 赫函数所定义。
Wannier 函数
满足正交关系
紧束缚作用: 如果晶体中原子之间的间距增大,当电子距某一原子较
近时,其行为类似孤立原子情形。 瓦尼尔函数也应接近孤立原子的波函数
电子波函数
满足
—— 薛定谔方程
无简并s态
用 应用
—— 重叠越多 形成能带越宽
紧束缚近似

(r ) ami (r Rm )
Rm
且近似认为:
*(r i
Rn )i (r
Rm )dr
mn
即:同一格点上的i 是归一化的,不同格点上的 i 因轨道
交叠甚小而正交。式中 Rm m1a1 m2a2 m3a3 格矢
eik•Rs iat i (k ) eik•Rs Jss
e J / ikRn sn
0
Rn
eik•Rs iat i (k ) eik•Rs Jss
e J / ikRn sn
0
e 等式两边同时除以 ik •Rs 得:
Rn
at i
i
(k
)
J ss
e J 0 / ik (Rn Rs ) sn
Rm
V r Vat (r Rn ) 'Vat (r Rm)
Rm
2
Hˆ
2 2m
Vat (r
Rn)
Rm
/Vat (r
Rm)
Hˆ 0
Hˆ '
2
Hˆ 0 2m 2 Vat (r Rn )
r
r Rn
Hˆ /Vat (r Rm ) Rm
0 Rn
4.方程与计算
如果不考虑原子间的相互影响,在格点 R n 附近的电子将以
( s )max
at s
J0
6J1
称为能带顶。
能带的宽度: (s )max (s )min 12J1
J0
12J1
原子能级分裂成能带
可见能带宽度由两个因素决定:
(1)重叠积分J的大小; (2)J前的数字,而数字的大小取决于最近邻格点的数目, 即晶体的配位数。
量子力学第三节、紧束缚近似

由孤立原子能级分裂形成的能带称为子能带 如果两个以上的子能带 相互交叠,则形成一个混合能带 如果能带之间没有发生交叠,就有能隙存在。 能隙就是能级分裂成能带之后余下的部分 4、近自由电子近似与紧束缚近似的适用范围 近自由电子近似适用于金属的价电子 紧束缚近似适用于绝缘体、半导体、金属的内层电子及过渡金属 的d电子。
孤立原子波函数是归一化的,因而
1当 R 0 n r r R d n o , n 0 当 R 0 n
a s a s
于是,方程的左侧成为ES(k)-Esa
方程的右侧分为Rn=0和Rn≠0两项 令
a a A r Vr d V r s c s c
n
ˆ V r R E K a r R 0 e ik R n H c n s n a s
a a e ik R n E V r R E K s c n s s r Rn 0
由 于 孤 立 原 子 满 足 : Hˆ a sa r R n E sa sa r R n 所以
第四节、实际的能带结构
晶体实际的能带结构,通过理论计算与实验相结合而得到 能带的计算 能带的简并 对于某一给定的波矢k,两个或两个以上的子能带的能量相等,于 是这些子能带在k处简并。 一、半导体Ge、Si等的能带结构 1、能带 结构
它是电子处在sa(r)态时,由微扰势VC(r)引起的静电势能, 且大于零. 令
B R r V r Rr R d n c n
a s a ns
它是Rn=0和Rn≠0处两个孤立原子中电子波函数相对微扰势 VC(r-Rn)的重叠积分,大于零 (1)相邻原子间波函数重叠很小,除了近邻以外,B(Rn)可以 认为是零 (2)由于S态波函数具有球对称性,所以B(Rn)与Rn无关
紧束缚近似名词解释

紧束缚近似名词解释
紧束缚近似(Tight-Binding Approximation)是一种在固体物理学和材料科学中常用的近似方法,用于描述电子在晶格结构中的行为。
该方法假设电子只在相邻原子之间的相互作用下运动,忽略了更远的相互作用。
这种近似方法特别适用于那些电子波函数重叠较少的材料,因为在这种情况下,电子的波函数主要集中在它们各自的原子附近。
在紧束缚近似下,电子的能量和波函数可以通过一个包含原子轨道和它们之间相互作用的模型来描述。
这种方法的一个优点是它可以处理大规模系统,因为它只需要考虑每个原子周围的有限数量的其他原子。
尽管紧束缚近似有许多优点,但它也有一些局限性。
例如,它不能很好地描述那些电子波函数重叠较大的材料,如金属和半金属。
此外,它也不能描述那些具有强电子关联效应的材料,如某些过渡金属氧化物。
以上信息仅供参考,如有需要,建议您咨询专业人士。
固体物理(第16课)紧束缚近似资料

V为晶体的体积
2. 微扰计算结果
k
(
r
)
1 N
N
e ikRn i
(r
Rn
)
n1
Ek Ei J ss
e J ik( Rn Rs ) sn
J SS
J SN
V V
* i
* i
(r (r
与sR近s邻)的Hˆn Rs )Hˆ
i i
(r (r
Rs )d Rn )d
E
k
Ei
J ss
ห้องสมุดไป่ตู้
e J ik( Rn Rs ) sn
与s近邻的n
E
k
Gh
Ei
J ss
e J i (k Gh )( Rn Rs ) sn
与s近邻的n
Ei J ss
e e J ik( Rn Rs )
iGh ( Rn Rs ) sn
与s近邻的n
Ek (3) Ek随k变化,它们构成了与Ei相联系的能带
能带的宽度取决于J sn
示意图
零级近似:
Hˆ 0
k
0
(r
)
Ek 0
k
0
(r
)
Ekk00(r)Ei
i
(r
Rn )
孤立原子
k
l1 N1
b1
l2 N2
b2
l3 N3
b3
其中
Ni 2
li
Ni 2
N为晶体中的原 子数或布喇菲晶 格的原胞数
在第一布里渊区有N个值不同的 值,对应这些准连续函数取值的 波矢k, E(k)构成一个准连续的能 带.
积分值才不为0,当Rs 0时,波函数重叠最大,
能带理论(3)(紧束缚近似)

把孤立原子的势场看成零级近似,而原子间相互作用看成微扰, 这种微扰是N重简并微扰,微扰后的状态是N个简并态的线性 组合。
(r) ami (r Rm )
m
代入晶体运动方程,得
am i U (r) V (r Rm )i (r Rm )
m
E ami (r Rm )
m
可以近似认为
i*(r Rm )i (r Rn )dr nm
comments
• 晶体电子共有化与紧束缚思想矛盾?共有化在 紧束缚态近似方法中如何体现?
• 紧束缚态近似用局域波函数和周期性的相因子 来构成满足Bloch函数的基函数
• 近自由电子用平面波基函数是自然的,因为平 面波本身就是非局域的,本身就是调幅为常数 的Bloch函数!
紧束缚态近似——原子轨道线性组合法
U (r) U (r Rm )
i* (Rn Rm )U ( ) V ( )i ( )d J (Rn Rm )
am J (Rn Rm ) (E i )an
m
令
am i
J (Rn
R )eik .(Rm Rn ) m
J (Rs )eik.Rs
2 2m
2
V
(r
Rm
)i
(r
Rm
)
ii
(r
Rm
)
(1)
V(r-Rm)为Rm格点的原子势场,i 为原子能级。
晶体中电子运动的波动方程为
2 2m
2
U
(r)
(r)
E
(r)
U(r)为周期势场,它是各格点原子势场之和。
在紧束缚态近似中,方程(1)看成0级近似,把
看成微扰。
U (r) V (r Rm )
紧束缚近似---原子轨道线性组合法

以
左乘上面方程 积分得到
化简后得到
am
i*
(r
Rn
)[U
(r )
V
(r
Rm
)]i
(r
Rm
)dr
(E
i
)an
m
—— N种可能选取,方程是N个联立方程中的一个方程
04_05_紧束缚近似-原子轨道线性组合法 —— 能带理论
am
i*
(r
Rn
)[U
(r)
V
(r
Rm
)]i
(r
Rm
)dr
—— Si的价带和导带是上面八个布洛赫和的线性组合
04_05_紧束缚近似-原子轨道线性组合法 —— 能带理论
—— 也可以看作是Si 原子进行轨道杂化, 形成四个杂化轨道
近邻原子的杂化轨道之 间形成成键态和反键态
h1
1 2
(
s
px
py
pz )
h2
1 2
(
s
px
py
pz )
h3
Orbitals
—— 原子轨道线性组合法
04_05_紧束缚近似-原子轨道线性组合法 —— 能带理论
—— 电子在第m个原子附近运动,其它原子的作用是微扰
—— 简单晶格原胞只有一个原子 电子在格矢
处原子附近运动
电子的束缚态波函数
04_05_紧束缚近似-原子轨道线性组合法 —— 能带理论
电子的束缚态波函数
函数的线性组合构成
晶体中电子的波函数
(r )
am
i
(r
Rm
)
m
电子的薛定谔方程
04_05_紧束缚近似-原子轨道线性组合法 —— 能带理论
紧束缚近似

定义:
i ( r Rm ) 表示位于格点 Rm 上的孤立原子波函数; i (k , r ) 紧束缚下晶体中电子波函数,可表示 为 i ( r Rm )的线性组合,即: (k , r ) am (k ) i (r Rm )
这里:
(k , r ) am (k ) i (r Rm ).......... .......... ......( 3)
m V U ( r ) V ( r Rm )......... .......... .......... .......... ......( 4)
例二、面心立方晶格中由原子s态形成的能带,并分 析其能带宽度;
例三、简立方晶格中由原子p态形成的能带。
13
紧束缚近似微扰计算——例一
例一、简立方晶格中由原子s态形成的能带,并分析其能 带宽度。 求解方法:利用公式计算 E s(k )
E k i J 0
公式中需要解决的是:
*
对应本征值为:
ik E (k ) i J ( Rs )e Rs s
特点:是准连续能级
11
化简J ( Rs ) :
紧束缚近似微扰计算
表示式:
* J ( Rs ) i -Rs U V i d
化简: am i i r Rm am V i r Rm E am i r Rm
m m m
i i r Rm
m
m
7
紧束缚近似微扰计算
继续化简得: am i V i r Rm E am i r Rm
固体物理(第16课)紧束缚近似

a (r R
m i m
m)
作为晶体中电子共有化状态的波函数,把原子间的相互 影响作为周期势场的微扰项. 于是晶体中电子的薛定鄂方程为: 2 2 [ U ( r )] E 2m
U (r)
V (r R ) U (r R )
n l
ˆ H k ( r ) E k k ( r )
l l l k 1 b1 2 b2 3 b3 N1 N2 N3 Ni Ni 其中 li 2 2
在第一布里渊区有N个值不同的 值,对应这些准连续函数取值的 波矢k, E(k)构成一个准连续的能 带.
N为晶体中的原 子数或布喇菲晶 格的原胞数
V为晶体的体积
2. 微扰计算结果
n m n m 0 s s 0
ik( Rn Rm ) ikRs
ikRs
令 r Rm J ( Rs )
* i (
( Rn Rm ))[U ( ) V ( )] i ( )d
式中 Rs=Rn-Rm,为原子的相对位置。 上式为晶体中作共有化运动的电子的能量本征值,与其 对应的波函数为:
1 (r ) k N E k Ei
s
e
n 1
N
ik Rn
i ( r Rn )
J ( R )e
s s 0
ikRs ikRs
Ei J 0
J ( R )e
s
3. 说明
( r )是布洛赫波函数 (1) k 1 k (r ) N
对上式乘以*i(r-Rm)并积分,经过变换后得到
( Ei E )an
解出 am Ce
3.3紧束缚近似

e
ik R s
iat
ik R s / ik R n i (k ) e J ss e J sn 0
等式两边同时除以
e
ik R s
得:
Rn
i
at
i ( k ) J ss
*iBiblioteka 即:同一格点上的 i 是归一化的,不同格点上的 i 因轨道 交叠甚小而正交。 式中 R m m1 a1 m 2 a 2 m 3 a 3 格矢
( r ) 的上述取法称为原子轨道线性组合法(LCAO)
即晶体中的电子作共有化运动,其共有化轨道由原子轨道
i (r Rm )
i (r Rm )
下面验证 k ( r ) 为布洛赫函数 按照布洛赫定理,只要证得:
ik R n k ( r R n ) e k ( r )
即可。
令:R n R m R l
k ( r R n ) 1 N 1 N e e 1 N
应。如2s、2p等能带。
Jsn 表示相距为 R s R n 的两个格点上的波函数的重叠积分, at at 它依赖于 i ( r R n ) 与 i ( r R s ) 的重叠程度,R R 重叠
s n
最完全,即Jss最大,其次是最近邻格点的波函数的重叠积分, 涉及较远格点的积分甚小,通常可忽略不计。
1 N
e
Rn
ik R n
i
at
(r Rn )
(r )
ˆ 注意到: H
2
2m
P-4.4 紧束缚近似-19

E(R) =εs − J0 + 6J1 M点:k = (π/a, π/a, 0)
E(M) =εs − J0 + 2J1
E (k )
[100] π/a
R
[111]
简立方情形
Γ点和R点分别对于能带底和能带顶,所以,能带宽度 ΔE = E(R) − E(Γ) = 12J1 由此可见,能带的 宽度决定于J1,而 J1的大小取决于近
的情况,这时的原子轨道只受到其它原子很
微弱的作用,过渡金属中很重要的3d能带就 是一例。
在N个原子相距较远时,每个原子有不同的原子能级,整个体系的单电子 态是N重简并的,当把它们放在一起形成晶体后,由于最紧邻原子波函数
的交叠,N重简并解除,展宽成能带。每个能带都包含N个k 值。
由于能带从原子的能
级演化而来,所以内 层电子能带常用原子 能级的量子数标记, 如3s,3p,3d等。
E n 是与本征态 U (r Rl )是第l个原子势, 其中,
级)。该式忽略了其它原子的影响。
n
相对应的本征能量(能
万尼尔函数
万尼尔函数
紧束缚近似
紧束缚近似
紧束缚近似
紧束缚近似
U
紧束缚近似
V
这是紧束缚近似给出的最有用的结论。
以简单立方晶格为例
在简单立方晶格的简约区中 Γ点:k=(0, 0, 0) E(Γ) =εs − J0 − 6J1 X点:k=(π/a, 0, 0) E(X) =εs − J0 − 2J1 R点:k =(π/a, π/a, π/a)
以上就是TBA模型的 主要结论。
紧束缚近似的出发点是:电子在一个原子附近时,将主要受到该原子势作
用,其它原子势作用弱,可当作微扰作用。此时晶体中电子的波函数不能用自
第18讲紧束缚近似

第十八讲:紧束缚近似紧束缚近似的出发点电子在一个原子附近时,将主要受到该原子场的作用,把其它原子场的作用看成是微扰作用,由此可以得到电子的原子能级与晶体中能带之间的相互联系。
紧束缚近似的模型和微扰计算如果完全不考虑原子之间的相互影响,在某格点R m =m 1a 1+m 2a 2+m 3a 3附近的电子将以原子束缚态ϕi (r −R m )的形式环绕点R m 运动,假定是简单晶格,每个原胞中只有一个原子。
ϕi 表示孤立原子的波动方程的本征态()()()222m i m i i m V m ϕεϕ −∇+−−=−r R r R r R (4-49) V (r −R m )为R m 格点的原子势场,εi 为某原子能级。
在紧束缚近似中,这些看作微扰的零级近似。
晶体中电子运动的波动方程为()()()222U E m ψψ−∇+=r r r U (r )为周期性势场,它是各格点原子势场之和。
U (r )− V (r −R m )看成微扰。
原子轨道线形组合L C A O环绕不同的N 个格点,将有N 个类似的波函数,它们具有相同的能量εi ,也就是说是N 重简并。
这实际上是把原子间相互影响看作微扰的简并微扰方法,微扰以后的状态是N 个简并态的线形组合,即用原子轨道ϕi (r −R m )的线形组合来构成晶体中电子共有化运动的轨道ψ(r ) ,因而也称为原子轨道线形组合L C A O 。
晶体中电子共有化运动的波函数为()()m m mr a ψϕ=−∑r R (4-50)代入波动方程(4-49)得到()()()()mi m i m m i m mmaU V E a εϕϕ+−−−=− ∑∑r r R r R r R (4-51)当原子间距比原子轨道半径大时,不同格点的ϕi 重叠很小,将近似认为()()inimmnd ϕϕδ∗−−=∫r R r R r (4-52)以()i n ϕ∗−r R 左乘波动方程式(4-51)并积分就得到()()()(){}mi mni n m i m n maU V d Ea εδϕϕ∗+−−−−= ∑∫r R r r R r R r (4-53)化简得()()()()()min m i m i nma U V d E aϕϕε∗−−−−=− ∑∫r R r r R r R r (4-53)注意()i n ϕ∗−r R 实际上有N 种可能的选取办法,上式实际上是N 个联立方程中的一个典型方程。
固体物理:6-3 紧束缚近似方法

哈佛-固体化学导论:LCAO (Linear Combination of Atomic Orbitals)
6.3.1 模型和微扰计算 6.3.2 一个简单的例子 6.3.3 原子能级与能带的对应 6.3.4 Wannier函数
➢ 6.3.4 Wannier函数
LCAO:
形式类似,只是现在一个二阶张量代替了
m
1 称其为倒有效质量张量。
m
倒有效质量张量的分量为:
1
1 2E
m
2
k k
20
选kx,ky,kz轴沿张量主轴方向,则有: 2 E 0,
k k 0, 这时倒有效质量张量是对角化的。
1 1 2E
m
2
k k
2E k x2
1
2
0
0
0
2E
k
2 y量大顶附近总是 Nhomakorabea负值。k
例1:以体心立方晶格,紧束缚近似下的s能带为例,讨论有效 质量的特点。
22
解:由紧束缚近似可得体心立方s能带的能量表达式:
Es(k )
E
a s
t
C
s
8J
cos
ak x 2
cos
ak 2
y
cos
akz 2
E 4Ja sin akx cos aky cos akz
k x
222
0
0
0
2E
k
2 z
下面以一维情况为例对电子有效质量进行简单的讨论。
21
(1)有效质量反比于能谱曲线的曲率,
d2E 大,有效质量小; dk 2
d2E dk 2
小,有效质量大。
紧束缚近似公式(一)

紧束缚近似公式(一)紧束缚近似公式紧束缚近似(Tight Binding Approximation)是一种描述电子在固体晶格中行为的数学方法。
在紧束缚近似中,电子波函数被表示为原子轨道的线性组合,通过求解薛定谔方程来得到能级结构和电子态密度等信息。
Bloch定理Bloch定理表明在理想晶体中,电子波函数可以表示为平面波和某个周期函数的乘积形式。
根据Bloch定理,电子波函数可以用下式表示:Ψk(r)=e ik⋅r u k(r)其中,e ik⋅r是平面波,u k(r)是周期函数。
紧束缚近似基本公式紧束缚近似基本公式是在Bloch定理的基础上,进一步假设电子波函数由最近邻原子的原子轨道线性组合构成。
根据紧束缚近似,电子在晶体中的波函数可以用下式表示:e ik⋅R n u n(r−R n)Ψk(r)=∑c nn其中,R n是最近邻原子的位置矢量,u n(r−R n)是最近邻原子的原子轨道。
紧束缚近似能带关系根据紧束缚近似基本公式,可以得到能带关系,即能量与波矢之间的关系。
能带关系可以用下式表示:E k=∑c n∗c n e ik⋅(R n−R m)ϵnmn其中,E k是能量,c n∗和c n是电子的系数,e ik⋅(R n−R m)是相位因子,ϵnm是最近邻原子间的相互作用能。
紧束缚近似的应用举例紧束缚近似在描述材料的能带结构和电子态密度等方面有广泛的应用。
以下是一些应用举例:1.能带计算:通过紧束缚近似,可以计算材料的能带结构,进而分析材料的导电性、绝缘性等特性。
2.电子态密度计算:紧束缚近似可以用于计算材料的电子态密度,这对于研究材料的化学反应等方面非常重要。
3.值得注意的是,紧束缚近似也有其局限性,适用于描述弱相互作用体系,如共价键、金属键等。
对于强相互作用系统,如强关联电子体系,紧束缚近似可能不适用。
总之,紧束缚近似是一种重要的描述电子在晶体中行为的方法,在材料科学和凝聚态物理等领域有着广泛的应用。
4-5紧束缚近似ppt课件

(3)孤立原子波函数作为零级近似;
2 2m
2
V
(r
Rm
) i
(r
Rm
)
i
i
(r
Rm
)
(3)其它原子场作用看成微扰处理。
V
U
(
r)
V
(
r
Rm
)
2
一、基本思想
(5)紧束缚近似的实质:把原子间相互作用影响看成
微性晶扰组体的合中简,的并即电微用子扰原共方子有法轨化,道运微动扰的i后轨(r的道 R状m )态(k的是, r线)N性个,组简也合并称来态原构的子成线
(k )
i
(r
Rm
)..........
..........
......(
3)
V
U
(
r)
m
V
(
r
Rm
).........
..........
..........
..........
......(
4)
6
紧束缚近似微扰计算
将(3)(4)式代入(2)式:
2 2m
2
V
r
Rm
U (r) V
E py (k )
p
J0
2J1
cos k ya
2J 2 (cos k x a
cos kza)
E pz (k )
p
J0
2J1
cos kza
2J 2 (cos k x a
cos k ya)
考虑到原子p态是奇宇称,
对于 px,有 px ( x) px ( x) ,可得到沿x轴的J1<0,
而沿y和z轴J2>0;
紧束缚近似

一.定性说明
二.微扰计算
三.原子能级与能带的对应
参考:黄昆书4.5节 p189
和近自由电子近似认为原子实对电子的作用很弱相反,本 节,我们假定原子实对电子的束缚作用很强,因此,当电子距 某个原子实比较近时,电子的运动主要受该原子势场的影响, 受其它原子势场的影响很弱。因此电子的行为同孤立原子中电 子的行为更为相似。
对这样一个由 N 个原子组成的晶体,其晶体势场应由各原 子势场相加而成,并具有和晶格相同的周期性:
U r V r Rm U r Rn
m
ur r r r Rn n1a1 n2a2 n3a3
于是,晶体的薛定鄂方程为:
h2 2m
2
U
r
r
E
r
将上面的结果代入求解,会得到晶体中能带的表达式。
每个能带都包 含 N个k 值。
由于能带从原 子的能级演化 而来,所以内 层电子能带常 用原子能级的 量子数标记, 如3s,3p,3d等
以上就是 TBA模型的主 要结论。
紧束缚近似的出发点是:电子在一个原子附近时,将主要 受到该原子势作用,其它原子势作用弱,可当作微扰作用。此 时晶体中电子的波函数不能用自由电子波函数表示,而是应由 所有原子的电子波函数的线性组合来表示,即:
m
J Rs eikRs
近的电子将以原子束缚态 i (r - Rm) 的形式环绕 Rm 点运动 (这里设为简单晶格,每个原胞中只有一个原子) j 表示孤
立原子波动方程的一个本征态。
ur
rrr
Rm m1a1 m2a2 m3a3
r-Rm
0
第 m 个孤立原子的波动方程:
h2 2m
2
V
r
固体电子2---紧束缚近似

重叠最完全的是Rs=0,我们用J0表示(教材上用):
J 0 j (ξ) [U (ξ) V (ξ)]dξ
2
其次是Rs为近邻格点的格矢量,一般只保留到最近邻项:
E (k ) E j J 0
最近邻
R s 0
e
ik R s
2 2 V (r R m )] [U (r) V (r R m )] (r) E (r) [ 2m N 1 ik Rm (r ) e j (r R m ) N m1
e
m 1
N
ik R m
N 2 2 ik R m [ V ( r R )] [ U ( r ) V ( r R )] ( r R ) E e j (r R m ) j m m m m 1 2m
eik R m J ( Rn Rm ) ( E E j )eik R n
m 1
N
E E j eik ( R m R n ) J ( Rn Rm )
m 1
N
令Rs=Rn-Rm
E E j e ik R s J (R s )
s
能量本征值仅由格位差Rs决定,与n、m无关。
孤立原子哈密顿量,H0 小量,微扰项,H
H0对应的电子波函数和能级已知:
2 2 [ V (r R m)] j (r R m ) E j j (r R m ) 2m
V(r-Rm)为Rm处原子在r处产生的势场。 Ej为原子能 级,相应的本征函数为j(rRm)为原子波函数。
10
令: r Rm , r Rm
3.3 紧束缚近似

§ 3.3.2 微扰作用与能带的形成 显然,在独立电子近似和周期场近似下Bravais晶格中的单电子 Hamilton算符可改写成如下形式
2 2 ˆ ˆ Ha r u (r Rl ) H ' U (r ) u (r Rl ) u(r R‘ l ) ve (r ) 2 me ‘ l ( l ) 于是,Bravais晶格中的单电子定态SchrÖdinger方程为 ˆ ˆ ˆ H (r ) ( H a H ' ) (r ) (r ) 如果将独立电子近似和周期场近似下Bravais晶格中的单个电子进 一步简化为紧束缚电子,则有 ˆ ' H ˆ H a
ˆ H ˆ H ˆ' H a
这样,在原子内束缚电子的定态SchrÖdinger方程的近似解的基础 上,应用量子力学中的微扰理论就可以近似地求解晶体中的单电子 定态SchrÖdinger方程
原子内束缚电子的定态SchrÖdinger方程在有关原子的量子力 学理论中已经近似解出,原子内束缚电子的各单电子能级及其相应 的定态波函数(在固体物理学中,通常又称为电子的原子轨道函数 或原子轨道)如表所示: 能级
§ 3.3 紧束缚近似
在本节中,将以绝缘体晶体和半导体晶体中的s、 p价电子以及过渡族金属晶体中的d价电子等价电子在
晶体中的行为特点为基础,建立起近似地求解独立电
子近似和周期场近似下晶体中单个电子运动的定态
SchrÖdinger方程的另一种近似方法——紧束缚电子
近似方法。其物理图象及结果较适用于过渡族金属中
Rl
其运动将遍及整个晶体体积区域,故而常将描述晶体中共有化电子 运动状态的单电子定态波函数称为电子的晶体轨道函数或晶体轨道。 与此同时,在其它离子实和其它价电子的微扰作用下,N重简 (a) 并的能级 i 将进一步分裂成N个密集的能级从而形成一个能带,
4第四章电子结构的紧束缚近似
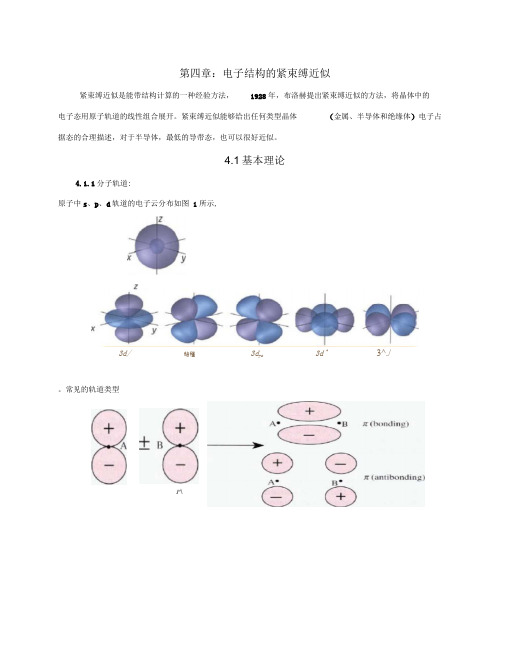
第四章:电子结构的紧束缚近似紧束缚近似是能带结构计算的一种经验方法,1928年,布洛赫提出紧束缚近似的方法,将晶体中的电子态用原子轨道的线性组合展开。
紧束缚近似能够给出任何类型晶体(金属、半导体和绝缘体)电子占据态的合理描述,对于半导体,最低的导带态,也可以很好近似。
4.1基本理论4.1.1分子轨道:原子中s、p、d轨道的电子云分布如图1所示,3d/站程3d yz3d^3^./。
常见的轨道类型P\4.1.1简单晶格:首先考虑简单格子构成的晶体,每个原胞只有一个原子,假定原子的轨道用 子数,晶体中其它原子的对轨道波函数表示为 ]r-R 。
由晶体中所有原子的相应轨道建立以k 为博士的晶体的布洛赫和,表示为:其中,N 为晶体原胞数。
在紧束缚近似中,以 k 为波失的晶体电子波函数,用所有以k 为波失的布洛赫和展开,表示如下:'i八 C i k i k,ri式中C i k ,为展开式系数,可以通过标准的矩阵对角化程序求出。
晶体的哈密顿量为如下形势:晶体的能量本征值和本征失(展开式系数)可以有下列行列式方程给出:M j k -ES j k =0式中M y (k )为由布洛赫和构建的晶体哈密顿矩阵元 Mj (k )=(叫(k,r |H |®j (k,r 》,q 为晶体布洛赫 之间的交叠积分 S jk,r < k,r :)。
这样求晶体的的电子态就主要转化为求上述(4-4)式中的哈密顿矩阵元和交叠积分,可以通过对原胞实空间进行具体积分求得,但计算复杂,计算代价高。
通常, 紧束缚近似方法中矩阵元是通过半经验的方法给出。
4.1.2半经验方法在半经验方法中,首先假定原子轨道具有高度局域性,这样以不同原子为中心的原子轨道之间的交 叠积分为零,又由于,相同原子的不同轨道正交,这样,式( 是计算哈密顿矩阵元:Mj (k )=丄瓦送 exp 「ik 依-Rm )WM r -Rm l H pU r -尺》(必)NR m R ni r 表示,其中i 为量i一卜 exp ik & i r — R(4-1)(4-2)(4-3)(4-4)4-4 )中的交叠积分 $二。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
积分值只有当它们有一定相互重叠时,才不为零。当 Rs =0 时,两波函数完全重叠。
J 0 i U V d
2
其次,考虑 Rs =近邻格矢,一般只需保留到近邻项,而略 去其他影响小的项,即可得
J0 由此可见,能带的 s 12J1 宽度决定于J1,而 J1的大小取决于近 邻原子波函数间的重叠,重叠越多,形成的能带就越宽。能
}
量越低,能带就越窄;能量越高,能带就越宽。这是由于能 量最低的带对应于最内层的电子,其电子轨道很小,不同原 子间波函数的重叠很少,因而能带较窄;而能量较高的能带 对应于外层电子,不同原子间波函数有较多的重叠,因此形 成的能带就较宽。
E k i J 0
Rs 近邻
J R exp ik R
s s
这是紧束缚近似给出的最有用的结论!
例1:求简单立方晶体中由电子的 s 态所形成的能带
由于 s 态的原子波函数是球对称的, 沿各个方向的重叠积分相同。因此, 对于不同方向的近邻,有相同的值:
J Rs J1
E k
100
a
3
a
111
简立方情形
以上的讨论只适用于原子的 s 态电子,即原子的能级非 简并的情况,这时一个能级只有一个态 i 而且还假设原子 波函数间的重叠很少,因此只适用于原子内层的 s 电子。对 于 p电子、d电子等,这些状态都是简并的,因此,其Bloch 函数应是孤立原子的有关状态波函数的线性组合。 例2:求简单立方晶体由原子 p 态所形成的能带 原子的 p 态为三重简并,其原子轨道可表为
Rs 近邻格矢
a
a
对于简单立方: Rs=(a, 0, 0), (0, a, 0), (0, 0, a)
E k s J 0 J1 e
ik x a
e
ik x a
e
ik y a
e
ik y a
eikz a eikz a
s J 0 2 J 1 cos k x a cos k y a cos k z a
将上面的结果代入求解,会得到晶体中能带的表达式。 微扰后的状态由这N 个简并态的线性组合而成,即用原
子轨道 i r Rm 的线性组合来构成晶体中电子共有化运动
的轨道 (r)。所以这种方法也称为原子轨道的线性组合法, 简称LCAO(Linear Combination of Atomic Orbitals)
r ami r Rm
式中, m m1a1 m2 a2 m3 a3 是晶体中第 m 个原子的位矢, R
i r Rm 是将该原子视为孤立原子时自由原子波函数。它应
该满足如下方程:
m
2 2 2m V r Rm i r Rm ii r Rm
6.4 紧束缚近似(TBA)
一.定性说明
二.微扰计算 三.原子能级与能带的对应
参考:黄昆书4.5节 p189
和近自由电子近似认为原子实对电子的作用很弱相反,本 节,我们假定原子实对电子的束缚作用很强,因此,当电子距 某个原子实比较近时,电子的运动主要受该原子势场的影响, 受其它原子势场的影响很弱。因此电子的行为同孤立原子中电 子的行为更为相似。
成的能带。
对这样一个由 N 个原子组成的晶体,其晶体势场应由各原 子势场相加而成,并具有和晶格相同的周期性:
U r V r Rm U r Rn
m
Rn n1 a1 n2 a2 n3 a3
于是,晶体的薛定鄂方程为:
2 2 2m U r r E r
这时可将孤立原子看成零级近似,而将其他原子势场的影 响看成小的微扰,由此可以给出电子的原子能级和晶体能带之 间的相互联系。这种方法称为紧束缚近似 (Tight Binding Approximation)。
一. 定性说明: 下图绘出了一维原子势,假定原子势很强,因此,当一 个电子在晶体中运动并被一个离子束缚住的时候,在它被释 放或隧穿到另一个离子之前,将会停留相当长的时间,在受 束缚期间,电子轨道主要是围绕单个离子,其态函数基本上 是一个原子轨道,受其它原子的影响很小。(图中表明,产 生的电子能量明显低于势垒顶点。) 该模型主要适合于晶体中原子间距较大时,或能带低而 窄、壳层半径比晶格常数小得多的情况,这时的原子轨道只 受到其它原子很微弱的作用,过渡金属中很重要的3d能带就 是一例。
由于能带从原 子的能级演化 而来,所以内 层电子能带常 用原子能级的 量子数标记, 如3s,3p,3d等 以上就是 TBA模型的主 要结论。
紧束缚近似的出发点是:电子在一个原子附近时,将主要 受到该原子势作用,其它原子势作用弱,可当作微扰作用。此 时晶体中电子的波函数不能用自由电子波函数表示,而是应由 所有原子的电子波函数的线性组合来表示,即:
{
p xf r
x
p yf r
y
p zf r
z
在简单立方晶体中,三个 p 轨道各自形成一个能带,
其波函数是各自原子轨道的线性组合。
kp C eikR p r R
x
{
x
k C eikR p r R
一维晶体势
原子波函数
相应的Bloch 波函数 Omar 一书对紧束缚模型的描述 (见该书 p210)
在N个原子相距较远时,每个原子有不同的原子能级,整个体 系的单电子态是N重简并的,当把它们放在一起形成晶体后, 由于最紧邻原子波函数的交叠,N重简并解除,展宽成能带。 每个能带都包 含 N个k 值。
二、微扰计算 如果完全不考虑原子间的相互影响,在某个格点 Rm 附 近的电子将以原子束缚态 i (r - Rm) 的形式环绕 Rm 点运动 (这里设为简单晶格,每个原胞中只有一个原子) j 表示孤 立原子波动方程的一个本征态。
Rm m1 a1 m2 a2 m3 a3
在紧束缚近似中,认为原子间距比原子轨道半径大,
因此可以认为不同格点的 j 重叠很少,可以近似地认为:
(这个近似只是为了数学表述上的简化,没有实质影响)
i r Rn i r Rm dr nm
以i*(r-Rn)同时乘方程两边,积分得
am inm i r Rn U r V r Rm i r Rm dr Ean
相应的能量本征值为
E k j J Rs eikRs
s
利用Born-Karman周期性边界条件,可得 k 的取值为
h3 h1 h2 k b1 b2 b3 N1 N2 N3
h1, h2, h3=整数
由此可知,在简约区中,波矢 k 共有 N 个准连续的取 值,即可得 N 个电子的本征态 k(r) 对应于N个准连续的 k 值。这样,E(k)将形成一个准连续的能带。
于是,对于一个确定的 k,电子运动的波函数为
1 k r N
k r e
e
m
ik Rm
j r Rm
1 C N
容易验证k(r)为Bloch函数
ikr
1 N
e
m
ik r Rm
ikr i r Rm e uk r
周期场 U(r) 是晶体中各格点原子势场之和,在紧束缚近 似中,我们将孤立原子看成零级近似,而将其他原子势场 [U(r)-V(r-Rl)] 的影响看成微扰。由于电子可以环绕不同的格 点运动,而环绕不同的格点可得到 N 个类似的原子波函数, 它们具有相同的能量 i ,即这 N 个态的能量是简并的,晶体 中的电子构成了一个 N 度简并的系统。
am CeikRm
ik Rn Rm
其中C为归一化因子。代入方程组得
E i J Rn Rm e
m
J Rs eikRs
s
Rs Rn Rm
由于上式与 n 或 m 都无关,这表明,这种形式的解对 所有联立方程组都化为同一条件。上式确定了这种形式 解所对应的能量本征值。
以上论述说明,形成固体时,一个原子能级将展宽为 一个相应的能带,其 Bloch 函数是各格点上原子波函数 j(r-Rm) 的线性组合。
通常,能量本征值 E(k) 的表达式可进一步简化。
J Rs i Rs U V i d
r-Rm
0
第 m 个孤立原子的波动方程:
2 2 2m V r Rm i r Rm ii r Rm
V(r-Rm)是 Rm 格点的原子势场, i 为其原子能级. 在晶体中,电子运动的波动方程为:
2 2 2m U r r E r
py
kp C eikR p r R
z
y
z
由于p轨道不是球对称的,因此,沿不同方向的近邻重叠积 分J(Rs)不完全相同。如 px ,电子主要集中在 x 轴方向, 在六个近邻重叠积分中,沿 x 轴方向的重叠积分较大,用 J1表示;沿 y 方向和 z 方向的重叠积分用 J2 表示。
M点:k= (/a, /a, 0)
ky
kx
E M s J 0 2J1
由于s态波函数是偶宇称,s(r)= s(-r), 所以,在 近邻重叠积分中波函数的贡献为正,即J1 > 0 。
点和R点分别对于能带底和能带顶,所以,能带宽度
E E R E 12J1
在简单立方晶格的简约区中 点:k=(0, 0, 0)
E s J 0 6 J1
