八年级上册数学 轴对称填空选择专题练习(解析版)
天津市汇森中学数学轴对称填空选择单元测试卷(解析版)

天津市汇森中学数学轴对称填空选择单元测试卷(解析版)一、八年级数学全等三角形填空题(难)1.如图,在ABC ∆和ADE ∆中,90BAC DAE ∠=∠=︒,AB AC =,AD AE =,C ,D ,E 三点在同一条直线上,连接BD ,则下列结论正确的是___________.①ABD ACE ∆≅∆②45ACE DBC ∠+∠=︒③BD CE ⊥④180EAB DBC ∠+∠=︒【答案】①②③④【解析】【分析】根据全等三角形的判定和性质,以及等腰三角形的性质解答即可.【详解】解:∵∠BAC=∠DAE=90°,∴∠BAC+∠DAC=∠DAE+∠DAC ,即:∠BAD=∠CAE ,∵AB=AC ,AE=AD ,∴△BAD ≌△CAE (SAS ),故①正确;∵△BAD ≌△CAE ,∴∠ABD=∠ACE ,∵∠ABD+∠DBC=45°,∴∠ACE+∠DBC=45°,故②正确;∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°,则BD ⊥CE ,故③正确;∵90BAC DAE ∠=∠=︒,∴∠BAE+∠DAC=180°,∵∠ADB=∠E=45°,∴DAC DBC ∠=∠,∴180EAB DBC ∠+∠=︒,故④正确;故答案为:①②③④.【点睛】此题主要考查了全等三角形的判定及性质,以及等腰三角形的性质,注意细心分析,熟练应用全等三角形的判定以及等腰三角形的性质是解决问题的关键.2.如图,P为等边△ABC内一点,∠APC=150°,且∠APD=30°,AP=6,CP=3,DP=7,则BD的长为______.【答案】234.【解析】【分析】将△CPA绕点C逆时针旋转60°得到△CEB,连接EP,由全等三角形的性质可得CE=CP,∠ECB=∠PCA,∠CEB=∠CPA=150°,BE=AP=6,结合等边三角形的性质可得出∠ECP=60°,进而证明△ECP为等边三角形,由等边△ECP的性质进而证明D、P、E三点共线以及∠DEB=90°,最后利用勾股定理求出BD的长度即可.【详解】将△CPA绕点C逆时针旋转60°得到△CEB,连接EP,∴CE=CP,∠ECB=∠PCA,∠CEB=∠CPA=150°,BE=AP=6,∵等边△ABC,∴∠ACP+∠PCB=60°,∴∠ECB+∠PCB=60°,即∠ECP=60°,∴△ECP为等边三角形,∴∠CPE=∠CEP=60°,PE=6,∴∠DEB=90°,∵∠APC=150°,∠APD=30°,∴∠DPC=120°,∴∠DPE=180°,即D、P、E三点共线,∴ED=3+7=10,∴BD=22DE BE=234.故答案为234.【点睛】本题主要考查全等三角形的性质、勾股定理、等边三角形的判定与性质以及三点共线的判定,运用旋转构造全等三角形是解题的关键.3.如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为48和36,求△EDF的面积________.【答案】6【解析】【分析】作DM=DE交AC于M,作DN⊥AC,利用角平分线的性质得到DN=DF,将三角形EDF的面积转化为三角形DNM的面积来求.【详解】作DM=DE交AC于M,作DN⊥AC,∵AD是△ABC的角平分线,DF⊥AB,∴DF=DN,∵DE=DG,∴DG=DM,∴Rt△DEF≌Rt△DMN(HL),∵DG=DM, DN⊥AC,∴MN=NG,∴△DMN≌△DNG,∵△ADG和△AED的面积分别为48和36,∴S△MDG=S△ADG-S△ADM=48-36=12,∴S△DEF=12S△MDG=1212=6,故答案为:6【点睛】本题考查了角平分线的性质及全等三角形的判定及性质,正确地作出辅助线,将所求的三角形的面积转化为另外的三角形的面积来求是解题关键.4.如图,在四边形ABCD 中,∠DAB =∠DCB =90°,CB =CD ,AC =6,则四边形ABCD 的面积是_________.【答案】18.【解析】【分析】根据已知线段关系,将△ACD 绕点C 逆时针旋转90°,CD 与CB 重合,得到△CBE ,证明A 、B 、E 三点共线,则△ACE 是等腰直角三角形,四边形面积转化为△ACE 面积.【详解】∵CD =CB ,且∠DCB =90°,∴将△ACD 绕点C 逆时针旋转90°,CD 与CB 重合,得到△CBE ,∴∠CBE =∠D ,AC =EC ,∠DCA =∠BCE .根据四边形内角和360°,可得∠D +∠ABC =180°,∴∠CBE +∠ABC =180°,∴A 、B 、E 三点共线,∴△ACE 是等腰直角三角形,∴四边形ABCD 面积=△ACE 面积= 12⨯AC 2=18.故答案为:18.【点睛】本题考查了旋转的性质以及转化思想,解决这类问题要结合已知线段间的数量关系和位置关系进行旋转,使不规则图形转化为规则图形.5.如图,已知ABC △是等边三角形,点D 在边BC 上,以AD 为边向左作等边ADE ,连结BE ,作BF AE ∥交AC 于点F ,若2AF =,4CF =,则AE =________.【答案】7【解析】【分析】证明△BAE ≌△CAD 得到ABE BAC ∠=∠,从而证得BEAF ,再得到AEBF 是平行四边形,可得AE=BF ,在三角形BCF 中求出BF 即可.【详解】作FH BC ⊥于H ,∵ABC 是等边三角形,2AF =,4CF =∴BC=AC=6在HCF 中, CF=4, 060BCF ∠=030,2CFD CH ∴∠==2224212FH ∴=-=22241227BF BH FH ∴++=∵ABC 是等边三角形,ADE 是等边三角形∴AC=AB ,AD=AE ,060CAB DAE ∠=∠=CAD BAE ∴∠=∠CAD BAE ∴∆≅∆060ABE ACD ∴∠=∠=ABE BAC ∴∠=∠BE AF ∴∵BF AE∴AEBF 是平行四边形∴AE=BF= 27【点睛】本题考查全等三角形的判定和性质、平行四边形的判定和性质、等边三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.6.AD 、BE 是△ABC 的高,这两条高所在的直线相交于点O ,若BO=AC ,则∠ABC=______.【答案】45°或135°【解析】【分析】分别讨论△ABC 为锐角三角形时、∠A 、∠B 、∠C 分别为钝角时和∠A 为直角时五种情况,利用AAS 证明△BOD ≌△ACD ,可得BD=AD ,根据等腰直角三角形的性质即可得答案.【详解】①如图,当△ABC为锐角三角形时,∵AD、BE为△ABC的两条高,∴∠CAD+∠AOE=90°,∠CBE+∠BOD=90°,∵∠BOD=∠AOE,∴∠CAD=∠OBD,又∵∠ODB=∠ADC=90°,OB=AC,∴△BOD≌△ACD,∴AD=BD,∵AD⊥BC,∴∠ABC=45°,②如图,当∠B为钝角时,∵∠C+∠CAD=90°,∠O+∠CAD=90°,∴∠C=∠O,又∵∠ADC=∠ODB=90°,OB=AC,∴△BOD≌△ACD,∴BD=AD,∵AD⊥BC,∴∠ABD=45°,∴∠ABC=180°-45°=135°.③如图,当∠A为钝角时,同理可证:△BOD≌△ACD,∴AD=BD.∴∠ABC=45°,④如图,当∠C为钝角时,同理可证:△BOD≌△ACD,∴AD=BD.∴∠ABC=45°.⑤当∠B为直角时,点O、D、B重合,OB=0,不符合题意,当∠C为直角时,点O、C、D、E重合,CD=0,不符合题意,如图,当∠A为直角时,点A、E、O重合,∵OB=AC,∠CAB=90°,∴△ABC是等腰直角三角形,∴∠ABC=45°.综上所述:∠ABC的度数为45°或135°.故答案为:45°或135°【点睛】本题主要考查全等三角形的判定与性质,全等三角形的判定方法有:SSS、AAS、ASA、SAS、HL等,注意:SAS时,角必须是两边的夹角,SSA和AAA不能判定两个三角形全等.灵活运用分类讨论的思想是解题关键.7.AD,BE是△ABC的高,这两条高所在的直线相交于点O,若BO=AC,BC=a,CD=b,则AD的长为______.【答案】AD的长为a-b或b-a或a+b或12a或b.【解析】【分析】分别讨论△ABC为锐角三角形时、∠A、∠B、∠C分别为钝角时和∠A为直角时五种情况,利用AAS证明△BOD≌△ACD,可得BD=AD,根据线段的和差关系即可得答案.【详解】①如图,当△ABC为锐角三角形时,∵AD、BE为△ABC的两条高,∴∠CAD+∠AOE=90°,∠CBE+∠BOD=90°,∵∠BOD=∠AOE,∴∠CAD=∠OBD,又∵∠ODB=∠ADC=90°,OB=AC,∴△BOD≌△ACD,∴AD=BD,∵BC=a,CD=b,∴AD=BD=BC-CD=a-b.②如图,当∠B为钝角时,∵∠C+∠CAD=90°,∠O+∠CAD=90°,∴∠C=∠O,又∵∠ADC=∠ODB=90°,OB=AC,∴△BOD≌△ACD,∴BD=AD,∴AD=CD-BC=b-a.③如图,当∠A为钝角时,同理可证:△BOD≌△ACD,∴AD=BC-CD=a-b.④如图,当∠C为钝角时,同理可证:△BOD≌△ACD,∴AD=BD=BC+CD=a+b.⑤当∠B为直角时,点O、D、B重合,OB=0,不符合题意,当∠C为直角时,点O、C、D、E重合,CD=0,不符合题意,如图,当∠A为直角时,点A、E、O重合,∵OB=AC,∠CAB=90°,∴△ABC是等腰直角三角形,∵AD⊥BC,∴AD是Rt△ABC斜边中线,∴AD=AD=12BC=12a=b.综上所述:AD的长为a-b或b-a或a+b或12a或b.故答案为:a-b或b-a或a+b或12a或b【点睛】本题主要考查全等三角形的判定与性质,全等三角形的判定方法有:SSS、AAS、ASA、SAS、HL等,注意:SAS时,角必须是两边的夹角,SSA和AAA不能判定两个三角形全等.灵活运用分类讨论的思想是解题关键.8.已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC; ②∠BCE+∠BCD=180°;③AF2=EC2﹣EF2; ④BA+BC=2BF.其中正确的是_____.【答案】①②③④.【解析】【分析】根据已知条件易证△ABD≌△EBC,可判定①正确;根据等腰三角形的性质、对顶角相等、结合全等三角形的性质及平角的定义即可判定②正确;证明AD=AE=EC,再利用勾股定理即可判定③正确;过E作EG⊥BC于G点,证明Rt△BEG≌Rt△BEF及Rt△CEG≌Rt△AFE,根据全等三角形的性质可得AF=CG,所以BA+BC=BF+FA+BG﹣CG=BF+BG=2BF,即可判定④正确.【详解】①∵BD为△ABC的角平分线,∴∠ABD=∠CBD,在△ABD和△EBC中,BD BCABD CBDBE BA=⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△EBC (SAS ),∴①正确;②∵BD 为△ABC 的角平分线,BD=BC ,BE=BA ,∴∠BCD=∠BDC=∠BAE=∠BEA ,∵△ABD ≌△EBC ,∴∠BCE=∠BDA ,∴∠BCE+∠BCD=∠BDA+∠BDC=180°,∴②正确;③∵∠BCE=∠BDA ,∠BCE=∠BCD+∠DCE ,∠BDA=∠DAE+∠BEA ,∠BCD=∠BEA , ∴∠DCE=∠DAE ,∴△ACE 为等腰三角形,∴AE=EC ,∵△ABD ≌△EBC ,∴AD=EC ,∴AD=AE=EC ,∵EF ⊥AB ,∴AF 2=EC 2﹣EF 2;∴③正确;④如图,过E 作EG ⊥BC 于G 点,∵E 是BD 上的点,∴EF=EG ,在Rt △BEG 和Rt △BEF 中,BE BE EF EG =⎧⎨=⎩, ∴Rt △BEG ≌Rt △BEF (HL ),∴BG=BF ,在Rt △CEG 和Rt △AFE 中,EF FG AE CE =⎧⎨=⎩, ∴Rt △CEG ≌Rt △AFE (HL ),∴AF=CG ,∴BA+BC=BF+FA+BG ﹣CG=BF+BG=2BF ,∴④正确.故答案为:①②③④.【点睛】本题考查了全等三角形的判定,考查了全等三角形的对应边、对应角相等的性质,本题中熟练求证三角形全等和熟练运用全等三角形对应角、对应边相等性质是解题的关键.9.如图,在等腰直角三角形ABC中,∠C=90 o,AC=BC=4,点D是AB的中点,E, F在射线AC与射线CB上运动,且满足AE=CF,∠EDF=90°;当点E运动到与点C的距离为1时,则△DEF的面积为___________.【答案】52或132【解析】解:①E在线段AC上.在△ADE和△CDF中,∵AD=CD,∠A=∠DCF,AE=CF,∴△ADE≌△CDF(SAS),∴同理△CDE≌△BDF,∴四边形CEDF面积是△ABC面积的一半.∵CE=1,∴CF=4﹣1=3,∴△CEF的面积=12CE•CF=32,∴△DEF的面积=12×22×22﹣32=52.②E'在AC延长线上.∵AE'=CF',AC=BC=4,∠ACB=90°,∴CE'=BF',∠ACD=∠CBD=45°,CD=AD=BD=22,∴∠DCE'=∠DBF'=135°.在△CDE'和△BDF'中,∵CD=BD,∠DCE′=DBF′,CE′=BF′,∴△CDE'≌△BDF'(SAS),∴DE'=DF',∠CDE'=∠BDF'.∵∠CDE'+∠BDE'=90°,∴∠BDE'+∠BDF'=90°,即∠E'DF'=90°.∵DE'2=CE'2+CD2﹣2CD•CE'cos135°=1+8+2×22×22=13,∴S△E'DF'=12DE'2=13 2.故答案为132或52.点睛:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ADE≌△CDF和△CDE≌△BCF是解题的关键.10.如图,在△ABC中,∠C=90°,AC=BC,AD是△ABC的角平分线,DE⊥AB,垂足为点E.已知AB=12,则△DEB的周长为_______.【答案】12【解析】根据角平分线的性质,由AD 是∠CAB 的平分线,DE ⊥AB ,∠C=90°,可得到CD=ED ,然后根据直角三角形的全等判定HL 证得Rt △ACD ≌Rt △AED ,再由全等的性质得到AC=AE ,然后根据AC=BC ,因此可得△DEB 的周长=BD+DE+BE=BD+CD+BE=BC+BE=AC+BE=AE+BE=AB=12.故答案为:12.点睛:此题主要考查了全等三角形的性质和角平分线的性质,解题时根据全等三角形的性质和角平分线的性质得到相等的线段,然后再代还求解即可.二、八年级数学全等三角形选择题(难)11.如图,ABC △是等边三角形,ABD △是等腰直角三角形,∠BAD =90°,AE ⊥BD 于点E .连CD 分别交AE ,AB 于点F ,G ,过点A 做AH ⊥CD 交BD 于点H ,则下列结论:①∠ADC =15°;②AF =AG ;③AH =DF ;④△ADF ≌△BAH ;⑤DF =2EH .其中正确结论的个数为( )A .5B .4C .3D .2【答案】B【解析】【分析】 ①根据△ABC 为等边三角形,△ABD 为等腰直角三角形,可以得出各角的度数以及DA=AC ,即可作出判断;②分别求出∠AFG 和∠AGD 的度数,即可作出判断;④根据三角形内角和定理求出∠HAB 的度数,求证EHG DFA ∠=∠,利用AAS 即可证出两个三角形全等;③根据④证出的全等即可作出判断;⑤证明∠EAH=30°,即可得到AH=2EH ,又由③可知AH DF =,即可作出判断.【详解】①正确:∵ABC △是等边三角形,∴60BAC ︒∠=,∴CA AB =.∵ABD △是等腰直角三角形,∴DA AB =.又∵90BAD ︒∠=,∴150CAD BAD BAC ︒∠=∠+∠=,∴DA CA =,∴()1180150152ADC ACD ︒︒︒∠=∠=-=; ②错误:∵∠EDF=∠ADB-∠ADC=30°∴∠DFE=90°-∠EDF=90°-30°=60°=∠AFG∵∠AGD=90°-∠ADG=90°-15°=75°∠AFG≠∠AGD∴AF≠AG③,④正确,由题意可得45DAF ABH ︒∠=∠=,DA AB =,∵AE BD ⊥,AH CD ⊥.∴180EHG EFG ︒∠+∠=.又∵180?DFA EFG ∠+∠=,∴EHG DFA ∠=∠,在DAF △和ABH 中 ()AFD BHA DAF ABHAAS DA AB ∠=∠⎧⎪∠=∠⎨⎪=⎩∴DAF △≌ABH .∴DF AH =.⑤正确:∵150CAD ︒∠=,AH CD ⊥,∴75DAH ︒∠=,又∵45DAF ︒∠=,∴754530EAH ︒︒︒∠=-=又∵AE DB ⊥,∴2AH EH =,又∵=AH DF ,∴2DF EH =【点睛】本题考查了等边三角形的性质,等腰三角形的性质,三角形的内角和定理,三角形外角的性质,全等三角形的判定与性质,综合性较强,属于较难题目.12.下列条件中,不能判定两个直角三角形全等的是( )A .两条直角边对应相等B .有两条边对应相等C .斜边和一锐角对应相等D .一条直角边和斜边对应相等【答案】B【解析】根据全等三角形的判定SAS ,可知两条直角边对应相等的两个直角三角形全等,故A 不正确;根据一条直角边和斜边对应相等的两个直角三角形,符合全等三角形的判定定理HL ,能判定全等;若两条直角边对应相等的两个直角三角形,符合全等三角形的判定定理SAS ,也能判全等,但是有两边对应相等,没说明是什么边对应,故不能判定,故B 正确.根据全等三角形的判定AAS ,可知斜边和一锐角对应相等的两直角三角形全等,故C 不正确;根据直角三角形的判定HL ,可知一条直角边和斜边对应相等两直角三角形全等,故D 不正确.故选B.点睛:此题主要考查了直角三角形全等的判定,解题时利用三角形全等的判定SSS ,SAS ,ASA ,AAS ,HL ,直接判断即可.13.已知OD 平分∠M ON ,点A 、B 、C 分别在OM 、OD 、ON 上(点A 、B 、C 都不与点O 重合),且AB=BC, 则∠OAB 与∠BCO 的数量关系为( )A .∠OAB+∠BCO=180°B .∠OAB=∠BCOC .∠OAB+∠BCO=180°或∠OAB=∠BCOD .无法确定【答案】C【解析】根据题意画图,可知当C 处在C 1的位置时,两三角形全等,可知∠OAB=∠BCO ;当点C 处在C 2的位置时,根据等腰三角形的性质和三角形的外角的性质,∠OAB+∠BCO=180°.故选C.14.如图,在ABC ∆中,AC BC =,90ACB ∠=︒,AE 平分BAC ∠交BC 于点E ,BD AE ⊥于点D ,DF AC ⊥交AC 的延长线于点F ,连接CD ,给出四个结论:①45ADC ∠=︒;②12BD AE =;③AC CE AB +=;④2AB BC FC -=;其中正确的结论有 ( )A .1个B .2个C .3个D .4个【答案】D【解析】试题解析:如图,过E 作EQ ⊥AB 于Q ,∵∠ACB=90°,AE 平分∠CAB ,∴CE=EQ ,∵∠ACB=90°,AC=BC ,∴∠CBA=∠CAB=45°,∵EQ ⊥AB ,∴∠EQA=∠EQB=90°,由勾股定理得:AC=AQ ,∴∠QEB=45°=∠CBA ,∴EQ=BQ ,∴AB=AQ+BQ=AC+CE ,∴③正确;作∠ACN=∠BCD ,交AD 于N , ∵∠CAD=12∠CAB=22.5°=∠BAD , ∴∠ABD=90°-22.5°=67.5°,∴∠DBC=67.5°-45°=22.5°=∠CAD ,∴∠DBC=∠CAD ,在△ACN 和△BCD 中, DBC CAD AC BCACN DCB ∠∠⎧⎪⎨⎪∠∠⎩===, ∴△ACN ≌△BCD ,∴CN=CD ,AN=BD ,∵∠ACN+∠NCE=90°,∴∠NCB+∠BCD=90°,∴∠CND=∠CDA=45°,∴∠ACN=45°-22.5°=22.5°=∠CAN ,∴AN=CN ,∴∠NCE=∠AEC=67.5°,∴CN=NE , ∴CD=AN=EN=12AE ,∵AN=BD,∴BD=12AE,∴①正确,②正确;过D作DH⊥AB于H,∵∠FCD=∠CAD+∠CDA=67.5°,∠DBA=90°-∠DAB=67.5°,∴∠FCD=∠DBA,∵AE平分∠CAB,DF⊥AC,DH⊥AB,∴DF=DH,在△DCF和△DBH中90F DHBFCD DBADF DH∠∠︒⎧⎪∠∠⎨⎪⎩====,∴△DCF≌△DBH,∴BH=CF,由勾股定理得:AF=AH,∴2,2 AC AB AC AH BH AC AM CM AC AF CF AF AF AF AM AF AF+++++++====,∴AC+AB=2AF,AC+AB=2AC+2CF,AB-AC=2CF,∵AC=CB,∴AB-CB=2CF,∴④正确.故选D15.如图,BD是∠ABC的角平分线,AD⊥AB,AD=3,BC=5,则△BCD的面积为()A.7.5 B.8 C.10D.15【答案】A【解析】作DE⊥BC于E,根据角平分线的性质,由BD是∠ABC的角平分线,AD⊥AB,DE⊥BC,求出DE=DA=3,根据三角形面积公式计算S△BCD=12×BC×DE=7.5,故选:A.16.如图,在等腰直角△ABC中,∠ACB=90°,点O为斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P,则下列结论:①图中全等三角形有三对;②△ABC的面积等于四边形CDOE面积的倍;③DE2+2CD•CE=2OA2;④AD2+BE2=2OP•OC.正确的有()个.A.1 B.2 C.3 D.4【答案】C【解析】【分析】结论(1)正确.因为图中全等的三角形有3对;结论(2)错误.由全等三角形的性质可以判断;结论(3)正确.利用全等三角形和等腰直角三角形的性质可以判断.结论(4)正确.利用相似三角形、全等三角形、等腰直角三角形和勾股定理进行判断.【详解】结论(1)正确,理由如下:图中全等的三角形有3对,分别为△AOC≌△BOC,△AOD≌△COE,△COD≌△BOE.由等腰直角三角形的性质,可知OA=OC=OB,易得△AOC≌△BOC.∵OC⊥AB,OD⊥OE,∴∠AOD=∠COE.在△AOD与△COE中,∴△AOD≌△COE(ASA),同理可证:△COD≌△BOE.结论(2)错误.理由如下:∵△AOD≌△COE,∴S△AOD=S△COE,∴S四边形CDOE=S△COD+S△COE=S△COD+S△AOD=S△AOC=S△ABC即△ABC的面积等于四边形CDOE的面积的2倍.结论(3)正确,理由如下:∵△AOD≌△COE,∴CE=AD,∴CD+CE=CD+AD=AC=OA,∴(CD+CE)2=CD2+CE2+2CD•CE=DE2+2CD•CE=2OA2;结论(4)正确,理由如下:∵△AOD≌△COE,∴AD=CE;∵△COD≌△BOE,∴BE=CD.在Rt△CDE中,由勾股定理得:CD2+CE2=DE2,∴AD2+BE2=DE2.∵△AOD≌△COE,∴OD=OE,又∵OD⊥OE,∴△DOE为等腰直角三角形,∴DE2=2OE2,∠DEO=45°.∵∠DEO=∠OCE=45°,∠COE=∠COE,∴△OEP∽△OCE,∴,即OP•OC=OE2.∴DE2=2OE2=2OP•OC,∴AD2+BE2=2OP•OC.综上所述,正确的结论有3个,故选C.【点睛】本题是几何综合题,考查了等腰直角三角形、全等三角形、相似三角形和勾股定理等重要几何知识点.难点在于结论(4)的判断,其中对于“OP•OC”线段乘积的形式,可以寻求相似三角形解决问题.=,D、E是斜边BC上两点,且∠DAE=45°,将17.如图,在Rt△ABC中,AB AC△ADC绕点A顺时针旋转90︒后,得到△AFB,连接EF.列结论:+=①△ADC≌△AFB;②△ABE≌△ACD;③△AED≌△AEF;④BE DC DE 其中正确的是( )A.②④B.①④C.②③D.①③【答案】D【解析】解:∵将△ADC 绕点A 顺时针旋转90︒后,得到△AFB ,∴△ADC ≌△AFB ,故①正确; ②无法证明,故②错误;③∵△ADC ≌△AFB ,∴AF =AD ,∠FAB =∠DAC .∵∠DAE =45°,∴∠BAE +∠DAC =45°,∠FA E =∠DAE =45°.在△FAE 和△DAE 中,∵AF =AD ,∠FAE =∠DAE ,AE =AE ,∴△FAE ≌△DAE ,故③正确;④∵△ADC ≌△AFB ,∴DC =BF ,∵△FAE ≌△DAE ,∴EF =ED ,∵BF +BE >EF ,∴DC +BE >ED .故④错误.故选D .18.如图,在▱ABCD 中,AD =2AB ,F 是AD 的中点,作CE ⊥AB ,垂足E 在线段AB 上,连接EF 、CF ,则下列结论中①∠DCF =123,1x x ==-∠BCD ;②EF =CF ;③S △BEC =2S △CEF ;④∠DFE =3∠AEF .一定成立的是( )A .①②B .①③④C .①②③D .①②④【答案】D【解析】①∵F 是AD 的中点,∴AF=FD , ∵在?ABCD 中,AD=2AB ,∴AF=FD=CD ,∴∠DFC=∠DCF ,∵AD ∥BC ,∴∠DFC=∠FCB ,∴∠DCF=∠BCF ,∴∠DCF=12∠BCD ,故此选项正确;延长EF ,交CD 延长线于M ,∵四边形ABCD 是平行四边形,∴AB ∥CD ,∴∠A=∠MDF ,∵F 为AD 中点,在△AEF 和△DFM 中,∠A =∠FDMAF =DF ∠AFE =∠DFM ,∴△AEF ≌△DMF (ASA ),∴FE=MF ,∠AEF=∠M ,∵CE ⊥AB ,∴∠AEC=90°,∴∠AEC=∠ECD=90°,∵FM=EF ,∴FC=FM ,故②正确;③∵EF=FM ,∴S △EFC=S △CFM ,∵MC >BE ,∴S △BEC <2S △EFC故S △BEC=2S △CEF 错误;④设∠FEC=x ,则∠FCE=x ,∴∠DCF=∠DFC=90°-x ,∴∠EFC=180°-2x ,∴∠EFD=90°-x+180°-2x=270°-3x ,∵∠AEF=90°-x ,∴∠DFE=3∠AEF ,故此选项正确.故正确的有:①②④.故选D.19.如图,Rt ACB 中,90ACB ︒∠=,ABC 的角平分线AD 、BE 相交于点P ,过P 作PF AD ⊥交BC 的延长线于点F ,交AC 于点H ,则下列结论:①135APB ︒∠=;②PF PA =;③AH BD AB +=;④S 四边形23ABDE S ABP =,其中正确的个数是( )A .4B .3C .2D .1【答案】B【解析】根据三角形全等的判定和性质以及三角形内角和定理逐一分析判断即可.【详解】解:∵在△ABC 中,∠ACB=90°,∴∠CAB+∠ABC=90°∵AD 、BE 分别平分∠BAC 、∠ABC ,∴∠BAD=12CAB ∠,∠ABE=12ABC ∠ ∴∠BAD+∠ABE=111+=()45222CAB ABC CAB ABC ∠∠∠+∠=︒ ∴∠APB=180°-(∠BAD+∠ABE )=135°,故①正确;∴∠BPD=45°,又∵PF ⊥AD ,∴∠FPB=90°+45°=135°∴∠APB=∠FPB又∵∠ABP=∠FBPBP=BP∴△ABP ≌△FBP (ASA )∴∠BAP=∠BFP ,AB=AB ,PA=PF ,故②正确;在△APH 与△FPD 中∵∠APH=∠FPD=90°∠PAH=∠BAP=∠BFPPA=PF∴△APH ≌△FPD (ASA ),∴AH=FD ,又∵AB=FB∴AB=FD+BD=AH+BD ,故③正确;连接HD ,ED ,∵△APH ≌△FPD ,△ABP ≌△FBP ∴APH FPD S S =,ABP FBP S S =,PH=PD ,∵∠HPD=90°,∴∠HDP=∠DHP=45°=∠BPD∴HD ∥EP ,∴EPH EPD S S =∵ABP BDP AEP EPD ABDE S S SS S =+++四边形 ()ABP AEP EPHPBD S S S S =+++ ABP APH PBDS S S =++ ABP FPD PBD S S S =++ABP FBP S S =+2ABP S =故④错误,∴正确的有①②③,故答案为:B .【点睛】本题考查了三角形全等的判定方法,判定两个三角形全等的方法有:SSS 、SAS 、AAS 、ASA 、HL ,注意AAA 和SAS 不能判定两个三角形全等.20.如图,四边形ABCD 中,∠A 、∠B 、∠C 、∠D 的角平分线恰相交于一点P ,记△APD 、△APB 、△BPC 、△DPC 的面积分别为S 1、S 2、S 3、S 4,则有( )A .1324S S S S +=+B .1234S S S S +=+C .1423S S S S +=+D .13S S =【答案】A【解析】【分析】作辅助线,利用角平分线性质定理,明确8个三角形中面积两两相等即可解题.【详解】四边形ABCD,四个内角平分线交于一点P,即点p 到四边形各边距离相等,(角平分线性质定理),如下图,可将四边形分成8个三角形,面积分别是a 、a 、b 、b 、c 、c 、d 、d,则S 1=a+d, S 2=a+b, S 3=b+c, S 4=c+d,∴S 1+S 3=a+b+c+d= S 2+S 4故选A【点睛】本题考查了角平分线性质定理,作高线和理解角平分线性质定理是解题关键.21.如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,DH⊥BC于H,交BE于G.下列结论:①BD=CD;②AD+CF=BD;③CE=12BF;④AE=BG.其中正确的是A.①②B.①③C.①②③D.①②③④【答案】C【解析】【分析】根据∠ABC=45°,CD⊥AB可得出BD=CD,利用AAS判定Rt△DFB≌Rt△DAC,从而得出DF=AD,BF=AC.则CD=CF+AD,即AD+CF=BD;再利用AAS判定Rt△BEA≌Rt△BEC,得出CE=AE=12AC,又因为BF=AC所以CE=12AC=12BF,连接CG.因为△BCD是等腰直角三角形,即BD=CD.又因为DH⊥BC,那么DH垂直平分BC.即BG=CG.在Rt△CEG中,CG是斜边,CE是直角边,所以CE<CG.即AE<BG.【详解】解:∵CD⊥AB,∠ABC=45°,∴△BCD是等腰直角三角形.∴BD=CD.故①正确;在Rt△DFB和Rt△DAC中,∵∠DBF=90°−∠BFD,∠DCA=90°−∠EFC,且∠BFD=∠EFC,∴∠DBF=∠DCA.又∵∠BDF=∠CDA=90°,BD=CD,∴△DFB≌△DAC.∴BF=AC;DF=AD.∵CD=CF+DF,∴AD+CF=BD ;故②正确; 在Rt △BEA 和Rt △BEC 中.∵BE 平分∠ABC ,∴∠ABE=∠CBE.又∵BE=BE,∠BEA=∠BEC=90°,∴Rt △BEA ≌Rt △BEC.∴CE=AE=12AC. 又由(1),知BF=AC ,∴CE=12AC=12BF ;故③正确; 连接CG.∵△BCD 是等腰直角三角形,∴BD=CD.又DH ⊥BC ,∴DH 垂直平分BC.∴BG=CG.在Rt △CEG 中,∵CG 是斜边,CE 是直角边,∴CE<CG.∵CE=AE ,∴AE<BG.故④错误.故选C.【点睛】本题考查了等腰直角三角形、等腰三角形的判定与性质、全等三角形的判定与性质.此类问题涉及知识点较多,需要对相关知识点有很高的熟悉度.22.如图,在等腰△ABC 中,90ACB ︒∠=,8AC =,F 是AB 边上的中点,点D 、E 分别在AC 、BC 边上运动,且保持AD CE =,连接DE 、DF 、EF 在此运动变化的过程中,下列结论:(1)DEF 是等腰直角三角形;(2)四边形CDFE 不可能为正方形,(3)DE 长度的最小值为4;(4)连接CF ,CF 恰好把四边形CDFE 的面积分成1:2两部分,则CE =13或143其中正确的结论个数是A.1个B.2个C.3个D.4个【答案】A【解析】【分析】连接CF,证明△ADF≌△CEF,根据全等三角形的性质判断①,根据正方形的判定定理判断②,根据勾股定理判断③,根据面积判断④.【详解】连接CF,∵△ABC是等腰直角三角形,∴∠FCB=∠A=45,CF=AF=FB;∵AD=CE,∴△ADF≌△CEF(SAS);∴EF=DF,∠CFE=∠AFD;∵∠AFD+∠CFD=90∘,∴∠CFE+∠CFD=∠EFD=90∘,又∵EF=DF∴△EDF是等腰直角三角形(故(1)正确).当D. E分别为AC、BC中点时,四边形CDFE是正方形(故(2)错误).由于△DEF是等腰直角三角形,因此当DE最小时,DF也最小;即当DF⊥AC时,DE最小,此时142DF BC== .∴242DE DF=故(3)错误).∵△ADF≌△CEF,∴S△CEF=S△ADF∴S四边形CDFE=S△AFC,∵CF恰好把四边形CDFE的面积分成1:2两部分∴S△CEF:S△CDF=1:2 或S△CEF:S△CDF=2:1即S△ADF:S△CDF=1:2 或S△ADF:S△CDF=2:1当S△ADF:S△CDF=1:2时,S△ADF=13S△ACF=111684323⨯⨯⨯=又∵S△ADF=1422AD AD ⨯⨯=∴2AD=16 3∴AD=83(故(4)错误).故选:A.【点睛】本题考查了全等三角形,等腰直角三角形,以及勾股定理,掌握全等三角形,等腰直角三角形,以及勾股定理是解题的关键.23.如图,与都是等边三角形,,下列结论中,正确的个数是( )①;②;③;④若,且,则.A.1 B.2 C.3 D.4【答案】C【解析】【分析】利用全等三角形的判定和性质一一判断即可.【详解】解:∵与都是等边三角形∴AD=AB,AC=AE,∠DAB=∠EAC=60°∴∠DAB+∠BAC=∠EAC +∠BAC即∠DAC=∠EAB∴∴,①正确;∵∴∠ADO=∠ABO∴∠BOD=∠DAB=60°,②正确∵∠BDA=∠CEA=60°,∠ADC≠∠AEB∴∠BDA-∠ADC≠∠CEA-∠AEB∴,③错误∵∴∠DAC+∠BCA=180°∵∠DAB=60°,∴∠BCA=180°-∠DAB-∠BAC=30°∵∠ACE=60°∴∠BCE=∠ACE+∠BCA=60°+30°=90°∴④正确故由①②④三个正确,故选:C【点睛】本题考查全等三角形的判定和性质、等边三角形的性质、角平分线的判定定理等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.24.如图,把ΔABC剪成三部分,边AB,BC,AC放在同一直线上,点O都落在直线MN 上,直线MN∥AB.在ΔABC中,若∠AOB=125°,则∠ACB的度数为()A.70°B.65°C.60°D.85°【答案】A【解析】【分析】利用平行线间的距离处处相等,可知点O到BC、AC、AB的距离相等,得出O为三条角平分线的交点,根据三角形内角和定理和角平分线的定义即可得出结论.【详解】如图1,过点O作OD⊥BC于D,OE⊥AC于E,OF⊥AB于F.∵MN∥AB,∴OD=OE=OF(平行线间的距离处处相等).如图2:过点O作OD'⊥BC于D',作OE'⊥AC于E',作OF'⊥AB于F'.由题意可知:OD=OD',OE=OE',OF=OF',∴OD'=OE'=OF',∴图2中的点O是三角形三个内角的平分线的交点.∵∠AOB=125°,∴∠OAB+∠OBA=180°-125°=55°,∴∠CAB+∠CBA=2×55°=110°,∴∠ACB=180°-110°=70°.故选A.【点睛】本题考查了三角形的内心,平行线间的距离处处相等,角平分线定义,解答本题的关键是判断出OD=OE=OF.25.如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,∠EAF=12∠BAD,若DF=1,BE=5,则线段EF的长为()A.3 B.4 C.5 D.6【答案】B【解析】【分析】在BE上截取BG=DF,先证△ADF≌△ABG,再证△AEG≌△AEF即可解答.【详解】在BE上截取BG=DF,∵∠B+∠ADC=180°,∠ADC+∠ADF=180°,∴∠B=∠ADF,在△ADF与△ABG中AB ADB ADFBG DF=⎧⎪∠=∠⎨⎪=⎩,∴△ADF≌△ABG(SAS),∴AG=AF,∠FAD=∠GAB,∵∠EAF=12∠BAD,∴∠FAE=∠GAE,在△AEG与△AEF中AG AFFAE GAEAE AE=⎧⎪∠=∠⎨⎪=⎩,∴△AEG≌△AEF(SAS)∴EF=EG=BE﹣BG=BE﹣DF=4.故选:B.【点睛】考查了全等三角形的判定与性质,证明三角形全等是解决问题的关键.26.具备下列条件的两个三角形,可以证明它们全等的是( ).A.一边和这一边上的高对应相等B.两边和第三边上的中线对应相等C.两边和其中一边的对角对应相等D.直角三角形的斜边对应相等【答案】B【解析】【分析】根据判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL分别进行分析.【详解】解:A、一边和这边上的高对应相等,无法得出它们全等,故此选项错误;B、两边和第三边上的中线对应相等,通过如图所示方式(倍长中线法)可以证明它们全等(△ABC≌△A′B′C′),故此选项正确..C、两边和其中一边的对角对应相等,无法利用ASS得出它们全等,故此选项错误;D、直角三角形的斜边对应相等,无法得出它们全等,故此选项错误.故选:B.【点睛】本题考查三角形全等的判定方法,注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.27.如图,AO OM,OA=8,点B为射线OM上的一个动点,分别以OB、AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF、等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,PB的长度是 ( )A.3.6 B.4 C.4.8 D.PB的长度随B点的运动而变化【答案】B【解析】【分析】作辅助线,首先证明△ABO≌△BEN,得到BO=ME;进而证明△BPF≌△MPE,即可解决问题.【详解】如图,过点E作EN⊥BM,垂足为点N,∵∠AOB=∠ABE=∠BNE=90°,∴∠ABO+∠BAO=∠ABO+∠NBE=90°,∴∠BAO=∠NBE,∵△ABE、△BFO均为等腰直角三角形,∴AB=BE,BF=BO;在△ABO与△BEN中,BAO NBEAOB BNEAB BE∠∠⎧⎪∠∠⎨⎪⎩===∴△ABO≌△BEN(AAS),∴BO=NE,BN=AO;∵BO=BF,∴BF=NE,在△BPF与△NPE中,FBP ENPFPB EPNBF NE∠∠⎧⎪∠∠⎨⎪⎩===∴△BPF≌△NPE(AAS),∴BP=NP=12BN;而BN=AO,∴BP=12AO=12×8=4,故选B.【点睛】本题考查了三角形内角和定理,全等三角形的性质和判定的应用,解题的关键是作辅助线,构造全等三角形,灵活运用有关定理来分析或解答.28.如图所示,△ABP 与△CDP 是两个全等的等边三角形,且PA ⊥PD ,有下列四个结论:①∠PBC =15°,②AD ∥BC ,③PC ⊥AB ,④四边形ABCD 是轴对称图形,其中正确的个数为( )A .1个B .2个C .3个D .4个 【答案】D【解析】【分析】 根据周角的定义先求出∠BPC 的度数,再根据对称性得到△BPC 为等腰三角形,∠PBC 即可求出;根据题意:有△APD 是等腰直角三角形;△PBC 是等腰三角形;结合轴对称图形的定义与判定,可得四边形ABCD 是轴对称图形,进而可得②③④正确.【详解】根据题意,BPC 36060290150∠=-⨯-= , BP PC =,()PBC 180150215∠∴=-÷=,①正确;根据题意可得四边形ABCD 是轴对称图形,④正确;∵∠DAB+∠ABC=45°+60°+60°+15°=180°,∴AD//BC ,②正确;∵∠ABC+∠BCP=60°+15°+15°=90°,∴PC ⊥AB ,③正确,所以四个命题都正确,故选D .【点睛】本题考查了等边三角形的性质、等腰直角三角形的性质、等腰三角形的判定与性质、轴对称图形的定义与判定等,熟练掌握各相关性质与定理是解题的关键.29.已知:如图,在长方形ABCD 中,AB=4,AD=6.延长BC 到点E ,使CE=2,连接DE ,动点P 从点B 出发,以每秒2个单位的速度沿BC-CD-DA 向终点A 运动,设点P 的运动时间为t 秒,当t 的值为_____秒时,△ABP 和△DCE 全等.A .1B .1或3C .1或7D .3或7【答案】C【解析】【分析】分两种情况进行讨论,根据题意得出BP=2t=2和AP=16-2t=2即可求得.【详解】解:因为AB=CD ,若∠ABP=∠DCE=90°,BP=CE=2,根据SAS 证得△ABP ≌△DCE , 由题意得:BP=2t=2,所以t=1, 因为AB=CD ,若∠BAP=∠DCE=90°,AP=CE=2,根据SAS 证得△BAP ≌△DCE ,由题意得:AP=16-2t=2,解得t=7.所以,当t 的值为1或7秒时.△ABP 和△DCE 全等.故选C .【点睛】本题考查全等三角形的判定,判定方法有:ASA ,SAS ,AAS ,SSS ,HL .30.如图,D 为BAC ∠的外角平分线上一点并且满足BD CD =,DBC DCB ∠=∠,过D 作DE AC ⊥于E ,DF AB ⊥交BA 的延长线于F ,则下列结论:①CDE △≌BDF ;②CE AB AE =+;③BDC BAC ∠=∠;④DAF CBD ∠=∠. 其中正确的结论有( ).A .1个B .2个C .3个D .4个【答案】D【解析】 BD=CD,AD 是角平分线,所以FD=DE,∠DFB =∠DEC =90°,所以CDE ≌BDF ;①正确.由全等得BF=CE ,因为FA=AE,FB=AB+FA ,所以CE=AB+AE , ②正确.由全等知,∠DCE=∠FBD,所以∠BAC=∠BDC. ③正确. ∴DBF DCE ∠=∠,∴A 、B 、C 、D 四点共圆,∴DAF CBD ∠=∠,④正确.故选D.。
人教版八年级数学上册《轴对称》测试卷(含答案)

人教版八年级数学上册《轴对称》测试卷(含答案)一、选择题(每小题3分,共30分)1.点A(m,3)与B(4,n)关于x轴对称,则m,n的值分别为( )A.4,3B.-4,-3C.-4,3D.4,-32.下列交通标志中,是轴对称图形的是( )3.下列轴对称图形中,对称轴最多的是( )A.线段B.等边三角形C.五角星D.圆4.下列三角形中,不是轴对称图形的是( )A.等腰直角三角形B.有一个角是30°的直角三角形C.两内角分别是30°,120°的三角形D.两内角分别是30°,75°的三角形5.如图,ABCD 是矩形纸片,翻折∠B、∠D,使AD、BC 边与对角线AC重叠,且顶点B、D恰好落在同一点0上,折痕分别是CE、AF,则AE等于( )EBA.√3B.2C.1.5D.√26.到三角形三个顶点距离相等的点是( )A.三条中线的交点B.三条高的交点C.三条角平分线的交点D.三边垂直平分线的交点7.如图,在等腰梯形ABCD中,AD //BC,AB=CD,AC=BD,AC平分∠BCD,若∠ABC=72°,则图中等腰三角形共有( )A.8个B.6个C.4个D.2个8.如图,在△ABC 中,AB<AC,BC边的垂直平分线交BC于D,交AC 于E,连BE,AB=6cm,△ABE 的周长为14cm,则AC的长为( )A.4cmB.6cmC.8cmD.10cm9.如图,已知AB=AC=BD,则∠1与∠2的关系是( )A.∠1=2∠2B.2∠1+∠2=180°C.∠1+3∠2=180°D.3∠1-∠2=180°10.如图,在△ABC中,∠BAC=90,AB=AC,BD平分∠ABC交AC于D,AE⊥BD,交BC于E,下列说法:①AB=BE;②∠CAE=1∠C;③AD=CE;④CD=CE.其中正确的是( )2A.①②③B.②③④C.①②④D.①②③④二、填空题(每小题3分,共18分)11.已知点A(m-1,3)与点B(2,n+1)关于x轴对称,则m=_________,n=__________.12.等腰三角形的一个角是80°,则它顶角的度数是_______________度.13.在△ABC 中.①若AB=BC=CA,则△ABC为等边三角形;②若∠A=∠B=∠C,则△ABC 为等边三角形;③有两个角都是60°的三角形是等边三角形;④一个角为60°的等腰三角形是等边三角形.上述结论中正确的有__个.14.如图,在△ABC 中,∠A=90°,∠ABC=60°,∠ABC,∠ACB的平分线交于点O,OE // AB交BC于E,OF //AC交BC于F,若AB=1,则△OEF 的周长为_____________.15.如图,AD是等边△ABC底边上的中线,AC的垂直平分线交AC 于点E,交AD于点F ,若AD=9,则DF长为____.16.已知Rt△ABC 中,∠C=90°,∠A=30°.在直线BC或AC上取一点P,使得△PAB是等腰三角形,则符合条件的P点有________个.三、解答题(72分)17.(8分)如图,△ABC 中,点D是BC边的中点,DE⊥AB于E,DF⊥AC于F,BE=CF.求证:∠BAD=∠CAD.18.(8分)如图,在△ABC中,D,E分别是AC,AB边上的点,BD,CE相交于点0,给出下列条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.(1)上述四个条件中,哪两个条件可判定△ABC是等腰三角形?(用序号写出所有的情形);(2)选择(1)中的一种情形,证明△ABC是等腰三角形.19.(8分)在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-3,0),B(-3,-4),C(-1,-4).(1)求△ABC的面积;(2)在图中作出△ABC关于x轴对称的图形△DEF,并写出D,E,F 的坐标.20.(8分)如图,在△ABC中,∠ACB=2∠B,∠BAC的平分线AD交BC于D,过C作CN⊥AD交AD于H,交AB于N.(1) 求证:△ANC为等腰三角形;(2)试判断BN与CD的数量关系,并说明理由.21.(8分)已知如图,在△ABC中,AB=BC=2,∠ABC=120°,BC//x轴,点B的坐标是(一3,1).(1)写出顶点C的坐标;(2)作出△ABC 关于y轴对称的△A'B'C';(3)求以点A,B,B',A'为顶点的四边形的周长.22.(10 分)在△ABC 中,AB=CB.(1)若AC=AB,如图1,CM⊥AB 于点M,MN⊥AC 于点N,NP ⊥BC 于点P.若CP=2,则BP=_______;(2)若∠BAC=45°,如图2,CD平分∠ACB交AB于点D,过边AC上一点E作EF //CD,交AB于点F,AG是△AEF的高,探究高AG与边EF的数量关系;(3)若∠ABC=90°,点E是射线BC上的一个动点,作AF⊥AE且AF=AE,连CF交直线AB于点G.若BCCE =53,则AGBG=__________.23.(10分)图1,在△ABC中,AB=AC,∠BAC=30°,点D 是△ABC内一点,DB=DC,∠DCB=30°,点E是BD延长线上一点,AE=AB.(1)直接写出∠ADE 的度数___________;(2)求证:DE=AD+DC;(3)作BP 平分∠ABE,EF⊥BP,垂足为F(如图2),若EF=3,求BP 的长.24.(12分)如图1,A 是OB 的垂直平分线上的一点,P为y轴上一点,且∠OPB=∠OAB.(1)若∠AOB=60°,PB=4,求点P的坐标;(2)在(1)的条件下,求证:PA+PO=PB;(3)如图2,若点A是OB 的垂直平分线上的一点,已知A(2,5),∠OPB=∠OAB,求PO+PB 的值.参考答案:。
八年级数学上册 轴对称填空选择单元测试卷附答案

一、八年级数学全等三角形填空题(难)1.如图,已知△ABC和△ADE均为等边三角形,点O是AC的中点,点D在射线BO上,连结OE,EC,则∠ACE=_____°;若AB=1,则OE的最小值=_____.【答案】301 4【解析】【分析】根据等边三角形的性质可得OC=12AC,∠ABD=30°,根据"SAS"可证△ABD≌△ACE,可得∠ACE=30°=∠ABD,当OE⊥EC时,OE的长度最小,根据直角三角形的性质可求OE 的最小值.【详解】解:∵△ABC的等边三角形,点O是AC的中点,∴OC=12AC,∠ABD=30°∵△ABC和△ADE均为等边三角形,∴AB=AC,AD=AE,∠BAC=∠DAE=60°,∴∠BAD=∠CAE,且AB=AC,AD=AE,∴△ABD≌△ACE(SAS)∴∠ACE=30°=∠ABD当OE⊥EC时,OE的长度最小,∵∠OEC=90°,∠ACE=30°∴OE最小值=12OC=14AB=14故答案为:30,1 4【点睛】本题考查了全等三角形的判定和性质,等边三角形的性质,熟练运用全等三角形的判定是本题的关键.2.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E ,交AC 于F ,过点O 作OD ⊥AC 于D ,下列四个结论:①EF =BE +CF ;②∠BOC =90°+12∠A ; ③点O 到△ABC 各边的距离相等;④设OD =m ,AE +AF =n ,则AEF S mn ∆=.其中正确的结论是____.(填序号)【答案】①②③【解析】【分析】由在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,根据角平分线的定义与三角形的内角和定理,即可求出②∠BOC =90°+12∠A 正确;由平行线的性质和角平分线的定义可得△BEO 和△CFO 是等腰三角形可得①EF =BE +CF 正确;由角平分线的性质得出点O 到△ABC 各边的距离相等,故③正确;由角平分线定理与三角形的面积求法,设OD=m ,AE+AF=n,则△AEF 的面积=12mn ,④错误. 【详解】在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,∴∠OBC=12∠ABC ,∠OCB=12∠ACB ,∠A+∠ABC+∠ACB=180°, ∴∠OBC+∠OCB=90°-12∠A , ∴∠BOC=180°-(∠OBC+∠OCB )=90°,故②∠BOC =90°+12∠A 正确; 在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,∴∠OBC=∠EOB ,∠OCB=∠OCF ,∵EF ∥BC ,∴∠OBC=∠EOB ,∠OCB=∠FOC ,∠EOB=∠OBE,∠FOC=∠OCF ,∴BE=OE,CF=OF,∴EF=OE+OF=BE+CF ,即①EF =BE +CF 正确;过点O 作OM ⊥AB 于M ,作ON ⊥BC 于点N ,连接AO ,∵在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,∴ON=OD=OM=m ,即③点O 到△ABC 各边的距离相等正确;∴S △AEF=S △AOE+ S △AOF=12AE·OM+12AF·OD=12OD·(AE+AF )=12mn ,故④错误; 故选①②③【点睛】此题主要考查角平分线的性质,解题的关键是熟知等腰三角形的判定与性质.3.如图,已知点I 是△ABC 的角平分线的交点.若AB +BI =AC ,设∠BAC =α,则∠AIB =______(用含α的式子表示)【答案】1206α︒-【解析】【分析】 在AC 上截取AD=AB ,易证△ABI ≌△ADI ,所以BI=DI ,由AB +BI =AC ,可得DI=DC ,设∠DCI=β,则∠ADI=∠ABI=2β,然后用三角形内角和可推出β与α的关系,进而求得∠AIB.【详解】解:如图所示,在AC 上截取AD=AB ,连接DI ,点I 是△ABC 的角平分线的交点所以有∠BAI=∠DAI ,∠ABI=∠CBI ,∠ACI=∠BCI ,在△ABI 和△ADI 中,AB=AD BAI=DAI AI=AI ⎧⎪∠∠⎨⎪⎩∴△ABI ≌△ADI (SAS )∴DI=BI又∵AB +BI =AC ,AB+DC=AC∴DI=DC∴∠DCI=∠DIC设∠DCI=∠DIC=β则∠ABI=∠ADI=2∠DCI=2β在△ABC 中,∠BAC+2∠ABI+2∠DCI=180°,即42180ββ︒++=a , ∴180=3066β︒︒=--a a 在△ABI 中,180︒∠=-∠-∠AIB BAI ABI121802αβ︒=-- 1=23160028αα︒︒⎛⎫--- ⎪⎝⎭ =1206α︒-【点睛】本题考查全等三角形的判定和性质,以及三角形角度计算,利用截长补短构造全等三角形是解题的关键.4.在Rt △ABC 中,∠C =90°,∠A 的平分线AD 分对边BD ,DC 的长度比为3:2,且BC =20cm ,则点D 到AB 的距离是_____cm .【答案】8【解析】【分析】根据题意画出图形,过点D 作DE ⊥AB 于点E ,由角平分线的性质可知DE =CD ,根据角平分线AD 分对边BC 为BD :DC =3:2,且BC =10cm 即可得出结论.【详解】解:如图所示,过点D 作DE ⊥AB 于点E ,∵AD 是∠BAC 的平分线,∠C =90°,∴DE =CD .∵BD :DC =3:2,且BC =10cm ,∴CD=20×25=8(cm).故答案为:8.【点睛】本题考查的是角平分线的性质,熟知角的平分线上的点到角的两边的距离相等是解答此题的关键.5.如图,已知点(,0)A a在x轴正半轴上,点(0,)B b在y轴的正半轴上,ABC∆为等腰直角三角形,D为斜边BC上的中点.若2OD=,则a b+=________.【答案】2【解析】【分析】根据等腰直角三角形的性质,可得AP与BC的关系,根据垂线的性质,可得答案【详解】如图:作CP⊥x轴于点P,由余角的性质,得∠OBA=∠PAC,在Rt△OBA和Rt△PAC中,OBA PACAOB CPABA AC∠∠⎧⎪∠∠⎨⎪⎩===,Rt △OBA ≌Rt △PAC (AAS ),∴AP=OB=b ,PC=OA=a .由线段的和差,得OP=OA+AP=a+b ,即C 点坐标是(a+b ,a ),由B (0,b ),C (a+b ,a ),D 是BC 的中点,得D (2a b +,2a b +), ∴OD=22a b +() ∴2a b +()=2, ∴a+b=2.故答案为2.【点睛】本题解题主要①利用了等腰直角三角形的性质;②利用了全等三角形的判定与性质;③利用了线段中点的性质.6.如图,△ABE ,△BCD 均为等边三角形,点A ,B ,C 在同一条直线上,连接AD ,EC ,AD 与EB 相交于点M ,BD 与EC 相交于点N ,下列说法正确的有:___________ ①AD=EC ;②BM=BN ;③MN ∥AC ;④EM=MB .【答案】①②③【解析】∵△ABE ,△BCD 均为等边三角形,∴AB=BE ,BC=BD ,∠ABE=∠CBD=60°,∴∠ABD=∠EBC ,在△ABD 和△EBC 中AB BE ABD EBC BD BC =⎧⎪∠=∠⎨⎪=⎩∴△ABD ≌△EBC(SAS),∴AD=EC ,故①正确;∴∠DAB=∠BEC ,又由上可知∠ABE=∠CBD=60°,∴∠EBD=60°,在△ABM 和△EBN 中MAB NEBAB BEABE EBN∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ABM≌△EBN(ASA),∴BM=BN,故②正确;∴△BMN为等边三角形,∴∠NMB=∠ABM=60°,∴MN∥AC,故③正确;若EM=MB,则AM平分∠EAB,则∠DAB=30°,而由条件无法得出这一条件,故④不正确;综上可知正确的有①②③,故答案为①②③.点睛:本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(即SSS、SAS、AAS、ASA和HL)和性质(即全等三角形的对应边相等,对应角相等).7.在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CDE=55°.如图,则∠EAB的度数为_________【答案】35°【解析】【分析】过点E作EF⊥AD于F,根据角平分线上的点到角的两边的距离相等可得CE=EF,再根据到角的两边距离相等的点在角的平分线上可得AE是∠BAD的平分线,然后求出∠AEB,再根据直角三角形两锐角互余求解即可.【详解】过点E作EF⊥AD于F.∵DE平分∠ADC,∴CE=EF.∵E是BC的中点,∴CE=BE,∴BE=EF,∴AE是∠BAD的平分线,∴∠EAB=∠FAE.∵∠B=∠C=90°,∴∠CDA+∠DAB=180°,∴2∠CDE+2∠EAB=180°,∴∠CDE+∠EAB=90°,∴∠EAB=90°-∠CDE=90°-55°=35°.故答案为:35°.【点睛】本题考查了角平分线上的点到角的两边的距离相等的性质,角平分线的判定,熟记性质并作辅助线是解题的关键.8.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,P、Q是边AC、BC上的两个动点,PD⊥AB于点D, QE⊥AB于点E.设点P、Q运动的时间是t秒(t>0).若点P从C点出发沿CA以每秒3个单位的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回到点C停止运动;点Q从点B出发沿BC以每秒1个单位的速度向点C匀速运动,到达点C后停止运动,当t= 时,△APD和△QBE全等.【答案】2或4.【解析】试题分析:①0≤t<83时,点P从C到A运动,则AP=AC=CP=8﹣3t,BQ=t,当△ADP≌△QBE时,则AP=BQ,即8﹣3t=t,解得:t=2;②t≥83时,点P从A到C运动,则AP=3t﹣8,BQ=t,当△ADP≌△QBE时,则AP=BQ,即3t﹣8=t,解得:t=4;综上所述:当t=2s或4s时,△ADP≌△QBE.考点:1.全等三角形的判定;2.动点型;3.分类讨论.9.如图,在△ABC中,∠BAC=90°, AB=AC=22,点D,E均在边BC上,且∠DAE=45°,若BD=1,则DE=__________.【答案】53【解析】分析:根据等腰直角三角形的性质得45B ACB∠=∠=,把△ABD绕点A逆时针旋转90得到△ACF,连接,EF 如图,根据旋转的性质得,,AD AF BAD CAF=∠=∠45,ABD ACF∠=∠=接着证明45,EAF∠=然后根据“SAS”可判断△ADE≌△AFE,得到DE=FE,由于90ECF ACB ACF∠=∠+∠=,根据勾股定理得222CE CF EF+=,设,DE EF x==则3CE x=-,则()22231,x x-+=由此即可解决问题.详解:90BAC AB AC∠==,,∴45B ACB∠=∠=,把△ABD绕点A逆时针旋转90得到△ACF,连接,EF如图,则△ABD≌△ACF,,,45,AD AF BAD CAF ABD ACF=∠=∠∠=∠=∵45DAE∠=,∴45BAD CAE∠+∠=,∴45,CAF CAE∠+∠=即45,EAF∠=∴∠EAD=∠EAF,在△ADE和△AFE中AE AEEAD EAFAD AF=⎧⎪∠=∠⎨⎪=⎩,∴△ADE≌△AFE,∴DE=FE,∵90ECF ACB ACF∠=∠+∠=,∴222CE CF EF+=,Rt△ABC中,∵22AB AC==,∴224BC AB AC+=,∵1BD=,设,DE EF x==则3CE x=-,则有()22231,x x -+=解得:5.3x =∴5.3DE = 故答案为5.3点睛:本题属于全等三角形的综合题,涉及三角形旋转,全等三角形的判定与性质,勾股定理等知识点,综合性较强,难度较大.10.如图,在△ABC 中,∠C =90°,AC =BC ,AD 是△ABC 的角平分线,DE ⊥AB ,垂足为点E .已知AB =12,则△DEB 的周长为_______.【答案】12【解析】根据角平分线的性质,由AD 是∠CAB 的平分线,DE ⊥AB ,∠C=90°,可得到CD=ED ,然后根据直角三角形的全等判定HL 证得Rt △ACD ≌Rt △AED ,再由全等的性质得到AC=AE ,然后根据AC=BC ,因此可得△DEB 的周长=BD+DE+BE=BD+CD+BE=BC+BE=AC+BE=AE+BE=AB=12.故答案为:12.点睛:此题主要考查了全等三角形的性质和角平分线的性质,解题时根据全等三角形的性质和角平分线的性质得到相等的线段,然后再代还求解即可.二、八年级数学全等三角形选择题(难)11.已知:如图,ABC ∆、CDE ∆都是等腰三角形,且CA CB =,CD CE =,ACB DCE α∠=∠=,AD 、BE 相交于点O ,点M 、N 分别是线段AD 、BE 的中点.以下4个结论:①AD BE =;②180DOB α∠=-;③CMN ∆是等边三角形;④连OC ,则OC 平分AOE ∠.正确的是( )A .①②③B .①②④C .①③④D .①②③④【答案】B【解析】【分析】 ①根据∠ACB=∠DCE 求出∠ACD=∠BCE,证出ACD BCE ≅△△即可得出结论,故可判断; ②根据全等求出∠CAD=∠CBE,根据三角形外角定理得∠DOB=∠OBA+∠BAO,通过等角代换能够得到∠DOB=∠CBA+∠BAC,根据三角形内角和定理即可求出∠CBA+∠BAC,即可求出∠DOB ,故可判断;③根据已知条件可求出AM=BN,根据SAS 可求出CAM CBN ≅,推出CM=CN ,∠ACM=∠BCN,然后可求出∠MCN=∠ACB=α,故可判断CMN ∆的形状;④在AD 上取一点P 使得DP=EO,连接CP ,根据ACD BCE ≅△△,可求出∠CEO=∠CDP ,根据SAS 可求出 CEO CDP ≅,可得∠COE=∠CPD,CP=CO,进而得到 ∠COP=∠COE ,故可判断.【详解】①正确,理由如下:∵ACB DCE α∠=∠=,∴∠ACB+∠BCD=∠DCE+∠BCD,即∠ACD=∠BCE,又∵CA=CB,CD=CE,∴ACD BCE ≅△△(SAS),∴AD=BE,故①正确;②正确,理由如下:由①知,ACD BCE ≅△△,∴∠CAD=∠CBE,∵∠DOB 为ABO 的外角,∴∠DOB=∠OBA+∠BAO=∠EBC+∠CBA+∠BAO=∠DAC+∠BAO+∠CBA=∠CBA+∠BAC, ∵∠CBA+∠BAC+∠ACB=180°,∠ACB=α,∴∠CBA+∠BAC=180°-α,即∠DOB=180°-α,故②正确;③错误,理由如下:∵点M 、N 分别是线段AD 、BE 的中点,∴AM=12AD,BN= 12BE, 又∵由①知,AD=BE,∴AM=BN,又∵∠CAD=∠CBE,CA=CB,∴CAM CBN ≅(SAS), ∴CM=CN ,∠ACM=∠BCN,∴∠MCN=∠MCB+∠CBN=∠MCB+∠ACM=∠ACB=α,∴MCN △为等腰三角形且∠MCN=α,∴MCN △不是等边三角形,故③错误;④正确,理由如下:如图所示,在AD 上取一点P 使得DP=EO,连接CP ,由①知,ACD BCE ≅△△,∴∠CEO=∠CDP ,又∵CE=CD,EO=DP ,∴CEO CDP ≅(SAS),∴∠COE=∠CPD,CP=CO,∴∠CPO=∠COP ,∴∠COP=∠COE,即OC 平分∠AOE,故④正确;故答案为:B.【点睛】本题考查了三角形全等的判定和性质,三角形内角和定理和外角定理,等边三角形的判定,根据已知条件作出正确的辅助线,找出全等三角形是解题的关键.12.已知OD 平分∠MON,点A 、B 、C 分别在OM 、OD 、ON 上(点A 、B 、C 都不与点O 重合),且AB=BC, 则∠OAB 与∠BCO 的数量关系为( )A .∠OAB+∠BCO=180°B .∠OAB=∠BCOC .∠OAB+∠BCO=180°或∠OAB=∠BCOD .无法确定【答案】C【解析】根据题意画图,可知当C 处在C 1的位置时,两三角形全等,可知∠OAB=∠BCO ;当点C 处在C 2的位置时,根据等腰三角形的性质和三角形的外角的性质,∠OAB+∠BCO=180°.故选C.13.如图,已知,BD 为△ABC 的角平分线,且BD=BC ,E 为BD 延长线上的一点,BE=BA .下面结论:①△ABD ≌△EBC ;②AC=2CD ;③AD=AE=EC ;④∠BCE+∠BCD=180°.其中正确的是( )A .①②③B .①②④C .①③④D .②③④【答案】C【解析】 已知BD 为△ABC 的角平分线,根据角平分线的定义可得∠ABD =∠CBD ,在△AB D 和△EB C 中,BD =BC ,∠ABD =∠CBD ,BE =BA ,由SAS 可判定△ABD ≌△EBC ,即可得①正确;根据已知条件,无法证明AC =2CD ,②错误; 已知BD 为△ABC 的角平分线,BD=BC ,BE=BA ,可得∠BCD =∠BDC =∠BAE =∠BEA , 再由∠BCE =∠BDA ,∠BCE =∠BCD +∠DCE ,∠BDA =∠DAE +∠BEA ,∠BCD =∠BEA ,可得∠DCE =∠DAE ,所以AE =EC ;再由△ABD ≌△EBC ,可得AD=EC ,所以AD=AE=EC ,即③正确;由△ABD ≌△EBC ,可得∠BCE =∠BDA ,所以∠BCE +∠BCD =∠BDA +∠BDC =180°,④正确.故选C.点睛:本题考查了全等三角形的判定及性质、等腰三角形的的性质、三角形外角的性质,本题中熟练求证三角形全等和熟练运用全等三角形对应角、对应边相等性质是解题的关键.14.如图,ABC △中,60BAC ∠=︒,ABC ∠、ACB ∠的平分线交于E ,D 是AE 延长线上一点,且120BDC ∠=︒.下列结论:①120BEC ∠=︒;②DB DE =;③2BDE BCE ∠=∠.其中所有正确结论的序号有( ).A .①②B .①③C .②③D .①②③【答案】D【解析】 分析:根据三角形内角和等于180°求出∠ABC+∠ACB ,再根据角平分线的定义求出∠EBC+∠ECB ,然后求出∠BEC=120°,判断①正确;过点D 作DF ⊥AB 于F ,DG ⊥AC 的延长线于G ,根据角平分线上的点到角的两边的距离相等可得DF=DG ,再求出∠BDF=∠CDG ,然后利用“角边角”证明△BDF 和△CDG 全等,根据全等三角形对应边相等可得BD=CD ,再根据等边对等角求出∠DBC=30°,然后根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义求出∠DBE=∠DEB ,根据等角对等边可得BD=DE ,判断②正确,再求出B ,C ,E 三点在以D 为圆心,以BD 为半径的圆上,根据同弧所对的圆周角等于圆心角的一半可得∠BDE=2∠BCE ,判断③正确.详解:∵60BAC ∠=︒,∴18060120ABC ACB ∠+∠=︒-︒=︒,∵BE 、CE 分别为ABC ∠、ACB ∠的平分线,∴12EBC ABC ∠=∠,12ECB ACB ∠=∠, ∴11()1206022EBC ECB ABC ACB ∠+∠=∠+∠=⨯︒=︒, ∴180()18060120BEC EBC ECB ∠=︒-∠+∠=︒-︒=︒, 故①正确.如图,过点D 作DF AB ⊥于F ,DG AC ⊥的延长线于G ,∵BE 、CE 分别为ABC ∠、ACB ∠的平分线,∴AD 为BAC ∠的平分线,∴DF DG =,∴36090260120FDG ∠=︒-︒⨯-︒=︒,又∵120BDC ∠=︒,∴120BDF CDF ∠+∠=︒,120CDG CDF ∠+∠=︒.∴BDF CDG ∠=∠,∵在BDF 和CDG △中,90BFD CGD DF DGBDF CDG ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩, ∴BDF ≌()CDG ASA ,∴DB CD =, ∴1(180120)302DBC ∠=︒-︒=︒, ∴30DBC DBC CBE CBE ∠=∠+∠=︒+∠,∵BE 平分ABC ∠,AE 平分BAC ∠,∴ABE CBE ∠=∠,1302BAE BAC ∠=∠=︒, 根据三角形的外角性质, 30DEB ABE BAE ABE ∠=∠+∠=∠+︒,∴DEB DBE ∠=∠,∴DB DE =,故②正确.∵DB DE DC ==,∴B 、C 、E 三点在以D 为圆心,以BD 为半径的圆上,∴2BDE BCE ∠=∠,故③正确,综上所述,正确结论有①②③,故选:D .点睛:本题考查了角平分线的性质,全等三角形的判定与性质,等角对等边的性质,圆内接四边形的判定,同弧所对的圆周角等于圆心角的一半性质,综合性较强,难度较大,特别是③的证明.15.如图,点 D 是等腰直角 △ABC 腰 BC 上的中点,点B 、B′ 关于 AD 对称,且 BB′ 交AD 于 F ,交 AC 于 E ,连接 FC 、 AB′,下列说法:① ∠BAD=30°; ② ∠BFC=135°;③ AF=2B′ C ;正确的个数是()A.1 B.2 C.3 D.4【答案】B【解析】【分析】依据点D是等腰直角△ABC腰BC上的中点,可得tan∠BAD=12,即可得到∠BAD≠30°;连接B'D,即可得到∠BB'C=∠BB'D+∠DB'C=90°,进而得出△ABF≌△BCB',判定△FCB'是等腰直角三角形,即可得到∠CFB'=45°,即∠BFC=135°;由△ABF≌△BCB',可得AF=BB'=2BF=2B'C;依据△AEF与△CEB'不全等,即可得到S△AFE≠S△FCE.【详解】∵点D是等腰直角△ABC腰BC上的中点,∴BD=12BC=12AB,∴tan∠BAD=12,∴∠BAD≠30°,故①错误;如图,连接B'D,∵B、B′关于AD对称,∴AD垂直平分BB',∴∠AFB=90°,BD=B'D=CD,∴∠DBB'=∠BB'D,∠DCB'=∠DB'C,∴∠BB'C=∠BB'D+∠DB'C=90°,∴∠AFB=∠BB'C,又∵∠BAF+∠ABF=90°=∠CBB'+∠ABF,∴∠BAF=∠CBB',∴△ABF≌△BCB',∴BF=CB'=B'F,∴△FCB'是等腰直角三角形,∴∠CFB'=45°,即∠BFC=135°,故②正确;由△ABF≌△BCB',可得AF=BB'=2BF=2B'C,故③正确;∵AF>BF=B'C,∴△AEF与△CEB'不全等,∴AE≠CE,∴S△AFE≠S△FCE,故④错误;故选B.【点睛】本题主要考查了轴对称的性质以及全等三角形的判定与性质的运用,如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.16.如图,在等腰直角△ABC中,∠ACB=90°,点O为斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P,则下列结论:①图中全等三角形有三对;②△ABC的面积等于四边形CDOE面积的倍;③DE2+2CD•CE=2OA2;④AD2+BE2=2OP•OC.正确的有()个.A.1 B.2 C.3 D.4【答案】C【解析】【分析】结论(1)正确.因为图中全等的三角形有3对;结论(2)错误.由全等三角形的性质可以判断;结论(3)正确.利用全等三角形和等腰直角三角形的性质可以判断.结论(4)正确.利用相似三角形、全等三角形、等腰直角三角形和勾股定理进行判断.【详解】结论(1)正确,理由如下:图中全等的三角形有3对,分别为△AOC≌△BOC,△AOD≌△COE,△COD≌△BOE.由等腰直角三角形的性质,可知OA=OC=OB,易得△AOC≌△BOC.∵OC⊥AB,OD⊥OE,∴∠AOD=∠COE.在△AOD与△COE中,∴△AOD ≌△COE (ASA ),同理可证:△COD ≌△BOE .结论(2)错误.理由如下:∵△AOD ≌△COE ,∴S △AOD =S △COE ,∴S 四边形CDOE =S △COD +S △COE =S △COD +S △AOD=S △AOC =S △ABC即△ABC 的面积等于四边形CDOE 的面积的2倍.结论(3)正确,理由如下:∵△AOD ≌△COE ,∴CE=AD , ∴CD+CE=CD+AD=AC=OA ,∴(CD+CE )2=CD 2+CE 2+2CD•CE=DE 2+2CD•CE=2OA 2;结论(4)正确,理由如下:∵△AOD ≌△COE ,∴AD=CE ;∵△COD ≌△BOE ,∴BE=CD .在Rt △CDE 中,由勾股定理得:CD 2+CE 2=DE 2,∴AD 2+BE 2=DE 2.∵△AOD ≌△COE ,∴OD=OE ,又∵OD ⊥OE ,∴△DOE 为等腰直角三角形,∴DE 2=2OE 2,∠DEO=45°.∵∠DEO=∠OCE=45°,∠COE=∠COE ,∴△OEP ∽△OCE ,∴,即OP•OC=OE 2.∴DE 2=2OE 2=2OP•OC ,∴AD 2+BE 2=2OP•OC .综上所述,正确的结论有3个,故选C .【点睛】本题是几何综合题,考查了等腰直角三角形、全等三角形、相似三角形和勾股定理等重要几何知识点.难点在于结论(4)的判断,其中对于“OP•OC”线段乘积的形式,可以寻求相似三角形解决问题.17.如图,D 为BAC ∠的外角平分线上一点并且满足BD CD =,DBC DCB ∠=∠,过D 作DE AC ⊥于E ,DF AB ⊥交BA 的延长线于F ,则下列结论:①CDE △≌BDF ;②CE AB AE =+;③BDC BAC ∠=∠;④DAF CBD ∠=∠. 其中正确的结论有( ).A.1个B.2个C.3个D.4个【答案】D【解析】BD=CD,AD是角平分线,所以FD=DE,∠DFB=∠DEC=90°,所以CDE≌BDF;①正确.由全等得BF=CE,因为FA=AE,FB=AB+FA,所以CE=AB+AE, ②正确.由全等知,∠=∠,∠DCE=∠FBD,所以∠BAC=∠BDC.③正确. ∴DBF DCE∴A、B、C、D四点共圆,∠=∠,④正确.∴DAF CBD故选D.18.如图,与都是等边三角形,,下列结论中,正确的个数是( )①;②;③;④若,且,则.A.1 B.2 C.3 D.4【答案】C【解析】【分析】利用全等三角形的判定和性质一一判断即可.【详解】解:∵与都是等边三角形∴AD=AB,AC=AE,∠DAB=∠EAC=60°∴∠DAB+∠BAC=∠EAC +∠BAC即∠DAC=∠EAB∴∴,①正确;∵∴∠ADO=∠ABO∴∠BOD=∠DAB=60°,②正确∵∠BDA=∠CEA=60°,∠ADC≠∠AEB∴∠BDA -∠ADC≠∠CEA -∠AEB∴,③错误 ∵∴∠DAC+∠BCA=180° ∵∠DAB=60°,∴∠BCA=180°-∠DAB -∠BAC=30°∵∠ACE=60°∴∠BCE=∠ACE+∠BCA=60°+30°=90°∴④正确 故由①②④三个正确, 故选:C【点睛】本题考查全等三角形的判定和性质、等边三角形的性质、角平分线的判定定理等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.19.已知111122,A B C A B C △△的周长相等,现有两个判断:①若21212112,A A B C B A A C ==,则111222A B C A B C △≌△;②若12=A A ∠∠,1122=A C A C ,则111222A B C A B C △≌△,对于上述的两个判断,下列说法正确的是( )A .①,②都正确B .①,②都错误C .①错误,②正确D .①正确,②错误 【答案】A【解析】【分析】根据SSS 即可推出△111A B C ≅△222A B C ,判断①正确;根据相似三角形的性质和判定和全等三角形的判定推出即可.【详解】解:①△111A B C ,△222A B C 的周长相等,1122A B A B =,1122AC A C =,1122B C B C ∴=,∴△111A B C ≅△222()A B C SSS ,∴①正确;②如图,延长11A B 到1D ,使1111B D B C =,,延长22A B 到2D ,使2222B D B C =,∴111111A D A B B C =+,222222A D A B B C =+,∵111122,A B C A B C △△的周长相等,1122=A C A C∴1122A D A D =,在△111A B D 和△222A B D 中1122121122==A D A D A A A C A C =⎧⎪∠∠⎨⎪⎩,∴ △111A B D ≅△222A B D (SAS )∴12=D D ∠∠,∵1111B D B C =,2222B D B C =∴1111=D D C B ∠∠,2222=D D C B ∠∠,又∵1111111=A B C D D C B ∠∠+∠,2222222=A B C D D C B ∠∠+∠,∴1112221==2A B C A B C D ∠∠∠,在△111A B C 和△222A B C 中111222121122===A B C A B C A A A C A C ∠∠⎧⎪∠∠⎨⎪⎩, ∴△111A B C ≅△222A B C (AAS ),∴②正确;综上所述:①,②都正确.故选:A .【点睛】本题考查了全等三角形的判定、等腰三角形的性质,能构造全等三角形、综合运用定理进行推理是解此题的关键,注意:全等三角形的判定定理有SAS ,ASA ,AAS ,SSS ,而AAA 和SSA 不能判断两三角形全等.20.如图,△ABC 中,AB ⊥BC ,BE ⊥AC ,∠1=∠2,AD =AB ,则下列结论不正确的是A .BF =DFB .∠1=∠EFDC .BF >EFD .FD ∥BC【答案】B【解析】【分析】根据余角的性质得到∠C=∠ABE,∠EBC=∠BAC.根据SAS推出△ABF≌△ADF,根据全等三角形的性质得到BF=DF,故A正确;由全等三角形的性质得到∠ABE=∠ADF,等量代换得到∠ADF=∠C,根据平行线的判定得到DF∥BC,故D正确;根据直角三角形的性质得到DF >EF,等量代换得到BF>EF;故C正确;根据平行线的性质得到∠EFD=∠EBC=∠BAC=2∠1,故B错误.【详解】∵AB⊥BC,BE⊥AC,∴∠C+∠BAC=∠ABE+∠BAC=90°,∴∠C=∠ABE.同理:∠EBC=∠BAC.在△ABF与△ADF中,∵12AD ABAF AF=⎧⎪∠=∠⎨⎪=⎩,∴△ABF≌△ADF,∴BF=DF,故A正确,∵△ABF≌△ADF,∴∠ABE=∠ADF,∴∠ADF=∠C,∴DF∥BC,故D正确;∵∠FED=90°,∴DF>EF,∴BF>EF;故C正确;∵DF∥BC,∴∠EFD=∠EBC.∵∠EBC=∠BAC=∠BAC=2∠1,∴∠EFD=2∠1,故B错误.故选B.【点睛】本题考查了全等三角形的判定和性质,平行线的判定和性质,证得△ABF≌△ADF是解题的关键.21.如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2,其中正确结论有()A.0个B.1个C.2个D.3个【答案】D【解析】分析:由四边形ABCD与四边形EFGC都为正方形,得到四条边相等,四个角为直角,利用SAS 得到三角形BCE与三角形DCG全等,利用全等三角形对应边相等即可得到BE=DG,利用全等三角形对应角相等得到∠CBM=∠MDO,利用等角的余角相等及直角的定义得到∠BOD为直角,利用勾股定理求出所求式子的值即可.详解:①∵四边形ABCD和EFGC都为正方形,∴CB=CD,CE=CG,∠BCD=∠ECG=90°,∴∠BCD+∠DCE=∠ECG+∠DCE,即∠BCE=∠DCG.在△BCE和△DCG中,CB=CD,∠BCE=∠DCG,CE=CG,∴△BCE≌△DCG,∴BE=DG,故结论①正确.②如图所示,设BE交DC于点M,交DG于点O.由①可知,△BCE≌△DCG,∴∠CBE=∠CDG,即∠CBM=∠MDO.又∵∠BMC=∠DMO,∠MCB=180°-∠CBM-∠BMC,∠DOM=180°-∠CDG-∠MDO,∴∠DOM=∠MCB=90°,∴BE⊥DG.故②结论正确.③如图所示,连接BD、EG,由②知,BE⊥DG,则在Rt△ODE中,DE2=OD2+OE2,在Rt△BOG中,BG2=OG2+OB2,在Rt△OBD中,BD2=OD2+OB2,在Rt△OEG中,EG2=OE2+OG2,∴DE2+BG2=(OD2+OE2)+(OB2+OG2)=(OD2+OB2)+(OE2+OG2)=BD2+EG2.在Rt△BCD中,BD2=BC2+CD2=2a2,在Rt△CEG中,EG2=CG2+CE2=2b2,∴BG2+DE2=2a2+2b2.故③结论正确.故选:D.点睛:本题考查了旋转的性质、全等三角形的判定与性质、正方形的性质.22.如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面四个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④AP垂直平分RS.其中正确结论的序号是().A.①②B.①②③C.①②④D.①②③④【答案】C【分析】如图,连接AP,根据HL 判定△APR 和△APS 全等,即可说明①正确;由△APR 和△APS 全等可得∠RAP=∠PAC,再根据等腰三角形性质推出∠QAP=∠QPA ,得到∠QPA=∠BAP ,根据平行线判定推出OP//AB ,即②正确;在Rt △BRP 和Rt △QSP 中,只有PR=PS.无法判断Rt △BRP 和Rt △QSP 是否全等;连接RS ,与AP 交于点D ,先证△ARD ≌△ASD ,即RD=SD ;运用等腰三角形的性质即可判定.【详解】解:如图,连接AP∵PR ⊥AB ,PS ⊥AC ,PR =PS∴△APR ≌△APS∴AS =AR ,∠RAP=∠PAC即①正确;又∵AQ=PQ∴∠QAP=∠QPA∴∠QPA=∠BAP∴OP//AB ,即②正确.在Rt △BRP 和Rt △QSP 中,只有PR=PS.无法判断Rt △BRP 和Rt △QSP 是否全等,故③错误.如图,连接PS∵△APR ≌△APS∴AR =AS ,∠RAP=∠PAC∴AP 垂直平分RS ,即④正确;故答案为C.【点睛】本题主要考查了全等三角形的性质和判定,角平分线性质的应用,熟练掌握全等三角形的判定和性质是解答本题的关键23.如图,在四边形ABCD 中,//AB CD .不能判定ABD CDB ∆≅∆的条件是( )A .AB CD = B .AD BC = C .//AD BC D .A C ∠=∠【解析】【分析】根据已知条件,分别添加选项进行排查,即可完成解答;注意BD是公用边这个条件.【详解】解:A.若添加AB=CD,根据AB∥CD,则∠ABD=∠CDB,依据SAS可得△ABD≌△CDB,故A选项正确;B.若添加AD=BC,根据AB∥CD,则∠ADB=∠CBD,不能判定△ABD≌△CDB,故B选项错误;C.若添加//AD BC,则四边形ABCD是平行四边形,能判定△ABD≌△CDB,故C选项正确;D.若添加∠A=∠C,根据AB∥CD,则∠ABD=∠CDB,且BD公用,能判定△ABD≌△CDB,故D选项正确;故选:B.【点睛】本题考查了全等三角形的判定:全等三角形的5种判定方法中,选用哪一种方法,取决于题目中的已知条件,若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.24.如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,∠EAF=12∠BAD,若DF=1,BE=5,则线段EF的长为()A.3 B.4 C.5 D.6【答案】B【解析】【分析】在BE上截取BG=DF,先证△ADF≌△ABG,再证△AEG≌△AEF即可解答.【详解】在BE上截取BG=DF,∵∠B+∠ADC=180°,∠ADC+∠ADF=180°,∴∠B=∠ADF,在△ADF与△ABG中AB ADB ADFBG DF=⎧⎪∠=∠⎨⎪=⎩,∴△ADF≌△ABG(SAS),∴AG=AF,∠FAD=∠GAB,∵∠EAF=12∠BAD,∴∠FAE=∠GAE,在△AEG与△AEF中AG AFFAE GAEAE AE=⎧⎪∠=∠⎨⎪=⎩,∴△AEG≌△AEF(SAS)∴EF=EG=BE﹣BG=BE﹣DF=4.故选:B.【点睛】考查了全等三角形的判定与性质,证明三角形全等是解决问题的关键.25.如图(1),已知AB AC=,D为BAC∠的角平分线上一点,连接BD,CD;如图(2),已知AB AC=,D,E为BAC∠的角平分线上两点,连接BD,CD,BE,CE;如图(3),已知AB AC=,D,E,F为BAC∠的角平分线上三点,连接BD,CD,BE,CE,BF,CF;……,依此规律,第6个图形中有全等三角形的对数是()A .21B .11C .6D .42【答案】A【解析】【分析】 根据条件可得图1中△ABD ≌△ACD 有1对三角形全等;图2中可证出△ABD ≌△ACD ,△BDE ≌△CDE ,△ABE ≌△ACE 有3对三角形全等;图3中有6对三角形全等,根据数据可分析出第6个图形中全等三角形的对数.【详解】解:∵AD 是∠BAC 的平分线,∴∠BAD=∠CAD .在△ABD 与△ACD 中,AB AC BAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△ACD .∴图1中有1对三角形全等;同理图2中,△ABE ≌△ACE ,∴BE=EC ,∵△ABD ≌△ACD .∴BD=CD ,又DE=DE ,∴△BDE ≌△CDE ,∴图2中有3对三角形全等,3=1+2;同理:图3中有6对三角形全等,6=1+2+3;∴第6个图形中有全等三角形的对数是1+2+3+4+5+6=21.故选:A .【点睛】此题主要考查了三角形全等的判定以及规律的归纳,解题的关键是根据条件证出图形中有几对三角形全等,然后寻找规律.26.如图,在△ABC 中,AB=BC ,90ABC ∠=︒,点D 是BC 的中点,BF ⊥AD ,垂足为E ,BF 交AC 于点F ,连接DF.下列结论正确的是()A .∠1=∠3B .∠2=∠3C .∠3=∠4D .∠4=∠5【答案】A【解析】【分析】如图,过点C 作BC 的垂线,交BF 的延长线于点G ,则CG BC ⊥,先根据直角三角形两锐角互余可得BAD CBG ∠=∠,再根据三角形全等的判定定理与性质推出1G ∠=∠,又根据三角形全等的判定定理与性质推出3G ∠=∠,由此即可得出答案.【详解】如图,过点C 作BC 的垂线,交BF 的延长线于点G ,则CG BC ⊥,即90BCG ∠=︒ ,90AB BC ABC =∠=︒45BAC ACB ∠∴∠==︒904545GCF BCG ACB ∴∠=∠-∠=︒-︒=︒BF AD ⊥1190BAD CBG ∴∠+∠=∠+∠=︒BAD CBG ∴∠=∠在BAD ∆和CBG ∆中,90BAD CBG AB BC ABD BCG ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩()BAD CBG ASA ∴∆≅∆,1BD CG G ∴=∠=∠点D 是BC 的中点CD BD CG ∴==在CDF ∆和CGF ∆中,45CD CG DCF GCF CF CF =⎧⎪∠=∠=︒⎨⎪=⎩()CDF CGF SAS ∴∆≅∆3G ∴∠=∠13∠∠∴=故选:A .【点睛】本题是一道较难的综合题,考查了直角三角形的性质、三角形全等的判定定理与性质等知识点,通过作辅助线,构造两个全等的三角形是解题关键.27.如图,AD 是ABC 的角平分线,DE AC ⊥;垂足为,//E BF AC 交ED 的延长线于点F ,若BC 恰好平分ABF ∠.给出下列三个结论:①DE DF =;②DB DC =;③AD BC ⊥.其中正确的结论共有( )个A .0B .1C .2D .3【答案】D【解析】【分析】 由BF ∥AC ,AD 是ABC 的角平分线,BC 平分ABF ∠得∠ADB=90︒;利用AD 平分∠CAB 证得△ADC ≌△ADB 即可证得DB=DC ;根据DE AC ⊥证明△CDE ≌△BDF 得到DE DF =.【详解】∵DE AC ⊥,BF ∥AC,∴EF ⊥BF ,∠CAB+∠ABF=180︒,∴∠CED=∠F=90︒,∵AD 是ABC 的角平分线,BC 平分ABF ∠,∴∠DAB+∠DBA=12(∠CAB+∠ABF)=90︒, ∴∠ADB=90︒,即AD BC ⊥,③正确; ∴∠ADC=∠ADB=90︒,∵AD 平分∠CAB,∴∠CAD=∠BAD,∵AD=AD,∴△ADC ≌△ADB,∴DB=DC ,②正确;又∵∠CDE=∠BDF ,∠CED=∠F ,∴△CDE ≌△BDF,∴DE=DF ,①正确;故选:D.【点睛】此题考查平行线的性质,三角形全等的判定及性质,角平分线的定义.28.如图,△ABC 是等边三角形,AQ =PQ ,PR ⊥AB 于点R ,PS ⊥AC 于点S ,PR =PS .下列结论:①点P 在∠A 的角平分线上;②AS =AR ;③QP ∥AR ;④△BRP ≌△QSP .其中,正确的有( )A .1个B .2个C .3个D .4个【答案】D【解析】∵△ABC 是等边三角形,PR ⊥AB ,PS ⊥AC ,且PR =PS ,∴P 在∠A 的平分线上,故①正确;由①可知,PB =PC ,∠B =∠C ,PS =PR ,∴△BPR ≌△CPS ,∴AS =AR ,故②正确;∵AQ =PQ ,∴∠PQC =2∠PAC =60°=∠BAC ,∴PQ ∥AR ,故③正确;由③得,△PQC 是等边三角形,∴△PQS ≌△PCS ,又由②可知,④△BRP ≌△QSP ,故④也正确,∵①②③④都正确,故选D .点睛:本题考查了角平分线的性质与全等三角形的判定与性质,准确识图并熟练掌握全等三角形的判定方法与性质是解题的关键.29.如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于( )A .150°B .180°C .210°D .225°【答案】B【解析】【分析】 根据SAS 可证得ABC ≌EDC ,可得出BAC DEC ∠∠=,继而可得出答案,再根据邻补角的定义求解. 【详解】由题意得:AB ED =,BC DC =,D B 90∠∠==, ABC ∴≌EDC ,BAC DEC ∠∠∴=,12180∠∠+=.故选B .【点睛】本题考查全等图形的知识,比较简单,解答本题的关键是判断出ABC ≌EDC..30.如图,点P是AB上任意一点,∠ABC=∠ABD,还应补充一个条件,才能推出△APC≌△APD.从下列条件中补充一个条件,不一定能推出△APC≌△APD的是( )A.BC=BD;B.AC=AD;C.∠ACB=∠ADB;D.∠CAB=∠DAB【答案】B【解析】根据题意,∠ABC=∠ABD,AB是公共边,结合选项,逐个验证得出:A、补充BC=BD,先证出△BPC≌△BPD,后能推出△APC≌△APD,故正确;B、补充AC=AD,不能推出△APC≌△APD,故错误;C、补充∠ACB=∠ADB,先证出△ABC≌△ABD,后能推出△APC≌△APD,故正确;D、补充∠CAB=∠DAB,先证出△ABC≌△ABD,后能推出△APC≌△APD,故正确.故选B.点睛:本题考查了三角形全等判定,三角形全等的判定定理:有AAS,SSS,ASA,SAS.注意SSA是不能证明三角形全等的,做题时要逐个验证,排除错误的选项.。
人教版八年级上册数学 轴对称解答题专题练习(解析版)

人教版八年级上册数学轴对称解答题专题练习(解析版)一、八年级数学轴对称解答题压轴题(难)1.在等边△ABC中,点D在BC边上,点E在AC的延长线上,DE=DA(如图1).(1)求证:∠BAD=∠EDC;(2)若点E关于直线BC的对称点为M(如图2),连接DM,AM.求证:DA=AM.【答案】(1)见解析;(2)见解析【解析】【分析】(1)根据等边三角形的性质,得出∠BAC=∠ACB=60°,然后根据三角形的内角和和外角性质,进行计算即可.(2)根据轴对称的性质,可得DM=DA,然后结合(1)可得∠MDC=∠BAD,然后根据三角形的内角和,求出∠ADM=60°即可.【详解】解:(1)如图1,∵△ABC是等边三角形,∴∠BAC=∠ACB=60°,∴∠BAD=60°﹣∠DAE,∠EDC=60°﹣∠E,又∵DE=DA,∴∠E=∠DAE,∴∠BAD=∠EDC.(2)由轴对称可得,DM=DE,∠EDC=∠MDC,∵DE=DA,∴DM=DA,由(1)可得,∠BAD=∠EDC,∴∠MDC=∠BAD,∵△ABD中,∠BAD+∠ADB=180°﹣∠B=120°,∴∠MDC+∠ADB=120°,∴∠ADM=60°,∴△ADM是等边三角形,∴AD=AM.【点睛】本题主要考察了轴对称和等边三角形的性质,解题的关键是熟练掌握这些性质.2.再读教材:宽与长的比是5-1(约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为2的矩形纸片折叠黄金矩形.(提示; MN=2)第一步,在矩形纸片一端.利用图①的方法折出一个正方形,然后把纸片展平.第二步,如图②.把这个正方形折成两个相等的矩形,再把纸片展平.第三步,折出内侧矩形的对角线 AB,并把 AB折到图③中所示的AD处,第四步,展平纸片,按照所得的点D折出 DE,使 DE⊥ND,则图④中就会出现黄金矩形,问题解决:(1)图③中AB=________(保留根号);(2)如图③,判断四边形 BADQ的形状,并说明理由;(3)请写出图④中所有的黄金矩形,并选择其中一个说明理由.(4)结合图④.请在矩形 BCDE中添加一条线段,设计一个新的黄金矩形,用字母表示出来,并写出它的长和宽.【答案】(15(2)见解析;(3)见解析; (4) 见解析.【解析】分析:(1)由勾股定理计算即可;(2)根据菱形的判定方法即可判断;(3)根据黄金矩形的定义即可判断;(4)如图④﹣1中,在矩形BCDE上添加线段GH,使得四边形GCDH为正方形,此时四边形BGHE为所求是黄金矩形.详解:(1)如图3中.在Rt△ABC中,AB22AC BC+2212+55(2)结论:四边形BADQ是菱形.理由如下:如图③中,∵四边形ACBF是矩形,∴BQ∥AD.∵AB∥DQ,∴四边形ABQD是平行四边形,由翻折可知:AB=AD,∴四边形ABQD是菱形.(3)如图④中,黄金矩形有矩形BCDE ,矩形MNDE .∵AD =5.AN =AC =1,CD =AD ﹣AC =5﹣1. ∵BC =2,∴CD BC =51-,∴矩形BCDE 是黄金矩形. ∵MN DN =15+=51-,∴矩形MNDE 是黄金矩形. (4)如图④﹣1中,在矩形BCDE 上添加线段GH ,使得四边形GCDH 为正方形,此时四边形BGHE 为所求是黄金矩形.长GH 51,宽HE =35点睛:本题考查了几何变换综合题、黄金矩形的定义、勾股定理、翻折变换等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考创新题目.3.已知:AD 是ABC ∆的高,且BD CD =. (1)如图1,求证:BAD CAD ∠=∠;(2)如图2,点E 在AD 上,连接BE ,将ABE ∆沿BE 折叠得到'A BE ∆,'A B 与AC 相交于点F ,若BE=BC ,求BFC ∠的大小;(3)如图3,在(2)的条件下,连接EF ,过点C 作CG EF ⊥,交EF 的延长线于点G ,若10BF =,6EG =,求线段CF 的长.图1. 图2. 图3.【答案】(1)见解析,(2)BFC ∠=60(3)8=CF . 【解析】 【分析】(1)根据等腰三角形三线合一,易得AB=AC ,BAD CAD ∠=∠;(2)在图2中,连接CE ,可证得BCE ∆是等边三角形,60BEC ∠= ,30BED ∠=且由折叠性质可知1'2ABE A BE ABF ∠=∠=∠,可得BFC FAB ABF ∠=∠+∠ ()2BAD ABE =∠+∠ 260BED =∠=;(3)连接CE ,过点E 分别作EH AB ⊥于点H ,EM BF ⊥于点M ,EN AC ⊥于点N ,可证得Rt BEM Rt CEN ∆≅∆,BM CN =,BF FM CF CN -=+,可得线段CF 的长. 【详解】解:(1)证明:如图1,AD BC ⊥,BD CD = AB AC ∴=BAD CAD ∴∠=∠;图1(2)解:在图2中,连接CEED BC ⊥,BD CD = BE CE ∴= 又BE BC = BE CE BC ∴== BCE ∴∆是等边三角形60BEC ∴∠= 30BED ∴∠=由折叠性质可知1'2ABE A BE ABF ∠=∠=∠ 2ABF ABE ∴∠=∠ 由(1)可知2FAB BAE ∠=∠BFC FAB ABF ∴∠=∠+∠ ()2BAD ABE =∠+∠ 223060BED =∠=⨯=图2(3)解:连接CE ,过点E 分别作EH AB ⊥于点H ,EM BF ⊥于点M ,EN AC ⊥于点N'ABE A BE ∠=∠,BAD CAD ∠=∠ EM EH EN ∴== AFE BFE ∴∠=∠ 又60BFC ∠= 60AFE BFE ∴∠=∠=在Rt EFM ∆中,906030FEM ∠=-= 2EF FM ∴=令FM m =,则2EF m = 62FG EG EF m ∴=-=- 同理12FN EF m ==,2124CF FG m ==-在Rt BEM ∆和Rt CEN ∆中,EM EN =,BE CE = Rt BEM Rt CEN ∴∆≅∆BM CN ∴=BF FM CF FN ∴-=+ 10124m m m ∴-=-+ 解得1m = 8CF ∴=图3故答案为(1)见解析,(2)BFC ∠= 60(3)8CF =. 【点睛】本题考查翻折的性质,涉及角平分线的性质、等腰三角形的性质和判定、等边三角形的判定和性质、含30度角的直角三角形、全等三角形的判定和性质等知识点,属于较难的题型.4.如图,在等边△ABC 中,线段AM 为BC 边上的中线.动点D 在直线AM 上时,以CD 为一边在CD 的下方作等边△CDE ,连结BE . (1)求∠CAM 的度数;(2)若点D 在线段AM 上时,求证:△ADC ≌△BEC ;(3)当动D 在直线..AM 上时,设直线BE 与直线AM 的交点为O ,试判断∠AOB 是否为定值?并说明理由.【答案】(1)30°;(2)答案见解析;(3)∠AOB 是定值,∠AOB =60°. 【解析】【分析】(1)根据等边三角形的性质可以直接得出结论;(2)根据等边三角形的性质就可以得出AC =BC ,DC =EC ,∠ACB =∠DCE =60°,由等式的性质就可以∠BCE =∠ACD ,根据SAS 就可以得出△ADC ≌△BEC ;(3)分情况讨论:当点D 在线段AM 上时,如图1,由(2)可知△ACD ≌△BCE ,就可以求出结论;当点D 在线段AM 的延长线上时,如图2,可以得出△ACD ≌△BCE 而有∠CBE =∠CAD =30°而得出结论;当点D 在线段MA 的延长线上时,如图3,通过得出△ACD ≌△BCE 同样可以得出结论. 【详解】(1)∵△ABC 是等边三角形,∴∠BAC =60°. ∵线段AM 为BC 边上的中线,∴∠CAM 12=∠BAC ,∴∠CAM =∠BAM =30°. (2)∵△ABC 与△DEC 都是等边三角形,∴AC =BC ,CD =CE ,∠ACB =∠DCE =60°,∴∠ACD +∠DCB =∠DCB +∠BCE ,∴∠ACD =∠BCE .在△ADC 和△BEC 中,∵AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△BCE (SAS );(3)∠AOB 是定值,∠AOB =60°.理由如下:①当点D 在线段AM 上时,如图1,由(2)可知△ACD ≌△BCE ,则∠CBE =∠CAD =30°,又∠ABC =60°,∴∠CBE +∠ABC =60°+30°=90°.∵△ABC 是等边三角形,线段AM 为BC 边上的中线,∴AM 平分∠BAC ,即11603022BAM BAC ∠∠==⨯︒=︒,∴∠BOA =90°﹣30°=60°.②当点D 在线段AM 的延长线上时,如图2. ∵△ABC 与△DEC 都是等边三角形,∴AC =BC ,CD =CE ,∠ACB =∠DCE =60°,∴∠ACB +∠DCB =∠DCB +∠DCE ,∴∠ACD =∠BCE .在△ACD 和△BCE 中,∵AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△BCE (SAS ),∴∠CBE =∠CAD =30°. 由(1)得:∠BAM =30°,∴∠BOA =90°﹣30°=60°. ③当点D 在线段MA 的延长线上时. ∵△ABC 与△DEC 都是等边三角形,∴AC =BC ,CD =CE ,∠ACB =∠DCE =60°,∴∠ACD +∠ACE =∠BCE +∠ACE =60°,∴∠ACD =∠BCE .在△ACD和△BCE中,∵AC BCACD BCECD CE=⎧⎪∠=∠⎨⎪=⎩,∴△ACD≌△BCE(SAS),∴∠CBE=∠CAD.由(1)得:∠CAM=30°,∴∠CBE=∠CAD=150°,∴∠CBO=30°,∠BAM=30°,∴∠BOA=90°﹣30°=60°.综上所述:当动点D在直线AM上时,∠AOB是定值,∠AOB=60°.【点睛】本题考查了等边三角形的性质的运用,直角三角形的性质的运用,等式的性质的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.5.已知如图1,在ABC∆中,AC BC=,90ACB∠=,点D是AB的中点,点E是AB边上一点,直线BF垂直于直线CE于点F,交CD于点G.(1)求证:AE CG=.(2)如图2,直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M,求证:BE CM=.【答案】(1)证明见解析;(2)证明见解析.【解析】【分析】(1)首先根据点D 是AB 中点,∠ACB =90°,可得出∠ACD =∠BCD =45°,判断出△AEC ≌△CGB ,即可得出AE =CG ;(2)根据垂直的定义得出∠CMA +∠MCH =90°,∠BEC +∠MCH =90°,再根据AC =BC ,∠ACM =∠CBE =45°,得出△BCE ≌△CAM ,进而证明出BE =CM . 【详解】(1)∵点D 是AB 中点,AC =BC ,∠ACB =90°,∴CD ⊥AB ,∠ACD =∠BCD =45°,∴∠CAD =∠CBD =45°,∴∠CAE =∠BCG . 又∵BF ⊥CE ,∴∠CBG +∠BCF =90°. 又∵∠ACE +∠BCF =90°,∴∠ACE =∠CBG .在△AEC 和△CGB 中,∵CAE BCG AC BC ACE CBG ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△AEC ≌△CGB (ASA ),∴AE =CG ;(2)∵CH ⊥HM ,CD ⊥ED ,∴∠CMA +∠MCH =90°,∠BEC +∠MCH =90°,∴∠CMA =∠BEC .在△BCE 和△CAM 中,BEC CMA ACM CBE BC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BCE ≌△CAM (AAS ),∴BE =CM .【点睛】本题考查了全等三角形的判定与性质,等腰直角三角形的性质.全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.6.如图,在平面直角坐标系中,点B 坐标为()6,0-,点A 是y 轴正半轴上一点,且10AB =,点P 是x 轴上位于点B 右侧的一个动点,设点P 的坐标为()0m ,.(1)点A 的坐标为___________;(2)当ABP △是等腰三角形时,求P 点的坐标;(3)如图2,过点P 作PE AB ⊥交线段AB 于点E ,连接OE ,若点A 关于直线OE 的对称点为A ',当点A '恰好落在直线PE 上时,BE =_____________.(直接写出答案) 【答案】(1)()0,8;(2)()4,0或()6,0或7,03⎛⎫ ⎪⎝⎭;(3)425【解析】 【分析】(1)根据勾股定理可以求出AO 的长,则可得出A 的坐标; (2)分三种情况讨论等腰三角形的情况,得出点P 的坐标; (3)根据PE AB ⊥,点A '在直线PE 上,得到EAGOPG ,利用点A ,A '关于直线OE 对称点,根据对称性,可证'OPG EAO ,可得'8OP OA ,82AP,设BE x =,则有6AE x ,根据勾股定理,有:22222BP BE EP AP AE解之即可. 【详解】解:(1)∵点B 坐标为6,0,点A 是y 轴正半轴上一点,且10AB =,∴ABO 是直角三角形,根据勾股定理有:22221068AOAB BO ,∴点A 的坐标为()0,8; (2)∵ABP △是等腰三角形, 当BPAB 时,如图一所示:∴1064OP BP BO ,∴P 点的坐标是()4,0; 当AP AB =时,如图二所示:∴6OP BO∴P 点的坐标是()6,0;当AP BP =时,如图三所示:设OP x =,则有6AP x∴根据勾股定理有:222OP AO AP +=即:22286x x解之得:73x = ∴P 点的坐标是7,03; (3)当ABP △是钝角三角形时,点A '不存在;当ABP △是锐角三角形时,如图四示:连接'OA ,∵PE AB ⊥,点A '在直线PE 上, ∴AEG △和GOP 是直角三角形,EGA OGP ∴EAG OPG ,∵点A ,A '关于直线OE 对称点, 根据对称性,有'8OA OA ,'EAEA ∴'FAO FAO ,'FAE FAE ∴'EAG EAO 则有:'OPGEAO ∴'AOP 是等腰三角形,则有'8OP OA , ∴22228882AP AO OP ,设BE x =,则有6AEx ,根据勾股定理,有: 22222BP BE EP AP AE 即:2222688210x x 解之得:425BEx 【点睛】 本题考查了三角形的综合问题,涉及的知识点有:解方程,等腰三角形的判定与性质,对称等知识点,能分类讨论,熟练运用各性质定理,是解题的关键.7.(1)问题发现:如图1, ABC 和ADE 均为等边三角形,点B D E 、、在同一直线上,连接.CE①求证: BD CE =; ②求BEC ∠的度数.(2)拓展探究:如图2, AB C 和ADE 均为等腰直角三角形,90BAC DAE ∠=∠=︒,点B D E 、、在同一直线上AF ,为ADE 中DE 边上的高,连接.CE①求BEC ∠的度数:②判断线段AF BE CE 、、之间的数量关系(直接写出结果即可).()3解决问题:如图3,AB 和ADE 均为等腰三角形,BAC DAE n ∠=∠=,点B D E 、、在同一直线上,连接CE .求AEC ∠的度数(用含n 的代数式表示,直接写出结果即可).【答案】(1)①证明见解析;②60°;(2)①90°;②BE =CE+2AF ;(3)∠AEC =90°+12n ︒. 【解析】【分析】(1)根据等边三角形的性质得AB=AC,AD=AE, ∠DAE=∠BAC=60°,根据SAS 进一步证明△BAD ≌△CAE,依据其性质可得 BD CE =,再根据对应角相等求出BEC ∠的度数;(2)根据等腰直角三角形的性质得AB=AC,AD=AE, ∠DAE=∠BAC=90°,根据SAS 进一步证明△BAD ≌△CAE ,根据对应角相等求出BEC ∠的度数;因为DE=2AF,BD=EC,结合线段的和差关系得出结论;(3)根据等腰三角形的性质得AB=AC,AD=AE, ∠DAE=∠BAC=n °,根据SAS 进一步证明△BAD ≌△CAE ,根据对应角相等求出得出∠ADB=BEC ∠的度数,结合内角和用n 表示∠ADE 的度数,即可得出结论.【详解】(1)①∵△ABC和△ADE均为等边三角形(如图1),∴ AB=AC,AD=AE,∠BAC=∠DAE=60°,∴∠BAC-∠DAC=∠DAE-∠DAC,∴∠BAD=∠CAE.∴△BAD≌△CAE(SAS)∴ BD=CE.②由△CAE≌△BAD,∴∠AEC=∠ADB=180°-∠ADE=120°.∴∠BEC=∠AEC-∠AED=120°-60°=60°.(2)①∵△ABC和△ADE均为等腰直角三角形(如图2),∴ AB=AC,AD=AE,∠ADE=∠AED=45°,∵∠BAC=∠DAE=90°,∴∠BAC-∠DAC=∠DAE-∠DAC,∴∠BAD=∠CAE.∴△BAD≌△CAE(SAS).∴ BD=CE,∠AEC=∠ADB=180°-∠ADE=135°.∴∠BEC=∠AEC-∠AED=135°-45°=90°.② BE=CE+2AF.(3)如图3:∠AEC=90°+12n ,理由如下,∵△ABC和△ADE均为等腰直角三角形,∴ AB=AC,AD=AE,∠ADE=∠AED=n°,∴∠BAC-∠DAC=∠DAE-∠DAC,∴∠BAD=∠CAE.∴△BAD≌△CAE(SAS).∴∠AEC=∠ADB=180°-∠ADE=180°-1801809022n n.∴∠AEC=90°+12n .【点睛】本题考查等边三角形、等腰直角三角形的性质及旋转型三角形全等,掌握全等常见模型及由特殊到一般找出解题规律是解答此题的关键.8.如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A.点B同时出发,沿三角形的边运动,已知点M的速度为2cm/s,点N的速度为3cm/s.当点N第一次到达B点时,M、N同时停止运动.(1)点M、N运动秒后,△AMN是等边三角形?(2)点M、N在BC边上运动时,运动秒后得到以MN为底边的等腰三角形△AMN?(3)M、N同时运动几秒后,△AMN是直角三角形?请说明理由.【答案】(1)125;(2)485;(3)点M、N运动3秒或127秒或10秒或9秒后,△AMN为直角三角形.【解析】【分析】(1)当AM=AN时,△MNA是等边三角形.设运动时间为t秒,构建方程即可解决问题;(2)点M、N在BC边上运动时,满足CM=BN时,可以得到以MN为底边的等腰三角形△AMN.构建方程即可解决问题;(3)据题意设点M、N运动t秒后,可得到直角三角形△AMN,分四种情况讨论即可.【详解】(1)当AM=AN时,△MNA是等边三角形,设运动时间为t秒则有:2t=12﹣3t解得t=12 5故点M、N运动125秒后,△AMN是等边三角形;(2)点M、N在BC边上运动时,满足CM=BN时,可以得到以MN为底边的等腰三角形△AMN则有:2t﹣12=36﹣3t解得t=48 5故运动485秒后得到以MN为底边的等腰三角形△AMN;(3)设点M、N运动t秒后,可得到直角三角形△AMN ①当M在AC上,N在AB上,∠ANM=90°时,如图∵∠A=60°∴∠AMN=30°∴AM=2AN则有2t=2(12﹣3t)∴t=3;②当M在AC上,N在AB上,∠AMN=90°时,如图∵∠A=60°∴∠ANM=30°∴2AM=AN∴4t=12﹣3t∴t=127;③当M、N都在BC上,∠ANM=90°时,如图CN =3t ﹣24=6解得t =10;④当M 、N 都在BC 上,∠AMN =90°时,则N 与B 重合,M 正好处于BC 的中点,如图此时2t =12+6解得t =9;综上所述,点M 、N 运动3秒或127秒或10秒或9秒后,△AMN 为直角三角形. 【点睛】本题主要考查了等边三角形的性质、等腰三角形的判定、全等三角形的判定与性质,熟练掌握相关知识点是解决本题的关键.9.如图,在△ABC 中,AB =AC =2,∠B =40°,点D 在线段BC 上运动(D 不与B 、C 重合),连接AD ,作∠ADE =40°,DE 交线段AC 于E 点.(1)当∠BDA =115°时,∠BAD =___°,∠DEC =___°;(2)当DC 等于多少时,△ABD 与△DCE 全等?请说明理由;(3)在点D 的运动过程中,△ADE 的形状可以是等腰三角形吗?若可以,请直接写出∠BDA 的度数;若不可以,请说明理由.【答案】(1) 25,115;(2)当DC =2时,△ABD ≌△DCE ,理由见解析;(3)可以;当∠BDA 的度数为110°或80°时,△ADE 的形状是等腰三角形.【解析】【分析】(1)根据三角形内角和定理,将已知数值代入即可求出BAD ∠,根据平角的定义,可求出EDC ∠的度数,根据三角形内和定理,即可求出DEC ∠.(2)当AB DC =时,利用AAS 可证明ABD DCE ∆≅∆,即可得出2AB DC ==.(3)假设ADE ∆是等腰三角形,分为三种情况讨论:①当AD AE =时,40ADE AED ∠=∠=︒,根据AED C ∠>∠,得出此时不符合;②当DA DE =时,求出70DAE DEA ∠=∠=︒,求出BAC ∠,根据三角形的内角和定理求出BAD ∠,根据三角形的内角和定理求出BDA ∠即可;③当EA ED =时,求出DAC ∠,求出BAD ∠,根据三角形的内角和定理求出ADB ∠.【详解】(1)在BAD 中,40B ∠= ,115BDA ∠=,1801804011525BAD ABD BDA ∴∠=︒-∠-∠=︒-︒-︒=︒,1801801154025EDC ADB ADE ∠=︒-∠-∠=︒-︒-︒=︒.AB AC =,40B ∠=,40B C ∴∠=∠=,1801804025115C E DC D E C ︒-∠-∠=︒-︒-︒=∠=︒.故答案为:25,115;(2)当2DC =时,ABD DCE ∆≅∆.理由如下:40C ∠=,140EDC DEC ∴∠+∠=︒,又40ADE ∠=,140ADB EDC ∴∠+∠=︒,ADB DEC ∴∠=∠.在ABD △和DCE ∆中,B C ∠=∠,ADB DEC ∠=∠,当AB DC =时,()ABD DCE AAS ∆≅∆,2AB DC ∴==;(3)AB AC =,40B C ∴∠=∠=︒,分三种情况讨论:①当AD AE =时,40ADE AED ∠=∠=︒,AED C ∠>∠,∴此时不符合; ②当DA DE =时,即1(18040)702DAE DEA ∠=∠=︒-︒=︒,1804040100BAC ∠=︒-︒-︒=︒,1007030BAD ∴∠=︒-︒=︒;1803040110BDA ∴∠=︒-︒-︒=︒;③当EA ED =时,40ADE DAE ∠=∠=︒,1004060BAD ∴∠=︒-︒=︒,180604080BDA ∴∠=︒-︒-︒=︒;∴当110ADB ∠=︒或80︒时,ADE ∆是等腰三角形.【点睛】本题考查了学生对等腰三角形的判定与性质,全等三角形的判定与性质,三角形内角和定理等知识点的理解和掌握,此题涉及到的知识点较多,综合性较强.10.(1)操作:如图,在已知内角度数的三个三角形中,请用直尺从某一顶点画一条线段,把原三角形分割成两个等腰三角形,并在图中标注相应的角的度数(2)拓展,△ABC中,AB=AC,∠A=45°,请把△ABC分割成三个等腰三角形,并在图中标注相应的角的度数.(3)思考在如图所示的三角形中∠A=30°.点P和点Q分别是边AC和BC上的两个动点.分别连接BP和PQ把△ABC分割成三个三角形.△ABP,△BPQ,△PQC若分割成的这三个三角形都是等腰三角形,求∠C的度数所有可能值直接写出答案即可.【答案】(1)见解析;(2)见解析;(3)∠C所有可能的值为10°、20°、25°,35°、40°、50°、80°、100°.【解析】【分析】(1)在图1、图2、图3中,分别作AB、AB、BC的垂直平分线,根据垂直平分线的性质及外角的性质求出各角度数即可;(2)分别作AB、BC的垂直平分线,交于点O,连接OA、OB、OC可得三角形OAB、OAC、OBC为等腰三角形,根据等腰三角形的性质及外角性质求出各角度数即可;(3)分PB=PA、AB=AP、BA=BP时,PB=PQ、BP=BQ、QB=QP,PQ=QC、PC=QC、PQ=PC等10种情况,根据等腰三角形的性质分别求出∠C的度数即可.【详解】(1)在图1、图2、图3中,分别作AB、AB、BC的垂直平分线,如图1,∵∠ABC=23°,∠BAC=90°,∴∠C=90°-23°=67°,∵MN垂直平分AB,∴BD=AD,∴△ABD是等腰三角形,∴∠BAD=∠ABC=23°,∴∠ADC=2∠ABC=46°,∵∠BAC=90°,∴∠DAC=∠BAC-∠BAD=67°,∴∠DAC=∠C,∴△DAC是等腰三角形,同理:图2中,∠ADC=46°,∠DAC=88°,∠C=46°,△ABD和△ACD是等腰三角形,图3中,∠BCD=23°,∠ADC=46°,∠ACD=46°,△BCD和△ACD是等腰三角形.(2)作AB、BC的垂直平分线,交于点O,连接OA、OB、OC,∵点O是三角形垂直平分线的交点,∴OA=OB=OC,∴△OAB、△OAC、△OBC是等腰三角形,∵AB=AC,∠BAC=45°,∴∠ABC=∠ACB=67.5°,∴AD是BC的垂直平分线,∴∠BAD=∠CAD=22.5°,∴∠OBA=∠OAB=22.5°,∠OCA=∠OAC=22.5°,∴∠OBC=∠OCB=45°.(3)①如图,当PB=PA,PB=PQ,PQ=CQ时,∵∠A=30°,PB=PQ,∴∠ABP=∠A=30°,∴∠APB=120°,∵PB=PQ,PQ=CQ,∴∠PQB=∠PBQ,∠C=∠CPQ,∴∠PBQ=2∠C,∴∠APB=∠PBQ+∠C=3∠C=120°,解得:∠C=40°.②如图,当PB=PA,PB=BQ,PQ=CQ时,∴∠PQB=2∠C,∠PQB=∠BPQ,∴∠PBQ=180°-2∠PQB=180°-4∠C,∴180°-4∠C+∠C=120°,解得:∠C=20°,③如图,当PA=PB,BQ=PQ,CQ=CP时,∵∠PQC=2∠PBQ,∠PQC=12(180°-∠C),∴∠PBQ=14(180°-∠C),∴14(180°-∠C)+∠C=120°,解得:∠C=100°.④如图,当PA=PB,BQ=PQ,PQ=CP时,∵∠PQC=∠C=2∠PBQ,又∵∠C+∠PBQ=120°,∴∠C=80°;⑤如图,当AB=AP,BP=BQ,PQ=QC时,∵∠A=30°,∴∠APB=12(180°-30°)=75°,∵BP=BQ,PQ=CQ,∴∠BPQ=∠BQP,∠QPC=∠QCP,∴∠BQP=2∠C,∴∠PBQ=180°-4∠C,∴∠C+180°-4∠C=75°,解得:∠C=35°.⑥如图,当AB=AP,BQ=PQ,PC=QC时,∴∠PQC=2∠PBC,∠PQC=12(180°-∠C),∴∠PBC=14(180°-∠C),∴14(180°-∠C)+∠C=75°,解得:∠C=40°.⑦如图,当AB=AP,BQ=PQ,PC=QP时,∵∠C=∠PQC=2∠PBC,∠C+∠PQC=75°,∴∠C=50°;⑧当AB=AP,BP=PQ,PQ=CQ时,∵AB=BP,∠A=30°,∴∠ABP=∠APB=75°,又∵∠PBQ=∠PQB=2∠C,且有∠PBQ+∠C=180°-30°-75°=75°,∴3∠C=75°,∴∠C=25°;⑨当AB=BP,BP=PQ,PQ=CQ时,∵AB=BP,∴∠BPA=∠A=30°,∵∠PBQ=∠PQB=2∠C,∴2∠C+∠C=30°,解得:∠C=10°.⑩当AB=BP,BQ=PQ,PQ=CQ时,∴∠PQC=∠C=2∠PBQ,∴12∠C+∠C=30°,解得:∠C=20°.综上所述:∠C所有可能的值为10°、20°、25°,35°、40°、50°、80°、100°.【点睛】本题考查复杂作图及等腰三角形的性质,熟练掌握等腰三角形的性质是解题关键.。
八年级上册数学 轴对称填空选择专题练习(解析版)

八年级上册数学 轴对称填空选择专题练习(解析版)一、八年级数学全等三角形填空题(难)1.如图,MN ∥PQ ,AB ⊥PQ ,点A ,D ,B ,C 分别在直线MN 和PQ 上,点E 在AB 上,AD +BC =7,AD =EB ,DE =EC ,则AB =_____.【答案】7 【解析】由MN ∥PQ ,AB ⊥PQ ,可知∠DAE=∠EBC=90°,可判定△ADE ≌△BCE ,从而得出AE=BC ,则AB=AE+BE=AD+BC=7.故答案为:7.点睛:本题考查了直角三角形全等的判定和性质以及平行线的性质,是基础知识,比较简单.2.如图,10AB =,45A B ∠=∠=︒,32AC BD ==.点E ,F 为线段AB 上两点.现存在以下条件:①4CE DF ==;②AF BE =;③CEB DFA ∠=∠;④5CE DF ==.请在以上条件中选择一个条件,使得ACE △一定..和BDF 全等,则这个条件可以为________.(请写出所有正确的答案)【答案】②③④【解析】【分析】根据三角形全等的判定定理逐个判断即可.【详解】①如图1,过点C 作CM AB ⊥,过点D 作DN AB ⊥32,45A B AC BD ∠=∠===︒3CM AM DN BN ∴====4CE DF ==由勾股定理得:22227,7ME CE CM NF DF DN =-==-=37,37AE AM ME BF BN NF ∴=-=-=+=+AE BF ≠此时,ACE ∆和BDF ∆不全等②AF BE=AF EF BE EF∴+=+,即AE BF=又452,3AC DA B B∠=∠=︒==则由SAS定理可得,ACE BDF∆≅∆③CEB DFACEB C ADFA D B∠=∠⎧⎪∠=∠+∠⎨⎪∠=∠+∠⎩C AD B∴∠+∠=∠+∠又A B∠=∠C D∴∠=∠32AC BD==则由ASA定理可得,ACE BDF∆≅∆④由(1)知,当5CE DF==时,22224,4ME CE CM NF DF DN=-==-=此时,,,CE CA DF BDME AM NF BN>>⎧⎨>>⎩则点E在点M的右侧,点F在点N的左侧又10AM BN ME AM BN NF AB++=++==则点E与点N重合,点F与点M重合,如图2所示因此必有347AE BF==+=由SSS定理可得,ACE BDF∆≅∆故答案为:②③④.【点睛】本题考查了三角形全等的判定定理,熟记各判定定理是解题关键.3.如图,△ABC是等边三角形,AE=CD,AD、BE相交于点P,BQ⊥DA于Q,PQ=3,EP=1,则DA的长是________.【答案】7【解析】试题解析:∵△ABC 为等边三角形,∴AB=CA ,∠BAE=∠ACD=60°;又∵AE=CD ,在△ABE 和△CAD 中,AB CA BAE ACD AE CD ⎧⎪∠∠⎨⎪⎩=== ∴△ABE ≌△CAD ;∴BE=AD ,∠CAD=∠ABE ;∴∠BPQ=∠ABE+∠BAD=∠BAD+∠CAD=∠BAE=60°;∵BQ ⊥AD ,∴∠AQB=90°,则∠PBQ=90°-60°=30°;∵PQ=3,∴在Rt △BPQ 中,BP=2PQ=6;又∵PE=1,∴AD=BE=BP+PE=7.故答案为7.4.如图,△ABE ,△BCD 均为等边三角形,点A ,B ,C 在同一条直线上,连接AD ,EC ,AD 与EB 相交于点M ,BD 与EC 相交于点N ,下列说法正确的有:___________ ①AD=EC ;②BM=BN ;③MN ∥AC ;④EM=MB .【答案】①②③【解析】∵△ABE ,△BCD 均为等边三角形,∴AB=BE ,BC=BD ,∠ABE=∠CBD=60°,∴∠ABD=∠EBC ,在△ABD 和△EBC 中AB BEABD EBCBD BC=⎧⎪∠=∠⎨⎪=⎩∴△ABD≌△EBC(SAS),∴AD=EC,故①正确;∴∠DAB=∠BEC,又由上可知∠ABE=∠CBD=60°,∴∠EBD=60°,在△ABM和△EBN中MAB NEBAB BEABE EBN∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ABM≌△EBN(ASA),∴BM=BN,故②正确;∴△BMN为等边三角形,∴∠NMB=∠ABM=60°,∴MN∥AC,故③正确;若EM=MB,则AM平分∠EAB,则∠DAB=30°,而由条件无法得出这一条件,故④不正确;综上可知正确的有①②③,故答案为①②③.点睛:本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(即SSS、SAS、AAS、ASA和HL)和性质(即全等三角形的对应边相等,对应角相等).5.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,BE平分∠ABC交AC于E,交AD于F,FG∥BC,FH∥AC,下列结论:①AE=AF;②AF=FH;③AG=CE;④AB+FG=BC,其中正确的结论有________________.(填序号)【答案】①②③④【解析】①正确.∵∠BAC=90°∴∠ABE+∠AEB=90°∴∠ABE=90°-∠AEB∵AD⊥BC∴∠ADB=90°∴∠DBE+∠BFD=90°∴∠DBE=90-∠BFD∵∠BFD=∠AFE∴∠DBE=90°-∠AFE∵BE 平分∠ABC∴∠ABE=∠DBE∴90°-∠AEB=90°-∠AFE∴∠AEB=∠AFE∴AE=AF②正确.∵∠BAC=90°∴∠BAF+∠DAC=90°∴∠BAF=90°-∠DAC∵AD ⊥BC∴∠ADC=90°∴∠C+∠DAC=90°∴∠C=90°-∠DAC∴∠C=∠BAF∵FH ∥AC∴∠C=∠BHF∴∠BAF=∠BHF在△ABF 和△HBF 中ABE CBE BAF BHF BF BF ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABF ≌△HBF∴AF=FH③正确.∵AE=AF ,AF=FH∴AE=FH∵FG ∥BC ,FH ∥AC∴四边形FHCG 是平行四边形∴FH=GC∴AE=GC∴AE+EG=GC+EG∴AG=CE④正确.∵四边形FHCG 是平行四边形∴FG=HC∵△ABF≌△HBF∴AB=HB∴AB+FG=HB+HC=BC故正确的答案有①②③④.6.如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②AF∥EB;③∠FAN=∠EAM;④△ACN≌△ABM其中正确的有.【答案】①③④【解析】【分析】由∠E=∠F=90°,∠B=∠C,AE=AF,利用“AAS”得到△ABE与△ACF全等,根据全等三角形的对应边相等且对应角相等即可得到∠EAB与∠FAC相等,AE与AF相等,AB与AC相等,然后在等式∠EAB=∠FAC两边都减去∠MAN,得到∠EAM与∠FAN相等,然后再由∠E=∠F=90°,AE=AF,∠EAM=∠FAN,利用“ASA”得到△AEM与△AFN全等,利用全等三角形的对应边相等,对应角相等得到选项①和③正确;然后再∠C=∠B,AC=AB,∠CAN=∠BAM,利用“ASA”得到△ACN与△ABM全等,故选项④正确;若选项②正确,得到∠F与∠BDN相等,且都为90°,而∠BDN不一定为90°,故②错误.【详解】解:在△ABE和△ACF中,∠E=∠F=90°,AE=AF,∠B=∠C,∴△ABE≌△ACF,∴∠EAB=∠FAC,AE=AF,AB=AC,∴∠EAB-∠MAN=∠FAC-∠NAM,即∠EAM=∠FAN,在△AEM和△AFN中,∠E=∠F=90°,AE=AF,∠EAM=∠FAN,∴△AEM≌△AFN,∴EM=FN,∠FAN=∠EAM,故选项①和③正确;在△ACN和△ABM中,∠C=∠B,AC=AB,∠CAN=∠BAM(公共角),∴△ACN≌△ABM,故选项④正确;若AF∥EB,∠F=∠BDN=90°,而∠BDN不一定为90°,故②错误,则正确的选项有:①③④.故答案为①③④7.如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1、l2之间的距离为2,l2、l3之间的距离为3,则AC的长是_________;【答案】217【解析】【分析】首先作AD⊥l3于D,作CE⊥l3于E,再证明△ABD≌△BCE,因此可得BE=AD=3,再结合勾股定理可得AC的长.【详解】作AD⊥l3于D,作CE⊥l3于E,∵∠ABC=90°,∴∠ABD+∠CBE=90°,又∠DAB+∠ABD=90°,∴∠BAD=∠CBE,又AB=BC,∠ADB=∠BEC.∴△ABD≌△BCE,∴BE=AD=3,在Rt△BCE中,根据勾股定理,得34在Rt△ABC中,根据勾股定理,得22342217+=⨯=AB CB故答案为17【点睛】本题主要考查直角三角形的综合问题,关键在于证明三角形的全等,这类题目是固定的解法,一定要熟练掌握.8.如图,Rt△ABC中,AB=AC,点D为BC中点.∠MDN=90°,∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF;⑤S四边形AEDF=14AD2,其中正确结论是_____(填序号)【答案】①②③【解析】【分析】先由ASA证明△AED≌△CFD,得出AE=CF,DE=FD;再由全等三角形的性质得到BE+CF=AB,由勾股定理求得EF与AB的值,通过比较它们的大小来判定④的正误;先得出S四边形AEDF=S△ADC=12AD2,从而判定⑤的正误.【详解】解:∵Rt△ABC中,AB=AC,点D为BC中点,∴∠C=∠BAD=45°,AD=BD=CD,∵∠MDN=90°,∴∠ADE+∠ADF=∠ADF+∠CDF=90°,∴∠ADE=∠CDF.在△AED与△CFD中,EAD CAD CDADE CDF∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△AED≌△CFD(ASA),∴AE=CF,ED=FD.故①②正确;又∵△ABD≌△ACD,∴△BDE≌△ADF.故③正确;∵△AED≌△CFD,∴AE=CF,ED=FD,∴BE+CF=BE+AE=AB2BD,∵EF2ED,BD>ED,∴BE+CF>EF.故④错误;∵△AED≌△CFD,△BDE≌△ADF,∴S四边形AEDF=S△ADC=12AD2.故⑤错误.综上所述,正确结论是①②③.故答案是:①②③.【点睛】考查了全等三角形的判定与性质,等腰直角三角形的性质,勾股定理,图形的面积等知识,综合性较强,有一定难度.9.已知:如图,在△ABC中,∠C=90°,∠B=30°,AB的垂直平分线交BC于D,垂足为E,BD=4cm,则DC=_______【答案】2cm【解析】试题解析:解:连接AD,∵ED是AB的垂直平分线,∴BD=AD=4c m,∴∠BAD=∠B=30°,∵∠C=90°,∴∠BAC=90°-∠B=90°-30°=60°,∴∠DAC=60°-30°=30°,在Rt△ACD中,∴DC=12AD==12× 4=2c m.故答案为2c m.点睛:本题考查了线段垂直平分线,在直角三角形中30度角所对的边等于斜边的一半,三角形内角和定理,主要考查学生运用性质进行计算的能力.10.如图,AD=AB,∠C=∠E,AB=2,AE=8,则DE=_________.【答案】6【解析】根据三角形全等的判定“AAS ”可得△ADC ≌△ABE ,可得AD=AB=2,由AE=8可得DE=AE-AD=6.故答案为:6.点睛:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS 、SAS 、SSA 、HL .注意:AAA 、SSA 不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.二、八年级数学全等三角形选择题(难)11.已知:如图,ABC ∆、CDE ∆都是等腰三角形,且CA CB =,CD CE =,ACB DCE α∠=∠=,AD 、BE 相交于点O ,点M 、N 分别是线段AD 、BE 的中点.以下4个结论:①AD BE =;②180DOB α∠=-;③CMN ∆是等边三角形;④连OC ,则OC 平分AOE ∠.正确的是( )A .①②③B .①②④C .①③④D .①②③④【答案】B【解析】【分析】 ①根据∠ACB=∠DCE 求出∠ACD=∠BCE,证出ACD BCE ≅△△即可得出结论,故可判断; ②根据全等求出∠CAD=∠CBE,根据三角形外角定理得∠DOB=∠OBA+∠BAO,通过等角代换能够得到∠DOB=∠CBA+∠BAC,根据三角形内角和定理即可求出∠CBA+∠BAC,即可求出∠DOB ,故可判断;③根据已知条件可求出AM=BN,根据SAS 可求出CAM CBN ≅,推出CM=CN ,∠ACM=∠BCN,然后可求出∠MCN=∠ACB=α,故可判断CMN ∆的形状;④在AD 上取一点P 使得DP=EO,连接CP ,根据ACD BCE ≅△△,可求出∠CEO=∠CDP ,根据SAS 可求出 CEO CDP ≅,可得∠COE=∠CPD,CP=CO,进而得到 ∠COP=∠COE ,故可判断.【详解】①正确,理由如下:∵ACB DCE α∠=∠=,∴∠ACB+∠BCD=∠DCE+∠BCD,即∠ACD=∠BCE,又∵CA=CB,CD=CE,∴ACD BCE ≅△△(SAS),∴AD=BE,故①正确;②正确,理由如下:由①知,ACD BCE ≅△△,∴∠CAD=∠CBE,∵∠DOB 为ABO 的外角,∴∠DOB=∠OBA+∠BAO=∠EBC+∠CBA+∠BAO=∠DAC+∠BAO+∠CBA=∠CBA+∠BAC, ∵∠CBA+∠BAC+∠ACB=180°,∠ACB=α,∴∠CBA+∠BAC=180°-α,即∠DOB=180°-α,故②正确;③错误,理由如下:∵点M 、N 分别是线段AD 、BE 的中点,∴AM=12AD,BN= 12BE, 又∵由①知,AD=BE,∴AM=BN,又∵∠CAD=∠CBE,CA=CB,∴CAM CBN ≅(SAS), ∴CM=CN ,∠ACM=∠BCN,∴∠MCN=∠MCB+∠CBN=∠MCB+∠ACM=∠ACB=α,∴MCN △为等腰三角形且∠MCN=α,∴MCN △不是等边三角形,故③错误;④正确,理由如下:如图所示,在AD 上取一点P 使得DP=EO,连接CP ,由①知,ACD BCE ≅△△,∴∠CEO=∠CDP ,又∵CE=CD,EO=DP ,∴CEO CDP ≅(SAS),∴∠COE=∠CPD,CP=CO,∴∠CPO=∠COP ,∴∠COP=∠COE,即OC 平分∠AOE,故④正确;故答案为:B.【点睛】本题考查了三角形全等的判定和性质,三角形内角和定理和外角定理,等边三角形的判定,根据已知条件作出正确的辅助线,找出全等三角形是解题的关键.12.如图,在△ABC 中,∠C=90°,∠B=30°,以A 为圆心,任意长为半径画弧分别交AB,AC 于点M 和N,再分别以M,N 为圆心,大于12MN 的长为半径画弧,两弧交于点P,连结AP 并延长交BC 于点D,则下列说法中正确的个数是( )①AD 平分∠BAC;②作图依据是S.A .S ;③∠ADC=60°; ④点D 在AB 的垂直平分线上A .1个B .2个C .3个D .4个【答案】C【解析】 ①根据作图的过程可以判定AD 是∠BAC 的∠平分线;②根据作图的过程可以判定出AD 的依据;③利用角平分线的定义可以推知∠CAD=30°,则由直角三角形的性质求∠ADC 的度数; ④利用等角对等边可以证得△ADB 的等腰三角形,由等腰三角形的“三合一”的性质可以证明点在AB的中垂线上.解:如图所示,①根据作图的过程可知,AD是∠BAC的∠平分线;故①正确;②根据作图的过程可知,作出AD的依据是SSS;故②错误;③∵在△ABC中,∠C=90°,∠B=30°,∴∠CBA=60°.又∵AD是∠BAC的平分线,∴∠1=∠2=12∠CAB=30°,∴∠3=90°-∠2=60°,即∠ADC=60°.故③正确;④∵∠1=∠B=30°,∴AD=BD,∴点D在AB的中垂线上.故④正确;故选C.“点睛”此题主要考查的是作图-基本作图,涉及到角平分线的作法以及垂直平分线的性质,熟练根据角平分线的性质得出∠ADC的度数是解题的关键.13.如图,在△ABC中,AB=6,AC=10,BC边上的中线..AD=4,则△ABC的面积..为()A.30B.48C.20D.24【答案】D【解析】延长AD到E,使DE=AD,连接BE,因为D为BC的中点,所以DC=BD,在△ADC和△EDB中,AD EDADC EDBDC BD=⎧⎪∠=∠⎨⎪=⎩,所以△ADC≌△EDB,所以BE=AC=10, ∠CAD=∠E,又因为AE=2AD=8,AB=6,所以222AB AE BE=+,所以∠CAD=∠E=90°,则11114646242222ABC ABD ADCS S S AD BE AD AC=+=⨯+⨯=⨯⨯+⨯⨯=,所以故选D.14.如图,在ABC∆中,AC BC=,90ACB∠=︒,AE平分BAC∠交BC于点E,BD AE⊥于点D,DF AC⊥交AC的延长线于点F,连接CD,给出四个结论:①45ADC∠=︒;②12BD AE=;③AC CE AB+=;④2AB BC FC-=;其中正确的结论有 ( )A.1个B.2个C.3个D.4个【答案】D【解析】试题解析:如图,过E 作EQ ⊥AB 于Q ,∵∠ACB=90°,AE 平分∠CAB ,∴CE=EQ ,∵∠ACB=90°,AC=BC ,∴∠CBA=∠CAB=45°,∵EQ ⊥AB ,∴∠EQA=∠EQB=90°,由勾股定理得:AC=AQ ,∴∠QEB=45°=∠CBA ,∴EQ=BQ ,∴AB=AQ+BQ=AC+CE ,∴③正确;作∠ACN=∠BCD ,交AD 于N , ∵∠CAD=12∠CAB=22.5°=∠BAD , ∴∠ABD=90°-22.5°=67.5°,∴∠DBC=67.5°-45°=22.5°=∠CAD ,∴∠DBC=∠CAD ,在△ACN 和△BCD 中, DBC CAD AC BCACN DCB ∠∠⎧⎪⎨⎪∠∠⎩===, ∴△ACN ≌△BCD ,∴CN=CD ,AN=BD ,∵∠ACN+∠NCE=90°,∴∠NCB+∠BCD=90°,∴∠CND=∠CDA=45°,∴∠ACN=45°-22.5°=22.5°=∠CAN ,∴AN=CN ,∴∠NCE=∠AEC=67.5°,∴CN=NE , ∴CD=AN=EN=12AE ,∵AN=BD ,∴BD=12AE , ∴①正确,②正确;过D 作DH ⊥AB 于H ,∵∠FCD=∠CAD+∠CDA=67.5°,∠DBA=90°-∠DAB=67.5°,∴∠FCD=∠DBA ,∵AE 平分∠CAB ,DF ⊥AC ,DH ⊥AB ,∴DF=DH ,在△DCF 和△DBH 中90F DHB FCD DBA DF DH ∠∠︒⎧⎪∠∠⎨⎪⎩====, ∴△DCF ≌△DBH ,∴BH=CF ,由勾股定理得:AF=AH , ∴2,2AC AB AC AH BH AC AM CM AC AF CF AF AF AF AM AF AF+++++++====, ∴AC+AB=2AF ,AC+AB=2AC+2CF ,AB-AC=2CF ,∵AC=CB ,∴AB-CB=2CF , ∴④正确.故选D15.如图,点P 、Q 分别是边长为6cm 的等边ABC △边AB 、BC 上的动点,点P 从顶点 A ,点Q 从顶点B 同时出发,且它们的速度都为1cm/s ,下面四个结论:①BQ AM =②ABQ △≌CAP △③CMQ ∠的度数不变,始终等于60︒④当第 2秒或第4秒时,PBQ △为直角三角形,正确的有( )个.A .1B .2C .3D .4【答案】C【解析】 ∵点P 、Q 速度相同,∴AP BQ =.在ACP △和ABQ △中,60AP BQ CAP ABQ AC BA =⎧⎪∠==︒⎨⎪=⎩, ∴ACP △≌BAQ △,故②正确.则AQC CPB ∠=∠.即B BAQ BAQ AMP ∠+∠=∠+∠.∴60AMP B ∠=∠=︒.则60CMQ AMP ∠=∠=︒,故③正确.∵APM ∠不一定等于60︒.∴AP AM ≠.∴BQ AM ≠.故①错误.设时间为t ,则AP=BQ=t ,PB=4-t①当∠PQB =90°时,∵∠B =60°,∴PB =2BQ ,得6-t =2t ,t =2 ;②当∠BPQ =90°时,∵∠B =60°,∴BQ =2BP ,得t =2(6-t ),t =4;∴当第2秒或第4秒时,△PBQ 为直角三角形.∴④正确.故选C.点睛:本题考查了等边三角形的性质、全等三角形的判定与性质、直角三角形的性质等知识点,综合性强,难度较大.16.在边长为1的正方形网格中标有A、B、C、D、E、F六个格点,根据图中标示的各点位置,与△ABC全等的是()A.△ACF B.△ACEC.△ABD D.△CEF【答案】C【解析】【分析】利用勾股定理先分别求得△ABC的各边长以及各选项中三角形的各边长,再根据三角形全等的判定方法进行判定即可得.【详解】在△ABC中,AB=22+=10,BC=2231+=2,AC=22,11A、在△ACF中,AF=22+=5≠10,5≠2,5≠22,则△ACF与△ABC不全21等,故不符合题意;B、在△ACE中,AE=3≠10,3≠2,3≠22,则△ACE与△ABC不全等,故不符合题意;C、在△ABD中,AB=AB,AD=2=BC,BD=22=AC,则由SSS可证明△ACE与△ABC全等,故符合题意;D、在△CEF中,CF=3≠10,3≠2,3≠22,则△CEF与△ABC不全等,故不符合题意,故选C.【点睛】本题考查了勾股定理以及全等三角形的判定,熟练掌握勾股定理以及全等三角形的判定方法是解题的关键.17.如图,点 D 是等腰直角△ABC 腰 BC 上的中点,点B 、B′ 关于 AD 对称,且BB′ 交AD 于 F,交 AC 于 E,连接 FC 、 AB′,下列说法:① ∠BAD=30°; ② ∠BFC=135°;③ AF=2B′C;正确的个数是()A.1 B.2 C.3 D.4【答案】B【解析】【分析】依据点D是等腰直角△ABC腰BC上的中点,可得tan∠BAD=12,即可得到∠BAD≠30°;连接B'D,即可得到∠BB'C=∠BB'D+∠DB'C=90°,进而得出△ABF≌△BCB',判定△FCB'是等腰直角三角形,即可得到∠CFB'=45°,即∠BFC=135°;由△ABF≌△BCB',可得AF=BB'=2BF=2B'C;依据△AEF与△CEB'不全等,即可得到S△AFE≠S△FCE.【详解】∵点D是等腰直角△ABC腰BC上的中点,∴BD=12BC=12AB,∴tan∠BAD=12,∴∠BAD≠30°,故①错误;如图,连接B'D,∵B、B′关于AD对称,∴AD垂直平分BB',∴∠AFB=90°,BD=B'D=CD,∴∠DBB'=∠BB'D,∠DCB'=∠DB'C,∴∠BB'C=∠BB'D+∠DB'C=90°,∴∠AFB=∠BB'C,又∵∠BAF+∠ABF=90°=∠CBB'+∠ABF,∴∠BAF=∠CBB',∴△ABF≌△BCB',∴BF=CB'=B'F,∴△FCB'是等腰直角三角形,∴∠CFB'=45°,即∠BFC=135°,故②正确;由△ABF≌△BCB',可得AF=BB'=2BF=2B'C,故③正确;∵AF>BF=B'C,∴△AEF与△CEB'不全等,∴AE≠CE,∴S△AFE≠S△FCE,故④错误;故选B.【点睛】本题主要考查了轴对称的性质以及全等三角形的判定与性质的运用,如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.18.如图,在等腰直角△ABC中,∠ACB=90°,点O为斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P,则下列结论:①图中全等三角形有三对;②△ABC的面积等于四边形CDOE面积的倍;③DE2+2CD•CE=2OA2;④AD2+BE2=2OP•OC.正确的有()个.A.1 B.2 C.3 D.4【答案】C【解析】【分析】结论(1)正确.因为图中全等的三角形有3对;结论(2)错误.由全等三角形的性质可以判断;结论(3)正确.利用全等三角形和等腰直角三角形的性质可以判断.结论(4)正确.利用相似三角形、全等三角形、等腰直角三角形和勾股定理进行判断.【详解】结论(1)正确,理由如下:图中全等的三角形有3对,分别为△AOC≌△BOC,△AOD≌△COE,△COD≌△BOE.由等腰直角三角形的性质,可知OA=OC=OB,易得△AOC≌△BOC.∵OC⊥AB,OD⊥OE,∴∠AOD=∠COE.在△AOD与△COE中,∴△AOD≌△COE(ASA),同理可证:△COD≌△BOE.结论(2)错误.理由如下:∵△AOD≌△COE,∴S△AOD=S△COE,∴S四边形CDOE=S△COD+S△COE=S△COD+S△AOD=S△AOC=S△ABC即△ABC的面积等于四边形CDOE的面积的2倍.结论(3)正确,理由如下:∵△AOD≌△COE,∴CE=AD,∴CD+CE=CD+AD=AC=OA,∴(CD+CE)2=CD2+CE2+2CD•CE=DE2+2CD•CE=2OA2;结论(4)正确,理由如下:∵△AOD≌△COE,∴AD=CE;∵△COD≌△BOE,∴BE=CD.在Rt△CDE中,由勾股定理得:CD2+CE2=DE2,∴AD2+BE2=DE2.∵△AOD≌△COE,∴OD=OE,又∵OD⊥OE,∴△DOE为等腰直角三角形,∴DE2=2OE2,∠DEO=45°.∵∠DEO=∠OCE=45°,∠COE=∠COE,∴△OEP∽△OCE,∴,即OP•OC=OE2.∴DE2=2OE2=2OP•OC,∴AD2+BE2=2OP•OC.综上所述,正确的结论有3个,故选C.【点睛】本题是几何综合题,考查了等腰直角三角形、全等三角形、相似三角形和勾股定理等重要几何知识点.难点在于结论(4)的判断,其中对于“OP•OC”线段乘积的形式,可以寻求相似三角形解决问题.19.如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则下列四个结论:①PA平分∠BAC;②AS=AR;③QP∥AR;④△BRP≌△CSP,其中结论正确的的序号为()A.①②③B.①②④C.②③④D.①②③④【答案】A【解析】【分析】根据角平分线性质即可推出②,根据勾股定理即可推出AR=AS,根据等腰三角形性质推出∠QAP=∠QPA,推出∠QPA=∠BAP,根据平行线判定推出QP∥AB即可;没有条件证明△BRP≌△QSP.【详解】试题分析:解:∵PR⊥AB,PS⊥AC,PR=PS,∴点P在∠A的平分线上,∠ARP=∠ASP=90°,∴∠SAP=∠RAP,在Rt△ARP和Rt△ASP中,由勾股定理得:AR2=AP2﹣PR2,AS2=AP2﹣PS2,∵AP=AP,PR=PS,∴AR=AS,∴②正确;∵AQ=QP,∴∠QAP=∠QPA,∵∠QAP=∠BAP,∴∠QPA=∠BAP,∴QP∥AR,∴③正确;没有条件可证明△BRP≌△QSP,∴④错误;连接RS,∵PR=PS,∵PR⊥AB,PS⊥AC,∴点P在∠BAC的角平分线上,∴PA平分∠BAC,∴①正确.故答案为①②③.故选A.点睛:本题考查了等边三角形的性质和判定,全等三角形的性质和判定,平行线的性质和判定,角平分线性质的应用,熟练掌握全等三角形的判定和性质是解题的关键.20.如图,△ABC中,AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则下列结论不正确的是A.BF=DF B.∠1=∠EFD C.BF>EF D.FD∥BC【答案】B【解析】【分析】根据余角的性质得到∠C=∠ABE,∠EBC=∠BAC.根据SAS推出△ABF≌△ADF,根据全等三角形的性质得到BF=DF,故A正确;由全等三角形的性质得到∠ABE=∠ADF,等量代换得到∠ADF=∠C,根据平行线的判定得到DF∥BC,故D正确;根据直角三角形的性质得到DF >EF,等量代换得到BF>EF;故C正确;根据平行线的性质得到∠EFD=∠EBC=∠BAC=2∠1,故B错误.【详解】∵AB⊥BC,BE⊥AC,∴∠C+∠BAC=∠ABE+∠BAC=90°,∴∠C=∠ABE.同理:∠EBC=∠BAC.在△ABF与△ADF中,∵12AD ABAF AF=⎧⎪∠=∠⎨⎪=⎩,∴△ABF≌△ADF,∴BF=DF,故A正确,∵△ABF≌△ADF,∴∠ABE=∠ADF,∴∠ADF=∠C,∴DF∥BC,故D正确;∵∠FED=90°,∴DF>EF,∴BF>EF;故C正确;∵DF∥BC,∴∠EFD=∠EBC.∵∠EBC=∠BAC=∠BAC=2∠1,∴∠EFD=2∠1,故B错误.故选B.【点睛】本题考查了全等三角形的判定和性质,平行线的判定和性质,证得△ABF≌△ADF是解题的关键.21.如图,在△ABC中,AB=AC,高BD,CE交于点O,AO交BC于点F,则图中共有全等三角形()A .8对B .7对C .6对D .5对【答案】B【解析】【分析】 易证△ABC 是关于AF 对称的图形,其中的小三角形也关于AF 对称,共可找出7对三角形.【详解】全等的三角形有:①△AFB≌△AFC;②△CEB≌△BDC;③△AEO≌△ADO;④△EOB≌△DOC;⑤△OBF≌△OFC;⑥△AOB≌△AOC;⑦△AEC≌△ADB证明①△AFB≌△AFC∵AB=AC,CE⊥AB,BD⊥AC 又∵1122ABC S AB CE AC BD == ∴CE=BD∴在Rt△BCE 和Rt△CBD 中BC BC CE BD=⎧⎨=⎩ ∴△BCE≌△C BD∴BE=CD,∴AE=AD在Rt△AEO 和Rt△ADO 中AE AD AO AO =⎧⎨=⎩∴△AEO≌△ADO∴∠EOD=∠DOA在△BAF 和△CAF 中AB AC BAF CAF AF AF =⎧⎪∠=∠⎨⎪=⎩∴△BAF≌△CAF,得证其余全等证明过程类似故选:B【点睛】本题考查全等的证明,解题关键是利用等腰三角形的性质,推导出图形中边的关系,为证全等作准备22.在和中,,高,则和的关系是( ) A.相等B.互补C.相等或互补D.以上都不对【答案】C【解析】试题解析:当∠C′为锐角时,如图1所示,∵AC=A′C′,AD=A′D′,AD⊥BC,A′D′⊥B′C′,∴Rt△ADC≌Rt△A′D′C′,∴∠C=∠C′;当∠C为钝角时,如图3所示,∵AC=A′C′,AD=A′D′,AD⊥BC,A′D′⊥B′C′,∴Rt△ACD≌Rt△A′C′D′,∴∠C=∠A′C′D′,∴∠C+∠A′C′B′=180°.故选C.23.如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面四个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④AP垂直平分RS.其中正确结论的序号是().A.①②B.①②③C.①②④D.①②③④【答案】C【解析】【分析】如图,连接AP,根据HL判定△APR和△APS全等,即可说明①正确;由△APR和△APS 全等可得∠RAP=∠PAC,再根据等腰三角形性质推出∠QAP=∠QPA,得到∠QPA=∠BAP,根据平行线判定推出OP//AB,即②正确;在Rt△BRP和Rt△QSP中,只有PR=PS.无法判断Rt△BRP和Rt△QSP是否全等;连接RS,与AP交于点D,先证△ARD≌△ASD,即RD=SD;运用等腰三角形的性质即可判定.【详解】解:如图,连接AP∵PR⊥AB,PS⊥AC,PR=PS∴△APR≌△APS∴AS=AR,∠RAP=∠PAC即①正确;又∵AQ=PQ∴∠QAP=∠QPA∴∠QPA=∠BAP∴OP//AB,即②正确.在Rt△BRP和Rt△QSP中,只有PR=PS.无法判断Rt△BRP和Rt△QSP是否全等,故③错误.如图,连接PS∵△APR≌△APS∴AR=AS,∠RAP=∠PAC∴AP垂直平分RS,即④正确;故答案为C.【点睛】本题主要考查了全等三角形的性质和判定,角平分线性质的应用,熟练掌握全等三角形的判定和性质是解答本题的关键24.如图,已知∠DCE=90°,∠DAC=90°,BE⊥AC于B,且DC=EC.若BE=7,AB=3,则AD 的长为()A.3 B.5 C.4 D.不确定【答案】C【解析】根据同角的余角相等求出∠ACD=∠E,再利用“角角边”证明△ACD≌△BCE,根据全等三角形对应边相等可得AD=BC,AC=BE=7,然后求解BC=AC-AB=7-3=4.故选:C.点睛:本题考查了全等三角形的判定与性质,等角的余角相等的性质,熟练掌握三角形全等的判定方法是解题的关键.25.如图,ABC∆中,45ABC∠=,CD AB⊥于D,BE平分ABC∠,且BE AC⊥于E,与CD相交于点F,H是BC边的中点,连接DH与BE相交于点G,下列结论正确的有( )个①BF AC=;②12AE BF=;③67.5A∠=;④DGF∆是等腰三角形;⑤ADGE GHCES S=四边形四边形.A.5个B.4个C.3个D.2个【答案】B【解析】【分析】只要证明△BDF≌△CDA,△BAC是等腰三角形,∠DGF=∠DFG=67.5°,即可判断①②③④正确,作GM⊥BD于M,只要证明GH<DG即可判断⑤错误.【详解】∵CD⊥AB,BE⊥AC,∴∠BDC=∠ADC=∠AEB=90°,∴∠A+∠ABE=90°,∠ABE+∠DFB=90°,∴∠A=∠DFB,∵∠ABC=45°,∠BDC=90°,∴∠DCB=90°−45°=45°=∠DBC,∴BD=DC,在△BDF和△CDA中BDF CDAA DFBBD CD∠∠⎧⎪∠∠⎨⎪⎩===,∴△BDF≌△CDA(AAS),∴BF=AC,故①正确.∵∠ABE=∠EBC=22.5°,BE⊥AC,∴∠A =∠BCA =67.5°,故③正确,∴BA =BC ,∵BE ⊥AC ,∴AE =EC =12AC =12BF ,故②正确, ∵BE 平分∠ABC ,∠ABC =45°,∴∠ABE =∠CBE =22.5°,∵∠BDF =∠BHG =90°,∴∠BGH =∠BFD =67.5°,∴∠DGF =∠DFG =67.5°,∴DG =DF ,故④正确.作GM ⊥AB 于M .∵∠GBM =∠GBH ,GH ⊥BC ,∴GH =GM <DG ,∴S △DGB >S △GHB ,∵S △ABE =S △BCE ,∴S 四边形ADGE <S 四边形GHCE .故⑤错误,∴①②③④正确,故选:B .【点睛】此题是三角形综合题,考查了等腰三角形的性质,直角三角形的性质,全等三角形的性质和判定,三角形的面积等知识点的综合运用,第五个问题难度比较大,添加辅助线是解题关键,属于中考选择题中的压轴题.26.如图,AD 是ABC 的角平分线,DE AC ⊥;垂足为,//E BF AC 交ED 的延长线于点F ,若BC 恰好平分ABF ∠.给出下列三个结论:①DE DF =;②DB DC =;③AD BC ⊥.其中正确的结论共有( )个A.0B.1C.2D.3【答案】D【解析】【分析】由BF∥AC,AD是ABC的角平分线,BC平分ABF∠得∠ADB=90︒;利用AD平分∠CAB证得△ADC≌△ADB即可证得DB=DC;根据DE AC⊥证明△CDE≌△BDF得到DE DF=.【详解】∵DE AC⊥,BF∥AC,∴EF⊥BF,∠CAB+∠ABF=180︒,∴∠CED=∠F=90︒,∵AD是ABC的角平分线,BC平分ABF∠,∴∠DAB+∠DBA=12(∠CAB+∠ABF)=90︒,∴∠ADB=90︒,即AD BC⊥,③正确;∴∠ADC=∠ADB=90︒,∵AD平分∠CAB,∴∠CAD=∠BAD,∵AD=AD,∴△ADC≌△ADB,∴DB=DC,②正确;又∵∠CDE=∠BDF,∠CED=∠F,∴△CDE≌△BDF,∴DE=DF,①正确;故选:D.【点睛】此题考查平行线的性质,三角形全等的判定及性质,角平分线的定义.27.如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE相交于点O,给出四个条件:①OB=OC;②∠EBO=∠DCO;③∠BEO=∠CDO;④BE=CD.上述四个条件中,选择两个可以判定△ABC是等腰三角形的方法有()A.2种B.3种C.4种D.6种【答案】C【解析】【分析】①②:求出OBC=∠OCB,推出∠ACB=∠ABC即可的等腰三角形;①③:证△EBO≌△DCO,得出∠EBO=∠DCO,求出∠ACB=∠ABC即可;②④:证△EBO≌△DCO,推出OB=OC,求出∠ABC=∠ACB即可;③④:证△EBO≌△DCO,推出∠EBO=∠DCO,OB=OC,求出∠OBC=∠OCB,推出∠ACB=∠ABC即可.【详解】解:有①②,①③,②④,③④,共4种,①②,理由是:∵OB=OC,∴∠OBC=∠OCB,∵∠EBO=∠DCO,∴∠EBO+∠OBC=∠DCO+∠OCB,即∠ABC=∠ACB,∴AB=AC,即△ABC是等腰三角形;①③,理由是:∵在△EBO和△DCO中BEO CDOEOB DOC OB OC∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△EBO≌△DCO,∴∠EBO=∠DCO,∵∠OBC=∠OCB(已证),∴∠EBO+∠OBC=∠DCO+∠OCB,即∠ABC=∠ACB,即AB=AC,∴△ABC是等腰三角形;②④,理由是:∵在△EBO和△DCO中BEO CDOEOB DOC BE CD∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△EBO≌△DCO,∴OB=OC,∴∠OBC=∠OCB,∴∠EBO+∠OBC=∠DCO+∠OCB,即∠ABC=∠ACB,即AB=AC,∴△ABC是等腰三角形;③④,理由是:∵在△EBO和△DCO中BEO CDOEOB DOCBE CD∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△EBO≌△DCO,∴∠EBO=∠DCO,OB=OC,∴∠OBC=∠OCB,∴∠EBO+∠OBC=∠DCO+∠OCB,即∠ABC=∠ACB,即AB=AC,∴△ABC是等腰三角形;故选C.28.如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF,给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有()A.4个B.3个C.2个D.1个【答案】A【解析】试题解析:∵BF∥AC,∴∠C=∠CBF,∵BC平分∠ABF,∴∠ABC=∠CBF,∴∠C=∠ABC,∴AB=AC,∵AD是△ABC的角平分线,∴BD=CD,AD⊥BC,故②③正确,在△CDE与△DBF中,{C CBFCD BDEDC BDF∠=∠=∠=∠,∴△CDE≌△DBF,∴DE=DF,CE=BF,故①正确;∵AE=2BF,∴AC=3BF,故④正确.故选A.考点:1.全等三角形的判定与性质;2.角平分线的性质;3.相似三角形的判定与性质.29.如图,已知AB=AC,AF=AE,∠EAF=∠BAC,点C、D、E、F共线.则下列结论,其中正确的是()①△AFB≌△AEC;②BF=CE ;③∠BFC=∠EAF;④AB=BC .A .①②③B .①②④C .①②D .①②③④【答案】A【解析】【分析】 根据题意结合图形证明△AFB≌△AEC ;利用四点共圆及全等三角形的性质问题即可解决.【详解】如图,∵∠EAF=∠BAC ,∴∠BAF=∠CAE ;在△AFB 与△AEC 中,AF AE BAF CAE AB AC ⎧⎪∠∠⎨⎪⎩===, ∴△AFB ≌△AEC (SAS ),∴BF=CE ;∠ABF=∠ACE ,∴A 、F 、B 、C 四点共圆,∴∠BFC=∠BAC=∠EAF ;故①、②、③正确,④错误.故选A..【点睛】本题主要考查了全等三角形的判定及其性质的应用问题;解题的关键是准确找出图形中隐含的全等三角形,灵活运用四点共圆等几何知识来分析、判断、推理或证明.30.如图,AC ⊥BE 于点C ,DF ⊥BE 于点F ,且BC =EF ,如果添上一个条件后,可以直接利用“HL ”来证明△ABC ≌△DEF ,则这个条件应该是( )A.AC=DE B.AB=DE C.∠B=∠E D.∠D=∠A【答案】B【解析】在Rt△ABC与Rt△DEF中,直角边BC=EF,要利用“HL”判定全等,只需添加条件斜边AB=DE.故选:B.。
(常考题)人教版初中数学八年级数学上册第三单元《轴对称》测试卷(包含答案解析)(1)

一、选择题1.若a ,b 是等腰ABC 的两边长,且满足()2370a b -+-=,此三角形的周长是( )A .13B .13或17C .17D .202.以下尺规作图中,点D 为线段BC 边上一点,一定能得到线段AD BD =的是( ) A . B .C .D .3.如图,已知ABC ∆中,,AB AC =点,D E 是射线AB 上的两个动点(点D 在点E 的右侧).且,CE DE =连结CD ,若ACE x ∠=,BCD y ∠=.则y 关于x 的函数关系式是( )A .()900180y x x =-<<︒B .()101802y x x =<<︒C .()39001802y x x =-<<︒D .()201803y x x =<<︒ 4.如图,在ABC ∆中,90,30C B ︒︒∠=∠= ,以A 为圆心,任意长为半径画弧分别交AB AC 、于点M 和N ,再分别以M N 、为圆心,大于12MN 的长为半径画弧,两弧交于点P ,连接AP ,并延长交BC 于点D ,则下列说法中正确的个数是( )①AD 是BAC ∠的平分线;②60ADC ︒∠=;③点D 在AB 的垂直平分线上﹔④若2AD =,则点D 到AB 的距离是1,:1:2DAC ABC S S ∆∆=A .2B .3C .4D .55.如图,等边ABC 的顶点(1,1)A ,(3,1)B ,规定把等边ABC “先沿x 轴翻折,再向左平移1个单位”为一次变换,这样连续经过2021次变换后,ABC 顶点C 的坐标为( )A .(2020,13)-+B .(2020,13)---C .(2019,13)-+D .(2019,13)--- 6.如图,在△ABC 中,∠BAC =90°,AD 是高,BE 是中线,CF 是角平分线,CF 交AD 于点G ,交BE 于点H ,下面说法:①△ABE 的面积=△BCE 的面积;②∠AFG =∠AGF ;③∠FAG =2∠ACF ;④BH =CH .其中正确的是( )A .①②③④B .①②③C .②④D .①③7.如图,在△ABC 纸片中,AB=9cm ,BC=5cm ,AC=7cm ,沿过点B 的直线折叠这个三角形,使点C 落在AB 边上的点E 处,折痕为BD ,则△ADE 的周长为是( )A .9cmB .11cmC .12cmD .14cm 8.下列推理中,不能判断ABC 是等边三角形的是( ) A .A B C ∠=∠=∠ B .,60AB AC B =∠=︒C .60,60A B ∠=︒∠=︒D .AB AC =,且B C ∠=∠ 9.如图,C 是线段AB 上的一点,ACD △和BCE 都是等边三角形,AE 交CD 于M ,BD 交CE 于N ,交AE 于O ,则①DB AE =;②AMC DNC ∠=∠;③60AOB ∠=︒;④DN AM =;⑤CMN △是等边三角形.其中,正确的有( )A .2个B .3个C .4个D .5个10.如图,是一个 3×4 的网格(由 12 个小正方形组成,虚线交点称之格点)图中有一个三角形,三个顶点都在格点上,在网格中可以画出( )个与此三角形关于某直线对称的格点三角形.A .6B .7C .8D .911.如图,AC AD =,BC BD =,则有( )A .AB 与CD 互相垂直平分B .CD 垂直平分ABC .CD 平分ACB ∠ D .AB 垂直平分CD12.如图,在等腰ABC 中,118ABC ︒∠=,AB 垂直平分线DE 交AB 于点D ,交AC 于点E ,BC 的垂直平分线PQ 交BC 于点P ,交AC 于点Q ,连接BE ,BQ ,则EBQ ∠=( )A .65︒B .60︒C .56︒D .50︒二、填空题13.如图,已知60AOB ︒∠=,点P 在边OA 上, 10OP =,点,M N 在边OB 上, PM PN =,若3,MN =则OM 的长是__________.14.如图,在平面直角坐标系中,直线l 与x 轴交于点1B ,与y 轴交点于D ,且111,60OB ODB =∠=︒,以1OB 为边长作等边三角形11AOB ,过点1A 作12A B 平行于x 轴,交直线l 于点2B ,以12A B 为边长作等边三角形212A A B ,过点2A 作23A B 平行于x 轴,交直线l 于点3B ,以23A B 为边长作等边三角形323A A B ,…,按此规律进行下去,则点6A 的横坐标是______.15.如图,ABC 中,AB BC =,点D 在线段BC 上(不与点,B C 重合). 作法如下:①连接AD ,作AD 的垂直平分线分别交直线,AB AC 于点,P Q ,连接,DP DQ ,则APQ DPQ △≌△;②过点D 作AC 的平行线交AB 于点P ,在线段AC 上截取AQ ,使AQ DP =,连接,PQ DQ ,则APQ DQP △≌△;③过点D 作AC 的平行线交AB 于点P ,过点D 作AB 的平行线交AC 于点Q ,连接PQ ,则APQ DQP △≌△;④过点D 作AB 的平行线交AC 于点Q ,在直线AB 上取一点P ,连接DP ,使DP AQ =,连接PQ ,则APQ DPQ △≌△.以上说法一定成立的是__________.(填写正确的序号)16.如图,在ABC 中,D 是BC 上一点,,105AC AD DB BAC ==∠=︒,则B ∠=________°.17.如图在钝角△ABC 中,已知∠BAC=135°,边AB 、AC 的垂直平分线分别交BC 于点D 、E ,连接AD 、AE ,则∠DAE=_____18.如图,在锐角△ABC 中,AB =62 ,∠BAC =45°,∠BAC 的平分线交BC 于点D ,M ,N 分别是AD 和AB 上的动点,则BM +MN 的最小值是_____________.19.如图,∠AOB =45°,OC 平分∠AOB ,点M 为OB 上一定点,P 为OC 上的一动点,N 为OB 上一动点,当PM +PN 最小时,则∠PMO 的度数为___________.20.如图,在等边三角形ABC 中,CM 平分ACB ∠交AB 于点M .(1)ACM ∠的大小=__________(度);(2)AMC ∠的大小=__________(度);(3)已知4AB =,点D 为射线CM 上一点,作∠DCE=60︒,()CE CD CD AB =≠,连接DE 交射线CB 于点F ,连接BD ,BE 当以B ,D ,M 为顶点的三角形与BEF 全等时,线段CF 的长为__________.三、解答题21.如图,,A B AE BE ∠=∠=,点D 在AC 边上,12,AE ∠=∠和BD 相交于点O . (1)求证:AEC BED ∆≅∆(2)若70BDE ︒∠=,求1∠的度数.22.如图,已知∠A =∠D =90°,E 、F 在线段BC 上,DE 与AF 交于点O ,且AB =CD ,BE =CF .求证:(1)Rt △ABF ≌Rt △DCE ;(2)OE =OF .23.如图:已知ABC 中AB AC =:(1)尺规作图:过A 点作//AE BC (不写作法,保留作图痕迹);(2)求证:AE 是ABC 的一个外角角平分线.24.已知ABC 是等边三角形,点D 是AC 的中点,点P 在射线BC 上,点Q 在线段AB 上,120PDQ ∠=︒.(1)如图1,若点Q 与点B 重合,求证:DB DP =;(2)如图2,若点P 在线段BC 上,8AC =,求AQ PC +的值.25.已知:90,A D AB DC ︒∠=∠==,点,E F 在直线BC 上,位置如图所示,且BE CF =.(1)求证:AF DE =;(2)若PO 平分EPF ∠,求证:PO 垂直平分线段BC .26.(1)如图①,已知:在ABC 中,90BAC ∠=︒,AB AC =,直线m 经过点A ,BD ⊥直线m ,CE ⊥直线m ,垂足分别为点D 、E .求证:DE BD CE =+.(2)如图②,将(1)中的条件改为:在ABC 中,AB AC =,D 、A 、E 三点都在直线m 上,并且有BDA AEC BAC a ∠=∠=∠=,其中a 为任意锐角或钝角.请问结论DE BD CE =+是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)拓展与应用:如图③,D 、E 是D 、A 、E 三点所在直线m 上的两动点(D 、A 、E 三点互不重合),点F 为BAC ∠平分线上的一点,且ABF 和ACF 均为等边三角形,连接BD 、CE ,若BDA AEC BAC ∠=∠=∠,试判断DEF 的形状.(不需要说明理由)【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】根据绝对值非负性的性质以及平方的非负性可知a和b的值,然后根据等腰三角形的性质分情况计算即可;【详解】∵()2-+-=,a b370∴ a=3,b=7,若腰为3时,3+3<7,三角形不成立;若腰为7时,则周长为7+7+3=17,故选:C.【点睛】本题考查了非负性的性质以及等腰三角形的性质,熟练掌握知识点是解题的关键;.2.D解析:D【分析】点D到点A、点B的距离相等可知点D在线段AB的垂直平分线上,据此可得答案.【详解】解:∵点D到点A、点B的距离AD=BD,∴点D在线段AB的垂直平分线上,故选择:D.【点睛】本题主要考查作图−复杂作图,解题的关键是掌握线段中垂线的性质与尺规作图.3.B解析:B【分析】根据等腰三角形的性质得出∠ACB=∠ABC=x+∠BCE和∠D=∠DCE=y+∠BCE,由三角形的外角性质得出∠ABC=∠D+∠BCD ,即x+∠BCE= y+∠BCE+ y ,即x=2y ,得出y 关于x 的函数关系式.【详解】解:∵AB AC =,ACE x ∠=,∴ ∠ACB=∠ABC=x+∠BCE ,∵CE DE =,BCD y ∠=∴∠D=∠DCE=y+∠BCE ,∵ ∠ABC 是△BCD 的一个外角,∴∠ABC=∠D+∠BCD ,即 x+∠BCE= y+∠BCE+ y ,即x=2y , ∴()101802y x x =<<︒, 故选:B .【点睛】 本题主要考查了等腰三角形的性质,三角形的外角性质,三角形的外角等于它不相邻的两个内角和.熟练掌握并运用各性质是解题的关键.4.B解析:B【分析】先根据三角形内角和计算出∠BAC=60°,再利用基本作图对①进行判断;利用∠BAD=∠CAD=30°得到∠ADC=60°,则可对②进行判断;利用∠B=∠BAD 得到DA=DB ,根据线段垂直平分线的性质定理的逆定理可对③进行判断.利用30度角所对的直角边是斜边的一半、三角形的面积计算公式即可得出两个三角形的面积之比.【详解】解:由作法得,AD 平分∠BAC ,所以①正确;∵∠C=90°,∠B=30°,∴∠BAC=60°,∴∠BAD=∠CAD=12×60°=30°, ∴∠ADC=90°-∠CAD=60°,所以②正确;∵∠B=∠BAD ,∴DA=DB ,∴点D 在AB 的垂直平分线上,所以③正确;在直角△ACD 中,∠CAD=30°,∴CD=12AD , ∴BC=CD+BD=12AD+AD=32AD ,1124DAC S AC CD AC AD ∆=⋅=⋅.∴11332224ABC S AC BC AC AD AC AD ∆=⋅=⋅=⋅, ∴13::1:344DAC ABC S S AC AD AC AD ∆∆=⋅⋅=,故④错误. 所以,正确的结论有3个故选:B .【点睛】 本题考查了角平分线的性质、线段垂直平分线的性质以及作图-基本作图.解题时需要熟悉等腰三角形的判定与性质.5.D解析:D【分析】先求出点C 坐标,第一次变换,根据轴对称判断出点C 变换后在x 轴下方然后求出点C 纵坐标,再根据平移的距离求出点C 变换后的横坐标,最后写出第一次变换后点C 坐标,同理可以求出第二次变换后点C 坐标,以此类推可求出第n 次变化后点C 坐标.【详解】∵△ABC 是等边三角形AB=3-1=2∴点C 到x 轴的距离为1+21=+2 ∴C(2,1+由题意可得:第1次变换后点C 的坐标变为(2-1,1),即(1,1-,第2次变换后点C 的坐标变为(2-21),即(0,1+第3次变换后点C 的坐标变为(2-3,1),即(-1,1--第n 次变换后点C 的坐标变为(2-n ,1)(n 为奇数)或(2-n ,1+为偶数), ∴连续经过2021次变换后,等边ABC 的顶点C 的坐标为(-2019,1-, 故选:D .【点睛】本题考查了利用轴对称变换(即翻折)和平移的特点求解点的坐标,在求解过程中找到规律是关键. 6.B解析:B【分析】根据等底等高的三角形的面积相等即可判断①;根据三角形内角和定理求出∠ABC =∠CAD ,根据三角形的外角性质即可推出②;根据三角形内角和定理求出∠FAG =∠ACD ,根据角平分线定义即可判断③;根据等腰三角形的判定判断④即可.【详解】∵BE 是中线,∴AE=CE,∴△ABE的面积=△BCE的面积(等底等高的三角形的面积相等),故①正确;∵CF是角平分线,∴∠ACF=∠BCF,∵AD为高,∴∠ADC=90°,∵∠BAC=90°,∴∠ABC+∠ACB=90°,∠ACB+∠CAD=90°,∴∠ABC=∠CAD,∵∠AFG=∠ABC+∠BCF,∠AGF=∠CAD+∠ACF,∴∠AFG=∠AGF,故②正确;∵AD为高,∴∠ADB=90°,∵∠BAC=90°,∴∠ABC+∠ACB=90°,∠ABC+∠BAD=90°,∴∠ACB=∠BAD,∵CF是∠ACB的平分线,∴∠ACB=2∠ACF,∴∠BAD=2∠ACF,即∠FAG=2∠ACF,故③正确;根据已知条件不能推出∠HBC=∠HCB,即不能推出BH=CH,故④错误;故选:B.【点睛】本题考查了三角形内角和定理,三角形的外角性质,三角形的角平分线、中线、高,等腰三角形的判定等知识点,能综合运用定理进行推理是解此题的关键,题目比较好,属于中考题型.7.B解析:B【分析】根据折叠的性质得到:DE=CD,BE=BC=5cm,求出AE=4cm,根据△ADE的周长为AD+DE+AE=AC+AE代入数值计算即可得解.【详解】由折叠得:DE=CD,BE=BC=5cm,∵AB=9cm,∴AE=AB-BE=9cm-5cm=4cm,∴△ADE的周长为AD+DE+AE=AC+AE=7cm+4cm=11cm,故选:B.【点睛】此题考查折叠的性质:折叠前后对应边相等,正确理解折叠的性质是解题的关键.8.D解析:D【分析】根据等边三角形的定义、判定定理以及三角形内角和定理进行判断.【详解】A 、由“三个角都相等的三角形是等边三角形”可以判断△ABC 是等边三角形,故本选项不符合题意;B 、由“有一个角是60°的等腰三角形是等边三角形”可以判断△ABC 是等边三角形,故本选项不符合题意;C 、由“∠A =60°,∠B =60°”可以得到“∠A =∠B =∠C =60°”,则由“三个角都相等的三角形是等边三角形”可以判断△ABC 是等边三角形,故本选项不符合题意;D 、由“AB =AC ,且∠B =∠C”只能判定△ABC 是等腰三角形,故本选项符合题意. 故选:D .【点睛】本题主要考查了等边三角形的判定和三角形内角和定理,属于基础题.(1)由定义判定:三条边都相等的三角形是等边三角形.(2)判定定理1:三个角都相等的三角形是等边三角形.(3)判定定理2:有一个角是60°的等腰三角形是等边三角形.9.C解析:C【分析】易证△ACE ≌△DCB ,可得①正确;即可求得∠AOB =120°,可得③错误;再证明△ACM ≌△DCN ,可得②④正确和CM =CN ,即可证明⑤正确;即可解题.【详解】解:∵ACD △和BCE 都是等边三角形∵∠ACD =∠BCE =60°,∴∠DCE =60°,在△ACE 和△DCB 中,AC DC ACE DCB CB CE =⎧⎪∠=∠⎨⎪=⎩,∴△ACE ≌△DCB (SAS ),∴∠BDC =∠EAC ,DB =AE ,①正确;∠CBD =∠AEC ,∵∠AOB =180°−∠OAB−∠DBC ,∴∠AOB =180°−∠AEC−∠OAB =120°,③错误;在△ACM 和△DCN 中,60BDC EAC DC ACACD DCN ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩, ∴△ACM ≌△DCN (ASA ),∴AM =DN ,④正确;∠AMC =∠DNC ,②正确;CM =CN ,∵∠ACD =∠BCE =60°,∴∠MCN =180°-∠ACD-∠BCE =60°,∴△CMN 是等边三角形,⑤正确;故有①②④⑤正确.故选:C .【点睛】本题考查了全等三角形的判定和全等三角形对应边、对应角相等的性质,本题中求证△ACE ≌△DCB 和△ACM ≌△DCN 是解题的关键.10.B解析:B【分析】先确定对称轴,再找到对称点进而可以找到符合题意的对称三角形即可.【详解】解:如图,左右对称的有4个,如图,上下对称的有1个,如图,关于正方形的对角线对称的有2个,∴一共有7个与原三角形关于某直线对称的格点三角形,故选:B .【点睛】本题考查了轴对称图形的性质,找到正确的对称轴,画出相应的对称三角形是解决本题的关键.11.D解析:D【分析】根据线段垂直平分线的判定定理解答.【详解】∵AC AD =,BC BD =,∴AB 垂直平分CD ,故D 正确,A 、B 错误,OC 不平分∠ACB ,故C 错误,故选:D .【点睛】此题考查线段垂直平分线的判定:到线段两个端点距离相等的点在这条线段的垂直平分线上.12.C解析:C【分析】根据等腰ABC ,118ABC ︒∠=,得到AB=CB ,∠A=∠C=1(180)312ABC ︒︒-∠=,由DE 垂直平分AB ,求得∠ABE=31A ∠=︒,同理:31QBC C ∠=∠=︒,根据∠EBQ=∠ABC-∠ABE-∠QBC 计算得出答案.【详解】在等腰ABC 中,118ABC ︒∠=,∴AB=CB ,∠A=∠C=1(180)312ABC ︒︒-∠=, ∵DE 垂直平分AB ,∴AE=BE ,∴∠ABE=31A ∠=︒,同理:31QBC C ∠=∠=︒,∴∠EBQ=∠ABC-∠ABE-∠QBC=56︒,故选:C.【点睛】此题考查等腰三角形的性质,线段垂直平分线的性质,三角形的内角和定理,熟记线段垂直平分线的性质是解题的关键.二、填空题13.5【分析】作PH⊥MN于H如图根据等腰三角形的性质得MH=NH=MN=15在Rt△POH中由∠POH=60°得到∠OPH=30°则根据在直角三角形中30°角所对的直角边等于斜边的一半可得OH=OP=解析:5【分析】作PH⊥MN于H,如图,根据等腰三角形的性质得MH=NH=12MN=1.5,在Rt△POH中由∠POH=60°得到∠OPH=30°,则根据在直角三角形中,30°角所对的直角边等于斜边的一半可得OH=12OP=5,然后计算OH-MH即可.【详解】作PH⊥MN于H,如图,∵PM=PN,∴MH=NH=12MN=1.5,在Rt△POH中,∵∠POH=60°,∴∠OPH=30°,∴OH=12OP=12×10=5,∴OM=OH-MH=5-1.5=3.5.故答案为:3.5.【点睛】本题考查了含30度角的直角三角形的性质:在直角三角形中,30°角所对的直角边等于斜边的一半.也考查了等腰三角形的性质.14.5【分析】过A1作A1A⊥OB1于A过A2作A2B⊥A1B2于B过A3作A3C⊥A2B3于C根据等边三角形的性质以及含30°角的直角三角形的性质分别求得A1的横坐标为A2的横坐标为A3的横坐标为进而解析:5【分析】过A1作A1A⊥OB1于A,过A2作A2B⊥A1B2于B,过A3作A3C⊥A2B3于C,根据等边三角形的性质以及含30°角的直角三角形的性质,分别求得A1的横坐标为1212-,,A2的横坐标为2212-,A3的横坐标为3212-,进而得到A n的横坐标为212n-,据此可得点A6的横坐标.【详解】解:如图所示,过A1作A1A⊥OB1于A,则OA=12OB1=12,即A1的横坐标为12=1212-,∵160ODB∠=°,∴∠OB1D=30°,∵A1B2//x轴,∴∠A1B2B1=∠OB1D=30°,∠B2A1B1=∠A1B1O=60°,∴∠A1B1B2=90°,∴A1B2=2A1B1=2,过A2作A2B⊥A1B2于B,则A1B=12A1B2=1,即A2的横坐标为12+1=2212-,过A3作A3C⊥A2B3于C,同理可得,A2B3=2A2B2=4,A2C=12A2B3=2,即A3的横坐标为12+1+2=3212-,同理可得,A4的横坐标为12+1+2+4=4212-,由此可得,A n的横坐标为212n-,∴点A6的横坐标是62163==31.522-,故答案为31.5.【点睛】本题是一道找规律问题,涉及到等边三角形的性质、含30度角的直角三角形,解题的关键要利用等边三角形的性质总结出关于点A的系列点的规律.15.①②③【分析】根据题意画出图形再根据垂直平分线的性质平行线的性质和三角形全等的判定可以得证【详解】解:①如图∵PQ为AD的垂直平分线∴PA=PDQA=QD∴在△APQ和△DPQ中∴△APQ≌△DPQ解析:①②③【分析】根据题意画出图形,再根据垂直平分线的性质,平行线的性质和三角形全等的判定可以得证.【详解】解:①如图,∵PQ为AD的垂直平分线,∴PA=PD,QA=QD,∴在△APQ和△DPQ中,PA PDPQ PQQA QD=⎧⎪=⎨⎪=⎩,∴△APQ≌△DPQ(SSS),①正确;②如图,∵PD ∥AC ,∴∠DPQ=∠AQP ,∴在△APQ 和△DQP 中,AQ DP AQP DPQ QP PQ =⎧⎪∠=∠⎨⎪=⎩,∴△APQ ≌△DQP (SAS ),②正确 ;③如图,∵PD ∥AC ,∴∠DPQ=∠AQP ,同理∠DQP=∠APQ ,∴在△APQ 和△DQP 中,DPQ AQP PQ PQDQP APQ ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△APQ ≌△DQP (ASA ),③正确 ;④如图,△APQ ≌△DPQ 不成立,④错误;故答案为①②③.【点睛】本题考查三角形与平行线的综合应用,熟练掌握垂直平分线的性质,平行线的性质和三角形全等的判定是解题关键.16.25【分析】设∠ADC =α然后根据AC =AD =DB ∠BAC =105°表示出∠B 和∠BAD 的度数最后根据三角形的内角和定理求出∠ADC 的度数进而求得∠B 的度数即可【详解】解:∵AC =AD =DB ∴∠B =解析:25【分析】设∠ADC =α,然后根据AC =AD =DB ,∠BAC =105°,表示出∠B 和∠BAD 的度数,最后根据三角形的内角和定理求出∠ADC 的度数,进而求得∠B 的度数即可.【详解】解:∵AC =AD =DB ,∴∠B =∠BAD ,∠ADC =∠C ,设∠ADC =α,∴∠B =∠BAD =2α , ∵∠BAC =105°,∴∠DAC =105°﹣2α, 在△ADC 中, ∵∠ADC +∠C +∠DAC =180°,∴2α+105°﹣2α=180°, 解得:α=50°,∴∠B =∠BAD =2α=25°, 故答案为:25.【点睛】 本题考查了等腰三角形的性质:①等腰三角形的两腰相等;②等腰三角形的两个底角相等,熟练掌握等腰三角形的性质是解题的关键.17.90°【分析】根据等腰三角形的性质和线段垂直平分线的性质即可得到结论【详解】解:连接DAEA 如图∵∠BAC=135°∴∠B+∠C=180°-135°=45°∵DF 是AB 的垂直平分线EG 是AC 的垂直平解析:90°【分析】根据等腰三角形的性质和线段垂直平分线的性质即可得到结论.【详解】解:连接DA、EA,如图,∵∠BAC=135°,∴∠B+∠C=180°-135°=45°,∵DF是AB的垂直平分线,EG是AC的垂直平分线,∴DA=DB,EA=EC,∴∠B=∠DAB,∠C=∠EAC,∴∠DAB +∠EAC =∠B+∠C=45°,∴∠DAE=∠BAC –(∠DAB +∠EAC)=135°-45°=90°.故答案为:90°.【点睛】本题考查线段的垂直平分线的性质,解题的关键是熟练掌握线段的垂直平分线的性质.18.6【分析】作BH⊥AC垂足为H交AD于M′点过M′点作M′N′⊥AB垂足为N′则BM′+M′N′为所求的最小值再根据AD是∠BAC的平分线可知M′H=M′N′再由锐角三角函数的定义即可得出结论【详解解析:6【分析】作BH⊥AC,垂足为H,交AD于M′点,过M′点作M′N′⊥AB,垂足为N′,则BM′+M′N′为所求的最小值,再根据AD是∠BAC的平分线可知M′H=M′N′,再由锐角三角函数的定义即可得出结论.【详解】解:如图,作BH⊥AC,垂足为H,交AD于M′点,过M′点作M′N′⊥AB,垂足为N′,则BM′+M′N′为所求的最小值.∵AD是∠BAC的平分线,∴M′H=M′N′,∴BH是点B到直线AC的最短距离(垂线段最短),∵AB=2∠BAC=45°,∴BH=AH∴222+=AH BH AB∴BH=6.∵BM+MN的最小值是BM′+M′N′=BM′+M′H=BH=6.故答案为6.【点睛】本题考查的是轴对称-最短路线问题,解答此类问题时要从已知条件结合图形认真思考,通过角平分线性质,垂线段最短,确定线段和的最小值.19.45°【分析】找到点M关于OC对称点M′过点M′作M′N⊥OB于点N交OC 于点P则此时PM+PN的值最小再根据角平分线的性质及三角形内角和即可得出答案【详解】解:如图找到点M关于OC对称点M′过点M解析:45°【分析】找到点M关于OC对称点M′,过点M′作M′N⊥OB于点N,交OC于点P,则此时PM+PN 的值最小,再根据角平分线的性质及三角形内角和即可得出答案.【详解】解:如图,找到点M关于OC对称点M′,过点M′作M′N⊥OB于点N,交OC于点P,则此时PM+PN 的值最小.∵PM=PM′,∴此时PM+PN=PM′+PN′=M′N′,∵点M与点M′关于OC对称,OC平分∠AOB,∴OM=OM′,∵∠AOB=45°,∴∠PM'O=∠AOB=45°,∴∠PMO=∠PM'O=45°,故答案为:45°.【点睛】本题考查了利用轴对称的知识寻找最短路径的知识,涉及到两点之间线段最短、垂线段最短的知识,有一定难度,正确确定点P及点N的位置是关键.20.2或6或【分析】(1)根据等边三角形的性质及角平分线的性质求解;(2)根据等边三角形的三线合一的性质解答;(3)根据题意分两种情况:当点D在线段CM上时当点D在线段CM的延长线上时分别画出图形利用全解析:3090 2或6或23【分析】(1)根据等边三角形的性质及角平分线的性质求解;(2)根据等边三角形的三线合一的性质解答;(3)根据题意分两种情况:当点D在线段CM上时,当点D在线段CM的延长线上时,分别画出图形,利用全等三角形的性质解答.【详解】(1)∵△ABC是等边三角形,∴∠ACB=60︒,∵CM平分ACB∠,∠ACB=30,∴∠ACM=12故答案为:30;∠,(2)∵△ABC是等边三角形,CM平分ACB∴CM⊥AB,∴∠AMC=90︒,故答案为:90︒;(3)∵∠DCE=60︒,CD=CE,∴△CDE是等边三角形,∴DE=CE=CD,∵∠BCM=∠ACM=30,∴∠BCE=30,∴CF平分∠DCE,∵CD=CE,∴CB垂直平分DE,①当点D在线段CM上时,当△BDM≌△BEF时,如图1,∴BF=BM=2,∴CF=CB-BF=4-2=2;当△BDM≌△EBF时,如图1,则EF=BM=2,∴CD=DE=4,,∵AB=4,CD<CM<4,∴此种情况不成立,舍去;②当点D在线段CM的延长线上时,当△BDM≌△BEF时,如图2,∴BF=BM=2,∴CF=BC+BF=4+2=6,;当△BDM≌△EBF时,如图3,则EF=BM=2,∴CE=2EF=4,∴2223CF CE EF =-=,故答案为: 2或6或23..【点睛】此题考查等边三角形的性质,利用三线合一的性质进行证明,全等三角形的性质,熟记等边三角形的性质是解题的关键.三、解答题21.(1)见解析;(2)40°【分析】(1)由12∠=∠得到BED AEC ∠=∠,然后根据ASA 即可证明AEC BED ∆≅∆; (2)由(1)得DE=CE ,70C BDE ∠=∠=︒,由三角形内角和即可求出1∠的度数.【详解】解:()11=2∠∠,BED AEC ∠=∠∴又,A B AE BE ∠=∠=()AEC BED ASA ∴∆≅∆;()2AEC BED ∆≅∆70,BDE C DE CE ∴∠=∠=︒=70C EDC ︒∴∠=∠=118027040︒︒︒∴∠=-⨯=;【点睛】本题考查了等腰三角形的性质,全等三角形的判定和性质,三角形的内角和定理,解题的关键是掌握全等三角形的判定和性质进行解题.22.(1)见解析;(2)见解析【分析】(1)由于△ABF 与△DCE 是直角三角形,根据直角三角形全等的判定的方法即可证明; (2)先根据三角形全等的性质得出∠AFB =∠DEC ,再根据等腰三角形的性质得出结论.【详解】证明:(1)∵BE =CF ,∴BE+EF=CF+EF,即BF=CE,∵∠A=∠D=90°,∴△ABF与△DCE都为直角三角形,在Rt△ABF和Rt△DCE中∵BF CE AB CD=⎧⎨=⎩,∴Rt△ABF≌Rt△DCE(HL);(2)∵Rt△ABF≌Rt△DCE(已证),∴∠AFB=∠DEC,∴OE=OF.【点睛】本题主要考查全等三角形的判定和性质以及等腰三角形的判定定理,掌握HL判断两个直角三角形全等,是解题的关键.23.(1)见解析;(2)见解析.【分析】(1)作∠CAE=∠C即可;(2)延长BA,根据两直线平行,同位角相等,有∠EAF=∠B,由(1)可知∠CAE=∠C,再根据AB=AC,可得∠B=∠C,等量替换之后即可得证.【详解】(1)射线AE为所求;(2)证明:如图所示,延长BA,∵//AE BC,∴∠EAF=∠B,∠CAE=∠C,∵AB=AC,∴∠B=∠C,∴∠EAF=∠CAE,∴AE是ABC的一个外角角平分线.【点睛】本题考查了平行线的性质和判定,等腰三角形的性质和角平分线的判定等知识,掌握相关知识是解题的关键.24.(1)证明见解析;(2)4.【分析】(1)由等边三角形的性质证明30DBC ∠=︒,再利用三角形的内角和定理求解30DPB ∠=︒,从而可得结论; (2)过点D 作//DE BC 交AB 于点E ,先证明ADE 为等边三角形,再证明QDE PDC ≌,可得QE PC =, 从而可得答案.【详解】证明:(1)∵ABC 为等边三角形,∴,60BA BC ABC =∠=︒∵D 为AC 的中点,∴DB 平分ABC ∠,∴30DBC ∠=︒. ∵120PDB ∠=︒,∴1801203030DPB ∠=︒-︒-︒=︒,∴DBC DPB ∠=∠,∴DB DP =.(2)过点D 作//DE BC 交AB 于点E .∵ABC 为等边三角形,8AC =,点D 是AC 的中点,∴4,60AD CD ABC ACB A ==∠=∠=∠=︒.∵//DE BC ,∴60AED B ∠=∠=︒.60ADE C ∠=∠=︒,∴ADE 为等边三角形,120EDC ∠=︒,∴4AD ED AE ===,∴ED CD 4==.∵120QDP EDC ∠=∠=︒,,QDE EDP EDP PDC ∴∠+∠=∠+∠∴QDE PDC ∠=∠.∵,60ED CD AED C =∠=∠=︒,∴QDE PDC ≌,∴EQ PC =,∴4AQ PC AQ QE AE +=+==.【点睛】本题考查的是等腰三角形的判定,等边三角形的性质与判定,三角形的全等的判定与性质,掌握以上知识是解题的关键.25.(1)证明见解析;(2)证明见解析.【分析】(1)根据已知条件证明Rt △ABF ≌Rt △DCE(HL)即可得出结论;(2)根据Rt △ABF ≌Rt △DCE 可得出∠E=∠F ,即△PEF 为等腰三角形,又因为PO 平分∠EPF ,根据三线合一可知PO 垂直平分EF ,从而得出PO 垂直平分BC .【详解】(1)证明:∵BE=CF ,BC=CB∴BF=CE ,在Rt △ABF 与Rt △DCE 中,BF CE AB DC =⎧⎨=⎩∴Rt △ABF ≌Rt △DCE(HL),∴AF=DE ;(2)∵Rt △ABF ≌Rt △DCE ,∴∠E=∠F∴△PEF 为等腰三角形,又∵PO 平分∠EPF∴PO ⊥BC(三线合一),EO=FO(三线合一)又∵EB=FC∴BO=CO ,∴PO 垂直平分线段BC.【点睛】本题考查的知识点是全等三角形的判定及性质、垂直平分线的判定、等腰三角形的性质,角平分线的性质,难度不大,但综合性较强,考验了学生综合分析问题的能力. 26.(1)见解析;(2)成立,证明见解析;(3)DEF 为等边三角形【分析】(1)根据BD ⊥直线m ,CE ⊥直线m 得∠BDA=∠CEA=90°,而∠BAC=90°,根据等角的余角相等得∠CAE=∠ABD ,然后根据“AAS”可判断△ADB ≌△CEA ,则AE=BD ,AD=CE ,于是DE=AE+AD=BD+CE ;(2)由∠BDA=∠AEC=∠BAC ,就可以求出∠BAD=∠ACE ,进而由AAS 就可以得出△BAD ≌△ACE ,就可以得出BD=AE ,DA=CE ,即可得出结论;(3)由等边三角形的性质,可以求出∠BAC=120°,就可以得出△BAD ≌△ACE ,就有BD=AE ,进而得出△BDF ≌△AEF ,得出DF=EF ,∠BFD=∠AFE ,而得出∠DFE=60°,即可推出△DEF 为等边三角形.【详解】(1)证明:∵BD ⊥直线m ,CE ⊥直线m ,∴90BDA CEA ∠=∠=︒∵90BAC ∠=︒,∴90BAD CAE ∠+∠=︒∵90BAD ABD ∠+∠=︒,∴CAE ABD ∠=∠.在ADB △和CEA 中:CAE ABD BDA CEA AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴ADB CEA AAS ≌()△△. ∴AE BD =,AD CE =.∴DE AE AD BD CE =+=+.(2)成立.证明如下:∵∠BDA=∠BAC=α,又∵DBA ADB BAC CAE ∠+∠=∠+∠∴∠DBA=∠CAE ,在ADB △和CEA 中:DBA CAE BDA AEC AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()ADB CEA AAS ≌△△. ∴AE BD =,AD CE =,∴DE AE AD BD CE =+=+.(3)DEF 为等边三角形.证明:∵△ABF 和△ACF 均为等边三角形,∴AB=AF=AC ,∠ABF=∠CAF=60°,BF=AF,∴由(2)可知,△ADB ≌△CEA ,∴BD=AE ,∠DBA=∠CAE ,∴∠DBA+∠ABF=∠CAE+∠CAF ,∴∠DBF=∠FAE ,∵在△DBF 和△EAF 中,BD AE DBF FAE BF AF ⎧⎪∠∠⎨⎪⎩=== ∴△DBF ≌△EAF (SAS ),∴DF=EF ,∠BFD=∠AFE ,∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,∴△DEF 为等边三角形.【点睛】本题属于三角形综合题,主要考查了全等三角形与等边三角形的综合应用,解题的关键是熟练掌握全等三角形的判定与性质以及等边三角形的判定与性质并灵活运用,属于中考常考题型.。
八年级数学上册 轴对称填空选择单元测试卷附答案

八年级数学上册轴对称填空选择单元测试卷附答案一、八年级数学全等三角形填空题(难)1.如图,AD⊥BC 于 D,且 DC=AB+BD,若∠BAC=108°,则∠C 的度数是______度.【答案】24【解析】【分析】在DC上取DE=DB.连接AE,在Rt△ABD和Rt△AED中,BD=ED,AD=AD.证明△ABD≌△AED即可求解.【详解】如图,在DC上取DE=DB,连接AE.在Rt△ABD和Rt△AED中,BD EDADB ADEAD AD=⎧⎪∠=∠⎨⎪=⎩∴△ABD≌△AED(SAS).∴AB=AE,∠B=∠AED.又∵CD=AB+BD,CD=DE+EC∴EC=AB∴EC=AE,∴∠C=∠CAE∴∠B=∠AED=2∠C又∵∠B+∠C=180°-∠BAC=72°∴∠C=24°,故答案为:24.【点睛】本题考查了全等三角形的判定与性质及三角形内角和定理,属于基础图,关键是巧妙作出辅助线.2.如图,△ABC的三边AB、BC、CA的长分别为30、40、15,点P是三条角平分线的交点,将△ABC分成三个三角形,则APBS∆︰BPCS∆︰CPAS∆等于____.【答案】6:8:3【解析】【分析】由角平分线性质可知,点P 到三角形三边的距离相等,即三个三角形的AB 、BC 、CA 边上的高相等,利用面积公式即可求解.【详解】解:过点P 作PD ⊥BC 于D ,PE ⊥CA 于E ,PF ⊥AB 于F∵P 是三条角平分线的交点∴PD=PE=PF∵AB=30,BC=40,CA=15∴APB S ∆︰BPC S ∆︰CPA S ∆=30∶40∶15=6∶8∶3故答案为6∶8∶3.【点睛】本题主要考查了角平分线的性质和三角形面积的求法. 角平分线上的点到两边的距离相等. 难度不大,作辅助线是关键.3.如图,在四边形ABCD 中,AD =4,CD =3,∠ABC =∠ACB =∠ADC =45°,则BD 的长为 .41.【解析】作AD′⊥AD ,AD′=AD ,连接C D′,DD′,如图:∵∠BAC+∠CAD=∠DAD′+∠CAD ,即∠BAD=∠CAD′,在△BAD 与△CAD′中,BA CA BAD CAD AD AD =⎧⎪∠=∠'⎨⎪='⎩, ∴△BAD ≌△CAD′(SAS),∴BD=CD′.∠DAD′=90°由勾股定理得DD′=22()=32=42AD AD +',∠D′DA+∠ADC=90°由勾股定理得CD′=22()=932=41DC DD +'+∴BD=CD′=41,故答案为41.4.如图,AD 是△ABC 的角平分线,DF⊥AB,垂足为F ,DE=DG ,△ADG 和△AED 的面积分别为48和36,求△EDF 的面积________.【答案】6【解析】【分析】作DM=DE 交AC 于M ,作DN ⊥AC ,利用角平分线的性质得到DN=DF ,将三角形EDF 的面积转化为三角形DNM 的面积来求.【详解】作DM=DE 交AC 于M ,作DN ⊥AC ,∵AD 是△ABC 的角平分线,DF ⊥AB ,∴DF=DN,∵DE=DG,∴DG=DM,∴Rt△DEF≌Rt△DMN(HL),∵DG=DM, DN⊥AC,∴MN=NG,∴△DMN≌△DNG,∵△ADG和△AED的面积分别为48和36,∴S△MDG=S△ADG-S△ADM=48-36=12,∴S△DEF=12S△MDG=1212=6,故答案为:6【点睛】本题考查了角平分线的性质及全等三角形的判定及性质,正确地作出辅助线,将所求的三角形的面积转化为另外的三角形的面积来求是解题关键.5.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,BE平分∠ABC交AC于E,交AD于F,FG∥BC,FH∥AC,下列结论:①AE=AF;②AF=FH;③AG=CE;④AB+FG=BC,其中正确的结论有________________.(填序号)【答案】①②③④【解析】①正确.∵∠BAC=90°∴∠ABE+∠AEB=90°∴∠ABE=90°-∠AEB∵AD⊥BC∴∠ADB=90°∴∠DBE+∠BFD=90°∴∠DBE=90-∠BFD∵∠BFD=∠AFE∴∠DBE=90°-∠AFE∵BE 平分∠ABC∴∠ABE=∠DBE∴90°-∠AEB=90°-∠AFE∴∠AEB=∠AFE∴AE=AF②正确.∵∠BAC=90°∴∠BAF+∠DAC=90°∴∠BAF=90°-∠DAC∵AD ⊥BC∴∠ADC=90°∴∠C+∠DAC=90°∴∠C=90°-∠DAC∴∠C=∠BAF∵FH ∥AC∴∠C=∠BHF∴∠BAF=∠BHF在△ABF 和△HBF 中ABE CBE BAF BHF BF BF ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABF ≌△HBF∴AF=FH③正确.∵AE=AF ,AF=FH∴AE=FH∵FG ∥BC ,FH ∥AC∴四边形FHCG 是平行四边形∴FH=GC∴AE=GC∴AE+EG=GC+EG∴AG=CE④正确.∵四边形FHCG 是平行四边形∴FG=HC∵△ABF ≌△HBF∴AB=HB∴AB+FG=HB+HC=BC故正确的答案有①②③④.6.在△ABC中,∠ABC=60°,∠ACB=70°,若点O到三边的距离相等,则∠BOC=_____°.【答案】115或65或22.5【解析】【分析】先画出符合的图形,再根据角平分线的性质和三角形的内角和定理逐个求出即可.【详解】解:①如图,∵点O到三边的距离相等,∴点O是△ABC的三角的平分线的交点,∵∠ABC=60°,∠ACB=70°,∴∠OBC=12∠ABC=30°,1OCB2∠=∠ACB=35°,∴∠BOC=180°﹣∠OBC﹣∠OCB=115°;②如图,∵∠ABC=60°,∠ACB=70°,∴∠EBC=180°﹣∠ABC=120°,∠FCB=180°﹣∠ACB=110°,∵点O到三边的距离相等,∴O是∠EBC和∠FCB的角平分线的交点,∴∠OBC=12∠EBC=60°,1OCB2∠=∠FCB=55°,∴∠BOC=180°﹣∠OBC﹣∠OCB=65°;③如图,∵∠ABC=60°,∠ACB=75°,∴∠A=180°﹣∠ABC﹣∠ACB=45°,∵点O到三边的距离相等,∴O是∠EBA和∠ACB的角平分线的交点,∴∠OBA=12∠EBA=12×(180°﹣60°)=60°,1OCB2∠=∠ACB=37.5°,∴∠BOC=180°﹣(∠OBA+∠ABC+∠OCB)=180°﹣(60°﹣60°﹣37.5°)=22.5°;如图,此时∠BOC=22.5°,故答案为:115或65或22.5.【点睛】此题主要考查三角形的内角和,解题的关键是根据题意分情况讨论.7.如图,平面直角坐标系中,A(0,3),B(4,0),BC∥y轴,且BC<OA,第一象限内有一点P(a,2a-3),若使△ACP是以AC斜边的等腰直角三角形,则点P的坐标为_______________.【答案】(103,113).【解析】【详解】解:∵点P的坐标为(a,2a-3),∴点P在直线y=2x-3上,如图所示,当点P在AC的上方时,过P作y轴的垂线,垂足为D,交BC的延长线于E,则∠E=∠ADP=90°,∵△ACP是以AC为斜边的等腰直角三角形,∴AP=PC,∠APD=∠PCE,∴△APD≌△PCE,∴PE=AD,又∵OD=2a-3,AO=3,∴AD=2a-6=PE,∵DE=OB=4,DP=a,又∵DP+PE=DE,∴a+(2a-6)=4,解得a=10 3∴2a-3=11 3,∴P(103,113);当点P在AC下方时,过P作y轴的垂线,垂足为D,交BC于E,a=2,此时,CE=2,BE=2,即BC=2+2=4>AO,不合题意;综上所述,点P的坐标为P(103,113)故答案为P(103,113).8.如图,Rt△ABC中,∠C=90°.E为AB中点,D为AC上一点,BF∥AC交DE的延长线于点F.AC=6,BC=5.则四边形FBCD周长的最小值是______.【答案】16【解析】四边形FBCD 周长=BC+AC+DF ;当DF BC ⊥ 时,四边形FBCD 周长最小为5+6+5=169.如图,在△ABC 中,∠ABC =50°,∠ACB =60°,点E 在BC 的延长线上,∠ABC 的平分线BD 与∠ACE 的平分线CD 相交于点D ,连接AD ,以下结论:①∠BAC =70°;②∠DOC =90°;③∠BDC =35°;④∠DAC =55°,其中正确的是__________.(填写序号)【答案】①③④【解析】【分析】根据三角形内角和定理、角平分线的定义、三角形外角的性质、角平分线的性质解答即可.【详解】解:∵∠ABC =50°,∠ACB =60°,∴∠BAC =180°﹣50°﹣60°=70°,①正确;∵BD 是∠ABC 的平分线,∴∠DBC =12∠ABC =25°,∴∠DOC =25°+60°=85°,②错误; ∠BDC =60°﹣25°=35°,③正确;∵∠ABC 的平分线BD 与∠ACE 的平分线CD 相交于点D ,∴AD 是∠BAC 的外角平分线,∴∠DAC =55°,④正确.故答案为①③④.【点睛】本题考查的是角平分线的定义和性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.10.把两个三角板如图甲放置,其中90ACB DEC ∠=∠=︒,45A ∠=︒,30D ∠=︒,斜边12AB =,14CD =,把三角板DCE 绕着点C 顺时针旋转15︒得到△11D CE (如图乙),此时AB 与1CD 交于点O ,则线段1AD 的长度为_________.【答案】10【解析】试题分析:如图所示,∠3=15°,∠1E =90°, ∴∠1=∠2=75°, 又∵∠B=45°,∴∠OF 1E =∠B+∠1=45°+75°=120° ∴∠1D FO=60° ∵∠C 11D E =30°,∴∠5=∠4=90°, 又∵AC=BC ,AB=12, ∴OA=OB=6 ∵∠ACB=90°,∴CO=12AB=6, 又∵C 1D =CD=14, ∴O 1D =C 1D -OC=14-6=8, 在Rt △A 1D O 中,222211A 6810D OA OD =+=+=点睛:本题主要考查的就是旋转的性质、三角形的外角性质、直角三角形的性质及判定以及勾股定理的应用.解决这个问题的关键就是首先根据三角形外角的性质以及旋转图形的性质得出△AO 1D 为直角三角形,然后根据直角三角形的性质得出AO 和O 1D 的长度,最后根据直角三角形的勾股定理得出答案.二、八年级数学全等三角形选择题(难)11.如图,在Rt △ABC 中,AB AC =,D 、E 是斜边BC 上两点,且∠DAE =45°,将△ADC 绕点A 顺时针旋转90︒后,得到△AFB ,连接EF .列结论:①△ADC ≌△AFB ;②△ABE ≌△ACD ;③△AED ≌△AEF ;④BE DC DE += 其中正确的是( )A .②④B .①④C .②③D .①③【答案】D【解析】解:∵将△ADC绕点A顺时针旋转90 后,得到△AFB,∴△ADC≌△AFB,故①正确;②无法证明,故②错误;③∵△ADC≌△AFB,∴AF=AD,∠FAB=∠DAC.∵∠DAE=45°,∴∠BAE+∠DAC=45°,∠FA E=∠DAE=45°.在△FAE和△DAE中,∵AF=AD,∠FAE=∠DAE,AE=AE,∴△FAE≌△DAE,故③正确;④∵△ADC≌△AFB,∴DC=BF,∵△FAE≌△DAE,∴EF=ED,∵BF+BE>EF,∴DC+BE>ED .故④错误.故选D.12.如图, AB=AC,AD=AE, BE、CD交于点O,则图中全等三角形共有()A.五对B.四对C.三对D.二对【答案】A【解析】如图,由已知条件可证:①△ABE≌△ACD;②△DBC≌△ECB;③△BDO≌△ECO;④△ABO≌△ACO;⑤△ADO≌△AEO;∴图中共有5对全等三角形.故选A.13.下列条件中,不能判定两个直角三角形全等的是( )A.两条直角边对应相等B.有两条边对应相等C.斜边和一锐角对应相等D.一条直角边和斜边对应相等【答案】B【解析】根据全等三角形的判定SAS,可知两条直角边对应相等的两个直角三角形全等,故A不正确;根据一条直角边和斜边对应相等的两个直角三角形,符合全等三角形的判定定理HL,能判定全等;若两条直角边对应相等的两个直角三角形,符合全等三角形的判定定理SAS,也能判全等,但是有两边对应相等,没说明是什么边对应,故不能判定,故B正确.根据全等三角形的判定AAS,可知斜边和一锐角对应相等的两直角三角形全等,故C不正确;根据直角三角形的判定HL,可知一条直角边和斜边对应相等两直角三角形全等,故D不正确.故选B.点睛:此题主要考查了直角三角形全等的判定,解题时利用三角形全等的判定SSS,SAS,ASA,AAS,HL,直接判断即可.14.如图所示,在Rt ABC∆中,E为斜边AB的中点,ED AB⊥,且:1:7CAD BAD∠∠=,则BAC∠=( )A.70B.45C.60D.48【答案】D【解析】根据线段的垂直平分线,可知∠B=∠BAD,然后根据直角三角形的两锐角互余,可得∠BAC+∠B=90°,设∠CAD=x,则∠BAD=7x,则x+7x+7x=90°,解得x=6°,因此可知∠BAC=∠CDA+∠BAD=6°+42°=48°.故选:D.点睛:此题主要考查了线段垂直平分线的性质,利用线段垂直平分线的性质和直角三角形的性质求角的关系,根据比例关系设出未知数,然后根据角的关系列方程求解是解题关键.15.如图,BD是∠ABC的角平分线,AD⊥AB,AD=3,BC=5,则△BCD的面积为()A.7.5 B.8 C.10D.15【答案】A【解析】作DE⊥BC于E,根据角平分线的性质,由BD是∠ABC的角平分线,AD⊥AB,DE⊥BC,求出DE=DA=3,根据三角形面积公式计算S△BCD=12×BC×DE=7.5,故选:A.16.如图,在Rt△ABC中,∠CBA=90°,∠CAB的角平分线AP和∠ACB外角的平分线CF相交于点D,AD交CB于点P,CF交AB的延长线于点F,过点D作DE⊥CF交CB的延长线于点G,交AB的延长线于点E,连接CE并延长交FG于点H,则下列结论:①∠CDA=45°;②AF-CG=CA;③DE=DC;④FH=CD+GH;⑤CF=2CD+EG;其中正确的有()A.①②④B.①②③C.①②④⑤D.①②③⑤【答案】D【解析】试题解析:①利用公式:∠CDA=12∠ABC=45°,①正确;②如图:延长GD与AC交于点P',由三线合一可知CG=CP',∵∠ADC=45°,DG⊥CF,∴∠EDA=∠CDA=45°,∴∠ADP=∠ADF,∴△ADP'≌△ADF(ASA),∴AF=AP'=AC+CP'=AC+CG,故②正确;③如图:∵∠EDA=∠CDA ,∠CAD=∠EAD ,从而△CAD ≌△EAD ,故DC=DE ,③正确;④∵BF ⊥CG ,GD ⊥CF ,∴E 为△CGF 垂心,∴CH ⊥GF ,且△CDE 、△CHF 、△GHE 均为等腰直角三角形,∴2CD ,故④错误;⑤如图:作ME ⊥CE 交CF 于点M ,则△CEM 为等腰直角三角形,从而CD=DM ,CM=2CD ,EM=EC ,∵∠MFE=∠CGE ,∠CEG=∠EMF=135°,∴△EMF ≌△CEG (AAS ),∴GE=MF ,∴CF=CM+MF=2CD+GE ,故⑤正确;故选D点睛:本题考查了角平分线的性质、等腰三角形的判定与性质、三角形垂心的定义和性质、全等三角形的判定与性质等多个知识点,技巧性很强,难度较大,要求学生具有较高的几何素养.对于这一类多个结论的判断型问题,熟悉常见的结论及重要定理是解决问题的关键,比如对第一个结论的判定,若熟悉该模型则可以秒杀.17.如图在ABC △中,P ,Q 分别是BC 、AC 上的点,作PR AB ⊥,PS AC ⊥,垂足分别是R ,S ,AQ PQ =,PR PS =,下面三个结论:①AS AR =;②PQ AB ∥;③BRP △≌CSP △.其中正确的是( ).A .①②B .②③C .①③D .①②③【答案】A【解析】连接AP ,由题意得,90ARP ASP ∠=∠=︒, 在Rt APR 和Rt APS 中,AP AP PR PS =⎧⎨=⎩, ∴△APR ≌()APS HL ,∴AS AR =,故①正确.BAP SAP ∠=∠,∴2SAB BAP SAP SAP ∠=∠+∠=∠,在AQP △中,∴AQ PQ =,∴QAP APQ ∠=∠,∴22CQP QAP APQ QAP SAP ∠=∠+∠=∠=∠,∴PQ AB ∥,故②正确; 在Rt BRP 和Rt CSP 中,只有PR PS =,不满足三角形全等的条件,故③错误.故选A .点睛:本题主要考查三角形全等的判定方法以及角平分线的判定和平行线的判定,准确作出辅助线是解决本题的关键.18.如图,ABC △中,60BAC ∠=︒,ABC ∠、ACB ∠的平分线交于E ,D 是AE 延长线上一点,且120BDC ∠=︒.下列结论:①120BEC ∠=︒;②DB DE =;③2BDE BCE ∠=∠.其中所有正确结论的序号有( ).A .①②B .①③C .②③D .①②③【答案】D【解析】 分析:根据三角形内角和等于180°求出∠ABC+∠ACB ,再根据角平分线的定义求出∠EBC+∠ECB ,然后求出∠BEC=120°,判断①正确;过点D 作DF ⊥AB 于F ,DG ⊥AC 的延长线于G ,根据角平分线上的点到角的两边的距离相等可得DF=DG ,再求出∠BDF=∠CDG ,然后利用“角边角”证明△BDF 和△CDG 全等,根据全等三角形对应边相等可得BD=CD ,再根据等边对等角求出∠DBC=30°,然后根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义求出∠DBE=∠DEB ,根据等角对等边可得BD=DE ,判断②正确,再求出B ,C ,E 三点在以D 为圆心,以BD 为半径的圆上,根据同弧所对的圆周角等于圆心角的一半可得∠BDE=2∠BCE ,判断③正确.详解:∵60BAC ∠=︒,∴18060120ABC ACB ∠+∠=︒-︒=︒,∵BE 、CE 分别为ABC ∠、ACB ∠的平分线,∴12EBC ABC ∠=∠,12ECB ACB ∠=∠, ∴11()1206022EBC ECB ABC ACB ∠+∠=∠+∠=⨯︒=︒, ∴180()18060120BEC EBC ECB ∠=︒-∠+∠=︒-︒=︒, 故①正确.如图,过点D 作DF AB ⊥于F ,DG AC ⊥的延长线于G ,∵BE 、CE 分别为ABC ∠、ACB ∠的平分线,∴AD 为BAC ∠的平分线,∴DF DG =,∴36090260120FDG ∠=︒-︒⨯-︒=︒,又∵120BDC ∠=︒,∴120BDF CDF ∠+∠=︒,120CDG CDF ∠+∠=︒.∴BDF CDG ∠=∠,∵在BDF 和CDG △中,90BFD CGD DF DGBDF CDG ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩, ∴BDF ≌()CDG ASA ,∴DB CD =, ∴1(180120)302DBC ∠=︒-︒=︒, ∴30DBC DBC CBE CBE ∠=∠+∠=︒+∠,∵BE 平分ABC ∠,AE 平分BAC ∠,∴ABE CBE ∠=∠,1302BAE BAC ∠=∠=︒, 根据三角形的外角性质, 30DEB ABE BAE ABE ∠=∠+∠=∠+︒,∴DEB DBE ∠=∠,∴DB DE =,故②正确.∵DB DE DC ==,∴B 、C 、E 三点在以D 为圆心,以BD 为半径的圆上,∴2BDE BCE ∠=∠,故③正确,综上所述,正确结论有①②③,故选:D .点睛:本题考查了角平分线的性质,全等三角形的判定与性质,等角对等边的性质,圆内接四边形的判定,同弧所对的圆周角等于圆心角的一半性质,综合性较强,难度较大,特别是③的证明.19.下列四组条件中,能够判定△ABC 和△DEF 全等的是( )A .AB=DE ,BC=EF ,∠A=∠DB .AC=EF ,∠C=∠F ,∠A=∠DC .∠A=∠D ,∠B=∠E ,∠C=∠FD .AC=DF ,BC=DE ,∠C=∠D【答案】D【解析】根据三角形全等的判定定理:SSS 、SAS 、ASA 、AAS 、HL ,逐一判断:A 、AB=DE ,BC=EF ,∠A=∠D ,不符合“SAS ”定理,不能判断全等;B 、AC=EF ,∠C=∠F ,∠A=∠D , 不符合“ASA”定理,不能判断全等;C、∠A=∠D,∠B=∠E,∠C=∠F ,“AAA”不能判定全等;不符合“SAS”定理,不对应,不能判断全等;D、AC=DF,BC=DE,∠C=∠D,可利用“SAS”判断全等;故选:D.点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.20.如图,,,,点D、E为BC边上的两点,且,连接EF、BF则下列结论:≌;≌;;,其中正确的有( )个.A.1B.2C.3D.4【答案】D【解析】【分析】根据∠DAF=90°,∠DAE=45°,得出∠FAE=45°,利用SAS证明△AED≌△AEF,判定①正确;由△AED≌△AEF得AF=AD,由,得∠FAB=∠CAD,又AB=AC, 利用SAS证明≌,判定②正确;先由∠BAC=∠DAF=90°,得出∠CAD=∠BAF,再利用SAS证明△ACD≌△ABF,得出CD=BF,又①知DE=EF,那么在△BEF中根据三角形两边之和大于第三边可得BE+BF>EF,等量代换后判定③正确;先由△ACD≌△ABF,得出∠C=∠ABF=45°,进而得出∠EBF=90°,判定④正确.【详解】‚解:①∵∠DAF=90°,∠DAE=45°,∴∠FAE=∠DAF-∠DAE=45°.在△AED与△AEF中,,∴△AED≌△AEF(SAS),①正确;②∵△AED≌△AEF,∴AF=AD,∵,∴∠FAB=∠CAD,∵AB=AC,∴≌,②正确;③∵∠BAC=∠DAF=90°,∴∠BAC-∠BAD=∠DAF-∠BAD,即∠CAD=∠BAF.在△ACD与△ABF中,,∴△ACD≌△ABF(SAS),∴CD=BF,由①知△AED≌△AEF,∴DE=EF.在△BEF中,∵BE+BF>EF,∴BE+DC>DE,③正确;④由③知△ACD≌△ABF,∴∠C=∠ABF=45°,∵∠ABE=45°,∴∠EBF=∠ABE+∠ABF=90°.④正确.故答案为D.【点睛】本题考查了勾股定理,全等三角形的判定与性质,等腰直角直角三角形的性质,三角形三边关系定理,相似三角形的判定,此题涉及的知识面比较广,解题时要注意仔细分析,有一定难度.21.如图,在△ABC中,AB=AC,高BD,CE交于点O,AO交BC于点F,则图中共有全等三角形()A.8对B.7对C.6对D.5对【答案】B【解析】【分析】易证△ABC是关于AF对称的图形,其中的小三角形也关于AF对称,共可找出7对三角形.【详解】全等的三角形有:①△AFB≌△AFC;②△CEB≌△BDC;③△AEO≌△ADO;④△EOB≌△DOC;⑤△OBF≌△OFC;⑥△AOB≌△AOC;⑦△AEC≌△ADB证明①△AFB≌△AFC∵AB=AC,CE⊥AB,BD⊥AC又∵1122ABCS AB CE AC BD==∴CE=BD∴在Rt△BCE和Rt△CBD中BC BCCE BD=⎧⎨=⎩∴△BCE≌△CBD∴BE=CD,∴AE=AD在Rt△AEO和Rt△ADO中AE ADAO AO=⎧⎨=⎩∴△AEO≌△ADO∴∠EOD=∠DOA在△BAF和△CAF中AB ACBAF CAFAF AF=⎧⎪∠=∠⎨⎪=⎩∴△BAF≌△CAF,得证其余全等证明过程类似故选:B【点睛】本题考查全等的证明,解题关键是利用等腰三角形的性质,推导出图形中边的关系,为证全等作准备22.在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,如图,那么下列各条件中,不能使Rt△AB C≌Rt△A′B′C′的是( )A.AB=A′B′=5,BC=B′C′=3B.AB=B′C′=5,∠A=∠B′=40°C.AC=A′C′=5,BC=B′C′=3D.AC=A′C′=5,∠A=∠A′=40°【答案】B【解析】∵在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°A选项:AB=A′B′=5,BC=B′C′=3,符合直角三角形全等的判定条件HL,∴A选项能使Rt△ABC≌Rt△A′B′C′;B选项:AB=B′C′=5,∠A=∠B′=40°,不符合符合直角三角形全等的判定条件,∴B选项不能使Rt△ABC≌Rt△A′B′C′;C选项符合Rt△ABC和Rt△A′B′C全等的判定条件SAS;∴C选项能使Rt△ABC≌Rt△A′B′C′;D选项符合Rt△ABC和Rt△A′B′C全等的判定条件ASA,∴D选项能使Rt△ABC≌Rt△A′B′C′;故选:B.点睛:此题主要考查学生对直角三角全等的判定的理解和掌握,解答此题不仅仅是掌握直角三角形全等的判定,还要熟练掌握其它判定三角形全等的方法,才能尽快选出此题的正确答案.23.如图,已知 AD 为△ABC 的高线,AD=BC,以 AB 为底边作等腰 Rt△ABE,连接 ED,EC,延长CE 交AD 于F 点,下列结论:①△ADE≌△BCE;②CE⊥DE;③BD=AF;④S△BDE=S△ACE,其中正确的有()A.①③B.①②④C.①②③④D.②③④【答案】C【解析】【分析】①易证∠CBE=∠DAE,即可求证:△ADE≌△BCE;②根据①结论可得∠AEC=∠DEB,即可求得∠AED=∠BEG,即可解题;③证明△AEF≌△BED即可;④易证△FDC是等腰直角三角形,则CE=EF,S△AEF=S△ACE,由△AEF≌△BED,可知S△BDE=S△ACE,所以S△BDE=S△ACE.【详解】∵AD为△ABC的高线,∴∠CBE+∠ABE+∠BAD=90°,∵Rt△ABE是等腰直角三角形,∴∠ABE=∠BAE=∠BAD+∠DAE=45°,AE=BE,∴∠CBE+∠BAD=45°,∴∠DAE=∠CBE,在△DAE和△CBE中,AE BE DAE CBE AD BC =⎧⎪∠=∠⎨⎪=⎩∴△ADE ≌△BCE (SAS );故①正确;②∵△ADE ≌△BCE ,∴∠EDA=∠ECB ,∵∠ADE+∠EDC=90°,∴∠EDC+∠ECB=90°,∴∠DEC=90°,∴CE ⊥DE ;故②正确;③∵∠BDE=∠ADB+∠ADE ,∠AFE=∠ADC+∠ECD ,∴∠BDE=∠AFE ,∵∠BED+∠BEF=∠AEF+∠BEF=90°,∴∠BED=∠AEF ,在△AEF 和△BED 中,BDE AFE BED AEF AE BE ∠∠⎧⎪∠∠⎨⎪⎩===∴△AEF ≌△BED (AAS ),∴BD=AF ;故③正确;④∵AD=BC ,BD=AF ,∴CD=DF ,∵AD ⊥BC ,∴△FDC 是等腰直角三角形,∵DE ⊥CE ,∴EF=CE ,∴S △AEF =S △ACE ,∵△AEF ≌△BED ,∴S △AEF =S △BED ,∴S △BDE =S △ACE .故④正确;综上①②③④都正确,故选:C .【点睛】本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△BFE ≌△CDE 是解题的关键.24.已知:如图,ABC ∆、CDE ∆都是等腰三角形,且CA CB =,CD CE =,ACB DCE α∠=∠=,AD 、BE 相交于点O ,点M 、N 分别是线段AD 、BE 的中点.以下4个结论:①AD BE =;②180DOB α∠=-;③CMN ∆是等边三角形;④连OC ,则OC 平分AOE ∠.正确的是( )A .①②③B .①②④C .①③④D .①②③④【答案】B【解析】【分析】 ①根据∠ACB=∠DCE 求出∠ACD=∠BCE,证出ACD BCE ≅△△即可得出结论,故可判断; ②根据全等求出∠CAD=∠CBE,根据三角形外角定理得∠DOB=∠OBA+∠BAO,通过等角代换能够得到∠DOB=∠CBA+∠BAC,根据三角形内角和定理即可求出∠CBA+∠BAC,即可求出∠DOB ,故可判断;③根据已知条件可求出AM=BN,根据SAS 可求出CAM CBN ≅,推出CM=CN ,∠ACM=∠BCN,然后可求出∠MCN=∠ACB=α,故可判断CMN ∆的形状;④在AD 上取一点P 使得DP=EO,连接CP ,根据ACD BCE ≅△△,可求出∠CEO=∠CDP ,根据SAS 可求出 CEO CDP ≅,可得∠COE=∠CPD,CP=CO,进而得到 ∠COP=∠COE ,故可判断.【详解】①正确,理由如下:∵ACB DCE α∠=∠=,∴∠ACB+∠BCD=∠DCE+∠BCD,即∠ACD=∠BCE,又∵CA=CB,CD=CE,∴ACD BCE ≅△△(SAS),∴AD=BE,故①正确;②正确,理由如下:由①知,ACD BCE ≅△△,∴∠CAD=∠CBE,∵∠DOB 为ABO 的外角,∴∠DOB=∠OBA+∠BAO=∠EBC+∠CBA+∠BAO=∠DAC+∠BAO+∠CBA=∠CBA+∠BAC,∵∠CBA+∠BAC+∠ACB=180°,∠ACB=α,∴∠CBA+∠BAC=180°-α,即∠DOB=180°-α,故②正确;③错误,理由如下:∵点M 、N 分别是线段AD 、BE 的中点,∴AM= 12AD,BN= 12BE, 又∵由①知,AD=BE,∴AM=BN,又∵∠CAD=∠CBE,CA=CB,∴CAM CBN ≅(SAS), ∴CM=CN ,∠ACM=∠BCN,∴∠MCN=∠MCB+∠CBN=∠MCB+∠ACM=∠ACB=α,∴MCN △为等腰三角形且∠MCN=α,∴MCN △不是等边三角形,故③错误;④正确,理由如下:如图所示,在AD 上取一点P 使得DP=EO,连接CP ,由①知,ACD BCE ≅△△,∴∠CEO=∠CDP ,又∵CE=CD,EO=DP ,∴CEO CDP ≅(SAS),∴∠COE=∠CPD,CP=CO,∴∠CPO=∠COP ,∴∠COP=∠COE,即OC 平分∠AOE,故④正确;故答案为:B.【点睛】本题考查了三角形全等的判定和性质,三角形内角和定理和外角定理,等边三角形的判定,根据已知条件作出正确的辅助线,找出全等三角形是解题的关键.25.如图,在△ABC中,∠ABC=45°, BC=4,以AC为直角边,点A为直角顶点向△ABC的外侧作等腰直角三角形ACD,连接BD,则△DBC的面积为( ) .A.8 B.10 C.42D.82【答案】A【解析】【分析】将△ABD绕着点A顺时针旋转90°得到△AEC,BD与EC交于点O,连接BE,根据旋转的性质得到AE=AB,∠BAE=∠DOC=90°,过D点作DF⊥BC,证△EBC≌BFD,可得DF=BC=4,再用三角形面积公式即可得出答案.【详解】解:如下图所示,将△ABD绕着点A顺时针旋转90°得到△AEC,BD与EC交于点O,连接BE,根据旋转的性质可知EC=BD,AE=AB,∠BAE=∠DOC=90°,∴△ABE是等腰直角三角形,∴∠ABE=45°,又∵∠ABC=45°,∴∠EBC=90°,∵∠BDF+∠DBF=90°,∠ECB+∠DBF=90°,∴∠BDF=∠ECB在△EBC和△BFD中EBC=BFD=90ECB=BDFEC=BD⎧∠∠⎪∠∠⎨⎪⎩∴△EBC≌△BFD(AAS)∴DF=BC=4∴△DBC的面积=11BC DF=44=8 22⋅⨯⨯故选A.【点睛】本题考查了旋转的性质,等腰直角三角形的性质,全等三角形的判定,是一道综合性较强的题,难度较大,关键是正确的作出辅助线构造全等三角形.26.如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②BF=BA;③PH=PD;④连接CP,CP平分∠ACB,其中正确的是()A.①②③B.①②④C.①③④D.①②③④【答案】D【解析】分析:根据三角形内角和定理以及角平分线定义判断①;根据全等三角形的判定和性质判断②③;根据角平分线的判定与性质判断④.详解:在△ABC中,∵∠ACB=90°,∴∠BAC+∠ABC=90°,又∵AD、BE分别平分∠BAC、∠ABC,∴∠BAD+∠ABE=(∠BAC+∠ABC)=45°,∴∠APB=135°,故①正确.∴∠BPD=45°,又∵PF⊥AD,∴∠FPB=90°+45°=135°,∴∠APB=∠FPB,又∵∠ABP=∠FBP,BP=BP,∴△ABP≌△FBP,∴∠BAP=∠BFP,AB=FB,PA=PF,故②正确.在△APH和△FPD中,∵∠APH=∠FPD=90°,∠PAH=∠BAP=∠BFP,PA=PF,∴△APH≌△FPD,∴PH=PD,故③正确.∵△ABC 的角平分线AD 、BE 相交于点P ,∴点P 到AB 、AC 的距离相等,点P 到AB 、BC 的距离相等,∴点P 到BC 、AC 的距离相等,∴点P 在∠ACB 的平分线上,∴CP 平分∠ACB,故④正确.故选D .点睛:本题考查了角平分线的判定与性质,三角形全等的判定方法,三角形内角和定理.掌握相关性质是解题的关键.27.具备下列条件的两个三角形,可以证明它们全等的是( ).A .一边和这一边上的高对应相等B .两边和第三边上的中线对应相等C .两边和其中一边的对角对应相等D .直角三角形的斜边对应相等【答案】B【解析】【分析】根据判定两个三角形全等的一般方法有:SSS 、SAS 、ASA 、AAS 、HL 分别进行分析.【详解】解:A 、一边和这边上的高对应相等,无法得出它们全等,故此选项错误;B 、两边和第三边上的中线对应相等,通过如图所示方式(倍长中线法)可以证明它们全等(△ABC ≌△A ′B ′C ′),故此选项正确. .C 、两边和其中一边的对角对应相等,无法利用ASS 得出它们全等,故此选项错误;D 、直角三角形的斜边对应相等,无法得出它们全等,故此选项错误.故选:B .【点睛】本题考查三角形全等的判定方法,注意:AAA 、SSA 不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.28.如图,ABC ∆中,45ABC ∠=,CD AB ⊥于D ,BE 平分ABC ∠,且BE AC ⊥于E,与CD相交于点F,H是BC边的中点,连接DH与BE相交于点G,下列结论正确的有( )个①BF AC=;②12AE BF=;③67.5A∠=;④DGF∆是等腰三角形;⑤ADGE GHCES S=四边形四边形.A.5个B.4个C.3个D.2个【答案】B【解析】【分析】只要证明△BDF≌△CDA,△BAC是等腰三角形,∠DGF=∠DFG=67.5°,即可判断①②③④正确,作GM⊥BD于M,只要证明GH<DG即可判断⑤错误.【详解】∵CD⊥AB,BE⊥AC,∴∠BDC=∠ADC=∠AEB=90°,∴∠A+∠ABE=90°,∠ABE+∠DFB=90°,∴∠A=∠DFB,∵∠ABC=45°,∠BDC=90°,∴∠DCB=90°−45°=45°=∠DBC,∴BD=DC,在△BDF和△CDA中BDF CDAA DFBBD CD∠∠⎧⎪∠∠⎨⎪⎩===,∴△BDF≌△CDA(AAS),∴BF=AC,故①正确.∵∠ABE=∠EBC=22.5°,BE⊥AC,∴∠A=∠BCA=67.5°,故③正确,∴BA=BC,∵BE⊥AC,∴AE=EC=12AC=12BF,故②正确,∵BE平分∠ABC,∠ABC=45°,∴∠ABE =∠CBE =22.5°,∵∠BDF =∠BHG =90°,∴∠BGH =∠BFD =67.5°,∴∠DGF =∠DFG =67.5°,∴DG =DF ,故④正确.作GM ⊥AB 于M . ∵∠GBM =∠GBH ,GH ⊥BC ,∴GH =GM <DG ,∴S △DGB >S △GHB ,∵S △ABE =S △BCE ,∴S 四边形ADGE <S 四边形GHCE .故⑤错误,∴①②③④正确,故选:B .【点睛】此题是三角形综合题,考查了等腰三角形的性质,直角三角形的性质,全等三角形的性质和判定,三角形的面积等知识点的综合运用,第五个问题难度比较大,添加辅助线是解题关键,属于中考选择题中的压轴题.29.如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于( )A .150°B .180°C .210°D .225°【答案】B【解析】【分析】 根据SAS 可证得ABC ≌EDC ,可得出BAC DEC ∠∠=,继而可得出答案,再根据邻补角的定义求解.【详解】由题意得:AB ED =,BC DC =,D B 90∠∠==,ABC ∴≌EDC ,BAC DEC ∠∠∴=, 12180∠∠+=.故选B .【点睛】本题考查全等图形的知识,比较简单,解答本题的关键是判断出ABC ≌EDC ..30.如图,等腰直角△ABC 中,∠BAC=90︒,AD ⊥BC 于D ,∠ABC 的平分线分别交AC 、AD 于E 、F 两点,M 为EF 的中点,延长AM 交BC 于点N ,连接DM .下列结论:①AE=AF ;②AM ⊥EF ;③AF=DF ;④DF=DN ,其中正确的结论有( )A .1个B .2个C .3个D .4个【答案】C【解析】 试题解析:∵∠BAC=90°,AC=AB ,AD ⊥BC ,∴∠ABC=∠C=45°,AD=BD=CD ,∠ADN=∠ADB=90°,∴∠BAD=45°=∠CAD ,∵BE 平分∠ABC ,∴∠ABE=∠CBE=12∠ABC=22.5°, ∴∠BFD=∠AEB=90°-22.5°=67.5°,∴∠AFE=∠BFD=∠AEB=67.5°,∴AF=AE ,故①正确;∵M 为EF 的中点,∴AM ⊥EF ,故②正确;过点F 作FH ⊥AB 于点H ,∵BE 平分∠ABC ,且AD ⊥BC , ∴FD=FH <FA ,故③错误; ∵AM ⊥EF ,∴∠AMF=∠AME=90°,∴∠DAN=90°-67.5°=22.5°=∠MBN , 在△FBD 和△NAD 中 {FBD DANBD ADBDF ADN∠∠∠∠=== ∴△FBD ≌△NAD , ∴DF=DN ,故④正确; 故选C .。
八年级数学上册 轴对称填空选择专题练习(解析版)

八年级数学上册 轴对称填空选择专题练习(解析版)一、八年级数学全等三角形填空题(难)1.如图,已知△ABC 和△ADE 均为等边三角形,点O 是AC 的中点,点D 在射线BO 上,连结OE ,EC ,则∠ACE =_____°;若AB =1,则OE 的最小值=_____.【答案】3014【解析】【分析】 根据等边三角形的性质可得OC =12AC ,∠ABD =30°,根据"SAS"可证△ABD ≌△ACE ,可得∠ACE =30°=∠ABD ,当OE ⊥EC 时,OE 的长度最小,根据直角三角形的性质可求OE 的最小值.【详解】解:∵△ABC 的等边三角形,点O 是AC 的中点,∴OC =12AC ,∠ABD =30° ∵△ABC 和△ADE 均为等边三角形,∴AB =AC ,AD =AE ,∠BAC =∠DAE =60°,∴∠BAD =∠CAE ,且AB =AC ,AD =AE ,∴△ABD ≌△ACE (SAS ) ∴∠ACE =30°=∠ABD当OE ⊥EC 时,OE 的长度最小,∵∠OEC =90°,∠ACE =30°∴OE 最小值=12OC =14AB =14 故答案为:30,14【点睛】 本题考查了全等三角形的判定和性质,等边三角形的性质,熟练运用全等三角形的判定是本题的关键.2.如图,在等腰三角形ABC 中,90ABC ∠=,D 为AD 边上中点,多D 点作DE DF ⊥,交AB 于E ,交BC 于F ,若3AE =,2CF =,则ABC ∆的面积为______.【答案】252【解析】【分析】 利用等腰直角三角形斜边中点D 证明AD=BD ,∠DBC=∠A=45︒,再利用DE DF ⊥证得∠ADE=∠BDF ,由此证明△ADE ≌△BDF ,得到BC 的长度,即可求出三角形的面积.【详解】∵90ABC ∠=︒,AB=BC,∴∠A=45︒,∵D 为AC 边上中点,∴AD=CD=BD ,∠DBC=∠A=45︒,∠ADB=90︒,∵DE DF ⊥,∴∠EDB+∠BDF=∠EDB+∠ADE=90︒,∴∠ADE=∠BDF,∴△ADE ≌△BDF,∴BF==AE=3,∵CF=2,∴AB=BC=BF+CF=5,∴ABC ∆的面积为212BC ⋅=252, 故答案为:252. 【点睛】此题考查等腰直角三角形的性质,三角形全等的判定及性质.3.如图,△ABE ,△BCD 均为等边三角形,点A ,B ,C 在同一条直线上,连接AD ,EC ,AD 与EB 相交于点M ,BD 与EC 相交于点N ,下列说法正确的有:___________ ①AD=EC ;②BM=BN ;③MN ∥AC ;④EM=MB .【答案】①②③【解析】∵△ABE ,△BCD 均为等边三角形,∴AB=BE ,BC=BD ,∠ABE=∠CBD=60°,∴∠ABD=∠EBC ,在△ABD 和△EBC 中AB BE ABD EBC BD BC =⎧⎪∠=∠⎨⎪=⎩∴△ABD ≌△EBC(SAS),∴AD=EC ,故①正确;∴∠DAB=∠BEC ,又由上可知∠ABE=∠CBD=60°,∴∠EBD=60°,在△ABM 和△EBN 中MAB NEB AB BEABE EBN ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ABM ≌△EBN(ASA),∴BM=BN ,故②正确;∴△BMN 为等边三角形,∴∠NMB=∠ABM=60°,∴MN ∥AC ,故③正确;若EM=MB ,则AM 平分∠EAB ,则∠DAB=30°,而由条件无法得出这一条件,故④不正确;综上可知正确的有①②③,故答案为①②③.点睛:本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(即SSS 、SAS 、AAS 、ASA 和HL )和性质(即全等三角形的对应边相等,对应角相等).4.如图,52A ∠=︒,O 是ABC ∠、ACB ∠的角平分线交点,P 是ABC ∠、ACB ∠外角平分线交点,则BOC ∠=______︒,BPC ∠=_____︒,联结AP ,则PAB ∠=______︒,点O ____(选填“在”、“不在”或“不一定在”)直线AP 上.【答案】116 64 26 在【解析】【分析】∠ABC+∠ACB=180°-∠A,∠OBC+∠OCB= 12(∠ABC+∠ACB), ∠BOC=180°-(∠OBC+∠OCB),据此可求∠BOC的度数;∠BCP= 12∠BCE=12(∠A+∠ABC),∠PBC=12∠CBF=12(∠A+∠ACB),由三角形内角和定理得:∠BPC=180°-∠BCP-∠PBC,据此可求∠BPC的度数;作PG⊥AB于G,PH⊥AC于H,PK⊥BC于K,利用角平分线的性质定理可证明PG=PH,于是可证得AP平分∠BAC,据此可求∠PAB的度数;同理可证OA平分∠BAC,故点O在直线AP上.【详解】解:∵O点是∠ABC和∠ACB的角平分线的交点,∴∠OBC+∠OCB= 12(∠ABC+∠ACB)= 12(180°-∠A)=90°- 12∠A,∴∠BOC=180°-(∠OBC+∠OCB)=180°-90°+ 12∠A=90°+ 12∠A=90°+26°=116°;如图,∵BP、CP为△ABC两外角的平分线,∴∠BCP= 12∠BCE=12(∠A+∠ABC),∠PBC= 12∠CBF=12(∠A+∠ACB),由三角形内角和定理得:∠BPC=180°-∠BCP-∠PBC=180°- 12[∠A+(∠A+∠ABC+∠ACB)]=180°- 12(∠A+180°)=90°- 12∠A=90°-26°=64°.如图,作PG⊥AB于G,PH⊥AC于H,PK⊥BC于K,连接AP,∵BP、CP为△ABC两外角的平分线,PG⊥AB,PH⊥AC,PK⊥BC,∴PG=PK,PK=PH,∴PG=PH,∴AP平分∠BAC,∴PAB∠=26°同理可证OA平分∠BAC,点O在直线AP上.故答案是:(1) 116 ;(2) 64;(3) 26;(4) 在.【点睛】此题主要考查了角平分线的性质定理和判定定理及三角形内角和定理,熟知定理并正确作出辅助线是解题关键.5.如图,在等边△ABC中,AB=10,BD=4,BE=2,点P从点E出发沿EA方向运动,连结PD,以PD为边,在PD的右侧按如图所示的方式作等边△DPF,当点P从点E运动到点A 时,点F运动的路径长是________.【答案】8【解析】【分析】作FG⊥BC于点G,DE’⊥AB于点E’,易证E点和E’点重合,则∠FGD=∠DEP=90°;由∠EDB+∠PDF=90°可知∠EDP+∠GFD=90°,则易得∠EPD=∠GDF,再由PD=DF易证△EPD≌△GDF,则可得FG=DE,故F点的运动轨迹为平行于BC的线段,据此可进行求解.【详解】解:作FG⊥BC于点G,DE’⊥AB于点E’,由BD=4、BE=2与∠B=60°可知DE⊥AB,即∠∵DE’⊥AB,∠B=60°,∴BE’=BD×1=2,2∴E点和E’点重合,∴∠EDB=30°,∴∠EDB+∠PDF=90°,∴∠EDP+∠GFD=90°=∠EDP+∠DPE,∴∠DPE=∠GFD∵∠DEP=∠FGD=90°,FD=GP,∴△EPD≌△GDF,∴FG=DE,DG=PE,∴F点运动的路径与G点运动的路径平行,即与BC平行,由图可知,当P点在E点时,G点与D点重合,∵DG=PE,∴F点运动的距离与P点运动的距离相同,∴F点运动的路径长为:AB-BE=10-2=8,故答案为8.【点睛】通过构造垂直线段构造三角形全等,从而确定F点运动的路径,本题有一些难度.6.如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②AF∥EB;③∠FAN=∠EAM;④△ACN≌△ABM其中正确的有.【答案】①③④【解析】【分析】由∠E=∠F=90°,∠B=∠C,AE=AF,利用“AAS”得到△ABE与△ACF全等,根据全等三角形的对应边相等且对应角相等即可得到∠EAB与∠FAC相等,AE与AF相等,AB与AC相等,然后在等式∠EAB=∠FAC两边都减去∠MAN,得到∠EAM与∠FAN相等,然后再由∠E=∠F=90°,AE=AF,∠EAM=∠FAN,利用“ASA”得到△AEM与△AFN全等,利用全等三角形的对应边相等,对应角相等得到选项①和③正确;然后再∠C=∠B,AC=AB,∠CAN=∠BAM,利用“ASA”得到△ACN与△ABM全等,故选项④正确;若选项②正确,得到∠F与∠BDN相等,且都为90°,而∠BDN不一定为90°,故②错误.【详解】解:在△ABE和△ACF中,∠E=∠F=90°,AE=AF,∠B=∠C,∴△ABE≌△ACF,∴∠EAB=∠FAC,AE=AF,AB=AC,∴∠EAB-∠MAN=∠FAC-∠NAM,即∠EAM=∠FAN,在△AEM和△AFN中,∠E=∠F=90°,AE=AF,∠EAM=∠FAN,∴△AEM≌△AFN,∴EM=FN,∠FAN=∠EAM,故选项①和③正确;在△ACN和△ABM中,∠C=∠B,AC=AB,∠CAN=∠BAM(公共角),∴△ACN≌△ABM,故选项④正确;若AF∥EB,∠F=∠BDN=90°,而∠BDN不一定为90°,故②错误,则正确的选项有:①③④.故答案为①③④7.已知在△ABC 中,两边AB 、AC 的中垂线,分别交BC 于E 、G .若BC =12,EG =2,则△AEG 的周长是________.【答案】16或12.【解析】【分析】根据线段垂直平分线性质得出AE =BE ,CG =AG ,分两种情况讨论:①DE 和FG 的交点在△ABC 内,②DE 和FG 的交点在△ABC 外.【详解】∵DE ,FG 分别是△ABC 的AB ,AC 边的垂直平分线,∴AE =BE ,CG =AG .分两种情况讨论: ①当DE 和FG 的交点在△ABC 内时,如图1.∵BC =12,GE =2,∴AE +AG =BE +CG =12+2=14,△AGE 的周长是AG +AE +EG =14+2=16. ②当DE 和FG 的交点在△ABC 外时,如图2,△AGE 的周长是AG +AE +EG = BE +CG+EG =BC =12.故答案为:16或12.【点睛】本题考查了线段垂直平分线性质,注意:线段垂直平分线上的点到线段两个端点的距离相等.8.如图,已知ABC △是等边三角形,点D 在边BC 上,以AD 为边向左作等边ADE ,连结BE ,作BF AE ∥交AC 于点F ,若2AF =,4CF =,则AE =________.【答案】7【解析】【分析】证明△BAE ≌△CAD 得到ABE BAC ∠=∠,从而证得BE AF ,再得到AEBF 是平行四边形,可得AE=BF ,在三角形BCF 中求出BF 即可.【详解】作FH BC ⊥于H ,∵ABC 是等边三角形,2AF =,4CF =∴BC=AC=6在HCF 中, CF=4, 060BCF ∠=030,2CFD CH ∴∠==2224212FH ∴=-=22241227BF BH FH ∴=+=+=∵ABC 是等边三角形,ADE 是等边三角形∴AC=AB ,AD=AE ,060CAB DAE ∠=∠=CAD BAE ∴∠=∠CAD BAE ∴∆≅∆060ABE ACD ∴∠=∠=ABE BAC ∴∠=∠BE AF ∴∵BF AE∴AEBF 是平行四边形∴AE=BF= 27【点睛】本题考查全等三角形的判定和性质、平行四边形的判定和性质、等边三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.9.如图所示,在平行四边形ABCD 中,2AD AB =,F 是AD 的中点,作CE AB ⊥,垂足E 在线段上,连接EF 、CF ,则下列结论2BCD DCE ①∠=∠;EF CF =②;3DFE AEF ③∠=∠,2BEC CEF SS =④中一定成立的是______ .(把所有正确结论的序号都填在横线上)【答案】②③【解析】分析:由在平行四边形ABCD中,AD=2AB,F是AD的中点,易得AF=FD=CD,继而证得①∠DCF=12∠BCD;然后延长EF,交CD延长线于M,分别利用平行四边形的性质以及全等三角形的判定与性质得出△AEF≌△DMF(ASA),得出对应线段之间关系,进而得出答案.详解:①∵F是AD的中点,∴AF=FD,∵在▱ABCD中,AD=2AB,∴AF=FD=CD,∴∠DFC=∠DCF,∵AD∥BC,∴∠DFC=∠FCB,∴∠DCF=∠BCF,∴∠DCF=12∠BCD,即∠BCD=2∠DCF;故此选项错误;②延长EF,交CD延长线于M,∵四边形ABCD是平行四边形,∴AB∥CD,∴∠A=∠MDF,∵F为AD中点,∴AF=FD,在△AEF和△DFM中,A FDMAF DFAFE DFM∠∠⎧⎪⎨⎪∠∠⎩===,∴△AEF≌△DMF(ASA),∴FE=MF,∠AEF=∠M,∵CE⊥AB,∴∠AEC=90°,∴∠AEC=∠ECD=90°,∵FM=EF,∴FC=FM,故②正确;③设∠FEC=x,则∠FCE=x,∴∠DCF=∠DFC=90°-x,∴∠EFC=180°-2x,∴∠EFD=90°-x+180°-2x=270°-3x,∵∠AEF=90°-x,∴∠DFE=3∠AEF,故此选项正确.④∵EF=FM,∴S△EFC=S△CFM,∵MC>BE,∴S△BEC<2S△EFC故S△BEC=2S△CEF错误;综上可知:一定成立的是②③,故答案为②③.点睛:此题主要考查了平行四边形的性质以及全等三角形的判定与性质等知识,得出△AEF≌△DME是解题关键.10.如图,已知AB∥CD,O为∠CAB、∠ACD的角平分线的交点,OE⊥AC于E,且OE=2,CO=3,则两平行线间AB、CD的距离等于________.【答案】4【解析】试题解析:如图,过点O作MN,MN⊥AB于M,交CD于N,∵AB∥CD,∴MN⊥CD,∵AO是∠BAC的平分线,OM⊥AB,OE⊥AC,OE=2,∴OM=OE=2,∵CO是∠ACD的平分线,OE⊥AC,ON⊥CD,∴ON=OE=2,∴MN=OM+ON=4,即AB与CD之间的距离是4.点睛:要明确:①角的平分线上的点到角的两边的距离相等,②从一条平行线上的任意一点到另一条直线作垂线,垂线段的长度叫两条平行线之间的距离,③平行线间的距离处处相等.二、八年级数学全等三角形选择题(难)11.如图,点P 是AB 上任意一点,∠ABC=∠ABD ,还应补充一个条件,才能推出△APC ≌△APD .从下列条件中补充一个条件,不一定能推出△APC ≌△APD 的是( )A .BC=BD ;B .AC=AD ;C .∠ACB=∠ADB ;D .∠CAB=∠DAB【答案】B【解析】根据题意,∠ABC=∠ABD ,AB 是公共边,结合选项,逐个验证得出:A 、补充BC=BD ,先证出△BPC ≌△BPD ,后能推出△APC ≌△APD ,故正确;B 、补充AC=AD ,不能推出△APC ≌△APD ,故错误;C 、补充∠ACB=∠ADB ,先证出△ABC ≌△ABD ,后能推出△APC ≌△APD ,故正确; D 、补充∠CAB=∠DAB ,先证出△ABC ≌△ABD ,后能推出△APC ≌△APD ,故正确. 故选B .点睛:本题考查了三角形全等判定,三角形全等的判定定理:有AAS ,SSS ,ASA ,SAS .注意SSA 是不能证明三角形全等的,做题时要逐个验证,排除错误的选项.12.在ABC 中,2,72A B ACB ∠=∠∠≠︒,CD 平分ACB ∠,P 为AB 的中点,则下列各式中正确的是( )A .AD BC CD =-B .AD BC AC =- C .AD BC AP =-D .AD BC BD =-【答案】B【解析】【分析】 可在BC 上截取CE=CA ,连接DE ,可得△ACD ≌△ECD ,得DE=AD ,进而再通过线段之间的转化得出线段之间的关系.【详解】解:∵∠A=2∠B,∴∠A﹥∠B∴BC﹥AC∴可在BC上截取CE=CA,连接DE(如图),,∴∠ACD=∠BCD∵CD平分ACB又∵CD=CD,CE=CA∴△ACD≌△ECD,∴AD=ED,∠CED=∠A=2∠B又∠CED=∠B+∠BDE∴∠B=∠BDE∴AD=DE=BE,∴BC=BE+EC=AD+AC所以AD=BC-AC故选:B若A选项成立,则CD=AC,∴∠A=∠CDA=∠CDE=∠CED=2∠B=2∠EDB∴∠CDA+∠CDE+∠EDB=180°即5∠EDB=180°∴∠EDB=36°∴∠A=72°,∠B=36°∴∠ACB=72°与已知∠ACB≠72°矛盾,故选项A不正确;假设C选项成立,则有AP=AC,作∠BAC的平分线,连接FP,∴△CAF≌△PAF≌△PBF,∴∠CFA=∠AFP=∠PFB=60°∠B=30°,∠ACB=90°当∠ACB=90°时,选项C才成立,∴当∠ACB≠72°时,选项C不一定成立;假设D选项成立,则AD=BC-BD由图可知AD=BA-BD∴AB=BC∴∠A=∠ACB=2∠B∴∠A+∠ACB+∠B=180°∴∠B=36°,∠ACB=72这与已知∠ACB≠72°矛盾,故选项D不成立.故选:B【点睛】本题考查的是考查的是利用角的平分线的性质说明线段之间的关系.,,13.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以M,N为圆心,大于12MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )①AD平分∠BAC;②作图依据是S.A.S;③∠ADC=60°;④点D在AB的垂直平分线上A.1个B.2个C.3个D.4个【答案】C【解析】①根据作图的过程可以判定AD是∠BAC的∠平分线;②根据作图的过程可以判定出AD的依据;③利用角平分线的定义可以推知∠CAD=30°,则由直角三角形的性质求∠ADC的度数;④利用等角对等边可以证得△ADB的等腰三角形,由等腰三角形的“三合一”的性质可以证明点在AB的中垂线上.解:如图所示,①根据作图的过程可知,AD是∠BAC的∠平分线;故①正确;②根据作图的过程可知,作出AD的依据是SSS;故②错误;③∵在△ABC中,∠C=90°,∠B=30°,∴∠CBA=60°.又∵AD是∠BAC的平分线,∴∠1=∠2=12∠CAB=30°,∴∠3=90°-∠2=60°,即∠ADC=60°.故③正确;④∵∠1=∠B=30°,∴AD=BD,∴点D在AB的中垂线上.故④正确;故选C.“点睛”此题主要考查的是作图-基本作图,涉及到角平分线的作法以及垂直平分线的性质,熟练根据角平分线的性质得出∠ADC的度数是解题的关键.14.在△ABC中,∠C=90°,D为AB的中点,ED⊥AB,∠DAE=∠CAE,则∠CAB=()A.30°B.60°C.80 °D.50°【答案】B【解析】试题解析:∵D为AB的中点,ED⊥AB,∴DE为线段AB的垂直平分线,∴AE=BE,∴∠DAE=∠DBE,∴∠DAE=∠DBE=∠CAE,在Rt△ABC中,∵∠CAB+∠DBE=90°,∴∠CAE+∠DAE+∠DBE=90°,∴3∠DBE=90°,∴∠DBE=30°,∴∠CAB=90°-∠DBE=90°-30°=60°.故选B.15.如图,已知,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA.下面结论:①△ABD≌△EBC;②AC=2CD;③AD=AE=EC;④∠BCE+∠BCD=180°.其中正确的是()A.①②③B.①②④C.①③④D.②③④【答案】C【解析】已知BD为△ABC的角平分线,根据角平分线的定义可得∠ABD=∠CBD,在△AB D和△EB C 中,BD=BC,∠ABD=∠CBD,BE=BA,由SAS可判定△ABD≌△EBC,即可得①正确;根据已知条件,无法证明AC=2CD,②错误;已知BD为△ABC的角平分线,BD=BC,BE=BA,可得∠BCD=∠BDC=∠BAE=∠BEA,再由∠BCE=∠BDA,∠BCE=∠BCD+∠DCE,∠BDA=∠DAE+∠BEA,∠BCD=∠BEA,可得∠DCE=∠DAE,所以AE=EC;再由△ABD≌△EBC,可得AD=EC,所以AD=AE=EC,即③正确;由△ABD≌△EBC,可得∠BCE=∠BDA,所以∠BCE+∠BCD=∠BDA+∠BDC=180°,④正确.故选C.点睛:本题考查了全等三角形的判定及性质、等腰三角形的的性质、三角形外角的性质,本题中熟练求证三角形全等和熟练运用全等三角形对应角、对应边相等性质是解题的关键.16.在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB于点E,AB=18cm,则△DBE的周长为()A.16cm B.8cm C.18cm D.10cm【答案】C【解析】因为∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,易证△ACD≌△AED,所以AE=AC=BC,ED=CD.△DBE的周长=BE+DE+DB=BE+CD+DB=BE+BC=BE+AE=AB.因为AB=12,所以△DBE的周长=12.故选C.点睛:本题主要考查了全等三角形的判定的性质及角平分线的性质定理,角的平分线上的点到角的两边的距离相等,运用这个性质,结合等腰三角形有性质,将△DBE的周长转化为AB的长.17.如图,BD是∠ABC的角平分线,AD⊥AB,AD=3,BC=5,则△BCD的面积为()A.7.5 B.8 C.10D.15【答案】A【解析】作DE⊥BC于E,根据角平分线的性质,由BD是∠ABC的角平分线,AD⊥AB,DE⊥BC,求出DE=DA=3,根据三角形面积公式计算S△BCD=12×BC×DE=7.5,故选:A.18.如图,在Rt△ABC中,∠CBA=90°,∠CAB的角平分线AP和∠ACB外角的平分线CF相交于点D,AD交CB于点P,CF交AB的延长线于点F,过点D作DE⊥CF交CB的延长线于点G,交AB的延长线于点E,连接CE并延长交FG于点H,则下列结论:①∠CDA=45°;②AF-CG=CA;③DE=DC;④FH=CD+GH;⑤CF=2CD+EG;其中正确的有()A.①②④B.①②③C.①②④⑤D.①②③⑤【答案】D【解析】试题解析:①利用公式:∠CDA=12∠ABC=45°,①正确;②如图:延长GD与AC交于点P',由三线合一可知CG=CP',∵∠ADC=45°,DG⊥CF,∴∠EDA=∠CDA=45°,∴∠ADP=∠ADF,∴△ADP'≌△ADF(ASA),∴AF=AP'=AC+CP'=AC+CG,故②正确;③如图:∵∠EDA=∠CDA,∠CAD=∠EAD,从而△CAD≌△EAD,故DC=DE,③正确;④∵BF⊥CG,GD⊥CF,∴E为△CGF垂心,∴CH⊥GF,且△CDE、△CHF、△GHE均为等腰直角三角形,∴2CD,故④错误;⑤如图:作ME⊥CE交CF于点M,则△CEM为等腰直角三角形,从而CD=DM,CM=2CD,EM=EC,∵∠MFE=∠CGE,∠CEG=∠EMF=135°,∴△EMF≌△CEG(AAS),∴GE=MF,∴CF=CM+MF=2CD+GE ,故⑤正确;故选D点睛:本题考查了角平分线的性质、等腰三角形的判定与性质、三角形垂心的定义和性质、全等三角形的判定与性质等多个知识点,技巧性很强,难度较大,要求学生具有较高的几何素养.对于这一类多个结论的判断型问题,熟悉常见的结论及重要定理是解决问题的关键,比如对第一个结论的判定,若熟悉该模型则可以秒杀.19.已知111122,A B C A B C △△的周长相等,现有两个判断:①若21212112,A A B C B A A C ==,则111222A B C A B C △≌△;②若12=A A ∠∠,1122=A C A C ,则111222A B C A B C △≌△,对于上述的两个判断,下列说法正确的是( )A .①,②都正确B .①,②都错误C .①错误,②正确D .①正确,②错误 【答案】A【解析】【分析】根据SSS 即可推出△111A B C ≅△222A B C ,判断①正确;根据相似三角形的性质和判定和全等三角形的判定推出即可.【详解】解:①△111A B C ,△222A B C 的周长相等,1122A B A B =,1122AC A C =,1122B C B C ∴=,∴△111A B C ≅△222()A B C SSS ,∴①正确;②如图,延长11A B 到1D ,使1111B D B C =,,延长22A B 到2D ,使2222B D B C =,∴111111A D A B B C =+,222222A D A B B C =+,∵111122,A B C A B C △△的周长相等,1122=A C A C∴1122A D A D =,在△111A B D 和△222A B D 中1122121122==A D A DA AA C A C=⎧⎪∠∠⎨⎪⎩,∴△111A B D≅△222A B D(SAS)∴12=D D∠∠,∵1111B D B C=,2222B D B C=∴1111=D D C B∠∠,2222=D D C B∠∠,又∵1111111=A B C D D C B∠∠+∠,2222222=A B C D D C B∠∠+∠,∴1112221==2A B C A B C D∠∠∠,在△111A B C和△222A B C中111222121122===A B C A B CA AA C A C∠∠⎧⎪∠∠⎨⎪⎩,∴△111A B C≅△222A B C(AAS),∴②正确;综上所述:①,②都正确.故选:A.【点睛】本题考查了全等三角形的判定、等腰三角形的性质,能构造全等三角形、综合运用定理进行推理是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,而AAA和SSA不能判断两三角形全等.20.如图,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE交于O,连结AO,则图中共有全等三角形的对数为()A.2对B.3对C.4对D.5对【答案】C【解析】【分析】先根据条件,利用AAS可知△ADB≌△AEC,然后再利用HL、ASA即可判断△AOE≌△AOD,△BOE≌△COD,△AOC≌△AOB.【详解】∵AB=AC,BD⊥AC于D,CE⊥AB于E,∴∠ADB=∠AEC=90°,∵∠A为公共角,∴△ADB≌△AEC,(AAS)∴AE=AD,∠B=∠C∴BE=CD,∵AE=AD,OA=OA,∠ADB=∠AEC=90°,∴△AOE≌△AOD(HL),∴∠OAC=∠OAB,∵∠B=∠C,AB=AC,∠OAC=∠OAB,∴△AOC≌△AOB.(ASA)∵∠B=∠C,BE=CD,∠ODC=∠OEB=90°,∴△BOE≌△COD(ASA).综上:共有4对全等三角形,故选C.【点睛】本题考查三角形全等的判定方法和全等三角形的性质,判定两个三角形全等的一般方法有:SSS、SAS、ASA、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.做题时要从已知条件开始结合全等的判定方法逐一验证,由易到难,不重不漏.21.如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,DH⊥BC于H,交BE于G.下列结论:①BD=CD;②AD+CF=BD;③CE=12BF;④AE=BG.其中正确的是A.①②B.①③C.①②③D.①②③④【答案】C【解析】【分析】根据∠ABC=45°,CD⊥AB可得出BD=CD,利用AAS判定Rt△DFB≌Rt△DAC,从而得出DF=AD,BF=AC.则CD=CF+AD,即AD+CF=BD;再利用AAS判定Rt△BEA≌Rt△BEC,得出CE=AE=12AC,又因为BF=AC所以CE=12AC=12BF,连接CG.因为△BCD是等腰直角三角形,即BD=CD.又因为DH⊥BC,那么DH垂直平分BC.即BG=CG.在Rt△CEG中,CG是斜边,CE是直角边,所以CE<CG.即AE<BG.【详解】解:∵CD⊥AB,∠ABC=45°,∴△BCD是等腰直角三角形.∴BD=CD.故①正确;在Rt△DFB和Rt△DAC中,∵∠DBF=90°−∠BFD,∠DCA=90°−∠EFC,且∠BFD=∠EFC,∴∠DBF=∠DCA.又∵∠BDF=∠CDA=90°,BD=CD,∴△DFB≌△DAC.∴BF=AC;DF=AD.∵CD=CF+DF,∴AD+CF=BD;故②正确;在Rt△BEA和Rt△BEC中.∵BE平分∠ABC,∴∠ABE=∠CBE.又∵BE=BE,∠BEA=∠BEC=90°,∴Rt△BEA≌Rt△BEC.∴CE=AE=12 AC.又由(1),知BF=AC,∴CE=12AC=12BF;故③正确;连接CG.∵△BCD是等腰直角三角形,∴BD=CD.又DH⊥BC,∴DH垂直平分BC.∴BG=CG.在Rt△CEG中,∵CG是斜边,CE是直角边,∴CE<CG.∵CE=AE,∴AE<BG.故④错误.故选C.【点睛】本题考查了等腰直角三角形、等腰三角形的判定与性质、全等三角形的判定与性质.此类问题涉及知识点较多,需要对相关知识点有很高的熟悉度.22.如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边三角形ABC 和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②AP=BQ;③PQ∥AE;④DE=DP;⑤∠AOE=120°;其中正确结论的个数为()A.2个B.3个C.4个D.5个【答案】C【解析】【分析】①由于△ABC和△CDE是等边三角形,可知AC=BC,CD=CE,∠ACB=∠DCE=60°,从而证出△ACD≌△BCE,可推知AD=BE,故①正确;②由△ACD≌△BCE得∠CBE=∠DAC,加之∠ACB=∠DCE=60°,AC=BC,得到△ACP≌△BCQ (ASA),所以AP=BQ;故②正确;③根据②△CQB≌△CPA(ASA),再根据∠PCQ=60°推出△PCQ为等边三角形,又由∠PQC=∠DCE,根据内错角相等,两直线平行,可知③正确;④根据∠QCP=60°,∠DPC=∠BCA+∠PAC>60°,可知PD≠CD,可知④错误;⑤利用等边三角形的性质,BC∥DE,再根据平行线的性质得到∠CBE=∠DEO,于是∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°,由平角的性质可得∠AOE=120°,可知⑤正确;【详解】①∵△ABC和△CDE为等边三角形∴AC=BC,CD=CE,∠BCA=∠DCB=60°∴∠ACD=∠BCE∴△ACD≌△BCE(SAS)∴AD=BE,故①正确;由(1)中的全等得∠CBE=∠DAC,且BC=AC,∠ACB=∠BCQ=60°∴△CQB≌△CPA(ASA),∴AP=BQ,故②正确;∵△CQB≌△CPA,∴PC=PQ,且∠PCQ=60°∴△PCQ为等边三角形,∴∠PQC=∠DCE=60°,∴PQ∥AE,故③正确,∵∠QCP=60°,∠DPC=∠BCA+∠PAC>60°,∴PD≠CD,∴DE≠DP,故④DE=DP错误;∵BC∥DE,∴∠CBE=∠BED,∵∠CBE=∠DAE,∴∠AOB=∠OAE+∠AEO=60°,∴∠AOE=120°,故⑤正确,故选C.【点睛】本题考查了全等三角形的判定与性质,利用了等边三角形的判定与性质,全等三角形的判定与性质,平行线的判定与性质,综合性较强,题目难度较大.23.如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,∠EAF=12∠BAD,若DF=1,BE=5,则线段EF的长为()A.3 B.4 C.5 D.6【答案】B【解析】【分析】在BE上截取BG=DF,先证△ADF≌△ABG,再证△AEG≌△AEF即可解答.【详解】在BE上截取BG=DF,∵∠B+∠ADC=180°,∠ADC+∠ADF=180°,∴∠B=∠ADF,在△ADF与△ABG中AB ADB ADFBG DF=⎧⎪∠=∠⎨⎪=⎩,∴△ADF≌△ABG(SAS),∴AG=AF,∠FAD=∠GAB,∵∠EAF=12∠BAD,∴∠FAE=∠GAE,在△AEG与△AEF中AG AFFAE GAEAE AE=⎧⎪∠=∠⎨⎪=⎩,∴△AEG≌△AEF(SAS)∴EF=EG=BE﹣BG=BE﹣DF=4.故选:B.【点睛】考查了全等三角形的判定与性质,证明三角形全等是解决问题的关键.24.如图,在△ABC中,AB=AC,∠BAC=45°,BD⊥AC,垂足为D点,AE平分∠BAC,交BD于点F交BC于点E,点G为AB的中点,连接DG,交AE于点H,下列结论错误的是()A.AH=2DF B.HE=BE C.AF=2CE D.DH=DF【答案】A【解析】【分析】通过证明△ADF≌△BDC,可得AF=BC=2CE,由等腰直角三角形的性质可得AG=BG,DG⊥AB,由余角的性质可得∠DFA=∠AHG=∠DHF,可得DH=DF,由线段垂直平分线的性质可得AH=BH,可求∠EHB=∠EBH=45°,可得HE=BE,即可求解.【详解】解:∵∠BAC=45°,BD⊥AC,∴∠CAB=∠ABD=45°,∴AD=BD,∵AB=AC,AE平分∠BAC,∴CE=BE=12BC,∠CAE=∠BAE=22.5°,AE⊥BC,∴∠C+∠CAE=90°,且∠C+∠DBC=90°,∴∠CAE=∠DBC,且AD=BD,∠ADF=∠BDC=90°,∴△ADF≌△BDC(AAS)∴AF=BC=2CE,故选项C不符合题意,∵点G为AB的中点,AD=BD,∠ADB=90°,∠CAE=∠BAE=22.5°,∴AG=BG,DG⊥AB,∠AFD=67.5°∴∠AHG=67.5°,∴∠DFA=∠AHG=∠DHF,∴DH=DF,故选项D不符合题意,连接BH,∵AG=BG,DG⊥AB,∴AH=BH,∴∠HAB=∠HBA=22.5°,∴∠EHB=45°,且AE⊥BC,∴∠EHB=∠EBH=45°,∴HE=BE,故选项B不符合题意,故选:A.【点睛】本题考查三角形全等的性质与判定,等腰直角三角形的性质,关键在于熟练掌握基本知识点,灵活运用知识点.25.如图,△ABC是等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS.下列结论:①点P在∠A的角平分线上;②AS=AR;③QP∥AR;④△BRP≌△QSP.其中,正确的有()A.1个 B.2个 C.3个 D.4个【答案】D【解析】∵△ABC 是等边三角形,PR ⊥AB ,PS ⊥AC ,且PR =PS ,∴P 在∠A 的平分线上,故①正确;由①可知,PB =PC ,∠B =∠C ,PS =PR ,∴△BPR ≌△CPS ,∴AS =AR ,故②正确;∵AQ =PQ ,∴∠PQC =2∠PAC =60°=∠BAC ,∴PQ ∥AR ,故③正确;由③得,△PQC 是等边三角形,∴△PQS ≌△PCS ,又由②可知,④△BRP ≌△QSP ,故④也正确,∵①②③④都正确,故选D .点睛:本题考查了角平分线的性质与全等三角形的判定与性质,准确识图并熟练掌握全等三角形的判定方法与性质是解题的关键.26.如图所示,△ABP 与△CDP 是两个全等的等边三角形,且PA ⊥PD ,有下列四个结论:①∠PBC =15°,②AD ∥BC ,③PC ⊥AB ,④四边形ABCD 是轴对称图形,其中正确的个数为( )A .1个B .2个C .3个D .4个【答案】D【解析】【分析】根据周角的定义先求出∠BPC 的度数,再根据对称性得到△BPC 为等腰三角形,∠PBC 即可求出;根据题意:有△APD 是等腰直角三角形;△PBC 是等腰三角形;结合轴对称图形的定义与判定,可得四边形ABCD 是轴对称图形,进而可得②③④正确.【详解】根据题意,BPC 36060290150∠=-⨯-= , BP PC =,()PBC 180150215∠∴=-÷=,①正确;根据题意可得四边形ABCD 是轴对称图形,④正确;∵∠DAB+∠ABC=45°+60°+60°+15°=180°,∴AD//BC ,②正确;∵∠ABC+∠BCP=60°+15°+15°=90°,∴PC ⊥AB ,③正确,所以四个命题都正确,故选D .【点睛】本题考查了等边三角形的性质、等腰直角三角形的性质、等腰三角形的判定与性质、轴对称图形的定义与判定等,熟练掌握各相关性质与定理是解题的关键.27.如图,在等腰△ABC 中,AB =AC ,∠A =20°,AB 上一点D ,且AD =BC ,过点D 作DE ∥BC 且DE =AB ,连接EC ,则∠DCE 的度数为( )A .80°B .70°C .60°D .45°【答案】B【解析】【分析】 连接AE .根据ASA 可证△ADE ≌△CBA ,根据全等三角形的性质可得AE=AC ,∠AED=∠BAC=20°,根据等边三角形的判定可得△ACE 是等边三角形,根据等腰三角形的判定可得△DCE 是等腰三角形,再根据三角形内角和定理和角的和差关系即可求解.【详解】如图所示,连接AE .∵AB=DE ,AD=BC∵DE ∥BC ,∴∠ADE=∠B ,可得AE=DE∵AB=AC ,∠BAC=20°,∴∠DAE=∠ADE=∠B=∠ACB=80°,在△ADE 与△CBA 中,DAE ACB AD BCADE B ∠∠⎧⎪⎨⎪∠∠⎩===, ∴△ADE ≌△CBA (ASA ),∴AE=AC ,∠AED=∠BAC=20°,∵∠CAE=∠DAE-∠BAC=80°-20°=60°,∴△ACE 是等边三角形,∴CE=AC=AE=DE ,∠AEC=∠ACE=60°,∴△DCE 是等腰三角形,∴∠CDE=∠DCE ,∴∠DEC=∠AEC-∠AED=40°,∴∠DCE=∠CDE=(180-40°)÷2=70°.故选B .【点睛】考查了等腰三角形的性质,全等三角形的判定和性质,等边三角形的判定和性质,等腰三角形的判定和性质,三角形内角和定理,平行线的性质,综合性较强,有一定的难度.28.如图,O 是正ABC 内一点,3OA =,4OB =,5OC =,将线段BO 以点B 为旋转中心逆时针旋转60°得到线段BO ',连接AO ',下列结论:①BO A '△可以由BOC 绕点B 逆时针旋转60°得到:②点O 与O '的距离为4;③150AOB ∠=︒;④S 四边形643AOBO ;⑤9634AOC AOB S S +=+△△.其中正确的结论是( )A .①②③④B .①②③⑤C .①②④⑤D .①②③④⑤【答案】D【解析】【分析】 证明△BO ′A ≌△BOC ,又∠OBO ′=60°,所以△BO ′A 可以由△BOC 绕点B 逆时针旋转60°得到,故结论①正确;由△OBO ′是等边三角形,可知结论②正确;在△AOO ′中,三边长为3,4,5,这是一组勾股数,故△AOO ′是直角三角形;进而求得∠AOB =150°,故结论③正确;643AOO OBO AOBO S S S '∆'∆'=+=+四边形④正确;如图②,将△AOB 绕点A 逆时针旋转60°,使得AB 与AC 重合,点O 旋转至O ″点.利用旋转变换构造等边三角形与直角三角形,将S △AOC +S △AOB 转化为S △COO ″+S △AOO ″,计算可得结论⑤正确.【详解】解:由题意可知,∠1+∠2=∠3+∠2=60°,∴∠1=∠3,又∵OB =O ′B ,AB =BC ,∴△BO ′A ≌△BOC ,又∵∠OBO ′=60°,∴△BO ′A 可以由△BOC 绕点B 逆时针旋转60°得到,故结论①正确;如图①,连接OO ′,∵OB =O ′B ,且∠OBO ′=60°,∴△OBO ′是等边三角形,∴OO ′=OB =4.故结论②正确;∵△BO ′A ≌△BOC ,∴O ′A =5.在△AOO ′中,三边长为3,4,5,这是一组勾股数,∴△AOO ′是直角三角形,∠AOO ′=90°,∴∠AOB =∠AOO ′+∠BOO ′=90°+60°=150°,故结论③正确;2313446432AOO OBO AOBO S S S '∆'∆'=+=⨯⨯+⨯=+四边形, 故结论④正确;如图②所示,将△AOB 绕点A 逆时针旋转60°,使得AB 与AC 重合,点O 旋转至O ″点.易知△AOO ″是边长为3的等边三角形,△COO ″是边长为3、4、5的直角三角形,则23193436324AOC AOB COO AOO AOCO S S S S S ∆∆∆''∆''''+==+=⨯⨯+⨯=+四边形, 故结论⑤正确.综上所述,正确的结论为:①②③④⑤.故选:D .【点睛】本题考查了旋转变换中等边三角形,直角三角形的性质.利用勾股定理的逆定理,判定勾股数3、4、5所构成的三角形是直角三角形,这是本题的要点.在判定结论⑤时,将△AOB 向不同方向旋转,体现了结论①﹣结论④解题思路的拓展应用.29.如图,在△ABC 中,AB=AC ,高BD ,CE 交于点O ,AO 交BC 于点F ,则图中共有全等三角形( )A .8对B .7对C .6对D .5对【答案】B【解析】【分析】易证△ABC 是关于AF 对称的图形,其中的小三角形也关于AF 对称,共可找出7对三角形.【详解】全等的三角形有:①△AFB≌△AFC;②△CEB≌△BDC;③△AEO≌△ADO;④△EOB≌△DOC;⑤△OBF≌△OFC;⑥△AOB≌△AOC;⑦△AEC≌△ADB证明①△AFB≌△AFC∵AB=AC,CE⊥AB,BD⊥AC 又∵1122ABC S AB CE AC BD == ∴CE=BD∴在Rt△BCE 和Rt△CBD 中BC BC CE BD =⎧⎨=⎩∴△BCE≌△CBD∴BE=CD,∴AE=AD在Rt△AEO 和Rt△AD O 中AE AD AO AO=⎧⎨=⎩ ∴△AEO≌△ADO∴∠EOD=∠DOA在△BAF 和△CAF 中AB AC BAF CAF AF AF =⎧⎪∠=∠⎨⎪=⎩∴△BAF≌△CAF,得证其余全等证明过程类似故选:B【点睛】本题考查全等的证明,解题关键是利用等腰三角形的性质,推导出图形中边的关系,为证全等作准备30.已知等边三角形ABC 的边长为12,点P 为AC 上一点,点D 在CB 的延长线上,且BD=AP ,连接PD 交AB 于点E ,PE ⊥AB 于点F ,则线段EF 的长为( )A.6 B.5C.4.5 D.与AP的长度有关【答案】A【解析】【分析】作DQ⊥AB,交直线AB的延长线于点Q,连接DE,PQ,根据全等三角形的判定定理得出△APE≌△BDQ,再由AE=BQ,PE=QD且PE∥QD,可知四边形PEDQ是平行四边形,进而可得出EF=12AB,由等边△ABC的边长为12可得出DE=6.【详解】解;如图,作DQ⊥AB,交AB的延长线于点F,连接DE,PQ,又∵PE⊥AB于E,∴∠BQD=∠AEP=90°,∵△ABC是等边三角形,∴∠A=∠ABC=∠DBQ=60°,在△APE和△BDQ中,A DBQAEP BQDAP BD∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△APE≌△BDQ(AAS),∴AE=BQ,PE=QD且PE∥QD,∴四边形PEDQ是平行四边形,∴EF=1EQ,2∵EB+AE=BE+BQ=AB,∴EF=1AB,2又∵等边△ABC的边长为12,∴EF=6.故选:A.【点睛】本题主要考查全等三角形的判定与性质,平行四边形的判定与性质,解此题的关键在于根据题中PE⊥AB作辅助线构成全等的三角形.。
人教版八年级数学上册第十三章 轴对称经典题型专项练习(含解析)
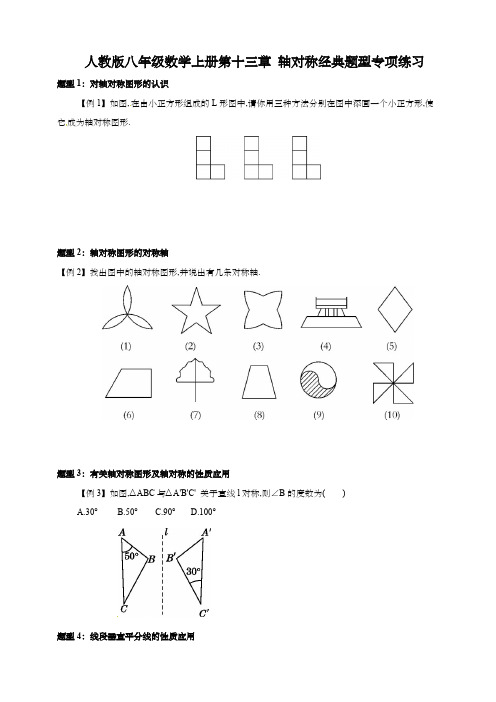
人教版八年级数学上册第十三章轴对称经典题型专项练习题型1:对轴对称图形的认识【例1】如图,在由小正方形组成的L形图中,请你用三种方法分别在图中添画一个小正方形,使它成为轴对称图形.题型2:轴对称图形的对称轴【例2】找出图中的轴对称图形,并说出有几条对称轴.题型3:有关轴对称图形及轴对称的性质应用【例3】如图,△ABC与△A'B'C' 关于直线l对称,则∠B的度数为( )A.30°B.50°C.90°D.100°题型4:线段垂直平分线的性质应用【例4】如图(1),有分别过A,B两个加油站的公路l1,l2,l1,l2相交于点O,现准备在∠AOB内建一个油库,要求油库的位置点P满足到A,B两个加油站的距离相等,而且P到两个公路l1,l2的距离也相等.请用尺规作图,作出点P.(不写作法,保留作图痕迹)(1) 题型5:利用线段垂直平分线的性质及判定解题【例5】如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )A.PA=PBB.PO平分∠APBC.OA=OBD.AB垂直平分OP题型6:作图形的对称轴【例6】如图,已知线段AB和线段A'B'关于某条直线对称,请你画出这条对称轴.题型7:利用作对称轴解决实际问题【例7】如图,校园内有两条路OA、OB,在交叉口附近有两块宣传牌C、D,学校准备在这里安装一盏路灯,要求灯柱的位置P离两块宣传牌一样远,并且到两条路的距离也一样远,请你帮忙画出灯柱的位置P,并说明理由.题型8:利用作图形的轴对称图形补全图形【例8】如图,把下列图形补成关于直线l对称的图形.题型9:利用轴对称图形的性质割补图形【例9】请你将一个等边三角形分割成三角形或四边形(至少4块),然后将它们重新组合,拼成不同形状的轴对称图形.题型10:坐标系中的轴对称变换【例10】在平面直角坐标系中,对于平面内任一点(m,n),规定以下两种变换:①f(m,n)=(m,-n),如f(2,1)=(2,-1);②g(m,n)=(-m,-n) ,如g(2,1)=(-2,-1).按照以上变换有:f=f=,那么g等于( )A.(3,2)B.(3,-2)C.(-3,2)D.(-3,-2)题型11:在坐标系中利用轴对称解决问题A(a,b)和点3a+3c+的值:利用三角形的性质解决实际问题A C(1)BC=AD;(2)△题型16:等边三角形的边角计算【例16】如图,过边长为1的等边三角形ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )A. B. C. D.不能确定题型17:利用等边三角形证线段和差【例17】如图,在△ABC中,AB=AC,D是CB延长线上的一点,∠ADB=60°,E是AD上的一点,且DE=DB.求证:AE=BE+BC.(1) (2) (3)题型18:含30°角的直角三角形的边角关系【例18】如图,△ABC为等边三角形,AE=CD,AD,BE相交于点P,BQ⊥AD于Q,PQ=3,PE=1.(1)求证:AD=BE.(2)求AD的长.题型19:特殊直角三角形性质的实际应用【例19】如图,一艘轮船早上8时从点A向正北方向出发,小岛P在轮船的北偏西15°方向,轮船每小时航行15海里,11时轮船到达点B处,小岛P此时在轮船的北偏西30°方向.(1)求PB的距离;(2)在小岛P的周围20海里范围内有暗礁,如果轮船不改变方向继续向前航行,是否会有触礁危险?请说明理由.题型20:解决实际生活中的最短路径问题【例20】如图,在河岸l的同侧有亚运村A和奥运村B,现计划在河边修建一座小型休闲中心P,使P到两村的距离之和最短;另在河两岸架起一座桥Q,使Q与A、B两村的距离相等,试画出P、Q 所在的位置.人教版八年级数学上册经典题型汇编第十三章轴对称题型1:对轴对称图形的认识【例1】如图,在由小正方形组成的L形图中,请你用三种方法分别在图中添画一个小正方形,使它成为轴对称图形.解:根据图中三个图形的特征,利用轴对称的知识可以得到如图13.1-14所示的补充后的轴对称图形.点拨:本题不同于直接作出一个图形的轴对称图形,而是需要先找准对称轴,然后才能把轴对称图形补充完整.题型2:轴对称图形的对称轴【例2】找出图中的轴对称图形,并说出有几条对称轴.点拨:轴对称图形的特征是将该图形沿某一条直线折叠,直线两旁的部分能够互相重合.因此,判定一个图形是不是轴对称图形的关键是看能否找到一条直线,使得沿此直线折叠时,直线两侧的部分能够重合.解:(1)是轴对称图形,有3条对称轴;(2)是轴对称图形,有5条对称轴;(3)是轴对称图形,有4条对称轴;(4)是轴对称图形,有1条对称轴;(5)是轴对称图形,有2条对称轴;(6)不是轴对称图形;(7)是轴对称图形,有1条对称轴;(8)是轴对称图形,有1条对称轴;(9)、(10)都不是轴对称图形.题型3:有关轴对称图形及轴对称的性质应用【例3】如图,△ABC与△A'B'C' 关于直线l对称,则∠B的度数为( )A.30°B.50°C.90°D.100°答案:D点拨:根据轴对称的定义可知,两个图形成轴对称,则它们是全等图形,从而对应元素相等.题型4:线段垂直平分线的性质应用【例4】如图(1),有分别过A,B两个加油站的公路l1,l2,l1,l2相交于点O,现准备在∠AOB内建一个油库,要求油库的位置点P满足到A,B两个加油站的距离相等,而且P到两个公路l1,l2的距离也相等.请用尺规作图,作出点P.(不写作法,保留作图痕迹)解:作出的点P如图(2)所示.(1) (2)点拨:到两点距离相等的点,在这两点所连线段的垂直平分线上.在角的内部到角两边距离相等的点在角的平分线上.这两条线的交点就是加油站的位置.题型5:利用线段垂直平分线的性质及判定解题【例5】如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )A.PA=PBB.PO平分∠APBC.OA=OBD.AB垂直平分OP答案:D点拨:∵OP平分∠AOB,PA⊥OA,PB⊥OB,∴在△AOP与△BOP中,∴△AOP≌△BOP,∴结论A,B,C均正确,故选D.题型6:作图形的对称轴【例6】如图,已知线段AB和线段A'B'关于某条直线对称,请你画出这条对称轴.解:如图所示:点拨:连接AA'或BB'作它们的线段垂直平分线,就是对称轴所在直线.题型7:利用作对称轴解决实际问题【例7】如图,校园内有两条路OA、OB,在交叉口附近有两块宣传牌C、D,学校准备在这里安装一盏路灯,要求灯柱的位置P离两块宣传牌一样远,并且到两条路的距离也一样远,请你帮忙画出灯柱的位置P,并说明理由.解:到∠AOB两边距离相等的点在这个角的平分线上,而到宣传牌C、D的距离相等的点则在线段CD的垂直平分线上,于是如图,交点P即为所求.点拨:本题根据角的平分线和线段的垂直平分线的性质作图即可.题型8:利用作图形的轴对称图形补全图形【例8】如图,把下列图形补成关于直线l对称的图形.解:如图:点拨:该图形均由线段构成,可以利用找特殊点(端点)的对称点的方法画轴对称图形,要注意图(2)中图形被直线l穿过的情况.题型9:利用轴对称图形的性质割补图形【例9】请你将一个等边三角形分割成三角形或四边形(至少4块),然后将它们重新组合,拼成不同形状的轴对称图形.解:答案不唯一,如图:点拨:根据轴对称图形的性质,先分割,再验证,最后确定分法.题型10:坐标系中的轴对称变换【例10】在平面直角坐标系中,对于平面内任一点(m,n),规定以下两种变换:①f(m,n)=(m,-n),如f(2,1)=(2,-1);②g(m,n)=(-m,-n) ,如g(2,1)=(-2,-1).按照以上变换有:f=f=,那么g等于( )A.(3,2)B.(3,-2)C.(-3,2)D.(-3,-2)解:由题意可得f(-3,2)=(-3,-2),从而g[f(-3,2)]=g(-3,-2)=(3,2),故选A.点拨:本题定义了两种变换,只要正确理解给出的定义,其中f(m,n)表示将一个点的横坐标不变,纵坐标变为原来的相反数,g(m,n)表示将一个点的横坐标与纵坐标均变为原来的相反数,从而模仿套写即可.题型11:在坐标系中利用轴对称解决问题【例11】已知点A(a,b)和点B(c,d)关于y轴对称,试求3a+3c+的值.解:∵ 点A(a,b)和点B(c,d)关于y轴对称,∴ a+c=0,b=d.∴ 3a+3c+=3+=0+2=2.点拨:两点关于y轴对称,横坐标互为相反数,纵坐标相等.题型12:在等腰三角形中求边的长度【例12】已知等腰三角形的底边长为10,周长不大于40,求腰长的取值范围.解:设腰长为x.∵ 等腰三角形两腰相等,∴ 2x+10≤40.∴ x≤15.又 底边长为10,两边之和要大于第三边,∴ x+x>10.∴ x>5.∴ 腰长的取值范围是5<x≤15.点拨:由等腰三角形的周长不大于40和三角形的两边之和大于第三边可确定两个不等式,腰长的取值范围就是这两个不等式的公共解.题型13:利用等腰三角形的性质求角的度数【例13】如图,△ABC中,AC=AD=BD,∠DAC=80°.则∠B的度数是( )A.40°B.35°C.25°D.20°点拨:法一:∵AC=AD,∠DAC=80°,∴∠A DC=∠ABD,∴∠ABD=25°,故选C.法二:设ABD=x°,∵∵AC=AD,ACD=∠∵∠2x+2x+80=180.C.欲求三角形中的某个内角可从已知条件出发也可利用方程思想设所求的角的度数为再执果索因A C(1)BC=AD;(2)△∵ AC⊥BC,BD⊥AD,B DA(HL) .∴ BC=AD.(2)由△ACB≌Rt△BDA得∠CAB=∠DBA,∴ △OAB是等腰三角形.点拨:(1)证△ACB≌Rt△BDA ,根据全等三角形的对应边相等可得;(2)证∠OAB=∠OB A,根据等角对等边可得.题型16:等边三角形的边角计算【例16】如图,过边长为1的等边三角形ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )A. B. C. D.不能确定答案:B点拨:如图所示,作PF∥BC交AC于F,∵△ABC是等边三角形,∴∠APF=∠ABC=60°,∠AFP=∠ACB=60°,∴△APF是等边三角形,∴AP=PF,∵PA=CQ,∴PF=CQ.在△DPF和△DQC中,∴△DPF≌△DQC,∴DF=DC,∵PE⊥AC,∴E是AF中点,从而ED=AC=,故选B.因为本题中DE与等边三角形ABC的边长之间无直接联系,所以通过分割,将其分成两部分后,分别证DF=DC和EF=EA,从而求之.题型17:利用等边三角形证线段和差【例17】如图,在△ABC中,AB=AC,D是CB延长线上的一点,∠ADB=60°,E是AD上的一点,且DE=DB.求证:AE=BE+BC.(1) (2) (3)证明:证法一:如图(1),延长DC到F,使CF=BD,连接AF,∵∠ADB=60°,DE=DB,∴△DBE是等边三角形,∴BE=DB.∴BE=CF.∵AB=AC,∴∠ABC=∠ACB,∴∠ABD=∠ACF.∵BD=CF,∴△ABD≌△ACF.∴∠F=∠D=60°,∴△ADF是等边三角形,∴AD=DF,∴AD-DE=DF-DB,即AE=BF,∴AE=BC+CF=BC+BE.证法二:如图(2),延长EB到P,使BP=BC,连接AP,CP.∵∠ADB=60°,DE=DB,∴△DBE是等边三角形,∴∠CBP=∠DBE=60°,∴△BPC为等边三角形,∴BP=PC.∵AB=AC,AP=AP,∴△BAP≌△CAP,∴∠BPA=∠CPA,∵∠PCB=∠D=60°,∴PC∥AD,∴∠CPA=∠EAP,∴∠EAP=∠BPA,∴AE=EP=BE+BC.证法三:如图(3),过C作CM∥BE,交AD于M.∵∠ADB=60°,DE=DB,∴△DBE是等边三角形,∴∠DBE=60°.∵CM∥BE,∴∠MCD=∠DBE=60°,∠DMC=∠DEB=60°,∴△DCM为等边三角形,∴CD=MD,∴CD-DB=DM-DE,即BC=EM.∵AB=AC,∴∠ABC=∠ACB.∴∠D+∠DAB=∠DCM+∠MCA.∵∠D=∠MCD=60°,∴∠DAB=∠MCA.∵MC∥BE,∴∠CMA=∠AEB,∴△ABE≌△CAM.∴AM=BE,∴AE=AM+EM=BE+BC.点拨:欲证一线段等于另两线段之和,可利用“截长补短”之法.本题条件蕴含着等边三角形,所以有相等的边与角,从而有全等的三角形,由此得证.题型18:含30°角的直角三角形的边角关系【例18】如图,△ABC为等边三角形,AE=CD,AD,BE相交于点P,BQ⊥AD于Q,PQ=3,PE=1.(1)求证:AD=BE.(2)求AD的长.解:(1)证明:∵△ABC为等边三角形,∴∠B AC=∠C=60°,AB=AC.又AE=CD,∴△ABE≌△CAD(SAS),∴BE=AD.(2)解:∵△ABE≌△CAD,∴∠ABE=∠CAD.∵∠BPQ=∠BAP+∠ABE=∠BAP+∠PAE=∠BAC=60°,又∵BQ⊥AD,∴∠PBQ=30°,∴PB=2PQ=6,∴BE=PB+PE=7,∴AD=BE=7.点拨:因为等边三角形的三条边都相等,三个角都等于60°,所以在等边三角形中容易找到全等三角形,本题第(1)题就是通过全等三角形证两线段相等;在第(1)题的基础上,可求得∠BPQ的度数,从而联想直角三角形中含30°角的性质求得PB之长,再求AD的长.题型19:特殊直角三角形性质的实际应用【例19】如图,一艘轮船早上8时从点A向正北方向出发,小岛P在轮船的北偏西15°方向,轮船每小时航行15海里,11时轮船到达点B处,小岛P此时在轮船的北偏西30°方向.(1)求PB的距离;(2)在小岛P的周围20海里范围内有暗礁,如果轮船不改变方向继续向前航行,是否会有触礁危险?请说明理由.解:(1)过点P作PE⊥AB,垂足为E,由题意,得∠PAB=15°,∠PBC=30°.∴ ∠BPA=∠PBC-∠A=15°.∴ BP=BA.又AB=3×15=45海里,∴ BP=45海里.(2)∵ PE⊥AB,∠PBC=30°,∴ PE=BP=22.5海里,∵ 22.5海里>20海里,∴ 如果轮船不改变方向继续向前航行,不会有触礁危险.点拨:过点P作PE垂直于AB的延长线,垂足为E,根据三角形的外角可知∠BPA=∠A,使得BP=AB,所以可以求出BP的距离;在(2)中,只要求出PE的长即可,可以根据直角三角形中30°角的性质解决.题型20:解决实际生活中的最短路径问题【例20】如图,在河岸l的同侧有亚运村A和奥运村B,现计划在河边修建一座小型休闲中心P,使P到两村的距离之和最短;另在河两岸架起一座桥Q,使Q与A、B两村的距离相等,试画出P、Q 所在的位置.解:如图.(1)作点B关于直线l的对称点B';(2)连接AB',交直线l于点P,则点P就是所求的小型休闲中心的位置;(3)连接AB;(4)作线段AB的垂直平分线,交直线l于点Q,则点Q就是所求的桥的位置.点拨:要使点P到两村的距离最短,可知点P一定是点B关于河岸l的对称点B'和点A的连线与河岸l的交点;点Q与A、B两村的距离相等,则表明点Q在线段AB的垂直平分线上.。
八年级数学上册轴对称填空选择单元复习练习(Word版 含答案)

八年级数学上册轴对称填空选择单元复习练习(Word版含答案)一、八年级数学全等三角形填空题(难)1.如图,ABE△,BCD均为等边三角形,点A,B,C在同一条直线上,连接AD,EC,AD与EB相交于点M,BD与EC相交于点N,连接OB,下列结论正确的有_________.①AD EC=;②BM BN=;③MN AC;④EM MB=;⑤OB平分AOC∠【答案】①②③⑤.【解析】【分析】由题意根据全等三角形的判定和性质以及等边三角形的性质和角平分线的性质,对题干结论依次进行分析即可.【详解】解:∵△ABE,△BCD均为等边三角形,∴AB=BE,BC=BD,∠ABE=∠CBD=60°,∴∠ABD=∠EBC,在△ABD和△EBC中,AB BEABD EBCBD BC⎧⎪∠∠⎨⎪⎩===∴△ABD≌△EBC(SAS),∴AD=EC,故①正确;∴∠DAB=∠BEC,又由上可知∠ABE=∠CBD=60°,∴∠EBD=60°,在△ABM和△EBN中,MAB NEBAB BEABE EBN∠∠⎧⎪⎨⎪∠∠⎩===∴△ABM ≌△EBN (ASA ),∴BM=BN ,故②正确;∴△BMN 为等边三角形,∴∠NMB=∠ABM=60°,∴MN ∥AC ,故③正确;若EM=MB ,则AM 平分∠EAB ,则∠DAB=30°,而由条件无法得出这一条件,故④不正确;如图作,,BG AD BH EC ⊥⊥∵由上可知△ABD ≌△EBC ,∴两个三角形对应边的高相等即BG BH =,∴OB 是AOC ∠的角平分线,即有OB 平分AOC ∠,故⑤正确.综上可知:①②③⑤正确.故答案为:①②③⑤.【点睛】本题考查全等三角形的判定和性质,熟练掌握全等三角形的判定和性质以及等边三角形的性质和角平分线的性质与平行线的判定是解题的关键.2.如图,点D 、E 、F 、B 在同一直线上,AB ∥CD 、AE ∥CF ,且AE=CF ,若BD=10,BF=2,则EF=__.【答案】6【解析】【分析】由于AB//CD、AE/CF,根据平行线的性质可以得到∠B=∠D,∠AEF=∠CFD,然后利用已知条件就可以证明△AEF≌△CFD,最后利用全等三角形的性质和已知条件即可求解.【详解】解:∵AB//CD、AE/CF,∴∠B=∠D,∠AEF=∠CFD,而AE=CF,∴△AEF≌△CFD,∴DF=EB,∴DE=BF,∴EF=BD-2BF=6.故答案为:6.【点睛】本题主要考查了全等三角形的性质与判定,解题时首先利用平行线的性质构造全等条件证明三角形全等,然后利用全等三角形的性质即可解决问题.3.如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④CO平分∠AOE;⑤∠AOB=60°.恒成立的结论有__.(把你认为正确的序号都填上)【答案】①②③④⑤【解析】【分析】根据等边三角形的性质及SAS即可证明△ACD≌△BCE即可求解.【详解】①△ABC和△DCE均是等边三角形,点A,C,E在同一条直线上,∴AC=BC,EC=DC,∠BCE=∠ACD=120°∴△ACD≌△ECB∴AD=BE,故本选项正确;②∵△ACD≌△ECB∴∠CBQ=∠CAP,又∵∠PCQ=∠ACB=60°,CB=AC,∴△BCQ≌△ACP,∴CQ=CP,又∠PCQ=60°,∴△PCQ为等边三角形,∴∠QPC=60°=∠ACB,∴PQ∥AE,故本选项正确;③∵∠ACB=∠DCE=60°,∴∠BCD=60°,∴∠ACP=∠BCQ,∵AC=BC,∠DAC=∠QBC,∴△ACP≌△BCQ(ASA),∴CP=CQ,AP=BQ,故本选项正确;④∵BC∥DE,∴∠CBE=∠BED,∵∠CBE=∠DAE,∴∠AOB=∠OAE+∠AEO=60°,同理可得出∠AOE=120°,∵D,O,C,E四点共圆,∴∠OCD=∠OED,∴∠OAC=∠OCD,∴∠DCE=∠AOC=60°,∴OC平分∠AOE,故④正确;⑤∵△ABC、△DCE为正三角形,∴∠ACB=∠DCE=60°,AC=BC,DC=EC,∴∠ACB+∠BCD=∠DCE+∠BCD,∴∠ACD=∠BCE,∴△ACD≌△BCE(SAS),∴∠CAD=∠CBE,∴∠AOB=∠CAD+∠CEB=∠CBE+∠CEB,∵∠ACB=∠CBE+∠CEB=60°,∴∠AOB=60°,故本选项正确.综上所述,正确的结论是①②③④⑤.【点睛】本题考查等边三角形的性质、全等三角形的判定与性质,利用旋转不变性,找到不变量,是解题关键.4.已知:四边形ABCD中,AB=AD=CD,∠BAD=90°,三角形ABC的面积为1,则线段AC 的长度是___________.【答案】2【解析】【分析】过B作BE⊥AC于E, 过D作DF⊥AC于F,构造得出BE=AF利用等腰三角形三线合一的性质得出:AF=可得BE=AF=,利用三角形ABC的面积为1进行计算即可.【详解】过B作BE⊥AC于E, 过D作DF⊥AC于F,∴∠BEA=∠AFD=90°∴∠2+∠3=90°∵∠BAD=90°∴∠1+∠2=90°∴∠1=∠3∵AB=AD∴∴BE=AF∵AD=CD,DF⊥AC∴AF=∴BE=AF=∴∴AC=2故答案为:2【点睛】本题考查了利用一线三等角构造全等三角形,以及利用三角形面积公式列方程求线段,熟练掌握辅助线做法构造全等是解题的关键.5.如图,AE平分∠BAC,BD=DC,DE⊥BC,EM⊥AB.若AB=9,AC=5,则AM的长为______.【答案】7【解析】【分析】过点E 作EN ⊥AC 的延长线于点N ,连接BE 、EC ,利用角平分线的性质、垂直平分线的性质得到EM=EN ,EB=EC ,证明Rt △BME ≌Rt △CNE (HL ),得到BM=CN ,证明Rt △AME ≌Rt △ANE (HL ),得到AM=AN ,由AM=AB-BM=AB-CN=AB-(AN-AC )=AB-AN+AC=AB-AM+AC ,即AM=9-AM+5,即可解答.【详解】解:如图,过点E 作EN ⊥AC 的延长线于点N ,连接BE 、EC ,∵BD=DC ,DE ⊥BC∵BE=EC .∵AE 平分∠BAC ,EM ⊥AB ,EN ⊥AC ,∴EM=EN ,∠EMB=∠ENC=90°.在Rt △BME 和Rt △CNE 中,BE EC EM EN =⎧⎨=⎩, ∴Rt △BME ≌Rt △CNE (HL )∴BM=CN ,在RtAME 和Rt △ANE 中,AE AE EM EN =⎧⎨=⎩, ∴Rt △AME ≌Rt △ANE (HL )∴AM=AN ,∴AM=AB-BM=AB-CN=AB-(AN-AC )=AB-AN+AC=AB-AM+AC ,即AM=9-AM+52AM=9+52AM=14AM=7.故答案为:7.【点睛】考查了全等三角形的性质与判定,解决本题的关键是证明Rt△BME≌Rt△CNE(HL),得到BM=CN,证明Rt△AME≌Rt△ANE(HL),得到AM=AN.6.如图,在ABC中,ACB90,CA CB∠==.点D在AB上,点F在CA的延长线上,连接FD并延长交BC于点E,若∠BED=2∠ADC,AF=2,DF=7,则ABC的面积为______.【答案】25 2【解析】【分析】作CD的垂直平分线交AD于M,交CD与N,根据垂直平分线的性质可得MC=MD,进而可得∠MDC=∠MCD,根据已知及外角性质可得∠AMC=∠BED,由等腰直角三角形的性质可得∠B=∠CAB=45°,根据三角形内角和定理可得∠ACM=∠BDE,进而可证明∠ADF=∠ACM,进而即可证明∠FCD=∠FDC,根据等腰三角形的性质可得CF=DF,根据已知可求出AC的长,根据三角形面积公式即可得答案.【详解】作CD的垂直平分线交AD于M,交CD与N,∵MN是CD的垂直平分线,∴MC=MD,∴∠MDC=∠MCD,∵∠AMC=∠MDC=∠MCD,∴∠AMC=2∠ADC,∵∠BED=2∠ADC,∴∠AMC=∠BED,∵∠ACB=90°,AC=BC,∴∠B=∠CAB=45°,∵∠ACM=180°-∠CAM-∠AMC,∠BDE=180°-∠B-∠BED,∴∠ACM=∠BDE,∵∠BDE=∠ADF,∴∠ADF=∠ACM,∴∠ADF+∠ADC=∠ACM+∠MCD,即∠FCD=∠FDC,∴FC=FD,∵AF=2,FD=7,∴AC=FC-AF=7-2=5,∴S△ABC=12×5×5=252.故答案为:25 2【点睛】本题考查了等腰三角形的判定与性质及线段垂直平分线的性质,线段垂直平分线上的点,到线段两端的距离相等;等腰三角形的两个底角相等;熟练掌握相关的定理及性质是解题关键.7.如图,OP平分∠AOB,∠AOP=15°,PC∥OA,PC=4,点D是射线OA上的一个动点,则PD的最小值为_____.【答案】2【解析】【分析】作PE⊥OA于E,根据角平分线的性质可得PE=PD,根据平行线的性质可得∠ACP=∠AOB=30°,由直角三角形中30°的角所对的直角边等于斜边的一半,可求得PE,即可求得PD.【详解】当PD⊥OA时,PD有最小值,作PE⊥OA于E,∵∠AOP=∠BOP,PD⊥OB,PE⊥OA,∴PE=PD(角平分线上的点到角两边的距离相等),∵∠BOP=∠AOP=15°,∴∠AOB=30°,∵PC∥OB,∴∠ACP=∠AOB=30°,∴在Rt△PCE中,PE=12PC=12×4=2(在直角三角形中,30°角所对的直角边等于斜边的一半),∴PD=PE=2,故答案是:2.【点睛】此题主要考查角平分线的性质和平行线的性质,难度一般,作辅助线是关键.8.如图,点E是等边△ABC内一点,且EA=EB,△ABC外一点D满足BD=AC,且BE平分∠DBC,则∠D=__________.【答案】30°【解析】试题解析:(1)连接CE,∵△ABC是等边三角形,∴AC=BC,在△BCE与△ACE中,{AC BCAE BECE CE===∴△BCE≌△ACE(SSS)∴∠BCE=∠ACE=30°∵BE平分∠DBC,∴∠DBE=∠CBE,在△BDE与△BCE中,{BD BCDBE CBE BE BE∠∠===∴△BDE ≌△BCE (SAS ),∴∠BDE=∠BCE=30°.9.已知△ABC 中,AB=BC ≠AC ,作与△ABC 只有一条公共边,且与△ABC 全等的三角形,这样的三角形一共能作出_____个.【答案】7 【解析】只要满足三边对应相等就能保证作出的三角形与原三角形全等,以腰为公共边时有6个,以底为公共边时有一个,答案可得.解:以AB 为公共边有三个,以CB 为公共边有三个,以AC 为公共边有一个,所以一共能作出7个.故答案为710.如图,AB =BC 且AB ⊥BC ,点P 为线段BC 上一点,PA ⊥PD 且PA =PD ,若∠A =22°,则∠D 的度数为_________.【答案】23°【解析】解:过D 作DE ⊥PC 于E .∵PA ⊥PD ,∴∠APB +∠DPE =90°.∵AB ⊥BC ,∴∠A +∠APB =90°,∴∠A =∠DPE =22°.在△ABP 和△PED 中,∵∠A =∠DPE ,∠B =∠E =90°,PA =PD ,∴△ABP ≌△PED ,∴AB =PE ,BP =DE .∵AB =BC ,∴BC =PE ,∴BP =CE .∵BP =DE ,∴CE =DE ,∴∠DCE =45°,∴∠PDC =∠DCE -∠DPC =45°-22°=23°.故答案为:23°.二、八年级数学全等三角形选择题(难)11.已知等边△ABC中,在射线BA上有一点D,连接CD,并以CD为边向上作等边△CDE,连接BE和AE,试判断下列结论:①AE=BD;②AE与AB所夹锐夹角为60°;③当D在线段AB或BA延长线上时,总有∠BDE-∠AED=2∠BDC;④∠BCD=90°时,CE2+AD2=AC2+DE2,正确的序号有()A.①②B.①②③C.①②④D.①②③④【答案】C【解析】【分析】由∠BCD=∠ACD+60°,∠ACE=∠ACD+60°可得∠BCD=∠ACE,利用SAS可证明△BCD≌△ACE,可得AE=BD,①正确;∠CBD=∠CAE=60°,进而可得∠EAD=60°,②正确,当∠BCD=90°时,可得∠ACD=∠ADC=30°,可得AD=AC,即可得CE2+AD2=AC2+DE2,④正确;当D点在BA延长线上时,∠BDE-∠BDC=60°,根据△BCD≌△ACE可得∠AEC=∠BDC,进而可得∠BDC+∠AED=∠AEC+∠AED=∠CED=60°,即可证明∠BDE-∠BDC=∠BDC+∠AED,即∠BDE-∠AED=2∠BDC,当点D在AB上时可证明∠BDE-∠AED=120°,③错误,综上即可得答案.【详解】∵∠BCA=∠DCE=60°,∴∠BCA+∠ACD=∠DCE+∠ACD,∴∠BCD=∠ACE,又∵AC=BC,CE=CD,∴△BCD≌△ACE,∴AE=BD,∠CBA=∠CAE=60°,∠AEC=∠BDC,①正确,∴∠BAE=120°,∴∠EAD=60°,②正确,∵∠BCD=90°,∠BCA=60°,∴∠ACD=∠ADC=30°,∴AC=AD,∵CE=DE ,∴CE 2+AD 2=AC 2+DE 2,④正确,当D 点在BA 延长线上时,∠BDE-∠BDC=60°,∵∠AEC=∠BDC ,∴∠BDC+∠AED=∠AEC+∠AED=∠CED=60°,∴∠BDE-∠BDC=∠BDC+∠AED∴∠BDE-∠AED=2∠BDC ,如图,当点D 在AB 上时,∵△BCD ≌△∠ACE ,∴∠CAE=∠CBD=60°,∴∠DAE=∠BAC+∠CAE=120°,∴∠BDE-∠AED=∠DAE=120°,③错误故正确的结论有①②④,故选C.【点睛】此题主要考查等边三角形的性质和全等三角形的判定与性质等知识点的理解和掌握 12.如图,A ABC CB =∠∠,AD 、BD 、CD 分别平分ABC 的EAC ∠、ABC ∠、ACF ∠,以下结论:①AD BC ∥;②2ACB ADB ∠=∠;③90ADC ABD ∠=︒-∠;④BD 分ADC ∠;⑤3BDC BAC ∠=∠。
8年级数学人教版上册同步练习 画轴对称图形-八年级数学人教版(上)(解析版)

第十三章轴对称13. 2画轴对称图形一、选择题目:在每小题给出的四个选项中,只有一项是符合题目要求的.1.如图,在3×3方格图中,在其中一个小方格的中心画上半径相等的圆,使整个图形为轴对称图形,方法有A.1种B.2种C.3种D.4种【答案】C【解析】共有3种,如图.故选C.学科&网2.点(4,3)与点(4,-3)的关系是A.关于原点对称B.关于x轴对称C.关于y轴对称D.不能构成对称关系【答案】B【解析】根据平面直角坐标系的特点,可知点(4,3)与点(4,-3)的关系是关于x轴对称.故选B.3.已知点P关于y轴的对称点1P的坐标是(2,3),则点P坐标是A.(-3,-2)B.(-2,3)C.(2,-3)D.(3,-2)【答案】B4.在平面直角坐标系中,点B的坐标是(4,-1),点A与点B关于x轴对称,则点A的坐标是A.(4,1)B.(-1,4)C.(-4,-1)D.(-1,-4)【答案】A【解析】∵点B的坐标是(4,-1),点A与点B关于x轴对称,∴点A的坐标是:(4,1),故选A.5.若点A(1+m,1-n)与点B(-3,2)关于y轴对称,则m+n的值是A.-5 B.-3 C.3 D.1【答案】D【解析】∵点A(1+m,1-n)与点B(-3,2)关于y轴对称,∴1+m=3,1-n=2,解得:m=2,n=-1,所以m+n=2-1=1,故选D.学科&网6.如图,△ABC与△DEF关于y轴对称,已知A(-4,6),B(-6,2),E(2,1),则点D的坐标为A.(-4,6)B.(4,6)C.(-2,1)D.(6,2)【答案】B【解析】∵△ABC与△DEF关于y轴对称,A(-4,6),∴D(4,6),故选B.二、填空题目:请将答案填在题中横线上.7.点A(-5,-6)与点B(5,-6)关于__________对称.【答案】y轴8.如图,在方格纸上建立的平面直角坐标系中,Rt△ABC关于y轴对称的图形为Rt△DEF,则点A的对应点D的坐标是__________.【答案】(2,1)【解析】∵点A的坐标为(-2,1),∴点A关于y轴对称的点D的横坐标为2,纵坐标为1,∴点A关于x轴对称的点D的坐标是(2,1),故答案为:(2,1).学科&网9.如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有__________个.【答案】5三、解答题:解答应写出文字说明、证明过程或演算步骤.10.在5×7的方格纸上,任意选出5个小方块涂上颜色,使整个图形(包括着色的“对称”)有:①1条对称轴;②2条对称轴;③4条对称轴.【解析】①如图1所示:②如图2所示:③如图3所示:11.如图,已知四边形ABCD的顶点坐标分别为A(1,1),B(5,1),C(5,4),D(2,4),分别写出四边形ABCD关于x轴、y轴对称的四边形A1B1C1D1和A2B2C2D2的顶点坐标.祝福语祝你考试成功!。
人教版八年级上册数学第13章《轴对称》单元测试卷(含答案解析)

人教版八年级上册数学第13章《轴对称》单元测试卷班级_________ 姓名__________ 考号_____________ 得分____________一、选择题(每小题3分,共30分)1、下列图形中一定是轴对称图形的是()A.B.C.D.2、点A(a﹣3,﹣1)与点B(2,b+2)关于x轴对称,则a,b的值分别是()A.a=1,b=﹣3 B.a=1,b=﹣1 C.a=5,b=﹣3 D.a=5,b=﹣13、如图,在△ABC中,AB=AD=DC,若∠BAD=36°,则∠C的大小为()A.36°B.38°C.40°D.42°4、等腰三角形的一个外角是140°,则其底角是()A.40°B.70°或40°C.70°D.140°5、等腰三角形的周长为15,其中一边长为3,则该等腰三角形的底边长为()A.3 B.4 C.5 D.66、如图,△ABC中,AB=AC,AD=DE,∠BAD=18°,∠EDC=12°,则∠DAE的度数为()A.58°B.56°C.62°D.60°7、如图,四边形ABCD中,AB=AD,点B关于AC的对称点B′恰好落在CD上,若∠BAD=100°,则∠ACB的度数为()A.40°B.45°C.60°D.80°8、如图,在△ABC中,∠C=90°,点A关于BC边的对称点为A′,点B关于AC边的对称点为B′,点C关于AB边的对称点为C′,则△ABC与△A′B′C′的面积之比为()A.B.C.D.9、在△ABC中,AB=AC,OB=OC,点A到BC的距离是6,O到BC的距离是4,则AO为()A.2 B.10 C.2或10 D.无法测量10、如图,在Rt△ABC中(AB>2BC),∠C=90°,以BC为边作等腰△BCD,使点D落在△ABC的边上,则点D的位置有()A.2个B.3个C.4个D.5个二、填空题(每小题4分,共24分)11、在平面直角坐标系中,点A的坐标是(﹣1,2),作点A关于y轴对称得到点A′,再将点A′向上平移2个单位,得到点A″,则点A″的坐标是(1,4).12、一个等腰三角形一腰上的中线把这个三角形的周长分为12和30两部分,则这个等腰三角形的腰长为20.13、如图,等腰△ABC中,AB=AC,∠A=54°,AB的垂直平分线MN交AC于点D,则∠DBC的度数是9°.14、如图,在△ABC中,∠C=∠ABC,BE⊥AC,垂足为点E,△BDE是等边三角形,若AD=4,则线段BE的长为.15、如图,在平面直角坐标系xOy中,已知点A(6,2),B(0,1).在x轴上找一点P,使得PA+PB最小,则点P的坐标是(2,0),此时△PAB的面积是4.16、在Rt△ABC中,∠ACB=90°,∠CAB=36°,在直线AC或BC上取点M,使得△MAB为等腰三角形,符合条件的M点有8个.。
八年级数学上册 全等三角形专题练习(解析版)

八年级数学上册全等三角形专题练习(解析版)一、八年级数学轴对称三角形填空题(难)1.在等腰△ABC中,AD⊥BC交直线BC于点D,若AD=12BC,则△ABC的顶角的度数为_____.【答案】30°或150°或90°【解析】试题分析:分两种情况;①BC为腰,②BC为底,根据直角三角形30°角所对的直角边等于斜边的一半判断出∠ACD=30°,然后分AD在△ABC内部和外部两种情况求解即可.解:①BC为腰,∵AD⊥BC于点D,AD=12 BC,∴∠ACD=30°,如图1,AD在△ABC内部时,顶角∠C=30°,如图2,AD在△ABC外部时,顶角∠ACB=180°﹣30°=150°,②BC为底,如图3,∵AD⊥BC于点D,AD=12 BC,∴AD=BD=CD,∴∠B=∠BAD,∠C=∠CAD,∴∠BAD+∠CAD=12×180°=90°,∴顶角∠BAC=90°,综上所述,等腰三角形ABC的顶角度数为30°或150°或90°.故答案为30°或150°或90°.点睛:本题考查了含30°交点直角三角形的性质,等腰三角形的性质,分类讨论是解题的关键.2.如图,P为∠AOB内一定点,M,N分别是射线OA,OB上一点,当△PMN周长最小时,∠OPM=50°,则∠AOB=___________.【答案】40°【解析】【分析】作P关于OA,OB的对称点P1,P2.连接OP1,OP2.则当M,N是P1P2与OA,OB的交点时,△PMN的周长最短,根据对称的性质可以证得:∠OP1M=∠OPM=50°,OP1=OP2=OP,根据等腰三角形的性质即可求解.【详解】如图:作P关于OA,OB的对称点P1,P2.连接OP1,OP2.则当M,N是P1P2与OA、OB 的交点时,△PMN的周长最短,连接P1O、P2O,∵PP1关于OA对称,∴∠P1OP=2∠MOP,OP1=OP,P1M=PM,∠OP1M=∠OPM=50°同理,∠P2OP=2∠NOP,OP=OP2,∴∠P1OP2=∠P1OP+∠P2OP=2(∠MOP+∠NOP)=2∠AOB,OP1=OP2=OP,∴△P1OP2是等腰三角形.∴∠OP2N=∠OP1M=50°,∴∠P1OP2=180°-2×50°=80°,∴∠AOB=40°,故答案为:40°【点睛】本题考查了对称的性质,正确作出图形,证得△P 1OP 2是等腰三角形是解题的关键.3.如图,在ABC ∆中,ABC ∠和ACB ∠的平分线相交于点O ,过点O 作//EF BC 交AB 于E ,交AC 于F ,过点O 作OD AC ⊥于D 下列结论:①EF BE CF =+;②点O 到ABC ∆各边的距离相等;③1902BOC A ∠=+∠;④设OD m =,AE AF n +=,则AEF S mn ∆=;⑤1()2AD AB AC BC =+-.其中正确的结论是.__________.【答案】①②③⑤【解析】【分析】由在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,根据角平分线的定义与三角形内角和定理,即可求得③∠BOC =90°+12∠A 正确;由平行线的性质和角平分线的定义得出△BEO 和△CFO 是等腰三角形得出EF =BE +CF 故①正确;由角平分线的性质得出点O 到△ABC 各边的距离相等,故②正确;由角平分线定理与三角形面积的求解方法,即可求得④设OD =m ,AE +AF =n ,则S △AEF =12mn ,故④错误,根据HL 证明△AMO ≌△ADO 得到AM =AD ,同理可证BM =BN ,CD =CN ,变形即可得到⑤正确.【详解】∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴∠OBC=12∠ABC,∠OCB=12∠ACB,∠A+∠ABC+∠ACB=180°,∴∠OBC+∠OCB=90°﹣12∠A,∴∠BOC=180°﹣(∠OBC+∠OCB)=90°+12∠A;故③正确;∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴∠OBC=∠OBE,∠OCB=∠OCF.∵EF∥BC,∴∠OBC=∠EOB,∠OCB=∠FOC,∴∠EOB=∠OBE,∠FOC=∠OCF,∴BE=OE,CF=OF,∴EF=OE+OF=BE+CF,故①正确;过点O作OM⊥AB于M,作ON⊥BC于N,连接OA.∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴ON=OD=OM=m,∴S△AEF=S△AOE+S△AOF=12AE•OM+12AF•OD=12OD•(AE+AF)=12mn;故④错误;∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴点O到△ABC各边的距离相等,故②正确;∵AO=AO,MO=DO,∴△AMO≌△ADO(HL),∴AM=AD;同理可证:BM=BN,CD=CN.∵AM+BM=AB,AD+CD=AC,BN+CN=BC,∴AD=12(AB+AC﹣BC)故⑤正确.故答案为:①②③⑤.【点睛】本题考查了角平分线的定义与性质,等腰三角形的判定与性质.此题难度适中,解题的关键是注意数形结合思想的应用.4.如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心,大于12MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上;④S△DAC:S△ABC=1:3.其中正确的是__________________.(填所有正确说法的序号)【答案】4【解析】【分析】①连接NP,MP,根据SSS定理可得△ANP≌△AMP,故可得出结论;②先根据三角形内角和定理求出∠CAB的度数,再由AD是∠BAC的平分线得出∠1=∠2=30°,根据直角三角形的性质可知∠ADC=60°;③根据∠1=∠B可知AD=BD,故可得出结论;④先根据直角三角形的性质得出∠2=30°,CD=12AD,再由三角形的面积公式即可得出结论.【详解】①连接NP,MP.在△ANP与△AMP中,∵AN AMNP MPAP AP=⎧⎪=⎨⎪=⎩,∴△ANP≌△AMP,则∠CAD=∠BAD,故AD是∠BAC的平分线,故此选项正确;②∵在△ABC中,∠C=90°,∠B=30°,∴∠CAB=60°.∵AD是∠BAC的平分线,∴∠1=∠2=12∠CAB=30°,∴∠3=90°﹣∠2=60°,∴∠ADC=60°,故此选项正确;③∵∠1=∠B=30°,∴AD=BD,∴点D在AB的中垂线上,故此选项正确;④∵在Rt△ACD中,∠2=30°,∴CD=12AD,∴BC=BD+CD=AD+12AD=32AD,S△DAC=12AC•CD=14AC•AD,∴S △ABC=12AC•BC=12AC•32AD=34AC•AD,∴S△DAC:S△ABC=1:3,故此选项正确.故答案为①②③④.【点睛】本题考查的是作图﹣基本作图,熟知角平分线的作法是解答此题的关键.5.如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA2=4,则△A n B n A n+1的边长为_____.【答案】2n.【解析】【分析】根据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3,以及A2B2=2B1A2,得出A3B3=4B1A2=8,A4B4=8B1A2=16,A5B5=16B1A2…进而得出答案.【详解】解:∵△A1B1A2是等边三角形,∴A1B1=A2B1,∵∠MON=30°,∵OA2=4,∴OA1=A1B1=2,∴A2B1=2,∵△A2B2A3、△A3B3A4是等边三角形,∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,∴A2B2=2B1A2,B3A3=2B2A3,∴A3B3=4B1A2=8,A4B4=8B1A2=16,A5B5=16B1A2=32,以此类推△A n B n A n+1的边长为 2n.故答案为:2n.【点睛】本题主要考查等边三角形的性质及含30°角的直角三角形的性质,由条件得到OA5=2OA4=4OA3=8OA2=16OA1是解题的关键.6.如图,在平面直角坐标系中,点 A,B 的坐标分别是(1,5)、(5,1),若点 C 在 x 轴上,且 A,B,C 三点构成的三角形是等腰三角形,则这样的 C 点共有_____________个【答案】5【解析】【分析】分别以A、B为圆心,AB为半径画圆,及作AB的垂直平分线,数出在x轴上的点C的数量即可【详解】解:由图可知:点 C 在 x 轴上,且 A,B,C 三点构成的三角形是等腰三角形,则这样的 C 点共有5个故答案为:5【点睛】本题考查了等腰三角形的存在性问题,掌握“两圆一线”找等腰三角形是解题的关键7.如图,30AOB ∠=︒,P 是AOB ∠内一点,10PO =.若Q 、R 分别是边OA 、OB 上的动点,则PQR ∆周长的最小值为_______.【答案】10【解析】【分析】作点P 关于OB 的对称点P′,点P 关于OA 的对称点P″,连接P′P″交OB 于R ,交OA 于Q ,连接PR 、PQ ,如图3,利用对称的性质得到△PQR 周长=P′P″,根据两点之间线段最短可判断此时△PQR 周长最小,最小值为P′P″的长,再证明△P′OP″为等边三角形得到P′P″=OP′=OP=10,从而得到△PQR 周长的最小值【详解】解:作点P关于OB的对称点P′,点P关于OA的对称点P″,连接P′P″交OB于R,交OA于Q,连接PR、PQ,如图3,则OP=OP′,OP=OP″,RP=RP′,QP=QP″,∴△PQR周长=PR+RQ+PQ=RP′+RQ+QP″=P′P″,∴此时△PQR周长最小,最小值为P′P″的长,∵由对称性可知OP=OP′,OP=OP″,PP′⊥OB,PP″⊥OA,∴∠1=∠2,∠3=∠4,∴∠P′OP″=∠1+∠2+∠3+∠4=2∠2+2∠3=2∠BOA=60°,∴△P′OP″为等边三角形,∴P′P″=OP′=OP=10,故答案是:10.【点睛】本题考查了几何变换综合题:熟练掌握轴对称的性质和等边三角形的性质;会利用两点之间线段最短解决最短路径问题.8.如图,过边长为1的等边三角形ABC的边AB上一点P,作PE⊥AC于点E,Q为BC延长线上一点,当AP=CQ时,PQ交AC于D,则DE的长为______.【答案】1 2【解析】过点Q作AD的延长线的垂线于点F.因为△ABC是等边三角形,所以∠A=∠ACB=60°.因为∠ACB=∠QCF,所以∠QCF=60°.因为PE⊥AC,QF⊥AC,所以∠AEP=∠CFQ=90°,又因为AP=CQ,所以△AEP≌△CFQ,所以AE=CF,PE=QC.同理可证,△DEP≌△DFQ,所以DE=DF.所以AC=AE+DE+CD=DE+CD+CF=DE+DF=2DE,所以DE=12AC=12.故答案为1 2 .9.如图,在四边形ABCD中,∠A=60°,∠ADC=∠ABC=90°,在AB、AD上分别找一点F、E,连接CE、EF、CF,当△CEF的周长最小时,则∠ECF的度数为______.【答案】60°【解析】【分析】此题需分三步:第一步是作出△CEF的周长最小时E、F的位置(用对称即可);第二步是证明此时的△CEF的周长最小(利用两点之间线段最短);第三步是利用对称性求此时∠ECF的值.【详解】分别作出C关于AD、AB的对称点分别为C1、C2,连接C1C2,分别交AD,AB于点E、F再连接CE、CF此时△CEF的周长最小,理由如下:在AD、AB上任意取E1、F1两点根据对称性:∴CE=C1E,CE1=C1E1,CF=C2F,CF1=C2F1∴△CEF的周长= CE+EF+CF= C1E+EF+C2F= C1C2而△CE1F1的周长= CE1+E1F1+CF1= C1E1+E1F1+C2F1根据两点之间线段最短,故C1E1+E1F1+C2F1>C1C2∴△CEF的周长的最小为:C1C2.∵∠A=60°,∠ADC=∠ABC=90°∴∠DCB=360°-∠A-∠ADC-∠ABC=120°∴∠C C1C2+∠C C2C1=180°-∠DCB=60°根据对称性:∠C C1C2=∠E CD,∠C C2C1=∠F CB∴∠E CD+∠F CB=∠C C1C2+∠C C2C1=60°∴∠ECF=∠DCB-(∠E CD+∠F CB)=60°故答案为:60°【点睛】此题考查的是周长最小值的作图方法(对称点),及周长最小值的证法:两点之间线段最短,掌握周长最小值的作图方法是解决此题的关键.10.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为_________【答案】8 5【解析】【分析】首先根据折叠可得CD=AC=6,B′C=BC=8,∠ACE=∠DCE ,∠BCF=∠B′CF ,CE ⊥AB ,然后求得△ECF 是等腰直角三角形,进而求得∠B′FD=90°,CE=EF=4.8,由勾股定理求出AE ,得出BF 的长,即 B′F 的长.【详解】解:根据折叠的性质可知:DE=AE ,∠ACE=∠DCE ,∠BCF=∠B′CF ,CE ⊥AB ,B′F=BF ,∴B′D=8-6=2,∠DCE+∠B′CF=∠ACE+∠BCF ,∵∠ACB=90°,∴∠ECF=45°,∴△ECF 是等腰直角三角形,∴EF=CE ,∠EFC=45°,∴∠BFC=∠B′FC=135°,∴∠B′FE=90°,∵S △ABC =12AC•BC=12AB•CE , ∴AC•BC=AB•CE , ∵根据勾股定理得:22226810ABAC BC ∴ 4.8AC BC CE AB⋅== ∴EF=4.8,22 3.6AE AC EC -=∴B′F=BF=AB -AE-EF=10-3.6-4.8=1.6=85, 故答案是:85.【点睛】此题主要考查了翻折变换,等腰三角形的判定和性质,勾股定理等知识;熟练掌握翻折变换的性质,由直角三角形的性质和勾股定理求出CE 、AE 是解决问题的关键.二、八年级数学轴对称三角形选择题(难)11.已知等边三角形的边长为3,点P 为等边三角形内任意一点,则点P 到三边的距离之和为( )A .32B .332C .32D .不能确定【答案】B 【解析】 已知,如图,P 为等边三角形内任意一点,PD 、PE 、PF 分别是点P 到边AB 、BC 、AC 的距离,连接AP 、BP 、CP ,过点A 作AH ⊥BC 于点H ,已知等边三角形的边长为3,可求得高线AH =332,因S △ABC =12BC •AH =12AB •PD+12BC•PE +12AC •PF ,所以12×3×AH =12×3×PD +12×3×PE +12×3×PF ,即可得PD +PE +PF =AH =332,即点P 到三角形三边距离之和为332.故选B.点睛:本题考查了等边三角形的性质,根据三角形的面积求点P 到三边的距离之和等于等边三角形的高是解题的关键,作出图形更形象直观.12.已知:如图,点D ,E 分别在△ABC 的边AC 和BC 上,AE 与BD 相交于点F ,给出下面四个条件:①∠1=∠2;②AD=BE ;③AF=BF ;④DF=EF ,从这四个条件中选取两个,不能判定△ABC 是等腰三角形的是( )A .①②B .①④C .②③D .③④【答案】C【解析】【分析】 根据全等三角形的判定和性质以及等腰三角形的判定进行判断即可.【详解】选取①②:在ADF ∆ 和BEF ∆ 中1=2{12AFD BFEAD BEADF BEFAF BFFAB FBACAB CBAAC BC∠∠∠=∠=∴∆≅∆∴=∴∠=∠∠=∠∴∠=∠∴=选取①④:在ADF ∆ 和BEF ∆ 中 1=2{12AFD BFEFD FEADF BEFAF BFFAB FBACAB CBAAC BC∠∠∠=∠=∴∆≅∆∴=∴∠=∠∠=∠∴∠=∠∴=选取③④:在ADF ∆ 和BEF ∆ 中 ={12AF BFAFD BFEFD FEADF BEFAF BFFAB FBACAB CBAAC BC∠=∠=∴∆≅∆∴=∴∠=∠∠=∠∴∠=∠∴=故选C.【点睛】本题考查了等腰三角形的性质和判定,全等三角形的性质和判定的应用,关键是熟练地运用定理进行推理,是一道开放性的题目,能培养学生分析问题的能力.13.如图所示,在ABC 中,AC BC =,90ACB ︒∠=,AD 平分BAC ∠,BE AD ⊥交AC 的延长线F ,E 为垂足.则有:①AD BF =;②CF CD =;③AC CD AB +=;④BE CF =;⑤2BF BE =,其中正确结论的个数是( )A .1B .2C .3D .4【答案】D【解析】【分析】 利用全等三角形的判定定理及其性质以及等腰三角形的三线合一的性质逐项分析即可得出答案.【详解】解:∵AC BC =,90ACB ︒∠=∴45CAB ABC ︒∠=∠=∵AD 平分BAC ∠∴22.5BAE EAF ︒∠=∠=∵90EAF F FBC F ︒∠+∠=∠+∠=∴EAF FBC ∠=∠∴ADC BFC ≅∴AD=BF ,CF=CD ,故①②正确;∵CD=CF,∴AC+CD=AC+CF=AF∵67.5F ︒∠=∵18018067.54567.5ABF F CAB ︒︒︒︒︒∠=-∠-∠=--=∴AF=AB ,即AC+CD=AB ,故③正确;由③可知,三角形ABF 是等腰三角形,∵BE AD ⊥∴12BE BF = 若BE CF =,则30CBF ∠=︒与②中结论相矛盾,故④错误;∵三角形ABF 是等腰三角形,∵BE AD ⊥∴12BE BF = ∴BF=2BE ,故⑤正确;综上所述,正确的选项有4个.故选:D .【点睛】本题考查的知识点是全等三角形的判定定理及其性质,等腰三角形的判定与性质,等腰直角三角形的性质,掌握以上知识点是解此题的关键.14.等边△ABC ,在平面内找一点P ,使△PBC 、△PAB 、△PAC 均为等腰三角形,具备这样条件的P 点有多少个?( )A .1个B .4个C .7个D .10个【答案】D【解析】试题分析:根据点P 在等边△ABC 内,而且△PBC 、△PAB 、△PAC 均为等腰三角形,可知P 点为等边△ABC 的垂心;由此可得分别以三角形各顶点为圆心,边长为半径,交垂直平分线的交点就是满足要求的.解:由点P 在等边△ABC 内,而且△PBC 、△PAB 、△PAC 均为等腰三角形,可知P 点为等边△ABC 的垂心;因为△ABC 是等边三角形,所以分别以三角形各顶点为圆心,边长为半径画弧,交垂直平分线的交点就是满足要求的,每条垂直平分线上得3个交点,再加三角形的垂心,一共10个.故选D .点评:此题主要考查等腰三角形的性质和等边三角形的性质,有一定的拔高难度,属于中档题.15.如图,AOB α∠=,点P 是AOB ∠内的一定点,点,M N 分别在OA OB 、上移动,当PMN ∆的周长最小时,MPN ∠的值为( )A .90α+B .1902α+C .180α-D .1802α-【答案】D【解析】【分析】 过P 点作角的两边的对称点,在连接两个对称点,此时线段与角两边的交点,构成的三角形周长最小.再根据角的关系求解.【详解】解:过P 点作OB 的对称点1P ,过P 作OA 的对称点2P ,连接12PP ,交点为M,N ,则此时PMN 的周长最小,且△1P NP 和△2PMP 为等腰三角形.此时∠12P PP =180°-α;设∠NPM=x°,则180°-x°=2(∠12P PP -x°) 所以 x°=180°-2α 【点睛】求出M,N 在什么位子△PMN 周长最小是解此题的关键.16.如图,ABC ∆中,60BAC ∠=︒,BAC ∠的平分线AD 与边BC 的垂直平分线MD 相交于点D ,DE AB ⊥交AB 的延长线于点E ,DF AC ⊥于点F ,现有下列结论:①DE DF =;②DE DF AD +=;③DM 平分EDF ∠;④2AB AC AE +=,其中正确的是( )A .①②B .①②③C .①②④D .①②③④【答案】C【解析】【分析】 ①由角平分线的性质可知①正确;②由题意可知∠EAD=∠FAD=30°,故此可知ED=12AD ,DF=12AD ,从而可证明②正确;③若DM 平分∠EDF ,则∠EDM=90°,从而得到∠ABC 为直角三角形,条件不足,不能确定,故③错误;④连接BD、DC,然后证明△EBD≌△DFC,从而得到BE=FC,从而可证明④.【详解】解:如图所示:连接BD、DC.①∵AD平分∠BAC,DE⊥AB,DF⊥AC,∴ED=DF.∴①正确.②∵∠EAC=60°,AD平分∠BAC,∴∠EAD=∠FAD=30°.∵DE⊥AB,∴∠AED=90°.∵∠AED=90°,∠EAD=30°,∴ED=12AD.同理:DF=12AD.∴DE+DF=AD.∴②正确.③由题意可知:∠EDA=∠ADF=60°.假设MD平分∠EDF,则∠ADM=30°.则∠EDM=90°,又∵∠E=∠BMD=90°,∴∠EBM=90°.∴∠ABC=90°.∵∠ABC是否等于90°不知道,∴不能判定MD平分∠EDF,故③错误.④∵DM是BC的垂直平分线,∴DB=DC.在Rt△BED和Rt△CFD中DE DFBD DC⎧⎨⎩==,∴Rt△BED≌Rt△CFD.∴BE=FC.∴AB+AC=AE-BE+AF+FC又∵AE=AF,BE=FC,∴AB+AC=2AE.故④正确.综上所述,①②④正确,故选:C.【点睛】本题主要考查的是全等三角形的性质和判定、角平分线的性质、线段垂直平分线的性质,掌握本题的辅助线的作法是解题的关键.17.如图,C 是线段 AB 上一点,且△ACD 和△BCE 都是等边三角形,连接 AE、BD 相交于点O,AE、BD 分别交 CD、CE 于 M、N,连接 MN、OC,则下列所给的结论中:①AE=BD;②CM=CN;③MN∥AB;④∠AOB=120º;⑤OC 平分∠AOB.其中结论正确的个数是()A.2 B.3 C.4 D.5【答案】D【解析】【分析】由题意易证:△ACE≅△DCB,进而可得AE=BD;由△ACE≅△DCB,可得∠CAE=∠CDB,从而△ACM ≅△DCN,可得:CM=CN;易证△MCN是等边三角形,可得∠MNC=∠BCE,即MN∥AB;由∠CAE=∠CDB,∠AMC=∠DMO,得∠ACM=∠DOM=60°,即∠AOB=120º;作CG⊥AE,CH⊥BD,易证CG=CH,即:OC 平分∠AOB.【详解】∵△ACD 和△BCE 都是等边三角形,∴AC=DC,CE=CB,∠ACE=∠DCB=120°,∴△ACE≅△DCB(SAS)∴AE=BD,∴①正确;∵△ACE≅△DCB,∴∠CAE=∠CDB,∵△ACD 和△BCE 都是等边三角形,∴∠ACD=∠BCE=∠DCE=60°,AC=DC,在△ACM 和△DCN中,∵60CAE CDB AC DCACD DCE ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩∴△ACM ≅△DCN (ASA ),∴CM =CN ,∴②正确;∵CM =CN ,∠DCE=60°,∴△MCN 是等边三角形,∴∠MNC=60°,∴∠MNC=∠BCE ,∴MN ∥AB ,∴③正确;∵△ACE ≅△DCB ,∴∠CAE=∠CDB ,∵∠AMC=∠DMO ,∴180°-∠CAE-∠AMC=180°-∠CDB-∠DMO ,即:∠ACM=∠DOM=60°,∴∠AOB =120º,∴④正确;作CG ⊥AE ,CH ⊥BD ,垂足分别为点G ,点H ,如图,在△ACG 和△DCH 中,∵90?AMC DHC CAE CDB AC DC ∠=∠=⎧⎪∠=∠⎨⎪=⎩∴△ACG ≅△DCH (AAS ),∴CG =CH ,∴OC 平分∠AOB ,∴⑤正确.故选D.【点睛】本题主要考查全等三角形的判定定理和性质定理,等边三角形的性质定理以及角平分线性质定理的逆定理,添加合适的辅助线,是解题的关键.18.如图,等腰三角形ABC的底边BC长为4,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,若△CDM周长的最小值为8,则△ABC的面积为()A.12 B.16 C.24 D.32【答案】A【解析】【分析】连接AD,由于△ABC是等腰三角形,点D是BC边的中点,故AD⊥BC,再根据EF是线段AC的垂直平分线可知,点C关于直线EF的对称点为点A,故AD的长为CM+MD的最小值,再根据三角形的周长求出AD的长,由此即可得出结论.【详解】连接AD,∵△ABC是等腰三角形,点D是BC边的中点,∴AD⊥BC,∵EF是线段AC的垂直平分线,∴点C关于直线EF的对称点为点A,∴AD的长为CM+MD的最小值,∵△CDM周长的最小值为8,∴AD=8-12BC=8-2=6∴S△ABC=12BC•AD=12×4×6=12,故选A.【点睛】本题考查的是轴对称-最短路线问题,熟知等腰三角形三线合一的性质是解答此题的关键.19.如图,已知,点A(0,0)、B(43,0)、C(0,4),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…则第2017个等边三角形的边长等于()A .201532B .201632C .3D .201932【答案】A【解析】【分析】【详解】根据锐角三函数的性质,由OB=43,OC=1,可得∠OCB=90°,然后根据等边三角形的性质,可知∠A 1AB=60°,进而可得∠CAA 1=30°,∠CA 1O=90°,因此可推导出∠A 2A 1B=30°,同理得到∠CA 2B 1=∠CA 3B 2=∠CA 4B 3=90°,∠A 2A 1B=∠A 3A 2B 2=∠A 4A 3B 3=30°,故可得后一个等边三角形的边长等于前一个等边三角形的边长的一半,即OA 1=OCcos ∠CAA 1=23,B 1A 2=1232⨯,以此类推,可知第2017个等边三角形的边长为:201713()432⨯=. 故选A.【点睛】此题主要考查了等边三角形的性质,属于规律型题目,解题关键是仔细审图,得出:后一个等边三角形的边长等于前一个等边三角形的边长的一半.20.如图,在△ABC 中,AB=AC=8,BC=5,AB 的垂直平分线交AC 于D ,则△BCD 的周长为( )A .13B .15C .18D .21【答案】A【解析】 根据线段垂直平分线的性质,可由AB=AC=8,BC=5,AB 的垂直平分线交AC 于D ,得到AD=BD ,进而得出△BCD 的周长为:CD+BD+BC=AC+BC=8+5=13.故选A .点睛:此题主要考查了线段垂直平分线的性质,关键是掌握垂直平分线上任意一点,到线段两端点的距离相等.。
八年级数学上册 轴对称填空选择专题练习(解析版)

八年级数学上册 轴对称填空选择专题练习(解析版)一、八年级数学全等三角形填空题(难)1.如图,在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,过点O 作EF ∥BC 交AB 于E ,交AC 于F ,过点O 作OD ⊥AC 于D ,下列四个结论:①EF =BE +CF ;②∠BOC =90°+12∠A ; ③点O 到△ABC 各边的距离相等;④设OD =m ,AE +AF =n ,则AEF S mn ∆=.其中正确的结论是____.(填序号)【答案】①②③【解析】【分析】由在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,根据角平分线的定义与三角形的内角和定理,即可求出②∠BOC =90°+12∠A 正确;由平行线的性质和角平分线的定义可得△BEO 和△CFO 是等腰三角形可得①EF =BE +CF 正确;由角平分线的性质得出点O 到△ABC 各边的距离相等,故③正确;由角平分线定理与三角形的面积求法,设OD=m ,AE+AF=n,则△AEF 的面积=12mn ,④错误. 【详解】在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,∴∠OBC=12∠ABC ,∠OCB=12∠ACB ,∠A+∠ABC+∠ACB=180°, ∴∠OBC+∠OCB=90°-12∠A , ∴∠BOC=180°-(∠OBC+∠OCB )=90°,故②∠BOC =90°+12∠A 正确; 在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,∴∠OBC=∠EOB ,∠OCB=∠OCF ,∵EF ∥BC ,∴∠OBC=∠EOB ,∠OCB=∠FOC ,∠EOB=∠OBE,∠FOC=∠OCF ,∴BE=OE,CF=OF,∴EF=OE+OF=BE+CF,即①EF=BE+CF正确;过点O作OM⊥AB于M,作ON⊥BC于点N,连接AO,∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴ON=OD=OM=m,即③点O到△ABC各边的距离相等正确;∴S△AEF=S△AOE+ S△AOF=12AE·OM+12AF·OD=12OD·(AE+AF)=12mn,故④错误;故选①②③【点睛】此题主要考查角平分线的性质,解题的关键是熟知等腰三角形的判定与性质.2.如图,MN∥PQ,AB⊥PQ,点A,D,B,C分别在直线MN和PQ上,点E在AB上,AD+BC=7,AD=EB,DE=EC,则AB=_____.【答案】7【解析】由MN∥PQ,AB⊥PQ,可知∠DAE=∠EBC=90°,可判定△ADE≌△BCE,从而得出AE=BC,则AB=AE+BE=AD+BC=7.故答案为:7.点睛:本题考查了直角三角形全等的判定和性质以及平行线的性质,是基础知识,比较简单.3.如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为_____.【答案】12.5【解析】过A作AE⊥AC,交CB的延长线于E,判定△ACD≌△AEB,即可得到△ACE是等腰直角三角形,四边形ABCD的面积与△ACE的面积相等,根据S△ACE=12×5×5=12.5,即可得出结论.【详解】如图,过A作AE⊥AC,交CB的延长线于E,∵∠DAB=∠DCB=90°,∴∠D+∠ABC=180°=∠ABE+∠ABC,∴∠D=∠ABE,又∵∠DAB=∠CAE=90°,∴∠CAD=∠EAB,又∵AD=AB,∴△ACD≌△AEB(ASA),∴AC=AE,即△ACE是等腰直角三角形,∴四边形ABCD的面积与△ACE的面积相等,∵S△ACE=12×5×5=12.5,∴四边形ABCD的面积为12.5,故答案为12.5.【点睛】本题主要考查了全等三角形的判定与性质,解题的关键是学会添加常用辅助线,构造全等三角形解决问题4.如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为48和36,求△EDF的面积________.【答案】6【解析】【分析】作DM=DE交AC于M,作DN⊥AC,利用角平分线的性质得到DN=DF,将三角形EDF的面积转化为三角形DNM的面积来求.作DM=DE交AC于M,作DN⊥AC,∵AD是△ABC的角平分线,DF⊥AB,∴DF=DN,∵DE=DG,∴DG=DM,∴Rt△DEF≌Rt△DMN(HL),∵DG=DM, DN⊥AC,∴MN=NG,∴△DMN≌△DNG,∵△ADG和△AED的面积分别为48和36,∴S△MDG=S△ADG-S△ADM=48-36=12,∴S△DEF=12S△MDG=1212=6,故答案为:6【点睛】本题考查了角平分线的性质及全等三角形的判定及性质,正确地作出辅助线,将所求的三角形的面积转化为另外的三角形的面积来求是解题关键.5.如图,在△ABC中,AC=BC,∠ACB=90°,M是AB边上的中点,点D、E分别是AC、BC 边上的动点,连接DM 、ME、CM、DE, DE与CM相交于点F且∠DME=90°.则下列5个结论: (1)图中共有两对全等三角形;(2)△DEM是等腰三角形; (3)∠CDM=∠CFE;(4)AD2+BE2=DE2;(5)四边形CDME的面积发生改变.其中正确的结论有( )个.A.2 B.3 C.4 D.5【答案】B【解析】【分析】根据等腰三角形的性质,三角形内角和定理,得出:△AMC≌△BMC、△AMD≌△CME、△CMD≌△BME,根据全等三角形的性质得出DM=ME得出△DEM是等腰三角形,及∠CDM=∠CFE,再逐个判断222AD+BE=DE CEM CDM ADM CDM ACM ABCCDME1S=S+S=S+S=S=S2△△△△△△四边形即可得出结论.【详解】解:如图在Rt△ABC中,∠ACB=90°,M为AB中点,AB=BC∴AM=CM=BM,∠A=∠B=∠ACM=∠BCM=45°,∠AMC=∠BMC=90°∵∠DME=90°.∴∠1+∠2=∠2+∠3=∠3+∠4=90°∴∠1=∠3,∠2=∠4在△AMC和△BMC中AM=BMMC MCAC BC⎧⎪=⎨⎪=⎩∴△AMC≌△BMC在△AMD和△CME中A=MCEAM=CM1=3∠∠⎧⎪⎨⎪∠∠⎩∴△AMD≌△CME在△CDM和△BEMDCM=BCM=BM2=4∠∠⎧⎪⎨⎪∠∠⎩∴△CMD≌△CME共有3对全等三角形,故(1)错误∵△AMD≌△BME∴DM=ME∴△DEM是等腰三角形,(2)正确∵∠DME=90°.∴∠EDM=∠DEM=45°,∴∠CDM=∠1+∠A=∠1+45°,∴∠EDM=∠3+∠DEM=∠3+45°,∴∠CDM=∠CFE,故(3)正确在Rt △CED 中,222CE CD DE +=∵CE=AD ,BE=CD∴222AD +BE =DE 故(4)正确(5)∵△ADM ≌△CEM∴ADM CEM S =S △△∴CEM CDM ADM CDM ACM ABC CDME 1S =S +S =S +S =S =S 2△△△△△△四边形 不变,故(5)错误 故正确的有3个故选:B【点睛】本题主要考查了等腰直角三角形的判定与性质、全等三角形的判定与性质、勾股定理等知识,通过推理论证每个命题的正误是解决此类题目的关键.6.已知在△ABC 中,AD 是BC 边上的中线,若AB=10,AC=4,则AD 的取值范围是_____.【答案】3<AD <7【解析】【分析】连接AD 并延长到点E ,使DE=DA ,连接BE ,利用SAS 证得△BDE ≌△CDA ,进而得到BE=CA=4,利用三角形两边之和大于第三边,两边之差小于第三边,即可求得AE 的取值范围,进而求出AD 的取值范围.【详解】如图,连接AD 并延长到点E ,使DE=DA ,连接BE ,∵在△ABC 中,AD 是BC 边上的中线∴BD=CD在△BDE 和△CDA 中BD CD BDE CDA DE DA =⎧⎪∠=∠⎨⎪=⎩∴△BDE ≌△CDA (SAS )∴BE=CA=4在△ABE 中,AB+BE>AE ,且AB ﹣BE <AE∵AB=10,AC=4,∴6<AE <14∴3<AD <7故答案为3<AD <7【点睛】本题考点涉及三角形全等的判定及性质、三角形的三边关系等知识点,熟练掌握相关性质定理是解题关键.7.已知在△ABC 中,两边AB 、AC 的中垂线,分别交BC 于E 、G .若BC =12,EG =2,则△AEG 的周长是________.【答案】16或12.【解析】【分析】根据线段垂直平分线性质得出AE =BE ,CG =AG ,分两种情况讨论:①DE 和FG 的交点在△ABC 内,②DE 和FG 的交点在△ABC 外.【详解】∵DE ,FG 分别是△ABC 的AB ,AC 边的垂直平分线,∴AE =BE ,CG =AG .分两种情况讨论: ①当DE 和FG 的交点在△ABC 内时,如图1.∵BC =12,GE =2,∴AE +AG =BE +CG =12+2=14,△AGE 的周长是AG +AE +EG =14+2=16. ②当DE 和FG 的交点在△ABC 外时,如图2,△AGE 的周长是AG +AE +EG = BE +CG+EG =BC =12.故答案为:16或12.【点睛】本题考查了线段垂直平分线性质,注意:线段垂直平分线上的点到线段两个端点的距离相等.8.如图,△ABC中,AB=AC,∠BAC=56°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为_____度.【答案】112.【解析】【分析】连接OB、OC,根据角平分线的定义求出∠BAO=28°,利用等腰三角形两底角相等求出∠ABC,根据线段垂直平分线上的点到两端点的距离相等可得OA=OB,再根据等边对等角求出∠OBA,然后求出∠OBC,再根据等腰三角形的性质可得OB=OC,然后求出∠OCE,根据翻折变换的性质可得OE=CE,然后利用等腰三角形两底角相等列式计算即可得解.【详解】如图,连接OB、OC,∵OA平分∠BAC,∠BAC=56°,∴∠BAO=12∠BAC=12×56°=28°,∵AB=AC,∠BAC=56°,∴∠ABC=12(180°﹣∠BAC)=12×(180°﹣56°)=62°,∵OD垂直平分AB,∴OA=OB,∴∠OBA=∠BAO=28°,∴∠OBC=∠ABC﹣∠OBA=62°﹣28°=34°,由等腰三角形的性质,OB=OC,∴∠OCE=∠OBC=34°,∵∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,∴OE=CE,∴∠OEC=180°﹣2×34°=112°.故答案是:112.【点睛】考查了翻折变换,等腰三角形的性质,线段垂直平分线上的点到两端点的距离相等的性质,三角形的内角和定理,熟记各性质并准确识图是解题的关键.9.如图,在△ABC中,∠ABC=50°,∠ACB=60°,点E在BC的延长线上,∠ABC的平分线BD与∠ACE的平分线CD相交于点D,连接AD,以下结论:①∠BAC=70°;②∠DOC=90°;③∠BDC=35°;④∠DAC=55°,其中正确的是__________.(填写序号)【答案】①③④【解析】【分析】根据三角形内角和定理、角平分线的定义、三角形外角的性质、角平分线的性质解答即可.【详解】解:∵∠ABC=50°,∠ACB=60°,∴∠BAC=180°﹣50°﹣60°=70°,①正确;∵BD是∠ABC的平分线,∴∠DBC=12∠ABC=25°,∴∠DOC=25°+60°=85°,②错误;∠BDC=60°﹣25°=35°,③正确;∵∠ABC的平分线BD与∠ACE的平分线CD相交于点D,∴AD是∠BAC的外角平分线,∴∠DAC=55°,④正确.故答案为①③④.【点睛】本题考查的是角平分线的定义和性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.10.如图,AB=BC且AB⊥BC,点P为线段BC上一点,PA⊥PD且PA=PD,若∠A=22°,则∠D的度数为_________.【答案】23°【解析】解:过D作DE⊥PC于E.∵PA⊥PD,∴∠APB+∠DPE=90°.∵AB⊥BC,∴∠A+∠APB=90°,∴∠A=∠DPE=22°.在△ABP和△PED中,∵∠A=∠DPE,∠B=∠E=90°,PA=PD,∴△ABP≌△PED,∴AB=PE,BP=DE.∵AB=BC,∴BC=PE,∴BP=CE.∵BP=DE,∴CE=DE,∴∠DCE=45°,∴∠PDC=∠DCE-∠DPC=45°-22°=2 3°.故答案为:23°.二、八年级数学全等三角形选择题(难)11.已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P的运动时间为t秒,当t的值为_____秒时,△ABP和△DCE全等.A.1 B.1或3 C.1或7 D.3或7【答案】C【解析】【分析】分两种情况进行讨论,根据题意得出BP=2t=2和AP=16-2t=2即可求得.【详解】解:因为AB=CD,若∠ABP=∠DCE=90°,BP=CE=2,根据SAS证得△ABP≌△DCE,由题意得:BP=2t=2,所以t=1,因为AB=CD,若∠BAP=∠DCE=90°,AP=CE=2,根据SAS证得△BAP≌△DCE,由题意得:AP=16-2t=2,解得t=7.所以,当t 的值为1或7秒时.△ABP 和△DCE 全等.故选C .【点睛】本题考查全等三角形的判定,判定方法有:ASA ,SAS ,AAS ,SSS ,HL .12.如图,A ABC CB =∠∠,AD 、BD 、CD 分别平分ABC 的EAC ∠、ABC ∠、ACF ∠,以下结论:①AD BC ∥;②2ACB ADB ∠=∠;③90ADC ABD ∠=︒-∠;④BD 分ADC ∠;⑤3BDC BAC ∠=∠。
八年级数学人教版上册同步练习5轴对称(单元检测)(解析版)

13.5轴对称(单元检测)一、单选题(共36分)1.(本题3分)如图所示的正方形网格中,网格线的交点为格点,已知A、B是两个定格点,如果C也是图中的格点,且使得ABC为等腰三角形,则点C的个数是()A.6个B.7个C.8个D.9个【答案】C【分析】分AB是腰长时,根据网格结构,找出一个小正方形与A、B顶点相对的顶点,连接即可得到等腰三角形,AB是底边时,根据线段垂直平分线上的点到线段两端点的距离相等,AB垂直平分线上的格点都可以作为点C,然后相加即可得解.【详解】①AB为等腰△ABC底边时,符合条件的C点有4个;②AB为等腰△ABC其中的一条腰时,符合条件的C点有4个.具体如图所示:故选:C.【点评】本题考查了等腰三角形的判定,熟练掌握网格结构的特点是解题的关键,要注意分AB是腰长与底边两种情况讨论求解.,连结BF,2.(本题3分)如图,AD是ABC的中线,E,F分别是AD和AD延长线上的点,且DE DFCE.下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有()A.1个B.2个C.3个D.4个【答案】C∆≅∆,则可对④进行判断;利用全等三角形的性质可对①进行判【分析】根据“SAS”可证明CDE BDF断;由于AE与DE不能确定相等,则根据三角形面积公式可对②进行判断;根据全等三角形的性质得到∠=∠,则利用平行线的判定方法可对③进行判断.ECD FBD∆的中线,【详解】AD是ABCCD BD∴=,∠=∠,=,CDE BDFDE DF∴∆≅∆,所以④正确;()CDE BDF SAS∴=,所以①正确;CE BF∵与DE不能确定相等,AE∆面积不一定相等,所以②错误;ACE∴∆和CDE∆≅∆,CDE BDF∴∠=∠,ECD FBD∴,所以③正确;BF CE//故选:C.【点评】本题考查了全等三角形的判定,熟悉全等三角形的5种判定方法是解题的关键.3.(本题3分)如图是一个台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔.若一个球按图中所示的方向被击出(球可以经过多次反射),则该球最后将落入的球袋是()A.1 号袋B.2 号袋C.3 号袋D.4 号袋【答案】B【分析】根据轴对称的性质画出图形即可得出正确选项.【详解】根据轴对称的性质可知,台球走过的路径为:∴最后落入2号球袋,故选B.【点评】本题考查轴对称图形的定义与判定,如果一个图形沿着一条直线对折,两侧的图形能完全重合,这个图形就是轴对称图形.折痕所在的这条直线叫做对称轴;画出图形是正确解答本题的关键.4.(本题3分)下列说法中,正确的有()①等腰三角形的两腰相等;②等腰三角形底边上的中线与底边上的高相等;③等腰三角形的两底角相等;④等腰三角形两底角的平分线相等.A.1个B.2个C.3个D.4个【答案】D【解析】分析:等腰三角形中顶角平分线,底边中线及高互相重合,即三线合一,两腰上的角平分线、中线及高都相等.详解:①等腰三角形的两腰相等;正确;②等腰三角形底边上的中线与底边上的高相等;正确;③等腰三角形的两底角相等;正确;④等腰三角形两底角的平分线相等.正确.故选D.点睛:本题主要考查了等腰三角形的性质以及命题与定理的概念,能够熟练掌握.,D是BC中点,下列结论,不一定正确的是()5.(本题3分)如图,△ABC中,AB ACA .AD BC ⊥B .AD 平分BAC ∠ C .2AB BD = D .B C ∠=∠【答案】C 【分析】根据等边对等角和等腰三角形三线合一的性质解答.【详解】∵AB=AC ,∴∠B=∠C ,∵AB=AC ,D 是BC 中点,∴AD 平分∠BAC ,AD ⊥BC ,所以,结论不一定正确的是AB=2BD .故选:C .【点评】本题考查了等腰三角形的性质,主要利用了等边对等角的性质以及等腰三角形三线合一的性质,熟记性质并准确识图是解题的关键.6.(本题3分)等腰三角形ABC 中,AB AC =,一边上的中线BD 将这个三角形的周长分为15和12两部分,则这个等腰三角形的底边长为( )A .7B .7或11C .11D .7或10【答案】B【分析】根据已知条件中的15或12两个部分,哪一部分是腰长与腰长一半的和不明确,则需分两种情况讨论.【详解】根据题意,如图所示:①当AC+12AC=15,解得AC=10,所以底边长=12-12×10=7; ②当AC+12AC=12,解得AC=8, 所以底边长=15-12×8=11. 所以底边长等于7或11.故选:B .【点评】考查了等腰三角形的性质和三角形的三边关系,解题关键抓住在已知条件没有明确给出哪一部分长要一定要想到两种情况,需采用分类进行讨论,还应验证各种情况是否能构成三角形.7.(本题3分)如图,点P 为∠AOB 内一点,分别作出点P 关于OA 、OB 的对称点P 1、P 2,连接P 1,P 2交 OA 于M ,交OB 于N ,若P 1P 2=6,则△PMN 的周长为( )A .4B .5C .6D .7【答案】C【解析】 试题分析:根据对称图形的性质可得:PM=1P M ,PN=2P N ,则△PMN 的周长=PM+MN+PN=1P M+MN+2P N=1P 2P =6.考点:对称的性质8.(本题3分)如果一个三角形的外角平分线与这个三角形一边平行,则这个三角形一定是( ) A .锐角三角形B .等腰三角形C .等边三角形D .等腰直角三角形 【答案】B【分析】可依据题意线作出图形,结合图形利用平行线的性质和角平分线的定义可得∠B=∠A ,利用“等角对等边”可得其为等腰三角形.【详解】如图,DC 平分∠ACE ,且AB ∥CD ,∴∠ACD =∠DCE ,∠A =∠ACD ,∠B =∠DCE ,∴∠B =∠A ,∴△ABC 为等腰三角形.故选B .【点评】本题考查了平行线的性质和等腰三角形的判定,进行角的等量代换是正确解答本题的关键. 9.(本题3分)将点A (2,3)向左平移2个单位长度得到点A’,点A’关于x 轴的对称点是A’’,则点A’’的坐标为( )A .(0,-3)B .(4,-3)C .(4,3)D .(0,3)【答案】A【详解】试题解析:∵点A (2,3)向左平移2个单位长度得到点A′,∴点A′的横坐标为2-2=0,纵坐标不变,即点A′的坐标为(0,3).点A ′关于x 轴的对称点是A ″,则点A ″的坐标为(0,-3).故选A .10.(本题3分)已知,在△ABC 中,AB AC =,如图,(1)分别以B ,C 为圆心,BC 长为半径作弧,两弧交于点D ; (2)作射线AD ,连接BD ,CD .根据以上作图过程及所作图形,下列结论中错误..的是( )A .BAD CAD ∠=∠B .△BCD 是等边三角形C .AD 垂直平分BCD .ABDC S AD BC =【答案】D 【分析】根据作图过程及所作图形可知BD BC CD ==,得出△BCD 是等边三角形;又因为AB AC =,,BD CD AD AD ==,推出ABD ACD ≅,继而得出BAD CAD ∠=∠;根据,BAD CAD ∠=∠,可知AD 为BAC ∠的角平分线,根据三线合一得出AD 垂直平分BC ;四边形ABCD 的面积等于ABD △的面积与ACD △的面积之和,为12AD BC ⋅. 【详解】∵BD BC CD ==∴△BCD 是等边三角形故选项B 正确;∵AB AC =,,BD CD AD AD ==∴ABD ACD ≅∴BAD CAD ∠=∠故选项A 正确;∵BAD CAD ∠=∠,AB AC =∴据三线合一得出AD 垂直平分BC故选项C 正确;∵四边形ABCD 的面积等于ABD △的面积与ACD △的面积之和 ∴12ABCD S AD BC =⋅ 故选项D 错误.故选:D .【点评】本题考查的知识点是等边三角形的判定、全等三角形的判定及性质、线段垂直平分线的判定以及四边形的面积,考查的范围较广,但难度不大.11.(本题3分)如图,在ABC ∆中,4BC =,BD 平分ABC ∠,过点A 作AD BD ⊥于点D ,过点D 作//DE CB ,分别交AB 、AC 于点E 、F ,若2EF DF =,则AB 的长为( )A .10B .8C .7D .6【答案】D【分析】延长AD 、BC 交于点G ,根据三线合一性质推出ABG ∆是等腰三角形,从而可得D 是AG 的中点,E 是AB 的中点,再利用中位线定理即可得.【详解】如图,延长AD 、BC 交于点G∵BD 平分ABC ∠,AD BD ⊥于点D,90ABD GBD ADB GDB ∴∠=∠∠=∠=︒∴BAD G ∠=∠AB BG ∴=,D 是AG 的中点∵//DE BG∴E 是AB 的中点,F 是AC 的中点,DE 是ABG ∆的中位线,EF 是ABC ∆的中位线 ∴12,22EF BC BG DE === 又∵2EF DF =∴1DF =∴3DE EF DF =+=∴26BG DE ==∴6AB =故选:D.【点评】本题考查了等腰三角形的判定定理与性质、中位线定理,通过作辅助线,构造等腰三角形是解题关键.错因分析:容易题.失分原因是对特殊三角形的性质及三角形的重要线段掌握不到位.12.(本题3分)如图,AB ⊥AC ,CD 、BE 分别是△ABC 的角平分线,AG ∥BC ,AG ⊥BG ,下列结论:①∠BAG =2∠ABF ;②BA 平分∠CBG ;③∠ABG =∠ACB ;④∠CFB =135°,其中正确的结论有( )个A.1 B.2 C.3 D.4【答案】C【分析】由已知条件可知∠ABC+∠ACB=90°,又因为CD、BE分别是△ABC的角平分线,所以得到∠FBC+∠FCB=45°,所以求出∠CFB=135°;有平行线的性质可得到:∠ABG=∠ACB,∠BAG=2∠ABF.所以可知选项①③④正确.【详解】∵AB⊥AC.∴∠BAC=90°,∵∠BAC+∠ABC+∠ACB=180°,∴∠ABC+∠ACB=90°∵CD、BE分别是△ABC的角平分线,∴2∠FBC+2∠FCB=90°∴∠FBC+∠FCB=45°∴∠BFC=135°故④正确.∵AG∥BC,∴∠BAG=∠ABC∵∠ABC=2∠ABF∴∠BAG=2∠ABF 故①正确.∵AB⊥AC,∴∠ABC+∠ACB=90°,∵AG⊥BG,∴∠ABG+∠GAB=90°∵∠BAG=∠ABC,∴∠ABG=∠ACB 故③正确.故选C.【点评】本题考查了等腰三角形的判定与性质,平行线的性质.掌握相关的判定定理和性质定理是解题的关键.二、填空题目(共12分)13.(本题3分)如图,在△ABC 中,AB =4,BC =6,∠B =60°,将△ABC 沿射线BC 的方向平移2个单位后,得到A B C ''',连接A C ',则A B C ''的周长为________.【答案】12【分析】根据平移的性质得2BB '=,4A B AB ''==,=60A B C B ∠''∠=︒,则可计算624B C BC BB '=-'=-=,则4A B B C ''='=,可判断A B C ''△为等边三角形,继而可求得A B C ''△的周长.【详解】ABC 平移两个单位得到的A B C ''',2BB ∴'=,AB A B ='',4AB =,6BC =,4A B AB ∴''==,624B C BC BB '=-'=-=,4A B B C ∴''='=,又60B ∠=︒,60A B C ∴∠''=︒,A B C ∴''是等边三角形,A B C ∴''的周长为4312⨯=.故答案为:12.【点评】本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.14.(本题3分)如图,在Rt △ACB 中,∠ACB =90°,∠A =25°,D 是AB 上一点,将Rt △ABC 沿CD 折叠,使点B 落在AC 边上的B ′处,则∠ADB ′等于_____.【答案】40°.【详解】∵将Rt△ABC沿CD折叠,使点B落在AC边上的B′处,∴∠ACD=∠BCD,∠CDB=∠CDB′,∵∠ACB=90°,∠A=25°,∴∠ACD=∠BCD=45°,∠B=90°﹣25°=65°,∴∠BDC=∠B′DC=180°﹣45°﹣65°=70°,∴∠ADB′=180°﹣70°﹣70°=40°.故答案为40°.15.(本题3分)如图,在△ABC中,AB=10,AC=8,∠ABC、∠ACB的平分线相交于点O,MN过点O,且MN∥BC,分别交AB、AC于点M、N.则△AMN的周长为_______.【答案】18【分析】由在△ABC中,∠ABC与∠ACB的平分线相交于点O,过点O作MN∥BC,易证得△BOM与△CON是等腰三角形,继而可得△AMN的周长等于AB+AC.【详解】∵在△ABC中,∠ABC、∠ACB的平分线相交于点O,∴∠ABO=∠OBC,∵MN∥BC,∴∠MOB=∠OBC,∴∠ABO=∠MOB,∴BM=OM,同理CN=ON,∴△AMN的周长是:AM+NM+AN=AM+OM+ON+AN=AM+BM+CN+AN=AB+AC=10+8=18.故答案为:18.【点评】本题考查等腰三角形的判定与性质,角平分线的性质,平行线的判定,三角形周长的求法,等量代换等知识点.16.(本题3分)如图所示,在等腰△ABC中,AB=AC,∠A=36°,将△ABC中的∠A沿DE向下翻折,使点A落在点C处.若,则BC的长是_____.【解析】【分析】由折叠的性质可知AE=CE,再证明△BCE是等腰三角形即可得到BC=CE,问题得解.【详解】∵AB=AC,∠A=36°,∴∠B=∠ACB=180362︒-︒=72°,∵将△ABC中的∠A沿DE向下翻折,使点A落在点C处,∴AE=CE,∠A=∠ECA=36°,∴∠CEB=72°,∴,【点睛】本题考查了等腰三角形的判断和性质、折叠的性质以及三角形内角和定理的运用,证明△BCE是等腰三角形是解题的关键.三、解答题(共72分)17.(本题8分)用一条长为18的绳子围成一个等腰三角形.(1)若等腰三角形有一条边长为4,它的其它两边是多少?(2)若等腰三角形的三边长都为整数,请直接写出所有能围成的等腰三角形的腰长.【答案】(1)其他两边分别为4和7;(2)y =2时,x =8,y =4时,x =7,y =8时,x =5.【分析】(1)根据等腰三角形的性质即可求出答案.(2)设等腰三角形的三边长为x 、x 、y ,根据题意可知y <9,y 是2的倍数,从而可求出答案.【详解】(1)当等腰三角形的腰长为4,∴底边长为18﹣4×2=10,∵4+4<10,∴4、4、10不能组成三角形,当等腰三角形的底边长为4,∴腰长为(18﹣4)÷2=7,∵4+7>7,∴4、7、7能组成三角形,综上所述,其他两边分别为4和7.(2)设等腰三角形的三边长为x 、x 、y ,由题意可知:2x +y =18,且2x >y ,∴y <9,∵x =18y 2-=9﹣y 2,x 与y 都是整数, ∴y 是2的倍数,∴y =2时,x =8,y =4时,x =7,y =8,x =5.【点评】本题考查等腰三角形,解题的关键是熟练运用等腰三角形的性质,本题属于基础题型. 18.(本题8分)如图,一个四边形纸片ABCD ,90B D ∠=∠=︒,把纸片按如图所示折叠,使点B 落在AD 边上的'B 点,AE 是折痕.(1)判断'B E 与DC 的位置关系,并说明理由;(2)如果130C ∠=︒,求AEB ∠的度数.【答案】(1)B′E ∥DC ,理由见解析;(2)65°【分析】(1)由于AB '是AB 的折叠后形成的,可得90AB E B D ∠'=∠=∠=︒,可得B′E ∥DC ; (2)利用平行线的性质和全等三角形求解.【详解】(1)由于AB '是AB 的折叠后形成的,90AB E B D ∠'=∠=∠=︒,//B E DC ∴';(2)折叠,ABE ∴∆≅△AB E ',AEB AEB ∴∠'=∠,即12AEB BEB ∠=∠', //B E DC ',130BEB C ∴∠'=∠=︒,1652AEB BEB ∴∠=∠'=︒. 【点评】本题考查了三角形全等的判定及性质;把纸片按如图所示折叠,使点B 落在AD 边上的B ′点,则ABE ∆≅△AB E ',利用全等三角形的性质和平行线的性质及判定求解.19.(本题8分)如图,点D ,E 在△ABC 的边BC 上,AB =AC ,AD =AE ,求证:BD =CE.【答案】见解析【分析】如图,过点 A 作 ⊥AP BC 于 P ,根据等腰三角形的三线合一得出BP=PC ,DP=PE ,进而根据等式的性质,由等量减去等量差相等得出BD=CE .【详解】如图,过点A 作⊥AP BC 于 P .∵AB AC =,∴BP PC =;∵AD AE =,∴DP PE =,∴BP DP PC PE -=-,∴BD=CE .【点评】本题考查了等腰三角形的性质,注意:等腰三角形的底边上的高,底边上的中线,顶角的平分线互相重合.20.(本题8分)如图所示,一个四边形纸片ABCD ,∠B=∠D=90°,把纸片按如图所示的方式折叠,使点B 落在AD 边上的B′点,AE 是折痕.(1)试判断B′E 与DC 的位置关系;(2)如果∠C=130°,求∠AEB 的度数.【答案】(1)B 'E//DC ;(2)∠AEB=65°【分析】(1)先由折叠性质可知90AB E B '∠=∠=︒,再由∠D=90°可得AB E D ∠'=∠,进而求解即可; (2)先运用平行线的性质可得130B EB C ∠=∠='︒,再由折叠的性质可得AEB AEB '∠=∠,进而求解即可.【详解】(1)B 'E ∥DC由折叠可知∠A B 'E=∠B=90°∵∠D=90°∴∠A B 'E=∠D∴B 'E ∥DC(2)∵B′E ∥DC∴∠B'EB=∠C=130°由折叠可知∠AEB=∠AE B',∴∠AEB=12∠B'EB=12×130°=65°故答案为:65°【点评】本题主要是折叠的性质以及平行线的判定和性质,根据折叠的性质,找到折叠后相等的角和边;同位角相等,两直线平行,两直线平行,同位角相等.21.(本题8分)如图,点P是∠AOB外的一点,点Q与P关于OA对称,点R与P关于OB对称,直线QR 分别交OA、OB于点M、N,若PM=PN=4,MN=5.(1)求线段QM、QN的长;(2)求线段QR的长.【答案】(1)4,1;(2)5【分析】(1)利用轴对称的性质求出MQ即可解决问题;(2)利用轴对称的性质求出NR即可解决问题.【详解】(1)∵P,Q关于OA对称,∴OA垂直平分线段PQ,∴MQ=MP=4,∵MN=5,∴QN=MN﹣MQ=5﹣4=1.(2)∵P,R关于OB对称,∴OB垂直平分线段PR,∴NR=NP=4,∴QR=QN+NR=1+4=5.【点评】本题考查轴对称的性质,解题的关键是理解题意,熟练掌握轴对称的性质属于中考常考题型. 22.(本题10分)如图,点O 是等边ABC 内一点,AOB 110∠=,BOC α∠=.将BOC 绕点C 逆时针旋转60得ADC ,连接OD .()1求证:DOC 是等边三角形;()2当AO 5=,BO 4=,α150=时,求CO 的长; ()3探究:当α为多少度时,AOD 是等腰三角形.【答案】()1证明见解析;()23CO =;()3125α=、110α=或140α=.【分析】()1由旋转的性质可以知道CO CD =,D 60OC ∠=,可判断COD 是等边三角形; ()2由()1可知D 60OC ∠=,当α150=时,90ADO ADC CDO ∠∠∠=-=,可判断AOD 为直角三角形; ()3?根据AOD 是等腰三角形,推出两腰相等,分三种情况进行讨论,利用旋转和全等的性质即可得出答案. 【详解】()1∵将BOC 绕点C 按顺时针方向旋转60得ADC ,∴BOC ADC ≅,D 60OC ∠=,∴CO CD =.∴COD 是等边三角形;()2∵ADC BOC ≅,∴4DA OB ==,∵COD 是等边三角形,∴60CDO ∠=,又150ADC ∠∠α==,∴90ADO ADC CDO ∠∠∠=-=,∴AOD 为直角三角形.又5AO =,4AD =,∴3OD =,∴3CO OD ==;()3若AOD 是等腰三角形,所以分三种情况:①AOD ADO ∠∠=②ODA OAD ∠∠=③AOD DAO ∠∠=,∵110AOB ∠=,60COD ∠=,∴36011060190BOC AOD AOD ∠∠∠=---=-,而BOC ADC ADO CDO ∠∠∠∠==+,由①AOD ADO ∠∠=可得60BOC AOD ∠∠=+,求得125α=;由②ODA OAD ∠∠=可得11502BOC AOD ∠∠=-求得110α=;由③AOD DAO ∠∠=可得2402BOC AOD ∠∠=-,求得140α=; 综上可知125α=、110α=或140α=.【点评】本题主要考查旋转的性质,全等三角形的判定与性质,等腰(边)三角形的判定与性质,掌握图形的关系是解题的关键.23.(本题10分)如图,在△ABC 中,AB=AC ,∠BAC 和∠ACB 的平分线相交于点D ,∠ADC=125°.求∠ACB 和∠BAC 的度数.【答案】70°、40°.【详解】试题分析:根据等腰三角形三线合一的性质可得AE ⊥BC ,再求出∠CDE ,然后根据直角三角形两锐角互余求出∠DCE ,根据角平分线的定义求出∠ACB ,再根据等腰三角形两底角相等列式进行计算即可求出∠BAC.试题解析:∵AB=AC,AE平分∠BAC,∴AE⊥BC(等腰三角形三线合一),∵∠ADC=125°,∴∠CDE=55°,∴∠DCE=90°﹣∠CDE=35°,又∵CD平分∠ACB,∴∠ACB=2∠DCE=70°,又∵AB=AC,∴∠B=∠ACB=70°,∴∠BAC=180﹣(∠B+∠ACB)=40°.【点睛】本题考查了等腰三角形三线合一的性质,等腰三角形两底角相等的性质,角平分线的定义,是基础题,准确识图并熟记性质是解题的关键.24.(本题12分)已知点C为线段AB上一点,分别以AC、BC为边在线段AB同侧作△ACD和△BCE,且CA=CD,CB=CE,∠ACD=∠BCE,直线AE与BD交于点F,(1)如图1,若∠ACD=60°,则∠AFB=;如图2,若∠ACD=90°,则∠AFB=;如图3,若∠ACD=120°,则∠AFB=;(2)如图4,若∠ACD=α,则∠AFB=(用含α的式子表示);(3)将图4中的△ACD绕点C顺时针旋转任意角度(交点F至少在BD、AE中的一条线段上),变成如图5所示的情形,若∠ACD=α,则∠AFB与α的有何数量关系?并给予证明.【答案】(1)120°,90°,60°;(2)180°﹣α;(3)∠AFB=180°﹣α,证明详见解析.【分析】(1)如图1,证明△ACE≌△DCB,根据全等三角形的性质可得∠EAC=∠BDC,再根据∠AFB是△ADF的外角求出其度数即可;如图2,证明△ACE≌△DCB,得出∠AEC=∠DBC,又有∠FDE=∠CDB,进而得出∠AFB=90°;如图3,证明△ACE≌△DCB,得出∠EAC=∠BDC,又有∠BDC+∠FBA=180°-∠DCB得到∠FAB+∠FBA=120°,进而求出∠AFB=60°;(2)由∠ACD=∠BCE得到∠ACE=∠DCB,再由三角形的内角和定理得∠CAE=∠CDB,从而得出∠DFA=∠ACD,得到结论∠AFB=180°-α;(3)由∠ACD=∠BCE得到∠ACE=∠DCB,通过证明△ACE≌△DCB得∠CBD=∠CEA,由三角形内角和定理得到结论∠AFB=180°-α.【详解】(1)如图1,CA=CD,∠ACD=60°,所以△ACD是等边三角形.∵CB=CE,∠ACD=∠BCE=60°,所以△ECB是等边三角形.∵AC=DC,∠ACE=∠ACD+∠DCE,∠BCD=∠BCE+∠DCE,又∵∠ACD=∠BCE,∴∠ACE=∠BCD.∵AC=DC,CE=BC,∴△ACE≌△DCB.∴∠EAC=∠BDC.∠AFB是△ADF的外角.∴∠AFB=∠ADF+∠FAD=∠ADC+∠CDB+∠FAD=∠ADC+∠EAC+∠FAD=∠ADC+∠DAC=120°.如图2,∵AC=CD,∠ACE=∠DCB=90°,EC=CB,∴△ACE≌△DCB.∴∠AEC=∠DBC,又∵∠FDE=∠CDB,∠DCB=90°,∴∠EFD=90°.∴∠AFB=90°.如图3,∵∠ACD=∠BCE,∴∠ACD﹣∠DCE=∠BCE﹣∠DCE.∴∠ACE=∠DCB.又∵CA=CD,CE=CB,∴△ACE≌△DCB.∴∠EAC=∠BDC.∵∠BDC+∠FBA=180°﹣∠DCB=180°﹣(180﹣∠ACD)=120°,∴∠FAB+∠FBA=120°.∴∠AFB=60°.故填120°,90°,60°.(2)∵∠ACD=∠BCE,∴∠ACD+∠DCE=∠BCE+∠DCE.∴∠ACE=∠DCB.∴∠CAE=∠CDB.∴∠DFA=∠ACD.∴∠AFB=180°﹣∠DFA=180°﹣∠ACD=180°﹣α.(3)∠AFB=180°﹣α;证明:∵∠ACD=∠BCE=α,则∠ACD+∠DCE=∠BCE+∠DCE,即∠ACE=∠DCB.在△ACE和△DCB中,则△ACE≌△DCB(SAS).则∠CBD=∠CEA,由三角形内角和知∠EFB=∠ECB=α.∠AFB=180°﹣∠EFB=180°﹣α.【点评】本题考查了全等三角形的性质和判定、三角形的外角性质及三角形的内角和定理,熟练运用三角形全等的判定方法证明三角形全等,利用全等三角形的性质解决问题是解决这类题目的基本思路.祝福语祝你考试成功!。
八年级数学轴对称解答题专题练习(解析版)

八年级数学轴对称解答题专题练习(解析版)一、八年级数学轴对称解答题压轴题(难)1.如图,在ABC△中,已知AD是BC边上的中线,E是AD上一点,且BE AC=,延长BE交AC于点F,求证:AF EF=.【答案】证明见解析【解析】【分析】延长AD到点G,使得AD DG=,连接BG,结合D是BC的中点,易证△ADC和△GDB 全等,利用全等三角形性质以及等量代换,得到△AEF中的两个角相等,再根据等角对等边证得AE=EF.【详解】如图,延长AD到点G,延长AD到点G,使得AD DG=,连接BG.∵AD是BC边上的中线,∴DC DB=.在ADC和GDB△中,AD DGADC GDBDC DB=⎧⎪∠=∠⎨⎪=⎩(对顶角相等),∴ADC≌GDB△(SAS).∴CAD G∠=∠,BG AC=.又BE AC=,∴BE BG=.∴BED G ∠=∠. ∵BED AEF ∠=∠∴AEF CAD ∠=∠,即AEF FAE ∠=∠ ∴AF EF =. 【点睛】本题考查的是全等三角形的判定与性质,根据题意构造全等三角形是解答本题的关键.2.如图,在ABC ∆中,CE 为三角形的角平分线,AD CE ⊥于点F 交BC 于点D (1)若9628BAC B ︒︒∠=∠=,,直接写出BAD ∠= 度 (2)若2ACB B ∠=∠, ①求证:2AB CF =②若,CF a EF b ==,直接写出BDCD= (用含,a b 的式子表示)【答案】(1)34;(2)①见详解;②2ba b- 【解析】 【分析】(1)由三角形内角和定理和角平分线定义即可得出答案;(2)①证明B BCE ∠=∠,得出BE=CE ,过点A 作//AH BC 交CE 与点H ,则,H BCE ACE EAH B ∠=∠=∠∠=∠,得出AH=AC ,H EAH ∠=∠,得出AE=HE ,由等腰三角形的性质可得出HF=CF ,即可得出结论;②证明AHF DCF ≅,得出AH=DC ,求出HF=CF=a ,HE=HF-EF=a-b ,CE=a+b ,由//AH BC 得出AH AE a bBC BE a b-==+,进而得出结论. 【详解】解:(1)∵9628BAC B ︒︒∠=∠=,, ∴180962856ACB ∠=︒-︒-︒=︒, ∵CE 为三角形的角平分线, ∴1282ACE ACB ∠=∠=︒, ∵AD CE ⊥,∴902862CAF ∠=︒-︒=︒, ∴966234BAD ∠=︒-︒=︒.故答案为:34;(2)①证明:∵22ACB B BCE∠=∠=∠∴B BCE∠=∠∴BE CE=过点A作//AH BC交CE与点H,如图所示:则,H BCE ACE EAH B∠=∠=∠∠=∠∴AH=AC,H EAH∠=∠∴AE=HE∵AD CE⊥∴HF=CF∴AB=HC=2CF;②在AHF△和DCF中,H DCFHF CFAFH DFC∠=∠⎧⎪=⎨⎪∠=∠⎩∴AHF DCF≅∴AH=DC∵,CF a EF b==∴HF CF a==,由①得AE HE HF EF a b==-=-,BE CE a b==+∵//AH BC∴AH AE a bBC BE a b-==+∴CD a bBC a b-=+∴2BD bCD a b=-.故答案为:2ba b-.【点睛】本题考查的知识点是全等三角形的判定及其性质、等腰三角形的判定及其性质、三角形的内角和定理、三角形的角平分线定理等,掌握以上知识点是解此题的关键.3.如图,在等边ABC∆中,点D,E分别是AC,AB上的动点,且AE CD=,BD 交CE于点P.(1)如图1,求证120BPC︒∠=;(2)点M是边BC的中点,连接PA,PM.①如图2,若点A,P,M三点共线,则AP与PM的数量关系是;②若点A,P,M三点不共线,如图3,问①中的结论还成立吗?若成立,请给出证明,若不成立,请说明理由.【答案】(1)证明过程见详解;(2)①2AP PM=;②结论成立,证明见详解【解析】【分析】(1)先证明()AEC CDB SAS≌,得出对应角相等,然后利用四边形的内角和和对顶角相等即可得出结论;(2)①2AP PM=;由等边三角形的性质和已知条件得出AM⊥BC,∠CAP=30°,可得PB=PC,由∠BPC=120°和等腰三角形的性质可得∠PCB=30°,进而可得AP=PC,由30°角的直角三角形的性质可得PC=2PM,于是可得结论;②延长BP至D,使PD=PC,连接AD、CD,根据SAS可证△ACD≌△BCP,得出AD=BP ,∠ADC=∠BPC=120°,然后延长PM至N,使MN=MP,连接CN,易证△CMN≌△BMP (SAS),可得CN=BP=AD,∠NCM=∠PBM,最后再根据SAS证明△ADP≌△NCP,即可证得结论.【详解】(1)证明:因为△ABC为等边三角形,所以60A ACB∠=∠=︒∵AC BCA ACBAE CD=⎧⎪∠=∠⎨⎪=⎩,∴()AEC CDB SAS≌,∴AEC CDB∠=∠,在四边形AEPD中,∵360AEC EPD PDA A∠+∠+∠+∠=︒,∴18060360AEC EPD CDB∠+∠+︒-∠+︒=︒,∴120EPD∠=︒,∴120BPC∠=︒;(2)①如图2,∵△ABC 是等边三角形,点M 是边BC 的中点, ∴∠BAC =∠ABC =∠ACB =60°,AM ⊥BC ,∠CAP =12∠BAC =30°,∴PB =PC , ∵∠BPC =120°,∴∠PBC =∠PCB =30°, ∴PC =2PM ,∠ACP =60°﹣30°=30°=∠CAP , ∴AP =PC ,∴AP =2PM ; 故答案为:2AP PM ;②AP =2PM 成立,理由如下:延长BP 至D ,使PD =PC ,连接AD 、CD ,如图4所示:则∠CPD =180°﹣∠BPC =60°, ∴△PCD 是等边三角形,∴CD =PD =PC ,∠PDC =∠PCD =60°,∵△ABC 是等边三角形,∴BC =AC ,∠ACB =60°=∠PCD , ∴∠BCP =∠ACD , ∴△ACD ≌△BCP (SAS ), ∴AD =BP ,∠ADC =∠BPC =120°, ∴∠ADP =120°﹣60°=60°,延长PM 至N ,使MN =MP ,连接CN , ∵点M 是边BC 的中点,∴CM =BM , ∴△CMN ≌△BMP (SAS ), ∴CN =BP =AD ,∠NCM =∠PBM , ∴CN ∥BP ,∴∠NCP +∠BPC =180°, ∴∠NCP =60°=∠ADP ,在△ADP 和△NCP 中,∵AD=NC ,∠ADP =∠NCP ,PD=PC , ∴△ADP ≌△NCP (SAS ), ∴AP =PN =2CM ;【点睛】本题是三角形的综合题,主要考查了等边三角形的判定与性质、全等三角形的判定与性质、含30°角的直角三角形的性质等知识;熟练掌握等边三角形的判定与性质,证明三角形全等是解题的关键.4.如图,在等边△ABC中,线段AM为BC边上的中线.动点D在直线AM上时,以CD为一边在CD的下方作等边△CDE,连结BE.(1)求∠CAM的度数;(2)若点D在线段AM上时,求证:△ADC≌△BEC;(3)当动D在直线..AM上时,设直线BE与直线AM的交点为O,试判断∠AOB是否为定值?并说明理由.【答案】(1)30°;(2)答案见解析;(3)∠AOB是定值,∠AOB=60°.【解析】【分析】(1)根据等边三角形的性质可以直接得出结论;(2)根据等边三角形的性质就可以得出AC=BC,DC=EC,∠ACB=∠DCE=60°,由等式的性质就可以∠BCE=∠ACD,根据SAS就可以得出△ADC≌△BEC;(3)分情况讨论:当点D在线段AM上时,如图1,由(2)可知△ACD≌△BCE,就可以求出结论;当点D在线段AM的延长线上时,如图2,可以得出△ACD≌△BCE而有∠CBE=∠CAD=30°而得出结论;当点D在线段MA的延长线上时,如图3,通过得出△ACD≌△BCE同样可以得出结论.【详解】(1)∵△ABC 是等边三角形,∴∠BAC =60°. ∵线段AM 为BC 边上的中线,∴∠CAM 12=∠BAC ,∴∠CAM =∠BAM =30°. (2)∵△ABC 与△DEC 都是等边三角形,∴AC =BC ,CD =CE ,∠ACB =∠DCE =60°,∴∠ACD +∠DCB =∠DCB +∠BCE ,∴∠ACD =∠BCE .在△ADC 和△BEC 中,∵AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△BCE (SAS );(3)∠AOB 是定值,∠AOB =60°.理由如下:①当点D 在线段AM 上时,如图1,由(2)可知△ACD ≌△BCE ,则∠CBE =∠CAD =30°,又∠ABC =60°,∴∠CBE +∠ABC =60°+30°=90°.∵△ABC 是等边三角形,线段AM 为BC 边上的中线,∴AM 平分∠BAC ,即11603022BAM BAC ∠∠==⨯︒=︒,∴∠BOA =90°﹣30°=60°.②当点D 在线段AM 的延长线上时,如图2. ∵△ABC 与△DEC 都是等边三角形,∴AC =BC ,CD =CE ,∠ACB =∠DCE =60°,∴∠ACB +∠DCB =∠DCB +∠DCE ,∴∠ACD =∠BCE .在△ACD 和△BCE 中,∵AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△BCE (SAS ),∴∠CBE =∠CAD =30°. 由(1)得:∠BAM =30°,∴∠BOA =90°﹣30°=60°. ③当点D 在线段MA 的延长线上时. ∵△ABC 与△DEC 都是等边三角形,∴AC =BC ,CD =CE ,∠ACB =∠DCE =60°,∴∠ACD +∠ACE =∠BCE +∠ACE =60°,∴∠ACD =∠BCE .在△ACD 和△BCE 中,∵AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△BCE (SAS ),∴∠CBE =∠CAD . 由(1)得:∠CAM =30°,∴∠CBE =∠CAD =150°,∴∠CBO =30°,∠BAM =30°,∴∠BOA =90°﹣30°=60°.综上所述:当动点D 在直线AM 上时,∠AOB 是定值,∠AOB =60°.【点睛】本题考查了等边三角形的性质的运用,直角三角形的性质的运用,等式的性质的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.5.已知如图1,在ABC ∆中,AC BC =,90ACB ∠=,点D 是AB 的中点,点E 是AB 边上一点,直线BF 垂直于直线CE 于点F ,交CD 于点G . (1)求证:AE CG =.(2)如图2,直线AH 垂直于直线CE ,垂足为点H ,交CD 的延长线于点M ,求证:BE CM =.【答案】(1)证明见解析;(2)证明见解析. 【解析】 【分析】(1)首先根据点D 是AB 中点,∠ACB =90°,可得出∠ACD =∠BCD =45°,判断出△AEC ≌△CGB ,即可得出AE =CG ;(2)根据垂直的定义得出∠CMA +∠MCH =90°,∠BEC +∠MCH =90°,再根据AC =BC ,∠ACM =∠CBE =45°,得出△BCE ≌△CAM ,进而证明出BE =CM . 【详解】(1)∵点D 是AB 中点,AC =BC ,∠ACB =90°,∴CD ⊥AB ,∠ACD =∠BCD =45°,∴∠CAD =∠CBD =45°,∴∠CAE =∠BCG . 又∵BF ⊥CE ,∴∠CBG +∠BCF =90°.又∵∠ACE+∠BCF=90°,∴∠ACE=∠CBG.在△AEC和△CGB中,∵CAE BCGAC BCACE CBG∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△AEC≌△CGB(ASA),∴AE=CG;(2)∵CH⊥HM,CD⊥ED,∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,∴∠CMA=∠BEC.在△BCE和△CAM中,BEC CMAACM CBEBC AC∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BCE≌△CAM(AAS),∴BE=CM.【点睛】本题考查了全等三角形的判定与性质,等腰直角三角形的性质.全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.6.如图,在平面直角坐标系中,点B坐标为()6,0-,点A 是y轴正半轴上一点,且10AB=,点P是x轴上位于点B右侧的一个动点,设点P的坐标为()0m,.(1)点A的坐标为___________;(2)当ABP△是等腰三角形时,求P点的坐标;(3)如图2,过点P作PE AB⊥交线段AB于点E,连接OE,若点A关于直线OE的对称点为A',当点A'恰好落在直线PE上时,BE=_____________.(直接写出答案)【答案】(1)()0,8;(2)()4,0或()6,0或7,03⎛⎫⎪⎝⎭;(3)425【解析】【分析】(1)根据勾股定理可以求出AO的长,则可得出A的坐标;(2)分三种情况讨论等腰三角形的情况,得出点P的坐标;(3)根据PE AB⊥,点A'在直线PE上,得到EAG OPG,利用点A,A'关于直线OE对称点,根据对称性,可证'OPG EAO,可得'8OP OA,82AP,设BE x=,则有6AE x,根据勾股定理,有:22222BP BE EP AP AE解之即可.【详解】AB=,解:(1)∵点B坐标为6,0,点A是y轴正半轴上一点,且10∴ABO是直角三角形,根据勾股定理有:2222AO AB BO,1068∴点A的坐标为()0,8;(2)∵ABP△是等腰三角形,当BP AB时,如图一所示:OP BP BO,∴1064∴P点的坐标是()4,0;=时,如图二所示:当AP ABOP BO∴6∴P点的坐标是()6,0;=时,如图三所示:当AP BP设OP x =,则有6AP x∴根据勾股定理有:222OP AO AP += 即:22286x x解之得:73x = ∴P 点的坐标是7,03; (3)当ABP △是钝角三角形时,点A '不存在;当ABP △是锐角三角形时,如图四示:连接'OA ,∵PE AB ⊥,点A '在直线PE 上,∴AEG △和GOP 是直角三角形,EGA OGP ∴EAG OPG ,∵点A ,A '关于直线OE 对称点, 根据对称性,有'8OA OA ,'EAEA ∴'FAO FAO,'FAE FAE ∴'EAG EAO则有:'OPG EAO ∴'AOP 是等腰三角形,则有'8OP OA , ∴22228882AP AO OP ,设BE x =,则有6AEx ,根据勾股定理,有: 22222BP BE EP AP AE 即:2222688210x x 解之得:425BEx 【点睛】 本题考查了三角形的综合问题,涉及的知识点有:解方程,等腰三角形的判定与性质,对称等知识点,能分类讨论,熟练运用各性质定理,是解题的关键.7.如图,已知DCE ∠与AOB ∠,OC 平分AOB ∠.(1)如图1,DCE ∠与AOB ∠的两边分别相交于点 D 、E ,90AOB DCE ∠=∠=︒,试判断线段CD 与CE 的数量关系,并说明理由.以下是小宇同学给出如下正确的解法:解:CD CE =.理由如下:如图1,过点 C 作 C F OC ⊥,交 O B 于点 F ,则90OCF ∠=︒,…请根据小宇同学的证明思路,写出该证明的剩余部分.(2)你有与小宇不同的思考方法吗?请写出你的证明过程.(3)若120AOB ∠=︒,60DCE ∠=︒.①如图3,DCE ∠与AOB ∠的两边分别相交于点 D 、E 时,(1)中的结论成立吗?为什么?线段 O D 、OE 、OC 有什么数量关系?说明理由.②如图4,DCE ∠的一边与 AO 的延长线相交时,请回答(1)中的结论是否成立,并请直接写出线段 O D 、OE 、OC 有什么数量关系;如图5,DCE ∠的一边与 BO 的延长线相交时,请回答(1)中的结论是否成立,并请直接写出线段 O D 、OE 、OC 有什么数量关系.【答案】(1)见解析;(2)证明见解析;(3)①成立,理由见解析;②在图4中,(1)中的结论成立,OE OD OC-=.在图5中,(1)中的结论成立,OD OE OC-=【解析】【分析】(1)通过ASA证明CDO CEF∆∆≌即可得到CD=CE;(2)过点C作CM OA⊥,CN OB⊥,垂足分别为M,N,通过AAS证明CMD CNE∆∆≌同样可得到CD=CE;(3)①方法一:过点C作C M OA⊥,CN OB⊥垂足分别为M,N,通过AAS得到CMD CNE∆∆≌,进而得到,CD CE DM EN==,利用等量代换得到=OE OD ON OM++,在Rt CMO∆中,利用30°角所对的边是斜边的一半得12OM OC=,同理得到12ON OC=,所以OE OD OC+=;方法二:以CO为一边作60FCO∠=︒,交O B于点F,通过ASA证明CDO CEF∆∆≌,得到,CD CE OD EF==,所以OE OD OE EF OF OC+=+==;②图4:以OC为一边,作∠OCF=60°与OB交于F点,利用ASA证得△COD≌△CFE,即有CD=CE,OD=EF得到OE=OF+EF=OC+OD;图5:以OC为一边,作∠OCG=60°与OA交于G点,利用ASA证得△CGD≌△COE,即有CD=CE,OD=EF,得到OE=OF+EF=OC+OD.【详解】解:(1)OC平分AOB∠,145∠=∠2=︒∴,390245,123︒︒∴∠=-∠=∴∠=∠=∠OC FC∴=又456590︒∠+∠=∠+∠=在CDO∆与CEF∆中,1346OC FC∠=∠⎧⎪=⎨⎪∠=∠⎩()CDO CEF ASA∴∆∆≌CD CE∴=(2)如图2,过点 C 作CM OA ⊥,CN OB ⊥,垂足分别为 M ,N ,∴90CMD CNE ∠=∠=︒,又∵OC 平分AOB ∠,∴CM CN =,在四边形 O DCE 中,12360AOB DCE ∠+∠+∠+∠=︒,又∵90AOB DCE ∠=∠=︒,∴12180∠+∠=︒,又∵13180∠+∠=︒,∴32∠=∠,在CMD ∆与CNE ∆中,32CMD CNE CM CN ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()CMD CNE AAS ∆∆≌,∴CD CE=.(3)①(1)中的结论仍成立.OE OD OC +=.理由如下:方法一:如图3(1),过点 C 作 C M OA ⊥,CN OB ⊥,垂足分别为 M ,N ,∴90CMD CNE ∠=∠=︒,又∵OC 平分AOB ∠,∴CM CN =,在四边形ODCE 中,12360AOB DCE ∠+∠+∠+∠=︒,又∵60120180AOB DCE ∠+∠=︒+︒=︒,∴12180∠+∠=︒,又∵23180∠+∠=︒,∴13∠=∠,在CMD ∆与CNE ∆中,13CMD CNE CM CN ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()CMD CNE AAS ∆∆≌,∴,CD CE DM EN ==.∴OE OD OE OM DM OE OM EN ON OM +=++=++=+.在 Rt CMO ∆中,1490590302AOB ∠=︒-∠=︒-∠=︒, ∴12OM OC =,同理1 2ON OC =, ∴1122OE OD OC OC OC +=+=. 方法二:如图3(2),以CO 为一边作60FCO ∠=︒,交 O B 于点 F ,∵OC 平分AOB ∠,∴1260∠=∠=︒,∴3180260FCO ∠=︒-∠-∠=︒,∴13∠=∠,32FCO ∠=∠=∠,∴COF ∆是等边三角形,∴CO CF =,∵4560DCE ∠=∠+∠=︒,6560FCO∠=∠+∠=︒,∴46∠=∠,在CDO∆与CEF∆中,1346CO CF∠=∠⎧⎪=⎨⎪∠=∠⎩∴()CDO CEF ASA∆∆≌,∴,CD CE OD EF==.∴OE OD OE EF OF OC+=+==.②在图4中,(1)中的结论成立,OE OD OC-=.如图,以OC为一边,作∠OCF=60°与OB交于F点∵∠AOB=120°,OC为∠AOB的角平分线∴∠COB=∠COA=60°又∵∠OCF=60°∴△COF为等边三角形∴OC=OF∵∠COF=∠OCD+∠DCF=60°,∠DCE=∠DCF+∠FCB=60°∴∠OCD=∠FCB又∵∠COD=180°-∠COA=180°-60°=120°∠CFE=180°-∠CFO=180°-60°=120°∴∠COD=∠CFE∴△COD≌△CFE(ASA)∴CD=CE,OD=EF∴OE=OF+EF=OC+OD即OE-OD=OC-=.在图5中,(1)中的结论成立,OD OE OC如图,以OC为一边,作∠OCG=60°与OA交于G点∵∠AOB=120°,OC为∠AOB的角平分线∴∠COB=∠COA=60°又∵∠OCG=60°∴△COG为等边三角形∴OC=OG∵∠COG=∠OCE+∠ECG=60°,∠DCE=∠DCG+∠GCE=60°∴∠DCG=∠OCE又∵∠COE=180°-∠COB=180°-60°=120°∠CGD=180°-∠CGO=180°-60°=120°∴∠CGD=∠COE∴△CGD≌△COE(ASA)∴CD=CE,OE=DG∴OD=OG+DG=OC+OE即OD-OE=OC【点睛】本题主要考查全等三角形的综合应用,有一定难度,解题关键在于能够做出辅助线证全等.8.如图,在等边三角形ABC的外侧作直线AP,点C关于直线AP的对称点为点D,连接AD,BD,其中BD交直线AP于点E.(1)依题意补全图形;(2)若∠PAC=20°,求∠AEB的度数;(3)连结CE ,写出AE ,BE ,CE 之间的数量关系,并证明你的结论.【答案】(1)补图见解析;(2)60°;(3)CE +AE =BE .【解析】【分析】(1)根据题意补全图形即可;(2)根据轴对称的性质可得AC =AD ,∠PAC =∠PAD=20°,根据等边三角形的性质可得AC =AB ,∠BAC =60°,即可得AB =AD ,在△ABD 中,根据等腰三角形的性质和三角形的内角和定理求得∠D 的度数,再由三角形外角的性质即可求得∠AEB 的度数;(3)CE +AE =BE ,如图,在BE 上取点M 使ME =AE ,连接AM ,设∠EAC =∠DAE =x ,类比(2)的方法求得∠AEB =60°,从而得到△AME 为等边三角形,根据等边三角形的性质和SAS 即可判定△AEC ≌△AMB ,根据全等三角形的性质可得CE =BM ,由此即可证得CE +AE =BE .【详解】(1)如图:(2)在等边△ABC 中,AC =AB ,∠BAC =60°由对称可知:AC =AD ,∠PAC =∠PAD ,∴AB =AD∴∠ABD =∠D∵∠PAC =20°∴∠PAD =20°∴∠BAD =∠BAC+∠PAC +∠PAD =100°()1180402D BAD ︒︒∴∠=-∠=. ∴∠AEB =∠D +∠PAD =60°(3)CE +AE =BE .在BE上取点M使ME=AE,连接AM,在等边△ABC中,AC=AB,∠BAC=60°由对称可知:AC=AD,∠EAC=∠EAD,设∠EAC=∠DAE=x.∵AD=AC=AB,∴()11802602D BAC x x︒︒∠=-∠-=-∴∠AEB=60-x+x=60°.∴△AME为等边三角形.∴AM=AE,∠MAE=60°,∴∠BAC=∠MAE=60°,即可得∠BAM=∠CAE.在△AMB和△AEC中,AB ACBAM CAEAM AE=⎧⎪∠=∠⎨⎪=⎩,∴△AMB≌△AEC.∴CE=BM.∴CE+AE=BE.【点睛】本题是三角形综合题,主要考查了轴对称的性质、三角形的内角和定理、等边三角形的性质及全等三角形的判定与性质等知识点,解决第三问时,通过做辅助线,把AE转化到BE 上,再证明CE=BM即可得结论.9.八年级的小明同学通到这样一道数学题目:△ABC为边长为4的等边三角形,E是边AB 边上任意一动点,点D在CB的延长线上,且满足AE=BD.(1)如图①,当点E 为AB 的中点时,DE = ;(2)如图②,点E 在运动过程中,DE 与EC 满足什么数量关系?请说明理由;(3)如图③,F 是AC 的中点,连接EF .在AB 边上是否存在点E ,使得DE +EF 值最小?若存在,求出这个最小值;若不存在,请说明理由.(直角三角形中,30°所对的边是斜边的一半)【答案】(1)23;(2)DE =CE ,理由见解析;(3)这个最小值为27;【解析】【分析】(1)如图①,过点E 作EH ⊥BC 于H ,由等边三角形的性质可得BE =DB =AE =2,由直角三角形的性质可求BH =1,EH 3=,由勾股定理可求解;(2)如图②,过E 作EF ∥BC 交AC 于F ,可证△AEF 是等边三角形,AE =EF =AF =BD ,由“SAS ”可证△DBE ≌△EFC ,可得DE =CE ;(3)如图③,将△ABC 沿AB 翻折得到△ABC ',连接C 'F 交AB 于点E ',连接CE ',DE ',过点F 作FH ⊥AC '于点H ,由“SAS ”可证△ACE '≌△AC 'E ',可得C 'E '=CE ',可得当点C ',点E ',点F 三点共线时,DE +EF 的值最小,由勾股定理可求最小值.【详解】(1)如图①,过点E 作EH ⊥BC 于H ,∵△ABC 为边长为4的等边三角形,点E 是AB 的中点,∴AE =BE =2=DB ,∠ABC =60°,且EH ⊥BC ,∴∠BEH =30°,∴BH =1,EH 3=BH 3=,∴DH =DB +BH =2+1=3,∴DE 2293DH EH =+=+=23.故答案为:23;(2)DE =CE.理由如下:如图②,过E 作EF ∥BC 交AC 于F .∵△ABC 是等边三角形,∴∠ABC =∠ACB =∠A =60°,AB =AC =BC.∵EF ∥BC ,∴∠AEF =∠ABC =60°,∠AFE =∠ACB =60°,∴∠AEF =∠AFE =∠A =60°,∴△AEF 是等边三角形,∴AE =EF =AF ,∴AB ﹣AE =AC ﹣AF ,∴BE =CF.∵∠ABC =∠ACB =∠AFE =60°,∴∠DBE =∠EFC =120°,且AE =EF =DB ,BE =CF ,∴△DBE ≌△EFC (SAS),∴DE =CE ,(3)如图③,将△ABC 沿AB 翻折得到△ABC ',连接C 'F 交AB 于点E ',连接CE ',DE ',过点F 作FH ⊥AC '于点H.∵将△ABC 沿AB 翻折得到△ABC ',∴AC =AC '=BC =BC '=4,∠BAC =∠BAC '=60°,且AE '=AE ',∴△ACE '≌△AC 'E '(SAS),∴C 'E '=CE ',由(2)可知:DE '=CE ',∴C 'E '=CE '=DE '.∵DE +EF =C 'E +EF =C 'E '+EF ,∴当点C ',点E ',点F 三点共线时,DE +EF 的值最小.∵F 是AC 的中点,∴AF =CF =2,且HF ⊥AC ',∠FAH =180°﹣∠CAB ﹣∠C 'AB =60°,∴AH =1,HF 3=3=∴C 'H =4+1=5,∴C 'F 22'253C H HF +=+=27∴DE +EF 的最小值为27【点睛】本题是三角形综合题,考查了等边三角形的判定和性质,直角三角形的性质,全等三角形的判定和性质,折叠的性质,添加恰当辅助线是解答本题的关键.10.(1)操作:如图,在已知内角度数的三个三角形中,请用直尺从某一顶点画一条线段,把原三角形分割成两个等腰三角形,并在图中标注相应的角的度数(2)拓展,△ABC中,AB=AC,∠A=45°,请把△ABC分割成三个等腰三角形,并在图中标注相应的角的度数.(3)思考在如图所示的三角形中∠A=30°.点P和点Q分别是边AC和BC上的两个动点.分别连接BP和PQ把△ABC分割成三个三角形.△ABP,△BPQ,△PQC若分割成的这三个三角形都是等腰三角形,求∠C的度数所有可能值直接写出答案即可.【答案】(1)见解析;(2)见解析;(3)∠C所有可能的值为10°、20°、25°,35°、40°、50°、80°、100°.【解析】【分析】(1)在图1、图2、图3中,分别作AB、AB、BC的垂直平分线,根据垂直平分线的性质及外角的性质求出各角度数即可;(2)分别作AB、BC的垂直平分线,交于点O,连接OA、OB、OC可得三角形OAB、OAC、OBC为等腰三角形,根据等腰三角形的性质及外角性质求出各角度数即可;(3)分PB=PA、AB=AP、BA=BP时,PB=PQ、BP=BQ、QB=QP,PQ=QC、PC=QC、PQ=PC等10种情况,根据等腰三角形的性质分别求出∠C的度数即可.【详解】(1)在图1、图2、图3中,分别作AB、AB、BC的垂直平分线,如图1,∵∠ABC=23°,∠BAC=90°,∴∠C=90°-23°=67°,∵MN垂直平分AB,∴BD=AD,∴△ABD是等腰三角形,∴∠BAD=∠ABC=23°,∴∠ADC=2∠ABC=46°,∵∠BAC=90°,∴∠DAC=∠BAC-∠BAD=67°,∴∠DAC=∠C,∴△DAC是等腰三角形,同理:图2中,∠ADC=46°,∠DAC=88°,∠C=46°,△ABD和△ACD是等腰三角形,图3中,∠BCD=23°,∠ADC=46°,∠ACD=46°,△BCD和△ACD是等腰三角形.(2)作AB、BC的垂直平分线,交于点O,连接OA、OB、OC,∵点O是三角形垂直平分线的交点,∴OA=OB=OC,∴△OAB、△OAC、△OBC是等腰三角形,∵AB=AC,∠BAC=45°,∴∠ABC=∠ACB=67.5°,∴AD是BC的垂直平分线,∴∠BAD=∠CAD=22.5°,∴∠OBA=∠OAB=22.5°,∠OCA=∠OAC=22.5°,∴∠OBC=∠OCB=45°.(3)①如图,当PB=PA,PB=PQ,PQ=CQ时,∵∠A=30°,PB=PQ,∴∠ABP=∠A=30°,∴∠APB=120°,∵PB=PQ,PQ=CQ,∴∠PQB=∠PBQ,∠C=∠CPQ,∴∠PBQ=2∠C,∴∠APB=∠PBQ+∠C=3∠C=120°,解得:∠C=40°.②如图,当PB=PA,PB=BQ,PQ=CQ时,∴∠PQB=2∠C,∠PQB=∠BPQ,∴∠PBQ=180°-2∠PQB=180°-4∠C,∴180°-4∠C+∠C=120°,解得:∠C=20°,③如图,当PA=PB,BQ=PQ,CQ=CP时,∵∠PQC=2∠PBQ,∠PQC=12(180°-∠C),∴∠PBQ=14(180°-∠C),∴14(180°-∠C)+∠C=120°,解得:∠C=100°.④如图,当PA=PB,BQ=PQ,PQ=CP时,∵∠PQC=∠C=2∠PBQ,又∵∠C+∠PBQ=120°,∴∠C=80°;⑤如图,当AB=AP,BP=BQ,PQ=QC时,∵∠A=30°,∴∠APB=12(180°-30°)=75°,∵BP=BQ,PQ=CQ,∴∠BPQ=∠BQP,∠QPC=∠QCP,∴∠BQP=2∠C,∴∠PBQ=180°-4∠C,∴∠C+180°-4∠C=75°,解得:∠C=35°.⑥如图,当AB=AP,BQ=PQ,PC=QC时,∴∠PQC=2∠PBC,∠PQC=12(180°-∠C),∴∠PBC=14(180°-∠C),∴14(180°-∠C)+∠C=75°,解得:∠C=40°.⑦如图,当AB=AP,BQ=PQ,PC=QP时,∵∠C=∠PQC=2∠PBC,∠C+∠PQC=75°,∴∠C=50°;⑧当AB=AP,BP=PQ,PQ=CQ时,∵AB=BP,∠A=30°,∴∠ABP=∠APB=75°,又∵∠PBQ=∠PQB=2∠C,且有∠PBQ+∠C=180°-30°-75°=75°,∴3∠C=75°,∴∠C=25°;⑨当AB=BP,BP=PQ,PQ=CQ时,∵AB=BP,∴∠BPA=∠A=30°,∵∠PBQ=∠PQB=2∠C,∴2∠C+∠C=30°,解得:∠C=10°.⑩当AB=BP,BQ=PQ,PQ=CQ时,∴∠PQC=∠C=2∠PBQ,∴12∠C+∠C=30°,解得:∠C=20°.综上所述:∠C所有可能的值为10°、20°、25°,35°、40°、50°、80°、100°.【点睛】本题考查复杂作图及等腰三角形的性质,熟练掌握等腰三角形的性质是解题关键.。
八年级上册数学 轴对称填空选择单元练习(Word版 含答案)

八年级上册数学轴对称填空选择单元练习(Word版含答案)一、八年级数学全等三角形填空题(难)1.如图,∠ACB=90°,AC=BC,点C(1,2)、A(-2,0),则点B的坐标是__________.【答案】(3,-1)【解析】分析:过C和B分别作CD⊥OD于D,BE⊥CD于E,利用已知条件可证明△ADC≌△CEB,再由全等三角形的性质和已知数据即可求出B点的坐标.详解:过C和B分别作CD⊥OD于D,BE⊥CD于E,∵∠ACB=90°,∴∠ACD+∠CAD=90°,∠ACD+∠BCE=90°,∴∠CAD=∠BCE,在△ADC和△CEB中,∠ADC=∠CEB=90°;∠CAD=∠BCE,AC=BC,∴△ADC≌△CEB(AAS),∴DC=BE,AD=CE,∵点C的坐标为(1,2),点A的坐标为(−2,0),∴AD=CE=3,OD=1,BE=CD=2,∴则B点的坐标是(3,−1).故答案为(3,−1).点睛:本题主要考查了全等三角形的判定与性质,解题关键在于结合坐标、图形性质和已经条件.2.如图,直角三角形ABC与直角三角形BDE中,点B,C,D在同一条直线上,已知AC=AE=CD,∠BAC和∠ACB的角平分线交于点F,连DF,EF,分别交AB、BC于M、N,已知点F到△ABC三边距离为3,则△BMN的周长为____________.【答案】6【解析】【分析】由角平分线和三角形的内角和定理可得∠AFC=135°,由△AFC≌△DFC可得∠DFC=∠AFC=135°,可得∠AFD=90°.同理可得∠CFE=90°,可求得∠MFN=45°,过点F作FP⊥AB于点P,FQ⊥BC于点Q,由正方形的半角模型可得MN=MP+NQ,由此即可得出答案.【详解】解:过点F作FP⊥AB于点P,FQ⊥BC于点Q,过点F作FG⊥FM,交BC于点G.∵点F是∠BAC和∠BCA的角平分线交点,∴FP=FQ=3,∵∠ABC=90°,∴四边形BPFQ是正方形,∴BP=BQ=3.在Rt△ABC中,∠BAC+∠BCA=90°,∵AF、CF是角平分线,∴∠FAC+∠FCA=45°,∴∠AFC=180°-45°=135°.易证△AFC≌△DFC(SAS),∴∠AFC=∠DFC=135°,∴∠ADF=90°,同理可得∠EFC=90°,∴∠MFN=360°-90°-90°-135°=45°.∵∠PFM+∠MFN=90°,∠MFN+∠QFG=90°,∴∠PMF=∠QFG,∵∠FPM=∠FQG=90°,FP=FQ,∴△FPM≌△FQG(ASA),∴PM=QG,FM=FG.在△FMN和△FGN中45FM FGMFN GFNFN FN=⎧⎪∠=∠=⎨⎪=⎩∴△FMN≌△FGN(SAS),∴MN=NG,∴MN=NG=NQ+QG=PM+QN,∴△BMN的周长为:BM+BN+MN= BM+BN+ PM+QN=BP+BQ=3+3=6.故答案为:6.【点睛】本题是一道全等三角形的综合题,主要考查了全等三角形的判定和性质的应用,角平分线的性质,以及全等三角形常用辅助线的作法,作出辅助线,准确的找出全等三角形是解决此题的关键.3.在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CDE=55°.如图,则∠EAB的度数为_________【答案】35°【解析】【分析】过点E作EF⊥AD于F,根据角平分线上的点到角的两边的距离相等可得CE=EF,再根据到角的两边距离相等的点在角的平分线上可得AE是∠BAD的平分线,然后求出∠AEB,再根据直角三角形两锐角互余求解即可.【详解】过点E作EF⊥AD于F.∵DE平分∠ADC,∴CE=EF.∵E是BC的中点,∴CE=BE,∴BE=EF,∴AE是∠BAD的平分线,∴∠EAB=∠FAE.∵∠B=∠C=90°,∴∠CDA+∠DAB=180°,∴2∠CDE+2∠EAB=180°,∴∠CDE+∠EAB=90°,∴∠EAB=90°-∠CDE=90°-55°=35°.故答案为:35°.【点睛】本题考查了角平分线上的点到角的两边的距离相等的性质,角平分线的判定,熟记性质并作辅助线是解题的关键.4.如图,Rt△ABC中,∠C=90°.E为AB中点,D为AC上一点,BF∥AC交DE的延长线于点F.AC=6,BC=5.则四边形FBCD周长的最小值是______.【答案】16【解析】四边形FBCD周长=BC+AC+DF;当DF BC时,四边形FBCD周长最小为5+6+5=165.AD,BE是△ABC的高,这两条高所在的直线相交于点O,若BO=AC,BC=a,CD=b,则AD的长为______.【答案】AD的长为a-b或b-a或a+b或12a或b.【解析】【分析】分别讨论△ABC为锐角三角形时、∠A、∠B、∠C分别为钝角时和∠A为直角时五种情况,利用AAS证明△BOD≌△ACD,可得BD=AD,根据线段的和差关系即可得答案.【详解】①如图,当△ABC为锐角三角形时,∵AD、BE为△ABC的两条高,∴∠CAD+∠AOE=90°,∠CBE+∠BOD=90°,∵∠BOD=∠AOE,∴∠CAD=∠OBD,又∵∠ODB=∠ADC=90°,OB=AC,∴△BOD≌△ACD,∴AD=BD,∵BC=a,CD=b,∴AD=BD=BC-CD=a-b.②如图,当∠B为钝角时,∵∠C+∠CAD=90°,∠O+∠CAD=90°,∴∠C=∠O,又∵∠ADC=∠ODB=90°,OB=AC,∴△BOD≌△ACD,∴BD=AD,∴AD=CD-BC=b-a.③如图,当∠A为钝角时,同理可证:△BOD≌△ACD,∴AD=BC-CD=a-b.④如图,当∠C为钝角时,同理可证:△BOD≌△ACD,∴AD=BD=BC+CD=a+b.⑤当∠B为直角时,点O、D、B重合,OB=0,不符合题意,当∠C为直角时,点O、C、D、E重合,CD=0,不符合题意,如图,当∠A为直角时,点A、E、O重合,∵OB=AC,∠CAB=90°,∴△ABC是等腰直角三角形,∵AD⊥BC,∴AD是Rt△ABC斜边中线,∴AD=AD=12BC=12a=b.综上所述:AD的长为a-b或b-a或a+b或12a或b.故答案为:a-b或b-a或a+b或12a或b【点睛】本题主要考查全等三角形的判定与性质,全等三角形的判定方法有:SSS、AAS、ASA、SAS、HL等,注意:SAS时,角必须是两边的夹角,SSA和AAA不能判定两个三角形全等.灵活运用分类讨论的思想是解题关键.6.如图,Rt△ABC中,AB=AC,点D为BC中点.∠MDN=90°,∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF;⑤S四边形AEDF=14AD2,其中正确结论是_____(填序号)【答案】①②③【解析】【分析】先由ASA证明△AED≌△CFD,得出AE=CF,DE=FD;再由全等三角形的性质得到BE+CF=AB,由勾股定理求得EF与AB的值,通过比较它们的大小来判定④的正误;先得出S四边形AEDF=S△ADC=12AD2,从而判定⑤的正误.【详解】解:∵Rt△ABC中,AB=AC,点D为BC中点,∴∠C=∠BAD=45°,AD=BD=CD,∵∠MDN=90°,∴∠ADE+∠ADF=∠ADF+∠CDF=90°,∴∠ADE=∠CDF.在△AED与△CFD中,EAD CAD CDADE CDF∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△AED≌△CFD(ASA),∴AE=CF,ED=FD.故①②正确;又∵△ABD≌△ACD,∴△BDE≌△ADF.故③正确;∵△AED≌△CFD,∴AE=CF,ED=FD,∴BE+CF=BE+AE=AB2BD,∵EF2ED,BD>ED,∴BE+CF>EF.故④错误;∵△AED≌△CFD,△BDE≌△ADF,∴S四边形AEDF=S△ADC=12AD2.故⑤错误.综上所述,正确结论是①②③.故答案是:①②③.【点睛】考查了全等三角形的判定与性质,等腰直角三角形的性质,勾股定理,图形的面积等知识,综合性较强,有一定难度.7.如图,四边形ABCD是正方形,直线l1、l2、l3分别过A、B、C三点,l1∥l2∥l3,若l1与l2之间的距离为4,l2与l3之间的距离为5,则正方形的边长为______.【答案】41【解析】解:过B作直线BF⊥l3于F,交直线l1于点E.∵l1∥l3,∴∠AEB=∠BFC=90°,∴BE=4,BF=5.∵ABCD是正方形,∴AB=BC,∠ABC=90°,∴∠ABE+∠CBF=90°.∵∠ABE+∠BAE=90°,∴∠BAE=∠CBF.在△ABE和△BCF中,∵∠BAE=∠CBF,∠AEB=∠BFC,AB=BC,∴△ABE≌△BCF,∴AE=BF=5.在Rt△AEB中,AB=22=41.故答案为41.AE BE=2254点睛:本题考查了全等三角形的性质和判定,正方形的性质的应用,解答本题的关键是能正确作出辅助线,并进一步求出△ABE≌△BCF,难度适中.8.如图,在△ABC中,∠ABC=50°,∠ACB=60°,点E在BC的延长线上,∠ABC的平分线BD与∠ACE的平分线CD相交于点D,连接AD,以下结论:①∠BAC=70°;②∠DOC=90°;③∠BDC=35°;④∠DAC=55°,其中正确的是__________.(填写序号)【答案】①③④【解析】【分析】根据三角形内角和定理、角平分线的定义、三角形外角的性质、角平分线的性质解答即可.【详解】解:∵∠ABC=50°,∠ACB=60°,∴∠BAC=180°﹣50°﹣60°=70°,①正确;∵BD是∠ABC的平分线,∴∠DBC=12∠ABC=25°,∴∠DOC=25°+60°=85°,②错误;∠BDC=60°﹣25°=35°,③正确;∵∠ABC的平分线BD与∠ACE的平分线CD相交于点D,∴AD是∠BAC的外角平分线,∴∠DAC=55°,④正确.故答案为①③④.【点睛】本题考查的是角平分线的定义和性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.9.如图,在△ABC中,AB AC=10,BC=12,AD是角平分线,P、Q分别是AD、AB边上的动点,则BP+PQ的最小值为_______.【答案】9.6【解析】∵AB=AC,AD是角平分线,∴AD⊥BC,BD=CD,∴B点,C点关于AD对称,如图,过C作CQ⊥AB于Q,交AD于P,则CQ=BP+PQ 的最小值,根据勾股定理得,AD=8,利用等面积法得:AB ⋅CQ=BC ⋅AD ,∴CQ=BC AD AB ⋅=12810⨯=9.6 故答案为:9.6. 点睛:此题是轴对称-最短路径问题,主要考查了角平分线的性质,对称的性质,勾股定理,等面积法,用等面积法求出CQ 是解本题的关键.10.如图:△ABC 中,∠ACB=90°,∠CAD=30°,AC=BC=AD ,CE ⊥CD ,且CE=CD ,连接BD ,DE ,BE ,则下列结论:①∠ECA=165°,②BE=BC ;③AD ⊥BE ;其中正确的是_________【答案】①②③【解析】如图,(1)∵AC=AD ,∠CAD=30°,∴∠ACD=∠ADC=18030752-=, ∵CE ⊥DC ,∴∠DCE=90°,∴∠ACE=∠ACD+∠DCE=165°.故①正确;(2)由(1)可知:∠ACB=∠DCE=90°,∴∠ACE-∠DCB=∠DCE-∠DCB ,即∠ACD=∠BCE ,在△ACD 和△BCE 中,AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩, ∴△ACD ≌△BCE ,∴BE=AD=BC.故②正确;(3)延长AD 交BE 于点F ,∵△ACD ≌△BCE ,∴∠2=∠CAD=30°,∵AC=BC ,∠ACB=90°,∴∠CAB=∠3=45°,∴∠1=∠CAB-∠CAD=15°,∴∠AFB=180°-∠1-∠2-∠3=90°,∴AD ⊥BE.故③正确;综上所述:正确的结论是①②③.二、八年级数学全等三角形选择题(难)11.如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面四个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④AP垂直平分RS.其中正确结论的序号是().A.①②B.①②③C.①②④D.①②③④【答案】C【解析】【分析】如图,连接AP,根据HL判定△APR和△APS全等,即可说明①正确;由△APR和△APS 全等可得∠RAP=∠PAC,再根据等腰三角形性质推出∠QAP=∠QPA,得到∠QPA=∠BAP,根据平行线判定推出OP//AB,即②正确;在Rt△BRP和Rt△QSP中,只有PR=PS.无法判断Rt△BRP和Rt△QSP是否全等;连接RS,与AP交于点D,先证△ARD≌△ASD,即RD=SD;运用等腰三角形的性质即可判定.【详解】解:如图,连接AP∵PR⊥AB,PS⊥AC,PR=PS∴△APR≌△APS∴AS=AR,∠RAP=∠PAC即①正确;又∵AQ=PQ∴∠QAP=∠QPA∴∠QPA=∠BAP∴OP//AB,即②正确.在Rt△BRP和Rt△QSP中,只有PR=PS.无法判断Rt△BRP和Rt△QSP是否全等,故③错误.如图,连接PS∵△APR≌△APS∴AR=AS,∠RAP=∠PAC∴AP垂直平分RS,即④正确;故答案为C.【点睛】本题主要考查了全等三角形的性质和判定,角平分线性质的应用,熟练掌握全等三角形的判定和性质是解答本题的关键12.如图,已知,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA.下面结论:①△ABD≌△EBC;②AC=2CD;③AD=AE=EC;④∠BCE+∠BCD=180°.其中正确的是()A.①②③B.①②④C.①③④D.②③④【答案】C【解析】已知BD为△ABC的角平分线,根据角平分线的定义可得∠ABD=∠CBD,在△AB D和△EB C 中,BD=BC,∠ABD=∠CBD,BE=BA,由SAS可判定△ABD≌△EBC,即可得①正确;根据已知条件,无法证明AC=2CD,②错误;已知BD为△ABC的角平分线,BD=BC,BE=BA,可得∠BCD=∠BDC=∠BAE=∠BEA,再由∠BCE=∠BDA,∠BCE=∠BCD+∠DCE,∠BDA=∠DAE+∠BEA,∠BCD=∠BEA,可得∠DCE=∠DAE,所以AE=EC;再由△ABD≌△EBC,可得AD=EC,所以AD=AE=EC,即③正确;由△ABD≌△EBC,可得∠BCE=∠BDA,所以∠BCE+∠BCD=∠BDA+∠BDC=180°,④正确.故选C.点睛:本题考查了全等三角形的判定及性质、等腰三角形的的性质、三角形外角的性质,本题中熟练求证三角形全等和熟练运用全等三角形对应角、对应边相等性质是解题的关键.13.如图,在△ABC中,P是BC上的点,作PQ∥AC交AB于点Q,分别作PR⊥AB,PS⊥AC,垂足分别是R,S,若PR=PS,则下面三个结论:①AS=AR;②AQ=PQ;③△PQR≌△CPS;④AC﹣AQ=2SC,其中正确的是()A.②③④B.①②C.①④D.①②③④【答案】B【解析】【分析】连接AP,由已知条件利用角平行线的判定可得∠1 = ∠2,由三角形全等的判定得△APR≌△APS,得AS=AR,由已知可得∠2 = ∠3,得QP=AQ,答案可得.【详解】解:如图连接AP,PR=PS,PR⊥AB,垂足为R,PS⊥AC,垂足为S,AP是∠BAC的平分线,∠1=∠2,△APR≌△APS.AS=AR,又QP/AR,∠2 = ∠3又∠1 = ∠2,∠1=∠3,AQ=PQ,没有办法证明△PQR≌△CPS,③不成立,没有办法证明AC-AQ=2SC,④不成立.所以B选项是正确的.【点睛】本题主要考查三角形全等及三角形全等的性质.14.如图,△ABC的两条外角平分线AP、CP相交于点P,PH⊥AC于H;如果∠ABC=60º,则下列结论:①∠ABP=30º;②∠APC=60º;③PB=2PH;④∠APH=∠BPC;其中正确的结论个数是()A.1 B.2 C.3 D.4【答案】B【解析】【分析】作PM ⊥BC 于M ,PN ⊥BA 于N .根据角平分线的性质定理可证得PN=PM ,再根据角平分线的判定定理可得PB 平分∠ABC ,即可判定①;证明△PAN ≌△PAH ,△PCM ≌△PCH ,根据全等三角形的性质可得∠APN=∠APH ,∠CPM=∠CPH ,由此即可判定②;在Rt △PBN 中,∠PBN=30°,根据30°角直角三角形的性质即可判定③;由∠BPN=∠CPA=60°即可判定④.【详解】如图,作PM ⊥BC 于M ,PN ⊥BA 于N .∵∠PAH=∠PAN ,PN ⊥AD ,PH ⊥AC ,∴PN=PH ,同理PM=PH ,∴PN=PM ,∴PB 平分∠ABC ,∴∠ABP=12∠ABC=30°,故①正确, ∵在Rt △PAH 和Rt △PAN 中, PA PA PN PH =⎧⎨=⎩, ∴△PAN ≌△PAH ,同理可证,△PCM ≌△PCH ,∴∠APN=∠APH ,∠CPM=∠CPH ,∵∠MPN=180°-∠ABC=120°,∴∠APC=12∠MPN=60°,故②正确, 在Rt △PBN 中,∵∠PBN=30°, ∴PB=2PN=2PH ,故③正确,∵∠BPN=∠CPA=60°,∴∠CPB=∠APN=∠APH ,故④正确.综上,正确的结论为①②③④.故选D.【点睛】本题考查了角平分线的性质定理及判定定理、全等三角形的判定与性质及30°角直角三角形的性质,熟练运用相关知识是解决问题的关键.15.已知等边△ABC 中,在射线BA 上有一点D ,连接CD ,并以CD 为边向上作等边△CDE ,连接BE 和AE ,试判断下列结论:①AE=BD ; ②AE 与AB 所夹锐夹角为60°;③当D 在线段AB或BA延长线上时,总有∠BDE-∠AED=2∠BDC;④∠BCD=90°时,CE2+AD2=AC2+DE2,正确的序号有()A.①②B.①②③C.①②④D.①②③④【答案】C【解析】【分析】由∠BCD=∠ACD+60°,∠ACE=∠ACD+60°可得∠BCD=∠ACE,利用SAS可证明△BCD≌△ACE,可得AE=BD,①正确;∠CBD=∠CAE=60°,进而可得∠EAD=60°,②正确,当∠BCD=90°时,可得∠ACD=∠ADC=30°,可得AD=AC,即可得CE2+AD2=AC2+DE2,④正确;当D点在BA延长线上时,∠BDE-∠BDC=60°,根据△BCD≌△ACE可得∠AEC=∠BDC,进而可得∠BDC+∠AED=∠AEC+∠AED=∠CED=60°,即可证明∠BDE-∠BDC=∠BDC+∠AED,即∠BDE-∠AED=2∠BDC,当点D在AB上时可证明∠BDE-∠AED=120°,③错误,综上即可得答案.【详解】∵∠BCA=∠DCE=60°,∴∠BCA+∠ACD=∠DCE+∠ACD,∴∠BCD=∠ACE,又∵AC=BC,CE=CD,∴△BCD≌△ACE,∴AE=BD,∠CBA=∠CAE=60°,∠AEC=∠BDC,①正确,∴∠BAE=120°,∴∠EAD=60°,②正确,∵∠BCD=90°,∠BCA=60°,∴∠ACD=∠ADC=30°,∴AC=AD,∵CE=DE,∴CE2+AD2=AC2+DE2,④正确,当D点在BA延长线上时,∠BDE-∠BDC=60°,∵∠AEC=∠BDC,∴∠BDC+∠AED=∠AEC+∠AED=∠CED=60°,∴∠BDE-∠BDC=∠BDC+∠AED∴∠BDE-∠AED=2∠BDC,如图,当点D 在AB 上时,∵△BCD ≌△∠ACE ,∴∠CAE=∠CBD=60°,∴∠DAE=∠BAC+∠CAE=120°,∴∠BDE-∠AED=∠DAE=120°,③错误故正确的结论有①②④,故选C.【点睛】此题主要考查等边三角形的性质和全等三角形的判定与性质等知识点的理解和掌握16.如图,D 为BAC ∠的外角平分线上一点并且满足BD CD =,DBC DCB ∠=∠,过D 作DE AC ⊥于E ,DF AB ⊥交BA 的延长线于F ,则下列结论:①CDE △≌BDF ;②CE AB AE =+;③BDC BAC ∠=∠;④DAF CBD ∠=∠. 其中正确的结论有( ).A .1个B .2个C .3个D .4个【答案】D【解析】 BD=CD,AD 是角平分线,所以FD=DE,∠DFB =∠DEC =90°,所以CDE ≌BDF ;①正确.由全等得BF=CE ,因为FA=AE,FB=AB+FA ,所以CE=AB+AE , ②正确.由全等知,∠DCE=∠FBD,所以∠BAC=∠BDC. ③正确. ∴DBF DCE ∠=∠,∴A 、B 、C 、D 四点共圆,∴DAF CBD ∠=∠,④正确.故选D.17.如图,与都是等边三角形,,下列结论中,正确的个数是( )①;②;③;④若,且,则.A.1 B.2 C.3 D.4【答案】C【解析】【分析】利用全等三角形的判定和性质一一判断即可.【详解】解:∵与都是等边三角形∴AD=AB,AC=AE,∠DAB=∠EAC=60°∴∠DAB+∠BAC=∠EAC +∠BAC即∠DAC=∠EAB∴∴,①正确;∵∴∠ADO=∠ABO∴∠BOD=∠DAB=60°,②正确∵∠BDA=∠CEA=60°,∠ADC≠∠AEB∴∠BDA-∠ADC≠∠CEA-∠AEB∴,③错误∵∴∠DAC+∠BCA=180°∵∠DAB=60°,∴∠BCA=180°-∠DAB-∠BAC=30°∵∠ACE=60°∴∠BCE=∠ACE+∠BCA=60°+30°=90°∴④正确故由①②④三个正确,故选:C【点睛】本题考查全等三角形的判定和性质、等边三角形的性质、角平分线的判定定理等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.18.如图,把ΔABC剪成三部分,边AB,BC,AC放在同一直线上,点O都落在直线MN 上,直线MN∥AB.在ΔABC中,若∠AOB=125°,则∠ACB的度数为()A.70°B.65°C.60°D.85°【答案】A【解析】【分析】利用平行线间的距离处处相等,可知点O到BC、AC、AB的距离相等,得出O为三条角平分线的交点,根据三角形内角和定理和角平分线的定义即可得出结论.【详解】如图1,过点O作OD⊥BC于D,OE⊥AC于E,OF⊥AB于F.∵MN∥AB,∴OD=OE=OF(平行线间的距离处处相等).如图2:过点O作OD'⊥BC于D',作OE'⊥AC于E',作OF'⊥AB于F'.由题意可知:OD=OD',OE=OE',OF=OF',∴OD'=OE'=OF',∴图2中的点O是三角形三个内角的平分线的交点.∵∠AOB=125°,∴∠OAB+∠OBA=180°-125°=55°,∴∠CAB+∠CBA=2×55°=110°,∴∠ACB=180°-110°=70°.故选A.【点睛】本题考查了三角形的内心,平行线间的距离处处相等,角平分线定义,解答本题的关键是判断出OD=OE=OF.19.在△ABC中,∠C=90°,D为AB的中点,ED⊥AB,∠DAE=∠CAE,则∠CAB=()A.30°B.60°C.80 °D.50°【答案】B【解析】试题解析:∵D为AB的中点,ED⊥AB,∴DE为线段AB的垂直平分线,∴AE=BE,∴∠DAE=∠DBE,∴∠DAE=∠DBE=∠CAE,在Rt△ABC中,∵∠CAB+∠DBE=90°,∴∠CAE+∠DAE+∠DBE=90°,∴3∠DBE=90°,∴∠DBE=30°,∴∠CAB=90°-∠DBE=90°-30°=60°.故选B.20.如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边三角形ABC 和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②AP=BQ;③PQ∥AE;④DE=DP;⑤∠AOE=120°;其中正确结论的个数为()A.2个B.3个C.4个D.5个【答案】C【解析】【分析】①由于△ABC和△CDE是等边三角形,可知AC=BC,CD=CE,∠ACB=∠DCE=60°,从而证出△ACD≌△BCE,可推知AD=BE,故①正确;②由△ACD≌△BCE得∠CBE=∠DAC,加之∠ACB=∠DCE=60°,AC=BC,得到△ACP≌△BCQ (ASA),所以AP=BQ;故②正确;③根据②△CQB≌△CPA(ASA),再根据∠PCQ=60°推出△PCQ为等边三角形,又由∠PQC=∠DCE,根据内错角相等,两直线平行,可知③正确;④根据∠QCP=60°,∠DPC=∠BCA+∠PAC>60°,可知PD≠CD,可知④错误;⑤利用等边三角形的性质,BC∥DE,再根据平行线的性质得到∠CBE=∠DEO,于是∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°,由平角的性质可得∠AOE=120°,可知⑤正确;【详解】①∵△ABC和△CDE为等边三角形∴AC=BC,CD=CE,∠BCA=∠DCB=60°∴∠ACD=∠BCE∴△ACD≌△BCE(SAS)∴AD=BE,故①正确;由(1)中的全等得∠CBE=∠DAC,且BC=AC,∠ACB=∠BCQ=60°∴△CQB≌△CPA(ASA),∴AP=BQ,故②正确;∵△CQB≌△CPA,∴PC=PQ,且∠PCQ=60°∴△PCQ为等边三角形,∴∠PQC=∠DCE=60°,∴PQ∥AE,故③正确,∵∠QCP=60°,∠DPC=∠BCA+∠PAC>60°,∴PD≠CD,∴DE≠DP,故④DE=DP错误;∵BC∥DE,∴∠CBE=∠BED,∵∠CBE=∠DAE,∴∠AOB=∠OAE+∠AEO=60°,∴∠AOE=120°,故⑤正确,故选C.【点睛】本题考查了全等三角形的判定与性质,利用了等边三角形的判定与性质,全等三角形的判定与性质,平行线的判定与性质,综合性较强,题目难度较大.21.如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,DH⊥BC于H,交BE于G.下列结论:①BD=CD;②AD+CF=BD;③CE=12BF;④AE=BG.其中正确的是A.①②B.①③C.①②③D.①②③④【答案】C【解析】【分析】根据∠ABC=45°,CD⊥AB可得出BD=CD,利用AAS判定Rt△DFB≌Rt△DAC,从而得出DF=AD,BF=AC.则CD=CF+AD,即AD+CF=BD;再利用AAS判定Rt△BEA≌Rt△BEC,得出CE=AE=12AC,又因为BF=AC所以CE=12AC=12BF,连接CG.因为△BCD是等腰直角三角形,即BD=CD.又因为DH⊥BC,那么DH垂直平分BC.即BG=CG.在Rt△CEG中,CG是斜边,CE是直角边,所以CE<CG.即AE<BG.【详解】解:∵CD⊥AB,∠ABC=45°,∴△BCD是等腰直角三角形.∴BD=CD.故①正确;在Rt△DFB和Rt△DAC中,∵∠DBF=90°−∠BFD,∠DCA=90°−∠EFC,且∠BFD=∠EFC,∴∠DBF=∠DCA.又∵∠BDF=∠CDA=90°,BD=CD,∴△DFB≌△DAC.∴BF=AC;DF=AD.∵CD=CF+DF,∴AD+CF=BD;故②正确;在Rt△BEA和Rt△BEC中.∵BE平分∠ABC,∴∠ABE=∠CBE.又∵BE=BE,∠BEA=∠BEC=90°,∴Rt△BEA≌Rt△BEC.∴CE=AE=12 AC.又由(1),知BF=AC,∴CE=12AC=12BF;故③正确;连接CG.∵△BCD是等腰直角三角形,∴BD=CD.又DH⊥BC,∴DH垂直平分BC.∴BG=CG.在Rt△CEG中,∵CG是斜边,CE是直角边,∴CE<CG.∵CE=AE,∴AE<BG.故④错误.故选C.【点睛】本题考查了等腰直角三角形、等腰三角形的判定与性质、全等三角形的判定与性质.此类问题涉及知识点较多,需要对相关知识点有很高的熟悉度.22.已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P的运动时间为t秒,当t的值为_____秒时,△ABP和△DCE全等.A.1 B.1或3 C.1或7 D.3或7【答案】C【解析】【分析】分两种情况进行讨论,根据题意得出BP=2t=2和AP=16-2t=2即可求得.【详解】解:因为AB=CD,若∠ABP=∠DCE=90°,BP=CE=2,根据SAS证得△ABP≌△DCE,由题意得:BP=2t=2,所以t=1,因为AB=CD,若∠BAP=∠DCE=90°,AP=CE=2,根据SAS证得△BAP≌△DCE,由题意得:AP=16-2t=2,解得t=7.所以,当t的值为1或7秒时.△ABP和△DCE全等.故选C.【点睛】本题考查全等三角形的判定,判定方法有:ASA,SAS,AAS,SSS,HL.23.如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,∠EAF=12∠BAD,若DF=1,BE=5,则线段EF的长为()A .3B .4C .5D .6【答案】B【解析】【分析】 在BE 上截取BG =DF ,先证△ADF ≌△ABG ,再证△AEG ≌△AEF 即可解答.【详解】在BE 上截取BG =DF ,∵∠B +∠ADC =180°,∠ADC +∠ADF =180°,∴∠B =∠ADF ,在△ADF 与△ABG 中AB AD B ADF BG DF =⎧⎪∠=∠⎨⎪=⎩,∴△ADF ≌△ABG (SAS ),∴AG =AF ,∠FAD =∠GAB ,∵∠EAF =12∠BAD , ∴∠FAE =∠GAE ,在△AEG 与△AEF 中AG AF FAE GAE AE AE =⎧⎪∠=∠⎨⎪=⎩,∴△AEG ≌△AEF (SAS )∴EF =EG =BE ﹣BG =BE ﹣DF =4.故选:B .【点睛】考查了全等三角形的判定与性质,证明三角形全等是解决问题的关键.24.如图(1),已知AB AC=,D为BAC∠的角平分线上一点,连接BD,CD;如图(2),已知AB AC=,D,E为BAC∠的角平分线上两点,连接BD,CD,BE,CE;如图(3),已知AB AC=,D,E,F为BAC∠的角平分线上三点,连接BD,CD,BE,CE,BF,CF;……,依此规律,第6个图形中有全等三角形的对数是()A.21 B.11 C.6 D.42【答案】A【解析】【分析】根据条件可得图1中△ABD≌△ACD有1对三角形全等;图2中可证出△ABD≌△ACD,△BDE≌△CDE,△ABE≌△ACE有3对三角形全等;图3中有6对三角形全等,根据数据可分析出第6个图形中全等三角形的对数.【详解】解:∵AD是∠BAC的平分线,∴∠BAD=∠CAD.在△ABD与△ACD中,AB ACBAD CADAD AD=⎧⎪∠=∠⎨⎪=⎩,∴△ABD≌△ACD.∴图1中有1对三角形全等;同理图2中,△ABE≌△ACE,∴BE=EC,∵△ABD≌△ACD.∴BD=CD,又DE=DE,∴△BDE≌△CDE,∴图2中有3对三角形全等,3=1+2;同理:图3中有6对三角形全等,6=1+2+3;∴第6个图形中有全等三角形的对数是1+2+3+4+5+6=21.故选:A.【点睛】此题主要考查了三角形全等的判定以及规律的归纳,解题的关键是根据条件证出图形中有几对三角形全等,然后寻找规律.25.如图,在△ABC中,AB=BC,90ABC∠=︒,点D是BC的中点,BF⊥AD,垂足为E,BF交AC于点F,连接DF.下列结论正确的是()A.∠1=∠3 B.∠2=∠3 C.∠3=∠4 D.∠4=∠5【答案】A【解析】【分析】如图,过点C作BC的垂线,交BF的延长线于点G,则CG BC⊥,先根据直角三角形两锐角互余可得BAD CBG∠=∠,再根据三角形全等的判定定理与性质推出1G∠=∠,又根据三角形全等的判定定理与性质推出3G∠=∠,由此即可得出答案.【详解】如图,过点C作BC的垂线,交BF的延长线于点G,则CG BC⊥,即90BCG∠=︒,90AB BC ABC=∠=︒45BAC ACB∠∴∠==︒904545GCF BCG ACB∴∠=∠-∠=︒-︒=︒BF AD⊥1190BAD CBG∴∠+∠=∠+∠=︒BAD CBG∴∠=∠在BAD∆和CBG∆中,90BAD CBGAB BCABD BCG∠=∠⎧⎪=⎨⎪∠=∠=︒⎩()BAD CBG ASA∴∆≅∆,1BD CG G∴=∠=∠点D是BC的中点CD BD CG∴==在CDF∆和CGF∆中,45CD CGDCF GCFCF CF=⎧⎪∠=∠=︒⎨⎪=⎩()CDF CGF SAS∴∆≅∆3G∴∠=∠13∠∠∴=故选:A .【点睛】本题是一道较难的综合题,考查了直角三角形的性质、三角形全等的判定定理与性质等知识点,通过作辅助线,构造两个全等的三角形是解题关键.26.已知:如图,在长方形ABCD 中,AB=4,AD=6.延长BC 到点E ,使CE=2,连接DE ,动点P 从点B 出发,以每秒2个单位的速度沿BC-CD-DA 向终点A 运动,设点P 的运动时间为t 秒,当t 的值为_____秒时,△ABP 和△DCE 全等.A .1B .1或3C .1或7D .3或7 【答案】C【解析】【分析】 分两种情况进行讨论,根据题意得出BP=2t=2和AP=16-2t=2即可求得.【详解】解:因为AB=CD ,若∠ABP=∠DCE=90°,BP=CE=2,根据SAS 证得△ABP ≌△DCE , 由题意得:BP=2t=2,所以t=1,因为AB=CD ,若∠BAP=∠DCE=90°,AP=CE=2,根据SAS 证得△BAP ≌△DCE ,由题意得:AP=16-2t=2,解得t=7.所以,当t 的值为1或7秒时.△ABP 和△DCE 全等.故选C .【点睛】本题考查全等三角形的判定,判定方法有:ASA ,SAS ,AAS ,SSS ,HL .27.如图,在等腰△ABC 中,AB =AC ,∠A =20°,AB 上一点D ,且AD =BC ,过点D 作DE ∥BC 且DE =AB ,连接EC ,则∠DCE 的度数为( )A .80°B .70°C .60°D .45°【答案】B【解析】【分析】 连接AE .根据ASA 可证△ADE ≌△CBA ,根据全等三角形的性质可得AE=AC ,∠AED=∠BAC=20°,根据等边三角形的判定可得△ACE 是等边三角形,根据等腰三角形的判定可得△DCE 是等腰三角形,再根据三角形内角和定理和角的和差关系即可求解.【详解】如图所示,连接AE .∵AB=DE ,AD=BC∵DE ∥BC ,∴∠ADE=∠B ,可得AE=DE∵AB=AC ,∠BAC=20°,∴∠DAE=∠ADE=∠B=∠ACB=80°,在△ADE 与△CBA 中,DAE ACB AD BCADE B ∠∠⎧⎪⎨⎪∠∠⎩===, ∴△ADE ≌△CBA (ASA ),∴AE=AC ,∠AED=∠BAC=20°,∵∠CAE=∠DAE-∠BAC=80°-20°=60°,∴△ACE 是等边三角形,∴CE=AC=AE=DE ,∠AEC=∠ACE=60°,∴△DCE 是等腰三角形,∴∠CDE=∠DCE ,∴∠DEC=∠AEC-∠AED=40°,∴∠DCE=∠CDE=(180-40°)÷2=70°.故选B.【点睛】考查了等腰三角形的性质,全等三角形的判定和性质,等边三角形的判定和性质,等腰三角形的判定和性质,三角形内角和定理,平行线的性质,综合性较强,有一定的难度.28.如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2,其中正确结论有()A.0个B.1个C.2个D.3个【答案】D【解析】分析:由四边形ABCD与四边形EFGC都为正方形,得到四条边相等,四个角为直角,利用SAS 得到三角形BCE与三角形DCG全等,利用全等三角形对应边相等即可得到BE=DG,利用全等三角形对应角相等得到∠CBM=∠MDO,利用等角的余角相等及直角的定义得到∠BOD为直角,利用勾股定理求出所求式子的值即可.详解:①∵四边形ABCD和EFGC都为正方形,∴CB=CD,CE=CG,∠BCD=∠ECG=90°,∴∠BCD+∠DCE=∠ECG+∠DCE,即∠BCE=∠DCG.在△BCE和△DCG中,CB=CD,∠BCE=∠DCG,CE=CG,∴△BCE≌△DCG,∴BE=DG,故结论①正确.②如图所示,设BE交DC于点M,交DG于点O.由①可知,△BCE≌△DCG,∴∠CBE=∠CDG,即∠CBM=∠MDO.又∵∠BMC=∠DMO,∠MCB=180°-∠CBM-∠BMC,∠DOM=180°-∠CDG-∠MDO,∴∠DOM=∠MCB=90°,∴BE⊥DG.故②结论正确.③如图所示,连接BD 、EG ,由②知,BE ⊥DG ,则在Rt △ODE 中,DE 2=OD 2+OE 2,在Rt △BOG 中,BG 2=OG 2+OB 2,在Rt △OBD 中,BD 2=OD 2+OB 2,在Rt △OEG 中,EG 2=OE 2+OG 2,∴DE 2+BG 2=(OD 2+OE 2)+(OB 2+OG 2)=(OD 2+OB 2)+(OE 2+OG 2)=BD 2+EG 2.在Rt △BCD 中,BD 2=BC 2+CD 2=2a 2,在Rt △CEG 中,EG 2=CG 2+CE 2=2b 2,∴BG 2+DE 2=2a 2+2b 2.故③结论正确.故选:D.点睛:本题考查了旋转的性质、全等三角形的判定与性质、正方形的性质.29.如图所示,OP 平分AOB ∠,PA OA ⊥,PB OB ⊥,垂足分别为A 、B .下列结论中不一定成立的是( ).A .PA PB =B .PO 平分APB ∠C .OA OB =D .AB 垂直平分OP【答案】D【解析】【分析】 根据角平分线上的点到角的两边距离相等可得出PA=PB ,再利用“HL ”证明△AOP 和△BOP 全等,可得出APO BPO ∠=∠,OA=OB ,即可得出答案.【详解】解:∵OP 平分AOB ∠,PA OA ⊥,PB OB ⊥∴PA PB =,选项A 正确;在△AOP 和△BOP 中,PO PO PA PB =⎧⎨=⎩, ∴AOP BOP ≅∴APO BPO ∠=∠,OA=OB ,选项B ,C 正确;由等腰三角形三线合一的性质,OP 垂直平分AB ,AB 不一定垂直平分OP ,选项D 错误.故选:D.【点睛】本题考查的知识点是角平分线的性质以及垂直平分线的性质,熟记性质定理是解此题的关键.30.如图,△ABC中,AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则下列结论不正确的是A.BF=DF B.∠1=∠EFD C.BF>EF D.FD∥BC【答案】B【解析】【分析】根据余角的性质得到∠C=∠ABE,∠EBC=∠BAC.根据SAS推出△ABF≌△ADF,根据全等三角形的性质得到BF=DF,故A正确;由全等三角形的性质得到∠ABE=∠ADF,等量代换得到∠ADF=∠C,根据平行线的判定得到DF∥BC,故D正确;根据直角三角形的性质得到DF >EF,等量代换得到BF>EF;故C正确;根据平行线的性质得到∠EFD=∠EBC=∠BAC=2∠1,故B错误.【详解】∵AB⊥BC,BE⊥AC,∴∠C+∠BAC=∠ABE+∠BAC=90°,∴∠C=∠ABE.同理:∠EBC=∠BAC.在△ABF与△ADF中,∵12AD ABAF AF=⎧⎪∠=∠⎨⎪=⎩,∴△ABF≌△ADF,∴BF=DF,故A正确,∵△ABF≌△ADF,∴∠ABE=∠ADF,∴∠ADF=∠C,∴DF∥BC,故D正确;∵∠FED=90°,∴DF>EF,∴BF>EF;故C正确;∵DF∥BC,∴∠EFD=∠EBC.∵∠EBC=∠BAC=∠BAC=2∠1,∴∠EFD=2∠1,故B错误.故选B.【点睛】本题考查了全等三角形的判定和性质,平行线的判定和性质,证得△ABF≌△ADF是解题的关键.。
人教版初中八年级数学上册第十三章《轴对称》经典练习(含答案解析)

一、选择题1.如图,在等腰三角形ABC 中,,36,AB AC A D =∠=是AC 的中点,ED AC ⊥交AB 于点E ,已知6,2AC DE ==,则BC 的长为( )A .13B .32C .40D .20 2.已知锐角AOB ∠,如图(1)在射线OA 上取一点C ,以点O 为圆心,OC 长为半径作弧MN ,交射线OB 于点D ,连接CD ;(2)分别以点,C D 为圆心,CD 长为半径作弧,两弧交于点P ,连接,CP DP ; (3)作射线OP 交CD 于点Q .根据以上作图过程及所作图形,有如下结论:①//CP OB ;②2CP QC =;③AOP BOP ∠=∠;④CD OP ⊥.其中正确的有( )A .①②③④B .②③④C .③④D .③ 3.已知一个等腰三角形两个内角度数之比为1:4,则这个等腰三角形顶角度数为( ) A .75° B .90° C .105° D .120°或20° 4.如图,在ABC 中,6AB =,8AC =,10BC =,EF 是BC 的垂直平分线,P 是直线EF 上的一动点,则PA PB +的最小值是( ).A .6B .8C .10D .115.下列命题中,假命题是( ) A .两条直角边对应相等的两个直角三角形全等B .等腰三角形顶角平分线把它分成两个全等的三角形C .相等的两个角是对顶角D .有一个角是60的等腰三角形是等边三角形6.下列命题正确的是( )A .全等三角形的对应边相等B .面积相等的两个三角形全等C .两个全等三角形一定成轴对称D .所有等腰三角形都只有一条对称轴 7.如图,在ABC 中,90C ∠=︒,30B ∠=︒,以点A 为圆心,任意长为半径画弧分别交AB ,AC 于点M 和N ,再分别以点M ,N 为圆心,大于12MN 的长为半径画弧,两弧交于点P ,连接AP 并延长交BC 于点D .则下列说法中正确的个数是( ) ①AD 是BAC ∠的平分线;②60ADC ∠=︒;③点D 在AB 的中垂线上;④:2:5DAC ABC S S =△△A .1B .2C .3D .48.如图,在ABC ∆中,90,30C B ︒︒∠=∠= ,以A 为圆心,任意长为半径画弧分别交AB AC 、于点M 和N ,再分别以M N 、为圆心,大于12MN 的长为半径画弧,两弧交于点P ,连接AP ,并延长交BC 于点D ,则下列说法中正确的个数是( )①AD 是BAC ∠的平分线;②60ADC ︒∠=;③点D 在AB 的垂直平分线上﹔④若2AD =,则点D 到AB 的距离是1,:1:2DAC ABC S S ∆∆=A .2B .3C .4D .59.如图,ABC 是等边三角形,D 是线段BC 上一点(不与点,B C 重合),连接AD ,点,E F 分别在线段,AB AC 的延长线上,且DE DF AD ==,点D 从B 运动到C 的过程中,BED 周长的变化规律是( )A .不变B .一直变小C .先变大后变小D .先变小后变大 10.如图,长方形纸片ABCD (长方形的对边平行且相等,每个角都为直角),将纸片沿EF 折叠,使点C 与点A 重合,下列结论:①AF AE =,②ABE AGF ≌,③AF CE =,④60AEF ∠=︒,其中正确的( )A .①②B .②③C .①②③D .①②③④ 11.如图,在ABC 与A B C ''△中,,90AB AC A B A C B B ==''='∠+∠'=︒,ABC ,A B C '''的面积分别为1S 、2S ,则( )A .12S S >B .12S SC .12S S <D .无法比较1S 、2S 的大小关系 12.若a b c 、、是ABC 的边,且222()()()0,a b a c b c -+-+-=则ABC 是( ). A .锐角三角形 B .直角三角形 C .钝角三角形 D .等边三角形 13.下列图案中,是轴对称图形的是( )A .B .C .D .14.如图,在等腰ABC 中,118ABC ︒∠=,AB 垂直平分线DE 交AB 于点D ,交AC 于点E ,BC 的垂直平分线PQ 交BC 于点P ,交AC 于点Q ,连接BE ,BQ ,则EBQ ∠=( )A .65︒B .60︒C .56︒D .50︒15.如图,在Rt ABC 中,∠BAC =90°,以点A 为圆心,以AB 长为半径作弧交BC 于点D ,再分别以点B ,D 为圆心,以大于12BD 的长为半径作弧,两弧交于点P ,作射线AP 交BC 于点E ,如果AB =3,AC =4,那么线段AE 的长度是( )A .125B .95C .85D .75二、填空题16.如图,在平面直角坐标系中,直线l 与x 轴交于点1B ,与y 轴交点于D ,且111,60OB ODB =∠=︒,以1OB 为边长作等边三角形11AOB ,过点1A 作12A B 平行于x 轴,交直线l 于点2B ,以12A B 为边长作等边三角形212A A B ,过点2A 作23A B 平行于x 轴,交直线l 于点3B ,以23A B 为边长作等边三角形323A A B ,…,按此规律进行下去,则点6A 的横坐标是______.17.如图,在ABC 中,AB 的垂直平分线DE 分别与,AB BC 交于点,D E ,AC 的垂直平分线FG 分别与,BC AC 交于点,F G ,10,3BC EF ==,则AEF 的周长是________.18.如图,在ABC 和ADE 中,90BAC DAE ∠=∠=︒,AB AC =,AD AE =,其中点C ,D ,E 在同一条直线上,连接BD ,BE .以下四个结论:①ACE DBC ∠=∠;②45ACE DBC ∠+∠=︒;③BD CE ⊥;④BD CE =.一定正确的是______.19.如图,∠MON=30°,点123A A A 、、…在射线ON 上,点123B B B 、、…在射线OM 上,△112A B A 、△223A B A 、△334A B A …均为等边三角形,从左起第1个等边三角形的边长记为1a ,第2个等边三角形的边长记为2a ,以此类推.若11OA =,则2021a =____.20.如图30AOB ∠=︒,OC 平分AOB ∠,P 为OC 上一点,//PD OA 交OB 于点D ,PE OA ⊥于E ,6cm OD =,则PE =________.21.如图,E 是腰长为2的等腰直角ABC 斜边上一点,且BE BC P =,为CE 上任意一点,PQ BC ⊥于点Q PR BE ⊥,于点R ,则PQ PR +的值是___________.22.如图,已知 O 为△ABC 三边垂直平分线的交点,且∠A =50°,则∠BOC 的度数为_____度.23.如图,在ABC 中,30EFD ∠=︒,且AEF AFE ∠=∠,CFD CDF ∠=∠,则B 的度数为______.24.如图,在△ABC 中,AB =AC ,∠BAC=36°,AD 、CE 是△ABC 的两条角平分线,BD=5,P 是AD 上的一个动点,则线段BP +EP 最小值的是____________.25.已知,点()1,3A a -与点()2,21B b --关于x 轴对称,则2a b +___________. 26.如图,在ABC 中,12 cm AB AC ==, 6 cm BC =,D 为AC 的中点,动点P 从点A 出发,以每秒1 cm 的速度沿A B C --的方向运动,设运动时间为t ,当过D ,P 两点的直线将ABC 的周长分成两部分,当其中一部分是另一部分的2倍时,t =_________.三、解答题27.如图,ABC 是边长为10的等边三角形,现有两点P 、Q 沿如图所示的方向分别从点A 、点B 同时出发,沿ABC 的边运动,已知点P 的速度为每秒1个单位长度,点Q 的运度为每秒2个单位长度,当点P 第一次到达B 点时,P 、Q 同时停止运动. (1)点P 、Q 运动几秒后,可得到等边三角形APQ ?(2)点P 、Q 运动几秒后,P 、Q 两点重合?(3)当点P 、Q 在BC 边上运动时,能否得到以PQ 为底边的等腰APQ ?如存在,请求出此时P 、Q 运动的时间.28.已知,在四边形ABCD 中,AB AD =,CB CD =,连接,AC BD ,判断,AC BD 的位置关系,并加以证明.29.如图,等边三角形ABC 中,AD BC ⊥,垂足为D ,点E 在线段AD 上,45EBC ∠=︒,求ACE ∠的度数.30.如图:已知ABC 中AB AC =:(1)尺规作图:过A 点作//AE BC (不写作法,保留作图痕迹);(2)求证:AE 是ABC 的一个外角角平分线.。
八年级数学上册全等三角形专题练习(解析版)

八年级数学上册全等三角形专题练习(解析版)一、八年级数学轴对称三角形填空题(难)1.如图,在锐角△ABC中,AB=5,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD,AB上的动点,则BM+MN的最小值是______.【答案】5【解析】【分析】作BH⊥AC,垂足为H,交AD于M点,过M点作MN⊥AB,垂足为N,则BM+MN为所求的最小值,再根据AD是∠BAC的平分线可知MH=MN,再由等腰直角三角形的性质即可得出结论.【详解】如图,作BH⊥AC,垂足为H,交AD于M点,过M点作MN⊥AB,垂足为N,则BM+MN 为所求的最小值.∵AD是∠BAC的平分线,∴MH=MN,∴BH是点B到直线AC的最短距离(垂线段最短).∵AB=5,∠BAC=45°,∴BH==5.∵BM+MN的最小值是BM+MN=BM+MH=BH=5.故答案为5.【点睛】本题考查了轴对称﹣最短路线问题,解答此类问题时要从已知条件结合图形认真思考,通过角平分线性质,垂线段最短,确定线段和的最小值.中取点P使得PA,PB,PC的长分别为3, 4, 5,则2.如图,在等边ABCAPC APB S S ∆∆+=_________.【答案】936 【解析】【分析】把线段AP 以点A 为旋转中心顺时针旋转60︒得到线段AD ,由旋转的性质、等边三角形的性质以及全等三角形的判定定理SAS 证得△ADB ≌△APC ,连接PD ,根据旋转的性质知△APD 是等边三角形,利用勾股定理的逆定理可得△PBD 为直角三角形,∠BPD =90︒,由△ADB ≌△APC 得S △ADB =S △APC ,则有S △APC +S △APB =S △ADB +S △APB =S △ADP +S △BPD ,根据等边3S △ADP +S △BPD =332+12×3×4=936+. 【详解】将线段AP 以点A 为旋转中心顺时针旋转60︒得到线段AD ,连接PD∴AD =AP ,∠DAP =60︒,又∵△ABC 为等边三角形,∴∠BAC =60︒,AB =AC ,∴∠DAB +∠BAP =∠PAC +∠BAP ,∴∠DAB =∠PAC ,又AB=AC,AD=AP∴△ADB ≌△APC∵DA =PA ,∠DAP =60︒,∴△ADP 为等边三角形,在△PBD 中,PB =4,PD =3,BD =PC =5,∵32+42=52,即PD 2+PB 2=BD 2,∴△PBD 为直角三角形,∠BPD =90︒,∵△ADB ≌△APC ,∴S △ADB =S △APC ,∴S △APC +S △APB =S △ADB +S △APB =S △ADP +S △BPD =34×32+12×3×4=9364+.故答案为:9364 .【点睛】本题考查了等边三角形的性质与判定,解题的关键是熟知旋转的性质作出辅助线进行求解.3.如图,在△ABC中,AB=10,∠B=60°,点D、E分别在AB、BC上,且BD=BE=4,将△BDE沿DE所在直线折叠得到△B′DE(点B′在四边形ADEC内),连接AB′,则AB′的长为______.【答案】2.【解析】【分析】【详解】过点D作DF⊥B′E于点F,过点B′作B′G⊥AD于点G,∵∠B=60°,BE=BD=4,∴△BDE是等边三角形,∵△B′DE≌△BDE,∴B′F=12B′E=BE=2,3,∴GD=B′F=2,∴3∵AB=10,∴AG=10﹣6=4,∴7考点:1轴对称;2等边三角形.4.如图,在ABC ∆中,点D 是BC 的中点,点E 是AD 上一点,BE AC =.若70C ∠=︒,50DAC ∠=︒ 则EBD ∠的度数为______.【答案】10︒【解析】【分析】延长AD 到F 使DF AD =,连接BF ,通过ACD FDB ≅,根据全等三角形的性质得到CAD BFD ∠=∠,AC BF =, 等量代换得BF BE =,由等腰三角形的性质得到F BEF ∠=∠,即可得到BEF CAD ∠=∠,进而利用三角形的内角和解答即可得.【详解】如图,延长AD 到F ,使DF AD =,连接BF :∵D 是BC 的中点∴BD CD =又∵ADC FDB ∠=∠,AD DF =∴ACD FDB ≅∴AC BF =, CAD F ∠=∠,C DBF ∠=∠∵AC BE =, 70C ︒∠=, 50CAD ︒∠=∴BE BF =, 70DBF ︒∠=∴50BEF F ︒∠=∠=∴180180505080EBF F BEF ︒︒︒︒︒∠=-∠-∠=--=∴807010EBD EBF DBF ︒︒︒∠=∠-∠=-=故答案为:10︒【点睛】本题主要考查的知识点有全等三角形的判定及性质、等腰三角形的性质及三角形的内角和定理,解题的关键在于通过倍长中线法构造全等三角形.5.如图,△ABC中,AB=8,AC=6,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC,分别交AB、AC于点D、E,则△ADE的周长为_____.【答案】14.【解析】【分析】先根据角平分线的定义及平行线的性质得BD=DF,CE=EF,则△ADE的周长=AB+AC=14.【详解】∵BF平分∠ABC,∴∠DBF=∠CBF,∵DE∥BC,∴∠CBF=∠DFB,∴∠DBF=∠DFB,∴BD=DF,同理FE=EC,∴△AED的周长=AD+AE+ED=AB+AC=8+6=14.故答案为:14.【点睛】此题考查角平分线的性质,平行线的性质,等腰三角形的等角对等边的性质.6.如图,已知每个小方格的边长为1,A 、B 两点都在小方格的格点(顶点)上,请在图中找一个格点C ,使△ABC 是等腰三角形,这样的格点C 有________个。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级上册数学轴对称填空选择专题练习(解析版)一、八年级数学全等三角形填空题(难)1.如图,AD⊥BC 于 D,且 DC=AB+BD,若∠BAC=108°,则∠C 的度数是______度.【答案】24【解析】【分析】在DC上取DE=DB.连接AE,在Rt△ABD和Rt△AED中,BD=ED,AD=AD.证明△ABD≌△AED即可求解.【详解】如图,在DC上取DE=DB,连接AE.在Rt△ABD和Rt△AED中,BD EDADB ADEAD AD=⎧⎪∠=∠⎨⎪=⎩∴△ABD≌△AED(SAS).∴AB=AE,∠B=∠AED.又∵CD=AB+BD,CD=DE+EC∴EC=AB∴EC=AE,∴∠C=∠CAE∴∠B=∠AED=2∠C又∵∠B+∠C=180°-∠BAC=72°∴∠C=24°,故答案为:24.【点睛】本题考查了全等三角形的判定与性质及三角形内角和定理,属于基础图,关键是巧妙作出辅助线.2.如图,△ABC是等边三角形,AE=CD,AD、BE相交于点P,BQ⊥DA于Q,PQ=3,EP=1,则DA的长是________.【答案】7【解析】试题解析:∵△ABC 为等边三角形,∴AB=CA ,∠BAE=∠ACD=60°;又∵AE=CD ,在△ABE 和△CAD 中,AB CA BAE ACD AE CD ⎧⎪∠∠⎨⎪⎩=== ∴△ABE ≌△CAD ;∴BE=AD ,∠CAD=∠ABE ;∴∠BPQ=∠ABE+∠BAD=∠BAD+∠CAD=∠BAE=60°;∵BQ ⊥AD ,∴∠AQB=90°,则∠PBQ=90°-60°=30°;∵PQ=3,∴在Rt △BPQ 中,BP=2PQ=6;又∵PE=1,∴AD=BE=BP+PE=7.故答案为7.3.如图,CA ⊥AB ,垂足为点A ,射线BM ⊥AB ,垂足为点B ,AB=12cm ,AC=6cm .动点E 从A 点出发以3cm/s 沿射线AN 运动,动点D 在射线BM 上,随着E 点运动而运动,始终保持ED=CB .当点E 经过______s 时,△DEB 与△BCA 全等.【答案】0、2、6、8【解析】∵CA ⊥AB ,垂足为点A ,射线BM ⊥AB ,垂足为点B ,∴ ∠CAB=∠DBE=90°,∴△CAB 和△EBD 都是Rt △,∵点E 运动过程中两三角形始终保持斜边ED=CB ,∴当BE=BA=12cm或BE=AC=6cm时,两三角形全等,如图共有四种情形,此时AE分别等于0cm、6cm、18cm、24cm,又∵点E每秒钟移动3cm,∴当点E移动的时间分别为0秒、2秒、6秒和8秒时,两三角形全等.4.如图,Rt△ABC中,∠C=90°.E为AB中点,D为AC上一点,BF∥AC交DE的延长线于点F.AC=6,BC=5.则四边形FBCD周长的最小值是______.【答案】16【解析】四边形FBCD周长=BC+AC+DF;当DF BC⊥时,四边形FBCD周长最小为5+6+5=165.如图,在四边形ABCD中,∠DAB=∠DCB=90°,CB=CD,AC=6,则四边形ABCD的面积是_________.【答案】18.【解析】【分析】根据已知线段关系,将△ACD绕点C逆时针旋转90°,CD与CB重合,得到△CBE,证明A、B、E三点共线,则△ACE是等腰直角三角形,四边形面积转化为△ACE面积.【详解】∵CD=CB,且∠DCB=90°,∴将△ACD绕点C逆时针旋转90°,CD与CB重合,得到△CBE,∴∠CBE=∠D,AC=EC,∠DCA=∠BCE.根据四边形内角和360°,可得∠D+∠ABC=180°,∴∠CBE+∠ABC=180°,∴A、B、E三点共线,∴△ACE是等腰直角三角形,∴四边形ABCD面积=△ACE面积= 12⨯AC2=18.故答案为:18.【点睛】本题考查了旋转的性质以及转化思想,解决这类问题要结合已知线段间的数量关系和位置关系进行旋转,使不规则图形转化为规则图形.6.如图,已知ABC △是等边三角形,点D 在边BC 上,以AD 为边向左作等边ADE ,连结BE ,作BF AE ∥交AC 于点F ,若2AF =,4CF =,则AE =________.【答案】27【解析】【分析】证明△BAE ≌△CAD 得到ABE BAC ∠=∠,从而证得BEAF ,再得到AEBF 是平行四边形,可得AE=BF ,在三角形BCF 中求出BF 即可. 【详解】作FH BC ⊥于H ,∵ABC 是等边三角形,2AF =,4CF =∴BC=AC=6在HCF 中, CF=4, 060BCF ∠=030,2CFD CH ∴∠==2224212FH ∴=-=22241227BF BH FH ∴++=∵ABC 是等边三角形,ADE 是等边三角形∴AC=AB ,AD=AE ,060CAB DAE ∠=∠=CAD BAE∴∠=∠∴∆≅∆CAD BAE∴∠=∠=ABE ACD60∴∠=∠ABE BACBE AF∴∵BF AE∴AEBF是平行四边形∴AE=BF= 27【点睛】本题考查全等三角形的判定和性质、平行四边形的判定和性质、等边三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.7.如图,在△ABD中,∠BAD=80°,C为BD延长线上一点,∠BAC=130°,△ABD的角平分线BE与AC交于点E,连接DE,则∠DEB=_____.【答案】40°【解析】【分析】做辅助线,构建角平分线的距离,根据角平分线的性质和逆定理可得:EF=EG=EH,设∠DEG=y,∠GEB=x,根据三角形内角和定理可得:∠GEA=∠FEA=40°,∠FEB=∠HEB,列方程为2y+x=80-x,y+x=40,可得结论:∠DEB=40°.【详解】如图,过E作EF⊥AB于F,EG⊥AD于G,EH⊥BC于H,∵BE平分∠ABD∴EH=EF∵∠BAC=130°,∠BAD=80°∴∠FAE=∠CAD=50°∴EF=EG∴EG=EH∴ED平分∠CDG∴∠HED=∠DEG设∠DEG=y,∠GEB=x,∵∠EFA=∠EGA=90°∴∠GEA=∠FEA=40°∵∠EFB=∠EHB=90°,∠EBH=∠EBF∴∠FEB=∠HEB∴2y+x=80-x,2y+2x=80y+x=40即∠DEB=40°.故答案为:40°.【点睛】本题考查三角形内角和定理和角平分线的性质,正确作辅助线是解题的关键.8.如图,Rt△ABC中,AB=AC,∠BAC=90°,BE⊥CE,垂足是E,BE交AC于点D,F是BE 上一点,AF⊥AE,且C是线段AF的垂直平分线上的点,AF=22,则DF=________.【答案】3.【解析】【分析】由题意可证的△ABF≌△ACE,可得△AEF为等腰直角三角形,取AF的中点O,连接CO交BE与点G,连接AG,可得△AGF, △AGE,△CEG均为等腰直角三角形,可得AG平行等于CE,可得四边形AGCE为平行四边形,可得FD的长.【详解】解:如图Rt△ABC中,AB=AC,∠BAC=90°,∴∠ABC=∠ACB=45°,又∠BAC=90°,BE⊥CE,∠DAE为∠BAC与EAF的公共角∴∠BAF=∠CAE,∠ABC=∠ACB=45°, BE⊥CE∴∠ABF+∠CBE=45°,∠CBE+∠ACB+∠ACE=90°,即: ∠CBE+∠ACE=45°,∴∠ABF=∠ACE,在△ABF与△ACE中,有AB ACBAF CAEABF ACE=⎧⎪∠=∠⎨⎪∠=∠⎩,∴△ABF≌△ACE,∴AE=AF, △AEF为等腰直角三角形, 取AF的中点O,连接CO交BE与点G,连接AG,C是线段AF的垂直平分线上的点,易得△AGF, △AGE,△CEG均为等腰直角三角形,AF=22∴AG=GE=CE=FG=2,又AG⊥BE,CE⊥BE,可得AG∥CE,∴四边形AGCE为平行四边形,∴GD=DE=1,∴DF=FG+GD=2+1=3.【点睛】本题主要考查三角形全等及性质,综合性强,需综合运用所学知识求解.9.如图,在△ABC中,∠ABC=50°,∠ACB=60°,点E在BC的延长线上,∠ABC的平分线BD与∠ACE的平分线CD相交于点D,连接AD,以下结论:①∠BAC=70°;②∠DOC=90°;③∠BDC=35°;④∠DAC=55°,其中正确的是__________.(填写序号)【答案】①③④【解析】【分析】根据三角形内角和定理、角平分线的定义、三角形外角的性质、角平分线的性质解答即可.【详解】解:∵∠ABC=50°,∠ACB=60°,∴∠BAC=180°﹣50°﹣60°=70°,①正确;∵BD是∠ABC的平分线,∴∠DBC=12∠ABC=25°,∴∠DOC=25°+60°=85°,②错误;∠BDC=60°﹣25°=35°,③正确;∵∠ABC的平分线BD与∠ACE的平分线CD相交于点D,∴AD是∠BAC的外角平分线,∴∠DAC=55°,④正确.故答案为①③④.【点睛】本题考查的是角平分线的定义和性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.10.如图,△ABC 与△DEF 为等边三角形,其边长分别为a ,b ,则△AEF 的周长为___________.【答案】a+b【解析】先根据全等三角形的判定AAS 判定△AEF≌△BFD,得出AE=BF ,从而得出△AEF 的周长=AF+AE+EF=AF+BF+EF=a+b .故答案为:a+b二、八年级数学全等三角形选择题(难)11.如图,在▱ABCD 中,AD =2AB ,F 是AD 的中点,作CE ⊥AB ,垂足E 在线段AB 上,连接EF 、CF ,则下列结论中①∠DCF =123,1x x ==-∠BCD ;②EF =CF ;③S △BEC =2S △CEF ;④∠DFE =3∠AEF .一定成立的是( )A .①②B .①③④C .①②③D .①②④【答案】D【解析】①∵F 是AD 的中点,∴AF=FD , ∵在?ABCD 中,AD=2AB ,∴AF=FD=CD ,∴∠DFC=∠DCF ,∵AD ∥BC ,∴∠DFC=∠FCB ,∴∠DCF=∠BCF ,∴∠DCF=12∠BCD ,故此选项正确;延长EF ,交CD 延长线于M ,∵四边形ABCD是平行四边形,∴AB∥CD,∴∠A=∠MDF,∵F为AD中点,∴AF=FD,在△AEF和△DFM中,∠A=∠FDMAF=DF∠AFE=∠DFM,∴△AEF≌△DMF(ASA),∴FE=MF,∠AEF=∠M,∵CE⊥AB,∴∠AEC=90°,∴∠AEC=∠ECD=90°,∵FM=EF,∴FC=FM,故②正确;③∵EF=FM,∴S△EFC=S△CFM,∵MC>BE,∴S△BEC<2S△EFC故S△BEC=2S△CEF错误;④设∠FEC=x,则∠FCE=x,∴∠DCF=∠DFC=90°-x,∴∠EFC=180°-2x,∴∠EFD=90°-x+180°-2x=270°-3x,∵∠AEF=90°-x,∴∠DFE=3∠AEF,故此选项正确.故正确的有:①②④.故选D.12.如图,在△ABC中,AB=6,AC=10,BC边上的中线..为..AD=4,则△ABC的面积()A .30B .48C .20D .24【答案】D【解析】 延长AD 到E ,使DE =AD ,连接BE ,因为D 为BC 的中点,所以DC =BD ,在△ADC 和△EDB 中,AD ED ADC EDB DC BD =⎧⎪∠=∠⎨⎪=⎩, 所以△ADC ≌△EDB ,所以BE =AC =10, ∠CAD =∠E ,又因为AE =2AD =8,AB =6,所以222AB AE BE =+,所以∠CAD =∠E=90°,则11114646242222ABC ABD ADC S S S AD BE AD AC =+=⨯+⨯=⨯⨯+⨯⨯=, 所以故选D.13.如图,已知等腰Rt △ABC 和等腰Rt △ADE ,AB=AC=4,∠BAC=∠EAD=90°,D 是射线BC 上任意一点,连接EC .下列结论:①△AEC △ADB ;② EC ⊥BC ; ③以A 、C 、D 、E 为顶点的四边形面积为8;④当BD=时,四边形AECB 的周长为10524++;⑤ 当BD=32B 时,ED=5AB ;其中正确的有( )A .5个B .4个C .3 个D .2个 【答案】B 【解析】解:∵∠BAC =∠EAD =90°,∴∠BAD =∠CAE ,∵AB =AC ,AD =AE ,∴△AEC ≌△ADB ,故①正确; ∵△AEC ≌△ADB ,∴∠ACE =∠ABD =45°,∵∠ACB =45°,∴J IAO ECB =90°,∴EC ⊥BC ,故②正确;∵四边形ADCE 的面积=△ADC 的面积+△ACE 的面积=△ADC 的面积+△ABD 的面积=△ABC 的面积=4×4÷2=8.故③正确;∵BD =2,∴EC =2,DC =BC -BD =422-=32,∴DE 2=DC 2+EC 2,=()()22322+=20,∴DE =25,∴AD =AE =252=10.∴AECB 的周长=AB +DC +CE +AE =442210+++=45210++,故④正确;当BD =32BC 时,CD =12BC ,∴DE =221322BC BC ⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭=102BC =52AB .故⑤错误. 故选B .点睛:此题是全等三角形的判定与性质的综合运用,熟练掌握等腰直角三角形的性质是解答此题的关键.14.如图,Rt ABC ∆中,90C =∠,3,4,5,AC BC AB ===AD 平分BAC ∠.则:ACD ABD S S ∆∆=( )A .3:4B .3:5C .4:5D .2:3【答案】B【解析】 如图,过点D 作DE ⊥AB 于点E ,由角平分线的性质可得出DE=CD ,由全等三角形的判定定理HL 得出△ADC ≌△ADE ,故可得出AE=AC=3,由AB=5求出BE=2,设CD=x ,则DE=x ,BD=4﹣x ,再根据勾股定理知DE 2+BE 2=BD 2,即x 2+22=(4﹣x )2,求出x=32,进而根据等高三角形的面积,可得出:S △ACD :S △ABD =CD :BD=12×32×3:12×32×5=3:5.故选:B .点睛:本题考查的是角平分线的性质,熟知角平分线上的点到角两边的距离相等是解答此题的关键.15.在△ABC 中, ∠C=90°,AC=BC ,AD 是∠BAC 的平分线,DE ⊥AB 于点E ,AB=18cm ,则△DBE 的周长为( )A .16cmB .8cmC .18cmD .10cm【答案】C【解析】因为 ∠C=90°,AC=BC ,AD 是∠BAC 的平分线,DE ⊥AB ,易证△ACD≌△AED,所以AE =AC=BC ,ED=CD.△DBE 的周长=BE+DE+DB=BE+CD+DB=BE+BC=BE+AE=AB.因为AB=12,所以△DBE 的周长=12.故选C.点睛:本题主要考查了全等三角形的判定的性质及角平分线的性质定理,角的平分线上的点到角的两边的距离相等,运用这个性质,结合等腰三角形有性质,将△DBE 的周长转化为AB 的长.16.如图在ABC △中,P ,Q 分别是BC 、AC 上的点,作PR AB ⊥,PS AC ⊥,垂足分别是R ,S ,AQ PQ =,PR PS =,下面三个结论:①AS AR =;②PQ AB ∥;③BRP △≌CSP △.其中正确的是( ).A .①②B .②③C .①③D .①②③【答案】A【解析】连接AP ,由题意得,90ARP ASP ∠=∠=︒,在Rt APR 和Rt APS 中,AP AP PR PS =⎧⎨=⎩, ∴△APR ≌()APS HL ,∴AS AR =,故①正确.BAP SAP ∠=∠,∴2SAB BAP SAP SAP ∠=∠+∠=∠,在AQP △中,∴AQ PQ =,∴QAP APQ ∠=∠,∴22CQP QAP APQ QAP SAP ∠=∠+∠=∠=∠,∴PQ AB ∥,故②正确;在Rt BRP 和Rt CSP 中,只有PR PS =,不满足三角形全等的条件,故③错误.故选A .点睛:本题主要考查三角形全等的判定方法以及角平分线的判定和平行线的判定,准确作出辅助线是解决本题的关键.17.如图所示,把腰长为1的等腰直角三角形折叠两次后,得到的一个小三角形的周长是( )A .2B .2C .2D 2-1【答案】B【解析】 第一次折叠后,等腰三角形的底边长为1,腰长为22; 第一次折叠后,等腰三角形的底边长为22,腰长为12,所以周长为112212222++=+.故答案为B.18.如图,AD是△ABC的外角平分线,下列一定结论正确的是()A.AD+BC=AB+CD,B.AB+AC=DB+DC,C.AD+BC<AB+CD,D.AB+AC<DB+DC【答案】D【解析】【分析】在BA的延长线上取点E,使AE=AC,连接ED,证△ACD≌△AED,推出DE=DC,根据三角形中任意两边之和大于第三边即可得到AB+AC<DB+DC.【详解】解: 在BA的延长线上取点E, 使AE=AC,连接ED,∵AD是△ABC的外角平分线,∴∠EAD=∠CAD,在△ACD和△AED中,AD ADEAD CADAC AE=⎧⎪∠=∠⎨⎪=⎩∴△ACD≌△AED(SAS)∴DE=DC,在△EBD中,BE<BD+DE,∴AB+AC<DB+DC故选:D.【点睛】本题主要考查三角形全等的证明,全等三角形的性质,三角形的三边关系,作辅助线构造以AB 、AC 、DB 、DC 的长度为边的三角形是解题的关键,也是解本题的难点.19.在ABC 中,2,72A B ACB ∠=∠∠≠︒,CD 平分ACB ∠,P 为AB 的中点,则下列各式中正确的是( )A .AD BC CD =-B .AD BC AC =- C .AD BC AP =-D .AD BC BD =-【答案】B【解析】【分析】 可在BC 上截取CE=CA ,连接DE ,可得△ACD ≌△ECD ,得DE=AD ,进而再通过线段之间的转化得出线段之间的关系.【详解】解:∵∠A=2∠B , ∴∠A ﹥∠B ∴BC ﹥AC∴可在BC 上截取CE=CA ,连接DE(如图),∵CD 平分ACB ∠,∴∠ACD=∠BCD又∵CD=CD,CE=CA∴△ACD ≌△ECD ,∴AD=ED ,∠CED=∠A=2∠B又 ∠CED=∠B+∠BDE∴∠B=∠BDE∴AD=DE=BE,∴BC=BE+EC=AD+AC所以AD=BC-AC故选:B若A选项成立,则CD=AC,∴∠A=∠CDA=∠CDE=∠CED=2∠B=2∠EDB∴∠CDA+∠CDE+∠EDB=180°即5∠EDB=180°∴∠EDB=36°∴∠A=72°,∠B=36°∴∠ACB=72°与已知∠ACB≠72°矛盾,故选项A不正确;假设C选项成立,则有AP=AC,作∠BAC的平分线,连接FP,∴△CAF≌△PAF≌△PBF,∴∠CFA=∠AFP=∠PFB=60°∠B=30°,∠ACB=90°当∠ACB=90°时,选项C才成立,∴当∠ACB≠72°时,选项C不一定成立;假设D选项成立,则AD=BC-BD由图可知AD=BA-BD∴AB=BC∴∠A=∠ACB=2∠B∴∠A+∠ACB+∠B=180°∴∠B=36°,∠ACB=72这与已知∠ACB≠72°矛盾,故选项D不成立.故选:B【点睛】本题考查的是考查的是利用角的平分线的性质说明线段之间的关系.,,20.如图,点 D 是等腰直角△ABC 腰 BC 上的中点,点B 、B′ 关于 AD 对称,且BB′ 交AD 于 F,交 AC 于 E,连接 FC 、 AB′,下列说法:① ∠BAD=30°; ② ∠BFC=135°;③ AF=2B′ C;正确的个数是()A.1 B.2 C.3 D.4【答案】B【解析】【分析】依据点D是等腰直角△ABC腰BC上的中点,可得tan∠BAD=12,即可得到∠BAD≠30°;连接B'D,即可得到∠BB'C=∠BB'D+∠DB'C=90°,进而得出△ABF≌△BCB',判定△FCB'是等腰直角三角形,即可得到∠CFB'=45°,即∠BFC=135°;由△ABF≌△BCB',可得AF=BB'=2BF=2B'C;依据△AEF与△CEB'不全等,即可得到S△AFE≠S△FCE.【详解】∵点D是等腰直角△ABC腰BC上的中点,∴BD=12BC=12AB,∴tan∠BAD=12,∴∠BAD≠30°,故①错误;如图,连接B'D,∵B、B′关于AD对称,∴AD垂直平分BB',∴∠AFB=90°,BD=B'D=CD,∴∠DBB'=∠BB'D,∠DCB'=∠DB'C,∴∠BB'C=∠BB'D+∠DB'C=90°,∴∠AFB=∠BB'C,又∵∠BAF+∠ABF=90°=∠CBB'+∠ABF , ∴∠BAF=∠CBB',∴△ABF ≌△BCB',∴BF=CB'=B'F ,∴△FCB'是等腰直角三角形,∴∠CFB'=45°,即∠BFC=135°,故②正确;由△ABF ≌△BCB',可得AF=BB'=2BF=2B'C ,故③正确;∵AF >BF=B'C ,∴△AEF 与△CEB'不全等,∴AE≠CE ,∴S △AFE ≠S △FCE ,故④错误;故选B .【点睛】本题主要考查了轴对称的性质以及全等三角形的判定与性质的运用,如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.21.如图,已知在正方形ABCD 中,点E F 、分别在BC CD 、上,△AEF 是等边三角形,连接AC 交EF 于G ,给出下列结论:①BE DF =; ② 15DAF ∠=;③AC 垂直平分EF ; ④BE DF EF +=.其中结论正确的共有( ).A .1个B .2个C .3个D .4个【答案】C【解析】试题分析:四边形ABCD 是正方形,∴AB=BC=CD=AD ,∠B=∠BCD=∠D=∠BAD=90°.∵△AEF 等边三角形,∴AE=EF=AF ,∠EAF=60°.∴∠BAE+∠DAF=30°.∴Rt △ABE ≌Rt △ADF (HL ),∴BE=DF (故①正确).∠BAE=∠DAF ,∴∠DAF+∠DAF=30°,即∠DAF=15°(故②正确),∵BC=CD ,∴BC ﹣BE=CD ﹣DF ,即CE=CF ,∵AE=AF ,∴AC 垂直平分EF .(故③正确). 设EC=x ,由勾股定理,得EF=x ,CG=x ,AG=AEsin60°=EFsin60°=2×CGsin60°=x , ∴AC=, ∴AB=, ∴BE=﹣x=,∴BE+DF=x ﹣x≠x .(故④错误).∴综上所述,正确的有3个.考点:正方形的性质;全等三角形的判定与性质;线段垂直平分线的性质;等边三角形的性质.22.如图,D 为BAC ∠的外角平分线上一点并且满足BD CD =,DBC DCB ∠=∠,过D 作DE AC ⊥于E ,DF AB ⊥交BA 的延长线于F ,则下列结论:①CDE △≌BDF ;②CE AB AE =+;③BDC BAC ∠=∠;④DAF CBD ∠=∠. 其中正确的结论有( ).A .1个B .2个C .3个D .4个【答案】D【解析】 BD=CD,AD 是角平分线,所以FD=DE,∠DFB =∠DEC =90°,所以CDE ≌BDF ;①正确.由全等得BF=CE ,因为FA=AE,FB=AB+FA ,所以CE=AB+AE , ②正确.由全等知,∠DCE=∠FBD,所以∠BAC=∠BDC. ③正确. ∴DBF DCE ∠=∠,∴A 、B 、C 、D 四点共圆,∴DAF CBD ∠=∠,④正确.故选D.23.如图,在等腰△ABC 中,90ACB ︒∠=,8AC =,F 是AB 边上的中点,点D 、E 分别在AC 、BC 边上运动,且保持AD CE =,连接DE 、DF 、EF 在此运动变化的过程中,下列结论:(1)DEF 是等腰直角三角形;(2)四边形CDFE 不可能为正方形,(3)DE 长度的最小值为4;(4)连接CF ,CF 恰好把四边形CDFE 的面积分成1:2两部分,则CE =13或143其中正确的结论个数是A .1个B .2个C .3个D .4个【答案】A【解析】【分析】连接CF,证明△ADF≌△CEF,根据全等三角形的性质判断①,根据正方形的判定定理判断②,根据勾股定理判断③,根据面积判断④.【详解】连接CF,∵△ABC是等腰直角三角形,∴∠FCB=∠A=45,CF=AF=FB;∵AD=CE,∴△ADF≌△CEF(SAS);∴EF=DF,∠CFE=∠AFD;∵∠AFD+∠CFD=90∘,∴∠CFE+∠CFD=∠EFD=90∘,又∵EF=DF∴△EDF是等腰直角三角形(故(1)正确).当D. E分别为AC、BC中点时,四边形CDFE是正方形(故(2)错误).由于△DEF是等腰直角三角形,因此当DE最小时,DF也最小;即当DF⊥AC时,DE最小,此时142DF BC== .∴242DE DF=故(3)错误).∵△ADF≌△CEF,∴S△CEF=S△ADF∴S四边形CDFE=S△AFC,∵CF恰好把四边形CDFE的面积分成1:2两部分∴S△CEF:S△CDF=1:2 或S△CEF:S△CDF=2:1即S△ADF:S△CDF=1:2 或S△ADF:S△CDF=2:1当S△ADF:S△CDF=1:2时,S△ADF=13S△ACF=111684323⨯⨯⨯=又∵S△ADF=1422AD AD ⨯⨯=∴2AD=16 3∴AD=83(故(4)错误).故选:A.【点睛】本题考查了全等三角形,等腰直角三角形,以及勾股定理,掌握全等三角形,等腰直角三角形,以及勾股定理是解题的关键.24.如图,点P是AB上任意一点,∠ABC=∠ABD,还应补充一个条件,才能推出△APC≌△APD.从下列条件中补充一个条件,不一定能推出△APC≌△APD的是( )A.BC=BD;B.AC=AD;C.∠ACB=∠ADB;D.∠CAB=∠DAB【答案】B【解析】根据题意,∠ABC=∠ABD,AB是公共边,结合选项,逐个验证得出:A、补充BC=BD,先证出△BPC≌△BPD,后能推出△APC≌△APD,故正确;B、补充AC=AD,不能推出△APC≌△APD,故错误;C、补充∠ACB=∠ADB,先证出△ABC≌△ABD,后能推出△APC≌△APD,故正确;D、补充∠CAB=∠DAB,先证出△ABC≌△ABD,后能推出△APC≌△APD,故正确.故选B.点睛:本题考查了三角形全等判定,三角形全等的判定定理:有AAS,SSS,ASA,SAS.注意SSA是不能证明三角形全等的,做题时要逐个验证,排除错误的选项.25.如图,Rt△ACB中,∠ACB=90°,∠ABC的平分线BE和∠BAC的外角平分线AD相交于点P,分别交AC和BC的延长线于E,D,过P作PF⊥AD交AC的延长线于点H,交BC的延长线于点F,连接AF交DH于点G,则下列结论:①∠APB=45°;②PF=PA;③BD﹣AH=AB;④DG=AP+GH,其中正确的是()A.1 B.2 C.3 D.4【答案】C【解析】【分析】①根据三角形的一个外角等于与它不相邻的两个内角的和与角平分线的定义表示出∠CAP ,再根据角平分线的定义∠ABP=12∠ABC ,然后利用三角形的内角和定理整理即可得解; ②先求出∠APB=∠FPB ,再利用“角边角”证明△ABP 和△FBP 全等,根据全等三角形对应边相等得到AB=BF ,AP=PF ;③根据直角的关系求出∠AHP=∠FDP ,然后利用“角角边”证明△AHP 与△FDP 全等,根据全等三角形对应边相等可得DF=AH ;④根据PF ⊥AD ,∠ACB=90°,可得AG ⊥DH ,然后求出∠ADG=∠DAG=45°,再根据等角对等边可得DG=AG ,再根据等腰直角三角形两腰相等可得GH=GF ,然后求出DG=GH+AF ,有直角三角形斜边大于直角边,AF >AP ,从而得出本小题错误.【详解】解:①∵∠ABC 的角平分线BE 和∠BAC 的外角平分线,∴∠ABP=12∠ABC , ∠CAP=12(90°+∠ABC )=45°+12∠ABC , 在△ABP 中,∠APB=180°-∠BAP-∠ABP ,=180°-(45°+12∠ABC+90°-∠ABC )-12∠ABC , =180°-45°- 12∠ABC-90°+∠ABC-12∠ABC , =45°,故本小题正确;②∵PF ⊥AD ,∠APB=45°(已证),∴∠APB=∠FPB=45°,∵∵PB 为∠ABC 的角平分线,∴∠ABP=∠FBP ,在△ABP 和△FBP 中, APB FPB PB PBABP FBP ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△ABP ≌△FBP (ASA ),∴AB=BF ,AP=PF ;故②正确;③∵∠ACB=90°,PF ⊥AD ,∴∠FDP+∠HAP=90°,∠AHP+∠HAP=90°,∴∠AHP=∠FDP ,∵PF ⊥AD ,∴∠APH=∠FPD=90°,在△AHP 与△FDP 中,90AHP FDPAPH FPDAP PF∠=∠⎧⎪∠=∠=︒⎨⎪=⎩∴△AHP≌△FDP(AAS),∴DF=AH,∵BD=DF+BF,∴BD=AH+AB,∴BD-AH=AB,故③小题正确;④∵PF⊥AD,∠ACB=90°,∴AG⊥DH,∵AP=PF,PF⊥AD,∴∠PAF=45°,∴∠ADG=∠DAG=45°,∴DG=AG,∵∠PAF=45°,AG⊥DH,∴△ADG与△FGH都是等腰直角三角形,∴DG=AG,GH=GF,∴DG=GH+AF,∵AF>AP,∴DG=AP+GH不成立,故本小题错误,综上所述①②③正确.故选:C.【点睛】本题考查了直角三角形的性质,全等三角形的判定,以及等腰直角三角形的判定与性质,等角对等边,等边对等角的性质,综合性较强,难度较大,做题时要分清角的关系与边的关系.26.如图,已知∠DCE=90°,∠DAC=90°,BE⊥AC于B,且DC=EC.若BE=7,AB=3,则AD 的长为()A.3 B.5 C.4 D.不确定【答案】C【解析】根据同角的余角相等求出∠ACD=∠E,再利用“角角边”证明△ACD≌△BCE,根据全等三角形对应边相等可得AD=BC,AC=BE=7,然后求解BC=AC-AB=7-3=4.故选:C.点睛:本题考查了全等三角形的判定与性质,等角的余角相等的性质,熟练掌握三角形全等的判定方法是解题的关键.27.如图,O 是正ABC 内一点,3OA =,4OB =,5OC =,将线段BO 以点B 为旋转中心逆时针旋转60°得到线段BO ',连接AO ',下列结论:①BO A '△可以由BOC 绕点B 逆时针旋转60°得到:②点O 与O '的距离为4;③150AOB ∠=︒;④S 四边形643AOBO ;⑤9634AOC AOB S S +=+△△.其中正确的结论是( )A .①②③④B .①②③⑤C .①②④⑤D .①②③④⑤【答案】D【解析】【分析】 证明△BO ′A ≌△BOC ,又∠OBO ′=60°,所以△BO ′A 可以由△BOC 绕点B 逆时针旋转60°得到,故结论①正确;由△OBO ′是等边三角形,可知结论②正确;在△AOO ′中,三边长为3,4,5,这是一组勾股数,故△AOO ′是直角三角形;进而求得∠AOB =150°,故结论③正确;643AOO OBO AOBO S S S '∆'∆'=+=+四边形④正确;如图②,将△AOB 绕点A 逆时针旋转60°,使得AB 与AC 重合,点O 旋转至O ″点.利用旋转变换构造等边三角形与直角三角形,将S △AOC +S △AOB 转化为S △COO ″+S △AOO ″,计算可得结论⑤正确.【详解】解:由题意可知,∠1+∠2=∠3+∠2=60°,∴∠1=∠3,又∵OB =O ′B ,AB =BC ,∴△BO ′A ≌△BOC ,又∵∠OBO ′=60°,∴△BO ′A 可以由△BOC 绕点B 逆时针旋转60°得到,故结论①正确;如图①,连接OO ′,∵OB =O ′B ,且∠OBO ′=60°,∴△OBO ′是等边三角形,∴OO ′=OB =4.故结论②正确;∵△BO ′A ≌△BOC ,∴O ′A =5.在△AOO ′中,三边长为3,4,5,这是一组勾股数,∴△AOO ′是直角三角形,∠AOO ′=90°,∴∠AOB =∠AOO ′+∠BOO ′=90°+60°=150°,故结论③正确;2313446432AOO OBO AOBO S S S '∆'∆'=+=⨯⨯+⨯=+四边形, 故结论④正确;如图②所示,将△AOB 绕点A 逆时针旋转60°,使得AB 与AC 重合,点O 旋转至O ″点.易知△AOO ″是边长为3的等边三角形,△COO ″是边长为3、4、5的直角三角形,则23193436324AOC AOB COO AOO AOCO S S S S S ∆∆∆''∆''''+==+=⨯⨯+⨯=+四边形, 故结论⑤正确.综上所述,正确的结论为:①②③④⑤.故选:D .【点睛】本题考查了旋转变换中等边三角形,直角三角形的性质.利用勾股定理的逆定理,判定勾股数3、4、5所构成的三角形是直角三角形,这是本题的要点.在判定结论⑤时,将△AOB 向不同方向旋转,体现了结论①﹣结论④解题思路的拓展应用.28.如图,在△ABC 中,AB=AC ,高BD ,CE 交于点O ,AO 交BC 于点F ,则图中共有全等三角形( )A .8对B .7对C .6对D .5对【答案】B【解析】【分析】 易证△ABC 是关于AF 对称的图形,其中的小三角形也关于AF 对称,共可找出7对三角形.【详解】全等的三角形有:①△AFB≌△AFC;②△CEB≌△BDC;③△AEO≌△ADO;④△EOB≌△DOC;⑤△OBF≌△OFC;⑥△AOB≌△AOC;⑦△AEC≌△ADB证明①△AFB≌△AFC∵AB=AC,CE⊥AB,BD⊥AC又∵1122ABCS AB CE AC BD==∴CE=BD∴在Rt△BCE和Rt△CBD中BC BCCE BD=⎧⎨=⎩∴△BCE≌△CB D∴BE=CD,∴AE=AD在Rt△AEO和Rt△ADO中AE ADAO AO=⎧⎨=⎩∴△AEO≌△ADO∴∠EOD=∠DOA在△BAF和△CAF中AB ACBAF CAFAF AF=⎧⎪∠=∠⎨⎪=⎩∴△BAF≌△CAF,得证其余全等证明过程类似故选:B【点睛】本题考查全等的证明,解题关键是利用等腰三角形的性质,推导出图形中边的关系,为证全等作准备29.如图所示,设甲、乙、丙、丁分别表示△ABC,△ACD,△EFG,△EGH.已知∠ACB=∠CAD=∠EFG=∠EGH=70°,∠BAC=∠ACD=∠EGF=∠EHG=50°,则叙述正确的是()A.甲、乙全等,丙、丁全等B.甲、乙全等,丙、丁不全等C.甲、乙不全等,丙、丁全等D.甲、乙不全等,丙、丁不全等【答案】B【解析】【分析】根据题意即是判断甲、乙是否全等,丙丁是否全等.运用判定定理解答.【详解】解:∵∠ACB=CAD=70°,∠BAC=∠ACD=50°,AC为公共边,∴△ABC≌△ACD,即甲、乙全等;△EHG中,∠EGH=70°≠∠EHG=50°,即EH≠EG,虽∠EFG=∠EGH=70°,∠EGF=∠EHG=50°,∴△EFG不全等于△EGH,即丙、丁不全等.综上所述甲、乙全等,丙、丁不全等,B正确,故选:B.【点睛】本题考查的是全等三角形的判定,但考生需要有空间想象能力.判定两个三角形全等的一般方法有:SSS、SAS、AAS、HL.找着∠EGH=70°≠∠EHG=50°,即EH≠EG是正确解决本题的关键.30.如图,等腰直角△ABC中,∠BAC=90 ,AD⊥BC于D,∠ABC的平分线分别交AC、AD 于E、F两点,M为EF的中点,延长AM交BC于点N,连接DM.下列结论:①AE=AF;②AM⊥EF;③AF=DF;④DF=DN,其中正确的结论有()A.1个B.2个C.3个D.4个【答案】C【解析】试题解析:∵∠BAC=90°,AC=AB,AD⊥BC,∴∠ABC=∠C=45°,AD=BD=CD,∠ADN=∠ADB=90°,∴∠BAD=45°=∠CAD,∵BE平分∠ABC,∴∠ABE=∠CBE=12∠ABC=22.5°,∴∠BFD=∠AEB=90°-22.5°=67.5°,∴∠AFE=∠BFD=∠AEB=67.5°,∴AF=AE,故①正确;∵M为EF的中点,∴AM⊥EF,故②正确;过点F作FH⊥AB于点H,∵BE平分∠ABC,且AD⊥BC,∴FD=FH<FA,故③错误;∵AM⊥EF,∴∠AMF=∠AME=90°,∴∠DAN=90°-67.5°=22.5°=∠MBN,在△FBD和△NAD中{FBD DANBD ADBDF ADN∠∠∠∠===∴△FBD≌△NAD,∴DF=DN,故④正确;故选C.。
