匈牙利解法C程序代码
匈牙利算法——精选推荐

匈⽛利算法0 - 相关概念0.1 - 匈⽛利算法 匈⽛利算法是由匈⽛利数学家Edmonds于1965年提出,因⽽得名。
匈⽛利算法是基于Hall定理中充分性证明的思想,它是⼆部图匹配最常见的算法,该算法的核⼼就是寻找增⼴路径,它是⼀种⽤增⼴路径求⼆分图最⼤匹配的算法。
0.2 - ⼆分图 若图G的结点集合V(G)可以分成两个⾮空⼦集V1和V2,并且图G的任意边xy关联的两个结点x和y分别属于这两个⼦集,则G是⼆分图。
1 - 基本思想1. 找到当前结点a可以匹配的对象A,若该对象A已被匹配,则转⼊第3步,否则转⼊第2步2. 将该对象A的匹配对象记为当前对象a,转⼊第6步3. 寻找该对象A已经匹配的对象b,寻求其b是否可以匹配另外的对象B,如果可以,转⼊第4步,否则,转⼊第5步4. 将匹配对象b更新为另⼀个对象B,将对象A的匹配对象更新为a,转⼊第6步5. 结点a寻求下⼀个可以匹配的对象,如果存在,则转⼊第1步,否则说明当前结点a没有可以匹配的对象,转⼊第6步6. 转⼊下⼀结点再转⼊第1步2 - 样例解析 上⾯的基本思想看完肯定⼀头雾⽔(很⼤程度是受限于我的表达能⼒),下⾯通过来就匈⽛利算法做⼀个详细的样例解析。
2.1 - 题⽬⼤意 农场主John有N头奶⽜和M个畜栏,每⼀头奶⽜需要在特定的畜栏才能产奶。
第⼀⾏给出N和M,接下来N⾏每⾏代表对应编号的奶⽜,每⾏的第⼀个数值T表⽰该奶⽜可以在多少个畜栏产奶,⽽后的T个数值为对应畜栏的编号,最后输出⼀⾏,表⽰最多可以让多少头奶⽜产奶。
2.1 - 输⼊样例5522532342153125122.2 - 匈⽛利算法解题思路2.2.1 - 构造⼆分图 根据输⼊样例构造如下⼆分图,蓝⾊结点表⽰奶⽜,黄⾊结点表⽰畜栏,连线表⽰对应奶⽜能在对应畜栏产奶。
2.2.2 - 模拟算法流程为结点1(奶⽜)分配畜栏,分配畜栏2(如图(a)加粗红边所⽰)为结点2(奶⽜)分配畜栏,由于畜栏2已经被分配给结点1(奶⽜),所以寻求结点1(奶⽜)是否能够分配别的畜栏,以把畜栏2腾给结点2(奶⽜)。
运筹学指派问题的匈牙利法

运筹学课程设计指派问题的匈牙利法专业:姓名:学号:1.算法思想:匈牙利算法的基本思想是修改效益矩阵的行或列,使得每一行或列中至少有一个为零的元素,经过修正后,直至在不同行、不同列中至少有一个零元素,从而得到与这些零元素相对应的一个完全分配方案。
当它用于效益矩阵时,这个完全分配方案就是一个最优分配,它使总的效益为最小。
这种方法总是在有限步內收敛于一个最优解。
该方法的理论基础是:在效益矩阵的任何行或列中,加上或减去一个常数后不会改变最优分配。
2.算法流程或步骤:1.将原始效益矩阵C的每行、每列各元素都依次减去该行、该列的最小元素,使每行、每列都至少出现一个0元素,以构成等价的效益矩阵C’。
2.圈0元素。
在C’中未被直线通过的含0元素最少的行(或列)中圈出一个0元素,通过这个0元素作一条竖(或横)线。
重复此步,若这样能圈出不同行不同列的n个0元素,转第四步,否则转第三步。
3.调整效益矩阵。
在C’中未被直线穿过的数集D中,找出最小的数d,D中所有数都减去d,C’中两条直线相交处的数都加的d。
去掉直线,组成新的等价效益矩阵仍叫C’,返回第二步。
X=0,这就是一种最优分配。
最低总4.令被圈0元素对应位置的X ij=1,其余ij耗费是C中使X=1的各位置上各元素的和。
ij算法流程图:3.算法源程序:#include<iostream.h>typedef struct matrix{float cost[101][101];int zeroelem[101][101];float costforout[101][101];int matrixsize;int personnumber;int jobnumber;}matrix;matrix sb;int result[501][2];void twozero(matrix &sb);void judge(matrix &sb,int result[501][2]);void refresh(matrix &sb);void circlezero(matrix &sb);matrix input();void output(int result[501][2],matrix sb);void zeroout(matrix &sb);matrix input(){matrix sb;int m;int pnumber,jnumber;int i,j;float k;char w;cout<<"指派问题的匈牙利解法:"<<endl;cout<<"求最大值,请输入1;求最小值,请输入0:"<<endl;cin>>m;while(m!=1&&m!=0){cout<<"请输入1或0:"<<endl;cin>>m;}cout<<"请输入人数(人数介于1和100之间):"<<endl;cin>>pnumber;while(pnumber<1||pnumber>100){cout<<"请输入合法数据:"<<endl;cin>>pnumber;}cout<<"请输入工作数(介于1和100之间):"<<endl;cin>>jnumber;while(jnumber<1||jnumber>100){cout<<"请输入合法数据:"<<endl;cin>>jnumber;}cout<<"请输入"<<pnumber<<"行"<<jnumber<<"列的矩阵,同一行内以空格间隔,不同行间以回车分隔,以$结束输入:\n";for(i=1;i<=pnumber;i++)for(j=1;j<=jnumber;j++){cin>>sb.cost[i][j];sb.costforout[i][j]=sb.cost[i][j];}cin>>w;if(jnumber>pnumber)for(i=pnumber+1;i<=jnumber;i++)for(j=1;j<=jnumber;j++){sb.cost[i][j]=0;sb.costforout[i][j]=0;}else{if(pnumber>jnumber)for(i=1;i<=pnumber;i++)for(j=jnumber+1;j<=pnumber;j++){sb.cost[i][j]=0;sb.costforout[i][j]=0;}}sb.matrixsize=pnumber;if(pnumber<jnumber)sb.matrixsize=jnumber;sb.personnumber=pnumber;sb.jobnumber=jnumber;if(m==1){k=0;for(i=1;i<=sb.matrixsize;i++)for(j=1;j<=sb.matrixsize;j++)if(sb.cost[i][j]>k)k=sb.cost[i][j];for(i=1;i<=sb.matrixsize;i++)for(j=1;j<=sb.matrixsize;j++)sb.cost[i][j]=k-sb.cost[i][j];}return sb;}void circlezero(matrix &sb){int i,j;float k;int p;for(i=0;i<=sb.matrixsize;i++)sb.cost[i][0]=0;for(j=1;j<=sb.matrixsize;j++)sb.cost[0][j]=0;for(i=1;i<=sb.matrixsize;i++)for(j=1;j<=sb.matrixsize;j++)if(sb.cost[i][j]==0){sb.cost[i][0]++;sb.cost[0][j]++;sb.cost[0][0]++;}for(i=0;i<=sb.matrixsize;i++)for(j=0;j<=sb.matrixsize;j++)sb.zeroelem[i][j]=0;k=sb.cost[0][0]+1;while(sb.cost[0][0]<k){k=sb.cost[0][0];for(i=1;i<=sb.matrixsize;i++){if(sb.cost[i][0]==1){for(j=1;j<=sb.matrixsize;j++)if(sb.cost[i][j]==0&&sb.zeroelem[i][j]==0)break;sb.zeroelem[i][j]=1;sb.cost[i][0]--;sb.cost[0][j]--;sb.cost[0][0]--;if(sb.cost[0][j]>0)for(p=1;p<=sb.matrixsize;p++)if(sb.cost[p][j]==0&&sb.zeroelem[p][j]==0){sb.zeroelem[p][j]=2;sb.cost[p][0]--;sb.cost[0][j]--;sb.cost[0][0]--;}}}for(j=1;j<=sb.matrixsize;j++){if(sb.cost[0][j]==1){for(i=1;i<=sb.matrixsize;i++)if(sb.cost[i][j]==0&&sb.zeroelem[i][j]==0)break;sb.zeroelem[i][j]=1;sb.cost[i][0]--;sb.cost[0][j]--;sb.cost[0][0]--;if(sb.cost[i][0]>0)for(p=1;p<=sb.matrixsize;p++)if(sb.cost[i][p]==0&&sb.zeroelem[i][p]==0){sb.zeroelem[i][p]=2;sb.cost[i][0]--;sb.cost[0][p]--;sb.cost[0][0]--;}}}}if(sb.cost[0][0]>0)twozero(sb);elsejudge(sb,result);}void twozero(matrix &sb){int i,j;int p,q;int m,n;float k;matrix st;for(i=1;i<=sb.matrixsize;i++)if(sb.cost[i][0]>0)break;if(i<=sb.matrixsize){for(j=1;j<=sb.matrixsize;j++){st=sb;if(sb.cost[i][j]==0&&sb.zeroelem[i][j]==0){sb.zeroelem[i][j]=1;sb.cost[i][0]--;sb.cost[0][j]--;sb.cost[0][0]--;for(q=1;q<=sb.matrixsize;q++)if(sb.cost[i][q]==0&&sb.zeroelem[i][q]==0){sb.zeroelem[i][q]=2;sb.cost[i][0]--;sb.cost[0][q]--;sb.cost[0][0]--;}for(p=1;p<=sb.matrixsize;p++)if(sb.cost[p][j]==0&&sb.zeroelem[p][j]==0){sb.zeroelem[p][j]=2;sb.cost[p][0]--;sb.cost[0][j]--;sb.cost[0][0]--;}k=sb.cost[0][0]+1;while(sb.cost[0][0]<k){k=sb.cost[0][0];for(p=i+1;p<=sb.matrixsize;p++){if(sb.cost[p][0]==1){for(q=1;q<=sb.matrixsize;q++)if(sb.cost[p][q]==0&&sb.zeroelem[p][q]==0)break;sb.zeroelem[p][q]=1;sb.cost[p][0]--;sb.cost[0][q]--;sb.cost[0][0]--;for(m=1;m<=sb.matrixsize;m++)if(sb.cost[m][q]=0&&sb.zeroelem[m][q]==0){sb.zeroelem[m][q]=2;sb.cost[m][0]--;sb.cost[0][q]--;sb.cost[0][0]--;}}}for(q=1;q<=sb.matrixsize;q++){if(sb.cost[0][q]==1){for(p=1;p<=sb.matrixsize;p++)if(sb.cost[p][q]==0&&sb.zeroelem[p][q]==0)break;sb.zeroelem[p][q]=1;sb.cost[p][q]--;sb.cost[0][q]--;sb.cost[0][0]--;for(n=1;n<=sb.matrixsize;n++)if(sb.cost[p][n]==0&&sb.zeroelem[p][n]==0){sb.zeroelem[p][n]=2;sb.cost[p][0]--;sb.cost[0][n]--;sb.cost[0][0]--;}}}}if(sb.cost[0][0]>0)twozero(sb);elsejudge(sb,result);}sb=st;}}}void judge(matrix &sb,int result[501][2]){int i,j;int m;int n;int k;m=0;for(i=1;i<=sb.matrixsize;i++)for(j=1;j<=sb.matrixsize;j++)if(sb.zeroelem[i][j]==1)m++;if(m==sb.matrixsize){k=1;for(n=1;n<=result[0][0];n++){for(i=1;i<=sb.matrixsize;i++){for(j=1;j<=sb.matrixsize;j++)if(sb.zeroelem[i][j]==1)break;if(i<=sb.personnumber&&j<=sb.jobnumber)if(j!=result[k][1])break;k++;}if(i==sb.matrixsize+1)break;elsek=n*sb.matrixsize+1;}if(n>result[0][0]){k=result[0][0]*sb.matrixsize+1;for(i=1;i<=sb.matrixsize;i++)for(j=1;j<=sb.matrixsize;j++)if(sb.zeroelem[i][j]==1){result[k][0]=i;result[k++][1]=j;}result[0][0]++;}}else{refresh(sb);}}void refresh(matrix &sb){int i,j;float k;int p;k=0;for(i=1;i<=sb.matrixsize;i++){for(j=1;j<=sb.matrixsize;j++)if(sb.zeroelem[i][j]==1){sb.zeroelem[i][0]=1;break;}}while(k==0){k=1;for(i=1;i<=sb.matrixsize;i++)if(sb.zeroelem[i][0]==0){sb.zeroelem[i][0]=2;for(j=1;j<=sb.matrixsize;j++)if(sb.zeroelem[i][j]==2){sb.zeroelem[0][j]=1;}}for(j=1;j<=sb.matrixsize;j++){if(sb.zeroelem[0][j]==1){sb.zeroelem[0][j]=2;for(i=1;i<=sb.matrixsize;i++)if(sb.zeroelem[i][j]==1){sb.zeroelem[i][0]=0;k=0;}}}}p=0;k=0;for(i=1;i<=sb.matrixsize;i++){if(sb.zeroelem[i][0]==2){for(j=1;j<=sb.matrixsize;j++){if(sb.zeroelem[0][j]!=2)if(p==0){k=sb.cost[i][j];p=1;}else{if(sb.cost[i][j]<k)k=sb.cost[i][j];}}}}for(i=1;i<=sb.matrixsize;i++){if(sb.zeroelem[i][0]==2)for(j=1;j<=sb.matrixsize;j++)sb.cost[i][j]=sb.cost[i][j]-k;}for(j=1;j<=sb.matrixsize;j++){if(sb.zeroelem[0][j]==2)for(i=1;i<=sb.matrixsize;i++)sb.cost[i][j]=sb.cost[i][j]+k;}for(i=0;i<=sb.matrixsize;i++)for(j=0;j<=sb.matrixsize;j++)sb.zeroelem[i][j]=0;circlezero(sb);}void zeroout(matrix &sb){int i,j;float k;for(i=1;i<=sb.matrixsize;i++){k=sb.cost[i][1];for(j=2;j<=sb.matrixsize;j++)if(sb.cost[i][j]<k)k=sb.cost[i][j];for(j=1;j<=sb.matrixsize;j++)sb.cost[i][j]=sb.cost[i][j]-k;}for(j=1;j<=sb.matrixsize;j++){k=sb.cost[1][j];for(i=2;i<=sb.matrixsize;i++)if(sb.cost[i][j]<k)k=sb.cost[i][j];for(i=1;i<=sb.matrixsize;i++)sb.cost[i][j]=sb.cost[i][j]-k;}}void output(int result[501][2],matrix sb) {int k;int i;int j;int p;char w;float v;v=0;for(i=1;i<=sb.matrixsize;i++){v=v+sb.costforout[i][result[i][1]];}cout<<"最优解的目标函数值为"<<v;k=result[0][0];if(k>5){cout<<"解的个数超过了限制."<<endl;k=5;}for(i=1;i<=k;i++){cout<<"输入任意字符后输出第"<<i<<"种解."<<endl;cin>>w;p=(i-1)*sb.matrixsize+1;for(j=p;j<p+sb.matrixsize;j++)if(result[j][0]<=sb.personnumber&&result[j][1]<=sb.jobnumber)cout<<"第"<<result[j][0]<<"个人做第"<<result[j][1]<<"件工作."<<endl;}}void main(){result[0][0]=0;sb=input();zeroout(sb);circlezero(sb);output(result,sb);}4. 算例和结果:自己运算结果为:->⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡3302102512010321->⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡330110241200032034526635546967562543----⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡可以看出:第1人做第4件工作;第2人做第1件工作;第3人做第3件工作;第4人做第2件工作。
vc++匈牙利命名法

匈牙利命名法是一种编程时的命名规范。
基本原则是:变量名=属性+类型+对象描述。
其中每一对象的名称都要求有明确含义,可以取对象名字全称或名字的一部分。
命名要基于容易记忆容易理解的原则。
目前在Windows程序开发和MFC程序开发中常用的命名规则是匈牙利命名法。
下面就是HN命名法的一般规则。
属性部分全局变量g_const常量c_c++类成员变量m_静态变量s_类型部分指针p函数fn无效v句柄h长整型l布尔b浮点型(有时也指文件) f双字dw字符串sz短整型n双精度浮点d计数c(通常用cnt)字符ch(通常用c)整型i(通常用n)字节by字w实型r无符号u描述部分最大Max最小Min初始化Init临时变量T(或Temp)源对象Src目的对象Dest这里顺便写几个例子:(1) hwnd :h 是类型描述,表示句柄,wnd 是变量对象描述,表示窗口,所以hwnd 表示窗口句柄;(2) pfnEatApple :pfn 是类型描述,表示指向函数的指针,EatApple 是变量对象描述,所以它表示指向EatApple 函数的函数指针变量。
(3) g_cch :g_ 是属性描述,表示全局变量,c 和ch 分别是计数类型和字符类型,一起表示变量类型,这里忽略了对象描述,所以它表示一个对字符进行计数的全局变量。
小结:匈牙利命名法MFC、句柄、控件及结构的命名规范Windows类型样本变量MFC类样本变量HWND hWnd;CWnd* pWnd;HDLG hDlg;CDialog* pDlg;HDC hDC;CDC* pDC;HGDIOBJ hGdiObj;CGdiObject* pGdiObj;HPEN hPen;CPen* pPen;HBRUSH hBrush;CBrush* pBrush;HFONT hFont;CFont* pFont;HBITMAP hBitmap;CBitmap* pBitmap;HPALETTE hPaltte;CPalette* pPalette;HRGN hRgn;CRgn* pRgn;HMENU hMenu;CMenu* pMenu;HWND hCtl;CState* pState;HWND hCtl;CButton* pButton;HWND hCtl;CEdit* pEdit;HWND hCtl;CListBox* pListBox;HWND hCtl;CComboBox* pComboBox;HWND hCtl;CScrollBar* pScrollBar;HSZ hszStr;CString pStr;POINT pt;CPoint pt;SIZE size;CSize size;RECT rect;CRect rect;一般前缀命名规范前缀类型实例C 类或结构CDocument,CPrintInfom_ 成员变量m_pDoc,m_nCustomers变量命名规范前缀类型描述实例ch char 8位字符chGradech TCHAR 如果_UNICODE定义,则为16位字符chNameb BOOL 布尔值bEnablen int 整型(其大小依赖于操作系统)nLengthn UINT 无符号值(其大小依赖于操作系统)nHeightw WORD 16位无符号值wPosl LONG 32位有符号整型lOffsetdw DWORD 32位无符号整型dwRangep * 指针pDoclp FAR* 远指针lpszNamelpsz LPSTR 32位字符串指针lpszNamelpsz LPCSTR 32位常量字符串指针lpszNamelpsz LPCTSTR 如果_UNICODE定义,则为32位常量字符串指针lpszName h handle Windows对象句柄hWndlpfn callback 指向CALLBACK函数的远指针资源类型命名规范前缀符号类型实例范围IDR_ 不同类型的多个资源共享标识IDR_MAIINFRAME 1~0x6FFFIDD_ 对话框资源IDD_SPELL_CHECK 1~0x6FFFHIDD_ 对话框资源的Help上下文HIDD_SPELL_CHECK 0x20001~0x26FF IDB_ 位图资源IDB_COMPANY_LOGO 1~0x6FFFIDC_ 光标资源IDC_PENCIL 1~0x6FFFIDI_ 图标资源IDI_NOTEPAD 1~0x6FFFID_ 来自菜单项或工具栏的命令ID_TOOLS_SPELLING 0x8000~0xDFFF HID_ 命令Help上下文HID_TOOLS_SPELLING 0x18000~0x1DFFFIDP_ 消息框提示IDP_INVALID_PARTNO 8~0xDEEFHIDP_ 消息框Help上下文HIDP_INVALID_PARTNO 0x30008~0x3DEFF IDS_ 串资源IDS_COPYRIGHT 1~0x7EEFIDC_ 对话框内的控件IDC_RECALC 8~0xDEEFMicrosoft MFC宏命名规范名称类型_AFXDLL 唯一的动态连接库(Dynamic Link Library,DLL)版本_ALPHA 仅编译DEC Alpha处理器_DEBUG 包括诊断的调试版本_MBCS 编译多字节字符集_UNICODE 在一个应用程序中打开UnicodeAFXAPI MFC提供的函数CALLBACK 通过指针回调的函数库标识符命名法标识符值和含义u ANSI(N)或Unicode(U)d 调试或发行:D = 调试;忽略标识符为发行。
求kM算法和匈牙利算法的程序代码

求kM算法和匈牙利算法的程序代码kM算法和匈牙利算法的程序代码,最好是用matlab给出的,用c语言亦可。
不要用其他的编程语言。
//二分图最佳匹配,kuhn munkras算法,邻接阵形式,复杂度O(m*m*n)//返回最佳匹配值,传入二分图大小m,n和邻接阵mat,表示权值//match1,match2返回一个最佳匹配,未匹配顶点match值为-1//一定注意m<=n,否则循环无法终止//最小权匹配可将权值取相反数#include <string.h>#define MAXN 310#define inf 1000000000#define _clr(x) memset(x,0xff,sizeof(int)*n)int kuhn_munkras(int m,int n,int mat[][MAXN],int* match1,int* match2){ int s[MAXN],t[MAXN],l1[MAXN],l2[MAXN],p,q,ret=0,i,j,k;for (i=0;i<m;i++)for (l1[i]=-inf,j=0;j<n;j++)l1[i]=mat[i][j]>l1[i]?mat[i][j]:l1[i];for (i=0;i<n;l2[i++]=0);for (_clr(match1),_clr(match2),i=0;i<m;i++){for (_clr(t),s[p=q=0]=i;p<=q&&match1[i]<0;p++)for (k=s[p],j=0;j<n&&match1[i]<0;j++)if (l1[k]+l2[j]==mat[k][j]&&t[j]<0){s[++q]=match2[j],t[j]=k;if (s[q]<0)for (p=j;p>=0;j=p)match2[j]=k=t[j],p=match1[k],match1[k]=j;}if (match1[i]<0){for (i--,p=inf,k=0;k<=q;k++)for (j=0;j<n;j++)if (t[j]<0&&l1[s[k]]+l2[j]-mat[s[k]][j]<p)p=l1[s[k]]+l2[j]-mat[s[k]][j];for (j=0;j<n;l2[j]+=t[j]<0?0:p,j++);for (k=0;k<=q;l1[s[k++]]-=p);}}for (i=0;i<m;i++)ret+=mat[i][match1[i]];return ret;}昨天帮一个同学完成了他的毕业论文上的指派问题的匈牙利算法程序。
匈牙利算法代码解析

匈牙利算法代码解析匈牙利算法又称作增广路算法,主要用于解决二分图最大匹配问题。
它的基本思想是在二分图中查找增广路,然后将这条增广路上的边反转,这样可以将匹配数增加一个,由此不断寻找增广路并反转边直到无法找到为止,最后所找到的就是二分图的最大匹配。
匈牙利算法的流程如下:1. 从左边开始选择一个未匹配的节点,将其标记为当前节点;2. 再从当前节点出发,依次寻找与它相连的未匹配节点;3. 如果找到了一个未匹配节点,则记录该节点的位置,并将当前节点标记为该节点;4. 如果当前节点的所有连边都不能找到未匹配节点,则退回到上一个节点,再往其他的连接点继续搜索;5. 如果到达已经匹配节点,则将该节点标记为新的当前节点,返回步骤4;6. 如果找到了一条增广路,则将其上的边反转,并将匹配数+1;7. 重复以上步骤,直至无法找到增广路为止。
在匈牙利算法中,增广路的查找可以使用DFS或BFS,这里我们以DFS为例进行解释。
匈牙利算法的时间复杂度为O(nm),n和m分别表示左边和右边的节点数,因为每条边至多遍历两次,所以最多需要执行2n次DFS。
以下为匈牙利算法的Python代码:```Pythondef findPath(graph, u, match, visited):for v in range(len(graph)):if graph[u][v] and not visited[v]:visited[v] = Trueif match[v] == -1 or findPath(graph, match[v], match, visited):# 如果v没有匹配或者匹配的右匹配节点能找到新的匹配match[v] = u # 更新匹配return Truereturn Falsedef maxMatching(graph):n = len(graph)match = [-1] * n # 右部节点的匹配数组,初始化为-1表示没有匹配count = 0return match, count```其中,findPath函数是用来查找增广路的DFS函数,match数组是右边节点的匹配数组,初始化为-1表示没有匹配,count则表示匹配数。
C语言第08讲匈牙利命名法

C语言第08讲匈牙利命名法第08讲匈牙利命名法一、匈牙利命名法匈牙利命名法计算机程序设计中的一种命名规则,用这种方法命名的变量显示了其数据类型。
匈牙利命名法有两种:系统匈牙利命名法和匈牙利应用命名法。
匈牙利命名法被设计成语言独立的,并且首次在BCPL语言中被大量使用。
由于BCPL只有机器字这一种数据类型,因此这种语言本身无法帮助程序员来记住变量的类型。
匈牙利命名法通过明确每个变量的数据类型来解决这个问题。
在匈牙利命名法中,一个变量名由n个小写字母开始,这些字母有助于记忆变量的类型和用处,紧跟着的就是程序员选择的任何名称。
这个后半部分的首字母可以大写以区别前面的类型指示字母(参见驼峰式大小写)。
二、系统匈牙利命名法与匈牙利应用命名法 1、系统命名法与应用命名法的区别在于前缀的目的在系统匈牙利命名法中,前缀代表了变量的实际数据类型。
例如:lAccountNum : 变量是一个长整型 ("l");arru8NumberList : 变量是一个无符号8位整型数组 ("arru8");szName : 变量是一个零结束字符串 ("sz"),这是西蒙尼最开始建议的前缀之一。
匈牙利应用命名法不表示实际数据类型,而是给出了变量目的的提示,或者说它代表了什么。
rwPosition : 变量代表一个行 ("rw")。
usName : 变量代表一个非安全字符串 ("us"),需要在使用前处理。
strName : 变量代表一个包含名字的字符串("str")但是没有指明这个字符串是如何实现的。
2、西蒙尼建议的大多数前缀都是自然语义的,但不是所有由于这种命名法通常使用小写字母开头用来助记,但是并没有对助记符本身作规定。
有几种被广泛使用的习惯(见下面的示例),但是任意字母组合都可以被使用,只要它们在代码主体中保持一致就可以了。
C++编程匈牙利命名法

匈牙利命名法匈牙利命名法是一种编程时的命名规范。
基本原则是:变量名=属性+类型+对象描述,其中每一对象的名称都要求有明确含义,可以取对象名字全称或名字的一部分。
命名要基于容易记忆容易理解的原则。
保证名字的连贯性是非常重要的。
据说这种命名法是一位叫Charles Simonyi的匈牙利程序员发明的,后来他在微软呆了几年,于是这种命名法就通过微软的各种产品和文档资料向世界传播开了。
现在,大部分程序员不管自己使用什么软件进行开发,或多或少都使用了这种命名法。
这种命名法的出发点是把量名变按:属性+类型+对象描述的顺序组合起来,以使程序员作变量时对变量的类型和其它属性有直观的了解,下面是HN变量命名规范,其中也有一些是我个人的偏向:属性部分:全局变量g_常量c_c++类成员变量m_静态变量s_类型部分:指针p函数fn无效v句柄h长整型l布尔b浮点型(有时也指文件)f双字dw字符串sz短整型n双精度浮点d计数c(通常用cnt)字符ch(通常用c)整型i(通常用n)字节by字w实型r无符号u描述部分最大Max最小Min初始化Init临时变量T(或Temp)源对象Src目的对象Dest这里顺便写几个例子:hwnd:h是类型,表示句柄描述,wnd是变量对象描述,表示窗口,所以hwnd表示窗口句柄;pfnEatApple:pfn是类型描述,表示指向函数的指针,EatApple是变量对象描述,所以它表示指向EatApple函数的函数指针变量。
g_cch:g_是属性描述,表示全局变量,c和ch分别是计数类型和字符类型,一起表示变量类型,这里忽略了对象描述,所以它表示一个对字符进行计数的全局变量。
上面就是HN命名法的一般规则。
小结:匈牙利命名法匈牙利命名法MFC、句柄、控件及结构的命名规范Windows类型样本变量MFC类样本变量HWND hWnd;CWnd*pWnd;HDLG hDlg;CDialog*pDlg;HDC hDC;CDC*pDC;HGDIOBJ hGdiObj;CGdiObject*pGdiObj;HPEN hPen;CPen*pPen;HBRUSH hBrush;CBrush*pBrush;HFONT hFont;CFont*pFont;HBITMAP hBitmap;CBitmap*pBitmap;HPALETTE hPaltte;CPalette*pPalette;HRGN hRgn;CRgn*pRgn;HMENU hMenu;CMenu*pMenu;HWND hCtl;CState*pState;HWND hCtl;CButton*pButton;HWND hCtl;CEdit*pEdit;HWND hCtl;CListBox*pListBox;HWND hCtl;CComboBox*pComboBox;HWND hCtl;CScrollBar*pScrollBar;HSZ hszStr;CString pStr;POINT pt;CPoint pt;SIZE size;CSize size;RECT rect;CRect rect;一般前缀命名规范前缀类型实例C类或结构CDocument,CPrintInfom_成员变量m_pDoc,m_nCustomers变量命名规范前缀类型描述实例ch char8位字符chGradech TCHAR如果_UNICODE定义,则为16位字符chNameb BOOL布尔值bEnablen int整型(其大小依赖于操作系统)nLengthn UINT无符号值(其大小依赖于操作系统)nHeightw WORD16位无符号值wPosl LONG32位有符号整型lOffsetdw DWORD32位无符号整型dwRangep*指针pDoclp FAR*远指针lpszNamelpsz LPSTR32位字符串指针lpszNamelpsz LPCSTR32位常量字符串指针lpszNamelpsz LPCTSTR如果_UNICODE定义,则为32位常量字符串指针lpszName h handle Windows对象句柄hWndlpfn callback指向CALLBACK函数的远指针前缀符号类型实例范围IDR_不同类型的多个资源共享标识IDR_MAIINFRAME1~0x6FFFIDD_对话框资源IDD_SPELL_CHECK1~0x6FFFHIDD_对话框资源的Help上下文HIDD_SPELL_CHECK0x20001~0x26FF IDB_位图资源IDB_COMPANY_LOGO1~0x6FFFIDC_光标资源IDC_PENCIL1~0x6FFFIDI_图标资源IDI_NOTEPAD1~0x6FFFID_来自菜单项或工具栏的命令ID_TOOLS_SPELLING0x8000~0xDFFF HID_命令Help上下文HID_TOOLS_SPELLING0x18000~0x1DFFFIDP_消息框提示IDP_INVALID_PARTNO8~0xDEEFHIDP_消息框Help上下文HIDP_INVALID_PARTNO0x30008~0x3DEFF IDS_串资源IDS_COPYRIGHT1~0x7EEFIDC_对话框内的控件IDC_RECALC8~0xDEEFMicrosoft MFC宏命名规范名称类型_AFXDLL唯一的动态连接库(Dynamic Link Library,DLL)版本_ALPHA仅编译DEC Alpha处理器_DEBUG包括诊断的调试版本_MBCS编译多字节字符集_UNICODE在一个应用程序中打开UnicodeAFXAPI MFC提供的函数CALLBACK通过指针回调的函数库标识符命名法标识符值和含义u ANSI(N)或Unicode(U)d调试或发行:D=调试;忽略标识符为发行。
最新C++之匈牙利命名法

C++之匈牙利命名法
在编程时,变量、函数的命名是一个极其重要的问题。
好的命名方法使变量易于记忆且程序可读性大大提高。
Microsoft采用匈牙利命名法来命名Windows API函数和变量。
匈牙利命名法是由Microsoft的著名开发人员、Excel的主要设计者查尔斯·西蒙尼在他的博士论文中提出来
我们先看一下我们低海拔的平原到底有多少。
图中国真正的平原地区
我们会发现中国几千年扩张的这么大的地盘,其实平原相比少的可怜,在没有获得四川盆地和东北平原的时代,我们所熟知的夏商西周春秋战国,其实主要的活动区域仅仅是上面的黄色区域(华北平原)和红色区域(渭河谷地)以及长江边缘的小型平原。
其实大家也发现了,上图中往往有河流的地方,才有所谓平原。
其实绝大部分的平原,都是一种叫做“冲积平原”的东西,也就是说河流携带大量泥沙,然后沉积在地表,形成平坦肥沃的土地。
所以我们可以看到,我们最大最古老的华北平原,其实就是黄河冲积形成的肥沃土地。
华北平原。
匈牙利命名法及实用规则.

一、匈牙利命名法:Windows 编程中用到的变量(还包括宏的命名规则匈牙利命名法,这种命名技术是由一位能干的 Microsoft 程序员查尔斯·西蒙尼 (Charles Simonyi 提出的。
基本原则是:变量名=属性+类型+对象描述⑴属性部分:全局变量:g_常量 :c_类成员变量:m_⑵类型部分:数组:a布尔型:b byte: bychar: c 字节计数 : cb 颜色引用值 : cr 坐标差(长度 : cx,cy双字 (DWORD: dw浮点型:f 函数 : fn句柄:h整数 (integer: i长整型 (long: l long 型指针 : lp短整型:n near 指针 : np指针:pstring: s 用 '\0'终止的字符串 : sz文本内容 : tm无符号:uWord: w坐标 : x,y⑶描述部分:初始化:Init临时变量:Tmp目的对象:Dst源对象:Src窗口:Wnd下边举例说明:hwnd :h 表示句柄, wnd 表示窗口,合起来为“窗口句柄” 。
m_bFlag:m 表示成员变量, b 表示布尔,合起来为:“某个类的成员变量,布尔型,是一个状态标志” 。
1,变量命名;2,常量命名、宏定义;3,资源名字定义格式;4,函数命名和命名空间、类的命名、接口的命名;5,结构体命名;6,控件的命名;7,注释;本文来自 CSDN 博客,转载请标明出处:/stkim/archive/2004/09/29/120347.aspx 匈牙利命名法通过在变量名前面加上相应的小写字母的符号标识作为前缀, 标识出变量的作用域, 类型等。
这些符号可以多个同时使用, 顺序是先 m_(成员变量 , 再指针, 再简单数据类型, 再其他。
例如:m_lpszStr, 表示指向一个以 0字符结尾的字符串的长指针成员变量。
匈牙利命名法关键是:标识符的名字以一个或者多个小写字母开头作为前缀;前缀之后的是首字母大写的一个单词或多个单词组合,该单词要指明变量的用途。
匈牙利匹配算法代码

匈牙利匹配算法代码匈牙利匹配算法(又称为二分图最大匹配算法)是一种常用于解决二分图最大匹配问题的算法。
它的时间复杂度为O(V*E),其中V表示顶点的个数,E表示边的个数。
下面是一个用C++实现的匈牙利匹配算法的示例代码,包含详细的注释说明。
```cpp#include <iostream>#include <vector>using namespace std;const int MAXN = 100; // 二分图中左侧和右侧顶点的最大数量vector<int> graph[MAXN]; // 二分图的邻接表表示bool used[MAXN]; // 用于记录右侧顶点是否已被匹配int match[MAXN]; // 记录右侧顶点的匹配int n, m; // 二分图中左侧和右侧顶点的数量//判断是否存在增广路径bool dfs(int u)for (int i = 0; i < graph[u].size(; i++)int v = graph[u][i]; // v表示与u相邻的右侧顶点if (!used[v]) { // 如果v还未被匹配,则找到一条增广路径used[v] = true;if (match[v] == -1 , dfs(match[v]))//如果右侧顶点v未匹配或右侧顶点v已经匹配但是可以找到增广路径,则将u和v进行匹配match[v] = u;return true;}}}return false;//计算二分图的最大匹配数int hungariaint res = 0;//初始化右侧顶点的匹配为-1,表示未匹配memset(match, -1, sizeof(match));for (int u = 0; u < n; u++)memset(used, 0, sizeof(used));if (dfs(u))res++;}}return res;int maicin >> n >> m; // 输入二分图中左侧和右侧顶点的数量//输入每个左侧顶点和右侧顶点之间的边for (int i = 0; i < n; i++)int u, v;cin >> u >> v;graph[u].push_back(v);}int maxMatching = hungarian(; // 计算最大匹配数cout << "Maximum matching: " << maxMatching << endl;return 0;```这是一个基本的匈牙利匹配算法的实现代码,你可以根据具体的需求进行修改和扩展。
超详细!!!匈牙利算法流程以及Python程序实现!!!通俗易懂
超详细匈⽛利算法流程以及Python程序实现通俗易懂前不久在⽆⼈机检测跟踪的项⽬中⽤到了多⽬标跟踪算法(该项⽬后续会发贴介绍),其中需要涉及多个⽬标在两帧之间的匹配问题,最初使⽤的是最简单的距离最⼩化原则进⾏帧间多⽬标的匹配。
后来通过实习和查阅论⽂等渠道了解到了多⽬标跟踪领域经典的Sort和DeepSort算法,其中都使⽤到了匈⽛利算法解决匹配问题,因此开此贴记录⼀下算法的学习过程。
指派问题概述⾸先,对匈⽛利算法解决的问题进⾏概述:实际中,会遇到这样的问题,有n项不同的任务,需要n个⼈分别完成其中的1项,每个⼈完成任务的时间不⼀样。
于是就有⼀个问题,如何分配任务使得花费时间最少。
通俗来讲,就是n*n矩阵中,选取n个元素,每⾏每列各有1个元素,使得和最⼩。
如下表所⽰上表可以抽象成⼀个矩阵,如果是如上表所⽰的求和最⼩问题,那么这个矩阵就叫做花费矩阵(Cost Matrix);如果要求的问题是使之和最⼤化,那么这个矩阵就叫做利益矩阵(Profit Matrix)。
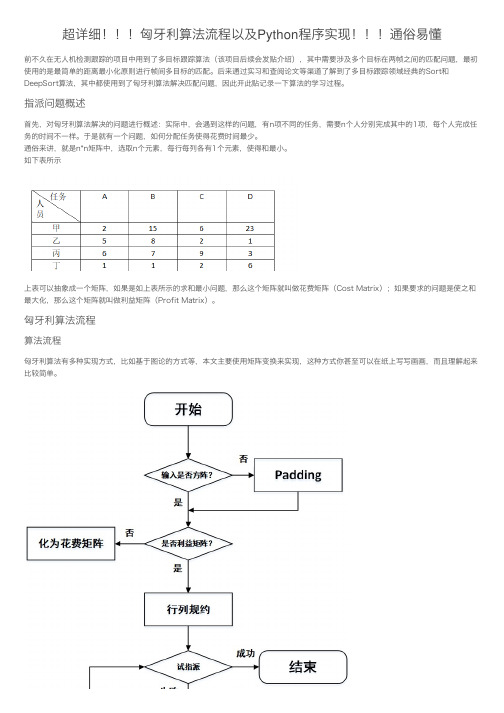
匈⽛利算法流程算法流程匈⽛利算法有多种实现⽅式,⽐如基于图论的⽅式等,本⽂主要使⽤矩阵变换来实现,这种⽅式你甚⾄可以在纸上写写画画,⽽且理解起来⽐较简单。
本⽂算法流程如上图所⽰,⾸先进⾏列规约,即每⾏减去此⾏最⼩元素,每⼀列减去该列最⼩元素,规约后每⾏每列中必有0元素出现。
接下来进⾏试指派,也就是划最少的线覆盖矩阵中全部的0元素,如果试指派的独⽴0元素数等于⽅阵维度则算法结束,如果不等于则需要对矩阵进⾏调整,重复试指派和调整步骤直到满⾜算法结束条件。
以上是我简要描述的算法流程,值得⼀提的是,⽤矩阵变换求解的匈⽛利算法也有多种实现,主要不同就在于试指派和调整矩阵这块,但万变不离其宗都是为了⽤最少的线覆盖矩阵中全部的零元素。
咱们废话少说,来看⼀个例⼦。
程序实现完整代码(带测试⽤例)'''@Date: 2020/2/23@Author:ZhuJunHui@Brief: Hungarian Algorithm using Python and NumPy'''import numpy as npimport collectionsimport timeclass Hungarian():""""""def__init__(self, input_matrix=None, is_profit_matrix=False):"""输⼊为⼀个⼆维嵌套列表is_profit_matrix=False代表输⼊是消费矩阵(需要使消费最⼩化),反之则为利益矩阵(需要使利益最⼤化) """if input_matrix is not None:# 保存输⼊my_matrix = np.array(input_matrix)self._input_matrix = np.array(input_matrix)self._maxColumn = my_matrix.shape[1]self._maxRow = my_matrix.shape[0]# 本算法必须作⽤于⽅阵,如果不为⽅阵则填充0变为⽅阵matrix_size =max(self._maxColumn, self._maxRow)pad_columns = matrix_size - self._maxRowpad_rows = matrix_size - self._maxColumnmy_matrix = np.pad(my_matrix,((0,pad_columns),(0,pad_rows)),'constant', constant_values=(0)) # 如果需要,则转化为消费矩阵if is_profit_matrix:my_matrix = self.make_cost_matrix(my_matrix)self._cost_matrix = my_matrixself._size =len(my_matrix)self._shape = my_matrix.shape# 存放算法结果self._results =[]self._totalPotential =0else:self._cost_matrix =Nonedef make_cost_matrix(self,profit_matrix):'''利益矩阵转化为消费矩阵,输出为numpy矩阵'''# 消费矩阵 = 利益矩阵最⼤值组成的矩阵 - 利益矩阵matrix_shape = profit_matrix.shapeoffset_matrix = np.ones(matrix_shape, dtype=int)* profit_matrix.max()cost_matrix = offset_matrix - profit_matrixreturn cost_matrixdef get_results(self):"""获取算法结果"""return self._resultsdef calculate(self):"""实施匈⽛利算法的函数"""result_matrix = self._cost_matrix.copy()# 步骤 1: 矩阵每⼀⾏减去本⾏的最⼩值for index, row in enumerate(result_matrix):result_matrix[index]-= row.min()# 步骤 2: 矩阵每⼀列减去本⾏的最⼩值for index, column in enumerate(result_matrix.T):result_matrix[:, index]-= column.min()#print('步骤2结果 ',result_matrix)#print('步骤2结果 ',result_matrix)# 步骤 3:使⽤最少数量的划线覆盖矩阵中所有的0元素# 如果划线总数不等于矩阵的维度需要进⾏矩阵调整并重复循环此步骤total_covered =0while total_covered < self._size:time.sleep(1)#print("---------------------------------------")#print('total_covered: ',total_covered)#print('result_matrix:',result_matrix)# 使⽤最少数量的划线覆盖矩阵中所有的0元素同时记录划线数量cover_zeros = CoverZeros(result_matrix)single_zero_pos_list = cover_zeros.calculate()covered_rows = cover_zeros.get_covered_rows()covered_columns = cover_zeros.get_covered_columns()total_covered =len(covered_rows)+len(covered_columns)# 如果划线总数不等于矩阵的维度需要进⾏矩阵调整(需要使⽤未覆盖处的最⼩元素)if total_covered < self._size:result_matrix = self._adjust_matrix_by_min_uncovered_num(result_matrix, covered_rows, covered_columns) #元组形式结果对存放到列表self._results = single_zero_pos_list# 计算总期望结果value =0for row, column in single_zero_pos_list:value += self._input_matrix[row, column]self._totalPotential = valuedef get_total_potential(self):return self._totalPotentialdef_adjust_matrix_by_min_uncovered_num(self, result_matrix, covered_rows, covered_columns):"""计算未被覆盖元素中的最⼩值(m),未被覆盖元素减去最⼩值m,⾏列划线交叉处加上最⼩值m"""adjusted_matrix = result_matrix# 计算未被覆盖元素中的最⼩值(m)elements =[]for row_index, row in enumerate(result_matrix):if row_index not in covered_rows:for index, element in enumerate(row):if index not in covered_columns:elements.append(element)min_uncovered_num =min(elements)#print('min_uncovered_num:',min_uncovered_num)#未被覆盖元素减去最⼩值mfor row_index, row in enumerate(result_matrix):if row_index not in covered_rows:for index, element in enumerate(row):if index not in covered_columns:adjusted_matrix[row_index,index]-= min_uncovered_num#print('未被覆盖元素减去最⼩值m',adjusted_matrix)#⾏列划线交叉处加上最⼩值mfor row_ in covered_rows:for col_ in covered_columns:#print((row_,col_))adjusted_matrix[row_,col_]+= min_uncovered_num#print('⾏列划线交叉处加上最⼩值m',adjusted_matrix)return adjusted_matrixclass CoverZeros():"""使⽤最少数量的划线覆盖矩阵中的所有零输⼊为numpy⽅阵""""""def__init__(self, matrix):# 找到矩阵中零的位置(输出为同维度⼆值矩阵,0位置为true,⾮0位置为false)self._zero_locations =(matrix ==0)self._zero_locations_copy = self._zero_locations.copy()self._shape = matrix.shape# 存储划线盖住的⾏和列self._covered_rows =[]self._covered_columns =[]def get_covered_rows(self):"""返回覆盖⾏索引列表"""return self._covered_rowsdef get_covered_columns(self):"""返回覆盖列索引列表"""return self._covered_columnsdef row_scan(self,marked_zeros):'''扫描矩阵每⼀⾏,找到含0元素最少的⾏,对任意0元素标记(独⽴零元素),划去标记0元素(独⽴零元素)所在⾏和列存在的0元素''' min_row_zero_nums =[9999999,-1]for index, row in enumerate(self._zero_locations_copy):#index为⾏号row_zero_nums = collections.Counter(row)[True]if row_zero_nums < min_row_zero_nums[0]and row_zero_nums!=0:#找最少0元素的⾏min_row_zero_nums =[row_zero_nums,index]#最少0元素的⾏row_min = self._zero_locations_copy[min_row_zero_nums[1],:]#找到此⾏中任意⼀个0元素的索引位置即可row_indices,= np.where(row_min)#标记该0元素#print('row_min',row_min)marked_zeros.append((min_row_zero_nums[1],row_indices[0]))#划去该0元素所在⾏和列存在的0元素#因为被覆盖,所以把⼆值矩阵_zero_locations中相应的⾏列全部置为falseself._zero_locations_copy[:,row_indices[0]]= np.array([False for _ in range(self._shape[0])])self._zero_locations_copy[min_row_zero_nums[1],:]= np.array([False for _ in range(self._shape[0])])def calculate(self):'''进⾏计算'''#储存勾选的⾏和列ticked_row =[]ticked_col =[]marked_zeros =[]#1、试指派并标记独⽴零元素while True:#print('_zero_locations_copy',self._zero_locations_copy)#循环直到所有零元素被处理(_zero_locations中没有true)if True not in self._zero_locations_copy:breakself.row_scan(marked_zeros)#2、⽆被标记0(独⽴零元素)的⾏打勾independent_zero_row_list =[pos[0]for pos in marked_zeros]ticked_row =list(set(range(self._shape[0]))-set(independent_zero_row_list))#重复3,4直到不能再打勾TICK_FLAG =Truewhile TICK_FLAG:#print('ticked_row:',ticked_row,' ticked_col:',ticked_col)TICK_FLAG =False#3、对打勾的⾏中所含0元素的列打勾for row in ticked_row:#找到此⾏row_array = self._zero_locations[row,:]#找到此⾏中0元素的索引位置#找到此⾏中0元素的索引位置for i in range(len(row_array)):if row_array[i]==True and i not in ticked_col:ticked_col.append(i)TICK_FLAG =True#4、对打勾的列中所含独⽴0元素的⾏打勾for row,col in marked_zeros:if col in ticked_col and row not in ticked_row:ticked_row.append(row)FLAG =True#对打勾的列和没有打勾的⾏画画线self._covered_rows =list(set(range(self._shape[0]))-set(ticked_row)) self._covered_columns = ticked_colreturn marked_zerosif __name__ =='__main__':#以下为3个测试⽤例cost_matrix =[[4,2,8],[4,3,7],[3,1,6]]hungarian = Hungarian(cost_matrix)print('calculating...')hungarian.calculate()print("Expected value:\t\t12")print("Calculated value:\t", hungarian.get_total_potential())# = 12print("Expected results:\n\t[(0, 1), (1, 0), (2, 2)]")print("Results:\n\t", hungarian.get_results())print("-"*80)profit_matrix =[[62,75,80,93,95,97],[75,80,82,85,71,97],[80,75,81,98,90,97],[78,82,84,80,50,98],[90,85,85,80,85,99],[65,75,80,75,68,96]]hungarian = Hungarian(profit_matrix, is_profit_matrix=True)hungarian.calculate()print("Expected value:\t\t543")print("Calculated value:\t", hungarian.get_total_potential())# = 543print("Expected results:\n\t[(0, 4), (2, 3), (5, 5), (4, 0), (1, 1), (3, 2)]")print("Results:\n\t", hungarian.get_results())print("-"*80)profit_matrix =[[62,75,80,93,0,97],[75,0,82,85,71,97],[80,75,81,0,90,97],[78,82,0,80,50,98],[0,85,85,80,85,99],[65,75,80,75,68,0]]hungarian = Hungarian(profit_matrix, is_profit_matrix=True)hungarian.calculate()print("Expected value:\t\t523")print("Calculated value:\t", hungarian.get_total_potential())# = 523print("Expected results:\n\t[(0, 3), (2, 4), (3, 0), (5, 2), (1, 5), (4, 1)]")print("Results:\n\t", hungarian.get_results())print("-"*80)print("-"*80)总结如开篇所⾔,匈⽛利算法具有多种实现⽅式,可见该算法多么优秀,本⽂的实现⽅式不⼀定是最优的,但相对⽽⾔⽐较通俗易懂。
C_C++程序编程规范(基于匈牙利命名法)

5
1.2 代码行
【规则1】一行代码只做一件事情,如只定义一个变量,或只写一条语句。这样 的代码容易阅读,并且方便于写注释。 【规则2】if、for、while 、do 等语句只占一行,执行语句不得紧跟其后。不 论执行语句有多少都要加{}。这样可以防止书写失误。 示例: 风格良好的代码行: int iWidth; // 宽度 int iHeight; // 高度 int iDepth; // 深度 x = a + b; y = c + d; z = e + f; if (width < height) { DoSomething(); } for (initialization; condition; update) { DoSomething(); } Other(); 【规范3】尽可能在定义变量的同时初始化该变量(就近原则) 如果变量的引用处和其定义处相隔比较远,变量的初始化很容易被忘记。如果 引用了未被初始化的变量,可能会导致程序错误。本规范可以减少隐患。例如 int iWidth = 10; // 定义并初绐化width int iHeight = 10; // 定义并初绐化height int iDepth = 10; // 定义并初绐化depth 风格不良的代码行: int width, height, depth; // 宽度高 度深度 x = a + b; y = c + d; z = e + f;
4
int ProgStart(void) { int iResult; long lPos[SYSTEM_MAX_AXIS_NUM]; //表明上面的是临时变量的定义块 if(GetFeedHoldFlag ()) { SetIIPOutputFlags(PROG_STOP); return 1; } //表明上面是if语句的结束 switch(GetSysTemMode()) { case SYS_MODE_AUTO: //自动 if(GetFlagCycle()) { SetIIPOutputFlags(PROG_STOP); } //表明上面是if语句的结束 break; case SYS_MODE_JOG: break; default: break; } //表明上面是switch语句的结束 SetCycleStat(1); //将上面的语句和下面的while循环分开 while(GetIIPOutputFlags() != PROG_IDLE) { Sleep(10); } //表明上面是while语句的结束 return 0; } //此空行将把相连的两个函数分开 int NextFun(void) { ……//函数的具体实现 } /然不会影响程序的功能,但会直接影响代码的可读性、质量、维护、重 用等等许多方面,因此再程序编写的过程中应该注意一下几个方面。
C语言匈牙利命名法
对话框资源的Help上下文
HIDD_SPELL_CHECK
0x20001~0x26FF
IDB_
位图资源
IDB_COMPANY_LOGO
1~0x6FFF
IDC_
光标资源
IDC_PENCIL
1~0x6FFF
IDI_
图标资源
IDI_NOTEPAD
1~0x6FFF
ID_
来自菜单项或工具栏的命令
ID_TOOLS_SPELLING
l
LONG
32位有符号整型
lOffset
dw
DWORD
32位无符号整型
dwRange
p
*
指针
pDoc
lp
FAR*
远指针
lpszName
lpsz
LPSTR
32位字符串指针
lpszName
lpsz
LPCSTR
32位常量字符串指针
lpszName
lpsz
LPCTSTR
如果_UNICODE定义,则为32位常量字符串指针
NAFXCW.LIB
发行版本:MFC静态连接库
UAFXCWD.LIB
调试版本:具有Unicode支持的MFC静态连接库
UAFXCW.LIB
发行版本:具有Unicode支持的MFC静态连接库
动态连接库命名规范
名称
类型
_AFXDLL
唯一的动态连接库(DLL)版本
WINAPI
Windows所提供的函数
?
?
0x8000~0xDFFF
HID_
命令Help上下文
HID_TOOLS_SPELLING
0x18000~0x1DFFF
C++之匈牙利命名法

w
WORD
16位无符号值
wPos
f
float
浮点型
fRadius
d
double
双精度型
dArea
l
LONG
长整型
lOffset
ld
long double
长双精度型
ldRate
dw
DWORD
32位无符号整型
dwRange
p
*
指针
pDoc
lp
FAR*
远指针
lpszName
lpsz
LPSTR
HBRUSH
hBrush;
CBrush*
pBrush;
HFONT
hFont;
CFont*
pFont;
HBITMAP
hBitmap;
CBitmap*
pBitmap;
HPALETTE
hPaltte;
CPalette*
pPalette;
HRGN
hRgn;
CRgn*
pRgn;
HMENU
hMenu;
CMenu*
pScrollBar;
HSZ
hszStr;
CString
pStr;
POINT
pt;
CPoint
pt;
SIZE
size;
CSize
size;
RECT
rect;
CRect
rect;
一般前缀命名规范
前缀
类型
实例
C
类或结构
CDocument,CPrintInfo
S
结构体
SAddress
m_
匈牙利算法-包括代码

匈⽛利算法-包括代码匈⽛利算法-包括代码转⾃:匈⽛利算法转载:求最⼤的⼀种的算法是:先找出全部匹配,然后保留匹配数最多的。
但是这个算法的复杂度为边数的指数级函数。
因此,需要寻求⼀种更加⾼效的算法。
增⼴路的定义(也称增⼴轨或交错轨):若P是图G中⼀条连通两个未匹配顶点的路径,并且属M的边和不属M的边(即已匹配和待匹配的边)在P上交替出现,则称P为相对于M的⼀条增⼴路径。
由增⼴路的定义可以推出下述三个结论:1-P的路径长度必定为奇数,第⼀条边和最后⼀条边都不属于M。
2-P经过取反操作可以得到⼀个更⼤的匹配M’。
3-M为G的最⼤匹配当且仅当不存在相对于M的增⼴路径。
⽤增⼴路求最⼤匹配(称作匈⽛利算法,Edmonds于1965年提出)算法轮廓:(1)置M为空(2)找出⼀条增⼴路径P,通过取反操作获得更⼤的匹配M’代替M(3)重复(2)操作直到找不出增⼴路径为⽌程序清单:#include<stdio.h>#include<string.h>bool g[201][201];int n,m,ans;bool b[201];int link[201];bool init(){int _x,_y;memset(g,0,sizeof(g));memset(link,0,sizeof(link));ans=0;if(scanf("%d%d",&n,&m)==EOF)return false;for(int i=1;i<=n;i++){scanf("%d",&_x);for(int j=0;j<_x;j++){scanf("%d",&_y);g[ i ][_y]=true;}}return true;}bool find(int a){for(int i=1;i<=m;i++){if(g[a][ i ]==1&&!b[ i ]){b[ i ]=true;if(link[ i ]==0||find(link[ i ])) {link[ i ]=a;return true;}}}return false;}int main(){while(init()){for(int i=1;i<=n;i++){memset(b,0,sizeof(b)); if(find(i))ans++;}printf("%d\n",ans);}}。
匈牙利算法--java

匈⽛利算法--java 先上例题bool 寻找从k出发的对应项出的可增⼴路{while (从邻接表中列举k能关联到顶点j){if (j不在增⼴路上){把j加⼊增⼴路;if (j是未盖点或者从j的对应项出发有可增⼴路){修改j的对应项为k;则从k的对应项出有可增⼴路,返回true;}}}则从k的对应项出没有可增⼴路,返回false;}void匈⽛利hungary(){for i->1 to n{if (则从i的对应项出有可增⼴路)匹配数++;}输出匹配数;}附上题解代码import java.util.*;public class Main {public int map[][]=new int [1010][1010];//男⽣和⼥的有关系数public int match[]=new int[1010]; //是否已经匹配数public int used[]=new int [1010]; //是否有关系public boolean find(int x,int n ){for(int i=1;i<=n;i++){if(used[i]==0&&map[x][i]==1){ //如果没有i男⽣是空闲的且x,i有关系used[i]=1;if(match[i]==-1||find(match[i],n)){ //如果i男⽣没有匹配或者她放弃男⽣i并且另外找到了⾃⼰的伴 match[i]=x;return true;}}}return false;} //该函数判断⼥⽣爱能不能找到伴public static void main(String[] args) {Scanner sc=new Scanner(System.in);int k,m,n;while(sc.hasNext()){k=sc.nextInt();if(k==0)System.exit(0);m=sc.nextInt();n=sc.nextInt();int cnt=0;Main lei=new Main();Arrays.fill(lei.match,-1);for(int i=0;i<lei.map.length;i++){for(int j=0;j<lei.map.length;j++){lei.map[i][j]=0;}}for(int i=1;i<=k;i++){int a,b;a=sc.nextInt();b=sc.nextInt();lei.map[a][b]=1;}for(int i=1;i<=m;i++){Arrays.fill(ed,0);if(lei.find(i,n))cnt++;}System.out.println(cnt);}}}匈⽛利算法精髓就是尽可能的多占,可以通过回溯来试,不过当试的时候破坏了之前的安排,则是⽆能为⼒的,只能要求尽可能的多。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
西安科技大学程序设计实训报告班级: ^^^^^^^^^^^学号: ^^^^^^^^^^姓名: ^^^^^^2012年6月20日题目指派问题的匈牙利法一、算法思想本程序根据课本上匈牙利算法思想做了如下操作:首先定义结构体ASS用于存储该矩阵中每个元素,并且定义结构体TrueOrForse用于判断矩阵中每个元素是否被标记。
并且定义了相应函数(例如:输出函数)来完成相关操作。
(注释:具体操作见第二步,算法流程与步骤。
具体结构体与相关函数祥见源程序首部定义)二、算法流程与步骤初始化:本程序首先根据用户输入转换为其相应的方阵(即行数等于列数)。
若人的数量乘以每个人最多工作的任务数量小于或等于任务数量,同时补n行0;否则补n列0。
(n 为任务数量减去人的数量乘以每个人最多工作的任务数量的绝对值)。
输出该方阵,方便用户检查输入是否正确。
标记:然后根据用户输入判断是按行减去每行最小值,还是减去每列最小值(注释:若人的数量乘以每个人最多工作的任务数量小于或等于任务数量,则减去每行最小值,否则则减去每列最小值)。
然后从中选择其中含0最多的行或列依次进行标记,若所标记的直线数量小于矩阵行数(或列数),则撤销所有标记,选择其中含0最少的行(或列)减去其中除0以外的最小值,并同时将该行出现负数所在列(或行)每个元素加上该负数的相反数。
重复以上操作,直到所标记的直线数等于矩阵行数(或列数)。
转换为0-1指派矩阵:从行与列中选择含零最少的行(或列),将该行(或列)中的零元素先转换为矩阵中不可能出现的一个很大的数,将零出现的行与列进行标记,然后从列(或行)中选择零最少的,并将其中未被标记零元素转化为很大的数,依此类推;直到标记完所有数,最后将很大的数转换为1,其余均转化为0。
即得0-1指派矩阵。
三、算法源程序#include <stdio.h>#include <malloc.h>#include <stdlib.h>#include <conio.h>#include <string.h>#define MAXCOUNT 50 // 最大的人数和任务数量#define TRUE 1#define FALSE 0#define INDEF 10000 //指派中不可能出现的数struct TrueOrForse{int marker;}; //用于记录某元素是否被标记typedef struct ASS{int assign[MAXCOUNT][MAXCOUNT];struct TrueOrForse sign[MAXCOUNT][MAXCOUNT];}Assign; //记录指派中各元素,及其是否被标记void Print(int a[][MAXCOUNT],int Row,int Col); // 输出0-1指派构成的矩阵void reduceRow(Assign*L,int Row,int Col); // 减去行中最小值void reduceCol(Assign*L,int Row,int Col); // 减去列中最小值int CountZero(Assign*L,int Row,int Col,int temp); // 计算其中的零元素,并返回最大(temp 若为0,则返回最小的)的行或列,若都标记完,则返回0void Zero_marker(Assign*L,int m,int n); // 若m<n 标记m行;若m>n标记m-n列void SearchAgainByRowReduce(Assign*L,int count,int m); // 搜索未被标记行元素继续操作使其出现0,并将所有数置为正数void SearchAgainByColReduce(Assign*L,int m,int count); // 搜索未被标记列元素继续操作使其出现0,并将所有数置为正数void removeMarker(Assign*L,int m); // 撤销所有标记void ToBest(Assign*L,int count,int m); // 最后化为0-1指派int main(void){Assign *L = NULL;int PersonCount = 0,ThingCount = 0; // 人数与任务数量int OneDoMaxThing = 0; // 一个人最多工作的任务数量int m; // 记录化成指派问题的行数与列数int i,j,k;int flag = 0; // 用于标记本题是人数多,还是任务数量多int count,count_Count = 0;int count1[MAXCOUNT] = {0},a[MAXCOUNT] = {0};L = (Assign*)malloc(sizeof(Assign));if(L == NULL){printf("存储空间不足。
");return 0;}memset(L->assign,0,sizeof(int)*MAXCOUNT*MAXCOUNT);//矩阵中所有元素置0 printf("----------------------------\n");printf("-----指派问题的匈牙利法-----\n");printf("----------------------------\n");printf("请输入工作的人数:");scanf("%d",&PersonCount);printf("请输入任务数量:");scanf("%d",&ThingCount);printf("请输入一个人最多工作的任务数量:");scanf("%d",&OneDoMaxThing);printf("请输入0-1指派,按行输入:\n");for(i=1; i<=PersonCount*OneDoMaxThing; ) // 初始化0-1指派(用户输入){for(j=1; j<=ThingCount; ++j){scanf("%d",&L->assign[i][j]);}i += OneDoMaxThing;for(k=i-OneDoMaxThing+1; k<i; ++k){for(j=1; j<=ThingCount; ++j){L->assign[k][j] = L->assign[k-1][j];}}}m = i - OneDoMaxThing;getch();system("cls");if(OneDoMaxThing*PersonCount < ThingCount){m = ThingCount;flag = 0;}else if(OneDoMaxThing*PersonCount > ThingCount) {m = OneDoMaxThing*PersonCount;flag = 1;}printf("该问题可化作如下矩阵:\n");Print(L->assign,m,m);if(flag == 0){for(i=1; i<=m; ++i){reduceRow(L,i,m);}}else{for(j=1; j<=m; ++j){reduceCol(L,m,j);}}printf("减去每行最小值后,其结果为:\n");Print(L->assign,m,m);count_Count = 1;do{count = CountZero(L,m,m,1);Zero_marker(L,count,m);++count_Count;if(count == 0){removeMarker(L,m);count = CountZero(L,m,m,0);if(count <= m){SearchAgainByRowReduce(L,count,m);}else{SearchAgainByColReduce(L,m,count);}removeMarker(L,m);count_Count = 1;getch();puts("");Print(L->assign,m,m);}}while(count_Count < m);do{for(i=1; i<=m; ++i){for(j=1; j<=m; ++j){if(L->assign[i][j] == 0){count1[i]++;}}}for(j=1; j<=m; ++j){for(i=1; i<=m; ++i){if(L->assign[i][j] == 0){count1[m+j]++;}}}for(k=1; k<m; ++k){count = 1;for(i=1; i<=m*2; ++i){if(count1[count] < count1[i]){count = i;}}Zero_marker(L,count,m);count1[count] = 0;for(i=1; i<=m; ++i){for(j=1; j<=m; ++j){if(L->assign[i][j] == 0 && L->sign[i][j].marker == FALSE){flag = 2;}}}for(i=1; i<=m; ++i){int t = 0;for(j=1; j<=m; ++j){if(L->assign[i][j] != 0){t++;}}if(t == m){flag = 1;break;}}if(flag != 2 ){removeMarker(L,m);count = CountZero(L,m,m,0);if(count <= m){SearchAgainByRowReduce(L,count,m);}else{SearchAgainByColReduce(L,m,count);}}}while(flag != 2);puts("");Print(L->assign,m,m);getch();printf("其结果为:\n");Print(L->assign,m,m);getch();system("cls");printf("本问题的最优解为:\n");removeMarker(L,m);count = CountZero(L,m,m,0);ToBest(L,count,m);for(i=1; i<=m; ++i){for(j=1; j<=m; ++j){if(L->assign[i][j] != 0){L->assign[i][j] = 1;}}}Print(L->assign,m,m);getch();free(L);L = NULL;return 0;}void Print(int a[][MAXCOUNT],int Row,int Col) {int i,j;for(i=1; i<=Row; ++i){for(j=1; j<=Col; ++j){printf("%-4d",a[i][j]);}puts("");}}void reduceRow(Assign*L,int Row,int Col){int j;int min;min = L->assign[Row][1];for(j=1; j<=Col; ++j){if(min>L->assign[Row][j]){min = L->assign[Row][j];}}for(j=1; j<=Col; ++j){L->assign[Row][j] -= min;}}void reduceCol(Assign*L,int Row,int Col){int i;int min;min = L->assign[1][Col];for(i=1; i<=Row; ++i){if(min>L->assign[i][Col]){min = L->assign[i][Col];}}for(i=1; i<=Row; ++i){L->assign[i][Col] -= min;}}int CountZero(Assign*L,int Row,int Col,int temp){int i,j,max_Zero = 1,flag = 0,count[2*(MAXCOUNT+1)] = {0};for(i=1; i<=Row; ++i){for(j=1; j<=Col; ++j){if(L->assign[i][j] == 0 && L->sign[i][j].marker == FALSE){count[i]++;flag = 1;}}}for(j=1; j<=Col; ++j){for(i=1; i<=Row; ++i){if(L->assign[i][j] == 0 && L->sign[i][j].marker == FALSE){count[Row+j]++;flag = 1;}}}if(flag == 1){for(i=2; i<=Row*2; ++i){if(temp == 1){if(count[i]>count[max_Zero]){max_Zero = i;}}else{if(count[i]<count[max_Zero]){max_Zero = i;}}}return max_Zero;}return 0;}void Zero_marker(Assign*L,int m,int n){int i,j;if(m <= n){for(j=1; j<=n; ++j){L->sign[m][j].marker = TRUE;}}else{for(i=1; i<=n; ++i){L->sign[i][m-n].marker = TRUE;}}}void SearchAgainByRowReduce(Assign*L,int count,int m){int j,t,temp,min = 1;while(L->assign[count][min] == 0){min++;}for(j=2; j<=m; ++j){if(L->assign[count][j] < L->assign[count][min] && L->assign[count][j] != 0){min = j;}}temp = L->assign[count][min];for(j=1; j<=m; ++j){L->assign[count][j] -= temp;}for(j=1; j<=m; ++j){if(L->assign[count][j] < 0){temp = L->assign[count][j] * -1;for(t=1; t<=m; ++t){L->assign[t][j] += temp;}}}}void SearchAgainByColReduce(Assign*L,int m,int count){int i,t,temp,min = 1;while(L->assign[min][count-m] == 0){min++;}for(i=2; i<=m; ++i){if(L->assign[i][count-m] < L->assign[min][count-m] && L->assign[min][count-m] != 0){min = i;}}temp = L->assign[min][count-m];for(i=1; i<=m; ++i){L->assign[i][count-m] -= temp;}for(i=1; i<=m; ++i){if(L->assign[i][count-m] < 0){temp = L->assign[i][count-m] * -1;for(t=1; t<=m; ++t){L->assign[i][t] += temp;}}}}void removeMarker(Assign*L,int m){int i,j;for(i=1; i<=m; ++i){for(j=1; j<=m; ++j){L->sign[i][j].marker = FALSE;}}}void ToBest(Assign*L,int count,int m){int i,j,t,a[MAXCOUNT] = {0};if(count <= m){for(j=1; j<=m; ++j){for(i=1; i<=m; ++i){if(L->assign[i][j] == 0 && L->sign[i][j].marker == FALSE){a[j+m]++;}}}for(j=m+1; j<=2*m; ++j){if(a[j] == 1){for(i=1; i<=m; ++i){if(L->assign[i][j-m] == 0 && L->sign[i][j-m].marker == FALSE){L->assign[i][j-m] = INDEF;for(t=0; t<=m; ++t){if(L->assign[i][t] != INDEF){L->assign[i][t] = 0;L->sign[i][t].marker = TRUE;}}L->sign[i][j-m].marker = TRUE;}else{L->assign[i][j-m] = 0;L->sign[i][j-m].marker = TRUE;}}ToBest(L,j,m);break;}}}else{for(i=1; i<=m; ++i){for(j=1; j<=m; ++j){if(L->assign[i][j] == 0 && L->sign[i][j].marker == FALSE){a[i]++;}}}for(i=1; i<=m; ++i){if(a[i] == 1){for(j=1; j<=m; ++j) { if(L->assign[i][j] == 0 && L->sign[i][j].marker == FALSE) { L->assign[i][j] = INDEF; for(t=1; t<=m; ++t) { if(L->assign[t][j] != INDEF) { L->assign[t][j] = 0; L->sign[t][j].marker = TRUE; } } L->sign[i][j].marker = TRUE; } else { L->assign[i][j] = 0; L->sign[i][j].marker = TRUE; } }ToBest(L,i,m); break;}}}}四、算例和结果本程序以课本上例4-10为例:例4-10 某商业公司计划开办五家新商店 54321,,,,B B B B B ,为了尽早建成营业,现有五家建筑公司54321,,,,A A A A A ,以便让每家新商店由一个建筑公司承建。
