2013年 江苏 南京 六城区 教师招聘考试 笔试 数学 真题答案解析分析新
2013年小学数学教师招聘试卷

2013年小学数学教师招聘试卷一、选择题(共14个小题,每小题4分,共56分.在每个小题给出的四个备选答案中,只有一个是符合题目要求的)1.-5的绝对值是().A.5 B.C.D.-52.计算的结果是().A.-9 B.-6 C.D.3.计算的结果是().A.B.a C.D.4.2002年我国发现首个世界级大气田,储量达6000亿立方米,6000亿立方米用科学记数法表示为().A.亿立方米B.亿立方米C.亿立方米D.亿立方米5.下列图形中,不是中心对称图形的是().A.菱形B.矩形C.正方形D.等边三角形6.如果两圆的半径分别为3 cm和5 cm,圆心距为10 cm,那么这两个圆的公切线共有().A.1条B.2条C.3条D.4条7.如果反比例函数的图象经过点P(-2,3),那么k的值是().A.-6 B.C.D.68.在△ABC中,∠C=90°.如果,那么sinB的值等于().A.B.C.D.9.如图,CA为⊙O的切线,切点为A,点B在⊙O上.如果∠CAB=55°,那么∠AOB等于().A.55°B.90°C.110°D.120°10.如果圆柱的底面半径为4 cm,母线长为5 cm,那么它的侧面积等于().A.20p B.40p C.20 D.4011.如果关于x的一元二次方程有两个不相等的实数根,那么k的取值范围是().A.k<1 B.k≠0 C.k<1且k≠0 D.k>112.在抗击“非典”时期的“课堂在线”学习活动中,李老师从5月8日至5月14日在网上答题个数的记录如下表:日期5月8日5月9日5月10日5月11日5月12日5月13日5月14日答题个数68555056544868在李老师每天的答题个数所组成的这组数据中,众数和中位数依次是().A.68,55 B.55,68 C.68,57 D.55,5713.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E.如果AB=10,CD=8,那么AE的长为().A.2 B.3 C.4 D.514.三峡工程在6月1日至6月10日下闸蓄水期间,水库水位由106米升至135米,高峡平湖初现人间.假设水库水位匀速上升,那么下列图象中,能正确反映这10天水位h(米)随时间t(天)变化的是().二、填空题(共4个小题,每小题4分,共16分)15.在函数中,自变量x的取值范围是________.16.如图,在等边三角形ABC中,点D、E分别在AB、AC边上,且DE∥BC.如果BC=8 cm,AD∶AB=1∶4,那么△ADE的周长等于________ cm.17.如图,B、C是河岸边两点,A是对岸岸边一点,测得∠ABC=45°,∠ACB=45°,BC=60米,则点A 到岸边BC的距离是________米.18.观察下列顺序排列的等式:9³0+1=1,9³1+2=11,9³2+3=21,9³3+4=31,9³4+5=41,……猜想:第n个等式(n为正整数)应为________.三、(共3个小题,共14分)19.(本小题满分4分)分解因式:.20.(本小题满分4分)计算:21.(本小题满分6分)用换元法解方程四、(本题满分5分)22.如图,在□ABCD中,点E、F在对角线AC上,且AE=CF.请你以F为一个端点,和图中已标明字母的某一点连成一条新线段,猜想并证明它和图中已有的某一条线段相等(只须证明一组线段相等即可).(1)连结________.(2)猜想:________=________.(3)证明:五、(本题满分6分)23.列方程或方程组解应用题:在社会实践活动中,某校甲、乙、丙三位同学一同调查了高峰时段北京的二环路、三环路、四环路的车流量(每小时通过观测点的汽车车辆数),三位同学汇报高峰时段的车流量情况如下:甲同学说:“二环路车流量为每小时10000辆.”乙同学说:“四环路比三环路车流量每小时多2000辆.”丙同学说:“三环路车流量的3倍与四环路车流量的差是二环路车流量的2倍.”请你根据他们所提供的信息,求出高峰时段三环路、四环路的车流量各是多少.六、(本题满分7分)24.已知:关于x的方程的两个实数根是、,且.如果关于x的另一个方程的两个实数根都在和之间,求m的值.七、(本题满分8分)25.已知:在ABC中,AD为∠BAC的平分线,以C为圆心,CD为半径的半圆交BC的延长线于点E,交AD 于点F,交AE于点M,且∠B=∠CAE,FE∶FD=4∶3.(1)求证:AF=DF;(2)求∠AED的余弦值;(3)如果BD=10,求△ABC的面积.更多资料到八、(本题满分8分)26.已知:抛物线与x轴的一个交点为A(-1,0).(1)求抛物线与x轴的另一个交点B的坐标;(2)D是抛物线与y轴的交点,C是抛物线上的一点,且以AB为一底的梯形ABCD的面积为9,求此抛物线的解析式;(3)E是第二象限内到x轴、y轴的距离的比为5∶2的点,如果点E在(2)中的抛物线上,且它与点A在此抛物线对称轴的同侧,问:在抛物线的对称轴上是否存在点P,使△APE的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.参考答案一、选择题(每小题4分,共56分)1.A 2.D 3.C 4.B 5.D 6.D 7.A 8.B 9.C 10.B 11.C 12.A 13.A 14.B二、填空题(每小题4分,共16分)15.x≥-3 16.6 17.30 18.9(n-1)+n=10n-9(或9(n-1)+n=10(n-1)+1)三、(共14分)19.解:…………………………………………………………………2分………………………………………………………4分20.解:……………………………………………………………3分= .…………………………………………………………………………4分21.解:设,…………………………………………………………………1分则原方程化为.………………………………………………………2分∴.解得,……………………………………………………………3分当y=-2时,.∴.解得,.…………………………………………………………………4分当y=-3时,.∴∵△=9-12<0,∴此方程无实数根.………………………………………………………………5分经检验,,都是原方程的根.…………………………………………6分∴原方程的根为,.四、(本题满分5分)22.答案一:(1)BF……………………………………………………………………1分(2)BF,DE……………………………………………………………………………2分(3)证法一:∵四边形ABCD为平行四边形,∴AD=BC,AD∥BC.∴∠DAE=∠BCF.……………………………………………………………………3分在△BCF和△DAE中,∴△BCF≌△DAE.……………………………………………4分∴BF=DE.……………………………………………………………………………5分证法二:连结DB、DF,设DB、AC交于点O.∵四边形ABCD为平行四边形,∴AO=OC,DO=OB.∵AE=FC,∴AO-AE=OC-FC.∴EO=OF.……………………………………………………………………………3分∴四边形EBFD为平行四边形.………………………………………………………4分∴BF=DE.……………………………………………………………………………5分答案二:(1)DF…………………………………………………………………………1分(2)DF,BE……………………………………………………………………………2分(3)证明:略(参照答案一给分).五、(本题满分6分)23.解法一:设高峰时段三环路的车流量为每小时x辆,…………………………1分则高峰时段四环路的车流量为每小时(x+2000)辆.………………………………2分根据题意,得3x-(x+2000)=2³10000.…………………………………………4分解这个方程,得x=11000.…………………………………………………………5分x+2000=13000.答:高峰时段三环路的车流量为每小时11000辆,四环路的车流量为每小时13000辆.…………………………………………………………………………………………………6分解法二:设高峰时段三环路的车流量为每小时x辆,四环路的车流量为每小时y辆.…………………………………………………………………………………………………1分根据题意,得……………………………………………………………………4分解这个方程组,得……………………………………………………………………………5分答:高峰时段三环路的车流量为每小时11000辆,四环路的车流量为每小时13000辆.…………………………………………………………………………………………………6分六、(本题满分7分)24.解:∵,是方程①的两个实数根,∴,.∵,∴.∴.解得,………………………………………………………………3分(ⅰ)当m=-1时,方程①为.∴,.方程②为.∴,.∵-5、3不在-3和1之间,∴m=-1不合题意,舍去.…………………………………………………………5分(ⅱ)当m=4时,方程①为.∴,.方程②为.∴,.∵2<3<5<6,即,∴方程②的两根都在方程①的两根之间.∵m=4.………………………………………………………………………………7分综合(ⅰ)(ⅱ),m=4.注:利用数形结合解此题正确的,参照上述评分标准给分.七、(本题满分8分)25.解法一:(1)证明:∵AD平分∠BAC,∴∠BAD=∠DAC.∵∠B=∠CAE,∴∠BAD+∠B=∠DAC+∠CAE.∵∠ADE=∠BAD+∠B,∴∠ADE=∠DAE.∴EA=ED.∵DE是半圆C的直径,∴∠DFE=90°.∴AF=DF.……………………………………………………………………………2分(2)解:连结DM.∵DE是半圆C的直径,∴∠DME=90°.∵FE∶FD=4∶3,∴可设FE=4x,则FD=3x.由勾股定理,得DE=5x.∴AE=DE=5x,AF=FD=3x.由切割线定理的推论,得AF²AD=AM²AE.∴3x(3x+3x)=AM²5x.∴.∴.在Rt△DME中,.………………………………………………………5分(3)解:过A点作AN⊥BE于N.由,得.∴.在△CAE和△ABE中,∵∠CAE=∠B,∠AEC=∠BEA,∴△CAE∽△ABE.∴.∴.∴.解得x=2.∴,.∴.…………………………………………8分解法二:(1)证明:同解法一(1).(2)解:过A点作AN⊥BE于N.在Rt△DFE中,∵FE∶FD=4∶3,∴可设FE=4x,则FD=3x.由勾股定理,得DE=5x.∴AE=DE=5x,AF=FD=3x.∵,∴.∴.∴∴由勾股定理,得.∴.…………………………………………………5分(3)解:在△CAE和△ABE中,∴∠CAE=∠B,∠AEC=∠BEA,∴△CAE∽△ABE.∴.∴∴.解得x=2.∴,.∴.…………………………………………8分八、(本题满分8分)26.解法一:(1)依题意,抛物线的对称轴为x=-2.∵抛物线与x轴的一个交点为A(-1,0),∴由抛物线的对称性,可得抛物线与x轴的另一个交点B的坐标为(-3,0).…………………………………………………………………………………………………2分(2)∵抛物线与x轴的一个交点为A(-1,0),∴.∴t=3a.∴.∴D(0,3a).∴梯形ABCD中,AB∥CD,且点C在抛物线上,∵C(-4,3a).∴AB=2,CD=4.∵梯形ABCD的面积为9,∴.∴.∴a±1.∴所求抛物线的解析式为或…………………5分(3)设点E坐标为(,)依题意,,,且.∴.①设点E在抛物线上,∴.解方程组得∵点E与点A在对称轴x=-2的同侧,∴点E坐标为(,).设在抛物线的对称轴x=-2上存在一点P,使△APE的周长最小.∵AE长为定值,∴要使△APE的周长最小,只须PA+PE最小.∴点A关于对称轴x=-2的对称点是B(-3,0),∴由几何知识可知,P是直线BE与对称轴x=-2的交点.设过点E、B的直线的解析式为,∴解得∴直线BE的解析式为.∴把x=-2代入上式,得.∴点P坐标为(-2,).②设点E在抛物线上,∴.解方程组消去,得.∴△<0∴此方程无实数根.综上,在抛物线的对称轴上存在点P(-2,),使△APE的周长最小.…………8分解法二:(1)∵抛物线与x轴的一个交点为A(-1,0),∴.∴t=3a.∴.令y=0,即.解得,.∴抛物线与x轴的另一个交点B的坐标为(-3,0).2分(2)由,得D(0,3a).∵梯形ABCD中,AB∥CD,且点C在抛物线上,∴C(-4,3a).∴AB=2,CD=4.∵梯形ABCD的面积为9,∴.解得OD=3.∴.∴a±1.∴所求抛物线的解析式为或.…………………5分(3)同解法一得,P是直线BE与对称轴x=-2的交点.∴如图,过点E作EQ⊥x轴于点Q.设对称轴与x轴的交点为F.由PF ∥EQ ,可得 .∴ .∴ .∴ 点P 坐标为(-2, ).选调小学数学教师试卷一、 填空题(每小题3分,共30分)1、 把56分解质因数是_____________.2、 100增加2000后再减少20%是______.3、 将一根长75米的绳子平均剪成若干段,一共剪了4次,每段长______米4、 书店图书按八五折出售,就是按______的______出售,也就是降价______出售.5、 函数=y 412--x x 的自变量x 的取值范围是_____________. 6、 点p (-2,1)关于x 轴对称的点的坐标是_________.7、 如果α是锐角,且αcos =54,那么()α-090cos =_______.8、 如果圆锥的底面半径为5,母线长为10,那么圆锥的侧面展开图的面积是_______.9、新教材的修订,旨在贯彻《中共中央国务院关于深化教育改革 全面推进素质教育的决定》的精神,使数学教育更加有利于提高学生的________,有利于培养学生的_____________和_____________.10、在教学过程中,老师应该按照_____________和_____________选择适当的方法进行教学.二、 判断题(正确的在括号里打“ ”,错误的打“ ” )(每小题2分,共10分)1、教学方法受特定的课堂内容的制约。
南京六城区教师招聘真题及答案

06年六城区考试十一五计划的农业发展目标加德那的多元智能理论三、简答题1. 5’ 对于节能型的社会,你有什么建议2. 5’ 一个小孩一年级时上课积极回答问题,二年级就不怎么举手发言了,三年级上课就不认真听讲了,让你想出对策。
3. 5’+5’ 一位新教师听了两位有经验的教师上了相同的内容的课,作了笔记,并做出了分析:其中一位上课结构型强,上课严厉,课堂气氛不是很好,但学生的学习成绩不错,学生的水平差不多。
另一位上课有活力,跟学生的互动很多,总体成绩跟前一个班差不多,但学生有两极分化的倾向。
(1).你得到什么启示,结论。
(2).作为新教师除了观察老教师的课,从中吸取经验之外,还可以通过什么途径。
4. 10’ 给了一张表格,对比新的课程理念与旧的课程理念。
如“以教师为中心”与“以学生为中心”2010年南京六城区教师招聘考试笔试试题试卷一教育基础综合 60分一、单项选择(1′×20)题目下面给出的只是选项中的一部分5.新课程教学改革要求我们首先确立起()的教学理念。
A.与新课程相适应的,体现素质教育精神 B. 以学生为中心C. 以教师为主导,学生为主体D. 以课程教学为中心6.为了改变课程管理过于集中的状况,本次课改实行()A. 国家,地方,学校三级课程管理B. 国家,省,县三级课程管理C. 省,县,乡三级课程管理D. 教育部,教育局,教务处三级课程管理7.通过创设良好的情境对学生进行潜移默化的影响,以培养学生品德的方法是()A.说服法 B. 榜样法 C. 锻炼法 D. 陶冶法8.新课程把教学过程看作是()A.知识传授与学生能力发展的过程B. 课程传授和执行的过程C. 教师的教与学生的学的过程D. 师生交往,积极互动,共同发展的过程9.多元智力理论是新课程改革的理论基础之一,其提出者为()A. 加德纳B. 艾宾浩斯C. 布鲁纳D. 杜威12.美国的国务卿相当于我国的()A.国务院总理 B.外交部部长C.全国人大常务委员会委员长 D.民政部部长14.蔬菜和水果长时间储存,保险所需要的条件应为()A.低温,干燥,低氧 B.低温,湿度适中,低氧C.高温,干燥,高氧 D.高温,湿度适中,高氧16.“嗯,我懂”,“我能体会”,“请继续讲”,“原来如此!”,采用如此之类的语言与学生展开评估性会谈,这种技术属于会谈的()A. 倾听技术B. 面质技术C. 询问技术D.鼓励技术17.右图是南京国民政府总统府办公桌上的台历,它用黄铜铸成,透过历史的尘埃还能看到上面写着“中华民国三十八年四月小,23,星期六”,作为历史它在此定格成为永恒。
2013年江苏教师资格证考试真题卷(1)(2)

2013年江苏教师资格证考试真题卷(1)•本卷共分为2大题50小题,作答时刻为180分钟,总分100分,60分及格。
一、单项选择题(共25题,每题2分。
每题的备选项中,只要一个最契合题意)1.__是发明性思想的主导成分。
A.形象思想B.发散思想C.直觉思想D.惯例思想参阅答案:B一般以为,发明性思想的主导成分是发散思想。
2.依据柯尔伯格的有关儿童道德判别展开阶段的研讨,威望与保持社会次序的道德阶段处于__。
A.后风俗水平B.风俗水平C.可逆水平D.前风俗水平参阅答案:B风俗水平包含寻求认可取向阶段和恪守法规取向阶段。
3.看到月亮的边上有一圈光晕,就推知即将刮风,这是__ A.感觉B.思想C.幻想D.错觉参阅答案:B思想能够进行推理,然后猜测未来。
4.教育心思学首要研讨的是校园教育中的__。
A.学生的学习B.教育办法C.校园环境D.学与教的规则参阅答案:D教育心思学是一门研讨校园情境中学与教的根本心思规则的科学。
5.教育心思学普遍以为西方榜首本《教育心思学》出书于__。
A.1903年B.1913年C.1914年D.1900年参阅答案:A1903年桑代克出书的《教育心思学》是西方榜首本以“教育心思学”命名的专著。
6.教师采纳的有用到达教育政策的全部活动方案叫__。
A.教育战略B.学习战略C.教育方案D.教育政策参阅答案:A教育战略指教师采纳的有用到达教育政策的全部活动方案。
7.彻悟说的重要代表人物是__。
A.桑代克B.巴甫洛夫C.斯金纳D.苛勒参阅答案:D彻悟说是认知学习理论格局塔学派的代表观念之一,其重要代表人物是苛勒。
8.品格的中心是__。
A.才干B.智力C.性情D.气质参阅答案:C品格的中心是性情。
9.奥苏伯尔提出的解说忘记原因的理论是__。
A.痕迹阑珊说B.搅扰说C.同化说D.动机说参阅答案:C同化说由奥苏伯尔提出,他以为,忘记就其本质来说,是常识的安排与认知结构简化的进程。
10.心情与道德构成进程阅历的第二阶段是__。
2013年江苏高考数学卷试卷及详细解析
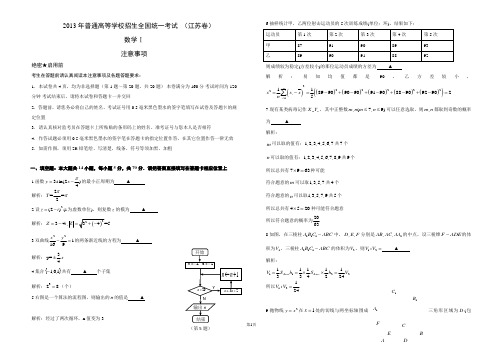
YN 输出n 开始1a 2n ←←,1n n ←+32a a ←+20a <结束 2013年普通高等学校招生全国统一考试 (江苏卷)数学Ⅰ 注意事项绝密★启用前考生在答题前请认真阅读本注意事项及各题答题要求:1.本试卷共4页,均为非选择题(第1题~第20题,共20题).本卷满分为160分.考试时间为120分钟.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请您务必将自己的姓名、考试证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与您本人是否相符.4.作答试题必须用0.5毫米黑色墨水的签字笔在答题卡的指定位置作答,在其它位置作答一律无效. 5.如需作图,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.一、填空题:本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应位置上......... 1.函数)42sin(3π-=x y 的最小正周期为 ▲ .解析:2==2T ππ 2.设2)2(i z -=(i 为虚数单位),则复数z 的模为 ▲ . 解析:()2234,34=5Z i Z =-=+-3.双曲线191622=-y x 的两条渐近线的方程为 ▲ . 解析:3y=4x ±4.集合{}1,0,1-共有 ▲ 个子集. 解析:328=(个)5.右图是一个算法的流程图,则输出的n 的值是 ▲解析:经过了两次循环,n 值变为36.抽样统计甲,乙两位射击运动员的5次训练成绩(单位:环),结果如下: 运动员 第1次 第2次 第3次 第4次 第5次 甲 87 91 90 89 93 乙8990918892则成绩较为稳定(方差较小)的那位运动员成绩的方差为 ▲ . 解析:易知均值都是90,乙方差较小,()()()()()()()22222221118990909091908890929025ni i s x xn ==-=-+-+-+-+-=∑7.现有某类病毒记作n m Y X ,其中正整数)9,7(,≤≤n m n m 可以任意选取,则n m ,都取到奇数的概率为 ▲ . 解析:m 可以取的值有:1,2,3,4,5,6,7共7个 n 可以取的值有:1,2,3,4,5,6,7,8,9共9个所以总共有7963⨯=种可能 符合题意的m 可以取1,3,5,7共4个 符合题意的n 可以取1,3,5,7,9共5个 所以总共有4520⨯=种可能符合题意 所以符合题意的概率为20638.如图,在三棱柱ABC C B A -111中,F E D ,,分别是1,,AA AC AB 的中点,设三棱锥ADE F -的体积为1V ,三棱柱ABC C B A -111的体积为2V ,则=21:V V ▲ . 解析:112211111334224ADE ABC V S h S h V ==⨯⨯=所以121:24V V =9.抛物线2x y =在1=x 处的切线与两坐标轴围成三角形区域为D (包1A1B1C含三角形内部和边界).若点),(y x P 是区域D 内的任意一点,则y x 2+的取值范围是 ▲ . 解析:易知切线方程为:21y x =-所以与两坐标轴围成的三角形区域三个点为()()()0,00.5,00,1A B C - 易知过C 点时有最小值2-,过B 点时有最大值0.510.设E D ,分别是ABC ∆的边BC AB ,上的点,AB AD 21=,BC BE 32=,若AC AB DE 21λλ+=(21,λλ为实数),则21λλ+的值为 ▲ .解析:易知()121212232363DE AB BC AB AC AB AB AC =+=+-=-+所以1212λλ+=11.已知)(x f 是定义在R 上的奇函数.当0>x 时,x x x f 4)(2-=,则不等式x x f >)(的解集用区间表示为 ▲ . 解析:因为)(x f 是定义在R 上的奇函数,所以易知0x ≤时,2()4f x x x =-- 解不等式得到x x f >)(的解集用区间表示为()()5,05,-+∞12.在平面直角坐标系xOy 中,椭圆C 的标准方程为)0,0(12222>>=+b a by a x ,右焦点为F ,右准线为l ,短轴的一个端点为B ,设原点到直线BF 的距离为1d ,F 到l 的距离为2d .若126d d =,则椭圆的离心率为 ▲ . 解析: 由题意知2212,bc a b d d c a c c==-= 所以有26b bcc a= 两边平方得到2246a b c =,即42246a a c c -= 两边同除以4a 得到2416e e -=,解得213e =,即33e = 13.平面直角坐标系xOy 中,设定点),(a a A ,P 是函数)0(1>=x xy 图像上一动点,若点A P ,之间最短距离为22,则满足条件的实数a 的所有值为 ▲ . 解析:由题意设()0001,,0P x x x ⎛⎫> ⎪⎝⎭则有()222222200000200000111112++2=+-2+22PA x a a x a x a x a x a x x x x x ⎛⎫⎛⎫⎛⎫⎛⎫=-+-=+-+- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ 令()001t 2x t x +=≥ 则()222=(t)=t 2222PA f at a t -+-≥ 对称轴t a = 1.2a ≤时,22min 2(2)2422428PA f a a a a ==-+∴-+=1a =- , 3a =(舍去) 2.2a >时,22min 2()228PA f a a a ==-∴-=10a = , 10a =-(舍去) 综上1a =-或10a = 14.在正项等比数列{}n a 中,215=a ,376=+a a .则满足n n a a a a a a a a ......321321>++++的最大正整数n 的值为 ▲ .解析:2252552667123123115521155223 (1),.222222011521312913236002292212n n n n n n nn n n a a a a a a a a a a q a q q a a n nq n q n q a -------=+=+-+=∴++++>∴->∴->>-∴->-+∴<<=>∴==n N +∈112,n n N +∴≤≤∈又12n =时符合题意,所以n 的最大值为12二、解答题:本大题共6小题,共计90分。
2013年 江苏 南京 六城区 教师招聘考试 笔试 公共知识 真题答案解析

2013年南京市六城区中小学新教师招聘考试公共知识真题试题一、选择题(15题,每题2分)1.2012年6月24日12时55分,在神舟()载人飞船航天员的精准操控下,飞船与天宫一号空间站手控交会对接取得圆满成功。
A.五号B.七号C.九号D.十号2.胡锦涛同志在十八大报告中提出,把()建设放在突出地位,融入经济建设.政治建设.文明建设.社会建设各方面和全过程,努力建设美丽中国,实现中华民族有序发展。
A.物质文明B.精神文明C.法治文明D.生态文明3.我国的国家元首是()。
A.中共中央总书记B.全国人大常委会委员长C.国家主席D.国务院总理4.大学英语等级考试是一种()测试。
A.总结性B.发展性C.常模参照性D.标准参照性5.马铃薯食用部分是植物的()。
A.根B.茎C.果实D.种子6.南京中山陵是伟大的革命先行者孙中山先生的陵墓,全局呈“警钟”形图案,其中祭堂为仿宫殿式建筑,建有三道拱门,门楣上分别刻有“()”横幅,即三民主义。
A..民主、民权、民生B.民族、民权、民生C.民主、民治、民生D.民族、民治、民生7.右图反映的中国古代重大发明是()。
A.造纸术B.雕版印刷术C. 活字印刷术D.指南针8.美国华盛顿儿童博物馆墙上有一条格言:“I hear and forget,I see and remember,I do and I understand.”对教师的启示是在教学过程中应()。
A.尊重儿童的个性B.重视儿童积极的情感体验C.重视儿童学习的自律性D.重视儿童的操作活动9.生活中常说的“白色污染”主要是指()。
A.白色烟尘B.白色建筑废料C.生活垃圾D.塑料垃圾10.义务教育阶段的教材编写、教学实施和教学评价的基本依据是()。
A.课程标准B.课程计划C.课程方案D.教学目标11.纳米是一种()。
A.技术B.粒子C.材料D.长度单位12.教师对自己的教育教学行为进行分析,提出改进意见或表达困惑,以便日后更正或引起他人思考而写的文字,称之为()。
南京六城区教师招聘真题

2010年数学专业知识卷(1)选择题1.已知a =(-2,1),b =(1,0),且 a +b 与a垂直,求2.《几何原本》的5条公设,以下哪个不是?( ) A.假设所有直角都相等B.假设平面上一点与另一点可以作直线C.平行。
D.整体大于部分 3.已知直线ax+by=4与圆x 2+y2=4相离,则点P(a,b)与圆x 2+y2=4的关系是( )A.在圆内B.在圆上C.在圆外4.已知cosx 和sin(x+ )在(0,2)上单调性相同, 可能的值是什么? ( ) A.3 B.4 C.2 D.65.已知函数y=f(x)的图像如右图所示,则函数f(x)的表达式可能为( ) A.f(x)=-x-sinx B.f(x)=-x-cosx C.f(x)=|x|sinx D.f(x)=x|cosx|6.将1,2,3三个数字放在三行三列的方格中,使得每行每列都恰好有一个数字的放法有多少种? ( )A.6种B.12种C.24种D.36种(2)填空1.已知 ABC ,圆I 是其内切圆,切点为E 、F 、G ,其中 EFG=52,求 A=_______。
C 2.甲、乙比赛每比一场甲赢的概率为32,乙赢的概率为31,谁先胜出三次,谁获胜。
问甲恰好第四次获胜的概率为_______。
3.如右图所示,图C1为等边三角形,边长为1,在图C1上构造图C2:把C1的各边三等分,并把中间段为边向外作等边三角形,再擦去中间这一段。
以此类推,问Cn 图的周长为_______。
4.已知:a=27,b=5,求225=1+a 5b +a 4-b a 44的非1和本身以外的任一约数________5.在直角坐标系中,12222 by a x 的焦距为2c ,以坐标原点O 为圆心,a 为半径作圆,椭圆的右准线上一点P ,过P 点作圆O 的两条切线互相垂直,求椭圆离心率的取值范围:_______。
6.化简))(())((c a b a c x b x +))(())((a b c b a x c x +))(())((b c a c b x a x =_________。
2013年中学数学教师招聘考试专业基础知识试卷(2)及答案

中学数学教师招聘考试专业基础知识试卷(二)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设B A ,是非空集合,定义B A ⨯={B A x x ∈且B A x ∉},己知{}20≤≤=x x A{}0≥=y y B ,则B A ⨯等于 ( )A .(2,+∞)B .[0,1]∪[2,+∞)C .[0,1)∪(2,+∞)D .[0,1]∪(2,+∞)2. 某林场有树苗30000棵,其中松树苗4000棵,为调查树苗的生长情况,采用分层抽样的方法抽取一个容量为150的样本,则样本中松树苗的数量为 ( )A .25B .30C .15D .20 3.已知1sin()43πα-=,则cos()4πα+的值等于( ) AC.13D.-134.如果复数212bii -+(其中i 为虚数单位,b R ∈)的实部和虚部互为相反数,则b 等于( ) A .23- B .23 C.25.已知三个平面,,αβγ,若βγ⊥,且αγ与相交但不垂直,,a b 分别为,αβ内的直线,则( )A .,a a αγ∃⊂⊥B .,//a a αγ∃⊂C .,b b βγ∀⊂⊥D .,//b b βγ∀⊂6.右图是一算法的程序框图,若此程序运行结果为720S =, 则在判断框中应填入关于k 的判断条件是 ( )A .6?k ≥B .7?k ≥C .8?k ≥D .9?k ≥7.设向量a 与b 的夹角为θ,定义a 与b 的“向量积”:a b ⨯是一个向量,它的模sin ab a b θ⨯=⋅⋅,若()()3,1,1,3a b =--=,则a b ⨯=( )AB .2C.D .48.过双曲线22221(0,0)x y a b a b-=>>的右顶点作斜率为-1的直线,该直线与双曲线的两条渐近线的交点分别为B,C.若12AB BC =,则双曲线的离心率是 ( )9.设数列{a n }的前n 项和为S n ,令12nn S S S T n+++=,称T n 为数列a 1,a 2,…,a n 的“理第6题想数”.已知a 1,a 2,…,a 500的“理想数”为1002,那么数列3,a 1,a 2,….a 500的“理想数”为( )A .1005B .1003C .1002D .999 10.函数221ln )(x x x f -=的图象大致是( )A .B .C .D .二、填空题:本大题共7小题,每小题4分,共28分.11.某大学对1000名学生的自主招生水平测试成绩进行统计,得到样本频率分布直方图如下图所示,现规定不低于70分为合格,则合格人数是 ▲12. 某几何体的三视图(单位:cm)如下图,则这个几何体的体积为_______cm 3.13.观察等式1555159739991591311513131313159131715717171717176,22,22,22,C C C C C C C C C C C C C C +=+++++++=-++++=+……由以等式推测到一个一般的结论: 对于*1594141414141,n n n n n n N C C C C +++++∈++++=_______________.14.已知△AOB,点P 在直线AB 上,且满足2,OP tOB tPA t R =+∈,则PA PB=_________正视图俯视图12题第11题教师考试网 国内最大的教师招聘资讯、试题免费分享平台ABMFEDCG 15.若不等式组0024x y y x s y x ≥⎧⎪≥⎪⎨+≤⎪⎪+≤⎩表示的平面区域是一个三角形,则s 的取值范围是 .16. 在一次招聘口试中,每位考生都要在5道备选试题中随机抽出3道题回答,答对其中2道题即为及格,若一位考生只会答5道题中的3道题,则这位考生能够及格的概率为 .17.设函数)(),(x g x f 的定义域分别为g f D D ,,且gfDD ⊂≠,若)()(,x f x g D x f =∈∀,则函数)(x g 为)(x f 在g D 上的一个延拓函数.已知()2(0)x f x x =<,上在是R x f x g )()(的一个延拓函数,且)(x g 是奇函数,则)(x g =________________三、解答题(本大题共5小题,共72分。
2013年下半年真题及答案解析(初中数学)

2013年下半年中小学教师资格考试 数学学科知识与教学能力试题(初级中学)注意事项:1.考试时间为120分钟,满分为150分。
2.请按规定在答题卡上填涂、作答。
在试卷上作答无效,不予评分。
一、单项选择题(本大题共8小题,每小题5分,共40分) 1.极限的值是( )。
A. -1B. OC. l D .正无穷 2.设f(x)是R 上的函数,则下列叙述正确的是( )。
A. f(x)f(-x)是奇函数B. f(x)| f(x)|是奇函数C. f(x)-f(-x)是偶函数D. f(x)+f(-x)是偶函数 3.定积分∫2dx 3−2的值是( )。
A. 254π B. 252πC. 256π D. 94π4.函数y=f(x)的导函数的图像如图所示,x 0=l ,则( )。
A.x 0不是驻点B.x 0是驻点,但不是极值点C.x 0是极小值点D.x 0是极大值点5.经过圆x 2+2x+y 2=0的圆心,与直线x+y=0垂直的直线方程是( )。
A.x+y+l=0 B.x-y-l=0 C.x+y-l=0 D.x-y+l=0 6.下列矩阵所对应的线性变换不是旋转变换的是( )。
A .(1101) B .(1001)C .√202−442) D .(cos θsin θ−sin θcos θ) 7.下列内容属于《义务教育数学课程标准(2011年版)》第三学段“数与式”的是( )。
①有理数②方程③实数④代数式⑤整式与分式A .①②③④B .①②④⑤ C.①③④⑤ D .①②③⑤ 8.下面哪位不是数学家?( )A .祖冲之B .秦九韶C .孙思邈D .杨辉二、简答题(本大题共5小题,每小题7分,共35分)9.设a 、b 为实数,O<a<b ,证明在开区间(a ,b)中存在有理数(提示取1n <b −a )。
10.已知矩阵M=,求曲线在矩阵M -1对应的线性变换作用下得到的曲线方程。
11.射手向区间[0,1]射击一次,落点服从均匀分布,若射中[0,12]区间,则观众甲中奖;若射中[x,35]区间,则观众乙中奖。
2013年教师招聘考试小学数学真题汇编试卷-教师资格小学教师专业知识试卷与试题

10. 教学的重点与难点是彼此独立的。[1分]-----正确答案(错) 对错
三、问答题 1. 结合实际谈谈新课程小学数学教材使用的策略。[5分]
参考答案: (1)多种境界探究教材;(2)多种方式呈现教材;(3)多种渠道开发教材
6. 有人认为接受学习已经过时了,对此,你有何看法?[5分] 参考答案: 学生的学习方式一般由接受和发现两种。两种学习方式都有其存在的价值,彼此也是相辅相成的关系。但粗昂同 的学习方式过分突出和强调接受和掌握,使学生学习纯粹被动地接受、记忆的过程。转变学习方式就是改变这种 装态。探究学习过程离不开有意义的接受学习。
5. 所谓在教学时要“用一把钥匙开一把锁”,是指教师要有()。[1分]-----正确答案(A) A 针对性 B 逻辑性 C 知识性 D 创造性
6. “时教必有正业,退息必有居学”体现的是()教育思想。[1分]-----正确答案(A) A 课内与课外相结合 B 因材施教 C 教学相长 D 启发式教学
7. 在教育情境的种种遭遇中每一个学生个性化的创造性表现为()[1分]-----正确答案(A) A 表现性课程目标 B 生成性课程目标 C 行为取向性目标 D 价值取向性目标
17. 学生数学学习内容的呈现采用不同的 表达方式 ,以满足 多样化 的学习需要。[每空1分]
18. 数学在提高人的 推理能力 、抽象能力、 想象力 和 创造力 等方面有着独特的作用。 [每空1分]
19. 《标准》倡导 自主探索 、 合作交流 、 实践创新 的数学学习方法。[每空1分]
20. 数学教学活动必须建立在学生的 认知发展水平 和 已有的知识经验 基础之上。[每空1分]
11. 在新课程理念下,如何使用教材?[5分] 参考答案: 领会教材的精神,做到心中有数 关注现实生活,挖掘丰富的课程资源 充分发挥教师在教学中的创造力来分析教材,挖掘教材,超越教材,发展教材
2013 江苏 南京 教师招聘考试笔试 美术 真题答案解析

南京六城区2013年美术笔试真题(本卷共150分,其中公共基础知识60分学科专业知识90分)学科知识部分一、选择题(共20题,每题1分)1、唐贞观之后,绘画艺术发展中( )被誉为“画圣”。
A、张萱B、顾恺之C、吴道子D、王维2、商朝晚期具有概括性、写实性的青铜器是()。
A、毛公鼎B、司母戊方鼎C、莲鹤方壶D、四羊方尊3、表现主义代表蒙克是()人。
A、意大利B、法国C、挪威D、德国4、马远、夏圭是()时期的山水画家。
A、明清B、南宋C、北宋D、唐代5、巴黎圣母院是属于西方美术上( )风格的建筑?A、罗马式B、巴洛克式C、哥特式D、拜占庭式6、被称为现代艺术之父的画家是:()A、毕加索B、梵高C、塞尚D、杜尚7、在塑造美术形象的艺术语言中,线条、形体、明暗色调属于美术的()A、艺术手法B、表现形式C、表现手段D、艺术规律8、《流民图》的作者是()A、蒋兆和B、徐悲鸿C、王式廓D、董希文9、、唐三彩常用的颜色主要是()。
A、红、黄、蓝B、红、绿、白C、绿、黄、紫D、黄、绿、白10、提出了品画的艺术标准“六法论”的魏晋南北朝时期著名美术理论家是( )A、王微B、宗炳C、谢赫D、顾恺之11浮世绘是日本17世纪兴起的一种艺术,它将民间日常生活作为创作题材,主要通过()的形式表现出来。
A、水彩画 B 、工笔画 C、版画 D、油画12、一件好的实用工艺品必须具备()A.功能性与实用性B.功能性与审美性C.功能性与耐用性D.实用性与灵活性13、风景画《蒙特方丹的回忆》的作者是()A、法国柯罗B、法国莫奈C、荷兰梵高D、俄国苏里科夫14、《掷铁饼者》是什么事期的雕塑作品()A、古埃及B、古罗马C、古希腊D、古印度15、《韩熙载夜宴图》分为()个场面A.2个B.3个C.4个D.5个16、59、美术创作原则“外师造化、中得心源”是()提出的。
A、王洽 B 、张璪C、王维D、张彦远17、下面属于海派画家的是:()A. 吴昌硕B. 高剑父C. 金农D. 黄慎18、17、黄河流域半坡彩陶纹饰最多的是()A、兽面纹B、凤鸟纹C、几何纹D、鱼纹19、属于长沙马王堆帛画的是()。
2013教师招聘考试试题及答案

2013年教师招聘考试全真模拟试题及答案大全•考试内容:公共知识(基础教育课程改革理论、教育学与心理学及其他综合知识)、学科专业知识。
•••试卷分值•第一份试题:公共知识60分•1、单项选择题(20道)每题1分;•2、判断题(10道)每题1分•3、简答题(3道)共30分•第二份试题:专业知识90分•1、教案设计1题30分•2、学科专业知识60分一、选择题:本大题共20个小题,每小题2分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的,把所选项前的字母填在括号内。
1.世界上最早的教育文献是我国的(C)A.《论语》B.《大学》C.《学记》D.《中庸》2.教育“生物起源论”的代表人物是(D)A.孟禄B.洛克C.卢梭D.利托尔诺3.教育要适应人的发展的顺序性规律,应做到(A)A.循序渐进B.因材施教C.教学相长D.防微杜渐4.在教育目的问题上,德国教育家赫尔巴特的主张体现了(A)A.社会本位论思想B.个人本位论思想C.社会效益论思想D.教育无目的论思想5.广义的教育制度是指(D)A.学校教育制度B.高等教育制度C.社会教育制度D.国民教育制度6.在下列主张中,比较准确地体现了启发性教学原则的是()A.学不躐等B.各因其材C.开而弗达D.温故而知新7.教师通过创设良好的环境和自身的教育因素,对学生进行熏陶和感染以培养学生良好思想品德的德育方法是()A.品德评价法B.榜样示范法C.实际锻炼法D.陶冶教育法8.尊重信任学生是教师的()A.知识素养之一B.能力素养之一C.思想品德素养之一D.基本任务之一9.在教学计划和教学大纲之外,利用课余时间,对学生实施的各种有目的、有计划、有组织的教育活动是()A.课外教育B.校外教育C.业余教育D.课外校外教育10.整个教学工作的中心环节是()A.备课B.上课C.布置作业D.成绩评定11.心理现象就其产生方式是()A.精神活动B.反射活动C.意识活动D.技能活动12,下列选项中哪种是一般能力? ()A.观察力B.曲调感C.节奏感D.色调感13.狼孩的心理障碍主要原因是()A.缺乏营养B.遗传因素C.狼的影响D.缺乏社会性刺激14.勤奋和懒惰属下列哪种特性? ()A.气质B.性格C.能力D.兴趣15.长时记忆的遗忘属于下列哪种障碍? ()A.生理性障碍B.心理性障碍C.存储性障碍D.提取性障碍16.注意的稳定性是注意品质的哪种特性? ()A.广度B.强度C.时间D.空间17.直观时运用变式方法的目的是()A.激发兴趣B.引起注意C.丰富想象D.区分本质与非本质特征18.“人逢喜事精神爽”是下列哪种情绪状态? ()A.心境B.激情C.应激D.热情19.个性结构的核心成分是()A.能力B.气质C.性格D.兴趣20.听觉中枢位于()A.额叶B.顶叶C.颞叶D.枕叶二、填空题:本大题共18个小题,每空1分,共36分。
2013南京六城区教师招考回忆版真题(英语)

2013年南京六城区教师招考回忆真题(英语)2013年1月2号,刚过了元旦,又到了南京六城区教师招考的日子,本人在火车上跨年,千里迢迢来到了南京参加考试,当然最最感谢的还是南京的一个高中同学的大力帮助和支持,感激不尽。
好了,进入正题。
今年南京教师招考仍然分为两个部分,公共知识部分和学科专业知识部分。
LZ报的是中学英语,在江苏教育学院附属高级中学考试。
两份试卷一起分发,考生可以自主选择先做哪个卷子,由于监考老师先发的学科专业知识,所以我先做的英语学科专业知识。
英语试卷共100分,单选,完型,阅读理解2篇,根据首字母写出单词,还有教材分析。
第一题是单选,忘记十个还是十五个了,跟高考题题型差不多吧,考查语法,词汇等,这部分就靠自己平时积累还有英语底子吧,还好,不算难。
第一个考的是should表惊讶的用法,第二个题是词汇选择,最后一个好像是谚语的语境用法吧,LZ选的是水滴石穿那个选项,其他的忘了,不知道对不对。
总之难度还好。
第二个题是完型填空,考的是关于Happiness 的一些观点看法,是stimulus还是response,人们认为有了想要的东西才会感到幸福,认为已有的东西是stimulus,而幸福则是response.作者的观点是相反,认为先有happiness 才有了其他想要的东西,即幸福是stimulus, 总之完型有点难度,需要理解,读两遍理解了也还好。
再就是两篇阅读理解,第一篇比较简单,第二篇讲的是达卡的服装厂的工人艰苦的工作条件。
哦,我以为是印度达卡,才知道是孟加拉国的,所以第三个题选错了,呜呜。
下一个题是一篇文章,根据首字母写出适当的单词,内容是关于毕业之后找工作之类的,这部分,个人感觉有点难度,有几个空,没填出来,之前也没听说有这样的题型,总之还是考自己的英语基础。
最后一题是教材分析,30分,分为小学和中学,小学的好像是一节听说课吧,LZ报的是中学英语,所以没怎么看小学的。
中学英语是一篇阅读课,National flags, colours and cultures.主要讲了美国国旗和法国国旗背后的含义,颜色代表的含义,及其相关文化背景。
2013年江苏教师资格证考试真题卷

2013年江苏教师资格证考试真题卷•本卷共分为2大题50小题,作答时刻为180分钟,总分100分,60分及格。
一、单项选择题(共25题,每题2分。
每题的备选项中,只要一个最契合题意)1.由特定集体的相对规范决议终究效果的检验是()。
A.规范参照检验B.常模参照检验C.描绘性检验D.集体检验参考答案:B[解析]常模参照检验是经过丈量团队的平均值,依照单个在团队中所在的方位来终究决议效果的。
2.“忘记不是坚持的消失而是回想被压抑”,这是哪一种理论对忘记的解说?()A.痕迹阑珊说B.搅扰说C.同化说D.动机说参考答案:D3.心思开展因进行的速度、抵达的时刻和终究抵达的高度而表现出多样化的开展方法,这表现了心思开展的什么特色。
()A.连续性与阶段性B.定向性与次序性C.不平衡性D.差异性参考答案:C[解析]心思开展因进行的速度、抵达的时刻和终究抵达的高度而表现出多样化的开展方法。
这表现了心思开展的不平衡性。
4.发明性思想的中心是()。
A.发明性B.聚合思想C.发散思想D.智力参考答案:C[解析]发散思想是发明性思想的中心。
5.第一个别系地研讨儿童品德判别开展的心思学家是()。
A.皮亚杰B.柯尔伯格C.加涅D.夸美纽斯参考答案:A[解析]皮亚杰是第一个别系地研讨儿童品德判别开展的心思学家。
6.校园心思教导首要服务的人群是()。
A.正常学生集体B.特别学生集体C.有心思问题的学生D.极单个学生参考答案:A[解析]校园心思教导的首要服务人群是正常的学生集体,并非限制有心思问题的特别集体。
7.在教师自编检验里,下面哪一类题型是主观题()。
A.选择题B.判别题C.填空题D.论说题参考答案:D[解析]所谓主观题,是指那些能更好地考察学生详细情况或特性的试题。
经过这类试题的考察,可以全面了解学生对某门课程的某个详细部分了解和把握的程度,可以测验学生精确地回想所学内容,灵敏地安排资料,清楚地表达问题,深刻地了解问题实质的才能。
2013年南京市六城区中小学新教师招聘考试《公共知识》真题试题及答案解析

2013年南京市六城区中小学新教师招聘考试公共知识真题试题一、选择题(15题,每题2分)1.2012年6月24日12时55分,在神舟()载人飞船航天员的精准操控下,飞船与天宫一号空间站手控交会对接取得圆满成功。
A.五号B.七号C.九号D.十号2.胡锦涛同志在十八大报告中提出,把()建设放在突出地位,融入经济建设.政治建设.文明建设.社会建设各方面和全过程,努力建设美丽中国,实现中华民族有序发展。
A.物质文明B.精神文明C.法治文明D.生态文明3.我国的国家元首是()。
A.中共中央总书记B.全国人大常委会委员长C.国家主席D.国务院总理4.大学英语等级考试是一种()测试。
A.总结性B.发展性C.常模参照性D.标准参照性5.马铃薯食用部分是植物的()。
A.根B.茎C.果实D.种子6.南京中山陵是伟大的革命先行者孙中山先生的陵墓,全局呈“警钟”形图案,其中祭堂为仿宫殿式建筑,建有三道拱门,门楣上分别刻有“()”横幅,即三民主义。
A..民主、民权、民生B.民族、民权、民生C.民主、民治、民生D.民族、民治、民生7.右图反映的中国古代重大发明是()。
A.造纸术B.雕版印刷术C. 活字印刷术D.指南针8.美国华盛顿儿童博物馆墙上有一条格言:“I hear and forget,I see and remember,I do and I understand.”对教师的启示是在教学过程中应()。
A.尊重儿童的个性B.重视儿童积极的情感体验C.重视儿童学习的自律性D.重视儿童的操作活动9.生活中常说的“白色污染”主要是指()。
A.白色烟尘B.白色建筑废料C.生活垃圾D.塑料垃圾10.义务教育阶段的教材编写、教学实施和教学评价的基本依据是()。
A.课程标准B.课程计划C.课程方案D.教学目标11.纳米是一种()。
A.技术B.粒子C.材料D.长度单位12.教师对自己的教育教学行为进行分析,提出改进意见或表达困惑,以便日后更正或引起他人思考而写的文字,称之为()。
2013年教师招聘考试数学真题试卷参考答案

2013年教师招聘考试数学真题试卷参考答案吉林教师考试交流群:279620409一、填空题1、知识与技能;过程与方法;情感态度与价值观2、动手实践;自主探索;合作交流3、认知发展水平;知识经验基础4、现代信息技术5、《周髀算经》6、一切为了学生的发展7、组织者;引导者;合作者8、生动活泼;主动的;富有个性9、基础性;普及型;发展性10、自主学习;合作学习;探究学习11、全面;持续;和谐12、现实的;有意义的;富有挑战性的13、数与代数14、研究性学习;社区服务与社会实践;信息技术教育;劳动与技术教育15、知识;生活经验16、重新发现;重新组合17、表达方式;多样化18、推理能力;想象力;创造力19、自主探索;合作交流;实践创新20、认知发展水平;已有的知识经验21、有价值;必需22、独立性;质疑;调查;富有个性23、属于代数;空间与图形;统计与概率;实践与综合应用24、开放;多样化25、知识与技能;数学思考;解决问题;情感与态度26、模仿与记忆;动手实践;自主探索;合作交流27、认知发展水平;已有的知识经验28、数学活动;师生之间;学生之间29、综合课程;均衡性;综合性;选择性30、现实的;有意义的;富有挑战性的31、主人;组织者;引导者;合作者32、导向;激励;评价33、能够帮助人们处理数据;推理和证明;有效地描述自然现象和社会现象34、自主学习;合作学习;探究学习35、多样化36、多元主义价值观二、判断题1.×2.×3.√4.×5.√6.√7.×8.×9.× 10.×三、问答题1、答案要点(1)多种境界探究教材;(2)多种方式呈现教材;(3)多种渠道开发教材2、答案要点所谓新课程小学数学教学设计就是指在《数学课程标准》的指导下,依据现代教育理论和教师的经验,基于对学生需求的理解,多课程性质的分析,而对教学内容、教学手段、教学方式、教学活动等进行规划安排的一种可操作的过程。
2013年下半年教师资格初中数学学科真题答案

考试时间:120 分钟考试总分:150 分1.【答案】C。
1。
2.【答案】D。
f x+f ﹣x是偶函数。
3.【答案】A。
4.【答案】B。
0 x 是驻点,但不是极值点。
5.【答案】D。
7.【答案】C。
①③④⑤。
8.【答案】C。
孙思邈。
12.【参考答案】解析:“四基”的内容是:数学的基础知识、基本技能、基本思想、基本活动经验。
基础知识一般是指数学课程中所涉及的基本概念、基本性质、基本法则、基本公式等。
比如,说明1/4,0.25 和25%的含义。
分数、小数和百分数是重要的数概念,它们有本身的特征,又有密切的联系。
真分数通常表示部分与整体的关系,所以理解什么是1/4,一定要知道是哪个整体的,如全班同学人数的1/4。
全班同学是40 人,其1/4 就是10 人,全班同学是32 人,其1/4 就是8 人。
小数通常表示具体的数量,如一支铅笔0.25 元,书桌的宽度是0.45 米。
百分数是同分母(统一标准)的比值,便于比较,如去年比前年增长21%,今年比去年增长25%。
基本技能内容包括基本的运算、测量、绘图等技能。
如20 以内加减法和表内乘法,每分钟完成8~10 题。
这一要求可以看作是一个参照,大多数学生经过一定的训练完全可以达到,不排除一些学生经过一段时间才能达到这一要求,也会有相当一些学生要高于这一要求。
这一要求可以成为平时考查学生的参考,也可以作为测验和考试的参考。
数学基本思想主要是指数学抽象的思想、数学推理的思想和数学模型的思想。
比如,数概念的形成与发展是数与代数中的重要内容,从整数、小数、分数到有理数的学习,是一个从具体事物和数量抽象为数的过程,是抽象水平不断提高的过程。
教学中应当结合具体教学内容的学习,把抽象的思想体现在教学活动之中,培养学生的抽象思维能力。
比如,最简单的10 以内数的认识,其中就蕴含了深刻的抽象的过程和抽象的思想。
数学基本活动经验的积累要和过程性目标建立联系。
如《标准(2011 年版)》规定,“经历数与代数的抽象、运算与建模等过程,掌握数与代数的基础知识和基本技能;经历图形的抽象、分类、性质探讨、运动、位置确定等过程,掌握图形与几何的基础知识和基本技能;经历在实际问题中收集和处理数据、利用数据分析问题、获取信息的过程,掌握统计与概率的基础知识和基本技能。
南京市六城区教师编制数学专业试题
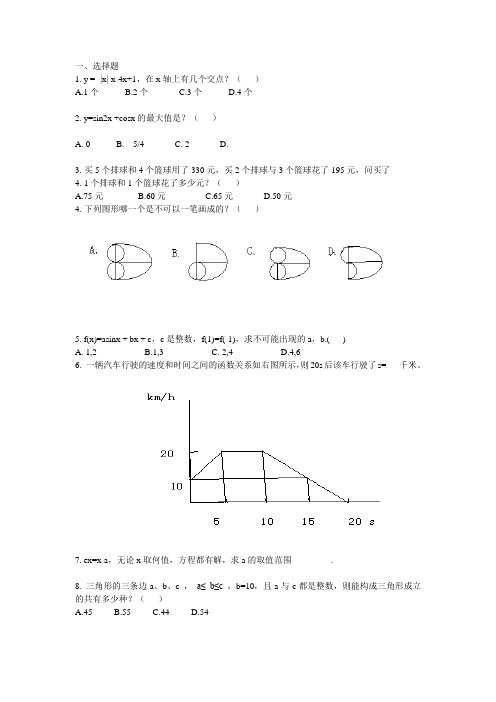
1. y = -|x|·x-4x+1,在x轴上有几个交点?()A.1个B.2个C.3个D.4个2. y=sin2x +cosx的最大值是?()A. 0B. 5/4C. 2D.3.买5个排球和4个篮球用了330元,买2个排球与3个篮球花了195元,问买了4.1个排球和1个篮球花了多少元?()A.75元B.60元C.65元D.50元4.下列图形哪一个是不可以一笔画成的?()5. f(x)=asinx + bx + c,c是整数,f(1)=f(-1),求不可能出现的a,b.( )A. 1,2B.1,3C. 2,4D.4,66. 一辆汽车行驶的速度和时间之间的函数关系如右图所示,则20s后该车行驶了s=___千米。
7. ex=x-a,无论x取何值,方程都有解,求a的取值范围_________.8. 三角形的三条边a、b、c ,a≤ b≤c ,b=10,且a与c都是整数,则能构成三角形成立的共有多少种?()A.45B.55C.44D.541. 已知正方体ABCD-A1B1C1D1,EF分别是CD,CB的中点,求AD1与EF的夹角为____.2. 直线方程为(2m+1)x+(m+1)y = 7m+4,随m的变化,直线恒过点_________ .3. 在△ABC中,AD⊥BC,求△ABC为等腰三角形,从下列选项任选一个条件可证明得到△ABC为等腰三角形的选项为_________.①∠BAD=∠DAC② BC=2BD③ AB+BD=AC+CD④点D到AB、AC的距离相等4. 已知{an}为等比数列,|q|< 1 ,bn=an+2,bn连续4个数{-52,-22,20,38,83},求q =_____.5. x2-2nx+m2=0,要使方程有实根,m,n在0,1,2,3中任取一个数,使方程有实根的概率是多少________.。
2013年江苏卷数学试题及答案

又AF⊂平面SAB,AF⊥SB,
所以AF⊥平面SBC.
因为BC⊂平面SBC,所以AF⊥BC.
又因为AB⊥BC,AF∩AB=A,AF,AB⊂平面SAB,所以BC⊥平面SAB.
因为SA⊂平面SAB,所以BC⊥SA.
17.如图1-3,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4.设圆C的半径为1,圆心在l上.
(1)若f(x)在(1,+∞)上是单调减函数,且g(x)在(1,+∞)上有最小值,求a的取值范围;
(2)若g(x)在(-1,+∞)上是单调增函数,试求f(x)的零点个数,并证明你的结论.
20.解:(1)令f′(x)= -a= <0,考虑到f(x)的定义域为(0,+∞),故a>0,进而解得x>a-1,即f(x)在(a-1,+∞)上是单调减函数.同理,f(x)在(0,a-1)上是单调增函数.由于f(x)在(1,+∞)上是单调减函数,故(1,+∞)⊆(a-1,+∞),从而a-1≤1,即a≥1.令g′(x)=ex-a=0,得x=lna.当x<lna时,g′(x)<0;当x>lna时,g′(x)>0.又g(x)在(1,+∞)上有最小值,所以lna>1,即a>e.
2013·江苏卷(数学)
1.函数y=3sin 的最小正周期为________.
1.π[解析]周期为T= =π.
2.设z=(2-i)2(i为虚数单位),则复数z的模为________.
2.5[解析]因为z=(2-i)2=4-4i+i2=3-4i,所以复数z的模为5.
3.双曲线 - =1的两条渐近线的方程为________.
13.-1, [解析]由题意知,若a<0,则a=-1满足题意;若a>0,则圆(x-a)2+(y-a)2=8与y= (x>0)相切.联立方程,消去y得
2013年高考江苏数学试题及答案(word解析版)

2014年普通高等学校招生全国统一考试(江苏卷)数学Ⅰ一、填空题:本大题共14小题,每小题5分,共计70分. 请把答案填写在答题卡相应位置上......... (1)【2014年江苏,1,5分】函数3sin(2)4y x π=-的最小正周期为_______.【答案】π【解析】函数π3sin 24y x ⎛⎫=+ ⎪⎝⎭的最小正周期2ππ2T ==.(2)【2014年江苏,2,5分】设2(2i)z =-(i 为虚数单位),则复数z 的模为_______. 【答案】5【解析】()222i 44i i 3i 54z =--+-====.(3)【2014年江苏,3,5分】双曲线221169x y -=的两条渐近线的方程为_______.【答案】34y x =±【解析】由题意可知所求双曲线的渐近线方程为34y x =±.(4)【2014年江苏,4,5分】集合{}1,0,1-共有 _______个子集. 【答案】8【解析】由于集合{}1,0,1-有3个元素,故其子集个数为328=.(5)【2014年江苏,5,5分】右图是一个算法的流程图,则输出的n 的值是_______. 【答案】3【解析】第一次循环后:82a n ←←,;第二次循环后:263a n ←←,;由于2620>,跳出循环,输出3n =.(6)【的那位运动员成绩的方差为 .【答案】2【解析】由题中数据可得=90x 甲,=90x 乙.()()()()()22222287909190909089909015394s -+-+-⎡⎤=⎣+-+-⎦=甲,()()()()()22222289909090919088909015292s -+-+-⎡⎤=⎣+-+-⎦=乙,由22>s s 甲乙,可知乙运动员成绩稳定.故应填2.(7)【2014年江苏,7,5分】现有某类病毒记作m n X Y ,其中正整数,(7,9)m n m n ≤≤可以任意选取,则,m n 都取到奇数的概率为________.【答案】2063【解析】由题意知m 的可能取值为1,2,3,…,7;n 的可能取值为1,2,3,…,9.由于是任取m ,n :若1m =时,n 可取1,2,3,…,9,共9种情况;同理m 取2,3,…,7时,n 也各有9种情况,故m ,n 的取值情况共有7963⨯=种.若m ,n 都取奇数,则m 的取值为1,3,5,7,n 的取值为1,3,5,7,9,因此满足条件的情形有4×5=20种.故所求概率为2063.(8)【2014年江苏,8,5分】如图,在三棱柱111A B C ABC -中,,,D E F 分别是1,,AB AC AA 的中点,设三棱锥F ADE -的体积为1V ,三棱柱111A B C ABC -的体积为2V ,则12:V V =_______. 【答案】1:24【解析】由题意可知点F 到面ABC 的距离与点1A 到面ABC 的距离之比为1:2,1:4ADE ABC S S =:.因此12131:242AED ABCAF S AF S V V ∆∆=⋅=⋅:. (9)【2014年江苏,9,5分】抛物线2y x =在1x =处的切线与两坐标轴围成三角形区域为D (包含三角形内部和边界).若点(,)P x y 是区域D 内的任意一点,则2x y +的取值范围是________.【答案】12,2⎡⎤-⎢⎥⎣⎦【解析】由题意可知抛物线2y x =在1x =处的切线方程为21y x =-.该切线与两坐标轴围成的区域如图中阴影部分所示:当直线20x y +=平移到过点1,02A ⎛⎫⎪⎝⎭时,2x y +取得最大值12.当直线20x y +=平移到过点1(0)B -,时,2x y +取得最小值2-. 因此所求的2x y +的取值范围为12,2⎡⎤-⎢⎥⎣⎦.(10)【2014年江苏,10,5分】设,D E 分别是ABC ∆的边,AB BC 上的点,12AD AB =,23BE BC =,若12DE AB AC λλ=+(12,λλ为实数),则12λλ+的值为________.【答案】12【解析】由题意作图如图.∵在ABC ∆中,1223DE DB BE AB BC =+=+12()23AB AC AB =+-121263AB AC AB AC λλ=-+=+,∴116λ=-,223λ=.故1212λλ+=.(11)【2014年江苏,11,5分】已知()f x 是定义在R 上的奇函数.当0x >时,2()4f x x x =-,则不等式()f x x >的解集用区间表示为________. 【答案】5,0)5()(∞-,+【解析】∵函数()f x 为奇函数,且0x >时,()24f x x x =-,则()22400040f x x x x x x x x =⎧->⎪=⎨⎪--<⎩∴原不等式等价于204x x x x >⎧⎨->⎩或204x x x x <⎧⎨-->⎩,由此可解得5x >或50x -<<. (12)【2014年江苏,12,5分】在平面直角坐标系xOy 中,椭圆C 的标准方程为22221(0,0)x y a b a b+=>>,右焦点为F ,右准线为l ,短轴的一个端点为B ,设原点到直线BF 的距离为1d ,F 到l 的距离为2d .若21d =,则椭圆的离心率为________.【解析】设椭圆C 的半焦距为c ,由题意可设直线BF 的方程为=1x yc b+,即0bx cy bc +-=.于是可知1bc d a ==,22222a a c b d c c c c -=-==.∵21d =,∴2b c =,即2ab =.∴()22246a a c c -=.∴42610e e +-=.∴213e =.∴e(13)【2014年江苏,13,5分】平面直角坐标系xOy 中,设定点(,)A a a ,P 是函数1(0)y x x=>图像上一动点,若点,P A 之间最短距离为a 的所有值为________.【答案】1-【解析】设P 点的坐标为1,x x ⎛⎫⎪⎝⎭,则222222111()=2=2x a a x a x a x x A x P ⎛⎫⎛⎫⎛⎫-+-+-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=.令12t x x =+≥,则()()2222222222PA t at a t a a t =-+-=-+-≥.结合题意可知(1)当2a ≤,2t =时,2PA 取得最小 值.此时()22228a a -+-=,解得1a =-,3a =(舍去).(2)当2a >,t a =时,2PA 取得最小值.此时228a -=,解得a =a =(舍去).故满足条件的实数a 1-.(14)【2014年江苏,14,5分】在正项等比数列{}n a 中,512a =,673a a +=.则满足123123......n n a a a a a a a a ++++>的最大正整数n 的值为_______. 【答案】12【解析】设正项等比数列{}n a 的公比为q ,则由()26753a a a q q +=+=可得2q =,于是62n n a -=,则1251(12)13221232n n n a a a --=-+=-++⋯.∵512a =,2q =,∴61a =, 111210261a a a a a ==⋯==.∴12111a a a ⋯=.当n 取12时,7612121211121213222a a a a a a a a ++⋯+=->⋯==成立;当n 取13时,86713121312111213121322132·22a a a a a a a a a a ++⋯+=-⋯===<.当13n >时,随着n 增大12n a a a ++⋯+将恒小于12n a a a ⋯.因此所求n 的最大值为12.二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内........作答,解答时应写出必要的文字说明、证明过程或演算步骤.(15)【2014年江苏,15,14分】已知()cos sin a αα=,,()cos sin b ββ=,,0βαπ<<<. (1)若2a b -=,求证:a b ⊥;(2)设()01c ,=,若a b c +=,求α,β的值. 解:(1)解法一:由||2a b -=,得:22||()2a b a b -=-=,即2222a a b b -⋅+=.又2222||||1a b a b ====, 所以222a b -⋅=,0a b ⋅=,故a b ⊥.解法二:(cos cos ,sin sin )a b αβαβ-=--,由||2a b -=,得:22||()2a b a b -=-=,即:22(cos cos )(sin sin )2αβαβ-+-=,化简,得:2(cos cos sin sin )0αβαβ+-=, cos cos sin sin 0a b αβαβ⋅=+-=,所以a b ⊥.(2)(cos cos ,sin sin )a b αβαβ+=++,可得:cos cos 0(1)sin sin 1(2)αβαβ+=⎧⎨+=⎩ 解法一:0(3)1(4),可得:2π=.代入(46π.ABC 中,平面AS AB =.过A 作AF SB ⊥,垂足为F ,点E ,G 分别是侧棱SA ,SC 的中点.求证:(1)平面EFG //平面ABC ; (2)BC SA ⊥. 解:(1)因为AS AB =,AF SB ⊥于F ,所以F 是SB 的中点.又E 是SA 的中点,所以//EF AB .因为EF ⊄平面ABC ,AB ⊂平面ABC ,所以//EF 平面ABC .同理可证//EG 平面ABC .又EF EG E =,所以平面//EFG 平面ABC .(2)因为平面SAB ⊥平面SBC 于SB ,又AF ⊂平面SAB ,AF SB ⊥,所以AF ⊥平面SBC .因为BC ⊂平面SBC ,所以AF BC ⊥.又因为AB BC⊥,AF AB A =,AF AB ⊂、平面SAB ,所以BC ⊥平面SAB .又因为SA ⊂平面SAB ,所以BC SA ⊥.(17)【2014年江苏,17,14分】如图,在平面直角坐标系xOy 中,点()03A ,,直线24l y x =-:.设圆的半径为1,圆心在l 上.(1)若圆心C 也在直线1y x =-上,过点A 作圆C 的切线,求切线的方程; (2)若圆C 上存在点M ,使2MA MO =,求圆心C 的横坐标a 的取值范围. 解:(1)由题设,圆心C 是直线24y x =-和1y x =-的交点,解得点2(3)C ,,于是切线的斜率必存在.设过3(0)A ,的圆C 的切线方程为3y kx =+1=,解得0k =或34-, 故所求切线方程为3y =或34120x y +-=.(2)因为圆心在直线24y x =-上,所以圆C 的方程为()()22221x a y a -+--⎤⎣⎦=⎡.设点()M x y ,, 因为2MA MO =22230x y y ++-=,即()2214x y ++=, 所以点M 在以1(0)D -,为圆心,2为半径的圆上.由题意,点()M x y ,在圆C 上,所以圆C 与圆D 有 公共点,则2121CD -≤≤+,即13≤.由251280a a -+≥,得R a ∈;由25120a a -≤,得0125a ≤≤.所以点C 的横坐标a 的取值范围为120,5⎡⎤⎢⎥⎣⎦. (18)【2014年江苏,18,16分】如图,游客从某旅游景区的景点处下山至C 处有两种路径. 一种是从沿A 直线步行到C ,另一种是先从A 沿索道乘缆车到B ,然后从B 沿直线步行到 C .现有甲、乙两位游客从A 处下山,甲沿AC 匀速步行,速度为50m/min .在甲出发2min 后,乙从A 乘缆车到B ,在B 处停留1min 后,再从B 匀速步行到C .假设缆车匀速直线运动的速度为130m/min ,山路AC 长为1260m ,经测量,12cos 13A =,3cos 5C =.(1)求索道AB 的长;(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?(3)为使两位游客在C 处相互等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?.解:(1)在ABC ∆中,因为3os 1c 12A =,cos 35C =,所以sin 513A =,sin 45C =.从而()()sin sin sin sin cos cos sin 531246313513565B AC A C A C A C π=-+=+=+⨯⨯⨯==⎡⎤⎣⎦. 由正弦定理sin sin AB ACC B=,得12604sin 104063sin 565AC AB C B =⨯=⨯=.所以索道AB 的长为1040 m . (2)假设乙出发t min 后,甲、乙两游客距离为d ,此时,甲行走了()10050 m t +,乙距离A 处130m t ,所以由余弦定理得()()()()2222121005013021301005020037705013d t t t t t t =++-⨯⨯+⨯=-+, 因10430001t ≤≤,即08t ≤≤,故当3537t =(min)时,甲、乙两游客距离最短. (3)由正弦定理sin sin BC ACA B=,得12605sin 500m 63sin 1365AC BC A B =⨯=⨯=. 乙从B 出发时,甲已走了()50281550⨯++=(m),还需走710 m 才能到达C .设乙步行的速度为v m/min ,由题意得5007103350v -≤-≤,解得12506254314v ≤≤,所以为使两位游客在C 处互相等待的时间不超过3min ,乙步行的速度应控制在1250625,4314⎡⎤⎢⎥⎣⎦(单位:m/min)范围内. (19)【2014年江苏,19,16分】设{}n a 是首项为a ,公差为d 的等差数列()0d ≠,n S 是其前n 项和.记2n n nSb n c=+,N n *∈,其中c 为实数.(1)若0c =,且1b ,2b ,4b 成等比数列,证明:()2N nk k S n S k,n *=∈;(2)若{}n b 是等差数列,证明:0c =. 解:由题设,(1)2n n n S na d -=+. (1)由0c =,得12n n S n b a d n -==+.又因为124b b b ,,成等比数列,所以1224b b b =,即23=22d a a a d ⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭, 化简得220d ad -=.因为0d ≠,所以2d a =.因此,对于所有的*N m ∈,有2m S m a =.从而对于所有的k ,*N n ∈,有()2222nk k S nk a n k a n S ===. (2)设数列{}n b 的公差是1d ,则()111n b b n d =+-,即()1121nb n nS n cd =+-+,*N n ∈,代入n S 的表达式,整理 得,对于所有的*N n ∈,有()111321111122d d n b d a d n cd n c d b ⎛⎫⎛⎫-+--++ ⎪ =⎪⎭⎭-⎝⎝.令112A d d =-,1112B d d b a =--+,()11D c d b =-,则对于所有的*N n ∈,有321An Bn cd n D ++=.(*)在(*)式中分别取1234n =,,,,得1111842279364164A B cd A B cd A B cd A B cd ++=++=++=++, 从而有11173019502150A B cd A B cd A B cd ++=⎧⎪++=⎨⎪++=⎩①②③,由②,③得0A =,15cd B =-,代入方程①,得0B =,从而10cd =.即1102d d -=,11102b d a d -+=-=0,10cd =.若d 1=0,则由1102d d -=,得0d =,与题设矛盾,所以10d ≠.又因为10cd =,所以0c =.(20)【2014年江苏,20,16分】设函数()ln f x x ax =-,()x g x e ax =-,其中a 为实数. (1)若()f x 在()1,+∞上是单调减函数,且()g x 在()1,+∞上有最小值,求a 的范围; (2)若()g x 在()1,-+∞上是单调增函数,试求()f x 的零点个数,并证明你的结论. 解:(1)令f ′(x )=()110axf x a x x-'=-=<,考虑到()f x 的定义域为(0)+∞,,故0a >,进而解得1x a ->,即()f x 在1()a -+∞,上是单调减函数.同理,()f x 在1(0)a -,上是单调增函数.由于()f x 在(1)+∞,上是单调减函数,故1()(1)a -∞∞⊆++,,,从而11a -≤,即1a ≥.令()0x g x e a '=-=,得ln x a =.当ln x a <时,()0g x '<;当ln x a >时,()0g x '>.又()g x 在(1)+∞,上有最小值,所以ln 1a >,即a e >.综上,有()a e ∈+∞,.(2)当0a ≤时,()g x 必为单调增函数;当0a >时,令()0x g x e a '=->,解得x a e <,即ln x a >.因为()g x 在()1-+∞,上是单调增函数,类似(1)有ln 1a ≤-,即10a e -<≤.结合上述两种情况,有1a e -≤. ①当0a =时,由()10f =以及()10f x x'=>,得()f x 存在唯一的零点; ②当0a <时,由于()()10a a a f e a ae a e =-=-<,()10f a =->,且函数()f x 在[1]a e ,上的图象不间断, 所以()f x 在(1)a e ,上存在零点.另外,当0x >时,()10f x a x'=->,故()f x 在(0)+∞,上是单调增 函数,所以f (x )只有一个零点.③当10a e -<≤时,令()10f x a x'=-=,解得1x a -=.当10x a -<<时,()0f x '>,当1x a ->时,()0f x '<,所以,1x a -=是()f x 的最大值点,且最大值为()1ln 1f a a -=--.当ln 10a --=,即1a e -=时,()f x 有一个零点x e =.当ln 10a -->,即10a e -<<时,()f x 有两个零点.实际上,对于10a e -<<,由于()1110f e ae --=--<,()10f a ->,且函数()f x 在11[]e a --,上的图象不间断,所以()f x 在11()e a --,上存在零点.另外,当1()0x a -∈,时, ()10a xf x =->',故()f x 在1(0)a -,上是单调增函数,所以()f x 在1(0)a -,上只有一个零点.下面考虑()f x 在1()a -+∞,上的情况.先证()()1210a a f e a a e ---=-<.为此,我们要证明:当x e >时,2x e x >.设()2x h x e x =-,则()2x h x e x '=-,再设()()2x l x h x e x ='=-,则()2x l x e '=-.当1x >时,()220x l x e e '=->->,所以()()l x h x ='在(1)+∞,上是单调增函数.故当2x >时,()()22240x h x e x h e '=->'=->,从而()h x 在(2)+∞,上是单调增函数,进而当x e >时,()()220x e h x e x h e e e =->=->.即当x e >时,2x e x >.当10a e -<<,即1a e ->时,()()111210a a a f e a ae a a e -----=-=-<,又()10f a ->,且函数()f x 在11[]a a e --,上的图象不间断,所以()f x 在11()a a e --,上存在零点.又当1x a ->时,()0f x a '=-<,故()f x 在(a -1,+∞)上是单调减函数,所以f (x )在(a -1,+∞)上只有一个零点.综合①,②,③,当0a ≤或1a e -=时,()f x 的零点个数为1,当10a e -<<时,()f x 的零点个数为2.数学Ⅱ【选做】本题包括A 、B 、C 、D 四小题,请选定其中两题......,并在相应的答题区域内作答............,若多做,则按作答 的前两题评分.解答时应写出文字说明、证明过程或演算步骤. (21-A )【2014年江苏,21-A ,10分】(选修4-1:几何证明选讲)如图,AB 和BC 分别与圆O 相切于点D C AC 、,经过圆心O ,且2BC OC =.求证:2AC AD =.解:连结OD .因为AB 和BC 分别与圆O 相切于点D ,C ,所以90ADO ACB ∠=∠=︒.又因为A A ∠=∠,所以Rt Rt ADO ACB ∆∆∽.所以BC ACOD AD=. 又22BC OC OD ==,故2AC AD =. (21-B )【2014年江苏,21-B ,10分】(选修4-2:矩阵与变换)已知矩阵1012,0206-⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦A B ,求矩阵1-A B . 解:设矩阵A 的逆矩阵为 a b c d ⎡⎤⎢⎥⎣⎦,则 1 00 2-⎡⎤⎢⎥⎣⎦ a b c d ⎡⎤⎢⎥⎣⎦=1 00 1⎡⎤⎢⎥⎣⎦,即 2 2a b c d --⎡⎤⎢⎥⎣⎦=1 00 1⎡⎤⎢⎥⎣⎦,故100a b c =-==,,,12d =,从而A 的逆矩阵为1 1 010 2--⎡⎤⎢⎥⎢⎥⎣⎦=A ,所以1 1 010 2--⎡⎤⎢⎥⎢⎥⎣=⎦A B 1 20 6⎡⎤⎢⎥⎣⎦= 1 20 3--⎡⎤⎢⎥⎣⎦. (21-C )【2014年江苏,21-C ,10分】(选修4-4:坐标系与参数方程)在平面直角坐标系xoy 中,直线l 的参数方程为12x t y t =+⎧⎨=⎩(t 为参数),曲线C 的参数方程为22tan 2tan x y θθ⎧=⎨=⎩(θ为参数).试求直线l 和曲线C 的普通方程,并求出它们的公共点的坐标.解:因为直线l 的参数方程为12x t y t =+⎧⎨=⎩(t 为参数),由1x t =+得1t x =-,代入2y t =,得到直线l 的普通方程为220x y --=.同理得到曲线C 的普通方程为22y x =.联立2212y x y x =(-)⎧⎨=⎩,解得公共点的坐标为(2)2,,1,12⎛⎫- ⎪⎝⎭. (21-D )【2014年江苏,21-D ,10分】(选修4-4:不等式选讲)已知0a b ≥>,求证:332222a b ab a b -≥-. 解:()()()()()()()()332222222222222a b ab a b a a b b a b a b a b a b a b a b ---=-+-=-+=-++.因为0a b ≥>,所以0a b -≥,0a b +>,20a b +>,从而()()()20a b a b a b -++≥,即332222a b ab a b -≥-. 【必做】第22、23题,每小题10分,计20分.请把答案写在答题卡的指定区域内............ (22)【2014年江苏,22,10分】如图,在直三棱柱111A B C ABC -中,AB AC ⊥,2AB AC ==,14AA =,点D 是BC 的中点.(1)求异面直线1A B 与1C D 所成角的余弦值;(2)求平面1ADC 与平面1ABA 所成二面角的正弦值. 解:(1)以A 为坐标原点,建立如图所示的空间直角坐标系A xyz -,则()000A ,,,()200B ,,,()020C ,,()110D ,,,14(0)0A ,,,14(0)2C ,,,所以1(20)4A B =-,,,1(11)4C D =--,,.因为111111cos ,20A B C D A B C D A B C D⋅===,所以异面直线1A B 与1C D .(2)设平面1ADC 的法向量为1()n x y z =,,,因为(1)10AD =,,,10()24AC =,,,所以10n AD ⋅=,110n AC ⋅=,即0x y +=且20y z +=,取1z =,得2x =,2y =-,所以,12()21n =-,,是平面1ADC 的一个法向量.取平面1AA B 的一个法向量为2(010)n =,,,设平面1ADC 与平面 1ABA所成二面角的大小为θ.由12122||||s 3co θ⋅===n n n n ,得sin θ=.因此,平面1ADC 与平面1ABA .,11(1),(1)k k k k k ----个,…n a ++(n ∈.对于l N *∈,定义(1)求11中元素个数; (2)求集合2000P 中元素个数.解:(1)由数列{}n a 的定义得123456789101223334444a a a a a a a a a a ==-=-====-=-=-=-,,,,,,,,,,,115a =,1234567891011113036226105S S S S S S S S S S S ∴==-=-=====-=-=-=-,,,,,,,,,,,从而11445566111102S a S a S a S a S a ==⨯===-,,,,,所以集合11P 中元素的个数为5. (2)先证:()()*2121()i i S i i i +=-+∈N .①当1i =时,()3213i i S S +==-,()213i i -+=-,故原等式成立; ②假设i m =时成立,即()()2121m m S m m +=-+,则1i m =+时,()()()()()()()()22222(113)21222143253123m m m m S S m m m m m m m m m +++=++-+=-+--=-++=-++.综合①②可得()()2121i i S i i +=-+.于是()()()()()()()2(221121)212121211i i i i S S i i i i i i +++=++=-+++=++. 由上可知()21i i S +是21i +的倍数,而()21(211221)i i j a i j i ++=+=⋯+,,,,所以()()(212)121i i i i j S S j i +++=++是 ()211)2(21i i j a j i ++=⋯+,,,的倍数.又()()()()121121i i S i i ++=++不是22i +的倍数,而()()()12122i i j a i +++=-+()1222j i =⋯+,,,,所以()()()()()()()()1211212221122i i j i i S S j i i i j i +++++=-+=++-+不是()()121i i j a +++ 122()2j i =⋯+,,,的倍数,故当()21l i i =+时,集合l P 中元素的个数为()21321i i ++⋯+-=,于是,当()()21121l i i j j i =++≤≤+时,集合l P 中元素的个数为2i j +. 又()200031231147=⨯⨯++,故集合2000P 中元素的个数为231471008+=.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
行为受到师生的一致好评,请你谈谈对这一行为的认识 一所小学的某个班级以: (不记得了)为班级公约,问: 1.这则公约有什么特点;2.制定 班级公约有什么需要注意的 南京有一所学校开设“玩”课,就是让孩子到南京各个景点去玩,请分析该校开设该课 程的目的,并谈谈开发校本课程对促进学校发展的意义。
3
专业知识(数学)
5
C(a,a) ,问 a 取何值时 ABC 周长最小?
B.如果数学家中有诗人,则诗人中也有数学家 C.诗人中年龄最大的数学家就是数学家中年龄最大的诗人 D.数学家中的诗人的人数少于诗人中数学家的人数 8. 下列选项中哪一组选项中的动词是体现三维目标中过程方法的? A 了解 理解 探索 四、教案书写 1.中学:必修四 任意角三角函数 2. 小学:五年级下册 分数的基本性质 B 经历 感受 探索
一.综合题 1. 已知数列 an : a, aq, aq 2 ,
, aq n1 ,
(1)求 a n 的前 n 项和 S n (2)用两种方法证明 S n
x2 y2 2. 在椭圆 1 上有一动点 , P , F 为椭圆的右焦点, 9 5
另有一定点 A (1,1)
y
3 (1)求 PA PF 的最小值,及 P 点的坐标 2
3.我国的国家元首是( A.军委主席
B.党的总书记 )测试
4.大学英语四级是( A.学能测验
B.成就测验
C.常模参照性
D.标准参照性
5.马铃薯的食用部分是() A.种子 B.茎 C.根 D.果实
6.孙中山先生的三民主义是指() A. 民主、民权、民生 C. 7.一幅图,问是什么技术 B.民族、民权、民生 D.
2013 年南京六城区中小学教师招聘考试 公共知识
一、选择题(15 题,每题 2 分) 1.6 月 24 日神舟( )号与天宫一号成功手动对接。 A.七 B.八 C.九 D.十
2.党的十八大,我党将( )加入建设社会主义现代化建设 A. 物质文明 B.精神文明 ) C. 国家主席 D.国家总理 C.政治文明 D.生态文明
A.
B.
C. 活字印刷术
D.雕版印刷术
8. 美 国 一 所 小 学 提 倡 “ I hear and I forget,I see and I remember,I do and I understand.”体现的是( )
1
A. 重视儿童的听觉活动 C. 重视儿童的情感活动 9.白色污染是( A. B. )
6
答案解析 公共知识
选择题解析: 1.选 C 2.选 D 3.选 C 4.选 D 【解析】标准参照评价是在被评价的集合之外确定一个标准,这个标准被称为客观标准。 大学英语四级考试是在被评价的集合之一确定的一个标准分数。 5.选 B 6.选 A 7.选 D 8.选 D 9.选 D 10.选 A 【解析】教材是依照课程标准编制、系统反映学科内容的教学用书。 11.选 D 12.选 A 【解析】所谓教学反思,是指教师对教育教学实践的再认识、再思考,并以此来总结经 验教训,进一步提高教育教学水平。教学反思一直以来是教师提高个人业务水平的一种有效 手段,教育上有成就的大家一直非常重视之。现在很多教师会从自己的教育实践中来反观自 己的得失,通过教育案例、教育故事、或教育心得等来提高教学反思的质量。 13.选 A 14.题目不完整,无答案 15.选 B 二、判断题解析
9
根据等比数列的通项公式 an a1q n1 ,则 Sn a1 a1q a1q 2 a1q n1 当 q =1 时, Sn na1 对①式等号两边同乘以 q 可得:
①
qSn a1q 3.朱自清的《背影》一文叙述的是发生在南京( A. 浦口 B.下关 C.中华门 ) D.
D.中央门
14.“化作春泥更护花”一诗体现了( A. 自然界的物质循环 B. C.
15. 一个棱长为 3 的正方体,将它的 6 个面涂上颜色,再分割成棱长为 1 的小正方体, 问只有一个面有颜色的正方体有( A. 0 B.6 )个 D.18
专业知识(数学)
一、综合题。 1. (1)解:由题目已知条件可知: an a1q n1 ,则数列 an 为等比数列,
a1 (1 q n ) (q 1) 因此 an 的前 n 项和 S n 1 q na (q 1) 1
(2)证明: 方法一 数列 an 的前 n 项和是: Sn a1 a2 a3 an
②
y
a a1q n 当 q 1 时,①-②得: (1 q) Sn a1 a1q n ,则 Sn 1 1 q
a1 (1 q n ) (q 1) 综上所述: S n 1 q na (q 1) 1
B.重视儿童的视觉活动 D.重视儿童的操作活动
C.废纸
D.塑料垃圾
10.教材是依据( )制定的 A. 课程标准 11.纳米是( A. 重量单位 B. ) B.面积单位 C.体积单位 D.长度单位 C. D.
12.教师将教学过程中的一些体会和细节写下来,供大家课后反思,改进教学的方式是 ( ) A.教学反思 B. C. D. )车站
C. 12
二、判断题(5 题,每题 1 分) 国家提倡素质教育是为了提高国民素质 国家课程具有规定性和强制性 班主任规定对迟到的学生处以 5 元的罚款,这一行为是违规而不是违法的 将学生的成长有关的信息资料统一收集作为评价的资料,是档案袋评价法 老师的一句鼓励,一个眼神使得学生学习更加努力,导致这种行为教育学上称为移情作 用 三、简答题(3 题,共 25 分) 一所施行小班化教学的小学,实施两只红笔的教学活动,教师带一只红笔进入课堂,当 堂批改学生的练习,学生带一只红笔进入课堂,对于老师改过的题目一律用红笔订正,这种
8
督促、相互教育,促使学生逐步由“他律”转变为“自律” ,提高学生遵纪守法的自觉性。 3.【解析】该校开设该课程的目的是推动校本课程的开发。校本课程有别于国家课程, 它更能凸显学校的办学理念,彰显学校的个性。更能突出学生的自主性、自愿性和灵活性。 它对培养学生的个性特长、创新思维和实践能力,培养学生分析和解决问题的能力,团结协 作的能力、社会活动能力,具有十分重要的意义。有利于学校更好的适应市场的需求,教育 是一项基础性投资的概念以被多数家长所接受。家长择校一方面受高考驱动,另一方面也在 为孩子选择一个合适的教育环境。在城市和发达的乡村,如今受教育但更要享受优质的教育 已成为普遍的教育需求。公立学校如果抱残守缺,裹足不前,很容易失去“市场的份额” 。校 本课程开发强调自主决策、自主开发,特别有利于公立学校提高其教育品质,更好地适应市 场的需求,并逐步提升自己在市场中的位置。 有利于形成学校特色, 校本课程开发强调学校利用自身的资源、自主规划、自我负责。 这十分有利于学校发挥各自的优势,形成自己的特色。过去,我们总是批判我国的学校“千 校一面” ,而如今,只要去一些实施校本课程开发的学校看看,我们便会感叹那里的“绝”和 “独” 。如“和田十二创造技法” 、大同中学的“知识论”课程、华东模范中学的“双通道” 办学模式级课程设计、华东师大附一中的“跨学科系列学习主题”的设计、北京北方交大二 附中的“环保课程” 、北京十一中学的综合实践活动系列,等等。
4
C D E A O B
2. 2013 减去它的
1 1 1 ,在减去剩下的 ,再减去剩下的 ,„„,减去 2 3 4
剩下的 3.
1 后,还剩_______. 2013
数学史三大变革_________ , ____________ , ____________。
2 f ( x) 满 足 一 定 条 件 后 , 可 表 示 成 a0 a1 x a 2 x n n a x
2.若函数 f ( x) x2 2 x 8 , 问使得 f (5a 1) f (a 2 5) 恒成立的整数 a 的值有几个? 3. 已知 AB BC AD 5 , ABC 60 , DAE 75 ,求 CD 。
D 75 A
C 60 B
4. 在 1,2,3,4 中取两个数,其中一个数是另一个数的 2 倍的概率( ) 5.甲在地铁站等乙,每隔几分钟有一辆地铁过去,甲第一次等乙 12 分钟,过去了 5 辆 地铁,甲第二次等乙 20 分钟,过去了 6 辆,甲第三次等乙 30 分钟,可能过去了几辆( ) 6. A (-4,-2), B (0,2), 7. 下列说法错误的是( ) A.如果诗人中没有数学家,则数学家中也没有诗人
(2)如何引导学生对此题进行反思(怎样解题)
P A 0 F
x
3.(中学)已知函数 f ( x) x 3 3 px 2 , 有两条平行直线分别与该函数相切于 A, B 两点 (1)若在 x 1处取极值,①求 p 的值 ②若直线 AB 的斜率为 1,求 AB 所在直线方程 (2)该函数图象是中心对称图形吗?若是,求出对称中心,若不是,说明理由 (小学)已知函数 f ( x) x 3 px, 在x 1 处取极小值
7
1.正确 实施素质教育,就是全面贯彻党的教育方针,以提高国民素质为根本宗旨。 2.正确 【解析】国家课程是指国家委托有关部门或机构制定的基础教育的必修课程或称核心课 程的课程标准或大纲.国家课程体现的是国家的意志具有统一规定性和强制性。 3.错误 【解析】此行为已经违法。 “罚款要有法律依据,并且得到物价部门核准,同时还必须是 有罚款权利的部门才能实施罚款。 ”客观上,这样的罚款已经成了“以罚代管” 。教育者的出 发点肯定是好的,但是在具体的管理过程中,简单粗暴的罚款不仅没有解决迟到与缺勤的问 题,反 而让大家看到这种管理方式的无力。 4.正确 【解析】它是指教师和学生有意地将各种有关学生表现的材料收集起来,并进行合理的 分析与解释,以反映学生在学习与发展过程中的努力、进步状况或成就。 5.错误 【解析】这属于罗森塔尔效应又叫做皮革马利翁效应,即老师对学生的一种积极的心理 暗示,会使学生的信心倍增,更加努力的学习。 三、简答题 1.【解析】 “两支红笔进课堂”教师课堂内就可以及时批改学生们的习题,面批面改,及 时提供反馈给学生,提高了课堂教学的效率。学生对于老师改过的题目一律用红笔订正,体 现了学生积极主动参与评价,增强了对知识的巩固能力同时也锻炼了自我教育的能力。在整 个教学活动中,首先小班教学有利于教师因材施教,提高教学效率。而两只红笔则增加了师 生之间的交流和互动性,同时也提高的学生的参与性。 2.【解析】一、体现了民主性、目标性、制约性、公开性。 二、制定班级公约时需要注意: (一)让学生参与制定班级公约,促进学生自主管理。班 级公约是全班共同信守的制度,是班级学生活动的指南。建设良好的班风,就要制定科学、 合理、符合学生特点的班级公约。 (二)建立和健全激励机制,让学生感受成功的乐趣。1、 开展活动,分享成功乐趣。2、树立榜样,帮助后进生纠正不良习气。 (三)开展竞争,提高 学生自律意识。现代社会发展要求培养学生的竞争意识、合作精神。在班级管理过程中也可 以充分利用学习小组的优势,开展小组间的良性竞争,并通过小组间成员的相互影响、相互
