基于Hopfield神经网络识别0~9

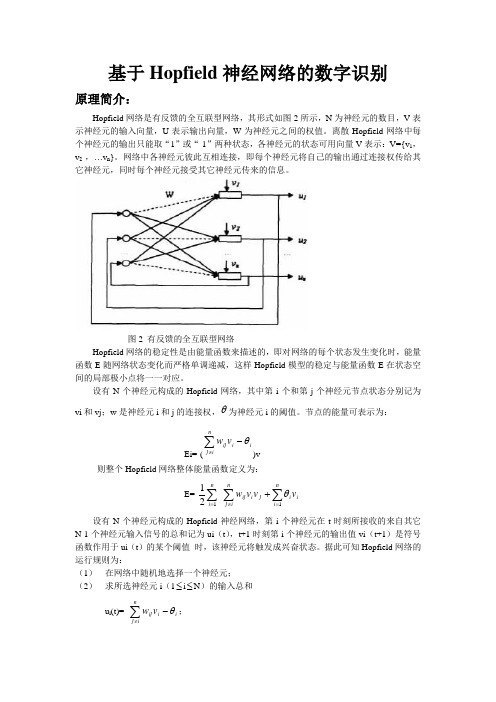
基于Hopfield 神经网络的数字识别 原理简介：
Hopfield 网络是有反馈的全互联型网络，其形式如图2所示，N 为神经元的数目，V 表示神经元的输入向量，U 表示输出向量，W 为神经元之间的权值。

离散Hopfield 网络中每个神经元的输出只能取“1”或“-1”两种状态，各神经元的状态可用向量V 表示：V={v 1，v 2 ，…v n }。

网络中各神经元彼此互相连接，即每个神经元将自己的输出通过连接权传给其它神经元，同时每个神经元接受其它神经元传来的信息。

图2 有反馈的全互联型网络
Hopfield 网络的稳定性是由能量函数来描述的，即对网络的每个状态发生变化时，能量函数E 随网络状态变化而严格单调递减，这样Hopfield 模型的稳定与能量函数E 在状态空间的局部极小点将一一对应。

设有N 个神经元构成的Hopfield 网络，其中第i 个和第j 个神经元节点状态分别记为vi 和vj ；w 是神经元i 和j 的连接权，θ为神经元i 的阈值。

节点的能量可表示为：
Ei=-(i i n i
j ij v w θ-∑≠)v 则整个Hopfield 网络整体能量函数定义为： E=-i n
i i j i n i j ij n
i v v v w ∑∑∑=≠=+1121θ 设有N 个神经元构成的Hopfield 神经网络，第i 个神经元在t 时刻所接收的来自其它N-1个神经元输入信号的总和记为ui （t ），t+1时刻第i 个神经元的输出值vi （t+1）是符号函数作用于ui （t ）的某个阈值 时，该神经元将触发成兴奋状态。

据此可知Hopfield 网络的运行规则为：
（1） 在网络中随机地选择一个神经元；
（2） 求所选神经元i （1≤i ≤N ）的输入总和
u i (t)= i i n i j ij v
w θ-∑≠；
（3） 根据u i (t)的值大小，更新神经元的状态
if （u i (t)）≥0
then v i （t+1）=1
else v i （t+1）=0；
（4） 神经元i 以外的神经元j 的状态不变化；
（5） 转向（1），直到网络达到稳定。

Hopfield 网络作为记忆的学习时，稳定状态是给定的，通过网络的学习求适合的权矩阵W （对称阵），学习完成后以计算的方式进行联想。

对给定的M 个模式，Hopfield 网络可按Hebb 规则来进行学习。

⎪⎩⎪⎨⎧≠==∑=M
k j i ij j i k v k v j i W 1
),()(,0 按上述规则求出权矩阵后，可认为网络已经将这M 个模式存入到网络的连接权中。

问题描述：
设计一个Hopfield 网络，使其具有联想记忆功能，能正确识别阿拉伯数字，当数字被噪声污染后仍可以正确地识别。

程序流程：
先设计好标准的数字点阵（本文采用10*10矩阵表示），根据这些标准的数字点阵创建并训练网络，使网络达到稳定状态，用带噪声的数字测试训练的网络。

噪声有两种形式：一种是固定噪声；另一种是随机噪声，本文对两种噪声都做讨论。

程序：
%数字0-9的标准点阵
zero=load('zero.txt');
one=load('one.txt');
two=load('two.txt');
three=load('three.txt');
four=load('four.txt');
five=load('five.txt');
six=load('six.txt');
seven=load('seven.txt');
eight=load('eight.txt');
nine=load('nine.txt');
%训练样本（目标向量）
T=[zero(:),one(:),two(:),three(:),four(:),five(:),six(:),seven(:),eight(:),nine(:)];
%输出数字0-9
figure
for ii=0:9,
subplot(2,5,ii+1);
imshow(reshape(T(:,ii+1),10,10));
title([' 当前数字：' num2str(ii)])
end
%数字带噪声数字点阵（固定法）
noise_matrix=load('noise_matrix.txt');
%数字带噪声数字点阵（随机法）
%noise_matrix=zero;
%for i=1:100
% a=rand;
% if a<0.1
% noise_matrix(i)=-zero(i);
%end
%end
figure
subplot(2,3,1)
imshow(noise_matrix);
title('带噪声的样本');
%关于hopfield网络的创建和仿真，参数形式参见Matlab的帮助
net=newhop(T);%创建hopfield网络，根据标准样本开始训练学习
No22=sim(net,{1,5},{},{noise_matrix(:)});%仿真5次，只有一个样本noise_matrix for ii=1:5
subplot(2,3,1+ii)
imshow(reshape(No22{ii},10,10));
title(['第' num2str(ii) '仿真结果'])
end
实验结果：
标准数字点阵
当前数字：0 当前数字：1 当前数字：2 当前数字：3 当前数字：4
当前数字：5 当前数字：6 当前数字：7 当前数字：8 当前数字：9
随机噪声的数字识别：（以带随机噪声的0为例）
带噪声的样本第1仿真结果第2仿真结果
第3仿真结果第4仿真结果第5仿真结果
固定噪声的数字识别：（以被污染的2为例）
带噪声的样本第1仿真结果第2仿真结果
第3仿真结果第4仿真结果第5仿真结果
结果分析：
本文对被污染的数字0-9都进行了实验，无论是带随机噪声还是固定噪声，训练过的Hopfield网络在仿真3次后都能被识别出来。

由于用来训练网络的各个样本并不是严格地正交，不符合Hopfield网络联想记忆的条件，当数字在噪声的污染下失真很严重时，Hopfield 网络识别会出现偏差。

改进方法：
当输入的训练样本不满足相互正交的条件时，可以在网络训练时，通过修改连接权值，使网络达到稳定状态，这样的话，Hopfield网络可以训练样本不是相互正交时也可以达到稳定状态，训练后的网络可以很好地识别带噪声的数字。