数学物理方法第二章

P P P
x
3
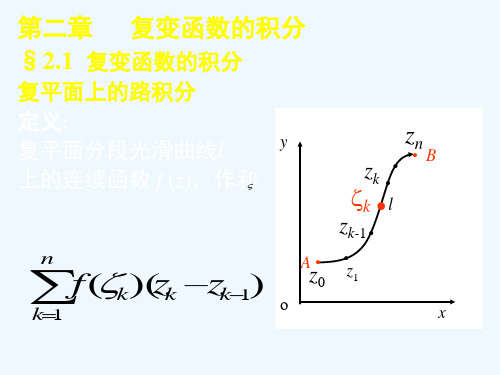
2.积分的定义:
设函数 w f ( z ) 定义在区域 D 内, C 为区域 D 内起点为 A 终点为 B的一条光滑的有向曲线 , 把曲线 C 任意分成 n 个弧段, 设分点为 A z0 , z1 , , zk 1 , zk ,, zn B ,
在每个弧段 zk 1 zk ( k 1,2,, n) 上任意取一点 k ,
C
证 设光滑曲线C由参数方程给出 z z ( t ) x( t ) i y( t ), t
正方向为参数增加的方向,
参数 及 对应于起点 A 及终点 B,
7
并且 z( t ) 0, t , 如果 f ( z ) u( x , y ) i v( x , y ) 在 D 内处处连续, 那么 u( x , y ) 和 v( x , y ) 在 D 内均为连续函数 ,
L L
常数因子可以移到积分号外
(3) f ( z ) g ( z )dz f ( z )dz g ( z )dz ;
L L L
函数的和的积分等于各函数积分之和
(4) f ( z )dz f ( z )dz f ( z )dz, 其中L是
L L1 L2
由L1和L2组成的
设 k k ik , 因为 zk zk zk 1 xk iyk ( xk 1 iyk 1 )
( xk xk 1 ) i ( yk yk 1 )
xk iyk ,
8
所以
f ( k ) zk
k 1 n k 1
i {v[ x ( t ), y( t )] x( t ) u[ x ( t ), y( t )] y( t )}dt


{u[ x( t ), y( t )] iv[ x( t ), y( t )]}{ x( t ) iy( t )}dt


f [ z( t )]z( t )dt .
0.
21
1 dz , C 为以 z0 为中心, r 为半 例4 求 n 1 C (z z ) 0 y 径的正向圆周 , n 为整数.
z
解
积分路径的参数方程为
(0 2π ),
o
0 z

r
z z0 re i
x
C
2π 1 ire i n 1 dz 0 n1 i ( n1) d ( z z0 ) r e i 2π in n e d , r 0
学习要求与内容提要
目的与要求：掌握复变函数积分的概念、柯西定理 不定 积分 柯西公式
重点： 1. 复积分的基本定理；
2. 柯西积分公式与高阶导数公式 难点： 复合闭路定理与复积分的计算
1
2.1复变函数的积分 ——复平面上的线积分
(与实函数积分相似，定义为和的极限)
1.有向曲线:
设C为平面上给定的一条光滑(或按段光滑) 曲线, 如果选定C的两个可能方向中的一个作 为正方向(或正向), 那么我们就把C理解为带 有方向的曲线, 称为有向曲线. 如果A到B作为曲线C的正向, 那么B到A就是曲线C的负向, 记为 C .
9
当 n 无限增大而弧段长度的最大值趋于零时,
不论对 C 的分法任何, 点 ( k , k ) 的取法如何, 下式两端极限存在 ,
f ( k )zk [u( k ,k )xk v( k ,k )yk ]
k 1 k 1
n
n
i [v ( k ,k )xk u( k ,k )yk ]
o
y
B
A
x
2
关于曲线方向的说明: 在今后的讨论中,常把两个端点中的一个 作为起点, 另一个作为终点, 除特殊声明外, 正方向总是指从起点到终点的方向. 简单闭曲线正向的定义:
y
简单闭曲线C的正向 P 是指当曲线上的点P顺此方 向前进时, 邻近P点的曲线 o 的内部始终位于P点的左方. 与之相反的方向就是曲线的负方向.
于是 Re z t , dz dt ,
1到1+i直线段的参数方程为 z ( t ) 1 it (0 t 1),
于是 Re z 1, dz idt ,
y
i
C
Re zdz tdt 1 idt
0 0
1
1
1 i
y x2
1 i. 2
o
1
x
20
例3 计算 z dz , 其中 C 为 : 圆周 z 2.
C
解 积分路径的参数方程为
z 2e
i
(0 2π ),
2π 0
dz 2ie d
i
C
z dz 2 2ie i d ( 因为 z 2 )
4i (cos i sin )d
0
2π
1 k n
如果不论对 C 的分法及 k 的取法如何 , Sn 有唯 一极限, 那么称这极限值为 记为
f ( k ) zk . C f ( z )dz lim n k 1
n
函数 f ( z ) 沿曲线 C 的积分,
y
A
1 2
z1 z2
k z k zk 1
C z n 1
于是 Re z t , dz (1 2ti )dt ,
C Re zdz 0 t (1 2it )dt
t 1 2 2i 3 2 3t 2 3 i; 0
2 1
i
1
y
1 i
y x2
o
1
x
19
(3) 积分路径由两段直线段构成 x轴上直线段的参数方程为 z ( t ) t (0 t 1),

12

C f ( z )dz

f [ z( t )]z( t )dt
如果 C 是由 C1 , C 2 , , C n 等光滑曲线依次 相互连接所组成的按段 光滑曲线, 则
C f ( z )dz C
1
f ( z )dz f ( z )dz f ( z )dz .
所以不论 C 是怎样从原点连接到点3 4i 的 曲线,
( 3 4i ) 2 C zdz 2 .
17
例2 计算 Re zdz , 其中 C 为 :
C
(1)从原点到点1 i 的直线段; (2) 抛物线 y x 2 上从原点到点1 i 的弧段; (3) 从原点沿 x 轴到点1 再到 1 i 的折线.
n
[u( k , k ) i v ( k , k )]( xk iyk )
[u( k ,k )xk v ( k ,k )yk ]
k 1
n
i [v ( k ,k )xk u( k ,k )yk ]
k 1
n
由于 u, v 都是连续函数, 根据线积分的存在定理,
L
全路径上的积分等于各段上积分之和
L
14
(5) f ( z )dz f ( z ) ds
注意到
dz dx idy (dx ) 2 (dy ) 2 ds
性质(5)可以写为

L
f ( z )dz f ( z ) dz
L
wenku.baidu.com
特别地，若在L上有 f ( z) M ，L的长记为L， 则性质(5)成为 (6) f ( z )dz ML
z1 z1
25
z2
z2
因此可得到复变函数的积分与路径无关的充要条件
udx vdy i vdx udy . 积分的计算法1 C C
11
积分的计算法2 函数的线 f ( z )dz 可以通过两个二元实变
C
积分来计算.
C f ( z )dz {u[ x( t ), y( t )] x( t ) v[ x( t ), y( t )] y( t )}dt
y
A
1 2
z1 z2
k z k zk 1
C z n 1
B
o
x
4
作和式 Sn f ( k ) ( zk zk 1 ) f ( k ) zk ,
k 1 k 1
n
n
这里 zk zk zk 1 , sk zk 1 zk的长度,
记 max{sk }, 当 n 无限增加且 0 时,
B
o
x
5
关于定义的说明:
(1) 如果 C 是闭曲线, 那么沿此闭曲线的积分 记为 f ( z )dz .
C
( 2) 如果 C 是 x 轴上的区间a x b, 而 f ( z ) u( x ), 这个积分定义就是一元 实变函数 定积分的定义.
6
3. 存在的条件和计算法
如果 f ( z ) 是连续函数而C 是光滑曲线时, 积分 f ( z )dz 一定存在.
n 0, n 0.
重要结论：积分值与路径圆周的中心和半径无关.
23
2.2 柯西定理
讨论复变函数积分与积分路径的关系 （一） 单通区域情形 单连通区域： 在区域中做任何简单闭合围道，围 道内的点都属于该区域 复连通区域，或称多连通区域
区别：区域中任一闭合曲线能否连续变形而缩成一 点。
连续变形：变形时曲线始终属于该区域。
k 1
n
C f ( z )dz C udx vdy iC vdx udy
10
公式
C f ( z )dz C udx vdy iC vdx udy
在形式上可以看成是
f ( z ) u iv 与 dz dx idy 相乘后求积分得到:
C f ( z )dz C (u iv )(dx idy ) udx ivdx iudy vdy C
C zdz 0 (3 4i ) tdt (3 4i ) 0 tdt
2 2
1
1
( 3 4i ) 2 . 2
又因为
C zdz C ( x iy )(dx idy )
16
C zdz C xdx ydy i C ydx xdy
这两个积分都与路线C 无关
解 (1) 积分路径的参数方程为
z ( t ) t it (0 t 1),
y
i
于是 Re z t , dz (1 i )dt ,
1 C Re zdz 0 t (1 i )dt 2 (1 i );
1
1 i
o
1
x
18
(2) 积分路径的参数方程为
z(t ) t it 2 (0 t 1),
22
当 n 0 时, 1 2π C ( z z0 )n1 dz i 0 d 2i; 当 n 0 时,
y
z
0 z
o

r
x
C
1 i 2π n 1 dz n 0 (cos n i sin n )d 0; ( z z0 ) r
2i , 1 所以 n1 dz ( z z0 ) 0, z z0 r
C2 Cn
在今后讨论的积分中, 总假定被积函数是连续的, 曲线 C 是按段光滑的.
13
性质：
设L是简单逐段光滑曲线，f,g在L上连续，则
(1) f ( z )dz f ( z )dz; 反转积分路径，积分反号 L L
(2) Rf ( z )dz R f ( z )dz , 其中 R为复常数
L
注意：数学分析中的积分中值定理不能推移到 复变函数积分上来，例如：

而
2
0
1 2 ei d ei 0 0 i
ei0 (2 0) 0 (0 0 2 )
15
例1 计算 zdz , C : 从原点到点3 4i 的直线段.
C
x 3t , 0 t 1, 解 直线方程为 y 4t , 在 C 上, z ( 3 4i )t , dz ( 3 4i )dt ,
24
复习：二元函数积分的格林公式
实变线积分 Pdx Qdy 在单连通区域B内与
L
路径无关的充要条件：
P( x, y ), Q( x, y)
在B内的偏导数
P Q , y x
连续，并且
P Q y x
由于复变函数的积分可转化为两个实变线积分
z2
z1
f ( z)dz udx vdy i vdx udy