圆周角导学案
圆周角导学案6

24.1.4 圆周角导学案【学习目标】学习目标:1、理解并掌握圆周角的定义2、能利用圆周角定理及其推论解题【学习重点】能利用圆周角定理及其推论解题【学习难点】分类思想证明圆周角定理【学习过程】一、知识链接1.什么叫圆心角?2. 圆心角、弧、弦三个量之间关系的一个结论,这个结论是什么?二、自主学习1.圆周角的定义:,并且两边都与圆相交的角叫做圆周角。
2.定理:在同圆或等圆中,所对的圆周角相等,都等于这条弧所对的。
3,推论:(1)(或直径)所对的圆周角是直角,的圆周角所对的弦是。
(2)在同圆或等圆中,的圆周角所对的。
4.圆内接多边形:圆内接四边形的,这个圆叫做圆内接四边形的性质:。
三、合作探究——圆周角定理的证明探究:如图,观察圆周角∠ABC与圆心角∠AOC,它们的大小有什么关系? 说说你的想法,并与同伴交流.推论:直径(或半圆)所对的圆周角是直角,90°的圆周角所对的弦是直径.在同圆或等圆中,如果两个圆周角相等,它们所对的弧一定相等。
请写出定理、推论的符号语言。
CCEBABA四、学以致用1.下列说法正确的是( )A 相等的圆周角所对弧相等形B 直径所对的角是直角C 顶点在圆上的角叫做圆周角D 如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
2.如图,△ABC 内接于⊙O ,若∠OAB=28°, 则∠C 的大小为( )A . 28° B. 56° C. 60° D. 62°3.如图,在⊙O 中, ∠ABC=40°,则∠ABC= °.4. 如图,AB 是⊙O 的直径,C,D,E 都是圆上的点, 则∠1+∠2= °.5.如图,AB 是⊙O 的直径,BD 是⊙O 的弦,延长BD 到C, 使AC=AB. 求证:BD=CD.三、当堂检测1. 如图,AB 是⊙O 的直径, BC,CD,DA 是⊙O 的弦,且 BC=CD=DA,则∠BCD=( ).A . 100° B. 110° C. 120° D130°BAED2. 如图,⊙O 是△ABC 的外接圆,AB 是直径, 若∠BOD=80°,则∠A=( )A . 60° B. 50° C. 40° D30°3.如图,A,B,C 是⊙O 上三点, ∠AOC=100°, 则∠ABC= °.4. 如图,正方形ABCD 内接于⊙O,点E 在劣弧AD 上, 则∠BEC 等于 °5.. 如图,在⊙O 中, ∠ACB=∠BDC=60°,AC=32,(1)求∠BAC 的度数;(2)求⊙O 的周长.三、当堂检测1、如图,在⊙O 中,ABC=50°,则∠AOC 等于( )A 、50°B 、80°C 、90°D 、100° 2、如图,△ABC 是等边三角形,动点P 在圆周的劣弧AB 上,且不与A 、B 重合,则∠BPC 等于( ) A 、30° B 、60° C 、90° D 、45°第1题图 第2题图 第3题图 3、图中的角x 的度数分别是 、 。
圆周角导学案(学生用)

圆周角(1)导学案绵竹市孝德中学:王伦平【学习目标】:1、 理解圆周角的概念,能运用概念进行辩识圆周角。
2、 探索圆周角与圆心角及其所对弧的关系。
3、 经历探索过程,体会分类、化归和完全归纳等数学思想方法。
4、 会运用圆周角定理解决简单问题。
【学习重点】:圆周角概念及圆周角定理.【学习难点】:圆周角定理的探索过程。
【学习过程】专题一:课前预习: 1、观察右图1.1右图中∠C,∠D 和∠E 是圆心角吗?它们是____________.1.2右图中∠C,∠D 和∠E 有什么共同特点?2、★圆周角定义:阅读教材P84内容,回答下列问题 2.1什么是圆周角?2.2你觉得识别圆周角要把握哪些件: ; 。
2.3运用圆周角的定义,判断下列各图中,各图中的角是不是圆周角?并说出判断理由.......(1)(2)(3)(4)(5)专题二:新知探究 3. ★探究圆周角定理 3.1 :量一量①还能再画一个与∠C 具有共同特点的角吗?观察演示(一): 观察»AB所对的圆周角有多少个? 结论:在同一个圆中,同弧所对的圆周角有_____个。
②同学乙、丙、丁看到的海洋范围(视角)一样吗?观察演示(二):观察»AB所对的圆周角的大小关系 结论:在同一个圆中,同弧所对的圆周角________。
③乙、丙、丁的视角∠C 、∠D 、∠E 与同学甲的视角∠AOB 又有什么关系?观察演示(三):»AB所对的圆周角与»AB 所对的圆心角的大小有什么关系? 结论:同弧所对的圆周角等于这条弧所对的圆心角的_______.④根据度量结果和观察结论猜想::在同圆或等圆中,同弧或等弧所对的圆周角_____ ,并且都等于这条弧所对的圆心角的__________。
玻璃丁乙玻璃丁乙3.2 定理证明已知:在⊙O 中,»BC所对的圆周角是∠A ,圆心角是∠BOC 求证:1= BOC 2A ∠∠观察演示(四):观察»AB所对圆心角的顶点O 与»AB 所对圆周角有几种不同的位置关系?Ⅰ:圆心在圆周角一边上时(图1) Ⅱ: 圆心在圆周角内部时(图2) 证明:如图1 证明:如图2_________21_____2O OA OCA BOC A BOC AA =∴∠=∠=∠+∴∠=∠∠=e Q Q 在中即: Ⅲ:圆心在圆周角外部时(图3)定理辩析:圆周角定理使用条件是什么?结论有几个?它们是?圆周角定理的三种语言:(1)文字语言:(在上面)(2)图形语言(如右图) (3)符号语言图11____=____(1)21____=____(2)22_______I ∠∠∠∠∠∠e 连接AO 并延长交O于点D 由证明易得:1由(1)___()得:_____=21____=____(1)21____=____(2)22_______I ∠∠∠∠∠∠e 连接AO 并延长交O 于点D 由证明易得:1由(1)___()得:_____=2»______O AB ∴∠=∠e Q 在中»1______21___2O ABD AOB∴∠=∠∠=∠e Q 在中图2图33.3 及时反溃1、如图,点A 、B 、C 、D 在⊙O 上,若∠C=60°,则∠D=____,∠O=____.2、如图,点A 、B 、C 、D 在同一个圆上,四边形的对角线把4个内角分成8个角,这些角中哪些是相等的角?3.4 例题讲解:例1:在⊙O 中, AB 是⊙O 的一条弦,圆周角∠CBD=30° ,∠BDC=20°, 求∠A想一想:(1)在圆周角定理中,能把 “同弧”能否改成“同弦”吗?为什么?专题三:学习小结请你选择下面一个或几个关键词谈本节课的体会:知识、方法、思想、收获、喜悦、困惑、成功……作业:必做:①87页 87页 习题21﹒4 第 4题、第5题 ②完成例1的解题过程;③选做:88页 第12题第2题图专题四:尝试练习1、如图1,AB 是⊙O 的直径,»»BCBD ,∠A=30°,则∠BOD=_______。
最新人教版初中九年级数学上册《圆周角》导学案

24.1.4 圆周角姓名:班级:组别:评定等级【自主学习】(一)复习巩固:1.圆周角的定义.2.圆周角定理.3.在半径为R的圆内,长为R的弦所对的圆周角为 .(二)新知导学1.直径(或半圆)所对的圆周角是 .2.900的圆周角所对的弦是 .3.圆的内接多边形,多边形的内接圆。
圆内接四边形的对角。
【合作探究】如图,AB是⊙O的直径,AB=AC,D、E在⊙O上.求证:BD=DE.【自我检测】1.如图,AB是⊙O的直径,∠AOD是圆心角,∠BCD是圆周角.若∠BCD=25°,则∠AOD= .2.如图,⊙O直径MN⊥AB于P,∠BMN=30°,则∠AON= .3.如图,A、B、C是⊙O上三点,∠BAC的平分线AM交BC于点D,交⊙O于点M.若∠BAC=60°,∠ABC=50°,则∠CBM= ,∠AMB= .4.如图,⊙O中,两条弦AB⊥BC,AB=6,BC=8,求⊙O的半径=.5.下列说法正确的是()A.顶点在圆上的角是圆周角 B.两边都和圆相交的角是圆周角C.圆心角是圆周角的2倍 D.圆周角度数等于它所对圆心角度数的一半6.下列说法错误的是()A.等弧所对圆周角相等 B.同弧所对圆周角相等C.同圆中,相等的圆周角所对弧也相等. D.同圆中,等弦所对的圆周角相等7.在⊙O中,同弦所对的圆周角()A.相等B.互补C.相等或互补 D.都不对8.如图,在⊙O中,弦AD=弦DC,则图中相等的圆周角的对数是()A.5对 B.6对 C.7对D.8对后序亲爱的朋友,你好!非常荣幸和你相遇,很乐意为您服务。
希望我的文档能够帮助到你,促进我们共同进步。
孔子曰,三人行必有我师焉,术业有专攻,尺有所长,寸有所短,希望你能提出你的宝贵意见,促进我们共同成长,共同进步。
每一个都花费了我大量心血,其目的是在于给您提供一份参考,哪怕只对您有一点点的帮助,也是我最大的欣慰。
如果您觉得有改进之处,请您留言,后期一定会优化。
《圆周角》导学案.docx

圆周角学习目标:理解圆周角的概念,了解并证明圆周角定理及其推论,体会定理证明屮的分类、转化,由特殊到一般等数学思想方法。
重点:定义的理解、定理的推导及运用难点:定理的发现与证明三.基础题1.如图,点A、B、C、D在。
0上,点A与点I)在点B、C所在直线的同侧,ZBAC=35°(1)ZBDC= __________ °,理由是_(2)ZBOC= __________ °,理由是—2.如图,占A、B、C在00上,(1)若ZBAC=60° ,求ZB0C=(2)若ZA0B=90°,求ZACB=_提高运用题(独立完成后小组合作交流)1. ______________________________ 如图,有一圆形展厅,在其图形边缘上的点A处安装了一台监视器,它的监控角度是65°,为了监控整个展厅,最少需要圆形人边缘上共安装这样的监视器台。
学具准备:量角器、圆规、直尺教学过程:一、知识链接:圆心角定义及性质二、圆周角定义(自学课木第15页的议一议)圆周角的定义:___________________________巩固练习(独立完成,说明理由)ACAB2. ____________________________________ 如图,量角器外沿上有A,B两点,它们的读数分别是70° ,40° ,则Z1的度数为____________________ o|TT1 谟晋小结本扫课我们盂有哪些收获? 知识:数学思想:解题:五、达标检测1.下列命题中是真命题的是()A顶点在圆周上,一边与圆相交的角叫圆周角B顶点在圆上,两边都与圆相交的角叫圆周角C圆周角是圆心角的一半D —条弧的度数为120。
,则它所对的圆周角度数为120。
2、如图,D是弧AC的中点,与ZABD相等的角的个数是()3、如图,A,B,C,D是00上四点,D是弧的中点,CD 交OB 于E, ZAOB=\OQ° , ZOBC=55° ,则ZOEC= ____________ ° .六、分类作业(每小组6人)A类作业:(每组1〜3号)习题4.5 第1题添加条件Z1 = Z2,找岀相等的角和相似的三角形2、一条弦分圆周成1:4两部分,那么这条弦所对的圆周角是多少度。
3.4圆周角导学案3

课题 3.4 圆周角3导学案时间:课型:新授【学习目标】1、掌握圆内接四边形的概念,掌握圆内接四边形的性质定理;2、初步会运用圆的内接四边形的性质定理证明和计算一些问题.3、培养学生观察、分析、概括的能力.【重点难点】重点:圆内接四边形的性质定理.难点:理解“内对角”这一重点词语的意思.【导学流程】一、知识铺垫:1、圆心角定理:圆心角的度数与它所对的弧的度数相等.2、圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半.二、引导知新:认真研读教材82页内容,完成:1、什么是圆内接多边形?2、圆内接四边形有什么性质?怎么证明?定理1 圆的内接四边形的对角互补.定理2 圆内接四边形的外角等于它的内对角.三、深入学习:例1、已知:如图,在⊙O中,∠CBD=30°, ∠BDC=20°,求∠A例2、已知:如图⊙O1与⊙O2相交于A、B两点,经过A的直线与⊙O1交于点C,与⊙O2交于点D.过B的直线与⊙O1交于点E,与⊙O2交于点F.课海拾贝我的困惑:我们的困惑:求证:CE∥DF.四、迁移运用:1、若圆内接四边形ABCD中,∠A,∠B,∠C的度数的比是2∶3∶6,则该四边形内角中最大度数是____.2、如图,四边形ABCD内接于圆,∠DCE=50°,则∠BOD=____.3、如图,已知:四边形ABCD内接于圆,BD平分∠ABC,且AB∥CD . 求证:CD=CB4、如图,已知AB=AC,∠APC=60°(1)求证:△ABC是等边三角形.(2)若BC=4cm,求⊙O的面积.课后反思。
《圆周角》 导学案

《圆周角》导学案一、学习目标1、理解圆周角的概念,掌握圆周角的两个特征。
2、经历探索圆周角定理的过程,理解并掌握圆周角定理及其推论。
3、能用圆周角定理及其推论解决简单的几何问题,培养逻辑推理能力和数学应用意识。
二、学习重点1、圆周角的概念和圆周角定理。
2、圆周角定理的推论及其应用。
三、学习难点1、圆周角定理的证明。
2、圆周角定理推论的灵活应用。
四、知识链接1、圆心角的定义:顶点在圆心的角叫做圆心角。
2、圆心角的度数等于它所对弧的度数。
五、学习过程(一)自主学习1、阅读教材,理解圆周角的定义:顶点在圆上,并且两边都与圆相交的角叫做圆周角。
2、观察下面的角,判断哪些是圆周角,哪些不是,并说明理由。
(二)合作探究1、画一画在同圆或等圆中,画出同弧所对的圆心角和圆周角,你能画出多少个?2、量一量用量角器测量所画的圆心角和圆周角的度数,你发现了什么?3、猜一猜同弧所对的圆周角和圆心角之间有什么数量关系?4、证一证(1)分情况讨论:当圆心在圆周角的一边上时,如何证明圆周角定理?当圆心在圆周角的内部时,如何证明圆周角定理?当圆心在圆周角的外部时,如何证明圆周角定理?(2)证明圆周角定理:同弧所对的圆周角等于它所对的圆心角的一半。
(三)圆周角定理的推论1、思考:在同圆或等圆中,如果两个圆周角相等,它们所对的弧相等吗?为什么?2、推论 1:在同圆或等圆中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等。
3、思考:半圆(或直径)所对的圆周角是多少度?为什么?4、推论 2:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径。
(四)例题讲解例 1:如图,AB 是⊙O 的直径,∠C = 30°,求∠ABD 的度数。
例 2:如图,⊙O 中,弦 AB 与 CD 相交于点 E,∠A = 40°,∠B = 30°,求∠APC 的度数。
(五)课堂练习1、如图,在⊙O 中,∠BOC = 50°,求∠A 的度数。
圆周角导学案(1)

3 题图
4 题图
5 题图
6. . 已知:∠A 是圆 O 的圆周角,∠A=40°. 求:∠OBC 的度数.
7.如图,点 A、B、C、D 在⊙O 上,∠ADC=∠BDC=60°.判断△ABC 的形状,并说 明理由.
8. . AB 是⊙O 的直径, C 、D 是圆上的两点,若∠ABD=40°,求∠BCD.
(2)求 DE 的长.
活动六,当堂测试
1、如图,点 A、B、C、D 在⊙O 上,点 A 与点 D 在点 B、C 所在直线的同侧,∠BAC=35 (1)∠BDC=_______°,理由是____________. (2)∠BOC=_______°,理由是_____________. 2、如图,点 A、B、C 在⊙O 上, (1) 若∠BAC=60°,求∠BOC=______°; (2) 若∠AOB=90°,求∠ACB=______
03. 如图所示,点 A、 Nhomakorabea、C 在⊙O 上,连接 OA、OB,若∠ABO=25°,则∠C=_____________.
4. 如图所示,AB 是⊙O 的直径,AC 是弦,若∠ACO=32°,则∠COB=___________。 5. 如图所示,OA 为⊙O 的半径,以 OA 为直径的圆⊙C 与⊙O 的弦 AB 相交于点 D,若 OD=5cm,则 BE= __________。
活动二,探究新知 圆周角的定义:像上面的三个张角∠ABC、 ∠ADC、∠AEC 的顶点在 ,其它两边都和圆 的角,叫做__________。 辨一辨:下列各图中哪些角是圆周角?是的打“√”,不是的打“×”。
探究一: (1)在上面的图中画出弧 AB 所对的圆周角,试试你能画出多少个?量一量你所画出 的圆周角,你发现了什么?由此你能得出什么结论? 于是我有了发现 1:____________________________________。 (2)在上面的图中画出弧 AB 所对的圆心角。 (3)量一量弧 AB 所对的圆周角和弧 AB 所对的圆心角,你发现它们有 什么关系? 于是我有了发现 2__________________________________。 (4)做一做:在圆上任取一个圆周角∠ACB,观察圆心与圆周角的位置关系有几种情况? ︵ 1 分别画出AB所对的圆心角∠AOB。求证:∠ACB= ∠AOB(分三种 2 情况进行证明) ①
九下数学《圆周角》导学案

图27.1.10《圆周角》导学案第1课时【学习目标】1、知道什么样的角是圆周角,了解圆周角和圆心角的关系,直径所对的圆周角的特征;2、能应用圆心角和圆周角的关系、直径所对的圆周角的特征解决相关问题,3、通过对圆心角和圆周角关系的探索,培养学生运用已有知识,进行实验、猜想、论证,从而得到新知。
【重难点预测】重点:认识圆周角,同一条弧的圆周角和圆心角的关系,直径所对的圆周角的特征。
难点:发现同一条弧的圆周角和圆心角的关系,利用这个关系进一步得到其他知识,运用所得到的知识解决问题。
【学习过程】一、课前展示,激趣导入:(5分钟)1、上节课作业典型错题展析2、如下图,同学们能找到圆心角吗?它具有什么样的特征?二、明确目标、自学指导:(2分钟)【自学指导】1、观察P40图27.1.8,圆周角的两要素:顶点在 上,两边都与 相交;2、P41“黑体字”定理可简记为“直径对 直角 ”或“半圆对直角 ”P43“推论1”可简记为“直角对 ”如图27.1.12,∵AB 是直径 ∴ 反之,∵∴AB 是直径 3、P43“黑体字”圆周角定理: 在同圆或等圆.....中, 同弧或等弧所对的圆周角等于该弧所对的圆心角的 。
可简记为:圆周角=21 前提条件:如图27.1.10,∠ACB =21∠图27.1.12∠ADB =21∠ 4、认真阅读P44“例2”三、自主学习,组内交流。
(12分钟)学生看书,完成[自学指导]问题,教师巡视、适当指导,了解普遍问题。
四、组间展评,达成共识(7分钟)小组代表展示,小组代表点评、质疑,教师点拨、拓展,控制秩序。
形成共识:圆周角的两要素:顶点在 上,两边都与 相交。
圆周角与直径(半圆)的关系:圆周角与圆心角的关系:五、检测反馈,拓展延伸(10分钟)P44练习 2、3、P45 习题6拓展:这是一个圆形的零件,你能告诉我,它的圆心的位置吗?你有什么简捷的办法?六、小结与课后作业。
人教版九年级数学上册《圆周角》导学案

BAOB MOA MOB M 《圆周角》导学稿一、教学目标:1、使学生理解圆周角概念,掌握圆周角和圆心角的关系定理。
2、使学生了解化归思想和分类思想。
3、养成善于合作,勇于探索的自主学习的好习惯。
二、教学重点:概念的引入,定理的发现和证明。
教学难点:定理的证明及应用。
三[新课必备] 1、圆心角的定义?如何度量圆心角所对弧的度数,根据是什么?直径所成的圆心角是多少度? 2、请画图说明一个角的顶点和一个圆的位置关系有哪些可能?四、预习导学、探究活动:问题1、如图是一个圆柱形的海洋馆的横截面示意图,人们可以通过其中的圆弧形玻璃窗弧AB 观看窗内的海洋动物,同学甲在圆心的位置,其他3人在圆上,这3人的视角与甲的视角有什么关系?这3人的视角有什么关系? 导学提示:由∠ANB 与∠AOB 的特殊关系入手分析如果圆心角∠AOB = 60º,∠ANB= 改变圆心角∠AOB 的大小,可以看到 结果。
可见当点N 在圆上时,∠ANB 具有特殊性。
N Q通过以上分析可以得到:定义:顶点 ,并且两边 叫做圆周角。
尝试练习1、下列各图中,哪一个角是圆周角?( )ABCD尝试练习2、图3中有几个圆周角?( ) (A )2个 (B )3个(C )4个(D )5个。
尝试练习3、写出图4中的圆周角:___________________________________图3图4BACDBCA练习4、在同圆中,一条弧所对的圆心角有几个?圆周角有几个?画图表示。
问题2、圆周角定理的证明导学提示:根据问题1对于具体给定的圆心角,同弧所对的所有圆周角都等于圆心角的 。
对于任意的圆心角是否也有上述关系呢?说出你的猜想B AOB M O AMOM请你利用圆周角和圆心角的如下三种位置关系给出证明DD(1) B(2)(3)OACACOB BC OA通过以上述证明,上述猜想: 正确 导学提示:1、圆心和圆周角是否还有其他不同的位置关系?2、面对这三种情况,能否找到一种统一的证明方法?3、如右图,∠N ,∠M ,∠Q 是同弧所对的圆周角,这三个角有什么关系?你能得出什么结论?Q4、等弧所对的圆周角有什么关系?总结以上推导过程,得出定理:------------ 问题3、定理的应用尝试练习5、如图6,已知∠ACB = 20º,则∠AOB = _______.尝试练习6、如图7,已知圆心角∠AOB=100,则∠ACB = _______。
圆周角 导学案

24.1.4圆周角定理主备:总课时数:周课时数:教学过程个性备课快乐元素:课前一首课情境引入:海洋馆是个让人流连往返的地方,人们可以通过圆弧形玻璃观看精彩的表演,现有C,D,E你会选择在哪一点观看呢?他们的视角一样吗?通过今天的学习就可以解决这个问题.前面学过顶点在圆心的角叫圆心角,你能用类别的方法给这三个角起个名字吗?你能不能给它下个定义呢?一、圆周角定义:顶点在圆上,且两边都与圆相交的角叫做圆周角.分析定义:○1圆周角需要满足两个条件;○2圆周角与圆心角的区别请写出上图中所有的圆周角:。
二、探究圆周角定理我们熟悉圆周角那么它和圆心角有什么关系呢?请同学们继续在纸片上画出圆心角,并探讨它们之间的关系?1.结合圆周角的概念通过度量思考问题:○1一条弧所对的圆周角有多少个?②同弧所对的圆周角的度数有何关系?③同弧所对的圆周角与圆心角有何数量关系吗?2.分情况进行几何证明教学目标知识技能1.了解圆周角的概念,理解圆周角的定理及其推论.2.熟练掌握圆周角的定理及其推论的灵活运用.3.体会分类思想.过程方法设置情景,给出圆周角概念,探究这些圆周角与圆心角的关系,运用数学分类思想给予逻辑证明定理,得出推导,让学生活动证明定理推论的正确性,最后运用定理及其推论解决问题.情感态度激发学生观察、探究、发现数学问题的兴趣和欲望.教学重点圆周角定理、圆周角定理的推导及运用它们解题.教学难点运用数学分类思想证明圆周角的定理.①当圆心O在圆周角∠ABC的一边BC上时,如图⑴所示,那么∠ABC=12∠AOC吗?②当圆心O在圆周角∠ABC的内部时,如图⑵,那么∠ABC=12∠AOC吗?③当圆心O在圆周角∠ABC的外部时,如图⑶,∠ABC=12∠AOC吗?可得到:一条弧所对的圆周角等于这条弧所对的圆心角的一半.根据得到的上述结论,证明同弧所对的圆周角相等. 得到:同弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.问题:将上述“同弧”改为“等弧”结论会发生变化吗?总结归纳出圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.于是,在同圆或等圆中,两个圆心角,两个圆周角、两条弧、两条弦中有一组量相等,则其它各组量都分别相等.半圆作为特殊的弧,直径作为特殊的弦,运用上述定理有什么新的结论?推论半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.三、圆内接多边形与多边形的内接圆1.圆内接多边形与多边形的内接圆的定义如何区别两个定义?(前者是特殊的多边形后者是特殊的圆)2.圆内接四边形性质这条性质的题设和结论分别是什么?怎样证明?四、圆周角与圆心角的计算.如图,点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,这些角中哪些是相等的角?教后反思(学习收获):。
人教版-数学-九年级上册24.1.4 圆周角 导学案

一、基础知识1、理解圆周角的概念掌握圆周角的两个特征、定理的内容及简单应用;理解圆周角概念,理解圆周用与圆心角的异同;2.掌握圆周角的性质和直径所对圆周角的特征;3.能灵活运用圆周角的性质解决问题;圆周角定义:顶点在圆上,并且两边都与圆相交的角叫做圆周角.(注意两点:1.角的顶点在圆上;2.角的两边都与圆相交,二者缺一不可.)圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论1:同圆或等圆中,如果两个圆周角相等,它们所对的弧一定相等。
(也是圆周角定理的逆定理,要通过圆心角来转换)推论2:半圆(或直径)所对的圆周角是直角,90的圆周角所对的弦是直径。
二、重难点分析本课教学重点:圆周角与圆心角的关系,圆周角的性质和直径所对圆周角的特征.本课教学难点:发现并证明圆周角定理.三、典例精析:例1:(2014•齐齐哈尔)如图,在⊙O中,OD⊥BC,∠BOD=60°,则∠CAD 的度数等于()A.15° B.20° C.25° D.30°例2.(2014年天津市)已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O 于点D.(Ⅰ)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;(Ⅱ)如图②,若∠CAB=60°,求BD的长.【点评】本题综合考查了圆周角定理,勾股定理以及等边三角形的判定与性质.此题利用了圆的定义、有一内角为60度的等腰三角形为等边三角形证得△OBD是等边三角形.四、感悟中考1、(2014•牡丹江)如图,⊙O的直径AB=2,弦AC=1,点D在⊙O上,则∠D的度数是( )A.30°B.45°C.60°D.75°【点评】本题可直接根据圆周角的性质和等边三角形性质来解答。
2、(2014•齐齐哈尔)如图,在⊙O中,OD⊥BC,∠BOD=60°,则∠CAD的度数等于()A.15°B.20°C.25°D.30°五、专项训练。
九年级数学 圆周角导学案
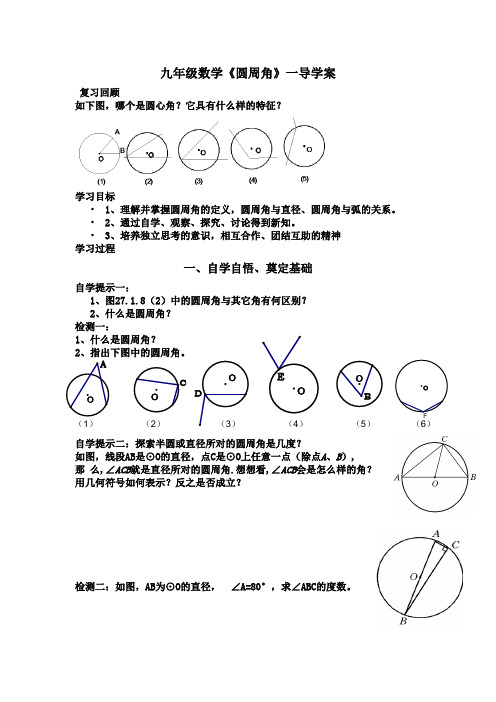
九年级数学《圆周角》一导学案复习回顾如下图,哪个是圆心角?它具有什么样的特征?学习目标• 1、理解并掌握圆周角的定义,圆周角与直径、圆周角与弧的关系。
• 2、通过自学、观察、探究、讨论得到新知。
• 3、培养独立思考的意识,相互合作、团结互助的精神 学习过程一、自学自悟、奠定基础自学提示一:1、图27.1.8(2)中的圆周角与其它角有何区别?2、什么是圆周角? 检测一:1、什么是圆周角?2、指出下图中的圆周角。
自学提示二:探索半圆或直径所对的圆周角是几度?如图,线段AB 是⊙O 的直径,点C 是⊙O 上任意一点(除点A 、B ), 那 么,∠ACB 就是直径所对的圆周角.想想看,∠ACB会是怎么样的角? 用几何符号如何表示?反之是否成立?检测二:如图,AB 为⊙O 的直径,∠A=80°,求∠ABC 的度数。
(1) (2) (4) (5) (6)自学提示三:• 1.一条弧所对的圆周角有几个?它们的大小有何关系? • 2.等弧所对的圆周角有何关系?• 3.在同圆或等圆中,相等的圆周角所对的弧有何关系? 检测三:试找出图中所有相等的圆周角。
二、探究归纳、提升能力1. 如图,P 是△ABC 的外接圆上的一点∠APC=∠CPB=60°。
求证:△ABC 是等边三角形。
2.已知:如图,在△ABC 中,AB=AC,以AB 为直径的圆交BC 于D,交AC 于E, 求证:弧BD=弧DED C AB CAD三、检测达标、总结提升归纳梳理:本节学到了什么数学知识?常作的辅助线是什么?当堂检测1、下图中是圆周角的有 .②2、如图,AB 是⊙O 的直径,∠ABC=30°,则∠BAC 的度数 是______.3、A 、B 、C 、D 四个点在同一个圆上,四边形ABCD 的对角线把四个内角分成的八个角中,相等的角有( )A.2对B.3对C.4对D.5对4、(08中招)已知:如图,AD•是⊙O•的直径,∠ABC=•30•°, 求∠CAD 的度数.D_C选做题、如图 AB 是⊙O 的直径, C ,D 是圆上的两点,若∠ABD=40°,求∠BCD 度数.思考题、(07中招) 如图,已知A 、B 、C 、D 是⊙O 上的四个点,AB =BC , BD 交AC 于点E ,连接CD 、AD . (1)求证:DB 平分∠ADC ;(2)若BE =3,ED =6,求AB 的长.BA。
圆周角及性质导学案

图1 圆周角及性质导学案班级_______姓名_________________学号_________________学习目标:1.理解圆周角的概念,掌握圆周角的性质及推论。
2.灵活运用圆周角的性质进行证明与计算。
活动一.温故知新 如图.顶点在圆心O 上的∠AOB ,叫做_________角.思考:∠ACB 的顶点C 在圆心上吗?∠ACB 是圆心角吗?活动二.探究新知 探究(一)圆周角的概念如图1,把顶点在 ,且两边都和圆 的角,叫做圆周角. 探究(二)圆周角的性质操作1.请你量一量图2中弧BC 所对的圆周角∠BAC 和弧BC 所对的 圆心角∠BOC 的度数,你发现它们有什么关系?结论:________.请你结合图2证明你的结论于是我发现了性质1:___________________________________________________。
思考:你能画出几种同弧(等弧)所对的圆周角和圆心角?请你在下面不同的类型。
操作2.请你在图3中画出弧AB 所对的圆周角,试试你能画出多少个?结论:_______; 请你量一量你所画出的圆周角,你发现了什么?于是我发现了性质2:____________________________________________。
操作3.请你在右图4中任意画出一个直径所对的圆周角,你能发现它是什么角吗?由此你能得出什么结论?结论:___________________________。
于是,我发现了性质3:(圆周角定理推论)__________________________________________________________________________.注意,要记住:1.同圆或等于圆中,如果两个圆周角相等,它们所对弧一定相等. 2.在同圆或等于圆中,圆心角的度数与所对弧的度数相等。
如果圆心角是800,那么所对弧的度数是800,所对的圆周角是400活动三.运用新知如图,⊙O 的直径AB 为10 cm ,弦AC 为6 cm ,∠ACB 的平分线交⊙O 于D , 求BC 、AD 、BD 的长.O CB C A O图2图3图4活动四.巩固练习AB、AC为⊙O的两条弦,延长CA到D,使AD=AB,如果∠ADB=35°.求∠BOC的度数活动五.拓展延伸如图,在△ABC中,AB=BC=2,以AB为直径的⊙O分别交BC,AC于点D,E,且点D为边BC的中点. (1)求证:△ABC为等边三角形; (2)求DE的长.活动六.课外作业1.如图所示,点A、B、C在⊙O上,连接OA、OB,若∠ABO=25°,则∠C=_____________.2. 如图所示,AB是⊙O的直径,AC是弦,若∠ACO=32°,则∠COB=___________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
24.1.4圆周角
学习目标:
1.了解圆周角的概念.
2.理解圆周角的定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,•都等于这条弧所对的圆心角的一半.
3.理解圆周角定理的推论:半圆(或直径)所对的圆周角是直角,90•°的圆周角所对的弦是直径.
4.熟练掌握圆周角的定理及其推理的灵活运用.
重点、难点
重点:圆周角的定理、圆周角的定理的推导及运用它们解题.
难点:运用数学分类思想证明圆周角的定理.
导学过程:阅读教材P84 — 85 , 完成课前预习
【课前预习】
1:知识准备
(1)什么叫圆心角?
(2)圆心角、弦、弧之间有什么内在联系呢? 2:探究1
圆周角: 在圆上,并且 都与圆相交的角叫做圆周角。
为了进一步研究上面发现的,在⊙O 任取一个圆周角∠BAC ,将圆对折,使
折痕经过圆心O 和∠BAC 的顶点A 。
由于点A 的位置的取法可能不同,这时折痕
可能会:
(1) 在圆周角的一边上; (2)在圆周角的内部; (3)在圆周角的外部。
(1)证明:在⊙O 中,∵OA=OC (2)证明: (3)证明:
∴∠A=∠
又∵∠BOC=∠A+∠C=2∠
∴∠A=2
1∠BOC
从(1)、(2)、(3),我们可以总结归纳出圆周角定理:
在同圆或等圆中,同弧或等弧所对的 相等,都等于这条弧所
对的 .
表达式:
在同圆或等圆中,如果两个圆周角相等,它们所对的弧一定 .
表达式: 进一步,我们还可以得到下面的推导:
半圆(或直径)所对的圆周角是 ,
90°的圆周角所对的弦是 .
表达式: 探究2:
如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做 ,
这个圆叫做这个多边形的
圆内接四边形的对角
已知:
求证:
证明: 【课堂活动】
活动1:预习反馈
活动2:典型例题
例1.如图,⊙O 的直径AB 为10cm ,弦AC 为6cm ,∠ACB 的平分线交⊙O 于D ,求BC ,AD ,BD
D
A B
活动3:随堂训练
1. 如图,点A,B,C,D在同一个圆上,四边形ABCD的对角线把4个内角分成8
2.如图,你能确定一个圆形纸片的圆心吗?你有多少种方法?
3.求证:如果三角形一条边上的中线等于这条边的一半,那么这个三角形是直角三角形。
(提示:作出以这条边为直径的圆)
活动4:课堂小结。
