六年级数学上册有理数课件
合集下载
1.5有理数的混合运算(有理数混合运算的实际应用)(教学课件)-六年级数学上册(沪教版2024)

通过计算,说明这个文具店去年总的盈利情况。
解: −1.2 × 3 + 4 × 3 + 3.4 × 3 + −1.5 × 3 = 14.1 万元
答:这个文具店去年盈利14.1万元。
课堂练习
2. 某冷冻厂一号库房的室温是 − 2℃,现在有一批食品需要在 − 23℃条件下冷冻,
如果该库房每小时能降低4℃,那么经过多久能降到所要求的温度?
.
240
2 要求人数增加4人后完成的天数,根据工作总量、工作效率和工作时间之间的关系,
1
可知增加4人后的工作
240
1
解:根据题意,每人每天修1 ÷ 8 ÷ 30 =
.
240
1
1
增加4人后的工作时间 = 1 ÷
× 4+8 =1÷
= 20 天 .
240
20
实际应用问题.(难点)
复习导入
做有理数的混合运算时,应注意以下运算顺序:
1. 先乘方,再乘除,最后加减;
2. 同级运算,从左到右进行;
3. 如有括号,先做括号内的运算,按小括号、
中括号、大括号依次进行.
复习导入
活学巧记
混合运算分三级,
运算顺序高到低;
乘方、乘除再加减,
若有括号它优先.
课本例题4
沪教版(2024)六年级数学上册 第一章 有理数
1.5 有理数的混合运算
第三课时 有理数混合运算的实际应用
目录/CONTENTS
学习目标
情景导入
新知探究
分层练习
课堂反馈
课堂小结
学习目标
1. 理解并熟练掌握有理数的混合运算的顺序,并会进行简单
有理数的混合运算.(重点)
解: −1.2 × 3 + 4 × 3 + 3.4 × 3 + −1.5 × 3 = 14.1 万元
答:这个文具店去年盈利14.1万元。
课堂练习
2. 某冷冻厂一号库房的室温是 − 2℃,现在有一批食品需要在 − 23℃条件下冷冻,
如果该库房每小时能降低4℃,那么经过多久能降到所要求的温度?
.
240
2 要求人数增加4人后完成的天数,根据工作总量、工作效率和工作时间之间的关系,
1
可知增加4人后的工作
240
1
解:根据题意,每人每天修1 ÷ 8 ÷ 30 =
.
240
1
1
增加4人后的工作时间 = 1 ÷
× 4+8 =1÷
= 20 天 .
240
20
实际应用问题.(难点)
复习导入
做有理数的混合运算时,应注意以下运算顺序:
1. 先乘方,再乘除,最后加减;
2. 同级运算,从左到右进行;
3. 如有括号,先做括号内的运算,按小括号、
中括号、大括号依次进行.
复习导入
活学巧记
混合运算分三级,
运算顺序高到低;
乘方、乘除再加减,
若有括号它优先.
课本例题4
沪教版(2024)六年级数学上册 第一章 有理数
1.5 有理数的混合运算
第三课时 有理数混合运算的实际应用
目录/CONTENTS
学习目标
情景导入
新知探究
分层练习
课堂反馈
课堂小结
学习目标
1. 理解并熟练掌握有理数的混合运算的顺序,并会进行简单
有理数的混合运算.(重点)
2022秋六年级数学上册 第二章 有理数及其运算全章热门考点整合应用课件 鲁教版五四制

=4221.
9 对于四个数“-8,-2,1,3”及四种运算“+,-, ×,÷”,列算式解答:
(1)求这四个数的和; 解:(-8)+(-2)+1+3=-10+4=-6;
(2)在这四个数中选出两个数,按要求进行下列计算, 使得:①两数差的结果最小,②两数积的结果最大; 解:①(-8)-3=-8-3=-11, ②(-8)×(-2)=16;
4 下面两个数互为相反数的是( D ) A.-(+2021)与+(-2021) B.-0.8 和-(+0.8) C.-1.25 和45 D.+(-0.02)与--510
5 已知a,b分别是两个不同的点A,B所表示的有理数, 且|a|=5,|b|=2,它们在数轴上的位置如图所示.
(1)试确定数a,b. 解:因为|a|=5,|b|=2,所以a=±5,b=±2. 由数轴可知a<b<0,所以a=-5,b=-2.
第一章 丰富的图形世界
全章热门考点整合应用
习题链接
温馨提示:点击 进入讲评
1C 2 3 4D
5 6 7D 8
答案呈现
9 10 11 12
习题链接
温馨提示:点击 进入讲评
13 14 15 16
17 D 18 B 19 20
答案呈现
1 在-3,-1,13,0,-37,2021 中,正数有( C )
(2)一只电子虫P从B点出发,以2个单位长度/秒的速度向 左运动,同时另一只电子虫Q从A点出发,以3个单位 长度/秒的速度向右运动,经过多长时间这两只电子虫 在数轴上相距40个单位长度?
解:相遇前,两只电子虫在数轴上相距40个单位长度时, (100-40)÷(2+3)=12(秒);相遇后,两只电子虫在数 轴上相距40个单位长度时,(40+100)÷(2+3)=28(秒), 即经过12秒或28秒,这两只电子虫在数轴上相距40个单 位长度.
9 对于四个数“-8,-2,1,3”及四种运算“+,-, ×,÷”,列算式解答:
(1)求这四个数的和; 解:(-8)+(-2)+1+3=-10+4=-6;
(2)在这四个数中选出两个数,按要求进行下列计算, 使得:①两数差的结果最小,②两数积的结果最大; 解:①(-8)-3=-8-3=-11, ②(-8)×(-2)=16;
4 下面两个数互为相反数的是( D ) A.-(+2021)与+(-2021) B.-0.8 和-(+0.8) C.-1.25 和45 D.+(-0.02)与--510
5 已知a,b分别是两个不同的点A,B所表示的有理数, 且|a|=5,|b|=2,它们在数轴上的位置如图所示.
(1)试确定数a,b. 解:因为|a|=5,|b|=2,所以a=±5,b=±2. 由数轴可知a<b<0,所以a=-5,b=-2.
第一章 丰富的图形世界
全章热门考点整合应用
习题链接
温馨提示:点击 进入讲评
1C 2 3 4D
5 6 7D 8
答案呈现
9 10 11 12
习题链接
温馨提示:点击 进入讲评
13 14 15 16
17 D 18 B 19 20
答案呈现
1 在-3,-1,13,0,-37,2021 中,正数有( C )
(2)一只电子虫P从B点出发,以2个单位长度/秒的速度向 左运动,同时另一只电子虫Q从A点出发,以3个单位 长度/秒的速度向右运动,经过多长时间这两只电子虫 在数轴上相距40个单位长度?
解:相遇前,两只电子虫在数轴上相距40个单位长度时, (100-40)÷(2+3)=12(秒);相遇后,两只电子虫在数 轴上相距40个单位长度时,(40+100)÷(2+3)=28(秒), 即经过12秒或28秒,这两只电子虫在数轴上相距40个单 位长度.
鲁教版六年级数学上册(五四制)电子课本课件【全册】

第一章 丰富的图形世界
鲁教版六年级数学上册(五四制)电 子课本课件【全册】
1 生活中的立体图形
鲁教版六年级数学上册(五四制)电 子课本课件【全册】
2 展开与折叠
鲁教版六年级数学上册(五四制)电 子课本课件【全册】
பைடு நூலகம்
鲁教版六年级数学上册(五四制) 电子课本课件【全册】目录
0002页 0056页 0058页 0106页 0128页 0168页 0225页 0261页 0307页 0346页 0393页 0427页 0443页 0490页
第一章 丰富的图形世界 2 展开与折叠 4 从三个方向看物体的形状 1 有理数 3 绝对值 5 有理数的减法 7 有理数的乘法 9 有理数的乘方 11 有理数的混合运算 13 用计算器进行运算 1 用字母表示数 3 整式 5 去括号 7 探索与表达规律
六年级数学上册第二章有理数及其运算3绝对值pptx课件鲁教版五四制

一个数的绝对值就是在这个数的两旁各画一条竖线,如+2的绝对值等于2,记作 |+2|=2。 数a的绝对值记作|a|。
如图,在数轴上表示-5的点与原点的距离是5,即-5的绝对值是5,记作|-5|=5。
合作探究 达成目标
活动一:1. 阅读教材,思考:+3与-3,-5与 +5,-1.5与1.5这三对数有什么共同点?还能列 举出这样的数吗?如何表示相反数? 2. 在数轴上,标出以下各数及它们的相反数-1, 0, 5 ,-4.思考:数轴上表示互为相反数的
-5
-2 3
2 3
5
-5 -4 -3 -2 -1 0 1 2 3 4 5
学习目标
1.借助数轴,初步理解绝对值和相反数的概念,能求 一个数的绝对值和相反数.
2.会利用绝对值比较两负数的大小;学习数形结合的 数学方法和分类讨论的思想.
结论
如果两个数只有符号不同,那么我们称其中 一个数为另一个数的相反数,也称这两个数 互为相反数。特别地,0的相反数是0。
合作探究 达成目标
活动二:阅读教材,探究解决:
画数轴,观察回答: 距原点1个单位长度的数是____+__1___和____-__1___, 距原点2个5 单位长度的数是____+__2______和____-__2____, 距原点 2 个单位长度的数是___+__52___和___-__52___,
3 绝对值
创设情景 明确目标
1、画出数轴,并用数轴上的点表示下列各数:
2 3
,-5,0,5,-4,- 2 3
解: -5 -4
-2 3
0
2 3
5
-5 -4 -3 -2 -1 0 1 2 3 4 5
如图,在数轴上表示-5的点与原点的距离是5,即-5的绝对值是5,记作|-5|=5。
合作探究 达成目标
活动一:1. 阅读教材,思考:+3与-3,-5与 +5,-1.5与1.5这三对数有什么共同点?还能列 举出这样的数吗?如何表示相反数? 2. 在数轴上,标出以下各数及它们的相反数-1, 0, 5 ,-4.思考:数轴上表示互为相反数的
-5
-2 3
2 3
5
-5 -4 -3 -2 -1 0 1 2 3 4 5
学习目标
1.借助数轴,初步理解绝对值和相反数的概念,能求 一个数的绝对值和相反数.
2.会利用绝对值比较两负数的大小;学习数形结合的 数学方法和分类讨论的思想.
结论
如果两个数只有符号不同,那么我们称其中 一个数为另一个数的相反数,也称这两个数 互为相反数。特别地,0的相反数是0。
合作探究 达成目标
活动二:阅读教材,探究解决:
画数轴,观察回答: 距原点1个单位长度的数是____+__1___和____-__1___, 距原点2个5 单位长度的数是____+__2______和____-__2____, 距原点 2 个单位长度的数是___+__52___和___-__52___,
3 绝对值
创设情景 明确目标
1、画出数轴,并用数轴上的点表示下列各数:
2 3
,-5,0,5,-4,- 2 3
解: -5 -4
-2 3
0
2 3
5
-5 -4 -3 -2 -1 0 1 2 3 4 5
2020鲁教版六年级数学上册(五四制)全册完整课件

第一章 丰富的图形世界
2020鲁教版六年级数学上册(五四 制)全册完整课件
1 生活中的立体图形
2020鲁教版六年级数学上册(五四 制)全册完整课件
2 展开与折叠
2020鲁教版六年级数学上册(五四 制)全册完整课件
2020鲁教版六年级数ቤተ መጻሕፍቲ ባይዱ上册(五四 制)全册完整课件目录
0002页 0038页 0064页 0103页 0141页 0190页 0248页 0264页 0280页 0338页 0368页 0426页 0442页 0502页 0520页 0551页
第一章 丰富的图形世界 2 展开与折叠 4 从三个方向看物体的形状 1 有理数 3 绝对值 5 有理数的减法 7 有理数的乘法 9 有理数的乘方 11 有理数的混合运算 13 用计算器进行运算 1 用字母表示数 3 整式 5 去括号 7 探索与表达规律 1 等式与方程 3 一元一次方程的应用
1.3 有理数的乘法与除法(第2课时 有理数的乘法运算律)(课件)-六年级数学上册(沪教版2024)

乘时,可以先把前两个数相乘,再把积与第三个数相乘;或者先把后两个数
相乘,再把积与第一个数相乘.按两种顺序得到的运算结果相等。
概念归纳
乘法交换律
乘法结合律
a× = ×
( a× ) × = × ( × )
其中a、b、c表示有理数.
注:三个或三个以上的有理数相乘,可以任意交换乘数的位置,也可
3
(
4
1
− )
6
解:方法一:0.12×
9
=0.12× (
12
7
=0.12×
12
2
− )
12
3
(
4
=0.07
3
1
方法二:0.12× ( − )
4
6
3
1
=0.12× − 0.12 × )
4
6
=0.09-0.02
=0.07
1
3
4
15
1
3
4
15
(2)( +
−
1
)
6
(2)( +
1
3
= × 30 +
=10+8-27
12
-15
-3
(−3)×(−4)+(−3)×5=_____+_____=_______.
由此,你发现了什么?
我们发现,一个有理数与两个有理数的和相乘,等于把这个数分别与这两
个加数相乘,再把积相加,即
乘法对加法的分配律a×(b+c)=a×b+a×c.
其中a、b、c表示有理数.
课本例题
例3计算:
(1) 0.12×
以先把其中的几个乘数相乘.
相乘,再把积与第一个数相乘.按两种顺序得到的运算结果相等。
概念归纳
乘法交换律
乘法结合律
a× = ×
( a× ) × = × ( × )
其中a、b、c表示有理数.
注:三个或三个以上的有理数相乘,可以任意交换乘数的位置,也可
3
(
4
1
− )
6
解:方法一:0.12×
9
=0.12× (
12
7
=0.12×
12
2
− )
12
3
(
4
=0.07
3
1
方法二:0.12× ( − )
4
6
3
1
=0.12× − 0.12 × )
4
6
=0.09-0.02
=0.07
1
3
4
15
1
3
4
15
(2)( +
−
1
)
6
(2)( +
1
3
= × 30 +
=10+8-27
12
-15
-3
(−3)×(−4)+(−3)×5=_____+_____=_______.
由此,你发现了什么?
我们发现,一个有理数与两个有理数的和相乘,等于把这个数分别与这两
个加数相乘,再把积相加,即
乘法对加法的分配律a×(b+c)=a×b+a×c.
其中a、b、c表示有理数.
课本例题
例3计算:
(1) 0.12×
以先把其中的几个乘数相乘.
1.5有理数的混合运算(课件)六年级数学上册(沪教版2024)

-
3
5
1
4
- )
1
3
)=
4
5
12
−(
20
-
5
20
3
)=
5
7 1
- =
20 4
本题还可这样计算:
3
5
3
5
1
4
−( - )
3
3
+(-1)×(
5
5
=
3
1
- 4 )(有理数的乘法法则)
3
1
= 5+(-1)× 5 +(-1)×(- 4)(乘法对加法的分配律)
3
5
1
=
4
3
5
= + ( − )+
1
4
新课讲授
括号前带负号,去掉负号和括号后,原括号内各数要变号,
4
4
(-38)×3
解: 按收入为正数,支出为负数,
5
5
(-4)×3
填写表格(表 1-3).
分析: 一般为了方便,我们把收入记为正数,把支出
记为负数.比如买了3 份午饭我们可以记为(一38)X3.
根据表 1-3,我们可以列出
85+(-72)+200+(-38)X3+(-4)X3=87(元).
答:小海回到家后还剩87元.
学以致用
基础巩固题
4.一出租车一天下午2小时内以鼓楼为出发地在东西方向营运,向东走为正,向西走为负,行车
里程(单位:公里)依先后次序记录如下:+9,−3,−5,+4,−8,+6.
(1)该车2小时内最远时在鼓楼什么方向?离鼓楼多远?直接写出结果即可;
鲁教版(五四制)初中数学六年级上册_《有理数的加减混合运算》第二课时参考课件

2 3 5 4
二、计算: -32 - (-12) +(-15)
解: -32 - (-12) +(-15) = -32+12+ -15
= -32 +12 - 15
= -47 +12 = -35
练习
将下列式子先统一成加法,再写成省略加 号和括号的和的形式,并把它读出来。
1.(-4 )-(+7 )+( - 9 )-(-3 ) 2. ( + 2.3 )-(-2.1)+(-3.2 )-4
1 2 = (- ) + (- ) + (-15) 3 3
1 2 例2 (1)(- ) - 15 + (- ) 3 3
6 7 = -12 - 8 + 5 10 1 = -20 + = (-1) +(-15) 有理数的加 2 39 =减混合运算 = -16 2 可以统一成
加法
一、把下列各式改写成代数和的形式
学以致用:
(1)把下面各式写成省略括号的和的形式:
①10+(+4)+(-6)-(-5); ②(-8)-(+4)+(-7)-(+9). 解:① 10+(+4)+(-6)-(-5) =10+4-6+5 ② (-8)-(+4)+(-7)-(+9)
= -8-4-7-9
7 6 (2)(-12) - - + (-8) 10 5 1 2 6 7 解: (1)(- ) - 15 + (- ) 解: (-12) - - + (-8) 3 3 10 5 6 7 1 2 = (- ) + (-15) + (- ) = -12 + - 8 3 3 5 10
二、计算: -32 - (-12) +(-15)
解: -32 - (-12) +(-15) = -32+12+ -15
= -32 +12 - 15
= -47 +12 = -35
练习
将下列式子先统一成加法,再写成省略加 号和括号的和的形式,并把它读出来。
1.(-4 )-(+7 )+( - 9 )-(-3 ) 2. ( + 2.3 )-(-2.1)+(-3.2 )-4
1 2 = (- ) + (- ) + (-15) 3 3
1 2 例2 (1)(- ) - 15 + (- ) 3 3
6 7 = -12 - 8 + 5 10 1 = -20 + = (-1) +(-15) 有理数的加 2 39 =减混合运算 = -16 2 可以统一成
加法
一、把下列各式改写成代数和的形式
学以致用:
(1)把下面各式写成省略括号的和的形式:
①10+(+4)+(-6)-(-5); ②(-8)-(+4)+(-7)-(+9). 解:① 10+(+4)+(-6)-(-5) =10+4-6+5 ② (-8)-(+4)+(-7)-(+9)
= -8-4-7-9
7 6 (2)(-12) - - + (-8) 10 5 1 2 6 7 解: (1)(- ) - 15 + (- ) 解: (-12) - - + (-8) 3 3 10 5 6 7 1 2 = (- ) + (-15) + (- ) = -12 + - 8 3 3 5 10
沪教版六年级数学上册 1.1.2 数轴 课件(16张PPT)
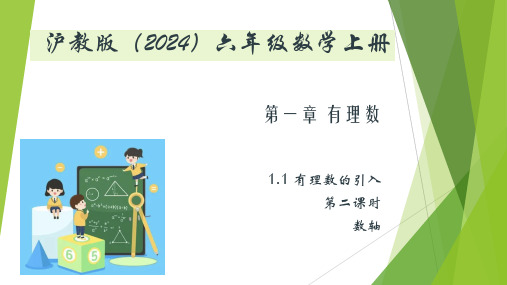
线叫作数轴。
数轴的三要素:原点、正方向和单位长度;
2.任何有理数,都可以用数轴上点表示。
反过来说,“数轴上的点表示的都是有理数”是错误的!
3.数形结合是一种数学思想方法,通过数与形之间的对应和
转化来解决数学问题。
THANKS
-3可以用数轴上位于原点左边、距离原点3个单位长度的点来表示;
3
3
- 可以用数轴上位于原点右边、距离原点 个单位长度的点来表示;
2
2
任何有理数,都可以用数轴上点表示。
反过来说,“数轴上的点表示的都是有理数”是错误的!
应用
例1
下图中,这些都是数轴吗?若不是,请说明理由.
缺少原点
1
2
3
缺少正方向
缺少单位长度
沪教版(2024)六年级数学上册
第一章 有理数
1.1 有理数的引入
第二课时
数轴
内容回顾
上节课我们学习了正数和负数,我们一起复习一下
1.正数和负数可以表示相反意义的量;
2.数字前面有“+”号(正号)或没有符号的数是
正数(0除外);
数字前面有“-”号(负号)的数是负数;
零既不是正数也不是负数!
3.正整数、零和负整数统称为整数;
二、可以说出数轴上的点所表示的数;可以在数轴上标
记出任意有理数;
三、数形结合,理解有理数与数轴上的点的对应关系,
初步了解数形结合的数学思想;
情景导入
我们已经知道,零上温度用正数表示,零下温度用负数表
示,如图1-1-7所示。
把温度计水平横置,那么在“0”右边的数都是正数,在
“0”的左边都是负数。
思考
为4,则B点表示的数是多少?
数轴的三要素:原点、正方向和单位长度;
2.任何有理数,都可以用数轴上点表示。
反过来说,“数轴上的点表示的都是有理数”是错误的!
3.数形结合是一种数学思想方法,通过数与形之间的对应和
转化来解决数学问题。
THANKS
-3可以用数轴上位于原点左边、距离原点3个单位长度的点来表示;
3
3
- 可以用数轴上位于原点右边、距离原点 个单位长度的点来表示;
2
2
任何有理数,都可以用数轴上点表示。
反过来说,“数轴上的点表示的都是有理数”是错误的!
应用
例1
下图中,这些都是数轴吗?若不是,请说明理由.
缺少原点
1
2
3
缺少正方向
缺少单位长度
沪教版(2024)六年级数学上册
第一章 有理数
1.1 有理数的引入
第二课时
数轴
内容回顾
上节课我们学习了正数和负数,我们一起复习一下
1.正数和负数可以表示相反意义的量;
2.数字前面有“+”号(正号)或没有符号的数是
正数(0除外);
数字前面有“-”号(负号)的数是负数;
零既不是正数也不是负数!
3.正整数、零和负整数统称为整数;
二、可以说出数轴上的点所表示的数;可以在数轴上标
记出任意有理数;
三、数形结合,理解有理数与数轴上的点的对应关系,
初步了解数形结合的数学思想;
情景导入
我们已经知道,零上温度用正数表示,零下温度用负数表
示,如图1-1-7所示。
把温度计水平横置,那么在“0”右边的数都是正数,在
“0”的左边都是负数。
思考
为4,则B点表示的数是多少?
六年级数学课件--近似数

, 或 叫精确
到
),
0.0001
万分位
……
精讲点拨
按括号内的要求,用四舍五入法对下列各数 取近似数:
(1)0.0158(精确到0.001); (2)304.35(精确到个位); (3)1.804(精确到0.1); (4)1.804(精确到0.01)
思路分析:按要求确定精确到的数位,再根据这个数位 右边的一位按四舍五入法进行取值。
六年级数学上册第二章有理数及其运算
2.12 近似数
教学目标
了解近似数的概念,能按要求取近似 数,体会近似数的意义及其在生活中 的作用。
预习诊断
对于参加同一个会议的人数,有两种报道: “会议秘书处宣布,参加今天会议的有513人”。 另一种报道说: “约有500人参加了今天的会 议” 。
这里数字513确切地反映了实际人数,它是一个准确数。
准确数-- 与实际完全符合的数
500这个数只是接近实际人数,但与实际人数还有差别, 它是一个近似数。
近似数-- 与实际非常接近的数
探究新知
下列各数,哪些是近似数?哪些是准确数? ⑴ 一小时有60分。 ⑵绿化队今年植树约2万棵。 ⑶小明到书店买了10本书。 ⑷一次数学测验中,有2人得100分。 ⑸某区在校中学生近75万人。 ⑹七年级二班有56人。
探究新知 关于近似数——精确度
(1)精确度-- 表示近 似数与准确数的接近 程度。
(2)按四舍五入法对圆 周率π取近似数。
π≈3 (精确到个位 )
π≈3.1( 精确到0.1,或叫精确到十分
位)
π≈3.14(精确到0.01,或叫精确到百分 位)
π≈3.142精确到
到),0.001Fra bibliotek,或叫精确
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
99国债 (1)
+0.01
99国债 (2)
-0.05
99国债 01通化债券 01三峡债
(3)
券
-1.24 +0.15 -2.01
99国债(1)_涨__0_.0_1_元____;99国债(2)_跌__0_._0_5_元__; 99国债(3)_跌__1_._2_4_元___;01通化债券_涨__0_.1_5_元__; 01三峡债券__跌__2_.0_1_元____.
用小学学过的数能表示下列数吗
零上5ºC
零下5ºC
用
小
学
学
过
的
数
能
表
示
下
列
数
吗
0
数怎么不够用了? 所以我们引进有理数的概念
某班进行知识竞赛,评分 标准是答对一题加1分, 答错一题扣1分,不答得0 分;每个队的基础分都是 0分
答对
答错
答题情况
第一队
第二队
不回答
加1分表示+1分
扣1分表示-1分
得0分表示0分
数的分类
有理数
正有理数 零
负有理数
正整数
正分数 负整数 负分数
说明:①分类的标准不同,结果也不同;②分类的结果应无遗漏、 无 重复;③零是整数,但零既不是正数,也不是负数.
1.零是整数吗?自然数一定是整数吗?自然数一定是 正整数吗?整数一定是自然数吗?
零是整数;自然数一定是整数;自然数不一定是 正整数,因为零也是自然数;整数不一定是自然 数,因为负整数不是自然数。
7
排名 2 46 66
111 120 153 184
财富全球500强中的主要零售企业
公司 沃尔玛 麦德龙 家乐福 特斯科 洋华堂
大荣 佳士客
年收入 166809.0 46663.6 39855.7 30351.9 28670.9 25230.1 22451.3
利润 5377.0 295.1 805.6 1088.4 423.6 -195.2 -25.2
练习:把下列各数分类,并填在表示相应 集合的大括号
里:
•
-11,4,8.6,+12,-6.4, 0. 4
2 ,π,0, 3 , 27
2.如果一个数是非负数(不是负数),那 么这数可能是_____正__数__或__零_____. 3.如果一个是非正数(不是正数),那么 这个数可能是____负___数__或__零___.
记住啰:零和正数统称为非负数!
练习1:下表是某日上海发行的部分债券行情表,试说明各债券当
天涨跌情况。
名称 涨跌/元
(2)在某次乒乓球质量检测中,一只乒乓球超出标准质 量0.02g记作+0.02g,那么-0.03g表示什么?
(3)某大米包装袋上标注着“净含量:10kg±150g”,这里 的“10kg±150g”表示什么?
解:(1)沿顺时针方向转了12圈记作-12圈; (2)-0.03g表示乒乓球的质量低于标准质量0.03g; (3)每袋大米的标准质量应为10kg,但实际每袋大米可能有150g的误差, 即最多超出标准质量150g,最少少于标准质量150g
特别注意:“-”不可以省略!
进一步理解:
1.形如8,2.6,150………这样的数叫做正数。 正数 >_ 0 (用“<”“>”“=”填空)
2.在正数前面加上“-”号的数叫做负数, 形如-8,-2.6,-150……
负数 _< 0(用“<”“>”“=”填空)
3.0 既不是正数,也不是负数.
我们学过的数中又来新成员了:
记住啦!
1, 2, 3,称为负整数; 1 , 2 , 5 ,称为负分数;
234 相应的, 1,2,3,称为正整数; 1 ,2 ,5 ,称为正分数。 234
数的分类
正整数、零和负整数统称整数;
正分数和负分数统称分数。
整数和分数统称有理数。
正整数
整数
零
有理数
分数
负整数 正分数
负分数
自然数
注意: 小数≠分数
用心理解!
为了表示具有相反意义的量,我们把一种意义的量规定为正,用 过去学过的数(零除外),如123,15,3.14等来表示,这样的数叫 做正数。正数前面可加正号“+”来表示(“+”常省略不写);把 另一种与之意义相反的量规定为负,用过去学过的数(零除外)前 面放上负号“-”来表示,
如 233, 60, 2 , 0.5等,这样的数叫做负数。 3
答对题得分
答错题得分
未回答题的得分
第一队
+6
-3
0
第二队
+8
-2
生活中你见过带有“-”号的数吗?
全国主要城市天气预报
城市 天气 高温 低温 城市 天气 高温 低温
哈尔滨 小雨 15
6
长春 多云 18
10
沈阳 小雨 19
7
天津 小雨 12
8
西宁 小雪 5
-4 银川 小雪
0
-3
兰州 小雪 3
-3 西安 小雨 16
(5)某粮店运进粮食1200千克,运出粮食800千克
获得新知
零上与零下
盈利与亏损 加分与扣分
具有相反意义的量
高出与低于
具有相反意义的量:上升与下降、增与减、收入与支出、胜与负、 进与退、多与少、盈利与亏损向东与向西、顺与逆、过剩与不足、 重与轻等
用正数和负数可以表示具有相反意义的量
(1)某人转动转盘,如果用+5圈表示沿逆时针方向转了 5圈,那么沿顺时针方向转了12圈怎样表示?
雇员人数 1140000 171440 297290 134896
97040 47953 34375
资料来源:2002年《财富》全球500统计
单位:百万美元
想一想:
生活中的“+”“-”的关系? “+”“-”表示具有相反的量
你能列举一些相反意义的量吗?
日常生活中,常会遇到的一些相反意义的量:
(1)汽车向东行驶3千米。向西行驶1千米 (2)某超市买进水果100公斤,卖出90公斤 (3)某天的最低气温是零下6°C,最高气温是零上7°C (4)小亮家今年上半年的收入) 在知识竞赛中,如果用+10 分表示加10分, 那么扣20分表示_-2_0 _。
(2)某人转动转盘,如果用+5圈表示沿逆时针方向转了5圈, 那么沿顺时针方向转了12圈表示_-1_2 _。
(3)小明在某个路口,以规定方向以向东为正,向西为负,如果 他向东走了100m,则可表示为_+10_0 ;如果向西走了150m,则 可表示为 _-15_0 _;如果他走了-50m,则表示_向_西走_了_50_m_ , 如果走了+200m,则表示_向_东走_了_20_0m___;如果小明先向西 走了180m,后又向东走了200m,则此时他在离路口 东_面_20_m。
