双曲线及其标准方程练习题一
(完整word版)双曲线及其标准方程练习题.doc

2.2.1 双曲线及其标准方程x 2 y 2 )1.已知方程1表示焦点在 y 轴上的双曲线,则 k 的取值范围是(9 kk 3A.3<k <9B.k >3C.k >9D.k <32.方程 x 2 +(k-1)y 2=k+1 表示焦点在 x 轴上的双曲线,则 k 的取值范围是 ( )A.k <-1B.k > 1C.-1< k <1D.k < -1 或 k > 13.方程x 2y 2 1表示焦点在坐标轴上的双曲线,则α是第几象限的角()sincosA.二B.四C.二或四D.一或三4.已知双曲线的焦点 F 1(-4,0),F 2( 4, 0),且经过点 M (2 6 ,2)的双曲线标准方程是 ______.5.双曲线的焦点在 x 轴上,且经过点 M (3,2)、N (-2,-1),则双曲线标准方程是 ______.双曲线x 2 y 2 1 上点 P 到左焦点的距离为 6,这样的点有 ______个.6.12437.双曲线 3x 2 -y 2=2 的右支上有一点 P , P 到 x 轴、 y 轴的距离之比为,则点 P 的坐标是______.8.若双曲线 x 2 -4y 2 =4 的焦点是 F 1、F 2 过 F 1 的直线交左支于 A 、B ,若|AB|=5,则△ AF 2B 的周长是 ______.1 / 39.已知双曲线 x2y 2 1 ,过它的焦点且垂直于 x 轴的弦长是 ______. 25 2410.在双曲线 x 2-y 2 =4 上的一点,使该点与焦点的连线互相垂直,则这个点坐标是______.11. 已知 12 是双曲线 x 2 21 的两个焦点,点 P 在双曲线上且满足∠ F 1 PF2 F 、 F y4=90°,求△ F 1PF 2 的面积 .2 / 3参考答案1. C2. C3. C4. y 2 x 2 15. x 2y 2 16. 39 77 73 57.(2 6, 6 ) 8. 189.483510.( 6 , 2 ),(- 6 , 2 ),( 6 ,- 2 ),(- 6 ,- 2 )∵ 为双曲线 x 2y 21 上的一个点且 F 1、2 为焦点. 11. P4F∴ ||PF 1|-|PF 2||=2a=4,|F 1 F 2|=2c=2 5∵∠ F 1PF 2=90°∴在 Rt △PF 1F 2 中 ,|PF 1|2+|PF 2|2=|F 1F 2|2=20∵( |PF 1|-|PF 2|)2=|PF 1 |2+|PF 2|2-2|PF 1||PF 2|=16∴20-2|PF 1||PF 2|=16∴ |PF 1| ·|PF 2|=2∴SF PF12|PF 1| |PF ·2|=1 12由此题可归纳出 S △ F1PF2=b 2cot ∠F 1PF223 / 3。
双曲线及其标准方程基础练习

双曲线及其标准方程基础练习一、选择题1.双曲线y2-x2=2的渐近线方程是()A.y=±x B.y=±2x C.y=±3x D.y=±2x2.设F1、F2是双曲线x2-y224=1的两焦点,P是双曲线上一点,且3|PF1|=4|PF2|,则△PF1F2的面积等于()A.42B.83C.24 D.483.(2011·湖南高考)设双曲线x2a2-y29=1(a>0)的渐近线方程为3x±2y=0,则a的值为()A.4 B.3 C.2 D.14.若双曲线x2a2-y2b2=1的焦点到其渐近线的距离等于实轴长,则该双曲线的离心率为()A. 5 B.5 C. 2 D.25.(2011·山东高考)已知双曲线x2a2-y2b2=1(a>0,b>0)的两条渐近线均和圆C:x2+y2-6x+5=0相切,且双曲线的右焦点为圆C的圆心,则该双曲线的方程为()A.x25-y24=1 B.x24-y25=1 C.x23-y26=1 D.x26-y23=16.(2012·江南十校联考)已知F1、F2为双曲线C:x2-y2=1的左右焦点,点P在C上,∠F1PF2=60°,则|PF1|·|PF2|= ( )A.2 B.4 C.6 D.87.(2012·豫南九校联考)设圆锥曲线r的两个焦点分别为F1,F2,若曲线r上存在点P满足|PF1|∶|F1F2|∶|PF2|=4∶3∶2,则曲线r的离心率等于()A.12或32 B.23或2 C.12或2 D.23或328.(2012·滨州模拟)已知F1、F2分别是双曲线x2a2-y2b2=1(a>0,b>0)的左、右焦点,过F1作垂直于x轴的直线交双曲线于A、B两点,若△ABF2为锐角三角形,则双曲线的离心率的范围是()A.(1,1+2) B.(1+2,+∞)C.(1-2,1+2) D.(2,2+1)二、填空题9.双曲线mx2+y2=1的虚轴长是实轴长的2倍,则m等于________.10.已知双曲线C:x2a2-y2b2=1(a>0,b>0)的离心率e=2,且它的一个顶点到相应焦点的距离为1,则双曲线C的方程为__________.11.(2012·泰安模拟)与双曲线x29-y216=1有共同的渐近线,并且过点A(6,82)的双曲线的标准方程为________________________.12.(2011·江西高考)若双曲线y216-x2m=1的离心率e=2,则m=________.三、解答题13.(2011·江西高考)P(x0,y0)(x0≠±a)是双曲线E:x2a2-y2b2=1(a>0,b>0)上一点,M,N分别是双曲线E 的左,右顶点,直线PM ,PN 的斜率之积为15. (1)求双曲线的离心率;(2)过双曲线E 的右焦点且斜率为1的直线交双曲线于A ,B 两点,O 为坐标原点,C 为双曲线上一点,满足OC OA OB λ=+,求λ的值.14.(2012·南昌模拟)已知双曲线x 2a 2-y 2b 2=1(b >a >0),O 为坐标原点,离心率e =2,点M (5,3)在双曲线上.(1)求双曲线的方程;(2)若直线l 与双曲线交于P 、Q 两点,且0OP OQ •=.求1|OP |2+1|OQ |2的值.15.(14分)(2011·广东高考)设圆C 与两圆(x +5)2+y 2=4,(x -5)2+y 2=4中的一个内切,另一个外切.(1)求C 的圆心轨迹L 的方程;(2)已知点M (355,455),F (5,0),且P 为L 上动点,求||MP |-|FP ||的最大值及此时点P 的坐标.。
双曲线练习题(含答案)

双曲线及其标准方程习题一、 单选题(每道小题 4分 共 56分 )1. 命题甲:动点P 到两定点A 、B 距离之差│|PA|-|PB|│=2a(a >0);命题乙; P 点轨迹是双曲线,则命题甲是命题乙的 [ ] A .充分非必要条件 B .必要非充分条件 C .充要条件 D .既非充分也非必要条件2.若双曲线的一个焦点是,,则等于 . . . .2kx ky =1(04)k [ ]A B C D 22---33258332583.点到点,与它关于原点的对称点的距离差的绝对值等于,则点的轨迹方程是 . .. .P (60)10P [ ]A y 11=1B y 25=1C y 6=1D y 25=12222-----x x x x 2222256125114.k 5+y 6k=1[ ]A B C D 2<是方程表示双曲线的 .既非充分又非必要条件 .充要条件.必要而非充分条件 .充分而非必要条件x k 25--5. 如果方程x 2sin α-y 2cos α=1表示焦点在y 轴上的双曲线,那么角α的终边在 [ ] A .第四象限 B .第三象限 C .第二象限 D .第一象限 6.下列曲线中的一个焦点在直线上的是 . .. .4x 5y +25=0[ ]A y 16=1B +y 16=1C x 16=1D +x 16=12222---x x y y 22229259257. 若a ·b <0,则ax 2-ay 2=b 所表示的曲线是 [ ] A .双曲线且焦点在x 轴上 B .双曲线且焦点在y 轴上 C .双曲线且焦点可能在x 轴上,也可能在y 轴上 D .椭圆 8.以椭圆的焦点为焦点,且过,点的双曲线方程为. .. .x x y y y 2222296109251150+y 25=1P(35)[ ]A y 10=1B x 6=1C x 3=1D x 2=122222----9.到椭圆的两焦点距离之差的绝对值等于椭圆短轴的点的轨迹方程是 . .. .x x x x x 2222225251697+y 9=1[ ]A y 9=1B y 9=1C y 7=1D y 9=122222----10.直线与坐标轴交两点,以坐标轴为对称轴,以其中一点为焦点且另一点为虚轴端点的双曲线的方程是 . .. .或2x 5y +20=0[ ]A y 16=1B y 84=1C y 84=1D y 84=1y 84=122222------x x x x x 2222284161001610011.以坐标轴为对称轴,过,点且与双曲线有相等焦距的双曲线方程是 .或 .或.或 .或A(34)y 20=1[ ]A y 20=1x 20=1B y 15=1x 15=1C y 20=1x 15=1D y 5=1x 10=1222222222x x y x y x y x y 22222222255510105102015---------12.与双曲线共焦点且过点,的双曲线方程是 . .. .x x x x x 2222215520916------y 10=1(34)[ ]A y 20=1B y 5=1C y 16=1D y 9=12222213. 已知ab <0,方程y=-2x +b 和bx 2+ay 2=ab 表示的曲线只可能是图中的 [ ]14.已知△一边的两个端点是、,另两边斜率的积是,那么顶点的轨迹方程是 . .. .ABC A(7,0)B(70)C [ ]A x +y =49B +x 49=1C =1D 5y 147=12222---,x 355147514749492222y y x二、 填空题(每道小题 4分 共 8分 )1.已知双曲线的焦距是,则的值等于 .x k 21+-y 5=18k 22.设双曲线,与恰是直线在轴与轴上的截距,那么双曲线的焦距等于 .x a 22--y b=1(a >0,b >0)a b 3x +5y 15=0x y 22双曲线的标准方程及其简单的几何性质1.平面内到两定点E 、F 的距离之差的绝对值等于|EF |的点的轨迹是( ) A .双曲线 B .一条直线 C .一条线段 D .两条射线 2.已知方程x 21+k -y 21-k =1表示双曲线,则k 的取值范围是( )A .-1<k <1B .k >0C .k ≥0D .k >1或k <-13.动圆与圆x 2+y 2=1和x 2+y 2-8x +12=0都相外切,则动圆圆心的轨迹为( ) A .双曲线的一支 B .圆 C .抛物线 D .双曲线4.以椭圆x 23+y 24=1的焦点为顶点,以这个椭圆的长轴的端点为焦点的双曲线方程是( )A.x 23-y 2=1 B .y 2-x 23=1 C.x 23-y 24=1D.y 23-x 24=1 5.“ab <0”是“曲线ax 2+by 2=1为双曲线”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件6.已知双曲线的两个焦点为F 1(-5,0)、F 2(5,0),P 是此双曲线上的一点,且PF 1⊥PF 2, |PF 1|·|PF 2|=2,则该双曲线的方程是( ) A.x 22-y 23=1 B.x 23-y 22=1 C.x 24-y 2=1 D .x 2-y 24=17.已知点F 1(-4,0)和F 2(4,0),曲线上的动点P 到F 1、F 2距离之差为6,则曲线方程为( ) A.x 29-y 27=1 B.x 29-y 27=1(y >0) C.x 29-y 27=1或x 27-y 29=1 D.x 29-y 27=1(x >0) 8.已知双曲线的左、右焦点分别为F 1、F 2,在左支上过F 1的弦AB 的长为5,若2a =8,那么△ABF 2的周长是( ) A .16B .18C .21D .269.已知双曲线与椭圆x 29+y 225=1共焦点,它们的离心率之和为145,双曲线的方程是( )A.x 212-y 24=1B.x 24-y 212=1 C .-x 212+y 24=1 D .-x 24+y 212=1 10.焦点为(0,±6)且与双曲线x 22-y 2=1有相同渐近线的双曲线方程是( )A.x 212-y 224=1 B.y 212-x 224=1 C.y 224-x 212=1 D.x 224-y 212=111.若0<k <a ,则双曲线x 2a 2-k 2-y 2b 2+k 2=1与x 2a 2-y 2b 2=1有( )A .相同的实轴B .相同的虚轴C .相同的焦点D .相同的渐近线12.中心在坐标原点,离心率为53的双曲线的焦点在y 轴上,则它的渐近线方程为( )A .y =±54xB .y =±45xC .y =±43xD .y =±34x13.双曲线x 2b 2-y 2a 2=1的两条渐近线互相垂直,那么该双曲线的离心率为( )A .2B. 3C. 2D.3214.双曲线x 29-y 216=1的一个焦点到一条渐近线的距离等于( )A. 3 B .3 C .4 D .2二、填空题15.双曲线的焦点在x 轴上,且经过点M (3,2)、N (-2,-1),则双曲线标准方程是________. 16.过双曲线x 23-y 24=1的焦点且与x 轴垂直的弦的长度为________.17.如果椭圆x 24+y 2a 2=1与双曲线x 2a -y 22=1的焦点相同,那么a =________.18.双曲线x 24+y 2b =1的离心率e ∈(1,2),则b 的取值范围是________.19.椭圆x 24+y 2a 2=1与双曲线x 2a2-y 2=1焦点相同,则a =________.20.双曲线以椭圆x 29+y 225=1的焦点为焦点,它的离心率是椭圆离心率的2倍,求该双曲线的方程为________.双曲线及其标准方程习题答案一、单选题1. B2. C3. A4. D5. B6. C7. B8. B9. C 10. A 11. C 12. A 13. B 14. D 二、填空题1. 10 2.234双曲线的标准方程及其简单的几何性质(答案)1、[答案] D2、[答案] A [解析] 由题意得(1+k )(1-k )>0,∴(k -1)(k +1)<0,∴-1<k <1.3、[答案] A [解析] 设动圆半径为r ,圆心为O , x 2+y 2=1的圆心为O 1,圆x 2+y 2-8x +12=0的圆心为O 2,由题意得|OO 1|=r +1,|OO 2|=r +2, ∴|OO 2|-|OO 1|=r +2-r -1=1<|O 1O 2|=4, 由双曲线的定义知,动圆圆心O 的轨迹是双曲线的一支.4、[答案] B [解析] 由题意知双曲线的焦点在y 轴上,且a =1,c =2, ∴b 2=3,双曲线方程为y 2-x 23=1. 5、[答案] C [解析] ab <0⇒曲线ax 2+by 2=1是双曲线,曲线ax 2+by 2=1是双曲线⇒ab <0. 6、[答案] C [解析] ∵c =5,|PF 1|2+|PF 2|2=|F 1F 2|2=4c 2, ∴(|PF 1|-|PF 2|)2+2|PF 1|·|PF 2|=4c 2,∴4a 2=4c 2-4=16,∴a 2=4,b 2=1. 7、[答案] D [解析] 由双曲线的定义知,点P 的轨迹是以F 1、F 2为焦点, 实轴长为6的双曲线的右支,其方程为:x 29-y 27=1(x >0)8、[答案] D [解析] |AF 2|-|AF 1|=2a =8,|BF 2|-|BF 1|=2a =8, ∴|AF 2|+|BF 2|-(|AF 1|+|BF 1|)=16,∴|AF 2|+|BF 2|=16+5=21, ∴△ABF 2的周长为|AF 2|+|BF 2|+|AB |=21+5=26.9、[答案] C [解析] ∵椭圆x 29+y 225=1的焦点为(0,±4),离心率e =45,∴双曲线的焦点为(0,±4),离心率为145-45=105=2, ∴双曲线方程为:y 24-x 212=1.10、[答案] B [解析] 与双曲线x 22-y 2=1有共同渐近线的双曲线方程可设为x 22-y 2=λ(λ≠0),又因为双曲线的焦点在y 轴上, ∴方程可写为y 2-λ-x 2-2λ=1.又∵双曲线方程的焦点为(0,±6),∴-λ-2λ=36.∴λ=-12. ∴双曲线方程为y 212-x 224=1.11、[答案] C [解析] ∵0<k <a ,∴a 2-k 2>0.∴c 2=(a 2-k 2)+(b 2+k 2)=a 2+b 2.12、[答案] D [解析] ∵c a =53,∴c 2a 2=a 2+b 2a 2=259,∴b 2a 2=169,∴b a =43,∴a b =34.又∵双曲线的焦点在y 轴上,∴双曲线的渐近线方程为y =±a b x ,∴所求双曲线的渐近线方程为y =±34x .13、[答案] C [解析] 双曲线的两条渐近线互相垂直,则渐近线方程为:y =±x ,∴b a =1,∴b 2a 2=c 2-a 2a 2=1,∴c 2=2a 2,e =ca= 2. 14、[答案] C[解析] ∵焦点坐标为(±5,0),渐近线方程为y =±43x ,∴一个焦点(5,0)到渐近线y =43x 的距离为4.15、[答案] x 273-y 275=1 [解析] 设双曲线方程为:x 2a 2-y 2b 2=1(a >0,b >0)又点M (3,2)、N (-2,-1)在双曲线上,∴⎩⎨⎧ 9a 2-4b 2=14a 2-1b 2=1,∴⎩⎨⎧a 2=73b 2=75.16、[答案]833[解析] ∵a 2=3,b 2=4,∴c 2=7,∴c =7, 该弦所在直线方程为x =7,由⎩⎪⎨⎪⎧x =7x 23-y 24=1得y 2=163,∴|y |=433,弦长为833.17、[答案] 1 [解析] 由题意得a >0,且4-a 2=a +2,∴a =1.18、[答案] -12<b <0 [解析] ∵b <0,∴离心率e =4-b2∈(1,2),∴-12<b <0. 19、[答案]62 [解析] 由题意得4-a 2=a 2+1,∴2a 2=3,a =62. 焦点为(0,±4),离心率e =c a =45,∴双曲线的离心率e 1=2e =85,∴c 1a 1=4a 1=85,∴a 1=52,∴b 21=c 21-a 21=16-254=394,∴双曲线的方程为y 2254-x 2394=1.20、[答案]y2254-x2394=1 [解析]椭圆x29+y225=1中,a=5,b=3,c2=16,。
双曲线及其标准方程练习

∵0<a<c,∴令c2-a2=b2(b>0)
x 2 y2 2 1 (a 0,b 0, 2 a b a不一定大于b) y2 x 2 2 1 2 a b
【典例训练】
1.双曲线2x2-y2=k的焦距为6,则k的值为___________.
x2 y2 1 表示双曲线,则m的取值范围为_____. 2.方程 2m m 3 2 2 3.讨论方程 x y 1 表示何种圆锥曲线?它们有何共同特 25 k 9 k
(2)焦点F1、F2的位置,是双曲线定位的条件,它决定了双曲 线标准方程的类型.“焦点跟着正项走”:若x2项的系数为正,
则焦点在x轴上;若y2项的系数为正,那么焦点在y轴上.
(3)当且仅当双曲线的中心在原点,其焦点在坐标轴上时,ຫໍສະໝຸດ 双曲线的方程才具有标准形式.
求双曲线的标准方程 【技法点拨】 1.求双曲线标准方程的三个关注点
x 2 y2 2.若方程 1 表示焦点在x轴上的双曲线,那么m,n的符 m n
号怎样? 提示:m>0,n<0.
3.对双曲线标准方程的三点说明
x 2 y2 y2 x 2 双曲线的标准方程有两种不同类型: 2 2 1, 2 2(a>0,b>0), 1 a b a b
分别表示焦点在x轴上和焦点在y轴上的双曲线. (1)标准方程中的两个参数a和b确定了双曲线的形状和大小, 是双曲线的定形条件,这里b2=c2-a2,与椭圆中b2=a2-c2(a>b>0) 相区别,且椭圆中a>b>0,而双曲线中,a、b大小不确定.
②
③
一般地,在△PF1F2中,通过以上三个等式,所求问题就会顺利 解决.
焦点三角形SPF1F2 b cot 2
最新双曲线及其标准方程练习题

课时作业(十)[学业水平层次]一、选择题1.方程x 22+m -y 22-m =1表示双曲线,则m 的取值范围( )A .-2<m <2B .m >0C .m ≥0D .|m |≥2【解析】 ∵已知方程表示双曲线,∴(2+m )(2-m )>0. ∴-2<m <2. 【答案】 A2.设动点P 到A (-5,0)的距离与它到B (5,0)距离的差等于6,则P 点的轨迹方程是( )A.x 29-y 216=1 B.y 29-x 216=1 C.x 29-y 216=1(x ≤-3)D.x 29-y 216=1(x ≥3)【解析】 由题意知,轨迹应为以A (-5,0),B (5,0)为焦点的双曲线的右支.由c =5,a =3,知b 2=16,∴P 点的轨迹方程为x 29-y 216=1(x ≥3). 【答案】 D3.(2014·福州高级中学期末考试)已知双曲线的中心在原点,两个焦点F 1,F 2分别为(5,0)和(-5,0),点P 在双曲线上,且PF 1⊥PF 2,△PF 1F 2的面积为1,则双曲线的方程为( )A.x 22-y 23=1 B.x 23-y 22=1 C.x 24-y 2=1 D .x 2-y 24=1【解析】由⎩⎨⎧|PF 1|·|PF 2|=2,|PF 1|2+|PF 2|2=(25)2,⇒(|PF 1|-|PF 2|)2=16,即2a =4,解得a =2,又c =5,所以b =1,故选C. 【答案】 C4.已知椭圆方程x 24+y 23=1,双曲线的焦点是椭圆的顶点,顶点是椭圆的焦点,则双曲线的离心率为( )A.2B. 3 C .2D .3【解析】 椭圆的焦点为(1,0),顶点为(2,0),即双曲线中a =1,c =2,所以双曲线的离心率为e =c a =21=2.【答案】 C 二、填空题5.设点P 是双曲线x 29-y 216=1上任意一点,F 1,F 2分别是其左、右焦点,若|PF 1|=10,则|PF 2|=________.【解析】 由双曲线的标准方程得a =3,b =4. 于是c =a 2+b 2=5.(1)若点P 在双曲线的左支上,则|PF 2|-|PF 1|=2a =6,∴|PF 2|=6+|PF 1|=16; (2)若点P 在双曲线的右支上, 则|PF 1|-|PF 2|=6, ∴|PF 2|=|PF 1|-6=10-6=4. 综上,|PF 2|=16或4. 【答案】 16或46.(2014·河南省洛阳高一月考)已知F 1(-3,0),F 2(3,0),满足条件|PF 1|-|PF 2|=2m -1的动点P 的轨迹是双曲线的一支,则m 可以是下列数据中的________.(填序号)①2;②-1;③4;④-3.【解析】 设双曲线的方程为x 2a 2-y 2b 2=1,则c =3,∵2a <2c =6,∴|2m -1|<6,且|2m -1|≠0,∴-52<m <72,且m ≠12,∴①②满足条件.【答案】 ①②7.(2014·哈尔滨高二检测)已知△ABP 的顶点A 、B 分别为双曲线C :x 216-y 29=1的左、右焦点,顶点P 在双曲线C 上,则|sin A -sin B |sin P 的值等于________.【解析】 由方程x 216-y 29=1知a 2=16,b 2=9,即a =4,c =16+9=5.在△ABP 中,利用正弦定理和双曲线的定义知,|sin A -sin B |sin P=||PB |-|P A |||AB |=2a 2c =2×42×5=45.【答案】 45 三、解答题8.求与双曲线x 24-y 22=1有相同焦点且过点P (2,1)的双曲线的方程.【解】 ∵双曲线x 24-y 22=1的焦点在x 轴上. 依题意,设所求双曲线为x 2a 2-y 2b 2=1(a >0,b >0). 又两曲线有相同的焦点, ∴a 2+b 2=c 2=4+2=6.①又点P (2,1)在双曲线x 2a 2-y 2b 2=1上, ∴4a 2-1b 2=1.②由①、②联立,得a 2=b 2=3, 故所求双曲线方程为x 23-y 23=1.9.已知方程kx 2+y 2=4,其中k 为实数,对于不同范围的k 值分别指出方程所表示的曲线类型.【解】 (1)当k =0时,y =±2,表示两条与x 轴平行的直线;(2)当k =1时,方程为x 2+y 2=4,表示圆心在原点,半径为2的圆;(3)当k <0时,方程为y 24-x 2-4k =1,表示焦点在y 轴上的双曲线;(4)当0<k <1时,方程为x 24k +y 24=1,表示焦点在x 轴上的椭圆;(5)当k >1时,方程为x 24k+y 24=1,表示焦点在y 轴上的椭圆.[能力提升层次]1.椭圆x 24+y 2a 2=1与双曲线x 2a -y 22=1有相同的焦点,则a 的值为( )A .1 B. 2 C .2 D .3【解析】 由题意知椭圆、双曲线的焦点在x 轴上,且 a >0.∵4-a 2=a +2,∴a 2+a -2=0, ∴a =1或a =-2(舍去).故选A. 【答案】 A2.(2014·桂林高二期末)已知F 1、F 2为双曲线C :x 2-y 2=1的左、右焦点,点P 在C 上,∠F 1PF 2=60°,则|PF 1|·|PF 2|等于( )A .2B .4C .6D .8【解析】 不妨设P 是双曲线右支上一点, 在双曲线x 2-y 2=1中,a =1,b =1,c =2,则|PF 1|-|PF 2|=2a =2,|F 1F 2|=22,∵|F 1F 2|2=|PF 1|2+|PF 2|2-2|PF 1|·|PF 2|·cos ∠F 1PF 2, ∴8=|PF 1|2+|PF 2|2-2|PF 1|·|PF 2|·12, ∴8=(|PF 1|-|PF 2|)2+|PF 1|·|PF 2|, ∴8=4+|PF 1||PF 2|, ∴|PF 1||PF 2|=4.故选B. 【答案】 B3.(2014·福建省厦门一中期末考试)已知双曲线x 216-y 225=1的左焦点为F ,点P 为双曲线右支上的一点,且PF 与圆x 2+y 2=16相切于点N ,M 为线段PF 的中点,O 为坐标原点,则|MN |-|MO |=________.【解析】 设F ′是双曲线的右焦点,连PF ′(图略),因为M ,O 分别是FP ,FF ′的中点,所以|MO |=12|PF ′|,又|FN |=|OF |2-|ON |2=5,且由双曲线的定义知|PF |-|PF ′|=8,故|MN |-|MO |=|MF |-|FN |-12|PF ′|=12(|PF |-|PF ′|)-|FN |=12×8-5=-1.【答案】 -14.已知双曲线x 216-y 24=1的两焦点为F 1、F 2.(1)若点M 在双曲线上,且MF 1→·MF 2→=0,求点M 到x 轴的距离; (2)若双曲线C 与已知双曲线有相同焦点,且过点(32,2),求双曲线C 的方程.【解】 (1)不妨设M 在双曲线的右支上,M 点到x 轴的距离为h ,MF 1→·MF 2→=0, 则MF 1⊥MF 2,设|MF 1|=m ,|MF 2|=n ,由双曲线定义知,m -n =2a =8,又m 2+n 2=(2c )2=80,②由①②得m ·n =8, ∴12mn =4=12|F 1F 2|·h , ∴h =255.(2)设所求双曲线C 的方程为x 216-λ-y 24+λ=1(-4<λ<16),由于双曲线C 过点(32,2),所以1816-λ-44+λ=1,解得λ=4或λ=-14(舍去).∴所求双曲线C 的方程为x 212-y 28=1.。
2.3.1 双曲线及其标准方程

2.3.1 双曲线及其标准方程1.若方程-=1表示双曲线,则实数m的取值范围是( B )(A)(-1,3) (B)(-1,+∞)(C)(3,+∞) (D)(-∞,-1)解析:依题意应有m+1>0,即m>-1.故选B.2.已知M(-2,0),N(2,0),||PM|-|PN||=3,则动点P的轨迹是( D )(A)圆 (B)椭圆 (C)射线 (D)双曲线解析:因为||PM|-|PN||=3<|MN|=4,所以由双曲线定义可知,点P的轨迹是双曲线.故选D.3.设F1,F2是双曲线x2-=1的两个焦点,P是双曲线上的一点,且3|PF1|=4|PF2|,则|PF1|等于( A )(A)8 (B)6 (C)4 (D)2解析:依题意得解得|PF2|=6,|PF1|=8,故选A.4.双曲线-=1的焦距为10,则实数m的值为( C )(A)-16 (B)4 (C)16 (D)81解析:因为2c=10,所以c2=25,所以9+m=25,所以m=16.故选C.5.在方程mx2-my2=n中,若mn<0,则方程表示的曲线是( D )(A)焦点在x轴上的椭圆(B)焦点在x轴上的双曲线(C)焦点在y轴上的椭圆(D)焦点在y轴上的双曲线解析:方程mx2-my2=n可化为-=1.因为mn<0,所以<0,->0.方程又可化为-=1,所以方程表示焦点在y轴上的双曲线.故选D.6.已知双曲线的方程为-=1(a>0,b>0),A,B在双曲线的右支上,线段AB经过双曲线的右焦点F2,|AB|=m,F1为另一焦点,则△ABF1的周长为( B )(A)2a+2m (B)4a+2m(C)a+m (D)2a+4m解析:由双曲线定义得|AF1|-|AF2|=2a,|BF1|-|BF2|=2a,所以|AF1|+|BF1|-(|AF2|+|BF2|)=4a.所以|AF1|+|BF1|=4a+m.所以△ABF1的周长是4a+2m.故选B.7.已知椭圆+=1与双曲线-=1有共同的焦点F 1,F 2,两曲线的一个交点为P,则·的值为( C )(A)3 (B)7 (C)11 (D)21解析:椭圆与双曲线同焦点,解得m=4, 设r 1=|PF 1|>r 2=|PF 2|,根据圆锥曲线定义 得r 1+r 2=10,r 1-r 2=4,解得r 1=7,r 2=3,而焦距为6,由余弦定理得cos ∠F 1PF 2==,因此·=3×7×=11.故选C.8.焦点分别为(-2,0),(2,0)且经过点(2,3)的双曲线的标准方程为( A )(A)x 2-=1 (B)-y 2=1 (C)y 2-=1 (D)-=1 解析:由双曲线定义知,2a=-=5-3=2,所以a=1.又c=2,所以b 2=c 2-a 2=4-1=3,因此所求双曲线的标准方程为x 2-=1.故选A.9.设m 是常数,若点F(0,5)是双曲线-=1的一个焦点,则m= .解析:由点F(0,5)可知双曲线-=1的焦点落在y轴上,所以m>0,且m+9=52,解得m=16.答案:1610.已知双曲线的两个焦点F1(-,0),F2(,0),P是双曲线上一点,且·=0,|PF1|·|PF2|=2,则双曲线的标准方程为.解析:由题意可设双曲线方程为-=1(a>0,b>0).由·=0,得PF1⊥PF2.根据勾股定理得|PF1|2+|PF2|2=(2c)2,即|PF1|2+|PF2|2=20.又根据双曲线定义有|PF1|-|PF2|=±2a,两边平方并代入|PF1|·|PF2|=2得20-2×2=4a2,解得a2=4,从而b2=5-4=1,所以双曲线方程为-y2=1. 答案:-y2=111.已知椭圆+=1与双曲线-y2=1的公共焦点为F1,F2,点P是两条曲线的一个公共点,则cos∠F1PF2的值为.解析:设P在第一象限,由椭圆与双曲线的定义可得⇒又|F1F2|=4,由余弦定理得cos∠F1PF2==.答案:12.从双曲线-=1(a>0,b>0)的左焦点F引圆x2+y2=a2的切线,切点为T,延长FT交双曲线右支于点P,若M是线段PF的中点,O为原点,则|MO|-|MT|的值是.解析:如图所示,设双曲线的右焦点为F1,连接PF1,则|PF|-|PF1|=2a, 在Rt△FTO中,|OF|=c,|OT|=a,所以|FT|===b,又M是线段PF的中点,O为FF1中点,所以|PF|=2|MF|=2(|MT|+b),所以|MO|=|PF1|=(|PF|-2a)=(2|MT|+2b-2a)=|MT|+b-a即|MO|-|MT|=b-a.答案:b-a13.求适合下列条件的双曲线的标准方程:(1)a=3,c=4,焦点在x轴上;(2)经过点(3,-4),(,5).解:(1)由题设知,a=3,c=4,由c2=a2+b2得,b2=c2-a2=42-32=7.因为双曲线的焦点在x轴上,所以所求双曲线的标准方程为-=1.(2)设双曲线的方程为mx2+ny2=1(mn<0),因为双曲线经过点(3,-4),(,5),所以解得故所求双曲线的标准方程为-=1.14.已知双曲线-=1的左、右焦点分别是F1,F2,若双曲线上一点P 使得∠F1PF2=60°,求△F1PF2的面积.解:由-=1,得a=3,b=4,c=5.由定义和余弦定理得|PF1|-|PF2|=±6,|F1F2|2=|PF1|2+|PF2|2-2|PF1||PF2|cos 60°,所以102=(|PF1|-|PF2|)2+|PF1|·|PF2|,所以|PF1|·|PF2|=64.所以=|PF1|·|PF2|·sin∠F1PF2=×64×=16.15.已知双曲线过点(3,-2)且与椭圆4x2+9y2=36有相同的焦点. (1)求双曲线的标准方程;(2)若点M在双曲线上,F1,F2分别为左、右焦点,且|MF1|=2|MF2|,试求△MF1F2的面积.解:(1)椭圆方程可化为+=1,焦点在x轴上,且c=,故设双曲线方程为-=1,则解得所以双曲线的标准方程为-=1.(2)因为点M在双曲线上,又|MF1|=2|MF2|,所以点M在双曲线的右支上,则有|MF1|-|MF2|=2,故解得|MF1|=4,|MF2|=2,又|F1F2|=2,因此在△MF1F2中,cos∠F1MF2==,所以sin∠F1MF2=,所以=|MF1|·|MF2|·sin∠F1MF2=×4×2×=2.16.已知双曲线的两个焦点为F1(-,0),F2(,0),M是此双曲线上的一点,且满足·=0,||·||=2,则该双曲线的方程是( A )(A)-y2=1 (B)x2-=1(C)-=1 (D)-=1解析:因为·=0,所以⊥,即MF1⊥MF2,所以|MF1|2+|MF2|2=40.则(|MF1|-|MF2|)2=|MF1|2-2|MF1|·|MF2|+|MF2|2=40-2×2=36.所以||MF1|-|MF2||=6=2a,即a=3.因为c=,所以b2=c2-a2=1.所以该双曲线的方程是-y2=1.故选A.17.已知两圆C1:(x+4)2+y2=2,C2:(x-4)2+y2=2,动圆M与两圆C1,C2都相切,则动圆圆心M的轨迹方程是( D )(A)x=0 (B)-=1(x≥)(C)-=1 (D)-=1或x=0解析:动圆M与两圆C1,C2都相切,有四种情况:①动圆M与两圆都外切;②动圆M与两圆都内切;③动圆M与圆C1外切,与圆C2内切;④动圆M与圆C1内切,与圆C2外切.在①②情况下,显然动圆圆心M的轨迹方程是x=0;在③的情况下,如图,设动圆M的半径为r,则|MC1|=r+,|MC2|=r-,故得|MC1|-|MC2|=2;在④的情况下,同理,得|MC2|-|MC1|=2.由③④得||MC1|-|MC2||=2<8=|C1C2|,根据双曲线定义,可知点M的轨迹是以C1(-4,0),C2(4,0)为焦点的双曲线,且a=,c=4,b2=c2-a2=14,所以此时动圆圆心M的轨迹方程为-=1.故选D.18.(2018·浙江衢州高三模拟)F1,F2分别是双曲线-=1的左、右焦点,P为双曲线右支上的一点,☉A是△PF1F2的内切圆,☉A与x轴相切于点M(m,0),则m的值为.解析:如图所示,易知|PB|=|PC|,|BF1|=|MF1|,|CF2|=|MF2|,|PF1|-|PF2|=|BF1|-|CF2|=|MF1|-|MF2|=2a,所以点M在双曲线上,因为a=4,所以M(4,0),即m=4.答案:419.已知F是双曲线-=1的左焦点,点A(1,4),P是双曲线右支上的动点,则|PF|+|PA|的最小值为.解析:设右焦点为F′,依题意,|PF|=|PF′|+4,所以|PF|+|PA|=|PF′|+4+|PA|=|PF′|+|PA|+4≥|AF′|+4=5+4=9. 答案:920.已知△ABC的两个顶点A,B分别为椭圆x2+5y2=5的左焦点和右焦点,且三个内角A,B,C满足关系式sin B-sin A=sin C.(1)求线段AB的长度;(2)求顶点C的轨迹方程.解:(1)将椭圆方程化为标准形式为+y2=1.所以a2=5,b2=1,c2=a2-b2=4,则A(-2,0),B(2,0),|AB|=4.(2)因为sin B-sin A=sin C,所以由正弦定理得|CA|-|CB|=|AB|=2<|AB|=4,即动点C到两定点A,B的距离之差为定值.所以动点C的轨迹是双曲线的右支,并且c′=2,a′=1,所以所求的点C的轨迹方程为x2-=1(x>1).。
2.2.1双曲线及其标准方程 高二上学期数学北师大版选择性必修第一册

2.1 双曲线及其标准方程1.双曲线方程为x 2-2y 2=1,则它的右焦点坐标为( )A.√22,0 B.√62,0C.√52,0D.(√3,0)2.已知双曲线x 2a 2−y 2b2=1(a>0,b>0)的左、右焦点分别为F 1,F 2,点P 在双曲线的右支上,若|PF 1|-|PF 2|=b ,且双曲线的焦距为2√5,则该双曲线的方程为( )A.x 24-y 2=1B.x 23−y 22=1 C.x 2-y 24=1D.x 22−y 23=13.已知双曲线x 2λ-3+y 22-λ=1,焦点在y 轴上,若焦距为4,则λ等于( )A.32B.5C.7D.124.已知双曲线x 24−y 25=1上一点P 到左焦点F 1的距离为10,则PF 1的中点N 到坐标原点O 的距离为( ) A.3或7 B.6或14C.3D.75.如图,已知双曲线的方程为x 2a 2−y 2b2=1(a>0,b>0),点A ,B 均在双曲线的右支上,线段AB 经过双曲线的右焦点F 2,|AB|=m ,F 1为双曲线的左焦点,则△ABF 1的周长为( ) A.2a+2m B.4a+2mC.a+mD.2a+4m 6.与圆x 2+y 2=1及圆x 2+y 2-8x+12=0都外切的圆P 的圆心在( )A.一个椭圆上B.一个圆上C.一条抛物线上D.双曲线的一支上7.以椭圆x 2+y 2=1的焦点为顶点,以这个椭圆的长轴的端点为焦点的双曲线的标准方程是 .8.已知点F 1,F 2分别是双曲线x 29−y 216=1的左、右焦点,若点P 是双曲线左支上的点,且|PF 1|·|PF 2|=32,则△F 1PF 2的面积为 . 9.已知与双曲线x 216−y 29=1共焦点的双曲线过点P -√52,-√6,求该双曲线的标准方程.能力达标10.“mn<0”是方程“mx 2+ny 2=1表示双曲线”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件D.既不充分也不必要条件11.已知平面内两定点A (-5,0),B (5,0),动点M 满足|MA|-|MB|=6,则点M 的轨迹方程是( ) A.x 216−y 29=1B.x 216−y 29=1(x ≥4)C.x 29−y 216=1 D.x 29−y 216=1(x ≥3)12.动圆与圆x 2+y 2=1和x 2+y 2-8x+12=0都外切,则动圆圆心的轨迹是( ) A.双曲线的一支 B.圆 C.椭圆D.双曲线13.若双曲线x 2n -y 2=1(n>1)的左、右焦点分别为F 1,F 2,点P 在双曲线上,且满足|PF 1|+|PF 2|=2√n +2,则△PF 1F 2的面积为( ) A.1B.12C.2D.414.已知左、右焦点分别为F 1,F 2的双曲线C :x 2a 2-y 2=1(a>0)过点√15,-√63,点P 在双曲线C 上,若|PF 1|=3,则|PF 2|=( ) A.3B.6C.9D.1215.若曲线C :mx 2+(2-m )y 2=1是焦点在x 轴上的双曲线,则m 的取值范围为 .16.焦点在x 轴上的双曲线经过点(4√2,-3),且Q (0,5)与两焦点的连线互相垂直,则此双曲线的标准方程为 .17.已知双曲线E :x 2−y 2=1的左、右焦点分别为F 1,F 2. (1)若点M 在双曲线上,且MF 1⃗⃗⃗⃗⃗⃗⃗⃗ ·MF 2⃗⃗⃗⃗⃗⃗⃗⃗ =0,求点M 到x 轴的距离;(2)若双曲线C 与双曲线E 有相同的焦点,且过点(3√2,2),求双曲线C 的方程.18.已知△OFQ 的面积为2√6,且OF ⃗⃗⃗⃗⃗ ·FQ ⃗⃗⃗⃗⃗ =m ,其中O 为坐标原点. (1)设√6<m<4√6,求OF ⃗⃗⃗⃗⃗ 与FQ ⃗⃗⃗⃗⃗ 的夹角θ的正切值的取值范围;(2)设以O 为中心,F 为其中一个焦点的双曲线经过点Q ,如图所示,|OF ⃗⃗⃗⃗⃗ |=c ,m=√64-1c 2,当|OQ ⃗⃗⃗⃗⃗⃗ |取得最小值时,求此双曲线的标准方程.1.双曲线方程为x 2-2y 2=1,则它的右焦点坐标为( )A.√22,0 B.√62,0C.√52,0D.(√3,0)答案B解析将双曲线方程化为标准方程为x 2-y 212=1,∴a 2=1,b 2=1,∴c 2=a 2+b 2=3,∴c=√6,故右焦点坐标为√62,0.2.已知双曲线x 2a 2−y 2b2=1(a>0,b>0)的左、右焦点分别为F 1,F 2,点P 在双曲线的右支上,若|PF 1|-|PF 2|=b ,且双曲线的焦距为2√5,则该双曲线的方程为( ) A.x 2-y 2=1 B.x 2−y 2=1 C.x 2-y 2=1 D.x 2−y 2=1答案C解析由题意得{|PF 1|-|PF 2|=2a =b ,c 2=a 2+b 2,2c =2√5,解得{a 2=1,b 2=4,则该双曲线的方程为x 2-y 24=1.3.已知双曲线x 2λ-3+y 22-λ=1,焦点在y 轴上,若焦距为4,则λ等于( ) A.32 B.5 C.7D.12答案D解析根据题意可知,双曲线的标准方程为y 22-λ−x 23-λ=1. 由其焦距为4,得c=2, 则有c 2=2-λ+3-λ=4,解得λ=12.4.已知双曲线x 24−y 25=1上一点P 到左焦点F 1的距离为10,则PF 1的中点N 到坐标原点O 的距离为( ) A.3或7 B.6或14C.3D.7答案A解析连接ON ,ON 是△PF 1F 2的中位线,∴|ON|=12|PF 2|,∵||PF 1|-|PF 2||=4,|PF 1|=10, ∴|PF 2|=14或|PF 2|=6, ∴|ON|=7或|ON|=3.5.如图,已知双曲线的方程为x 2a 2−y 2b2=1(a>0,b>0),点A ,B 均在双曲线的右支上,线段AB 经过双曲线的右焦点F 2,|AB|=m ,F 1为双曲线的左焦点,则△ABF 1的周长为( ) A.2a+2m B.4a+2mC.a+mD.2a+4m答案B解析由双曲线的定义,知|AF 1|-|AF 2|=2a ,|BF 1|-|BF 2|=2a.又|AF 2|+|BF 2|=|AB|,所以△ABF 1的周长为|AF 1|+|BF 1|+|AB|=4a+2|AB|=4a+2m. 6.与圆x 2+y 2=1及圆x 2+y 2-8x+12=0都外切的圆P 的圆心在( ) A.一个椭圆上 B.一个圆上 C.一条抛物线上 D.双曲线的一支上答案D解析由x 2+y 2-8x+12=0, 得(x-4)2+y 2=4,画出圆x 2+y 2=1与(x-4)2+y 2=4的图象如图, 设圆P 的半径为r ,∵圆P 与圆O 和圆M 都外切,∴|PM|=r+2,|PO|=r+1,则|PM|-|PO|=1<4,∴点P 在以O ,M 为焦点的双曲线的左支上.7.以椭圆x 23+y 24=1的焦点为顶点,以这个椭圆的长轴的端点为焦点的双曲线的标准方程是 . 答案y 2-x 23=1解析由题意知,双曲线的焦点在y 轴上,设双曲线的标准方程为y 2a2−x 2b2=1,则a=1,c=2,所以b 2=3,所以双曲线的标准方程为y 2-x 2=1.8.已知点F 1,F 2分别是双曲线x 2−y 2=1的左、右焦点,若点P 是双曲线左支上的点,且|PF 1|·|PF 2|=32,则△F 1PF 2的面积为 . 答案16解析因为P 是双曲线左支上的点, 所以|PF 2|-|PF 1|=6,两边平方得|PF 1|2+|PF 2|2-2|PF 1|·|PF 2|=36,所以|PF 1|2+|PF 2|2=36+2|PF 1|·|PF 2|=36+2×32=100. 在△F 1PF 2中,由余弦定理,得cos ∠F 1PF 2=|PF 1|2+|PF 2|2-|F 1F 2|22|PF 1|·|PF 2|=100-1002|PF 1|·|PF 2|=0,所以∠F 1PF 2=90°,所以S △F 1PF 2=12|PF 1|·|PF 2|=12×32=16.9.已知与双曲线x 216−y 29=1共焦点的双曲线过点P -√52,-√6,求该双曲线的标准方程.解已知双曲线x 216−y 29=1, 则c 2=16+9=25,∴c=5. 设所求双曲线的标准方程为x 2a 2−y 2b2=1(a>0,b>0).依题意知b 2=25-a 2,故所求双曲线方程可写为x 2a 2−y 225-a 2=1.∵点P -√52,-√6在所求双曲线上, ∴代入有(-√52) 2a 2−(-√6)225-a 2=1,化简得4a 4-129a 2+125=0, 解得a 2=1或a 2=1254. 当a 2=1254时,b 2=25-a 2=25-1254=-254<0, 不合题意,舍去,∴a 2=1,b 2=24,∴所求双曲线的标准方程为x 2-y 224=1.能力达标10.“mn<0”是方程“mx 2+ny 2=1表示双曲线”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件D.既不充分也不必要条件 答案C解析因为mn<0,所以m ,n 均不为0且异号,方程mx 2+ny 2=1,可化为x 21m+y 21n=1,因为1m 与1n异号,所以方程x 21m+y 21n=1表示双曲线,故“mn<0”是“方程mx 2+ny 2=1表示双曲线”的充分条件;反之,若mx 2+ny 2=1表示双曲线,则其方程可化为x 21m+y 21n=1,可知1m 与1n异号,则必有mn<0,故“mn<0”是“方程mx 2+ny 2=1表示双曲线”的必要条件.综上可得,“mn<0”是方程“mx 2+ny 2=1表示双曲线”的充要条件. 11.已知平面内两定点A (-5,0),B (5,0),动点M 满足|MA|-|MB|=6,则点M 的轨迹方程是( ) A.x 2−y 2=1B.x 2−y 2=1(x ≥4)C.x 29−y216=1 D.x29−y216=1(x≥3)答案D解析由|MA|-|MB|=6,且6<|AB|=10,得a=3,c=5,b2=c2-a2=16.故其轨迹为以A,B为焦点的双曲线的右支.所以点M的轨迹方程为x 29−y216=1(x≥3).12.动圆与圆x2+y2=1和x2+y2-8x+12=0都外切,则动圆圆心的轨迹是()A.双曲线的一支B.圆C.椭圆D.双曲线答案A解析设动圆的圆心为M,半径为r,圆x2+y2=1与x2+y2-8x+12=0的圆心分别为O1和O2,半径分别为1和2,由两圆外切的充要条件,得|MO1|=r+1,|MO2|=r+2.∴|MO2|-|MO1|=1,又|O1O2|=4,∴动点M的轨迹是双曲线的一支(靠近O1).13.若双曲线x 2n-y2=1(n>1)的左、右焦点分别为F1,F2,点P在双曲线上,且满足|PF1|+|PF2|=2√n+2,则△PF1F2的面积为()A.1B.12C.2D.4答案A解析设点P在双曲线的右支上,则|PF1|-|PF2|=2√n,已知|PF1|+|PF2|=2√n+2,解得|PF1|=√n+2+√n,|PF2|=√n+2−√n,|PF1|·|PF2|=2.又|F1F2|=2√n+1,则|PF1|2+|PF2|2=|F1F2|2,∴△PF1F2为直角三角形,∠F1PF2=90°,∴S△PF1F2=12|PF1|·|PF2|=12×2=1.14.已知左、右焦点分别为F1,F2的双曲线C:x 2a2-y2=1(a>0)过点√15,-√63,点P在双曲线C上,若|PF1|=3,则|PF2|=()A.3B.6C.9D.12答案C解析由左、右焦点分别为F 1,F 2的双曲线C :x 2a2-y 2=1(a>0)过点√15,-√63,可得15a 2−69=1,解得a=3,b=1,c=√10,a+c>3,点P 在双曲线C 上,若|PF 1|=3,可得P 在双曲线的左支上,则|PF 2|=2a+|PF 1|=6+3=9.故选C. 15.若曲线C :mx 2+(2-m )y 2=1是焦点在x 轴上的双曲线,则m 的取值范围为 . 答案(2,+∞)解析由曲线C :mx 2+(2-m )y 2=1是焦点在x 轴上的双曲线,可得x 21m−y 21m -2=1, 即有m>0,且m-2>0,解得m>2.16.焦点在x 轴上的双曲线经过点(4√2,-3),且Q (0,5)与两焦点的连线互相垂直,则此双曲线的标准方程为 .答案x 216−y 29=1解析设焦点F 1(-c ,0),F 2(c ,0)(c>0), 则由QF 1⊥QF 2,得k QF 1·k QF 2=-1,∴5c ·5-c =-1,∴c=5,设双曲线的标准方程为x 2a 2−y 2b2=1(a>0,b>0),∵双曲线过点(4√2,-3),∴32a 2−9b2=1.又c 2=a 2+b 2=25,∴a 2=16,b 2=9,∴双曲线的标准方程为x 2−y 2=1. 17.已知双曲线E :x 2−y 2=1的左、右焦点分别为F 1,F 2.(1)若点M 在双曲线上,且MF 1⃗⃗⃗⃗⃗⃗⃗⃗ ·MF 2⃗⃗⃗⃗⃗⃗⃗⃗ =0,求点M 到x 轴的距离;(2)若双曲线C 与双曲线E 有相同的焦点,且过点(3√2,2),求双曲线C 的方程.解(1)如图所示,不妨设点M 在双曲线E 的右支上,点M 到x 轴的距离为h ,MF 1⃗⃗⃗⃗⃗⃗⃗⃗ ·MF 2⃗⃗⃗⃗⃗⃗⃗⃗ =0, 则MF 1⊥MF 2, 设|MF 1|=m ,|MF 2|=n , 由双曲线定义,知m-n=2a=8,①又m 2+n 2=(2c )2=80, ②由①②得mn=8,∴12mn=4=12|F 1F 2|·h , ∴h=2√55. (2)设所求双曲线C 的方程为x 216-λ−y 24+λ=1(-4<λ<16), 由于双曲线C 过点(3√2,2),∴1816-λ−44+λ=1,解得λ=4或λ=-14(舍去),∴所求双曲线C 的方程为x 212−y 28=1.18.已知△OFQ 的面积为2√6,且OF ⃗⃗⃗⃗⃗ ·FQ ⃗⃗⃗⃗⃗ =m ,其中O 为坐标原点. (1)设√6<m<4√6,求OF⃗⃗⃗⃗⃗ 与FQ ⃗⃗⃗⃗⃗ 的夹角θ的正切值的取值范围; (2)设以O 为中心,F 为其中一个焦点的双曲线经过点Q ,如图所示,|OF ⃗⃗⃗⃗⃗ |=c ,m=√64-1c 2,当|OQ ⃗⃗⃗⃗⃗⃗ |取得最小值时,求此双曲线的标准方程.解(1)因为{12|OF ⃗⃗⃗⃗⃗ ||FQ ⃗⃗⃗⃗⃗|sin (π-θ)=2√6,|OF ⃗⃗⃗⃗⃗ ||FQ⃗⃗⃗⃗⃗ |cosθ=m ,所以tan θ=4√6. 又√6<m<4√6, 所以1<tan θ<4,即tan θ的取值范围为(1,4).(2)设双曲线的标准方程为x 2a 2−y 2b2=1(a>0,b>0),Q (x 1,y 1),则FQ⃗⃗⃗⃗⃗ =(x 1-c ,y 1), 所以S △OFQ =12|OF ⃗⃗⃗⃗⃗|·|y 1|=2√6,则y 1=±4√6.又OF⃗⃗⃗⃗⃗ ·FQ ⃗⃗⃗⃗⃗ =m , 即(c ,0)·(x 1-c ,y 1)=√64-1c 2, 解得x 1=√64c ,所以|OQ ⃗⃗⃗⃗⃗⃗ |=√x 12+y 12=√38c 2+96c 2≥√12=2√3,当且仅当c=4时,取等号,此时|OQ ⃗⃗⃗⃗⃗⃗ |最小, 这时Q 的坐标为(√6,√6)或(√6,-√6).因为{6a 2-6b 2=1,a 2+b 2=16,所以{a 2=4,b 2=12.于是所求双曲线的标准方程为x 24−y 212=1.。
双曲线及其标准方程习题

5.若点 M 在双曲线错误!-错误!=1 上,双曲线的焦点为 F1,F2,且|MF1|=3|MF2|,则|MF2|
等于
A.2
B.4
C.8
D.12
解析:选 B.双曲线中 a2=16,a=4,2a=8,由双曲线定义知||MF1|-|MF2||=8,又|MF1|=
3|MF2|,所以 3|MF2|-|MF2|=8,解得|MF2|=4.
以对于所求双曲线 a=1,c=2,b2=3,焦点在 y 轴上,双曲线的方程为 y2-错误!=1.
4.在方程 mx2-my2=n 中,若 mn<0,则方程表示的曲线是 A.焦点在 x 轴上的椭圆 B.焦点在 x 轴上的双曲线 C.焦点在 y 轴上的椭圆 D.焦点在 y 轴上的双曲线
解析:选 D.将方程化为错误!-错误!=1.
A.5,10 C.10,+∞
B.-∞,5 D.-∞,5∪10,+∞
解析:选 A.由题意得 10-k5-k<0,解得 5<k<10.
3.以椭圆错误!+错误!=1 的焦点为顶点,以这个椭圆的长轴的端点为焦点的双曲线的 方程是
-y2=1 -错误=1
B.y2-错误!=1 -错误!=1
解析:选 B.椭圆错误!+错误!=1 的焦点为 F10,1,F20,-1,长轴的端点 A10,2,A20,-2,所
由错误!·错误!=0,得 PF1⊥PF2.根据勾股定理得 |PF1|2+|PF2|2=2c2,即|PF1|2+|PF2|2=20. 根据双曲线定义有|PF1|-|PF2|=±2a. 两边平方并代入|PF1|·|PF2|=2 得 20-2×2=4a2,解得 a2=4,从而 b2=5-4=1, 所以双曲线方程为错误!-y2=1. 答案:错误!-y2=1 3.设圆 C 与两圆 x+错误!2+y2=4,x-错误!2+y2=4 中的一个内切,另一个外切.求 C 的圆心轨迹 L 的方程. 解:设两圆 x+错误!2+y2=4,x-错误!2+y2=4 的圆心分别为 F1-错误!,0,F2错误!,0, 两圆相离, 由题意得||CF1|-|CF2||=4<2错误!=|F1F2|, 从而得动圆的圆心 C 的轨迹是双曲线, 且 a=2,c=错误!,所以 b=错误!=1, 所求轨迹 L 的方程为错误!-y2=1. 4.如图,若 F1,F2 是双曲线错误!-错误!=1 的两个焦点. 1 若双曲线上一点 M 到它的一个焦点的距离等于 16,求点 M 到另一个焦点的距离; 2 若 P 是双曲线左支上的点,且|PF1|·|PF2|=32,试求△F1PF2 的面积. 解:双曲线的标准方程为错误!-错误!=1, 故 a=3,b=4,c=错误!=5. 1 由双曲线的定义得||MF1|-|MF2||=2a=6,又双曲线上一点 M 到它的一个焦点的距离等 于 16,假设点 M 到另一个焦点的距离等于 x,则|16-x|=6,解得 x=10 或 x=22. 故点 M 到另一个焦点的距离为 10 或 22. 2 将||PF2|-|PF1||=2a=6,两边平方得 |PF1|2+|PF2|2-2|PF1|·|PF2|=36, ∴|PF1|2+|PF2|2=36+2|PF1|·|PF2|=36+2×32=100. 在△F1PF2 中,由余弦定理得 cos∠F1PF2=错误! =错误!=0, ∴∠F1PF2=90°, ∴S△F1PF2=错误!|PF1|·|PF2|=错误!×32=16.
双曲线及其标准方程(作业)

①曲线 C 不可能是圆; ②若 1<k<4,则曲线 C 为椭圆; ③若曲线 C 为双曲线,则 k<1 或 k>4; ④若曲线 C 表示焦点在 x 轴上的椭圆,则 1<k<52. 其中正确命题的序号是________(写出所有正确的命题的序号)
三、解答题 9.求与双曲线x42-y22=1 有相同焦点且过点 P(2,1)的双曲线的方程.
10.已知方程 kx2+y2=4,其中 k 为实数,对于不同范围的 k 值分别指出方 程所表示的曲线类型.
11.某部队进行军事演习,一方指挥中心接到其正西、正东、正北方向三 个观测点 A,B,C 的报告:正西、正北两个观测点同时听到了炮弹的爆炸声, 正东观测点听到爆炸声的时间比其他两观测点晚 4 s,已知各观测点到该中心的 距离都是 1 020 m,试确定该枚炮弹的袭击位置.(声音的传播速度为 340 m/s, 相关各点均在同一平面内).
A.x22-y32=1
B.x32-y22=1
C.x2-y42=1 D.x42-y2=1
二、填空题 6.双曲线m2+x2 12-4-y2m2=1 的焦距为________.
7.(2013·郑州高二检测)设点 P 是双曲线x92-1y26=1 上任意一点,F1,F2 分 别是其左、右焦点,若|PF1|=10,则|PF2|=________.
双曲线及其标准方程
一、选择题
1.(2013·东营高二检测)方程2+x2m-2-y2m=1 表示双曲线,则 m 的取值范
围( )
A.-2<m<2
B.m>0
C.m≥P 到 A(-5,0)的距离与它到 B(5,0)距离的差等于 6,则 P 点的轨
3.2.1 双曲线及其标准方程 练习册正文

3.2 双曲线3.2.1 双曲线及其标准方程一、选择题1.双曲线y 24-x 25=1的焦距为( ) A .6B .3C .2D .12.焦点分别为(-2,0),(2,0),且经过点(2,3)的双曲线的标准方程为( ) A .x 2-y 23=1B .x 23-y 2=1C .y 2-x 23=1D .x 22-y 22=13.已知F 1,F 2是平面内两个不同的定点,则“||MF 1|-|MF 2||为定值”是“动点M 的轨迹是双曲线”的( ) A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4.[2024·益阳高二期末] 点M (x ,y )的坐标满足√(x +5)2+y 2-√(x -5)2+y 2=8,则点M 的轨迹方程为 ( )A .x 216+y 29=1B .x 216-y 29=1C .x 216-y 29=1(x>0)D .y 216-x 29=1(y>0) 5.若F 1,F 2分别是双曲线8x 2-y 2=8的左、右焦点,点P 在该双曲线上,且△PF 1F 2是等腰三角形,则△PF 1F 2的周长为( ) A .17B .16或12C .20D .16或206.[2024·福建南平一中高二月考] 设双曲线C 2与椭圆C 1:x 216+y 212=1有公共焦点F 1,F 2.若双曲线C 2经过点A (1,0),设P 为双曲线C 2与椭圆C 1的一个交点,则∠F 1PF 2的余弦值为( )A .35B .23C .34D .457.已知F 1,F 2分别是双曲线C :x 24-y 24=1的左、右焦点,P 是C 上一点,且位于第一象限,PF 1⃗⃗⃗⃗⃗⃗⃗ ·PF 2⃗⃗⃗⃗⃗⃗⃗ =0,则P 的纵坐标为 ( )A .1B .2C .√2D .√38.(多选题)[2024·河南商丘高二期中] 已知方程x 2m 2-1+y 22m+2=1(m ≠±1)表示曲线C ,则下列结论正确的是 ( ) A .若m=3,则曲线C 是圆B .若曲线C 是椭圆,则m>3C .若曲线C 是双曲线,则m<1且m ≠-1D .若m<-1,则曲线C 是焦点在x 轴上的双曲线9.(多选题)已知双曲线x 2a 2-y 2b 2=1(a>0,b>0)的左、右顶点分别是A 1,A 2,左、右焦点分别是F 1,F 2,P 是双曲线上异于A 1,A 2的任意一点,给出下列结论,其中正确的是( )A .||PA 1|-|PA 2||=2aB .直线PA 1,PA 2的斜率之积等于定值b 2a 2C .使得△PF 1F 2为等腰三角形的点P 有且仅有四个D .若PA 1⃗⃗⃗⃗⃗⃗⃗ ·PA 2⃗⃗⃗⃗⃗⃗⃗⃗ =b 2,则PF 1⃗⃗⃗⃗⃗⃗⃗ ·PF 2⃗⃗⃗⃗⃗⃗⃗ =0 二、填空题10.若双曲线y 22-x 2m =1的焦点与椭圆x 24+y 29=1的焦点重合,则m= .11.[2024·天津西青区高二期末] 已知双曲线x 2a 2-y 236=1(a>0)的两个焦点为F 1,F 2,焦距为20,点P 是双曲线上一点,|PF 1|=17,则|PF 2|= .12.已知O 为坐标原点,设F 1,F 2分别是双曲线x 2-y 2=1的左、右焦点,P 为双曲线上任意一点,过点F 1作∠F 1PF 2的平分线的垂线,垂足为H ,则|OH|= .三、解答题13.(1)求与双曲线x 22-y 2=1有公共焦点,且过点(√2,√2)的双曲线的标准方程.(2)已知圆C 1:(x+2)2+y 2=254,圆C 2:(x-2)2+y 2=14,动圆P 与圆C 1,C 2都外切,求动圆圆心P 的轨迹方程.14.[2024·安徽芜湖一中高二月考] 已知点A (-2,0)与点B (2,0),P 是动点,且直线AP 与BP 的斜率之积等于34.(1)求动点P 的轨迹方程;(2)若点O 为原点,P 在第二象限,当|OP|=√232时,求点P 的坐标.15.双曲线定位法是通过测定待定点到至少三个已知点的两个距离差所进行的一种无线电定位.通过船(待定点)接收到三个发射台的电磁波的时间差计算出距离差,两个距离差即可形成两条位置双曲线,两者相交便可确定船位.我们来看一种简单的“特殊”状况,如图所示,已知三个发射台分别为A,B,C且刚好三点共线,已知AB=34海里,AC=20海里,现以AB的中点为原点,AB所在直线为x轴建立平面直角坐标系.根据船P接收到C发射台与A发射台发出的电磁波的时间差计算出距离差,得知船P在双曲线(x-27)236-y264=1的左支上,根据船P接收到A发射台与B发射台发出的电磁波的时间差,计算出船P到B发射台的距离比到A发射台的距离远30海里,则点P的坐标为( )A.(907,±32√117)B.(1357,±32√27)C.(17,±323) D.(45,±16√2)16.已知椭圆x 2a2+y2b2=1(a>b>0)与双曲线x2m2-y2n2=1(m>0,n>0)的一个交点为P,且有公共的焦点F1,F2,若∠F1PF2=2α,求证:tan α=nb.。
双曲线及其标准方程练习题.doc

课时作业(十)[学业水平层次]1表示双曲线,则加的取值范围(D. |m|^2【解析】 T 已知方程表示双曲线,(2+加)(2—加)>0. /. —2<m<2.【答案】A2. 设动点P 到A (—5,0)的距离与它到B (5,0)距离的差等于6,则 戶点的轨迹方程是()2 2 2 2 A 」丄=1=1 宀9 16-116_i 2 2 22 C.g —話=l (xW —3) D.g —牯=1(x23)【解析】 由题意知,轨迹应为以A (-5,0), B (5,0)为焦点的双 曲线的右支.由c=5, a=3,知b 2= 16,2 2:.P 点的轨迹方程为寺一話=1(心3).【答案】D3. (2014-福州高级中学期末考试)已知双曲线的中心在原点,两 个焦点円,兄分别为(书,0)和(一书,0),点P 在双曲线上,且PF1 丄戶尸2,AP^F O 的面积为1,则双曲线的方程为() 一、选择题A. —2<加<2B. m >0A •厂c.j-y 2=i【解析】由S 〔|PF1F+|PF2|2 = (2书)2,即2a=4,解得a=2,又c=\[5,所以b=l,故选C.【答案】C2 24. 已知椭圆方程予+牙=1,双曲线的焦点是椭圆的顶点,顶点 是椭圆的焦点,则双曲线的离心率为()A.^2B.^3C. 2D. 3【解析】 椭圆的焦点为(1,0),顶点为(2,0),即双曲线中a=l,c 2 c=2,所以双曲线的离心率为e=~=^=2.【答案】C二、填空题2 25. 设点P 是双曲线牙一話=1上任意一点,F”巧分别是其左、 右焦点,若|戶刊=10,则戶刊= ___________ .【解析】 由双曲线的标准方程得a=3, b=4. 于是 c=-\/a 2+b 2=5.(1) 若点P 在双曲线的左支上,则\PF2\-\PFr | = 2a=6, \PF 2\ = 6+|戶円| = 16;(2) 若点P 在双曲线的右支上,贝川阳一|阳 =6,•••1戶尸21 = 1戶尸11一6= 10—6=4.在△4BP中,利用正弦定理和双曲线的定义知, |sin A—sin B\sin P综上,IPF2| = 16 或4.【答案】16或46.(2014-河南省洛阳高一月考)已知Fi(—3,0), F2(3,0),满足条件|MiM“2l = 2加一1的动点P的轨迹是双曲线的一支,则m可以是下列数据中的______________ •(填序号)①2;②一1;③4;④一3.2 2【解析】设双曲线的方程为孑一右=1,则c=3, V2a<2c=6,5 7 1|2m—1|<6,且|2加一1|工0, •••—㊁SV刁且加工刁.••①②满足条件.【答案】①②7・(2014-哈尔滨高二检测)已知的顶点4、B分别为双曲线c:看—的左、右焦点,顶点P在双曲线C上,则回書严 1 的值等于.2 2 ________________________________________________________【解析】由方程話—卷=1知cr=l6,kr=9,即a=4, c=#16+9||PB|-|B4||_2a_2X4_4\AB\=2c=2X5 = 5-4【答案】|三、解答题8.求与双曲线予一号=1有相同焦点且过点戶(2,1)的双曲线的方程.【解】*.*双曲线予一号=1的焦点在兀轴上.2 2依题意,设所求双曲线为寺一缶=l(a>0, Z?>0).又两曲线有相同的焦点,•I /+F=4+2 = 6.①2 2又点P(2,l)在双曲线歩一*=1上,4 1••厂产②由①、②联立,得a2=b2=3,2 2故所求双曲线方程为专一'=】•9.已知方程2+y2=4,其中R为实数,对于不同范围的E值分别指出方程所表示的曲线类型.【解】(1)当k=0时,y=±2,表示两条与x轴平行的直线;(2)当k=l时,方程为H+y2=4,表示圆心在原点,半径为2的圆;V2%2(3)当kVO时,方程为;一~^=1,表示焦点在y轴上的双曲线;k2 2(4)当OVkVl时,方程为才+才=1,表示焦点在兀轴上的椭圆;k2 2(5)当E>1时,方程为才+眷=1,表示焦点在y轴上的椭圆.k[能力提升层次]2 2 2 21.椭圆牙+^2=1与双曲线乡一牙=1有相同的焦点,则a的值为()A. 1B.^2C. 2D. 3【解析】由题意知椭圆、双曲线的焦点在兀轴上,且a>0.4—a?=a+2, a2a—2=0,.'.a= 1或a=—2(舍去).故选A.【答案】A2.(201牛桂林高二期末)已知Fi、局为双曲线C:x~y2=l的左、右焦点,点P 在C 上,ZF i PF2=6Q°,则PF I|-|PF2|^于()A. 2B. 4C. 6D. 8【解析】不妨设P是双曲线右支上一点,在双曲线x~y= 1 中,a=l, b=l, c=y[2,则|PK| —|戶尸21 = 2°=2, |尸1局1 = 2返,\F}F^= \PF X |2+|PF2|2 - 2|PF! | • |PF2| • cos Z F!PF2,8 = |PF1|2+|PF2|2-2|PF]|-|PF2|-|,••.8=4+|"i||PF2l, A |PF I||PF2|=4.故选B.【答案】B2 23.(2014•福建省厦门一中期末考试)已知双曲线話一去=1的左焦点为尸,点P为双曲线右支上的一点,且PF与圆X2+/=16相切于点N, M 为线段PF的中点,0为坐标原点,则|MN —|M0| =【解析】设F是双曲线的右焦点,连PF'(图略),因为M,0分别是FP, FF'的中点,所^\MO\=^\PF' I,又0州=yJ\OFf~\ONf = 5,且由双曲线的定义知\PF\~\PF' \ = &故\MN\-\MO\ = \MF\-\FN\~^\PF' \=^(\PF\~\PF' |)-|FN|=|x8 —5 = —1.【答案】一12 24.已知双曲线話一才=1的两焦点为尸1、尸2.—►—►(1)若点M在双曲线上,且MF l MF2=0,求点M到x轴的距离;(2)若双曲线C与已知双曲线有相同焦点,且过点(3迈,2),求双曲线C的方程.【解】(1)不妨设M在双曲线的右支上,M点到x轴的距离为h,—►―►MF2=0,MFV则MF]丄M”2,设\MF^\=m, \MF2\ = n,由双曲线定义知,m—n=2a=&又m+ “2 = (2c)2 = 80,②由①②得加•“ = &1 1 =4=刁円尸2|•力,⑵设所求双曲线C的方程为由于双曲线C 过点(3返,2), 所以 16_久—4+1=1,解得久=4或久=—14(舍去).2 2所求双曲线C 的方程为診一竟=1. 16——A 4+久 =1(—4<2<16),。
课时作业3:3.2.1 双曲线及其标准方程

3.2.1 双曲线及其标准方程A 组 基础巩固练一、选择题1.已知平面内两定点A (-5,0),B (5,0),动点M 满足|MA |-|MB |=6,则点M 的轨迹方程是( )A .x 216-y 29=1 B .x 216-y 29=1(x ≥4) C .x 29-y 216=1 D .x 29-y 216=1(x ≥3) 2.若ax 2+by 2=b (ab <0),则这个曲线是( )A .双曲线,焦点在x 轴上B .双曲线,焦点在y 轴上C .椭圆,焦点在x 轴上D .椭圆,焦点在y 轴上3.已知双曲线的中心在原点,两个焦点F 1,F 2分别为(5,0)和(-5,0),点P 在双曲线上,且PF 1⊥PF 2,△PF 1F 2的面积为1,则双曲线的方程为( )A .x 22-y 23=1 B .x 23-y 22=1 C .x 24-y 2=1 D .x 2-y 24=1 4.双曲线x 225-y 29=1上的点P 到一个焦点的距离为12,则到另一个焦点的距离为( ) A .22或2B .7C .22D .25.已知F 是双曲线C :x 2-y 23=1的右焦点,P 是C 上一点,且PF 与x 轴垂直,点A 的坐标是(1,3),则△APF 的面积为( )A .13B .12C .23D .32二、填空题6.若方程x 22-m +y 2|m |-3=1表示双曲线,则实数m 的取值范围为________.7.已知双曲线的左、右焦点分别为F 1,F 2,过F 1的直线与双曲线的左支交于A ,B 两点,线段AB 的长为5.若2a =8,那么△ABF 2的周长是________.8.如图所示,已知双曲线以长方形ABCD 的顶点A ,B 为左、右焦点,且双曲线过C ,D 两顶点.若AB =4,BC =3,则此双曲线的标准方程为________.三、解答题9.已知方程kx 2+y 2=4,其中k 为实数,对于不同范围的k 值,分别指出方程所表示的曲线类型.10.已知双曲线x 24-y 29=1,F 1,F 2是其两个焦点,点M 在双曲线上. (1)若∠F 1MF 2=90°,求△F 1MF 2的面积;(2)若∠F 1MF 2=120°,△F 1MF 2的面积是多少?若∠F 1MF 2=60°,△F 1MF 2的面积又是多少?(3)观察以上计算结果,你能看出随∠F 1MF 2的变化,△F 1MF 2的面积将怎样变化吗?试证明你的结论.B 组 素养提升练11.(多选题)设θ是三角形的一个内角,对于方程x 2sin θ+y 2cos θ=1的说法正确的是( ) A .当0<θ<π2时,方程表示椭圆 B .当θ=π2时,方程不表示任何图形 C .当π2<θ<3π4时,方程表示焦点在x 轴上的双曲线 D .当3π4<θ<π时,方程表示焦点在y 轴上的双曲线 12.(多选题)已知方程x 24-t +y 2t -1=1表示的曲线为C .给出以下判断,正确的是( ) A .当1<t <4时,曲线C 表示椭圆B .当t >4或t <1时,曲线C 表示双曲线C .若曲线C 表示焦点在x 轴上的椭圆,则1<t <52D .若曲线C 表示焦点在y 轴上的双曲线,则t >413.(一题两空)已知△ABC 的两个顶点A ,B 分别为椭圆x 2+5y 2=5的左焦点和右焦点,则|AB |=________.又三个内角A ,B ,C 满足关系式sin B -sin A =12sin C .则点C 的轨迹方程为________.14.过双曲线x 2144-y 225=1的一个焦点作x 轴的垂线,则垂线与双曲线的一个交点到两焦点的距离分别为________.C 组 思维提升练15.设圆C 与两圆(x +5)2+y 2=4,(x -5)2+y 2=4中的一个内切,另一个外切.(1)求C 的圆心轨迹L 的方程;(2)已知点M ⎝⎛⎭⎫355,455,F (5,0),且P 为L 上动点.求||MP -|FP ||的最大值.参考答案A 组 基础巩固练一、选择题1.【答案】D【解析】由题意知,轨迹应为以A (-5,0),B (5,0)为焦点的双曲线的右支.由c =5,a =3,知b 2=16,∴M 点的轨迹方程为x 29-y 216=1(x ≥3). 2.【答案】B【解析】因为ab <0,方程可化为x 2b a+y 2=1,∴b a<0,方程表示的曲线为焦点在y 轴上的双曲线,故选B.3.【答案】C【解析】由⎩⎨⎧ |PF 1|·|PF 2|=2,|PF 1|2+|PF 2|2=252,⇒(|PF 1|-|PF 2|)2=16, 即2a =4,解得a =2,又c =5,所以b =1,故选C.4.【答案】A【解析】根据双曲线的方程得2a =2×5=10,由定义知||PF |-12|=10,可解得|PF |=22或2,故选A. 5.【答案】D【解析】因为F 是双曲线C :x 2-y 23=1的右焦点,所以F (2,0). 因为PF ⊥x 轴,所以可设P 的坐标为(2,y P ).因为P 是C 上一点,所以4-y 2P 3=1,解得y P =±3, 所以P (2,±3),|PF |=3.又因为A (1,3),所以点A 到直线PF 的距离为1,所以S △APF =12×|PF |×1=12×3×1=32.故选D. 二、填空题6.【答案】(-3,2)∪(3,+∞)【解析】依题意有⎩⎪⎨⎪⎧ 2-m >0,|m |-3<0或⎩⎪⎨⎪⎧2-m <0,|m |-3>0,解得-3<m <2或m >3.所以实数m 的取值范围是(-3,2)∪(3,+∞).7.【答案】26【解析】根据双曲线定义知,|AF 2|-|AF 1|=8,|BF 2|-|BF 1|=8.∴|AF 2|+|BF 2|=16+|AF 1|+|BF 1|=16+|AB |=16+5=21.所以△ABF 2的周长是|AF 2|+|BF 2|+|AB |=21+5=26.8.【答案】x 2-y 23=1 【解析】设双曲线的标准方程为x 2a 2-y 2b 2=1(a >0,b >0). 由题意得B (2,0),C (2,3),所以⎩⎪⎨⎪⎧ 4=a 2+b 2,4a 2-9b 2=1,解得⎩⎪⎨⎪⎧a 2=1,b 2=3, 所以双曲线的标准方程为x 2-y 23=1. 三、解答题 9.解:(1)当k =0时,y =±2,表示两条与x 轴平行的直线;(2)当k =1时,方程为x 2+y 2=4,表示圆心在原点,半径为2的圆;(3)当k <0时,方程为y 24-x 2-4k=1,表示焦点在y 轴上的双曲线; (4)当0<k <1时,方程为x 24k+y 24=1,表示焦点在x 轴上的椭圆; (5)当k >1时,方程为x 24k+y 24=1,表示焦点在y 轴上的椭圆. 10.解:设|MF 1|=r 1,|MF 2|=r 2(不妨设r 1>r 2),θ=∠F 1MF 2,因为S △F 1MF 2=12r 1r 2sin θ, θ已知,所以只要求r 1r 2即可,因此考虑到用双曲线定义及余弦定理的知识,求出r 1r 2.(1)当θ=90°时,S △F 1MF 2=12r 1r 2sin θ=12r 1r 2.由双曲线方程知a =2,b =3,c =13, 由双曲线定义,得|r 1-r 2|=2a =4,两边平方,得r 21+r 22-2r 1r 2=16,又r 21+r 22=|F 1F 2|2,即|F 1F 2|2-4S △F 1MF 2=16,也即52-16=4S △F 1MF 2,求得S △F 1MF 2=9. (2)若∠F 1MF 2=120°,在△MF 1F 2中,|F 1F 2|2=r 21+r 22-2r 1r 2cos 120°=(r 1-r 2)2+3r 1r 2=52,所以r 1r 2=12,求得S △F 1MF 2=12r 1r 2sin 120°=3 3. 同理,可求得若∠F 1MF 2=60°,S △F 1MF 2=9 3. (3)由以上结果可见,随着∠F 1MF 2的增大,△F 1MF 2的面积将减小.证明如下:由双曲线定义及余弦定理,得⎩⎪⎨⎪⎧(r 1-r 2)2=4a 2, ①r 21+r 22-2r 1r 2cos θ=4c 2. ② ②-①,得r 1r 2=4c 2-4a 22(1-cos θ), 所以S △F 1MF 2=12r 1r 2sin θ=(c 2-a 2)sin θ1-cos θ=b 2cot θ2. 因为0<θ<π,所以0<θ2<π2, 在⎝⎛⎭⎫0,π2内,cot θ2是减函数. 因此当θ增大时,S △F 1MF 2=b 2cot θ2减小. B 组 素养提升练11.【答案】BC【解析】当0<θ<π2时,sin θ>0,cos θ>0,但当θ=π4时,sin θ=cos θ>0表示圆,故A 错误;当θ=π2时,cos θ=0,方程无意义,所以不表示任何图形,故B 正确;当π2<θ<π时,sin θ>0,cos θ<0,所以不论π2<θ<3π4还是3π4<θ<π时,方程表示焦点在x 轴上的双曲线,所以C 正确,D 错误,故选BC.12.【答案】BCD【解析】A 错误,当t =52时,曲线C 表示圆;B 正确,若C 为双曲线,则(4-t )(t -1)<0,∴t <1或t >4;C 正确,若曲线C 为焦点在x 轴上的椭圆,则4-t >t -1>0,∴1<t <52;D 正确,若曲线C 为焦点在y 轴上的双曲线,则⎩⎪⎨⎪⎧4-t <0,t -1>0,∴t >4.] 13.【答案】4 x 2-y 23=1(x >1) 【解析】将椭圆方程化为标准形式为x 25+y 2=1. ∴a 2=5,b 2=1,c 2=a 2-b 2=4,则A (-2,0),B (2,0),|AB |=4.又∵sin B -sin A =12sin C ,∴由正弦定理得 |CA |-|CB |=12|AB |=2<|AB |=4, 即动点C 到两定点A ,B 的距离之差为定值.∴动点C 的轨迹是双曲线的右支,并且c =2,a =1,∴所求的点C 的轨迹方程为x 2-y 23=1(x >1). 14.【答案】2512,31312【解析】因为双曲线方程为x 2144-y 225=1,所以c =144+25=13,设F 1,F 2分别是双曲线的左、右焦点,则F 1(-13,0),F 2(13,0).设过F 1且垂直于x 轴的直线l 交双曲线于A (-13,y )(y >0),则y 225=132144-1=25144, 所以y =2512,即|AF 1|=2512.又|AF 2|-|AF 1|=2a =24, 所以|AF 2|=24+2512=31312.即所求距离分别为2512,31312. C 组 思维提升练15.解:(1)两圆的圆心分别为A (-5,0),B (5,0),半径为2,设圆C 的半径为r . 由题意得|CA |=r -2,|CB |=r +2或|CA |=r +2,|CB |=r -2,两式相减得|CA |-|CB |=-4或|CA |-|CB |=4,即||CA |-|CB ||=4.则圆C 的圆心轨迹为双曲线,其中2a =4,c =5,b 2=1,∴圆C 的圆心轨迹L 的方程为x 24-y 2=1. (2)由(1)知F 为双曲线L 的一个焦点,如图,连接MF 并延长交双曲线于一点P ,此时|PM |-|PF |=|MF |为||PM |-|FP ||的最大值.又|MF |=⎝⎛⎭⎫355-52+⎝⎛⎭⎫4552=2, ∴||MP |-|FP ||的最大值为2.。
双曲线标准方程及其性质经典题型分类总结
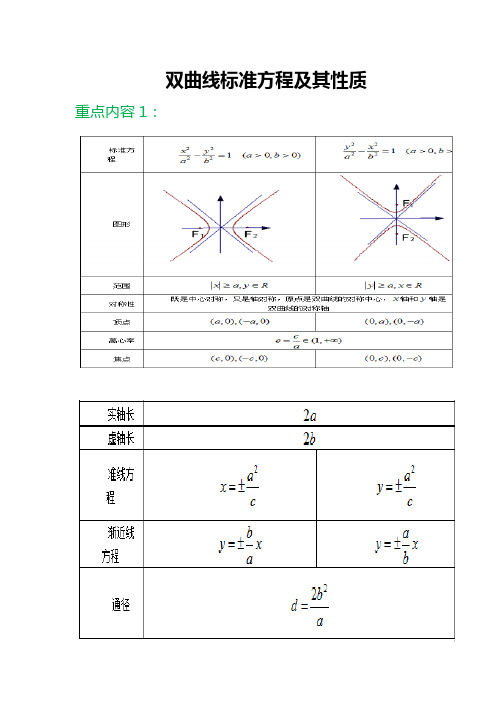
双曲线标准方程及其性质重点内容1:基础专练:1. 双曲线116922=-y x 的a=______、b=______、c=______;实轴长为______、虚轴长为______、焦点坐标______、离心率为______、渐近线方程为___________。
2. 双曲线1162522=-x y ,实半轴长为_____、虚半轴长为______、焦距为______、离心率为______、渐近线方程为____________。
3. 已知,双曲线上的动点到距离之差为6,则双曲线的方程为:4.双曲线的渐近线为,则离心率为5.已知双曲线的渐近线方程是,焦点在x 轴上且焦距是10,则此双曲线的方程为 ;6.(烟台调研)与椭圆x 24+y 2=1共焦点且过点P (2,1)的双曲线方程是( )A.x 24-y 2=1 B.x 22-y 2=1 12(5,0),(5,0)F F -P 21,F F x y 23±=2xy ±=C.x 23-y 23=1 D .x 2-y 22=1题型(一):求轨迹(定义法)例1:已知动圆M 与圆C 1:(x+4)2+y 2=16外切,与圆C 2:(x-4)2+y 2=64外切,求动圆圆心M 的轨迹方程.练习1 :动圆与两圆和都外切,求动圆圆心的轨迹?变式1:在△ABC 中,已知|AB|=42,且三内角A 、B 、C 满足2sinA+sinC=2sinB ,建立适当的坐标系,求顶点C 的轨迹方程.122=+y x 012822=+-+x y x题型(二):求双曲线方程1.(重庆高考)已知双曲线x 2a 2-y 2b2=1 (a >0,b >0)的一条渐近线为y =kx (k >0),离心率e =5k ,则双曲线方程为( ) A.x 2a 2-y 24a 2=1 B.x 2a 2-y 25a 2=1 C.x 24b 2-y 2b 2=1 D.x 25b 2-y 2b2=12.已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的两条渐近线方程为y =±33x ,若顶点到渐近线的距离为1,则双曲线方程为____________.3.已知双曲线)0,0(12222>>=-b a b y a x 的一条渐近线平行于直线,102:+=x y l 双曲线的一个焦点在直线l 上,则双曲线的方程为( ) 120522=-y x B.152022=-y x C.1100325322=-y x D.1253100322=-y x4.已知双曲线1C 、2C 的顶点重合,1C 的方程为1422=-y x ,若2C 的一条渐近线的斜率是1C 的一条渐近线的斜率的2倍,则2C 的方程为 .题型(三):利用双曲线定义求参数范围例1.若方程x2|k|-2+y25-k =1表示双曲线,则实数k 的取值范围是( )A .k<-2,或2<k<5B .-2<k<5C .k<-2,或k>5D .-2<k<2,或k>5练习1:若实数k 满足05k <<,则曲线221165x y k -=-与曲线221165x y k -=-的( )A.实半轴长相等B.虚半轴长相等C.离心率相等D.焦距相等 变式1:已知π04θ<<,则双曲线1C :22221sin cos x y θθ-=与2C :22221cos sin y x θθ-=的( )A .实轴长相等B .虚轴长相等C .离心率相等D .焦距相等 题型(四):共焦点求双曲线方程例1.与椭圆1422=+y x 共焦点且过点P(2,1)的双曲线方程是( )A. 1422=-y xB.1222=-y xC.13y 322=-x D .1222=-y x练习1: 已知双曲线22221(0b 0)x y a a b -=>,>和椭圆22x y =1169+有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为 ?例2:求与双曲线有公共焦点,且过点(,2)的双曲线方程。
双曲线及其标准方程练习题一

《双曲线及其标准方程》练习题一1.设动点P 到A (-5,0)的距离与它到B (5,0)距离的差等于6,则P 点的轨迹方 程是( )A.x 29-y 216=1B.y 29-x 216=1C.x 29-y 216=1(x ≤-3)D.x 29-y 216=1(x ≥3) 2.“ab<0”是“方程c by ax =+22表示双曲线”的( )A .必要不充分条件B .充分不必要条件C .充要条件D .既不充分又不必要条件3.双曲线的两焦点坐标是F 1(3,0),F 2(-3,0),2b =4,则双曲线的标准方程是( )A.x 25-y 24=1B.y 25-x 24=1C.x 23-y 22=1D.x 29-y 216=1 4.方程x =3y 2-1所表示的曲线是( )A .双曲线B .椭圆C .双曲线的一部分D .椭圆的一部分5.双曲线x 216-y 29=1上一点P 到点(5,0)的距离为15,那么该点到点(-5,0)的距 离为( )A .7B .23C .5或25D .7或236.圆P 过点,且与圆 外切,则动圆圆心P 的轨迹方程( ).A .; B .C .D . 7.椭圆x 24+y 2a 2=1与双曲线x 2a -y 22=1有相同的焦点,则a 的值是( ) A.12 B .1或-2 C .1或12D .1 8. 已知ab<0,方程y= —2x+b 和bx 2+ay 2=ab 表示的曲线只可能是图中的( )9.双曲线m y x =-222的一个焦点是)3,0(,则m 的值是_______。
10.过双曲线)0,0(12222>>=-b a by a x 的焦点且垂直于x 轴的弦的长度为_____。
11.已知双曲线的焦点在x 轴上,且a +c =9,b =3,则它的标准方程是________.12.过点(1,1)且b a =2的双曲线的标准方程为________.13.根据下列条件,求双曲线的标准方程.(1)过点P ⎝ ⎛⎭⎪⎫3,154,Q ⎝ ⎛⎭⎪⎫-163,5且焦点在坐标轴上; (2)c =6,经过点(-5,2),焦点在x 轴上.14.已知方程x 22-k +y 2k -1=1表示的图形是:(1)双曲线;(2)椭圆;(3)圆.试分别求出k 的取值范围.15.已知双曲线过点A (-2,4)、B (4,4),它的一个焦点是)0,1(1F ,求它的另 一个焦点2F 的轨迹方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《双曲线及其标准方程》练习题一
1.设动点P 到A (-5,0)的距离与它到B (5,0)距离的差等于6,则P 点的轨迹方
程是( ) -y 216=1 -x 216=1 C.x 29-y 216=1(x ≤-3) -y 2
16=1(x ≥3)
2.“ab<0”是“方程c by ax =+22表示双曲线”的( )
A .必要不充分条件
B .充分不必要条件
C .充要条件
D .既不充分又不必要条件
3.双曲线的两焦点坐标是F 1(3,0),F 2(-3,0),2b =4,则双曲线的标准方程是( )
-y 24=1 -x 24=1 C.x 23-y 22=1 -y 2
16=1
4.方程x =3y 2-1所表示的曲线是( )
A .双曲线
B .椭圆
C .双曲线的一部分
D .椭圆的一部分
5.双曲线x 216-y 2
9=1上一点P 到点(5,0)的距离为15,那么该点到点(-5,0)的距
离为( )
A .7
B .23
C .5或25
D .7或23
6.圆P 过点
,且与圆 外切,则动圆圆心P 的轨迹方程( ). A .
; B . C .
D . 7.椭圆x 24+y 2a 2=1与双曲线x 2a -y 2
2=1有相同的焦点,则a 的值是( )
B .1或-2
C .1或12
D .1
8. 已知ab<0,方程y= —2x+b 和bx 2+ay 2=ab 表示的曲线只可能是图中的( )
9.双曲线m y x =-222的一个焦点是)3,0(,则m 的值是_______。
10.过双曲线)0,0(122
22>>=-b a b
y a x 的焦点且垂直于x 轴的弦的长度为_____。
11.已知双曲线的焦点在x 轴上,且a +c =9,b =3,则它的标准方程是________.
12.过点(1,1)且b a =2的双曲线的标准方程为________.
13.根据下列条件,求双曲线的标准方程.
(1)过点P ⎝ ⎛⎭⎪⎫3,154,Q ⎝ ⎛⎭
⎪⎫-163,5且焦点在坐标轴上; (2)c =6,经过点(-5,2),焦点在x 轴上.
14.已知方程x 22-k +y 2
k -1
=1表示的图形是:(1)双曲线;(2)椭圆;(3)圆.试分别求出k 的取值范围.
15.已知双曲线过点A (-2,4)、B (4,4),它的一个焦点是)0,1(1F ,求它的另 一个焦点2F 的轨迹方程。
16.如图所示,在△ABC 中,已知|AB |=42,且三内角A ,B ,C 满足 2sin A +sin C =2sin B ,建立适当的坐标系,求顶点C 的轨迹方程.。
