第05章__刚体力学基础补充汇总
刚体力学基础

mA
第5章 刚体力学基础
2.7
刚体力学基础
解:研究对象:A、B、圆柱 用隔离法分别对各物体作受力 分析,如图所示。
mB
N
mA
f
mB m Bg
TB
TA
mA
aB T 'B
aA
mAg
T 'A
第5章 刚体力学基础
2.7
刚体力学基础
N
f
mB m Bg
TB
TA
T 'B
T 'A
mA mAg
aA
aB
A: mA g TA mAaA TB f mB aB B: N mB g 0
2.7
定点转动:
刚体力学基础
运动中刚体上只有一点固定不动,整个刚体绕过该
固定点的某一瞬时轴线转动. 如:陀螺的运动
i3
(转轴方向(2),绕轴转角(1))
第5章 刚体力学基础
2.7
刚体力学基础
二 刚体定轴转动的运动学描述 定轴转动:刚体上任意点都绕同一 轴在各自的转动平面内作圆周运动
特征:刚体各个部分在相同时间内绕 转轴转过的角度(角位移)都相同 引入角量描述将非常方便。
oo mi vi 垂直于z轴。
i
th
刚体 mi
oo mi vi ri mi vi
z
我们只对z方向的分量感兴趣:
Liz ri mi vi mi ri 2
Lz Liz mi ri
2
ω,α vi
△ mi
ri O’ × 刚体 × O
刚体定轴转动的动能=绕质心转动的动能+
刚体携总质量(质心)绕定轴作圆周运动的动能
大学物理第5章 刚体力学基础ppt课件

z
or
d
F
P
Mz的方向平行于转轴,由右手螺旋定则确定。
2、F不在转轴平面内 把F分解为三个分量 Fz, Fr, Ft, Fr的力矩为零, Fz的力矩不为零, 但不影响刚体的定轴转动, Ft的力矩沿轴向, 它对角动量有贡献。
z
Fz
F
r
o
P Fr
Ft
3、多个力作用于刚体 各外力作用点各不相同,外力对转轴
1、转动定律适用条件:刚体定轴转动。 2、M 一定:作用不同刚体上,J 大时,β 小, 转速不宜
改变,转动惯性大。反之,J 小,转动惯性小。 — 转动惯量是物体转动惯性大小的量度。
M J 类比 F ma
3、刚体转动定律是解决刚体转动问题的重要定律。 应用时应注意以下问题: ① 力矩和转动惯量必须对同一转轴而言。
M
r
m1
对重物应用牛顿第二定律,得
T f m 2 g si n m 2 a
N
T
对滑轮应用转动定律,得
f
• o
T
MTrJ
m2g
关联方程为: a r
J
1 2
m1r 2
TT fN m 2gco s
联立得:
Mm2grsinm2gcos
1 2m1r2m2r2
由于 为常量,故滑轮作匀变速转动.则
2 2
an
l2
9gcos
4
例题5-10 一恒力矩M作用于斜面顶点的滑轮上,滑轮的半径为r,
质量为m1,质量为m2的重物通过一不可伸长的轻绳固定在轮的边
缘,重物沿倾角为α的斜面上升.重物与斜面间的摩擦系数为μ。
求:轮子由静止开始转过角 后获得多大的角速度?
第五章_刚体力学_习题解答

5.1、一长为l 的棒AB ,靠在半径为r 的半圆形柱面上,如图所示。
今A 点以恒定速度0v沿水平线运动。
试求:(i)B 点的速度B v;(ii)画出棒的瞬时转动中心的位置。
解:如图,建立动直角系A xyz -,取A 点为原点。
B A AB v v r ω=+⨯ ,关键是求ω法1(基点法):取A 点为基点,sin C A AC A CO A A v v r v v v v ωθ=+⨯=+=+即sin AC A r v ωθ⨯=,AC r ω⊥ ,化成标量为ω在直角三角形OCA ∆中,AC r rctg θ=所以200sin sin sin cos A AC v v v r rctg r θθθωθθ===即20sin cos v k r θωθ=取A 点为基点,那么B 点的速度为:2002300sin [(cos )sin ]cos sin sin (1)cos B A AB v v v r v i k l i l j r v l l v i jr rθωθθθθθθ=+⨯=+⨯-+=--法2(瞬心法):如图,因棒上C 点靠在半圆上,所以C 点的速度沿切线方向,故延长OC ,使其和垂直于A 点速度线交于P 点,那么P 点为瞬心。
在直角三角形OCA ∆中,sin OA r r θ=在直角三角形OPA ∆中,2cos sin AP OA r r r ctg θθθ==02cos ()sin A PA PA PA r v r k r j r i i v i θωωωωθ=⨯=⨯-===,即20sin cos v r θωθ= 取A 点为基点,那么B 点的速度为:2002300sin [(cos )sin ]cos sin sin (1)cos B A AB v v v r v i k l i l j r v l l v i jr rθωθθθθθθ=+⨯=+⨯-+=--5.2、一轮的半径为r ,竖直放置于水平面上作无滑动地滚动,轮心以恒定速度0v前进。
第05章刚体力学基础学习知识补充

第五章 刚体力学基础一、选择题1 甲乙两人造卫星质量相同,分别沿着各自的圆形轨道绕地球运行,甲的轨道半径较小,则与乙相比,甲的:(A)动能较大,势能较小,总能量较大; (B)动能较小,势能较大,总能量较大; (C)动能较大,势能较小,总能量较小;(D)动能较小,势能较小,总能量较小;[ C ]难度:易2 一滑冰者,以某一角速度开始转动,当他向内收缩双臂时,则: (A)角速度增大,动能减小; (B)角速度增大,动能增大; (C)角速度增大,但动能不变;(D)角速度减小,动能减小。
[ B ]难度:易3 两人各持一均匀直棒的一端,棒重W ,一人突然放手,在此瞬间,另一个人感到手上承受的力变为:(A)3w ; (B) 2w (C) 43w; (D) 4w 。
[ D ]难度:难4 长为L 、质量为M 的匀质细杆OA 如图悬挂.O 为水平光滑固定转轴,平衡时杆竖直下垂,一质量为m 的子弹以水平速度0v 击中杆的A 端并嵌入其内。
那么碰撞后A 端的速度大小:(A)M m mv +12120; (B) Mm mv +330;(C) Mm mv +0; (D) M m mv +330。
[ B ]难度:中L5 一根质量为m 、长为l 的均匀直棒可绕过其一端且与棒垂直的水平光滑固定轴转动.抬起另一端使棒竖直地立起,如让它掉下来,则棒将以角速度ω撞击地板。
如图将同样的棒截成长为2l的一段,初始条件不变,则它撞击地板时的角速度最接近于:(A)ω2; (B)ω2; (C) ω; (D) 2ω。
[ A ]难度:难6 如图:A 与B 是两个质量相同的小球,A 球用一根不能伸长的绳子拴着,B 球用橡皮拴着,把它们拉到水平位置,放手后两小球到达竖直位置时绳长相等,则此时两球的线速度:(A)B A v v = (B) B A v v < (C) B A v v > (D)无法判断。
[ C ]难度:中7 水平圆转台上距转轴R 处有一质量为m 的物体随转台作匀速圆周运动。
大学物理 第五章 刚体力学基础

v i ri
ri
mi
Lz Liz mi vi ri ( mi ri 2 ) J z
Lz J z
说明
动量矩与质点动量 P mv 对比, Jz — m, — v
三、 刚体定轴转动的动量矩定理 dLO 质点系角动量定理 MO dt
mg T ma
Tr J a r
r
O
T
21.8
F
mg
例 均匀细直棒m 、l ,可绕轴 O 在竖直平面内转动,初始时 它在水平位置 m l O 求 它由此下摆 角时的 m 解 dm dx dm 质元 l x dM gdm x cos dm 重力矩 gdm 1 M dM 2 mgl cos 重力对棒的合力矩等于重力全部集中于质心所产生的力矩 M 转动定律 3 g cos J 3g cos 1 2 2l J ml d 2l d d d 3 0 0 dt d 2 3g sin / l
1 1 2 2 mgh mv J 2 2 1 2 J mr 2
O
v r
mgh v 2 M 2m
mg
例 均匀细直棒m 、l ,可绕轴 O 在竖直平面内转动,初始时 它在水平位置 m l O 求 它由此下摆 角时的 。
解一 机械能守恒( 以初始位置为0势能点)
h
1 2 J mgh 2 l 3g sin 1 2 2 h sin J ml 2 l 3 解二 定轴转动动能定理 m 动能的增量等于重力做的功 1 2 0 Md 2 J 0 3 g sin 2 1 l 重力矩 M mgl cos 2
5第五章-刚体力学基础

①总质量; ②质量分布; ③转轴位置。
上页 下页 返回 退出
2. 转动惯量J
(1)质点 J mr2
r1
m1 O
(2)质点系 J miri2
i
例:J m1r12 +m2r22
r2
m2
(3)刚体 dJ dm r2
J dJ
r dm
上页 下页 返回 退出
dl
dm
dS
dV
线分布 面分布 体分布
一、力矩的功 M 1 2
dA F dr Fdscos Fdssin F sin rd Md
d
r
dr
F
A dA 2 Md 1
功率 P dA Md M
dt dt
上页 下页 返回 退出
二、 刚体的转动动能
第i个质点
Ek
1 2
J2
Eki
1 2
mi vi 2
1 2
mi
ri
2
2
上页 下页 返回 退出
三、 动量矩守恒定律的应用
当 M合外 0 时,L 恒量
讨论:
(1)动量矩守恒条件:
M外 0 或 M内 M外
(2)也适用于非刚体,是自然界最普遍规律之一
J 恒量 J , J ,
上页 下页 返回 退出
上页 下页 返回 退出
上页 下页 返回 退出
z
F
M rF 0
上页 下页 返回 退出
§1、2 刚体的转动定律
一、刚体和刚体的运动
1. 刚体: 形状、大小不变的理想模型。 2. 刚体的运动: (1)平动。 看作质点。
上页 下页 返回 退出
(2)转动。 定轴; 非定轴(瞬时轴)。
第5章刚体力学基础
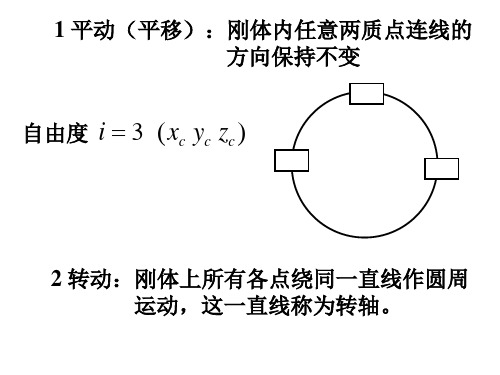
i
1 刚体为分裂的不连续结构 J
mi ri2
i
2 刚体为连续体 J r 2dm
J与质量,质量分布有关,与转轴有关
单位: SI kg m2
例: 均质棒:m, l 求它对通过中心与棒垂直 的转轴的转动惯量。
解: dm m dx l
J x2dm
dm
o dx
x
l 2
m x2dx
1
ml2
l
mvRcos J o
y
m(黏土块)
(2)
J 1 MR2 mR2 2mR2
(3)
2
h
由 (1)(2)(3) 得:
o
2gh cos
2R
(4)
对 m+M+地球系统,只有重力做功,
E 守恒.
P
M
R
Oθ
光滑轴
x
(水平)
令 P、x 重合时 E =0。
则:mgR
sin
1 2
P
J
2 o
1 2
J 2
(5)
3 平面平行运动:刚体上每一质元的运动都 平行于某一固定平面
可以分解为刚体随质心的平移(2)和绕 质心垂直于运动平面的定轴转动(1)
i3
如:车轮滚动 i 11
4 刚体的一般运动可以分解为随质心的平移 和绕质心的定点转动
i 33
二 、定轴转动的描述 角量
p点:角位置 角位移
转动平面 p
d
dt
Li
ri
vi
mi
Ri
由于 oo vi 垂直于z轴
o
y
Liz ri mivi mi ri2 x
Lz Liz ri mivi
上海理工大学 大学物理 第五章_刚体力学答案

一、选择题[ C ] 1、基础训练(2)一轻绳跨过一具有水平光滑轴、质量为M 的定滑轮,绳的两端分别悬有质量为m 1和m 2的物体(m 1<m 2),如图5-7所示.绳与轮之间无相对滑动.若某时刻滑轮沿逆时针方向转动,则绳中的张力(A) 处处相等. (B) 左边大于右边. (C) 右边大于左边. (D) 哪边大无法判断.参考答案:逆时针转动时角速度方向垂直于纸面向外, 由于(m 1<m 2),实际上滑轮在作减速转动,角加速度方向垂直纸面向内,所以,由转动定律21()T T R J β-=可得:21T T >[ B ] 2、基础训练(5)如图5-9所示,一静止的均匀细棒,长为L 、质量为M ,可绕通过棒的端点且垂直于棒长的光滑固定轴O 在水平面内转动,转动惯量为231ML .一质量为m 、速率为v 的子弹在水平面内沿与棒垂直的方向射出并穿出棒的自由端,设穿过棒后子弹的速率为v 21,则此时棒的角速度应为(A)MLm v . (B)MLm 23v . (C)MLm 35v . (D)MLm 47v .图5-9[ C ] 3、基础训练(7)一圆盘正绕垂直于盘面的水平光滑固定轴O 转动,如图5-11射来两个质量相同,速度大小相同,方向相反并在一条直线上的子弹,子弹射入圆盘并且留在盘内,则子弹射入后的瞬间,圆盘的角速度 (A) 增大. (B) 不变. (C) 减小. (D) 不能确定.图5-7m图5-11v21v俯视图[ C ] 4、自测提高(2)将细绳绕在一个具有水平光滑轴的飞轮边缘上,现在在绳端挂一质量为m 的重物,飞轮的角加速度为 .如果以拉力2mg 代替重物拉绳时,飞轮的角加速度将(A) 小于 . (B) 大于 ,小于2 . (C) 大于2 . (D) 等于2 .[ A ] 5、自测提高(7)质量为m 的小孩站在半径为R 的水平平台边缘上.平台可以绕通过其中心的竖直光滑固定轴自由转动,转动惯量为J .平台和小孩开始时均静止.当小孩突然以相对于地面为v 的速率在台边缘沿逆时针转向走动时,则此平台相对地面旋转的角速度和旋转方向分别为(A) ⎪⎭⎫ ⎝⎛=R J mR v 2ω,顺时针. (B) ⎪⎭⎫⎝⎛=R J mR v 2ω,逆时针.(C) ⎪⎭⎫ ⎝⎛+=R mR J mR v 22ω,顺时针. (D) ⎪⎭⎫⎝⎛+=R mR J mR v 22ω,逆时针.二、填空题6、基础训练(8)绕定轴转动的飞轮均匀地减速,t =0时角速度为05rad ω=,t =20s 时角速度为00.8ωω=,则飞轮的角加速度β=-0.05 rad/s 2 ,t =0到 t =100 s 时间内飞轮所转过的角度θ= 250rad .7、基础训练(9)一长为l ,质量可以忽略的直杆,可绕通过其一端的水平光滑轴在竖直平面内作定轴转动,在杆的另一端固定着一质量为m 的小球,如图5-12所示.现将杆由水平位置无初转速地释放.则杆刚被释放时的角加速度β0= g/l ,杆与水平方向夹角为60°时的角加速度β= g/2l .图 5-128、基础训练(10)如图5-13所示,P 、Q 、R 和S 是附于刚性轻质细杆上的质量分别为4m 、3m 、2m 和m 的四个质点,PQ =QR =RS =l ,则系统对O O '轴的转动惯量为 50ml 2 。
大学物理:第 05 章 刚体力学基础

j
i
设作用在质元Dmi上的外力
位于转动平面内。
z
合外力对刚体做的元功: P
力矩的功:
功率:
三、刚体定轴转动的动能定理
合外力矩对刚体所作的功等于刚体转动动能的增量。
四、刚体的重力势能
以地面为势能零点,刚体和地球 系统的重力势能:
z
i O
五、 刚体定轴转动的功能原理
将重力矩作的功用重力势能差表示:
如:直立旋转陀螺不倒。
o
此时,即使撤去轴承的支撑作用, 刚体仍将作 定轴转动——定向回转仪—— 可以作定向装置。
二、非刚体( J 可变)的角动量守恒
当 J 增大, 就减小,当 J 减小, 就增大。
如:芭蕾舞,花样滑冰中的转动, 恒星塌缩 (R0,0) (R,) 中子星 的形成等。
[例5-11] 水平转台(m1 、 R ) 可绕竖直的中心轴转动,初角 速度0,一人(m2 )立在台中心,相对转台以恒定速度u沿 半径向边缘走去,计算经时间 t,台转过了多少角度。 解:人与转台组成的系统对竖直 轴的角动量守恒:
(2)
(3) (4)
[例5-16] 细杆A : (m , L)可绕轴转动,水平处静止释放, 在竖直位置与静止物块B : (m) 发生弹性碰撞,求碰后: (1)物块B的速度 vB ,(2)细杆A 的角速度2 , (3)细杆A 转过的最大角度 θmax 。 解: B
A
碰后反方向转动。
A
B
[例5-17] 圆锥体R,h,J,表面有浅槽,令以ω0转动, 小滑块m 由静止从顶端下滑,不计摩擦,求滑到底部滑 块相对圆锥体的速度、圆锥体角速度。
是关于刚体定轴转动的动力学方程。 (与 F = ma 比较) 推广到 J 可变情形: ——刚体定轴转动的角动量定理
第五章 刚体力学基础

第五章 刚体力学基础一、选择题1 甲乙两人造卫星质量相同,分别沿着各自的圆形轨道绕地球运行,甲的轨道半径较小,则与乙相比,甲的:(A)动能较大,势能较小,总能量较大; (B)动能较小,势能较大,总能量较大; (C)动能较大,势能较小,总能量较小;(D)动能较小,势能较小,总能量较小;[ C ]难度:易2 一滑冰者,以某一角速度开始转动,当他向内收缩双臂时,则: (A)角速度增大,动能减小; (B)角速度增大,动能增大; (C)角速度增大,但动能不变;(D)角速度减小,动能减小。
[ B ]难度:易3 两人各持一均匀直棒的一端,棒重W ,一人突然放手,在此瞬间,另一个人感到手上承受的力变为:(A)3w ; (B) 2w (C) 43w; (D) 4w 。
[ D ]难度:难4 长为L 、质量为M 的匀质细杆OA 如图悬挂.O 为水平光滑固定转轴,平衡时杆竖直下垂,一质量为m 的子弹以水平速度0v 击中杆的A端并嵌入其内。
那么碰撞后A 端的速度大小: (A)M m mv +12120; (B) Mm mv +330;(C) Mm mv +0; (D) M m mv +330。
[ B ]难度:中5 一根质量为m 、长为l 的均匀直棒可绕过其一端且与棒垂直的水平光滑固定轴转动.抬起另一端使棒竖直地立起,如让它掉下来,则棒将以角速度ω撞击地板。
如图将同样的棒截成长为2l的一段,初始条件不变,则它撞击地板时的角速度最接近于:(A)ω2; (B)ω2; (C) ω; (D) 2ω。
[ A ]难度:难6 如图:A 与B 是两个质量相同的小球,A 球用一根不能伸长的绳子拴着,B 球用橡皮拴着,把它们拉到水平位置,放手后两小球到达竖直位置时绳长相等,则此时两球L的线速度:(A)B A v v = (B) B A v v <(C) B A v v > (D)无法判断。
[ C ]难度:中7 水平圆转台上距转轴R 处有一质量为m 的物体随转台作匀速圆周运动。
第五章 刚体力学基础

§5.1
刚体和刚体的基本运动
一、什么是刚体?
橡皮泥
不锈钢
刚体:受力时形状和体积都不发生改变的物体
大学物理 第三次修订本
第5章 刚体力学基础 动量矩
刚体可以看作是由许多质 点组成的,每一个质点叫 做刚体的一个质元,刚体 这个质点系的特点是: 在外力作用下各质元之间 的相对位置保持不变。
mj
mi
w w0 t 4π rad/s
飞轮边缘上一点 线速度:
v rw 2.5m/s
2
切向加速度:a r 0.105m s
2 2
法向加速度:an v / r rw 31.6m s
大学物理 第三次修订本
2
15
第5章 刚体力学基础 动量矩
例2 设圆柱型电机转子由静止经300s后达 18000r/min已知转子的角加速度α与时间成 正比。 求: 转子在这段时间内转过的圈数。 解: 因角加速度α 随时间而增大, ct 设
在刚体转动过程中,如果转轴固定不动,则称这种 转动为定轴转动。
特点:
① 各质元的线速度、加速度 不同。 ② 由于各质元的相对位置保持 不变,且都绕同一转轴作圆 周运动,因此具有相同的角 速度和角加速度;在相同的 时间内有相同的角位移。
大学物理 第三次修订本
第5章 刚体力学基础 动量矩 大小: 方向:
大学物理 第三次修订本
h θ
F Fn
F
23
第5章 刚体力学基础 动量矩
力不在垂直于轴的平面内
z
r
F//
M z ( F ) F r sin F h Fτ r
2.力对点的力矩
h θ
F
大学物理第五章刚体力学1

机械能守恒定律是物理学中的基本定律之一,对于刚体而言同样适用。如果一个刚体在 运动过程中不受外力矩作用,则其动能和势能之和保持不变。这意味着,如果刚体的动
能增加,则其势能必定减少,反之亦然。
05
刚体的振动和波动
简谐振动
简谐振动定义
物体在平衡位置附近做周期性往复运动的现象。
简谐振动方程
x=A*sin(ωt+φ),其中A为振幅,ω为角频率,φ为初相角。
THANK YOU
感谢聆听
转动惯量的计算
对于细长均匀杆,转动惯量I=mr^2/2;对于质量均匀分布的圆盘, I=mr^2/4。
03
刚体的角动量守恒定律
角动量守恒定律
角动量守恒定律
一个不受外力矩作用或者所受 外力矩的矢量和为零的刚体, 其角动量保持不变。
角动量
刚体绕某一定点的转动惯量与 刚体相对该点的角速度的乘积 。
角动量守恒的条件
刚体定义与特性
80%
刚体定义
刚体是一个理想化的物理模型, 在实际中并不存在。
100%
刚体特性
刚体具有不变形、不可压缩、无 摩擦等特性。
80%
刚体运动
刚体的运动可以用质点和刚体的 运动学来描述,其动力学则由牛 顿第二定律和转动定律来描述。
02
刚体的转动定律
刚体的角速度和角动量
角速度
描述刚体绕固定点转动的速度,用矢 量表示,单位为弧度/秒。
总结词
刚体的动能在数值上等于刚体 转动惯量与刚体角速度平方乘 积的一半。
详细描述
除了平动运动外,刚体还可以 进行转动运动。在转动运动中 ,刚体的动能等于刚体的转动 惯量与刚体角速度平方乘积的 一半。
刚体的势能
大学物理第5章刚体
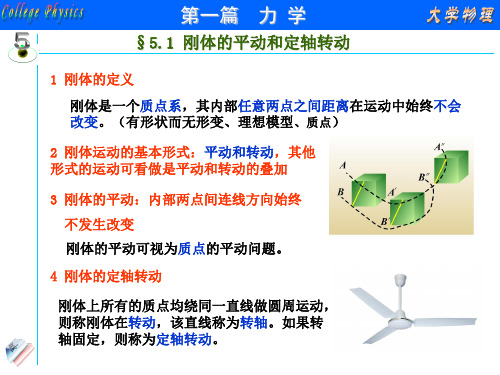
B C
分析受力和力矩情况
第一篇 力 学
解:由ABC和绳子组成系统为研究对象,分析受力和力矩情况。
系统受到的合力矩: M m2 gr m3gr
对整个系统列出角动量定理积分形式
t
Mdt Lt L0
t0
分别计算,有 Mdt (m2gr m1gr)t
L0 0
0
L
LA
若质量连续分布 J r2dm
一维
二维
三维
dm
dl
线密度 dm dl
J r2dl
面密度 dm dS
J r2dS
体密度 dm dV
J r2dV
第一篇 力 学
例1.求长为L、质量为m的均匀细棒对图中不同轴的转动惯量。
解:取如图坐标,dm=dx
J A
L x2dx mL2 / 3
0
L
JC
2 L
x2dx
mL2
/12
2
A L
A
C
L/2
B X
B L/2 X
例2.求质量为m、半径为R的均匀圆环的转动惯量。轴与圆环平面垂
直并通过圆心。
解:
J R2dm R2 dm mR2
O
R
dm
第一篇 力 学
例3.求长求质量为m、半径为R均匀圆盘的转动惯量。轴与盘平面垂 直并通过盘心。
解:取半径为r宽为dr 的薄圆环
dm 2rdr
dJ r2dm 2r3dr
dr rR
J dJ R 2r3dr 1 R4
0
2
m
R 2
理论力学第五章 点的运动和刚体的基本运动 [同济大学]
![理论力学第五章 点的运动和刚体的基本运动 [同济大学]](https://img.taocdn.com/s3/m/9038a70db52acfc788ebc909.png)
dv v2 τ n dt
a
r
O
`
v vτ
r
dv 2 v2 ) ( )2 dt ρ
tan
aτ an
1
例5-2 汽车以匀速度v=10m/s过拱桥,桥面曲线 y=4fx(L–x)/L2, f=1m,求车到桥最高点时的加速度。
解: aτ
例5-3 销钉A由导杆B带动沿固定圆弧槽运动。导杆B沿轴螺旋 立柱以不变的速度v0 =2m/s向上运动。试计算当θ=30° 时,销钉 A的切向和法向加速度。 解: 建立弧坐标s和直角坐标Oxy如图。 因 s=Rθ,
销钉A的加速度为
aτ v sin θ v0 θ cos θ
2 2 sin θ v0 12.32m/s 2 R cos3 θ
an
2 v2 v0 21.33m/s 2 R R cos 2 θ
例5-4
判别下图示曲线中加速度、速度矢量是否正确。
§5-4 刚体的基本运动平动,转动
则vD=vA=2rω
aDn=aAn=2rω2 aDτ=aAτ=2ra
0 dt
0
t
y x
θ θ0 ω0t
t
0 0
t
αdtdt
角加速度为常量:
两个独立方程
0 t,
1 θ θ0 ω0 t t 2 2
1 θ θ0 (ω0 ω)t , 2
t 0
'2 1 1 y " k y
切线
v r S M* + M
dτ s v lim n d t lim t 0 t t 0 s t
an
05.刚体力学

a at R
联立四式解得:
---- (4)
m1 g
m2 g
Mf m2 m1 g R a 1 m1 m2 m 2
Mf m2 m1 g R a 1 m1 m2 m 2 m1 M f m 2 m 2 m1 g 2 R T1 m1 g a m m1 m 2 2 m2 M f m 2 m1 m 2 g 2 R T2 m 2 g a m m1 m 2 2
P
vP
4
y
单位均为cm s
3
o
x
2 k rad s1
z
5
rP 3i 4 j 5 k cm
该时刻P点的速度为: 3
rP
P
vP
4
y
o
v r 0 3
i
j 0 4
k 2 5
x
-1 v 25.1i 18.8 j (cm s )
* 简化为研究转动平面内的运动
* 用角量作整体描述
* 在轴上选正方向,各角量均表示为代数量
四.角速度矢量
角速度:
旋转方向 O
d lim t 0 t dt
角速度矢量
R
P
v
方向:右手螺旋法则 垂直于运动平面,沿轴
o
r
v r
2 3L 4
z
A L4
m o
L
C
B
解1:
解2: J z J C m L 1 mL2 m L 7 mL2 48 4 12 4
刚体力学课件

l
rR
其质量为
显然:转动惯量与l 无关。所以,实心圆柱对其
轴的转动惯量也是mR2/2。
14
例3.如图所示,一个均匀半圆薄板的质量为m, 半径 为R.以其直径边为转轴, 它的转动惯量多大?
解: 设面密度为 .
取窄条状面元dS. dh
dq 对应的弧长为Rdq
dS h
?
15
例4.求长为L、质量为m的均匀细棒
转轴
刚体
p x
参考 方向
(4)
角加速度
b
=
dw
dt
=
d 2q
dt 2
6
定轴转动中角量与线量的基本关系
矢量式
类似一维运动,各角量的方向 由“+”,“–”号表示。 注意: 这里的角量单位都用弧度(rad)
7
第2节 刚体定轴转动定律
Principle of Rotation of a Rigid
1. 力矩
19
例:一细绳跨过一轴承光滑的定滑轮,绳的两端分别悬有质量为m1和m2的物体(m1<m2), 如图所示.设滑轮和绳的质量可忽略不计,绳不能伸长,试求物体的加速度以及悬挂滑轮
的绳中张力.
解:选取对象m1、m2及滑轮 分析运动
m1,以加速度a1向上运动 m2,以加速度a2向下运动 分析受力
T1 a
1
m1g
解: 以棒和小球为系统. 在碰撞过程中, 对轴O的
外力矩只有小球的重力矩mgL .因碰撞时间
极短, 此重力矩对时间的累积可忽略不计.
碰前
o
u
m
碰后
o
于是,系统对转轴o
v
m
的角动量守恒:
40
工程力学_05空间力系

0, MO 0 时,空间力系为平衡力系。 当 FR
§5–1 空间任意力系向一点的简化· 主矢和主矩
空间任意力系向任一点简化可得到一个力和一个力偶。 这个力通过简化中心,称为力系的主矢,它等于各 个力的矢量和,并与简化中心的选择无关。 这个力偶的力偶矩矢称为力系对简化中心的主矩, 并等于力系中各力对简化中心之矩矢的矢量和,并 与简化中心的选择有关。
§5–1 空间任意力系向一点的简化· 主矢和主矩
§5–1 空间任意力系向一点的简化· 主矢和主矩
空间任意力系:作用线在空间任意分布的力系。
空间汇交力系
空间任意力系
空间力偶系
§5–1 空间任意力系向一点的简化· 主矢和主矩
空间任意力系:作用线在空间任意分布的力系。 一、空间任意力系向一点的简化
其中,各 Fi Fi ,
Fx 0, FAx Fx 0 (1) Fy 0, FAy Fy 0 (2) Fz 0, FAz Fz 0 (3) M x ( F ) 0, M y ( F ) 0, M z ( F ) 0,
FAz MAz
O
z
MAy FAx
FAy Fz
y 200 Fy
MAx
M Ax 0.075Fz 0 M Ay 0.2 Fz 0
x 75 Fx
M Az 0.075Fx 0.2 Fy 0
P 20 kN
§5–2 空间任意力系的平衡条件
解题步骤、技巧与注意问题: 1、解题步骤: ①选研究对象
O
11
§5–1 空间任意力系向一点的简化· 主矢和主矩
三、补充:空间任意力系的简化结果分析(最后结果)
第05章__刚体力学基础补充

第05章__刚体⼒学基础补充第五章刚体⼒学基础⼀、选择题1 甲⼄两⼈造卫星质量相同,分别沿着各⾃的圆形轨道绕地球运⾏,甲的轨道半径较⼩,则与⼄相⽐,甲的:(A)动能较⼤,势能较⼩,总能量较⼤; (B)动能较⼩,势能较⼤,总能量较⼤; (C)动能较⼤,势能较⼩,总能量较⼩;(D)动能较⼩,势能较⼩,总能量较⼩;[ C ]难度:易2 ⼀滑冰者,以某⼀⾓速度开始转动,当他向内收缩双臂时,则: (A)⾓速度增⼤,动能减⼩; (B)⾓速度增⼤,动能增⼤;(C)⾓速度增⼤,但动能不变;(D)⾓速度减⼩,动能减⼩。
[ B ]难度:易3 两⼈各持⼀均匀直棒的⼀端,棒重W ,⼀⼈突然放⼿,在此瞬间,另⼀个⼈感到⼿上承受的⼒变为:(A)3w ; (B) 2w (C) 43w ; (D) 4w 。
[ D ]难度:难4 长为L 、质量为M 的匀质细杆OA 如图悬挂.O 为⽔平光滑固定转轴,平衡时杆竖直下垂,⼀质量为m 的⼦弹以⽔平速度0v 击中杆的A端并嵌⼊其内。
那么碰撞后A 端的速度⼤⼩: (A)M m mv +12120; (B) Mm mv +330;(C) M m mv +0; (D) Mm mv +330。
[ B ]难度:中5 ⼀根质量为m 、长为l 的均匀直棒可绕过其⼀端且与棒垂直的⽔平光滑固定轴转动.抬起另⼀端使棒竖直地⽴起,如让它掉下来,则棒将以⾓速度ω撞击地板。
如图将同样的棒截成长为2l的⼀段,初始条件不变,则它撞击地板时的⾓速度最接近于:(A)ω2; (B)ω2; (C) ω; (D) 2ω。
[ A ]难度:难6 如图:A 与B 是两个质量相同的⼩球,A 球⽤⼀根不能伸长的绳⼦拴着,B 球⽤橡⽪拴着,把它们拉到⽔平位置,放⼿后两⼩球到达竖直位置时绳长相等,则此时两球L的线速度:(A)B A v v = (B) B A v v <(C) B A v v > (D)⽆法判断。
[ C ]难度:中7 ⽔平圆转台上距转轴R 处有⼀质量为m 的物体随转台作匀速圆周运动。
刚体力学补充内容ppt

y
C
q mg O x
1 2 2 cos q m l q m glcosq m l cosq l sin q q q 3 2 cosq sin q mglcosq ml2q 1 g 2 cos q q sin q cosq q cosq 0 3 l
5 v0 0 2R
此后,质心速度为负,质心后退,但角速度仍沿原方向 质心向左加速,球转动继续减慢 摩擦力方向不变 到某个时刻t2,A点速度为零,球开始做纯滚动
5m g vA vC R v0 m gt2 0 t2 R 0 2R 2v0 R0 t2 7 mg 3 此时 vC v0 m gt2 v0 7 1 v0 R0 4
0 m
R
v0
球相对P点角动量守恒
P
(2)
2 2 mR 0 mv0 R 0 (1) 5 2 v0 R0 5 2 2 2 2 mR 0 mv0 R mvR mR 5 5 3v0 3 代入即得 以 v v0 7 7R 1 v0 R0 4
刚体力学补充内容
若外力为保守力,则机械能守恒: 不是独立方程!
上海交通大学物理系高景jgao@
刚体力学补充内容
一圆柱质量为m,半径为R。静 止地放在摩擦系数为 m 的粗糙水平面上。若沿水平方 向过质心加恒定外力F, 求其运动。
F
[分析] 受力:外力F,重力mg,支持力N,摩擦力f
如何运动与F、f 有关,而f 又与运动情况有关
x
若应用运动定理
为
y px y qx 型方程
通解
ye
pdx
qe pdx dx c
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3一、选择题1甲乙两人造卫星质量相同,分别沿着各自的圆形轨道绕地球运行,与乙相比,甲的:(A) 动能较大,势能较小, (B) 动能较小,势能较大, (C) 动能较大,势能较小, (D) 动能较小,势能较小,4长为L 、质量为M 的匀质细杆 轴,平衡时杆竖直下垂,一质量为 端并嵌入其内。
那么碰撞后 A 端的速度大小:5 一根质量为m 、长为I 的均匀直棒可绕过其一端且与棒垂直 的水平光滑固定轴转动.抬起另一端使棒竖直地立起,如让它 掉下来,则棒将以角速度 ⑷撞击地板。
如图将同样的棒截成长 为少2的一段,初始条件不变,则它撞击地板时的角速度最接近 于:6如图:A 与B 是两个质量相同的小球, A 球用一根不 能伸长的绳子拴着,B 球用橡皮拴着,把它们拉到水平位 置,放手后两小球到达竖直位置时绳长相等,则此时两球第五章刚体力学基础甲的轨道半径较小,总能量较大; 总能量较大; 总能量较小;总能量较小;C ]难度:2 一滑冰者,以某一角速度开始转动, (A) 角速度增大,动能减小; (B) 角速度增大,动能增大; (C) 角速度增大,但动能不变; (D) 角速度减小,动能减小。
当他向内收缩双臂时,则:3两人各持一均匀直棒的一端,棒重 受的力变为:(A)% ; W , —人突然放手,在此瞬间, 另一个人感到手上承(B) W 2OA 如图悬挂.0为水平光滑固定转 m 的子弹以水平速度v 0击中杆的12mv 0 (A)12m+M3mv 0 (B)3m + MV omv o(C)mmM(D)倍。
(A) 2 ;(B) 42^:A ]难度:难(C)(D)的线速度: (A) V A =V B (C) V A >V B :C ]难度:中 (B) V A C V B (D)无法判断。
7水平圆转台上距转轴 R 处有一质量为 m 的物体随转台作匀速圆周运动。
间的静摩擦因数为 1 (A) E k 兰-卩mgR 4 卩,若物体与转台间无相对滑动,则物体的转动动能为: 1 (B) E^-kmgR (C) E k < 4mgR (D) E k I ,质量为m 。
杆两端用线吊起,保持水平,现有一条 8 一匀质细杆长为 线突然断开,如图所示,则断开瞬间另一条绳的张力为: 3 (A) — mg4 1 (B)4mg(C) 2 mg (D) mg :B ]难度:难 已知物体与转台<2PmgR:B ]难度:中9 一根均匀棒AB ,长为 1 摆动,已知转动惯量为 -mgl 2 .开始时棒静止在水 3 平位置,当它自由下摆到 0角时,B 端速度的大小 为: (A )J gl sin9(C) J 3gl sin e I ,质量为m ,可绕通过A 端且与其垂直的固定轴在竖直面内自由 (B) J 6glsin 0 (D) J 2gl sin 日 转动惯量为J , 开始时转台以匀角速度 O 0转动,此时有一质量为 m 的人站在转台中心.随后人沿半径向外 跑去,当人到达转台边缘时, J (A) ------------- 2J +mR 2 10 有一半径为 R 的水平圆转台,可绕通过其中心的竖直固定光滑轴转动, 转台的角速度为 J (B) (J +m R 2 J(C) F mR :A ]难度:中 11 一质量为M 、半径为 (D)叫.作幅度很小的简谐振动.r 的均匀圆环挂在一光滑得的钉子上,以钉子为轴在自身平面内 一 2 1 已知圆环对轴的转动惯量 J = 2Mr 2,若测得其振动周期为一兀s , 2 则r 的值为 (A) g/32. g(B)丽.(C) J2g/16 . (D) g/4.:A ]难度:中12、质量和长度都相同的均匀铝细圆棒A 和铁细圆棒B ,它们对穿过各自中心且垂直于棒的轴的转动惯量各为 J A 和J B ,则(A) J A > J B . (B) J B > J A .(C) J A = J B .(D) J A 、J B 哪个大,不能确定.13、两个质量和厚度相等的均匀木质圆盘 A 和均匀铁质圆盘 B , 面轴的转动惯量各为 J A 和J B ,则(A) J A > J B .(C) J A = J B .:A ]难度:易15、一质量均匀分布的圆盘,质量为M ,半径为R ,放在一粗糙水平面上,圆盘与水平面之间的摩擦系数为 出圆盘可绕通过其中心的竖直固定光滑轴转动.开始时,圆盘的角速度为(A)空 ()4g3%R(C)茁16、均匀细棒 OA 可绕通过其一端 0而与棒垂直的水平固定光滑轴转动,开始时自然悬挂 于竖直位置若给棒一水平冲力,则棒在绕轴转动过程中:(A) (B) (C) (D) 17、一个转动惯量为J 的圆盘绕一固定轴转动, 起初角速度为©0.设它所受阻力矩与转动角1速度成正比,即M = — k ⑷(k 为正的常数),则圆盘的角速度从 时0变为一⑷0时所需的时间(SI2制):(B) 丄k1(D) -k .2:C]难度:易(B) J B > J A . (D) J A 、J B 哪个大,不能确定. 设两盘对通过盘心垂直于盘14、两根细棒的质量、长度均相同,且都半截木质、半截钢质,一根的转动轴木质端,另一根的转动轴在钢质端。
今在棒的另一端施 F ,两细棒得到的角加速度满足:俄> fe . (B) fe > 3A .仇=fe .(D)无法确定.:B ]难度:, 木 钢相同的力 (A) (C) ©0,当圆盘角速度变为所需时间为(SI 制):2角速度逐渐增大,角加速度逐渐减小; 角速度和角加速度都逐渐增大; 角速度和角加速度都逐渐减小; 角速度逐渐减小,角加速度逐渐增大。
1 (A)2 .J l n2 (C)"TA机械能和角动量守恒,动量不守恒. 机械能守恒,动量和角动量不守恒. 动量和机械能不守恒•角动量守恒. 机械能不守恒.动量和角动量守恒. :C ]难度:易21、一质量为 M 的水平匀质圆盘可绕通过其中心的固定竖直轴转动, 量为m 的人.把人和圆盘取作系统,开始时,该系统的角速度为 圆盘中心,在走动过程中(忽略轴的摩擦),此系统的(A) 转动惯量不变; (B) 角速度减小; (C) 机械能不变; (D) 角动量不变。
:D]难度:易22、一质量为 M 的水平匀质圆盘可绕通过其中心的固定竖直轴转动,圆盘边缘站着一个质 量为m 的人.把人和圆盘取作系统,开始时,该系统的角速度为C o ,接着此人沿着半径走到圆盘中心,此系统的角速度将为::C ]难度:中 18、一个转动惯量为J 的圆盘绕一固定轴转动, 起初角速度为O 0.设它所受阻力矩与转动角速度成正比,即 M =—加(k 为正的常数),则圆盘的角速度从 ⑷0变为丄⑷0时,阻力距所作2的功(SI 制): (A)学 4 J 阮(D):B ]难度:中19、一花样滑冰运动员绕通过自身的竖直轴转动,开始时以转动动能 些旋转,当他向内21 收缩双臂时,他的转动惯量减少为 -J .这时他转动动能变为: 3 (B)孃. 6 9J 0:in(D) . 2(A)畔 2 (C) 2 C ]难度:中20、一人双手握着重物伸开双臂站在可绕中心轴无摩擦转动的平台上, 系统的转动惯量为 J ,角速度为©.当此人突然将两臂收回,使系统的转动惯量减少为1一J o .3 则该系统:(A) (B) (C) (D) 圆盘边缘站着一个质 C o ,接着此人沿着半径走到2m八(A) 一%;M(B) (1 +一)矶;M(C) (1 + m 、冷2M (D) m 個0。
]难度:中23、一飞轮从静止开始作均加速转动,飞轮边上一点的法向加速度 a n 和切向加速度a t 值的变化为: (A) a n 不变, a t 为零; (B) a n 不变, a t 不变; (C) a n 增大, a t 为零; (D) a n 增大, a t 不变;。
]难度:中 24、一根均匀棒,长为I ,质量为m , —端固定,由水平位置可绕通过其固定端且与其垂直 的固定轴在竖直面内自由摆动•则在水平位置时其质心 过其一端垂直于棒的轴的转动惯量为 丄ml 2 ): 3(B)0 • (D) -g • 2 C 的加速度为(已知均匀棒对于通 (A) g • 3(C) -g •4:C ]难度:中 25、一根长为I 、质量为m 的均匀细直棒在地上竖立着,如果让其以下端与地的接触处为轴 自由倒下,当上端到达地面时, 上端的速率为(已知均匀棒对于通过其一端垂直于棒的轴的 1 2转动惯量为—ml ): 3 (A) J6gl • (C) J2gl • ]难度:中根长为I 、质量为m 的的杆如图悬挂.0为水平光滑固定转轴, m 、速度为V o 的子弹从与水平方向成 击中杆的中点且留在杆中,则杆的中点 C 的速度为: v_2 •3 m ^V o COS 屮•3m一 V 0COS 屮•4 3 .①-v 0sin 屮•26、 平衡时杆竖直下垂,一质量为角处飞来, (A)(B) (C) (D) :B ]难度:中27、在经典力学中,下列哪个说法是错误的:质点的位置、速度、加速度都是矢量. 刚体定轴转动的转动惯量是标量. 质点运动的总机械能是标量. 刚体转动的角速度是标量. :D ]难度:易 1 一飞轮以角速度O 0绕光滑固定轴旋转,飞轮对轴的转动惯量为J 1;另一静止飞轮突然和上述转动的飞轮啮合,绕同一转轴转动,该飞轮对轴的转动惯量为前者的二倍. 啮合后整 个系统的角速度为①则—%1答案:-3难度:中2 一电唱机的转盘以 n = 78 rev/min 的转速匀速转动,则转盘上与转轴相距 P 的线速度v = _________________________________ .(A) (B) (C) (D) r = 15 cm 的一点 难度:中3 一电唱机的转盘以n = 78 rev/min 的转速匀速转动,则转盘上与转轴相距 P 的法向加速度a n =— 答案:10%2 难度:中4 一电唱机的转盘开始以 阻力矩作用下减速,并在r = 15 cm 的一点n = 78 rev/min 的转速匀速转动,在电动机断电后, t = 15 s 内停止转动,则转盘在停止转动前的角加速度转盘在恒定的难度:中5 一电唱机的转盘开始以 阻力矩作用下减速,并在 n = 78 rev/min 的转速匀速转动,在电动机断电后,转盘在恒定的 t = 15 s 内停止转动,则转盘在停止转动前转过的圈数答案:9.75rev 难度:难6如图所示,半径为 =0.75 m 的B 轮带动, 轮与皮带间无滑动发生. 的时间t= ____________ 答案:40 难度:中r 1= 0.3 m 的A 轮通过皮带被半径为B 轮以匀角加速度 兀rad /s 2由静止起动, 则 A 轮达到转速3000 rev/min 所需要 s. 的角速度绕中心轴转动,对该轴转动惯量为24 kg 'm ,由于恒力矩的作用, 答案: 难度: 16 中答案:8.17 答案:-0.545 7、圆柱体以80在10s 内其角速度变为 40,则力矩的大小为在10s 内其角速度变为40ra 叹,则圆柱体损失的动能为9、 如图所示,A 和B 两飞轮的轴杆在同一中心线上, 设A 轮 的转动惯量J = 10 kg • m 2 .开始时,A 轮转速为600 rev/min , B 轮静止.C 为摩擦啮合器,其转动惯量可忽略不计. A 、B 分别与C 的左、右两个组件相连,当 C 的左右组件啮合时, i 石 B 轮得到加速而 A 轮减速,直到两轮的转速都达到 200 rev/min 为止.设轴光滑,则B 轮的转动惯量 J = __________________________________ kg • m 2. 答案:20难度:中10、 一半径 R = 1.0m 的飞轮可绕通过其中心且与盘面垂直的固定转轴转 动,一根细绳绕在飞轮的边缘,绳末端悬一质量为 m = 1kg 的物体.设在 t = 0 s 时物体在重力作用下从静止开始作匀加速下降,在 t = 2 s 时下降高 度h = 0.4m ,贝y t = 4 s 时飞轮的边缘任意点的切向加速度 a t =答案:0.2 难度:中答案:0.64 难度:中12、一半径 R = 1.0m 的飞轮可绕通过其中心且与盘面垂直的固定转轴转 动,一根细绳绕在飞轮的边缘,绳末端悬一质量为m = 1kg 的物体.设在t = 0 s 时物体在重力作用下从静止开始作匀加速下降,在t = 2 s 时下降高度 h = 0.4m ,则飞轮关于其固定轴的转动惯量kg 'm 2 .答案:48 难度:中作用,的角速度绕中心轴转动,对该轴转动惯量为4kg .m 2,由于恒力矩的答案: 难度: 9600 中---- 旺 ⑥A 11、一半径 R = 1.0m 的飞轮可绕通过其中心且与盘面垂直的固定转轴转 动,一根细绳绕在飞轮的边缘,绳末端悬一质量为m = 1kg 的物体.设在t = 0 s 时物体在重力作用下从静止开始作匀加速下降,在t = 2 s 时下降高度h = 0.4m ,贝y t = 4 s 时飞轮的边缘任意点的法向加速度叹2 .(3a n =c mJ=8、圆柱体以801 物体A 和B 叠放在水平桌面上,由跨过定滑轮的轻质 细绳相互连接,如图所示.今用大小为 F 的水平力拉A .A 、B 和滑轮的质量都为 m ,滑轮的半径为 R ,对轴的转动1惯量J = _ mR 2 . AB 之间、A 与桌面之间、滑轮与其轴之间2的摩擦都可以忽略不计,绳与滑轮之间无相对的滑动且绳不可伸长•已知kg , R = 0.050 m .求:(1) 滑轮的角加速度;(2) 物体A 与滑轮之间的绳中的张力;(3) 物体B 与滑轮之间的绳中的张力.解:各物体受力情况如图.F —T = ma T ‘ = ma(T -T')R = J a = —mR 2a绕00/轴转动,如图所示.若在转动过程中细线被拉断,套管将 沿着杆滑动.求在套管滑动过程中,该系统转动的角速度05与套管离轴的距离 x 的函数关系.(已知杆本身对 00 /轴的转动惯量为1 .2-ml 3难度:设/"O RF = 10 N , m = 8.0a = Ra由上述方程组解得:FRa = -----------------J +2mR 2 3T =3F =6N5 2T' = 2F =4N5中(1) =10 rad /(5mR难度:2在一水平放置的质量为 量也为m 的套管B(可看作质点 1滑固定轴00 /的距离为一l ,2m 、 长度为I 的均匀细杆上,套着一质 ),套管用细线拉住,它到竖直的光杆和套管所组成的系统以角速度豹0O'JC o答案:4(l 2 +3x 2)3长为I 、质量为M 的匀质杆可绕通过杆一端 0的水平光滑固定轴转动, 1 2转动惯量为-Ml 2,开始时杆竖直下垂,如图所示.有一质量为 3 弹以水平速度v ;射入杆上A 点,并嵌在杆中,0A = 2l / 3,求子弹射入后 瞬间杆的角速度©。
