基本体的投影作图
中职机械制图教案:基本体的投影作图(全2课时)
中等专业学校2024-2025-1教案编号:备课组别机械组课程名称机械制图所在年级主备教师授课教师授课系部授课班级授课日期课题基本体的投影作图(第一课时)教学目标1.了解基本体的含义、分类及用途;2.掌握基本体的投影作图及尺寸标注;3.培养学生的空间想象能力;4.培养学生绘制和识读基本体三视图的能力。
重点基本体的含义与分类、作图与尺寸标注、对基本体进行点、线、面投影分析。
难点对基本体的线、面分析、回转体素线的投影、培养学生的空间想象能力。
教法启发式、讨论式、直观演示、比较法、练习法等多种教法,讲练结合教学设备多媒体设备、教师用绘图工具、学生用绘图工具、A4幅面的绘图纸教学环节教学活动内容及组织过程个案补充教学内容【组织教学】检查出勤情况,稳定情绪【教学引入】螺栓毛坯的三维图用AutoCAD绘图软件或SolidWorks实体设计软件动态展示物体(螺栓毛坯)的三维图。
提出问题:(1)物体是由哪些基本体组成?(2)如何用三视图表达?【新课教学】教学内容任何物体均可以看成是由若干基本体组合而成。
基本体包括平面体和曲面体两类。
平面体:棱柱、棱锥等;曲面体:如圆柱、圆锥、圆球等,也称回转体通过动画演示,引导学生观察分析:物体是由六棱柱、圆柱和圆锥台三部分基本体构成。
所以基本体的投影作图是后学学习组合体及零件图的重要基础。
一、棱柱特征:侧棱线相互平行,侧面是矩形;两端面相等的多边形正六棱柱为例,分析其投影特征和作图方法分析:顶面和底面是相互平行的正六边形;六个侧棱面均为矩形按图示位置分析三个视图作图(1)作正六棱柱的对称中心线和底面基线,定位;(2)画出反映主要形状特征的俯视图的正六边形(按外接圆尺寸φ30)。
教学内容(3)按三等规律画出主视图和左视图(高12)。
分析:俯视图正六边形,也是顶面和底面的重合投影,且反映实形;六条边分别是六个棱面有积聚性的投影。
主视图为三个矩形线框组合,中间的矩形是前、后棱面的重合投影,反映实形;顶面和底面投影积聚为上、下两条水平线。
基本体的投影作图

(1)作基线,确定视图位置
(2)画反映主要形状的视图,俯视图 按长对正的投影关系和五棱柱的高度 画出主视图
(3)按高平齐、宽 相 等的投影关系画出左视图
2-3 基本体的投影作图
一、课堂作业
1、在正三棱柱、正四棱 柱、正六棱柱中,请你选 择一个棱柱画其三视图, 棱柱的长宽高可以自己定。 棱柱的位置是顶面和底面 与水平面平行,后棱面平 行于正面
2-3 基本体的投影作图
基本体
平面体
曲面体
基本体的投影作图
一、棱柱
三棱柱 四棱柱 五棱柱 六棱柱
2-3 基本体的投影作图
正五棱柱 分析:
1、两端面平行于水平面
2、后棱面平行于正面且所
有棱面垂直于水平面
V
投影特征:顶面和底面 水平投影重合,并反映 实形——正五边形
2-3 基本体的投影作图
2、4人一组,选出组长, 画好后组长代表本组展示作 品
3、考核标准: 其中选择正三棱柱、六棱柱画加10分 评分标准 1)视图对称中心线,确定视图位置10分 2)画出俯视图30分 3)主视图30分 4)左视图30 5)视图画不完整画错要减分
2-3 基本体的投影作图
课堂作业评讲
正三棱柱投影图
正四棱柱投影图
2-3 基本体的投影作图
正六棱柱投影图
2-3 基本体的投影作图
一、课堂总结:
通过正五棱柱投影图的学习我们知道了棱柱投影图的画 法,首先分析位置,然后根据俯视图、主视图、左视图 投影关系画出投影图
二、作业布置:预习棱锥的投影
图画法
谢 谢!
《基本体的作图投影》教案

何特点?生:讨论师:平面体的每个表面都是平面,例如长方体,棱柱和棱锥等,曲面体至少有一个表面是曲面,如圆柱、圆锥和球二、圆球13min师:展示模型(球)引导学生思考日常生活见到实例?生:思考回答(篮球、乒乓球、跳棋的溜溜珠子、佛珠等等)师:展示上述并补充说明讲:(1)圆球的形成展示模型(球)圆球的表面可看做是由一条圆母线绕其直径回转而成。
简单来说球的表面无直线。
(2)圆球的放置在三投影面体系中展示篮球(3)圆球的作图1、视图分析正面投影的圆是球体正面投影的转向轮廓线,也是前后两半球可见与不可见的分界线,水平面投影的圆是球体水平面投影的转向轮廓标识正面投影圆的三面投影,形象直观,为下面学生的练习起好示范和铺垫作用。
言传身教,规范作图。
讲练结合,激发学生参与热情。
体现了教为主导,学为主体的教育理念。
在绘图的过程中,不仅使学生的逻辑思维得锻炼,更有助于提高其自信心,对其他学生也有很好的榜样作用。
线,也是上下两半球可见与不可见的分界线,侧面投影的圆是球体侧面投影的转向轮廓线,也是左右两半球可见与不可见的分界线。
2、作图步骤1)、绘制定位基准线、对称中心线及反映圆的视图2)、根据“三等”关系绘制其他视图,检查,整理,加深师:圆的投影是与圆球直径相等的三个圆,这三个圆分别是三个不同方向球的轮廓素线圆的投影,不能认为是球面上同一圆的三个投影。
师:让学生对照模型想象三视图如何绘制并讲解引导。
学生互动找一名同学在黑板上画圆球三视图,其余同学在本子上画师:巡回指导,现场指正讲评:1.该生作图,完成较好应该掌声鼓励(此处应该有掌声)2.其他同学完成情况,进一步强调作图正确性和规范问题教师:将自己事先绘制的圆球三视图展示并张贴在黑板上。
三、六棱柱15min师:展示摆放好的模型(六棱柱),学生通过模型想象三视图投影讲:(1)分析:正六棱柱由顶面、底面和六个侧棱面组成。
正六棱柱的顶面、底面为水平面,在俯视图中反映实形。
直观图投影图(2)作图步骤1、绘制对称中心线、轴线和底面等作图基准线,确定各视图的位置2、绘制反映底面实形的视图即俯视图的正六边形,按长对正的投影关系及六棱柱的高度绘制主视图3、根据高平齐宽相等的投影关系画出左视图,检查,整理加深师:边画边讲解生:跟着老师一起画师:现场指导发现问题:1、共性问题分析2、个性问题分析板书设计基本体的投影作图一、形体的分类二、圆球三、六棱柱(1)圆球的形成展示模型(球)(1)结构组成平面体(2)圆球的作图方法(2)作图步骤曲面体图略图略。
第3章-机械制图基本体

资讯
3.1 基本体的投影
立体按构成不同可分为基本体和组合体。 通常将棱柱、棱锥、圆柱、圆锥、球体等简单几何体称为基本体。 按表面性质不同,又可将立体分为平面立体和曲面立体。 3.1.1 平面立体 由平面围成的立体称为平面立体,立体上相邻侧表面的交线称为 棱线。 1. 棱柱 (1) 棱柱的三视图 图3-1所示一放置在三投影面体 系中的正六棱柱。
图3-2 三棱锥的三视图
资讯
3.1.2 曲面立体 曲面立体的表面由曲面或曲面和平面组成。常见的曲面立体有圆 柱、圆锥和球体。 由于组成立体的曲面为回转面,故上述曲面立体也称为回转体。 有关回转面的几个概念如下。 回转面:一条线绕另一直线旋转所形成的运动轨迹。 回转面的轴线:不动的直线。 母线:即运动的线,回转面的母线可以是 直线也可以为任意曲线。 素线:母线位于回转面上任一位置时的线。
(a) 截切的圆锥
(b) 截切圆锥的视图
图3-17 圆锥的截交线
资讯
[例3-4] 完成被截切圆锥的视图。
(a) 求作截交线
(b) 整理图形 图3-18 圆锥的截交线
资讯
3. 球体的截交线 球体的截交线为圆,如图3-19所示。 由于截切的位置关系,球体截交线圆的投影可能为圆、直线或椭圆。 球体截交线的作图分析:当截交线的投影为圆或直线时,作图较为 简便。如是椭圆,则要利用找点的方法求得椭圆上若干点的投影后 再光滑连接各点。
资讯
若是沿圆柱轴线开一通孔,便称为圆筒。圆筒有内、外两个表面。 当截平面截切圆筒时,就会在内外表面上产生形状相同的截交线, 如图3-14所示。
(a)
(b)
图3-14 圆筒的截交线
资讯
圆筒被截切和开槽的情况如图3-15所示。
第3章基本形体的投影

a
2 m
s
3 b
圆锥的投影及表面上的点
例:已知圆锥表面 上点M及N的正面投影 m′和n′,求它们的 其余两投影。
m
(n ) (n )
m
a’ (a”)
n
a
m
在圆锥表面上取点
①特殊点:特殊素线+三等关系 ②一般点:利用辅助素线法、纬圆法+三等关系
3.圆球
⑴ 圆球的形成
圆母线以它的直 径为轴旋转而成。
s
s
b
a c
a(c)
b
b
棱锥的三视图
Z V s' S a' s"
如图为一正三棱锥,锥 顶为S,其底面为△ABC, 呈水平位置,水平投影 △abc反映实形。
棱面△SAB、 △SBC是 一般位置平面,它们的 各个投影均为类似形。 棱面△SAC为侧垂面, 其侧面投影s”a”c”重影 为一直线。
⑴ 圆柱体的组成 由圆柱面和两个底面组成。 圆柱面是由直线AA1绕与 它平行的轴线OO1旋转而成。 直线AA1称为母线。 圆柱面上与轴线平行的任 一直线称为圆柱面的素线。
O1 A1
(1) 圆柱的投影
(1) 先绘出圆柱的对 称线、回转轴线。 (2)绘出圆柱的顶面 和底面。 (3)画出正面转向轮 廓线和侧面转向轮廓线。
1.4 体的三面投影—三视图 3.基本形体的三视图
结束放映
1.4 三面投影图
正立面图 ——由前向后投影,实体的正面投影
Z
V
平面图 ——由上向下投影, 实体的水平投影
左侧立面图 ——由左向右 投影,实体的侧面投影
W X
O
H
Y
2.投影体系的展开
基本体的三视图

五棱柱旳三视图
9
正五边形作图措施:
10
正五边形作图措施:
11
二、棱锥
S
A
C
B
12
注意:
三棱锥旳三视图
三棱锥左视图不
是一种等腰三角形。
s'
s"
a’ b' c' a"(c") b"
a
c
s
b
13
三、圆柱
转向(侧影)轮廓线旳投影。
转向(侧影) 转向(侧影)
轮廓线
轮廓线
14
孔转向(侧影)轮廓线旳投影
截交线为圆 截交线为矩形 截交线为椭圆 截交线为部分椭
圆
截交线为部分椭 圆
41
[例题一] 求侧平面与圆柱旳截交线
y
截平面平行圆柱轴线 截交线为矩形
42
y
[例题二]圆柱体被切片
y1 y
侧平面R 水平面Q 立体旋装90˚ 怎么体现?
43
y y1
[例题三]圆柱体开槽
y1 y
侧平面R
y y1
水平面Q
44
空心圆柱开圆孔
70
空心圆柱开马蹄槽
空心圆柱开键槽
71
60
[例题一] 完毕正方体与半圆柱相交旳主视图
61
[例题二] 求三棱柱穿孔后旳投影
c' b'
c" b"
a' a"
a c
b
62
[例题三] 完毕两圆柱旳相贯线
清除!
a'
b'
1'
2'
c'Leabharlann a" b" 1"
基本形体投影作图.ppt

(a)空间投影体系中正四棱台的投影
(b)正四棱台的三面投影图
为了作图简便,投影轮廓清晰,而将投影 轴省略不画,但三投影之间仍应符合“长 对正、高平齐、宽相等”的投影关系。
五.常见基本形体投影作图
曲面立体的投影——圆柱体
圆柱投影特点分析(如右图所示): ① 圆柱体的顶面和底面平行于H面,故在H面上的投影为圆,
们在W面上的投影均积聚为一直线,在另外两个面 上的投影均为空间平面形状矩形的类似形。
图2.1.19
五.常见基本形体投影作图
平面立体的投影——棱柱体[例6]
如图2.1.19(b)所示,已知正三棱柱表面上M和N点的H面投影,求V、W面投影。
注:பைடு நூலகம்的可见性判别。
m’ (n)’
(m)” (n)”
具体画法 (点击播放)
称为回转曲面,运动着的直线或曲线称为母线,母线在曲面上任一位置称为素线。由回转曲 面或由回转曲面与平面所围成的立体称为回转体。常见的回转体有圆柱体、圆锥体、球体等。
平面立体
曲面立体
五.常见基本形体投影作图
平面立体的投影
由于平面立体的表面是由若干平面多边形围成,故求作平面立体的投影,就是作出围成该形体的 各个表面或其表面与表面相交棱线或顶点的投影,因而体的投影仍然符合点、线、面的正投影规 律,作图时应注意重影性和可见性。
V面和W面投影都积聚为平行于OX轴和OY轴的直线, 其长度等于底圆的直径; ② 圆锥面为光滑的曲面,其H面投影是一个圆,与底面 圆的投影相重合,其底圆圆心与锥顶的投影S相重合; ③ 作V面投影时,锥面上最左、最右两条素线SA和SB 为正平线,其投影分别为s′a′、s′b′,即圆锥面在V面 上投影的轮廓线,等腰△s′a′b′即为圆锥体在V面上的 投影; ④ 圆锥体在W面上的投影与V面投影相同,但等腰三角 形中s″c″、s″d″分别为圆锥体最前、最后两条素线的 投影。
第三章基本几何体的投影
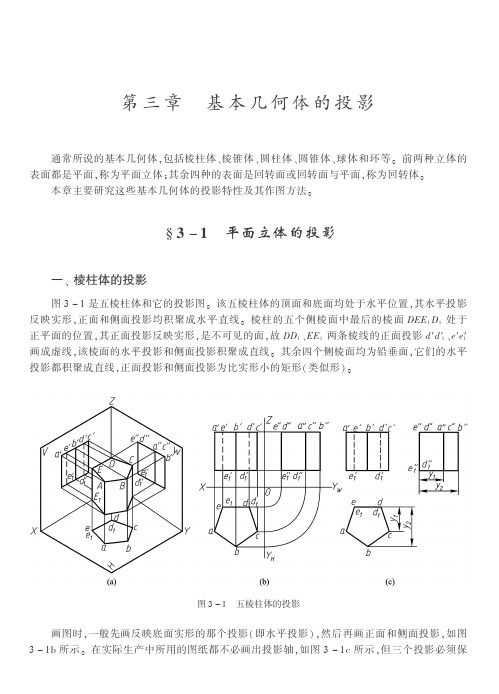
第三章 基本几何体的投影通常所说的基本几何体,包括棱柱体、棱锥体、圆柱体、圆锥体、球体和环等。
前两种立体的表面都是平面,称为平面立体;其余四种的表面是回转面或回转面与平面,称为回转体。
本章主要研究这些基本几何体的投影特性及其作图方法。
§3-1 平面立体的投影一、棱柱体的投影图3-1是五棱柱体和它的投影图。
该五棱柱体的顶面和底面均处于水平位置,其水平投影反映实形,正面和侧面投影均积聚成水平直线。
棱柱的五个侧棱面中最后的棱面DEE1D1处于正平面的位置,其正面投影反映实形,是不可见的面,故DD1、EE1两条棱线的正面投影d′d′1、e′e′1画成虚线,该棱面的水平投影和侧面投影积聚成直线。
其余四个侧棱面均为铅垂面,它们的水平投影都积聚成直线,正面投影和侧面投影为比实形小的矩形(类似形)。
图3-1 五棱柱体的投影画图时,一般先画反映底面实形的那个投影(即水平投影),然后再画正面和侧面投影,如图3-1b所示。
在实际生产中所用的图纸都不必画出投影轴,如图3-1c所示,但三个投影必须保持左右、上下、前后的对应关系,即V 、H 两面投影左右对正,V 、W 两面投影上下平齐,H 、W 两面投影前后相等。
二、棱锥体的投影图3-2是正三棱锥体和它的投影图。
该三棱锥体的底面处于水平位置,其水平面投影反映实形,正面和侧面投影积聚成水平直线。
三棱锥的右侧棱面SBC 为正垂面,其正面投影s ′b ′c ′积聚成直线,水平面投影sbc 和侧面投影s ″b ″c ″为类似形。
前棱面SAB 和后棱面SAC 均为一般位置平面,因而,它们的三面投影均为类似形(正面投影两个三角形重合)。
图3-2 正三棱锥体的投影画图时,先画出底面三角形ABC 和锥顶S 的投影,然后顺次连接各棱线SA 、SB 、SC 的同面投影,如图3-2b所示。
通过棱柱和棱锥体的投影分析,可归纳如下几点:1)由于平面立体的棱线是直线,所以画平面立体的投影图就是先画出各棱线交点的投影,然后顺次连线,并注意区分可见性。
高校高等职业教育《建筑工程制图与识图》教学课件 第3章 基本体的投影

§3.3
3.3.1平面体的截交线
截割体的投影
由于平面体是由平面围成,所以平面体的截交线是封闭的平面折线, 即平面多边形。
求平面立体截交线的步骤:
(1)分析 截交线形状及投影形状; (2)求点 利用截平面的积聚性求棱线与截平面的交点; (3)连线 按一定顺序并根据可见性连线。
§3.3 截割体的投影
圆锥与各种平面立体的相贯线; ➢ 用辅助平面法可求: 圆球与各种平面立体的相贯线。
圆环与各种平面立体的相贯线。
§3.4 相贯体的投影
[例题15] 已知圆柱体与四棱柱相贯的俯视图,补全V、W面投影。
易多线 1’
2’
解题步骤:
1’’(2’’)
3’(5’)
4’(6’)
5’’(6’’)
3’’(4’’)
二、圆锥
投影分析和画法 圆锥的底圆平面为水平面,其
水平投影为圆,且反映实形; 正面投影和侧面投影均积聚为
直线段,长度等于底圆的直径。
投影特点: 一个视图为圆,另两个为三角形。
§3.2
二、圆锥
圆锥表面上取点:
回转体的投影
素线法取点
§3.2
二、圆锥
圆锥表面上取点:
回转体的投影
纬圆法取点
四、圆环
圆环的三视图:
回转体的投影
§3.2
四、圆环
圆环表面取点:
已知圆环面上的 点A、B 的一个 投影,求它们的 另一个投影
回转体的投影
§3.2
四、圆环
回转体的投影
圆环表面取曲线:
已知圆环面上的 曲线AD 水平投 影,求正面投影
§3.1 基本体的投影
[例题3] 补全属于基本回转体表面的点和线段的三面投影。
04基本体的投影

(1)圆柱面的形成 圆柱面由直线AA1绕与其平行的轴线回转而 成。
(2)投影 当圆柱的轴线垂直于H面时,圆柱的顶面、底面是水平 面,所以水平投影反映圆的实形,其正面投影和侧面投影积聚为直 线,直线的长度等于圆的直径;由于圆柱的轴线垂直于水平面,圆柱 面的所有素线都是铅垂线,故其水平投影积聚为圆,与上下底面圆 的投影重合;在圆柱的正面投影中,前后两半圆柱面的投影重合为 一矩形,矩形的左右两边分别是圆柱面最左、最右素线的投影,这
4.2.2.2 圆锥
圆锥(cone)由圆锥面和底面所围成,如图4-11(a)所示。
(1)圆锥面的形成 圆锥面由直线SA绕与它相交的轴线回转而成, 其上所有素线均交于锥顶S点,且面上任一点与顶点的连线均为属 于圆锥表面的直线。
(2)投影 当圆锥的轴线垂直于H面时,底面为水平面,水平投影反 映实形,其正面投影、侧面投影均积聚成直线;圆锥面在水平面上 的投影为圆内区域,与底面的水平投影重影,另两个投影为等腰三 角形,三角形两腰为锥面的转向轮廓线的投影;最左和最右素线
通常把棱柱、棱锥、圆柱、圆锥、圆球、圆环 等简单立体称为基本几何体,简称基本体(elementary soild)。
4.2.1 平面立体及其表面上的点和线
平面立体的表面都是平面,平面由直线围成,所以绘制平面立 体的投影可归结为绘制各种直线、平面及它们之间相对位 置的投影,再判别可见性,将可见轮廓线的投影画成粗实线,不 可见轮廓线的投影画成细虚线,当粗实线和细虚线重合时画 粗实线,当轮廓线与细点画线重合时画轮廓线。
[例4-2] 已知图4-7所示棱锥外表面上K点的正面投影k'(可见),试 作K点的其他投影。
【作图】
方法一:如图4-7(a)所示。
① 过锥顶S点和K点作一辅助线SD,即在视图上作s'k'延长交b'c'于 点d'。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)作基线,确定视图位置 (2)画反映主要形状的视图,俯视图 按长对正的投影关系和五棱柱的高度 画出主视图
(3)按高平齐、宽 相 等的投影关系画出左视图
2-3
一、课堂作业
基本体的投影作图
1、在正三棱柱、正四棱 柱、正六棱柱中,请你选 择一个棱柱画其三视图, 棱柱的长宽高可以自己定。 棱柱的位置是顶面和底面 与水平面平行,后棱面平 行于正面 2、4人一组,选出组长, 画好后组长代表本组展示作 品
一、课堂总结:
通过正五棱柱投影图的学习我们知道了棱柱投影图的画 法,首先分析位置,然后根据俯视图、主视图左视图 投影关系画出投影图
二、作业布置:预习棱锥的投影
图画法
谢 谢!
3、考核标准: 其中选择正三棱柱、六棱柱画加10分 评分标准 1)视图对称中心线,确定视图位置10分 2)画出俯视图30分 3)主视图30分 4)左视图30 5)视图画不完整画错要减分
2-3
正三棱柱投影图
基本体的投影作图
正四棱柱投影图
课堂作业评讲
2-3
正六棱柱投影图
基本体的投影作图
2-3
基本体的投影作图
2-3
基本体的投影作图
基本体
平面体
曲面体
2-3
一、棱柱
三棱柱 四棱柱 五棱柱 六棱柱
基本体的投影作图
2-3 基本体的投影作图
正五棱柱 分析:
1、两端面平行于水平面 2、后棱面平行于正面且所 有棱面垂直于水平面
V
投影特征:顶面和底面 水平投影重合,并反映 实形——正五边形
2-3 基本体的投影作图
