2018-2019学年浙江省宁波市镇海区镇海中学高一上学期期中数学试题(解析版)
2019届浙江省宁波市镇海中学高三上学期期中考试数学试卷及解析

2019届宁波市镇海中学高三上学期期中考试数学试卷注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、单选题1.设全集,集合,则集合A. B.C. D.2.某几何体的三视图如图所示,图中的四边形都是边长为的正方形,两条虚线互相垂直,则该几何体的体积是A. B. C. D.3.记为等差数列的前项和,若, 则A. B. C. D.4.4.满足线性约束条件23,23,{0,x yx yxy+≤+≤≥≥的目标函数z x y=+的最大值是A.1 B.32C.2 D.35.已知函数,则函数的图象为A. B.C. D.6.若、是两个相交平面,则在下列命题中,真命题的序号为①若直线,则在平面内一定不存在与直线平行的直线.②若直线,则在平面内一定存在无数条直线与直线垂直.③若直线,则在平面内不一定存在与直线垂直的直线.④若直线,则在平面内一定存在与直线垂直的直线.A.①③ B.②③ C.②④ D.①④7.已知,那么A. B. C. D.8.已知正项等比数列满足,若存在两项,使得,则的最小值为A. B. C. D.9.已知双曲线的左右焦点分别为,为双曲线上一点,为双曲线渐近线上一点,均位于第一象限,且,,则双曲线的离心率为A. B. C. D.10.如图,在三棱柱中,底面为边长为的正三角形,在底面的射影为中点且到底面的距离为,已知分别是线段与上的动点,记线段中点的轨迹为,则等于(注:表示的测度,本题中若分别为曲线、平面图形、空间几何体,分别对应为其长度、面积、体积)。
2019学年镇海中学高三上期中
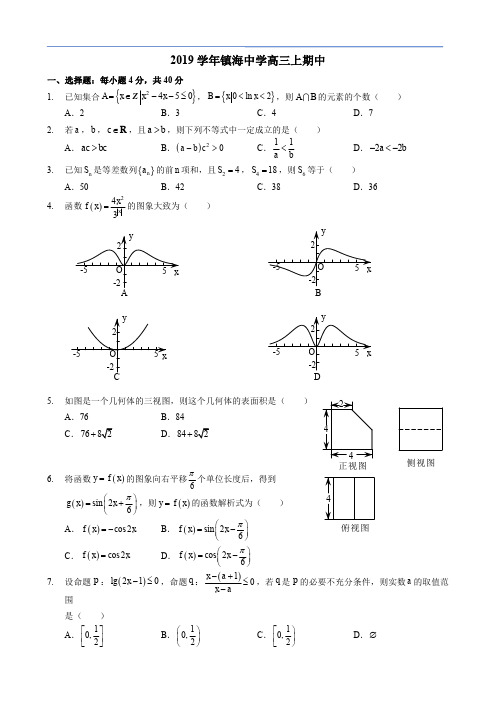
2019学年镇海中学高三上期中一、选择题:每小题4分,共40分1. 已知集合{}2450A x x x =∈--≤Z ,{}0ln 2B x x =<<,则A B 的元素的个数( )A .2B .3C .4D .72. 若a ,b ,c ∈R ,且a b >,则下列不等式中一定成立的是( )A .ac bc >B .()20a b c ->C .11a b<D .22a b -<-3. 已知n S 是等差数列{}n a 的前n 项和,且24S =,418S =,则6S 等于( )A .50B .42C .38D .364. 函数()243xx f x =的图象大致为( )5. 如图是一个几何体的三视图,则这个几何体的表面积是( )A .76B .84C.76+D.84+6. 将函数()y f x =的图象向右平移6π个单位长度后,得到 ()sin 26g x x π⎛⎫=+ ⎪⎝⎭,则()y f x =的函数解析式为( )A .()cos 2f x x =-B .()sin 26f x x π⎛⎫=- ⎪⎝⎭C .()cos 2f x x =D .()cos 26f x x π⎛⎫=- ⎪⎝⎭7. 设命题p :()lg 210x -≤,命题q :()10x a x a-+≤-,若q 是p 的必要不充分条件,则实数a 的取值范围是( )A .10,2⎡⎤⎢⎥⎣⎦B .10,2⎛⎫ ⎪⎝⎭C .10,2⎡⎫⎪⎢⎣⎭D .∅BD俯视图侧视图正视图8. 已知22ππαβ-<-<,sin 2cos 1αβ-=,cos 2sin αβ+=sin 6πβ⎛⎫+= ⎪⎝⎭( )ABC. D. 9. 已知椭圆和双曲线有相同的焦点1F ,2F ,设点P 是该椭圆和双曲线的一个公共点,且123F PF π∠=,若椭圆和双曲线的离心率分别为1e ,2e ,则2212e e +的最小值为( )AB.4+C.2+ D.110. 设a ,b 为正实数,且121322a b a b +++=,则12a b +的最大值与最小值之和为( )A .2B .92C .132D .9二、填空题:单空题每题4分,多空题每题6分11. 抛物线22y x =的焦点坐标为 ,准线方程为 .12. 已知点()1,0A ,()0,2B ,点(),P a b 在线段AB 上,则直线AB 的斜率为 , ⋅a b 的最大值为 .13. 若实数(),x y 满足约束条件20201x y x y y --≤⎧⎪+-≥⎨⎪≤⎩,则2x y -的最小值为 ,的最小值为 .14. 已知长方体1111ABCD A B C D -中,112AA =,1AB =,AD ,则直线1AA 与平面1A BD 所成的角为 ,若空间的一条直线l 与直线1AA 所成的角为4π,则直线l 与平面1A BD 所成的最大角为 .15. 已知{}n a 是等比数列且0n a >,243546225a a a a a a ++=,则4a 的最大值为 . 16. 已知圆O :221x y +=,设点P 是恒过点()0,4的直线l 上任意的一点,若在该圆上存在点A 使得3OPA π∠≤,则直线l 的斜率k 的取值范围为 .17. 已知()11,A x y ,()22,B x y 为单位圆上两点,且满足12OA OB ⋅=,则1122x y x y +++的取值范围为 .三、解答题:5小题,共74分18. 已知()sin cos sin 222x x x f x a ⎛⎫=⋅++ ⎪⎝⎭.(1)求实数a 的值;(2)若44f a f a ππ⎛⎫⎛⎫++-= ⎪ ⎪⎝⎭⎝⎭,求2141tan παα⎛⎫-+ ⎪⎝⎭+的值.19. 在锐角ABC △中,角A ,B ,C 所对的边分别为a ,b ,c .已知3b =,2239a c c =-+.(1)求A ;(2)求22sin sin B C +的取值范围.20. 如图,在三棱锥P ABC -中,PAB △与ABC △都为等腰直角三角形,PA PB ⊥,AB AC ⊥,M 为AC的中点,且PM AC =.(1)求二面角P AB C --的大小;(2)求直线PM 与平面PBC 所成角的正弦值.M PCBA21. 已知数列{}n a 的前n 项和为{}n S ,且满足:12a =,()*132n n a S n +=-+∈N .(1)求数列{}n a 的通项公式;(2)数列{}n b 满足12b =-,()()()2131n n n b b n n n a +-+=+,求数列{}n b 的通项公式.22. 在平面直角坐标系中,已知()2,0F ,()2,P t -,若线段FP 的中垂线l 与抛物线()2:20C y px p =>总是相切.(1)求抛物线C 的方程;(2)若过点()2,1Q 的直线l '交抛物线C 于M 、N 两点,过M ,N 分别作抛物线的切线1l ,2l 相交于点A ,1l ,2l 分别与y 轴交于点B ,C ;(i )证明:当l '变化时,ABC △的外接圆过定点,并求出定点的坐标; (ii )求ABC △的外接圆面积的最小值.。
浙江省宁波市镇海中学2018-2019学年高一上学期期末考试数学试题 Word版含解析

已知点在第二象限,则角【详解】由题意,点在第二象限,对于向量,和实数,则或若,则,则或,则【答案】B;由向量的平方即,即可得到答案.,则或或,则或是正确的;,则,不能得到,所以不正确;,则,不一定得到,可能是已知向量,,若,则实数B. C. D.,即可得出,进行数量积的运算即可得出,在由向量的,所以,整理得,,解得【点睛】本题主要考查了向量的模的运算,以及向量的数量积的坐标运算,其中解答中根据向量的运算,求得推理与运算能力,属于基础题函数的图象关于直线对称,则实数B. C. D.【答案】【详解】由题意,函数又由函数的图象关于对称,所以,解得,故选D.【点睛】本题主要考查了三角函数的辅助角公式的应用,以及三角函数的图象与性质的应用,的图象上各点横坐标伸长到原来的倍,然后将图象向右平移重合,则(B. C. D.【答案】A【详解】由题意,可采用逆向思维,首先对函数向左平移的图象,进一步把图象上所有的点的横坐标缩短为原来的【点睛】本题主要考查了三角函数的图象变换的应用,其中解答中熟记三角函数的图象变换已知函数,,则是(最小正周期为最小正周期为最小正周期为最小正周期为利用三角函数的恒等变换化简函数为【详解】由函数所以函数为偶函数,且最小正周期为,故选B.【点睛】本题主要考查了三角函数的恒等变换以及三角函数的图象与性质,其中解答中熟练若向量,,且B. C. D.由题意,,求得式,化简为齐次式,即可求解【详解】由题意,,所以,解得又由向量,,【点睛】本题主要考查了平面向量的数量积的运算性质,以及利用三角函数的基本关系式化已知,是方程的两个实数根,则B. C. D.,是方程,是方程的两个实数根,,【点睛】本题主要考查了一元二次方程的根和系数的应用,以及三角函数关系式的恒等变换的应用,其中解答中熟记两角和的正切函数的公式,合理、准确运算是解答的关键,着重考已知单位向量的夹角为,若向量满足,则B. C. D.【答案】A,由,化简得,表示圆心为的最大值【详解】由题意,设单位向量,且,,所以,化简得,表示圆心为由图形可知,的最大值为,故选A.【点睛】本题主要考查了平面向量的模的计算,以及向量的坐标运算表示的图形,结合图象求解是解答的关键,着重考查了数形结合思想,以及推理与计算能力,属于基础题①函数的对称中心是②若函数(,对于任意都有;③函数在上的函数()时,成立.则其中正确的叙述有(个 B. C. 个 D.的导数判断单调性,结【详解】由题意,①中,函数的对称中心是,所以不正确;若函数对于任意都有可得函数关于对称,则③中,函数的导数为,可得函数在在有且只有一个零点,所以是正确的;④中,已知定义在上的函数时,即时,;时,即时,和,时,即当时,成立,所以是正确的,故选【点睛】本题主要考查了三角函数的图象与性质,以及函数与方程的应用,其中解答中熟记的值为(2)..【点睛】本题主要考查了三角函数的化简求值问题,其中解答中熟记三角函数的诱导公式和已知扇形的周长为,当它的半径为(2).设扇形的半径与中心角分别为,可得,在利用扇形的面积为,利用基本不等【详解】设扇形的半径与中心角分别为,则,可得,可得扇形的面积为当且仅当是取等号.【点睛】本题主要考查了扇形的弧长和面积公式,以及基本不等式的性质的应用,其中解答已知,,若,则实数的值是;若与的夹角为锐角,则实数或 (2).,得到方程即可解答得值,和,不同向,列出不等式,即可求解,所以,解得或,和的夹角为锐角,所以,且,所以且的取值范围为且【点睛】本题主要考查了向量的共线的应用,以及向量的数量积的应用问题,其中解答中熟,是单位向量,且,的夹角为,若,;在(2).与的模【详解】由平面向量的数量积的定义,可得,,即,所以在方向上的投影为.【点睛】本题主要考查了平面向量的数量积的定义,以及向量的投影的应用,其中解答中熟记平面向量的数量积的计算公式,以及向量的投影的计算是解答本题的关键,着重考查了推已知的终边上的一点,且,则实数的值为【答案】由三角函数的定义,即可求解,解得,所以.若函数则实数【答案】或由题意,,,把原函数转化为两个不同的零点,进而转化为方程在上有唯一的实根或在上有两相等的实根,利用二次函数的性质,即可求解.令,,则原函数转化为有两个不同的零点,在在(0,1)转化为函数,与函数有唯一交点或所以或【点睛】本题主要考查了函数与方程的综合应用,其中解答中根据题意令有两个不同的零点,进而转化为方程在根或在(0,1)上有两相等的实根,利用二次函数的性质求解是解答的关键,着重考查了转化思已知的外心,,若(的取值范围是【答案】,建立平面直角坐标系,利用向量的坐标运算,得到法二,由奔弛定理和向量的运算,得,进而得,利用三角函【详解】法一:设圆的半径为,如图所示建立平面直角坐标系,则,法二,由奔弛定理由已知转化为:,所以变形为,.【点睛】与性质的应用,其中解答中熟记向量的坐标运算,把已知,(Ⅰ)求的夹角(Ⅱ)当为何值时,与())由向量的数量积的运算,列出方程,求得,即可求解结果)由,利用向量的数量积的运算,即可求解【详解】(1)由题意,根据向量的运算,得解得:(2),..时,与垂直【点睛】本题主要考查了向量的数量积的化简、运算,其中解答中熟记平面向量的数量积的已知函数.(Ⅰ)求函数的最小正周期;在)函数的最小正周期是)利用三角函数恒等变换的公式,化简)由,根据三角函数的性质,得到)由题意,函数,即函数的最小正周期是.(2),,所以函数在的单调递增区间是【点睛】本题主要考查了三角恒等变换,以及三角函数的图象与性质的应用,其中解答中利的解析式,,且,(Ⅰ)求的值;(Ⅱ)求())法一:根据两角和的正切函数的公式,化简得法二:令,求得)由三角函数的基本关系式,求得的值,进而可求解.)法一:,法二:令,则,(2),,,,,.【点睛】本题主要考查了三角恒等变换,及三角函数基本关系式和诱导公式的化简求值,其已知的夹角为,且满足.(Ⅰ)求所有满足条件的所组成的集合;,,对于集合中的任意一个,在集合中总存在着一个,使得成立,求实数的取值范围())由向量的数量积的公式,求得,进而根据题设条件,得到)根据三角恒等变换的公式,化简,令,利用二次函数的性质,即可求解.【详解】(1)由题意,,;,得,故所求集合)由题意,根据三角恒等变换的公式,得;令,,由题意,得,.【点睛】本题主要考查了向量的数量积的运算,以及三角函数的图象与性质的应用,其中解已知实数,,,若向量满足. (Ⅰ)若;(Ⅱ)若)求实数的取值范围;)若恒成立,求的取值范围或(2)(Ⅰ)设,即可得到向量的坐标;(Ⅱ)(1,又由函数也是增函数,得到,即可求解得取值范围;)由对恒成立,进而转化为,由,,所以,即,,又,所以,故或(Ⅱ)(1)根据向量的模的公式,化简得在上为增函数,即,;,对对恒成立,解得.。
【数学】浙江省镇海中学2018-2019学年高三上学期期中考试数学试卷(精校版)

镇海中学2018学年第一学期期中考试高三年级数学试卷一、选择题:(本大题共10个小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.设全集U R =,集合{}{}|,|053A x x B x x ==≤<≥,则集合()U C A B ( )A .{}|03x x ≤≤B .{}|03x x <<C .{}|03x x <≤D .{}|03x x ≤<2.某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,两条虚线互相垂直,则该几何体的体积是( )A .83π-B .163C .86π-D .2033.记n S 为等差数列{}n a 的前n 项和,若93845,12S a a =+=,则7a 等于( )A .10B .9C .8D .74.满足线性约束条件23230,0x y x y x y +≤⎧⎪+≤⎨⎪≥≥⎩的目标函数z x y =+的最大值是( )A . 1B .32C .2D .35.已知函数()2||In x f x x x=-,则函数()f x 的图象为( )A .B .C .D .6.若,αβ是两个相交的平面,则下列命题中,真命题的序号为( ) ①若直线m α⊥,则在平面β内,一定不存在与直线m 平行的直线 ②若直线m α⊥,则在平面β内,一定存在无数条直线与直线m 垂直 ③若直线m α⊆,则在平面β内,不一定存在与直线m 垂直的直线 ④若直线m α⊆,则在平面β内,一定存在与直线m 垂直的直线A .①③B .②③C .②④D .①④7.已知sin 63πα⎛⎫-=-⎪⎝⎭,那么cos22αα=( ) A .109B .109-C .59-D .598.已知正项等比数列{}n a 满足7652a a a =+,若存在两项,m n a a ,使得2116m n a a a ⋅=,则19m n+的最小值为( )A .32B .114C .83D .1039.已知双曲线()2222:10,0x y C a b a b-=>>的左右交点分别为12,F F ,P 为双曲线C 上一点,Q 为双曲线渐近线C 上一点,,P Q 均位于第一象限,且2122,0QP PF QF QF →→→→=⋅=,则双曲线C 的离心率为( )A 1B 1C 2D 210.如图,在三棱柱111ABC A B C -中,底面为边长为2的正三角形,1B 在底面的射影为AC 中点且1B 到,E F 分别是线段1AB 与1CA 上的动点,记线段EF 中点M 的轨迹为L ,则L 等于( )(注:L 表示L 的测度,本题中L 若分别为曲线、平面图形、空间几何体,分别对应为其长度、A .1BCD二、填空题:(本大题共7个小题,多空题每题6分,单空题每小题4分,共36分.)11.中国古代数学著作《九章算术》中有一个这样的问题:“某贾人擅营,月入益功疾(注:从第2月开始,每月比前一月多入相同量的铜钱,3月入25贯,全年(按12个月计)共入510贯“,则该人每月比前一月多入_________________贯,第12月营收贯数为_________________. 12.sin 26y x π⎛⎫=+⎪⎝⎭的最小正周期为_________________,为了得到函数sin 26y x π⎛⎫=+⎪⎝⎭的图象,可以将函数cos 2y x =的图象向左最小移动_________________个单位13.已知直线()12:210,:20l ax a y l x ay +++=++=,其中a R ∈,若12l l ⊥,则a =_________________,若12//l l ,则a =_________________.14.已知,x y R ∈,且2241x y xy ++=,则224x y +的最小值_________________,此时x 的值为_________________.15.已知两个不共线的非零向量,a b →→,满足2,1a a b →→→=-=,则向量,a b →→夹角的最大值是_________________.16.已知数列{}n a 为等差数列,其前n 项和为n S ,且13623a a S +=,给出以下结论:①100a =②10S 最小③712S S =④190S =,正确的有_________________.17.设函数()()2|124|1,12,1x x f x x x a x -+≤⎧⎪=⎨-+>⎪⎩,若存在互不相等的4个实数1234,,,x x x x,使得()()()()123412347f x f x f x f x x x x x ====,则a 的取值范围为_________________. 三、解答题:(本大题共个5小题,共74分.解答应写出文字说明、证明过程或演算步骤)18.(本小题满分14分)已知函数()2sin cos 333x x x f x =+ (1)求函数()f x 图象对称中心的坐标;(2)如果ABC ∆的三边,,a b c 满足2b ac =,且边b 所对的角为B ,求()f B 的取值范围.19.(本小题满分15分)已知数列{}n a 的前n 项和为n S ,且32,2n n n S a n N *=-∈,12n n nb a =- (1)求证:数列{}n b 为等比数列,并求出数列{}n a 的通项公式;(2)是否存在实数λ,对任意,m n N *∈,不等式m nS b λ>恒成立?若存在,求出λ的取值范围,若不存在请说明理由.-的底面ABCD为平行四边形,平面PAB⊥平面ABCD,20.(本小题满分15分)如图,四棱锥P ABCDPB PC ABC︒=∠=,点E是线段PA上靠近点A的三等分点,45⊥(1)求证:AB PC∆是边长为2的等边三角形,求直线DE与平面PBC所成角的正弦值(2)若PAB21.(本小题满分15分)如图,O 为坐标原点,点F 为抛物线()21:20C x py p =>的焦点,且抛物线1C 上点P 处的切线与圆222:1C x y +=相切于点Q(1)当直线PQ的方程为0x y -=时,求抛物线1C 的方程; (2)当正数p 变化时,记12,S S 分别为,FPQ FOQ ∆∆的面积,求12S S 的最小值22.(本小题满分15分)已知a R ∈,函数()1x f x e ax -=-在点()1,1a -处与x 轴相切 (1)求a 的值,并求()f x 的单调区间(2)当1x >时,()()1f x m x Inx >-,求实数m 的取值范围参考答案:1——5DDBCD 6——10CABCD11.5;70 12.56ππ; 13.0或3-;2或-1 14.45±; 15.030 16.①③④ 17.(6,18)18.(1)2()sin()33f x x π=++,对称中心3(,0),22k k Z ππ-+∈(2)()f B ∈+⎦19.(1)证明略;1122n n na -=+(2)92λ<20.(1)略 (2)sin θ=21.(1)21:C x =(2)解析如下:2001110111200022111111001200011221121121(,),(,)20100:1:02-1==-=-=-222=-11=-2Q P P Q x P x Q x y px x y Q l x x y y x x P l x y p p l l x p px px px y y x x x x x x x x p px x y p y x x <<⎧>⎨<⎩+=--=⎧⎪⎪⎧⎪⎪∴⇒⎨⎨⎪⎪-=⎩⎪⎪⎩⎧+=⎪⎨⎪⎩∴设根据对称性:仅取和研究过处切线方程过处切线方程与重合221)p=10101111112111122)()1222()()PQ x x x x x x x x y x px x ==-=-=-=-=-=-F 到PQ l距离为:221141p x d +==2211121121221122211112222111221121122421112211224222211112122()(1)2412212()(1)442(1)(1)441=-2141,(1)4421421(1)(1)4(1p S x x px x p S x p x x S px x p x p S p x x x x y p y x p x x x x p S S p x x p x x p =⨯-⨯+=⨯⨯-⨯+∴==-⨯+⨯⎧+=⎪⎨⎪⎩∴+==-∴=-⨯=-⨯-221121(1)1)x x =-⨯-将21221)x p=带入上式:122222222212221(1)221)11)1)1,1(1)21331111,S S p p t p t S t t t t t S t t t t p 令当且仅当:=-⨯-=-⨯==>=-++===-++≥---==22.(1)解析过程略()()11,,1a =+∞-∞增区间:减区间:(2)12m ≤解析如下:11''1''''''12''11(1)ln ()(1)ln ,1(1)0()0,(1)01()1ln ,1(1)0(1)0,(1)0(),11(1)120,212()(1)ln x x x x x x e x m x xh x e x m x x x h h x h x h x e m x m x x h h h m mh x e x x x h m m m h x e x m x x ----->->-=--->=>≥-=--->=>≥=-->∴=-≥∴≤≤=---时,令由于欲使需要欲使需要接下来证明:'1''12'''123,11()1ln ,1(),12(),1x x x x x h x e m x m x x m mh x e x x x m mh x e x x x --->-=--->=-->=++>①当102m <≤时'''123''1''2'1'12()0()(1)1201()1ln (1)0()(1)ln (1)0102x x x x mm h x e x x m mh x e h m x x x h x e m x m h x h x e x m x x h m ----=++>∴=-->=-≥-∴=--->=∴=--->=∴<≤成立②当0m ≤时1()0,(1)ln 0()(1)ln ,112x f x e x m x x f x m x x x m -=->-≤∴>->≤综上:备注:此题考查的是导数的端点效应。
2018-2019学年浙江省宁波市镇海中学高三(上)期中数学试卷

2018-2019学年浙江省宁波市镇海中学高三(上)期中数学试卷试题数:22.满分:1501.(单选题.5分)设全集U=R.集合A={x|x≥3}.B={x|0≤x <5}.则集合(∁U A )∩B=( )A.{x|0<x <3}B.{x|0≤x <3}C.{x|0<x≤3}D.{x|0≤x≤3}2.(单选题.5分)某几何体的三视图如图所示(单位:cm ).图中的四边形都是边长为2的正方形.两条虚线互相垂直.则该几何体的体积(单位:cm 3)是( )A. 163B. 203C. 8−π6D. 8−π3 3.(单选题.5分)记S n 为等差数列{a n }的前n 项和.若S 9=45.a 3+a 8=12.则a 7等于( )A.10B.9C.8D.74.(单选题.5分)满足线性约束条件 {2x +y ≤3x +2y ≤3x ≥0y ≥0.的目标函数z=x+y 的最大值是( )A.1B. 32C.2D.3.则函数y=f(x)的大致图象为()5.(单选题.5分)已知函数f(x)=x2−ln|x|xA.B.C.D.6.(单选题.5分)若α.β是两个相交的平面.则下列命题中.真命题的序号为()① 若直线m⊥α.则在平面β内.一定不存在与直线m平行的直线② 若直线m⊥α.则在平面β内.一定存在无数条直线与直线m垂直③ 若直线m⊆α.则在平面β内.不一定存在与直线m垂直的直线④ 若直线m⊆α.则在平面β内.一定存在与直线m垂直的直线A. ① ③B. ② ③C. ② ④D. ① ④7.(单选题.5分)已知 sin (π6−α)=−√23 .那么 cos2α+√3sin2α =( ) A. 109B. −109C. −59D. 598.(单选题.5分)已知正项等比数列{a n }满足:a 7=a 6+2a 5.若存在两项a m 、a n .使得a m a n =16a 12.则 1m + 9n 的最小值为( )A. 32B. 83C. 114D.不存在9.(单选题.5分)已知双曲线C : x 2a 2 - y 2b 2 =1(a >0.b >0)的左右焦点分别为F 1.F 2.P 为双曲线C 上一点.Q 为双曲线C 渐近线上一点.P.Q 均位于第一象限.且2 QP ⃗⃗⃗⃗⃗ = PF 2⃗⃗⃗⃗⃗⃗⃗ . QF 1⃗⃗⃗⃗⃗⃗⃗ •QF 2⃗⃗⃗⃗⃗⃗⃗ =0.则双曲线C 的离心率为( )A. √3 -1B. √3+1C. √13 -2D. √13 +210.(单选题.5分)如图.在三棱柱ABC-A 1B 1C 1中.底面为边长为2的正三角形.B 1在底面的射影为AC 中点且B 1到底面的距离为 √3 .已知E.F 分别是线段AB 1与CA 1上的动点.记线段EF 中点M 的轨迹为L.则|L|等于( )(注:|L|表示L 的测度.本题中L 若分别为曲线、平面图形、空间几何体.分别对应为其长度、面积、体积)A.1B. √102C. √32D. √39411.(填空题.4分)中国古代数学著作《九章算术》中有一个这样的问题:“某贾人擅营.月入益功疾(注:从第2月开始.每月比前一月多入相同量的铜钱.3月入25贯.全年(按12个月计)共入510贯“.则该人每月比前一月多入___ 贯.第12月营收贯数为___ .12.(填空题.4分)y=sin(2x+ π6)的最小正周期为___ .为了得到函数y=sin(2x+ π6)的图象.可以将函数y=cos2x的图象向左最小移动___ 个单位.13.(填空题.4分)已知直线l1:ax+(a+2)y+1=0.l2:x+ay+2=0.其中a∈R.若l1⊥l2.则a=___ .若l1 || l2.则a=___ .14.(填空题.4分)已知x.y∈R.且4x2+y2+xy=1.则4x2+y2的最小值___ .此时x的值为___ .15.(填空题.4分)已知两非零向量a,b⃗满足|a|=2 . |a−b⃗|=1 .则向量a,b⃗夹角的最大值是___ .16.(填空题.4分)已知数列{a n}为等差数列.其前n项和为S n.且2a1+3a3=S6.给出以下结论:① a10=0 ② S10最小③ S7=S12④ S19=0.正确的有___ .17.(填空题.4分)设函数f(x)={|12x−4|+1,x≤1x(x−2)2+a,x>1.若存在互不相等的4个实数x1.x2.x3.x4.使得f(x1)x1=f(x2)x2=f(x3)x3=f(x4)x4=7 .则a的取值范围为___ .18.(问答题.12分)已知函数f(x)=sin x3cos x3+√3cos2x3.(1)求函数f(x)图象对称中心的坐标;(2)如果△ABC的三边a.b.c满足b2=ac.且边b所对的角为B.求f(B)的取值范围.19.(问答题.15分)已知数列{a n}的前n项和为S n.且S n=2a n−32n ,n∈N∗ . b n=a n−12n(1)求证:数列{b n}为等比数列.并求出数列{a n}的通项公式;(2)是否存在实数λ.对任意m.n∈N*.不等式S m>λb n恒成立?若存在.求出λ的取值范围.若不存在请说明理由.20.(问答题.15分)如图.四棱锥P-ABCD的底面ABCD为平行四边形.平面PAB⊥平面ABCD.PB=PC.∠ABC=45°.点E是线段PA上靠近点A的三等分点.(Ⅰ)求证:AB⊥PC;(Ⅱ)若△PAB是边长为2的等边三角形.求直线DE与平面PBC所成角的正弦值.21.(问答题.15分)如图.O为坐标原点.点F为抛物线C1:x2=2py(p>0)的焦点.且抛物线C1上点P处的切线与圆C2:x2+y2=1相切于点Q.(Ⅰ)当直线PQ的方程为x-y- √2 =0时.求抛物线C1的方程;(Ⅱ)当正数p变化时.记S1.S2分别为△FPQ.△FOQ的面积.求S1S2的最小值.22.(问答题.15分)已知a∈R.函数f(x)=e x-1-ax在点(1.1-a)处与x轴相切.(1)求a的值.并求f(x)的单调区间;(2)当x>1时.f(x)>m(x-1)lnx.求实数m的取值范围.2018-2019学年浙江省宁波市镇海中学高三(上)期中数学试卷参考答案与试题解析试题数:22.满分:1501.(单选题.5分)设全集U=R.集合A={x|x≥3}.B={x|0≤x<5}.则集合(∁U A)∩B=()A.{x|0<x<3}B.{x|0≤x<3}C.{x|0<x≤3}D.{x|0≤x≤3}【正确答案】:B【解析】:先根据补集的定义求出集合A的补集∁U A.然后和集合B进行交集运算.可求(∁U A)∩B.【解答】:解:因为A={x|x≥3}.所以∁U A={x|x<3}.所以(∁U A)∩B={x|0≤x<3}.故选:B.【点评】:本题的考点是集合的补集和交集运算.比较基础.2.(单选题.5分)某几何体的三视图如图所示(单位:cm).图中的四边形都是边长为2的正方形.两条虚线互相垂直.则该几何体的体积(单位:cm3)是()A. 163B. 203C. 8−π6D. 8−π3【正确答案】:B【解析】:由三视图知原几何体是一个棱长为2的正方体挖去一四棱锥得到的.根据所提供的数据可求出正方体、锥体的体积.从而得到答案.【解答】:解:由三视图知原几何体是一个棱长为2的正方体挖去一四棱锥得到的.该四棱锥的底为正方体的上底.高为1.如图所示:所以该几何体的体积为23- 13 ×22×1= 203.故选:B.【点评】:本题考查三视图.考查柱体、锥体的体积计算.解决该类问题的关键是由三视图还原得到原几何体.画三视图的要求为:“长对正.高平齐.宽相等”.3.(单选题.5分)记S n为等差数列{a n}的前n项和.若S9=45.a3+a8=12.则a7等于()A.10B.9C.8D.7【正确答案】:B【解析】:利用等差数列的通项公式与求和公式即可得出.【解答】:解:设等差数列{a n}的公差为d.∵S9=45.a3+a8=12.∴9a1+ 9×82d=45.2a1+9d=12.联立解得a1=-3.d=2.则a7=-3+6×2=9.故选:B.【点评】:本题考查了等差数列的通项公式与求和公式.考查了推理能力与计算能力.属于中档题.4.(单选题.5分)满足线性约束条件 {2x +y ≤3x +2y ≤3x ≥0y ≥0.的目标函数z=x+y 的最大值是( )A.1B. 32C.2D.3【正确答案】:C 【解析】:先根据约束条件画出可行域.再利用几何意义求最值.只需求出直线z=x+y 过点B (1.1)时.z 最大值即可.【解答】:解:先根据约束条件画出可行域.当直线z=x+y 过点B (1.1)时.z 最大值为2.故选:C .【点评】:本题主要考查了简单的线性规划.以及利用几何意义求最值.属于基础题.5.(单选题.5分)已知函数 f (x )=x 2−ln|x|x .则函数y=f (x )的大致图象为( )A.B.C.D.【正确答案】:A【解析】:可得函数为奇函数.排除选项.利用特殊点的位置判断选项即可.【解答】:解:由题意可得函数的定义域为(-∞.0)∪(0.+∞).函数f(x)=x2−ln|x|x.可得f(-x)≠±f(x).故函数为非奇非偶函数.排除:B、C;当x=- 1e 时.y= 1e2+lne−11e= 1e2−e<0.排除D;综上可得选项A符合题意.故选:A.【点评】:本题考查函数的性质.由函数的性质入手是解决问题的关键.属中档题.6.(单选题.5分)若α.β是两个相交的平面.则下列命题中.真命题的序号为()① 若直线m⊥α.则在平面β内.一定不存在与直线m平行的直线② 若直线m⊥α.则在平面β内.一定存在无数条直线与直线m垂直③ 若直线m⊆α.则在平面β内.不一定存在与直线m垂直的直线④ 若直线m⊆α.则在平面β内.一定存在与直线m垂直的直线A. ① ③B. ② ③C. ② ④D. ① ④【正确答案】:C【解析】:若直线m⊥α.则在平面β内.一定存在无数条直线与直线m垂直;若直线m⊆α.则在平面β内.一定存在与直线m垂直的直线.【解答】:解:由α.β是两个相交的平面.知:在① 中.若直线m⊥α.则在平面β内.存在与直线m平行的直线.故① 错误;在② 中.若直线m⊥α.则在平面β内.一定存在无数条直线与直线m垂直.故② 正确;在③ 中.若直线m⊆α.则在平面β内.一定存在与直线m垂直的直线.故③ 错误;在④ 中.若直线m⊆α.则在平面β内.一定存在与直线m垂直的直线.故④ 正确.故选:C.【点评】:本题考查命题真假的判断.考查空间中线线、线面、面面间的位置关系等基础知识.考查运算求解能力.是中档题.7.(单选题.5分)已知sin(π6−α)=−√23.那么cos2α+√3sin2α =()A. 109B. −109C. −59D. 59【正确答案】:A【解析】:由题意利用辅助角公式、诱导公式.二倍角公式.求得cos2α+√3sin2α的值.【解答】:解:∵已知sin(π6−α)=−√23.∴ cos2α+√3sin2α =2sin(2α+ π6)=2cos(π3-2α)=2[1-2 sin2(π6−α) ]=2(1-2× 29)= 109.故选:A.【点评】:本题主要考查辅助角公式、诱导公式.二倍角公式的应用.属于基础题.8.(单选题.5分)已知正项等比数列{a n}满足:a7=a6+2a5.若存在两项a m、a n.使得a m a n=16a12.则1m + 9n的最小值为()A. 32 B. 83 C. 114 D.不存在 【正确答案】:C【解析】:设{a n }的公比为q (q >0).由等比数列的通项公式化简a 7=a 6+2a 5.求出q.代入a m a n =16a 12化简得m.n 的关系式.由“1”的代换和基本不等式求出式子的范围.验证等号成立的条件.由m 、n 的值求出式子的最小值.【解答】:解:设正项等比数列{a n }的公比为q.且q >0. 由a 7=a 6+2a 5得:a 6q=a 6+2a 6q. 化简得.q 2-q-2=0.解得q=2或q=-1(舍去). 因为a m a n =16a 12.所以 (a 1q m−1) (a 1q n−1) =16a 12. 则q m+n-2=16.解得m+n=6.所以 1m +9n = 16 (m+n )( 1m +9n )= 16 (10+ nm +9m n )≥ 16(10+2√nm•9m n ) = 83. 当且仅当 nm=9mn时取等号.此时 {nm =9m nm +n =6.解得 {m =32n =92 . 因为m n 取整数.所以均值不等式等号条件取不到.则 1m +9n > 83 . 验证可得.当m=2、n=4时. 1m +9n 取最小值为 114 . 故选:C .【点评】:本题考查等比数列的通项公式.利用“1”的代换和基本不等式求最值问题.考查化简、计算能力.注意等号的成立的条件.属于易错题. 9.(单选题.5分)已知双曲线C : x 2a 2 - y 2b 2 =1(a >0.b >0)的左右焦点分别为F 1.F 2.P 为双曲线C 上一点.Q 为双曲线C 渐近线上一点.P.Q 均位于第一象限.且2 QP ⃗⃗⃗⃗⃗ = PF 2⃗⃗⃗⃗⃗⃗⃗ . QF 1⃗⃗⃗⃗⃗⃗⃗ •QF 2⃗⃗⃗⃗⃗⃗⃗ =0.则双曲线C 的离心率为( ) A. √3 -1 B. √3+1 C. √13 -2 D. √13 +2【正确答案】:C【解析】:设Q (m. bam ).(m >0).P (s.t ).F 1(c.0).F 2(c.0).由向量共线的坐标表示.以及点满足双曲线方程.向量垂直的条件:数量积为0.可得a.b.c 的关系.再由离心率公式.计算可得所求值.【解答】:解:设Q (m. ba m ).(m >0).P (s.t ).F 1(-c.0).F 2(c.0).QP ⃗⃗⃗⃗⃗ = 12 PF 2⃗⃗⃗⃗⃗⃗⃗ .可得 m+12c 1+12=s. bma1+12=t. 由P 在双曲线上.可得 (m+12c)294a 2 -b 2m 294a 2b 2=1.化为c 2+4mc=9a 2. m=9a 2−c 24c. 由 QF 1⃗⃗⃗⃗⃗⃗⃗ •QF 2⃗⃗⃗⃗⃗⃗⃗ =0.可得 bma m−c • bm am+c =-1. 即c 2-m 2=b 2m 2a 2. 即c 2=m 2•a 2+b 2a 2=m 2• c 2a 2 . 可得m=a. 则4ca=9a 2-c 2.由e= ca 可得e 2+4e-9=0. 可得e=-2+ √13 (负的舍去). 故选:C .【点评】:本题考查双曲线的方程和性质.主要是渐近线和离心率的求法.考查向量共线和垂直的条件.考查运算化简能力.属于中档题.10.(单选题.5分)如图.在三棱柱ABC-A 1B 1C 1中.底面为边长为2的正三角形.B 1在底面的射影为AC 中点且B 1到底面的距离为 √3 .已知E.F 分别是线段AB 1与CA 1上的动点.记线段EF 中点M 的轨迹为L.则|L|等于( )(注:|L|表示L 的测度.本题中L 若分别为曲线、平面图形、空间几何体.分别对应为其长度、面积、体积)A.1B.√102C. √32 D.√394【正确答案】:D【解析】:取特殊点得到M 的轨迹为平行四边形区域.建立空间直角坐标系.再由三角形面积求解.【解答】:解:当E 位于B 1.A.而F 在A 1C 上移动时.M 的轨迹为平行于A 1C 的两条线段. 当F 位于A 1.C.而E 在AB 1上移动时.M 的轨迹为平行于AB 1的两条线段. 其它情况下.M 的轨迹构成图中平行四边形内部区域.以O 为坐标原点.分别以OC.OB 1所在直线为x.z 轴建立空间直角坐标系. 则A (-1.0.0).B 1(0.0. √3 ).C (1.0.0).A 1 (-1. √3 . √3 ). ∴ AB 1⃗⃗⃗⃗⃗⃗⃗ =(1,0,√3) . CA 1⃗⃗⃗⃗⃗⃗⃗ =(−2,√3,√3) . 则 |AB 1⃗⃗⃗⃗⃗⃗⃗ |=2 . |CA 1⃗⃗⃗⃗⃗⃗⃗ |=√10 .cos <AB 1⃗⃗⃗⃗⃗⃗⃗ ,CA 1⃗⃗⃗⃗⃗⃗⃗ > = AB 1⃗⃗⃗⃗⃗⃗⃗⃗ •CA 1⃗⃗⃗⃗⃗⃗⃗⃗|AB 1⃗⃗⃗⃗⃗⃗⃗⃗ |•|CA 1⃗⃗⃗⃗⃗⃗⃗⃗ | = √1020 .则异面直线AB 1与CA 1所成角的正弦值为sinθ= √1−(√1020)2=√39020. ∴|L|=2× 12 × |12AB 1⃗⃗⃗⃗⃗⃗⃗ | × |12CA 1⃗⃗⃗⃗⃗⃗⃗ | = 1×√102×√39020=√394. 故选:D .【点评】:本题考查棱柱的结构特征.考查空间想象能力和思维能力.利用特殊点得到M的轨迹是解答该题的关键.是中档题.11.(填空题.4分)中国古代数学著作《九章算术》中有一个这样的问题:“某贾人擅营.月入益功疾(注:从第2月开始.每月比前一月多入相同量的铜钱.3月入25贯.全年(按12个月计)共入510贯“.则该人每月比前一月多入___ 贯.第12月营收贯数为___ .【正确答案】:[1]5; [2]70【解析】:由题意可知.每个月的收入构成等差数列{a n}.由已知列式求得首项与公差.再由等差数列的通项公式求得a12.【解答】:解:由题意可知.每个月的收入构成等差数列{a n}.设公差为d.则a3=25.S12=510.∴a1+2d=25.12a1+ 12×112d=510.解得a1=15.d=5.∴a12=15+11×5=70.∴该人每月比前一月多入5贯.第12月营收贯数为70.故答案为:5;70.【点评】:本题考查了等差数列的通项公式与求和公式.考查了推理能力与计算能力.是基础题.12.(填空题.4分)y=sin(2x+ π6)的最小正周期为___ .为了得到函数y=sin(2x+ π6)的图象.可以将函数y=cos2x的图象向左最小移动___ 个单位.【正确答案】:[1]π; [2] 56π【解析】:根据正弦图象性质即可求出最小正周期.结合三角函数平移变换规律即可得到结论【解答】:解:函数y=sin(2x+π6)的最小正周期T= 2π2=π;将函数y=cos2x=sin(2x+ π2)的图象向左平移φ个单位(φ>0).可得:y=sin(2x+2φ+π2);∴2φ+ π2 = π6+2kπ.则φ=k π−π6.φ>0∴k=1时.可得φ= 5π6故答案为:π;5π6.【点评】:本题主要考查三角函数性质和平移变换的规律应用.属于基础题.13.(填空题.4分)已知直线l1:ax+(a+2)y+1=0.l2:x+ay+2=0.其中a∈R.若l1⊥l2.则a=___ .若l1 || l2.则a=___ .【正确答案】:[1]0或-3; [2]-1或2【解析】:利用直线与直线垂直、直线与直线平行的性质直接求解.【解答】:解:∵直线l1:ax+(a+2)y+1=0.l2:x+ay+2=0.其中a∈R.l1⊥l2.∴a×1+(a+2)a=0.解得a=0或a=-3;当l1 || l2时. a1=a+2a≠12.解得a=-1或a=2.故答案为:0或-3.-1或2.【点评】:本题考查实数值的求法.考查直线与直线垂直、直线与直线平行的性质等基础知识.考查运算求解能力.考查函数与方程思想.是基础题.14.(填空题.4分)已知x.y∈R.且4x2+y2+xy=1.则4x2+y2的最小值___ .此时x的值为___ .【正确答案】:[1] 45 ; [2] ±√1010【解析】:由重要不等式4x2+y2≥4xy.解不等式可得4x2+y2的最小值和x的值.【解答】:解:由4x2+y2≥4xy.即有xy≤ 4x 2+y2 4.由4x2+y2+xy=1.可得1≤4x2+y2+ 4x2+y24.可得4x2+y2≥ 45.当且仅当2x=y即x=± √1010时.取得等号.则4x2+y2的最小值为45.故答案为:45 .± √1010.【点评】:本题考查基本不等式的运用:求最值.考查不等式的解法和运算能力.属于基础题.15.(填空题.4分)已知两非零向量a,b⃗满足|a|=2 . |a−b⃗|=1 .则向量a,b⃗夹角的最大值是___ .【正确答案】:[1] π6【解析】:设向量a,b⃗夹角为θ.由余弦定理求得cosθ= 3+x24x.再利用基本不等式求得cosθ取得最小值.即可求得θ的最大值.【解答】:解:∵两非零向量a,b⃗满足|a|=2 . |a−b⃗|=1 .设向量a,b⃗夹角为θ.由于非零向量a,b⃗以及a−b⃗构成一个三角形.设| b⃗ |=x.则由余弦定理可得1=4+x2-4x•cosθ.解得cosθ= 3+x24x =3x+x4≥ √32.当且仅当x= √3时.cosθ取得最小值为√32.角θ取得最大值为π6.故答案为π6.【点评】:本题主要考查两个向量的加减法的法则.以及其几何意义.余弦定理以及基本不等式的应用.属于中档题.16.(填空题.4分)已知数列{a n}为等差数列.其前n项和为S n.且2a1+3a3=S6.给出以下结论:① a10=0 ② S10最小③ S7=S12④ S19=0.正确的有___ .【正确答案】:[1] ① ③ ④【解析】:先求出a1=-9d.再表示出求和公式.即可判断.【解答】:解:设等差数列{a n}的公差为d.∵2a1+3a3=S6.∴5a1+6d=6a1+15d.化为:a1+9d=0.即a10=0.给出下列结论:① a10=0.正确;② S 10=10a 1+10(10−1)d2=-45d.可能大于0.也可能小于0.因此不正确;③ S 12-S 7=12a 1+ 12×112 d-7a 1- 7×62d=5a 1+45d=5(a 1+9d )=0.正确. ④ S 19=19(a 1+a 19)2=19a 10=0.正确; 其中正确结论的个数是 ① ③ ④ . 故答案为: ① ③ ④【点评】:本题考查了等差数列的通项公式与求和公式及其性质.考查了推理能力与计算能力.属于中档题.17.(填空题.4分)设函数 f (x )={|12x −4|+1,x ≤1x (x −2)2+a ,x >1.若存在互不相等的4个实数x 1.x 2.x 3.x 4.使得f (x 1)x 1=f (x 2)x 2=f (x 3)x 3=f (x 4)x 4=7 .则a 的取值范围为___ .【正确答案】:[1](6.18)【解析】:由题意可得f (x )=7x 有4个不同实根.讨论x≤1时.x >1时.由解方程和运用导数判断单调性和极值、最值.解不等式即可得到所求范围.【解答】:解:由f (x 1)x 1=f (x 2)x 2=f (x 3)x 3=f (x 4)x 4=7 .可得f (x )=7x 有4个不同实根. 当x≤1时.f (x )=|12x-4|+1=7x. 解得x= 35 或x= 519 .故当x >1时.f (x )=7x 有2个不同实根. 设g (x )=f (x )-7x=x (x-2)2-7x+a (x >1). g′(x )=(3x+1)(x-3).当1<x <3时.g′(x )<0.g (x )递减; 当x >3时.g′(x )>0.g (x )递增. 则g (x )min =g (3)=a-18.又g (1)=a-6. 由a-18<0.且a-6>0. 解得6<a <18. 即a 的范围是(6.18). 故答案为:(6.18).【点评】:本题考查函数和方程的转化思想.考查分类讨论思想方法.以及导数的运用:求单调区间和极值、最值.考查运算能力.属于中档题.18.(问答题.12分)已知函数f(x)=sin x3cos x3+√3cos2x3.(1)求函数f(x)图象对称中心的坐标;(2)如果△ABC的三边a.b.c满足b2=ac.且边b所对的角为B.求f(B)的取值范围.【正确答案】:【解析】:(1)运用二倍角公式和两角和的正弦公式.由正弦函数的对称中心.解方程可得所求;(2)运用三角形的余弦定理和基本不等式.可得12≤co sB<1.即有0<B≤ π3.运用正弦函数的图象和性质.即可得到所求范围.【解答】:解:(1)f(x)=sin x3cos x3+√3cos2x3.= 12sin23x+√32(cos23x+1) .=sin(23x+π3)+ √32.令23x+π3=kπ(k∈Z).解得:x= 3kπ2−π2(k∈Z).所以函数的图象的对称中心为:(3kπ2−π2,√32)(k∈Z).(2)由于b2=ac.所以:cosB= a 2+c2−b22ac≥2ac−ac2ac=12.则:0 <B≤π3.所以:π3<2B3+π3≤5π9.则:√32<sin(2B3+π3)≤1 .所以:√3<f(B)≤1+√32.则:f(B)的取值范围为:(√3,1+√32].【点评】:本题考查三角函数的恒等变换的运用.考查正弦函数的图象和性质.同时考查解三角形的余弦定理和基本不等式的运用.19.(问答题.15分)已知数列{a n}的前n项和为S n.且S n=2a n−32n ,n∈N∗ . b n=a n−12n(1)求证:数列{b n}为等比数列.并求出数列{a n}的通项公式;(2)是否存在实数λ.对任意m.n∈N*.不等式S m>λb n恒成立?若存在.求出λ的取值范围.若不存在请说明理由.【正确答案】:【解析】:(1)直接利用递推关系式求出数列的通项公式.进一步证明数列为等比数列.(2)利用(1)的结论.进一步利用分组法和恒成立问题求出实数λ的取值范围.【解答】:证明:(1)已知数列{a n}的前n项和为S n.且S n=2a n−32n,n∈N∗ . ①当n=1时. a1=32.则:当n≥2时. S n−1=2a n−1−32n−1. ②① - ② 得:a n=2a n-2a n-1- 32n + 62n.整理得:a n=2a n−1−32n.所以:a n−12n =2(a n−1−12n−1) .故:a n−12na n−1−12n−1=2(常数).故:数列{a n}是以a1−12=1为首项.2为公比的等比数列.故:a n−12n=1•2n−1=2n−1 .所以:a n=2n−1+12n.由于:b n=a n−12n=2n−1 .所以:b nb n−1=2n−12n−2=2(常数).故:数列{b n}为等比数列.(2)由(1)得:a n=2n−1+12n.所以:S n=(1+21+22+⋯+2n−1) +(121+122+⋯+12n).= (2n−1)2−1+12(1−12n)1−12.= 2n−12n.假设存在实数λ.对任意m.n∈N*.不等式S m>λb n恒成立.即:λb n<(S m)min .由于:S m=2m−12m为增函数 .故当m=1时. S1=32.所以:λ<2n−1•32.当n=1时. λ<32.故存在实数λ.且λ<32.【点评】:本题考查的知识要点:数列的通项公式的求法及应用.分组法在数列求和中的应用.主要考查学生的运算能力和转化能力.属于中档题.20.(问答题.15分)如图.四棱锥P-ABCD的底面ABCD为平行四边形.平面PAB⊥平面ABCD.PB=PC.∠ABC=45°.点E是线段PA上靠近点A的三等分点.(Ⅰ)求证:AB⊥PC;(Ⅱ)若△PAB是边长为2的等边三角形.求直线DE与平面PBC所成角的正弦值.【正确答案】:【解析】:(Ⅰ)作PO⊥AB于O.连接OC.可得PO⊥面ABCD.由△POB≌△POC.∠ABC=45°.得OC⊥AB.即得AB⊥面POC.可证得AB⊥PC.(Ⅱ)以O 为原点建立空间坐标系. P(0,0,√3),B(1,0,0),C(0,1,0),A(−1,0,0) .利用向量求解.【解答】:解:(Ⅰ)作PO⊥AB 于O… ① .连接OC.∵平面PAB⊥平面ABCD.且面PAB∩面ABCD=AB.∴PO⊥面ABCD .…(2分)∵PB=PC .∴△POB≌△POC .∴OB=OC .又∵∠ABC=45°.∴OC⊥AB… ②又PO∩CO=O .由 ① ② .得AB⊥面POC.又PC⊂面POC.∴AB⊥PC .…(6分)(Ⅱ)∵△PAB 是边长为2的等边三角形.∴ PO =√3,OA =OB =OC =1 . 如图建立空间坐标系. P(0,0,√3),B(1,0,0),C(0,1,0),A(−1,0,0)设面PBC 的法向量为 n ⃗ =(x ,y ,z) .PB ⃗⃗⃗⃗⃗ =(1,0,−√3),BC ⃗⃗⃗⃗⃗ =(−1,1,0) .由 {n ⃗ •PB ⃗⃗⃗⃗⃗ =x −√3z =0n ⃗ •BC ⃗⃗⃗⃗⃗ =−x +y =0.令 x =√3 .得 n ⃗ =(√3,√3,1) ;AP ⃗⃗⃗⃗⃗ =(1,0,√3),AE ⃗⃗⃗⃗⃗ =13AP ⃗⃗⃗⃗⃗ =(13,0,√33) . CB ⃗⃗⃗⃗⃗ =DA ⃗⃗⃗⃗⃗ =(1,−1,0) . DE ⃗⃗⃗⃗⃗ =DA ⃗⃗⃗⃗⃗ +AE ⃗⃗⃗⃗⃗ =(43,−1,√33) .设DE 与面PBC 所成角为θ.sinθ=|cos〈n ⃗ ,DE ⃗⃗⃗⃗⃗ 〉|=n⃗ •DE ⃗⃗⃗⃗⃗⃗ |n ⃗ ||DE ⃗⃗⃗⃗⃗⃗ |=4√33−√3+√33√169+1+39×√3+3+1=√37∴直线DE 与平面PBC 所成角的正弦值 √37 .…(12分)【点评】:本题考查了空间线线垂直的判定.向量法求线面角.属于中档题.21.(问答题.15分)如图.O 为坐标原点.点F 为抛物线C 1:x 2=2py (p >0)的焦点.且抛物线C 1上点P 处的切线与圆C 2:x 2+y 2=1相切于点Q .(Ⅰ)当直线PQ 的方程为x-y- √2 =0时.求抛物线C 1的方程;(Ⅱ)当正数p 变化时.记S 1.S 2分别为△FPQ .△FOQ 的面积.求 S1S 2 的最小值.【正确答案】:【解析】:(Ⅰ)设点P (x 0. x 022p ).代入直线PQ 的方程得一方程.再根据抛物线在P 处切线斜率为1列一方程.解方程组即可求得p 值;(Ⅱ)易表示出点p 处切线方程.据线圆相切得一方程.再与圆联立方程组可表示出Q 坐标.据弦长公式可表示出|PQ|.利用点到直线的距离公式可表示出点F 到切线PQ 的距离d.则S 1可表示.又 S 2=12|OF ||x Q | = p 2|x 0| .所以 S1S 2 可表示为关于x 0的函数.据函数结构特点利用基本不等式即可求得其最小值.【解答】:解:(Ⅰ)设点P (x 0. x 022p ).由x 2=2py (p >0)得.y= x 22p .求导y′= x p . 因为直线PQ 的斜率为1.所以 x 0p =1且x 0- x 022p - √2 =0.解得p=2 √2 .所以抛物线C 1 的方程为 x 2=4√2y .(Ⅱ)因为点P 处的切线方程为:y- x 022p = x 0p(x-x 0).即2x 0x-2py- x 02 =0. 根据切线与圆切.得d=r.即 02√4x 02+4p 2 =1.化简得 x 04=4x 02+4p 2 .由方程组 {2x 0x −2py −x 02=0x 2+y 2=1x 04−4x 02−4p 2=0.解得Q ( 2x 0 . 4−x 022p ). 所以|PQ|= √1+k 2 |x P -x Q |= √1+x 02p 2 |x 0−2x 0| = √p 2+x 02p |x 02−2x 0| . 点F (0. p 2 )到切线PQ 的距离是d=202√4x 02+4p 2 = 12 √x 02+p 2 . 所以 S 1=12|PQ |•d = 12 ×√p 2+x 02p |x 02−2x 0| × 12 √x 02+p 2 = x 02+p 24p |x 02−2x 0| . S 2=12|OF ||x Q | = p2|x 0| .而由 x 04=4x 02+4p 2 知.4p 2= x 04−4x 02>0 .得|x 0|>2.所以 S 1S 2 = x 02+p 24p |x 02−2x 0|×2|x 0|p = (x 02+p 2)(x 02−2)2p 2 = (4x 02+x 04−4x 02)(x 02−2)2(x 04−4x 02) = x 02(x 02−2)2(x 02−4) = x 02−42+4x 02−4 +3≥2 √2 +3.当且仅当 x 02−42=4x 02−4 时取“=”号.即 x 02=4+2√2 .此时.p= √2+2√2 .所以 S1S 2 的最小值为2 √2 +3.【点评】:本题主要考查抛物线几何性质、直线与抛物线的位置关系.同时考查解析几何的基本思想方法和运算求解能力.综合性强.难度大.22.(问答题.15分)已知a∈R .函数f (x )=e x-1-ax 在点(1.1-a )处与x 轴相切.(1)求a 的值.并求f (x )的单调区间;(2)当x >1时.f (x )>m (x-1)lnx.求实数m 的取值范围.【正确答案】:【解析】:(1)求出函数的导数.利用已知条件列出方程.求出a.判断导函数的繁符号.然后求解单调区间.(2)令g (x )=f (x )-m (x-1)lnx.x >0.求出 g′(x )=e x−1−m (lnx +x−1x )−1 .令h (x )=g'(x ).求出导数.通过(i )若 m ≤12 .(ii )若 m >12 .判断函数的单调性求解最值.然后求解m的取值范围.【解答】:解:(1)函数f (x )的定义域为R.f'(x )=e x-1-a 因为f (x )在点(1.1-a )处与x 轴相切.所以f'(1)=e 1-1-a=1-a=0∴a=1f'(x )=e x-1-1当f'(x )=e x-1-1>0时.x >1.当f'(x )=e x-1-1<0时.x <1.故函数f (x )的递增区间为(1.+∞).递减区间为(-∞.1);(2)令g (x )=f (x )-m (x-1)lnx.x >0.则 g′(x )=e x−1−m (lnx +x−1x )−1 .令h (x )=g'(x ). ℎ′(x )=e x−1−m (1x +1x 2)(i )若 m ≤12 .因为当x >1时.e x-1>1. m (1x +1x 2)<1 .所以h'(x )>0.所以h(x)即g'(x)在(1.+∞)上单调递增.又因为g'(1)=0.所以当x>1时.g'(x)>0.从而g(x)在[1.+∞)上单调递增.而g(1)=0.所以g(x)>0.即f(x)>m(x-1)lnx成立..可以h'(x)在(0.+∞)上单调递增.( ii)若m>12因为h'(1)=1-2m<0.h'(1+ln(2m))>0.所以存在x1∈(1.1+ln(2m)).使得h'(x1)=0.且当x∈(1.x1)时.h'(x)<0.所以h(x)即g′(x)在x∈(1.x1)上单调递减.又因为g′(1)=0.所以当x∈(1.x1).g′(x)<0.从而g(x)在[1.x1)上单调递减.而g(1)=0.所以当x∈(1.x1)时.g(x)<0.即f(x)>m(x-1)lnx不成立.].综上所述.m的取值范围为(−∞,12【点评】:本题考查函数的导数的应用.函数的单调性、切线方程函数的最值的求法.考查分析问题解决问题的能力.。
2018-2019浙江省宁波市高一上学期期中考试数学试卷(2-7班)

2018-2019学年浙江省宁波市北仑中学高一上学期期中考试数学试卷一、选择题:(本大题共10小题,每题4分,共计40分,在每题给出的四个选项中,只有一个是正确的)1.已知集合={0,1,2,3,4}M ,2={1<log (x+2)<2}N x ,则M N = ( )A .{0,1}B .{2,3}C .{1}D .{2,3,4}2.若sin 0θ>且tan 0θ<,则θ是 ( ) A .第一象限角 B .第二象限角 C .第三象限角 D .第四象限角3.若扇形的面积为38π,半径为1,则扇形的圆心角为 ( ) A .32π B .34π C .38π D .316π4.设4log , 2 ,3.03.03.02===c b a ,则 ( ) A .b a c << B .c b a << C .b c a << D .c a b << 5.函数1(0,1)xy a a a a=->≠的图象可能是 ( )6.函数2()ln(1)f x x x=--的零点所在的大致区间是 ( ) A .(1,2)B .(2,3)C .(3,4)D .(1,2)或(2,3)7.设偶函数()f x 在(0,)+∞上为减函数,且(2)0f =,则不等式()()0f x f x x+->的解集为 ( )A .(2,0)(2,)-+∞B .(2,0)(0,2)-C .(,2)(0,2)-∞-D .(,2)(2,)-∞-+∞8.在锐角ABC ∆中,若m A =+)sin 1lg( , 且n A=-sin 11lg ,则A cos lg 等于( )A .21(m -n) B .m -n C .21( m +n 1) D .m +n1 9.设0a >且1a ≠,函数2()log a f x ax x =-在[3,4]上是增函数,则a 的取值范围是( )A .1(0,)(1,)4+∞ B .11[,](1,)84+∞ C .11[,)(1,)86+∞ D .11[,)(1,)64+∞10.已知函数22123(),(),()2()f x x f x x f x x x ===-,(0,1,2,,8,9)9i i a i ==⋅⋅⋅,记102198()()()()()()(1,2,3)k k k k k k k L f a f a f a f a f a f a k =-+-+⋅⋅⋅+-=,则( ) A .312L L L <= B .213L L L << C .312L L L << D .123L L L << 二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分 11.计算:(1)20.530.018( 4.3)-++-= ;(2)4log 21lg lg 2042++= .12.已知角α的终边经过点(4,3)P -,则sin α= ;tan α= .13.已知函数23,0()log ,0x x f x x x ⎧≤=⎨>⎩,则1[()]4f f = ;若1()2f a =,则实数a = .14.已知函数()f x 是定义在R 上的奇函数,当0x >时,2()3f x x x =-,则当0x <时,()f x = ;函数()()3g x f x x =-+零点的集合为 .15.函数2lg(16)y x =-+的定义域为 .16.已知t 为常数,函数24y x x t =--在区间[0,6]上的最大值为10,则t = . 17.已知函数212,1(),1ax a x f x x ax x +-<⎧=⎨-≥⎩,若存在12,x x R ∈,12x x ≠,使12()()f x f x =成立,则实数a 的取值范围是 .三、解答题:(本题共5小题,共74分,解答应写出文字说明,证明过程或演算步骤.) 18. (本小题满分14分)已知集合2{3100}A x x x =--<,{121}B x a x a =+<<+.(Ⅰ)若2a =,求()()R A C B R 为实数集;(Ⅱ)若A B A =,求实数a 的取值范围.19. (本小题满分15分) 已知cos 2sin 5αα+=. (Ⅰ)求tan α的值; (Ⅱ)求227sin sin cos cos αααα+⋅+的值.20. (本小题满分15分)已知奇函数21()21x x a f x ⋅-=+的定义域为[2,]a b --.(Ⅰ)求实数,a b 的值;(Ⅱ)判断函数()f x 的单调性,并用定义给出证明;(Ⅲ)若实数m 满足(1)(21)0f m f m -+-<,求m 的取值范围.21. (本小题满分15分) 已知函数xxx f 212)(-=.(Ⅰ)若2)(=x f ,求x 的值;(Ⅱ)若0)()2(2≥+t mf t f t对于]2,1[∈t 恒成立,求实数m 的取值范围.22. (本小题满分15分)设函数2()12,f x x x a a R =+-+∈.(Ⅰ)若方程()3f x x =在区间(1,2)内有实数根,求a 的取值范围; (Ⅱ)设2()log (41)x ag x +=-+,若对任意的12,(0,2)x x ∈,都有1221()()4g x f x <+,求实数a 的取值范围.参考答案 一、选择题: CBBDD CBADA 二、填空题15.[4,)[0,]ππ--三、解答题19.略21.略。
精品解析:【全国百强校】浙江省宁波市镇海中学2019届高三上学期期中考试数学试题(解析版)

浙江省镇海中学2018-2019学年高三上学期期中考试数学试卷一、选择题:(本大题共10个小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.设全集U R =,集合{}{}|3,|05A x x B x x =??,则集合()U C A B?( )A. {}|03x x# B. {}|03x x <<C. {}|03x x <?D. {}|03x x ?【答案】D 【解析】 【分析】先根据补集的定义求出集合A 的补集U C A ,然后和集合B 进行交集运算,可求()U C A B Ç 【详解】因为A={x|x≥3}, 所以U C A ={x|x <3},所以(U C A )∩B═{x|0≤x<3}. 故选:D .【点睛】本题的考点是集合的补集和交集运算,比较基础.2.某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,两条虚线互相垂直,则该几何体的体积是( )A. 83p -B. 163C. 86p -D. 203【答案】D 【解析】 【分析】由三视图知原几何体是一个棱长为2的正方体挖去一四棱锥得到的,根据所提供的数据可求出正方体、锥体的体积,从而得到答案.【详解】由三视图知原几何体是一个棱长为2的正方体挖去一四棱锥得到的,该四棱锥的底为正方体的上底,高为1, 如图所示:所以该几何体的体积为23﹣13×22×1=203. 故选:D .【点睛】本题考查三视图,考查柱体、锥体的体积计算,解决该类问题的关键是由三视图还原得到原几何体,画三视图的要求为:“长对正,高平齐,宽相等”. 3.记n S 为等差数列{}n a 的前n 项和,若945S =,3812a a +=,则7a 等于( )A. 10B. 9C. 8D. 7 【答案】B 【解析】由题意可得:955945,5S a a ==\=,由等差数列的性质可得:385666512,7a a a a a a +=+=+=\=, 该数列的公差:652d a a =-=,故76729a a d =+=+=. 本题选择B 选项.4.满足线性约束条件23,23,0,0x y x y x y ì+?ïï+?ïí³ïï³ïî的目标函数z x y =+的最大值是 ( ) A. 1 B. 32C. 2D. 3 【答案】C 【解析】画出可行域如图阴影部分所示,易得1,1A ()z x y =+在1,1A ()处取得最大值2max z = 故选C点睛:本题主要考查线性规划中利用可行域求目标函数的最值,属简单题.求目标函数最值的一般步骤是“一画、二移、三求”:(1)作出可行域(一定要注意是实线还是虚线);(2)找到目标函数对应的最优解对应点(在可行域内平移变形后的目标函数,最先通过或最后通过的顶点就是最优解);(3)将最优解坐标代入目标函数求出最值.视频5.已知函数()2In x f x x x=-,则函数()f x 的图象为( )A.B.C.D.【答案】D 【解析】 【分析】写出分段函数,分段求导后利用导函数的符号或导函数的零点判断函数f (x )的图象的形状.【详解】()2ln x f x x x =-=()2200lnxx x x ln x x x x ì-ïïí-ï-ïî,>,<, 当x <0时,()()212ln x f x x x--¢=-=()3221x ln x x-+-.令g (x )=2x 3﹣1+ln (﹣x ), 由()3216160x g x x x x =¢+=+=,得x =- 当x∈(﹣∞,-x )>0,当x∈(-0)时,g′(x )<0. 所以g (x)有极大值为32(1g -=?-+=416033ln --<.又x 2>0,所以f′(x )的极大值小于0. 所以函数f (x )在(﹣∞,0)上为减函数.当x >0时,()212lnx f x x x -¢=-=3221x lnx x -+.令h(x)=2x3﹣1+lnx,()2160h x xx¢=+>.所以h(x)在(0,+∞)上为增函数,而h(1)=1>0,h(12)=﹣3204ln-<.又x2>0,所以函数f′(x)在(0,+∞)上有一个零点,则原函数有一个极值点.综上函数f(x)的图象为D中的形状.故选:D.【点睛】函数图象的辨识可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置;(2)从函数的单调性,判断图象的变化趋势;(3)从函数的奇偶性,判断图象的对称性;(4)从函数的特征点,排除不合要求的图象.6.若a、b是两个相交平面,则在下列命题中,真命题的序号为()①若直线m a^,则在平面b内一定不存在与直线m平行的直线.②若直线m a^,则在平面b内一定存在无数条直线与直线m垂直.③若直线m aÌ,则在平面b内不一定存在与直线m垂直的直线.④若直线m aÌ,则在平面b内一定存在与直线m垂直的直线.A. ①③B. ②③C. ②④D. ①④【答案】C【解析】试题分析:对于①,若直线m a^,如果a,b互相垂直,则在平面b内,存在与直线m平行的直线,所以①是错误的;对于②,若直线m a^,则直线m垂直于平面a内的所有直线,则在平面b内,一定存在无数条直线与直线m垂直,所以②正确;对于③,若直线m aÌ,则在平面b内,一定存在与直线m垂直的直线,所以③是错误的;对于④,若直线m aÌ,则在平面b内,一定存在与直线m垂直的直线,所以④是正确的.故应选C.考点:1、直线与平面之间的位置关系.7.已知sin 6pa 骣琪-琪桫cos22a a =( ) A.109 B. 109- C. 59- D. 59【答案】A 【解析】分析:先把cos 22a a 变形为2sin 26p a 骣琪+琪桫,而22626p ppa a 骣琪+=--琪桫,故可以利用诱导公式和二倍角公式求解.详解:因为cos 222sin 26pa a a 骣琪=+琪桫,故cos 222sin 22cos 2266pppa a a a 轾轾骣骣犏犏琪琪=--=-琪琪犏犏桫桫臌臌21024sin 69p a 骣琪=--=琪桫,故选A.点睛:本题考查诱导公式和两角和差的余弦、正弦公式的逆用,属于基础题.解题中注意根据正弦、余弦前面的系数选择合适的辅助角变形,另外在求值过程中注意寻找已知的角和未知的角之间的联系. 8.已知正项等比数列{}n a 满足7652a a a =+,若存在两项,m n a a ,使得2116m n a a a ?,则19m n+的最小值为( ) A.32 B. 114 C. 83 D. 103【答案】B 【解析】 【分析】设{a n }的公比为q (q >0),由等比数列的通项公式化简a 7=a 6+2a 5,求出q ,代入a m a n =16a 12化简得m ,n 的关系式,由“1”的代换和基本不等式求出式子的范围,验证等号成立的条件,由m 、n 的值求出式子的最小值.【详解】设正项等比数列{a n }的公比为q ,且q >0, 由7652a a a =+得:6a q=6a +62a q, 化简得,q 2﹣q ﹣2=0,解得q=2或q=﹣1(舍去), 因为a m a n =16a 12,所以()()1111m n a q a q --=16a 12,则q m+n ﹣2=16,解得m+n=6,所以19m n +=16(m+n )(19m n +)=16(10+9n m m n +)≥1106骣琪+琪桫=83,当且仅当9n m m n =时取等号,此时96n m m n m n ì=ïíï+=î,解得3292m n ì=ïïíï=ïî, 因为m n 取整数,所以均值不等式等号条件取不到,则19m n +>83, 验证可得,当m=2、n=4时,19m n +取最小值为114, 故选:B .【点睛】本题考查等比数列的通项公式,利用“1”的代换和基本不等式求最值问题,考查化简、计算能力,注意等号的成立的条件,属于易错题.9.已知双曲线()2222:10,0x y C a b a b-=>>的左右焦点分别为12,F F ,P 为双曲线C 上一点,Q 为双曲线C 渐近线上一点,,P Q 均位于第一象限,且22QP PF =,120QF QF ?,则双曲线C 的离心率为( )1122 【答案】C 【解析】分析:设()(),0Q at bt t >,根据12FQF D 为直角三角形可以得到1t =,再根据22QP PF =得2323c am b m ì+=ïïíï=ïî,代入双曲线方程可得到离心率. 详解:设()(),0Q at btt >,(),P m n ,注意到1290FQF ??,从而OQ c =,故22222b t a t c +=即1t =,故(),QP m a n b =--,()2,PF c m n =--.又2222m a c m n b n ì-=-ïí-=-ïî,解得2323c am b m ì+=ïïíï=ïî,代入双曲线方程,则有()222224199c a b a b +-=,2ca=,故选C. 点睛:离心率的计算,关键在合理构建关于,,a b c 的等量关系,本题中Q 的坐标与,,a b c 有关联,这种关联可以通过向量关系式转化到P ,最后根据P 在双曲线上可以得到离心率的大小.10.如图,在三棱柱111ABC A B C -中,底面为边长为2的正三角形,1B 在底面的射影为AC 中点且1B 到底,E F 分别是线段1AB 与1CA 上的动点,记线段EF 中点M 的轨迹为L ,则L 等于( )(注:L 表示L 的测度,本题中L 若分别为曲线、平面图形、空间几何体,分别对应为其长度、面积、体积)A. 1B.C.D.【答案】D 【解析】由题意画出图形,取特殊点得到M 的轨迹为平行四边形区域,再建立空间坐标系求出面积即可. 【详解】当E 位于B 1(或A ),而F 在A 1C 上移动时,M 的轨迹为平行于A 1C 的一条线段, 当F 位于A 1(或C ),而E 在AB 1上移动时,M 的轨迹为平行与AB 1的一条线段. 其它情况下,M 的轨迹构成图中平行四边形内部区域. 设异面直线AB 1与CA 1所成角为θ, ∴|L|=2×12|12AB 1|•|12CA 1|•sin θ=14|AB 1|•|CA 1|•sin θ.以O 为原点,OB 、OC 、O 1B 为x 轴,y 轴,z 轴建立空间坐标系, 则()()((11A 01,0C 0,1,0,?B A ---,,, ∴()(110,1332AB AC ==-,,,∴11210AB AC ==,111110cos θAB AC AB AC ==,sinθ=∴|L|=124创故选:D【点睛】本题考查棱柱的结构特征,考查空间想象能力和思维能力,利用特殊点得到M 的轨迹是解答该题的关键,是压轴题.二、填空题:(本大题共7个小题,多空题每题6分,单空题每小题4分,共36分.)11.中国古代数学著作《九章算术》中有一个这样的问题:“某贾人擅营,月入益功疾(注:从第2月开始,每月比前一月多入相同量的铜钱,3月入25贯,全年(按12个月计)共入510贯“,则该人每月比前一月多入_________________贯,第12月营收贯数为_________________. 【答案】 (1). 5 (2). 70 【解析】 【分析】设每个月的收入为等差数列{a n }.公差为d .可得a 3=25,S 12=510.利用等差数列的通项公式与求和公式即【详解】设每个月的收入为等差数列{a n }.公差为d . 则a 3=25,S 12=510. ∴a 1+2d=25,12a 1+12112´d=510,解得a 1=15,d=5, ∴12a = a 1+11d=15+55=70 故答案为:5,70【点睛】本题考查了等差数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题. 12.sin 26y x p骣琪=+琪桫的最小正周期为_________________,为了得到函数sin 26y x p 骣琪=+琪桫的图象,可以将函数cos 2y x =的图象向左最小移动_______个单位 【答案】 (1). p (2).56p【解析】 【分析】利用正弦型周期公式得到最小周期性,先根据诱导公式进行化简y=cos2x 为正弦函数的类型,再由左加右减上加下减的原则可确定平移的方案. 【详解】sin 26y x p骣琪=+琪桫的最小正周期为22p p =,由题意y=cos2x=sin (2x +2p ), 函数y=sin (2x +2p )的图象经过向左平移56p ,得到函数y=sin [2(x+56p )+2p ]=1326sin x p 骣琪+琪桫=sin 26x p 骣琪+琪桫的图象, 故答案为:π,56p .【点睛】本题主要考查三角函数的平移.三角函数的平移原则为左加右减上加下减,注意x 的系数的应用,以及诱导公式的应用.13.已知直线()12:210,:20l ax a y l x ay +++=++=,其中a R Î,若12l l ^,则a =______,若12//l l ,则a =__________.【答案】 (1). 0或3- (2). 2或-1 【解析】 【分析】根据直线垂直的等价条件进行求解即可,根据直线的平行关系求出a 的值. 【详解】∵l 1⊥l 2,∴a+a(a+2)=0, 即a (a+3)=0,解得a=0或a=﹣3, ∵l 1∥l 2,∴a 2﹣a ﹣2=0,解得:a=2或a=﹣1, 经检验均适合题意, 故答案为:0或3- ,2或-1【点睛】两直线位置关系的判断: 1111:0l A x B y C ++=和2222:0l A x B y C ++=的平行和垂直的条件属于常考题型,如果只从斜率角度考虑很容易出错,属于易错题题型,应熟记结论: 垂直: 12120A AB B +=; 平行: 1221A B A B =,同时还需要保证两条直线不能重合,需要检验. 14.已知,x y R Î,且2241x y xy ++=,则224x y +的最小值_________,此时x 的值为___________.【答案】 (1). 45 (2). ±【解析】 【分析】利用均值不等式可得224224x y x yxy +?,即22222241444x y x y xy xy +=++?+从而得到224x y +的最小值及相应的x 值.【详解】∵224224x y x y xy +?,∴2244x y xy +£,当且仅当2x=y 时,等号成立, 又2214x y xy =++,∴22222241444x y x y xy x y +=++?+, ∴22445x y +?,即224x y +的最小值45由22241x y x y xy ì=ïí++=ïî,解得:x =?故答案为:45,±【点睛】本题考查基本不等式以及一元二次不等式的解法,属中档题.15.已知两不共线的非零向量,a b 满足2a =,1a b -=,则向量a 与b 夹角的最大值是__________. 【答案】6p 【解析】 【分析】设向量,a b 夹角为q ,由余弦定理求得23cos 4x xq +=,再利用基本不等式求得cos q 取得最小值,即可求得q 的最大值,得到结果.【详解】因为两非零向量,a b 满足2a =,1a b -=,设向量,a b 夹角为q , 由于非零向量,a b 以及a b -构成一个三角形,设b x =, 则由余弦定理可得2144cos x x q =+-,解得233cos 44x x x x q ++==?,当且仅当x cos q所以q 的最大值是6p ,故答案是6p.【点睛】该题考查的是有关向量夹角的大小问题,在解题的过程中,涉及到的知识点有余弦定理,基本不等式,注意当什么情况下取得最值,再者就是需要明确角取最大值的时候其余弦值最小.16.已知数列{}na 为等差数列,其前n 项和为n S ,且13623a a S +=,给出以下结论:①100a =②10S 最小③712S S =④190S =,正确的有_________________. 【答案】①③④ 【解析】 【分析】先求出a 1=﹣9d ,再表示出求和公式,即可判断.【详解】设等差数列{a n }的公差为d ,∵2a 1+3a 3=S 6,∴5a 1+6d=6a 1+15d , 化为:a 1+9d=0,即a 10=0, 给出下列结论:①a 10=0,正确; ②S 10=10a 1+()101012d-=﹣45d ,可能大于0,也可能小于0,因此不正确;③S 12﹣S 7=12a 1+12112´d ﹣7a 1﹣762´d=5a 1+45d=5(a 1+9d )=0,正确. ④S 19=()119192a a +=19a 10=0,正确;其中正确结论的个数是①③④. 故答案为:①③④【点睛】本题考查了等差数列的通项公式与求和公式及其性质,考查了推理能力与计算能力,属于中档题.17.设函数()()21241,12,1x x f x x x a x ì-+?ï=íï-+>î,若存在互不相等的4个实数1234,,,x x x x ,使得()()()()123412347f x f x f x f x x x x x ====,则a 的取值范围为__________.【答案】(6,18) 【解析】 【分析】由题意可得f (x )=7x 有4个不同实根,讨论x ≤1时,x >1时,由解方程和运用导数判断单调性和极值、最值,解不等式即可得到所求范围.【详解】由()11f x x =()22f x x =()33f x x =()44f x x =7,可得f (x )=7x 有4个不同实根,当x ≤1时,f (x )=|12x ﹣4|+1=7x ,解得x=35或x=519, 故当x >1时,f (x )=7x 有2个不同实根, 设g (x )=f (x )﹣7x=x (x ﹣2)2﹣7x+a (x >1), g′(x )=(3x+1)(x ﹣3),当1<x <3时,g′(x )<0,g (x )递减; 当x >3时,g′(x )>0,g (x )递增. 则g (x )min =g (3)=a ﹣18,又g (1)=a ﹣6, 由a ﹣18<0,且a ﹣6>0, 解得6<a <18. 故答案为:()6,18.【点睛】本题考查函数和方程的转化思想,考查分类讨论思想方法,以及导数的运用:求单调区间和极值、最值,考查运算能力,属于中档题.三、解答题:(本大题共个5小题,共74分.解答应写出文字说明、证明过程或演算步骤)18.已知函数()2sincos 333x x xf x = (1)求函数()f x 图象对称中心的坐标;(2)如果ABC D 的三边,,a b c 满足2b ac =,且边b 所对的角为B ,求()f B 的取值范围.【答案】(1)对称中心3,22k k Z p p 骣琪-+?琪桫(2)()f B ? 【解析】 【分析】(1)运用二倍角公式和两角和的正弦公式,由正弦函数的对称中心,解方程可得所求;(2)运用三角形的余弦定理和基本不等式,可得12≤cosB<1,即有0<B≤3p,运用正弦函数的图象和性质,即可得到所求范围.【详解】(1)()2333x x xf x sin cos =.=12212323sin x cos x +桫,=sin (233x p +)令233x k p p +=(k∈Z), 解得:x=322k p p -(k∈Z),所以函数的图象的对称中心为:3,22k k Z p p 骣琪-+?琪桫.(2)由于b 2=ac ,所以:cosB=22221222a cb ac acac ac+--?,则:03B p £<. 所以:253339B p p p +?<,2133B sin p 骣琪+?琪桫,()1f B ?.则:f (B )的取值范围为:2]. 【点睛】本题考查三角函数的恒等变换的运用,考查正弦函数的图象和性质,同时考查解三角形的余弦定理和基本不等式的运用.19.已知数列{}na 的前n 项和为n S ,且32,2n n n S a n N *=-?,12n n nb a =-(1)求证:数列{}n b 为等比数列,并求出数列{}n a 的通项公式; (2)是否存在实数l ,对任意,m n N *Î,不等式m nS b l>恒成立?若存在,求出l 的取值范围,若不存在请说明理由.【答案】(1)证明略;1122n n n a -=+ (2)32l < 【解析】 【分析】(1)直接利用递推关系式求出数列的通项公式,进一步证明数列为等比数列; (2)利用(1)的结论,进一步利用分组法和恒成立问题求出实数λ的取值范围. 【详解】证明:(1)已知数列{a n }的前n 项和为S n ,且*322n n n S a n N =-?,,① 当n=1时,132a =, 则:当n ≥2时,111322n n n S a ---=-,② ①﹣②得:a n =2a n ﹣2a n ﹣1﹣32n +62n ,整理得:1322n n n a a -=-,所以:11112()22n n n n a a ---=-,故:1112212n nn n a a ---=-(常数), 故:数列{a n }是以1112a -=为首项,2为公比的等比数列.故:1111222n n n n a ---=?,所以:1122n n n a -=+.由于:1122n n n n b a -=-=,所以:121222n n n n b b ---==(常数).故:数列{b n }为等比数列. (2)由(1)得:1122n n na -=+, 所以:()1211222n n S -=+++++(12111222n +++), =()111212212112n n 骣??琪-桫+--, =122n n-,假设存在实数λ,对任意m ,n ∈N *,不等式m nS b l>恒成立, 即:()m min nS b l <, 由于:122m m m S =-为增函数, 故当m=1时,132S =,所以:1322n l -×<,当n=1时,32l <.故存在实数λ,且32l <.【点睛】本题考查的知识要点:数列的通项公式的求法及应用,分组法在数列求和中的应用,主要考查学生的运算能力和转化能力,属于中档题.20.如图,四棱锥P ABCD -的底面ABCD 为平行四边形,平面PAB ^平面ABCD ,,45PB PC ABC °=?,点E 是线段PA 上靠近点A 的三等分点(1)求证:AB PC ^(2)若PAB D 是边长为2的等边三角形,求直线DE 与平面PBC 所成角的正弦值 【答案】(Ⅰ)见解析;【解析】试题分析:(Ⅰ)由平面PAB ^面ABCD ÞPO ^ 面ABCD 再证POB POC D @DOB OC OCAB AB ?轣轣面POC AB PC 轣 ;(Ⅱ)建立空间坐标系, 求得面PBC 的法向量为()4333,3,1,,1,cos ,37n DE n DE n DE n DE骣×琪==-掎?=琪桫. 试题解析:(Ⅰ)作PO AB ^于O ……①,连接OC , ∵平面PAB ^平面ABCD ,且PAB ABCD AB ?面面 ,∴PO ^面ABCD.∵PB PC =,∴POB POC D @D ,∴OB OC =, 又∵45ABC °?,∴OC AB ^……②又PO COO ?,由①②,得AB ^面POC ,又PC Ì面POC ,∴AB PC ^.(Ⅱ)∵PAB D 是边长为2的等边三角形,∴1PO OA OB OC ===如图建立空间坐标系,(()()(),1,0,0,0,1,0,1,0,0P B C A - 设面PBC 的法向量为(),,n xy z =,()()1,0,3,1,1,0PB BC =-=- 0{n PBx n BC x y ?-=?-+=,令x =()3,3,1n =()111,0,3,33AP AE AP 骣琪===琪桫,()1,1,0CB DA ==-4,3DE DA AE 骣琪=+=-琪桫,设DE 与面PBC 所成角为qsin cos ,16n DE n DE nDEq -×=狁===∴直线DE 与平面PBC21.如图,O 为坐标原点,点F 为抛物线()21:20C x py p =>的焦点,且抛物线1C 上点P 处的切线与圆222:1C x y +=相切于点Q(1)当直线PQ 的方程为0x y --=时,求抛物线1C 的方程;(2)当正数p 变化时,记12,S S 分别为,FPQ FOQ D D 的面积,求12S S 的最小值。
宁波中学2018学年第一学期高一期中考试卷答案与解析成品

的最小值是_________ (解析提供者 衢州汪强)
【解析】作出函数
f
(x)
x
1 2
,0
x
1 2
的图象,如下图所示
2 x 1 ,
1 2
x
2
13.函数 f (x) a x1 (0 a 1) 的定义域为____________,图像必过定点_________
17.求“方程 (3)x ( 4)x 1的解”有如下解题思路:设 f (x) (3)x ( 4)x ,则 f (x) 在 R 上单调递减,且 f (2) 1 ,
55
55
所以原方程有唯一解 x 2 ,类比上述解题思路,方程 x6 x2 (x 2)3 x 2 的解集为__________
(答案与解析提供:浙江湖州莫国良)
【答案】(1) f (x) x2 x 1 ;(2) t 9 或 t 3 ;(3) m 0 或1 m 4
2
2
【解析】①设 f (x) ax2 bx c ,代入 f (x 1) f (x) 2x 得
a x 12 b(x 1) c ax 2 bx c 2x 2ax a b=2x a 1,b 1
(答案提供: 宁波汪灿泉)
存在 x1, x2 ,当 0 x1 x2 2 时, f (x1) f (x2 ) ,
0
x1
1 2
由图可知,
x1
f
(x2 )
f
(x2 )
x1
f
(x1)
f
( x1 )
2019学年镇海中学高一上学期期中数学试卷

2019学年镇海中学高一上学期期中试卷一、选择题:本大题共10小题,每小题4分,共40分1.设全集U R =,集合{}2|20A x x x =-<,{}|1B x x =>,则()U A C B = A. {}|12x x << B. {}|12x x ≤< C. {}|01x x << D. {}|01x x <≤2.函数()23x f x x =+的零点所在的一个区间是A. ()2,1--B. ()1,0-C. ()0,1D. ()1,2 3.下列四组函数中,表示同一函数的是A .()f x =与()g x =B .()f x =()g x =C .2()lg f x x =与()2lg g x x = D .0()f x x =与01()g x x =4.已知0.250.5log 2,log 0.2,0.5a b c ===,则,,a b c 的大小关系为 A .a c b <<B .a b c <<C .b c a <<D .c a b <<5.关于函数21()45f x x x =++,下列说法正确的是 A .()f x 的最小值为1B .()f x 的图象不具备对称性C .()f x 在[2,)-+∞上单调递增D .对任意x R ∈,均有()1f x ≤6.若函数()212()log 45=-++f x x x 在区间()32,2-+m m 内单调递增,则实数m 的取值范围为A. 4,33⎡⎤⎢⎥⎣⎦B.4,23⎡⎤⎢⎥⎣⎦C. 4,23⎡⎫⎪⎢⎣⎭D. 4,3⎡⎫+∞⎪⎢⎣⎭7.设a 为实数,若函数()22=-+f x x x a 有零点,则函数()=⎡⎤⎣⎦y f f x 零点的个数是 A.1或3 B.2或3 C.2或4 D.3或4 8.已知函数()(),--=-=+x x x x f x e e g x e e ,则下列结论正确的是 A.任意的 12,∈x x R 且12≠x x ,都有()()12120-<-f x f x x xB.任意的 12,∈x x R 且12≠x x ,都有()()12120-<-g x g x x xC.()f x 有最小值,无最大值D.()g x 有最小值,无最大值 9.函数()()=+∈af x x a R x的图像不可能是A B C D10.已知函数()()21.043,0+≤⎧⎪=⎨+->⎪⎩x x e f x x x x ,函数()y f x a =-有四个不同零点,从小到大依次为1234,,,x x x x ,则1234-++x x x x 的取值范围为A. ()3,3eB. (]3,3+eC. (]3,3eD. [)3,3+e二、填空题:本大题共7小题,多空题每空6分,单空题每空4分,共36分 11. 已知集合123A x N y Z x ⎧⎫=∈=∈⎨⎬+⎩⎭,则列举法表示集合A = ,集合A 的真子集有 个. 12.函数y =的定义域是 ,值域是 .13.已知函数,0()0x x f x x ⎧≤⎪=⎨>,则((2))f f -= ;若()2f a =,则实数a = .14. 已知集合{}1,2,3A B ==,设:f A B →为从集合A 到集合B 的函数,则这样的函数一共有 个,其中函数的值域一共有 种不同情况.15. 若函数2(2)3,14(),142,4a x a x f x x xx ax x -+≤⎧⎪⎪=<≤⎨⎪⎪-+>⎩是R 上的单调函数,则实数a 的取值范围为 .16. 若12x ≤且0x ≠时,不等式22ax x a x --≥恒成立,则实数a 的取值范围为 .17. 已知集合{}210A x Z x =∈->,{}2210B x x tx =--≤,若{}12,A B x x = ,求t 的取值范围 .三、解答题:本大题共5小题:共74分18.计算求值:(1)()1122330213129.60.134864--⎛⎫⎛⎫⎛⎫--+-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭;(2)1lg3lg94lg81lg 27+-+-.19.已知集合{}221A x a x a =≤≤+,()(){}2312310B x x a x a =-+++≤,其中a R ∈. (1)若4A ∈,3A ∉,求实数a 的取值范围; (2)若A B ⊆,求实数a 的取值范围.20.定义在R 上的函数()f x 满足()()f x f x -=,且当0x ≥时,()21,0122,1xx x f x x ⎧-+≤<⎪=⎨-≥⎪⎩. (1)求当0x <时,()f x 的解析式;(2)若对任意的[]1,x m m ∈-,不等式()()2f x f x m -≤+恒成立,求实数m 的取值范围.21.已知函数()33x x af x b+=+(1)当5a =,3b =-时,求满足()3x f x =的x 的值;(2)若函数()f x 是定义在R 上的奇函数,函数()g x 满足()()333x xf xg x -⋅+=-⎡⎤⎣⎦,若对任意x R ∈且0x ≠,不等式()()210g x m g x ≥⋅-恒成立,求实数m 的最大值22.已知函数()21f x x a =-+,()1g x x a =-+,x R ∈ (1)若2a =且[]2,3x ∈,求函数()()()f xg x x ee=+最小值;(2)若()()g x f x ≥对于任意[),x a ∈+∞恒成立,求a 的取值范围; (3)若[]1,6x ∈,求函数()()(){}max ,f x g x h x e e =的最小值。
【100所名校】2019届浙江省宁波市镇海中学高三上学期期中考试数学试题(含答案)

2019届浙江省宁波市镇海中学 高三上学期期中考试数学试题数学注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、单选题1.设全集U =R ,集合A ={x|x ≥3},B ={x|x ≤0<5},则集合(C U A )∩B = A .{x|0≤x ≤3} B .{x|0<x <3} C .{x|0<x ≤3} D .{x|0≤x <3}2.某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,两条虚线互相垂直,则该几何体的体积是A .8−π3B .163C .8−π6D .2033.记S n 为等差数列{a n }的前n 项和,若S 9=45,a 3+a 8=12, 则a 7= A .10 B .9 C .8 D .74.4.满足线性约束条件23,23,{ 0,0x y x y x y +≤+≤≥≥的目标函数z x y =+的最大值是A .1B .32C .2D .3 5.已知函数f (x )=x 2−In|x|x,则函数f (x )的图象为A .B .C .D .6.若α、β是两个相交平面,则在下列命题中,真命题的序号为①若直线m ⊥α,则在平面β内一定不存在与直线m 平行的直线.②若直线m ⊥α,则在平面β内一定存在无数条直线与直线m 垂直. ③若直线m ⊂α,则在平面β内不一定存在与直线m 垂直的直线. ④若直线m ⊂α,则在平面β内一定存在与直线m 垂直的直线. A .①③ B .②③ C .②④ D .①④ 7.已知sin (π6−α)=√23,那么cos2α+√3sin2α=A .109 B .−109 C .−59 D .598.已知正项等比数列{a n }满足a 7=a 6+2a 5,若存在两项a m ,a n ,使得a m ⋅a n =16a 12,则1m+9n 的最小值为 A .32 B .114 C .83 D .103 9.已知双曲线C:x 2a 2−y 2b 2=1(a >0,b >0)的左右焦点分别为F 1,F 2,P 为双曲线C 上一点,Q 为双曲线C 渐近线上一点,P,Q 均位于第一象限,且2QP ⃑⃑⃑⃑⃑ =PF 2⃑⃑⃑⃑⃑⃑⃑ ,QF 1⃑⃑⃑⃑⃑⃑⃑ ⋅QF 2⃑⃑⃑⃑⃑⃑⃑ =0,则双曲线C 的离心率为A .√3−1B .√3+1C .√13−2D .√13+210.如图,在三棱柱ABC −A 1B 1C 1中,底面为边长为2的正三角形,B 1在底面的射影为AC 中点且B 1到底面的距离为√3,已知E,F 分别是线段AB 1与CA 1上的动点,记线段EF 中点M 的轨迹为L ,则|L |等于(注:|L |表示L 的测度,本题中L 若分别为曲线、平面图形、空间几何体,分别对应为其长度、面积、体积)此卷只装订不密封班级 姓名 准考证号 考场号 座位号A.1B.√102C.√32D.√394二、填空题11.中国古代数学著作《九章算术》中有一个这样的问题:“某贾人擅营,月入益功疾(注:从第2月开始,每月比前一月多入相同量的铜钱,3月入25贯,全年(按12个月计)共入510贯“,则该人每月比前一月多入_________________贯,第12月营收贯数为_________________.12.y=sin(2x+π6)的最小正周期为_________________,为了得到函数y=sin(2x+π6)的图象,可以将函数y=cos2x的图象向左最小移动_______个单位13.已知直线l1:ax+(a+2)y+1=0,l2:x+ay+2=0,其中a∈R,若l1⊥l2,则a=______,若l1//l2,则a=__________.14.已知x,y∈R,且4x2+y2+xy=1,则4x2+y2的最小值_________,此时x的值为___________.15.已知两不共线的非零向量a ,b⃑满足|a|=2,|a−b⃑|=1,则向量a与b⃑夹角的最大值是__________.16.已知数列{a n}为等差数列,其前n项和为S n,且2a1+3a3=S6,给出以下结论:①a10= 0②S10最小③S7=S12④S19=0,正确的有_________________.17.设函数f(x)={|12x−4|+1,x≤1x(x−2)2+a,x>1,若存在互不相等的4个实数x1,x2,x3,x4,使得f(x1)x1=f(x2) x2=f(x3)x3=f(x4)x4=7,则a的取值范围为__________.三、解答题18.已知函数f(x)=sin x3cos x3+√3cos2x3(1)求函数f(x)图象对称中心的坐标;(2)如果ΔABC的三边a,b,c满足b2=ac,且边b所对的角为B,求f(B)的取值范围.19.已知数列{a n}的前n项和为S n,且S n=2a n−32n,n∈N∗,b n=a n−12n(1)求证:数列{b n}为等比数列,并求出数列{a n}的通项公式;(2)是否存在实数λ,对任意m,n∈N∗,不等式S m>λb n恒成立?若存在,求出λ的取值范围,若不存在请说明理由.20.如图,四棱锥P−ABCD的底面ABCD为平行四边形,平面PAB⊥平面ABCD,PB=PC,∠ABC=45°,点E是线段PA上靠近点A的三等分点(1)求证:AB⊥PC(2)若ΔPAB是边长为2的等边三角形,求直线DE与平面PBC所成角的正弦值21.如图,O为坐标原点,点F为抛物线C1:x2=2py(p>0)的焦点,且抛物线C1上点P处的切线与圆C2:x2+y2=1相切于点Q(1)当直线PQ的方程为x−y−√2=0时,求抛物线C1的方程;(2)当正数p变化时,记S1,S2分别为ΔFPQ,ΔFOQ的面积,求S1S2的最小值。
镇海中学2018学年第一学期期中考试高一年级数学试卷参考答案2018.11(1)

x2
x22 a
1
( a
1)x2
1
(
,2 a 2)
因为 2a 2 2 a 1 a
综上所述,
当 a 4 时, x1 x1 的取值范围为 ( , 2 a 1 a] [2 a 1 a, ) ;
x2
当4 a
1 时, x1 x1 的取值范围为 (
x2
, 2 a 1 a] (1 a , 2
);
当 1 a 0 时, x1 x1 的取值范围为 (
1
( Ⅰ)
2
(Ⅱ)若 a 0 ,则 f (x) 在 R 上为增函数,符合题意;
若 a 0 ,不合题意;
若 a 0 ,则 a 2
1,从而 a
综上,实数 a 的取值范围为 a
2 2或 a 0。
高一数学 第 6 页 共 4 页
(Ⅲ)因为 a 0 ,则 f (x) 在 (
, a) 上为减函数,在 ( a ,
f (x1)
f ( x2 ) ,求 x1 x2
x1 的取值范围 .
高一数学 第 4 页 共 4 页
镇海中学 2018 学年第一学期期中考试
高一年级数学试卷参考答案
一、选择题:本大题共 10 小题,每小题 4 分,共 40 分.在每小题给出的四个选项中,只有一项 是符合题目要求的.
序号
1
2
3
4
5
6
7
(2) 当 4 a
1 时, a 2
a且 a
a , 则 g ( x) 在 (0,
a a] ,[ ,0) 上为增函数,
2
高一数学 第 7 页 共 4 页
在 [ a , a] 上为减函数
a
从而当
2
2018-2019学年浙江省宁波市镇海区镇海中学高一上学期期中考试数学试题 Word版含解析

2018学年第一学期镇海中学高一年级数学期中试卷一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.集合}{1,2,3,4,5,6U =,}{1,4,5S =,}{2,3,4T =,则()U S C T ⋂的子集个数为( ) A. 1 B. 2 C. 3 D. 4【答案】D 【解析】 【分析】先求出U C T ,再求()U S C T ⋂中元素的个数,进而求出子集的个数。
【详解】由题可得{}1,5,6U C T =,所以(){}1,5U S C T ⋂=,里面有2个元素,所以子集个数为224=个 故选D【点睛】本题考查集合的基本运算,子集的个数为2n 个,n 指元素个数2.已知α是锐角,那么2α是( ) A. 第一象限角 B. 第一象限角或第二象限角 C. 第二象限角 D. 小于180的正角【答案】D 【解析】 【分析】根据α是锐角求出2α的取值范围,进而得出答案。
【详解】因为α是锐角,所以02πα<< ,故02απ<<故选D.【点睛】本题考查象限角,属于简单题。
3.下列根式与分数指数幂的互化,正确的是 ( )A. 12()(0)x x =-≥13(0)x x =≤C. 340)xx -=>D. 130)xx -=≠【答案】C 【解析】 【分析】利用根式与分数指数幂的关系化简计算即可。
【详解】12(0)x x =-≥,故A 错13x =,故B 错130)xx -=≠,故D 错 所以选C【点睛】本题考查根式与分数指数幂的化简计算,属于基础题。
4.设0.3113211log 2,log ,()32a b c ===,则( ) A. a b c <<B. a c b <<C. b c a <<D. b a c <<【答案】D 【解析】试题分析:根据我们所学的指数函数和对数函数的性质可知,1133log 2log 10a =<=,112211log log 132b =>=,0.30110()()122c <=<=,因此可知a c b <<,故选B. 考点:对数函数性质点评:解决的关键是对于不同底数的对数和指数式比较大小,一般找中间量即可,1,0为常用的常数,属于基础题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.设
a
log 1
3
2, b
log 1
2
1 3
,c
( 1 )0.3 2
,则(
)
A. a b c
B. a c b
C. b c a
D. b a c
【答案】D
【解析】试题分析:根据我们所学的指数函数和对数函数的性质可知,
a
log 1
3
2
log1 1
3
0
,b
log 1
2
1 3
log 1
2
1 2
【答案】A
【解析】对函数求导,求函数的单调性,再考虑趋向性。
【详解】
由题可得
y
1
ln x2
x
x
0
, y 0 即1 ln x 0
,解得 0 x e
y 0 即1 ln x 0 ,解得 x e
所以在 0, e 上函数单调递增,在 e, 上函数单调递减,且当 x 0 时, y
x 时, y 0
【点睛】
本题主要考查双勾函数,解题的关键时得出 3x
4y
y
6
1
4
y
1
13
,属于一般
题。
二、填空题
11.计算: sin
2 3
=_______;
1 1log2 5 2
ln
e =_______.
【答案】 3
3
25
【解析】(1)由三角函数的诱导公式计算即可
(2)有指数与对数的运算法则计算即可。
【详解】
当 x 0 时, x 0 ,所以 f x ln x 2 f x ,即 f x ln x 2 ,
所以
f
(x)
在
x
0
上的解析式为
f
(x)
0, x ln(2
0
x)
,
x
0
【点睛】
本题考查由函数的奇偶性求函数值和解析式,解题的关键是熟练掌握奇偶性的性质,属
于一般题。
第 7 页 共 14 页
1 y
y 1
y 1
令t
y
1 ,则 t
1,
2 3
0,
则有 g t 6 4t (双勾函数),令 6 4t ,解得 t 6
t
t
2
又因为
t
1,
2 3
0,
,
所以当 t
2 3
g t
时,
min
6 2
4
2 3
9
8 3
35 3
3
所以 3x 4 y 的最小值为 35 13 4
3
3
故选 D.
又因为
f (0)
1
,所以
2
f
2
f
1
0
2
故选 C.
【点睛】
本题考查函数的周期性,解题的关节是求出函数的周期,属于一般题。
8.已知函数
f
(x)
1
ex
x ex
的最大值为 M
,最小值为 m
,则 M
m 的值等于
()
A.1
B.2
C.1
1
e e2
D.
2
1
e e2
【答案】B
【解析】令
g x
ex
x ex
当 x 1时, f (x) x2 2x ,
所以当 x 1 时, f (x) x2 6x 8
当 x2
2x
1 2
时,可得
x1
x2
2
当
x2
6x
8
1 2
时,可得
x3
x4
6
所以 f (x) 1 的所有根之和为 6 2 4 2
故选 A
【点睛】
本题考查函数的奇偶性以及求函数的解析式,解题的关键是得出函数 y f (x) 的图像
1,0
c
( 1 )0.3 2
( 1 )0 2
1 ,因此可
知 a c b ,故选 B.
【考点】对数函数性质
点评:解决的关键是对于不同底数的对数和指数式比较大小,一般找中间量即可,1,0
为常用的常数,属于基础题。
5.函数 y ln x 的大致图象是 ( ) x
A.
B.
C.
D.
第 2 页 共 14 页
3
的性质判断单调区间
【详解】
因为 y log1 (x2 3x 2) ,所以 x2 3x 2 0 ,解得 x 1或 x 2 3
令 t x2 3x 2 ,因为 y x2 3x 2 的图像开口向上,对称轴方程为 x 3 , 2
所以内函数 t x2 3x 2 在 2, 上单调递增,
2018-2019 学年浙江省宁波市镇海区镇海中学高一上学期期 中数学试题
一、单选题
1.集合U 1, 2,3, 4,5, 6 , S 1, 4,5,T 2,3, 4 ,则 S CUT 的子集个数为
()
A.1
B.2
C.3
D.4
【答案】D
【解析】先求出 CUT ,再求 S CUT 中元素的个数,进而求出子集的个数。
【详解】
由题可得 CUT 1,5, 6 ,所以 S CUT 1,5 ,里面有 2 个元素,所以子集个数为
22 4 个
故选 D
【点睛】
本题考查集合的基本运算,子集的个数为 2n 个, n 指元素个数 2.已知 是锐角,那么 2 是( )
A.第一象限角
B.第一象限角或第二象限角
C.第二象限角
D.小于180 的正角
【答案】D
【解析】根据 是锐角求出 2 的取值范围,进而得出答案。
【详解】
因为 是锐角,所以 0 ,故 0 2 2
故选 D.
【点睛】
本题考查象限角,属于简单题。
3.下列根式与分数指数幂的互化,正确的是 ( )
1
A. x (x)2 (x 0)
1
B. 6 x2 x3 (x 0)
C.
(x 1) 是 , 上的增函数,则实数 a 的
loga x
(x 1)
取值范围为_____.
【答案】 5 a 3 2
第 8 页 共 14 页
【解析】因为函数
f
(x)
1 a 2
x2
2x
5 4
(x 1) 是 , 上的增函数,所以当
loga x
(x 1)
x
1,时
f
x
loga
x
是增函数,当 x
,根据奇函数的性质即可求出
g x min
g x max
0 ,进
而得出答案。
【详解】
令 gx
ex
x ex
,则 g x
x ex ex
ex
x ex
gx
所以 g x 是奇函数,即 g x g x 0
min
max
所以 M m g x g x 2 2
min
max
故选 B
令t
y
1 ,则 t
1,
2 3
0, ,利用双勾函数的性质得出答案。
【详解】
第 5 页 共 14 页
由题可得 x 1 y 1 3y ,当 y 1时上式不成立,故 y 1
所以
x
13y 1 y
且 x, y 0 ,则 y 1 或 0 y 1 3
所以 3x 4 y 31 3y 4 y 9 y 3 4 y 6 4 y 1 13
外函数 y log1 t 单调递减,
3
所以由复合函数单调性的性质可知函数 y log1 (x2 3x 2) 的单调递减区间为
3
2,
故选 A. 【点睛】 本题考查复合函数的单调性,解题的关键是掌握复合函数单调性同增异减的方法,属于 一般题。
第 3 页 共 14 页
7.已知函数 f x 对于任意实数 x 满足条件 f (x 2) 1 ,若 f (0) 1 ,则
,分子分母同时除以 cos2
,再
将 tan 2 代入即可。
【详解】
将 sin cos 的分子分母同时除以 cos 得 tan 1 ,将 tan 2 代入可得
2sin cos
2 tan 1
tan 1 2 1 1 ;故 sin cos 1 2 tan 1 4 1 5 2sin cos 5
3
x4
4
1 x
3
(
x
0)
D.
1
x3
3
x(x
0)
第 1 页 共 14 页
【答案】C
【解析】利用根式与分数指数幂的关系化简计算即可。
【详解】
1
x x2 (x 0) ,故 A 错
1
6 x2 x3 ,故 B 错
1
x3
3
1 (x
0) ,故 D 错
x
所以选 C
【点睛】
本题考查根式与分数指数幂的化简计算,属于基础题。
当 x 0 时, x 0 ,所以 f x ln x 2 f x ,又因为 f 0 0 ,进而可
得答案。 【详解】
f (x) 是定义在 R 上的奇函数,所以 f x f x , f 0 0
当 x 0 时, f x ln x 2 ,所以 f 1 f 1 ln 1 2 ln 3 ;
故选 A 【点睛】
本题考查有函数解析式判断函数的图像,一般方法是利用函数的特殊值,单调性,奇偶
性,趋向性等,属于一般题。
6.函数 y log1 (x2 3x 2) 的单调递减区间为( )
3
A. 2,
B.
3 2
,
C. ,1
D.
,
3 2
