最小元素法
管理运筹学基础 答案

《管理运筹学基础》判断正误线性规划问题的一般模型中不能出现等式约束。
正确答案:说法错误2.在线性规划模型的标准型中,b j(j=1,2,…m)一定是非负的。
正确答案:说法正确解答参考:3.判断正误线性规划问题的基本解一定是基本可行解正确答案:说法错误解答参考:5.判断正误同一问题的线性规划模型是唯一的。
正确答案:说法错误解答参考:12.第一个顶点和最后一个顶点相同的闭链叫回路。
正确答案:说法错误解答参考:14.判断正误Djisktra算法可求出非负赋权图中一顶点到任一顶点的最短距离。
正确答案:说法正确解答参考:15.简述编制统筹图的基本原则。
参考答案:统筹图是有向图,箭头一律向右;统筹图只有一个起始点。
一个终点,没有缺口;两个节点之间只能有一个作业相连;统筹图中不能出现闭合回路。
17.简述西北角法、最小元素法、差值法确定运输问题初始基本可行解的过程并指出那种方法得出的解较优。
参考答案:西北角法:按照地图中的上北下南,左西右东的判断,对调运表中的最西北角上的空格优先满足最大供应,之后划去一行或一列,重复这种做法,直至得到初始可行解。
最小元素法:对调运表中的最小运价对应的空格优先没醉最大供应,之后划去一行或一列,重复这种做法,直至得到初始可行解。
差值法:在运价表中,计算各行和各列的最小运价和次最小运价之差,选出最大者,它所在某行或某列中的最小运价对应的空格优先满足最大供应,重复这种做法,直至得到初始可行解。
一般来讲,用差值法求出的初始可行解最接近最优解,也就是最优的。
2.用图解法求最优解时,只需求出可行域顶点对应的目标值,通过比较大小,就能找出最优解。
正确答案:说法正确单纯形法计算中,选取最大正检验数对应的变量作为换入变量,将使目标函数的值增加更快。
正确答案:说法错误解答参考:6.若原问题有无穷多最优解,则其对偶问题也一定有无穷多最优解。
正确答案:说法正确解答参考:8.表上作业法中,任何一种确定初始基本可行解的方法都必须保证有(m + n -1)个变量。
3运输问题及其解法

m
n
m
(3.1-4)
将后 n 个约束相加,得
∑∑ xij = ∑ b j ,
j =1 i =1 j =1 m n
m
n
(3.1-5)
因为,
(3.1-4)式与(3.1-5)式是相同的.由此可见,这 m + n 个约束 ∑ ai = ∑ b j ,所以,
i =1 j =1
不是独立的.我们可以证明:当所有的 ai , b j 都大于零时,任何 m + n − 1 个约束都是相互独立 的.即,系数矩阵 A 的秩 r ( A) = m + n − 1 ,事实上,
位(称为需求量), 设 cij (i = 1, 2,L , m, j = 1, 2,L , n) 为由产地 Ai 运往销地 B j 的单位运费, xij 为从 Ai 调往 B j 的物资数量,试问如何调运,求能使总运费最小. 为了清楚起见,通常将上述数据列在一张表上,该表称为运输表(见表3.1-1).
初看起来,最小元素法十分合理,但是,有时按某一最小单位运价优先安排物品调运时, 却可能导致不得不采用运费很高的其他供销点对,从而使整个运输费用增加.对每一个供应地 或销售地, 均可由它到各销售地或到各供应地的单位运价中找出最小单位运价和次小单位运价, 并称这两个单位运价之差为该供应地或销售地的罚数.若罚数的值不大,当不能按最小单位运 价安排运输时造成的运费损失不大;反之,如果罚数的值很大,不按最小运价组织运输就会造 成很大损失,故应尽量按最小单位运价安排运输,元素差额法就是基于这种考虑提出来的. 现结合上例说明这种方法: 首先计算运输表中每一行和每一列的次小单位运价和最小单位运价之间的差值,并分别称 之为行罚数和列罚数;将算出的行罚数填入位于运输表右侧行罚数栏的左边第一列的相应格子 中,列罚数填人位于运输表下边列罚数栏的第一行的相应格子中. A1 行中的次小和最小单位运 价分别为8和6,故其行罚数为2, B1 列中次小单位运价和最小单位运价分别为9和8,故其列罚 数为1,如此进行,可计算出 A1 , A2 , A3 的行罚数分别为2,2和4, B1 , B2 , B3 , B4 列的列罚数分别 为1,3,3,2.在这些罚数中最大者为4(在表4.2 - 6中用小圆圈标出),它位于 A3 行,由于在
最小元素法

什么是最小元素法[1]最小元素法是找出运价表中最小的元素,在运量表内对应的格填入允许取得的最大数,若某行(列)的产量(销量)已满足,则把运价表中该运价所在行(列)划去;找出未划去的运价中的最小数值,按此办法进行下去,直至得到一个基本可行解的方法。
注:应用西北角法和最小元素法,每次填完数,都只划去一行或一列,只有最后一个元素例外(同时划去一行和一列)。
当填上一个数后行、列同时被满足(也就是出现退化现象)时,也只任意划去一行(列)。
需要填入“0”的位置不能任意确定,而要根据规则来确定。
所谓退化现象是指:当在平衡表中某一处填入一数字后,该数字所在的行和列同时被满足,即需方的需求得到满足,同时供方的供应数量也已经供完的现象。
最小元素法的基本思想是:运价最小的优先调运,即从单位运价中最小的运价开始确定供销关系,然后次小,一直到给出初始基本可行解为止。
[编辑]最小元素法的例子[1]第一步:列出运价表和调运物资平衡表。
运用表上作业法时,首先要列出被调运物资的运价表和供需平衡表(简称平衡表),如表1,2所示。
第二步:编制初始调运方案。
首先,在运价表中找出最小的数值(若几个同为最小,则任取其中一个),A2B1最小,数值为1,这表示先将A2产品供应给B1 是最便宜的,故应给C21所对应的变量x21以尽可能大的数值。
显然x21=min{4,3}=3。
在表4中的A2B1处填上“3”。
B1列被满足,已不需要A1和A3再向它供货,故运价表2中的第一列数字已不起作用,因此将原运价表1中的第一列划去,并标注①(见表3)。
然后,在运价表中未划去的元素中找最小运价A 2B 3 = 2,让A 2 尽量供应满足B 3的需要,由于A 2的4已经供应了3T 给B 1,最多只能供应1T 给B 3。
于是在平衡表的A 2B 3格中填上“1”;相应地由于A 2所生产的产品已全部供应完毕,因此,在运价表中与A 2 同行的运价也不再起作用,所以也将它们划去,并标注②。
伏格尔法

什么是伏格尔法最小元素法的缺点是,为了节约一处的费用,有时造成在其他处要多花几倍的运费。
伏格尔法又称差值法,该方法考虑到,某产地的产品如不能按最小运费就近供应,就考虑次小运费,这就有一个差额。
差额越大,说明不能按最小运费调运时,运费增加越多。
因而对差额最大处,就应当采用最小运费调运。
伏格尔法的步骤伏格尔法一般能得到一个比用西北角法和最小元素法两种方法所得的初始基本可行解更好的初始基本可行解。
伏格尔法要求首先计算出各行各列中最小的cij,与次小的cij之间的差的绝对值,在具有最大差值的那行或列中,选择具有最小的cij的方格来决定基变量值。
这样就可以避免将运量分配到该行(或该列)具有次小的cij的方格中,以保证有较小的目标函数值。
所以,伏格尔法的基本步骤如下。
1、算出各行各列中最小元素和次小元素的差额,并标出差额最大的(若几个差额同为最大,则可任取其一)。
2、在差额最大的行或列中的最小元素处填上尽可能大的数。
3、对未划去的行列重复以上步骤,直到得到一个初始解。
由此可见,伏格尔法同最小元素法除在确定供求关系的原则上不同外,其余步骤相同。
伏格尔法给出的初始解比用最小元素法给出的初始解更接近最优解。
伏格尔法案例分析[编辑]案例一:伏格尔法的实例分析[1]例:某公司有三个加工厂A 1,A 2,A 3 生产某产品,每日的产量分别为7T ,4T ,9T ,该公司把这些产品分别运往四个销售点B 1,B 2,B 3,B 4,各销售点的每日销量分别为3T ,6T ,5T ,6T 。
从各工厂到各销售点的单位运价如表1所示。
问该公司如何调运产品,才能在满足各销售点需要量的前提下,使总费用最少?表1:第一步:求各行各列最小和次小元素的差值。
在表2中,各行的差值分别为0,1,1,各列的差值分别为2,5,1,3。
可见第二列差值最大,首先考虑第二列,在第二列中最小的cij 为c32=4,令x32=min{6,9}=6,填入表5-10 中,第二列饱和,划去该列。
运输问题(最小元素法+位势法)

运输问题教案某单位有三个工厂A1,A2,A3生产同一产品,有四个销售点,有四个销售点B1,B2,B3,B4进行销售。
各工厂的产量,各销售点的销量(吨)以及各加工厂到各销售点的单位运价(元/吨)见下表。
问:如何调运才能使总运费最少?解:第一步:确定初始方案(最小元素法)最小元素法:就近供应,即从单位运价表中最小的运价开始确定供销关系,依次类推,一直到给出全部方案为止。
产销平衡问题:∑(∑x ijnj=1)mi=1=总产量模型最多有m+n-1个独立约束方程第二步:解的最优性检验(位势法)检验数σij运费=现在的方案运费+非基变量*x ijσij意义:当从产地i调往销地j,1单位物资时,总运费的该变量。
若存在σij≤0,说明总费用有下降调整的空间。
位势法:对运输表上的每一行赋予一个数值u i,每一列赋予一个数值v j,使之满足:σij=C ij−(u i+u i)。
称u i为行位势,v j为列位势。
(1)基变量的检验数σij=0,填入。
(2)任取对偶问题变量为自由变量,设定其取值,不妨设u1=0。
(3)利用σij=C ij−(u i+u i),基变量检验数等于0,算出所有的u i和v j。
判断所有非基变量的检验数是否都大于等于零。
若是,为最优调运方案;否则,寻找下一个调运方案。
σij=C ij−(u i+u i)第三步解的调整优化,直至最优解调入格(入基变量):选择σij≤0的基变量入基,即x24调出格:偶数顶点小的那个改进方案表显然,检验数均大于等于0.因此,最佳调运方案即改进方案表中的调运方案。
即,A1运往B3地12吨,运往B4地4吨;A2运往B1地 8吨,运往B4地 2吨;A3运往B2地14吨,运往B4地8吨;。
运筹学【运输问题】考研必备

22
13
12 0
最小元素法(2)
1 6 1 8 2 5 3 22 9 4 7
2 5
3 3
4 14 1
132 712来自10 62715
19 13 12 0 13 0
最小元素法(3)
1 6 1 8 2 5 3 22 9 4 7
2 5
3 3
4 14 1
13
2 7
13
10
12
6
27
2
19 13 0 12 0 13 0
解: 西北角法
销地 产地
B1 6 4 7 2
B2 5 4 6 4
B3 3 7 5 3
B4 4 5 8 4
产量
A1 A2 A3
销量
4 6 3 13
(1) 从图的西北角开始, 填入a1与b1较小的值,b1=2, 即从A1运 给B1(2吨)B1已满足, 划去b1列, 并将a1=4-2=2
销地 产地
B1 26 4 7 2-2
例2
供应地 运价 销售地 1 a1=14 供 应 量 1 6 7 5
b1=22
a2=27
2
a3=19
3
3 8 4 2 7 5 9 10 6
2
b2=13
销 售 量
3
b3=12
4
b4=13
解:
初始基础可行解—最小元素法(1)
1 1 6 7
2 5
3 3
4 14
2
8
4
2
7
27
15
12
3 5 9 10 6 19 13
如何调运产品才能使总运费最小?
销地 产地
B1 6 4 7 2
B2 5 4 6 4
运筹学:运输问题

运输问题运输问题(transportation problem)一般是研究把某种商品从若干个产地运至若干个销地而使总运费最小的一类问题。
然而从更广义上讲,运输问题是具有一定模型特征的线性规划问题。
它不仅可以用来求解商品的调运问题,还可以解决诸多非商品调运问题。
运输问题是一种特殊的线性规划问题,由于其技术系数矩阵具有特殊的结构,这就有可能找到比一般单纯形法更简便高效的求解方法,这正是单独研究运输问题的目的所在。
§1运输问题的数学模型[例4-1] 某公司经营某种产品,该公司下设A、B、C三个生产厂,甲、乙、丙、丁四个销售点。
公司每天把三个工厂生产的产品分别运往四个销售点,由于各工厂到各销售点的路程不同,所以单位产品的运费也就不同案。
各工厂每日的产量、各销售点每日的销量,以及从各工厂到各销售点单位产品的运价如表4-1所示。
问该公司应如何调运产品,在满足各销售点需要的前提下,使总运费最小。
表4-1设代表从第个产地到第个销地的运输量(;),用代表从第个产地到第个销地的运价,于是可构造如下数学模型:(;运出的商品总量等于其产量)(;运来的商品总量等于其销量)通过该引例的数学模型,我们可以得出运输问题是一种特殊的线性规划问题的结论,其特殊性就在于技术系数矩阵是由“1”和“0”两个元素构成的。
将该引例的数学模型做一般性推广,即可得到有个产地、个销地的运输问题的一般模型。
注意:在此仅限于探讨总产量等于总销量的产销平衡运输问题,而产销不平衡运输问题将在本章的后续内容中探讨。
(;运出的商品总量等于其产量)(;运来的商品总量等于其销量)供应约束确保从任何一个产地运出的商品等于其产量,需求约束保证运至任何一个销地的商品等于其需求。
除非负约束外,运输问题约束条件的个数是产地与销地的数量和,即;而决策变量个数是二者的积,即。
由于在这个约束条件中,隐含着一个总产量等于总销量的关系式,所以相互独立的约束条件的个数是个。
管理运筹学运输问题最小元素法的思政元素

管理运筹学运输问题最小元素法的思政元素管理运筹学中的运输问题是一种特殊的线性规划问题,其目的是寻找满足运输需求的最小化运输费用的运输方案。
最小元素法是一种常用的求解运输问题的简单方法,其主要思想是按照单位运输成本从小到大的顺序选择运输方案,直到满足需求或者达到最大运输能力为止。
在管理运筹学中,思政元素可以渗透到运输问题的最小元素法中,以实现立德树人、成效驱动的教育理念。
以下是一些可能的思政元素:1.唯物主义世界观、人生观、价值观的体现:最小元素法在运输问题中的应用是基于客观存在的运输需求和实际存在的运输能力,这体现了唯物主义世界观。
同时,最小元素法选择单位运输成本最小的方案,这体现了实用主义的人生观和价值观。
2.爱国主义教育:在讲解最小元素法时,可以引入我国在交通运输领域的成就和贡献,例如我国的高铁建设、高速公路建设等。
这可以激发学生的爱国热情和民族自豪感。
3.职业道德教育:在讲解最小元素法时,可以强调在运输问题中需要遵循职业道德原则,例如合理规划运输路线、保证运输安全等。
这可以帮助学生树立职业道德意识。
4.创新精神教育:最小元素法是一种简单而实用的方法,但在实际应用中可能需要进行一些创新性的调整和改进。
例如,可以引导学生思考如何根据实际情况对最小元素法进行改进或创新,以更好地满足运输需求和降低运输成本。
5.团队合作教育:在讲解最小元素法时,可以强调团队合作的重要性。
例如,在应用最小元素法解决运输问题时,需要各个部门或人员的协作和配合,这需要学生具备团队合作意识和能力。
总之,将思政元素融入管理运筹学中的运输问题最小元素法中,可以帮助学生树立正确的世界观、人生观和价值观,提高其综合素养和创新精神,同时也能够激发其爱国热情和民族自豪感。
经济管理决策分析方法第六章2-运输问题-表上作业法

A B C
销量(bj)
3
6
5
6
第三步:在表4-5中再找出最小运价“3”, 这样一步步地进行下去,直到单位运价表上 的所有元素均被划去为止。
表4-6 A B C 销量(bj) 表4-7 甲 乙 甲 3 1 7 3 乙 11 9 4 6 丙 3 2 10 5 丙 4 1 6 6 3 5 6 丁 10 8 5 6 丁 3 产量(ai) 7 4 9
表上作业法
第一步 确定初始基可行解
与一般的线性规划不同,产销平衡的运输问
题一定具有可行解(同时也一定存在最优 解)。 最小元素法(the least cost rule)。
最小元素法
最小元素法的基本思想是就近供应,即从单位 运价表中最小的运价开始确定产销关系,依此 类推,一直到给出基本方案为止.
450
非基变量X12的检验数:
12 =(c12+c23)-(c13+c22)
=70+75-(100+65)=-20, 非基变量X21的检验数:
21 =(c +c )-(c +c ) 21 13 11 23
=80+100-(90+75)=15。 经济含义:在保持产销平衡的条件下,该非 基变量增加一个单位运量而成为基变量时目 标函数值的变化量。
表4-30 A B
甲 11 = 1 3
31 = 10 3 销量(bj) C
乙 12 = 2 22 = 1 6 6
丙 4 1 33 = 12 5
丁 3
24 = -1 3 6
产量(ai) 7 4 9
表4-33 乙 12 = 2 22 = 1 6 31 = 10 3 6 销量(bj) A B C 表4-34 甲 乙 丙 4 1 丁 3
数组最小值c语言

数组最小值c语言
数组最小值是数组中最小的元素值。
对于数组最小值的求解,在C语言中有多种方法。
一、遍历法
遍历法是最基本的求解数组最小值的方法。
遍历数组,依次比较每个元素的大小,如果当前元素小于最小值,则将当前元素赋值为最小值。
这种方法简单易懂,但时间复杂度较高,为O(n)。
二、排序法
排序法是将数组进行排序,然后取出最小值。
这种方法时间复杂度较低,为O(nlogn),但需要对数组进行排序,对数组的元素顺序会造成影响。
三、递归法
递归法采用分治策略,将数组分成两部分,分别求解左半部分和右半部分的最小值,然后将两部分的最小值进行比较,取出最小值。
这种方法时间复杂度为O(logn),但需要递归求解,比较复杂。
四、二分法
二分法是在有序数组中查找最小值的一种方法。
通过不断地将数组分成两部分,找到最小值所处的区间,直到区间缩小到只剩一个元素为止。
这种方法时间复杂度为O(logn),但需要对数组进行排序。
综上所述,选择方法要根据实际情况进行选择。
若数组长度较小,可以采用遍历法;若需要排序操作,可以采用排序法;若要求时间复杂度较低,可以采用递归法或二分法。
运筹学知识点
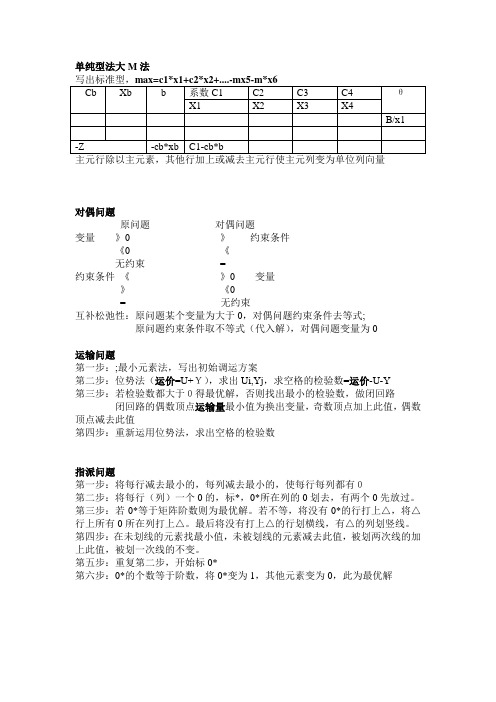
单纯型法大M法写出标准型,max=c1*x1+c2*x2+....-mx5-m*x6Cb Xb b 系数C1 C2 C3 C4 θX1 X2 X3 X4B/x1-Z -cb*xb C1-cb*b主元行除以主元素,其他行加上或减去主元行使主元列变为单位列向量对偶问题原问题对偶问题变量》0 》约束条件《0 《无约束=约束条件《》0 变量》《0= 无约束互补松弛性:原问题某个变量为大于0,对偶问题约束条件去等式;原问题约束条件取不等式(代入解),对偶问题变量为0运输问题第一步:;最小元素法,写出初始调运方案第二步:位势法(运价=U+Y),求出Ui,Yj,求空格的检验数=运价-U-Y第三步:若检验数都大于0得最优解,否则找出最小的检验数,做闭回路闭回路的偶数顶点运输量最小值为换出变量,奇数顶点加上此值,偶数顶点减去此值第四步:重新运用位势法,求出空格的检验数指派问题第一步:将每行减去最小的,每列减去最小的,使每行每列都有0第二步:将每行(列)一个0的,标*,0*所在列的0划去,有两个0先放过。
第三步:若0*等于矩阵阶数则为最优解。
若不等,将没有0*的行打上△,将△行上所有0所在列打上△。
最后将没有打上△的行划横线,有△的列划竖线。
第四步:在未划线的元素找最小值,未被划线的元素减去此值,被划两次线的加上此值,被划一次线的不变。
第五步:重复第二步,开始标0*第六步:0*的个数等于阶数,将0*变为1,其他元素变为0,此为最优解最小部分树破圈法:每次取一圈,从圈中划掉最大边,一直到无圈为止。
避圈法:选择最小的边存储问题R为需求速度,P为生产速度,C1存储费,C2缺货费,C3为固定费(进货,生产),K为货物的单位成本,Q为每次的批量模型一;不允许缺货单位时间费用C0= KR+√2*C1*C3*R最佳存储时间t0=√2*C3 / C1*R最佳批量Q0 =√2*C3*R / C1模型二;生产速度需求速度问题单位时间费用C=1/t*[C3+KQ+0.5*C1*t(P-R)*t]由于q=rt=pt上式C=C3/T+C1*(P-R)*R*T/2P +KR最佳生产批量Q=r *t0=√2*c3r*p/c1(p-r)最小总费用c=K*P+√2C1C3R*(P-R)/C1*P模型三:允许缺货单位时间费用c0=1/t[C3+KQ+0.5C1*T1+0.5C2*(T1-T2)*S]化简为;c0=minc(q,s)=KR+√2C1C2C3R/(C1+C2)最佳生产批量为Q=√2*C3*R(C1+C2)/C1*C2最佳周期为t0=√2*C3(C1+C2)/R*C1*C2单纯型法大M法写出标准型,max=c1*x1+c2*x2+....-mx5-m*x6Cb Xb b 系数C1 C2 C3 C4 θX1 X2 X3 X4B/x1-Z -cb*xb C1-cb*b主元行除以主元素,其他行加上或减去主元行使主元列变为单位列向量对偶问题原问题对偶问题变量》0 》约束条件《0 《无约束=约束条件《》0 变量》《0= 无约束互补松弛性:原问题某个变量为大于0,对偶问题约束条件去等式;原问题约束条件取不等式(代入解),对偶问题变量为0运输问题第一步:;最小元素法,写出初始调运方案第二步:位势法(运价=U+Y),求出Ui,Yj,求空格的检验数=运价-U-Y第三步:若检验数都大于0得最优解,否则找出最小的检验数,做闭回路闭回路的偶数顶点运输量最小值为换出变量,奇数顶点加上此值,偶数顶点减去此值第四步:重新运用位势法,求出空格的检验数指派问题第一步:将每行减去最小的,每列减去最小的,使每行每列都有0第二步:将每行(列)一个0的,标*,0*所在列的0划去,有两个0先放过。
最小元素法例题详解

最小元素法例题详解最小元素法是一种常用的数学方法,用于求解最优化问题。
其基本思想是将原问题分解成若干个子问题,然后对每个子问题求解得到最小元素,最后将这些最小元素组合起来得到原问题的最优解。
本文将通过详细的例题解析,帮助读者更好地理解和掌握最小元素法。
例题一某公司有三个部门,每个部门需要雇佣若干名员工。
已知每个员工的工资和能力值,要求在满足每个部门的人数要求的前提下,使得公司的总工资最小。
假设每个部门需要的员工人数分别为5人、8人和10人,且公司共有15名员工。
解答:首先,将原问题分解成三个子问题:在第一个部门中雇佣5名员工的最小工资和;在第二个部门中雇佣8名员工的最小工资和;在第三个部门中雇佣10名员工的最小工资和。
为了方便起见,我们可以将每个部门的员工按照能力值从小到大排序,然后选取前n名员工。
这样,每个子问题就可以转化为一个选择问题。
例如,在第一个部门中,我们需要选择5名员工,可以从前15名员工中进行选择,共有C(15,5)种选择方式。
接下来,我们需要确定每个子问题的最小元素。
在第一个部门中,我们可以按照工资从小到大排序,然后选择前5名员工,这样得到的工资和就是第一个部门的最小工资和。
同理,在第二个部门中,我们可以按照工资从小到大排序,然后选择前8名员工,这样得到的工资和就是第二个部门的最小工资和。
在第三个部门中,我们可以按照工资从小到大排序,然后选择前10名员工,这样得到的工资和就是第三个部门的最小工资和。
最后,我们将这些最小元素相加,得到公司总工资的最小值。
需要注意的是,这个最小值并不一定是唯一的,因为在每个子问题中,选取员工的方式可能不同,从而得到不同的最小元素。
例题二有n个任务需要完成,每个任务需要花费一定的时间和费用,每个任务只能被一个人完成。
现在有m个人可以进行任务,每个人有一定的时间和费用限制。
要求在满足每个人的时间和费用限制的前提下,完成所有任务的最小总费用。
解答:这是一个典型的分配问题,我们可以将其分解成n个子问题。
生产计划与控制运输表法的计算方法

生产计划与控制运输表法的计算方法下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by theeditor.I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!生产计划与控制:运输表法的计算方法解析在生产管理中,生产计划与控制是关键的一环,它涉及到资源的有效分配、生产效率的提升以及成本的控制。
最小元素法

最小元素法
最小元素法是一种用于查找排序数组中最小项的搜索算法,它通过检查数组中的每一
个元素,来找到最小值。
它相对于其他搜索算法更有效,因为它最多需要检查n个元素就
能找到最小值,其中n是数组的大小,而其他算法需要检查更多的数据。
1. 首先,从数组中获取第一个元素;
2. 然后,从剩余的数组中取出第二个元素,并与第一个元素比较;
4. 重复步骤2和3,直到所有的元素都已经检查过;
5. 最终,从比较的结果中留下最小的元素,这就是最小值。
最小元素法的时间复杂度为O(n),空间复杂度也为O(n),其中n为数组大小。
因此,它是一种比较快速而高效的搜索算法,可以快速检索出数组中最小元素,不需要比较太多
的元素就可以找到结果。
它适用于搜索已排序好的数组,但是它不能处理未排序的数组,
所以它只能用于特定的情况。
最小元素法

什么是最小元素法[1]最小元素法是找出运价表中最小的元素,在运量表内对应的格填入允许取得的最大数,若某行(列)的产量(销量)已满足,则把运价表中该运价所在行(列)划去;找出未划去的运价中的最小数值,按此办法进行下去,直至得到一个基本可行解的方法。
注:应用西北角法和最小元素法,每次填完数,都只划去一行或一列,只有最后一个元素例外(同时划去一行和一列)。
当填上一个数后行、列同时被满足(也就是出现退化现象)时,也只任意划去一行(列)。
需要填入“0”的位置不能任意确定,而要根据规则来确定。
所谓退化现象是指:当在平衡表中某一处填入一数字后,该数字所在的行和列同时被满足,即需方的需求得到满足,同时供方的供应数量也已经供完的现象。
最小元素法的基本思想是:运价最小的优先调运,即从单位运价中最小的运价开始确定供销关系,然后次小,一直到给出初始基本可行解为止。
[编辑]最小元素法的例子[1]第一步:列出运价表和调运物资平衡表。
运用表上作业法时,首先要列出被调运物资的运价表和供需平衡表(简称平衡表),如表1,2所示。
第二步:编制初始调运方案。
首先,在运价表中找出最小的数值(若几个同为最小,则任取其中一个),A2B1最小,数值为1,这表示先将A2产品供应给B1 是最便宜的,故应给C21所对应的变量x21以尽可能大的数值。
显然x21=min{4,3}=3。
在表4中的A2B1处填上“3”。
B1列被满足,已不需要A1和A3再向它供货,故运价表2中的第一列数字已不起作用,因此将原运价表1中的第一列划去,并标注①(见表3)。
然后,在运价表中未划去的元素中找最小运价A2B3 = 2,让A2尽量供应满足B3的需要,由于A2的4已经供应了3T给B1,最多只能供应1T给B3。
于是在平衡表的A2B3格中填上“1”;相应地由于A2所生产的产品已全部供应完毕,因此,在运价表中与A2同行的运价也不再起作用,所以也将它们划去,并标注②。
仿照上面的做法,一直做下去,就可以得到表4。
最小元素法

什么是最小元素法⑴址小兀倉法足找岀运价农中址小的儿瓠住公笊&内对稅的惰细入ft许取得的俎人数・拓朵行(缚的产趴锚”心满足.H'ICifi价左f诔运价所们“尺)划山恂I;木划人的运价屮的第小数ffl.按此〃比进行下£・W至側乳个以木对厅駢的力M.注,应用杓北m”・和址小兀素比.何次坝完tt祁只划上行或列•只冇址际个元食例外仆d时划厶行和列)■ -un上个«t*;tf•列制两故洒足(也祯建出现迢化現彖>时•也只任盘划上<列〉。
需枕境入•()•的位買水址任息的定•闻徃帜挟现创來的宅。
所ifliHtt.现策圧怡=在丫衞农叩果处堆入数丫垢•谡飲丫所在的仃棚列创时桃褂也即濡方的寿球符列满足・网时供方的e^aw也己经供完的现跟。
Md'kt法的棊▲思魁址;运价放水的优先调运•即从m椅运价中於小的运价歼始确定倪舖关系.体麻次小.nmiiiw 始前本吋行解为止・(«»«]最小元索法的例子⑴SR…步■列出运价表和调运ttftYtt*.运用农1件〃浓时.首先変列岀孩调运韧茨的运价农和供需丫衝农《简称丫衛农〉.帕衣1・2所示•« •步:编制初&试运方*.占先./";价次中找出时小的裁你片JI个M为站小.期仟取茸中个).ARM小.质侑为1.这衣示先将A・产呂供应給B1 ilMftn的.故应始G.所对疵的x,U尽叫後大的散仿,«^x;l Tnin{4.3}.3. 4衣4中的/I几处览 E 弘列被満足.已不芮耍儿和儿再瀚它供货• 故迄价& 2中的雄列政7已Hl Wilt将廉远价&1中的第刊划山并休注①<见& 3入此时,在运份龙中只有也对应的运价10没台划抻.血BM有3TIMU为门芮足供需T ft,所以W^6:T»J A上对应仏乩处应Ml入T.这样就得判点5:对J编:M初始力案说明以卜儿点:门用域小儿*也编:M初始说辽方纭这里的■加小*指馬曹両三8USU 4、M 定足域小的.可以作为初始方为•傑.其填有盘庁的方格供应点个敢如咼求点个1.即(m・ri・1)•第三步,初始方案的检鲨与诉號・西北角法的例子⑴从左1中可知.总的产升.总的错駅敏产销足半衡的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
什么是最小元素法[1]
最小元素法是找出运价表中最小的元素,在运量表内对应的格填入允许取得的最大数,若某行(列)的产量(销量)已满足,则把运价表中该运价所在行(列)划去;找出未划去的运价中的最小数值,按此办法进行下去,直至得到一个基本可行解的方法。
注:应用西北角法和最小元素法,每次填完数,都只划去一行或一列,只有最后一个元素例外(同时划去一行和一列)。
当填上一个数后行、列同时被满足(也就是出现退化现象)时,也只任意划去一行(列)。
需要填入“0”的位置不能任意确定,而要根据规则来确定。
所谓退化现象是指:当在平衡表中某一处填入一数字后,该数字所在的行和列同时被满足,即需方的需求得到满足,同时供方的供应数量也已经供完的现象。
最小元素法的基本思想是:运价最小的优先调运,即从单位运价中最小的运价开始确定供销关系,然后次小,一直到给出初始基本可行解为止。
[编辑]
最小元素法的例子[1]
第一步:列出运价表和调运物资平衡表。
运用表上作业法时,首先要列出被调运物资的运价表和供需平衡表(简称平衡表),如表1,2所示。
第二步:编制初始调运方案。
首先,在运价表中找出最小的数值(若几个同为最小,则任取其中一个),A
2B1最小,数值为1,这表示先将A2产品供应给B1 是最便宜的,故应给C21所对应的变量x21以尽可能大的数值。
显然x
21=min{4,3}=3。
在表4中的A2B1处填上“3”。
B1列被满足,已不需要A1和A3再向它供货,故运价表2中的第一列数字已不起作用,因此将原运价表1中的第一列划去,并标注①(见表3)。
然后,在运价表中未划去的元素中找最小运价A
2B3 = 2,让A2尽量供应满足B3的需要,由
于A
2的4已经供应了3T给B1,最多只能供应1T给B3。
于是在平衡表的A2B3格中填上“1”;相
应地由于A
2所生产的产品已全部供应完毕,因此,在运价表中与A2同行的运价也不再起作用,所以也将它们划去,并标注②。
仿照上面的做法,一直做下去,就可以得到表4。
此时,在运价表中只有A
1B4对应的运价10没有划掉,而B4尚有3T需求,为了满足供需平
衡,所以最后在平衡表上对应A
1B4处应填入“3”,这样就得到表5。
对于编制初始方案说明以下几点:应用最小元素法编制初始调运方案,这里的“最小”系指局部而言,就整体考虑的运费不见得一定是最小的。
可以作为初始方案的调运方案,其填有数字的方格数应是供应点个数加需求点个数之和再减1,即(m+n-1)。
第三步:初始方案的检验与调整。
西北角法的例子[1]
从表1中可知,总的产量=总的销量,故产销是平衡的。
第一步:列出运价表和调运物资平衡表。
运用表上作业法时,首先要列出被调运物资的运价表和供需平衡表(简称平衡表),如表1,2所示。
第二步:编制初始调运方案。
首先在表2的西北角方格(即左上角方格,对应变量x
11),尽可能取最大值:
x
11=min{3,7}=3
将数值3填入该方格(见表3)。
由此可见x
21,x31必须为0,即第一列其他各方格都不能取非零
值,划去第一列。
在剩下的方格中,找出其西北角方格x
12,
x
12=min{6,7-3}=4
将4填入它所对应方格,第一行饱和,划去该行。
再找西北角方格x
22,
x
22=min{6-4,4}=2
将2填入x
22所对应方格,于是第二列饱和,划去该列。
继续寻找西北方格为x23,
x
23=min{5,4-2}=2
将2填入x
23所对应方格,第二行饱和,划去该行。
剩下方格的西北角方格为x33,
x
33=min{5-2,9}=3
将3填入x
33所对应方格,第三列饱和,划去该列。
最后剩下x34方格,取x34 = 6。
这样我们就找到了m+n-1=3+4-1=6个基变量,它们为:x
11 = 3,x12 = 4,x22 = 2,x23 = 2,x33 = 3,x34 = 6。
显然它们用折线连接后不形成闭回路。
这就是西北角法所找初始基可行解,所对应的目标值为:
2×200+1×250+3×150+1×150+3×250+3×300+4×200=4000
我们找到的初始基可行解可通过各行方格中数值之和是否等于产量,各列方格中数值之和是否等于销量来简单验证。
利用西北角法找初始基可行解简单可行,但也存在问题。
例如在表3中可见c
35 = 4,单价高于该行其他各方格,最简单想法是单价小的情况下多运些货物,这样总运费会更小些,最小元素法就改进了西北角法的缺点。
