积分、线性回归、2乘2列联表、频率分布直方图高考双向细目表
近6年高考双向细目表包括2019(2020冲刺利器)高考数学

线性规划
双曲线椭圆 渐近线
二项式系数 排列组合
三角函数性 质
三视图面积 逻辑推理 程序框图
程序框图 程序框图 圆柱球体积
三角函数相 关
双曲线圆离 心率
等差数列和
抛物线最小 直三棱柱异 椭圆圆直线
值
线角
离心率
方程不等式
极值点极小 值
零点求参
推理新概念
三角形向量 数量积
矩形圆向量 最值
向量夹角模
二项分布方 差
解三角形
解三角形面 积
保险统计概 率
面面垂直二 面角
线性回归分 析
面面垂异线 角
概率均值茎 叶图
统计正态分 布
平行二面角 体积
垂直线面角
平行二面角
线面垂直二 分布列方案 线面平行线 回归分析回 立几作图线 立几垂直二 统计回归方 互斥分布列 函数直方图
面角
优选
面角
归方程 面角
面角
程
期望
概率
椭圆面积范 围
对立独立概 率
二项分布
数列递推 双曲线的几何性质
解三角形面 正弦定理,余弦定
积
理,三角恒等变换
分段函数分 直四棱柱,空间中
布列
平行关系,二面角
垂直二面角
直线与抛物线的位 置关系,弦长问题
圆抛物线讨 利用导数研究函数
论
的极值、零点
导数单调性 最值
相互独立事件,分 布列,等比数列定 义及求和公式
参数方程极坐标与
等比数列 函数的图象与性质
程序框图 古典概型,组合数
三视图体积 平面向量的数量积
双曲线抛物 循环结构的程序框
线
图
三角函数单 等差数列的通项公
数学双向细目表

√ √
√
## 确定物体的位置
√
## 证明的含义
√
## 证明的必要性
√
证 ## 定义、命题、定理的含义 √
明 ## 命题的条件(题设)和结论 √ √
的 ## 逆命题的概念
√
含 ## 互逆命题
√√
义 ## 反证法的含义
√
## 综合证明法
√
√
##
一条直线截两条平行直线所 得的同位角相等
√
两条直线被第三条直线所
√
√
## 多边形的内角和外角和公式 √
√
## 正多边形的概念
√
##
平行四边形、矩形、菱形、 正方形、梯形的概念和性质
√
√
图
## 四边形的不稳定性
√
形
## 平行四边形的性质和判定
√
√
的 认 识
四 边 形
##
矩形、菱形、正方形的性质 和判定
##
等腰梯形及直角梯形的有关 性质和判定
√
√
√ √
##
线段、矩形、平行四边形、 三角形的重心及物理意义
60 一次函数的意义
√
61 确定一次函数表达式 一 62 画一次函数的图象 函次 数函
√ √
第 3 页,共 13 页
数
难度及系数7:2:1 基础题 稍难题 难题
√ √
√
√
√
√ √
初中数学知识点考试双向细目表
知知
知识与技能
过程与方法
题型
分值
识识编 领单号 域 元一
知识内容
了解 理解 掌握
灵活 应用
经历 体验 探索 选择题 填空题 解答题
初中数学知识点考试双向细目表
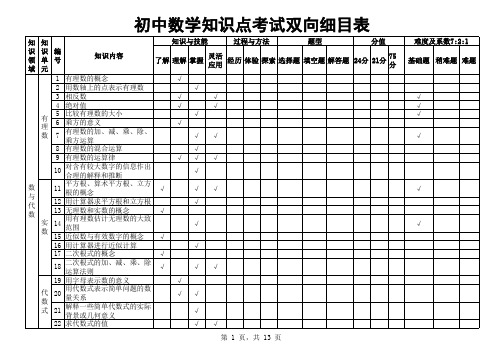
√ √
初中数学知识点考试双向细目表
知 识 领 域 知识与技能 过程与方法 题型 分值 难度及系数7:2:1 知 识 编 知识内容 灵活 单 了解 理解 掌握 经历 体验 探索 选择题 填空题 解答题 24分 21分 75分 基础题 稍难题 难题 角 号 应用 元 86 补角、余角、对顶角 √ 等角的余角相等、等角的补 87 √ 角相等、对顶角相等 88 垂线、垂线段 √ 89 垂线段最短的性质 √ √ 90 点到直线距离的意义 √ 过一点有且仅有直线垂直于 91 √ √ 已知直线 相 用三角尺或量角器过一点画 交 92 √ 一条直线的垂线 线 93 线段垂直平分线及其性质 √ 与 94 两直线平行,同位角相等 √ √ √ 平 过直线外一点有且仅有一条 行 95 √ 直线平行于已知直线 线 用三角尺和直尺过已知直线 96 √ 外一点画这条直线的平行线 两条平行直线之间距离的意 97 √ √ 义 98 度量两条平行线之间的距离 √ 三角形有关概念(内角、外 99 √ 角、中线、高、角平分线) 画任意三角形的角平分线、 ## √ √ 中线和高 ## 三角形的稳定性 √ ## 三角形中位线的性质 √ √ ## 全等三角形的概念 √ 三 ## 两个三角形全等的判定 √ √ √ √ 角 ## 等腰三角形的有关概念 √ 形 ## 等腰三角形性质和判定 √ √ 第 5 页,共 13 页
45 不等式的基本性质 46 一元一次不等式的解法 在数轴上表示不等式(组) 47 的解集 48 解一元一次不等式组 根据具体问题中的数量关 系,列出一元一次不等式或 49 一元一次不等式组,解决简 单的问题 具体问题中的两个变量之间 50 的关系 从表格、图象中分析某些变 51 量之间的关系 用表格或关系式表示某些变 52 量之间的关系 53 常量、变量的意义 √ 54 函数的概念及其表示方法 √ 函 对简单实际问题中的函数关 数 55 系进行分析 56 确定函数的自变量取值范围 57 求函数值 用适当的函数表示法刻画某 58 些实际问题中变量之间的关 系 对变量的变化规律进行初步 59 预测 60 一次函数的意义 61 确定一次函数表达式 一 62 画一次函数的图象 函 次 数 函 数
高考数学双向细目表模板

高考数学双向细目表模板江西高考数学自主命题知识双向细目表(理工农医类)备考试内容能力层次高考要求 05年 06年 07年 08年注有关集合的概念和理解意义集合与集合运算有关术语和符号,1 1 6 2掌握能正确地表示出一些简单的-集合逻辑联结词"或". " 逻辑联结词与四且" "非"的含义;理解种命题四种命题及其相互关系充分条件与必要掌握充要条件的意义条件映射与函数理解有关概念函数的定义17(1) 17(1) 3,12 域?解析式?值掌握有关概念域判断一些简单函数函数的单调性掌握单调性的方法能利用函数的奇13偶性与图象的对函数的奇偶性掌握称性的关系描述函数图象反函数的概念及了解互为反函数图象间的关系反函数会求一些简单函 14 13 理解数的反函数解决有关数学问 6 二次函数掌握题指数函数与对数10 指数函数与对掌握函数的概念图象数函数和性质函数的图象理解有关概念 12 利用函数知识应用函数知识解掌握解应用题决实际难度问题函数的综合问综合运用函数知 22 掌握题识解决数学问题数列、通项公式的理解概念数列的概念 Sa掌握由求的公式 nnwhen the Terminal level when installed on the line number (Word) should be arranged from top to bottom. 6.4.4 cable core must be completely loose and straight, but not damage the insulation and core. Core bundle of the same plate vertically or horizontally arranged 等差数列的通项公掌握式,前n项和公式等差数列等差数列的性质解熟练应用题等比数列的通项公掌握式,前n项和公式等比数列等比数列的性质解 21 19 熟练应用题有关概念及解决实21 22 22 5 数列的综合应用掌握际问题任意角的正弦、余弦、正切的定义,用三角函数线表三角函数概念示正弦、余弦和正掌握公式切;同角三角函数的基本关系式;正弦、余弦的诱导公式通过公式的推导, 3了解它们的内在和差倍公式掌握联系,从而培养逻辑推理能力会用三角函数线5 19(2) 5 6画正弦函数,正切函数的图象,由诱图象与性质掌握导公式画余弦函数的图象;理解它们的性质; 会用"五点法"A,、、的物,理解yAx,,sin(),, 理意义的图象用"五点法"画函数yAx,,sin(),,掌握的简图三角最值及综利用三角知识求11 掌握合应用最值运用所学二角知18 18 应用掌握识解决实际问题向量、向量的加共线向量,平面向 15 了解法与减法、实数量基本定理when the Terminal level when installed on the line number (Word) should be arranged from top to bottom. 6.4.4 cable core must be completely loose and straight, but not damage the insulation and core. Core bundle of the same plate vertically or horizontally arranged 与向量的积向量,向量共线的 7理解充要条件,平面向量的坐标向量的几何表示,实数与向量的积,掌握向量加法与减法,乎面向量的坐标运算用平面向量的数量积可以处理有了解关长度、角度和垂数量积直等问题平面向量的数量6 13掌握积及其几何意义;向量垂直的条件平面两点间的距离公式,线段的定掌握距离公式、定比比分点和中点坐分点标公式,灵活运平移公式用正弦定理、余弦 19(1) 17 正余弦定理掌握定理,并能运用它们解斜三角形不等式的概念理解不等式的性质性质两个(不扩展到三 11个)正数的算术平均数不小于它们的几何平均数的均值不等式掌握定理.并会简单的应用; 分析法、综合法、比较法证明简单的不等式二次不等式、简单17(2) 17(2) 17(2) 14 解不等式掌握的分式不等式的解法不等式理解 ||||||||||ababab,,,,,绝对值不等式简单的绝对值不掌握等式的解法不等式的应用灵活运用有关概念 22直线的倾斜角和直线方程及位理解斜率置关系掌握两点斜率公式:一when the Terminal level when installed on the line number (Word) should be arranged from top to bottom. 6.4.4 cable core must be completely loose and straight, but not damage the insulation and core. Core bundle of the same plate vertically or horizontally arranged点和斜率求出直线方程的方法;点斜式、两点式和一般式,熟练求出直线方程.两条直线平行与垂直的条件,两条直线成的角、点到直线的距离公式,两条直线的位直关系简单的线性规划了解问题,线性规划的意义线性规化二元一次不等式掌握表示平面区域,简单线性规划问题了解参数方程的概念理解圆的参数方程圆的方程圆的标准方程和 16 掌握一般方程直线与圆掌握相关概念 3 16椭圆的标准方程16 21 9 掌握椭圆及其几何性质了解椭圆的参数方程双曲线的标准方 9 21 21 双曲线掌握程及其几何性质抛物线的标准方22 4 15 抛物线掌握程及其几何性质直线与圆锥曲线掌握综合 16 21 21 21轨迹方程掌握综合 22 21 21 21综合应用熟练掌握综合 22 21 21 21平面的基本性质,斜二侧的画法;画出空间两条直线的各种位置关系的图空间直线理解形,根据图形想象它们的位置关系;直线与直线所成角、距离when the Terminal level when installed on the line number (Word) should be arranged from top to bottom. 6.4.4 cable core must be completely loose and straight, but not damage the insulation and core. Core bundle of the same plate vertically or horizontally arranged 画出空间直线和平面的各种位置关系的图形,根据图形想象它们的位置关直线与平面掌握系;直线和平面平行、垂直的判定定理和性质定理,线面角和距离,三垂线定理及其逆定理平面与平面所成的角、距离,掌握两平面与平面掌握个平面平行和垂直的判定定理和性质定理(多面体、凸多面体、棱柱棱锥的概念、了解正多面体、欧拉公式棱柱的性质,会画11,15 15 7 16 出直棱柱的直观简单多面体图,正棱锥的性质,会画正棱锥的直观掌握图,会求几何体的表面积、体积,会处理几何体的侧面展开图问题了解球的概念球的性质、表面积、9 8 10 球掌握体积公式,球面距离通过空间图形的20 20 20 20 各种位置关系间的教学,培养空间综合应用掌握想像能力,发展逻辑思维能力,并培养辩证唯物主义观点理解排列、组合的意义分类、分步计数原理,排列数计算公排列组合式,组合数计算公掌握式和组合数的性质,并能用它们解决一些简单的应用when the Terminal level when installed on the line number (Word) should be arranged from top to bottom. 6.4.4 cable core must be completely loose and straight, but not damage the insulation and core. Core bundle of the same plate vertically or horizontally arranged 问题(二项式展开式的性4 8 4 8质,并能用它们计二项式掌握算和证明一些简单的问题等可能性事件的概率,互斥事件的意了解义,相互独立事件的意义,随机事件计算等可能性事件12 10 10的概率,会用互斥事件的概率加法公概率式和相互独立事件的概率乘法公式计掌握算一些事件的概率,会计算事件在n次独立重复试验中恰好发生k次的概率离散型随机变量的了解意义及其期望值和方差的意义会求出某些简单的19 18 19 18随机变量离散型随机变量的分布列;会根据离掌握散型随机变量的分布列求出期望值、方差正态分布的意义及主要性质;线性回了解归的方法和简单应用会用随机抽样、系统计统抽样、分层抽样等常用的抽样方法掌握从总体中抽取样本;会用样本频率分布去估计总体分布数学归纳法的原理解理数学归纳法能用数学归纳法证掌握明一些简单的数学命题when the Terminal level when installed on the line number (Word) should be arranged from top to bottom. 6.4.4 cable core must be completely loose and straight, but not damage the insulation and core. Core bundle of the same plate vertically or horizontally arranged 从数列和函数的变化趋势了解数了解列和函数的极限的概念;连续的意义借助数学直观理17(1) 极限解闭区间上连续理解函数有最值的性质极限的四则运算法8 13 2 4 掌握则(会求某些数列与函数的极限导数的概念;复合了解函数求导法则理解导函数的概念函数在一点处的导 5 11数的定义和导数的导数几何意义;基本导掌握数公式;和、差、积、商的求导法则;会求某些简单函数的导数;可导函数的单调性17(1) 7 12与其导数的关系;了解可导函数在某点取导数应用得极值的必要条件和充分条件会求一些实际问题掌握的最大值和最小值复数的有关概念及了解复数的代数表示和几何意义复数运算法则,能进行2 2 1 1复数代数形式的加掌握法、减法、乘法、除法运算when the Terminal level when installed on the line number (Word) should be arranged from top to bottom. 6.4.4 cable core must be completely loose and straight, but not damage the insulation and core. Core bundle of the same plate vertically or horizontally arranged。
最新高考理科数学双向细目表

最新高考理科数学双向细目表模块知识点考查内容知识要求2017 分值2018 分值2019 分值备注了解理解掌握集合集合的含义与表示集合的含义、元素与集合的属于关系√列举法、描述法√集合间的基本关系包含与相等的含义√识别给定集合子集√全集与空集√集合的基本运算并集与交集含义与运算√补集含义与运算√韦恩图表达集合的关系与运算√函数概念与基本初等函数I 函数简单定义域值域,了解映射√图像法、列表法、解析法表示函数√分段函数√函数单调性、最值及几何意义√函数奇偶性√函数图像研究函数性质√指数函数指数函数模型背景√有理、实数指数幂、幂的运算√指数函数概念、单调性√指数函数图像过定点√对数函数对数的概念及其运算√换底公式、自然对数、常用对数√对数函数的概念、单调性√对数函数图像过定点√指数函数与对数函数互为反函数√幂函数幂函数概念√幂函数图像√函数与方程二次函数、零点与方程根√一元二次方程根的存在性及根的个数√结合图像,用二分法求近似解√函数模型及应用指、对、幂的增长特征√函数模型的应用√立体几何初步空间几何体柱锥台的结构特征√三视图√斜二测画出直观图√平行、中心投影√会画视图和直观图√球柱锥台的表面积和体积公式√点线面位置关系线面位置关系定义√线面平行判定√面面平行判定√线面垂直判定√面面垂直判定√线面平行性质√面面平行性质√线面垂直性质√面面垂直性质√用已获结论证明空间图形的位置关系√平面解析几何初步直线与方程结合图形,确定直线位置的几何要素√直线倾斜角和斜率√过两点的直线斜率计算公式√判定直线平行或垂直√点斜式、两点式、一般式√斜截式与一次函数的关系√两条相交直线的交点坐标√两点间距离公式√点到直线距离公式√两条平行直线间距离√圆与方程圆的几何要素,标准方程和一般方程√判断直线与圆的位置关系√判断两圆的位置关系√应用直线与圆的方程√代数方法处理几何问题的思想√空间直角坐标系空间直角坐标表示点的位置√空间两点间距离公式√算法初步算法的含义、程序框图算法的含义和思想√顺序、条件分支、循环逻辑结构√基本算法语句输入、输出、赋值、条件、循环语句√统计随机抽样会用简单随机抽样从总体中抽取样本√分层抽样和系统抽样√用样本估计总体频率分布表、频率分布直方图、折线图√茎叶图√数据标准差意义和作用√平均数和标准差√用样本估计总体思想√变量的相关性会画散点图,并认识变量间的相关关系√最小二乘法,线性回归方程√概率事件与概率频率与概率的意义√互斥事件的概率加法公式√古典概型古典概型计算公式√随机事件所含的基本事件数及发生概率√几何概型随机数的意义,运用模拟方法估计概率√几何概型的意义√基本初等函数II 任意角的概念、弧度制任意角的概念√弧度制的概念、弧度与角度的互化√三角函数理解正弦、余弦、正切的定义√单位圆的三角函数线√诱导公式√会画三角函数图像√三角函数周期性√正余弦单调性、最值与X轴交点等性质√正切函数性质√同角三角函数的基本关系式√正弦型函数参数对图像变化的影响√平面向量平面向量的实际背景及基本概念向量的实际背景√平面向量的概念√两个向量相等√向量的几何表示√向量的线性运算加法、减法、几何意义√数乘的运算、几何意义√两个向量共线的含义√线性运算的性质和几何意义√平面向量基本定理和坐标表示平面向量基本定理及意义√正交分解及坐标表示√加法、减法、数乘坐标运算√用坐标表示平面向量共线的条件√平面向量的数量积平面向量的数量积含义与物理意义√平面向量的数量积与向量投影关系√数量积坐标表达式与运算√用数量积表示夹角√用数量积判断两个向量的垂直关系√向量的应用解决平面几何问题√解决实际问题√三角恒等变换和与差的三角函数公式两角和与差的余弦、正弦、正切公式√二倍角公式√三角恒等变换积化和差、和差化积√半角公式√解三角形正弦定理余弦定理正弦定理√余弦定理√应用三角形度量问题√数列数列的概念与简单表示法数列的概念√列表、图像、通项公式表示方法√数列是自变量为正整数的函数√等差数列、等比数列等差数列概念√等差数列通项公式和求和公式√等比数列概念√等比数列通项公式和求和公式√等差数列与一次函数√等比数列与指数函数√不等式不等关系实际背景√一元二次不等实际情景中抽象√式与二次函数、一元二次方程联系√会解一元二次不等式,设计程序框图√二元一次不等式组与简单的线性规划问题实际情景抽象出二元一次不等式组√二元一次不等式组表示平面区域√二元线性规划问题√基本不等式了解证明过程√解决最值问题√常用基本逻辑用语命题及其关系命题的概念√四种命题及其关系√充分、必要、充要条件√简单的逻辑联结词或、且、非√全称量词与存在量词全称量词√存在量词√含有量词命题的否定√圆锥曲线与方程圆锥曲线实际背景√椭圆定义几何图形标准方程、简单性质√抛物线定义几何图形标准方程简单性质√双曲线定义几何图形标准方程简单性质√简单应用、数形结合思想√曲线与方程方程的曲线与曲线的方程√空间向量与立体几何空间向量及其运算空间向量概念、基本定理、坐标√空间向量线性运算√空间向量数量积√用空间向量数量积表示共线与垂直√空间向量的应用直线方向向量与平面的法向量√线线、线面、面面平行关系√线线、线面、面面垂直关系√三垂线定理√线线、线面、面面夹角计算√导数及其应用导数概念及几何意义导数概念实际背景√导数的几何意义√导数的运算求导运算法则√基本初等函数导数公式√在研究函数中应用单调性与导数关系√函数取极值的必要条件和充分条件√会求函数的极值√会求闭区间上的最值√生活中的优化问题实际问题√定积分与微积分定积分概念、实际背景、思想√微积分基本定理√推理与证明合情推理与演绎推理归纳和类比推理√演绎推理的基本模式√联系和差异√直接证明与间接证明分析法与综合法√反证法√数学归纳法数学归纳法√数系的扩充与复数的引入复数的概念复数的概念√复数相等的充要条件√复数代数表示法与几何意义√复数的四则运算四则运算√加减法运算的几何意义√计数原理分类加法、分步乘法分类加法√分步乘法√排列与组合排列概念与公式√组合概念与公式√二项式定理证明二项式定理√展开式有关问题√概率与离散型随机变量与分布列√统计概率超几何分布√条件概率√两个事件相互独立√N次独立重复试验与二项分布√均值、方差√正态分布曲线特点及意义√统计案例独立性检验√回归分析√坐标系与参数方程坐标系用极坐标表示点的位置√极坐标与直角坐标互化√简单图形的方程√柱坐标系、球坐标系表示空间中点位置√参数方程参数方程和参数的意义√直线、圆、圆锥曲线的参数方程√平摆线与渐开线√不等式选讲含绝对值不等式几何意义√绝对值三角不等式√柯西不等式不同形式√几何意义√柯西不等式一般情参数配方法√排序不等式向量递归法√伯努利不等式数学归纳法√均值不等式求极值√证明不等式方法比较、综合、分析、反证、放缩√。
2019级高三二诊数学双向细目表及打分板

了解理解掌握权重比例集合的交集、补集运算选择题150.85√三角恒等变换选择题350.8√向量的投影选择题450.7√充分必要条件选择题650.65√三角函数的图象与性质选择题750.65√函数的基本性质选择题1050.5√解三角形选择题1150.4√导数的几何意义选择题1250.25√复数的运算填空题1350.85√新定义问题(二元变量)填空题1550.5√等比数列的通项公式解答题17(I)60.7√数列求和解答题17(II)60.4√不等式恒成立问题解答题21(I)60.4√函数与不等式综合问题解答题21(II)60.2√双曲线的基本性质选择题250.8√直线与圆的位置关系选择题950.5√直线与抛物线综合问题填空题1650.25√椭圆的标准方程解答题20(I)50.7√直线与椭圆的位置关系解答题20(II)70.3√空间线线关系、线面关系选择题850.6√三棱锥的外接球问题填空题1450.75√空间直线与直线的垂直关系解答题19(I)50.6√三棱锥的体积解答题19(II)70.5√茎叶图,数字特征分析选择题550.7√独立性检验解答题18(I)60.7√古典概型解答题18(II)60.6√圆的普通方程,直线的极坐标方程解答题22(I)50.6√直线极坐标方程的应用解答题22(II)50.4√绝对值不等式的化简解答题23(I)50.6√不等式的证明解答题23( II)50.4√1500.56269628100%解析几何27分(18%)22分(14.7%)2016级高三二诊考试文科数学命题双向细目表能力层次分值难度预估题型题号内容板块具体内容立体几何数与代数74分(49.3%)概率/算法/统计17分(11.3%)10分(6.7%)不等式选讲统计百分比坐标系与参数方程吾将上下而求索吾将上下而求索2016级高三二诊考试数学网上评卷题组切分计划切分题组号阅卷任务(题号)打分板分值分值区间1一二、13~16420均为0~52二三、17212文理科均为(Ⅰ)0~6,(Ⅱ)0~6。
高考数学知识点双向细目表

高考数学知识点双向细目表在高中阶段,数学是学生们的重要学科之一,也是高考必考科目之一。
为了顺利备战高考,了解数学知识点是非常重要的。
本文将为大家提供一份高考数学知识点双向细目表,以帮助同学们更好地了解数学知识体系和复习规划。
首先,我们来了解一下高考数学知识点的分类。
数学高考知识点主要包括代数、几何、三角学、概率与统计以及数学思维能力等五个方面。
每个方面又包含了具体的知识点。
下面将以这五个方面进行详细介绍。
代数部分是数学中的基础内容,主要包括函数、方程与不等式、数列与数学归纳法、概率与统计等几个知识点。
其中函数是代数部分的核心,包括一次函数、二次函数、指数函数、对数函数等。
函数的性质、图像与应用都是需要掌握的内容。
方程与不等式也是非常重要的知识点,包括一元一次方程、二元一次方程、二次方程、绝对值不等式以及分式方程等。
此外,数列与数学归纳法是代数部分的另一重点,需要了解等差数列与等比数列的概念与性质,以及如何利用数学归纳法证明数学命题。
最后,概率与统计是数学中的实际应用部分,需要了解基本的概率与统计方法,如频率、概率、条件概率、正态分布等。
几何部分是数学中的空间内容,主要包括平面几何、立体几何和空间解析几何。
平面几何包括了直线、曲线、多边形、圆等基本图形的性质与应用。
立体几何则需要了解体积、表面积等概念,要掌握球、圆锥、棱柱、棱台等几何体的性质。
空间解析几何是几何部分的进阶内容,需要掌握平面与直线的表示方法、位置关系与求交点的方法。
三角学是数学中的三角函数部分,主要包括三角函数的定义与性质、三角函数的图像与变换、三角恒等式与解三角方程等。
在此部分,还涉及到向量的概念与性质,包括向量的表示方法、运算法则、点积与叉积等。
概率与统计部分是数学中的实际应用部分,需要了解概率的基本概念与性质,条件概率、事件独立性的判定与计算方法等。
统计部分则包括数据的收集与整理、频数分析与频率分析、正态分布与抽样调查等内容。
(完整版)初中数学知识点双向细目表

知识领域知识单元编号知识内容知识与技能过程与方法题型分值难度及系数7:2:1了解理解掌握灵活应用经历体验探索选择题填空题解答题24分21分75分基础题稍难题难题数与代数有理数1有理数的概念√2用数轴上的点表示有理数√3相反数√√√4绝对值√√√5比较有理数的大小√√6乘方的意义√7有理数的加、减、乘、除、乘方运算√√√8有理数的混合运算√9有理数的运算律√√√10对含有较大数字的信息作出合理的解释和推断√实数11平方根、算术平方根、立方根的概念√√√√12用计算器求平方根和立方根√13无理数和实数的概念√14用有理数估计无理数的大致范围√√15近似数与有效数字的概念√16用计算器进行近似计算√17二次根式的概念√18二次根式的加、减、乘、除运算法则√√√代数式19用字母表示数的意义√20用代数式表示简单问题的数量关系√√21解释一些简单代数式的实际背景或几何意义√22求代数式的值√√方程与不等式整式与分式23整数指数幂的意义和基本性质√√24用科学记数法√√25整式的概念√26整式加、减、乘、除运算√27乘法公式:完全平方√√√28提公因式法、公式法(直接用公式不超过2次)进行因式分解√√29分式的概念√30分式的基本性质√√√√31约分和通分√√32分式加、减、乘、除运算√√√√方程与方程组33根据具体问题中的数量关系列方程√√√34用观察、画图或计算器等手段估计方程的解√35一元一次方程及相关概念√36解一元一次方程√√√37二元一次方程组及其解法√√√38分式方程的概念√√√39解可化为一元一次方程的分式方程√√40一元二次方程及其相关概念√√√41配方法√√√√42因式分解法、公式法√√√43根据具体问题的实际意义检验结果是否合理√44不等式的意义√知识领域知识单元编号知识内容知识与技能过程与方法题型分值难度及系数7:2:1了解理解掌握灵活应用经历体验探索选择题填空题解答题24分21分75分基础题稍难题难题45不等式的基本性质√√√46一元一次不等式的解法√√√√√47在数轴上表示不等式(组)的解集√√48解一元一次不等式组√√√√49根据具体问题中的数量关系,列出一元一次不等式或一元一次不等式组,解决简单的问题√√√函数50具体问题中的两个变量之间的关系√√√51从表格、图象中分析某些变量之间的关系√52用表格或关系式表示某些变量之间的关系√53常量、变量的意义√54函数的概念及其表示方法√√55对简单实际问题中的函数关系进行分析√56确定函数的自变量取值范围√√57求函数值√58用适当的函数表示法刻画某些实际问题中变量之间的关系√59对变量的变化规律进行初步预测√一60一次函数的意义√√61确定一次函数表达式√√62画一次函数的图象√等式不等式与不等式组初中数学知识点考试双向细目表知识领域知识单元编号知识内容知识与技能过程与方法题型分值难度及系数7:2:1了解理解掌握灵活应用经历体验探索选择题填空题解答题24分21分75分基础题稍难题难题63一次函数的性质√√64正比例函数√√65根据一次函数的图象求二元一次方程组的近似解√66用一次函数解决实际问题√√反比例函数67反比例函数的意义√68确定反比例函数的表达式√√69画反比例函数的图像√70反比例函数的性质√71用反比例函数解决某些实际问题√√√二次函数72二次函数的意义√73确定二次函数的表达式√√√74用描点法画出二次函数的图像√75二次函数的性质√√√76根据解析式确定图像的顶点、开口方向和对称轴√77利用二次函数的图像求一元二次方程的近似解√78利用二次函数解决简单的实际问题√√79点、线、面√角80角√81比较角的大小√82估计一个角的大小√83计算角度的和与差√84度、分、秒及其简单换算√√85角平分线及其性质√函数一次函数知识领域知识单元编号知识内容知识与技能过程与方法题型分值难度及系数7:2:1了解理解掌握灵活应用经历体验探索选择题填空题解答题24分21分75分基础题稍难题难题86补角、余角、对顶角√87等角的余角相等、等角的补角相等、对顶角相等√相交线与平行线88垂线、垂线段√89垂线段最短的性质√√90点到直线距离的意义√91过一点有且仅有直线垂直于已知直线√√92用三角尺或量角器过一点画一条直线的垂线√93线段垂直平分线及其性质√94两直线平行,同位角相等√√√95过直线外一点有且仅有一条直线平行于已知直线√96用三角尺和直尺过已知直线外一点画这条直线的平行线√97两条平行直线之间距离的意义√√98度量两条平行线之间的距离√三角形99三角形有关概念(内角、外角、中线、高、角平分线)√##画任意三角形的角平分线、中线和高√√##三角形的稳定性√##三角形中位线的性质√√##全等三角形的概念√##两个三角形全等的判定√√√√##等腰三角形的有关概念√##等腰三角形性质和判定√√知识领域知识单元编号知识内容知识与技能过程与方法题型分值难度及系数7:2:1了解理解掌握灵活应用经历体验探索选择题填空题解答题24分21分75分基础题稍难题难题##等边三角形的概念√##等边三角形的性质√√##直角三角形的概念√##直角三角形的性质和判定√√√√##勾股定理√√√√√##用勾股定理的逆定理判定直角三角形√√四边形##多边形的内角和外角和公式√√##正多边形的概念√##平行四边形、矩形、菱形、正方形、梯形的概念和性质√√√##四边形的不稳定性√##平行四边形的性质和判定√√√##矩形、菱形、正方形的性质和判定√√√##等腰梯形及直角梯形的有关性质和判定√√√##线段、矩形、平行四边形、三角形的重心及物理意义√√##平面图形的镶嵌√##任意一个三角形、四边形或正六边形可以镶嵌平面√##简单的镶嵌设计√##圆及其有关概念√##弧、弦、圆心角的关系,√√##点与圆、直线与圆以及圆与圆的位置关系√√##圆的性质√√##圆周角与圆心角的关系√√图形的认识角形知识领域知识单元编号知识内容知识与技能过程与方法题型分值难度及系数7:2:1了解理解掌握灵活应用经历体验探索选择题填空题解答题24分21分75分基础题稍难题难题##直径所对圆周角的特征√##三角形的内心和外心√##切线的概念√##切线与过切点的半径之间的关系√√##切线的判定√##画圆的切线√##计算弧长及扇形的面积,√##计算圆锥的侧面积和全面积√√##圆及其有关概念√√##作一条线段等于已知线段√##作一个角等于已知角√##作角平分线√√##作线段的垂直平分线√##已知三边作三角形√尺规作图##已知两边及其夹角作三角形√##已知两角及其夹边作三角形√##已知底边及底边上的高作等腰三角形√##过一点、两点和笔在同一条直线上的三点作圆√##尺规作图的步骤√√##画基本几何体(直棱柱、圆柱、圆锥、球)的三视图,会判断简单物体的三视图,√##能根据三视图描述基本几何体或实物原型√√##直棱柱、圆锥的侧面积展开图√圆知识领域知识单元编号知识内容知识与技能过程与方法题型分值难度及系数7:2:1了解理解掌握灵活应用经历体验探索选择题填空题解答题24分21分75分基础题稍难题难题##根据展开图判断立体模型制作立体模型√##基本几何体与其三视图,展开图(球除外)之间的关系及其应用√√##一些有趣的图形(如雪花曲线、莫比乌斯带)√##物体阴影的形成√##根据光线的方向辨认实物的阴影√##视点视角及盲区的含义√√##中心投影和平行投影√图形的轴对称##轴对称√√##轴对称的基本性质√√##要求作简单平面图形的轴对称关系√##简单图形之间的轴对称关系√##基本图形(等腰三角形、矩形、菱形、等腰梯形、正多边形、圆)的轴对称性及其相关性质√##利用轴对称进行图案设计√##现实生活中的轴对称图形√图形的平移##认识平移√##平移的对应点连线平行且相等的性质√√##按要求作简单平面图形平移后的图形√##利用平移进行图案设计√√视图与投影知识领域知识单元编号知识内容知识与技能过程与方法题型分值难度及系数7:2:1了解理解掌握灵活应用经历体验探索选择题填空题解答题24分21分75分基础题稍难题难题##平移在生活中的应用√图形的旋转##旋转√##旋转的基本性质√√##平行四边形、圆是中心对称图形√##作简单平面图形旋转后的图形√√##旋转在现实生活中的应用√##图形之间的变换关系(轴对称、平移、旋转及其组合)√√√##用轴对称、平移和旋转的组合进行图案设计√√图形的相似##比例基本性质√##线段的比、成比例线段、黄金分割√##图形的相似√##相似图形的性质√√√##三角形相似的概念√##两个三角形相似的条件√√##图形的位似√##利用位似将一个图形放大或缩小√##利用图形的相似解决实际问题√√√##锐角三角函数(sinA,cosA,tanA)√√##30°,45°,60°角的三角函数值√图形与变换形的平移知识领域知识单元编号知识内容知识与技能过程与方法题型分值难度及系数7:2:1了解理解掌握灵活应用经历体验探索选择题填空题解答题24分21分75分基础题稍难题难题##使用计算器求三角函数值;由已知三角函数值求它对应的锐角√##用三角函数解决与直角三角形有关的简单实际问题√√√√图形与坐标图形与坐标##平面直角坐标系√##根据坐标描点的位置、由点的位置写出它的坐标√√##在方格纸上建立适当的直角坐标系,描述物体的位置√##在同一直角坐标系中,图形变换后点的坐标的变化√√##确定物体的位置√证明的含义##证明的含义√##证明的必要性√##定义、命题、定理的含义√##命题的条件(题设)和结论√√##逆命题的概念√##互逆命题√√##反证法的含义√##综合证明法√√证明的##一条直线截两条平行直线所得的同位角相等√##两条直线被第三条直线所截,若同位角相等,那么这两条直线平行√形的相似初中数学知识点考试双向细目表知识领域知识单元编号知识内容知识与技能过程与方法题型分值难度及系数7:2:1了解理解掌握灵活应用经历体验探索选择题填空题解答题24分21分75分基础题稍难题难题##若两个三角形的两边及其夹角(或两角及其夹边或三边)对应相等,则这两个三角形全等√##全等三角形的对应边、对应角分别相等√证明命题##平行线的性质定理(内错角相等、同旁内角互补)和判定定理(内错角相等或同旁内角互补,则两直线相等√##三角形的内角和定理及推论√##直角三角形全等的判定定理√##角平分线性质定理及逆定理;三角形的三条角平分线交于一点(内心)√##垂直平分线性质定理及其逆定理;三角形的三边的垂直平分线交于一点(外心)√##三角形中位线定理√##等腰三角形、等边三角形、直角三角形的性质和判定定理√##平行四边形、矩形、菱形、正方形、等腰梯形的性质和判定定理√图形与证明证明的依据初中数学知识点考试双向细目表知识领域知识单元编号知识内容知识与技能过程与方法题型分值难度及系数7:2:1了解理解掌握灵活应用经历体验探索选择题填空题解答题24分21分75分基础题稍难题难题##几何的演绎体系对数学发展和人类文明的价值√统计与概率统计##收集、整理、描述和分析数据√##用计算器处理较为复杂的统计数据√##抽样的必要性√√√##总体、个体、样本√√##用条形、扇形统计图表示数据√√##计算加权平均数√√##选择合适的统计量表示数据的集中程度√##表示一组数据的离散 程度√√√##计算极差和方差√√##频数、频率的概念√##频数分布的意义和作用√##列频数分布表,画频数分布直方图和频数折线图,解决简单的实际问题√##用样本估计总体的思想√##用样本的平均数\方差来估计总体的平均数和方差√##根据统计结果作出合理的判断和预测√##统计对决策的作用√##根据问题查找有关资料,获得数据信息;对日常生活中的某些数据发表自己的看法√题初中数学知识点考试双向细目表知识领域知识单元编号知识内容知识与技能过程与方法题型分值难度及系数7:2:1了解理解掌握灵活应用经历体验探索选择题填空题解答题24分21分75分基础题稍难题难题##统计在社会生活及科学领域中的应用√√√概率##概率的意义√##用列举法(包括列表\画树状图)计算简单事件发生的概率√√√##频率√##大量重复实验时频率可作为事件发生概率的估计值√##解决一些实际问题√课题学习课题学习##"问题情境--建立模型--求解--解释与应用"的基本过程√##数学知识之间的内在联系√√##一些研究问题的方法和经验√√##成功的体验和克服困难的经历√##增强应用数学的自信心√与概率初中数学知识点考试双向细目表知识领域知识单元编号知识内容知识与技能过程与方法题型分值难度及系数7:2:1了解理解掌握灵活应用经历体验探索选择题填空题解答题24分21分75分基础题稍难题难题。
积分、线性回归、2乘2列联表、频率分布直方图高考双向细目表

图1 图2 正相关,u与v正相关
正相关,u与v负相关
负相关,u与v正相关
图1 A类工人生产能力的频率分布直方图
永和九年,岁在癸丑,暮春之初,会于会稽山阴之兰亭,修禊事也。
群贤毕至,少长咸集。
此地有崇山峻岭,茂林修竹;又有清流激湍,映带左右,引以为流觞曲水,列坐其次。
虽无丝竹管弦之盛,一觞一咏,亦足以畅叙幽情。
是日也,天朗气清,惠风和畅,仰观宇宙之大,俯察品类之盛,所以游目骋怀,足以极视听之娱,信可乐也。
夫人之相与,俯仰一世,或取诸怀抱,晤言一室之内;或因寄所托,放浪形骸之外。
虽取舍万殊,静躁不同,当其欣于所遇,暂得于己,快然自足,不知老之将至。
及其所之既倦,情随事迁,感慨系之矣。
向之所欣,俯仰之间,已为陈迹,犹不能不以之兴怀。
况修短随化,终期于尽。
古人云:“死生亦大矣。
”岂不痛哉!
每览昔人兴感之由,若合一契,未尝不临文嗟悼,不能喻之于怀。
固知一死生为虚诞,齐彭殇为妄作。
后之视今,亦犹今之视昔。
悲夫!故列叙时人,录其所述,虽世殊事异,所以兴怀,其致一也。
后之览者,亦将有感于斯文。
-高考数学双向细目表(精)

2020届理科数学双向细目表模块知识点考查内容知识要求2015 分值2016 分值2017 分值备注了解理解掌握集合集合的含义与表示集合的含义、元素与集合的属于关系√列举法、描述法√集合间的基本关系包含与相等的含义√识别给定集合子集√全集与空集√集合的基本运算并集与交集含义与运算√补集含义与运算√韦恩图表达集合的关系与运算√函数概念与基本初等函数I 函数简单定义域值域,了解映射√图像法、列表法、解析法表示函数√分段函数√函数单调性、最值及几何意义√函数奇偶性√函数图像研究函数性质√指数函数指数函数模型背景√有理、实数指数幂、幂的运算√指数函数概念、单调性√指数函数图像过定点√对数函数对数的概念及其运算√换底公式、自然对数、常用对数√对数函数的概念、单调性√对数函数图像过定点√指数函数与对数函数互为反函数√幂函数幂函数概念√幂函数图像√函数与方程二次函数、零点与方程根√一元二次方程根的存在性及根的个数√结合图像,用二分法求近似解√函数模型及应用指、对、幂的增长特征√函数模型的应用√立体几何初步空间几何体柱锥台的结构特征√三视图√斜二测画出直观图√平行、中心投影√会画视图和直观图√球柱锥台的表面积和体积公式√点线面位置关系线面位置关系定义√线面平行判定√面面平行判定√线面垂直判定√面面垂直判定√线面平行性质√面面平行性质√线面垂直性质√面面垂直性质√用已获结论证明空间图形的位置关系√平面解析几何初步直线与方程结合图形,确定直线位置的几何要素√直线倾斜角和斜率√过两点的直线斜率计算公式√判定直线平行或垂直√点斜式、两点式、一般式√斜截式与一次函数的关系√两条相交直线的交点坐标√两点间距离公式√点到直线距离公式√两条平行直线间距离√圆与方程圆的几何要素,标准方程和一般方程√判断直线与圆的位置关系√判断两圆的位置关系√应用直线与圆的方程√代数方法处理几何问题的思想√空间直角坐标系空间直角坐标表示点的位置√空间两点间距离公式√算法初步算法的含义、程序框图算法的含义和思想√顺序、条件分支、循环逻辑结构√基本算法语句输入、输出、赋值、条件、循环语句√统计随机抽样会用简单随机抽样从总体中抽取样本√分层抽样和系统抽样√用样本估计总体频率分布表、频率分布直方图、折线图√茎叶图√数据标准差意义和作用√平均数和标准差√用样本估计总体思想√变量的相关性会画散点图,并认识变量间的相关关系√最小二乘法,线性回归方程√概率事件与概率频率与概率的意义√互斥事件的概率加法公式√古典概型古典概型计算公式√随机事件所含的基本事件数及发生概率√几何概型随机数的意义,运用模拟方法估计概率√几何概型的意义√基本初等函数II 任意角的概念、弧度制任意角的概念√弧度制的概念、弧度与角度的互化√三角函数理解正弦、余弦、正切的定义√单位圆的三角函数线√诱导公式√会画三角函数图像√三角函数周期性√正余弦单调性、最值与X轴交点等性质√正切函数性质√同角三角函数的基本关系式√正弦型函数参数对图像变化的影响√平面向量平面向量的实际背景及基本概念向量的实际背景√平面向量的概念√两个向量相等√向量的几何表示√向量的线性运算加法、减法、几何意义√数乘的运算、几何意义√两个向量共线的含义√线性运算的性质和几何意义√平面向量基本定理和坐标表示平面向量基本定理及意义√正交分解及坐标表示√加法、减法、数乘坐标运算√用坐标表示平面向量共线的条件√平面向量的数量积平面向量的数量积含义与物理意义√平面向量的数量积与向量投影关系√数量积坐标表达式与运算√用数量积表示夹角√用数量积判断两个向量的垂直关系√向量的应用解决平面几何问题√解决实际问题√三角恒等变换和与差的三角函数公式两角和与差的余弦、正弦、正切公式√二倍角公式√三角恒等变换积化和差、和差化积√半角公式√解三角形正弦定理余弦定理正弦定理√余弦定理√应用三角形度量问题√数列数列的概念与简单表示法数列的概念√列表、图像、通项公式表示方法√数列是自变量为正整数的函数√等差数列、等比数列等差数列概念√等差数列通项公式和求和公式√等比数列概念√等比数列通项公式和求和公式√等差数列与一次函数√等比数列与指数函数√不等式不等关系实际背景√一元二次不等式实际情景中抽象√与二次函数、一元二次方程联系√会解一元二次不等式,设计程序框图√二元一次不等式组与简单的线性规划问题实际情景抽象出二元一次不等式组√二元一次不等式组表示平面区域√二元线性规划问题√基本不等式了解证明过程√解决最值问题√常用基本逻辑用语命题及其关系命题的概念√四种命题及其关系√充分、必要、充要条件√简单的逻辑联结词或、且、非√全称量词与存在量词全称量词√存在量词√含有量词命题的否定√圆锥曲线与方程圆锥曲线实际背景√椭圆定义几何图形标准方程、简单性质√抛物线定义几何图形标准方程简单性质√双曲线定义几何图形标准方程简单性质√简单应用、数形结合思想√曲线与方程方程的曲线与曲线的方程√空间向量与立体几何空间向量及其运算空间向量概念、基本定理、坐标√空间向量线性运算√空间向量数量积√用空间向量数量积表示共线与垂直√空间向量的应用直线方向向量与平面的法向量√线线、线面、面面平行关系√线线、线面、面面垂直关系√三垂线定理√线线、线面、面面夹角计算√导数及其应用导数概念及几何意义导数概念实际背景√导数的几何意义√导数的运算求导运算法则√基本初等函数导数公式√在研究函数中应用单调性与导数关系√函数取极值的必要条件和充分条件√会求函数的极值√会求闭区间上的最值√生活中的优化问题实际问题√定积分与微积分定积分概念、实际背景、思想√微积分基本定理√推理与证明合情推理与演绎推理归纳和类比推理√演绎推理的基本模式√联系和差异√直接证明与间接证明分析法与综合法√反证法√数学归纳法数学归纳法√数系的扩充与复数的引入复数的概念复数的概念√复数相等的充要条件√复数代数表示法与几何意义√复数的四则运算四则运算√加减法运算的几何意义√计数原理分类加法、分步乘法分类加法√分步乘法√排列与组合排列概念与公式√组合概念与公式√二项式定理证明二项式定理√展开式有关问题√概率与统计概率离散型随机变量与分布列√超几何分布√条件概率√两个事件相互独立√N次独立重复试验与二项分布√均值、方差√正态分布曲线特点及意义√统计案例独立性检验√回归分析√坐标系与参数方程坐标系用极坐标表示点的位置√极坐标与直角坐标互化√简单图形的方程√柱坐标系、球坐标系表示空间中点位置√参数方程参数方程和参数的意义√直线、圆、圆锥曲线的参数方程√平摆线与渐开线√不等式选讲含绝对值不等式几何意义√绝对值三角不等式√柯西不等式不同形式√几何意义√柯西不等式一般情参数配方法√排序不等式向量递归法√伯努利不等式数学归纳法√均值不等式求极值√证明不等式方法比较、综合、分析、反证、放缩√。
全国数学双向细目表
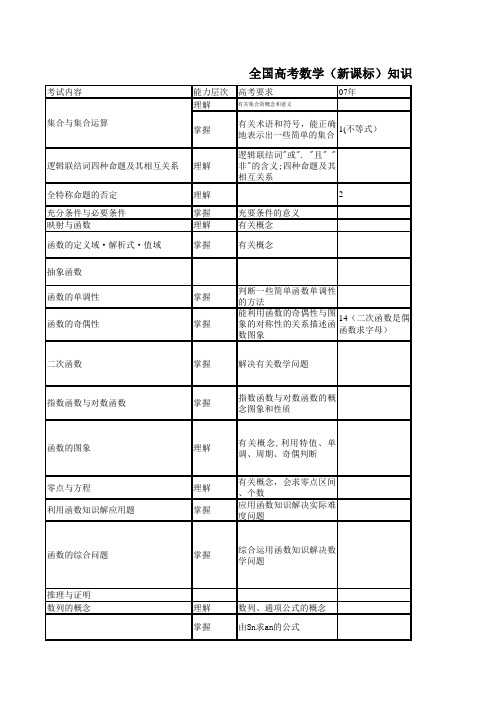
考试内容能力层次高考要求07年理解有关集合的概念和意义逻辑联结词四种命题及其相互关系理解逻辑联结词"或"."且""非"的含义;四种命题及其相互关系全特称命题的否定理解2充分条件与必要条件掌握充要条件的意义映射与函数理解有关概念抽象函数函数的单调性掌握判断一些简单函数单调性的方法二次函数掌握解决有关数学问题指数函数与对数函数掌握指数函数与对数函数的概念图象和性质函数的图象理解有关概念,利用特值、单调、周期、奇偶判断零点与方程理解有关概念,会求零点区间、个数利用函数知识解应用题掌握应用函数知识解决实际难度问题函数的综合问题掌握综合运用函数知识解决数学问题推理与证明数列的概念理解数列、通项公式的概念集合与集合运算掌握有关术语和符号,能正确地表示出一些简单的集合1(不等式)掌握能利用函数的奇偶性与图象的对称性的关系描述函数图象14(二次函数是偶函数求字母)函数的奇偶性函数的定义域·解析式·值域掌握有关概念掌握由Sn求an的公式全国高考数学(新课标)知识双等比数列掌握等比数列的通项公式,前n项和公式6(等比性质)掌握差比裂项求和三角函数概念公式掌握任意角的正弦、余弦、正切的定义,用三角函数线表示正弦、余弦和正切;同角三角函数的基本关系式;正弦、余弦的诱导公式和差倍公式掌握通过公式的推导,了解它们的内在联系,从而培养逻辑推理能力9(二倍角、和差公式约分,含π/4的)求值图象与性质掌握会用三角函数线画正弦函数,正切函数的图象,由诱导公式画余弦函数的图象;理解它们的性质;会用"五点法"3(一个半周期闭区间上图象)用"五点法"画函数y=Asin(ωx+Φ)的简图图象变换掌握利用三角知识求范围最值掌握运用所学三角知识解决实际问题等差数列掌握等差数列的通项公式,前n项和公式16(基本量求d)掌握有关概念及解决实际问题数列的综合应用理解A、ω、Φ的物理意义y=Asin(ωx+Φ)的图象三角最值及综合应用掌握了解共线向量,平面向量基本定理理解向量,向量共线的充要条件,平面向量的坐标掌握向量的几何表示,实数与向量的积,向量加法与减法,平面向量的坐标运算4(线性运算的坐标表示)了解用平面向量的数量积可以处理有关长度、角度和垂直等问题掌握平面向量的数量积及其几何意义;向量垂直的条件向量综合掌握综合不等式的概念性质理解不等式的性质不等式证明分析法、综合法、比较法证明简单的不等式均值不等式掌握并会简单的应用;解不等式掌握二次不等式、简单的分式不等式的解法掌握简单的绝对值不等式的解法直线方程及位置关系理解直线的倾斜角和斜率掌握两点斜率公式:一点和斜率求出直线方程的方法;点斜式、两点式和一般式,熟练求出直线方程.两条直线平行与垂直的条件,两条直线成的角、点到直线的距离公式,两条直线的位直关系了解简单的线性规划问题,线性规划的意义掌握二元一次不等式表示平面区域,简单线性规划问题绝对值不等式理解不等式|a+b|≤|a|+|b|线性规化不等式的应用灵活运用有关概念掌握正弦定理、余弦定理,并能运用它们解斜三角形17(实际测量,用字母表示)正余弦定理向量、向量的加法与减法、实数与向量的积数量积圆与圆理解16(外切)直线与圆掌握直线与圆的位置关系21(交点个数,结合向量共线类似椭圆问题)掌握椭圆的标准方程及其几何性质理解椭圆的定义、概念双曲线了解双曲线的标准方程及其几何性质13(几何性质应用求离心率)抛物线了解抛物线的标准方程及其几何性质7(从坐标考抛物线定义)轨迹方程了解直线与圆锥曲线掌握综合综合应用熟练掌握综合线面、面面平行线面、面面垂直18(面面垂直化为线面垂直,存在问题)三视图掌握三视图8(体积)体积计算了解会求几何体的表面积、体积,会处理几何体的侧面展开图问题8,11了解球的概念11(球内接三棱锥)掌握球的性质、表面积、体积公式,球面距离综合掌握圆的标准方程和一般方程椭圆球圆的方程算法初步掌握程序框图5(求和)古典概型掌握计算等可能性事件的概率,会用互斥事件的概率加法公式和相互独立事件的概率乘法公式计算一些事件的概率20(1)几何概型了解计算几何概型概率20(2)了解独立性检验了解线性回归的方法简单应用了解茎叶图掌握频率分布直方图抽样导数概念运算掌握函数在一点处的导数的定义和导数的几何意义;基本导数公式;和、差、积、商的求导法则;会求某些简单函数的导数;掌握导数求切线10统计掌握平均数与方差计算12了解可导函数的单调性与其导数的关系;可导函数在某点取得极值的必要条件和充分条件19导数应用掌握会求一些实际问题的最大值和最小值19掌握导数证明不等式、恒成立了解复数的有关概念及复数的代数表示和几何意义掌握运算法则,能进行复数代数形式的加法、减法、乘法、除法运算15说明21题必考有选修选考复数08年09年10年11年12年备注4(全特称命题的真假)321(2)(二次函数最值及解含参二次不等式)11(指对都有的不等式)12(画图象求最值)12(综合周期、奇偶绝对值画图求交点个数)11(指对都有的不等式)10(求零点区间)18(1)9(奇偶与指数不等式结合)12(图象与对数运算结合)1(不等式)1(有限集)1(不等式)316(奇偶性求和)知识双向细目表(文史类)1(绝对值不等式与有限集)1(有限集)8(和与项的比)1517(1)14(由和求公比)7(用到定义)11(二倍角化为二次函数求最值)17(1)107、11(用到)17(1)6(由定义得解析式并判断图象)11(单调区间、对称轴)13(通项应用)8(性质应用)17(求完通项、和后求和最值)17(2)9(由图象求ω、Φ)12(求和)16(由图象求ω、Φ进而求值)9(共线条件)2(用数量积坐标运算求夹角)5(由垂直求字母)7(由垂直求字母)13(由垂直求字母,非坐标)7(二次不等式解法,三个范围公共解)21(2)(讨论解含参二次不等式)20(斜率取值范围,化为不等式问题)10(线段点到原点距离)61114517(2)17(实际测量求值)16(解三角形求线段长)15(解三角形后求面积)17(2)20(1)(1次比2次型不等式求范围)20(2)(分成弧的比)20(2)(结合OA、OB垂直类似椭圆问题)20(1)由定义性质求方程20(1)椭圆定义4(离心率)42(直接求焦距)5(渐近线求离心率)1014(弦中点求抛物线方程)4(知切点求切线)9(定义应用求距离)10(用到)20(2)(切线方程)20(2)代入法求轨迹并讨论什么曲线16(求交点与原点组成三角形面积)20(2)(弦长问题)12(平行垂直判断)1812(平行垂直判断)18(线线垂直与线面垂直、面面垂直转化,求体积)18(1)1819(1)1811(三视图求全面积)1587(三视图求体积)1818(2)19(2)14(球内接正六棱柱求球的体积)7(知内接长方体求表面积)16(球中直角三角形)18(由直观图得三视图计算体积,证线面平行)9(平行、垂直,体积计算)20(1)(结合抛物线条件求圆的方5(求关于直线对称的圆)13(求圆的方程)20(1)(由三点定方程)6(三数输出最大)10(条件结构)56(图的含义)19(2)14(估计古典概型)618(2)19(2)3(散点图观察正负相关)3(相关系数的理解)16(说明直观含义)19(2)(画图并由图估计平均数)19(1)(分层抽样人数)19(1)(估计比例)(3)(用分层更好)421(切线求字母,切线与定直线围成面积)1321(1)(切线求字母)13(知切点求切线)19(1)21(1)(求极值)21(1)(单调区间)21(1)(2)(恒成立求字母范围)。
2020高考数学艺体生文化课第十章概率与统计第2节频率直方图、2x2列联表茎叶图线性回归方程、相关关系课件

(参考公式: K 2
n(ad bc)2
,其中n=a+b+c+d)
(a b)(c d )(a c)(b d )
(2)由已知数据可求得 : K 2 30(618 2 4)2 8.523 7.879, 10 208 22
因此有99.5%的把握认为肥胖与常喝碳酸饮料有关.
(3)现从常喝碳酸饮料且肥胖的学生中(其中有2名为女生),抽取2 人参加电视节目,则正好抽到一男一女的概率是多少?
(3)设常喝碳酸饮料的肥胖者男生为A、B、C、D, 女生为E、F , 则任取两人有AB, AC, AD, AE, AF, BC, BD, BE, BF,CD,CE,CF, DE, DF, EF, 共15种. 其中一男一女有AE, AF, BE, BF,CE,CF, DE, DF. 故抽出一男一女的概率是p 8 .
3.求方差公式:S 2
1 n [(x1
x)2
( x2
x)2
( x3
x)2
... (xn
x)2 ].
频率分布直方图中求方差的参考公式: S 2 (x1 x)2 f1 (x2 x)2 f2 (x3 x)2 f3 ... (xn x)2 fn (其中x1,x2,…,xn取各分段的中间值)
t.
(ti t)2
i 1
【解析】 (1)由折线图中数据和附注中参考数据得t 4,
7
7
(ti t)2 28, ( yi y)2 0.55.
i 1
i 1
7
7
7
(ti t)( yi y) ti yi t yi 40.17 4 9.32 2.89,
一部高三(理科)数学双向细目表

推 理 证 明
任意角三角函数 同角三角函数的基本 关系式、诱导公式 三角函数的周期性 三角函数的图像 三角函数的单调性、 最值、对称性 图像变换 三角函数模型 两角和与差的三角函 数 二倍角公式 三角恒等变换 正弦定理、余弦定理 面积公式 等差数列、等比数列 的概念. 通项公式与前n项和公 式 综合应用 错位相减 裂项相消 并项求和 分组求和 数学归纳法 归纳和类比 新定义 反证法等证明方法
算 法
框图
基本逻辑结构
了解算法的含义,了解算法 的思想;理解程序框图的三 种基本逻辑结构:顺序结构 、条件分支结构、循环结 构;
平 面 向 量
线性运算及其几何意 义 向量的运算 坐标运算、数量积的 坐标运算 基底运算 解决某些简单的平面 向量的应用 几何问题 三视图、直观图 面积与体积 表面积和体积 空间直线、平面位置 关系 直线、平面 的位置关系 线面平行的有关性质 与判定定理 线面垂直的有关性质 与判定定理 异面直线所成角 空间角 线面角 二面角 距离公式、点到直线 直线与方程 的距离、斜率与倾斜 角 圆的标准方程与一般 方程 圆与方程 直线与圆的位置关系 两圆的位置关系. 圆锥曲线的实际背景 及作用 椭圆的定义及简单性 质 抛物线的定义及简单 圆锥曲线 性质 双曲线的定义和标准 方程 双曲线的简单几何性 质.
√ √ √
)数学高考双向细目表
能力层次 掌握 全国卷 全国 全国卷 全国卷 全国卷 (I) 2014(I 2015 (I) (I) 2013 ) (I) 2016 2017
题号
全国 全国 全国 全国2015 2013(Ⅱ 2014(Ⅱ 2016(Ⅱ (Ⅱ) ) ) ) 题号 题号 题号 题号
题号
题号
√
2
2
2017-2020高考数学双向细目表

√
四、数列
等比数列
5512..等 等差 差数 数列 列、 的等 通比 项数 公列式与与函前数n 项关和系公 式 53.等比数列的通项公式与前n 项和公 式 54.等差数列、等比数列解决相应问题
√
√
√
√
√
等差数列与一次函数,等比数列与指 数函数的关系
√
近4年 2018年 2019年
√ √
√
√
√
√
√
√
√
√ √ √
2020年高考数学(理科)双向细目表
考试内容 (三十八)加法原理
、乘法原理
127.分类加法计数原理或分步乘法计
十四、计
数原理的简单应用
数原理
(三十九)排列与组 合
128.排列、组合的概念 129.排列数公式、组合数公式
130排列与组合的简单应用
(四十)二项式定理 131二项式定理及其简单应用
√
2017年
√ √
(二十八)点、直线 92.空间线、面平行或垂直的判定 、平面间的位置关系 93.空间线、面平行或垂直的性质
√
√
√
线面平行、面面平行、线面垂直、面 面垂直的判定和性质定理
√
√
94.异面直线所成的角、直线与平面所 成的角、二面角的概念及求解
√
95.空间图形的位置关系的简单命题的
证明
√
√
√
√
√
√
√
2020年 √
√
√
2020年
√ √
2020年高考数学(理科)双向细目表
考试内容
要求层次 了解 理解 掌握
(十四)不等式与不 等关系
55.不等式关系,不等式的性质
近10年高考数学双向细目表(10-19年新课标全国卷高考统计 )
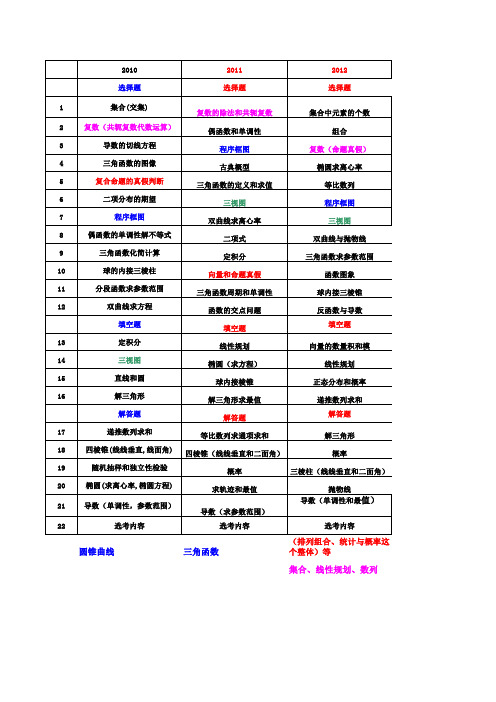
2011 选择题
2012 选择题
1
集合(交集)
复数的除法和共轭复数
集合中元素的个数
2
复数(共轭复数代数运算)
偶函数和单调性
组合
3
导数的切线方程
程序框图
复数(命题真假)
4
三角函数的图像
古典概型
椭圆求离心率
5
复合命题的真假判断
三角函数的定义和求值
等比数列
6
二项分布的期望
三视图
程序框图
7
程序框图
双曲线求离心率
三视图
8
偶函数的单调性解不等式
二项式
双曲线与抛物线
9
三角函数化简计算
定积分
三角函数求参数范围
10
球的内接三棱柱
向量和命题真假
函数图象
11
分段函数求参数范围
三角函数周期和单调性
球内接三棱锥
12
双曲线求方程
函数的交点问题
反函数与导数
填空题
填空题
填空题
13
定积分
线性规划
向量的数量积和模
14
三视图
集合(交集)
复数的运算和虚部
复数(除法运算)
抽样方法
等比数列
双曲线的渐近线
线面关系
程序框图
二项式求参数
球的组合体
程序框图
等差数列
三视图
三视图
对数比较大小
二项式求参数
线性规划求参数
椭圆方程
导数
分段函数求参数范围
抛物线与圆
递推数列研究单调性
直线与三角形面积问题
填空题
填空题
向量运算求参数
2015-2017高考数学双向细目表

韦恩图表达集合的关系与运算
√
函数概念与基本初等函数
函数
简单定义域值域,了解映射
√
图像法、列表法、解析法表示函数
√
分段函数
√
函数单调性、最值及几何意义
√
函数奇偶性
√
函数图像研究函数性质
√
指数函数
指数函数模型背景
√
有理、实数指数幂、幂的运算
√
指数函数概念、单调性
√
指数函数图像过定点
√
对数函数
对数的概念及其运算
√
分步乘法
√
排列与组合
排列概念与公式
√
组合概念与公式
√
二项式定理
√
简单应用、数形结合思想
√
曲线与方程
方程的曲线与曲线的方程
√
空间向量与立体几何
空间向量及其运算
空间向量概念、基本定理、坐标
√
空间向量线性运算
√
空间向量数量积
√
用空间向量数量积表示共线与垂直
√
空间向量的应用
直线方向向量与平面的法向量
√
线线、线面、面面平行关系
√
线线、线面、面面垂直关系
√
三垂线定理
√
线线、线面、面面夹角计算
√
加法、减法、数乘坐标运算
√
用坐标表示平面向量共线的条件
√
平面向量的数量积
平面向量的数量积含义与物理意义
√
平面向量的数量积与向量投影关系
√
数量积坐标表达式与运算
√
用数量积表示夹角
√
用数量积判断两个向量的垂直关系
√
向量的应用
解决平面几何问题
考点22 回归方程和2×2联表(新高考地区专用)(原卷版)

考点22 回归方程和2×2联表一.线性关系 1.变量间的相关关系(1)常见的两变量之间的关系有两类:一类是函数关系,另一类是相关关系;与函数关系不同,相关关系是一种非确定性关系.(2)从散点图上看,点散布在从左下角到右上角的区域内,两个变量的这种相关关系称为正相关;点散布在左上角到右下角的区域内,两个变量的这种相关关系为负相关. 2.两个变量的线性相关(1)从散点图上看,如果这些点从整体上看大致分布在通过散点图中心的一条直线附近,称两个变量之间具有线性相关关系,这条直线叫做回归直线.(2)回归方程: 是两个具有线性相关关系的变量的一组数据的回归方程,其中是待定参数. 的计算公式.注意:回归方程必过样本中心,这也是做小题的依据和检验所求回归方程是否正确。
(3)相关系数:当r >0时,表明两个变量正相关; 当r <0时,表明两个变量负相关.r 的绝对值越接近于1,表明两个变量的线性相关性越强.r 的绝对值越接近于0,表明两个变量之间几乎不存在线性相关关系.通常|r |大于0.75时,认为两个变量有很强的线性相关性. 二.独立性检验 (1)2×2列联表设X ,Y 为两个变量,它们的取值分别为{x 1,x 2}和{y 1,y 2},其样本频数列联表(2×2列联表)如下:y 1 y 2 总计x 1 a b a +b x 2c d c +d 总计a +cb +da +b +c +d(2)独立性检验利用随机变量K 2(也可表示为χ2)的观测值(其中n =a +b +c +d 为样本容量)来判断“两个变量有关系”的方法称为独立性检验.1122()()()n n x y x y x y ,,,,,,知识理解考向一 一次线性关系【例1-1】(2020·山东高三专题练习)某工厂的每月各项开支与毛利润(单位:万元)之间有如下关系,与的线性回归方程,则( )A .17.5B .17C .15D .15.5【例1-2】(2021·全国高三专题练习)西尼罗河病毒(WNV )是一种脑炎病毒,WNV 通常是由鸟类携带,经蚊子传播给人类.1999年8-10月,美国纽约首次爆发了WNV 脑炎流行.在治疗上目前尚未有什么特效药可用,感染者需要采取输液及呼吸系统支持性疗法,有研究表明,大剂量的利巴韦林含片可抑制WNV 的复制,抑制其对细胞的致病作用.现某药企加大了利巴韦林含片的生产,为了提高生产效率,该药企负责人收集了5组实验数据,得到利巴韦林的投入量x (千克)和利巴韦林含片产量y (百盒)的统计数据如下:由相关系数可以反映两个变量相关性的强弱,||[0.75,1]r ∈,认为变量相关性很强;||[0.3,0.75]r ∈,认为变量相关性一般;||[0,0.25]r ∈,认为变量相关性较弱. (1)计算相关系数r ,并判断变量x 、y 相关性强弱;(2)根据上表中的数据,建立y 关于x 的线性回归方程;为了使某组利巴韦林含片产量达到150百盒,估计该组应投入多少利巴韦林? 参考数据:.考向分析参考公式:相关系数()()niix x y y r --=∑()()()121niii nii x x y y b x x ==--=-∑∑,.【举一反三】1.(2020·全国高三专题练习)某工厂某产品产量(千件)与单位成本(元)满足回归直线方程77.36 1.82y x =-,则以下说法中正确的是( )A .产量每增加件,单位成本约下降元B .产量每减少件,单位成本约下降元C .当产量为千件时,单位成本为元D .当产量为千件时,单位成本为元2.(2020·安徽省六安中学高三开学考试)“关注夕阳、爱老敬老”—某马拉松协会从年开始每年向敬老院捐赠物资和现金.下表记录了第年(年是第一年)与捐赠的现金(万元)的对应数据,由此表中的数据得到了关于的线性回归方程ˆ0.35ymx =+,则预测年捐赠的现金大约是( )A .万元B .万元C .万元D .万元3.(2020·全国高三专题练习)基于移动互联技术的共享单车被称为“新四大发明”之一,短时间内就风靡全国,带给人们新的出行体验、某共享单车运营公司的市场研究人员为了解公司的经营状况,对该公司最近六个月内的市场占有率进行了统计,结果如下表:(1)请在给出的坐标纸中作出散点图,并用相关系数说明可用线性回归模型拟合月度市场占有率与月份代码之间的关系;(2)求关于的线性回归方程,并预测该公司年月份的市场占有率;(3)根据调研数据,公司决定再采购一批单车扩大市场,现有采购成本分别为元/辆和元/辆的、两款车型报废年限各不相同,考虑到公司的经济效益,该公司决定先对两款单车各辆进行科学模拟测试,得到两款单车使用寿命频数表如下:经测算,平均每辆单车每年可以为公司带来收入元.不考虑除采购成本之外的其他成本,假设每辆单车的使用寿命都是整数年,且用频率估计每辆单车使用寿命的概率,以每辆单车产生利润的期望值为决策依据、如果你是该公司的负责人,你会选择采购哪款车型? 参考数据:,61()()35iii x x y y =--=∑36.5≈参考公式:相关系数;回归直线方程为,其中121()()ˆ()niii nii x x y y bx x ==--=-∑∑,4.(2020·全国高三专题练习)近年来,“双11”网购的观念逐渐深入人心.某人统计了近年某网站“双11”当天的交易额,,统计结果如下表:(1)请根据上表提供的数据,用相关系数说明与的线性相关程度,线性相关系数保留三位小数.(统计中用相关系数来衡量两个变量之间线性关系的强弱.若相应于变量的取值,变量的观测值为(),则两个变量的相关系数的计算公式为:.统计学认为,对于变量,如果[]1,0.75r -∈-,那么负相关很强;如果[]0.751r ∈,,那么正相关很强;如果(]0.75,0.30r ∈--或[)0.30,0.75r ∈,那么相关性一般;如果[]0.25,0.25r ∈-,那么相关性较弱);(2)求出关于x 的线性回归方程,并预测年该网站“双11”当天的交易额.参考公式:121()()()ˆniii ni i x x y y bx x ==--=-∑∑,;参考数据:.考向二独立性检验【例2】(2021·江苏泰州市·高三期末)2020年是脱贫攻坚的收官之年,国务院扶贫办确定的贫困县全部脱贫摘帽,脱贫攻坚取得重大胜利,为确保我国如期全面建成小康社会,实现第一个百年奋斗目标打下了坚实的基础在产业扶贫政策的大力支持下,西部某县新建了甲、乙两家玩具加工厂,加工同一型号的玩具质监部门随机抽检了两个厂的各100件玩具,在抽取中的200件玩具中,根据检测结果将它们分成“A”、“B”、“C”三个等级,A、B等级都是合格品,C等级是次品,统计结果如下表所示:(表一)(表二)在相关政策扶持下,确保每件合格品都有对口销售渠道,但从安全起见,所有的次品必须由原厂家自行销. (1)请根据所提供的数据,完成上面的2×2列联表(表二),并判断是否有95%的把握认为产品的合格率与厂家有关?(2)每件玩具的生产成本为30元,A、B等级产品的出厂单价分别为60元、40元.另外已知每件次品的销毁费用为4元.若甲厂抽检的玩具中有10件为A等级,用样本的频率估计概率,试判断甲、乙两厂能否都能盈利,并说明理由.=+++.附:,其中n a b c d【举一反三】1.(2021·山东高三专题练习)共享单车进驻城市,绿色出行引领时尚.某市有统计数据显示,2020年该市共享单车用户年龄等级分布如图1所示,一周内市民使用单车的频率分布扇形图如图2所示.若将共享单车用户按照年龄分为“年轻人”(20岁-39岁)和“非年轻人”(19岁及以下或者40岁及以上)两类,将一周内使用的次数为6次或6次以上的称为“经常使用单车用户”,使用次数为5次或不足5次的称为“不常使用单车用户”.已知在“经常使用单车用户”中有是“年轻人”.(1)现对该市市民进行“经常使用共享单车与年龄关系”的调查,采用随机抽样的方法,抽取一个容量为200的样本,请你根据图表中的数据,补全下列列联表,并根据列联表的独立性检验,判断是否有85%的把握认为经常使用共享单车与年龄有关?(2)将(1)中频率视为概率,若从该市市民中随机任取3人,设其中经常使用共享单车的“非年轻人”人数为随机变量,求的分布列与期望.参考数据:独立性检验界值表=+++其中,,n a b c d【举一反三】1.(2021·全国高三专题练习)某工厂为了提高生产效率,对生产设备进行了技术改造,为了对比技术改造后的效果,采集了技术改造前后各20次连续正常运行的时间长度(单位:天)数据,整理如下:改造前:19,31,22,26,34,15,22,25,40,35,18,16,28,23,34,15,26,20,24,21改造后:32,29,41,18,26,33,42,34,37,39,33,22,42,35,43,27,41,37,38,36 (1)完成下面的列联表,并判断能否有99%的把握认为技术改造前后的连续正常运行时间有差异?(2)工厂的生产设备的运行需要进行维护,工厂对生产设备的生产维护费用包括正常维护费,保障维护费两种.对生产设备设定维护周期为T天(即从开工运行到第kT天,k∈N*)进行维护.生产设备在一个生产周期内设置几个维护周期,每个维护周期相互独立.在一个维护周期内,若生产设备能连续运行,则只产生一次正常维护费,而不会产生保障维护费;若生产设备不能连续运行,则除产生一次正常维护费外,还产生保障维护费.经测算,正常维护费为0.5万元/次;保障维护费第一次为0.2万元/周期,此后每增加一次则保障维护费增加0.2万元.现制定生产设备一个生产周期(以120天计)内的维护方案:T=30,k=1,2,3,4.以生产设备在技术改造后一个维护周期内能连续正常运行的频率作为概率,求一个生产周期内生产维护费的分布列及均值.附:2.(2020·四川成都市·高三一模)一网络公司为某贫困山区培养了名“乡土直播员”,以帮助宣传该山区文化和销售该山区的农副产品,从而带领山区人民早日脱贫致富.该公司将这名“乡土直播员”中每天直播时间不少于小时的评为“网红乡土直播员”,其余的评为“乡土直播达人”.根据实际评选结果得到了下面列联表:(1)根据列联表判断是否有的把握认为“网红乡土直播员”与性别有关系?(2)在“网红乡土直播员”中按分层抽样的方法抽取人,在这人中选人作为“乡土直播推广大使”.设被选中的名“乡土直播推广大使”中男性人数为,求的分布列和期望.=+++.附:,其中n a b c d考向三非一次性回归方程【例3-1】(2021·全国高三专题练习)在一项调查中有两个变量和,下图是由这两个变量近8年来的取值数据得到的散点图,那么适宜作为关于的回归方程的函数类型是( )A.B.C.D.()【例3-2】.(2020·全国高三专题练习)根据公安部交管局下发的通知,自2020年6月1日起,将在全国开展“一盔一带”安全守护行动,其中就要求骑行摩托车、电动车需要佩戴头盔,为的就是让大家重视交通安全.某地交警部门根据某十字路口的监测数据,从穿越该路口的骑行者中随机抽查了200人,得到如图所示的列联表:(1)是否有97.5%的把握认为自觉带头盔行为与性别有关?(2)通过一定的宣传和相关处罚措施出台后,交警在一段时间内通过对某路口不带头盔的骑行者统计,得到上面的散点图和如下数据: 观察散点图,发现两个变量不具有线性相关关系,现考虑用函数对两个变量的关系进行拟合,通过分析得y 与有一定的线性相关关系,并得到以下参考数据(其中):请选择合适的参考数据,求出y 关于x 的回归方程. 参考公式:. 对于一组数据,,…,,其回归直线的斜率和截距的最小二乘估计分别为:1221ˆni i i ni i u v nuvunuβ==-=-∑∑,.【举一反三】1.(2020·河南周口市·高三月考)已知变量关于变量的回归方程为,其一组数据如下表所示:若,则()A.5 B.6 C.7 D.82.(2021·全国高三专题练习)近期,济南公交公司分别推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,用表示活动推出的天数,表示每天使用扫码支付的人次(单位:十人次),统计数据如表所示:表:根据以上数据,绘制了散点图.(1)根据散点图判断,在推广期内与(,均为大于零的常数)哪一个适宜作为扫码支付的人次关于活动推出天数的回归方程类型?(给出判断,不必说明理由);(2)根据(1)的判断结果及表中的数据,建立关于的回归方程,并预测活动推出第8天使用扫码支付的人次;(3)推广期结束后,车队对乘客的支付方式进行统计,结果如下表:车队为缓解周边居民出行压力,以80万元的单价购进了一批新车,根据以往的经验可知,每辆车每个月的运营成本约为0.66万元.已知该线路公交车票价为2元,使用现金支付的乘客无优惠,使用乘车卡支付的乘客享受8折优惠,扫码支付的乘客随机优惠,根据统计结果得知,使用扫码支付的乘客中有的概率享受7折优惠,有的概率享受8折优惠,有的概率享受9折优惠,预计该车队每辆车每个月有1万人次乘车,根据所给数据以事件发生的频率作为相应事件发生的概率,在不考虑其它因素的条件下,按照上述收费标准,假设这批车需要年才能开始盈利,求的值.参考数据:其中,=+的斜率和截距的最小二乘估计公式分别为:,. 参考公式:对于一组数据,,…,,其回归直线v a uβ3.(2021·全国高三专题练习)某公司研发了一种帮助家长解决孩子早教问题的萌宠机器人.萌宠机器人语音功能让它就像孩子的小伙伴一样和孩子交流,记忆功能还可以记住宝宝的使用习惯,很快找到宝宝想听的内容.同时提供快乐儿歌、国学经典、启蒙英语等早期教育内容,且云端内容可以持续更新.萌宠机器人一投放市场就受到了很多家长欢迎.为了更好地服务广大家长,该公司研究部门从流水线上随机抽取100件萌宠机器人(以下简称产品),统计其性能指数并绘制频率分布直方图(如图1):产品的性能指数在的适合托班幼儿使用(简称A类产品),在的适合小班和中班幼儿使用(简称B类产90,110的适合大班幼儿使用(简称C类产品),A,B,C,三类产品的销售利润分别为每件品),在[]1.5,3.5,5.5(单位:元).以这100件产品的性能指数位于各区间的频率代替产品的性能指数位于该区间的概率.(1)求每件产品的平均销售利润;(2)该公司为了解年营销费用(单位:万元)对年销售量(单位:万件)的影响,对近5年的年营销费用,和年销售量()1,2,3,4,5i y i =数据做了初步处理,得到的散点图(如图2)及一些统计量的值.表中,,,.根据散点图判断,可以作为年销售量(万件)关于年营销费用(万元)的回归方程. (i )建立关于的回归方程;(ii )用所求的回归方程估计该公司应投入多少营销费,才能使得该产品一年的收益达到最大? (收益=销售利润-营销费用,取). 参考公式:对于一组数据()()()1122,,,,,,n n u u u υυυ,其回归直线的斜率和截距的最小二乘估计分别为,.1.(2021·全国高三专题练习)给出下列说法: ①回归直线恒过样本点的中心,且至少过一个样本点; ②两个变量相关性越强,则相关系数就越接近1;③将一组数据的每个数据都加一个相同的常数后,方差不变;④在回归直线方程ˆ20.5yx =-中,当解释变量增加一个单位时,预报变量平均减少0.5个单位. 其中说法正确的是( ) A .①②④B .②③④C .①③④D .②④2.(2020·全国高三专题练习)对两个变量、进行线性相关检验,得线性相关系数10.7859r =,对两个变量、进行线性相关检验,得线性相关系数20.9568r =-,则下列判断正确的是( ) A .变量与正相关,变量与负相关,变量与的线性相关性较强 B .变量与负相关,变量与正相关,变量与的线性相关性较强 C .变量与正相关,变量与负相关,变量与的线性相关性较强 D .变量与负相关,变量与正相关,变量与的线性相关性较强3.(2020·河南新乡市·高三一模)年的“金九银十”变成“铜九铁十”,全国各地房价“跳水”严重,但某地二手房交易却“逆市”而行.下图是该地某小区年月至年月间,当月在售二手房均价(单位:万元/平方米)的散点图.(图中月份代码分别对应年月2020年月)根据散点图选择和ln y c d x =+两个模型进行拟合,经过数据处理得到的两个回归方程分别为0.9369y =+0.95540.0306ln y x =+,并得到以下一些统计量的值:注:是样本数据中的平均数,是样本数据中的平均数,则下列说法不一定成立的是( ) A .当月在售二手房均价与月份代码呈正相关关系强化练习B .根据0.9369y =+ 1.0509万元/平方米C .曲线0.9369y =+0.95540.0306ln y x =+的图形经过点D .0.95540.0306ln y x =+回归曲线的拟合效果好于0.9369y =+4.(2020·全国高三专题练习)对四组数据进行统计,获得以下散点图,关于其相关系数的比较,正确的是( )A .24310r r r r <<<<B .42130r r r r <<<<C .42310r r r r <<<<D .24130r r r r <<<<5.(2020·邵阳市第二中学高三其他模拟(文))某种产品的广告费支出与销售额(单位:万元)之间有如表关系,与的线性回归方程为,当广告支出5万元时,随机误差的效应(残差)为( )A .10B .20C .30D .406.(2020·全国高三专题练习)为研究某种细菌在特定环境下,随时间变化的繁殖情况,得到如下实验数据:由最小二乘法得与的线性回归方程为ˆˆ0.7yx a =+,则当时,繁殖个数的预测值为( ) A .4.9 B .5.25 C .5.95D .6.157.(2020·全国高三专题练习)已知某种商品的广告费支出x (单位:万元)与销售额y (单位:万元)之间有如下对应数据:根据上表可得回归方程,计算得,则当投入10万元广告费时,销售额的预报值为A.75万元B.85万元C.99万元D.105万元8.(2020·全国高三专题练习)随着国家二孩政策的全面放开,为了调查一线城市和非一线城市的二孩生育意愿,某机构用简单随机抽样方法从不同地区调查了100位育龄妇女,结果如下表.由,得22100(45222013)9.61665355842K⨯⨯-⨯=≈⨯⨯⨯.参照下表,下列结论正确的是()A.在犯错误的概率不超过0.1%的前提下,认为“生育意愿与城市级别有关”B.在犯错误的概率不超过0.1%的前提下,认为“生育意愿与城市级别无关”C.有99%以上的把握认为“生育意愿与城市级别有关”D.有99%以上的把握认为“生育意愿与城市级别无关”9.(2020·全国高三专题练习)为考察高中生的性别与是否喜欢数学课程之间的关系,利用2×2列联表进行检验,经计算K2的观测值k=7.069,参考下表,则认为“性别与是否喜欢数学课程有关”犯错误的概率不超过()A.0.001 B.0.01 C.0.99 D.0.99910.(多选)(2021·全国高三专题练习)因防疫的需要,多数大学开学后启用封闭式管理.某大学开学后也启用封闭式管理,该校有在校学生9000人,其中男生4000人,女生5000人,为了解学生在封闭式管理期间对学校的管理和服务的满意度,随机调查了40名男生和50名女生,每位被调查的学生都对学校的管理和服务给出了满意或不满意的评价,经统计得到如下列联表:附表:附:以下说法正确的有()A.满意度的调查过程采用了分层抽样的抽样方法B.该学校学生对学校的管理和服务满意的概率的估计值为0.6C.有99%的把握认为学生对学校的管理和服务满意与否与性别有关系D.没有99%的把握认为学生对学校的管理和服务满意与否与性别有关系11.(2021·山东高三专题练习)某沙漠地区经过治理,生态系统得到很大改善,野生动物数量有所增加.为调查该地区某种野生动物的数量,将其分成面积相近的200个地块,从这些地块中用简单随机抽样的方法抽取20个作为样区,调查得到样本数据(x i,y i)(i=1,2,…,20),其中x i和y i分别表示第i个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得,,,2021)9000iiy y=-=∑(,201))800 iiix yx y=--=∑((.(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数);(2)求样本(x i,y i)(i=1,2,…,20)的相关系数(精确到0.01);(3)根据现有统计资料,各地块间植物覆盖面积差异很大.为提高样本的代表性以获得该地区这种野生动物数量更准确的估计,请给出一种你认为更合理的抽样方法,并说明理由.附:相关系数r))niix y x y --∑((,≈1.414.12.(2020·江苏南通市·高三期中)利用简单随机抽样的方法,从某校高一年级男生体验表格中抽取名同学的胸围与肺活量的样本,计算平均值,,并求出线性回归方程为ˆ32.26yx a =+. 高一男生胸围与肺活量样本统计表(1)求的值;(2)求样本与的相关系数,并根据相关性检验的临界值表,判断有无把握认为肺活量与胸围线性关系是有意义的(精确到);(3)将肺活量不低于4500ml 视为大肺活量,用样本大肺活量的频率作为全校高一男生大肺活量的概率,求从本校高一年级任意抽取名男同学,恰有两名是大肺活量的概率.(参考公式及数据:()()()121ˆniii nii x x y y bx x ==--=-∑∑2040.)附:相关性检验的临界值表13.(2020·江苏扬州市·高三期中)某校从高二年级随机抽取了20名学生的数学总评成绩和物理总评成绩,记第i 位学生的成绩为() (i =1,2,3...20),其中分别为第i 位学生的数学总评成绩和物理总评成绩.抽取的数据列表如下( 按数学成绩降序整理):(1)根据统计学知识,当相关系数|r |≥0.8时,可视为两个变量之间高度相关.根据抽取的数据,能否说明数学总评成绩与物理总评成绩高度相关?请通过计算加以说明. 参考数据:参考公式:相关系数12211()().()()niii n niii i x x y y r x x x y ===--=--∑∑∑(2)规定:总评成绩大于等于85分者为优秀,小于85分者为不优秀,对优秀赋分1,对不优秀赋分0,从这20名学生中随机抽取2名学生,若用X 表示这2名学生两科赋分的和,求X 的分布列和数学期望.14.(2020·全国高三专题练习)近年来,“双11”网购的观念逐渐深入人心.某人统计了近年某网站“双11”当天的交易额,统计结果如下表:(1)请根据上表提供的数据,用相关系数说明与的线性相关程度,线性相关系数保留三位小数.(统计中用相关系数来衡量两个变量之间线性关系的强弱.若相应于变量的取值,变量的观测值为(),则两个变量的相关系数的计算公式为:()()niix x y y r --=∑.统计学认为,对于变量,如果[]1,0.75r ∈--,那么负相关很强;如果[]0.751r ∈,,那么正相关很强;如果(]0.75,0.30r ∈--或[)0.30,0.75r ∈,那么相关性一般;如果[]0.25,0.25r ∈-,那么相关性较弱);(2)求出关于的线性回归方程,并预测年该网站“双11”当天的交易额.参考公式:121()()()ˆniii ni i x x y y bx x ==--=-∑∑,;参考数据:.15.(2020·陕西高三零模)年月日,国家统计局公布全国规模以上工业企业月累计营业收入利润率数据如表:(1)根据表中有关数据请在下图中补充完整与的折线图,判断与哪一个更适宜作为关于的回归方程类型,并说明理由;(2)根据(1)的判断结果及表中数据,建立关于的回归方程(系数精确到); (3)根据(2)得出的回归方程,预测月月累计营业收入利润率的值为多少?参考公式:对于一组数据、、、,其回归直线的斜率和截距的最小二乘估计分别为,v u αβ=-. 参考数据:表中,,.16.(2020·河北邢台市·邢台一中高三月考)近年来,国资委、党委高度重视扶贫开发工作,坚决贯彻落实中央扶贫工作重大决策部署,在各个贫困县全力推进定点扶贫各项工作,取得了积极成效.某贫困县为了响应国家精准扶贫的号召,建了一些蔬菜大棚供村民承包管理,已知土地的使用面积以及相应的管理时间的关系如下表所示:并调查了某村300名村民参与管理的意愿,得到的部分数据如下表所示:(1)求出相关系数r(保留三位小数)的大小,并判断管理时间y与土地使用面积x是否有较强的相关关系?若有,求出线性回归方程.(2)是否有99.9%的把握认为村民的性别与参与管理的意愿有关?=+++参考公式:,;,n a b c d参考数据:。
全国高考数学理科II双向细目表

11/5
抛物线
掌握
抛物线的标准方程及其几何性质
、
11/5
10/5
11/5
直线与圆锥曲线
掌握
综合
8/5
20
轨迹方程
掌握
综合
20
23
23
23
综合应用
熟练掌握
综合
20
空间直线
理解
平面的基本性质,斜二侧的画法;画出空间两条直线的各种位置关系的图形,根据图形想象它们的位置关系;直线与直线所成角、距离
10/5
9/5
14/5
13/5
图象与性质
掌握
会用三角函数线画正弦函数,正切函数的图象,由诱导公式画余弦函数的图象;理解它们的性质;会用"五点法"
12/5
的图象
理解
、 、 的物理意义
掌握
用"五点法"画函数 的简图;函数的平移问题
7/5
三角最值及综合应用
掌握
利用三角知识求最值
14/5
12/5
应用
掌握
运用所学二角知识解决实际问题
3/5
距离公式、定比分点
掌握
平面两点间的距离公式,线段的定比分点和中点坐标公式,
灵活运用
平移公式
正余弦定理
掌握
正弦定理、余弦定理,并能运用它们解斜三角形
13/5
17
4/5
17
不等式的概念性质
理解
不等式的性质
均值不等式
掌握
两个(不扩展到三个)正数的算术平均数不小于它们的几何平均数的定理.并会简单的应用;分析法、综合法、比较法证明简单的不等式
向量、向量的加法与减法、实数与向量的积
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图1 图2 正相关,u与v正相关
正相关,u与v负相关
负相关,u与v正相关
图1 A类工人生产能力的频率分布直方图图2 B类工人生产能力的频率分布直方图
亲贤臣,远小人,此先汉所以兴隆也;亲小人,远贤臣,此后汉所以倾颓也。
先帝在时,每与臣论此事,未尝不叹息痛恨于桓、灵也。
侍中、尚书、长史、参军,此悉贞良死节之臣,愿陛下亲之、信之,则汉室之隆,可计日而待也。
臣本布衣,躬耕于南阳,苟全性命于乱世,不求闻达于诸侯。
先帝不以臣卑鄙,猥自枉屈,三顾臣于草庐之中,咨臣以当世之事,由是感激,遂许先帝以驱驰。
后值倾覆,受任于败军之际,奉命于危难之间,尔来二十有一年矣。
先帝知臣谨慎,故临崩寄臣以大事也。
受命以来,夙夜忧叹,恐托付不效,以伤先帝之明;故五月渡泸,深入不毛。
今南方已定,兵甲已足,当奖率三军,北定中原,庶竭驽钝,攘除奸凶,兴复汉室,还于旧都。
此臣所以报先帝而忠陛下之职分也。
至于斟酌损益,进尽忠言,则攸之、祎、允之任也。
愿陛下托臣以讨贼兴复之效,不效,则治臣之罪,以告先帝之灵。
若无兴德之言,则责攸之、祎、允等之慢,以彰其咎;陛下亦宜自谋,以咨诹善道,察纳雅言,深追先帝遗诏。
臣不胜受恩感激。
今当远离,临表涕零,不知所言。
