第5章机械的效率和自锁
孙桓《机械原理》笔记和课后习题(含考研真题)详解(机械的效率和自锁)【圣才出品】

第5章机械的效率和自锁5.1 复习笔记一、机械的效率1.功和效率(1)机械效率①驱动功机械上的驱动功(输入功)为W d,有效功(输出功)为W r,损失功为W f。
则有W d=W r+W f②机械效率a.定义机械的输出功与输入功之比称为机械效率,反映了输入功在机械中的有效利用程度,以η表示。
b.计算方法用功计算时η=W r/W d=1-W f/W d;用功率计算时η=P r/P d=1-P f/P d;式中,P d——输入功率;P r——输出功率;P f——损失功率。
(2)损失率①定义机械的损失功与输入功之比称为损失率,以ξ表示。
②计算方法由定义有ξ=W f/W d=P f/P d。
注:η+ξ=1,由于摩擦损失不可避免,故必有ξ>0和η<1。
(3)效率的简便计算方法为便于效率的计算,可应用下式进行计算η=理想驱动力/实际驱动力=理想驱动力矩/实际驱动力矩①斜面机构正反行程的机械效率分别为η=tanα/tan(α+φ)η′=tan(α-φ)/tanα式中,α——斜面夹角;φ——总反力与法向反力的夹角。
②螺旋机构拧紧和放松螺母时的效率计算式分别为η=tanα/tan(α+φv)η′=tan(α-φv)/tanα式中,α——中径升角;φv——螺旋副的摩擦角。
2.机器(或机组)的效率已知各机构的效率可计算确定整个机构的效率。
常用机构的效率见教材表5-1。
(1)串联①计算公式由k个机器串联组成的机组,设各机器的效率分别为η1、η2、…、ηk,机组的输入功率为P d,输出功率为P r。
则整个串联机组的机械效率为η=P r/P d=(P1/P d)(P2/P1)…(P k/P k-1)=η1η2…ηk②特点a.前一机器的输出功率即为后一机器的输入功率;b.只要串联机组中任一机器的效率很低,就会使整个机组的效率极低;c.串联机器的数目越多,机械效率也越低。
③提高串联机组效率的措施a.减少串联机器的数目;b.优先提高效率最低机器的效率。
第5章机械的效率和自锁

P1 1
P’1
P2
Pk
2
k
P’2
P’k
Pr
总效率η不仅与各机器的效率ηi有关,而且与传递的功率 Pi有关。
设各机器中效率最高最低者分别为ηmax和ηmin 则有:
ηmin<η <ηmax
3.)混联 先分别计算,合成后按串联或并联计算。
P1 1
P2 P’d23‘ P’d3 4‘P’r 2
Pd
P”d23“ P”d3 P4“kP”r
无论F多大,滑块在F的作用下不可能运动
FR Ft F Fn
φβ 1
Ff
2
当驱动力的作用线落在摩擦角(锥)内时,则机械发生 自锁。
5.4.2转动副的自锁
a
对仅受单力F作用的回转运动副产 生的力矩为: Md=F·a
最大摩擦力矩为: Mf =FRρ
1F FR
2
当力F的作用线穿过摩擦圆(a<ρ)时,发生自锁。
Ff 21
简单平面移动副
2 FN21 G
Ff 21 fFN21 fG
v FN21
12
F 1
G
●槽面接触: fv= f / sinθ
G=(FN21 /2)sinθ+(FN21 /2)sinθ FN21 = G / sinθ Ff21= f FN21
= G (f / sinθ) =G fv
fv─当量摩擦系数。
第5章 机械的效率和自锁
本章教学内容
5.1运动副中摩擦力的确定 5.2考虑摩擦时机构的受力分析 5.3机构的效率 5.4机构的自锁
5.1 运动副中的摩擦力的确定
5.1.1移动副中摩擦力的确定
●水平面接触:
Ff 21 fFN21
《机械原理》课件-第5章②机械自锁
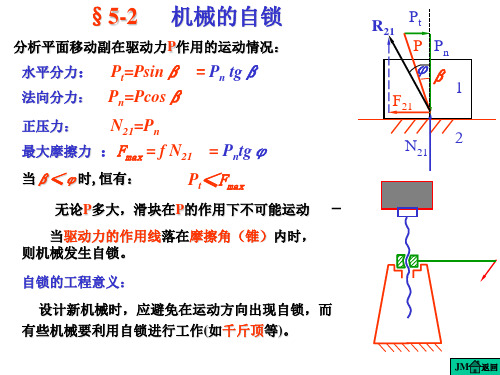
分析平面移动副在驱动力P作用的运动情况:
水平分力: Pt=Psinβ = Pn tgβ 法向分力: Pn=Pcosβ
正压力:
N21=Pn
最大摩擦力 :Fmax = f N21 = Pntgφ
当β≤φ时,恒有:
Pt≤Fmax
无论P多大,滑块在P的作用下不可能运动
R21 Pt P PnOE来自PδA
e
C R23
φD
3
O
B
2
E
δ-φ
A
C
1
φ
esin(δ-φ)-(Dsinφ)/2≤ρ
B
JM 返回
当机械出现自锁时,无论驱动力多大,都不能运动,从能量的观点来看, 就是驱动力所做的功永远≤由其引起的摩擦力所做的功。即:
η≤0
设计机械时,上式可用于判断是否自锁及出现自锁条件。 说明: η≤0时,机械已不能动,外力根本不做功,η已失去一般效 率的意义。仅表明机械自锁的程度。且η越小表明自锁越可靠。
a
1P R
应用实例:图示偏心夹具在P力加紧,去掉P后要求
2
不能松开,即反行程具有自锁性,
s
若总反力R23穿过摩擦圆--发生自锁
s1
由此可求出夹具各参数的几何条件为:
s-s1≤ρ
在直角△ABC中有:
s1 =AC =(Dsinφ) /2
在直角△OEA中有:
s =OE=esin(δ-φ)
该夹具反行程具有自锁条件为:
②令η≤0;
③令生产阻力Q≤0; ④驱动力在运动方向上的分力Pt≤F摩擦力。
JM 返回
f =0.15
(2)斜面压榨机
φv =8.7°
Q
R13 3 1
孙桓《机械原理》【教材精讲+考研真题解析】(第五章机械的效率与自锁)【圣才出品】

第5章机械的效率与自锁[视频讲解]5.1本章要点详解本章要点■机械效率的定义及其计算方法■提高机械效率的措施■机械的自锁现象及其应用■机械的自锁条件及其确定重难点导学一、机械的效率1.机械效率的概念及意义(1)概念①机械效率机械的输出功与输入功之比称为机械效率,它反映了输入功在机械中的有效利用程度,以 表示。
②损失率机械的损失功(W f)与输入功(W d)的比值称为机械损失系数或损失率,以ξ表示。
(2)意义①机械效率反映了输入功在机械中的有效利用的程度。
②机械效率是机械中的一个主要性能指标。
③因摩擦损失是不可避免的,故必有ξ>0和η<1。
2.机械效率的确定(1)机械效率的计算确定①以功表示的计算公式式中W r表示有效功、W f表示损失功、W d表示总功。
②以功率表示的计算公式式中P r表示有效功率、P f表示损失功率、P d表示总功率。
③以力或力矩表示的计算公式η=F0/F=M0/M式中M0和M分别表示为了克服同样生产阻力所需的理想驱动力矩和实际驱动力矩,所以其计算公式也可表示为(2)机械效率的实验测定机械效率的确定除了用计算法外,更常用实验法来测定,许多机械尤其是动力机械在制成后,往往都需作效率实验。
3.机组的机械效率计算已知机构的效率可计算确定整个机构的效率。
常用机构的效率见如表5-1-1所示。
表5-1-1简单传动机构和运动副的效率(1)机组的定义由若干个机器组成的机械系统称为机组。
当已知机组各台机器的机械效率时,则该机械的总效率可由计算求得。
(2)机组的分类①串联机组如图5-1-1所示,由k个机器串联组成的机组,设各机器的效率分别为1η、2η、…、η,则串联机组的效率为k图5-1-1串联机组由此可见,只要串联机组中任一机器的效率很低,就会使整个机组的效率极低;且串联机器的数目越多,机器的效率也越低。
因此,提高串联机组机械效率的方法有:a.减少串联机构的数目;η。
b.提高机组中最小的机械效率min②并联机组如图5-1-2所示,由k个机构并联组成的机组,设各机构的效率分别为1η、2η、……kη,则并联机组的效率为图5-1-2并联机组由此可见,并联机组的特点有:a.机组的输入功率为各机器的输入功率之和,而其输出功率为各机器的输出功率之和。
机械原理 第五章机械的效率

(机械自锁时已不能运动,它已不能克服任何工作阻力(即使很小),工作阻力
G〈 0 意味着只有工作阻力反向而变成驱动力后,才可能使机械运动,即G〈 0 机 械自锁)
机械原理
第5章机械的效率和自锁
例1偏心夹具
确定当作用在手柄上的力去 掉后夹具不至松开的条件 (即自锁条件)
7。 风 力 发 电 机 中 的 叶 轮 受 到 流 动 空 气 的 作 用 力,
此力在机械中属于
。
A) 驱 动 力;B) 生 产 阻 力; C) 有 害 阻 力; D) 惯 性 力。
8。在机械中阻力与 其作用点速度方向
。
A).相 同; B).一定相反; C).成锐角; D).相反或成钝角 。
机械原理
第5章机械的效率和自锁
思考题:
1。移动副的自锁条件是—————————,转动副的自锁条件是—————— ———,螺旋副的自锁条件是—————————。
2。机械中V带比平带应用广泛,从摩擦角度来看,其主要原因是——————。
3。在由 若 干机 器 并 联 构 成 的 机 组 中, 若 这 些 机 器 的 单 机 效
A) 都 不 可 能;B) 不 全 是;C) 一 定 都。
6。在 车 床 刀 架 驱 动 机 构 中, 丝 杠 的 转 动 使 与 刀 架 固
联 的 螺 母 作 移 动, 则 丝 杠 与 螺 母 之 间 的 摩 擦 力 矩
属于
。
A)驱 动 力;B)生 产 阻 力;C)有 害 阻 力;D)惯 性 力。
(2)并联:由几种机器并联组成的机组。
(3)混联:包含串、并联。
机械原理
第5章机械的效率和自锁
机械原理复习题(第3、4、5、8章)

第3章平面机构的运动分析第4章平面机构的力分析第5章机械的效率和自锁第8章平面连杆机构及其设计一、填空题:α=,则传动角γ=___________度,传动角越大,1、铰链四杆机构的压力角040传动效率越___________。
2、下图为一对心曲柄滑块机构,若以滑块3为机架,则该机构转化为机构;若以构件2为机架,则该机构转化为机构。
3、移动副的自锁条件是;转动副的自锁条件是。
4、曲柄摇杆机构中,当和共线时出现死点位置。
:5、曲柄摇杆机构中,只有取为主动件时,才有可能出现死点位置。
处于死点位置时,机构的传动角γ=__________度。
6、平行四边形机构的极位夹角θ=,它的行程速比系数K=。
7、曲柄滑块机构中,若增大曲柄长度,则滑块行程将。
8、如下图所示铰链四杆机构,70mm,150mm,110mm,90mm====。
若以a b c da杆为机架可获得机构,若以b杆为机架可获得机构。
9、如图所示铰链四杆机构中,若机构以AB杆为机架时,为机构;以CD 杆为机架时,为机构;以AD杆为机架时,为机构。
~10、在平面四杆机构中,和为反映机构传力性能的重要指标。
11、在曲柄摇杆机构中,如果将杆作为机架,则与机架相连的两杆都可以作运动,即得到双曲柄机构。
12、在摆动导杆机构中,若以曲柄为原动件,该机构的压力角为,其传动角为。
13、相对瞬心与绝对瞬心的相同点是,不同点是;在由N个构件组成的机构中,有个相对瞬心,有个绝对瞬心。
/二、判断题:1、对于铰链四杆机构,当机构运动时,传动角是不变的。
()2、在四杆机构中,若有曲柄存在,则曲柄必为最短杆。
()3、平面四杆机构的行程速度变化系数K 1,且K值越大,从动件急回越明显。
()4、曲柄摇杆机构中,若以摇杆为原动件,则当摇杆与连杆共线时,机构处于死点位置。
()5、曲柄的极位夹角θ越大,机构的急回特性也越显著。
()6、在实际生产中,机构的“死点”位置对工作都是不利的,处处都要考虑克服。
机械原理5机械效率与自锁

一、机械的效率
机械在稳定运转阶段恒有: Wd= Wr+Wf η =Wr / Wd =(Wd-Wf) /Wd =1-Wf /Wd
比值Wr / Wd反映了驱动功的有效利用程度, 称为机械效率。
用功率表示:η =Nr / Nd =(Nd-Nf) /Nd
=1-Nf /Nd
分析:η 总是小于 1,当Wf 增加时将导致η 下降。
以上为效率计算方法,工程上更多地是用实验法
测定η ,表5-1列出由实验所得简单传动机构和运
动副的机械效率(P69-P70)。
表5-1 简单传动机械和运动副的效率
名称
传动形式
效率值
备注
圆柱齿 轮传动
6~7级精度齿轮传动
8级精度齿轮传动 9级精度齿轮传动 切制齿、开式齿轮传动
铸造齿、开式齿轮传动
6~7级精度齿轮传动
拧紧时:
M
d2 2
Gtg(
v )
理想机械: M0=(d2 G tgα) / 2 η=M0 / M =tgα/tg(α+φv )
拧松时,驱动力为G,M’为阻力矩,则有:
实际驱动力:
G=2M’/d2 tg(α-φv )
理想驱动力: ∴
G0=2M’/d2 tgα η’=G0/G =tg(α-φv ) / tgα
良好跑合、稀油润滑 稀油润滑 干油润滑
0.40~0.45 0.70~0.75
0.75~0.82 0.80~0.92 0.85~0.95
润滑良好
名称 带传动
链传动 摩擦轮
传动 滑动轴承 滚动轴承
螺旋传动
续表5-1 简单传动机械和运动副的效率
传动形式
效率值
备注
第五章机构的效率与自锁

计算公式:
η= Nr /Nd =G vG/(F vF) 设: η0=1的理想机械 η0=1= G vG/ (F0 vF) 则有: η= F0/ F 或η= M0/ M
(F0/ M0不考虑摩擦时的理想驱动力/矩)
斜面机构的效率
正行程:F=G*tg(α+ φ)
φ)
反行程 F’=G*tg(α-
(F为驱动力)
3。利用效率≤0(驱动力所作的功不足克服其所引起的最 大损失功 因驱动力G=FR32 G=FR32 = F sin(90+) /sin(-2) =F cos / sin(-2) G0 = F / sin = G0/G = (F/sin)/(Fcos /sin(-2)) = sin(-2)/ (sin cos ) ≤0 sin(-2) ≤0 -2≤0 即自锁条件为 ≤ 2
2、驱动力F ≤0(即必须加一个反向的作用力才能将楔形块拉出 对上例中楔形块2,F+FR12+FR32=0 利用正弦定律: F/sin(-2)= FR32 /sin(90+) = FR12 /sin(90-+) 因为 F ≤0 所以 sin(-2) ≤0 即自锁条件为: ≤ 2
3)混联系统
§5-2机构的自锁
一.定义 由于摩擦力的存在,使机构无论在多大的驱动力的作用下 都无法运动的现象,称为自锁. 例: 1、螺旋千斤顶 A 旋转螺母,使重物上升 B 撤去旋转力F,则无论 重物多重,都不能使螺 母反转,使重物下降。 - - - - - -可利用的自锁
二、自锁的条件
1、移动副 分析右图所示滑块机构,要使滑块 向右滑动或有向右滑动的趋势, 则:Ff<Ft 因 Ft=Fsin Fn=Fcos Ff=Fn tg= F cos tg 有 F sin> F cos tg tg > tg 故 > 反之,当≤时,无论作用在滑 块上的力有多大,Ff≥Ft,机构自锁, 也即当驱动力作用在摩擦锥内时, 机构自锁。
机械的效率与自锁

3.生产阻抗力G等于或小于零; G 0
机电工程学院电子机械系
第四章 运动副中的摩擦和机械效率
例3:已知机构位置、摩擦圆半径ρ、摩擦角φ如图所示。图中Q 为已知生产阻力。
(1)在图中画出各运动副总反力作用线。
(2)求出机构在图示位置的驱动力P及瞬时效率η。
α
机电工程学院电子机械系
Nd
N1 N2 NK
并联系统的总效率不仅与各组成机器的效率有关,而且与
各机器所传递的功率也有关。设ηmax和ηmin为各个机器中效 率的最大值和最小值,则ηmin<η<ηmax。
若各台机器的效率均相等,并联系统的总效率等于 任一台机器的效率。
机电工程学院电子机械系
3.混联
由串联和并联组成的混联式机械系统。其 总效率的求法按其具体组合方式而定。
如果判断反行程自锁条件,则
P0 tg ( ) P tg ( )
根据斜面机构可推出反行程的 P'
P' Q tg ( )
机电工程学院电子机械系
P' 0
作业及思考:
1、习题4-5、5-8、4-13、4-20、4-22。 2、思考什么实际工作情况下应该考虑或 者不考虑摩擦力?举例说明,并分析考虑 与否对结果产生的影响的程度。
第四章 运动副中的摩擦和机械效率
2.自锁条件
机构是许多构件由运动副联接起来的,如机构 中有一个运动副发生自锁,则该机构出现自锁,即 机械发生自锁的实质是运动副发生自锁。
1)运动副的自锁条件 FR21
①移动副的自锁条件
P
β Pn
Pt P sin Pn tan
V12
Ff 21 f Pn Pn tan
机械的效率和自锁机械原理

第五章机械的效率和自锁研究内容:1 机械的效率2 机械的自锁第1讲机械的效率5.1.1 机械效率的概念5.1.2机械效率的计算5.1.3机组效率的计算机械效率的概念及意义:(1) 概念: 机械效率 η 机械损失率 ξ η=W r W d 摩擦损失是不可避免的,总有 ξ >0 和 η < 1;机械效率反映了输入功在机械中的有效利用的程度。
(2) 意义: 降耗节能是国民经济可持续发展的重要任务之一。
机械效率的高低是机械中的一个主要性能指标。
—— 机械的输出功(W r )与输入功(W d )之比—— 机械的损失功(W f )与输入功(W d )之比=1−Wf W d =1−ξ机械效率的计算:1) 以功表示的计算公式 η=W r W d =1−W f W d2) 以功率表示的计算公式 η=P r P d =1−P f P d 3) 以力或力矩表示的计算公式η=F 0F =M 0M实际机械装置 ηF 0v F机械传动装置 Gv Gη=P r P d =Gv G Fv F η0=Gv G F 0v F =1即 η=理想驱动力实际驱动力=理想驱动力矩实际驱动力矩机组 ——由若干个机器组成的机械系统整机 ——由若干个机构组成的整台机器 已知机组各机器的效率,便可计算该机组的总效率。
1. 串联机组1) 功率传动特点: 前一机器的输出功率即为后一机器的输入功率。
2) 总机械效率:η=P r P d =P 1P d P 2P 1…P k P k−1=η1η2…ηn⋯1 2kP dP 1P 2P k -1P k串联机组模型结论:串联机组中任一机器效率很低,整个机械效率就会极低;且串联机器的数目越多,机械效率也越低。
2.并联机组1)传动功率特点:机组的输入功率为各机器的输入功率之和,而输出功率为各机器的输出功率之和。
2) 总机械效率:η=P riP di=P1η1+P2η2+⋯+P kηkP1 +P2 +⋯+P kη1 η2 ηkP1η1P1 P2 P kP dP2η2Pkηk结论:⏹并联机组的总效率与各机器的效率和传动功率大小均有关;⏹其总效率主要取决于传动功率大的机器的效率;⏹要提高并联机组的总效率,应着重提高传动功率大的路线的效率。
机械原理课件第4-5章机械的受力分析、效率与自锁

受力分析的方法
1
平衡分析法
平衡分析法是分析力的平衡状态,建立方程并解方程的方法。
2Байду номын сангаас
变形分析法
变形分析法是利用物体的变形和位移来分析内力和外力的方法。
3
虚功原理法
虚功原理法是利用机身位移和外力所做的功的原理,来分析内力和外力平衡的方 法。
自锁的概念
自锁是机械一种特殊的现象,当一种机械的某些部件因运动而产生内部力矩时,其本身所固有的特性导致自身 所承受的内部力矩增大,从而在不依靠外力的情况下产生锁定作用。
3 弯曲力 & 正应力
弯曲力作用在物体上时会导致形变以及正应力的产生。
提高机械效率的途径
保持润滑状态
润滑状态对机械效率的影响非常大。
选择合适的材料
材料的选择应该考虑机械运行的环境和作用力。
减小摩擦损失
尽可能地降低内摩擦和外摩擦的损失。
优化设计
通过分析机械结构,寻求机械优化方案,以提高 机械效率。
机械效率的计算方法
结论
通过学习,我们了解了机械受力分析、效率和自锁的相关知识。同时,我们也深入了解了提高机械效率的途径 以及常见的自锁装置等等,这些能够有助于我们更好地理解机械的性能和使用。
机械原理课件第4-5章机 械的受力分析、效率与自 锁
欢迎大家来到机械原理课件的第四至第五章。今天我们将学习机械的受力分 析、效率以及自锁的原理。
机械力的分类
1 张力 & 压力
张力是物体前后两端受到的同向拉力,压力则是相反的方向。
2 剪力 & 扭力
剪力是垂直于物体截面方向的力,而扭力是绕物体轴旋转的力。
功率输入 传动装置输入功率的总和
功率输出 传动装置输出功率除以效率
机械原理(第5章 机械中的摩擦、机械效率及自锁)

二、转动副中摩擦力:
轴 轴承
轴径
Northwest A&F University
第五章 机械中的摩擦、机械效率及自锁
二、转动副中摩擦力:
1.轴径摩擦: 轴用于承受径向力放在轴承中的部分称为轴径。 1)摩擦力矩的确定: 设有径向载荷G作用的轴径1,在驱 动力矩Md的作用下,在轴承2中等速运动。 此时转动副两元素必将产生摩擦力以阻 止轴径向对于轴承的滑动。则:
Northwest A&F University
第五章 机械中的摩擦、机械效率及自锁
一、移动副中摩擦力的确定:
2)三角形螺纹螺旋中的摩擦:
β
β △N β △N
Q
△N
△N
β
Q
β-牙形半角
Northwest A&F University
第五章 机械中的摩擦、机械效率及自锁
一、移动副中摩擦力的确定:
2)三角形螺纹螺旋中的摩擦: 螺母和螺纹的相对运动完全相同两者受力分析的方法一致。 运动副元素的几何形状不同在轴向载荷完全相同的情况下, 两者在运动副元素间的法向反力不同接触面间产生的摩擦力不 同。 引入当量摩擦系数: 当量摩擦角: fv = f / cosβ
第五章 机械中的摩擦、机械效率及自锁
二、研究机械中摩擦的内容:
1.几种常见的运动副中摩擦的分析; 2.考虑摩擦时机构的受力分析; 3.机械效率的计算; 4.由于摩擦的存在而可能发生的所谓机械的“自锁” 现 象,以及自锁现象发生的条件。
Northwest A&F University
第五章 机械中的摩擦、机械效率及自锁
Northwest A&F University
第五章 机械中的摩擦、机械效率及自锁
第五章 机械的效率和自锁武汉理工大学,机械原理,课件

2. 并联 图示为几种机器并联组成的机组。
Nd1 Nd2
1 2 总输入功率为: Nr1 Nr2 Nd = Nd1 + Nd2 + …+ NdK 总输出功率为: Nr = Nr1 + Nr2 + …+ NrK ∵hi= Nri/Ndi 而 Nr = Nd1h1 + Nd2h2 + …+ NdKhK
Nd Nd3 NdK
c. 力(矩)表示 设:F——实际驱动力;Q——实 际生产阻力;VF、VQ作用点沿力方向线 速度。 Q 设想机器中无有害阻力——理想机器。设F0为对应(克服)同一生产 阻力Q时的理想阻力。对于理想机器,有
h = Nr / Nd = QVQ /FVF
vQ
vF F
h0= QVQ /F0VF = 1
即: QVQ = F0VF
越大,表明自锁越可靠。
四、楔形面自锁条件 与平面摩擦相对应,对于楔形面摩擦可
θ 1
θ
以直接用fv代替f,相应地可以用jv代替j。
结论:自锁条件——a≤jv 五、斜面自锁条件
N′ n R21 1 F
2 Q N′
1. 等速上升
建立力平衡条件,有P = Q tg (a + j) 于是: P0 = Q tg a 即斜面的机械效率为
h
h
h3
Nr3 Nr
hK
NrK
∴h =
=
(Nd1h1 + Nd2h2 + …+ NdKhK) (Nd1 + Nd2 + …+ NdK) (Nd1h1 + Nd2h2 + …+ NdKhK) Nd
∴h = (Nd1h1 + Nd2h2 + …+ NdKhK) / (Nd1 + Nd2 + …+ NdK) = (Nd1h1 + Nd2h2 + …+ NdKhK) / Nd
05 机构的效率与自锁

并联系统
总输入功率
Pd = P1 +P+ Pk P1 1 h1 P’1 2 P2 h2 P’2
Pd Pk k hk P’k
总输出功率
Pr = P’1 + P’2 + P’k
效率 h Pr P1h1 P2h 2 Pkh k Pd P 1P 2 P k • 总效率不仅与各台机器的效率有关,而且与各台机器 传递的功率大小有关 • 总效率主要取决于传递功率最大的机器 若各台机器的输入功率相等 h (h1 h 2 h k ) / k
§5-1 机械的效率
一、机械效率的概念
作用在机械上的力: 驱动力F、 生产阻力Q、 有害阻力Ff 作用力所作的功: 输入功 Wd 、 输出功 Wr 、 损耗功 Wf 力所具有的功率: 输入功率 Nd 、输出功率 Nr 、损耗功率 Nf 通常,将驱动力做的功称为输入功(Wd);克服生产阻力做的功称 为输出功(Wr);克服有害阻力做的功称为损耗功 (Wf)。
Wd Wd / t Pd Pd
Pd
由于实际中,损耗功率不可能为零,故效率始终小于1 减小损耗功率(主要减小摩擦损耗),可以提高效率
简单传动机构和运动副的效率 :表5-1/P69
2 力或力矩形式表达效率
Pr GvG h Pd FvF 对理想机械:不存在摩擦 理想驱动力:F0<F 理想机械的效率:
•尽量简化机械系统。采用最简单的机构满足工作要求,使传递功率通过 的运动副最少 •选择适当的运动副形式。转动副易保证精度,效率高;移动副不易保证 精度,效率低 •减小构件尺寸。如轴径增大时会使摩擦力矩增大,机械易发生自锁 •减少运动副中的摩擦。如矩形螺纹效率高于三角螺纹;平面摩擦效率高 于槽面摩擦;滚动摩擦效率高于滑动摩擦;表面精度高效率高于表面精 度低;选用摩擦系数小的材料;合理润滑等 •减少动载荷
第5章运动副中的摩擦和机械效率

5.4 转动副中的摩擦
径向轴颈与轴承 止推轴颈与轴承
5.4.1径向轴颈与轴承
平衡条件:
Q R 21 0
M M
f
令 : f1
T21 N
21
0
Q R 21 N
2 21
M
M
f
R 21
T21 N
2
21
1 f1
2
f
T 21 r f1 N
21
r
螺纹
螺纹的牙型
30º 15º 3º 30º
矩形螺纹
三角形螺纹
梯形螺纹
锯齿形螺纹
内螺纹
内外螺纹相互旋 合构成螺旋副
外螺纹
假定:螺钉与螺母间的压力 1. 螺母沿螺旋面等速上升 作用在螺旋平均半径r0(直 M F r0 径d0)的螺旋线上;螺旋副 中力的作用(a)与滑块和斜 F Q tg ( ) 面间力的作用(b)相同.
5.4.3止推径向轴颈或轴承
1、非跑合的止推轴承:轴 端各处的压强相等
M
f
2 3
R r
3
3 2
R r
2
fQ
2、跑合的止推轴承:轴端 各处的压强不相等,离中心 远的部分磨损较快,因而压 强减小;离中心近的部分磨 损较慢,因而压强增大。
M 1 ( R r) f Q 2
f
螺旋机构正反 行程效率不同
5.5.3机械的效率与自锁
在实际机械中,由于摩擦的存在以及驱动力作用方向的问 题,有时会出现无论驱动力如何增大,机械都无法运转的 现象,这种现象称为机械的自锁。
机械自锁的条件:
0
0
空转
自锁
孙恒《机械原理》(第八版)学习辅导书第5章 机械的效率和自锁【圣才出品】

第5章 机械的效率和自锁5.1 复习笔记本章主要介绍了机械的效率和自锁条件的计算。
考试时,常与第4章摩擦力的计算及机构的受力分析综合考察,主要是计算题。
复习时需要把握其具体内容,重点掌握。
一、机械的效率1.功和效率(见表5-1-1)表5-1-1 功和效率注:η+ξ=1,由于实际情况下,摩擦损失不可避免,故必有η<1和ξ>0。
2.机器(或机组)的效率(见表5-1-2)表5-1-2 机器(或机组)的效率注:①若已知各机构的效率,则可计算确定整个机构的效率。
常用机构的效率见教材表5-1。
②设各机器的效率分别为η1、η2、…、ηk,输入功率分别为P1、P2、…P k,则各机器的输出功率分别为P1η1、P2η2、…、P kηk。
3.提高机械的效率的方法(1)减小介质阻力①使用流线型外形设计;②应注意高速旋转零件的结构设计,减小风阻。
(2)减小运动副中的摩擦①用滚动摩擦代替滑动摩擦;②注意各运动副的润滑;③对高速轴承可采用空气轴承、磁悬浮轴承等。
二、机械的自锁(见表5-1-3)表5-1-3 机械的自锁图5-1-1 移动副的自锁图5-1-2 转动副的自锁5.2 课后习题详解5-1 眼镜用小螺钉(M1×0.25)与其他尺寸螺钉(例如M8×1.25)相比,为什么更易发生自动松脱现象(螺纹中径=螺纹大径-0.65×螺距)?解:(1)求眼镜用小螺钉的螺纹升角M1×0.25型螺纹,其大径d′为1mm,螺距P′为0.25mm。
则M1×0.25螺钉的螺纹中径为d′2=(1-0.65×0.25)mm=0.8375mm;螺纹升角为α′=arctan(P′/d′2)=arctan(0.25/0.8375)=16.62°(2)求其他尺寸螺钉的螺纹升角同理,M8×1.25型螺钉,其大径d″为8mm,螺距P″为1.25mm。
则M8×1.25螺钉的螺纹中径为d″2=(8-0.65×1.25)mm=7.1875mm;螺纹升角为α′′=arctan(P′′/d′′2)=arctan(1.25/7.1875)=9.87°<α′。
机械原理第五章机械的效率和自锁

机械效率和机械自锁的关系
机械效率和机械自锁密切相关,一些自锁机构的应用可 以提高机械效率,更加安全可靠。
机械自锁的定义和分类
机械自锁是指机械装置自身具有防止倒退或松动的特性,分为正向自锁和反向自锁。正向自锁是 防止负载向反向移动,反向自锁是防止负载向正向移动载倒退。
自锁蜗轮机构
利用蜗轮和蜗杆的摩擦阻力,确保负载在停止状态下不会移动。
丝杠自锁机构
利用丝杠和螺母的摩擦阻力,防止负载向下滑动。
自锁机构的应用范围
自锁机构被广泛应用于各种机械装置中,如起重机、传送带、滑车、石材切割机等。它们可以防止因负载运动产 生的安全事故,提高设备效率和可靠性。
双蜗杆自锁机构
棘轮与制动器自锁机构
双蜗杆自锁机构通过两个蜗杆不同的螺旋角度实现自锁。 棘轮与制动器自锁机构通过摩擦力和弹簧力实现自锁。
自锁机构的设计和计算
自锁机构的设计和计算需要考虑多个因素,如负载大小和重量、自锁机构的类型和材料、以及工 作环境和要求等。设计过程需要综合材料力学、机械结构、热力学和工程力学等知识。
材料选择
材料选择需要考虑自锁机构的使用环境和要求,如机械性能、耐磨性、耐腐蚀性等。
自锁角计算
自锁角是指自锁机构能保持自锁状态的最大倾斜角度。当自锁角大于工作角度时,自锁机构 才能起到良好的效果。
弹簧力计算
有些自锁机构需要利用弹簧力来实现自锁,弹簧力的大小和设计也需要计算和考虑。
机械效率和自锁的关系
1
石材切割机
在切割大理石或花岗岩的时候,自锁机构可以确保切割刀不发生倒退或滑动。
2
电梯传动系统
在电梯传动系统中,自锁机构可以保证电梯不会发生自由下落。
机械原理第五章 机械的效率和自锁.

机械的效率(2/10)
2.机械效率的确定 (1)机械效率的计算确定 1)以功表示的计算公式
实际机械装置 理论机械装置
F0 vF
h0
h=Wr/Wd=1-Wf/Wd
2)以功率表示的计算公式
G0
vG
h = Pr /Pd=GvG /FvF
h=Pr/Pd=1-Pf/Pd
3)以力或力矩表示的计算公式 h=F0/F=M0/M=G/G0=Mr/Mr0 即
2)实验方法 实验时,可借助于磅秤测定出定子平衡杆的压力F来确定出 主动轴上的力矩M主, 即 M主=Fl。 同时,根据弹性梁上的千分表读数(即代表Q力)来确定 制动轮上的圆周力Ft=Q-G, 从而确定出从动轴上的力矩M从,
M从=FtR=(Q-G)R 该蜗杆的传动机构的效率公式为 η =P从/P主 =ω从M从/(ω主M主) =M从/(iM主) 式中 i为蜗杆传动的传动比。 对于正在设计和制造的机械,虽然不能直接用实验法测定其 机械效率,但是由于各种机械都不过是由一些常用机构组合而成 的,而这些常用机构的效率又是可通过实验积累的资料来预先估 定的(如表5-1 简单传动机构和运动副的效率)。 据此,可通过 计算确定出整个机械的效率。
0.94 0.94 0.42
解 机构1、2、3′ 及4′串联的部分
′ 4 )′ =5 kW/(0.982×0.962)=5.649 kW P′d=P′r /(η1η2η3 η 机构1、2、3" 、4"及5"串联的部分 " =Pr"/(η1η2η3 " "5 )" =0.2 kW/(0.982×0.942×0.42)=0.561 kW Pd η4 η 故该机械的总效率为 η = ∑Pr /∑Pd =(5+0.2) kW/(5.649+0.561) kW=0.837
机械原理第05章

ω:0↗ωm,
2、稳定运转阶段
1) ω=const——等速稳定运转 W=∆E=0,即在任一时间间隔内,Wd=Wc ; 条件:作用于机械上的力或力矩均为常矢。 2) ω= ω(t)= ω(t+T)——周期性的稳定运转 T——周期:完成一个运动循环所需的时 间。 运动循环:机器的运动状态(包括位移、 速度和加速度等)从某一原始值开始, 经过一个运动过程又变回到该原始值。 这个运动过程称为机器的一个运动循环。
上海海运大学专用
v
b、轴颈自锁的条件:α≤ρ 其中,α为作用于轴颈1上的外主动力
系的合力F离轴颈中心的O的距离; ρ为摩擦圆半径,如图5-9所示。 几何意义:轴颈自锁 的条件是:作用于 轴颈1上的外主动力 系的合力F的作用 线切于或割于摩擦 圆。
上海海运大学专用
图5-9
例1a
例1推导图5-10所示偏心夹具的自锁条件。 解 要求在夹紧工件并撤去 手柄力F后,保证偏心盘 不能松转。 显然,使偏心盘发生松转 的力是FR23 ,而FR23 是作 用在轴颈O上的主动外 力。由轴颈的自锁条件 知,应保证: a=s-s1≤ρ
1、串联 2、并联 3、混联
上海海运大学专用
1、串联
如图5-3所示为k个机器串联组成的机组。 设各机器的效率分别为η1、η2、…、ηk, 机组的输入功率为Pd,输出功率为Pr=Pk。 串联特点:前一机器的输出功率为后一机 器的输入功率。
图5-3
上海海运大学专用
<min(η1、η2、…、ηk)
P P P P 1 2 r η= = ⋅ ⋅ ⋅ k =η1η2 ⋅ ⋅ ⋅ηk P P P P −1 1 d d k
上海海运大学专用
3、停车阶段
Wc,输入功小于阻抗功。 为加速制动,一般都要撤去驱动力;有时, 还需另加制动力,以缩短停车时间。 机器运转三个阶段的主轴角速度的变化曲 线如图5-1所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
r2)
=
f
G(R+r)/2
r
5.1考虑摩擦时机构的受力分析
●考虑摩擦时,机构受力分析的步骤: 1)计算出摩擦角和摩擦圆半径,并画出摩擦圆; 2)从二力杆着手分析,根据杆件受拉或受压及该杆相对于 另一杆件的转动方向,求得作用在该构件上的二力方向;
3)对有已知力作用的构件作力分析; 4)对未知力所在构件作力分析、求解。
方向:与ω12相反。
——摩擦圆半径
G' Md
12
1
2
总反力
FR21恒切于摩擦圆。 对轴心矩的方向与ω12相反。
G G'G' G'
FR21FR21 Mf
FN21
Ff21
●转动副总反力方位线的确定
FR21
12
FR21
12
FR21
1
2
1
2
1
2
G
G
G
1) FR21与载荷G大小相等,方向相反; 2) FR21的作用线必切于摩擦圆; 3) FR21产生的摩擦力矩与12转动方向相反。
【例5-2】已知机构简图、各摩擦角、摩擦圆半径、
驱动力矩Md ,阻力Fr。试画出各运动副静力图。
Md
1
2
3
Fr
4
【解】 1.从二力杆(连杆)入手,注意拉压杆。
Md 1
21 23
2
3
Fr
4
Md 1
21 23
2
3
Fr
4
21
Md 1
23
2
3
Fr
4
【解】 1.从二力杆(连杆)入手,注意拉压杆。 2.分析滑块,注意三力汇交。 3.分析曲柄,注意力偶平衡力拒。
= fr
2
F
45
3
2.确定各轮的转向,并标在
4
图上。
3.取1构件为分离体进行力分析。
5
G
3.取1构件为分离体进行力分析。
6
FR61 16
16
1
R T21 F R
23
1
T21
F
4.取2构件为分离体进行力分析。 45
2
F
T62 23
T12
FR12
Md 1
FR41
2
4
90o+ 34
3
Fr
FR43
FR32
FR12
Md
1
FR41
21
23
2
FR43 Fr
4 3
V34
FR32
【例5-2】如图滑轮组,已 知r、R分别为轴肖和滑轮 半径,f为轴销摩擦系数, F为滑轮组的驱动力,试 求G=?。
6
16
23
1
【解】1.计算摩擦圆半径,并
画在图上。
R
fpds
2f
R
p 2d
r
r
●新轴端,p=常数: p G / (R2 r2 )
2R
dρ ω ρr
M f
2
fp
R 2d
r
= 2 fp(R3 r3 )
3
2 3
R3 r3 fG R2 r2
R
●跑合轴端, pρ=常数
R
G pds 2p(R r) r
M f 2fp
R
d
fp(R2
F
【例5-1】滑块等速在斜面运动,确定驱动力。
●正行程
【解】1.确定总反力的方向
2.根据滑块力系平衡列方程:
φα
V12
F R21
1
FR21 G F 0
F
3.做图求解未知力
α
G
2
F Gtan( +)
F
α+ φ G
F R21
●反行程
【解】1.确定总反力的方向
F R21
2.根据滑块力系平衡列方程:
槽面接触: Ff21= ( f / sinθ) G 半圆柱面接触: Ff21= f kG
非平面接触时 , 摩擦力增大。
应用:当需要增大滑动摩擦力时,可将接触面设计成槽面或柱面。 如圆形皮带(缝纫机)、三角形皮带、螺栓联接中采用的三角形 螺纹。
fv=3.24 f
θθ
对于三角带:
θ=18°
5.1.2移动副中总反力的确定
FR21 G F 0
3.做图求解未知力
F Gtan( -)
分析
φ
V12
α
α
1 F
G
2
F
若α>φ,F 为阻力。
若α<φ, F 方向相反,为驱动力。
F R21 G
α-φ
5.1.2螺旋副中摩擦力的确定
1、矩形螺纹螺旋中的摩擦 ●矩形螺纹螺旋副的简化 斜面其升角为:
tgα =l /πd2=zp /πd2
22
放松力与力矩为:
F ' Gtg( )
M ' F ' d2 d2 Gtg( )
22
G
d2 M F
d2 v
F
l
α
Gπd2
5.1.2转动副中摩擦力的确定
轴 轴承
轴径 轴端
1.转动副(轴径)
Ff21 = fvG FR21=G 摩擦力矩的大小
Mf= Ff21 r = fvGr
令 = fvr Mf = G = FR21
注意 FR21是构件2作用到构件1上的力,是构件1所受的力。
12是构件1相对于构件2的角速度。
2. 轴端摩擦
取环形面积: ds=2πρdρ 设ds上的压强为p,正压力为:dFN=pds,
Gω
Mf 1
M
摩擦力为:dFf= fdFN = fpds
2
2r
摩擦力矩:dMf =ρdFf =ρfpds
总摩擦力矩:M f
Ff 21
简单平面移动副
2 FN21 G
Ff 21 fFN21 fG
v FN21
12
F 1
G
●槽面接触: fv= f / sinθ
G=(FN21 /2)sinθ+(FN21 /2)sinθ FN21 = G / sinθ Ff21= f FN21
= G (f / sinθ) =G fv
fv─当量摩擦系数。
总反力——法向反力与摩擦力的合力
FR21 Ff 21 FN 21
FR21
tan Ff 21 / FN 21
fFN 21 / FN 21 f
(v )─摩擦角(当量摩擦角)
摩擦锥—以 FR21为母线所作圆锥。
● FR21与v12夹钝角(90+)
● FR21恒切于摩擦锥。
1 Ff21
2 G
FN21 v12
θ
FN 21 2
②
G θ
FN
①
21
2
●半圆柱面接触: fv =f k
FN21=kG Ff21= f kG
2
=G fv
理论分析和实验结果有: k =1~π/2
结论:不论何种运动副元素,有计算通式:
Ff21= f FN21
= fvG
fv-称为当量摩擦系数
FN21 1
G
总结:
水平面接触: Ff 21 fG
第5章 机械的效率和自锁
本章教学内容
5.1运动副中摩擦力的确定 5.2考虑摩擦时机构的受力分析 5.3机构的效率 5.4机构的自锁
5.1 运动副中的摩擦力的确定
5.1.1移动副中摩擦力的确定
●水平面接触:
Ff 21 fFN21
G一定时,决定 Ff21 的两个因素:
1. f
2. 运动副元素的几何形状
式中:l-导程,z-螺纹头数,p-螺距
假定螺母与螺杆间的作用力集 中在一小段螺纹上,这样就可以把 螺旋副中摩擦的研究简化为滑块在 倾斜平面上的摩擦来研究。
G
G
G
d2
v
F
l
α
Gπd2
●拧紧力矩与放松力矩 根据滑块在斜面的运动 拧紧力与力矩为:
F Gtg( )
M F d2 d2 Ftg( )
