安徽省江南十校2019届高三文科数学下册3月份综合素质检测文数试题卷(含答案)
安徽省江南十校2019届高三3月综合素质测试语文试卷(解析版)

安徽省江南十校2019届高三3月综合素质测试语文试卷一、现代文阅读(36分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成各题。
影戏源于中国,这是世界公认的观点。
一般把汉代方士设帐弄影招魂,视为影戏的肇始,李少翁为汉武帝早逝的宠姬招魂就是一例。
比较可信的说法是唐代中晚期或稍晚的五代时期是影戏的滥觞期。
当时影戏是为佛教宣示轮回报应的佛法服务的。
寺院中的俗讲僧在超度亡灵时,用影人作为死者的灵魂。
宋代的《都城纪胜》一书中介绍了影戏制作材料的演变和表演的内容:“凡影戏乃京师人初以素纸雕镂,后用彩色装皮(羊皮)为之,其话本与讲史书者颇同。
”宋代都城汴梁的市井游乐中,就有傀儡戏之类的表演。
宋代影戏相当繁荣表现在出现了专门制作镂刻影人的艺人。
宋《武林旧事》有“小径纪,一项,记载有“镞影人”即刻镂影人的行业。
“武林”是南宋都城临安的别称,这说明从北宋至南宋,影戏又有了新的发展。
因为需要众多,才会有专门刻镂影人的行业。
当时影戏还有不同的种类,《东京梦华录》“京瓦伎艺”章说“丁仪、瘦吉等弄‘乔影戏’(滑稽影)”;《都城纪胜》“杂手艺”条说“有‘手影戏’一种”;《武林旧事》“元夕”条云“或戏于小楼,以人为‘大影戏’,儿童喧呼,终夕不绝”;在南曲曲谱中有“大影戏”曲调一种。
元代统治者把影戏作为宫廷和军中之乐。
成吉思汗的大军远征到欧亚大陆的广大地区,中国影戏也被传到波斯等阿拉伯国家,后又辗转传入土耳其、希腊等国家,至今希腊和土耳其称影戏为“中国皮影”。
明代影戏在民间广泛流传,它不只受到广大下层民众的喜爱,也受到文人欣赏。
《剪灯新语》作者瞿佑有《影戏》诗一首,诗中描写影戏的情景,结句说“线索重看傀儡喜”,由此可知明代有称影人为傀儡的习惯,正如近代有人称“皮影”为“平面傀儡”一样。
经过明代二百多年的发展,至清代,中国皮影进入了空前的繁盛时期,形成了历史上从未有过的成熟和繁荣局面。
其一,流传全国,形成了七大影系,北到黑龙江,南至广东、海南,西至青海、甘肃,几乎是遍布城乡,处处皆有影戏,而且酬神祭社、节庆娱乐,具有多种功能。
2019届安徽省江南十校高三下学期联考文科数学试卷【含答案及解析】

2019届安徽省江南十校高三下学期联考文科数学试卷【含答案及解析】姓名___________ 班级____________ 分数__________一、选择题1. 已知集合,,则中的元素个数为(A)(B)____________________ (C)(D)2. 已知复数满足(为虚数单位),则(A)(B)(C)(D)3. 随机抛掷一枚质地均匀的骰子,记正面向上的点数为,则函数有两个不同零点的概率为(A)(B)(C)(D)4. 已知函数,则(A)(B)______________ (C)(D)5. 已知双曲线的右焦点与抛物线的焦点重合,且其渐近线方程为,则双曲线的方程为(A)(B)(C)(D)6. 设,则下列说法错误的是( A )是奇函数___________________________________(B)在上单调递增( C )的值域为___________________________________(D)是周期函数7. 设满足约束条件则的最小值为(A)(B)(C)(D)8. 在平面直角坐标系中,满足的点的集合对应的平面图形的面积为;类似的,在空间直角坐标系中,满足,的点的集合对应的空间几何体的体积为(A)(B)(C)(D)9. 已知各项均为正数的等比数列中,,则数列的前项和为(A)________________________ (B)(C)________________________ (D)10. 执行如图所示的程序框图,如果输入的,则输出的(A)(B)(C)(D)11. 已知函数的最小正周期为,且,则的一个对称中心坐标是(A)(B)___________(C)(D)12. 已知函数,若的图象与轴正半轴有两个不同的交点,则实数的取值范围为(A)(B)(C)(D)二、填空题13. 已知向量,,若,则实数=____________________ .14. 在数列中,,为的前项和.若,则______________ .15. 椭圆的右顶点为,是椭圆上一点,为坐标原点.已知,且,则椭圆的离心率为___________________________________ .16. 某几何体的三视图如图所示,其中侧视图的下半部分曲线为半圆弧,则该几何体的表面积为___________________________________ .三、解答题17. 如图,平面四边形中,,,,,,求(Ⅰ );(Ⅱ ).18. 第31届夏季奥林匹克运动会将于2016年8月5日—21日在巴西里约热内卢举行.下表是近五届奥运会中国代表团和俄罗斯代表团获得的金牌数的统计数据(单位:枚).p19. ly:Calibri; font-size:10.5pt"> 第30届伦敦第29届北京第28届雅典第27届悉尼第26届亚特兰大中国 38 51 32 28 16 俄罗斯 24 23 27 32 26(Ⅰ )根据表格中两组数据完成近五届奥运会两国代表团获得的金牌数的茎叶图,并通过茎叶图比较两国代表团获得的金牌数的平均值及分散程度(不要求计算出具体数值,给出结论即可);(Ⅱ )下表是近五届奥运会中国代表团获得的金牌数之和(从第26届算起,不包括之前已获得的金牌数)随时间变化的数据:p20. ly:宋体; font-size:10.5pt">时间x(届) 26 27 28 29 30 金牌数之和y(枚)16 44 76 127 165作出散点图如下:( i )由图可以看出,金牌数之和与时间之间存在线性相关关系,请求出关于的线性回归方程;( ii )利用( i )中的回归方程,预测今年中国代表团获得的金牌数.参考数据:,,,附:对于一组数据,,……, ,其回归直线的斜率和截距的最小二乘估计分别为:,21. 设函数.( 1 )当时,讨论的单调性;( 2 )当时,设在处取得最小值,求证:.22. 如图,过外一点作的两条切线,其中为切点,为的一条直径,连并延长交的延长线于点.(Ⅰ )证明:;(Ⅱ)若 ,求的值.23. 在平面直角坐标系中,以坐标原点为极点,轴的正半轴为极轴建立极坐标系,已知在极坐标系中,,圆的方程为( 1 )求在平面直角坐标系中圆的标准方程;( 2 )已知为圆上的任意一点,求面积的最大值.24. 已知函数,记的解集为.( 1 )求;( 2 )已知 ,比较与的大小.参考答案及解析第1题【答案】第2题【答案】第3题【答案】第4题【答案】第5题【答案】第6题【答案】第7题【答案】第8题【答案】第9题【答案】第10题【答案】第11题【答案】第12题【答案】第13题【答案】第14题【答案】第15题【答案】第16题【答案】第17题【答案】第18题【答案】第19题【答案】第22题【答案】。
安徽省江南十校2019届高三3月份综合素质检测文科数学

2019年安徽省“江南十校”综合素质检测数学(文科)一、选择题:本大题共12小题,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A ={x|0≤x <2},B =Z (Z 为整数集),则A∩B = A .{1} B .{0,1} C .{1,2} D .{0,1,2} 2.复数z 满足(i -2)z =4+3i ,则|z|=A B .3 C D .53.已知命题p :0x ∀>,3x +x 2>1,则¬p 为 A .0x ∃>,3x +x 2≤1 B .0x ∃≤,3x +x 2≤1 C .0x ∀>,3x +x 2≤1 D .0x ∀≤,3x +x 2≤14.双曲线22221y x a b-=(a >0,b >0)的渐近线方程为y =,则其离心率为A B C D 5.曲线12ln ()xf x x-=在点P (1,f (1))处的切线l 的方程为 A .x +y -2=0 B .2x +y -3=0 C .3x +y +2=0 D .3x +y -4=0 6.某圆锥的正视图是腰长为2的等腰三角形,且母线与底面所成的角为60°,则其侧面积为A .2πB .C .3πD .4π7.已知样本甲:x 1,x 2,x 3,…,x n 与样本乙:y 1,y 2,y 3,…,y n ,满足321i i y x =+(i=1,2,…,n ),则下列叙述中一定正确的是 A .样本乙的极差等于样本甲的极差 B .样本乙的众数大于样本甲的众数C .若某个x i 为样本甲的中位数,则y i 是样本乙的中位数D .若某个x i 为样本甲的平均数,则y i 是样本乙的平均数 8.已知函数f (x )=x (|x|+1),则不等式f (x 2)+f (x -2)>0的解集为 A .(-2,1) B .(-1,2) C .(-∞,-1)∪(2,+∞) D .(-∞,-2)∪(1,+∞)9.已知函数2()cos()(0)3f x x ωωπ=+>的最小正周期为4π,则下列叙述中正确的是 A .函数f (x )的图象关于直线3x π=-对称B .函数f (x )在区间(0,π)上单调递增C .函数f (x )的图象向右平移3π个单位长度后关于原点对称D .函数f (x )在区间[0,π]上的最大值为10.如图所示,正方体ABCD -A 1B 1C 1D 1中,点E ,F ,G ,P ,Q 分别为棱AB ,C 1D 1,D 1A 1,D 1D ,C 1C 的中点.则下列叙述中正确的是A .直线BQ ∥平面EFGB .直线A 1B ∥平面EFGC .平面APC ∥平面EFGD .平面A 1BQ ∥平面EFG 11.△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若232cos cos 22A B C -+=,且△ABC 的面积为214c ,则C = A .6π B .3π C .6π,65π D .3π,32π12.已知函数21()(21)22x x f x a x bx =+--+(a ,b ∈R ),若函数y =f (x )与函数y =f(f (x ))的零点相同,则a -b 的取值范围为 A .[0,2) B .(-2,0] C .(-∞,-2]∪[0,+∞) D .(-∞,0]∪[2,+∞) 二、填空题:本大题共4小题。
安徽省江南十校2019届高三3月联考文科数学试题

2019年安徽省“江南十校”综合素质检测=,∴侧面积为2cos60112. B 【解析】:由题:(0)0f a ==,∴2()2f x x bx =−+,令()00f x x =⇒=或2b , 若0b =,()f x 仅有一个零点0x =,符合题意;若0b ≠,∵22(())(2)(22)f f x x bx x bx b =−+−+,则2220x bx b −+=无实数根,故2(2)42002b b b ∆=−−⨯<⇒<<; 综上:[0,2)b ∈,∴(2,0]a b b −=−∈−,故选B.二、填空题:本题共4小题,每小题5分,共20分.13. 2−或3【解析】:∵(3,1)a b m −=−−,∴()()6(1)0a a ba ab m m ⊥−⇔⋅−=−+−=, 故2m =−或3.【解析】:目标函数2z x y =−在(2,3)−处取得最小值8−.【解析】:122||||2||||6(||||)[5,7]PF PQ a PF PQ PQ PF +=−+=+−∈.【解析】:法一:111336O ABC C OAB OAB OAB V V S OC S −−∆∆==⋅≤≤当且仅当,,OA OB OC 两两垂直时,三棱锥O ABC −体积最大,此时ABC ∆为边长为,∴面积为28()33ππ⋅=.法二:易知三棱锥O ABC −为正三棱锥,如图所示:D 为BC 中点,OG ⊥平面ABC ,且G 为BC ∆的重心,设AB x =,则2233AG AD x ===,∴OG ==213O ABC V −==令2(0,12)t x =∈,2()(12)g t t t =−,()3(8)08g t t t t '=−=⇒=,且(0,8)t ∈时,()g t 单调递增,(8,12)t ∈时,()g t 单调递减,∴28x t ==时三棱锥O ABC −体积最大,此时228)3AG x ==, ∴平面ABC 截球O 所得的截面圆的面积为283AG ππ⋅=. 三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.17.(12分)解析:(1)∵2log n a ,211log 2n a +,1 成等差数列, ∴21212log log 12n n a a +⨯=+,∴12n n a a +=,且0n a >, ∴数列{}n a 是等比数列,…………………………………………………………………3分 由2664a a =得,48a =,∴11a =,公比2q =,∴12n n a −=.…………………………6分(2)由(1)知,111211(21)(21)2121n n n n n n b −−−==−++++,……………………………9分 ∴011223111111()()()212121212121n T =−+−+−+++++++ 211111111()()21212121221n n n n n −−−+−+−=−+++++.…………………………………12分 G C D A O18.(12分)解析:(1)∵2AB =,1A B =,160A AB ∠=,由余弦定理:22211112cos A B AA AB AA AB A AB =+−⋅∠,即21112303AA AA AA −−=⇒=或1−,故13AA =.………2分取BC 中点O ,连接1,OA OA ,∵ABC ∆是边长为2的正三角形,∴AO BC ⊥,且AO =,1BO =,又11A AB A AC ∆≅∆,∴11A B AC ==1A O BC ⊥,且1AO ,∵22211AO A O AA +=,∴1AO A O ⊥,…………………4分又BC AO O =,故1A O ⊥平面ABC ,∵1A O ⊂平面1A BC ,∴平面1A BC ⊥平面ABC .………………………………………6分(2)由(1)12111233A ABC ABC V S AO −=⋅==……………………………9分 ∵11113ABC A B C A ABC V V −−=,∴11112A BCC B A ABC V V −−==.…………………………………12分 (其他正确解答酌情给分)19.(12分)解析:(1)在2014—2018近五年的相关数据中任取3年的取法有10n =,依条件知,年返修率不超过千分之一....的有2014,2016,2018三年的数据, ………2分 ∴任意选取3年的数据,其中恰有1年生产部门考核优秀的取法有3m =,故至少有2年生产部门考核优秀的概率7110m P n =−=.…………………………5分 (2)∵41144i i x x ===∑,411484i i y y ===∑,42194i i x ==∑,41952i i i x y ==∑, ∴4124222149524448184 6.139444304ii i i i x y x y b xx ==−⋅−⨯⨯===≈−⨯−∑∑, ∴218448423.4730a =−⨯≈(写248 6.13423.48a =−⨯=也可)……………………10分 ∴211ˆ||6%10%ˆb b b −≈<,211ˆˆ||34%10%ˆa a a −≈>,不符合条件, 故若生产部门希望2019年考核优秀,不能同意2019年只生产该产品1万台. …12分20.(12分)解析:(1)由题: E :22x y =. ………………………………………………………3分 (2)∵(0,2)Q −,设2222(,),(,),(,),(,)2222a b c d A a B b C c D d (,,,a b c d 互不相等), 则221222a b a b k a b −+==−,同理22c d k +=; ……………………………………………5分∵,,A P C 三点共线,∴AP CP k k =, A C O A 1C 1B 1B即22112()222a c a c a c c a c ac a −−−=⇒−=−⇒=−,同理2d b =−, ……………………8分 ∴1222()02222a b a b a b ab a b k k ab λλλλ−−++++=+=−=⇒=,联立1:2AB l y k x =−与得21240x k x −+=,由韦达定理:4ab =,故22ab λ==. …………………………………………………12分(其他正确解答酌情给分)21.(12分)解析:(Ⅰ)()[(1)]x f x ax a e '=−−(0x >,a R ∈),当1a ≥时,()0f x '≥,()f x 在(0,)+∞上递增; ……………………………………3分当01a <<时,()f x 在1(0,)a a −上递减, 在1(,)a a−+∞上递增; 当0a ≤时,()0f x '≤,()f x 在(0,)+∞上递减.………………………………………6分 (2)依题意得(1)2x x e kx −>−对于0x >恒成立,方法一、令()(1)2x g x x e kx =−−+(0x ≥),则()x g x xe k '=−(0x ≥), ………7分 当0k ≤时, ()g x 在(0,)+∞上递增,且(0)10g =>,符合题意;当0k >时,易知0x ≥时,()g x '单调递增.则存在00x >,使得000()0x g x x e k '=−=, 且()g x 在0(0,]x 上递减,在0[,)x +∞上递增, ∴0000()()(1)20x min g x g x x e kx ==−−+>,∴000120x k kx x −−+>,0021()1k x x <+−, …………………………………………10分 由0012x x +≥得,02k <<,又k Z ∈,∴ 整数k 的最大值为1. 另一方面,1k =时,1'()10,'(1)e 102g g <=−> ∴01(,1)2x ∈ ,002(1,2)()1x x ∈+−,1k ∴=时成立.………………………………12分 方法二、(1)2x x e k x −+<(0x >)恒成立,令(1)2()x x e h x x−+=(0x >), 则22(1)2()x x x e h x x−+−'=(0x >),…………………………………………………8分 令2()(1)2x t x x x e =−+−(0x >),则()(1)0x t x x x e '=+>,∴()t x 在(0,)+∞上递增,又(1)0t >,1()202t =<, ∴存在01(,1)2x ∈,使得20000()()(1)20x h x t x x x e '==−+−=, 且()h x 在在0(0,]x 上递减,在0[,)x +∞上递增,∴min 0002()()11h x h x x x ==+−,…10分又01(,1)2x ∈,∴00131(1,)2x x +−∈, ∴04()(,2)3h x ∈,∴2k <, 又k Z ∈,∴ 整数k 的最大值为1. …………………………………………………12分 (其他正确解答酌情给分)(二)选考题:共10分。
安徽“江南十校”2019年高三3月联考(数学文)word版

安徽“江南十校”2019年高三3月联考(数学文)word版数学〔文科〕第I卷〔选择题共50分〕一.选择题:本大题共10小题,每题5分,共50分.在每题给出的四个选项中,只有一项为哪一项符合题目要求的.(l)i为虚数单位,复数,那么复数z在复平面上的对应点位于〔〕A.第一象限B.第二象限C.第三象限D.第四象限(2) 假设集合,那么=〔 )A. B. C. D.都是减函数,那么在上是减函数,以下说法中正确的选项是〔〕A.“p或q”是真命题B.“p或q”是假命题C.为假命题D.为假命题⑷下面框图所给的程序运行结果为s=28,那么判断框中应填入的关于k的条件是〔〕A. B. C. D.(5)在下图的表格中,如果每格填上一个数后,每一横行成等差数列,每一纵列成等比数列,那么的值为〔〕A.1B.2C.3D.4(6)据第六次全国人口普查的数据,得到我国人口的年龄频率分布直方图如下图所示:那么在一个总人口数为300万的城市中,年龄在[20,60)之间的人口数大约有〔〕A. 158万B. 166万C. 174万D. 132万(7)关于X的方程的解集为P,那么P中所有元素的和可能是〔〕A.3,6,9B.6,9,12C.9,12,15D.6,12,15(8)在中,角A,B,C所对的边分别为a,b,c,,C=,那么=()A.30°B.450C.45°或1350D.60°(9)定直线l与平面a成60°角,点P是平面a内的一动点,且点p到直线l的距离为3,那么动点P的轨迹是〔〕A.圆B.椭圆的一部分C.抛物线的一部分D.椭圆(10)x,y满足记目标函数z=+的最大值为7,最小值为1,那么b,c的值分别为〔)A.-1,-4B.-1,-3C.-2,-1D.-1,-2第II卷〔非选择题共100分〕二.填空题:本大题共5小题,每题5分,共25分.(11)假设,且,那么与的夹角是__________.(12)假设某多面体的三视图(单位:cm)如下图,其中正视图与俯视图均为等腰三角形,那么此多面体的表面积为________cm2.v(13)定义在[-2,2]上的奇函数在(0,2]上的图象如下图,那么不等式的解集为________,(14)令.如果对,满足为整数,那么称k为“好数”,那么区间[l,2018]内所有的“好数”的和M=________.(15)如图,正方体棱长为1,点,,且,有以下四个结论:①,②;③.;④MN与是异面直线、其中正确结论的序号是________(注:把你认为正确命题的序号都填上〕三.解答题:本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤.(16)(本小题总分值12分己知函数.(I)假设,,求的值;(I I)求函数的最大值和单调递增区间.(17)(本小题总分值12分〕2017.年广州亚运会的一组志愿者全部通晓中文,并且每个志愿者还都通晓英语、日语和韩语中的一种〔但无人通晓两种外语).从中任抽一人,其通晓中文和英语的概率为,通晓中文和日语的概率为.假设通晓中文和韩语的人数不超过3人.(I)求这组志愿者的人数;(II)现从这组志愿者中选出通晓英语的志愿者1名,通晓韩语的志愿者1名,假设甲通晓英语,乙通晓韩语,求甲和乙不全被选中的概率.(18)(本小题总分值12分〕如图1所示,在边长为12的正方形中,点B、C在线段AD上,且AB=3,BC=4,作分别交于点B,P,作分别交于点,将该正方形沿折叠,使得与重合,构成如图2所示的三棱柱(I)求证:平面;〔I I)求多面体的体积.(19)(本小题总分值12分〕假设数列满足:(I)证明数列是等差数列;.(II)求使成立的最小的正整数n.(20)(本小题总分值13分〕 焦点在X 轴上的椭圆C 为.,F 1、F 2分别是椭圆C的左、右焦点,离心率e=.(I)求椭圆C 的方程;(II)设点Q 的坐标为〔1,0),椭圆上是否存在一点P ,使得直线都与以Q 为圆心的一个圆相切,如存在,求出P 点坐标及圆的方程,如不存在,请说明理由. (21) (本小题总分值14分〕设M 是由满足以下条件的函数f(X)构成的集合: ①方程有实数根;②函数的导数(满足”(I)假设函数为集合M 中的任一元素,试证明万程只有一个实根;(II) 判断函^是否是集合M 中的元素,并说明理由; (III)“对于〔I I )中函数定义域内的任一区间,都存在,使得”,请利用函数的图象说明这一结论.安徽省2018年“江南十校”高三第一次联考(文科数学)答案与解析一.选择题:本大题共10小题,每题5分,共50分.在每题给出的四个选项中,只有一项为哪一项符合题目要求的. 〔1〕解析∵()()()()13113133121112i i i i i z ii i i +⋅++++-====-+--⋅+,∴选B〔2〕解析:∵{}11R C A x x =-≤≤,{}0B y y =≥,∴()R C A ∩B ={}10|≤≤x x ,应选C〔3〕解析:∵0a b →→⋅>时,a →与b→的夹角为锐角或零度角,∴命题p 是假命题;又∵函数()f x 在(],0-∞及(0,)+∞上都是减函数时,可能()f x 在0处是个跳跃点,∴命题q也是假命题,∴选B〔4〕解析:起始10k=通过条件框要满足“是”,110,9S k=+=和1109,8S k=++=仍然满足“是”,1109828,7S k=+++==达到题目要求,通过条件框要满足“否”,所以选D〔5〕解析:先算出三角函数值,然后根据每一横行成等差数列,每一纵列成等比数列,填所以选A〔6〕解析:年龄在[)20,60之间的人所占频率为:()0.0180.011200.58+⨯=,所以年龄在[)20,60之间的人大约有0.58300174⨯=万,应选C〔7〕解析:26y x x=-的图象是把2的图象在x轴下方的部分翻到上方,上方由图可知,画任意一条横线,根总是关于3x=对称,从下往上移动可知:P中所有元素的和可能是,所以选B〔8〕解析:由tan1tanAB+=和正弦定理得:1cos,602A A=∠=,又由正弦定理得:,sinsinCC=又∵c a<,∴060C∠<,∴45C∠=,应选B〔9〕解析:到直线l的点的轨迹是以直线l为旋转轴,以3为半径的无限延伸的圆柱面,不难想象,它应该是一个椭圆,所以选D图为〔10〕解析:由图分析知:直线0x by c++=经过274x yx y+=⎧⎨+=⎩和211x yx+=⎧⎨=⎩的交点,即4 62O经过()3,1和()1,1-点,所以3010b c b c ++=⎧⎨-+=⎩,∴1b =-,2c =-,应选D二.填空题:本大题共5小题,每题5分,共25分. 〔11〕解析:∵()→→→+⊥a b a,∴2()00→→→→→→+⋅=⇒+⋅=a b a a a b 4→→⇒⋅=-a b cos 4θ→→⇒⋅=-a b1cos 2θ⇒=-∴23πθ=〔12〕解析:由三视图知:多面体为右图所示,其表面积为:2111645426(32222S cm=⨯⨯+⨯⨯⨯+⨯⨯=+ 〔13〕解析:画出()y f x =与y x =的图象为:解出坐标为:22,33⎛⎫ ⎪⎝⎭和22,33⎛⎫-- ⎪⎝⎭,由图知,解集为22,3⎡⎫--⎪⎢⎣⎭∪20,3⎛⎫ ⎪⎝⎭ 〔14〕解析:对任意正整数k ,有231(1)(2)()log 3log 4log (2)k f f f k k +⋅⋅ ⋅⋅⋅ ⋅=⋅⋅⋅⋅+ lg3lg 4lg(2)lg 2lg3lg(1)k k +=⋅⋅ ⋅⋅⋅ ⋅+lg(2)lg 2k +=2log (2)k =+、假设k 为“好数”,那么2log (2)k Z +∈,从而必有22()l k l N *+=∈、令1222012l ≤-≤,解得210l ≤≤、所以[]1,2012内所有“好数”的和为()()()231222222M =-+-+⋅⋅⋅+-()2310222292026=+⋅⋅⋅+-⨯=、〔15〕解析:过N 作1NP BB ⊥于点P ,连接MP ,可证1AA ⊥面MNP ∴①对 过M 、N 分别作11MR A B ⊥、11NS B C ⊥于点R 、S ,那么当M 、N 不是1AB 、1BC 的中点时,11A C 与RS 相交;当M 、N 是1AB 、1BC 的中点时,11A C ∥RS ∴11C A 与MN 可以异面,也可以平行,故②④错由①正确知:面MNP ∥面111A B C D ,故③对应选①③三.解答题:本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤. 〔16〕解析:〔Ⅰ〕∵()sin cos f x x x =+,∴()cos sin f x x x -=-、┄┄┄┄┄1分又∵()2()f x f x =-, ∴()sin cos 2cos sin x x x x +=-且cos 0x ≠1tan 3x ⇒=、┄┄┄┄┄┄┄┄3分∴22cos sin cos 1sin x x xx-+222cos sin cos 2sin cos x x x x x-=+21tan 2tan 1x x -=+611=;┄┄┄┄┄┄6分 〔Ⅱ〕由题知22()cos sin 12sin cos F x x x x x =-++()cos 2sin 21F x x x ⇒=++()214F x x π⎛⎫⇒=++ ⎪⎝⎭、┄┄┄┄┄┄┄10分∴当sin 214x π⎛⎫+= ⎪⎝⎭时,max ()1F x 、┄┄┄┄┄┄┄┄┄┄┄┄┄┄11分由222242k x k πππππ-+≤+≤+解得,单调递增区间为3,()88k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦、┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄12分〔17〕解析:〔Ⅰ〕设通晓中文和英语的人数为x 人,通晓中文和日语的人数为y 人,通晓中文和韩语的人数为z 人,且,,x y z N *∈,那么12310x x y z y x y z ⎧=⎪++⎨=⎪++⎩且03z <≤,┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄4分 那么依题意有:5,3,2.x y z =⎧=⎨=⎩所以这组志愿者有53210++=人;┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄6分 〔Ⅱ〕设通晓中文和英语的人为12345,,,,A A A A A ,甲为1A ,通晓中文和韩语的人为12,B B ,乙为1B ,那么从这组志愿者中选出通晓英语和韩语的志愿者各1名的所有情况为:()()()()()()()()()()11122122313241425152,,,,,,,,,,,,,,,A B A B A B A B A B A B A B A B A B A B 共10个,┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄10分同时选中甲、乙只有()11,A B 1个、┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄11分所以甲和乙不全被选中的概率为1911010-=、┄┄┄┄┄┄┄┄┄┄┄┄┄┄12分 〔18〕〔Ⅰ〕证明:由题知:3AB =,4BC =,5CA =,∴AB BC ⊥、┄┄┄┄┄2分又∵1AB BB ⊥,∴AB ⊥平面11BCC B ;┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄5分〔Ⅱ〕解析:由题知:三棱柱111ABC A B C -的体积13412722=⨯⨯⨯=、┄┄┄┄┄6分 ∵ABP ∆和ACQ ∆都是等腰直角三角形,∴3AB BP ==,7AC CQ ==,┄7分 ∴13A CQPBV S -=四边形11(37)432032CQPB AB ⨯=⨯⨯+⨯⨯=、┄┄┄┄┄┄┄10分∴多面体111A B C APQ -的体积111ABC A B C V -=-A CQPB V -722052=-=、┄12分〔19〕解析:〔Ⅰ〕由()11322n n n a a a +--+=可得:11223n n n a a a +--+=,即()()1123n n n n a a a a +----=,┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄4分所以数列{}1n n a a +-是以2143a a -=为首项,23为公差的等差数列;┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄5分 〔Ⅱ〕由〔1〕知1422(1)(1)333n n a a n n +-=+-=+,┄┄┄┄┄┄┄┄┄┄┄┄┄┄6分1C 11111于是累加求和得:121(23)(1)33n a a n n n =+++⋅⋅⋅+=+,┄┄┄┄┄┄┄┄┄┄8分 所以11131n a n n ⎛⎫=- ⎪+⎝⎭,┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄10分进而123111135312n a a a a n +++⋅⋅⋅+=->+5n ⇒>,∴最小的正整数为6n =、┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄12分〔20〕解析:〔Ⅰ〕由题可知:2c aa ⎧=⎪⎨⎪=⎩,解得2c a =⎧⎪⎨=⎪⎩,┄┄┄┄┄┄┄┄┄┄┄2分∴22242b a c b =-=⇒=、┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄3分 ∴椭圆C 的方程为22184x y +=;┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄4分 〔Ⅱ〕假设存在椭圆上的一点()00,P x y ,使得直线1PF ,2PF 与以Q 为圆心的圆相切,那么Q 到直线1PF ,2PF 的距离相等,()()122,0,2,0F F -,()1000:220PF x y y x y +--=, ()2000:220PF x y y x y --+=、12d d ===,┄┄┄┄┄┄┄┄┄┄┄┄┄7分化简整理得:220008403280x x y -++=、┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄9分∵点在椭圆上,∴220028x y +=、解得:02x =或08x =〔舍〕, 02x =时,0y =1r =、∴椭圆上存在点P ,其坐标为(或(2,,使得直线1PF ,2PF 与以Q 为圆心的圆()2211x y -+=相切、┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄13分〔21〕解析:〔Ⅰ〕令()()h x f x x =-,那么()()10h x f x ''=-<,即()h x 在区间(1,)+∞上单调递减所以,使()0h x =,即()0f x x -=成立的x 至多有一解,┄┄┄┄┄┄┄┄┄3分 又由题设①知方程()0f x x -=有实数根,所以,方程()0f x x -=只有一个实数根;┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄4分 〔Ⅱ〕由题意易知,111()(0,)(0,1)222g x x '=-∈⊂,满足条件②┄┄┄┄┄┄┄┄┄6分 令ln ()()3(1)22x xF x g x x x =-=--+>, 那么225()0,()20222e e F e F e =-+>=-+<,┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄8分又()F x 在区间2[,]e e 上连续,所以()F x 在2[,]e e 上存在零点0x ,即方程()0g x x -=有实数根20[,]x e e ∈,故()g x 满足条件①,综上可知,()g x M ∈;┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄9分 〔Ⅲ〕由〔Ⅱ〕知:11()()()(ln ln )22g n g m n m n m -=---, 而0011()()()()22n m g x n m x '-=--,所以原式等价于ln ln 1n m n m x -=-,┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄11分该等式说明函数ln (1)y x x =>上任意两点(,ln )A m m 和(,ln )B n n 的连线段AB 〔如下图〕,在曲线ln ()y x m x n =≤≤上都一定存在一点00(,ln )P x x ,使得该点处的切线平行于AB ,根据ln (1)y x x =>图象知该等式一定成立.┄┄┄┄┄14分。
安徽省江南十校2019届高三3月综合素质检测文科综合试题 扫描版含答案

政治参考答案和评分说明业榨菜产品价格上升不会引起其替代品需求量的大幅变化,A不选;决定商品价值量的是社会必要劳动时间,B不选;企业营利能力可能下降,也可能增强,C不选。
榨菜需求弹性较小,若该品牌榨菜的调价在消费者承受的合理区间内,对消费者的品牌忠诚度影响不大,D 正确。
13.A【解析】从液态金属机器人原型机到新的软体机器人研发方向的“研发路径”指向生产什么(消费对象)和生产目的,不能直接体现消费动力和引发消费热点,①②符合题意,A正确。
14.B【解析】我国民营经济的发展壮大表明非公有制经济是我国经济社会发展的重要基础,也表明我国对非公有制经济的政策态度,①④入选,B正确。
②错在“控制力”,③表述不完整。
15.C【解析】图4表示2010-2017年我国财政支出增速总体上高于财政收入的增速。
分析其原因:面对经济下行压力,我国实行积极的财政政策,增加财政支出,刺激需求,促进宏观经济向好;同时,政府减税降费,降低企业税负,有利于增强企业活力,促进经济提质增效,②④正确。
图表不能体现财政收支失衡,①不合题意;③与财政收支增速无关,不合题意。
16.B【解析】全国人大常委会修改刑诉法,①正确;建立刑事缺席审判制度,为反腐追赃提供了司法支持,③正确。
人大代表不能行使决定权,人民法院行使审判权,②④错误。
17.B【解析】综合国力的重要标志和国家统一的基础是民族团结,国家统一领导是实行民族区域自治制度的前提,②③表述错误。
18.C【解析】我国外交政策的基本目标是维护我国的主权、安全和发展利益,促进世界的和平与发展,未改变;中非合作论坛峰会、中非命运共同体不是国际组织,①③表述错误。
19.C【解析】举办庆祝活动是为了提升农民幸福感和获得感,汇聚兴农富农力量,展示中国农民的伟大创造,表达农民丰收喜悦,②③正确。
文化遗产是历史文化成就的重要标志,①不选;发展公益性文化事业保障基本文化权益,④表述错误,不选。
20.A【解析】传统文化的现代表达,实现了传统文化的创造性转化和创新性发展,A正确。
安徽省江南十校高三下学期文数3月一模联考试卷附解析
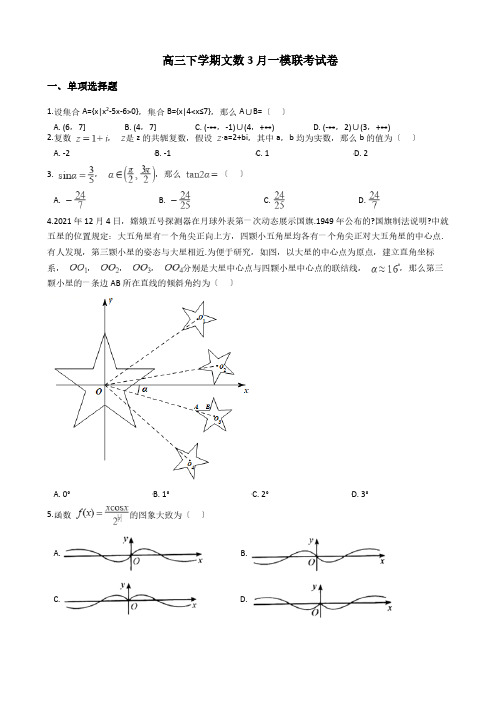
高三下学期文数3月一模联考试卷一、单项选择题1.设集合A={x|x2-5x-6>0},集合B={x|4<x≤7},那么A∪B=〔〕A. (6,7]B. (4,7]C. (-∞,-1)∪(4,+∞)D. (-∞,2)∪(3,+∞)2.复数,是z的共轭复数,假设·a=2+bi,其中a,b均为实数,那么b的值为〔〕A. -2B. -1C. 1D. 23. ,,那么〔〕A. B. C. D.4.2021年12月4日,嫦娥五号探测器在月球外表第一次动态展示国旗.1949年公布的?国旗制法说明?中就五星的位置规定:大五角星有一个角尖正向上方,四颗小五角星均各有一个角尖正对大五角星的中心点.有人发现,第三颗小星的姿态与大星相近.为便于研究,如图,以大星的中心点为原点,建立直角坐标系,,,,分别是大星中心点与四颗小星中心点的联结线,,那么第三颗小星的一条边AB所在直线的倾斜角约为〔〕A. 0°B. 1°C. 2°D. 3°5.函数的图象大致为〔〕A. B.C. D.6.椭圆的左、右焦点分别为、,过的直线与椭圆交于、两点,假设的周长为,那么面积的最大值为〔〕A. B. C. D. 37.设、两条直线,那么的充要条件是〔〕A. 、与同一个平面所成角相等B. 、垂直于同一条直线C. 、平行于同一个平面D. 、垂直于同一个平面8.假设直线y=kx与曲线(x- )2+(|y|-1)2=1有交点,那么k的取值范围是〔〕A. [- ,]B. [-1,1]C. [- ,]D. [- ,]9.将数列{3n+1}与{9n-1}的公共项从小到大排列得到数列{an},那么〔〕A. 319B. 320C. 321D. 32210. ,记,那么〔〕A. B. C. D.11.如图,在ABC中,∠BAC= ,点D在线段BC上,AD⊥AC,,那么sinC=〔〕A. B. C. D.12.当x>1时,函数y=(lnx)2+alnx+1的图象在直线y=x的下方,那么实数a的取值范围是〔〕A. (-∞,e)B. (-∞,)C. (-∞,)D. (-∞,e-2)二、填空题13.函数的最小正周期为,那么ω=________.14.非零向量满足,且,那么和的夹角为________.15.如图,分别为双曲线的右顶点和右焦点,过作轴的垂线交双曲线于,且在第一象限,到同一条渐近线的距离分别为,且是和的等差中项,那么的离心率为________·16.如图,在三棱锥中,是边长为的等边三角形,,点分别在棱上,平面平面,假设,那么三棱锥的外接球被平面所截的截面面积为________.三、解答题17.某家水果店的店长为了解本店苹果的日销售情况,记录了近期连续120天苹果的日销售量(单位:),并绘制频率分布直方图如下:〔1〕请根据频率分布直方图估计该水果店苹果日销售量的众数和平均数;(同一组中的数据以这组数据所在区间中点的值作代表)〔2〕一次进货太多,水果会变得不新鲜;进货太少,又不能满足顾客的需求.店长希望每天的苹果尽量新鲜,又能80%地满足顾客的需求(在10天中,大约有8天可以满足顾客的需求).请问每天应该进多少千克苹果?(精确到整数位)18.各项均为正数的等差数列{a n}满足a1=1,.〔1〕求{a n}的通项公式;〔2〕记b n= ,求数列{b n}的前n项和S n.19.菱形边长为,,以为折痕把和折起,使点到达点的位置,点到达点的位置,,不重合.〔1〕求证:;〔2〕假设,求点到平面的距离.20.函数f(x)=a x-ax(a>0且a≠1).〔1〕当a=e时,求函数f(x)的最值;〔2〕设g(x)是f(x)的导函数,讨论函数g(x)在区间(0,1)零点的个数.2+(y-2)2=4相外切,圆心P在x轴的上方,P点的轨迹为曲线C.〔1〕求C的方程;〔2〕E(4,2),过点(0,4)作直线交曲线C于A,B两点,分别以A,B为切点作曲线C的切线相交于D,当△ABE 的面积S1与△ABD的面积S2之比取最大值时,求直线AB的方程.22.在直角坐标系xOy中,曲线的参数方程为(t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线的极坐标方程为.〔1〕当时,求和的直角坐标方程;〔2〕当时,与交于A,B两点,设P的直角坐标为(0,1),求的值.23.函数f(x)=|x-2|+|x+1|.〔1〕解不等式f(x)>x+2;〔2〕记f(x)的最小值为m,正实数a,b,c满足a+b+c=m,证明:答案解析局部一、单项选择题1.【解析】【解答】因为B={x|4<x≤7},所以故答案为:C【分析】利用条件结合一元二次不等式求解集的方法,进而求出集合A,再利用并集的运算法那么,进而求出集合A和集合B的并集。
[首发]安徽省江南十校2019届高三3月综合素质检测数学(文)答案
![[首发]安徽省江南十校2019届高三3月综合素质检测数学(文)答案](https://img.taocdn.com/s3/m/d0d9153df18583d04864591e.png)
2 3 36
2
f
(x
−
3
)
=
cos
1 2
(
x
−
3
)
+
2 3
=
cos(
1 2
x
+
2
)
=
−
sin
1 2
x
,故
C
正确.
10. B【解析】:过点 E, F,G 的截面如图所示( H , I 分别为 A1A, BC 的中点),∵ A1B // HE ,
A1B 平面 EFG , HE 平面 EFG ,故直线 A1B// 平面 EFG ,故选 B.
=
1 3
3 x2 4
4 − 1 x2 = 1 3 12
x4 (12 − x2 ) ,
B
令 t = x2 (0,12) , g(t) = t2 (12 − t) , g(t) = 3t(8 − t) = 0 t = 8 ,
且 t (0,8) 时, g(t) 单调递增, t (8,12) 时, g(t) 单调递减,
D1 G A1
P
F
C1
B1 Q
H D
A
E
C I B
11. A【解析】:∵ 2cos2 A − B + cos C = cos( A − B) − cos(A + B) + 1 = 2sin Asin B + 1 = 3 ,
2
2
∴ sin
Asin
B
=
1 4
,又 SABC
=
1 2
absin C
=
1 c2 4
安徽省江南十校2019届高三3月综合素质测试语文试题 word

2019年安徽省“江南十校”综合素质检测语文一、现代文阅读(36分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成1—3题。
影戏源于中国,这是世界公认的观点。
一般把汉代方士设帐弄影招魂,视为影戏的肇始,李少翁为汉武帝早逝的宠姬招魂就是一例。
比较可信的说法是唐代中晚期或稍晚的五代时期是影戏的滥觞期。
当时影戏是为佛教宣示轮回报应的佛法服务的。
寺院中的俗讲僧在超度亡灵时,用影人作为死者的灵魂。
‘宋代的《都城纪胜》一书中介绍了影戏制作材料的演变和表演的内容:“凡影戏乃京师人初以素纸雕镂,后用彩色装皮(羊皮)为之,其话本与讲史书者颇同。
”宋代都城汴梁的市井游乐中,就有傀儡戏之类的表演。
宋代影戏相当繁荣表现在出现了专门制作镂刻影人的艺人。
宋《武林旧事》有“小径纪,,一项,记载有“镞影人”即刻镂影人的行业。
“武林”是南宋都城临安的别称,这说明从北宋至南宋,影戏又有了新的发展。
因为需要众多,才会有专门刻镂影人的行业。
当时影戏还有不同的种类,《东京梦华录》“京瓦伎艺”章说“丁仪、瘦吉等弄‘乔影戏’(滑稽影)”;《都城纪胜》“杂手艺”条说“有‘手影戏’一种”;《武林旧事》“元夕”条云“或戏于小楼,以人为‘大影戏’,儿童喧呼,终夕不绝”;在南曲曲谱中有“大影戏”曲调一种。
元代统治者把影戏作为宫廷和军中之乐。
成吉思汗的大军远征到欧亚大陆的广大地区,中国影戏也被传到波斯等阿拉伯国家,后又辗转传入土耳其、希腊等国家,至今希腊和土耳其称影戏为“中国皮影”。
明代影戏在民间广泛流传,它不只受到广大下层民众的喜爱,也受到文人欣赏。
《剪灯新语》作者瞿佑有《影戏》诗一首,诗中描写影戏的情景,结句说“线索重看傀儡喜”,由此可知明代有称影人为傀儡的习惯,正如近代有人称“皮影”为“平面傀儡”一样。
经过明代二百多年的发展,至清代,中国皮影进入了空前的繁盛时期,形成了历史上从未有过的成熟和繁荣局面。
其一,流传全国,形成了七大影系,北到黑龙江,南至广东、海南,西至青海、甘肃,几乎是遍布城乡,处处皆有影戏,而且酬神祭社、节庆娱乐,具有多种功能。
安徽省2019届高三江淮十校第三次联考文科数学试卷

A,256
B.255
C。 16
D.31
【D-019】 数学(文 科)试 卷 第 1页 (共 4页 )
7.已 知 函 数 灭 多)=3⒍ n佛 ∞s锑 -JIcos2仍 (ω )0)的 最 小 正 周 期 为 π,且 r【 ε)〓 ÷ ,贝刂r{ε 一毋 }〓
⒈ A· -钅
:· -钅|
C· -讠;
D∶ -讠:
(Ⅱ
)当
Bε
∥平面
⒕‘
`时
,求
四棱锥 灶-BDEC的 体积。
【D-019】 数学(文 科)试 卷 第3页 (共 4页 )
19.(本 小题满分 ⒓ 分 )
已知数列 {Gn}的 前 n项 的和 SⅡ =′ +2尼 ,{3n}是 等差数列 ,且 GⅡ =bⅡ +bⅡ +1。 (I)求 数列 {bⅡ }的 通项公式 ;
(Ⅱ )证 明:当 艿)0时 矿+2钐 ≥′ +“ +1.
【D-019】 数学(文 科)试卷 第4页 (共 4页 )
(Ⅱ )完 成下 面 2× 2列 联表 ,并 回答是否有 ” %的 把握认 为 “农村 中学 和城镇 中学 的学生对交通安
全
知识
的掌握情况有显
著差异
”
?
成绩小于 ω 分人数 成绩不小于 ω 分人数 合 计
农村 中学
城镇 中学
合计
附 :Kz=
(Ω
刀(cd-bc)2
+b)(c+J)(c+c)(b+d)
临界值表 :
姓名
座位号
(在 此卷上答题无效 )
数 学 (文 科 )
本试卷分第 I卷 (选 择题 )和 第 Ⅱ卷(非 选择题 )两 部分。第 I卷 第 1至第 2页 ,第 Ⅱ卷第 2至 第 4 页。全卷满分 150分 ,考 试时间 1z0分钟。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C.平面 APC∥平面 EFG D.平面 A1BQ∥平面 EFG
11.△ABC 中,角 A,B,C 所对的边分别为 a,b,c,若 2 cos2 A B cos C 3 ,且△ABC
2
2
的面积为 1 c2 ,则 C= 4
A.
6
B.
3
C. ,
66
D. ,
33
12.已知函数
f
(x)
a(2x
1 2x
为
A.2π B. 2 3 C.3π D.4π
7.已知样本甲:x1,x2,x3,…,xn 与样本乙:y1,y2,y3,…,yn,满足 yi 2xi3 1 (i
=1,2,…,n),则下列叙述中一定正确的是
A.样本乙的极差等于样本甲的极差
B.样本乙的众数大于样本甲的众数
C.若某个 xi 为样本甲的中位 数,则 yi 是样本乙的中位数 D.若某个 xi 为样本甲的平均数,则 yi 是样本乙的平均数 8.已知函数 f(x)=x(|x|+1),则不等式 f(x2)+f(x-2)>0 的解集为
函数
y=f(x)与函数
y=f
(f(x))的零点相同,则 a-b 的取值范围为
A.[0,2) B.(-2,0] C.(-∞,-2]∪[0,+∞) D.(-∞,0]∪[2,+∞)
二、填空题:本大题共 4 小题。
13.已知向量 a (2, m) , b (5,1) ,且 a (a b) ,则 m=________.
A. 3 B.3 C. 5 D.5
3.已知命题 p: x 0 ,3x+x2 >1,则¬p 为 A. x 0 ,3x+x2≤1 B. x 0 ,3x+x2≤1 C. x 0 ,3x+x2≤1 D. x 0 ,3x+x2≤1
4.双曲线
y2 a2
x2 b2
1(a>0,b>0)的渐近线方程为
y
率才可低于 千分之一.若生产部门希望 2019 年考核优秀,能否同意 2019 年只生产该产品 1 万台?请说明理由.
log2an,
1 2
log 2
an1
,1(n∈N*)成等差数列.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足 bn
(an
an 1)(an 1
1)
,数列{bn}的前
n
项和为
Tn,求
Tn.
18.斜三棱柱 ABC-A1B1C1 中,底面△ABC 是边长为 2 的正三角形, A1B 7 ,∠A1AB
则当三棱锥 O-ABC 的体积最大时,平面 ABC 截球 O 所得的截面圆的面积为________.
三、解答题:解答应写出文字说明、证明过程或演算步骤。17~21 题为必考题,每个试题
考生都必须作答。22、23 题为选考题,考生根据要求作答。
(一)必考题:
17.已知数列{an}中,a2a6=64,且
=∠A1AC=60°.
(1)证明:平面 A1BC⊥平面 ABC;
(2)求四棱锥 A1-BCC1B1 的体积.
19.某公司生产的某种产品,如果年返修率低于千分之一,则其生产部门当年考核优秀.现
获得该公司 2014-2018 年的相关数据如下表所示:
年份
2014 2015 2016 2017 2018
年生产台数x(万台)
A.(-2,1) B.(-1,2)
C.(-∞,-1)∪(2,+∞)
D.(-∞,-2)∪(1,+∞)
1
9.已知函数 f (x) cos(x 2)( 0) 的最小正周期为 4π,则下列叙述中正确的是 3
A.函数 f(x)的图象关于直线 x 对称 3
B.函数 f(x)在区间(0,π)上单调递增
方程是 y=6.5x+17.5①.现该公司计划从 2019 年开始转型,并决定 2019 年只生产该产品 1 万台,且预计 2019 年可获利 32(百万元);但生产部门发现,若用预计的 2019 年的数据与
2014-2018 年中考核优秀年份的数据重新建立回归方程,只有当重新估算的 b 2 ,a 2 的值(精 确到 0.01),相对于①中 b1 , a1 的值的误差的绝对值都不超过 10%时,2019 年该产品返修
2x ,则其离心率为
A. 5 2
B. 6 2
C. 3
D. 5
5.曲线 f (x) 1 2 ln x 在点 P(1,f(1))处的切线 l 的方程为 x
A.x+y-2=0 B.2x+y-3=0 C.3x+y+2=0 D.3x+y-4=0
6.某圆锥的正视图是腰长为 2 的等腰三角形,且母线与底面所成的角为 60°,则其侧面积
24568
该产品的年利润y(百万元) 30 40 60 50 70
年返修台数(台)
19 58 45 71 70
注: 年返修率 年返修台数 . 年生产台数
3
(1)从该公司 2014-2018 年的相关数据中任意选取 3 年的数据,求这 3 年中至少有 2 年生 产部门考核优秀的概率.
(2)利用上表中五年的数据求出年利润 y(百万元)关于年生产台数 x(万台)的回归直线
x y 2 0
14.设变量
x,y
满足约束条件
x
2
y
4
0
,则目标函数
z=x-2y
的最小值为________.
y 3 0
2
x2
15.已知椭圆 C:
y2
1的左、右焦点分别为 F1、F2,以 F2 为圆心作半径为 1 的圆 F2,
96
P 为椭圆 C 上一点,Q 为圆 F2 上一点,则|PF1|+|PQ|的取值范围为________. 16.已知点 A,B,C 在半径为 2 的球 O 的球面上,且 OA,OB,OC 两两所成的角相等,
C.函数 f(x)的图象向右平移 个单位长度后关于原点对称
3
D.函数 f(x)在区间[0,π]上的最大值为 3 2
10.如图所示,正方体 ABCD-A1B1C1D1 中,点 E,F,G,P,Q 分别为棱 AB,C1D1,D1A1,
D1D,C1C 的中点.则下列叙述中正确的是
A.直线 BQ∥平面 EFG B.直线 A1B∥平面 EFG
2019 年安徽省“江南十校”综合素质检测
数学(文科) 一、选择题:本大题共 12 小题,在每小题给出的四个选项中,只有一项是符合题目要求的。 1.已知集合 A={x|0≤x< 2},B=Z(Z 为整数 集),则 A∩B= A.{1} B.{0,1} C.{1,2} D.{0,1,2} 2.复数 z 满足(i-2)z=4+3i,则|z|=
