矩阵理论研究生课程大作业
学年工科硕士研究生期末考试矩阵论试题

武汉大学数学与统计学院2005-2006学年工科硕士研究生学位课程期末考试《矩阵论》 试题 (A 卷,150分钟)专业 电气工程 班号 姓名 学号注:所有的答题内容必须写在答题纸上,凡写在其它地方的一律无效;交卷时将试卷连同答题纸、草稿纸一并上交。
一、 是非题(满分12“√”,否则打“×”)(√A 是n m ⨯的实矩阵,x 为n 维向量,则⇔=0Ax A T 0=Ax ;()()212200*0*000T T T m j mjm ji A Ax x A Ax Ax a a a Y Ax ⨯=∴==⎛⎫⎪ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭⇔=⇔==∑∑Tij m n j=1j=1令Y=(y ),则Y Y=0,即 ( × ) 2.设n 阶方阵A 满足E A =2,则A 的特征值只能是1;也可能是-1,如令1001A ⎛⎫= ⎪-⎝⎭证明:21111111A E A AAx x A Ax A x x A x Ax Ax x λλλλλλλλ----=⇒==⇒=⇒==⇒=⇒=⇒=±(√ ) 3.欧氏空间n R 上的任意两种向量范数都是等价的; 在线性空间中所任意两种范数等价而欧氏空间是一种特殊的线性空间(√ ) 4.设A 为n m ⨯矩阵,B 为n 阶可逆方阵,则---=A B AB 1)(.()()()111()AB B A AB ABB A AB AA AB ABAB B A--------===∴=二、 填空题(本题满分12分,每空3分).设有三个四维向量T T T Z Y X )3,1,1,2(,)1,1,1,1(,)1,1,1,1(=--=-=.则它们的2-范数分别为=2X2 ; =2Y2 ;2Z 且与Z Y X ,,都正交的所有向量为 (4013)k -. 即求1234111101111021130x x x x ⎛⎫-⎛⎫⎛⎫ ⎪ ⎪ ⎪⎪--= ⎪ ⎪⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭的解。
矩阵论大作业

“矩阵论”课程研究报告科目:矩阵理论及其应用教师:姓名:学号:专业:机械设计及理论类别:上课时间: 2013年2月至2013年5月考生成绩:阅卷评语:阅卷教师(签名)利用矩阵论相关知识求解传动轴固有频率的有限元分析法摘要:在结构力学中,求解结构自由振动的固有频率是十分重要的内容。
本文通过对某机器传动轴各个单元进行单元刚度矩阵、单元质量矩阵等特性分析,再把各个单元的特性矩阵组集起来组成结构的总刚度矩阵、总质量矩阵,从而形成结构的自由振动方程式。
最后利用矩阵论相关知识求解自由振动方程式的广义特征值,并通过广义特征值与固有频率的关系求得传动轴的固有频率。
正文一、问题描述已知某机器传动轴两端固定,其传动轴受扭长度L为1500mm,传动轴的横截面积是环形,其外径D为50mm,内径d为45mm,弹性模量E为52。
利2.110/N mm用矩阵论及有限元分析法求解传动轴的固有频率。
二、方法简述1.建立传动轴的有限元分析模型由于传动轴两端固定,采用平面梁单元分析该传动轴。
考虑到本次计算是手算,为了简化计算,将该传动轴划分为(1)、(2)两个单元,共1、2、3三个结点。
由于该结构中一个结点有两个自由度,故总共有1、2、3、4、5、6六个自由度。
建立有限元分析模型及各个部分编号如图1所示。
图1 传动轴有限元分析模型2.平面梁单元的单元刚度矩阵由《机械结构有限元分析》[1]中形状函数N 的构造方法可知,对于该结构的平面梁单元,它有两个节点,四个自由度,采用自然坐标系,通过构造计算可得单元的形函数为()()()()v iiv j j N N N N N θθ⎡⎤=⎣⎦23232332(132)(2)(32)()ξξξξξξξξξ⎡⎤=-+-+--⎣⎦ (1)其中,i j 为结点编号,v 为结点位移,θ为结点转角,xlξ=,l 为梁单元的长度。
平面梁单元的单元刚度矩阵T lk E I B B d x=⎰ (2) 其中E 为弹性模量,I 为惯性矩。
矩阵理论研究生课程大作业

研究生“矩阵论”课程课外作业姓名:学号:学院:专业:类别:组数:成绩:人口迁移问题和航班问题(重庆大学 机械工程学院,机械传动国家重点实验室)摘要:随着人类文明的进程,一些关于数学类的问题越来越贴近我们的生活,越发觉得数学与我们息息相关。
本文将利用矩阵理论的知识对人口迁移问题和航班问题进行分析。
人口迁移问题假设有两个地区——如南方和北方,之间发生人口迁移。
每一年北方50%的人口迁移到南方,同时有25%的南方人口迁移到北方,直观上可由下图表示:问题:如果这个移民过程持续下去,北方的人会不会全部都到南方?如果会请说明理由;如果不会,那么北方的最终人口分布会怎样?解 设n 年后北方和南方的人口分别为n x 和n y , 我们假设最初北方有0x 人,南方有0y 人。
则我们可得,1=n 时,一年后北方和南方的人口为⎩⎨⎧+=+=00100175.05.025.05.0y x y y x x (1-1)将上述方程组(1-1)写成矩阵的形式⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛0011y x A y x其中 ⎥⎦⎤⎢⎣⎡=75.05.025.05.0A2=n 时,两年后北方和南方的人口为⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛0021122y x A y x A y x依次类推下去,n 年后北方和南方的人口为⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛00y x A y x n n n (1-2) N S 0.5 0.25 0.5 0.75现在只需求出n A 就可得出若干年后北方和南方的人口数。
下面将使用待定系数法[1]求n A)1)(25.0(25.025.125.05.0)75.0)(5.0(75.05.025.05.02--=+-=⨯---=----=-λλλλλλλλλA E所以 1,25.021==λλ矩阵A 的最小多项式为 )1)(25.0()(--=λλλm 设A a E a A n 10+= 由此可得方程组⎩⎨⎧=+=+125.025.01010a a a a n解方程组得⎪⎪⎩⎪⎪⎨⎧-=+-=75.025.0175.025.025.010n na a 所以⎥⎦⎤⎢⎣⎡+⨯--⨯+=-++-=+=++111025.05.025.05.05.025.025.025.05.025.075.0175.025.0175.025.025.0n n n n nn nAE A a E a A 所以由式(1-2),我们得到n 年后北方和南方的人口北方:01075.025.025.075.025.05.025.0y x x n n n +-+⨯+=南方:01075.025.05.075.025.05.05.0y x y n n n +++⨯-=当∞→n 时,得)(31)75.025.025.075.025.05.025.0(lim lim 00010y x y x x n n n n n +=-+⨯+=+∞→∞→()000103275.025.05.075.025.05.05.0lim lim y x y x y n n n n n +=⎪⎪⎭⎫⎝⎛++⨯-=+∞∞→∞→ 由上面计算可以得到,如果移民过程持续下去,北方的人不会全部都到南方。
研究生矩阵理论课后答案4,5章习题
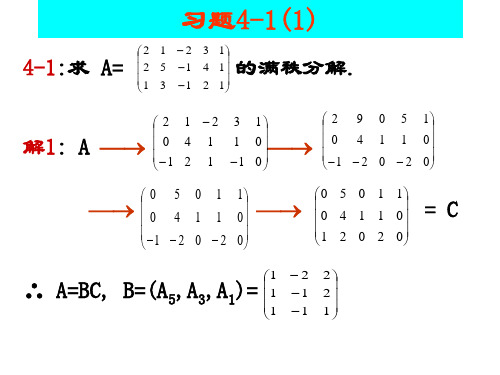
2 1 − 2 3 1 0 4 1 1 0 −1 2 1 −1 0
0 5 0 1 1 0 4 1 1 0 −1 −2 0 −2 0
→
1 1 1 −2 −1 −1
0 5 0 1 1 0 4 1 1 0 1 2 0 2 0
同一向量的三种范数之间的大小关系 习题#5-4:对n维线性空间的任意向量x成 习题#5维线性空间的任意向量x #5
‖x‖∞ ≤‖x‖2 ≤‖x‖1 ≤ n‖x‖∞ ≤ n‖x‖2 ≤ n‖x‖1 ≤ n2‖x‖∞ ≤ …
立
证: |,…,|x ‖x‖∞= max{|x1|, ,|xn|} ≤(Σi=1n|xi|2)1/2 = ‖x‖2 |+…+|x ≤((|x1|+ +|xn|)2)1/2 = ‖x‖1 |,…,|x ≤ n max{|x1|, ,|xn|} = n‖x‖∞
习题#5是正定矩阵,x ,x∈ 习题#5-6A∈Cn×n是正定矩阵,x∈Cn #5
是向量范数. •证明:‖x‖=(x*Ax)1/2 是向量范数. 证明:‖x‖=(x
解1:因A是正定Hermite矩阵A,故存在可逆矩阵B 是正定Hermite矩阵A,故存在可逆矩阵B Hermite矩阵A,故存在可逆矩阵 使得A=B B.则 的上述表示式可写为: 使得A=B*B.则x的上述表示式可写为: (Bx)) ‖x‖=(x*Ax)1/2 =((Bx)*(Bx))1/2 =‖Bx‖2 其中‖‖ 是向量2 范数.再注意可逆矩阵B 其中‖‖2 是向量2-范数.再注意可逆矩阵B的性 Bx=0,即可直接推出非负性 即可直接推出非负性. 质:x=0 ⇔ Bx=0,即可直接推出非负性. ‖kx‖=‖B(kx)‖2=|k|‖Bx‖2=|k|‖x‖ 推出齐次性;三角不等式则由下式推出: 推出齐次性;三角不等式则由下式推出: ‖x+y‖=‖B(x+y)‖2≤‖Bx‖2+‖By‖2
研究生矩阵论课后习题答案(全)习题二

习题二1.化下列矩阵为Smith 标准型:(1)222211λλλλλλλλλ⎡⎤-⎢⎥-⎢⎥⎢⎥+-⎣⎦; (2)22220000000(1)00000λλλλλλ⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥-⎣⎦; (3)2222232321234353234421λλλλλλλλλλλλλλ⎡⎤+--+-⎢⎥+--+-⎢⎥⎢⎥+---⎣⎦;(4)23014360220620101003312200λλλλλλλλλλλλλλ⎡⎤⎢⎥++⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥---⎣⎦. 解:(1)对矩阵作初等变换133122222222111001100(1)c c r r λλλλλλλλλλλλλλλλλλλλλ+-⎡⎤⎡⎤⎡⎤-⎢⎥⎢⎥⎢⎥-−−−→-−−−→-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥+---+⎣⎦⎣⎦⎣⎦23221311(1)1010000000(1)00(1)c c c c c c r λλλλλλλλλ+--⨯-⎡⎤⎡⎤⎢⎥⎢⎥−−−→-−−−→⎢⎥⎢⎥⎢⎥⎢⎥-++⎣⎦⎣⎦,则该矩阵为Smith 标准型为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+)1(1λλλ; (2)矩阵的各阶行列式因子为44224321()(1),()(1),()(1),()1D D D D λλλλλλλλλλ=-=-=-=,从而不变因子为222341234123()()()()1,()(1),()(1),()(1)()()()D D D d d d d D D D λλλλλλλλλλλλλλλλ===-==-==-故该矩阵的Smith 标准型为2210000(1)0000(1)0000(1)λλλλλλ⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥-⎣⎦;(3)对矩阵作初等变换1332212132132222222222242322(2)2(2)323212332212435323443322421221762450110221c c c c r r r r c c c λλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλ-------⎡⎤⎡⎤+--+----⎢⎥⎢⎥+--+-−−−→---⎢⎥⎢⎥⎢⎥⎢⎥+-----⎣⎦⎣⎦⎡⎤-+--++-⎢⎥−−−−→--⎢⎥⎢⎥--⎣⎦3122131211342322(2)3232(1)32(5)(1)27624501100011245001000110010001001000100(1)(c c c r r r r r c c λλλλλλλλλλλλλλλλλλλλλλλλλ---+↔+--⨯-↔⎡⎤-+--++-⎢⎥−−−−−→--⎢⎥⎢⎥⎣⎦⎡⎤-+---++-⎢⎥−−−−→-⎢⎥⎢⎥⎣⎦⎡⎤--+⎢⎥−−−−−→-−−−→-⎢⎥⎢⎥-⎣⎦1)⎡⎤⎢⎥⎢⎥⎢⎥+⎣⎦故该矩阵的Smith 标准型为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+--)1()1(112λλλ; (4)对矩阵作初等变换152323230100014360220002206200020101001010033122003312200c c c c λλλλλλλλλλλλλλλλλλλλλλλλ--⎡⎤⎡⎤⎢⎥⎢⎥+++⎢⎥⎢⎥⎢⎥⎢⎥−−−→⎢⎥⎢⎥----⎢⎥⎢⎥⎢⎥⎢⎥------⎣⎦⎣⎦12213231322000100010002200000020002010100100000100001000c c r r c c c c λλλλλλλλλλλλλλ+-+-⎡⎤⎡⎤⎢⎥⎢⎥+⎢⎥⎢⎥⎢⎥⎢⎥−−−→−−−→⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦2143145425222000101000000000000000000001000000010010000001r r c c c c c c c c λλλλλλλλλλ--↔-↔⎡⎤⎡⎤⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥−−−→−−−→⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦在最后的形式中,可求得行列式因子3254321()(1),()(1),()()()1D D D D D λλλλλλλλλ=-=-===,于是不变因子为2541234534()()()()()1,()(1),()(1)()()D D d d d d d D D λλλλλλλλλλλλλ=====-==-故该矩阵的Smith 标准形为2100000100000100000(1)00000(1)λλλλ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥-⎣⎦. 2.求下列λ-矩阵的不变因子:(1)210021002λλλ--⎡⎤⎢⎥--⎢⎥⎢⎥-⎣⎦;(2)10010000λαββλαλαββλα+⎡⎤⎢⎥-+⎢⎥⎢⎥+⎢⎥-+⎣⎦; (3)100100015432λλλλ-⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥+⎣⎦; (4)0012012012002000λλλλ+⎡⎤⎢⎥+⎢⎥⎢⎥+⎢⎥+⎣⎦. 解:(1)该λ-矩阵的右上角的2阶子式为1,故12()()1,D D λλ==而33()(2)D λλ=-,所以该λ-矩阵的不变因子为2123()()1,()(2)d d d λλλλ===-;(2)当0β=时,由于4243()(),()()D D λλαλλα=+=+,21()()1D D λλ==,故不变因子为12()()1d d λλ==,2234()(),()()d d λλαλλα=+=+当0β≠时,由于224()[()]D λλαβ=++,且该λ-矩阵中右上角的3阶子式为2(),βλα-+且4(2(),())1D βλαλ-+=,则3()1D λ=,故21()()1D D λλ==,所以该λ-矩阵的不变因子为123()()()1,d d d λλλ===224()[()]d λλαβ=++;(3)该λ-矩阵的右上角的3阶子式为1-,故123()()()1,D D D λλλ===而4324()2345D λλλλλ=++++,所以该λ-矩阵的不变因子为123()()()1,d d d λλλ=== 4324()2345d λλλλλ=++++;(4)该λ-矩阵的行列式因子为123()()()1,D D D λλλ===44()(2)D λλ=+,所以该λ-矩阵的不变因子为123()()()1,d d d λλλ===44()(2)d λλ=+.3.求下列λ-矩阵的初等因子:(1)333232212322λλλλλλλλ⎡⎤++⎢⎥--+--+⎣⎦; (2)3223222212122122λλλλλλλλλλ⎡⎤-+--+⎢⎥-+--⎣⎦. 解:(1)该λ-矩阵的行列式因子为212()1,()(1)(1)D D λλλλ==+-,故初等因子为21,(1)λλ+-;(2) 该λ-矩阵的行列式因子为212()1,()(1)(1)D D λλλλλ=-=+-,故不变因子为12()1,()(1)(1),d d λλλλλ=-=+-因此,初等因子为1,1,1λλλ+--.4.求下列矩阵的Jordan 标准形:(1)131616576687⎡⎤⎢⎥---⎢⎥⎢⎥---⎣⎦;(2)452221111-⎡⎤⎢⎥--⎢⎥⎢⎥--⎣⎦;(3)3732524103-⎡⎤⎢⎥--⎢⎥⎢⎥--⎣⎦; (4)111333222-⎡⎤⎢⎥--⎢⎥⎢⎥--⎣⎦;(5)03318621410⎡⎤⎢⎥-⎢⎥⎢⎥--⎣⎦;(6)1234012300120001⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦. 解:(1)设该矩阵为A ,则210001000(1)(3)E A λλλ⎡⎤⎢⎥-→⎢⎥⎢⎥-+⎣⎦,故A 的初等因子为2(1)(3)λλ-+,则A 的Jordan 标准形为300011001-⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦; (2)设该矩阵为A ,则310001000(1)E A λλ⎡⎤⎢⎥-→⎢⎥⎢⎥-⎣⎦,故A 的初等因子为3(1)λ-,从而A 的Jordan 标准形为110011001⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦;(3)设该矩阵为A ,则210001000(1)(1)E A λλλ⎡⎤⎢⎥-→⎢⎥⎢⎥-+⎣⎦,故A 的初等因子为1,,,i i λλλ-+-从而A 的Jordan 标准形为1000000i i ⎡⎤⎢⎥-⎢⎥⎢⎥⎣⎦; (4)设该矩阵为A ,则21000000E A λλλ⎡⎤⎢⎥-→⎢⎥⎢⎥⎣⎦,故A 的初等因子为2,λλ,从而A 的Jordan 标准形为000001000⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦; (5)设该矩阵为A ,则210001000(1)E A λλλ⎡⎤⎢⎥-→⎢⎥⎢⎥+⎣⎦,故A 的初等因子为2,(1)λλ+,从而A 的Jordan 标准形为000011001⎡⎤⎢⎥-⎢⎥⎢⎥-⎣⎦; (6)设该矩阵为A ,则1234012300120001E A λλλλλ----⎡⎤⎢⎥---⎢⎥-=⎢⎥--⎢⎥-⎣⎦, 该λ-矩阵的各阶行列式因子为123()()()1,D D D λλλ===44()(1)D λλ=-,则不变因子为123()()()1,d d d λλλ===44()(1)d λλ=-,故初等因子为4(1)λ-,则A 的Jordan 标准形为1100011000110001⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦. 5.设矩阵142034043A ⎡⎤⎢⎥=--⎢⎥⎢⎥⎣⎦,求5A .解:矩阵A 的特征多项式为2()(1)(5)A f I A λλλλ=-=--,故A 的特征值为11λ=,235λλ==.属于特征值11λ=的特征向量为1(1,0,0)Tη=,属于235λλ==的特征向量为23(2,1,2),(1,2,1)T Tηη==-.设123121[,,]012021P ηηη⎡⎤⎢⎥==-⎢⎥⎢⎥⎣⎦,100050005⎡⎤⎢⎥Λ=⎢⎥⎢⎥⎣⎦,则1A P P -=Λ.,故4455144441453510354504535A P P -⎡⎤⨯⨯-⎢⎥=Λ=-⨯⨯⎢⎥⎢⎥⨯⨯⎣⎦. 6.设矩阵211212112A --⎡⎤⎢⎥=--⎢⎥⎢⎥-⎣⎦,求A 的Jordan 标准形J ,并求相似变换矩阵P ,使得1P AP J -=.解:(1) 求A 的Jordan 标准形J .221110021201011200(1)I A λλλλλλ-⎡⎤⎡⎤⎢⎥⎢⎥-=-+→-⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦,故其初等因子为21,(1)λλ--,故A 的Jordan 标准形100011001J ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦.(2)求相似变换矩阵P .考虑方程组()0,I A X -=即1231112220,111x x x -⎡⎤⎛⎫⎪⎢⎥-= ⎪⎢⎥ ⎪⎢⎥--⎣⎦⎝⎭解之,得12100,111X X ⎛⎫⎛⎫⎪ ⎪== ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭.其通解为1122k X k X +=1212k k k k ⎛⎫⎪⎪ ⎪-⎝⎭,其中21,k k 为任意常数.考虑方程组1122312111222,111x k x k x k k -⎡⎤⎛⎫⎛⎫ ⎪ ⎪⎢⎥-= ⎪ ⎪⎢⎥ ⎪ ⎪⎢⎥---⎣⎦⎝⎭⎝⎭11212121211111122200021110002k k k k k k k k k --⎡⎤⎡⎤⎢⎥⎢⎥-→-+⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦,故当1220k k -=时,方程组有解.取121,2k k ==,解此方程组,得3001X ⎛⎫⎪= ⎪ ⎪⎝⎭.则相似变换矩阵123100[,,]010111P X X X ⎡⎤⎢⎥==⎢⎥⎢⎥-⎣⎦.7.设矩阵102011010A ⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦,试计算8542234A A A A I -++-. 解: 矩阵A 的特征多项式为3()21A f I A λλλλ=-=-+,由于8542320234(21)()(243710)f λλλλλλλλλ-++-=-++-+,其中532()245914f λλλλλ=+-+-. 且32A A I O -+=,故8542234A A A A I -++-=2348262437100956106134A A I --⎡⎤⎢⎥-+=-⎢⎥⎢⎥-⎣⎦.8.证明:任意可逆矩阵A 的逆矩阵1A -可以表示为A 的多项式. 证明:设矩阵A 的特征多项式为12121()n n n A n n f I A a a a a λλλλλλ---=-=+++++,则12121n n n n n A a A a A a A a I O ---+++++=,即123121()n n n n n A A a A a A a I a I ----++++=-,因为A 可逆,故(1)0nn a A =-≠,则11231211()n n n n nA A a A a A a I a -----=-++++9.设矩阵2113A -⎡⎤=⎢⎥⎣⎦,试计算4321(5668)A A A A I --++-.解: 矩阵A 的特征多项式为2()57A f I A λλλλ=-=-+,则227A A I O -+=,而432225668(57)(1)1λλλλλλλλ-++-=-+-+-,故14321111211(5668)()12113A A A A I A I ----⎡⎤⎡⎤-++-=-==⎢⎥⎢⎥-⎣⎦⎣⎦. 10.已知3阶矩阵A 的三个特征值为1,-1,2,试将2nA 表示为A 的二次式. 解: 矩阵A 的特征多项式为()(1)(1)(2)A f I A λλλλλ=-=-+-,则设22()()n f g a b c λλλλλ=+++,由(1)0,(1)0,(2)0,f f f =-==得21,1,422.n a b c a b c a b c ++=⎧⎪--=⎨⎪++=⎩解之,得2211(21),0,(24)33n n a b c =-==--,因此2222211(21)(24)33n n n A aA bA cI A I =++=---.11.求下列矩阵的最小多项式:(1)311020111-⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦;(2)422575674-⎡⎤⎢⎥--⎢⎥⎢⎥--⎣⎦; (3)n 阶单位阵n I ;(4)n 阶方阵A ,其元素均为1;(5)0123103223013210a a a a a a a a B a a a a a a a a ⎡⎤⎢⎥--⎢⎥=⎢⎥--⎢⎥--⎣⎦. 解:(1) 设311020111A -⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,则 231110002002011100(2)I A λλλλλλ--⎡⎤⎡⎤⎢⎥⎢⎥-=-→-⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦,故该矩阵的最小多项式为2(2)λ-.(2) 设422575674A -⎡⎤⎢⎥=--⎢⎥⎢⎥--⎣⎦,则 2(2)(511)I A λλλλ-=--+,故该矩阵有三个不同的特征值,因此其最小多项式为2(2)(511)λλλ--+(3) n 阶单位阵n I 的最小多项式为()1m λλ=-. (4) 因为1()n I A n λλλ--=-,又2A nA =,即2A nA O -=,故该矩阵的最小多项式为()n λλ-.(5)因为22222200123[2()]I B a a a a a λλλ-=-++++,而2222200123()2()m a a a a a λλλ=-++++是I B λ-的因子,经检验知()m λ是矩阵B 的最小多项式.。
研究生 矩阵论 课后答案
|
xk
|2
)
1 2
是范数.
k =1
(2)证明函数 || x ||∞ = max{| x1 |,| x2 |,...,| xn |}是范数.
2.设
x∈R2,
A=
⎛4 ⎜⎝1
1⎞ 4⎟⎠
,请画出由不等式||
x
||
A
≤
1决定的x的全
体所对应的几何图形.
3.在平面 R2中将一个棍子的一端放在原点,另一端放
生成子空间V,求V的正交补空间V ⊥.
15.(MATLAB)将以下向量组正交化.
(1) x1 = (1,1,1)T , x2 = (1,1, 0)T , x3 = (1, −1, 2);T
(2) f (t) = 1, g(t) = t, h(t) = t2是[0,1]上的多项式空间
的基,并且定义(
f
9.把下面矩阵A对应的λ -矩阵化为Smith标准形,并且写
出与A相似的Jordan标准形.
⎛1 −1 2 ⎞
(1)
⎜ ⎜
3
−3
6
⎟ ⎟
⎜⎝ 2 − 2 4⎟⎠
⎛ −4 2 10⎞
(2)
⎜ ⎜⎜⎝
−4 −3
3 1
7 7
⎟ ⎟⎟⎠
⎧ dx1
⎪ ⎪
dt
=
3x1
+ 8x3
10.(MATLAB)求解微分方程:
α3 = (0,1,1)T 的矩阵为: ⎡ 1
A=⎢ 1 ⎢⎣−1
0 1⎤ 1 0⎥ 2 1⎥⎦
求在基e1 = (1,0,0)T ,e2 = (0,1,0)T ,e3 = (0,0,1)T下的矩阵.
10.设S = {ε1,ε2 ,ε3,ε4}是四维线性空间V的一个基,已知
华中科技大学研究生数学矩阵论练习和习题省名师优质课赛课获奖课件市赛课一等奖课件

L L{1,2,···,m }
W
W1+W2
矩 矩阵AF m×n,两个子空间
不不变子空间
线线性变换旳数量关系:
➢线性变换旳表达 ➢线性变换旳数量关系 ➢主要旳线性变换
第1章习题选讲
P31,习题一 1(3),2,4,9,10,11 ,17,20, 23(4),26,29,30
第2章推荐习题
P58 1,2,3,6,8,9,11, 12, 13,16,19,20
第2章习题选讲
P58 1,3,6,8,9,11, 13,16, 19,20
线性空间旳问题
线性空间旳表达形式:
集合表达形式:Vn(F)={ 满足旳性质} 向量生成形式:L{1,2,···,m }
子空间类型:
L{1,2,···,m } W1+W2 矩阵AF m×n,两个子空间 不变子空间
线性空间旳数量关系与矩阵
线性变换旳数量关系
线性变换旳给定方式 线性变换旳变换矩阵 空间分解与矩阵分解
复习与习题
2023 级矩阵论考试信息
考试时间:第16周六(12月22日),
考试地点:西12楼(详见网上告知) 答疑时间:第16周三、四、五:下午 答疑地点:逸夫科技楼(北)913#
矩阵论复习(07)
要点:
线性空间旳问题 线性变换旳数量关系 JA,mA() ,f() =|I-A | 之间旳关系 A与f(A)在Jordan原则形上旳关系 正规矩阵旳性质与应用 向量范数与矩阵范数 矩阵幂级数和矩阵函数
试题旳构造
习题选讲
P31,习题一 2,4,10,11 ,17, 23(4),26,29,30 P57,习题二 3,6,11,13, 20
试题旳构造
填空题 25% 计算题60% 证明题 15% 试题样板
研究生矩阵理论课后答案矩阵分析所有习题

其中1,…,n是A的特征值的任意排列. ∵ A2=E=Udiag(1,…,1)U* 和
A2=Udiag(1,…,n)U*Udiag(1,…,n)U* =Udiag(12,…,n2)U*
∴ i2=1,即i=1,i=1,…,n,. 取1,…,n的排列使特征值1(设共有r个)全排在
2 5
5 0 1 5
0 1 0
1
5
0
2 5
习题3-9
#3-9:若S,T分别为实对称,反实对称矩阵,则 A=(E+T+iS)(E-T-iS)-1为酉矩阵.
证: A*A=((E-T-iS)*)-1(E+T+iS)*(E+T+iS)(E-T-iS)-1
=((E+T+iS)-1(E-(T+iS))(E+(T+iS))(E-T-iS)-1 =(E+T+iS)-1(E+T+iS)(E-T-iS)(E-T-iS)-1 =E
∴ A+B是正定Hermite矩阵.
习题3-22设A,B均是正规矩阵,试证:A 与B相似的充要条件是A与B酉相似
证:因为A,B是正规矩阵,所以存在U,VUnn 使得 A=Udiag(1,…,n)U*, B=Vdiag(1,…,n)V*,
其中1,…, n,,1,…,n分别是A,B的特征值集 合的任意排列.
证:因为A是正规矩阵,所以存在UUnn 使得 其中1,…, ArA=n是=UUdAdi的iaag特g((征1r1,,值…….,,于nn是r))U,U**,=0 蕴∴涵Air==U0d,iia=g1(,0…,…,n,.0后)U者*=又0.蕴涵 1=…=n=0.
研究生矩阵理论课后答案第5章

按范数收敛
定义:赋范空间V的序列{x(n)|n=1,2,…}按范数 ‖‖α收敛于aV,如果 limn‖x(n)-a‖α=0 命题:对赋范空间V的任意两个等价向量范数 ‖‖α, ‖‖β, 都有 limn‖x(n)-a‖α=0 limn‖x(n)-a‖β=0 (即按任意两个向量范数的收敛实质上等价) 因 0 limn‖x(n)-a‖α d limn‖x(n)-a‖β 0 limn‖x(n)-a‖β(1/c)limn‖x(n)-a‖α
1=|yk|(i=1n|yi|p)1/p =‖y‖p n1/p (*) (i|yi|=|xi|/|xk|1) 1=limp1limp‖y‖p limpn1/p=n0=1 1=limp‖y‖p=limp‖x‖p/‖x‖ ‖x‖=limp‖x‖p
同一向量的三种范数之间的大小关系
Frobenius 矩阵范数
例5.2.2:矩阵的Frobenius范数定义为 ‖A‖F=(i=1mj=1n|aij|2)1/2. (ACmn的向量2-范数蕴含前3条公理)不难证明4 条范数公理全部满足.因非负性和齐次性是显 然的;③的证明见课本.我们只讲④的证明. ‖AB‖F2=i=1mj=1n|k=1paikbkj|2 i=1mj=1n((k=1p|aik|2)(k=1p|bkj|2))(C-S不等
则
n
1 ak 1 bk a k bk a b p q q b p a
1 a k bk a b k 1 pa
p
n k 1
ak
p
1 qb
q
b k 1 k
n q
1 1 ab ab q xn|}=|k‖x‖; ‖x+y‖= max{|x1+y1|,…,|xn+yn|} max{|x1|+|y1|,…,|xn|+|yn|} max{|x1|,…,|xn|}+max{|y1|,…,|yn|} =‖x‖+‖y‖
重庆大学研究生“矩阵论”课程课外作业

2 3 0 1 3 , 0 2 3 0 。
如果豌豆初始位置在 #2,#4 ,经过奇数无穷多次移动后,概率分布为
运用 Hamilton-Cayley 定理求解
f ( ) I A
1
1 2 0 1 2 0 0
0 1 2
1
0 0 1 1 ( 1)( 1)( )( ) 1 2 2 2
1 0 0 0 1 2 0 1 2 0 p4 (k 1) 0 1 2 0 1 2 0 1 0 0
P(k 1) A , k 1,2,3,
以此类推,则有
P(k ) P(k 1) A P(k 2) AA P(k 2) A2 P(k 3) A2 A P(k 3) A3 P(2) Ak 2 P(1) Ak 1 P(0) Ak
0 2 3 0 1 3 1 3 0 2 3 0 。 lim P(k ) P(0) k 0 2 3 0 1 3 1 3 0 2 3 0 也就是说,如果豌豆初始位置在 #1,#3 ,经过奇数无穷多次移动后,概率 分布为
0 1 3
方法 2 首先,A 的特征多项式为:
把 A 的四个特征值带入上式,得出方程组:
(1) k q 0 q1 q 2 q3 1k q 0 q1 q 2 q3 1 k 1 1 1 ( ) q 0 q1 q 2 q3 2 4 8 2 1 1 1 1 ( ) k q 0 q1 q 2 q3 2 4 8 2
一、欲解决的题目内容:
如图所示, 一颗豌豆被放置在四个壳里中的其中一个的里面,一个敏捷的操 纵者通过一系列迅速的移动将它们重新排列。每一次的移动,含有豌豆的壳要么 向左或向右移壳在位置#1 时,就只能移动到位置#2,如果含有豌豆的壳在 位置#4 时,就只能移动到位置#3。当含有豌豆的壳在位置#2 或#3 时,就有可能 向左或右移动。 问题 1:假定我们知道含有豌豆的壳的初始位置,那么经过 k 次移动后,含 有豌豆的壳在这四个位置的概率各是多少? 问题 2:经过无数次( k )移动后,含有豌豆的壳出现在每个位置的概 率又是多少?
研究生课程-《矩阵分析》试题及答案

第一套试题答案一(10分)、证明:(1)设11k x +22k x +33k x =0, ①用σ作用式①两端,有111k x λ+222k x λ+333k x λ=0 ②1λ⨯①-②,有21223133()()0k x k x λλλλ-+-= ③再用σ作用式③两端,有2122231333()()0k x k x λλλλλλ-+-= ④ ③⨯2λ-④,有313233()()0k x λλλλ--=。
由于123,,λλλ互不相等,30x ≠,因此30k =,将其代入④,有20k =,利用①,有10k =。
故1x ,2x ,3x 是线性无关的。
(2)用反证法。
假设1x +2x +3x 是σ的属于特征值λ的特征向量,于是有123123()()x x x x x x σλ++=++即112223123()x x x x x x λλλλ++=++112223()()()0x x x λλλλλλ-+-+-=由于1x ,2x ,3x 线性无关,因此123λλλλ===,这与123,,λλλ互不相等矛盾。
所以,1x +2x +3x 不是σ的特征向量。
二(10分)、解:2312321232()()1;()(2);()(2)()1;()(2);()(2)1()(2)(2)A D D D d d d A λλλλλλλλλλλλλλλλλλλλ==-=-==-=-⎛⎫⎪- ⎪ ⎪-⎝⎭的行列式因子分别为,不变因子分别为,于是的Smith 标准形为.三(10分)、解:11121634E A λλλλ+⎛⎫ ⎪-= ⎪ ⎪---⎝⎭210001000(1)λλ⎛⎫ ⎪≅- ⎪ ⎪-⎝⎭A λλ2矩阵的初等因子为: -1, (-1),100:011001J ⎛⎫⎪= ⎪ ⎪⎝⎭故约当标准形为。
四(12分)、解:令()()()1120,E A λλλλ-=-++=得特征值123112λλλ==-=-,,,解齐次方程组()0,E A x -=()2;Tii α=1得基础解系解齐次方程组()0,E A x --=()101;Tα=-2得基础解系解齐次方程组()20,E A x --=()1;T ii α=-3得基础解系αααααα123123由于,,已两两正交,将,,单位化得()()()11121011623T T Tp i i p p i i --123=,=,= ()1,(2)1.3H U p p p U AU ⎛⎫⎪==- ⎪ ⎪⎝⎭123令分,则五(10分)、解:(){}11(1),01,()TAx o i N A span ξξ===解齐次方程组得基础解系,,;又(){}{}()232323010,,,,100,,00H H R A span o span A o i ξξξξξξ⎛⎫⎪===-= ⎪ ⎪-⎝⎭这里,; 显然(),0,iji j ξξ=≠当时;()().HN A R A ⊥故有()()()()()()()()()333(2)dim dim dim 3dim ,Q H H H H N A R A C N A R A N A R A C N A R A C ++=+==+=是的子空间且故。
研究生矩阵论课后习题答案(全)习题一

解
(1)设 Eij 是第 i 行第 j 列的元素为 1 而其余元素全为 0 的 n 阶方阵.
①令 Fij = ⎨
⎧ Eii , i = j , 则 Fij 是对称矩阵, 易证 F11 ,L , F1n , F22 , L , F2 n , ⎩ Eij + E ji , i ≠ j
L , Fnn 线 性 无 关 , 且 对 任 意 n 阶 对 称 矩 阵 A = (aij ) n×n , 其 中 aij = a ji , 有
1 −1 −1
= aa −1 = 1
⑥ k o (l o a ) = k o a = (a ) = a
l l k
lk
= (lk ) o a
⑦ (k +;l
= a k a l = a k ⊕ a l = (k o a) ⊕ (l o a )
k k k
⑧ k o ( a ⊕ b) = k o ( ab) = ( ab) = a b = ( k o a ) ⊕ (k o b) 所以 R+对这两种运算构成实数域 R 上的线性空间. (5)否.设 V2 = y ( x ) y ′′ + a1 y ′ + a 0 y = f ( x ), f ( x ) ≠ 0 ,则该集合对函数的 加法和数乘均不封闭.例如对任意的 y1 , y 2 ∈ V2 , y1 + y 2 ∉ V2 .故不构成线性空间. (6)是.集合 V 对函数的加法和数乘显然封闭.零函数是 V 的零元素;对任意
研究生矩阵论试题及答案与复习资料大全

矩阵论试题(2011级硕士试题)一、(10分)设函数矩阵 ()⎪⎪⎭⎫⎝⎛-=t t t t t A sin cos cos sin 求:()⎰tdt t A 0和(()⎰20t dt t A )'。
解:()⎰t dt t A 0=()⎪⎪⎪⎭⎫ ⎝⎛-⎰⎰⎰⎰tttt tdt tdt dt t dtt 00sin cos cos sin =⎪⎪⎭⎫⎝⎛---t t t t cos 1sin sin cos 1 (()⎰2t dt t A )'=()⎪⎪⎭⎫⎝⎛-=⋅22222sin cos cos sin 22t t t t t t t A 二、(15分)在3R 中线性变换σ将基⎪⎪⎪⎭⎫ ⎝⎛-=1111α,⎪⎪⎪⎭⎫ ⎝⎛-=1202α,⎪⎪⎪⎭⎫⎝⎛-=1013α变为基 ⎪⎪⎪⎭⎫⎝⎛-=0111β,⎪⎪⎪⎭⎫ ⎝⎛-=1102β,⎪⎪⎪⎭⎫ ⎝⎛-=2303β(1)求σ在基321,,ααα下的矩阵表示A ;(2)求向量()T 3,2,1=ξ及()ξσ在基321,,ααα下的坐标; (3)求向量()()ξσξ及T 3,2,1=在基321,,βββ下的坐标。
解:(1)不难求得:()2111ααβασ-==()32122αααβασ++-== ()321332αααβασ++-== 因此σ在321,,ααα下矩阵表示为⎪⎪⎪⎭⎫ ⎝⎛---=110211111A(2)设()⎪⎪⎪⎭⎫ ⎝⎛=321321,,k k k αααξ,即⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎪⎭⎫ ⎝⎛321111021101321k k k解之得:9,4,10321-=-==k k k 所以ξ在321,,ααα下坐标为()T 9,4,10--。
()ξσ在321,,ααα下坐标可得⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎪⎭⎫ ⎝⎛133223*********1111321y y y (3)ξ在基321,,βββ下坐标为⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛---6151941001111110194101A()ξσ在基321,,βββ下坐标为⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛---94101332230111111011332231A三、(20分)设⎪⎪⎪⎭⎫ ⎝⎛-=301010200A ,求At e 。
重庆大学矩阵论大作业

矩阵分析在-------机械振动中的应用摘要:随着科学技术的迅速发展,古典的线性代数知识已不能满足现代科技的需要,矩阵的理论和方法业已成为现代科技领域必不可少的工具。
诸如数值分析、优化理论、微分方程、概率统计、控制论、力学、电子学、网络等学科领域都与矩阵理论有着密切的联系,甚至在经济管理、金融、保险、社会科学等领域,矩阵理论和方法也有着十分重要的应用。
本文采用了矩阵论中所学的矩阵相似变换、矩阵正交化及特征方程等相关知识,对多自由度系统的自振动的运动微分方程进行了研究分析,引入正则坐标并采用坐标变化法求得了振动系统的自由响应。
关键词:多自由度系统,正则坐标,自由响应一、引言20世纪60年代,随着计算机技术的进步,航空航天技术和综合自动化的发展需要,对于复杂的机械结构特性分析也越来越重要。
而对于像航天器等复杂的机械结构需要用更多的自由度来描述,多自由度系统的振动方程式二阶常微分方程组。
建立系统方程是振动分析的前提,但随着自由度的增多,所建立的系统运动微分方程也越来越复杂,对于离散系统运用牛顿第二定律的方式来对方程进行求解也越来越困难,为此发展了柔度系数法和刚度系数法,而拉尔朗日方程是建立系统控制方程的最通用方法,他使用功、能和广义力等物理量,得到了完全刻画系统的最少方程。
本文只考虑阻尼矩阵能够被无阻尼振形矩阵对角化的情形,分析其基本理论方程,并用实例进行论证求解。
二、多自由度系统的自由振动理论本文主要对多自由度系统的自由振动进行求解,在介绍多自由度系统的振动之前,先介绍单自由度无阻尼的自由振动以便了解机械振动理论的基本原理。
1.单自由度无阻尼系统的自由振动图1 单自由度无阻尼系统对于单自由度系统而言,当系统受到激励时,根据牛顿第二定律,可以列出的运动微分方程为:0mx kx += (1.1)其中,m 为物体的质量;k 为弹簧的刚度;x 为物体的加速度;x 为弹簧的伸缩量。
该方程是一个二阶齐次线性常系数微分方程。
北航矩阵论大作业

2019--2020第二学期大作业一.(10分)判断正误(1) 列向量X 的模长||X 满足公式2||H X X X =,也有2||H H X A AX AX =. ( )而且如果0HA AX =,则有可能0AX ≠ ( ) (2)设()ij m n A a ⨯= 则有迹公式:2()()||HHij tr A A tr AA a ==∑ ( )而且若()0H tr A A =,则可能有0A ≠ ( )(3)若B 是列满秩(高阵), C 是行满秩, 则11(), ()H H H H B B B B C C CC +−+−==( ) (4) 若A BC =是满秩分解(高低分解),则A C B +++= ( ) (5) 若矩阵()ij A a =的秩为()1rank A =,则21(||)H ij A a A +−=∑ ( )(6)设,()ij n n A a =特征值为1,,n λλ,则有许尔不等式:221,1nnk ijk i j aλ==≤∑∑( )(7)若A 是酉矩阵(HHA A AA I ==), 则1H A AA +−== ( )(8)若A 是正规阵, P 是同阶酉矩阵,则HP AP 也是正规阵. ( ) (9)若A 是正规阵, 则存在酉矩阵P 使HP AP D =为对角阵. ( ) (10)若正规阵A 特征根为1{,,}n λλ,则它的全体奇异值为1{||,,||}n λλ ( )(11)若A 是n 阶方阵, 则行列式()det()Atr A ee = 且A A e e I−=(单位阵) ( )(12) ,A B 是任意矩阵,则()H H H A B A B ⊗=⊗,()A B A B +++⊗=⊗ ( ) (13)方阵A 的特征根λ,谱半径()A ρ满足1||()||||A A λρ≤≤且33[()]()A A ρρ= ( ) (14)设,n p p n A A B B ⨯⨯==,则AB ,BA 有相同的非0特征根,且()()tr BA tr AB = ( ) (15) ||||•是矩阵范数, I 是单位阵, 则可能有 ||||1I < ( )(16)许尔定理说:若A 是n 阶方阵, 则存在酉矩阵P 使HP AP D =为对角阵. ( ) (17)若x=b A 无解(不相容), 则x=b H H A A A 也无解(不相容) ( )(18)111, ,002a A B b ⎛⎫⎛⎫==⎪ ⎪⎝⎭⎝⎭张量积A B ⊗的全体特征根为{ , 2a b } ( )二. 化简与计算(10分)1.设A 的QR 分解是A QR =,其中H Q Q I =,化简H R Q A −2. 已知2A A =, 化简2323!AA A eI A =++++=?3. 0c ≠为复数,求正规阵00c A c ⎛⎫= ⎪⎝⎭谱半径A ρ();写出0kk A ∞=∑收敛的条件4. 已知2()0A I −=,化简23(())(())()23!()?t A I t A I t A I eI t A I −−−=+−+++=且()()?tA t A I tI t A I tI e e e e −+−===5.111A −⎛⎫⎪⎝⎭3=,化简2(2)A I −,(2)t A I e −,(2)2?tA t A I tI e e e −==二. 计算(15分)1. 211421A ⎛⎫⎪− ⎪ ⎪⎝⎭=.求A 的正SVD (正奇值分解)与奇异值分解.2. 212,(1)1i i i A ⎛⎫=− ⎪⎝⎭= 求QR 分解A QR =三. 计算(15分)1.已知cos3sin 3sin 3cos3tAt t e t t −⎛⎫= ⎪⎝⎭, 求tAe −,0?, ?tA t de A dt =⎛⎫== ⎪⎝⎭ 2.求解微分方程:1d , (0),1d XAX X t ⎛⎫== ⎪⎝⎭其中0330A −⎛⎫= ⎪⎝⎭3.1()1i A i i ⎛⎫== ⎪⎝⎭求:A + ,特征根()H A A λ,谱范数2A 4.用盖尔圆盘定理估计111999111999111416161111010102468A ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭的谱半径()A ρ的范围 四. (15分)说明01110-11-10A ⎛⎫ ⎪= ⎪ ⎪⎝⎭是否正规阵? 并求A 与1A −的谱分解,计算100A五. (10分) 设列向量1(,,)0T n X x x =≠,令(镜面阵)22||H XX P I X =−,其中2||HX X X =. (1)21, , , ? H P P P I P P PX P −−−−=计算:是否酉阵,(优阵)? (2)用秩1方法求H XX 的特征根()HXXλ,)P P λ(求全体特征根的;(3)已知1||322, 00,22002X ααβαβ−⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪====−= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭令求22?, ||HXX P I P P X αββα=−=== 验证六.计算与证明(13分)1.设110011001A ⎛⎫ ⎪= ⎪ ⎪⎝⎭,求一个矩阵B , 使10B A =2.若n 阶Hermite 阵A 的互异特征值只有1,-1,计算20202021A A 与3.证明:若列向量,x y 满足H H A Ax A Ay =,则必有Ax Ay =七.简述题(12分)写出你对正奇值分解(正SVD)或奇异值分解(SVD)的理解;试用一个例子说明它的应用.。
矩阵理论其应用大作业

矩阵奇异值分解在图像压缩上的应用摘要矩阵的奇异值理论提出至今己经有很长的一段时间。
奇异值分解理论由Beltrami和Jordan于十九世纪七十年代提出至今,由于其内在的一些良好特性,奇异值分解正成为应用数学和数学模型领域的一个极有价值的工具。
奇异值分解在很多领域得到了应用,它在数据挖掘及搜索引擎中被用来对数据库文件进行规类,近年来,它在图像压缩方面的应用也越来越受到相关学者的重视。
关键字:图像压缩;奇异值分解第一章总论数字图像处理技术中的数字图像压缩,或者叫图像编码。
二维形式呈现的数字图像,其信息量很大,给传输、处理、储存、显示等都带来了不少的问题。
另一方面,图像中又有很多冗余信息,根据香农(Shannon)的率失真理论。
无论在传输或者储存时,都可对数字图像进行一定方式编码,删除其中冗余信息,实现不失真压缩,或在容许失真限度内进行有失真压缩,以换取更大的压缩率。
对于供人观看的图像,如电视信号,这时人是通信系统中的一环,人的视觉特征,如掩盖效应,对灰度分辨率和空间分辨率的有限性等,也可以用来为压缩服务。
数字图像以数据矩阵形式储存在存储器中,这就使得通过操作数据矩阵的方式压缩图像成为可能。
事实上矩阵的奇异值本身具有可降维的特性,若能合理的利用矩阵奇异值的这一特性,SVD方法在图像压缩领域必将会有广阔的应用前景。
矩阵的奇异值分解(SVD)目前在信号处理、模式分析等领域得到了较为广泛的应用。
由于数字图像矩阵通常是由数据量较大的阵列矩阵所构成,这就给基于SVD变换的算法构造添加了很大的难度,所以SVD变换目前在数据压缩领域得到的应用还不是很多,从SVD变换算法的研究着手,研究大矩阵奇异值的分布情况以及他们在图像恢复时所起到的作用,并在此基础上展开对SVD变换算法在数据压缩领域应用的研究,构造能将SVD变换实际应用到数据压缩领域的快速、高效的算法是十分必要的。
第二章 矩阵奇异值分解理论2.1奇异值分解及其解释2.1.1奇异值分解奇异值分解最早由Beltrami 在1873年针对实正方矩阵提出来的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
研究生“矩阵论”课程课外作业
姓名:学号:
学院:专业:
类别:组数:
成绩:
人口迁移问题和航班问题
(重庆大学 机械工程学院,机械传动国家重点实验室)
摘要:随着人类文明的进程,一些关于数学类的问题越来越贴近我们的生活,越发觉得数学与我们息息相关。
本文将利用矩阵理论的知识对人口迁移问题和航班问题进行分析。
人口迁移问题
假设有两个地区——如南方和北方,之间发生人口迁移。
每一年北方50%的人口迁移到南方,同时有25%的南方人口迁移到北方,直观上可由下图表示:
问题:如果这个移民过程持续下去,北方的人会不会全部都到南方?如果会请说明理由;如果不会,那么北方的最终人口分布会怎样?
解 设n 年后北方和南方的人口分别为n x 和n y , 我们假设最初北方有0x 人,南方有0y 人。
则我们可得,1=n 时,一年后北方和南方的人口为
⎩⎨⎧+=+=001
00175.05.025.05.0y x y y x x (1-1)
将上述方程组(1-1)写成矩阵的形式
⎪⎪⎭
⎫ ⎝⎛=
⎪⎪⎭
⎫
⎝⎛0011y x A y x 其中 ⎥⎦
⎤
⎢⎣⎡=75.05.025.05.0A
2=n 时,两年后北方和南方的人口为
⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛0021122y x A y x A y x
依次类推下去,n 年后北方和南方的人口为
⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛00y x A y x n n n (1-2) 现在只需求出n A 就可得出若干年后北方和南方的人口数。
下面将使用待定系数法[1]求n A
)1)(25.0(25
.025.125
.05.0)75.0)(5.0(75
.05.025
.05
.02--=+-=⨯---=----=
-λλλλλλλλλA E
所以 1,25.021==λλ
矩阵A 的最小多项式为 )1)(25.0()(--=λλλm 设A a E a A n 10+= 由此可得方程组
⎩⎨⎧=+=+125.025.01010a a a a n
解方程组得
⎪⎪⎩
⎪⎪⎨⎧-=
+-=75.025.0175.025.025.010n
n
a a 所以
⎥⎦
⎤⎢⎣⎡+⨯--⨯+=-++-=+=++11
1025.05.025.05.05.025.025.025.05.025.075.0175
.025.0175.025.025.0n n n n n
n n
A
E A a E a A 所以由式(1-2),我们得到n 年后北方和南方的人口
北方:01
075.025.025.075.025.05.025.0y x x n n n +-+⨯+=
南方:01
075
.025.05.075.025.05.05.0y x y n n n +++⨯-=
当∞→n 时,得
)(3
1
)75.025.025.075.025.05.025.0(lim lim 0001
0y x y x x n n n n n +=-+⨯+=+∞→∞→ ()000103
2
75.025.05.075.025.05.05.0lim lim y x y x y n n n n n +=⎪⎪⎭⎫
⎝⎛++⨯-=+∞∞→∞→ 由上面计算可以得到,如果移民过程持续下去,北方的人不会全部都到南方。
最终北方的人口是移民前南北人口之和的1/3。
南方人口是北方人口的两倍。
结论
本文论述的南北方人口迁移问题是一个比较理想化的问题,但还是有一些实际的参考价值,通过本问题的演算过程,我们可以推论,若一个地区有人口迁出(迁出率<1),那么只要有人口迁入,则该地区始终有人口住居。
航班问题
一家航空公司经营A 、B 、C 、D 和H 五个城市的航线业务,其中H 为中心城市。
各个城市间的路线见图1。
图 1
假设你想从A 城市飞往B 城市,因此要完成这次路线,至少需要两个相连的航班,即
A →H 和H →
B 。
如果没有中转站的话,就不得不要至少三个相连的航班。
那么问题如下:
(1)从A 到B ,有多少条路线刚好是三个相连的航班; (2)从A 到B ,有多少条路线要求不多于四个相连的航班。
解 为了方便计算,设1、2、3、4、5分别代表A 、B 、C 、D 、H 五个城市。
令()ij a A =,其中ij a 表示i 城市到j 城市单连航班的路线条数()5,4,3,2,1,=j i ,若1=ij a 表示i 城市到j 城市的单连航班有1条,若0=ij a 表示i 城市到j 城市的单连航班有0条[2]。
则表示i 城市到j 城市单连航班的路线条数用矩阵A 表示为
⎥⎥⎥⎥⎥⎥⎦
⎤⎢⎢⎢⎢⎢
⎢⎣⎡=01
111
1001011000
100011010
A 令()2A b
B ij ==,则ij b 表示i 城市到j 城市两个相连航班的路线条数
⎥⎥⎥
⎥⎥⎥⎦
⎤
⎢⎢⎢⎢⎢
⎢⎣⎡==41111
1111211121
1121112111
2A B
令()3A c C ij ==,则ij c 表示i 城市到j 城市三个相连航班的路线条数
⎥⎥⎥
⎥⎥⎥⎦
⎤
⎢⎢⎢⎢⎢⎢⎣⎡==45555
5232252223
53222522323
A C
令()4A d D ij ==,则ij c 表示i 城市到j 城市四个相连航班的路线条数
⎥⎥⎥
⎥⎥
⎥⎦
⎤⎢⎢⎢⎢⎢
⎢⎣⎡==209999
9877797877
97
78797
7784A D
(1)由上面的计算可得,12c 代表从A 到B 刚好是三个相连的航班路线条数。
所以,从A 到B ,有3条路线刚好是三个相连的航班。
(2)要求从A 到B ,不多于四个相连的航班路线条数,即是要把单个相连、两个相连、三 个相连和四个相连的全部航班路线条数加起来。
即 11731012121212=+++=+++d c b a
所以,从A 到B ,有11条路线不多于四个相连的航班。
参考文献
[1]李新,何传江.矩阵理论及其应用[M].重庆:重庆大学出版社,2005.8:117-120 [2]同济大学数学系.工程数学.线性代数[M].北京:高等教育出版社,2007.5:30-37 如有侵权请联系告知删除,感谢你们的配合!
如有侵权请联系告知删除,感谢你们的配合!。
