-2大学高数历年期末试题

合集下载

数学高数期末试题及答案

数学高数期末试题及答案第一部分：选择题1. 设函数 $f(x) = e^x + \ln x$，则 $f'(1) =$ ( )A. $e$B. $e+1$C. $1$D. $0$2. 设二元函数 $z=f(x,y)$ 在点 $(1,2)$ 处可微，则 $\frac{\partialz}{\partial x}$ 在该点的值为 ( )A. $f_x(1,2)$B. $f_y(1,2)$C. $0$D. $f(1,2)$3. 设平面$2x+y+z=2$，直线$L$ 过点$(1,1,1)$，且与该平面平行，则直线 $L$ 的方程为 ( )A. $x=y=z$B. $2x+y+z=4$C. $x=y=z=1$D. $x+y+z=3$第二部分: 简答题1. 解释什么是极限？极限是一个函数在某一点或者无穷远处的值或趋近于的值。

对于一个给定的函数，当自变量趋近某一特定值时，函数的值也会趋近于某个特定的值。

2. 什么是导数？导数是函数在某一点的切线斜率。

在数学中，导数表示函数在给定点的变化率。

第三部分: 解答题1. 计算函数 $f(x) = \sin(x) - \cos(x)$ 在区间 $[0, \frac{\pi}{4}]$ 上的最大值和最小值。

首先，我们求解导数 $f'(x)$，然后令其等于零，解得$x=\frac{\pi}{4}$。

此时，我们可以计算得到 $f(\frac{\pi}{4}) =\sqrt{2}-1$。

另外，我们可以计算 $f(0) = 1$ 和 $f(\frac{\pi}{4}) = \sqrt{2}-1$。

所以，函数 $f(x)$ 在区间 $[0, \frac{\pi}{4}]$ 上的最大值为 $1$，最小值为 $\sqrt{2}-1$。

2. 计算二重积分 $\iint_D x^2 y \,dA$，其中 $D$ 是由直线 $x=0$，$y=0$ 和 $x+y=1$ 所围成的区域。

高等数学2期末复习题与答案(可编辑修改word版)

x 2 + y 2 - 1 3 1- y 2《高等数学》2 期末复习题一、填空题：1. 函数 z = + ln(3 - x 2 - y 2 ) 的定义域是 1≦X^2+Y^2<3 . 2.设 z = (1 + x ) y, 则∂z =∂y(1+ x ) yln(1+ x ) .3.函数 z = ln(1+ x 2 + y 2 ) 在点(1, 2) 的全微分dz = 1dx + 2 dy(1,2)3 34．设 f (x + y , xy ) = x 2 + y 2 , 则 f (x , y ) =.设 f (x + y , y) = x 2 - y 2 , 则 f (x , y ) = .x5. 设 z = e u sin v 而 u = xy v = x + y 则 ∂z =∂ye xy [x sin(x + y ) + cos(x + y )]6. 函数 z = x 2 + y 2 在点（1，2）处沿从点（1，2）到点（2，2 + ）的方向导数是1+ 222 y 17. 改换积分次序⎰0dy ⎰y 2f (x , y )dx =； ⎰0 dy ⎰y -1f (x , y )dx = .8. 若 L 是抛物线 y 2 = x 上从点 A (1,-1) 到点 B (1,1) 的一段弧，则⎰xydx =L9. 微分方程(1+ e 2x )dy + ye 2x dx = 0 的通解为.二、选择题： 1.lim ( x , y )→(2,0) tan(xy )y 等于（）（上下求导）A ．2，B. 12C.0D.不存在2. 函数 z = 的定义域是（ D ）A． {(x , y ) x ≥ 0, y ≥ 0} C. {(x , y ) y ≥ 0, x 2 ≥ y }B. {(x , y ) x 2 ≥ y } D． {(x , y ) x ≥ 0, y ≥ 0, x 2 ≥ y }3 x - y23.∂f (x , y ) | ∂x( x0 ,y 0 ) = （ B ）A. lim ∆x →0 f (x 0 + ∆x , y 0 + ∆y ) - f (x 0 , y 0 )∆xB. lim∆x →0f (x 0 + ∆x , y 0 ) - f (x 0 , y 0 )∆xC. lim ∆x →0 f (x 0 + ∆x , y 0 + ∆y ) - f (x 0 + ∆x , y 0 )∆xD. lim∆x →0 f (x 0 + ∆x , y 0 ) ∆x5. 设 z = F (x 2 + y 2 ) ，且 F 具有导数，则∂z + ∂z= （D ）∂x ∂yA. 2x + 2 y ；B. (2x + 2 y )F (x 2 + y 2 ) ；C. (2x - 2 y )F '(x 2 + y 2 ) ；D. (2x + 2 y )F '(x 2 + y 2 ) .6. 曲线 x = a cos t ， y = a sin t ， z = amt ，在 t = 处的切向量是（ D ）4A ． (1,1, 2)B. (-1,1, 2)C. (1,1, 2m )D. (-1,1, 2m )7. 对于函数 f (x , y ) = x 2 + xy ，原点(0,0)（ A ）A ．是驻点但不是极值点B.不是驻点C.是极大值点D.是极小值点8．设 I= ⎰⎰5Dx 2 + y 2 -1dxdy ，其中 D 是圆环1 ≤ x 2 + y 2 ≤ 4 所确定的闭区域，则必有（） A ．I 大于零 B.I 小于零C.I 等于零D.I 不等于零，但符号不能确定。

第二学期高数下期末考试试卷及答案

第二学期期末高数（下）考试试卷及答案1一、填空题(每空 3 分，共 15 分) 1.设()=⎰22t xFx e dt ，则()F x '=-22x xe.2.曲面sin cos =⋅z x y 在点,,⎛⎫⎪⎝⎭1442ππ处的切平面方程是--+=210x y z .3.交换累次积分的次序：=(),-⎰⎰2302xxdx f x y dy.4.设闭区域D 是由分段光滑的曲线L 围成,则：使得格林公式： ⎛⎫∂∂-=+ ⎪∂∂⎝⎭⎰⎰⎰ÑD LQ P dxdy Pdx Qdy x y 成立的充分条件是：()(),,和在D上具有一阶连续偏导数P x y Q x y .其中L 是D 的取正向曲线;5.级数∞=-∑1nn 的收敛域是(],-33.二、单项选择题 (每小题3分,共15分)1.当→0x ，→0y 时,函数+2423x yx y 的极限是()DA.等于0;B. 等于13;C. 等于14; D. 不存在.2.函数(),=zf x y 在点(),00x y 处具有偏导数(),'00x f x y ，(),'00y f x y 是函数在该点可微分的()CA.充分必要条件;B.充分但非必要条件;C.必要但非充分条件;D. 既非充分又非必要条件.3.设()cos sin =+x ze y x y ，则==10x y dz()=BA.e ;B. ()+e dx dy ;C. ()-+1edx dy ; D. ()+x e dx dy .4.若级数()∞=-∑11nn n a x 在=-1x 处收敛,则此级数在=2x处()AA.绝对收敛;B.条件收敛;C.发散;D.收敛性不确定.5.微分方程()'''-+=+3691x y y y x e 的特解*y 应设为()DA. 3xae ; B.()+3x ax b e ;C. ()+3x xax b e ; D. ()+23x x ax b e .三.（8分）设一平面通过点(),,-312,而且通过直线-+==43521x y z,求该平面方程. 解：()(),,,,,--312430QA B(),,∴=-142u u u rAB 平行该平面∴该平面的法向量()()(),,,,,,=⨯-=--5211428922rn∴所求的平面方程为：()()()----+=83912220x y z即：---=8922590x y z四.（8分）设(),=yz fxy e ,其中(),f u v 具有二阶连续偏导数,试求∂∂z x 和∂∂∂2zx y. 解：令=u xy ，=y v e五.（8分）计算对弧长的曲线积分⎰L其中L 是圆周+=222xy R 与直线,==00x y在第一象限所围区域的边界.解：=++123L L L L其中： 1L ：(),+=≥≥22200xy R x y2L ：()=≤≤00x y R3L ：()=≤≤00y x R而Re ==⎰⎰1202RR L e Rdt ππ故：()Re =+-⎰212R R Le π六、（8分）计算对面积的曲面积分∑⎛⎫++ ⎪⎝⎭⎰⎰423z x y dS ,其中∑为平面++=1234x y z在第一卦限中的部分. 解：Q xy D ：≤≤⎧⎪⎨≤≤-⎪⎩023032x y x=3-==⎰⎰323200x dx七.（8分）将函数()=++2143f x x x ,展开成x 的幂级数.解：()⎛⎫=-=⋅-⋅ ⎪+++⎝⎭+111111121321613Q f x xx x x , 而 ()∞=⋅=-+∑01111212n nn x x , (),-11 ()∞=-⋅=+∑01116313nn n n x x , (),-33 ()()∞+=⎛⎫∴=-+ ⎪⎝⎭∑10111123nnn n f x x , (),-11八.（8分）求微分方程：()()+-+-+=42322253330xxy y dx x y xy y dy 的通解.解：∂∂==-∂∂263Q P Qxy y y x,∴原方程为：通解为：++-=532231332x y x y y x C九.幂级数：()()!!!!=++++⋅⋅⋅++⋅⋅⋅246212462nx x x x y x n1.试写出()()'+y x y x 的和函数;（4分）2.利用第1问的结果求幂级数()!∞=∑202nn x n 的和函数.（8分）解：1、()()!!!-'=+++⋅⋅⋅++⋅⋅⋅-35213521n x x x y x x n (),-∞∞于是()()!!'+=++++⋅⋅⋅=23123x x x y x y x x e (),-∞∞ 2、令：()()!∞==∑202nn x S x n由1知：()()'+=x S x S x e 且满足：()=01S通解：()()--=+=+⎰12x x x xx Sx e C e e dx Ce e 由()=01S ，得：=12C ；故：()()-=+12xx S x e e十.设函数()f t 在(),+∞0上连续,且满足条件其中Ωt 是由曲线⎧=⎨=⎩2z ty x ,绕z 轴旋转一周而成的曲面与平面=zt (参数>0t )所围成的空间区域。

高等数学二期末复习题及答案

高等数学二期末复习题及答案_28171462418361700(共19页) -本页仅作为预览文档封面，使用时请删除本页-《高等数学（二）》期末复习题一、选择题1、若向量b 与向量)2,1,2(-=a 平行，且满足18-=⋅b a ，则=b （）（A ） )4,2,4(-- （B ）(24,4)--，（C ） (4,2,4)- （D ）(4,4,2)--.2、在空间直角坐标系中，方程组2201x y z z ⎧+-=⎨=⎩代表的图形为 ( )（A ）直线 (B) 抛物线（C ）圆 (D)圆柱面 3、设22()DI x y dxdy =+⎰⎰，其中区域D 由222x y a +=所围成，则I =（）(A) 2240ad a rdr a πθπ=⎰⎰ (B) 22402ad a adr a πθπ=⎰⎰(C) 223023ad r dr a πθπ=⎰⎰(D) 2240012a d r rdr a πθπ=⎰⎰4、设的弧段为：230,1≤≤=y x L ，则=⎰Lds 6 （）（A ）9 (B) 6 （C ）3 (D)23 5、级数∑∞=-11)1(n nn的敛散性为（）（A ）发散 (B) 条件收敛 (C) 绝对收敛 (D) 敛散性不确定6、二重积分定义式∑⎰⎰=→∆=ni i i i Df d y x f 10),(lim ),(σηξσλ中的λ代表的是（）（A ）小区间的长度 (B)小区域的面积 (C)小区域的半径 (D)以上结果都不对7、设),(y x f 为连续函数，则二次积分⎰⎰-1010d ),(d xy y x f x 等于 ( )（A ）⎰⎰-1010d ),(d xx y x f y (B) ⎰⎰-1010d ),(d yx y x f y(C)⎰⎰-x x y x f y 1010d ),(d (D)⎰⎰101d ),(d x y x f y8、方程222z x y =+表示的二次曲面是 ( )（A ）抛物面（B ）柱面（C ）圆锥面（D ）椭球面9、二元函数),(y x f z =在点),(00y x 可微是其在该点偏导数存在的（）. （A ）必要条件（B ）充分条件（C ）充要条件（D ）无关条件10、设平面曲线L 为下半圆周 21,y x =--则曲线积分22()Lx y ds +=⎰( )(A) 0 (B) 2π (C) π (D)4π11、若级数1n n a ∞=∑收敛，则下列结论错误的是（）(A)12n n a ∞=∑收敛 (B) 1(2)n n a ∞=+∑收敛 (C)100nn a∞=∑收敛 (D) 13n n a ∞=∑收敛 12、二重积分的值与（）（A ）函数f 及变量x,y 有关； (B) 区域D 及变量x,y 无关；（C ）函数f 及区域D 有关； (D) 函数f 无关，区域D 有关。

【经典期末卷】大学高数(下)期末测试题及答案

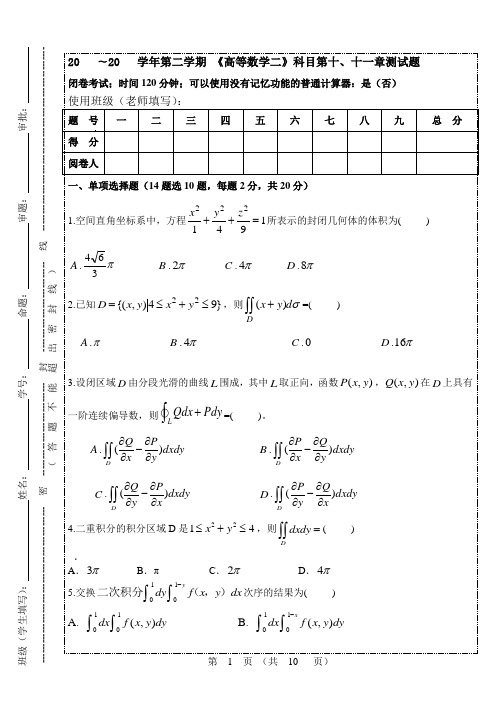
第 1 页（共 10 页）班级（学生填写）：姓名：学号：命题：审题：审批： ----------------------------------------------- 密 ---------------------------- 封 --------------------------- 线 ------------------------------------------------------- （答题不能超出密封线）LQdx Pdy +⎰=( )dxdy )P dxdy x 二重积分的积分区域D 是221≤+x y π C ．2π+⎰L Pdx Qdy在A．∂∂-=∂∂P Qy x第 2 页（共10 页）第 3 页（共 10 页）班级（学生填写）：姓名：学号： ----------------------------------------------- 密 ---------------------------- 封 --------------------------- 线 ------------------------------------------------------- （答题不能超出密封线）()Lx y ds +⎰＝ ()Lx y ds +⎰= Lydx xdy +⎰= 2sin y t =上对应22xy De dxdy --⎰⎰= 2.第 4 页（共 10 页）三. 计算题（一）（每小题6分，共36分）1.计算：22xy De d σ+⎰⎰，其中D 是由圆周224x y +=所围成的闭区域。

2.计算三重积分xdxdydz Ω⎰⎰⎰，其中Ω为三个坐标面及平面21x y z ++=所围成的闭区域。

3.计算xyzdxdydz Ω⎰⎰⎰，其中Ω是由曲面2221x y z ++=，0,0,0x y z ≥≥≥所围成.第 5 页（共 10 页）班级（学生填写）：姓名：学号： ----------------------------------------------- 密 ---------------------------- 封 --------------------------- 线 ------------------------------------------------------- （答题不能超出密封线）4.求2d d Dxx y y⎰⎰，其中D 为1xy =，y x =及2x =所围成的区域。

高数期末考试题及答案大全

高数期末考试题及答案大全试题一：极限的概念与计算问题：计算极限 $\lim_{x \to 0} \frac{\sin x}{x}$。

答案：根据洛必达法则，当分子分母同时趋向于0时，可以对分子分母同时求导，得到：\[\lim_{x \to 0} \frac{\sin x}{x} = \lim_{x \to 0} \frac{\cosx}{1} = \cos(0) = 1.\]试题二：导数的应用问题：设函数 $f(x) = x^3 - 3x^2 + 2x$，求其在 $x=1$ 处的切线方程。

答案：首先求导数 $f'(x) = 3x^2 - 6x + 2$。

在 $x=1$ 处，导数值为 $f'(1) = -1$，函数值为 $f(1) = 0$。

切线方程为 $y - 0 = -1(x - 1)$，即 $y = -x + 1$。

试题三：不定积分的计算问题：计算不定积分 $\int \frac{1}{x^2 + 1} dx$。

答案：这是一个基本的三角换元积分问题，令 $x = \tan(\theta)$，$dx = \sec^2(\theta) d\theta$。

则 $\int \frac{1}{x^2 + 1} dx = \int \frac{1}{\tan^2(\theta) + 1} \sec^2(\theta) d\theta = \int \cos^2(\theta) d\theta$。

利用二倍角公式，$\cos^2(\theta) = \frac{1 +\cos(2\theta)}{2}$。

积分变为 $\int \frac{1}{2} d\theta + \frac{1}{2} \int\cos(2\theta) d\theta = \frac{\theta}{2} +\frac{\sin(2\theta)}{4} + C$。

高数(二)期末考试试卷及答案

2017学年春季学期《高等数学Ⅰ（二）》期末考试试卷(B）注意: 1、本试卷共 3 页；2、考试时间110分钟; 3、姓名、学号必须写在指定地方一、单项选择题（8个小题，每小题2分,共16分）将每题的正确答案的代号A、B、C或D填入下表中．1．a与b是向量，若baba+=+,则必有（）(A)⊥a b(B)0,0==a b或(C)a=b(D)⋅=a b a b2。

()(),0,1sin()limx yxyx→=( ）。

（A）不存在（B）1（C) 0（D) ∞3．二元函数),(yxfz=在),(yx处可微的充要条件是（）（A）),(yxf在),(yx处连续（B）),(yxfx'，),(yxfy'在),(yx的某邻域内存在（C）),(yxfx'，),(yxfy'在),(yx的某邻域内连续（D）当0)()(22→∆+∆yx时，yyxfxyxfzyx∆'-∆'-∆),(),(是4．对函数(,)f x y=(0,0)是(,)f x y的( )。

（A）驻点与极值点（B）驻点，非极值点(C）极值点，非驻点（D）非驻点，非极值点5．设平面区域D：1)1()2(22≤-+-yx，若21()dDI x yσ=+⎰⎰，32()dDI x yσ=+⎰⎰则有（）（A)21II<（B）21II=（C）21II>（D）不能比较6．设椭圆L:13422=+yx的周长为l，则()dLx y s+=⎰（）(A）0 （B）l（C) l3 (D）l47．下列结论正确的是（）（A）若11nnuu+<(1,2,)n=成立,则正项级数1nnu∞=∑收敛（B)当0lim=∞→nnu时，交错级数1(1)nnnu∞=-∑收敛(C)若级数1nnu∞=∑收敛,则对级数的项任意加括号后所成的新级数也收敛（D）若对级数1nnu∞=∑的项适当加括号后所成的新级数收敛，则原级数也收敛8。

设∑∞=1nnnxa的收敛半径为(0)R R>，则∑∞=12nnnxa的收敛半径为（ A ）(A) （B）R(C）2R（D) 不能确定二、填空题(7个小题，每小题2分，共14分）．1．过点(1,2,3)且方向向量为(1,2,3)=n的直线方程为；2。

高等数学第二学期期末考试试题真题及完整答案(第2套)

高等数学第二学期期末考试试题真题及完整答案一、填空题（将正确答案填在横线上)(本大题共5小题，每小题4分，总计20分)1、设函数，则=2、曲面在点处的切平面方程为____3、= .4、曲面积分= ，其中，为与所围的空间几何形体的封闭边界曲面，外侧.5、幂级数的收敛域为。

二、选择题（将选项填在括号内）(本大题共5小题，每小题4分，总计20分）1、函数在(1,1）点沿方向的方向导数为（ )。

（A） 0 （B） 1 （C) 最小 (D）最大2、函数在处( ）.(A）不连续，但偏导数存在 (B)不连续，且偏导数不存在（C)连续，但偏导数不存在 (D)连续，且偏导数存在3、计算=（ )，其中为（按逆时针方向绕行)．（A）0 (B）（C） (D)4、设连续,且,其中D由所围成，则（ )。

（A）（B) （C） (D)5、设级数收敛，其和为，则级数收敛于( )。

（A）(B）(C）（D）三、解答下列各题(本大题共3小题，每小题8分,总计24分)1、设函数由方程所确定，计算，。

2、计算，其中,为曲线,．3、求幂级数的和函数．三、解答下列各题(本大题共3小题，每小题8分，总计24分）1、求内接于半径为的球面的长方体的最大体积．2、计算，其中平面区域．3、计算，其中为平面被柱面所截得的部分.五、解答下列各题(本大题共2小题,每小题6分，总计12分）1、计算其中为上从点到点．2、将函数展开成的幂级数.答案及评分标准一、填空题 (本大题分5小题，每小题4分，共20分)1、 2、3、 4、 5、二、选择题（将选项填在括号内）(本大题共5小题，每小题4分，共20分）1、C2、A3、B4、D5、B三、解答下列各题(本大题共3小题,每小题8分，共24分)1、解：方程两端同时对分别求偏导数，有，………………6分解得：.…………………………………………8分2、解:作图（略）。

原式=………………………2分.………………………8分3、解：经计算，该级数的收敛域为。

2-2大学高数历年期末试题word资料10页

2019-2019年一. 填空题 (共4小题，每小题4分，共计16分) 1．22(1,0)ln(),y z xe x y dz =++=设则2．设xy y x y x f sin ),(+-=,则dx x x f dy y ⎰⎰110 ),(=3．设函数21cos ,0()1,0xx f x xx x πππ+⎧<<⎪=-⎨⎪+-≤≤⎩以2π为周期，()s x 为的()f x 的傅里叶级数的和函数，则(3)s π-= .4．设曲线C 为圆周222Ry x =+,则曲线积分dsx y x C ⎰+）—（322=二.选择题（共4小题，每小题4分，共计16分）1. 设直线L 为32021030,x y z x y z ++=⎧⎨--+=⎩平面π为4220x y z -+-=,则（） .(A) L 平行于平面π (B) L 在平面π上(C) L 垂直于平面π (D) L 与π相交，但不垂直2．设有空间区域2222:x y z R Ω++≤，则Ω等于（）.(A) 432R π (B) 4R π (C) 434R π (D) 42R π3．下列级数中，收敛的级数是（）.(A)∑∞=+-1)1()1(n nnn n (B) ∑∞=+-+11)1(n nn n(C)nn en -∞=∑13(D)∑∞=+1)11ln(n nnn4. 设∑∞=1n na是正项级数，则下列结论中错误的是（）（A ）若∑∞=1n na收敛，则∑∞=12n na也收敛（B ）若∑∞=1n na收敛，则11+∞=∑n n naa 也收敛（C ）若∑∞=1n n a 收敛，则部分和n S 有界（D ）若∑∞=1n n a 收敛，则1lim 1<=+∞→ρnn n a a三．计算题（共8小题，每小题8分，共计64分）1．设函数f 具有二阶连续偏导数，),(2y x y x f u +=，求y x u∂∂∂2.2．求函数y x xy z +-=23在曲线12+=x y 上点（1,2）处，沿着曲线在该点偏向x 轴正向的切线方向的方向导数. 解：3．计算,)(2dxdy y x D⎰⎰+其中}4),({22≤+=y x y x D . 4. 设立体Ω由锥面z =及半球面1z =围成.已知Ω上任一点(),,x y z 处的密度与该点到x y o 平面的距离成正比（比例系数为0K >），试求立体Ω的质量.6. 计算第二类曲面积分⎰⎰∑++dxdy zx xydxdz xyzdydz 2，其中∑为球面2x 的外侧．7．求幂级数nn x n ∑∞=+111的和函数。

高数期末考试题及答案选择

高数期末考试题及答案选择一、选择题（每题2分，共20分）1. 函数 $ f(x) = x^2 $ 在 $ x = 0 $ 处的导数是：A. 0B. 1C. 2D. 4答案： A2. 定积分 $ \int_{0}^{1} x^2 dx $ 的值是：A. $ \frac{1}{3} $B. $ \frac{1}{2} $C. $ \frac{2}{3} $D. $ \frac{3}{4} $答案： A3. 若 $ \lim_{x \to 0} \frac{f(x)}{g(x)} $ 存在，则$ \lim_{x \to 0} f(x) $ 与 $ \lim_{x \to 0} g(x) $ 必须：A. 都存在B. 都不存在C. 至少有一个存在D. 至少有一个不存在答案： D4. 函数 $ y = \sin(x) $ 的周期是：A. $ 2\pi $B. $ \pi $C. $ \frac{\pi}{2} $D. $ \frac{1}{2} $答案： A5. 根据泰勒公式，函数 $ e^x $ 在 $ x = 0 $ 处的泰勒展开式为：A. $ 1 + x $B. $ 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots $C. $ 1 - x + \frac{x^2}{2!} - \frac{x^3}{3!} + \cdots $D. $ 1 + x - \frac{x^2}{2!} + \frac{x^3}{3!} - \cdots $答案： B6. 级数 $ \sum_{n=1}^{\infty} \frac{1}{n^2} $ 收敛于：A. $ \frac{1}{2} $B. $ \frac{\pi^2}{6} $C. $ \frac{e}{2} $D. $ \frac{1}{e} $答案： B7. 若 $ \lim_{x \to \infty} f(x) = L $，则函数 $ f(x) $ 必须：A. 在 $ x $ 足够大时，值接近 $ L $B. 在 $ x $ 足够大时，值等于 $ L $C. 在 $ x $ 足够大时，值小于 $ L $D. 在 $ x $ 足够大时，值大于 $ L $答案： A8. 函数 $ y = x^3 - 3x^2 + 2x $ 的拐点是：A. $ x = 0 $B. $ x = 1 $C. $ x = 2 $D. $ x = 3 $答案： B9. 若 $ f(x) $ 在区间 $ I $ 上连续，则 $ \int_{a}^{b}f(x) dx $ 存在，其中 $ a, b $ 是区间 $ I $ 上的任意两点：A. 正确B. 错误答案： A10. 函数 $ y = \ln(x) $ 的定义域是：A. $ x > 0 $B. $ x < 0 $C. $ x \geq 0 $D. $ x \leq 0 $答案： A二、填空题（每题2分，共20分）11. 函数 $ f(x) = \frac{1}{x} $ 在 $ x = 1 $ 处的导数是_______。

高数(2-2)历年期末试题参考答案

2006—2007学年第二学期高等数学（2-2）期末试卷(A)参考答案一、选择题（本题共6小题，每小题4分，满分24分.每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内）. 1．设三向量→→→c b a ,,满足关系式→→→→⋅=⋅c a b a ，则（ D ）. （A ）必有→→=0a 或者→→=c b ；（B ）必有→→→→===0c b a ；（C ）当→→≠0a 时，必有→→=c b ；（D ）必有)(→→→-⊥c b a . 2. 已知2,2==→→b a ，且2=⋅→→b a ，则=⨯→→b a （ A ）.（A ）2 ；（B ）22；（C ）22；（D ）1 . 3. 设曲面)0,0(:2222>≥=++a z a z y x S ，1S 是S 在第一卦限中的部分，则有（ C ）.（A ）⎰⎰⎰⎰=14S SxdS xdS ；（B ）⎰⎰⎰⎰=14S SxdS ydS ；（C ）⎰⎰⎰⎰=14S SxdS zdS ；（D ）⎰⎰⎰⎰=14S SxyzdS xyzdS .4. 曲面632222=++z y x 在点)1,1,1(--处的切平面方程是：（D ）. （A ）632=+-z y x ；（B ）632=-+z y x ；（C ）632=++z y x ；（D ）632=--z y x .5. 判别级数∑∞=⋅1!3n nn n n 的敛散性，正确结果是：（ B ）.（A ）条件收敛；（B ）发散；（C ）绝对收敛；（D ）可能收敛，也可能发散.6. 平面0633=--y x 的位置是（B ）.（A ）平行于xoy 平面；（B ）平行于z 轴，但不通过z 轴；（C ）垂直于z 轴；（D ）通过z 轴 .二、填空题（本题共4小题，每小题5分，满分20分）. 1. 已知xy e z =，则2x xdy ydx e dz xy -⋅-=.2. 函数zx yz xy u ++=在点)3,2,1(P 处沿向量→OP 的方向导数是71411，函数u 在点P 处的方向导数取最大值的方向是}3,4,5{，该点处方向导数的最大值是25.3. 已知曲线1:22=+y x L ，则π2)(2=+⎰Lds y x .4. 设函数展开傅立叶级数为：)(,cos 02ππ≤≤-=∑∞=x nx ax n n，则12=a .三、解答下列各题（本题共7小题，每小题7分，满分49分）. 1. 求幂级数∑∞=+01n nn x 收敛域及其和函数. 解 nn n a a 1lim+∞→ ,121lim =++=∞→n n n ∴收敛半径为1，当1=x 时，级数∑∞=+011n n 发散，当1-=x 时，级数∑∞=+-01)1(n nn 收敛，故所求的收敛域为)1,1[-；令;)1,1[,1)(0-∈+=∑∞=x n x x S n n于是.1,1)(01<+=∑∞=+x n x x S x n n 逐项求导，得.1,11)1(])([001<-=='+='∑∑∞=∞=+x x x n x x S x n n n n.1),1ln(1])([)(00<--=-='=∴⎰⎰x x t dtdt t tS x xS x x1,)1ln(1)(<--=∴x x xx S 且.0≠x而,2ln )1ln(1lim )(lim )1(11=--==-++-→-→x x x S S x x 1)0(=S ，故⎪⎩⎪⎨⎧=<<<≤---=.01,1001,)1ln()(x x x xx x S 2. 计算二重积分⎰⎰≤++42222y x y xdxdy e.解令⎩⎨⎧==θθsin cos r y r x ，则⎰⎰≤++42222y x y x dxdy e⎰⎰=20202rdr e d r πθ ⎰=22)(2r d e r π202r eπ=).1(4-=e π3. 已知函数),(y x f z =的全微分ydy xdx dz 22-=，并且2)1,1(=f . 求),(y x f z =在椭圆域}14),{(22≤+=y x y x D 上的最大值和最小值.解由,22ydy xdx dz -=得),1(2x xf=∂∂ ),2(2y y f -=∂∂)1(两边关于x 积分，得)(2),(y C xdx y x f +=⎰)(2y C x +=，此式两边关于y 求偏导，再由)2(知,2)(y y C -=',)(2C y y C +-=⇒.),(22C y x y x f +-=∴ 由2)1,1(=f 知，2=C ,故.2),(22+-=y x y x f令,0202⎪⎪⎩⎪⎪⎨⎧=-=∂∂==∂∂y yf x x f得驻点)0,0(在D 内部，且2)0,0(=f ，在D 的边界1422=+y x 上：.11,252)44(222≤≤--=+--=x x x x z 其最大值是,3)0,1(1=±=±=f z x 最小值是2)2,0(0-=±==f z x ；故),(y x f z =在椭圆域}14),{(22≤+=y x y x D 上的最大值是3}2,3,2max{=-，最小值是.2}2,3,2min{-=-.4. 设Ω是由4,22=+=z y x z ，所围成的有界闭区域，计算三重积分⎰⎰⎰Ω++dxdydz z y x)(22.解令,sin cos ⎪⎩⎪⎨⎧===z z r y r x θθ则.4,20,20:2≤≤≤≤≤≤Ωz r r πθ⎰⎰⎰⎰⎰⎰+=++∴Ω422020222)()(rdz z r rdr d dxdydz z y x πθ⎰⎰+=42202)(2rdz z r rdr π⎰==+=204222]2[2dr z z r r z r z π⎰-+=2053)2384(2dr r r r π.32]44[220624ππ=-+=r r r 5. 设AB L 为从点)0,1(-A 沿曲线21x y -=到点)0,1(B 一段曲线，计算⎰++ABL y x ydy xdx 22. 解 ⎩⎨⎧-=-=≤≤-==,2,1.11,,:2xdx dy x y x dx dx x x L AB.0)1()2)(1(11222222=-+--+=++∴⎰⎰-dx x x x x x y x ydy xdx ABL6. 设∑是上半球面221y x z --=的下侧，计算曲面积分⎰⎰∑++-+dxdy z y xy dzdx z y x dydz xz)2()(2322.解 ,2,,2322z y xy R z y x Q xz P +=-== ,222z y x zRy Q x P ++=∂∂+∂∂+∂∂ 作.1,0:22≤+=∑y x z 上补与下∑所围成的立体为Ω，由高斯公式，⎰⎰∑++-+dxdy z y xy dzdx z y x dydz xz )2()(2322 ⎰⎰∑+∑++-+=上补下dxdy z y xy dzdx z y x dydz xz )2()(2322⎰⎰∑++-+-上补dxdy z y xy dzdx z y x dydz xz )2()(2322⎰⎰⎰⎰⎰≤+Ω⋅+---∂∂+∂∂+∂∂-=1222)02(00y x dxdy y xy dxdydz z R y Q x P ）（000222---++-=⎰⎰⎰Ωdxdydz z y x ）（（作球面坐标变换）⎰⎰⎰⋅-=1222020sin ρϕρρϕθππd d d .52sin 21420πρρϕϕππ-=-=⎰⎰d d 7. 将函数61)(2--=x x x f 展开成关于1-x 的幂级数 .解.1,110<=-∑∞=x x x n n.1,)1(110<-=+∑∞=x x x n n n )2131(51)3)(2(161)(2+--=-+=--=∴x x x x x x x f ]3)1(12)1(1[51+----=x x]311131211121[51-+⋅---⋅-=x x ]311131211121[51-+⋅+--⋅-=x x∑∞=+--=012)1(51n n n x ∑∞=+---013)1()1(51n n nn x ( 121<-x 且131<-x ) 21,)1](3)1(21[51011<---+-=∑∞=++x x n n n nn 即).3,1(-∈x四、证明题（7分）. 证明不等式:2)sin (cos 122≤+≤⎰⎰Dd x yσ，其中D 是正方形区域：.10,10≤≤≤≤y x证D 关于y x =对称，⎰⎰∴Dd yσ2(cos ⎰⎰=D d x σ2cos ，⎰⎰+∴Dd x y σ)sin (cos 22.)sin (cos 22⎰⎰+=Dd x x σ又 ),4sin(2)cos 21sin 21(2cos sin 22222π+=+=+x x x x x而,102≤≤x ,2)4sin(22212≤+≤=∴πx 即 ,2cos sin 122≤+≤x x,22)cos (sin 1122=≤+≤⋅=∴⎰⎰⎰⎰⎰⎰DDDd d x x d σσσ即 .2)sin (cos 122≤+≤⎰⎰Dd x y σ2007—2008学年第二学期高等数学（2-2）期末试卷(A)参考答案一、填空题：1~6小题，每小题4分，共24分. 请将答案写在指定位置上. 1. 平面1:0y z -=∏与平面2:0x y +=∏的夹角为3π.2. 函数22y x z +=在点)2,1(处沿从点)2,1(到点)32,2(+的方向的方向导数为321+.3. 设(,)f x y 是有界闭区域222:a y x D ≤+上的连续函数，则当0→a 时，=⎰⎰→Da dxdy y x f a ),(1lim20π)0,0(f .4. 区域Ω由圆锥面222x y z +=及平面1=z 围成，则将三重积分f dv ⎰⎰⎰Ω在柱面坐标系下化为三次积分为211()πθ⎰⎰⎰rd dr f r rdz .5. 设Γ为由曲线32,,t z t y t x ===上相应于t 从0到1的有向曲线弧，R Q P ,,是定义在Γ上的连续三元函数，则对坐标的曲线积分化为对弧长的曲线积分有：Pdx Qdy Rdz Γ++=⎰6. 将函数()1(0)f x x x π=+≤≤展开成余弦级数为)0()5cos 513cos 31(cos 412122πππ≤≤+++-+=+x x x x x .二、单项选择题：7~12小题，每小题3分，共18分。

2-2大学高数历年期末试题

2010-2011年一. 填空题(共4小题，每小题4分，共计16分)1．22(1,0)ln(),yz xe x y dz=++=设则2．设xyyxyxf sin),(+-=,则dxxxfdyy⎰⎰11),(=3．设函数21cos,0()1,0xxf x xx xπππ+⎧<<⎪=-⎨⎪+-≤≤⎩以2π为周期，()s x为的()f x的傅里叶级数的和函数，则(3)sπ-= .4．设曲线C为圆周222Ryx=+,则曲线积分dsxyxC⎰+）—（322=二.选择题（共4小题，每小题4分，共计16分）1.设直线L为32021030,x y zx y z++=⎧⎨--+=⎩平面π为4220x y z-+-=,则（） .(A) L平行于平面π (B) L在平面π上(C) L垂直于平面π (D) L与π相交，但不垂直2．设有空间区域2222:x y z RΩ++≤，则Ω等于（）.(A)432Rπ(B) 4Rπ (C)434Rπ(D) 42Rπ3．下列级数中，收敛的级数是（）.(A) ∑∞=+-1)1()1(nnnnn(B)∑∞=+-+11)1(nnnn(C)nnen-∞=∑13(D)∑∞=+1)11ln(nn nn4. 设∑∞=1nna是正项级数，则下列结论中错误的是（）（A）若∑∞=1nna收敛，则∑∞=12nna也收敛（B）若∑∞=1nna收敛，则11+∞=∑nnnaa也收敛（C）若∑∞=1nna收敛，则部分和nS有界（D）若∑∞=1nna收敛，则1lim1<=+∞→ρnnn aa三．计算题（共8小题，每小题8分，共计64分）1．设函数f 具有二阶连续偏导数，),(2y x y x f u +=，求y x u∂∂∂2.2．求函数y x xy z +-=23在曲线12+=x y 上点（1,2）处，沿着曲线在该点偏向x 轴正向的切线方向的方向导数. 解：3．计算,)(2dxdy y x D⎰⎰+其中}4),({22≤+=y x y x D .4. 设立体Ω由锥面z =及半球面1z =围成.已知Ω上任一点(),,x y z 处的密度与该点到x y o 平面的距离成正比（比例系数为0K >），试求立体Ω的质量.6. 计算第二类曲面积分⎰⎰∑++dxdy zx xydxdz xyzdydz 2，其中∑为球面1222=++z y x 的外侧．7．求幂级数nn x n ∑∞=+111的和函数。

大一第二学期高数期末考试题(含答案)

大一第二学期高数期末考试一、单项选择题 (本大题有4小题, 每小题4分, 共16分)1. )(0),sin (cos )(　处有则在设=+=x x x x x f .（A ）(0)2f '= （B ）(0)1f '=（C ）(0)0f '= （D ）()f x 不可导.2. ）时（　，则当，设133)(11)(3→-=+-=x x x x xx βα.（A ）()()x x αβ与是同阶无穷小，但不是等价无穷小；（B ）()()x x αβ与是等价无穷小；（C ）()x α是比()x β高阶的无穷小；（D ）()x β是比()x α高阶的无穷小.3.若()()()02xF x t x f t dt=-⎰，其中()f x 在区间上(1,1)-二阶可导且'>()0f x ，则（）.（A ）函数()F x 必在0x =处取得极大值；（B ）函数()F x 必在0x =处取得极小值；（C ）函数()F x 在0x =处没有极值，但点(0,(0))F 为曲线()y F x =的拐点；（D ）函数()F x 在0x =处没有极值，点(0,(0))F 也不是曲线()y F x =的拐点。

4.)()( , )(2)( )(1=+=⎰x f dt t f x x f x f 则是连续函数，且设（A ）22x （B ）222x +（C ）1x - （D ）2x +.二、填空题（本大题有4小题，每小题4分，共16分）5. =+→xx x sin 2)31(lim .6. ,)(cos 的一个原函数是已知x f xx=⋅⎰x xxx f d cos )(则.7.lim(cos cos cos )→∞-+++=22221L n n nnn n ππππ .8.=-+⎰21212211arcsin －dx xx x .三、解答题（本大题有5小题，每小题8分，共40分）9. 设函数=()y y x 由方程sin()1x ye xy ++=确定，求'()y x 以及'(0)y . 10. .d )1(177x x x x ⎰+-求11. ．　求，，设⎰--⎪⎩⎪⎨⎧≤<-≤=1 32)(1020)(dx x f x x x x xe x f x12.设函数)(x f 连续，=⎰1()()g x f xt dt，且→=0()lim x f x A x ，A 为常数. 求'()g x并讨论'()g x 在=0x 处的连续性.13. 求微分方程2ln xy y x x '+=满足=-1(1)9y 的解.四、解答题（本大题10分）14. 已知上半平面内一曲线)0()(≥=x x y y ，过点(,)01，且曲线上任一点M x y (,)00处切线斜率数值上等于此曲线与x 轴、y 轴、直线x x =0所围成面积的2倍与该点纵坐标之和，求此曲线方程. 五、解答题（本大题10分）15. 过坐标原点作曲线x y ln =的切线，该切线与曲线x y ln =及x 轴围成平面图形D.(1) 求D 的面积A ；(2) 求D 绕直线x = e 旋转一周所得旋转体的体积V . 六、证明题（本大题有2小题，每小题4分，共8分）16. 设函数)(x f 在[]0,1上连续且单调递减，证明对任意的[,]∈01q ，1()()≥⎰⎰q f x d x q f x dx.17. 设函数)(x f 在[]π,0上连续，且0)(0=⎰πx d x f ，cos )(0=⎰πdx x x f .证明：在()π,0内至少存在两个不同的点21,ξξ，使.0)()(21==ξξf f （提示：设⎰=xdxx f x F 0)()(）解答一、单项选择题(本大题有4小题, 每小题4分, 共16分) 1、D 2、A 3、C 4、C二、填空题（本大题有4小题，每小题4分，共16分）5.6e . 6.cx x +2)cos (21　.7. 2π. 8.3π.三、解答题（本大题有5小题，每小题8分，共40分） 9. 解：方程两边求导(1)cos()()0x y e y xy xy y +''+++= cos()()cos()x y x ye y xy y x e x xy +++'=-+0,0x y ==，(0)1y '=- 10. 解：767u x x dx du == 1(1)112()7(1)71u du duu u u u -==-++⎰⎰原式 1(ln ||2ln |1|)7u u c =-++ 7712ln ||ln |1|77x x C =-++11.解：10330()x f x dx xe dx ---=+⎰⎰⎰3()x xd e --=-+⎰⎰00232cos (1sin )x x xe e d x πθθθ----⎡⎤=--+-=⎣⎦⎰　令3214e π=--12. 解：由(0)0f =，知(0)0g =。

高数(二)期末考试试卷及答案

2017学年春季学期《高等数学Ⅰ（二）》期末考试试卷（B）注意：1、本试卷共 3 页；2、考试时间110分钟； 3、姓名、学号必须写在指定地方一、单项选择题（8个小题，每小题2分，共16分）将每题的正确答案的代号A、B、C或D填入下表中．1．a与b是向量，若baba+=+，则必有（）(A)⊥a b(B)0,0==a b或(C)a=b(D)⋅=a b a b2.()(),0,1sin()limx yxyx→=( ).（A）不存在（B）1（C）0（D）∞3．二元函数),(yxfz=在),(yx处可微的充要条件是（）（A）),(yxf在),(yx处连续（B）),(yxfx'，),(yxfy'在),(yx的某邻域内存在（C）),(yxfx'，),(yxfy'在),(yx的某邻域内连续（D）当0)()(22→∆+∆yx时，yyxfxyxfzyx∆'-∆'-∆),(),(是4．对函数(,)f x y=(0,0)是(,)f x y的( ).（A）驻点与极值点（B）驻点，非极值点（C）极值点，非驻点（D）非驻点，非极值点5．设平面区域D：1)1()2(22≤-+-yx，若21()dDI x yσ=+⎰⎰，32()dDI x yσ=+⎰⎰则有（）（A）21II<（B）21II=（C）21II>（D）不能比较6．设椭圆L：13422=+yx的周长为l，则()dLx y s+=⎰（）(A)0 (B) l (C) l3 (D) l47．下列结论正确的是( )(A)若11nnuu+<(1,2,)n=成立，则正项级数1nnu∞=∑收敛(B)当0lim=∞→nnu时，交错级数1(1)nnnu∞=-∑收敛(C)若级数1nnu∞=∑收敛，则对级数的项任意加括号后所成的新级数也收敛(D) 若对级数1nnu∞=∑的项适当加括号后所成的新级数收敛，则原级数也收敛8.设∑∞=1nnnxa的收敛半径为(0)R R>，则∑∞=12nnnxa的收敛半径为( A )(A) (B) R(C) 2R(D) 不能确定二、填空题(7个小题，每小题2分，共14分)．1．过点(1,2,3)且方向向量为(1,2,3)=n的直线方程为；2.设z是方程e zx y z+-=所确定的,x y的隐函数，则(1,0,0)zx∂=∂；3.设22(,)f x y x y=-，则(1,1)f=grad；4. 交换积分1d(,)dyy f x y x⎰的积分次序，变为；5．设L是直线21y x=+上从点（0，1）到点（1，3）的线段，将(,)(,)LP x y dx Q x y dy+⎰转换成对弧长的曲线积分为；6.幂级数11(1)nnnxn∞-=-∑的收敛域是；7.设有周期为π2的函数，它在(,]ππ-上的表达式为()⎩⎨⎧≤<+≤<--=ππxxxxf,1,1，其傅里叶级数在点π=x处收敛于.三峡大学试卷纸教学班号序号学号姓名……………………．……答题不要超过密封线…………．………………………………三、综合解答题一（5个小题，每小题7分，共35分.解答题应写出文字说明、证明过程或演算步骤）1．设(,)z z x y =由方程(23,2)0F x z y z --=所确定，其中F 是可微函数，求d z ．解： 2.求曲面32=++xy z e z在点)0,1,2(处的切平面方程与法线方程. 解：3.计算二重积分22()d Dxxy y σ++⎰⎰，其中D 由1,0,0=+==y x y x 所围成．解：4．计算(1)d I x v Ω=+⎰⎰⎰，其中Ω是以原点(0,0,0)为形心，边长为a 正立方体．解：5．求幂级数01nn x n ∞=+∑的收敛域与和函数．解：三峡大学试卷纸教学班号序号学号姓名……………………．……答题不要超过密封线…………．………………………………四、综合解答题二（5个小题，每小题7分，共35分.解答题应写出文字说明、证明过程或演算步骤）1．在椭圆4422=+y x 上求一点，使其到直线0632=-+y x 的距离最短．解： 2.计算d d Ly x x y -+⎰，其中L 是沿圆周1)1()1(22=-+-y x 正向一周．解：3．计算d Lxy s ⎰，其中L 为从（0，0）到（2，0）的上半圆弧：)0(222≥=+y x y x ．解：4．计算积分d I z S =∑⎰⎰，其中∑是上半球面222y x a z --=，(0)a >.解：5．利用高斯公式计算对坐标的曲面积分(cos cos cos )d x y z S ∑αβγ++⎰⎰，其中∑为锥面222x y z +=介于平面0z =及1z =之间的部分的下侧， (cos ,cos ,cos αβγ)是∑上点(,,)x y z 处的法向量的方向余弦．解：三峡大学试卷纸教学班号序号学号姓名……………………．……答题不要超过密封线…………．………………………………2017学年春季学期《高等数学Ⅰ（二）》期末考试试卷(B)答案及评分标准一、单项选择题（8个小题，每小题2分，共16分）1．a 与b 是向量，若b a b a +=+，则必有（D ）(A)⊥a b ； (B)0,0==a b 或； (C)a =b ； (D)⋅=a b a b ．2.()(),0,1sin()limx y xy x →=( B ).（A ）不存在；（B ） 1；（C ） 0；（D ） ∞ .3．二元函数),(y x f z =在),(00y x 处可微的充要条件是（ C ）（A ）),(y x f 在),(00y x 处连续；（B ）),(y x f x '，),(y x f y '在),(00y x 的某邻域内存在；（C ）),(y x f x '，),(y x f y '在),(00y x 的某邻域内连续； (D)当0)()(22→∆+∆y x 时，y y x f x y x f z y x ∆'-∆'-∆),(),(0000是比4．对函数(,)f x y =(0,0)是(,)f x y 的( C ). （A ）驻点与极值点；（B ）驻点，非极值点；（C ）极值点，非驻点；（D ）非驻点，非极值点. 5．设平面区域D ：1)1()2(22≤-+-y x ，若21()d DI x y σ=+⎰⎰，32()d DI x y σ=+⎰⎰则有（ A ）（A ）21I I <；（B ） 21I I =；（C ）21I I >；（D ）不能比较．6．设椭圆L ：13422=+y x 的周长为l ，则()d L x y s +=⎰（A ） (A)0； (B) l ； (C) l 3； (D) l 4．7．下列结论正确的是 ( C )(A) 若11n n u u +<(1,2,)n =成立，则正项级数1n n u ∞=∑收敛； (B) 当0lim =∞→n n u 时，交错级数1(1)nnn u∞=-∑收敛；(C) 若级数1nn u∞=∑收敛，则对级数的项任意加括号后所成的新级数也收敛； (D) 若对级数1nn u∞=∑的项适当加括号后所成的新级数收敛，则原级数也收敛．8.设∑∞=1n nnx a的收敛半径为(0)R R >，则∑∞=12n n n x a 的收敛半径为 ( A )(A)(B) R ； (C) 2R ； (D) 不能确定．二、填空题(7个小题，每小题2分，共14分)．1．过点(1,2,3)且方向向量为(1,2,3)=n 的直线方程为123123x y z ---==．2.设z 是方程e zx y z +-=所确定的,x y 的隐函数，则(1,0,0)z x ∂=∂_______12_____ 3.设22(,)f x y x y =-，则(1,1)f =grad （2，-2）． 4.交换积分10d (,)d yy f x y x ⎰的积分次序为______21d (,)d xxx f x y y ⎰⎰___．5．设L 是直线21y x =+上从点（0，1）到点（1，3）的线段，将(,)(,)LP x y dx Q x y dy+⎰转换成对弧长的曲线积分为2)P Q ds +⎰． 6.幂级数11(1)nn n x n∞-=-∑的收敛域是 (1,1]- . 7.设有周期为π2的函数，它在(,]ππ-上的表达式为()⎩⎨⎧≤<+≤<--=ππx x x x f 0,10,1，其傅里叶级数在点π=x 处收敛于2π. 三、综合解答题一（5个小题，每小题7分，共35分.解答题应写出文字说明、证明过程或演算步骤）1．设(,)z z x y =由方程(23,2)0F x z y z --=所确定，其中F 是可微函数，求d z ．解：d d d x y z z x z y =+………………2分12121222d d 33F F x y F F F F =-+-----………………5分12122d 2d 3F x F y F F +=+．………………7分或解：由12(2d 3d )(2d d )0F x z F y z ⋅-+⋅-=，得12122d 2d d 3F x F yz F F +=+．2.求曲面32=++xy z e z在点)0,1,2(处的切平面方程与法线方程. 解：令32),,(-++=xy z e z y x F z，………………2分则2,,+===z z y x e F x F y F ，故(2,1,0)(1,2,3)n………………4分所求切平面的方程为 03)1(2)2(=+-+-z y x ，即432=++z y x ， ………………6分法线方程为32112zy x =-=-.………………7分 3.计算二重积分22()d Dx xy y σ++⎰⎰，其中D 由1,0,0=+==y x y x 所围成．解：22()d Dxxy y σ++⎰⎰=1-1220d ()d x x x xy y y +++⎰⎰………………4分1320515()d 62324x x x x =-+-+=⎰．………………7分4．计算(1)d I x v Ω=+⎰⎰⎰，其中Ω是以原点(0,0,0)为形心，边长为a 正立方体．解：Ω的形心为(0,0,0)，Ω的体积V 为3a ，………………4分故3I xV V V a =+==.………………7分5．求幂级数01nn x n ∞=+∑的收敛域与和函数．解：因为11limlim 12n n n n a n a n ρ+→∞→∞+===+，所以1R = ． ………………1分在左端点1x =-，幂级数成为0(1)1nn n ∞=-+∑，它是收敛的；在右端点1x =，幂级数成为011n n ∞=+∑，它是发散的，故该幂级数收敛域为[1,1)-． ………………3分令0()1nn xs x n ∞==+∑，[1,1)x ∈-，于是1()1n n x xs x n +∞==+∑，[1,1)x ∈-，逐项求导，得(())xs x '=101n n x n +∞='⎛⎫ ⎪+⎝⎭∑=101n n x n +∞='⎛⎫ ⎪+⎝⎭∑=0n n x ∞=∑=11x -，(1,1)x ∈- 将上式两端从0到x 积分，得01()d ln(1),111xxs x x x x x==---≤<-⎰，（根据和函数的连续性，当1x =-时，此式也成立）．于是，当0x ≠时，1()ln(1)s x x x=--，又(0)1s =．故 1ln(1), [-1,0)(0,1),()1, 0.x x s x xx ⎧--∈⎪=⎨⎪=⎩ ………………7分四、综合解答题二（5个小题，每小题7分，共35分.解答题应写出文字说明、证明过程或演算步骤）1．在椭圆4422=+y x 上求一点，使其到直线0632=-+y x 的距离最短．解：设),(y x 为椭圆4422=+y x 上任一点，则该点到直线0632=-+y x 的距离为13326yx d --=；令)44()326(222-++--=y x y x L λ，………………2分于是由224(623)20,6(623)80,440,x y L x y x L x y y L x y λλλ⎧=---+=⎪=---+=⎨⎪=+-=⎩ 得驻点 183(,)35M ，283(,)55M -，383(,)55M --，483(,)55M -，………………5分依题意，椭圆到直线一定有最短距离存在，其中1313133261min =--=M yx d 即为所求．………………7分 2.计算d d Ly x x y -+⎰，其中L 是沿圆周1)1()1(22=-+-y x 正向一周．解：圆周1)1()1(22=-+-y x 所围区域D 的面积为 π⋅21，………………3分由格林公式得d d (11)d d LDy x x y x y -+=+⎰⎰⎰=π2．………………7分3．计算d Lxy s ⎰，其中L 为从（0，0）到（2，0）的上半圆弧：)0(222≥=+y x y x ．解： :L 1cos {,[0,]sin x t t y tπ=+∈=，………………3分d (1cos )sin d 2Lxy s t t t π=+=⎰⎰．………………7分4．计算积分d I z S =∑⎰⎰，其中∑是上半球面222y x a z --=，(0)a >.解：d d S x y =d x y ………………3分d DI x y =………………5分3d d d DDx y a x y a π===⎰⎰．………………7分5．利用高斯公式计算对坐标的曲面积分(cos cos cos )d x y z S ∑αβγ++⎰⎰，其中∑为锥面222x y z +=介于平面0z =及1z =之间的部分的下侧，（cos ,cos ,cos αβγ）是∑上点(,,)x y z 处的法向量的方向余弦．解：设∑1为221(1)z x y =+≤的上侧，………………2分则∑与∑1一起构成一个闭曲面，记它们围成的空间闭区域为1=∑∑Ω+，由高斯公式得 1(cos cos cos )d x y z S ∑∑αβγ+++⎰⎰3d d d x y z Ω=⎰⎰⎰=π………………4分而 22111(cos cos cos )d d d d d x y x y z S z x y x y ∑αβγπ∑+≤++===⎰⎰⎰⎰⎰⎰，………………6分因此 (cos cos cos )d x y z S ∑αβγ++⎰⎰=0 ………………7分。

大学高等数学期末考试试题与答案

大学高等数学期末考试试题与答案下列哪个公式不是牛顿-莱布尼茨公式的应用？B) (4x3 + 5x2 + 6x + 7)′D) (e2x + 3y)′答案：D) (e2x + 3y)′填空题(每题3分，共18分)略解答题(每题10分，共60分)略综合题(每题15分，共30分)略当谈论数学时，大家可能会想到那些复杂的公式和令人头疼的问题。

然而，数学在我们的日常生活中无处不在，它不仅是一门学科，更是一种思维方式。

在吉林大学，高等数学课程一直受到高度重视。

本文将通过学生们的期末试题来展示数学的魅力和应用。

试题是数学学习的重要组成部分。

通过做题，学生不仅可以巩固所学知识，还可以培养解决问题的能力和举一反三的思维方式。

以下是一道吉林大学高等数学的期末试题：求函数 y=x^3-3x^2+2在区间 [0,4]上的最大值和最小值。

这道题目的答案是：最大值为28，最小值为-16。

要解决这个问题，我们需要对函数进行求导，并确定函数的极值点。

然后，我们可以在给定的区间内找到函数的最大值和最小值。

除了在高等数学中学习数学基础知识，我们还可以将这些知识应用到实际生活中。

例如，在经济学的课程中，学生们可以使用数学模型来分析股票市场的波动；在工程学中，可以使用数学方法来设计桥梁和建筑的结构等。

数学是人类文化的重要组成部分，它为我们的日常生活提供了很多帮助。

通过学习高等数学，我们可以更好地理解数学的应用价值，提高我们的思维能力和解决问题的能力。

在未来的学习和工作中，这些能力将是我们不可或缺的竞争优势。

吉林大学高等数学期末试题不仅考察了学生的数学知识，还体现了数学在生活中的应用价值。

通过学习数学，我们可以培养举一反三的思维方式，提高解决问题的能力和竞争力。

让我们一起感受数学的魅力吧！下列哪个选项是高等数学中“极限”的概念？ ( )下列哪个选项是高等数学中“导数”的概念？( )下列哪个选项是高等数学中“积分”的概念？( )积分在高等数学中是一个非常广泛的概念，它涉及到面积、体积、平均值等多个方面，但不能简单地说积分就是求面积或体积或平均值。

大学高数期末复习卷试卷与答案1

第二学期高等数学练习题（二）一、选择题1、在点处),(y x f 可微的充分条件是（）（A ）),(y x f 的所有二阶偏导数存在（B ）),(y x f 连续（C ）),(y x f 的所有一阶偏导数连续（D ）),(y x f 连续且),(y x f 对y x ,的偏导数都存在。

2．设22),(y xy x y x f -+=的驻点为)0,0(,则)0,0(f 是),(y x f 的（）(A)极大值; (B) 极小值; (C) 非极值; (D) 不能确定.3．微分方程x xey y y 2'"65=+-的特解形式是（） (A) bx ae x +2 (B) x e b ax 2)(+(C) x e b ax x 2)(+ (D) x e b ax x 22)(+4．曲面1232222=++z y x 上，点)1,2,1(-处的切平面方程是（）A 、24682=-+z y xB 、2068=+-z y xC 、1234=-+z y xD 、1234=+-z y x5．下列级数条件收敛的是（）（A ）)1(1)1(1+-∑∞=n n n n（B ）211)1(n n n ∑∞=- （C ）1)1(1+-∑∞=n n n n （D ）n n n 1sin )1(1∑∞=- 6．设n 是曲面632222=++z y x 在点P(1,1,1)处指向外侧的法向量，则z y x u 2286+=在点P 沿方向n 的方向导数为（）（A ）0 （B ）711 （C ）117 （D ）2 。

7．设),(y x f 在点),(b a 处的偏导数存在，则xb x a f b x a f x ),(),(lim 0--+→= 。

A. 0； B 、),2(b a f x ； C 、),(b a f x ； D 、),(2b a f x 。

二、填空题1、微分方程 x y y x cos =+' 的通解是2．交换积分⎰⎰--x x dy y x f dx 1110),(的次序成为。

第二学期高数（下）期末考试试卷及答案

第⼆学期⾼数（下）期末考试试卷及答案第⼆学期期末⾼数（下）考试试卷及答案⼀、填空题?每空 ? 分，共 ?? 分? ?设()=?22t xFx e dt ，则()F x '=-22x xe曲⾯sin cos =?z x y 在点,,??1442ππ处的切平⾯⽅程是--+=210x y z交换累次积分的次序：()(),,-+12330010xdy f x y dx dy f x y dx=(),-??2302x x dx f x y dy设闭区域是由分段光滑的曲线?围成则：使得格林公式： ??-=+ D LQ P dxdy Pdx Qdy x y 成⽴的充分条件是：()(),,和在D上具有⼀阶连续偏导数P x y Q x y其中?是的取正向曲线级数∞=-∑1nn 的收敛域是(],-33⼆、单项选择题 ?每⼩题分共 ?分?当→0x ，→0y 时函数+2423x yx y 的极限是()D等于 ? ?? 等于13等于14不存在函数(),=zf x y 在点(),00x y 处具有偏导数(),'00x f x y ，(),'00y f x y 是函数在该点可微分的()C充分必要条件 ??充分但⾮必要条件 ?必要但⾮充分条件 ?? 既⾮充分⼜⾮必要条件 ?设()cos sin =+x z e y x y ，则==10x y dz()=Be ()+e dx dy ?? ()-+1e dx dy ?? ()+x e dx dy若级数()∞=-∑11nn n a x 在=-1x 处收敛则此级数在=2x处()A绝对收敛 ??条件收敛发散 ??收敛性不确定 ?微分⽅程()'''-+=+3691x y y y x e 的特解*y 应设为()D3xae ??()+3x ax b e()+3xx ax b e ??()+23xx ax b e三（分）设⼀平⾯通过点(),,-312 ⽽且通过直线-+==43521x y z求该平⾯⽅程解：()(),,,,,--312430A B(),,∴=-142AB 平⾏该平⾯∴该平⾯的法向量()()(),,,,,,=?-=--5211428922n ∴所求的平⾯⽅程为：()()()----+=83912220x y z 即：---=8922590xy z四（分）设(),=yz f xy e其中(),f u v 具有⼆阶连续偏导数试求??zx和2zx y解：令=uxy ，=y v e=u zyf x ()()==++2y u u uu uvz yf f y xf e f x y y五（分）计算对弧长的曲线积分L其中L 是圆周+=222xy R 与直线,==00x y在第⼀象限所围区域的边界解：=++123L L L L其中： 1L ：(),+=≥≥2 2200xy R x y2L ：()=≤≤00x y R 3L ：()=≤≤00y x R∴===123LL L L⽽Re ==1202RR L e Rdt ππ==-??201Ry R L e dy ex R L e dx e故：()Re =+-?212R R Le π六、（分）计算对⾯积的曲⾯积分∑? ++423z x y dS其中∑为平⾯++=1234x y z在第⼀卦限中的部分解：xy D ：≤≤≤≤-??023032x yx=3∑?∴++== ??42433xyDz x y dS dxdy-==??32七（分）将函数()=++2 143f x x x 展开成x 的幂级数解：()??=-=?-? ?+++??+1111111 21321613f x xx x x ⽽ ()∞=?=-+∑01111212n nn x x (),-11 ()∞=-?=+∑01116313nn n n x x (),-33()()∞+=??∴=-+ ∑10 111123nnn n f x x (),-11⼋（分）求微分⽅程：()()+-+-+=4 2322253330xxy y dx x y xy y dy 的通解解：==-263P Q∴原⽅程为：()()??++-+-=??4223225333x dx y dy xy y dx x y xy dy =++-= ?532231332dx d y d x y y x=++-= ?5322313032d x y x y y x通解为：++-=532231332x y x y y x C 九幂级数：()()=++++++246212462nx x x x y x n()(),∈-∞∞x试写出()()'+y x y x 的和函数（分）利⽤第问的结果求幂级数()!∞=∑202nn x n 的和函数（分）解：、()()-'=+++++-35213521n x x x y x x n (),-∞∞ 于是()()!!'+=++++=23123x x x y x y x x e (),-∞∞、令：()()!∞==∑202nn x S x n由知：()()'+=x S x S x e 且满⾜：()=01S 通解：()()--=+=+?12xx xxx Sx eC e e dx Cee 由()=01S ，得：=12C ；故：()()-=+12x x S x e e⼗设函数()f t 在(),+∞0上连续且满⾜条件()Ω=+11tf t fdv π其中Ωt 是由曲线?=?=?2z ty x 绕z 轴旋转⼀周⽽成的曲⾯与平⾯=zt ?参数>0t ?所围成的空间区域。

高数二期末考试题

高数二期末考试题第一篇：高数二期末考试题高数是我们比较难学的一个科目，下面是小编整理的高数二期末考试题，希望对你有帮助。

一、填空。

（28分值）1、1米=（）厘米 45厘米-6厘米=（）厘米37厘米+5厘米=（）厘米23米-8米=（）米2、6个3相加，写成乘法算式是（），这个式子读作（）。

3、在下面的（）里最大能填几？（）×6＜27（）＜3×74×（）＜15 35＞7×（）4、在算式4×7=28中，4是（），7是（），28是（）。

5、先把下面的口诀补充完整，再根据口诀写出两道乘法算式。

八九（）（）二十四6、小芳和小伙伴们计划两天做100颗星，昨天做了58颗，今天他们大约要做（）颗。

7、一把三角板上有（）个角，其中（）个是直角。

8、算得积是18的口诀有（）和（）。

9、在○里填上“+”、“-”、“×”或“＜”、“＞”、“=”。

8○6=48 36○73-37 9×7○652○2=4 43○6×7 18○9=9二、判断。

（5分值）1、9个相加的和是13。

（）2、小强身高大约是137厘米。

（）3、角都有一个顶点，两条边。

（）4、计算48+29，得数大约是70。

（）5、1米和100厘米一样长。

（）三、选择题。

（把正确答案的序号填在括号里，5分值）1、5个3相加是多少？正确的列式是（）Ａ、5+5+5=15 B、5＋3=８ C、5×3=152、用2、6、0三个数字组成的两位数有（）个。

Ａ、２ B、４Ｃ、６3、小明有50元钱，买故事书花了28元，他大约还剩（）元。

A、22B、30C、204、5+5+5+4，不可以改写成算式（）。

A、5×4B、5×3+4C、4×5-15、4个好朋友见面互相拥抱一次，共要拥抱（）次。

A、3次B、4次C、6次四、计算。

（26分值）1、用竖式计算。

（15分值）90-47= 59+26= 63-28=37+46-54= 81-32-27= 42-34+57=2、列式计算。

高数期末试题及答案

高数期末试题及答案1. 选择题（每题2分，共40分）
1.1 选择题题干
答案：选项A
解析：解析内容
1.2 选择题题干
答案：选项B
解析：解析内容
......
2. 填空题（每题4分，共40分）
2.1 填空题题干
答案：填空答案
解析：解析内容
2.2 填空题题干
答案：填空答案
解析：解析内容
......
3. 计算题（每题10分，共80分）3.1 计算题题干
解答：
计算过程
3.2 计算题题干
解答：
计算过程
......
4. 证明题（每题20分，共80分）4.1 证明题题干
解答：
证明过程
4.2 证明题题干
解答：
证明过程
......
5. 应用题（每题15分，共60分）5.1 应用题题干
解答：
解题思路和步骤
5.2 应用题题干
解答：
解题思路和步骤
......
综上所述，这是一份高数期末试题及答案，包括选择题、填空题、计算题、证明题和应用题。

每道题目都提供了准确的答案和解析，以帮助同学们检验和巩固他们的数学知识。

请同学们认真阅读每道题目并按照正确的解题思路和步骤进行答题。

祝大家期末考试顺利！
（文章结束，共计xxx字）。

-2大学高数历年期末试题

数学高数期末试题及答案

高等数学2期末复习题与答案(可编辑修改word版)

第二学期高数下期末考试试卷及答案

高等数学二期末复习题及答案

【经典期末卷】大学高数(下)期末测试题及答案

高数期末考试题及答案大全

高数(二)期末考试试卷及答案

高等数学第二学期期末考试试题真题及完整答案(第2套)

2-2大学高数历年期末试题word资料10页

高数期末考试题及答案选择

高数(2-2)历年期末试题参考答案

2-2大学高数历年期末试题

大一第二学期高数期末考试题(含答案)

高数(二)期末考试试卷及答案

大学高等数学期末考试试题与答案

大学高数期末复习卷 试卷与答案1

第二学期高数（下）期末考试试卷及答案

高数二期末考试题

高数期末试题 及答案

大学高数期末复习卷试卷与答案1

高数期末试题及答案