蒲丰氏投针问题的模拟过程
蒲丰投针――MonteCarlo算法

蒲丰投针 ―― Monte Carlo 算法背景:蒙特卡罗方法(Monte Carlo ),也称统计模拟方法,是在二次世界大战期间随着科学技术的发展和电子计算机的发明,而被提出的一种以概率统计理论为基础的一类非常重要的数值计算方法。
蒙特卡罗方法在应用物理、原子能、固体物理、化学、生态学、社会学以及经济行为等领域中得到广泛利用。
蒙特卡罗方法的名字来源于世界著名的赌城 —— 摩纳哥的蒙特卡罗。
其历史起源可追溯到1777年法国科学家蒲丰提出的一种计算圆周的方法 —— 随机投针法,即著名的蒲丰投针问题。
问题:设在平面上有一组平行线,间距为d ,把一根长L 的针随机投上去,则这根针和平行线相交的概率是多少?(其中 L < d )分析:由于 L < d ,所以这根针至多只能与一条平行线相交。
设针的中点与最近的平行线之间的距离为 y ,针与平行线的夹角为 θ (0 ≤ θ ≤ π)。
相交情形 不相交情形易知针与平行线相交的充要条件是:sin 2Ly x θ≤=由于1[0,], [0, ]2y d θπ∈∈,且它们的取值均满足平均分布。
建立直角坐标系,则针与平行线的相交条件在坐标系下就是曲线所围成的曲边梯形区域(见右图)。
所以有几何概率可知针与平行线相交的概率是sin d 2212LL p d d πθθππ==⎰Monte Carlo 方法:随机产生满足平均分布的 y 和 θ,其中1[0,], [0, ]2y d θπ∈∈,判断 y 是否在曲边梯形内。
重复上述试验,并统计 y 在曲边梯形内的次数 m ,其与试验次数 n 的比值即为针与平行线相交的概率的近似值。
clear;n = 100000; L = 1; d = 2; m = 0;for k = 1 : ntheta = rand(1)*pi; y = rand(1)*d/2;if y < sin(theta)*L/2m = m + 1; end endfprintf('针与平行线相交的概率大约为 %f\n', m/n)计算π的近似值利用该方法可以计算 π 的近似值:sin d 22 22 1n LL m p d m d L d n πθθπππ⇒≈==≈⎰下面是一些通过蒲丰投针实验计算出来的 π 的近似值:蒲丰投针问题的重要性并非是为了求得比其它方法更精确的π值,而是在于它是第一个用几何形式表达概率问题的例子。
蒲丰投针试验讲解课件

该试验不仅在理论上具有重要意义,对 于理解随机性和几何规律的本质有重要 贡献,而且在实际应用中也有广泛的应
用价值。
蒲丰投针试验可以应用于统计学、物理 学、计算机科学等多个领域,为相关领
域的研究提供了重要的启示和工具。
蒲丰投针试验的局限性
01
02
03
04
蒲丰投针试验虽然是一个经典 的试验,但是它也存在一些局
针方向与平行线垂直。
重复投掷蒲丰投针N次,记录每 次投掷的结果。
测量与计算阶段
测量投掷后蒲丰投针 与平行线之间的距离 ,记录下来。
根据公式π=2*n/N ,计算π的近似值, 其中n为相交次数, N为投掷次数。
根据记录的数据,计 算蒲丰投针与平行线 相交的次数。
CHAPTER 03
试验结果分析
蒲丰投针试验的预期结果
蒲丰投针试验是一种估算π值的方法,其预期结果是通过投掷 一根针到一张白纸上,然后统计针与白纸边缘相交的次数, 来估算π的值。
蒲丰投针试验的预期结果是根据概率论和几何学原理推导出 来的,即当投掷次数足够多时,针与白纸边缘相交的频率接 近于π/4。
实际结果与预期结果的比较
在实际进行蒲丰投针试验时,需要记录针与白纸边缘相交的次数,并计 算出相应的π值。
限性。
首先,该试验的结果受到投针 方式、试验环境等因素的影响 ,可能导致结果存在误差。
其次,蒲丰投针试验的应用范 围相对有限,主要适用于一些 特定的几何形状和随机性问题
。
最后,蒲丰投针试验的结论仅 适用于理想化的模型,与实际
情况可能存在差异。
未来研究方向与展望
随着科学技术的发展和研究的深入, 蒲丰投针试验在未来仍有广阔的研究 前景。
蒲丰投针试验讲解课 件
投针实验详解

一、 问题的提出在人类数学文化史中,对圆周率π精确值的追求吸引了许多学者的研究兴趣。
在众多的圆周率计算方法中,最为奇妙的是法国物理学家布丰(Boffon )在1777年提出的“投针实验”。
与传统的“割圆术”等几何计算方法不同的是,“投针实验”是利用概率统计的方法计算圆周率的值,进而为圆周率计算开辟了新的研究途径,也使其成为概率论中很有影响力的一个实验。
本节我们将借助于MATLAB 仿真软件,对“投针实验”进行系统仿真,以此来研究类比的系统建模方法和离散事件系统仿真。
二、 系统建模“投针实验”的具体做法是:在一个水平面上画上一些平行线,使它们相邻两条直线之间的距离都为a ;然后把一枚长为l (0<l <a )的均匀钢针随意抛到这一平面上。
投针的结果将会有两种,一种是针与这组平行线中的一条直线相交,一种是不相交。
设n 为投针总次数,k 为相交次数,如果投针次数足够多,就会发现公式2ln ak计算出来的值就是圆周率π。
当然计算精度与投针次数有关,一般情况下投针次数要到成千上万次,才能有较好的计算精度。
有兴趣的读者可以耐心地做一下这个实验。
为了能够快速的得到实验结果,我们可以通过编写计算机程序来模拟这个实验,即进行系统仿真。
所谓的系统仿真是指以计算机为工具,对具有不确定性因素的、可模型化的系统的一种研究方法。
建立能够反映实验情况的数学模型是系统仿真的基础。
系统建模中需解决两个问题,一个是如何模拟钢针的投掷结果,另一个是如何判断钢针与平行线的位置关系。
这里,设O 为钢针中点,y 为O 点与最近平行线之间的距离,θ为钢针与平行线之间的夹角(0180θ≤< )。
首先,由于人的投掷动作是随机的,钢针落下后的具体位置也是随机的,因此可用按照均匀分布的两个随机变量y 和θ来模拟钢针投掷结果。
其次,人工实验时可以用眼睛直接判断出钢针是否与平行线相交,而计算机仿真实验则需要用数学的方法来判别。
如下图所示,如果y 、l 和θ满足关系式1sin 2y l θ≤,那么钢针就与平行线相交,否则反之,进而可以判断钢针与平行线的位置关系。
蒲丰投针实验原理

蒲丰投针实验原理
蒲丰投针实验是一种检测泥沙粒径分布的实验方法,它是利用悬浮在水中的粒度分布模拟藉由空气流抛掷及落入平板上的控制情形来模拟河流中悬浮颗粒的粒径分布,从而进行检测的。
该实验流程是:将检测的粒料悬浮于水中,利用抛掷及落入平板上的控制条件来模拟河流中悬浮颗粒的粒径分布,然后借助投针实验来观测平面上粒料的分布情况。
最后,根据获得的结果计算出每种粒径的百分率,从而可以得出泥沙粒径分布情况。
蒲丰投针最简单的代码

蒲丰投针最简单的代码
蒲丰投针是一种概率统计实验,可以用来求圆周率。
这里介绍一下最简单的蒲丰投针代码。
首先,需要导入Python中的random模块来生成随机数。
然后,定义需要用到的变量和常数,如针长(L)和两根地板板缝之间的距离(d)。
接下来,生成两个随机数,分别表示针的中心点距离地板板缝的距离(x)和针与竖直方向的夹角(theta)。
利用这两个随机数可以计算出针与地板板缝相交的情况。
再用一个计数器变量count来记录针与地板板缝相交的次数,重复这个实验若干次后,圆周率的近似值就可以通过下面的公式计算出来:
pi = 2 * L / (d * p)
其中,p为相交次数与总次数之比。
代码如下:
import random
L = 1 # 针长
d = 2 # 地板板缝间距
n = 10000000 # 实验次数
count = 0 # 相交次数
for i in range(n):
x = random.uniform(0, d) # 针中心距地板板缝距离
theta = random.uniform(0, 180) # 针与竖直方向的夹角
if x <= L * 0.5 * math.sin(theta / 180 * math.pi): # 判断是否相交
count += 1
p = count / n # 相交次数与总次数之比
pi = 2 * L / (d * p) # 计算圆周率
print(pi)
需要注意的是,模拟次数越多,计算出的圆周率越接近真实值。
但是过多的模拟次数会导致程序运行时间增长,因此需要根据实际情况来选择合适的实验次数。
蒲丰(Buffon)投针试验

一、利用Matlab计算机语言验证蒲丰(Buffon)投针试验问题给定a=10,b=5时,模拟100万次投针实验的Matlab程序如下:a=10;b=5;n=1000000;p=10; % a为平行线间距,b为针的长度,n为投掷次数,p为有效数字位数x=unifrnd(0,a/2,[n,1]);phi=unifrnd(0,pi,[n,1]); % 产生均匀分布的随机数,分别模拟针的中点与最近平行线的距离和针的倾斜角y=x<0.5*b*sin(phi); m=sum(y); % 计数针与平行线相交的次数PI=vpa(2*b*n/(a*m),p)运行结果PI =3.138919145二、利用C++计算机语言编程通过大量重复实验验证以下结论:三个阄,其中一个阄内写着“有”字,两个阄内不写字,三人依次抓取,各人抓到“有”字阄的概率均为1/3。
程序如下:#include<stdio.h>#include<stdlib.h>#include<time.h>void main(){int n=500000;int i,a[3]={0};srand(time(NULL));for(i=0;i<n;i++)a[rand()%3]++;printf("共测试%d次,其中有字事件有%d次, 占%.2f%%\n""抓到无字事件1有%d次,占%.2f%%\n""抓到无字事件2有%d次,占%.2f%%\n""抓到无字事件共%d次,占%.2f%%",n,a[0],a[0]*100.0/n,a[1],a[1]*100.0/n,a[2],a[2]*100.0/n,a[1]+a[2],(a[1]+a[2])*100.0/n);return 0;}。
蒲丰投针实验模拟

蒲丰投针求兀问题一、蒲丰投针问题在平面上画有等距离的一些平行线,平行线间的距离为a(a>0),向平面上随机投…长为l(lva)的针,针与平行线相交的概率p,结果发现Ji =2*l/(a*p)・二、试验方法可以采用MATLAB软件进行模拟实验,即用MATLAB编写程序来进行“蒲丰投针实验”。
1、基本原理由丁•针投到纸上的时候,有各种不同方向和位置,但是,每一次投针时,其位置和方向都可以由两个量唯一确定, 那就是针的小点和偏离水平的角度。
以x表示针的中点到最近的一条平行线的距离,B表示针与平行线的交角。
显然有0<=x<=a/2, 0<=f3<=Pi o用边长为a/2及Pi 的长方形表示样本空间。
为使针与平行线相交, 必须x<=l*sin 3 *0.5,满足这个关系的区域面积是从0到Pi 的严sin B对B的积分,可计算出这个概率值是(21)/(Pi*a)o只要随机牛成n对这样的x和P,就可以模拟n次的投针实验, 然后统计满足x<=l*sin B *0.5的x的个数,就可以认为这是相交的次数。
然后利用公式求得兀值。
2、MATLAB 编程clear ('n')clearCa')clear('x')clear(T)clear ('y‘)clear ('m')dis"本程序用来进行投针实验的演示」代衣两线间的宽度, 针的长度l=a/2, n代表实验次数a=input(f iH 输入a: *);n=input(*W输入n: *);x=unifrnd(0,a/2,[n, 1 ]);f=unifmd(O,p i,[n,l]);y=x<0.25*a*sin(f);m=sum(y);PI=vpa(a* n/(a* m))三、实验数据(部分程序截屏见后)四、实验结论从上述数据分析可知,随着模拟次数的越来越多,PI的值逐渐稳定在H值附近,即越来越趋近于匚,故蒲丰投针实验确实可以模拟出兀的值。
蒲丰投针概率推导过程

蒲丰投针概率推导过程蒲丰投针是一个经典的概率问题,它的推导过程非常有趣。
本文将从一个人的视角进行叙述,以增加读者的情感共鸣。
我要向大家介绍一下蒲丰投针的背景和问题。
蒲丰投针是由法国数学家蒲丰在18世纪提出的,他提出了一个问题:如果有一根长度为L的针,将其随机地投在一块有平行线的地板上,那么这根针与平行线相交的概率是多少?现在,让我们来推导一下这个概率。
首先,我们需要假设一些条件。
假设针的长度L小于等于平行线的间距D,且针的中点与平行线之间的距离为x(0<=x<=D/2)。
这样,我们可以将针的位置分为两种情况:一种是针与平行线相交,另一种是针与平行线不相交。
让我们来计算针与平行线不相交的情况。
在这种情况下,针的中点到最近的平行线的距离大于针的半径。
针的半径可以用L/2来表示,所以针的中点到最近的平行线的距离大于L/2。
我们可以将这个问题转化为一个几何问题,即计算一个长度为L/2的线段与两条平行线之间不相交的概率。
假设针的中点到最近的平行线的距离为y(L/2<=y<=D/2),那么不相交的情况可以表示为y >= L/2。
由于y的取值范围是L/2到D/2,所以不相交的概率可以表示为 (D/2 - L/2)/(D/2)。
接下来,让我们来计算针与平行线相交的情况。
在这种情况下,针的中点到最近的平行线的距离小于等于针的半径。
也就是说,针的中点到最近的平行线的距离小于等于L/2。
我们可以将这个问题转化为一个几何问题,即计算一个长度为L/2的线段与两条平行线之间相交的概率。
假设针的中点到最近的平行线的距离为y(0<=y<=L/2),那么相交的情况可以表示为y <= L/2。
由于y的取值范围是0到L/2,所以相交的概率可以表示为 (L/2)/L/2。
现在,我们可以将不相交的概率和相交的概率相加,得到针与平行线相交的概率。
即 P = (D/2 - L/2)/(D/2) + (L/2)/L/2。
蒲丰投针原理
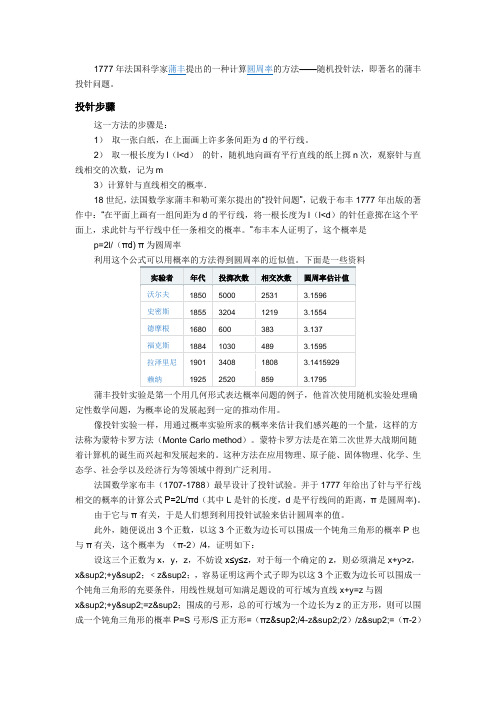
/4.因为对于每一个z,这个概率都为(π-2)/4,因此对于任意的正数x,y,z,有P=(π-2)/4,命题得证。
为了估算π的值,我们需要通过实验来估计它的概率,这一过程可交由计算机编程来实现,事实上x+y>z,x²+y²;﹤z²;等价于(x+y-z)(x²+y²-z²;)﹤0,因此只需检验这一个式子是否成立即可。
若进行了m 次随机试验,有n次满足该式,当m足够大时,n/m趋近于(π-2)/4,令n/m=(π-2)/4,解得π=4n/m+2,即可估计出π值。
值得注意的是这里采用的方法:设计一个适当的试验,它的概率与我们感兴趣的一个量(如π)有关,然后利用试验结果来估计这个量,随着计算机等现代技术的发展,这一方法已经发展为具有广泛应用性的蒙特卡罗方法。
计算π最稀奇方法之一计算π的最为稀奇的方法之一,要数18世纪法国的博物学家C·布丰和他的投针实验:在一个平面上,用尺画一组相距为d的平行线;一根长度小于d的针,扔到画了线的平面上;如果针与线相交,则该次扔出被认为是有利的,否则则是不利的.布丰惊奇地发现:有利的扔出与不利的扔出两者次数的比,是一个包含π的表示式.如果针的长度等于d,那么有利扔出的概率为2/π.扔的次数越多,由此能求出越为精确的π的值.公元1901年,意大利数学家拉兹瑞尼作了3408次投针,给出π的值为3.1415929——准确到小数后6位.不过,不管拉兹瑞尼是否实际上投过针,他的实验还是受到了美国犹他州奥格登的国立韦伯大学的L·巴杰的质疑.通过几何、微积分、概率等广泛的范围和渠道发现π,这是着实令人惊讶的!证明下面就是一个简单而巧妙的证明。
找一根铁丝弯成一个圆圈,使其直径恰恰等于平行线间的距离d。
可以想象得到,对于这样的圆圈来说,不管怎么扔下,都将和平行线有两个交点。
蒲丰投针概率推导过程

蒲丰投针概率推导过程蒲丰投针是一种古老的传统技艺,也是一项非常有挑战性的技巧活动。
它要求将一个小针投入到一个竹筒中,而这个竹筒的直径通常只有针的两倍大小。
这项技艺的成功率非常低,但是许多人仍然对此感兴趣,并且希望了解一下成功的概率是多少。
那么,蒲丰投针的成功概率是多少呢?要回答这个问题,我们需要做一些概率推导。
首先,我们可以假设竹筒的直径为d,针的直径为r。
为了成功投针,针必须以正确的角度进入竹筒,而且针的位置必须足够准确以免碰到竹筒的边缘。
假设针的投射角度为α,我们可以将投射角度分为两个范围:一个是α1,表示针的一端离开竹筒的范围;另一个是α2,表示针的另一端离开竹筒的范围。
这两个范围的和必须小于等于竹筒的直径d。
根据几何原理,我们可以得到以下关系:2r*sin(α1)+2r*sin(α2)≤d。
这个关系表明,针的两端在竹筒中的投射范围之和不能超过竹筒的直径。
现在,我们可以进一步推导出针的投射角度α的范围。
假设针的长度为l,我们可以得到以下关系:2r*sin(α1)+2r*sin(α2)≤l。
这个关系表明,针的两端在竹筒中的投射范围之和不能超过针的长度。
现在,我们可以将这个关系进一步转化为概率问题。
假设针的长度l=2r,我们可以得到以下关系:2*sin(α1)+2*sin(α2)≤1。
这个关系表明,针的两端在竹筒中的投射范围之和不能超过1。
为了计算针的成功概率,我们需要确定针的投射角度α的范围。
根据上述关系,我们可以得到以下范围:0≤α1≤π/2,0≤α2≤π/2。
这个范围表明,针的投射角度α的范围在0到π/2之间。
现在,我们可以计算针的成功概率。
假设针的投射角度α的范围在0到π/2之间均匀分布,我们可以得到以下概率:P(针成功)=∫[0,π/2]∫[0,π/2]2*sin(α1)*2*sin(α2)dα1dα2。
由于文章要求不包含数学公式或计算公式,我们不再具体计算上述积分。
但是,我们可以肯定地说,这个积分是一个正值,因此针的成功概率是一个大于零的数。
浦丰投针试验--MATLAB仿真

浦丰投针试验一,试验内容试验步骤是:1)取一张白纸,在上面画上许多条间距为d的平行线。
2)取一根长度为l(l<d)的针,随机地向画有平行直线的纸上掷n 次,观察针与直线相交的次数,记为m3)计算针与直线相交的概率.其概率的值freq=2*l/(π*d)根据这一公式和大量测试结果,即可估算出圆周率π=2*l/(d*freq)。
下面我们将用MATLAB来模拟这一试验,估算出圆周率的值,并探讨影响其准确率的因素。
二,试验过程试验程序如下:>>clear>> d=3;>> r=1;>>NoI=0;>> n=100;>> x=d/2*rand(1,n);>> p=pi*rand(1,n);>>fori=1:nif x(i)<r*sin(p(i))NoI=NoI+1endend;>>freq=NoI/n;>>estpi=4*r/(d*freq);>>delta=abs(estpi-pi)/pi;>>freqfreq =0.4700>>estpiestpi =2.8369>>delta=0.0970注:d为两平行线之间的距离,r为针的长度的一半,NoI(numbers of intersction)表示相交次数,n表示投针次数,相交概率为freq,估算出的π的值为estpi,最后是计算出来的相对误差。
由于试验次数越多所得到的概率更有普遍性,于是我们首先尝试改变n的取值,观察其对所得到π值得影响。
1)当取n=1000时>> n=1000;>>freqfreq =0.4370>>estpiestpi =3.0511>>deltadelta =0.02882)当取n=2000时>> n=2000;freq =0.4285>>estpiestpi =3.1116>>deltadelta =0.00953)当取n=5000时>> n=2000;>>freqfreq =0.4230>>estpiestpi =3.1521>>deltadelta =0.0033又猜想其结果可能与针的长度和平行线之间的距离有关,现保持针的长度不变,改变平行线之间的距离以达到改变d/r的值,观察其影响。
蒲丰氏投针问题的模拟过程

蒲丰氏投针问题的模拟过程,随机数发生器也是自编的,以供大家参考和提出建议。
谢谢。
(seed1和seed2最好选择3和5,为了使投针次数达到1000000,CVF进行如下设置Project->settings->link->output,将stack allocations reserve:设为1000000000)program getpiimplicit nonereal,parameter::a=5,L=4,pi=3.14159integer::n1,i,counter=0real,allocatable::R1(:),R2(:)real::theta,x,pi1write(*,*) 'input the size of the array:'read(*,*) n1allocate(R1(n1))allocate(R2(n1))call random(n1,R1,R2)do i=1,n1x=a*(2*R1(i)-1)theta=pi*R2(i)if(abs(x)<L*sin(theta)) counter=counter+1end dopi1=(1.0*n1)/(counter*1.0)*(2.0*L/a)write(*,*) 'this is PI:'write(*,*) piwrite(*,"('this is ratio of counter to total number',F10.6)")1.0&*counter/n1stopend programsubroutine random(n,R1,R2)implicit noneinteger n,seed1,seed2,i,little,mreal::R1(n),R2(n)integer::temp1(n),temp2(n)write(*,*) 'input seed1'read(*,*) seed1write(*,*) 'input seed2'read(*,*) seed2m=2**30m=m*2-1temp1(1)=397204094temp2(1)=temp1(1)R1(1)=(1.0*temp1(1))/(1.0*m)R2(1)=(1.0*temp2(1))/(1.0*m)little=0if(R1(1)<0.5) little=little+1do i=1,n-1temp1(i+1)=mod(seed1*temp1(i),m)R1(i+1)=(1.0*temp1(i+1))/(1.0*m)temp2(i+1)=mod(seed2*temp2(i),m)R2(i+1)=(1.0*temp2(i+1))/(1.0*m)if(R1(i+1)<0.5) little=little+1 .end do ;write(*,*) 'ratio of number which is little than 0.5'write(*,*) 1.0*little/nreturnend subroutine拟蒙特卡洛方法(Quasi-Monte Carlo)积分实例%使用Matlab提供的函数求积分,exp(-1/2*x^2)在(0,1)间积分 format long; syms xa = sym(1/2);f = exp(-a*x^2);ezplot(f)disp(int(f,-1,1));fprintf('integral result:%1.18f.\n',double(int(f,0,1)));%disp(double(int(f,0,1)));复制代码%使用拟蒙特卡洛方法积分%得到拟蒙特卡洛序列,即低偏差序列,halton法%如果有相关的工具箱的话,可以用Matlab里面的haltonset,faureset,sobolset 函数实现,x=halton(10000,2,5577);n=length(x);mju=0;for i=1:nmju=mju + exp(-0.5*x(i)^2);endmju=mju/n;fprintf('Quasi-Monte Carlo result:%1.18f.\n',mju);%disp(mju);%使用蒙特卡洛方法积分%得到Uniform序列,x=random('unif',0,1,10000,1);n=length(x);mju=0;for i=1:nmju=mju + exp(-0.5*x(i)^2);endmju=mju/n;fprintf('Monte Carlo result:%1.18f.\n',mju);%=============生成HALTON序列======================== function result = halton( m,base,seeder )%生成HALTON序列% Check inputsif nargin < 3seeder = 0;if nargin < 2error('MATLAB:Halton:NotEnoughInputs',...'Not enough input arguments. See Halton.'); endendres=0;n=length(base);for i=1:mfor j=1:nelement=0;temp=seeder+i;k=1;while temp>0element(k)=rem(temp,base(j));temp=fix(temp/base(j));k=k+1;endres(i,j)= 0;for k=1:length(element)res(i,j)=res(i,j)+element(k)/(base(j)^k); endendendresult=res;。
综合实验三 蒲丰投针问题实验

综合实验三 蒲丰投针问题实验一、实验目的1. 掌握几何概型、熟悉Monte Carlo 方法的基本思想;3.会用MATLAB 实现简单的计算机模拟二、实验内容在用传统方法难以解决的问题中,有很大一部分可以用概率模型进行描述.由于这类模型含有不确定的随机因素,分析起来通常比确定性的模型困难.有的模型难以作定量分析,得不到解析的结果,或者是虽有解析结果,但计算代价太大以至不能使用.在这种情况下,可以考虑采用Monte Carlo 方法。
下面通过例子简单介绍Monte Carlo 方法的基本思想.Monte Carlo 方法是计算机模拟的基础,它的名字来源于世界著名的赌城——摩纳哥的蒙特卡洛,其历史起源于1777年法国科学家蒲丰提出的一种计算圆周π的方法——随机投针法,即著名的蒲丰投针问题。
这一方法的步骤是:1) 取一张白纸,在上面画上许多条间距为d 的平行线,见图8.1(1)2) 取一根长度为()l l d <的针,随机地向画有平行直线的纸上掷n 次,观察针与直线相交的次数,记为m3)计算针与直线相交的概率.由分析知针与平行线相交的充要条件是 ϕs i n 21≤x 其中πϕ≤≤≤≤0,20d x 建立直角坐标系),(x ϕ,上述条件在坐标系下将是曲线所围成的曲边梯形区域,见图 8.l (2).由几何概率知(*)22s i n 210d l d d G g p ππϕϕπ===⎰的面积的面积 4)经统计实验估计出概率,n m P ≈由(*)式即?2=⇒=ππd l n m Monte Carlo 方法的基本思想是首先建立一个概率模型,使所求问题的解正好是该模型的参数或其他有关的特征量.然后通过模拟一统计试验,即多次随机抽样试验(确定m 和n ),统计出某事件发生的百分比.只要试验次数很大,该百分比便近似于事件发生的概率.这实际上就是概率的统计定义.利用建立的概率模型,求出要估计的参数.蒙特卡洛方法属于试验数学的一个分支.问题:(1) 经过n次试验后圆周率估计与的圆周 之间的差的绝对值的规律是?其中n分别取100,1000,2000,5000,10000,20000,50000(2) 参数l,d的不同选择,会对圆周率的估计有什么影响?可以选择d为l.5倍,2倍,3倍,4倍,5倍,8倍,10倍,20倍,50倍三、实验要求写出实验步骤、结果显示及分析四、实验分析以x 表示针的中点与最近一条平行线的距离,以j表示针与此线间的交角.显然0≤x≤a/20≤j≤p针与平行线相交的充要条件是x≤lsin(j)/2因(x,j)在图(4)中下面的矩形中等可能地取点,可见针与平行线相交的概率p 为图(4)正弦曲线线段与横轴围成的面积同图(4)中矩形面积的比.经计算得p= 另一方面得到如大量得投针实验,利用大数定理知:随着实验次数的增加,针与平行线相交的频率依概率收敛到概率p.那么在上式中以频率代替相应的概率p,则可以获得圆周率p的近似值.下面的程序是用matlab语言编写的计算机模拟投针以计算p 的近似值的程序.五、实验步骤1.编写MATLAB程序cleard=2l=0.5counter=0n=100x=unifrnd(0,d/2,1,n)fi=unifrnd(0,pi,1,n)for i=1:nif x(i)<1*sin(fi(i))/2counter=counter+1endendfren=counter/npihat=2*1/(d*fren)sqrt((pihat-pi)^2)结果显示:fren = 0.3300pihat =3.0303ans =0.1113以此类推:将n=1000,2000,5000,10000,20000,50000分别代入,可得:当n=1000时,fren =0.3240pihat =3.0864ans =0.0552当n=2000时,fren =0.3230pihat =3.0960ans =0.0456当n=5000时,fren =0.3204pihat =3.1211ans =0.0205当n=10000时,fren =0.3190pihat =3.1348ans =0.0068当n=20000时,fren =0.3172pihat =3.1521ans =0.0105当n=50000时,fren =0.3177pihat =3.1478ans =0.00622.改变d的取值,分别为1.5,2 ,3 ,4,5,8,10,20,50倍仍用1中的程序:cleard=3l=0.5counter=0n=100x=unifrnd(0,d/2,1,n)fi=unifrnd(0,pi,1,n)for i=1:nif x(i)<1*sin(fi(i))/2counter=counter+1endendfren=counter/npihat=2*1/(d*fren)sqrt((pihat-pi)^2)结果显示:d为1.5倍时fren =0.2300pihat =2.8986ans =0.2430d为2倍时fren =0.1700pihat =2.9412ans =0.2004d为3倍时fren =0.1100pihat =3.0303ans =0.1113d为4倍时fren =0.0800pihat =3.1250ans =0.0166d为5倍时fren =0.0600pihat =3.3333ans =0.1872d为8倍时fren =0.0400pihat =3.1250ans =0.0211d为10倍时fren =0.0300pihat =3.3333ans =0.1872d为20倍时fren =0.0100pihat =5ans =1.8539d为50倍时fren =0pihat =Infans =Inf六、结果分析1.经过n次试验后圆周率估计与的圆周π之间的差的绝对值的规律是:n的次数取值越多,圆周率估计与的圆周π之间的差的绝对值越小:圆周率越接近真值。
关于用蒲丰投针求∏值的实验报告

关于用蒲丰投针求∏值的实验报告实验目的理解蒲丰投针的模型,逐渐掌握用数学知识解决实际问题的能力掌握运用matlab 进行一般的数学运算培养团队合作精神实验原理在一张纸上画出间距为l 的多条直线,随机在上面投放长度为 a 的针,投放n 次,记与直线相交的次数为m ,当n 相当大之后,则针与线相交的概率n m p =如下图,通过分析,针与线相交的条件简化为 ϕsin 21≤x 而πϕ≤≤≤≤0,20dx这是一个几何特型的概率问题,通过推理可得(*)22s i n 210d l dd G g p ππϕϕπ===⎰的面积的面积所以,实验过程及结果用matlab 模拟投针过程求∏值 的函数:function f=fun(a,l,n)x=pi.*rand(1,n);y=(a/2).*rand(1,n);c=(y<=((l/2).*sin(x)));m=sum(c);f=2*l*n/(m*a);随机一次实验求得的∏值>> a=input('a=');l=input('l=');n=input('n=');a=20l=15n=1000>> fun(a,l,n)ans =3.131524008350731>>以上得到的∏值不是十分精确,这是由于实验次数有限导致的误差,当实验的次数相当大之后,所得结果必定会更加逼近∏的精确值。
缺点和改进上述模拟实验还不是十分精确,而且没有绘图,不够直观,下次会注意模拟的更加精确,更加直观。
蒲丰投针与蒙特卡洛(MonteCarlo)方法

蒲丰投针与蒙特卡洛(Monte —Carlo)方法1777年法国科学家蒲丰(Buffon )提出并解决了如下的投针问题:桌面上画有一些平行线,它们之间的距离都是,一根长为a )(a l l ≤的针随机地投在桌面上。
问:此针与任一直线相交的概率是多少?设表示针的中点到最近的一条平行线的距离,Y 表示针与平行线的夹角(如图),如果X 2sin l Y X <, 或Y lX sin 2<时,针与一条直线相交。
由于向桌面投针是随机的,所以用来确定针在桌面上位置的是二维随机向量。
并且在),(Y X X ⎟⎠⎞⎜⎝⎛2,0a 上服从均匀分布,在Y ⎟⎠⎞⎜⎝⎛2,0π上服从均匀分布,与Y 相互独立。
由此可以写出的联合概率密度函数:X ),(Y X⎪⎩⎪⎨⎧<<<<=其它20,204),(ππy ax ay x f 于是,所求概率为:∫∫∫∫===⎭⎬⎫⎩⎨⎧<<20sin 20sin 224),(sin 2πππal dxdy adxdy y x f Y l X P y ly lx ①由于最后的结果与π有关,因此有些人想利用它来计算π的值。
其方法是向桌面投针次,若针与直线相交次,则针与直线相交的频率为n k n k ,以频率代替概率,则有al n k π2=,所以aknl2=π。
下表列举了这些试验的有关资料。
投针试验的历史资料(折算为1)a 试验者 年份 针长投针次数n 相交次数k π的试验值Wolf 1850 0.85000 2532 3.1596 Smith1855 0.63204 1219 3.1554 De.Morgan 1860 1600 383 3.137 Fox 1884 0.751030 489 3.1595 Lazzerini 1901 0.833408 1801 3.1415929 Reina1925 0.5425208593.1795这个思路已被人们发展成为统计学的一个分支—随机试验法或称为蒙特卡洛(Monte—Carlo )方法,其中随机试验可借助计算机大量重复,以致结果更接近真值。
实验报告3蒲丰投针
0
1.79821
2.30682
1.111713993
0
1.76922
1.13937
1.36255246
0
1.91693
0.85702
1.133839234
0
0.02899
0.71090
0.978779676
1
0.81484
1.90012
1.419389613
1
1.72649
1.19545
在历史上人们对 的计算非常感兴趣性,发明了许多求 的近似值的方法,其中用蒲丰投针问题来解决求 的近似值的思想方法在科学占有重要的位置,人们用这一思想发现了随机模拟的方法.
蒲丰投针问题:平面上画有间隔为 的等距平行线,向平面任意投一枚长为 的针,求针与任一平行线相交的概率.进而求 的近似值.
对于 =50,100,500,1000,3000各做5次试验,分别求出 的近似值.写出书面报告、总结出随机模拟的思路.
在历史上人们对的计算非常感兴趣性发明了许多求的近似值的方法其中用蒲丰投针问题来解决求的近似值的思想方法在科学占有重要的位置人们用这一思想发现了随机模拟的方法
数学实验报告
实验序号:3日期:2015年4月20日
班级
13A
姓名
徐文婕
学号
134080041
实验
名称
随机模拟计算 的值----蒲丰投针问题
问题的背景:
实验过程:(含解决方法和基本步骤,主要程序清单及异常情况记录等)
n=
d=
ห้องสมุดไป่ตู้l=
10000
4
3
相交计数
相交次数
π≈2nl/kd
蒲丰投针试验---------概率论与数理统计

蒲丰资料
1777年,法国科学家蒲丰(Buffon)提ห้องสมุดไป่ตู้了投针 试验问题.平面上画有等距离为a(a>0)的一些平行直 线,现向此平面任意投掷一根长为b( b<a )的针,试求 针与某一平行直线相交的概率. 解 以 x表示针投到平面上时,
针的中点M到最近的一条平行
a
M x
直线的距离, 表示针与该平行直线的夹角.
1.0
0.75 0.83 0.5419
600
1030 3408 2520
382
489 1808 859
3.137
3.1595 3.1415929 3.1795
利用蒙特卡罗(Monte Carlo)法进行计算机模拟. 单击图形播放/暂停 ESC键退出 取a 1, b 0.85.
利用上式可计算圆周率π 的近似值.
历史上一些学者的计算结果(直线距离a=1)
试验者 Wolf Smith 时间 1850 1855 针长 0.8 0.6 投掷次数 相交次数 π的近似值 5000 3204 2532 1218 3.1596 3.1554
De Morgan 1860
Fox Lazzerini Reina 1884 1901 1925
那么针落在平面上的位置可由( x , )完全确定.
投针试验的所有可能结果与 矩形区域
a S {( x , ) 0 x ,0 π} 2 中的所有点一一对应 . 由投掷的任意性可知 这是一个几何概型问题.
a
M x
所关心的事件
o
A { 针与某一平行直线相交} 发生的充分必要条件为S 中的点满足 b 0 x sin , 0 π . 2
蒲丰(Buffon)投针随机试验的讨论 (修改稿)

(2006-3-7, 2009-9-18再修改)例 ( 蒲丰(Buffon )投针随机试验的讨论 ) 在平面上画有相互距离均为2a 的平行线束,向平面上随机投一枚长为2l 的针,为了避免针与两平行线同时相交的复杂情况,假定0>>l a , 设M 为针的中点,y 为M 与最近平行线的距离,φ为针与平行线的交角(如图1)a y ≤≤0, πϕ≤≤0. 于是,很明显,针与平行线相交的充要条件是ϕsin l y ≤(如图2),故相交的概率为ald l a dy d a p l πϕϕπϕπϕππ2 sin 1 1sin 000===⎰⎰⎰ (1) 我们用n 表示投针次数, n S 表示针与平行线相交次数,由大数定理知,当n 充分大时,频率接近于概率,即aln S n π2≈ 于是有naS nl2≈π (2)这就是上面所说的用随机试验求π值的基本公式。
根据公式(2),19—20世纪,曾有不少学者做了随机投针试验,并得到了π的估计值 . 其中最详细的有如下两个 :其中π的估计值就是利用π的近似公式(8)得到的,即1596.363320002532455000362≈=⨯⨯⨯≈π (Wolf )1415929.31133551808334085.22≈=⨯⨯⨯≈π (Lazzarini )一般情况下,随机抽样试验的精度是不高的,Wolf 的试验结果是π≈3.1596,只准确两位有效数字 .精度是由方差n p p n S D n )1(-=⎪⎭⎫⎝⎛决定的,为了确定概率p ,不妨取l =a 这一极限情况,这时π2≈p =0.6366,n n S D n 2313.0≈⎪⎭⎫⎝⎛,由积分极限定理, dx n p p p n S P x n n ⎰-∞→=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧≤--λλπλ221-e21)1(lim即频率n S n /近似地服从正态分布律()n p p p N /)1(,- . 如果要求以大于95%的概率(96.1=λ),保证以频率n S n /作为p 的近似值精确到三位有效数字,001.0≤-=p nS nε 即≈⎪⎪⎭⎫⎝⎛≤-001,0p n S P n 95.021/)1(001.0)1(001.0212≥⎰----np p np p x dx eπ则必须有96.1/)1(001.0=≥-λnp p根据上式,要求试验次数7.88001.0/231.096.122≈⨯≥n 万次 .至于Lazzarini 的试验,为什么实验次数少反而精确度却很高呢?这是由于这一试验结果恰好和祖冲之密率355/113相合,而祖冲之密率为无理数π的连分式,属于π的最佳有理逼近 . 很明显,作为一种具有随机性质的试验,其结果恰好与最佳有理逼近的结果一致是非常偶然的;顾及到上述讨论,故Lazzarini 的试验结果是不大可能的 .注:以上的讨论是第6章“假设检验”方法的一个有实际意义的例子。
蒲丰投针问题与无理数π的模拟

5、在C4输入=3*SIN(C4)/2。下托到C1003;在D4输入=IF(D4<=1,"1","0")下托到D1003,在E4输入=COUNTIF(E4:E10003,"1")在下托到E1003,在F4输入=2*10000*3/(F4*4)。
教师评语与成绩:
实验结果总结:计算机上模拟蒲丰投针试验,可以求出π的近似的值.我的到的值为3.225133和3.123367.他与.31415926存在了差别.可能是由于计算机取的1000个随机数的差别.虽然它们存在差别,但是它们已经很接近啦,这比人工或其它方法计远的快和准确于人的计算.
本实验旨在让实验者在计算机上模拟蒲丰投针试验,掌握无理数 的近似计算方法,理解随机模拟法的基本原理,从中体会到新思想、新方法产生的过程。
实验内容:
蒲丰投针问题:平面上画有间隔为 的等距平行线,向平面任意投一枚长为 的针,求针与任一平行线相交的概率,进而求 的近似值。若做了 次投针试验,有 次针与线相交,那么由教材例1.2.9结论知所求概率为 ,而 ,故有 。
2、单击数据/数据分析/随机数发生器,选择变量个数2,随机数1000,均匀分布,介于-1到1,输出区域$A$2,确定;
3、在C2输入=A2^2+B2^2;
4、在D2输入=IF(C6<=1,"1","0"),在E2输入=COUNTIF(D2:D10002,"1");
5、在F2输入=4*E2/10000。
实验二、蒲丰投针问题与无理数π的模拟
布丰的投针试验

布丰的投针试验公元1777年的一天,法国科学家D·布丰(707~1788)的家里宾客满堂,原来他们是应主人的邀请前来观看一次奇特试验的。
试验开始,但见年已古稀的布丰先生兴致勃勃地拿出一张纸来,纸上预先画好了一条条等距离的平行线。
接着他又抓出一大把原先准备好的小针,这些小针的长度都是平行线间距离的一半。
然后布丰先生宣布:“请诸位把这些小针一根一根往纸上扔吧! 不过,请大家务必把扔下的针是否与纸上的平行线相交告诉我。
”客人们不知布丰先生要玩什么把戏,只好客随主意,一个个加入了试验的行列。
一把小针扔完了,把它捡起来又扔,而布丰先生本人则不停地在一旁数着、记着,如此这般地忙碌了将近一个钟头。
最后,布丰先生高声宣布:“先生们,我这里记录了诸位刚才的投针结果,共投针2212次,其中与平行线相交的704次。
总数2212与相交数704的比值为3.142。
”说到这里,布丰先生故意停了停,并对大家报以神秘的一笑,接着有意提高声调说:“先生们,这就是圆周率π的近似值!”众客哗然,一时疑议纷纷,大家全部感到莫名期妙:“圆周率π? 这可是与圆半点也不沾边的呀!”布丰先生似乎猜透了大家的心思,得意洋洋地解释道:“诸位,这里用的是概率的原理,如果大家有耐心的话,再增加投针的次数,还能得到π的更精确的近似值。
不过,要想弄清其间的道理,只好请大家去看敝人的新作了。
”随着布丰先生扬了扬自己手上的一本《或然算术试验》的书。
π在这种纷纭杂乱的场合出现,实在是出乎人们的意料,然而它却是千真万确的事实。
由于投针试验的问题,是布丰先生最先提出的,所以数学史上就称它为布丰问题,布丰得出的一般结果是:如果纸上两平行线间相距为d,小针长为l,投针的次数为n,所以投的针当中与平行线相交的次数的m,那么当n相当大时有:π≈(2ln)/(dm)在上面故事中,针长l恰等于平行线间距离d的一半,所以代入上面公式简化得:π≈n/m值得一提的是,后来有不少人步布丰先生的后尘,用同样的方法来计算π值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
蒲丰氏投针问题的模拟过程,随机数发生器也是自编的,以供大家参考和提出建议。
谢谢。
(seed1和seed2最好选择3和5,为了使投针次数达到1000000,CVF进行如下设置Project->settings->link->
output,将stack allocations reserve:设为1000000000)
program getpi
implicit none
real,parameter::a=5,L=4,pi=3.14159
integer::n1,i,counter=0
real,allocatable::R1(:),R2(:)
real::theta,x,pi1
write(*,*) 'input the size of the array:'
read(*,*) n1
allocate(R1(n1))
allocate(R2(n1))
call random(n1,R1,R2)
do i=1,n1
x=a*(2*R1(i)-1)
theta=pi*R2(i)
if(abs(x)<L*sin(theta)) counter=counter+1
end do
pi1=(1.0*n1)/(counter*1.0)*(2.0*L/a)
write(*,*) 'this is PI:'
write(*,*) pi
write(*,"('this is ratio of counter to total number',F10.6)")
1.0
&*counter/n1
stop
end program
subroutine random(n,R1,R2)
implicit none
integer n,seed1,seed2,i,little,m
real::R1(n),R2(n)
integer::temp1(n),temp2(n)
write(*,*) 'input seed1'
read(*,*) seed1
write(*,*) 'input seed2'
read(*,*) seed2
m=2**30
m=m*2-1
temp1(1)=397204094
temp2(1)=temp1(1)
R1(1)=(1.0*temp1(1))/(1.0*m)
R2(1)=(1.0*temp2(1))/(1.0*m)
little=0
if(R1(1)<0.5) little=little+1
do i=1,n-1
temp1(i+1)=mod(seed1*temp1(i),m)
R1(i+1)=(1.0*temp1(i+1))/(1.0*m)
temp2(i+1)=mod(seed2*temp2(i),m)
R2(i+1)=(1.0*temp2(i+1))/(1.0*m)
if(R1(i+1)<0.5) little=little+1 .
end do ;
write(*,*) 'ratio of number which is little than 0.5'
write(*,*) 1.0*little/n
return
end subroutine
拟蒙特卡洛方法(Quasi-Monte Carlo)积分实例
%使用Matlab提供的函数求积分,exp(-1/2*x^2)在(0,1)间积分 format long; syms x
a = sym(1/2);
f = exp(-a*x^2);
ezplot(f)
disp(int(f,-1,1));
fprintf('integral result:%1.18f.\n',double(int(f,0,1)));
%disp(double(int(f,0,1)));
复制代码%使用拟蒙特卡洛方法积分
%得到拟蒙特卡洛序列,即低偏差序列,halton法
%如果有相关的工具箱的话,可以用Matlab里面的haltonset,faureset,sobolset 函数实现,
x=halton(10000,2,5577);
n=length(x);
mju=0;
for i=1:n
mju=mju + exp(-0.5*x(i)^2);
end
mju=mju/n;
fprintf('Quasi-Monte Carlo result:%1.18f.\n',mju);
%disp(mju);
%使用蒙特卡洛方法积分
%得到Uniform序列,
x=random('unif',0,1,10000,1);
n=length(x);
mju=0;
for i=1:n
mju=mju + exp(-0.5*x(i)^2);
end
mju=mju/n;
fprintf('Monte Carlo result:%1.18f.\n',mju);
%=============生成HALTON序列======================== function result = halton( m,base,seeder )
%生成HALTON序列
% Check inputs
if nargin < 3
seeder = 0;
if nargin < 2
error('MATLAB:Halton:NotEnoughInputs',...
'Not enough input arguments. See Halton.'); end
end
res=0;
n=length(base);
for i=1:m
for j=1:n
element=0;
temp=seeder+i;
k=1;
while temp>0
element(k)=rem(temp,base(j));
temp=fix(temp/base(j));
k=k+1;
end
res(i,j)= 0;
for k=1:length(element)
res(i,j)=res(i,j)+element(k)/(base(j)^k); end
end
end
result=res;。
