资料分析计算公式整理

资料分析公式汇总

资料分析公式汇总在进行资料分析时，掌握一些关键的公式可以帮助我们更高效、准确地处理和解读数据。

以下是为大家汇总的一些常用公式：一、增长相关公式1、增长量＝现期量基期量增长量用于衡量数据在一定时期内的绝对增长幅度。

2、增长率＝增长量÷基期量×100%这个公式反映了数据增长的相对速度。

3、基期量＝现期量÷（1 ＋增长率）当我们已知现期量和增长率，要求出之前某个时期的量时，就会用到这个公式。

4、现期量＝基期量×（1 ＋增长率）通过基期量和增长率来计算当前时期的量。

二、比重相关公式1、比重＝部分÷整体×100%比重表示部分在整体中所占的比例。

2、整体＝部分÷比重已知部分和其占整体的比重，可求出整体的量。

3、部分＝整体×比重根据整体的量和部分所占的比重，能计算出部分的量。

三、平均数相关公式1、平均数＝总数÷个数这是计算平均数最基本的公式。

2、总数＝平均数×个数当已知平均数和个数时，可求出总数。

四、倍数相关公式1、 A 是 B 的几倍：A÷B直接用 A 的数值除以 B 的数值，得到 A 是 B 的倍数。

2、 A 比 B 多几倍：（A B）÷B先计算 A 与 B 的差值，再除以 B 的数值。

五、隔年增长相关公式1、隔年增长率＝现期增长率＋间期增长率＋现期增长率×间期增长率例如，今年的增长率为 r1，去年的增长率为 r2，那么隔年增长率就是 r1 ＋ r2 ＋ r1×r2 。

2、隔年基期量＝现期量÷（1 ＋隔年增长率）六、年均增长相关公式1、年均增长量＝（末期量初期量）÷年份差用于计算在一定年份内平均每年的增长量。

2、年均增长率＝（末期量÷初期量）＾（1÷年份差) 1七、混合增长率相关公式整体增长率介于部分增长率之间，且偏向于基期量大的部分增长率。

资料分析常考公式

资料分析常考公式一、基期与现期1.基期量=现期量-增长量=现期量/（1+r），当|r|≤5%，可化除为乘，现期量/（1+r）≈现期量×（1-r）2.现期量=基期量+增长量=基期量×（1+r）常见考法：基期量或现期量计算，基期量、现期量和差计算及大小比较。

基期比较：①当现期相差比较大，直接看量级；②现期相差不大，给出了现期和增长率，直接截位直除（根据选项差距来判断截取几位）。

二、增长量1.增长量=现期量-基期量（选项与材料精确度一样且尾数不同，可用尾数法；选项差距较大，首位法或者截位相加减）2.增长量=现期量×增长率/（1+增长率）（常用特殊分数法，增长率为正，用n+1；增长率为负，用n-1）3.年（月）均增长量=（末期-初期）/年（月）份差常见考法：增长量的计算及大小比较。

增长量比较口诀：“大大则大”，即当现期和增长率都大时，增长量也大；“一大一小”，主要看现期×增长率。

三、增长率r =（现期量-基期量）/基期量=增长量/基期量=现期量/基期量-1=增长量/（现期量-增长量）常见考法：增长率计算及大小比较增长率比较：①直接用现期量/基期量进行比较；②当基期量相差不大时，直接比较增长量大小；③分数比较（主要方法：首位法、截位直除、差分法）特殊增长率1.混合增长率：混合增长率介于部分增长率之间，且偏向基期较大的一方（用于判断大小范围）；用线段法或十字交叉法估算具体数值。

2.间隔增长率：r=r1+r2+r1r2。

3.年均增长率：（1+年均增速）^n=末期/基期，n为年份差，计算时长代入10%、20%等中间值来判断年均增速的范围，进而确定选项。

四、比重1.比重=部分量/整体量，部分量=整体量×比重，整体量=部分量/比重2.现期比重=B/A （B为部分量，A为整体量）3.基期比重=B/A×（1+a）/（1+b）（B为部分量，b为部分量增速，A为整体量，a为整体量增速）4.两期比重差=B/A×（b-a）/（1+b）常见考法：比重计算和比较；两期比重判断：部分量增速大于整体量增速，比重上升；部分量增速小于整体量增速，比重下降。

资料分析公式汇总

资料分析公式汇总速算技巧一、估算法精度要求不高的情况下，进行粗略估值的速算方式。

选项相差较大，或者在被比较的数字相差必须比较大，差距的大小将直接决定对“估算”时对精度的要求。

二、直除法在比较或者计算较复杂的分数时，通过“直接相除”的方式得到商的首位（首一位、首两位、首三位），从而得出正确答案的速算方式。

常用形式： 1.比较型：比较分数大小时，若其量级相当，首位最大∕小数为最大∕小数2.计算型：计算分数大小时，选项首位不同，通过计算首位便可得出答案。

难易梯度：1.基础直除法：①可通过直接观察判断首位的情形；②需要通过手动计算判断首位的情形。

2.多位直除法：通过计算分数的“首两位”或“首三位”判断答案情形。

三、插值法1.“比较型”插值法如果A与B的比较，若可以找到一个数C，使得A﹥C，而B﹤C，既可以判定A﹥B；若可以找到一个数C，使得A﹤C，而B﹥C，既可以判定A﹤B；2.“计算型”插值法若A﹤C﹤B，则如果f﹥C，则可以得到f=B;如果f﹤C，则可以得到f=A；若A﹥C﹥B，则如果f﹥C，则可以得到f=A;如果f﹤C，则可以得到f=B。

四、放缩法当计算精度要求不高时，可以将中间结果进行大胆的“放”（扩大）或者“缩”（缩小），从而迅速得到精度足够的结果。

常用形式：1. A﹥B,C﹥D,则有A+C﹥B+D；A-D﹥B-C；2. A﹥B﹥0，C﹥D﹥0，则有A×C﹥B×D；A÷D﹥B÷C五、割补法在计算一组数据的平均值或总和值时，首先选取一个中间值，根据中间值将这组数据“割”（减去）或“补”（追上），进而求取平均值或总和值。

常用形式:1.根据该组数据，粗略估算一个中间值；2.将该组值分别减去中间值得到一组数值；3.将得到的新数值相加得到和值，用和值除以该组数值的项数得到商值，将商值加上中间值，即为该组数值的精确平均值；4.用中间值乘以数据项数再加上最后的和值即为总和值。

资料分析计算公式整理

资料分析计算公式整理在进行资料分析时，掌握一些关键的计算公式是至关重要的。

这些公式能够帮助我们快速、准确地从大量的数据中提取有价值的信息，做出合理的判断和决策。

下面，我将为大家整理一些常见且实用的资料分析计算公式。

一、增长率相关公式1、增长率＝（现期量基期量）÷基期量× 100%这是最基本的增长率计算公式。

例如，某公司去年的销售额为 100 万元，今年为 120 万元，那么今年的销售额增长率为（120 100）÷ 100 × 100% ＝ 20%。

2、间隔增长率＝ r1 ＋ r2 ＋ r1×r2当涉及到间隔年份的增长率计算时，就需要用到这个公式。

假设第一年的增长率为 r1，第二年的增长率为 r2，那么从第一年到第二年的间隔增长率就是 r1 ＋ r2 ＋ r1×r2。

3、年均增长率＝＼（＼sqrtn{＼frac{现期量}｛基期量}｝ 1 ＼）（n 为年份差）如果要计算一段时间内的平均增长率，就用这个公式。

比如，某地区 2010 年的 GDP 为 100 亿元，2020 年为 200 亿元，年份差为 10 年，那么年均增长率＝＼（＼sqrt10{＼frac{200}｛100}｝ 1 ＼）。

1、比重＝部分量÷整体量× 100%比如，某班级共有 50 名学生，其中男生 25 人，那么男生在班级中的比重就是 25÷50× 100% ＝ 50%。

2、整体量＝部分量÷比重已知部分量和比重，求整体量时使用。

假设某企业某产品的销售额占总销售额的 30%，该产品销售额为 100 万元，那么企业总销售额＝100÷30% 。

3、部分量＝整体量×比重当已知整体量和比重，求部分量时运用。

比如一个城市总人口为100 万人，其中老年人占比 20%，那么老年人的数量＝ 100×20% ＝ 20 万人。

资料分析常用公式

资料分析常用公式1. 平均数公式平均数（Mean）是表示一组数据集中趋势的量数，计算公式为：$$\text{平均数} = \frac{\sum_{i=1}^{n} x_i}{n}$$其中，$ x_i $ 表示第 $ i $ 个数据，$ n $ 表示数据总数。

平均数适用于描述一组数据的总体水平，常用于市场调研、人口统计等领域。

2. 中位数公式中位数（Median）是将一组数据按大小顺序排列后位于中间位置的数，计算公式为：$$\text{中位数} =\begin{cases}\frac{x_{\frac{n+1}{2}} + x_{\frac{n}{2}}}{2} & \text{当 } n \text{ 为偶数时} \\x_{\frac{n+1}{2}} & \text{当 } n \text{ 为奇数时}\end{cases}$$其中，$ x_i $ 表示第 $ i $ 个数据，$ n $ 表示数据总数。

中位数适用于描述一组数据的中间水平，常用于描述收入、房价等分布不均的数据。

3. 标准差公式标准差（Standard Deviation）是衡量一组数据离散程度的量数，计算公式为：$$\sigma = \sqrt{\frac{\sum_{i=1}^{n} (x_i \mu)^2}{n}}$$其中，$ x_i $ 表示第 $ i $ 个数据，$ \mu $ 表示平均数，$ n $ 表示数据总数。

标准差适用于描述一组数据的波动程度，常用于质量控制、风险评估等领域。

4. 相关系数公式相关系数（Correlation Coefficient）用于衡量两个变量之间的线性关系程度，计算公式为：$$r = \frac{\sum_{i=1}^{n} (x_i \bar{x})(y_i\bar{y})}{\sqrt{\sum_{i=1}^{n} (x_i \bar{x})^2}\sqrt{\sum_{i=1}^{n} (y_i \bar{y})^2}}$$其中，$ x_i $ 和 $ y_i $ 分别表示两个变量中的第 $ i $ 个数据，$ \bar{x} $ 和 $ \bar{y} $ 分别表示两个变量的平均数，$ n $ 表示数据总数。

资料分析公式汇总

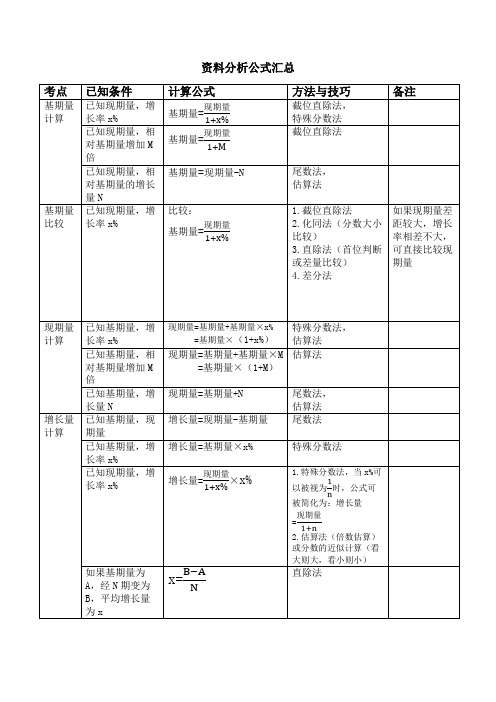
资料分析公式汇总考点已知条件计算公式方法与技巧备注基期量计算已知现期量，增长率x%基期量=截位直除法，特殊分数法已知现期量，相对基期量增加M倍基期量=截位直除法已知现期量，相对基期量的增长量N基期量=现期量-N尾数法，估算法基期量比较已知现期量，增长率x%比较：基期量=1.截位直除法2.化同法（分数大小比较）3.直除法（首位判断或差量比较）4.差分法如果现期量差距较大，增长率相差不大，可直接比较现期量现期量计算已知基期量，增长率x%现期量=基期量+基期量×x%=基期量×特殊分数法，估算法（1+x%）已知基期量，相对基期量增加M倍现期量=基期量+基期量×M=基期量×（1+M）估算法已知基期量，增长量N 现期量=基期量+N尾数法，估算法增长量计算已知基期量，现期量增长量=现期量-基期量尾数法已知基期量，增长率x%增长量=基期量×x%特殊分数法已知现期量，增长率x%增长量=×x% 1.特殊分数法，当x%可以被视为时，公式可被简化为：增长量=2.估算法（倍数估算）或分数的近似计算（看大则大，看小则小）如果基期量为A，经N期变为B，平均增长量为xx=直除法增长量比较已知现期量，增长率x%增长量=×x% 1.特殊分数法，当x%可以被视为时，公式可被简化为：增长量=2.公式可变换为：增长量=现期量×，其中为增函数，所以现期量大，增长率大的情况下，增长量一定大增长率计算已知基期量，增长量增长率=截位直除法，插值法已知现期量，基期量增长率=截位直除法求平均增长率：如果基期量为A，第n+1期（或经n期）变为B,平均增长率为x%x%=-1代入法，公式法B=A（1+X%）n当x%较小时可简化为B=A（1+nx%）求两期混合增长率：如果第一期和第二期增长率分别为r1和r2，那么第三期相对第一期增长率为r3r3= r1+r2+r1r2简单记忆口诀：连续增长，最终增长大于增长率之和；连续下降，最终下降小于增长率之和（正负号带进公式计算）求总体增长率：整体分为A,B两个部分，分别增长a%与b%，整体增长率x%x%=x%=a%+已知总体增长率和其中一个部分的增长率，求另一部分的增长率求混合增长率：整体为A，增长率为a%，分为两个部分B,C，增长率为b%和c%混合增长率a%介于b%和c%之间混合增长率大小居中增长率比较已知现期量与增长量比较增长率=代替增长率进行大小比较相当于分数大小比较发展速度已知现期量与基期量发展速度==1+增长率截位直除法，插值法增长贡献率已知部分增长量与整体增长量增长贡献量=截位直除法，插值法贡献率贡献率%=贡献率是指有效或有用成果数量与资源消耗及占用量之比，即投入量与产出量之比拉动增长求B拉动A增长几个百分点:如果B是A的一部分，B拉动A增长x%x%=截位直除法，插值法比重计算某部分现期量为A，整体现期量为为B现期比重=截位直除法，插值法某部分基期量为A，增长率a%，整体基期量为B，增长率b%现期比重=一般先计算，然后根据a和b的大小判断大小某部分现期量为A，增长率a%，整体现期量为B，增长基期比重=×一般先计算，然后根据a和b的大小判断大小率b%求基期比重-现期比重：某部分现期量为A增长率a%,整体现期量为B，增长率b%两期比重差值计算：现期比重-基期比重=-×=×（1-）=×1.先根据a与b的大小判断差值计算结果是正数还是负数；2.答案小于|a-b|3.估算法（近似取整估算）4.直除法比重比较某部分现期量为A，整体现期量为B现期比重=相当于分数大小比较，同上述做法基期比重与现期比重比较：某部分现期量为A，增长率a%，整体现期量为B，增长率b%基期比重=×直除法，当部分增长率大于整体增长率，则现期比重大于基期比重。

(完整版)资料分析公式汇总

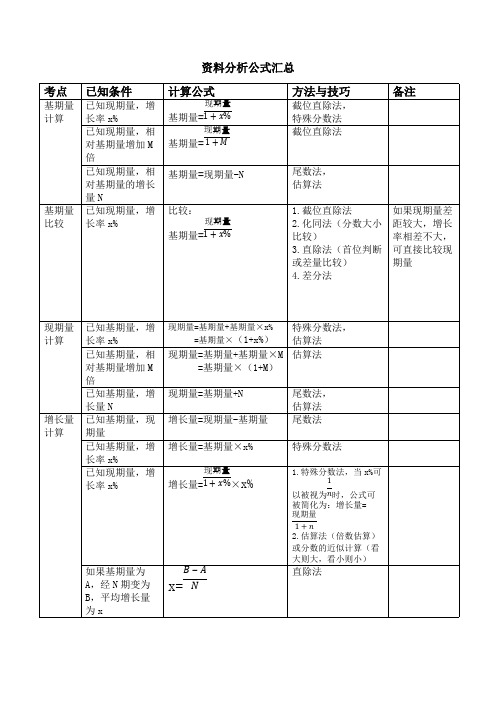
资料分析公式汇总考点已知条件计算公式方法与技巧备注已知现期量，增长率x%基期量=现期量1+x%截位直除法，特殊分数法已知现期量，相对基期量增加M 倍基期量=现期量1+M截位直除法基期量计算已知现期量，相对基期量的增长量N基期量=现期量-N尾数法，估算法基期量比较已知现期量，增长率x%比较：基期量=现期量1+x%1.截位直除法2.化同法（分数大小比较）3.直除法（首位判断或差量比较）4.差分法如果现期量差距较大，增长率相差不大，可直接比较现期量已知基期量，增长率x%现期量=基期量+基期量×x%=基期量×（1+x%）特殊分数法，估算法已知基期量，相对基期量增加M 倍现期量=基期量+基期量×M =基期量×（1+M ）估算法现期量计算已知基期量，增长量N现期量=基期量+N 尾数法，估算法已知基期量，现期量增长量=现期量-基期量尾数法已知基期量，增长率x%增长量=基期量×x%特殊分数法已知现期量，增长率x%增长量=×x%现期量1+x% 1.特殊分数法，当x%可以被视为时，公式可1n 被简化为：增长量=现期量1+n2.估算法（倍数估算）或分数的近似计算（看大则大，看小则小）增长量计算如果基期量为A ，经N 期变为B ，平均增长量为xx=B ‒A N直除法增长量比较已知现期量，增长率x%增长量=×x%现期量1+x%1.特殊分数法，当x%可以被视为时，公式可1n被简化为：增长量=现期量1+n2.公式可变换为：增长量=现期量×，其中为x%1+x%x%1+x%增函数，所以现期量大，增长率大的情况下，增长量一定大已知基期量，增长量增长率=增长量基期量截位直除法，插值法已知现期量，基期量增长率=现期量‒基期量基期量截位直除法求平均增长率：如果基期量为A，第n+1期（或经n期）变为B,平均增长率为x%x%=-1nBA代入法，公式法B=A（1+X%）n当x%较小时可简化为B=A（1+nx%）求两期混合增长率：如果第一期和第二期增长率分别为r1和r2，那么第三期相对第一期增长率为r3r3= r1+r2+r1r2简单记忆口诀：连续增长，最终增长大于增长率之和；连续下降，最终下降小于增长率之和（正负号带进公式计算）求总体增长率：整体分为A,B两个部分，分别增长a%与b%，整体增长率x%x%=A×a%+B×b%A+B x%=a%+B(b%-a%)A+B已知总体增长率和其中一个部分的增长率，求另一部分的增长率增长率计算求混合增长率：整体为A，增长率为a%，分为两个部分B,C，增长率为b%和c%混合增长率a%介于b%和c%之间混合增长率大小居中增长率比较已知现期量与增长量比较增长率=代替增现期量基期量长率进行大小比较相当于分数大小比较发展速度已知现期量与基期量发展速度==1+增长率现期量基期量截位直除法，插值法已知部分增长量与整体增长量增长贡献量=部分增长量整体增长量截位直除法，插值法增长贡献率贡献率贡献率%=贡献量（产出量，所得量）投入量（消耗量，占用量）贡献率是指有效或有用成果数量与资源消耗及占用量之比，即投入量与产出量之比拉动增长求B拉动A增长几个百分点:如果B是A的一部分，B拉动A增长x%x%=B的增长量A的基期量截位直除法，插值法某部分现期量为A，整体现期量为为B现期比重=AB截位直除法，插值法某部分基期量为A，增长率a%，整体基期量为B，增长率b%现期比重=AB×1+a%1+b%一般先计算，然后AB根据a和b的大小判断大小某部分现期量为A，增长率a%，整体现期量为B，增长率b%基期比重=×AB1+b%1+a%一般先计算，然后AB根据a和b的大小判断大小比重计算求基期比重-现期比重：某部分现期量为A增长率a%,整体现期量为B，增长率b%两期比重差值计算：现期比重-基期比重=-×ABAB1+b%1+a%=×（1-）AB1+b%1+a%=×ABa%‒b%1+a%1.先根据a与b的大小判断差值计算结果是正数还是负数；2.答案小于|a-b|3.估算法（近似取整估算）4.直除法某部分现期量为A，整体现期量为B 现期比重=AB相当于分数大小比较，同上述做法比重比较基期比重与现期比重比较：某部分现期量为A，增长率a%，整体现期量为B，增长率b%基期比重=×AB1+b%1+a%直除法，当部分增长率大于整体增长率，则现期比重大于基期比重。

(完整版)资料分析公式汇总

资料分析公式汇总考点已知条件计算公式方法与技巧备注已知现期量，增长率x%基期量=现期量1+x%截位直除法，特殊分数法已知现期量，相对基期量增加M 倍基期量=现期量1+M截位直除法基期量计算已知现期量，相对基期量的增长量N基期量=现期量-N尾数法，估算法基期量比较已知现期量，增长率x%比较：基期量=现期量1+x%1.截位直除法2.化同法（分数大小比较）3.直除法（首位判断或差量比较）4.差分法如果现期量差距较大，增长率相差不大，可直接比较现期量已知基期量，增长率x%现期量=基期量+基期量×x%=基期量×（1+x%）特殊分数法，估算法已知基期量，相对基期量增加M 倍现期量=基期量+基期量×M =基期量×（1+M ）估算法现期量计算已知基期量，增长量N现期量=基期量+N 尾数法，估算法已知基期量，现期量增长量=现期量-基期量尾数法已知基期量，增长率x%增长量=基期量×x%特殊分数法已知现期量，增长率x%增长量=×x%现期量1+x% 1.特殊分数法，当x%可以被视为时，公式可1n 被简化为：增长量=现期量1+n2.估算法（倍数估算）或分数的近似计算（看大则大，看小则小）增长量计算如果基期量为A ，经N 期变为B ，平均增长量为xx=B ‒A N直除法增长量比较已知现期量，增长率x%增长量=×x%现期量1+x%1.特殊分数法，当x%可以被视为时，公式可1n被简化为：增长量=现期量1+n2.公式可变换为：增长量=现期量×，其中为x%1+x%x%1+x%增函数，所以现期量大，增长率大的情况下，增长量一定大已知基期量，增长量增长率=增长量基期量截位直除法，插值法已知现期量，基期量增长率=现期量‒基期量基期量截位直除法求平均增长率：如果基期量为A，第n+1期（或经n期）变为B,平均增长率为x%x%=-1nBA代入法，公式法B=A（1+X%）n当x%较小时可简化为B=A（1+nx%）求两期混合增长率：如果第一期和第二期增长率分别为r1和r2，那么第三期相对第一期增长率为r3r3= r1+r2+r1r2简单记忆口诀：连续增长，最终增长大于增长率之和；连续下降，最终下降小于增长率之和（正负号带进公式计算）求总体增长率：整体分为A,B两个部分，分别增长a%与b%，整体增长率x%x%=A×a%+B×b%A+B x%=a%+B(b%-a%)A+B已知总体增长率和其中一个部分的增长率，求另一部分的增长率增长率计算求混合增长率：整体为A，增长率为a%，分为两个部分B,C，增长率为b%和c%混合增长率a%介于b%和c%之间混合增长率大小居中增长率比较已知现期量与增长量比较增长率=代替增现期量基期量长率进行大小比较相当于分数大小比较发展速度已知现期量与基期量发展速度==1+增长率现期量基期量截位直除法，插值法已知部分增长量与整体增长量增长贡献量=部分增长量整体增长量截位直除法，插值法增长贡献率贡献率贡献率%=贡献量（产出量，所得量）投入量（消耗量，占用量）贡献率是指有效或有用成果数量与资源消耗及占用量之比，即投入量与产出量之比拉动增长求B拉动A增长几个百分点:如果B是A的一部分，B拉动A增长x%x%=B的增长量A的基期量截位直除法，插值法某部分现期量为A，整体现期量为为B现期比重=AB截位直除法，插值法某部分基期量为A，增长率a%，整体基期量为B，增长率b%现期比重=AB×1+a%1+b%一般先计算，然后AB根据a和b的大小判断大小某部分现期量为A，增长率a%，整体现期量为B，增长率b%基期比重=×AB1+b%1+a%一般先计算，然后AB根据a和b的大小判断大小比重计算求基期比重-现期比重：某部分现期量为A增长率a%,整体现期量为B，增长率b%两期比重差值计算：现期比重-基期比重=-×ABAB1+b%1+a%=×（1-）AB1+b%1+a%=×ABa%‒b%1+a%1.先根据a与b的大小判断差值计算结果是正数还是负数；2.答案小于|a-b|3.估算法（近似取整估算）4.直除法某部分现期量为A，整体现期量为B 现期比重=AB相当于分数大小比较，同上述做法比重比较基期比重与现期比重比较：某部分现期量为A，增长率a%，整体现期量为B，增长率b%基期比重=×AB1+b%1+a%直除法，当部分增长率大于整体增长率，则现期比重大于基期比重。

资料分析公式汇总

考点已知条件计算公式方法与技巧备注基期量计算已知现期量，增长率x%基期量=截位直除法，特殊分数法已知现期量，相对基期量增加M倍基期量=截位直除法已知现期量，相对基期量的增长量N基期量=现期量-N尾数法，估算法基期量比较已知现期量，增长率x%比较：基期量=1.截位直除法2.化同法（分数大小比较）3.直除法（首位判断或差量比较）4.差分法如果现期量差距较大，增长率相差不大，可直接比较现期量现期量计算已知基期量，增长率x%现期量=基期量+基期量×x%=基期量×（1+x%）特殊分数法，估算法已知基期量，相对基期量增加M倍现期量=基期量+基期量×M=基期量×（1+M）估算法已知基期量，增长量N现期量=基期量+N尾数法，估算法增长量计算已知基期量，现期量增长量=现期量-基期量尾数法已知基期量，增长率x%增长量=基期量×x%特殊分数法已知现期量，增长率x%增长量=×x% 1.特殊分数法，当x%可以被视为时，公式可被简化为：增长量=2.估算法（倍数估算）或分数的近似计算（看大则大，看小则小）如果基期量为A，经N期变为B，平均增长量为xx=直除法增长量比较已知现期量，增长率x%增长量=×x% 1.特殊分数法，当x%可以被视为时，公式可被简化为：增长量=2.公式可变换为：增长量=现期量×，其中为增函数，所以现期量大，增长率大的情况下，增长量一定大增长率计算已知基期量，增长量增长率=截位直除法，插值法已知现期量，基期量增长率=截位直除法求平均增长率：如果基期量为A，第n+1期（或经n期）变为B,平均增长率为x%x%=-1代入法，公式法B=A（1+X%）n当x%较小时可简化为B=A（1+nx%）求两期混合增长率：如果第一期和第二期增长率分别为r1和r2，那么第三期相对第一期增长率为r3= r1+r2+r1r2简单记忆口诀：连续增长，最终增长大于增长率之和；连续下降，最终下降小于增长率之和（正负号带进公式计算）r3求总体增长率：整体分为A,B两个部分，分别增长a%与b%，整体增长率x%x%=x%=a%+已知总体增长率和其中一个部分的增长率，求另一部分的增长率求混合增长率：整体为A，增长率为a%，分为两个部分B,C，增长率为b%和c%混合增长率a%介于b%和c%之间混合增长率大小居中增长率比较已知现期量与增长量比较增长率=代替增长率进行大小比较相当于分数大小比较发展速度已知现期量与基期量发展速度==1+增长率截位直除法，插值法增长贡献率已知部分增长量与整体增长量增长贡献量=截位直除法，插值法贡献率贡献率%=贡献率是指有效或有用成果数量与资源消耗及占用量之比，即投入量与产出量之比拉动增长求B拉动A增长几个百分点:如果B是A的一部分，B拉动A增长x%x%=截位直除法，插值法比重计算某部分现期量为A，整体现期量为为B现期比重=截位直除法，插值法某部分基期量为A，增长率a%，整体基期量为B，增长率b%现期比重=一般先计算，然后根据a和b的大小判断大小某部分现期量为A，增长率a%，整体现期量为B，增长率b%基期比重=×一般先计算，然后根据a和b的大小判断大小求基期比重-现期比重：某部分现期量为A增长率a%,整体现期量为B，增长率b%两期比重差值计算：现期比重-基期比重=-×=×（1-）=×1.先根据a与b的大小判断差值计算结果是正数还是负数；2.答案小于|a-b|3.估算法（近似取整估算）4.直除法比重比较某部分现期量为A，整体现期量为B现期比重=相当于分数大小比较，同上述做法基期比重与现期比重比较：某部分现期量为A，增长率a%，整体现期量为B，增长率b%基期比重=×直除法，当部分增长率大于整体增长率，则现期比重大于基期比重。

资料分析公式汇总

资料分析公式汇总速算技巧一、估算法精度要求不高的情况下，进行粗略估值的速算方式。

选项相差较大，或者在被比较的数字相差必须比较大，差距的大小将直接决定对“估算”时对精度的要求。

二、直除法在比较或者计算较复杂的分数时，通过“直接相除”的方式得到商的首位（首一位、首两位、首三位），从而得出正确答案的速算方式。

常用形式： 1.比较型：比较分数大小时，若其量级相当，首位最大∕小数为最大∕小数2.计算型：计算分数大小时，选项首位不同，通过计算首位便可得出答案。

难易梯度：1.基础直除法：①可通过直接观察判断首位的情形；②需要通过手动计算判断首位的情形。

2.多位直除法：通过计算分数的“首两位”或“首三位”判断答案情形。

三、插值法1.“比较型”插值法如果A与B的比较，若可以找到一个数C，使得A﹥C，而B﹤C，既可以判定A﹥B；若可以找到一个数C，使得A﹤C，而B﹥C，既可以判定A﹤B；2.“计算型”插值法若A﹤C﹤B，则如果f﹥C，则可以得到f=B;如果f﹤C，则可以得到f=A；若A﹥C﹥B，则如果f﹥C，则可以得到f=A;如果f﹤C，则可以得到f=B。

四、放缩法当计算精度要求不高时，可以将中间结果进行大胆的“放”（扩大）或者“缩”（缩小），从而迅速得到精度足够的结果。

常用形式：1. A﹥B,C﹥D,则有A+C﹥B+D；A-D﹥B-C；2. A﹥B﹥0，C﹥D﹥0，则有A×C﹥B×D；A÷D﹥B÷C五、割补法在计算一组数据的平均值或总和值时，首先选取一个中间值，根据中间值将这组数据“割”（减去）或“补”（追上），进而求取平均值或总和值。

常用形式:1.根据该组数据，粗略估算一个中间值；2.将该组值分别减去中间值得到一组数值；3.将得到的新数值相加得到和值，用和值除以该组数值的项数得到商值，将商值加上中间值，即为该组数值的精确平均值；4.用中间值乘以数据项数再加上最后的和值即为总和值。

行测资料分析常用公式

行测资料分析常用公式
1.百分比计算公式：
百分比=（部分/全部）×100%
2.平均数计算公式：
平均数=总和/数量
3.增长率计算公式：
增长率=（增加量/原始量）×100%
4.比例计算公式：
比例=（部分/全部）×100%
5.环比增长率计算公式：
环比增长率=（本期数-上期数）/上期数×100%
6.季度增长率计算公式：
季度增长率=（本季度数-上季度数）/上季度数×100% 7.面积计算公式：
矩形面积=长×宽
圆的面积=π×半径^2
三角形面积=底×高/2
8.速度计算公式：
速度=路程/时间
9.利息计算公式：
利息=本金×利率×时间
10.折扣率计算公式：
折扣率=（原价-折扣价）/原价×100%
11.投资收益率计算公式：
投资收益率=（收益-成本）/成本×100%
12.年增长率计算公式：
年增长率=（今年数-去年数）/去年数×100%
13.运动距离计算公式：
运动距离=初速度×时间+加速度×时间^2/2
14.分数计算公式：
百分数=数分/总分×100%
15.概率计算公式：
概率=指定事件发生的次数/总事件的次数
以上是一些行测资料分析中常用的计算公式，考生在应用这些公式的时候，需要灵活运用，并且注意理解题目中给出的信息和要求，正确选择合适的公式进行计算。

在考试前做好公式的记忆和理解，对于提高行测得分是非常有帮助的。

资料分析计算公式整理

资料分析计算公式整理在进行资料分析时，掌握一些常用的计算公式能够帮助我们更高效、准确地处理数据和得出结论。

以下是对一些重要的资料分析计算公式的整理。

一、增长类计算公式1、增长量＝现期量基期量例如，2022 年某公司的销售额为 100 万元，2021 年为 80 万元，那么增长量就是 100 80 ＝ 20 万元。

2、增长率＝增长量 ÷基期量 × 100%用上例的数据，增长率为（20 ÷ 80）× 100% ＝ 25% 。

3、基期量＝现期量 ÷（1 ＋增长率）假设 2023 年某产品的销量为 120 万件，同比增长 20%，则 2022 年的销量（基期量）为 120 ÷（1 ＋ 20%）＝ 100 万件。

4、现期量＝基期量 ×（1 ＋增长率）如果已知 2021 年某地区的人口为 50 万人，预计每年以 5%的速度增长，那么 2025 年的人口（现期量）为 50 ×（1 ＋ 5%）＾4 万人。

二、比重类计算公式1、比重＝部分量 ÷整体量 × 100%比如，某班级男生有 20 人，全班共有 50 人，那么男生所占比重为（20 ÷ 50）× 100% ＝ 40% 。

2、部分量＝整体量 ×比重若已知某公司总利润为 1000 万元，其中 A 产品的利润占比为 30%，则 A 产品的利润为 1000 × 30% ＝ 300 万元。

3、整体量＝部分量 ÷比重比如某企业中研发部门的人数为 50 人，占总人数的 20%，则该企业总人数为 50 ÷ 20% ＝ 250 人。

三、平均数类计算公式1、平均数＝总数 ÷个数例如，某班级5 名学生的数学成绩分别为80、90、85、95、75 分，那么平均成绩为（80 ＋ 90 ＋ 85 ＋ 95 ＋ 75）÷ 5 ＝ 85 分。

资料分析计算公式整理

资料分析计算公式整理在进行数据分析时，计算公式是一个非常重要的工具。

它们可以帮助我们对数据进行深入的理解和解释。

本文将整理一些常用的资料分析计算公式，以供参考使用。

一、中心趋势测量1. 平均值（Mean）平均值是最常用的中心趋势测量指标，用于衡量一组数据的集中程度。

计算公式如下：\[ \bar{x} = \frac{{x_1 + x_2 + \cdots + x_n}}{n} \]其中，$ x_1, x_2, \cdots, x_n $ 为数据集中的数据值，$ n $ 为数据点的个数。

2. 加权平均值（Weighted Mean）加权平均值是在计算平均值时，根据每个数据点的权重给予不同的重要程度。

计算公式如下：\[ \bar{x} = \frac{{w_1x_1 + w_2x_2 + \cdots + w_nx_n}}{w_1 + w_2 + \cdots + w_n} \]其中，$ w_1, w_2, \cdots, w_n $ 表示每个数据点的权重。

3. 中位数（Median）中位数是一组数据中的中间值，能够较好地反映数据的集中程度。

计算公式如下：若数据个数 $ n $ 为奇数：\[ \text{Median} = x_{\frac{n+1}{2}} \]若数据个数 $ n $ 为偶数：\[ \text{Median} = \frac{{x_{\frac{n}{2}} + x_{\frac{n}{2} + 1}}}{2} \]4. 众数（Mode）众数是一组数据中出现次数最多的数据值。

一组数据可能有一个或多个众数，也可能没有众数。

二、离散趋势测量1. 范围（Range）范围是一组数据的最大值与最小值之间的差异程度。

计算公式如下：\[ \text{Range} = \text{最大值} - \text{最小值} \]2. 四分位距（Interquartile Range，IQR）四分位距用于描述数据的分散程度，它是上四分位数与下四分位数之间的差异程度。

资料分析公式汇总

欢迎共阅资料分析公式汇总考点已知条件计算公式方法与技巧备注基期量计算已知现期量，增长率x%基期量=截位直除法，特殊分数法已知现期量，相对基期量增加M倍基期量=截位直除法已知现期量，相对基期量的增长量N基期量=现期量-N 尾数法，估算法基期量比较已知现期量，增长率x%比较：基期量=1.截位直除法2.化同法（分数大小比较）3.直除法（首位判断或差量比较）4.差分法如果现期量差距较大，增长率相差不大，可直接比较现期量现期量计算已知基期量，增长率x%现期量=基期量+基期量×x%=基期量×（1+x%）特殊分数法，估算法已知基期量，相对基期量增加M倍现期量=基期量+基期量×M=基期量×（1+M）估算法已知基期量，增长量N现期量=基期量+N 尾数法，估算法增长量计算已知基期量，现期量增长量=现期量-基期量尾数法已知基期量，增长率x%增长量=基期量×x% 特殊分数法已知现期量，增长率x%增长量=×x%1.特殊分数法，当x%可以被视为时，公式可被简化为：增长量=2.估算法（倍数估算）或分数的近似计算（看大则大，看小则小）如果基期量为A，经N期变为B，平均增长量为xx=直除法增长量已知现期量，增 1.特殊分数法，当x%可被简化为：增长量=2.公式可变换为：增长量=现期量×，其中为增函数，所以现期量大，增长率大的情况下，增长量一定大增长率计算已知基期量，增长量增长率=截位直除法，插值法已知现期量，基期量增长率=截位直除法求平均增长率：如果基期量为A，第n+1期（或经n期）变为B,平均增长率为x%x%=-1代入法，公式法B=A（1+X%）n当x%较小时可简化为B=A（1+nx%）求两期混合增长率：如果第一期和第二期增长率分别为r1和r2，那么第三期相对第一期增长率为r3r3=r1+r2+r1r2 简单记忆口诀：连续增长，最终增长大于增长率之和；连续下降，最终下降小于增长率之和（正负号带进公式计算）求总体增长率：整体分为A,B两个部分，分别增长a%与b%，整体增长率x%x%=x%=a%+已知总体增长率和其中一个部分的增长率，求另一部分的增长率求混合增长率：整体为A，增长率为a%，分为两个部分B,C，增长率为b%和c%混合增长率a%介于b%和c%之间混合增长率大小居中增长率比较已知现期量与增长量比较增长率=代替增长率进行大小比较相当于分数大小比较发展速度已知现期量与基期量发展速度==1+增长率截位直除法，插值法增长贡已知部分增长量截位直除法，=数量与资源消耗及占用量之比，即投入量与产出量之比拉动增长求B拉动A增长几个百分点:如果B是A的一部分，B拉动A增长x%x%=截位直除法，插值法比重计算某部分现期量为A，整体现期量为为B现期比重=截位直除法，插值法某部分基期量为A，增长率a%，整体基期量为B，增长率b%现期比重=一般先计算，然后根据a和b的大小判断大小某部分现期量为A，增长率a%，整体现期量为B，增长率b%基期比重=×一般先计算，然后根据a和b的大小判断大小求基期比重-现期比重：某部分现期量为A增长率a%,整体现期量为B，增长率b%两期比重差值计算：现期比重-基期比重=-×=×（1-）=×1.先根据a与b的大小判断差值计算结果是正数还是负数；2.答案小于|a-b|3.估算法（近似取整估算）4.直除法比重比较某部分现期量为A，整体现期量为B现期比重=相当于分数大小比较，同上述做法基期比重与现期比重比较：某部分现期量为A，增长率a%，整体现期量为B，增长率b%基期比重=×直除法，当部分增长率大于整体增长率，则现期比重大于基期比重。

资料分析报告计算公式整理

平均数计算
（29）已知N个量的值，求平均数
凑整法
直接读数类
（30）方法：读题做标记，辅助工具（直尺）
综合分析题
（31）四项基本原则：题干短原则，不计算原则（时间与材料时间一致），信息易得原则，简单计算原则
比较代替增长率进行大小比较
相当于分数大小比较，同上述做法
发展速度
（20）已知今年量与去年量
（1）截位直除法
（2）插值法
增长贡献率
（21）已知部分增长量与整体增长量
（1）截位直除法
（2）插值法
拉动增长
（22）如果B是A的一部分，B拉动A增长x%
（1）截位直除法
（2）插值法
比重计算
（23）某部分今年量为A，整体今年量为B
（2）公式可变换为：，其中为增函数，所以今年量大，增长率大的情况下，增长量一定大
(大大则大)
增长率计算
（13）已知去年量与增长量
（1）截位直除法
（2）插值法
（14）已知今年量与去年量
截位直除法
（15）如果去年量为A，经N期变为B，平均增长率为x%
代入法或公式法
（16）两期混合增长率：如果第二期与第三期增长率分别为与，那么第三期相对第一期增长率
简单记忆口诀：连续增长，最终增长大于增长率之和；连续下降，最终下降小于增长率之和
（17）合成增长率：整体分为A、B两个部分，分别增长a%与b%，整体增长率r%
（18）混合增长率：整体为A，增长率为，分为两个部分B和C，增长率为和
则介于和之间
混合增长率大小居中
增长率比较
（19）已知今年量与增长量
资料分析计算公式整理
考点
已知条件
计算公式

资料分析常用公式

资料分析常用公式1. 平均数公式平均数（Mean）是表示一组数据集中趋势的量数，计算公式为：$$\text{平均数} = \frac{\sum_{i=1}^{n} x_i}{n}$$其中，$ x_i $ 表示第 $ i $ 个数据，$ n $ 表示数据的总数。

平均数适用于描述数据的中心位置，常用于市场调查、产品评价等领域。

2. 中位数公式中位数（Median）是将一组数据从小到大（或从大到小）排列，位于中间位置的数值。

计算公式为：$$\text{中位数} = \begin{cases}x_{\frac{n+1}{2}} & \text{当 } n \text{ 为奇数时} \\\frac{x_{\frac{n}{2}} + x_{\frac{n}{2}+1}}{2} & \text{当 } n \text{ 为偶数时}\end{cases}$$中位数适用于描述数据的中心位置，特别适用于数据分布不均匀或存在异常值的情况。

3. 标准差公式标准差（Standard Deviation）是衡量一组数据离散程度的量数，计算公式为：$$\sigma = \sqrt{\frac{\sum_{i=1}^{n} (x_i \mu)^2}{n}}$$其中，$ \sigma $ 表示标准差，$ x_i $ 表示第 $ i $ 个数据，$ \mu $ 表示平均数，$ n $ 表示数据的总数。

标准差越大，表示数据的离散程度越大，反之越小。

4. 相关系数公式相关系数（Correlation Coefficient）用于衡量两个变量之间的线性关系程度，计算公式为：$$r = \frac{n(\sum xy) (\sum x)(\sum y)}{\sqrt{[n\sum x^2 (\sum x)^2][n\sum y^2 (\sum y)^2]}}$$其中，$ r $ 表示相关系数，$ x $ 和 $ y $ 分别表示两个变量，$ n $ 表示数据的总数。