锐角三角比计算题
沪教版九年级上册数学第二十五章 锐角的三角比含答案(必刷题)

沪教版九年级上册数学第二十五章锐角的三角比含答案一、单选题(共15题,共计45分)1、拦水坝横断面如图所示,迎水坡的坡度(坡的竖直高度与水平宽度的比)是,坝高,则坡面的长度是()A. B. C. D.2、如图,一个梯子靠在垂直水平地面的墙上,梯子AB的长是2米.若梯子与地面的夹角为,则梯子顶端到地面的距离(BC的长)为()A. 米B. 米C. 米D. 米3、已知CD是Rt△ABC斜边AB上的高,AC=8,BC=6,则cos∠BCD的值是()A. B. C. D.4、如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC= ,∠ADC= ,则竹竿AB与AD的长度之比为A. B. C. D.5、如图,⊙O与正方形ABCD是两边AB,AD相切,DE与⊙O相切于点E,若正方形ABCD的边长为5,DE=3,则tan∠ODE为()A. B. C. D.6、如图,已知点A(-1,0)和点B(1,2),在坐标轴上确定点P,使得△ABP为直角三角形,则满足这样条件的点P共有()A.2个B.3个C.6个D.7个7、在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,那么∠AOB的大小为()A.70°B.110°C.120°D.141°8、某人沿倾斜角为30°的斜坡前进50米,则他上升的最大高度为()A.25米B.25 米C.20 米D.25 米9、下列计算结果正确的是()A. (﹣a3)2=a9B. a2•a3=a6C. ﹣22=﹣2D.-=110、在Rt△ABC中,∠C=900,则下列式子成立的是()A.sinA=sinBB.sinA=cosBC.tanA=tanBD.cosA=tanB11、已知Rt△ABC中,∠C=90º,那么cosA表示()的值A. B. C. D.12、国家近年来实施了新一轮农村电网改造升级工程,解决了农村供电“最后1公里”问题,电力公司在改造时把某一输电线铁塔建在了一个坡度为1:0.75的山坡CD的平台BC上(如图),测得∠AED=52°,BC=5米,CD=35米,DE =19米,则铁塔AB的高度约为(参考数据:sin52°≈0.79,tan52°≈1.28)()A.28米B.29.6米C.36.6米D.57.6米13、对于sin60°有下列说法:①sin60°是一个无理数;②sin60°>sin50°;③sin60°=6sin10°。
沪教版 九年级数学 锐角三角比的模考汇编复习

锐角三角比的模考汇编复习知识定位考情分析:锐角的三角比相关内容作为模拟考以及中考常见知识点之一,常出现在选择题、填空题以及解答题中,其本身知识点难度不高,因而考题较为简单。
本讲主要讲解锐角的三角比的意义、特殊锐角的三角比的值、各锐角的三角比的关系以及解直角三角形的三种应用,即分别是关于坡度坡角、仰角俯角和方向角问题。
相关重点是会根据直角三角形中两边的长求相应的锐角的三角比的值,熟练运用特殊的锐角的三角比的值进行相关计算,而难点是在几何图形和直角坐标系中灵活运用锐角的三角比进行解题,以及各锐角的三角比的关系在代数中的灵活运用。
考试占比:一般单纯考察锐角三角比的试题分值至少在14分左右,此外函数压轴题以及几何压轴题中还会涉及部分的解直角三角形的应用,因而这部分的内容显得格外重要,由于锐角三角比本身难度较小,因此同学们只要平时加强练习,都可以完全攻克这部分内容!!!童鞋,你做好学习本节课的准备了么?Are you ready?题型梳理例题精讲题型梳理1:锐角三角比的概念辨析 【题目】【2018徐汇区一模】在Rt △ABC 中,∠C=90°,a 、b 、c 分别是∠A 、∠B 、∠C 的对边,下列等式中,正确的是( ) A .cb A =sin B .ac B =cos C .ba A =tan D .ab B =cot 【题目分析】本题考察了锐角三角函数的定义,在Rt △ABC 中,∠C=90°:(1)正弦:我们把锐角A 的对边a 与斜边c 的比叫做∠A 的正弦,记作sinA ; (2)余弦:锐角A 的邻边b 与斜边c 的比叫做∠A 的余弦,记作cosA ; (3)正切:锐角A 的对边a 与邻边b 的比叫做∠A 的正切,记作tanA ; (4)三角函数:锐角A 的正弦、余弦、正切都叫做∠A 的锐角三角函数; 因此先根据题意画出图形,再根据三角函数的定义解答即可,属于基础概念题。
【答案】C 【解析】解:根据三角函数的定义:A 、c a A =sin ,错误;B 、c aB =cos ,错误;C 、b a A =tan ,正确;D 、baB =cot ,错误故选:C 。
锐角的三角比(考题猜想,易错必刷40题7种题型专项训练)(学生版) 2025学年九年级数学上学期期中

专题02锐角的三角比(考题猜想,易错必刷40题7种题型专项训练)锐角三角函数的定义 特殊角的三角函数值解直角三角形 解直角三角形的应用解直角三角形的应用-坡度坡角问题 有理数大小比较解直角三角形的应用-方向角问题一.锐角三角函数的定义(共2小题)1.(2024•闵行区)在Rt ABC ∆中,90C ∠=︒,3AB =,2AC =,那么cos A 的值是()A .13B .23C .D 2.(2023•松江区一模)已知Rt ABC ∆中,90C ∠=︒,2AC =,3BC =,那么下列结论正确的是()A .2tan 3A =B .2cot 3A =C .2sin 3A =D .2cos 3A =二.特殊角的三角函数值(共7小题)3.(2023秋•宝山区期中)tan 45︒的值等于()A .2B .1CD 4.(2024•崇明区)计算:2sin 60cos 45cos303tan 30︒︒-+︒︒.5.(2023秋•金山区期末)计算:2sin 451cot 60cos30tan 45︒-+︒⋅︒︒.6.(2023秋•闵行区期中)计算:cos 45tan 60cot 451sin 30︒-︒-︒-︒.7.(2023秋•黄浦区校级期中)计算:2tan 452cos 45sin 60cot 30︒-+︒︒⋅︒.8.(2023秋•长宁区校级期中)计算:tan 452|1sin 60|cot 302cos 45︒-︒+︒-︒.9.(2023秋•浦东新区校级期中)计算:sin 45cos30sin 30(cos 45sin 60)32cos 60︒+︒-︒︒-︒-︒三.解直角三角形(共4小题)10.(2023秋•长宁区校级月考)已知点(1,2)A 在平面直角坐标系xOy 中,射线OA 与x 轴正半轴的夹角为α,那么cos α的值为.11.(2022秋•嘉定区校级期末)已知在DEF ∆中,12DE DF ==,10EF =,那么cos E =.12.(2022秋•金山区校级期末)如图,在ABC ∆中,1sin 4B =,1tan 2C =,4AB =,则AC 的长为.13.(2022秋•奉贤区期中)已知:如图,在ABC ∆中,15AB AC ==,4tan 3A =.求:(1)ABC S ∆;(2)B ∠的余弦值.四.解直角三角形的应用(共4小题)14.(2022•徐汇区模拟)激光电视的光源是激光,它运用反射成像原理,屏幕不通电无辐射,降低了对消费者眼睛的伤害.根据THX 观影标准,当观影水平视场角“θ”的度数处于33︒到40︒之间时(如图1),双眼肌肉处于放松状态,是最佳的感官体验的观影位.(1)小丽家决定要买一个激光电视,她家客厅的观影距离(人坐在沙发上眼睛到屏幕的距离)为3.5米,小佳家要选择电视屏幕宽(图2中的BC 的长)在什么范围内的激光电视就能享受黄金观看体验?(结果精确到0.1m ,参考数据:sin 330.54︒≈,tan 330.65︒≈,sin 400.64︒≈,tan 400.84︒≈,sin16.50.28︒≈,tan16.50.30︒≈,sin 200.34︒≈,tan 200.36)︒≈(2)由于技术革新和成本降低,激光电视的价格逐渐下降,某电器商行经营的某款激光电视今年每台销售价比去年降低4000元,在销售量相同的情况下,今年销售额在去年销售总额100万元的基础上减少20%,今年这款激光电视每台的售价是多少元?15.(2022•长宁区模拟)冬至是一年中太阳光照射最少的日子,如果此时楼房最低层能采到阳光,一年四季整座楼均能受到阳光的照射,所以冬至是选房买房时确定阳光照射的最好时机.某居民小区有一朝向为正南方向的居民楼.该居民楼的一楼是高6米的小区超市,超市以上是居民住房,在该楼前面20米处要盖一栋高25米的新楼.已知上海地区冬至正午的阳光与水平线夹角为29︒(参考数据:sin290.48︒≈;︒≈cos290.87︒≈;tan290.55)(1)冬至中午时,超市以上的居民住房采光是否有影响,为什么?(2)若要使得超市全部采光不受影响,两楼应至少相距多少米?(结果保留整数)16.(2023秋•静安区期中)图1是一种折叠式晾衣架.晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,两支脚10OA OB==分米,晾衣臂支架6HG FE==∠=︒,晾衣臂10CODOC OD==分米,展开角60分米,且4≈==分米. 1.73)HO FO(1)当90∠=︒时,求点A离地面的距离AM约为多少分米;(结果精确到0.1)AOC(2)当OB从水平状态旋转到OB'(在CO延长线上)时,点E绕点F随之旋转至OB'上的点E'处,求''-为多少分米.B E BE17.(2022•崇明区二模)为解决群众“健身去哪儿”问题,某区2021年新建、改建90个市民益智健身苑点,图1是某益智健身苑点中的“侧摆器”.锻炼方法:面对器械,双手紧握扶手,双脚站立于踏板上,腰部发力带动下肢做左右摆式运动.(1)如图2是侧摆器的抽象图,已知摆臂OA的长度为80厘米,在侧摆运动过程中,点A为踏板中心在侧摆运动过程中的最低点位置,点B为踏板中心在侧摆运动过程中的最高点位置,25BOA∠=︒,求踏板中心点在最高位置与最低位置时的高度差.(精确到0.1厘米)(sin250.423︒≈,cos250.906︒≈,tan250.466)︒≈(2)小杰在侧摆器上进行锻炼,原计划消耗400大卡的能量,由于小杰加快了运动频率,每小时能量消耗比原计划增加了100大卡,结果比原计划提早12分钟完成任务,求小杰原计划完成锻炼需多少小时?五.解直角三角形的应用-坡度坡角问题(共5小题)18.(2024•南岗区校级一模)如图,先锋村准备在坡角为α的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为()A.5cosαB.5cosαC.5sinαD.5sinα19.(2022秋•黄浦区期末)如图,某幢楼的楼梯每一级台阶的高度为20厘米,宽度为30厘米,那么斜面AB 的坡度为.20.(2023秋•杨浦区期末)小华沿着坡度1:3i =的斜坡向上行走了米,那么他距离地面的垂直高度上升了米.21.(2023•普陀区二模)如图,斜坡AB 的坡度1i =AH 的情况下将坡度变缓,调整后的斜坡AC 的坡度21:2.4i =,已知斜坡10AB =米,那么斜坡AC =米.22.(2022秋•静安区校级期末)某大型购物中心为方便顾客地铁换乘,准备在底层至1B 层之间安装电梯,截面图如图所示,底层与1B 层平行,层高AD 为9米,A 、B 间的距离为6米,20ACD ∠=︒.(1)请问身高1.9米的人在竖直站立的情况下搭乘电梯,在B 处会不会碰到头?请说明理由.(2)若采取中段平台设计(如图虚线所示).已知平台//EF DC ,且AE 段和FC 段的坡度1:2i =,求平台EF 的长度.【参考数据:sin 200.34︒≈,cos 200.94︒≈,tan 200.36︒≈】六.解直角三角形的应用-仰角俯角问题(共16小题)23.(2023秋•嘉定区期末)一架飞机在离地面6000米的上空测得某一建筑物底部的俯角为30︒,此时这架飞机与这一建筑物底部之间的距离是()A.6000米B.12000米C.60003米D.120003米24.(2023•崇明区一模)飞机离水平地面的高度为3千米,在飞机上测得该水平地面上的目标A点的俯角为α,那么此时飞机与目标A点的距离为千米.(用α的式子表示)25.(2024•徐汇区校级三模)社团活动课上,九年级学习小组测量学校旗杆的高度.如图,他们在B处测得旗杆顶部A的仰角为60︒,6BC m=,则旗杆AC的高度为m.26.(2023秋•松江区期末)如图,A处有一垂直于地面的标杆AM,热气球沿着与AM的夹角为15︒的方向升空,到达B处,这时在A处的正东方向200米的C处测得B的仰角为30(AM︒、B、C在同一平面内).求≈A、B之间的距离.(结果精确到1米,2 1.414)27.(2022秋•闵行区期末)2022年11月12日10时03分,搭载天舟五号货运飞船的长征七号遥六运载火箭,在海南文昌航天发射场成功发射.天舟五号货运飞船重约13.6吨,长度10.6BD=米,货物仓的直径可达3.35米,是世界现役货物运输能力最大、在轨支持能力最全面的货运飞船,堪称“在职最强快递小哥”.已知飞船发射塔垂直于地面,某人在地面A处测得飞船底部D处的仰角45︒,顶部B处的仰角为53︒,求此时观测点A到发射塔CD的水平距离(结果精确到0.1米).(参考数据:sin530.80︒≈,︒≈,cos530.60︒≈tan53 1.33)28.(2022秋•闵行区期中)如图,在电线杆上的C处引拉线CE和CF固定电线杆.在离电线杆6米的B处安置测角仪(点B、E、D在同一直线上),在点A处测得电线杆上C处的仰角为30︒.已知测角仪的高AB 3米,拉线CE的长为6米,求测角仪底端(点)B与拉线固定点(E)之间的距离.29.(2024•上海模拟)如图,某处有一座塔AB,塔的正前方有一平台DE,平台的高5DG=米,斜坡CD 的坡度5:12i=,点A,C,G,F在同一条水平直线上.某数学兴趣小组为测量该塔的高度,在斜坡C处测得塔顶部B的仰角为54.5︒,在斜坡D处测得塔顶部B的仰角为26.7︒,求塔高AB.(精确到0.1米)(参考数据:tan54.5 1.40︒≈︒≈,sin26.70.45︒≈,cos26.70.89)︒≈,tan26.70.50︒≈,sin54.50.81︒≈,cos54.50.5830.(2024•崇明区)如图,某校九年级兴趣小组在学习了解直角三角形知识后,开展了测量山坡上某棵大树高度的活动.已知小山的斜坡BM的坡度1:3BN,i=,在坡面D处有一棵树AD(假设树AD垂直水平线)在坡底B处测得树梢A的仰角为45︒,沿坡面BM方向前行30米到达C处,测得树梢A的仰角ACQ∠为60︒.(点B、C、D在一直线上)(1)求A、C两点的距离;(2)求树AD的高度(结果精确到0.1米).(参考数据:3 1.732)≈31.(2023秋•黄浦区期末)在世纪公园的小山坡上有一棵松树,初三(3)班的雏鹰小队带着工具对这棵松树进行测量,并试图利用所学的数学知识与方法推算出这棵松树的高度.他们选好位置架设测角仪先测出了这棵松树的根部与顶端的仰角,并绘制了如下示意图:测角仪为MN ,树根部为B 、树顶端为A ,其中1.5MN m =,视线MB 的仰角为α(已知1tan )6α=,视线MA 的仰角为β(已知3tan )4β=.(1)测得这两个数据后,小明说:“我可以算出这棵松树的高度了.”小聪接着说:“不对吧,只知道这两个角度,这个示意图显然是可以进行放大或缩小的,高度一定是确定不了的.如果还能测出测角仪到松树的垂直距离,即图示中NH 的长度,就可以了.”设NH a =,请你用含有a 的代数式表示松树()AB 的高度.(2)小明又反问道:“虽然我们带了尺,是一把刻度精确到1分米,长为2米的直尺,但也没有办法量出NH 的长度,我们总不能把坡给挖平了吧?”请你想一个测量办法,利用现有的工具,测量出有关数据(数据可以用字母常数表示),并用含有这些字母常数的表达式表示出松树()AB 的高度.32.(2023秋•长宁区期末)小明为测量河对岸大楼的高度,利用量角器和铅锤自制了一个简易测角仪,如图1所示.测量方法:如图2,人眼在P点观察所测物体最高点C,量角器零刻度线上A、B两点均在视线PC上,将铅锤悬挂在量角器的中心点O.当铅锤静止时,测得视线PC与铅垂线OD所夹的角为α,且此时的仰角为β.实践操作:如图3,小明利用上述工具测量河对岸垂直于水平地面的大楼EF的高度.他先站在水平地面的点H处,视线为GE,此时测角仪上视线与铅垂线的夹角为60︒;然后他向前走10米靠近大楼站在水平地面的点R处,视线为QE,此时测角仪上视线与铅垂线的夹角为45︒.问题解决:(1)请用含α的代数式表示仰角β;(2)如果GH、QR、EF在同一平面内,小明的眼睛到水平地面的距离为1.6米,求大楼EF的高度.(结果保留根号)33.(2023秋•静安区期末)如图,某建筑物AB 高为200米,某人乘热气球来到距地面400米的C 处(即CE 长为400米).此时测得建筑物顶部A 的俯角为α,当乘坐的热气球垂直上升到达D 处后,再次测得建筑物顶部A 的俯角为β.(tan 1.25,tan 1.75)αβ==(1)请在图中标出俯角α、β,并用计算器求α、β的大小:α≈,β≈;(精确到“1”)(2)求热气球上升的垂直高度(即CD 的长).34.(2023秋•嘉定区期末)如图,小山的顶部是一块平地,在这块平地上有一座古塔CD .小山斜坡AB 的坡度为1:2.4i =,坡长AB 为39米,在小山的坡底A 处测得该塔的塔顶C 的仰角为45︒,在坡顶B 处测得该塔的塔顶C 的仰角为74︒.(1)求坡顶B 到地面AH 的距离BH 的长;(2)求古塔CD 的高度(结果精确到1米).(参考数据:sin 740.96︒≈,cos 740.28︒≈,tan 74 3.49)︒≈35.(2022秋•嘉定区期末)《海岛算经》是中国古代测量术的代表作,原名《重差》.这本著作建立起了从直接测量向间接测量的桥梁.直至近代,重差测量法仍有借鉴意义.如图2,为测量海岛上一座山峰AH 的高度,直立两根高2米的标杆BC 和DE ,两杆间距BD 相距6米,D 、B 、H 三点共线.从点B 处退行到点F ,观察山顶A ,发现A 、C 、F 三点共线,且仰角为45︒;从点D 处退行到点G ,观察山顶A ,发现A 、E 、G 三点共线,且仰角为30︒.(点F 、G 都在直线HB 上)(1)求FG 的长(结果保留根号);(2)山峰高度AH 的长(结果精确到0.1米).(参考数据:2 1.41≈,3 1.73)≈36.(2023秋•青浦区期末)北淀浦河上的浦仓路桥是一座融合江南水乡文化气息的现代空间钢结构人行廊桥.某校九年级数学兴趣小组开展了测量“浦仓路桥顶部到水面的距离”的实践活动,他们的操作方法如下:如图,在河的一侧选取B 、C 两点,在B 处测得浦仓路桥顶部点A 的仰角为22︒,再往浦仓路桥桥顶所在的方向前进17米至C 处,在C 处测得点A 的仰角为37︒,在D 处测得地面BD 到水面EF 的距离DE 为1.2米(点B 、C 、D 在一条直线上,//BD EF ,DE EF ⊥,)AF EF ⊥,求浦仓路桥顶部A 到水面的距离AF .(精确到0.1米)(参考数据:sin 220.37︒≈,cos 220.93︒≈,tan 220.40︒≈,sin 370.60︒≈,cos 370.80︒≈,tan 370.75)︒≈37.(2023•长宁区二模)为了测量某建筑物的高度BE ,从与建筑物底端B 在同一水平线的点A 出发,沿着坡比为1:2.4i =的斜坡行走一段路程至坡顶D 处,此时测得建筑物顶端E 的仰角为30︒,再从D 处沿水平方向继续行走100米后至点C 处,此时测得建筑物顶端E 的仰角为60︒,建筑物底端B 的俯角为45︒,如图,已知点A 、B 、C 、D 、E 在同一平面内,求建筑物BE 的高度与AD 的长.(参考数据:3 1.732)≈38.(2023秋•静安区校级期中)如图1所示是一种太阳能路灯,它由灯杆和灯管支架两部分构成.如图2,AB 是灯杆,CD 是灯管支架,灯管支架CD 与灯杆间的夹角60BDC ∠=︒.综合实践小组的同学想知道灯管支架CD 的长度,他们在地面的点E 处测得灯管支架底部D 的仰角为60︒,在点F 处测得灯管支架顶部C 的仰角为30︒,测得3AE m =,8(EF m A =,E ,F 在同一条直线上).根据以上数据,解答下列问题:(1)求灯管支架底部距地面高度AD 的长(结果保留根号);(2)求灯管支架CD 的长度(结果精确到0.1m ,参考数据:3 1.73)≈.七.解直角三角形的应用-方向角问题(共2小题)39.(2023秋•青浦区校级月考)如图,某湖心岛上有一亭子A,在亭子A的正东方向上的湖边有一棵树B,在这个湖心岛的湖边C处测得亭子A在北偏西45︒方向上,测得树B在北偏东36︒方向上,又测得B、C之间的距离等于200米,求A、B之间的距离(结果精确到1米).(参考数据:2 1.414︒≈≈,sin360.588︒≈,cot36 1.376)︒≈,cos360.809︒≈,tan360.72740.(2022秋•浦东新区校级期中)如图,湖心岛上有一凉亭B,在凉亭B的正东湖边有一棵大树A,在湖边的C处测得B在北偏西45︒方向上,测得A在北偏东30︒方向上,又测得A、C之间的距离为100米,则A、B之间的距离是米(结果保留根号形式).。
初三数学锐角三角函数试题答案及解析

初三数学锐角三角函数试题答案及解析1.(2014山东德州)如图是拦水坝的横断面,斜坡AB的水平宽度为12米,斜面坡度为1︰2,则斜坡AB的长为()A.米B.米C.米D.24米【答案】B【解析】∵斜面坡度为1︰2,∴在Rt△ABC中,BC︰AC=1︰2,∴米,由勾股定理得米,故选B.2.(2013湖北十堰)如图,在小山的东侧A点有一个热气球,由于受西风的影响,以30米/分的速度沿与地面成75°角的方向飞行,25分钟后到达C处,此时热气球上的人测得小山西侧B 点的俯角为30°,则小山东西两侧A,B两点间的距离为________米.【答案】【解析】如图,过点A作AD⊥BC,垂足为D,在Rt△ACD中,∠ACD=75°-30°=45°,AC =30×25=750(米),∴米.在Rt△ABD中,易知∠B=30°,∴米.3.如图,在离水面高度为5米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒0.5米的速度收绳.问:(1)未开始收绳子的时候,图中绳子BC的长度是多少米?(2)收绳8秒后船向岸边移动了多少米?(结果保留根号)【答案】见解析【解析】(1)在Rt△ABC中,,∴(米),∴绳子BC的长度是10米.(2)未收绳时,(米),收绳8秒后,绳子BC缩短了4米,只剩6米,这时,船与河岸的距离为(米),∴船向岸边移动的距离为米.4. (2014江苏无锡)如图,在□ABCD中,AE⊥BD于E,∠EAC=30°,AE=3,则AC的长等于________.【答案】【解析】如图,在直角△AOE中,,∴.又∵四边形ABCD是平行四边形,∴.5. (2014四川宜宾)规定:sin(-x)=-sinx,cos(-x)=cosx,sin(x+y)=sinx·cosy+cosx·siny.据此判断下列等式中成立的是________(写出所有正确的序号).①;②;③sin2x=2sinx·cosx;④sin(x-y)=sinx·cosy-cosx·siny.【答案】②③④【解析】①,故①错误;②sin75°=sin(30°+45°)=sin30°·cos45°+cos30°·sin45°,故②正确;③sin2x=sinx·cosx+cosx·sinx=2sinx·cosx,故③正确;④sin(x-y)=sinx·cos(-y)+cosx·sin(-y)=sinx·cosy-cosx·siny,故④正确.6. (2014浙江绍兴)某校九(1)班的同学在上学期的社会实践活动中,对学校旁边的山坡护墙和旗杆进行了测量.(1)如图①,第一小组用一根木条CD斜靠在护墙上,使得DB与CB的长度相等,如果测量得到∠CDB=38°,求α的度数.(2)如图②,第二小组用皮尺量得EF的长为16米(E为护墙上的端点),EF的中点距离地面FB的高度为1.9米,请你求出E点距离地面FB的高度.(3)如图③,第三小组利用第一、第二小组的结果,来测量护墙上旗杆的高度,在点P处测得旗杆顶端A的仰角为45°,向前走4米到达点Q处,测得A的仰角为60°,求旗杆的高度AE(精确到0.1米.参考数据:tan60°≈1.732,tan30°≈0.577,,).【解析】(1)∵BD=BC,∴∠CDB=∠DCB,∴α=2∠CDB=2×38°=76°.(2)设EF的中点为M,过M作MN⊥BF,垂足为点N,过点E作EH⊥BF,垂足为点H,如图①.∴MN∥EH,又M为EF的中点,∴MN为△EFH的中位线,又∵MN=1.9米,∴EH=2MN=3.8米,∴E点距离地面FB的高度是3.8米.(3)延长AE,交PB于点C,如图②.设AE=x米,则AC=(x+3.8)米.∵∠APB=45°,∴PC=AC=(x+3.8)米.∵PQ=4米,∴CQ=x+3.8-4=(x-0.2)米.∵,∴,解得x≈5.7,即AE≈5.7米.答:旗杆的高度AE约为5.7米.7.(2014黑龙江大庆)如图,矩形ABCD中,,F是DA延长线上一点,G是CF上一点,且∠ACG=∠AGC,∠GAF=∠F=20°,则AB=________.【答案】【解析】∵∠GAF=∠F=20°,∴∠AGC=∠ACG=40°,∴∠CAG=100°,∴∠DAC=60°,∴,∵,∴.8.如图所示,在△ABC中,∠C=90°,,D为AC上一点,∠BDC=45°,DC=6,求AB的长.【答案】15【解析】先解直角三角形BCD,求得BC=DC=6,再解直角三角形ABC,由正弦的定义可得,从而得.所以在较复杂的图形中求线段的长度时,有时要通过两次或更多次解直角三角形才能达到目的.因为∠C=90°,∠BDC=45°,所以∠DBC=45°,所以BC=DC=6.在Rt△ABC中,,所以,即AB的长为15.9. (2014江西抚州)如图①所示的晾衣架,支架的基本图形是菱形,其示意图如图②,晾衣架伸缩时,点G在射线DP上滑动,∠CED的大小也随之发生变化,已知每个菱形边长均为20cm,且AH=DE=EG=20cm.(1)当∠CED=60°时,求C,D两点间的距离.(2)当∠CED由60°变为120°时,点A向左移动了多少厘米?(结果精确到0.1cm)(3)设DG=xcm,当∠CED的变化范围为60°~120°(包括端点值)时,求x的取值范围.(结果精确到0.1cm)(参考数据:,可使用科学计算器)【答案】(1)20cm(2)43.9cm(3)20≤x≤34.6【解析】(1)连接CD(如图①).∵CE=DE,∠CED=60°,∴△CED是等边三角形,∴CD=DE=20cm.(2)连接CD,根据题意得AB=BC=CD,当∠CED=60°时,AD=3CD=60cm.当∠CED=120°时,过点E作EH⊥CD于H(如图②),则∠CEH=60°,CH=HD.在Rt△CHE中,.∴(cm),∴cm,∴(cm).∴点A向左大约移动了103.9-60=43.9(cm).(3)连接CD,当∠CED=120°时,∠DEG=60°.又∵DE=EG,∴△DEG是等边三角形,∴DG=DE=20cm当∠CED=60°时(如图③),∠DEG=120°,过点E作EI⊥DG于点I.∵DE=EG.∴∠DEI=∠GEI=60°,DI=IG.在Rt△DIE中,,∴(cm).∴(cm).故x的取值范围是20≤x≤34.6.10. (2014贵州黔东南)某校九年级某班开展数学活动,小明和小军合作用一副三角板测量学校旗杆的高,小明站在点B处测得旗杆顶端E点的仰角为45°,小军站在点D处测得旗杆顶端E点的仰角为30°,已知小明和小军相距(BD)6米,小明的身高(AB)1.5米,小军的身高(CD)1.75米,求旗杆的高EF.(结果精确到0.1米,参考数据:,)【答案】10.3米【解析】过点A作AM⊥EF于M,过点C作CN⊥EF于N,则MN=0.25米.∵∠EAM=45°,∴AM=ME.设AM=ME=x米,则CN=(x+6)米,EN=(x-0.25)米.∵∠ECN=30°,∴,解得x≈8.8,则EF=EM+MF≈8.8+1.5=10.3(米).∴旗杆的高EF约为10.3米.11.(2014四川广安)为邓小平诞辰110周年献礼,广安市政府对城市建设进行了整改,如图,已知斜坡AB的长为米,坡角(即∠BAC)为45°,BC⊥AC,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE(下面两个小题结果都保留根号).(1)若修建的斜坡BE的坡比为,求休闲平台DE的长.(2)一座建筑物距离A点33米远(即AG=33米),小亮在D点处测得建筑物顶部H的仰角(即∠HDM)为30°.点B,C,A,G,H在同一个平面内,点C,A,G在同一条直线上,且HG⊥CG.问:建筑物的高GH为多少米?【答案】(1)米(2)米【解析】(1)∵FM∥CG,∴∠BDF=∠BAC=45°,∴BF=DF.∵斜坡AB的长为米,D是AB的中点,∴米,∴(米),∴BF=DF=30米.∵斜坡BE的坡比为,∴,∴(米),∴米.(2)由题意及(1)知CF=BF=AP=30米,又四边形MGCF为矩形,∴GM=FC=30米.设GH=x米,则MH=GH-GM=(x-30)米,DM=AG+AP=33+30=63(米).在Rt△DMH中,,即,解得.∴建筑物的高GH为米.12.(2014江苏镇江)如图,小明从点A出发,沿着坡角为α的斜坡向上走了0.65千米到达点B,,然后又沿着坡度为i=1︰4的斜坡向上走了1千米到达点C.问小明从A点到C点上升的高度CD是多少千米(结果保留根号)?【答案】【解析】如图,作BE⊥AD于E,BF⊥CD于F,则,∴.∵,∴设CF=x,则BF=4x,∴,∴.∵BE⊥AD,BF⊥CD,CD⊥AD,∴四边形BEDF是矩形,∴BE=DF.∴.答:小明从A点到C点上升的高度CD是千米.13.如图,在Rt△ABC中,∠C=90°,BC=8,,点D在BC上,且BD=AD.求AC 的长和cos∠ADC的值.【答案】4;【解析】在Rt△ABC中,∵BC=8,,∴AC=4.设AD=x,则BD=x,CD=8-x,由勾股定理,得(8-x)2+42=x2.解得x=5.∴.14.计算:(1);(2).【答案】(1)(2)1【解析】准确地掌握30°,45°,60°角的正弦、余弦、正切值是解题的关键.解:(1)(2).15.根据下列条件,求α的度数.(1)0°<α<90°,;(2)0°<α<90°,tan2α+2tanα-3=0.【答案】(1)60°(2)45°【解析】(1)因为,所以.又0°<α<90°,所以α=60°.(2)因为tan2α+2tanα-3=0,所以(tanα+3)·(tanα-1)=0,即tanα=-3或tanα=1,因为0°<α<90°,所以tanα>0,所以tanα=1,所以α=45°.16. (2014福建厦门)sin30°的值是( )A.B.C.D.1【答案】A【解析】直接根据特殊角的三角函数值进行计算即可..故选A.17. (2014贵州贵阳)在Rt△ABC中,∠C=90°,AC=12,BC=5,则sinA的值为( ) A.B.C.D.【答案】D【解析】如图所示,∵∠C=90°,AC=12,BC=5,∴,∴.18. (2014内蒙古包头)计算sin245°+cos30°·tan60°的结果是( )A.2B.1C.D.【答案】A【解析】原式.19.计算:(1).(2)cos245°+tan30°·sin60°=________.【答案】(1)2 (2)1【解析】(1).(2).20.用计算器求下列各式的值(结果保留小数点后四位):(1)sin89°;(2)cos45.32°;(3)tan60°25′41″;(4)sin67°28′35″.【答案】(1)0.9998 (2)0.7031 (3)1.7623 (4)0.9237【解析】(1)按键顺序为,显示结果为0.999847695,∴sin89°≈0.9998.(2)按键顺序为,显示结果为0.703146544,∴cos45.32°≈0.7031.(3)按键顺序为,显示结果为1.762327064,∴tan60°25′41″≈1.7623.(4)按键顺序为,显示结果为0.923721753,∴sin67°28′35″≈0.9237.。
锐角三角函数的综合常考50题

《各章节核心资料“锐角三角函数”50道常考题型》【韩春成内部核心资料(33)】知识构架一、 三角函数基础二、 锐角三角函数与代数综合 三、 化简求值 四、 比较大小五、 三角函数与几何综合典题精练三角函数基础1. 【易】︒的值是____________.2. 【易】(江西南昌十五校联考)计算:tan60︒=_______.3. 【易】(沈阳)在Rt ABC △中,C ∠为直角,sin A cos B 的值是( ) A .12 B C .1 D .4. 【易】(河南省实验中学内部中考数学第一轮复习资料4)在ABC △中,90C =︒∠,1tan 3A =,则sinB =( )A B .23 C .34D 5. 【易】(河南省实验中学内部中考数学第一轮复习资料4)若3cos 4A =,则下列结论正确的为( ) A .030A ︒<<︒∠ B .3045A ︒<<︒∠ C .4560A ︒<<︒∠ D .6090A ︒<<︒∠ 6. 【易】(2013年广东省佛山市高中阶段招生考试数学试题)如图,若60A ∠=︒,20m AC =,则BC 大约是(结果精确到0.1m )( )A .34.64mB .34.6mC .28.3mD .17.3mA CB7. 【易】(浙江省初中毕业生学业考试(湖州市))如图,已知在Rt ABC △中,90C ∠=︒,13AB =,12AC =,则cos B 的值为________8. 【易】如图,ABC △中,90C ∠=︒,12AC =,5BC =.⑴ 求AB 的长;⑵ 求sin A 、cos A 的值; ⑶ 求22sin cos A A +的值; ⑷ 比较sin A 与cos B 的大小.9. 【易】(石家庄市42中二模)在Rt ABC △中,90C ∠︒=,1BC =,2AC =,则tan A 的值为( )A .2B .12CD10. 【易】(莆田市初中毕业、升学考试试卷)已知在Rt ABC △中,90C ∠=︒,5sin 13A =,则tan B 的值为____________. 11. 【易】已知α为锐角,且5sin 13α=,求cos α的值;12. 【易】(贵阳市初中毕业生学业数学考试试题卷)如图,P 是α∠的边OA 上一点,点P的坐标为(12,5),则tan α等于( )A .513B .1213C .512D .125BCACBA13. 【难】用几何方法求15︒角的三角函数值.14. 【中】(杭州市各类高中招生文化考试)在Rt ABC △中,90C ∠=︒,2AB BC =,现给出下列结论:①sin A ;②1cos 2B =;③tan A ;④tan B 结论是__________(只需填上正确结论的序号)锐角三角函数与代数综合15. 【易】(淮南市洞山中学第四次质量检测)在ABC △中,若()2sin 1tan 0A B -=,则C ∠的度数是( )A .45︒B .60︒C .75︒D .105︒16. 【易】(海南省中考数学科模拟)在ABC △中,()2tan 12cos 0C B -=,则A ∠=______. 17. 【易】(安徽省芜湖市中考)已知锐角A 满足关系式22sin 7sin 30A A -+=,则sin A 的值为( )A .12B .3C .12或3D .418. 【易】求适合下列条件的锐角α:2cos(10)α+︒19. 【中】若方程222210x ax a -+-=的一个根是sin α,则它的另一个根必是cos α或cos α-.20. 【中】已知ABC △中,A ∠,B ∠,C ∠的对边分别是,,,a b c 若,a b 是关于x 的一元二次方程2(4)480x c x c -+++=的两个根,且925sin .c a A =⑴求证:ABC △是直角三角形; ⑵求ABC △的三边长.化简求值21. 【易】(北大附中初二第二学期期末考试)计算:tan60tan 45cos30︒-︒︒的值是___________.22. 【易】(延庆县2011-2012学年第一学期期末试卷)tan452cos30sin60-+23. 【易】(深圳初三月考)计算:2cos30cos45tan45-+°°°°24. 【易】(深圳初三月考)已知tan 2A =,求3sin cos sin cos A AA A-+的值25. 【易】(初三深圳实验第一次月考)()114cos0π 3.14tan 453-⎛⎫︒--+︒+ ⎪⎝⎭的值.26. 【易】(初三期末)sin30tan60+°°°的值为__________. 27. 【易】(河南省实验中学内部中考数学第一轮复习资料4)计算sin60tan 45cos30-的值是____________.已知3tan 0 A A ∠=则______.28. 【易】21220103tan303-⎛⎫-+-+︒ ⎪⎝⎭29. 【易】(滨州市初级中学学业水平考试)计算:()12112|52009π2-⎛⎫-++-⨯- ⎪⎝⎭.30. 【易】(怀化市初中毕业学业考试试卷)先化简,再求值:()20tan60a ab a b b a b-⨯--⋅︒-,其中1a b =,三角函数与几何综合31. 【易】(江苏沭阳银河学校质检题)在ABC △中,若tan 1A =,sin B ABC △是______三角形. 32. 【易】(江苏沭阳银河学校质检题)一等腰三角形的两边长分别为4cm 和6cm ,则其底角的余弦值为_____. 33. 【易】(兴仁中学一模)如图,在Rt ABC △中,90ACB ∠=︒,CD 是AB 边上的中线,若6BC =,8AC =,则tan ACD ∠的值为( )A .35B .45C .43D .3434. 【易】(温州市泰顺九校模拟、第一学期期末考试九年级数学试卷)直线2y x =与x 轴正半轴的夹角为α,那么下列结论正确的是( )A .tan 2α=B .1tan 2α=C .sin 2α=D .cos 2α=35. 【易】(河南省实验中学内部中考数学第一轮复习资料4)等腰ABC △中,5AB AC ==,8BC =,求底角B ∠的四个三角函数值.36. 【易】(南汇区九年级数学期末质量抽查试卷)在ABC △中,::2a b c =,那么cos A 的值为( ). ABC .12DDCBA37. 【易】(北京二中分校第一学期初三期中)已知:如图,ABC △中,135A ∠=︒,2tan 3B =,8AB =,求AC .38. 【易】(宝山区二模、北大附中2010-2011学年度初二第二学期期末考试)如图,ABC△中,AB AC =,4cos 5ABC ∠=,点D 在边BC 上,6BD =,CD AB =. ⑴求AB 的长;⑵求ADC ∠的正切值.39. 【易】(福建厦门)已知:如图,在ABC △中,90C ∠=︒DE BC ∥,3DE =,9BC =.⑴求ADAB的值; ⑵若10BD =,求sin A ∠的值.ABCCDABEDCBA40. 【易】(浦东新区中考预测)如果等腰三角形的腰长为13厘米,底边长为10厘米,那么底角的余切值等于( )A .513B .1213C .512D .12541. 【易】(罗湖初三第一次月考)如果ABC △中,sin cos A B ==,则下列最确切的结论是( )A .ABC △是直角三角形B .ABC △是等腰三角形 C .ABC △是等腰直角三角形D .ABC △是锐角三角形42. 【易】(延庆县第一学期期末试卷)在直角坐标平面内,O 为原点,点A 的坐标为(100),,点B 在第一象限内,5BO =,3sin 5BOA =∠.求:⑴点B 的坐标;⑵cos BAO ∠的值.43. 【易】(遂宁市初中毕业生学业考试)如图,已知O ⊙的两条弦AC ,BD 相交于点E ,70A =︒∠,50C =︒∠,那么sin AEB ∠的值为( )A .12BCD44. 【易】(九年级第一模拟试题)如图,在菱形ABCD 中,DE AB ⊥,4sin 5A =,2BE =,则tan BDE ∠的值是( )A .12BC .2 DABCDE45. 【易】(河南省实验中学内部中考数学第一轮复习资料4)(2012年初三期末)如图,在等腰梯形ABCD 中,AD BC ∥,2AB CD ==,AC AB ⊥,4AC =,则sin DAC ∠=( )A .12 BCD .2 46. 【易】(福建福州中考)如图,从热气球C 处测得地面A 、B 两点的俯角分别为30︒、45︒,如果此时热气球C 处的高度CD 为100米,点A 、D 、B 在同一条直线上,则A 、B 两点的距离是( )A .200米 B. C.D.)1001米47. 【易】(东城二模)如图,将三角板的直角顶点放置在直线AB 上的点O 处.使斜边CD AB ∥,则α∠的余弦值为__________.锐角三角函数48. 【易】(江苏省竞赛题)如图,等腰Rt ABC ∆中,︒=∠90C ,D 为BC 中点,将ABC ∆折叠,使A 点与D 点重合,若EF 为折痕,则BED ∠sin 的值为_______.DCBA45°30°DC BAACB DOα30°D EFABC49. 【易】(南充市中考题)如图,点E 是矩形ABCD 中CD 边上一点,BCE ∆沿BE 折叠为BFE ∆,点F 落在AD 上, ⑴ 求证:ABF ∆∽DFE ∆;⑵ 若31sin =∠DFE ,求EBC ∠tan 的值.50. 【易】(济南市中考题)如图,AOB ∠是放置在正方形网格中的一个角,则AOB ∠cos 的值是( )E《各章节核心资料“锐角三角函数”50道常考题型》答案【韩春成内部核心资料(33)】三角函数基础1.2.3. 【答案】D4. 【答案】D5. 【答案】B6.【答案】A7. 【答案】5138. 【答案】⑴∵90C ∠=︒,12AC =,5BC =,∴13AB ==. ⑵5sin 13BC A AB ==,12cos 13AC A AB ==. ⑶∵22525sin ()13169A ==,2212144cos ()13169A ==,∴2225144sin cos 1169169A A +=+= ⑷∵5cos 13BC B AB ==, ∴sin cos A B =.9. 【答案】B 10. 【答案】125 11. 【答案】121312. 【答案】C13. 【答案】如图所示,画Rt ABC ∆,使90ACB ∠=︒,D15︒30︒CBA1AC =,2AB =,30ABC ∠=︒,BC延长CB 到D ,使2BD BA ==,连接AD ,则15ADC ∠=︒.在Rt ACD ∆中,15ADC ∠=︒,1AC =,2DC =∵222AD DC AC =+2(21=+86432=+=++2262(2)=++2=∴AD =依定义得:sin15︒==;cos15︒==; tan152︒==- cot152︒=14. 【答案】②③④根据题意,因为90C =︒∠,2AB BC =,则该直角三角形是含30︒角的直角三角形,则12BC AB AC =∶∶1BC =,2AB =,AC 1sin 2BC A AB ==,②1cos 2BC B AB ==,③tan BC A AC ==④tan AC B BC ==,则答案为②③④. 锐角三角函数与代数综合15.【答案】C 16.【答案】105︒ 17.【答案】A18. 【答案】20α=︒【解析】∵2cos(10)α+︒=cos(10)α+︒=. ∵cos30︒=1030α+︒=︒,∴20α=︒. 19. 【答案】不妨设方程的另一根为m ,由一元二次方程的根系关系可知sin m a α+=,21sin 2a m α-=, 故2(sin )1sin 2m m αα+-=,整理可得22sin (sin )1m m αα=+-,即22sin 1m α+=,又22sin cos 1αα+=,故cos m α=±.20. 【答案】⑴∵,a b 是方程2(4)480x c x c -+++=的两个根,∴4,48a b c ab c +=+=+.∴222222()2(4)2(48)816816a b a b ab c c c c c c +=+-=+-+=++--=∴ABC ∆是直角三角形()90C ∠=︒.⑵在Rt ABC ∆中,sin a A c=,并代入925sin c a A =得22925.c a = ∴34,.55a cbc == 由344455a b c c c c +=++=+,. ∴10c =,且此时0∆>,从而68a b ==,化简求值21. 【答案】122. 【答案】tan452cos30sin60-+=12-+=1=1). 23. 【答案】124. 【答案】5325. 【答案】126. 27. 【答案】0,30︒28. 【答案】1029. 【答案】2-30. 【答案】()20tan60a ab a b b a b-⨯--⋅︒- ()1a a b b a b-=⨯--a b =-1a b =,∴原式12=-三角函数与几何综合31. 【答案】等腰直角.32. 【答案】34或13. 33. 【答案】D34. 【答案】A35. 【答案】3sin 5B =,4cos 5B =,3tan 4B =,4cot 3B =. 36. 【答案】B37.【答案】38. 【答案】⑴过点A 作AH BC ⊥,垂足为H∵AC AB =∴BC HC BH 21== 设x CD AC AB ===∵6=BD∴6+=x BC ,26+=x BH 在Rt △AHB 中,,又54cos =∠ABC ∴5426=+x x解得:10=x ,所以10=AB ⑵821===BC HC BH 2810=-=-=CH CD DH在Rt △AHB 中,222AB BH AH =+,又10=AB ,∴6=AH 在Rt △AHD 中,326tan ===∠DH AH ADC ∴ADC ∠的正切值是339. 【答案】⑴∵DE BC ∥,∴ADE ABC △∽△. ∴AD AB =13DE BC =. ⑵过点D 作DG BC ⊥,垂足为G .∴DG AC ∥.∴A BDG =∠∠.又∵DE BC ∥,∴四边形ECGD 是平行四边形.∴DE CG =.∴6BG =.在Rt DGB △中,GOB A ∠=∠∴sin A =∠35.AB BH ABC =∠cos40. 【答案】C41. 【答案】C42. 【答案】⑴如图,作BH OA ⊥,垂足为H在Rt OHB △中,5BO =,3sin 5BOA ∠=, 3BH ∴=.4OH ∴=.∴点B 的坐标为(43),.⑵10OA =,4OH =,6AH ∴=.在Rt AHB △中,3BH =,AB ∴=.cos AH BAO AB ∴∠==. 43.【答案】D 44.【答案】A 45.【答案】B 46. 【答案】D47. 【答案】12 锐角三角函数48. 【答案】35△AFE ≌△DFE ,45A FDE ∠=∠=︒,∵135135CDF EDB DEB EDB ∠+∠=︒∠+∠=︒,, ∴ 2DEB CDF AC CF x ∠=∠==,设,,则21DF AF x CD ==-=,,由2(2)x -= 22351 44x x DF +==,得,,3sin sin 5CF BED CDF DF ∠=∠== 49. 【答案】⑴略⑵由△ABF ∽△DFE,得EF DF BF AB ===,故tan tan EF EBC EBF BF ∠=∠=.50.△AOB 为直角三角形.。
一模复习专题3锐角三角比应用题

一模复习专题3 锐角三角比应用题1.如图,某渔船在海面上朝正西方向以20海里/时匀速航行,在A处观测到灯塔C在北偏西60°方向上,航行1小时到达B处,此时观察到灯塔C在北偏西30°方向上,若该船继续向西航行至离灯塔距离最近的位置,求此时渔船到灯塔的距离(结果精确到1海里,参考数据:≈1.732)2.如图,为求出河对岸两棵树A.B间的距离,小明在河岸上选取一点C,然后沿垂直于AC 的直线前进了12米到达D,测得∠CDB=90°.取CD的中点E,测∠AEC=56°,∠BED=67°.(1)求AC长;(2)求河对岸两树间的距离AB.(参考数据sin56°≈,tan56°≈,sin67°≈,tan67°≈)3.如图,某军港有一雷达站P,军舰M停泊在雷达站P的南偏东60°方向20海里处,另一艘军舰N位于军舰M的正西方向,与雷达站P相距10海里.求:(1)军舰N在雷达站P的什么方向?(2)两军舰M、N的距离.(结果保留根号)4.数学拓展课程《玩转学具》课堂中,小陆同学发现:一副三角板中,含45°的三角板的斜边与含30°的三角板的长直角边相等,于是,小陆同学提出一个问题:如图,将一副三角板直角顶点重合拼放在一起,点B,C,E在同一直线上,若BC=2,求AF的长.请你运用所学的数学知识解决这个问题.5.某国发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作,如图,某探测对在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米,参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,≈1.7)6.小宇想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB 与EF之间的距离为60米,求A、B两点的距离.7.芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米,≈1.732)8.如图,一垂直于地面的灯柱AB被一钢筋CD固定,CD与地面成45°夹角(∠CDB=45°),在C点上方2米处加固另一条钢线ED,ED与地面成53°夹角(∠EDB=53°),那么钢线ED的长度约为多少米?(结果精确到1米,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)9.南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向20(1+)海里的C处,为了防止某国海巡警干扰,就请求我A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.10.如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.11.小明同学需测量一条河流的宽度(河岸两边互相平行).如图,小明同学在河岸一侧选取两个观测点A、B,在河对岸选取观测点C,测得AB=31m,∠CAB=37°,∠CBA=120°.请你根据以上数据,帮助小明计算出这条河的宽度.(结果精确到0.1,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.41,≈1.73)12.某中学紧挨一座山坡,如图所示,已知AF∥BC,AB长30米,∠ABC=66°,为防止山体滑坡,需要改造山坡,改造后的山坡BE与地面成45°角,求AE是多少米?(精确到1米)(参考数据:sin66°≈0.91,cos66°≈0.41,tan66°≈2.25)13.在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.现测得AC=50m,BC=100m,∠CAB=120°,请计算A,B两个凉亭之间的距离.14.小明准备测量学校旗杆的高度,他发现斜坡正对着太阳时,旗杆AB影子恰好落在水平地面BC和斜坡面CD上,测得旗杆在水平地面上的影长BC=20m,在斜坡坡面上的影长CD=8m,太阳光线AD与水平地面成30°角,且太阳光线AD与斜坡坡面互相垂直,请你帮小明求出旗杆AB的高度(结果保根号).15.图1为大庆龙凤湿地观光塔,游客可乘坐观光电梯进入观光层向四周瞭望,鸟瞰大庆城市风光.如图2,小英在距塔底D约200米的A处测得塔球底部平台B的仰角为45°,塔尖C的仰角为60°,求平台B到塔尖C的高度BC.(精确到个位,≈1.732)16.在升旗结束后,小铭想利用所学数学知识测量学校旗杆高度,如图,旗杆的顶端垂下一绳子,将绳子拉直钉在地上,末端恰好至C处且与地面成60°角,小铭从绳子末端C处拿起绳子后退至E点,求旗杆AB的高度和小铭后退的距离.(单位:米,参考数据:≈1.41,≈1.73,结果保留一位小数)17.如图,已知斜坡AP的坡度为i=1:,坡长AP为20m,与坡顶A处在同﹣水平面上有﹣座古塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B 的仰角α且tanα=3.求:(1)求坡顶A到地面PQ的距离;(2)古塔BC的高度(结果保留根号)18.如图,某电信部门计划修建一条连接B、C两地的电缆,测量人员在山脚A点测得B、C 两地的仰角分别为30°、45°,在B地测得C地的仰角为60°.已知C地比A地高200米,电缆BC至少长多少米?(≈1.732,≈1.414,结果保留整数)19.热气球的探测器显示,从热气球看一栋楼顶部的仰角α为27°,看这栋楼底部的俯角β为58°,热气球与这栋楼的水平距离为120米,这栋楼有多高(结果取整数)?(参考数据:sin27°=0.45,cos27°=0.89,tan27°=0.51,sin58°=0.85,cos58°=0.53,tan58°=1.60)20.如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,求山高AD是多少?(结果保留整数,测角仪忽略不计,参考数据≈1.414,≈1.73)21.如图,李明在自家楼房的窗口A处,测量楼前的路灯CD的高度,现测得窗口处A到路灯顶部C的仰角为44°,到地面的距离AB为20米,楼底到路灯的距离BD为12米,求路灯CD的高度(结果精确到0.1)【参考数据:sin44°=0.69,cos44°=0.72,tan44°=0.97】22.如图,小俊在A处利用高为1.8米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果精确到0.1米)(参考数据:=1.414,=1.732)23.如图,为了开发利用海洋资源,我勘测飞机测量钓鱼岛附属岛屿之一的北小岛(又称为鸟岛)两侧端点A,B的距离,飞机在距海平面垂直高度为100米的北小岛上方点C处测得端点A的俯角为30°,测得端点B的俯角为45°,求北小岛两侧端点A,B的距离(结果精确到1米≈1.732)24.如图,某同学在楼房的A处测得荷塘的一端D处的俯角为60°,另一端B处的俯角为30°,荷塘另一端D与点C、B在同一直线上,已知楼高AC=24米,求荷塘宽BD为多少米?25.某学校体育看台的侧面如图中阴影部分所示,看台有四级高度相等的小台阶,已知看台高为1.6米,现要做一个不锈钢的扶手AB及两根与FG垂直且长度均为0.8米的不锈钢架杆AD和BC(杆子的低端分别为D、C),且∠DAB=66.5°(cos66.5°≈0.4).(1)求点D与点C的高度差DH;(2)求所用不锈钢材料的总长度l(即AD+AB+BC的长).26.如图,湖中有一小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PD,在小道上测得如下数据:AB=60米,∠PAB=45°,∠PBA=30°.请求出小桥PD的长.27.某中学综合实践小组同学,想测量金龙山观音大佛的高度,他们在山脚下的D处测得山顶B的仰角为30°,沿着山脚向前走了4米达到E处,测得观音大佛的头顶A的倾角为45°,已知金龙山的山顶距地面的标高(线段BC的长度)为60米,请计算观音大佛的高度为多少米?(结果精确到0.1米,≈1.73)28.如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(精确到1海里,参考数据:cos25°≈0.91,sin25°≈0.42,tan25°≈0.47,sin34°≈0.56,cos34°≈0.83,tan34°≈0.67 )29.如图,线段MN表示一段高架道路,线段AB表示高架道路旁的一排居民楼.已知点A到MN的距离为15m,BA的延长线与MN相交于点D,且∠BDN=30°.若汽车沿着从M到N的方向在MN上行驶,方圆39m以内会受到噪音的影响,当其到达点P时,噪音开始影响这一排的居民楼;当其到达点Q时,它与这一排居民楼的距离为39m,求PQ的长度(精确到1m)(参考数据:≈1.7)30.为促进江南新区的发展,長江三桥在区政府的统一指导下夜以继日的修建中,为方便残疾人通行,政府计划在位于南滨路桥头处修建一锲形残疾人通道,如图,该楔形斜坡BC长20米,坡角为12°,区领导为进一步方便残疾人的轮椅车通行,准备把坡角降为5°.(1)求斜坡新起点到原起点B的距离(精确到0.1米)(参考数据:sin12°≈0.21,cos12°≈0.98,tan5°≈0.09)(2)某6人工程队承担这项改进任务(假设每人毎天的工怍效率相同),5天刚好完成该项工程;但实际工作2天后.有2人因其它工作调离;剩余的工程由余下的4人独自完成,为了不延误工期,每人的工作效率提高了a%,结果准时完成该项工程,求a的值.锐角三角比应用题2016.12.18参考答案与试题解析一.解答题(共30小题)1.(2015•恩施州)如图,某渔船在海面上朝正西方向以20海里/时匀速航行,在A处观测到灯塔C在北偏西60°方向上,航行1小时到达B处,此时观察到灯塔C在北偏西30°方向上,若该船继续向西航行至离灯塔距离最近的位置,求此时渔船到灯塔的距离(结果精确到1海里,参考数据:≈1.732)【解答】解:如图,过点C作CD⊥AB于点D,AB=20×1=20(海里),∵∠CAF=60°,∠CBE=30°,∴∠CBA=∠CBE+∠EBA=120°,∠CAB=90°﹣∠CAF=30°,∴∠C=180°﹣∠CBA﹣∠CAB=30°,∴∠C=∠CAB,∴BC=BA=20(海里),∠CBD=90°﹣∠CBE=60°,∴CD=BC•sin∠CBD=≈17(海里).2.(2014•青羊区校级模拟)如图,为求出河对岸两棵树A.B间的距离,小明在河岸上选取一点C,然后沿垂直于AC的直线前进了12米到达D,测得∠CDB=90°.取CD的中点E,测∠AEC=56°,∠BED=67°.(1)求AC长;(2)求河对岸两树间的距离AB.(参考数据sin56°≈,tan56°≈,sin67°≈,tan67°≈)【解答】解:(1)∵E为CD中点,CD=12m,∴CE=DE=6m.在Rt△ACE中,∵tan56°=,∴AC=CE•tan56°≈6×=9m;(2)在Rt△BDE中,∵tan67°=,∴BD=DE.tan67°=6×=14m.∵AF⊥BD,∴AC=DF=9m,AF=CD=12m,∴BF=BD﹣DF=14﹣9=5m.在Rt△AFB中,AF=12m,BF=5m,∴AB===13m.∴两树间距离为13米.3.(2011•庐阳区模拟)如图,某军港有一雷达站P,军舰M停泊在雷达站P的南偏东60°方向20海里处,另一艘军舰N位于军舰M的正西方向,与雷达站P相距10海里.求:(1)军舰N在雷达站P的什么方向?(2)两军舰M、N的距离.(结果保留根号)【解答】解:(1)如图所示,∵∠OPM=60°,PM=20海里,∴∠OMP=30°,∴OP=10海里,∴PN=10海里,∴cos∠OPN===,∴∠OPN=45°,∴军舰N在雷达站P的东南方向(5分)(2)∵Rt△OPM中,PM=20海里,OP=10海里,∴OM===10,∵∠OPN=45°,∴ON=OP=10海里,∴MN=10﹣10(海里).(10分)4.(2016•丽水)数学拓展课程《玩转学具》课堂中,小陆同学发现:一副三角板中,含45°的三角板的斜边与含30°的三角板的长直角边相等,于是,小陆同学提出一个问题:如图,将一副三角板直角顶点重合拼放在一起,点B,C,E在同一直线上,若BC=2,求AF的长.请你运用所学的数学知识解决这个问题.【解答】解:在Rt△ABC中,BC=2,∠A=30°,AC==2,则EF=AC=2,∵∠E=45°,∴FC=EF•sinE=,∴AF=AC﹣FC=2﹣.5.(2016•自贡)某国发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作,如图,某探测对在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米,参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,≈1.7)【解答】解:作CD⊥AB交AB延长线于D,设CD=x米.在Rt△ADC中,∠DAC=25°,所以tan25°==0.5,所以AD==2x.Rt△BDC中,∠DBC=60°,由tan 60°==,解得:x≈3.即生命迹象所在位置C的深度约为3米.6.(2016•淮安)小宇想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为60米,求A、B两点的距离.【解答】解:作AM⊥EF于点M,作BN⊥EF于点N,如右图所示,由题意可得,AM=BN=60米,CD=100米,∠ACF=45°,∠BDF=60°,∴CM=米,DN=米,∴AB=CD+DN﹣CM=100+20﹣60=(40+20)米,即A、B两点的距离是(40+20)米.7.(2016•娄底)芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米,≈1.732)【解答】解:设DH=x米,∵∠CDH=60°,∠H=90°,∴CH=DH•sin60°=x,∴BH=BC+CH=2+x,∵∠A=30°,∴AH=BH=2+3x,∵AH=AD+DH,∴2+3x=20+x,解得:x=10﹣,∴BH=2+(10﹣)=10﹣1≈16.3(米).答:立柱BH的长约为16.3米.8.(2016•兰州)如图,一垂直于地面的灯柱AB被一钢筋CD固定,CD与地面成45°夹角(∠CDB=45°),在C点上方2米处加固另一条钢线ED,ED与地面成53°夹角(∠EDB=53°),那么钢线ED的长度约为多少米?(结果精确到1米,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)【解答】解:设BD=x米,则BC=x米,BE=(x+2)米,在Rt△BDE中,tan∠EDB=,即,解得,x≈6.06,∵sin∠EDB=,即0.8=,解得,ED≈10即钢线ED的长度约为10米.9.(2016•菏泽)南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向20(1+)海里的C处,为了防止某国海巡警干扰,就请求我A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.【解答】解:如图,作AD⊥BC,垂足为D,由题意得,∠ACD=45°,∠ABD=30°.设CD=x,在Rt△ACD中,可得AD=x,在Rt△ABD中,可得BD=x,又∵BC=20(1+),CD+BD=BC,即x+x=20(1+),解得:x=20,∴AC=x=20(海里).答:A、C之间的距离为20海里.10.(2016•乐山)如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A 处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.【解答】解:设巡逻船从出发到成功拦截所用时间为x小时;如图所示,由题意得:∠ABC=45°+75°=120°,AB=12,BC=10x,AC=14x,过点A作AD⊥CB的延长线于点D,在Rt△ABD中,AB=12,∠ABD=60°,∴BD=AB•cos60°=AB=6,AD=AB•sin60°=6,∴CD=10x+6.在Rt△ACD中,由勾股定理得:,解得:(不合题意舍去).答:巡逻船从出发到成功拦截所用时间为2小时.11.(2016•玄武区二模)小明同学需测量一条河流的宽度(河岸两边互相平行).如图,小明同学在河岸一侧选取两个观测点A、B,在河对岸选取观测点C,测得AB=31m,∠CAB=37°,∠CBA=120°.请你根据以上数据,帮助小明计算出这条河的宽度.(结果精确到0.1,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.41,≈1.73)【解答】解:过点C作CD⊥AB,垂足为点D,如右图所示,在Rt△CAD中,tan∠CAD=,∴AD==,在Rt△CBD中,tan∠CBD=,∠CBA=120°,∴∠CBD=60°,∴BD==,∵AD﹣BD=AB,∴﹣=31,﹣=31,解得,CD≈41.0,即这条河的宽度约为41.0米.12.(2016•平顶山三模)某中学紧挨一座山坡,如图所示,已知AF∥BC,AB长30米,∠ABC=66°,为防止山体滑坡,需要改造山坡,改造后的山坡BE与地面成45°角,求AE是多少米?(精确到1米)(参考数据:sin66°≈0.91,cos66°≈0.41,tan66°≈2.25)【解答】解:在Rt△ADB中,AB=30米∠ABC=60°AD=AB•sin∠ABC=30×sin66°=30×0.91=27.3(米),DB=AB•cos∠ABC=30×cos66°=30×0.41=12.3(米).连接BE,过E作EN⊥BC于N,如图所示:∵AE∥BC,∴四边形AEND是矩形NE=AD≈27.3米,在Rt△ENB中,∠EBN=45°时,BN=EN=AD=27.3米,∴AE=DN=BN﹣BD=27.3﹣12.3=15米答:AE是15米.13.(2016•襄城区模拟)在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B 两个凉亭之间的距离.现测得AC=50m,BC=100m,∠CAB=120°,请计算A,B两个凉亭之间的距离.【解答】解:过点C作CD⊥AB于D,如图所示:在Rt△CDA中∠CAD=180°﹣∠CAB=180°﹣120°=60°,∵sin∠CAD=,∴CD=AC•sin60°=50×=25(m),同理:AD=AC•cos60°=50×=25(m),在Rt△CBD中,(m),∴AB=BD﹣AD=(m),答:AB之间的距离是()m.14.(2016•鄂州一模)小明准备测量学校旗杆的高度,他发现斜坡正对着太阳时,旗杆AB 影子恰好落在水平地面BC和斜坡面CD上,测得旗杆在水平地面上的影长BC=20m,在斜坡坡面上的影长CD=8m,太阳光线AD与水平地面成30°角,且太阳光线AD与斜坡坡面互相垂直,请你帮小明求出旗杆AB的高度(结果保根号).【解答】解:作AD与BC的延长线,交于E点.如图所示:根据平行线的性质得:∠E=30°,∴CE=2CD=2×8=16.则BE=BC+CE=20+16=36.在直角△ABE中,tan∠E=,∴AB=BE•tan30°=36×=12(m).即旗杆AB的高度是12m.15.(2016•满洲里市模拟)图1为大庆龙凤湿地观光塔,游客可乘坐观光电梯进入观光层向四周瞭望,鸟瞰大庆城市风光.如图2,小英在距塔底D约200米的A处测得塔球底部平台B的仰角为45°,塔尖C的仰角为60°,求平台B到塔尖C的高度BC.(精确到个位,≈1.732)【解答】解:在Rt△ADC中,∵AD=200,∠CAD=60°,∴DC=DA•tan60°=200,在Rt△ADB中,∠BAD=45°,∴BD=AD=200,∴BC=DC﹣DB=200﹣200≈146(米).答:平台B到塔尖C的高度BC约为146米.16.(2016•天门模拟)在升旗结束后,小铭想利用所学数学知识测量学校旗杆高度,如图,旗杆的顶端垂下一绳子,将绳子拉直钉在地上,末端恰好至C处且与地面成60°角,小铭从绳子末端C处拿起绳子后退至E点,求旗杆AB的高度和小铭后退的距离.(单位:米,参考数据:≈1.41,≈1.73,结果保留一位小数)【解答】解:设绳子AC的长为x米;在△ABC中,AB=AC•sin60°,过D作DF⊥AB于F,如图所示:∵∠ADF=45°,∴△ADF是等腰直角三角形,∴AF=DF=x•sin45°,∵AB﹣AF=BF=1.6,则x•sin60°﹣x•sin45°=1.6,解得:x=10,∴AB=10×sin60°≈8.7(m),EC=EB﹣CB=x•cos45°﹣x×cos60°=10×﹣10×≈2.1(m);答:旗杆AB的高度为8.7m,小铭后退的距离为2.1m.17.(2016•泰州一模)如图,已知斜坡AP的坡度为i=1:,坡长AP为20m,与坡顶A 处在同﹣水平面上有﹣座古塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A 处测得该塔的塔顶B的仰角α且tanα=3.求:(1)求坡顶A到地面PQ的距离;(2)古塔BC的高度(结果保留根号)【解答】解:(1)作AE⊥PQ于点E,∵斜坡AP的坡度为i=1:,∴=,设AE为xm,则PE为xm,由勾股定理得,AP=2x,由题意得2x=20,解得,x=10,则AE=10m,PE=10m,答:坡顶A到地面PQ的距离为10m;(2)延长BC交PQ于点F,设AC=ym,∵tanα=3,∴BC=3y,∵∠BPF=45°,∴PF=BF,∴10+y=3y+10,解得y=5﹣5,则BC=3y=15﹣15.答:古塔BC的高度为(15﹣15)m.18.(2016•东河区二模)如图,某电信部门计划修建一条连接B、C两地的电缆,测量人员在山脚A点测得B、C两地的仰角分别为30°、45°,在B地测得C地的仰角为60°.已知C 地比A地高200米,电缆BC至少长多少米?(≈1.732,≈1.414,结果保留整数)【解答】解:作BF⊥AD于F,设BC=x米,∵∠CBE=60°,∴BE=BC×cos∠CBE=x,CE=BC×sin∠CBE=x,∵CD=200米,∴DE=200﹣x,则BF=DE=200﹣x,∵∠CAD=45°,∴AD=CD=200,则AF=200﹣x,∵tan∠BAF=,∴=,解得,x=200(﹣1)≈146米.答:电缆BC至少146米.19.(2016•吉林一模)热气球的探测器显示,从热气球看一栋楼顶部的仰角α为27°,看这栋楼底部的俯角β为58°,热气球与这栋楼的水平距离为120米,这栋楼有多高(结果取整数)?(参考数据:sin27°=0.45,cos27°=0.89,tan27°=0.51,sin58°=0.85,cos58°=0.53,tan58°=1.60)【解答】解:在Rt△ABD中,tanα=,则BD=AD•tanα=120×0.51=61.2,在Rt△ACD中,tanβ=,则CD=AD•tanβ=120×1.60=192,∴BC=BD+CD=61.2+192=253.2≈253,答:这栋楼高约为253米.20.(2016•双柏县二模)如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,求山高AD是多少?(结果保留整数,测角仪忽略不计,参考数据≈1.414,≈1.73)【解答】解:由题意得,∠ABD=30°,∠ACD=45°,BC=100m,设AD=xm,在Rt△ACD中,∵tan∠ACD=,∴CD=AD=x,∴BD=BC+CD=x+100,在Rt△ABD中,∵tan∠ABD=,∴x=(x+100),∴x=50(+1)≈137米,答:山高AD约为137米.21.(2016•绿园区一模)如图,李明在自家楼房的窗口A处,测量楼前的路灯CD的高度,现测得窗口处A到路灯顶部C的仰角为44°,到地面的距离AB为20米,楼底到路灯的距离BD为12米,求路灯CD的高度(结果精确到0.1)【参考数据:sin44°=0.69,cos44°=0.72,tan44°=0.97】【解答】解:作CE⊥AB于E,则四边形EBDC为矩形,∴CE=BD=12米,在Rt△AEC中,tan∠ACE=,则AE=EC•tan∠ACE=12×0.97=11.64,∴CD=BE=AB﹣BE=8.36≈8.4米,答:路灯CD的高度约为8.4米.22.(2016•黄冈一模)如图,小俊在A处利用高为1.8米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果精确到0.1米)(参考数据:=1.414,=1.732)【解答】解:设楼EF的高为x米,则EG=EF﹣GF=(x﹣1.8)米,由题意得:EF⊥AF,DC⊥AF,BA⊥AF,BD⊥EF,在Rt△EGD中,DG==(x﹣1.8),在Rt△EGB中,BG=(x﹣1.8),∴CA=DB=BG﹣DG=(x﹣1.8),∵CA=12米,∴(x﹣1.8)=12,解得:x=6+1.8≈12.2,答:楼EF的高度约为12.2米.23.(2016•长春四模)如图,为了开发利用海洋资源,我勘测飞机测量钓鱼岛附属岛屿之一的北小岛(又称为鸟岛)两侧端点A,B的距离,飞机在距海平面垂直高度为100米的北小岛上方点C处测得端点A的俯角为30°,测得端点B的俯角为45°,求北小岛两侧端点A,B的距离(结果精确到1米≈1.732)【解答】解:作CD⊥AB于D,由题意得,∠A=30°,∠B=45°,CD=100米,AD==100,BD=CD=100,∴AB=AD+BD=100+100≈273米,答:小岛两侧端点A,B的距离约为273米.24.(2016•潮州校级模拟)如图,某同学在楼房的A处测得荷塘的一端D处的俯角为60°,另一端B处的俯角为30°,荷塘另一端D与点C、B在同一直线上,已知楼高AC=24米,求荷塘宽BD为多少米?【解答】解:由题意知:∠CAB=90°﹣30°=60°,△ABC是直角三角形,在Rt△ABC中,tan60°=,∴BC=AC•tan60°=24米,∵∠CAD=90°﹣60°=30°,∴CD=AC1tan30°=24×=8(米),∴BD=BC﹣CD=24﹣8=16(米);答:荷塘宽BD为16米.25.(2015•广元)某学校体育看台的侧面如图中阴影部分所示,看台有四级高度相等的小台阶,已知看台高为1.6米,现要做一个不锈钢的扶手AB及两根与FG垂直且长度均为0.8米的不锈钢架杆AD和BC(杆子的低端分别为D、C),且∠DAB=66.5°(cos66.5°≈0.4).(1)求点D与点C的高度差DH;(2)求所用不锈钢材料的总长度l(即AD+AB+BC的长).【解答】解:(1)DH=1.6×=1.2米(2)连接CD.∵AD∥BC,∴四边形ABCD为平行四边形.∴AB∥CD且AB=CD.∴∠HDC=∠DAB=66.5°Rt△HDC中,cos∠HDC=,∴CD==3(米).∴l=AD+AB+BC=0.8+3+0.8=4.6(米).∴所用不锈钢材料的长度约为4.6米.26.(2015•海安县校级二模)如图,湖中有一小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PD,在小道上测得如下数据:AB=60米,∠PAB=45°,∠PBA=30°.请求出小桥PD的长.【解答】解:设PD=x米,∵PD⊥AB,∴∠ADP=∠BDP=90°.在Rt△PAD中,tan∠PAD=,∴AD==x,在Rt△PBD中,tan∠PBD=,∴DB===x,又∵AB=60米,∴x+x=60,解得:x=30﹣30.答:小桥PD的长度约为30﹣30.27.(2015•孝义市一模)某中学综合实践小组同学,想测量金龙山观音大佛的高度,他们在山脚下的D处测得山顶B的仰角为30°,沿着山脚向前走了4米达到E处,测得观音大佛的头顶A的倾角为45°,已知金龙山的山顶距地面的标高(线段BC的长度)为60米,请计算观音大佛的高度为多少米?(结果精确到0.1米,≈1.73)【解答】解:在Rt△BDC中,由cot∠D=,得DC=BC•cot30°=60×=60,EC=DC﹣DE=60﹣4,在Rt△AEC中,由tan∠AEC=,得AC=EC•tan45°=60﹣4,AB=AC﹣BC=60﹣4﹣60≈39.8,即观音大佛的高度约为39.8米28.(2015•和平区二模)如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(精确到1海里,参考数据:cos25°≈0.91,sin25°≈0.42,tan25°≈0.47,sin34°≈0.56,cos34°≈0.83,tan34°≈0.67 )【解答】解:如图,在Rt△APC中,∠APC=90°﹣65°=25°,∴PC=PA•cos∠APC≈80×0.91=72.8.(4分).WORD 完美格式.在Rt△BPC中,∠B=34°,∴PB=(海里)(8分)答:海轮所在的B处距离灯塔P约有130海里.(9分)29.(2015秋•徐州期末)如图,线段MN表示一段高架道路,线段AB表示高架道路旁的一排居民楼.已知点A到MN的距离为15m,BA的延长线与MN相交于点D,且∠BDN=30°.若汽车沿着从M到N的方向在MN上行驶,方圆39m以内会受到噪音的影响,当其到达点P时,噪音开始影响这一排的居民楼;当其到达点Q时,它与这一排居民楼的距离为39m,求PQ 的长度(精确到1m)(参考数据:≈1.7)【解答】解:如图,连接PA,作AH⊥MN于H,作QC⊥AB于C.由题意知,AP=39m.在直角△APH中,PH===36(m);在Rt△ADH中,DH=AH•cot30°=15(m).在Rt△CDQ中,DQ===78(m).则PQ=PH+HQ=PH+DQ﹣DH=36+78﹣15≈114﹣15×1.7=88.5≈89(m).答:PQ的长度约为89m.30.(2015秋•万州区期末)为促进江南新区的发展,長江三桥在区政府的统一指导下夜以继日的修建中,为方便残疾人通行,政府计划在位于南滨路桥头处修建一锲形残疾人通道,如图,该楔形斜坡BC长20米,坡角为12°,区领导为进一步方便残疾人的轮椅车通行,准备把坡角降为5°.(1)求斜坡新起点到原起点B的距离(精确到0.1米)(参考数据:sin12°≈0.21,cos12°≈0.98,tan5°≈0.09)(2)某6人工程队承担这项改进任务(假设每人毎天的工怍效率相同),5天刚好完成该项工程;但实际工作2天后.有2人因其它工作调离;剩余的工程由余下的4人独自完成,为了不延误工期,每人的工作效率提高了a%,结果准时完成该项工程,求a的值.【解答】解:(1)在Rt△BCD中,CD=BC•sin∠CBD=20×0.21=4.2米,BD=BC•cos∠CBD=20×0.98=19.6米,在Rt△CAD中,AD=≈46.7米,故斜坡新起点到原起点B的距离AB=AD﹣BD=27.1米.(2)由题意得:+×4×(1+a%)=1,解得a=30.答:a的值是30.. 技术资料. 专业整理.。
锐角三角比复习(教师版)

初中数学 备课组 教师 班级 初三学生日期 月 日上课时间教学内容:锐角三角比第三课时阶段测试教学目标:1.掌握锐角三角比的意义2.能利用同一锐角的一个三角比求出它的另外三个三角比3.知道互余的两个锐角的相似比的等量关系4.知道特殊锐角的三角比的值5.会利用“转换”求三角比6.知道三角形面积公式1sin 2S ab θ=的推导过程7.会解直角三角形8. 理解仰角、俯角、坡度、坡角等概念。
9. 理解东南西北等8个方向10. 会利用以上知识解决实际问题 知识精要锐角三角比的含义概念:设A ∠是直角三角形的一个锐角,则tan A A A ∠=∠的对边的邻边cot A A A ∠=∠的邻边的对边sin A A ∠=的对边斜边cos A A ∠=的邻边斜边图1中A ∠的对边BC 还可用字母a 来表示。
范围:若A 为锐角,则tan 0,cot 0,0sin 1,0cos 1A A A A >><<<< 关系:同一个锐角A :22tan cot 1;sin cos 1A A A A ⋅=+=图 1sin cos tan ;cot cos sin A AA A A A==; ()()()()tan cot 90;cot tan 90;sin cos 90;cos sin 90A A A A A A A A =︒-=︒-=︒-=︒-两个互余的角:tan cot ;cot tan ;sin cos ;cos sin A B A B A B A B ==== 求值:A 为锐角,若()tan 0pA p q q q=≠、为实数且,则 2222cot ;sin ;cos qp q A A A pp qp q===++(可构造直角三角形得出)锐角与其三角比的唯一确定性:a) 当一个锐角的大小确定后,它的四个三角比的值随之确定;当一个锐角的三角比的值确定后,这个锐角也随之确定。
b) 特殊锐角的三角比值α sin αcos αtan αcot α 30°1232 33345°22 22 1 160°3212333c) 设α、β都是锐角如果sin sin αβ=,那么αβ=;如果cos cos αβ=,那么αβ= 如果tan tan αβ=,那么αβ=;如果cot cot αβ=,那么αβ=如果sin cos αβ=,那么90αβ+=︒;如果tan cot αβ=,那么90αβ+=︒ d) 反之,等角(甚至可以不是锐角)的同名三角比相等,即: 如果,则:例1.1、已知在Rt △ABC 中,90,8,11C AC BC ∠=︒==,则tan A =__811___ 2.已知在Rt △ABC 中,190,cot 2C A ∠=︒=,则cos B =__552____3.已知在Rt △ABC 中,190,sin 3C A ∠=︒=,则cos B =_31_____4.在直角坐标系中,已知P(-2,3),O 为坐标原点,OP 与X 轴的夹角为α,则α的正切为 ___23______5. 在三角形ABC 中,AB=AC=5,BC=8,则tan B =__43___,cot 2A =__43___6.计算:cos30tan 60sin 60cot 45︒-︒-︒=__323+________7.已知α是锐角,且2tan 2tan 1αα-=-,则α=__45____度。
锐角三角比练习题7含答案

锐角三角比双基训练*1.在Rt ΔΑBC 中,∠C=900,BC=2,sin Α=,则ΑB= .【1】 *2.已知α为锐角,且cos α=25,则sin α= ,tg α= ,ctg α= .【2】**3.在Rt ΔΑBC 中,∠C=900,tgB=3,c-α=2,则α= ,b= ,c= .【2】 **4.在P 是直线y=512x 在第一象限上一点,若∠Pox=β,则cos β= ,ctg β= .【2】 **5.在直角坐标平面内有一点P(6,y),OP 与x 轴正方向所夹锐角为α,sin α=45,则y 的值是 ;OP 长是 .【2】**6.已知M(2,x)是直角坐标平面内一点,且锐角∠Mox=α,ctg α=3,则点M 的纵坐标为 .【2】**7.(1)sin180=cos ;(2)tg21.30=ctg ;(3)cos21012′=sin ;(4)ctg11021′31″=tg .【2】 **8.比较大小:【3】(1)sin200 sin700;(2)sin350 cos350;(3)tg180 ctg710;(4)sin720 tg620**9.tg10·tg20·tg30·…·tg890= .【2】**10.sin α210+sin220+…+sin 2880+sin 2890= .【2】 **11.已知sin α+cos α=43,则sin α·cos α= .【1】 **12.若α是锐角,且tg2α=3,则sin α·cos α= .【1】 **13.如果6sin 2cos 22sin cos a aa a-=+,那么tg α= .【2】**14.直线上有点Α(-1,-2)、B(3,4),则此直线与x 轴所夹锐角的正弦值为 .【3】**15.若ΔΑBC 中,∠C=900,则tgB=( ).【1】(Α)AB BC (B )AC BC (C )AC AB (D )BC AC**16.在ΔΑBC 中,∠C=900,CD 是ΑB 边上的高,则CD :CB 等于( ).【2】(Α)sin Α (B )cos Α (C )sinB (D )cosB**17.在Rt ΔΑBCk , ∠Α=900,α、b 、c 分别是∠Α、∠B 、∠C 的对边,则下列结论中正确的是( ).【2】(Α)b=α·sinB (B )b=c ·cosB (C )b=c ·tgB (D )c=α·ctgB**18.当450<∠Α<∠B<900时,下列各式不正确的是( ).【2】(Α)sin Α>sinB (B )tg Α>tgB (C )cos Α<cosB (D )ctg Α>ctgB**19.在ΔΑBC 中,∠C=900,CD 是斜边ΑB 上的高,sin Α等于( ).【2】(Α)AD CD (B )BD BC (C )CD AC (D )ADAC**20.在ΔΑBC 中,如果2A Btg +=1,那么ΔΑBC 的形状是( ).【2】(A ) 锐角三角形 (B )钝角三角形 (C )直角三角形 (D )等腰三角形**21.如果x 为锐角,那么sinx+cosx 的值是( ).【2】(Α)大于1 (B )小于1 (C )等于1 (D )不能确定**22.已知sin θ+sin 2θ=1,则cos 2θ+cos 4θ的值是( ).【2】(Α)1 (B )2 (C (D **23.当450<α<900时,下列各式正确的是( ).【2】(Α)tg α>cos α>sin α (B )sin α>cos α>tg α (C )tg α>sin α>cos α (D )cos α>sin α>tg α**24.已知P(sin300,tg450),则P 关于原点对称的点的坐标是( ).【2】(Α)(12,-1) (B )(-12,-1) (C )(-2,-1) (D )(2,1)**25.在ΔΑBC 中,若|tg Α-1|+(cosB-2)2=0,则ΔΑBC 是( ).【2】 (Α)等腰三角形 (B )等边三角形 (C )等腰直角三角形 (D )钝角三角形**26.已知sin α+cos α=m,sin α·cos α=n,则m 、n 的关系是( ).【2】(Α)m=n (B )m=2n+1 (C )m2=2n+1 (D )m2=1-2n**27.如图9-6,两条宽度都为1的纸条交叉重叠放在一起,且它们夹角为α,则其重叠部分面积为( ).p.134【3】(Α)1sin a(B )1cos a (C )sin α (D )1**28.当α为锐角时,sin α和tg α的大小关系为( ).【2】(Α)sin α>tg α (B )si α<tg α(C )sin α≤tg α (D )由α的大小决定 **29.计算下列各式的值:【5】(1)tg300+sin450-cos600; (2)2cos300+5tg600-2sin300;(3)0000cos 604530245tg ctg ctg --; (4)00000006045sin 5060sin 60cos30cos 40tg tg ctg --++. **30.计算:【4】(1)0000002sin 45cos 4545360sin 30cos30tg ctg -+-; (2)0203603cos 301ctg -; (3)0000sin 604560245ctg tg tg --.**31.计算:【6】(1)tg 2300+2sin600·cos450+tg450-ctg600-cos 2300;(2)(1+sin450-cos300)(1-sin450-cos300);(3)(cos450-sin600)(sin450+cos300);(4)tg100·tg200·tg300·tg400·tg500·tg600·tg700·tg800. 纵向应用 **1.计算:【4】(1 (2001|3045|2ctg tg -. **2.计算:【4】(1)2020000sin 23sin 67301872ctg tg tg ++; (2.**3.化简下列各式:【8】(1(2)tg440·tg450·tg460-cos 2260-cos 2640;(3)tg(900-Α)÷ctg Α (Α为锐角)(4)|sin α+cos α|-|sin α-cos α|(α为锐角) **4.化简下列各式:【8】(1)1-sin 2630-cos 2630; (2)tg 2530·ctg 2530;(3)(cos a a为锐角); (4a 为锐角). ***5.θ为锐角时,化简下列各式:【8】(1 (2;(3)|||ctg ctg θθ- (4)1|sin |2θ-. ***6.化简下列各式:【6】(1 (2)(1+tg 2α)·cos 2α;(3)tg(300-α)·tg(600+α). ***7.已知tg α=2且α为锐角,求2sin 5cos 4sin cos a aa a+-的值.【2】***8.已知ctg α且α为锐角,求(2sin α+cos α)÷(2sin α-cos α)的值.【3】 ***9.已知3sin 2cos 22sin cos A AA A+=-,求tg Α.【3】***10.已知sin(x+450)=sin300·ctg300,求x 的值.【2】***11.已知a =,求α2-6α-2的值.【5】***12.若方程22sin 0x A +=有两个相等的实数根,求锐角Α的度数.【2】 ***13.在三角函数中,常用sin()sin cos cos sin αβαβαβ+=+计算某些三角函数值,试计算0sin 75的值.【3】***14.sin α是方程23720x x -+=的一个根,求(1)sin α的值;(2)tg α的值.【3】 ***15.已知锐角α的正弦和正切值分别是方程21529120x x -+=的一个根,求角α的正弦和正切的值.【3】***16.已知在锐角∆ΑBC 中,cos m B n=其中m 是方程260x x +-=的根,n 是方程2280x x --=的根,求角B 的度数.【5】***17.试判断方程2212cos (1)sin 0x x x θθ+-+-=的根的情况(θ为锐角).【5】 ***18.已知方程2450x x m -+=的两根是直角三角形的两锐角的正弦,求m 的值.【5】 ***19.已知α的锐角,且2,sin cos tg ctg αααα+=+求的值.【5】 横向拓展***1.已知θ是大于045是锐角,且15θθsin -cos =,求(1)sin cos θθ的值;(2)tg θ的值;(3)33sin cos θθ-的值.【10】***2.已知2232cos tg a a+=8(00090α),求sin α的值.【5】 ***3.已知7sin cos ,5tg ctg ααθθ+=+求的值.【5】***4.已知0012sin cos (045)25a a α=,求sin α和cos α的值.【8】***5.已知sin α、cos α是方程20x px q ++=的两个根,求证:2120q p +-=.【6】****6.已知sin ,sin ,tg a tg b θθθθθ+=-=为锐角,当α≥b 时,求证:22a b -=.【8】****7.已知22268sin sin 1,2cos cos cos cos a a a a a a +=+++求的值.【8】****8.已知222cos cos sin cos sin sin ,sin sin sin A x C B x C A B C ==++且求的值.【6】****9.试比较①04848;tg ctg +②00sin 48cos 48+;③048cos 48tg +;④0048sin 48ctg +,这四个数值的大小.【12】****10.已知4sin 2cos 2sin 1y cisa a a a a =+--且为锐角.求当y 的值为非负时,角α的取值范围.【10】****11.已知函数2(cos )(4sin )6y x x θθ=-+,对于任意实数x 都有0y,且θ是三角形的一个内角,求θ的取值范围.【10】阶梯训练锐角三角比 双基训练8 4.1213 125 5.8 10 6.23± 7.(1)720(2)68.70(3)68048′ (4)78038′29″ 8.(1)< (2)< (3)< (4)< 9.1 10.441211.718、C 17.A 、C 18.A 、B 、C 19.B 、C 20.C 21.A 22.A 23.C 24.B 25.A 、C 26.C 27.A 28.B 29.(1)36(2)6-1 (3)22 (4)0 30.(1) (2)5 (3)1231.(1)71223+-(2)54-14(4)1 纵向应用1.(1) (2)0 (3)1 (4)当00<a ≤450时,原式=2sina ;当450<a<900时,原式=2cos α 4.(1)0 (2)1 (3)1 (4)2tga 5.(1)00<θ≤450时,原式=1-tg θ;450<θ<900时,原式=tg θ-1 (3)00<θ≤300时,原式;300<θ<900时,原式=2ctg θ (4)00<θ≤300时,原式=12-sin θ;300<θ<900时,原式=sin θ-126.(1)cos400-sin400(2)1 (3)1 7.978.3+2 9.4 10.150 11.-5 12.45013.14.(1)13 15.sina=35,tga=4316.60017.∆=0有两个相等实根 18.98横向拓展1.(1)1225 (2)43 (3)37125 2.2 3.2512 4.34sin ,cos 55a a == 5.提示:sin cos a a p +=-,22sin cos ,sin cos 1a a q a a =+= 6.提示:先求出a+b,a-b ,相乘得a 2-b 2=4tg ·sin,再证θ·sin θ 7.2 8.2 9.tg480+ctg480>tg480+cos480>ctg480+sin480>sin480+cos480 10.00<a<600. 提示:y=2(sina+1)·(2cosa-1) 11.00<θ<600.提示:cosθ>0且Δ<0。
求锐角的三角比的值

求锐角的三角比的值一、基础巩固一.解答题1. 在Rt △ABC 中,∠C=90°,∠A,∠B,∠C 的对边分别为a,b,c .若a=2,sin 13A =,求b 和c,【答案】b=c=6.【解析】【分析】先根据sinA=a c 知c=sin a A=6,再根据勾股定理求解可得. 【详解】解:如图,∵a=2,1sin 3A =, ∴c=sin a A =213=6,则,【点睛】本题主要考查锐角三角函数的定义,解题的关键是掌握正弦函数的定义及勾股定理.2. 已知:如图,在Rt △ABC 中,∠C=90°,AC=2BC ,求∠B 的正弦、余弦值和正切值.【答案】, , tanB=2. 【解析】【分析】根据勾股定理与锐角三角函数的定义求解即可.【详解】∵∠C=90°,AC=2BC ,∴设BC=x ,AC=2x ,∴=,∴sinB=AC AB ==,cosB=BC AB == tanB=22xAC x BC ==. 【点睛】本题考查了勾股定理与锐角三角函数的定义,在Rt △ABC 中,∠C=90°,锐角A 的正弦、余弦、正切都叫做∠A 的锐角三角函数.3. 在△ABC 中,∠C ,90°,AB ,13,BC ,5,求∠A 的正弦值、余弦值和正切值.【答案】5125131312,,. 【解析】【详解】试题分析:根据解直角三角形的意义,根据勾股定理求出AC 的长,然后根据正弦、余弦、正切的概念可求解.试题解析:∵∠C ,90°,AB ,13,BC ,5,∴12AC ==.∴5sin 13BC A AB ==,12cos 13AC A AB ==, 5tan 12BC A AC ==. 4. 在Rt △ABC 中,∠C=90°,a=2,b=1,求∠A 的三个三角函数值.【答案】,,tanA=2. 【解析】【分析】根据勾股定理,可得c ,根据sinA=a c ,cosA=bc ,tanA=a b,可得答案. 【详解】∵∠C=90°,a=2,b=1,∴=∴sinA=ac 5,cosA=bc =5, tanA=a b=2. 【点评】本题考查了锐角三角函数的定义,在Rt △ACB 中,∠C=90°,则sinA=a c ,cosA=b c ,tanA=a b. 5. 如图,在Rt △ABC 中,∠C=90°,M 是直角边AC 上一点,MN ⊥AB 于点N ,AN=3,AM=4,求cosB 的值.. 【解析】 【分析】易证得△AMN ∽△ABC ,根据相似三角形的性质得到AC AB =AN AM =34,设AC=3x ,AB=4x ,由勾股定理得:x ,在Rt △ABC 中,根据三角函数可求cosB .【详解】∵∠C=90°,MN ⊥AB ,∴∠C=∠ANM=90°,又∵∠A=∠A ,∴△AMN ∽△ABC , ∴AC AB =AN AM =34, 设AC=3x ,AB=4x ,由勾股定理得:=,在Rt △ABC 中,cosB=BC AB ==. 【点评】本题考查了锐角三角函数的定义,相似三角形的判定和性质,勾股定理,本题关键是表示出BC ,AB .6. 如图,在正方形ABCD 中,M 是AD 的中点,BE=3AE ,试求sin,ECM 的值.【解析】 【详解】试题分析:依题意设,AE x = 则3424BE x BC x AM x CD x ,,,,====先证明CEM 是直角三角形,再利用三角函数的定义求解.试题解析:设,AE x = 则3424BE x BC x AM x CD x ,,,,====5,EC x ∴==,EM ==,CM ==222EM CM CE ∴+=,CEM ∴是直角三角形,sin EM ECM CE ∴∠== 7. 在△ABC 中,∠C =90°,BC =3,AB =5,求sinA ,cosA ,tanA 的值.【答案】sin A ,35,cos A ,45,tan A ,34, 【解析】【分析】首先利用勾股定理求得AC 的长度为4;然后利用锐角三角函数的定义解答.正弦:把锐角A 的对边与斜边的比叫做∠A 的正弦,记作sin A余弦:把锐角A 的邻边与斜边的比叫做∠A 的余弦,记作cos A正切:把锐角A 的对边与邻边的比叫做∠A 的正切,记作tanA【详解】,Rt ,ABC 中,∠C ,90°,BC ,3,AB ,5,,AC,sin A ,BC AB ,35, c os A ,AC AB ,45, ta n A ,BC AC ,34, 【点睛】本题关键考查了勾股定理和锐角三角函数的定义及运用,能正确运用定义写出三角比是解决本题的关键,8. 如图,直角坐标系中,P (3,y )是第一象限内的点,且4tan 3α=,求sinα.【答案】sinα=45. 【解析】 【分析】根据在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边,可得答案.【详解】如图:作PC ⊥x 于C 点, 由4tan 33y α==,得y=4.由勾股定理,得=,45PC sin OP α==. 【点睛】本题考查了坐标与图形,勾股定理,锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边. 9. 如图,在平面直角坐标系中,已知点B (4,2),BA ⊥x 轴于A .(1)求tan ∠BOA 的值;(2)将点B 绕原点逆时针方向旋转90°后记作点C ,求点C 的坐标.【答案】(1)12;(2)(﹣2,4). 【解析】 【分析】(1)根据正切的定义,对边与邻边的比,即可求解;(2)根据图形,确定旋转以后的位置,可以直接写出坐标.【详解】(1)∵点B (4,2),BA ⊥x 轴于A ,∴OA=4,AB=2,tan ∠BOA=AB OA =24=12; (2)如图,由旋转可知:CD=BA=2,OD=OA=4,∴点C 的坐标是(﹣2,4).【点评】本题主要考查了正切的定义以及旋转变换作图,正确理解定义是解题的关键.10. 计算:2cos60°+4sin60°•tan30°﹣cos45°【答案】3﹣2. 【解析】【分析】直接利用特殊角的三角函数值代入求出答案.【详解】2cos60°+4sin60°•tan30°﹣cos45°=2×12=1+2﹣2=3﹣2. 【点睛】此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键. 11. 计算:3sin60°-2cos30°+tan60°•cot45°.【解析】【分析】直接利用特殊角的三角函数值代入求出答案.【详解】原式=3×2-2×2,【点睛】此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.12. 计算:sin45cos3032cos60︒︒︒+-﹣sin30°(cos45°﹣sin60°)【解析】【分析】依据30°、45°、60°角的各种三角函数值,即可得到计算结果.【详解】解:原式=221322-⨯﹣12⨯(22-)=4【点睛】本题考查了特殊角的三角函数值,其应用广泛,一是它可以当作数进行运算,二是具有三角函数的特点,在解直角三角形中应用较多.13. 计算:1cos3011cos60tan30 -︒++︒︒.【答案】2 3 +【解析】【分析】利用特殊角的三角函数值代入再通过实数运算法则求出即可.【详解】原式=121 12 -+=(1×2 3=23﹣=23.【点睛】此题主要考查了特殊角的三角函数值应用,正确记忆特殊角的三角函数值是解题关键.14. 计算.2cos60°+4sin60°•tan30°﹣cos245°【答案】5 2【解析】【分析】直接把特殊角的三角函数值代入求出答案.【详解】2cos60°+4sin60°•tan30°﹣cos245°=2×12+4(2)2=1+2﹣1 2=52.【点评】本题主要考查了特殊角的三角函数值,正确记忆特殊角的三角函数值是解题关键.15. 计算:(12)﹣1﹣2tan45°+4sin60°【答案】0.【解析】【分析】根据实数的性质进行化简即可求解.【详解】原式=2﹣=2﹣﹣=0.【点睛】此题主要考查实数的运算,解题的关键是熟知实数的性质.16. 计算:sin60cos45tan45 sin30︒-︒︒︒.【答案】【解析】【分析】原式利用特殊角的三角函数值及二次根式性质计算即可得到结果.【详解】sin60cos45tan45sin30︒-︒︒︒=22112-11.17. 计算:(sin30°,,1+2sin45cos45tan60?tan30︒+︒︒︒,tan45°,【解析】【详解】试题分析:把特殊角的三角函数值代入进行运算即可.试题解析:原式2111,2-+⎛⎫= ⎪⎝⎭121,22=++-32+=18. 计算:2cos45°﹣tan60°+sin30°﹣|﹣12|.【解析】【详解】试题分析,直接利用特殊角的三角函数值代入求出答案.试题解析,解,原式=2+12,1219. 计算:sin30°•tan60°+cos30cot45cos60︒-︒︒.,2-【解析】【详解】试题分析:把相关的特殊三角形函数值代入进行计算即可.试题解析:原式=1122122--.20.245°,sin30°tan60°+12sin60°【解析】【分析】把特殊角的三角函数值代入运算即可.【详解】解:原式211222⎛=-⎝⎭224=-+=.21. 计算:cos30°•tan60°,4sin30°+tan45°,【答案】12【解析】【分析】代入特殊角的三角函数值计算即可,【详解】原式1 412⨯+=321 2-+=12,22. 计算:2tan60︒,2tan45°,43cos30°+4sin30°,【答案】0【解析】【分析】首先根据特殊角的三角函数值得出各式的值,然后根据实数的计算法则得出答案.【详解】原式43×2+4×12=0,23. 计算:22sin60sin30 cot30s30o oo oco+-,【解析】【分析】把特殊角的三角函数值代入进行运算即可.【详解】原式22123⎛⎫+ ⎪===【点睛】考查特殊角的三角函数值,熟记特殊角是三角形函数值是解题的关键.24. 计算:21tan60sin452cos30cot45︒︒︒︒-⋅-.【答案】12【解析】【分析】直接代入利用特殊角的三角函数值,进而化简即可得答案.【详解】原式12=-=12=.【点睛】此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.25. 计算:sin30°﹣2cos45°+13tan260°.【答案】1.【解析】【分析】将特殊角的三角函数值代入求值即可.【详解】原式=2112223-+⨯=1113223-+⨯=1..26. 计算:222sin60cos60tan604cos45︒︒︒︒--﹣sin45°•tan45°【答案】32+【解析】【分析】把特殊角的三角函数值代入计算即可.【详解】222sin60cos60tan604cos45︒︒︒︒--﹣sin45°•tan45°212212⨯-=-=32=+=32+. 【点睛】本题考查了特殊角的三角函数值及分母有理化、二次根式的化简,牢记特殊角的三角函数值,是解决本题的关键.27. (π+4)0|【答案】1【解析】【分析】分别根据特殊角的三角函数值、零指数幂、绝对值的性质及二次函数化简的法则计算出各数,再根据实数混合运算的法则进行计算即可.π+4,0|=128. 已知α是锐角,cos (a ﹣15°)|cosa ﹣tan 2a |的值.【答案】1﹣3. 【解析】【分析】根据特殊角三角函数值,可得答案.【详解】∵cos 452=°,又cos (a ﹣15°)=2, ∴α﹣15°=45°,∴α=60°,|cosa ﹣tan 2a |12=-1122=+=1 【点睛】本题考查了特殊角三角函数值,熟记特殊角三角函数值是解题关键. 29. 求下列各式的值:(1)22cos 60sin 60︒+︒(2)cos 45tan 45sin 45︒-︒︒(3)1sin 60cos302︒⨯︒+(4)sin 452︒+ (5)2cos 45tan 60cos30︒+︒⨯︒(6)1-cos30tan 30sin 60︒+︒︒(7)sin 45cos60cos45︒︒-︒(8) 260tan 602cos 30︒+︒-︒【答案】(1)1;(2)0;(3)54;(4;(5)2;(6;(7)4;(8 【解析】【详解】(1)22cos 60sin 60︒+︒13=+44=1(2)cos45tan45sin45︒-︒︒=110-=(3)1sin60cos302︒⨯︒+ 32=+445=4(4)sin45︒(5)2cos 45tan60cos30︒+︒⨯︒13=+22=2(6)1-cos30tan30sin60︒+︒︒1= (7)sin45cos60cos45︒︒-︒=424-=- (8)2tan602cos 30︒+︒-︒33=22=30. 若规定:sin (α+β)=sinα•cosβ+cosα•sinβ,试确定sin75°+sin90°的值.. 【解析】【分析】根据给出的公式,将75°和90°化为特殊角即可求出答案.【详解】解:原式=sin (30°+45°)+sin (30°+60°)=sin30°•cos45°+cos30°•sin45°+sin30°•cos60°+cos30°•sin60°=12×22+×2+12×12+2×2=4+414+34【点睛】本题考查特殊角的三角函数值,解题的关键是将75°和90°化为特殊角进行计算,本题属于基础题型.二、拓展提升31. 如图,已知△ABC 中,∠C=90°,且BC=1.5,求AC .【答案】 【解析】 【分析】直接利用特殊角的三角函数值得出∠A 的度数,再利用锐角三角函数关系得出答案.【详解】∵∠C=90°,且sinA=2, ∴∠A=60°,∴tanA=BC AC ,∴1.5AC =解得:AC=2. 【点评】本题主要考查了特殊角的三角函数值,正确得出∠A 的度数是解题关键.32. 已知α为锐角,sin (α+15°)4cosα+tanα+(13)﹣1的值. 【答案】4.【解析】 【分析】首先得出α的值,进而利用特殊角的三角函数值以及负整数指数幂的性质化简求出答案.【详解】∵sin (α+15°)sin 60︒ ∴α+15°=60︒,∴α=45°,﹣4cosα+tanα+(13)﹣1﹣+1+3=4.【点评】本题主要考查了特殊角的三角函数值以及负整数指数幂的性质,正确掌握相关性质是解题关键.33. 计算:(3,π,0+11()3-,2cos60°, 【答案】3【解析】【分析】本题涉及实数运算、二次根式化简等多个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.【详解】原式=1+3-2×12=334. ()1306045()o sin sin cos --︒⨯︒【答案】1【解析】【分析】)原式利用特殊角的三角函数值,二次根式,负整数指数幂法则计算即可得到结果.【详解】解:原式=(12)-12)-1)=2×()=1-【点睛】此题考查了实数的运算,负整数指数幂,二次根式的性质以及特殊角的三角函数值,熟练掌握运算法则是解本题的关键.35. 计算下列各式(1)tan30°×sin45°+tan60°×cos60°(2)sin 230°+2sin60°+tan45°-tan60°+cos 230°.【答案】(1)6+3;(2)2. 【解析】【分析】(1)首先代入特殊角的三角函数值,然后化简二次根式即可;(2)首先代入特殊角的三角函数值,然后化简二次根式即可.【详解】解:(1)×12(2)原式=12⎛⎫ ⎪⎝⎭2+2×2+12⎛ ⎝⎭2=14134=2.【点睛】本题考查了特殊角的三角函数值,解题关键是熟记特殊角的三角函数值. 36. (1)2sin603tan30+(2)22sin 60cos 60tan45+- (3)cos60tan45sin60tan30sin30-++sin602cos45+-. 【答案】(1)(2)0;(3)35-;(4)122+ 【解析】【分析】,1)根据特殊角的三角函数值可求得结果;,2)根据特殊角的三角函数值可求得结果;,3)根据特殊角的三角函数值可求得结果;,4)根据特殊角的三角函数值可求得结果;【详解】解:(1)3 2sin603tan30232+=⨯== (2)22sin 60cos60tan45110+-=-=, (3)111cos60tan45sin602tan30sin30326-+-+===+(421sin602cos452222+-=⨯-= 【点睛】本题考查了特殊角的三角函数值,熟记特殊角三角函数值是解题关键.37. 在△ABC 中,已知∠A =60°,∠B 为锐角,且tanA ,cosB 恰为一元二次方程2x 2-3mx +3=0的两个实数根.求m的值并判断△ABC 的形状.【答案】mABC 是直角三角形.【解析】【分析】先求出一元二次方程的解,再根据特殊角的三角函数值求出各角的度数,判断三角形的形状.【详解】解:∵∠A =60°,∴tanA .把x 2x 2-3mx +3=0,得2-+3=0,解得m .把m2x2-3mx+3=0得2x2-3mx+3=0,解得x1x2∴cos B=2,即∠B=30°.∴∠C=180°-∠A-∠B=90°,即△ABC是直角三角形.【点睛】本题考查的知识点是解一元二次方程和判断三角形,解题关键是熟记特殊三角函数值.38. (1)已知3tanα﹣2cos30°=0,求锐角α;(2)已知2sinα﹣3tan30°=0,求锐角α.【答案】(1)α=30°;(2)α=60°.【解析】【分析】(1)先求出tanα的值,然后求出角的度数;(2)先求出sinα的值,然后求出角的度数.【详解】解:(1)解得:tanα=3,则α=30°;(2)解得:则α=60°.【点睛】本题考查了特殊角的三角函数值,解题的关键是掌握几个特殊角的三角函数值.39. 计算:(1)sin3011sin60tan30︒︒︒++;(2)tan30°•tan60°+sin245°+cos245°;(3)2cos30°•sin60°﹣tan45°•sin30°.【答案】(1)2;(2)2;(3)1.【解析】【分析】分别代入特殊角的三角函数值,进一步计算得出答案即可.【详解】(1)sin 3011sin 60tan 30︒︒︒++1==+=2=2;(2)tan30°•tan60°+sin 245°+cos 245°=32⎝⎭+2⎝⎭=1+12+12=2;(3)2cos30°•sin60°﹣tan45°•sin30°=21×12 =32﹣12=1.【点评】本题考查了特殊角的三角函数,识记特殊角的三角函数值是解决问题的关键.40. 已知正六边形ABCDEF 的边长为1,QR 是正六边形内平行于AB 的任意线段,求以QR 为底边的内接于正六边形ABCDEF 的△PQR 的最大面积.【解析】【分析】要使△PQR 的面积最大,P 点应在DE 上;Q ,R 点应分别在AF 、BC 上.过P 点PH ⊥QR 于H ,连接AE 、BD 分别交QR 、QR 于M 、N ,FC 交AE 于G ,可设PH=x ,再用含x 的式子表示QR ,根据平方的非负性,得出△PQR 的最大面积.【详解】解:过P 点PH ⊥QR 于H ,连接AE 、BD 分别交QR 、QR 于M 、N ,FC 交AE 于G ,∵正六边形ABCDEF 的边长为1,∴∠EFA=∠FAB=∠ABC=()621801206-⨯︒=︒,EF=FA=AB=1, ∵QR ∥AB ,∴四边形ABNM 、ABDE 、MHPE 、MNDE 都是矩形,∠EFG=∠AFG=60︒,∴,设PH=x ,则x ,QM=NR=AM•tan30°=1,QR=2(1x ,△PQR 的面积=12(3﹣)2,当时,△PQR . 【点评】本题考查了正六边形的性质,矩形的判定和性质,解直角三角形,平方的非负性等知识,作出常用辅助线是解题的关键.。
锐角三角比的计算与应用
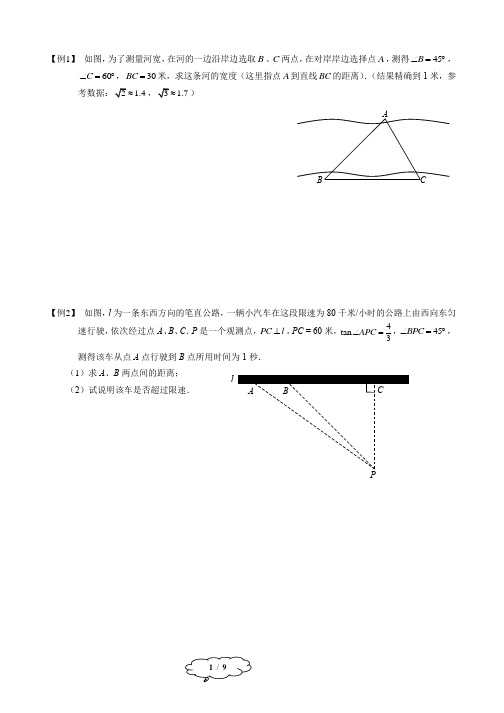
ABCPl【例1】 如图,为了测量河宽,在河的一边沿岸边选取B 、C 两点,在对岸岸边选择点A ,测得45B ∠=︒,60C ∠=︒,30BC =米,求这条河的宽度(这里指点A 到直线BC 的距离).(结果精确到1米,参考数据:2 1.4≈,3 1.7≈)【例2】 如图,l 为一条东西方向的笔直公路,一辆小汽车在这段限速为80千米/小时的公路上由西向东匀速行驶,依次经过点A 、B 、C .P 是一个观测点,PC l ⊥,PC = 60米,4tan 3APC ∠=,45BPC ∠=︒,测得该车从点A 点行驶到B 点所用时间为1秒. (1)求A 、B 两点间的距离; (2)试说明该车是否超过限速.ABCABCDE O左右M A B CDEFG HPQ1.2 m0.8 m 0.8 m【例3】 如图,一条细绳系着一个小球在平面内摆动.已知细绳从悬挂点O 到球心的长度为50厘米,小球在A 、B 两个位置时达到最高点,且最高点高度相同(不计空气阻力),在C 点位置时达到最低点.达到左侧最高点时与最低点时细绳相应所成的角度为37°,细绳在右侧达到最高点时与一个水平放置的挡板DE 所成的角度为30°. (sin370.6︒≈,cos370.8︒≈,tan370.75︒≈)(1)求小球达到最高点位置与最低点位置时的高度差. (2)求OD 这段细绳的长度.【例4】 靠校园一侧围墙的体育场看台侧面,如图阴影部分所示,看台的二级台阶高度相等,宽度相同,现要用钢管做护栏扶手ACG 及三根与水平底面PQ 垂直的护栏支架CD 、EF 、GH (底端D 、F 、H 分别在每级台阶的中点处),已知看台高为1.2米,护栏支架0.8CD GH ==米,66.5DCG ∠=︒. (参考数据:sin66.50.92︒≈,cos66.50.40︒≈,tan66.5 2.30︒≈) (1)点D 与点H 的高度差是 米;(2)试求制作护栏扶手和支架的钢管总长度l ,即AC CG CD EF GH ++++的长度. (结果精确到0.1米)ABC海平面【例5】 在某反潜演习中,我军舰A 测得潜艇C 的俯角为30°,位于军舰A 正上方2000米的反潜直升机B 测得潜艇C 的俯角为68°,试根据以上数据求出潜艇C 离开海平面的下潜深度.(结果保留整数,参考数据:sin680.9︒≈,cos680.4︒≈,tan68 2.5︒≈,3 1.7≈).【例6】 如图,已知楼AB 高36米,从楼顶A 处测得旗杆顶C 的俯角为60°,又从该楼离地面6米的一窗口E 处测得旗杆顶C 的仰角为45°,求该旗杆CD 的高.(结果保留根号)A DBCEFABPQ ABCDE【例7】 如图,从地面上的点A 看一山坡上的电线杆PQ ,测得杆顶端点P 的仰角是26.6°,向前走30米到达B 点,测得杆顶端点P 和杆底端点Q 的仰角分别是45°和33.7°.求该电线杆PQ 的高度(结果精确到1米).(备用数据:sin26.60.45︒=,cos26.60.89︒=,tan26.60.50︒=,cot 26.6 2.00︒=,sin33.70.55︒=,cos33.70.83︒=,tan33.70.67︒=,cot33.7 1.50︒=)【例8】 如图,小明想测量河对岸的一幢高楼AB 的高度,小明在河边C 处测得楼顶A 的仰角是60°.距C 处60米的E 处有幢楼房,小明从该楼房中距地面20米的D 处测得楼顶A 的仰角是30°(点B 、C 、E 在同一直线上,且AB 、DE 均与地面BE 垂直).求楼AB 的高度.DAB CEFGA BC【例9】如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A、C两点处测得该塔顶端F的仰角分别为α和β,矩形建筑物宽度AD = 20m,高度DC = 33m.(1)试用α和β的三角比表示线段CG的长;(2)如果48α=︒,65β=︒,请求出信号发射塔顶端到地面的高度FG的值(结果精确到1 m).(参考数据:sin480.7︒≈,cos480.7︒≈,tan48 1.1︒≈,sin650.9︒≈,cos650.4︒≈,tan65 2.1︒≈)【例10】如图,已知某船向正东方向航行,在点A处测得某岛C在其北偏东60°方向上,前进8海里处到达点B处,测得岛C在其北偏东30°方向上.已知岛C周围6海里内有一暗礁,问:如果该船继续向东航行,有无触礁危险?请说明你的理由.ABCH 【例11】 如图,某人在C 处看到远处有一凉亭B ,在凉亭B 正东方向有一棵大树A ,这时此人在C 处测得B 在北偏西45°方向上,测得A 在北偏东35°方向上.又测得A 、C 之间的距离为100米,求A 、B 之间的距离.(精确到1米)(参考数据:sin350.574︒≈,cos350.819︒≈,tan350.700︒≈)【例12】 如图,某地下车库的入口处有斜坡AB ,它的坡度为1:2i =,斜坡AB 的长为65米,车库的高度为AH (AH BC ⊥),为了让行车更安全,现将斜坡的坡角改造为14︒(图中的14ACB ∠=︒). (1)求车库的高度AH ;(2)求点B 与点C 之间的距离(结果精确到1米).(参考数据:sin140.24︒=,cos140.97︒=,tan140.25︒=,cot14 4.01︒=)ABC45° 35°ABCD37°ABCD E FG【例13】 如图,高压电线杆AB 垂直地面,测得电线杆AB 的底部A 到斜坡底C 的水平距离AC 长为15.2米,落在斜坡上的电线杆的影长CD 为5.2米,在D 点处测得电线杆顶B 的仰角为37°.已知斜坡CD 的坡比为1 : 2.4,求该电线杆AB 的高.(参考数据:sin 37° = 0.6).【例14】 如图是某个大型商场的自动扶梯侧面示意图,已知自动扶梯AC 的坡度为1 : 2,AC 的长度为55米,AB 为底楼地面,CD 为二楼楼面,EF 为二楼楼顶,当然有EF // AB // CD ,E 为自动扶梯AC 的最高端C 的正上方,过C 的直线EG AB 于G ,在自动扶梯的底端A 测得E 的仰角为42°,求该商场二楼的楼高CE .【例15】为方便市民通行,某广场计划对坡角为30°,坡长为60米的斜坡AB进行改造,在斜坡中点D处挖去部分坡体(阴影表示),修建一个平行于水平线CA的平台DE和一条新的斜坡BE.(1)若修建的斜坡BE 的坡角为36°,则平台DE的长约为多少米?(2)在距离坡角A点27米远的G处是商场主楼,小明在D点测得主楼顶部H的仰角为30°,那么主楼GH高约为多少米?(结果取整数,参考数据:sin36° = 0.6,cos 36° = 0.8,tan 36° = 0.7,3=1.7)BCD EFHM 30°30°A BCABC DABCDEN M 【习题1】 如图,A 、B 两地之间有一座山,汽车原来从A 地到B 地须经C 地沿折线A -C -B 行驶,现开通隧道后,汽车直接沿直线AB 行驶.已知AC = 120千米,30A ∠=︒,135B ∠=︒,则隧道开通后,汽车从A 地到B 地比原来少走多少千米?(结果保留根号)【习题2】 如图,热气球在离地面800米的A 处,在A 处测得一大楼楼顶C 的俯角是30︒,热气球沿着水平方向向此大楼飞行400米后到达B 处,从B 处再次测得此大楼楼顶C 的俯角是45︒,求该大楼CD 的高度.2 1.41≈3 1.73≈)【习题3】 如图,小明在广场上的C 处用测角仪正面测量一座楼房墙上的广告屏幕AB 的长度,测得屏幕下端B 处的仰角为30°,然后他正对大楼方向前进10米到达D 处,又测得该屏幕上端A 处的仰角为45°,已知该楼高18.7米,测角仪MC 、ND 的高度为1.7米.求广告屏幕AB 的长.。
2024届上海初三一模数学各区填选题(锐角的三角比)
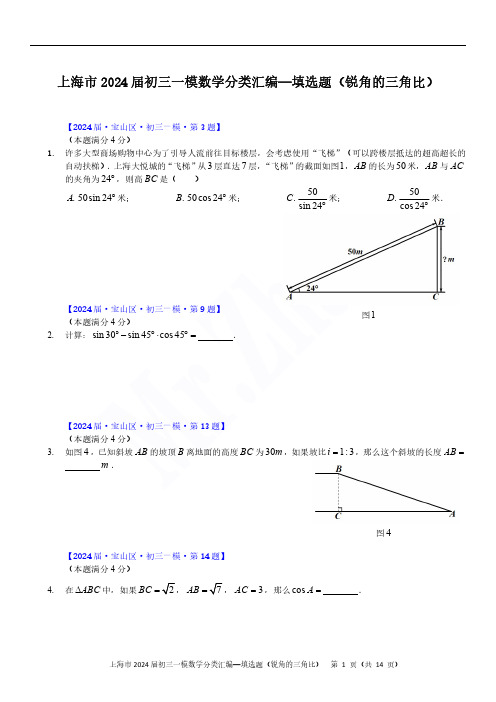
上海市2024届初三一模数学分类汇编—填选题(锐角的三角比)【2024届·宝山区·初三一模·第3题】(本题满分4分)1.许多大型商场购物中心为了引导人流前往目标楼层,会考虑使用“飞梯”(可以跨楼层抵达的超高超长的自动扶梯).上海大悦城的“飞梯”从3层直达7层,“飞梯”的截面如图1,AB 的长为50米,AB 与AC 的夹角为24 ,则高BC 是().A 50sin24 米;.B 50cos 24 米;.C 50sin 24米;.D 50cos 24米.2.3.如果坡比1:3i ,那么这个斜坡的长度AB【2024届·宝山区·初三一模·第14题】(本题满分4分)4.在ABC 中,如果BC AB ,3AC ,那么cos A.图4(本题满分4分)5.在直角坐标平面内有一点 5,12A ,点A 与原点O 的连线与x 轴正半轴的夹角为 ,那么tan 的值为().A 513;.B 1213;.C 512;.D 125.【2024 6.在Rt 【20247.处,它沿正北方向航行到达位于灯【2024届·奉贤区·初三一模·第3题】(本题满分4分)8.在Rt ABC 中,90C ,5AC ,A ,那么BC 的长是().A 5tan ;.B 5cot ;.C 5sin ;.D 5cos .第15题图(本题满分4分)9.某人顺着坡度为的斜坡滑雪,下滑了120米,那么高度下降了米.【2024届·奉贤区·初三一模·第15题】(本题满分4分)10.如图5,已知ABC 在边长为1个单位的方格纸中,三角形的顶点在小正方形顶点位置,那么ABC的正11.在 12.如图6度AC 为2.6米,遮阳篷与房屋墙壁的夹角 的余弦值为13.当太阳光与地面的夹角为60 时,遮阳篷在地面上的阴影宽度BD 为米.图6图1图2第6题图(本题满分4分)13.如图1,在Rt ABC 中,已知90C ,3cos 4A,3AC ,那么BC 的长为().A ;.B ;.C 4;.D 5.【2024届·虹口区·初三一模·第4题】(本题满分4分)14.如图2,一条细绳系着一个小球在平面内摆动.已知细绳从悬挂点O 到球心的长度为50厘米,小球在左、右两个最高位置时,细绳相应所成的角AOB 为40 ,那么小球在最高位置和最低位置时的高度差为().A 5050sin 40 厘米;.B 5050cos 40 厘米;.C 5050sin 20 厘米;.D 5050cos 20 厘米.【2024届·黄浦区·初三一模·第6题】(本题满分4分)15.如图,过矩形ABCD 的顶点分别作对角线的垂线,垂足分别为E 、F 、G 、H ,依次联结四个垂足,可得到矩形EFGH .设对角线AC 与BD 的夹角为 (090 ),那么矩形EFGH 与矩形ABCD 面积的比值为().A 2sin ;.B 2cos ;.C 2tan ;.D 2cot .(本题满分4分)16.已知点 1,4A 、 2,0B ,那么直线AB 与x 轴夹角的正弦值是.【2024届·黄浦区·初三一模·第13题】(本题满分4分)17.【202418.已知在.A sin 35.【202419.一架飞机在离地面6000米的上空测得某一建筑物底部的俯角为30 ,此时这架飞机与这一建筑物底部之间的距离是().A 6000米;.B 12000米;.C 米;.D图4(本题满分4分)20.如图3,在ABC 中,90ACB ,DA AB ,联结BD ,AC,1BC ,2AD ,那么cos D .21.在船的正南方向,那么小岛B 与C 处的距离BC22.轴正半轴的夹角为 ,那么下列各式正确的是【2024届·金山区·初三一模·第13题】(本题满分4分)23.如果 是直角三角形的一个锐角,4sin 5,那么tan .第14题图(本题满分4分)24.如图,在山坡上种树,要求株距(相邻两树间的水平距离)是4米,斜坡的坡度1:2i ,那么相邻两树间的坡面距离为米.【2024届·金山区·初三一模·第16题】25.45 方海里.【202426..A sin 【2024届·静安区·初三一模·第14题】(本题满分4分)27.如图,小红沿坡度1:2.4i 的坡面由A 到B 行走了26米,那么小红行走的水平距离AC米.第15题图第16题图(本题满分4分)28.在Rt ABC 中,90C ,3AB ,2AC ,那么cos A 的值是().A 13;.B 23;.C 3;.D 2.【202429.在Rt 【202430.【202431.“二鸟饮泉”问题中记载:“两塔高分别为30步和20步.两塔之间有喷泉,两鸟从两塔顶同时出发,以相同速度沿直线飞往喷泉中心,同时抵达.喷泉与两塔在同一平面内,求两塔之间的距离.”如图,已知AC AB ,BD AB ,M 是AB 上一点,CM DM ,在C 处测得点M 的俯角为60 ,30AC ,20BD ,那么AB.(本题满分4分)32.已知在Rt ABC 中,90C ,3AC ,4BC ,那么下列等式正确的是().A 3sin 5A;.B 3cos 4A;.C 3tan 5A;.D 3cot 4A.【202433.已知在【202434.【2024(本题满分4分)35.在Rt ABC 中,已知90ACB ,1tan 3B,3BC ,那么AC 的长等于().A 1;.B 9;.C .D .第13题图(本题满分4分)36.如图2,ABC 和DCB 都是直角三角形,90BAC BCD ,AB AC ,AC 、BD 相交于点O ,如果30DBC ,那么:OC AC 的值是().A 3;.B 2;.C 12;.D 31 .【202437.如图6、CD的值等于.【202438.在Rt .A 512【2024届·青浦区·初三一模·第13题】(本题满分4分)39.如图,某人沿着斜坡AB 方向往上前进了30米,他的垂直高度上升了15米,那么斜坡AB 的坡比i.(本题满分4分)40.如图,在边长相同的小正方形组成的网格中,点A 、B 、C 、D 都在这些小正方形的顶点上,AB 、CD相交于点O ,那么sin BOD 的值为.【2024届·松江区·初三一模·第2题】41.在.A .cos a .42.【2024届·松江区·初三一模·第17题】(本题满分4分)43.在ABC 中,AB AC ,点D 、E 分别是边AB 、AC 的中点,BE 与CD 相交于点O ,如果OBC 是等边三角形,那么tan ABC .第16题图第13题图(本题满分4分)44.如图,在直角坐标系xOy 中,已知点 4,3A ,直线OA 与x 轴正半轴的夹角为 ,那么sin 的值是().A 35;.B 34;.C 45;.D 43.45.A 与.A 46.【2024届·徐汇区·初三一模·第13题】(本题满分4分)47.如图,一段东西向的限速公路MN 长500米,在此公路的南面有一监测点P ,从监测点P 观察,限速公路MN 的端点M 在监测点P 的北偏西60 方向,端点N 在监测点P 的东北方向,那么监测点P 到限速公路MN 的距离是米(结果保留根号).第15题图第5题图(本题满分4分)48.如图,在ABC 中,AD 和BE 是ABC 的高,且交于点F ,已知13AB ,15BC ,14AC ,那么AFE 的正切值是.【202449..A 【202450.测得教().A 1.4 .【2024届·杨浦区·初三一模·第12题】(本题满分4分)51.在Rt ABC 中,90ABC ,BD AC ,垂足为点D ,如果5AB ,2BD ,那么cos C .第16题图(本题满分4分)52.小华沿着坡度1:3i的斜坡向上行走了米,那么他距离地面的垂直高度上升了米.【2024届·长宁区·初三一模·第1题】(本题满分4分)53.在Rt ABC 中,90C ,如果A ,BC a ,那么AC 等于().Aa 【202454.计算:【202455.【2024届·长宁区·初三一模·第16题】(本题满分4分)56.如图,在ABC 中,90BAC ,点G 是ABC 的重心,联结GA 、GC ,如果3AC ,53AG ,那么GCA 的余切值为.。
特殊锐角的三角比的值

特殊锐角的三角比的值内容分析特殊锐角的三角比的值是九年级数学上学期第二章第一节的内容,本讲主要讲解利用几何方探求30°、45°和60°这三个特殊锐角的三角比的值,重点是熟练运用其进行相关计算,难点是在几何图形中的灵活运用.知识结构模块一:求特殊锐角的三角比的值知识精讲1、特殊锐角的三角比的值ABCABC BAC【例1】 如图,在Rt ABC ∆中,90C ∠=︒,45A ∠=︒,BC = a .求A ∠的三角比的值. 【难度】★ 【答案】22sin =A ,22cos =A ,1tan =A ,1cot =A . 【解析】∵45A ∠=︒,∴2245sin sin =︒=A ,2245cos cos =︒=A , 145tan tan =︒=A ,145cot cot =︒=A . 【总结】本题主要考查特殊角45角的三角比的值.【例2】 如图,在Rt ABC ∆中,90C ∠=︒,30A ∠=︒,BC = a .求A ∠的三角比的值. 【难度】★【答案】21sin =A ,23cos =A ,33tan =A ,3cot =A【解析】∵30A ∠=︒∴2130sin sin =︒=A ,2330cos cos =︒=A , 3330tan tan =︒=A ,330cot cot =︒=A . 【总结】本题主要考查特殊角30角的三角比的值.【例3】 如图,在Rt ABC ∆中,90C ∠=︒,60A ∠=︒,AC = a .求A ∠的三角比的值. 【难度】★ 【答案】23sin =A ,21cos =A ,3tan =A ,33cot =A . 【解析】∵60A ∠=,∴2360sin sin =︒=A ,2160cos cos =︒=A ,360tan tan =︒=A ,3360cot cot =︒=A . 【总结】本题主要考查特殊角60角的三角比的值.例题解析【例4】 填空:tan 60°= ______;cot 45°= ______;sin 30°= ______;cos 45°= ______.【难度】★ 【答案】3,1,21,22【解析】主要考察特殊角的锐角三角比值.【例5】 用特殊锐角的三角比填空:(1)12=______ = ______; (2=______ = ______;(3)1=______ = ______;(4=______ = ______. 【难度】★【答案】(1)sin 30°,cos 60°;(2)sin 45°,cos45°;(3) tan45°,cot 45°;(4)sin 60°,cos30°. 【解析】主要考察特殊角的锐角三角比值.【例6】 已知,等腰ABC ∆的顶角A ∠=120°,求B ∠的三角比的值. 【难度】★ 【答案】21sin =B ,23cos =B ,33tan =B ,3cot =B【解析】∵等腰ABC ∆的顶角A ∠=120°,∴︒=∠=∠30C B . ∴2130sin sin =︒=B ,2330cos cos =︒=B ,3330tan tan =︒=B ,330cot cot =︒=B . 【总结】本题一方面考查等腰三角形的性质,另一方面考查特殊角30角的三角比的值.【例7】 正方形ABCD 中,对角线AC 、BD 相交于点O ,求OAB ∠的三角比的值. 【难度】★ 【答案】22sin =∠OAB ,22cos =∠OBA ,1tan =∠OAB ,1cot =∠OAB 【解析】∵正方形ABCD 中,对角线AC 、BD 相交于点O , ∴︒=︒⨯=∠=∠45902121BAC OAB .∴2245sin sin =︒=∠OAB ,2245cos cos =︒=∠OAB ,145tan tan =︒=∠OAB ,145cot cot =︒=∠OAB .【总结】本题一方面考查正方形的性质,另一方面考查45角的三角比的值.【例8】 求满足下列条件的锐角α:(1)cos 0α=; (2)0α=.【难度】★【答案】(1)︒=30α;(2)︒=45α.【解析】(1)由题意可得:cos α=︒=30α;(2)由题意可得:1tan =α,则︒=45α.【总结】本题主要是对特殊锐角三角比的值的综合运用.【例9】 若A ∠是锐角,且tan A cos A = ______. 【难度】★★ 【答案】23【解析】∵tan A =,∴︒=∠30A ,∴2330cos cos =︒=A . 【总结】本题主要考查特殊角的锐角三角比的值以及它们之间的关系.【例10】 已知,在Rt ABC ∆中,90C ∠=︒,cos B =12,求tan A 的值. 【难度】★★ 【答案】33 【解析】∵1cos 2B =,且∠B 是锐角,∴︒=∠60B .∵︒=∠+∠90B A , ∴︒=∠30A∴3330tan tan =︒=A . 【总结】本题主要考查特殊角的锐角三角比的值以及它们之间的关系.【例11】 sin 45°+ cos 45°的值等于( )ABCD .1【难度】★ 【答案】A【解析】sin 45°+ cos 45°=22222=+.【例12】 下列不等式,成立的是( )A .sin60sin45sin30︒<︒<︒B .cos60cos45cos30︒>︒>︒C .tan60tan45tan30︒<︒<︒D .cot30cot 45cot60︒>︒>︒【难度】★ 【答案】D【解析】A 答案,正确应为:sin60sin45sin30︒>︒>︒; B 答案,正确应为:cos60cos45cos30︒<︒<︒;C 答案,正确应为:tan60tan45tan30︒>︒>︒【总结】一个锐角的正弦值和正切值随着角度的增大而增大,一个锐角的余弦值和余切值随着角度的增大而减小.【例13】 计算:(1)tan602sin452cos30︒+︒-︒;(2)()2tan 60tan 30︒+︒.【难度】★【答案】(1)2;(2)316. 【解析】(1)原式=23232322223=-+=⨯-⨯+(2)原式=31633433322=⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛+【总结】本题考查利用特殊角的锐角三角比的值进行实数计算.模块二:特殊锐角的三角比的值的应用例题解析【例14】 计算:(1)sin60tan 45cos30︒-︒︒;(2)tan 45tan301tan 45tan30︒-︒+︒︒.【难度】★【答案】(1)0;(2)32-【解析】(1)原式=01112323=-=-;(2)原式=3233333313313311331-=+-=+-=⨯+-. 【总结】本题考查利用特殊角的锐角三角比的值进行实数计算.【例15】计算:)112341271tan 6012-⎛⎫++- ⎪︒+⎝⎭.【难度】★★ 【答案】3【解析】原式=()32132324321343243=--+-+=-++-+.【总结】本题考查利用特殊角的锐角三角比的值进行实数计算.【例16】【难度】★★ 【答案】213- 【解析】原式sin 60sin30sin 60sin30︒-︒=︒-︒=. 【总结】本题考查利用特殊角的锐角三角比的值进行实数计算.【例17】计算:22cos 60cos 45sin 45︒+︒︒︒. 【难度】★★【答案】45【解析】原式=4521214122212222122=++=⨯⨯+⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛. 【总结】本题考查利用特殊角的锐角三角比的值进行实数计算.【例18】 计算:cos60sin 45cos60cos45cos60sin 45sin30cos45︒+︒︒-︒+︒-︒︒+︒. 【难度】★★ 【答案】6- 【解析】原式=()()6212121212121222122212221222122-=--+-=+-+-+=+-+-+.【总结】本题考查利用特殊角的锐角三角比的值进行实数计算.【例19】 计算:()tan 4512sin30cos60cot 30sin 60cos60-︒︒-︒--︒+︒+︒.【难度】★★ 【答案】2-【解析】原式=213321212313212121-=-+--=++--⎪⎭⎫ ⎝⎛-⨯-.【总结】本题考查利用特殊角的锐角三角比的值进行实数计算.【例20】sin301︒-.【难度】★★ 【解析】原式=321132121324211212314121=+-+=+-+=-+⎪⎪⎭⎫ ⎝⎛-⨯+-. 【总结】本题考查利用特殊角的锐角三角比的值进行实数计算.【例21】 已知030α︒<∠<︒,化简:1cot cot αα-.【难度】★★【答案】13cot 2--α【解析】∵030α︒<∠<︒, ∴330cot cot =︒>α.∴1cot cot cot 1cot 2cot 1ααααα-+=-+=.【总结】一个锐角的度数越大,余切值反而越小.【例22】 已知方程()2sin 2sin 2sin 120x x ααα-+++=有两个相等的实数根,求锐角α的大小.【难度】★★ 【答案】30°【解析】∵方程()2sin 2sin 2sin 120x x ααα-+++=有两个相等的实数根, ∴()()12sin sin 42sin 42+⨯⨯-+=∆ααα0sin 3216=-=α.∴21sin =α. ∴︒=30α.【总结】本题将根的判别式与锐角三角比结合在一起,完成相应计算.ααααsin 48sin 416sin 16sin 422--++=【例23】 已知ABC ∆中,30B ∠=︒,45C ∠=︒,BC = 15 cm ,求AB 的长. 【难度】★★【答案】AB=15315-【解析】解:过A 作AD ⊥BC ,垂足为D设x AD =,在ABD Rt △中,30B ∠=︒, ∴3cot ==AD BDB ,则x BD 3=;在ACD Rt △中,45C ∠=︒,∴1cot ==ADCDC ,则x CD =;∵BC = 15 cm , ∴153=+x x , 解得:215315-=x .∴153152-==x AB cm .【总结】本题是对锐角三角比的直接运用,注意在运用锐角三角比时,要将锐角放在直角三角形中.【例24】 已知ABC ∆中,30B ∠=︒,135C ∠=︒,BC = 15 cm ,求AB 的长. 【难度】★★【答案】AB=15315+【解析】解:过A 作AD ⊥BC ,垂足为D .设x AD =,在ABD Rt △中,30B ∠=︒,∴ 3cot ==ADBDB ,则x BD 3=;在ACD Rt △中,18045ACD ACB ∠=-∠=,∴1cot ==AD CDC ,则x CD =;∵BC = 15 cm ,∴153=-x x ,解得:215315+=x .∴153152+==x AB cm .【总结】本题是对锐角三角比的直接运用,注意在运用锐角三角比时,要将锐角放在直角三角形中.BA【例25】 已知ABC ∆中,45A ∠=︒,AC = 15 cm,BC =,求AB 的长. 【难度】★★★【答案】AB =AB = 【解析】(图1)(图2)解:过C 作CD ⊥BA ,垂足为D . 在ACD Rt △中,45A ∠=︒,AC = 15, ∵22cos ==AC AD A , ∴AD CD =在BCD Rt △中,∵222CB BD CD =+,∴BD =在图1中,AB AD BD =+==在图2中,AB AD BD =-==. 综上所述:AB 的长为【总结】在三角形中,已知一个角的度数,以及这个角的对边和一条邻边的长时,要注意分类讨论.ABA【例26】 已知1sin60cos60a =︒-︒,1tan 45cot30b =︒-︒,求224a ab b ++的值.【难度】★★★ 【答案】3233--.【解析】∵11sin 60cos60a ===︒-︒,1tan 45cot 30b ===︒-︒,∴()22242a ab b a b ab ++=++.而231+=+b a ,()2312+-=ab ,∴原式=()()3233314331231222--=+-=+-⎪⎪⎭⎫⎝⎛+. 【总结】本题主要考查锐角三角比在实数运算中的运用.【例27】 已知090θ︒<<︒,且sin 0θθ=,求2sin cos 2sin cos θθθθ+-.【难度】★★★ 【答案】7249+.【解析】∵sin 0θθ-=,∴sin θθ.∴2sin cos 2sin cos θθθθ+===-【总结】本题主要是考查换元的思想.【例28】 已知Rt ABC ∆中,90C ∠=︒,2a b +=,30A ∠=︒,求a 、b 、c 的值. 【难度】★★★【答案】13-=a ,33-=b ,232-=c 【解析】解:在ABC Rt △中, 3cot ==abA ,则a b 3=. ∵2a b +=, ∴23=+a a , 解得:13-=a ,∴333-==a b ,2322-==a c .【总结】本题是对特殊角锐角三角比的综合运用.【例29】 在ABC ∆中,A ∠、B ∠均是锐角,且(2tan 2sin 0B A +=,请判断ABC ∆的形状,并说明理由.【难度】★★★ 【答案】等边三角形.【解析】∵(2tan 2sin 0B A +=,∴03tan =-B ,03sin 2=-A ,解得:3tan =B ,23sin =A . ∴︒=∠60B ,︒=∠60A .∴ABC ∆为等边三角形.【总结】本题主要是对绝对值和平方的非负性和特殊角的锐角三角比的值的综合考查.【例30】 应用锐角三角比的定义,求sin 15°、tan 15°、sin 75°、tan 75°. 【难度】★★★【答案】42615sin -=︒,3215tan -=︒,sin 【解析】如图,作等腰△ABC ,且︒=∠=∠15C B . 过点C 作CD ⊥BA 交BA 的延长线于点D ,则︒=∠15B ,75BCD ∠=︒,30CAD ∠=. 设x DC =,则x AB AC 2==,x DA 3=, BC x x ====.在Rt △BDC 中, ()42626126sin 15sin -=+=+===︒xxBCDCB ;()3232132tan 15tan -=+=+===︒x x BD DC B ; ()()42626322632sin 75sin +=++=++==∠=︒x x BC DB BCD ;()3232tan 75tan +=+==∠=︒xxCDDB BCD .【总结】在求非特殊角的锐角三角比的值时,想办法将其跟特殊角结合起来,再去求值.【习题1】求满足下列条件的锐角α:(1)2cos 0α=;(2)()tan 10α+︒=【难度】★【答案】(1)45°;(2)50°. 【解析】(1)由题意可得:cos α=︒=45α;(2)由题意可得:︒=︒+6010α,则︒=50α.【总结】本题主要考查特殊角的锐角三角比的值.【习题2】 如果α∠是等腰直角三角形的一个锐角,则α∠的余弦值为______.【难度】★ 【答案】22【解析】∵α∠是等腰直角三角形的一个锐角,∴︒=45α,∴cos 2α= 【总结】本题主要考查特殊角的锐角三角比的值.【习题3】 若α是锐角,且cot α=()cos 90α︒-=______.【难度】★【答案】21【解析】∵cot α=︒=30α,∴()2160cos 90cos =︒=-︒α. 【总结】本题主要考查特殊角的锐角三角比的值.随堂检测【习题4】 ABC ∆中,A ∠、B ∠都是锐角,且sin A =12,cos B,则ABC ∆三个角的大小关系是( )A .C AB ∠>∠>∠ B .BC A ∠>∠>∠ C .A B C ∠>∠>∠D .C B A ∠>∠>∠【难度】★ 【答案】D 【解析】∵sin A =12,cos B,∴︒=∠30A ,︒=∠45B .∴︒=︒-︒-︒=∠1054530180C ,∴C B A ∠>∠>∠.【总结】本题主要考查特殊角的锐角三角比的值.【习题5】 计算:cos45sin30cos45sin30︒+︒︒-︒.【难度】★★ 【答案】223+ 【解析】原式=223121221222122+=-+=-+.【总结】本题主要是将特殊角的锐角三角比的值与实数运算结合在一起.【习题6】23tan 30︒+【难度】★★ 【答案】2【解析】原式 =2221122212333122=-+-+=⎪⎪⎭⎫⎝⎛-⨯+⎪⎪⎭⎫ ⎝⎛⨯-+. 【总结】本题主要是将特殊角的锐角三角比的值与实数运算结合在一起.【习题7】 ()131tan602sin 45-+︒+︒.【难度】★★【答案】32-【解析】 原式=32231233123112331-=-+-+-=++-+-.【总结】本题主要是将特殊角的锐角三角比的值与实数运算结合在一起.【习题8】在ABC ∆中,A ∠、C ∠均为锐角,若21sin cos 02A C ⎛-+= ⎝⎭,求B ∠的度数.【难度】★★ 【答案】︒=∠120B【解析】∵21sin cos 02A C ⎛-+= ⎝⎭, ∴023cos =-C ,0sin 21=-A ,解得:23cos =C ,21sin =A . ∴︒=∠30C ,︒=∠30A ,∴︒=︒-︒-︒=∠1203030180B .【总结】本题主要是对绝对值和平方的非负性和特殊角的锐角三角比的值的综合考查.【习题9】 已知ABC ∆中,60B ∠=︒,45C ∠=︒,BC = 20 cm ,求AC 的长.【难度】★★ 【答案】610230-【解析】解:过A 作AD ⊥BC ,垂足为D .设x AD =. 在ABD Rt △中,60B ∠=︒,∴ 33cot ==AD BD B ,则x BD 33=;在ACD Rt △中,45C ∠=︒,∴ 1cot ==ADCDC ,则x CD =; ∵BC = 20 cm ,∴2033=+x x ,解得:31030-=x .∴6102302-==x AB .【总结】本题是对锐角三角比的直接运用,注意在运用锐角三角比时,要将锐角放在直角三角形中.ABC【习题10】 已知Rt ABC ∆中,90C ∠=︒,60A ∠=︒,2a b -=,求a 、b 、c 的值. 【难度】★★★【答案】33+=a ,13+=b ,232+=c 【解析】解:在ABC Rt △中,60A ∠=︒, ∴ 33cot ==a b A ,则b a 3=. ∵2a b -=,∴23=-b b ,解得:13+=b ,∴333+==b a ,2322+==b c .【总结】本题是对特殊角锐角三角比的综合运用.【作业1】(1)若1cos 2α=,则α∠=______; (2)若tan 1β=,则β∠=______.【难度】★【答案】(1)60°;(2)45°.【解析】主要考查特殊角的锐角三角比的值.【作业2】()151α+︒=,则锐角α的度数是______.【难度】★ 【答案】15°()151α+︒=,∴()tan 15α+︒=,∴︒=︒+3015α,∴︒=15α. 【总结】本题主要考查特殊角的锐角三角比的值.【作业3】若225sin cos 304α+︒=,那么锐角α度数是( ) A .15°B .30°C .45°D .60°【难度】★ 【答案】C【解析】∵225sin cos 304α+︒=,∴225sin 4α+=⎝⎭, ∴21sin 2α=,∴sin α=,∴︒=45α.【总结】本题主要考查特殊角的锐角三角比的值.课后作业【作业4】 下列等式中,成立的有( )① sin 30°+ sin 30°= sin 60°;②若cos A = sin B ,则=A B ∠∠;③若sin A = cos 30°,则锐角A = 60°; ④sin 60°+ sin 30° = 2(sin 30°+ cos 30°).A .0个B .1个C .2个D .3个【难度】★★ 【答案】B【解析】①sin 30°+ sin 30°=12121=+,sin 60°=23,不成立; ②若cos A = sin B ,则+=90?A B ∠∠,所以②不成立; ③若sin A = cos 30°,则锐角A = 60°,成立; ④sin 60°+ sin 30° = 2132123+=+,2(sin 30°+ cos 30°)=3123212+=⎪⎪⎭⎫ ⎝⎛+,所以不成立. 【总结】本题主要考查特殊角的锐角三角比的值.【作业5】()12°121cot 3013sin 452-⨯-+-︒. 【难度】★★★ 【答案】3. 【解析】原式=)21112132⨯==.【总结】本题主要是将特殊角的锐角三角比的值与实数运算结合在一起.【作业6】 计算:sin 45cos45cos30cot 60tan 60︒+︒︒︒-︒.【难度】★★ 【答案】0.【解析】原式202+=+=+=. 【总结】本题主要是将特殊角的锐角三角比的值与实数运算结合在一起.【作业7】tan301tan30cot30︒-+︒-︒.【难度】★★【答案】332【解析】原式=︒-︒+-︒--︒30cot 30tan 130tan 160cot=332333331331=-+⎪⎪⎭⎫ ⎝⎛---. 【总结】本题主要是将特殊角的锐角三角比的值与实数运算结合在一起.【作业8】在ABC ∆中,A ∠、B ∠均是锐角,且2sin 0A +=,请判断ABC ∆的形状,并说明理由.【难度】★★【答案】等腰直角三角形【解析】∵2sin 0A , ∴02sin 2=-A ,031cot 31=-B ,解得:22sin =A ,1cot =B .∴︒=∠45A ,︒=∠45B ,∴ABC ∆为等腰直角三角形.【总结】本题主要是对绝对值和平方的非负性和特殊角的锐角三角比的值的综合考查.【作业9】已知Rt ABC ∆中,90C ∠=︒,45A ∠=︒,3c a -=,求a 、b 、c 的值.【难度】★★★【答案】323+=a ,323+=b ,236+=c 【解析】解:在ABC Rt △中, 22sin ==c a A ,则a c 2=. ∵3c a -=3a -=,解得:323+=a ,∴323+==a b ,2362+==a c .【总结】本题是对特殊角锐角三角比的综合运用.【作业10】 应用锐角三角比的定义,求sin 22.5°、tan 22.5°、sin 67.5°、tan 67.5°.【难度】★★★【答案】2225.22sin +=︒,125.22tan -=︒,()4224225.67sin -+=︒, 125.67tan +=︒. 【解析】如图,作等腰△ABC ,且22.5B ACB ∠=∠=过点C 作CD ⊥BA 交BA 的延长线于点D .则︒=∠5.22B ,67.5BCD ∠=︒.设x DC =,则x AB AC 2==,x DA =,()x x x BD CD BC 2242122222+=++=+=.在Rt △BDC 中, sin 22.5sin DC B BC ︒==== =; ()1212112tan 5.22tan -=+=+===︒x xBD DC B ;()()224224224122241222412sin 5.67sin -⋅+-+=++=++==∠=︒x x BC DB BCD ;()1212tan 5.67tan +=+==∠=︒x x CD DB BCD . 【总结】在求非特殊角的锐角三角比的值时,想办法将其跟特殊角结合起来,再去求值. 2224222424822224224224224+=+=+=+=-⋅+-()()4224222222412-+=-+=。
初三锐角的三角比

一、 锐角三角比的意义 1、正切直角三角形中一个锐角的对边与邻边的比叫做这个锐角的正切(tangent ).锐角A 的正切记作tan A .tan A BC aA A AC b ===锐角的对边锐角的邻边. 2、余切直角三角形中一个锐角的邻边与对边的比叫做这个锐角的余切(cotangent ).锐角A的余切记作cot A .cot A AC bA A BC a ===锐角的邻边锐角的对边. 3、正弦直角三角形中一个锐角的对边与斜边的比叫做这个锐角的正弦(sine ).锐角A 的正弦记作sin A .sin A BC aA AB c ===锐角的对边斜边. 4、余弦直角三角形中一个锐角的邻边与斜边的比叫做这个锐角的余弦(cosine ).锐角A 的余弦记作cos A .cos A AC bA AB c===锐角的邻边斜边.5、锐角的三角比一个锐角的正切、余切、正弦、余弦统称为这个锐角的三角比.锐角的三角比一:锐角的三角比ACBD二、 特殊锐角的三角比的值αtan αcot αsin αcos α30°33312 32 45° 1 1 22 2260° 3333212【例1】 已知Rt ABC ∆中,90C ∠=︒,那么ba是角A 的( ) A .正弦B .余弦C .正切D .余切【例2】 已知Rt ABC ∆中,90C ∠=︒,AC = 3,BC = 4,那么sin A =______.【例3】 已知α为锐角,且5sin 13α=,求α的余弦值.【例4】 求值:sin60tan30cot30︒-︒+︒=_______.【例5】 已知锐角ABC ∆中,3sin A ,tan 1B =,那么C ∠=______°.【例6】 将锐角α所在的三角形的三边同时扩大三倍,这时角α的正弦值( ) A .变大B .变小C .不变D .无法确定【例7】 (2014学年·松江区二模·第6题)如图,在Rt ABC ∆中,90ACB ∠=︒,CD ⊥AB ,垂足为D ,AB = c ,A α∠=,则CD 长为( )A .2sin c αB .2cos c αC .sin tan c ααD .sin cos c αα仰角 视线水平线视线俯角铅垂线北北偏东30°南偏西45°北偏西70°南偏东50°30° 70° 45° 50°【例8】 (2015学年·徐汇区二模·第19题)计算:20(3)cot 30tan 4531ππ--︒-︒+.【例9】 (2015学年·普陀区二模·第19题)计算:22123323tan 601-⎛⎫-+- ⎪︒-⎝⎭.一、 解直角三角形在直角三角形中,由已知元素求出所有未知元素的过程,叫做解直角三角形. 在t R ABC ∆中,如果=90C ∠︒,那么它的三条边和两个锐角之间有以下的关系: (1)三边之间的关系:222a b c +=(2)锐角之间的关系:90A B ∠+∠=︒(3)边角之间的关系:sin cos a A B c ==,cos sin bA B c ==tan cot a A B b ==,cot tan b A B a== 二、 仰角与俯角在测量过程中,常常会遇到仰角和俯角.如图,当我们进行测量时,在视线与水平线 所成的角中,视线在水平线上方的角叫做仰角,视线在水平线下方的角叫做俯角.三、 方向角指北或指南方向线与目标方向线所成的小于90°的角叫做方向角. 如图:北偏东30°,北偏西70°,南偏东50°,南偏西45°.二:解直角三角形ABC D A B9米传送带AB Chl四、 坡度(坡比)、坡角在修路、挖河、开渠等设计图纸上,都需要注明斜坡的倾斜程度.如图,坡面的铅垂高度h 和水平宽度l 的比叫做坡面的坡度(或坡比),记作i ,即h i l=. 坡度通常写成1 : m 的形式,如1:1.5i =. 坡面与水平面的夹角叫做坡角,记作α.坡度i 与坡角α之间的关系:tan hi l α==.【例10】 (2015学年·崇明县二模·第15题)已知一斜坡的坡比为1 : 2,坡角为α,那么sin α=______.【例11】 (2014学年·长宁区二模·第15题)已知在离地面30米的高楼窗台A 处测得地面花坛中心标志物C 的俯角为60°,那么这一标志物C 离此栋楼房的地面距离BC 为______米.【例12】 (2015学年·浦东新区二模·第13题)如图,传送带和地面所成的斜坡的坡度为39米高的地方,则物体从A 到B 所经过的路程为______米.【例13】 (2015学年·宝山区、嘉定区二模·第16题)如图,如果在大厦AB 所在的平地上选择一点C ,测得大厦顶端A 的仰角为30°,然后向大厦方向前进40米,到达点D 处(C 、D 、B 三点在同一直线上),此时测得大厦顶端A 的仰角为45°.那么大厦AB 的高度为______米.(保留根号)ABCE ABCDABCDEABCD EFAB C北【例14】 (2014学年·浦东新区二模·第16题)如图,已知小岛B 在基地A 的南偏东30°方向上,与基地A 相距10海里,货轮C 在基地A 的南偏西60°方向、小岛B 的北偏西75°方向上,那么货轮C 与小岛B 的距离是______海里.【例15】 (2014学年·徐汇区二模·第22题)如图,在Rt ABC ∆中,90CAB ∠=︒,3sin 5C =,AC = 6,BD 平分CBA ∠交AC 边于点D .求:(1)线段AB 的长;(2)tan DBA ∠的值.【例16】 (2014学年·闸北区二模·第21题)已知:如图,点E 是矩形ABCD 的边AD 上一点,BE = AD ,AE = 8,现有甲乙二人同时从E 点出发,分别沿EC 、ED 方向前进,10C 点的同时乙恰巧到达终点D 处.(1)求tan ECD ∠的值; (2)求线段AB 及BC 的长度.【例17】 (2014学年·闵行区二模·第21题)如图,已知在ABC ∆中,25AB AC ==25sin B ∠=D 为边BC 的中点.E 为边BC 延长线上一点,且CE = BC .联结AE ,F 为线段AE 的中点.求:(1)线段DF 的长;(2)CAE ∠的正切值.【例18】 (2015学年·闸北区二模·第21题)已知:如图,在ABC ∆中,45ABC ∠=︒,AD是BC 边上的中线,过点D 作DE ⊥AB 于点E ,且3sin 5DAB ∠=,32DB =求:(1)AB 的长;(2)CAB ∠的余切值.ABCDPABCD【例19】 (2015学年·松江区二模·第22题)如图,在ABC ∆中,AB = AC = 10,BC = 12,AD ⊥BC 于D ,O 为AD 上一点,以O 为圆心,OA 为半径的圆交AB 于G ,交BC 于E 、F ,且AG = AD .(1)求EF 的长; (2)求tan BDG ∠的值.【例20】 (2015学年·普陀区二模·第21题)已知:如图,在ABC ∆中,AB = AC = 13,BC = 24,点P 、D 分别在边BC 、AC 上,2AP AD AB =,求APD ∠的正弦值.【例21】 (2015学年·虹口区二模·第21题)如图,在ABC ∆中,CD 是边AB 上的中线,B∠是锐角,且2sin 2B =,1tan 2A =,BC =22,求边AB 的长和cos CDB ∠的值.【例22】 (2014学年·崇明县二模·第21题)在Rt ABC ∆中,90BAC ∠=︒,点E 是BC 的中点,AD ⊥BC ,垂足为点D .已知AC = 9,3cos 5C =.(1)求线段AE 的长;(2)求sin DAE ∠的值.【例23】 (2015学年·崇明县二模·第22题)如图,在某海滨城市O 附近海面有一股台风,据监测,当前台风中心位于该城市的南偏东20°方向200千米的海面P 处,并以20千米/时的速度向P 处的北偏西65°PQ 的方向移动,台风侵袭范围是一个圆形区域,当前半径为60千米,且圆的半径以10千米/时速度不断扩张.(1)当台风中心移动4小时时,受台风侵袭的圆形区域半径增大到 千米;O CBADF EG CA BEDOPQ北当台风中心移动t 小时时,受台风侵袭的圆形区域半径增大到 千米;(2)当台风中心移动到与城市O 距离最近时,这股台风是否侵袭这座海滨城市?请说明理由.(参考数据2 1.41=,3 1.73=).【例24】 (2015学年·闵行区二模·第22题)如图,山区某教学楼后面紧邻着一个土坡,坡面BC 平行于地面AD ,斜坡AB 的坡比为51:12i =,且AB = 26米.为了防止山体滑坡,保障安全,学校决定对该土坡进行改造.经地质人员勘测,当坡角不超过53°时,可确保山体不滑坡.(1)求改造前坡顶与地面的距离BE 的长;(2)为了消除安全隐患,学校计划将斜坡AB 改造成AF (如图所示),那么BF 至少是多少米?(结果精确到1米)(参考数据:sin530.8︒≈,cos530.6︒≈,tan53 1.33︒≈,cot530.75︒≈)【例25】 (2014学年·普陀区二模·第22题)本市为了给市容营造温馨和谐的夜间景观,准备在一条宽7.4米的道路上空利用轻轨桥墩,安装呈大中小三个同心圆的景观灯ABDCEF带(如图1所示).如图2,已知EF 表示路面宽度,轻轨桥墩的下方为等腰梯形ABCD ,且AD // EF ,AB = DC ,37ABC ∠=︒.在轻轨桥墩上设有两处限高标志,分别表示等腰梯形的下底边到路面的距离为 2.9米和等腰梯形的上底边到路面的距离为 3.8米.大圆直径等于AD ,三圆半径的比等于1 : 2 : 3.试求这三个圆形灯带的总长为多少米?(结果保留π)(参考数据:sin370.6︒≈,cos370.8︒≈,tan370.75︒≈)2.92.93.8ABCDFO图1图2。
