SOR迭代法
6.4超松弛迭代法

表6.3 Gauss-Seidel迭代法与SOR迭代法比较
Gauss-Seidel迭代法
SOR迭代法(ω=1.25)
k
x1
0
1.0000000
x2 1.0000000
x3 1.0000000
x1 1.0000000
x2 1.0000000
x3 1.0000000
1
5.2500000
3.1825000
第六章 线性方程组迭代解法
§ 6.4 超松弛迭代法(SOR)
§ 6.4超松弛迭代法(SOR)
SOR(Successive Over-Relaxation)法, 即超松弛迭代法,是目前解大型线性方程 组的一种最常用的方法,是Gauss-Seidel迭 代法的一种加速方法。
一、SOR法迭代公式
例6.6 用SOR法求解线性方程组
前面我们看到,SOR法收敛与否或收敛速度都 与松弛因子ω 有关,关于ω 的范围,有如下定理。
SOR法收敛与收敛速度有关定理
定理6.5 设A∈Rnn,满足a ii≠0 (i=1,2,,n),则有 ρ(Bω)≥ |1-ω| 。
推论 解线性方程组,SOR法收敛的必要条件是 |1-ω| <1 ,即 0<ω <2。
4.0009262
-4.9982822
7 3.0134110
3.9888241
-5.0027940
3.0000498
4.0002586
-5.0003486
迭代法若要精确到七位小数, Gauss-Seidel迭代法需要34次迭代; 而用SOR迭代法(ω=1.25),只需要14次迭代。
可见,若选好参数ω,SOR迭代法收敛速度会很 快。
sor迭代法手算例题

sor迭代法手算例题SOR迭代法是求解线性方程组的一种经典方式,其基本思想是通过不断迭代来逼近方程组的解。
这种方法在大规模问题上具有很好的效率,因此得到了广泛的应用。
本文将介绍SOR迭代法的基本原理,并以一个手算例题来展示其具体步骤和计算结果。
一、SOR迭代法的基本原理在介绍SOR迭代法的原理之前,我们先来看一下迭代法本身的思想。
假设有一个线性方程组:$$Ax=b$$其中,A是一个$n\times n$的系数矩阵,b是一个$n\times 1$的常数向量,x是一个$n\times 1$的未知向量。
迭代法的基本思想是将方程组表示为:$$x^{(k+1)}=Tx^{(k)}+C$$其中,$x^{(k)}$表示第k次迭代的近似解,$T$是一个$n\times n$的矩阵,$C$是一个$n\times 1$的常数向量。
迭代法的步骤是从一个初始点$x^{(0)}$开始,不断应用上述公式来寻找更好的解$x^{(k+1)}$。
当接近真解时,迭代的过程会不断收敛,即$x^{(k+1)}$会不断逼近真解$x$。
那么,如何确定矩阵$T$和向量$C$呢?最简单的方法是将方程组表示为:$$x^{(k+1)}=(I-\omega A)x^{(k)}+\omega b$$其中,I是$n\times n$的单位矩阵,$\omega$是一个常数,称作松弛因子。
当$\omega=1$时,这就是最基本的迭代法——雅克比迭代法。
但是,雅克比迭代法的收敛速度比较慢,因此需要调整$\omega$的值,从而得到更好的迭代效果。
SOR迭代法就是一种改良的迭代方法,其基本思想是通过加速松弛因子的变化来改善雅克比迭代法的效率。
具体来说,SOR迭代法的公式为:$$x_i^{(k+1)}=(1-\omega)x_i^{(k)}+\frac{\omega}{a_{ii}}\left(b_i-\sum_{j<i}a_{ij}x_j^{(k+1)}-\sum_{j>i}a_{ij}x_j^{(k)}\right)$$其中,$i=1,2,\cdots,n$。
SOR迭代(算法分析和数值算例)

SOR 迭代基本思想Gauss-Seidel 迭代(1)1()(1)()()k k x D L U xD L +--=-+-的结果作为中间值,记为(1)k x+ 。
SOR 方法是将(1)k x+ 与上次计算的结果()k x 做加权平均作为最后结果。
迭代格式为:1(1)(1)()()111[](1),1,2i nk k k k ii ij jij j ij j i iix b a x a x x i na ωω-++==+=--+-=∑∑或者1(1)()(1)()11[],1,2i nk k k k iii ij jij j j j iiix x b a x a x i na ω-++===+--=∑∑算法: 1.0,,,A b x t e ω输入迭代初值松弛参数,为迭代次数初始值为0,为记录误差2. 当1,2in= 时,11:[]ni i i i j j j iix x b a x a ω==+-∑,结果仍然存储在ix 中。
迭代次数:1t t =+ 3.计算误差*e x x=-(真解已知)4.如果6510e -<⨯,则已达到精确度要求,否则继续第2步数值结果041010141,4,001430A b x -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=--== ⎪ ⎪ ⎪⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭迭代初值,用Gauss 消去法求的其真解为*12112x ⎛⎫⎪ ⎪=⎪ ⎪- ⎪⎝⎭依次取1,1.03,1.1ω=,数值结果见下表总结从实验结果可以看出,当取松弛参数为1.03时只需五步就能达到所需精度。
附录(M文件)function [t,x]=successiive_over_Rellaxatiion(A,b,x0,w,rx)n=length(A);x=x0; %% x0为迭代初值e=norm(rx-x0,inf); %% rx为真解,e为误差t=0; %% t为迭代次数while e>5*10^(-6)for i=1:ntemp=0;for j=1:ntemp=temp+A(i,j)*x(j,1);endx(i,1)=x(i,1)+w*(b(i,1)-temp)/A(i,i);ende=norm(rx-x,inf);t=t+1;xend。
sor方法

sor方法
SOR方法是一种迭代数值解法,主要被用于求解线性系统Ax=b,其中A是系数矩阵,b是右端向量。
SOR方法的全称为"Successive Over-Relaxation Method",意为迭代超松弛法。
在使用SOR方法求解线性方程组时,首先需要将系数矩阵A分解为L、D和U 三个部分,其中L是A的严格下三角矩阵,D是A的对角线矩阵,U是A的严格上三角矩阵。
同时,SOR方法还需要一个松弛因子w。
SOR方法的迭代公式为:
x(k+1) = (1-w)x(k) + w(D-wL)^(-1)(b-Ux(k))
其中x(k)表示第k次迭代求得的解向量,x(k+1)表示x(k)的下一次迭代,^(−1)表示逆矩阵。
可以发现,SOR方法是基于Gauss-Seidel方法的改进,它在每一次迭代中添加了一个松弛因子w,从而使得解向量的迭代更快、更稳定。
在实际应用中,我们需要选择一个合适的松弛因子w,以使得SOR方法能够收敛并且收敛速度较快。
一般来说,选择一个小于1的w能够保证SOR方法的收敛性,而选择一个大于1的w能够加快SOR方法的收敛速度。
需要注意的是,SOR方法只能够求解特定条件下的线性方程组,如系数矩阵为对称正定矩阵、对角占优矩阵等。
当系数矩阵不满足这些条件时,SOR方法可能出现发散的情况。
总的来说,SOR方法是一种简单而有效的数值解法,被广泛应用于工程计算等领域。
在使用时,需要根据具体问题选择合适的松弛因子w,并且注意其收敛性和收敛速度。
用sor法解方程组

用SOR法解方程组引言方程组是数学中常见的问题,解决方程组可以帮助我们理解和预测各种实际问题。
解方程组的方法有很多种,其中一种常用的方法是SOR(Successive Over Relaxation)法。
SOR法是一种迭代法,通过不断迭代逼近解的过程来求解方程组。
本文将对SOR法进行详细的介绍和分析。
SOR法概述SOR法是一种求解线性方程组的迭代算法,其基本思想是通过引入松弛因子来加速收敛速度。
对于线性方程组Ax=b,SOR法的迭代公式为:x^(k+1) = (1-w)x^(k) + w * D^(-1) * (b - L * x^(k+1) - U * x^(k))其中,x(k)表示第k次迭代的解向量,x(k+1)表示第k+1次迭代的解向量,w为松弛因子(0 < w< 2),A被分解为下三角矩阵L、上三角矩阵U和对角矩阵D。
算法流程SOR法的算法流程如下:1.初始化解向量x^(0)2.对于每次迭代k = 0, 1, 2, …–计算下一次迭代的解向量x^(k+1): x^(k+1) = (1-w)x^(k) + w * D^(-1) * (b - L * x^(k+1) - U * x^(k))–判断迭代是否收敛:如果迭代误差小于预设的阈值就停止迭代,否则继续迭代3.返回最终的解向量x^(k+1)SOR法特点SOR法具有以下几个特点:1.相对于传统的迭代法,SOR法引入了松弛因子,能够加速迭代的收敛速度。
2.当松弛因子w=1时,SOR法等价于高斯-赛德尔迭代法。
3.大部分情况下,SOR法是收敛的。
收敛速度与松弛因子w有关,一般来说,选择一个合适的松弛因子可以加快算法的收敛速度。
4.SOR法对于对角占优的线性方程组具有较好的收敛性能,但对于一般的线性方程组效果可能不理想。
SOR法的数值实验为了验证SOR法的性能,我们进行了一系列的数值实验。
我们选取了不同规模的线性方程组,通过对比SOR法的迭代次数和收敛速度来评估其性能。
SOR迭代法求解线性方程组

SOR迭代法求解线性方程组一实验名称:实验四:逐次超松弛迭代法。
二实验题目:求解下面的三元一次线性方程组:2x-y+2z=4;x+2y+3z=9;2x-2y-3z=-3;要求选取不同的松弛因子进行计算,并估计最优松弛因子的大小。
三实验目的:1.熟悉掌握逐次超松值迭代法的基本原理和基本方法。
2.学会用逐次超松弛迭代法解简单的方程组。
3.选取不同的w值(0<w<2)进行试探性的计算,从中摸索出近似的最佳松弛因子。
四基础理论:超松弛迭代法以及所涉及的主要算法为:Xi^(k+1)←(1-w)*Xi^(k)+w*Xi的共轭的(k+1)次幂。
五实验环境:Visual C++6.0。
六实验过程:1. 在程序中输入不同的数据时,会得到不同的结果。
2.大于1的时候的松弛因子,被称作超松弛法。
小于则被称做低松弛法。
由于松弛因子对方程组的收敛速度影响很大,所以在一定的误差范围内,选择不同的松弛因子时,迭代次数也会不同。
3. 按照实验题目中的数据输入时,比较结果当w=0.6时,会出现下面的结果:当w=0.7时得当w=0.8时得当w=0.9时,会出现下面的结果当w=1.0时得七结果分析:当在一定的误差范围内,有以上运行结果可以得出答案,最优松弛因子的范围为0.8。
八逐次超松弛迭代法程序代码:#include<iostream.h>#include<stdlib.h>#include<stdio.h>#include<math.h>void SOR(double w, double a[3][3], double b[3], double x[3], double esp) {double t[3];int flag=0;int n=0;while(!flag){flag=1;n++;t[0]=x[0]; t[1]=x[1]; t[2]=x[2];for(int i=0;i<3;i++){double m=b[i];for(int j=0;j<3;j++){m-=(a[i][j]*x[j]);}x[i]=x[i]+w*m/a[i][i];}for(int k=0;k<3;k++){if(fabs(x[k]-t[k])>=esp){flag=0;break;}}}printf("%d\n",n);}void main(){double a[3][3];double b[3];double x[3];double w,esp;a[0][0]=2; a[0][1]=-1; a[0][2]=2;a[1][0]=1; a[1][1]=2; a[1][2]=3;a[2][0]=2; a[2][1]=-2; a[2][2]=-3;b[0]=4; b[1]=9; b[2]=-3;x[0]= x[1]= x[2]=0;w=0.6;esp=0.0001;SOR(w,a,b,x,esp);for(int i=0;i<3;i++)printf("%f\n",x[i]);}。
sor迭代法

SOR迭代法的Matlab程序function [x]=SOR_iterative(A,b)% 用SOR迭代求解线性方程组,矩阵A是方阵x0=zeros(1,length(b)); % 赋初值tol=10^(-2); % 给定误差界N=1000; % 给定最大迭代次数[n,n]=size(A); % 确定矩阵A的阶w=1; % 给定松弛因子k=1;% 迭代过程while k<=Nx(1)=(b(1)-A(1,2:n)*x0(2:n)')/A(1,1);for i=2:nx(i)=(1-w)*x0(i)+w*(b(i)-A(i,1:i-1)*x(1:i-1)'-A(i,i+1:n)*x0(i+1:n)')/A(i,i);endif max(abs(x-x0))<=tolfid = fopen('SOR_iter_result.txt', 'wt');fprintf(fid,'\n********用SOR迭代求解线性方程组的输出结果********\n\n');fprintf(fid,'迭代次数: %d次\n\n',k);fprintf(fid,'x的值\n\n');fprintf(fid, '%12.8f \n', x);break;endk=k+1;x0=x;endif k==N+1fid = fopen('SOR_iter_result.txt', 'wt');fprintf(fid,'\n********用SOR迭代求解线性方程组的输出结果********\n\n');fprintf(fid,'迭代次数: %d次\n\n',k);fprintf(fid,'超过最大迭代次数,求解失败!');fclose(fid);end常微分方程的数值解法实验目的:熟悉在Matlab平台上直接求解常微分方程初值问题试验方法1、利用改进欧拉法解方程:程序内容为:fun=@(x,y)x^(-2)-y/x;h=0.05;X=1:h:2;Y(1)=1;for i=2:21Y(i)=Y(i-1)+h/2*(fun(X(i-1),Y(i-1))+fun(X(i),Y(i-1))+h*fun(X(i-1),Y(i-1))); end;Y运行结果为:Y =Columns 1 through 91.0000 0.9989 0.9957 0.9909 0.9848 0.9778 0.9701 0.9618 0.9530Columns 10 through 180.9440 0.9348 0.9254 0.9160 0.9065 0.8971 0.8876 0.8783 0.8690Columns 19 through 210.8598 0.8508 0.8418真实解的求法为:x=1:0.05:2;y=1./x.*(log(x)+1)y =Columns 1 through 81.0000 0.9988 0.9957 0.9911 0.9853 0.9785 0.9710 0.9630Columns 9 through 160.9546 0.9459 0.9370 0.9279 0.9188 0.9096 0.9004 0.8912Columns 17 through 210.8821 0.8731 0.8641 0.8553 0.8466用四阶R-K算法解常微分方程的程序为:fun=@(x,y)x^(-2)-y/x;h=0.1;X=1:h:2;Y(1)=1;for n=2:11k1=fun(x(n-1),Y(n-1));k2=fun(x(n-1)+h/2,Y(n-1)+h/2*k1);k3=fun(x(n-1)+h/2,Y(n-1)+h/2*k2);k4=fun(x(n-1)+h,Y(n-1)+h*k3);Y(n)=Y(n-1)+h/6*(k1+2*k2+2*k3+k4)end;Y运行后了结果为:Y =Columns 1 through 91.0000 0.9957 0.9853 0.9710 0.9546 0.9370 0.9188 0.9004 0.8821Columns 10 through 110.8641 0.8466真实解的求法为:x=1:0.1:2;y=1./x.*(log(x)+1)y =Columns 1 through 91.0000 0.9957 0.9853 0.9710 0.9546 0.9370 0.9188 0.9004 0.8821Columns 10 through 110.8641 0.8466可见其精确度至少已达到0.0012、MATLAB中数值解法“ode45”为:[x1,y1] = ode45(@(x,y)x^(-2)-y/x,[1,2],y0);符号解法“dsolve”求解为:dsolve('Dy=x^(-2)-y/x','y(1) = 1','x')ans =(log(x)+1)/x画出两种算法的图形位:[x1,y1] = ode45(@(x,y)x^(-2)-y/x,[1,2],1);fplot('(log(x)+1)/x',[1,2]);hold on, plot(x1,y1,'ro');数值算法同解析算法几乎完全吻合。
逐次超松弛迭代法

(3.7)
图6.1
12
我们在 (x, y) 平面上作两组平行直线
x x0 ih, y y0 jh i, j 0,1,2,
(3.8)
(x0 , y0 ) 是平面 (x, y) 上的任意一点,通常取 (x0 , y0 ) 为坐标原点, h( 0) 称为步长.这样,整
个平面就被这两组平行直线构成的正方形网格所覆盖,所讨论的区域 G+P 可被有限个正
x1(k )
1 (4 5
x (k 1) 2
x (k 1) 3
x4(k 1) )
x2(k )
1 10
(12
x1(k
)
x (k 1) 3
x (k 1) 4
)
x3(k )
1 (8 5
x1(k )
x2(k )
x4(k 1) )
x4(k )
1 (34 10
x1(k )
x2(k )
x3(k ) )
k 1,2,
输出 近似解 x1, x2 ,xn 或迭代次数超过 m 的信息.
step 1 对 k 1,, n 做 step2—4.
step 2 对 i 1,2,, n
step 3 step 4
i 1
n
(bi aij x j aij xoj
xi (1 )x0i
j 1
j i 1
若 x x0 TOL ,则输出 (x1,, xn ) ;停机.
图表6.2
5
从表6.2得到
x6x
5.5 61 04
算法6.3 应用SOR方法解方程组 Axb
输人 方程组的阶数 n ; A 的元素 aij (i, j 1,, n) ;b 的分量 bi (i 1,, n) ;初始向量 x0 的分量
超松弛迭代法(SOR方法)

解:SOR迭代公式
x1( k
1)
(1 )x1(k )
4
(10 2x2(k )
4x3(k ) )
x
(k 2
1)
(1 )x2(k )
17
(3
2
x1(
k
1)
10x3(k ) )
x3( k
1)
(1 )x3(k )
9
(7 4x1(k 1)
10
x
(k 2
1)
)
初值 x (0) (0,0,0)T k = 0,1,2,…,
例该4方.4程用组S的OR精法确求解解线x (性*) 方 程(2组,1,1)T
如值只果需x(0取)迭ω取代(0=,04ω21,00x(=42)即1次T1xx,要11.高4便26达x斯11,可207到—xx要达22同4塞求到x样319德精0x精x3尔度130度迭要x,(3k7代求需1) 法要x)迭(和k) 代同1一1100初6次
数值计算方法
超松弛迭代法(SOR方法) 使用迭代法的困难在于难以估计其计算
量。有时迭代过程虽然收敛,但由于收敛速 度缓慢,使计算量变得很大而失去使用价值 。因此,迭代过程的加速具有重要意义。逐 次超松弛迭代(Successive Over relaxatic Method,简称SOR方法)法,可以看作是带参 数的高斯—塞德尔迭代法,实质上是高斯-塞 德尔迭代的一种加速方法。
或 Dx(k1) (1)Dx(k) (b Lx(k1) Ux(k) )
故 (D L)x(k1) (1)D Ux(k) b
显然对任何一个ω值,(D+ωL)非奇异,(因为假设 aii 0,i 1,2,, n )于是超松弛迭代公式为
x(k1) (D L)1 (1)D U x(k) (D L)1b
关于逐次超松弛迭代法(SOR方法)的教学

关于“逐次超松弛迭代法(SOR 方法)”的教学一、SOR 迭代公式逐次超松弛(Successive Over Relaxation)迭代法,简称SOR 方法,它是在GS 法基础上为提高收敛速度,采用加权平均而得到的新算法,设求解线性代数方程组b Ax =的GS 法记为(1)再由与加权平均得这里ω>0称为松弛参数,将(1)代入则得(2)称为SOR 迭代法,ω>0称为松弛因子,当ω=1时,(2)即为GS 法,将(2)写成矩阵形式则得即,于是得SOR 迭代的矩阵表示(3)其中(4)亦可作矩阵分解ωωN M A -=,其中有.从而SOR 迭代矩阵 ωωωN M G 1-=. 例1 给定方程组精确解,用SOR法求解,分别取ω=1及ω=125.解用SOR迭代公式(2)可得取,迭代7次后分别为若要精确到小数后7位,对ω=1(即GS法)需迭代34次,而对ω=1.25的SOR法,只需迭代14次.它表明松弛因子ω选择的好坏,对收敛速度影响很大。
二、SOR迭代法收敛性根据迭代法收敛性定理,SOR法收敛的充分必要条件为,收敛的充分条件为,但要计算比较复杂,通常都不用此结论,而直接根据方程组的系数矩阵A 判断SOR迭代收敛性,下面先给出收敛必要条件定理1设,则解方程的SOR迭代法收敛的必要条件是0<ω<2.证明因为SOR迭代矩阵为,于是另一方面,设的特征值为,由特征根性质,有若SOR法收敛,则,由,则得0<ω<2.定理2若对称正定,且0<ω<2,则解Ax=b的SOR迭代法(3)对迭代收敛。
证明设的特征值为(可能是复数),对应特征向量x≠0, 由(4)得因为实对称矩阵,故, 上式两边与x作内积,得(5)因A正定,故D也正定,记.又记,,由内积性质得于是由(5)有由于A正定及0<ω<2,故,于是。
注一:当ω=1时SOR法即为GS法,故GS法也收敛,此即为GS法的收敛定理结论。
对于SOR迭代法,松弛因子的选择对收敛速度影响较大,关于最优松弛因子研究较为复杂,且已有不少理论结果。
数值计算 SOR方法
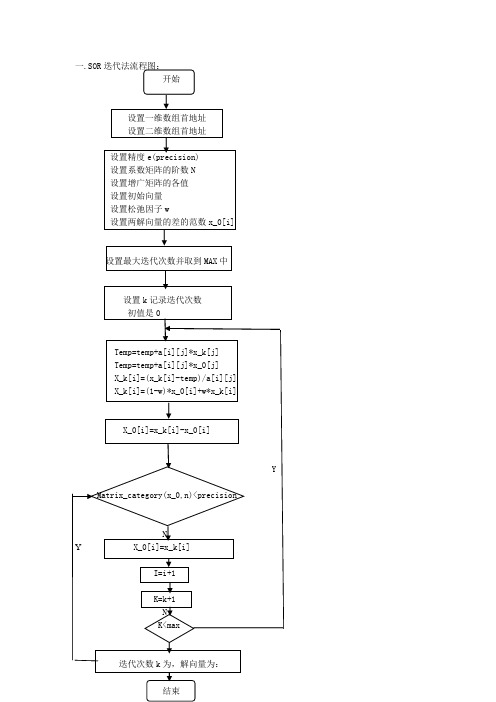
一.SOR迭代法流程图:开始设置一维数组首地址设置二维数组首地址设置精度e(precision)设置系数矩阵的阶数N设置增广矩阵的各值设置初始向量设置松弛因子w设置两解向量的差的范数x_0[i]设置最大迭代次数并取到MAX中设置k记录迭代次数初值是0Temp=temp+a[i][j]*x_k[j]Temp=temp+a[i][j]*x_0[j]X_k[i]=(x_k[i]-temp)/a[i][j]X_k[i]=(1-w)*x_0[i]+w*x_k[i]X_0[i]=x_k[i]-x_0[i]YMatrix_category(x_0,n)<precisionNY X_0[i]=x_k[i]I=i+1K=k+1NK<max实验名称: 松弛法实验解题小组成员(班级:09医软(1)班):姚飞 :09713047 参与程序的编写闫化晴 :09713046 参与搜集资料与编写程序余雷 :09713049 参与搜集资料与后期运行调试张珊 :09713051 参与程序的编写实验内容:二.SOR 迭代法理论:松弛法是 Gauss -Seidel 迭代 迭代法的一种加速方法.若记△X = X (K+1) - X (K) = LX (K+1) + UX (K) + f - X (K)则X (K+1) = X (K) + △X ,这样X (K+1) 可以看作是 X (K)加上修正项 △X 而得到.若在修正项△X 前面添加一个因子ω= 1,就是Gauss -Seidel 迭代.通过选择ω可使迭代法收敛的更快.松弛法简称SOR 方法,它的计算格式为:(1)()()()111122111(1)()(1)()()222211233222(1)()(1)()1111(1)(),(1)(),(1)(),k k k k n n k k k k k n n k k k k n n n n nn n nn x x b a x a x a x x b a x a x a x a x x b a x a x a ωωωωωω+++++--=-+---=-+----=-+---这里ω称为松弛因子.当ω< 1时称为低松弛迭代,当1 < ω <2时称为超松弛迭代.实验素材及结果:三、SOR 迭代法例1、用SOR 迭代法求解线性方程组:⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----------74.012.018.168.072.012.006.016.012.001.103.014.006.003.088.001.016.014.001.076.04321x x x x取初始点T x )0,0,0,0()0(=,松弛因子05.1=ω,精度要求610-=ε.解 :根据上面程序运行结果如下:例2、用SOR迭代法求解方程组:8X1 + X2- 2X3 = 9,3X1 - 10X2 +X3 = 19,5X1 - 2X2 +20X3 = 72,取初始点X(0) = (0,0,0)T,松弛因子ω= 1,精度要求ε= 10-5.解:根据上面程序运行结果如下:。
SOR迭代法

aij x(jk )
3.1
若记
i1
n
r(k)
i
(bi
a x(k 1) ij j
aij
x
(k j
)
),
j 1
j i
i 1,2,L ,n
则 3.1 式可写为
x( k 1) i
x(k) i
1 aii
r(k)
i
3.2
由此可以看出, Gauss Seidel 迭代法的第 k 1
步 ,相当于在第 k 步的基础上每一个分量增加
SOR迭代法常以这种形式进行计算。
格式(3.4)的矩阵形式为
X (k1) (1 ) X k D1 b LX k UX (k) ,
3.5
其中
a11
D
a22
O
0
0
,
ann
0 a12 L
U
0O
O
0
a1n
an1,n
0
显然,A D L U.
0
0
L
a21
O
OO
上述定理说明,对于任何系数矩阵 A,若要 SOR
法收敛,必须选取松弛因子 0,2 , 然而,当松
弛因子满足条件 0 2 时,并不是对所有系数矩 阵 A 来说,SOR 法都是收敛的。但是,对一些特殊矩 阵来说,这一条件是充分的。
定理7 如果矩阵 A 是对称正定的,则 SOR 法 对于0 2 是收敛的。
其 Gauss Seidel 迭 代 格 式 可写为 (aii 0) :
x(k1) i
x(k) i
1 aii
bi
a x(k1) i1 1
L
a x(k1) i,i1, i1
sor迭代法matlab

sor迭代法matlabSOR迭代法(Successive Over-Relaxation)是一种用于求解线性方程组的迭代算法,在MATLAB中有广泛的应用。
它广泛应用于科学计算、工程技术等领域,被用于求解各种复杂的数学模型和物理问题。
我们需要了解什么是线性方程组。
线性方程组是由一系列线性方程组成的方程组,其中每个方程都是关于未知数的一次多项式。
线性方程组的求解是求解未知数的一组值,使得所有方程都成立。
解线性方程组的传统方法有高斯消元法和LU分解法等,但这些方法的计算量较大,尤其是对于大规模的线性方程组,计算效率较低。
而SOR迭代法通过将线性方程组转化为递推形式,通过不断迭代逼近解,从而提高了计算效率。
SOR迭代法的基本思想是通过使用逐点松弛因子来迭代求解线性方程组。
逐点松弛因子是指在每次迭代中,对于每个未知数,根据当前已知的其他未知数的值进行修正。
这种逐点松弛的策略可以加快迭代收敛速度。
在MATLAB中,实现SOR迭代法的过程如下:1. 首先,给定一个初始解向量x0,并初始化迭代次数k和松弛因子ω。
2. 对于每个未知数xi,使用如下公式进行迭代更新:xi(k+1) = (1-ω)xi(k) + (ω/aii)(bi - Σ(aijxj(k)), j≠i)其中,aii表示系数矩阵A中第i行第i列的元素,bi表示等式右侧的常数项。
3. 重复步骤2,直到满足收敛条件为止。
一般来说,可以设置一个收敛判据,比如设定一个误差阈值,当两次迭代之间的误差小于该阈值时,迭代停止。
4. 返回最终的解向量x(k)。
需要注意的是,SOR迭代法的收敛性与松弛因子ω的选择有关。
一般来说,如果松弛因子取值在(0,1)之间,则迭代过程是收敛的。
当松弛因子取值为1时,SOR迭代法等价于高斯-赛德尔迭代法。
在实际应用中,选择合适的松弛因子是非常重要的。
如果选择的松弛因子过小,收敛速度会很慢;而如果选择的松弛因子过大,迭代可能会发散。
sor迭代法

sor迭代法Sor迭代法是一种求解线性方程组的算法,它是Jacobi迭代法和Gauss-Seidel迭代法的改进。
在本文中,我们将深入探讨Sor迭代法的原理、优缺点以及应用。
一、原理1.1 Sor迭代法的基本思想Sor迭代法是通过对Jacobi迭代法和Gauss-Seidel迭代法进行改进得到的。
其基本思想是在Jacobi迭代和Gauss-Seidel迭代中引入一个松弛因子,使得每次更新后的值更接近于真实解。
1.2 Sor迭代公式Sor迭代公式如下:$x^{(k+1)}_i=(1-\omega)x^{(k)}_i+\frac{\omega}{a_{ii}}\left(b_i-\sum_{j=1,j\neq i}^n a_{ij}x^{(k+1)}_j\right)$其中,$x^{(k+1)}_i$表示第$k+1$次迭代中第$i$个未知数的值;$x^{(k)}_i$表示第$k$次迭代中第$i$个未知数的值;$\omega$为松弛因子;$a_{ii}$为系数矩阵中第$i$行第$i$列元素;$\sum_{j=1,j\neq i}^n a_{ij}x^{(k+1)}_j$表示第$k+1$次迭代中除第$i$个未知数外的其他未知数的值的和;$b_i$为方程组中第$i$个方程的常数项。
1.3 松弛因子松弛因子$\omega$是Sor迭代法中一个重要的参数,它控制了每次迭代后更新值与真实解之间的距离。
一般情况下,松弛因子取值在0和2之间。
当$\omega=1$时,Sor迭代法退化成Gauss-Seidel迭代法;当$\omega=0$时,Sor迭代法退化成Jacobi迭代法。
二、优缺点2.1 优点(1)收敛速度快:相比于Jacobi迭代法和Gauss-Seidel迭代法,Sor迭代法具有更快的收敛速度。
(2)适用范围广:Sor迭代法适用于大多数线性方程组求解问题,并且不需要对系数矩阵做任何特殊处理。
2.2 缺点(1)松弛因子需要调整:松弛因子是影响Sor迭代法收敛速度和精度的关键参数,因此需要通过试验或经验来确定最优值。
用SOR迭代法

一、数值求解如下正方形域上的Poisson 方程边值问二、2222(,)2,0,1(0,)(1,)(1),01(,0)(,1)0,01u u f x y x y x y u y u y y y y u x u x x ⎧⎛⎫∂∂-+==<<⎪ ⎪∂∂⎪⎝⎭⎨==-≤≤⎪⎪==≤≤⎩二、用椭圆型第一边值问题的五点差分格式得到线性方程组为2,1,1,,1,10,1,,0,141,?,?,?,?0,1i j i j i j i j i j ijj N j i i N u u u u u h f i j N u u u u i j N -+-+++----=≤≤====≤≤+,写成矩阵形式Au=f 。
其中 三、基本原理程序步骤:所有的步骤基本一致 1. 设置u ,n ,并给u ,n 赋初值; 2. While 语句循环,到的6步 3. Up 我第K 次迭代的值; 4. 分别进行计算,sum=0; 例如:Jacobi :sun= sum+A(i,j)*Ub; SOR 和Gauss_Seidel= sum+A(i,j)*u; 各自进行相应的下不运算。
5. 计算|Up-u|<ep 的绝对值,判断是否停机 6. 如果小于规定误差,迭代终止; 7. 输出结果u 和迭代次数k8. 在块的迭代中调用了追赶法的求解子程序zg ,在SOR 设计了A 得自动生成子程序creat_matix.1122N N v b v b u f v b ⎛⎫⎛⎫ ⎪ ⎪ ⎪⎪== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭4114114ii A -⎛⎫ ⎪- ⎪= ⎪- ⎪-⎝⎭11,12,1,121,22,2,21,2,,2211,12,1,121,22,2,221,2,,(,,...,),(,,...,),......,(,,...,)(,,...,)?,(,,...,)?,......,(,,...,)?1,999,0.10.011T T N N TN N N N N T T N N T N N N N N v u u u v u u u v u u u b h f f f b h f f f b h f f f h N h N ====+=+=+===+取或则或,2,,1,2,...,i j f i j N==1122NN A I I A A I IA -⎛⎫ ⎪-⎪= ⎪- ⎪-⎝⎭四、编写求解线性方程组Au=f的算法程序,用下列方法编程计算,并比较计算速度。
第五章 第三节 SOR迭代法

3.1
若记
ri
(k )
(bi aij x
j 1
i 1
( k 1) j
aij x (j k ) ),
j i
n
i 1, 2,, n
则 3.1 式可写为
xi( k 1) xi( k ) 1 (k ) ri aii
3.2
由此可以看出, Gauss Seidel 迭代法的第 k 1 步 ,相当于在第 k 步的基础上每一个分量增加 一个修正量
xi
k 1
x
(k ) i
i 1 n 1 ( k 1) (k ) bi aij x j aij x j aii j 1 j i
有
xi
k 1
x
(k ) i
xi
k
bi aij x aii j 1
i 1
用 SOR 法进行迭代,取不同的松弛因子 ,收 敛速度不同,见下表
ω
迭代次数
0.6
16
0.8
10
1
8
1.1
7
1.15
8
1.25
11
1.3
15
1.5
15
1.8
15
近似解与 准确解重 复合位数
5
5
5
5
5
5
5
4
1
使 SOR 法收敛最快的松弛因子通常称为最 优 松 弛因子。目前,只有少数特殊类型的矩阵,才有确定 的最优松弛因子的理论公式,但实际使用时也有一定 困难。通常的办法,是选不同的 进行试算,以确定 最佳 的近似值,或者先取一个 0 2 ,然后根 据迭代过程的收敛快慢,不断修正 ,这样逐步寻 找最佳 ,直到满意后再固定下来,继续迭代,以 达到加速的目的。
SOR迭代法求解线性方程组

实验三:用SOR迭代法求解线性方程组
取初始点 ,松弛因子 ,精度要求 。
1,建立SOR.m函数文件,此函数文件可调用,程序源码如下:
function [x,n]=SOR(A,b,x0,w,eps,M)
U=-triu(A,1); %求A的上三角阵
B=inv(D-L*w)*((1-w)*D+w*U);
f=w*inv((D-L*w))*b;
x=B*x0+f;
n=1; %迭代次数
whix0+f;
n=n+1;
if(n>=M)
disp('Warning:迭代次数太多,可能不收敛!');
if nargin==4
eps= 1.0e-6;%精度要求
M = 200;
elseif nargin<4
error;
return
elseif nargin ==5
M = 200;
end
if(w<=0 || w>=2)
error;
return;
end
D=diag(diag(A)); %求A的对角矩阵
L=-tril(A,-1); %求A的下三角阵
return;
end
end
2,输入矩阵。并根据要求调用函数,运行结果如下图所示:
即经过7次迭代算出结果,且求得:
sor迭代法手算例题

sor迭代法手算例题農迭代法是一種重要的數學方法,在農業、經濟學、生物學、物理學等領域中都有廣泛的應用。
本文將通過手算例題,深入探討農迭代法的原理、應用和注意事項。
一、農迭代法的原理農迭代法是一種通過不斷迭代,逐步逼近真實值的方法,其基本原理是:假設一個初始值,然後通過一系列計算,得到一個新的值,再以此新值為初始值,重複進行計算,直到得到一個足夠接近真實值的結果。
以求解方程f(x)=0為例,農迭代法的基本步驟如下:(1)選擇一個初始值x0;(2)根據f(x)=0的形式,將x表示為x=g(x),即x=g(x0);(3)用x0的值代入g(x)中,得到新的值x1=g(x0);(4)重複步驟(3),得到x2=g(x1),x3=g(x2),直到得到一個足夠接近真實值的結果。
需要注意的是,農迭代法的收斂性和速度都與選擇初始值有關,通常需要通過觀察函數圖像、分析函數性質等方法,選擇一個合適的初始值,才能獲得較好的結果。
二、農迭代法的應用1. 求解方程農迭代法在求解方程方面有廣泛的應用。
例如,對於方程f(x)=0,可以通過農迭代法求解,其中g(x)可以選擇為f(x)+x,即x=g(x)=f(x)+x。
2. 求解最小值農迭代法在求解最小值方面也有應用。
例如,對於函數f(x),可以通過農迭代法求解其最小值,其中g(x)可以選擇為f(x+1)。
3. 求解微分方程農迭代法在求解微分方程方面也有應用。
例如,對於微分方程y'=f(x,y),可以通過農迭代法求解其解析解,其中g(y)可以選擇為y0+∫f(x,y)dx。
三、手算例題下面通過手算例題,深入探討農迭代法的具體應用。
例題1:求解方程x^3-3x+1=0的根。
解答:根據農迭代法的原理,可以將方程表示為x=(3x-1)/x^2,即g(x)=(3x-1)/x^2。
選擇初始值x0=1,代入g(x)中,得到x1=g(x0)=(3-1)/1^2=2。
再將x1代入g(x)中,得到x2=g(x1)=(3*2-1)/2^2=5/4。
sor理论

sor理论
SOR理论(Successive Over-Relaxation)是一种基于迭代的技术,用来求解线性方程组。
它使用可变步长迭代法,其中步长由SOR系数决定。
SOR系数是一个实数,取值在[1,2]之间,缺省值通常为1.25或者1.5。
SOR法尝试不断减少系数和方程之间的差异,以及将这些方程求解为0。
要实现这一目标,它首先对方程组中的每个方程做出一个估计,然后逐步修正这些估计,以便最终达到收敛状态。
SOR理论的优点是可以更快地收敛,并能够解决更大规模的线性方程组。
另外,它也可以用来求解非线性方程组,但是要求这些方程组有适当的结构。
