电磁场与电磁波_第四版_第三章

合集下载

谢处方《电磁场与电磁波》(第4版)课后习题-第3章静态电磁场及其边值问题的解【圣才出品】

第3章　静态电磁场及其边值问题的解（一）思考题3.1 电位是如何定义的？中的负号的意义是什么？答：由静电场基本方程▽×E＝0和矢量恒等式可知，电场强度E 可表示为标量函数φ的梯度，即式中的标量函数φ称为静电场的电位函数，简称电位；式中负号表示场强方向与该点电位梯度的方向相反。

3.2“如果空间某一点的电位为零，则该点的电场强度也为零”，这种说法正确吗？为什么？答：不正确。

因为电场强度大小是该点电位的变化率。

3.3“如果空间某一点的电场强度为零，则该点的电位为零”，这种说法正确吗？为什么？答：不正确。

此时该点电位可能是任一个不为零的常数。

3.4 求解电位函数的泊松方程或拉普拉斯方程时，边界条件有何意义？答：边界条件起到给方程定解的作用。

3.5 电容是如何定义的？写出计算电容的基本步骤。

答：两导体系统的电容为任一导体上的总电荷与两导体之间的电位差之比，即其基本计算步骤：①根据导体的几何形状，选取合适坐标系；②假定两导体上分别带电荷＋q和－q；③根据假定电荷求出E；④由求得电位差；⑤求出比值3.6 多导体系统的部分电容是如何定义的？试以考虑地面影响时的平行双导线为例，说明部分电容与等效电容的含义。

答：多导体系统的部分电容是指多导体系统中一个导体在其余导体的影响下，与另一个导体构成的电容。

计及大地影响的平行双线传输线，如图3-1-1所示，它有三个部分电容C11、C12和C22，导线1、2间的等效电容为；导线1和大地间的等效电容为；导线2和大地间的等效电容为图3-1-13.7 计算静电场能量的公式和之间有何联系？在什么条件下二者是一致的？答：表示连续分布电荷系统的静电能量计算公式，虽然只有ρ≠0的区域才对积分有贡献，但不能认为静电场能量只存在于有电荷区域，它只适用静电场。

表示静电场能量存在于整个电场区域，所有E≠0区域对积分都有贡献，既适用于静电场，也用于时变电磁场，当电荷分布在有限区域内，闭合面S无限扩大时，有限区内的电荷可近似为点电荷时，二者是一致的。

电磁场与电磁波(第四版)习题解答

电磁场与电磁波(第四版）习题解答第1章习题习题1．1给定三个矢量A 、B 和C 如下:23x y z =+-A e e e ．4y z=-+B e e ，52x z =-C e e ,解:(1）22323)12(3)A x y z e e e A a e e e A+-===+-++- （2）2641x y z A B e e e -=+-==(3)(23)(4)11x y z y z A B e e e e e •=+-•-+=-（4）arccos135.5A B AB θ•===︒ (５)1711cos -=⋅=⋅⋅==B B A A B B A A A A AB Bθ(６）12341310502xy zx Y Z e e e A C e e e ⨯=-=---- (７)0418520502xy zx Y Z e e e B C e e e ⨯=-=++-()(23)(8520)42x Y Z x Y Z A B C e e e e e e •⨯=+-•++=-123104041xy zx Y Z e e e A B e e e ⨯=-=---- ()(104)(52)42x Y Z x Z A B C e e e e e ⨯•=---•-=-(8）()10142405502x y zx Y Z e e e A B C e e e ⨯⨯=---=-+-()1235544118520xy zx Y Z e e e A B C e e e ⨯⨯=-=-- 习题1．4给定两矢量 234x y z =+-A e e e 和 456x y z =-+B e e e ,求它们之间的夹角和 A 在Ｂ上的分量。

解：29)4(32222=-++=A776)5(4222=+-+=B31)654()432(-=+-⋅-+=⋅z y x z y x e e e e e e B A则A 与B之间的夹角为131772931cos =⎪⎪⎭⎫ ⎝⎛⋅-=⎪⎪⎪⎭⎫⎝⎛⋅⋅=ar BA B A arcis ABθ A 在B上的分量为532.37731cos -=-=⋅=⋅⋅⋅==B B A BA B A A A A AB Bθ习题1.９用球坐标表示的场225rr =E e ， (1）求在直角坐标中点(3,4,5)--处的E 和x E ；(2）求在直角坐标中点(3,4,5)--处E 与矢量22x y z =-+B e e e 构成的夹角。

《电磁场与电磁波》(第四版)课后习题解答(全)

第一章习题解答【习题1.1解】222222222222222222222222222222222222cos cos cos cos cos cos 1xx x y z yx y z z x y z x y z x y z x y z x y z x y z x y z 矢径r 与轴正向的夹角为，则同理，矢径r 与y 轴正向的夹角为，则矢径r 与z 轴正向的夹角为，则可得从而得证a a b b g g a b g =++=++=++++=++++++++++==++ 【习题1.2解】924331329(243)54(9)(243)236335x y z x y z x y z x y z x y z x y z x y z x y z A B e e e e e e e e e A B e e e e e e e e e A B e e e e e e A B +=--+-+=-+=----+=---∙=--∙-+=+-=⨯（）（）－（）(9)(243)19124331514x y z x y z x y z x y ze e e e e e e e e e e e =--⨯-+=---=--+【习题1.3解】已知,38,x y z x y z A e be ce B e e e =++=-++ （1）要使A B ⊥，则须散度 0A B =所以从 1380A B b c =-++=可得：381b c +=即只要满足3b+8c=1就可以使向量错误！未找到引用源。

和向量错误！未找到引用源。

垂直。

（2）要使A B ，则须旋度 0A B ⨯= 所以从1(83)(8)(3)0138xy zx y z e e e A B b c b c e c e b e ⨯==--+++=-可得 b=-3，c=-8 【习题1.4解】已知129x y z A e e e =++，x y B ae be =+，因为B A ⊥，所以应有0A B ∙= 即()()1291290xy z x y ee e ae be a b ++∙+=+= ⑴又因为 1B =; 所以221=； ⑵由⑴，⑵ 解得 34,55a b =±=【习题1.5解】由矢量积运算规则123233112()()()x y zx y z x x y y z ze e e A Ca a a a z a y e a x a z e a y a x e xyzB e B e B e B =?=-+-+-=++取一线元：x y z dl e dx e dy e dz =++则有xy z xyz e e e dlB B B dx dy dzB ?=则矢量线所满足的微分方程为 x y zd x d y d z B B B == 或写成233112()dx dy dzk a z a y a x a z a y a x==---＝常数求解上面三个微分方程：可以直接求解方程，也可以采用下列方法k xa a y a a z a d z a a x a a y a d y a a z a a x a d =-=-=-323132132231211)()()( （1）k x a y a z zdzz a x a y ydy y a z a x xdx =-=-=-)()()(211332 （2）由（1）（2）式可得)()(31211y a a x a a k x a d -=)()(21322z a a x a a k y a d -= （3）)()(32313x a a y a a k z a d -= )(32xy a xz a k xdx -=)(13yz a xy a k ydy -= （4）)(21xz a yz a k zdz -=对（3）（4）分别求和0)()()(321=++z a d y a d x a d 0)(321=++z a y a x a d0=++zdz ydy xdx 0)(222=++z y x d所以矢量线方程为1321k z a y a x a =++ 2222k z y x =++【习题1.6解】已知矢量场222()()(2)x y z A axz x e by xy e z z cxz xyz e =++++-+- 若 A 是一个无源场，则应有 div A =0即： div A =0y x zA A A A x y z∂∂∂∇⋅=++=∂∂∂ 因为 2x A axz x =+ 2y A by xy =+ 22z A z z cxz xyz =-+- 所以有div A =az+2x+b+2xy+1-2z+cx-2xy =x(2+c)+z(a-2)+b+1=0 得 a=2, b= -1, c= - 2 【习题1.7解】设矢径 r的方向与柱面垂直，并且矢径 r到柱面的距离相等（r ＝a ）所以，2sssr ds rds a ds a ah πΦ===⎰⎰⎰＝22a h π=【习题1.8解】已知23x y φ=,223y z A x yze xy e =+而 A A A A rot⨯∇+⨯∇=⨯∇=φφφφ)()(2222(6)3203xy zx y ze e e A xy x y e y e xyze x y z x yz xy ∂∂∂∇⨯==--+∂∂∂ 2223[(6)32]x y z A x y xy x y e y e xyze φ∴∇⨯=--+又y x z y x e x e xy ze y e x e 236+=∂∂+∂∂+∂∂=∇φφφφ 232233222630918603xy z x y z e e e A xyx x y e x y e x y ze x yz xy φ∇⨯==-+所以222()3[(6)32]x y z rot A A A x y xy x y e y e xyze φφφ=∇⨯+∇⨯=--+ +z y x e z y x e y x e y x 2332236189+-=]49)9[(3222z y x e xz e y e x x y x+--【习题1.9解】已知 222(2)(2)(22)x y zA y x z e x y z e x z y z e =++-+-+ 所以()()1144(22)0xyzyy x x z z x y z x yzx y z A A A A A A rot A A x y z y z z x x y A A A xz xz y y e e ee e e e e e ∂∂⎛⎫⎛⎫∂∂∂∂∂∂∂⎛⎫=∇⨯==-+-+- ⎪ ⎪ ⎪∂∂∂∂∂∂∂∂∂⎝⎭⎝⎭⎝⎭-++-+-=由于场A 的旋度处处等于0，所以矢量场A 为无旋场。

电磁场与电磁波课后习题答案第3章(杨儒贵编着)

第三章静电场3-1 已知在直角坐标系中四个点电荷分布如习题图3-1所示，试求电位为零的平面。

解已知点电荷q 的电位为rq 4πεϕ=，令)0,1,0(1q q -=，)0,1,3(2q q +=，)0,0,1(3q q -=，)0,0,0(4q q +=，那么，图中4个点电荷共同产生的电位应为∑=414ii r q πεϕ令0=ϕ，得 0 4 4 4 44321=+-+-r qr q r q r q πεπεπεπε 由4个点电荷的分布位置可见，对于x =1.5cm 的平面上任一点，4321 ,r r r r ==，因此合成电位为零。

同理，对于x =0.5cm 的平面上任一点，3241 ,r r r r ==，因此合成电位也为零。

所以，x =1.5cm 及x =0.5cm 两个平面的电位为零。

3-2 试证当点电荷q 位于无限大的导体平面附近时，导体表面上总感应电荷等于)(q -。

证明建立圆柱坐标，令导体表面位于xy 平面，点电荷距离导体表面的高度为h ，如图3-2所示。

那么，根据镜像法，上半空间的电场强度为32023101 4 4r q r q πεπεr r E -=X 习题图3-1(r , z )习题图3-2电通密度为)(43223110r r q r r E D -==πε 式中 232231])([h z r r -+=； 232232])([h z r r ++=那么，⎥⎥⎥⎦⎤⎪⎪⎪⎭⎫ ⎝⎛+++-++-+⎢⎢⎢⎣⎡⎪⎪⎪⎭⎫ ⎝⎛++--+=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧++++--+-+=z z zh z r hz h z r h z h z r r h z r r q h z r h z r h z r h z r q e e e e e e D r r r 232223222322232223222322])([])([ ])([])([4 ])([)(])([)(4ππ 已知导体表面上电荷的面密度n s D =ρ，所以导体表面的感应电荷为2322232223220)(2][][4h r qh h r h h r h q D z zs +-=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧++-+-===ππρ 则总的感应电荷为q h r r r qh r r S q s ss -=+-===⎰⎰⎰∞∞2322)(d d 2d 'πρρ3-3 根据镜像法，说明为什么只有当劈形导体的夹角为π的整数分之一时，镜像法才是有效的？当点电荷位于两块无限大平行导体板之间时，是否也可采用镜像法求解。

电磁场与电磁波(第四版)课后答案__谢处方

电磁场与电磁波（第四版）课后答案第一章习题解答1.1 给定三个矢量A 、B 和C 如下： 23x y z =+-A e e e4y z =-+B e e 52x z =-C e e求：（1）A a ；（2）-A B ；（3）A B ；（4）AB θ；（5）A 在B 上的分量；（6）⨯A C ；（7）()⨯A B C 和()⨯A B C ；（8）()⨯⨯A B C 和()⨯⨯A B C 。

解（1）23A x y z +-===+-e e e A a e e e A （2）-=A B (23)(4)x y z y z +---+=e e e ee 64x y z +-=e e e （3）=A B (23)x y z +-e e e (4)y z -+=e e －11 （4）由c o sAB θ=11238=A B A B ，得1c o s AB θ-=(135.5= （5）A 在B 上的分量 B A =A c o s AB θ==A B B （6）⨯=A C 123502xyz-=-e e e 41310x y z ---e e e （7）由于⨯=B C 041502xyz-=-e e e 8520x y z ++e e e⨯=A B 123041xyz-=-e e e 1014x y z ---e e e所以 ()⨯=A B C (23)x y z +-e e e (8520)4x y z ++=-e e e ()⨯=A B C (1014)x y z ---e e e (52)42x z -=-e e （8）()⨯⨯=A B C 1014502xyz---=-e e e 2405x y z -+e e e()⨯⨯=A B C 1238520x y z -=e e e 554411x y z --e e e1.2 三角形的三个顶点为1(0,1,2)P -、2(4,1,3)P -和3(6,2,5)P 。

电磁场与电磁波第四版第三章部分答案

电磁场与电磁波第四版第三章部分答案电磁场与电磁波第三章3.7无限大导体平板分别置于x =0和x =d 处，板间充满电荷，其体电荷密度为ρ=ρ0x d,极板间的电位分别为0和U 0，如图所示，求两级板之间的电位和电场强度。

解：由泊松定理得d 2φdx 2=?1ε0ρ0xd解得φ=?ρ0x 36ε0d+x +B在x =0处，φ=0，故B =0 在x =d 处，φ=U 0，故U 0=?ρ0x 36ε0d+d故=U 0d+ρ0d 6ε0φ=?ρ0x 36ε0d+(U 0d+ρ0d 6ε0)xE =??φ=?e x ?φ?x=e x [ρ0x 22ε0d?(U 0d+ρ0d 6ε0)]3.8证明：同轴线单位长度的静电储能W e =q l 22C。

式中q l 为单位长度上的电荷量，C 为单位长度上的电容。

解：由高斯定理可知：E (ρ)=q l 2περ故内外导体间的电压为U =∫Edρ=∫q l 2περbb dρ=q l 2πεln b则电容为C =q l U=2πεlnbW e =12∫εE 2dV =12∫εb (q l 2περ)22πρdρ=12q l 22πεln b =q l22C3.9有一半径为,带电量q 的导体球，其球心位于介电常数分别为ε1和ε2的两种介质的分界面上，该分界面为无限大平面。

试求：（1）导体球的电容；（2）总的静电常量。

解：根据边界条件则E 1t =E 2t ,故有E 1=E 2=E ,由于D 1=ε1E 1,D 2=ε2E 2,所以D 1≠D 2，由高斯定理可得D 1S 1+D 2S 2=q即2πr 2ε1E +2πr 2ε2E =qE =q212 导体球的电位为φ( )=∫Edr =∞q2π(ε1+ε2)∫1r ∞dr =q 2π(ε1+ε2)电容为C =q φ( )=2π(ε1+ε2)(2)总的静能量为W e =12qφ( )=q 24π(ε1+ε2)3.13在一块厚度为d 的导电板上，由两个半径分别为r 1和r 2的圆弧和夹角为α的两半径割出的一块扇形体，如图所示。

电磁场与电磁波答案(第四版)谢处方之欧阳治创编

欧阳治创编 2021.03.10 一章习题解答1.1给定三个矢量A 、B 和C 如下：求：（1）A a ；（2）-A B ；（3）A B ；（4）AB θ；（5）A 在B 上的分量；（6）⨯A C ；（7）()⨯A B C 和()⨯A B C ；（8）()⨯⨯A B C 和()⨯⨯A BC 。

解（1）23A x y z +-===+e e e A a e e e A（）-=A B (23)(4)xy z y z +---+=e e e e e 64x y z +-=e e e （3）=A B (23)x y z +-e e e (4)y z -+=e e －11（4）由cos AB θ=14==⨯A B A B ，得1cosAB θ-=(135.5= （5A 在B 上的分量欧阳治创编 2021.03.10B A =A cos AB θ=17=-A B B （6）⨯=A C 123502xyz-=-e e e 41310x y z ---e e e （7）由于⨯=B C 041502x yz-=-e e e 8520x y z ++e e e所以()⨯=A B C (23)x y z +-e e e (8520)42x y z ++=-e e e（8）()⨯⨯=A B C 1014502xyz---=-e e e 2405x y z -+e e e1.2三角形的三个顶点为1(0,1,2)P -、2(4,1,3)P -和3(6,2,5)P 。

（1）判断123PP P ∆是否为一直角三角形；（2）求三角形的面积。

解（1）三个顶点1(0,1,2)P -、2(4,1,3)P -和3(6,2,5)P 的位置矢量分别为 12y z =-r e e ，243x y z =+-r e e e ，3625x y z =++r e e e则12214x z=-=-R r r e e ，233228x y z =-=++R r r e e e ，欧阳治创编 2021.03.10 由此可见故123PP P ∆为一直角三角形。

电磁场与电磁波(第四版)(王家礼) (4)

• E • (j ) 2j 0
第三章恒定电流的电场和磁场 3.1.6 恒定电流场的边界条件
将恒定电流场基本方程的积分形式应用到两种不同导体的界面上(如图 3-4所示)，可得出恒定电流场的边界条件为
n×(E2－E1)=0
(3-20)
n·(J2－J1)=0
(3-21)
或
J1n=J2n
(3-22)
3.1 恒定电流的电场
3.1.1 电流密度我们知道，导体内的自由电子在电场的作用下，会沿着与
电场相反的方向运动，这样就形成电流。习惯上，规定正电荷运动的方向为电流的方向，用电流强度描述一根导线上电流的强弱(电流强度定义为单位时间内通过某导线截面的电荷量)。
第三章恒定电流的电场和磁场电流强度只能描述一根导线上总电流的强弱。为了描述电荷在空间的流动情况(即考虑导体截面的大小)，要引入电流密度的概念。电流密度是一个矢量，它的方向与导体中某点的正电荷运动方向相同（实际上是自由电子移动方向的反方向），大小等于与正电荷运动方向垂直的单位面积上的电流强度。若
C0
2π
ln b
a
可以直接得出同轴线单位长度的漏电导为
G0
2π
ln b
a
例 3-3 计算深埋地下半径为a的导体半球的接地电阻(如图
3-7 所示)。设土壤的电导率为σ；接地半球的电导率为无穷大。
第三章恒定电流的电场和磁场
图 3-7 半球形接地器
第三章恒定电流的电场和磁场解：导体球的电导率一般总是远大于土壤的电导率，可将
流场的矢量线叫做电流线。
第三章恒定电流的电场和磁场
图 3-1 电流密度
第三章恒定电流的电场和磁场
可以从电流密度J求出流过任意面积S的电流强度。一般情况下，电流密度J和面积元dS的方向并不相同。此时，通过面积 S的电流就等于电流密度J在S上的通量，即

电磁场与电磁波（第4版）第3章部分习题参考解答

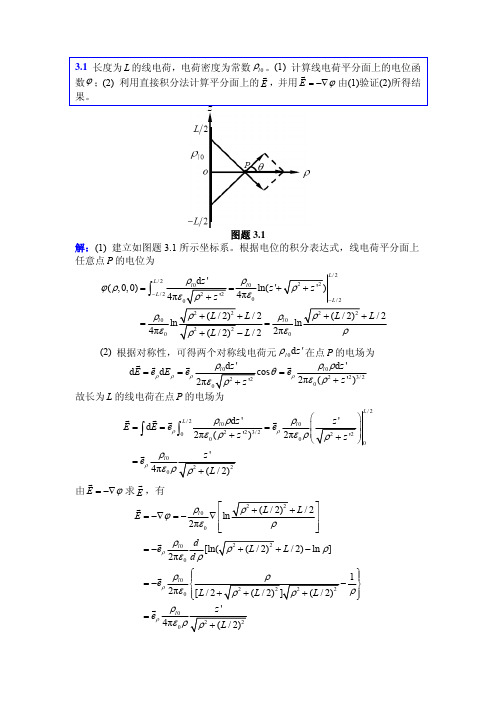
ρ ≥ a 时， E = −∇ϕ = −eρ
G
G ∂ ∂ρ
3.4 已知 y > 0 的空间中没有电荷，试判断下列函数中哪些是可能的电位解？ (1) e− y cosh x ；(2) e− y cos x ；(3) e− 2 sin x cos x ；(4) sin x sin y sin z 。解：在电荷体密度 ρ = 0 的空间，电位函数应满足拉普拉斯方程 ∇ 2ϕ = 0 。
∂2 − y ∂2 − y ∂2 − y (e cosh x) + 2 (e cosh x) + 2 (e cosh x) = 2e− y cosh x ≠ 0 (1) ∂x 2 ∂y ∂z −y 所以函数 e cosh x 不是 y > 0 空间中的电位解； ∂2 − y ∂2 − y ∂2 − y (e cos x) + 2 (e cos x) + 2 (e cos x) = −e− y cos x + e− y cos x = 0 (2) ∂x 2 ∂y ∂z −y 所以函数 e cos x 是 y > 0 空间中可能的电位解； ∂ − 2 ∂ ∂ (e sin x cos x) + 2 (e− 2 sin x cos x) + 2 (e − 2 sin x cos x) (3) 2 ∂x ∂y ∂z
G ρ = −eρ l 0 2πε 0 G = eρ
ρl 0 4πε 0 ρ
⎧ ρ 1⎫ ⎪ ⎪ − ⎬ ⎨ 2 2 2 2 ρ⎪ ⎪[ L / 2 + ρ + ( L / 2) ] ρ + ( L / 2) ⎩ ⎭ z'
ρ 2 + ( L / 2) 2
3.2 点电荷 q1 = q 位于 P 1 ( − a, 0, 0) ，另一点电荷 q2 = −2q 位于 P 2 ( a, 0, 0) ，求空间的零电位面。解：两个点电荷 + q 和 −2q 在空间产生的电位 ⎤ q 1 ⎡ 2q ϕ ( x, y , z ) = − ⎢ ⎥ 2 2 2 2 2 2 4 πε 0 ⎢ ( ) ( ) ⎥ x a y z x a y z + + + − + + ⎣ ⎦ 1 2 − =0 令 ϕ ( x, y, z ) = 0 ，则有 2 2 2 2 ( x + a) + y + z ( x − a) + y 2 + z 2

《电磁场与电磁波》第4版(谢处方编)课后习题答案高等教育出版社三章习题解答

三章习题解答3.1 真空中半径为a 的一个球面，球的两极点处分别设置点电荷q 和q -，试计算球赤道平面上电通密度的通量Φ(如题3.1图所示)。

解由点电荷q 和q -共同产生的电通密度为33[]4q R R π+-+-=-=R R D 22322232()(){}4[()][()]r z r z r z a r z a q r z a r z a π+-++-+-++e e e e 则球赤道平面上电通密度的通量d d zz SSS Φ====⎰⎰D S D e223222320()[]2d 4()()aq a ar r r a r a ππ--=++⎰ 22121)0.293()aqaq q r a =-=-+ 3.2 1911年卢瑟福在实验中使用的是半径为a r 的球体原子模型，其球体内均匀分布有总电荷量为Ze -的电子云，在球心有一正电荷Ze （Z 是原子序数，e 是质子电荷量），通过实验得到球体内的电通量密度表达式为02314ra Ze r r r π⎛⎫=- ⎪⎝⎭D e ，试证明之。

解位于球心的正电荷Ze 球体内产生的电通量密度为 124rZer π=D e 原子内电子云的电荷体密度为333434a a Ze Zer r ρππ=-=- 电子云在原子内产生的电通量密度则为 32234344r ra r Ze rr r ρπππ==-D e e 故原子内总的电通量密度为 122314ra Ze r r r π⎛⎫=+=- ⎪⎝⎭D D D e 3.3 电荷均匀分布于两圆柱面间的区域中，体密度为30C m ρ, 两圆柱面半径分别为a 和b ，轴线相距为c )(a b c -<，如题3.3图()a 所示。

求空间各部分的电场。

解由于两圆柱面间的电荷不是轴对称分布，不能直接用高斯定律求解。

但可把半径为a 的小圆柱面内看作同时具有体密度分别为0ρ±的两种电荷分布，这样在半径为b 的整个圆柱体内具有体密度为0ρ的均匀电荷分布，而在半径为a 的整个圆柱体内则具有体密度为0ρ-的均匀电荷分布，如题 3.3图()b 所示。

电磁场与电磁波课程教学大纲

《电磁场与电磁波》课程教学大纲一、课程基本信息课程代码：课程名称：电磁场与电磁波英文名称：Electromagnetic Fields and Electromagnetic Waves课程类别：专业基础课学时：63学分：3适用对象: 电子信息专业考核方式：考试先修课程：大学物理、高等数学与工程数学(包括矢量分析,场论和数理方程等)二、课程简介电磁场与电磁波是通信技术的理论基础，是电子信息专业本科学生的知识结构中重要组成部分。

本课程使学生掌握电磁场的有关定理、定律、麦克斯韦方程等的物理意义及数学表达式。

使学生熟悉一些重要的电磁场问题的数学模型（如波动方程、拉氏方程等）的建立过程以及分析方法。

培养学生正确的思维方法和分析问题的能力，使学生学会用"场"的观点去观察、分析和计算一些简单、典型的场的问题。

为后续课程打下坚实的理论基础。

Electromagnetic Field and Electromagnetic Wave is the theoretical foundation of communication technology, it is one of the most important components of the knowledge structerue for undergraduate students who major in information and electronic. Electromagnetic Field and Electromagnetic Wave make students grasp the theorem and the physical meaning of the Maxwell equations and mathematical expressions. It also make students grasp building method and analyzing method of some important mathematical model (such as wave equation,Laplace equation). This course trains students on the proper ways of thinking and ability to analyze issues, It also provides a solid theoretical foundation for following courses.三、课程性质与教学目的一切电现象，都会产生电磁场，而电磁波的辐射与传播规律，更是一切无线电活动的基础。

电磁场与电磁波答案(第四版)

第一章习题解答1.1 给定三个矢量A 、B 和C 如下： 23x y z =+-A e e e4y z =-+B e e52x z =-C e e求：（1）A a ；（2）-A B ；（3）A B g ；（4）AB θ；（5）A 在B 上的分量；（6）⨯A C ；（7）()⨯A B C g 和()⨯A B C g ；（8）()⨯⨯A B C 和()⨯⨯A B C 。

解（1）23A x y z +-===+e e e A a e e e A （2）-=A B (23)(4)x y z y z +---+=e e e ee 64x y z +-=e e e（3）=A B g (23)x y z +-e e e (4)y z -+=e e g －11 （4）由cos AB θ===A B A B g ，得1cos AB θ-=(135.5=o （5）A 在B 上的分量 B A =A cos ABθ==A B B g （6）⨯=A C 123502x yz-=-e e e 41310x y z ---e e e（7）由于⨯=B C 041502x yz-=-e e e 8520x y z ++e e e⨯=A B 123041xyz-=-e e e 1014x y z ---e e e所以 ()⨯=A B C g (23)x y z +-e e e g (8520)42x y z ++=-e e e ()⨯=A B C g (1014)x y z ---e e e g (52)42x z -=-e e（8）()⨯⨯=A B C 1014502x yz---=-e e e 2405x y z -+e e e()⨯⨯=A B C 1238520x y z -=e e e 554411x y z --e e e1.2 三角形的三个顶点为1(0,1,2)P -、2(4,1,3)P -和3(6,2,5)P 。

（1）判断123PP P ∆是否为一直角三角形；（2）求三角形的面积。

电磁场与电磁波第四版

电磁场与电磁波第四版引言《电磁场与电磁波》是一本经典的电磁学教材，被广泛应用于大学电子信息类专业的教学。

本书第四版对前三版进行了全面修订和更新，并添加了一些新的内容，以便更好地满足读者的需求。

本文将介绍《电磁场与电磁波第四版》的主要内容，并对其中涉及的一些重要主题进行简要概述。

主要内容第一章：电磁场的基本概念本章介绍了电磁场的基本概念，包括电场和磁场的定义、电场强度、磁感应强度等基本量的引入，并通过一些简单的例子来解释这些概念。

第二章：电磁场的基本规律本章介绍了电磁场的基本规律，包括电场和磁场的基本方程、电场和磁场的高斯定律、安培环路定理等。

通过这些规律，读者可以深入理解电磁场的本质和特性。

第三章：静电场本章主要讨论静电场的性质和特点，包括静电场的产生、电势、电场强度分布等。

此外，还介绍了一些与静电场相关的重要定理，如电势差定理、电场强度叠加原理等。

第四章：静电场的应用本章介绍了静电场在工程和科学中的应用，包括静电场的能量和能量密度，以及静电场在电容器和电磁屏蔽中的应用。

第五章：恒定电流本章讨论了恒定电流的概念和性质，包括导体中的电流分布、欧姆定律、电阻和电阻器等。

此外，还介绍了一些与恒定电流相关的重要定理，如基尔霍夫定律和焦耳定律。

第六章：恒定磁场本章主要讨论恒定磁场的性质和特点，包括磁场的产生、磁力、磁感应强度等。

此外，还介绍了一些与恒定磁场相关的重要定理，如比奥-萨伐尔定律、洛伦兹力和安培环路定理等。

第七章：电磁感应本章介绍了电磁感应的基本原理和应用，包括法拉第电磁感应定律、楞次定律、自感和互感等。

此外，还介绍了一些与电磁感应相关的重要概念，如感应电动势和感应电磁力。

第八章：交流电路本章主要讨论交流电路的性质和特点，包括交流电源、交流电路中的电压和电流关系、交流电路的频率等。

此外，还介绍了一些与交流电路相关的重要定理，如波形和相位关系等。

结语本文简要介绍了《电磁场与电磁波第四版》的主要内容。

电磁场与电磁波(第四版)课后答案_电科习题

3)
v C

evx
3y2 - 2x
+ evy x2 + evz 2z
问：1.哪些矢量可以由一个标量函数的梯度表示？哪些
矢量可以由一个矢量函数的旋度表示？
2.求出这些矢量的源分布。
1.28利用直角坐标，证明
v fA
vv f A Af
1.29：矢量
在Av由 evρ=52， evzz验2=z0证和散z=度4围定成理的。圆柱形区域,
分量，根据边界条件可知，两种介质的
2
磁感应强度
uv B1
rr

uv B2

r B

er B
但磁场
强度 H1 H2
3.23一电荷量为 q 质量为 m 的小带电体，放置在无限长导体
平面下方，与平面距离h 。求 q 的值以使带电体上受到的
静电力恰好与重力相平衡（设 m 2103 kg, h 0.02m）。
对
第二章
2.1已知半径为a的导体球面上分布着电荷密度为 s s0 cos 的电荷，式中的 s0
为常数。试计算球面上的总电荷量。
2.6 一个平行板真空二极管内的电荷体位密于度x=为0，阳极94 板0U0位(d 于43 )xx23=，d，式极中间阴电极压板为U0。如果U0 ＝40V，d＝lcm，横截面积s =10cm2。求：
验
A
证散度定理
1.21 求矢量
v A

erx
x

ery
x2

erz
y
2
z
沿xy平面上的一个边长为2的正
形再回求路的Av线对积此分回，路此所正包方围形的的表两面个积边分分，别验与证x斯轴托和克y轴斯相定重理合

电磁场与电磁波_第四版_第三章

能量。
静电场能量来源于建立电荷系统的过程中外源提供的能量任何形式的带电系统，都要经过从没有电荷分布到某个最终电荷分布的建立(或充电)过程。在此过程中，外加电源必须克服
电荷之间的相互作用力而作功。
如果充电过程进行得足够缓慢，就不会有能量辐射，充电过程中外加电源所作的总功将全部转换成电场能量，或者说电场能
Da
电磁场与电磁波
第3章静态电磁场及其边值问题的解
16
例3.3 同轴线内导体半径为a，外导体半径为为b，内外导体间
填充的介电常数为的均匀介质，求同轴线单位长度的电容。解设同轴线的内、外导体单位长度带电量分别为 l 和 l ，应用高斯定理可得到内外导体间任一点的电场强度为
l E ( ) e 2
1 0 q d 2 q 根据能量守恒定律，此功也就是电量为 q 的带电体具有的电
1
场能量We ，即
1 We q 2 对于电荷体密度ρ为的体分布电荷，体积元dV中的电荷ρdV具 1 dWe dV 2
有的电场能量为
电磁场与电磁波
第3章静态电磁场及其边值问题的解
19
1 We dV 2 V 对于面分布电荷，电场能量为 W 1 dS e S S 2 对于多导体组成的带电系统，则有
电磁场与电磁波
第3章静态电磁场及其边值问题的解
3
3.1 静电场分析
学习内容 3.1.1 静电场的基本方程和边界条件
3.1.2 电位函数
3.1.3 3.1.4 导体系统的电容静电场的能量
电磁场与电磁波
第3章静态电磁场及其边值问题的解
4
3.1.1 静电场的基本方程和边界条件 1. 基本方程
D dS q D S 微分形式：积分形式： E dl 0 E 0 C 本构关系： D E D1n D2 n S 2. 边界条件 en ( D1 D2 ) S 或 E1t E2t 0 e ( E E ) 0 1 2 n

电磁场与电磁波(第四版)课后答案_第三章习题

习题三答案及解析
B选项
$( - frac{1}{2} + frac{3}{2}i)( frac{1}{2} + frac{3}{2}i)$ 可以
化简为 $-i$。
C选项
$( - frac{1}{2} - frac{3}{2}i)( frac{1}{2} + frac{3}{2}i)$ 可以
化简为 $-i$。
D选项
$frac{-2i}{-2i + 1}$ 可以化简为 $-i$。
习题三答案及解析
答案
A. $-frac{1}{4}$
习题三答案及解析
B. $-i$
1
C. $-i$
2
D. $-i$
3
习题三答案及解析
01
解析
02
此题考查复数的乘法运算，根据复数乘法的定义和性质，可以得出答案。
03
A选项：$( - frac{1}{2} + frac{3}{2}i)( - frac{1}{2} - frac{3}{2}i)$ 可以化简为 $-frac{1}{4}$。
• 下一章将介绍电磁场与电磁波的基本原理和概念，包括电场、磁场、电磁感应等。同时，还将介绍电磁波的传播方式和在不同介质中的传播特性，以及电磁波的应用和影响。
THANKS
感谢观看
D选项
$100e^{- frac{pi i}{2}}$ 可以化简为 $100(cosfrac{3pi}{2} + isinfrac{3pi}{2})$，与题目中的形式一致。
习题二答案及解析
答案
A. $-frac{1}{2}$
习题二答案及解析
B. $-i$ C. $-i$ D. $-i$

谢处方《电磁场与电磁波》(第4版)章节习题-第3章静态电磁场及其边值问题的解【圣才出品】

第3章　静态电磁场及其边值问题的解一、判断题1．为了简化空间电位分布的表达式，总可以将电位参考点选择在无穷远处。

（）【答案】×2．焦耳定律只适用于传导电流，不适应于运流电流。

（）【答案】√3．绝缘介质与导体分界面上，在静电情况下导体外的电力线总是垂直于导体表面的。

（）【答案】√4．位移电流的假说就是变化的磁场产生电场的假说。

（）【答案】×5．任意两个带电导体之间都存在电容，对电容有影响的因素包括导体几何形状，导体上的电荷量、两导体相对位置和空间介质。

（）【答案】×6．恒定电场中理想导体内的电场强度为零。

（）【答案】√7．空间体积中有电流时，该空间内表面上便有面电流。

（）【答案】×8．应用分离变量法求解电、磁场问题时，要求整个场域内媒质必须是均匀、线性的。

（）【答案】×9．一个点电荷Q放在球形高斯面中心处。

如果此电荷被移开原来的球心，但仍在球内，则通过这个球面的电通量将会改变。

（）【答案】×台10．在线性磁介质中，由的关系可知，电感系数不仅与导线的几何尺寸、材料L Iψ=特性有关，还与通过线圈的电流有关。

（）【答案】×二、填空题1．镜像法是在所求场的区域之外，用_______来代替场问题的边界。

假想电荷和场区域原有的电荷一起产生的电场必须要满足_______。

【答案】一些假想电荷；原问题的边界条件。

2．磁介质中恒定磁场的基本方程为：_______。

【答案】，；，.d 0S B S =⎰v v Ñ0B ∇⋅=v d 0CH l ⋅=⎰v v ÑH J ∇⨯=v v 3．位移电流假说的实质是_______。

【答案】变化的电场可以产生磁场4．位移电流和真实电流（如传导电流和运流电流）的区别在于_______。

【答案】位移电流不对应任何带电质点的运动，只是电场随时间的变化率5．已知磁感应强度为，则m 的值为_______。

电磁场与电磁波答案(第四版)谢处方

一章习题解答1.1 给定三个矢量A 、B 和C 如下： 23x y z =+-A e e e4y z =-+B e e52x z =-C e e求：1A a ；2-A B ；3A B ；4AB θ；5A 在B 上的分量；6⨯A C ；7()⨯A B C 和()⨯AB C ；8()⨯⨯A BC 和()⨯⨯A B C ..解 123A x y z+-===+e e e A a e e e A 2-=A B (23)(4)x y z y z +---+=e e e e e 64x y z +-=e e e 3=A B (23)x y z +-e e e (4)y z -+=ee －114由 cos AB θ=14-==⨯A B A B ;得 1cos AB θ-=(135.5=5A 在B 上的分量 B A =A cos AB θ=1117=-A B B 6⨯=A C 123502xy z-=-e e e 41310x y z ---e e e 7由于⨯=B C 041502x yz-=-e e e 8520x y z ++e e e ⨯=A B 123041xyz-=-e e e 1014x y z ---e e e所以 ()⨯=A B C (23)x y z +-e e e (8520)42x y z ++=-e e e ()⨯=A B C (1014)x y z ---e e e (52)42x z -=-e e8()⨯⨯=A B C 1014502x y z---=-e e e 2405x y z -+e e e()⨯⨯=A B C 1238520xy z -=e e e 554411x y z --e e e1.2 三角形的三个顶点为1(0,1,2)P -、2(4,1,3)P -和3(6,2,5)P .. 1判断123PP P ∆是否为一直角三角形； 2求三角形的面积..解 1三个顶点1(0,1,2)P -、2(4,1,3)P -和3(6,2,5)P 的位置矢量分别为 12y z =-r e e ;243x y z =+-r e e e ;3625x y z =++r e e e 则 12214x z =-=-R r r e e ; 233228x y z =-=++R r r e e e ;311367x y z =-=---R r r e e e由此可见1223(4)(28)0x z x y z =-++=R R e e e e e故123PP P ∆为一直角三角形.. 2三角形的面积122312231117.1322S =⨯=⨯==R R R R 1.3 求(3,1,4)P '-点到(2,2,3)P -点的距离矢量R 及R 的方向..解 34P x y z '=-++r e e e ;223P x y z =-+r e e e ;则 53P P P P x y z ''=-=--R r r e e e 且P P 'R 与x 、y 、z 轴的夹角分别为11cos ()cos 32.31x P P xP P φ--''===eR R 11cos ()cos 120.47y P P y P P φ'--'===e R R11cos ()cos (99.73z P P z P P φ--''===e R R1.4给定两矢量234x y z =+-A e e e 和456x y z =-+B e e e ;求它们之间的夹角和A 在B 上的分量..解 A 与B 之间的夹角为11cos ()cos 131θ--===AB A B A B A 在B 上的分量为 313.53277B A -===-B AB 1.5 给定两矢量234x y z =+-A e e e 和64x y z =--+B e e e ;求⨯A B 在x y z=-+C e e e 上的分量..解 ⨯=A B 234641x y z-=--e e e 132210x y z -++e e e所以⨯A B 在C 上的分量为 ()⨯=C A B ()2514.433⨯=-=-A B C C1.6 证明：如果A B =A C 和⨯=A B ⨯A C ;则=B C ；解由⨯=A B ⨯A C ;则有()()⨯⨯=⨯⨯A A B A A C ;即()()()()-=-A B A A A B A C A A A C由于A B =A C ;于是得到 ()()=A A B A A C 故 =B C1.7 如果给定一未知矢量与一已知矢量的标量积和矢量积;那么便可以确定该未知矢量..设A 为一已知矢量;p =A X 而=⨯P A X ;p 和P 已知;试求X ..解由=⨯P A X ;有()()()()p ⨯=⨯⨯=-=-A P A A X A X A A A X A A A X 故得 p -⨯=A A P X A A 1.8 在圆柱坐标中;一点的位置由2(4,,3)3π定出;求该点在：1直角坐标中的坐标；2球坐标中的坐标..解 1在直角坐标系中 4cos(22x π==-、4sin(2y π==、3z =故该点的直角坐标为(2,-..2在球坐标系中 435r =+=、1tan (453.1θ-==、23120φπ== 故该点的球坐标为(5,53.1,120)1.9 用球坐标表示的场225rr =E e ; 1求在直角坐标中点(3,4,5)--处的E 和x E ；2求在直角坐标中点(3,4,5)--处E 与矢量22x y z =-+B e e e 构成的夹角.. 解 1在直角坐标中点(3,4,5)--处;2222(3)4(5)50r =-++-=;故22512rr ==E e1cos220x x rx E θ====-e E E2在直角坐标中点(3,4,5)--处;345x y z =-+-r e e e ;所以233452525r r -+-===e e e r E故E 与B 构成的夹角为11cos ()cos (153.63θ--===EB E B E B 1.10 球坐标中两个点111(,,)r θφ和222(,,)r θφ定出两个位置矢量1R 和2R ..证明1R 和2R 间夹角的余弦为121212cos cos cos sin sin cos()γθθθθφφ=+-解由 111111111sin cos sin sin cos x y z r r r θφθφθ=++R e e e222222222sin cos sin sin cos x y z r r r θφθφθ=++R e e e得到 1212cos γ==R R R R1122112212sin cos sin cos sin sin sin sin cos cos θφθφθφθφθθ++=121211212sin sin (cos cos sin sin )cos cos θθφφφφθθ++= 121212sin sin cos()cos cos θθφφθθ-+1.11 一球面S 的半径为5;球心在原点上;计算： (3sin )d r Sθ⎰e S 的值..解 (3sin )d (3sin )d r r r SSS θθ==⎰⎰e S e e 2220d 3sin 5sin d 75ππφθθθπ⨯=⎰⎰1.12 在由5r =、0z =和4z =围成的圆柱形区域;对矢量22r z r z =+A e e 验证散度定理.. 解在圆柱坐标系中 21()(2)32rr z r r r z∂∂∇=+=+∂∂A 所以 4250d d d (32)d 1200z r r r πττφπ∇=+=⎰⎰⎰⎰A 又2d (2)(d d d )rz r r z z SSrz S S S φφ=+++=⎰⎰A S e e e e e42522000055d d 24d d 1200z r r ππφφπ⨯+⨯=⎰⎰⎰⎰故有d 1200ττπ∇=⎰A d S=⎰A S 1.13 求1矢量22222324x y z x x y x y z =++A e e e 的散度；2求∇A 对中心在原点的一个单位立方体的积分；3求A 对此立方体表面的积分;验证散度定理..解 12222232222()()(24)2272x x y x y z x x y x y z x y z∂∂∂∇=++=++∂∂∂A 2∇A 对中心在原点的一个单位立方体的积分为1212122222121121d (2272)d d d 24x x y x y z x y z ττ---∇=++=⎰⎰⎰⎰A 3A 对此立方体表面的积分1212112221212121211d ()d d ()d d 22Sy z y z ----=--+⎰⎰⎰⎰⎰A S12121212222212121212112()d d 2()d d 22x x z x x z ------+⎰⎰⎰⎰1212112232231212121211124()d d 24()d d 2224x y x y x y x y ------=⎰⎰⎰⎰故有1d 24ττ∇=⎰A d S=⎰A S1.14 计算矢量r 对一个球心在原点、半径为a 的球表面的积分;并求∇r 对球体积的积分..解223d d d sin d 4r SSS aa a ππφθθπ===⎰⎰⎰⎰r S r e 又在球坐标系中;221()3r r r r∂∇==∂r ;所以 223000d 3sin d d d 4ar r a ππττθθφπ∇==⎰⎰⎰⎰r 1.15 求矢量22x y z x x y z =++A e e e 沿xy 平面上的一个边长为2的正方形回路的线积分;此正方形的两边分别与x 轴和y 轴相重合..再求∇⨯A 对此回路所包围的曲面积分;验证斯托克斯定理..解22222d d d 2d 0d 8Cx x x x y y =-+-=⎰⎰⎰⎰⎰A l又 2222x y z x z yz x x y z x x y z∂∂∂∇⨯==+∂∂∂e e e A e e 所以 2200d (22)d d 8xzzSyz x x y ∇⨯=+=⎰⎰⎰A S e e e故有d 8C=⎰A l d S=∇⨯⎰A S1.16 求矢量2x y x xy =+A e e 沿圆周222x y a +=的线积分;再计算∇⨯A 对此圆面积的积分..解2d d d CCx x xy y =+=⎰⎰A l 242422(cos sin cos sin )d 4a aa ππφφφφφ-+=⎰d ()d yx z z S SA A S x y ∂∂∇⨯=-=∂∂⎰⎰A S e e 2422200d sin d d 4a S a y S r r r ππφφ==⎰⎰⎰ 1.17 证明：13∇=R ；2∇⨯=R 0；3()∇=A R A ..其中x y z x y z =++R e e e ;A 为一常矢量..解 13x y z x y z∂∂∂∇=++=∂∂∂R 2 x y z x y z x y y∂∂∂∇⨯==∂∂∂e e e R 03设x x y y z z A A A =++A e e e ;则x y z A x A y A z =++A R ;故()()()xx y z y x y z A x A y A z A x A y A z x y ∂∂∇=++++++∂∂A R e e ()z x y z A x A y A z z∂++=∂e x x y y z z A A A ++=e e e A 1.18 一径向矢量场()r f r =F e 表示;如果0∇=F ;那么函数()f r 会有什么特点呢解在圆柱坐标系中;由 1d [()]0d rf r r r∇==F 可得到()Cf r r=C 为任意常数.. 在球坐标系中;由 221d [()]0d r f r r r ∇==F 可得到 2()C f r r =1.19 给定矢量函数x y y x =+E e e ;试求从点1(2,1,1)P -到点2(8,2,1)P -的线积分d ⎰E l ：1沿抛物线2x y =；2沿连接该两点的直线..这个E 是保守场吗解 1 d d d x y CCE x E y =+=⎰⎰E l d d Cy x x y +=⎰2221d(2)2d y y y y +=⎰2216d 14y y =⎰ 2连接点1(2,1,1)P -到点2(8,2,1)P -直线方程为2812x x y y --=-- 即 640x y -+= 故21d d d d(64)(64)d xy CCEx E y y y y y =+=-+-=⎰⎰⎰E l 21(124)d 14y y-=⎰由此可见积分与路径无关;故是保守场..1.20 求标量函数2x yz ψ=的梯度及ψ在一个指定方向的方向导数;此方向由单位矢量xy ze e e (2,3,1)点的方向导数值.. 解 222()()()x y z x yz x yz x yz x y zψ∂∂∂∇=++=∂∂∂ee e222x y z xyz x z x y ++e e e故沿方向l x y z=e e e e 的方向导数为 22650l xyz l ψψ∂=∇=+∂e 点(2,3,1)处沿l e 的方向导数值为lψ∂==∂1.21试采用与推导直角坐标中yx zAA Ax y z∂∂∂∇=++∂∂∂A相似的方法推导圆柱坐标下的公式1()zrA ArAr r r zφφ∂∂∂∇=++∂∂∂A..解在圆柱坐标中;取小体积元如题1.21图所示..矢量场A沿re方向穿出该六面体的表面的通量为()d d d dz z z zr r r r r rz zA r r r A r rφφφφφφψφφ+∆+∆+∆+∆+∆=+∆-≈⎰⎰⎰⎰[()(,,)(,,)]r rr r A r r z rA r z zφφφ+∆+∆-∆∆≈()()1r rrA rAr zr r rφτ∂∂∆∆∆=∆∂∂同理d d d dr r z z r r z zr z r zA r z A r zφφφφφφψ+∆+∆+∆+∆+∆=-≈⎰⎰⎰⎰[(,,)(,,)]A r z A r z r zφφφφφ+∆-∆∆≈A Ar zrφφφτφφ∂∂∆∆∆=∆∂∂d d d dr r r rz z z z z zr rA r r A r rφφφφφφψφφ+∆+∆+∆+∆+∆=-≈⎰⎰⎰⎰[(,,)(,,)]z zA r z z A r z r r zφφφ+∆-∆∆∆≈z zA Ar r zz zφτ∂∂∆∆∆=∆∂∂因此;矢量场A穿出该六面体的表面的通量为()1[]r zr zArA AΨΨΨΨr r r zφφτφ∂∂∂=++≈++∆∂∂∂故得到圆柱坐标下的散度表达式()1lim r zArA Ar r r zφτψτφ∆→∂∂∂∇⋅==++∆∂∂∂A1.22方程222222x y zua b c=++给出一椭球族..求椭球表面上任意点的单位法向矢量..解由于222222x y zx y zua b c∇=++e e eu∇=故椭球表面上任意点的单位法向矢量为222(x y zu x y za b cu∇==++∇n e e e1.23现有三个矢量A、B、C为sin cos cos cos sin r θφθφθφφ=+-A e e e22sin cos 2sin r z z z rz φφφφ=++B e e e22(32)2x y z y x x z =-++C e e e1哪些矢量可以由一个标量函数的梯度表示哪些矢量可以由一个矢量函数的旋度表示 2求出这些矢量的源分布.. 解1在球坐标系中22111()(sin )sin sin r A r A A r r r r φθθθθθφ∂∂∂∇=++=∂∂∂A22111(sin cos )(sin cos cos )(sin )sin sin r r r r r θφθθφφθθθφ∂∂∂++-=∂∂∂ 2cos 2sin cos cos sin cos 0sin sin r r r r φθφφθφθθ+--= 2sin 1sin sin r r r r r r A rA r A θφθφθθθφθ∂∂∂∇⨯==∂∂∂e e e A2sin 10sin sin cos cos cos sin sin rr r r rr r θφθθθφθφθφθφ∂∂∂=∂∂∂-e e e故矢量A 既可以由一个标量函数的梯度表示;也可以由一个矢量函数的旋度表示；在圆柱坐标系中11()z r B B rB r r r z φφ∂∂∂∇++=∂∂∂B =2211(sin )(cos )(2sin )rz z rz r r r z φφφφ∂∂∂++=∂∂∂22sin sin 2sin 2sin z z r r r r φφφφ-+= 22110sin cos 2sin r z r z r z r r r r z r r z B rB B z rz rz θθθφφφφφ∂∂∂∂∂∂∇⨯===∂∂∂∂∂∂e e e e e e B故矢量B 可以由一个标量函数的梯度表示；直角在坐标系中y x z C C C x y z∂∂∂∇++=∂∂∂C =22(32)()(2)0y x x z x y z∂∂∂-++=∂∂∂22(26)322x y z z x y x y z y x x z∂∂∂∇⨯==-∂∂∂-e e e C e故矢量C 可以由一个矢量函数的旋度表示.. 2这些矢量的源分布为0∇=A ;0∇⨯=A ；2sin r φ∇B =;0∇⨯=B ；0∇=C ;(26)z x y ∇⨯=-C e1.24 利用直角坐标;证明()f f f ∇=∇+∇A A A解在直角坐标中()()y x z x y z A A A f f ff f f A A A x y z x y z∂∂∂∂∂∂∇+∇=+++++=∂∂∂∂∂∂A A()()()y x z x y z A A A f f ff A f A f A x x y y z z ∂∂∂∂∂∂+++++=∂∂∂∂∂∂()()()()x y z fA fA fA f x y z∂∂∂++=∇∂∂∂A 1.25 证明()∇⨯=∇⨯-∇⨯A H H A A H解根据∇算子的微分运算性质;有()()()A H ∇⨯=∇⨯+∇⨯A H A H A H式中A ∇表示只对矢量A 作微分运算;H ∇表示只对矢量H 作微分运算..由()()⨯=⨯a b c c a b ;可得()()()A A ∇⨯=∇⨯=∇⨯A H H A H A同理 ()()()H H ∇⨯=-∇⨯=-∇⨯A H A H A H 故有 ()∇⨯=∇⨯-∇⨯A H H A A H1.26 利用直角坐标;证明()f f f ∇⨯=∇⨯+∇⨯G G G解在直角坐标中[()()()]yy x x z z x y z G G G G G G f f y z z x x y ∂∂∂∂∂∂∇⨯=-+-+-∂∂∂∂∂∂G e e ef ∇⨯=G [()()()]x zy y x z z y x f f f f f f G G G G G G y z z x x y∂∂∂∂∂∂-+-+-∂∂∂∂∂∂e e e 所以f f ∇⨯+∇⨯=G G [()()]y z x zy G G f fG f G f y y z z∂∂∂∂+-++∂∂∂∂e [()()]x z y x z G G f fG f G f z z x x∂∂∂∂+-++∂∂∂∂e[()()]y x z y x G G f fG f G f x x y y ∂∂∂∂+-+=∂∂∂∂e()()[]y z x fG fG y z ∂∂-+∂∂e ()()[]x z y fG fG z x ∂∂-+∂∂e ()()[]y x z fG fG x y∂∂-=∂∂e ()f ∇⨯G1.27 利用散度定理及斯托克斯定理可以在更普遍的意义下证明()0u ∇⨯∇=及()0∇∇⨯=A ;试证明之..解 1对于任意闭合曲线C 为边界的任意曲面S ;由斯托克斯定理有()d d d d 0SCCCuu u l u l ∂∇⨯∇=∇===∂⎰⎰⎰⎰S l 由于曲面S 是任意的;故有()0u ∇⨯∇=2对于任意闭合曲面S 为边界的体积τ;由散度定理有12()d ()d ()d ()d SS S ττ∇∇⨯=∇⨯=∇⨯+∇⨯⎰⎰⎰⎰A A S A S A S 其中1S 和2S 如题1.27图所示..由斯托克斯定理;有11()d d S C ∇⨯=⎰⎰A S A l ; 22()d d S C ∇⨯=⎰⎰A S A l由题1.27图可知1C 和2C 是方向相反的同一回路;则有 12d d C C =-⎰⎰A l A l所以得到1222()d d d d d 0C C C C ττ∇∇⨯=+=-+=⎰⎰⎰⎰⎰A A l A l A l A l 由于体积τ是任意的;故有 ()0∇∇⨯=A二章习题解答2.1 一个平行板真空二极管内的电荷体密度为43230049U d x ρε--=-;式中阴极板位于0x =;阳极板位于x d =;极间电压为0U ..如果040V U =、1cm d =、横截面210cm S =;求：10x =和x d =区域内的总电荷量Q ；22x d =和x d=区域内的总电荷量Q '..1题1.27图解 1 420004d ()d 9dQ U d x S x τρτε--==-=⎰⎰110044.7210C 3U S dε--=-⨯ 2 4323004d ()d 9dd Q U d x S x τρτε--''==-=⎰⎰11004(10.9710C 3U S d ε---=-⨯ 2.2 一个体密度为732.3210C m ρ-=⨯的质子束;通过1000V 的电压加速后形成等速的质子束;质子束内的电荷均匀分布;束直径为2mm ;束外没有电荷分布;试求电流密度和电流..解质子的质量271.710kg m -=⨯、电量191.610C q -=⨯..由212mv qU = 得61.3710v ==⨯ m 故 0.318J v ρ== 2A m26(2)10I J d π-== A2.3 一个半径为a 的球体内均匀分布总电荷量为Q 的电荷;球体以匀角速度ω绕一个直径旋转;求球内的电流密度..解以球心为坐标原点;转轴一直径为z 轴..设球内任一点P 的位置矢量为r ;且r 与z 轴的夹角为θ;则P 点的线速度为sin r φωθ=⨯=v r e ω球内的电荷体密度为343Qa ρπ=故 333sin sin 434Q Q r r a aφφωρωθθππ===J v e e 2.4 一个半径为a 的导体球带总电荷量为Q ;同样以匀角速度ω绕一个直径旋转;求球表面的面电流密度..解以球心为坐标原点;转轴一直径为z 轴..设球面上任一点P 的位置矢量为r ;且r 与z 轴的夹角为θ;则P 点的线速度为sin a φωθ=⨯=v r e ω球面的上电荷面密度为24Q a σπ=故 2sin sin 44S Q Q a a aφφωσωθθππ===J v e e 2.5 两点电荷18C q =位于z 轴上4z =处;24C q =-位于y 轴上4y =处;求(4,0,0)处的电场强度..解电荷1q 在(4,0,0)处产生的电场为1113014q πε'-=='-r r E r r电荷2q 在(4,0,0)处产生的电场为222302444q πε-'-=='-e e r r E r r 故(4,0,0)处的电场为122+-=+=e e e E E E2.6 一个半圆环上均匀分布线电荷l ρ;求垂直于圆平面的轴线上z a =处的电场强度(0,0,)a E ;设半圆环的半径也为a ;如题2.6 图所示..解半圆环上的电荷元d d l l l a ρρφ''=在轴线上z a =处的电场强度为d φ'==E(cos sin )φφφ''-+'e e e在半圆环上对上式积分;得到轴线上z a =处的电场强度为(0,0,)d a ==⎰E E2[(cos sin )]d z xy ππφφφ'''-+=⎰e ee 2.7 三根长度均为L ;均匀带电荷密度分别为1l ρ、2l ρ和3l ρ地线电荷构成等边三角形..设1l ρ=22l ρ=32l ρ;计算三角形中心处的电场强度..解建立题2.7图所示的坐标系..三角形中心到各边的距离为3tan 3026L d L == 则111003(cos30cos150)42ll yyd Lρρπεπε=-=E e e 2120033(cos30sin 30)()28l l x y y L L ρρπεπε=-+=-E e e e e 3130033(cos30sin 30)()28l lx y y L Lρρπεπε=-=E e e e e 故等边三角形中心处的电场强度为123=++=E E E E111000333()()288l l l yy y L L Lρρρπεπεπε-+=e e e e e 1034l yL ρπεe 2.8 －点电荷q +位于(,0,0)a -处;另－点电荷2q -位于(,0,0)a 处;空间有没有电场强度0=E 的点题 2.6图1lo 题2.7图解电荷q +在(,,)x y z 处产生的电场为1222320()4[()]x y z x a y zqx a y z πε+++=+++e e e E电荷2q -在(,,)x y z 处产生的电场为2222320()24[()]x y z x a y z q x a y z πε-++=--++e e e E (,,)x y z 处的电场则为12=+E E E ..令0=E ;则有22232()[()]x y z x a y z x a y z +++=+++e e e 222322[()][()]x y z x a y z x a y z -++-++e e e由上式两端对应分量相等;可得到2223222232()[()]2()[()]x a x a y z x a x a y z +-++=-+++ ① 2223222232[()]2[()]y x a y z y x a y z -++=+++ ②222322232[()]2[()]z x a y z z x a y z -++=+++ ③当0y ≠或0z ≠时;将式②或式③代入式①;得0a =..所以;当0y ≠或0z ≠时无解；当0y =且0z =时;由式①;有33()()2()()x a x a x a x a +-=-+解得(3x a =-±但3x a =-+不合题意;故仅在(3,0,0)a --处电场强度0=E ..2．9 一个很薄的无限大导电带电面;电荷面密度为σ..证明：垂直于平面的z 轴上0z z =处的电场强度E 中;有一半是有平面上半径为03z 的圆内的电荷产生的..解半径为r 、电荷线密度为d l r ρσ=的带电细圆环在z 轴上0z z =处的电场强度为0223200d d 2()zr z rr z σε=+E e故整个导电带电面在z 轴上0z z =处的电场强度为002232221200000d 12()2()2z z zr z r z r z r z σσσεεε∞∞==-=++⎰E e e e 而半径为03z 的圆内的电荷产生在z 轴上0z z =处的电场强度为022320000d 12()42zz zr z r r z σσεε'==-==+⎰E e e e E 2.10 一个半径为a 的导体球带电荷量为Q ;当球体以均匀角速度ω绕一个直径旋转;如题2.10图所示..求球心处的磁感应强度B ..解球面上的电荷面密度为24Q a σπ=题2.10图当球体以均匀角速度ω绕一个直径旋转时;球面上位置矢量r a =r e 点处的电流面密度为S z r a σσσω==⨯=⨯=J v ωr e esin sin 4Qa aφφωωσθθπ=e e将球面划分为无数个宽度为d d l a θ=的细圆环;则球面上任一个宽度为d d l a θ=细圆环的电流为 d d sin d 4S QI J l ωθθπ==细圆环的半径为sin b a θ=;圆环平面到球心的距离cos d a θ=;利用电流圆环的轴线上的磁场公式;则该细圆环电流在球心处产生的磁场为202232d d 2()z b Ib d μ==+B e 230222232sin d 8(sin cos )z Qa a a μωθθπθθ=+e 30sin d 8zQ aμωθθπe 故整个球面电流在球心处产生的磁场为 3000sin d 86z zQ Q a aπμωθμωθππ==⎰B e e 2.11 两个半径为b 、同轴的相同线圈;各有N 匝;相互隔开距离为d ;如题2.11图所示..电流I 以相同的方向流过这两个线圈..1求这两个线圈中心点处的磁感应强度x x B =B e ； 2证明：在中点处d d x B x 等于零；3求出b 与d 之间的关系;使中点处22d d x B x 也等于零.. 解 1由细圆环电流在其轴线上的磁感应强度 2022322()zIa a z μ=+B e得到两个线圈中心点处的磁感应强度为 202232(4)xNIb b d μ=+B e2两线圈的电流在其轴线上x )0(d x <<处的磁感应强度为2200223222322()2[()]x NIb NIb b x b d x μμ⎧⎫=+⎨⎬++-⎩⎭B e 所以 220022522252d 33()d 2()2[()]x B NIb x NIb d x x b x b d x μμ-=-+++- 故在中点2d x =处;有220022522252d 32320d 2[4]2[4]x B NIb d NIb d x b d b d μμ=-+=++ 3 222200222722252d 153d 2()2()x B NIb x NIb x b x b x μμ=-+++ 222002272225215()32[()]2[()]NIb d x NIb b d x b d x μμ--+-+- 令 0d d 222==d x x xB ;有 0]4[1]4[45252227222=+-+d b d b d题2.11图即 5222d b d += 故解得 b d =2.12 一条扁平的直导体带;宽为a 2;中心线与z 轴重合;通过的电流为I ..证明在第一象限内的磁感应强度为 04x I B aμαπ=-;021ln 4yI r B a r μπ= 式中α、1r 和2r 如题2.12图所示..解将导体带划分为无数个宽度为x 'd 的细条带;每一细条带的电流x aII '=d 2d ..由安培环路定理;可得位于x '处的细条带的电流I d 在点),(y x P 处的磁场为00d d d 24I I x B R aRμμππ'===02212d 4[()]I x a x x y μπ''-+ 则 022d d d sin 4[()]x Iy x B B a x x y μθπ'=-=-'-+ 022()d d d cos 4[()]y I x x x B B a x x y μθπ''-=='-+ 所以022d 4[()]ax aIy x B a x x y μπ-'=-='-+⎰0arctan 4a aI x x a y μπ-'⎛⎫--= ⎪⎝⎭0arctan arctan 4I a x a x a y y μπ⎡⎤⎛⎫⎛⎫-----=⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎣⎦0arctan arctan 4I x a x a a y y μπ⎡⎤⎛⎫⎛⎫+---=⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎣⎦021()4I a μααπ--=04I aμαπ- 022()d 4[()]a y aI x x x B a x x y μπ-''-=='-+⎰220ln[()]8aa I x x y a μπ-'--+=22022()ln 8()I x a y a x a y μπ++=-+021ln 4I r a r μπ 2.13 如题2.13图所示;有一个电矩为1p 的电偶极子;位于坐标原点上;另一个电矩为2p 的电偶极子;位于矢径为r 的某一点上..试证明两偶极子之间相互作用力为121212403(sin sin cos 2cos cos )4r p p F r θθφθθπε=-式中11,θ=<>r p ;22,θ=<>r p ;φ是两个平面1(,)r p 和2(,)r p 间的夹角..并问两个偶极子在怎样的相对取向下这个力值最大解电偶极子1p 在矢径为r 的点上产生的电场为1115303()1[]4r rπε=-p r r p E 所以1p 与2p 之间的相互作用能为1212215303()()1[]4e W r rπε=-=--p r p r p p p E题 2.12图因为11,θ=<>r p ;22,θ=<>r p ;则111cos p r θ=p r222cos p r θ=p r又因为φ是两个平面1(,)r p 和2(,)r p 间的夹角;所以有2121212()()sin sin cos r p p θθφ⨯⨯=r p r p另一方面;利用矢量恒等式可得1212()()[()]⨯⨯=⨯⨯=r p r p r p r p 2112[()]r -=p r p r p 21212()()()r -p p r p r p因此12121221()[()()()()]r=⨯⨯+=p p r p r p r p r p 1212sin sin cos p p θθφ+1212cos cos p p θθ 于是得到 =eW 12304p p r πε12sin sin cos θθφ-122cos cos θθ 故两偶极子之间的相互作用力为e r q constW F r=∂=-=∂1204p p πε-12sin sin cos θθφ-122cos cos θθ3d 1()d r r= 124034p p r πε12sin sin cos θθφ-122cos cos θθ由上式可见;当120θθ==时;即两个偶极子共线时;相互作用力值最大..2.14 两平行无限长直线电流1I 和2I ;相距为d ;求每根导线单位长度受到的安培力m F .. 解无限长直线电流1I 产生的磁场为 0112I rφμπ=B e 直线电流2I 每单位长度受到的安培力为 1012122112d 2m z I I I z dμπ=⨯=-⎰F e B e 式中12e 是由电流1I 指向电流2I 的单位矢量..同理可得;直线电流1I 每单位长度受到的安培力为 0122112122m m I I dμπ=-=F F e 2.15 一根通电流1I 的无限长直导线和一个通电流2I 的圆环在同一平面上;圆心与导线的距离为d ;如题2.15图所示..证明：两电流间相互作用的安培力为012(sec 1)m F I I μα=- 这里α是圆环在直线最接近圆环的点所张的角..解无限长直线电流1I 产生的磁场为0112I rφμπ=B e 圆环上的电流元22d I l 受到的安培力为0122212d d d 2m y I II xμπ=⨯=⨯F l B l e1I由题2.15图可知 2d (sin cos )d x z a θθθ=-+l e ecos x d a θ=+所以 2012(sin cos )d 2(cos )m z x aI I d a πμθθθπθ=--=+⎰F e e 20120cos d 2(cos )x aI I d a πμθθπθ-=+⎰e 0120122((sec 1)2xx aI I I I a μπμαπ--=--e e 2.16 证明在不均匀的电场中;某一电偶极子p 绕坐标原点所受到的力矩为()⨯∇+⨯r p E p E ..解如题2.16图所示;设d q =p l (d 1)l <<;则电偶极子p 绕坐标原点所受到的力矩为2211()()q q =⨯-⨯=T r E r r E rd d d d ()()()()2222q q +⨯+--⨯-=l l l l r E r r E rd d d d [()()]d [()()]22222q q ⨯+--+⨯++-l l l lr E r E r l E r E r当d 1l <<时;有d d ()()()()22+≈+⋅∇l lE r E r E rd d ()()()()22-≈-⋅∇l lE r E r E r故得到(d )()d ()q q ≈⨯⋅∇+⨯=T r l E r l E r()⨯∇+⨯r p E p E三章习题解答3.1 真空中半径为a 的一个球面;球的两极点处分别设置点电荷q 和q -;试计算球赤道平面上电通密度的通量Φ如题3.1图所示..解由点电荷q 和q -共同产生的电通密度为33[]4q R R π+-+-=-=R R D 22322232()(){}4[()][()]r z r z r z a r z a q r z a r z a π+-++-+-++e e e e 则球赤道平面上电通密度的通量x 题2.16 图d d zz SSS Φ====⎰⎰D S D e223222320()[]2d 4()()aq a ar r r a r a ππ--=++⎰ 22121)0.293()aqaq q r a =-=-+ 3.2 1911年卢瑟福在实验中使用的是半径为a r 的球体原子模型;其球体内均匀分布有总电荷量为Ze -的电子云;在球心有一正电荷ZeZ 是原子序数;e 是质子电荷量;通过实验得到球体内的电通量密度表达式为02314r a Ze r r r π⎛⎫=- ⎪⎝⎭D e ;试证明之..解位于球心的正电荷Ze 球体内产生的电通量密度为 124rZerπ=D e 原子内电子云的电荷体密度为333434a a Ze Zer r ρππ=-=-电子云在原子内产生的电通量密度则为 32234344r ra r Ze rr r ρπππ==-D e e 故原子内总的电通量密度为 122314ra Ze r r r π⎛⎫=+=- ⎪⎝⎭D D D e 3.3 电荷均匀分布于两圆柱面间的区域中;体密度为30C m ρ; 两圆柱面半径分别为a 和b ;轴线相距为c )(a b c -<;如题3.3图()a 所示..求空间各部分的电场..解由于两圆柱面间的电荷不是轴对称分布;不能直接用高斯定律求解..但可把半径为a 的小圆柱面内看作同时具有体密度分别为0ρ±的两种电荷分布;这样在半径为b 的整个圆柱体内具有体密度为0ρ的均匀电荷分布;而在半径为a 的整个圆柱体内则具有体密度为0ρ-的均匀电荷分布;如题3.3图()b 所示..空间任一点的电场是这两种电荷所产生的电场的叠加..在b r >区域中;由高斯定律0d Sqε=⎰E S ;可求得大、小圆柱中的正、负电荷在点P 产生的电场分别为 2200120022rb b r r πρρπεε==r E e 2200120022r a a r r πρρπεε'-''==-''r E e 题3. 3图()a点P 处总的电场为 2211220()2b a r r ρε''=+=-'r r E E E 在b r <且a r >'区域中;同理可求得大、小圆柱中的正、负电荷在点P 产生的电场分别为220022r r r πρρπεε==r E e 22220022r a a r r πρρπεε'-''==-''r E e点P 处总的电场为 202220()2a r ρε''=+=-'r E E E r 在a r <'的空腔区域中;大、小圆柱中的正、负电荷在点P 产生的电场分别为20030022r r r πρρπεε==r E e 20030022r r r πρρπεε''-''==-'r E e 点P 处总的电场为 003300()22ρρεε''=+=-=E E E r r c 3.4 半径为a 的球中充满密度()r ρ的体电荷;已知电位移分布为32542()()r r Ar r a D a Aa r a r ⎧+≤⎪=⎨+≥⎪⎩ 其中A 为常数;试求电荷密度()r ρ..解：由ρ∇=D ;有 221d ()()d r r r D r rρ=∇=D 故在r a <区域 23220021d ()[()](54)d r r r Ar r Ar r rρεε=+=+ 在r a >区域 5420221d ()()[]0d a Aa r r r r rρε+== 3.5 一个半径为a 薄导体球壳内表面涂覆了一薄层绝缘膜;球内充满总电荷量为Q 为的体电荷;球壳上又另充有电荷量Q ..已知球内部的电场为4()r r a =E e ;设球内介质为真空..计算：1球内的电荷分布；2球壳外表面的电荷面密度..解 1 由高斯定律的微分形式可求得球内的电荷体密度为20021d [()]d r E r r ρεε=∇==E 432002441d [()]6d r r r r r a aεε=题3. 3图()b＝＋2球体内的总电量Q 为 3220040d 64d 4ar Q r r a a τρτεππε===⎰⎰球内电荷不仅在球壳内表面上感应电荷Q -;而且在球壳外表面上还要感应电荷Q ;所以球壳外表面上的总电荷为2Q ;故球壳外表面上的电荷面密度为 02224Qaσεπ== 3.6 两个无限长的同轴圆柱半径分别为r a =和r b =()b a >;圆柱表面分别带有密度为1σ和2σ的面电荷..1计算各处的电位移0D ；2欲使r b >区域内00=D ;则1σ和2σ应具有什么关系解 1由高斯定理d Sq =⎰DS ;当r a <时;有 010=D当a r b <<时;有 02122rD a ππσ= ;则 102ra rσ=D e 当b r <<∞时;有 0312222rD a b ππσπσ=+ ;则 1203r a b rσσ+=D e 2令 12030ra b rσσ+==D e ;则得到 12b a σσ=- 3.7 计算在电场强度x y y x =+E e e 的电场中把带电量为2C μ-的点电荷从点1(2,1,1)P -移到点2(8,2,1)P -时电场所做的功：1沿曲线22x y =；2沿连接该两点的直线..解 1d d d d x y CCCW q q E x E y ===+=⎰⎰⎰F l E l2221d d d(2)2d Cq y x x y q y y y y +=+=⎰⎰22616d 142810()q y y q J -==-⨯⎰2连接点1(2,1,1)P -到点2(8,2,1)P -直线方程为2812x x y y --=-- 即 640x y -+= 故W =21d d d(64)(64)d Cq y x x y q y y y y +=-+-=⎰⎰261(124)d 142810()q y y q J --==-⨯⎰3.8 长度为L 的细导线带有均匀电荷;其电荷线密度为0l ρ..1计算线电荷平分面上任意点的电位ϕ；2利用直接积分法计算线电荷平分面上任意点的电场E ;并用ϕ=-∇E 核对..解 1建立如题3.8图所示坐标系..根据电位的积分表达式;线电荷平分面上任意点P 的电位为2(,0)L L r ϕ-==⎰22ln(4L l L z ρπε-'=L rρ04l ρπε=02l ρπε2根据对称性;可得两个对称线电荷元z l 'd 0ρ在点P 的电场为d d r r rE θ===E e e 022320d 2()l rr z r z ρπε''+e故长为L 的线电荷在点P 的电场为20223200d d 2()L l r r z r z ρπε'==='+⎰⎰E Ee 20002L l r r ρπε=e re由ϕ=-∇E 求E ;有002l ρϕπε⎡⎢=-∇=-∇=⎢⎥⎣⎦E(00d ln 2ln 2d l rL r r ρπε⎡⎤--=⎢⎥⎣⎦e0012l r r ρπε⎧⎫⎪-=⎬⎪⎭e r e 3.9 已知无限长均匀线电荷l ρ的电场02lrr ρπε=E e ;试用定义式()d Pr rr ϕ=⎰E l 求其电位函数..其中P r 为电位参考点..解000()d d ln ln 222PPPr r rl l l P r rrr r r r r rρρρϕπεπεπε====⎰⎰E l 由于是无限长的线电荷;不能将P r 选为无穷远点..3.10一点电荷q +位于(,0,0)a -;另一点电荷2q -位于(,0,0)a ;求空间的零电位面.. 解两个点电荷q +和2q -在空间产生的电位1(,,)4x y zϕπε=令(,,)0x y z ϕ=;则有0=即 2222224[()]()x a y z x a y z +++=-++故得 222254()()33x a y z a +++= 由此可见;零电位面是一个以点5(,0,0)3a -为球心、43a 为半径的球面..3.11 证明习题3.2的电位表达式为 2013()()422a aZe r r r r r ϕπε=+- 解位于球心的正电荷Ze 在原子外产生的电通量密度为 124rZerπ=D e 电子云在原子外产生的电通量密度则为 32224344a r r r Zer rρπππ==-D e e 所以原子外的电场为零..故原子内电位为230011()d ()d 4aa r ra r r Ze rr D r r r r ϕεπε==-=⎰⎰2013()422a aZe r r r r πε+- 3.12 电场中有一半径为a 的圆柱体;已知柱内外的电位函数分别为2()0()()cos r r a a r A r r a rϕϕφ=≤⎧⎪⎨=-≥⎪⎩ 1求圆柱内、外的电场强度；2这个圆柱是什么材料制成的表面有电荷分布吗试求之..解 1由ϕ=-∇E ;可得到 r a <时; 0ϕ=-∇=Er a >时; ϕ=-∇=E 22[()cos ][()cos ]r a a A r A r r r r rφφφφ∂∂----=∂∂e e2222(1)cos (1)sin r a a A A r rφφφ-++-e e2该圆柱体为等位体;所以是由导体制成的;其表面有电荷分布;电荷面密度为0002cos r r a r a A σεεεφ=====-n E e E3.13 验证下列标量函数在它们各自的坐标系中满足20ϕ∇=1sin()sin()hz kx ly e - 其中222h k l =+； 2[cos()sin()]n r n A n φφ+ 圆柱坐标； 3cos()n r n φ- 圆柱坐标； 4cos r φ 球坐标； 52cos r φ- 球坐标..解 1在直角坐标系中 2222222x y zϕϕϕϕ∂∂∂∇=++∂∂∂而 22222[sin()sin()]sin()sin()hz hz kx ly e k kx ly e x xϕ--∂∂==-∂∂22222[sin()sin()]sin()sin()hz hzkx ly e l kx ly e y y ϕ--∂∂==-∂∂ 22222[sin()sin()]sin()sin()hz hz kx ly e h kx ly e z zϕ--∂∂==∂∂ 故 2222()sin()sin()0hzk l h kx ly e ϕ-∇=--+=2在圆柱坐标系中 2222221()r r r r r zϕϕϕϕφ∂∂∂∂∇=++∂∂∂∂而11(){[cos()sin()]}n r r r n A n r r r r r r ϕφφ∂∂∂∂=+=∂∂∂∂22[cos()sin()]n n r n A n φφ-+ 222221[cos()sin()]}n n r n A n r ϕφφφ-∂=-+∂ 2222[cos()sin()]0nr n A n z zϕφφ-∂∂=+=∂∂ 故 20ϕ∇=3 2211(){[cos()]}cos()n n r r r n n r n r r r r r rϕφφ---∂∂∂∂==∂∂∂∂222221cos()n n r n r ϕφφ--∂=-∂ 2222[cos()]0nr n z zϕφ-∂∂==∂∂ 故 20ϕ∇=4在球坐标系中 22222222111()(sin )sin sin r r r r r r ϕϕϕϕθθθθθφ∂∂∂∂∂∇=++∂∂∂∂∂ 而 2222112()[(cos )]cos r r r r r r r r r r ϕθθ∂∂∂∂==∂∂∂∂ 2211(sin )[sin (cos )]sin sin r r r ϕθθθθθθθθθ∂∂∂∂==∂∂∂∂ 2212(sin )cos sin r r rθθθθ∂-=-∂ 2222222211(cos )0sin sin r r r ϕθθφθφ∂∂==∂∂故 20ϕ∇=5 222222112()[(cos )]cos r r r r r r r r r rϕθθ-∂∂∂∂==∂∂∂∂ 22211(sin )[sin (cos )]sin sin r r r ϕθθθθθθθθθ-∂∂∂∂==∂∂∂∂222412(sin )cos sin r r rθθθθ-∂-=-∂ 22222222211(cos )0sin sin r r r ϕθθφθφ-∂∂==∂∂ 故 20ϕ∇=3.14 已知0>y 的空间中没有电荷;下列几个函数中哪些是可能的电位的解1cosh y e x -； 2x e y cos -；3cos sin e x x 4z y x sin sin sin ..解 1222222(cosh )(cosh )(cosh )y y ye x e x e x x y z---∂∂∂++=∂∂∂2cosh 0y e x -≠所以函数x e y cosh -不是0>y 空间中的电位的解；2 222222(cos )(cos )(cos )y y y e x e x e x x y z---∂∂∂++=∂∂∂cos cos 0y y e x e x ---+= 所以函数x e y cos -是0>y 空间中可能的电位的解；3222222(cos sin )(cos sin )(cos sin )e x x e x x e x x x y z∂∂∂++=∂∂∂4cos sin 2cos sin 0e x x e x x -+≠所以函数x x e y sin cos 2-不是0>y 空间中的电位的解；4 222222(sin sin sin )(sin sin sin )(sin sin sin )x y z x y z x y z x y z∂∂∂++=∂∂∂ 3sin sin sin 0x y z -≠所以函数z y x sin sin sin 不是0>y 空间中的电位的解..3.15 中心位于原点;边长为L 的电介质立方体的极化强度矢量为0()x y z P x y z =++P e e e ..1计算面束缚电荷密度和体束缚电荷密度；2证明总的束缚电荷为零..解 1 03P P ρ=-∇=-P220()22P x L x x L L L x P σ======n Pe P220()22P x L x x L L L x P σ=-=-=-==-=n P e P同理 0()()()()22222P P P P L L L L Ly y z z P σσσσ===-====-=2 320d d 3602P P P SL q S P L L P τρτσ=+=-+⨯=⎰⎰ 3.16 一半径为0R 的介质球;介电常数为0r εε;其内均匀分布自由电荷ρ;证明中心点的电位为20021()23r r R ερεε+ 解由d Sq =⎰D S ;可得到0r R <时; 321443r r D ππρ=即 13r D ρ=; 11003r r D r E ρεεεε== 0r R >时; 3202443R r D ππρ=即 30223R D rρ= ; 30122003R D E r ρεε== 故中心点的电位为00301220000(0)d d d d 33R R r R RR r E r E r r r r ρρϕεεε∞∞=+=+=⎰⎰⎰⎰22200000021()6323r r r R R R ρρερεεεεε++= 3.17 一个半径为R 的介质球;介电常数为ε;球内的极化强度r K r =P e ;其中K 为一常数..1 计算束缚电荷体密度和面密度；2 计算自由电荷密度；3计算球内、外的电场和电位分布..解 1 介质球内的束缚电荷体密度为 2221d ()d p K Kr r r r r ρ=-∇=-=-P 在r R =的球面上;束缚电荷面密度为 p r r Rr R KRσ=====n P e P2由于0ε=+D E P ;所以 00εεε∇=∇+∇=∇+∇D E P D P 即 0(1)εε-∇=∇D P 由此可得到介质球内的自由电荷体密度为 20()p Kr εεερρεεεεεε=∇=∇=-=---D P总的自由电荷量 2200014d 4d R K RK q r r r τεπερτπεεεε===--⎰⎰ 3介质球内、外的电场强度分别为100()r Krεεεε==--P E e ()r R < 2220004()r rq RKr r επεεεε==-E e e ()r R > 介质球内、外的电位分别为112d d d RrrRE r E r ϕ∞∞==+=⎰⎰⎰E l。

电磁场与电磁波_第四版_第三章

谢处方《电磁场与电磁波》(第4版)课后习题-第3章 静态电磁场及其边值问题的解【圣才出品】

电磁场与电磁波(第四版)习题解答

《电磁场与电磁波》(第四版)课后习题解答(全)

电磁场与电磁波课后习题答案第3章(杨儒贵编着)

电磁场与电磁波(第四版)课后答案__谢处方

电磁场与电磁波第四版第三章部分答案

电磁场与电磁波答案(第四版)谢处方之欧阳治创编

电磁场与电磁波(第四版)(王家礼) (4)

电磁场与电磁波（第4版）第3章部分习题参考解答

《电磁场与电磁波》第4版(谢处方 编)课后习题答案 高等教育出版社三章习题解答

电磁场与电磁波课程教学大纲

电磁场与电磁波答案(第四版)

电磁场与电磁波第四版

电磁场与电磁波(第四版)课后答案_电科习题

电磁场与电磁波_第四版_第三章

电磁场与电磁波(第四版)课后答案_第三章习题

谢处方《电磁场与电磁波》(第4版)章节习题-第3章 静态电磁场及其边值问题的解【圣才出品】

电磁场与电磁波答案(第四版)谢处方

谢处方《电磁场与电磁波》(第4版)课后习题-第3章静态电磁场及其边值问题的解【圣才出品】

《电磁场与电磁波》第4版(谢处方编)课后习题答案高等教育出版社三章习题解答

谢处方《电磁场与电磁波》(第4版)章节习题-第3章静态电磁场及其边值问题的解【圣才出品】