第五章水力学详解
合集下载
流体力学 水力学 第五章
7 H [H0 ] 9m 0.75
§5.3 有压管道恒定流 5.3.1 短管水力计算（Q、d、H） 有压流：水沿管道满管流动的水力现象。 特点：水流充满管道过水断面，管道内不存在自 由水面，管壁上各点承受的压强一般不等于大 气压强。
短管：局部水头损失和 速度水头在总水头损失 中占有相当的比重，计 算时不能忽略的管道. （一般局部损失和速度 水头大于沿程损失 的5% ~ 10%）。一般L/d 1000
1 vc c 0
v
2 0 0
2 gH 0 2 gH 0
v hw h j 2g p c pa
2 c
1 1 流速系数： c 0 1 0
1 1 流速系数： c 0 1 0
实验得： 0.97 ~ 0.98 1 推求： 0 2 1 1 0.06 2 0.97 1
2
d2
5.126m 2g
例5 3：如图所示圆形有压涵管，管长50m, 上下游水位差3m 沿程阻力系数为0.03，局部阻力系数：进口 1＝0.5。 第一个转弯 2＝0.71，第二个转弯 3＝0.65，出口
4＝1.0，要求涵管通过流量大约3m 3 / s, 试设计管径d。
2 1 1
2g
v
v
2 2 2
2 2 2
2g
hw
2g
hw
H0 H
v
2 1 1
2g
v
2 2 2
2g
hw
hw h f h j (
l v
v d 2g 2g
2
2
l
v ) d 2g
水力学第五章 有旋流动和有势流动
定义
数。
M(x,y,z)
( x, y, z ) = + u x d x + u y d y + u z d z
M 0 ( x0 , y0 , z 0 )
u x =
x
u y =
y
u z =
z
无旋流动
ij ×u=
xy
xy
无旋流动
k
=0 z
z
等价
有势流动
u=
有势流动
u(t)
u(t+dt)
L是由确定流体质点组成的封闭线，是 一个系统，在流动中会改变位置和形状。
简要的证明
dΓ
du
dt
+ d t d l
L
d dt
+
L
u
δ
l
d
+ d t (u δ l)
L
+
L
d
t
δ
d
lL++
δu
2
du
dl
du
+ d t δ l + + u δ d t + d t δ l + + u δ u
=
( uz
u y) + ( ux
uz ) +
uy (
xy z yz x zx
ux ) = 0 y
由于涡管侧壁没有涡 通量，所以根据涡量场是 无源场可得如下结论：
结论 在同一时刻，穿 过同一涡管的各断面的涡 通量都是相同的。即同一 时刻，一根涡管对应一个 涡管强度。
回答了前面的问题
水力学-第5章 明渠恒定均匀流1113
工程中采用最多的是梯形断面， 工程中采用最多的是梯形断面，其边坡系数 m 由 边坡稳定要求确定。 边坡稳定要求确定。在 m 已定的情况下，同样的过水 要求确定 已定的情况下， 面积 A ，湿周的大小因底宽与水深的比值 b / h 而异 。根据水力最佳断面的条件： 根据水力最佳断面的条件： 即
χ = 最小值 A = 常数
解：将已知条件代入基本公式，并用曼宁公 将已知条件代入基本公式， 式计算谢才系数， 式计算谢才系数，整理后可得
nQ( β + 2 1 + m 2 ) 2 / 3 h= 5 / 3 1/ 2 ( β + m) i
3/8
当为水力最佳断面时: 当为水力最佳断面时
β = 2( 1 + m 2 − m) = 2( 1 + 1.252 − 1.25) = 0.702
2
15
用 β m 代替上式中的 β 值，整理后得 即梯形水力最佳断面的水力半径等于水深的一半。 即梯形水力最佳断面的水力半径等于水深的一半。
hm Rm = 2 的梯形断面。 矩形断面可以看成为 m = 0 的梯形断面。以 m = 0
代入以上各式可求得矩形水力最佳断面的 β m 及 Rm .
bm βm = = 2 即 bm = 2hm hm
χ = b + 2 h 1 + m 2 = 34 m + 2 × ( 2 . 7 m ) 1 + 1 . 5 2 = 43 . 74 m
102 . 74 m 2 R= = = 2 . 35 m χ 43 . 74 m A
查表可知， 查表可知，对渠线弯曲并已滋生杂草的土 n =0.03
1 1/ 6 1 C= R = (2.35)1/ 6 = 38.4m1/ 2 / s n 0.03
第五章_给水管网水力分析
管段的水力特性方程： 管段的水力特性方程：hi=siqin 可将管段流量与水头相互转换， 个方程。 可将管段流量与水头相互转换，即N 个未知量对应 N 个方程。 管段流量 相互转换
（3）必须至少有一个定压节点 ）
• 管网中无定压节点（R=0）时，恒定流方程组无 管网中无定压节点（ ） 解。 • 因为若 j*为方程组解， Hj* +∆H仍为方程组的 因为若H 为方程组解 为方程组解， 仍为方程组的 解，即方程组无解。 即方程组无解。
(H + ∆H ) − (H + ∆H ) = H − H = h
* Fi * Ti * Fi * Ti
* i
5.3 单定压节点树状管网水力分析
比较简单， 比较简单，管段流量可以由节点流量连续性方程 组直接求出，不要求解非线性的能量方程组。 组直接求出，不要求解非线性的能量方程组。 水力分析计算分两步（P89例题 ）： 例题5.1）： 水力分析计算分两步（ 例题 • 1、用流量连续性条件计算管段流量，并计算出管 、用流量连续性条件计算管段流量， 段压降； 段压降； • 2、根据管段能量方程和管段压降，从定压节点出 、根据管段能量方程和管段压降， 发推求各节点水头。 发推求各节点水头。
可以看出：树状网中，各管段流量 可以看出：树状网中，各管段流量qi可以用节点流 表示出来。 量Qj表示出来。
5.1.2 管段能量方程（根据能量守恒定律） 根据能量守恒定律）
管段两端节点水头之差等于该管段的压降： 管段两端节点水头之差等于该管段的压降： HFi –HTi= hi i-1,2,…,M
HFi——管段 的上端点水头； 管段i的上端点水头 管段 的上端点水头； HTi——管段 的下端点水头； 管段i的下端点水头； 管段 的下端点水头 hi——管段 的压降； 管段i的压降 管段 的压降； M——管段模型中的管段总数。 管段模型中的管段总数。 管段模型中的管段总数
（3）必须至少有一个定压节点 ）
• 管网中无定压节点（R=0）时，恒定流方程组无 管网中无定压节点（ ） 解。 • 因为若 j*为方程组解， Hj* +∆H仍为方程组的 因为若H 为方程组解 为方程组解， 仍为方程组的 解，即方程组无解。 即方程组无解。
(H + ∆H ) − (H + ∆H ) = H − H = h
* Fi * Ti * Fi * Ti
* i
5.3 单定压节点树状管网水力分析
比较简单， 比较简单，管段流量可以由节点流量连续性方程 组直接求出，不要求解非线性的能量方程组。 组直接求出，不要求解非线性的能量方程组。 水力分析计算分两步（P89例题 ）： 例题5.1）： 水力分析计算分两步（ 例题 • 1、用流量连续性条件计算管段流量，并计算出管 、用流量连续性条件计算管段流量， 段压降； 段压降； • 2、根据管段能量方程和管段压降，从定压节点出 、根据管段能量方程和管段压降， 发推求各节点水头。 发推求各节点水头。
可以看出：树状网中，各管段流量 可以看出：树状网中，各管段流量qi可以用节点流 表示出来。 量Qj表示出来。
5.1.2 管段能量方程（根据能量守恒定律） 根据能量守恒定律）
管段两端节点水头之差等于该管段的压降： 管段两端节点水头之差等于该管段的压降： HFi –HTi= hi i-1,2,…,M
HFi——管段 的上端点水头； 管段i的上端点水头 管段 的上端点水头； HTi——管段 的下端点水头； 管段i的下端点水头； 管段 的下端点水头 hi——管段 的压降； 管段i的压降 管段 的压降； M——管段模型中的管段总数。 管段模型中的管段总数。 管段模型中的管段总数
水力学基础课件——第五章 明渠恒定均匀流
A
(b mh)h
R
x b 2h 1 m2
第五章 明渠恒定均匀流
二、明渠的底坡 底坡：明渠渠底倾斜的程度称为底坡。以符号i表
示，i等于渠底线与水平线夹角口的正弦即i＝Sinθ。 明渠有三种底坡：顺坡、平坡和逆坡
第五章 明渠恒定均匀流
➢顺坡： i>0，明槽槽底沿程降低者称为正坡或顺坡。 ➢平坡： i=0，明槽槽底高程沿程不变者称为平坡。 ➢逆坡： i<0，明槽槽底沿程增高者称为反坡或逆坡。
第五章 明渠恒定均匀流
5.1 明渠的类型及其对水流运动的影响
明渠的渠身及其沿流动方向的倾斜程度( 称作底坡 )， 是水流边界的几何条件。一定形式的边界几何条件，给 予水流运动一定的影响。所以为了了解水流运动的特征， 必须先对影响明渠水流运动的边界几何条件进行分析。
第五章 明渠恒定均匀流
一、明渠的横断面 人工明渠的横断面，通常作成对称的几何形状。例如
二、允许流速
允许流速是为了保持渠道安全稳定运行在流速上的限 制，包括不冲流速、不淤流速和其它运行管理要求的流 速限制。在实际明渠均匀流计算中必须结合工程要求进 行校核。
第五章 明渠恒定均匀流
➢在设计中，要求渠道流速v在不冲、不淤的允许
流速范围内，即：
式中：
——不冲允许流速（m/s），根据壁面材料定。
➢ 如果您有任何问题， 请毫不犹豫地提出 !
In case of you have any question, DO NOT hesitate to ask me !
第五章 明渠恒定均匀流
5.2 明渠均匀流特性及其产生条件
一、明渠均匀流的特性： 1、均匀流过水断面的形状、尺寸沿流程不变，特别
是水深h沿程不变，这个水深也称为正常水深。 2、过水断面上的流速分布和断面平均流速沿流程不
水力学-第5章 明渠恒定均匀流
R/m 1.625 1.866 2.090 2.310
C /( m
1/2
/ s)
Q AC
Ri /( m / s )
42.6 59.3 78.6 100.9
3
21.25 27.00 33.25 40.00
44.5 45.5 46.5 47.0
由上表绘出 h ~ Q 曲线。从曲线查得： 当 Q =70 m3/s 时，h = 3.3 m 。
5
nK
3 8 1 h 3 h m b b
根据上式就可绘出另一组曲线
h b
～
b
2 .6 7
（见附图II）
nK
现应用附图 II 解本例，
K Q i 70 m / s 1 800
3
1980 m / s
3
b
2 . 67
(6 m )
2 . 67 3
第五章
5.5
明渠恒定均匀流
明渠均匀流的水力计算
对于梯形渠道，各水力要素间存在着下列函数关系:
Q AC
Ri f ( m , b , h , i , n )
主要有下列几种类型：
一、已知渠道的断面尺寸b、m、h及底坡i、粗糙 系数n，求通过的流量（或流速）。 二、已知渠道的设计流量Q、底坡i、底宽b、边坡 系数m和粗糙系数n，求水深h。 三、已知渠道的设计流量Q、底坡i、水深h、边坡 系数m及粗糙系数n，求渠道底宽b。 四、已知渠道的设计流量Q，水深h、底宽b、粗糙 系数n及边坡系数m，求底坡i。 五、已知流量Q、流速v、底坡i、粗糙系数n和边 坡系数m，要求设计渠道断面尺寸。
i
（1）试算～图解法
可假设一系列 h 值，代入上式计算相应的 Q 值，并 绘成 h ~ Q曲线，然后根据已知流量，在曲线上即可查 出要求的 h 值。
水力学第五章
逐步充满整个断面。
一、圆柱形外管嘴的恒定出流
1
v H 0 00 n 2g 2g 2g 1 v 2gH n 2gH n
n
1
v
2 0 0
v
2
2
l (3 ~ 4)d
H
0 d
c
2
0
பைடு நூலகம்
c
2
n
1
Q v n 2 gH 0
n n 0.82
§5.3 短管的水力计算
1.虹吸管的水力计算
例题2
§5.3 短管的水力计算
2.水泵吸水管的水力计算 hv ，求水泵安装高度 H 。 计算内容：已知 Q、d、l吸、、 进、 弯、
例题3
例题1
在 H 孔口 H n , d 孔口 d n 及流量。 1.流速比较 条件下，试分别比较孔口和管嘴出流的流速
流体力学
主 讲：赵 超
第五章 孔口、管嘴出流和有压管路
§5.1 液体经薄壁孔口的恒定出流 §5.2 液体经管嘴的恒定出流 §5.3 短管的水力计算
第五章 孔口、管嘴出流和有压管路
常用公式 连续性方程： 伯努利方程： 损失公式：
A1v1 A2 v2
2 p1 1v12 p2 2 v2 z1 z2 hw12 g 2g g 2g
2gH0 2gH0
1
c 0
速度系数 收缩系数 流量系数
Q Ac vc A 2 gH 0 A 2 gH 0
c /
三、薄壁小孔口的 淹没出流
2 2 vc vc H1 0 0 H2 0 0 0 se 2g 2g
l 3 ~ 4 d
一、圆柱形外管嘴的恒定出流
1
v H 0 00 n 2g 2g 2g 1 v 2gH n 2gH n
n
1
v
2 0 0
v
2
2
l (3 ~ 4)d
H
0 d
c
2
0
பைடு நூலகம்
c
2
n
1
Q v n 2 gH 0
n n 0.82
§5.3 短管的水力计算
1.虹吸管的水力计算
例题2
§5.3 短管的水力计算
2.水泵吸水管的水力计算 hv ，求水泵安装高度 H 。 计算内容：已知 Q、d、l吸、、 进、 弯、
例题3
例题1
在 H 孔口 H n , d 孔口 d n 及流量。 1.流速比较 条件下，试分别比较孔口和管嘴出流的流速
流体力学
主 讲：赵 超
第五章 孔口、管嘴出流和有压管路
§5.1 液体经薄壁孔口的恒定出流 §5.2 液体经管嘴的恒定出流 §5.3 短管的水力计算
第五章 孔口、管嘴出流和有压管路
常用公式 连续性方程： 伯努利方程： 损失公式：
A1v1 A2 v2
2 p1 1v12 p2 2 v2 z1 z2 hw12 g 2g g 2g
2gH0 2gH0
1
c 0
速度系数 收缩系数 流量系数
Q Ac vc A 2 gH 0 A 2 gH 0
c /
三、薄壁小孔口的 淹没出流
2 2 vc vc H1 0 0 H2 0 0 0 se 2g 2g
l 3 ~ 4 d
水力学课件第五章
紊流
管中为石油时
vd 100 2 333.3 2300 Re 0.6 ν
层流
作业
1、2
均匀流沿程水头损失与切应力的关系
沿程水头损失与切应力的关系 在管道恒定均匀流中，取总流流段1-1到2-2，各 作用力处于平衡状态：F=0。
P1
1
0 0
2
P2 2 z2
z1 z2 sin l
p1 p2 hf g g
m 13600 ( 1)hp ( 1) 0.3 4.23m 900
设流动为层流
4Q v 2.73m / s 2 d
l v 2 64 l v 2 64 l v 2 hf d 2 g Re d 2 g vd d 2 g
Re
d 1.175 0.075 979 < 2300 4 0.9 10
层流
1 2 1 Q 1.175 d 3600 1.175 3.14 0.075 2 3600 18.68m 3 / h 4 4
2、求沿程水头损失
64 64 0.0654 Re 979
T
T
u x u x u x
T
1 1 1 ' ux (ux ux )dt ux dt ux dt ux ux 0 T0 T0 T0
其它运动要素也同样处理：
1 p T 1 p T
T
pdt
0 T 0
p p p
pdt 0
脉动值说明：
—局部损失系数(无量纲)
一般由实验测定
实际液体流动的两种形态
雷诺试验
实验条件：
短管--《水力学》第五章
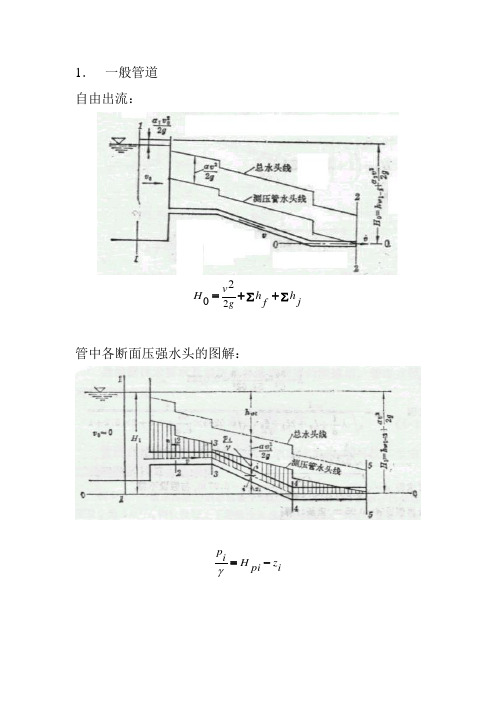
1． 一般管道 自由出流：
∑∑++=j
h f h v H g 22
管中各断面压强水头的图解：
i
z pi H i p
-=γ
淹没出流
∑∑+=j h f
h H 0
2．虹吸管
负压段（利用水头线判断）
最大真空断面位置
例如在下图中
3．离心泵
吸水管、压力管
流量Q
扬程H：水泵提供给单位重量水体的能量
扬程H=提水高度z +管路全部水头损失h w
允许吸水真空度：决定水泵安装高度z s 。
功率：
轴功率（输入功率）N ——电机传递给泵的功率。
有效功率N e ——水体从泵实际获得的功率，HQ e N γ=。
效率：N e N
=η
转速：一般固定（恒速泵）。
离心泵性能曲线：
管道性能曲线：
管道单位重量水体所需能量
2
2)2
21221(SQ g H Q gA gA d l g H j h
f
h g H w
h g H H +=∑++++=+=∑=∑∑ζλ 对于给定管道系统，S 为定值。
水泵选用及工作点的确定：
初选：流量、扬程为主要参数；校核：力求高效运行。
【精品】第五章-明渠恒定均匀流---水力学课程主页
第五章-明渠恒定均匀流---水力学课程主页第五章 明渠恒定均匀流第一节 概 述一．明渠水流1、明渠定义：人工渠道、天然河道、未充满水流的管道统称为明渠。
2、明渠水流是指在明渠中流动，具有显露在大气中的自由表面，水面上各点的压强都等于大气压强。
故明渠水流又称为无压流。
明渠水流的运动是在重力作用下形成的。
在流动过程中，自由水面不受固体边界的约束（这一点与管流不同），因此，在明渠中如有干扰出现，例如底坡的改变、断面尺寸的改变、粗糙系数的变化等，都会引起自由水面的位置随之升降，即水面随时空变化，这就导致了运动要素发生变化，使得明渠水流呈现出比较多的变化。
在一定流量下，由于上下游控制条件的不同，同一明渠中的水流可以形成各种不同形式的水面线。
正因为明渠水流的上边界不固定，故解决明渠水流的流动问题远比解决有压流复杂得多。
明渠水流可以是恒定流或非恒定流，也可以是均匀流或非均匀流，非均匀流也有急变流和渐变流之分。
本章首先学习恒定均匀流。
明渠恒定均匀流是一种典型的水流，其有关的理论知识是分析和研究明渠水流各种现象的基础，也是渠道断面设计的重要依据。
对明渠水流而言，当然也有层流和紊流之分，但绝大多数水流（渗流除外）为紊流，并且接近或属于紊流阻力平方区。
因此，本章及以后各章的讨论将只限于此种情况。
二、渠槽的断面形式（一）按横断面的形状分类渠道的横断面形状有很多种。
人工修建的明渠，为便于施工和管理，一般为规则断面，常见的有梯形断面、矩形断面、U 型断面等，具体的断面形式还与当地地形及筑渠材料有关。
天然河道 一般为无规则，不对称，分为主槽与滩地。
在今后的分析计算中，常用的是渠道的过水断面的几何要素，主要包括：过水断面面积A 、湿周χ、水力半径R 、水面宽度B 。
对梯形断面而言，其过水断面几何要素计算公式如下：2)()h m h mh b A +=+=β（h m m h b )12(1222++=++=βχχA R = h m mh b B )2(2+=+=β式中，b 为底宽；m 为边坡系数；h 为水深；β为宽深比，定义为h b =β（二）按横断面形状尺寸沿流程是否变化分类棱柱体明渠是指断面形状尺寸沿流程不变的长直明渠。
水力学第五章明渠恒定均匀流
6
在平底渠道中i＝0，流段重力在顺流方向 分力Gsinθ＝0；
在逆坡渠道中，流段重力的分力Gsinθ与摩 阻力Ff的方向一致，因而都不可能满足Gsinθ ＝ Ff的平衡条件，故在平底及逆坡渠段中， 不可能产生均匀流动，只有在顺坡渠道中， 才有可能产生均匀流。
7
5.2 明渠均匀流特性及其生条件
一、明渠均匀流的特性： 1、均匀流过水断面的形状、尺寸沿流程不变，特
18
3、梯形过水断面渠道的水力最佳断面
根据水力最佳断面的条件
19
3、梯形过水断面渠道的水力最佳断面
以上二式，消去db/dh，得：梯形水力最佳断面的宽深比值
因为 故
梯形水力最佳断面的水力半径等于水深的一半。
矩形断面可以看成为m＝o的梯形断面，得：
20
结论：
1）梯形水力最佳断面的宽深比仅是边
坡系数 m 的函数。
9
实际工程中的渠道并不是都能严格满足上述要求的， 特别是许多渠道中总有这种或那种建筑物存在，因 此，大多数明渠中的水流都是非均匀流。但是，在 顺直棱柱体渠道中的恒定流，当流量沿程不变时， 只要渠道有足够的长度，在离开渠道进口、出口或 建筑物一定距离的渠段，水流仍近似于均匀流。
10
5.3 明渠均匀流的计算公式
2
当明渠修在土质地基上肘，往往作成梯形断面，其
两侧的倾斜程度用边坡系数m(m＝cotα)表示，m的大 小应根据土的种类或护面情况而定(如表5.1)。材料的 坚硬程度越高，m越小。
矩形断面常用于岩石中开凿或两侧用条石砌筑面成 的渠道；混凝土渠或木渠也常作成矩形。
圆形断面通常用于无压隧洞。
3
第五章 明渠恒定均匀流
➢工程中应用最广的是梯形渠道，其过水断面的诸水利要素关系 如下：
在平底渠道中i＝0，流段重力在顺流方向 分力Gsinθ＝0；
在逆坡渠道中，流段重力的分力Gsinθ与摩 阻力Ff的方向一致，因而都不可能满足Gsinθ ＝ Ff的平衡条件，故在平底及逆坡渠段中， 不可能产生均匀流动，只有在顺坡渠道中， 才有可能产生均匀流。
7
5.2 明渠均匀流特性及其生条件
一、明渠均匀流的特性： 1、均匀流过水断面的形状、尺寸沿流程不变，特
18
3、梯形过水断面渠道的水力最佳断面
根据水力最佳断面的条件
19
3、梯形过水断面渠道的水力最佳断面
以上二式，消去db/dh，得：梯形水力最佳断面的宽深比值
因为 故
梯形水力最佳断面的水力半径等于水深的一半。
矩形断面可以看成为m＝o的梯形断面，得：
20
结论：
1）梯形水力最佳断面的宽深比仅是边
坡系数 m 的函数。
9
实际工程中的渠道并不是都能严格满足上述要求的， 特别是许多渠道中总有这种或那种建筑物存在，因 此，大多数明渠中的水流都是非均匀流。但是，在 顺直棱柱体渠道中的恒定流，当流量沿程不变时， 只要渠道有足够的长度，在离开渠道进口、出口或 建筑物一定距离的渠段，水流仍近似于均匀流。
10
5.3 明渠均匀流的计算公式
2
当明渠修在土质地基上肘，往往作成梯形断面，其
两侧的倾斜程度用边坡系数m(m＝cotα)表示，m的大 小应根据土的种类或护面情况而定(如表5.1)。材料的 坚硬程度越高，m越小。
矩形断面常用于岩石中开凿或两侧用条石砌筑面成 的渠道；混凝土渠或木渠也常作成矩形。
圆形断面通常用于无压隧洞。
3
第五章 明渠恒定均匀流
➢工程中应用最广的是梯形渠道，其过水断面的诸水利要素关系 如下：
水力学 第五章_有压管道的恒定流
式中 hw ——为管嘴的水头损失,等于进口损失与收缩断面后的 进口损失与收缩断面后的 扩大损失之和(管嘴沿程水头损失忽略),也就是相 扩大损失之和 当于管道锐缘进口的损失情况. ζn——管嘴阻力系数,即管道锐缘进口局部阻力系数, 一股取ζn =0.5; n ——管嘴流速系数 n = 1 / α + ζ n ≈ 1 / 1 + 0.5 = 0.82 μn——管嘴流量系数,因出口无收缩,故 n = n = 0.82
各种流速下的k值计算,其结果见表5—2. 为了计算方便,编制出各种管材,各种管径的比阻A的计算表 .钢管的 见表 钢管的A见表 见表5-4. 钢管的 见表5—3,铸铁管的 见表 ,铸铁管的A见表 .
2.串联管路 . 由直径不同的几段管路依次连接而成的管路,称为串联 由直径不同的几段管路依次连接而成的管路 管路.串联管路各管段通过的流量可能相同,也可能不同. 根据能量方程得(各管段的流量Q,直径d,流速v不同,整个 整个 串联管路的水头损失应等于各管段水头损失之和): 串联管路的水头损失应等于各管段水头损失之和
= ε = 0.54 × 0.97 = 0.62
2.大孔口的自由出流 大孔口的自由出流
适用上式, Ho为大孔口中心的水头, = ε
中ε较大.
在水利工程中,闸孔出流可按大孔口出流计算,其流量系数列 于表51中.
§5—2 液体经管嘴的恒定出流
1.圆柱形外管嘴的恒定出流 . 圆柱形外管嘴: 圆柱形外管嘴: 在孔口断面处接一直径与孔口直径完全相同 的圆柱形短管,其长度L=(3～4)d. 收缩断面C-C处水流与管壁分离,形成漩涡区;在管嘴出口断 面上,水流已完全充满整个断面. 列 管嘴为自由出流时的 伯努利方程 以通过管嘴断面形心的水平面为 基准面; 基准面; 对 断面 断面0-0 和 管嘴出口断面 b-b列方程.
各种流速下的k值计算,其结果见表5—2. 为了计算方便,编制出各种管材,各种管径的比阻A的计算表 .钢管的 见表 钢管的A见表 见表5-4. 钢管的 见表5—3,铸铁管的 见表 ,铸铁管的A见表 .
2.串联管路 . 由直径不同的几段管路依次连接而成的管路,称为串联 由直径不同的几段管路依次连接而成的管路 管路.串联管路各管段通过的流量可能相同,也可能不同. 根据能量方程得(各管段的流量Q,直径d,流速v不同,整个 整个 串联管路的水头损失应等于各管段水头损失之和): 串联管路的水头损失应等于各管段水头损失之和
= ε = 0.54 × 0.97 = 0.62
2.大孔口的自由出流 大孔口的自由出流
适用上式, Ho为大孔口中心的水头, = ε
中ε较大.
在水利工程中,闸孔出流可按大孔口出流计算,其流量系数列 于表51中.
§5—2 液体经管嘴的恒定出流
1.圆柱形外管嘴的恒定出流 . 圆柱形外管嘴: 圆柱形外管嘴: 在孔口断面处接一直径与孔口直径完全相同 的圆柱形短管,其长度L=(3～4)d. 收缩断面C-C处水流与管壁分离,形成漩涡区;在管嘴出口断 面上,水流已完全充满整个断面. 列 管嘴为自由出流时的 伯努利方程 以通过管嘴断面形心的水平面为 基准面; 基准面; 对 断面 断面0-0 和 管嘴出口断面 b-b列方程.
水力学资料第五章
解：（1）写出自由涡的流速分布r C r /,0==θμμ将m r r 3.00==处流速值u(0r )=2m/s 带入上式，得常数C=0.9，有 r /6.0=θμ在弯道内侧，;/3,2.011s m m r r ===θμ在弯道外侧，s m m r r /5.1,4.022===θμ。
依据同心圆弯道的压强微分式，有dr rdp 2θμρ=由1r r =和2r r =积分该式，得 ⎪⎪⎭⎫⎝⎛-==⎰⎰22212321122121r r dr rdp r r r r θθρμμρ故弯管内、外壁之压差为pa pa p p 33754.012.01210006.022212=⎪⎭⎫ ⎝⎛-⨯⨯=- （2）压强水头差m m g p p 344.010008.9337512=⨯=-ρ 流速水头差m m g 344.08.9235.12222122=⨯-=-θθμμ 可见，压强水头差等于流速水头差，故总机械能在弯道内、外壁处相等。
第五章 层流、紊流及其能量损失5-1（1）某水管的直径d=100mm,通过流量Q=4L/s,水温T=20C 0;(2)条件与以上相同，但水管中流过的是重燃油，其运动粘度s m /1015026-⨯=ν。
试判断以上两种情况下的流态。
解：（1）2000504251001.11.0004.0444Re 62>=⨯⨯⨯⨯====-πνππνd Q v d Qd Vd 流动为紊流流态。
（2）20005.339101501.0004.044Re 6<=⨯⨯⨯⨯===-πνπνd Q Vd 流动为层流流态。
5-2（2）温度为0C 0的空气，以4m/s 的速度在直径为100mm 的圆管中流动，试确定其流态（空气的运动粘度为s m /1037.125-⨯）。
若管中的流体换成运动粘度为s m /10792.126-⨯的水，问水在观众管中呈何流态？解 流体为空气时，有2000291971037.11.04Re 5>=⨯⨯==-νVd 紊流流态流体为水时，有200022321410792.11.04Re 6>=⨯⨯==-νVd 紊流流态 5-3（1）一梯形断面排水沟，底宽0.5m ，边坡系数5.1cot =θ(θ为坡角)，水温为C 020，水深0.4m ，流速为0.1m/s ，试判别流态；（2）如果水温保持不变，流速减小到多大时变为层流？ 解（1）梯形断面面积 2244.0)5.14.05.0(4.0)(m m hm b h A =⨯+⨯=+= 湿周 ()m m m h b 942.15.114.025.01222=+⨯⨯+=++=χ 水力半径 m m A R 2266.0942.144.0===χ雷诺数 5001024.21001.12266.01.0Re 46>⨯=⨯⨯==-νVR紊流流态 （2）层流的上界雷诺数500Re ==νVR。
水力学系统讲义课件第五章(1)-流动形态及水头损失
1
v1≈0 进口
0 1
转弯 突扩
突缩 阀门
H
2 V0 Q
2
h w12 hf hj
过水断面的形状和尺寸对沿程水头损失的影响
A
A
A
A1
A2
Χ1
Χ2
Χ3
Χ4
Χ5
圆形
正方形
长方形
(a)
(b)
湿周：过水断面上被液体湿润的固体周界长度，
记为χ。
1 2 3
hf1 hf 2 hf 3
产生原因：液体的粘滞性和液体质点间的动量 交换而引起的。
1
v1≈0 进口
0 1
转弯 突扩
突缩 阀门
H
2 V0 Q
2
局部水头损失：在水流方向、断面形状和尺寸 改变以及障碍处产生，记为hj。
产生原因：局部地区产生漩涡。漩涡的产生及 维持，漩涡水体与主流之间的动量交换，漩涡 间的碰撞与摩擦均需消耗能量而引起水头损失。
形过水断面渠道的水 力半径为
b
矩形过水断面渠道的水力 半径，令m=0，则
R bh mh2 b 2h 1 m2
R bh b 2h
对于h/b<1/10的宽矩形过水断面渠道的水力半径
R h h 1 2 h b
§5-2 均匀流中沿程水头损失的计算 公式
圆管总流中取出长度为s的一段作为控制体，研 究其平衡。假设流动是恒定的均匀流，且液体 是不可压缩的。
实验结论
1.同一种液体在同一个管道中流动，当流速不 同时液体有两种不同的运动型态：
（1）层流：是指在流速较小时，液体质点作有 条不紊的直线运动，水流各层上的质点互不掺 混。 （2）紊流（湍流）：是指在流速较大时，流层 逐渐不稳定，质点相互掺混，液体质点运动轨 迹极不规则的流动。
水力学 第五章 有压管路(道)
液体经薄壁孔口的恒定出流 液体经管嘴的恒定出流 短管的水力计算 长管的水力计算 离心水泵的水力计算
教学重点：
１.孔口出流及管嘴出流的计算。 ２.短管水力计算方法。
教学难点：
１.孔口出流及管嘴出流的流动现象。 ２.管嘴的长短为什么会影响管嘴的流动。 3.短管的计算要点。
§5-1 液体经薄壁孔口的恒定出流 （自由出流）
①对水来说，为防止汽化的容许真空度hv=7mH2O，因此， 其水头H就不能高于7/0.75=9.5m
②为达到增加外管嘴流量的目的，不应使管嘴太长或太短， 因此一般管嘴长度l=3-4d为宜。
3、常用管嘴的出流
1）流线型管嘴： 0.97
适用于要求流量大，水头损失小的情况。
2）收缩管嘴：出流量与收缩角度θ有关。
第五章 有压管路的 恒定流动
本章主要研究液体经孔口、管嘴、管路流动时 的特性，确定流速，流量及有关的影响因素。
有压管路：
液体在压差作用下流动时，液体整个周围都和固体 壁面相接触，没有自由表面。
在这样的流动中，固体壁面处处受到液体压强的作 用，并且压强的大小一般不等于大气压强。
§5-1 §5-2 §5-3 §5-4 §5-5
面处称为缩脉，用ωc来表示，ωc与小孔面积ω的比值
称为收缩系数ε 。
0v02
c
1 pa
2g
HH
0
c
如图列1-c截面间伯氏方程
0
d
c
H
p1
1v12
2g
0
pc
c vc2
2g
hm
1
此时只考虑局部水头损失，忽略沿程水头损失
∵ pc p1 pa
∴
H
1v12
水力学 第五章
故
H0
2v 2
2g
hf hj
上式表明，管道的总水头将全部消耗于管道的水头损 失和保持出口的动能。
l v2 因为沿程损失 h f d 2g
局部水头损失
v2 h j 2 g
有
l v2 H 0 ( 2 ) d 2g
3
取 2 1 管中流速 通过管道流量
K Q H l
由表4-1即可查出所
若为短管
d
4Q
c 2 gH
17
流量系数 c 与管径有关，需用试算法确定。
三、管线布置已定，当要求输送一定流量时， 确定所需的断面尺寸（圆形管道即确定管道直 径）。这时可能出现下述两种情况：
2．管道的输水量 Q，管长l 已知，要求选定所需的管径 及相应的水头。从技术和经济条件综合考虑。 (1) 管道使用要求： 管中流速大产生水击，流速小泥沙 淤积。 (2) 管道经济效益：管径小，造价低，但流速大，水头 损失也大，抽水耗费也增加。反之管径大，流速小，水头 损失减少，运转费用少，但管道造价高。 当根据技术要求确定流速后管 4Q d 道直径即可由右式计算： v 18
水利工程的有压输水管道水流一般属于紊流的水力粗糙
区，其水头损失可直接按谢齐公式计算，用 8 g 2
H 8g l v 8gl Q2 Q l 2 2 2 2 2 C d 2 g C 4R 2 gA AC R
2 2
C
则
令 K AC R ，即得
Q2 H hf 2 l K
或
QK
23
4-3 简单管道水力计算特例—— 虹吸管及水泵装置的水力计算
一、虹吸管的水力计算
虹吸管是一种压 力输水管道，其顶 部高程高于上游供 水水面。 特点：顶部真空理 论上不能大于10m H2g，一般其真空 值小于(7~8m )；虹 吸管长度一般不大，应按短管计算。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
μc =
1
α
+
∑
λ
l d
+
∑
ζ
两公式的比较。
μc =
1
∑
λ
l d
+
∑ζ
§5-4 短管出流的水力计算
1
1
自由出流
O 1
2 H 淹没出流
O 2
1
Z
O
2 O
2
μc =
1
α
+
∑
λ
l d
+
∑ζ
两公式的比较。
μc =
1
∑
λ
l d
+
∑ζ
自由出流的作用水头一部分消耗于水流的沿程水头损失和 局部损失，另一部分转化为管道出口的流速水头。
+ hw
得
H0
=
H1
−
H2
=
H
=
hw
=ξ′
vc2 2g
因为 ζ ′ = ζ 0 + ζ se = ζ 0 +1
vc =
1
1+ζc
2gH = ϕ 2gH
Q = ϕε A 2gH = μ A 2gH
与自由出流的公式进行比较：
流量公式虽然与薄壁孔口出流相同， 但意义不一样。 孔口淹没出流的流量和流速与孔口 离液面的距离无关。
管嘴出流的局部损失由两部分组成，即孔口的局部水头损失 及收缩断面后扩展产生的局部损失，水头损失大于孔口出流。但 是管嘴出流为满流，收缩系数为1，因此流量系数仍比孔口大。
§5-2 液体经管嘴的恒定出流
v=
1
α +ζc
2gH0 = ϕn A 2gH
管嘴出流的局部损失由两部分组成，即孔口的局部 水头损失及收缩断面后扩展产生的局部损失，水头损 失大于孔口出流。但是管嘴出流为满流，收缩系数为 1，因此流量系数仍比孔口大。
3.已知H=1.2m、d，求H2（稳定工作条件 下）
H H2
§5-3 孔口、管嘴的非恒定出流
容器水面随时间变化而变化，形成非恒定流动（容器放 水、船闸泄水、充水等。）
分析思路： 在某一微小时段dt内，将流动看成恒定流动，然后在整 个时间段上进行积分，进行求解。
t = 2Ω (
μA 2g
H1 −
H2 )
vc2 2g
+ζ0
vc2 2g
= (αc
+
ζ
0
)
vc2 2g
vc =
1
αc +ζ0
2gH0 = ϕ 2gH0
其中：ϕ =
1
αc +ζ0
ϕ：孔口的流速系数，0.97~0.98
ζ 0 = 0.06
薄壁锐缘小孔口的自由出流
流量Q：
Q = vc × Ac
= ϕ 2gH0 ×ε A = μ A 2gH0 = μ A 2gH
pv
γ
=
pc
γ
= 0.75H0
1.真空度一般限制在7m以下，相应的作用水头限制在H<9m。 2.管嘴的长度一般为管径的3~4倍。
§5-2 液体经管嘴的恒定出流
其他形式的管嘴
思考题： 1.开口面积、作用水头相同的孔口与管 嘴出流相比较：
流速，流量
2.孔口、管嘴的流量系数，流速系数， 收缩系数的大小。
第五章 孔口、管嘴出流和有压管路
孔口出流：在容器壁上开孔，水经孔 口流出的水力现象，称为孔口出流。
管嘴出流：若在孔口上连 接长为3~4倍孔径的短管， 水经过短管并在出口断面 满管流出的水力现象，称 为管嘴出流。
§5-1 薄壁孔口的恒定出流
孔口出流的分类：
小孔口出流、大孔口出流（按H/D 是否大于10来判
容器放空时间： T = 2ΩH1 = 2V
μ A 2gH1 Qmax
按照最大水头流量流出时间的2倍。
H(t) H
§5-4 短管出流的水力计算
1.短管出流的概念
不能忽略hj和hf，基本一样大， hj和hf均要计算的管路。 2.自由出流及淹没出流。
1
1
自由出流
O 1
2 H 淹没出流
O 2
1
Z
O
2 O
2
§5-2 液体经管嘴的恒定出流
管嘴出流流量系数的加大也可以从管嘴收缩断面 处存在的真空来解释，由于收缩断面在管嘴内，压强 要比孔口出流时的零压低，必然会提高吸出流量的能 力。
§5-2 液体经管嘴的恒定出流
管嘴正常工作的条件：
对C-C断面与出口断面列能量方程
根据公式：
pc
γ
=
pa
γ
− 0.75H0
薄壁大孔口出流
采用积分思想，取一单元，看作小孔口， 对整个断面进行积分。
Q = μbd 2gH
A l2
l1
由于边壁的整流作用，它的
B
此边不完全收缩 存在会影响收缩系数， 故有完全收缩与非完全收缩
之分，
D
C
视孔口边缘与容器边壁距离
此边无收缩
与孔口尺寸之比的大小而
定，
大于3则可认为完全收缩。
厚壁孔口出流
§5-2 液体经管嘴的恒定出流
管嘴及管嘴出流特点
当孔壁厚等于3~4倍孔径d， 或者在孔口处外接一段长度l= （3~4）d的短管时，液流流经 短管的出流。
特点：水流进入管嘴以前与孔口出流相同；进入管嘴后，先形成 收缩断面，收缩断面附近水流与管壁分离，形成漩涡区；然后逐 渐扩大，直至充满整个水管断面。
成，而后再扩展成满流流出管嘴。管嘴出流的能量损失只考虑局部损 失，如果管嘴再长，以致必须考虑沿程损失时就是短管了。
薄壁锐缘小孔口的自由出流
对0-0，c-c断面列能量方程：
H
+
pa
γ
+ α0v02
2g
=0+
pc
γ
+ αcvc2
2g
+ hw
令
H0
=
H
+
α 0 v02
2g
所以
H0
=
H
+ α0v02
2g
= αc
淹没出流的作用水头完全消耗在克服水流的沿程阻力和局 部阻力上。
§5-4 短管出流
水头线的绘制：
1.先画总水头线；
对各控制断面计算水头损失，绘出总水头线。
2.再画测压管水头线；
总水头线再减去该断面的流速水头，再把各断面的测压管水头线连 接起来。
定）； 恒定出流、非恒定出流； 淹没出流、非淹没出流； 薄壁出流、厚壁出流。
薄壁出流确切地讲就是锐缘孔口出流，流体与孔壁只有周线上接 触，孔壁厚度不影响射流形态，否则就是厚壁出流，如孔边修圆的情 况，此时孔壁参与了出流的收缩，但收缩断面还是在流出孔口后形成。
如果壁厚达到3～4D，孔口就可以称为管嘴，收缩断面将会在管嘴内形
厚壁孔口出流与薄壁 孔口出流的差别在于收缩 系数和边壁性质有关，
注意到收缩系数定义 中的A为孔口外侧面积， 容易看出孔边修圆后，
收缩减小，收缩系数 和流量系数都增大。
例题
图示水箱侧壁同一竖线上开两个孔口，上孔距水面 为a，下孔距地面为c，量孔口流速系数相等，若 c=a，两股水流是否会相遇在地面上同一点。
参数的定义和大小：
ε：断面收缩系数，ε = 0.64 μ：孔口的流量系数 μ = εϕ = 0.64×（0.97~0.98）=0.60~0.62
与理想流动的理论流量 Q = A 2gH 进行比较。
淹没出流
对1-1，2-2断面列能量方程：
H1
+ 0 + α1v12
2g
=
H2
+ 0 + α2v22
2g