第三章 高斯光束及其特性
合集下载
高斯光束的特点
高斯光束的特点高斯光束是一种常见的光束形式，它具有一些独特的特征和性质。
在这篇文章中，我将详细介绍高斯光束的特点和应用。
高斯光束的产生首先，让我们了解高斯光束的产生机制。
高斯光束是由激光器产生的，其中的光源是一个能够将能量转换为光的物质。
在激光器内部，光被引导通过透镜并被聚焦在一个非常小的点上。
这个非常小的点就是所谓的高斯光束。
高斯光束的特性接下来是高斯光束的一些重要特性：1. 对称性：高斯光束在垂直和水平方向上具有相同的亮度分布，呈现完美的对称性。
2. 聚焦性：高斯光束能够通过透镜聚焦到一个非常小的点上，这使得它在许多领域都具有广泛的应用。
3. 窄束宽：高斯光束的光束宽度非常窄，这意味着它能够将光精确地聚焦在一个非常小的区域内。
这使其在制造领域中应用越来越广泛，比如在半导体微处理器和纳米加工中使用。
4. 相位一致性：高斯光束中的光波具有相位一致性。
这意味着高斯光束中的光波可以相互干涉，并且具有非常大的干涉强度，使其在干涉仪和光学器件中应用广泛。
5. 光束稳定性：高斯光束的光束是稳定的，它不会像其他类型的光束一样发生绕射或扩散。
这使得它在通信和传输领域中应用广泛。
应用领域高斯光束在许多领域中都得到了广泛应用，以下是其中一些领域：1. 通信和传输：在光纤通信和光学传输系统中使用高斯光束可以提供更好的性能和可靠性。
高斯光束产生的光束非常窄，可以提供更高的传输速率和更少的数据丢失。
2. 制造和加工：高斯光束的光束聚焦非常精确，因此它在制造和加工领域中使用越来越广泛。
例如，它可以用于微加工、纳米加工、刻蚀和切割。
3. 治疗和医学：高斯光束已被用于医学成像和激光治疗。
它可以用于照射和去除组织中的癌细胞。
4. 科学研究：高斯光束在科学研究领域中应用广泛。
它可以用于干涉仪、单光子实验、冷却原子、微分析和高分辨率成像等。
总结在本文中，我详细介绍了高斯光束的特点和应用领域。
高斯光束通过激光器产生，具有对称性、聚焦性、窄束宽、相位一致性和光束稳定性等特点，其应用领域包括通信和传输、制造和加工、治疗和医学和科学研究等。
高斯光束的基本性质及特征参数r讲解
1/ e
2
2 ( z ) lim z 0 z
高斯光束的发散度由束腰半径ω 0决定。
综上所述，基模高斯光束在其传播轴线附近， 可以看作是一种非均匀的球面波，其等相位面是曲 率中心不断变化的球面，振幅和强度在模截面内保 持高斯分布。
photomultiplier
photodiode
z
2
z 0 1 f
f2 R( z ) z z
高斯光束的共焦参数
2 0 f Z0
与传播轴线相 交于Z点的高斯光束 等相位面的曲率半 径
高斯光束的基本特征： (1)基模高斯光束在横截面内的光电场振幅分 布按照高斯函数的规律从中心（即传播轴线）向外 平滑地下降，如图1-6所示。由中心振幅值下降到 1/e点所对应的宽度，定义为光斑半径。
Avalanche photodiode
R(z)随Z变化规律为：
2 2 f f R z z 1 2 z z z
结论： a)当Z=0时，R(z)→∞，表明束腰所在处的等 相位面为平面。 b) 当Z→±∞时，│R(z)│≈z→∞表明离束腰无 限远处的等相位面亦为平面，且曲率中心就在束腰 处； c)当z=±f时，│R(z)│=2f，达到极小值 。
决定了基模高斯光束的空间相移特性。 其 中 ， kz 描 述 了 高 斯 光 束 的 几 何 相 移 ； arctan(z/f)描述了高斯光束在空间行进距离z处， 相对于几何相移的附加相移；因子kr2/(2R(z))则表 示与横向坐标 r 有关的相移，它表明高斯光束的等 相位面是以R(z)为半径的球面。
高斯光束的基本性质及特征参数
基模高斯光束
高斯光束在自由空间的传播规律
高斯光束衍射极限
高斯光束衍射极限引言在现代光学中，高斯光束是一种重要的光学现象。
高斯光束是指在空间中传播的电磁波的一种特殊形式，它具有高度集中的能量分布和自聚焦特性。
高斯光束的衍射极限是指在特定条件下，高斯光束经过衍射后的最小尺寸限制。
本文将详细探讨高斯光束的衍射极限及其相关内容。
高斯光束的特点高斯光束具有以下几个重要特点：1.高度集中的能量分布：高斯光束的能量在空间中呈现出高度集中的分布，大部分能量集中在光束的中心区域。
这使得高斯光束在很多应用中具有重要的作用，比如激光器、光纤通信等。
2.自聚焦特性：高斯光束在传播过程中会出现自聚焦的现象。
这是由于高斯光束的折射率与光强度之间存在非线性关系，使得光束在传播过程中会自动聚焦在一个点上。
这种自聚焦现象在激光切割、激光打孔等领域得到了广泛应用。
3.良好的相干性：高斯光束具有良好的相干性，即波前的相位关系在空间中保持稳定。
这使得高斯光束在干涉、衍射等现象中表现出优越的性能。
高斯光束的衍射极限高斯光束经过衍射后会出现一定的扩散现象，其衍射极限即为高斯光束经过衍射后的最小尺寸限制。
衍射极限的大小与光束的波长、光束直径和衍射距离等因素有关。
衍射极限的计算方法衍射极限可以通过一些数学模型进行计算。
其中，最常用的是菲涅尔衍射和夫琅禾费衍射模型。
菲涅尔衍射模型菲涅尔衍射模型适用于光源到衍射屏的距离与衍射屏到观察点的距离相近的情况。
在菲涅尔衍射模型中，衍射极限的计算公式为：D=2λL d其中，D为衍射极限的直径，λ为光束的波长，L为光源到衍射屏的距离，d为光束的直径。
夫琅禾费衍射模型夫琅禾费衍射模型适用于光源到衍射屏的距离远大于衍射屏到观察点的距离的情况。
在夫琅禾费衍射模型中，衍射极限的计算公式为：D=2λf d其中，D为衍射极限的直径，λ为光束的波长，f为焦距，d为光束的直径。
影响衍射极限的因素衍射极限的大小受到多种因素的影响，主要包括：1.波长：波长越短，衍射极限越小。
这是由于波长与衍射极限的计算公式中呈反比关系。
第三章--高斯光束及其特性
qM
AqM B 1 CqM D qM
D Ai 2B
1 (D A)2 4 B
§3.2 高斯光束与球面谐振腔的自再现模式
1 D A 1 (D A)2 4
i
qM 2B
B
1 q(z)
1 R(z)
i
2 (z)
R(z) 2B (D A)
(z) (
)1 2
B12
1
D
2
A
2
2
0 (z)
z
R(z
)
1
1
2(z) R(z)
R(z) 2
2
(
z
)
§3.1 基模高斯光束
3）基模高斯光束的特征参数：
➢ 用q参数表征高斯光束
u00
(
x
,
y
,
z
)
c00
0 (z
)
exp[
x2
2(
y2 z)
]exp{
i[k
(
z
x2 y2 ) arctg 2R(z)
1 11
q2 q1 F
q2
Aq1 Cq1
B D
复曲率半径q
§3.1 基模高斯光束
出射光束的束腰位置和尺寸： 入射高斯光束的光腰在l处， 出射高斯光束的光腰在l ’处
q q0
if
02
q
q0
if
02
等和式实两部端对的应虚相部等
f l
(l
F2 f F )2
l(l F ) f (l F )2 f
z f
]}
u00 ( x,
y, z) c00
0 exp{ik (z)
x2
高斯光束的传播特性ppt课件
复习：共焦腔内或腔外的一点的行波场的解析式：
umn x, y, z CmnHm
2 1
2
2 ws
x Hn
2 1
2
2 ws
y
exp
1
2
2
x2 y2 ws2
exp ix,
y, z
1. Hm
2 1
2
2 ws
x Hn
2 1 2
2 ws
y
exp
2 1
2
x2 y2 ws2
行波场横向振幅分布因子
束腰半径
0
1 2
s
L 2
f
等相面曲率半径 R(z) z [1 ( L )2 ] z [1 ( f )2 ] z [1 (02 )2 ]
2z
z
z
任意位置光斑 半径
(z) 0
1
(
z 02
)2
高斯光束的束腰半 径的大小和位置确
镜面光斑半径 远场发散角
s
20
L
2 2 0
定，就可以确定整
2、光斑尺寸
当场振幅为轴上( x2 y2 0 )的值的e-1倍，即强度为轴上的值的e-2倍时，
所对应的横向距离 z 即z 处截面内基模的光斑半径为
(z)
x2 y2 s
2
1 2 s
2
4z2 1 L2
§3.3.1 高斯光束的振幅和强度分布
(z) s 1 2 s
2
2
ωs xs2 ys2 L
k
L 2
1
2z L
1
2z L 2z
2
x2
L
y
2
2
z
k
umn x, y, z CmnHm
2 1
2
2 ws
x Hn
2 1
2
2 ws
y
exp
1
2
2
x2 y2 ws2
exp ix,
y, z
1. Hm
2 1
2
2 ws
x Hn
2 1 2
2 ws
y
exp
2 1
2
x2 y2 ws2
行波场横向振幅分布因子
束腰半径
0
1 2
s
L 2
f
等相面曲率半径 R(z) z [1 ( L )2 ] z [1 ( f )2 ] z [1 (02 )2 ]
2z
z
z
任意位置光斑 半径
(z) 0
1
(
z 02
)2
高斯光束的束腰半 径的大小和位置确
镜面光斑半径 远场发散角
s
20
L
2 2 0
定，就可以确定整
2、光斑尺寸
当场振幅为轴上( x2 y2 0 )的值的e-1倍，即强度为轴上的值的e-2倍时，
所对应的横向距离 z 即z 处截面内基模的光斑半径为
(z)
x2 y2 s
2
1 2 s
2
4z2 1 L2
§3.3.1 高斯光束的振幅和强度分布
(z) s 1 2 s
2
2
ωs xs2 ys2 L
k
L 2
1
2z L
1
2z L 2z
2
x2
L
y
2
2
z
k
高斯光束的传播特性
zz 0
0
zz 0
0
——共焦腔的等相面是凹面向着腔的中心的球面 结论:在z ＜ 0 处,光束是沿着z的方向传播的会聚球面波; 在z = 0处变成一个平面波;
在z＞0处又变成发散球面波。
三.共焦场的等相位面的分布图
物理意义： ①波阵面对共焦腔中心呈对称分布 ②等相位面为球面，但球心不固定
③腔内波阵面对应的“发光点”在 腔外，且随着波阵面由镜面向腔中心 接近，波阵面的曲率半径逐渐增大。 共焦场中等相面的分布 “发光点”由镜面中心移向无穷远处， 腔中心处的波阵面是个平面。 ④腔外波阵面对应的“发光点”在腔内，且随着波阵面由镜 面远离腔体，波阵面的曲率半径逐渐增大。“发光点”由镜 面中心向腔中心靠近，即无穷远处波阵面对应的“发光点” 是中心。 ⑤镜面本身也是波阵面，且曲率半径最小，对应的“发光 点”在另一镜面的中心。
3、等相位面的特点
2 z0 2z 2 2 x y x2 y 2 x2 y 2 L L z z0 2 2 L L L 2 2z 2 z0 1 1 2 z0 1 L L 2z 0
1
2 2 x H n 1 2 w s
2 x2 y2 y exp 1 2 w2 行波场横向振幅分布因子 s
—厄米—高斯函数 在横截面内的场振幅分布按高斯函数所描述的规律从 中心(即传输轴线)向外平滑地降落。 花样：沿x方向有m条节线，沿y方向有n条节线。
s 20
2 2 0
1. 高斯光束在其轴线附近可看作是一种非均匀的高 斯球面波， 2.在其传播过程中曲率中心不断改变 3.其振幅在横截面内为一高斯光束
4.强度集中在轴线及其附近
高斯光束的基本性质及特征参数r
0
综上所述，基模高斯光束在其传播轴线附近， 能够看作是一种非均匀旳球面波，其等相位面是曲 率中心不断变化旳球面，振幅和强度在模截面内保 持高斯分布。
photomultiplier
photodiode
Avalanche photodiode
高斯光束旳基本性质及特征参数
基模高斯光束 高斯光束在自由空间旳传播规律
高斯光束旳参数特征
4、高斯光束
由激光器产生旳激光束既不是上面讨论旳均匀平 面光波，也不是均匀球面光波，而是一种振幅和等 相位面在变化旳高斯球面光波，即高斯光束。
以基模TEM00高斯光束为例，体现式为：
E0
ωγ2 2zeik
z
γ2
2 z z2
02 f 2 1
如图1-7所示。
在Z=0处，ω（z）=ω0到达极小值，称为束 腰半径。
(2)基模高斯光束场旳相位因子
00 r, z
k z
2R
2
z
arctan
z f
决定了基模高斯光束旳空间相移特征。
其中，kz描述了高斯光束旳几何相移； arctan(z/f)描述了高斯光束在空间行进距离z处， 相对于几何相移旳附加相移；因子kr2/(2R(z))则表 达与横向坐标r有关旳相移，它表白高斯光束旳等 相位面是以R(z)为半径旳球面。
R(z)随Z变化规律为：
Rz
z 1
f2 z2
z
f2 z
结论：
a)当Z=0时，R(z)→∞，表白束腰所在处旳等 相位面为平面。
b) 当Z→±∞时，│R(z)│≈z→∞表白离束腰无 限远处旳等相位面亦为平面，且曲率中心就在束腰 处；
c)当z=±f时，│R(z)│=2f，到达极小值 。
综上所述，基模高斯光束在其传播轴线附近， 能够看作是一种非均匀旳球面波，其等相位面是曲 率中心不断变化旳球面，振幅和强度在模截面内保 持高斯分布。
photomultiplier
photodiode
Avalanche photodiode
高斯光束旳基本性质及特征参数
基模高斯光束 高斯光束在自由空间旳传播规律
高斯光束旳参数特征
4、高斯光束
由激光器产生旳激光束既不是上面讨论旳均匀平 面光波，也不是均匀球面光波，而是一种振幅和等 相位面在变化旳高斯球面光波，即高斯光束。
以基模TEM00高斯光束为例，体现式为：
E0
ωγ2 2zeik
z
γ2
2 z z2
02 f 2 1
如图1-7所示。
在Z=0处，ω（z）=ω0到达极小值，称为束 腰半径。
(2)基模高斯光束场旳相位因子
00 r, z
k z
2R
2
z
arctan
z f
决定了基模高斯光束旳空间相移特征。
其中，kz描述了高斯光束旳几何相移； arctan(z/f)描述了高斯光束在空间行进距离z处， 相对于几何相移旳附加相移；因子kr2/(2R(z))则表 达与横向坐标r有关旳相移，它表白高斯光束旳等 相位面是以R(z)为半径旳球面。
R(z)随Z变化规律为：
Rz
z 1
f2 z2
z
f2 z
结论：
a)当Z=0时，R(z)→∞，表白束腰所在处旳等 相位面为平面。
b) 当Z→±∞时，│R(z)│≈z→∞表白离束腰无 限远处旳等相位面亦为平面，且曲率中心就在束腰 处；
c)当z=±f时，│R(z)│=2f，到达极小值 。
《激光原理》3.3高斯光束的传播特性(新)
共焦腔的反射镜面是两个等 相位面，与场的两个等相位 面重合,且曲率半径达到最小 值。
z = f, 即镜面处R最小,且等于镜面本身曲率半径
证 R(z) z f 2
z
dR
f2
dz 1 z2 0
zf
R( f ) ( f f 2 ) 2 f R f
z
-f 0
f
R02 x2 y2 z z0 R0 2
1.当 z0 0 时，R(z0 ) 2.当 z0 时，R(z0 ) 3.当 z0 f 时，R(z0 ) z0 4.当 z0 f 时，R(z0 ) L 2 f
束腰处的等相位面为平面， 曲 率中心在无穷远处
无穷远处等相位面为平 面，曲率中心在z=0处
光束可近似为一个 由z=0点发出的半径 为z的球面波。
由 0s 20 可知,镜面上的光斑尺寸,基模体积和远
V000
L
2 0
发散角等高斯光束的参数都可以通过
2 2 基模腰斑半径(“腰粗”)ω0来表征,故 0 “腰粗”是高斯光束的一个特征参数.
计算表明： 2 内含86.5%的光束总功率
Area
立体角的单位为sr，称为球面度。1sr是这样的 立体角：其顶点位于球心，它在球面上所截取 的面积等于以球半径为边长的正方形面积。
f ' z0 f 2 2 2z0
可以证明，在近轴情况下，共焦场的在z0处的等相位面近 似为球面，其曲率半径为：
R0
2
f
'
z0 [1
(
f z0
)2 ]
z0 [1
(L 2z0
)2 ]
(3 38)
则有：
z
z0
x2 y2 2R0
R0
x2 y2 1 R02 R0
z = f, 即镜面处R最小,且等于镜面本身曲率半径
证 R(z) z f 2
z
dR
f2
dz 1 z2 0
zf
R( f ) ( f f 2 ) 2 f R f
z
-f 0
f
R02 x2 y2 z z0 R0 2
1.当 z0 0 时，R(z0 ) 2.当 z0 时，R(z0 ) 3.当 z0 f 时，R(z0 ) z0 4.当 z0 f 时，R(z0 ) L 2 f
束腰处的等相位面为平面， 曲 率中心在无穷远处
无穷远处等相位面为平 面，曲率中心在z=0处
光束可近似为一个 由z=0点发出的半径 为z的球面波。
由 0s 20 可知,镜面上的光斑尺寸,基模体积和远
V000
L
2 0
发散角等高斯光束的参数都可以通过
2 2 基模腰斑半径(“腰粗”)ω0来表征,故 0 “腰粗”是高斯光束的一个特征参数.
计算表明： 2 内含86.5%的光束总功率
Area
立体角的单位为sr，称为球面度。1sr是这样的 立体角：其顶点位于球心，它在球面上所截取 的面积等于以球半径为边长的正方形面积。
f ' z0 f 2 2 2z0
可以证明，在近轴情况下，共焦场的在z0处的等相位面近 似为球面，其曲率半径为：
R0
2
f
'
z0 [1
(
f z0
)2 ]
z0 [1
(L 2z0
)2 ]
(3 38)
则有：
z
z0
x2 y2 2R0
R0
x2 y2 1 R02 R0
3-3激光器的输出特性-高斯光束传播特性
§ .
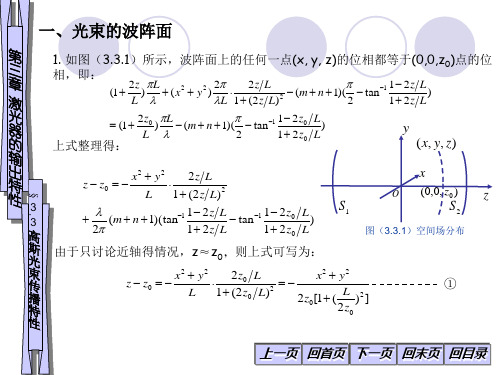
图（3.3.1）空间场分布
由于只讨论近轴得情况，z≈z0，则上式可写为：
2 z0 L x2 y2 x2 y2 z z0 L 2 L 1 ( 2 z0 L) 2 2 z0 [1 ( ) ] 2 z0
①
上一页 回首页 下一页 回末页 回目录
第 三 章 激 光 器 的 输 出 特 性
由于激光的发散角比普通光源的发散角小得多，因此激光的亮度要大得多。
5. 对高阶横模来说，光束的发散角比基横模大。 6. 高斯光束与球面波的区别：
2 0 L R0 z0 [1 ( )] z 0 1 ( z02 ) 2 7. 总结： 0 2 z0 0 1 2 20 2 2 0
x2 y2 2z L z z0 L 1 ( 2 z L) 2 1 2 z0 L 1 2z L (m n 1)(tan1 tan1 ) 2 1 2z L 1束 传 播 特 性
3 3
S1
(0,0, z0 )
S2
z
3 3
L 2 L2 R0 z0 z0 ( ) 2 z0 4 z0 R0 z0 越小。 看出，z0 越大，
高 斯 光 束 传 播 特 性
§ .
即波阵面离中心越远，其曲率中 心离腔中心越近，如图(3.3.5)所 示。
上一页 回首页 下一页 回末页 回目录
第 三 章 激 光 器 的 输 出 特 性
0
§ .
对近轴的波面有z≈z0，则上式可写为：
U 0 ( x, y, z ) U 0 ( x, y, z0 )
令
z
L [1 (2 z0 L) 2 ] 2
上一页 回首页 下一页 回末页 回目录
高斯光束的基本性质及特征参数
高阶高斯光束
(Higher-order Gaussian modes)) Higher• 厄米特-高斯光束 • 其横向场分布由高斯函数和厄米特多项式 (Hermite polynomial)的乘积决定，沿x方向有m 条节线，沿y方向有n条节线
e
− r2
ω2
2 2 Hm x H n ω ω
q( z ) = R( z ) −i
πω 2 ( z )
用q参数分析高斯光束的传输问题
• 已知：入射高斯光束腰斑半径为ω0 ，束腰与透 镜的距离为l，透镜的焦距为F。 • 求：通过透镜L后在与透镜相距lC处的高斯光束 参数ωC和RC。
• • • • •
思路1：思路2？ 在z=0处 q(0)=iπ ω02 /λ 在A处（紧靠透镜的左方）qA=q(0)+l 在B处（紧靠透镜的右方）1/qB=1/qA-1/F 在C处 qC=qB+lC qC ⇒ ωC、RC
高斯光束腰斑的变换规律
• 若将C点取在像方束腰处，则有RC→∞、 Re[1/qC]=0，可以求出像方束腰到透镜的 距离l′和像方腰斑的大小ω0′ 。
(l − F ) F 2
2 πω 0 2 (l − F ) 2 + ( ) λ
l′ = F +
′ ω 02 =
2 πω 0 2 (F − l)2 + ( ) λ
• Transformation for the Gaussian beam---the ABCD law • The great power of the ABCD law is that it enables us to trace the Gaussian beam parameter q(z) through a complicated sequence of lenslike elements. The beam radius R(z) and spot size ω(z) at any plane z can be recovered through the use of the following expression 1 1 λ
高斯光束
物理与光电信息科技学院
《激光原理与技术》
Lasers Principles and Technologies
主讲教师：陈 建 新 、朱莉莉、陈荣
福建师范大学物理与光电信息科技学院
（第三章）
物理与光电信息科技学院
《激光原理与技术》
第三章 高斯光束
赫姆霍兹方程在缓慢振幅近似下的一个特解，对应着具有 圆对称光学谐振腔的振荡模式。
（第三章）
物理与光电信息科技学院
《激光原理与技术》
在垂直于光束的任意一个横截面上，振幅的分布为:
2 r l l 2r 2 r 2 cosl Apl r , , z [ ] L p [ 2 ] exp 2 sin l w( z ) w z w z
（第三章）
物理与光电信息科技学院
《激光原理与技术》
高斯光束的基本性质
波动方程的基模解 在标量近似下稳态传播的电磁场满足的赫姆霍茨方程：
u0 k u0 0
2
在z的缓变振幅近似下（忽略 解出上式微分方程的一个特解：
2 z 2
），利用“试探法”
此特解叫做基模高斯光束
光斑半径随z的变化规律为：wz w 0 当
z z 1 w 1 0 z w 2 0 0
2 2
z z0 时 wz0 2w0
从最小光斑面 积增大到它的 二倍的范围是 瑞利范围， 从最小光斑处 算起的这个长 度叫瑞利长度
（第三章）
物理与光电信息科技学院
《激光原理与技术》
w0 r2 z r2 u0 x , y , z { exp i kz arctan( 2 ) exp[i ] w 2 z exp w z 2 R ( z ) w 0
《激光原理与技术》
Lasers Principles and Technologies
主讲教师：陈 建 新 、朱莉莉、陈荣
福建师范大学物理与光电信息科技学院
（第三章）
物理与光电信息科技学院
《激光原理与技术》
第三章 高斯光束
赫姆霍兹方程在缓慢振幅近似下的一个特解，对应着具有 圆对称光学谐振腔的振荡模式。
（第三章）
物理与光电信息科技学院
《激光原理与技术》
在垂直于光束的任意一个横截面上，振幅的分布为:
2 r l l 2r 2 r 2 cosl Apl r , , z [ ] L p [ 2 ] exp 2 sin l w( z ) w z w z
（第三章）
物理与光电信息科技学院
《激光原理与技术》
高斯光束的基本性质
波动方程的基模解 在标量近似下稳态传播的电磁场满足的赫姆霍茨方程：
u0 k u0 0
2
在z的缓变振幅近似下（忽略 解出上式微分方程的一个特解：
2 z 2
），利用“试探法”
此特解叫做基模高斯光束
光斑半径随z的变化规律为：wz w 0 当
z z 1 w 1 0 z w 2 0 0
2 2
z z0 时 wz0 2w0
从最小光斑面 积增大到它的 二倍的范围是 瑞利范围， 从最小光斑处 算起的这个长 度叫瑞利长度
（第三章）
物理与光电信息科技学院
《激光原理与技术》
w0 r2 z r2 u0 x , y , z { exp i kz arctan( 2 ) exp[i ] w 2 z exp w z 2 R ( z ) w 0
第三章 高斯光束及其特性
§3.1 基模高斯光束
出射光束的束腰位置和尺寸
随入射光束的变化：
l (l F ) f 2 l F 2 2 (l F ) f
0
F ( l F )2 f 2
0
§3.1 基模高斯光束
0 F (l F ) f
2 2
0
l固定的情况下：
1 2
1 1 i q2 R2 22
高斯光束是非均匀的、 曲率中心不断变化的球面波
注意区别f与F
q C q z2 lC
1 1 1 1 i 2 R1 F 1 q1 F
§3.1 基模高斯光束
束腰距离透镜分 别为l和l’
§3.1 基模高斯光束
傍轴波面通过焦距为f的薄透镜： (应用牛顿公式)其波前曲率半径 满足：
1 1 1 R2 ( z ) R1 ( z ) f
A B 1 AR1 ( z ) B R2 ( z ) , CR1 ( z ) D C D 1/ f 0 1
§3.1 基模高斯光束
2）高斯光束在自由空间的传输规律：
( z ) 0
z 2 ( z ) 1 , lim 2 z z f f
2
( z ) 的渐近线夹角θ定义为光束的发散角
§3.1 基模高斯光束
,z 0 f R ( z ) z 等相位面的曲率半径 2 f ,z f 近似球面波！ z 曲率中心随z变化 z , z f
§3.1 基模高斯光束
3）基模高斯光束的特征参数： 用q参数表征高斯光束
0 x2 y2 x2 y2 z u00 ( x, y, z ) c00 exp[ 2 ]exp{ i[k ( z ) arctg ]} ( z) (z) 2 R( z ) f
高斯光束的基本性质及特征参数课件
变换方法
通过使用各种光学元件，如反射镜、 棱镜等，可以对高斯光束进行各种形 式的变换，如旋转、平移、缩放等。
高斯光束的操控与调制
操控技术
利用光学元件对高斯光束进行操控，如改变光束方向、实现光束分裂等。
调制方法
通过在光束中加入外部信号，可以对高斯光束进行调制，实现信息传输和信号 处理等功能。
05
CHAPTER
高斯光束的聚焦
通过透镜可以将高斯光束聚焦到一点 ，聚焦点处的光强最大过程中，其传播方向呈发散状。
光强分布
高斯光束的光强呈高斯型分布，中心光强最大，向外逐渐减小。
衍射极限
高斯光束的衍射极限由波长和束腰宽度决定，短波长、小束腰宽度 的高斯光束具有更好的聚焦性能。
高斯光束的模拟与仿真
高斯光束的数值模拟方法
有限差分法
通过离散化高斯光束的波动方程，使用差分公式 求解离散点上的场值。
有限元法
将高斯光束的波动方程转化为变分问题，利用分 片多项式逼近解。
谱方法
将高斯光束的波动方程转化为频域或谱域的方程 ，通过傅里叶变换求解。
高斯光束的物理仿真实验
光学实验平台
搭建光学实验装置，通过实际的光路系统模拟高斯光束的传播。
光学成像
1 2 3
高分辨率成像
高斯光束在光学成像领域可用于实现高分辨率、 高清晰度的成像，从而提高图像的细节表现力和 清晰度。
荧光显微镜
高斯光束作为激发光，能够均匀地激发样品中的 荧光物质，提高荧光显微镜的成像质量和稳定性 。
光学共聚焦显微镜
利用高斯光束的聚焦和扫描特性，可以实现光学 共聚焦显微镜的高精度、高灵敏度成像。
激光加工
高效加工
01
高斯光束具有较高的亮度和能量集中度，能够实现高效、高精
通过使用各种光学元件，如反射镜、 棱镜等，可以对高斯光束进行各种形 式的变换，如旋转、平移、缩放等。
高斯光束的操控与调制
操控技术
利用光学元件对高斯光束进行操控，如改变光束方向、实现光束分裂等。
调制方法
通过在光束中加入外部信号，可以对高斯光束进行调制，实现信息传输和信号 处理等功能。
05
CHAPTER
高斯光束的聚焦
通过透镜可以将高斯光束聚焦到一点 ，聚焦点处的光强最大过程中，其传播方向呈发散状。
光强分布
高斯光束的光强呈高斯型分布，中心光强最大，向外逐渐减小。
衍射极限
高斯光束的衍射极限由波长和束腰宽度决定，短波长、小束腰宽度 的高斯光束具有更好的聚焦性能。
高斯光束的模拟与仿真
高斯光束的数值模拟方法
有限差分法
通过离散化高斯光束的波动方程，使用差分公式 求解离散点上的场值。
有限元法
将高斯光束的波动方程转化为变分问题，利用分 片多项式逼近解。
谱方法
将高斯光束的波动方程转化为频域或谱域的方程 ，通过傅里叶变换求解。
高斯光束的物理仿真实验
光学实验平台
搭建光学实验装置，通过实际的光路系统模拟高斯光束的传播。
光学成像
1 2 3
高分辨率成像
高斯光束在光学成像领域可用于实现高分辨率、 高清晰度的成像，从而提高图像的细节表现力和 清晰度。
荧光显微镜
高斯光束作为激发光，能够均匀地激发样品中的 荧光物质，提高荧光显微镜的成像质量和稳定性 。
光学共聚焦显微镜
利用高斯光束的聚焦和扫描特性，可以实现光学 共聚焦显微镜的高精度、高灵敏度成像。
激光加工
高效加工
01
高斯光束具有较高的亮度和能量集中度，能够实现高效、高精
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
q z2 q z1 z2 z1 q z1 L
高斯光束的复数曲率半径q与普通球面波的曲率半径遵循 相同的传播规律
Aq1 B q2 Cq1 D
§3.1 基模高斯光束
高斯光束通过薄透镜的变换
q(0) q0 if q1 l q0 1 1 1 R2 R1 F
0 F l 腰斑放大率 k 0 l F l
可用几何光学处理傍轴光线的方法来处理高斯光束 特殊情况：当 l F l F
与几何光学迥然不同
§3.1 基模高斯光束
如果复参数q1的高斯光束顺次通过传输矩阵
A1 M1 C1 B1 A2 , M 2 D1 C 2 B2 , D2 An Mn C n Bn Dn
1）沿z轴方向传播的基模高斯光束
0 x2 y2 x2 y2 z u00 ( x, y, z ) c00 exp[ 2 ]exp{ i[k ( z ) arctg ]} (z) (z) 2 R( z ) f
其中，c为常数，k=2/， 0为基模高斯光束的腰斑半径，f 为高斯光束的共焦参数。曲率中心不断变化的球面波
R1 ( z ) R z1 z1 R2 ( z ) R z2 z2 R2 ( z ) R1 z z2 z1 R1 z L
A B 1 L AR1 ( z ) B R2 ( z ) , CR1 ( z ) D C D 0 1
§3.1 基模高斯光束
Aq1 B 高斯光束 q2 Cq1 D
结论：高斯光束经任何光学系统变换时服从ABCD公式， 由光学系统对傍轴光线的变换矩阵所决定 优点：能通过任意复杂的光学系统追踪高斯光束的q参数值 (将q称为复曲率半径)
§3.1 基模高斯光束
研究对象
特点 在自由空间的传输规律 通过薄透镜的变换
§3.1 基模高斯光束
2）高斯光束在自由空间的传输规律：
( z ) 0
z 2 ( z ) 1 , lim 2 z z f f
2
( z ) 的渐近线夹角θ定义为光束的发散角
§3.1 基模高斯光束
,z 0 f R ( z ) z 等相位面的曲率半径 2 f ,z f 近似球面波！ z 曲率中心随z变化 z , z f
q q1 l q q2 l
l ll (1 )q ( l l ) F F q 可以得到l’处的q’ : q l (1 ) F F
已知透镜的焦距，只要知道入射高斯光束的q和l，就可 求得出射高斯光束在l/处的q/
1 1 1 q2 q1 F
第三章 高斯光束及其特性
本章大纲
§3.1 基模高斯光束 掌握高斯光束q参数的表达 高斯光束在线性光学系统中的变换 高斯光束的自再现变换与稳定球面腔模式的关系 §3.2 高阶高斯光束 了解高阶高斯光束的特性。
§3.3 高斯光束的准直与聚焦 了解高斯光束的准直的与聚焦特点。
§3.1 基模高斯光束
2
傍轴，谐振腔 外较远距离
z 0处， R( z ) ，束腰所在处的等相位面为平面； z f 处， R( z ) z; z , R( z ) ， R( z ) 极大值 z f 处， R( z ) 2 f ， R( z ) 极小值 当 z f 时, z R( z ) f ，曲率中心的位置 z R( z )在共焦腔腔外； 当 z f 时, z R( z ) f ，曲率中心的位置在共焦腔腔内
0
f
, ( z ) 0 z f ) f z
z 2 1 ( ) f
R( z ) f (
对称共焦腔镜面上 z f ：0 s ( z ) 20
重要！通过练习来加强理解和记忆
§3.1 基模高斯光束
振幅分布 、光斑半径
x2 y2 2( x 2 y 2 ) A( x , y, z ) A0 exp ， I ( x, y, z ) I 0 exp 2 2 ( z ) ( z )
§3.1 基模高斯光束
傍轴波面通过焦距为f的薄透镜： (应用牛顿公式)其波前曲率半径 满足：
1 1 1 R2 ( z ) R1 ( z ) f
A B 1 AR1 ( z ) B R2 ( z ) , CR1 ( z ) D C D 1/ f 0 1
1 1 i 引入一个新的参数q(z)，定义为 2 q( z ) R( z ) ( z )
§3.1 基模高斯光束
1 1 i 2 q( z ) R( z ) ( z )
q：复曲率半径
参数q将(z)和R(z)统一在一个表达式中，知道了高斯光束在 某位置处的q参数值，可由下式求出该位置处(z)和R(z)的数值 1 1 1 1 Re[ ], 2 Im[ ] R( z ) q( z ) (z) q( z ) 用q0=q(0)表示z=0处的参数值，得出 1 1 1 i ， R(0) ， (0) 0 2 q0 q(0) R(0) (0)
02 q0 i if
f
（q0 是纯虚数）
用q参数研究高斯光束传输更为方便
§3.1 基模高斯光束
4） 高斯光束q参数的变换规律 普通球面波的传播规律 高斯光束q参数的变换规律——ABCD公式 用q参数分析高斯光束的传输问题
§3.1 基模高斯光束
普通球面波在自由空间的传播规律 O点发出的球面波波前曲率 半径随传播过程的变化为：
§3.1 基模高斯光束
l (l F ) f 2 F l F , 0 0 2 2 (l F ) f ( l F )2 f 2
当满足 f l F ，即物高斯光束束腰离透镜足够远时
l lF 1 1 1 lF ( ) f
( z ) 0
§3.1 基模高斯光束
3）基模高斯光束的特征参数： 用参数(z)和R(z)表征高斯光束 如果知道了某给定位置处的(z)和R(z)，可决定高斯光 束腰斑的大小0和位置z
2 2 2 (z) z z ( z ) 1 0 ( z ) 1 0 1 0 2 R ( z ) f 0 2 2 2 2 R( z ) 0 f z 1 R( z ) z z R( z ) 1 2 ( z ) z z
入射高斯光束的光腰在l处，
出射高斯光束的光腰在l ’处
2 2 F f 0 f 2 2 q q0 if 等式两端的虚部 (l F ) f 和实部对应相等 2 0 l (l F ) f 2 if l F q q0 2 2 (l F ) f l ll F (1 ) q ( l l ) 0 0 2 2 F F (l F ) f q q l (1 ) F F
1 2
1 1 i q2 R2 22
高斯光束是非均匀的、 曲率中心不断变化的球面波
注意区别f与F
q C q z2 lC
1 1 1 1 i 2 R1 F 1 q1 F
§3.1 基模高斯光束
束腰距离透镜分 别为l和l’
§3.1 基模高斯光束
3）基模高斯光束的特征参数： 用q参数表征高斯光束
0 x2 y2 x2 y2 z u00 ( x, y, z ) c00 exp[ 2 ]exp{ i[k ( z ) arctg ]} ( z) (z) 2 R( z ) f
0 x2 y2 1 z u00 ( x, y, z ) c00 exp{ik [ i 2 ]}exp[ i (kz arctg )] (z) 2 R( z ) ( z ) f
普通球面波
曲率中心固定的 R2=R1+L
高斯球面波
曲率中心变化的 q2=q1+L
1 1 1 R2 R1 F
AR1 B R2 CR1 D
曲率半径R
1 1 1 q2 q1 F Aq1 B q2 Cq1 D
复曲率半径q
总的变换规律
§3.1 基模高斯光束
出射光束的束腰位置和尺寸：
A B An 总矩阵元 M C D C n
Bn A2 Dn C2
B2 A1 C D2 1
B1 D1
Aq1 B q2 Cq1 D
§3.1 基模高斯光束
高斯光束在其传输轴线附近 可近似看作是一种非均匀球面波
曲率中心随着传输过程而不断改变
振幅和强度在横截面内始终保持高斯分布特性 等相位面始终保持为球面 强度集中在轴线及其附近
§3.1 基模高斯光束
3）基模高斯光束的特征参数： 用参数0（或f）及束腰位置表征高斯光束
2 0
i
2 ( / 0 )f2 z 2 i 2 2 2 2 z f z f z f
z if z q(0) z
§3.1 基模高斯光束
02 q z i z if z q(0) z
高斯光束在自由空间由z1经距离L传播到z2
2 z f2 1 ， R z z z f
z 0
1 q z 1 z f z
2
1 z if 1 2 q 2 z f if z