抛物线与平行四边形
抛物线中平行四边形存在性问题的求解策略

4
9
(3)∵ PQ 的 长 为 0<PQ≤ 的 整
4
数,
∴PQ=1 或 PQ=2.
①如图 2,当 PQ=1 时,分别过点
D、Q、P 作 PQ、DP、DQ 的平行线,平
行线两两相交于点 R1、R2、R3,∵PQ⊥
图2
x 轴,∴R1R2 ⊥x 轴,根据平行四边形
的性质,得 D R1=D R2=1,∵D(-2,-3),∴点 R(-2,
OC=4,OA=2,OB=3,点 P 是 CD 上一点,求 2PA+PB 的最
小值,画出示意图并写出求解过程 .
图6
解析:如图 6,在 AB 上截取 BF=1,连接 PF,PC,∵AB
PB 1 BF
=9,PB=3,BF=1,∴
= =
,且 ∠ABP= ∠ABP,∴
AB
3 BP
FP BP 1
1
1
△ ABP∽ △ PBF,∴
=
= ,∴ PF= AP,∴ AP +
AP AB 3
3
3
1
PC=PF+PC,∴当点 F,P,C 三点共线时, AP+PC 的值
3
1
最小,∴CF= BF 2 + BC 2 = 1 + 49 = 5 2 ,∴ AP+PC
3
的最小值为 5 2 .
评注:本题中系数不为 1 的线段中的系数 k 决定了
1
构造相似三角形的相似比 . 若系数 k 是 ,就构造一个相
(1)求直线 AD 及抛物线的解析式;
(2)过点 P 的直线垂直于 x 轴,交抛物线于点 Q,求
线段 PQ 的长度 l 与 m 的关系式,m 为何
难点攻关 抛物线与平行四边形【含答案】

难点攻关 抛物线与平行四边形
近年中考试题中常常出现抛物线与平行四边形组合的压轴题,
1. 在平面直角坐标系xoy 中,点C ,B 的坐标分别为(-4,0),(0,2).四边形ABCO 是平行四边形,抛物线过A ,B ,C 三点,与x 轴交于另一点D .一动点P 以每秒1个单位长度的速度从B 点出发沿BA 向点A 运动,运动到点A 停止,同时一动点Q
从点D 出发,以每秒3个单位长度的速度沿DC 向点C 运动,与点P 同
时停止.
(1)求抛物线的解析式;
(2)若抛物线的对称轴与AB 交于点E ,与x 轴交于点F ,当点P 运动时间t
为何值时,四边形POQE 是等腰梯形?
(3)当t 为何值时,以P ,B ,O 为顶点的三角形与以点Q ,B ,O 为顶点的三角形相似? 解:(1)∵四边形ABCO 是平行四边形,∴OC=AB=4.
∴A(4,2),B(0,2),C(-4,0).
∵抛物线y=ax 2+bx+c 过点B(0,2),∴c=2.
由题意,有⎩⎨⎧16a−4b+2=0
16a+4b+2=2 解得: ⎪⎨⎪⎧a=-1
16
b=14
∴⎩⎪⎨⎪⎧a−b+c =025a+5b+c =0c =−52 解得 : ⎩⎨⎧a=12b=-2c=-52。
抛物线中平行四边形问题精选课件

类型二 两定两动
例2. 如图,平面直角坐标系中,y=-0.25x2+x与x轴相交于点B(4,0),点 Q在抛物线的对称轴上,点P在抛物线上,且以点O,B,Q,P为顶点的四边 形为平行四边形,写出相应的点P 的坐标
已知B(4,0), O(0,0)
设Q(2,a), P(m,-0.25m2+m)
①点B与点O相对
动点,点Q是直线y=-x上的动点,判断有几个位置能使以点P,Q,B,O为顶点的四
边形为平行四边形,写出相应的Q的坐标
已知B(0,-4), O(0,0)
设Q(a,-a), P(m,0.5m2+m-4)
①点B与点O相对
00ma 400.5m2m4a
a1 a
2
4 0
舍
②点B与点P相对
0m0a 40.5m2m40a
分两种情况讨论(1)AB为平行四边形的边,将AB上下左右平移,确定P,Q的位置 (2)若AB为平行四边形的对角线,取AB中点,旋转经过中点的直线确定P,Q的位置
A B
A B
二、集思广益 探究发现
• 1、线段的中点公式
平面直标 角面 中 坐, Ax1,y1,Bx2,y2,则线A段 B的中P点 的
坐标P为 x1x2 y1y2 ,
402m
m
00a0.25m2
m
a
2 1
②点B与点Q相对 420m
m 6
0a00.25m2 m a 3
③点B与点P相对
4m02 00.25m2 m0a
m
a
2 3
∴P1(2,1), P2(6,-3), P3(-2,-3)
变式训练2
如图,平面直角坐标系中,y=0.5x2+x-4与y轴相交于点B(0,-4),点P是抛物线上的
1.抛物线与平行四边形

抛物线与平行四边形问题1.中点坐标公式如左图,在平面直角坐标系xOy 中,11(,)A x y ,22(,)B x y ,点M 为线段AB 的中点,则1212(,)22x x y y M ++.水平线段=左右x x -竖直线段=下上y y - 2.对角线互相平分的四边形是平行四边形.如右图,在平面直角坐标系xOy 中,□ABCD 的对角线AC 、BD 相交于点M ,则M 的坐标可以表示为(,)22A C A C x x y y M ++,也可以表示为(,)22B D B D x x y y M ++.若四边形ABCD 为平行四边形,则AC BD x x x x +=+且A C B D y y y y +=+;重点:若A C B D x x x x +=+且A C B D y y y y +=+,则四边形ABCD 为平行四边形.1.如图,直线y=-3x+3与x 轴、y 轴分别交于点A,B.抛物线y=a(x-2)²+k 经过A,B,并与x 轴交于另一点C,求点Q 坐标,使得以A,B,C,Q 为顶点的四边形是平行四边形.变式1:如图,直线y=-3x+3与x 轴、y 轴分别交于点A,B.抛物线y=a(x-2)²+k 经过A,B,并与x 轴交于另一点C,M,N 分别是抛物线及其对称轴上的点,求点M 坐标,使得以A,C,M,N 为顶点的四边形是平行四边形.2.抛物线c bx x ++=221y 经过点A(-4,0),点B 在y 轴上,且OA=OB,直线AB 与抛物线交于点C,且点C 的横坐标为2,求点N 坐标,使得以A,O,C,N 为顶点的四边形是平行四边形.变式2:抛物线c bx x ++=221y 经过点A(-4,0),点B 在y 轴上,且OA=OB,直线AB 与抛物线交于点C,且点C 的横坐标为2,M,N 分别是抛物线及其对称轴上的点,求点M 坐标,使得以A,0,M,N 为顶点的四边形是平行四边形.3.如图,抛物线c bx ax ++=2y 与直线623y +-=x 交于B,C 两点,抛物线的对称轴为直线x=1,点D 是抛物线上一点,且点D 横坐标为3,若M 是x 轴上一动点,N 是抛物线上一动点,求点M 坐标,使得以B,D,M,N 为顶点的四边形是平行四边形?4.如图,抛物线32y 2--=x x 与x 轴相交于A,B 两点,与y 轴相交于点C ,若点D 是抛物线对称轴上一动点,点G 为抛物线上的一点,求点G 坐标,使得以B,C,D,G 为顶点的四边形是平行四边形?5.如图,在平面直角坐标系中,已知抛物线经过A(-4,0)、B(0,-4)、C(2,0)三点.(1)求抛物线的解析式;(2)若点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.。
九年级数学抛物线中平行四边形存在性问题习题

抛物线中平行四边形存在性问题习题1.如图2-1,在平面直角坐标系中,已知抛物线y =-x 2+2x +3与x 轴交于A 、B 两点,点M 在这条抛物线上,点P 在y 轴上,如果以点P 、M 、A 、B 为顶点的四边形是平行四边形,求点M 的坐标.2.(2019·内蒙古中考真题)已知,如图,抛物线2(0)y ax bx c a =++≠的顶点为(1,9)M ,经过抛物线上的两点(3,7)A --和(3,)B m 的直线交抛物线的对称轴于点C .(1)求抛物线的解析式和直线AB 的解析式.(2)若点P 在抛物线上,点Q 在x 轴上,当以点,,,A M P Q 为顶点的四边形是平行四边形时,直接写出满足条件的点P 的坐标.3.(2019·广西中考真题)如图,已知抛物线2y ax bx c =++的顶点为()4,3A ,与y 轴相交于点()0,5B -,对称轴为直线l ,点M 是线段AB 的中点.(1)求抛物线的表达式;(2)写出点M 的坐标并求直线AB 的表达式;(3)设动点P ,Q 分别在抛物线和对称轴l 上,当以A ,P ,Q ,M 为顶点的四边形是平行四边形时,求P ,Q 两点的坐标.4.(2019·甘肃中考真题)如图,已知二次函数y =x 2+bx+c 的图象与x 轴交于点A (1,0)、B (3,0),与y 轴交于点C .(1)求二次函数的解析式;(2)若点P 为抛物线上的一点,点F 为对称轴上的一点,且以点A 、B 、P 、F 为顶点的四边形为平行四边形,求点P 的坐标;5.(2019·四川中考真题)如图,抛物线25(0)y ax bx a =+-≠经过x 轴上的点A (1,0)和点B 及y 轴上的点C ,经过B 、C 两点的直线为y x n =+. ①求抛物线的解析式.于点M,过抛物线上一动点N(不与点B、C重合)作直线③过点A作AM BCAM的平行线交直线BC于点Q.若点A、M、N、Q为顶点的四边形是平行四边形,求点N的横坐标.。
两定两动畅游在抛物线上的平行四边形课件

数学建模中两定两动平行四边形的应用有助于解决实际问题。
详细描述
在数学建模中,两定两动平行四边形可以用于解决一些实际问题,如建筑设计、机械运动等。通过设定两个定点 和两个动点,可以构建出满足特定条件的平行四边形,进一步建立数学模型,为解决实际问题提供理论支持。
总结与展望
本章总结
01
02
介绍了抛物线的基本概 念和平行四边形的性质。
平行四边形的相对边平行于抛 物线的对称轴,且相对顶点沿 抛物线轨迹运动。
随着相对顶点的移动,平行四 边形的大小和形状会发生变化, 但仍然保持平行四边形的特性。
两定两动平行四边形在抛物线上的运动轨迹
固定在抛物线对称轴上的两个顶 点,其运动轨迹是垂直于对称轴
的两条直线。
另外两个顶点沿抛物线轨迹运动, 其运动轨迹是抛物线的一部分。
两定两动平行四边形在抛 物线上的应用
两定两动平行四边形在几何作图中的应用
总结词
几何作图中的两定两动平行四边形是解决复杂几何问题的重 要工具。
详细描述
在几何作图中,两定两动平行四边形可以用于解决一些复杂 的几何问题,如作图、证明等。通过合理设定两个定点和两 个动点,可以构造出满足特定条件的平行四边形,进而解决 一系列的几何问题。
两定两动平行四边形的性质
01
02
03
性质1
两定两动平行四边形具有 平行四边形的所有性质, 如对边相等、对角相等、 对角线互相平分等。
性质2
由于其中一个顶点是动点, 因此两定两动平行四边形 具有一个顶点在抛物线上 的性质。
性质3
两定两动平行四边形的面 积等于两个定点之间的距 离乘以顶点到定点的距离。
通过两定两动的设定, 详细阐述了如何在抛物 线上构造平行四边形。
探究平行四边形的存在性问题——以2016_年安顺市中考的一道抛物线题为例

探究平行四边形的存在性问题以2016年安顺市中考的一道抛物线题为例刘利果(河北省邢台市沙河市第三中学ꎬ河北邢台054100)摘㊀要:抛物线中的动点问题ꎬ尤其是与存在性有关的动点问题ꎬ是中考的一个难点.文章以2016年贵州省安顺市的一道中考题为例ꎬ借助网络画板ꎬ从试验探究㊁思路分析㊁一题多解的角度来进行深度探究.关键词:抛物线ꎻ动点ꎻ平行四边形ꎻ存在性ꎻ探究中图分类号:G632㊀㊀㊀文献标识码:A㊀㊀㊀文章编号:1008-0333(2023)35-0092-03收稿日期:2023-09-15作者简介:刘利果(1981.10-)ꎬ女ꎬ河北省邢台人ꎬ本科ꎬ中小学高级教师ꎬ从事初中数学教学研究.㊀㊀抛物线中平行四边形的存在性问题ꎬ是中考的一个难点ꎬ也是热点ꎬ常常以压轴题的形式出现.如何突破这一类试题呢?笔者以2016年安顺市一道中考题为例进行探究.1试题呈现抛物线经过A(-1ꎬ0)ꎬB(5ꎬ0)ꎬC0ꎬ-52æèçöø÷三点.(1)求抛物线的解析式.(2)在抛物线的对称轴上有一点Pꎬ使PA+PC的值最小ꎬ求点P的坐标.(3)若M为x轴上一动点ꎬ在抛物线上是否存在一点Nꎬ使AꎬCꎬMꎬN四点构成的四边形为平行四边形?若存在ꎬ求点N的坐标ꎻ若不存在ꎬ请说明理由[1].2思路分析第(1)(2)问略.第(3)问:①如图1所示ꎬAC为对角线时ꎬ取AC中点Oᶄꎬ连接M4Oᶄꎬ交抛物线于点N4ꎻ如图2所示ꎬ若AC为边ꎬ平移AC得到另外三种情况.过四边形顶点作横平坚直线(平行于坐标轴)构造全等三角形解决问题.图1㊀AC为对角线②设M(xꎬ0)ꎬ分别以ACꎬAMꎬAN为对角线ꎬ分三种情况根据平行四边形两组相对顶点横坐标之和相等ꎬ纵坐标之和也相等ꎬ表示出点N的坐标ꎬ代入抛物线解析式求解即可.③如图3所示ꎬ从路径(轨迹)角度分析.假设以AꎬCꎬMꎬN为顶点的平行四边形存在.在x轴上任取一动点Mꎬ把M看作定点ꎬ然后分别以AMꎬACꎬCM为对角线作出三个平行四边形ꎬ设第四个顶点分别为N1ꎬN2ꎬN3.若拖动动点M可以发现ꎬ动点N1ꎬN2ꎬN3运动的路径均为与x轴平行的直线.易得N1ꎬN3到x轴的距离等于OC=52ꎬ到x轴的距离为2952的直线有两条.易知ꎬ点N1的路径为直线y=52ꎬ点N2ꎬN3的路径为直线y=-52.所以求点N的坐标就可以转化为由抛物线的解析式与点N的路径解析式组成的方程组的解的问题.图2㊀AC为边3一题多解解㊀(1)y=12x2-2x-52.(2)点P的坐标是2ꎬ-32æèçöø÷.过程略.(3)解法1㊀存在点Nꎬ使AꎬCꎬMꎬN四点为顶点构成的四边形为平行四边形.①当AC为边时ꎬ如图2所示ꎬ若点N在x轴下方.图3㊀让M运动又对称轴为直线x=2ꎬC0ꎬ-52æèçöø÷ꎬ所以点N14ꎬ-52æèçöø÷.当点N在x轴上方时ꎬ过点N2作N2Dʅx轴于点D.ȵAC=M2N2ꎬøCAO=øN2M2DꎬøCOA=øN2DM2ꎬʑәAOC≅әM2DN2ꎬʑN2D=OC=52ꎬ即N2点的纵坐标为52.ʑ12x2-2x-52=52ꎬ解得x=2+14或x=2-14ꎬʑN22+14ꎬ52æèçöø÷ꎬN32-14ꎬ52æèçöø÷.②如图1所示ꎬ当AC为对角线时ꎬ由四边形AM4CN4为平行四边形ꎬ知CN4ʊAM4ꎬ所以点N4的纵坐标为-52ꎬʑN44ꎬ-52æèçöø÷.综上所述ꎬ符合条件的点N的坐标为4ꎬ-52æèçöø÷或2+14ꎬ52æèçöø÷或2-14ꎬ52æèçöø÷.解法2㊀设M(xꎬ0)ꎬNxNꎬyN().①若AC为对角线ꎬ则有-1+0=x+xNꎬ0-52=0+yNꎬìîíïïï即xN=-1-xꎬyN=-52.ìîíïïï将N-1-xꎬ-52æèçöø÷代入抛物线表达式ꎬ得12(-1-x)2-2(-1-x)-52=-52ꎬ解得x=-1或-5ꎬ即xN=0或xN=4ꎬ所以N0ꎬ-52æèçöø÷(与C重合ꎬ舍去)或N4ꎬ-52æèçöø÷.②若AN为对角线ꎬ则有-1+xN=x+0ꎬ0+yN=0-52ꎬìîíïïï即xN=x+1ꎬyN=-52.ìîíïïïꎬ将Nx+1ꎬ-52æèçöø÷代入抛物线表达式ꎬ即12(x+1)2-2(x+1)-52=-52ꎬ解得x=-1或3ꎬ即xN=0或xN=4ꎬ所以N0ꎬ-52æèçöø÷(与C重合ꎬ舍去)或N4ꎬ-52æèçöø÷.③若AM为对角线ꎬ则有-1+x=xN+0ꎬ0+0=yN-52ꎬìîíïïï即xN=x-1ꎬyN=52.ìîíïïï将Nx-1ꎬ52æèçöø÷代入抛物线表达式ꎬ即12(x-1)2-2(x-1)-52=52ꎬ解得x1=3+1439或x2=3-14ꎬ即xN=2+14或xN=2-14ꎬ所以N2+14ꎬ52æèçöø÷或N2-14ꎬ52æèçöø÷.综上所述ꎬ符合条件的点N的坐标为4ꎬ-52æèçöø÷或2+14ꎬ52æèçöø÷或2-14ꎬ52æèçöø÷.解法3㊀如图4所示ꎬ在x轴上任取一点Mꎬ连接CMꎬ分别过点AꎬCꎬM作CMꎬAMꎬAC的平行线ꎬ得平行四边形ACMN1ꎬ四边形CMAN2ꎬ四边形ACN3Mꎬ分别过N1ꎬN2ꎬN3作x轴的垂线ꎬ垂足分别为FꎬGꎬE.过点M作MHʅN2N3于点H.易证明N1F=N2G=N3E=OC=52.图4㊀探究点N的路径所以N1运动的路径为直线y=52ꎬN2ꎬN3运动的路径为直线y=-52.因为N1ꎬN2ꎬN3在抛物线y=12x2-2x-52上ꎬ所以N的坐标满足y=52ꎬy=12x2-2x-52ìîíïïïï或y=-52ꎬy=12x2-2x-52ꎬìîíïïïï解得x1=2+14ꎬy1=52ꎬìîíïïïx2=2-14ꎬy2=52ꎬìîíïïïx3=0ꎬy3=-52ìîíïïï(舍去)ꎬx4=4ꎬy3=-52.ìîíïïï综上所述ꎬ符合条件的点N的坐标为4ꎬ-52æèçöø÷ꎬ2+14ꎬ52æèçöø÷或2-14ꎬ52æèçöø÷.解法4㊀如图3所示ꎬ因为A(-1ꎬ0)ꎬC0ꎬ-52æèçöø÷ꎬ所以AꎬC两点间的水平距离为1ꎬ坚直距离为52.设点M的坐标为(mꎬ0)ꎬ将点M按CңA方向平移ꎬ得到点N1m-1ꎬ52æèçöø÷ꎬ将点C按MңA方向平移ꎬ得到点N2-m-1ꎬ-52æèçöø÷ꎬ将点M按AңC方向平移ꎬ得到点N3m+1ꎬ-52æèçöø÷.将点N1m-1ꎬ52æèçöø÷ꎬN2-m-1ꎬ-52æèçöø÷ꎬN3m+1ꎬ-52æèçöø÷分别代代入抛物线的解析式y=12x2-2x-52得①12(m-1)2-2(m-1)-52=52ꎬ解得m=3-14或m=14+3ꎬʑN12+14ꎬ52æèçöø÷或N12-14ꎬ52æèçöø÷.②12(-m-1)2-2(-m-1)-52=-52ꎬ解得m=-1或m=-5ꎬʑN20ꎬ-52æèçöø÷(与C重合ꎬ舍去)或N24ꎬ-52æèçöø÷.③12(m+1)2-2(m+1)-52=-52ꎬ解得m=-1或m=3ꎬʑN30ꎬ-52æèçöø÷(与C重合ꎬ舍去)或N34ꎬ-52æèçöø÷.综上所述ꎬ符合条件的点N的坐标为4ꎬ-52æèçöø÷ꎬ2+14ꎬ52æèçöø÷或2-14ꎬ52æèçöø÷.对于平行四边形的存在性问题中已知两个定点ꎬ先虚拟一个动点ꎬ围成一个三角形ꎬ过三角形的每一个顶点画对边的平行线ꎬ三条直线两两相交ꎬ就可以确定平行四边形的第四个顶点.按照虚拟的第三个点ꎬ第四个顶点存在三种情况.但是第四个点到底有几个ꎬ要具体问题具体分析.参考文献:[1]董红凤.有效解决函数中动点型综合题教学探究[J].数学学习ꎬ2016(01):25-30.[责任编辑:李㊀璟]49。
难点攻关 抛物线与平行四边形

难点攻关 抛物线与平行四边形
近年中考试题中常常出现抛物线与平行四边形组合的压轴题,
1. 在平面直角坐标系xoy 中,点C ,B 的坐标分别为(-4,0),(0,2).四边形ABCO 是平行四边形,抛物线过A ,B ,C 三点,与x 轴交于另一点D .一动点P 以每秒1个单位长度的速度从B 点出发沿BA 向点A 运动,运动到点A 停止,同时一动点Q 从点D 出发,以每秒3个单位长
度的速度沿DC 向点C 运动,与点P 同时停止.
(1)求抛物线的解析式;
(2)若抛物线的对称轴与AB 交于点E ,与x 轴交于点F ,当点P 运动时间t
为何值时,四边形POQE 是等腰梯形?
(3)当t 为何值时,以P ,B ,O 为顶点的三角形与以点Q ,B ,O 为顶点的三角形相似?
解:(1)∵四边形ABCO 是平行四边形,∴OC=AB=4.
∴A(4,2),B(0,2),C(-4,0).
∵抛物线y=ax 2+bx+c 过点B(0,2),∴c=2.
由题意,有⎩⎨⎧16a−4b+2=016a+4b+2=2 解得: ⎩⎪⎨⎪⎧a=-116b=14
∴⎩⎪⎨⎪⎧a−b+c =025a+5b+c =0c =−52
解得 :
⎨⎧a=12b=-2c=-52。
抛物线中平行四边形问题品质课件PPT

402m
m
00a0.25m2
m
a
2 1
②点B与点Q相对 420m
m 6
0a00.25m2 m a 3
③点B与点P相对
4m02 00.25m2 m0a
m
a
2 3
∴P1(2,1), P2(6,-3), P3(-2,-3)
变式训练2
如图,平面直角坐标系中,y=0.5x2+x-4与y轴相交于点B(0,-4),点P是抛物线上的
• 例1 如图,平面直角坐标系中,已知点A(-1,0),B(1,-2),C(3,1),点D
是平面内一动点,若以点A,B,C,D为顶点的四边形是平行四边
形,则点D的坐标是__(-_3_,-_3)_,(_1_,3_),_(5,-1)
设点D(x,y)
①点A与点B相对 11 3 x 02 1 y
②点A与点C相对13 1 x 01 2 y
抛物线中 平行四边形存在性问题
一、画图引领 温故知新
• 1、已知平面上不共线三点A、B、C,求一 点D,使得A、B、C、D四个点组成平行四
边形
连接AB,AC,BC,分别过点A,B,C作对边的平行线,三条平行线的交点即为所有点D
D1
A
D2
B
C
D3
• 2、已知平面上两个点A,B,求两点P,Q,使 得A,B,P,Q四个点组成平行四边形(题目中 P,Q的位置有具体的限制)
x 3
y
3
D2 C
A
x 1
y
3
D1
B
D3
说明:若题中四边形ABCD是平行四边形,
则点D的坐标只有一个结果__(1,3)
③点A与点D相对 1 x 13 x 5
2020年中考数学压轴题专题之抛物线上的特殊平行四边形问题探究

抛物线上的特殊平行四边形问题探究专题导入导图:给出两点确定平行四边形关系如下图:导例如图1,在平面直角坐标系中,已知抛物线经过A(-4,0)、B(0,-4)、C(2,0)三点.(1)求抛物线的解析式;(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△MAB的面积为S,求S关于m的函数关系式,并求出S的最大值;(3)若点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.图1 图2思路点拨1.求抛物线的解析式,设交点式比较简便.2.把△MAB分割为共底MD的两个三角形,高的和为定值O A.3.当PQ与OB平行且相等时,以点P、Q、B、O为顶点的四边形是平行四边形,按照P、Q 的上下位置关系,分两种情况列方程.答案:(1) 因为抛物线与x轴交于A(-4,0)、C(2,0)两点,设y=a(x+4)(x-2).代入点B(0,-4),求得12a =.所以抛物线的解析式为211(4)(2)422y x x x x =+-=+-. (2)如图2,直线AB 的解析式为y =-x -4.过点M 作x 轴的垂线交AB 于D ,那么2211(4)(4)222MD m m m m m =---+-=--.所以2142MDA MDB S S S MD OA m m ∆∆=+=⋅=--2(2)4m =-++.因此当2m =-时,S 取得最大值,最大值为4.(3) 如果以点P 、Q 、B 、O 为顶点的四边形是平行四边形,那么PQ //OB ,PQ =OB =4. 设点Q 的坐标为(,)x x -,点P 的坐标为21(,4)2x x x +-. ①当点P 在点Q 上方时,21(4)()42x x x +---=.解得225x =-±.此时点Q 的坐标为(225,225)-+-(如图3),或(225,225)--+(如图4). ②当点Q 在点P 上方时,21()(4)42x x x --+-=.解得4x =-或0x =(与点O 重合,舍去).此时点Q 的坐标为(-4,4) (如图5).图3 图4 图5典例类型一:已知“两点”判断平行四边形存在性问题例1、如图,在平面直角坐标系中,抛物线y =x 2+mx +n 经过点A (3,0)、B (0,﹣3),点P 是直线AB 上的动点,过点P 作x 轴的垂线交抛物线于点M ,设点P 的横坐标为t . (1)分别求出直线AB 和这条抛物线的解析式.(2)若点P 在第四象限,连接AM 、BM ,当线段PM 最长时,求△ABM 的面积.(3)是否存在这样的点P ,使得以点P 、M 、B 、O 为顶点的四边形为平行四边形?若存在,请直接写出点P 的横坐标;若不存在,请说明理由.【分析】:(1)分别利用待定系数法求两函数的解析式:把A(3,0)B(0,﹣3)分别代入y=x2+mx+n 与y=kx+b,得到关于m、n的两个方程组,解方程组即可;(2)设点P的坐标是(t,t﹣3),则M(t,t2﹣2t﹣3),用P点的纵坐标减去M的纵坐标得到PM 的长,即PM=(t﹣3)﹣(t2﹣2t﹣3)=﹣t2+3t,然后根据二次函数的最值得到当t=﹣=32时,PM最长为=94,再利用三角形的面积公式利用S△ABM=S△BPM+S△APM计算即可;(3)由PM∥OB,根据平行四边形的判定得到当PM=OB时,点P、M、B、O为顶点的四边形为平行四边形,然后讨论:当P在第四象限:PM=OB=3,PM最长时只有,所以不可能;当P在第一象限:PM=OB=3,(t2﹣2t﹣3)﹣(t﹣3)=3;当P在第三象限:PM=OB=3,t2﹣3t=3,分别解一元二次方程即可得到满足条件的t的值.类型二:菱形的存在性问题例2 如图2所示,直线y=x+c与x轴交于点A(-4,0),与y轴交于点C,抛物线y=-x2+bx+c 经过点A,C.(1)求抛物线的解析式;(2)点E在抛物线的对称轴上,求CE+OE的最小值;(3)如图2所示,点M是线段OA上的一个动点,过点M作垂直于x轴的直线与直线AC和抛物线分别交于点P,N.若点P恰好是线段MN的中点,点F是直线AC上一个动点,在坐标平面内是否存在点D,使以点D,F,P,M为顶点的四边形是菱形?若存在,请直接写出点D的坐标;若不存在,请说明理由.注:二次函数y=ax2+bx+c(a≠0)的顶点坐标为(﹣,)【分析】(1)把已知点坐标代入解析式;(2)取点C关于抛物线的对称轴直线l的对称点C′,由两点之间线段最短,最小值可得;(3)①由已知,注意相似三角形的分类讨论.②设出M坐标,求点P坐标.注意菱形是由等腰三角形以底边所在直线为对称轴对称得到的.本题即为研究△CPN为等腰三角形的情况.类型三:正方形的存在性问题例3如图1,在平面直角坐标系中,直线y=x+4与抛物线y=﹣x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.(1)求该抛物线的解析式;(2)P 是抛物线上一动点(不与点A 、B 重合),①如图2,若点P 在直线AB 上方,连接OP 交AB 于点D ,求的最大值;②如图3,若点P 在x 轴的上方,连接PC ,以PC 为边作正方形CPEF ,随着点P 的运动,正方形的大小、位置也随之改变.当顶点E 或F 恰好落在y 轴上,直接写出对应的点P 的坐标.【分析】(1)利用直线解析式求出点A 、B 的坐标,再利用待定系数法求二次函数解析式解答; (2)作PF ∥BO 交AB 于点F ,证△PFD ∽△OBD ,得比例线段,则PF 取最大值时,求得的最大值;(3)(i )点F 在y 轴上时,P 在第一象限或第二象限,如图2,3,过点P 作PH ⊥x 轴于H ,根据正方形的性质可证明△CPH ≌△FCO ,根据全等三角形对应边相等可得PH =CO =2,然后利用二次函数解析式求解即可;(ii )点E 在y 轴上时,过点PK ⊥x 轴于K ,作PS ⊥y 轴于S ,同理可证得△EPS ≌△CPK ,可得PS =PK ,则P 点的横纵坐标互为相反数,可求出P 点坐标;点E 在y 轴上时,过点PM ⊥x 轴于M ,作PN ⊥y 轴于N ,同理可证得△PEN ≌△PCM ,可得PN =PM ,则P 点的横纵坐标相等,可求出P 点坐标.由此即可解决问题. 专题突破1、如图,抛物线2y x bx c =-++与直线122y x =+交于,C D 两点,其中点C 在y 轴上,点D 的坐标为7(3,)2。
与抛物线有关的平行四边形存在性问题(两动两定)

2
8
2
8
ii)当DE ∥QP, EP ∥ DQ时,则点P的坐标为(4m 2,3m 7).
把P点坐标代入抛物线的解析式中,得- 1(4m 2)2 (4m 2) 3 3m 7
4
解得m1
-
7 4
, m2
-1(舍去). 因此,点Q的坐标为(- 7,-
9 ). 4
(2)DE为平行四边形的对角线 ,则点P的坐标为( - 6 - 4m,1 3m).
xA, yA
xB, yB
xD, yD
xC , yC
xA xC xB xD , yA yC yB yD
2
2
2
ห้องสมุดไป่ตู้
2
即xA xC xB xD , yA yC yB yD.
有xD xA xC xB , yD yA yC yB.
二、用我们熟悉的知识解决不太熟悉的问题,……
(1)DE为平行四边形的一边,
i)当DE ∥QP, EQ ∥ DP时,则点P的坐标为(4m 2,3m 1).
把P点坐标代入抛物线的解析式中,得- 1(4m 2)2 (4m 2) 3 3m 1 4
解得m1
3 8
89
, m2
3 8
89
因此,点 Q的坐标为( - 3 89 ,15 3 89 )或( - 3 - 89 ,15 - 3 89 ).
2
8
2
8
4
4
三、再看看下面的问题,……
四、想想今天所学,你有何收获?
1.今天是研究什么问题? 2.在研究这个问题的过程中,你熟悉了哪些知识? 3.这类问题通常是可以怎么解决的呢?
与抛物线有关的平行四边形存在性问题
两动两定 两定—— 两个坐标确定的点. 两动—— 一个是在抛物线上的动点,另一个在一条直线(X轴 / Y轴 / 对称轴 / 一次函数的图象 )上的动点.
抛物线中平行四边形存在性问题答案

抛物线中平行四边形存在性问题习题1.解:先求出A (-1,0),B (2,0),C (0,2) 设点M (x ,y )A 与点B 相对 -1+2= 0+x 且 0+0= 2+yA 与点C 相对 -1+0= 2+x 且 0+2= 0+yA 与点M 相对 -1+x = 2+0 且 0+y = 0+2所以,M 1(3,2), M 2 (-3,2),M 3 (1,-2)2.解答:(1)二次函数表达式为:()219y a x =-+,将点A 的坐标代入上式并解得:1a =-,故抛物线的表达式为:228y x x =-++…①,则点()3,5B ,将点,A B 的坐标代入一次函数表达式并解得:直线AB 的表达式为:21y x =-;(2)设点(),0Q m 、点P (s,-s 2+2s+8)且点(3,7)A --和(3,)B m 点A 与点B 相对 m+s=0且m-7=-s 2+2s+8点A 与点P 相对 s-3=m+3且-s 2+2s+8-7=m点A 与点Q 相对 m-3=s=3且-7=-s 2+2s+8+m解得,点()6,16P -或()4,16--或()12+或()12.3.解析:(1)函数表达式为:()243y a x ==+,将点B 坐标代入上式并解得:12a =-, 故抛物线的表达式为:21452=-+-y x x ; (2)()4,3A 、()0,5B -,则点()2,1-M ,设直线AB 的表达式为:5y kx =-,将点A 坐标代入上式得:345k =-,解得:2k =,故直线AB 的表达式为:25y x =-;(3)设点()4,Q s 、点21,452P m m m ⎛⎫-+- ⎪⎝⎭, ①当AM 是平行四边形的一条边时,点A 向左平移2个单位、向下平移4个单位得到M ,同样点21,452P m m m ⎛⎫-+- ⎪⎝⎭向左平移2个单位、向下平移4个单位得到()4,Q s , 即:24m -=,214542m m s -+--=, 解得:6m =,3s =-,故点P 、Q 的坐标分别为()6,1、()4,3-;②当AM 是平行四边形的对角线时,由中点定理得:424m +=+,2131452m m s -=-+-+, 解得:2m =,1s =,故点P 、Q 的坐标分别为()2,1、()4,1;故点P 、Q 的坐标分别为()6,1,()4,3-或()2,1、()4,3-,()2,1或()4,1.4.解析:(1)用交点式函数表达式得:y =(x ﹣1)(x ﹣3)=x 2﹣4x+3; 故二次函数表达式为:y =x 2﹣4x+3;(2)①当AB 为平行四边形一条边时,如图1,则AB =PE =2,则点P 坐标为(4,3),当点P 在对称轴左侧时,即点C 的位置,点A 、B 、P 、F 为顶点的四边形为平行四边形,故:点P (4,3)或(0,3);②当AB 是四边形的对角线时,如图2,AB 中点坐标为(2,0)设点P 的横坐标为m ,点F 的横坐标为2,其中点坐标为:22m + , 即:22m +=2,解得:m =2, 故点P (2,﹣1);故:点P (4,3)或(0,3)或(2,﹣1);5. 解析:①∵点B 、C 在直线为y x n =+上, ∴B(﹣n ,0)、C (0,n ),∵点A (1,0)在抛物线上,∴250505a b an bn n +-=⎧⎪+-=⎨⎪=-⎩,∴1a =-,6b =,∴抛物线解析式:265y x x =-+-;②由①知,BC 所在直线为:5y x =-,∴点A 到直线BC 的距离22d =过点N 作x 轴的垂线交直线BC 于点P ,交x 轴于点H . 设()2,65N m m m -+-,则(,0)H m 、(,5)P m m -, 易证△PQN 为等腰直角三角形,即22NQ PQ == ∴4PN =,Ⅰ.4NH HP +=,∴265(5)4m m m -+---=解得11m =,24m =,∵点A 、M 、N 、Q 为顶点的四边形是平行四边形, ∴4m =;Ⅱ.4NH HP +=,∴()25654m m m ---+-=解得152m =,252m =, ∵点A 、M 、N 、Q 为顶点的四边形是平行四边形, 5m >,∴52m =, Ⅲ.4NH HP -=,∴()265[(5)]4m m m --+----=,解得152m =,252m =, ∵点A 、M 、N 、Q 为顶点的四边形是平行四边形, 0m <,∴52m =,综上所述,若点A 、M 、N 、Q 为顶点的四边形是平行四边形,点N 的横坐标为:4.。
初中数学精品试题:抛物线中的平行四边形练习

抛物线中的平行四边形练习1、如图,抛物线y=ax2+2ax+c(a>0)与y轴交于点C,与x轴交于A、B两点,A点在B 点左侧.若点E在x轴上,点P在抛物线上,且以A、C、E、P为顶点的四边形是平行四边形,则符合条件的点P有()A .1个B.2个C.3个D.4个2、已知抛物线C1:y=﹣x2+2mx+1(m为常数,且m≠0)的顶点为A,与y轴交于点C;抛物线C2与抛物线C1关于y轴对称,其顶点为B.若点P是抛物线C1上的点,使得以A、B、C、P为顶点的四边形为菱形,则m为()A .B.C.D.3、如图,抛物线y=ax2+bx+c交x轴于点A、B,交y轴于点D(0,3),其对称轴为直线x=4,点C为对称轴上一点,若四边形ABCD为平行四边形,则抛物线的解析式为.4、如图,对称轴为直线x=的抛物线经过点A(﹣6,0)和点B(0,4).(1)求抛物线的解析式和顶点坐标;(2)设点E(x,y)是抛物线上的一个动点,且位于第三象限,四边形OEAF是以OA为对角线的平行四边形,求▱OEAF的面积S与x的函数关系式,并写出自变量x的取值范围;①当▱OEAF的面积为24时,请判断▱OEAF是否为菱形?②是否存在点E,使▱OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.5、已知经过原点的抛物线y=﹣2x2+4x(如图所示)与x的另一交点为A现将它向右平移m (m>0)位,所得抛物线与x轴交于C、D点,与原抛物线交于点P(1)求点P的坐标(可用含m式子表示);(2)设△PCD的面积为s,求s关于m关系式;(3)过点P作x轴的平行线交原抛物线于点E,交平移后的抛物线于点F.请问是否存在m,使以点E、O、A、F为顶点的四边形为平行四边形?若存在,求出m的值;若不存在,请说明理由.6、如图,直线y=x+m与抛物线y=﹣x2+bx+c交于C、D两点,其中点C在y轴上,点D 的坐标为(3,),点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.(1)求一次函数和抛物线的解析式;(2)若点P的横坐标为t,当t为何值时,四边形OCPE是平行四边形?请说明理由;(3)在CD上方是否存在点P,使∠PCF=45°?若存在,求出相应的点P的坐标;若不存在,试说明理由.。
中考压轴题——抛物线平行四边形(含详细答案分析)
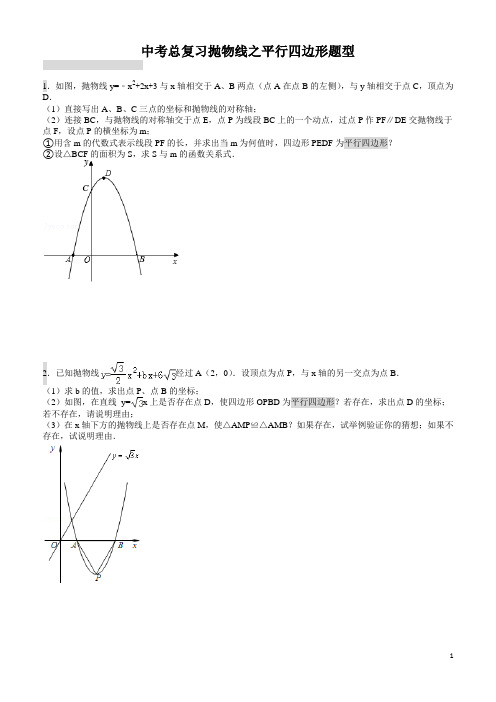
中考总复习抛物线之平行四边形题型1.如图,抛物线y=﹣x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.(1)直接写出A、B、C三点的坐标和抛物线的对称轴;(2)连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m;①用含m的代数式表示线段PF的长,并求出当m为何值时,四边形PEDF为平行四边形?②设△BCF的面积为S,求S与m的函数关系式.2.已知抛物线经过A(2,0).设顶点为点P,与x轴的另一交点为点B.(1)求b的值,求出点P、点B的坐标;(2)如图,在直线y=x上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐标;若不存在,请说明理由;(3)在x轴下方的抛物线上是否存在点M,使△AMP≌△AMB?如果存在,试举例验证你的猜想;如果不存在,试说明理由.3.如图,抛物线y=x2﹣2x+c的顶点A在直线l:y=x﹣5上.(1)求抛物线顶点A的坐标;(2)设抛物线与y轴交于点B,与x轴交于点C、D(C点在D点的左侧),试判断△ABD的形状;(3)在直线l上是否存在一点P,使以点P、A、B、D为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.4.已知抛物线y=﹣mx2+4x+2m与x轴交于点A(α,0),B(β,0),且=﹣2,(1)求抛物线的解析式.(2)抛物线的对称轴为l,与y轴的交点为C,顶点为D,点C关于l的对称点为E,是否存在x轴上的点M,y轴上的点N,使四边形DNME的周长最小?若存在,请画出图形(保留作图痕迹),并求出周长的最小值;若不存在,请说明理由.(3)若点P在抛物线上,点Q在x轴上,当以点D、E、P、Q为顶点的四边形是平行四边形时,求点P的坐标.5.已知抛物线y=﹣x2﹣2x+a(a≠0)与y轴相交于A点,顶点为M,直线y=x﹣a分别与x轴、y轴相交于B,C两点,并且与直线MA相交于N点.(1)若直线BC和抛物线有两个不同交点,求a的取值范围,并用a表示交点M,A的坐标;(2)将△NAC沿着y轴翻转,若点N的对称点P恰好落在抛物线上,AP与抛物线的对称轴相交于点D,连接CD,求a的值及△PCD的面积;(3)在抛物线y=﹣x2﹣2x+a(a>0)上是否存在点P,使得以P,A,C,N为顶点的四边形是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.6.边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点E 在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点.(1)求抛物线的解析式;(2)点P从点C出发,沿射线CB每秒1个单位长度的速度运动,运动时间为t秒.过点P作PF⊥CD于点F,当t为何值时,以点P,F,D为顶点的三角形与△COD相似?(3)点M为直线AB上一动点,点N为抛物线上一动点,是否存在点M,N,使得以点M,N,D,E为顶点的四边形是平行四边形?若存在,请直接写出满足条件的点的坐标;若不存在,请说明理由.7.如图,边长为1的正方形ABCD一边AD在x负半轴上,直线l:y=x+2经过点B(x,1)与x轴,y轴分别交于点H,F,抛物线y=﹣x2+bx+c.(1)求A,D两点的坐标及抛物线经过A,D两点时的解析式;(2)当抛物线的顶点E(m,n)在直线l上运动时,连接EA,ED,试求△EAD的面积S与m之间的函数解析式,并写出m的取值范围;(3)设抛物线与y轴交于G点,当顶点E在直线l上运动时,以A,C,E,G为顶点的四边形能否成为平行四边形?若能,求出E点坐标;若不能,请说明理由.8.已知抛物线:(1)求抛物线y1的顶点坐标.(2)将抛物线y1向右平移2个单位,再向上平移1个单位,得到抛物线y2,求抛物线y2的解析式.(3)如图,抛物线y2的顶点为P,x轴上有一动点M,在y1、y2这两条抛物线上是否存在点N,使O(原点)、P、M、N四点构成以OP为一边的平行四边形?若存在,求出N点的坐标;若不存在,请说明理由.9.如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.(1)求AD的长及抛物线的解析式;(2)一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO 以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动.设运动时间为t秒,当t 为何值时,以P、Q、C为顶点的三角形与△ADE相似?(3)点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使以M,N,C,E为顶点的四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.10.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N.其顶点为D.(1)抛物线及直线AC的函数关系式;(2)设点M(3,m),求使MN+MD的值最小时m的值;(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;(4)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.11.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0),B(3,0)两点,与y轴交于点C(0,﹣3).(1)求该抛物线的解析式及顶点M坐标;(2)求△BCM面积与△ABC面积的比;(3)若P是x轴上一个动点,过P作射线PQ∥AC交抛物线于点Q,随着P点的运动,在抛物线上是否存在这样的点Q,使以A,P,Q,C为顶点的四边形为平行四边形?若存在,请求出Q点坐标;若不存在,请说明理由.12.如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于点A和点B,其中点A的坐标为(﹣2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.(1)求抛物线的解析式;(2)若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形ABFC的面积为17,若存在,求出点F的坐标;若不存在,请说明理由;(3)平行于DE的一条动直线l与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标.13.如图,抛物线y=x2+bx+c与x轴交于A(5,0)、B(﹣1,0)两点,过点A作直线AC⊥x轴,交直线y=2x于点C;(1)求该抛物线的解析式;(2)求点A关于直线y=2x的对称点A′的坐标,判定点A′是否在抛物线上,并说明理由;(3)点P是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.14.如图,直线y=2x+2与x轴交于点A,与y轴交于点B,把△AOB沿y轴翻折,点A落到点C,过点B 的抛物线y=﹣x2+bx+c与直线BC交于点D(3,﹣4).(1)求直线BD和抛物线的解析式;(2)在第一象限内的抛物线上,是否存在一点M,作MN垂直于x轴,垂足为点N,使得以M、O、N为顶点的三角形与△BOC相似?若存在,求出点M的坐标;若不存在,请说明理由;(3)在直线BD上方的抛物线上有一动点P,过点P作PH垂直于x轴,交直线BD于点H,当四边形BOHP 是平行四边形时,试求动点P的坐标.15.综合与探究:如图,在平面直角坐标系xOy中,四边形OABC是平行四边形,A、C两点的坐标分别为(4,0),(﹣2,3),抛物线W经过O、A、C三点,D是抛物线W的顶点.(1)求抛物线W的解析式及顶点D的坐标;(2)将抛物线W和▱OABC一起先向右平移4个单位后,再向下平移m(0<m<3)个单位,得到抛物线W′和▱O′A′B′C′,在向下平移的过程中,设▱O′A′B′C′与▱OABC的重叠部分的面积为S,试探究:当m为何值时S有最大值,并求出S的最大值;(3)在(2)的条件下,当S取最大值时,设此时抛物线W′的顶点为F,若点M是x轴上的动点,点N是抛物线W′上的动点,试判断是否存在这样的点M和点N,使得以D、F、M、N为顶点的四边形是平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.16.如图,抛物线与x轴交于点A(﹣5,0)和点B(3,0).与y轴交于点C(0,5).有一宽度为1,长度足够的矩形(阴影部分)沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和Q,交直线AC于点M和N.交x轴于点E和F.(1)求抛物线的解析式;(2)当点M和N都在线段AC上时,连接MF,如果sin∠AMF=,求点Q的坐标;(3)在矩形的平移过程中,当以点P,Q,M,N为顶点的四边形是平行四边形时,求点M的坐标.17.如图,在平面直角坐标系xOy中,抛物线y=a(x+1)2﹣3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C(0,﹣),顶点为D,对称轴与x轴交于点H,过点H的直线l交抛物线于P,Q两点,点Q在y轴的右侧.(1)求a的值及点A,B的坐标;(2)当直线l将四边形ABCD分为面积比为3:7的两部分时,求直线l的函数表达式;(3)当点P位于第二象限时,设PQ的中点为M,点N在抛物线上,则以DP为对角线的四边形DMPN能否为菱形?若能,求出点N的坐标;若不能,请说明理由.1.解:(1)A(﹣1,0),B(3,0),C(0,3).抛物线的对称轴是:直线x=1.(2)①设直线BC的函数关系式为:y=kx+b.把B(3,0),C(0,3)分别代入得:解得:.所以直线BC的函数关系式为:y=﹣x+3.当x=1时,y=﹣1+3=2,∴E(1,2).当x=m时,y=﹣m+3,∴P(m,﹣m+3).在y=﹣x2+2x+3中,当x=1时,y=4.∴D(1,4)当x=m时,y=﹣m2+2m+3,∴F(m,﹣m2+2m+3)∴线段DE=4﹣2=2,线段PF=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m∵PF∥DE,∴当PF=ED时,四边形PEDF为平行四边形.由﹣m2+3m=2,解得:m1=2,m2=1(不合题意,舍去).因此,当m=2时,四边形PEDF为平行四边形.②设直线PF与x轴交于点M,由B(3,0),O(0,0),可得:OB=OM+MB=3.∵S=S△BPF+S△CPF即S=PF•BM+PF•OM=PF•(BM+OM)=PF•OB.∴S=×3(﹣m2+3m)=﹣m2+m(0≤m≤3).方法二:(3)∵B(3,0),C(0,3),D(1,4),∴,∴,∵∠DEC=∠COB=90°,∴△DEC∽△COB,∴∠DCE=∠CBO,∴∠DCE+∠OCB=90°,∴DC⊥BC,∴△BCD的外接圆圆心M为BD中点,∴M X==2,M Y==2,∴△BCD的外接圆圆心M(2,2).2.(2012•东营)已知抛物线经过A(2,0).设顶点为点P,与x轴的另一交点为点B.(1)求b的值,求出点P、点B的坐标;(2)如图,在直线y=x上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐标;若不存在,请说明理由;(3)在x轴下方的抛物线上是否存在点M,使△AMP≌△AMB?如果存在,试举例验证你的猜想;如果不存在,试说明理由.【解答】解:(1)由于抛物线经过A(2,0),所以,解得.所以抛物线的解析式为,①将①式配方,得,所以顶点P的坐标为(4,﹣2),令y=0,得,解得x1=2,x2=6.所以点B的坐标是(6,0).(2)在直线y=x上存在点D,使四边形OPBD为平行四边形.理由如下:设直线PB的解析式为y=kx+b,把B(6,0),P(4,﹣2)分别代入,得,解得,所以直线PB的解析式为.又因为直线OD的解析式为,所以直线PB∥OD.设直线OP的解析式为y=mx,把P(4,﹣2)代入,得,解得.如果OP∥BD,那么四边形OPBD为平行四边形.设直线BD的解析式为,将B(6,0)代入,得0=,所以所以直线BD的解析式为,解方程组,得,同样还存在第二种情况,如图所示,D′点和D关于原点对称,因此D′的坐标为(﹣2,﹣2),所以D点的坐标为(2,2)或(﹣2,﹣2).(3)符合条件的点M存在.验证如下:过点P作x轴的垂线,垂足为C,则PC=2,AC=2,由勾股定理,可得AP=4,PB=4,又AB=4,所以△APB是等边三角形,只要作∠PAB的平分线交抛物线于M点,连接PM,BM,由于AM=AM,∠PAM=∠BAM,AB=AP,可得△AMP≌△AMB.因此即存在这样的点M,使△AMP≌△AMB.方法二:(4)过点G作x轴垂线,垂足为H,∵⊙G为△OBD的外接圆,∴点G在线段OH的垂直平分线上,且GO=GD,∵B(6,0),∴l GH:x=3,设G点坐标为(3,m),O(0,0),D(2,2),∴(3﹣0)2+(m﹣0)2=(3﹣2)2+(m﹣2)2,∴m=,∴G点的坐标为(3,).3.(2012•宜宾)如图,抛物线y=x2﹣2x+c的顶点A在直线l:y=x﹣5上.(1)求抛物线顶点A的坐标;(2)设抛物线与y轴交于点B,与x轴交于点C、D(C点在D点的左侧),试判断△ABD的形状;(3)在直线l上是否存在一点P,使以点P、A、B、D为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.【解答】方法一:解:(1)∵顶点A的横坐标为x=﹣=1,且顶点A在y=x﹣5上,∴当x=1时,y=1﹣5=﹣4,∴A(1,﹣4).(2)△ABD是直角三角形.将A(1,﹣4)代入y=x2﹣2x+c,可得,1﹣2+c=﹣4,∴c=﹣3,∴y=x2﹣2x﹣3,∴B(0,﹣3)当y=0时,x2﹣2x﹣3=0,x1=﹣1,x2=3∴C(﹣1,0),D(3,0),BD2=OB2+OD2=18,AB2=(4﹣3)2+12=2,AD2=(3﹣1)2+42=20,BD2+AB2=AD2,∴∠ABD=90°,即△ABD是直角三角形.(3)存在.由题意知:直线y=x﹣5交y轴于点E(0,﹣5),交x轴于点F(5,0)∴OE=OF=5,又∵OB=OD=3∴△OEF与△OBD都是等腰直角三角形∴BD∥l,即PA∥BD则构成平行四边形只能是PADB或PABD,如图,过点P作y轴的垂线,过点A作x轴的垂线交过P且平行于x轴的直线于点G.设P(x1,x1﹣5),则G(1,x1﹣5)则PG=|1﹣x1|,AG=|5﹣x1﹣4|=|1﹣x1|PA=BD=3由勾股定理得:(1﹣x1)2+(1﹣x1)2=18,x12﹣2x1﹣8=0,x1=﹣2或4∴P(﹣2,﹣7)或P(4,﹣1),存在点P(﹣2,﹣7)或P(4,﹣1)使以点A、B、D、P为顶点的四边形是平行四边形.方法二:(1)略.(2)把A(1,﹣4)代入y=x2﹣2x+c,得c=3,∴y=x2﹣2x+3=(x﹣3)(x+1),∴D(3,0),B(0,﹣3),A(1,﹣4),K BD==1,K AB==﹣1,∴K BD•K AB=﹣1,∴AB⊥BD,即△ABD为直角三角形.(3)略.(4)∵,解得:x1=1(舍),x2=2,∴G(2,﹣3),∵A(1,﹣4),B(0,﹣3),D(3,0),∴GA==,BD==3,AB==,∴S△BDG==4.4.(2015•德州)已知抛物线y=﹣mx2+4x+2m与x轴交于点A(α,0),B(β,0),且=﹣2,(1)求抛物线的解析式.(2)抛物线的对称轴为l,与y轴的交点为C,顶点为D,点C关于l的对称点为E,是否存在x轴上的点M,y轴上的点N,使四边形DNME的周长最小?若存在,请画出图形(保留作图痕迹),并求出周长的最小值;若不存在,请说明理由.(3)若点P在抛物线上,点Q在x轴上,当以点D、E、P、Q为顶点的四边形是平行四边形时,求点P的坐标.【解答】解:(1)由题意可得:α,β是方程﹣mx2+4x+2m=0的两根,由根与系数的关系可得,α+β=,αβ=﹣2,∵=﹣2,∴=﹣2,即=﹣2,解得:m=1,故抛物线解析式为:y=﹣x2+4x+2;(2)存在x轴上的点M,y轴上的点N,使得四边形DNME的周长最小,∵y=﹣x2+4x+2=﹣(x﹣2)2+6,∴抛物线的对称轴l为x=2,顶点D的坐标为:(2,6),又∵抛物线与y轴交点C的坐标为:(0,2),点E与点C关于l对称,∴E点坐标为:(4,2),作点D关于y轴的对称点D′,点E关于x轴的对称点E′,则D′的坐标为;(﹣2,6),E′坐标为:(4,﹣2),连接D′E′,交x轴于M,交y轴于N,此时,四边形DNME的周长最小为:D′E′+DE,如图1所示:延长E′E,′D交于一点F,在Rt△D′E′F中,D′F=6,E′F=8,则D′E′===10,设对称轴l与CE交于点G,在Rt△DGE中,DG=4,EG=2,∴DE===2,∴四边形DNME的周长最小值为:10+2;(3)如图2,P为抛物线上的点,过点P作PH⊥x轴,垂足为H,若以点D、E、P、Q为顶点的四边形为平行四边形,则△PHQ≌△DGE,∴PH=DG=4,∴|y|=4,∴当y=4时,﹣x2+4x+2=4,解得:x1=2+,x2=2﹣,当y=﹣4时,﹣x2+4x+2=﹣4,解得:x3=2+,x4=2﹣,故P点的坐标为;(2﹣,4),(2+,4),(2﹣,﹣4),(2+,﹣4).5.(2015•绵阳)已知抛物线y=﹣x2﹣2x+a(a≠0)与y轴相交于A点,顶点为M,直线y=x﹣a分别与x轴、y轴相交于B,C两点,并且与直线MA相交于N点.(1)若直线BC和抛物线有两个不同交点,求a的取值范围,并用a表示交点M,A的坐标;(2)将△NAC沿着y轴翻转,若点N的对称点P恰好落在抛物线上,AP与抛物线的对称轴相交于点D,连接CD,求a的值及△PCD的面积;(3)在抛物线y=﹣x2﹣2x+a(a>0)上是否存在点P,使得以P,A,C,N为顶点的四边形是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.【解答】解:(1)由题意得,,整理得2x2+5x﹣4a=0.∵△=25+32a>0,解得a>﹣.∵a≠0,∴a>﹣且a≠0.令x=0,得y=a,∴A(0,a).由y=﹣(x+1)2+1+a得,M(﹣1,1+a).(2)设直线MA的解析式为y=kx+b(k≠0),∵A(0,a),M(﹣1,1+a),∴,解得,∴直线MA的解析式为y=﹣x+a,联立得,,解得,∴N(,﹣).∵点P是点N关于y轴的对称点,∴P(﹣,﹣).代入y=﹣x2﹣2x+a得,﹣=﹣a2+a+a,解得a=或a=0(舍去).∴A(0,),C(0,﹣),M(﹣1,),|AC|=,∴S△PCD=S△PAC﹣S△ADC=|AC|•|x p|﹣|AC|•|x0|=••(3﹣1)=;(3)①当点P在y轴左侧时,∵四边形APCN是平行四边形,∴AC与PN互相平分,N(,﹣),∴P(﹣,);代入y=﹣x2﹣2x+a得,=﹣a2+a+a,解得a=,∴P1(﹣,).②当点P在y轴右侧时,∵四边形ACPN是平行四边形,∴NP∥AC且NP=AC,∵N(,﹣),A(0,a),C(0,﹣a),∴P(,﹣).代入y=﹣x2﹣2x+a得,﹣=﹣a2﹣a+a,解得a=,∴P2(,﹣).综上所述,当点P1(﹣,)和P2(,﹣)时,A、C、P、N能构成平行四边形.6.(2015•湖北)边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点E在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点.(1)求抛物线的解析式;(2)点P从点C出发,沿射线CB每秒1个单位长度的速度运动,运动时间为t秒.过点P作PF⊥CD于点F,当t为何值时,以点P,F,D为顶点的三角形与△COD相似?(3)点M为直线AB上一动点,点N为抛物线上一动点,是否存在点M,N,使得以点M,N,D,E为顶点的四边形是平行四边形?若存在,请直接写出满足条件的点的坐标;若不存在,请说明理由.【解答】解:(1)方法一:过点E作EG⊥x轴于G点.∵四边形OABC是边长为2的正方形,D是OA的中点,∴OA=OC=2,OD=1,∠AOC=∠DGE=90°.∵∠CDE=90°,∴∠ODC+∠GDE=90°.∵∠ODC+∠OCD=90°,∴∠OCD=∠GDE.在△OCD和△GED中,∴△ODC≌△GED (AAS),∴EG=OD=1,DG=OC=2.∴点E的坐标为(3,1).∵抛物线的对称轴为直线AB即直线x=2,∴可设抛物线的解析式为y=a(x﹣2)2+k,将C、E点的坐标代入解析式,得.解得,抛物线的解析式为y=(x﹣2)2+;方法二:过点E作EG⊥x轴于G点.DE⊥DC⇒∠CDO+∠EDH=90°,EG⊥x轴⇒∠DEH+∠EDH=90°,∴∠CDO=∠DEH,DC=DE,∴△ODC≌△GED⇒DG=OC=2,EG=OD=1,∴E(3,1),∴9a+3b+2=0,∵﹣=2,抛物线的解析式为y=(x﹣2)2+;(2)方法一:①若△DFP∽△COD,则∠PDF=∠DCO,∴PD∥OC,∴∠PDO=∠OCP=∠AOC=90°,∴四边形PDOC是矩形,∴PC=OD=1,∴t=1;②若△PFD∽△COD,则∠DPF=∠DCO,=.∴∠PCF=90°﹣∠DCO=90﹣∠DPF=∠PDF.∴PC=PD,∴DF=CD.∵CD2=OD2+OC2=22+12=5,∴CD=,∴DF=.∵=,∴PC=PD=×=,t=,综上所述:t=1或t=时,以点P,F,D为顶点的三角形与△COD相似;方法二:过点F作x轴的垂线,分别交BC,OA于G,H,PF⊥CD⇒∠PFG+∠DFH=90°,GH⊥OA⇒∠FDH+∠DFH=90°,∴∠PFG=∠FDH⇒△PFG∽△FDH⇒,∵PF⊥CD⇒K PF×K CD=﹣1,∴l CD:y=﹣2x+2,∴F(m,﹣2m+2),P(t,2),∴,∴m=,∴F(,﹣),∴=,∴以P,F,D为顶点的三角形与△COD相似,①,∴,∴t=,②,∴,∴t=1,综上所述:t=1或t=时,以点P,F,D为顶点的三角形与△COD相似;方法三:若以P,F,D为顶点的三角形与△COD相似,则∠OCD=∠PDF或∠ODC=∠PDF,①∠OCD=∠PDF⇒PD∥OC,∴CP=OD=1,∴t=1,②∠ODC=∠PDF,作OO′⊥CD交CD于H,∴K OO′×K CD=﹣1,∴l CD:y=﹣2x+2,∴H(m,﹣2m+2),∴﹣2×=﹣1,∴m=,∴H(,),∵H为OO′中点,∴O′(,),∴l O′D:y=,令y=2,∴x=,即P(,2),∴t=.(3)存在,四边形MDEN是平行四边形时,M1(2,1),N1(4,2);四边形MNDE是平行四边形时,M2(2,3),N2(0,2);四边形NDME是平行四边形时,M3(2,),N3(2,).7.(2015•广安)如图,边长为1的正方形ABCD一边AD在x负半轴上,直线l:y=x+2经过点B(x,1)与x轴,y轴分别交于点H,F,抛物线y=﹣x2+bx+c.(1)求A,D两点的坐标及抛物线经过A,D两点时的解析式;(2)当抛物线的顶点E(m,n)在直线l上运动时,连接EA,ED,试求△EAD的面积S与m之间的函数解析式,并写出m的取值范围;(3)设抛物线与y轴交于G点,当顶点E在直线l上运动时,以A,C,E,G为顶点的四边形能否成为平行四边形?若能,求出E点坐标;若不能,请说明理由.【解答】解:(1)∵直线l:y=x+2经过点B(x,1),∴1=x+2,解得x=﹣2,∴B(﹣2,1),∴A(﹣2,0),D(﹣3,0),∵抛物线经过A,D两点,∴,解得,∴抛物线经过A,D两点时的解析式为y=﹣x2﹣5x﹣6;(2)∵点E(m,n)在直线l上,∴n=m+2,∴S=×1×[±(m+2)]=±(m+1),即S=m+1(m>﹣4)或S=﹣m﹣1(m<﹣4);(3)如图,若以A,C,E,G为顶点的四边形能成为平行四边形,则AC=EG,AC∥EG,作EH∥y轴交过G点平行于x轴的直线相交于H,则EH⊥GH,△EHG≌△CDA,∴GH=AD=1,∴E的横坐标为±1,∵点E在直线l上,∴y=×(﹣1)+2=,或y=×1+2=当AC为对角线时,有E和G的横坐标之和等于A和C的横坐标之和,故可求得E(﹣5,﹣1/2)∴E(﹣1,);(1,)或(﹣5,﹣1/2);由于E为抛物线的顶点,G为抛物线与y轴的交点,故将其坐标代入y=﹣x2+bx+c,检验可知当E取(1,)或(﹣5,﹣1/2)时,与此时的A、C、E构成平行四边形的G点并不是y轴与抛物线的交点,与前提相矛盾;综上,满足题意的E的坐标为(﹣1,).8.(2012秋•义乌市校级期中)已知抛物线:(1)求抛物线y1的顶点坐标.(2)将抛物线y1向右平移2个单位,再向上平移1个单位,得到抛物线y2,求抛物线y2的解析式.(3)如图,抛物线y2的顶点为P,x轴上有一动点M,在y1、y2这两条抛物线上是否存在点N,使O(原点)、P、M、N四点构成以OP为一边的平行四边形?若存在,求出N点的坐标;若不存在,请说明理由.【解答】解:(1)依题意把抛物线:y1=﹣x2+2x=﹣(x2﹣4x)=﹣[(x﹣2)2﹣4]=﹣(x﹣2)2+2,故抛物线y1的顶点坐标为:(2,2);(2)∵抛物线y1向右平移2个单位,再向上平移1个单位,得到y2=﹣(x﹣4)2+3,整理得y2=﹣x2+4x﹣5;(3)符合条件的N点存在.如图:作PA⊥x轴于点A,NB⊥x轴于点B,∴∠PAO=∠MBN=90°,若四边形OPMN为符合条件的平行四边形,则OP∥MN,且OP=MN,∴∠POA=∠BMN,在△POA和△NMB中∴△POA≌△NMB(AAS),∴PA=BN,∵点P的坐标为(4,3),∴NB=PA=3,∵点N在抛物线y1、y2上,且P点为y1、y2的最高点∴符合条件的N点只能在x轴下方,①点N在抛物线y1上,则有:﹣x2+2x=﹣3解得:x1=2﹣,x2=2+,②点N在抛物线y2上,则有:﹣(x﹣4)2+3=﹣3解得:x3=4﹣2或x4=4+2故符合条件的N点有四个:N1(2﹣,﹣3),N2(4﹣2,﹣3),N3(2+,﹣3),N4(4+2,﹣3).9.(2012•襄阳)如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B 落在OA边上的点E处.分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c 经过O,D,C三点.(1)求AD的长及抛物线的解析式;(2)一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO 以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动.设运动时间为t秒,当t 为何值时,以P、Q、C为顶点的三角形与△ADE相似?(3)点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使以M,N,C,E为顶点的四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.【解答】方法一:解:(1)∵四边形ABCO为矩形,∴∠OAB=∠AOC=∠B=90°,AB=CO=8,AO=BC=10.由题意,△BDC≌△EDC.∴∠B=∠DEC=90°,EC=BC=10,ED=BD.由勾股定理易得EO=6.∴AE=10﹣6=4,设AD=x,则BD=ED=8﹣x,由勾股定理,得x2+42=(8﹣x)2,解得,x=3,∴AD=3.∵抛物线y=ax2+bx+c过点D(3,10),C(8,0),O(0,0)∴,解得∴抛物线的解析式为:y=﹣x2+x.(2)∵∠DEA+∠OEC=90°,∠OCE+∠OEC=90°,∴∠DEA=∠OCE,由(1)可得AD=3,AE=4,DE=5.而CQ=t,EP=2t,∴PC=10﹣2t.当∠PQC=∠DAE=90°,△ADE∽△QPC,∴=,即=,解得t=.当∠QPC=∠DAE=90°,△ADE∽△PQC,∴=,即=,解得t=.∴当t=或时,以P、Q、C为顶点的三角形与△ADE相似.(3)假设存在符合条件的M、N点,分两种情况讨论:①EC为平行四边形的对角线,由于抛物线的对称轴经过EC中点,若四边形MENC是平行四边形,那么M点必为抛物线顶点;则:M(4,);而平行四边形的对角线互相平分,那么线段MN必被EC中点(4,3)平分,则N(4,﹣);②EC为平行四边形的边,则EC MN,设N(4,m),则M(4﹣8,m+6)或M(4+8,m﹣6);将M(﹣4,m+6)代入抛物线的解析式中,得:m=﹣38,此时N(4,﹣38)、M(﹣4,﹣32);将M(12,m﹣6)代入抛物线的解析式中,得:m=﹣26,此时N(4,﹣26)、M(12,﹣32);综上,存在符合条件的M、N点,且它们的坐标为:①M1(﹣4,﹣32),N1(4,﹣38);②M2(12,﹣32),N2(4,﹣26);③M3(4,),N3(4,﹣).方法二:(1)略.(2)∵E(0,6),C(8,0),∴l EC:y=﹣x+6,∵,EP=2t,∴P x=t,∴P(t,﹣t+6),Q(8﹣t,0),∵△PQC∽△ADE,且∠ECO=∠AED,∴PQ⊥OC或PQ⊥PC.当PQ⊥OC时,Px=Qx,即t=8﹣t,∴t1=,当PQ⊥PC时,K PQ•K PC=﹣1,∴t2=.(3)M,N,C,E为顶点的四边形是平行四边形.设N(4,t),C(8,0),E(0,6),∴,∴M1(4,6﹣t),同理M2(﹣4,t+6),M3(12,t﹣6),∴﹣t,∴t=﹣,﹣×(﹣4)2+(﹣4)=t+6,∴t=﹣38,﹣×122+×12=t﹣6,∴t=﹣26,综上,存在符合条件的M、N点,且它们的坐标为:①M1(4,),N1(4,﹣);②M2(12,﹣32),N2(4,﹣26);③M3(﹣4,﹣32),N3(4,﹣38).10.(2012•恩施州)如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N.其顶点为D.(1)抛物线及直线AC的函数关系式;(2)设点M(3,m),求使MN+MD的值最小时m的值;(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;(4)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.【解答】解:(1)由抛物线y=﹣x2+bx+c过点A(﹣1,0)及C(2,3)得,,解得,故抛物线为y=﹣x2+2x+3又设直线为y=kx+n过点A(﹣1,0)及C(2,3)得,解得故直线AC为y=x+1;(2)如图1,作N点关于直线x=3的对称点N′,则N′(6,3),由(1)得D(1,4),故直线DN′的函数关系式为y=﹣x+,当M(3,m)在直线DN′上时,MN+MD的值最小,则m=﹣×=;(3)由(1)、(2)得D(1,4),B(1,2),∵点E在直线AC上,设E(x,x+1),①如图2,当点E在线段AC上时,点F在点E上方,则F(x,x+3),∵F在抛物线上,∴x+3=﹣x2+2x+3,解得,x=0或x=1(舍去)∴E(0,1);②当点E在线段AC(或CA)延长线上时,点F在点E下方,则F(x,x﹣1)由F在抛物线上∴x﹣1=﹣x2+2x+3解得x=或x=∴E(,)或(,)综上,满足条件的点E的坐标为(0,1)、(,)或(,);(4)方法一:如图3,过点P作PQ⊥x轴交AC于点Q,交x轴于点H;过点C作CG⊥x轴于点G,设Q (x,x+1),则P(x,﹣x2+2x+3)∴PQ=(﹣x2+2x+3)﹣(x+1)=﹣x2+x+2又∵S△APC=S△APQ+S△CPQ=PQ•AG=(﹣x2+x+2)×3=﹣(x﹣)2+∴面积的最大值为.方法二:过点P作PQ⊥x轴交AC于点Q,交x轴于点H;过点C作CG⊥x轴于点G,如图3,设Q(x,x+1),则P(x,﹣x2+2x+3)又∵S△APC=S△APH+S直角梯形PHGC﹣S△AGC=(x+1)(﹣x2+2x+3)+(﹣x2+2x+3+3)(2﹣x)﹣×3×3=﹣x2+x+3=﹣(x﹣)2+∴△APC的面积的最大值为.11.(2014•赤峰)如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0),B(3,0)两点,与y轴交于点C(0,﹣3).(1)求该抛物线的解析式及顶点M坐标;(2)求△BCM面积与△ABC面积的比;(3)若P是x轴上一个动点,过P作射线PQ∥AC交抛物线于点Q,随着P点的运动,在抛物线上是否存在这样的点Q,使以A,P,Q,C为顶点的四边形为平行四边形?若存在,请求出Q点坐标;若不存在,请说明理由.【解答】方法一:解:(1)设抛物线解析式为y=a(x+1)(x﹣3),∵抛物线过点(0,﹣3),∴﹣3=a(0+1)(0﹣3),∴a=1,∴抛物线解析式为y=(x+1)(x﹣3)=x2﹣2x﹣3,∵y=x2﹣2x﹣3=(x﹣1)2﹣4,∴M(1,﹣4).(2)如图1,连接BC、BM、CM,作MD⊥x轴于D,∵S△BCM=S梯形OCMD+S△BMD﹣S△BOC=•(3+4)•1+•2×4﹣•3•3=+﹣=3S△ABC=•AB•OC=•4•3=6,∴S△BCM:S△ABC=3:6=1:2.(3)存在,理由如下:①如图2,当Q在x轴下方时,作QE⊥x轴于E,∵四边形ACQP为平行四边形,∴PQ平行且相等AC,∴△PEQ≌△AOC,∴EQ=OC=3,∴﹣3=x2﹣2x﹣3,解得x=2或x=0(与C点重合,舍去),∴Q(2,﹣3).②如图3,当Q在x轴上方时,作QF⊥x轴于F,∵四边形ACPQ为平行四边形,∴QP平行且相等AC,∴△PFQ≌△AOC,∴FQ=OC=3,∴3=x2﹣2x﹣3,解得x=1+或x=1﹣,∴Q(1+,3)或(1﹣,3).综上所述,Q点为(2,﹣3)或(1+,3)或(1﹣,3)方法二:(1)略.(2)连接BC、BM、CM,作MD⊥x轴于D,交BC于H,∵B(3,0),C(0,﹣3),∴l BC:y=x﹣3,当x=1时,y=﹣2,∴H(1,﹣2)∴S△BCM=(3﹣0)(﹣2+4)=3,∵S△ABC=AB×OC=×3×4=6,∴S△BCM:S△ABC=3:6=1:2,(3)∵PQ∥AC,∴当PQ=AC时,A、P、Q、C为顶点的四边形为平行四边形,即|Q Y|=|C Y|,设Q(t,t2﹣2t﹣3),∴|t2﹣2t﹣3|=3,①t2﹣2t﹣3=3,解得:t1=1+,t2=1﹣,②t2﹣2t﹣3=﹣3,解得:t1=0(舍),t2=2,综上所述,Q点为(2,﹣3)或(1+,3)或(1﹣,3).12.(2014•潍坊)如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于点A和点B,其中点A的坐标为(﹣2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.(1)求抛物线的解析式;(2)若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形ABFC的面积为17,若存在,求出点F的坐标;若不存在,请说明理由;(3)平行于DE的一条动直线l与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标.【解答】方法一:解:(1)∵抛物线y=ax2+bx+c(a≠0)过点C(0,4),∴c=4 ①.∵对称轴x=﹣=1,∴b=﹣2a ②.∵抛物线过点A(﹣2,0),∴0=4a﹣2b+c ③,由①②③解得,a=﹣,b=1,c=4,∴抛物线的解析式为y=﹣x2+x+4;(2)假设存在满足条件的点F,如图所示,连结BF、CF、OF,过点F作FH⊥x轴于点H,FG⊥y轴于点G.设点F的坐标为(t,﹣t2+t+4),其中0<t<4,则FH=﹣t2+t+4,FG=t,∴S△OBF=OB•FH=×4×(﹣t2+t+4)=﹣t2+2t+8,S△OFC=OC•FG=×4×t=2t,∴S四边形ABFC=S△AOC+S△OBF+S△OFC=4﹣t2+2t+8+2t=﹣t2+4t+12.令﹣t2+4t+12=17,即t2﹣4t+5=0,则△=(﹣4)2﹣4×5=﹣4<0,∴方程t2﹣4t+5=0无解,故不存在满足条件的点F;(3)设直线BC的解析式为y=kx+n(k≠0),∵B(4,0),C(0,4),∴,解得,∴直线BC的解析式为y=﹣x+4.由y=﹣x2+x+4=﹣(x﹣1)2+,∴顶点D(1,),又点E在直线BC上,则点E(1,3),于是DE=﹣3=.若以D、E、P、Q为顶点的四边形是平行四边形,因为DE∥PQ,只须DE=PQ,设点P的坐标是(m,﹣m+4),则点Q的坐标是(m,﹣m2+m+4).①当0<m<4时,PQ=(﹣m2+m+4)﹣(﹣m+4)=﹣m2+2m,由﹣m2+2m=,解得:m=1或3.当m=1时,线段PQ与DE重合,m=1舍去,∴m=3,P1(3,1).②当m<0或m>4时,PQ=(﹣m+4)﹣(﹣m2+m+4)=m2﹣2m,由m2﹣2m=,解得m=2±,经检验适合题意,此时P2(2+,2﹣),P3(2﹣,2+).综上所述,满足题意的点P有三个,分别是P1(3,1),P2(2+,2﹣),P3(2﹣,2+).方法二:(1)略.(2)∵B(4,0),C(0,4),∴l BC:y=﹣x+4,过F点作x轴垂线,交BC于H,设F(t,﹣t2+t+4),∴H(t,﹣t+4),∵S四边形ABFC=S△ABC+S△BCF=17,∴(4+2)×4+(﹣t2+t+4+t﹣4)×4=17,∴t2﹣4t+5=0,∴△=(﹣4)2﹣4×5<0,∴方程t2﹣4t+5=0无解,故不存在满足条件的点F.(3)∵DE∥PQ,∴当DE=PQ时,以D、E、P、Q为顶点的四边形是平行四边形,∵y=﹣x2+x+4,∴D(1,),∵l BC:y=﹣x+4,∴E(1,3),∴DE=﹣3=,设点F的坐标是(m,﹣m+4),则点Q的坐标是(m,﹣m2+m+4),∴|﹣m+4+m2﹣m﹣4|=,∴m2﹣2m=或m2﹣2m=﹣,∴m=1,m=3,m=2+,m=2﹣,经检验,当m=1时,线段PQ与DE重合,故舍去.∴P1(3,1),P2(2+,2﹣),P3(2﹣,2+).13.(2014•济宁)如图,抛物线y=x2+bx+c与x轴交于A(5,0)、B(﹣1,0)两点,过点A作直线AC⊥x轴,交直线y=2x于点C;(1)求该抛物线的解析式;(2)求点A关于直线y=2x的对称点A′的坐标,判定点A′是否在抛物线上,并说明理由;(3)点P是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.【解答】方法一:解:(1)∵y=x2+bx+c与x轴交于A(5,0)、B(﹣1,0)两点,∴,解得.∴抛物线的解析式为y=x2﹣x﹣.(2)如答图所示,过点A′作A′E⊥x轴于E,AA′与OC交于点D,∵点C在直线y=2x上,∴C(5,10)∵点A和A′关于直线y=2x对称,∴OC⊥AA′,A′D=AD.∵OA=5,AC=10,∴OC===.∵S△OAC=OC•AD=OA•AC,∴AD=.∴AA′=,在Rt△A′EA和Rt△OAC中,∵∠A′AE+∠A′AC=90°,∠ACD+∠A′AC=90°,∴∠A′AE=∠ACD.又∵∠A′EA=∠OAC=90°,∴Rt△A′EA∽Rt△OAC.∴,即.∴A′E=4,AE=8.∴OE=AE﹣OA=3.∴点A′的坐标为(﹣3,4),当x=﹣3时,y=×(﹣3)2+3﹣=4.所以,点A′在该抛物线上.(3)存在.理由:设直线CA′的解析式为y=kx+b,则,解得∴直线CA′的解析式为y=x+设点P的坐标为(x,x2﹣x﹣),则点M为(x,x+).∵PM∥AC,∴要使四边形PACM是平行四边形,只需PM=AC.又点M在点P的上方,∴(x+)﹣(x2﹣x﹣)=10.解得x1=2,x2=5(不合题意,舍去)当x=2时,y=﹣.∴当点P运动到(2,﹣)时,四边形PACM是平行四边形.方法二:(1)略.(2)设AA′与直线OC的交点为H,∵点A,点A′关于直线OC:y=2x对称,∴AA′⊥OC,K OC•K AA′=﹣1,∵K OC=2,∴K AA′=﹣,∵A(5,0),∴l AA′:y=﹣x+,l OC:y=2x,∴H(1,2),∵H为AA′的中点,∴⇒,∴A′X=﹣3,A′Y=4,∴A′(﹣3,4),当x=﹣3时,y=×(﹣3)2+3﹣=4,∴点A在抛物线上.(3)∵PM∥AC,要使四边形PACM是平行四边形,只需PM=AC,∵直线AC⊥x轴,∴C x=A x,∵A(5,0),∴C x=5,∵l OC:y=2x,∴C Y=10,∴C(5,10),∵A′(﹣3,4),∴l CA′:y=x+,∵M在线段CA′上,点M在点P的上方,∴设M(t,),∴P(t,t2﹣t﹣),∴﹣(t2﹣t﹣)=10,∴t1=2,t2=5(舍),∴P(2,﹣).14.(2014•东营)如图,直线y=2x+2与x轴交于点A,与y轴交于点B,把△AOB沿y轴翻折,点A落到点C,过点B的抛物线y=﹣x2+bx+c与直线BC交于点D(3,﹣4).(1)求直线BD和抛物线的解析式;(2)在第一象限内的抛物线上,是否存在一点M,作MN垂直于x轴,垂足为点N,使得以M、O、N为顶点的三角形与△BOC相似?若存在,求出点M的坐标;若不存在,请说明理由;(3)在直线BD上方的抛物线上有一动点P,过点P作PH垂直于x轴,交直线BD于点H,当四边形BOHP 是平行四边形时,试求动点P的坐标.。
抛物线与平行四边形教学设计

初中九年数学教学设计课题:抛物线与平行四边形教师导学:教师将26题代几综合题的常见考点带着学生梳理,提炼解题策略。
本节课目标导学:点动、线动、面动构成的问题称为动态题.近几年来中考26题多是二次函数与几何图形相结合的代几综合题。
(一)常见考点:(1)确定二次函数解析式(2)与动点有关的存在性问题(直角、等角、等腰三角形、直角三角形、等腰三角形全等三角形、相似三角形、特殊四边形等)(3)函数类最值问题(4)运动问题中特殊位置的数量和位置关系(大胆猜想)本节课主要解决与动点有关的平行四边形问题的研究方法和策略(二)解题策略:动点(线、面)→画出符合条件的静态图形→设出关键点坐标→由点坐标表示线段长→建立模型(方程)→解方程求解符合条件的点坐标→验证符合题意教学过程设计、如图,抛物线课后作业必做题1、已知抛物线的顶点为A(2,1),且经过原点O,与x轴的另一个交点为B,若点C在抛物线的对称轴上,点D在抛物线上,且以O,C,D,B四点为顶点的四边形为平行四边形,则D点的坐标为.2.如图,抛物线y=(x-1)(x-5)交x轴于A、B 两点,P 为顶点,四边形ABCP是平行四边形,则经过P、B、C三点且对称轴平行于y轴的抛物线的解析式为.第2题第3题3.如图,抛物线y=x2-2x-3与x轴分别交于A,B两点.(1)求A,B两点的坐标;(2)求抛物线顶点M关于x轴对称的点M′的坐标,并判断四边形AMBM′是何特殊平行四边形.(不要求说明理由)4.经过点A(-4,5)的抛物线y=-x2+bx+5与y轴交于点B.点M在抛物线的对称轴上,点N在抛物线上,且以A,B,M,N为顶点的四边形是平行四边形.则点N的坐标为.5.如图,在平面直角坐标系中,抛物线A(-1,0),B(3,0),C(0,-1)三点.(1)求该抛物线的表达式;(2)点Q在y轴上,点P在抛物线上,要使Q、P、A、B为顶点的四边形是平行四边形,求所有满足条件点P的坐标.选做题6.如图,抛物线y=x2+bx+c经过A(-2、0)B(2、4)两点,与x轴的另一交点为D,点P(x、y)是线段AB上的一个动点,过P点的直线PQ⊥x轴,与抛物线相交于点Q.(1)求b、c的值(2)求线段PQ长度的最大值(3)当PQ 的长度取最大值时,在抛物线上是否存在M 、N 两点(点M 的横坐标小于N 的横坐标),使得P 、D 、M 、N 为顶点的四边形是平行四边形?若存在,求出M 、N 的坐标;若不存在,请说明理由.7、如图,直线3+-=x y 与x 轴交于点C ,与y 轴交于点A ,点B 的坐标为(2,3),抛物线c bx x y ++-=2经过A,C 两点。
抛物线中动点问题讲义

文档根源为:从网络采集整理.word版本可编写.支持.第一讲抛物线中的动点问题一、利用动点(图形)地点进行分类,把运动问题切割成几个静态问题,而后运用转变的思想和方法将几何问题转变为函数和方程问题二、利用函数与方程的思想和方法将所解决图形的性质(或所求图形面积)直接转变为函数或方程。
一、平行四边形与抛物线【例】如图甲,在平面直角坐标系中,A、B的坐标分别为(4,0)、(0,3),抛物线y=x2+bx+c经过点B,且对称轴是直线x=﹣.1)求抛物线对应的函数分析式;2)将图甲中△ABO沿x轴向左平移到△DCE(如图乙),当四边形ABCD是菱形时,请说明点C和点D都在该抛物线上;3)在(2)中,若点M是抛物线上的一个动点(点M不与点C、D重合),经过点M作MN∥y轴交直线CD于N,设点M的横坐标为t,MN的长度为l,求l与t之间的函数分析式,并求当t为什么值时,以M、N、C、E为极点的四边形是平行四边形.变式操练【变式】如图,在平面直角坐标系中,已知Rt△AOB的两条直角边OA、OB分别在y轴和x轴上,而且OA、OB的长分别是方程x2﹣7x+12=0的两根(OA<OB),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点0运动;同时,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动,设点P、Q运动的时间为t秒.(1)求A、B两点的坐标.(2)求当t为什么值时,△APQ与△AOB相像,并直接写出此时点Q的坐标.(3)当t=2时,在座标平面内,能否存在点M,使以A、P、Q、M为极点的四边形是平行四边形?若存在,请直接写出M点的坐标;若不存在,请说明原因.【变式】如图,已知抛物线y=﹣x2+bx+c与向来线订交于A(﹣1,0),C(2,3)两点,与y轴交于点N.其极点为D.文档根源为:从网络采集整理.word版本可编写.支持.(1)抛物线及直线AC的函数关系式;(2)设点M(3,m),求使MN+MD的值最小时m的值;(3)若抛物线的对称轴与直线AC订交于点B,E为直线AC上的随意一点,过点E作EF∥BD 交抛物线于点F,以B,D,E,F为极点的四边形可否为平行四边形?若能,求点若不可以,请说明原因;E的坐标;(4)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.二、梯形与抛物线【例】已知,在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2.若以O为坐标原点,OA所在直线为x轴,成立如下图的平面直角坐标系,点B在第一象限内.将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.(1)求点C的坐标;2(2)若抛物线y=ax+bx(a≠0)经过C、A两点,求此抛物线的分析式;(3)若上述抛物线的对称轴与OB交于点D,点P为线段DB上一动点,过P作y轴的平行线,交抛物线于点M,问:能否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,恳求出此时点P的坐标;若不存在,请说明原因.变式操练【变式】如图,O为坐标原点,直线l绕着点A(0,2)旋转,与经过点C(0,1)的二次函数y=x2+h的图象交于不一样的两点P、Q.(1)求h的值;(2)经过操作、察看,算出△POQ的面积的最小值(不用说理);(3)过点P、C作直线,与x轴交于点B,试问:在直线l的旋转过程中,四边形AOBQ能否为梯形?假如,请说明原因;若不是,请指出四边形的形状.【变式】如图,在平面直角坐标系xOy中,矩形AOCD的极点A的坐标是(0,4),现有两动点P,Q,点P从点O出发沿线段OC(不包含端点O,C)以每秒2个单位长度的速度匀速向点C运动,点Q从点C出发沿线段CD(不包含端点C,D)以每秒1个单位长度的速度匀速向点D运动.点P,Q同时出发,同时停止,设运动时间为t(秒),当t=2(秒)时,PQ=2 .(1)求点D的坐标,并直接写出t的取值范围.(2)连结AQ并延伸交x轴于点E,把AE沿AD翻折交CD延伸线于点F,连结EF,则△AEF的面积S能否随t的变化而变化?若变化,求出 S与t的函数关系式;若不变化,求出S的值.(3)在(2)的条件下,t为什么值时,四边形APQF是梯形?三、等腰三角形、菱形与抛物线【例】在平面直角坐标系xOy中,一块含60°角的三角板作如图摆放,斜边AB在x轴上,直角极点C在y轴正半轴上,已知点A(﹣1,0).(1)请直接写出点B、C的坐标:B 、C ;并求经过A、B、C三点的抛物线解析式;(2)现有与上述三角板完整同样的三角板DEF(此中∠EDF=90°,∠DEF=60°),把极点E放在线段AB上(点E是不与A、B两点重合的动点),并使ED所在直线经过点C.此时,EF所在直线与(1)中的抛物线交于点M.①设AE=x,当x为什么值时,△OCE∽△OBC;②在①的条件下研究:抛物线的对称轴上能否存在点P使△PEM是等腰三角形?若存在,请写出点P的坐标;若不存在,请说明原因.变式操练【变式】如图,在平面直角坐标系中,直角三角形AOB的极点A、B分别落在座标轴上.O为原点,点A 的坐标为(6,0),点B的坐标为(0,8).动点M从点O出发.沿OA向终点A以文档根源为:从网络采集整理.word版本可编写.支持.每秒1个单位的速度运动,同时动点N从点A出发,沿AB向终点B以每秒个单位的速度运动.当一个动点抵达终点时,另一个动点也随之停止运动,设动点M、N运动的时间为t秒(t>0).(1)当t=3秒时.直接写出点N的坐标,并求出经过O、A、N三点的抛物线的分析式;(2)在此运动的过程中,△MNA的面积能否存在最大值?若存在,恳求出最大值;若不存在,请说明原因;(3)当t为什么值时,△MNA是一个等腰三角形?【变式】如图,直线l1经过点A(﹣1,0),直线l2经过点B(3,0),l1、l2均为与y轴交于点C(0,),抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.(1)求抛物线的函数表达式;(2)抛物线的对称轴挨次与x轴交于点D、与l2交于点E、与抛物线交于点F、与l1交于点G.求证:DE=EF=FG;(3)若l1⊥l2于y轴上的C点处,点P为抛物线上一动点,要使△PCG为等腰三角形,请写出切合条件的点P 的坐标,并简述原因.【变式】如图,在平面直角坐标系中,直角梯形OABC的边OC、OA分别与x轴、y轴重合,AB∥OC,∠AOC=90°,∠BCO=45°,BC=12 ,点C的坐标为(﹣18,0).(1)求点B的坐标;(2)若直线DE交梯形对角线BO于点D,交y轴于点E,且OE=4,OD=2BD,求直线DE的分析式;(3)若点P是(2)中直线DE上的一个动点,在座标平面内能否存在点Q,使以O、E、P、Q为极点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明原因.【变式】如图,已知抛物线经过原点O和x轴上一点A(4,0),抛物线极点为E,它的对称轴与x轴交于点D.直线y=﹣2x﹣1经过抛物线上一点B(﹣2,m)且与y轴交于点C,与抛物线的对称轴交于点F.(1)求m的值及该抛物线对应的分析式;(2)P(x,y)是抛物线上的一点,若S△ADP=S△ADC,求出所有切合条件的点P的坐标;(3)点Q是平面内随意一点,点M从点F出发,沿对称轴向上以每秒1个单位长度的速度匀速运动,设点M的运动时间为t秒,能否能使以 Q、A、E、M四点为极点的四边形是菱形?若能,请直接写出点M的运动时间t的值;若不可以,请说明原因.四、直角三角形与抛物线【例】如图,抛物线y=与x轴交于A、B两点(点A在点B的左边),与y轴交于点C.(1)求点A、B的坐标;(2)设D为已知抛物线的对称轴上的随意一点,当△ACD的面积等于△ACB的面积时,求点的坐标;(3)若直线l过点E(4,0),M为直线l上的动点,当以A、B、M为极点所作的直角三角形有且只有三个时,求直线l的分析式.【变式】如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直均分线和BC所在的直线成立平面直角坐标系,抛物线y=﹣x2+x+4经过A、B两点.文档根源为:从网络采集整理.word版本可编写.支持.(1)写出点A、点B的坐标;(2)若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA和抛物线于点E、M和点P,连结PA、PB.设直线l挪动的时间为t(0<t<4)秒,求四边形PBCA的面积S(面积单位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积;(3)在(2)的条件下,抛物线上能否存在一点P,使得△PAM是直角三角形?若存在,恳求出点P的坐标;若不存在,请说明原因.【变式】如图,极点为P(4,﹣4)的二次函数图象经过原点(0,0),点A在该图象上,OA交其对称轴l于点M,点M、N对于点P对称,连结AN、ON,(1)求该二次函数的关系式;(2)若点A在对称轴l右边的二次函数图象上运动时,请解答下边问题:①证明:∠ANM=∠ONM;②△ANO可否为直角三角形?假如能,恳求出全部切合条件的点A的坐标;假如不可以,请说明原因.【变式】如图,在平面直角坐标系中,直线y=x+2交x轴于点P,交y轴于点A.抛物线y=x2+bx+c的图象过点E(﹣1,0),并与直线订交于A、B两点.(1)求抛物线的分析式(关系式);(2)过点A作AC⊥AB交x轴于点C,求点C的坐标;(3)除点C外,在座标轴上能否存在点M,使得△MAB是直角三角形?若存在,恳求出点M的坐标;若不存在,请说明原因.五、相像三角形与抛物线2(1)求抛物线的分析式;(2)将直线OB向下平移m个单位长度后,获得的直线与抛物线只有一个公共点值及点D的坐标;D,求m的(3)如图2,若点N在抛物线上,且∠NBO=∠ABO,则在(2)的条件下,求出全部知足△POD∽△NOB的点P坐标(点P、O、D分别与点N、O、B对应).变式操练【变式】如图,已知抛物线y=ax2+bx+c(a≠0)的图象经过原点O,交x轴于点A,其极点B的坐标为(3,﹣).(1)求抛物线的函数分析式及点A的坐标;(2)在抛物线上求点P,使S△POA=2S△AOB;(3)在抛物线上能否存在点Q,使△AQO与△AOB相像?假如存在,恳求出Q点的坐标;假如不存在,请说明原因.【变式】如图,已知抛物线的方程C1:y=﹣(x+2)(x﹣m)(m>0)与x轴订交于点B、C,与y轴订交于点E,且点B在点C的左边.(1)若抛物线C1过点M(2,2),务实数m的值;(2)在(1)的条件下,求△BCE的面积;(3)在(1)条件下,在抛物线的对称轴上找一点H,使BH+EH最小,并求出点H的坐标;(4)在第四象限内,抛物线C1上能否存在点F,使得以点B、C、F为极点的三角形与△BCE相像?若存在,求m的值;若不存在,请说明原因.文档根源为:从网络采集整理.word版本可编写.支持.【变式】如图,已知二次函数的图象过点A(﹣4,3),B(4,4).(1)求二次函数的分析式:(2)求证:△ACB是直角三角形;(3)若点P在第二象限,且是抛物线上的一动点,过点P作PH垂直x轴于点H,能否存在以P、H、D为极点的三角形与△ABC相像?若存在,求出点P的坐标;若不存在,请说明原因.【变式】如图,直线AB交x轴于点B(4,0),交y轴于点A(0,4),直线DM⊥x轴正半轴于点M,交线段AB于点C,DM=6,连结DA,∠DAC=90°.(1)直接写出直线AB的分析式;(2)求点D的坐标;(3)若点P是线段MB上的动点,过点P作x轴的垂线,交AB于点F,交过O、D、B三点的抛物线于点E,连结CE.能否存在点P,使△BPF与△FCE相像?若存在,恳求出点P的坐标;若不存在,请说明原因.【变式】在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C.(1)求这个二次函数的关系分析式;(2)点P是直线AC上方的抛物线上一动点,能否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明原因;(3)在平面直角坐标系中,能否存在点Q,使△BCQ是以BC为腰的等腰直角三角形?若存在,直接写出点Q的坐标;若不存在,说明原因;(4)点Q是直线AC上方的抛物线上一动点,过点Q作QE垂直于x轴,垂足为E.能否存在点Q,使以点B、Q、E为极点的三角形与△AOC相像?若存在,直接写出点Q的坐标;若不存在,说明原因;(5)点M为抛物线上一动点,在x轴上能否存在点Q,使以A、C、M、Q为极点的四边形是平行四边形?若存在,直接写出点Q的坐标;若不存在,说明原因.六、抛物线中的翻折问题【例】如图,抛物线y=ax2+bx+2交x轴于A(﹣1,0),B(4,0)两点,交y轴于点C,与过点C且平行于x轴的直线交于另一点D,点P是抛物线上一动点.(1)求抛物线分析式及点D坐标;(2)点E在x轴上,若以A,E,D,P为极点的四边形是平行四边形,求此时点P的坐标;(3)过点P作直线CD的垂线,垂足为Q,若将△CPQ沿CP翻折,点Q的对应点为Q′.能否存在点P,使Q′恰巧落在x轴上?若存在,求出此时点P的坐标;若不存在,说明原因.变式操练【变式】如图,在平面直角坐标系中,二次函数点在原点的左边,B点的坐标为(3,0),与y抛物线上一动点.(1)求这个二次函数的表达式.y=x2+bx+c的图象与x轴交于A、B两点,A轴交于C (0,﹣3)点,点P是直线BC下方的(2)连结PO、PC,并把△POC沿CO翻折,获得四边形POP′C,那么能否存在点P,使四边形POP′C为菱形?若存在,恳求出此时点P的坐标;若不存在,请说明原因.(3)当点P运动到什么地点时,四边形ABPC的面积最大并求出此时P点的坐标和四边形ABPC的最大面积.。
抛物线中的平行四边形存在性问题

抛物线中的平行四边形存在性问题作者:娄霖林来源:《速读·下旬》2017年第03期抛物线中的平行四边形存在性问题是中考中常考题型,其解决办法的突破口在于寻找分类标准,分类标准寻找的恰当,可以使解的个数又快又准确,然后再画图,最后通过计算解决问题。
如果已知三个定点,则平行四边形的第四个顶点有三种情况,以已知三个定点为三角形的顶点,过每个点画对边的平行线,三条直线两两相交,产生3个交点。
如果已知两个定点,一般是把确定的一条线段按边或对角线分为两种情况,然后利用平行四边形的性质找到相等关系而解决问题。
下面通过几道中考例题具体说明抛物线中的平行四边形存在性的解题策略。
一、已知三个定点,一个动点,探究平行四边形的存在性例1.已知抛物线[y=-ax2+2ax+b]与x轴的一个交点为A(-1,0),与y轴的正半轴交于点C。
(1)直接写出抛物线的对称轴,及抛物线与x轴的另一个交点B的坐标。
(2)当点C在以AB为直径的⊙P上时,求抛物线的解析式。
(3)坐标平面内是否存在点M,使得以点M和(2)中抛物线上的三点A、B、C为顶点的四边形是平行四边形?若存在,请求出点M的坐标;若不存在,请说明理由。
解:(1)对称轴是直线:x=1,点B的坐标是(3,0)。
(2)[y=-33x2+233x+3]。
(3)存在。
理由:连接AC、BC,设点M的坐标为M(x,y)①当以AC或BC为对角线时,点M在x轴上方,此时CM∥AB,且CM=AB,AB=4∴|x|=4,[y=OC=3]。
∴点M的坐标为[M4,3]或[-4,3]。
②当以AB为对角线时,点M在x轴下方过M作MN⊥AB于N,则∠MNB=∠AOC=90°∵四边形AMBC是平行四边形,∴AC=MB,且AC∥MB∴∠CAO=∠MBN,∴△AOC≌△BNM,∴BN=AO=1,[MN=CO=3]∵OB=3,∴ON=3-1=2,∴点M的坐标为[M2,-3]综上所述,[M14,3],[M2-4,3],[M32,-3]点评:本题已知三个定点坐标的具体数值,如果没有规定由三点构成的三条线段中哪条为边或对角线,则三种情况都必须考虑。
抛物线中平行四边形形状的判定

抛物线中平行四边形形状的判定
抛物线中平行四边形形状的判定涉及数学中的几何含义。
它是一个经验的过程,由复杂的数学公式构成。
判断抛物线中平行四边形形状的关键是要理解相关概念和数学方程式,遵循确定的步骤。
首先,在确定抛物线中平行四边形形状的过程中,要先找到抛物线的两个顶点,并利用竪边中点绘制出抛物线上的第三个点。
这样就能确定抛物线的軓点形状。
接下来,要求出抛物线的解析式,通过调整抛物线上两个点坐标,确定它的系数值,从而得到抛物线的公式。
最后,需要进行验证,计算出抛物线上第三个点具体坐标值,主要是由竪边中点坐标计算出来的,和它的解析式相比较,如果该坐标值完全符合抛物线的解析式,那么就可以确定抛物线上的形状为”平行四边形“。
总之,确定抛物线中平行四边形形状是一个涉及数学公式和步骤的复杂过程,有许多变量和步骤需要精确运算和验证,但只要错都步进行耐心细致的工作,就能够确定抛物线上的平行四边形形状。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、(2011陕西)如图,二次函数x x y 3
1
322-=
的图象经过△AOB 的三个顶点,其中A (-1,m ),B (n ,n )。
(1)求点A 、B 的坐标;
(2)在坐标平面上找点C ,使以A 、O 、B 、C 为顶点的四边形是平行四边形。
①这样的点C 有几个?
②能否将抛物线x x y 3
1
322-=平移后经过A 、C 两点?若能,
求出平移后经过A 、C 两点的一条抛物线的解析式,若不能,
说明理由。
2.(2011广东)如图,抛物线14
17
452++-
=x y 与y 物线交于另一点B ,过点B 作BC ⊥x 轴,垂足为点C (3,(1)求直线AB 的函数关系式;
(2)动点P 在线段OC 点P 作PN ⊥x 轴,交直线AB 于点M ,交抛物线于点N . 为t 秒,MN 的长度为s 个单位,求s 与t 的函数关系式,围;
(3)设在(2)的条件下(不考虑点P 与点O ,点C CM ,BN ,当t 为何值时,四边形BCMN 为平行四边形?
问对于所求的t 值,平行四边形BCMN 由.
3.(2011兰州)如图所示,在平面直角坐标系X0Y 中,正方形OABC 的边长为2cm ,点A 、C 分别在y 轴的负半轴和x 轴的正半轴上,抛物线2
y ax bx c =++经过点A 、B 和D (4,23
-
). (1)求抛物线的表达式.
(2)如果点
P 由点A 出发沿AB 边以2cm/s 的速度向点C 运动,当其中一点到达终点时,
另一点也随之停止运动,设S=2PQ (2
cm ).
①试求出S 与运动时间t 之间的函数关系式,并写出t 的取值范围; ②当S 取
5
4
时,在抛物线上是否存在点R ,使得以点P 、B 、Q 、R 为顶点的四边形是平行四边形?如果存在,求出R 点的坐标;如果不存在,请说明理由.
(3)在抛物线的对称轴上求点M ,使得M 到D 、A 的距离之差最大,求出点M 的坐标. 4.(2011南宁)如图,在平面直角坐标系中,抛物线y =x 2
+mx +n 经过点A (3,0)、B (0,
-3),点P 是直线AB 上的动点,过点P 作x 轴的垂线交抛物线于点M ,设点P 的横坐标为t .
(1)分别求出直线AB 和这条抛物线的解析式.
(2)若点P 在第四象限,连接AM 、BM ,当线段PM 最长时,求△ABM 的面积.
(3)是否存在这样的点P ,使得以点P 、M 、B 、O 为顶点的四边形为平行四边形?若存在,请直接写出点P 的横坐标;若不存在,请说明理由.
5.(2009江西)如图,抛物线2
23y x x =-++与x 轴相交于A 、在点B 的左侧),与y 轴相交于点C ,顶点为D .
(1)直接写出A 、B 、C 三点的坐标和抛物线的对称轴;
(2)连接BC ,与抛物线的对称轴交于点E ,点P 为线段BC 动点,过点P 作PF DE ∥交抛物线于点F ,设点P 的横坐标为①用含m 的代数式表示线段PF 的长,并求出当m 为何值时,四边形PEDF 为平行四边形?
②设BCF △的面积为S ,求S 与m 的函数关系式.
6.如图,在平面直角坐标系中,已知抛物线经过点A(-4,0),B(0,-4),C (2,0)三点
(1)求抛物线的解析式
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S,求S关于m的函数关系式,并求出S的最大值
(3)若点P时抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能使点P,Q,B,O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标。
