抛物线中平行四边形问题精选课件
难点攻关 抛物线与平行四边形【含答案】

难点攻关 抛物线与平行四边形
近年中考试题中常常出现抛物线与平行四边形组合的压轴题,
1. 在平面直角坐标系xoy 中,点C ,B 的坐标分别为(-4,0),(0,2).四边形ABCO 是平行四边形,抛物线过A ,B ,C 三点,与x 轴交于另一点D .一动点P 以每秒1个单位长度的速度从B 点出发沿BA 向点A 运动,运动到点A 停止,同时一动点Q
从点D 出发,以每秒3个单位长度的速度沿DC 向点C 运动,与点P 同
时停止.
(1)求抛物线的解析式;
(2)若抛物线的对称轴与AB 交于点E ,与x 轴交于点F ,当点P 运动时间t
为何值时,四边形POQE 是等腰梯形?
(3)当t 为何值时,以P ,B ,O 为顶点的三角形与以点Q ,B ,O 为顶点的三角形相似? 解:(1)∵四边形ABCO 是平行四边形,∴OC=AB=4.
∴A(4,2),B(0,2),C(-4,0).
∵抛物线y=ax 2+bx+c 过点B(0,2),∴c=2.
由题意,有⎩⎨⎧16a−4b+2=0
16a+4b+2=2 解得: ⎪⎨⎪⎧a=-1
16
b=14
∴⎩⎪⎨⎪⎧a−b+c =025a+5b+c =0c =−52 解得 : ⎩⎨⎧a=12b=-2c=-52。
专题6二次函数与平行四边形存在性问题(解析版)

专题6 二次函数与平行四边形存在性问题以二次函数为载体的平行四边形存在性问题是中考的热点难点之一,其图形复杂,知识覆盖面广,综合性较强,对学生分析问题和解决问题的能力要求高.对这类题,常规解法是先画出平行四边形,再依据“平行四边形的一组对边平行且相等”或“平行四边形的对角线互相平分”来解决.由于先要画出草图,若考虑不周,很容易漏解.解决抛物线中的平行四边形存在性问题,常用的结论和方法有:线段中点坐标公式、平行四边形顶点坐标公式、画平行四边形.1. 平面直角坐标系中,点 A 的坐标是11(,)x y ,点B 的坐标是22(,)x y ,则线段AB 的中点坐标是1212(,)22x x y y ++. 2. 平行四边形ABCD 的顶点坐标分别为(,)A A x y 、(,)B B x y 、(,)C C x y 、(,)D D x y ,则A C B D x x x x +=+,A CB D y y y y +=+.3.已知不在同一直线上的三点A、B、C,在平面内找到一个点D,使以A、B、C、D为顶点的四边形是平行四边形,有三种情况:【例1】(2020•甘孜州)如图,在平面直角坐标系xOy中,直线y=kx+3分别交x轴、y轴于A,B两点,经过A,B两点的抛物线y=﹣x2+bx+c与x轴的正半轴相交于点C(1,0).(1)求抛物线的解析式;(2)若P为线段AB上一点,∠APO=∠ACB,求AP的长;(3)在(2)的条件下,设M是y轴上一点,试问:抛物线上是否存在点N,使得以A,P,M,N为顶点的四边形为平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.【分析】(1)利用待定系数法解决问题即可.(2)求出AB ,OA ,AC ,利用相似三角形的性质求解即可.(3)分两种情形:①P A 为平行四边形的边时,点M 的横坐标可以为±2,求出点M 的坐标即可解决问题.②当AP 为平行四边形的对角线时,点M ″的横坐标为﹣4,求出点M ″的坐标即可解决问题.【解析】(1)∵直线y =kx +3分别交y 轴于B ,令x =0,得到y =3,∴B (0,3)由题意抛物线经过B (0,3),C (1,0),∴{c =3−1+b +c =0, 解得,{b =−2c =3, ∴抛物线的解析式为y =﹣x 2﹣2x +3;(2)对于抛物线y =﹣x 2﹣2x +3,令y =0,解得x =﹣3或1,∴A (﹣3,0),∵B (0,3),C (1,0),∴OA =OB =3,OC =1,AB =3√2,∵∠APO =∠ACB ,∠P AO =∠CAB ,∴△P AO ∽△CAB ,∴AP AC =AO AB , ∴AP 4=3√2, ∴AP =2√2.(3)由(2)可知,P (﹣1,2),AP =2√2,①当AP 为平行四边形的边时,点N 的横坐标为2或﹣2,∴N (﹣2,3),N ′(2,﹣5),②当AP 为平行四边形的对角线时,点N ″的横坐标为﹣4,∴N ″(﹣4,﹣5),综上所述,满足条件的点N 的坐标为(﹣2,3)或(2,﹣5)或(﹣4,﹣5).【点评】本题考查二次函数综合题,考查了待定系数法,相似三角形的判定和性质,平行四边形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考压轴题.【例2】(2020•天水)如图所示,拋物线y =ax 2+bx +c (a ≠0)与x 轴交于A 、B 两点,与y 轴交于点C ,且点A 的坐标为A (﹣2,0),点C 的坐标为C (0,6),对称轴为直线x =1.点D 是抛物线上一个动点,设点D 的横坐标为m (1<m <4),连接AC ,BC ,DC ,DB .(1)求抛物线的函数表达式;(2)当△BCD 的面积等于△AOC 的面积的34时,求m 的值; (3)在(2)的条件下,若点M 是x 轴上一动点,点N 是抛物线上一动点,试判断是否存在这样的点M ,使得以点B ,D ,M ,N 为顶点的四边形是平行四边形.若存在,请直接写出点M 的坐标;若不存在,请说明理由.【分析】(1)由题意得出方程组,解方程组即可;(2)过点D 作DE ⊥x 轴于E ,交BC 于G ,过点C 作CF ⊥ED 交ED 的延长线于F ,求出点B 的坐标为(4,0),由待定系数法求出直线BC 的函数表达式为y =−32x +6,则点D 的坐标为(m ,−34m 2+32m +6),点G 的坐标为(m ,−32m +6),求出S △BCD =−32m 2+6m =92,解方程即可;(3)求出点D 的坐标为(3,154),分三种情况,①当DB 为对角线时,证出DN ∥x 轴,则点D 与点N关于直线x =1对称,得出N (﹣1,154)求出BM =4,即可得出答案;②当DM 为对角线时,由①得N (﹣1,154),DN =4,由平行四边形的性质得出DN =BM =4,进而得出答案; ③当DN 为对角线时,点D 与点N 的纵坐标互为相反数,N (1+√14,−154)或N (1−√14,−154),再分两种情况解答即可.【解析】(1)由题意得:{−b 2a =14a −2b +c =0c =6, 解得:{ a =−34b =32c =6, ∴抛物线的函数表达式为:y =−34x 2+32x +6; (2)过点D 作DE ⊥x 轴于E ,交BC 于G ,过点C 作CF ⊥ED 交ED 的延长线于F ,如图1所示: ∵点A 的坐标为(﹣2,0),点C 的坐标为(0,6),∴OA =2,OC =6,∴S △AOC =12OA •OC =12×2×6=6,∴S △BCD =34S △AOC =34×6=92,当y =0时,−34x 2+32x +6=0,解得:x 1=﹣2,x 2=4,∴点B 的坐标为(4,0),设直线BC 的函数表达式为:y =kx +n ,则{0=4k +n 6=n, 解得:{k =−32n =6, ∴直线BC 的函数表达式为:y =−32x +6,∵点D 的横坐标为m (1<m <4),∴点D 的坐标为:(m ,−34m 2+32m +6),点G 的坐标为:(m ,−32m +6),∴DG =−34m 2+32m +6﹣(−32m +6)=−34m 2+3m ,CF =m ,BE =4﹣m ,∴S △BCD =S △CDG +S △BDG =12DG •CF +12DG •BE =12DG ×(CF +BE )=12×(−34m 2+3m )×(m +4﹣m )=−32m 2+6m ,∴−32m 2+6m =92,解得:m 1=1(不合题意舍去),m 2=3,∴m 的值为3;(3)由(2)得:m =3,−34m 2+32m +6=−34×32+32×3+6=154, ∴点D 的坐标为:(3,154), 分三种情况讨论:①当DB 为对角线时,如图2所示:∵四边形BDNM 是平行四边形,∴DN ∥BM ,∴DN ∥x 轴,∴点D 与点N 关于直线x =1对称,∴N (﹣1,154),∴DN =3﹣(﹣1)=4,∴BM =4,∵B (4,0),∴M (8,0);②当DM 为对角线时,如图3所示:由①得:N (﹣1,154),DN =4,∵四边形BDNM 是平行四边形,∴DN =BM =4,∵B (4,0),∴M (0,0);③当DN 为对角线时,∵四边形BDNM 是平行四边形,∴DM =BN ,DM ∥BN ,∴∠DMB =∠MBN ,∴点D 与点N 的纵坐标互为相反数,∵点D (3,154),∴点N 的纵坐标为:−154, 将y =−154代入y =−34x 2+32x +6中, 得:−34x 2+32x +6=−154, 解得:x 1=1+√14,x 2=1−√14,当x =1+√14时,如图4所示:则N (1+√14,−154), 分别过点D 、N 作x 轴的垂线,垂足分别为E 、Q ,在Rt △DEM 和Rt △NQB 中,{DM =BN DE =NQ, ∴Rt △DEM ≌Rt △NQB (HL ),∴BQ =EM ,∵BQ =1+√14−4=√14−3,∴EM=√14−3,∵E(3,0),∴M(√14,0);当x=1−√14时,如图5所示:则N(1−√14,−15 4),同理得点M(−√14,0);综上所述,点M的坐标为(8,0)或(0,0)或(√14,0)或(−√14,0).【点评】本题是二次函数综合题目,考查了待定系数法求函数的解析式、坐标与图形性质、平行四边形的性质、全等三角形的判定与性质等知识;本题综合性强,有一定难度.【例3】(2020•青海)如图1(注:与图2完全相同)所示,抛物线y=−12x2+bx+c经过B、D两点,与x轴的另一个交点为A,与y轴相交于点C.(1)求抛物线的解析式.(2)设抛物线的顶点为M,求四边形ABMC的面积.(请在图1中探索)(3)设点Q在y轴上,点P在抛物线上.要使以点A、B、P、Q为顶点的四边形是平行四边形,求所有满足条件的点P的坐标.(请在图2中探索)【分析】(1)用待定系数法解答便可;(2)求出抛物线与坐标轴的交点A、C坐标及抛物线顶点M的坐标,再将四边形ABMC的面积分为三角形的面积的和,进行计算便可;(3)分两种情况:AB为平行四边形的边;AB为平行四边形的对角线.分别解答便可.【解析】(1)把B (3,0)和D (﹣2,−52)代入抛物线的解析式得, {−92+3b +c =0−2−2b +c =−52, 解得,{b =1c =32, ∴抛物线的解析式为:y =−12x 2+x +32;(2)令x =0,得y =−12x 2+x +32=32, ∴C(0,32),令y =0,得y =−12x 2+x +32=0, 解得,x =﹣1,或x =3,∴A (﹣1,0),∵y =−12x 2+x +32=−12(x −1)2+2, ∴M (1,2),∴S 四边形ABMC =S △AOC +S △COM +S △MOB=12OA ⋅OC +12OC ⋅x M +12OB ⋅y M=12×1×32+12×32×1+12×3×2=92;(3)设Q (0,n ),①当AB 为平行四边形的边时,有AB ∥PQ ,AB =PQ , a ).P 点在Q 点左边时,则P (﹣4,n ),把P (﹣4,n )代入y =−12x 2+x +32,得n =−212,∴P (﹣4,−212); ②当AB 为平行四边形的边时,有AB ∥PQ ,AB =PQ , 当P 点在Q 点右边时,则P (4,n ), 把P (4,n )代入y =−12x 2+x +32,得 n =−52, ∴P (4,−52);③当AB 为平行四边形的对角线时,如图2,AB 与PQ 交于点E , 则E (1,0), ∵PE =QE , ∴P (2,﹣n ),把P (2,﹣n )代入y =−12x 2+x +32,得 ﹣n =32, ∴n =−32, ∴P (2,32).综上,满足条件的P 点坐标为:(﹣4,−212)或(4,−52)或(2,32).【点评】本题是二次函数的综合题,主要考查了待定系数法,二次函数的图象与性质,四边形的面积计算,平行四边形的性质,第(2)题关键是把四边形分割成三角形进行解答,第(3)题关键是分情况讨论.【例4】(2020•玉林)如图,已知抛物线:y 1=﹣x 2﹣2x +3与x 轴交于A ,B 两点(A 在B 的左侧),与y 轴交于点C .(1)直接写出点A ,B ,C 的坐标;(2)将抛物线y1经过向右与向下平移,使得到的抛物线y2与x轴交于B,B'两点(B'在B的右侧),顶点D的对应点为点D',若∠BD'B'=90°,求点B'的坐标及抛物线y2的解析式;(3)在(2)的条件下,若点Q在x轴上,则在抛物线y1或y2上是否存在点P,使以B′,C,Q,P 为顶点的四边形是平行四边形?如果存在,求出所有符合条件的点P的坐标;如果不存在,请说明理由.【分析】(1)令x=0或y1=0,解方程可得结论.(2)设平移后的抛物线的解析式为y2=﹣(x﹣a)2+b,如图1中,过点D′作D′H⊥OB′于H.,连接BD′,B′D′.构建方程组解决问题即可.(3)观察图象可知,当点P的纵坐标为3或﹣3时,存在满足条件的平行四边形.分别令y1和y2等于3或﹣3,解方程即可解决问题.【解析】(1)对于y1=﹣x2﹣2x+3,令y1=0,得到﹣x2﹣2x+3=0,解得x=﹣3或1,∴A(﹣3,0),B(1,0),令x=0,得到y1=3,∴C(0,3).(2)设平移后的抛物线的解析式为y2=﹣(x﹣a)2+b,如图1中,过点D′作D′H⊥OB′于H,连接BD′.∵D′是抛物线的顶点,∴D′B=D′B′,D′(a,b),∵∠BD′B′=90°,D′H⊥BB′,∴BH=HB′,∴D′H=BH=HB′=b,∴a=1+b,又∵y2=﹣(x﹣a)2+b,经过B(1,0),∴b=(1﹣a)2,解得a=2或1(不合题意舍弃),b=1,∴B′(3,0),y2=﹣(x﹣2)2+1=﹣x2+4x﹣3.(3)如图2中,观察图象可知,当点P的纵坐标为3或﹣3时,存在满足条件的平行四边形.对于y1=﹣x2﹣2x+3,令y1=3,x2+2x=0,解得x=0或﹣2,可得P1(﹣2,3),令y1=﹣3,则x2+2x﹣6=0,解得x=﹣1±√7,可得P2(﹣1−√7,﹣3),P3(﹣1+√7,﹣3),对于y2=﹣x2+4x﹣3,令y2=3,方程无解,令y2=﹣3,则x2﹣4x=0,解得x=0或4,可得P4(0,﹣3),P5(4,﹣3),综上所述,满足条件的点P的坐标为(﹣2,3)或(﹣1−√7,﹣3)或(﹣1+√7,﹣3)或(0,﹣3)或(4,﹣3).【点评】本题属于二次函数综合题,考查了二次函数的性质,平行四边形的判定和性质,等腰直角三角形的性质等知识,解题的关键是学会利用参数构建方程组解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.【例5】(2020•绵阳)如图,抛物线过点A (0,1)和C ,顶点为D ,直线AC 与抛物线的对称轴BD 的交点为B (√3,0),平行于y 轴的直线EF 与抛物线交于点E ,与直线AC 交于点F ,点F 的横坐标为4√33,四边形BDEF 为平行四边形.(1)求点F 的坐标及抛物线的解析式;(2)若点P 为抛物线上的动点,且在直线AC 上方,当△P AB 面积最大时,求点P 的坐标及△P AB 面积的最大值;(3)在抛物线的对称轴上取一点Q ,同时在抛物线上取一点R ,使以AC 为一边且以A ,C ,Q ,R 为顶点的四边形为平行四边形,求点Q 和点R 的坐标.【分析】(1)由待定系数法求出直线AB 的解析式为y =−√33x +1,求出F 点的坐标,由平行四边形的性质得出﹣3a +1=163a ﹣8a +1﹣(−13),求出a 的值,则可得出答案; (2)设P (n ,﹣n 2+2√3n +1),作PP '⊥x 轴交AC 于点P ',则P '(n ,−√33n +1),得出PP '=﹣n 2+73√3n ,由二次函数的性质可得出答案;(3)联立直线AC 和抛物线解析式求出C (73√3,−43),设Q (√3,m ),分两种情况:①当AQ 为对角线时,②当AR 为对角线时,分别求出点Q 和R 的坐标即可. 【解析】(1)设抛物线的解析式为y =ax 2+bx +c (a ≠0), ∵A (0,1),B (√3,0), 设直线AB 的解析式为y =kx +m , ∴{√3k +m =0m =1,解得{k =−√33m =1,∴直线AB 的解析式为y =−√33x +1,∵点F 的横坐标为4√33,∴F 点纵坐标为−√33×4√33+1=−13, ∴F 点的坐标为(43√3,−13), 又∵点A 在抛物线上, ∴c =1,对称轴为:x =−b2a =√3, ∴b =﹣2√3a ,∴解析式化为:y =ax 2﹣2√3ax +1, ∵四边形DBFE 为平行四边形. ∴BD =EF , ∴﹣3a +1=163a ﹣8a +1﹣(−13), 解得a =﹣1,∴抛物线的解析式为y =﹣x 2+2√3x +1;(2)设P (n ,﹣n 2+2√3n +1),作PP '⊥x 轴交AC 于点P ',则P '(n ,−√33n +1), ∴PP '=﹣n 2+73√3n ,S △ABP =12OB •PP '=−√32n 2+72n =−√32(n −76√3)2+4924√3, ∴当n =76√3时,△ABP 的面积最大为4924√3,此时P (76√3,4712). (3)∵{y =−√33x +1y =−x 2+2√3x +1,∴x =0或x =73√3, ∴C (73√3,−43), 设Q (√3,m ), ①当AQ 为对角线时, ∴R (−43√3,m +73),∵R 在抛物线y =−(x −√3)2+4上, ∴m +73=−(−43√3−√3)2+4,解得m =−443,∴Q (√3,−443),R (−43√3,−373); ②当AR 为对角线时, ∴R (103√3,m −73), ∵R 在抛物线y =−(x −√3)2+4上, ∴m −73=−(103√3−√3)2+4, 解得m =﹣10, ∴Q (√3,﹣10),R (103√3,−373).综上所述,Q (√3,−443),R (−43√3,−373);或Q (√3,﹣10),R (103√3,−373).【点评】本题是二次函数综合题,考查了待定系数法,二次函数的性质,二次函数图象上点的坐标特征,平行四边形的性质等知识,熟练掌握二次函数的性质及方程思想,分类讨论思想是解题的关键. 【例6】(2020•雅安)已知二次函数y =ax 2+2x +c (a ≠0)的图象与x 轴交于A 、B (1,0)两点,与y 轴交于点C (0,﹣3),(1)求二次函数的表达式及A 点坐标;(2)D 是二次函数图象上位于第三象限内的点,求点D 到直线AC 的距离取得最大值时点D 的坐标; (3)M 是二次函数图象对称轴上的点,在二次函数图象上是否存在点N ,使以M 、N 、B 、O 为顶点的四边形是平行四边形?若有,请写出点N 的坐标(不写求解过程).【分析】(1)利用待定系数法解决问题即可.(2)如图1中连接AD ,CD .由题意点D 到直线AC 的距离取得最大,推出此时△DAC 的面积最大.过点D 作x 轴的垂线交AC 于点G ,设点D 的坐标为(x ,x 2+2x ﹣3),则G (x ,﹣x ﹣3),推出DG =﹣x ﹣3﹣(x 2+2x ﹣3)=﹣x ﹣3﹣x 2﹣2x +3=﹣x 2﹣3x ,利用二次函数的性质求解即可. (3)分两种情形:OB 是平行四边形的边或对角线分别求解即可. 【解析】(1)把B (1,0),C (0,﹣3)代入y =ax 2+2x +c 则有{c =−3a +2+c =0,解得{a =1c =−3,∴二次函数的解析式为y =x 2+2x ﹣3,令y =0,得到x 2+2x ﹣3=0,解得x =﹣3或1, ∴A (﹣3,0).(2)如图1中连接AD ,CD . ∵点D 到直线AC 的距离取得最大, ∴此时△DAC 的面积最大, 设直线AC 解析式为:y =kx +b , ∵A (﹣3,0),C (0,﹣3), ∴{b =−3−3k +b =0, 解得,{k =−1b =−3,∴直线AC 的解析式为y =﹣x ﹣3,过点D 作x 轴的垂线交AC 于点G ,设点D 的坐标为(x ,x 2+2x ﹣3),则G(x,﹣x﹣3),∵点D在第三象限,∴DG=﹣x﹣3﹣(x2+2x﹣3)=﹣x﹣3﹣x2﹣2x+3=﹣x2﹣3x,∴S△ACD=12•DG•OA=12(﹣x2﹣3x)×3=−32x2−92x=−32(x+32)2+278,∴当x=−32时,S最大=278,点D(−32,−154),∴点D到直线AC的距离取得最大时,D(−32,−154).(3)如图2中,当OB是平行四边形的边时,OB=MN=1,OB∥MN,可得N(﹣2,﹣3)或N′(0,﹣3),当OB为对角线时,点N″的横坐标为2,x=2时,y=4+4﹣3=5,∴N″(2,5).综上所述,满足条件的点N的坐标为(﹣2,﹣3)或(0,﹣3)或(2,5).【点评】本题考查待定系数法求二次函数解析式、二次函数的性质、二次函数的最值,解答本题的关键是明确题意,利用二次函数的性质和数形结合的思想解答.1.(2020•齐齐哈尔)综合与探究在平面直角坐标系中,抛物线y=12x2+bx+c经过点A(﹣4,0),点M为抛物线的顶点,点B在y轴上,且OA=OB,直线AB与抛物线在第一象限交于点C(2,6),如图①.(1)求抛物线的解析式;(2)直线AB的函数解析式为y=x+4,点M的坐标为(﹣2,﹣2),cos∠ABO=√22;连接OC,若过点O的直线交线段AC于点P,将△AOC的面积分成1:2的两部分,则点P的坐标为(﹣2,2)或(0,4);(3)在y轴上找一点Q,使得△AMQ的周长最小.具体作法如图②,作点A关于y轴的对称点A',连接MA'交y轴于点Q,连接AM、AQ,此时△AMQ的周长最小.请求出点Q的坐标;(4)在坐标平面内是否存在点N,使以点A、O、C、N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.【分析】(1)将点A 、C 的坐标代入抛物线表达式即可求解;(2)点A (﹣4,0),OB =OA =4,故点B (0,4),即可求出AB 的表达式;OP 将△AOC 的面积分成1:2的两部分,则AP =13AC 或23AC ,即可求解;(3)△AMQ 的周长=AM +AQ +MQ =AM +A ′M 最小,即可求解; (4)分AC 是边、AC 是对角线两种情况,分别求解即可.【解析】(1)将点A 、C 的坐标代入抛物线表达式得:{12×16−4b +c =012×4+2b +c =6,解得{b =2c =0,故抛物线的表达式为:y =12x 2+2x ;(2)点A (﹣4,0),OB =OA =4,故点B (0,4), 设直线AB 的解析式为y =kx +4, 将点A 坐标代入得,﹣4k +4=0, ∴k =1.∴直线AB 的表达式为:y =x +4; 则∠ABO =45°,故cos ∠ABO =√22;对于y =12x 2+2x ,函数的对称轴为x =﹣2,故点M (﹣2,﹣2); OP 将△AOC 的面积分成1:2的两部分,则AP =13AC 或23AC ,则y P y C=13或23,即y P 6=13或23,解得:y P =2或4,故点P (﹣2,2)或(0,4); 故答案为:y =x +4;(﹣2,﹣2);√22;(﹣2,2)或(0,4);(3)△AMQ 的周长=AM +AQ +MQ =AM +A ′M 最小, 点A ′(4,0),设直线A ′M 的表达式为:y =kx +b ,则{4k +b =0−2k +b =−2,解得{k =13b =−43, 故直线A ′M 的表达式为:y =13x −43,令x=0,则y=−43,故点Q(0,−43);(4)存在,理由:设点N(m,n),而点A、C、O的坐标分别为(﹣4,0)、(2,6)、(0,0),①当AC是边时,点A向右平移6个单位向上平移6个单位得到点C,同样点O(N)向右平移6个单位向上平移6个单位得到点N(O),即0±6=m,0±6=n,解得:m=n=±6,故点N(6,6)或(﹣6,﹣6);②当AC是对角线时,由中点公式得:﹣4+2=m+0,6+0=n+0,解得:m=﹣2,n=6,故点N(﹣2,6);综上,点N的坐标为(6,6)或(﹣6,﹣6)或(﹣2,6).【点评】本题考查的是二次函数综合运用,涉及到一次函数的性质、平行四边形的性质、图形的平移、面积的计算等,其中(4),要注意分类求解,避免遗漏.2.(2020•平顶山二模)如图,已知二次函数y=−38x2+bx+c的图象与x轴交于点A、C,与y轴交于点B,直线y=34x+3经过A、B两点.(1)求b、c的值.(2)若点P是直线AB上方抛物线上的一动点,过点P作PF⊥x轴于点F,交直线AB于点D,求线段PD的最大值.(3)在(2)的结论下,连接CD,点Q是抛物线对称轴上的一动点,在抛物线上是否存在点G,使得以C、D、G、Q为顶点的四边形是平行四边形,若存在,请直接写出点G的坐标;若不存在,请说明理由.【分析】(1)由直线AB 的解析式可求出点A ,B 的坐标,将A ,B 两点的坐标代入y =−38x 2+bx +c 可得出答案;(2)设点P (m ,−38m 2−34m +3),则D (m ,34m +3),可得出PD =−38m 2−32m ,由二次函数的性质可得出答案;(3)分类讨论,一是当CD 为平行四边形对角线时,二是当CD 为平行四边形一边时,利用中点坐标公式及平移规律即可求出点G 的坐标.【解析】(1)∵直线y =34x +3经过A 、B 两点. ∴当x =0时,y =3,当y =0时,x =﹣4,∴直线y =34x +3与坐标轴的交点坐标为A (﹣4,0),B (0,3).分别将x =0,y =3,x =﹣4,y =0代入y =−38x 2+bx +c 得,{c =30=−38×(−4)2−4b +c , 解得,b =−34,c =3,(2)由(1)得y =−38x 2−34x +3,设点P (m ,−38m 2−34m +3),则D (m ,34m +3),∴PD =−38m 2−34m +3−(34m +3)=−38m 2−32m =−38(m +2)2+32, ∴当m =﹣2时,PD 最大,最大值是32.(3)存在点G ,使得以C 、D 、G 、Q 为顶点的四边形是平行四边形,G 点的坐标为(1,158)或(3,−218)或(−5,−218); ∵y =−38x 2−34x +3, ∴y =0时,x =﹣4或x =2, ∴C (2,0),由(2)可知D (﹣2,32),抛物线的对称轴为x =﹣1,设G (n ,−38n 2−34n +3),Q (﹣1,p ),CD 与y 轴交于点E ,E 为CD 的中点, ①当CD 为对角线时, n +(﹣1)=0, ∴n =1, 此时G (1,158).②当CD 为边时,若点G 在点Q 上边,则n +4=﹣1,则n =﹣5,此时点G 的坐标为(﹣5,−218). 若点G 在点Q 上边,则﹣1+4=n ,则n =3,此时点G 的坐标为(3,−218).综合以上可得使得以C 、D 、G 、Q 为顶点的四边形是平行四边形的G 点的坐标为(1,158)或(3,−218)或(−5,−218);【点评】本题是二次函数综合题,考查了二次函数的有关性质、一次函数的性质、平行四边形的判定和性质,熟练掌握二次函数的性质是解题的关键.3.(2020•菏泽)如图,抛物线y =ax 2+bx ﹣6与x 轴相交于A ,B 两点,与y 轴相交于点C ,OA =2,OB =4,直线l 是抛物线的对称轴,在直线l 右侧的抛物线上有一动点D ,连接AD ,BD ,BC ,CD . (1)求抛物线的函数表达式;(2)若点D 在x 轴的下方,当△BCD 的面积是92时,求△ABD 的面积;(3)在(2)的条件下,点M 是x 轴上一点,点N 是抛物线上一动点,是否存在点N ,使得以点B ,D ,M ,N 为顶点,以BD 为一边的四边形是平行四边形,若存在,求出点N 的坐标;若不存在,请说明理由.【分析】(1)根据OA =2,OB =4确定点A 和B 的坐标,代入抛物线的解析式列方程组解出即可; (2)如图1,过D 作DG ⊥x 轴于G ,交BC 于H ,利用待定系数法求直线BC 的解析式,设D (x ,34x 2−32x﹣6),则H (x ,32x ﹣6),表示DH 的长,根据△BCD 的面积是92,列方程可得x 的值,因为D 在对称轴的右侧,所以x =1不符合题意,舍去,利用三角形面积公式可得结论; (3)分两种情况:N 在x 轴的上方和下方,根据y =±154确定N 的坐标,并正确画图. 【解析】(1)∵OA =2,OB =4, ∴A (﹣2,0),B (4,0),把A (﹣2,0),B (4,0)代入抛物线y =ax 2+bx ﹣6中得:{4a −2b −6=016a +4b −6=0,∴抛物线的解析式为:y =34x 2−32x ﹣6;(2)如图1,过D 作DG ⊥x 轴于G ,交BC 于H ,当x =0时,y =﹣6, ∴C (0,﹣6),设BC 的解析式为:y =kx +n ,则{n =−64k +n =0,解得:{k =32n =−6, ∴BC 的解析式为:y =32x ﹣6,设D (x ,34x 2−32x ﹣6),则H (x ,32x ﹣6),∴DH =32x ﹣6﹣(34x 2−32x ﹣6)=−34x 2+3x ,∵△BCD 的面积是92,∴12DH ⋅OB =92,∴12×4×(−34x 2+3x)=92,解得:x =1或3,∵点D 在直线l 右侧的抛物线上, ∴D (3,−154),∴△ABD 的面积=12AB ⋅DG =12×6×154=454;(3)分两种情况:①如图2,N 在x 轴的上方时,四边形MNBD 是平行四边形,∵B (4,0),D (3,−154),且M 在x 轴上, ∴N 的纵坐标为154,当y =154时,即34x 2−32x ﹣6=154,解得:x =1+√14或1−√14, ∴N (1−√14,154)或(1+√14,154);②如图3,点N 在x 轴的下方时,四边形BDNM 是平行四边形,此时M 与O 重合,∴N(﹣1,−15 4);综上,点N的坐标为:(1−√14,154)或(1+√14,154)或(﹣1,−154).【点评】此题主要考查二次函数的综合问题,会求函数与坐标轴的交点,会利用待定系数法求函数解析式,会利用数形结合的思想解决平行四边形的问题,并结合方程思想解决问题.4.(2020•东莞市校级一模)已知,抛物线y=x2+bx+c与x轴交点为A(﹣1,0)和点B,与y轴交点为C (0,﹣3),直线L:y=kx﹣1与抛物线的交点为点A和点D.(1)求抛物线和直线L的解析式;(2)如图,点M为抛物线上一动点(不与A、D重合),当点M在直线L下方时,过点M作MN∥x轴交L于点N,求MN的最大值;(3)点M为抛物线上一动点(不与A、D重合),M'为直线AD上一动点,是否存在点M,使得以C、D、M、M′为顶点的四边形是平行四边形?如果存在,请直接写出点M的坐标,如果不存在,请说明理由.【分析】(1)用待定系数法即可求解;(2)设点M的坐标为(m,m2﹣2m﹣3),则点N(﹣m2+2m+2,m2﹣2m﹣3),则MN=﹣m2+m+2,进而求解;(3)分CD 为边、CD 为对角线两种情况,利用图象平移和中点公式求解即可. 【解析】(1)将点A 、C 的坐标代入抛物线表达式得{1−b +c =0c =−3,解得:{b =−2c =−3,故抛物线的表达式为:y =x 2﹣2x ﹣3①,将点A 的坐标代入直线L 的表达式得:0=﹣k ﹣1,解得:k =﹣1, 故直线L 的表达式为:y =﹣x ﹣1②;(2)设点M 的坐标为(m ,m 2﹣2m ﹣3), 点N 的纵坐标与点M 的纵坐标相同,将点N 的纵坐标代入y =﹣x ﹣1得:m 2﹣2m ﹣3=﹣x ﹣1, 解得:x =﹣m 2+2m +2,故点N (﹣m 2+2m +2,m 2﹣2m ﹣3), 则MN =﹣m 2+2m +2﹣m =﹣m 2+m +2,∵﹣1<0,故MN 有最大值,当m =−b2a =12时,MN 的最大值为94;(3)设点M (m ,n ),则n =m 2﹣2m ﹣3③,点M ′(s ,﹣s ﹣1), ①当CD 为边时,点C 向右平移2个单位得到D ,同样点M (M ′)向右平移2个单位得到M ′(M ), 即m ±2=s 且n =﹣s ﹣1④,联立③④并解得:m =0(舍去)或1或1±√172, 故点M 的坐标为(1,﹣4)或(1+√172,1−√172)或(1−√172,1+√172); ②当CD 为对角线时,由中点公式得:12(0+2)=12(m +s )且12(﹣3﹣3)=12(n ﹣s ﹣1)⑤,联立③⑤并解得:m =0(舍去)或﹣1,故点M (1,﹣4); 综上,点M 的坐标为(1,﹣4)或(1+√172,1−√172)或(1−√172,1+√172). 【点评】本题考查的是二次函数综合运用,涉及到一次函数的性质、平行四边形的性质等,其中(3),要注意分类求解,避免遗漏.【题组二】5.(2020•雁塔区校级二模)已知抛物线L :y =x 2+bx +c 经过点A (﹣1,0)和(1,﹣2)两点,抛物线L 关于原点O 的对称的为抛物线L ′,点A 的对应点为点A ′. (1)求抛物线L 和L ′的表达式;(2)是否在抛物线L 上存在一点P ,抛物线L ′上存在一点Q ,使得以AA ′为边,且以A 、A ′、P 、Q 为顶点的四边形是平行四边形?若存在,求出P 点坐标;若不存在,请说明理由.【分析】(1)利用待定系数法可求抛物线L 解析式,由中心对称的性质可求抛物线L ′的表达式; (2)分两种情况讨论,由平行四边形的性质可求解.【解析】(1)∵抛物线L :y =x 2+bx +c 经过点A (﹣1,0)和(1,﹣2)两点, ∴{0=1−b +c −2=1+b +c , 解得:{b =−1c =−2,∴抛物线L 的解析式为:y =x 2﹣x ﹣2, ∵y =x 2﹣x ﹣2=(x −12)2−94, ∴顶点坐标为(12,−94),∵抛物线L 关于原点O 的对称的为抛物线L ′, ∴抛物线L ′的解析式为:y =﹣(x +12)2+94; (2)∵点A 关于原点O 对应点为点A ′, ∴点A '(1,0), ∴AA '=2,∵以AA ′为边,且以A 、A ′、P 、Q 为顶点的四边形是平行四边形, ∴PQ =AA '=2,PQ ∥AA ', 设点P (x ,x 2﹣x ﹣2), 当点P 在点Q 的左侧, ∴点Q 的横坐标为x +2, ∴x 2﹣x ﹣2=﹣(x +2+12)2+94, ∴x =﹣1,∴点P (﹣1,0)(不合题意舍去);当点P在点Q的右侧,∴点Q的横坐标为x﹣2,∴x2﹣x﹣2=﹣(x﹣2+12)2+94,∴x1=√2+1,x2=−√2+1,∴点P1(√2+1,√2),P2(−√2+1,−√2).【点评】本题是二次函数综合题,考查了二次函数的性质,中心对称的性质,平行四边形的性质,灵活运用这些性质解决问题是本题的关键.6.(2020•怀化)如图所示,抛物线y=x2﹣2x﹣3与x轴相交于A、B两点,与y轴相交于点C,点M为抛物线的顶点.(1)求点C及顶点M的坐标.(2)若点N是第四象限内抛物线上的一个动点,连接BN、CN,求△BCN面积的最大值及此时点N的坐标.(3)若点D是抛物线对称轴上的动点,点G是抛物线上的动点,是否存在以点B、C、D、G为顶点的四边形是平行四边形.若存在,求出点G的坐标;若不存在,试说明理由.(4)直线CM交x轴于点E,若点P是线段EM上的一个动点,是否存在以点P、E、O为顶点的三角形与△ABC相似.若存在,求出点P的坐标;若不存在,请说明理由.【分析】(1)令抛物线解析式中x=0即可求出C点坐标,写出抛物线顶点式,即可求出顶点M坐标;(2)过N点作x轴的垂线交直线BC于Q点,设N(n,n2﹣2n﹣3),求出BC解析式,进而得到Q点坐标,最后根据S△BCN=S△NQC+S△NQB即可求解;(3)设D点坐标为(1,t),G点坐标为(m,m2﹣2m﹣3),然后分成①DG是对角线;②DB是对角线;③DC是对角线时三种情况进行讨论即可求解;(4)连接AC ,由CE =CB 可知∠EBC =∠E ,求出MC 的解析式,设P (x ,﹣x ﹣3),然后根据△PEO 相似△ABC ,分成EO BA=EP BC和EO BC=EP BA讨论即可求解.【解析】(1)令y =x 2﹣2x ﹣3中x =0,此时y =﹣3, 故C 点坐标为(0,﹣3), 又∵y =x 2﹣2x ﹣3=(x ﹣1)2﹣4, ∴抛物线的顶点M 的坐标为(1,﹣4);(2)过N 点作x 轴的垂线交直线BC 于Q 点,连接BN ,CN ,如图1所示: 令y =x 2﹣2x ﹣3=0, 解得:x =3或x =﹣1, ∴B (3,0),A (﹣1,0), 设直线BC 的解析式为:y =ax +b ,将C (0,﹣3),B (3,0)代入直线BC 的解析式得:{−3=b 0=3a +b ,解得:{a =1b =−3,∴直线BC 的解析式为:y =x ﹣3,设N 点坐标为(n ,n 2﹣2n ﹣3),故Q 点坐标为(n ,n ﹣3),其中0<n <3,则S △BCN =S △NQC +S △NQB =12⋅QN ⋅(x Q −x C )+12⋅QN ⋅(x B −x Q )=12⋅QN ⋅(x Q −x C +x B −x Q )=12⋅QN ⋅(x B −x C ),(其中x Q ,x C ,x B 分别表示Q ,C ,B 三点的横坐标),且QN =(n ﹣3)﹣(n 2﹣2n ﹣3)=﹣n 2+3n ,x B ﹣x C =3,故S △BCN =12⋅(−n 2+3n)⋅3=−32n 2+92n =−32(n −32)2+278,其中0<n <3, 当n =32时,S △BCN 有最大值为278,此时点N 的坐标为(32,−154),(3)设D 点坐标为(1,t ),G 点坐标为(m ,m 2﹣2m ﹣3),且B (3,0),C (0,﹣3) 分情况讨论:①当DG 为对角线时,则另一对角线是BC ,由中点坐标公式可知:线段DG 的中点坐标为(x D +x G 2,y D +y G 2),即(1+m 2,t+m 2−2m−32),线段BC 的中点坐标为(x B +x C 2,y B +y C 2),即(3+02,0−32),此时DG 的中点与BC 的中点为同一个点,∴{1+m 2=32t+m 2−2m−32=−32,解得{m =2t =0, 经检验,此时四边形DCGB 为平行四边形,此时G 坐标为(2,﹣3);②当DB 为对角线时,则另一对角线是GC ,由中点坐标公式可知:线段DB 的中点坐标为(x D +x B 2,y D +y B 2),即(1+32,t+02), 线段GC 的中点坐标为(x G +x C 2,y G +y C 2),即(m+02,m 2−2m−3−32), 此时DB 的中点与GC 的中点为同一个点,∴{1+32=m+02t+02=m 2−2m−3−32,解得{m =4t =2, 经检验,此时四边形DCBG 为平行四边形,此时G 坐标为(4,5);③当DC 为对角线时,则另一对角线是GB ,由中点坐标公式可知:线段DC 的中点坐标为(x D +x C 2,y D +y C 2),即(1+02,t−32), 线段GB 的中点坐标为(x G +x B 2,y G +y B 2),即(m+32,m 2−2m−3+02), 此时DC 的中点与GB 的中点为同一个点,∴{1+02=m+32t−32=m 2−2m−3+02,解得{m =−2t =8, 经检验,此时四边形DGCB 为平行四边形,此时G 坐标为(﹣2,5);综上所述,G 点坐标存在,为(2,﹣3)或(4,5)或(﹣2,5);(4)连接AC ,OP ,如图2所示:设MC 的解析式为:y =kx +m ,将C (0,﹣3),M (1,﹣4)代入MC 的解析式得:{−3=m −4=k +m, 解得:{k =−1m =−3∴MC 的解析式为:y =﹣x ﹣3,令y =0,则x =﹣3,∴E 点坐标为(﹣3,0),∴OE =OB =3,且OC ⊥BE ,∴CE =CB ,∴∠CBE =∠E ,设P (x ,﹣x ﹣3),又∵P 点在线段EM 上,∴﹣3<x <1,则EP =√(x +3)2+(−x −3)2=√2(x +3),BC =√32+32=3√2,由题意知:△PEO 相似于△ABC ,分情况讨论:①△PEO ∽△CBA ,∴EOBA=EP BC , ∴34=√2(x+3)3√2, 解得x =−34,满足﹣3<x <1,此时P 的坐标为(−34,−94);②△PEO ∽△ABC ,∴EO BC =EP BA , ∴3√2=√2(x+3)4, 解得x =﹣1,满足﹣3<x <1,此时P 的坐标为(﹣1,﹣2).综上所述,P 点的坐标为(−34,−94)或(﹣1,﹣2).【点评】本题是二次函数综合题目,考查了二次函数的图象和性质、待定系数法求直线的解析式、平行四边形的性质、相似三角形的性质和判定、等腰三角形的判定与性质等知识;本题综合性较强,具有一定的难度,熟练掌握二次函数的图形和性质,学会用代数的方法求解几何问题.7.(2020•碑林区校级三模)在平面直角坐标系中,O为坐标原点,抛物线L:y=ax2﹣4ax(a>0)与x轴正半轴交于点A.抛物线L的顶点为M,对称轴与x轴交于点D.(1)求抛物线L的对称轴.(2)抛物线L:y=ax2﹣4ax关于x轴对称的抛物线记为L',抛物线L'的顶点为M',若以O、M、A、M'为顶点的四边形是正方形,求L'的表达式.(3)在(2)的条件下,点P在抛物线L上,且位于第四象限,点Q在抛物线L'上,是否存在点P、点Q使得以O、D、P、Q为顶点的四边形是平行四边形,若存在,求出点P坐标,若不存在,请说明理由.【分析】(1)根据抛物线的对称轴公式计算即可.(2)利用正方形的性质求出点M,M′的坐标即可解决问题.(3)分OD是平行四边形的边或对角线两种情形求解即可.【解析】(1)∵抛物线L:y=ax2﹣4ax(a>0),∴抛物线的对称轴x=−−4a2a=2.(2)如图1中,对于抛物线y=ax2﹣4ax,令y=0,得到ax2﹣4ax=0,解得x=0或4,∴A(4,0),∵四边形OMAM′是正方形,∴OD=DA=DM=DM′=2,∴M((2,﹣2),M′(2,2)把M(2,﹣2)代入y=ax2﹣4ax,可得﹣2=4a﹣8a,∴a=1 2,∴抛物线L′的解析式为y=−12(x﹣2)2+2=−12x2+2x.(3)如图3中,由题意OD=2.当OD 为平行四边形的边时,PQ =OD =2,设P (m ,12m 2﹣2m ),则Q [m ﹣2,−12(m ﹣2)2+2(m ﹣2)]或[m +2,−12(m +2)2+2(m +2)],∵PQ ∥OD ,∴12m 2﹣2m =−12(m ﹣2)2+2(m ﹣2)或12m 2﹣2m =−12(m +2)2+2(m +2), 解得m =3±√3或1±√3,∴P (3+√3,√3)或(3−√3,−√3)或(1−√3,√3)和(1+√3,−√3),当OD 是平行四边形的对角线时,点P 的横坐标为1,此时P (1,−32),∵点P 在第四象限,∴满足条件的点P 的坐标为(3−√3,−√3)或(1+√3,−√3)或(1,−32).【点评】本题属于二次函数综合题,考查了二次函数的性质,正方形的性质,平行四边形的判定和性质等知识,解题的关键是理解题意,学会利用参数构建方程解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.8.(2020•泰安二模)如图①抛物线y =ax 2+bx +4(a ≠0)与x 轴,y 轴分别交于点A (﹣1,0),B (4,0),点C 三点.(1)试求抛物线解析式;(2)点D (3,m )在第一象限的抛物线上,连接BC ,BD .试问,在对称轴左侧的抛物线上是否存在一点P ,满足∠PBC =∠DBC ?如果存在,请求出点P 的坐标;如果不存在,请说明理由;(3)点N 在抛物线的对称轴上,点M 在抛物线上,当以M 、N 、B 、C 为顶点的四边形是平行四边形时,请直接写出点M 的坐标.【分析】(1)把已知点A 、B 代入抛物线y =ax 2+bx +4中即可求解;(2)将二次函数与方程、几何知识综合起来,先求点D 的坐标,再根据三角形全等证明∠PBC =∠DBC ,最后求出直线BP 解析式即可求出P 点坐标;(3)根据平行四边形的判定即可写出点M 的坐标.【解析】如图:(1)∵抛物线y =ax 2+bx +3(a ≠0)与x 轴,y 轴分别交于点A (﹣1,0),B (4,0),点C 三点. ∴{a −b +4=016a +4b +4=0, 解得{a =−1b =3. ∴抛物线的解析式为y =﹣x 2+3x +4.(2)存在.理由如下:y =﹣x 2+3x +4=﹣(x ﹣1.5)2+6.25.∵点D (3,m )在第一象限的抛物线上,∴m =4,∴D (3,4),∵C (0,4)∵OC =OB ,∴∠OBC =∠OCB =45°.连接CD ,∴CD ∥x 轴,∴∠DCB =∠OBC =45°,∴∠DCB =∠OCB ,在y 轴上取点G ,使CG =CD =3,再延长BG 交抛物线于点P ,。
两定两动畅游在抛物线上的平行四边形课件

数学建模中两定两动平行四边形的应用有助于解决实际问题。
详细描述
在数学建模中,两定两动平行四边形可以用于解决一些实际问题,如建筑设计、机械运动等。通过设定两个定点 和两个动点,可以构建出满足特定条件的平行四边形,进一步建立数学模型,为解决实际问题提供理论支持。
总结与展望
本章总结
01
02
介绍了抛物线的基本概 念和平行四边形的性质。
平行四边形的相对边平行于抛 物线的对称轴,且相对顶点沿 抛物线轨迹运动。
随着相对顶点的移动,平行四 边形的大小和形状会发生变化, 但仍然保持平行四边形的特性。
两定两动平行四边形在抛物线上的运动轨迹
固定在抛物线对称轴上的两个顶 点,其运动轨迹是垂直于对称轴
的两条直线。
另外两个顶点沿抛物线轨迹运动, 其运动轨迹是抛物线的一部分。
两定两动平行四边形在抛 物线上的应用
两定两动平行四边形在几何作图中的应用
总结词
几何作图中的两定两动平行四边形是解决复杂几何问题的重 要工具。
详细描述
在几何作图中,两定两动平行四边形可以用于解决一些复杂 的几何问题,如作图、证明等。通过合理设定两个定点和两 个动点,可以构造出满足特定条件的平行四边形,进而解决 一系列的几何问题。
两定两动平行四边形的性质
01
02
03
性质1
两定两动平行四边形具有 平行四边形的所有性质, 如对边相等、对角相等、 对角线互相平分等。
性质2
由于其中一个顶点是动点, 因此两定两动平行四边形 具有一个顶点在抛物线上 的性质。
性质3
两定两动平行四边形的面 积等于两个定点之间的距 离乘以顶点到定点的距离。
通过两定两动的设定, 详细阐述了如何在抛物 线上构造平行四边形。
专题22 二次函数中的平行四边形问题(解析版)

专题22 二次函数中的平行四边形问题1、如图,在平面直角坐标系中,抛物线y =x 2+mx +n 经过点A(3,0)、B(0,-3),点P 是直线AB 上的动点,过点P 作x 轴的垂线交抛物线于点M ,设点P 的横坐标为t .(1)分别求出直线AB 和这条抛物线的解析式.(2)若点P 在第四象限,连接AM 、BM ,当线段PM 最长时,求△ABM 的面积.(3)是否存在这样的点P ,使得以点P 、M 、B 、O 为顶点的四边形为平行四边形?若存在,请直接写出点P 的横坐标;若不存在,请说明理由.【答案】(1)抛物线的解析式是.直线AB 的解析式是.(2). (3)P. 【解析】解:(1)把A (3,0)B (0,-3)代入,得解得 所以抛物线的解析式是.设直线AB 的解析式是,把A (3,0)B (0,)代入,得解得 所以直线AB 的解析式是.(2)设点P 的坐标是(),则M (,),因为在第四象限,所以PM=223y x x =--3y x =-2782y x mx n =++093{3m n n =++-=2{3m n =-=-223y x x =--y kx b =+3-y kx b =+03{3k b b =+-=1{3k b ==-3y x =-3p p -,p 223p p --p,当PM 最长时,此时 ==. (3)若存在,则可能是:△P 在第四象限:平行四边形OBMP ,PM=OB=3, PM 最长时,所以不可能. △P 在第一象限平行四边形OBPM : PM=OB=3,,解得,(舍去),所以P 点的横坐标是. △P 在第三象限平行四边形OBPM :PM=OB=3,,解得(舍去), △,所以P. 所以P 点的横坐标是或.2、如图,在平面直角坐标系中,抛物线y =ax 2+bx+3经过A (﹣3,0)、B(1,0)两点,其顶点为D ,连接AD ,点P 是线段AD 上一个动点(不与A 、D 重合). (1)求抛物线的函数解析式,并写出顶点D 的坐标;(2)如图1,过点P 作PE△y 轴于点E .求△PAE 面积S 的最大值;(3)如图2,抛物线上是否存在一点Q ,使得四边形OAPQ 为平行四边形?若存在求出Q 点坐标,若不存在请说明理由.【答案】(1)抛物线的解析式为y =﹣x 2﹣2x+3,顶点D 的坐标为(﹣1,4);(2)△PAE 面积S 的最大值22(3)(23)3p p p p p ----=-+94PM =3,2p =ABMBPMAPMSSS=+19324⨯⨯27894PM =233p p -=132p +=232p -=32+233p p -=132p +=2p =32+32-是94;(3)点Q 的坐标为(﹣2+√7,2√7﹣4).【解析】解:(1)△抛物线y =ax 2+bx+3经过A (﹣3,0)、B (1,0)两点, △{9a −3b +3=0a +b +3=0,得{a =−1b =−2 ,△抛物线解析式为y =﹣x 2﹣2x+3=﹣(x+1)2+4, △抛物线的顶点坐标为(﹣1,4),即该抛物线的解析式为y =﹣x 2﹣2x+3,顶点D 的坐标为(﹣1,4); (2)设直线AD 的函数解析式为y =kx+m , {−3k +m =0−k +m =4 ,得{k =2m =6, △直线AD 的函数解析式为y =2x+6,△点P 是线段AD 上一个动点(不与A 、D 重合), △设点P 的坐标为(p ,2p+6), △S △PAE =−p⋅(2p+6)2=﹣(p+32)2+94,△﹣3<p <﹣1,△当p =﹣32时,S △PAE 取得最大值,此时S △PAE =94, 即△PAE 面积S 的最大值是94;(3)抛物线上存在一点Q ,使得四边形OAPQ 为平行四边形, △四边形OAPQ 为平行四边形,点Q 在抛物线上, △OA =PQ , △点A (﹣3,0), △OA =3, △PQ =3,△直线AD 为y =2x+6,点P 在线段AD 上,点Q 在抛物线y =﹣x 2﹣2x+3上, △设点P 的坐标为(p ,2p+6),点Q (q ,﹣q 2﹣2q+3), △{q −p =32p +6=−q 2−2q +3,解得,{p =−5+√7q =−2+√7 或{p =−5−√7q =−2−√7(舍去),当q =﹣2+√7时,﹣q 2﹣2q+3=2√7﹣4,即点Q 的坐标为(﹣2+√7,2√7﹣4).3、如图,抛物线y =-x 2+bx +c 与x 轴交于A 、B 两点,且B 点的坐标为(3,0),经过A 点的直线交抛物线于点D (2, 3).(1)求抛物线的解析式和直线AD 的解析式;(2)过x 轴上的点E (a ,0) 作直线EF △AD ,交抛物线于点F ,是否存在实数a ,使得以A 、D 、E 、F 为顶点的四边形是平行四边形?如果存在,求出满足条件的a ;如果不存在,请说明理由.【答案】(1) y=-x 2+2x+3;y=x+1;(2)a 的值为-3或. 【解析】解:(1)把点B 和D 的坐标代入抛物线y=-x 2+bx+c 得: 解得:b=2,c=3,△抛物线的解析式为y=-x 2+2x+3; 当y=0时,-x 2+2x+3=0, 解得:x=3,或x=-1, △B (3,0), △A (-1,0);设直线AD 的解析式为y=kx+a , 把A 和D 的坐标代入得:解得:k=1,a=1,△直线AD 的解析式为y=x+1;(2)分两种情况:△当a <-1时,DF△AE 且DF=AE , 则F 点即为(0,3),4930423b c b c -++=⎧⎨-++=⎩23k a k a -+=⎧⎨+=⎩△AE=-1-a=2, △a=-3;△当a >-1时,显然F 应在x 轴下方,EF△AD 且EF=AD , 设F (a -3,-3),由-(a -3)2+2(a -3)+3=-3, 解得:a=;综上所述,满足条件的a 的值为-3或.4、如图1,在平面直角坐标系xOy 中,抛物线W 的函数表达式为y=﹣421x 2+1621x+4.抛物线W 与x 轴交于A ,B 两点(点B 在点A 的右侧,与y 轴交于点C ,它的对称轴与x 轴交于点D ,直线l 经过C 、D 两点. (1)求A 、B 两点的坐标及直线l 的函数表达式.(2)将抛物线W 沿x 轴向右平移得到抛物线W′,设抛物线W′的对称轴与直线l 交于点F ,当△ACF 为直角三角形时,求点F 的坐标,并直接写出此时抛物线W′的函数表达式.(3)如图2,连接AC ,CB ,将△ACD 沿x 轴向右平移m 个单位(0<m≤5),得到△A′C′D′.设A′C 交直线l 于点M ,C′D′交CB 于点N ,连接CC′,MN .求四边形CMNC′的面积(用含m 的代数式表示).【答案】(1)点A 坐标为(﹣3,0),点B 的坐标为(7,0),y=﹣2x+4;(2) 点F 的坐标为(5,﹣6),y=﹣421x 2+4021x ;(3) 四边形CMNC′的面积为45m 2.【解析】(1)当y =0时,﹣421x 2+1621+4=0,解得x 1=﹣3,x 2=7, △点A 坐标为(﹣3,0),点B 的坐标为(7,0). △﹣b2a =−16212×(−421)△抛物线w 的对称轴为直线x =2,44±△点D 坐标为(2,0). 当x =0时,y =4, △点C 的坐标为(0,4). 设直线l 的表达式为y =kx +b ,{b=42k+b=0解得{k=-2b=4△直线l 的解析式为y =﹣2x +4;(2)△抛物线w 向右平移,只有一种情况符合要求, 即△F AC =90°,如图.此时抛物线w ′的对称轴与x 轴的交点为G , △△1+△2=90°△2+△3=90°, △△1=△3, △tan△1=tan△3,△FG AG =AOCO .设点F 的坐标为(x F ,﹣2x F +4),△−(2x F +4)x F−(−3)=34,解得x F =5,﹣2x F +4=﹣6, △点F 的坐标为(5,﹣6),此时抛物线w ′的函数表达式为y =﹣421x 2+4021x ;(3)由平移可得:点C ′,点A ′,点D ′的坐标分别为C ′(m ,4),A ′(﹣3+m ,0),D ′(2+m ,0),CC ′△x 轴,C ′D ′△CD , 可用待定系数法求得直线A ′C ′的表达式为y =43x +4﹣43m ,直线BC 的表达式为y =﹣47x +4,直线C ′D ′的表达式为y =﹣2x +2m +4, 分别解方程组{y=43x+4-43m y=-2x+4 和{y=-2x+2m+4y=-47x+4解得{x=25my=-45m+4和{x=75my=-45m+4 △点M 的坐标为(25m ,﹣45m +4),点N 的坐标为(75m ,﹣45 m +4), △y M =y N △MN △x 轴, △CC ′△x 轴, △CC ′△MN . △C ′D ′△CD ,△四边形CMNC ′是平行四边形, △S =m [4﹣(﹣45m +4)]=45m 25、如图,三角形ABC 是以BC 为底边的等腰三角形,点A 、C 分别是一次函数334y x =-+的图象与y 轴、x 轴的交点,点B 在二次函数218y x bx c =++的图象上,且该二次函数图象上存在一点D 使四边形ABCD能构成平行四边形.(1)试求b 、c 的值,并写出该二次函数表达式;(2)动点P 沿线段AD 从A 到D ,同时动点Q 沿线段CA 从C 到A 都以每秒1个单位的速度运动,问: △当P 运动过程中能否存在PQ AC ⊥?如果不存在请说明理由;如果存在请说明点的位置? △当P 运动到何处时,四边形PDCQ 的面积最小?此时四边形PDCQ 的面积是多少?【答案】(1)143b c ⎧=-⎪⎨⎪=-⎩,211384y x x =--;(2) △当点P 运动到距离A 点259个单位长度处,有PQ AC ⊥;△当点P 运动到距离点A 52个单位处时,四边形PDCQ 面积最小,最小值为818. 【解析】 【分析】(1)根据一次函数解析式求出A 和C 的坐标,再由△ABC 是等腰三角形可求出点B 的坐标,根据平行四边形的性质求出点D 的坐标,利用待定系数法即可得出二次函数的表达式;(2)△设点P 运动了t 秒,PQ△AC ,进而求出AP 、CQ 和AQ 的值,再由△APQ△△CAO ,利用对应边成比例可求出t 的值,即可得出答案;△将问题化简为△APQ 的面积的最大值,根据几何关系列出APQS关于时间的二次函数,根据二次函数的性质,求出函数的最大值,即求出△APQ 的面积的最大值,进而求出四边形PDCQ 面积的最小值. 【详解】解:(1)由334y x =-+,令0x =,得3y =,所以点()0,3A ; 令0y =,得4x =,所以点()4,0C , △ABC ∆是以BC 为底边的等腰三角形, △B 点坐标为()4,0-,又△四边形ABCD 是平行四边形, △D 点坐标为()8,3,将点()4,0B -、点()8,3D 代入二次函数218y x bx c =++,可得240883b c b c -+=⎧⎨++=⎩,解得:143b c ⎧=-⎪⎨⎪=-⎩,故该二次函数解析式为:211384y x x =--. (2)△3OA =,4OB =, △5AC =.△设点P 运动了t 秒时,PQ AC ⊥,此时AP t =,CQ t =,5AQ t =-, △PQ AC ⊥,△90AQP AOC ∠=∠=︒,PAQ ACO ∠=∠, △APQ CAO ∆∆∽,△AP AQ AC CO =,即554t t-=, 解得:259t =. 即当点P 运动到距离A 点259个单位长度处,有PQ AC ⊥.△△APQ APQ ACD PDCQ S S S S ∆∆∆==+四边形,且183122ACD S ∆=⨯⨯=,△当APQ ∆的面积最大时,四边形PDCQ 的面积最小, 当动点P 运动t 秒时,AP t =,CQ t =,5AQ t =-, 设APQ ∆底边AP 上的高为h ,作QH AD ⊥于点H , 由AQH CAO ∆∆∽可得:535h t -=, 解得:()355h t =-, △()()2133552510APQ S t t t t ∆=⨯-=-+235151028t ⎛⎫=--+ ⎪⎝⎭, △当52t =时,APQ S ∆达到最大值158,此时15811288PDCQ S =-=四边形, 故当点P 运动到距离点A 52个单位处时,四边形PDCQ 面积最小,最小值为818.6、如图,在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点.(1)求抛物线的解析式;(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S,求S关于m的函数关系式,并求出S的最大值;(3)若点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能使以点P,Q,B,O为顶点的四边形为平行四边形(要求PQ△OB),直接写出相应的点Q的坐标.【答案】(1)y=12x2+x-4;(2)当m=-2时,S有最大值,S最大=4;(3)满足题意的Q点的坐标有三个,分别是(-2+2-,(-2-2+,(-4,4).【思路引导】(1)已知抛物线与x轴的两个交点的横坐标,一般选用两点式,利用待定系数法求解即可;(2)利用抛物线的解析式表示出点M的纵坐标,从而得到点M到x轴的距离,然后根据三角形面积公式表示并整理即可得解,根据抛物线的性质求出第三象限内二次函数的最值,然后即可得解;(3)利用直线与抛物线的解析式表示出点P、Q的坐标,然后求出PQ的长度,再根据平行四边形的对边相等列出算式,然后解关于x的一元二次方程即可得解.【解析】(1)设抛物线的解析式为y=a(x+4)(x-2),把B(0,-4)代入得,-4=a×(0+4)(0-2),解得a=12, △抛物线的解析式为:y=12(x+4)(x -2),即y=12x 2+x -4; (2)过点M 作MD△x 轴于点D ,设M 点的坐标为(m ,n ), 则AD=m+4,MD=-n ,n=12m 2+m -4, △S=S △AMD +S 梯形DMBO -S △ABO =111(4)()(4)()44222m n n m +-+-+--⨯⨯= -2n -2m -8=-2×(12m 2+m -4)-2m -8=-m 2-4m =-(m+2)2+4(-4<m <0);△S 最大值=4.(3)设P (x ,12x 2+x -4). △如图1,当OB 为边时,根据平行四边形的性质知PQ△OB ,△Q 的横坐标等于P 的横坐标,又△直线的解析式为y=-x ,则Q (x ,-x ).由PQ=OB ,得|-x -(12x 2+x -4)|=4,解得x=0,-4,-x=0不合题意,舍去. 由此可得Q (-4,4)或(-2--2-;△如图2,当BO 为对角线时,知A 与P 应该重合,OP=4.四边形PBQO 为平行四边形则BQ=OP=4,Q 横坐标为4,代入y=-x 得出Q 为(4,-4).故满足题意的Q 点的坐标有四个,分别是(-4,4),(4,-4),(-,2-,(-2-.【方法总结】本题是二次函数综合题,交点式求解析式,二次函数与三角形面积最值问题的公共底的辅助线的做法要注意,二次函数中存在平行四边形的方法,要分别对已知边的分别为平行四边形的边或是对角线进行分类讨论.7、如图,二次函数的图象与x 轴交于A 、B 两点,与y 轴交于点C ,已知点A (﹣4,0).(1)求抛物线与直线AC 的函数解析式;(2)若点D (m ,n )是抛物线在第二象限的部分上的一动点,四边形OCDA 的面积为S ,求S 关于m 的232(0)2y ax x a =-+≠函数关系式;(3)若点E 为抛物线上任意一点,点F 为x 轴上任意一点,当以A 、C 、E 、F 为顶点的四边形是平行四边形时,请求出满足条件的所有点E 的坐标.【答案】(1)(2)S=﹣m 2﹣4m+4(﹣4<m <0)(3)(﹣3,2)、(,﹣2)、(,﹣2)【解析】 (1)△A (﹣4,0)在二次函数y=ax 2﹣x+2(a≠0)的图象上, △0=16a+6+2,解得a=﹣, △抛物线的函数解析式为y=﹣x 2﹣x+2; △点C 的坐标为(0,2),设直线AC 的解析式为y=kx+b ,则, 解得, △直线AC 的函数解析式为:; (2)△点D (m ,n )是抛物线在第二象限的部分上的一动点,△D (m ,﹣m 2﹣m+2),122y x =+32-32-3212123204{2k b b=-+=1{22k b ==122y x =+1232过点D 作DH△x 轴于点H ,则DH=﹣m 2﹣m+2,AH=m+4,HO=﹣m , △四边形OCDA 的面积=△ADH 的面积+四边形OCDH 的面积,△S=(m+4)×(﹣m 2﹣m+2)+(﹣m 2﹣m+2+2)×(﹣m ), 化简,得S=﹣m 2﹣4m+4(﹣4<m <0);(3)△若AC 为平行四边形的一边,则C 、E 到AF 的距离相等,△|y E |=|y C |=2,△y E =±2.当y E =2时,解方程﹣x 2﹣x+2=2得, x 1=0,x 2=﹣3,△点E 的坐标为(﹣3,2);当y E =﹣2时,解方程﹣x 2﹣x+2=﹣2得, x 1=,x 2=, △点E 的坐标为(,﹣2)或(,﹣2); △若AC 为平行四边形的一条对角线,则CE△AF ,△y E =y C =2,△点E 的坐标为(﹣3,2).综上所述,满足条件的点E 的坐标为(﹣3,2)、,﹣2)、,﹣2).8、如图,抛物线y =x 2−2x −3与x 轴交A 、B 两点(A 点在B 点左侧),直线l 与抛物线交于A 、C 两点,其中C 点的横坐标为2.12321212321212321232123232-32-+32--32-+(1)求A 、B 两点的坐标及直线AC 的函数表达式;(2)P 是线段AC 上的一个动点,过P 点作y 轴的平行线交抛物线于E 点,求线段PE 长度的最大值;(3)点G 是抛物线上的动点,在x 轴上是否存在点F ,使A 、C 、F 、G 四个点为顶点的四边形是平行四边形?如果存在,写出所有满足条件的F 点坐标(请直接写出点的坐标,不要求写过程);如果不存在,请说明理由.【答案】(1)A(−1,0),B(3,0),y =−x −1。
探究平行四边形的存在性问题——以2016_年安顺市中考的一道抛物线题为例

探究平行四边形的存在性问题以2016年安顺市中考的一道抛物线题为例刘利果(河北省邢台市沙河市第三中学ꎬ河北邢台054100)摘㊀要:抛物线中的动点问题ꎬ尤其是与存在性有关的动点问题ꎬ是中考的一个难点.文章以2016年贵州省安顺市的一道中考题为例ꎬ借助网络画板ꎬ从试验探究㊁思路分析㊁一题多解的角度来进行深度探究.关键词:抛物线ꎻ动点ꎻ平行四边形ꎻ存在性ꎻ探究中图分类号:G632㊀㊀㊀文献标识码:A㊀㊀㊀文章编号:1008-0333(2023)35-0092-03收稿日期:2023-09-15作者简介:刘利果(1981.10-)ꎬ女ꎬ河北省邢台人ꎬ本科ꎬ中小学高级教师ꎬ从事初中数学教学研究.㊀㊀抛物线中平行四边形的存在性问题ꎬ是中考的一个难点ꎬ也是热点ꎬ常常以压轴题的形式出现.如何突破这一类试题呢?笔者以2016年安顺市一道中考题为例进行探究.1试题呈现抛物线经过A(-1ꎬ0)ꎬB(5ꎬ0)ꎬC0ꎬ-52æèçöø÷三点.(1)求抛物线的解析式.(2)在抛物线的对称轴上有一点Pꎬ使PA+PC的值最小ꎬ求点P的坐标.(3)若M为x轴上一动点ꎬ在抛物线上是否存在一点Nꎬ使AꎬCꎬMꎬN四点构成的四边形为平行四边形?若存在ꎬ求点N的坐标ꎻ若不存在ꎬ请说明理由[1].2思路分析第(1)(2)问略.第(3)问:①如图1所示ꎬAC为对角线时ꎬ取AC中点Oᶄꎬ连接M4Oᶄꎬ交抛物线于点N4ꎻ如图2所示ꎬ若AC为边ꎬ平移AC得到另外三种情况.过四边形顶点作横平坚直线(平行于坐标轴)构造全等三角形解决问题.图1㊀AC为对角线②设M(xꎬ0)ꎬ分别以ACꎬAMꎬAN为对角线ꎬ分三种情况根据平行四边形两组相对顶点横坐标之和相等ꎬ纵坐标之和也相等ꎬ表示出点N的坐标ꎬ代入抛物线解析式求解即可.③如图3所示ꎬ从路径(轨迹)角度分析.假设以AꎬCꎬMꎬN为顶点的平行四边形存在.在x轴上任取一动点Mꎬ把M看作定点ꎬ然后分别以AMꎬACꎬCM为对角线作出三个平行四边形ꎬ设第四个顶点分别为N1ꎬN2ꎬN3.若拖动动点M可以发现ꎬ动点N1ꎬN2ꎬN3运动的路径均为与x轴平行的直线.易得N1ꎬN3到x轴的距离等于OC=52ꎬ到x轴的距离为2952的直线有两条.易知ꎬ点N1的路径为直线y=52ꎬ点N2ꎬN3的路径为直线y=-52.所以求点N的坐标就可以转化为由抛物线的解析式与点N的路径解析式组成的方程组的解的问题.图2㊀AC为边3一题多解解㊀(1)y=12x2-2x-52.(2)点P的坐标是2ꎬ-32æèçöø÷.过程略.(3)解法1㊀存在点Nꎬ使AꎬCꎬMꎬN四点为顶点构成的四边形为平行四边形.①当AC为边时ꎬ如图2所示ꎬ若点N在x轴下方.图3㊀让M运动又对称轴为直线x=2ꎬC0ꎬ-52æèçöø÷ꎬ所以点N14ꎬ-52æèçöø÷.当点N在x轴上方时ꎬ过点N2作N2Dʅx轴于点D.ȵAC=M2N2ꎬøCAO=øN2M2DꎬøCOA=øN2DM2ꎬʑәAOC≅әM2DN2ꎬʑN2D=OC=52ꎬ即N2点的纵坐标为52.ʑ12x2-2x-52=52ꎬ解得x=2+14或x=2-14ꎬʑN22+14ꎬ52æèçöø÷ꎬN32-14ꎬ52æèçöø÷.②如图1所示ꎬ当AC为对角线时ꎬ由四边形AM4CN4为平行四边形ꎬ知CN4ʊAM4ꎬ所以点N4的纵坐标为-52ꎬʑN44ꎬ-52æèçöø÷.综上所述ꎬ符合条件的点N的坐标为4ꎬ-52æèçöø÷或2+14ꎬ52æèçöø÷或2-14ꎬ52æèçöø÷.解法2㊀设M(xꎬ0)ꎬNxNꎬyN().①若AC为对角线ꎬ则有-1+0=x+xNꎬ0-52=0+yNꎬìîíïïï即xN=-1-xꎬyN=-52.ìîíïïï将N-1-xꎬ-52æèçöø÷代入抛物线表达式ꎬ得12(-1-x)2-2(-1-x)-52=-52ꎬ解得x=-1或-5ꎬ即xN=0或xN=4ꎬ所以N0ꎬ-52æèçöø÷(与C重合ꎬ舍去)或N4ꎬ-52æèçöø÷.②若AN为对角线ꎬ则有-1+xN=x+0ꎬ0+yN=0-52ꎬìîíïïï即xN=x+1ꎬyN=-52.ìîíïïïꎬ将Nx+1ꎬ-52æèçöø÷代入抛物线表达式ꎬ即12(x+1)2-2(x+1)-52=-52ꎬ解得x=-1或3ꎬ即xN=0或xN=4ꎬ所以N0ꎬ-52æèçöø÷(与C重合ꎬ舍去)或N4ꎬ-52æèçöø÷.③若AM为对角线ꎬ则有-1+x=xN+0ꎬ0+0=yN-52ꎬìîíïïï即xN=x-1ꎬyN=52.ìîíïïï将Nx-1ꎬ52æèçöø÷代入抛物线表达式ꎬ即12(x-1)2-2(x-1)-52=52ꎬ解得x1=3+1439或x2=3-14ꎬ即xN=2+14或xN=2-14ꎬ所以N2+14ꎬ52æèçöø÷或N2-14ꎬ52æèçöø÷.综上所述ꎬ符合条件的点N的坐标为4ꎬ-52æèçöø÷或2+14ꎬ52æèçöø÷或2-14ꎬ52æèçöø÷.解法3㊀如图4所示ꎬ在x轴上任取一点Mꎬ连接CMꎬ分别过点AꎬCꎬM作CMꎬAMꎬAC的平行线ꎬ得平行四边形ACMN1ꎬ四边形CMAN2ꎬ四边形ACN3Mꎬ分别过N1ꎬN2ꎬN3作x轴的垂线ꎬ垂足分别为FꎬGꎬE.过点M作MHʅN2N3于点H.易证明N1F=N2G=N3E=OC=52.图4㊀探究点N的路径所以N1运动的路径为直线y=52ꎬN2ꎬN3运动的路径为直线y=-52.因为N1ꎬN2ꎬN3在抛物线y=12x2-2x-52上ꎬ所以N的坐标满足y=52ꎬy=12x2-2x-52ìîíïïïï或y=-52ꎬy=12x2-2x-52ꎬìîíïïïï解得x1=2+14ꎬy1=52ꎬìîíïïïx2=2-14ꎬy2=52ꎬìîíïïïx3=0ꎬy3=-52ìîíïïï(舍去)ꎬx4=4ꎬy3=-52.ìîíïïï综上所述ꎬ符合条件的点N的坐标为4ꎬ-52æèçöø÷ꎬ2+14ꎬ52æèçöø÷或2-14ꎬ52æèçöø÷.解法4㊀如图3所示ꎬ因为A(-1ꎬ0)ꎬC0ꎬ-52æèçöø÷ꎬ所以AꎬC两点间的水平距离为1ꎬ坚直距离为52.设点M的坐标为(mꎬ0)ꎬ将点M按CңA方向平移ꎬ得到点N1m-1ꎬ52æèçöø÷ꎬ将点C按MңA方向平移ꎬ得到点N2-m-1ꎬ-52æèçöø÷ꎬ将点M按AңC方向平移ꎬ得到点N3m+1ꎬ-52æèçöø÷.将点N1m-1ꎬ52æèçöø÷ꎬN2-m-1ꎬ-52æèçöø÷ꎬN3m+1ꎬ-52æèçöø÷分别代代入抛物线的解析式y=12x2-2x-52得①12(m-1)2-2(m-1)-52=52ꎬ解得m=3-14或m=14+3ꎬʑN12+14ꎬ52æèçöø÷或N12-14ꎬ52æèçöø÷.②12(-m-1)2-2(-m-1)-52=-52ꎬ解得m=-1或m=-5ꎬʑN20ꎬ-52æèçöø÷(与C重合ꎬ舍去)或N24ꎬ-52æèçöø÷.③12(m+1)2-2(m+1)-52=-52ꎬ解得m=-1或m=3ꎬʑN30ꎬ-52æèçöø÷(与C重合ꎬ舍去)或N34ꎬ-52æèçöø÷.综上所述ꎬ符合条件的点N的坐标为4ꎬ-52æèçöø÷ꎬ2+14ꎬ52æèçöø÷或2-14ꎬ52æèçöø÷.对于平行四边形的存在性问题中已知两个定点ꎬ先虚拟一个动点ꎬ围成一个三角形ꎬ过三角形的每一个顶点画对边的平行线ꎬ三条直线两两相交ꎬ就可以确定平行四边形的第四个顶点.按照虚拟的第三个点ꎬ第四个顶点存在三种情况.但是第四个点到底有几个ꎬ要具体问题具体分析.参考文献:[1]董红凤.有效解决函数中动点型综合题教学探究[J].数学学习ꎬ2016(01):25-30.[责任编辑:李㊀璟]49。
难点攻关 抛物线与平行四边形

难点攻关 抛物线与平行四边形
近年中考试题中常常出现抛物线与平行四边形组合的压轴题,
1. 在平面直角坐标系xoy 中,点C ,B 的坐标分别为(-4,0),(0,2).四边形ABCO 是平行四边形,抛物线过A ,B ,C 三点,与x 轴交于另一点D .一动点P 以每秒1个单位长度的速度从B 点出发沿BA 向点A 运动,运动到点A 停止,同时一动点Q 从点D 出发,以每秒3个单位长
度的速度沿DC 向点C 运动,与点P 同时停止.
(1)求抛物线的解析式;
(2)若抛物线的对称轴与AB 交于点E ,与x 轴交于点F ,当点P 运动时间t
为何值时,四边形POQE 是等腰梯形?
(3)当t 为何值时,以P ,B ,O 为顶点的三角形与以点Q ,B ,O 为顶点的三角形相似?
解:(1)∵四边形ABCO 是平行四边形,∴OC=AB=4.
∴A(4,2),B(0,2),C(-4,0).
∵抛物线y=ax 2+bx+c 过点B(0,2),∴c=2.
由题意,有⎩⎨⎧16a−4b+2=016a+4b+2=2 解得: ⎩⎪⎨⎪⎧a=-116b=14
∴⎩⎪⎨⎪⎧a−b+c =025a+5b+c =0c =−52
解得 :
⎨⎧a=12b=-2c=-52。
抛物线中平行四边形问题品质课件PPT

402m
m
00a0.25m2
m
a
2 1
②点B与点Q相对 420m
m 6
0a00.25m2 m a 3
③点B与点P相对
4m02 00.25m2 m0a
m
a
2 3
∴P1(2,1), P2(6,-3), P3(-2,-3)
变式训练2
如图,平面直角坐标系中,y=0.5x2+x-4与y轴相交于点B(0,-4),点P是抛物线上的
• 例1 如图,平面直角坐标系中,已知点A(-1,0),B(1,-2),C(3,1),点D
是平面内一动点,若以点A,B,C,D为顶点的四边形是平行四边
形,则点D的坐标是__(-_3_,-_3)_,(_1_,3_),_(5,-1)
设点D(x,y)
①点A与点B相对 11 3 x 02 1 y
②点A与点C相对13 1 x 01 2 y
抛物线中 平行四边形存在性问题
一、画图引领 温故知新
• 1、已知平面上不共线三点A、B、C,求一 点D,使得A、B、C、D四个点组成平行四
边形
连接AB,AC,BC,分别过点A,B,C作对边的平行线,三条平行线的交点即为所有点D
D1
A
D2
B
C
D3
• 2、已知平面上两个点A,B,求两点P,Q,使 得A,B,P,Q四个点组成平行四边形(题目中 P,Q的位置有具体的限制)
x 3
y
3
D2 C
A
x 1
y
3
D1
B
D3
说明:若题中四边形ABCD是平行四边形,
则点D的坐标只有一个结果__(1,3)
③点A与点D相对 1 x 13 x 5
中考数学 专题17 函数动点问题中平行四边形存在性(解析版)

专题17 函数动点问题中平行四边形存在性类型一、平行四边形存在性结论:A C B DA CB Dx x x xy y y y+=+⎧⎨+=+⎩类型二、特殊平行四边形存在性1. 矩形存在性常用解题思路:构造一线三直角(借助相似或三角函数求解);利用矩形对角线相等(直角三角形斜边的中线等于斜边的一半)借助勾股定理求解等.2. 菱形存在性常用解题思路:利用菱形四条边相等,对角线互相垂直,借助勾股定理等求解.3. 正方形存在性常用解题思路:兼具矩形和菱形二者.【例1】(2018·郑州预测卷)如图,直线y=334x-+与x轴交于点C,与y轴交于点B,抛物线y= 234ax x c++经过B、C两点.(1)求抛物线的解析式;(2)如图,点E是直线BC上方抛物线上的一个动点,当△BEC的面积最大时,求出点E的坐标和最大值;(3)在(2)条件下,过点E作y轴的平行线交直线BC于点M,连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使以点P、Q、A、M为顶点的四边形是平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.【答案】见解析.【解析】解:(1)∵直线y =334x -+与x 轴交于点C ,与y 轴交于点B ,∴B (0,3),C (4,0),将B (0,3),C (4,0)代入y = 234ax x c ++得: 16303a c c ++=⎧⎨=⎩,解得:383a c ⎧=-⎪⎨⎪=⎩, ∴抛物线的解析式为:233384y x x =-++.(2)过点E 作EF ⊥x 轴于F ,交BC 于M ,设E (x ,233384x x -++),则M (x ,334x -+),∴ME =233384x x -++-(334x -+)=23382x x -+∴S △BEC =12×EM ×OC =2EM=2(23382x x -+)=()23234x --+,∴当x =2时,△BEC 的面积取最大值3,此时E (2,3).(3)由题意得:M (2,32),抛物线对称轴为:x =1,A (-2,0),设P (m ,y ),y =233384m m -++,Q (1,n )①当四边形APQM 为平行四边形时,有:212m -+=+,解得:m =-3, 即P (-3,218-); ②当四边形AMPQ 为平行四边形时,有:-2+m =2+1,即m =5 即P (5, 218-); ③当四边形AQMP 为平行四边形时,有:2-2=1+m ,得:m =-1, 即P (-1,158); 综上所述,抛物线上存在点P ,使以点P 、Q 、A 、M 为顶点的四边形是平行四边形,点P 的坐标为:(-3,218-),(5, 218-),(-1,158).【变式1-1】(2018·河师大附中模拟)如图,抛物线y =ax 2+bx +c (a ≠0)与x 轴交于点A (-1,0)、B (3,0)两点,与y 轴交于点C (0,-3).(1)求抛物线的解析式与顶点M 的坐标; (2)求△BCM 的面积与△ABC 面积的比;(3)若P 是x 轴上一个动点,过P 作射线PQ ∥AC 交抛物线于点Q ,随着P 点的运动,在x 轴上是否存在这样的点P ,使以点A 、P 、Q 、C 为顶点的四边形为平行四边形?若存在请直接写出点P 的坐标;若不存在,请说明理由.【答案】见解析.【解析】解:(1)将A (-1,0),B (3,0), C (0,-3)代入y =ax 2+bx +c ,得:9303a b c a b c c -+=⎧⎪++=⎨⎪=-⎩, 解得:a =1,b =-2,c =-3,即抛物线的解析式为:y=x2-2x-3,顶点M的坐标为:(1,-4);(2)连接BC,BM,CM,过M作MD⊥x轴于D,如图所示,S△BCM=S梯形ODMC+S△BDM-S△BOC=3,S△ACB=6,∴S△BCM:S△ACB=1:2;(3)存在.①当点Q在x轴上方时,过Q作QF⊥x轴于F,如图所示,∵四边形ACPQ为平行四边形,∴QP∥AC,QP=AC∴△PFQ≌△AOC,∴FQ=OC=3,∴3=x2﹣2x﹣3,解得x或x=1,∴Q,3)或(1,3);②当点Q在x轴下方时,过Q作QE⊥x轴于E,如图所示,同理,得:△PEQ≌△AOC,∴EQ=OC=3,∴﹣3=x2﹣2x﹣3,解得:x=2或x=0(与C点重合,舍去),∴Q(2,﹣3);综上所述,点Q的坐标为:,3)或(1,3)或(2,﹣3).【例2】(2018·郑州三模)如图所示,在平面直角坐标系中,已知抛物线y=ax2+bx-5与x轴交于A(-1,0),B(5,0)两点,与y轴交于点C.(1)求抛物线的解析式;(2)如图2所示,CE∥x轴与抛物线相交于点E,点H是直线CE下方抛物线上的动点,过点H且与y轴平行的直线与BC、CE分别交于点F、G,试探究当点H运动到何处时,四边形CHEF的面积最大,求点H的坐标及最大面积;(3)点M是(1)中所求抛物线对称轴上一动点,点N是反比例函数y=kx图象上一点,若以点B、C、M、N为动点的四边形是矩形,请直接写出满足条件的k的值.【答案】见解析.【解析】解:(1)将A (-1,0),B (5,0)代入y =ax 2+bx -5得:5025550a b a b --=⎧⎨+-=⎩,解得:14a b =⎧⎨=-⎩, 即抛物线的解析式为:y =x 2-4x -5.(2)在y =x 2-4x -5中,当x =0时,y =-5,即C (0,-5), ∵CE ∥x 轴,则C 、E 关于直线x =2对称, ∴E (4,-5), CE =4,由B (5,0), C (0,-5)得直线BC 的解析式为:y =x -5, 设H (m ,m 2-4m -5), ∵FH ⊥CE , ∴F (m ,m -5),∴FH = m -5-(m 2-4m -5)= -m 2+5m , S 四边形CHEF =12·FH ·CE =12(-m 2+5m )×4 =-2(m -52)2+252,当m =52时,四边形CHEF 的面积取最大值252,此时H (52,354-).(3)设M (2,m ),N (n ,kn),B (5,0),C (0,-5), ①当BC 为矩形对角线时,此时:2+n =5+0,m +kn=0-5,即n =3,设BC 与MN 交于点H ,则H (52,52-),MH =12BC =2,∴222552222m ⎛⎛⎫⎛⎫-++= ⎪ ⎪ ⎝⎭⎝⎭⎝⎭, 解得:m =1或m =-6,当m =1时,k =-18;m =-6时,k =3, ②当BC 为矩形边时,分两种情况讨论:(i )当点M 在直线BC 下方时,即四边形BCMN 为矩形,则∠BCM=90°,2+5=n+0,m=kn-5,过M作MH⊥y轴于H,则由OB=OC知,∠OCB=45°,∴∠MCH=∠CMH=45°,即CH=MH,∴-5-m=2,解得:m=-7,n=7,k=-14;(ii)当点M在直线BC上方时,即四边形BCNM为矩形,则∠CBM=90°,n+5=2,kn=m-5,设对称轴与x轴交于点H,同理可得:BH=MH,∴3=m,n=-3,k=6;综上所述,k的值为:-18,3,-14或6.【变式2-1】(2019·驻马店二模)如图,抛物线y=-x2+bx+c经过A(-1,0),B(3,0)两点,且与y轴交于点C,点D是抛物线的顶点,抛物线的对称轴DE交x轴于点E,连接BD.(1)求经过A,B,C三点的抛物线的函数表达式.(2)点P是线段BD上一点,当PE=PC时,求点P的坐标.(3)在(2)的条件下,过点P作PF⊥x轴于点F,G为抛物线上一动点,M为x轴上一动点,N 为直线 PF 上一动点,当以 F ,M ,G ,N 为顶点的四边形是正方形时,请求出点 M 的坐标.【答案】见解析.【解析】解:(1)∵抛物线 y =-x 2+bx +c 经过 A (-1,0),B (3,0)两点,∴10930b c b c --+=⎧⎨-++=⎩,解得:23b c =⎧⎨=⎩,即抛物线的解析式为:y =-x 2+2x +3.(2)由y =-x 2+2x +3知,C (0,3),E (1,0),D (1,4), 可得直线BD 的解析式为:y =-2x +6,设P (m ,-2m +6),由勾股定理得:PE 2=()()22126m m -+-+,PC 2=()22263m m +-+-, 由PE =PC ,得:()()22126m m -+-+=()22263m m +-+-, 解得:m =2,即P (2,2).(3)∵M 在x 轴上,N 在直线PF 上, ∴∠NFM =90°,由四边形MFNG 是正方形,知MF =MG , 设M (n ,0),则G (n ,-n 2+2n +3), MG =|-n 2+2n +3|,MF =|n -2|, ∴|-n 2+2n +3|=|n -2|,解得:n n n n ,故点M 的坐标为:0),0),(12,0),(12-,0).【变式2-2】(2019·大联考)如图1,抛物线y =ax 2+bx +c 经过点A (-4,0),B (1,0),C (0,3),点P 在抛物线上,且在x 轴的上方,点P 的横坐标记为t .(1)求抛物线的解析式;(2)如图2,过点P 作y 轴的平行线交直线AC 于点M ,交x 轴于点N ,若MC 平分∠PMO ,求t 的值.(3)点D 在直线AC 上,点E 在y 轴上,且位于点C 的上方,那么在抛物线上是否存在点P ,使得以点C 、D 、E 、P 为顶点的四边形是菱形?若存在,请直接写出菱形的面积.图1 图2【答案】见解析.【解析】解:(1)∵抛物线y =ax 2+bx +c 经过点A (-4,0),B (1,0),C (0,3),∴301640c a b c a b c =⎧⎪++=⎨⎪-+=⎩,解得:39434c b a ⎧⎪=⎪⎪=-⎨⎪⎪=-⎪⎩,即抛物线的解析式为:y =34-x 294-x +3. (2)由A (-4,0),C (0,3)得直线AC 的解析式为:y =334x +, ∵点P 的横坐标为t , ∴M (t ,334t +), ∵PN ∥y 轴, ∴∠PMC =∠MCO , ∵MC 平分∠PMO , ∴∠PMC =∠OMC , ∴∠MCO =∠OMC , 即OM =OC =3,∴OM 2=9,即223394t t ⎛⎫++= ⎪⎝⎭,解得:t =0(舍)或t =7225,∴当MC 平分∠PMO 时,t =7225. (3)设P (t , 34-t 294-t +3), ①当CE 为菱形的边时,四边形CEPD 为菱形,则PD ∥y 轴,CD =PD ,则D (t ,334t +),∴PD =34-t 294-t +3-(334t +)=34-t 23-t , 由勾股定理得:CD =54t -,∴34-t 23-t =54t -,解得:t =0(舍)或t =73-, 即PD =3512,菱形面积为:3512×73=24536; ②当CE 为菱形的对角线时,此时P 与D 点关于y 轴对称,则D (-t , 34-t 294-t +3),将D 点坐标代入y =334x +,得: 34-t 294-t +3=()334t -+,解得:t =0(舍)或t =-2, PD =4,CE =3,菱形的面积为:12×4×3=6;综上所述,菱形的面积为:24536或6.1.(2019·南阳毕业测试)如图1,抛物线y =ax 2+bx +2与x 轴交于A ,B 两点,与y 轴交于点C ,AB =4,矩形OBDC 的边CD =1,延长DC 交抛物线于点E .(1)求抛物线的解析式;(2)如果点N 是抛物线对称轴上的一点,抛物线上是否存在点M ,使得以M ,A ,C ,N 为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的点M 的坐标;若不存在,请说明理由.【答案】见解析.【解析】解:(1)∵矩形OBDC 的边CD =1, ∴OB =1,由AB =4,得OA =3, ∴A (﹣3,0),B (1,0),∵抛物线y =ax 2+bx +2与x 轴交于A ,B 两点, ∴a +b +2=0,9a -3b +2=0, 解得:a =23-,b =43-, ∴抛物线解析式为y =23-x 243-x +2; (2)以AC 为边或对角线分类讨论: A (﹣3,0),C (0,2),抛物线y =23-x 243-x +2的对称轴为x =﹣1, 设M (m , y M ),N (-1,n ),y M =23-m 243-m +2 ①当四边形ACMN 为平行四边形时,有:312Mm y n -+=-⎧⎨=+⎩,解得:m =2,y M =103-,即M (2,103-); ②当四边形ACNM 为平行四边形时,有:312Mmy n --=⎧⎨+=⎩,解得:m =-4,y M =103-,即M (-4,103-); ③当四边形AMCN 为平行四边形时,有:312Mm y n -=-⎧⎨=+⎩,解得:m =-2,y M =2,即M (-2,2); 综上所述,点M 的坐标为(2,103-)或(﹣4,103-)或(﹣2,2). 2.(2019·开封模拟)如图,直线y =﹣x +4与抛物线y =﹣12x 2+bx +c 交于A ,B 两点,点A 在y 轴上,点B 在x 轴上.(1)求抛物线的解析式;(2)在x 轴下方的抛物线上存在一点P ,使得∠ABP =90°,求出点P 坐标;(3)点E 是抛物线对称轴上一点,点F 是抛物线上一点,是否存在点E 和点F 使得以点E ,F ,B ,O 为顶点的四边形是平行四边形?若存在,求出点F 的坐标;若不存在,请说明理由.【答案】见解析.【解析】解:(1)在y=﹣x+4中,当x=0时,y=4,当y=0时,x=4,即点A、B的坐标分别为(0,4)、(4,0),将(0,4)、(4,0),代入二次函数表达式,并解得:b=1,c=4,抛物线的解析式为:y=﹣12x2+x+4;(2)∵OA=OB=4,∴∠ABO=45°,∵∠ABP=90°,则∠PBO=45°,若直线PB交y轴于点M,则OM=OB=4,可得直线BP的解析式为:y=x-4,联立:y=x-4,y=﹣12x2+x+4,得:x=4,y=0(即B点);x=-4,y=-8,即P(-4,-8).(3)存在;由y=﹣12x2+x+4知抛物线的对称轴为:x=1,设E(1,m),F(n,﹣12n2+n+4),O(0,0),B(4,0),①当四边形OBEF是平行四边形时,有:EF=4,∴n-1=-4,即n=-3,F点坐标为(-3,72 -);②当四边形OBFE是平行四边形时,有:EF=4,n-1=4,即n=5,F点坐标为(5,72 -);③当四边形OFBE 是平行四边形时,有:410Fn m y =+⎧⎨=+⎩,即n =3,F 点坐标为(3,52);综上所述:点F 的坐标为(5,72-),(﹣3,72-),(3,52). 3.(2019·开封二模)如图,抛物线y =ax 2+bx +2与直线y =﹣x 交第二象限于点E ,与x 轴交于A (﹣3,0),B 两点,与y 轴交于点C ,EC ∥x 轴.(1)求抛物线的解析式;(2)如果点N 是抛物线对称轴上的一个动点,抛物线上存在一动点M ,若以M ,A ,C ,N 为顶点的四边形是平行四边形,请直接写出所有满足条件的点M 的坐标.【答案】见解析.【解析】解:(1)由题意知:A (﹣3,0),C (0,2),EC ∥x 轴 ∴点E 的纵坐标为2, ∵点E 在直线y =﹣x 上, ∴点E (﹣2,2),∵将A (﹣3,0)、E (﹣2,2)代入y =ax 2+bx +2,得:93204222a b a b -+=⎧⎨-+=⎩,解得:2343a b ⎧=-⎪⎪⎨⎪=-⎪⎩抛物线的解析式为:224233y x x =--+;(2)由224233y x x =--+知,抛物线的对称轴为x =-1,设N (-1,n ),M (m ,224233m m --+),∵A (﹣3,0),C (0,2),(1)当四边形ACNM 是平行四边形时,有:312Mm n y --=⎧⎨=+⎩,得:m =-4,y M = 103-; 即M (-4,103-). (2)当四边形ACMN 是平行四边形时,有:312Mm n y -+=-⎧⎨+=⎩,得:m =2,y M = 103-; 即M (2,103-). (3)当四边形ANCM 是平行四边形时,有:312Mmn y -=-+⎧⎨=+⎩,得:m =-2,y M = 2; 即M (-2,2).综上所述,M 点的坐标是(-4,103-),(2,103-),(-2,2). 4.(2019·名校模考)如图,抛物线y =ax 2+bx ﹣1(a ≠0)交x 轴于A ,B (1,0)两点,交y 轴于点C ,一次函数y =x +3的图象交坐标轴于A ,D 两点,E 为直线AD 上一点,作EF ⊥x 轴,交抛物线于点F(1)求抛物线的解析式;(2)在平面直角坐标系内存在点G ,使得G ,E ,D ,C 为顶点的四边形为菱形,请直接写出点G 的坐标.【答案】见解析.【解析】解:(1)将y =0代入y =x +3,得x =﹣3.∴A(﹣3,0).∵抛物线y=ax2+bx﹣1交x轴于A(﹣3,0),B(1,0)两点,∴109310a ba b+-=⎧⎨--=⎩,解得:1323ab⎧=⎪⎪⎨⎪=⎪⎩抛物线的解析式为y=13x2+23x﹣1;(2)点G的坐标为(2,1),(﹣,﹣1),(﹣1),(﹣4,3).①当四边形DCEG是菱形时,CD=CE=EG=4,设E(m,m+3),则G(m,m+7),由C(0,-1),E(m,m+3),得:CE2=m2+(m+4)2=16,解得:m=0(舍)或m=-4,此时G(-4,3);②当四边形DCGE是菱形时,CG2=16,设E(m,m+3),则G(m,m-1),即m2+ m2=16,解得:m=m=-此时,G(1)或G(--1);③当四边形DGCE是菱形时,设E(m,m+3),则G(-m,-m-1),此时E在CD的垂直平分线上,即m+3=1,m=-2,此时G(2,1);综上所述,点G的坐标为:(-4,3)、(1)、(--1)、(2,1).5.(2019·枫杨外国语三模)(2019·枫杨外国语三模)如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C,点A的坐标为(-1,0),点C的坐标为(0,3),点D和点C关于抛物线的对称轴对称,直线AD与y轴交于点E.(1)求抛物线的解析式;(2)点M是抛物线的顶点,点P是y轴上一点,点Q是坐标平面内一点,以A,M,P,Q为顶点的四边形是以AM为边的矩形.若点T和点Q关于AM所在直线对称,求点T的坐标.【答案】见解析.【解析】解:(1)将(-1,0),(0,3)代入y=﹣x2+bx+c,得:-1-b+c=0,c=3,解得:b=2,c=3,即抛物线的解析式为:y=﹣x2+2x+3.(2)由y=﹣x2+2x+3知,点M(1,4),分两种情况讨论,①当四边形MAPQ是矩形时,过M作MH⊥x轴于H,则MH=4,AH=2,易证得:∠APO=∠MAH,∴tan∠APO= tan∠MAH,即OA MHOP AH=2,∴OP=12,即P(0,-12),由A(-1,0)、M(1,4),P(0,-12)得:点Q坐标为(2,72),∵点T和点Q关于AM所在直线对称,即点Q与点T关于点M(1,4)对称,∴T(0,92 );②当四边形AMPQ是矩形时,同理可得:T(0,12 -);综上所述,点T的坐标为(0,92),(0,12-).6.(2019·焦作二模)如图,在平面直角坐标系中,一次函数y=x+b的图象经过点A(-2,0),与反比例函数kyx=(x>0)的图象交于点B(a,4).(1)求一次函数和反比例函数的表达式;(2)设M是直线AB上一点,过M作MN∥x轴,交反比例函数kyx=(x>0)的图象于点N,若以A,O,M,N为顶点的四边形是平行四边形,求点M的横坐标.【答案】见解析.【解析】解:(1)将A(-2,0)代入y=x+b,得:b=2,即一次函数的解析式为:y=x+2,将B(a,4)代入y=x+2,得:a=2,即B(2,4),将B(2,4)代入kyx=得:x=8,即反比例函数的解析式为:8 yx =.(2)设M(m,m+2),则N(82m+,m+2),由题意知,MN∥OA,则需MN=OA=2时,以A,O,M,N为顶点的四边形是平行四边形,∴82mm-+=2,解得:m=2或m=-2(舍)或m=m=-(舍),∴点M的坐标为:(2,+2).7.(2019·许昌月考)如图1,二次函数y=43x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.(1)求该二次函数的解析式;(2)设该抛物线的顶点为D,求△ACD的面积(请在图1中探索);(3)若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动,当P,Q运动到t秒时,△APQ沿PQ所在的直线翻折,点A恰好落在抛物线上E点处,请直接判定此时四边形APEQ的形状,并求出E点坐标(请在图2中探索).图1 图2【答案】见解析.【解析】解:(1)∵二次函数y=43x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0),∴493034103b cb c⎧⨯++=⎪⎪⎨⎪⨯-+=⎪⎩,解得:834bc⎧=-⎪⎨⎪=-⎩,即抛物线的解析式为:y=43x2﹣83x﹣4;(2)过点D作DM⊥y轴于点M,y =43x 2﹣83x ﹣4 =43(x ﹣1)2﹣163, ∴点D (1,﹣163)、点C (0,﹣4), S △ACD =S 梯形AOMD ﹣S △CDM ﹣S △AOC=12×(1+3)×163﹣12×(163﹣4)×1﹣12×3×4 =4;(3)四边形APEQ 为菱形,理由如下:E 点关于PQ 与A 点对称,过点Q 作QF ⊥AP 于F ,由折叠性质知: AP =EP ,AQ =EQ ∵AP =AQ =t , ∴AP =AQ =QE =EP , ∴四边形AQEP 为菱形, ∵FQ ∥OC ,∴AF FQ AQOA OC AC ==, ∴345AF FQ t ==∴AF =35t ,FQ =45t ,Q (3﹣35t ,﹣45t ),E (3﹣35t ﹣t ,﹣45t ),∵E 在二次函数y =43x 2﹣83x ﹣4上,∴﹣45t =43(3﹣85t )2﹣83(3﹣85t )﹣4,∴t =14564或t =0(舍去), ∴E (﹣58,﹣2916).8.(2018·新乡一模)如图,一次函数122y x =-+分别交y 、x 轴于A 、B 两点,抛物线2y x bx c=-++过A ,B 两点.(1)求这个抛物线的解析式;(2)作垂直于x 轴的直线x =t ,在第一象限交直线AB 于M ,交这个抛物线于N . 求当t 取何值时,MN 有最大值?最大值是多少?(3)在(2)的情况下,以A ,M 、N 、D 为顶点作平行四边形,直接写出第四个顶点D 的坐标.【答案】见解析【解析】解:(1)在122y x =-+得,当x =0时,y =2;y =0时,x =4,即A (0,2),B (4,0),把A (0,2),B (4,0)代入2y x bx c =-++,得: 21640c b c =⎧⎨++=⎩-,解得722b c ⎧=⎪⎨⎪=⎩, ∴抛物线解析式为2722y x x =-++. (2)由题意知,1(,2)2M t t -+,27(,2)2N t t t -++,∴MN =2712(2)22t t t -++--+=2(2)4t --+, ∴当t =2时,MN 有最大值4.(3)根据平行四边形的性质,得:D 点坐标为:(0,6),(0,-2)或(4,4).9.(2019·周口二模)如图,在平面直角坐标系中,抛物线y =ax 2+bx +4与x 轴交于A (-1,0),B (4,0)两点,与y 轴交于点C .(1)求这个抛物线的解析式;(2)设E 是该抛物线上位于对称轴右侧的一个动点,过点E 作x 轴的平行线交抛物线于另一点F ,过点E 作EH ⊥x 轴于点H ,再过点F 作FG ⊥x 轴于点G ,得到矩形EFGH .在点E 的运动过程中,当矩形EFGH 为正方形时,直接写出该正方形的边长.【答案】见解析.【解析】解:(1)∵抛物线y =ax 2+bx +4与x 轴交于A (-1,0),B (4,0)两点,∴4016440a b a b -+=⎧⎨++=⎩,解得:13a b =-⎧⎨=⎩,即抛物线的解析式为:y =-x 2+3x +4. (2)∵四边形EFGH 是矩形,∴当EF =EH 时,四边形EFGH 是正方形,设E(m, -m2+3m+4),则F(3-m,-m2+3m+4),m>32,∴EF=2m-3,EH=|-m2+3m+4|,∴2m-3=|-m2+3m+4|,解得:m或m(舍)或m或m(舍)∴正方形的边长EF2,综上所述,正方形EFGH的边长为:2.10.(2019·郑州一中模拟)如图所示,平面直角坐标系中直线y=x+1交坐标轴于点A、D两点,抛物线y=ax2+bx-3经过A、C两点,点C坐标为(a,5). 点M为直线AC上一点,过点M作x轴的垂线,垂足为F,交抛物线于点N.(1)求抛物线解析式;(2)是否存在点M,使得以点D、E、M、N为顶点的四边形为平行四边形,如果有,求点M的坐标,如果没有,请说明理由.【解析】解:∵直线y =x +1交坐标轴于点A 、D 两点, ∴A (-1,0),D (0,1),∵点C (a ,5)在直线y =x +1上, ∴a =4,即C (4,5),将A (-1,0),C (4,5)代入y =ax 2+bx -3得:3016435a b a b --=⎧⎨+-=⎩,解得:12a b =⎧⎨=-⎩, ∴抛物线的解析式为:y =x 2-2x -3. (2)存在,E (0,-3),∴DE =4, 由题意知:DE ∥MN ,∴当DE =MN =4时,四边形DENM 是平行四边形, 设N (m , m 2-2m -3),则M (m , m +1), ∴| m +1-(m 2-2m -3)|=4,解得:m =0(舍)或m =3或m =或m = ,综上所述,点M 的坐标为:(3,4),,).11.(2019·郑州模拟)如图,已知二次函数23234y ax a x ⎛⎫=--+ ⎪⎝⎭的图象经过点A (4,0),与y 轴交于点B ,在x 轴上有一动点C (m ,0) (0<m <4),过点C 作x 轴的垂线交直线AB 于点E ,交该二次函数图象于点D .(1)求a 的值和直线AB 的解析式;(2)过点D 作DF ⊥AB 于点F ,设△ACE ,△DEF 的面积分别为S 1,S 2,若S 1=4S 2,求m 的值; (3)点H 是该二次函数图象上第一象限内的动点,点G 是线段AB 上的动点,当四边形DEGH 是平行四边形,且平行四边形DEGH 的周长取最大值时,求点G 的坐标.【答案】见解析.【解析】解:(1)将A (4,0)代入23234y ax a x ⎛⎫=--+ ⎪⎝⎭得:a =34-,∴抛物线的解析式为:239344y x x =-++,设直线AB 的解析式为:y =kx +b , ∴4k +b =0,b =3,即k =34-,b =3, ∴直线AB 的解析式为:y =34-x +3. (2)∵点C 的横坐标为m ,∴D (m , 239344m m -++),E (m , 34-m +3),AC =4-m ,DE =239344m m -++-(34-m +3)= 2334m m -+,∵BC ∥y 轴, ∴43AC OA CE OB ==,即443m CE -=, ∴CE =()344m -,AE =()544m -, ∵∠DF A =∠DCA =90°,∠DBF =∠AEC , ∴△DFE ∽△ACE , ∵S 1=4S 2, ∴AE =2DE , 即()544m -=2(2334m m -+),解得:m =4(舍)或m =56, 即m 的值为56.(3)如图,过点G 作GM ⊥DC 于M ,设G 、H 点横坐标为n ,由DE =2334m m -+,得GH =2334n n -+,2334m m -+=2334n n -+,得:m =n (舍)或n =4-m ,∴MG =4-2m ,由45MG EG =得:EG =()5424m -, ∴C 四边形DEGH =2()25342344m m m ⎡⎤--+⎢⎥⎣⎦=23102m m -++=23161236m ⎛⎫--+ ⎪⎝⎭,∴当m =13时,C 最大,此时n =113,即G (113,14),E (13,114), 由图象可知当E 、G 互换位置时满足题意,即G (13,114),E (113,14),综上所述,G 点坐标为:(13,114),(113,14).13.(2018·郑州模拟)如图,抛物线y =﹣x 2+bx +c 与x 轴交于点A 和点B (3,0),与y 轴交于点C (0,3),点D 是抛物线的顶点,过点D 作x 轴的垂线,垂足为E ,连接DB .(1)求此抛物线的解析式及顶点D 的坐标;(2)点M 是抛物线上的动点,设点M 的横坐标为m . ①当∠MBA =∠BDE 时,求点M 的坐标;②过点M 作MN ∥x 轴,与抛物线交于点N ,P 为x 轴上一点,连接PM ,PN ,将△PMN 沿着MN 翻折,得△QMN ,若四边形MPNQ 恰好为正方形,直接写出m 的值.【答案】见解析.【解析】解:(1)将点B(3,0),C(0,3)代入y=﹣x2+bx+c,并解得:b=2,c=3,∴抛物线的解析式为y=﹣x2+2x+3.顶点D(1,4).(2)①过点M作MG⊥x轴于G,连接BM.则∠MGB=90°,设M(m,﹣m2+2m+3),∴MG=|﹣m2+2m+3|,BG=3﹣m,∵DE⊥x轴,D(1,4),B(3,0),∴∠DEB=90°,DE=4,OE=1,BE=2,∵∠MBA=∠BDE,∴tan∠MBA=tan∠BDE=12,∴2233m mm-++-=12解得:m=12-或m=32-或m=3(舍)∴满足条件的点M坐标(12-,74)或(32-,94-);②∵MN∥x轴,∴点M、N关于抛物线的对称轴对称,∵四边形MPNQ是正方形,∴OP=1,由∠QPM=∠MPO=45°,得:GM=GP,即|﹣m2+2m+3|=|1﹣m|,解得:m或m或m或m即满足条件的m.14.(2017·信阳二模)如图,抛物线y=ax2+bx﹣4与x轴交于A(﹣2,0)、B(8,0)两点,与y轴交于点C,连接BC,以BC为一边,点O为对称中心做菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.(1)求抛物线的解析式;(2)当点P在线段OB上运动时,直线l分别交BD、BC于点M、N,试探究m为何值时,四边形CQMD 是平行四边形,此时,请判断四边形CQBM的形状,并说明理由.【答案】见解析.【解析】解:(1)将A(﹣2,0)、B(8,0)代入y=ax2+bx﹣4并解得:a=14,b=32-,即抛物线的解析式为:y=14x232-x-4.(2)由y=14x232-x-4知,C(0,-4),由菱形的性质可知:D(0,4),设直线BD的解析式为:y=kx+n,将点B(8,0)、D(0,4)代入得:k=12-,n=4,即直线BD的解析式为:y=12-x+4,由M(m,12-m+4),Q(m,14m232-m-4).当MQ=DC时,四边形CQMD为平行四边形.∴12-m+4﹣(14m232-m-4)=8,解得m=4或m=0(舍去).∴MD∥CQ,MD=CQ,M(4,2),∴M为BD的中点,∴MD=MB.∴CQ=MB,又∵MB∥CQ,∴四边形CQBM为平行四边形.。
2020年中考数学压轴题专题之抛物线上的特殊平行四边形问题探究

抛物线上的特殊平行四边形问题探究专题导入导图:给出两点确定平行四边形关系如下图:导例如图1,在平面直角坐标系中,已知抛物线经过A(-4,0)、B(0,-4)、C(2,0)三点.(1)求抛物线的解析式;(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△MAB的面积为S,求S关于m的函数关系式,并求出S的最大值;(3)若点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.图1 图2思路点拨1.求抛物线的解析式,设交点式比较简便.2.把△MAB分割为共底MD的两个三角形,高的和为定值O A.3.当PQ与OB平行且相等时,以点P、Q、B、O为顶点的四边形是平行四边形,按照P、Q 的上下位置关系,分两种情况列方程.答案:(1) 因为抛物线与x轴交于A(-4,0)、C(2,0)两点,设y=a(x+4)(x-2).代入点B(0,-4),求得12a =.所以抛物线的解析式为211(4)(2)422y x x x x =+-=+-. (2)如图2,直线AB 的解析式为y =-x -4.过点M 作x 轴的垂线交AB 于D ,那么2211(4)(4)222MD m m m m m =---+-=--.所以2142MDA MDB S S S MD OA m m ∆∆=+=⋅=--2(2)4m =-++.因此当2m =-时,S 取得最大值,最大值为4.(3) 如果以点P 、Q 、B 、O 为顶点的四边形是平行四边形,那么PQ //OB ,PQ =OB =4. 设点Q 的坐标为(,)x x -,点P 的坐标为21(,4)2x x x +-. ①当点P 在点Q 上方时,21(4)()42x x x +---=.解得225x =-±.此时点Q 的坐标为(225,225)-+-(如图3),或(225,225)--+(如图4). ②当点Q 在点P 上方时,21()(4)42x x x --+-=.解得4x =-或0x =(与点O 重合,舍去).此时点Q 的坐标为(-4,4) (如图5).图3 图4 图5典例类型一:已知“两点”判断平行四边形存在性问题例1、如图,在平面直角坐标系中,抛物线y =x 2+mx +n 经过点A (3,0)、B (0,﹣3),点P 是直线AB 上的动点,过点P 作x 轴的垂线交抛物线于点M ,设点P 的横坐标为t . (1)分别求出直线AB 和这条抛物线的解析式.(2)若点P 在第四象限,连接AM 、BM ,当线段PM 最长时,求△ABM 的面积.(3)是否存在这样的点P ,使得以点P 、M 、B 、O 为顶点的四边形为平行四边形?若存在,请直接写出点P 的横坐标;若不存在,请说明理由.【分析】:(1)分别利用待定系数法求两函数的解析式:把A(3,0)B(0,﹣3)分别代入y=x2+mx+n 与y=kx+b,得到关于m、n的两个方程组,解方程组即可;(2)设点P的坐标是(t,t﹣3),则M(t,t2﹣2t﹣3),用P点的纵坐标减去M的纵坐标得到PM 的长,即PM=(t﹣3)﹣(t2﹣2t﹣3)=﹣t2+3t,然后根据二次函数的最值得到当t=﹣=32时,PM最长为=94,再利用三角形的面积公式利用S△ABM=S△BPM+S△APM计算即可;(3)由PM∥OB,根据平行四边形的判定得到当PM=OB时,点P、M、B、O为顶点的四边形为平行四边形,然后讨论:当P在第四象限:PM=OB=3,PM最长时只有,所以不可能;当P在第一象限:PM=OB=3,(t2﹣2t﹣3)﹣(t﹣3)=3;当P在第三象限:PM=OB=3,t2﹣3t=3,分别解一元二次方程即可得到满足条件的t的值.类型二:菱形的存在性问题例2 如图2所示,直线y=x+c与x轴交于点A(-4,0),与y轴交于点C,抛物线y=-x2+bx+c 经过点A,C.(1)求抛物线的解析式;(2)点E在抛物线的对称轴上,求CE+OE的最小值;(3)如图2所示,点M是线段OA上的一个动点,过点M作垂直于x轴的直线与直线AC和抛物线分别交于点P,N.若点P恰好是线段MN的中点,点F是直线AC上一个动点,在坐标平面内是否存在点D,使以点D,F,P,M为顶点的四边形是菱形?若存在,请直接写出点D的坐标;若不存在,请说明理由.注:二次函数y=ax2+bx+c(a≠0)的顶点坐标为(﹣,)【分析】(1)把已知点坐标代入解析式;(2)取点C关于抛物线的对称轴直线l的对称点C′,由两点之间线段最短,最小值可得;(3)①由已知,注意相似三角形的分类讨论.②设出M坐标,求点P坐标.注意菱形是由等腰三角形以底边所在直线为对称轴对称得到的.本题即为研究△CPN为等腰三角形的情况.类型三:正方形的存在性问题例3如图1,在平面直角坐标系中,直线y=x+4与抛物线y=﹣x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.(1)求该抛物线的解析式;(2)P 是抛物线上一动点(不与点A 、B 重合),①如图2,若点P 在直线AB 上方,连接OP 交AB 于点D ,求的最大值;②如图3,若点P 在x 轴的上方,连接PC ,以PC 为边作正方形CPEF ,随着点P 的运动,正方形的大小、位置也随之改变.当顶点E 或F 恰好落在y 轴上,直接写出对应的点P 的坐标.【分析】(1)利用直线解析式求出点A 、B 的坐标,再利用待定系数法求二次函数解析式解答; (2)作PF ∥BO 交AB 于点F ,证△PFD ∽△OBD ,得比例线段,则PF 取最大值时,求得的最大值;(3)(i )点F 在y 轴上时,P 在第一象限或第二象限,如图2,3,过点P 作PH ⊥x 轴于H ,根据正方形的性质可证明△CPH ≌△FCO ,根据全等三角形对应边相等可得PH =CO =2,然后利用二次函数解析式求解即可;(ii )点E 在y 轴上时,过点PK ⊥x 轴于K ,作PS ⊥y 轴于S ,同理可证得△EPS ≌△CPK ,可得PS =PK ,则P 点的横纵坐标互为相反数,可求出P 点坐标;点E 在y 轴上时,过点PM ⊥x 轴于M ,作PN ⊥y 轴于N ,同理可证得△PEN ≌△PCM ,可得PN =PM ,则P 点的横纵坐标相等,可求出P 点坐标.由此即可解决问题. 专题突破1、如图,抛物线2y x bx c =-++与直线122y x =+交于,C D 两点,其中点C 在y 轴上,点D 的坐标为7(3,)2。
第三讲动点形成平行四边形问题

第三讲 动点形成平行四边形问题的讨论【知识点说明】一般是以二次函数为背景,由点的运动,形成平行四边形。
由于这种图形边及顶点较三角形多,所以更复杂,要有一定的想象能力,打破空间上的思维定势,一般尽量把可能出现的情况想象出来,先画草图,再根据情况解决。
当然该问题仍然有其规律,题中一般会有三个或两个定点。
我们在确定定点的情况下,也就可以确定一些定边,以定边为标准,分别以它“做边或对角线”两种情况进行讨论,下面我们通过问题来体会。
(一)已知三个定点,再找一个定点构成平行四边形(平面内有三个点满足)例1、已知抛物线b ax ax y ++-=22与x 轴的一个交点为A(-1,0),与y 轴的正半轴交于点C .⑴ 接写出抛物线的对称轴,及抛物线与x 轴的另一个交点B 的坐标; ⑵ 点C 在以AB 为直径的⊙P 上时,求抛物线的解析式;⑶ 标平面内是否存在点M ,使得以点M 和⑵中抛物线上的三点A 、B 、C 为点的四边形是平行四边形?若存在,请求出点M 的坐标;若不存在,请说明理由.(二)、已知两个定点,再找两个点构成平行四边形①确定两定点连接的线段为一边,则两动点连接的线段应和已知边平行且相等)例2、已知,如图抛物线23(0)y ax ax c a =++>与y 轴交于C 点,与x 轴交于A 、B 两点,A 点在B 点左侧。
点B 的坐标为(1,0),OC=30B . (1) 求抛物线的解析式;(2) 若点D 是线段AC 下方抛物线上的动点,求四边形ABCD 面积的最大值:(3) 若点E 在x 轴上,点P 在抛物线上。
是否存在以A 、C 、E 、P 为顶点且以AC 为一边的平行四边形?若存在,求点P 的坐标;若不存在,请说明理由.②两定点连接的线段没确定为平行四边形的边,则这条线段可能为平行四边形的边或对角线例3、如图,抛物线223y x x =--与x 轴交A 、B 两点(A 点在B 点左侧),直线l 与抛物线交于A 、C 两点,其中C 点的横坐标为2.(1)求A 、B 两点的坐标及直线AC 的函数表达式;(2)P 是线段AC 上的一个动点,过P 点作y 轴的平行线交抛物线于E 点,求线段PE长度的最大值;(3)点G 抛物线上的动点,在x 轴上是否存在点F ,使A 、C 、F 、G 这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F 点坐标;如果不存在,请说明理由.【巩固练习】1、已知抛物线22y x x a =-+(0a <)与y 轴相交于点A ,顶点为M .直线12y x a =-分别与x 轴,y 轴相交于B C ,两点,并且与直线AM 相交于点N . (1)填空:试用含a 的代数式分别表示点M 与N 的坐标, 则()()M N , , , ;(2)如图,将NAC △沿y 轴翻折,若点N 的对应点N ′恰好落在抛物线上,AN ′与x 轴交于点D ,连结CD ,求a 的值和四边形ADCN 的面积;(3)在抛物线22y x x a =-+(0a <)上是否存在一点P ,使得以P A C N ,,,为顶点的四边形是平行四边形?若存在,求出P 点的坐标;若不存在,试说明理由.2.已知抛物线:x x y 22121+-= (1)求抛物线1y 的顶点坐标.(2)将抛物线1y 向右平移2个单位,再向上平移1个单位,得到抛物线2y ,求抛物线2y的解析式.(3)如下图,抛物线2y 的顶点为P ,x 轴上有一动点M ,在1y 、2y 这两条抛物线上是否存在点N ,使O (原点)、P 、M 、N 四点构成以OP 为一边的平行四边形,若存在,求出N 点的坐标;若不存在,请说明理由.第1题备用图3、已知:如图所示,关于x 的抛物线2(0)y ax x c a =++≠与x 轴交于点(20)A -,、点(60)B ,,与y 轴交于点C .(1)求出此抛物线的解析式,并写出顶点坐标;(2)在抛物线上有一点D ,使四边形ABDC 为等腰梯形,写出点D 的坐标,并求出直线AD 的解析式;(3)在(2)中的直线AD 交抛物线的对称轴于点M ,抛物线上有一动点P ,x 轴上有一动点Q .是否存在以A M P Q 、、、为顶点的平行四边形?如果存在,请直接写出点Q 的坐标;如果不存在,请说明理由.课后作业1、已知一个二次函数的图像经过)3,0(A 、 )3,4(B 、)0,1(C 三点(如图1).(1)求这个二次函数的解析式; (2)求BAC ∠tan 的值;(3)若点D 在x 轴上,点E 在(1)中所求出的二次函数的图像上,且以点A 、C 、D 、E 为顶点的四边形是平行四边形,求点D 、E2、如图,在梯形ABCD 中,24AD BC AD BC ==∥,,,点M 是AD 的中点,MBC △是等边三角形.(1)求证:梯形ABCD 是等腰梯形;(2)动点P 、Q 分别在线段BC 和MC 上运动,且60MPQ =︒∠保持不变.设PC x MQ y ==,,求y 与x 的函数关系式;(3)在(2)中:①当动点P 、Q 运动到何处时,以点P 、M 和点A 、B 、C 、D 中的两个点为顶点的四边形是平行四边形?并指出符合条件的平行四边形的个数;②当y 取最小值时,判断PQC △的形状,并说明理由.图1ADCBPMQ60第三讲 动点形成平行四边形问题的讨论(教师)【知识点说明】一般是以二次函数为背景,由点的运动,形成平行四边形。
中考压轴题——抛物线平行四边形(含详细答案分析)
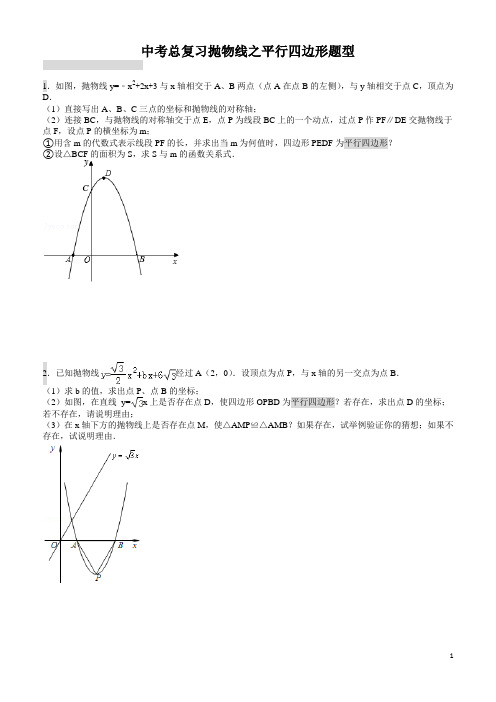
中考总复习抛物线之平行四边形题型1.如图,抛物线y=﹣x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.(1)直接写出A、B、C三点的坐标和抛物线的对称轴;(2)连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m;①用含m的代数式表示线段PF的长,并求出当m为何值时,四边形PEDF为平行四边形?②设△BCF的面积为S,求S与m的函数关系式.2.已知抛物线经过A(2,0).设顶点为点P,与x轴的另一交点为点B.(1)求b的值,求出点P、点B的坐标;(2)如图,在直线y=x上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐标;若不存在,请说明理由;(3)在x轴下方的抛物线上是否存在点M,使△AMP≌△AMB?如果存在,试举例验证你的猜想;如果不存在,试说明理由.3.如图,抛物线y=x2﹣2x+c的顶点A在直线l:y=x﹣5上.(1)求抛物线顶点A的坐标;(2)设抛物线与y轴交于点B,与x轴交于点C、D(C点在D点的左侧),试判断△ABD的形状;(3)在直线l上是否存在一点P,使以点P、A、B、D为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.4.已知抛物线y=﹣mx2+4x+2m与x轴交于点A(α,0),B(β,0),且=﹣2,(1)求抛物线的解析式.(2)抛物线的对称轴为l,与y轴的交点为C,顶点为D,点C关于l的对称点为E,是否存在x轴上的点M,y轴上的点N,使四边形DNME的周长最小?若存在,请画出图形(保留作图痕迹),并求出周长的最小值;若不存在,请说明理由.(3)若点P在抛物线上,点Q在x轴上,当以点D、E、P、Q为顶点的四边形是平行四边形时,求点P的坐标.5.已知抛物线y=﹣x2﹣2x+a(a≠0)与y轴相交于A点,顶点为M,直线y=x﹣a分别与x轴、y轴相交于B,C两点,并且与直线MA相交于N点.(1)若直线BC和抛物线有两个不同交点,求a的取值范围,并用a表示交点M,A的坐标;(2)将△NAC沿着y轴翻转,若点N的对称点P恰好落在抛物线上,AP与抛物线的对称轴相交于点D,连接CD,求a的值及△PCD的面积;(3)在抛物线y=﹣x2﹣2x+a(a>0)上是否存在点P,使得以P,A,C,N为顶点的四边形是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.6.边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点E 在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点.(1)求抛物线的解析式;(2)点P从点C出发,沿射线CB每秒1个单位长度的速度运动,运动时间为t秒.过点P作PF⊥CD于点F,当t为何值时,以点P,F,D为顶点的三角形与△COD相似?(3)点M为直线AB上一动点,点N为抛物线上一动点,是否存在点M,N,使得以点M,N,D,E为顶点的四边形是平行四边形?若存在,请直接写出满足条件的点的坐标;若不存在,请说明理由.7.如图,边长为1的正方形ABCD一边AD在x负半轴上,直线l:y=x+2经过点B(x,1)与x轴,y轴分别交于点H,F,抛物线y=﹣x2+bx+c.(1)求A,D两点的坐标及抛物线经过A,D两点时的解析式;(2)当抛物线的顶点E(m,n)在直线l上运动时,连接EA,ED,试求△EAD的面积S与m之间的函数解析式,并写出m的取值范围;(3)设抛物线与y轴交于G点,当顶点E在直线l上运动时,以A,C,E,G为顶点的四边形能否成为平行四边形?若能,求出E点坐标;若不能,请说明理由.8.已知抛物线:(1)求抛物线y1的顶点坐标.(2)将抛物线y1向右平移2个单位,再向上平移1个单位,得到抛物线y2,求抛物线y2的解析式.(3)如图,抛物线y2的顶点为P,x轴上有一动点M,在y1、y2这两条抛物线上是否存在点N,使O(原点)、P、M、N四点构成以OP为一边的平行四边形?若存在,求出N点的坐标;若不存在,请说明理由.9.如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.(1)求AD的长及抛物线的解析式;(2)一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO 以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动.设运动时间为t秒,当t 为何值时,以P、Q、C为顶点的三角形与△ADE相似?(3)点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使以M,N,C,E为顶点的四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.10.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N.其顶点为D.(1)抛物线及直线AC的函数关系式;(2)设点M(3,m),求使MN+MD的值最小时m的值;(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;(4)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.11.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0),B(3,0)两点,与y轴交于点C(0,﹣3).(1)求该抛物线的解析式及顶点M坐标;(2)求△BCM面积与△ABC面积的比;(3)若P是x轴上一个动点,过P作射线PQ∥AC交抛物线于点Q,随着P点的运动,在抛物线上是否存在这样的点Q,使以A,P,Q,C为顶点的四边形为平行四边形?若存在,请求出Q点坐标;若不存在,请说明理由.12.如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于点A和点B,其中点A的坐标为(﹣2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.(1)求抛物线的解析式;(2)若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形ABFC的面积为17,若存在,求出点F的坐标;若不存在,请说明理由;(3)平行于DE的一条动直线l与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标.13.如图,抛物线y=x2+bx+c与x轴交于A(5,0)、B(﹣1,0)两点,过点A作直线AC⊥x轴,交直线y=2x于点C;(1)求该抛物线的解析式;(2)求点A关于直线y=2x的对称点A′的坐标,判定点A′是否在抛物线上,并说明理由;(3)点P是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.14.如图,直线y=2x+2与x轴交于点A,与y轴交于点B,把△AOB沿y轴翻折,点A落到点C,过点B 的抛物线y=﹣x2+bx+c与直线BC交于点D(3,﹣4).(1)求直线BD和抛物线的解析式;(2)在第一象限内的抛物线上,是否存在一点M,作MN垂直于x轴,垂足为点N,使得以M、O、N为顶点的三角形与△BOC相似?若存在,求出点M的坐标;若不存在,请说明理由;(3)在直线BD上方的抛物线上有一动点P,过点P作PH垂直于x轴,交直线BD于点H,当四边形BOHP 是平行四边形时,试求动点P的坐标.15.综合与探究:如图,在平面直角坐标系xOy中,四边形OABC是平行四边形,A、C两点的坐标分别为(4,0),(﹣2,3),抛物线W经过O、A、C三点,D是抛物线W的顶点.(1)求抛物线W的解析式及顶点D的坐标;(2)将抛物线W和▱OABC一起先向右平移4个单位后,再向下平移m(0<m<3)个单位,得到抛物线W′和▱O′A′B′C′,在向下平移的过程中,设▱O′A′B′C′与▱OABC的重叠部分的面积为S,试探究:当m为何值时S有最大值,并求出S的最大值;(3)在(2)的条件下,当S取最大值时,设此时抛物线W′的顶点为F,若点M是x轴上的动点,点N是抛物线W′上的动点,试判断是否存在这样的点M和点N,使得以D、F、M、N为顶点的四边形是平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.16.如图,抛物线与x轴交于点A(﹣5,0)和点B(3,0).与y轴交于点C(0,5).有一宽度为1,长度足够的矩形(阴影部分)沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和Q,交直线AC于点M和N.交x轴于点E和F.(1)求抛物线的解析式;(2)当点M和N都在线段AC上时,连接MF,如果sin∠AMF=,求点Q的坐标;(3)在矩形的平移过程中,当以点P,Q,M,N为顶点的四边形是平行四边形时,求点M的坐标.17.如图,在平面直角坐标系xOy中,抛物线y=a(x+1)2﹣3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C(0,﹣),顶点为D,对称轴与x轴交于点H,过点H的直线l交抛物线于P,Q两点,点Q在y轴的右侧.(1)求a的值及点A,B的坐标;(2)当直线l将四边形ABCD分为面积比为3:7的两部分时,求直线l的函数表达式;(3)当点P位于第二象限时,设PQ的中点为M,点N在抛物线上,则以DP为对角线的四边形DMPN能否为菱形?若能,求出点N的坐标;若不能,请说明理由.1.解:(1)A(﹣1,0),B(3,0),C(0,3).抛物线的对称轴是:直线x=1.(2)①设直线BC的函数关系式为:y=kx+b.把B(3,0),C(0,3)分别代入得:解得:.所以直线BC的函数关系式为:y=﹣x+3.当x=1时,y=﹣1+3=2,∴E(1,2).当x=m时,y=﹣m+3,∴P(m,﹣m+3).在y=﹣x2+2x+3中,当x=1时,y=4.∴D(1,4)当x=m时,y=﹣m2+2m+3,∴F(m,﹣m2+2m+3)∴线段DE=4﹣2=2,线段PF=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m∵PF∥DE,∴当PF=ED时,四边形PEDF为平行四边形.由﹣m2+3m=2,解得:m1=2,m2=1(不合题意,舍去).因此,当m=2时,四边形PEDF为平行四边形.②设直线PF与x轴交于点M,由B(3,0),O(0,0),可得:OB=OM+MB=3.∵S=S△BPF+S△CPF即S=PF•BM+PF•OM=PF•(BM+OM)=PF•OB.∴S=×3(﹣m2+3m)=﹣m2+m(0≤m≤3).方法二:(3)∵B(3,0),C(0,3),D(1,4),∴,∴,∵∠DEC=∠COB=90°,∴△DEC∽△COB,∴∠DCE=∠CBO,∴∠DCE+∠OCB=90°,∴DC⊥BC,∴△BCD的外接圆圆心M为BD中点,∴M X==2,M Y==2,∴△BCD的外接圆圆心M(2,2).2.(2012•东营)已知抛物线经过A(2,0).设顶点为点P,与x轴的另一交点为点B.(1)求b的值,求出点P、点B的坐标;(2)如图,在直线y=x上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐标;若不存在,请说明理由;(3)在x轴下方的抛物线上是否存在点M,使△AMP≌△AMB?如果存在,试举例验证你的猜想;如果不存在,试说明理由.【解答】解:(1)由于抛物线经过A(2,0),所以,解得.所以抛物线的解析式为,①将①式配方,得,所以顶点P的坐标为(4,﹣2),令y=0,得,解得x1=2,x2=6.所以点B的坐标是(6,0).(2)在直线y=x上存在点D,使四边形OPBD为平行四边形.理由如下:设直线PB的解析式为y=kx+b,把B(6,0),P(4,﹣2)分别代入,得,解得,所以直线PB的解析式为.又因为直线OD的解析式为,所以直线PB∥OD.设直线OP的解析式为y=mx,把P(4,﹣2)代入,得,解得.如果OP∥BD,那么四边形OPBD为平行四边形.设直线BD的解析式为,将B(6,0)代入,得0=,所以所以直线BD的解析式为,解方程组,得,同样还存在第二种情况,如图所示,D′点和D关于原点对称,因此D′的坐标为(﹣2,﹣2),所以D点的坐标为(2,2)或(﹣2,﹣2).(3)符合条件的点M存在.验证如下:过点P作x轴的垂线,垂足为C,则PC=2,AC=2,由勾股定理,可得AP=4,PB=4,又AB=4,所以△APB是等边三角形,只要作∠PAB的平分线交抛物线于M点,连接PM,BM,由于AM=AM,∠PAM=∠BAM,AB=AP,可得△AMP≌△AMB.因此即存在这样的点M,使△AMP≌△AMB.方法二:(4)过点G作x轴垂线,垂足为H,∵⊙G为△OBD的外接圆,∴点G在线段OH的垂直平分线上,且GO=GD,∵B(6,0),∴l GH:x=3,设G点坐标为(3,m),O(0,0),D(2,2),∴(3﹣0)2+(m﹣0)2=(3﹣2)2+(m﹣2)2,∴m=,∴G点的坐标为(3,).3.(2012•宜宾)如图,抛物线y=x2﹣2x+c的顶点A在直线l:y=x﹣5上.(1)求抛物线顶点A的坐标;(2)设抛物线与y轴交于点B,与x轴交于点C、D(C点在D点的左侧),试判断△ABD的形状;(3)在直线l上是否存在一点P,使以点P、A、B、D为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.【解答】方法一:解:(1)∵顶点A的横坐标为x=﹣=1,且顶点A在y=x﹣5上,∴当x=1时,y=1﹣5=﹣4,∴A(1,﹣4).(2)△ABD是直角三角形.将A(1,﹣4)代入y=x2﹣2x+c,可得,1﹣2+c=﹣4,∴c=﹣3,∴y=x2﹣2x﹣3,∴B(0,﹣3)当y=0时,x2﹣2x﹣3=0,x1=﹣1,x2=3∴C(﹣1,0),D(3,0),BD2=OB2+OD2=18,AB2=(4﹣3)2+12=2,AD2=(3﹣1)2+42=20,BD2+AB2=AD2,∴∠ABD=90°,即△ABD是直角三角形.(3)存在.由题意知:直线y=x﹣5交y轴于点E(0,﹣5),交x轴于点F(5,0)∴OE=OF=5,又∵OB=OD=3∴△OEF与△OBD都是等腰直角三角形∴BD∥l,即PA∥BD则构成平行四边形只能是PADB或PABD,如图,过点P作y轴的垂线,过点A作x轴的垂线交过P且平行于x轴的直线于点G.设P(x1,x1﹣5),则G(1,x1﹣5)则PG=|1﹣x1|,AG=|5﹣x1﹣4|=|1﹣x1|PA=BD=3由勾股定理得:(1﹣x1)2+(1﹣x1)2=18,x12﹣2x1﹣8=0,x1=﹣2或4∴P(﹣2,﹣7)或P(4,﹣1),存在点P(﹣2,﹣7)或P(4,﹣1)使以点A、B、D、P为顶点的四边形是平行四边形.方法二:(1)略.(2)把A(1,﹣4)代入y=x2﹣2x+c,得c=3,∴y=x2﹣2x+3=(x﹣3)(x+1),∴D(3,0),B(0,﹣3),A(1,﹣4),K BD==1,K AB==﹣1,∴K BD•K AB=﹣1,∴AB⊥BD,即△ABD为直角三角形.(3)略.(4)∵,解得:x1=1(舍),x2=2,∴G(2,﹣3),∵A(1,﹣4),B(0,﹣3),D(3,0),∴GA==,BD==3,AB==,∴S△BDG==4.4.(2015•德州)已知抛物线y=﹣mx2+4x+2m与x轴交于点A(α,0),B(β,0),且=﹣2,(1)求抛物线的解析式.(2)抛物线的对称轴为l,与y轴的交点为C,顶点为D,点C关于l的对称点为E,是否存在x轴上的点M,y轴上的点N,使四边形DNME的周长最小?若存在,请画出图形(保留作图痕迹),并求出周长的最小值;若不存在,请说明理由.(3)若点P在抛物线上,点Q在x轴上,当以点D、E、P、Q为顶点的四边形是平行四边形时,求点P的坐标.【解答】解:(1)由题意可得:α,β是方程﹣mx2+4x+2m=0的两根,由根与系数的关系可得,α+β=,αβ=﹣2,∵=﹣2,∴=﹣2,即=﹣2,解得:m=1,故抛物线解析式为:y=﹣x2+4x+2;(2)存在x轴上的点M,y轴上的点N,使得四边形DNME的周长最小,∵y=﹣x2+4x+2=﹣(x﹣2)2+6,∴抛物线的对称轴l为x=2,顶点D的坐标为:(2,6),又∵抛物线与y轴交点C的坐标为:(0,2),点E与点C关于l对称,∴E点坐标为:(4,2),作点D关于y轴的对称点D′,点E关于x轴的对称点E′,则D′的坐标为;(﹣2,6),E′坐标为:(4,﹣2),连接D′E′,交x轴于M,交y轴于N,此时,四边形DNME的周长最小为:D′E′+DE,如图1所示:延长E′E,′D交于一点F,在Rt△D′E′F中,D′F=6,E′F=8,则D′E′===10,设对称轴l与CE交于点G,在Rt△DGE中,DG=4,EG=2,∴DE===2,∴四边形DNME的周长最小值为:10+2;(3)如图2,P为抛物线上的点,过点P作PH⊥x轴,垂足为H,若以点D、E、P、Q为顶点的四边形为平行四边形,则△PHQ≌△DGE,∴PH=DG=4,∴|y|=4,∴当y=4时,﹣x2+4x+2=4,解得:x1=2+,x2=2﹣,当y=﹣4时,﹣x2+4x+2=﹣4,解得:x3=2+,x4=2﹣,故P点的坐标为;(2﹣,4),(2+,4),(2﹣,﹣4),(2+,﹣4).5.(2015•绵阳)已知抛物线y=﹣x2﹣2x+a(a≠0)与y轴相交于A点,顶点为M,直线y=x﹣a分别与x轴、y轴相交于B,C两点,并且与直线MA相交于N点.(1)若直线BC和抛物线有两个不同交点,求a的取值范围,并用a表示交点M,A的坐标;(2)将△NAC沿着y轴翻转,若点N的对称点P恰好落在抛物线上,AP与抛物线的对称轴相交于点D,连接CD,求a的值及△PCD的面积;(3)在抛物线y=﹣x2﹣2x+a(a>0)上是否存在点P,使得以P,A,C,N为顶点的四边形是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.【解答】解:(1)由题意得,,整理得2x2+5x﹣4a=0.∵△=25+32a>0,解得a>﹣.∵a≠0,∴a>﹣且a≠0.令x=0,得y=a,∴A(0,a).由y=﹣(x+1)2+1+a得,M(﹣1,1+a).(2)设直线MA的解析式为y=kx+b(k≠0),∵A(0,a),M(﹣1,1+a),∴,解得,∴直线MA的解析式为y=﹣x+a,联立得,,解得,∴N(,﹣).∵点P是点N关于y轴的对称点,∴P(﹣,﹣).代入y=﹣x2﹣2x+a得,﹣=﹣a2+a+a,解得a=或a=0(舍去).∴A(0,),C(0,﹣),M(﹣1,),|AC|=,∴S△PCD=S△PAC﹣S△ADC=|AC|•|x p|﹣|AC|•|x0|=••(3﹣1)=;(3)①当点P在y轴左侧时,∵四边形APCN是平行四边形,∴AC与PN互相平分,N(,﹣),∴P(﹣,);代入y=﹣x2﹣2x+a得,=﹣a2+a+a,解得a=,∴P1(﹣,).②当点P在y轴右侧时,∵四边形ACPN是平行四边形,∴NP∥AC且NP=AC,∵N(,﹣),A(0,a),C(0,﹣a),∴P(,﹣).代入y=﹣x2﹣2x+a得,﹣=﹣a2﹣a+a,解得a=,∴P2(,﹣).综上所述,当点P1(﹣,)和P2(,﹣)时,A、C、P、N能构成平行四边形.6.(2015•湖北)边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点E在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点.(1)求抛物线的解析式;(2)点P从点C出发,沿射线CB每秒1个单位长度的速度运动,运动时间为t秒.过点P作PF⊥CD于点F,当t为何值时,以点P,F,D为顶点的三角形与△COD相似?(3)点M为直线AB上一动点,点N为抛物线上一动点,是否存在点M,N,使得以点M,N,D,E为顶点的四边形是平行四边形?若存在,请直接写出满足条件的点的坐标;若不存在,请说明理由.【解答】解:(1)方法一:过点E作EG⊥x轴于G点.∵四边形OABC是边长为2的正方形,D是OA的中点,∴OA=OC=2,OD=1,∠AOC=∠DGE=90°.∵∠CDE=90°,∴∠ODC+∠GDE=90°.∵∠ODC+∠OCD=90°,∴∠OCD=∠GDE.在△OCD和△GED中,∴△ODC≌△GED (AAS),∴EG=OD=1,DG=OC=2.∴点E的坐标为(3,1).∵抛物线的对称轴为直线AB即直线x=2,∴可设抛物线的解析式为y=a(x﹣2)2+k,将C、E点的坐标代入解析式,得.解得,抛物线的解析式为y=(x﹣2)2+;方法二:过点E作EG⊥x轴于G点.DE⊥DC⇒∠CDO+∠EDH=90°,EG⊥x轴⇒∠DEH+∠EDH=90°,∴∠CDO=∠DEH,DC=DE,∴△ODC≌△GED⇒DG=OC=2,EG=OD=1,∴E(3,1),∴9a+3b+2=0,∵﹣=2,抛物线的解析式为y=(x﹣2)2+;(2)方法一:①若△DFP∽△COD,则∠PDF=∠DCO,∴PD∥OC,∴∠PDO=∠OCP=∠AOC=90°,∴四边形PDOC是矩形,∴PC=OD=1,∴t=1;②若△PFD∽△COD,则∠DPF=∠DCO,=.∴∠PCF=90°﹣∠DCO=90﹣∠DPF=∠PDF.∴PC=PD,∴DF=CD.∵CD2=OD2+OC2=22+12=5,∴CD=,∴DF=.∵=,∴PC=PD=×=,t=,综上所述:t=1或t=时,以点P,F,D为顶点的三角形与△COD相似;方法二:过点F作x轴的垂线,分别交BC,OA于G,H,PF⊥CD⇒∠PFG+∠DFH=90°,GH⊥OA⇒∠FDH+∠DFH=90°,∴∠PFG=∠FDH⇒△PFG∽△FDH⇒,∵PF⊥CD⇒K PF×K CD=﹣1,∴l CD:y=﹣2x+2,∴F(m,﹣2m+2),P(t,2),∴,∴m=,∴F(,﹣),∴=,∴以P,F,D为顶点的三角形与△COD相似,①,∴,∴t=,②,∴,∴t=1,综上所述:t=1或t=时,以点P,F,D为顶点的三角形与△COD相似;方法三:若以P,F,D为顶点的三角形与△COD相似,则∠OCD=∠PDF或∠ODC=∠PDF,①∠OCD=∠PDF⇒PD∥OC,∴CP=OD=1,∴t=1,②∠ODC=∠PDF,作OO′⊥CD交CD于H,∴K OO′×K CD=﹣1,∴l CD:y=﹣2x+2,∴H(m,﹣2m+2),∴﹣2×=﹣1,∴m=,∴H(,),∵H为OO′中点,∴O′(,),∴l O′D:y=,令y=2,∴x=,即P(,2),∴t=.(3)存在,四边形MDEN是平行四边形时,M1(2,1),N1(4,2);四边形MNDE是平行四边形时,M2(2,3),N2(0,2);四边形NDME是平行四边形时,M3(2,),N3(2,).7.(2015•广安)如图,边长为1的正方形ABCD一边AD在x负半轴上,直线l:y=x+2经过点B(x,1)与x轴,y轴分别交于点H,F,抛物线y=﹣x2+bx+c.(1)求A,D两点的坐标及抛物线经过A,D两点时的解析式;(2)当抛物线的顶点E(m,n)在直线l上运动时,连接EA,ED,试求△EAD的面积S与m之间的函数解析式,并写出m的取值范围;(3)设抛物线与y轴交于G点,当顶点E在直线l上运动时,以A,C,E,G为顶点的四边形能否成为平行四边形?若能,求出E点坐标;若不能,请说明理由.【解答】解:(1)∵直线l:y=x+2经过点B(x,1),∴1=x+2,解得x=﹣2,∴B(﹣2,1),∴A(﹣2,0),D(﹣3,0),∵抛物线经过A,D两点,∴,解得,∴抛物线经过A,D两点时的解析式为y=﹣x2﹣5x﹣6;(2)∵点E(m,n)在直线l上,∴n=m+2,∴S=×1×[±(m+2)]=±(m+1),即S=m+1(m>﹣4)或S=﹣m﹣1(m<﹣4);(3)如图,若以A,C,E,G为顶点的四边形能成为平行四边形,则AC=EG,AC∥EG,作EH∥y轴交过G点平行于x轴的直线相交于H,则EH⊥GH,△EHG≌△CDA,∴GH=AD=1,∴E的横坐标为±1,∵点E在直线l上,∴y=×(﹣1)+2=,或y=×1+2=当AC为对角线时,有E和G的横坐标之和等于A和C的横坐标之和,故可求得E(﹣5,﹣1/2)∴E(﹣1,);(1,)或(﹣5,﹣1/2);由于E为抛物线的顶点,G为抛物线与y轴的交点,故将其坐标代入y=﹣x2+bx+c,检验可知当E取(1,)或(﹣5,﹣1/2)时,与此时的A、C、E构成平行四边形的G点并不是y轴与抛物线的交点,与前提相矛盾;综上,满足题意的E的坐标为(﹣1,).8.(2012秋•义乌市校级期中)已知抛物线:(1)求抛物线y1的顶点坐标.(2)将抛物线y1向右平移2个单位,再向上平移1个单位,得到抛物线y2,求抛物线y2的解析式.(3)如图,抛物线y2的顶点为P,x轴上有一动点M,在y1、y2这两条抛物线上是否存在点N,使O(原点)、P、M、N四点构成以OP为一边的平行四边形?若存在,求出N点的坐标;若不存在,请说明理由.【解答】解:(1)依题意把抛物线:y1=﹣x2+2x=﹣(x2﹣4x)=﹣[(x﹣2)2﹣4]=﹣(x﹣2)2+2,故抛物线y1的顶点坐标为:(2,2);(2)∵抛物线y1向右平移2个单位,再向上平移1个单位,得到y2=﹣(x﹣4)2+3,整理得y2=﹣x2+4x﹣5;(3)符合条件的N点存在.如图:作PA⊥x轴于点A,NB⊥x轴于点B,∴∠PAO=∠MBN=90°,若四边形OPMN为符合条件的平行四边形,则OP∥MN,且OP=MN,∴∠POA=∠BMN,在△POA和△NMB中∴△POA≌△NMB(AAS),∴PA=BN,∵点P的坐标为(4,3),∴NB=PA=3,∵点N在抛物线y1、y2上,且P点为y1、y2的最高点∴符合条件的N点只能在x轴下方,①点N在抛物线y1上,则有:﹣x2+2x=﹣3解得:x1=2﹣,x2=2+,②点N在抛物线y2上,则有:﹣(x﹣4)2+3=﹣3解得:x3=4﹣2或x4=4+2故符合条件的N点有四个:N1(2﹣,﹣3),N2(4﹣2,﹣3),N3(2+,﹣3),N4(4+2,﹣3).9.(2012•襄阳)如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B 落在OA边上的点E处.分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c 经过O,D,C三点.(1)求AD的长及抛物线的解析式;(2)一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO 以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动.设运动时间为t秒,当t 为何值时,以P、Q、C为顶点的三角形与△ADE相似?(3)点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使以M,N,C,E为顶点的四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.【解答】方法一:解:(1)∵四边形ABCO为矩形,∴∠OAB=∠AOC=∠B=90°,AB=CO=8,AO=BC=10.由题意,△BDC≌△EDC.∴∠B=∠DEC=90°,EC=BC=10,ED=BD.由勾股定理易得EO=6.∴AE=10﹣6=4,设AD=x,则BD=ED=8﹣x,由勾股定理,得x2+42=(8﹣x)2,解得,x=3,∴AD=3.∵抛物线y=ax2+bx+c过点D(3,10),C(8,0),O(0,0)∴,解得∴抛物线的解析式为:y=﹣x2+x.(2)∵∠DEA+∠OEC=90°,∠OCE+∠OEC=90°,∴∠DEA=∠OCE,由(1)可得AD=3,AE=4,DE=5.而CQ=t,EP=2t,∴PC=10﹣2t.当∠PQC=∠DAE=90°,△ADE∽△QPC,∴=,即=,解得t=.当∠QPC=∠DAE=90°,△ADE∽△PQC,∴=,即=,解得t=.∴当t=或时,以P、Q、C为顶点的三角形与△ADE相似.(3)假设存在符合条件的M、N点,分两种情况讨论:①EC为平行四边形的对角线,由于抛物线的对称轴经过EC中点,若四边形MENC是平行四边形,那么M点必为抛物线顶点;则:M(4,);而平行四边形的对角线互相平分,那么线段MN必被EC中点(4,3)平分,则N(4,﹣);②EC为平行四边形的边,则EC MN,设N(4,m),则M(4﹣8,m+6)或M(4+8,m﹣6);将M(﹣4,m+6)代入抛物线的解析式中,得:m=﹣38,此时N(4,﹣38)、M(﹣4,﹣32);将M(12,m﹣6)代入抛物线的解析式中,得:m=﹣26,此时N(4,﹣26)、M(12,﹣32);综上,存在符合条件的M、N点,且它们的坐标为:①M1(﹣4,﹣32),N1(4,﹣38);②M2(12,﹣32),N2(4,﹣26);③M3(4,),N3(4,﹣).方法二:(1)略.(2)∵E(0,6),C(8,0),∴l EC:y=﹣x+6,∵,EP=2t,∴P x=t,∴P(t,﹣t+6),Q(8﹣t,0),∵△PQC∽△ADE,且∠ECO=∠AED,∴PQ⊥OC或PQ⊥PC.当PQ⊥OC时,Px=Qx,即t=8﹣t,∴t1=,当PQ⊥PC时,K PQ•K PC=﹣1,∴t2=.(3)M,N,C,E为顶点的四边形是平行四边形.设N(4,t),C(8,0),E(0,6),∴,∴M1(4,6﹣t),同理M2(﹣4,t+6),M3(12,t﹣6),∴﹣t,∴t=﹣,﹣×(﹣4)2+(﹣4)=t+6,∴t=﹣38,﹣×122+×12=t﹣6,∴t=﹣26,综上,存在符合条件的M、N点,且它们的坐标为:①M1(4,),N1(4,﹣);②M2(12,﹣32),N2(4,﹣26);③M3(﹣4,﹣32),N3(4,﹣38).10.(2012•恩施州)如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N.其顶点为D.(1)抛物线及直线AC的函数关系式;(2)设点M(3,m),求使MN+MD的值最小时m的值;(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;(4)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.【解答】解:(1)由抛物线y=﹣x2+bx+c过点A(﹣1,0)及C(2,3)得,,解得,故抛物线为y=﹣x2+2x+3又设直线为y=kx+n过点A(﹣1,0)及C(2,3)得,解得故直线AC为y=x+1;(2)如图1,作N点关于直线x=3的对称点N′,则N′(6,3),由(1)得D(1,4),故直线DN′的函数关系式为y=﹣x+,当M(3,m)在直线DN′上时,MN+MD的值最小,则m=﹣×=;(3)由(1)、(2)得D(1,4),B(1,2),∵点E在直线AC上,设E(x,x+1),①如图2,当点E在线段AC上时,点F在点E上方,则F(x,x+3),∵F在抛物线上,∴x+3=﹣x2+2x+3,解得,x=0或x=1(舍去)∴E(0,1);②当点E在线段AC(或CA)延长线上时,点F在点E下方,则F(x,x﹣1)由F在抛物线上∴x﹣1=﹣x2+2x+3解得x=或x=∴E(,)或(,)综上,满足条件的点E的坐标为(0,1)、(,)或(,);(4)方法一:如图3,过点P作PQ⊥x轴交AC于点Q,交x轴于点H;过点C作CG⊥x轴于点G,设Q (x,x+1),则P(x,﹣x2+2x+3)∴PQ=(﹣x2+2x+3)﹣(x+1)=﹣x2+x+2又∵S△APC=S△APQ+S△CPQ=PQ•AG=(﹣x2+x+2)×3=﹣(x﹣)2+∴面积的最大值为.方法二:过点P作PQ⊥x轴交AC于点Q,交x轴于点H;过点C作CG⊥x轴于点G,如图3,设Q(x,x+1),则P(x,﹣x2+2x+3)又∵S△APC=S△APH+S直角梯形PHGC﹣S△AGC=(x+1)(﹣x2+2x+3)+(﹣x2+2x+3+3)(2﹣x)﹣×3×3=﹣x2+x+3=﹣(x﹣)2+∴△APC的面积的最大值为.11.(2014•赤峰)如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0),B(3,0)两点,与y轴交于点C(0,﹣3).(1)求该抛物线的解析式及顶点M坐标;(2)求△BCM面积与△ABC面积的比;(3)若P是x轴上一个动点,过P作射线PQ∥AC交抛物线于点Q,随着P点的运动,在抛物线上是否存在这样的点Q,使以A,P,Q,C为顶点的四边形为平行四边形?若存在,请求出Q点坐标;若不存在,请说明理由.【解答】方法一:解:(1)设抛物线解析式为y=a(x+1)(x﹣3),∵抛物线过点(0,﹣3),∴﹣3=a(0+1)(0﹣3),∴a=1,∴抛物线解析式为y=(x+1)(x﹣3)=x2﹣2x﹣3,∵y=x2﹣2x﹣3=(x﹣1)2﹣4,∴M(1,﹣4).(2)如图1,连接BC、BM、CM,作MD⊥x轴于D,∵S△BCM=S梯形OCMD+S△BMD﹣S△BOC=•(3+4)•1+•2×4﹣•3•3=+﹣=3S△ABC=•AB•OC=•4•3=6,∴S△BCM:S△ABC=3:6=1:2.(3)存在,理由如下:①如图2,当Q在x轴下方时,作QE⊥x轴于E,∵四边形ACQP为平行四边形,∴PQ平行且相等AC,∴△PEQ≌△AOC,∴EQ=OC=3,∴﹣3=x2﹣2x﹣3,解得x=2或x=0(与C点重合,舍去),∴Q(2,﹣3).②如图3,当Q在x轴上方时,作QF⊥x轴于F,∵四边形ACPQ为平行四边形,∴QP平行且相等AC,∴△PFQ≌△AOC,∴FQ=OC=3,∴3=x2﹣2x﹣3,解得x=1+或x=1﹣,∴Q(1+,3)或(1﹣,3).综上所述,Q点为(2,﹣3)或(1+,3)或(1﹣,3)方法二:(1)略.(2)连接BC、BM、CM,作MD⊥x轴于D,交BC于H,∵B(3,0),C(0,﹣3),∴l BC:y=x﹣3,当x=1时,y=﹣2,∴H(1,﹣2)∴S△BCM=(3﹣0)(﹣2+4)=3,∵S△ABC=AB×OC=×3×4=6,∴S△BCM:S△ABC=3:6=1:2,(3)∵PQ∥AC,∴当PQ=AC时,A、P、Q、C为顶点的四边形为平行四边形,即|Q Y|=|C Y|,设Q(t,t2﹣2t﹣3),∴|t2﹣2t﹣3|=3,①t2﹣2t﹣3=3,解得:t1=1+,t2=1﹣,②t2﹣2t﹣3=﹣3,解得:t1=0(舍),t2=2,综上所述,Q点为(2,﹣3)或(1+,3)或(1﹣,3).12.(2014•潍坊)如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于点A和点B,其中点A的坐标为(﹣2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.(1)求抛物线的解析式;(2)若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形ABFC的面积为17,若存在,求出点F的坐标;若不存在,请说明理由;(3)平行于DE的一条动直线l与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标.【解答】方法一:解:(1)∵抛物线y=ax2+bx+c(a≠0)过点C(0,4),∴c=4 ①.∵对称轴x=﹣=1,∴b=﹣2a ②.∵抛物线过点A(﹣2,0),∴0=4a﹣2b+c ③,由①②③解得,a=﹣,b=1,c=4,∴抛物线的解析式为y=﹣x2+x+4;(2)假设存在满足条件的点F,如图所示,连结BF、CF、OF,过点F作FH⊥x轴于点H,FG⊥y轴于点G.设点F的坐标为(t,﹣t2+t+4),其中0<t<4,则FH=﹣t2+t+4,FG=t,∴S△OBF=OB•FH=×4×(﹣t2+t+4)=﹣t2+2t+8,S△OFC=OC•FG=×4×t=2t,∴S四边形ABFC=S△AOC+S△OBF+S△OFC=4﹣t2+2t+8+2t=﹣t2+4t+12.令﹣t2+4t+12=17,即t2﹣4t+5=0,则△=(﹣4)2﹣4×5=﹣4<0,∴方程t2﹣4t+5=0无解,故不存在满足条件的点F;(3)设直线BC的解析式为y=kx+n(k≠0),∵B(4,0),C(0,4),∴,解得,∴直线BC的解析式为y=﹣x+4.由y=﹣x2+x+4=﹣(x﹣1)2+,∴顶点D(1,),又点E在直线BC上,则点E(1,3),于是DE=﹣3=.若以D、E、P、Q为顶点的四边形是平行四边形,因为DE∥PQ,只须DE=PQ,设点P的坐标是(m,﹣m+4),则点Q的坐标是(m,﹣m2+m+4).①当0<m<4时,PQ=(﹣m2+m+4)﹣(﹣m+4)=﹣m2+2m,由﹣m2+2m=,解得:m=1或3.当m=1时,线段PQ与DE重合,m=1舍去,∴m=3,P1(3,1).②当m<0或m>4时,PQ=(﹣m+4)﹣(﹣m2+m+4)=m2﹣2m,由m2﹣2m=,解得m=2±,经检验适合题意,此时P2(2+,2﹣),P3(2﹣,2+).综上所述,满足题意的点P有三个,分别是P1(3,1),P2(2+,2﹣),P3(2﹣,2+).方法二:(1)略.(2)∵B(4,0),C(0,4),∴l BC:y=﹣x+4,过F点作x轴垂线,交BC于H,设F(t,﹣t2+t+4),∴H(t,﹣t+4),∵S四边形ABFC=S△ABC+S△BCF=17,∴(4+2)×4+(﹣t2+t+4+t﹣4)×4=17,∴t2﹣4t+5=0,∴△=(﹣4)2﹣4×5<0,∴方程t2﹣4t+5=0无解,故不存在满足条件的点F.(3)∵DE∥PQ,∴当DE=PQ时,以D、E、P、Q为顶点的四边形是平行四边形,∵y=﹣x2+x+4,∴D(1,),∵l BC:y=﹣x+4,∴E(1,3),∴DE=﹣3=,设点F的坐标是(m,﹣m+4),则点Q的坐标是(m,﹣m2+m+4),∴|﹣m+4+m2﹣m﹣4|=,∴m2﹣2m=或m2﹣2m=﹣,∴m=1,m=3,m=2+,m=2﹣,经检验,当m=1时,线段PQ与DE重合,故舍去.∴P1(3,1),P2(2+,2﹣),P3(2﹣,2+).13.(2014•济宁)如图,抛物线y=x2+bx+c与x轴交于A(5,0)、B(﹣1,0)两点,过点A作直线AC⊥x轴,交直线y=2x于点C;(1)求该抛物线的解析式;(2)求点A关于直线y=2x的对称点A′的坐标,判定点A′是否在抛物线上,并说明理由;(3)点P是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.【解答】方法一:解:(1)∵y=x2+bx+c与x轴交于A(5,0)、B(﹣1,0)两点,∴,解得.∴抛物线的解析式为y=x2﹣x﹣.(2)如答图所示,过点A′作A′E⊥x轴于E,AA′与OC交于点D,∵点C在直线y=2x上,∴C(5,10)∵点A和A′关于直线y=2x对称,∴OC⊥AA′,A′D=AD.∵OA=5,AC=10,∴OC===.∵S△OAC=OC•AD=OA•AC,∴AD=.∴AA′=,在Rt△A′EA和Rt△OAC中,∵∠A′AE+∠A′AC=90°,∠ACD+∠A′AC=90°,∴∠A′AE=∠ACD.又∵∠A′EA=∠OAC=90°,∴Rt△A′EA∽Rt△OAC.∴,即.∴A′E=4,AE=8.∴OE=AE﹣OA=3.∴点A′的坐标为(﹣3,4),当x=﹣3时,y=×(﹣3)2+3﹣=4.所以,点A′在该抛物线上.(3)存在.理由:设直线CA′的解析式为y=kx+b,则,解得∴直线CA′的解析式为y=x+设点P的坐标为(x,x2﹣x﹣),则点M为(x,x+).∵PM∥AC,∴要使四边形PACM是平行四边形,只需PM=AC.又点M在点P的上方,∴(x+)﹣(x2﹣x﹣)=10.解得x1=2,x2=5(不合题意,舍去)当x=2时,y=﹣.∴当点P运动到(2,﹣)时,四边形PACM是平行四边形.方法二:(1)略.(2)设AA′与直线OC的交点为H,∵点A,点A′关于直线OC:y=2x对称,∴AA′⊥OC,K OC•K AA′=﹣1,∵K OC=2,∴K AA′=﹣,∵A(5,0),∴l AA′:y=﹣x+,l OC:y=2x,∴H(1,2),∵H为AA′的中点,∴⇒,∴A′X=﹣3,A′Y=4,∴A′(﹣3,4),当x=﹣3时,y=×(﹣3)2+3﹣=4,∴点A在抛物线上.(3)∵PM∥AC,要使四边形PACM是平行四边形,只需PM=AC,∵直线AC⊥x轴,∴C x=A x,∵A(5,0),∴C x=5,∵l OC:y=2x,∴C Y=10,∴C(5,10),∵A′(﹣3,4),∴l CA′:y=x+,∵M在线段CA′上,点M在点P的上方,∴设M(t,),∴P(t,t2﹣t﹣),∴﹣(t2﹣t﹣)=10,∴t1=2,t2=5(舍),∴P(2,﹣).14.(2014•东营)如图,直线y=2x+2与x轴交于点A,与y轴交于点B,把△AOB沿y轴翻折,点A落到点C,过点B的抛物线y=﹣x2+bx+c与直线BC交于点D(3,﹣4).(1)求直线BD和抛物线的解析式;(2)在第一象限内的抛物线上,是否存在一点M,作MN垂直于x轴,垂足为点N,使得以M、O、N为顶点的三角形与△BOC相似?若存在,求出点M的坐标;若不存在,请说明理由;(3)在直线BD上方的抛物线上有一动点P,过点P作PH垂直于x轴,交直线BD于点H,当四边形BOHP 是平行四边形时,试求动点P的坐标.。
抛物线中的平行四边形

若点A坐标为(-1,0),点B坐 标为(2,-2) 。你能写出 点D的坐标吗?
D2
C1
A
C3 C2
D1
B
01
已知平行四边形的两定点,
确定另两点构成平行四边形。
02
根据两定点确定的线段,分
为平行四边形的边或对角线
03
理一理:
例2、抛物线 yx22x3 与x轴交A,B两
点(A点在B点左侧),直线l与抛物线交于A,C两点, 其中C点的横坐标为2。点D是抛物线上的动点,在 x轴上是否存在点E,使以A、C、D、E为顶点的四 边形是平行四边形?如果存在,求出所有满足条件 的点D的坐标,若不存在,请说明理由。y
抛物线 y=x2-2x-3与x轴交于A,B点,与y轴交于C点,
顶轴点 交是 点NM,在.坐若标经平过面C,内M是两否点存作在直这线样yC 的M 点P,x使以3点与x P,A,C,N为顶点四边形是平行四边形?若存在,请求出 点P的坐标. 若不存在,请说明理由;
y
N
O1
Bx
C
M
解:令x=0,得y=-3. 令y=0,得x 2 2 x 3 0 , x 1 1 ,x 2 3
使以A、B、C、D为
D2
顶点的四边形是平行
四边形。
A
D1
算一算:
若这三点的坐标分别 为A(1,3)、B(-2,0)、 C(2,0),你能求出点 D的坐标吗?
Q B
P
C
D3
理一理:
已知平行四边形三定点,确定第四点构成平行四边形。
根据三点确定三角形,然后分别以这个三角形 的三边分别为平行四边形的对角线,有三种情况,得到 三个平行四边形。
点Q在y轴上,点P在抛物线上,要使Q、P、A、B为顶 点的四边形是平行四边形求所有满足条件点P的坐标。
中考复习专题6二次函数与平行四边形存在性问题(含解析)

专题6二次函数与平行四边形存在性问题解决抛物线中的平行四边形存在性问题,常用的结论和方法有:线段中点坐标公式、平行四边形顶点坐标公式、画平行四边形.1.平面直角坐标系中,点A 的坐标是11(,)x y ,点B 的坐标是22(,)x y ,则线段AB 的中点坐标是1212(,22x x y y ++.2.平行四边形ABCD 的顶点坐标分别为(,)A A x y 、(,)B B x y 、(,)C C x y 、(,)D D x y ,则A C B D x x x x +=+,A C B D y y y y +=+.3.已知不在同一直线上的三点A 、B 、C ,在平面内找到一个点D ,使以A 、B 、C 、D 为顶点的四边形是平行四边形,有三种情况:【例1】(2022•娄底)如图,抛物线y =x 2﹣2x ﹣6与x 轴相交于点A 、点B ,与y 轴相交于点C .(1)请直接写出点A ,B ,C 的坐标;(2)点P (m ,n )(0<m <6)在抛物线上,当m 取何值时,△PBC 的面积最大?并求出△PBC 面积的最大值.(3)点F 是抛物线上的动点,作FE ∥AC 交x 轴于点E ,是否存在点F ,使得以A 、C 、E 、F 为顶点的四边形是平行四边形?若存在,请写出所有符合条件的点F 的坐标;若不存在,请说明理由.【分析】(1)将x=0及y=0代入抛物线y=x2﹣2x﹣6的解析式,进而求得结果;,S△BOP,计算出S△BOC,根据S△PBC=S (2)连接OP,设点P(m,﹣2m﹣6),分别表示出S△POC﹣S△BOC,从而得出△PBC的函数关系式,进一步求得结果;四边形PBOC(3)可分为▱ACFE和▱ACEF的情形.当▱ACFE时,点F和点C关于抛物线对称轴对称,从而得出F点坐标;当▱ACED时,可推出点F的纵坐标为6,进一步求得结果.【解析】(1)当x=0时,y=﹣6,∴C(0,﹣6),当y=0时,x2﹣2x﹣6=0,∴x1=6,x2=﹣2,∴A(﹣2,0),B(6,0);(2)方法一:如图1,连接OP,设点P(m,﹣2m﹣6),=x P==3m,∴S△POCS△BOP=|y P|=+2m+6),==18,∵S△BOC=S四边形PBOC﹣S△BOC∴S△PBC+S△POB)﹣S△BOC=(S△POC=3m+3(﹣+2m+6)﹣18=﹣(m﹣3)2+,=;∴当m=3时,S△PBC最大方法二:如图2,作PQ⊥AB于Q,交BC于点D,∵B(6,0),C(0,﹣6),∴直线BC的解析式为:y=x﹣6,∴D(m,m﹣6),∴PD=(m﹣6)﹣(﹣2m﹣6)=﹣+3m,===﹣(m﹣3)2+,∴S△PBC=;∴当m=3时,S△PBC最大(3)如图3,当▱ACFE时,AE∥CF,∵抛物线对称轴为直线:x==2,∴F1点的坐标:(4,﹣6),如图4,当▱ACEF时,作FG⊥AE于G,∴FG=OC=6,当y=6时,x2﹣2x﹣6=6,∴x1=2+2,x2=2﹣2,∴F2(2+2,6),F3(2﹣2,6),综上所述:F(4,﹣6)或(2+2,6)或(2﹣2,6).【例2】.(2022•毕节市)如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于A,B两点,与y 轴交于点C,顶点为D(2,1),抛物线的对称轴交直线BC于点E.(1)求抛物线y=﹣x2+bx+c的表达式;(2)把上述抛物线沿它的对称轴向下平移,平移的距离为h(h>0),在平移过程中,该抛物线与直线BC始终有交点,求h的最大值;(3)M是(1)中抛物线上一点,N是直线BC上一点.是否存在以点D,E,M,N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.【分析】(1)利用抛物线的顶点式可直接得出抛物线的表达式;(2)先根据(1)中抛物线的表达式求出点A,B,C的坐标,进而可得出直线BC的表达式;设出点平移后的抛物线,联立直线BC和抛物线的表达式,根据根的判别式可得出结论;(3)假设存在以点D,E,M,N为顶点的四边形是平行四边形,分别以DE为边,以DE为对角线,进行讨论即可.【解析】(1)∵抛物线y=﹣x2+bx+c的顶点为D(2,1),∴抛物线的表达式为:y=﹣(x﹣2)2+1=﹣x2+4x﹣3.(2)由(1)知,抛物线的表达式为:y=﹣x2+4x﹣3,令x=0,则y=﹣3,∴C(0,﹣3);令y=0,则x=1或x=3,∴A(1,0),B(3,0).∴直线BC的解析式为:y=x﹣3.设平移后的抛物线的解析式为:y=﹣(x﹣2)2+1﹣h,令﹣(x﹣2)2+1﹣h=x﹣3,整理得x2﹣3x+h=0,∵该抛物线与直线BC始终有交点,∴Δ=9﹣4h≥0,∴h≤.∴h的最大值为.(3)存在,理由如下:由题意可知,抛物线的对称轴为:直线x=2,∴E(2,﹣1),∴DE=2,设点M(m,﹣m2+4m﹣3),若以点D,E,M,N为顶点的四边形是平行四边形,则分以下两种情况:①当DE为边时,DE∥MN,则N(m,m﹣3),∴MN=|﹣m2+4m﹣3﹣(m﹣3)|=|﹣m2+3m|,∴|﹣m2+3m|=2,解得m=1或m=2(舍)或m=或m=.∴N(1,﹣2)或(,)或(,).②当DE为对角线时,设点N的坐标为t,则N(t,t﹣3),∴,解得m或(舍),∴N(3,0).综上,点N的坐标为N(1,﹣2)或(,)或(,)或(3,0).【例3】(2022•聊城)如图,在直角坐标系中,二次函数y=﹣x2+bx+c的图象与x轴交于A,B两点,与y 轴交于点C(0,3),对称轴为直线x=﹣1,顶点为点D.(1)求二次函数的表达式;(2)连接DA,DC,CB,CA,如图①所示,求证:∠DAC=∠BCO;(3)如图②,延长DC交x轴于点M,平移二次函数y=﹣x2+bx+c的图象,使顶点D沿着射线DM方向平移到点D1且CD1=2CD,得到新抛物线y1,y1交y轴于点N.如果在y1的对称轴和y1上分别取点P,Q,使以MN为一边,点M,N,P,Q为顶点的四边形是平行四边形,求此时点Q的坐标.【分析】(1)根据抛物线对称轴和点C坐标分别确定b和c的值,进而求得结果;(2)根据点A,D,C坐标可得出AD,AC,CD的长,从而推出三角形ADC为直角三角形,进而得出∠DAC和∠BCO的正切值相等,从而得出结论;(3)先得出y1的顶点,进而得出先抛物线的表达式,N的坐标,根据三角形相似或一次函数可求得点M 坐标,以MN为边,点M,N,P,Q为顶点的四边形是▱MNQP和▱MNPQ根据M,N和点P的横坐标可以得出Q点的横坐标,进而求得结果.【解答】(1)解:由题意得,,∴,∴二次函数的表达式为:y=﹣x2﹣2x+3;(2)证明:∵当x=﹣1时,y=﹣1﹣2×(﹣1)+3=4,∴D(﹣1,4),由﹣x2﹣2x+3=0得,x1=﹣3,x2=1,∴A(﹣3,0),B(1,0),∴AD2=20,∵C(0,3),∴CD2=2,AC2=18,∴AC2+CD2=AD2,∴∠ACD=90°,∴tan∠DAC===,∵∠BOC=90°,∴tan∠BCO==,∴∠DAC=∠BCO;(3)解:如图,作DE⊥y轴于E,作D1F⊥y轴于F,∴DE∥FD1,∴△DEC∽△D1FC,∴=,∴FD1=2DE=2,CF=2CE=2,∴D1(2,1),∴y1的关系式为:y=﹣(x﹣2)2+1,当x=0时,y=﹣3,∴N(0,﹣3),同理可得:,∴,∴OM=3,∴M(3,0),设P(2,m),当▱MNQP时,∴MN∥PQ,PQ=MN,∴Q点的横坐标为﹣1,当x=﹣1时,y=﹣(﹣1﹣2)2+1=﹣8,∴Q(﹣1,8),当▱MNPQ时,同理可得:点Q横坐标为:5,当x=5时,y=﹣(5﹣2)2+1=﹣8,∴Q′(5,﹣8),综上所述:点Q(﹣1,﹣8)或(5,﹣8).【例4】(2022•郴州)已知抛物线y=x2+bx+c与x轴相交于点A(﹣1,0),B(3,0),与y轴相交于点C.(1)求抛物线的表达式;(2)如图1,将直线BC向上平移,得到过原点O的直线MN.点D是直线MN上任意一点.①当点D在抛物线的对称轴l上时,连接CD,与x轴相交于点E,求线段OE的长;②如图2,在抛物线的对称轴l上是否存在点F,使得以B,C,D,F为顶点的四边形是平行四边形?若存在,求出点F与点D【分析】(1)根据点A、B的坐标利用待定系数法即可求出抛物线的解析式;(2)①方法一:求出直线CD的解析式为y=4x﹣3,当y=0时,求出x的值,则可得出答案;方法二:求出OD=3,证明△DEO∽△CEB,由相似三角形的性质得出,设OE=x,则BE=3﹣x,列出方程求出x的值,则可得出答案;②分别以已知线段BC为边、BC为对角线,画出图形,利用平行四边形的性质及全等三角形的性质求点F的坐标和点D的坐标即可.【解析】(1)将A(﹣1,0)、B(3,0)代入y=x2+bx+c得,,解得,∴抛物线的解析式为y=x2﹣2x﹣3;(2)①由(1)可知,C(0,﹣3),设直线BC的解析式为y=kx+m,将C(0,﹣3),B(3,0)代入得,,∴,∴直线BC的解析式为y=x﹣3,∴直线MN的解析式为y=x,∵抛物线的对称轴为x=﹣=﹣=1,把x=1代入y=x,得y=1,∴D(1,1),方法一:设直线CD的解析式为y=k1x+b1,将C(0,﹣3),D(1,1)代入得,,解得,∴直线CD的解析式为y=4x﹣3,当y=0时,4x﹣3=0,∴x=,∴E(,0),∴OE=.方法二:由勾股定理得OD==,BC==3,∵BC∥MN,∴△DEO∽△CEB,∴,设OE=x,则BE=3﹣x,∴,解得x=,∴OE=.②存在点F,使得以B,C,D,F为顶点的四边形是平行四边形.理由如下:(Ⅰ)若平行四边形以BC为边时,由BC∥FD可知,FD在直线上,∴点F是直线MN与对称轴l的交点,即F(1,1),由点D在直线MN上,设D(t,t),如图,若四边形BCFD是平行四边形,则DF=BC,过点D作y轴的垂线交对称轴l于点G,则G(1,t),∵BC∥MN,∴∠OBC=∠DOB,∵GD∥x轴,∴∠GDF=∠DOB,∴∠OBC=∠GDF,又∵∠BOC=∠DGF=90°,∴△DGF≌△BOC(AAS),∴GD=OB,GF=OC,∵GD=t﹣1,OB=3,∴t﹣1=3,∴t=4,∴D(4,4),如图,若四边形BCDF是平行四边形,则DF=CB,同理可证△DKF≌△COB(AAS),∴KD=OC,∵KD=1﹣t,OC=3,∴1﹣t=3,∴t=﹣2,∴D(﹣2,﹣2);(Ⅱ)若平行四边形以BC为对角线时,由于D在BC的上方,则点F一定在BC的下方,如图,四边形BFCD为平行四边形,设D(t,t),F(1,n),同理可证△DHC≌△BPF(AAS),∴DH=BP,HC=PF,∵DH=t,BP=3﹣1=2,HC=t﹣(﹣3)=t+3,PF=0﹣n=﹣n,∴,∴,∴D(2,2),F(1,﹣5),综上所述,存在点F,使得以B,C,D,F为顶点的四边形是平行四边形.当点F的坐标为(1,1)时,点D的坐标为(4,4)或(﹣2,﹣2);当点F的坐标为(1,﹣5)时,点D的坐标为(2,2).1.(2021•滨城区一模)如图,抛物线y=ax2+bx﹣5(a≠0)经过x轴上的点A(1,0)和点B(5,0)及y 轴上的点C,经过B、C两点的直线为y=kx+b(k≠0).(1)求抛物线的解析式.(2)点P从A出发,在线段AB上以每秒1个单位的速度向B运动,同时点E从B出发,在线段BC上以每秒2个单位的速度向C运动.当其中一个点到达终点时,另一点也停止运动.设运动时间为t秒,求t为何值时,△PBE的面积最大并求出最大值.(3)过点A作AM⊥BC于点M,过抛物线上一动点N(不与点B、C重合)作直线AM的平行线交直线BC于点Q.若点A、M、N、Q为顶点的四边形是平行四边形,求点N的横坐标.【分析】(1)将A(1,0)和点B(5,0)代入y=ax2+bx﹣5计算出a,b的值即可;,利用二次函数求最值;(2)作ED⊥x轴于D,表示出ED,从而表示出S△BEP(3)过A作AE∥y轴交直线BC于E点,过N作NF∥y轴交直线BC于点F,则NF=AE=4,设N(m,﹣m2+6m﹣5),则F(m,m﹣5),从而有NF=|﹣m2+5m|=4,解方程即可求出N的横坐标.【解析】(1)将A(1,0)和点B(5,0)代入y=ax2+bx﹣5得:,解得,∴抛物线y=﹣x2+6x﹣5,(2)作ED⊥x轴于D,由题意知:BP=4﹣t,BE=2t,∵B(5,0),C(0,﹣5),∴OB=OC=5,∴∠OBC=45°,∴ED=sin45°×2t=,==﹣,∴S△BEP最大为2.当t=﹣时,S△BEP最大为2.∴当t=2时,S△BEP(3)过A作AE∥y轴交直线BC于E点,过N作NF∥y轴交直线BC于点F,则NF=AE=4,设N(m,﹣m2+6m﹣5),则F(m,m﹣5),∴NF=|﹣m2+5m|=4,∴m2﹣5m+4=0或m2﹣5m﹣4=0,∴m1=1(舍),m2=4,或m3=,m4=,∴点N的横坐标为:4或或.2.(2021•九龙坡区模拟)如图1,抛物线y=ax2+bx+4交x轴于A(﹣3,0),B(4,0)两点,与y轴交于点C,连接AC,BC.点P是第一象限内抛物线上的一个动点,设点P的横坐标为m,过点P作PM ⊥x轴,垂足为点M,PM交BC于点Q,过点P作PN⊥BC,交BC于点N.(1)求此抛物线的解析式;(2)请用含m的代数式表示PN,并求出PN的最大值以及此时点P的坐标;(3)如图2,将抛物线y=ax2+bx+4沿着射线CB的方向平移,使得新抛物线y'过原点,点D为原抛物线y与新抛物线y'的交点,若点E为原抛物线的对称轴上一动点,点F为新抛物线y'上一动点,求点F使得以A,D,E,F为顶点的四边形为平行四边形,请直接写出点F的坐标,并写出一个F点的求解过程.【分析】(1)将点A(﹣3,0),B(4,0)代入y=ax2+bx+4,即可求函数解析式;(2)先求出BC的解析式为y=﹣x+4,设P(m,﹣m2+m+4),Q(m,﹣m+4),=×BC×PN=×PQ×OB,可得PN=﹣(m﹣2)2+,所以当m=2时,PN 由面积S△BCP有最大值,P(2,);(3)由抛物线沿着射线CB的方向平移,可设抛物线沿x轴正方向平移t(t>0)个单位,则沿y轴负半轴平移t个单位,则平移后的函数解析式为y'=﹣+﹣t,再由新抛物线y'过原点,可求t=2,则可求新的抛物线解析式为y'=﹣x2+x,联立﹣x2+x=﹣x2+x+4,求出D(3,2),由点E在y'上,则E点的横坐标为,由点F为新抛物线y'上,设F点横坐标为n,当以A,D,E,F为顶点的四边形为平行四边形时,有三种情况:①当AE与DF为平行四边形的对角线时,﹣3+=n+3,得F(﹣,﹣);②当AF与ED为平行四边形对角线时,﹣3+n=3+,得F(,﹣);③当AD与EF为平行四边形对角线时,﹣3+3=n+,得F(﹣,﹣).【解析】(1)将点A(﹣3,0),B(4,0)代入y=ax2+bx+4,得:,解得:,∴y=﹣x2+x+4;(2)∵抛物线与y轴交于点C,∴C(0,4),设直线BC的解析式为y=kx+d,将点B与点C代入可得,,解得,∴y=﹣x+4,∵点P的横坐标为m,PM⊥x轴,∴P(m,﹣m2+m+4),Q(m,﹣m+4),=×BC×PN=×PQ×OB,∴S△BCP∵B(4,0),C(0,4),∴BC=8,∴8PN=(﹣m2+m+4+m﹣4)×4,∴PN=﹣(m﹣2)2+,∴当m=2时,PN有最大值,∴P(2,);(3)y=﹣x2+x+4=﹣+,∵抛物线沿着射线CB设抛物线沿x轴正方向平移t(t>0)个单位,则沿y轴负半轴平移t个单位,平移后的函数解析式为y'=﹣+﹣t,∵新抛物线y'过原点,∴0=﹣+﹣t,解得t=2或t=﹣6(舍),∴y'=﹣+=﹣x2+x,∵点D为原抛物线y与新抛物线y'的交点,联立﹣x2+x=﹣x2+x+4,∴x=3,∴D(3,2),∵y=﹣x2+x+4的对称轴为直线x=,∴E点的横坐标为,∵点F为新抛物线y'上一动点,设F点横坐标为n,①当AE与DF为平行四边形的对角线时,∴﹣3+=n+3,∴n=﹣,∴F(﹣,﹣);②当AF与ED为平行四边形对角线时,∴﹣3+n=3+,∴n=,∴F(,﹣);③当AD与EF为平行四边形对角线时,∴﹣3+3=n+,∴n=﹣,∴F(﹣,﹣);综上所述:以A,D,E,F为顶点的四边形为平行四边形时,F的坐标为(﹣,﹣)或(,﹣)或(﹣,﹣).3.(2021•碑林区校级模拟)如图,抛物线M:y=ax2+bx+b﹣a经过点(1,﹣3)和(﹣4,12),与两坐标轴的交点分别为A,B,C,顶点为D.(1)求抛物线M的表达式和顶点D的坐标;(2)若抛物线N:y=﹣(x﹣h)2+与抛物线M有一个公共点为E,则在抛物线N上是否存在一点F,使得以B、C、E、F为顶点的四边形是以BC为边的平行四边形?若存在,请求出h的值;若不存在,请说明理由.【分析】(1)将点代入抛物线解析式求出a,b的值,即可求出抛物线解析式,再将抛物线解析式转化为顶点式,求出顶点D的坐标;(2)先求出B,C的坐标,再设E,F的坐标,根据平移的特点列出关系式,求出h的值.【解析】(1)将(1,﹣3),(﹣4,12)代入y=ax2+bx+b﹣a,得,解得,∴,∴抛物线M的表达式为,顶点D的坐标为.(2)存在.∵,当x=0时,y=﹣2,当y=0时,,解得x1=﹣1,x2=4,∴C(0,﹣2),B(4,0),设,,当四边形BCFE是平行四边形时,可看出是E,F可看成分别是B,C平移相同的单位得到,则②﹣③得m+n=2h﹣1④,(①+④)÷2得⑤,(④﹣①)÷2得⑥,将⑤,⑥代入③得h=±,当四边形BCEF是平行四边形时,可看出是E,F可看成分别是C,B平移相同的单位得到,则②﹣③得m+n=2h﹣1④,(①+④)÷2得⑤,(④﹣①)÷2得⑥,将⑤,⑥代入③得h=或,当h=时,m=h+=+=8,n=h﹣=﹣=4,∴E(4,0),F(8,2),此时点E与点B重合,不符合题意,舍去;综上,h的值为或±.4.(2021•本溪模拟)如图,平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于A(﹣,0),B(3,0)两点,与y轴交于点C,抛物线的顶点为点E.(1)填空:△ABC的形状是直角三角形.(2)求抛物线的解析式;(3)经过B,C两点的直线交抛物线的对称轴于点D,点P为直线BC上方抛物线上的一动点,当△PCD 的面积最大时,求P点坐标;(4)M在直线BC上,N在抛物线上,以M、N、E、D为顶点的四边形为平行四边形,直接写出符合条件的点M的坐标.【分析】(1)由tan∠ACO==,故∠ACO=30°,同理可得,∠BCO=60°,即可求解;(2)用待定系数法即可求解;(3)当△PCD的面积最大时,若直线l和抛物线只要一个交点P,则点P为所求点,进而求解;(4)当ED是边时,点D向上平移2个单位得到点E,同样,点M(N)向上平移2个单位得到点N(M),进而求解;②当ED为对角线时,由中点坐标公式得:=m+n且4+2=﹣n2+n+3+3,即可求解.【解析】(1)由抛物线的表达式知,c=3,OC=3,则tan∠ACO==,故∠ACO=30°,同理可得,∠BCO=60°,故△ABC为直角三角形,故答案为:直角三角形;(2)由题意得:,解得,故抛物线的表达式为y=﹣x2+x+3①;(3)由点B、C的坐标得,直线BC的表达式为y=﹣x+3,则设直线l∥BC,则设直线l的表达式为:y=﹣x+c②,当△PCD的面积最大时,直线l和抛物线只要一个交点P,则点P为所求点,联立①②并整理得:﹣x2+x+3﹣c=0③,则△=()2﹣4×(﹣)(3﹣c)=0,解得:c=,将c的值代入③式并解得x=,故点P的坐标为(,);(4)由抛物线的表达式知,点E的坐标为(,4),∵直线BC的表达式为y=﹣x+3,故点D(,2),设点M的坐标为(m,﹣m+3),点N的坐标为(n,﹣n2+n+3),①当ED是边时,点D向上平移2个单位得到点E,同样,点M(N)向上平移2个单位得到点N(M),则m=n且﹣m+3±2=﹣n2+n+3,解得:m=(舍去)或2或;②当ED为对角线时,由中点坐标公式得:=m+n且4+2=﹣n2+n+3﹣m+3,解得m=(舍去)或0,综上,m=0或2或或,故点M的坐标为(0,3)或(2,1)或(,)或(,).5.(2021•深圳模拟)如图,抛物线y=ax2+bx﹣3与x轴交于A,B两点,与y轴交于C点,且经过点(2,﹣3a),对称轴是直线x=1,顶点是M.(1)求抛物线对应的函数表达式;(2)经过C,M两点作直线与x轴交于点N,在抛物线上是否存在这样的点P,满足以点P,A,C,N 为顶点的四边形为平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由;(3)设直线y=﹣x+3与y轴的交点是D,在线段BD上任取一点E(不与B,D重合),经过A,B,E 三点的圆交直线BC于点F,试判断△AEF的形状,并说明理由.【分析】(1)因为抛物线经过点(2,﹣3a),代入到解析式中,得到关于a和b的方程,由于抛物线对称轴为直线x=1,所以,联立两个方程,解方程组,即可求出a和b;(2)先将解析式配成顶点式,求出M坐标,然后求出C点坐标,利用待定系数法,求出直线MC的解析式,再求出MC和x轴交点N的坐标,利用抛物线解析式分别求出A和C坐标,以A,C,N,P为顶点构造平行四边形,并且P点必须在抛物线上,通过构图可以发现,只有当AC为对角线时,才有可能构造出符合条件的P点,所以过C作CP∥AN,使CP=AN,由于AN=2,所以可以得到P(2,﹣3),将P代入到抛物线解析式中,满足解析式,P即为所求;(3)利用y=﹣x+3,可以求出直线与y轴交点D的坐标,可以证得△DOB是等腰直角三角形,同理可以证得△BOC也是等腰直角三角形,根据题意画出图形,利用同弧所对的圆周角相等,可以证得∠AEF =∠AFE=45°,所以△AEF是等腰直角三角形.【解析】(1)∵抛物线经过点(2,﹣3a),∴4a+2b﹣3=﹣3a①,又因为抛物线对称为x=1,∴②,联立①②,解得,∴抛物线对应的函数表达式为y=x2﹣2x﹣3;(2)如图1,∵y=(x﹣1)2﹣4,∴M(1,﹣4),令x=0,则y=x2﹣2x﹣3=﹣3,∴C(0,﹣3),设直线MC为y=kx﹣3,代入点M得k=﹣1,∴直线MC为y=﹣x﹣3,令y=0,则x=﹣3,∴N(﹣3,0),令y=0,则x2﹣2x﹣3=0,∴x=﹣1或3,∴A(﹣1,0),B(3,0),过C作CP∥AN,使CP=AN,则四边形ANCP为平行四边形,∴CP=AN=﹣1﹣(﹣3)=2,∴P(2,﹣3),∵P的坐标满足抛物线解析式,∴P(2,﹣3)在抛物线上,即P(2,﹣3);(3)如图2,令x=0,则y=﹣x+3=3,∴D(0,3),∴OB=OD=3,又∠DOB=90°,∴∠DBO=45°,同理,∠ABC=45°,∵同弧所对的圆周角相等,∴∠AEF=∠ABC=45°,∠AFE=∠DBO=45°,∴∠AEF=∠AFE=45°,∴△AEF为等腰直角三角形.6.(2021•铜梁区校级一模)已知抛物线y=ax2+bx+3与x轴交于A、B两点(点A在点B的左侧).与y轴交于点C.其中OC=OB,tan∠CAO=3.(1)求抛物线的解析式;(2)P是第一象限内的抛物线上一动点,Q为线段PB的中点,求△CPQ面积的最大值时P点坐标:(3)将抛物线沿射线CB方向平移2个单位得新抛物线y'.M为新抛物线y′的顶点.D为新抛物线y'上任意一点,N为x轴上一点.当以M、N、C、D为顶点的四边形是平行四边形时,直接写出所有符合条件的点N的坐标.并选择一个你喜欢的N点.写出求解过程.【分析】(1)第一题将ABC三个点坐标表示后,代入求值即可.(2)第二题求面积最大值,可用铅锤法将面积转化为求铅垂高的最大值.(3)第三题平行四边形存在性问题,利用平行四边形对角线互相平分,套用中点坐标公式即可求出相应的点.【解析】(1)∵抛物线解析式为y=ax2+bx+3,令x=0得y=3,∴点C坐标为(0,3),∵OG﹣OB=3,∴B坐标为(3,0),∵tan∠CAO=3,∴=3,∴OA=1,∴点A坐标为(﹣1,0),∴设解析式为y=a(x+1)(x﹣3),代入(0,3)得a=﹣1,∴y=﹣(x+1)(x﹣3),=﹣(x2﹣2x﹣3)=﹣x2+2x+3=﹣(x﹣1)2+4,∴抛物线解析式为:y=﹣(x﹣1)2+4;(2)∵Q为线段PB中点,=S△CPB,∴S△CPQ面积最大时,△CPQ面积最大.当S△CPB设P坐标(a,﹣a2+2a+3),过点P作PH∥y轴交BC于点H,H坐标为(a,﹣a+3),∴PH=(﹣a2+2a+3)﹣(﹣a+3)=﹣a2+2a+3+a﹣3=﹣a2+3a,S△CPB=•PH•(x B﹣x C)=•PH•3=PH=(﹣a2+3a)=﹣(a2﹣3a+﹣)=﹣(a﹣)2+,当a=时,即P坐标为(,)时,=S△CPB=,最大S△CPQ∴P坐标为(,);(3)沿CB方向平移2个单位,即向右2个单位,向下2个单位,∴新抛物线解析式为y=﹣(x﹣3)2+2,M坐标为(3,2)C坐标为(0,3),点N坐标设为(n,0),∵=,∴=,∴y D=1,则1=﹣(x﹣3)2+2﹣1=﹣(x﹣3)2,(x﹣3)2=1,x﹣3=±1,∴x=4或2,∴x D=4或x D=2,=⇒=,∴x N=7,或=,∴x N=5,∴N坐标为(7,0)或(5,0),或=⇒=,得y D=﹣1,则﹣1=﹣(x﹣3)2+2,(x﹣3)2=3,x=±+3,∴x D=3﹣或x D=3+,即x N=﹣或,N坐标为(﹣,0)或(,0).7.(2021•盘龙区二模)如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点A(﹣4,0),点M为抛物线的顶点,点B在y轴上,且OA=OB,直线AB与抛物线在第一象限交于点C(2,6).(1)求抛物线的解析式及顶点M的坐标;(2)求直线AB的函数解析式及sin∠ABO的值;连接OC.若过点O的直线交线段AC于点P,将三角形AOC的面积分成1:2的两部分,请求出点P的坐标;(3)在坐标平面内是否存在点N,使以点A、O、C、N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.【分析】(1)将A(﹣4,0),C(2,6)代入y=x2+bx+c,用待定系数法可得解析式,从而可得顶点M的坐标;(2)由OA=OB可得B(0,4),设直线AB的函数解析式解析式为y=kx+b,将A(﹣4,0)、B(0,4)代入可求得AB为y=x+4,Rt△AOB中,可得sin∠ABO==,过点O的直线交线段AC于点P,将三角形AOC的面积分成1:2的两部分,过P作PQ⊥x轴于Q,过C作CH⊥x轴于H,分两种情况:①当S△AOP:S△COP=1:2时,PQ:CH=1:3,可求PQ=2,从而:S△AOP=1:2时,S△AOP:S△AOC=2:3,同理可求P坐标;求得P坐标,②当S△COP(3)设N(m,n),利用平行四边形对角线互相平分,即对角线的中点重合,分三种情况分别列方程组求解即可.【解析】(1)将A(﹣4,0),C(2,6)代入y=x2+bx+c得:,解得,∴抛物线的解析式为y=x2+2x,对称轴x==﹣2,当x=﹣2时,y=×4+2×(﹣2)=﹣2,∴顶点M的坐标为(﹣2,﹣2);(2)∵A(﹣4,0),∴OA=4,∵OA=OB,∴OB=4,B(0,4),设直线AB的函数解析式解析式为y=kx+b,将A(﹣4,0)、B(0,4)代入得:,解得,∴直线AB的函数解析式解析式为y=x+4,Rt△AOB中,AB==4,∴sin∠ABO===,过点O的直线交线段AC于点P,将三角形AOC的面积分成1:2的两部分,过P作PQ⊥x轴于Q,过C作CH⊥x轴于H,分两种情况:①当S△AOP:S△COP=1:2时,如图::S△COP=1:2,∵S△AOP:S△AOC=1:3,∴S△AOP∴PQ:CH=1:3,而C(2,6),即CH=6,∴PQ=2,即y P=2,在y=x+4中,令y=2得2=x+4,∴x=﹣2,∴P(﹣2,2);②当S△COP:S△AOP=1:2时,如图::S△AOP=1:2,∵S△COP:S△AOC=2:3,∴S△AOP∴PQ:CH=2:3,∵CH=6,∴PQ=4,即y P=4,在y=x+4中,令y=4得4=x+4,∴x=0,∴P(0,4);综上所述,过点O的直线交线段AC于点P,将三角形AOC的面积分成1:2的两部分,则P坐标为(﹣2,2)或(0,4);(3)点A、O、C、N为顶点的四边形是平行四边形时,设N(m,n),分三种情况:①以AN、CO为对角线,此时AN中点与CO中点重合,∵A(﹣4,0)、O(0,0),C(2,6),∴AN的中点为(,),OC中点为(,),∴,解得,∴N(6,6),②以AC、NO为对角线,此时AC中点与NO中点重合,同理可得:解得,∴N(﹣2,6),③以AO、CN为对角线,此时AO中点与CN中点重合,同理可得:,解得,∴N(﹣6,﹣6),综上所述,点A、O、C、N为顶点的四边形是平行四边形,N的坐标为:(6,6)或(﹣2,6)或(﹣6,﹣6).8.(2021•海州区一模)如图,抛物线y=ax2+bx﹣3的图象与x轴交于A(﹣1,0),B(3,0)两点,与y 轴交于点C,直线l与抛物线交于点B,交y轴于点D(0,3).(1)求该抛物线的函数表达式;(2)点P(m,0)为线段OB上一动点,过点P作x轴的垂线EF,分别交抛物线于直线l于点E,F,连接CE,CF,BE,求四边形CEBF面积的最大值及此时m的值;(3)点M为y轴右侧抛物线上一动点,过点M作直线MN∥AC交直线l于点N,是否存在点M,使以A,C,M,N四点为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标;若不存在,请说明理由.【分析】(1)将A,B坐标代入y=ax2+bx﹣3中,利用待定系数法可求;=S△CEF+S△BEF (2)求出直线l的解析式,用m表示点E,F的坐标,进而表示线段EF,根据S四边形CEBF=EF•OP+•BP=FE•OB,用含m的代数式表示四边形CEBF的面积,利用二次函数的性质,通过配方法得出结论;(3)分点M在直线BD的下方和点M在直线BD的上方时两种情形讨论解答;依据题意画出图形,①过M作ME⊥y轴于E,过N作NF⊥ME于F,通过说明△AOC≌△MFN,得出NF=3,设出点M的坐标,用坐标表示相应线段,利用线段与坐标的关系,用相同的字母表示点N的坐标后,用坐标表示出线段NG,GF,利用NG+GF=NF=3,列出方程,解方程,点M坐标可求;②利用①中相同的方法求得点M在直线BD的上方时点M的坐标.【解析】(1)将A(﹣1,0),B(3,0)代入y=ax2+bx﹣3中得:.解得:.∴该抛物线的函数表达式为:y=x2﹣2x﹣3.(2)设直线l的解析式为y=kx+n,将B(3,0),D(0,3)代入上式得:.解得:.∴直线l的解析式为:y=﹣x+3.∵点P(m,0),EF⊥x轴,∴E点坐标为(m,m2﹣2m﹣3),点F的坐标为(m,﹣m+3).∴EF=﹣m+3﹣m2+2m+3=﹣m2+m+6.∵B(3,0),∴OB=3.=S△CEF+S△BEF=EF•OP+•BP×EF=FE•OB,∵S四边形CEBF∴=﹣.∵<0,有最大值=.∴当m=时,S四边形CEBF即:当m=时,四边形CEBF面积的最大值为.(3)存在.①当点M在直线BD的下方时,如图,令x=0,则y=﹣3.∴C(0,﹣3).∴OC=3.∵A(﹣1,0),∴OA=1.过M作ME⊥y轴于E,过N作NF⊥ME于F,交x轴于点G,∵四边形ACMN为平行四边形,∴AC∥MN,AC=MN.∵NF⊥ME,ME⊥OE,∴NF∥OE.∴∠ACO=∠MNF.在△AOC和△MFN中,.∴△AOC≌△MFN(AAS).∴NF=OC=3,MF=OA=1.设M(h,h2﹣2h﹣3),则ME=h,GF=OE=﹣h2+2h+3.∴OG=EF=ME﹣MF=h﹣1.∴N(h﹣1,﹣h+4).∴NG=﹣h+4,∵NG+GF=NF=3,∴﹣h+4﹣h2+2h+3=3.解得:h=(负数不合题意,舍去).∴h=.∴M().②当点M在直线BD的上方时,如图,过N作NE⊥y轴于E,过M作MF⊥NE于F,交x轴于点G,由①知:△MNF≌△CAO(AAS),可得NF=OA=1,MF=OC=3.设M(h,h2﹣2h﹣3),则OG=FE=h,GM=h2﹣2h﹣3.∴NE=EF+NF=h+1.∴N(h+1,﹣h+2).∴GF=OE=h﹣2.∵MG+GF=MF=3,∴h﹣2+h2﹣2h﹣3=3.解得:h=(负数不合题意,舍去).∴h=.∴M().综上所述,存在点M,使以A,C,M,N四点为顶点的四边形是平行四边形,此时点M的坐标为()或().9.(2021•南昌县一模)如图,已知二次函数L1:y=mx2+2mx﹣3m+1(m≥1)和二次函数L2:y=﹣m(x ﹣3)2+4m﹣1(m≥1)图象的顶点分别为M,N,与x轴分别相交于A、B两点(点A在点B的左边)和C、D两点(点C在点D的左边).(1)函数y=mx2+2mx﹣3m+1(m≥1)的顶点坐标为(﹣1,﹣4m+1);当二次函数L1,L2的y 值同时随着x的增大而增大时,则x的取值范围是﹣1<x<3;(2)当AD=MN时,判断四边形AMDN的形状(直接写出,不必证明);(3)抛物线L1,L2均会分别经过某些定点:①求所有定点的坐标;②若抛物线L1位置固定不变,通过左右平移抛物线L2的位置使这些定点组成的图形为菱形,则抛物线L2应平移的距离是多少?【分析】(1)将已知抛物线解析式转化为顶点式,直接得到点M的坐标;结合函数图象填空;(2)利用抛物线解析式与一元二次方程的关系求得点A、B、C、D的横坐标,可得AD的中点为(1,0),MN的中点为(1,0),则AD与MN互相平分,可证四边形AMDN是矩形;(3)根据菱形的性质可得EH1=EF=4即可,设平移的距离为x,根据平移后图形为菱形,由勾股定理可得方程即可求解.【解析】(1)x=﹣=﹣1,顶点坐标M为(﹣1,﹣4m+1),由图象得:当﹣1<x<3时,二次函数L1,L2的y值同时随着x的增大而增大.故答案为:(﹣1,﹣4m+1);﹣1<x<3(2)结论:四边形AMDN由二次函数L1:y=mx2+2mx﹣3m+1(m≥1)和二次函数L2:y=﹣m(x﹣3)2+4m﹣1(m≥1)解析式可得:A点坐标为(,0),D点坐标为(,0),顶点M坐标为(﹣1,﹣4m+1),顶点N 坐标为(3,4m﹣1),∴AD的中点为(1,0),MN的中点为(1,0),∴AD与MN互相平分,∴四边形AMDN是平行四边形,又∵AD=MN,∴▱AMDN是矩形.(3)①∵二次函数L1:y=mx2+2mx﹣3m+1=m(x+3)(x﹣1)+1,故当x=﹣3或x=1时y=1,即二次函数L1:y=mx2+2mx﹣3m+1经过(﹣3,1)、(1,1)两点,∵二次函数L2:y=﹣m(x﹣3)2+4m﹣1=﹣m(x﹣1)(x﹣5)﹣1,故当x=1或x=5时y=﹣1,即二次函数L2:y=﹣m(x﹣3)2+4m﹣1经过(1,﹣1)、(5,﹣1)两点,②∵二次函数L1:y=mx2+2mx﹣3m+1经过(﹣3,1)、(1,1)两点,二次函数L2:y=﹣m(x﹣3)2+4m﹣1经过(1,﹣1)、(5,﹣1)两点,如图:四个定点分别为E(﹣3,1)、F(1,1),H(1,﹣1)、G(5,﹣1),则组成四边形EFGH为平行四边形,设平移的距离为x,根据平移后图形为菱形,由勾股定理可得:42=22+(4﹣x)2.解得:x=,抛物线L1位置固定不变,通过左右平移抛物线L2的位置使这些定点组成的图形为菱形,则抛物线L2向左平移或.10.(2022•渝中区校级模拟)如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3(a≠0)与y轴交于点C,与x轴交于A、B两点,且点A的坐标为(﹣1,0),连接BC,OB=2OC.(1)求抛物线的表达式;(2)如图1,点P是直线BC下方抛物线上一点,过点P作直线BC的垂线,垂足为H,过点P作PQ ∥y轴交BC于点Q,求△PHQ周长的最大值及此时点P坐标;(3)如图2,将抛物线水平向左平移4个单位得到新抛物线y';点D是新抛物线y'上的点且横坐标为﹣3,点M为新抛物线y'上一点,点E、F为直线AC上的两个动点,请直接写出使得以点D、M、E、F为顶点的四边形是平行四边形的点M的横坐标,并把求其中一个点M的横坐标的过程写出来.【分析】(1)求出B、C点坐标,将B、C点代入y=ax2+bx﹣3,即可求解;(2)先求出BC的解析式,设P(t,t2﹣t﹣3),则Q(t,t﹣3),PQ=﹣t2+3t,由PQ∥CO,可得∠HQP=∠OCB,利用直角三角形三角函数求出HP==PQ,HQ=PQ,则△PHQ周长=HP+PQ+HQ=(1+)PQ=(1+)[﹣(t﹣3)2+],当t=3时,△PHQ周长有最大值+,此时P(3,﹣6);(3)求出平移后的函数解析式为y'=x2+x﹣5,则D(﹣3,﹣5),设M(m,=m2+m﹣5),E (x1,﹣3x1﹣3),F(x2,﹣3x2﹣3),分三种情况讨论:①以EF为平行四边形的对角线时,M(,)或(,);②以EM为平行四边形的对角线时,M(﹣6,4);③以ED为平行四边形的对角线时,求得M(﹣6,4).【解析】(1)令x=0,则y=﹣3,∴C(0,﹣3),∴OC=3,∵OB=2OC,∴OB=6,∴B(6,0),将B、C点代入y=ax2+bx﹣3,∴,解得,∴y=x2﹣x﹣3;(2)设直线BC的解析式为y=kx+b,,解得,∴y=x﹣3,∴设P(t,t2﹣t﹣3),则Q(t,t﹣3),∴PQ=﹣t2+3t,∵CO=3,BO=6,∴BC=3,在Rt△ABC中,sin∠BCO=,cos∠BCO=,∵PQ∥CO,∴∠HQP=∠OCB,∴sin∠HQP==,cos∠HQP==,∴HP=PQ,HQ=PQ,∴△PHQ周长=HP+PQ+HQ=(1+)PQ=(1+)(﹣t2+3t)=(1+)[﹣(t﹣3)2+],∵点P是直线BC下方,∴0<t<6,∴当t=3时,△PHQ周长有最大值+,此时P(3,﹣6);(3)∵y=x2﹣x﹣3=(x﹣)2﹣,∴平移后的函数解析式为y'=(x+)2﹣=x2+x﹣5,∴D(﹣3,﹣5),设M(m,﹣m2+m﹣5),设直线AC的解析式为y=kx+b,,解得,∴y=﹣3x﹣3,设E(x1,﹣3x1﹣3),F(x2,﹣3x2﹣3),①以EF为平行四边形的对角线时,.解得m=或m=,∴M(,)或(,);②以EM为平行四边形的对角线时,,解得m=﹣3(舍)或m=﹣6,∴M(﹣6,4);③以ED为平行四边形的对角线时,,解得m=﹣3(舍)或m=﹣6,∴M(﹣6,4);综上所述:M点坐标为(,)或(,)或(﹣6,4).11.(2022•平桂区二模)如图,抛物线y=ax2+bx+c与x轴交于A(﹣1,0)、B(3,0)两点,与直线y =﹣x+3交于点B、C(0,n).(1)求点C的坐标及抛物线的对称轴;(2)求该抛物线的表达式;(3)点P在抛物线的对称轴上,纵坐标为t.若平移BC使点B与P重合,求点C的对应点C′的坐标(用含t的代数式表示);若点Q在抛物线上,以B、C、P、Q为顶点的四边形是平行四边形,且PQ∥BC,求点P的坐标.【分析】(1)把C(0,n)代入y=﹣x+3得n=3,即知C(0,3),根据抛物线y=ax2+bx+c与x轴交于A(﹣1,0)、B(3,0)两点,得抛物线y=ax2+bx+c的对称轴为直线x=1;(2)用待定系数法可得抛物线的表达式为y=﹣x2+2x+3;(3)由P(1,t),B(3,0)可知C(0,3)的对应点C'坐标为(﹣2,3+t),设Q(m,﹣m2+2m+3),分两种情况:①当PQ∥BC,BQ∥CP时,BP的中点即为CQ的中点,可得,P(1,﹣2);②当PQ∥BC,BP∥CQ时,BQ中点即为CP中点,,得P(1,﹣8).【解析】(1)把C(0,n)代入y=﹣x+3得:n=3,∴C(0,3),∵抛物线y=ax2+bx+c与x轴交于A(﹣1,0)、B(3,0)两点,∴抛物线y=ax2+bx+c的对称轴为直线x==1,答:C(0,3),抛物线y=ax2+bx+c的对称轴为直线x=1;(2)把A(﹣1,0)、B(3,0),C(0,3)代入y=ax2+bx+c得:,解得,∴抛物线的表达式为y=﹣x2+2x+3;(3)∵点P在抛物线的对称轴上,纵坐标为t,∴P(1,t),∵平移BC使点B与P重合,B(3,0),∴C(0,3)的对应点C'坐标为(﹣2,3+t),设Q(m,﹣m2+2m+3),①当PQ∥BC,BQ∥CP时,BP的中点即为CQ的中点,如图:。
抛物线中动点问题讲义

文档根源为:从网络采集整理.word版本可编写.支持.第一讲抛物线中的动点问题一、利用动点(图形)地点进行分类,把运动问题切割成几个静态问题,而后运用转变的思想和方法将几何问题转变为函数和方程问题二、利用函数与方程的思想和方法将所解决图形的性质(或所求图形面积)直接转变为函数或方程。
一、平行四边形与抛物线【例】如图甲,在平面直角坐标系中,A、B的坐标分别为(4,0)、(0,3),抛物线y=x2+bx+c经过点B,且对称轴是直线x=﹣.1)求抛物线对应的函数分析式;2)将图甲中△ABO沿x轴向左平移到△DCE(如图乙),当四边形ABCD是菱形时,请说明点C和点D都在该抛物线上;3)在(2)中,若点M是抛物线上的一个动点(点M不与点C、D重合),经过点M作MN∥y轴交直线CD于N,设点M的横坐标为t,MN的长度为l,求l与t之间的函数分析式,并求当t为什么值时,以M、N、C、E为极点的四边形是平行四边形.变式操练【变式】如图,在平面直角坐标系中,已知Rt△AOB的两条直角边OA、OB分别在y轴和x轴上,而且OA、OB的长分别是方程x2﹣7x+12=0的两根(OA<OB),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点0运动;同时,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动,设点P、Q运动的时间为t秒.(1)求A、B两点的坐标.(2)求当t为什么值时,△APQ与△AOB相像,并直接写出此时点Q的坐标.(3)当t=2时,在座标平面内,能否存在点M,使以A、P、Q、M为极点的四边形是平行四边形?若存在,请直接写出M点的坐标;若不存在,请说明原因.【变式】如图,已知抛物线y=﹣x2+bx+c与向来线订交于A(﹣1,0),C(2,3)两点,与y轴交于点N.其极点为D.文档根源为:从网络采集整理.word版本可编写.支持.(1)抛物线及直线AC的函数关系式;(2)设点M(3,m),求使MN+MD的值最小时m的值;(3)若抛物线的对称轴与直线AC订交于点B,E为直线AC上的随意一点,过点E作EF∥BD 交抛物线于点F,以B,D,E,F为极点的四边形可否为平行四边形?若能,求点若不可以,请说明原因;E的坐标;(4)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.二、梯形与抛物线【例】已知,在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2.若以O为坐标原点,OA所在直线为x轴,成立如下图的平面直角坐标系,点B在第一象限内.将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.(1)求点C的坐标;2(2)若抛物线y=ax+bx(a≠0)经过C、A两点,求此抛物线的分析式;(3)若上述抛物线的对称轴与OB交于点D,点P为线段DB上一动点,过P作y轴的平行线,交抛物线于点M,问:能否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,恳求出此时点P的坐标;若不存在,请说明原因.变式操练【变式】如图,O为坐标原点,直线l绕着点A(0,2)旋转,与经过点C(0,1)的二次函数y=x2+h的图象交于不一样的两点P、Q.(1)求h的值;(2)经过操作、察看,算出△POQ的面积的最小值(不用说理);(3)过点P、C作直线,与x轴交于点B,试问:在直线l的旋转过程中,四边形AOBQ能否为梯形?假如,请说明原因;若不是,请指出四边形的形状.【变式】如图,在平面直角坐标系xOy中,矩形AOCD的极点A的坐标是(0,4),现有两动点P,Q,点P从点O出发沿线段OC(不包含端点O,C)以每秒2个单位长度的速度匀速向点C运动,点Q从点C出发沿线段CD(不包含端点C,D)以每秒1个单位长度的速度匀速向点D运动.点P,Q同时出发,同时停止,设运动时间为t(秒),当t=2(秒)时,PQ=2 .(1)求点D的坐标,并直接写出t的取值范围.(2)连结AQ并延伸交x轴于点E,把AE沿AD翻折交CD延伸线于点F,连结EF,则△AEF的面积S能否随t的变化而变化?若变化,求出 S与t的函数关系式;若不变化,求出S的值.(3)在(2)的条件下,t为什么值时,四边形APQF是梯形?三、等腰三角形、菱形与抛物线【例】在平面直角坐标系xOy中,一块含60°角的三角板作如图摆放,斜边AB在x轴上,直角极点C在y轴正半轴上,已知点A(﹣1,0).(1)请直接写出点B、C的坐标:B 、C ;并求经过A、B、C三点的抛物线解析式;(2)现有与上述三角板完整同样的三角板DEF(此中∠EDF=90°,∠DEF=60°),把极点E放在线段AB上(点E是不与A、B两点重合的动点),并使ED所在直线经过点C.此时,EF所在直线与(1)中的抛物线交于点M.①设AE=x,当x为什么值时,△OCE∽△OBC;②在①的条件下研究:抛物线的对称轴上能否存在点P使△PEM是等腰三角形?若存在,请写出点P的坐标;若不存在,请说明原因.变式操练【变式】如图,在平面直角坐标系中,直角三角形AOB的极点A、B分别落在座标轴上.O为原点,点A 的坐标为(6,0),点B的坐标为(0,8).动点M从点O出发.沿OA向终点A以文档根源为:从网络采集整理.word版本可编写.支持.每秒1个单位的速度运动,同时动点N从点A出发,沿AB向终点B以每秒个单位的速度运动.当一个动点抵达终点时,另一个动点也随之停止运动,设动点M、N运动的时间为t秒(t>0).(1)当t=3秒时.直接写出点N的坐标,并求出经过O、A、N三点的抛物线的分析式;(2)在此运动的过程中,△MNA的面积能否存在最大值?若存在,恳求出最大值;若不存在,请说明原因;(3)当t为什么值时,△MNA是一个等腰三角形?【变式】如图,直线l1经过点A(﹣1,0),直线l2经过点B(3,0),l1、l2均为与y轴交于点C(0,),抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.(1)求抛物线的函数表达式;(2)抛物线的对称轴挨次与x轴交于点D、与l2交于点E、与抛物线交于点F、与l1交于点G.求证:DE=EF=FG;(3)若l1⊥l2于y轴上的C点处,点P为抛物线上一动点,要使△PCG为等腰三角形,请写出切合条件的点P 的坐标,并简述原因.【变式】如图,在平面直角坐标系中,直角梯形OABC的边OC、OA分别与x轴、y轴重合,AB∥OC,∠AOC=90°,∠BCO=45°,BC=12 ,点C的坐标为(﹣18,0).(1)求点B的坐标;(2)若直线DE交梯形对角线BO于点D,交y轴于点E,且OE=4,OD=2BD,求直线DE的分析式;(3)若点P是(2)中直线DE上的一个动点,在座标平面内能否存在点Q,使以O、E、P、Q为极点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明原因.【变式】如图,已知抛物线经过原点O和x轴上一点A(4,0),抛物线极点为E,它的对称轴与x轴交于点D.直线y=﹣2x﹣1经过抛物线上一点B(﹣2,m)且与y轴交于点C,与抛物线的对称轴交于点F.(1)求m的值及该抛物线对应的分析式;(2)P(x,y)是抛物线上的一点,若S△ADP=S△ADC,求出所有切合条件的点P的坐标;(3)点Q是平面内随意一点,点M从点F出发,沿对称轴向上以每秒1个单位长度的速度匀速运动,设点M的运动时间为t秒,能否能使以 Q、A、E、M四点为极点的四边形是菱形?若能,请直接写出点M的运动时间t的值;若不可以,请说明原因.四、直角三角形与抛物线【例】如图,抛物线y=与x轴交于A、B两点(点A在点B的左边),与y轴交于点C.(1)求点A、B的坐标;(2)设D为已知抛物线的对称轴上的随意一点,当△ACD的面积等于△ACB的面积时,求点的坐标;(3)若直线l过点E(4,0),M为直线l上的动点,当以A、B、M为极点所作的直角三角形有且只有三个时,求直线l的分析式.【变式】如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直均分线和BC所在的直线成立平面直角坐标系,抛物线y=﹣x2+x+4经过A、B两点.文档根源为:从网络采集整理.word版本可编写.支持.(1)写出点A、点B的坐标;(2)若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA和抛物线于点E、M和点P,连结PA、PB.设直线l挪动的时间为t(0<t<4)秒,求四边形PBCA的面积S(面积单位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积;(3)在(2)的条件下,抛物线上能否存在一点P,使得△PAM是直角三角形?若存在,恳求出点P的坐标;若不存在,请说明原因.【变式】如图,极点为P(4,﹣4)的二次函数图象经过原点(0,0),点A在该图象上,OA交其对称轴l于点M,点M、N对于点P对称,连结AN、ON,(1)求该二次函数的关系式;(2)若点A在对称轴l右边的二次函数图象上运动时,请解答下边问题:①证明:∠ANM=∠ONM;②△ANO可否为直角三角形?假如能,恳求出全部切合条件的点A的坐标;假如不可以,请说明原因.【变式】如图,在平面直角坐标系中,直线y=x+2交x轴于点P,交y轴于点A.抛物线y=x2+bx+c的图象过点E(﹣1,0),并与直线订交于A、B两点.(1)求抛物线的分析式(关系式);(2)过点A作AC⊥AB交x轴于点C,求点C的坐标;(3)除点C外,在座标轴上能否存在点M,使得△MAB是直角三角形?若存在,恳求出点M的坐标;若不存在,请说明原因.五、相像三角形与抛物线2(1)求抛物线的分析式;(2)将直线OB向下平移m个单位长度后,获得的直线与抛物线只有一个公共点值及点D的坐标;D,求m的(3)如图2,若点N在抛物线上,且∠NBO=∠ABO,则在(2)的条件下,求出全部知足△POD∽△NOB的点P坐标(点P、O、D分别与点N、O、B对应).变式操练【变式】如图,已知抛物线y=ax2+bx+c(a≠0)的图象经过原点O,交x轴于点A,其极点B的坐标为(3,﹣).(1)求抛物线的函数分析式及点A的坐标;(2)在抛物线上求点P,使S△POA=2S△AOB;(3)在抛物线上能否存在点Q,使△AQO与△AOB相像?假如存在,恳求出Q点的坐标;假如不存在,请说明原因.【变式】如图,已知抛物线的方程C1:y=﹣(x+2)(x﹣m)(m>0)与x轴订交于点B、C,与y轴订交于点E,且点B在点C的左边.(1)若抛物线C1过点M(2,2),务实数m的值;(2)在(1)的条件下,求△BCE的面积;(3)在(1)条件下,在抛物线的对称轴上找一点H,使BH+EH最小,并求出点H的坐标;(4)在第四象限内,抛物线C1上能否存在点F,使得以点B、C、F为极点的三角形与△BCE相像?若存在,求m的值;若不存在,请说明原因.文档根源为:从网络采集整理.word版本可编写.支持.【变式】如图,已知二次函数的图象过点A(﹣4,3),B(4,4).(1)求二次函数的分析式:(2)求证:△ACB是直角三角形;(3)若点P在第二象限,且是抛物线上的一动点,过点P作PH垂直x轴于点H,能否存在以P、H、D为极点的三角形与△ABC相像?若存在,求出点P的坐标;若不存在,请说明原因.【变式】如图,直线AB交x轴于点B(4,0),交y轴于点A(0,4),直线DM⊥x轴正半轴于点M,交线段AB于点C,DM=6,连结DA,∠DAC=90°.(1)直接写出直线AB的分析式;(2)求点D的坐标;(3)若点P是线段MB上的动点,过点P作x轴的垂线,交AB于点F,交过O、D、B三点的抛物线于点E,连结CE.能否存在点P,使△BPF与△FCE相像?若存在,恳求出点P的坐标;若不存在,请说明原因.【变式】在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C.(1)求这个二次函数的关系分析式;(2)点P是直线AC上方的抛物线上一动点,能否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明原因;(3)在平面直角坐标系中,能否存在点Q,使△BCQ是以BC为腰的等腰直角三角形?若存在,直接写出点Q的坐标;若不存在,说明原因;(4)点Q是直线AC上方的抛物线上一动点,过点Q作QE垂直于x轴,垂足为E.能否存在点Q,使以点B、Q、E为极点的三角形与△AOC相像?若存在,直接写出点Q的坐标;若不存在,说明原因;(5)点M为抛物线上一动点,在x轴上能否存在点Q,使以A、C、M、Q为极点的四边形是平行四边形?若存在,直接写出点Q的坐标;若不存在,说明原因.六、抛物线中的翻折问题【例】如图,抛物线y=ax2+bx+2交x轴于A(﹣1,0),B(4,0)两点,交y轴于点C,与过点C且平行于x轴的直线交于另一点D,点P是抛物线上一动点.(1)求抛物线分析式及点D坐标;(2)点E在x轴上,若以A,E,D,P为极点的四边形是平行四边形,求此时点P的坐标;(3)过点P作直线CD的垂线,垂足为Q,若将△CPQ沿CP翻折,点Q的对应点为Q′.能否存在点P,使Q′恰巧落在x轴上?若存在,求出此时点P的坐标;若不存在,说明原因.变式操练【变式】如图,在平面直角坐标系中,二次函数点在原点的左边,B点的坐标为(3,0),与y抛物线上一动点.(1)求这个二次函数的表达式.y=x2+bx+c的图象与x轴交于A、B两点,A轴交于C (0,﹣3)点,点P是直线BC下方的(2)连结PO、PC,并把△POC沿CO翻折,获得四边形POP′C,那么能否存在点P,使四边形POP′C为菱形?若存在,恳求出此时点P的坐标;若不存在,请说明原因.(3)当点P运动到什么地点时,四边形ABPC的面积最大并求出此时P点的坐标和四边形ABPC的最大面积.。
中考数学二次函数复习类型五特殊四边形存在性问题课件

类型五 特殊四边形存在性问题
(3)存在.
①当点 P 在 x 轴上方时,要使以 A、C、P、N 为顶点的四边形为平行四
边形,如解图,过点 C 作 CP1∥x 轴,交对称轴于点 P1,对称轴与 x 轴交
于点 D,
∵点 P1 在对称轴直线 x=-3 上,点 C 的坐标为(0,5),
∴点 P1(-3,5),
由勾股定理得 OG2=OD2+DG2=9+g2,AG2=AD2+GD2=4+g2,
∵GK∥AO,
①当 OG=AO=5,且 GK=AO 时,四边形 OGKA 是菱形,
此时有 9+g2=25,
解得 g1=4,g2=-4, ∴点 G 的坐标为(-3,4)或(-3,-4),
则相对应的点 K 的坐标为(-8,4)或(-8,-4);
解得 g1=6,g2=-1, 此时点 G 的坐标为(-3,6)或(-3,-1);
例题图⑦
综上所述,存在满足题意的点 G,点 G 的坐标为(-3,8)或(-3,-2)或
(-3,6)或(-3,-1);
类型五 特殊四边形存在性问题 (8)设 P 是抛物线上一点,Q 是 x 轴上一点,R 为坐标平面内一点,若以 A、 P、Q、R 为顶点的四边形是正方形,求出点 Q 的坐标.
∴x1=0,x2=-6, ∴CP1=AN1=6, ∴ON1=6+5=11, 此时 N1(-11,0). 若点 P 在 x 轴下方,不存在;
例题解图
类型五 特殊四边形存在性问题
②当 AC 为平行四边形的对角线时,如解图,
满足 AN2=P2C=6,
∴ON2=6-5=1,
此时 N2(1,0).
例题解图
综上所述,存在满足题意的点 N,点 N 的坐标为(-11,0)或(1,0);
专题04 二次函数中的平行四边形存在性问题(老师版)
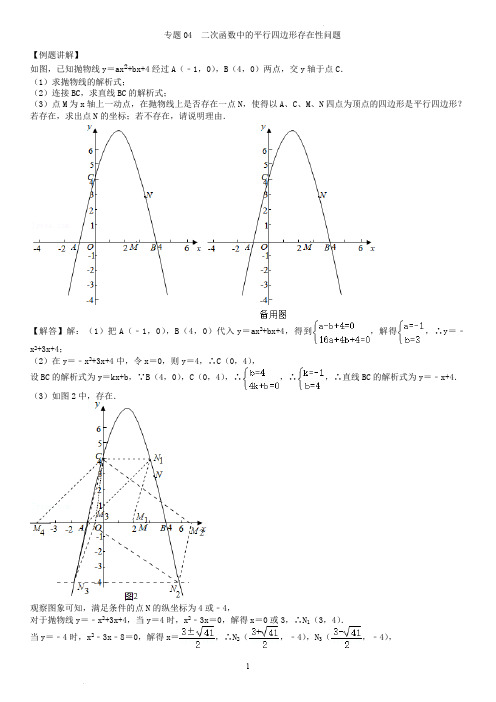
专题04 二次函数中的平行四边形存在性问题【例题讲解】如图,已知抛物线y=ax2+bx+4经过A(﹣1,0),B(4,0)两点,交y轴于点C.(1)求抛物线的解析式;(2)连接BC,求直线BC的解析式;(3)点M为x轴上一动点,在抛物线上是否存在一点N,使得以A、C、M、N四点为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.【解答】解:(1)把A(﹣1,0),B(4,0)代入y=ax2+bx+4,得到,解得,∴y=﹣x2+3x+4;(2)在y=﹣x2+3x+4中,令x=0,则y=4,∴C(0,4),设BC的解析式为y=kx+b,∵B(0),C(0,4),∴,∴,∴直线BC的解析式为y=﹣x+4.(3)如图2中,存在.观察图象可知,满足条件的点N的纵坐标为4或﹣4,对于抛物线y=﹣x2+3x+4,当y=4时,x2﹣3x=0,解得x=0或3,∴N1(3,4).当y=﹣4时,x2﹣3x﹣8=0,解得x=,∴N2(,﹣4),N3(,﹣4),综上所述,满足条件的点N 的坐标为(3,4)或(,﹣4)或(,﹣4).【模型解读】考虑到求证平行四边形存在,必先了解平行四边形性质:(1)对应边平行且相等;(2)对角线互相平分.这是图形的性质,我们现在需要的是将其性质运用在在坐标系中:(1)对边平行且相等可转化为:,可以理解为点B 移动到点A ,点C 移动到点D ,移动路径完全相同.(2)对角线互相平分转化为:,可以理解为AC 的中点也是BD 的中点.【小结】虽然由两个性质推得的式子并不一样,但其实可以化为统一:,→.当AC 和BD 为对角线时,结果可简记为:(各个点对应的横纵坐标相加)以上是对于平行四边形性质的分析,而我们要求证的是平行四边形存在性问题,此处当有一问:若坐标系中的4个点A 、B 、C 、D 满足“A+C=B+D”,则四边形ABCD 是否一定为平行四边形?反例如下:之所以存在反例是因为“四边形ABCD 是平行四边形”与“AC 、BD 中点是同一个点”并不是完全等价的转化,故存在反例.虽有反例,但并不影响运用此结论解题,另外,还需注意对对角线的讨论:(1)四边形ABCD 是平行四边形:AC 、BD 一定是对角线.(2)以A 、B 、C 、D四个点为顶点是四边形是平行四边形:对角线不确定需要分类讨论.y D -y Cx D -x Cy A -y Bx A -x BABC DDCBAD A B D CAB DC x x x x y y y y -=-⎧⎨-=-⎩2222A CB DAC BD x x x x y y y y ++⎧=⎪⎪⎨++⎪=⎪⎩A B D C A C D BA B D C AC D B x x x x x x x x y y y y y y y y -=-+=+⎧⎧→⎨⎨-=-+=+⎩⎩2222A CB DAC BD x x x x y y y y ++⎧=⎪⎪⎨++⎪=⎪⎩A C B D A C B D x x x x y y y y +=+⎧⎨+=+⎩A C B D +=+【题型分类】1.三定一动已知A (1,2)B (5,3)C (3,5),在坐标系内确定点D 使得以A 、B 、C 、D 四个点为顶点的四边形是平行四边形.思路1设D 点坐标为(m ,n ),又A (1,2)B (5,3)C (3,5),可得:(1)BC 为对角线时,,可得;(2)AC 为对角线时,,解得;(3)AB 为对角线时,,解得.当然,如果对这个计算过程非常熟悉的话,也不用列方程解,直接列算式即可.比如:,,.(此处特指点的横纵坐标相加减)2.两定两动已知A (1,1)、B (3,2),点C 在x 轴上,点D 在y 轴上,且以A 、B 、C 、D 为顶点的四边形是平行四边形,求C 、D 坐标.【分析】设C 点坐标为(m ,0),D 点坐标为(0,n ),又A (1,1)、B (3,2).(1)当AB 为对角线时,,解得,故C (4,0)、D (0,3);531352mn +=+⎧⎨+=+⎩()17,6D 135253mn +=+⎧⎨+=+⎩()21,4D -153235mn +=+⎧⎨+=+⎩()33,0D 1=D B C A +-2=D A C B +-3D A B C =+-130120m n +=+⎧⎨+=+⎩43m n =⎧⎨=⎩(2)当AC 为对角线时,,解得,故C (2,0)、D (0,-1);(3)当AD 为对角线时,,解得,故C (-2,0)、D (0,1).“三定一动”的动点和“两定两动”的动点性质并不完全一样,“三定一动”中动点是在平面中,横纵坐标都不确定,需要用两个字母表示,这样的我们姑且称为“全动点”,而有一些动点在坐标轴或者直线或者抛物线上,用一个字母即可表示点坐标,称为“半动点”.从上面例子可以看出,虽然动点数量不同,但本质都是在用两个字母表示出4个点坐标.若把一个字母称为一个“未知量”也可理解为:全动点未知量=半动点未知量×2.找不同图形的存在性最多可以有几个未知量,都是根据图形决定的,像平行四边形,只能有2个未知量.究其原因,在于平行四边形两大性质:(1)对边平行且相等;(2)对角线互相平分.但此两个性质统一成一个等式: ,两个等式,只能允许最多存在两个未知数,即我们刚刚所讲的平行四边形存在性问题最多只能存在2个未知量.由图形性质可知未知量,由未知量可知动点设计,由动点设计可化解问题.【模型实例】1.如图,抛物线y =ax 2+bx+c (a ≠0)与x 轴交于A 、B 两点,与y 轴交于C 点,AC =,OB =OC =3OA .(1)求抛物线的解析式;(2)在第二象限内的抛物线上确定一点P ,使四边形PBAC 的面积最大,求出点P 的坐标;(3)在(2)的结论下,点M 为x 轴上一动点,抛物线上是否存在一点Q ,使点P 、B 、M 、Q 为顶点的四边形是平行四边形,若存在,请直接写出Q 点的坐标;若不存在,请说明理由.【解答】解:(1)∵OC =3OA ,AC =,∠AOC =90°,∴OA 2+OC 2=AC 2,即OA 2+(3OA )2=()2,解得:OA =1,∴OC =3,∴A (1,0),C (0,3),∵OB =OC =3,∴B (﹣3,0),设抛物线解析式为y =a (x+3)(x ﹣1),将C (0,3)代入,得:﹣3a =3,解得:a =﹣1,130102m n +=+⎧⎨+=+⎩21m n =⎧⎨=-⎩103120m n +=+⎧⎨+=+⎩21m n =-⎧⎨=⎩A CB DA CB D x x x x y y y y +=+⎧⎨+=+⎩∴y=﹣(x+3)(x﹣1)=﹣x2﹣2x+3,∴该抛物线的解析式为y=﹣x2﹣2x+3;(2)如图1,过点P作PK∥y轴交BC于点K,设直线BC解析式为y=kx+n,将B(﹣3,0),C(0,3)代入,得:,解得:,∴直线BC解析式为y=x+3,设P(t,﹣t2﹣2t+3),则K(t,t+3),∴PK=﹣t2﹣2t+3﹣(t+3)=﹣t2﹣3t,∴S△PBC=S△PBK+S△PCK=PK•(t+3)+PK•(0﹣t)=PK=(﹣t2﹣3t),S△ABC=AB•OC=×4×3=6,∴S四边形PBAC=S△PBC+S△ABC=(﹣t2﹣3t)+6=﹣(t+)2+,∵﹣<0,∴当t=﹣时,四边形PBAC的面积最大,此时点P的坐标为(﹣,);(3)存在.如图2,分两种情况:点Q在x轴上方或点Q在x轴下方.①当点Q在x轴上方时,P与Q纵坐标相等,∴﹣x2﹣2x+3=,解得:x1=﹣,x2=﹣(舍去),∴Q1(﹣,),②当点Q在x轴下方时,P与Q纵坐标互为相反数,∴﹣x2﹣2x+3=﹣,解得:x1=﹣,x2=,∴Q2(﹣,﹣),Q3(,﹣),综上所述,Q点的坐标为Q1(﹣,),Q2(﹣,﹣),Q3(,﹣).2.如图1,在平面直角坐标系中,直线y=x+1分别与x轴、y轴交于点A,C,经过点C的抛物线y=x2+bx+c 与直线y=x+1的另一个交点为点D,点D的横坐标为6.(1)求抛物线的表达式.(2)M为抛物线上的动点,N为x轴上一点,当四边形CDMN为平行四边形时,求点M的坐标;【解答】解:(1)令x=0,则y=x+1=1,∴C点坐标为(0,1),令y=0,则,∴,∴A点坐标为(,0),令x=6,则y=,∴D点坐标为(),将C,D两点坐标代入到抛物线解析式中得,,解得,∴抛物线的表达式为:y=;(2)①设N(n,0),∵四边形CDMN为平行四边形,∴由平移与坐标关系可得M(n+6,),∵点M在抛物线上,∴+1=,∴n2+9n+4=0,∴n=,∴点M的坐标为(,)或(,);3.如图,抛物线y=ax2﹣2x+c(a≠0)与x轴交于A、B(3,0)两点,与y轴交于点C(0,﹣3),抛物线的顶点为D.(1)求抛物线的解析式;(2)点P在抛物线的对称轴上,点Q在x轴上,若以点P、Q、B、C为顶点,BC为边的四边形为平行四边形,请直接写出点P、Q的坐标;【解答】解:(1)将点B(3,0),C(0,﹣3)分别代入y=ax2﹣2x+c中,得:,解得,∴抛物线的函数关系为y=x2﹣2x﹣3;(2)由抛物线的表达式知,其对称轴为x=﹣=1,故设点P(1,m),点Q(x,0),B(3,0),C(0,﹣3),①以PB为对角线时,,解得:,∴P(1,﹣3),Q(4,0);②以PC为对角线时,,解得:,∴P(1,3),Q(﹣2,0);故点P、Q的坐标分别为(1,﹣3)、(4,0)或(1,3)、(﹣2,0);4.如图,抛物线过点A(0,1)和C,顶点为D,直线AC与抛物线的对称轴BD的交点为B(,0),平行于y轴的直线EF与抛物线交于点E,与直线AC交于点F,点F的横坐标为,四边形BDEF为平行四边形.(1)求点F的坐标及抛物线的解析式;(2)在抛物线的对称轴上取一点Q,同时在抛物线上取一点R,使以AC为一边且以A,C,Q,R为顶点的四边形为平行四边形,求点Q和点R的坐标.【解答】解:(1)设抛物线的解析式为y=ax2+bx+c(a≠0),∵A(0,1),B(,0),设直线AB的解析式为y=kx+m,∴,解得,∴直线AB的解析式为y=﹣x+1,∵点F的横坐标为,∴F点纵坐标为﹣+1=﹣,∴F点的坐标为(,﹣),又∵点A在抛物线上,∴c=1,对称轴为:x=﹣,∴b=﹣2a,∴解析式化为:y=ax2﹣2ax+1,∵四边形DBFE为平行四边形.∴BD=EF,∴﹣3a+1=a﹣8a+1﹣(﹣),解得a=﹣1,∴抛物线的解析式为y=﹣x2+2x+1;(2)∵,∴x=0或x=,∴C(,﹣),设Q(,m),①当AQ为对角线时,∴R(﹣),∵R在抛物线y=+4上,∴m+=﹣+4,解得m=﹣,∴Q,R;②当AR为对角线时,∴R(),∵R在抛物线y=+4上,∴m﹣+4,解得m=﹣10,∴Q(,﹣10),R().综上所述,Q,R;或Q(,﹣10),R().5.如图,抛物线y=ax2+bx+c(a≠0)的图象经过A(1,0),B(3,0),C(0,6)三点.(1)求抛物线的解析式.(2)P为抛物线上的一动点,Q为对称轴上动点,抛物线上是否存在一点P,使A、D、P、Q为顶点的四边形为平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.【解答】解:(1)∵抛物线y=ax2+bx+c(a≠0)的图象经过A(1,0),B(3,0),∴设抛物线解析式为:y=a(x﹣1)(x﹣3),∵抛物线y=a(x﹣1)(x﹣3)(a≠0)的图象经过点C(0,6),∴6=a(0﹣1)(0﹣3),∴a=2,∴抛物线解析式为:y=2(x﹣1)(x﹣3)=2x2﹣8x+6;(2)若AD为平行四边形的边,∵以A、D、P、Q为顶点的四边形为平行四边形,∴AD=PQ,∴x D﹣x A=x P﹣x Q或x D﹣x A=x Q﹣x P,∴x P=4﹣1+2=5或x P=2﹣4+1=﹣1,∴点P坐标为(5,16)或(﹣1,16);若AD为平行四边形的对角线,∵以A、D、P、Q为顶点的四边形为平行四边形,∴AD与PQ互相平分,∴,∴x P=3,∴点P坐标为(3,0),综上所述:当点P坐标为(5,16)或(﹣1,16)或(3,0)时,使A、D、P、Q为顶点的四边形为平行四边形.6.如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,过点A的直线l交抛物线于点C(2,m).(1)求抛物线的解析式.(2)点F是抛物线上的动点,在D,使得以点A,C,D,F为顶点的四边形是平行四边形?如果存在,请直接写出所有满足条件的点D的坐标;如果不存在,请说明理由.【解答】解:(1)将A(﹣1,0),B(3,0)代入y=x2+bx+c,得到解得,∴y=x2﹣2x﹣3.(2)存在.理由:如图,设抛物线与y的交点为K,由题意K(0,﹣3),∵C(2,﹣3),∴CK∥x轴,CK=2,当AC是平行四边形ACF1D1的边时,可得D1(﹣3,0).当AC是平行四边形AF1CD2的对角线时,AD2=CK,可得D2(1,0),当点F在x轴的上方时,令y=3,3=x2﹣2x﹣3,解得x=1±,∴F3(1﹣,3),F4(1+,3),由平移的性质可知D3(4﹣,0),D4(4+,0).综上所述,满足条件的点D的坐标为(﹣3,0)或(1,0)或(4﹣,0)或(4+,0).7.在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于A,B两点.与y轴交于点C.且点A的坐标为(﹣1,0),点C的坐标为(0,5).(1)求该抛物线的解析式;(2)如图,若点M是抛物线上一点,点N是抛物线对称轴上一点,是否存在点M使得以B,C,M,N为顶点的四边形是平行四边形?若存在,请求出点M的坐标;若不存在,请说明理由.【解答】解:(1)将A的坐标(﹣1,0),点C的坐(0,5)代入y=﹣x2+bx+c得:,解得,∴抛物线的解析式为y=﹣x2+4x+5;(2)存在,理由如下:抛物线y=﹣x2+4x+5对称轴为直线x=2,设M(s,﹣s2+4s+5),N(2,t),而B(5,0),C(0,5),①以MN、BC为对角线,则MN、BC的中点重合,如图:∴,解得,∴M(3,8),②以MB、NC为对角线,则MB、NC的中点重合,如图:∴,解得,∴M(﹣3,﹣16),③以MC、NB为对角线,则MC、NB中点重合,如图:,解得,∴M(7,﹣16);综上所述,M的坐标为:(3,8)或(﹣3,﹣16)或(7,﹣16).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
类型二 两定两动
例2. 如图,平面直角坐标系中,y=-0.25x2+x与x轴相交于点B(4,0),点 Q在抛物线的对称轴上,点P在抛物线上,且以点O,B,Q,P为顶点的四边 形为平行四边形,写出相应的点P 的坐标
已知B(4,0), O(0,0)
设Q(2,a), P(m,-0.25m2+m)
①点B与点O相对
动点,点Q是直线y=-x上的动点,判断有几个位置能使以点P,Q,B,O为顶点的四
边形为平行四边形,写出相应的Q的坐标
已知B(0,-4), O(0,0)
设Q(a,-a), P(m,0.5m2+m-4)
①点B与点O相对
00ma 400.5m2m4a
a1 a
2
4 0
舍
②点B与点P相对
0m0a 40.5m2m40a
分两种情况讨论(1)AB为平行四边形的边,将AB上下左右平移,确定P,Q的位置 (2)若AB为平行四边形的对角线,取AB中点,旋转经过中点的直线确定P,Q的位置
A B
A B
二、集思广益 探究发现
• 1、线段的中点公式
平面直标 角面 中 坐, Ax1,y1,Bx2,y2,则线A段 B的中P点 的
坐标P为 x1x2 y1y2 ,
402m
m
00a0.25m2
m
a
2 1
②点B与点Q相对 420m
m 6
0a00.25m2 m a 3
③点B与点P相对
4m02 00.25m2 m0a
m
a
2 3
∴P1(2,1), P2(6,-3), P3(-2,-3)
变式训练2
如图,平面直角坐标系中,y=0.5x2+x-4与y轴相交于点B(0,-4),点P是抛物线上的
先求出A(-1,0),B(2,0),C(0,2),设点M(x,y)
①点A与点B相对 12 0 x 00 2 y
x 1
y
2
②点A与点C相对 10 2 x 02 0 y
x 3
y
2
1 x 20 ③点A与点M相对 0 y 0 2
x 3
y
2
∴M1(1,-2), M2(-3,2), M3(3,2)
抛物线中 平行四边形存在性问题
一、画图引领 温故知新
• 1、已知平面上不共线三点A、B、C,求一 点D,使得A、B、C、D四个点组成平行四
边形
连接AB,AC,BC,分别过点A,B,C作对边的平行线,三条平行线的交点即为所有点D
D1
A
D2
B
C
D3
• 2、已知平面上两个点A,B,求两点P,Q,使 得A,B,P,Q四个点组成平行四边形(题目中 P,Q的位置有具体的限制)
a22 5
0a0m ③点B与点Q相对 4a00.5m2m4
a1 4
a 2 0舍
∴ Q (4 Q ( , - 2 5 4 2 ,- 2 ) 5 ), Q ,( - 2 5 2 , 2 2 5 ) Q , (-4
1
2
3
4
合作探究
已知抛物线y=-x2-2x+a(a<0)与y轴相交于点A,顶点为M,直线y=-0.5x-a与y轴相交 于点C,并且与直线AM相交于点N。若P为抛物线上一动点,求出使得以P,A,C,N为 顶点的四边形是平行四边形的点P的坐标
先求 A 0,a,出 C 0,a,N 4a,1a 设 P m ,m 2 2 m a 3 3 ①点A与点C相对
②点A与点N相对
③点A与点P相对
向你的美好的希冀和追求撒开网吧,九百九十九次落空了,还有一千次呢人若软弱就是自己最大的敌人游手好闲会使人心智生锈。故天将降大任于斯人也,必先苦其心 乏其身,行拂乱其所为,所以动心忍性,增益其所不能。让生活的句号圈住的人,是无法前时半步的。少一点预设的期待,那份对人的关怀会更自在。榕树因为扎根于 越长越茂盛。稗子享受着禾苗一样的待遇,结出的却不是谷穗。进取乾用汗水谱烈军属着奋斗和希望之歌。患难可以试验一个人的品格,非常的境遇方可以显出非常的 角度来看它。机会只对进取有为的人开放,庸人永远无法光顾。困苦能孕育灵魂和精神的力量骄傲,是断了引线的风筝,稍纵即逝;自卑,是剪了双翼的飞鸟,难上青 圆规的两只脚都动,永远也画不出一个圆。有困难是坏事也是好事,困难会逼着人想办法,困难环境能锻炼出人才来。只存在於蠢人的字典里。青,取之于蓝而青于蓝 然后知松柏之后凋也。积极的人在每一次忧患中都看到一个机会,而消极的人则在每个机会都看到某种忧患。一个能从别人的观念来看事情,能了解别人心灵活动的人 志当存高远。绳锯木断,水滴石穿让我们将事前的忧虑,换为事前的思考和计划吧!锲而舍之,朽木不折;锲而不舍,金石可镂。没有天生的信心,只有不断培养的信 下而求索天行健,君子以自强不息。会当凌绝顶,一览众山小。丈夫志四海,万里犹比邻。也,而不可夺赤。信言不美,美言不信。善者不辩,辩者不善。知者不博, 和其光,同其尘,是谓“玄同”。故不可得而亲,不可得而疏;不可得而利,不可得而害;不可得而贵,不可得而贱。故为天下贵。天下之至柔,驰骋天下之至坚。无 益。知者不言,言者不知。更多老子名言敬请关注习古堂国学网的相关文章。柔弱胜刚强。鱼不可脱於渊,国之利器不可以示人。善为士者,不武;善战者,不怒;善 之下。是谓不争之德,是谓用人之力,是谓配天古之极是以圣人后其身而身先,外其身而身存无为而无不为。取天下常以无事,及其有事,不足以取天下。合抱之木, 土;千里之行,始於足下。多言数穷,不如守中。天下莫柔弱於水,而攻坚强者莫之能胜,以其无以易之。天长地久。天地所以能长且久者,以其不自生,故能长生。 身而身存。非以其无故能成其私。譬道之在天下,犹川谷之於江海。江海之所以能为百谷王者,以其善下之,故能为百谷王。是以圣人欲上民,必以言下之;欲先民, 民不重,处前而民不害。是以天下乐推而不厌。以其不争,故天下莫能与之争。是以圣人抱一为天下式。不自见,故明;不自是,故彰;不自伐,故有功;不自矜,故 之争。故道大,天大,地大,人亦大。域中有四大,而人居其一焉修之於身,其德乃真;修之於家,其德乃余;修之於乡,其德乃长;修之於邦,其德乃丰;修之於天 以家观家,以乡观乡,以邦观邦,以天下观天下。吾何以知天下然哉?以此。慈故能勇;俭故能广;不敢为天下先,故能成器长。今舍慈且勇;舍俭且广;舍後且先; 将救之,以慈卫之。道生一,一生二,二生三,三生万物。知人者智,自知者明。胜人者有力,自胜者强。知足者富。强行者有志。一个实现梦想的人,就是一个成功 完全投入于权力和仇恨中,你怎么能期望他还有梦梦想无论怎样模糊,总潜伏在我们心底,使我们的心境永远得不到宁静,直到这些梦想成为事实。落叶——树叶撒下 腰拾起;与其肩负苦涩的回忆,不如走向明天,淋浴春雨梦想绝不是梦,两者之间的差别通常都有一段非常值得人们深思的距离。一个人要实现自己的梦想,最重要的 和行动。一个人如果已经把自己完全投入于权力和仇恨中,你怎么能期望他还有梦?如果一个人不知道他要驶向哪个码头,那么任何风都不会是顺风。最初的梦想紧握 让一切都曾失去过。谁不曾迷茫?谁有不曾坠落呢?安逸的日子谁不想有呢?如果骄傲没被现实大海冷冷拍下,如果梦想不曾坠落悬崖千钧一发,又怎会懂得要多努力 著的人拥有隐形翅膀?现在的一切都是为将来的梦想编织翅膀,让梦想在现实中展翅高飞。很多时候,我们富了口袋,但穷了脑袋;我们有梦想,但缺少了思想。、一 微,但是不可以没有梦想。只要梦想一天,只要梦想存在一天,就可以改变自己的处境乐理知识和乐器为我的音乐梦想插上了一双希望的翅膀。长大以后,我要站在真 风采,为大家带来欢乐。没有一颗心会因为追求梦想而受伤,当你真心想要某样东西时,整个宇宙都会联合起来帮你完成。青年时准备好材料,想造一座通向月亮的桥 宇。活到中年,终于决定搭一个棚。一个人有钱没钱不一定,但如果这个人没有了梦想,这个人穷定了。梦想无论怎样模糊,总潜伏在我们心底,使我们的心境永远得 事实。如果失去梦想,人类将会怎样?不要怀有渺小的梦想,它们无法打动人心。最初所拥有的只是梦想,以及毫无根据的自信而已。但是,所有的一切就从这里出发 福,有时梦想破灭也是一种幸福。人生最苦痛的是梦醒了无路可走。做梦的人是幸福的;倘没有看出可以走的路,最要紧的是不要去惊醒他。在每一个想你的日子里, 更难。想你,已成为我的习惯。努力向上吧,星星就躲藏在你的灵魂深处;做一个悠远的梦吧,每个梦想都会超越你的目标。要想成就伟业,除了梦想,必须行动。人 实际上人们每天在安排着自己的一切活动家都是梦想家。悲观的人,先被自己打败,然后才被生活打败;乐观的人,先战胜自己,然后才战胜生活。
2 2
(x1,y1)
平行四边形顶点坐标规律
A
D (x4,y4)
x1
x x x x 12
x3
3x 2
2
x4
2
4
y y y y
y 1 12
y 3
y2
3
2
y4
2
4
E
B (x2,y2)
C(x3,y3)
对点法 平面直角坐标系中,平行四边形两组相对顶点
的横坐标之和相等,纵坐标之和也相等
三、学以致用 解决问题 三定一动
• 例1 如图,平面直角坐标系中,已知点A(-1,0),B(1,-2),C(3,1),点D
是平面内一动点,若以点A,B,C,D为顶点的四边形是平行四边
形,则点D的坐标是__(-_3_,-_3)_,(_1_,3_),_(5,-1)
设点D(x,y)
①点A与点B相对 11 3 x 02 1 y
②点A与点C相对13 1 x 01 2 y
x 3
y
3
D2 C
A
x 1
y
3
D1
B
D3
说明:若题中四边形ABCD是平行四边形,
则点D的坐标只有一个结果__(1,3)
③点A与点D相对 1 x 13 x 5
0 y 21
y
1
四、解决问题
变式训练1. 已知抛物线y=-x2+x+2与x轴的交点为A,B,与y轴的 交点为C,点M是平面内一点,判断M有几个位置能使以点 M,A,B,C为顶点的四边形是平行四边形,请写出相应的坐标
