高中数学函数压轴题精制
完整)上海高中数学三角函数大题压轴题练习

完整)上海高中数学三角函数大题压轴题练习三角函数大题压轴题练1.已知函数$f(x)=\cos(2x-\frac{\pi}{3})+2\sin(x-\frac{\pi}{4})\sin(x+\frac{\pi}{4})$。
Ⅰ)求函数$f(x)$的最小正周期和图象的对称轴方程。
解:(1)$f(x)=\cos(2x-\frac{\pi}{3})+2\sin(x-\frac{\pi}{4})\sin(x+\frac{\pi}{4})$frac{1}{3}\cos(2x-\frac{\pi}{3})+\frac{4}{3}\sin x\cos x$frac{1}{3}(\cos^2x-\sin^2x-\frac{1}{2})+\frac{4}{3}\sin x\cos x$frac{1}{6}(3\cos2x-1)+\frac{4}{3}\sin x\cos x$frac{1}{6}(3\cos2x+2\sin x\cos x-\frac{2}{3})$frac{1}{6}(3\cos2x+\sin(2x-\frac{\pi}{3})-\frac{2}{3})$frac{1}{6}(3\cos2x+\sin2x\cos\frac{\pi}{3}-\cos2x\sin\frac{\pi}{3}-\frac{2}{3})$frac{1}{6}(2\cos2x+\sqrt{3}\sin2x-\frac{2}{3})$frac{1}{3}(\cos2x+\frac{\sqrt{3}}{2}\sin2x)-\frac{1}{3}$frac{2}{3}\sin(2x+\frac{\pi}{3})-\frac{1}{3}$所以,函数$f(x)$的最小正周期为$\pi$,图象的对称轴方程为$x=k\pi+\frac{\pi}{3}$($k\in Z$)。
2)在区间$[-\frac{5\pi}{6},\frac{\pi}{2}]$上,$f(x)$单调递增,而在区间$[\frac{\pi}{2},\frac{7\pi}{6}]$上单调递减。
高中数学_函数类压轴题6大题型精讲

导数与函数类压轴题精讲(前三讲)题型一切线型1.求在某处的切线方程2.求过某点的切线方程3.已知切线方程求参数题型二单调型1.主导函数需“二次求导”型2.主导函数为“一次函数”型3.主导函数为“二次函数”型4.已知函数单调性,求参数范围题型三极值最值型1.求函数的极值2.求函数的最值3.已知极值求参数4.已知最值求参数题型四零点型1.零点(交点,根)的个数问题2.零点存在性定理的应用3.极值点偏移问题题型五恒成立与存在性问题1.单变量型恒成立问题2.单变量型存在性问题3.双变量型的恒成立与存在性问题4.等式型恒成立与存在性问题题型六与不等式有关的证明问题1.单变量型不等式证明2.含有e x 与lnx 的不等式证明技巧3.多元函数不等式的证明4.数列型不等式证明的构造方法题型一切线型1.求在某处的切线方程例1.【2015重庆理20】求函数f (x )=3x ²e x 在点(1,f (1))处的切线方程.解:由f (x )=3x ²e x ,得f ′(x )=6x -3x ²e x,切点为(1,3e ),斜率为f ′(1)=3e 由f (1)=3e ,得切点坐标为(1,3e ),由f ′(1)=3e ,得切线斜率为3e ;∴切线方程为y -3e =3e (x -1),即3x -ey =0.例2.求f (x )=e x (1x+2)在点(1,f (1))处的切线方程.解:由f (x )=e x (1x +2),得f ′(x )=e x (-1x ²+1x+2)由f (1)=3e ,得切点坐标为(1,3e ),由f ′(1)=2e ,得切线斜率为2e ;∴切线方程为y -3e =2e (x -1),即2ex -y +e =0.例3.求f (x )=ln 1-x 1+x在点(0,f (0))处的切线方程.解:由f (x )=ln 1-x 1+x=ln (1-x )-ln (1+x ),得f ′(x )=-11-x -11+x 由f (0)=0,得切点坐标为(0,0),由f ′(0)=-2,得切线斜率为-2;∴切线方程为y =-2x ,即2x +y =0.例4.【2015全国新课标理20⑴】在直角坐标系xoy 中,曲线C :y =x ²4与直线l :y =kx +a (a >0)交于M ,N 两点,当k =0时,分别求C 在点M 与N 处的切线方程.解:由题意得:a =x ²4,则x =±2a ,即M (-2a ,a ),N (2a ,a ),由f (x )=x ²4,得f ′(x )=x 2,当切点为M (-2a ,a )时,切线斜率为f ′(-2a )=-a ,此时切线方程为:ax +y +a =0;当切点为N (2a ,a )时,切线斜率为f ′(2a )=a ,此时切线方程为:ax -y -a =0;解题模板一求在某处的切线方程⑴写出f (x );⑵求出f ′(x );⑶写出切点(x 0,f (x 0));⑷切线斜率k =f ′(x 0);⑸切线方程为y -f (x 0)=f ′(x 0)(x -x 0).2.求过某点的切线方程Step 1设切点为(x 0,f (x 0)),则切线斜率f ′(x 0),切线方程为:y -f (x 0)=f ′(x 0)(x -x 0)Step 2因为切线过点(a ,b ),所以b -f (x 0)=f ′(x 0)(a -x 0),解得x 0=x 1或x 0=x 2Step 2当x 0=x 1时,切线方程为y -f (x 1)=f ′(x 0)(x -x 1)当x 0=x 2时,切线方程为y -f (x 2)=f ′(x 0)(x -x 2)例1.求f (x )=13x 3+43过点P (2,4)的切线方程.O o O o Oo P P P 点P 不在曲线上不是切点点P 在曲线上不确定是切点点P 在曲线上切点解:设切点为(x 0,13x 03+43),则切线斜率f ′(x 0)=x 0²,所以切线方程为:y -13x 03+43=x 0²(x -x 0),由切线经过点P (2,4),可得4-13x 03+43=x 0²(2-x 0),整理得:x 03-3x 0²+4=0,解得x 0=-1或x 0=2当x 0=-1时,切线方程为:x -y +2=0;当x 0=2时,切线方程为:4x -y -4=0.例2.求f (x )=x 3-4x ²+5x -4过点(2,-2)的切线方程.解:设切点为(x 0,x 03-4x 0²+5x 0-4),则切线斜率f ′(x 0)=3x 0²-8x 0+5,所以切线方程为:y -(x 03-4x 0²+5x 0-4)=(3x 0²-8x 0+5)(x -x 0),由切线经过点P (2,4),可得4-(x 03-4x 0²+5x 0-4)=(3x 0²-8x 0+5)(2-x 0),解得x 0=1或x 0=2当x 0=1时,切线方程为:2x +y -2=0;当x 0=2时,切线方程为:x -y -4=0.例3.过A (1,m )(m ≠2)可作f (x )=x 3-3x 的三条切线,求m 的取值范围.解:设切点为(x 0,x 03-3x 0),则切线斜率f ′(x 0)=3x 0²-3,切线方程为y -(x 03-3x 0)=(3x 0²-3)(x -x 0)∵切线经过点P (1,m ),∴m -(x 03-4x 0²+5x 0-4)=(3x 0²-8x 0+5)(1-x 0),即:-2x 03+3x 0²-3-m =0,即m =-2x 03+3x 0²-3∵过点A (1,m )(m ≠2)可作f (x )=x 3-3x 的三条切线,∴方程m =-2x 03+3x 0²-3,有三个不同的实数根.∴曲线H (x 0)=-2x 03+3x 0²-3与直线y =m 有三个不同交点,H ′(x 0)=-6x 0²+6x 0=-6x 0(x 0-1)令H ′(x 0)>0,则0<x 0<1;令H ′(x 0)<0,则x 0<0或x 0>1∴H (x 0)在(-∞,0)递减,在(0,1)递增,在(1,+∞)递减,∴H (x 0)的极小值=H (0)=-3,H (x 0)的极大值=H (1)=-2,由题意得-3<x <-2.例4.由点(-e ,e -2)可向曲线f (x )=lnx -x -1作几条切线,并说明理由.解:设切点为(x 0,lnx 0-x 0-1),则切线斜率f ′(x 0)=1x 0-1,切线方程为y -(lnx 0-x 0-1)=(1x 0-1)(x -x 0),∵切线经过点(-e ,e -2),∴e -2-(lnx 0-x 0-1)=(1x 0-1)(-e -x 0),即lnx 0=e x 0∵y =lnx 与y =e x 只有一个交点∴方程lnx 0=e x 0有唯一的实数根∴由点(-e ,e -2)可向曲线f (x )=lnx -x -1作一条切线.解题模板二求过某点的切线方程⑴设切点为(x0,f(x0)),则切线斜率f′(x0),切线方程为:y-f(x0)=f′(x0)(x-x0)⑵因为切线过点(a,b),所以b-f(x0)=f′(x0)(a-x0),解得x0=x1或x0=x2⑶当x0=x1时,切线方程为y-f(x1)=f′(x0)(x-x1)当x0=x2时,切线方程为y-f(x2)=f′(x0)(x-x2)3.已知切线方程求参数解题模板三已知切线方程求参数已知直线Ax+By+C=0与曲线y=f(x)相切⑴设切点横坐标为x0,则切线斜率=切线斜率(x0)=-Ax0+CBf′(x0)=-AB⑵解方程组得x0及参数的值.例1.函数f(x)=alnxx+1+bx在(1,f(1))处的切线方程为x+2y-3=0,求a,b的值.解:∵f(x)=alnxx+1+bx,∴f′(x)=a(x+1)x-alnx(x+1)²-bx²f(1)=1′(1)=-12,即b=1b=-12∴a=b=1例2.f(x)=ae x lnx+be x-1x在(1,f(1))处的切线方程为y=e(x-1)+2,求a,b的值.解:∵f(x)=ae x lnx+be x-1x,∴f′(x)=aex(1x+lnx)+bex-1(-1x²+1x)f(1)=2′(1)=-e=2=e∴a=1,b=2例3.若直线y=kx+b是y=lnx+2的切线,也是y=ln(x+1)的切线,求b.解:设y=kx+b与y=lnx+2相切的切点横坐标为x1,y=kx+b与y=ln(x+1)相切的切点横坐标为x2,2=kx1+b①②1)=kx2+b③k④,由②③得:x1=x2+1,由①-③得:lnx1-ln(x2+1)+2=k(x1-x2),将上式代入得:k=2∴x1=12,代入①得:-ln2+2=1+b∴b =1-ln 2.例4.若f (x )=x 与g (x )=a lnx 相交,且在交点处有共同的切线,求a 和该切线方程.解:设切点横坐标为x 0alnx 0①=a x 0②,由②得x 0=2a ,代入①得:x 0=e ²,∴a =e 2∵切点为(e ²,e ),切线斜率为12e,∴切线方程为x -2ey +e ²=0.例5.已知函数f (x )=x 3+ax +14,当a 为何值时,x 轴为曲线方程y =f (x )的切线.例6.已知函数f (x )=x ²+ax +b 和g (x )=e x (cx +d )都过点P (0,2)且在P 处有相同切线y =4x +2,求a ,b ,c ,d 的值.题型二单调型1.主导函数需“二次求导”型I 不含参求单调区间例1.求函数f (x )=x (e x -1)-12x ²的单调区间.解:f (x )的定义域为Rf ′(x )=e x (1+x )-1-x =(x +1)(e x +1)令f ′(x )>0,得x <-1或x >0;令f ′(x )<0,得-1<x <0f (x )的增区间为(-∞,-1)和(0,+∞),减区间为(-1,0)。
2023-2024学年高考数学专项复习——压轴题(附答案)

决胜3.已知函数,曲线在处的切线方程为.()2e xf x ax =-()y f x =()()1,1f 1y bx =+(1)求的值:,a b (2)求在上的最值;()f x []0,1(3)证明:当时,.0x >()e 1e ln 0x x x x +--≥4.已知函数,.()()ln 1f x x x a x =-++R a ∈(1)若,求函数的单调区间;1a =()f x (2)若关于的不等式在上恒成立,求的取值范围;x ()2f x a≤[)2,+∞a (3)若实数满足且,证明.b 21a b <-+1b >()212ln f x b <-5.椭圆的离心率是,点是椭圆上一点,过点2222:1(0)x y E a b a b +=>>22()2,1M E 的动直线与椭圆相交于两点.()0,1P l ,A B (1)求椭圆的方程;E (2)求面积的最大值;AOB (3)在平面直角坐标系中,是否存在与点不同的定点,使恒成立?存在,xOy P Q QA PAQB PB=求出点的坐标;若不存在,请说明理由.Q 6.已知函数,.()21ln 2f x a x x⎛⎫=-+ ⎪⎝⎭()()()2R g x f x ax a =-∈(1)当时,0a =(i )求曲线在点处的切线方程;()y f x =()()22f ,(ii )求的单调区间及在区间上的最值;()f x 1,e e ⎡⎤⎢⎥⎣⎦(2)若对,恒成立,求a 的取值范围.()1,x ∀∈+∞()0g x <(1)求抛物线的表达式和的值;,t k (2)如图1,连接AC ,AP ,PC ,若△APC 是以(3)如图2,若点P 在直线BC 上方的抛物线上,过点的最大值.12CQ PQ +(1)【基础训练】请分别直接写出抛物线的焦点坐标和准线l 的方程;22y x =(2)【技能训练】如图2所示,已知抛物线上一点P 到准线l 的距离为6,求点P 的坐218y x =标;(3)【能力提升】如图3所示,已知过抛物线的焦点F 的直线依次交抛物线及准()20y ax a =>线l 于点,若求a 的值;、、A B C 24BC BF AF ==,(4)【拓展升华】古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点C 将一条线段分为两段和,使得其中较长一段是全线段与另一AB AC CB AC AB 段的比例中项,即满足:,后人把这个数称为“黄金分割”,把CB 512AC BC AB AC -==512-点C 称为线段的黄金分割点.如图4所示,抛物线的焦点,准线l 与y 轴AB 214y x=(0,1)F 交于点,E 为线段的黄金分割点,点M 为y 轴左侧的抛物线上一点.当(0,1)H -HF 时,求出的面积值.2MH MF=HME 10.已知双曲线的一条渐近线方程的倾斜角为,焦距为4.2222:1(0,0)x y C a b a b -=>>60︒(1)求双曲线的标准方程;C (2)A 为双曲线的右顶点,为双曲线上异于点A 的两点,且.C ,M N C AM AN ⊥①证明:直线过定点;MN ②若在双曲线的同一支上,求的面积的最小值.,M N AMN(1)试用解析几何的方法证明:(2)如果将圆分别变为椭圆、双曲线或抛物线,你能得到类似的结论吗?13.对于数集(为给定的正整数),其中,如果{}121,,,,n X x x x =-2n ≥120n x x x <<<< 对任意,都存在,使得,则称X 具有性质P .,a b X ∈,c d X ∈0ac bd +=(1)若,且集合具有性质P ,求x 的值;102x <<11,,,12x ⎧⎫-⎨⎬⎩⎭(2)若X 具有性质P ,求证:;且若成立,则;1X ∈1n x >11x =(3)若X 具有性质P ,且,求数列的通项公式.2023n x =12,,,n x x x 14.已知,是的导函数,其中.()2e xf x ax =-()f x '()f x R a ∈(1)讨论函数的单调性;()f x '(2)设,与x 轴负半轴的交点为点P ,在点P()()()2e 11x g x f x x ax =+-+-()y g x =()y g x =处的切线方程为.()y h x =①求证:对于任意的实数x ,都有;()()g x h x ≥②若关于x 的方程有两个实数根,且,证明:()()0g x t t =>12,x x 12x x <.()2112e 11e t x x --≤+-15.在平面直角坐标系中,一动圆经过点且与直线相切,设该动圆圆心xOy 1,02A ⎛⎫ ⎪⎝⎭12x =-的轨迹为曲线K ,P 是曲线K 上一点.(1)求曲线K 的方程;(2)过点A 且斜率为k 的直线l 与曲线K 交于B 、C 两点,若且直线OP 与直线交//l OP 1x =于Q 点.求的值;||||AB ACOP OQ ⋅⋅(3)若点D 、E 在y 轴上,的内切圆的方程为,求面积的最小值.PDE △()2211x y -+=PDE △16.已知椭圆C :,四点中恰有三()222210x y a b a b +=>>()()1234331,1,0,1,1,,1,22P P P P ⎛⎫⎛⎫- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭点在椭圆C 上.(1)求椭圆C 的方程;(2)设直线l 不经过P 2点且与C 相交于A ,B 两点,若直线与直线的斜率的和为,2P A 2P B 1-证明:l 过定点.18.给定正整数k ,m ,其中,如果有限数列同时满足下列两个条件.则称2m k ≤≤{}n a 为数列.记数列的项数的最小值为.{}n a (,)k m -(,)k m -(,)G k m 条件①:的每一项都属于集合;{}n a {}1,2,,k 条件②:从集合中任取m 个不同的数排成一列,得到的数列都是的子列.{}1,2,,k {}n a 注:从中选取第项、第项、…、第项()形成的新数列{}n a 1i 2i 5i 125i i i <<<…称为的一个子列.325,,,i i i a a a ⋯{}n a (1)分别判断下面两个数列,是否为数列.并说明理由!(33)-,数列;1:1,2,3,1,2,3,1,2,3A 数列.2:1,2,3,2,1,3,1A (2)求的值;(),2G k (3)求证.234(,)2k k G k k +-≥答案:1.(1)极大值为,无极小值2e (2)证明见解析【分析】(1)求导,根据导函数的符号结合极值的定义即可得解;(2)构造函数,利用导数求出函数的最小值,再()21()()()2ln 12F x f x g x x x x x x =+=+->证明即可或者转换不等式为,通过构造函数可得证.()min0F x >()112ln 012x x x +->>【详解】(1)的定义域为,,()f x (0,)+∞()2(1ln )f x x '=-+当时,,当时,,10e x <<()0f x '>1e x >()0f x '<所以函数在上单调递增,在上单调递减,()f x 10,e ⎛⎫ ⎪⎝⎭1,e ⎛⎫+∞ ⎪⎝⎭故在处取得极大值,()f x 1e x =12e e f ⎛⎫= ⎪⎝⎭所以的极大值为,无极小值;()f x 2e (2)设,()21()()()2ln 12F x f x g x x x x x x =+=+->解法一:则,()2ln 1F x x x '=--令,,()()2ln 11h x x x x =-->22()1x h x x x -'=-=当时,,单调递减,当时,,单调递增,12x <<()0h x '<()h x 2x >()0h x '>()h x 又,,,(2)1ln 40h =-<(1)0h =(4)32ln 40h =->所以存在,使得,即.0(2,4)x ∈0()0h x =002ln 10x x --=当时,,即,单调递减,01x x <<()0h x <()0F x '<()F x 当时,,即,单调递增,0x x >()0h x >()0F x '>()F x 所以当时,在处取得极小值,即为最小值,1x >()F x 0x x =故,22000000(11()()12ln )222F x F x x x x x x ≥=+-=-+设,因为,2000122()p x x x =-+0(2,4)x ∈由二次函数的性质得函数在上单调递减,2000122()p x x x =-+(2,4)故,0()(4)0p x p >=所以当时,,即.1x >()0F x >()()0f x g x +>解法二:要证,即证,()0F x >()1()12ln 012p x x x x =+->>因为,所以当时,,单调递减,()124()122x p x x x x -'=-=>()1,4x ∈()0p x '<()p x 当时,,单调递增,()4,x ∞∈+()0p x '>()p x 所以,所以,即.()()4212ln 434ln 20p x p ≥=+-=->()0F x >()()0f x g x +>方法点睛:利用导数证明不等式问题,方法如下:(1)直接构造函数法:证明不等式(或)转化为证明()()f xg x >()()f xg x <(或),进而构造辅助函数;()()0f xg x ->()()0f xg x -<()()()h x f x g x =-(2)适当放缩构造法:一是根据已知条件适当放缩;二是利用常见放缩结论;(3)构造“形似”函数,稍作变形再构造,对原不等式同解变形,根据相似结构构造辅助函数.2.(1)0(2)证明详见解析(3)2a ≤【分析】(1)利用导数求得的最小值.()g x (2)根据(1)的结论得到,利用放缩法以及裂项求和法证得不等式成立.2211ln 1n n ⎛⎫+≤ ⎪⎝⎭(3)由不等式分离参数,利用构造函数法,结合导数求得的取ln (2)10xx x x a x -+--≥a a 值范围.【详解】(1)依题意,,()21ln (,0)2f x x x x t t x =-+∈>R 所以,()()()()ln 1ln 10g x f x x x x x x '==-+=-->,所以在区间上单调递减;()111x g x x x -'=-=()g x ()0,1()()0,g x g x '<在区间上单调递增,()1,+∞()()0,g x g x '>所以当时取得最小值为.1x =()g x ()11ln110g =--=(2)要证明:对任意正整数,都有,(2)n n ≥222211111111e 234n ⎛⎫⎛⎫⎛⎫⎛⎫+⋅+⋅++< ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ 即证明,22221111ln 1111ln e234n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+⋅+⋅++< ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ 即证明,222111ln 1ln 1ln 1123n ⎛⎫⎛⎫⎛⎫++++++< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 由(1)得,即()()()10f xg x g '=≥=ln 10,ln 1x x x x --≥≤-令,所以, *211,2,N x n n n =+≥∈222111ln 111n n n ⎛⎫+≤+-= ⎪⎝⎭所以222222111111ln 1ln 1ln 12323n n ⎛⎫⎛⎫⎛⎫++++++≤+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ ,()111111111122312231n n n n <+++=-+-++-⨯⨯-- 111n=-<所以对任意正整数,都有.(2)n n ≥222211111111e 234n ⎛⎫⎛⎫⎛⎫⎛⎫+⋅+⋅++< ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ (3)若不等式恒成立,此时,ln (2)10xx x x a x -+--≥0x >则恒成立,ln 21x x x x x a x -+-≤令,()ln 21xx x x x h x x -+-=令,()()()e 10,e 10x x u x x x u x '=--≥=-≥所以在区间上单调递增,()u x[)0,∞+所以,当时等号成立,()0e 010,e 10,e 1x x u x x x ≥--=--≥≥+0x =所以,()ln e ln 21ln 1ln 212x x x x x x x x x x h x x x -+-+-+-=≥=当时等号成立,所以.ln 0,1x x x ==2a ≤利用导数求函数的最值的步骤:求导:对函数进行求导,得到它的导函数.导函数()f x ()f x '表示了原函数在不同点处的斜率或变化率.找出导数为零的点:解方程,找到使得导()0f x '=数为零的点,这些点被称为临界点,可能是函数的极值点(包括最大值和最小值),检查每个临界点以及区间的端点,并确认它们是否对应于函数的最值.3.(1),1a =e 2b =-(2);()max e 1f x =-()min 1f x =(3)证明见解析【分析】(1)利用切点和斜率列方程组,由此求得.,a b (2)利用多次求导的方法求得在区间上的单调性,由此求得在上的最值.()f x []0,1()f x []0,1(3)先证明时,,再结合(2)转化为,从0x >()()e 21f x x ≥-+()21e ln e x x x x x+--≥+而证得不等式成立.【详解】(1),()e 2x f x ax'=-∴,解得:,;()()1e 21e 1f a b f a b ⎧=-=⎪⎨=-=+'⎪⎩1a =e 2b =-(2)由(1)得:,()2e xf x x =-,令,则,()e 2x f x x '=-()e 2x h x x=-()e 2x h x '=-是增函数,令解得.()h x ()0h x '=ln 2x =∴,也即在上单调递减,()h x ()f x '()0,ln2()()0,h x h x '<在上单调递增,()ln2,+∞()()0,h x h x '>∴,∴在递增,()()ln 2ln222ln20h f ==->'()f x []0,1∴;;()()max 1e 1f x f ==-()()min 01f x f ==(3)∵,由(2)得过,()01f =()f x ()1,e 1-且在处的切线方程是,()y f x =1x =()e 21y x =-+故可猜测且时,的图象恒在切线的上方,0x >1x ≠()f x ()e 21y x =-+下面证明时,,设,,0x >()()e 21f x x ≥-+()()()e 21g x f x x =---()0x >∴,∴令,()()e 2e 2x g x x =---'()()()e 2e 2x x x g m x '--==-,()e 2x m x '=-由(2)得:在递减,在递增,()g x '()0,ln2()ln2,+∞∵,,,∴,()03e 0g '=->()10g '=0ln21<<()ln20g '<∴存在,使得,()00,1x ∈()0g x '=∴时,,时,,()()00,1,x x ∈⋃+∞()0g x '>()0,l x x ∈()0g x '<故在递增,在递减,在递增.()g x ()00,x ()0,1x ()1,+∞又,∴当且仅当时取“”,()()010g g ==()0g x ≥1x ==()()2e e 210x g x x x =----≥故,,由(2)得:,故,()e e 21x x xx+--≥0x >e 1x x ≥+()ln 1x x ≥+∴,当且仅当时取“=”,∴,1ln x x -≥1x =()e e 21ln 1x x x x x+--≥≥+即,∴,()21ln 1e e x x x x+--≥+()21e ln e x x x x x+--≥+即成立,当且仅当时“=”成立.()1ln 10e e x x x x +---≥1x =求解切线的有关的问题,关键点就是把握住切点和斜率.利用导数研究函数的单调性,如果一次求导无法求得函数的单调性时,可以考虑利用多次求导来进行求解.利用导数证明不等式恒成立,如果无法一步到位的证明,可以先证明一个中间不等式,然后再证得原不等式成立.4.(1)单调增区间为,单调减区间为;()0,1()1,+∞(2)(],2ln 2-∞(3)证明见解析【分析】(1)求导,再根据导函数的符号即可得解;(2)分离参数可得,构造函数,利用导数求出函数的最小ln 1x x a x ≤-ln (),21x xg x x x =≥-()g x 值即可得解;(3)由,得,则,要证21a b <-+21a b -<-2112()(e )e e 1a a b f x f a b ---≤=+<-+,即证,即证,构造函数()212ln f x b<-222e112ln bb b --+<-22212ln 0eb b b +-<,证明即可.()()()12ln e x h x x x x =>-()1h x <-【详解】(1)当时,,1a =()ln 1,0f x x x x x =-++>,由,得,由,得,()ln f x x '=-()0f x '>01x <<()0f x '<1x >故的单调增区间为,单调减区间为;()f x ()0,1()1,+∞(2),()ln 2,1x xf x a a x ≤∴≤- 令,ln (),21x x g x x x =≥-则,21ln ()(1)x xg x x --'=-令,则,()ln 1t x x x =-+11()1xt x x x -'=-=由,得,由,得,()0t x '>01x <<()0t x '<1x >故在递增,在递减,,()t x ()0,1()1,+∞max ()(1)0t x t ==,所以,()0t x ∴≤ln 1≤-x x 在上单调递增,,()0,()g x g x '≥∴[)2,+∞()min ()2g x g ∴=,(2)2ln 2a g ∴≤=的取值范围;a ∴(],2ln 2-∞(3),221,1b a b a <-+∴-<- 又,在上递增,11()(e )e a a f x f a --≤=+1e a y a -=+ R a ∈所以,2112()(e )e e 1a a b f x f a b ---≤=+<-+下面证明:,222e 112ln b b b --+<-即证,22212ln 0ebb b +-<令,则,21x b =>12ln 0e x x x +-<即,(2ln )e 1xx x -⋅<-令,则,()()()12ln e xh x x x x =>-()22ln 1e xh x x x x '⎛⎫=-+-⋅ ⎪⎝⎭令,则,()2()2ln 11x x x x x ϕ=-+->()()2221122()101x x x x x x ϕ---=--=<>∴函数在上单调递减,()x ϕ()1,+∞,()(1)0x ϕϕ∴<=在递减,()()0,h x h x '∴<(1,)+∞,()()1e 1h x h ∴<=-<-所以.()212ln f x b <-方法点睛:利用导数证明不等式问题,方法如下:(1)直接构造函数法:证明不等式(或)转化为证明()()f xg x >()()f xg x <(或),进而构造辅助函数;()()0f xg x ->()()0f xg x -<()()()h x f x g x =-(2)适当放缩构造法:一是根据已知条件适当放缩;二是利用常见放缩结论;(3)构造“形似”函数,稍作变形再构造,对原不等式同解变形,根据相似结构构造辅助函数.5.(1)22142x y +=(2)2(3)存在,.()0,2Q 【分析】(1)由离心率及过点列方程组求解.()2,1M,a b (2)设直线为与椭圆方程联立,将表达为的函数,由基本不l 1y kx =+1212AOB S x x =⋅- k 等式求最大值即可.(3)先讨论直线水平与竖直情况,求出,设点关于轴的对称点,证得()0,2Q B y B '三点共线得到成立.,,Q A B 'QA PAQB PB=【详解】(1)根据题意,得,解得,椭圆C 的方程为.2222222211c a a b c a b ⎧=⎪⎪⎪=+⎨⎪⎪+=⎪⎩222422a b c ⎧=⎪=⎨⎪=⎩22142x y +=(2)依题意,设,直线的斜率显然存在,()()1122,,,A x y B x y l 故设直线为,联立,消去,得,l 1y kx =+221142y kx x y =+⎧⎪⎨+=⎪⎩y ()2212420k x kx ++-=因为直线恒过椭圆内定点,故恒成立,,l ()0,1P 0∆>12122242,1212k x x x x k k +=-=-++故,()2221212221224212111214414222122AOBk S x x x x x x k k k k ⋅+⎛⎫⎛⎫=⋅=⨯-=⨯-⨯= ⎪ ⎪+⎝-+-⎝++⎭⎭- 令,所以,当且仅当,即时取得214,1t k t =+≥22222211AOB t S t t t=×=×£++1t =0k =等号,综上可知:面积的最大值为.AOB 2(3)当平行于轴时,设直线与椭圆相交于两点,如果存在点满足条件,l x ,C D Q 则有,即,所以点在轴上,可设的坐标为;||||1||||QC PC QD PD ==QC QD =Q y Q ()00,y 当垂直于轴时,设直线与椭圆相交于两点,如果存在点满足条件,l x ,M N Q 则有,即,解得或,||||||||QM PM QN PN =00221212y y --=++01y =02y =所以若存在不同于点的定点满足条件,则点的坐标为;P Q Q ()0,2当不平行于轴且不垂直于轴时,设直线方程为,l x x l 1y kx =+由(2)知,12122242,1212k x x x x k k --+==++又因为点关于轴的对称点的坐标为,B y B '()22,x y -又,,11111211QA y kx k k x x x --===-22222211QB y kx k k x x x '--===-+--.方法点睛:直线与椭圆0Ax By C ++=时,取得最大值2222220a A b B C +-=MON S 6.(1)(i );(322ln 220x y +--=(2)11,22⎡⎤-⎢⎥⎣⎦故曲线在点处的切线方程为,()y f x =()()22f ,()()32ln 222y x --+=--即;322ln 220x y +--=(ii ),,()21ln 2f x x x =-+()0,x ∈+∞,()211x f x x x x -'=-+=令,解得,令,解得,()0f x ¢>()0,1x ∈()0f x '<()1,x ∈+∞当时,,1,e e x ⎡⎤∈⎢⎥⎣⎦()()max 112f x f ==-又,,221111ln 1e 2e e 2e f ⎛⎫=-+=-- ⎪⎝⎭()2211e e ln e e 122f =-+=-+其中,()222211111e 1e 1e 20e 2e 222ef f ⎛⎫⎛⎫-=----+=--> ⎪ ⎪⎝⎭⎝⎭故,()()2min 1e e 12f x f ==-+故的单调递增区间为,单调递减区间为;()f x ()0,1()1,+∞在区间上的最大值为,最小值为;()f x 1,e e ⎡⎤⎢⎥⎣⎦12-21e 12-+(2),()21ln 22xg x a x x a ⎭-+⎛=⎪-⎫ ⎝对,恒成立,()1,x ∀∈+∞21ln 202a x x ax ⎛⎫-+-< ⎪⎝⎭变形为对恒成立,ln 122x a xa x<--⎛⎫ ⎪⎝⎭()1,x ∀∈+∞令,则,()(),1,ln x h x x x ∈=+∞()21ln xh x x -'=当时,,单调递增,()1,e x ∈()0h x '>()ln xh x x =当时,,单调递减,()e,+x ∈∞()0h x '<()ln xh x x =其中,,当时,恒成立,()10h =()ln e 1e e e h ==1x >()ln 0x h x x =>故画出的图象如下:()ln x h x x =其中恒过点122y xa a ⎛⎫ ⎪⎝=⎭--(2,1A 又,故在()210111h -'==()ln x h x x =又在上,()2,1A 1y x =-()对于2111644y x x =-+-∴点,即()0,6C -6OC =∵2114,14P m m m ⎛-+- ⎝∴点,3,64N m m ⎛⎫- ⎪⎝⎭∴,22111316624444PN m m m m m⎛⎫=-+---=-+ ⎪⎝⎭∵轴,PN x ⊥∴,//PN OC ∴,PNQ OCB ∠=∠∴,Rt Rt PQN BOC ∴,PN NQ PQ BC OC OB ==∵,8,6,10OB OC BC ===∴,34,55QN PN PQ PN==∵轴,NE y ⊥∴轴,//NE x ∴,CNE CBO ∴,5544CN EN m ==∴,2215111316922444216CQ PQ m m m m ⎛⎫+=-+=--+⎪⎝⎭当时,取得最大值.132m =12CQ PQ+16916关键点点睛:熟练的掌握三角形相似的判断及性质是解决本题的关键.8.(1)详见解析;(2)①具有性质;理由见解析;②P 1346【分析】(1)当时,先求得集合,由题中所给新定义直接判断即可;10n =A (2)当时,先求得集合, 1010n =A ①根据,任取,其中,可得,{}2021|T x x S =-∈02021t x T =-∈0x S ∈0120212020x ≤-≤利用性质的定义加以验证,即可说明集合具有性质;P T P ②设集合有个元素,由(1)可知,任给,,则与中必有个S k x S ∈12020x ≤≤x 2021x -1不超过,从而得到集合与中必有一个集合中至少存在一半元素不超过,然后利1010S T 1010用性质的定义列不等式,由此求得的最大值.P k【详解】(1)当时,,10n ={}1,2,,19,20A = 不具有性质,{}{}|910,11,12,,19,20B x A x =∈>= P 因为对任意不大于的正整数,10m 都可以找到该集合中的两个元素与,使得成立,110b =210b m =+12||b b m -=集合具有性质,{}*|31,N C x A x k k =∈=-∈P 因为可取,对于该集合中任一元素,110m =<,(),都有.112231,31c k c k =-=-*12,N k k ∈121231c c k k -=-≠(2)当时,集合,1010n ={}()*1,2,3,,2019,2020,1010N A m m =≤∈ ①若集合具有性质,那么集合一定具有性质.S P {}2021|T x x S =-∈P 首先因为,任取,其中.{}2021|T x x S =-∈02021t x T =-∈0x S ∈因为,所以.S A ⊆{}01,2,3,,2020x ∈ 从而,即,所以.0120212020x ≤-≤t A ∈T A ⊆由具有性质,可知存在不大于的正整数,S P 1010m 使得对中的任意一对元素,都有.s 12,s s 12s s m -≠对于上述正整数,从集合中任取一对元素,m {}2021|T x x S =-∈112021t x -=,其中,则有.222021t x =-12,x x S ∈1212t t s s m --≠=所以,集合具有性质P ;{}2021|T x x S =-∈②设集合有个元素,由(1)可知,若集合具有性质,S k S P 那么集合一定具有性质.{}2021|T x x S =-∈P 任给,,则与中必有一个不超过.x S ∈12020x ≤≤x 2021x -1010所以集合与中必有一个集合中至少存在一半元素不超过.S T 1010不妨设中有个元素不超过.S 2k t t ⎛⎫≥ ⎪⎝⎭12,,,t b b b 1010由集合具有性质,可知存在正整数.S P 1010m ≤使得对中任意两个元素,都有.S 12,s s 12s s m -≠所以一定有.12,,,t b m b m b m S +++∉ 又,故.100010002000i b m +≤+=121,,,b m b m b m A +++∈ 即集合中至少有个元素不在子集中,A t S 因此,所以,得.20202k k k t +≤+≤20202k k +≤1346k ≤当时,取,{}1,2,,672,673,,1347,,2019,2020S = 673m =则易知对集合中的任意两个元素,都有,即集合具有性质.S 12,y y 12673y y -≠S P 而此时集合S 中有个元素,因此,集合元素个数的最大值为.1346S 1346解新定义题型的步骤:(1)理解“新定义”——明确“新定义”的条件、原理、方法、步骤和结论.(2)重视“举例”,利用“举例”检验是否理解和正确运用“新定义”;归纳“举例”提供的解题方法.归纳“举例”提供的分类情况.(3)类比新定义中的概念、原理、方法,解决题中需要解决的问题.9.(1),10,8⎛⎫ ⎪⎝⎭18y =-(2)或()42,4()42,4-(3)14a =(4)或51-35-【分析】(1)根据焦点和准线方程的定义求解即可;(2)先求出点P 的纵坐标为4,然后代入到抛物线解析式中求解即可;(3)如图所示,过点B 作轴于D ,过点A 作轴于E ,证明,推BD y ⊥AE y ⊥FDB FHC ∽出,则,点B 的纵坐标为,从而求出,证明16FD a =112OD OF DF a =-=112a 36BD a =,即可求出点A 的坐标为,再把点A 的坐标代入抛物线解析式AEF BDF ∽123,24a ⎛⎫ ⎪⎝+⎭-中求解即可;(4)如图,当E 为靠近点F 的黄金分割点的时候,过点M 作于N ,则,MN l ⊥MN MF=先证明是等腰直角三角形,得到,设点M 的坐标为,则MNH △NH MN=21,4m m ⎛⎫⎪⎝⎭过点B 作轴于D ,过点BD y ⊥由题意得点F 的坐标为F ⎛ ⎝1FH =当E 为靠近点F 的黄金分割点的时候,过点∵在中,Rt MNH △sin MHN ∠∴,∴是等腰直角三角形,45MHN ︒=MNH △双曲线方程联立,利用韦达定理及题目条件可得,后由题意可得AM AN ⋅= ()()222131t t m -+=-所过定点坐标;②结合①及图形可得都在左支上,则可得,后由图象可得,M N 213m <,后通过令,结合单调性229113m S m +=-223113m λλ⎛⎫+=≤< ⎪⎝⎭()423313f x x x x ⎛⎫=-≤< ⎪⎝⎭可得答案.【详解】(1)设双曲线的焦距为,C 2c 由题意有解得.2223,24,,ba c c ab ⎧=⎪⎪=⎨⎪=+⎪⎩1,3,2a b c ===故双曲线的标准方程为;C 2213y x -=(2)①证明:设直线的方程为,点的坐标分别为,MN my x t =+,M N ()()1122,,,x y x y 由(1)可知点A 的坐标为,()1,0联立方程消去后整理为,2213y x my x t ⎧-=⎪⎨⎪=+⎩x ()222316330m y mty t --+-=可得,2121222633,3131mt t y y y y m m -+==--,()212122262223131m t tx x m y y t t m m +=+-=-=--,()()()()222222222121212122223363313131m t m t m t x x my t my t m y y mt y y t t m m m -+=--=-++=-+=----由,()()11111,,1,AM x y AN x y =-=-有()()()1212121212111AM AN x x y y x x x x y y ⋅=--+=-+++,()()()()22222222222222222132331313131313131t t t t t t m t t t m m m m m m -----++-=--++===------由,可得,有或,AM AN ⊥0AM AN ⋅=1t =-2t =当时,直线的方程为,过点,不合题意,舍去;1t =-MN 1my x =-()1,0当时,直线的方程为,过点,符合题意,2t =MN 2my x =+()2,0-②由①,设所过定点为121224,31x x x x m +==-若在双曲线的同一支上,可知,M N 有12240,31x x x m +=<-关键点睛:求直线所过定点常采取先猜后证或类似于本题处理方式,设出直线方程,通过题一方面:由以上分析可知,设椭圆方程为一方面:同理设双曲线方程为()22221y m x a b +-=,()2222221b x a k x m a b -+=化简并整理得()(2222222112ba k x a mk x a m ---+一方面:同理设抛物线方程为(22x p y =,()212x p k x n =+化简并整理得,由韦达定理可得12220pk x x pn --=2,2x x pk x x pn +=⋅=-(2)构造,故转化为等价于“对任()()()()()13131931x x xx f x k k g x f x +--==+++()()()123g x g x g x +>意,,恒成立”,换元后得到(),分,和1x 2x 3R x ∈()()11k g x q t t -==+3t ≥1k >1k =三种情况,求出实数k 的取值范围.1k <【详解】(1)由条件①知,当时,有,即在R 上单调递增.12x x <()()12f x f x <()f x 再结合条件②,可知存在唯一的,使得,从而有.0R x ∈()013f x =()093x x f x x --=又上式对成立,所以,R x ∀∈()00093x x f x x --=所以,即.0001393x x x --=0009313x x x ++=设,因为,所以单调递增.()93x x x xϕ=++()9ln 93ln 310x x x ϕ'=++>()x ϕ又,所以.()113ϕ=01x =所以;()931x x f x =++(2)构造函数,()()()()()13131931x x xx f x k k g x f x +--==+++由题意“对任意的,,,1x 2x 3R x ∈均存在以,,为三边长的三角形”()()()11113x f x k f x +-()()()22213x f x k f x +-()()()33313x f x k f x +-等价于“对任意,,恒成立”.()()()123g x g x g x +>1x 2x 3R x ∈又,令,()111313x x k g x -=+++1131231333x x x x t ⋅=++≥+=当且仅当时,即时取等号,91x=0x =则(),()()11k g x q t t -==+3t ≥当时,,因为且,1k >()21,3k g x +⎛⎤∈ ⎥⎝⎦()()122423k g x g x +<+≤()3213k g x +<≤所以,解得,223k +≤4k ≤即;14k <≤当时,,满足条件;1k =()()()1231g x g x g x ===当时,,因为且,1k <()2,13k g x +⎡⎫∈⎪⎢⎣⎭()()122423k g x g x ++<≤()3213k g x +<≤所以,即.2413k +≤112k -≤<综上,实数k 的取值范围是.1,42⎡⎤-⎢⎥⎣⎦复合函数零点个数问题处理思路:①利用换元思想,设出内层函数;②分别作出内层函数与外层函数的图象,分别探讨内外函数的零点个数或范围;③内外层函数相结合确定函数交点个数,即可得到复合函数在不同范围下的零点个数.13.(1)14x =(2)证明过程见解析(3),()112023k n k x --=1k n≤≤【分析】(1)由题意转化为对于,都存在,使得,其中(),m a b =(),n c d =0m n ⋅= ,选取,,通过分析求出;,,,a b c d X ∈()1,,2m a b x ⎛⎫== ⎪⎝⎭ ()(),1,n c d d ==- 14x =(2)取,,推理出中有1个为,则另一个为1,即,()()11,,m a b x x == (),n c d =,c d 1-1X ∈再假设,其中,则,推导出矛盾,得到;1k x =1k n <<101n x x <<<11x =(3)由(2)可得,设,,则有,记11x =()11,m s t =()22,n s t =1212s t t s =-,问题转化为X 具有性质P ,当且仅当集合关于原点对称,得到,,s B s X t X s t t ⎧⎫=∈∈>⎨⎬⎩⎭B ,共个数,由对称性可知也有个数,(){}234,0,,,,n B x x x x -∞=---- ()1n -()0,B +∞ ()1n -结合三角形数阵得到,得到数列为首项为1的等比123212321n n n n n n x x x x x x x x x x -----===== 12,,,n x x x 数列,设出公比为,结合求出公比,求出通项公式.q 2023n x =【详解】(1)对任意,都存在,使得,,a b X ∈,c d X ∈0ac bd +=即对于,都存在,使得,其中,(),m a b =(),n c d =0m n ⋅= ,,,a b c d X ∈因为集合具有性质P ,11,,,12x ⎧⎫-⎨⎬⎩⎭选取,,()1,,2m a b x ⎛⎫== ⎪⎝⎭ ()(),1,n c d d ==-则有,12x d -+=假设,则有,解得,这与矛盾,d x =102x x -+=0x =102x <<假设,则有,解得,这与矛盾,1d =-12x --=12x =-102x <<假设,则有,解得,这与矛盾,1d =12x -+=12x =102x <<假设,则有,解得,满足,12d =14x -+=14x =102x <<故;14x =(2)取,,()()11,,m a b x x == (),n c d =则,()10c d x +=因为,所以,即异号,120n x x x <<<< 0c d +=,c d 显然中有1个为,则另一个为1,即,,c d 1-1X ∈假设,其中,则,1k x =1k n <<101n x x <<<选取,,则有,()()1,,n m a b x x ==(),n s t =10n sx tx +=则异号,从而之中恰有一个为,,s t ,s t 1-若,则,矛盾,1s =-11n x tx t x =>≥若,则,矛盾,1t =-1n n x sx s x =<≤故假设不成立,所以;11x =(3)若X 具有性质P ,且,20231n x =>由(2)可得,11x =设,,则有,()11,m s t =()22,n s t =1212s t t s =-记,则X 具有性质P ,当且仅当集合关于原点对称,,,s B s X t X s t t ⎧⎫=∈∈>⎨⎬⎩⎭B 注意到是集合中唯一的负数,1-X 故,共个数,(){}234,0,,,,n B x x x x -∞=---- ()1n -由对称性可知也有个数,()0,B +∞ ()1n -由于,已经有个数,123421n n n n n nn n n n x x x x x x x x x x x x ----<<<<<< ()1n -对于以下三角形数阵:123421n n n n n n n n n n x x x x x xx x x x x x ----<<<<<< 1111123421n n n n n n n n x x x x xx x x x x --------<<<<< ……3321x x x x <21x x 注意到,123211111n n n x x x x x x x x x x -->>>>> 所以有,123212321n n n n n n x x x x x x x x x x -----===== 从而数列为首项为1的等比数列,设公比为,12,,,n x x x q 由于,故,解得,2023n x =112023n nx q x -==()112023n q -=故数列的通项公式为,.12,,,n x x x ()112023k n k x --=1k n ≤≤集合新定义问题,命题新颖,且存在知识点交叉,常常会和函数或数列相结合,很好的考虑了知识迁移,综合运用能力,对于此类问题,一定要解读出题干中的信息,正确理解问题的本质,转化为熟悉的问题来进行解决,要将“新”性质有机地应用到“旧”性质上,创造性的解决问题.14.(1)答案见解析(2)①证明见解析;②证明见解析【分析】(1)求出的导数,结合解不等式可得答案;()e 2x f x ax'=-(2)①,利用导数的几何意义求得的表达式,由此构造函数,()y h x =()()()F x g x h x =-利用导数判断其单调性,求其最小值即可证明结论;②设的根为,求得其表达式,()h x t=1x '并利用函数单调性推出,设曲线在点处的切线方程为,设11x x '≤()y g x =()0,0()y t x =的根为,推出,从而,即可证明结论.()t x t=2x '22x x '≥2121x x x x ''-≤-【详解】(1)由题意得,令,则,()e 2x f x ax'=-()e 2x g x ax=-()e 2x g x a'=-当时,,函数在上单调递增;0a ≤()0g x '>()f x 'R 当时,,得,,得,0a >()0g x '>ln 2x a >()0g x '<ln 2x a <所以函数在上单调递减,在上单调递增.()f x '(),ln 2a -∞()ln 2,a +∞(2)①证明:由(1)可知,令,有或,()()()1e 1x g x x =+-()0g x ==1x -0x =故曲线与x 轴负半轴的唯一交点P 为.()y g x =()1,0-曲线在点处的切线方程为,()1,0P -()y h x =则,令,则,()()()11h x g x '=-+()()()F x g x h x =-()()()()11F x g x g x '=--+所以,.()()()()11e 2e x F x g x g x '''=-=+-()10F '-=当时,若,,1x <-(],2x ∈-∞-()0F x '<若,令,则,()2,1x --()1()e 2e x m x x =+-()()e 30xm x x '=+>故在时单调递增,.()F x '()2,1x ∈--()()10F x F ''<-=故,在上单调递减,()0F x '<()F x (),1-∞-当时,由知在时单调递增,1x >-()()e 30x m x x '=+>()F x '()1,x ∈-+∞,在上单调递增,()()10F x F ''>-=()F x ()1,-+∞设曲线在点处的切线方程为()y g x =()0,0令()()()()(1e x T x g x t x x =-=+当时,2x ≤-()()2e x T x x =+-'()()2e xn x x =+-设,∴()()1122,,,B x y C x y 1x 又1211,22AB x AC x =+=+依题意,即,则,0bc <02x >()()220220004482x y c x x b =+---因为,所以,2002y x =0022x b c x -=-所以,()()00000242248122424S b c x x x x x -⋅=-++≥-⋅+=-=-当且仅当,即时上式取等号,00422x x -=-04x =所以面积的最小值为8.PDE △方法点睛:圆锥曲线中最值或范围问题的常见解法:(1)几何法,若题目的条件和结论能明显体现几何特征和意义,则考虑利用几何法来解决;(2)代数法,若题目的条件和结论能体现某种明确的函数关系,则可首先建立目标函数,再求这个函数的最值或范围.16.(1)2214x y +=(2)证明见解析(3)存在,7,,777⎛⎫⎛⎫-∞- ⎪ ⎪ ⎪ ⎪⎝+∞⎝⎭⎭ 【分析】(1)根据椭圆的对称性,得到三点在椭圆C 上.把的坐标代入椭圆234,,P P P 23,P P C ,求出,即可求出椭圆C 的方程;22,a b (2)当斜率不存在时,不满足;当斜率存在时,设,与椭圆方程联立,利():1l y kx t t =+≠用判别式、根与系数的关系,结合已知条件得到,能证明直线l 过定点;21t k =--()2,1-(3)利用点差法求出直线PQ 的斜率,从而可得直线PQ 的方程,与抛物线方程联14PQ k t =立,由,及点G 在椭圆内部,可求得的取值范围,设直线TD 的方程为,0∆>2t 1x my =+与抛物线方程联立,由根与系数的关系及,可求得m 的取值范围,进而可求得直线11DA TB k k =的斜率k 的取值范围.2l【详解】(1)根据椭圆的对称性,两点必在椭圆C 上,34331,,1,22P P ⎛⎫⎛⎫- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭又的横坐标为1,4P ∴椭圆必不过,()11,1P ∴三点在椭圆C 上.()234330,1,1,,1,22P P P ⎛⎫⎛⎫- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭把代入椭圆C ,()3231,20,1,P P ⎛⎫- ⎪ ⎪⎝⎭得,解得,222111314b a b ⎧=⎪⎪⎨⎪+=⎪⎩2241a b ⎧=⎨=⎩∴椭圆C 的方程为.2214x y +=(2)证明:①当斜率不存在时,设,,:l x m =()(),,,A A A m y B m y -∵直线与直线的斜率的和为,2P A 2P B 1-∴,221121A A P A P B y y k k m m m ----+=+==-解得m =2,此时l 过椭圆右顶点,不存在两个交点,故不满足.②当斜率存在时,设,,,:l y kx t =+1t ≠()()1122,,,A x y B x y 联立,消去y 整理得,22440y kx tx y =+⎧⎨+-=⎩()222148440k x ktx t +++-=则,,122814kt x x k -+=+21224414t x x k -=+则()()()()222112************111111P A P B x y x y x kx t x kx t y y k k x x x x x x -+-+-++---+=+==,()()()()()()12121222222448218114141144411142t k k kx x t tk t k t k k t t x t x x x +-+=--⋅+-⋅-++===--+-+又,∴,此时,1t ≠21t k =--()()222222644144464161664k t k t k t k ∆=-+-=-+=-故存在k ,使得成立,0∆>∴直线l 的方程为,即21y kx k =--()12y k x +=-∴l 过定点.()2,1-(3)∵点P ,Q 在椭圆上,所以,,2214P P x y +=2214Q Q x y +=两式相减可得,()()()()04PQ P Q P Q P Q y xy x x x y y +-++-=又是线段PQ 的中点,()1,G t -∴,2,2P Q P Q x x x x t+=-=∴直线PQ 的斜率,()144P Q P QP Q P QPQ x x k ty y x y y x +==-=--+∴直线PQ 的方程为,与抛物线方程联立消去x 可得,()114y x t t =++()22164410y ty t -++=由题可知,∴,()2161210t ∆=->2112t >又G 在椭圆内部,可知,∴,故,2114t +<234t <213124t <<设,,由图可知,,221212,,,44y y A y B y ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭223434,,,44y y T y D y ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭2134,y y y y >>∴,()2121216,441y y t y y t +==+当直线TD 的斜率为0时,此时直线TD 与抛物线只有1个交点,不合要求,舍去,设直线TD 的方程为,与抛物线方程联立,消去x 可得,()10x my m =+≠2440y my --=∴,34344,4y y m y y +==-由,可知,即,11//ATB D 11DA TB k k =3142222234214444y y y y y y y y --=--∴,即,1342y y y y +=+1243y y y y -=-∴,()()221212343444y y y y y y y y +-=+-∵,()()()()()222212124161641161210,128y y y y t t t +-=-+=-∈∴,解得,即,()()223434416160,128y y y y m +-=+∈27m <()7,7m ∈-∴直线TD 即的斜率.2l 771,77,k m ⎛⎫⎛⎫=∈-∞- ⎪ ⎪ ⎪ ⎪⎝+∞⎝⎭⎭ 思路点睛:处理定点问题的思路:(1)确定题目中的核心变量(此处设为),k (2)利用条件找到与过定点的曲线的联系,得到有关与的等式,k (),0F x y =k ,x y (3)所谓定点,是指存在一个特殊的点,使得无论的值如何变化,等式恒成立,()00,x y k 此时要将关于与的等式进行变形,直至找到,k ,x y ()00,x y ①若等式的形式为整式,则考虑将含的式子归为一组,变形为“”的形式,让括号中式k ()k ⋅子等于0,求出定点;②若等式的形式是分式,一方面可考虑让分子等于0,一方面考虑分子和分母为倍数关系,可消去变为常数.k 17.(1)1y =-(2)2ln23-+【分析】(1)由题意,将代入函数的解析式中,对函数进行求导,得到1m =()f x ()f x 和,代入切线方程中即可求解;()1f '()1f (2)得到函数的解析式,对进行求导,利用根的判别式以及韦达定理对()g x ()g x 进行化简,利用换元法,令,,可得,12122()()y x x b x x =--+12x t x =01t <<2(1)ln 1t y t t -=-+根据,求出的范围,构造函数,对进行求导,利用导数得到322m ≥t 2(1)()ln 1t h t tt -=-+()h t 的单调性和最值,进而即可求解.()h t 【详解】(1)已知(为常数),函数定义域为,()ln f x x mx =-m (0,)+∞当时,函数,1m =()ln f x x x =-可得,此时,又,11()1x f x x x -'=-=()=01f '()11=f -所以曲线在点处的切线方程为,即.()y f x =()()1,1f (1)0(1)y x --=⨯-1y =-(2)因为,函数定义域为,22()2()2ln 2g x f x x x mx x =+=-+(0,)+∞可得,222(1)()22x mx g x m x x x -+=-+='此时的两根,即为方程的两根,()0g x '=1x 2x 210x mx -+=因为,所以,由韦达定理得,,322m ≥240m ∆=->12x x m +=121=x x 又,所以1212lnx x b x x =-121212121212ln 22()()()()xx y x x b x x x x x x x x =--=--++-,11211211222212()ln 2ln 1x x x x x x x x x x x x --=-=⨯-++令,,所以,12x t x =01t <<2(1)ln 1t y t t -=-+因为,整理得,2212()x x m +=22212122x x x x m ++=因为,则,121=x x 2221212122x x x x m x x ++=等式两边同时除以,得,12x x 212212=x x m x x ++可得,因为,212t m t ++=322m ≥所以,,152t t +≥()()2252=2210t t x x -+--≥解得 或,则,12t ≤2t ≥102t <≤不妨设,函数定义域为,2(1)()ln 1t h t t t -=-+10,2⎛⎤⎥⎝⎦可得,22(1)()0(1)t h t t t -'=-<+所以函数在定义域上单调递减,()h t 此时,min 12()()ln223h t h ==-+故的最小值为.12122()()y x x b x x =--+2ln23-+利用导数求解在曲线上某点处的切线方程,关键点有两点,第一是切线的斜率,第二是切点。
(完整)高一数学第一学期函数压轴[大题]练习[含答案及解析],推荐文档
![(完整)高一数学第一学期函数压轴[大题]练习[含答案及解析],推荐文档](https://img.taocdn.com/s3/m/0e4f6c50eff9aef8941e06cb.png)
10. (本题 16 分)已知函数 f (x) log9 (9x 1) kx ( k R )是偶函数.
(1)求 k 的值;
(2)若函数 y f (x) 的图象与直线 y 1 x b 没有交点,求 b 的取值范围; 2
(3)设 h(x) log9
f
1 ()
2
.
1 x2
25
(1) 求实数 a , b 的值;
(2) 用定义证明:函数 f (x) 在区间 (1,1) 上是增函数;
(3) 解关于 t 的不等式 f (t 1) f (t) 0 .
4. (14 分)定义在 R 上的函数 f(x)对任意实数 a,b R ,均有 f(ab)=f(a)+f(b)成立,且当 x>1 时,f(x)
技术资料.整理分享
WORD 格式.可编辑
13.(本小题满分 16 分)
设 a 0 , b 0 ,已知函数 f (x) ax b . x 1
(Ⅰ)当 a b 时,讨论函数 f (x) 的单调性(直接写结论);
(Ⅱ)当 x 0 时,(i)证明 f (1) f ( b ) [ f ( b )]2 ;
6. (12 分)设函数 f (x) loga (x 3a)(a 0,且a 1) ,当点 P(x, y) 是函数 y f (x) 图象上的点时,
点 Q(x 2a, y) 是函数 y g(x) 图象上的点. (1)写出函数 y g(x) 的解析式; (2)若当 x [a 2, a 3] 时,恒有 | f (x) g(x) |„ 1 ,试确定 a 的取值范围; (3)把 y g(x) 的图象向左平移 a 个单位得到 y h(x) 的图象,函数
WORD 格式.可编辑
(word完整版)必修一函数压轴题

函数压轴题 一、函数的性质1.已知函数)1()(xx e e x x f -=,若f (x 1)<f (x 2),则( ) A .x 1>x 2 B .x 1+x 2=0 C .x 1<x 2 D .2221x x <2。
f (x )是定义在(0,+∞)上的单调增函数,满足f (xy )=f (x )+f (y ),f (3)=1,若f (x )+f (x -8)≤2,则x 的取值范围为________.3。
要使函数22)(-+=x kx x f 与y =log 3(x -2)在(3,+∞)上具有相同的单调性,则实数k 的取值范围是________.4.已知函数f (x )是(-∞,+∞)上的奇函数,且f (x )的图象关于x =1对称,当x ∈[0,1]时,f (x )=2x -1,①求证:f (x )是周期函数;②当x ∈[1,2]时,求f (x )的解析式;③计算f (0)+f (1)+f (2)+…+f (2 017)的值.5.已知f (x )是定义在R 上的偶函数,g (x )是定义在R 上的奇函数,且g (x )=f (x -1),则f (2 013)+f (2 015)的值为( )A .-1B .1C .0D .无法计算6.设f (x )是定义在R 上的奇函数,且对任意实数x ,恒有f (x +2)=-f (x ).当x ∈[0,2]时,f (x )=2x -x 2.(1)求证:f (x )是周期函数;(2)当x ∈[2,4]时,求f (x )的解析式; (3)计算f (0)+f (1)+f (2)+…+f (2 014).7.奇函数f (x )的定义域为R ,若f (x +2)为偶函数,且f (1)=1,则f (8)+f (9)=( )A .-2B .-1C .0D .18。
若函数)1ln()(2++=x x x x f 为偶函数,则a =________. 9.若函数))(12()(a x x xx f -+=为奇函数,则a =________10.已知f (x )是定义在R 上的奇函数,当x ≥0时,f (x )=3x +m (m 为常数),则f (-log 35)的值为( )A .4B .-4C .6D .-611.已知函数f (x )是定义在R 上的偶函数,且在区间[0,+∞)上单调递增.若实数a 满足)1(2)(log )(log 212f a f a f ≤+,则a 的取值范围是( )A .[1,2]B 。
数学函数几何综合压轴题(精选16题)
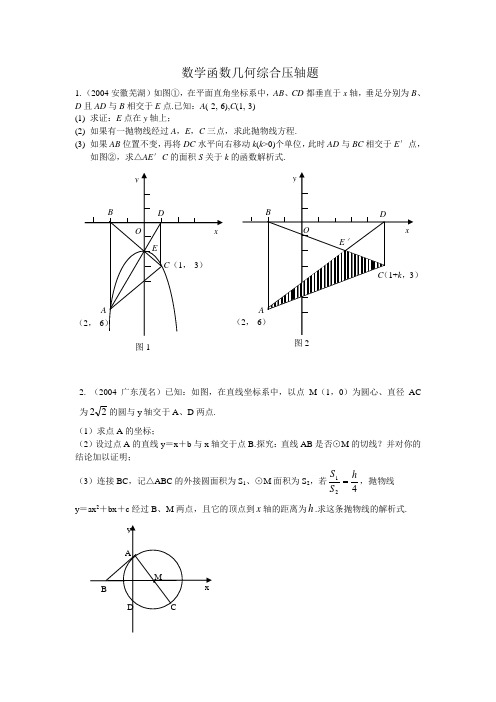
数学函数几何综合压轴题1.(2004安徽芜湖)如图①,在平面直角坐标系中,AB 、CD 都垂直于x 轴,垂足分别为B 、D 且AD 与B 相交于E 点.已知:A (-2,-6),C (1,-3) (1) 求证:E 点在y 轴上;(2) 如果有一抛物线经过A ,E ,C 三点,求此抛物线方程. (3) 如果AB 位置不变,再将DC 水平向右移动k (k >0)个单位,此时AD 与BC 相交于E ′点,如图②,求△AE ′C 的面积S 关于k 的函数解析式.2. (2004广东茂名)已知:如图,在直线坐标系中,以点M (1,0)为圆心、直径AC 为22的圆与y 轴交于A 、D 两点.(1)求点A 的坐标;(2)设过点A 的直线y =x +b 与x 轴交于点B.探究:直线AB 是否⊙M 的切线?并对你的结论加以证明;(3)连接BC ,记△ABC 的外接圆面积为S 1、⊙M 面积为S 2,若421hS S ,抛物线 y =ax 2+bx +c 经过B 、M 两点,且它的顶点到x 轴的距离为h .求这条抛物线的解析式.图1 图23.(2004湖北荆门)如图,在直角坐标系中,以点P (1,-1)为圆心,2为半径作圆,交x 轴于A 、B 两点,抛物线)0(2>++=a c bx ax y 过点A 、B ,且顶点C 在⊙P 上. (1)求⊙P 上劣弧⌒AB 的长;(2)求抛物线的解析式;(3)在抛物线上是否存在一点D ,使线段OC与PD在,请说明理由.4.(2004湖北襄樊)如图,在平面直角坐标系内,Rt △ABC 的直角顶点C (0在y 轴的正半轴上,A 、B 是x 轴上是两点,且OA ∶OB =3∶1,以OA 、OB 为直径的圆分别交AC 于点E ,交BC 于点F .直线EF 交OC 于点Q . (1)求过A 、B 、C 三点的抛物线的解析式;(2)请猜想:直线EF 与两圆有怎样的位置关系?并证明你的猜想.(3)在△AOC 中,设点M 是AC 边上的一个动点,过M 作MN ∥AB 交OC 于点N .试问:在x 轴上是否存在点P ,使得△PMN 是一个以MN 为一直角边的等腰直角三角形?若存在,求出P 点坐标;若不存在,请说明理由.5.(2004湖北宜昌)如图,已知点A(0,1)、C(4,3)、E(415,823),P 是以AC 为对角线的矩形ABCD 内部(不在各边上)的—个动点,点D 在y 轴,抛物线y =ax 2+b x +1以P 为顶点. (1)说明点A 、C 、E 在一条条直线上;(2)能否判断抛物线y =ax 2+b x +1的开口方向?请说明理由;(3)设抛物线y =ax 2+b x +1与x 轴有交点F 、G(F 在G 的左侧),△GAO 与△FAO 的面积差为3,且这条抛物线与线段AE 有两个不同的交点.这时能确定a 、b 的值吗?若能,请求出a 、b 的值;若不能,请确定a 、b 的取值范围. (本题图形仅供分析参考用)6.(2004湖南长沙)已知两点O(0,0)、B(0,2),⊙A 过点B 且与x 轴分别相交于点O 、C ,⊙A 被y 轴分成段两圆弧,其弧长之比为3∶1,直线l 与⊙A 切于点O ,抛物线的顶点在直线l 上运动.(1)求⊙A 的半径;(2)若抛物线经过O 、C 两点,求抛物线的解析式;(3)过l 上一点P 的直线与⊙A 交于C 、E 两点,且PC =CE ,求点E 的坐标;(4)若抛物线与x 轴分别相交于C 、F 两点,其顶点P 的横坐标为m ,求△PEC 的面积关于m 的函数解析式.7.(2006江苏连云港)如图,直线4+=kx y 与函数)0,0(>>=m x xmy 的图像交于A 、B 两点,且与x 、y 轴分别交于C 、D 两点.(1)若COD ∆的面积是AOB ∆的面积的2倍,求k 与m 之间的函数关系式;(2)在(1)的条件下,是否存在k 和m ,使得以AB 为直径的圆经过点)0,2(P .若存在,求出k 和m 的值;若不存在,请说明理由.8.(2004江苏镇江)已知抛物线2(5)5(0)y mx m x m =--->与x 轴交于两点1(,0)A x 、2(,0)B x 12()x x <,与y 轴交于点C ,且AB =6.(1)求抛物线和直线BC 的解析式.(2)在给定的直角坐标系中,画抛物线和直线BC . (3)若P e 过A 、B 、C 三点,求P e 的半径.(4)抛物线上是否存在点M ,过点M 作MN x ⊥轴于点N ,使MBN ∆被直线BC 分成面积比为13:的两部分?若存在,请求出点M 的坐标;若不存在,请说明理由。
高一数学第一学期函数压轴(大题)练习(含答案)

高一数学第一学期函数压轴(大题)练习(含答案)1.已知不等式 $2(\log_2 x)^2+7\log_2 x+3\leqslant 0$,求函数 $f(x)=\log_2 x\cdot \log_2 x$ 的最大值、最小值及相应的$x$ 值。
2.已知定义域为 $\mathbb{R}$ 的函数$f(x)=\dfrac{2x+1}{x^2+1}$ 是奇函数。
1)求 $a$ 的值;2)判断并证明该函数在定义域 $\mathbb{R}$ 上的单调性;3)若对任意的 $t\in\mathbb{R}$,不等式 $f(t-2t)+f(2t-k)<0$ 恒成立,求实数 $k$ 的取值范围。
3.已知定义在区间 $(-1,1)$ 上的函数 $f(x)=\dfrac{(1-a)x^2+b}{1-x^2}$。
1)求实数 $a,b$ 的值;2)用定义证明:函数$f(x)$ 在区间$(-1,1)$ 上是增函数;3)解关于 $t$ 的不等式 $\dfrac{(1-a)t^2+b}{1-t^2}>0$。
4.定义在 $\mathbb{R}^+$ 上的函数 $f(x)$ 对任意实数$a,b\in \mathbb{R}^+$,均有 $f(ab)=f(a)+f(b)$ 成立,且当$x>1$ 时,$f(x)<0$。
1)求 $f(1)$;2)求证:$f(x)$ 为减函数;3)当 $f(4)=-2$ 时,解不等式$f(x)+f\left(\dfrac{1}{2}x\right)>0$。
5.已知函数$f(x)=x-2bx+\dfrac{4}{b}$,定义域为$[1,4]$,$b\geqslant 1$。
I)求 $f(x)$ 的最小值 $g(b)$;II)求 $g(b)$ 的最大值 $M$。
6.设函数 $f(x)=\log_a (x-3)$,$a>0$ 且 $a\neq 1$,当点$P(x,y)$ 是函数 $y=f(x)$ 图象上的点时,点 $Q(x-2a,-y)$ 是函数 $y=g(x)$ 图象上的点。
高考数学压轴题100题汇总(含答案)

高考数学压轴题100题汇总(含答案)1. 设函数f(x) = x^3 3x + 1,求f(x)的极值点和极值。
答案:f(x)的极值点为x = 1和x = 1,极值分别为f(1) = 1和f(1) = 3。
2. 已知等差数列{an}的前n项和为Sn = n^2 + n,求该数列的通项公式。
答案:an = 2n + 1。
3. 已知三角形ABC中,AB = AC = 5,BC = 8,求三角形ABC的面积。
答案:三角形ABC的面积为12。
4. 设直线y = kx + b与圆x^2 + y^2 = 1相切,求k和b的值。
答案:k = ±√3/3,b = ±√6/3。
5. 已知函数f(x) = log2(x^2 + 1),求f(x)的导数。
答案:f'(x) = 2x/(x^2 + 1)ln2。
6. 已知向量a = (2, 3),向量b = (1, 4),求向量a和向量b的夹角。
答案:向量a和向量b的夹角为arccos(1/√5)。
7. 已知矩阵A = [1 2; 3 4],求矩阵A的逆矩阵。
答案:矩阵A的逆矩阵为[4 2; 3 1]。
8. 已知函数f(x) = x^3 6x^2 + 9x + 1,求f(x)的零点。
答案:f(x)的零点为x = 1和x = 3。
9. 已知函数f(x) = sin(x) cos(x),求f(x)在区间[0, π/2]上的最大值。
答案:f(x)在区间[0, π/2]上的最大值为√2。
10. 已知函数f(x) = x^2 + 4x + 4,求f(x)的顶点坐标。
答案:f(x)的顶点坐标为(2, 0)。
高考数学压轴题100题汇总(含答案)11. 已知函数f(x) = e^x 2x,求f(x)的导数。
答案:f'(x) = e^x 2。
12. 已知函数f(x) = x^2 4x + 4,求f(x)的极值点和极值。
答案:f(x)的极值点为x = 2,极值为f(2) = 0。
函数压轴题,100道高难度函数试题解法赏析

间1,12éùêúëû上单调递减,因此()max142g x g æö==ç÷èø,从而a ≥4;当x <0 即[)1,0-时,()331f x ax x =-+≥0可化为a £2331x x -,()()'4312x g x x -=0>()g x 在区间[)1,0-上单调递增,因此()()ma 14ng x g =-=,从而a ≤4,综上a =4 特殊方法:抓住îíì³£Þïîïíì³³-440)21(0)1(a a f f 例1.函数1)3()(2+-+=x m mx x f 的图象与x 轴的交点至少有一个在原点的右侧,则实数m 的取值范围为_______1£m 解析:显然0£m 成立,当0>m 时,10023£<Þïîïíì>--³D m mm例2.设函数)(x f y =在),(+¥-¥内有定义.对于给定的正数K ,定义函数îíì>£=K x f K K x f x f x f k)(,)(),()(,取函数xe x xf ---=2)(,若对任意的),(+¥-¥Îx ,恒有)()(x f x f k =,则K 的取值范围是_______1³K解析:2009湖南理,由定义知,若对任意的),(+¥-¥Îx ,恒有)()(x f x f k =即为K x f £)(恒成立,即求)(x f 的最大值,由'()10,xf x e-=-=知0x =,所以(,0)x Î-¥时,'()0f x >,当(0,)x Î+¥时,'()0f x <,所以max ()(0)1,f x f ==即()f x 的值域是(,1]-¥例3.已知函数()log (2)a f x ax =+的图象和函数1()log (2)ag x a x =+(0,1a a >¹)的图象关于直线y b =对称(b 为常数),则a b += 2解析:b x g x f 2)()(=+b x a ax a a 2)2(log )2(log =+-+Þ,2,1;0,1====a x b x例4.已知定义在R 上的函数)(x F 满足()()()F x y F x F y +=+,当0x >时,()0F x <. . 若若对任意的[0,1]x Î,不等式组22(2)(4)()(3)F kx x F k F x kx F k ì-<-ïí-<-ïî均成立,则实数k 的取值范围是 .(3,2)-解析:0)0(=F ,令x y -=得)(x F 奇函数,设)()()(,121221x F x F x x F x x -+=-<0)()(12<-=x F x F ,)(x F 减函数,ïîïíì->-->-34222k kx x k x kx ïïîïïíì<Þ££-+=++<<<-Þîíì<<Þ<-+-Þ2)21(2413430)1(0)0(0)4(222k t t t x x k k F f k kx x 例5.已知函数31++-=x x y 的最大值为M ,最小值为m ,则M m 的值为的值为__________22 解析:法一:平方解析:法一:平方 ; 法二:向量)3,1(),1,1(+-x x 数量积数量积 例6.设函数31()12x f x x -=--的四个零点分别为1234x x x x 、、、,1234()f x x x x =+++ . 19 解析:令)0(2)(,13³-==-t t t g t x t画出ty t y 2,3==图象,它们在第一象限有两个交点,则,11t x =-21t x =-242312111,1,1,1t x t x t x t x -=+=-=+=Þ,44321=+++x x x x 19)4(=f例7.定义在R 上的函数()y f x =,若对任意不等实数12,x x 满足1212()()0f x f x x x -<-,且y x ,满足不等式22(2)(2)0f x x f y y -+-£成立函数(1)y f x =-的图象关于点(1,0)对称,则当则当 14x ££时,y x 的取值范围为________]121-[,解析:)(222y x y x -³-,(1)0=-y x 时,1=xy 成立;(2)121-20££Þîíì³+³-xy y x y x(3)ïîïí죣£+<-4120x y x y x 无解无解例8.已知1,0¹>a a ,若函数)(log )(2x ax x f a-=在]4,3[是增函数,则a 的取值范围是________),1(+¥解析:x ax x g -=2)(对称轴是a x 21=,当321£a 时,10)3(161>Þïïîïïíì>>³a g a a ;当421³a 时,f Þïïîïïíì><<£0)4(1081g a a例9.若直角坐标平面内两点Q P ,满足条件:①Q P ,都在函数)(x f 图象上;②Q P ,关于原点对称,则称点对),(Q P 是函数)(x f 的一个“友好点对”(点对),(Q P 与),(P Q 看作同一个“友好点对”).已知函数ïîïíì³<++=0,20,142)(2x ex x x x f x ,则)(x f 的“友好点对”有____个 2个解析:数形结合,即看0,2³=x e y x 关于原点对称函数0,2£-=x e y x 与0,1422<++=x x x y 有几个交点。
高一数学第一学期函数压轴(大题)练习(含答案)

欢迎阅读高一数学第一学期函数压轴(大题)练习(含答案)1.(本小题满分12分)已知x 满足不等式211222(log )7log 30x x ++≤,求22()log log 42x xf x =⋅的最大值与最小值及相应x 值. 2.(14分)已知定义域为R 的函数2()12x xaf x -+=+是奇函数(1)求a 值;(2)判断并证明该函数在定义域R 上的单调性;(3)若对任意的t R ∈,不等式22(2)(2)0f t t f t k -+-<恒成立,求实数k 的取值范围; 3.(1) (2) (3) 4. (14(1)求5.(I)求(II)求6. (12是函数(y g =(1(2(3)把)在1[,4]4的最大值为54,求a 的值.7. (12分)设函数124()lg()3x xa f x a R ++=∈.(1)当2a =-时,求()f x 的定义域;(2)如果(,1)x ∈-∞-时,()f x 有意义,试确定a 的取值范围; (3)如果01a <<,求证:当0x ≠时,有2()(2)f x f x <. 8. (本题满分14分)已知幂函数(2)(1)()()k k f x x k z -+=∈满足(2)(3)f f <。
(1)求整数k 的值,并写出相应的函数()f x 的解析式;(2)对于(1)中的函数()f x ,试判断是否存在正数m ,使函数()1()(21)g x mf x m x =-+-,在区间[]0,1上的最大值为5。
若存在,求出m 的值;若不存在,请说明理由。
9. (本题满分14分)已知函数1()(0x f x a a -=>且1)a ≠(Ⅰ)若函数()y f x =的图象经过()4,3P 点,求a 的值;(Ⅱ)当a 变化时,比较1(lg)( 2.1)100f f -与大小,并写出比较过程; (Ⅲ)若(lg )100f a =,求a 的值.10. (本题16分)已知函数()log (91)xf x kx =++()是偶函数.(1)(2)(3)11. (112.((Ⅰ)求(Ⅱ)定数.设)(x F 13.(设0a >(Ⅰ)当(Ⅱ)当14.(本小题满分16分) 设函数])1(lg[)(22x a ax x f +-=的定义域区间为I,其中0a >.(Ⅰ)求I 的长度)(a L (注:区间(,)αβ的长度定义为βα-);(Ⅱ)判断函数)(a L 的单调性,并用单调性定义证明; (Ⅲ)给定常数(0,1)k ∈,当[]k k a +-∈1,1时,求区间I 长度)(a L 的最小值.1.解:由211222(log )7log 30x x ++≤,∴1213log 2x -≤≤-, ∴21log 32x ≤≤,而2222()log log (log 2)(log 1)42x xf x x x =⋅=--=222(log )3log 2x x -+=2231(log )24x --,当23log 2x =时min 1()4f x =- 此时x =322=当2log 3x =时max 91()244f x =-=,此时8x =. 2. 解:(1)由题设,需12(0)0,1a f a -+==∴=,1212()xxf x -+∴=经验证,()f x 为奇函数,1a ∴=---------(2分)(2)减函数--------------(3分)由(1∴3. 则(f (2) -∴(f 故函数(3)函数在区间上是增函数 111t ⎨⎪-<-<⎩2故关于t 的不等式的解集为1(0,2. 4(1) 由条件得f(1)=f(1)+f(1),所以f(1)=0 (2) 法一:设k 为一个大于1的常数,x ∈R+,则 f(kx)=f(x)+f(k)因为k>1,所以f(k)<0,且kx>x所以kx>x,f(kx)<f(x)对x ∈R+恒成立,所以 f(x)为R+上的单调减函数 法二:设()2121,0,x x x x <+∞∈且令1,12>=k kx x 则有题知,f(k)<0)()(0)()(2121x f x f x f x f >>-∴即所以f(x)在(0,+∞)上为减函数 法三:设()2121,0,x x x x <+∞∈且)()(0)()(2121x f x f x f x f >>-∴即 所以f(x)在(0,+∞)上为减函数 5解:f(x)=(x-b)2-b 2+4b的对称轴为直线x =b ( b ≥1), (I) ①当1≤b ≤4时,g(b)=f(b)=-b 2+b ; ②当b >4时,g(b)=f(4)=16-31,(II) b ②当b 6. 解:∵点(P ∴'y -(2)又0a >∵()f x ∵01a <<∴22a a +>,则22()43r x x ax a =-+在[2,3]a a ++上为增函数, ∴函数22()log (43)a u x x ax a =-+在[2,3]a a ++上为减函数,从而max [()](2)log (44)a u x u a a =+=-。
(精校版)高一数学第一学期函数压轴(大题)练习(含答案)

(直打版)高一数学第一学期函数压轴(大题)练习(含答案)(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((直打版)高一数学第一学期函数压轴(大题)练习(含答案)(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(直打版)高一数学第一学期函数压轴(大题)练习(含答案)(word版可编辑修改)的全部内容。
高一数学第一学期函数压轴(大题)练习(含答案)1.(本小题满分12分)已知x 满足不等式,211222(log )7log 30x x ++≤求的最大值与最小值及相应x 值.22()log log 42x xf x =⋅2。
(14分)已知定义域为的函数是奇函数R 2()12x x af x -+=+ (1)求值;a (2)判断并证明该函数在定义域上的单调性;R (3)若对任意的,不等式恒成立,求实数的取值范围;t R ∈22(2)(2)0f t t f t k -+-<k 3. (本小题满分10分)已知定义在区间上的函数为奇函数,且.(1,1)-2()1ax b f x x +=+12(25f =(1) 求实数,的值;a b (2) 用定义证明:函数在区间上是增函数;()f x (1,1)-(3) 解关于的不等式.t (1)()0f t f t -+<4. (14分)定义在R 上的函数f (x)对任意实数a,b ,均有f (ab )=f(a)+f(b)成立,且当x>1时,f ++∈R (x)<0,(1)求f (1) (2)求证:f(x)为减函数。
(3)当f(4)= -2时,解不等式1)5()3(-≥+-f x f 5。
高考数学压轴题精选100题汇总(含答案)

7. 已知动圆过定点 P(1,0),且与定直线 L:x=-1 相切,点 C 在 l 上. (1)求动圆圆心的轨迹 M 的方 程; (2)设过点 P,且斜率为 3 的直线与曲线 M 相交于 A, B 两点. (i)问:△ABC 能否为正三角形?若能,求点 C 的坐标;若不能,说明理由 (ii)当△ABC 为钝角三角形时,求这种点 C 的纵坐标的取值范围.
1
1
n 1 1
(Ⅱ)已知各项不为零的数列an 满足 4Sn f ( ) 1 ,求证: ln
;
an
an1
n
an
(Ⅲ)设 bn 1 , Tn 为数列bn 的前 n 项和,求证: T2008 1 ln 2008 T2007 .
ba b a
2
(1)求椭圆的方程;
(2)若直线 AB 过椭圆的焦点 F(0,c),(c 为半焦距),求直线 AB 的斜率 k 的值;
(3)试问:△AOB 的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
5.已知数列{an}中各项为: 12、1122、111222、……、111 22 2 ……
n
T 2n 1 .
n
3
26. 对于函数 f (x) ,若存在 x0 R ,使 f (x0 ) x0 成立,则称 x0 为 f (x) 的不动点.如果函数
f (x) x2 a (b, c N*) 有且仅有两个不动点 0 、 2 ,且 f (2) 1 .
bx c
2
(Ⅰ)试求函数 f (x) 的单调区间;
a2 a3
an1 3
14.已知函数gx a2 x3 a x 2 cxa 0,
32
(I)当a 1 时,若函数 gx在区间1,1上是增函数,求实数c的取值范围;
高中数学函数压轴题(精制)

⾼中数学函数压轴题(精制)⾼考数学函数压轴题:1. 已知函数31()(,)3f x x ax b a b R =++∈在2x =处取得的极⼩值是43-.(1)求()f x 的单调递增区间;(2)若[4,3]x ∈-时,有210()3f x m m ≤++恒成⽴,求实数m 的取值范围.2. 某造船公司年最⾼造船量是20艘. 已知造船x 艘的产值函数R (x)=3700x + 45x 2– 10x 3(单位:万元), 成本函数为C (x) = 460x + 5000 (单位:万元). ⼜在经济学中,函数f(x)的边际函数Mf (x)定义为: Mf (x) = f (x+1) – f (x). 求:(提⽰:利润 = 产值 – 成本)(1) 利润函数P(x) 及边际利润函数MP(x);(2) 年造船量安排多少艘时, 可使公司造船的年利润最⼤?(3) 边际利润函数MP(x)的单调递减区间, 并说明单调递减在本题中的实际意义是什么?3. 已知函数155)(2++=x x x ?)(R x ∈,函数)(x f y =的图象与)(x ?的图象关于点)21,0(中⼼对称。
(1)求函数)(x f y =的解析式;(2)如果)()(1x f x g =,)2,)](([)(1≥∈=-n N n x g f x g n n ,试求出使0)(2⽴的x 取值范围;(3)是否存在区间E ,使{}Φ=N n ∈,且2≥n 时,都有0)(4.已知函数:)(1)(a x R a xa a x x f ≠∈--+=且(Ⅰ)证明:f(x)+2+f(2a -x)=0对定义域内的所有x 都成⽴.(Ⅱ)当f(x)的定义域为[a+21,a+1]时,求证:f(x)的值域为[-3,-2];(Ⅲ)设函数g(x)=x 2+|(x -a)f(x)| ,求g(x) 的最⼩值 .5. 设()f x 是定义在]1,0[上的函数,若存在*x )1,0(∈,使得()f x 在],0[*x 上单调递增,在]1,[*x 上单调递减,则称()f x 为]1,0[上的单峰函数,*x 为峰点,包含峰点的区间为含峰区间.对任意的]1,0[上的单峰函数()f x ,下⾯研究缩短其含峰区间长度的⽅法.(1)证明:对任意的21,x x )1,0(∈,21x x <,若)()(21x f x f ≥,则),0(2x 为含峰区间;若)()(21x f x f ≤,则)1,(1x 为含峰区间;(2)对给定的)5.00(<6. 设关于x 的⽅程0222=--ax x 的两根分别为α、β()βα<,函数14)(2+-=x a x x f(1)证明)(x f 在区间()βα,上是增函数;(2)当a 为何值时,)(x f 在区间[]βα,上的最⼤值与最⼩值之差最⼩7. 甲⼄两公司⽣产同⼀种新产品,经测算,对于函数()8+=x x f ,()12+=x x g ,及任意的0≥x ,当甲公司投⼊x 万元作宣传时,⼄公司投⼊的宣传费若⼩于()x f 万元,则⼄公司有失败的危险,否则⽆失败的危险;当⼄公司投⼊x 万元作宣传时,甲公司投⼊的宣传费若⼩于()x g 万元,则甲公司有失败的危险,否则⽆失败的危险. 设甲公司投⼊宣传费x 万元,⼄公司投⼊宣传费y 万元,建⽴如图直⾓坐标系,试回答以下问题: (1)请解释()()0,0g f ;(2)甲、⼄两公司在均⽆失败危险的情况下尽可能少地投⼊宣传费⽤,问此时各应投⼊多少宣传费?(3)若甲、⼄分别在上述策略下,为确保⽆失败的危险,根据对⽅所投⼊的宣传费,按最少投⼊费⽤原则,投⼊⾃⼰的宣传费:若甲先投⼊121=a 万元,⼄在上述策略下,投⼊最少费⽤1b ;⽽甲根据⼄的情况,调整宣传费为2a ;同样,⼄再根据甲的情况,调整宣传费为2b ,, 如此得当甲调整宣传费为n a 时,⼄调整宣传费为n b ;试问是否存在lim n n a →∞,n n b ∞→lim 的值,若存在写出此极限值(不必证明),若不存在,说明理由.8. 设)(x f 是定义域在]1,1[-上的奇函数,且其图象上任意两点连线的斜率均⼩于零.(l )求证)(x f 在]1,1[-上是减函数;(ll )如果)(c x f -,)(2c x f -的定义域的交集为空集,求实数c 的取值范围;(lll )证明若21≤≤-c ,则)(c x f -,)(2c x f -存在公共的定义域,并求这个公共的空义域.9. 已知函数f (x )=ax 2+bx +c ,其中a ∈N *,b ∈N ,c ∈Z 。
数学高考压轴题含答案

数学高考压轴题学校:___________姓名:___________班级:___________考号:___________评卷人得分一、解答题1.已知函数()x f x e ax =-和()ln g x ax x =-有相同的最小值.(1)求a ;(2)证明:存在直线y b =,其与两条曲线()y f x =和()y g x =共有三个不同的交点,并且从左到右的三个交点的横坐标成等差数列.2.已知点(2,1)A 在双曲线2222:1(1)1x y C a a a -=>-上,直线l 交C 于P ,Q 两点,直线,AP AQ 的斜率之和为0.(1)求l 的斜率;(2)若tan PAQ ∠=PAQ △的面积.3.已知函数()e e ax x f x x =-.(1)当1a =时,讨论()f x 的单调性;(2)当0x >时,()1f x <-,求a 的取值范围;(3)设n *∈Nln(1)n ++>+ .4.已知双曲线2222:1(0,0)x y C a b a b -=>>的右焦点为(2,0)F ,渐近线方程为y =.(1)求C 的方程;(2)过F 的直线与C 的两条渐近线分别交于A ,B 两点,点()()1122,,,P x y Q x y 在C 上,且1210,0x x y >>>.过P 且斜率为Q M .从下面①②③中选取两个作为条件,证明另外一个成立:①M 在AB 上;②PQ AB ∥;③||||MA MB =.注:若选择不同的组合分别解答,则按第一个解答计分.5.已知函数()e ln(1)x f x x =+.(1)求曲线()y f x =在点(0,(0))f 处的切线方程;(2)设()()g x f x '=,讨论函数()g x 在[0,)+∞上的单调性;(3)证明:对任意的,(0,)s t ∈+∞,有()()()f s t f s f t +>+.6.如图,已知椭圆22112x y +=.设A ,B 是椭圆上异于(0,1)P 的两点,且点0,21Q ⎛⎫ ⎪⎝⎭在线段AB 上,直线,PA PB 分别交直线132y x =-+于C ,D两点.(1)求点P 到椭圆上点的距离的最大值;(2)求||CD 的最小值.7.设函数e()ln (0)2f x x x x=+>.(1)求()f x 的单调区间;(2)已知,a b ∈R ,曲线()y f x =上不同的三点()()()()()()112233,,,,,x f x x f x x f x 处的切线都经过点(,)a b .证明:(ⅰ)若e a >,则10()12e a b f a ⎛⎫<-<- ⎪⎝⎭;(ⅱ)若1230e,a x x x <<<<,则22132e 112e e 6e 6ea ax x a --+<+<-.(注:e 2.71828= 是自然对数的底数)参考答案:1.(1)1a =(2)见解析【解析】【分析】(1)根据导数可得函数的单调性,从而可得相应的最小值,根据最小值相等可求a.注意分类讨论.(2)根据(1)可得当1b >时,e x x b -=的解的个数、ln x x b -=的解的个数均为2,构建新函数()e ln 2x h x x x =+-,利用导数可得该函数只有一个零点且可得()(),f x g x 的大小关系,根据存在直线y b =与曲线()y f x =、()y g x =有三个不同的交点可得b 的取值,再根据两类方程的根的关系可证明三根成等差数列.(1)()e x f x ax =-的定义域为R ,而()e '=-x f x a ,若0a ≤,则()0f x '>,此时()f x 无最小值,故0a >.()ln g x ax x =-的定义域为()0,∞+,而11()ax g x a x x'-=-=.当ln x a <时,()0f x '<,故()f x 在(),ln a -∞上为减函数,当ln x a >时,()0f x '>,故()f x 在()ln ,a +∞上为增函数,故()min ()ln ln f x f a a a a ==-.当10x a <<时,()0g x '<,故()g x 在10,a ⎛⎫⎪⎝⎭上为减函数,当1x a >时,()0g x '>,故()g x 在1,a ⎛⎫+∞ ⎪⎝⎭上为增函数,故min 11()1ln g x g a a ⎛⎫==- ⎪⎝⎭.因为()e x f x ax =-和()ln g x ax x =-有相同的最小值,故11lnln a a a a-=-,整理得到1ln 1a a a -=+,其中0a >,设()1ln ,01a g a a a a -=->+,则()()()222211011a g a a a a a --'=-=≤++,故()g a 为()0,∞+上的减函数,而()10g =,故()0g a =的唯一解为1a =,故1ln 1aa a-=+的解为1a =.综上,1a =.(2)由(1)可得e ()x x f x =-和()ln g x x x =-的最小值为11ln11ln 11-=-=.当1b >时,考虑e x x b -=的解的个数、ln x x b -=的解的个数.设()e xS x x b =--,()e 1x S x '=-,当0x <时,()0S x '<,当0x >时,()0S x '>,故()S x 在(),0∞-上为减函数,在()0,∞+上为增函数,所以()()min 010S x S b ==-<,而()e0bS b --=>,()e 2b S b b =-,设()e 2b u b b =-,其中1b >,则()e 20bu b '=->,故()u b 在()1,+∞上为增函数,故()()1e 20u b u >=->,故()0S b >,故()e xS x x b =--有两个不同的零点,即e x x b -=的解的个数为2.设()ln T x x x b =--,()1x T x x-'=,当01x <<时,()0T x '<,当1x >时,()0T x '>,故()T x 在()0,1上为减函数,在()1,+∞上为增函数,所以()()min 110T x T b ==-<,而()ee0bbT --=>,()e e 20b b T b =->,()ln T x x x b =--有两个不同的零点即ln x x b -=的解的个数为2.当1b =,由(1)讨论可得ln x x b -=、e x x b -=仅有一个零点,当1b <时,由(1)讨论可得ln x x b -=、e x x b -=均无零点,故若存在直线y b =与曲线()y f x =、()y g x =有三个不同的交点,则1b >.设()e ln 2x h x x x =+-,其中0x >,故1()e 2xh x x'=+-,设()e 1x s x x =--,0x >,则()e 10xs x '=->,故()s x 在()0,∞+上为增函数,故()()00s x s >=即e 1x x >+,所以1()1210h x x x'>+-≥->,所以()h x 在()0,∞+上为增函数,而(1)e 20h =->,31e 333122(e 3e 30e e eh =--<--<,故()h x 在()0,∞+上有且只有一个零点0x ,0311ex <<且:当00x x <<时,()0h x <即e ln x x x x -<-即()()f x g x <,当0x x >时,()0h x >即e ln x x x x ->-即()()f x g x >,因此若存在直线y b =与曲线()y f x =、()y g x =有三个不同的交点,故()()001b f x g x ==>,此时e x x b -=有两个不同的零点1010,(0)x x x x <<,此时ln x x b -=有两个不同的零点0404,(01)x x x x <<<,故11e xx b -=,00e x x b -=,44ln 0x x b --=,00ln 0x x b --=所以44ln x b x -=即44ex bx -=即()44e0x bx b b ----=,故4x b -为方程e x x b -=的解,同理0x b -也为方程e x x b -=的解又11e x x b -=可化为11e xx b =+即()11ln 0x x b -+=即()()11ln 0x b x b b +-+-=,故1x b +为方程ln x x b -=的解,同理0x b +也为方程ln x x b -=的解,所以{}{}1004,,x x x b x b =--,而1b >,故0410x x b x x b =-⎧⎨=-⎩即1402x x x +=.【点睛】思路点睛:函数的最值问题,往往需要利用导数讨论函数的单调性,此时注意对参数的分类讨论,而不同方程的根的性质,注意利用方程的特征找到两类根之间的关系.2.(1)1-;(2)9.【解析】【分析】(1)由点(2,1)A 在双曲线上可求出a ,易知直线l 的斜率存在,设:l y kx m =+,()()1122,,,P x y Q x y ,再根据0AP BP k k +=,即可解出l 的斜率;(2)根据直线,AP AQ 的斜率之和为0可知直线,AP AQ的倾斜角互补,再根据tan PAQ ∠=,AP AQ 的斜率,再分别联立直线,AP AQ 与双曲线方程求出点,P Q 的坐标,即可得到直线PQ 的方程以及PQ 的长,由点到直线的距离公式求出点A 到直线PQ 的距离,即可得出PAQ △的面积.(1)因为点(2,1)A 在双曲线2222:1(1)1x yC a a a -=>-上,所以224111a a -=-,解得22a =,即双曲线22:12x C y -=易知直线l 的斜率存在,设:l y kx m =+,()()1122,,,P x y Q x y ,联立2212y kx m x y =+⎧⎪⎨-=⎪⎩可得,()222124220k x mkx m ----=,所以,2121222422,2121mk m x x x x k k ++=-=--,()()22222216422210120m k m k m k ∆=++->⇒-+>.所以由0AP BP k k +=可得,212111022y y x x --+=--,即()()()()122121210x kx m x kx m -+-+-+-=,即()()()1212212410kx x m k x x m +--+--=,所以()()2222242124102121m mk k m k m k k +⎛⎫⨯+-----= ⎪--⎝⎭,化简得,()2844410k k m k +-++=,即()()1210k k m +-+=,所以1k =-或12m k =-,当12m k =-时,直线():21l y kx m k x =+=-+过点()2,1A ,与题意不符,舍去,故1k =-.(2)不妨设直线,PA PB 的倾斜角为(),αβαβ<,因为0AP BP k k +=,所以παβ+=,因为tan PAQ ∠=,所以()tan βα-=,即tan 2α=-,2tan 0αα-=,解得tan α,于是,直线):21PA y x =-+,直线):21PB y x =-+,联立)222112y x x y ⎧=-+⎪⎨-=⎪⎩可得,(23211002x x +-+-=,因为方程有一个根为2,所以103P x -=,P y=53,同理可得,103Q x +=,Q y=53-.所以5:03PQ x y +-=,163PQ =,点A 到直线PQ的距离3d =,故PAQ △的面积为11623⨯=3.(1)()f x 的减区间为(),0-∞,增区间为()0,+∞.(2)12a ≤(3)见解析【解析】【分析】(1)求出()f x ¢,讨论其符号后可得()f x 的单调性.(2)设()e e 1ax xh x x =-+,求出()h x '',先讨论12a >时题设中的不等式不成立,再就102a <≤结合放缩法讨论()h x '符号,最后就0a ≤结合放缩法讨论()h x 的范围后可得参数的取值范围.(3)由(2)可得12ln t t t<-对任意的1t >恒成立,从而可得()ln 1ln n n +-的*n N ∈恒成立,结合裂项相消法可证题设中的不等式.(1)当1a =时,()()1e x f x x =-,则()e xf x x '=,当0x <时,()0f x ¢<,当0x >时,()0f x ¢>,故()f x 的减区间为(),0-∞,增区间为()0,+∞.(2)设()e e 1ax xh x x =-+,则()00h =,又()()1e e ax x h x ax '=+-,设()()1e e ax xg x ax =+-,则()()22e e ax xg x a a x '=+-,若12a >,则()0210g a '=->,因为()g x '为连续不间断函数,故存在()00,x ∈+∞,使得()00,x x ∀∈,总有()0g x ¢>,故()g x 在()00,x 为增函数,故()()00g x g >=,故()h x 在()00,x 为增函数,故()()01h x h >=-,与题设矛盾.若102a <≤,则()()()ln 11e e ee ax ax ax xx h x ax ++'=+-=-,下证:对任意0x >,总有()ln 1x x +<成立,证明:设()()ln 1S x x x =+-,故()11011x S x x x-'=-=<++,故()S x 在()0,+∞上为减函数,故()()00S x S <=即()ln 1x x +<成立.由上述不等式有()ln 12e e e e e e 0ax ax x ax ax x ax x +++-<-=-≤,故()0h x '≤总成立,即()h x 在()0,+∞上为减函数,所以()()01h x h <=-.当0a ≤时,有()e e e 1100ax x axh x ax '=-+<-+=,所以()h x 在()0,+∞上为减函数,所以()()01h x h <=-.综上,12a ≤.(3)取12a =,则0x ∀>,总有12e e 10x x x -+<成立,令12e x t =,则21,e ,2ln x t t x t >==,故22ln 1t t t <-即12ln t t t<-对任意的1t >恒成立.所以对任意的*n N ∈,有<整理得到:()ln 1ln n n +-()ln 2ln1ln 3ln 2ln 1ln n n +-+-+++- ()ln 1n =+,故不等式成立.【点睛】思路点睛:函数参数的不等式的恒成立问题,应该利用导数讨论函数的单调性,注意结合端点处导数的符号合理分类讨论,导数背景下数列不等式的证明,应根据已有的函数不等式合理构建数列不等式.4.(1)2213y x -=(2)见解析【解析】【分析】(1)利用焦点坐标求得c 的值,利用渐近线方程求得,a b 的关系,进而利用,,a b c 的平方关系求得,a b 的值,得到双曲线的方程;(2)先分析得到直线AB 的斜率存在且不为零,设直线AB 的斜率为k ,M (x 0,y 0),由③|AM |=|BM |等价分析得到200283k x ky k +=-;由直线PM 和QM 的斜率得到直线方程,结合双曲线的方程,两点间距离公式得到直线PQ 的斜率03x m y =,由②//PQ AB 等价转化为003ky x =,由①M在直线AB 上等价于()2002ky k x =-,然后选择两个作为已知条件一个作为结论,进行证明即可.(1)右焦点为(2,0)F ,∴2c =,∵渐近线方程为y =,∴ba=b ,∴222244c a b a =+==,∴1a =,∴b =∴C 的方程为:2213y x -=;(2)由已知得直线PQ 的斜率存在且不为零,直线AB 的斜率不为零,若选由①②推③或选由②③推①:由②成立可知直线AB 的斜率存在且不为零;若选①③推②,则M 为线段AB 的中点,假若直线AB 的斜率不存在,则由双曲线的对称性可知M 在x 轴上,即为焦点F ,此时由对称性可知P 、Q 关于x 轴对称,与从而12x x =,已知不符;总之,直线AB 的斜率存在且不为零.设直线AB 的斜率为k ,直线AB 方程为()2y k x =-,则条件①M 在AB 上,等价于()()2000022y k x ky k x =-⇔=-;两渐近线的方程合并为2230x y -=,联立消去y 并化简整理得:()22223440k x k x k --+=设()()3334,,,A x y B x y ,线段中点为(),N N N x y ,则()2342226,2233N N N x x k kx y k x k k +===-=--,设()00,M x y ,则条件③AM BM =等价于()()()()222203030404x x y y x x y y -+-=-+-,移项并利用平方差公式整理得:()()()()3403434034220x x x x x y y y y y ⎡⎤⎡⎤--++--+=⎣⎦⎣⎦,()()3403403434220y y x x x y y y x x -⎡⎤⎡⎤-++-+=⎣⎦⎣⎦-,即()000N N x x k y y -+-=,即200283k x ky k +=-;由题意知直线PM 的斜率为直线QM ,∴由))10102020,y y x x y y x x -=--=-,∴)121202y y x x x -=+-,所以直线PQ的斜率)1201212122x x x y y m x x x x +--==--,直线)00:PM y x x y =-+,即00y y =,代入双曲线的方程22330x y --=,即)3yy +-=中,得:()()00003y y ⎡⎤-=⎣⎦,解得P的横坐标:100x y ⎛⎫=+⎪⎪⎭,同理:200x y ⎛⎫=⎪⎪⎭,∴0012012002222000033,2,33y x x x y x x x x y x y x ⎛⎫-=++-=--⎪--⎭∴03x m y =,∴条件②//PQ AB 等价于003m k ky x =⇔=,综上所述:条件①M 在AB 上,等价于()2002ky k x =-;条件②//PQ AB 等价于003ky x =;条件③AM BM =等价于200283kx ky k +=-;选①②推③:由①②解得:2200002228,433k k x x ky x k k =∴+==--,∴③成立;选①③推②:由①③解得:20223k x k =-,20263k ky k =-,∴003ky x =,∴②成立;选②③推①:由②③解得:20223k x k =-,20263k ky k =-,∴02623x k -=-,∴()2002ky k x =-,∴①成立.5.(1)y x=(2)()g x 在[0,)+∞上单调递增.(3)证明见解析【解析】【分析】(1)先求出切点坐标,在由导数求得切线斜率,即得切线方程;(2)在求一次导数无法判断的情况下,构造新的函数,再求一次导数,问题即得解;(3)令()()()m x f x t f x =+-,(,0)x t >,即证()(0)m x m >,由第二问结论可知()m x 在[0,+∞)上单调递增,即得证.(1)解:因为()e ln(1)x f x x =+,所以()00f =,即切点坐标为()0,0,又1()e (ln(1))1xf x x x=+++',∴切线斜率(0)1k f '==∴切线方程为:y x =(2)解:因为1()()e (ln(1))1xg x f x x x=++'=+,所以221()e (ln(1))1(1)xg x x x x =++++',令221()ln(1)1(1)h x x x x =++-++,则22331221()01(1)(1)(1)x h x x x x x +=-+=>++++',∴()h x 在[0,)+∞上单调递增,∴()(0)10h x h ≥=>∴()0g x '>在[0,)+∞上恒成立,∴()g x 在[0,)+∞上单调递增.(3)解:原不等式等价于()()()(0)f s t f s f t f +->-,令()()()m x f x t f x =+-,(,0)x t >,即证()(0)m x m >,∵()()()e ln(1)e ln(1)x t x m x f x t f x x t x +=+-=++-+,e e ()e ln(1)e ln(1)()()11x t x x tx m x x t x g x t g x x t x++=++++-=+-++'+,由(2)知1()()e (ln(1))1xg x f x x x=++'=+在[)0,∞+上单调递增,∴()()g x t g x +>,∴()0m x '>∴()m x 在()0,∞+上单调递增,又因为,0x t >,∴()(0)m x m >,所以命题得证.6.(1)11;(2)5.【解析】【分析】(1)设,sin )Q θθ是椭圆上任意一点,再根据两点间的距离公式求出2||PQ ,再根据二次函数的性质即可求出;(2)设直线1:2AB y kx =+与椭圆方程联立可得1212,x x x x +,再将直线132y x =-+方程与PA PB 、的方程分别联立,可解得点,C D 的坐标,再根据两点间的距离公式求出CD ,最后代入化简可得231CD k =⋅+,由柯西不等式即可求出最小值.(1)设,sin )Q θθ是椭圆上任意一点,(0,1)P ,则222221144144||12cos (1sin )1311sin 2sin 11sin 111111PQ θθθθθ⎛⎫=+-=--=-+≤⎭+⎪⎝,当且仅当1sin 11θ=-时取等号,故||PQ (2)设直线1:2AB y kx =+,直线AB 方程与椭圆22112x y +=联立,可得22130124k x kx ⎛⎫++-= ⎪⎝⎭,设()()1122,,,A x y B x y ,所以12212211231412k x x k x x k ⎧+=-⎪+⎪⎪⎨⎪=-⎛⎫⎪+ ⎪⎪⎝⎭⎩,因为直线111:1y PA y x x -=+与直线132y x =-+交于C ,则111114422(21)1C x x x x y k x ==+-+-,同理可得,222224422(21)1D x x x x y k x ==+-+-.则224||(21)1C D x CD x k x =-=+-2=35161656565231555k =⋅=≥=+,当且仅当316k =时取等号,故CD 的最小值为5.【点睛】本题主要考查最值的计算,第一问利用椭圆的参数方程以及二次函数的性质较好解决,第二问思路简单,运算量较大,求最值的过程中还使用到柯西不等式求最值,对学生的综合能力要求较高,属于较难题.7.(1)()f x 的减区间为e 02⎛⎫⎪⎝⎭,,增区间为e ,2⎛⎫+∞ ⎪⎝⎭.(2)(ⅰ)见解析;(ⅱ)见解析.【解析】【分析】(1)求出函数的导数,讨论其符号后可得函数的单调性.(2)(ⅰ)由题设构造关于切点横坐标的方程,根据方程有3个不同的解可证明不等式成立,(ⅱ)31x k x =,1e a m =<,则题设不等式可转化为()()()2131313122236m m m t t m m t t --++--<+,结合零点满足的方程进一步转化为()()()()211312ln 0721m m m m m m ---++<+,利用导数可证该不等式成立.(1)()22e 12e 22xf x x x x -'=-+=,当e02x <<,()0f x ¢<;当e 2x >,()0f x ¢>,故()f x 的减区间为e 02⎛⎫⎪⎝⎭,,()f x 的增区间为e ,2⎛⎫+∞ ⎪⎝⎭.(2)(ⅰ)因为过(),a b 有三条不同的切线,设切点为()(),,1,2,3i i x f x i =,故()()()i i i f x b f x x a '-=-,故方程()()()f x b f x x a '-=-有3个不同的根,该方程可整理为()21e e ln 022x a x b x x x ⎛⎫----+= ⎪⎝⎭,设()()21e e ln 22g x x a x b x x x ⎛⎫=---+ ⎪⎝⎭,则()()22321e 1e 1e22g x x a x x x x x x⎛⎫'=-+-+--+ ⎪⎝⎭()()31e x x a x =---,当0e x <<或x a >时,()0g x ¢<;当e x a <<时,()0g x ¢>,故()g x 在()()0,e ,,a +∞上为减函数,在()e,a 上为增函数,因为()g x 有3个不同的零点,故()e 0g <且()0>g a ,故()21e e e ln e 0e 2e 2e a b ⎛⎫----+< ⎪⎝⎭且()21e e ln 022a a a b a a a ⎛⎫---+> ⎪⎝⎭,整理得到:12e a b <+且()e ln 2b a f a a >+=,此时()1e 13e11ln ln 2e 2e 22e 222a a a b f a a a a a ⎛⎫⎛⎫---<-+-+=-- ⎪ ⎪⎝⎭⎝⎭,设()3e ln 22u a a a =--,则()2e-202au a a '=<,故()u a 为()e,+∞上的减函数,故()3eln e 022eu a <--=,故()1012e a b f a ⎛⎫<-<- ⎪⎝⎭.(ⅱ)当0e a <<时,同(ⅰ)中讨论可得:故()g x 在()()0,,e,a +∞上为减函数,在(),e a 上为增函数,不妨设123x x x <<,则1230e x a x x <<<<<,因为()g x 有3个不同的零点,故()0g a <且()e 0g >,故()21e e e ln e 0e 2e 2e a b ⎛⎫----+> ⎪⎝⎭且()21e e ln 022a a a b a a a ⎛⎫---+< ⎪⎝⎭,整理得到:1ln 2e 2ea ab a +<<+,因为123x x x <<,故1230e x a x x <<<<<,又()2e e 1ln 2a ag x x b x x+=-+-+,设e t x =,()0,1e a m =∈,则方程2e e 1ln 02a ax b x x+-+-+=即为:2e ln 0e 2ea at t t b +-+++=即为()21ln 02m m t t t b -++++=,记123123e e e ,,,t t t x x x ===则113,,t t t 为()21ln 02m m t t t b -++++=有三个不同的根,设3131e 1x t k t x a ==>>,1eam =<,要证:22122e 112e e 6e 6e a a x x a --+<+<-,即证13e 2e e 26e 6ea at t a --+<+<-,即证:13132166m mt t m --<+<-,即证:131********m m t t t t m --⎛⎫⎛⎫+-+-+< ⎪⎝⎭⎝⎭,即证:()()()2131313122236m m m t t m m t t --++--<+,而()21111ln 02m m t t t b -++++=且()23331ln 02mm t t t b -++++=,故()()()22131313ln ln 102m t t t t m t t -+--+-=,故131313ln ln 222t t t t m m t t -+--=-⨯-,故即证:()()()21313131312ln ln 236m m m t t m t t m t t --+--⨯<-+,即证:()()()1213313ln1312072t t t m m m t t t +--++>-即证:()()()213121ln 0172m m m k k k --+++>-,记()()1ln ,11k k k k k ϕ+=>-,则()()2112ln 01k k k kk ϕ⎛⎫'=--> ⎪⎝⎭-,设()12ln u k k k k =--,则()2122210u k k k k k'=+->-=即()0k ϕ'>,故()k ϕ在()1,+∞上为增函数,故()()k m ϕϕ>,所以()()()()()()22131213121ln 1ln 172172m m m m m m k k m m k m --+--++++>+--,记()()()()()211312ln ,01721m m m m m m m m ω---+=+<<+,则()()()()()()()2232322132049721330721721m mm m m mm m m m m ω---+-+'=>>++,所以()m ω在()0,1为增函数,故()()10m ωω<=,故()()()()211312ln 0721m m m m m m ---++<+即()()()213121ln 0172m m m m m m --+++>-,故原不等式得证:【点睛】思路点睛:导数背景下的切线条数问题,一般转化为关于切点方程的解的个数问题,而复杂方程的零点性质的讨论,应该根据零点的性质合理转化需求证的不等式,常用的方法有比值代换等.。
精品 高考数学压轴题函数训练+答案分析

9. 函数 f ( x) 的定义域为 R,并满足以下条件:
1 ①对任意 x R ,有 f ( x) 0 ;②对任意 x 、 y R ,有 f ( xy ) [ f ( x)] y ;③ f ( ) 1. 3 (1)求 f (0) 的值; (2)求证: f ( x) 在 R 上是单调增函数; (3)若 a b c 0, 且b 2 ac ,求证: f (a ) f (c) 2 f (b).
1 2
2
高中数学
4.已知函数: f ( x)
x 1 a (a R且x a ) ax
(Ⅰ)证明:f(x)+2+f(2a-x)=0 对定义域内的所有 x 都成立. (Ⅱ)当 f(x)的定义域为[a+
1 ,a+1]时,求证:f(x)的值域为[-3,-2]; 2
(Ⅲ)设函数 g(x)=x2+|(x-a)f(x)| ,求 g(x) 的最小值 .
6
高中数学
12. 某造船公司年最高造船量是 20 艘. 已知造船 x 艘的产值函数 R (x)=3700x + 45x2 – 10x3(单位:万 元), 成本函数为 C (x) = 460x + 5000 (单位:万元). 又在经济学中,函数 f(x)的边际函数 Mf (x)定义 为: Mf (x) = f (x+1) – f (x). 求:(提示:利润 = 产值 – 成本) (1) 利润函数 P(x) 及边际利润函数 MP(x); (2) 年造船量安排多少艘时, 可使公司造船的年利润最大? (3) 边际利润函数 MP(x)的单调递减区间, 并说明单调递减在本题中的实际意义是什么?
15.设函数 f ( x) 定义在 R 上, 对任意的 m, n R , 恒有 f (m n) f (m) f (n) , 且当 x 1 时, f ( x) 0 。 试解决以下问题: (1)求 f (1) 的值,并判断 f ( x) 的单调性; (2)设集合 A ( x, y ) | f ( x y ) f ( x y ) 0 , B ( x, y ) | f (ax y 2) 0, a R ,若 A B ,求实 数 a 的取值范围; (3)若 0 a b ,满足 | f (a ) || f (b) | 2 | f (
2025届高考数学复习:压轴好题专项(构造函数证明不等式)练习(附答案)

2025届高考数学复习:压轴好题专项(构造函数证明不等式)练习1. (2024届云南省昆明市第一中学高三上学期第一次月考)已知函数()()2ln f x x a x =-,R a ∈. (1)若()10f '=,求a ;(2)若()1,e a ∈,()f x 的极大值大于b2e <.2.(2024届全国名校大联考高三上学期第一联考)已知函数()2ln f x x ax =+(a ∈R ). (1)若()0f x ≤在()0,∞+上恒成立,求a 的取值范围:(2)设()()3g x x f x =-,1x ,2x 为函数()g x 的两个零点,证明:121x x <.3.(2024届山东省青岛市高三上学期期初调研检测)已知1ea ≥,函数()e ln ln xf x a x a =-+.(1)若1a =,求()f x 在点()()1,1f 处的切线方程; (2)求证:()44f x x ≥-+;(3)若β为()f x 的极值点,点()(),f ββ在圆22117416x y ⎛⎫++= ⎪⎝⎭上.求a .4.(2024届湖南省株洲市第二中学教育集团2高三上学期开学联考)已知函数()21e 12xf x x x =---, (1)证明:当0x >时,()0f x >恒成立; (2)若关于x 的方程()sin 2f x xa x x +=在()0,π内有解,求实数a 的取值范围. 5.(2024届辽宁省十校联合体高三上学期八月调研考试)设方程()22e x x a -=有三个实数根123123,,()x x x x x x <<.(1)求a 的取值范围;(2)请在以下两个问题中任选一个进行作答,注意选的序号不同,该题得分不同.若选①则该小问满分4分,若选②则该小问满分9分.①证明:12(2)(2)4x x --<;②证明:1231231113e 2x x x x x x +++++<. 6.(2024届安徽省江淮十校高三第一次联考)已知函数()2k f x x x=+,0k ≠.(1)讨论()f x 的单调性;(2)设函数()3ln g x x x =-n m ≤<,当13k =-时,证明:()()()()332g m g n f m f n m n -+<-. 7.(2024届内蒙古包头市高三上学期调研考试)设函数()()ln 1f x a x =+-,已知2x =是函数()()2y x f x =-的极值点.(1)求a ; (2)设函数()()()()22x f x g x x f x -=-+,证明:()1g x >.8.(2024届北京市景山学校高三上学期开学考试)已知函数())(0)f x x b a =+≠,曲线()y f x =在点(1,(1))f 处的切线方程是1y x =-.(1)求a 、b 的值; (2)求证:()f x x <;(3)若函数()2()()g x f x t x x =+-在区间(1,)+∞上无零点,求t 的取值范围.9.(2024届山西省大同市高三上学期质量检测)已知函数2()ln (R)af x ax x a x=--∈. (1)讨论()f x 的单调性;(2)若()f x 的两个极值点分别为1x ,2x ,证明:12|()()|2f x f x a-<.10.(2024届黑龙江省哈尔滨市第三中学校高三上学期开学测试)已知函数()()111ln f x ax a x x=+--+.(1)讨论函数()f x 的单调性;(2)求证:n *∀∈N ,)21+⋅⋅⋅++>.参考答案1. (2024届云南省昆明市第一中学高三上学期第一次月考)已知函数()()2ln f x x a x =-,R a ∈. (1)若()10f '=,求a ;(2)若()1,e a ∈,()f x 的极大值大于b 2e <.【过程详解】(1)()212()ln ()f x x a x x a x'=-+-⋅,由()10f '=,即202(1)ln1(1)a a --=+,解得1a =. (2)()()(2ln 1)af x x a x x'=--+, 令()2ln 1ag x x x=-+, ()1,e a ∈ ,111(,1e ),a a a∴∈∴<,()21()2ln 11)2ln (10g a a a a a a=--+=-++-<, ()2ln 112ln 0g a a a =-+=>, 22()0ag x x x+'=>在(0,)+∞恒成立, 故()g x 在(0,)+∞递增,而1lg()0,()0g a a <>,01(,)x a a∴∃∈,使得g 0()0,x =令()0f x '=,有1201,,x a x x x =<=故0(0,)x x ∈时()0f x ¢>,0(,)x x a ∈时()0f x '<,(,)x a ∈+∞时()0f x ¢>, 故()f x 在0(0,)x 上递增,在0(,)x a 上递减,在(,)a +∞上递增,∴()f x 极大值2000()()ln ,f x x a x b =->由000()2ln 10,ag x x x =-+=得0002ln ,a x x x =+ 故23004(ln ),b x x <则230028(ln ),ab ax x <01,e 1e x a a<<<< 0e,e a x ∴<<,23233008(ln )8e e 18e ax x ∴<⋅⋅⋅=,328e ,ab ∴<2e <.2.(2024届全国名校大联考高三上学期第一联考)已知函数()2ln f x x ax =+(a ∈R ). (1)若()0f x ≤在()0,∞+上恒成立,求a 的取值范围:(2)设()()3g x x f x =-,1x ,2x 为函数()g x 的两个零点,证明:121x x <.【过程详解】(1)若()0f x ≤在()0,∞+上恒成立,即2ln xa x≤-, 令()2ln x u x x =-,所以()()222ln 122ln x x u x x x --'=-=, 所以当0e x <<时,()0u x '<,当e x >时,()0u x '>, 所以()u x 在()0,e 上单调递减,在()e,+∞上单调递增, 所以()()min 2e eu x u ==-,所以2a e ≤-,即a 的取值范围是2,e ⎛⎤-∞- ⎝⎦.(2)令()0g x =,即22ln 0xx a x--=, 令()22ln x h x x a x =--,则()()()3222ln 121ln 2x x x h x x x x +--'=-=, 令()3ln 1r x x x =+-,所以()2130r x x x'=+>,所以()r x 在()0,∞+上单调递增,又()10r =,所以当01x <<时,()0r x <,所以()0h x '<, 当1x >时,()0r x >,所以()0h x '>,所以()h x 在()0,1上单调递减,在()1,+∞上单调递增. 不妨设12x x <,则1201x x <<<,2101x <<, 因为()()120h x h x ==,所以()()22212222222212ln 2ln 1111x x h x h h x h x a a x x x x x ⎛⎫ ⎪⎛⎫⎛⎫⎛⎫ ⎪-=-=----- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ ⎪⎝⎭22222112ln x x x x x ⎛⎫⎛⎫=+--- ⎪ ⎪⎝⎭⎝⎭. 设函数()12ln x x x x ϕ=--(1x >),则()()22211210x x x x xϕ-'=+-=>在()1,+∞上恒成立, 所以()x ϕ在()1,+∞上单调递增,所以()()222212ln 10x x x x ϕϕ=-->=, 所以()1210h x h x ⎛⎫-> ⎪⎝⎭,即()121h x h x ⎛⎫> ⎪⎝⎭.又函数()22ln xh x x a x=--在()0,1上单调递减, 所以12101x x <<<,所以121x x <. 3.(2024届山东省青岛市高三上学期期初调研检测)已知1ea ≥,函数()e ln ln xf x a x a =-+.(1)若1a =,求()f x 在点()()1,1f 处的切线方程; (2)求证:()44f x x ≥-+;(3)若β为()f x 的极值点,点()(),f ββ在圆22117416x y ⎛⎫++= ⎪⎝⎭上.求a .【过程详解】(1)1a =,()e ln xf x x =-,0x >由()11e ln1e f =-=,得切点为()1,e由()1e xf x x'=-,有()1e 1f '=-,即()f x 在点()1,e 处的切线斜率为e 1-,所以()f x 在点()1,e 处的切线方程为:()e 11y x =-+. (2)证明:因为()1e xf x a x '=-(1ea ≥,0x >),设函数()()g x f x '=,则()21e 0xg x a x '=+>(1e a ≥,0x >),所以()f x '在()0,∞+上单调递增又因为()212e 02f a '=->,112e2e 1e 2e e 2e 02e a a f a a a a ⎛⎫⎛⎫'=-=-< ⎪ ⎪⎝⎭⎝⎭, 所以存在1,22e a β⎛⎫∈⎪⎝⎭,使得()0f β'=, 即1e a ββ=,1e a ββ=,所以,当()0,x ∈β时,()0f x '<,()f x 在()0,β上单调递减; 当(),x β∈+∞时,()0f x ¢>,()f x 在(),β+∞上单调递增;所以()()1e ln ln 2lnf x f a a ββββββ≥=-+=--令()12ln =--h x x x x ,()()()()14432ln 40x h x x x x x xϕ=--+=+-->, 则()()()2131x x x x ϕ-+'=,()0x ϕ'<解得01x <<,()0x ϕ'>解得1x >,所以,()x ϕ在()0,1上单调递减,在()1,+∞上单调递增; 所以,()()10x ϕϕ≥=,所以,()h x 的图像在44y x =-+的上方,且()h x 与44y x =-+唯一交点为()1,0, 所以,()44f x x ≥-+.(3)圆22117416x y ⎛⎫++= ⎪⎝⎭的圆心坐标为10,4⎛⎫- ⎪⎝⎭,半径r =圆心到直线44y x =-+的距离174d ===, 所以直线44y x =-+为圆22117416x y ⎛⎫++= ⎪⎝⎭的切线,由2211741644x y y x ⎧⎛⎫++=⎪ ⎪⎨⎝⎭⎪=-+⎩解得切点坐标为()1,0, 显然,圆22117416x y ⎛⎫++= ⎪⎝⎭在直线44y x =-+的下方又因为()44f x x ≥-+,且点()(),f ββ在圆22117416x y ⎛⎫++= ⎪⎝⎭上,则点()(),f ββ即为切点为()1,0,所以1β=,1ea =.4.(2024届湖南省株洲市第二中学教育集团2高三上学期开学联考)已知函数()21e 12xf x x x =---, (1)证明:当0x >时,()0f x >恒成立;(2)若关于x 的方程()sin 2f x xa x x +=在()0,π内有解,求实数a 的取值范围. 【过程详解】(1)函数21()e 12xf x x x =---,0x >,求导得()e 1x f x x '=--,令e 1x y x =--,0x >,求导得e 10x y '=->, 则函数()f x '在(0,)+∞上单调递增,()(0)0f x f ''>=, 因此函数()f x 在(0,)+∞上单调递增,()(0)0f x f >=, 所以当0x >时,()0f x >恒成立.(2)设sin y x x =-,()0,πx ∈,则1cos 0y x '=->, 则sin y x x =-在()0,π上递增,0y >,即sin 0x x >>, 方程()sin 2f x xa x x +=等价于e sin 10x ax x x ---=,()0,πx ∈, 令()e sin 1xg x ax x x =---,原问题等价于()g x 在()0,π内有零点,由()0,πx ∈,得2sin x x x <, 由(1)知,当12a ≤时,()21e sin 1e 102x xg x ax x x x x =--->--->, 当()0,πx ∈时,函数()y g x =没有零点,不合题意; 当12a >时,由()e sin 1x g x ax x x =---,求导得()()e cos sin 1xg x a x x x '=-+-, 令()()()e cos sin 1x t x g x a x x x '==-+-,则()()e sin 2cos xt x a x x x '=+-,当π[,π)2x ∈时,()0t x '>恒成立,当π(0,)2x ∈时,令()()()e sin 2cos x s x t x a x x x '==+-,则()()e 3sin cos xs x a x x x '=++,因为e 0x >,()3sin cos 0a x x x +>,则()0s x '>,即()t x '在π(0,2上单调递增,又()0120t a '=-<,π2ππ(e 022t a '=+>,因此()t x '在π(0,)2上存在唯一的零点0x ,当()00,x x ∈时,()0t x '<,函数()g x '单调递减,当()0,πx x ∈时,()0t x '>,函数()g x '单调递增,显然()()000g x g ''<=,()ππe π10g a '=+->,因此()g x '在()0,π上存在唯一的零点1x ,且()10,πx x ∈,当()10,x x ∈时,()0g x '<,函数()g x 单调递减,当()1,πx x ∈时,()0g x '>,()g x 单调递增, 又()00g =,()()100g x g <=,由(1)知,21e 112x x x x >++>+,则()ππe π10g =-->,所以()g x 在()10,x 上没有零点,在()1,πx 上存在唯一零点,因此()g x 在()0,π上有唯一零点, 所以a 的取值范围是1(,)2+∞.5.(2024届辽宁省十校联合体高三上学期八月调研考试)设方程()22e x x a -=有三个实数根123123,,()x x x x x x <<.(1)求a 的取值范围;(2)请在以下两个问题中任选一个进行作答,注意选的序号不同,该题得分不同.若选①则该小问满分4分,若选②则该小问满分9分.①证明:12(2)(2)4x x --<;②证明:1231231113e2x x x x x x +++++<. 【过程详解】(1)由题意设()()22e x f x x =-(x ∈R ),则()f x '=()2e xx x -,x ∈R ,令()0f x '=,得0x =或2x =,当0x <或2x >时,()0f x ¢>,所以()f x 在(),0∞-,()2,+∞上单调递增; 当02x <<时,()0f x '<,所以()f x 在()0,2上单调递减;又()20f =,()04f =,()33e 4f =>,且()()22e 0x f x x =-≥,当x 趋向于+∞时,()f x 也趋向于+∞,又方程()22e x x a -=有三个实数根123123,,()x x x x x x <<, 等价于直线y a =与()y f x =的函数图像有三个交点, 即04a <<,所以a 的取值范围为()0,4.(2)选①,证明如下:由(1)得:1202x x <<<,则122220x x -<-<-<, 设112t x =-,222t x =-,则1220t t <-<<, 不妨设121t k t =>,则12t kt =(1k >), 又()()1222122e 2e x x x x a -=-=,即12222212e e t t t t a ++==,故22222222e e 0e kt ta k t t ==>,即222e e kt t k =,所以22ln 1k t k=-,212ln 1k k t kt k ==-,1k >, 则()()()2222121222ln 2ln 22111k x x t t k k ⎛⎫⎫ ⎪⎛⎫⎪--==⋅==⎪ ⎪ ⎪-⎝⎭⎪⎪-⎪⎝⎭⎭,设()l 1n 2x g x x x=-+,1x >, 则()()222121=10x g x x x x -'--=-≤,所以()g x 在()1,+∞上单调递减,即()()10g x g <=,1>,则0<,即,0>2<,故()()212122241x x t t ⎛⎫ ⎪--==<⎪ ⎪⎪⎝⎭. 选②,证明如下:由(1)得:1202x x <<<,则122220x x -<-<-<, 设112t x =-,222t x =-,则1220t t <-<<, 不妨设121t k t =>,则12t kt =(1k >), 又()()1222122e 2e x x x x a -=-=,即12222212e e t t t t a ++==,故22222222e e 0e kt ta k t t ==>,即222e e kt t k =,所以22ln 1k t k=-,212ln 1k k t kt k ==-(1k >),则()()()2222121222ln 2ln 22111k x x t t k k ⎛⎫⎫ ⎪⎛⎫⎪--==⋅==⎪ ⎪ ⎪-⎝⎭⎪⎪-⎪⎝⎭⎭1>), 设()l 1n 2x g x x x=-+,1x >, 则()()222121=10x g x x x x -'--=-≤,所以()g x 在()1,+∞上单调递减,即()()10g x g <=,1>,则0<,即,0>2<,故()()212122241x x t t ⎛⎫ ⎪--==<⎪ ⎪⎪⎝⎭. 所以()()()12121222244x x x x x x --=-++<,则()12122x x x x <+, 又因为1202x x <<<,所以120x x <,从而()12121221121x x x x x x +⎛⎫=+< ⎪⎝⎭,故121112x x +<①,下证120x x +<, 有12122ln 2ln 44011k k kx x t t k k+=++=++<--(1k >), 即证1k >时,()()1ln 21k k k +>-,即()214ln 211k k k k ->=-++, 即证4ln 21k k +>+(1k >), 设()4ln 1h x x x =++(1x >),则()()()()22211411x h x x x x x -'=-=++,当1x >时,()0h x '>,所以()h x 在()1,+∞上单调递增, 则()()12h x h >=,所以120x x +<②,又()()33e 0f f =>,所以得323x <<,设()1x x xϕ=+,(23x <<),则()211x x ϕ'=-,当23x <<时,()0x ϕ'>,所以()x ϕ在()2,3上单调递增, 则331103x x +<③, 联立①②③得:123123*********e 042362x x x x x x +++++<++=<<,故1231231113e2x x x x x x +++++<. 6.(2024届安徽省江淮十校高三第一次联考)已知函数()2k f x x x=+,0k ≠.(1)讨论()f x 的单调性;(2)设函数()3ln g x x x =-n m ≤<,当13k =-时,证明:()()()()332g m g n f m f n m n -+<-. 【过程详解】(1)解:函数()f x 的定义域为{}|0x x ≠,()32222k x kf x x x x -='-=, 令()0f x '=,则x =①当0k<时,当x <()0f x '<,()f x0x <<时,()0f x ¢>,()f x 单调递增;当0x >时,()0f x ¢>,()f x 单调递增;②当0k>时,当0x <时,()0f x '<,()f x 单调递减;当0x <<()0f x '<,()f x 单调递减;当x >时,()0f x ¢>,()f x 单调递增.综上:当0k <时,单调增区间为⎫⎪⎪⎭,()0,∞+,单调递减区间为⎛-∞ ⎝; 当0k >时,单调递增区间为⎫+∞⎪⎪⎭,单调递减区间为(),0∞-,⎛ ⎝. (2)对任意的m,n ⎫∈+∞⎪⎭,且m n >,令mt n =(1t >),因为()()()()()()()32m n f m f n g m g n -+--()22333311ln 2222m m n m n m n m n n ⎛⎫⎛⎫=-+----- ⎪ ⎪⎝⎭⎝⎭33221133ln 222222n m m m n mn m n m n n=-+-+-+ 323111332ln 22m m m m n m n n n n n mn ⎡⎤⎛⎫⎛⎫⎛⎫=-+⋅----⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦()332331*********ln (1)2ln 2222n t t t t t n t t t t t ⎛⎫⎛⎫=-+----=---- ⎪ ⎪⎝⎭⎝⎭ ()33211111(1)2ln 33132ln 626t t t t t t t t t t ⎡⎤⎛⎫⎛⎫≥----=-+---- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ 321336ln 16t t t t ⎛⎫=-++- ⎪⎝⎭, 记()32336ln 1h t t t t t =-++-,则()22226311113636320h t t t t t t t t t t t t t ⎛⎫⎛⎫⎛⎫⎛⎫=-+-=---'=-+-> ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭,所以()h t 在()1,+∞单调递增,所以()()10h t h >=,故32336ln 10t t t t-++->,所以()()()()()()()302m n f m f n g m g n -+-->, 故()()()()332g m g n f m f n m n-+<-.7.(2024届内蒙古包头市高三上学期调研考试)设函数()()ln 1f x a x =+-,已知2x =是函数()()2y x f x =-的极值点.(1)求a ; (2)设函数()()()()22x f x g x x f x -=-+,证明:()1g x >.【过程详解】(1)由题意可知,()()()()22ln 1y x f x x a x =-=-+-,则()2ln 11xy a x a x-'=+-++-,因为2x =是函数()()2ln 1y x a x =-+-的极值点, 所以()ln 120a +-=,解得2a =, 经检验满足题意,故2a =;(2)由(1)得()()ln 3f x x =-,(),3x ∞∈-, 设()()()22ln 3h x x f x x x =-+=-+-,则()12133x h x x x -'=-=--, 当2x <时,203x x ->-,即()0h x '>,所以()h x 在区间(),2-∞单调递增; 当23x <<时,203x x -<-,即()0h x '<,所以()h x 在区间()2,3单调递减, 因此当(),3x ∞∈-时,()()20h x h ≤=,因为()g x 的定义域要求()f x 有意义,即(),3x ∞∈-,同时还要求()2ln 30x x -+-≠,即要求2x ≠,所以()g x的定义域为{|3x x < 且}2x ≠, 要证()()()()212x f x g x x f x -=>-+,因为()20x f x -+<,所以需证()()()22x f x x f x -<-+, 即需证()()23ln 30x x x -+-->,令3x t -=,则0t >且1t ≠,则只需证1ln 0t t t -+>,令()1ln m t t t t =-+,则()ln m t t '=,令()ln 0m t t '==,可得1t =, 所以()0,1t ∈,()0m t '<;()1,t ∈+∞,()0m t '>;所以()m t 在区间()0,1上单调递减,在区间()1,+∞上单调递增, 所以()()10m t m >=,即()1g x >成立.8.(2024届北京市景山学校高三上学期开学考试)已知函数())(0)f x x b a =+≠,曲线()y f x =在点(1,(1))f 处的切线方程是1y x =-.(1)求a 、b 的值; (2)求证:()f x x <;(3)若函数()2()()g x f x t x x =+-在区间(1,)+∞上无零点,求t 的取值范围.【过程详解】(1)()()f x x b '=+由切线方程知()()1110f f ⎧=⎪⎨='⎪⎩,即()()1110b b +=+=,注意到0a ≠,解得1a =,0b =.(2)由(1)可知()f x x,若要()f x x x =<且注意到0x >,所以只需ln x < 构造函数()ln h x x =()122h x x x '==,令()0h x '=得4x =,所以()h x 、()h x '随x 的变化情况如下表:()0,4 ()4,+∞()h x '+-()h x所以()h x 有极大值()244ln 42ln 0eh =-=<,综上()0h x <,结合分析可知命题得证. (3)由题意分以下三种情形讨论:情形一:注意到当0t ≥且1x >0x >,()10txx -≥,此时有()0g x >,即()g x 在区间(1,)+∞上无零点,符合题意.情形二:对()2()g x x t x x =+-求导得()()21g xt x x '=+-,所以有()11g t '=+;进一步对()()21g x t x x '=++- 求导得()32ln 24x g x t x-''=+,注意到当1t ≤-且1x >时,有20t <,32ln 04x x-< ,进而有()0g x ''<,所以()g x '单调递减,所以()()110g x g t ''<=+≤,因此()g x 单调递减,故()()10g x g <=,即()g x 在区间(1,)+∞上无零点,符合题意.情形三:由(2)可知1x >lnx <,且注意到当10t -<<时有()()()1()21211212g x t x t x t x '=-<+-<++-成立, 所以11(02a g a a -'<-<,此时()110g t '=+>, 所以存在011,a x a -⎛⎫∈ ⎪⎝⎭使得()00g x '=,且注意到此时有()32ln 204x g x t x -''=+<成立, 所以()g x 、()g x '随x 的变化情况如下表:()01,x ()0,x +∞()g x ' +-()g x故一方面当0x x =时,()g x 取极大值(或最大值)()0g x ,显然有()()010g x g >=;ln x <可得()()()22()1g x x t x x x t x x x tx t +-<+-=+-,所以有10a g a -⎛⎫< ⎪⎝⎭,由零点存在定理并结合这两方面可知函数()g x 在区间(1,)+∞上存在零点.综上所述,符合题意的t 的取值范围为(][),10,-∞-⋃+∞.9.(2024届山西省大同市高三上学期质量检测)已知函数2()ln (R)af x ax x a x=--∈. (1)讨论()f x 的单调性;(2)若()f x 的两个极值点分别为1x ,2x,证明:12|()()|f x f x -<. 【过程详解】(1)依题意,222122()(0)a ax x af x a x x x x -+'=-+=>,当0a ≤时,()0f x '<,所以()f x 在(0,)+∞上单调递减;当0a <<()0f x '>,解得102x a <<或12x a>,令()0f x '<,解得112x a <<,所以()f x在1(0,2a 上单调递增,在11(22a a上单调递减,在)+∞上单调递增;当a ≥时,()0f x '≥,所以()f x 在(0,)+∞上单调递增. (2)不妨设120x x <<,由(1)知,当04a <<时,()f x 在1(0,)x 上单调递增,在12(,)x x 上单调递减,在2(,)x +∞上单调递增,所以1x 是()f x 的极大值点,2x 是()fx的极小值点,所以12()()f x f x >,所以1212|()()|()()f x f x f xf x -=-.由(1)知,122x x =,121x x a+=,则21x xa-==.要证12|()()|f x f x -<1221()())2f x f x x x -<-.因为22121122121112()()()()()ln 222x x xx x f x f x x x a x x a x x x ---+=-+--+⋅2212212111212()2()()ln ln 2x x x x a x x x x x x x x -=-+--=+ 2122112(1)ln 1x x xx x x -=+, 设211x t x =>,2(1)()ln 1t g t t t -=++.所以222414()0(1)(1)g t t t t '==>++, 所以()g t 在(1,)+∞上单调递增,所以()(1)0g t g >=.所以2112)()()02x x f x f x --+>,即得1221()()()2f x f x x x -<-成立. 所以原不等式成立.10.(2024届黑龙江省哈尔滨市第三中学校高三上学期开学测试)已知函数()()111ln f x ax a x x=+--+.(1)讨论函数()f x 的单调性;(2)求证:n *∀∈N ,)21+⋅⋅⋅++>.【过程详解】(1)()f x 的定义域为()0,∞+,()()()221111ax x a f x a x x x --+'=+-=, 当0a ≤时,10ax -<,令()0f x ¢>,解得01x <<,令()0f x '<,解得1x >,所以()f x 在()0,1上单调递增,()1,+∞上单调递减;当01a <<时,令()0f x ¢>,解得01x <<或1x a >,令()0f x '<,解得11x a <<,所以()f x 在()0,1,1,a ⎛⎫+∞ ⎪⎝⎭上单调递增,11,a ⎛⎫⎪⎝⎭上单调递减;当1a =时,()0f x '≥恒成立,所以()f x 在()0,∞+上单调递增;当1a >时,令()0f x ¢>,解得10x a <<或1x >,令()0f x '<,解得11x a <<,所以()f x 在10,a ⎛⎫⎪⎝⎭,()1,+∞上单调递增,1,1a ⎛⎫⎪⎝⎭上单调递减;综上所述,当0a ≤时,()f x 在()0,1上单调递增,()1,+∞上单调递减;当01a <<时,()f x 在()0,1,1,a ⎛⎫+∞ ⎪⎝⎭上单调递增,11,a ⎛⎫⎪⎝⎭上单调递减;当1a =时,()f x 在()0,∞+上单调递增;当1a >时,()f x 在10,a ⎛⎫⎪⎝⎭,()1,+∞上单调递增,1,1a ⎛⎫ ⎪⎝⎭上单调递减.(2)当0a =时,由(1)可得()()11ln 10f x x f x=--<=,()1x >,因为N n *∈1>,则10<,即11>>所以n ++>-+L L2n =-L2n =-)21=-,即)2ln 1+>L .。
高考函数压轴精典题型以及答案

函数专题训练复习目标:通过对函数综合题的分类,使学生在解函数题中牢固掌握:反函数的求法及其与原函数的关系的应用、函数的单调性、函数的奇偶性、求函数的定义域与值域常用方法、函数的解析式求法、二次函数的根的分布情况的充要条件运用、函数中的新题型的新解法、函数与方程的思想方法等。
重点与难点: 反函数、值域、单调性、奇偶性、求解析式、分段函数、根的分布、函数与方程思想方法、函数图象等过程:一、反函数 ●有奖征解① 若函数f(x)的图像过点(0,1),则函数f(x+2)的反函数过定点(1,-2)② 若函数f(x)的图像过(0,1),则)4(1x f --过点(-1,0); ③若函数f(x)的图像过点(0,1),则f(4-x)的反函数过点(1,4),y=f(4-x)的反函数为)(41x fy --=。
●例子分析例1①已知函数()x x x f +-=121,函数y=g(x)的图像与)1(1--x f 的图像关于直线y=x 对称,则g(x)的解析式为12+-=x xy 。
②给定实数a,a ≠0,且a ≠1,设函数⎪⎭⎫⎝⎛≠∈--=a x R x ax x y 1,11,证明这个函数图关于y=x对称。
① 已知函数()ax x x f ++=12存在反函数,求α的取值。
(α≠1/2)说明:④小题可以据③小题去求,但也可以据通常方法去求。
二、周期性、循环 ● 有奖征解设x 为整数,给出一个流程图如右图:按此流程图计算,刚好处理3次 ,则输入的x 值是例1(2004年福建省高考)定义在R 上的偶函数f(x)满足f(x)=f(x+2),当x ∈[3,5]时,f(x)=2-|x-4|,则(D )(A )f(sin6π)<f(cos 6π) (B )f(sin1)>f(cos1) 输入x 与y 值 用2与x+3的几何平均值代替y开始用x+1代x 表示出x 终了 不是是 y 是否大于是x(C )f(cos32π)<f(sin 32π) (D )f(cos2)>f(sin2)例2 f(x)定义域为(-∞,+∞)上以2为周期的函数,对k ∈Z,用I k 表示区间(]12,12+-k k ,已知当x ∈I 0时,f(x)=x 2, ① 求f(x)在I k 上的解析式;② 对自然数k ,求集合M k ={a|使方程f(x)=ax 在I k 上有两个不同的实根}。
2025届高考数学复习:压轴好题专项(三次函数)练习(附答案)

2025届高考数学复习:压轴好题专项(三次函数)练习1.(2024届江苏省镇江市丹阳市高三上学期期初检测)已知函数()()3222f x x mx m x m =-+∈R 在6x =处有极小值. (1)求m 的值;(2)求函数()y f x =在[]0,t 上的最大值.2.(2023河南省新未来3月联考)已知函数()()3211132f x x a x ax =+--. (1)若2a =,求函数()f x 的极值;(2)当1a >时,若对0x ∀≥,()e 0xf x x b ++≥恒成立,求4b a -的最小值.3.(2023届安徽省卓越县中联盟高三上学期第一次联考)已知函数()3223=+f x x ax ,a ∈R .(1)若()f x 在[]1,3-上的值域为[]8,0-,求()f x 在R 上的单调区间;(2)若函数()()()6cos 6sin g x f x x a x x =++-,则当0a ≥时,求()g x 的零点个数.4.(2023届湖南省湘潭市部分学校高三上学期期末联考)已知函数()313f x mx kx =-,其中,m k ∈R .(1)当1k =时,求函数()f x 的单调区间;(2)已知函数()2ln g x x x =-(e 是自然对数的底数),若0k ∀>,曲线()y f x '=与曲线()y g x =都有唯一的公共点,求实数m 的取值范围.5.(2023届北京市第五中学高三下学期3月检测)设函数()()23f x x x x a =-+,R a ∈(1)当9a =-时,求函数()f x 的单调增区间;(2)若函数()f x 在区间()1,2上为减函数,求a 的取值范围;(3)若函数在区间()0,2内存在两个极值点1x ,2x ,且()()()()2121f x f x f x f x ->+,求a 的取值范围. 6.已知函数32()1f x x ax bx =+++(0,a b R >∈)有极值,且导函数()f x '的极值点是()f x 的零点.(1)求b 关于a 的函数关系式,并写出定义域; (2)求证:23b a >;(3)若(),()f x f x '这两个函数的所有极值之和不小于72-,求a 的取值范围.7.已知()3222,f x x ax a x a =+-+∈R .(1)当a<0时,求函数()y f x =的单调减区间;(2)当0a =时,曲线()y f x =在相异的两点,A B 点处的切线分别为1l 和21,l l 和2l 的交点位于直线2x =上,证明:,A B 两点的横坐标之和小于4.8.(2024届江西省稳派上进教育高三上学期摸底考试)已知函数()321132f x x x ax =++,()1e ln x g x x x x -=+,()f x ',()g x '分别为()f x ,()g x 的导函数,且对任意的(]10,1x ∈,存在(]20,1x ∈,使()()122f x g x ''≤-.(1)求实数a 的取值范围;(2)证明:0x ∀>,有()()'≥g x f x .9.已知函数()331f x x ax =++,[]1,1x ∈-,a R ∈,(1)若函数()f x 在区间[]1,1-上不单调,求a 的取值范围; (2)求()f x 的最大值;(3)若()1f x b +≤对任意[]1,1x ∈-恒成立,求a b +的取值范围.10.已知函数32()3f x x x ax b =-++在1x =-处的切线与x 轴平行. (1)求a 的值和函数()f x 的单调区间; (2)若函数()y f x =的图象与抛物线231532y x x =-+恰有三个不同交点,求b 的取值范围. 11.已知函数.0)0,(,2)(,)()(22<-∞∈=-=a x x a x g a x x x f 且 (1)(i )求函数)()(x g y x f y ==与的图象的交点A 的坐标;(ii )设函数)(),(x g y x f y ==的图象在交点A 处的切线分别为,,21l l 是否存在这样的实数a, 使得21l l ⊥?若存在,请求出a 的值和相应的点A 坐标;若不存在,请说明理由. (2)记[)0,1)(-=在x f y 上最小值为F (a ),求aa F )(的最小值. 12.已知函数32()1f x x ax bx =-+++在1x =时有极小值. (1)当4a =时,求()f x 在0x =处的切线方程;(2)求()f x 在33,2⎡⎤-⎢⎥⎣⎦上的最小值.13.已知函数()3222312f x x ax a x =+-,其中a ∈R .(1)求函数()f x 的单调区间;(2)设函数()f x 在区间2,2a a ⎡⎤⎣⎦上的最大值为()g a ,证明:()32g a <.14.已知函数()3221f x x ax a x =---,其中0a <.(1)求曲线()y f x =在点()(),a f a 处的切线方程;(2)若存在实数t ,使得不等式()0f x <的解集为(),t -∞,求a 的取值范围.15.已知函数()()33R f x x ax a a =-+∈.(1)讨论函数()f x 的单调性;(2)若函数()f x 在区间[]0,3上的最大值与最小值之差为()g a ,求()g a 的最小值. 16.已知函数3211()()32f x x ax a =-∈R 在[]0,1上的最小值为16-.(1)求a 的值;(2)讨论函数()()2()g x f x x b b =-+∈R 的零点个数.参考答案1.(2024届江苏省镇江市丹阳市高三上学期期初检测)已知函数()()3222f x x mx m x m =-+∈R 在6x =处有极小值. (1)求m 的值;(2)求函数()y f x =在[]0,t 上的最大值.【过程详解】(1)因为()3222f x x mx m x =-+,则()()()22343x mx m f x x m x m =-+'=--,又因为()f x 在6x =处有极小值,则()()()61860f m m '=--=,解得6m =或18m =, (i )当6m =时,则()()()326f x x x -'=-, 当(),2x ∈-∞时,()0f x ¢>,()f x 单调递增, 当()2,6x ∈时,()0f x '<,()f x 单调递减, 当()6,x ∞∈+时,()0f x ¢>,()f x 单调递增, 所以当6x =时,()f x 取得极小值,符合题意; (ii )当18m =时,()()()3618f x x x '=--, 当(),6x ∈-∞时,()0f x ¢>,()f x 单调递增, 当()6,18x ∈时,()0f x '<,()f x 单调递减, 当()18,x ∞∈+时,()0f x ¢>,()f x 单调递增, 所以当6x =时,()f x 取得极大值,不符合题意,舍去 综上所述:6m =.(2)由(1)可知:()321236f x x x x =-+,且()f x 在[)()0,2,6,+∞上单调递增,在()2,6上单调递减,()()8232f f ==,如图所示:又因为[]0,x t ∈,则有:(i )当02t <≤时,则()f x 在[]0,t 上单调递增,所以函数()y f x =在[]0,t 上的最大值为()()32max 1236f x f t t t t ==-+⎡⎤⎣⎦;(ii )当28t <≤时,结合图象可知:函数()y f x =在[]0,t 上的最大值为()()max 232f x f ==⎡⎤⎣⎦; (iii )当8t >时,则()f x 在[)(]0,2,6,t 上单调递增,在()2,6上单调递减,且()()8f t f >,所以函数()y f x =在[]0,t 上的最大值为()()32max 1236f x f t t t t ==-+⎡⎤⎣⎦;综上所述:()(]()(]32max1236,0,28,32,2,8t t t t f x t ∞⎧-+∈⋃+⎪⎡⎤=⎨⎣⎦∈⎪⎩. 2.(2023河南省新未来3月联考)已知函数()()3211132f x x a x ax =+--. (1)若2a =,求函数()f x 的极值;(2)当1a >时,若对0x ∀≥,()e 0xf x x b ++≥恒成立,求4b a -的最小值.【过程详解】(1)若2a =,可得()3211232f x x x x =--, 有()()()2212f x x x x x =--=+-',令()0f x '<,可得12x -<<,令()0f x ¢>,则1x <-或2x >, 故函数()f x 的增区间为(),1-∞-,()2,+∞,减区间为()1,2-, 函数()f x 的极小值为()1023f =-,极大值为()716f -=; (2)令()()()e 0xg x x x x f b =++≥,有()()()()()()()()211e 11e 1e x x xg x a x a x x x a x x x a x '=+--++=+-++=++-,由函数()e x h x x a =+-单调递增及()010h a =-<,()e 0ah a =>,可知存在()0,m a ∈,使得()0h m =,即e m a m =+, 当x >m 时,()0g x '>,当0x m <<时,()0g x '<, 所以函数()g x 的减区间为[)0,m ,增区间为(),m +∞, 可得()()()32min 111e 32mg m m a m am m b g x ==+--++()()32322111111e e e e 32622m m m m m m m m m m b m m m b =+---+++=---+, 由0x ∀≥,()e 0xf x x b ++≥恒成立,有()0g m ≥,可得322111e 622mb m m m ≥++, 有()3221114e 4e 622mm b a m m m m -≥++-+, 可得3221114e 44e 622mm b a m m m m -≥++--, 令()()322111e 44e 0622xx x x x x x x ϕ=++-->, 有()()()2221112e 44e 4e 1222x x x x x x x x x x ϕ⎛⎫'=+++--=+-+ ⎪⎝⎭()()()124e 12x x x =-++, 令()0x ϕ'>,则2x >,令()0x ϕ'<,则02x <<, 所以函数()x ϕ的减区间为()0,2,增区间为()2,+∞, 所以()()222414222e 84e 2e 33x ϕϕ≥=++--=--, 故4b a -的最小值为2142e 3--. 3.(2023届安徽省卓越县中联盟高三上学期第一次联考)已知函数()3223=+f x x ax ,a ∈R .(1)若()f x 在[]1,3-上的值域为[]8,0-,求()f x 在R 上的单调区间;(2)若函数()()()6cos 6sin g x f x x a x x =++-,则当0a ≥时,求()g x 的零点个数.【过程详解】(1)因为()3223=+f x x ax ,所以2()666()f x x ax x x a '=+=+,令()0f x '=,解得0x =或x a =-,当0a ->,即a<0时,令()0f x '<,得0x a <<-;令()0f x '>,得0x <或x a >-;所以()f x 在(),0∞-,(),a -+∞上单调递增,在()0,a -上单调递减,此时0x =是()f x 的极大值点; 当0a -<,即0a >时,令()0f x '<,得0a x -<<;令()0f x '>,得x a <-或0x >;所以()f x 在(),0a -上单调递减,在(),a -∞-,()0,∞+上单调递增,此时0x =是()f x 的极小值点; 当0a =时,()0f x '≥恒成立,则()f x 在[]1,3-上单调递增,此时()32f x x =,易得()12f -=-,()354f =,不满足题意;又(0)0f =,()f x 在[]1,3-上的值域为[8,0]-,所以()f x 在[]1,3-上的最值为(0)0f =,故0x =是()f x 的极大值点, 所以a<0,此时,有()8f a -=-或(1)8f -=-两种情况,都有2a =-,故2a =-满足题意,所以由上述分析可知,()f x 的单调递增区间为(),0∞-和()2,+∞,单调递减区间为()0,2. (2)令()sin t x x x =-,则()1cos 0t x x =-≥', 所以()t x 在R 上单调递增,又()00t =,所以当0x >时,()0t x >,即sin x x >,当0x <时,()0t x <,即sin x x <;因为()()()()326cos 6sin 236cos 6sin g x f x x a x x x ax x a x x =++-=+++-,令()0g x =,则()3211cos sin 032x ax x a x x +++-=,令()()3211cos sin 32h x x ax x a x x =+++-,则()()()sin h x x x x a ='-+, 令()0h x '=,解得0x =或x a =-.①若0a =,则()()sin 0h x x x x =-≥',此时()hx 在R 上单调递增.又()00h =,所以()h x 有且仅有1个零点,即()g x 有且仅有1个零点.②若0a >,0a -<,则当(),x a ∈-∞-时,()0h x '>,当(),0x a ∈-时,()0h x '<,当()0,x ∈+∞时,()0h x '>,故()h x 在(),a -∞-上单调递增,在(),0a -上单调递减,在()0,∞+上单调递增, 则()(0)0h a h a ->=>,故()h x 在(),a -+∞上没有零点,下证3302h a ⎛⎫--< ⎪⎝⎭.当x a <-时,0x a +<.因为cos 1x ≥-,所以()()cos x a x x a +≤-+. 因为sin x x >,所以sin x x -<-, 所以()()32323211111122323232h x x ax x a x x ax x a x ax x <+-+-=+--<+-213632x x ax ⎛⎫=+- ⎪⎝⎭,所以3913310222h a a a ⎛⎫⎛⎫⎛⎫--<-++< ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭.从而()h x 在33,2a a ⎛⎫--- ⎪⎝⎭上有唯一零点,所以()h x 在(),a -∞-上有唯一零点,在(),a -+∞上没有零点,综上所述,当0a ≥时,()h x 有且仅有1个零点,故()g x 有且仅有1个零点.4.(2023届湖南省湘潭市部分学校高三上学期期末联考)已知函数()313f x mx kx =-,其中,m k ∈R .(1)当1k =时,求函数()f x 的单调区间;(2)已知函数()2ln g x x x =-(e 是自然对数的底数),若0k ∀>,曲线()y f x '=与曲线()y g x =都有唯一的公共点,求实数m 的取值范围.【过程详解】(1)因为1k =,所以()331133f x mx kx mx x =-=-,所以()2f x m x '=-,当0m ≤时,()20f x m x '=-≤,所以()f x 在R 上单调递减;当0m >时,令()0f x '<,得x <或x >;令()0f x ¢>,得x <<所以()f x 在(,-∞和)+∞上单调递减,在(上单调递增;综上:当0m ≤时,()f x 的单调递减区间为R ;当0m >时,()f x 的单调递减区间为(,-∞和)+∞,单调递增区间为(.(2)因为()313f x mx kx =-,所以()2f x m kx '=-,因为0k ∀>,曲线()y f x '=与曲线()y g x =都有唯一的公共点,所以0k ∀>,方程22ln m kx x x -=-有唯一解,即方程22ln kx x x m +-=有唯一解,令()()22ln 0x kx x x x ϕ=+->,则()222221kx x x kx x xϕ-+'=+-=,对于222y kx x =-+, 当1160k ∆=-≤,即116k ≥时,()0x ϕ'≥,故函数()x ϕ在R 上单调递增, 易知,当x 趋向于0时,ln y x =趋向于无穷小,2y kx x =-趋向于0,故()22ln x kx x x ϕ=+-趋向于无穷小;当x 趋向于无穷大时,ln y x =趋向于无穷大,2y kx x =-趋向于无穷大,故()22ln x kx x x ϕ=+-趋向于无穷大;所以()x ϕ的值域为R ,所以R m ∀∈,()x ϕ与y m =有且只有一个交点,满足题意; 当1160k ∆=->,即1016k <<时,2220kx x -+=有两个实根12,x x ,且12182x x k +=>,12116x x k =>, 若124x x <<,则当10x x <<或2x x >时,()0x ϕ'>,当12x x x <<时,()0x ϕ'<, 所以()x ϕ先增后减再增,存在一个极大值和一个极小值,要使22ln kx x x m +-=有唯一实数根,则m 大于()x ϕ的极大值或小于()x ϕ的极小值,记3x 为极大值点,则304x <<,()233332ln x kx x x m ϕ=+-<恒成立,又233220kx x -+=,即23322kx x =-,则()x ϕ的极大值为()()2333333333112ln 22ln 2ln 122x kx x x x x x x x ϕ=+-=--+=--, 令()()12ln 1042m x x x x =--<<,则()2102m x x '=->,故()m x 在()0,4上单调递增,故()()44ln 23m x m <=-,则()34ln 23x ϕ<-,故4ln 23m ≥-,记4x 为极小值点,则44x >,()244442ln x kx x x m ϕ=+->恒成立,又244220kx x -+=,即24422kx x =-,则()x ϕ的极小值为()44412ln 12x x x ϕ=--, 令()()12ln 142n x x x x =-->,则()2102n x x '=-<, 故()n x 在()4,+∞上单调递减,因为()4M ∀-<-,即4M >,取e 4M x =>,则()11e2ln ee 12e 122MMM M n M =--=--,所以()1e 3e 12M M n M M +=--, 令()()13e 142x h x x x =-->,则()13e 02xh x '=-<,所以()h x 在()4,+∞上单调递减,故()()41412e 102h x h <=-⨯-<,所以()e0Mn M +<,即()e Mn M <-,所以()n x 趋向于无穷小,则()4x ϕ趋向于无穷小,所以不存在R m ∈,使得24442ln kx x x m +->恒成立;若124<<x x ,记5x 为极大值点,则54x >,同理可得()255552ln x kx x x m ϕ=+-<恒成立,因为()n x 在()4,+∞上单调递减,所以()()44ln 23n x n <=-,则()54ln 23x ϕ<-,故4ln 23m ≥-,记6x 为极小值点,则64x >,同理可得不存在R m ∈,使得26662ln kx x x m +->恒成立;综上:要使0k ∀>,曲线()y f x '=与曲线()y g x =都有唯一的公共点,4ln 23m ≥-,即m 的取值范围为[)4ln 23,-+∞.5.(2023届北京市第五中学高三下学期3月检测)设函数()()23f x x x x a =-+,R a ∈(1)当9a =-时,求函数()f x 的单调增区间;(2)若函数()f x 在区间()1,2上为减函数,求a 的取值范围;(3)若函数在区间()0,2内存在两个极值点1x ,2x ,且()()()()2121f x f x f x f x ->+,求a 的取值范围. 【过程详解】(1)当9a =-时,239()()f x x x x =--,则2()3693(1)(3)f x x x x x ==+'---,由()0f x '>解得:1x <-或3x >,所以函数()f x 的单调增区间是(,1)-∞-,(3,)+∞.(2)函数2())3(f x x a x x =-+,则2()36f x x x a '=-+,因函数()f x 在区间()1,2上为减函数,则(1,2)x ∀∈,()0f x '≤成立,即(1,2)x ∀∈,2236036x x a a x x -+≤⇔≤-+,显然236x x -+在()1,2上单调递减,即(1,2)x ∀∈,2360x x -+>,则0a ≤,所以a 的取值范围是0a ≤.(3)由(2)知,2()36f x x x a '=-+,因函数()f x 在区间()0,2内存在两个极值点1x ,2x ,则()0f x '=在区间()0,2内有两个不等根1x ,2x ,即有(0)(2)0(1)30f f a f a '''==>⎧⎨=-+<⎩,解得0<<3a ,且有12122,3a x x x x +==,不妨令1202x x <<<,则123()())(f x x x x x '=--,当10x x <<或22x x <<时,()0f x '>,当12x x x <<时,()0f x '<,则()f x 在1x 处取得极大值1()f x ,在2x 取得极小值2()f x ,显然,12()()f x f x >, 由1212()()()()f x f x f x f x ->+两边平方得12()()0f x f x ⋅<,而2211112222()()()03)3(x x x a x x x f f x a x -+-+⋅=⋅<,即221122()()330x x a x x a +-+<-,整理得:22212121212121212()3()[()2]93()0x x x x x x a x x x x x x a x x a -+++-+-++<,把12122,3a x x x x +==代入上述不等式并整理得:2409a a -<,解得904a <<,综上得904a <<, 所以实数a 的取值范围是904a <<. 6.已知函数32()1f x x ax bx =+++(0,a b R >∈)有极值,且导函数()f x '的极值点是()f x 的零点. (1)求b 关于a 的函数关系式,并写出定义域; (2)求证:23b a >;(3)若(),()f x f x '这两个函数的所有极值之和不小于72-,求a 的取值范围.【过程详解】(1)因为32()1f x x ax bx =+++所以2()32f x x ax b '=++,令()()g x f x '=,所以()62g x x a =+' 令()0g x '=,解得3ax =- 由于当3a x >-时,()0g x '>,所以()()g x f x '=在3ax >-时为单调递增; 当3a x <-时,()0g x '<,所以()()g x f x '=在3ax <-时为单调递减;所以()f x '的极小值点为3ax =-; 由于导函数()f x '的极值点是原函数()f x 的零点,所以(03a f -=,即33102793a a ab-+-+=,所以2239a b a=+;因为()f x 有极值,所以2()32f x x ax b '=++有两个不等的实根,所以24120a b >﹣,即21093a a>-,解得3a >,所以223(3).9a b a a=+>(2)证明:由(13).a =+>设函数23()9t h t t =+,则22227()9t h t t -'=;当t ⎫∈+∞⎪⎪⎝⎭时,()0h t '>,所以()h t 在t ⎫∈+∞⎪⎪⎝⎭上单调递增;又因为3a >,所以2>>,故(h h >=>因此23b a >.(3)设()f x 的极值点是12,x x ,由(1)知,12122,33a b x x x x +=-=,所以22212469a b x x -+=所以323212111222()()11f x f x x ax bx x ax bx +=+++++++即2222121212121212()()()()()()2f x f x x x x x x x a x x b x x +=++-+++++整理得31242()()20273a abf x f x +=-+=所以函数()f x 的两个极值之和为0,()f x '的极值为2213339a a f b a a ⎛⎫-=-=-'+ ⎪⎝⎭, 设(),'()f x f x 这两个函数的所有极值之和为()a ϕ,所以213(),(3)9a a a a ϕ=-+>,而223()09a a a ϕ'=--<;即()a ϕ在()3,+∞上单调递减,而7(6)2ϕ=-,所以由())a ϕϕ≥(6,即得6a ≤; 因此a 的取值范围为(]3,6.7.已知()3222,f x x ax a x a =+-+∈R .(1)当a<0时,求函数()y f x =的单调减区间;(2)当0a =时,曲线()y f x =在相异的两点,A B 点处的切线分别为1l 和21,l l 和2l 的交点位于直线2x =上,证明:,A B 两点的横坐标之和小于4. 【过程详解】(1)()f x 的定义域为R ,()()()22323f x x ax a x a x a '=+-=-+,0a < ,()0f x '∴<的解集为,3a a ⎛⎫- ⎪⎝⎭,故函数()y f x =的单调减区间为,3a a ⎛⎫- ⎪⎝⎭.(2)证明:当0a =时,()32f x x =+,()23f x x '=,设()()331122,2,,2A x x B x x ++,12x x ≠, 点A 处切线方程为()()3211123y x x x x -+=-,点B 处切线方程为()()3222223y x x x x -+=-,故()()()()23231112223232xx x xx x x x -++=-++,解得()()2212121223x x x x x x x ++=+,故两切线交点的横坐标为()()2212121223x x x x x x +++,由题意()()22121212223xx x x x x ++=+()221212123x x x x x x ∴++=+,结合12x x ≠,()()221212121232x x x x x x x x +⎛⎫∴+-+=< ⎪⎝⎭,解得1204x x <+<.故A ,B 两点的横坐标之和小于4.8.(2024届江西省稳派上进教育高三上学期摸底考试)已知函数()321132f x x x ax =++,()1e ln x g x x x x -=+,()f x ',()g x '分别为()f x ,()g x 的导函数,且对任意的(]10,1x ∈,存在(]20,1x ∈,使()()122f x g x ''≤-.(1)求实数a 的取值范围;(2)证明:0x ∀>,有()()'≥g x f x .【过程详解】(1)因为()321132f x x x ax =++,所以()221124f x x x a x a ⎛⎫'=++=++- ⎪⎝⎭,所以()f x '在区间(]0,1上单调递增, 故()()max 12f x f a ''==+. 因为()1e ln x g x x x x -=+,所以()()111ee ln 11e ln 1x x x g x x x x x ---'=+++=+++.令()()11e ln 1x h x x x -=+++,则()()112e x h x x x-'=++, 又(]0,1x ∈,所以()0h x '>, 故()g x '在区间(]0,1上单调递增, 所以()()max 13g x g ''==.又对任意的(]10,1x ∈,存在(]20,1x ∈,使()()122f x g x ''≤-, 所以()()max max 2f x g x ''≤-, 即232a +≤-,解得1a ≤-, 故实数a 的取值范围为(],1-∞-. (2)令()1e-=-x s x x ,0x >,则()1e 1-'=-x s x .令()0s x '=,解得1x =,则当()0,1x ∈时,()0s x '<,()s x 单调递减; 当()1,x ∈+∞时,()0s x '>,()s x 单调递增,所以()()10s x s ≥=,即1e x x -≥(当且仅当1x =时,等号成立). 令()1ln 1F x x x =+-,则()22111x F x x x x-'=-=. 令()0F x '=,解得1x =,则当()0,1x ∈时,()0F x '<,()F x 单调递减;当()1,x ∈+∞时,()0F x '>,()F x 单调递增,所以()()10F x F ≥=,即1ln 1x x≥-+(当且仅当1x =时,等号成立),故11eln 1x x x x-+≥-+(当且仅当1x =时,等号成立). 又0x >,所以12e ln 1x x x x x x -+≥+-. 因为1a ≤-,所以221x x x x a +-≥++, 故12e ln x x x x x x a -+≥++,即()()'≥g x f x .9.已知函数()331f x x ax =++,[]1,1x ∈-,a R ∈,(1)若函数()f x 在区间[]1,1-上不单调,求a 的取值范围; (2)求()f x 的最大值;(3)若()1f x b +≤对任意[]1,1x ∈-恒成立,求a b +的取值范围. 【过程详解】(1)由题意可知,函数()f x 在()1,1-上有极值点, ()331f x x ax =++ ,则()233f x x a '=+,所以,函数()f x '在()1,0-上递减,在()0,1上递增, 所以,()()1330030f a f a ⎧=+>⎪⎨=<''⎪⎩,可得10a -<<; (2)若1a ≤-时,对任意的[]1,1x ∈-,()0f x '≤,()f x 在[]1,1-上递减,()130f a -=->,()123f a =+,()()()2222112391240f f a a a --=+-=+<⎡⎤⎡⎤⎣⎦⎣⎦, 所以,()()11f f <-,则()()max 13f x f a =-=-; 若0a ≥,对任意的[]1,1x ∈-,()0f x '≥,()f x 在[]1,1-上递增,()13f a -=-,()1230f a =+>,()()()2222112391240f f a a a --=+-=+>⎡⎤⎡⎤⎣⎦⎣⎦,所以,()()11f f >-,则()()max 123f x f a ==+;若10a -<<,由()0f x '>,可得1x -<<1x <;由()0f x '<,可得<<x则()f x 在(1,-上递增,在(上递减,在)上递增;()130f a -=->,(21f =-,21f=,()123f a =+.因为()()3331312f x f x x ax x ax +-=++--+=,所以,函数()f x 关于()0,1对称,())212121f f=-=+≥=,则(){}max a 21,2x 3m a f x -=+,若213a -<≤-,230a +≤,()()()()212321232330a a a --+=-+++=-+>,则(){}max 1m 3ax 22,21f x a -+=-+=; 若2134a -<≤-,230a +>,()()()22123101a --+=≥,则2123a -≥+,则()max 21x f -=;若104a -<<,230a +>,()()()22123101a --+=<+,则2123a -<+,则()max 23f x a =+.综上()max3,1121,14123,4a a f x a a a ⎧⎪-≤-⎪⎪=--<≤-⎨⎪⎪+>-⎪⎩;(3)先考虑必要性,若()1f x b +≤对任意[]1,1x ∈-恒成立, 首先必须满足()()max min 2-≤f x f x .①若1a ≤-,()()()max min 332622f x f x a a a -=--+=--≤,可得23a ≥-,不合乎题意; ②若0a ≥,()()()max min 323622f x f x a a a -=++=+≤,解得0a ≤,此时0a =;③若10a -<<时,(()()4211622f f f f a ⎧-=-≤⎪⎨--=+≤⎪⎩,解得0a ≤,此时0a ≤<.综上0a ≤,此时函数()f x在1,⎡-⎣上单调递增,在(上单调递减,在⎤⎦上单调递增. 若104a -≤≤,由(2)可知,()max 23f x a =+,则()()min 13f x f a =-=-,由()()maxmin11f x bf x b⎧+≤⎪⎨+≥-⎪⎩,则231141231b aa ab aa b++≤⎧⇒-+≤+≤--⎨-+≥-⎩,所以12,2a b⎡⎤+∈--⎢⎥⎣⎦若14a-≤,则()max21f x=-,()min21f x=,由()()maxmin11f x bf x b⎧+≤⎪⎨+≥-⎪⎩,则211211bb⎧-+≤⎪⎨+≥-⎪⎩,则222a ab a--++≤≤令12t⎡⎢⎣,则3232222t t a b t t--≤+≤--,对于函数()3222g t t t=-+-,()()2622310g t t t t t'=-=->对任意的12t⎡∈⎢⎣恒成立,所以,函数()g t在12⎡⎢⎣上单调递增,所以,()min122g t g⎛⎫==-⎪⎝⎭,对于函数()232h t t t=--,()2260h t t t'=--<对任意的12t⎡∈⎢⎣恒成立,所以,函数()h t在区间12⎡⎢⎣上单调递减,则()max1122h t h⎛⎫==-⎪⎝⎭,因此,12,2a b⎡⎤+∈--⎢⎥⎣⎦.综上:12,2a b⎡⎤+∈--⎢⎥⎣⎦.10.已知函数32()3f x x x ax b=-++在1x=-处的切线与x轴平行.(1)求a的值和函数()f x的单调区间;(2)若函数()y f x=的图象与抛物线231532y x x=-+恰有三个不同交点,求b的取值范围.【过程详解】(1)由已知得2()36f x x x a'=-+,∵在1x=-处的切线与x轴平行∴(1)0f'-=,解得9a=-.这时2()3693(1)(3)f x x x x x==+'---由()0f x'>,解得3x>或1x<-;由()0f x'<,解13x-<<.∴()f x 的单调增区间为(,1)-∞-和(3,)+∞;单调减区间为(1,3)-.(2)令23239()()1536322g x f x x x x x x b ⎛⎫=--+=-++- ⎪⎝⎭,则原题意等价于()g x 图象与x 轴有三个交点.∵2()3963(1)(2)g x x x x x '=-+=--, ∴由()0g x '>,解得2x >或1x <;由()0g x '<,解得12x <<.∴()g x 在1x =时取得极大值1(1)2g b =-;()g x 在2x =时取得极小值(2)1g b =-. 依题意得1210b b ⎧->⎪⎨⎪-<⎩,解得112b <<. 故b 的取值范围为1,12⎛⎫⎪⎝⎭.11.已知函数.0)0,(,2)(,)()(22<-∞∈=-=a x x a x g a x x x f 且 (1)(i )求函数)()(x g y x f y ==与的图象的交点A 的坐标;(ii )设函数)(),(x g y x f y ==的图象在交点A 处的切线分别为,,21l l 是否存在这样的实数a, 使得21l l ⊥若存在,请求出a 的值和相应的点A 坐标;若不存在,请说明理由.(2)记[)0,1)(-=在x f y 上最小值为F (a ),求aa F )(的最小值. 【过程详解】(I )(i )设点A 的坐标为022(,2)(),,(2222=++-=-a x a a x x a a x x y x 得由得.2,2;8,2,2,232231121a y a x a y a x a x a x ======时当时且当故函数)(x f y =与)(x g y =图象的交点A 坐标为)2,2(),8,2(33a a a a(ii ),43)(',)('22a ax x x f ax x g +-==若存在a,使得.21l l ⊥则当点A 坐标为,12(')2(',8,2(3-=⋅af ag a a 时又8)243(2)2(')2('4222a a a a a a a f a g -=+-⨯⋅⋅=⋅,则8,0,1844-=<=a a a 故又,此时点A 坐标为)22,28(44--当点A 坐标为,1)2(')2(',)2,2(3-=⋅a f a g a a 时又422210)843()2()2(')2('a a a a a a a f a g =+-⨯⋅⋅=⋅, 则1104-=a ,无解.综上,存在)22,28(,,844214--⊥-=A l l a 此时使得(2)令,2742,3.,30)('322321a x a ax x a x a x a x x f =+-====时当得整理得 )(274,03)(34(32x f y a y a x a x ===--与即直线图象另一交点横坐标.34a x =结合图象可得:(1)若;)1()1()()(,3,132min +-=-==-<-<a f x f a F a a时即 (2)若;274)3()()(,433,31343min a a f x f a F a a ===-<≤-≤-<时即 (3)若.)1()1()()(,043,1342min +-=-==<≤--≥a f x f a F a a 时即综上⎪⎪⎩⎪⎪⎨⎧⎪⎭⎫⎢⎣⎡--∈⎪⎭⎫⎢⎣⎡---∞∈+-=43,3,2740,43)3,(,)1()(32a a a a a F所以⎪⎪⎩⎪⎪⎨⎧⎪⎭⎫⎢⎣⎡--∈⎪⎭⎫⎢⎣⎡---∞∈---=43,3,2740,43)3,(,21)(2a a a a a a a F当,1212)1()(21)(,0,43)3,(≥--+-=---=⎪⎭⎫⎢⎣⎡---∞∈a a a a a a F a 时且当43-=a 时取到“=”;当⎪⎭⎫⎢⎣⎡--∈43,3a 时,函数2274)(a a a F =单调递减,此时.121)(>a a F 综上,.121)((min =a a F 12.已知函数32()1f x x ax bx =-+++在1x =时有极小值. (1)当4a =时,求()f x 在0x =处的切线方程;(2)求()f x 在33,2⎡⎤-⎢⎥⎣⎦上的最小值.【过程详解】 (1)因为函数32()1f x x ax bx =-+++在1x =时有极小值, 故2()32f x x ax b '=-++,(1)320f a b '=-++=,解得:23a b +=. 当4a =时,5b =-,故32()451f x x x x =-+-+,2()385f x x x '=-+-, 则(0)1,(0)5f f '==-,则()f x 在0x =处的切线方程为:15(0)y x -=--,整理得:510x y +-=. 故()f x 在0x =处的切线方程为510x y +-=.(2)由(1)得2()32f x x ax b '=-++,且23a b +=, 故2()3(3)(1)(332)f x x b x b x x a '=-+-+=--+-, 令()0f x '=,解得12231,3a x x -==, 因为32()1f x x ax bx =-+++,所以(1)3f a =-,(3)1519f a -=+,3317(248f a =-+.又函数()f x 在1x =时有极小值,当2313a -<时,23(,3a x -∈-∞或(1,)+∞,()0f x '<,函数()f x 单调递减, 当23(,1)3a x -∈时,()0f x '>,函数()f x 单调递增, 故函数()f x 在11x =有极大值,与题意不符,故12x x <,即2313a ->,即3a >,所以,当(,1)x ∞∈-或23(,)3a -+∞,()0f x '<,函数()f x 单调递减,当23(1,3a x -∈时,()0f x '>,函数()f x 单调递增, 故函数()f x 在2233a x -=有极大值. 当23332a -≥,即154a ≥时,函数()f x 在区间[)3,1-单调递减,在区间31,2⎛⎤⎥⎝⎦单调递增,故在区间33,2⎡⎤-⎢⎥⎣⎦上得最小值为min ()(1)3f x f a ==-, 当233132a -<<,即1534a <<时,函数()f x 在区间[)3,1-和233,32a -⎛⎤⎥⎝⎦单调递减,在区间231,3a -⎛⎫ ⎪⎝⎭单调递增,且3317(248f a =-+,(1)3f a =-, 37(1)(284a f f -=-. 故当732a <≤时,3(1)()02f f -≥,min 3176()()28a f x f -==, 当71524a <<时,3(1)(02f f -<,min ()(1)3f x f a ==-. 综上所述:当732a <≤时,函数()f x 在33,2⎡⎤-⎢⎥⎣⎦上的最小值为1768a -, 当72a <时,函数()f x 在33,2⎡⎤-⎢⎥⎣⎦上的最小值为3a -. 13.已知函数()3222312f x x ax a x =+-,其中a ∈R .(1)求函数()f x 的单调区间;(2)设函数()f x 在区间2,2a a ⎡⎤⎣⎦上的最大值为()g a ,证明:()32g a <.【过程详解】 (1)因为()3222312f x x ax a x =+-,R x ∈,所以()()()22661262f x x ax a x a x a '=+-=+-.①若0a >,当2a x a -<<时,()0f x '<;当2x a <-或x a >时,()0f x '>.即()f x 在()2,a a -上单调递减,在(),2a -∞-和(),a +∞上单调递增;②若0a =,恒有()0f x '≥.即()f x 在定义域R 上单调递增;③若0a <,当2a x a <<-时,()0f x '<;当x a <或2x a >-时,()0f x '>.即()f x 在(),2a a -上单调递减,在(),a -∞和()2,a -+∞上单调递增;综上,当0a >时,函数()f x 的单调递减区间为()2,a a -,单调递增区间为(),2a -∞-,(),a +∞; 当0a =时,函数()f x 的单调递增区间为(),-∞+∞;当0a <时,函数()f x 的单调递减区间为(),2a a -,单调递增区间为(),a -∞,()2,a -+∞.(2)由题意,有22a a <,∴()0,2a ∈.由(1)知①当12a ≤<时,()f x 在2,2a a ⎡⎤⎣⎦上单调递增.∴()()32432g a f a a ==<.②当01a <<时,()f x 在)2,a a ⎡⎣上单调递减,在(],2a a 上单调递增. 由()324f a a =,01a <<,∴()024f a <<;又()()26544223122312f a a a a a a a =+-=+-.∵01a <<,∴223120a a +-<.∴()20f a <. ∴()()324432g a f a a ==<<.综上,有()32g a <.14.已知函数()3221f x x ax a x =---,其中0a <.(1)求曲线()y f x =在点()(),a f a 处的切线方程;(2)若存在实数t ,使得不等式()0f x <的解集为(),t -∞,求a 的取值范围.【过程详解】由()3221f x x ax a x =---得()2232f x x ax a '=--.(1)所以()0f a ¢=.又因为()31f a a =--.故所求的切线方程为31y a =--.(2)因为()()()22323f x x ax a x a x a =--+=-'令()0f x '=,得13a x =-,2x a =, 此时()f x ',()f x 随x 的变化如下:由题意,要想存在实数t ,使得不等式()0f x <的解集为(),t -∞只需()003f a a f ⎧>⎪⎨⎛⎫-> ⎪⎪⎝⎭⎩或()003f a a f ⎧<⎪⎨⎛⎫-< ⎪⎪⎝⎭⎩ 因为3510327a f a ⎛⎫-=-< ⎪⎝⎭, 所以()310f a a =--<所以a 的取值范围为()1,0-.15.已知函数()()33R f x x ax a a =-+∈.(1)讨论函数()f x 的单调性;(2)若函数()f x 在区间[]0,3上的最大值与最小值之差为()g a ,求()g a 的最小值.【过程详解】 (1)因为()()33f x x ax a a R =-+∈,所以()()22'333f x x a x a =-=-.①当0a ≤时,()'0f x ≥恒成立,()f x 在R 上单调递增;②当0a >时,(),x ∈-∞+∞ 时,()'0f x >;(x ∈时,()'0f x <; 故()f x在(,-∞和)+∞上单调递增,在(上单调递减. (2)由(1)可知:①当0a ≤时,()f x 在[]0,3上单调递增,()()()30279g a f f a =-=-;②3≥,即9a ≥时,()f x 在[]0,3上单调递减,()()()0927g a f f a a =-=-; ③当03<<,即09a <<时,()f x在⎡⎣上单调递减,在⎤⎦上单调递增, 于是()min 2f x f a ==-+,又()0f a =,()3278f a =-.故当0<<3a 时,()2792g a a =-+39a ≤<时,()2g a =综上可得:279,027923()29927,9a a a a g a a a a -≤⎧⎪-+<<⎪=⎨≤<⎪⎪-≥⎩,当0<<3a 时,()2792g a a =-+x 则0x <<,设23()2792h x x x =-+,2()6186(3)0h x x x x x '=-=-<,所以()h x 在上递减,又x ,所以()g a 在(0,3)上递增,所以()g a 在(3),-∞上递减,在(3,)+∞上递增,所以故()g a 的最小值为()3g =16.已知函数3211()()32f x x ax a =-∈R 在[]0,1上的最小值为16-. (1)求a 的值; (2)讨论函数()()2()g x f x x b b =-+∈R 的零点个数.【过程详解】(1)由3211()32f x x ax =-,2()()f x x ax x x a =--'=, 当0a …时,()'f x 在[0,)+∞上恒大于等于0,所以()f x 在[0,1]上单调递增,min ()(0)0f x f ==,不合题意;当01a <<时,则[0,]x a ∈时,()0f x '<,()f x 单调递减;[,1]x a ∈时,()0f x '>,()f x 单调递增, 所以333min 111()()326f x f a a a a ==-=-,31166a -=-, 所以1a =,不满足01a <<;当1a =时,在[0,1]上,()0f x '…且不恒为0,所以()f x 在[0,1]上单调递减,min 111()(1)326f x f ==-=-,适合题意; 当1a >时,在[0,1]上,()0f x '<,所以()f x 在[0,1]上单调递减,min 111()(1)326f x f a ==-=-,所以1a =,不满足1a >; 综上,1a =.(2)由(1)3211()232g x x x x b =--+,所以3211232b x x x =-++, 令3211()232h x x x x =-++,则2()2(2)(1)h x x x x x =-++=--+', 所以(2)0,(1)0h h ''=-=,且当1x <-时,()0h x '<;当12x -<<时,()0h x '>;当2x >时,()0h x '<,所以()()11712326h x h =-=+-=-极小,()()11102844323h x h ==-⨯+⨯+=极大, 如图:当76b<-或103b>时,函数()g x有1个零点;当76b=-或103b=时,函数()g x有2个零点;当71063b-<<时,函数()g x有3个零点.。
2025届高考数学复习:压轴好题专项(用导数研究函数的最值)练习(附答案)

2025届高考数学复习:压轴好题专项(用导数研究函数的最值)练习1.(2024届江苏省镇江市高三上学期阶段检测)已知函数()()2e xf x x a x =--.(1)若[]1,0,1a x =∈,求函数()f x 的最值;(2)若Z a ∈,函数()f x 在[0,)x ∞∈+上是增函数,求a 的最大整数值.2.(2023届江苏省南通市如皋市2高三上学期模拟)设*n ∈N ,函数()ln n x f x x =,函数()()e ,0,x n g x x x∞=∈+ (1)求函数g (x )的单调区间和最值;(2)若当3n =时,对任意的1x ,()20,x ∈+∞,都有()()12f x t g x ≤≤成立,求实数t 的取值范围.3.(2024届四川省成都市高三上学期开学考试)已知函数()e xf x ax =-,a ∈R .(1)讨论()f x 的单调性;(2)若当1x ≥-时,()f x ax >,求a 的取值范围.(3)若存在实数a 、b ,使得()2f x ax b ax +≥-恒成立,求a b -的最小值.4.(2024届百师联盟高三上学期开学摸底联考)已知函数()2ln 1f x x mx x =-+,m ∈R 且0m ≠.(1)当1m =时,求曲线()y f x =在点()()1,1f 处的切线方程; (2)若关于x 的不等式()2ef x x ≥恒成立,其中e 是自然对数的底数,求实数m 的取值范围. 5.(2024届宁夏银川一中高三上学期月考)已知函数()()212ln 1R 2f x x mx m =-+∈.(1)当1m =时,证明:()1f x <;(2)若关于x 的不等式()()2f x m x <-恒成立,求整数m 的最小值.6.(2024届湖北省腾云联盟高三上学期联考)已知函数2()(4)ln 2f x x x x ax =-++-. (1)证明:()f x 有唯一的极值点;(2)若()0f x ≥恒成立,求实数a 的取值范围.7(2023届黑龙江省哈尔滨市高三上学期月考)设函数322()33f x x ax b x =-+ (1)若1a =,0b =,求曲线()y f x =在点()()1,1f 处的切线方程;(2)若0a b <<,不等式1ln 1x k f f x x +⎛⎫⎛⎫> ⎪ ⎪-⎝⎭⎝⎭对任意()1,x ∈+∞恒成立,求整数k 的最大值.8.(2023届河南省南阳市高三上学期期中)已知()21e 12xf x x x =---. (1)讨论函数()f x 的单调性;(2)设()f x '是()f x 的导数.当[]1,1x ∈-时,记函数()f x 的最大值为M ,函数()f x '的最大值为N .求证:M N <.9.(2023届福建省三明市高三上学期期末)已知函数()1sin e x x f x x -=+,ππ,2x ⎛⎫∈- ⎪⎝⎭.(1)求证:()f x 在()ππ,2-上单调递增;(2)当()π,0-时,()sin e cos sin xf x x x k x --⎡⎤⎣⎦≤恒成立,求k 的取值范围. 10.(2023届河南省开封市模拟)设函数()()22e x f x x x =-,()2e ln eg x x a x =-.(1)若函数()g x 在()e,+∞上存在最大值,求实数a 的取值范围; (2)当2a =时,求证:()()f x g x >.11.已知函数()()e ,ln 1xh x x mx g x x x =-=++.(1)当1m =时,求函数()h x 的单调区间:(2)若()()h x g x …在()0,x ∈+∞恒成立,求实数m 的取值范围. 12.已知()ln f x x ax =+(a R ∈) (1)讨论()f x 的单调性;(2)当1a =时,若()()1f x k x b ≤++在()0,∞+上恒成立,证明:221k b k +--的最小值为1e -+.参考答案【例1】(2024届陕西省西安中学高三上学期月考)已知函数()()ln 20f x x ax a =--≠. (1)讨论函数()f x 的单调性;(2)若0a >时函数()f x 有最大值M ,且4M a >-,求实数a 的取值范围. 【过程详解】(1)()f x 的定义域为()0,∞+, 由()()ln 20f x x ax a =--≠可得()1f x a x'=-, 当0a <时,()0f x ¢>,所以()f x 在()0,∞+上单调递增, 当0a >时,令()0f x '=,得1x a=, 所以当10,x a ⎛⎫∈ ⎪⎝⎭时,()0f x ¢>,()f x 单调递增;当1,x a ⎛⎫∈+∞ ⎪⎝⎭时,()0f x '<,()f x 单调递减,综上所述,当0a <时,()f x 在()0,∞+上单调递增;当0a >时,()f x 在10,a ⎛⎫ ⎪⎝⎭上单调递增,在1,a ⎛⎫+∞ ⎪⎝⎭上单调递减.(2)当0a >时,()f x 在10,a ⎛⎫ ⎪⎝⎭上单调递增,在1,a ⎛⎫+∞ ⎪⎝⎭上是单调递减,所以当1x a=时,()f x 取得极大值,也是最大值, 即()max 1111ln 2ln 3ln 3f x f a a a a a a ⎛⎫==-⨯-=-=-- ⎪⎝⎭,因此有ln 34a a -->-,得ln 10a a +-<, 设()ln 1g a a a =+-, 则()110g a a'=+>, 所以()g a 在()0,∞+上单调递增,又()10g =,所以()()1g a g <,得01a <<, 故实数a 的取值范围是()0,1.【例2】(2024届宁夏吴忠市高三上学期月考)已知函数()e xf x ax =+在()()0,0f 处的切线与直线l :240x y -+=垂直.(1)求()f x 的单调区间;(2)若对任意实数x ,()232f x x b ≥--+恒成立,求整数b 的最大值.【过程详解】(1)由()e xf x a '=+,得()01k f a '==+,又切线与直线l :240x y -+=垂直,所以2k =-,即3a =-.所以()e 3xf x '=-,令()0f x '=,得ln3x =,当ln3x <时,()0f x '<,()f x 单调递减; 当ln3x >时,()0f x ¢>,()f x 单调递增.所以()f x 的单调递减区间为(),ln 3-∞,单调递增区间为()ln 3,+∞.(2)对任意实数x ,()232f x x b ≥--+恒成立,即对任意实数2,e332xx x x b +-+≥恒成立.设()2e 33x g x x x =+-+,即()min 12b g x ≤. ()e 23x g x x =+-',令()()e 23x h x g x x '==+-,所以()e 20'=+>xh x 恒成立,所以()e 23x g x x =+-'在R 上单调递增.又1202g ⎛⎫'=-< ⎪⎝⎭,()1e 10g '=->,所以存在01,12x ⎛⎫∈ ⎪⎝⎭,使得()00g x '=,即00e 230xx +-=,所以00e 32xx =-.当()0,x x ∈-∞时,()00g x '<,()g x 单调递减;当()0,x x ∈+∞时,()00g x '>,()g x 单调递增.所以()()02000min e 33xg x g x x x ==+-+2220000005132335624x x x x x x ⎛⎫=-+-+=-+=-- ⎪⎝⎭,当01,12x ⎛⎫∈ ⎪⎝⎭时,200152564x x <-+<,所以()01151,28g x ⎛⎫∈ ⎪⎝⎭,由题意知()012b g x ≤且b ∈Z所以1b ≤,即整数b 的最大值为1.【例3】(2024届江苏省南通市如皋市高三上学期诊断测试)已知函数()ln e xf x x x x=--.(1)求()f x 的最大值;(2)证明:()313e xx x f x x++≥-【过程详解】(1)()ln e xf x x x x=--,定义域为(0,)+∞,则21e (1)()1x x f x x x -'=--2(1)(e )x x x x --=, 令()(),e 1e 1x xg x x g x '=--=-,因为()()0,,0x g x '∈+∞>恒成立,所以()g x 在()0,+∞上单调递增, 所以()()0=0g x g >,即当0x >时,e 1x x x >+>,令()0f x ≥',可得01x <≤,得()f x 在(]0,1上单调递增,在(1,)+∞上单调递减, 所以max ()(1)1e f x f ==-.(2)要证3e 13()xx x f x x++≥-,即证321ln x x x -+≥,令()()11ln 1,h x x x h x x'=--=-令0()h x '≥得1x ≥,即()h x 在()0,1上单调递减,在()1,+∞上单调递增, ()()1=0h x h ≥,即1ln x x -≥,即欲证321ln x x x -+≥,只需证321 1.x x x -+≥-也就是证明3320.(*)x x -+≥ 设3()32(0)x x x x ϕ=-+>,则2()33x x ϕ'=-,令()0x ϕ'=,得 1.x = 当(0,1)x ∈时,()0x ϕ'<;当(1,)x ∈+∞时,()0.x ϕ'>∴当1x =时,()ϕx 取到最小值(1)0.ϕ=故(*)式成立,从而3e13()x x x f x x++≥-成立.【例4】(2023届北京名校高三二轮复习检测)已知函数()()3222213x x x a x f =-+-+,其中R a ∈. (1)若2a =,求曲线()y f x =在点()()1,1f 处的切线方程; (2)求()f x 在区间[]2,3上的最大值和最小值.【过程详解】(1)当2a =时,322()213f x x x =-+,求导得2()24f x x x '=-,则(1)2f '=-,而1(1)3f =-,所以曲线()y f x =在点(1,(1))f 处的切线方程为12(1)3y x +=--,即6350x y +-=. (2)依题意,22()2422(1)f x x x a x a '=-+-=--,而[2,3]x ∈,则2[2,8]2(1)x ∈-, ①当2a ≤时,()0f x '≥,当且仅当2,2a x ==时取等号,函数()f x 在[]2,3上单调递增, 则min 7()(2)23f x f a ==-,max ()(3)73f x f a ==-; ②当8a ≥时,()0f x '≤,当且仅当8,3a x ==时取等号,函数()f x 在[]2,3上单调递减, 则min ()(3)73f x f a ==-,max 7()(2)23f x f a ==-;③当28a <<时,函数()f x '在[]2,3上单调递增,由()0f x '=,得1x =,当[2,1x ∈时,()0,()'<f x f x 递减,当(1x ∈时,()0,()'>f x f x 递增,min 513()(3f a x f -==-, 由714(3)(2)(73)(2)033f f a a a -=---=-≥,得1423a <≤,max ()(3)73f x f a ==-,由14(3)(2)03f f a -=-<,得1483a <<,max 7()(2)23f x f a ==-, 所以当2a ≤时,()f x 的最小值是723a -,最大值是73a -;当1423a <≤时,()f x 的最小值是533a --73a -;当1483a <<时,()f x 的最小值是53a -723a -; 当8a ≥时,()f x 的最小值是73a -,最大值是723a -.四、跟踪检测1.(2024届江苏省镇江市高三上学期阶段检测)已知函数()()2e xf x x a x =--.(1)若[]1,0,1a x =∈,求函数()f x 的最值;(2)若Z a ∈,函数()f x 在[0,)x ∞∈+上是增函数,求a 的最大整数值.【过程详解】(1)若1a =,则函数()()21e x f x x x =--,()()()e 1e 2e 2x x xf x x x x =+--=-'.令()0f x '=,则0x =或ln 2x =,由于[]0,1x ∈,因而当()0,ln2x ∈时.()()0,f x f x '<单调递减, 当()ln2,1x ∈时.()()0,f x f x '>单调递增,所以()f x 的最小值为()()2ln21ln21f =---,最大值为()()011f f ==-(2)()()()e e 21e 2x x xf x x a x x a x =+--=--'+,由()f x 在[0,)x ∞∈+上是增函数, 得()0f x '≥在[0,)x ∞∈+上恒成立,即()[)1e 200,xx a x x ∞+--≥∈+,,分离参数得[)210e xxa x x ∞-≥-∈+,, 设()2e x x g x x =-,则()2222e 1e e xx xx x g x ---=='-, ()0g x '=,即22e 0x x --=设()22e xh x x =--,由于()1010102h h ⎛⎫=>=< ⎪⎝⎭,,因而方程22e 0x x --=在10,2⎛⎫⎪⎝⎭上有解,设为0x ,则00e 22xx =-,且当()00,x x ∈时,()0g x '>,当()0,x x ∈+∞时()0g x '<,,所以()g x 的最大值为()02000000002e 11x x x x g x x x x x =-=-=--.因而20011x a x -≥-,即20000113111x a x x x ≤+=++---, 又00110,11,22x x ⎛⎫⎛⎫∈-∈-- ⎪ ⎪⎝⎭⎝⎭,, 又001131,112x x ⎛⎫++-∈ ⎪-⎝⎭所以a 的最大整数值为0.2.(2023届江苏省南通市如皋市2高三上学期模拟)设*n ∈N ,函数()ln n x f x x =,函数()()e ,0,xn g x x x∞=∈+(1)求函数g (x )的单调区间和最值;(2)若当3n =时,对任意的1x ,()20,x ∈+∞,都有()()12f x t g x ≤≤成立,求实数t 的取值范围. 【过程详解】(1)()()e ,0,xn g x x x ∞=∈+,则()()1e x n x n g x x+='-,令()0g x '=,解得x n =, 当x 变化时,()g x '与()g x 的变化如下表所示:所以函数()g x 在区间()0,n 上为单调递减,区间(),n +∞上为单调递增, 所以()mine nn g x n=,无最大值. (2)当3n =时,函数()()33ln e ,,0xx f x g x x x x==>,由题意,若对任意的1x ,()20,x ∈+∞,都有()()12f x t g x ≤≤恒成立, 只需当()0,x ∞∈+时,()()max min f x t g x ≤≤, 因为()413ln xf x x-'=,令()0f x '=,解得13e x =, 当x 变化时,f (x )与f (x )的变化如下表所示:所以()13max1e 3ef x f ⎛⎫== ⎪⎝⎭,又因为()()4e 3x x g x x-'=,令()0g x '=,解得3x =, 由(1)知所以函数()g x 在区间()0,3上为单调递减,区间()3,+∞上为单调递增, 所以()()3mine 327g x g ==, 综上所述,得31e 3e 27t ≤≤. 3.(2024届四川省成都市高三上学期开学考试)已知函数()e xf x ax =-,a ∈R .(1)讨论()f x 的单调性;(2)若当1x ≥-时,()f x ax >,求a 的取值范围.(3)若存在实数a 、b ,使得()2f x ax b ax +≥-恒成立,求a b -的最小值.【过程详解】(1)解:因为()e x f x ax =-,其中x ∈R ,则()e xf x a '=-,若0a ≤,则()0f x >恒成立,此时()f x 的增区间为(),-∞+∞,无减区间; 若0a >,由()0f x '<,得ln x a <,由()0f x ¢>,得ln x a >, 此时函数()f x 的减区间为(),ln a -∞,增区间为()ln ,a +∞.综上所述,当0a ≤时,函数()f x 的增区间为(),-∞+∞,无减区间; 当0a >时,函数()f x 的减区间为(),ln a -∞,增区间为()ln ,a +∞. (2)解:由()f x ax >得2e x ax <, 当0x =时,显然成立;当[)1,0x ∈-时,20x <,可得e 2x a x >,令()e 2x g x x =,则()()2e 102x x g x x -=<',则()g x 在[)1,0-上递减,故()()112e g x g ≤-=-,此时12ea >-; 当()0,x ∈+∞时,20x >,可得e 2xa x <,令()()2e 102x x g x x -=='得1x =, 由()0g x '<,可得01x <<,由()0g x '>,可得1x >. 此时,函数()g x 在()0,1上单调递减,在()1,+∞上单调递增, 所以,()g x 在1x =处取得最小值,即()()e12g x g ≥=,此时e 2a <. 综上,a 的取值范围是1e ,2e 2⎛⎫- ⎪⎝⎭.(3)解:当a<0时,对任意的x <, ()()221e 111111x bf x ax ax a b b b a-=+<+<+⋅=--≤--=, 所以对任意的实数b ,()f x b ≥不可能恒成立;当0a =时,()e xf x =,要使()f x b ≥恒成立,只需0b ≤,所以0a b b -=-≥,当0a >时,由题意,()e 2xf x ax '=+,因为函数e x y =、2y ax =在R 上均为增函数,所以()f x '在R 上单调递增,因为121e 102a f a -⎛⎫'-=-< ⎪⎝⎭,()010f '=>,所以存在唯一的01,02x a ⎛⎫∈- ⎪⎝⎭,使得()00f x '=,由()0f x '<可得0x x <,由()0f x ¢>可得0x x >,所以()f x 在()0,x -∞上单调递减,在()0,x +∞上单调递增,从而()()0200min e x f x f x ax ==+,因为()f x b ≥恒成立,所以020e x ax b +≥,故020e x a b a ax -≥--①,又()000e 20x f x ax '=+=,所以0e 2x a x =-,代入不等式①可得0002000e e e 22x x x a b x x x ⎛⎫-≥--- ⎪⎝⎭,整理得:0200021e 2x x x a b x ---≥, 设()()221e 02x x x g x x x --=<,则()()()23222111e e 22x x x x x x x g x x x -+--+'==, 所以()010g x x '>⇔-<<,()01g x x '<⇔<-, 故()g x 在(),1-∞-上单调递减,在()1,0-上单调递增,从而()()11e g x g ≥-=-,所以()01e a b g x -≥≥-,当12e a =,32e b =时取等号,综上所述,a b -的最小值为1e-.4.(2024届百师联盟高三上学期开学摸底联考)已知函数()2ln 1f x x mx x =-+,m ∈R 且0m ≠.(1)当1m =时,求曲线()y f x =在点()()1,1f 处的切线方程; (2)若关于x 的不等式()2ef x x ≥恒成立,其中e 是自然对数的底数,求实数m 的取值范围. 【过程详解】(1)由题,当1m =时,()2ln 1f x x x x =-+,()2ln 1f x x x '=--,()11f '=,()12f =,所以切线方程为21y x -=-,化简得10x y -+=,即曲线()f x 在点()()1,1f 处的切线方程为10x y -+=.(2)()2ef x x ≥,即22ln 1e x mx x x -+≥,即12ln 0e x m x x +--≥在()0,∞+上恒成立, 令()12ln eg x x m x x =+--,则()222111m x mx g x x x x --'=--=. 对于21y x mx =--,240m ∆=+>,故其必有两个零点,且两个零点的积为1-,则两个零点一正一负,设其正零点为()00,x ∈+∞,则20010x mx --=,即001m x x =-, 且在()00,x 上时210,y x mx =--<则()0g x '<,此时()g x 单调递减,在()0,x +∞上,210,y x mx =-->()0g x '>,此时()g x 单调递增,因此当0x x =时,()g x 取最小值,故()00g x ≥,即00000112ln 0e x x x x x ⎛⎫+---≥ ⎪⎝⎭. 令()112ln e h x x x x x x ⎛⎫=+--- ⎪⎝⎭,则()2222111111ln 11ln h x x x x x x x ⎛⎫⎛⎫⎛⎫'=--+--=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 当()0,1x ∈时,()0h x '>,当()1,x ∈+∞时,()0h x '<,则()h x 在()0,1上单调递增,在()1,+∞上单调递减,又()1e 0e h h ⎛⎫== ⎪⎝⎭,故01,e e x ⎡⎤∈⎢⎥⎣⎦, 显然函数001m x x =-在1,e e ⎡⎤⎢⎥⎣⎦上是关于0x 的单调递增函数,则11e,e ee m ⎡⎤∈--⎢⎥⎣⎦, 所以实数m 的取值范围为11e,00e ,e e ⎡⎫⎛⎤--⎪ ⎢⎥⎣⎭⎝⎦U 5.(2024届宁夏银川一中高三上学期月考)已知函数()()212ln 1R 2f x x mx m =-+∈. (1)当1m =时,证明:()1f x <;(2)若关于x 的不等式()()2f x m x <-恒成立,求整数m 的最小值.【过程详解】(1)当1m =时,()212ln 1(0)2f x x x x =-+>, ()222(0)x f x x x x x-'∴=-=>, 令()0f x '=,得x ,当(x ∈时,()()0,f x f x '>单调递增;当)x ∈+∞时,()()0,f x f x '<单调递减, 所以()f x在x 处取得唯一的极大值,即为最大值,所以max 1()21ln22f x f ==⨯+=, 所以()ln2f x ≤,而ln2lne 1<=,所以()1f x <.(2)令()()()()2122ln 212G x f x m x x mx m x =--=-+-+. 则()()()22222mx m x G x mx m x x-+-+=-+-='. 当0m ≤时,因为0x >,所以()0G x '>,所以()G x 在()0,∞+上单调递增,又因为()31302G m =-+>. 所以关于x 的不等式()0G x <不能恒成立;当0m >时,()()21m x x m G x x⎛⎫-+ ⎪'⎝⎭=-. 令()0G x '=,得2x m =,所以当20,x m ⎛⎫∈ ⎪⎝⎭时,()0G x '>; 当2,x m ⎛⎫∈+∞ ⎪⎝⎭时,()0G x '<. 因此函数()G x 在20,m ⎛⎫ ⎪⎝⎭上单调递增,在2,m ⎛⎫+∞ ⎪⎝⎭上单调递减. 故函数()G x 的最大值为222ln 2ln21G m m m ⎛⎫=-+- ⎪⎝⎭. 令()22ln 2ln21h m m m=-+-, 因为()()()1112ln20,20,32ln22ln303h h h =+>==--<, 又因为()h m 在()0,∞+上单调递减,所以当3m ≥时,()0h m <.所以整数m 的最小值为3.6.(2024届湖北省腾云联盟高三上学期联考)已知函数2()(4)ln 2f x x x x ax =-++-.(1)证明:()f x 有唯一的极值点;(2)若()0f x ≥恒成立,求实数a 的取值范围.【过程详解】(1)证明:()f x 定义域为()0,∞+,由2()(4)ln 2f x x x x ax =-++-,得()44ln 2ln 21x f x x x a x x a x x -=+++=-+++', 令()()4ln 21x f x x x a x ϕ==-+++',则()21420x x xϕ'=++>, 所以()f x '在()0,∞+上单调递增,因为()4ln 1f x x a x <-++',且4ln 1R x a x ⎛⎫-++∈ ⎪⎝⎭,()ln 21f x x x a >+++',且当(1,)x ∈+∞时,()ln 21(3,)x x a a +++∈++∞,所以()f x '的值域为R ,所以()f x '有唯一的零点()00,x ∈+∞,使得()00f x '=,当()00,x x ∈时,()0f x '<,()f x 单调递减;当()0,x x ∈+∞时,()0f x ¢>,()f x 单调递增,所以()f x 有唯一的极值点,(2)由(1)知,()f x 在0x x =取得极小值点,也是最小值点,由()00f x '=得0004ln 21a x x x =--+-, 所以()()2000004ln 2f x x x x ax =-++-()2000000044ln ln 212x x x x x x x ⎛⎫=-++--+-- ⎪⎝⎭ ()()20000004ln 24ln 21x x x x x x =---+=--+-,当001x <≤时,04ln 0x -≥,()()00210x x -+-≥,所以()00f x ≥;当01x >时,04ln 0x -<,()()00210x x -+-<,所以()00f x <,因为()00f x ≥,所以001x <≤设()()4ln 2101h x x x x x=--+-<≤,则()()2142001h x x x x '=---<<≤ 所以()h x 在(0,1]上单调递减,所以()()011a h x h =≥=,即1a ≥7(2023届黑龙江省哈尔滨市高三上学期月考)设函数322()33f x x ax b x =-+(1)若1a =,0b =,求曲线()y f x =在点()()1,1f 处的切线方程;(2)若0a b <<,不等式1ln 1x k f f x x +⎛⎫⎛⎫> ⎪ ⎪-⎝⎭⎝⎭对任意()1,x ∈+∞恒成立,求整数k 的最大值. 【过程详解】(1)当1a =,0b =时,32()3f x x x =-,所以(1)2f =-,即切点为()1,2P - 因为2()36f x x x '=-,所以(1)363f '=-=-,所以切线方程为()231y x +=--,即31y x =-+,(2)22()363f x x ax b '=-+,由0a b <<,所以22363636()()0a b a b a b ∆=-=+-<, 所以函数()f x 在R 上单调递增 不等式1ln 1x k f f x x -⎛⎫⎛⎫> ⎪ ⎪-⎝⎭⎝⎭1ln (1ln )11x k x x k x x x --⇔>⇔>--,对()1,x ∈+∞恒成立, 构造(1ln )()1x x h x x -=-,22(2ln )(1)(ln )ln 2()(1)(1)x x x x x x x h x x x +--+--'==--, 构造()ln 2g x x x =--,11()1x g x x x-'=-=,对()1,x ∈+∞有()0g x '>, 所以()ln 2g x x x =--在()1,x ∈+∞递增,()31ln 30g =-<,()42ln 40g =->,所以0(3,4)x ∃∈,()000ln 20g x x x =--=,所以()01,x x ∈,()0g x <,即()0h x '<,()h x 在()01,x 递减,()0,x x ∈+∞,()0g x >,即()0h x '>,()h x 在()0,x +∞递增,所以()()00min 001ln ()1x x h x h x x +==-,结合00ln 2x x =-,故min 0()(3,4)h x x =∈, 所以(1ln )1x x k x +<-对(1,)x ∈+∞恒成立min ()k h x ⇔<,故3k ≤, 所以整数k 的最大值为3;8.(2023届河南省南阳市高三上学期期中)已知()21e 12x f x x x =---. (1)讨论函数()f x 的单调性;(2)设()f x '是()f x 的导数.当[]1,1x ∈-时,记函数()f x 的最大值为M ,函数()f x '的最大值为N .求证:M N <.【过程详解】(1)函数()f x 的定义域为R ,()e 1x f x x '=--,令()()(),e 1x x f x x ϕϕ''==-,当()()0,0,x x x ϕϕ'>>单调递增,当()()0,0,x x x ϕϕ'<<单调递减,所以()(0)0x ϕϕ≥=,即()e 10x f x x ¢=--?故函数()f x 在R 上单调递增(2)由(1)知()f x 在[]1,1x ∈-时,单调递增,且()00f =,故()()[]()(],0,1,1,0f x x y f x f x x ⎧∈⎪==⎨-∈-⎪⎩, 所以()(){}max 1,1M f f =-,由于()()115111e 3e 0e 22ef f --=---=--<, 所以()()11f f -<,故()51e 2M f ==-, 而()51e 2e 2N f M '≥=->-=, 因此M N < 9.(2023届福建省三明市高三上学期期末)已知函数()1sin e x x f x x -=+,ππ,2x ⎛⎫∈- ⎪⎝⎭. (1)求证:()f x 在()ππ,2-上单调递增; (2)当()π,0-时,()sin e cos sin x f x x x k x --⎡⎤⎣⎦≤恒成立,求k 的取值范围.【过程详解】(1)()1sin e x x f x x -=+,ππ,2x ⎛⎫∈- ⎪⎝⎭,()2cos e x x f x x -'=+, 由()π,0x ∈-,有22x -≥,11e x >,则22e x x ->,又1cos 1x -≤≤, 则()2cos 120e xx f x x -'=+>-+>. 当π0,2x ⎛⎫∈ ⎪⎝⎭时,cos 0x ≥,20x ->,所以()2cos 0e x x f x x -'=+> 所以当()ππ,2-时,()0f x ¢>,综上,()f x 在()ππ,2-上单调递增. (2)()sin e cos sin x f x x x k x --⎡⎤⎣⎦≤.化简得1cos sin x x k x --≤.当()π,0x ∈-时,sin 0x <,所以1cos sin x x k x --≤, 设()1cos sin x x g x x --=, ()()()221sin sin cos 1cos sin 1cos cos sin sin x x x x x x x x x g x x x +-+='--+-=设()sin 1cos cos h x x x x x =+-+,()()cos cos sin sin 1sin h x x x x x x x x =-+-=-'.()π,0x ∈- ,10x ∴-<,sin 0x <,()0h x '∴>()h x ∴在()π,0-上单调递增, 又由π02h ⎛⎫-= ⎪⎝⎭,所以当ππ,2x ⎛⎫∈-- ⎪⎝⎭时,()0h x <,()0g x '<, ()g x ∴在ππ,2⎛⎫-- ⎪⎝⎭上单调递减; 当π,02x ⎛⎫∈- ⎪⎝⎭时,()0h x ∴>,()0g x '>,()g x ∴在π,02⎛⎫- ⎪⎝⎭上单调递增, 所以()min π1ππ21212g x g --⎛⎫=-==+ ⎪-⎝⎭, 故π12k ≤+. 10.(2023届河南省开封市模拟)设函数()()22e x f x x x =-,()2e ln e g x x a x =-.(1)若函数()g x 在()e,+∞上存在最大值,求实数a 的取值范围;(2)当2a =时,求证:()()f x g x >.【过程详解】(1)由2()e ln e g x x a x =-得:()22e e e e a x g x a x x -=='-(0x >), ①当0a ≤时,()0g x '>,所以()g x 在(0,)+∞上单调递增,在(e,)+∞不存在最大值, ②当0a >时,令()0g x '=,解得:e 0x a=>, 当,e 0x a ⎛⎫∈ ⎪⎝⎭时,()0g x '>,()g x 在e 0,a ⎛⎫ ⎪⎝⎭上单调递增, 当,e x a ⎛⎫∈+∞ ⎪⎝⎭时,()0g x '<在e ,a ⎛⎫+∞ ⎪⎝⎭上单调递减, 所以()g x 在e x a =时,取得最大值e g a ⎛⎫ ⎪⎝⎭, 又由函数()g x 在(e,)+∞上存在最大值, 因此e e a>,解得:1a <,所以a 的取值范围为(0,1).(2)证明:当2a =时,2()e ln 2e g x x x =-,且函数()g x 的定义域为()0,∞+,要证明()()f x g x >,即证明0x >时,()222e e ln 2e x x x x x ->-, 只需要证明:0x >时,()222e 2e e ln x x x x x -+>, 因为0x >,所以不等式等价于2ln (2)e 2e e xx x x -+> 设()(2)e 2e x x x ϕ=-+(0x >),则()()1e xx x ϕ-'=, 令()0x ϕ'=得:1x =,当01x <<时,()0x ϕ'<,当1x >时,()0x ϕ'>,所以()ϕx 在(0,1)上单调递减,在(1,)+∞上单调递增,故()(1)e x ϕϕ≥=,且当1x =时,等号成立; 又设2e ln ()x h x x=(0x >),则22e (1ln )()x h x x -'=, 令()0h x '=得:e x =,当0e x <<时,()0h x '>,当e x >时,()0h x '<,所以()h x 在(0,e)上单调递增,在(e,)+∞上单调递减,故()(e)e h x h ≤=,且当e x =时,等号成立;综上可得:0x >时,()()x h x ϕ≥,且等号不同时成立,所以0x >时,()()x h x ϕ>,即当2a =时,()()f x g x >得证.11.已知函数()()e ,ln 1x h x x mx g x x x =-=++.(1)当1m =时,求函数()h x 的单调区间:(2)若()()h x g x …在()0,x ∈+∞恒成立,求实数m 的取值范围. 【过程详解】 (1)当1m =时()()()e ,1e 1x x h x x x h x x =+'=--设()()()1e 1x x h x x μ=+'=-,则()()2e 02x x x x μ=+≥⇒≥-'()()2e 02x x x x μ=+<⇒<-'()x μ∴即()h x '在(),2-∞-递减,在[)2,-+∞递增,当()()(),2,1e 10x x h x x ∞∈--=+⋅-<',当[)()()2,0,00x h x h '<'∈-=而当[)()()0,,00x h x h ∞''∈+≥=所以当()()(),0,0,x h x h x ∞'∈-<递减;[)()()0,,0,x h x h x ∞'∈+≥递增.故函数增区间为[)0,∞+,减区间为(),0∞- (2)ln 1e ln 11e x xx x x m x x x --+≤--=,()0,x ∈+∞ 令()()()22e ln 1e ln ,,0,x x x x x xf x f x x x x ∞--+==∈+' ()()()()221e ln ,e 20,0,x x p x x x p x x x x x ∞=+++>∈'=+令 ()p x ∴在()0,∞+递增,而()12e 1e 10,10e p p -⎛⎫=-<> ⎪⎝⎭, 11,1e x ⎛⎫∴∃∈ ⎪⎝⎭,使()10p x =,即()1211e ln 0*x x x += 当()10,x x ∈时,()()0,f x f x '<在()10,x 递减,当()1,x x ∈+∞时,()()0,f x f x '>在()1,x +∞递增 ()11min 111ln 1()e x x f x f x x x ∴==-- 因为()1211e ln 0*x x x +=可变形为()111ln 1111111111e ln ln e ln **x x x x x x x x =-== 又()e ,1e 0,e x x x y x y x y x ==+>∴='Q 在()0,∞+递增,由(**)可得1111111ln ln ,e x x x x x ==-= ()11min 11111ln 111()e 11110x x f x f x m m x x x x ∴==--=+-=∴+≤∴≤ 故m 取值范围为(],0-∞12.已知()ln f x x ax =+(a R ∈)(1)讨论()f x 的单调性;(2)当1a =时,若()()1f x k x b ≤++在()0,∞+上恒成立,证明:221k b k +--的最小值为1e -+.【过程详解】(1)因为()()10f x a x x'=+>, 当0a ≥时,()0f x '>,所以()f x 在()0,∞+上单调递增,当0a <时,若10,x a ⎛⎫∈- ⎪⎝⎭时,()0f x '>,()f x 单调递增; 若1,x a ⎛⎫∈-+∞ ⎪⎝⎭时,()0f x '<,()f x 单调递减, 综上:0a ≥时,()f x 在()0,∞+上单调递增;0a <时,()f x 在10,a ⎛⎫- ⎪⎝⎭上单调递增,在1,a ⎛⎫-+∞ ⎪⎝⎭上单调递减; (2)因为()ln 1x x k x b +≤++在()0,∞+上恒成立,所以()ln 1b x x k x ≥+-+在()0,∞+上恒成立, 设()()ln 1g x x x k x =+-+,所以()()110g x k x x'=+->, 当1k ≤时,()0g x '>,所以()g x 在()0,∞+上单调递增,此时()b g x ≥显然不恒成立;当1k >时,若10,1x k ⎛⎫∈ ⎪-⎝⎭时,()0g x '>,()g x 单调递增;若1,1x k ⎛⎫∈+∞ ⎪-⎝⎭时,()0g x '<,()g x 单调递减, 所以()()max 1111ln 1ln 111111g x g k k k k k k k ⎛⎫⎛⎫==+-+=---- ⎪ ⎪----⎝⎭⎝⎭, 所以()ln 11b k k ≥----, 又因为()()ln 11ln 12222211111k k k k b b k k k k -----++-=+≥+=-----, 令10t k =->,()ln 21t h t t +=-,所以()2ln 1t h t t +'=, 当10,e t ⎛⎫∈ ⎪⎝⎭时,()0h t '<,()h t 单调递减;当1,t e ⎛⎫∈+∞ ⎪⎝⎭时,()0h t '>,()h t 单调递增; 所以()min 11h t h e e ⎛⎫==-+ ⎪⎝⎭, 所以221k b k +--的最小值为1e -+.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考数学函数压轴题:1. 已知函数31()(,)3f x x ax b a b R =++∈在2x =处取得的极小值是43-. (1)求()f x 的单调递增区间; (2)若[4,3]x ∈-时,有210()3f x m m ≤++恒成立,求实数m 的取值范围. 2. 某造船公司年最高造船量是20艘. 已知造船x 艘的产值函数R (x)=3700x + 45x 2 – 10x 3(单位:万元), 成本函数为 C (x) = 460x + 5000 (单位:万元). 又在经济学中,函数f(x)的边际函数Mf (x)定义为: Mf (x) = f (x+1) – f (x). 求:(提示:利润 = 产值 – 成本)(1) 利润函数P(x) 及边际利润函数MP(x);(2) 年造船量安排多少艘时, 可使公司造船的年利润最大(3) 边际利润函数MP(x)的单调递减区间, 并说明单调递减在本题中的实际意义是什么3. 已知函数155)(2++=x x x ϕ)(R x ∈,函数)(x f y =的图象与)(x ϕ的图象关于点)21,0(中心对称。
(1)求函数)(x f y =的解析式;(2)如果)()(1x f x g =,)2,)](([)(1≥∈=-n N n x g f x g n n ,试求出使0)(2<x g 成立的x 取值范围;(3)是否存在区间E ,使{}Φ=<⋂0)(x f x E 对于区间内的任意实数x ,只要N n ∈,且2≥n 时,都有0)(<x g n 恒成立 4.已知函数:)(1)(a x R a xa ax x f ≠∈--+=且 (Ⅰ)证明:f(x)+2+f(2a -x)=0对定义域内的所有x 都成立.(Ⅱ)当f(x)的定义域为[a+21,a+1]时,求证:f(x)的值域为[-3,-2]; (Ⅲ)设函数g(x)=x 2+|(x -a)f(x)| ,求g(x) 的最小值 .5. 设()f x 是定义在]1,0[上的函数,若存在*x )1,0(∈,使得()f x 在],0[*x 上单调递增,在]1,[*x 上单调递减,则称()f x 为]1,0[上的单峰函数,*x 为峰点,包含峰点的区间为含峰区间. 对任意的]1,0[上的单峰函数()f x ,下面研究缩短其含峰区间长度的方法.(1)证明:对任意的21,x x )1,0(∈,21x x <,若)()(21x f x f ≥,则),0(2x 为含峰区间;若)()(21x f x f ≤,则)1,(1x 为含峰区间;(2)对给定的)5.00(<<r r ,证明:存在21,x x )1,0(∈,满足r x x 212≥-,使得由(1)所确定的含峰区间的长度不大于r +5.0;6. 设关于x 的方程0222=--ax x 的两根分别为α、β()βα<,函数14)(2+-=x ax x f (1)证明)(x f 在区间()βα,上是增函数;(2)当a 为何值时,)(x f 在区间[]βα,上的最大值与最小值之差最小7. 甲乙两公司生产同一种新产品,经测算,对于函数()8+=x x f ,()12+=x x g ,及任意的0≥x ,当甲公司投入x 万元作宣传时,乙公司投入的宣传费若小于()x f 万元,则乙公司有失败的危险,否则无失败的危险;当乙公司投入x 万元作宣传时,甲公司投入的宣传费若小于()x g 万元,则甲公司有失败的危险,否则无失败的危险. 设甲公司投入宣传费x 万元,乙公司投入宣传费y 万元,建立如图直角坐标系,试回答以下问题: (1)请解释()()0,0g f ;(2)甲、乙两公司在均无失败危险的情况下尽可能少地投入宣传费用,问此时各应投入多少宣传费(3)若甲、乙分别在上述策略下,为确保无失败的危险,根据对方所投入的宣传费,按最少投入费用原则,投入自己的宣传费:若甲先投入121=a 万元,乙在上述策略下,投入最少费用1b ;而甲根据乙的情况,调整宣传费为2a ;同样,乙再根据甲的情况,调整宣传费为2b ,, 如此得当甲调整宣传费为n a 时,乙调整宣传费为n b ;试问是否存在lim n n a →∞,n n b ∞→lim 的值,若存在写出此极限值(不必证明),若不存在,说明理由.8. 设)(x f 是定义域在]1,1[-上的奇函数,且其图象上任意两点连线的斜率均小于零.(l )求证)(x f 在]1,1[-上是减函数;(ll )如果)(c x f -,)(2c x f -的定义域的交集为空集,求实数c 的取值范围; (lll )证明若21≤≤-c ,则)(c x f -,)(2c x f -存在公共的定义域,并求这个公共的空义域.9. 已知函数f (x )=ax 2+bx +c ,其中a ∈N *,b ∈N ,c ∈Z 。
(1)若b>2a ,且f (sinx )(x ∈R )的最大值为2,最小值为-4,试求函数f (x )的最小值;(2)若对任意实数x ,不等式4x ≤f (x )≤2(x 2+1)恒成立,且存在x 0,使得f (x 0)<2(x 02+1)成立,求c 的值。
10. 已知函数14)(234-+-=ax x x x f 在区间[0,1]上单调递增,在区间[1,2]上单调递减; (1)求a 的值;(2)求证:x=1是该函数的一条对称轴;(3)是否存在实数b ,使函数1)(2-=bx x g 的图象与函数f(x)的图象恰好有两个交点若存在,求出b 的值;若不存在,请说明理由.11. 定义在区间(0,∞)上的函f(x)满足:(1)f(x)不恒为零;(2)对任何实数x 、q,都有)()(x qf x f q =.(1)求证:方程f(x)=0有且只有一个实根;(2)若a>b>c>1,且a 、b 、c 成等差数列,求证:)()()(2b f c f a f •; (3)(本小题只理科做)若f(x) 单调递增,且m>n>0时,有)2(2)()(nm f n f m f +==,求证:322m <<12. 已知三次函数c bx ax x x f +++=23)(在y 轴上的截距是2,且在),2(),1,(+∞--∞上单调递增,在(-1,2)上单调递减. (Ⅰ)求函数f (x)的解析式; (Ⅱ)若函数)ln()1()2(3)()(m x m x x f x h ++--'=,求)(x h 的单调区间.13. 已知函数33(1)()x a f x -=(0a ≠且1a ≠). (1) 试就实数a 的不同取值,写出该函数的单调递增区间;(2) 已知当0x >时,函数在6)上单调递减,在(6,)+∞上单调递增,求a 的值并写出函数的解析式;(3) (理)记(2)中的函数的图像为曲线C ,试问是否存在经过原点的直线l ,使得l 为曲线C 的对称轴若存在,求出l 的方程;若不存在,请说明理由.(文) 记(2)中的函数的图像为曲线C ,试问曲线C 是否为中心对称图形若是,请求出对称中心的坐标并加以证明;若不是,请说明理由.14. 已知函数()log a f x x =和()2log (22),(0,1,)a g x x t a a t R =+->≠∈ 的图象在2x =处的切线互相平行.(Ⅰ) 求t 的值;(Ⅱ)设)()()(x f x g x F -=,当[]1,4x ∈时,()2F x ≥恒成立,求a 的取值范围.15. 设函数()f x 定义在R +上,对任意的,m n R +∈,恒有()()()f m n f m f n ⋅=+,且当1x >时,()0f x <。
试解决以下问题:(1)求(1)f 的值,并判断()f x 的单调性;(2)设集合{}{}(,)|()()0,(,)|(2)0,A x y f x y f x y B x y f ax y a R =++->=-+=∈,若A B ≠∅,求实数a 的取值范围;(3)若0a b <<,满足|()||()|2|()|2a bf a f b f +==,求证:322b <<+ 16. (理科)二次函数f(x)=)(2R b a b ax x ∈++、 (I )若方程f(x)=0无实数根,求证:b>0;(II )若方程f(x)=0有两实数根,且两实根是相邻的两个整数,求证:f(-a)=)1(412-a ; (III )若方程f(x)=0有两个非整数实根,且这两实数根在相邻两整数之间,试证明存在整数k ,使得41)(≤k f .(文科)已知函数f(x)=c bx ax ++2,其中.,,*Z c N b N a ∈∈∈(I )若b>2a,且 f(sinx)(x ∈R)的最大值为2,最小值为-4,试求函数f(x)的最小值; (II )若对任意实数x ,不等式)1(2)(42+≤≤x x f x 恒成立,且存在)1(2)(0200+<x x f x 使得成立,求c 的值。
17. 定义在(-1,1)上的函数f(x)满足:对任意x 、y (-1,1)都有。
(I )求证:函数f(x)是奇函数; (II )如果当时,有f(x)>0,判断f(x)在(-1,1)上的单调性,并加以证明;(III )设-1<a<1,解不等式:18. 已知二次函数),,0(1)(2R b a bx ax x f ∈>++=设方程f(x)=x 有两个实数根x 1、x 2. (Ⅰ)如果4221<<<x x ,设函数f(x)的对称轴为x =x 0,求证x 0>—1; (Ⅱ)如果201<<x ,且f(x)=x 的两实根相差为2,求实数b 的取值范围. 19. 函数)(x f 的定义域为R ,并满足以下条件:①对任意R x ∈,有0)(>x f ; ②对任意x 、R y ∈,有y x f xy f )]([)(=;③.1)31(>f 则(1)求)0(f 的值; (4分) (2)求证:)(x f 在R 上是单调增函数; (5分) (3)若ac b c b a =>>>2,0且,求证:).(2)()(b f c f a f >+ 20. (理)已知)0()1()(2≤++=a ax x In x f(1)讨论)(x f 的单调性;(2)证明:2),()11()311)(211(*444≥∈<+++n N n e n其中无理数)71828.2 =e . (文)设函数)(31)(23c b a cx bx ax x f <<++=,其图象在点))(,()),1(,1(m f m B f A 处的切线的斜率分别为a o -,.(1)求证:10<≤ab; (2)若函数)(x f 的递增区间为],[t s ,求]-[t s 的取值范围.21.设函数)10(3231)(223<<+-+-=a b x a ax x x f(1)求函数f(x)的单调区间,并求函数f(x)的极大值和极小值; (2)当x ∈[a+1, a+2]时,不等a x f ≤'|)(|,求a 的取值范围. 22. 已知函数1x x716x )x (f --+=,函数m x ln 6)x (g +=. (1)当1x >时,求函数f(x)的最小值;(2)设函数h(x)=(1-x)f(x)+16,试根据m 的取值分析函数h(x)的图象与函数g(x)的图象交点的个数.23. 已知二次函数t t t t y l c bx ax x f .20(8:,)(212≤≤+-=++=其中直线为常数);2:2=x l .若直线l 1、l 2与函数f (x )的图象以及l 1,y 轴与函数f (x )的图象所围成的封闭图形如阴影所示.(Ⅰ)求a 、b 、c 的值;(Ⅱ)求阴影面积S 关于t 的函数S (t )的解析式;(Ⅲ)若,ln 6)(m x x g +=问是否存在实数m ,使得y=f (x )的图象与y=g (x )的图象有且只有两个不同的交点若存在,求出m 的值;若不存在,说明理由.24. 已知()()()f x x x a x b =--,点A(s,f(s)), B(t,f(t)) (I) 若1a b ==,求函数()f x 的单调递增区间;(II)若函数()f x 的导函数()f x '满足:当|x|≤1时,有|()f x '|≤23恒成立,求函数()f x 的解析表达式;(III)若0<a<b, 函数()f x 在x s =和x t =处取得极值,且a b +=证明:与不可能垂直.25. 已知函数().)(2R m xx m x f ∈-=(1)设x x f x g ln )()(+=,当m ≥41时,求g(x)在[221,]上的最大值;(2)若),1[)](8[log 31+∞-=在x f y 上是单调减函数,求实数m 的取值范围.26. (本小题满分12分)已知常数a > 0, n 为正整数,f n ( x ) = x n – ( x + a)n ( x > 0 )是关于x 的函数.(1) 判定函数f n ( x )的单调性,并证明你的结论.(2) 对任意n ? a , 证明f `n + 1 ( n + 1 ) < ( n + 1 )f n `(n)答案:1.解:(1)2()f x x a '=+,由题意(2)404844(2)233f a a b f a b '=+=⎧=-⎧⎪⇒⎨⎨==++=-⎩⎪⎩, 令2()40f x x '=->得()f x 的单调递增区间为(,2)-∞-和(2,)∞.(2) 31()443f x x x =-+,当x 变化时,()f x '与()f x 的变化情况如下表:- 4(-4,-2(-2,2(2,33-2)2) )单调递增单调递减单调递增1所以[4,3]x ∈-时,max 28()3f x =.于是210()3f x m m ≤++在[4,3]x ∈-上恒成立等价于2102833m m ++≥,求得(,3][2,)m ∈-∞-⋃+∞. 2.解:(1) P(x) = R (x) – C (x) = – 10x 3 + 45x 2 + 3240x – 5000 (x?N 且x?[1, 20]); 2分MP (x) = P ( x + 1 ) – P (x) = – 30x 2 + 60x +3275 (x?N 且x?[1, 20]). 4分(2) P`(x) = – 30x 2 + 90x + 3240 = – 30( x +9 )(x – 12) (x?N 且x?[1, 20]) 7分当1< x < 12时, P`(x) > 0, P(x)单调递增, 当 12 <x < 20时, P`(x) < 0 , P ( x ) 单调递减.∴ x = 12 时, P(x)取最大值, 10分 即, 年建造12艘船时, 公司造船的年利润最大. 11分 (3) 由MP(x ) = – 30( x – 1) 2 + 3305 (x?N 且x?[1, 20]).∴当1< x ? 20时,MP (x)单调递减. 12分 MP (x)是减函数说明: 随着产量的增加,每艘利润与前一台比较,利润在减少.1 3.解:(1)255)(x x x f -= ………………………………………………………………(6分) (2)由0)(5)(5)(2112<-=x g x g x g 解得1)(0)(11><x g x g 或即15505522>-<-x x x x 或解得1055105510+<<-><x x x 或或…………………………………(12分) (1) 由{}}{100)(><=<x x x x f x 或,又{}Φ=><⋂+-10)1055,1055(x x x 或, 当)1055,1055(+-∈x 时,0)(2<x g ,0)(5)(5)(2223<-=x g x g x g , ∴对于3,2=n 时,)1055,1055(+-⊆E ,命题成立。
