第6章--函数--参考答案
C语言程序设计 第六章 函数 试题及答案

B)形参可以是常量、变量或表达式
C)实参可以是任意类型
D)实参应与其对应的形参类型一致
参考答案:B
6.8以下正确的说法是。
A)定义函数时,形参的类型说明可以放在函数体内
B)return后面的值不能为表达式
C)如果函数的类型与返回值类型不一致,以函数类型为准
D)如果形参与实参的类型不一致,以实参类型为准
A)float型B)int型C)long型D)double型
参考答案:B
6.12 C语言规定,函数返回值的类型是由所决定。
A)return语句中的表达式类型
B)调用该函数时的主调函数类型
C)调用该函数是系统临时指定
D)在定义该函数时所指定的函数类型
参考答案:D
*6.13下面函数调用语句含有实参的个数为。
if(m!=-1) n=m;
}
printf("\nn=%d",n);
}
【1】A)k*10 B)k%10 C)k/10 D)k*10%10
【2】A)a2*10 B)a2 C)a2/10 D)a2%10
参考答案:【1】C【2】A
6.18以下是有关汉诺塔问题的程序段,若在main函数中有调用语句hanoi(3,'A','B','C');则符合程序段运行结果的选项是。
A-->C A-->C B-->C B-->C
A-->B A-->B A-->C A-->C
参考答案:C
6.19若用数组名作为函数调用的实参,传递给形参的是。
A)数组的首地址B)数组第一个元素的值
C)数组中全部元素的值D)数组元素的个数
c语言《程序设计基础》课后习题参考答案与解析

c语言《程序设计基础》课后习题参考答案与解析《程序设计基础》习题参考答案与部分解析第1章 C 语言概述一、填空a) C源程序的基本单位是函数。
b) 一个C程序中至少应包括一个 main函数。
c) 在C语言中,输出操作是有库函数 printf( )函数完成。
二、单选题1、A2、C3、B解析:第1题答案:A 。
因为一个C程序总是从main函数开始执行的,而不论main函数在程序中的位置。
且到main函数结束。
第2题答案:C 。
因为 main函数没有限制必须位于程序的最前面。
C程序书写自由,一行内可写几个语句。
在对一个C 程序进行编译的过程中,无法检查注释当中的拼写错误。
不过C语言本身并没有输入输出语句,输入输出是由函数完成的。
第3题答案:B。
因为一个C语言程序是由若干个函数组成的。
但至少包含一个main 函数,且main函数的位置不限。
三、编程题1、编写一个输出“Welcome to C!”信息的小程序。
解:程序如下#include “stdio.h”main( ){1printf(“Welcome to C!”) ;}2、已知三角形的三边长分别为3,4,5,试用海轮公式编程求其面积。
海伦公式为:S?= ,其中s= (a+b+s)/2 ;解:程序如下#include “math.h”#include “stdio.h”main( ){int a , b , c ; /* a ,b,c 3个整型变量表示三角形的3条边。
*/float s ,s1 ; /* s1作为面积变量,s 作为中间变量是都应该是实形*/a=3 ; b= 4; c=5 ;s= (a+b+c)/2.0 ;s1= sqrt(s*(s-a)*(s-b)*(s-c)); /* sqrt函数完成开平方根功能。
*/printf(“area=%f\n”,s1);}2第2章程序设计基础知识一、单选题1、C2、A3、C4、A5、C6、C7、D8、C9、D 10、A 11、D 12、A 13、C 14、C 15、B A 16、B 17 D解析:1. 答案:C。
C语言程序设计(第3版)第6章习题参考答案

gets(stridiom1);
printf("\nplease input the second idiom: ");
gets(stridiom2);
fnConcat(stridiom1,stridiom2);
printf("\nthe result is: %s",stridiom1)=0;
while(b[j] != '\0') /*把第二个字符串的内容连接到第一个字符串的后面*/
{
a[i+j] = b[j];
j++;
}
a[i+j]= '\0'; /*添加字符串结束符*/
}
void main()
{ char stridiom1[80],stridiom2[80];
i++;
}
a[j]= '\0'; /*添加字符串结束符*/
}
void main()
{ char stridiom1[80];
printf("\nplease input the first idiom: ");
gets(stridiom1);
fnConvert(stridiom1);
printf("\nthe result is: %s",stridiom1);
scanf("%d",&n);
printf("%ld",fnF(n));
getch();
}
(4)编一函数判别某一数是否为素数,若是,返回值为1,否则,返回值为0。
数学分析(上册)答案-张勇 杨光崇-第六章一元函数积分学

思考与练习 6-11. 回答下列问题:① 定积分作为积分和的极限,能否表示为()∑=∞→∆nk kkn xf 1lim ξ?答:不能.因为n →∞并不能推出0T →.② 积分和()∑=∆nk k k x f 1ξ的值与哪些因素有关?定积分()⎰badx x f 的值与哪些因素有关?答:()∑=∆nk k k x f 1ξ与函数,区间和区间的分割和取的点有关。
()⎰badx x f 只与函数和区间有关.③ 将区间[]b a ,n 等分,[].,,2,1,,,1n k x x n ab x k k k k =∈-=∆-ξ,积分和()∑=∆nk k k x f 1ξ是否为定值?答:不是.因为和()∑=∆nk kkxf 1ξ还与k ξ的取法有关.④ 在定积分的定义给出之前,如下说法是否合理?为什么?“曲边梯形()x f y ≤≤0”,[]b a x ,∈的面积不大于矩形[]b a x M y ,,0∈≤≤的面积,其中[](){}x f M b a x ,max ∈=.答: 不合理.因为在定积分定义给出之前,曲边梯形的面积没有定义,当然也就不能与矩形的面积比较大小.⑤ 0→T 是什么意思?当0→T 时,积分和()∑=∆nk kkxf 1ξ的极限是J 是什么意思?答:}{max 1i ni x T ∆=≤≤,0→T 表示对区间分割后最大的区间的长度都趋于0.设f 是定义在],[b a 上的一个有界函数,J 是一个确定的实数.若对任给的正数ε,总存在某一正数δ,使得对],[b a 的任何分割T ,以及在其上任意选取的点集}{i ξ,只要δ<T ,就有εξ<-∆∑=ni iiJ xf 1)(,则称函数f 在区间],[b a 上可积或黎曼可积;数J 称为f 在],[b a 上的定积分或黎曼积分,记作()baJ f x dx =⎰.2. 按定积分定义证明:⎰-=baa b k kdx )(.证明:0ε∀>,对[,]a b 作任意分割T ,并在其上任意选取点集{}i ξ,因为111(),[,],()()n n ni i i i i i i f x k x a b f x k x k x k b a ξ===≡∈∆=∆=∆=-∑∑∑,对任意的0ε>,任意取定0δ>,当T δ<时,有()1()()()0niii f x k b a k b a k b a ξε=∆--=---=<∑,所以函数()f x k =在[,]a b 上可积,且()bakdx k b a =-⎰3. 通过对积分区间作等分分割,并取适当的点集}{i ξ,把定积分看作是对应的积分和的 极限,来计算下列定积分:①⎰13dx x ; ②⎰<<bab a x dx)0(2, 提示:()i i i i i i i i x x x x x x x x 111112212-=-+∆---; ()i i i i i i i i x x x x x x x x 1111212121-=-+∆----. 解 ①将[0,1]n 等分,分点为,0,1,2,,1k n =-.在区间1,k k n n -⎡⎤⎢⎥⎣⎦上取k n 作为k ξ 而 313011l i m nn k k x d x n n →∞=⎛⎫=⋅ ⎪⎝⎭∑⎰3411l i m n n k k n →∞==∑224111lim (1)44n n n n →∞=⋅+=.②取i ξ=后211110111111()nn i i i i i i n x x x x x x a b -==-⎛⎫⎛⎫-=-=-=-⎪⎝⎭∑∑ 将[,]a b n 等分,分点为()ka b a n+-,0,1,2,,k n =.在区间1[,]k k x x -作为k ξ则212111lim ()n b k k a n k dxx x x a b -→∞=⎛⎫=-=-∑⎰ 4. 已知一质量不均匀分布的棒的线密度x =ρ,长为l ,试求该棒的质量.解:所求质量为:22l xdx M l==⎰思考与练习 6-21. 计算下列积分:①⎰+10)32(dx x ; ②⎰+10211dx x ; ③⎰22e e x dx ; ④⎰--102dx e e xx ; ⑤⎰-3211πdx x; ⑥⎰⎪⎪⎭⎫⎝⎛+942123dx x x ; ⑦()⎰+π0sin 2cos dx x x . ⑧⎰1dx a x; ⑨⎰22sin πxdx ; ⑩ ⎰+21211dx x.解①()()112(23)313004x dx x x +=+=+-+=⎰;②4arctan 111102π==+⎰x dx x ; ③()()22222ln 2ln ln 2212e e e e dx x e e x==-=-=⎰;④()()111001001111()122222x x x x e e dx e e e e e e e e -----=+=+-+=+-⎰;⑤3arcsin arcsin 1130302πππ==-⎰x dx x;⑥()93131319222222449944301020dx x x ⎡⎤⎛⎫⎛⎫⎛⎫+=+=+-+=-=⎢⎥ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦⎰; ⑦()()()00cos 2sin (sin 2cos )sin 2cos sin02cos04x x dx x x ππππ+=-=---=⎡⎤⎣⎦⎰; ⑧aa a a dx a x xln 1ln 1010-==⎰;⑨()22011sin 2cos2cos cos0122xdx x πππ⎛⎫=-=--= ⎪⎝⎭⎰;⑩()2211ln ln(2ln(1x =+=+-+=⎰。
高中数学第6章幂函数、指数函数和对数函数6.1幂函数高一第一册数学

堂 小
导
学
(1)求幂函数的定义域,再判定奇偶性;
结 提
探
新 知
(2)先研究第一象限的图象与性质,再根据奇偶性(对称性)研究
素 养
其它象限的图象.
课
合
时
作
2.幂函数在第一象限的图象与性质
分
探
层
究 释
(1)α>0,幂函数的图象恒经过(0,0),(1,1),在[0,+∞)是增函
作 业
疑
难 数.
返
首
12/9/2021
课 堂 小
导
结
学 探 新 知
∴1312>1412.
提 素 养
(2)∵y=x-1是(-∞,0)上的减函数, 课
合 作 探
且-23<-35,
时 分 层
究
作
释 疑 难
∴-23-1>-53-1.
业
返
首
12/9/2021
页
第二十一页,共五十五页。
课
情 景 导 学
(3)0.25-14=14-14=212,
堂 小 结 提
返 首 页
第五页,共五十五页。
2.幂函数的图象和性质
课
情
堂
景
小
导
结
学
提
探
新
素
知
养
课
合
时
作
分
探
层
究
作
释
业
疑
难
返
首
12/9/2021
页
第六页,共五十五页。
课
情
堂
景
小
导
结
学
提
通信原理(陈启兴版) 第6章作业和思考题参考答案
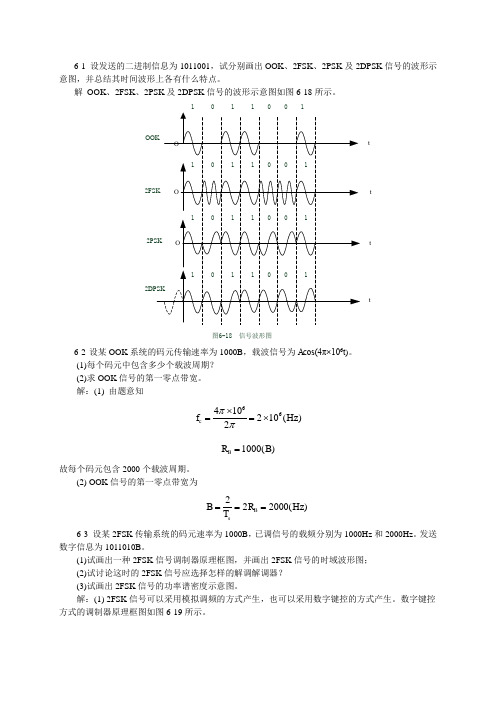
6-1 设发送的二进制信息为1011001,试分别画出OOK 、2FSK 、2PSK 及2DPSK 信号的波形示意图,并总结其时间波形上各有什么特点。
解 OOK 、2FSK 、2PSK 及2DPSK 信号的波形示意图如图6-18所示。
tttt图6-18 信号波形图6-2 设某OOK 系统的码元传输速率为1000B ,载波信号为A cos(4π×106t )。
(1)每个码元中包含多少个载波周期? (2)求OOK 信号的第一零点带宽。
解:(1) 由题意知66410210()2c f Hz ππ⨯==⨯1000()B R B =故每个码元包含2000个载波周期。
(2) OOK 信号的第一零点带宽为222000()B sB R Hz T === 6-3 设某2FSK 传输系统的码元速率为1000B ,已调信号的载频分别为1000Hz 和2000Hz 。
发送数字信息为1011010B 。
(1)试画出一种2FSK 信号调制器原理框图,并画出2FSK 信号的时域波形图; (2)试讨论这时的2FSK 信号应选择怎样的解调解调器? (3)试画出2FSK 信号的功率谱密度示意图。
解:(1) 2FSK 信号可以采用模拟调频的方式产生,也可以采用数字键控的方式产生。
数字键控方式的调制器原理框图如图6-19所示。
图6-19键控法产生2FSK 信号的原理图由题意知,码元传输速率R B =1000B ,若设“1”码对应的载波频率为f 1=1000Hz ,“0”码对应的载波频率为f 1=2000Hz ,则在2FSK 信号的时间波形中,每个“1”码元时间内共有1个周期的载波,每个“0”码元时间内有2个周期的载波。
2FSK 信号的时间波形如图6-20所示。
【注:实际中键控法的波形一般不连续。
】t2FSK图6-20 2FSK 信号的时间波形(2) 由于2FSK 信号的频谱有较大的重叠,若采用非相干解调是上下支路有较大串扰,使解调性能下降。
苏科版八年级数学上册第6章 一次函数的应用——动点问题(解析版)

一次函数的应用——动点问题一、单选题1.在平面直角坐标系中,已知一次函数y=﹣34x+6与x,y轴分别交于A,B两点,点C (0,n)是y轴上一点,把坐标平面沿直线AC折叠,点B刚好落在x轴上,则点C的坐标是()A. (0,3)B. (0,43) C. (0,83) D. (0,73)【答案】C【解析】【解答】解:过C作CD⊥AB于D,如图,对于直线y=﹣34x+6,当x=0,得y=6;当y=0,x=8,∴A(8,0),B(0,6),即OA=8,OB=6,∴AB=10,又∵坐标平面沿直线AC折叠,使点B刚好落在x轴上,∴AC平分∠OAB,∴CD=CO=n,则BC=6﹣n,∴DA=OA=8,∴DB=10﹣8=2,在Rt△BCD中,DC2+BD2=BC2,∴n2+22=(6﹣n)2,解得n= 83,∴点C的坐标为(0,83).故答案为:C.2.如图,函数y=mx﹣4m(m是常数,且m≠0)的图象分别交x轴、y轴于点M,N,线段MN上两点A,B(点B在点A的右侧),作AA1⊥x轴,BB1⊥x轴,且垂足分别为A1,B1,若OA1+OB1>4,则△OA1A的面积S1与△OB1B的面积S2的大小关系是()A. S1>S2B. S1=S2C. S1<S2D. 不确定的【答案】A【解析】【解答】解:由题意可得,m<0,设A(a,ma﹣4m),B(b,mb﹣4m),a<b,∵S1= 12a×(ma﹣4m),S2= 12b(mb﹣4m)∴S1﹣S2= 12(ma2﹣mb2)﹣124m(a﹣b)=(a﹣b){ 12m(a+b)﹣124m}.又∵OA1+OB1>4,∴12m(a+b)﹣124m= 12m(a+b﹣4)<0,∴S1﹣S2>0,故选A.3.如图,正方形ABCD的边长为4,P为正方形边上一动点,沿A→D→C→B→A 的路径匀速移动,设P点经过的路径长为x,△APD的面积是y,则下列图象能大致反映y与x的函数关系的是()A. B.C. D.【答案】B【解析】【解答】解:①当点P由点A向点D运动时,y的值为0;②当点P在DC上运动时,y随着x的增大而增大;③当点p 在CB 上运动时,y=AB•AD ,y 不变; ④当点P 在BA 上运动时,y 随x 的增大而减小. 故选B .二、填空题4.如图,直线y=﹣ 12 x+3与坐标轴分别交于点A 、B ,与直线y=x 交于点C ,线段OA 上的点Q 以每秒1个长度单位的速度从点O 出发向点A 作匀速运动,运动时间为t 秒,连接CQ .若△OQC 是等腰直角三角形,则t 的值为________.【答案】2或4【解析】【解答】∵由 {y =−12x +3y =x,得 {x =2y =2 , ∴C (2,2);如图1,当∠CQO=90°,CQ=OQ ,∵C (2,2), ∴OQ=CQ=2, ∴t=2;如图2,当∠OCQ=90°,OC=CQ , 过C 作CM ⊥OA 于M ,∵C (2,2), ∴CM=OM=2, ∴QM=OM=2, ∴t=2+2=4,即t的值为2或4,故答案为:2或4.5.如图,已知点C为直线y=x上在第一象限内一点,直线y=2x+1交y轴于点A,交x轴于B,将直线AB沿射线OC方向平移√2个单位,则平移后直线的解析式为________。
高级语言程序设计第6章参考答案

1.6.3习题解答编程题1.写两个函数,分别求两个整数的最大公约数和最小公倍数,用主调函数调用这两个函数,并输出结果。
两个整数由键盘输入。
分析:求两个数a和b的最大公约数:设这个数为x,则x一定小于等于a和b中的较小者min(a,b)。
在区间[1, min(a,b)]中能找到的最后一个同时被a和b整除的那个数,就是a和b的最大公约数x。
求两个数a和b的最小公倍数:设这个数为x,则x一定大于等于a和b中的较大者max(a,b),而小于等于a*b。
在区间[max(a,b), a*b ]中找到的第一个能同时整除a和b的那个数,就是a和b的最小公倍数x。
参考程序代码:#include "stdio.h"f1(int a, int b)/*求最大公约数*/{int x,i;for(i=1;i<=(a<=b?a:b);i++){if(a%i==0&&b%i==0){x=i;}}printf("\n最大公约数为: %d\n",x);}f2(int a, int b)/*求最小公倍数*/{int i,x;for(i=((a>b)?a:b);i<=a*b;i++){if(i%a==0&&i%b==0){x=i;break;}}printf("\n最小公倍数为: %d\n",x);}void main(){int a,b;printf("\n请输入两个数:\n");printf("a=");scanf("%d", &a);printf("b=");scanf("%d", &b);f1(a, b);f2(a, b);}运行结果:请输入两个数:a=4b=16最大公约数为:4最小公倍数为:162.编写一个函数,其功能是对于给定的一个时间数(秒为单位),以“时:分:秒”的格式输出。
第6章 二次函数--习题解析

(2008•上海)如图,在平面直角坐标系中,点O为坐标原点,以点A(0,-3)为圆心,5为半径作圆A,交x轴于B,C两点,交y轴于点D,E两点.(1)求点B,C,D的坐标;(2)如果一个二次函数图象经过B,C,D三点,求这个二次函数解析式;(3)P为x轴正半轴上的一点,过点P作与圆A相离并且与x轴垂直的直线,交上述二次函数图象于点F,当△CPF中一个内角的正切之为12时,求点P的坐标.由题意可知AC=5,OA=3,根据勾股定理可知,OC=4,可知C点坐标,同理求出B点坐标,OA=3,AD=5,求出OD=2,求出D点坐标.(1)∵点A的坐标为(0,-3),线段AD=5,∴点D的坐标(0,2).连接AC,在Rt△AOC中,∠AOC=90°,OA=3,AC=5,∴OC=4.∴点C的坐标为(4,0);同理可得点B坐标为(-4,0).(2)已知B,C,D三点坐标,设出解析式,代入即可求出函数解析式.设所求二次函数的解析式为y=ax2+bx+c,由于该二次函数的图象经过B,C,D三点,则0=16a-4b+c0=16a+4b+c2=c解得a=-18b=0c=2∴所求的二次函数的解析式为y=-18x2+2;(3)根据图象可知,正切为1,则∠cpf为直角,设出P点坐标,然后表示出CP,PF的长度,然后分情况讨论PFCP=12还是CPPF=12,或是两者都可,求出P点坐标.设点P坐标为(t,0),由题意得t>5,且点F的坐标为(t,-18t2+2),PC=t-4,PF=18t2-2,∵∠CPF=90°,∴当△CPF中一个内角的正切值为12时,①若CPPF=12时,即t-418t2-2=12,解得t1=12,t2=4(舍);②当PFCP12时,18t2-2t-4=12解得t1=0(舍),t2=4(舍),所以所求点P的坐标为(12,0).解答解:(1)∵点A的坐标为(0,-3),线段AD=5,∴点D的坐标(0,2).(1分)连接AC,在Rt△AOC中,∠AOC=90°,OA=3,AC=5,∴OC=4.(1分)∴点C的坐标为(4,0);(1分)同理可得点B坐标为(-4,0).(1分)(2)设所求二次函数的解析式为y=ax2+bx+c,由于该二次函数的图象经过B,C,D三点,则0=16a-4b+c0=16a+4b+c2=c(3分)解得a=-18b=0c=2∴所求的二次函数的解析式为y=-18x2+2;(1分)(3)设点P坐标为(t,0),由题意得t>5,(1分)且点F的坐标为(t,-18t2+2),PC=t-4,PF=18t2-2,∵∠CPF=90°,∴当△CPF中一个内角的正切值为12时,①若CPPF=12时,即t-418t2-2=12,解得t1=12,t2=4(舍);(1分)②当PFCP=12时,18t2-2t-4=12解得t1=0(舍),t2=4(舍),(1分)所以所求点P的坐标为(12,0).(1分)。
第6章-6.3-对数函数高中数学必修第一册苏教版

A.
B.
)
C.
D.
【解析】
若0 < < 1,则函数 = 的图象下降且过点 0,1 ,而函数
= log − 的图象上升且过点 −1,0 ,与题中所给图象均不符合.若 > 1,
首先函数 = 的图象只可能在轴上方,函数 = log − 的图象只可能
在轴左侧,从而A,D中图象不正确;再看单调性, = 与 = log − 的单调性
∴ = + 1.
又 的图象过点 1,3 ,
∴ 3 = + 1,即 = 2,
∴ = 2 + 1(【另解】至此,也可令2 + 1 = 9,解得 = 3,即 −1 9 = 3).
∴ −1 = log 2 − 1 , > 1.
故 −1 9 = log 2 8 = 3.
(1) = lg − 1 + lg − 2 ;
【解析】要使函数式有意义,需满足ቊ
− 1 > 0,
解得 > 2.
− 2 > 0,
所以函数 = lg − 1 + lg − 2 的定义域是{| > 2}.
(2) = log
1−
5;
【解析】要使函数式有意义,需满足ቊ
所以函数 = log
log 0.5 4 − 3
ln 4−
−3
3
的定义域是{|
4
< ≤ 1}.
.
4 − > 0,
【解析】要使函数式有意义,需满足ቊ
解得 < 4且 ≠ 3.
− 3 ≠ 0,
所以函数 =
ln 4−
−3
(完整word)高等代数(北大版)第6章习题参考答案

第六章 线性空间1.设,N M ⊂证明:,M N M M N N ==I U 。
证 任取,M ∈α由,N M ⊂得,N ∈α所以,N M I ∈α即证M N M ∈I 。
又因,M N M ⊂I 故M N M =I 。
再证第二式,任取M ∈α或,N ∈α但,N M ⊂因此无论哪 一种情形,都有,N ∈α此即。
但,N M N Y ⊂所以M N N =U 。
2.证明)()()(L M N M L N M I Y I Y I =,)()()(L M N M L N M Y I Y I Y =。
证 ),(L N M x Y I ∈∀则.L N x M x Y ∈∈且在后一情形,于是.L M x N M x I I ∈∈或所以)()(L M N M x I Y I ∈,由此得)()()(L M N M L N M I Y I Y I =。
反之,若)()(L M N M x I Y I ∈,则.L M x N M x I I ∈∈或 在前一情形,,,N x M x ∈∈因此.L N x Y ∈故得),(L N M x Y I ∈在后一情形,因而,,L x M x ∈∈x N L ∈U ,得),(L N M x Y I ∈故),()()(L N M L M N M Y I I Y I ⊂于是)()()(L M N M L N M I Y I Y I =。
若x M N L M N L ∈∈∈UI I (),则x ,x 。
在前一情形X x M N ∈U , X M L ∈U 且,x M N ∈U 因而()I U (M L )。
,,N L x M N X M L M N M M N M N ∈∈∈∈∈⊂U U U I U U I U U U U I U I U 在后一情形,x ,x 因而且,即X (M N )(M L )所以 ()(M L )(N L )故 (L )=()(M L )即证。
3、检验以下集合对于所指的线性运算是否构成实数域上的线性空间:1) 次数等于n (n ≥1)的实系数多项式的全体,对于多项式的加法和数量乘法;2) 设A 是一个n ×n 实数矩阵,A 的实系数多项式f (A )的全体,对于矩阵的加法和数量乘法;3) 全体实对称(反对称,上三角)矩阵,对于矩阵的加法和数量乘法; 4) 平面上不平行于某一向量所成的集合,对于向量的加法和数量乘法; 5) 全体实数的二元数列,对于下面定义的运算:212121121112b a b a a b b a a k k b a ⊕+=+++-1111(a ,)((,)()k 。
浙教版八年级下册数学第六章 反比例函数含答案

浙教版八年级下册数学第六章反比例函数含答案一、单选题(共15题,共计45分)1、以正方形ABCD两条对角线的交点O为坐标原点,建立如图所示的平面直角坐标系,双曲线y=经过点D,则正方形ABCD的面积是()A.10B.11C.12D.132、如图,在平面直角坐标系中,△OAB的顶点A在x轴正半轴上,OC是△OAB 的中线,点B,C在反比例函数的图象上,则△OAB的面积等于()A.2B.3C.4D.63、反比例函数y=(k≠0)的图象经过点(-2,3),则该反比例函数图象在()A.第一、三象限B.第二、四象限C.第二、三象限D.第一、二象限4、在闭合电路中,电流I,电压U,电阻R之间的关系为:I=.电压U(伏特)一定时,电流I(安培)关于电阻R(欧姆)的函数关系的大致图象是()A. B. C. D.5、若是反比例函数,则a的取值为()A.1B.-1C.±1D.任意实数6、下列说法正确的是A.两条对角线互相垂直且相等的四边形是正方形B.任意两个等腰三角形相似 C.一元二次方程,无论a取何值,一定有两个不相等的实数根 D.关于反比例函数,y的值随x值的增大而减小7、如图,双曲线与直线交于点M,N,并且点M坐标为(1,3)点N坐标为(-3,-1),根据图象信息可得关于x的不等式的解为( )A. B. C. D.8、某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强p(Pa)是气球体积V(m3)的反比例函数,且当V=1.5m3时,p=16000Pa,当气球内的气压大于40000Pa时,气球将爆炸,为确保气球不爆炸,气球的体积应( )A.不小于0.5m 3B.不大于0.5m 3C.不小于0.6m 3D.不大于0.6m 39、若点M(x,y)满足,则点M所在象限是()A.第一、三象限B.第二、四象限C.第一、二象限D.不能确定10、反比例函数y=的图象上有两个点为(1,y1),(2,y2),则y1与y2的关系是( )A.y1>y2B.y1<y2C.y1=y2D.无法判断11、一次函数与反比例函数( )的图象的形状大致是()A. B. C.D.12、如果点(-a,-b)在反比例函数y=的图象上,那么下列各点中,在此图象上的是()A.(a,b)B.(b,-a)C.(-a,b)D.(-b,a)13、如图,在平面直角坐标系中,将一块含有45°的直角三角板按照如图方式摆放,顶点A、B的坐标为(1,4)、(4,1),直角顶点C的坐标为(4,4),若反比例函数的图象与直角三角板的边有交点,则k的取值范围为()A. B. C. D.14、如图,反比例函数y=的图象经过直角三角形OAB的顶点A,D为斜边OA 的中点,则过点D的反比例函数的解析式是()A.y=B.y=-C.y=D.y=15、若反比例函数的图象位于第二、四象限内,则m的取值范围是()A.m>0B.m<0C.m>1D.m<1二、填空题(共10题,共计30分)16、如图,已知点A,C在反比例函数y= (a>0)的图象上,点B,D在反比例函数y= (b<0)的图象上,AB∥CD∥x轴,AB,CD在x轴的两侧,AB=3,CD=2,AB与CD的距离为5,则a﹣b的值是________.17、已知函数的图象经过点(1,3),且与x轴没有交点,写出一个满足题意的函数的解析式________.18、已知,是反比例函数图象上两个点的坐标,且,请写出一个符合条件的反比例函数的解析式________.19、在平面直角坐标系中,点A的坐标为(5,0),点C的坐标为(0,4),四边形ABCO为矩形,点P为线段BC上的一动点,若△POA为等腰三角形,且点P在双曲线y= 上,则k值可以是________.20、在平面直角坐标系中,A为反比例函数y=﹣(x>0)图象上一点,点B的坐标为(4,0),O为坐标原点,若的面积为6,则点A的坐标为________.21、如图,直线y=x向下平移b个单位后得直线l,l与函数y=(x>0)相交于点A,与x轴相交于点B,则OA2﹣OB2=________ .22、如图,过反比例函数y=图象上三点A、B、C分别作直角三角形和矩形,图中S1+S2=5,则S3=________ .23、如图,A(4,0),B(3,3),以AO,AB为边作平行四边形OABC,则经过C点的反比例函数的解析式为________.24、若反比例函数的图象经过第一、三象限,则 k的取值范围是________.25、如果反比例函数y=(k是常数,k≠0)的图象经过点(2,3),那么在这个函数图象所在的每个象限内,y的值随x值的增大而________.(填“增大”或“减小”)三、解答题(共5题,共计25分)26、已知, 与成正比例, 与成反比例,且当时,; 时, .试求当时, 的值.27、水池内有水40m3,经过排水管的时间y(h)与每小时流出的水量xm3之间的关系是反比例函数吗?28、已知一个长方体的体积是100cm3,它的长是ycm,宽是10cm,高是xcm.(1)写出y与x之间的函数关系式;(2)当x=2cm时,求y的值.29、如图,一次函数y=kx+b与反比例函数的图象交于A(m,6),B(3,n)两点.(Ⅰ)求一次函数的解析式;(Ⅱ)根据图象直接写出的x的取值范围;(Ⅲ)求△AOB的面积.30、如果y是z的反比例函数,z是x的反比例函数,那么y与x具有怎样的函数关系?参考答案一、单选题(共15题,共计45分)1、C2、B3、B4、A5、A6、C7、D9、B10、A11、C12、A13、C14、C15、D二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、28、30、。
No3.第6章习题及答案

2) 对于 FH→E,由于有 F→E,则为多余的:
-4-
第六章习题答案
5
F2={ E→G,G→E,F→E,F→G,H→E,H→G }
3) 在 F2 中的 F→E 和 F→G 以及 H→E 和 H→G 之一是多余的,则为:
R 属于______ NF。
答案:AB,2
-1-
第六章习题答案
2
二、选择题:
1.在二元关系模式 R(U,F)中,X、Y 都是单一属性,如果 X→Y,则 R 一定可以达到( )
A.2NF B. 3NF C. BCNF D. 4NF
答案:D
2.在关系模式 )
F3={ E→G,G→E,F→G, H→G }
F3={ E→G,G→E,F→G, H→E }
F3={ E→G,G→E,F→E, H→E }
F3={ E→G,G→E,F→E, H→G }
3).设有关系模式 R(A,B,C,D),其上的函数依赖集:F={A→C,C→A,B→AC,D→AC},试计算: A)(AD)+; B)F的最小等价依赖集F‘; C)R 的关键字; 答案: 1) 令X={AD},X(0)={AD},X(1)={ACD},X(2)={ACD},故(AD)+={ACD}。 2)
第六章习题答案
1
《数据库系统概论》第 6 章习题答案
题型:
1、填空题: 10 题 2、选择题: 10 题 2、综合题: 3 题
一、填空
1. 与 1NF 相比,2NF 消除了非主属性对候选关键字的_________。
答案:部分函数依赖
2.与 2NF 相比,3NF 消除了非主属性对候选关键字的_________。
(完整)人教版数学八年级上册第6章一次函数单元测试题(含答案),推荐文档

2 1 初二数学第六单元测试题一、选择题:(本题共 10 小题,每小题 3 分,共 30 分)1.如果 y = (m -1)x 2-m 2+ 3 是一次函数,那么 m 的值是…………………………( )A. 1 ;B. -1;C. ±1 ;D. ± ;2. (2015•南平)直线 y=2x+2 沿 y 轴向下平移 6 个单位后与 x 轴的交点坐标是 ............... ( ) A .(-4,0);B .(-1,0);C .(0,2);D .(2,0);13. 若点 A (-2,m )在正比例函数 y = - 2x 的图象上,则 m 的值是………………()A . ;B . - 1; C .1; D .-1;4 44. 若一次函数 y=(2-m )x-2 的函数值 y 随 x 的增大而减小,则 m 的取值范围是 …………( )A .m <0;B .m >0;C .m <2 ;D .m >2; 5. 直线 y=kx+b 不经过第四象限,则…………………………………………………()A .k >0,b >0;B .k <0,b >0;C .k≥0,b≥0;D .k <0,b≥0; 6. (2014.深圳)已知函数 y=ax+b 经过(1,3),(0,-2),则 a-b=… .......... ( )A .-1;B .-3;C .3;D .7;7. 如图,直线 y=-x+m 与 y=nx+4n (n≠0)的交点的横坐标为-2,则关于 x 的不等式- x+m >nx+4n >0 的整数解为……………………………………………………………( ) A .-1; B .-5; C .-4; D .-3;第 7 题图第 9 题 图 第 10 题 图8.已知直线l 经过点 A (1,0),且与直线 y = x 垂直,则直线l 的函数表达式为 ......................................... ( )A. y = -x +1 ;B. y = -x -1;C. y = x +1 ;D. y = x -1;9. 小明从家出发,外出散步,到一个公共阅报栏前看了一会报后,继续散步了一段时间, 然后回家,如图描述了小明在散步过程汇总离家的距离 s (米)与散步所用时间 t (分)之间的函数关系,根据图象,下列信息错误的是 ............................................................... ( )A. 小明看报用时 8 分钟;B .公共阅报栏距小明家 200 米;5. (2015•无锡)一次函数标为 .与两坐标 6.如图,已 x - y = 2 的解是 2x + y = 1 值, C .小明离家最远的距离为 400 米; D .小明从出发到回家共用时 16 分钟;10. (2014•黑龙江)如图,在平面直角坐标系中,边长为 1 的正方形 ABCD 中,AD 边的中点处有一动点 P ,动点 P 沿 P→D→C→B→A→P 运动一周,则 P 点的纵坐标 y 与点 P 走过的路程 s 之间的函数关系用图象表示大致是……………………………………( )A.B. C. D.二、填空题:(本题共 8 小题,每小题 3 分,共 24 分)211.函数 y =x -1中自变量 x 的取值范围是 .12.已知 m 是整数,且一次函数 y = (m + 4)x + m + 2 的图像不经过第二象限,则 m =.13.已知一次函数 y = kx + k - 3 的图像经过点(2,3),则 k 的值为.14.请你写出一个图像过点(0,2),且 y 随 x 的增大而减小的一次函数的解析式 .1 y=2x-6 的图象与 x 轴的交点坐标为 .与 y 轴的交点坐 轴围成的三角形面积为 . 1 知函数 y=x-2 和 y=-2x+1 的图象交于点 P ,根据图象可得方程组⎧⎨.⎩第 16 题图第 17 题图17. (2013 春•玉田县期中)在矩形 ABCD 中,动点 P 从点 B 出发,沿 BC 、CD 、DA 运动至点 A 停止,设点 P 运动的路程为 x ,△ABP 的面积是 . 18.如图,点 Q 在直线 y=-x 上运动,点 A 的坐标为(1,0),当线段 AQ 最短时,点 Q 的坐标为 .三、解答题:(本大题共 10 题,满分 76 分)19.(本题满分 8 分)已知一次函数 y = (1- 2m )x + m +1 ,求当 m 为何时 (1) y 随着 x 的增大而增大?(2)图像经过一、二、四象限? (3)图像经过一、三象限? (4)图像与 y 轴的交点在 x 轴上方?第 18 题图20.(本题满分 6 分)已知一次函数y=kx+b的图像经过 A(1,1),B(2,-1)两点,求这个函数的表达式.21.(本题满分 7 分)在平面直角坐标系中,点 O 是坐标原点,过点 A(1,2)的直线y=kx+b 与x 轴交于点 B,且S AOB=4,求k 的值.22.(本题满分 7 分)如图,直线 y=2x+3 与x 轴交于点 A,与y 轴交于点 B.(1)求A、B 两点的坐标;(2)过B 点作直线 BP 与x 轴交于点 P,且使 OP=2OA,求△ABP的面积.23.(本题满分 7 分)已知:y+2 与3x 成正比例,且当 x=1 时,y 的值为 4.(1)求y 与x 之间的函数关系式;(2)若点(-1,a)、点(2,b)是该函数图象上的两点,试比较 a、b 的大小,并说明理由.24.(本题满分 8 分)如图,在平面直角坐标系中,点 A(0,4),B(3,0),连接 AB,将△AOB沿过点 B 的直线折叠,使点 A 落在x 轴上的点A′处,折痕所在的直线交 y 轴正半轴于点 C,求直线 BC 的解析式.25.(本题满分 7 分)如图,直线l1:y =x +1与直线l2:y =mx +n 相交于点P(1,b).(1)求b 的值;⎧y =x +1(2)不解关于 x,y 的方程组⎨y =mx +n ,请你直接写出它的解;⎩(3)直线l3:y =nx +m 是否也经过点 P?请说明理由.26.(本题满分 6 分)已知直线 y=kx+b 经过点 A(5,0),B(1,4).(1)求直线 AB 的解析式;(2)若直线 y=2x-4 与直线 AB 相交于点 C,求点 C 的坐标;(3)根据图象,写出关于 x 的不等式 2x-4>kx+b 的解集.27.(本题满分 10 分)某社区活动中心为鼓励居民加强体育锻炼,准备购买 10 副某种品牌的羽毛球拍,每副球拍配 x(x≥2)个羽毛球,供社区居民免费借用.该社区附近 A、B 两家超市都有这种品牌的羽毛球拍和羽毛球出售,且每副球拍的标价均为 30 元,每个羽毛球的标价为 3 元,目前两家超市同时在做促销活动:A 超市:所有商品均打九折(按标价的 90%)销售;B 超市:买一副羽毛球拍送 2 个羽毛球.设在 A 超市购买羽毛球拍和羽毛球的费用为 yA(元),在 B 超市购买羽毛球拍和羽毛球的费用为 yB(元).请解答下列问题:(1)分别写出 yA、yB 与x 之间的关系式;(2)若该活动中心只在一家超市购买,你认为在哪家超市购买更划算?(3)若每副球拍配 15 个羽毛球,请你帮助该活动中心设计出最省钱的购买方案.28.(本题满分 10 分)为倡导低碳生活,绿色出行,某自行车俱乐部利用周末组织“远游骑行”活动.自行车队从甲地出发,途径乙地短暂休息完成补给后,继续骑行至目的地丙地,自行车队出发 1 小时后,恰有一辆邮政车从甲地出发,沿自行车队行进路线前往丙地,在丙地完成 2 小时装卸工作后按原路返回甲地,自行车队与邮政车行驶速度均保持不变,并且邮政车行驶速度是自行车队行驶速度的 2.5 倍,如图表示自行车队、邮政车离甲地的路程y (km)与自行车队离开甲地时间 x(h)的函数关系图象,请根据图象提供的信息解答下列各题:(1)自行车队行驶的速度是;(2)邮政车出发多少小时与自行车队首次相遇?(3)邮政车在返程途中与自行车队再次相遇时的地点距离甲地多远?4 ⎩2017-2018 学年第一学期初二数学第六单元测试题参考答案一 、 选 择 题 : 1.B ;2.D ;3.C ;4.D ;5.A ;6.D ;7.D ;8.A ;9.A ;10.D ; 二、填空题:11.x ≠ 1;12.-3 或-2;13.2;14. y = -x + 2 (答案不唯一);15.(3,0),⎧x = 1 ⎛ 1 1 ⎫(0,-6,9;16. ⎨ y = -1;17.10;18. 2 , - ; ⎩⎝ ⎭ 三、解答题:19.(1) m < 1 ;(2) m > 1 ;(3) m = -1;(4) m > -1且m ≠ 1;20.2y = -2x + 3 ;21. 2 2 k = - 2 或 2 ; 3 522.(1)A ⎛ -2 3 ,⎪0 ⎫ ;B (0, 3);(24) 27 或 9 ; ⎝ ⎭ 23.(1) y = 6x - 2 ;(2) a < b ; 24. y = - 1 x + 3;2 2⎧x = 125. (1) b = 2 ;(2) ⎨ y = 2 ;(3)直线 y=nx+m 也经过点 P .理由如下: ∵当 x=1 时,y=nx+m=m+n=2,∴(1,2)满足函数 y=nx+m 的解析式,则直线经过点 P . 26. (1) y = -x + 5 ;(2) (3, 2);(3)x > 3 ; 27. 解:(1)由题意,得 yA=(10×30+3×10x)×0.9=27x+270; yB=10×30+3(10x-20)=30x+240;(2)当 yA=yB 时,27x+270=30x+240,得 x=10; 当 yA >yB 时,27x+270>30x+240,得 x <10; 当 yA <yB 时,27x+270<30x+240,得 x >10∴当2≤x<10 时,到B 超市购买划算,当 x=10 时,两家超市一样划算, 当 x >10 时在 A 超市购买划算.(3)由题意知 x=15,15>10,∴选择 A 超市,yA=27×15+270=675(元), 先选择 B 超市购买 10 副羽毛球拍,送 20 个羽毛球,然后在 A 超市购买剩下的 羽毛球:(10×15-20)×3×0.9=351(元),共需要费用 10×30+351=651(元) .∵651 元<675 元,∴最佳方案是先选择 B 超市购买 10 副羽毛球拍,然后在 A 超市购买 130 个羽毛球.28. 解:(1)由题意得自行车队行驶的速度是:72÷3=24km/h. 故答案为:24;(2) 由题意得邮政车的速度为:24×2.5=60km/h .2设邮政车出发 a 小时两车相遇,由题意得 24(a+1)=60a ,解得:a= .32答:邮政车出发 小时与自行车队首次相遇;39(3) 由题意,得邮政车到达丙地的时间为:135÷60= ,4∴邮政车从丙地出发的时间为: 9 + 2 +1 = 21,∴B4 49 + 2 +1 = 21,C (7.5,0). 4 445 49 ,∴D⎛ 49 ⎫ 自行车队到达丙地的时间为:135÷24+0.5= +0.5= 888 ,135⎪ . ⎝ ⎭⎪⎧135 = 21 k + b设 BC 的解析式为 y = k x + b ,由题意得 1 1 1 ⎨4 1 1 ,∴ k 1 =−60, b 1 =450, ∴ y 1 = -60x + 450 ,⎩0 = 7.5k 1 + b 1设 ED 的解析式为 y 2 = k 2 x + b 2 ,由题意得⎧72 = 3.5k 2 + b 2 ,解得: ⎧k 2 = 24 ,∴ y = 24x -12 .当 y = y 时 , ⎨⎪ 49 ⎨ 135 = ⎩b = -122 1 2 ⎩⎪8 k 2 + b 2 2 -60x+450=24x-12,解得:x=5.5. y 1 =-60×5.5+450=120. 答:邮政车在返程途中与自行车队再次相遇时的地点距离甲地 120km .“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。
数字信号处理课后答案+第6章(第三版)

比较分子各项系数可知, A1、 A2应满足方程:
A1 A 2 1 A1 s 2 A 2 s1 a
解之得, A1=1/2, A2=1/2, 所以
H a (s) 1/ 2 s ( a jb ) 1/ 2 s ( a jb )
套用教材(6.3.4)式, 得到
(2) H a ( s )
Ha(s)的极点为
b (s a) b
2 2
s1=-a+jb,
s2=-a-jb
将Ha(s)部分分式展开:
j H a (s) j
2 2 s ( a jb ) s ( a jb )
套用教材(6.3.4)式, 得到
j H (z) 2 1 e
H a (s) H a ( p) |
p s
c
c
5 4 2 3
5 3 2 4 5
s 3 .2 3 6 1 c s 5 .2 3 6 1 c s 5 .2 3 6 1 c s 3 .2 3 6 1 c s c
对分母因式形式, 则有
H a (s) H a ( p) |
式中 Ωc=2πfc=2π×20×103=4π×104 rad/s
4. 已知模拟滤波器的系统函数Ha(s)如下: (1)
H a (s) sa (s a) b
2 2
(2)
H a (s)
b (s a) b
2 2
式中a、 b为常数, 设Ha(s)因果稳定, 试采用脉冲响应不变 法将其转换成数字滤波器H(z)。
H (z)
1 e
k 1
2
Ak
skT
z
1
第6章 反比例函数 浙教版数学八年级下册期末试题选编(含答案)

第6章反比例函数一、单选题1.(2022春·浙江金华·八年级统考期末)如图,在平面直角坐标系中,矩形ABCO,点B(10,8),点D在BC边上,连接AD,把ABD沿AD折叠,使点B恰好落在OC边上点E处,反比例函数(k≠0)的图象经过点D,则k的值为( )A.20B.30C.40D.482.(2022春·浙江丽水·八年级统考期末)反比例函数的图象必经过点()A.B.C.D.3.(2022春·浙江杭州·八年级统考期末)已知是关于的反比例函数,,和,是自变量与函数的两组对应值.则下列关系式中,成立的是()A.B.C.D.4.(2022春·浙江嘉兴·八年级统考期末)若反比例函数的图象经过点,则该反比例函数的表达式是()A.B.C.D.5.(2022春·浙江丽水·八年级统考期末)已知点,,都在反比例函数(a是常数)的图象上,且,则,,的大小关系为()A.B.C.D.6.(2022春·浙江湖州·八年级统考期末)已知反比例函数的图象经过点(2,﹣4),那么这个反比例函数的解析式是( )A.y=B.y=﹣C.y=D.y=﹣7.(2022春·浙江湖州·八年级统考期末)如图,和都是等腰直角三角形,,反比例函数在第一象限的图象经过点B,则与的面积差为().A.32B.16C.8D.48.(2022春·浙江金华·八年级统考期末)已知反比例函数的图象位于第一、三象限,则a的取值范围是()A.B.C.D.二、填空题9.(2022春·浙江绍兴·八年级统考期末)若点A(2,m)在反比例函数y=的图像上,则m 的值为________.10.(2022春·浙江宁波·八年级统考期末)如图,已知在平面直角坐标系中,直线分别交轴,轴于点和点,分别交反比例函数,的图象于点和点,过点作轴于点,连结. 若的面积与的面积相等,则的值是_____.11.(2022春·浙江宁波·八年级统考期末)若点在反比例函数的图象上,则____(填“>”或“<”或“=”)12.(2022春·浙江绍兴·八年级统考期末)如图,直线与反比例函数的图象相交于A、C 两点,与x轴交于点D,过点D作轴交反比例函的图象于点E,连结,点B为y 轴上一点,满足,且恰好平行于x轴.若,则k的值为________.13.(2022春·浙江金华·八年级统考期末)如图,在平面直角坐标系中,已知点的坐标为,射线与反比例函数的图像交于点,过点作轴的垂线交双曲线于点,过点作轴的垂线交双曲线于点,联结,那么的值是__________14.(2022春·浙江杭州·八年级统考期末)已知反比例函数,当时,的最大值与最小值之差是4,则________.15.(2022春·浙江绍兴·八年级统考期末)如图,在平面直角坐标系中,矩形的顶点A在x轴上,顶点C在y轴上,矩形的边在上,.反比例函数的图象经过点B,若阴影部分面积为6,则k的值为______________.16.(2022春·浙江嘉兴·八年级统考期末)如图,直线交反比例函数的图象于点A,交y轴于点B,将直线向下平移个单位后得到直线,交反比例函数的图象于点C.若的面积为,则k的值为____.17.(2022春·浙江丽水·八年级统考期末)如图,的顶点在轴正半轴上,反比例函数在第一象限经过点,与交于点,且,若的面积为9,则的值是______.18.(2022春·浙江宁波·八年级统考期末)如图,平面直角坐标系放置有两个三角板ABO和ACO,其中、为直角,,,和分别经过B、C两点,则的值为______.三、解答题19.(2022春·浙江丽水·八年级统考期末)已知是关于的反比例函数,当时,.(1)求此函数的表达式;(2)当时,函数值是,求的值.20.(2022春·浙江宁波·八年级统考期末)如图,一次函数y1=kx+b(k≠0)与反比例函数y2=(m≠0)的图象交于点A(1,2)和B(﹣2,a),与y轴交于点M.(1)求一次函数和反比例函数的解析式;(2)在y轴上取一点N,当△AMN的面积为3时,求点N的坐标;(3)求不等式kx+b﹣<0的解集.(请直接写出答案)21.(2022春·浙江杭州·八年级校考期末)如图,一次函数的图象与反比例四数的图象相交于A(1,3),B(-3,n)两点.(1)求一次函数和反比例函数的表达式;(2)当一次函数的值大于反比例函数的值时,直接写出的取值范围.(3)直线交轴于点,点是轴上的点,的面积等于的面积,求点的坐标.22.(2022春·浙江金华·八年级统考期末)如图,在平面直角坐标系中,点B在第一象限,BA⊥x轴于A,BC⊥y轴于C,BA=3,BC=5,有一反比例函数图像刚好过点B.(1)分别求出过点B的反比例函数和过A,C两点的一次函数的表达式.(2)动点P在射线CA(不包括C点)上,过点P作直线l⊥x轴,交反比例函数图像于点D.是否存在这样的点Q,使得以点B,D,P,Q为顶点的四边形为菱形?若存在,求出点Q的坐标;若不存在,请说明理由.23.(2022春·浙江嘉兴·八年级统考期末)如图,经过坐标原点O的直线交反比例函数的图象于点,B.点C是x轴上异于点O的动点,点D与点C关于y轴对称,射线交y轴于点E,连结,,.(1)①写出点B的坐标.②求证:四边形是平行四边形.(2)当四边形是矩形时,求点C的坐标.(3)点C在运动过程中,当A,C,E三点中的其中一点到另两点的距离相等时,求的值.24.(2022春·浙江湖州·八年级统考期末)如图一次函数y=kx+b的图像与反比例函数的图像交于点A(2,5)和点B(n,2).(1)求m,n的值;(2)连接OA,OB,求△OAB的面积.25.(2022春·浙江舟山·八年级统考期末)背景:点A在反比例函数的图象上,轴于点B,轴于点C,分别在射线上取点D,E,使得四边形为正方形.如图1,点A在第一象限内,当时,小李测得.探究:通过改变点A的位置,小李发现点D,A的横坐标之间存在函数关系.请有助小李解决下列问题.(1)求k的值.(2)设点A,D的横坐标分别为x,z,将z关于x的函数称为“Z函数”.如图2,小李画出了时“Z函数”的图象.①求这个“Z函数”的表达式.②补画时“Z函数”的图象,并写出这个函数的性质(两条即可).26.(2022春·浙江温州·八年级统考期末)如图,某校劳动小组计划利用已有的一堵长为6m的墙,用篱笆围成一个面积为的矩形劳动基地,边的长不超过墙的长度,在边上开设宽为1m的门(门不需要消耗篱笆).设的长为(m),的长为(m).(1)求关于的函数表达式.(2)若围成矩形劳动基地三边的篱笆总长为10m,求和的长度(3)若和的长都是整数(单位:m),且围成矩形劳动基地三边的篱笆总长小于10m,请直接写出所有满足条件的围建方案.27.(2022春·浙江衢州·八年级统考期末)如图1,将一长方体放置于一水平玻璃桌面上,按不同的方式摆放,记录桌面所受压强与受力面积的关系如下表所示:桌面所受压强P(Pa)400受力面积S()0.5根据表中数据,求出压强()的函数表达式及10cm,且与原长方体相同重量的长方体放置于该水平28.(2022春·浙江杭州·八年级统考期末)在探究欧姆定律时,小明发现小灯泡电路上的电压保持不变,通过小灯泡的电流越大,灯就越亮.设选用小灯泡的电阻为,通过的电流强度为.(1)若电阻为,通过的电流强度为,求关于的函数表达式.(2)如果电阻小于,那么与原来的相比,小灯泡的亮度将发生什么变化?参考答案:1.B【分析】根据翻折变换的性质,可得AE=AB=5,DE=BD;然后设点D的坐标是(10,b),在Rt△CDE 中,根据勾股定理,求出CD的长度,进而求出k的值.【详解】解:∵△ABD沿AD折叠,使点B恰好落在OC边上点E处,点B(10,8),∴AE=AB=10,DE=BD,∵AO=8,AE=10,∴OE==6,CE=10﹣6=4,设点D的坐标是(10,b),则CD=b,DE=8﹣b,∵CD2+CE2=DE2,∴b2+42=(8﹣b)2,解得b=3,∴点D的坐标是(10,3),∵反比例函数的图象经过点D,∴k=10×3=30,故选:B.【点睛】本题考查了求反比例函数的解析式,同时也考查了矩形的翻折问题.须熟练掌握待定系数法求反比例函数的解析式,轴对称的性质.其中求点D的坐标是解题的关键.2.B【分析】利用代入法,把坐标一一代入反比例函数解析式,即可得出结果.【详解】解:A.把代入反比例函数,可得:,故该选项不符合题意;B.把代入反比例函数,可得:,故该选项符合题意;C.把代入反比例函数,可得:,故该选项不符合题意;.把代入反比例函数,可得:,故该选项不符合题意.故选:B【点睛】本题考查了反比例函数的定义及解析式,解本题的关键在充分利用反比例函数解析式进行分【详解】解:设该反比例函数的表达式是,把点代入得:,解得:,∴该反比例函数的表达式是.故选:【点睛】本题主要考查了求反比例函数解析式,熟练掌握待定系数法求函数解析式是解题的关键.【分析】根据,判断反比例函数的图象所在位置,结合图象分析函数增减性,利用函数增减性比较自变量的大小.∵,反比例函数(当时,,故选:D.【点睛】本题考查反比例函数的自变量大小的比较,解题的关键是结合图象,根据反比例函数的增减性分析自变量的大小.=,代入点求出即可.【详解】解:设反比例函数解析式为=,-4=,所以这个反比例函数解析式为=-.【点睛】本题主要考查待定系数法求反比例函数解析式,求反比例函数解析式只需要知道其图像上一点的【分析】已知反比例函数的解析式为,根据系数)再结合已知条件求解即可;【详解】解:如图,设点,因为点B在反比例函数的图象上,所以设点,),)−=m2−2=n−(=−m mn=−(BAD=8.【点睛】本题考查了反比例函数系数的几何意义、等腰三角形的性质以及面积公式,解题的关键是掌握反比例函数系数的几何意义.【分析】根据反比例函数经过第一、三象限,可知,据此作答即可.反比例函数的图象位于第一、三象限,∴,解得:,故选:C.函数的(当时,反比例函数的(当时,反比例函数的()的图象经过二、四象限.【详解】解:将点()代入反比例函数得,==3点睛:本题主要考查反比例函数图象上点的坐标特征,所有在反比例函数上的点的横纵坐标符合函数的解【分析】过点作轴于.根据代入即可求得的值.【详解】如图,过点作轴于.代入得:由反比例函数比例系数的几何意义,可得,.∵,∴,∴.易证,从而,即的横坐标为,而在直线上,∴∴.故答案为2.【分析】先确定的图像在一,三象限,且在每一象限内,随的增大而减小,再利用反比例函数的性质可得答案.【详解】解:>的图像在一,三象限,且在每一象限内,随的增大而减小,><故答案为:【点睛】本题考查的是反比例函数的性质,掌握利用反比例函数的图像与性质比较函数值的大小是解题的【分析】由等腰三角形的性质可得,即点C的纵坐标得出,进而利用全等三角形得出点,利用反比例函数图象上点的坐标特征得出点E的纵坐标,再利用三角形的面积可得【详解】解:如图,过点作轴,交于点作轴,垂足为∵,∴,由于点A、点C在反比例函数的图象上,可设点,即,,∴,∴点,即,∴,∴,在和中,,∴,∴,∴点E的横坐标为,在反比例函数的图象上,的纵坐标为,即,∵,即,∴,∴,故答案为:6.【点睛】本题考查反比例函数图象上点的坐标特征,以及一次函数与反比例函数的交点坐标,利用坐标表【分析】求出的直线解析式,联立,求出,,过点作交于点,交于点,则,,分别求出,,,,即可求,,再求即可.【详解】解:设的解析式为,,,,联立,解得,,,过点作交于点,交于点,,,,,,,,,,故答案为:1.【点睛】本题考查反比例函数的图象及性质,解题的关键是熟练掌握反比例函数的图象及性质.,∴△CMO≌△EMF(AAS)∴,∴,则ab=12,=,=k =12故答案为【点睛】本题考查待定系数法求反比例函数,矩形的性质和全等三角形的性质和判定,不规则图形面积,【分析】向下平移个单位后得到直线,可得到的函数表达式,将点A分别作轴得垂线,与y轴交于点P,则,即可求的坐标,最后将点的坐标代入反比例函数的表达式,求出k即可.∵向下平移个单位后得到直线直线=0代入得;y=,)的横坐标为m,则,)的横坐标为,)AP=m,CQ=n,PQ=-()= PB==,BQ=====∵的面积为∴==(,4(,)代入解得:k=6=四边形OACB=BC∴,∵∴,∴,∴k=12,.【分析】过点,分别做轴的垂线,交于点,,令长为,根据直角三角形的性质,勾股定理,得,,,的值,得到点,点的坐标;将点的坐标代入,点的坐代入标,求出,,即可.【详解】如图,过点,分别做轴的垂线,交于点,,设长为∴在,中,∴,∴∴∴在,中,∴;∴;∴,∴,∴故答案为:.反比例函数解析式为(2)【分析】()首先设反比例函数解析式为,然后把,代入反比例函数,即可得出)中反比例函数解析式,把代入解析式,即可得出)解:设反比例函数解析式为,把,代入反比例函数解析式,可得:,反比例函数解析式为.)可得:,当时,函数值是,∵当时,,∴,解得:.【点睛】本题考查了用待定系数法求反比例函数表达式、反比例函数的定义,解本题的关键在正确求出反比例函数表达式.),;)或;)或【分析】(1)先由点A(1,)在反比例函数图象上求解反比例函数的解析式,再求解的坐标代入一次函数的解析式,求解一次函数的解析式即可;)先求解设点,可得)结合函数图象,根据一次函数的图象在反比例函数的图象的下方,从而可得答案)=(反比例函数的解析式为:)代入可得:把代入y1=(k≠0),解得:所以一次函数的解析式为:)令则则设点,解得:或或(3)kx+b﹣<0,所以一次函数值小于反比例函数值,即一次函数的图象在反比例函数图象的下方,所以或【点睛】本题考查的利用待定系数法求解一次函数与反比例函数的图象,坐标与图形的面积,利用函数图(1),(2)或(3)或【分析】(1)将点A坐标代入反比例解析式求出解析式求出n的值,确定出点)代入反比例解析式得:,,∴反比例解析式为,)代入反比例解析式得:,∴,∴B(-3,)代入中,得:,解得:,一次函数解析式为;)解:由图象得:一次函数值大于反比例函数值的的取值范围为或;)解:对于一次函数,令,得到,即0),∴.∵的面积等于的面积,,,∵点是轴上的点,∴设点P(∴,解得,.∴或.【点睛】此题考查了一次函数与反比例函数的交点问题,涉及的知识有:坐标与图形性质,待定系数法求函数解析式,利用了数形结合的思想,熟练掌握待定系数法是解本题的关键.22.(1),存在,Q点的坐标为(5,-)或(-)或(,)根据题意分别求出A点和C点的坐标,然后用待定系数法求出函数解析式即可;点和D点的坐标,分点在直线BA=,3=,的反比例函数的解析式为=,点坐标得,,解得,A,C两点的一次函数的表达式为=-x)解:存在,(m,-m,)若以点B,为顶点的四边形为菱形则点∴-(-m+3=,整理得,解得=或,经检验,m的值是方程的解,=时,=--m==此时Q5,3-),Q(5-);=时,=-(-m==此时(5,3-),Q(5-);B,D,P,,且=3=,经检验,m的值是方程的解,,=,(,综上所述,若以点-)或(-)或(,3【点睛】本题主要考查反比例函数的综合题,熟练掌握待定系数法求解析式,一次函数的性质,反比例函数的性质,菱形的性质,解一元二次方程等知识是解题的关键.23.(1);证明见解析(2)(3)或或【分析】(1)①根据反比例函数图象是中心对称图形可得点②根据中心对称的性质可得正比例函数与反比例函数的图象于点,∴;②∵点A、∴OA=OB,∵,∴,∴,∴;(3)当点E作AH⊥x轴于∴,∴,∵,∴点D与H重合,∴,∴,当点A为CE的中点时,如图,则,同理可得,∴,∵四边形ACBD是平行四边形,∴,∴,∴,当点C为AE的中点时,,则,,由勾股定理得,∴,综上:或或.【点睛】本题是反比例函数综合题,主要考查了反比例函数的性质,平行四边形的判定,矩形的性质,三角形中位线定理等知识,熟练掌握反比例函数图象是中心对称图形是解题的关键,同时注意分类讨论思想的运用.(2)【分析】2)利用待定系数法求得一次函数的解析式,即可求得直线与)代入中,得到y,y中,得到=5;)解:如图所示:∴,解得,∴一次函数为+7,令y=0,则﹣0,解得∴C(7,0),BOC.【点睛】本题考查待定系数法确定函数关系式以及平面直角坐标系下三角形面积,掌握待定系数法以及坐①;而增大.,,=(A(∴;②图象如图:性质1:x>0时,y随x的增大而增大;性质2:x<0时,y随x的增大而增大.【点睛】此题考查待定系数法求反比例函数解析式,画函数图象,函数的性质,熟练掌握各知识点并应用解决问题是解题的关键.26.(1)(2)(3)或,进而可得出:;均为整数,围成矩形劳动基地三边的篱笆总长小于10m,可得出∴.又∵墙长为∴,∴.∴y关于的函数表达式为:.)解:依题意得:,∴或,∵,∴,∴;(3)解:依题意得:,,∴,∵和的长都是正整数,∴或,∴则满足条件的围建方案为:或【点睛】本题考查了根据实际问题列出反比例函数关系式,根据各数量之间的关系,找出关系式以及根据x(1),这种摆放方式不安全,理由见解析()的函数表达式为,)代入得:,)关于受力面积S()的函数表达式为,时,,)解:这种摆放方式不安全,理由如下:=0.1×0.2=0.02()将长方体放置于该水平玻璃桌面上的压强为,(1)小灯泡的亮度将变亮【分析】(1)根据题意列出关系即可求解;电压不变,,∴,;(2),,随的增大而减小,若电阻小于,那么与原来的相比,小灯泡的亮度将变亮.【点睛】本题考查了反比例函数的应用,根据题意列出函数关系式是解题的关键.。
第6章 递归(C++版)

• 例6.18 用递归方法求两个数m和n的最大公约数。(m>0,n>0) 【分析】求两个数的最大公约数,可以用枚举因子的方法,从两者中 较小的数枚举到能被两个数同时整除且是最大的约数的方法;也可以 用辗转相除法,这里采用递归实现辗转相除算法: ①求m除以n的余数; ②如果余数不为0,则让m=n,n=余数,重复步骤①,即调用子程序; ③如果余数为0,则终止调用子程序; ④输出此时的n值。
2.函数的调用 声明了函数原型之后,便可以按如下形式调用函数: 函数名(实参列表) 例如语句sum+=js(i); 实参列表中应给出与函数原型形参个数相同、类型相 符的实参。在主调函数中的参数称为实参,实参一般应具 有确定的值。实参可以是常量、表达式,也可以是已有确 定值的变量,数组或指针名。函数调用可以作为一条语句 ,这时函数可以没有返回值。函数调用也可以出现在表达 式中,这时就必须有一个明确的返回值。
它的执行流程如下图所示:
采用有参函数编写程序如下: #include<iostream> using namespace std; int fac(int ); int main() { int x; cin>>x; cout<<x<<"!="<<fac(x)<<endl; //主程序调用fac(x) 求x ! return 0; } int fac(int n) //函数fac(n) 求n ! { return n==0 ? 1 : n*fac(n-1); //调用函数fac(n-1)递归求(n-1) ! } 【说明】: 这里出现了一个小东西,三元运算符“?:”。a?b:c的含义是:如果 a为真,则表达式的值是b,否则是c。所以n==0 ? 1 : n*fac(n-1)很好地 表达了刚才的递归定义。
信号与系统 第6章-作业参考答案

Hd
(z)
=
Hc(z)
s
=1− 1+
z z
−1 −1
证明:H������(z)有一个位于单位圆内的极点和一个位于单位圆外的零点
c)对于系统函数H������(z),证明�H�������ejω�� = 1
证明:
16
第六章 z 变换
第 6 章 习题参考答案
6-4 计算机设计题 答案暂略
17
和 x2(n) = �14�n u(n)
设序列x1(n)的单边和双边 变换分别为 X1( X2(z) 和 X2d (z) 。
1) 根据双边 z 变换的定义和卷积定理,求出g(n) = x1(n) ∗ x2(n); 2) 根据单边 z 变换的定义和卷积定理,求出g(n) = x1(n) ∗ x2(n); 3) 解释 1)和 2)的结果为何不同。 解:
,试用
z
变换的初值
和终值性质确定离散序列 x(n) 的初值 x(0) 和终值 x(∞) 。
6
第六章 z 变换 解:直接求出。
第 6 章 习题参考答案
6-2-26 某离散LTI系统由差分方程
y(n)
−
10 3
y(n)
+
y(n
+
1)
=
x(n)
描述。试求系统的单位样值响应 h(n) ,并确定系统的稳定性。
解:
5
第六章 z 变换
第 6 章 习题参考答案
∞
∑ 6-2-21 序列 x(n) 的自相关序列定义为φxx (n) = x(k)x(n + k) 。试利用 x(n) 的 z 变换 k =−∞
求出φxx (n) 的 z 变换。
解:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.在C语言中,全局变量的存储类别是:A) sta tic B) externC) void D) registerA2.C语言中,凡未指定存储类别的局部变量的隐含存储类别是:A) 自动(auto) B) 静态(static)C) 外部(extern) D) 寄存器(register)A3. 在一个C源程序文件中,要定义一个只允许本源文件中所有函数使用的全局变量,则该变量需要使用的存储类别是:________。
A) extern B) register?C) auto D) staticD4. 若有以下调用语句,则正确的fun函数首部是main(){ ∶∶int a;float x;∶∶fun(x,a);`∶∶}A) void fun(int m,float x) B) void fun(float a,int x)C) void fun(int m,float x[]) D) void fun(int x,float a)B5. 有如下函数调用语句func(rec1,rec2+rec3,(rec4,rec5));该函数调用语句中,含有的实参个数是A) 3 B) 4C) 5 D) 有语法错误、A6. 以下程序的运行结果是。
#include <>main(){ int k=4,m=1,p;p=func(k,m); printf("%d, ",p);p=func(k,m); printf("%d\n",p); }func(int a,int b){ static int m=0,i=2;i+=m+1;^m=i+a+b;return m; }A) 8,17, B) 8,17C) 8,8 D) 4,1B7. 函数fun的功能是:根据以下公式计算并返回S,n通过形参传入,n的值大于等于0。
划线处应填________。
1 1 1 1S=1 - ─+ ─- ─+ …───@3 5 7 2n-1float fun(int n){ float s=,w,t,f=;int i;for(i=0;i<n;i++){f=-f;w=f/(2*i+1);s+=w; }____________; }A) return (f) B) return (S)】C) return (s) D) return (w)C8. 有如下程序int func(int a,int b){ return(a+b); }main(){ int x=2,y=5,z=8,r;r=func(func(x,y),z);printf("%d\n",r); }该程序的输出结果是__________。
?A) 12 B) 13C) 14 D) 15D9. 以下函数返回a数组中最小值所在的下标,在划线处应填入的是________。
fun( int a[],int n){ int i,j=0,p;p=j;for(i=j;i<n;i++))if(a[i]<a[p])_______________;return (p); }A) i=p B) a[p]=a[i]C) p=j D) p=iD10. 设在主函数中有以下定义和函数调用语句,且fun函数为void类型;正确的fun函数的首部应为________(要求形参名为b)。
main(){ double s[10][22];'int n;∶∶fun(s);∶∶}A) void fun(double b[22])B) void fun(double b[][22])C) void fun(double b[][])&D) void fun(double b[22][])B11. 以下程序的输出结果是________。
void fun(){ static int a=0;a+=2;printf("%d",a); }main(){ int cc;for(cc=1;cc<4;cc++) fun( );>printf("\n"); }A) 2222 B) 2468C) 222 D) 246D12. 以下程序的输出结果是#include <>main(){ char a[]="abcdefghi"; int k;fun(a); puts(a); },fun( char s[]){ int x,y; char c;for(x=0,y=(strlen(s)-1)/2; x<y;x++,y--){c=s[y];s[y]=s[x];s[x]=c; } }A) ihgfedcba B) abcdefghiC) edcbafghi D) ihgfefghiC…13. 以下程序的输出结果是________。
int d=1;fun( int p){ static int d=5;d+=p;printf("%d ",d);return (d); }main(){ int a=3; printf("%d \n",fun(fun(d))); }A) 6 11 11 B) 6 6 9。
C) 6 12 12 D) 6 6 15C14. 下列程序的输出结果是________。
int t(int x,int y,int cp,int dp){ cp=x*x+y*y; dp=x*x-y*y; }main(){ int a=4,b=3,c=5,d=6;$t(a,b,c,d);printf("%d %d\n",c,d); }A) 16 9 B) 4 3C) 5 6 D) 25 9C15. 下列叙述中正确的是________。
A) C语言编译时不检查语法B) C语言的子程序有过程和函数两种C) C语言的函数可以嵌套定义D) C语言所有的函数都是外部函数&D16. 以下所列的各函数首部中,正确的是________。
A) void play(var a:Integer,var b:Integer)B) void play(int a,b)C) void play(int a,int b)D) void play(a as integer,b as integer)C17. 以下程序的输出结果是fun(int x,int y,int z){ z=x*x+y*y;}%main(){ int a=31;fun(5,2,a);printf("%d",a); }A) 0 B) 29C) 31 D) 无定值C18. 以下程序输出的结果是________。
long fun(int n)~{ long s;if(n==1||n==2) s=2;else s=n-fun(n-1);return s; }main(){ printf("%ld\n",fun(3));}A) 1 B) 2C) 3 D) 4A;19. 请读程序:#include <>char fun(char c){ if (c<='Z' && c>='A') c-='A'-'a';return (c); },main(){ char s[81]; int k=0;gets(s);while(s[k]){ s[k]=fun(s[k]); putchar(s[k]); k++;}putchar('\n'); }若运行时从键盘上输入OPEN THE DOOR<CR>(<CR>表示回车),则上面程序的输出结果是________。
A) oPEN tHE dOOR B) open the doorC) OPEN THE DOOR D) Open The Door<B20. 请读程序:#include <>f(int b[ ],int n){ int i,r;r=1;for (i=0;i<=n;i++) r=r*b[i];return r; }main(){ int x,a[]={2,3,4,5,6,7,8,9};;x=f(a,4);printf("%d\n",x); }上面程序的输出结果是________。
A) 720 B) 120C) 24 D) 6A21. 有以下程序#inclde <>main()《{int k=4,m=1,p;p=func(k,m); printf("%d, ",p);p=func(k,m); printf("%d\n",p); } func(int a,int b){ static int m=0,i=2;i=m+1;m=i+a+b;return(m); }输出结果是________。
A) 6,6 B) 6,12>C) 6,8 D) 8,8B22. 以下程序的输出结果是________。
#include ""space(char str[ ]){int i,t; char ts[81];"for(i=0,t=0;str[i]!= '\0';i+=2)if(!isspace(str[i]) && str[i]!= 'a')ts[t++]=toupper(str[i]);ts[t]= '\0';strcpy(str,ts); }main(){char s[81]={ "a b c d ef g"};space(s);puts(s);}A) abcdeg B) bcde,C) ABCDE D) BCDED23. 下面函数的功能是________。
sss(char s[ ],char t[ ]){ int i=0;while( t[i]) { s[i]=t[i]; i++ ; }s[i]= '\0'; }A) 求字符串的长度B) 比较两个字符串的大小%C) 将字符串s复制到字符串t中D) 将字符串t复制到字符串s中D24. 下面函数的功能是________。
sss(char s[ ]){ int i=0;while( s[i]) i++ ;return i; }A) 求字符串的长度B) 比较两个字符串的大小*C) 将字符串s逆序存放D) 功能无法确定A25. 设有如下的函数ggg(float x){printf("\n%d",x*x);}则函数的类型________。
