空间几何体的表面积和体积练习题
高一数学空间几何体的表面积与体积试题答案及解析

高一数学空间几何体的表面积与体积试题答案及解析1. 已知正方体的棱长为1,且其顶点都在一个球面上,则该球的表面积为( ) A .π B .2π C .3π D .4π【答案】C.【解析】正方体的对角线长为外接球的直径,因此,,因此.【考点】球的表面积公式.2. 如图,在四边形ABCD 中,∠DAB =90°,∠ADC =135°,AB =5,CD =2,AD =2,求四边形ABCD 绕AD 旋转一周所成几何体的表面积及体积.【答案】S 表面=(60+4)π.V =π.【解析】该图形旋转后是一个圆台除去一个倒放的圆锥, 则S 表面=S 下底面+S 台侧面+S 锥侧面 , 设圆台上,下地面半径是r 1,r 2,则 S 表面=π×r 22+π×(r 2+r 1)×5+π×r 1×CDV =V 台-V 锥=π(+r 1r 2+)AE -πr 2DE ,将数据代入计算即可。
试题解析:如图,设圆台上,下地面半径是r 1,r 2,过C 点作CF ⊥AB ,由∠ADC =135°,CE ⊥AD, CD=2得∠EDC =45°,r 1=" CE=" 2,则CF=4,BF=3,CF ⊥AB ,得BC=5,r 2=" AB=" 5, ∴S 表面=S 下底面+S 台侧面+S 锥侧面 =π×r 22+π×(r 2+r 1)×5+π×r 1×CD =π×52+π×(2+5)×5+π×2×2 =(60+4)π. V =V 台-V 锥=π(+r 1r 2+)AE -πDE =π(+2×5+)4-π×2=π.【考点】圆台,圆锥的表面积和体积.3.如图,在长方体ABCD—A1B1C1D1中,AB=2,BB1=BC=1,E为D1C1的中点,连结ED,EC,EB和DB.(1)求证:ED⊥平面EBC;(2)求三棱锥E-DBC的体积.【答案】(1)见解析;(2)【解析】(1)易得△DD1E为等腰直角三角形DE⊥EC,BC⊥平面 BC⊥DE,所以DE⊥平面EBC平面DEB⊥平面EBC.(2)需要做辅助线,取CD中点M,连接EM∥,DCB(这个证明很关键),然后根据公式.试题解析:(1)在长方体ABCD-A1B1C1D1中,AB=2,BB1=BC=1,E为D1C1的中点.∴△DD1E为等腰直角三角形,∠D1ED=45°.同理∠C1EC=45°.∴,即DE⊥EC.在长方体ABCD-中,BC⊥平面,又DE平面,∴BC⊥DE.又,∴DE⊥平面EBC.又∴平面DEB⊥平面EBC.(2)取CD中点M,连接EM,E为D1C1的中点,∥,且,又DCB.【考点】线面垂直,三棱锥的体积.4.设甲、乙两个圆柱的底面积分别为,体积分别为,若它们的侧面积相等,且,则的值是.【答案】【解析】设甲、乙两个圆柱的底面半径为,母线长,由于侧面积相等,,,,.【考点】圆柱的体积公式应用.5.如果两个球的体积之比为8:27,那么两个球的表面积之比为()A.8:27B.2:3C.4:9D.2:9【答案】C【解析】由题意,故选C【考点】球的体积和表面积6.棱长为4的正方体的八个顶点都在同一个球面上,则此球的表面积为_____________.【答案】48【解析】正方体的外接球的球心为正方体的中心,球的直径为正方体的对角线,所以球的表面积为【考点】正方体的外接球7.如图是从上下底面处在水平状态下的棱长为的正方体中分离出来的.有如下结论:①在图中的度数和它表示的角的真实度数都是;②;③与所成的角是;④若,则用图示中这样一个装置盛水,最多能盛的水.其中正确的结论是(请填上你所有认为正确结论的序号).【答案】①④【解析】①∵在正视图的等腰直角中,在图中的度数和它表示的角的真实度数都是,故①正确;②补全正方体如图所示:连接.∵,∴是正三角形,故.而==,故②错;③连接、,∵,∴是正三角形,所以与所成的角是,故③错;④用图示中这样一个装置来盛水,那么盛最多体积的水时应是三棱锥的体积.又===,故④正确,故填①④.【考点】1、正方体的性质;2、异面直线所成角;3、三棱锥的体积.8.已知一个正三棱锥的三条侧棱两两垂直且相等,底面边长为,则该三棱锥的外接球的表面积是()A.B.C.D.【答案】A【解析】设该正三棱锥为,依题意两两垂直且,所以,且该正三棱锥的外接球与以为邻边的正方体的外接球是相同的,正方体的边长为,体对角线长为,故球的半径为,所以球的表面积为,故选A.【考点】1.三棱锥的外接球;2.球的表面积公式.9.如图,已知直三棱柱中,,,,D为BC的中点.(1)求证:∥面;(2)求三棱锥的体积.【答案】(1)略(2)【解析】(1)连接交于点O,连接OD,在中可根据中位线证得∥,再根据线面平行的性质定理可证得∥面。
高二数学空间几何体的表面积与体积试题答案及解析

高二数学空间几何体的表面积与体积试题答案及解析1.正四棱锥的五个顶点在同一个球面上,若其底面边长为4,侧棱长为,则此球的表面积为()A.B.C.D.【答案】B【解析】设球的半径为,正方形的ABCD的对角线的交点 M,则球心在直线PM上.,由勾股定理得,再由射影定理得即∴此球的表面积为.【考点】球的表面积.2.一个圆柱形的罐子半径是4米,高是9米,将其平放,并在其中注入深2米的水,截面如图所示,水的体积是()平方米.A.B.C.D.【答案】D.【解析】所求几何体的体积为阴影部分的面积与高的乘积,在中,,则,,体积.【考点】组合体的体积.3.一个四棱锥的侧棱长都相等,底面是正方形,其正视图如图所示,则该四棱锥的侧面积是_________.【答案】【解析】由正视图可知四棱锥的底面边长为2,高为2,可求出斜高为,因此四棱锥的侧面积,答案为.【考点】1.几何体的三视图;2.锥体的侧面积计算4.已知球的直径SC=4,A.,B是该球球面上的两点,AB=2,∠ASC=∠BSC=45°,则棱锥S-ABC的体积为_________【答案】【解析】设AB的中点为D,球心为O,连结SD,CD,OD,由SC=4为球的直径知,∠SBC=∠SAC=90o,因为∠ASC=∠BSC=45°,所以SA=BC=SB=AC=,所以SD⊥AB,DC⊥AB,所以AB⊥面SDC,因为AB=2,所以SD=DC==,所以DO= =,所以= ===.考点:球的性质,线面垂直判定,三棱锥的体积公式,转化思想5.如图,一个盛满水的三棱锥容器,不久发现三条侧棱上各有一个小洞,且知,若仍用这个容器盛水,则最多可盛水的体积是原来的 .【答案】【解析】过作截面平行于平面,可得截面下体积为原体积的,若过点F,作截面平行于平面,可得截面上的体积为原体积的,若C为最低点,以平面为水平上面,则体积为原体积的,此时体积最大.【考点】体积相似计算.6.一个半径为1的小球在一个内壁棱长为的正四面体封闭容器内可向各个方向自由运动,则该小球表面永远不可能接触到的容器内壁的面积是.【答案】【解析】如图甲,考虑小球挤在一个角时的情况,记小球半径为,作平面//平面,与小球相切于点,则小球球心为正四面体的中心,,垂足为的中心.因,故,从而.记此时小球与面的切点为,连接,则.考虑小球与正四面体的一个面(不妨取为)相切时的情况,易知小球在面上最靠近边的切点的轨迹仍为正三角形,记为,如图乙.记正四面体的棱长为,过作于.因,有,故小三角形的边长.小球与面不能接触到的部分的面积为(如答图2中阴影部分).又,,所以.由对称性,且正四面体共4个面,所以小球不能接触到的容器内壁的面积共为.【考点】(1)三棱锥的体积公式;(2)分情况讨论及割补思想的应用。
空间几何体的综合计算测试题

空间几何体的综合计算测试题1. 综合计算题求以下空间几何体的表面积和体积:1.1 直方体已知直方体的长、宽、高分别为10 cm、6 cm、8 cm,求其表面积和体积。
解答:该直方体的表面积可通过公式2*(长×宽 + 长×高 + 宽×高)计算,代入数值计算得:表面积 = 2*(10 × 6 + 10 × 8 + 6 × 8) = 2*(60 + 80 + 48) = 376 cm²。
该直方体的体积可通过公式长×宽×高计算,代入数值计算得:体积 = 10 × 6 × 8 = 480 cm³。
1.2 正方体已知正方体的边长为5 cm,求其表面积和体积。
解答:该正方体的表面积可通过公式6×边长²计算,代入数值计算得:表面积 = 6×5² = 6×25 = 150 cm²。
该正方体的体积可通过公式边长³计算,代入数值计算得:体积 = 5³ = 125 cm³。
1.3 圆柱体已知圆柱体的底面半径为4 cm,高为10 cm,求其表面积和体积(π取3.14)。
解答:该圆柱体的表面积可分为两部分计算:侧面积和底面积。
侧面积可通过公式2×π×半径×高计算,代入数值计算得:侧面积 = 2×3.14×4×10 = 251.2 cm²。
底面积为圆的面积,可通过公式π×半径²计算,代入数值计算得:底面积 = 3.14×4² = 50.24 cm²。
因此,该圆柱体的表面积为251.2 + 50.24 = 301.44 cm²。
该圆柱体的体积可通过公式π×半径²×高计算,代入数值计算得:体积 = 3.14×4²×10 = 502.4 cm³。
必修二_1.3_空间几何体的表面积和体积同步练习和详细答案

1.3空间几何体的表面积和体积【知识总结】1. 多面体的面积和体积公式名称 侧面积(S 侧) 全面积(S 全)体积(V )棱 棱柱 直截面周长x IS 侧+2S 底S底• h=S 直截面• h柱直棱柱 chS 底• h「棱锥棱锥 各侧面积之和1S 底• h3 正棱锥 1『 —ch 2S 侧+S 底棱台各侧面面积之和1—h(S 上底+S 下底+3棱 台正棱台1一 (c+c ' )h '2S 侧+S 上底+S 下底S 下底’S 下底)表中表示面积,'、分别表示上、下底面周长,表斜咼,'表示斜咼,表示侧棱长。
2 .旋转体的面积和体积公式名称圆柱圆锥圆台球S 侧 2 n rl n rl n (r 1+「2)lS 全 2 n r(l+r) n r(l+r) 2 2n (r 1+r 2)l+ n (r 1+r24 n RVn r 2h(即 n r 2l)1r 2h —n r h312 2—n h(r 1+r 1「2+r 2)3 43—n R3 表中I 、h 分别表示母线、咼,r 表示圆柱、圆锥与球冠的底半径,r i 、「2分别表示圆台上、下底面半径,R 表示半径。
【知能训练】A:多面体的表面积和体积 一•选择题1.如图,在直三棱柱 ABC-ABC i 中,AA=AB=2 BC=1, / ABC=90,若规 定主(正)视方向垂直平面 ACCA ,则此三棱柱的左视图的面积为 ( )A.—— B . 2 - C . 4 D . 22•某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底 边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、 高为4的等腰三角形,则该几何体的表面积为()3.—个棱锥被平行于底面的平面所截,如果截面面积与底面面积之比为1: 2,则截面把棱锥的一条侧棱分成的两段之比是()A . 1 : 4B . 1 : 2C . 1 : ( "- 1 )D . 1: ( 一+1 ) 4.正六棱台的两底边长分别为1cm, 2cm,高是1cm,它的侧面积为()A . 80B . 24 一+88C. 24 一+40 D . 118A .9 ~ 2cm2B . 9 cmC. - cm 22D. 3 cm5. 要制作一个容积为 4卅,高为1m 的无盖长方体容器,已知该容器的底面造价是每平方米 20元,侧面造价是每平方米 10元,则该容器的最低总造价是( )A . 80 元B . 120 元C . 160 元D. 240 元6. (文) 四棱锥S-ABCD 的底面是矩形,锥顶点在底面的射影是矩形对角线的交点,四棱 锥及其三视图如图(AB 平行于主视图投影平面)则四棱锥 A . 24 B . 18 C . - - D . 87. 某空间组合体的三视图如图所示,则该组合体的体积为( A . 48B . 56C . 64D. 72&各棱长均为a 的三棱锥的表面积为( )A. 4 _a 2B . 3 "a 2C .2 _a 2D9.已知一个四棱锥的高为 3,其底面用斜二测画法所画出的水平放置的直观图是一个边长为1的正方形,则此四棱锥的体积为()10. 如图,在三棱柱 ABC-ABC 中,D, E , F 分别是AB, AC, AA 的中点,设三棱锥 F-ADE的体积为V 1,三棱柱 ABG-ABC 的体积为V 2,则V 1: V ___________________________________ .11. _______ 将边长为2的正方形沿对角线 AC 折起,以A, B, C, D 为顶点的三棱锥的体积最大值等 于 ____ .12.如图,一个三棱柱形容器中盛有水,且侧棱AA=8.若AAB 1B 水平放置时,液面恰好过AC BC, AC , BC 的中点,则当底面 ABC 水平放置时,液面的高为 _________________ . 13. 四棱锥P-ABCD 的底面ABCE 为正方形,且PD 垂直于底面 ABCD N 为PB 中点,则三棱锥 P-ANC 与四棱锥P-ABCD 的体积比为 ________________ .14.已知某四棱锥,底面是边长为2的正方形,且俯视图如图所示.若该四棱锥的侧视图为S-ABCD 的体积=( )A .B . 6C. -D . 2直角三角形,则它的体积为_________________15.如图所示,在三棱柱ABC-ABQ 中,AB=AC=AA=2, BC=2 ;且/ AAB=/ A i AC=60,则该三棱柱的体积是_________________________ .B:旋转体的表面积和体积1•如果圆锥的底面半径为,高为2,那么它的侧面积是()A. 4 n B . 2 n C . 2 n D . 4 n2.一圆锥的侧面展开图是半径为2的半圆,则该圆锥的全面积是()A. 5 nB. 4 nC. 3 nD. 2 n3•如果圆锥的轴截面是正三角形(此圆锥也称等边圆锥),则此圆锥的侧面积与全面积的比是()A. 1 : 2 B. 2: 3 C. 1 : 一 D. 2: _4•圆锥侧面积为全面积的,则圆锥的侧面展开图圆心角等于()A. - nB. nC. 2 nD.以上都不对5.圆台的上、下底面半径和高的比为 1 : 4: 4,母线长为10,则圆台的侧面积为()A. 81 nB. 100 nC. 14 nD. 169 n6.已知球的直径SC=8 A, B是该球球面上的两点,AB=2 ,/ SCAN SCB=60,则三棱锥S-ABC 的体积为()A. 2 ~B. 4 ~C. 6 ~D. 8 ~7.若圆柱的底面直径和高都与球的直径相等,圆柱、球的表面积分别记为S、S,则S:Sa=()A. 1 : 1B. 2: 1C. 3: 2D. 4: 1&若两个球的表面积之比为1: 4,则这两个球的体积之比为()A. 1 : 2B. 1 : 4C. 1 : 8D. 1 : 169.体积相等的正方体、球、等边圆柱(即底面直径与母线相等的圆柱)的全面积分别为S , S, S3,那么它们的大小关系为()A. S1 v S2 v S3B. S1 v S3V S2C. S2V S3 v S1D. S2 v S1 v S3二.填空题(共5小题)10.圆锥和圆柱的底面半径和高都是R,则圆锥的全面积与圆柱的全面积之比为________________n和n的矩形, 11 .已知一个圆柱的侧面展开图是一个长和宽分别为则该圆柱的体积是____________________12.在如图所示的斜截圆柱中,已知圆柱底面的直径为40cm,母线长最短50cm,最长80cm,则斜截圆柱的侧面面积S= cm 2.13.球的体积与其表面积的数值相等,则球的半径等于14•已知一圆柱内接于球O,且圆柱的底面直径与母线长均为2,则球为O的表面积为15.已知A, B, C是球面上三点,且AB=AC=4cm/ BAC=90,若球心O到平面ABC的距离为2 ,则该球的表面积为cm3.11.正三角形ABC的边长为2,将它沿高AD翻折,使点B与点C间的距离为1,此时四面体ABCD7卜接球表面积为三.解答题(共3小题)16•如图,某种水箱用的“浮球”,是由两个半球和一个圆柱筒组成•已知球的直径是6cm,圆柱筒长2cm.(1)这种“浮球”的体积是多少cm (结果精确到0.1 ) ?(2 )要在这样2500个“浮球”表面涂一层胶质,如果每平方米需要涂胶100克,共需胶多少?17.(文)如图,球O的半径长为10(1)求球O的表面积;(2)求球O的体积;(3)若球O的小圆直径AB=3Q求A、B两点的球面距离.18.设底面直径和高都是4厘米的圆柱的内切球为O.(1)求球O的体积和表面积;(2)与底面距离为1的平面和球的截面圆为M AB是圆M内的一条弦,其长为2 ,求AB 两点间的球面距离.参考答案: A:I、A 2、B 3、C 4、A 5、C 6、D 7、C 8、D 9、D10、解:因芮D,E,分S]是Ab肌的中自所以血虫DE;S AA BC=1:仆又F是宜納的中点,所以A T aS面的范离H为F到虧面距离h的2倍• 即三複栓盘卩1门-2匚的壽是三棱穩F-ME高的7倍-斷以如;畑空兰空=4T=1:西.故答案为1; 24.II、铅:妇也肪示,评正方也就口叭対術钱M * 3DSt + iO>甲n折更启的位豈为F・连揺即‘ *苛一TAZJLBC,AC l-BD* - BaflD- QrO--ACX 耶®IT g匡b> =楼帕的作祗対V D -kBC"v^EOC' -^Vc-BCC~ ;BCD' k AO*j52kBOD' x J S^ISOD_卞航:王方世的迪丢为2・可J?■■- BOD ft AH - To LABC谜劉昴尢值■*:S/\ 二 0D* =? x j^x忑小血乂目□力'二w in上aoii *’,丄i ?rv「.q-TTY-M' l「=丄工」•王5V.怡巧「此t」导.乂RJ农虻-土故告案为;半12、解:不妨令此三棱柱为直三棱柱,如图当侧面AA1B1B水平放置时,水的形状为四棱柱形,底面是梯形.设△ ABC的面积为S,贝U S梯形ABFE= S,V水=S? AA1=6S .当底面ABC水平放置时,水的形状为三棱柱形,设水面高为h,则有V水=Sh,••• 6S=Sh,.•• h=6 .故当底面ABC水平放置时,液面高为6 .故答案为:613、1:4 14、15、2解:團柱的側面展开囹星长利员务别为和TT的矩用,当毋线为戈氏时,區1桂的庙面半襌是扌此时囿桂体粮是(l)1 2Ttx3it=^;当母线为H时,圆柱酌展面半轻是学此时圆柱的体釈是(芥II"二竺匕£-t 4综上所求圈柱的体稅杲:—16、解:(1 )T该“浮球”的圆柱筒直径d=6cm ,•••半球的直径也是6cm,可得半径R=3cm,•两个半球的体积之和为V球=-冗R = - n ? 27 = 6 n cm3 * S 6…(2分)斗412、解:将相同的两个几何体,对接为圆柱,则圆柱的侧面展开,侧面展开图的面积 S=[ ( 50+80) X 20 n x 2]/2=2600 n cm2. 故答案为:2600 n13、 3 14、8 n 15、64 n学习参考而V 圆柱=n R ? h= n X 9X = n cm3…(2 分)•该“浮球”的体积是:V=V球+V圆柱=36 n +18 n =54 n" 169.6cm 3…(4分)(2)根据题意,上下两个半球的表面积是S 球表= n R = Xn X 9= 6 n cm?…(6 分)而“浮球”的圆柱筒侧面积为:S圆柱侧=2 n Rh=2 Xn X 3 X 2=12 n cm2…(8分)6 n n n• 1个“浮球”的表面积为S = —0一= —m因此,2500个“浮球”的表面积的和为2500 S = 00 X —= n m2…(10分)•/每平方米需要涂胶100克,•总共需要胶的质量为:100 X 12 n =1200 n (克)…(12分)答:这种浮球的体积约为169.6cm 3;供需胶1200 n克.…(13分)17、解:(1)球的表面积为4 n r 2=1200 n ; …(4分)(2)球的体积V=-n r3= 4000 _n ; …(8 分)(3)设球心为O,在△ AOB中,球O的小圆直径AB=30,球O的半径长为10解得Z AOB=",所以A、B两点的球面距离为0 n n . …(15分)18、解:(1)•••底面直径和高都是4厘米的圆柱的内切球为O,•球O的半径为2cm,.•.球O的体积为-n ? 2=,表面积4 n ? 22=16 n ;(2)•/ AB是圆M内的一条弦,其长为2 ,• Z AOB= n , • AB两点间的球面距离为".。
几何体的体积与表面积试题

几何体的体积与表面积试题一、选择题1. 下面关于体积和表面积的说法,正确的是:A. 体积是指几何体的外部空间,表面积是指几何体的内部空间。
B. 箱子的体积和表面积一定是相等的。
C. 体积和表面积都是用立方单位来计量的。
D. 几何体的体积是几何体的表面积的两倍。
2. 一个长方体的长、宽、高分别为3cm、4cm、5cm,它的体积是:A. 60cm³B. 48cm³C. 40cm³D. 20cm³3. 一个正方体的表面积是96平方厘米,它的边长是:A. 8厘米B. 12厘米C. 16厘米D. 24厘米4. 一个圆柱体的底面半径为2cm,高为6cm,它的表面积是:A. 24π平方厘米B. 28π平方厘米C. 32π平方厘米D. 36π平方厘米5. 一个球体的表面积是100π平方厘米,它的半径是:A. 2厘米B. 4厘米C. 6厘米D. 8厘米二、解答题1. 计算一个直方体的体积和表面积,并给出结果的单位。
解答:设直方体的长、宽、高分别为a、b、c,则直方体的体积V为 V = a * b * c,表面积S为 S = 2(a * b + a * c + b * c)。
根据具体的数值,计算出V和S,并注明单位。
2. 已知一个圆柱体的表面积为48π平方厘米,底面半径为3厘米,求圆柱体的高。
解答:设圆柱体的底面半径为r,高为h。
根据题意,可列出方程:2πr^2 + 2πrh = 48π化简得 r^2 + rh = 24代入r=3,解方程得 h = 6厘米。
3. 一个球体的表面积是200π平方厘米,求它的体积。
解答:设球体的半径为r。
根据题意,可列出方程:4πr^2 = 200π化简得 r^2 = 50代入r=√50,计算得体积V = (4/3)πr^3。
三、应用题1. 小明家的水缸是一个圆柱体,底面半径为50厘米,高为120厘米。
他要知道这个水缸最多可以盛多少升水。
解答:水缸的体积为圆柱体的体积V = πr^2h。
空间几何体的表面积与体积

第2节空间几何体的表面积与体积课时训练练题感提知能【选题明细表】一、选择题1.(2013湖北黄冈4月调研)某三棱锥的三视图如图所示,该三棱锥的体积为( B )(A)20 (B)(C)56 (D)60解析:空间几何体是底面为直角三角形的三棱锥,底面直角三角形的直角边边长分别为4,5,三棱锥的高为4,故其体积为××4×5×4=.故选B.2.(2013山东枣庄一模)一个几何体的三视图如图所示,其中长度单位为cm,则该几何体的体积为( D )(A)18 cm3(B)48 cm3(C)45 cm3(D)54 cm3解析:由题中三视图可知,该几何体是四棱柱,底面为直角梯形其上底为4,下底为5,高为3.棱柱的高为4,所以四棱柱的体积为×3×4=54(cm3),故选D.3.(2013河南省十所名校三联)某几何体的三视图如图所示,则该几何体的表面积为( B )(A)π (B)2π(C)(2+1)π(D)(2+2)π解析:由题中三视图可知该几何体是两个底面半径为1,高为1的圆锥的组合体,圆锥的母线长度为,故其表面积是2×π×1×=2π.故选B.4.(2013成都市模拟)一个几何体的三视图如图所示,且其侧视图是一个等边三角形,则这个几何体的体积为( B )(A)(B)(C)(D)(4+π)解析:此几何体是由半圆锥和一个四棱锥构成,则几何体体积V=××π×12×+×22×=.故选B.5.(2014山东烟台高三期末)一个几何体的三视图如图所示,则该几何体的表面积是( C )(A)6+8 (B)12+7(C)12+8(D)18+2解析:该空间几何体是一个三棱柱.底面等腰三角形的高是1,两腰长为2,所以其底边长是2,两个底面三角形的面积之和是2,侧面积是(2+2+2)×3=12+6,故其表面积是12+8.故选C.6.(2013河南开封二检)已知三棱锥O ABC,A,B,C三点均在球心为O的球表面上,AB=BC=1,∠ABC=120°,三棱锥O ABC的体积为,则球O 的表面积是( A )(A)64π(B)16π(C)π(D)544π解析:△ABC的面积是,设球心O到平面ABC的距离为h,则××h=,所以h=.△ABC外接圆的直径2r==2,所以r=1.球的半径R==4,故所求的球的表面积是4π×42=64π.故选A.7.(2013江西南昌一模)已知正三角形ABC三个顶点都在半径为2的球面上,球心O到平面ABC的距离为1,点E是线段AB的中点,过点E作球O的截面,则截面面积的最小值是( C )(A)π(B)2π(C)π(D)3π解析:所作的截面与OE垂直时,截面圆的面积最小.设正三角形ABC的高为3a,则4a2+1=4,即a=,此时OE2=12+=,截面圆半径r2=22-=,故截面面积为.故选C.8.(2014绵阳南山中学高三月考)有一个几何体的三视图及其尺寸如图所示(单位:cm),则该几何体的表面积为( C )(A)12π cm2(B)15π cm2(C)24π cm2(D)36π cm2解析:由三视图可知,该几何体为底面半径为3 cm的圆锥,∴S表=π×32+π×3×5=24π cm2.故选C.二、填空题9.有一根长为3π cm,底面直径为2 cm的圆柱形铁管,用一段铁丝在铁管上缠绕2圈,并使铁丝的两个端点落在圆柱的同一母线的两端,则铁丝的最短长度为cm.解析:把圆柱侧面及缠绕其上的铁丝展开,在平面上得到矩形ABCD(如图),由题意知BC=3π cm,AB=4π cm,点A与点C分别是铁丝的起、止位置,故线段AC的长度即为铁丝的最短长度.AC==5π(cm),故铁丝的最短长度为5π cm.答案:5π10.(2013年高考江苏卷)如图,在三棱柱A1B1C1ABC中,D,E,F分别是AB,AC,AA1的中点.设三棱锥F ADE的体积为V1,三棱柱A1B1C1ABC的体积为V2,则V1∶V2= .解析:==··=×××=.答案:1∶2411.(2013吉林省吉林市二模)已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥外接球的表面积等于cm2.解析:由题中三视图知该几何体为三棱锥C1ABC,可补成长方体如图所示,其外接球的直径AC1=,其中AB=3,BC=1,CC故其外接球的表面积为14π cm2.答案:14π12.(2013成都外国语学校高三月考)已知三棱柱ABC A1B1C1的侧棱与底面边长都相等且为1,A1在底面ABC内的射影为△ABC的中心O,则三棱柱ABC A1B1C1体积等于.解析:∵△ABC为正三角形,且边长为1,∴AO=×=,∴A1O===,∴=×12×=.答案:13.如图在底面半径为2,母线长为4的圆锥中内接一个高为的圆柱,则圆柱的表面积为.解析:由圆锥的底面半径为2,母线长为4,得圆锥的高h==2,由圆柱高为,则圆柱的底面半径r=1.S 表面=2S底面+S侧面=2π+2π×=(2+2)π.答案:(2+2)π三、解答题14.如图所示,在边长为5+的正方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M,N,K为切点,以扇形为圆锥的侧面,以圆O 为圆锥底面,围成一个圆锥,求圆锥的表面积与体积.解:设圆锥的母线长为l,底面半径为r,高为h,由已知条件解得r=,l=4,S=πrl+πr2=10π,h==,V=πr2h=.15.一个几何体的三视图如图所示.已知正视图是底边长为1的平行四边形,侧视图是一个长为,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.(1)求该几何体的体积V;(2)求该几何体的表面积S.解:(1)由三视图可知,该几何体是一个平行六面体(如图),其底面是边长为1的正方形,高为,所以V=1×1×=.(2)由题中三视图可知,该平行六面体中,A1D⊥平面ABCD,CD⊥平面BCC1B1,所以AA1=2,侧面ABB1A1,CDD1C1均为矩形,S=2×(1×1+1×+1×2)=6+2.16.(2013安徽黄山三校联考)如图(1)所示,△ABC是等腰直角三角形,AC=BC=4,E、F分别为AC、AB的中点,将△AEF沿EF折起,使A′在平面BCEF上的射影O恰为EC的中点,得到图(2).(1)求证:EF⊥A′C;(2)求三棱锥F A′BC的体积.(1)证明:在△ABC中,EF是等腰直角△ABC的中位线,∴EF⊥AC,在四棱锥A′BCEF中,EF⊥A′E,EF⊥EC,又EC∩A′E=E,∴EF⊥平面A′EC,又A′C⊂平面A′EC,∴EF⊥A′C.(2)解:在直角梯形BCEF中,EC=2,BC=4,∴S△FBC=BC·EC=4,∵A′O⊥平面BCEF,∴A′O⊥EC,又∵O为EC的中点,∴△A′EC为正三角形,边长为2,∴A′O=,A′O=×4×=.∴==S。
2023年新高考数学一轮复习8-2 空间几何体的表面积和体积(真题测试)解析版

专题8.2 空间几何体的表面积和体积(真题测试)一、单选题1.(2020·天津·高考真题)若棱长为 ) A .12π B .24π C .36π D .144π【答案】C【解析】【分析】求出正方体的体对角线的一半,即为球的半径,利用球的表面积公式,即可得解.【详解】这个球是正方体的外接球,其半径等于正方体的体对角线的一半,即3R =,所以,这个球的表面积为2244336S R πππ==⨯=.故选:C.2.(2020·北京·高考真题)某三棱柱的底面为正三角形,其三视图如图所示,该三棱柱的表面积为(). A .63+ B .623+ C .123+ D .1223+【答案】D【解析】【分析】首先确定几何体的结构特征,然后求解其表面积即可.【详解】由题意可得,三棱柱的上下底面为边长为2的等边三角形,侧面为三个边长为2的正方形,则其表面积为:()1322222sin 60122S ⎛⎫=⨯⨯+⨯⨯⨯⨯︒=+ ⎪⎝⎭故选:D.【点睛】(1)以三视图为载体考查几何体的表面积,关键是能够对给出的三视图进行恰当的分析,从三视图中发现几何体中各元素间的位置关系及数量关系.(2)多面体的表面积是各个面的面积之和;组合体的表面积应注意重合部分的处理.(3)圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将这个曲面展为平面图形计算,而表面积是侧面积与底面圆的面积之和.3.(2022·浙江·高考真题)某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:3cm )是( )A .22πB .8πC .22π3D .16π3【答案】C【解析】【分析】根据三视图还原几何体可知,原几何体是一个半球,一个圆柱,一个圆台组合成的几何体,即可根据球,圆柱,圆台的体积公式求出.【详解】由三视图可知,该几何体是一个半球,一个圆柱,一个圆台组合成的几何体,球的半径,圆柱的底面半径,圆台的上底面半径都为1cm ,圆台的下底面半径为2cm ,所以该几何体的体积(322214122ππ1π122π2π12333V =⨯⨯+⨯⨯+⨯⨯⨯+⨯=3cm .故选:C .4.(2022·全国·高考真题)已知正三棱台的高为1,上、下底面边长分别为面上,则该球的表面积为( )A .100πB .128πC .144πD .192π【答案】A【解析】【分析】根据题意可求出正三棱台上下底面所在圆面的半径12,r r ,再根据球心距,圆面半径,以及球的半径之间的关系,即可解出球的半径,从而得出球的表面积.【详解】设正三棱台上下底面所在圆面的半径12,r r ,所以123432,260sin 60r r ==,即123,4r r ==,设球心到上下底面的距离分别为12,d d ,球的半径为R ,所以1d =2d =121d d -=或121d d +=,即1=1,解得225R =符合题意,所以球的表面积为24π100πS R ==. 故选:A .5.(2021·浙江·高考真题)某几何体的三视图如图所示,则该几何体的体积是( )A .32B .3C .2D .【答案】A【解析】【分析】根据三视图可得如图所示的几何体,根据棱柱的体积公式可求其体积.【详解】几何体为如图所示的四棱柱1111ABCD A B C D -,其高为1,底面为等腰梯形ABCD ,1=故1111131222ABCD A B C D V -=⨯⨯=, 故选:A. 6.(2021·全国·高考真题(理))已如A ,B ,C 是半径为1的球O 的球面上的三个点,且,1AC BC AC BC ⊥==,则三棱锥O ABC -的体积为( )A B C D A 【解析】【分析】由题可得ABC 为等腰直角三角形,得出ABC 外接圆的半径,则可求得O 到平面ABC 的距离,进而求得体积.【详解】,1AC BC AC BC ⊥==,ABC ∴为等腰直角三角形,AB ∴=,则ABC 1, 设O 到平面ABC 的距离为d ,则2d =所以11111332O ABC ABC V S d -=⋅=⨯⨯⨯= 故选:A.7.(2022·全国·高考真题(文))已知球O 的半径为1,四棱锥的顶点为O ,底面的四个顶点均在球O 的球面上,则当该四棱锥的体积最大时,其高为( )A .13B .12CD 【答案】C【解析】【分析】先证明当四棱锥的顶点O 到底面ABCD 所在小圆距离一定时,底面ABCD 面积最大值为22r ,进而得到四棱锥体积表达式,再利用均值定理去求四棱锥体积的最大值,从而得到当该四棱锥的体积最大时其高的值.【详解】设该四棱锥底面为四边形ABCD ,四边形ABCD 所在小圆半径为r ,设四边形ABCD 对角线夹角为α, 则2111sin 222222ABCD S AC BD AC BD r r r α=⋅⋅⋅≤⋅⋅≤⋅⋅= (当且仅当四边形ABCD 为正方形时等号成立)即当四棱锥的顶点O 到底面ABCD 所在小圆距离一定时,底面ABCD 面积最大值为22r又22r h 1+=则2123O ABCDV r h -=⋅⋅=当且仅当222r h =即h 时等号成立,故选:C8.(2022·全国·高考真题)已知正四棱锥的侧棱长为l ,其各顶点都在同一球面上.若该球的体积为36π,且3l ≤≤ ) A .8118,4⎡⎤⎢⎥⎣⎦ B .2781,44⎡⎤⎢⎥⎣⎦ C .2764,43⎡⎤⎢⎥⎣⎦ D .[18,27]【答案】C【解析】【分析】设正四棱锥的高为h ,由球的截面性质列方程求出正四棱锥的底面边长与高的关系,由此确定正四棱锥体积的取值范围.【详解】∵ 球的体积为36π,所以球的半径3R =,设正四棱锥的底面边长为2a ,高为h ,则2222l a h =+,22232(3)a h =+-,所以26h l =,2222a l h =- 所以正四棱锥的体积42622411214()=333366936l l l V Sh a h l l ⎛⎫==⨯⨯=⨯-⨯- ⎪⎝⎭, 所以5233112449696l l V l l ⎛⎫⎛⎫-'=-= ⎪ ⎪⎝⎭⎝⎭,当3l ≤≤0V '>,当l ≤0V '<,所以当l =V 取最大值,最大值为643,又3l =时,274V =,l =814V =, 所以正四棱锥的体积V 的最小值为274, 所以该正四棱锥体积的取值范围是276443⎡⎤⎢⎥⎣⎦,. 故选:C.二、多选题9.(2022·广东茂名·二模)某一时段内,从天空降落到地面上的液态或固态的水,未经蒸发,而在水平面上积聚的深度称为这段时间的降雨量.24h 降雨量的等级划分如下:在一次暴雨降雨过程中,小明用一个大容量烧杯(如图,瓶身直径大于瓶口直径,瓶身高度为50cm ,瓶口高度为3cm )收集雨水,容器内雨水的高度可能是( )A .20cmB .22cmC .25cmD .29cm【答案】CD【解析】【分析】设降雨量为x ,容器内雨水高度为h,根据雨水的体积相等关系可得到h,x 之间的关系49h x =,结合题意可得4200400[,)999x ∈,由此判断出答案. 【详解】设降雨量为x ,容器内雨水高度为h,根据体积相等关系可得:22π100π150x h ⨯=⨯,解得49h x = , 由于[50,100)x ∈ ,故4200400[,)999x ∈, 故20040020040020,22[,),25,29[,)9999∉∈故选:CD .10.(2023·湖北·高三阶段练习)折扇是我国古老文化的延续,在我国已有四千年左右的历史,“扇”与“善”谐音,折扇也寓意“善良”“善行”.它常以字画的形式体现我国的传统文化,也是运筹帷幄、决胜千里、大智大勇的象征(如图1).图2是一个圆台的侧面展开图(扇形的一部分),若两个圆弧,DE AC 所在圆的半径分别是3和9,且120ABC ∠=,则该圆台的( )A .高为42B .体积为5023π C .表面积为34πD .上底面积、下底面积和侧面积之比为1:9:22【答案】AC【解析】 【分析】设圆台的上底面半径为r ,下底面半径为R ,求出1,3r R ==,即可判断选项A 正确;利用公式计算即可判断选项BCD 的真假得解.【详解】解:设圆台的上底面半径为r ,下底面半径为R ,则11223,22933r R ππππ=⨯⨯=⨯⨯,解得1,3r R ==.圆台的母线长6l =,圆台的高为h ==,则选项A 正确;圆台的体积()22133113π=⨯+⨯+=,则选项B 错误; 圆台的上底面积为π,下底面积为9π,侧面积为()13624ππ+⨯=,则圆台的表面积为92434ππππ++=,则C 正确;由前面可知上底面积、下底面积和侧面积之比为1:9:24,则选项D 错误.故选:AC .11.(2022·湖南·长沙一中模拟预测)传说古希腊数学家阿基米德的墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等.“圆柱容球”是阿基米德最为得意的发现;如图是一个圆柱容球,12O O ,为圆柱上下底面的圆心,O 为球心,EF 为底面圆1O 的一条直径,若球的半径2r =,则( )A .球与圆柱的表面积之比为12:B .平面DEF 截得球的截面面积最小值为165π C .四面体CDEF 的体积的取值范围为3203⎛⎤ ⎥⎝⎦,D .若P 为球面和圆柱侧面的交线上一点,则PE PF +的取值范围为2⎡+⎣【答案】BCD【解析】【分析】利用球的表面积公式及圆柱的表面积公式可判断A ,由题可得O 到平面DEF 的距离为1d 平面DEF 截得球的截面面积最小值可判断B ,由题可得四面体CDEF 的体积等于12E DCO V -可判断C ,设P 在底面的射影为P ',设2t P E '=,PE PF +PE PF +的取值范围可判断D.【详解】由球的半径为r ,可知圆柱的底面半径为r ,圆柱的高为2r ,则球表面积为24r π,圆柱的表面积222226r r r r πππ+⋅=, 所以球与圆柱的表面积之比为23,故A 错误;过O 作1OG DO ⊥于G ,则由题可得12OG == 设O 到平面DEF 的距离为1d ,平面DEF 截得球的截面圆的半径为1r ,则1d OG ≤,22221114164455r r d d =-=-≥-=, 所以平面DEF 截得球的截面面积最小值为165π,故B 正确; 由题可知四面体CDEF 的体积等于12E DCO V -,点E 到平面1DCO 的距离(0,4]d ∈, 又114482DCO S =⨯⨯=,所以123228(0,]33E DCO V d -=⨯∈,故C 正确; 由题可知点P 在过球心与圆柱的底面平行的截面圆上,设P 在底面的射影为P ', 则2222222,2,2,16PP PE P E PF P F P E P F '''''==+=++=,设2t P E '=,则20,4t ⎡⎤∈⎣⎦,PE PF +所以()2224PE PF +==+2424⎡⎤=++⎣⎦,所以2PE PF ⎡+∈+⎣,故D 正确.故选:BCD.12.(2022·全国·高考真题)如图,四边形ABCD 为正方形,ED ⊥平面ABCD ,,2FB ED AB ED FB ==∥,记三棱锥E ACD -,F ABC -,F ACE -的体积分别为123,,V V V ,则( )A .322V V =B .31V V =C .312V V V =+D .3123V V =【答案】CD【解析】【分析】直接由体积公式计算12,V V ,连接BD 交AC 于点M ,连接,EM FM ,由3A EFM C EFM V V V --=+计算出3V ,依次判断选项即可.【详解】设22AB ED FB a ===,因为ED ⊥平面ABCD ,FB ED ,则()2311114223323ACD V ED S a a a =⋅⋅=⋅⋅⋅=, ()232111223323ABC V FB S a a a =⋅⋅=⋅⋅⋅=,连接BD 交AC 于点M ,连接,EM FM ,易得BD AC ⊥, 又ED ⊥平面ABCD ,AC ⊂平面ABCD ,则ED AC ⊥,又ED BD D =,,ED BD ⊂平面BDEF ,则AC ⊥平面BDEF ,又12BM DM BD ==,过F 作FG DE ⊥于G ,易得四边形BDGF 为矩形,则,FG BD EG a ===,则,EM FM ===,3EF a =,222EM FM EF +=,则EM FM ⊥,212EFM SEM FM =⋅=,AC =, 则33123A EFM C EFM EFM V V V AC S a --=+=⋅=,则3123V V =,323V V =,312V V V =+,故A 、B 错误;C 、D 正确.故选:CD.三、填空题 13.(2021·全国·高考真题(文))已知一个圆锥的底面半径为6,其体积为30π则该圆锥的侧面积为________.【答案】39π【解析】【分析】利用体积公式求出圆锥的高,进一步求出母线长,最终利用侧面积公式求出答案.【详解】∵216303V h ππ=⋅=∴52h =∴132l =∴136392S rl πππ==⨯⨯=侧. 故答案为:39π.14.(2020·江苏·高考真题)如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2 cm ,高为2 cm ,内孔半径为0.5 cm ,则此六角螺帽毛坯的体积是 ____ cm 3. 【答案】1232π-【解析】【分析】先求正六棱柱体积,再求圆柱体积,相减得结果.【详解】正六棱柱体积为262⨯ 圆柱体积为21()222ππ⋅=所求几何体体积为2π故答案为: 2π15.(2019·天津·高考真题(文)若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为__________. 【答案】4π. 【解析】【分析】根据棱锥的结构特点,确定所求的圆柱的高和底面半径.【详解】借助勾股定理,2=,.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,圆柱的底面半径为12,一个底面的圆心为四棱锥底面的中心,故圆柱的高为1,故圆柱的体积为21124ππ⎛⎫⨯⨯= ⎪⎝⎭. 16.(2022·吉林·长春市第二实验中学高三阶段练习)在三棱锥P ABC -中,点P 在底面的射影是ABC 的外心,2,3BAC BC PA π∠===___________. 【答案】12548π 【解析】【分析】先由正弦定理得,ABC 外接圆的半径,再由勾股定理,即可求出半径,从而可得外接球体积.【详解】解:设ABC 的外心为1O ,连接1PO ,则球心O 在1PO 上,连接1O A ,则1O A 为ABC 外接圆的半径r ,连接OA ,设外接球的半径为R ,则OA OP R ==,在ABC 中,由正弦定理得2,BC r sin BAC ==∠解得1r =,即11O A =, 在1Rt PAO 中,12,PO =在1Rt AOO ,中22211OO AO AO +=,即()22221R R -+=,解得:54R =, 所以外接球的体积为:3344125334854R V πππ⎛⎫⋅ ⎪⎝⎭===, 故答案为:12548π 四、解答题17.(2022·安徽芜湖·高一期末)如图①,有一个圆柱形状的玻璃水杯,底面圆的直径为20cm ,高为30cm ,杯内有20cm 深的溶液.如图①,现将水杯倾斜,且倾斜时点B 始终不离开桌面,设直径AB 所在直线与桌面所成的角为α.要使倾斜后容器内的溶液不会溢出,求α的最大值. 【答案】4π【解析】【分析】当水杯倾斜过程中,溶液恰好不溢出时,此时α最大;在这个临界条件下,结合溶液的体积不变,可以得到关于α的一个不等式,即可求出α的取值范围,得到最大值.【详解】如图所示,在Rt △CDE 中20tan DE α=,()2221020tan 103020tan 10202παπαπ⨯⨯⨯⨯-+≥⨯⨯解得tan 1α≤,即α的最大值4π. 18.(2022·全国·南宁二中高三期末(文))图1是由矩形ABGF ,Rt ADE △和菱形ABCD 组成的一个平面图形,其中2AB =,1==AE AF ,60BAD ∠=︒,将该图形沿AB ,AD 折起使得AE 与AF 重合,连接CG ,如图2.(1)证明:图2中的C ,D ,E ,G 四点共面;(2)求图2中三棱锥C BDG -的体积.【答案】(1)证明见解析【解析】【分析】(1)依题意可得//AB FG ,//AB CD ,即可得到//AB GE ,从而得到//CD EG ,即可得证;(2)依题意可得AE AD ⊥、AE AB ⊥,即可得到AE ⊥平面ABCD 从而得到BG ⊥平面ABCD ,再根据13C BDG G BCD BCD V V BG S --==⋅计算可得;(1)证明:在矩形ABGF 和菱形ABCD 中,//AB FG ,//AB CD ,所以//AB GE ,所以//CD EG ,所以C 、D 、E 、G 四点共面;(2)解:在Rt ADE △中AE AD ⊥,矩形ABGE 中AE AB ⊥,AD AB A ⋂=,,AD AB ⊂平面ABCD ,所以AE ⊥平面ABCD ,又//BG EA ,所以BG ⊥平面ABCD ,又11sin 2222BCD S BC CD BCD =⋅⋅∠=⨯⨯=所以11133C BDG G BCD BCD V V BG S --==⋅=⨯ 19.(2022·山西吕梁·高一期末)如图是某种水箱用的“浮球”,它是由两个半球和一个圆柱筒组成.已知球的半径是2cm ,圆柱筒的高是2cm .(1)求这种“浮球”的体积;(2)要在100个这种“浮球”的表面涂一层防水漆,每平方厘米需要防水漆0.5g ,共需多少防水漆?【答案】(1)356(cm)3π (2)1200g π【解析】【分析】(1)由球的体积公式和圆柱的体积公式求解即可;(2)由球的表面积公式和圆柱的侧面积公式求解即可.(1)因为该“浮球”的圆柱筒底面半径和半球的半径2cm r =,圆柱筒的高为2cm ,所以两个半球的体积之和为331432(cm)33V r ππ==, 圆柱的体积2328(cm)V r h ππ==,∴该“浮球”的体积是31256(cm)3V V V π=+=; (2)根据题意,上下两个半球的表面积是221416(cm)S r ππ==,而“浮球”的圆柱筒侧面积为2228(cm)S rh ππ==,∴“浮球”的表面积为21224(cm)S S S π=+=;所以给100个这种浮球的表面涂一层防水漆需要100240.51200g ππ⨯⨯=.20.(2022·全国·高三专题练习)如图1,在直角梯形ABCD 中,//AD BC ,∠BAD =90°,12AB BC AD a ,E 是AD 的中点,O 是AC 与BE 的交点.将△ABE 沿BE 折起到图2中1A BE 的位置,使平面1A BE ⊥平面BCDE ,得到四棱锥1A BCDE -.当四棱锥1A BCDE -的体积为a 的值.【答案】6a =.【解析】【分析】在直角梯形ABCD 中,证明BE AC ⊥,在四棱锥1A BCDE -中,由面面垂直的性质证得1A O ⊥平面BCDE ,再利用锥体体积公式计算作答.【详解】如图,在直角梯形ABCD 中,连接CE ,因E 是AD 的中点,12BC AD a ,有//,AE BC AE BC =,则四边形ABCE 是平行四边形,又,90BAD AB BC ∠==,于是得ABCE 是正方形,BE AC ⊥,在四棱锥1A BCDE -中,1BE AO ⊥,因平面1A BE ⊥平面BCDE ,且平面1A BE 平面BCDE BE =,1A O ⊂平面1A BE ,因此1A O ⊥平面BCDE ,即1A O 是四棱锥1A BCDE -的高,显然112AO AO CO AC ====,平行四边形BCDE 的面积2S CO BE a =⋅==,因此,四棱锥1A BCDE -的体积为2311133V S AO a =⋅===6a =, 所以a 的值是6.21.(2022·北京·高一期末)《九章算术》中对一些特殊的几何体有特定的称谓,例如:将底面为直角三角形的直三棱柱称为堑堵,将一堑堵沿其一顶点与相对的棱刨开,得到一个阳马(底面是长方形,且有一条侧棱与底面垂直的四棱锥)和一个鳖臑 (四个面均为直角三角形的四面体).在如图所示的堑堵111ABC A B C -中,已知3AB =,4BC =,5AC =.当阳马111C ABB A -体积等于24时, 求:(1)堑堵111ABC A B C -的侧棱长;(2)鳖臑1C ABC -的体积;(3)阳马111C ABB A -的表面积.【答案】(1)6(2)12 (3)51313【解析】【分析】(1)设堑堵111ABC A B C -的侧棱长为x ,根据阳马111C ABB A -体积等于24求解即可;(2)根据棱锥的体积计算即可;(3)分别计算111C ABB A -的侧面积与底面积即可(1)因为3AB =,4BC =,5AC =,所以222AB BC AC +=.所以△ABC 为直角三角形.设堑堵111ABC A B C -的侧棱长为x ,则113A ABB S x 矩形,则111143243AA BB V x C , 所以6x =,所以堑堵111ABC A B C -的侧棱长为6.(2)因为13462ABC S =⨯⨯=△, 所以1111661233ABC ABC V S CC C . 所以鳖臑1C ABC -的体积为12.(3) 因为11113462A B C S,11164122BB C S , 11165152AA C S ,1132133132ABC S , 113618A ABB S 矩形,所以阳马111C ABB A -的表面积的表面积为612151831351313. 22.(2022·重庆市巫山大昌中学校高一期末)如图,AB 是圆柱OO '的一条母线,BC 过底面圆心O ,D 是圆O 上一点.已知5,3AB BC CD ===,(1)求该圆柱的表面积;(2)将四面体ABCD 绕母线AB 所在的直线旋转一周,求ACD △的三边在旋转过程中所围成的几何体的体积.【答案】(1)75π2(2)15π【解析】【分析】(1)由题意求出柱的底面圆的半径即可求解;(2)ACD △绕AB 旋转一周而成的封闭几何体的体积为两个圆锥的体积之差,结合圆锥体积公式求解即可(1)由题意知AB 是圆柱OO '的一条母线,BC 过底面圆心O ,且5AB BC ==, 可得圆柱的底面圆的半径为52R =, 则圆柱的底面积为221525πππ24S R ⎛⎫==⨯= ⎪⎝⎭, 圆柱的侧面积为252π2π525π2S Rl ==⨯⨯= 所以圆柱的表面积为12257522π25ππ42S S S =+=⨯+=. (2) 由线段AC 绕AB 旋转一周所得几何体为以BC 为底面半径,以AB 为高的圆锥,线段AD 绕AB 旋转一周所得的几何体为BD 为底面半径,以AB 为高的圆锥,所以以ACD △绕AB 旋转一周而成的封闭几何体的体积为:22221111πππ55π4515π3333V BC AB BD AB =⋅⋅-⋅⋅=⋅⋅-⋅⋅=.。
空间几何体的表面积和体积经典例题

空间几何体的表面积和体积一•课标要求:了解球、棱柱、棱锥、台的表面积和体积的计算公式(不要求记忆公式)。
二. 命题走向近些年来在高考中不仅有直接求多面体、旋转体的面积和体积问题,也有已知面积或体积求某些元素的量或元素间的位置关系问题。
即使考查空间线面的位置关系问题,也常以几何体为依托•因而要熟练掌握多面体与旋转体的概念、性质以及它们的求积公式•同时也要学会运用等价转化思想,会把组合体求积问题转化为基本几何体的求积问题,会等体积转化求解问题,会把立体问题转化为平面问题求解,会运用"割补法”等求解。
由于本讲公式多反映在考题上,预测2016年高考有以下特色:(1)用选择、填空题考查本章的基本性质和求积公式;(2)考题可能为:与多面体和旋转体的面积、体积有关的计算问题;与多面体和旋转体中某些元素有关的计算问题;三. 要点精讲1.多面体的面积和体积公式棱长。
2 .旋转体的面积和体积公式i2下底面半径,R表示半径。
四. 典例解析题型1 :柱体的体积和表面积例1 •一个长方体全面积是20cm2,所有棱长的和是24cm,求长方体的对角线长例2 .如图1所示,在平行六面体ABCD —A1B1C1D1中,已知AB=5,AD=4,AA i=3, AB 丄AD,/ A1AB= / A1AD= —。
3(1)求证:顶点A1在底面ABCD上的射影0在/ BAD的平分线上;(2)求这个平行六面体的体积。
图1 图2题型2:柱体的表面积、体积综合问题例3 •一个长方体共一顶点的三个面的面积分别是 ,2, . 3, . 6,这个长方体对角线的长是( ) A • 2 . 3B • 3.2C . 6D •. 6例 6. (2015 北京,19) • (本小题满分12分)如图,在四棱锥 P ABCD 中,平面PAD 平面ABCD , AB // DC , △ PAD 是等边三 角形,已知 BD 2AD 8,AB 2DC 4「5 •(I)设M 是PC 上的一点,证明:平面 MBD 平面PAD ; (n)求四棱锥 P ABCD 的体积.例4•如图,三棱柱 ABC-ABC 中,若E 、F 分别为 AB AC 的中点,平面 柱分成体积为 V 、V 2的两部分,那么 V : V 2= _______题型3:锥体的体积和表面积 (2015湖北卷3)用与球心距离为1的平面去截球,所得的截面面积为,则球 的体积为 A. 83C. 8,2D.32 3EBC i 将三棱PCPM C题型4:锥体体积、表面积综合问题例7. ABCD是边长为4的正方形,E、F分别是AB、AD的中点,GC垂直于正方形ABCD所在的平面,且GC= 2,求点B到平面EFG的距离?E7BC例8 (2015江西理,12)如图,在四面体 ABCD 中,截面AEF 经过四面体的内切球(与四个面都相切的球)球心 O, 且与BC, DC 分别截于E 、F ,如果截面将四面体分成体积相等的两部分,设四棱锥 A- BEFD与三棱锥A - EFC 的表面积分别是 S i , S 2,则必有()A. S i S 2 B . Si S 2C. S i =$D. S i , S 2的大小关系不能确定题型5:棱台的体积、面积及其综合问题例9. (2015四川理,19) (本小题满分12分)如图,面ABEFL 面ABCD 四边形ABEF 与四边形 ABCD 都是直角梯形,/ BAD / FAB=90 , BC L 丄AD, BE £-AF , G H 分别是FA 、FD 的中点。
高二数学空间几何体的表面积与体积试题

高二数学空间几何体的表面积与体积试题1. 已知四边形ABCD 是矩形,AB=,BC=,将△ABC 沿着对角线AC 折起来得到△AB 1C ,且顶点B 1在平面AB=CD 上射影O 恰落在边AD 上,如图所示. (1)求证:AB 1⊥平面B 1CD ;(2)求三棱锥B 1﹣ABC 的体积V B1﹣ABC .【答案】(1)见解析;(2)【解析】(1)平面ABCD ,平面ABCD ,所以,又CD AD ,AD=O ,所以平面,又平面,所以,又,且平面 (2)由于平面,平面ABCD ,所以在中,,又由得,所以试题解析:(1)平面ABCD ,平面ABCD ,,又CD AD ,AD =O 平面,又平面 ,又,且 平面 (2)由于平面,平面ABCD ,所以在中,, 又由得,所以【考点】1.空间线面垂直;2.锥体的体积2. 设一个扇形的半径为,圆心角为,用它做成一个圆锥的侧面,则这个圆锥的体积是_________. 【答案】【解析】因为一个扇形的半径为,圆心角为弧度,用它做成一个圆锥的侧面,设这个圆锥的底面半径为,高为,依题意圆锥的母线,由,即,所以,从而,进而有该圆锥的体积().【考点】圆锥及圆锥的体积计算.3. 如图,一个盛满水的三棱锥容器,不久发现三条侧棱上各有一个小洞,且知,若仍用这个容器盛水,则最多可盛水的体积是原来的 .【答案】【解析】过作截面平行于平面,可得截面下体积为原体积的,若过点F,作截面平行于平面,可得截面上的体积为原体积的,若C为最低点,以平面为水平上面,则体积为原体积的,此时体积最大.【考点】体积相似计算.4.一个空间几何体的三视图如右图所示,其中主视图和侧视图都是半径为的圆,且这个几何体是实心球体的一部分,则这个几何体的体积为.【答案】.【解析】由三视图可知,原几何体是球体沿其直径切去四分之一部分,所以其体积是四分之三球体积,即,其中【考点】由已知三视图还原为原几何体,球的体积公式.5.如图,正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB//CD,AB=AD=,点M在线段EC上且不与E、C垂合.(1)当点M是EC中点时,求证:BM//平面ADEF;(2)当平面BDM与平面ABF所成锐二面角的余弦值为时,求三棱锥M—BDE的体积【答案】(1)详见解析;(2)【解析】以、、分别为轴建立空间直角坐如图,(1)要证面,只要证明向量与平面的法向量垂直即可;(2)设,设面的法向量,利用向量的数量积求得,而平面的法向量由,解出的值,从而确定点位置,进而求出也即三棱锥M—BDE的体积.试题解析:(1)以、、分别为轴建立空间直角坐标系则所以,面的一个法向量所以,即面 4分(2)依题意设,设面的法向量则,令,则,面的法向量,解得为EC的中点,,到面的距离12分【考点】1、空间直角坐标系;2、向量法解决空间的平行、垂直与夹角问题;3、空间几何体的体积.6.三角形中,,以边所在直线为旋转轴,其余各边旋转一周而形成的曲面所围成的几何体的体积为()A.B.C.D.【答案】B【解析】依题意可知,旋转体的形状如下图,是一个圆锥,其中圆锥的高为,底面圆的半径为,所以该圆锥的体积为,故选B.【考点】旋转体的体积.7.如图,在正方体中,点在面对角线上运动,给出下列四个命题:①∥平面;②;③平面⊥平面;④三棱锥的体积不变.则其中所有正确的命题的序号是.【答案】①③④.【解析】可以以D为原点,以DA,DC,为坐标轴建立空间直角坐标系,利用向量的坐标运算可以证明(1),(3)成立;对于(4)如右图,三棱锥的底面△面积为定值,高BP也为定值,所以三棱锥的体积不变.【考点】(1)空间垂直平行的证明;(2)三棱锥的体积公式.8.如图,是圆柱体的一条母线,过底面圆的圆心,是圆上不与点、重合的任意一点,已知棱,,.(1)求证:;(2)将四面体绕母线转动一周,求的三边在旋转过程中所围成的几何体的体积.【答案】(1)详见解析。
高考专题练习: 空间几何体的表面积与体积
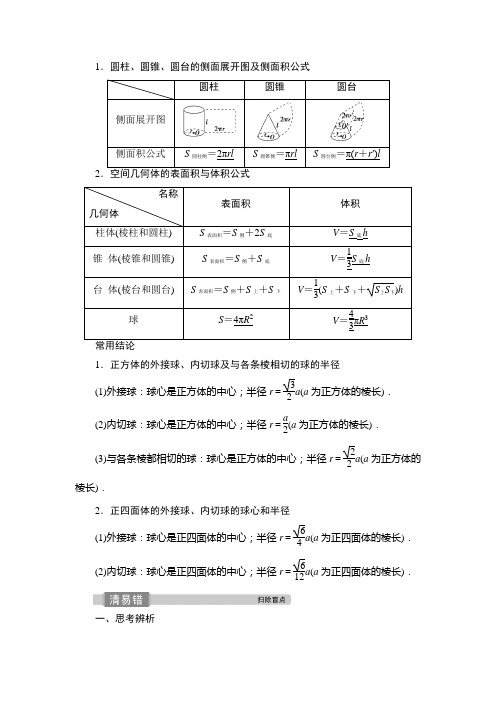
1.圆柱、圆锥、圆台的侧面展开图及侧面积公式圆柱圆锥圆台侧面展开图侧面积公式S圆柱侧=2πrl S圆锥侧=πrl S圆台侧=π(r+r′)l2.空间几何体的表面积与体积公式名称几何体表面积体积柱体(棱柱和圆柱)S表面积=S侧+2S底V=S底h锥体(棱锥和圆锥)S表面积=S侧+S底V=13S底h台体(棱台和圆台)S表面积=S侧+S上+S下V=13(S上+S下+S上S下)h球S=4πR2V=43πR3常用结论1.正方体的外接球、内切球及与各条棱相切的球的半径(1)外接球:球心是正方体的中心;半径r=32a(a为正方体的棱长).(2)内切球:球心是正方体的中心;半径r=a2(a为正方体的棱长).(3)与各条棱都相切的球:球心是正方体的中心;半径r=22a(a为正方体的棱长).2.正四面体的外接球、内切球的球心和半径(1)外接球:球心是正四面体的中心;半径r=64a(a为正四面体的棱长).(2)内切球:球心是正四面体的中心;半径r=612a(a为正四面体的棱长).一、思考辨析判断正误(正确的打“√”,错误的打“×”) (1)多面体的表面积等于各个面的面积之和.( ) (2)锥体的体积等于底面积与高之积.( ) (3)球的体积之比等于半径比的平方.( )(4)简单组合体的体积等于组成它的简单几何体体积的和或差.( ) (5)长方体既有外接球又有内切球.( ) 答案:(1)√ (2)× (3)× (4)√ (5)× 二、易错纠偏常见误区| (1)考虑不周,忽视分类讨论; (2)锥体的底面及其对应高不清楚; (3)组合体的表面积没注意衔接部分.1.将一个相邻边长分别为4π,8π的矩形卷成一个圆柱,则这个圆柱的表面积是________.解析:当底面周长为4π时,底面圆的半径为2,两个底面的面积之和是8π;当底面周长为8π时,底面圆的半径为4,两个底面的面积之和为32π.无论哪种方式,侧面积都是矩形的面积32π2,故所求的表面积是32π2+8π或32π2+32π.答案:32π2+8π或32π2+32π2.已知三棱锥S -ABC 中,∠SAB =∠ABC =π2,SB =4,SC =213,AB =2,BC =6,则三棱锥S -ABC 的体积是________.解析:由∠ABC =π2,AB =2,BC =6,得AC =210.由∠SAB =π2,AB =2,SB =4,得SA =2 3.由SA 2+AC 2=SC 2,得SA ⊥AC ,又SA ⊥AB ,所以SA ⊥平面ABC .所以三棱锥S -ABC 的体积为13S △ABC ·SA =13×12×2×6×23=4 3.答案:4 33.已知一几何体的三视图如图所示,它的侧视图与正视图相同,则该几何体的表面积为________.解析:由三视图知,该几何体是一个正四棱柱与半球的组合体,且正四棱柱的高为2,底面对角线长为4,球的半径为2,所以该正四棱柱的底面正方形的边长为22,该几何体的表面积S=12×4π×22+π×22+22×2×4=12π+16.答案:12π+16空间几何体的表面积(师生共研)(1)在梯形ABCD中,∠ABC=π2,AD∥BC,BC=2AD=2AB=2.将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的表面积为()A.(5+2)πB.(4+2)πC.(5+22)πD.(3+2)π(2)(2021·吉林梅河口五中模拟)阳马和鳖臑(biē nào)是《九章算术·商功》里对两种锥体的称谓.如图所示,取一个长方体,按下图斜割一分为二,得两个一模一样的三棱柱,称为堑堵.再沿其中一个堑堵的一个顶点与相对的棱剖开,得四棱锥和三棱锥各一个,有一棱与底面垂直的四棱锥称为阳马(四棱锥S-ABCD),余下三棱锥称为鳖臑(三棱锥S-ECD),若将某长方体沿上述切割方法得到一个阳马和一个鳖臑,且该阳马的正视图和鳖臑的侧视图如图所示,则该阳马和鳖臑的表面积之和为()A.12+13+3 5 B.11+13+3 5 C.12+313+ 5 D.11+313+ 5【解析】(1)因为在梯形ABCD中,∠ABC=π2,AD∥BC,BC=2AD=2AB=2,所以将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体是一个底面半径为AB=1,高为BC=2的圆柱挖去一个底面半径为AB=1,高为BC-AD=1的圆锥,所以该几何体的表面积S=π×12+2π×1×2+π×1×12+12=(5+2)π.故选A.(2)由三视图可知,在阳马中,AS=2,AD=3,CD=1,SD=13,SB=5,所以S阳马=S△SAD+S△SCD+S△SBC+S△SAB+S矩形ABCD=3×22+1×132+3×52+1×2 2+3=7+13+352.S鳖臑=S△SCD+S△CDE+S△SDE+S△SCE=132+1×22+2×32+3×52=4+13+352,所以所求表面积之和=11+13+35,故选B.【答案】(1)A(2)B空间几何体表面积的求法(1)以三视图为载体的几何体的表面积问题,关键是分析三视图确定几何体中各元素之间的位置关系及数量.(2)多面体的表面积是各个面的面积之和;组合体的表面积注意衔接部分的处理.(3)旋转体的表面积问题注意其侧面展开图的应用.某几何体的三视图如图所示,其中正视图和侧视图均为直角梯形,俯视图为两个正方形,则该几何体的表面积为()A.992B.61C.62 D.73解析:选C.由三视图画出几何体的直观图如图所示,上、下底面分别为边长是1,4的正方形;图中朝里的两个侧面是上底为1,下底为4,高为4的梯形;图中朝外的两个侧面是上底为1,下底为4,高为5的梯形,其表面积为S=1×1+4×4+12×(1+4)×4×2+12×(1+4)×5×2=62.空间几何体的体积(多维探究)角度一求简单几何体的体积(1)(2020·石家庄质量检测)某几何体的三视图如图所示(图中小正方形网格的边长为1),则该几何体的体积是()A .8B .6C .4D .2(2)如图,在直四棱柱ABCD -A 1B 1C 1D 1中,底面ABCD 是平行四边形,点E 是棱BB 1的中点,点F 是棱CC 1上靠近C 1的三等分点,且三棱锥A 1AEF 的体积为2,则四棱柱ABCD -A 1B 1C 1D 1的体积为( )A .12B .8C .20D .18【解析】 (1)由三视图可得该几何体为底面是直角梯形的直四棱柱(如图所示),其中底面直角梯形的上、下底分别为1,2,高为2,直四棱柱的高为2,所以该几何体的体积为(1+2)×22×2=6,故选B .(2)设点F 到平面ABB 1A 1的距离为h ,由题意得V A 1AEF=VF A 1AE.又VF A 1AE=13S△A 1AE ·h =13×⎝ ⎛⎭⎪⎫12AA 1·AB ·h =16(AA 1·AB )·h =16S 四边形ABB 1A 1·h =16V ABCD A 1B 1C 1D1,所以VABCD A 1B 1C 1D 1=6VA 1AEF=6×2=12.所以四棱柱ABCD -A 1B 1C 1D 1的体积为12.故选A .【答案】 (1)B (2)A 角度二 求组合体的体积(1)(2020·高考浙江卷)某几何体的三视图(单位:cm)如图所示,则该几何体的体积(单位:cm3)是()A.73B.143C.3 D.6(2)(2021·贵阳市第一学期监测考试)某几何体的三视图如图所示,则该几何体的体积为(俯视图中弧线是14圆弧)()A.4-πB.π-2C.1-π2D.1-π4【解析】(1)由三视图可知,该几何体是三棱柱和三棱锥的组合体,结合图中数据可得该几何体的体积V=12×2×1×2+13×12×2×1×1=73(cm3),故选A.(2)由题设知,该几何体是棱长为1的正方体被截去底面半径为1的14圆柱后剩下的部分,直观图如图所示,该几何体的体积V=1×1×1-14×π×12×1=1-π4,故选D.【答案】(1)A (2)D(1)处理体积问题的思路(2)求体积的常用方法直接法对于规则的几何体,利用相关公式直接计算割补法把不规则的几何体分割成规则的几何体,然后进行体积计算;或者把不规则的几何体补成规则的几何体,不熟悉的几何体补成熟悉的几何体,便于计算等体积法选择合适的底面来求几何体体积,常用于求三棱锥的体积,即利用三棱锥的任一个面作为三棱锥的底面进行等体积变换1.《九章算术》卷五商功中有如下问题:今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈,问积几何?刍甍:底面为矩形的屋脊状的几何体(网格纸中粗线部分为其三视图,设网格纸上每个小正方形的边长为1),那么该刍甍的体积为()A.4 B.5C.6 D.12解析:选B.如图所示,由三视图可还原得到几何体ABCDEF,过E,F分别作垂直于底面的截面EGH和FMN,可将原几何体切割成三棱柱EHG-FNM,四棱锥EADHG和四棱锥F-MBCN,易知三棱柱的体积为12×3×1×2=3,两个四棱锥的体积相同,都为13×1×3×1=1,则原几何体的体积为3+1+1=5.故选B.2.学生到工厂劳动实践,利用3D打印技术制作模型.如图,该模型为长方体ABCD-A1B1C1D1挖去四棱锥O-EFGH后所得的几何体,其中O为长方体的中心,E,F,G,H分别为所在棱的中点,AB=BC=6 cm,AA1=4 cm.3D打印所用原料密度为0.9 g/cm3.不考虑打印损耗,制作该模型所需原料的质量为________g.解析:由题易得长方体ABCD-A1B1C1D1的体积为6×6×4=144(cm3),四边形EFGH为平行四边形,如图所示,连接GE,HF,易知四边形EFGH的面积为矩形BCC1B1面积的一半,即12),所以V四棱锥O-EFGH=13×3×122×6×4=12(cm=12(cm3),所以该模型的体积为144-12=132(cm3),所以制作该模型所需原料的质量为132×0.9=118.8(g).答案:118.8球与空间几何体的接、切问题(多维探究) 角度一 外接球(1)已知三棱柱ABC -A 1B 1C 1的底面是边长为6的正三角形,侧棱垂直于底面,且该三棱柱的外接球的表面积为12π,则该三棱柱的体积为________.(2)已知三棱锥S -ABC 的所有顶点都在球O 的球面上,SC 是球O 的直径.若平面SCA ⊥平面SCB ,SA =AC ,SB =BC ,三棱锥S -ABC 的体积为9,则球O 的表面积为________.【解析】 (1)设球的半径为R ,上,下底面中心设为M ,N ,由题意,外接球球心为MN 的中点,设为O ,则OA =R ,由4πR 2=12π,得R =OA = 3.又易得AN =2,由勾股定理可知ON =1,所以MN =2,即棱柱的高h =2,所以该三棱柱的体积为34×(6)2×2=3 3.(2)设球O 的半径为R ,因为SC 为球O 的直径,所以点O 为SC 的中点,连接AO ,OB ,因为SA =AC ,SB =BC ,所以AO ⊥SC ,BO ⊥SC ,因为平面SCA ⊥平面SCB ,平面SCA ∩平面SCB =SC ,所以AO ⊥平面SCB ,所以V S ABC =V A SBC =13×S △SBC ×AO =13×⎝ ⎛⎭⎪⎫12×SC ×OB ×AO ,即9=13×⎝ ⎛⎭⎪⎫12×2R ×R ×R ,解得R =3,所以球O 的表面积为S =4πR 2=4π×32=36π.【答案】 (1)33 (2)36π(1)求解多面体的外接球时,经常用到截面圆.如图所示,设球O的半径为R,截面圆O′的半径为r,M为截面圆上任意一点,球心O到截面圆O′的距离为d,则在Rt△OO′M中,OM2=OO′2+O′M2,即R2=d2+r2.(2)求解球的内接正方体、长方体等问题的关键是把握球的直径即是几何体的体对角线.(3)若球面上四点P,A,B,C的连线中P A,PB,PC两两垂直或三棱锥的三条侧棱两两垂直,则可构造长方体或正方体解决问题.角度二内切球(1)(2021·重庆七校联考)已知正三棱锥的高为6,内切球(与四个面都相切)的表面积为16π,则其底面边长为()A.18 B.12C.6 3 D.4 3(2)(2020·高考全国卷Ⅲ)已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为________.【解析】(1)如图,由题意知,球心在三棱锥的高PE上,设内切球的半径为R,则S球=4πR2=16π,所以R=2.所以OE=OF=2,OP=4.在Rt△OPF中,PF=OP2-OF2=2 3.因为△OPF∽△DPE,所以OFDE=PFPE,得DE=23,AD=3DE=63,AB=23AD=12.故选B.(2)易知半径最大的球即为该圆锥的内切球.圆锥PE及其内切球O如图所示,设内切球的半径为R,则sin∠BPE=ROP =BEPB=13,所以OP=3R,所以PE=4R=PB2-BE2=32-12=22,所以R=22,所以内切球的体积V=43πR3=23π,即该圆锥内半径最大的球的体积为2 3π.【答案】(1)B(2)2 3π(1)在求四面体内切球的半径时,应重视分割的思想方法,即将该四面体分割为以球心为顶点,各面为底面的四个三棱锥,通过其体积关系求得半径.(2)与球有关的组合体问题,一种是内切,一种是外接.球与旋转体的组合通常作出它们的轴截面解题;球与多面体的组合,一般通过多面体的一条侧棱和球心,并结合“切点”或“接点”作出截面图,把空间问题化归为平面问题求解.1.已知正四棱锥P-ABCD内接于一个半径为R的球,则正四棱锥P-ABCD 体积的最大值是()A.16R381B.32R381C.64R381D.R3解析:选C.如图,记O为正四棱锥PABCD外接球的球心,O1为底面ABCD 的中心,则P,O,O1三点共线,连接PO1,OA,O1A.设OO 1=x ,则O 1A =R 2-x 2,AB =2·R 2-x 2,PO 1=R +x ,所以正四棱锥P -ABCD 的体积V =13AB 2·PO 1=13×2(R 2-x 2)(R +x )=23(-x 3-Rx 2+R 2x +R 3),求导得V ′=23(-3x 2-2Rx +R 2)=-23(x +R )·(3x -R ),当x =R3时,体积V 有最大值64R 381,故选C .2.设球O 内切于正三棱柱ABC -A 1B 1C 1,则球O 的体积与正三棱柱ABC -A 1B 1C 1的体积的比值为________.解析:设球O 的半径为R ,正三棱柱ABC -A 1B 1C 1的底面边长为a ,则R =33×a 2=36a ,即a =23R .又正三棱柱ABC -A 1B 1C 1的高为2R ,所以球O 的体积与正三棱柱ABC -A 1B 1C 1的体积的比值为43πR 334a 2×2R =43πR 334×12R 2×2R =23π27.答案:23π27核心素养系列14 直观想象——确定球心位置的三种方法决定球的几何要素是球心的位置和球的半径,在球与其他几何体的结合问题中,通过位置关系的分析,找出球心所在的位置是解题的关键,不妨称这个方法为球心位置分析法.方法一 由球的定义确定球心若一个多面体的各顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球.也就是说如果一个定点到一个简单多面体的所有顶点的距离都相等,那么这个定点就是该简单多面体外接球的球心.(1)长方体或正方体的外接球的球心是其体对角线的中点; (2)正三棱柱的外接球的球心是上、下底面中心连线的中点;(3)直三棱柱的外接球的球心是上、下底面三角形外心连线的中点;(4)正棱锥的外接球球心在其高上,具体位置可通过建立直角三角形运用勾股定理计算得到;(5)若棱锥的顶点可构成共斜边的直角三角形,则公共斜边的中点就是其外接球的球心.已知各顶点都在同一个球面上的正四棱柱的高为4,体积为16,则这个球的表面积是()A.16πB.20πC.24πD.32π【解析】已知各顶点都在同一个球面上的正四棱柱的高为4,体积为16,可求得底面边长为2,故球的直径为22+22+42=26,则半径为6,故球的表面积为24π,故选C.【答案】 C方法二构造长方体或正方体确定球心(1)正四面体、三条侧棱两两垂直的正三棱锥、四个面都是直角三角形的三棱锥,可将三棱锥补形成长方体或正方体;(2)同一个顶点上的三条棱两两垂直的四面体、相对的棱相等的三棱锥,可将三棱锥补形成长方体或正方体;(3)若已知棱锥含有线面垂直关系,则可将棱锥补形成长方体或正方体;(4)若三棱锥的三个侧面两两垂直,则可将三棱锥补形成长方体或正方体.如图,边长为2的正方形ABCD中,点E,F分别是边AB,BC的中点,将△AED,△EBF,△FCD分别沿DE,EF,FD折起,使A,B,C三点重合于点A′,若四面体A′EFD的四个顶点在同一个球面上,则该球的半径为()A. 2 B.6 2C.112D.52【解析】 易知四面体A ′EFD 的三条侧棱A ′E ,A ′F ,A ′D 两两垂直,且A ′E =1,A ′F =1,A ′D =2,把四面体A ′EFD 补成从顶点A ′出发的三条棱长分别为1,1,2的一个长方体,则长方体的外接球即为四面体A ′EFD 的外接球,球的半径为r =1212+12+22=62.故选B .【答案】 B方法三 由性质确定球心利用球心O 与截面圆圆心O ′的连线垂直于截面圆及球心O 与弦中点的连线垂直于弦的性质,确定球心.正三棱锥A -BCD 内接于球O ,且底面边长为3,侧棱长为2,则球O 的表面积为________.【解析】 如图,M 为底面△BCD 的中心,易知AM ⊥MD ,DM =1,AM = 3.在Rt △DOM 中,OD 2=OM 2+MD 2,即OD 2=(3-OD )2+1,解得OD =233,故球O 的表面积为4π×⎝ ⎛⎭⎪⎫2332=163π.【答案】 163π[A 级 基础练]1.(2020·高考全国卷Ⅲ)如图为某几何体的三视图,则该几何体的表面积是( )A .6+42B .4+4 2C .6+2 3D .4+2 3解析:选C .由三视图知该几何体为如图所示的三棱锥P -ABC ,其中P A ⊥平面ABC ,AB ⊥AC ,AB =AC =AP =2,故其表面积S =⎝ ⎛⎭⎪⎫12×2×2×3+12×(22)2×sin 60°=6+2 3.2.(2021·贵阳市适应性考试)某几何体的三视图如图所示,已知正视图和侧视图是全等的直角三角形,俯视图是圆心角为90°的扇形,则该几何体的体积是( )A .2πB .π2C .3π2D .3π解析:选D .依题意,题中的几何体是一个圆锥的14(其中该圆锥的底面半径为23,高为3),如图所示,因此该几何体的体积为14×⎣⎢⎡⎦⎥⎤13×π×(23)2×3=3π,选D .3.(2020·高考全国卷Ⅰ)已知A,B,C为球O的球面上的三个点,⊙O1为△ABC的外接圆.若⊙O1的面积为4π,AB=BC=AC=OO1,则球O的表面积为()A.64πB.48πC.36πD.32π解析:选A.如图所示,设球O的半径为R,⊙O1的半径为r,因为⊙O1的面积为4π,所以4π=πr2,解得r=2,又AB=BC=AC=OO1,所以ABsin 60°=2r,解得AB=23,故OO1=23,所以R2=OO21+r2=(23)2+22=16,所以球O的表面积S=4πR2=64π.故选A.4.(2021·东北三校第一次联考)如图,四边形ABCD是边长为2的正方形,ED⊥平面ABCD,FC⊥平面ABCD,ED=2FC=2,则三棱锥A-BEF的体积为()A.13B.23C.1 D.4 3解析:选B.如图,分别取BC,ED,AD的中点G,P,Q,连接FG,FP,PQ,QG,因为ED⊥平面ABCD,FC⊥平面ABCD,ED=2FC=2,所以PD∥=FC,所以四边形FCDP为平行四边形,所以PF∥DC.又Q,G分别为DA,CB的中点,所以QG ∥DC ,且QG =DC ,所以QG ∥PF ,且QG =PF ,所以四边形QGFP 为平行四边形,所以PQ ∥FG .又P 为DE 的中点,所以PQ ∥EA ,所以FG ∥EA ,因为EA ⊂平面EAB ,FG ⊄平面EAB ,所以FG ∥平面EAB .连接EG ,AG ,则V 三棱锥A -BEF =V 三棱锥F -ABE =V 三棱锥G -ABE =V 三棱锥E -ABG =13·ED ·S △ABG=23,故选B .5.(2021·福建省质量检测)某学生到工厂实践,欲将一个底面半径为2,高为3的实心圆锥体工件切割成一个圆柱体,并使圆柱体的一个底面落在圆锥体的底面内.若不考虑损耗,则得到的圆柱体的最大体积是( )A .16π9 B .8π9 C .16π27D .8π27解析:选A .方法一:如图,OC =2,OA =3,由△AED ∽△AOC 可得EDOC =AEAO .设圆柱体的底面半径r =ED =2x (0<x <1),可得AE =3x ,则圆柱体的高h =OE =3-3x ,圆柱体的体积V =π(2x )2(3-3x )=12π(x 2-x 3),令V (x )=12π(x 2-x 3),则V ′(x )=12π(2x -3x 2),令V ′(x )=0,解得x =23或x =0(舍去),可得V (x )在⎝ ⎛⎭⎪⎫0,23上单调递增,在⎝ ⎛⎭⎪⎫23,1上单调递减,故当x =23时,V (x )取得最大值,V (x )max =16π9,即圆柱体的最大体积是16π9.方法二:同方法一,则圆柱体的体积V =12πx 2(1-x )=6π·x ·x (2-2x )≤6π·⎣⎢⎡⎦⎥⎤x +x +(2-2x )33=16π9,当且仅当x =2-2x ,即x =23时等号成立,故圆柱体的最大体积是16π9.6.已知圆柱的底面积为S ,侧面展开图是一个正方形,那么圆柱的侧面积是________.解析:由πr 2=S 得圆柱的底面半径是Sπ,故侧面展开图的边长为2π·S π=2πS ,所以圆柱的侧面积是4πS .答案:4πS7.(2020·高考浙江卷)已知圆锥的侧面积(单位:cm 2)为2π,且它的侧面展开图是一个半圆,则这个圆锥的底面半径(单位:cm)是________.解析:方法一:设该圆锥的母线长为l ,因为圆锥的侧面展开图是一个半圆,其面积为2π,所以12πl 2 =2π,解得l =2,所以该半圆的弧长为2π.设该圆锥的底面半径为R ,则2πR =2π,解得R =1.方法二:设该圆锥的底面半径为R ,则该圆锥侧面展开图中的圆弧的弧长为2πR .因为侧面展开图是一个半圆,设该半圆的半径为r ,则πr = 2πR ,即r =2R ,所以侧面展开图的面积为12·2R ·2πR =2πR 2=2π,解得R =1.答案:18.(2021·长沙市统一模拟考试)在四面体P ABC 中,△ABC 为等边三角形,且边长为6,P A =6,PB =8,PC =10,则四面体P ABC 的体积为________.解析:如图,延长CA 到D ,使得AD =6,连接DB ,PD .因为AD =AB =6,所以△ADB 为等腰三角形,又∠DAB =180°-∠CAB =120°,所以∠ABD =12(180°-120°)=30°,所以∠ABD +∠CBA =90°,即∠DBC =90°,故CB ⊥DB .因为PB =8,PC =10,BC =6,所以PC 2=PB 2+BC 2,所以CB ⊥PB .因为DB ∩PB =B ,DB ⊂平面PBD ,PB ⊂平面PBD ,所以CB ⊥平面PBD ,所以V三棱锥C -PBD=13×CB ×S △PBD .因为DA =AC =AP =6,所以△PDC 为直角三角形,所以PD =CD 2-PC 2=144-100=211.又DB =3AD =63,PB =8,所以DB 2=PD 2+PB 2,故BP ⊥DP ,即△PBD 为直角三角形,所以S △PBD =12×8×211=811.因为A 为DC 的中点,所以V 四面体P ABC =12V 三棱锥P -CBD =12V 三棱锥C -PBD =12×13×6×811=811.答案:8119.已知一个几何体的三视图如图所示.(1)求此几何体的表面积;(2)如果点P ,Q 在正视图中所示位置,P 为所在线段的中点,Q 为顶点,求在几何体表面上,从P 点到Q 点的最短路径的长.解:(1)由三视图知该几何体是由一个圆锥与一个圆柱组成的组合体,其表面积是圆锥的侧面积、圆柱的侧面积和圆柱的一个底面积之和.S 圆锥侧=12(2πa )·(2a )=2πa 2, S 圆柱侧=(2πa )·(2a )=4πa 2, S 圆柱底=πa 2,所以S 表=2πa 2+4πa 2+πa 2=(2+5)πa 2.(2)沿P点与Q点所在母线剪开圆柱侧面,如图.则PQ=AP2+AQ2=a2+(πa)2=a1+π2,所以从P点到Q点在侧面上的最短路径的长为a1+π2.10.如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.(1)证明:平面AEC⊥平面BED;(2)若∠ABC=120°,AE⊥EC,三棱锥E-ACD的体积为63,求该三棱锥的侧面积.解:(1)证明:因为四边形ABCD为菱形,所以AC⊥BD.因为BE⊥平面ABCD,所以AC⊥BE.因为BD∩BE=B,BD⊂平面BED,BE⊂平面BED,所以AC⊥平面BED.又AC⊂平面AEC,所以平面AEC⊥平面BED.(2)设AB=x,在菱形ABCD中,由∠ABC=120°,可得AG=GC=32x,GB=GD=x 2.因为AE⊥EC,所以在Rt△AEC中,可得EG=32x.由BE⊥平面ABCD,知△EBG为直角三角形,可得BE=22x.由已知得,三棱锥E-ACD的体积V三棱锥E-ACD=13×12·AC·GD·BE=624x3=63,故x=2.从而可得AE=EC=ED= 6.所以△EAC的面积为3,△EAD的面积与△ECD的面积均为 5.故三棱锥E-ACD的侧面积为3+2 5.[B级综合练]11.(2021·安徽省部分重点学校联考)已知三棱锥D-ABC的体积为2,△ABC 是边长为2的等边三角形,且三棱锥D-ABC的外接球的球心O恰好是CD的中点,则球O的表面积为()A.52π3B.24πC.56π3D.20π3解析:选A.设球O的半径为R,球心O到平面ABC的距离为d,因为O是CD的中点,所以点D到平面ABC的距离为2d,则V DABC=13S△ABC2d=13×34×22×2d=2,解得d= 3.过点O向平面ABC作垂线,垂足为O′,则O′为等边三角形ABC的外心,连接O′A,则O′A=2×32×23=233,R2=d2+O′A2=3+43=133,所以球O的表面积S=4πR2=52π3.12.(2021·南充市第一次适应性考试)如图,在正三棱锥A-BCD中,AB=BC,E为棱AD的中点.若△BCE的面积为2,则三棱锥A-BCD的体积为()A.23B.33C.233D.223解析:选D.因为AB=BC,所以正三棱锥A-BCD为正四面体,因为E为AD 的中点,所以AD ⊥BE ,AD ⊥CE ,又CE ∩BE =E ,所以AD ⊥平面BCE .设AD =a ,则BE =CE =32a ,所以等腰三角形BCE 的面积S △BCE =12×BC × BE 2-⎝ ⎛⎭⎪⎫BC 22=12×a ×⎝ ⎛⎭⎪⎫32a 2-⎝ ⎛⎭⎪⎫a 22=12×22a 2=2,所以a =2,所以V 三棱锥A -BCD =V 三棱锥A -BCE +V 三棱锥D -BCE =2V 三棱锥A -BCE =2×13S △BCE ×AE =2×13×2×a 2=223.13.如图所示是一个几何体的三视图,根据图中所给的数据,这个几何体的表面积为________,体积为________.解析:如图所示是还原后的几何体的直观图,分别取BC ,AD 的中点E ,F ,连接SE ,EF ,SF ,由图中数据有AB =BC =CD =DA =SE =EF =2,BE =EC =1,因为△SBC 是等腰三角形,所以SB =SC = 5. 因为△SBA 为直角三角形,所以SA =3. 又因为△SAD 是等腰三角形,所以SF ⊥AD . 所以SF =2 2.所以S 正方形ABCD =4,S △SBC =2,S △SAB =S △SCD =5,S △SAD =2 2. 所以S S ABCD =6+2(2+5). 所以V S ABCD =13·S 正方形ABCD ·SE =83. 答案:6+2(2+5) 8314.(2020·河北九校第二次联考)如图,正方体ABCD -A 1B 1C 1D 1的棱长为a ,E ,F ,G 分别是DD 1,AB ,BC 的中点,过点E ,F ,G 的截面将正方体分割成两部分,则较大几何体的体积为________.解析:如图所示,延长GF ,DA 交于点M ,延长FG ,DC 交于点N ,连接EM ,EN 分别与A 1A ,C 1C 交于点P ,Q ,连接PF ,QG ,则五边形EPFGQ 即为过点E ,F ,G 的平面与正方体的截面图形.易得P A =QC =a6,连接EA ,EC ,截面下面部分可分割成三部分,分别是三棱锥E -P AF 、三棱锥E -CGQ 、五棱锥E -AFGCD ,则截面下面部分的体积V 1=V E P AF +V E CGQ +V E AFGCD =13×12×a 6×a2×a +13×12×a 6×a 2×a +13(a 2-12×a 2×a 2)×a 2=25144a 3,则较大几何体的体积V =a 3-25144a 3=119144a 3.答案:119144a 3[C级提升练]15.设A,B,C,D是同一个半径为4的球的球面上的四点,△ABC为等边三角形且其面积为93,则三棱锥D-ABC体积的最大值为() A.12 3 B.18 3C.24 3 D.54 3解析:选B.如图,E是AC的中点,M是△ABC的重心,O为球心,连接BE,OM,OD,BO.因为S△ABC=34AB2=93,所以AB=6,BM=23BE=23AB2-AE2=2 3.易知OM⊥平面ABC,所以在Rt△OBM中,OM=OB2-BM2=2,所以当D,O,M三点共线且DM=OD+OM时,三棱锥D-ABC的体积取得最大值,且最大值V max=13S△ABC×(4+OM)=13×93×6=18 3.故选B.16.如图,正方体ABCD-A1B1C1D1的棱长为3,线段B1D1上有两个动点E,F且EF=1,则当E,F移动时,下列结论正确的有________.(填序号)①AE∥平面C1BD;②四面体ACEF的体积为定值;③三棱锥A-BEF的体积为定值;④四面体ACDF 的体积为定值.解析:对于①,如图1,AB 1∥DC 1,易证AB 1∥平面C 1BD ,同理AD 1∥平面C 1BD ,且AB 1∩AD 1=A ,所以平面AB 1D 1∥平面C 1BD ,又AE ⊂平面AB 1D 1,所以AE ∥平面C 1BD ,①正确;对于②,如图2,S △AEF =12EF ·h 1=12×1×(32)2-⎝⎛⎭⎪⎫3222=364,点C 到平面AEF 的距离为点C 到平面AB 1D 1的距离d 为定值,所以V A CEF =V C AEF =13×364×d =64d 为定值,所以②正确;对于③,如图3,S △BEF =12×1×3=32,点A 到平面BEF 的距离为A 到平面BB 1D 1D 的距离d 为定值,所以V A BEF =13×32×d =12d 为定值,③正确;对于④,如图4,四面体ACDF 的体积为V A CDF =V F ACD =13×12×3×3×3=92为定值,④正确.答案:①②③④。
高三数学空间几何体的表面积与体积试题

高三数学空间几何体的表面积与体积试题1.四面体ABCD的四个顶点都在球O的表面上,平面BCD,是边长为3的等边三角形.若,则球O的表面积为()A.B.C.D.【答案】C【解析】取的中点E,连结AE,BE,∵在四面体ABCD中,AB⊥平面BCD,△BCD是边长为3的等边三角形.∴Rt△ABC≌Rt△ABD,△ACD是等腰三角形,△BCD的中心为G,作OG∥AB交AB的中垂线HO于O,O为外接球的中心,,,四面体ABCD外接球的表面积为:,故选C.【考点】球的体积和表面积.2.已知ABC的三个顶点在以O为球心的球面上,且,BC=1,AC=3,三棱锥O- ABC的体积为,则球O的表面积为__________。
【答案】【解析】设球的半径为R,ABC的外接圆半径为r,球心O到截面ABC的距离为,由得,=,=,解得AB=,所以==,所以===,解得=,由正弦定理知,2r===3,所以r=,由球的截面性质知,=2,所以球O的表面积为=.【考点】球的截面性质,球的表面积公式,棱锥的体积公式,正弦定理,余弦定理,运算求解能力3.如图,多面体的直观图及三视图如图所示,分别为的中点.(1)求证:平面;(2)求多面体的体积.【答案】(1)证明:见解析;(2)多面体的体积.【解析】(1)由多面体的三视图知,三棱柱中,底面是等腰直角三角形,,平面,侧面都是边长为的正方形.连结,则是的中点,由三角形中位线定理得,得证.(2)利用平面,得到,再据⊥,得到⊥平面,从而可得:四边形是矩形,且侧面⊥平面. 取的中点得到,且平面.利用体积公式计算.所以多面体的体积. 12分试题解析:(1)证明:由多面体的三视图知,三棱柱中,底面是等腰直角三角形,,平面,侧面都是边长为的正方形.连结,则是的中点,在△中,,且平面,平面,∴∥平面. 6分(2)因为平面,平面,,又⊥,所以,⊥平面,∴四边形是矩形,且侧面⊥平面 8分取的中点,,且平面. 10分所以多面体的体积. 12分【考点】三视图,平行关系,垂直关系,几何体的体积.4.若将一个圆锥的侧面沿一条母线剪开,其展开图是半径为2 cm的半圆,则该圆锥的体积为 .【答案】【解析】由题意得:,所以圆锥的体积为【考点】圆锥的体积及展开图5.若长方体三个面的面积分别为,,,则此长方体的外接球的表面积是________.【答案】6π【解析】设长方体的过同一顶点的三条棱长分别为a、b、c,则解得长方体外接球半径为R==,外接球的表面积为S=4π=6π6.如图所示,正方体ABCD A1B1C1D1的棱长为2,动点E,F在棱A1B1上,点Q是棱CD的中点,动点P在棱AD上.若EF=1,DP=x,A1E=y(x,y大于零),则三棱锥P EFQ的体积()A.与x,y都有关B.与x,y都无关C.与x有关,与y无关D.与y有关,与x无关【答案】C【解析】三棱锥P EFQ 的体积可以看作是以△PEF 为底面,而△PEF 的底EF=1,高A 1P=,与x 有关,三棱锥P EFQ 的高为点Q 到平面PEF 的距离.∵CD ∥EF,∴CD ∥平面PEF.∴点Q 到平面PEF 的距离等于点D 到平面PEF 的距离,与y 无关,故选C.7. 已知一个圆柱内接于球O 中,其底面直径和母线都是2,则球O 的体积是 . 【答案】π【解析】设球的半径为R,则2R==2,∴R=, ∴V=πR 3=π.8. 如图,AA 1,BB 1为圆柱OO 1的母线,BC 是底面圆O 的直径,D ,E 分别是AA 1,CB 1的中点,DE ⊥面CBB 1.(1)证明:DE ∥面ABC ; (2)求四棱锥C-ABB 1A 1与圆柱OO 1的体积比. 【答案】(1)见解析 (2)【解析】解:(1)证明:连接EO ,OA. ∵E ,O 分别为B 1C ,BC 的中点, ∴EO ∥BB 1.又DA ∥BB 1,且DA =BB 1=EO ,∴四边形AOED 是平行四边形,即DE ∥OA.又DE ⊄平面ABC ,AO ⊂平面ABC , ∴DE ∥平面ABC.(2)由题意知DE ⊥平面CBB 1,且由(1)知DE ∥AO , ∴AO ⊥平面CBB 1, ∴AO ⊥BC , ∴AC =AB.∵BC 是底面圆O 的直径, 得CA ⊥AB ,且AA 1⊥CA ,∴CA ⊥平面AA 1B 1B ,即CA 为四棱锥C-ABB 1A 1的高.设圆柱高为h ,底面半径为r , 则V OO 1=πr 2h ,V C-ABB 1A1=h(r)·(r)=hr 2.∴V C-ABB 1A1∶V OO 1=.9. 若长方体的顶点都在半径为3的球面上,则该长方体表面积的最大值为 . 【答案】【解析】设长方体的边长为,那么长方体的表面积为:,又由于:,而,所以该长方体表面积的最大值为.【考点】长方体的表面积;基本不等式的变形.10.已知Rt△ABC,其三边分别为a,b,c(a>b>c).分别以三角形的边a,b,c所在直线为轴,其余各边旋转一周形成的曲面围成三个几何体,其表面积和体积分别为S1,S2,S3和V1,V2,V3.则它们的大小关系为()A.S1>S2>S3,V1>V2>V3B.S1<S2<S3,V1<V2<V3C.S1>S2>S3,V1=V2=V3D.S1<S2<S3,V1=V2=V3【答案】B【解析】S1=π (b+c),V1=πa,S2=πac+πc2,V2=πbc2,S3=πab+πb2,V3=πb2c.由于a>b>c,可得S1<S2<S3,V1<V2<V3.11.在三棱锥中,,,,二面角的余弦值是,若都在同一球面上,则该球的表面积是 .【答案】【解析】取中点,连接,∵,∴,∵,∴,平面.∴为二面角.在中,,,∴.取等边的中心,作平面,过作平面,为外接球球心,∴,二面角的余弦值是,所以,,∴,∴点为四面体的外接球球心,其半径为,表面积为.【考点】三棱锥的外接球.12.已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,PD⊥底面ABCD,E,F分别为棱BC,AD的中点.(1)求证:DE∥平面PFB;(2)已知二面角P-BF-C的余弦值为,求四棱锥P-ABCD的体积.【答案】(1)见解析(2)【解析】(1)因为E,F分别为正方形ABCD的两边BC,AD的中点,所以BE綉FD,即BEDF 为平行四边形,∴ED∥FB,∵FB⊂平面PFB,且ED⊄平面PFB,∴DE∥平面PFB.(2)以D为原点,直线DA,DC,DP分别为x,y,z轴建立空间直角坐标系.如图,设PD=a,可得如下点的坐标P(0,0,a),F(1,0,0),B(2,2,0).则有=(1,0,-a),=(1,2,0).因为PD⊥底面ABCD,所以平面ABCD的一个法向量为m=(0,0,1).设平面PFB的法向量为n=(x,y,z),则可得即.,令x=1, 得z=,y=-,所以n=.由已知二面角P-BF-C的余弦值为,所以得cos〈m,n〉==,∴a=2,∴V=×2×2×2=P-ABCD13.如图,四棱锥中,底面是菱形,,,是的中点,点在侧棱上.(1)求证:⊥平面;(2)若是的中点,求证://平面;(3)若,试求的值.【答案】(1)详见解析(2)详见解析(3)【解析】(1)由线面垂直判定定理,要证线面垂直,需证垂直平面内两条相交直线,由,是的中点,易得垂直于,再由底面是菱形,得三角形为正三角形,所以垂直于,(2)由线面平行判定定理,要证线面平行,需证平行于平面内一条直线,根据是的中点,联想到取AC中点O所以OQ为△PAC中位线.所以OQ // PA注意在写定理条件时,不能省,要全面.例如,线面垂直判定定理中有五个条件,线线垂直两个,相交一个,线在面内两个;线面平行判定定理中有三个条件,平行一个,线在面内一个,线在面外一个,(3)研究体积问题关键在于确定高,由于两个底面共面,所以求的值就转化为求对应高的长度比.试题解析:(1)因为E是AD的中点,PA=PD,所以AD⊥PE.因为底面ABCD是菱形,∠BAD=,所以AB=BD,又因为E是AD的中点,所以 AD⊥BE.因为PE∩BE=E,所以AD⊥平面PBE. 4分(2)连接AC交BD于点O,连结OQ.因为O是AC中点,Q是PC的中点,所以OQ为△PAC中位线.所以OQ//PA. 7分因为PA平面BDQ,OQ平面BDQ.所以PA//平面BDQ. 9分(3)设四棱锥P-BCDE,Q-ABCD的高分别为,,所以VP-BCDE =SBCDE,VQ-ABCD=SABCD. 10分因为VP-BCDE =2VQ-ABCD,且底面积SBCDE=SABCD. 12分所以,因为,所以. 14分【考点】线面垂直判定定理, 线面平行判定定理,锥的体积.14.如图1,一个密闭圆柱体容器的底部镶嵌了同底的圆锥实心装饰块,容器内盛有升水.平放在地面,则水面正好过圆锥的顶点,若将容器倒置如图2,水面也恰过点.以下命题正确的是( ).A.圆锥的高等于圆柱高的;B.圆锥的高等于圆柱高的;C.将容器一条母线贴地,水面也恰过点;D.将容器任意摆放,当水面静止时都过点.【答案】C【解析】本题考查体积公式与空间想象能力,设圆锥的高为,圆柱的高为,则利用倒置前后水的体积不变这个性质知,化简得,均错,现在水的容积正好是圆柱内部空间的一半,因此把圆柱的母线贴地,则水面过点,但过点的平面不可能总是平分圆柱内部除去圆锥的那部分,故错误.【考点】体积公式.15.如图,PA平面ABCD,四边形ABCD为矩形,PA=AB=,AD=1,点F是PB的中点,点E在边BC上移动.(I)求三棱锥E—PAD的体积;(II)试问当点E在BC的何处时,有EF//平面PAC;(1lI)证明:无论点E在边BC的何处,都有PE AF.【答案】见解析【解析】(Ⅰ)注意到PA平面ABCD,得知的长即为三棱锥的高,而三棱锥的体积等于的体积,计算即得.(Ⅱ)当点为的中点时,与平面平行.利用三角形中位线定理,得到,进一步得出∥平面.(Ⅲ)证明:根据等腰三角形得出,根据平面,平面,得到,又因为且,⊂平面,得到平面,又平面,.再根据,平面,及平面,根据,作出结论.试题解析:(Ⅰ)由已知PA平面ABCD,所以的长即为三棱锥的高,三棱锥的体积等于的体积= = .(Ⅱ)当点为的中点时,与平面平行.∵在中,分别为的中点,连结,又平面,而平面,∴∥平面.(Ⅲ)证明:因为,所以等腰三角形中,∵平面,平面,∴又因为且,⊂平面,∴平面,又平面,∴.又∵,∴平面.PB,BE⊂平面PBE,∵平面,∴,即无论点E在边的何处,都有.【考点】几何体的体积,垂直关系,平行关系.16.已知D、E是边长为3的正三角形的BC边上的两点,且,现将、分别绕AD和AE折起,使AB和AC重合(其中B、C重合).则三棱锥的内切球的表面积是()A. B. C. D.【答案】B【解析】如下图所示,,,,.设内切球的半径为r,则,所以内切球的表面积为:.【考点】空间几何体的体积及表面积.17.如图,平面四边形中,,,,将其沿对角线折成四面体,使平面平面,若四面体顶点在同一球面上,则该球的体积为( )A.B.C.D.【答案】A【解析】由题意平面四边形ABCD中,AB=AD=CD=1,BD=,BD⊥CD,将其沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,若四面体A′-BCD顶点在同一个球面上,可知A′B⊥A′C,所以BC 是外接球的直径,所以BC=,球的半径为:,所以球的体积为:,选A.【考点】1.球内接多面体;2.球的体积和表面积18.在正三棱锥中,、分别是、的中点,且,若侧棱,则正三棱锥外接球的表面积是()A.B.C.D.【答案】C【解析】∵三棱锥是正棱锥,∴SB⊥AC(对棱互相垂直)∴,又∵而,∴平面,即平面,∴,将此三棱锥补成正方体,则它们有相同的外接球,∴,故选C.【考点】垂直关系,几何体的体积19.在三棱锥S−ABC中,,二面角S−AC−B的余弦值是,若S、A、B、C都在同一球面上,则该球的表面积是.【答案】【解析】如图,取AC的中点D,由已知易证二面角S−AC−B的平面角是∠SDB,,故由余弦定理可得,由勾股定理的逆定理可得,补体得正方体,∴三棱锥S−ABC的外接球的半径为,∴该球的表面积是.【考点】立体几何的二面角,球的表面积20.已知三棱锥的顶点都在球的球面上,且平面,则三棱锥的体积等于____.【答案】12【解析】由平面可得,又所以是平面,可以发现线段的中点为球心,取的中点,则,于是.【考点】立体几何中线线垂直、线面垂直的证明,以及椎体体积的求解等知识,考查学生的分析、知识迁移能力21.棱长为的正方体的个顶点都在球的表面上,分别是棱、的中点,则过两点的直线被球截得的线段长为____________【答案】【解析】设过两点的直线与球球交于均为等腰直角三角形,,点到的距离为棱长一半【考点】正方体与外接球点评:求解本题首先要把握住正方体的外接球的球心为正方体的中心,球心与弦中点的连线垂直于弦,从而解直角三角形求出弦长22.点在同一个球的球面,,,若四面体体积的最大值为,则这个球的表面积为()A.B.C.D.【答案】C【解析】∵,∴是直角三角形,∴的外接圆的圆心是边AC的中点O,如图所示,若使四面体ABCD体积的最大值只需使1点D到平面ABC的距离最大,又平面ABC,所以点D是直线与球的交点设球的半径为R,则由体积公式有:在中,,解得:,故选C。
高一数学空间几何体的表面积与体积试题

高一数学空间几何体的表面积与体积试题1.设甲、乙两个圆柱的底面积分别为,体积分别为,若它们的侧面积相等,且,则的值是.【答案】【解析】设甲、乙两个圆柱的底面半径为,母线长,由于侧面积相等,,,,.【考点】圆柱的体积公式应用.2.如图所示,在四棱锥中,平面,,,是的中点,是上的点且,为△中边上的高.(1)证明:平面;(2)若,,,求三棱锥的体积;(3)证明:平面.【答案】(1)见解析;(2)体积(3)见解析【解析】试题分析:(1)利用线面垂直的判断定理证明线面垂直,条件齐全.(2)利用棱锥的体积公式求体积.(3)证明线面垂直的方法:一是线面垂直的判定定理;二是利用面面垂直的性质定理;三是平行线法(若两条平行线中的一条垂直于这个平面,则另一条也垂直于这个平面.解题时,注意线线、线面与面面关系的相互转化.(4)在求三棱柱体积时,选择适当的底作为底面,这样体积容易计算.试题解析:(1)证明:因为平面,所以。
因为为△中边上的高,所以。
因为,所以平面。
4分(2)连结,取中点,连结。
因为是的中点,所以。
因为平面,所以平面。
则,。
8分(3)证明:取中点,连结,。
因为是的中点,所以。
因为,所以,所以四边形是平行四边形,所以。
因为,所以。
因为平面,所以。
因为,所以平面,所以平面。
13分【考点】(1)空间中线面垂直和平行的判定(2)几何体的体积.3.如果两个球的体积之比为8:27,那么两个球的表面积之比为()A.8:27B.2:3C.4:9D.2:9【答案】C【解析】由题意,故选C【考点】球的体积和表面积4.已知正方体的棱长为1,则该正方体外接球的体积为()A.B.C.D.【答案】A【解析】因为正方体的对角线长就是外接球的直径,而正方体的对角线长为,所以球的半径为,所以正方体的外接球的体积为,故选A.【考点】1、球与正方体的组合体;2、球的体积.5.棱长为1的正方体的8个顶点都在球的表面上,分别是棱的中点,点,分别是线段,(不包括端点)上的动点,且线段平行于平面,则(1)直线被球截得的线段长为(2)四面体的体积的最大值是【答案】(1);(2).【解析】(1)因为点在圆上,为中点,所以直线被球截得的线段长为正方形的外接圆直径,等于,(2)过做与点,连接∵,,平面∥平面,为平面与两平行平面的交线,,又,,平面,设正方体的棱长为1,,则,当时,最大值为.【考点】组合体6.已知直三棱柱中,,是中点,是中点.(1)求三棱柱的体积;(2)求证:;(3)求证:∥面.【答案】(1);(2)证明详见解析;(3)证明详见解析.【解析】(1)这是一个直三棱柱,直接由体积计算公式即可求解;(2)要证,只须证明面,注意到面与底面垂直且交线为,而依题意又有,由面面垂直的性质可得面,问题得证;(3)要证∥面,有两种思路:一是在平面内找一条直线与平行,这时只须取的中点,连接,证明四边形为平行四边形即可;二是先证经过直线的一个平面与面平行,这时可取中点,连结,,先证明面∥面,再由面面平行的性质即可证明∥面.试题解析:(1) 3分(2)∵,∴为等腰三角形∵为中点,∴ -4分∵为直棱柱,∴面面 5分∵面面,面∴面 6分∴ 7分(3)取中点,连结, 8分∵分别为的中点∴∥,∥, 9分∴面∥面 11分面∴∥面 12分.【考点】1.空间几何体的体积计算;2.空间中的平行关系;3.空间中的垂直关系.7.已知一个正三棱锥的三条侧棱两两垂直且相等,底面边长为,则该三棱锥的外接球的表面积是()A.B.C.D.【答案】A【解析】设该正三棱锥为,依题意两两垂直且,所以,且该正三棱锥的外接球与以为邻边的正方体的外接球是相同的,正方体的边长为,体对角线长为,故球的半径为,所以球的表面积为,故选A.【考点】1.三棱锥的外接球;2.球的表面积公式.8.已知正方体的外接球的体积是,则这个正方体的棱长是()A.B.C.D.【答案】D【解析】先求球的半径,直径就是正方体的对角线,然后求出正方体的棱长.正方体外接球的体积是,则外接球的半径正方体的对角线的长为2,棱长等于,故选D.【考点】球内接多面体;球的体积和表面积.9.正方体的体积是64,则其表面积是()A.64B.16C.96D.无法确定【答案】C【解析】由正方体的体积是64,能求出正方体的边长为4,由此能求出正方体的表面积.解:∵正方体的体积是64,∴正方体的边长为4,∴它的表面积S=6×42=96.故选C【考点】正方体的体积和表面积点评:本题考查正方体的体积和表面积的求法,是基础题,解题时要认真审题,注意等价转化思想的合理运用.10.一个空间几何体的三视图如图所示,则该几何体的表面积为()A.48B.32+8C.48+8D.80【答案】C【解析】观察三视图可知,这是一个四棱柱,底面梯形两底分别为2,4,高为4,几何体的高为4,底面梯形的腰长为,所以,几何体表面积为,48+8,故选C。
高三数学空间几何体的表面积与体积试题答案及解析

高三数学空间几何体的表面积与体积试题答案及解析1.如图, 四棱柱的底面ABCD是正方形, O为底面中心, ⊥平面ABCD,.(1)证明: // 平面;(2)求三棱柱的体积.【答案】(1)证明详见解析;(2)体积为1.【解析】本题主要考查线线平行、面面平行、线面垂直、柱体的体积等基础知识,考查学生的空间想象能力、逻辑推理能力、计算能力.第一问,由图象可得到,,,所以得到四边形为平行四边形,所以,利用面面平行的判定得证;第二问,由面ABCD,所以得到是三棱柱的高,利用体积转化法,得到三棱柱的体积.试题解析:(1)设线段的中点为,∵BD和是的对应棱,∴,同理,∵AO和是棱柱的对应线段,∴,且,且四边形为平行四边形且,面面.(2)∵面ABCD,∴是三棱柱的高,在正方形ABCD中,,在中,,,所以,.【考点】线线平行、面面平行、线面垂直、柱体的体积.2.(正四棱锥与球体积选做题)棱长为1的正方体的外接球的体积为________.【答案】.【解析】正方体的体对角线,就是正方体的外接球的直径,所以球的直径为:所以球的半径为:,∴正方体的外接球的体积V=.【考点】1.球的体积;2.球内接多面体.3.如图,ABCD是边长为2的正方形,ED⊥平面ABCD,ED=1,EF∥BD且EF=BD.(1)求证:BF∥平面ACE;(2)求证:平面EAC⊥平面BDEF(3)求几何体ABCDEF的体积.【答案】(1)见解析;(2)见解析;(3)2【解析】(1)利用线线平行,推证线面平行;(2)利用一个面内一条直线与另一个平面垂直,则这两个平面垂直,证明面面垂直;(3)将不规则几何体转化为主题或椎体的体积求解.试题解析:(1)证明:记AC与BD的交点为O,则DO=BO=BD,连接EO,∵EF∥BD且EF=BD,∴EF∥BO且EF=BO,则四边形EFBO是平行四边形,∴BF∥EO,又∵面ACE,面ACE,∴BF∥平面ACE;(2)证明:∵ED⊥平面ABCD,平面ABCD,∴ED⊥AC.∵ABCD为正方形,∴BD⊥AC,又ED∩BD=D,∴AC⊥平面BDEF,又平面EAC,∴平面EAC⊥平面BDEF;(3)解:∵ED⊥平面ABCD,∴ED⊥BD,又∵EF∥BD且EF=BD,∴BDEF是直角梯形,又∵ABCD是边长为2的正方形,BD=2,EF=,∴题型BDEF的面积为,由(1)知AC⊥平面BDEF,∴几何体的体积VABCDEF =2VA-BDEF=2×S BDEF·AO=.【考点】空间直线与平面位置关系,几何体的体积4.如图,多面体的直观图及三视图如图所示,分别为的中点.(1)求证:平面;(2)求多面体的体积.【答案】(1)证明:见解析;(2)多面体的体积.【解析】(1)由多面体的三视图知,三棱柱中,底面是等腰直角三角形,,平面,侧面都是边长为的正方形.连结,则是的中点,由三角形中位线定理得,得证.(2)利用平面,得到,再据⊥,得到⊥平面,从而可得:四边形是矩形,且侧面⊥平面. 取的中点得到,且平面.利用体积公式计算.所以多面体的体积. 12分试题解析:(1)证明:由多面体的三视图知,三棱柱中,底面是等腰直角三角形,,平面,侧面都是边长为的正方形.连结,则是的中点,在△中,,且平面,平面,∴∥平面. 6分(2)因为平面,平面,,又⊥,所以,⊥平面,∴四边形是矩形,且侧面⊥平面 8分取的中点,,且平面. 10分所以多面体的体积. 12分【考点】三视图,平行关系,垂直关系,几何体的体积.5.正三棱柱的底面边长为,侧棱长为,为中点,则三棱锥的体积为A.B.C.D.【答案】C【解析】如下图所示,连接,因为是正三角形,且为中点,则,又因为面,故,且,所以面,所以是三棱锥的高,所以.【考点】1、直线和平面垂直的判断和性质;2、三棱锥体积.6.棱长为的正四面体的外接球半径为.【答案】【解析】记正四面体棱长为,外接球半径为,在正四面体中,利用棱,与棱共顶点的高及这条棱在对面上的射影构成的直角三角形可解得,因此中本题中.【考点】正四面体(正棱锥的性质).7.如图,已知平面,,,且是的中点,.(1)求证:平面;(2)求证:平面平面;(3)求此多面体的体积.【答案】(1)详见解析;(2)详见解析;(3).【解析】(1)取的中点,连结、,利用中位线证明,利用题中条件得到,进而得到,于是说明四边形为平行四边形,得到,最后利用直线与平面平行的判定定理证明平面;(2)由平面得到,再利用等腰三角形三线合一得到,利用直线与平面垂直的判定定理证明平面,结合(1)中的结论证明平面,最后利用平面与平面垂直的判定定理证明平面平面;(3)利用已知条件得到平面平面,然后利用平面与平面垂直的性质定理求出椎体的高,最后利用椎体的体积公式计算该几何体的体积.(1)取中点,连结、,为的中点,,且,又,且,且,为平行四边形,,又平面,平面,平面;(2),,所以为正三角形,,平面,,平面,又平面,,又,,平面,又,平面,又平面,平面平面;(3)此多面体是一个以为定点,以四边形为底边的四棱锥,,平面平面,等边三角形边上的高就是四棱锥的高,.【考点】1.直线与平面平行;2.平面与平面垂直;3.椎体体积的计算8.如图,在三棱锥中,,,°,平面平面,,分别为,中点.(1)求证:∥平面;(2)求证:;(3)求三棱锥的体积.【答案】(1)证明过程详见解析;(2)证明过程详见解析;(3).【解析】本题主要考查线线平行、线面平行、线线垂直、线面垂直、面面垂直、三棱锥的体积等基础知识,考查学生的空间想象能力、逻辑推理能力.第一问,由于D、E分别为AB、AC中点,所以利用三角形的中位线得出∥,再利用线面平行的判定直接得到结论;第二问,由,而∥得,而D为AB中点,PA=PB,得,所以利用线面垂直的判定得平面,再利用线面垂直的性质得;第三问,由于,利用面面垂直的性质得平面,所以PD是三棱锥的高,而,所以. (1)因为,分别为,中点,所以∥,又平面,平面,所以∥平面. 4分(2)连结,因为∥,又°,所以.又,为中点,所以.所以平面,所以. 9分(3)因为平面平面,有,所以平面,所以. 14分【考点】线线平行、线面平行、线线垂直、线面垂直、面面垂直、三棱锥的体积.9.棱长为1的正方体及其内部一动点,集合,则集合构成的几何体表面积为 .【答案】【解析】 .【考点】几何体的表面积.10.已知等腰梯形PDCB中(如图),PB=3,DC=1,PD=BC=,A为PB边上一点,且PA=1,将△PAD沿AD折起,使平面PAD⊥平面ABCD(如图).(1)证明:平面PAD⊥平面PCD.(2)试在棱PB上确定一点M,使截面AMC把几何体分成的两部分VPDCMA ∶VMACB=2∶1.(3)在M满足(2)的情况下,判断直线PD是否平行平面AMC.【答案】(1)见解析(2)M为线段PB的中点时(3)不平行【解析】(1)因为PDCB为等腰梯形,PB=3,DC=1,PA=1,则PA⊥AD,CD⊥AD.又因为面PAD⊥面ABCD,面PAD∩面ABCD=AD,CD⊂面ABCD,故CD⊥面PAD. 又因为CD⊂面PCD,所以平面PAD⊥平面PCD.(2)所求的点M即为线段PB的中点.证明如下:设三棱锥M-ACB的高为h1,四棱锥P-ABCD的高为h2,当M为线段PB的中点时,==,所以===,所以截面AMC把几何体分成的两部分VPDCMA ∶VMACB=2∶1.(3)当M为线段PB的中点时,直线PD与面AMC不平行.证明如下:(反证法)假设PD∥面AMC,连接DB交AC于点O,连接MO.因为PD⊂面PBD,且面AMC∩面PBD=MO,所以PD∥MO.因为M为线段PB的中点时,则O为线段BD的中点,即=,而AB∥DC,故==,故矛盾.所以假设不成立,故当M为线段PB的中点时,直线PD与平面AMC不平行.11.棱长为2的三棱锥的外接球的表面积为()A.6πB.4πC.2πD.π【答案】A【解析】由题意知,此三棱锥为正四面体,以此正四面体的各棱为正方形的对角线拓展出一个正方体,则三棱锥外接球的半径为正方体外接球的半径.因三棱锥棱长为2,所以正方体棱长为,其外接球的直径为所以三棱锥的外接球的表面积为6π.12.如图,在三棱锥中,,,平面平面,为中点,点分别为线段上的动点(不含端点),且,则三棱锥体积的最大值为________.【答案】【解析】因为且为中点,所以,因为平面平面,由面面垂直的性质定理可得,即。
高三数学空间几何体的表面积与体积试题

高三数学空间几何体的表面积与体积试题1.设△ABC的三边长分别为a、b、c,△ABC的面积为S,内切圆半径为r,则r=;类比这个结论可知:四面体S -ABC的四个面的面积分别为S1、S2、S3、S4,内切球的半径为R,四面体S -ABC的体积为V,则R=.【答案】.【解析】设四面体的内切球的球心为O,则球心O到四个面的距离都是R,所以四面体的体积等于以O为顶点,分别以四个面为底面的4个三棱锥体积的和.则四面体的体积为 V四面体A−BCD=∴.【考点】类比推理.2.已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8,高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6,高为4的等腰三角形.(1)求该几何体的体积V;(2)求该几何体的侧面积S.【答案】(1)64 (2)40+24【解析】解:本题考查由三视图求几何体的侧面积和体积,由正视图和侧视图的三角形结合俯视图可知该几何体是一个底面为矩形,高为4,顶点在底面的射影是矩形中心的四棱锥,如图.(1)V=×(8×6)×4=64.(2)四棱锥的两个侧面VAD、VBC是全等的等腰三角形,取BC的中点E,连接OE,VE,则△VOE为直角三角形,VE为△VBC边上的高,VE==4.同理侧面VAB、VCD也是全等的等腰三角形,AB边上的高h==5.∴S侧=2×(×6×4+×8×5)=40+24.3.某圆锥体的侧面展开图是半圆,当侧面积是时,则该圆锥体的体积是 .【答案】【解析】设圆锥的母线长为,底面半径为,则,,,,所以圆锥的高为,体积为.【考点】圆锥的侧面展开图与体积.4. (2014·荆州模拟)湖面上漂着一个小球,湖水结冰后将球取出,冰面上留下了一个直径为12cm,深2cm的空穴,则该球的半径是________cm,表面积是________cm2.【答案】10 400π【解析】设球的半径为r,如图:由勾股定理可知,r2=(r-2)2+36,解得r=10cm.所以表面积为4πr2=4π×100=400π(cm2).5.如图甲,在平面四边形ABCD中,已知,,现将四边形ABCD沿BD折起,使平面ABD平面BDC(如图乙),设点E,F分别为棱AC,AD的中点.(1)求证:DC平面ABC;(2)设,求三棱锥A-BFE的体积.【答案】(1)证明:见解析;(2).【解析】(1)注意分析折叠前后变化的关系及不变化的关系.在图甲中可得;在图乙中,可得AB⊥CD.根据DC⊥BC,即可得到DC⊥平面ABC.(2)首先根据E,F分别为AC,AD的中点,得到EF//CD,根据(1)知,DC⊥平面ABC,得到EF⊥平面ABC,从而得到在图甲中,根据给定角度及长度,计算“不变量”,得,BD=2,BC=,EF=CD=,利用体积公式计算即得所求.解答本题的关键是确定“垂直关系”,这也是难点所在,平时学习中,应特别注意转化意识的培养,等体积转化的方法,是立体几何中常用方法之一.(1)证明:在图甲中∵且∴,即 1分在图乙中,∵平面ABD⊥平面BDC ,且平面ABD∩平面BDC=BD4分又,,且,∴DC⊥平面ABC. 6分(2)解:, 7分又由(1)知,DC⊥平面ABC,∴EF⊥平面ABC, 8分所以, 9分在图甲中,由得,, 10分,11分12分【考点】平行关系,垂直关系,几何体的体积.6.某几何体的三视图如图所示,则该几何体的体积是.【答案】【解析】直观图是圆柱中抽出正四棱柱∴该几何体的体积是7.已知圆锥的母线长为,侧面积为,则此圆锥的体积为__________.(结果中保留)【答案】【解析】由圆锥的母线长为,侧面积为.则根据.即可求出圆锥的底面周长.从而解出底面半径.再求出圆锥的高.根据体积公式.【考点】1.圆锥曲线的侧面积.2.圆锥曲线的体积公式.3.图形的展开前后的变化.8.已知函数将的图像与轴围成的封闭图形绕轴旋转一周,所得旋转体的体积为___________.【答案】【解析】.【考点】旋转体的体积.9.正四棱锥的五个顶点在同一球面上,若该正四棱锥的底面边长为2,侧棱长为,则这个球的表面积为_________.【答案】【解析】如图是正四棱锥外接球的球心,是底面中心,,,设球半径为,在中,,解得,所以.【考点】正棱锥的外接球.10.若长方体三个面的面积分别为,,,则此长方体的外接球的表面积是________.【答案】6π【解析】设长方体的过同一顶点的三条棱长分别为a、b、c,则解得长方体外接球半径为R==,外接球的表面积为S=4π=6π11.四面体的六条棱中,有五条棱长都等于a.(1)求该四面体的体积的最大值;(2)当四面体的体积最大时,求其表面积.【答案】(1)a3(2)a2【解析】(1)如图,在四面体ABCD中,设AB=BC=CD=AC=BD=a,AD=x,取AD的中点为P,BC的中点为E,连结BP、EP、CP.得到AD⊥平面BPC,∴V-BCD=V A-BPC+V D-BPC=·S△BPC·AP+S△BPC·PD=·S△BPC·AD=··aA≤·=a3(当且仅当x=a时取等号).∴该四面体的体积的最大值为a3.(2)由(1)知,△ABC和△BCD都是边长为a的正三角形,△ABD和△ACD是全等的等腰三角形,其腰长为a,底边长为a,∴S=2×a2+2××a×=a2+a×=a2+=a2.表12.如图,四棱锥P ABCD中,PA⊥底面ABCD,PA=2,BC="CD=2," ∠ACB=∠ACD=.(1)求证:BD⊥平面PAC;(2)若侧棱PC上的点F满足PF=7FC,求三棱锥P BDF的体积.【答案】(1)见解析 (2)【解析】(1)证明:因为BC=CD,所以△BCD为等腰三角形,又∠ACB=∠ACD,故BD⊥AC.因为PA⊥底面ABCD,所以PA⊥BD.从而BD与平面PAC内两条相交直线PA,AC都垂直,所以BD⊥平面PAC.=BC·CD·sin∠BCD=×2×2×sin =.(2)解:三棱锥P BCD的底面BCD的面积S△BCD由PA⊥底面ABCD,得=·S·PA=××2=2.△BCD由PF=7FC,得三棱锥F BCD的高为PA,故=·S△BCD·PA=×××2=,所以=-=2-=.13.一个与球心距离为1的平面截球体所得的圆面面积为π,则球的体积为() A.B.C.D.8π【答案】A【解析】由题意,球的半径为R=,故其体积V=π()3=,选A.14.如图所示,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为线段AA1,B1C上的点,则三棱锥D1-EDF的体积为________.【答案】【解析】因为E点在线段AA1上,所以S△DED1=×1×1=,又因为F点在线段B1C上,所以点F到平面DED1的距离为1,即h=1,所以VD1-EDF=VF-DED1=·S△DED1·h=××1=.15.若长方体的顶点都在半径为3的球面上,则该长方体表面积的最大值为.【答案】【解析】设长方体的边长为,那么长方体的表面积为:,又由于:,而,所以该长方体表面积的最大值为.【考点】长方体的表面积;基本不等式的变形.16.若圆锥底面半径为1,高为2,则圆锥的侧面积为.【答案】【解析】根据圆锥底面半径、高、母线长构成一个直角三角形,所以母线长为再根据圆锥的侧面积公式圆锥的侧面积公式可结合圆锥展开图为扇形,由相应扇形面积公式理解记忆.【考点】圆锥的侧面积.17.已知四面体的四个顶点都在球的球面上,若平面,,且,,则球的表面积为( )A.B.C.D.【答案】C【解析】因为平面,,在四面体的基础上构造长方体如图,可知长方体的外接球与四面体的外接球相同,长方体的对角线就是外接球的直径,即,球的表面积,故选C.【考点】1、空间几何体的位置关系;2、球的表面积.18.如图,一只蚂蚁由棱长为1的正方体ABCD-A1B1C1D1的点出发沿正方体的表面到达点的最短路程为.【答案】【解析】采用侧面展开法,展开后,在矩形中,,.【考点】立体几何表面距离最短问题.19.如图,平面四边形中,,,,将其沿对角线折成四面体,使平面平面,若四面体顶点在同一球面上,则该球的体积为( )A.B.C.D.【答案】A【解析】由题意平面四边形ABCD中,AB=AD=CD=1,BD=,BD⊥CD,将其沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,若四面体A′-BCD顶点在同一个球面上,可知A′B⊥A′C,所以BC 是外接球的直径,所以BC=,球的半径为:,所以球的体积为:,选A.【考点】1.球内接多面体;2.球的体积和表面积20.如图,在底面为平行四边形的四棱柱中,底面,,,.(Ⅰ)求证:平面平面;(Ⅱ)若,求四棱锥的体积.【答案】(Ⅰ)详见解析;(Ⅱ).【解析】(Ⅰ)由,,,易得,从而平面,由此可得平面平面.(Ⅱ)思路一、由(Ⅰ)知,平面,所以,即是一个直角三角形,这样可得四边形的面积.又平面平面,所以过D作的垂线,该垂线即垂直于平面,由此可得该棱锥的高,从而求得其体积.思路二、将四棱锥分割为以下两部分:三棱锥和,这两个三棱锥的体积相等,我们可先求其中的一个. 而三棱锥即为三棱锥,这个三棱锥的体积就很易求了.试题解析:(Ⅰ)证明:在中,由余弦定理得:,所以,所以,即, 3分又四边形为平行四边形,所以,又底面,底面,所以,又,所以平面, 5分又平面,所以平面平面. 6分(Ⅱ)法一:连结,∵,∴∵平面,所以, 8分所以四边形的面积, 10分取的中点,连结,则,且,又平面平面,平面平面,所以平面,所以四棱锥的体积:. 12分法二: 四棱锥的体积, 8分而三棱锥与三棱锥底面积和高均相等, 10分所以. 12分【考点】1、空间两平面的垂直;2、空间几何体的体积.21.一个圆锥过轴的截面为等边三角形,它的顶点和底面圆周在球O的球面上,则该圆锥的表面积与球O的表面积的比值为_____________.【答案】【解析】圆锥与球的截面如下图,设球的半径为,则圆锥底面圆的直径为,圆锥底面面积为,圆锥的侧面面积为,所以圆锥的表面积为,球的表面积为,所以其面积比为.【考点】1.圆锥与球的表面积;2.球与其内接几何体的关系.22.一个所有棱长均为1的正四棱锥的顶点与底面的四个顶点均在某个球的球面上,则此球的体积为()A.B.C.D.【答案】D【解析】设四棱锥是满足条件的,连结、交于,球心在上,令球的半径为,则,由正四棱锥所有棱长为1,易求得四棱锥的高,在中,,即,解得,故球的体积为. 选D.【考点】正四棱锥的性质,球的体积.23.如图,设是棱长为的正方体的一个顶点,过从顶点出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,截去个三棱锥,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:①有个顶点;②有条棱;③有个面;④表面积为;⑤体积为.其中正确的结论是(写出所有正确结论的编号).【答案】①②⑤【解析】根据几何体的特点可知,有12个顶点,24条棱,16个面,所以①、②都对,③错;表面积为故④错;其体积为故⑤成立.【考点】几何体的体积和表面积.24.如图,在三棱柱中,,,分别为,,的中点,设三棱锥体积为,三棱柱的体积为,则【答案】【解析】依题意,,三棱锥的高为三棱柱的高的. ∴.【考点】三棱柱与三棱锥的体积,三角形中位线定理,相似三角形的面积比等于相似比的平方.空间想象能力.中等题.25.如图是某几何体的三视图,则该几何体的体积为A.1B.C.D.【答案】B【解析】由三视图可知,该几何体是一个有一条侧棱垂直于底面的四棱锥,所以该几何体的体积为【考点】本小题主要考查三视图.点评:此类问题,主要考查学生的空间想象能力,解决此类问题的关键是根据三视图正确还原几何体.26.如果一个几何体的三视图如图所示,则该几何体的表面积为()A.B.C.96D.80【答案】A【解析】由三视图知:原几何体为正方体和一个四棱锥的组合体,正方体的棱长为4,正四棱锥的底面边长为4,高为2,所以正四棱锥的斜高为。
2023年高考数学微专题练习专练40空间几何体的表面积和体积含解析理

专练40 空间几何体的表面积和体积命题范围:空间几何体的表面积与体积.[基础强化]一、选择题1.已知圆柱的上、下底面的中心分别为O 1,O 2,过直线O 1O 2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( )A .122πB .12πC .82πD .10π2.[2022·全国甲卷(理),4]如图,网格纸上绘制的是一个多面体的三视图,网格小正方形的边长为1,则该多面体的体积为( )A .8B .12C .16D .203.已知某几何体的三视图如图所示(俯视图中曲线为四分之一圆弧),则该几何体的表面积为( )A .1-π4B .3+π2C .2+π4D .44.在梯形ABCD 中,∠ABC =π2,AD ∥BC ,BC =2AD =2AB =2.将梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )A.2π3B .4π3C .5π3D .2π5.[2022·江西省南昌市高三模拟]圆柱形玻璃杯中盛有高度为10cm 的水,若放入一个玻璃球(球的半径与圆柱形玻璃杯内壁的底面半径相同)后,水恰好淹没了玻璃球,则玻璃球的半径为( )A .203cmB .15cmC .103cmD .20cm6.已知圆锥的底面半径为R ,高为3R ,在它的所有内接圆柱中,全面积的最大值是( ) A .2πR 2B .94πR 2C .83πR 2D .32πR 2 7.某几何体的三视图如图所示,其中正视图是边长为4的正三角形,俯视图是由边长为4的正三角形和一个半圆构成,则该几何体的体积为( )A .8+43π3B .8+23π3C .4+43π3D .4+83π38.[2022·全国乙卷(理),9]已知球O 的半径为1,四棱锥的顶点为O ,底面的四个顶点均在球O 的球面上,则当该四棱锥的体积最大时,其高为( )A .13B.12 C .33D .229.[2021·全国甲卷]已知A ,B ,C 是半径为1的球O 的球面上的三个点,且AC ⊥BC ,AC =BC =1,则三棱锥O -ABC 的体积为( )A .212B . 312C .24D .34二、填空题10.[2020·全国卷Ⅲ]已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为________.11.已知圆锥的顶点为S ,母线SA ,SB 互相垂直,SA 与圆锥底面所成角为30°.若△SAB 的面积为8,则该圆锥的体积为________.12.[2022·安徽省高三联考]在三棱锥P ABC 中,侧棱PA =PB =PC =10,∠BAC =π4,BC =22,则此三棱锥外接球的表面积为________.[能力提升]13.[2022·全国甲卷(理),9]甲、乙两个圆锥的母线长相等,侧面展开图的圆心角之和为2π,侧面积分别为S 甲和S 乙,体积分别为V 甲和V 乙.若S 甲S 乙=2,则V 甲V 乙=( ) A .5B.2 2 C.10D.510414.[2022·江西省赣州市一模]在半径为2的球O 的表面上有A ,B ,C 三点,AB =2 2.若平面OAB ⊥平面ABC ,则三棱锥O ABC 体积的最大值为( )A .23B .223C .43D .42315.[2022·安徽省高三一模]半正多面体亦称阿基米德多面体,是由边数不全相同的正多边形为面的多面体.如图所示,将正方体沿交于一顶点的三条棱的中点截去一个三棱锥,如此共可截去八个三棱锥,得到一个有十四个面的半正多面体,其中八个面为正三角形,六个面为正方形,它们的边长都相等,称这样的半正多面体为二十四等边体.现有一个体积为V 1的二十四等边体,其外接球体积为V 2,则V 2V 1=________.16.[2022·江西省高三质量监测]如图,在棱长为4的正方体ABCDA1B1C1D1中,点P 在面AA1B1B内,记PD,PC与平面DD1C1C所成角分别为α、β,且tanβ=3tanα,则四棱锥PAB1C1D体积的最小值是________.专练40 空间几何体的表面积和体积1.B 设圆柱的底面半径为r,由题意得高h=2r,∴(2r)2=8,得r=2,∴S圆柱表=2πr2+2πrh=4π+8π=12π.2.B 如图,将三视图还原成直观图.该直观图是一个侧放的直四棱柱ABCD-A1B1C1D1,底面ABCD是直角梯形,AD⊥AB,AB∥DC,AD=DC=2,AB=4,AA1=2.所以底面面积S=(2+4)×2=6,设该直四棱柱的高为h,则该几何体的体积V=Sh=6×2=12.故选B.23.D由三视图可知该几何体是棱长为2的正方体截去一个以1为底面圆的半径,高为1的圆柱的14,如图所示,故其表面积S =1×1+1×1+2×⎝ ⎛⎭⎪⎫1×1-π4+2π4×1=1+1+2-π2+π2=4.4.C过点C 作CE 垂直AD 所在直线于点E ,梯形ABCD 绕AD 所在直线旋转一周而形成的旋转体是由以线段AB 的长为底面圆半径,线段BC 为母线的圆柱挖去以线段CE 的长为底面圆半径,ED 为高的圆锥,如图所示.由于V 圆柱=π·AB 2·BC =π×12×2=2π,V 圆锥=13π·CE 2·DE =13π×12×(2-1)=π3,所以该几何体的体积V =V 圆柱-V 圆锥=2π-π3=5π3.5.B 由题意玻璃球的体积等于放入玻璃球后的体积减去原来的体积.设玻璃球的半径为r ,即圆柱形玻璃杯的底面半径为r ,则玻璃球的体积为4πr 33,圆柱的底面面积为πr 2,若放入一个玻璃球后,水恰好淹没了玻璃球,则此时水面高度为2r ,所以4πr 33=πr 2(2r -10),解得r =15 (cm).6.B 设内接圆柱的底面半径为r (0<r <R ),母线长为h ,则r R =3R -h3R,即h =3R -3r ,则该圆柱的全面积为S =2πr (r +3R -3r )=2π(-2r 2+3Rr ),因为S =2π(-2r 2+3Rr )=2π⎣⎢⎡⎦⎥⎤-2(r -3R 4)2+9R 28,所以当r =3R 4时,内接圆柱的全面积的最大值为94πR 2.7.A8.C 设四棱锥的底面为四边形ABCD .设四边形ABCD 的外接圆圆心为O ′,半径为r .S四边形ABCD=S △AO ′B +S △AO ′D +S △BO ′C +S △CO ′D =12r 2sin∠AO ′B +12r 2sin∠AO ′D +12r 2sin∠BO ′C +12r 2sin∠CO ′D =12r 2(sin∠AO ′B +sin∠AO ′D +sin∠BO ′C +sin∠CO ′D ).因为∠AO ′B +∠AO ′D +∠BO ′C +∠CO ′D =2π,且当θ=π2时,sin θ取最大值1,所以当∠AO ′B =∠AO ′D =∠BO ′C =∠CO ′D =π2时,S四边形ABCD最大,即当四棱锥O -ABCD 的底面为正方形时,四棱锥O -ABCD 的体积取得最大值.设AB =a (a >0),则正方形ABCD 的外接圆的半径r =22a ,四棱锥O -ABCD 的高h =1-12a 2,则1-12a 2>0,解得0<a <2,所以V O -ABCD =13a 2h =13a 4-12a 6.令f (x )=x 4-12x 6(0<x <2),则f ′(x )=4x 3-3x 5=x 3(4-3x 2).当x ∈(0,233)时,f ′(x )>0;当x ∈(233,2)时,f ′(x )<0.所以f (x )在(0,233)上单调递增,在(233,2)上单调递减.当x 2=43时,f (x )取得极大值,也是最大值,即V O -ABCD 取得最大值,此时四棱锥O -ABCD 的高h =1-12a 2=33.故选C.9.A 如图所示,因为AC ⊥BC ,所以AB 为截面圆O 1的直径,且AB = 2.连接OO 1,则OO 1⊥面ABC ,OO 1=1-⎝ ⎛⎭⎪⎫AB 22=1-(22)2=22,所以三棱锥O -ABC 的体积V =13S △ABC ×OO 1=13×12×1×1×22=212. 10.2π3解析:如图为圆锥内球半径最大时的轴截面图. 其中球心为O ,设其半径为r ,AC =3,O 1C =1, ∴AO 1=AC 2-O 1C 2=2 2.∵OO 1=OM =r ,∴AO =AO 1-OO 1=22-r , 又∵△AMO ∽△AO 1C ,∴OM O 1C =AO AC ,即r 1=22-r 3,故3r =22-r ,∴r =22.∴该圆锥内半径最大的球的体积V =43π·⎝ ⎛⎭⎪⎫223=2π3.11.8π 解析:由题意画出图形,如图,设AC 是底面圆O 的直径,连接SO ,则SO 是圆锥的高.设圆锥的母线长为l ,则由SA ⊥SB ,△SAB 的面积为8,得12l 2=8,得l =4.在Rt△ASO 中,由题意知∠SAO =30°,所以SO =12l =2,AO =32l =2 3.故该圆锥的体积V =13π×AO 2×SO =13π×(23)2×2=8π.12.50π3解析:因为PA =PB =PC =10,所以点P 在底面ABC 的射影为△ABC 的外心O 1, 所以球心O 在直线PO 1上,设三棱锥外接球的半径为R ,因为2AO 1=22sinπ4,所以AO 1=2,PO 1=6,由AO 2=OO21+AO 21 可得,R 2=(6-R )2+4,解得R =56, 故此三棱锥外接球的表面积为4πR 2=4π×256=50π3.13.C 设甲、乙两个圆锥的母线长都为l ,甲、乙两个圆锥的底面半径分别为r 1,r 2,高分别为h 1,h 2.因为两圆锥的侧面展开图的圆心角之和为2π,所以2πr 1l +2πr 2l=2π,则r 1+r 2=l .又S 甲S 乙=2,所以πr 1l =2πr 2l ,所以r 1=2r 2,所以r 1=23l ,r 2=13l ,所以h 1=l 2-⎝ ⎛⎭⎪⎫23l 2=53l ,h 2=l 2-⎝ ⎛⎭⎪⎫13l 2=223l ,所以V 甲V 乙=13πr 21h 113πr 22 h 2=49l 2·53l 19l 2·223l =10.故选C.14.B作出如图三棱锥O ABC ,OA =OB =OC =2,取AB 中点D ,连接DC ,DO ,则OD ⊥AB , 又平面OAB ⊥平面ABC ,平面OAB ∩平面ABC =AB ,OD ⊂平面OAB ,所以OD ⊥平面ABC ,CD ⊂平面ABC ,则OD ⊥CD ,又AB =22,OA 2+OB 2=AB 2,所以OD =2,OA ⊥OB , 所以CD =22-(2)2=2=12AB ,所以AC ⊥BC ,S △OAB =12×2×2=2,要使三棱锥O ABC 体积最大,则C 到平面OAB 的距离h 最大,显然h ≤CD ,当CD ⊥AB 时,平面OAB ∩平面ABC =AB ,CD ⊂平面ABC ,所以CD ⊥平面OAB ,此时h =CD =2,为最大值,V max =13×2×2=223.15.22π5解析:设该半多面体是由棱长为2的正方体沿正方体各棱的中点截去8个三棱锥所得,内侧即为二十四等边体,其体积V 1=2×2×2-8×13×12×1×1×1=203;由二十四等边体的对称性可知, 如图所示,其外接球的球心即为正方体中心O ,半径为中心到一个顶点的距离,则R =OA 2+AB 2=1+1=2,故V 2=43π(2)3=82π3,从而V 2V 1=22π5.16.24-8 2解析:依题意DA ⊥平面ABB 1A 1,所以∠DPA 即为DP 与平面ABB 1A 1所成的角,又平面ABB 1A 1∥平面DCC 1D 1,所以∠DPA 即为DP 与平面DCC 1D 1所成的角,同理可得∠CPB 为PC 与平面DCC 1D 1所成的角,即α=∠DPA ,β=∠CPB ,因为tan β=3tan α,所以BC PB =3ADAP,又BC =AD ,所以AP =3BP ,在平面AA 1B 1B 内建立以点A 为原点,AB ,AA 1所在直线分别为x 轴,y 轴的直角坐标系,设点P (x ,y ),则x 2+y 2=3(x -4)2+y 2,即x 2+y 2-9x +18=0,即(x -92)2+y 2=94,直线AB 1的方程为y =x ,即x -y =0,所以圆心到直线的距离d =9212+(-1)2=924,所以点P 到直线AB 1的距离的最小值为92-64,又|AB 1|=|AB |2+|BB 1|2=42,SAB 1C 1D =4×42=162,所以四棱锥P AB 1C 1D 体积的最小值是13×162×92-64=24-8 2.。
高一数学空间几何体的表面积与体积试题

高一数学空间几何体的表面积与体积试题1.已知正三角形的边长为2,沿着上的高将正三角形折起,使得平面平面,则三棱锥的体积是【答案】【解析】∵AD⊥BD,AD⊥CD,BD∩CD=D,∴AD⊥平面BCD,∵平面ABD⊥平面ACD,且∠BDC是二面角B-AD-C的平面角∴∠BDC=90°,∵AD是边长为2的正三角形的高,可得BD=CD=1,AD=∴△BCD的面积S=×1×1=△BCD因此三棱锥A-BCD的体积V=×S×AD=××=△BCD故答案为:【考点】正三角形的性质;线面垂直的判定与性质;锥体体积求法.2.已知正方体的棱长为1,则该正方体外接球的体积为()A.B.C.D.【答案】A【解析】因为正方体的对角线长就是外接球的直径,而正方体的对角线长为,所以球的半径为,所以正方体的外接球的体积为,故选A.【考点】1、球与正方体的组合体;2、球的体积.3.如图,在三棱柱中,侧棱底面, 为的中点,.(1)求证:平面;(2)若,求三棱锥的体积.【答案】(1)详见解析;(2)1.【解析】(1)通过证明线线平行,线面平行的判定定理,在面中找到平行于的线,连接,设与相交于点,连接,证即证;(2)通过等体积转化=试题解析:证明:(1)连接,设与相交于点,连接. 1分∵四边形是平行四边形,∴点为的中点.∵为的中点,∴为△的中位线,∴. 4分∵平面,平面,∴平面. 6分解:(2)∵三棱柱,∴侧棱,又∵底面,∴侧棱,故为三棱锥的高,, 8分10分12分【考点】1.线面平行的判定定理;2.几何题的体积.4.若两个球的表面积之比为1:4,则这两个球的体积之比为()A.1:2,B.1:4,C.1:8,D.1:16【答案】C【解析】球的表面积公式,两个球的表面积之比是,所以半径之比是,球的体积公式是,所以体积之比是.【考点】球的表面积和体积公式5.如图所示,圆锥的轴截面为等腰直角,为底面圆周上一点.(1)若的中点为,,求证平面;(2)如果,,求此圆锥的全面积.【答案】(1)详见解析;(2).【解析】(1)要证平面,即证垂直于平面内的两条相交直线,是已知,转化为证平面,利用母线相等,利用底面半径相等,为中点,证得平面,证得,,得证;(2),求出底面半径,以及母线长,根据全面积公式,,求出全面积.试题解析:解:①连接OC,∵OQ=OB,C为QB的中点,∴OC⊥QB 2分∵SO⊥平面ABQ,BQ平面ABQ∴SO⊥BQ,结合SO∩OC=0,可得BQ⊥平面SOC∵OH⊂平面SOC,∴BQ⊥OH, 5分∵OH⊥SC,SC、BQ是平面SBQ内的相交直线,∴OH⊥平面SBQ; 6分②∵∠AOQ=60°,QB=,∴直角△ABQ中,∠ABQ=30°,可得AB==4 8分∵圆锥的轴截面为等腰直角△SAB,∴圆锥的底面半径为2,高SO=2,可得母线SA=2,因此,圆锥的侧面积为S侧=π×2×2=4π 10分∴此圆锥的全面积为S侧+S底=4π+π×22=(4+4)π 12分【考点】1.线面垂直的判定;2.线面垂直的性质;3.几何体的表面积.6.在正三棱锥中,、分别是棱、的中点,且,若侧棱,则正三棱锥外接球的表面积是()A.B.C.D.【答案】C【解析】∵三棱锥为正棱锥,∴⊥,∴⊥.又∵⊥,,∴平面,即⊥平面,∴,将此三棱锥补成正方体,则它们有相同的外接球,∴,解得,∴.【考点】三棱锥的外接球表面积.7.已知直三棱柱中,,是中点,是中点.(1)求三棱柱的体积;(2)求证:;(3)求证:∥面.【答案】(1);(2)证明详见解析;(3)证明详见解析.【解析】(1)这是一个直三棱柱,直接由体积计算公式即可求解;(2)要证,只须证明面,注意到面与底面垂直且交线为,而依题意又有,由面面垂直的性质可得面,问题得证;(3)要证∥面,有两种思路:一是在平面内找一条直线与平行,这时只须取的中点,连接,证明四边形为平行四边形即可;二是先证经过直线的一个平面与面平行,这时可取中点,连结,,先证明面∥面,再由面面平行的性质即可证明∥面.试题解析:(1) 3分(2)∵,∴为等腰三角形∵为中点,∴ -4分∵为直棱柱,∴面面 5分∵面面,面∴面 6分∴ 7分(3)取中点,连结, 8分∵分别为的中点∴∥,∥, 9分∴面∥面 11分面∴∥面 12分.【考点】1.空间几何体的体积计算;2.空间中的平行关系;3.空间中的垂直关系.8.球的表面积与它的内接正方体的表面积之比是( )A.B.C.D.【答案】B【解析】因为球的直径2R就是球的内接正方体的体对角线的长.即.所以球的表面积为.因为内接正方体的表面积为.所以球的表面积与它的内接正方体的表面积之比是.故选B.【考点】1.球的与内接正方体的关系.2.球的表面积公式.3.正方体的表面积公式.9.如图,已知直三棱柱中,,,,D为BC的中点.(1)求证:∥面;(2)求三棱锥的体积.【答案】(1)略(2)【解析】(1)连接交于点O,连接OD,在中可根据中位线证得∥,再根据线面平行的性质定理可证得∥面。
数学空间几何体的表面积与体积试题

数学空间几何体的表面积与体积试题1.如果一个正三棱锥的底面边长为6,且侧棱长为,那么这个三棱锥的体积是 .【答案】【解析】根据题意可作图如下,其中 ,则在中,, ,在中,由根据勾股定理得:,所以2.(本小题满分12分)如图,在三棱锥中,⊿是等边三角形,是以为斜边的等腰直角三角形.(Ⅰ)证明:AB⊥PC;(Ⅱ),求三棱锥体积.【答案】(Ⅰ)见解析(Ⅱ)【解析】(Ⅰ)如图,取中点,连结,. 2分因为是等边三角形,是以为斜边的等腰直角三角形,故,,所以平面,所以. 6分(Ⅱ)在中,因为,故,在中,,因为在中,,故,所以, 10分又平面,所以. 12分【命题意图】本题考查直线和平面垂直、四面体的体积等基础知识,意在考察学生空间向量能力、推理论证能力和基本的运算能力.3.如图,三棱柱中,,,.(1)证明:;(2)若,,求三棱柱的体积.【答案】(1)证明见详解;(2)3.【解析】(1)取AB的中点,连接、、,因为CA=CB,所以,由于,,故为等边三角形,所以,因为,所以平面.又,故.(2)由题设知都是边长为2的等边三角形,所以4.如图,在三棱锥中,是等边三角形,.(1)证明::;(2)证明:;(3)若,且平面平面,求三棱锥体积.【答案】(1)详见解析;(2)详见解析;(3).【解析】(1)因为是等边三角形,,所以,可得;(2)如图,取中点,连结、,则,,所以平面,所以;(3)作,垂足为,连结,因为,所以,,由已知,平面平面,故,因为,所以、、都是等腰直角三角形.由已知,得,的面积,因为平面,所以三棱锥的体积.5.如图,体积为V的大球内有4个小球,每个小球的球面过大球球心且与大球球面有且只有一个交点,4个小球的球心是以大球球心为中心的正方形的4个顶点.V1为小球相交部分(图中阴影部分)的体积,V2为大球内、小球外的图中黑色部分的体积,则下列关系中正确的是A.V1=B.V2=C.V1> V2D.V1< V2【答案】D【解析】设大球半径为,小球半径为,根据题意,所以,于是,即,所以。
高二数学空间几何体的表面积与体积试题答案及解析

高二数学空间几何体的表面积与体积试题答案及解析1.已知圆锥的高与底面半径相等,则它的侧面积与底面积的比为________.【答案】.【解析】设圆锥的底面半径和高为,则其母线长;所以圆锥的侧面积,底面面积,则它的侧面积与底面积的比为.【考点】圆锥的侧面积公式.2.一个与球心距离为1的平面截球所得的圆面面积为,则球的表面积为 .【答案】【解析】球的截面圆的半径为:π=πr2,r=1,球的半径为:R= ,所以球的表面积:4πR2=4π×( )2=8π.【考点】球的表面积.3.三棱锥P−ABC中,PA⊥平面ABC,AB⊥BC。
(1)证明:平面PAB⊥平面PBC;(2)若,,PB与底面ABC成60°角,分别是与的中点,是线段上任意一动点(可与端点重合),求多面体的体积.【答案】(1)证明见解析;(2).【解析】(1)证明两个平面垂直,首先考虑直线与平面垂直,也可以简单记为“证面面垂直,找线面垂直”,是化归思想的体现,这种思想方法与空间中的平行关系的证明类似,掌握化归与转化思想方法是解决这类题的关键;(2)证明线面垂直的方法:一是线面垂直的判定定理;二是利用面面垂直的性质定理;三是平行线法(若两条平行线中的一条垂直于这个平面,则另一条也垂直于这个平面.解题时,注意线线、线面与面面关系的相互转化;(3)在求三棱柱体积时,选择适当的底作为底面,这样体积容易计算.试题解析:(1)证明:,,且,而中,(2)解:(2)与底面成角即,在中,,又,在中,分别是的中点,面.【考点】(1)平面与平面垂直的判断;(2)求几何体的体积.4.如图,菱形ABCD的边长为4,∠BAD=60°,AC∩BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B﹣ACD,点M是棱BC的中点,DM=2.(1)求证:OM∥平面ABD;(2)求证:平面DOM⊥平面ABC;(3)求三棱锥B﹣DOM的体积.【答案】(1)∵O为AC的中点,M为BC的中点,∴OM∥AB.又∵OM⊄平面ABD,AB⊂平面ABD,∴OM∥平面ABD.(2)∵在菱形ABCD中,OD⊥AC,∴在三棱锥B-ACD中,OD⊥AC.在菱形ABCD中,AB=AD=4,∠BAD=60°,可得BD=4.∵O为BD的中点,∴,BD=2.∵O为AC的中点,M为BC的中点,∴,AB=2.因此,,可得OD⊥OM.∵AC、OM是平面ABC内的相交直线,∴OD⊥平面ABC.∵OD⊂平面DOM,∴平面DOM⊥平面ABC.(3).【解析】(1)利用三角形中位线定理,证出OM∥AB,结合线面平行判定定理,即可证出OM∥平面ABD.(2)根据题中数据,算出,BD=2,,AB=2,从而得到,可得OD⊥OM.结合OD⊥AC利用线面垂直的判定定理,证出OD⊥平面ABC,从而证出平面DOM⊥平面ABC.(3)由(2)得到OD为三棱锥D-BOM的高.算出△BOM的面积,利用锥体体积公式算出三棱锥D-BOM的体积,即可得到三棱锥B-DOM的体积.试题解析:(1)∵O为AC的中点,M为BC的中点,∴OM∥AB.又∵OM⊄平面ABD,AB⊂平面ABD,∴OM∥平面ABD.(2)∵在菱形ABCD中,OD⊥AC,∴在三棱锥B-ACD中,OD⊥AC.在菱形ABCD中,AB=AD=4,∠BAD=60°,可得BD=4.∵O为BD的中点,∴DO=,BD=2.∵O为AC的中点,M为BC的中点,∴OM=,AB=2.因此,,可得OD⊥OM.∵AC、OM是平面ABC内的相交直线,∴OD⊥平面ABC.∵OD⊂平面DOM,∴平面DOM⊥平面ABC.(3)由(2)得,OD⊥平面BOM,所以OD是三棱锥D-BOM的高.由OD=2,,所以.【考点】线面平行问题;面面垂直问题;三棱锥的体积.5.四面体ABCD中,已知AB=CD=,AC=BD=,AD=BC=,则四面体ABCD的外接球的表面()A.25p B.45p C.50p D.100p【答案】C【解析】作长方体,AB=CD=,AC=BD=,AD=BC=,该长方体和四面体有共同的外接球,长方体的对角线长为直径长,,表面积【考点】四面体的外接球的体积.6.如图,三棱柱中,侧棱垂直底面,,,是棱的中点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、知识回顾(1)棱柱、棱锥、棱台的表面积= 侧面积+ ______________;(2)圆柱:r为底面半径,l为母线长侧面积为_______________;表面积为_______________.圆锥:r为底面半径,l为母线长侧面积为_______________;表面积为_______________.圆台:r’、r分别为上、下底面半径,l为母线长侧面积为_______________;表面积为_______________.(3)柱体体积公式:________________________;(S为底面积,h为高)锥体体积公式:________________________;(S为底面积,h为高)台体体积公式:________________________;(S’、S分别为上、下底面面积,h为高)二、例题讲解题1:如图(1)所示,直角梯形ABCD绕着它的底边AB所在的直线旋转一周所得的几何体的表面积是______________;体积是______________。
8图(1)题2:若一个正三棱柱的三视图如图(2)所示, 求这个正三棱柱的表面积与体积图(2)题3:如图(3)所示,在多面体ABCDEF 中,已知ABCD 是边长为1的正方形,且ADE ∆,BCF ∆均为正三角形,EF//AB ,EF=2,则该多面体的体积为( )A .32B .33C .34D .23EABDCF左视图俯视图 主视图图(3)1、若圆柱的侧面积展开图是长为6cm ,宽为4cm 的矩形,则该圆柱的体积为2、如图(4),在正方体1111D C B A ABCD -中,棱长为2,E 为11B A 的中点,则 三棱锥11D AB E -的体积是____________.图(4)CBADC 1B 1EA 1D 13、已知某几何体的俯视图是如图(5)所示的矩形,正 视图(或称主视图)是一个底边长为8、高为4的等腰三 角形,侧视图(或称左视图)是一个底边长为6、高为4 的等腰三角形.(1)求该几何体的体积V ; (2)求该几何体的侧面积S 。
图(5)(选做题)4、如图(6),一个圆锥的底面半径为2cm , 高为6cm ,在其中有一个高为xcm 的内接圆柱。
(1)试用x 表示圆柱的侧面积;(2)当x 为何值时,圆柱的侧面积最大?一、选择题(每小题5分,共计60分。
请把选择答案填在答题卡上。
)1.以三棱锥各面重心为顶点,得到一个新三棱锥,它的表面积是原三棱锥表面积的 A.31B.41C.91D.161 2.正六棱锥底面边长为a ,体积为323a ,则侧棱与底面所成的角等于A.6πB.4πC.3πD.125π 3.有棱长为6的正四面体S-ABC ,C B A ''',,分别在棱SA ,SB ,SC 上,且S A '=2,S B '=3,S C '=4,则截面C B A '''将此正四面体分成的两部分体积之比为 A.91B.81C.41D.31 4.长方体的全面积是11,十二条棱长的和是24,则它的一条对角线长是A .32. B. 14 C. 5 D.65.圆锥的全面积是侧面积的2倍,侧面展开图的圆心角为α,则角α的取值范围是 A .(]︒︒90,0 B (]︒︒270,180 C (]︒︒180,90 D Φ6. 正四棱台的上、下底面边长分别是方程01892=+-x x 的两根,其侧面积等于两底面积的和,则其斜高与高分别为 A .25与2 B.2与23C.5与4D.2与3 7.已知正四面体A-BCD 的表面积为S ,其四个面的中心分别为E 、F 、G 、H ,设四面体E-FGH 的表面积为T ,则ST等于A .91 B.94 C. 41 D.318.三个两两垂直的平面,它们的三条交线交于一点O ,点P 到三个平面的距离比为1∶2∶3,PO=214,则P 到这三个平面的距离分别是A .1,2,3B .2,4,6C .1,4,6D .3,6,99.把直径分别为cm cm cm 10,8,6的三个铁球熔成一个大铁球,这个大铁球的半径是 A .cm 3 B.cm 6 C. cm 8 D.cm 12 9. 如图,在多面体ABCDEF 中,已知ABCD 是边长为1的正方形,且BCF ADE ∆∆、均为正三角形,EF ∥AB ,EF=2,则该多面体的体积为A.3/2B.33C.34D.2310.如图,在四面体ABCD 中,截面AEF 经过四面体的内切球(与四个面都相切的球)球心O ,且与BC ,DC 分别交于E 、F ,如果截面将四面体分成体积相等的两部分,设四棱锥A -BEFD 与三棱锥A -EFC 的表面积分别是21S S 、,则必有 A.S 1<S 2 B. S 1>S 2 C. S 1=S 2D.21S 与S 的大小关系不能确定11.三角形ABC 中,AB=32,BC=4,︒=∠120ABC ,现将三角形ABC 绕BC 旋转一周,所得简单组合体的体积为A .π4 B.π)34(3+ C.12π D.π)34(+12.棱台的上、下底面面积分别为4和9,则这个棱台的高和截得棱台的原棱锥的高的比是 A .21 B.31 C.32 D.43 DBAO EF二、填空题:请把答案填在题中横线上(每小题5分,共20分).13. 一个四面体的所有棱长都为2,四个顶点在同一个球面上,则此球的表面积为3π. 14.已知底面半径为r 的圆柱被一个平面所截,剩下部分母线长的最大值为a ,最小值为b ,那么这个圆柱被截后剩下部分的体积是2)(2πr b a +.15. (江西卷)在直三棱柱ABC -A 1B 1C 1中,底面为直角三角形,∠ACB =90︒,AC =6, BC =CC 1=2,P 是BC 1上一动点,则CP +PA 1的最小值是137+. 16.圆柱的轴截面的对角线长为定值,为使圆柱侧面积最大,轴截面对角线与底面所成的角为450.三、解答题:解答应写出文字说明、证明过程或演算步骤(本大题共4个大题,共20分). 17.圆锥的底面半径为cm 5 ,高为12cm ,当它的内接圆柱的底面半径为何值时,圆锥的内接圆柱全面积有最大值?最大值是多少? 当r=30/7cm 时,S 的最大值是π736018.如图,已知正三棱柱ABC —A 1B 1C 1的侧面对角线A 1B 与侧面ACC 1A 1成45°角,AB=4,求棱柱的侧面积. 棱柱的侧面积为242练习11 空间几何体的表面积与体积A 组1.一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比是(). (A )122ππ+ (B )144ππ+ (C )12ππ+ (D )142ππ+ 2.在棱长为 1 的正方体上,分别用过共顶点的三条棱中点的平面截该正方体,则截去与8个顶点相关的8个三棱锥后 ,剩下的几何体的体积是( ). (A )32 (B )43 (C )54 (D )65 题号 1 2 3 4 56789 10 11 12 答案CBBCDAABB ACCB3.一个直棱柱(侧棱垂直于底面的棱柱)的底面是菱形,对角线长分别是6cm 和8cm ,高是5cm ,则这个直棱柱的全面积是。
4.已知两个母线长相等的圆锥的侧面展开图恰能拼成一个圆,且它们的侧面积之比为1:2,则它们的高之比为。
5.已知三棱锥的三条侧棱两两互相垂直,且长度分别为1cm ,2cm ,3cm ,则此棱锥的体积_______________。
6.矩形两邻边的长为a 、b ,当它分别绕边a 、b 旋转一周时, 所形成的几何体的体积之比为。
7.球面上有三点,其中任意两点间的球面距离都等于大圆周长的16,经过这三点的小圆周长为4π,则这个球的表面积为。
B 组1.四面体ABCD 四个面的重心分别为E 、F 、G 、H ,则四面体EFGH 的表面积与四面体ABCD 的表面积的比值是。
2.半径为R 的半球,一正方体的四个顶点在半球的底面上,另四个顶点在半球的球面上,则该正方体的表面积是。
3.如图,一个棱锥S -BCD 的侧面积是Q ,在高SO 上取一点A ,使SA =31SO ,过点A 作平行于底面的截面得一棱台,求这个棱台的侧面积.4.如图,在四棱锥P -ABCD 中,底面ABCD 是正方形,边长AB =a ,且PD =a ,PA =PC =2a ,若在这个四棱锥内放一个球,求球的最大半径.练习七参考答案A 组 1.答案:A解:设展开图的正方形边长为a ,圆柱的底面半径为r ,则2πr =a ,2ar π=,底面圆的面积是24a π,于是全面积与侧面积的比是2221222a a a πππ++=,选A . 2.答案:D解:正方体的体积为1,过共顶点的三条棱中点的平面截该正方体截得的三棱锥的体积是111111()3222248⨯⨯⨯⨯=,于是8个三棱锥的体积是61,剩余部分的体积是65,选D .3.答案:148 cm 2解:底面菱形中,对角线长分别是6cm 和8cm ,所以底面边长是5cm ,侧面面积是4×5×5=100cm 2,两个底面面积是48cm 2, 所以棱柱的全面积是148cm 2. 4.答案:22:5解:设圆柱的母线长为l ,因为两个圆锥的侧面展开图恰能拼成一个圆,且它们的侧面积之比为1:2,所以它们的展开图即扇形的圆心角分别是23π和43π, 由圆锥侧面展开图扇形的圆心角的计算公式2r l πθ=,得13l r =,223lr =,所以它们的高的比是=. 5.答案:1cm 3解:转换一个角度来认识这个三棱锥,即把它的两条侧棱(如长度为1cm ,2cm 的两条)确定的侧面看作底面,另一条侧棱作为高,则此三棱锥的底面面积是1,高为3,则它的体积是31×1×3=1cm 3.6.答案:ba解:矩形绕a 边旋转,所得几何体的体积是V 1=πb 2a ,矩形绕b 边旋转,所得几何体的体积是V 2=πa 2b ,所以两个几何体的体积的比是2122V b a bV a b aππ==.7.答案:48π解:小圆周长为4π,所以小圆的半径为2,又这三点A 、B 、C 之间距离相等,所以每两点间的距离是AB =BC =AC =23, 又A 、B 之间的大圆劣弧长等于大圆周长的61,所以A 、B 在大圆中的圆心角是60°,所以大圆的半径R =23,于是球的表面积是4πR 2=48π.B 组 1.答案:1:9解:如图,不难看出四面体EFGH 与四面体ABCD 是相似的。
所以关键是求出它们的相似比,连接AF 、AG 并延长与BC 、CD 相交于M 、N , 由于F 、G 分别是三角形的重心,所以M 、N 分别是BC 、CD 的中点,且AF :AM =AG :AN =2:3,所以FG :MN =2:3,又MN :BD =1:2,所以FG :BD =1:3,即两个四面体的相似比是1:3, 所以两个四面体的表面积的比是1:9. 2.答案:24R解:如图,过正方体的对角面AC 1作正方体和半球的截面。
