湘教版九年级数学上册期末复习课件全套
合集下载
新湘教版九年级上册数学全册课件

新湘教版九年级上册数学 全册课件
只本 供课 免件 费来 交源 流于 使网 用络
第1章 反比例函数
1.1 反比例函数
学习目标 1. 理解并掌握反比例函数的概念. (重点) 2. 从实际问题中抽象出反比例函数的概念,能根据已 知 条件确定反比例函数的解析式. (重点、难点)
导入新课
情境引入 新学期伊始,小明想买一些笔记本为以 后的学习做准备. 妈妈给了小明 30 元钱,小 明可以如何选择笔记本的价钱和数量呢?
x 解析:通过上节课学习可知画图象的三个步骤为
列表 描点
连线
需要注意的是在反比例函数中自变量x不能为0.
解:列表如下
x … -6 -5 -4 -3 -2 -1 1 3 2 3 4 5 6 … y … 1 1.2 1.5 2 6 -6 -3 -2 -1.5 -1.2 -1 …
y
6 5 4 3 2 1 -6 -5 -4 -3 -2 -1 -1 -2 -3 -4 -5 -6
1463 例如,在前面得到的第一个解析式 v 因为 x 作为分母,不能等于零,因此自变量 t x 的取值范围是所有非零实数. 中,t 的取值范围是 t>0,且当 t 取每一个确定的
范围 . 值时, v
但实际问题中,应根据具体情况来确定反比例函数自变量的取值
都有唯一确定的值与其对应.
k 想一想 反比例函数除了可以用 y (k ≠ 0) 的形式 x : 表示,还有没有其他表达方式?
是 (2) 若
m≠1
.
m m 2 是反比例函数,则m的取值范 y 围是 . x
(3) 若
m ≠ 0 且是反比例函数,则 m ≠ -2 m的取值范围
x
2
是 y m 2. m m 1 m = -1
只本 供课 免件 费来 交源 流于 使网 用络
第1章 反比例函数
1.1 反比例函数
学习目标 1. 理解并掌握反比例函数的概念. (重点) 2. 从实际问题中抽象出反比例函数的概念,能根据已 知 条件确定反比例函数的解析式. (重点、难点)
导入新课
情境引入 新学期伊始,小明想买一些笔记本为以 后的学习做准备. 妈妈给了小明 30 元钱,小 明可以如何选择笔记本的价钱和数量呢?
x 解析:通过上节课学习可知画图象的三个步骤为
列表 描点
连线
需要注意的是在反比例函数中自变量x不能为0.
解:列表如下
x … -6 -5 -4 -3 -2 -1 1 3 2 3 4 5 6 … y … 1 1.2 1.5 2 6 -6 -3 -2 -1.5 -1.2 -1 …
y
6 5 4 3 2 1 -6 -5 -4 -3 -2 -1 -1 -2 -3 -4 -5 -6
1463 例如,在前面得到的第一个解析式 v 因为 x 作为分母,不能等于零,因此自变量 t x 的取值范围是所有非零实数. 中,t 的取值范围是 t>0,且当 t 取每一个确定的
范围 . 值时, v
但实际问题中,应根据具体情况来确定反比例函数自变量的取值
都有唯一确定的值与其对应.
k 想一想 反比例函数除了可以用 y (k ≠ 0) 的形式 x : 表示,还有没有其他表达方式?
是 (2) 若
m≠1
.
m m 2 是反比例函数,则m的取值范 y 围是 . x
(3) 若
m ≠ 0 且是反比例函数,则 m ≠ -2 m的取值范围
x
2
是 y m 2. m m 1 m = -1
湘教版九年级数学上册教学课件-《反比例函数》课件

特别地,当b=0时,称y是x的正比例函数.
即:y=kx (k ≠ 0 ),其中k叫做比例系数.
期末考试结束了,王老师想请几个同学帮忙批改60张 试卷的填空和选择题,如果请2个同学,平均每人帮老师 改几张试卷?3个,4个,5个,10个呢?
学生人数x(人) 2
3
4
ห้องสมุดไป่ตู้
5 10
每人批改的张数y 30 20
15
能用一个数学解析式表示吗?
x y =1661
y 1661 x
问题:学校课外生物小组的 同学准备自己动手,用旧围栏建一个 面积为24平方米的矩形饲养场.设它 的一边长为x(米),请写出另一边的长 y(米)与x的关系式.
x y=24, 即
根据矩形面积可知
y
24
x
由以上的实例中可得到如下的函数关系式:
3.当函数y (m 1)xm22m4是反比例函数时,
-3
同桌讨论:数学来源于生活,请 同学们找出生活中的反比例函数关系, 并举例:
小明同学用50元钱买学习用品,单价y(元)时与数
量x(件),那么变量y是x的函数吗?是反比例函数
吗?为什么?
,是,是
一个矩形的面积是20cm2,相邻的两条边长为xcm和
y 60 x
y 1661 x
y 24 x
小组讨论: 它们有什么共同的特 点?
一般地,如果两个变量x,y之间的关系可以表示
成:y k(K为常数,且K不为0)的形式,那么 x
称y是x的反比例函数 ,且K为比例系数.
注意:
常数 k 0
自变量X不能为零(因为分母为零时,该分式 无意义) xy = k
1.什么叫函数?
一般地.在某个变化中,有两个变量x 和y,如果给定一个x的值,相应地就确定 了y的一个值,那么我们称y是x的函数,其 中x叫自变量,y叫因变量.
即:y=kx (k ≠ 0 ),其中k叫做比例系数.
期末考试结束了,王老师想请几个同学帮忙批改60张 试卷的填空和选择题,如果请2个同学,平均每人帮老师 改几张试卷?3个,4个,5个,10个呢?
学生人数x(人) 2
3
4
ห้องสมุดไป่ตู้
5 10
每人批改的张数y 30 20
15
能用一个数学解析式表示吗?
x y =1661
y 1661 x
问题:学校课外生物小组的 同学准备自己动手,用旧围栏建一个 面积为24平方米的矩形饲养场.设它 的一边长为x(米),请写出另一边的长 y(米)与x的关系式.
x y=24, 即
根据矩形面积可知
y
24
x
由以上的实例中可得到如下的函数关系式:
3.当函数y (m 1)xm22m4是反比例函数时,
-3
同桌讨论:数学来源于生活,请 同学们找出生活中的反比例函数关系, 并举例:
小明同学用50元钱买学习用品,单价y(元)时与数
量x(件),那么变量y是x的函数吗?是反比例函数
吗?为什么?
,是,是
一个矩形的面积是20cm2,相邻的两条边长为xcm和
y 60 x
y 1661 x
y 24 x
小组讨论: 它们有什么共同的特 点?
一般地,如果两个变量x,y之间的关系可以表示
成:y k(K为常数,且K不为0)的形式,那么 x
称y是x的反比例函数 ,且K为比例系数.
注意:
常数 k 0
自变量X不能为零(因为分母为零时,该分式 无意义) xy = k
1.什么叫函数?
一般地.在某个变化中,有两个变量x 和y,如果给定一个x的值,相应地就确定 了y的一个值,那么我们称y是x的函数,其 中x叫自变量,y叫因变量.
湘教版九年级数学上册课件ppt《反比例函数的图象和性质》

oA
x 长方形面积 SAOP
k 2
︳m n︱ =︳K︱
三角形的面积
湖南教育出版社九年级 | 上册
y
课内练习:
1.如图,点P是反比例函数
y
4图象上的一点,PD⊥x轴于D.
则△POD的面积为 2 .
x
o
P D
x
2.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作
垂线,若阴影部分面积为3,则这个反比例函数的
3、对于函数 第 __三___象限.
y 1 2x
,当 x<0时,图象在
湖南教育出版社九年级 | 上册
例题解析,当堂练习
例1:已知反比例函数y= (k≠0)k的图象的一支如图。
x
(1)判断k是正数还是负数;
y
(-4,2)
(2)求这个反比例函数的解析式;
0
x
(3)补画这个反比例函数图象的另一支。 y (-4,2)
3、双曲线的两个分支无限接近x轴和y轴,但永远不会与x轴 和y轴相交。
4、图象的两个分支关于直角坐标系的原点成中心对称。
湖南教育出版社九年级 | 上册
1、函数
y 5 的图象在第___二__、__四___象限, x
2、函数 y m 的2 图象在二、四象限, x
则m的取值范围是 __m__<_2__ .
从点注光折画法意滑线反还:曲。比应②线例注描顺函意点次数什时连图么自结象左,? 看住切右忌,描用用
湖南教育出版社九年级 | 上册
议一议:
y
1. 反比例函数y 6
们相同吗?
x
和y 6x的图象在哪两个象限?它
0
2.
新湘教版九上数学课件:本章复习课

故直线的解析式为 y=x+1. (2)y2>y3>y1. (3)x<-2 或 0<x<1.
类型之三 反比例函数与一次函数的综合运用 6.[2018·柳州]如图 2,一次函数 y=mx+b 的图象与反比例函数 y=kx的图象 交于点 A(3,1)与点 B-12,n. (1)求该反比例函数的解析式; (2)求 n 的值及该一次函数的解析式.
解:(1)∵双曲线 y1=kx经过点 A(-4,1), ∴k=-4×1=-4. ∴双曲线的解析式为 y1=-4x. ∵双曲线 y1=-4x经过点 B(m,-4), ∴-4m=-4.∴m=1,∴B(1,-4).
∵直线 y2=ax+b 经过点 A(-4,1)和点 B(1,-4), ∴a-+4ba=+-b=4.1, 解得ab= =- -13, . ∴直线的解析式为 y2=-x-3. (2)AB=5 2.-4<x<0 或 x>1.
解得mn==150,,
∴直线 AD 的解析式为 y=5x+10.
当 y=15 时,15=5x+10,解得 x=1. 对于 y=24x0,当 y=15 时,x=16. ∴16-1=15(h). 答:恒温系统在一天内保持大棚里温度在 15 ℃及 15 ℃以上的时间有 15 h.
类型之五 反比例函数比例系数 k 的几何意义 10.如图 6,已知点 P(6,3),过点 P 作 PM⊥x 轴于点 M,PN⊥y 轴于点 N, 反比例函数 y=kx的图象交 PM 于点 A,交 PN 于点 B.若四边形 OAPB 的面积为 12, 则 k= 6 .
类型之四 运用反比例函数解决实际问题 9.我市某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为 15 ℃~20 ℃的新品种,图 5 是某天恒温系统从开启到关 闭及关闭后,大棚里温度 y(℃)随时间 x(h)变化的函数 图象,其中 AB 段是恒温阶段,BC 段是双曲线 y=kx的 一部分,请根据图中信息解答下列问题:
类型之三 反比例函数与一次函数的综合运用 6.[2018·柳州]如图 2,一次函数 y=mx+b 的图象与反比例函数 y=kx的图象 交于点 A(3,1)与点 B-12,n. (1)求该反比例函数的解析式; (2)求 n 的值及该一次函数的解析式.
解:(1)∵双曲线 y1=kx经过点 A(-4,1), ∴k=-4×1=-4. ∴双曲线的解析式为 y1=-4x. ∵双曲线 y1=-4x经过点 B(m,-4), ∴-4m=-4.∴m=1,∴B(1,-4).
∵直线 y2=ax+b 经过点 A(-4,1)和点 B(1,-4), ∴a-+4ba=+-b=4.1, 解得ab= =- -13, . ∴直线的解析式为 y2=-x-3. (2)AB=5 2.-4<x<0 或 x>1.
解得mn==150,,
∴直线 AD 的解析式为 y=5x+10.
当 y=15 时,15=5x+10,解得 x=1. 对于 y=24x0,当 y=15 时,x=16. ∴16-1=15(h). 答:恒温系统在一天内保持大棚里温度在 15 ℃及 15 ℃以上的时间有 15 h.
类型之五 反比例函数比例系数 k 的几何意义 10.如图 6,已知点 P(6,3),过点 P 作 PM⊥x 轴于点 M,PN⊥y 轴于点 N, 反比例函数 y=kx的图象交 PM 于点 A,交 PN 于点 B.若四边形 OAPB 的面积为 12, 则 k= 6 .
类型之四 运用反比例函数解决实际问题 9.我市某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为 15 ℃~20 ℃的新品种,图 5 是某天恒温系统从开启到关 闭及关闭后,大棚里温度 y(℃)随时间 x(h)变化的函数 图象,其中 AB 段是恒温阶段,BC 段是双曲线 y=kx的 一部分,请根据图中信息解答下列问题:
湘教版九年级数学上册全课件

143 20.98
149 20.13
4
随着时间t 的变化, 平均速度v发生了怎样的变化? v 随着t的增大而变小,随着t 的减小而变大.
(3)平均速度v是时间t 的函数吗?为什么?
5
问题2:我们知道,导体中的电流I,与导体的电阻R、导体两端的 电压之间满足关系式U=IR,当U=220V时, (1)请用含有R的代数式表示I.
D. 无法确定
解析:由题可知反比例函数解析式为
,因为yA、B6两点
x 均在函数图象上,并且都在第一象限内,根据xA>xB,得y1 < y2
故选C.
40
例2:如图所示的曲线是函数 (1)求常数m的取值范围;
y(m为常m数x)5图象的一支.
(2)若该函数的图象与正比例函数y=2x的图象在第一象限的交点为A(2,n),求点A
的坐标及反比例函数的解析式.
解:(1)由题意可得,m-5>0,解得m>5.
(2)∴∵两个函n数n的m交解24点得,为5 ,A(2,n),mn
4, 13.
∴ 点A的坐标为(2,4);反比例函数的
解析式为y= . 8
x
41
当堂练习
1.已知反比例函数
y 的m图象2在第一、三象限内,则m的取值范围是
正比例函数
y=kx(k是常数,k≠0) 直线(经过原点)
反比例函数
y=
k x
(
k是数,k≠0
)x
≠0
位 第一、三 置 象限 k>0 增 从左到右上升,y随x 减 的增大而增大 性
位 第二、四 置 象限
k<0
增 减 性
从左到右下降,y随 x的增大而减小
30
最新2019-湘教版九年级上数学课件 期末知识盘点 一、反比例函数的综合应用-PPT课件

尝试解答:(1)设反比例函数的解析式为 y=kx(k>0),∵A(m,-2)在 y=2x 上, ∴-2=2m,∴m=-1,∴A(-1,-2),又∵点 A 在 y=xk上,∴k=2,∴反 比例函数的解析式为 y=2x; (2)观察图象可知正比例函数值大于反比例函数值时自变量 x 的取值范围为- 1<x<0 或 x>1; (3)四边形 OABC 是菱形.证明:∵A(-1,-2),∴OA= 12+22= 5,由题
(2)结合图象直接写出:当 x>0 时,不等式 kx+b>mx 的解集. 解:x>2
8.如图,一次函数 y=-x+2 的图象与反比例函数 y=-x3的图象交于 A、B 两点,与 x 轴交于 D 点,且 C、D 两点关于 y 轴对称.
(1)求 A、B 两点的坐标; (2)求△ABC 的面积.
y=-x+2 解:(1)根据题意得y=-3x
A.36 C.6
(第 6 题图) B.12 D.3
重热点 4 反比例函数与一次函数 7.如图,在平面直角坐标系 xOy 中,已知一次函数 y=kx+b 的图象经过点 A(1,0)与反比例函数 y=mx (x>0)的图象相交于点 B(2,1).
(1)求 m 的值和一次函数的解析式;
解:(1)把点 B(2,1)代入 y=mx ,得 m=1×2=2,∵一次函数 y=kx+b 的图象 经过点 A(1,0)、B(2,1),∴k2+k+b=b=01 ,解得kb= =-1 1 ,∴一次函数解析式为 y=x-1
期末知识盘点
一、反比例函数的综合应用
【经典例题回放】 例 1:如图,已知正比例函数 y=2x 和反比例函数的图象交于点 A(m,-2).
(1)求反比例函数的解析式; (2)观察图象,直接写出正比例函数值大于反比例函数值时自变量 x 的取值范 围; (3)若双曲线上点 C(2,n)沿 OA 方向平移 5个单位长度得到点 B,判断四边 形 OABC 的形状并证明你的结论.
湘教版九年级数学上册作业课件 第2章 一元二次方程 章末复习(二)

(2)由BP2+BQ2=52,得(5-x)2+(2x)2=52,整理得x2-2x=0, 解方程得x=0(舍去),x=2. 所以2秒后PQ的长度等于5 cm;
(3)不可能.设12 (5-x)×2x=7,整理得x2-5x+7=0, ∵b2-4ac=-3<0,∴方程没有实数根, 所以△BPQ的面积为的面积不可能等于7 cm2.
11.甲、乙两同学解方程x2+px+q=0,甲看错了一次项,得根2和7, 乙看错了常数项,得根1和-10,则原方程为(D ) A.x2-9x+14=0 B.x2+9x-14=0 C.x2-9x+10=0 D.x2+9x+14=0
12.(2019·贵港)若α,β是关于x的一元二次方程x2-2x+m=0的
方程可化为x2-24x+150=0,Δ=(-24)2-4×150<0,
∴方程无实数解,∴不能围成花圃; (3)∵用n道篱笆隔成小矩形,且这些小矩形为正方形,∴AB=2n4+-2x , 而正方形的边长也为n+x 1 ,∴关系式为2n4+-2x =n+x 1 .
6.(开福区校级期中)一元二次方程x(x-2)=x-2的根是( C ) A.x=2 B.x1=0,x2=2 C.x1=2,x2=1 D.x=-1
7.解一元二次方程: (1)x2-3x=0; 解:x1=0,,x2=3.
(2)(x+1)2-4=0; 解:x1=1, x2=-3;
(3)2x解2-:3x=1=5x-12 , (4)3xx(22=x+3.121)=4x+2.
解:(1)设x秒后,△BPQ的面积为4 cm2,此时AP=x cm,
BP=(5-x)cm,BQ=2x cm,由12 BP×BQ=4,得12 (5-x)×2x=4, 整理得x2-5x+4=0,解得x=1或x=4(舍去).当x=4时,2x=8>7, 说明此时点Q越过点C,不合要求,舍去. 答:1秒后△BPQ的面积为4 cm2.
湘教版九年级上册数学期末复习课件第1章

第1章 反比例函数
1.2 反比例函数的图象与性质 第1课时
反比例函数 y=kx(k>0) 的图象与性质
1.画反比例函数的图象的三个基本步骤是: ①列表;②__描__点____;③连线.
2.一般地,当 k>0 时,反比例函数 y=kx的图象由分别在第 ____一____、____三____象限内的两支曲线组成,它们与 x 轴、 y 轴都不相交,在每个象限内,函数值 y 随自变量 x 的增大 而__减__小____.
_y_=__1x____.
9.在生活中不难发现这样的例子:三个量 a,b 和 c 之间存在数 量关系 a=bc.例如:长方形的面积=长×宽,匀速运动的路 程=速度×时间.
(1)如果三个量 a,b 和 c 之间存在数量关系 a=bc,那么: ①当 a=0 时,必须且只需_b_和__c_中__至__少__有__一___个__为__0____; ②当 b(或 c)为非零定值时,a 与 c(或 b)成_正__比__例___关系; ③当 a(a≠0)为定值时,b 与 c 成_反__比__例___关系.
1.反比例函数 y=53x的图象可能是( D )
2.【中考·柳州】反比例函数 y=2x的图象位于( A ) A.第一、三象限 B.第二、三象限 C.第一、二象限 D.第二、四象限
【点拨】∵k=2>0,∴反比例函数的图象位于第一、三象限.
3.已知反比例函数 y=kxb的图象与一次函数 y=-kx+b 的图象 在同一坐标系中的大致位置如图所示,则下列结论中正确的 是( ) A.k>0,b>0 B.k<0,b<0 C.k>0,b<0 D.k<0,b>0
【点拨】设反比例函数的表达式为 y=kx(k≠0), ∵当 x=-3 时,y=4,∴4=-k3,解得 k=-12. ∴反比例函数的表达式为 y=-x12.∴当 x=6 时,y=-612=-2.
湘教版 九年级数学 上册 第一章 反比例函数 复习课件(共29张PPT)

2、如图,一次函数与反比例函数的图象相交于A、 B两点,则图中使反比例函数的值小于一次函数的 值的x的取值范围 是( D ). A、x<-1 B、x>2 C、-1<x<0或x>2 D、x<-1或0<x<2
变式练习
1.(2012 广州)如图 ,正比例函数 y1=k1x 和反
k2 比例函数 y2= x 的图象交于 A(-1,2),B(1,-2)两点,若 y1<
面积为矩形,则它的面积为_
__ 2
解析:延长 BA 与 y 轴相交于点E,则矩形OC BE 的面积 为3,同理矩形 ODAE 的面积为 1,所以矩形 ABC D 的 面积为2.
变式练习
k 3.如图 262,点 A 在双曲线 y=x上,AB⊥x 轴于 B,且 -4 △AOB 的面积 S△AOB=2,则 k=__________.
可知AE=1,BF=4,
1 1 SV BOC OC BF 3 4 6 2 2 1 1 3 SV AOC OC AE 3 1 2 2 2 3 15 SVOAB SV BOC SV AOC 6 2 2
15 ∴△OAB的面积为 2
解:(1)当 0≤x≤2 时,y 与 x 成正比例函数关系. 设 y=kx,由于点(2,4)在直线上, 所以 4=2k,k=2,即 y=2x. (2)当 x>2 时,y 与 x 成反比例函数关系. 设 y=k/x,由于点(2,4)反比例函数的图象上, 所以 k=2×4=8,即 y=8/x. (3)当 0≤x≤2 时,含药量不低于 2 毫克, 即 2x≥2,x≥1.即服药 1 小时后; 当 x>2 时,含药量不低于 2 毫克, 8 即x ≥2,x≤4.即 2<x≤4. 所以服药一次,治疗疾病的有效时间是 1+2=3(小时). 忽略自变量的取值范围.
最全最新湘教版初中数学九年级上册数学知识点大全 ppt课件

7. 相似三角形的应用 (1) 测高 (不能直接使用皮尺或刻度尺量的) 测量不能到达顶部的物体的高度,通常用“在 同一时刻物高与影长成比例”的原理解决.
(2) 测距 (不能直接测量的两点间的距离) 测量不能到达两点间的距离,常构造相似三角形 求解.
8. 位似 (1) 如果两个图形不仅相似,而且对应顶点的连 线相交于一点,那么这样的两个图形叫做位 似图形,这个点叫做位似中心. (这时的相似 比也称为位似比) (2) 性质:位似图形上任意一对对应点到位似中心 的距离之比等于位似比;对应线段平行或者在 一条直线上.
一次项: ax2 一次项系数:a 二次项: bx 二次项系数:b 常数项:c
4.注意事项: (1)含有一个未知数; (2)未知数的最高次数为2; (3)二次项系数不为0; (4)整式方程.
二、解一元二次方程的方法 各种一元二次方程的解法及使用类型
一元二次方程的解法 直接开平方法 配方法 公式法 因式分解
3. 黄金分割
A
C
B
点C把线段AB分成两条线段AC和BC,如果
AC ABBC AC Nhomakorabea那么称线段AB被点C 黄金分割
点C叫做线段AB的 黄金分割点
AC与AB(或BC与AC)的比叫做 黄金比
黄金比
5 1 ≈0.618 2
4. 图形的相似 (1) 形状相同的图形
(2) 相似多边形
①表象:大小不等, 形状相同. ②实质:各对应角相 等、各对应边成比例.
适用的方程类型 (x+m)2=n(n ≥ 0)
x2 + px + q = 0 (p2 - 4q ≥0) ax2 + bx +c = 0(a≠0 , b2 - 4ac≥0)
2019年秋湘教版九年级数学上册课件:第4章 本章复习课(共25张PPT)
3.如图 2,在下面的网格中,小正方形的边长均为 1,点 A,B,O 都在格点 上,则∠AOB 的正弦值是( D ) 3 10 A. 10 1 C. 3 1 B. 2 10 D. 10
图2
5 4. 如图 3, 已知在 Rt△ACB 中, ∠C=90° , AB=13, AC=12, 则 cos B= 13 .
13.[2018· 湘潭]随着航母编队的成立,我国海军日益强大,2018 年 4 月 12 日, 中央军委在南海海域降重举行海上阅兵,在阅兵之前我军加强了海上巡逻.如图 8, 我军巡逻舰在某海域航行到 A 处时,该舰在观测点 P 的南偏东 45° 的方向上,且与 观测点 P 的距离 PA 为 400 海里;巡逻舰继续沿正北方向航行一 段时间后,到达位于观测点 P 的北偏东 30° 方向上的 B 处.问此时 巡逻舰与观测点 P 的距离 PB 为多少海里?(参考数据: 2≈1.414, 3≈1.732,结果精确到 1 海里)
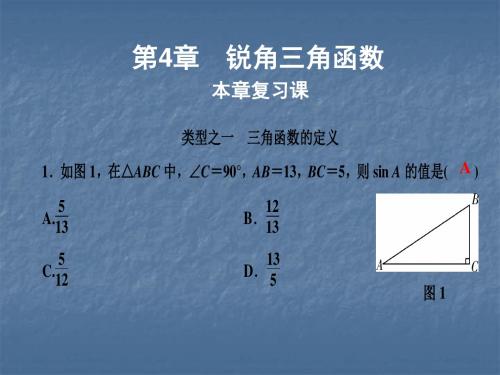
第4章 锐角三角函数
本章复习课
类型之一 三角函数的定义 1.如图 1,在△ABC 中,∠C=90° ,AB=13,BC=5,则 sin A 的值是( A )
5 A. 13 5 C. 12
12 B. 13 13 D. 5
图1
2 2.在 Rt△ABC 中,∠C=90° ,tan A= ,BC=6,则 AC=( A ) 3 A.9 C.18 B.4 D.12
11.如图 6,在△ABC 中,∠A=30° ,∠B=45° ,AC=2 3,求 AB 的长.
图6
解:如答图,过点 C 作 CD⊥AB 于点 D, ∴∠ADC=∠BDC=90° . ∵∠B=45° ,∴∠BCD=∠B=45° , ∴CD=BD. ∵∠A=30° ,AC=2 3, 1 ∴CD= AC= 3,∴BD=CD= 3. 2 由勾股定理得 AD= AC2-CD2=3, ∴AB=AD+BD=3+ 3.
湘教版数学九年级上册 期末备考PPT(135张PPT)

保持不变
期末备考
知识点
内容
要点
反比例 函数的
实际应 用
(1)作实际问题中函数的
根据实际问题建立反比例函数模型的 图像时,要注意两个变量
方法:(1)利用所学公式建立反比例函 的取值范围;
数模型;(2)利用问题情境中给出的数
量关系建立反比例函数模型
(2)在解决实际问题时, 要
注意应用数形结合思想
期末备考
期末备考
知识点
内容
解直角三 角形的应 用的常见
角
俯角与仰角 在实际计算中注意区分仰角和俯角
期末备考
知识点
内容
解直角三 角形的应 用的常见
角
坡度与坡 角 坡角是坡面与水平面的夹角, 它与坡度是两个不同的 概念;坡度i与坡角α的关系:tanα=i=
期末备考
知识点
内容
如图所示, 在平面上过观测点O画一条水平线(向右为
解直角三 角形的应 用的常见
角
东)和一条铅垂线(向上为北), 则从点O出发的视线与 铅垂线(南北方向线)的夹角, 方向角 叫作点O的方向角, 例如, 图中点A的方向角为北 偏东30°, 点B的方向角为南
偏西45°(或称为西南方向)
期末备考
第五章 用样本推断总体
期末备考
知识点
内容
要点
在反比例函数 的图像上任取一点, 过
反比例 函数
比例系 数的
几何意 义
这点向x轴和y轴分别作垂线, 与坐标轴围 与反比例函数图像相 成的矩形的面积是定值|k|. 反比例函数图 关的求面积的题目,
往往转化为与之有关 像上的这一点和x轴或y轴上的垂足以及坐 的三角形或矩形的面
标原点所构成的三角形的面积是 |k|, 且 积问题来解决
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A. 3
1 C. 3
B. -3
1 D. 3
a2 2
3. 若 y a 1 x A. 1
是反比例函数,则 a 的值为 ( A) C. ±1 D. 任意实数
B. -1
考点二 反比例函数的图象和性质 例1 已知点 A(1,y1),B(2,y2),C(-3,y3) 都在反比 6 例函数y 的图象上,则y1,y2,y3的大小关系是 x ( D)
九年级数学上(XJ) 教学课件
第1章 反比例函数
小结与复习
要点梳理
考点讲练
课堂小结
课后作业
要点梳理
1. 反比例函数的概念 k y x (k为常数,k≠0) 的函数称为反 定义:形如________
比例函数,其中x是自变量,y是x的函数,k是比例 系数. k 三种表达式方法:y 或 xy=kx 或y=kx-1 (k≠0). x 防错提醒:(1)k≠0;(2)自变量x≠0;(3)函数y≠0.
x 轴于点A,交C2于点B,则△POB的面积为 1 .
针对训练 如图,在平面直角坐标系中,点 M 为 x 轴正半 轴上一点,过点 M 的直线 l∥ y 轴,且直线 l 分别与 8 k 反比例函数 y (x>0)和 y (x>0) 的图象交于 x x P,Q两点,若 S△POQ=14, 则 k 的值为 20 .
2. 反比例函数的图象和性质
k (1) 反比例函数的图象:反比例函数y x
(k≠0)的
图象是 双曲线 ,它既是轴对称图形又是中心 对称图形. 反比例函数的两条对称轴为直线 y = x 和 y=-x ; 对称中心是: 原点 .
(2) 反比例函数的性质
图象 k> 0
k y x (k≠0) k<0
A
C O
(2) 求一次函数解析式及 m 的值;
1 解:把A(-4, ),B(-1,2)代入 y = kx + b中,得 2 1 1 k= , - 4k + b = , 2 2 解得 5 b= , -k + b =2, 2 1 5 所以一次函数的解析式为 y = x + . 2 2 m 把 B (-1,2)代入 y 中,得 m =-1×2=-2. x
规律:过双曲线上任意一点,向两坐标轴作垂线,
一条垂线与坐标轴、原点所围成的三角形的面积
k 为常数 . 2
3. 反比例函数的应用
◑利用待定系数法确定反比例函数:
k ① 根据两变量之间的反比例关系,设 y ; x ② 代入图象上一个点的坐标,即 x、y 的一对
对应值,求出 k 的值; ③ 写出解析式.
所在象限 y o
性质
一、三象 在每个象 限(x,y 限内,y 同号) 随 x 的增 x 大而减小
y o
二、四象 在每个象 限(x,y 限内,y 异号) 随 x 的增 x 大而增大
(3) 反比例函数比例系数 k 的几何意义 k 的几何意义:反比例函数图象上的点 (x,y) 具有 两坐标之积 (xy=k) 为常数这一特点,即过双曲线 上任意一点,向两坐标轴作垂线,两条垂线与坐 标轴所围成的矩形的面积为常数 |k|.
考点四 反比例函数的应用
1 例3 如图,已知 A (-4, ),B (-1,2) 是一次函数 2 m y =kx+b 与反比例函数 y (m<0)图象的两个交点, x
AC⊥x 轴于点 C,BD⊥y 轴于点 D. (1) 根据图象直接回答:在第二象限内,当 x 取何值 y 时,一次函数的值大于反比例函数的值; 解:当-4< x <-1时,一 次函数的值大于反比例 函数的值. B D x
针对训练 已知点 A (x1,y1),B (x2,y2) (x1<0<x2)都在反比
k 例函数 y (k<0) 的图象上,则 y1 与 y2 的大小关系 x
(从大到小) 为 y1 >0>y2 .
考点三 与反比例函数 k 有关的问题
4 2 例2 如图,两个反比例函数 y 和 y 在第一象 x x 限内的图象分别是 C1 和 C2,设点 P 在 C1 上,PA ⊥
C
O
ቤተ መጻሕፍቲ ባይዱ
x
方法总结:此类一次函数,反比例函数,二元一次方 程组,三角形面积等知识的综合运用,其关键是理清 解题思路. 在直角坐标系中,求三角形或四边形面积 时,是要选取合适的底边和高,正确利用坐标算出线 段长度.
3k 如图,设反比例函数的解析式为 y (k>0). x (1) 若该反比例函数与正比例函数 y =2x 的图象有一个
A. y3<y1<y2 C. y2<y1<y3
B. y1<y2<y3 D. y3<y2<y1
解析:方法①分别把各点代入反比例函数求出y1,y2, y3的值,再比较出其大小即可. 方法②:根据反比例函数的图象和性质比较.
方法总结:比较反比例函数值的大小,在同一个象限 内根据反比例函数的性质比较,在不同象限内,不能 按其性质比较,函数值的大小只能根据特征确定.
◑反比例函数与一次函数的图象的交点的求法 k2 求直线 y=k1x+b (k1≠0) 和双曲线 y (k2≠0) x 的交点坐标就是解这两个函数解析式组成的方 程组. ◑利用反比例函数相关知识解决实际问题
过程:分析实际情境→建立函数模型→明确 数学问题 注意:实际问题中的两个变量往往都只能取 非负值.
考点讲练
考点一 反比例函数的概念 针对训练 1. 下列函数中哪些是正比例函数?哪些是反比例函数? ① y = 3x-1 ②y= 2x2
1 ③ y x 1 ⑦y 3x 2x ④y 3 3 ⑧y 2x
⑤ y = 3x
1 ⑥y x
k 2. 已知点 P(1,-3) 在反比例函数 y 的图象上, x 则 k 的值是 ( B)
(3) P 是线段 AB 上的一点,连接 PC,PD,若△PCA 和 △PDB 面积相等,求点 P 坐标.
1 5 解:设点 的坐标为 ( tPDB , t面积相等, + ),P点到直线 AC 的 ∵ △P PCA 面积和△ 2 2 1 1 t-(-4),P 点到直线 1 5 2- 距离为 BD 的距离为 ∴ AC· [t-(-4)]= BD· [2-[ 2-( t+ )] , 2 2 2 2 y 1 5 5 ( t + ) . . 解得: t = 2 2 2 5 B ∴ 点 P 的坐标为 ( ,5 ). D 2 4 P A
