三角函数大题综合训练Word版
(完整版)三角函数综合练习题

1、若点P在的终边上,且OP=2,则点P的坐标()
A.B.C.D.
2、已知()
A.B.C.D.
3、下列函数中,最小正周期为的是()
A.B.C.D.
4、()
A.B.C.D.
5、若是三角形的内角,且,则等于()
A.B.或C.D.或
6、下列函数中,最小值为-1的是()
A.B.C.D.
7、设的值是()
A.B.C.D.
8、的值是()
A.B.C.D.
9、将函数的图象向左平移个单位,得到的图象,则等于()
ቤተ መጻሕፍቲ ባይዱA.B.C.D.
10、的值等于()
A.B.C.D.
11、化简等于()
A.B.C.D.
12、若在()
A.第一、二象限B.第一、三象限C.第一、四象限D.第二、四象限
13、函数()
A.周期为的奇函数B.周期为的偶函数C.周期为的奇函数D周期为的偶函数
A.B.
C.D.
8.(2009全国I文,1)°的值为
A. B. C. D.
9.(2007江西)若,,则等于( )
A.B.C.D.
11.(2009辽宁文,8)已知,则()
A.B.C.D.
12.(2009全国II文,9)若将函数的图像向右平移个单位长度后,与函数的图像重合,则的最小值为()
A. B. C. D.
3.(2007全国I)是第四象限角,,则()
A.B.C.D.
4.(2009临沂一模)使奇函数f(x)=sin(2x+θ)+cos(2x+θ)在[,0]上为减函数的θ值为
A、B、C、D、
5.(2009枣庄一模)已知的值是A.B.C.D.
三角函数基础测试题及答案(可编辑修改word版)

2 ⎪三角函数单元测试题一、选择题:(12ⅹ5 分=60 分)1. 若点 P 在角的终边的反向延长线上,且 OP = 1 ,则点P 的坐标为( )A (-cos , s in )B (cos , s in )C (cos,-sin )D (-cos ,-sin );2. 已知角的终边经过点 P (-3,-4),则cos(2+) 的值为()4 343A. -B.C.D. - 555 53. 已知、是第二象限的角,且cos> cos ,则 ()A.< ; B. s in> sin ; C. tan> tan ;D.以上都不对4. 函数 y = 5sin(2x + ) 图象的一条对称轴方程是() 6( A ) x = -; 12 (B) x = 0; (C) x = 6 (D) x = 3 5. 已知函数 y = A sin(x +) + B 的一部分图象如右图所示,如果 A > 0,> 0,||<,则( )2A. A = 4B.= 1 C.=6D. B = 46. 已 知 函 数 f (x ) = 2 s in(x +) 对 任 意 x 都 有 f ( + x ) = f ( - x ), 则 f ( ) 等 于6 6 6() A. 2 或0B. -2 或2C. 0D. -2 或03⎧cos x , (-≤ x < 0) 7. 设 f (x ) 是定义域为 R ,最小正周期为 2 15的函数,若 f (x ) = ⎨ ⎪⎩ 2, sin x , (0 ≤ x < )则 f (- ) 等于( ) 4A. 1B.C. 0 2D. -28. 若点 P (sin - c os , t an ) 在第一象限,则在[0, 2) 内的取值范围是()3 5 5 A . ( , ) (, )2 4 4 B. ( , ) (, )4 2 4 35 3 3 3 C. ( , ) ( , )2 4 4 2 D. ( , ) ( ,)2 4 42; ;6 6 + 9. 在函数 y = sin x 、 y = sin x 、 y = sin(2x + 为的函数的个数为() 2 ) 、 y = cos(2x + 3 2) 中,最小正周期 3A.1个B . 2 个C . 3 个D . 4 个10. 已知 A 1 , A 2 ,… A n 为凸多边形的内角,且lgsin A 1 + lgsin A 2 + ..... + lgsin A n = 0 ,则这个多边形是() A. 正六边形B .梯形C .矩形D .含锐角菱形11. 同时具有性质“(1)最小正周期是;(2)图像关于直线 x = 上是增函数”的一个函数是()对称;(3)在[- , ]3 6 3A. y = sin( x2 6B.y = cos(2x +3C.y = sin(2x - )6D.y = cos(2x - )6π π12. 已知函数 f (x )=f (π-x ),且当 x ∈(- =f (3),则( ) , ) 时,f (x )=x +sin x ,设 a =f (1),b =f (2),c2 2A. a <b<cB.b<c<aC.c<b<aD.c<a<b 二、填空题(4x4 分=16 分)13. 函数 y =14. 函数 y = 2 s in(2x + 的定义域是∈[-,0] 的单调递减区间是15. 已知函数 y =6 f (x ) 的图象上的每一点的纵坐标扩大到原来的4 倍,横坐标扩大到原来的2 倍,然后把所得的图象沿 x 轴向左平移,这样得到的曲线和 y = 2 sin x 的图象相同,2则已知函数 y = f (x ) 的解析式为.16. 关于函数 f (x ) = ⎛ + ⎫(x ∈ R ), 有下列命题: 4 sin 2x ⎪⎝ 3 ⎭① 由 f (x 1 ) = f (x 2 ) = 0 可得 x 1 - x 2 必是π的整数倍; ② y = f (x )的表达式可改写为 f (x ) =⎛ - ⎫ ; ③ y = f (x )的图象关于点⎛-4 cos 2x ⎪⎝ ⎭⎫ 对称;,0⎪ ⎝ ⎭④ y = f (x )的图象关于直线x = -对称.以上命题成立的序号是.6三.解答题:(5ⅹ12 分+14 分=74 分)log sin ⎛- 2x ⎫ 1 23 ⎝ ⎪ ⎭ )(x ) )) cos( ) cos( ) sin(2-) cos(+ + 11-) 17.(本题共 12 分)化简: 2 2cos(-) sin(3-) sin(--) sin(9+)218.(本题共 12 分)已知sin、cos是方程4x 2 + 2 6x + m = 0 的两实根,求:(1) m 的值; (2) sin 3+ cos 3的值.1 19.(本题共 12 分)已知函数 y = 2 s in( -x) ,(1)求它的单调区间;(2)当 x 为何值 6 3时,使 y > 1?20.(本题共 12 分)函数 f (x ) = A sin(wx +),( A > 0, w > 0, <的2图象如右,求出它的解析式,并说出它的周期、振幅、初相。
(完整word版)三角函数的定义、诱导公式、同角三角函数的关系练习题-

三角函数的定义、诱导公式、同角三角函数的关系练习题学校:___________姓名:___________班级:___________考号:___________一、单选题1.已知角α的终边经过点P(4,—3),则的值为( )A. B. C. D.2.已知角α的始边与x轴非负半轴重合,终边在射线4x-3y=0(x≤0)上,则cos α-sin α的值为( ) A. B.C. D.3.已知角α的终边与单位圆的交点P,则sinα·tanα=( )A.- B.± C.- D.±4.若tanα〈0,且sinα〉cosα,则α在()A.第一象限 B.第二象限C.第三象限 D.第四象限5.若,且,则角是( )A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角6.若,且为第二象限角,()A. B. C. D.7.已知,则等于A .B .C .D .8.若,且为第二象限角,则( )A .B .C .D .二、填空题9.已知 ,则___________三、解答题10.已知,且是第四象限的角。
(1)求; (2). 11.(1)已知,求的值;(2)已知, ,求的值.12.已知tan α2,= (1)求值: sin cos sin cos αααα+- (2)求值: ()()()()π5πsin cos cos π22cos 7πsin 2πsin παααααα⎛⎫⎛⎫+--+ ⎪ ⎪⎝⎭⎝⎭+-+ 13.已知角α终边上的一点()7,3P m m - ()0m ≠。
(1)求()cos sin 2119cos sin 22παπαππαα⎛⎫+-- ⎪⎝⎭⎛⎫⎛⎫-+ ⎪ ⎪⎝⎭⎝⎭的值; (2)求22sin cos cos ααα+-的值。
14.已知0θπ<<,且1sin cos 5θθ+=,求 (1)sin cos θθ-的值;(2)tan θ的值.15.已知tan 2α=.(1)求3sin 2cos sin cos αααα+-的值; (2)求()()()()3cos cos sin 22sin 3sin cos πππαααπααππα⎛⎫⎛⎫-+- ⎪ ⎪⎝⎭⎝⎭+-+的值; 16.已知,计算:(1); (2)。
三角函数综合练习.docx
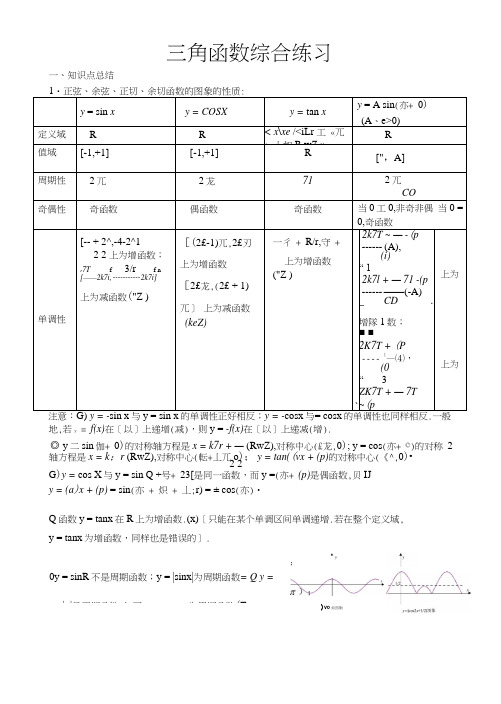
0y = sinR 不是周期函数;y = |sinx|为周期函数= Q y = cos|x|是周期函数(如图);y = cos 为周期函数(T =三角函数综合练习一、知识点总结1・正弦、余弦、正切、余切函数的图象的性质:y = sin xy = COSX y = tan x y = A sin (亦+ 0) (A 、e>0)定义域 R R < x\xe /<iLr 工 «兀 + 丄如R wZ »R 值域 [-1,+1] [-1,+1] R[",A]周期性 2兀2龙712兀CO奇偶性奇函数偶函数奇函数 当0工0,非奇非偶 当0 = 0,奇函数单调性[-- + 2^,-4-2^12 2 上为增函数;r 7T f3/r f n [——2k7i, ----------- 2k7i]上为减函数("Z )[(2£-1)兀,2£刃上为增函数[2£龙,(2£ + 1)兀] 上为减函数(keZ)一彳 + R/r,守 + 上为增函数("Z )、 2k7T ~ — -(p ------ (A),(i) “ 12k7l + — 71 -(p ------ ——(-A) _ CD .增隊1数;■ ■2K7T + (P---- 1—⑷,(0 “ 3ZK7T + — 7T ~(p 上为上为注意:G) y = -sin x 与y = sin x 的单调性正好相反;y = -cosx 与= cosx 的单调性也同样相反.一般地,若y = f(x)在[以]上递增(减),则y = -f(x)在[以]上递减(增).◎ y 二sin 伽+ 0)的对称轴方程是x = k7r + — (RwZ),对称中心(£龙,0); y = cos (亦+ ©)的对称 2 轴方程是x = k ;r (RwZ),对称中心(転+丄兀o ); y = tan((vx + (p)的对称中心(《^,0)•2 2G )y = cos X 与y = sin Q +号+ 23[是同一函数,而y =(亦+ (p)是偶函数,贝IJ y = (a )x + (p) = sin (亦 + 炽 + 丄;r) = ± cos (亦)•Q 函数y = tanx 在R 上为增函数.(x)[只能在某个单调区间单调递增.若在整个定义域, y = tanx 为增函数,同样也是错误的].)vo 如图勒"2嗚的周期为冗(如图) 2. 图像平移变换由丫="口的图象上的点的横坐标保持不变,纵坐标伸长(当|A|>1)或缩短(当0<|A|V1)到 原来的|A|倍,得到y=Asinx 的图彖,叫做振幅变换或叫沿Y 轴的伸缩变换.(用y/A 替换y )由y=sinx 的图象上的点的纵坐标保持不变,横坐标仲长(0<|^|<1)或缩短(|^|>1)到原 来的|丄I 倍,得到y=sinco x 的图彖,叫做周期变换或叫做沿x 轴的伸缩变换.(用3x 替换x )(0由丫=$脳 的图象上所有的点向左(当(p>0)或向右(当(p<0)平行移动丨(P I 个单位,得到y = sin (x+(p )的图彖,叫做相位变换或叫做沿x 轴方向的平移.(用x+(p 替换x )由y=sinx 的图象上所有的点向上(当b>0)或向下(当b<0)平行移动I b I 个单位,得到y = sinx+b 的图象叫做沿y 轴方向的平移.(用y+(・b )替换y )由y=sinx 的图象利用图象变换作函数y=Asin ((Qx+(p ) (A>0, >0) (xWR )的图象, 要特别注意:当周期变换和相位变换的先后顺序不同时,原图彖延x 轴量伸缩量的区别。
(完整word)1.4三角函数的图像与性质(真题)

1.4三角函数的图像与性质(真题)一、选择题(本大题共29小题,共145。
0分)1.已知sin(75°+α)=,则cos(15°—α)的值为()A. -B.C. —D。
2.若α是第三象限角,则y=+的值为()A. 0B. 2 C。
-2 D。
2或-23.角α是第一象限角,且sinα=,那么cosα()A。
B. —C。
D. -4.已知角α的终边经过点P(0,3),则α是()A。
第一象限角B。
终边在x轴的非负半轴上的角C。
第四象限角 D. 终边在y轴的非负半轴上的角5.已知,且,则tanφ=()A. B. C。
D。
6.将函数y=2sin(2x+)的图象向右平移个周期后,所得图象对应的函数为( )A。
y=2sin(2x+) B。
y=2sin(2x+)C。
y=2sin(2x—)D。
y=2sin(2x-)7.已知函数f(x)=sin(ωx+φ)(ω>0,|φ|≤),x=-为f(x)的零点,x=为y=f(x)图象的对称轴,且f(x)在(,)上单调,则ω的最大值为()A. 11B. 9C. 7 D。
58.函数y=A sin(ωx+φ)的部分图象如图所示,则()A。
y=2sin(2x-)B。
y=2sin(2x—)C。
y=2sin(x+)D。
y=2sin(x+)9.若将函数y=2sin2x的图象向左平移个单位长度,则平移后的图象的对称轴为()A。
x=—(k∈Z) B。
x=+(k∈Z)C. x=-(k∈Z)D。
x=+(k∈Z)10.函数f(x)=cos2x+6cos(—x)的最大值为( )A。
4 B. 5 C. 6 D. 711.已知曲线C1:y=cos x,C2:y=sin(2x+),则下面结论正确的是( )A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线C2B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线C2C. 把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线C2D. 把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线C212.设函数f(x)=cos(x+),则下列结论错误的是()A。
三角函数(Word有答案)

三角函数(一)选择题1、(07山东理5)函数sin 2cos 263y x x ππ⎛⎫⎛⎫=+-+ ⎪ ⎪⎝⎭⎝⎭的最小正周期和最大值分别为( )A .π,1B .πC .2π,1D .2π答案:A2、(07山东文4)要得到函数sin y x =的图象,只需将函数cos y x π⎛⎫=-⎪3⎝⎭的图象( )A .向右平移π6个单位 B .向右平移π3个单位 C .向左平移π3个单位D .向左平移π6个单位答案:A3.(08山东卷5)已知cos (α-6π)+sin α7sin()6πα+则的值是 (A )-532 (B )532 (C)-54 (D) 54答案:C4.(2009山东卷理)将函数sin 2y x =的图象向左平移4π个单位, 再向上平移1个单位,所得图象的函数解析式是( ).A.cos 2y x =B.22cos y x = C.)42sin(1π++=x y D.22sin y x =【解析】:将函数sin 2y x =的图象向左平移4π个单位,得到函数sin 2()4y x π=+即sin(2)cos 22y x x π=+=的图象,再向上平移1个单位,所得图象的函数解析式为21cos 22cos y x x =+=,故选B.答案:B【命题立意】:本题考查三角函数的图象的平移和利用诱导公式及二倍角公式进行化简解析式的基本知识和基本技能,学会公式的变形. 5.(2009山东卷文)将函数sin 2y x =的图象向左平移4π个单位, 再向上平移1个单位,所得图象的函数解析式是( ).A. 22cos y x = B. 22sin y x = C.)42sin(1π++=x y D. cos 2y x =【解析】:将函数sin 2y x =的图象向左平移4π个单位,得到函数sin 2()4y x π=+即sin(2)cos 22y x x π=+=的图象,再向上平移1个单位,所得图象的函数解析式为21cos 22cos y x x =+=,故选A.答案:A【命题立意】:本题考查三角函数的图象的平移和利用诱导公式及二倍角公式进行化简解析式的基本知识和基本技能,学会公式的变形.6、(2010山东文数)(10)观察2'()2x x =,4'3()4x x =,'(cos )sin x x =-,由归纳推理可得:若定义在R 上的函数()f x 满足()()f x f x -=,记()g x 为()f x 的导函数,则()g x -=(A )()f x (B)()f x - (C) ()g x (D)()g x - 答案:D7、(2011山东3)若点(a,9)在函数3xy =的图象上,则tan6a π的值为A .0BC .1D答案:D8、(2011山东理数6)若函数()sin f x x ω= (ω>0)在区间0,3π⎡⎤⎢⎥⎣⎦上单调递增,在区间,32ππ⎡⎤⎢⎥⎣⎦上单调递减,则ω=A .3B .2C .32D .23 答案:C9、(2011山东文数6)若函数()sin f x x ω= (ω>0)在区间0,3π⎡⎤⎢⎥⎣⎦上单调递增,在区间,32ππ⎡⎤⎢⎥⎣⎦上单调递减,则ω=A .23 B .32C .2D .3答案:B10、(2012山东卷文(5))设命题p :函数sin 2y x =的最小正周期为2π;命题q :函数cos y x =的图象关于直线2x π=对称.则下列判断正确的是(A)p 为真 (B)q ⌝为假 (C)p q ∧为假 (D)p q ∨为真 答案:C11、(2012山东卷文(8))函数2sin (09)63x y x ππ⎛⎫=-≤≤ ⎪⎝⎭的最大值与最小值之和为A(A)23- (B)0 (C)-1 (D)13-- 答案:A12(2013山东数学理)8.函数cos sin y x x x =+的图象大致为答案:8.D13、(2013山东数学文)(9)、函数x x x y sin cos +=的图象大致为答案:D(二)填空题1.(08山东卷15)已知a ,b ,c 为△ABC 的三个内角A ,B ,C 的对边,向量m =(1,3-),n =(cos A ,sin A ).若m ⊥n ,且a cos B +b cos A =c sin C ,则角B =答案:6π. 2、(2010山东数)2、已知a ,b ,c 为△ABC 的三个内角A ,B ,C 的对边,a=2b=2sin +cos =2=B B A 若,,,则(三)解答题1、(07山东理20)如图,甲船以每小时2海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于1A 处时,乙船位于甲船的北偏西105方向的1B 处,此时两船相距20海里,当甲船航行20分钟到达2A 处时,乙船航行到甲船的北偏西120方向的2B 处,此时两船相距102 解法一:如图,连结11A B ,由已知22102A B =122030210260A A ==, 1221A A AB ∴=,又12218012060A A B =-=∠,122A A B ∴△是等边三角形,1212102A B A A ∴==,由已知,1120A B =,1121056045B A B =-=∠,在121A B B △中,由余弦定理,22212111212122cos 45B B A B A B A B A B =+-22220(102)2201022=+-⨯⨯ 200=.北1B2B1A2A 120 105 乙 甲北 1B2B1A2A120 105甲12B B ∴=60=/小时).答:乙船每小时航行解法二:如图,连结21A B ,由已知1220A B =,122060A A ==,112105B A A =∠,cos105cos(4560)=+ cos 45cos60sin 45sin 60=-=sin105sin(4560)=+ sin 45cos60cos 45sin 60=+=在211A A B △中,由余弦定理,22221221211122cos105A B A B A A A B A A =+-2220220=+-⨯100(4=+.1110(1A B ∴=.由正弦定理11121112222(13)2sin sin 210(13)A B A A B B A A A B +===+∠∠, 12145A A B ∴=∠,即121604515B A B =-=∠,1A2A120 105 乙2(1cos15sin105+==.在112B A B △中,由已知12A B =22212112221222cos15B B A B A B A B A B =++22210(1210(1=+-⨯+⨯200=.12B B ∴=60=海里/小时.答:乙船每小时航行2、(07山东文17)在ABC △中,角A B C ,,的对边分别为tan a b c C =,,,(1)求cos C ;(2)若52CB CA =,且9a b +=,求c .解:(1)sin tan cos CC C=∴= 又22sin cos 1C C +=解得1cos 8C =±. tan 0C >,C ∴是锐角.1cos 8C ∴=.(2)52CB CA =,5cos 2ab C ∴=,20ab ∴=.又9a b +=22281a ab b ∴++=.2241a b ∴+=.2222cos 36c a b ab C ∴=+-=.6c ∴=.3.(08山东卷17)(本小题满分12分)已知函数f (x )=)0,0)(cos()sin(3><<+-+ωϕϕωϕωπx x 为偶函数,且函数y =f (x )图象的两相邻对称轴间的距离为.2π(Ⅰ)美洲f (8π)的值; (Ⅱ)将函数y =f (x )的图象向右平移6π个单位后,再将得到的图象上各点的横坐标舒畅长到原来的4倍,纵坐标不变,得到函数y =g (x )的图象,求g (x )的单调递减区间. 解:(Ⅰ)f (x )=)cos()sin(3ϕωϕω+-+x x=⎥⎦⎤⎢⎣⎡+-+)cos(21)sin(232ϕωϕωx x=2sin(ϕω+x -6π) 因为 f (x )为偶函数,所以 对x ∈R ,f (-x )=f (x )恒成立,因此 sin (-ϕω+x -6π)=sin (ϕω+x -6π). 即-sin x ωcos(ϕ-6π)+cos x ωsin(ϕ-6π)=sin x ωcos(ϕ-6π)+cos x ωsin(ϕ-6π),整理得 sin x ωcos(ϕ-6π)=0.因为 ω>0,且x ∈R ,所以 cos (ϕ-6π)=0.又因为 0<ϕ<π,故 ϕ-6π=2π.所以 f (x )=2sin(x ω+2π)=2cos x ω.由题意得 .2,222 = 所以 ωπωπ⋅=故 f (x )=2cos2x . 因为 .24cos2)8(==ππf(Ⅱ)将f (x )的图象向右平移个6π个单位后,得到)6(π-x f 的图象,再将所得图象横坐标伸长到原来的4倍,纵坐标不变,得到)64(ππ-f 的图象.).32(cos 2)64(2cos 2)64()(ππππππ-=⎥⎦⎤⎢⎣⎡-=-=f f x g 所以 当 2k π≤32ππ-≤2 k π+ π (k ∈Z),即 4k π+≤32π≤x ≤4k π+38π(k ∈Z)时,g (x )单调递减.因此g (x )的单调递减区间为 ⎥⎦⎤⎢⎣⎡++384,324ππππk k (k ∈Z) 4.(2009山东卷理)(本小题满分12分)设函数f(x)=cos(2x+3π)+sin 2x. (1) 求函数f(x)的最大值和最小正周期. (2) 设A,B,C 为∆ABC 的三个内角,若cosB=31,1()24c f =-,且C 为锐角,求sinA.解: (1)f(x)=cos(2x+3π)+sin 2x.=1cos 21cos 2cos sin 2sin 233222x x x x ππ--+=-所以函数f(x),最小正周期π.(2)()2c f =12C =-41, 所以sin C =, 因为C 为锐角, 所以3C π=,又因为在∆ABC 中, cosB=31, 所以 sin B = 所以11sin sin()sin cos cos sin 23A B C B C B C =+=+=+=【命题立意】:本题主要考查三角函数中两角和差的弦函数公式、二倍角公式、三角函数的性质以及三角形中的三角关系. 5.(2009山东卷文)(本小题满分12分)设函数f(x)=2)0(sin sin cos 2cos sin 2πϕϕϕ<<-+x x x 在π=x 处取最小值.(3) 求ϕ.的值;(4) 在∆ABC 中,c b a ,,分别是角A,B,C 的对边,已知,2,1==b a 23)(=A f ,求角C.. 解: (1)1cos ()2sin cos sin sin 2f x x x x ϕϕ+=⋅+- sin sin cos cos sin sin x x x x ϕϕ=++- sin cos cos sin x x ϕϕ=+ sin()x ϕ=+因为函数f(x)在π=x 处取最小值,所以sin()1πϕ+=-,由诱导公式知sin 1ϕ=,因为0ϕπ<<,所以2πϕ=.所以()sin()cos 2f x x x π=+=(2)因为23)(=A f ,所以3cos A =,因为角A 为∆ABC 的内角,所以6A π=.又因为,2,1==b a 所以由正弦定理,得sin sin a bA B=,也就是sin 12sin 22b A B a ==⨯=, 因为b a >,所以4π=B 或43π=B .当4π=B 时,76412C ππππ=--=;当43π=B 时,36412C ππππ=--=.【命题立意】:本题主要考查了三角函数中两角和差的弦函数公式、二倍角公式和三角函数的性质,并利用正弦定理解得三角形中的边角.注意本题中的两种情况都符合. 6、(2010山东文数)(17)(本小题满分12分) 已知函数2()sin()cos cos f x x x x πωωω=-+(0ω>)的最小正周期为π, (Ⅰ)求ω的值;(Ⅱ)将函数()y f x =的图像上各点的横坐标缩短到原来的12,纵坐标不变,得到函数()y g x =的图像,求函数()y g x =在区间0,16π⎡⎤⎢⎥⎣⎦上的最小值.7、(2010山东理数)8、(2011山东理数17)在∆ABC 中,内角A ,B ,C 的对边分别为a ,b ,c .已知cos A-2cosC 2c-a=cos B b . (I )求sin sin CA的值;(II )若cosB=14,b=2,ABC ∆的面积S 。
三角函数练习题100题(Word版,含解析)

三角函数习题100题练兵(1-20题为三角函数的基本概念及基本公式,包括同角三角函数关系,诱导公式等,21-40题三角函数的图象与性质,41-55题为三角恒等变形,56-70为三角函数基本关系及角度制与弧度制等,包括象限角弧长与扇形面积公式等,71-90题为三角函数的综合应用,91-100为高考真题。
其中1-55为选择题,56-70为填空题,71-100为解答题。
)1.函数且的图象恒过点,且点在角的终边上,则A. B. C. D.【解答】解:函数且的图象恒过定点,角的终边经过点,,,.故选B2.已知角的终边上有一点,则A. B. C. D.【解答】解:角的终边上有一点,,则.故选C.3.若,且,则角的终边位于A.第一象限B.第二象限C.第三象限D.第四象限【解答】解:,则角的终边位于一二象限,由,角的终边位于二四象限,角的终边位于第二象限.故选择.4.已知是第二象限角,为其终边上一点且,则的值A. B. C. D.【解答】解:是第二象限角,为其终边上一点且,,解得,,.故选A.5.已知角的终边过点,且,则的值为A. B. C. D.【解答】解:由题意,角的终边过点,可得,,,所以,解得,故选A.6.若点在角的终边上,则A. B. C. D.【解析】解:点在角的终边上,,则,,.故选B.7.在平面直角坐标系中,,点位于第一象限,且与轴的正半轴的夹角为,则向量的坐标是A. B. C. D.【解答】解:设,则,,故故选C.8.的大小关系为A. B. C. D.【解答】解:,,,,.故选C.9.已知角的终边上有一点,则的值为A. B. C. D.【解答】解:根据三角函数的定义可知,根据诱导公式和同角三角函数关系式可知,故选A.10.已知角的顶点为坐标原点,始边与轴的非负半轴重合,若角的终边过点,,且,则A. B. C. D.【解答】解:因为角的终边过点,所以是第一象限角,所以,,因为,,所以为第一象限角,,所以,所以,故选:.11.若角的终边经过点,则A. B. C. D.【解答】解:由题意,,,因为的正负不确定,则正负不确定.故选C.12.下列结论中错误的是A.B.若是第二象限角,则为第一象限或第三象限角C.若角的终边过点,则D.若扇形的周长为,半径为,则其圆心角的大小为弧度【解答】解:.,故A正确;B.因为为第二象限角,,所以,当为偶数时,为第一象限的角,当为奇数时,为第三象限角,故B正确;C.当时,,此时,故C错误;D.若扇形的周长为,半径为,则弧长为,其圆心角的大小为弧度,故正确.故选C.13.我国古代数学家赵爽利用弦图巧妙地证明了勾股定理,弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形如图如果内部小正方形的内切圆面积为,外部大正方形的外接圆半径为,直角三角形中较大的锐角为,那么A. B. C. D.【解答】解:因为内部小正方形的内切圆面积为,所以内部小正方形的内切圆的半径为,所以内部小正方形的边长为,外部大正方形的外接圆半径为,所以大正方形的边长为,设大直角三角形中长直角边为,斜边为,则,则,所以,所以大直角三角形中短直角边为,所以,,则.故选D.14.己知是第四象限角,化简为A. B. C. D.【解答】解:是第四象限角,故,又,,则.故选B.15.函数的最小正周期为A. B. C. D.【解答】解:,所以的最小正周期.故选C.16.函数的值域是A. B. C. D.【解答】解:,令,,则,,由二次函数的性质可得函数在上单调递减,在上单调递增,当时取的最小值,其最小值为,当时取得最大值,其最大值为.故函数的值域为.故选B.17.已知,,且,,则A. B. C. D.【解答】解:由题可知,,,所以,所以,又,所以,所以,当时,.因为,所以,不符合题意,当时,同理可得,故选:.18.已知,则的值为A. B. C. D.【解答】解:因为,所以,所以,所以,所以.故选A.19.在中,角、、的对边分别是、、,若,则的最小值为A. B. C. D.【解答】解:,由正弦定理化简得:,整理得:,,;则.当且仅当时等号成立,可得的最小值为.故选:.20.若的内角满足,则的值为.A. B. C. D.【解答】解:因为为的内角,且,所以为锐角,所以.所以,所以,即.所以.故选A.21.已知函数给出下列结论:①的最小正周期为;②是的最大值;③把函数的图象上的所有点向左平移个单位长度,可得到函数的图象.其中所有正确结论的序号是A.①B.①③C.②③D.①②③【解答】解:因为,①由周期公式可得,的最小正周期,故①正确;②,不是的最大值,故②错误;③根据函数图象的平移法则可得,函数的图象上的所有点向左平移个单位长度,可得到函数的图象,故③正确.故选:.22.将函数的图象先向右平移个单位长度,再将该图象上各点的横坐标缩短到原来的一半纵坐标不变,然后将所得图象上各点的纵坐标伸长到原来的倍横坐标不变,得函数的图象,则解析式是A. B.C. D.【解答】解:由题意函数的图象上各点向右平移个单位长度,得到新函数解析式为,再把所得函数的图象上各点横坐标缩短为原来的一半,得到新函数解析式为,再把所得函数的图象上各点纵坐标伸长为原来的倍,得到新函数解析式为.故选A.23.如图函数的图象与轴交于点,在轴右侧距轴最近的最高点,则不等式的解集是A.,B.,C.,D.,【解答】解:由在轴右边到轴最近的最高点坐标为,可得.再根据的图象与轴交于点,可得,结合,.由五点法作图可得,求得,不等式,即,,,求得,,故选:.24.函数的图像的一条对称轴是A. B. C. D.【解答】解:令,解得,函数图象的对称轴方程为,时,得为函数图象的一条对称轴.故选C25.已知函数,若相邻两个极值点的距离为,且当时,取得最小值,将的图象向左平移个单位,得到一个偶函数图象,则满足题意的的最小正值为A. B. C. D.【解答】解:函数,所以,,相邻两个极值点的横坐标之差为,所以,所以,又,所以,当时,取得最小值,所以,,而,所以,所以,将的图象向左平移个单位得为偶函数,所以,,即.所以的最小正值为.故选A.26.函数的定义域为A. B.C. D.【解答】解:根据对数的真数大于零,得,可知:当时,,故函数的定义域为.故选A.27.设函数若是偶函数,则A. B. C. D.【解答】解:,因为为偶函数,所以当时,则,,所以,,又,所以.故选B.28.函数的部分图像如图所示,则A. B. C. D.【解答】解:由题意,因为,所以,,由时,可得,所以,结合选项可得函数解析式为.故选A.29.已知函数,给出下列命题:①,都有成立;②存在常数恒有成立;③的最大值为;④在上是增函数.以上命题中正确的为A.①②③④B.②③C.①②③D.①②④【解答】解:对于①,,,①正确;对于②,,由,即存在常数恒有成立,②正确;对于③,,令,,则设,,令,得,可知函数在上单调递减,在上单调递增,在上单调递减,且,,则的最大值为,③错误;对于④,当时,,所以在上为增函数,④正确.综上知,正确的命题序号是①②④.故选:.30.已知,,直线和是函数图象的两条相邻的对称轴,则A. B. C. D.【解答】解:由题意得最小正周期,,即,直线是图象的对称轴,,又,,故选A.31.已知函数向左平移半个周期得的图象,若在上的值域为,则的取值范围是A. B. C. D.【解答】解:函数向左平移半个周期得的图象,由,可得,由于在上的值域为,即函数的最小值为,最大值为,则,得.综上,的取值范围是.故选D.32.若,则实数的取值范围是A. B. C. D.解:,,,.,,.33.如图,过点的直线与函数的图象交于,两点,则等于A. B. C. D.【解答】解:过点的直线与函数的图象交于,两点,根据三角函数的对称性得出;,,,,.是的中点,,.故选B.34.已知函数,若函数恰有个零点,,,,且,为实数,则的取值范围为A. B. C. D.解:画出函数的图象,如图:结合图象可知要使函数有个零点,则,因为,所以,所以,因为,所以,且,可设,其中,所以,所以,所以的取值范围是.故选A.35.函数的部分图象如图所示,现将此图象向左平移个单位长度得到函数的图象,则函数的解析式为A. B. C. D.【解答】解:根据函数的部分图象,则:,,所以:,解得:,当时,,即:解得:,,因为,当时,,故:,现将函数图象上的所有点向左平移个单位长度得到:函数的图象.故选C.36.已知曲线:,:,则下面结论正确的是A.把上各点的横坐标伸长到原来的倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线B.把上各点的横坐标伸长到原来的倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线C.把上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线D.把上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线【解答】解:把上各点的横坐标缩短到原来的倍,纵坐标不变,得到函数图象,再把得到的曲线向左平移个单位长度,得到函数的图象,即曲线,故选D.37.设,则函数的取值范围是A. B. C. D.【解答】解:,因为,所以,所以故选A.38.人的心脏跳动时,血压在增加或减少.血压的最大值、最小值分别称为收缩压和舒张压,血压计上的读数就是收缩压和舒张压,读数为标准值设某人的血压满足函数式,其中为血压单位:,为时间单位:,则下列说法正确的是A.收缩压和舒张压均高于相应的标准值B.收缩压和舒张压均低于相应的标准值C.收缩压高于标准值、舒张压低于标准值D.收缩压低于标准值、舒张压高于标准值【解答】解:某人的血压满足函数式,其中为血压单位:,为时间单位:则此人收缩压;舒张压,所以此人的收缩压高于标准值、舒张压低于标准值.故选C.39.设函数,下述四个结论:①的图象的一条对称轴方程为;②是奇函数;③将的图象向左平移个单位长度可得到函数的图象;④在区间上单调递增.其中所有正确结论的编号是A.①②B.②③C.①③D.②③④【解答】解:由题意.对①,的对称轴为,即,故是的对称轴故①正确;对②,,故为偶函数,故②错误;对③,将的图象向左平移个单位长度得到故③正确;对④,当时,,因为是的减区间,故④错误.综上可得①③正确.故选C.40.如图,某港口一天时到时的水深变化曲线近似满足函数,据此可知,这段时间水深单位:的最大值为A. B. C. D.【解答】解:由图象知.因为,所以,解得,所以这段时间水深的最大值是.故选C.41.若,且,则等于A. B. C. D.【解答】解:,,则,又,,则.故选:.42.若,则A. B. C. D.【解答】解:,且,,,两边同时平方得,解得或舍去,,故选B.43.,,则的值为.A. B. C. D.【解答】解:,,,,.故选:.44.若,均为锐角,,,则A. B. C.或 D.【解答】解:为锐角,,,且,,且,,,.45.在中,已知,那么的内角,之间的关系是A. B. C. D.关系不确定【解答】解:由正弦定理,即,所以,即,所以,则,所以.故选B.46.设,,则A. B. C. D.【解答】解:根据二倍角公式可得,解得,由,可得,所以,故选A.47.设,,且,则下列结论中正确的是A. B. C. D.【解答】解:,因为,所以.故选A.48.已知是锐角,若,则A. B. C. D.【解答】解:已知是锐角,,若,,则.故选A.49.化简的值等于A. B. C. D.【解答】解:,,.故选A.50.已知,,则的值为A. B. C. D.【解答】解:,,由得..故选B.51.已知函数,若函数在上单调递减,则实数的取值范围是A. B. C. D.【解答】解:函数,由函数在上单调递减,且,得解得,又,,实数的取值范围是.故选A.52.函数的最大值为A. B. C. D.【解答】解:函数,其中,函数的最大值为,故选C.53.计算:等于A. B. C. D.【解答】解:,,.故选A.54.在中,角,,的对边分别为,,,已知,,则的值为A. B. C. D.【解答】解:,,即,即,,由正弦定理可得,又,所以由余弦定理可得,故选D.55.函数取最大值时,A. B. C. D.【解答】解:,其中由确定.由与得.若,则,,,此时.所以,最大值时,,,.故选.56.已知点在第一象限,且在区间内,那么的取值范围是___________.【解答】解:由题意可知,,,借助于三角函数线可得角的取值范围为.故答案为.57.已知角的终边经过点,则实数的值是【解答】解:设,由于正切函数周期为,则,又终边经过点,所以,解得,故答案为.58.在平面直角坐标系中,角的顶点是,始边是轴的非负半轴,,若点是角终边上的一点,则的值是____.【解答】解:因为点是角终边上的一点,所以,由,,则在第一象限,又,所以.故答案为.59.已知,,则____________.【解答】解:,,,,.故答案为.60.已知角的终边与单位圆交于点,则的值为__________.【解答】解:由题意可得,则.故答案为.61.若扇形的圆心角为,半径为,则扇形的面积为__________.【解答】解:因为,所以扇形面积公式.故答案为.62.如果一扇形的弧长变为原来的倍,半径变为原来的一半,则该扇形的面积为原扇形面积的________.【解答】解:由于,若,,则.63.某中学开展劳动实习,学生加工制作零件,零件的截面如图所示,为圆孔及轮廓圆弧所在圆的圆心,是圆弧与直线的切点,是圆弧与直线的切点,四边形为矩形,,垂足为,,到直线和的距离均为,圆孔半径为,则图中阴影部分的面积为___________.【解答】解:设上面的大圆弧的半径为,连接,过作交于,交于,交于,过作于,记扇形的面积为,由题中的长度关系易知,同理,又,可得为等腰直角三角形,可得,,,,,解得,,故答案为.64.已知相互啮合的两个齿轮,大轮有齿,小轮有齿.当小轮转动两周时,大轮转动的角度为______________写正数值:如果小轮的转速为转分,大轮的半径为,则大轮周上一点每秒转过的弧长为______________.【解答】解:因为大轮有齿,小轮有齿,当小轮转动两周时,大轮转动的角为,如果小轮的转速为转分,则每秒的转速为转秒,由于大轮的半径为,那么大轮周上一点每转过的弧长是.故答案为.65.终边在直线上的所有角的集合是____________.【解答】解:由终边相同的角的定义,终边落在射线的角的集合为,终边落在射线的角的集合为:,终边落在直线的角的集合为:.故答案为.66.已知直四棱柱的棱长均为,以为球心,为半径的球面与侧面的交线长为________.【解答】解:如图:取的中点为,的中点为,的中点为,因为,直四棱柱的棱长均为,所以为等边三角形,所以,,又四棱柱为直四棱柱,所以平面,所以,因为,所以侧面,设为侧面与球面的交线上的点,则,因为球的半径为,,所以,所以侧面与球面的交线上的点到的距离为,因为,所以侧面与球面的交线是扇形的弧,因为,所以,所以根据弧长公式可得.故答案为.67.用弧度制表示终边落在如图所示阴影部分内的角的集合是_________________________.【解答】解:由题意,得与终边相同的角可表示为,与终边相同的角可表示为,故角的集合是,故答案为.68.给出下列命题:第二象限角大于第一象限角三角形的内角是第一象限角或第二象限角不论是用角度制还是用弧度制度量一个角,它们与扇形的半径的大小无关若,则与的终边相同若,则是第二或第三象限的角.其中正确的命题是填序号【解答】解:①是第二象限角,是第一象限角,但,①错误;②三角形内角有的直角,但它不是象限角,不属于任何象限,②错误;③角的度量是角所在扇形中它所对的弧长与相应半径的比值,与扇形半径无关,③正确④与的正弦值相等,但它们终边关于轴对称,④错误;⑤余弦值小于零,的终边在第二或第三象限或非正半轴上,⑤错误.故答案为③69.已知扇形的圆心角为,周长为,则扇形的面积为______ .解:设扇形的半径为,圆心角为,弧长,此扇形的周长为,,解得:,则扇形的面积为.故答案为.70.地球的北纬线中国段被誉为中国最美风景走廊,东起舟山东经,西至普兰东经,“英雄城市”武汉东经也在其中,假设地球是一个半径为的标准球体,某旅行者从武汉出发,以离普兰不远的冷布岗日峰东经为目的地,沿纬度线前行,则该行程的路程为__________用含的代数式表示【解答】解:地球半径为,所以北纬的纬度圈半径为,因为武汉和冷布岗日峰的经度分别为东经和东经,相差,即,所以两地在北纬的纬线长是.故答案为.71.如图,在平面直角坐标系中,以轴正半轴为始边的锐角的终边与单位圆交于点,且点的纵坐标是.求的值;若以轴正半轴为始边的钝角的终边与单位圆交于点,且点的横坐标为,求的值.【参考答案】解:因为锐角的终边与单位圆交于点,且点的纵坐标是,所以由任意角的三角函数的定义可知.从而.,.因为钝角的终边与单位圆交于点,且点的横坐标是,所以,从而.于是.因为为锐角,为钝角,所以,从而.72.如图,有一块扇形草地,已知半径为,,现要在其中圈出一块矩形场地作为儿童乐园使用,其中点、在弧上,且线段平行于线段若点为弧的一个三等分点,求矩形的面积;当在何处时,矩形的面积最大?最大值为多少?【参考答案】解:如图,作于点,交线段于点,连接、,,,,,,设,则,,,,,,即时,,此时在弧的四等分点处.73.如图,圆的半径为,,为圆上的两个定点,且,为优弧的中点,设,在右侧为优弧不含端点上的两个不同的动点,且,记,四边形的面积为.求关于的函数关系;求的最大值及此时的大小.解:如下图所示:圆的半径为,,为圆上的两个定点,且,,到的距离,若,则,到的距离,故令则,,的图象是开口朝上,且以直线为对称的抛物线,故当,即时,取最大值.74.如图,在中,,,为,,所对的边,于,且.求证:;若,求的值.【参考答案】证明:,,,,,在直角三角形中,,在直角三角形中,,则,即,,,由此即得证.解:,,,则,由知,,故的值为.75.已知角的终边经过点.求的值;求的值.【参考答案】解:Ⅰ因为角终边经过点,设,,则,所以,,..Ⅱ.76.已知向量,.当时,求的值;若,且,求的值.【参考答案】解:首先,.当时,.由知,.因为,得,所以.所以.77.如图,在平面直角坐标系中,以轴为始边做两个锐角,它们的终边分别与单位圆相交于、两点,已知、的横坐标分别为求的值;求的值.【参考答案】解:由已知得,,,因为为锐角,故,从而,同理可得,因此,,所以,,又,,,得.78.已知化简若是第二象限角,且,求的值.【参考答案】解:.是第二象限角,且,,是第二象限角,.79.如图,某市拟在长为的道路的一侧修建一条运动赛道,赛道的前一部分为曲线段,该曲线段为函数的图象,且图象的最高点为;赛道的后一部分为折线段,为保证参赛运动员的安全,限定.求,的值和,两点间的距离;应如何设计,才能使折线段最长?【参考答案】解:因为图象的最高点为,所以,由图象知的最小正周期,又,所以,所以,所以,,故,两点间的距离为,综上,的值为,的值为,,两点间的距离为;在中,设,因为,故,由正弦定理得,所以,.设折线段的长度为,则,所以的最大值是,此时的值为.故当时,折线段最长.80.已知函数.Ⅰ求的最小正周期;Ⅱ求在区间上的最大值和最小值.【参考答案】解:Ⅰ,所以的最小正周期为.Ⅱ因为,所以.于是,当,即时,取得最大值;当,即时,取得最小值.81.已知函数求函数的最小正周期;若函数对任意,有,求函数在上的值域.【参考答案】解:,的最小正周期;函数对任意,有,,当时,则,则,即,解得.综上所述,函数在上的值域为:.82.已知向量,.当时,求的值;设函数,且,求的最大值以及对应的的值.【参考答案】解:因为,所以,因为否则与矛盾,所以,所以;,因为,所以,所以当,即时,函数的最大值为.83.已知函数.求的值;从①;②这两个条件中任选一个,作为题目的已知条件,求函数在上的最小值,并直接写出函数的一个周期.【参考答案】解:Ⅰ由函数,则;Ⅱ选择条件①,则的一个周期为;由;,因为,所以;所以,所以;当,即时,在取得最小值为.选择条件②,则的一个周期为;由;因为,所以;所以当,即时,在取得最小值为.,,84.已知函数.求函数的最小正周期和单调递增区间;若存在满足,求实数的取值范围.【参考答案】解:,函数的最小正周期.由,得,的单调递增区间为.当时,可得:,令.所以若存在,满足,则实数的取值范围为.85.已知函数.求函数的单调减区间;将函数的图象向左平移个单位,再将所得的图象上各点的横坐标缩短为原来的倍,纵坐标不变,得到函数的图象,求在上的值域.【参考答案】解:函数,当,解得:,因此,函数的单调减区间为;将函数的图象向左平移个单位,得的图象,再将所得的图象上各点的横坐标缩短为原来的倍,纵坐标不变,得到函数的图象,,,故的值域为.86.函数的部分图象如图所示.求的解析式;设,求函数在上的最大值,并确定此时的值.【参考答案】解:由图知,,则,,,,,,,,的解析式为;由可知:,,,,当即时,.87.已知函数的一系列对应值如下表:根据表格提供的数据求函数的一个解析式.根据的结果,若函数周期为,当时,方程恰有两个不同的解,求实数的取值范围.【参考答案】解:设的最小正周期为,则,由,得.又由解得令,即,解得,.函数的最小正周期为,且,.令.,,的图像如图.在上有两个不同的解时,,方程在时恰有两个不同的解,则,即实数的取值范围是.88.已知函数的部分图象如图所示.求函数的解析式;求函数在区间上的最大值和最小值.【参考答案】解:由题意可知,,,得,解得.,即,,,所以,故;当时,,得;当时,即有时,函数取得最小值;当时,即有时,函数取得最大值.故,;89.已知函数.求的值;当时,不等式恒成立,求实数的取值范围.【参考答案】解:Ⅰ,.Ⅱ,..由不等式恒成立,得,解得.实数的取值范围为.90.设函数,.已知,函数是偶函数,求的值;求函数的值域.【参考答案】解:由,得,为偶函数,,,或,,,,,函数的值域为:.高考真题91.(2016山东)设.求的单调递增区间;把的图象上所有点的横坐标伸长到原来的倍纵坐标不变,再把得到的图象向左平移个单位,得到函数的图象,求的值.【参考答案】解:由,由,得,所以的单调递增区间是.由知,把的图象上所有点的横坐标伸长到原来的倍纵坐标不变,得到的图象,再把得到的图象向左平移个单位,得到的图象,即.所以.92.(2020安徽)在平面四边形中,,,,.求;若,求.解:,,,.由正弦定理得:,即,,,,.,,,.93.(2105重庆)已知函数求的最小正周期和最大值;讨论在上的单调性.【参考答案】解:.所以的最小正周期,当时,最大值为.当时,有,从而时,即时,单调递增,时,即时,单调递减,综上所述,单调增区间为,单调减区间为94.(2020上海)已知.求的值求的值.【解答】解:原式原式.95.(2017山东)设函数,其中,已知.Ⅰ求;Ⅱ将函数的图象上各点的横坐标伸长为原来的倍纵坐标不变,再将得到的图象向左平移个单位,得到函数的图象,求在上的最小值.解:Ⅰ函数,又,,,解得,又,Ⅱ由Ⅰ知,,,将函数的图象上各点的横坐标伸长为原来的倍纵坐标不变,得到函数的图象;再将得到的图象向左平移个单位,得到的图象,函数当时,,,当时,取得最小值是.96(2019上海)已知等差数列的公差,数列满足,集合.若,求集合;若,求使得集合恰好有两个元素;若集合恰好有三个元素:,是不超过的正整数,求的所有可能的值.【参考答案】解:等差数列的公差,数列满足,集合.当,集合,数列满足,集合恰好有两个元素,如图:根据三角函数线,①等差数列的终边落在轴的正负半轴上时,集合恰好有两个元素,此时,②终边落在上,要使得集合恰好有两个元素,可以使,的终边关于轴对称,如图,,此时,综上,或者.①当时,,数列为常数列,仅有个元素,显然不符合条件;②当时,,,数列的周期为,中有个元素,显然不符合条件;③当时,,集合,情况满足,符合题意.④当时,,,,,或者,,当时,集合,符合条件.⑤当时,,,,,或者,,因为,取,,集合满足题意.⑥当时,,,所以,,或者,,,取,,,满足题意.⑦当时,,,所以,,或者,,,故取,,,,当时,如果对应着个正弦值,故必有一个正弦值对应着个点,必然存在,有,,,,,不符合条件.当时,如果对应着个正弦值,故必有一个正弦值对应着个点,必然存在,有,,不是整数,不符合条件.当时,如果对应着个正弦值,故必有一个正弦值对应着个点,必然存在,有或者,,或者,此时,均不是整数,不符合题意.综上,,,,.97.(2017全国)已知集合是满足下列性质的函数的全体:存在非零常数,对任意,有成立.函数是否属于集合?说明理由;设函数,且的图象与的图象有公共点,证明:;若函数,求实数的取值范围.【参考答案】解:对于非零常数,,.因为对任意,不能恒成立,所以;因为函数且的图象与函数的图象有公共点,所以方程组:有解,消去得,显然不是方程的解,所以存在非零常数,使.于是对于有故;当时,,显然.当时,因为,所以存在非零常数,对任意,有成立,即.因为,且,所以,,。
2022年高考数学三角函数大题精品专题专练(word版)01面积问题1

面积问题11.在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c ,且2(cos )b a C -=. (Ⅰ)求A ;(Ⅱ)若2a =,求ABC ∆面积的最大值.解:(Ⅰ)由正弦定理得2(sin sin cos )B A C C -=,又 sin sin()sin cos cos sin B A C A C A C =+=+,2cos sin A C C ∴,又sin 0C ≠,2cos A ∴=,cos A ∴= 故在ABC ∆中,30A =︒;(Ⅱ)由余弦定理得:2222cos a b c bc A =+-,222242cos30(23)b c bc b c bc ∴=+-︒=+-,44(223bc ∴=+-,ABC ∴∆面积11sin 2324S bc A bc ==+.故ABC ∆面积的最大值为2+. 2.在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c ,sin cos()6b A a B π=-. (1)求角B 的大小;(2)若b =ABC ∆面积的最大值.解:(1)由正弦定理得sin sin sin cos()6B A A B π=-, 由于0A π<<,sin 0A ≠,所以1sin cos()sin 62B B B B π=-=+,即1sin 2B B ,则tan B 0B π<<,所以3B π=.(2)由余弦定理,得22122c a ca ac ca ac =+--=(当且仅当a c =时,取“=” ), 从而1sin 3323S ca π=,所以ABC ∆的面积取得最大值3.如图所示,在梯形ABCD 中,//AB CD ,2BAD π∠=,点E 是AD 上的一点,24DE AE ==,2cos cos cos BC BEC BE EBC CE ECB ∠=∠+∠. (1)求BEC ∠的大小;(2)若BCE ∆的面积S 为83,求BC .解:(1)2cos cos cos BC BEC BE EBC CE ECB ∠=∠+∠,22222222BE BC CE CE BC BE BE CE BC BE BC CE BC+-+-=⋅+⋅=⋅⋅, 所以1cos 2BEC ∠=,即3BEC π∠=; (2)设AEB α∠=,则23DEC πα∠=-,2(0)3πα<<, 因为24DE AE ==,所以2cos cos AE DE αα==,422cos()cos()33DE CE ππαα==--, BCE ∆的面积12383sin 8323cos cos()2sin(2)136S BE CE πππααα=⋅⋅==--- 所以sin(2)16πα-=,即262ππα-=, 所以3πα=,此时4BE =,8CE =,BCE ∆中,由余弦定理得2222cos BC BE CE BE CE BEC =+-⋅∠, 11664248482=+-⨯⨯⨯=. 故43BC =4.已知平面四边形ABCD 内接于圆O ,3AB BC ==,60ABC ∠=︒.(1)若3CD ,求ABD ∠所对的圆弧AD 的长;(2)求四边形ABCD 面积的最大值.解:(1)连接AC ,3AB BC ==,60ABC ∠=︒,ABC ∴∆为等边三角形,3AC =,平面四边形ABCD 内接于圆O ,180ABC ADC ∴∠+∠=︒(四点共圆),120ADC ∴∠=︒,由余弦定理可得,2222AD DC AC AD DC +-=⋅.COS ADC ∠, ∴3AD ,设ABC ∆的外接圆半径为R ,2sin ACR ABC =∠,3AC =,60ABC ∠=︒3R ∴OAD ∴∆为等边三角形,∴圆弧AD 所对于应的角3πα=,333AD R ππα==.(2)在ACD ∆中,2222AD DC AC AD DC ADC +-=⋅⋅∠, 120ADC ∠=︒,3AC =,229AD DC AD CD ∴+=-⋅,222AD CD AD CD +⋅,3AD CD ∴⋅,当且仅当3AD CD == ∴四边形ABCD 面积1111sin 60sin1203332222ABC ACD S S S AB BC AD DC =+=⋅⋅︒+⋅⋅︒⨯⨯⨯= ∴四边形ABCD 面积S =5.在ABC ∆中,a ,b ,c 分别是角A ,B ,C的对应边,已知cos cos a C b c A =+.(1)求A ;(2)若sin()B A -=,c =ABC ∆的面积. 解:(1)cos cos a C b c A =+,由正弦定理可得:sin cos sin sin cos A C CB C A =+, 又A B C π++=,sin sin[()]sin()B A C A Cπ∴=-+=+,∴sin cos sin cos cos sin sin cos A C C A C A C CA =++, ∴2sin cos C C A =,又(0,)C π∈,sin0C ∴>, ∴cosA = (0,)A π∈,∴4A π=.(2)sin()B A -=,即sin()4Bπ-=, 304B π<<,可得442B πππ-<-<,∴cos()4B π-==, ∴sinsin()sin()sin[()]cos()4424CA B B B Bππππ=+=+=-+=-= 又∴sin sin[()])cos()]4444B B B B ππππ=-+=-+-==, 在ABC ∆中,由正弦定理可知:25sin c R C ===, ∴52R =,(其中R 为ABC ∆外接圆半径),∴221523102515sin 2sin sin sin 2()2221052ABC S ab C R A B C ∆===⨯⨯⨯⨯=. 6.(1)如图,在直径为10cm 的轮子上有一长为6cm 的弦,P 是弦的中点,轮子以4弧度/秒的速度旋转,求点P 经过5s 所转过的弧长. (2)在ABC ∆中,已知1tan 2A =,1tan 3B =且最长边为1,求ABC ∆的面积.解:(1)因为P 是弦的中点,所以OP AB ⊥,因为10AO cm =,6AB cm =,所以4OP cm =, 因为轮子以4弧度/秒的速度旋转,选择5s ,所以所转过的弧长45480l cm cm =⨯⨯=;(2)因为1tan 2A =,1tan 3B =,所以tan tan tan tan()1tan tan 1A BC A B A B +=-+==--, 所以34C π=, 所以C ∠为最大角,所以1c =,由1tan 2A =,1tan 3B =可得5sin A =,10sin B =, 由正弦定理可得sin sin sin a b c A B C ==,所以sin sin c A a C =,sin sin c B b C =, 所以ABC ∆的面积251011sin sin sin sin 1510sin 22sin sin 2sin 1022c A c B c A B S ab C C C C ==⨯⨯===⨯. 7.如图,半圆O 的直径为2cm ,A 为直径延长线上的-点,2OA cm =,B 为半圆上任意一点,以AB 为一边作等边三角形ABC .设AOB α∠=.(1)当3πα=时,求四边形OACB 的周长;(2)点B 在什么位置时,四边形OACB 的面积最大?最大值为多少?解:(1)在OAB ∆中,由余弦定理得2222cos 14212cos 33AB OA OB OA OB πα=+-⋅=+-⨯⨯=, 即3AB =,于是四边形OACB 的周长为421343353OA OB AB AB +++=+++=+;(2)在OAB ∆中,由余弦定理得2222cos 14212cos 54cos AB OA OB OA OB ααα=+-⋅=+-⨯⨯⨯=-, 所以54cos AB α=-,0απ<<,于是四边形OACB 的面积为2133sin sin (54cos )244AOB ABC S S S OA OB AB ααα∆∆=+=⋅+=+- 5353sin 3cos 2sin()434πααα=-+=-+, 当32ππα-=,即56πα=时,四边形OACB 的面积取得最大值5324+. 8.已知ABC ∆中,3sin cos AC A BC B ⋅=⋅. (Ⅰ)求B 的大小;(Ⅱ)已知3C π=,1003AB =,若D 、E 是边BC 上的点,使6DAE π∠=,求当ADE ∆面积的最小时,BAD∠的大小.解:(Ⅰ)3sin cos AC A BC B ⋅=⋅, ∴3sin sin sin cos B A A B ⋅=⋅,(0,)A π∈,sin 0A ∴≠,得3tan B =,又(0,)B π∈,6B π∴=; (Ⅱ)由(Ⅰ)知,6B π=,又3C π=,ABC ∴∆为直角三角形,且2BAC π∠=,AB =100AC ∴=,设BAD α∠=,[0α∈,]3π, 则56BDA πα∠=-,在ABD ∆中,由5sin sin()66AD AB ππα=-,得sin()6AD α=-, 由3CAE πα∠=-,3C π∠=,得3AEC πα∠=+, 在ACE ∆中,由sin sin()33AEAC ππα=+,得sin()3AE α=+,由11sin 24ADE S AD AE DAE ∆=⋅⋅∠==. [0α∈,]3π,2[0α∴∈,2]3π,可得当sin 21α=,即4πα=时,S 取得最小值, 故当ADE ∆面积的最小时,4BAD π∠=.。
最全三角函数概念综合训练完整版.doc

三角函数综合训练一、 教材分析:三角函数作为高中数学的重要内容,其变换手段丰富多彩,所涉及到的数学 想,数学方法趣味横生在高考,会考中都把考查学生驾驭数字思想方法的能力放在首位。
本章涉及的数学思想和方法主要有:(1)数形结合的思想。
(2)函数与方程的思想。
(3)转化的思想。
(4)消之的思想。
(5)换元法。
(6)构造法等。
二、 基础训练题: 1.选择题(1)角α的终边与角β的终边关于y 轴对称,则β为( )A.-αB.л-αC.(2k л+1)л-α(k ∈Z)D.k л-α(k ∈Z ) (2)若sin αtg α≥0,k ∈Z ,则角α的集合为( ) A .[2k л-2л,2k л+л] B.(2k л-2л,2k л+2л) C.(2k л-2л,2k л+2л)∪}{лл-k 2 D.以上都不对(3)已知集合M=}{R x x x y y ∈+=,cos sin ,N=}{R x x x y y ∈=,cos sin л则MUN 等于( )A .M B.N C.ф D.}{22≤≤-y y(4)下列四个命题中的假命题是( )A. 存在这样的α和β的值,使得cos(α+β=cos αcos β+sin αsin βB. 不存在无数个α和β的值, 使得cos(α+β)=cos αcos β+sin αsin βC. 对于任意的α和β的值,使得cos(α+β)=cos αcos β-sin αsin βD. 不存在这样的α和β的值,使得cos(α+β)≠cos αcos β-sin αsin β(5)若cos(A+B)cos(A-B)-sin(A+B)sin(A-B)=53,A ∈(0,2л),则tgA=( ) A.2 B.21 C.-2 D.-21(6)若sin α+cos α=2,则tg α+ctg α=( )A.1B.2C.-1D.-2(7)已知α,β为锐角,且tg α=71,sin β=53,则α+β等于( ) A.43лB.32л C 4л D.3л(8)已知sin α+sin β=1,cos α+cos β=0,那么cos2α+cos2β等于( ) A.1 B.23 C.32 D.43 (9)当0<x <л时,则方程cos (лcosx)=0的解集为( )A. ⎭⎬⎫⎩⎨⎧65,6лл B.⎭⎬⎫⎩⎨⎧32,3лл C.⎩⎨⎧⎭⎬⎫3л D.⎩⎨⎧⎭⎬⎫32л (10)下列四个值:sin3,cos3,tg3,ctg3的大小关系是( )A.cos3<tg3<ctg3<sineB.sin3>cos3>tg3>ctg3C.ctg3<tg3<cos3<sin3D.sin3>tg3>cos3>ctg3 (11)已知2л<α<л<,sin α=54,则cos 2α的值为( ) A.25或-55 B.- 55 C. 55 D.以上都不对(12)在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,已知c=3,∠C=60°,a+b=5,则2BA -等于( ) A .125 B.65 C.43 D.32 (13)△ABC 中,A=60°,b=1,这个三角形的面积为3,则△ABC 外接圆的直径为( ) A.33 B.3326 C.3392 D.239(14)在Rt △ABC 中,C=90°,则sinAcos2(45°-2B )-sin 2A cos 2AA.有最大值41和最小值0B.有最大值41但无最小值C.即无最大值也无最小值D.有最大值21但无最小值(15)函数y=θθsin 2cos 52-在区间(0,л)上的最小值为( )A.223 B.2 C.1 D.25(16)若0≤x ≤2л,则y=7sinx+3cosx 的最小值是( ) A.1 B.2 C.7 D.0(17)已知函数f (x)=3sin 22xл+1,使得f (x+c)=f (x)成立c 的最小正整数为( )A.1B.2C.4D.以上都不对 (18)若θ是第四限的角,且sin θ=-54,那么2θ是( ) A.第一象限的角 B.第二象限的角 C.第三象限的角 D.第四象限的角(19)函数y=xxx sin 1cos sin 22+的值是( )A.y ≤21 B.-4≤y ≤21 C.y ≥-4 D.-4<y ≤21 (20)要得到y=sin2x 的图象,只需将y=cos(2x-4л)的图象 ( )A.向右平移8лB.向左平移8лC.向右平移4лD.向左平移4л(21)函数y=cos 2(x-12л+sin 2(x+12л)-1是( ) A.周期为2л的奇函数 B .周期为л的偶函数C.周期为л的奇函数D.周期为2л的偶函数 (22)设方程cos2x+3sin2x=α+1,d [0,2л]上有两个不同的实数角,则α的取值范围是( )A.[-3,1]B.[-л1]C.[0,1]D.[0,1] 2.填空题:(1)已知θ=5л,则tg `3433343θθθθtg tg tg ++= . (2)计算sin 10лsin 1013л= .(3)若f (tgx)=x sin ,则f (ctgx)= .(4)已知α=arcsin 426+则cos2α= . (5)在△ABC 中,sin2sin 2sin 2C B A =81,则△ABC 的形状为 . (6)直角三角形的周长为定值2l ,则斜边的最小值是 .(7)已知sin(4л+α)sin(4л-α)=61,α∈(2л,л),则sin4α= . (8)已知x ∈(0, 2л),则下面四式:①sinx <x <tgx ②sin(cosx)<cosx <cos(sinx)③sin 3x+cos 3x <1 ④cos(sinx)<sin(cosx)<cosx 中正确命题的序号是 .(9)︒︒-︒20cos 10sin 310cos 22 .(10)[2sin50°+sin10°(+3tg10°)]︒+20cos 1= . 3.解答题(1) 求函数y=2cos θsin θ-cos θ-sin θ(θ∈[0,л])的值域(2) 已知tg α=log 3525,tg β=log 725,求2sin(α-β)+sin α+sin β的值(3) 改sinA=asinB,cosA=bcosB,A 、B 为锐角且a >1,0<b <1,求tgAr 的值 (4) 已知0<α<л,0<β<л,tg αtg β是方程x 2+5x+6=0的两根。
(完整版)三角函数综合测试题(含答案)(3),推荐文档

三角函数综合测试题一、选择题(每小题5分,共70分)1. sin2100 =A .B . -C .D . -232321212.是第四象限角,,则 α5tan 12α=-sin α=A . B . C .D .1515-513513-3. =12sin12(cos ππ-12sin12(cosππ+ A .-B .-C .D .232121234. 已知sinθ=,sin2θ<0,则tanθ等于53 A .- B .C .-或D .43434343545.将函数的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再sin(3y x π=-将所得的图象向左平移个单位,得到的图象对应的僻析式是3πA .B . 1sin2y x =1sin(22y x π=-C . D .1sin(26y x π=-sin(26y x π=-6. ()2tan cot cos x x x +=A .B .C .D . tan x sin x cos x cot x 7.函数y = 的值域是xx sin sin-A. { 0 } B. [ -2 , 2 ]C. [ 0 , 2 ]D.[ -2 , 0 ]8.已知sin cos ,且,则sin +cos 的值为α81=α)2,0(πα∈ααA.B. -C.D.2525±25239. 是2(sin cos )1y x x =--A .最小正周期为的偶函数B .最小正周期为的奇函数2π2πC .最小正周期为的偶函数D .最小正周期为的奇函数ππ10.在内,使成立的取值范围为)2,0(πx x cos sin >x A . B .C .D .)45,()2,4(ππππ ),4(ππ45,4(ππ23,45(),4(ππππ 11.已知,函数y =2sin(ωx +θ)为偶函数(0<θ<π) 其图象与直线y =2的交点的横坐标为x 1,x 2,若| x 1-x 2|的最小值为π,则A .ω=2,θ=B .ω=,θ=C .ω=,θ=D .ω=2,θ=2π212π214π4π12. 设5sin7a π=,2cos 7b π=,2tan 7c π=,则A .a b c << B .a c b << C .b c a <<D .b a c<<13.已知函数的图象关于直线对称,则可能是()sin(2)f x x ϕ=+8x π=ϕA .B .C .D .2π4π-4π34π14. 函数f (x )=xxcos 2cos 1- A .在 、上递增,在、上递减⎪⎭⎫⎢⎣⎡20π,⎥⎦⎤ ⎝⎛ππ,2⎪⎭⎫⎢⎣⎡23,ππ⎥⎦⎤ ⎝⎛ππ2,23B .在、上递增,在、上递减⎪⎭⎫⎢⎣⎡20π,⎥⎦⎤ ⎝⎛23ππ,⎥⎦⎤ ⎝⎛ππ,2⎥⎦⎤ ⎝⎛ππ223,C .在、上递增,在、 上递减⎪⎭⎫⎢⎣⎡ππ,2⎥⎦⎤ ⎝⎛ππ223⎪⎭⎫⎢⎣⎡20π,⎥⎦⎤⎝⎛23ππ,D .在、上递增,在、上递减⎪⎭⎫⎢⎣⎡23,ππ⎥⎦⎤⎝⎛ππ2,23⎪⎭⎫⎢⎣⎡20π,⎥⎦⎤⎝⎛ππ,2二.填空题(每小题5分,共20分,)15. 已知,求使sin =成立的= ⎪⎭⎫⎝⎛-∈2,2ππαα32α16.sin15°cos75°+cos15°sin105°=_________17.函数y=Asin(x+)(>0,||< ,x ∈R )的部分图象如图,ωϕωϕ2π则函数表达式为 18.已知为锐角,且cos = cos = , 则cos =_________βα,α71)(βα+1411-β19.给出下列命题:(1)存在实数,使 (2)存在实数,使α1cos sin=ααα23cos sin=+αα(3)函数是偶函数 (4)若是第一象限的角,且,则)23sin(x y +=πβα、βα>.其中正确命题的序号是________________________________βαsin sin >三.解答题(每小题12分,共60分,)20.已知函数y =3sin 421(π-x (1)用五点法在给定的坐标系中作出函数一个周期的图象;(2)求此函数的振幅、周期和初相;(3)求此函数图象的对称轴方程、对称中心.21.已知 )cos(2-)sin(πθπθk k +=+Z k ∈求:(1);(2)θθθθsin 3cos 5cos 2sin 4+-θθ22cos 52sin 41+22.设,若的最大值为0,最小值为-4,试求与的值,0≥a b x a x y +-=sin cos 2a b并求的最大、最小值及相应的值.y x 23.已知,,且,求的值.21)tan(=-βα71tan -=β),0(,πβα∈βα-224.设函数(其中>0,),且f (x )的图象在a x x x x f ++=ωωωcos sin cos 3)(2ωR a ∈y 轴右侧的第一个最高点的横坐标为.6π(1)求的值;ω(2)如果在区间的最小值为,求的值.)(x f 65,3[ππ-3a 测试题答案.一.DDDA,CDDA,DCAD,CA二arcsin1 y=(3)32)48sin(4-ππ+x 21三、解答题:20.已知函数y=3sin 421(π-x (1)用五点法作出函数的图象;(2)求此函数的振幅、周期和初相;(3)求此函数图象的对称轴方程、对称中心.解 (1)列表:x2π23π25π27π29421π-x 02πππ232π3sin 421(π-x 030-3描点、连线,如图所示:…………………………………………………………………………………………5(2)周期T===4,振幅A=3,初相是-. ωπ2212ππ4π………………………………………………………….8(3)令=+k (k ∈Z ),421π-x 2ππ得x=2k +(k ∈Z ),此为对称轴方程.π23π令x-=k (k ∈Z )得x=+2k (k ∈Z ).214ππ2ππ对称中心为)0,22(ππ+k (k ∈Z )…………………………………………………………………………..1221.已知sin(+k )=-2cos(+k ) (k ∈Z ).θπθπ求:(1);θθθθsin 3cos 5cos 2sin 4+-(2)sin 2+cos 2.41θ52θ解:由已知得cos(+k )≠0,θπ∴tan(+k )=-2(k ∈Z ),即tan =-θπθ2..................................................................................................2(1)………………………………………………………………10tan 352tan 4sin 3cos 5cos 2sin 4=+-=+-θθθθθθ…7(2)sin 2+cos 2==………………………………….1241θ52θθθθθ2222cos sin cos 52sin 41++2571tan 52tan 4122=++θθ22.设a≥0,若y =cos 2x -asinx +b 的最大值为0,最小值为-4,试求a 与b 的值,并求出使y 取得最大、最小值时的x 值.解:原函数变形为y =- (2)412(sin 22a b a x ++++∵-1≤sinx≤1,a≥0∴若0≤a≤2,当sinx =-时2a y max =1+b +=0①42a 当sinx =1时,y min =-41)21(22a b a ++++=-a +b =-4 ②联立①②式解得a =2,b =-2…………………………………………………………7y 取得最大、小值时的x 值分别为:x =2kπ-(k ∈Z),x =2kπ+(k ∈Z)2π2π若a >2时,∈(1,+∞)2a ∴y max =-=0 ③b a a b a +=+++-41)21(22y min =- ④441)21(22-=+-=++++b a a b a 由③④得a =2时,而=1 (1,+∞)舍去 (112)a 故只有一组解a =2,b =-2 (12)23.已知tan(α-β)=,β=-,且α、β∈(0,),求2α-β的值.21tan 71π解:由tanβ=- β∈(0,π) 得β∈(, π)① (2)712π由tanα=tan[(α-β)+β]= α∈(0,π)∴310<α< (6)2π∴ 0<2α<π由tan2α=>0∴知0<2α<②432π∵tan(2α-β)==1 (10)βαβαtan 2tan 1tan 2tan +-由①②知 2α-β∈(-π,0)∴2α-β=- (124)3π24.设函数(其中ω>0,a ∈R ),且f(x)的图象在y a x x x x f ++=ϖϖϖcos sin cos 3)(2轴右侧的第一个最高点的横坐标为.6π(1)求ω的值;(2)如果在区间的最小值为,求a 的值.)(x f 65,3[xπ-3解:(1) f(x)=cos2x +sin2x ++a……………………………….223ω21ω23=sin(2x +)++a…………………………………………………..4ω3π23依题意得2·+=解得= (6)ω6π3π2πω21(2) 由(1)知f(x)=sin(2x +)++a ω3π23又当x ∈时,x +∈…………………………………8⎦⎤⎢⎣⎡-65,3ππ3π⎥⎦⎤⎢⎣⎡67,0π故-≤sin(x +)≤1 (10)213π从而f(x)在上取得最小值-++a ⎥⎦⎤⎢⎣⎡-65,3ππ2123因此,由题设知-++a =故a = (122)1233213+。
(完整word版)精选三角函数解答题30道带答案

三角函数综合练习三学校:___________姓名:___________班级:___________考号:___________一、解答题1(0ω>) (1)求()f x 在区间 (2)将函数()f x 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得个单位,得到函数()g x 的图象,若关于x 的方程()0g x k +=在区上有且只有一个实数根,求实数k 的取值范围. 2.其中,m x R ∈.(1)求()f x 的最小正周期;(2)求实数m 的值,使函数()f x 的值域恰为并求此时()f x 在R 上的对称中心.3 (1)求)(x f 的最小正周期;(2. 4 (1)求()f x 的最小正周期;(2)求()f x 在区间 5.已知函数.(1)求最小正周期; (2)求在区间上的最大值和最小值.6 (1)求()f x 的最小正周期;(2)若将()f x 的图象向右平移个单位,得到函数()g x 的图象,求函数()g x 在区间[]0,π上的最大值和最小值.7 (Ⅰ)(Ⅱ)8(1)求()f x 的定义域与最小正周期;(2求α的大小.9, x R ∈(1)求函数()f x 的最小正周期及在区间 (2,求0cos 2x 的值。
10.(本小题满分12 (1)求()f x 单调递增区间;(2)求()f x 在.11 (Ⅰ)求)(x f 的最小正周期;(Ⅱ)求)(x f 在.12 (I )求()f x 的最小正周期及其图象的对称轴方程;(II )将函数()f x 的图象向右平移个单位长度,得到函数()g x 的图象,求()g x 在的值域.13 (1)求()f x 的最小正周期;(2)求()f x 在区间 14(其中x ∈R ),求: (1)函数()f x 的最小正周期;(2)函数()f x 的单调区间;15 (1)求函数()f x 的最小正周期和图象的对称轴方程;(2)求函数()f x 在区间16 (1及()f x 的单调递增区间; (2)求()f x 在闭区间17(1(2成立的x 的取值集合.18 (Ⅰ)求函数()f x 的单调递减区间;19 (Ⅰ)求函数)(x f 的最小正周期T 及在],[ππ-上的单调递减区间;(Ⅱ)若关于x 的方程0)(=+k x f ,在区间上且只有一个实数解,求实数k 的取值范围.20 (1)求函数)(x f 的最小正周期和单调递减区间;(2)若将函数)(x f 的图象向左平移)0(>m m 个单位后,得到的函数)(x g 的图象关于轴对称,求实数m 的最小值.21(x R ∈). (1)求函数()f x 的最小正周期和单调减区间;(2)将函数()f x 的图象向右平移个单位长度后得到函数()g x 的图象,求函数()g x22(1)求函数()f x 的最小正周期;(2)求函数()f x 取得最大值的所有x 组成的集合.23 (Ⅰ)求()f x 的最小正周期;(Ⅱ)求()f x 在. 24.已知函数()22sin 2sin cos cos f x x x x x =+-.(Ⅰ)求函数()f x 的最小正周期; 时,求函数()f x 的最大值和最小值. 25.已知函数()()cos sin cos f x x x x =-. (Ⅰ)求函数()f x 的最小正周期; 时,求函数()f x 的最大值和最小值.26(1)求()f x 的周期和单调递增区间;(2)若关于x 的方程()2f x m -=在m 的取值范围.27(1)求函数()y f x =的最大、最小值以及相应的x 的值;(2)若y >2,求x 的取值范围.28 (1)求函数()f x 的最大值;(2)若直线x m =是函数()f x 的对称轴,求实数m 的值.29.函数()2cos (sin cos )f x x x x =+.(1 (2)求函数()f x 的最小正周期及单调递增区间.30 (1)求()f x 的最小正周期和最大值;(2)讨论()f x 在参考答案1.(1(2或1k =-. 【解析】试题分析:(1时,()f x 为减函数⇒所以()f x 的减区间为(2()y g x =的图象与直线y k =-在区间上只有一个交点⇒或1k =-.试题解析:(1因为()f x 的最小正周期为时,()f x 为减函数, 所以()f x 的减区间为 (2)将函数()f x 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到再将的图象向右平移个单位,得到若关于x 的方程()0g x k +=在区间 即函数()y g x =的图象与直线y k =-在区间上只有一个交点, 或1k -=,即或1k =-. 考点:三角函数的图象与性质.2.(1)T π=;(2,Z k ∈∈. 【解析】试题分析:(1)则最小正周期T π=;(2)时,)(x f 值域为]3,[m m +解得函数)(x f 对称中心为,Z k ∈∈. 试题解析:(1)最小正周期T π=;(2考点:三角函数图象的性质.3.(1)π=T ;(2)()f x 在【解析】试题分析:(1)根据正弦二倍角公式、余弦二倍角公式以及两角和的正弦公式可将)(x f 化可得)(x f 的最小正周期为π;(2)进而得)(x f . 试题解析:(1所以f(x)f(x)考点:1、正弦二倍角公式、余弦二倍角公式以及两角和的正弦公式;2、三角函数的周期性及单调性.4.(1)函数的最小正周期为π(2时,)(x f 取最大值2时,)(x f 取得最小值1-【解析】试题分析:(1最小正周期及其图象的对称中心的坐标;(2从而可求求f (x试题解析::(Ⅰ)因为f (x )=4cosxsin (-1=4cosx )-12x-1=2sin (, 所以f (x )的最小正周期为π,由于是,当2;当f (x )取得最小值-1 考点:三角函数的最值;三角函数中的恒等变换应用;三角函数的周期性及其求法【答案】(1)π=T ;(2【解析】试题分析:(1)借助题设条件和两角和的正弦公式化简求解;(2)借助题设条件及正弦函数的有界性求解.试题解析:(1)因()()2sin cos cos 2f x x x x =++考点:三角变换的有关知识及综合运用.6.(1)π;(2)2,1.【解析】试题分析:(1)利用二倍角公式、诱导公式、两角和的正弦函数化为一个角旳一个三角函数的形式,即可求()f x 的最小正周期;(2)将()f x 的图象向右平移求出函数()g x 的解析式, 然后根据三角函数有界性结合三角函数图象求()g x 在区间[]0,π上的最大值和最小值.考点:1、三角函数的周期性;2、三角函数的图象变换及最值.【方法点晴】本题主要考查三角函数的周期性、三角函数的图象变换及最值,属于难题.三角恒等变换的综合应用主要是将三角变换与三角函数的性质相结合,通过和、差、倍角公式的形式再研究其性质,解题时注意观察角、名、结构等特征,注意利用整体思想解决相关问题.7.(Ⅰ)2π(Ⅱ【解析】试题分析:(Ⅰ)先利用二倍角公式、配角公式将函数化为基本三角函数:()fx ,再根据正弦函数性质求周期(Ⅱ))的基础上,利用正弦函数性质求试题解析:(Ⅰ)(1)()f x 的最小正周期为(()f x 取得最小值为:考点:二倍角公式、配角公式8.(1(2 【解析】试题分析:(1)利用正切函数的性质,可求得()f x 的定义域,由其周期公式可求最小正周期;(2)利用同三角函数间的关系式及正弦、余弦的二倍角公式,,从而可求得α的大小. 试题解析:解:(1所以()f x 的定义域为.()f x 的最小正周期为考点:1、两角和与差的正切函数;2、二倍角的正切.9.(1)π=T,()[]2,1-∈xf;(2【解析】试题分析:(1)再利用周,,利用正弦函数图像可得值域;(2)先利用求出,再由角的关系.试题解析:(1所以π=T由函数图像知()[]2,1-∈xf.(2考点:三角函数性质;同角间基本关系式;两角和的余弦公式10.(1(2【解析】试题分析:(1)利用两角和的正弦公式、二倍角公式和辅助角公式,化简(2)试题解析:(1(2)由得f x在,因此,()考点:三角恒等变换,三角函数图象与性质. 11.(I )T π=;(II【解析】试题分析:(I )利用两角和的正弦公式,降次公式,辅助角公式,将函数化简为,由此可知函数最小周期T π=;(II)试题解析:∴()fx 的最小正周期考点:三角恒等变换.12.(I )π=T ,(II【解析】试题分析:(I )利用和差角公式对()x f 可化为:,解出x 可得对称轴方程;(II )由x 的范围可得x 2范围,从而得x 2cos 的范围,进而得()x g 的值域. 试题解析:(1)即函数()x g 在区间考点:(1)三角函数中恒等变换;(2)三角函数的周期;(3)复合函数的单调性.【方法点晴】本题考查三角函数的恒等变换、三角函数的周期及其求法、三角函数的图象变换等知识,熟练掌握有关基础知识解决该类题目的关键,高考中的常考知识点.于三角函数解答题中,当涉及到周期,单调性,单调区间以及最值等都属于三角函数的性质,首先都应把它化为三角函数的基本形式即()ϕω+=x A y sin ,然后利用三角函数u A y sin =的性质求解.13.(1)π=T ;(2) -2.【解析】 试题分析:(1)首先将函数进行化简,包括两角和的正弦公式展开,以及二倍角公式以及x x 2cos 1cos 22=-,然后合并同类项,最后利用辅助角公式(2. 试题解析:(1)由题意可得∴()f x 的最小正周期为T π=;(2∴()f x 在区间-2. 考点:1.三角函数的恒等变形;2.三角函数的性质.14.(1)π(2【解析】试题分析:f (x )的最小正周期.x 的范围,即可得到f (x )的单调增区间,同理可得减区间试题解析:(1所以()f x 的单调减区间为考点:三角函数中的恒等变换应用;三角函数的周期性及其求法;正弦函数的单调性15.(1)π,(2 【解析】试题分析:(1)先根据两角和与差的正弦和余弦公式将函数()f x 展开再整理, 可将函数化简为()sin y A x ωρ=+的形式, 根据可求出最小正周期, 令求出x 的值即可得到对称轴方程;(2)先根据x 的范围求出, 进而得到函数()f x 在区试题解析:(1(2时,()f x 取最大值1,时,()f x 取最小值所以函数()f x 在区间 考点:1、三角函数的周期性及两角和与差的正弦和余弦公式;2、正弦函数的值域、正弦函数的对称性.16.(1(2)最大值为1,最小值为 【解析】试题分析:(1)将原函数()f x 由倍角公式和辅助角公式,,利用正弦函数的单调递区间求得此函数的单调增区间;(2)先求出,再进一步得出对应的正弦值的取值,可得函数值的取值范围,可得函数最值. 试题解析:(1),则,(2)所以最大值为1,考点:1.三角恒等变换;2.三角函数性质.【知识点睛】本题主要考查辅助角公式及三角函数的性质.对于函数()()sin 0,0y A x A ωϕω=+>>的单调区间的确定,基本思路是把x ωϕ+视做一个整体,解出x 的范围所得区间即为增区间,由x 的范围,所得区间即为减区间.若函数中()0,0A ω><,可用诱导公式先将函数变为()()sin 0,0y A x A ωϕω=--->>,则()()sin 0,0y A x A ωϕω=-->>的增区间为原函数的减区间,减区间为原函数的增区间.17.(1)(2)【解析】试题分析:(1)直接代入解析式即可;(2)由两角差的余弦公式,及正余弦二倍角公式和辅,k Z ∈,从而求解.试题解析:(1(2)f (x )=cos xcos x因f (x )于是2k2x2kk ∈Z. 解得kx <kk ∈Z.故使f (xx 的取考点:1、二倍角公式;2、辅助角公式;3、余弦函数图象与性质. 18.,k Z ∈;(Ⅱ)()f x 取得最大值1,()f x 取得最小值 【解析】试题分析:,k Z ∈,可解得单调减区间;(Ⅱ)最小值.试题解析:,k Z ∈.,k Z ∈.时,()f x 取得最小值时,()f x 取得最大值1. 考点:(1)降幂公式;(2)辅助角公式;(3)函数()ϕω+=x A y sin 的性质.【方法点晴】本题主要考查了三角函数的化简,以及函数()ϕω+=x A y sin 的性质,属于基础题,强调基础的重要性,是高考中的常考知识点;对于三角函数解答题中,当涉及到周期,单调性,单调区间以及最值等都属于三角函数的性质,首先都应把它化为三角函数的基本形式即()ϕω+=x A y sin ,然后利用三角函数u A y sin =的性质求解.19. 【解析】试题分析:(Ⅰ)借助题设条件运用正弦函数的图象和性质求解;(Ⅱ)借助题设条件运用正弦函数的图象建立不等式求解. 试题解析:(Ⅰ)由已知又因为.当0=k 时 当1-=k 时∴函数)(x f 在[]ππ,-的单调递减区间为(Ⅱ) ,0)(=+k x f 在区与2--=∴k y 在区间考点:正弦函数的图象和性质等有关知识的综合运用.【易错点晴】三角函数的图象和性质是高中数学中重要内容,也高考和各级各类考试的重要内容和考点.用问题为背景,要求运用三角变换的公式将其化为k x A y ++=)sin(ϕω的形式,再借助正弦函数的图象和性质求解.解答本题时,首先要用二倍角公式将其化简为再运用正弦函数的图象即可获得答案.这里运用二倍角公式进行变换是解答本题的关键.20.(1)π,(2【解析】试题分析:(1)将展开后再次合并,化简得(2)先按题意平移,得到试题解析:∴函数)(x f 的最小正周期函数)(x f 单调递减.考点:三角函数图象与性质.21.(1)T π=,单调减区间(k Z ∈);(2【解析】试题分析:(1)利用降次公式和两角和的余弦公式,先展开后合并,化简函数,故周期T π=,代入余弦函数单调减区间[]2,2k k πππ-,可求(2)函数()f x 的图象向右平移试题解析:(1(k Z ∈).(2,()g x 在 考点:三角恒等变换、三角函数图象与性质.22.(1)π;(2【解析】试题分析:(1)利用降次公式,和辅助角公式,故周期等于π;(23.试题解析:(1)∴函数()f x 的最小正周期为(2)当()f x 取最大值时,考点:三角恒等变换.23.(I )π;(II )函数()f x 的单调递增区间是 【解析】试题分析:(I数的最小正周期;(II )函数2sin y z =的单调递增区间,即可求解函数的单调递增区间.试题解析:函数2sin y z =的单调递增区间是所以,,()f x . 考点:三角函数的图象与性质.【方法点晴】本题主要考查了三角函数的恒等变换、三角函数的图象与性质及三角函数的单调区间的求解,本题的解答中利用三角恒等变换的公式求解函数的解析式查了学生分析问题和解答问题的能力,以及学生的化简与运算能力. 24.(Ⅰ)π;,最小值1- 【解析】试题分析:(Ⅰ)化简函数解析式,可得最小正周期为π;(Ⅱ)可得()f x 在和1-试题解析:(Ⅰ)()22sin 2sin cos cos f x x x x x =+-sin 2cos2x x =-所以()f x 的最小正周期时,()f x 取得最大值,即0x =时,()f x 取得最小值1-所以()f x 在和1- 考点:三角函数求值.【思路点睛】本题主要考查三角函数恒等变换,考查了)sin(ϕω+=x A y 型函数的图象与性质,属中档题.通过展开三角函数关系式,利用正弦二倍角公式和降幂公式,辅助角公式,由x 的范围求得相位. 25.(Ⅰ)π;(Ⅱ)最大值0,最小值 【解析】试题分析:,可得最小正周期为π;,可得()f x 在最小值分别为0和 试题解析:(Ⅰ)因为()()cos sin cos f x x x x =-所以函数()f x 的最小正周期时,函数()f x 取得最大值0,时,函数()f x 取得最小值所以()f x 在0考点:三角函数求值.【思路点睛】本题主要考查三角函数恒等变换,考查了)sin(ϕω+=x A y 型函数的图象与性质,属中档题.通过展开三角函数关系式,利用正弦二倍角公式和降幂公式,将函数解析式化为y ,再用辅助角公式将函数化简为y ,由x 的范围求得相位的范围,进一.26.(1)周期为π,(2)[]0,1m ∈ 【解析】试题分析:(1)利用倍角公式,两角和的正余弦公式将函数转化为()sin()f x A x bωϕ=++的形式,进一步求函数的周期和单调性;(2得()f x 的取值范围,进一步得2m +的取值范围,可解得实数m 的取值范围.试题解析:(k ∈Z ). (2,所以()f x 的值域为[]2,3.而()2f x m =+,所以[]22,3m +∈,即[]0,1m ∈.考点:1.倍角公式;2.辅助角公式;3.函数()sin()f x A x b ωϕ=++的性质. 27.(1时有最大值3;时,取最小值1-;(2【解析】试题分析:(1)由函数()sin()f x A x k ωϕ=++的最值取值情况求所给函数的最值;(2)对于2y >,利用特殊角的三角函数值与正弦函数的单调性,可将不等式转化为关于x 的不等式,解不等式可得x 的取值范围. 试题解析:(1)设sin (1,此时函数f (x )=2sin (+1取最大值3.当u=2kπx=kπsin (-1,此时函数f (x )=2sin (+1取最小值-1.(2)∵y=2sin((k∈Z)(k∈Z)∴x (k∈Z) 考点:1.()sin()f x A x k ωϕ=++的性质;2.特殊角的三角函数性质.28.(1)最大值是2;(2 【解析】试题分析:(1)从而化简函数解析式,然后利用正弦函数的性质求出函数的最大值;(2)利用sin y x =的对称轴,列出关系式,解出x ,即可求得m 的值.试题解析:(1)所以()f x 的最大值是2.(2而直线x m =是函()y f x =的对称轴,所以 考点:1、诱导公式;2、正弦函数的图象与性质. 【方法点睛】三角函数的性质由函数的解析式确定,在解答三角形函数性质的综合试题时要抓住函数解析式这个关键,在函数解析式较为复杂时要注意使用三角恒等变换公式把函数解析式化为一个角的一个三角函数形式,然后利用正弦(余弦)函数的性质求解.29.(1)2;(2)π, 【解析】试题分析:(1)借助题设直接运用诱导公式化简求解;(2)借助题设条件和二倍角公式求解. 试题解析:(1(2所以()f x 的单调递增区间为 考点:三角函数的图象及诱导公式二倍角公式的运用.30.(1)π,1;(2)()f x 在 【解析】试题分析:(1)()f x 整理得由公式可求得()f x 的周期和最大值;(2)求函数()f x 在R 上的单调区间,分别与.(1)()f x 的最小正周期为π,最大值为1;(2)当()f x 递增时,()k Z ∈,当()f x ()k Z ∈所以,()f x 在 考点:两角的正弦公式;函数sin()y A x ωϕ=+的性质.。
(完整word)三角函数计算题期末复习(含答案),推荐文档

2sin 45 3 tan 30 cos 60 3
30.计算:
2.
31.计算: 2sin 60 3tan 30 2 tan 60 cos 45
试卷第 2 页,总 4 页
…………○…………外…………○…………装…………○…………订…………○…………线…………○………… 学校:___________姓名:___________班级:___________考号:___________
25.计算: 2 sin45°-tan60°·cos30°.
26.计算:
1 1 2
2sin 60
3 20150 .
27.计算: 8 tan 30 cos 60 2sin 45 .
28.计算:
1 2015
sin30
3.140
1 2
1
.
29.计算:2tan45 ∘ + sin60 ∘ - cos30 ∘ .
3
7.计算: 22 2cos30 tan60 3.140 .
8.计算: 2 1 2sin45 8 tan2 60 .
9.计算: 2sin30 ° 2cos45 ° 8 .
10.计算:
(1) sin2 60 cos2 60 ;
(2) 4cos45 tan60 8 12 .
11.计算: sin45 0 1 3 1 cos30 tan60 3 1 . 2
17.(2015 秋•合肥期末)计算:tan260°﹣2sin30°﹣ cos45°.
18.计算:2cos30°-tan45°- 1 tan 602 .
19.(本题满分 6 分)
计算: 22
9
2 cos
60o
1 3
1
(完整word版)三角函数图像与性质试题及配套答案

xO y1 2 3三角函数测试题一、选择题1、函数)32sin(2π+=x y 的图象( )A .关于原点对称B .关于点(-6π,0)对称C .关于y 轴对称D .关于直线x=6π对称 2、函数sin(),2y x x R π=+∈是 ( )A .[,]22ππ-上是增函数 B .[0,]π上是减函数C .[,0]π-上是减函数D .[,]ππ-上是减函数 3、如图,曲线对应的函数是 ( ) A .y=|sin x | B .y=sin |x |C .y=-sin |x |D .y=-|sin x |4.下列函数中,最小正周期为π,且图象关于直线3x π=对称的( ). A 。
)62sin(+=x y B.sin()26x y π=+ C.sin(2)6y x π=- D.sin(2)3y x π=-5.函数)sin(ϕω+=x y 的部分图象如右图,则ω,ϕ可以取的一组值是( )。
A 。
,24ωϕππ== B.,36ωϕππ==C.5,44ωϕππ==D.,44ωϕππ==6。
要得到3sin(2)4y x π=+的图象,只需将x y 2sin 3=的图象( ).A.向左平移4π个单位B.向右平移4π个单位C 。
向左平移8π个单位 D.向右平移8π个单位7。
设tan()2απ+=,则sin()cos()sin()cos()αααα-π+π-=π+-π+( ).A.3 B 。
13C 。
1D 。
1- 8。
A 为三角形ABC 的一个内角,若12sin cos 25A A +=,则这个三角形的形状为( ).A. 锐角三角形B. 钝角三角形C. 等腰直角三角形D. 等腰三角形9.定义在R 上的函数)(x f 既是偶函数又是周期函数,若)(x f 的最小正周期是π,且当[0,]2x π∈时,x x f sin )(=,则5()3f π的值为( ).A.21-B.23 C.23-D 。
2110.函数2cos 1y x =+的定义域是( )。
(word完整版)三角函数综合测试题(含答案),推荐文档

11.B 12.C 13.B 14.D 15.C 16.D 17.B 18.C 二、填空题:把答案填在答题卡相应题号后的横线上(本大题共 5 小题,每小题 3 分,共 15 分).
19.(08 北京卷 9)若角 的终边经过点 P(1, 2) ,则 tan 2 的值为
.
20.(08
江苏卷
1)
f
x
cos
x
6
的最小正周期为
5
,其中
0
,则
=
.
21.(08
辽宁卷
16)设
x
0,
2
,则函数
y
2sin2 x 1 sin 2x
的最小值为
.
22.(08
浙江卷
12)若 sin(
)
3
,则 cos2ຫໍສະໝຸດ _________。2
5
23.(08 上海卷 6)函数 f(x)= 3sin x +sin(2+x)的最大值是
24. 解: y 7 4sin x cos x 4 cos2 x 4 cos4 x
7 2sin 2x 4 cos2 x 1 cos2 x
7 2sin 2x 4 cos2 x sin2 x
7 2sin 2x sin2 2x
1 sin 2x2 6
由于函数 z u 12 6 在1,1中的最大值为
()
A.
B.
2
3
C.
2
D. 2
18.(08 浙江卷 7)在同一平面直角坐标系中,函数 y cos( x 3 )(x [0,2 ]) 的图象 22
和直线 y 1 的交点个数是 2
()
A.0
B.1
C.2
《三角函数练习题》word版

三角函数练习题一、选择题1.函数)352sin(π+x y =的最小正周期是( )A5π B 25π C π2 D π52.函数]),0[)(26sin(2ππ∈-=x x y 为增函数的区间是A ]3,0[πB ]127,12[ππC ]65,3[ππD ],65[ππ3.函数)23sin(2x y -=π的单调递增区间是( )A [])(22,22Z K K K ∈+-ππππ B [])(232,22Z K K K ∈++ππππC [])(1211,125Z K K K ∈+-ππππ D [])(1252,12Z K K K ∈+-ππππ 4.若tan 4f x x π=+()(),则 A 1f -()>f (0)>f (1) B f (0)>f (1)>f (-1)C 1f ()>f (0)>f (-1) D f (0)>f (-1)>f (1) 5.函数x y 2cos =在下列哪个区间上是减函数() A ]4,4[ππ-B ]43,4[ππC ]2,0[πD ],2[ππ6.满足)()(),()(x f x f x f x f =--=+π的函数)(x f 是( )A x x f 2cos )(=B x x f sin )(=C 2sin)(xx f = D x x f cos )(= 7.把函数)42sin(π+=x y 的图象向右平移8π个单位,再把所得图象上各点的横坐标缩短到原来的一半,则所得图象的函数是( ) A )834sin(π+=x y B )84sin(π+=x y C x y 4sin = D x y sin = 8.将函数)3cos(π+=x y 的图象向左平衡移个m 单位)0(>m ,所得图象关于Y 轴对称,则m 的最小值为( )A 1B 2C 3D 49.把函数x x y 2cos 2sin +=的图象适当变动,可以得到x x y 2cos 2sin -= 的图象,这种变动可以沿着X 轴( ) A 向左平移3π B 向右平移4π C 向左平移2π D 向右平移2π10.为了得到函数)62sin(π-=x y 的图象,可以将函数x y 2cos =的图象( )A 向右平移6π个单位长度 B 向右平移3π个单位长度 C 向左平移6π个单位长度D 向左平移3π个单位长度二、填空题11.函数216lg(sin )(x x x f -)+=的定义域是 12.若,3tan =α则2cos sin sin 32+-ααα= 13.00220270sin 30sin 3sin 434sin230sin +++-ππ= 14.函数)42sin(π+=x y 的图象的一条对称轴方程是(写一条即可)三、解答题15(10分)求函数3sin 2cos 2)(2-+=x x x f 的最大值与最小值,并求相应的x 值16(10分)设函数)(),0( )2sin()(x f y x x f =<<-+=ϕπϕ图像的一条对称轴是直线8π=x 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角函数大题综合训练1.已知函数()2sin()cos f x x x π=-.(Ⅰ)求()f x 的最小正周期;(Ⅱ)求()f x 在区间,62ππ⎡⎤-⎢⎥⎣⎦上的最大值和最小值.2.设函数f (x )=cos(2x +3π)+sin 2x .(1)求函数f(x)的最大值和最小正周期.(2)设A ,B ,C 为∆ABC 的三个内角,若cos B =31,1()24c f =-,且C 为锐角,求sin A .3.已知函数2()sin cos cos 2.222x x xf x =+- (Ⅰ)将函数()f x 化简成sin()(0,0,[0,2))A x B A ωϕωϕπ++>>∈的形式,并指出()f x 的周期; (Ⅱ)求函数17()[,]12f x ππ在上的最大值和最小值4.已知函数()2sin cos 442x x x f x =+.(Ⅰ)求函数()f x 的最小正周期及最值;(Ⅱ)令π()3g x f x ⎛⎫=+ ⎪⎝⎭,判断函数()g x 的奇偶性,并说明理由.5.已知函数()cos(2)2sin()sin()344f x x x x πππ=-+-+(Ⅰ)求函数()f x 的最小正周期和图象的对称轴方程(Ⅱ)求函数()f x 在区间[,]122ππ-上的值域6.设2()6cos 2f x x x =-.(Ⅰ)求()f x 的最大值及最小正周期;Ⅱ)若锐角α满足()3f α=-4tan 5α的值.7.已知0αβπ<<4,为()cos 2f x x π⎛⎫=+ ⎪8⎝⎭的最小正周期,1tan 14αβ⎛⎫⎛⎫=+- ⎪ ⎪⎝⎭⎝⎭,,a (cos 2)α=,b ,且m =·a b .求22cos sin 2()cos sin ααβαα++-的值.8.设a ∈R ,f (x )=cos x (a sin x -cos x )+cos 2()π2-x 满足f ()-π3=f (0).求函数f (x )在[]π4,11π24上的最大值和最小值.9.已知函数2π()cos 12f x x ⎛⎫=+ ⎪⎝⎭,1()1sin 22g x x =+.(I )设0x x =是函数()y f x =图象的一条对称轴,求0()g x 的值.(II )求函数()()()h x f x g x =+的单调递增区间.10.已知函数()sin(),f x x ωϕ=+其中0ω>,||2πϕ<(I )若coscos sinsin 0,44ππϕϕ3-=求ϕ的值; (Ⅱ)在(I )的条件下,若函数()f x 的图像的相邻两条对称轴之间的距离等于3π,求函数()f x 的解析式;并求最小正实数m ,使得函数()f x 的图像象左平移m 个单位所对应的函数是偶函数。
11. 已知函数f (x )=)0,0)(cos()sin(3><<+-+ωϕϕωϕωπx x 为偶函数,且函数y =f (x )图象的两相邻对称轴间的距离为.2π(Ⅰ)求f (8π)的值;(Ⅱ)将函数y =f (x )的图象向右平移6π个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y =g (x )的图象,求g (x )的单调递减区间. 12.22()(sin cos )2cos (0)f x x x x ωωωω=++>的最小正周期为23π.(Ⅰ)求ω的值.(Ⅱ)若函数()y g x =的图像是由()y f x =的图像向右平移2π个单位长度得到,求()y g x =的单调递增区间.1.解(Ⅰ)∵()()2sin cos 2sin cos sin 2f x x x x x x π=-==,∴函数()f x 的最小正周期为π. (Ⅱ)由2623x x ππππ-≤≤⇒-≤≤,∴3sin 212x -≤≤,∴()f x 在区间,62ππ⎡⎤-⎢⎥⎣⎦上的最大值为1,最小值为32-. 2解: (1)f(x)=cos(2x+3π)+sin 2x.=1cos 213cos 2cos sin 2sinsin 233222x x x x ππ--+=- 所以函数f(x)的最大值为132+,最小正周期π.(2)()2c f =13sin 2C -=-41, 所以3sin C =, 因为C 为锐角, 所以3C π=,又因为在∆ABC 中, cosB=31, 所以 2sin 33B =, 所以 2113223sin sin()sin cos cos sin 232326A B C B C B C +=+=+=⨯+⨯=. 3.【解析】(Ⅰ)f (x )=21sin x +23)4sin(2223)cos (sin 2122cos 1-+=-+=-+πx x x x . 故f (x )的周期为2k π{k ∈Z 且k ≠0}.(Ⅱ)由π≤x ≤1217π,得πππ35445≤+≤x .因为f (x )=23)4sin(22-+πx 在[45,ππ]上是减函数,在[1217,45ππ]上是增函数.故当x =45π时,f (x )有最小值-223+;而f (π)=-2,f (1217π)=-466+<-2,所以当x =π时,f (x )有最大值-2.4.【解析】(Ⅰ)()f x sin322x x =+π2sin 23x ⎛⎫=+ ⎪⎝⎭.()f x ∴的最小正周期2π4π12T ==当πsin 123x ⎛⎫+=- ⎪⎝⎭时,()f x 取得最小值2-;当πsin 123x ⎛⎫+= ⎪⎝⎭时,()f x 取得最大值2.(Ⅱ)由(Ⅰ)知π()2sin 23x f x ⎛⎫=+ ⎪⎝⎭.又π()3g x f x ⎛⎫=+ ⎪⎝⎭. ∴1ππ()2sin 233g x x ⎡⎤⎛⎫=++ ⎪⎢⎥⎝⎭⎣⎦π2sin 22x ⎛⎫=+ ⎪⎝⎭2cos 2x =.()2cos 2cos ()22x x g x g x ⎛⎫-=-== ⎪⎝⎭.∴函数()g x 是偶函数.5.()cos(2)2sin()sin()344f x x x x πππ=-+-+31cos 22(sin cos )(sin cos )2x x x x x x =++-+2231cos 22sin cos 2x x x x =++-31cos22cos2sin(2)26x x x x π=-=- ∴周期22T ππ==.由2()62x k k Z πππ-=+∈,得()23k x k Z ππ=+∈.∴函数图象的对称轴方程为()23k x k Z ππ=+∈(II )∵[,]122x ππ∈-,∴52[,]636x πππ-∈-.因为()sin(2)6f x x π=-在区间[,]123ππ-上单调递增,在区间[,]32ππ上单调递减,所以当3x π=时,()f x 取得最大值1;又1()()1222f f ππ-=<=,∴当12x π=-时,()f x 取得最小值.函数()f x 在[,]122ππ-上的值域为[.6.【解析】(Ⅰ)1cos 2()622xf x x +=3cos 223x x =+12sin 232x x ⎫=-+⎪⎪⎭236x π⎛⎫=++ ⎪⎝⎭.故()f x 的最大值为3;最小正周期22T π==π.(Ⅱ)由()3f α=-2336απ⎛⎫++=- ⎪⎝⎭cos 216απ⎛⎫+=- ⎪⎝⎭.又由02απ<<得2666απππ<+<π+,故26απ+=π,解得512α=π.从而4tan tan 53απ==. 7.解:因为β为π()cos 28f x x ⎛⎫=+ ⎪⎝⎭的最小正周期,故πβ=.因m =·a b ,又1cos tan 24ααβ⎛⎫=+- ⎪⎝⎭ab ··. 故1cos tan 24m ααβ⎛⎫+=+ ⎪⎝⎭·.由于π04α<<,所以222cos sin 2()2cos sin(22π)cos sin cos sin ααβαααααα++++=--22cos sin 22cos (cos sin )cos sin cos sin ααααααααα++==--1tan π2cos 2cos tan 2(2)1tan 4m ααααα+⎛⎫==+=+ ⎪-⎝⎭·8【解答】 f (x )=a sin x cos x -cos 2x +sin 2x =a 2sin2x -cos2x .由f ()-π3=f (0)得-32·a 2+12=-1,解得a =2 3. 因此f (x )=3sin2x -cos2x =2sin ()2x -π6.当x ∈[]π4,π3时,2x -π6∈[]π3,π2,f (x )为增函数,当x ∈[]π3,11π24时 ,2x -π6∈[]π2,3π4,f (x )为减函数.所以f (x )在[]π4,11π24上的最大值为f ()π3=2.又因f ()π4=3,f ()11π24=2,故f (x )在[]π4,11π24上的最小值为f ()11π24= 2.9解:(I )由题设知1π()[1cos(2)]26f x x =++.因为0x x =是函数()y f x =图象的一条对称轴,所以0π26x +πk =,即0 π2π6x k =-(k ∈Z ).所以0011π()1sin 21sin(π)226g x x k =+=+-.当k 为偶数时,01π13()1sin 12644g x ⎛⎫=+-=-= ⎪⎝⎭, 当k 为奇数时,01π15()1sin 12644g x =+=+=.(II )1π1()()()1cos 21sin 2262h x f x g x x x ⎡⎤⎛⎫=+=++++ ⎪⎢⎥⎝⎭⎣⎦1π3113cos 2sin 2sin 2262222x x x x ⎫⎡⎤⎛⎫=+++=++⎪ ⎪⎢⎥⎪⎝⎭⎣⎦⎝⎭1π3sin 2232x ⎛⎫=++ ⎪⎝⎭. 当πππ2π22π232k x k -++≤≤,即5ππππ1212k x k -+≤≤(k ∈Z )时,函数1π3()sin 2232h x x ⎛⎫=++ ⎪⎝⎭是增函数,故函数()h x 的单调递增区间是5ππππ1212k k ⎡⎤-+⎢⎥⎣⎦,(k ∈Z ). 10.【解析】方法一:(I )由3coscos sinsin 044ππϕϕ-=得cos cos sin sin 044ππϕϕ-=即cos()04πϕ+=又||,24ππϕϕ<∴=(Ⅱ)由(I )得,()sin()4f x x πω=+依题意,得23T π= 又2,T πω=故3,()sin(3)4f x x πω=∴=+函数()f x 的图像向左平移m 个单位后所对应的函数为()sin 3()4g x x m π⎡⎤=++⎢⎥⎣⎦()g x 是偶函数当且仅当3()42m k k Z πππ+=+∈ 即()312k m k Z ππ=+∈ 从而,最小正实数12m π=方法二:(I )同方法一(Ⅱ)由(I )得,()sin()4f x x πω=+ w 依题意,得23T π=又2T πω=,故3,()sin(3)4f x x πω=∴=+函数()f x 的图像向左平移m 个单位后所对应的函数为()sin 3()4g x x m π⎡⎤=++⎢⎥⎣⎦ ()g x 是偶函数当且仅当()()g x g x -=对x R ∈恒成立亦即sin[(33)]sin(33)44x m x m ππ-++=++对x R ∈恒成立sin(3)cos(3)cos(3)sin(3)44x m x m ππ∴-++-+sin 3cos(3)cos3sin(3)44x m x m ππ=+++ 即2sin 3cos(3)04x m π+=对x R ∈恒成立。
