平面直角坐标系(第二课时)ppt课件
合集下载
《平面直角坐标系》第2课时 公开课教学PPT课件【初中数学人教版七年级下册】

第七章 平面直角坐标系
7.1 平面直角坐标系 第 2 课时
一、复习引入
-3
B
4
1.数轴的三要素是什么?
原点、正方向、单位长度
2.数轴上的点与什么是一一对应的? 实数
3.A、B两点表示的数分别为多少? -4、2
4.能否将-3和4分别标在数轴上?
一、复习引入
数轴上的点可以用一个数表示,这个数叫做这个点的坐标.
限,第二象限,第三象限和第四象限.
y
4
第二象限 3
2
第一象限
1
-4 -3 -2 -1 o 1 2 3 4 5
x
-1
第三象限 -2
-3
第四象限
-4
-5
三、应用新知
在平面直角坐标系中描出下列各点: A(4,5),B(-2,3),C(-4,-1),D(2.5,-2),E(0,-4).
y
5
A
4
B
3
2
1
x
-4 -3 -2 -1 o
1.平面直角坐标系的画法. 2.平面直角坐标系内点的表示. 3.平面直角坐标系内的点与有序实数对一一对应. 4.平面直角坐标系内各象限及坐标轴上点的特点.
再见
解:(3)由题意得(m-1)-(2m+4)=3,解得m=-8. ∴点P(-12,-9).
(4)∵点P经过点A,且与x轴平行,∴m-1=-3,∴m=-2. ∴点P(0,-3).
四、巩固新知
4.若m是任意实数,则点(m-4,m+1)一定不在( D )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
五、归纳小结
C
-1
1 2 3 45
-2
7.1 平面直角坐标系 第 2 课时
一、复习引入
-3
B
4
1.数轴的三要素是什么?
原点、正方向、单位长度
2.数轴上的点与什么是一一对应的? 实数
3.A、B两点表示的数分别为多少? -4、2
4.能否将-3和4分别标在数轴上?
一、复习引入
数轴上的点可以用一个数表示,这个数叫做这个点的坐标.
限,第二象限,第三象限和第四象限.
y
4
第二象限 3
2
第一象限
1
-4 -3 -2 -1 o 1 2 3 4 5
x
-1
第三象限 -2
-3
第四象限
-4
-5
三、应用新知
在平面直角坐标系中描出下列各点: A(4,5),B(-2,3),C(-4,-1),D(2.5,-2),E(0,-4).
y
5
A
4
B
3
2
1
x
-4 -3 -2 -1 o
1.平面直角坐标系的画法. 2.平面直角坐标系内点的表示. 3.平面直角坐标系内的点与有序实数对一一对应. 4.平面直角坐标系内各象限及坐标轴上点的特点.
再见
解:(3)由题意得(m-1)-(2m+4)=3,解得m=-8. ∴点P(-12,-9).
(4)∵点P经过点A,且与x轴平行,∴m-1=-3,∴m=-2. ∴点P(0,-3).
四、巩固新知
4.若m是任意实数,则点(m-4,m+1)一定不在( D )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
五、归纳小结
C
-1
1 2 3 45
-2
平面直角坐标系(2)PPT课件

(-4,8),(-5,7),(-6,8),(-6,6),
(-5,5),(-6.5,3.5),(-5,2),
(-52,020年110)月2日,(-6,0),(-3,0).
6
如图,已知等腰三角形ABCD中, ∠DAB=60°,AD=4,DC=2, 建立适当的直角坐标系。
1)求A、B、C、D各点坐标;
2)求出梯形面积;
课内练习。
2020年10月2日
5
先画一个直角坐标系,然后按顺序描出点,
并用线段连接,说出图形的形状。
1、(5,2),(5,5),(6,3),
(5,2),(7,2),(5,1),(3,1),
(2,2),(5,2)
2、(-3,0),(-2,0),(-1,1),(-2,1)
(-3,0),(-3,3),(-5,5),(-4,6),
南-3教学楼
“餐厅”的坐标。
行政楼 -4 -5
体育楼 思考:若坐标系的单位 长度为10米,分别求
-6
2020年10月2日
-7
“体育楼”“南教学楼 “北教学楼”的距2离
在建立直角坐标系表示点或物体的位置时, 一般应选择适当的点作为坐标原点,适当的 距离为单位长度; 有时 x 轴上与y轴上的 单位长度可以不同,但同一坐标轴上的单位 长度必须统一.
D
C
2020年10月2日
A
B7
本节课你的收获是什么?
2020年10月2日
8
演讲完毕,谢谢观看!
Thank you for reading! In order to facilitate learning and use, the content of this document can be modified, adjusted and printed at will after downloading. Welcome to download!
冀教版八年级下册数学 19.2《平面直角坐标系(二)》 课件(共21张PPT)

•分析:由一个点到x轴的距离是该点 纵坐标的绝对值,所以a的绝对值等 于2,这样a的值应等于±2。
解:因为P到X轴的距离是2 ,所以, a的值可以等于±2,因此P(3,2) 或P(3,-2)。
巩固练习
1.点 M(- 8,12)到 x轴的距离是____8_____, 到 y轴的距离是___1_2____.
第4题
y
平行于x轴的直线上的各点的纵坐标相同,横坐标不同. 1
-1 0 1
x
-1
平行于y轴的直线上的各点的横坐标相同,纵坐标不同.
• (5)坐标平面内点P(m,2)与点Q(3,-2)关 于原点对称,则m=
(6)已知,点A(3a+5,-6a-2)在第二四象限的角 平分线上,求a2005-a的值
(7)若点P(x,y)满足xy﹥0,则点p在第几象 限?
C(-4,-1)
-1 -2
D(2.5,-2)
-3
-4
D (0,5) A(O) (0,0)
如图,正方形 ABCD的边长为5, 如果以点A为原点, AB所在直线为x轴,
C (5,5) 建立平面直角坐标系,
那么y轴是那条线? 写出正方形的顶点A、 B、C、D的坐标。
请再建立一个直 角坐标系。这时顶点 坐标又是多少?
x
B (5,0)
李强同学家在学校以东 100m再往北150m处, 张明同学家在学校以西 100m再往南50m处, 王玲同学家在学校以南 150m处,如图,再在 坐标系中画出这三位同 学家的位置,并用坐标 表示出来.
北
单位:m 李强
(100,150)
50
张明O 50
东
(-100,-50)
王玲 (0,-150)
第5题
解:因为P到X轴的距离是2 ,所以, a的值可以等于±2,因此P(3,2) 或P(3,-2)。
巩固练习
1.点 M(- 8,12)到 x轴的距离是____8_____, 到 y轴的距离是___1_2____.
第4题
y
平行于x轴的直线上的各点的纵坐标相同,横坐标不同. 1
-1 0 1
x
-1
平行于y轴的直线上的各点的横坐标相同,纵坐标不同.
• (5)坐标平面内点P(m,2)与点Q(3,-2)关 于原点对称,则m=
(6)已知,点A(3a+5,-6a-2)在第二四象限的角 平分线上,求a2005-a的值
(7)若点P(x,y)满足xy﹥0,则点p在第几象 限?
C(-4,-1)
-1 -2
D(2.5,-2)
-3
-4
D (0,5) A(O) (0,0)
如图,正方形 ABCD的边长为5, 如果以点A为原点, AB所在直线为x轴,
C (5,5) 建立平面直角坐标系,
那么y轴是那条线? 写出正方形的顶点A、 B、C、D的坐标。
请再建立一个直 角坐标系。这时顶点 坐标又是多少?
x
B (5,0)
李强同学家在学校以东 100m再往北150m处, 张明同学家在学校以西 100m再往南50m处, 王玲同学家在学校以南 150m处,如图,再在 坐标系中画出这三位同 学家的位置,并用坐标 表示出来.
北
单位:m 李强
(100,150)
50
张明O 50
东
(-100,-50)
王玲 (0,-150)
第5题
3.2平面直角坐标系(第二课时)(共29张PPT)

有些烦恼都是自找的,因为怀里揣着过去而放弃了 努力。有些痛苦的,不是靠天,也不 气,而是坚持和付出,是不停地做,重复的做,用 当你真的努力了付出了,你会发现自己潜力无限! 事,到了明天就是小事,再深的痛,过去了就把它 就算全世界都抛弃了你,——你依然也要坚定前行 你就是自己最大的底气。埋怨只是一种懦弱的表现 才是人生的态度。不安于现状,不甘于平庸,就可 于进取的奋斗中奏响人生壮美的乐间。原地徘徊一 抵不上向前迈出第一步;心中想过无数次,不如撸 干一次。世界上从不缺少空想家,缺的往往是开拓 和勤勉的实干。不要被内心的犹疑和怯懦束缚,行 你终将成为更好的自己。人生就要活得漂亮,走得 自己不奋斗,终归是摆设。无论你是谁,宁可做拼 败者,也不要做安于现状的平凡人。不谈以前的艰
4.2平面直角坐标系(2) 课件

M
Q(- 4,4)
1
M1
6 5 4 3 2 1O 1 2 3 4 5 6 7
x
1
3叫做点M的横坐标,
2
2叫做点M的纵坐标。
3
合起来叫做点
4
M在平面的坐标,记
5
做M(3,2)
.P
一般,先在x轴上得 到横坐标,再在y轴
上得到纵坐标。
回教顾学旧目知
标
(三) 由坐标找点:
21cnjy
(1)在平面直角坐标系中画出下列各点:A(-2,-1)、
答案不唯一,如:以火车站为坐标原 点,南北方向为y轴,东西方向为x轴 建立平面直角坐标系(如图).设图中每 个小正方形的边长为1000 m,则火车 站(0,0),体育场(-4000,2000), 华侨宾馆(-3000,-2000),乐源超 市(2000,-3000).
达教标学测目评
标
21cnjy
1.如图,若在象棋盘上建立平面直角坐标系,使“将”位于
达教标学测目评
标
21cnjy
3.如图,在平面直角坐标系中,四边形ABCD各顶点的坐标分别 为A(0,0),B(9,0),C(7,5),D(2,7),求四边形ABCD的 面积.
达教标学测目评
标
4.排列做操队形时,甲、乙、丙位置如图所示,甲对乙说,如果 我的位置用(0,0)来表示,你的位置用(2,1)表示,那么 丙的位置是(A ) A.(5,4) B.(4,5) C.(3,4) D.(4、3)
重点 难点
根据要表示的图形的需要建立适当的直角坐标系,并在直角坐标系中画出 图形. 例3的思路比较复杂,需要学生有较高的综合运用知识的能力,是本节教学 的难点.
回教顾学旧目知
浙教版八年级上册4.2 平面直角坐标系(2) 课件(共20张PPT)
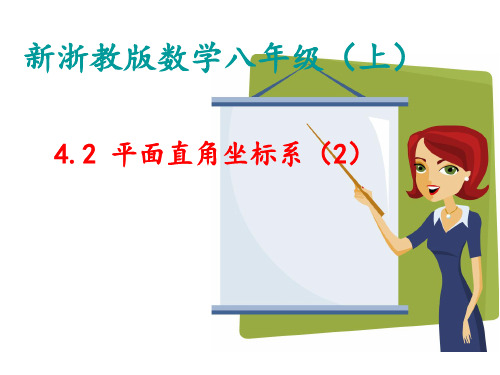
拓展
2.如图,点A的坐标是(2,2),若 点P在x轴上,且△APO是等腰 三角形,求点P的坐标.
y
2
A
1
-1 0
x
P
1 2 34
达标
3.若点P在第三象限且到x轴的距 离为2, 到y轴的距离为1.5,则点 P的坐标是____(_-1_._5,__-2_)______. 4.若点(a,b-1)在第二象限,则a的
点如的何坐选标择分y轴别?为(2)根据所 根据上述坐标在直角坐标系中 标注(的-1尺,寸0,)如,何(选2择,0坐)标 作点A,B,C,D,并用线段依次连 (轴2的.单5位,1长.度5?),(0,3.5)结各点,
如图中的四边形ABCD就是所求作的图形
若以A为坐标原点, 建立适当的坐标系,你能
D
写出ABCD各点的y坐标吗?
3.在点A(-2,-4)、B(-2,4)、C(3,-4)、D(3,4) 中,属第一象限的点是 点D ,属第二象限的点是 点B , 属第三象限的点是 点A , 属第四象限的点是 点C .
纵轴 y
4
第二象限 3
(-,+) 2
1
-4 -3 -2 -1 o
原点
-1
第三象限 -2
(-,-) -3
-4
第一象限
解:A点在第二象限;B点在第四象限;
C点在第三象限;D点在第一象限;
E点在x轴上;F点在y轴上
3、已知点P(0,a)在y轴的负半轴,则Q(-a2-2,-a+2)在( B ) (A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
4.如xy>0,且x+y<0,那么P(x,y)在( C ) A.第一象限 B.第二象限 C.第三象限 D.第四象限
北师大版数学八上3.2 平面直角坐标系(第2课时)特殊点的横纵坐标关系 课件(共14张PPT)

1.已知点P(m+3,m+1)在平面直角坐标系X轴上, 则m=________.
2.已知线段MN平行于Y轴, 且M,N的坐标分别 为(3,-5) 和(x,2),那么x=_________.
3.平面直角坐标系中,已知点P(1-2a,a-2) 在第三象限角平分线上,求a的值和该点坐 标。
ห้องสมุดไป่ตู้
课后作业:
1.已知A(0,2m)和点B(-1,m+1),且直线AB//X 轴,则m=_________.
2.在直角坐标系XOY中,点P坐标为 (2,2),点Q 在Y轴上,Δ PQO是等腰三角形,则满足条件的Q点 有______个。
3.在直角坐标系XOY中,已知点A(0,8)和点B(6,8)。 ①尺规作图:求作一个点P,使点P到A、B两点的距离 相等,同时使P到两坐标轴的距离也相等。 ②写出点P的坐标。
1.若P(x,y)满足x+y<0,xy>0,则点P在第______象限; 若P(x,y)满足xy<0,则点P在第______象限; 若P(x,y)满足xy=0,则点P在_________位置.
2.直角坐标系中, (1)点M(a,b)在第二象限且点M到X轴和Y轴的距 离分别为3和5,则点M的坐标为_____________; (2)若点M到X轴和Y轴的距离分别为3和5, 则点M的坐标为_____________.
北师大版八年级数学上册第三章第二节
平面直角坐标系中特殊点的 横纵坐标关系
同学们,你们了解自己的 家乡吗?知道自己的学校是在 抚州的什么位置吗?
你还知道学校周边的景点 在哪儿吗?
人民公园
拟砚台
金巢实验学校
名人雕塑园
革命纪念馆
M
平面直角坐标系(第二课时)ppt课件

(1) A(5,1) B(2,1) C(2,-3)
(2) A(-1,2) B(-2,-1) C(2,-1) D(3,2)
精选ppt
5
(1) A(5,1) B(2,1) C(2,-3)
y
4
2
B
A
-4 -2 0 -2 -4
24
C
精选ppt
x
直角三角形
S 134 6 2
6
(2) A(-1,2) B(-2,-1) C(2,-1) D(3,2)
平面直角坐系
(第二课时)
回顾与思考
1、什么是平面直角坐标系? 2、坐标轴分平面为四个部分,分别叫做什么?
平面直角坐标系 第二象限
y y轴或纵轴
6
5
4 第一象限
3
2
1 原点
x轴或横轴
-6 -5 -4 -3 -2 -1-o1
-2
第三象限 -3
1 23 4 5 6 X
第四象限
-4
注 意:坐标轴上的点--65不属于任何象限。 ①两条数轴 ②互相垂直 ③公共原点 叫平面直角坐标系
y
4
A 2
D
-4 -2 0 B -2
24 C
-4
精选ppt
x
平行四边形
S3412
7
1.如图, 长方形ABCD的长宽分别是6 , 4 , 建立适 当的坐标系,并写出各个顶点的坐标.
y
解: 如图,以点C为坐标 原点, 分别以CD , CB所 在的直线为x 轴,y 轴建 立直角坐标系. 此时C点 坐标为( 0 , 0 ).D , B , A 的坐标分别为D( 6 , 0 ),
B( 0 , 4 ),A( 6 , 4 ) .
B (0,4)
(2) A(-1,2) B(-2,-1) C(2,-1) D(3,2)
精选ppt
5
(1) A(5,1) B(2,1) C(2,-3)
y
4
2
B
A
-4 -2 0 -2 -4
24
C
精选ppt
x
直角三角形
S 134 6 2
6
(2) A(-1,2) B(-2,-1) C(2,-1) D(3,2)
平面直角坐系
(第二课时)
回顾与思考
1、什么是平面直角坐标系? 2、坐标轴分平面为四个部分,分别叫做什么?
平面直角坐标系 第二象限
y y轴或纵轴
6
5
4 第一象限
3
2
1 原点
x轴或横轴
-6 -5 -4 -3 -2 -1-o1
-2
第三象限 -3
1 23 4 5 6 X
第四象限
-4
注 意:坐标轴上的点--65不属于任何象限。 ①两条数轴 ②互相垂直 ③公共原点 叫平面直角坐标系
y
4
A 2
D
-4 -2 0 B -2
24 C
-4
精选ppt
x
平行四边形
S3412
7
1.如图, 长方形ABCD的长宽分别是6 , 4 , 建立适 当的坐标系,并写出各个顶点的坐标.
y
解: 如图,以点C为坐标 原点, 分别以CD , CB所 在的直线为x 轴,y 轴建 立直角坐标系. 此时C点 坐标为( 0 , 0 ).D , B , A 的坐标分别为D( 6 , 0 ),
B( 0 , 4 ),A( 6 , 4 ) .
B (0,4)
7.1.2平面直角坐标系(第二课时)课件

人教版七年级数学下册
7.1.2平面直角坐标系 (第二课时)
中华路中学 田金莲
回顾与思考
1、什么是平面直角坐标系? 2、两条坐标轴如何称呼,方向如何确定? 3、坐标轴分平面为四个部分,分别叫做什么? 4、什么是点的坐标?平面内点的坐标有几部分组成?
平面直角坐标
系的概念
5 4
满足以下条件的两条数 轴叫做平面直角坐标系
B(1O)2 3 4
x
-1 -1
-2 -2
以正方形的中心为原点
A(-3,-3) B(3,-3)
y
7
4
D
C
3
2
C(3,3)
1
-4 -3 -2 -1 O 1 2 3 4xຫໍສະໝຸດ D(-3,3)-1
-2
A
-3
B
-4
以图中的O点为坐标原点呢? y
7
6
D
C
5
A(-2,-1)
4
3
B(4,-1)
2
1
C(4,5)
-4 -3 -2 -1 O 1 2 3 4 5
x
D(-2,5)
A -1
B
-2
结论:对同一图形,坐标原点取的不同,相 应点的坐标不同。
0
下列各点分别在坐标平面的什么位置上?
A(3,6) 第一象限 B(0,-8) Y 轴上 C(-7,-5) 第三象限 D(-6,0) X 轴上 E(-3.6,5) 第二象限 F(5,-6) 第四象限 G(0,0) 原点
1.已知mn=0,则点(m,n)在__坐_标__轴__上___
2.已知点A(a,0)在x轴正半轴上,点B(0,b)在y轴负 半轴上,那么点C(-a, b)在第__三___象限.
7.1.2平面直角坐标系 (第二课时)
中华路中学 田金莲
回顾与思考
1、什么是平面直角坐标系? 2、两条坐标轴如何称呼,方向如何确定? 3、坐标轴分平面为四个部分,分别叫做什么? 4、什么是点的坐标?平面内点的坐标有几部分组成?
平面直角坐标
系的概念
5 4
满足以下条件的两条数 轴叫做平面直角坐标系
B(1O)2 3 4
x
-1 -1
-2 -2
以正方形的中心为原点
A(-3,-3) B(3,-3)
y
7
4
D
C
3
2
C(3,3)
1
-4 -3 -2 -1 O 1 2 3 4xຫໍສະໝຸດ D(-3,3)-1
-2
A
-3
B
-4
以图中的O点为坐标原点呢? y
7
6
D
C
5
A(-2,-1)
4
3
B(4,-1)
2
1
C(4,5)
-4 -3 -2 -1 O 1 2 3 4 5
x
D(-2,5)
A -1
B
-2
结论:对同一图形,坐标原点取的不同,相 应点的坐标不同。
0
下列各点分别在坐标平面的什么位置上?
A(3,6) 第一象限 B(0,-8) Y 轴上 C(-7,-5) 第三象限 D(-6,0) X 轴上 E(-3.6,5) 第二象限 F(5,-6) 第四象限 G(0,0) 原点
1.已知mn=0,则点(m,n)在__坐_标__轴__上___
2.已知点A(a,0)在x轴正半轴上,点B(0,b)在y轴负 半轴上,那么点C(-a, b)在第__三___象限.
3.2平面直角坐标系(第二课时)平面直角坐标系 课件(共17张PPT) 北师大版八年级数学上册

课堂小结
1.坐标轴上点的坐标
坐标轴上的点的坐标中至少有一个是0,即横轴上的点的纵坐标为0,纵轴上 的点的横坐标为0.
2.各个象限内的点的坐标特征:
第一象限(+,+),第二象限(-,+), 第三象限(-,-),第四象限(+,-).
3.平行x轴的直线上的点的 纵坐标相同 ,平行于y轴的直线上的 点的 横坐标相同 .
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.如果点P(x,y)满足xy=0,那么点P必定在( D )
A.原点上 B.x轴上 C.y轴上 D.坐标轴上
4.点P(m+3,m+1)在直角坐标系的x轴上,则点P的坐标为( B )
A.(0,-2) B.(2,0) C.(4,0) D.(0,-4)
探究新知
任务二:利用平面直角坐标系内点的坐标确定字母的值
例3 已知在平面直角坐标系中,点P(m,m-2)在第一象限内,
则m的取值范围是__m__>___2_.
解析:根据第一象限内点的坐标的符号特征,横坐标为正,纵坐
标为正,可得关于m的一元一次不等式组
m 0, m 2 0,
解得m>2.
求点的坐标中字母的取值范围的方法:根据各个象限内点的坐标的符号 特征,列出关于字母的不等式或不等式组,解不等式或不等式组即可求 出相应字母的取值范围.
第三章 位置与坐标
3.2平面直角坐标系(第二课时)
学习目标
3. 进一步体会平面直角坐标系中点与坐标之间 的一一对应关系. 2. 能够分析某些特殊点(坐标轴上的点、与坐 标轴平行的直线上的点等)的特征. 1. 熟练地根据坐标确定点的位置以及写出给定 点的坐标.Fra bibliotek复习导入
1.什么是平面直角坐标系? 2.作平面直角坐标系 3.指出四个象限 4.写出 P 点坐标 P(3,4)
平面直角坐标系课件(共15张PPT)
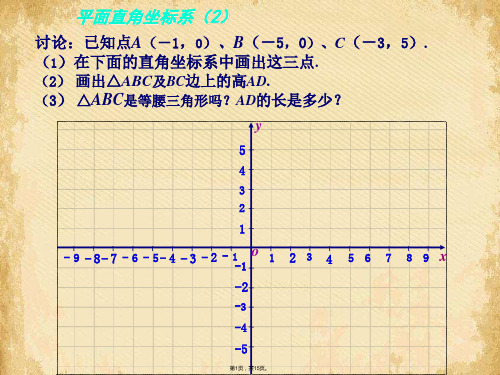
平面直角坐标系(2)
讨论:已知点A(-1,0)、B(-5,0)、C(-3,5).
(1)在下面的直角坐标系中画出这三点.
(2) 画出△ABC及BC边上的高AD.
(3) △ABC是等腰三角形吗?AD的长是多少?
y
5 4
3 2
1
-
9
- 8- 7
-
6
-
5- 4
-3
-2
-
1 -1
o
1
23
4
56
7
89x
-2
-3
-4
-5
第3页,共15页。
平面直角坐标系(2)
解:点B、点C的坐标分别为B(1,0)、C(5,0). 因为BC=4,△ABC面积为10,所以△ABC的高为5. 又因为△ABC是等腰三角形,所以点A的横坐标 是3, 纵坐标是5,即A(3,5). 在第一象限内画出△ABC.
y
5
A.
4
3 2
. . 1
B
(2) 画出△ABC及BC边上的高AD.
1
平面直角坐标系(2)
. .o . 平面直角坐标系(2)
. . . . - 9 - 8 - 7 - 6 - 5 - 4 - 3 - 2 - 1 (3)点P(a , b)关于x轴对称点的坐标为 ________,
. -1 解:点B、点C的坐标分别为B(1,0)、C(5,0).
平面直角坐标系(2)
y
5
B′(5,5)
.B(-42,3) 3
. A′(3,3) (5,3)
.2
A(-4,1)1
.(3,1)
- 9- 8- 7 - 6- 5- 4- 3 - 2- 1-1 o 1 2 3 4 5 6 7 8 9 x
讨论:已知点A(-1,0)、B(-5,0)、C(-3,5).
(1)在下面的直角坐标系中画出这三点.
(2) 画出△ABC及BC边上的高AD.
(3) △ABC是等腰三角形吗?AD的长是多少?
y
5 4
3 2
1
-
9
- 8- 7
-
6
-
5- 4
-3
-2
-
1 -1
o
1
23
4
56
7
89x
-2
-3
-4
-5
第3页,共15页。
平面直角坐标系(2)
解:点B、点C的坐标分别为B(1,0)、C(5,0). 因为BC=4,△ABC面积为10,所以△ABC的高为5. 又因为△ABC是等腰三角形,所以点A的横坐标 是3, 纵坐标是5,即A(3,5). 在第一象限内画出△ABC.
y
5
A.
4
3 2
. . 1
B
(2) 画出△ABC及BC边上的高AD.
1
平面直角坐标系(2)
. .o . 平面直角坐标系(2)
. . . . - 9 - 8 - 7 - 6 - 5 - 4 - 3 - 2 - 1 (3)点P(a , b)关于x轴对称点的坐标为 ________,
. -1 解:点B、点C的坐标分别为B(1,0)、C(5,0).
平面直角坐标系(2)
y
5
B′(5,5)
.B(-42,3) 3
. A′(3,3) (5,3)
.2
A(-4,1)1
.(3,1)
- 9- 8- 7 - 6- 5- 4- 3 - 2- 1-1 o 1 2 3 4 5 6 7 8 9 x
《平面直角坐标系》第二课时PPT课件

(–, +) 2 (+, +)
(x, 0)
1
(0, 0)
-2 -1 O 1 2 3 x
-1 (–, –)
-2
(+, –)
(0, y) “原点及两轴上点”的坐标特征:
范例讲解
例1、在如图的平面直角坐标系中描出下列各组点, 并将各组内的点用线段依次连接起来。
观察所得的图形,你觉得它像什么?
范例讲解
例1、在如图的平面直角坐标系中描出下列各组点, 并将各组内的点用线段依次连接起来。
CD∥y轴
C 、D的横坐标相同
O
x
B (2) 平行于y轴的直线 (–3, –3) 上的点:横坐标相同。
C (3, –6)
合作交流
ⅰ、在图中,点A、B 、C、D分别在哪个象限?
它们的坐标有什么特征?为什么? y
A
(–3, 6)
(3, 3)
D
O
B (–3, –3)
x
C (3, –6)
新知归纳
y “四个象限上点”的坐标特征:3
汇报人:XXX 汇报日期:20XX年10月10日
2020年9月28日
17
新知探究
Ⅲ、写出图中的平 行四边形ABCD各 个顶点的坐标。
y A (–3, 6)
(3, 3) D
O
B (–3, –3)
x
C (3, –6)
Ⅳ、在图中,观察线段AB与线段CD与y轴有怎样 的位置关系?点A与B,C与D的坐标有什么特征?
y
AB∥y轴
A
(–3, 6)
A、B的横坐标相同
(3, 3) D
(9, 4) (6, –2)
Ⅱ、在图中,观察线段AD与线段BC与x轴有怎样 的位置关系?点A与D,B与C的坐标有什么特征? A与B,C与D的坐标相同吗?为什么?
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
距离为1.5,则点P的坐标是(__-_1_.5_,___-。2)
4.点A(1-a,5),B(3 ,b)关于y轴对称,
则a=_4__,b=_5___。
6.如果同一直角坐标系下两个点的横坐标相同,
那么过这两点的直线( B )
(A)平行于x轴 (B)平行于y轴 (C)经过原点 (D)以上都不对
7.若点(a,b-1)在第二象限,则a的取值范
平面直角坐系
(第二课时)
回顾与思考
1、什么是平面直角坐标系? 2、坐标轴分平面为四个部分,分别叫做什么?
平面直角坐标系 第二象限
y y轴或纵轴
6
5
4 第一象限
3
2
1 原点
x轴或横轴
-6 -5 -4 -3 -2 -1-o1
-2Leabharlann 第三象限 -31 23 4 5 6 X
第四象限
-4
注 意:坐标轴上的点--65不属于任何象限。 ①两条数轴 ②互相垂直 ③公共原点
叫平面直角坐标系
结论1
1、第一、二、三、四象限内的坐标的 符号分别是(+,+),(-,+),(-,-),(+, -)
2、坐标轴上的点坐标至少有一个是0
横轴上的点的纵坐标为0,表示为(x,0) 纵轴上的点的横坐标为0.表示为(0,y) 原点的坐标为(0,0)
.
例:在平面直角坐标系中描出下列各组点, 并将各组内的点用线段依次连接起来得到 一个封闭图形,说说你得到的是什么图形, 并计算它们的面积.
围是__a_<_0_,b的取值范围_b__>_1____。
本节课你学到了什么?
平行坐标轴的点坐标的特点,关于X轴,Y轴 及原点对称的坐标的特点
点到坐标轴的距离 点A(a,b)到X轴的距离为b ,到Y轴的距离为 a
如何根据实际,建立平面直角坐标系,使问 题简单、快捷
.
感谢亲观看此幻灯片,此课件部分内容来源于网络, 如有侵权请及时联系我们删除,谢谢配合!
y
4
A 2
D
-4 -2 0 B -2
24 C
-4
.
x
平行四边形
S3412
1.如图, 长方形ABCD的长宽分别是6 , 4 , 建立适 当的坐标系,并写出各个顶点的坐标.
y
解: 如图,以点C为坐标 原点, 分别以CD , CB所 在的直线为x 轴,y 轴建 立直角坐标系. 此时C点 坐标为( 0 , 0 ).D , B , A 的坐标分别为D( 6 , 0 ),
01
C (-3, -2 )
A ( 3, 2 )
x
D ( 3 , -2)
你能说出点P关于x轴、y轴、原点的对称 点坐标吗?
5
4
B(-4,2) 3
·2
·P(4,2)
1
· -4
-3
-2
-1
O
-1
· · C(-4,- 2 ) -2
12345
X
-3
A(4,-2)
-4
.
若设点M(a,b), M点关于X轴的对称点M1( a,-b ) M点关于Y轴的对称点M2( - a, b ), M点关于原点O的对称点M3( -a,-b)
(1) A(5,1) B(2,1) C(2,-3) (2) A(-1,2) B(-2,-1) C(2,-1) D(3,2)
.
(1) A(5,1) B(2,1) C(2,-3)
y
4
2
B
A
-4 -2 0 -2 -4
24
C
.
x
直角三角形
S 134 6 2
(2) A(-1,2) B(-2,-1) C(2,-1) D(3,2)
B( 0 , 4 ),A( 6 , 4 ) .
B (0,4)
A (6,4)
1 C (0 , 0 )
01
D ( 6 , 0)
x
点A与点D关于X轴对称
横坐标相同, 纵坐标互为相反数
点A与点B关于Y轴对称
纵坐标相同, 横坐标互为相反数
点A与点C关于原点对称
横坐标、纵坐标 均互为相反数
y
B ( -3 , 2) 1
.
巩固练习 1.点(3,-2)在第_四____象限;点(-1.5,-1) 在第__三_____象限;点(0,3)在__y__轴上; 若点(a+1,-5)在y轴上,则a=__-1____.
2.点 M(4,-7)到 x轴的距离是______7___, 到 y轴的距离是___4_____.
3.若点P在第三象限且到x轴的距离为 2 ,到y轴的
4.点A(1-a,5),B(3 ,b)关于y轴对称,
则a=_4__,b=_5___。
6.如果同一直角坐标系下两个点的横坐标相同,
那么过这两点的直线( B )
(A)平行于x轴 (B)平行于y轴 (C)经过原点 (D)以上都不对
7.若点(a,b-1)在第二象限,则a的取值范
平面直角坐系
(第二课时)
回顾与思考
1、什么是平面直角坐标系? 2、坐标轴分平面为四个部分,分别叫做什么?
平面直角坐标系 第二象限
y y轴或纵轴
6
5
4 第一象限
3
2
1 原点
x轴或横轴
-6 -5 -4 -3 -2 -1-o1
-2Leabharlann 第三象限 -31 23 4 5 6 X
第四象限
-4
注 意:坐标轴上的点--65不属于任何象限。 ①两条数轴 ②互相垂直 ③公共原点
叫平面直角坐标系
结论1
1、第一、二、三、四象限内的坐标的 符号分别是(+,+),(-,+),(-,-),(+, -)
2、坐标轴上的点坐标至少有一个是0
横轴上的点的纵坐标为0,表示为(x,0) 纵轴上的点的横坐标为0.表示为(0,y) 原点的坐标为(0,0)
.
例:在平面直角坐标系中描出下列各组点, 并将各组内的点用线段依次连接起来得到 一个封闭图形,说说你得到的是什么图形, 并计算它们的面积.
围是__a_<_0_,b的取值范围_b__>_1____。
本节课你学到了什么?
平行坐标轴的点坐标的特点,关于X轴,Y轴 及原点对称的坐标的特点
点到坐标轴的距离 点A(a,b)到X轴的距离为b ,到Y轴的距离为 a
如何根据实际,建立平面直角坐标系,使问 题简单、快捷
.
感谢亲观看此幻灯片,此课件部分内容来源于网络, 如有侵权请及时联系我们删除,谢谢配合!
y
4
A 2
D
-4 -2 0 B -2
24 C
-4
.
x
平行四边形
S3412
1.如图, 长方形ABCD的长宽分别是6 , 4 , 建立适 当的坐标系,并写出各个顶点的坐标.
y
解: 如图,以点C为坐标 原点, 分别以CD , CB所 在的直线为x 轴,y 轴建 立直角坐标系. 此时C点 坐标为( 0 , 0 ).D , B , A 的坐标分别为D( 6 , 0 ),
01
C (-3, -2 )
A ( 3, 2 )
x
D ( 3 , -2)
你能说出点P关于x轴、y轴、原点的对称 点坐标吗?
5
4
B(-4,2) 3
·2
·P(4,2)
1
· -4
-3
-2
-1
O
-1
· · C(-4,- 2 ) -2
12345
X
-3
A(4,-2)
-4
.
若设点M(a,b), M点关于X轴的对称点M1( a,-b ) M点关于Y轴的对称点M2( - a, b ), M点关于原点O的对称点M3( -a,-b)
(1) A(5,1) B(2,1) C(2,-3) (2) A(-1,2) B(-2,-1) C(2,-1) D(3,2)
.
(1) A(5,1) B(2,1) C(2,-3)
y
4
2
B
A
-4 -2 0 -2 -4
24
C
.
x
直角三角形
S 134 6 2
(2) A(-1,2) B(-2,-1) C(2,-1) D(3,2)
B( 0 , 4 ),A( 6 , 4 ) .
B (0,4)
A (6,4)
1 C (0 , 0 )
01
D ( 6 , 0)
x
点A与点D关于X轴对称
横坐标相同, 纵坐标互为相反数
点A与点B关于Y轴对称
纵坐标相同, 横坐标互为相反数
点A与点C关于原点对称
横坐标、纵坐标 均互为相反数
y
B ( -3 , 2) 1
.
巩固练习 1.点(3,-2)在第_四____象限;点(-1.5,-1) 在第__三_____象限;点(0,3)在__y__轴上; 若点(a+1,-5)在y轴上,则a=__-1____.
2.点 M(4,-7)到 x轴的距离是______7___, 到 y轴的距离是___4_____.
3.若点P在第三象限且到x轴的距离为 2 ,到y轴的
